Phương pháp giải nhanh bài toán mặt cầu hình chóp | Trường Đại học Sư phạm Hà Nội
Phương pháp giải nhanh bài toán mặt cầu hình chóp | Trường Đại học Sư phạm Hà Nộivới những kiến thức và thông tin bổ ích giúp sinh viên tham khảo, ôn luyện và phục vụ nhu cầu học tập của mình cụ thể là có định hướng, ôn tập, nắm vững kiến thức môn học và làm bài tốt trong những bài kiểm tra, bài tiểu luận, bài tập kết thúc học phần, từ đó học tập tốt và có kết quả cao cũng như có thể vận dụng tốt những kiến thức mình đã học vào thực tiễn cuộc sống.
Preview text:
PP GIẢI NHANH BÀI TOÁN MẶT CẦU NGOẠI TIẾP HÌNH CHÓP
PP tính nhanh bán kính mặt cầu ngoại tiếp các loại
Loại 1 : Hình chóp có các đỉnh nhìn đoạn thẳng nối 2 đỉnh còn lại dưới 1 góc vuông. Rd 2
Ví dụ : Cho hình chóp SABC có tam giác ABC vuông tại B , SA vuông góc
với mặt phẳng (ABC) và SC=2a . Tính diện tích và thể tích mặt cầu ngoài tiếp hình chóp trên Giải :
Dễ thấy tam giác SAC vuông tại A , tam giác SBC vuông tại B từ đó hình chóp này loại 1 nên R 2
Ví dụ : Cho hình chóp SABCD có đáy ABCD là hình vuông , SA vuông góc
với mặt phẳng (ABCD) và SC=2a . Tính diện tích và thể tích mặt cầu ngoài tiếp hình chóp trên Giải :
Dễ thấy tam giác SAC vuông tại A , tam giác SBC vuông tại B và giác SDC
vuông tại D từ đó hình chóp này loại 1 nên : R 2 Loại 2 : Hình chóp đều X
Ví dụ : Cho hình chóp tam giác đều S.ABC , có AB=a và cạnh bên SA=2a ,
tính diện tích và thể tích mặt cầu ngoại tiếp hình chóp trên
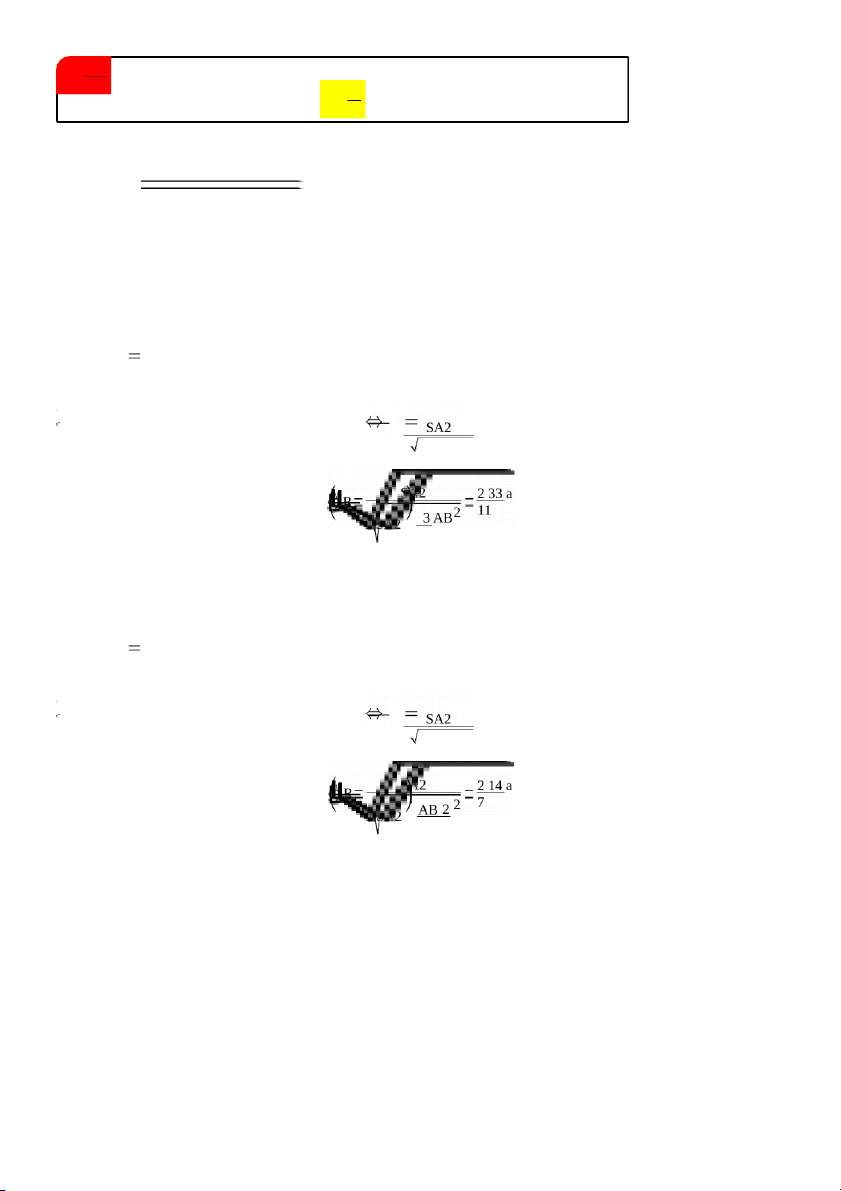
Giải : gọi G là trọng tâm tam giác thì ta có SG vuông góc với mặt phẳng (ABC) Thế thì SA k,SG h nên R mặt cầu : X R 2 SA2AG2 Ví dụ: Cho hình chóp tứ giác đều S.ABCD , 3 có AB=a và cạnh bên
SA=2a , tính diện tích và thể tích mặt cầu ngoại tiếp hình chóp trên
Giải : gọi O là tâm hình vuông ABCD thì ta có SO vuông góc với mặt
phẳng (ABCD) Thế thì SA k,SO h nên R mặt cầu : X R 2 SA2AO2 2
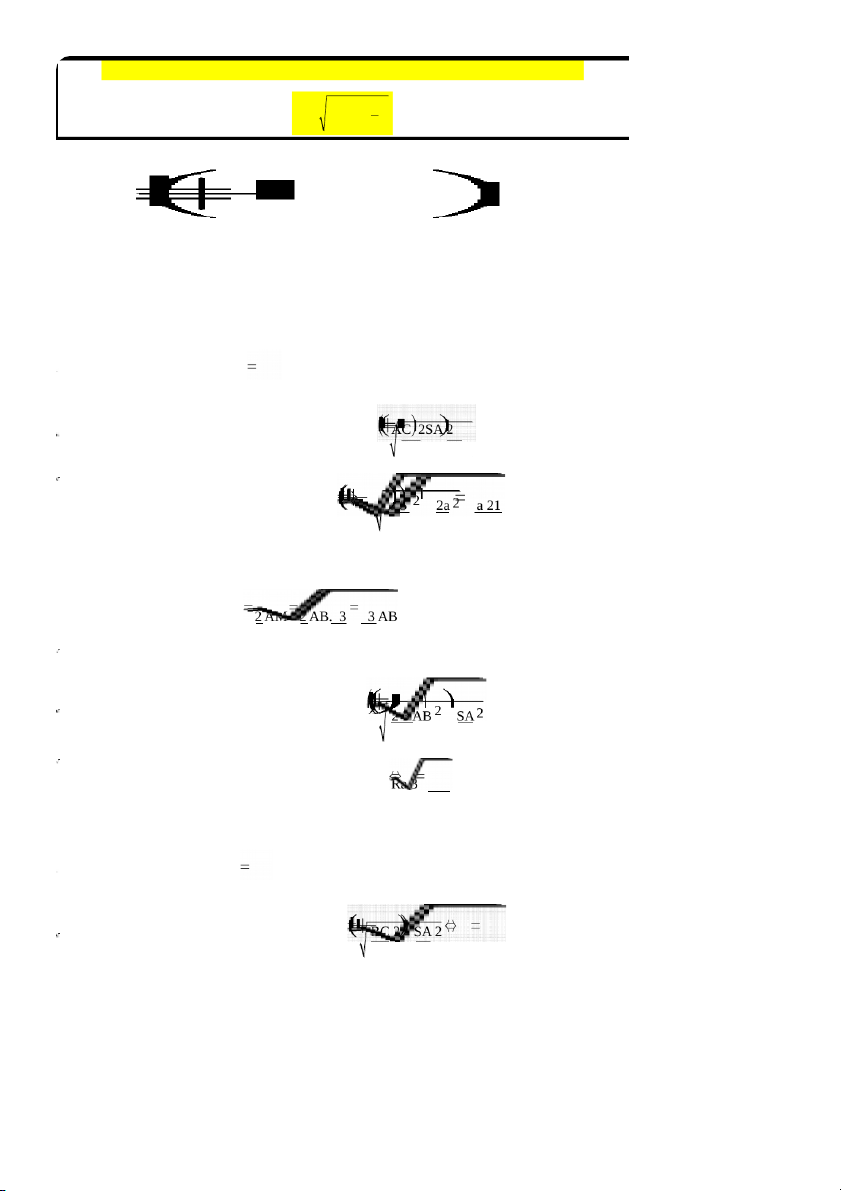
Loại 3 : Hình chóp có cạnh bên vuông góc với đáy X
Ví dụ : cho hình chóp SABCD có cạnh SA vuông góc với đáy , ABCD là hình chữ nhật
có đường chéo dài a , SA=2a . Tính diện 5
tích và thể tích mặt cầu ngoại tiếp SABCD Giải : Ta có : AC R
và SA=hÁp dụng công thức ta có : day2 R 22 Ví dụ : cho hình chóp R 2 a 2 SABC có cạnh SA vuông
góc với đáy , ABC là tam giác đều cạnh = a , SA dài 2a . Tính diện tích và
thể tích mặt cầu ngoại tiếp SABCD Giải : Ta R và SA=h da có y 3 32 3
Áp dụng công thức ta có : R 6 2
Ví dụ : cho hình chóp SABC có 3
cạnh SA vuông góc với đáy , ABC là tam giác vuông tại A và BC=2a , SA
dài 2a . Tính diện tích và thể tích mặt cầu ngoại tiếp SABCD Giải : Ta có BC R
và SA=h .Áp dụng công thức ta có : day2 R 2 2 Ra 2
Ví dụ : cho hình chóp SABC có cạnh SA vuông góc với đáy , ABC là tam
giác cân tại A và AB=a và góc A =120 độ , SA dài 2a . Tính diện tích và thể
tích mặt cầu ngoại tiếp SABC Giải : Ta có : AB . BC . CA a . a 3. a R a và SA=2a day 1 3 4S 4. a.a. ABC 2 2
Áp dụng công thức ta có : Rday R 2 R aa 22 a 2 2 4 (a 2)28 a2 Diện tích : S , thể tích V a3 3 3
Loại 4: Hình chóp có mặt bên vuông góc với đáy
Đối với loại này thì mặt bên vuông góc thường là tam giác vuông , tam giác cân hoặc đều
Ví dụ : cho hình chóp SABCD có đáy ABCD là hình vuông cạnh a , tam giác
SAB đều và nằm trong mặt phẳng vuông góc với đáy . Tính thể tích mặt cầu ngoại tiếp khối chóp
Giải : Giao tuyến của mặt bên và đáy là : GT AB , bán kính 22 đáy Rd , bán S kính mặt bên (SAB) là Rb
, Áp dung công thức ta có : R Rb2 Rd2 4 R 3 2 4 6
Ví dụ : cho hình chóp SABC có đáy ABC là tam giác đều cạnh a, tam giác
SAB cân tại S và có cạnh SA=2a, Tính thể tích mặt cầu ngoại tiếp khối chóp
Giải : Giao tuyến của mặt bên và đáy là : GT AB , bán kính 33 đáy Rd , bán kính mặt bên (SAB) SA . SB . A 4 15 là
a , Áp dung công thức ta có : Rb B 15 4S SAB GT 2 R Rb2 Rd2 4 R 15 3 4 10
Các loại mặt cầu khác thì ta nên sử dụng hệ trục cho dễ xử lý hơn là làm thuần túy Bài Tập vận dụng
Câu 1: Hình cầu ngoại tiếp hình lăng trụ đều tam giác có cạnh đáy bằng a, cạnh bên bằng 2a là 4 3a 3 32 3a 32 2a 32 3a 3 3 3 A. D. B. C. 27 27 9 2 7 a ; a 3
Câu 2: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại , B AB BC ; SA a
(ABC) . Thể tích hình cầu ngoại tiếp hình chóp S.ABC là 5 và SA 9 a 3 27 a 3 3 a 3 B. C. A. D. 36 2 2 2 a3
Câu 3: Thể tích của hình cầu nội tiếp hình lập phương cạnh bằng a là A. B. C. 3a 3 D. 6 3 2a 3 3 3 a 3 a 3 4 a 3
Câu 4: Thể tích hình cầu ngoại tiếp hình chóp tứ giác đều có tất cả các cạnh đều 2a 3 bằng a là a 3 A. 2a 3 B. C. D. 6 12 3 3
Câu 5: Thể tích hình cầu ngoại tiếp hình tứ diện đều có cạnh bằng a là 2a 3 2a 3 A. B. C. D. 3a 3 4 12 3a 3 12 4
Câu 6: Cho hình lăng trụ tam giác đều ABC.A' B 'C ' có AB a , góc giữa
hai mặt phẳng (A' BC ) và (ABC ) bằng 600. Gọi G là trọng tâm tam giác
A' BC . Thể tích của hình cầu ngoại tiếp tứ diện GABC là 49 a 3 A. 343 a 3 B. 343 a 3 C. 343 a 3 D. 108 432 5184 1296 3a 3
Câu 7: Thể tích của hình cầu ngoại tiếp hình lập phương cạnh bằng 4 a 3 a là A. C. a 3 D. D. 3a3 B. 3 4 2
Câu 8. Mặt cầu nội tiếp hình lập phương cạnh a (mặt cầu tiếp xúc với tất cả các mặt của
hình lập phương) có thể tích bằng: 4 a 3 A. 8 a 3 C. a 3 6 3 B. D. 3 E. 2 pa3
Câu 9. Cho hình lăng trụ tam giác đều có tất cả các cạnh đều bằng a. Thể tích khối cầu
ngoại tiếp ngoại tiếp khối lăng trụ đã cho là: A. B. 7 a 3 21 7 a 3 21 7 a 3 7 a2 3 C. D. 5 96 3 4
Câu 10. Cho hình chóp S.ABC có tam giác ABC vuông tại A, tam giác SBC vuông tại S, 3 AB=SC=a, AC=SB = a
. Thể tích của khối cầu ngoại tiếp hình chóp là: 4 a 3 4 a 3 2 A. C. D. 4 a 3 3 E. 2pa3 B. 3 3 3
Câu 11. Cho hình chóp S.ABCD đều có tất cả các cạnh đều bằng a. Diện
tích mặt cầu ngoại tiếp hình chóp bằng: A. B. C. pa2 D. 2pa2 4 a2 a2 2 4 3
Câu 12. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AC = a , 2
SA^(ABC), SC tạo với đáy một góc 450. Bán kính mặt cầu ngoại tiếp hình chóp bằng: