Phương pháp giải phương trình, bất phương trình, hệ phương trình vô tỉ

Tài liệu gồm có 109 trang được tổng hợp bởi thầy Trần Mạnh Tường hướng dẫn phương pháp giải phương trình, bất phương trình, hệ phương trình vô tỉ (cách gọi khác: phương trình, bất phương trình, hệ phương trình chứa căn; viết tắt: PT – HPT – BPT vô tỉ, PT – HPT – BPT chứa căn), đây là dạng toán điển hình trong chương trình Đại số 10 chương 3 (phương trình và hệ phương trình) và Đại số 10 chương 4 (bất đẳng thức và bất phương trình); tài liệu được phân dạng dựa theo các phương pháp giải toán; các bài toán trong tài liệu được phân tích và giải chi tiết.

118 59 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu chung Toán 10

Môn: Toán 10

Thông tin:

109 trang 7 tháng trước

Tác giả:

Profile Mai Nguyệt
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 1
Contents
I.  GII B .......................... 1
 THÊM BT THÀNH HNG THC ................................................... 6
III. S DT N PH .................................................. 11
1. T N PH HOÀN TOÀN .............................................................................................................. 11
2. T N PH KHÔNG HOÀN TOÀN .............................................................................................. 14
3. T N PH   ............................................................................. 14
4. T N PH  H ................................................................................................................ 15
 NHÂN LIÊN HP .......................................................................................... 19
1.   NHÂN LIÊN HP TRC TIP CÁC BIU THC CÓ SN TRONG
 ....................................................................................................................................... 19
2.  NHÂN LIÊN HP THÊM BT HNG S ............................................. 22
3.  NHÂN LIÊN HP THÊM BT BIU THC BC NHT .................... 25
 GII B .......................................................... 26
   DNG
f u f v
...................................................................... 32
 S D  ................................................................. 38
 S D ........................................................... 42
 S D ................................................................................... 46
 T S DU CA HÀM S ............................................... 50
  S DNG S NG THNG .. 65
 S DNG GIÁC HÓA .................................... 70
XI.  CÓ THAM S ................................................................................................ 71
XIV. TRC NGHITRÌNH VÔ T .......................................................................................... 78
I. PHƯƠNG TRÌNH VÔ TỈ GIẢI BẰNG PHƯƠNG PHÁP BIẾN ĐỔI TƯƠNG ĐƯƠNG
 
2
0B
AB
AB

.
0B
AB
AB

.
2
0
0
0
A
B
AB
B
AB


.
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 2
2
0
0
B
A B A
AB
.
0B
AB
AB

.
 




Bài 1: Gi
2
2 1 3 1 0 1x x x
( Khi D 2006)
Li gii
ng
.AB
2
2
22
3 1 0
(1) 2 1 3 1
2 1 ( 3 1)
xx
x x x
x x x
Kt lum
1, 2 2.xx
Nhận xét: ng tng quát:
2
, ( , 0)mx n ax bx c m a
u gic theo dng
.AB
Nc nghim hu t thì s ti phân tích thành tích
s i, nhân ti, cng chéo). Còn nu ra nghim vô t ta s tin hành s dng ch a máy
tính b  ng nhân t chung b    dng tích s bc hai nhân bc
hai mà d c nghim.
Bài 2: Gitrình:
32
5 4 2 2x x x x x
Li gii
u kinh:
2x 
.
Ta có:
32
5 4 2x x x x x
2
2
32
5 4 2x x x x x
6 5 4 3 2
2 9 22 7 0x x x x x x
Vy:
2 4 3 2
3 1 3 7 0x x x x x x
Vì
4 3 2 2 2 2
3 7 1 2 7 0x x x x x x x x x x
.

2
3 1 0xx
Vi
2
3 13
3 1 0
2
x x x
.
Th li nghic
3 13
2
x
là nghim duy nht tha mãn.
Kết luận: m duy nht
3 13
2
x
.
Nhận xét:  phân tích ta dùng máy tính casio
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 3
S dc:
12
3.302775638, 0.3027756377xx
o:
1 2 1 2
3, 1x x x x
Nhân t c:
2
31xx
Nhp máy tính:
6 5 4 3 2
2
2 9 22 7
31
x x x x x x
xx

Calc 100
Bài 3: Gi
22
7 5 3 2x x x x x
Li gii

2
22
3 2 0
()
7 5 3 2
xx
x x x x x

31
2
5
x
x
x
x
(do
0x
không là nghim c
32
2 2 2
31
20
31
2
0 2 0 1.
1
4
16 16 0
( 5) ( 2)
x
x
x
x
xx
x
x
x
x x x
x x x


Kt lum duy nht
1.x 
Nhận xét:      n:
0 0
,
A hay B
AB
AB


      n
0A
hay
0.B
D   m ca bài toán, ta nên ch     n nht, tc chn
2
3 2 0B x x
Bài 4: Gi
3 3 3
1 2 2 3.x x x
Li gii
i:
3
33
1 2 2 3x x x
33
3
3 1 2 1 2 0x x x x
3
1
3 1 2 2 3 0 2
3
2
x
x x x x
x
Th li ta thy các giá tr
3
1; 2;
2
x x x
u th
- Kt lun. Tp nghim c
3
1;2; .
2
T



Bài 5. Gi
3
2
8
2 -2 4 2 1.
21
x
x x x x
x
Li gii
u kin
1
.
2
x 
i:
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 4
3
2
8
2 1 2 4 2
21
x
x x x x
x
3
3 2 2
8
2 8 2 1 2 4 2 2 2 4 2
21
x
x x x x x x x x
x
32
5 7 3 0x x x
1
3
x
x
Th li ta thy nghim c có giá tr
1.x
Bài 6. Tng các nghim c
3
2
1
3 1 1
3
x
x x x x
x
là
A.
0
. B.
2
. C.
2
. D.
1
.
Li gii

u kin
1.x 
i:
2
3
2
2
1
3 1 1
3
x
x x x x
x




3
3 2 2
1
2 1 3 1 2 1 1 1
3
x
x x x x x x x x
x
3
22
1
1 2 2 0 1 3.
3
x
x x x x x
x
- Tp nghim c
1 3;1 3 .T
Vy tng các nghim là:
1 3 1 3 2
Bài 7:   
3 2 2
27 18 9 27 2 1 2 1 125 0x x x x x x
. Gi s nghim c 
trình có dng
ab
x
c
vi
,,abc
là các s 
a
c
ti gin. Tính
S a b c
.
A.
46S
. B.
47S
. C.
48S
. D.
49S
.
Li gii

Ta có:
3 2 2
27 18 9 27 2 1 2 1 125 0x x x x x x
3
2 1 3 125xx
2 1 3 5xx
16 22
9
x

Suy ra:
16, 22, 9a b c
Vy
47S
Bài 8: Bit r
3 2 2
4 4 2 2020 2 1009 3x x x x x x
có mt nghi
nht dng
b c d
xa
e


,,a b d
,
,ce
là các s nguyên t
a b c d e
bng:
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 5
A.
901.
B.
902
. C.
903
. D.
904
.
Li gii
C
3 2 2
4 4 2 2020 2 1009 3x x x x x x
42
1 1 2019 2019xx
4 2 2 2
11
1 1 1 2019 1 2019
44
x x x x
22
22
11
1 1 2019
22
xx
22
11
1 1 2019
22
xx
42
1 1 2018 0xx
2
1 3 897
1
2
x

1 3 897
1
2
1 3 897
1
2
x
x


Vy
1, 1, 3, 897, 2 904.a b c d e a b c d e
Bài 9: Gi s  
2
2 1 3 1 0x x x
có mt nghiêm có dng
x a b c
 
*
,,abc

abc
có kt qu là
A.
5.
B.
1
. C.
0
. D.
4
.
Li gii
u kin
1
.
2
x
i:
2
3 1 2 1x x x
2
2
2
3 1 0
3 1 2 1.
xx
x x x
2
4 3 2
3 1 0
6 11 8 2 0
xx
x x x x
2
22
3 1 0
2 1 4 2 0
xx
x x x x
3 5 3 5
22
1
22
x
x
x



1
2 2.
x
x

Vy
2, 1, 2 5.a b c a b c
Bài 10: 
2 2 2 2 3 2
2018
1 1 1 1 1 1 1 1
8 4 5 5 1
16 2 16 2 16 2 2 16
can
x x x x x x x x
(1)
Tm cng
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 6
A.
25 8 5
16
. B.
25 8 5
16
. C.
49
16
. D. 3.
Li gii
Chn B
T 
3 2 2
1
4 5 5 1 4 1 1 0
4
x x x x x x x
Ta có
2
2 2 2 3 2
2018
1 1 1 1 1 1 1
(1) 8 4 5 5 1
16 2 16 2 16 2 4
can
x x x x x x x



2 2 2 3 2
2017
1 1 1 1 1 1
8 4 5 5 1
16 2 16 2 2 16
can
x x x x x x x
2 3 2
11
8 4 5 5 1
2 16
x x x x x
2
1
8 4 1 1
4
x x x x



2
1
4
4 1 1 0
51
2
x
x x x
x

m bng
25 8 5
16
II.  THÊM BT THÀNH HNG THC
Bài 1: Gi
2
4 14 1 4 6 10 x x x
Li gii
2
2
2
2
4 14 1 4 6 10
4 20 25 6 10 4 6 10 4
2 5 6 10 2
2 5 6 10 2
x x x
x x x x
xx
xx
Bài 2.
2
7
3 6 3
3
x
xx
Li gii
Cách 1: t
7
0
3
x
tt

ta có:
2
2
3 6 3
37
x x t
tx

.
t
1yx
h  thành
2
2
36
36
yt
ty


.
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 7
Cách 2:         
2
3 21
63
9
x
xx
2
9 18 9 3 21x x x
2
49 1
9 21 3 21 3 21
44
x x x x
22
71
3 3 21
22
xx
Bài t: 1)
2
49
77
28
x
xx

. 2)
2
3
24
2
x
xx

. 3)
2
4
27 18
3
x x x
.
Bài 3. [

2
2
2
2 4 5 11
2 4 5 11
2 4 5 11
x y z y z
y z x z x
z x y x y
Li gii

24x
Cách 1: Nhân 2 v ca mi 2 và cng vi v theo vé, ta có
2 2 2
2 2 2 2 2 2 2 2 2 2 4 2 4 2 4
2 2 2 10 10 10 66
x y z x y z x y z
x y z x y z
[]
2 2 2
2 2 2
2 2 2
2 3 2 3 2 3 2 1 2 1 2 1
4 1 4 1 4 1 0
x y z x y z
x y z
3x y z
.
ng bng thc
2 2 2
2 4 2 4 2 4 6 11 6 11 6 11 *x x y y z z x x y y z z
Ta có:
2
2 4 2 2 4 4x x x x
2 4 2xx
Suy ra
*6VT
, du
""
xy ra khi
3x y z
.
Mt khác,
*6VP
, dy ra khi
3x y z
.
Vy
3x y z
.
Bài 4: Bi
22
8 8 3 8 2 3 1x x x x x
có 3 nghim
1 2 3 1 2 3
, , ( )x x x x x x
Tính
1 2 3
( 7 1)T x x x
?
A.
57
4
T
. B.
3
2
T
. C.
3T
. D.
8T
.
Li gii
C
u kin :
2
2 3 1 0xx
2 2 2 2 2
8 8 3 8 2 3 1 4( 2 3 1) (2 1)Pt x x x x x x x x x
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 8
2
2
33
2 2 3 1 1
4
71
2 2 3 1 4 1
4
x
xx
x x x
x

Vy
3 3 7 1 3 3
7 1 3
4 4 4
T
Bài 5: Nghim nh nht ca 
2
( 3) 8 48 24x x x x
có dng
x m n p
(vi
,mn
và
p
là s nguyên t). Tính giá tr
T m n p
.
A.
25T
. B.
27T
. C.
3T
. D.
7T
.
Li gii
A
u kin:
12 4x
.
i
2
2 3 8 48 2 24x x x x
2 2 2
6 9 2 3 8 48 8 48 9x x x x x x x
2
2
3 8 48 9x x x


2
2
3 8 48 3 1
3 8 48 3 2
x x x
x x x
2
0
0
1 2 2 7
2 2 7
2 8 48 0
2 2 7
x
x
x
x
xx
x

(tha mãn).
2
6
6
2 5 31
5 31
2 20 12 0
5 31
x
x
x
x
xx
x



(tha mãn).
Nghim nh nht s là
5 31x

5 1 31 25m n p
.
[Các Bài ]
Bài 6.
2
2 3 9 4x x x
. HD: PT
2
22
3 2 3 1 9 3 1 9x x x x x
.
Bài 7.
2
9x 20 2 3 10xx
. HD: PT
2
3 10 2 3 10 1 6 9 0x x x x
.
Bài 8.
2
2 1 3 1x x x
. HD: PT
2
4 2 1 4 2 1 1 4 4 1x x x x
.
Bài 9.
2
10 1 80 10x x x
.
HD: PT
2
4 4 40 1 80 40x x x
22
4 2.2 .19 19 1 80 40 1 80 400x x x x
2
2
2 19 1 80 20xx
.
Bài 10.
2
49
77
28
x
xx

.
HD: PT
22
196 196 28. 4 9 196 196 2. 28 63x x x x x x
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 9
2
196 224 64 28 63 2. 28 63 1x x x x
2
2
14 8 28 63 1xx
.
Bài 11.
4 3 10 3 2xx
.
HD: PT
2
2
4 3 10 3 2 *
x
xx
.
+
22
* 3 10 3 4 12 10 3 4 16x x x x x x
2
4 10 3 12 10 3 9 4 28 49x x x x
2
2
2 10 3 3 2 7xx
.
Bài 12.
22
4 1 1 2 2 1x x x x
.
HD: PT
22
8 4 1 1 16 16 8x x x x
2
2 2 2
4 1 8 4 1 1 16 1 16 24 9x x x x x x
2
2
2
4 1 4 1 4 3x x x
.
Bài 13. 
22
1 2 3 1 3 1 x x x x x x
.
Li gii
22
1 2 1 4 3 1 2 2 6 x x x x x x
2 2 2
2 1 1 3 1 2 3 1 1 0 x x x x x x x x
2
2
2
1 3 1 1 0 x x x x
2
1 0 1
10
3 1 1 0
3 1 1 0


xx
x x x
xx
x
.
Vy m.
H thng bài t:
1.
2
2 2 1 2 x x x
.
2.
2
1 4 5 x x x
.
3.
2
22 xx
.
4.
2
12 1 36 x x x
.
5.
2
2 2 1 4 1 x x x
.
6.
2
3 2 4 21 22 x x x
.
7.
42
33 xx
.
8.
2
11 xx
.
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 10
9.
2
5 4 2 1 x x x
.
10.
2
3
84
2

x
xx
.
11.
22
1 2 2 x x x x
.
12.
3 4 12 28 x x x x
.
13.
22
3 1 3 1 x x x x
.
14.
22
1 3 3 2 3 x x x x x
.
15.
22
2 2 2 1 x x x x x
.
16.
22
1 2 3 1 x x x x
.
17.
22
2 1 2 1 2 1 x x x x x
.
18.
4 3 2 3 2 11 x x x
.
19.
22
2 9 2 1 4 x x x x x
.
20.
2
2 2 4 4 2 9 16 x x x
.
21.
2
4 3 3 4 3 2 2 1 x x x x x
.
22.
22
1 2 4 4 1 2 1 x x x x
.
Bài 14: 
2
2
27 2
1 1 1
8
x x x x
Li gii
ng: S dpháp phân tích hng tht n ph.
u kin:
1x
.
Nhân 2 v vi
2,
c
2
27
1 2 1 1 1 1 1
4
x x x x x x
2
2
27
1 1 1 1
4
x x x x
2
27
1 1 1 1
4
x x x x
(1)
Chia c hai v cho
1x
c
2
1 27
11
14
x
x
x
(2).
t
2
2
2
2
1
1 2 1
01
1 1 4
1
x
x
t t t
xx
t

.
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 11
4 3 2
2
2
27
2 1 2 3 4 6 13 0
1
t t t t t t
t
5
2
3
tx
.
Vy
5
3
S



.
III. S DT N PH
chung
  v dt n
2
00at bt c a
.
  v u n ph.
Dng 1.
. . 0
n
a f x b f x c
Dng 2.
. . 2 . .a f x b g x ab f x g x h x
Dng 3.
nm
a f x b f x c
Dng 4.
22
.0
nn
n
a A b A B c B
Dng 5.
. . . .a f x b g x c f x g x
Dng 6.
22
. . . . .a f x b g x c d f x e g x
Dng 7.
n
n
f x b x a x a x f x b x
Dng 8.
..
n
n
ax b p cx d q x r
Dng 9.
22
22x a x b a b x a x b a b cx d
Dng 10. t n ph không hoàn toàn
1. ĐẶT ẨN PHỤ HOÀN TOÀN
Bài 1: Gii :
22
4 2 2 4 5x x x x
.
2 2 2S 
Bài 2: Gii :
2
5 2 4 5 3 0
5
x
x x x
x
.
3 53 3 85
;
22
S





Bài 3: Gii :
2
7 7 7 6 2 49 7 42 181 14x x x x x
.
t
7 7 7 6t x x
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 12
Bài 4. Gii b
1 2 2 3 2 2 1x x x

1x
t
2
1 1 0t x x t t
c b




2
22
4 3 2
4 3 2
0
20
1
2 2 1 2
2
4 4 7 4 0
4 4 7 4 0 2
t
tt
t
t t t
t t t
t t t
+Vi
0t
. Kt hu kin thì
0t
không tha mãn (2)
+Vi
1
2
t
thì (2)
32
2 4 4 2 0 2 1 2 3t t t t t x x TMDK
Tp nghim ca b

3;S
Bài 5: Gii b
2
3
7 8 1 2 1 1 1xx

1
2
x
t
2
1
2 1 0
2
t
t x x t
 thành
2
2
3
79
11
2
t
t
2
3
2 2 2
3
79
2 7 9 2 2
2
t
t t t t t
4 3 2
1 3 2 4 2 4 3 0t t t t t t
Ta có
2
4 2 2 2
2 4 2 4 3 2 4 3 0, 0t t t t t t t t
.
T 
1 3 0 1 3t t t
1 2 1 3 1 5xx
.
Bài 6:
2
7 7 7 6 2 49 7 42 181 14 (1)x x x x x
u kin:
6
7
x

2
(1) 14 181 7 7 7 6 2 49 7 42 0x x x x x
7 7 7 6 2 7 7 7 6 7 7 7 6 182 0x x x x x x
2
7 7 7 6 7 7 7 6 182 0x x x x
.
t
7 7 7 6 0x x t

2
182 0 14 13 0 13t t t t
.
Suy ra
7 7 7 6 13 0xx
vì hàm s v ng bin nên ta có
7 7 7 6 13 0 6x x x
.
Bài 7:
2
1 4 1 3 (1)x x x x
.
u kin:
0 2 3
23
x
x

.
Nhn xét:
0x
là mt nghim.
Vi
0x
, chia hai v cho
x
c
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 13
1 1 1 1
4 3 4 3 (2)x x x x
xx
xx
.
t
2
11
( 2) 2x t t x t
x
x
.
T (2), ta có
2
5
63
2
t t t
.
Suy ra
1
1
15
2
2 5 2 0
4
2
4
2
x
x
x x x
x
x
x
.
Vy bp nghim là
1
0; 4;
4



.
Bài 8:
2
1 (1)
1 2 1
xx
xx
.
u kin:
0x
.
Nhn xét:
2
2 2 2
2 1 1 1 1 1 2 1 0x x x x x x
.

22
1 2 1 2 1 1x x x x x x x x
(2).
Ta có
0x
không phi là nghim ca b
Vi
0x
, chia hai v cho
x
c
11
2 2 1xx
x
x






(3)
t
2
11
2x t x t
x
x
 thành
2
2 2 1 1t t t
1 3 5
1
2
xx
x
Bài 9: 
4 3 2 3 2
2 6 10 6 8 1 2 1x x x x x x x x
Li gii
u kin:
22
4 3 2
3
1 2 6 8 0
2 6 10 6 8 0
0
0
0
x x x
x x x x
x
xx
x



.

2 2 2 2
1. 2 6 8 1 1 2 0x x x x x x x
2
2 6 8 2 0 2x x x x
Nhn xét
0x
không phi là nghim nên chia cho
x
, ta có:
42
2 6 1 0 3xx
x
x






t
2
24
4x t x t
x
x
Ta có
2
2
1
2 2 1
2 1 0
t
tt
tt

1t
2
1x
x
4x
.
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 14
2. ĐẶT ẨN PHỤ KHÔNG HOÀN TOÀN
Bài 1: Gii :
2
2012 4 3 2011 4 3x x x x
.
t
43tx
22
2012 2011 0x xt t
2012
xt
t
x
Bài 2: Gii :
22
1 2 3 1x x x x
.
t
2
23t x x
2
11x t x
2
2 3 1 2 1 0x x x t x
2
1 2 1 0t x t x
2
2
t
tx

3. T N PH  
Bài 1: 
2
2010 1 1x x x
.
u kin:
0x
.
t
1 0 1t x t
2
22
11x t x t
.
c
2
2
22
1 2011 1t t t
2
2
2 1 1005 0t t t
2
10t
(Vì
01t
nên
2
1005 0tt
)
Bài 2: [trình tích] 
23
2 2 5 1xx
t
2
1; 1u x v x x
22
2 5 2 2 0u v uv u v u v
.
Bài 3: [] 
33
22
3
7 1 8 8 1 2x x x x x
.

33
22
3
7 1; 8; 8 1a x b x x c x x
3
28a b c a b c
Và
3 3 3
8abc
3
3 3 3
0a b c a b c
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 15
30a b b c c a
Bài 4: 
2 2 4 2
2 2 1 1 1 3 1 1x x x x
Li gii
u kin
11x
.
t
22
1 0, 1 0x a x b
Suy ra
2 2 2 4
3 1 2 ; 1x a b x ab
.
Ta có:
22
2 2 2 2 2 0a b ab a b a b a b
.
Vì
0 2 0a b a b

20ab
Suy ra
22
1 1 2xx
0x
.
Bài 5: 
4 2 2 2
2
2
1 1 1
21
1
1
x x x x x
xx
xx
Li gii
u kin
0x
Ta có
2 2 2 2
2 2 2
1 1 1 1
1 . 2 2
11
x x x x x x x
x x x x

t
22
22
11
0, 0,
11
x x x x
ab
xx


2
2
2
1
1
x
b
x

2
2 1 1 1 0 1ab a b b a b b
2
2
1
1 1 0
xx
x
x


Vy nghim ca b
0;
.
4. T N PH  H
Bài 1. 
Gii h 
33
2 1 2 5 1
2 1 2 2 1
9 2 21
5 11
x y x y
x y x y
xy
x
.
Li gii
t
22
2
2 2 2
2 11
2 1 0
21
5
2 1 2 3
2 1 0
5
ab
x
x y a
x y a
x y b a b
x y b
y



1
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 16
2 2 2 2
5 11 2 ; 9 2 21 4x a b x y a b
.
  thành
33
33
2 2 2 2
22
22
41
41
2
2 4 2
4
2
ab
ab
ab
a b a b a b
ab
ab






2
3 3 2 2 2 2
0
0
2 4 4 2 2 0
2
a
b
a b a b a b a b ab a b a b
ab
ab
.
TH1:
3
3
3
3
3
3
1 11 2
2 2 1 0
1
62
0
1
25
4
8 2 1
22
62
x
xy
ab
xy
y



.
TH2:
5
2 2 1 1
3
01
2 5 0 5
3
x
xy
ba
xy
y


.
TH3:
3
3
3
3
3
1
3 11 5
2 2 1
1
5
65
1
5
4
25
5
3
xy
x
ab
xy
y




.
TH4:
3
3
3
3
3
3
2
4 11 12
2 2 1
2
12
6 12
2
1
12
1 4 12
25
12
3
xy
x
ab
xy
y




.
Bài 2. 

2 2 2
2 2 2
7 2 1 2
2 7 2 1 3
x y x y y xy y
x x x y y xy x
Li gii
t
2
2
7
21
xu
yv


.
  thành
2
2
2
2
23
x y u yv xy y
uy
vx
xu x y v xy x


2 2 2
2
2 2 2
2
7 4 9
72
3
2 1 4
2
00
21
00
x y x
xy
x
y x y
y
xx
yx
yy








.
Bài 19. [] 
3
24 12 6xx
.
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 17

3
22
6
24 ; 12
36
uv
u x v x
uv


.

88; 24;3S
.
Bài 20. [] 
3
3
1 2 2 1xx
.

3
3
3
12
21
12
xt
tx
tx


.

15
1;
2
S






.
Bài 21. [] 
2
2 2 2 1xx
.

2
2
2 2 1
1 2 1
2 2 1
x x y
yx
y y x
.

22S 
.
Bài 22. 
1)
2
1 4 5 5 28x x x x
.
2)
2
4 4 2 2 12x x x x
.
3).
51
5 2 4
2
2
xx
x
x
4).
2
3 2 1 4 9 2 3 5 2x x x x x
.
5).
1
3 1 4 3 3 0
3
x
x x x
x
.
6).
2 2 2
3 2 1 2 2x x x x
.
7).
2
12 1 36x x x
.
8).
22
2 1 2 1 2 1x x x x x
.
9).
5 1 0xx
.
10).
2
39
24
xx
.
11).
3
2
5 3 5 2 4x x x x
.
12).
4
22
1 1 2x x x x
.
13).
22
4 5 1 2 1 9 3x x x x x
.
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 18
14).
23
2 3 2 3 8x x x
.
15).
2 2 4 2
3 1 1x x x x
.
16).
22
5 14 9 20 5 1x x x x x
.
17).
3 3 3 3
3 1 5 2 9 4 3 0x x x x
.
18).
2 . 3 3 . 5 5 . 2x x x x x x
.
19).
33
22
33
3 2011 3 7 2012 6 20 13 2012x x x x x
.
20).
3
3
3
. 25 25 30x x x x
.
21).
44
57 40 5xx
.
22).
2011 1 2012xx
.
23).
3
11
1
22
xx
.
24).
2
55xx
.
25).
2011 2011xx
.
26).
2
2 6 1 4 5x x x
.
27).
3
3
2 3 3 2xx
.
28).
2
49
77
8
x
xx

.
Bài 14.
2
7
3 6 3
3
x
xx
Li gii
Cách 1: t
7
0
3
x
tt

ta có:
2
2
3 6 3
37
x x t
tx

.
t
1yx
h  thành
2
2
36
36
yt
ty


.
Cách 2:         
2
3 21
63
9
x
xx
2
9 18 9 3 21x x x
2
49 1
9 21 3 21 3 21
44
x x x x
22
71
3 3 21
22
xx
Bài t: 1)
2
49
77
28
x
xx

. 2)
2
3
24
2
x
xx

. 3)
2
4
27 18
3
x x x
.
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 19
IV.  NHÂN LIÊN HP
1.  NHÂN LIÊN HP TRC TIP CÁC BIU THC CÓ SN

Bài 1. Gi
2 2 2 2
2 1 3 2 2 2 3 2x x x x x x x
ng dn gii
u kinh:
2
2
2 1 0
3 2 0
x
xx

.

2 2 2 2
2 1 3 2 2 2 3 2x x x x x x x
2 2 2 2
2 2 2 2
2 2 2 2
2 1 2 2 3 3 2 2 0
2 4 2 4
0
2 1 2 2 3 3 2 2
11
2 4 0
2 1 2 2 3 3 2 2
2 4 0 2.
x x x x x x x
xx
x x x x x x x
x
x x x x x x x
xx



Kt hp vu kin và th lc nghim c
2x 
.
Bài 2. Gi
22
2 16 18 1 2 4x x x x
ng dn gii
u kinh:
2
2
2 16 18 0
10
xx
x


22
2 16 18 1 2 4x x x x
22
2
2
2
2
22
1 2 4 2 16 18 1
21
1
2 4 2 16 18
1 0 2
2 1 2 4 2 16 18 3
x x x x
x
x
x x x
x
x x x x

Gii (2): .
Cng (1) vc
2
2
2
4 8 0
3 1 4 8
9 1 4 8
x
xx
xx

2
2
32 3 57
2
32 3 57
7
7
7 64 73 0
32 3 57
7
x
x
x
x
xx
x






.
Kt hp vu kin và th c các nghim là
1x 
và
32 3 57
7
x

.
2
1 0 1xx
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 20
Bài 3. Gi
2
3 1 2 3 7 2 4 4 2x x x x x
ng dn gii
u kinh:
1
3
x 

2
2
2
3 1 2 3 7 2 4 4 2
2 1 3 7 2 4 4 2 3 1 2
2 1 3 7 2 4 2 3 1 2 0
1
2
2 1 3 1 2 2 2 0 1
2
x x x x x
x x x x x x
x x x x x
x
x x x x
x


Vm
1
2
x
,
1x
và
2x
.
Bài 4. Gi
4 4 4
1 1 1
2 1 2
x
x x x


ng dn gii
u kinh:
0x
.
i:
44
4
4
4
3 2 2 3
4 4 4 4
4
2 2 1 1
2 1 2
11
2 1 2 2 2 2 1 2 2 1 2 1
x x x
x
xx
xx
x
x x x x x x x x



4
3 2 2 3
4 4 4 4
4
11
10
2 1 2 2 2 2 1 2 2 1 2 1
1.
x
x
x x x x x x x x
x






Vy m
1x
.
Bài 5: Gi
u kin
2x
ng dn nhân chia liên hp v trái xut hin nhân t chung
3 16x
Gii ra nghim
16
3
x
Bài 6: Gi
2
11
2 2 1xx
xx

1
2
0
x
x
3
3
2 2 5 14 3 16 2x x x x
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 21
2
11
2 1 2xx
xx
ng dn nhân chia liên hp xut hin nhân t chung
1x

1x
Bài 7: Gi
2 3 5 2 3x x x
ng dn nhân chia liên hp vt xut hin nhân t chung
23x

3
2
x
Bài 8: Gi
2
2
2
21
3 9 2
x
x
x
(1)
ng dn thy
3 9 2
2
3 9 2
xx
x
thay vào (1)
:
97
; 0 0 ;
22
Bài 9: Cho
;xy
tha mãn :
22
2011 2011 2011x x y y
Tính
?xy
Ta có:
22
22
2011 2011
2011 2011
x x y y
y y x x
Cng v vi v ta có
0xy
.
Luyn tp : Gi
2
2 2 2
22
2
2 2 2 2
2 2 2 2
1) 2 2 2 1 21 2
2) 2 5 3 5 8
3)2 3 8 6 4 1
4) 10 1 3 5 9 4 2 2
5)1 4 3 3 2 2
6) 15 3 2 8
7) 5 2 1 7 10 3
8) 3 7 3 2 3 5 1 3 4
9) 2 1 3 1 4 3 2 4
x x x
x x x x
x x x
x x x x
x x x x x x
x x x
x x x x
x x x x x x x
x x x x x x x x
2
2
2
2
3
10) 4
11
11) 1 1
1 1 4
12) 3
x
x
x
x x x
x
x
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 22
Bài 10: Gi
2
1 1 4


xy x y xy x y y
x y xy x x
Ta có:
2
1 1 4
(1) 2 0
2
0
2


xy x y xy x y y
x y xy x x
xy x y xy y x y
x y y xy
xy
xy
xy
xy x y xy y
Vi
xy
.T 
2
2
1 1 2 2
1



y xy x x
x
Bài 11. [
4
4
22
1 1 2 1
2 1 6 1 0 2
x x y y
x x y y x
Li gii
2
2 4 1 0y x y y
44
4
4
44
4
44
4
4
1 1 2 1
1 2 1
12
11
x y y x
x y y x
xy
y x y x

44
2
4
74
1 0 1
0
4
24
y x x y
y
y y y
y y y
Nu
01y
thì
74
24y y y
m
Nu
1y
thì
74
24y y y
m
2.  NHÂN LIÊN HP THÊM BT HNG S
Bài 1. 
22
5 3 12 5x x x
.
Li gii
Ta có:
22
5 3 3 6 4 12 0x x x
Bài 2. Gii h 
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 23
2
2
9 9 5 4 9 7 1
2 1 9 7 7 2
x xy x y y
x y x y x y
Li gii
u kin:
0; 0.y x y
t:
0x y t
. T
2
2 2 1 9 7t t t
2
2 3 1
9 1 0 0
72
t
tt
tt

(s dng nhân liên hp).
11
33
x y y x
.Th vào
1
ta có:
2
1 1 1
9 9 5 4 9 7
3 3 3
2
2 9 4 9 4 9 3 1 0
3
23
9 4 2 0.
3
9 3 1
x x x x x x
x x x x
xx
x





41
.
99
xy
Vy h có nghim:
41
; ; .
99
xy



Bài 3. Gip
Gi
2
6 2 6 6 5 2 5x x x x x
.
Li gii
u kin
5
6
6
x
.

2
6 1 2 6 4 6 5 5 2 15x x x x x
5 2 10 6 30
35
6 1 2 6 4 6 5 5
x x x
xx
x x x
1 2 6
5 3 0
6 1 2 6 4 6 5 5
xx
x x x



*
Vi
5
6
6
x
ta có
2 6 2 6
3 3 0
45
2 6 4 6 5 5xx
.

*5x
.
Vm duy nht
5x
.
Bài 4: Gi
2
3 1 6 3 14 8 0x x x x
(4)
 i hc khi B-2010)
Li gii
u kin:
1
6
3
x

2
3 1 4 1 6 3 14 5 0x x x x
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 24
35
5
3 1 5 0
3 1 4 6 1
x
x
xx
xx
5
3 1 0
31
3 1 4 6 1
x
x
xx
Ta th
31
3 1 0
3 1 4 6 1
x
xx
vô nghim vì
3 1 1
3 1 0, ;6
3
3 1 4 6 1
xx
xx



Vm duy nht x=5
Bài 5: Gii bp s thc:
2
1 1 2 0x x x
Li gii
u kinh:
1x
.
Ta có:
2
1 1 2 0x x x
2
2 1 2 1 2 2 0x x x
2
2x 5x 2 2 1 1 2 2 2 0x x x
22
2 2x 1 2 2 2 0
11
x
x x x
x

2 2 2 2
2 2x 1 0
1 1 2 2
x x x
x
xx
22
2 2x 1 0
1 1 2 2
x
x
xx




.
Vì:
22
2x 1 0, 1
1 1 2 2
x
x
xx

12x
.
Kết luận: Tp nghim ca b
1;2S
.
Bài 6: 
3
2 2 2
3 8 2 15x x x
. Gi
S
là tm thc ca

S
.
A.
0S
. B.
1S
. C.
2S
. D.
4S
.
Li gii

Ta d c nghim
1x 
, và ta vit l
3
2 2 2
3 1 8 3 15 4x x x
2
22
33
4 2 2 2
31
11
1 8 3 15 4
x
xx
x x x x

2
33
4 2 2 2
11
3 1 1
2
1 8 3 15 4
x
x x x x


11x
.
Gi
2
. Vì
33
42
3
0
1xx

;
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 25
2 2 2 2
22
11
15 8 15 4 8 3
15 4 8 3
x x x x
xx

2
vô nghim.
Vm
1, 1xx
. Suy ra
2
2
1 1 2S
.
Bài 7: Gii bp s thc:
3 2 3x 4 3 2x 1 3xx
c tp nghim là
a;bS

.ab
có kt qu là.
A.
3
. B.
3
. C.
12
. D.
12
.
Li gii
C
u kinh:
3x
.
Ta có:
3 2 3x 4 3 2x 1 3xx
3 4 3x 4 4 3 2x 1 3 3 1 0xx
3 4 6 4
4
3 4 0
3x 4 4 2x 1 3 3 1
xx
x
x
x

3 6 1
4 3 0
3x 4 4 2x 1 3 3 1
x
x



3 6 1
4 2 1 0
3x 4 4 2x 1 3 3 1
x
x



3 2 2x 1 3
40
3x 4 4 2x 1 3 3 1
x
x
x





34x
.
Kết luận: Tp nghim ca b
3;4S
.
3. PHƯƠNG TRÌNH VÔ TỈ NHÂN LIÊN HỢP THÊM BỚT BIỂU THỨC BẬC NHẤT
Bài 1: Gii bp s thc:
3 2 2
3 2 2 4 2 11x x x x x x
Li gii
u kinh:
4x 
.
Ta có:
3 2 2
3 2 2 4 2 11x x x x x x
3 2 2
3 2 2 4 2 11 0x x x x x x
2
3 2 4 2 2 11 0x x x x x
22
2
3 4 4 2 2 11
0
3 2 4 2 2 11
x x x x
x
x x x x
22
2
2 7 2 7
0
3 2 4 2 2 11
x x x x
x
x x x x
2
2
1
2 7 0
3 2 4 2 2 11
x
xx
x x x x



.
u kin có nghim:
32
4
3 2 0
x
x x x

32
4
3 3 0
x
x x x

3x
.
Vì
3 2 4 2 0
3
2 2 11 1 5 0
xx
x
xx
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 26
2
1
0
3 2 4 2 2 11
x
x x x x

2
2 7 0
1 2 2
3
xx
x
x

.
Kết luận: Tp nghim ca b
1 2 2;S
.
Nhận xét: S dc:
1.828427124x
.
c tìm nhân t:
2 4 4.828427125 3
2 11 3.828427125 2
xx
xx
.
Bài 2: Gi  
22
2 3 21 17x x x x x
 c
2
nghim
1 2 1 2
, ( )x x x x
  
22
21
xx
có kt qu là:
A.
3
. B.
4
. C.
2
. D.
8
.
Li gii
A
u kin
17
.
21
x
i:
22
2 3 1 3 1 21 17 3 2 0.x x x x x x x
2
2
2
2
9 3 2
32
3 2 0.
3 1 21 17
2 3 1
xx
xx
xx
xx
x x x


2
2
19
3 2 1 0
3 1 21 17
2 3 1
xx
xx
x x x



2
3 2 0xx
1
2
x
x
Do
2
1 9 17
1 0, .
21
3 1 21 17
2 3 1
x
xx
x x x
- Vy:
2 2 2 1
21
2 1 3xx
Nhn xét: Ta nhc rm
1; 2xx
. Do v  có
nhân t
2
1 2 3 2x x x x
nh s dng liên h giu quan tâm
là cách tách - ng có tron
Gi s ta s nhóm
2
1 1 2 2
2 3 21 17 .x x a x b a x b x
Thay các giá tr
1; 2xx
vào các
ng thc
2
11
22
2 3 0
,
21 17 0
x x a x b
a x b x
ta s  c
11
11
20
3 2 0
ab
ab
1
1
1
;
1
a
b
22
22
20
2 5 0
ab
ab
2
2
3
.
1
a
b

V.  GII B
Bài 1: 
22
9 9 10
8
xy
xy

Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 27
Li gii
Cách 1:
Tr 2 v
8xy
th vào
2
22
9 9 10 3xy
.
t
4tx
t n ph khéo léo)
4xt
và
4yt
th vào
3
ta có
22
8 25 8 25 10 4t t t t
2
2 2 2 2
25 64 25 , 25t t t t
.
4 2 2 2 4
50 625 64 625 50t t t t t
0t
4xy
.
Cách 2: 
Ta có
22
9 9 10
8
xy
xy

t
;3 ;3 8;6u x v y u v
22
99u x v y
Áp d
22
9 9 10u v u v x y
Du bng xy ra
;uv
c là
4
84
x y x
x y y




.
CÁC BÀI TP GI
1)
3 3 6
3 7 3 7 8
xy
xy

2)
1 1 4
6 4 6
xy
xy
3)
10
24 24 14
xy
xy

Bài 2: 
22
2 5 2 10 29 1x x x x
.
Li gii
Trong mt phng t
Oxy

1;2
1 ;3
ux
vx

.

2
2
| | 2 5
| | 2 10
2;5 | | 29
u x x
v x x
u v u v
.
2
2
| | 2 5
| | 2 10
( 2;5) | | 29
u x x
v x x
u v u v
Suy ra
1
| | | | | |u v u v
.
.0u v u k v k 
.
11
2 .3
x k x
k
2
3
2
11
3
k
xx
2
3
3 3 2 2
k
xx
2
3
1
5
k
x
.
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 28
Bài 3: 
2 2 2
2 2 4 12 26 9 12 29x x x x x x
.
Li gii:
Trong mt phng t
Oxy

1;1
2 3;4
ux
vx


.
3 2;5u v x
thì
2
2
2
22
4 12 25
9 12 29
u x x
v x x
u v x x
   
1 u v u v
0u kv k
1 2 3
1 .4
x k x
k
1
4
1
1 2 3
4
k
xx
1
4
4 4 2 3
k
xx
1
4
7
2
k
x
.
V
1
có nghim duy nht
7
2
x
.
Bài 4: Gii b
2
1 3 2 3 2 2x x x x
1
(B  Tuyn sinh)
Li gii
u kin
1x
Xét trong mt phng t
Oxy

2
31
3; 1
2
1;1
. 1 3
u x x
u x x
v
v
u v x x



.
Suy ra b  
1.u v u v
uv 
31xx
2
6 9 1
3
x x x
x
2
7 10 0
3
xx
x
2
5
5
3
x
x
x
x

.
Vy
5x
là nghim duy nht c
1
.
Bài 5.
31
1 1 4 2
x y xy
xy
Li gii

0 ; 1 ; 1xy x y
Cách 1
T
2
ta có :
2 2 1 16x y x y xy
3
T
1
ta có :
33x y xy x y xy
t
0xy t t
3x y t
Th vào
3
ta có
2
6
2 4 11 3 3
9
xy
t t t t x y
xy

.
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 29
Cách 2
D thy
0 ; 0xy
Áp d
3 3 6
2
xy
x y xy x y
T
2
ta có :
4 1 1 2 1 1 4x y x y



6
3
11
xy
xy
xy

.
Các Bài 
1)
3 3 2 8
7 7 6
x y xy
xy
2)
2 3 4 1 2 3 4 1 2 2 3 2 3
4
x x y y x y
x y xy

3)
2 2 2
2 3 4
4 1 25 9 4 3
x y z
x y z
4)
3
3
2 6 2
34
x y y
y x x
Bài 6. :
2
3 2 4 2 1 3x x x x x
2.1
.
Li gii
iu kin:
2
4
3
x
.
t
;1ux
và
3 2; 4 0v x x
.
Khi ,
. 3 2 4u v x x x
2
. 2 1 3u v x x
Suy ra, phng trình
2.1
tr thành
. . 0: .u v u v k u k v
.
32
4 3 2
14
x k x
x x x
kx


2
32
0
0
4 3 2
4 3 2 0
x
x
x x x
x x x


0
2
2;1 2;1 2
12
x
x
x
x


.
Vy tp nghim ca phng trình là
2;1 2S 
.
Bài 7. Gi
2 2 2
45
2 5 4 40 5 (2.2)
4
x x x x x x
Li gii
nh
x
.
t
1; 2ux
và
2 ;6vx

3;4 5u v u v
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 30
22
2
1 2 2 5u x x x
2
22
2 6 4 40v x x x
22
2 5 4 40 5u v u v x x x x
 m thì:
2
2
45 5 5
5 5 0
4 2 2
x x x x



Thay
5
2
x 
y tha mãn.
Vm duy nht
5
2
x 
.
Bài 8. Giải phương trình:
2
4 6 6
3 1 2sin 2 2 40 4 sin os 1 5 11 1x x c x


.
Li gii
t
2
4 6 6
3 1 2sin 2 2 40 4 sin os 1T x x c x


.
Ta có:
3
6 6 2 2 2 2 2 2
4 sin os 1 4 sin os 3sin cos sin os 1x c x x c x x x x c x



2 2 2 2
4 12sin cos 1 3 1 sin 2 3cos 2x x x x
.

4 4 4 4 4
9 18sin 2 160 36cos 2 9 9sin 2 9sin 2 144 16 36cos 2T x x x x x

22
3;3sin 2 ;3sin 2u x x
và
2
12;4;6 os 2v c x
.
44
9 9sin 2 9sin 2u x x
;
4
144 16 36 os 2v c x
.
22
2 2 2
225 3sin 2 4 3sin 2 6cos 2T u v u v T x x x
.
Mt khác theo bng thc Bunhiacopski ta có:
2 2 2
2 2 2 2 2 2 2 2
3sin 2 4 3sin 2 6cos 2 1 1 3sin 2 4 3sin 2 6cos 2 100x x x x x x



Suy ra:
22
2 2 2
3sin 2 4 3sin 2 6cos 2 50 5 11x x x T



.

1
có nghim khi và ch khi:
22
2
2 2 2
3 3sin 2 3sin 2
12 4
6 os 2
3sin 2 4 3sin 2 6cos 2
xx
cx
x x x

2
2 4 1 1
os 2 1 os4 os4 arccos ,
3 3 3 3 2
k
c x c x c x x k
.
V
1
có nghim là:
1
arccos ,
32
k
xk
.
Bài 9. 
2
1 3 2 10 16 * x x x x
.
Li gii
u kin
2
1
1
2 10 16 0

x
x
xx
.
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 31
Xét
1; 3
u x x
và
1;1 0
u
.
Ta có
. 1 3 u v x
,
2
2
. 1 3 . 2 2 10 16
u v x x x x
.
B
*
tr thành:
..u v u v
, mt khác
..u v u v
nên ta có
. . 0: u v u v k u kv

1
13
3


xk
xx
xk
2
3
30
5
2
13
5



x
x
x
x
xx
x
(thu kin).
Vy bm duy nht là
5x
.
Bài 10: Gii h:
1 2 2008
1 2 2008
2009
1 1 ... 1 2008
2008
2007
1 1 ... 1 2008
2008
x x x
x x x
1
Li gii
u kin:
1, i 1,2008
i
x
Trong mt phng t
Oxy

1 ; 1
i
ii
a x x
,
1,2008i
.

2008
1
2, 1,2008 2008 2
ii
i
a i a
2008 2008 2008
11
1 1 1
1 ; 1
i
i i i
a x x
22
2008 2008 2008
1 1 1
11
i i i
i i i
a x x
2008.2009 2008.2007 2008 2
2008 2008
11
i i i j
ii
a a a a
.
, 1,2008ij
.
a:
2, , 1,2008
ij
a a i j
Nên
, , 1,2008
ij
a a i j
, , 1,2008
ij
x x i j
2009
1 , 1,2008
2008
i
xi
2009
1 , 1,2008
2008
i
xi
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 32
1
, 1,2008
2008
i
xi
Vy h m duy nht là
1 2 2008
1
...
2008
x x x
Bài 11: Gii h 
2
1 3 2 1
2
21
x y x y x y x y
xy
xy
1
Li gii
Trong không gian
Oxy

;1
1 ; 3
a x y
b x y x y
(Vu kin
13xy
)
2
1
2
. 1 3
a x y
b
a b x y x y x y
. . 1 3a b a b a b x y x y x y
32
2 theo gt
3 1 0
xy
x y x y x y
2
2
1 2 1 0
21
xy
x y x y x y
xy
Kt hp vi
21xy
ta gic
2
1
x
y
.
VI.   DNG
f u f v
Bài 1:  h m:
3 3 2
2 2 2
3 3 2 0 1
1 3 2 0 2
x y y x
x x y y m
có nghim.
ng dn gii
u kinh:
1 1,0 2xy
.
Ta có:
3
3
1 3 1 3 1x x y y
. Xét hàm s
3
3f t t t
nghch bin trên khong
1;1
.
   ng
1 1 1f x f y x y y x
   
c
2 2 2 2
2 1 0 2 1 3x x m x x m
.
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 33
H có nghin
1;1
.
Xét hàm s
22
21g x x x
n
1;1
. Ta có:
2
22
2 1 1
2
2 0 0
11
xx
x
g x x g x x
xx


Ta có bng bin thiên:
T bng bin thiên suy ra yêu cu Bài tha mãn khi
12m
.
Bài 2: Gii h b:
2
17 3 5 3 4 4 0 1
2 2 5 3 3 2 1 6 13 2
x x y y
x y x y x x
.
Li gii.
1 3 5 2 5 3 4 2 4x x y y
.
t
32f t t t
, ta có
ft
ng bin
5 4 1x y y x
thay vào
2
2
2 3 4 3 5 9 6 13x x x x
2
2 3 4 2 2 3 5 9 3 3x x x x x x
23
1 1 0
3 4 2 5 9 3
xx
x x x x



10
23
10
3 4 2 5 9 3
xx
x x x x

0
10
x
x

0
1
x
x

H m:
0; 1 ; 1; 2
Bài 3. 
4
4
22
1 1 2 1
2 1 6 1 0 2
x x y y
x x y y y
Li gii
 .
 .
Suy ra .
2
2 1 4 0x y y y
4 4 4
4
4
1 1 1 1 1 1 1 1x x y y x y
2
4 7 4
4 2 4 0y y y y y y y
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 34
Vi
Vi , hàm s ng bin có duy nht nghim .
Bài 4. 
2
ax bx c k dx e

2
u ku dx e k dx e
Bài56: Gi
2
3 1 2 1x x x
Li gii
22
3 1 2 1 ( 2) 2( 2) 1 2 1x x x x x x x
t
2; 1u x v x
c:
22
22
2
uv
u u v v
uv
t 
Bài 5: Gi
2
2 2 1 4 1x x x
Li gii
2 2 2
2 2 1 4 1 4 4 2 2 4 1 (2 1) 2(2 1) 4 1 2 4 1x x x x x x x x x x
t
2 1; 4 1u x v x
c:
22
22
2
uv
u u v v
uv
t 
Bài 6: Gi
2
1 8 1x x x
Li gii
2 2 2
1 8 1 4 4 4 4 8 1 (2 1) 4(2 1) 8 1 4 8 1x x x x x x x x x x
t
2 1; 8 1u x v x
c:
22
44
4
uv
u u v v
uv
t 
Bài 7: Gi
2
4 21 22 3 2x x x
Li gii
2 2 2
4 21 22 3 2 4 21 22 3 2 (2 4) (2 4) 3 2 3 2x x x x x x x x x x
t
2 4; 3 2u x v x
c:
22
1
uv
u u v v
uv

t 
Bài 8: Gi
2
4
27 18
3
x x x
Li gii
2 2 2
4
27 18 81 54 9 12 (9 3) (9 3) 9 12 9 12
3
x x x x x x x x x x
Bài61: Gi
42
33xx
Li gii
2
4 2 2 2 2 2
3 3 3 3x x x x x x
...
Bài 9. [
33
u ku v kv
]
Gi
32
3
8 36 53 25 3 5 x x x x
.
Li gii
01yx
74
2 4 0y y y
1y
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 35
32
3
8 36 53 25 3 5 x x x x
3
3
2 3 2 3 3 5 3 5x x x x
.
t
23ux
;
3
35vx
.
33
u u v v
22
10u v u uv v
uv
.
3
2 3 3 5xx
32
8 36 51 22 0x x x
2
53
4
x
x
.
Bài 10. [
33
u ku v kv
]
Gi
32
3
4 6 4 1 2 1x x x x
.
Li gii
32
3
4 6 4 1 2 1x x x x
3
3
2 1 2 2 1 2 1 2 2 1x x x x
.
t
21ux
,
3
21vx
.
33
22u u v v
22
20u v u uv v
uv
.
3
2 1 2 1xx
32
8 12 4 0x x x
0
1
1
2
x
x
x

.
Bài 11. [
33
u ku v kv
]
Gi
32
3
20
9 9 1 1 2
3
x x x x
.
Li gii
32
3
20
9 9 1 1 2
3
x x x x
3
3
3 1 3 3 1 1 2 3 1 2x x x x
.
t
31ux
,
3
12vx
.
33
33u u v v
22
30u v u uv v
uv
.
3
3 1 1 2xx
32
27 27 11 0x x x
0x
.
Bài 12. [
33
u ku v kv
]
Gi
32
3
4 18 30 17 2 1x x x x
.
Li gii
32
3
4 18 30 17 2 1x x x x
3
3
3 2 2 3 2 2 1 2 2 1x x x x
.
t
32ux
,
3
21vx
.
33
22u u v v
22
20u v u uv v
uv
.
3
3 2 2 -1xx
32
8 36 56 28 0x x x
1x
.
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 36
Bài 13.      
2
ax bx c k dx e
 
22
u au v av
]
2
3 1 2 1x x x
Li gii
u kin:
1x 
.
t
1, 0y x y
.
 thành h
2
2
3 1 2
1
x x y
xy

.
Cng hai v cc
22
2 2 2 0
2
yx
x x y y x y x y
yx


.
Thay l t các giá tr
y
v       u, ta nhn hai nghim
5 13
2
x
và
15
2
x
.
Bài 14. 
2
ax bx c k dx e

22
u au v av
]
2
1 8 1x x x
Li gii
u kin:
1
8
x 
.
t
8 1, 0y x y
.
 thành h
22
22
1 4 4 4 4
8 1 8 1
x x y x x y
x y x y





.
Cng hai v cc
22
22
21
4 4 3 4 2 1 2
23
yx
x x y y x y
yx

.
Thay lt các giá tr
y
vu, ta nhn nghim
3x
.
Bài 15.      
2
ax bx c k dx e
 
22
u au v av
]
2
4
27 18
3
x x x
Li gii
u kin:
4
3
x 
.
t
4
,0
3
y x y
.
 thành h
2
2
2
2
27 18
81 54 3
4
9 12 9
3
x x y
x x y
xy
yy






.
Cng hai v cc
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 37
22
22
81 63 12 9 3 9 3 9 3 3 3
31
9 3 3 9 3 4 0
4
3
3
x x y y x x y y
yx
x y x y
yx

.
Thay l t các giá tr
y
v       u, ta nhn hai nghim
7 33
18
x

và
5 37
8
x

.
Bài 16.      
2
ax bx c k dx e
 
22
u au v av
]
32
3
8 36 53 25 3 5x x x x
Li gii
t
3
35yx
.
 thành h
32
3
8 36 53 25
35
x x x y
xy

.
Cng hai v cc
3
3 2 3 3
2
2
2
2
8 36 56 30 2 3 2 3
2 3 2 3 2 3 1 0
23
2 3 2 3 1 0
x x x y y x x y y
x y x y x y
yx
x y x y



D thy
2
2
2 3 2 3 1 0x y x y
.
Thay
23yx
u, ta nhn hai nghim
2x
và
53
4
x
.
Bài 17:
3
3
8 4 1 6 1x x x
, ta có
3
3
8 4 1
61
x x y
xy

Li gii
Cng v :
33
82x x y y
22
2 4 2 1 0x y x xy y
2yx

33
3
2 6 1 8 6 1 0 4 3 os
3
x x x x x x c
.
57
cos , cos , cos
9 9 9
x x x
.
BTLT : Gi
1)
2
4 2 2 4xx
2)
2
21
5 1 2
55
x
x
3)
2
4 4 1 2 4 2x x x
4)
2
49 65 17 3 2 1x x x
5)
2
75 79 28 2 3 4x x x
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 38
6)
32
3
6 10 13 2 4 1x x x x
7)
32
3
8 12 7 5 2 3 2x x x x
8)
32
3
128 288 218 61 2x x x x
.
VII.  S D 
Bài 1:
2 2 2
9 7 22 28 13 43 37 3 3 3x x x x x x x
Li gii.
Ta có
2
2
1 75 5 3
9
2 4 2
x x x



2 2 2
2
7 22 28 2 1 3 3 3 3 3 3x x x x x x
2 2 2
2
1 7 7 7
13 43 37 3 2 3 2 3 2
2 2 2 2
x x x x x x
Cng tng v c
VT VP
1
0
2
2 1 0
1
30
2
7
20
2
x
x
x
x
x




Bài 2: Gi
22
6 1 1 2 1 3 2 x x x x x x
D thy
1x
không là nghim c

2
2
2
6 1 1 2 1 3
6 1 1 2 1 2
x x x x x
x x x x
Nhn xét:
2 2 2 2
22
2
1 3 3 1
2 2 1 0 2 2 1
2 1 3 6 1 1
2 1 3 6 1 1
x x x
x x x x
x x x x x
x x x x x
Vm
Bài 3: Gi
33
22
22
66
6
23

x xy y
xy
x x y
x xy y
Nhn xét:
0, 0xy
không phi là nghim
Nu
0, 0xy
thì v trái ca mãn
,0xy
.
Vì
2 xy x y
nên
1 6 6 3 4 2x xy y x x y y x y
2 3 3xy
.
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 39
Mt khác
22
22
22
3
22
xy
xy
xy x xy y
3 3 3 3
2 2 2 2
32
4
x y x y
x y xy x y


.
Ta chng minh
33
22
22
2
25
xy
xy
xy

.
Ta có
3
3 3 2 2
52x y x y
6 6 3 3 4 2 2 4
4 3 3x y x y x y x y
.
D thy
6 3 3 3 3 4 2
6 3 3 3 3 2 4
3
3
x x y x y x y
y x y x y x y
5
.
Kt hp vi
2
và
22
2 x y x y
ta có
33
22
22
6
32
xy
x x y
x xy y

22
2 2 6x x y x x y x y
.
T
3
và
6
23xy
và
xy
1
1
x
y
.
Bài 4. 
2 2 2 2
3
5 2 2 2 2 5 3 1
2 1 7 12 8 2 5 2
x xy y x xy y x y
x y x y xy y
.
Li gii
Ta có:
2 2 2 2
2 2 2 2
5 2 2 2 2 5 2 2x xy y x xy y x y x y x y x y
2 2 3 3 3x y x y x y x y
.
0
1 2 0 0
20
xy
x y x y
xy


.
Th vào (2) ta có:
2
3
3 1 2 19 8 2 5x x x x
2
3
2 2 1 3 1 2 2 19 8 0x x x x x x


2
2
2
2
2
33
24
22
1 3 1
2 2 19 8 19 8
x x x
xx
xx
xx
x x x x

2
00
0
11
xy
x x TM
xy
. Vy h m.
Bài 5. [] Gii h 
11
3
44
11
3
16 16
99
3
16 16
xy
yz
zx
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 40
Li gii
u kin: .
t: . Ta có:
Do nên:
Nu thì Vô nghim.
Nu thì Vô nghim.
Vy  . Suy ra .
D thy nu mt s bng thì hai s còn lng .
Suy ra .
Bài 6. 
3 2 3
21
2 2 2

x x y y
x y y x
.
Li gii
u kin
0, 0xy
 ca
1
, ta có
2
33
4 4 2 3 x x y y x xy xy y
.
Thay
3
vào
2
c
3 2 3
4 2 2 2 xy xy y y y x
32
2 y xy xy x y
2
2 y y x x y y x y
.
T
1
suy ra
2
2 y y x x x y y y
2
x y y x x y
Ta có
2
2
2


x x x x
y y y y
2
x y x y y x y y x x y x x y
do (4).

2
1 1 2 2x y x y
2
22x y y x y y x y y x y y x x y
do (4).
2x x y y
.
9
,,
16
x y z
9 7 13
;;
12 12 12
a x b y c z
41
3
33
25 49
3
48 48
25 49
3
48 48
ab
bc
ca
4 1 25 49
3; 3
3 3 48 48
0, 0ab
41
3
33
ab
0, 0ab
41
3
33
ab
.0ab
. 0; . 0b c a c
2 2 2
. . 0abc
0abc
0
0
0abc
19 7 13
; ; ; ;
12 12 12
x y z



Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 41
ng thc xy ra
2
2
1
1
1
1
x x y y
x
x
y
y


.
Bài 7.
2 2 2 3
2
2 2 2
4 1 1 3 2 1
1 2 2
x x x y y
x y x y
Li gii
T
2
2
2 2 2 2
2 1 0x y x y y
22
01
1, 1.
xy
xy
Nu
2
1 1 0 0xx
ta có
1y 
h có nghim
0
1
x
y
.
Nu
2
1 1 0 0xx
, nhân 2 v ca
1
vi
2
11x 
ta có
1
2 2 2 2 3
4 1 1 3 2x x x x y y
2 2 3
4 1 1 3 2 3x x y y
2 2 3
1 4 1 3 3 2x x y y
2
22
1 1 . 1 3 2 1 4x x y y
.
Vi
0x
;
1x
;
1y
; ta có
2
1 1 0x
,
2
1 3 0x
,
2
1 1 0yy
nên
4
vô
nghim.
Bài 8. 

3 3 2 2
2 2 4 4
1
13 3
6 2 2
44
x y x xy y
x y x y x y xy
Li gii
Nhn xét:
0xy
không phi là nghim ca h nên
22
0x xy y
(1)
22
22
2 2 2 2
22
22
1
33
3
3
x y x y
x xy y
xy
x xy y x xy y
x xy y



.
T (3)
1
3*
3
xy
.
Li có
2
2 2 4 4 2 2 2 2
6 4 2 4x y x y x y x y xy
T (2) và (4)
13 3
2 2 5
44
x y xy xy
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 42
Nu
0xy
thì t (5) ta có :
13 3 3 1
22
4 4 13 3
x y xy xy x y
(mâu thun)
0xy
. T (5) ta có:
2 2 2
13 3
13 3
2 2 4
4 4 4
xy
x y xy xy xy x y x y x y

1
30
4
x y x y



.
Do
11
3
34
x y x y
i chiu vi (*) ta thng thc xy ra
0
3
2
3
xy
x y x y
xy

.
VIII.  T S D
Bài 1:
2
4 6 10 27 x x x x
Li gii

46x
.

2
46
10 27
f x VT x x
g x VP x x

2
2
10 27 5 2 2 1f x x x x

""

5x
.
..
2
22
1 4 1 6 1 1 4 6 2 2
B C S
g x x x x x




""

46
5
11
xx
x

.

2
4 6 2
,
10 27 2
xx
xx

""
trong
1 , 2

5x
.
 
5x
.


2
2
10 27 5 2 2
4 6 2
x x x
xx


Bài 2:
2 2 2
1 1 2 1x x x x x x
Li gii

2
2
10
1 5 1 5
22
1 0,
xx
xx
x x x
.
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 43

22
1; 1; 1; 1x x x x

2 2 2 2 2 2
1 1 1 1 1 1 2VT x x x x x x x x x


.
Hay
22
1 1 2 2x x x x x

2
2
2
2 2 2 1 1 0VT x x x x x x
Hay
2
2 2 3x x x

1 , 2 , 3
22
2
1 1 2
22
x x x x x
x x x

""
trong
2,3

22
11
1
11
x x x x
x
.

1x
.

AB


Bài 3. Gii h 
4
4
4
4
3
2 4 1
32
3
2 4 1
32
x
y
y
x
Li gii
Nu
xy
thì
44
44
33
2 4 2 4 1 1
3 3 2 2
xy
yx
yx
mâu thun.
 vi
xy
ta có
.xy
Ta có:
44
2
4
3 3 3
4 1 4. 4 1 2. 2 .
3 2 3 2 2
xx
x x x
Theo bng thc Bunhiacosky, ta có:
4 4 2 2
2
66
4. 4 4 4 4 2 4 3 .
3 3 3 3
x x x
x
T
2
22
33
2 ; 3 2 4 1 2. 6 0 6 6.
22
x x x x x x
Vy h có hai
4
nghim:
;xy
là:
6; 6 ; 6; 6 ; 6; 6 ; 6; 6 .
Bài 4: 
2 2 6 3 2
13 2 2 5 2 4 4 1 0x x x x x x x x
Li gii
ng: 
Nhn xét
22
6 3 2 3
1 1 1
10
2 2 2
x x x x x x
Nên b
22
13 2 2 5 2 4 4 0x x x x
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 44
22
2 2 5 2 4 4 13 1x x x x
D thy
22
2 2 2 2
a b c d a c b d
Nên
22
2
2 2 2
13
2 2 5 2 4 4 2 1 1
22
x x x x x x




22
15
2 13
22
.
Vy (1) xy ra
1
14
2
3
15
2
x
x
x
.
Bài 5: 
2
1 3 2 3 2 1x x x x
Li gii
2
2
1 3 2 3 1 1x x x x

..
2
2
22
1. 1 1. 3 1 1 . 3 1
B C S
x x x x
2
2
1 3 2 3 1 2x x x x

""

2
30
13
11
1 6 9
x
xx
x x x



2
3
3
5 3
52
7 10 0
x
x
x
xx
xx

.

1 , 2 , 3

5x
.
Bài 6: 
23
4
44
6 8 2 4 6 3 30 1x x x x x x x
  
2
4
4
6 8 4 2 4 2x x x x x x
 
           
2
ab
ab

44
24xx
 
AB
   
      
 
63xx
  

3
x
  

3
6 3 2. 27.x x x
.
Li gii
 
24x
.
 
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 45
2
4
42
6 8 4 2 1 2
2
xx
x x x x
33
6 3 2. 27. 27 3x x x x
  
..
22
44
2 4 1. 2 1. 4 1 1 2 4
B C S
x x x x x x
22
44
2 4 2 1. 2 1. 4 2 1 1 2 4x x x x x x
44
2 4 2 4 2 4xx

23
4
44
2 3 4 6 8 2 4 6 3 30 5x x x x x x x

1 , 5


""
trong
2 , 3 , 4

3
42
27 3
24
11
xx
xx
xx


.
   
3x
.
Bài 7: Gi
2 4 2 4
13 2 9 2 32x x x x
Li gii
Cách 1: Áp dng bng thc AM-GM
Ta có:
22
2 4 2 2
13 13 8 3 39
13 2 (8 4 ) 26
2 2 2 4
xx
x x x x
(1)
22
2 4 2 2
3 3 8 13 39
9 2 9 (8 4 ) 6
2 2 2 4
xx
x x x x
(2)
T (1) và (2) ta có
2 4 2 4
13 2 9 2 32x x x x
Vy
22
2 4 2 4 2
22
84
2 10
13 2 9 2 32 5 8
5
9 8 4
xx
x x x x x x
xx


Cách 2: Áp dng bng thc Bunhiacopxki
Ta có
2
2 2 4 2 4
32 13 2 9 2x x x x
2
2 2 2
. 13 26 13 3 3 6 3x x x
2 2 2
. 13 27 26 6 13 3x x x
22
16.5 . 16 5xx
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 46
2
22
2
5 16 5
16. 32
4
xx

IX.  S D
Bài 1: Gi
2 4 2 4
13 2 9 2 32x x x x
Li gii
Cách 1: Áp dng bng thc AM-GM
Ta có:
22
2 4 2 2
13 13 8 3 39
13 2 (8 4 ) 26
2 2 2 4
xx
x x x x
(1)
22
2 4 2 2
3 3 8 13 39
9 2 9 (8 4 ) 6
2 2 2 4
xx
x x x x
(2)
T (1) và (2) ta có
2 4 2 4
13 2 9 2 32x x x x
Vy
22
2 4 2 4 2
22
84
2 10
13 2 9 2 32 5 8
5
9 8 4
xx
x x x x x x
xx


Cách 2: Áp dng bng thc Bunhiacopxki
Ta có
2
2 2 4 2 4
32 13 2 9 2x x x x
2
2 2 2
. 13 26 13 3 3 6 3x x x
2 2 2
. 13 27 26 6 13 3x x x
22
16.5 . 16 5xx
2
22
2
5 16 5
16. 32
4
xx

Bài 2.
Gi
32
4
4 4 5 9 4 16 8 1x x x x
Li gii
u kin:
1
2
x
.
Ta có :
4
4
4 16 8 4 2.2.2. 2 1 2 2 2 2 1 2 7x x x x
.
ng thc xy ra
1
2 1 2
2
xx
.
T (1)
2
32
1
4 4 5 9 2 7 2 2 1 0 .
2
x x x x x x x
Bài 3: Nghim c
11
1xx
xx
có dng
2
a b c
vi
,,abc

2 3 4a b c
có kt qu là
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 47
A.
25
. B.
7
. C.
10
. D.
20
.
Li gii
Chn A.

1x
.

1
1
11
1.
11
2
1 2
1
1
11
1 1
2
Cauchy
Cauchy
x
x
xx
xx
xx
xx
x
x
x
xx









1 , 2

""
trong
2

2
1
1
1 5 1 5
1 0
1
22
1
x
x
x x x x
x
x



.

15
2
x
.
Vy
1
1 2 3 4 25
5
a
b a b c
c
Bài 4. 
3 3 2 2
7( ) 8 2( ) (1)
2 3 6 2 (2)
x y x y xy xy x y
y x x
Li gii
u kin
T (1)

ng thc xy ra th vào (2)
Do
3
,0
2
xy
2 2 2 2
( )( 6 ) 8 2 ( )x y x y xy xy xy x y
2 2 2
22
2 ( )
0 2 ( )
22
xy x y x y
xy x y
2 2 2 2
6 4 ( ) 2 4 ( ) 4( )x y xy xy x y xy x y x y xy
2
2 2 2 2
(x y)
( 6 ) 2 ( )4( )
2
x y xy xy x y x y xy
2 2 2 2
( )( 6 ) 8 2 ( )x y x y xy xy xy x y
xy
1
2 3 2 6 ( 3) 2 0
23
x x x x
xx




3
2
x
3 6 1
2 2 2
x
11
2 3 2 0
2
23
xx
xx




Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 48
Bài 5. 
3 3 2 2
2
2( ) (1)
4 1 9( 1) 2 2 (2)
x y xy x y
x x y x
Li gii
u kin:
T (2) Ta có
2 2 2 2
2xy x y x y x y xy
.

2 2 2 2
12x y x y xy xy x y x y
.
Ta có
2
2 1 2 1 1 9 1 1x x x x x
32
11
5
2 1 9 11 1
9
3
81 279 315 125 0
x
x x x x
x x x
Bài 6 . 
22
1 1 2
1
12
1 2 1 2
3 2 1
2 2 1 2 1 2 2
2
xy
xy
x y x y


Li gii
u kin
1
, 0; *
2
xy



.
Ta có
22
11
,
44
xy
suy ra
22
2 1 1 2
2 2 2 1
3
12
1 2 1 2
xy
xy
xy


1
, 0;
2
ab




thì
. 1 **ab
và ta có
22
1 1 2
3
1
11
ab
ab


.
   : Ta có
2
22
2 2 2 2
1 1 4 1 1 2 4
30
1 1 1 1
1 1 1 . 1
ab a b ab
a b a b



Theo B.C.S. ta có
22
22
22
1 1 1 4
1
11
a b ab
ab
ab


2
22
22
1
1 1 2
05
1 1 1
1 1 1
a b ab
a b ab
ab a b

.

ab
.

2 , 2a x b y
ta có :
3 0 3 3x x y
1x
1y
22
2 2 2 2 2 2
2
0 ;0 2 2
22
x y xy x y
xy xy x y x y x y xy
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 49
22
1 1 2
12
1 2 1 2
xy
xy



xy
. Thay vào (2) ta có
21
1 2 2 2 1 2 2 1
2
x x x x
 t
0
1 2 0
ux
vx

 c h  
22
1
2 2 2 1
2
2 1 2
2
u
uv
uv
v



hoc
2 2 1
6
24
6
u
v
suy ra
1
4
1
4
x
y
hoc
9 4 2
36
9 4 2
36
x
y
Bài 7. Gii h 

33
3
3
2 2 1 1
8 2 1 2
xy
x y x y


0
0
x
y
Ta có th chng minh bng thc
3
3 3 3 3
3
3
4
4
xy
x y x y x y
Bng thc xy ra
xy
Áp d trái cc

33
3
3
2
8
4
xy
xy
(*)
Li có



2
2
11
2 1 0 2 2 1 * *
22
x y x y x y
T (*) (**) ta có :
33
3
4 8 2 1x y x y
33
3
3
8 2 1x y x y
Suy ra (2) vô nghim. Vy h m.
Bài 8. Gii h 
3 3 2 2
2 3 2 6 (1)
7 8 2 (2)
x y x
x y x y xy xy x y
u kin:
3
2
0
x
y
Áp d     


33
33
2
2 2 2 2 2 2
7 4 2 .4 .
4 4 2 4 .2 .2 8 2
x y x y xy x y x y xy x y x y xy
x y xy xy x y xy xy x y xy xy x y
ng thc xy ra
xy
  (2)
xy
. Thay vào (1) ta có



31
2 3 2 6 2 3 3 2 0
2 3 2 3
x
x x x x x
x x x x
3x
(Vì
3
2
x
nên
11
2 2 0
2 3 2 3x x x x
)
Tp nghim ca h 
3S
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 50
X.  S DU CA HÀM S
Bài 1. 
3
3
3
3
2 2 2 2 6 6 6 6xx
. 
2x 
Li gii


3
2 ; 6f x x g x x

f f f f x g g g g x
.
Do
2
3
11
0; 0 ,
22
36
f x g x f x g x
x
x
ng bin trên
2; 
.
Vi
2x
thì
2f x g x
2
2
2
f f x f g x g g x
f f f x f g g x g g g x
f f f f x f g g g x g g g g x
VT VP

Vi
22x
thì
2f x g x
lp lu ta có
VT VP
.
Nhn thy
2x
là nghim c
2x
là nghim duy nht c
Bài 2:
3
4
3 2 1 4x x x
Li gii

1
2
x

3
4
3 2 1 4 0x x x
D thy khi
x
ng bin.
Pt có nghim duy nht
1x
.
Bài 3:
5
3 1 4 2 1x x x
Li gii

5
3 1 4 2 1 0x x x

1x
là nghim )
Bài 4:
55
2 1 5 2 5 2 2 1x x x x
Li gii

55
2 1 2 1 5 2 5 2x x x x
Xét
5
f t t t
nhn thy khi
t

ft

ft
ng bin.
2 1 5 2xx
1
3
x
( loi )
vô nghim.
Bài 5:
2 2 1 3 1 3x x x x
Li gii
u kin:
1
2
x 
.

2 1 2 1 3 1 1 3x x x x
Hàm s
f t t t
ng bin
2 1 3 1 .......xx
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 51
Bài 6. 
2
2 7 3 2 1 8 1 1 8x x x x x
Li gii
u kin:
1
8
x 
i
2
2
3 3 1 1 8 1 1 8x x x x
Hàm s
2
f t t t
ng bin trên khong
0;
nên
3 1 1 8xx
, gi
c
1; 3 /x x t m
Bài 7. 
3
33
3
55
1
2
2
x y y y x x
xy

Li gii
3
33
3
1 x x x y y y
. Hàm s
3
3
f t t t t
ng bin trên nên
xy
.
Th
xy
vào
2
c
1xy
.
Bài 8. 
55
3
3
1
2
1 3 2 3
x y y x
xy
Li gii
u kin:
1x
55
3
3
1 x x y y
. Hàm s
5
3
f t t t
ng bin trên nên
xy
.
Th
xy
vào
2
c
1 3 2 3 *xx
.
V trái ca
*
là hàm s ng bin trên khong
1; 
m duy nht
2 / 2x t m y
Bài 9. 
4
4
22
1
2
2
2
x y y x xy
xy

Li gii
u kin:
0; 0xy
.
Th
22
2 xy
vào
1
c
2 2 3 3
44
44
x y y x xy x y x x y y
Hàm s
3
4
f t t t
ng bin trên nên
xy
.
Th
xy
vào
2
c
1xy
(t/m) hoc
1xy
( loi).
Bài 10. 
3
2 1 2 1
1
2
2 2 1 1 0
x x y y
xy
Li gii
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 52
u kin:
1
2
y 
.
3
1 2 1 2 1 2 1x x y y y
. Hàm s
3
f t t t
ng bin trên
0; 
nên
21xy
.
Th
21xy
vào
2
c
1 0 /x y t m
.
Bài 11
4
4
22
x 1 x 1 y 2 y 1
x 2x y 1 y 6y 1 0 2
Li gii
u kin:
x1
4
4
44
1 x 1 2 x 1 y 2 y
Hàm s
4
f t f 2 t
ng bin
t0
4
4
x 1 y x y 1
và
y0
Th vào
6 5 3
0
2 y y 1 y y 3y 3y 9 0
y0
hoc
y1
Bài 12
3
2
2y y 2x 1 x 3 1 x 1
y 2y 1 4 x 4 2
Li gii
u kin:
4 x 4
t
2
1 x t 1 x t
;
t0

3
2x 1 x 2t 2t
3 3 2
1 2y y 2t t y t y 1 x y 1 x;y 0
Th vào
2
, ta có:
1 x 3 2x 4 x 4
3 2x 3 1 x 2 x 4 1 0
x 3 .... 0
x 3...
Bài 13. Gii h 
3 2 3 2
2
3 2 3 (1)
3 2 8 (2)
x x y y
x y y
*/ Cách thc mà trong thc t bn thân 
Hãy la chn bi  v dng
( ) ( )f x f y
.
Nhn xét gì v tp giá tr ca (x - 1) và ca
3y
?
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 53
Hàm s  u trên tc xét không ?
Li gii
u kin :
32
2
30
2
8 0 (*)
0
20
yy
x
yy
y
x



Ta có :
3
3 2 3
(1) 3 3 ( 1) 3( 1) 3 3 3 (1')x x y y x x y y
Xét hàm s
3
( ) 3f t t t
trên tp
[1; )
2
'( ) 3 3 0, 1f t t t
f(t) là hàm s ng bin trên khong
(1; )

2
(1') ( 1) 3 1 3 1 3f x f y x y x y
kt hp v
c :
2
2
2
2
2 1 3
2 2 (1')
9( 2) 8 (2')
3 2 8
x x y
x x y
x y y
x y y


Th c :
2
22
4 3 2
32
9 18 2 2 8 2 2
4 8 17 6 0
( 3)( 5 2) 0
x x x x x
x x x x
x x x x
3 2 2
3 0 3
3 1( )
5 2 0 ( 1) 4 ( 2) 0(VN)
xx
x y Tm
x x x x x x x



Vy h có nghim duy nht :
3
1
x
y
Bài 14. Gii h 
3
2 3 2
8 3 2 1 4 0 (1)
4 8 2 2 3 0(2)
x x y y
x x y y y
Li gii
u kin :
1
2
x
3
33
(1) 4(2 1) 1 2 1 4 4 2 1 2 1 4 (1')x x y y x x y y
Xét hàm s :
3
( ) 4f t t t
trên tp
[0; )
2
'( ) 12 1 0, 0f t t t
Hàm s f(t) ng bin trên khong
(0; )

2
(1') 2 1 ( ) 2 1 1 2f x f y x y y x
th c :
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 54
2
2 2 3 2
4 3 2
1 4 1 2 2 3 0
0
1
2 2 0 ( 1)(y 1)(y 2) 0
2
1
y y y y y
y
y
y y y y y y
y
y


Khi
1
0
2
yx
(thu kin)
Khi
11yx
(thu kin)
Khi
5
2
2
yx
(thu kin)
Khi
11yx
(thu kin)
Vy tp nghim ca h 
15
( ; ) (1; 1);(1; 1); ;0 ; ; 2
22
xy



Bài 15. Gii h 
2 2 2 2
3 3 8 ( )( 6) (1)
( 13)( 3 14 1) 5 (2)
x y y x y xy x
x y y x
*/ Cách thc mà trong thc t blàm:
Hãy la chn bi  v dng
( ) ( )f x f y
.
Nhn xét gì v tp giá tr ca (x + 1) và ca (y - 1) ?
Hàm s  u trên tc xét không ?
Li gii
u kin :
1
10
(*)
14
3 14 0
3
x
x
y
y




Ta có :
33
(1) 1 3 1 1 3 1 (1')x x y y
Xét hàm s
32
( ) 3 '( ) 3 3 0,f t t t f t t t R
Hàm s f(t) ng bin trên R

(1') ( 1) ( 1) 1 1 2f x f y x y y x
th   c :
(2 11)( 3 8 1) 5 (3)x x x
5
3 8 1 0 (4)
2 11
xx
x
(Do
11
2
x
không là nghim ca (3)
Xét hàm s
5
( ) 3 8 1
2 11
g x x x
x

trên
8 11 11
;;
3 2 2
D

2
2
3 1 10
'( )
2 3 8 2 1
2 11
6 17 10 8 11 11
0, ; ;
3 2 2
2 (3 8)( 1)(3 1 3 8)
2 11
gx
xx
x
x
x
x x x x
x


Hàm s g(x) ng bin trên
8 11
;
32



và
11
;
2




Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 55
- Khi
8 11
;
32
x



:
(4) ( ) (3) 3 5g x g x y
(thu kin (*))
-Khi
11
;
2
x




:
(4) ( ) (8) 8 10g x g x y
(thu kin (*))
Vy h m :
38
;
5 10
xx
yy





Bài 16. Gii h 
2
3
1 3 4
3 1 (1)
1
9 2 7 2 2 2 3 (2)
x
x y y
y
x
y x y y
Li gii
u kin :
1
10
(*)
2
9 2 0
9
x
x
y
y




Ta có :
2
11
(1) 3 ( 1) 3 1 (1')
1
y y x x
y
x
Xét hàm s
2
1
( ) 3f t t t
t
trên khong
(0; )
2
22
2 1 1
1
'( ) 2 3 0, (0; )
tt
f t t t
tt


Hàm s f(t) ng bin trên
(0; )

2
(1') ( ) 1 1 1f y f x y x x y
th c :
2
3
9 2 7 2 5 2 3y y y y
2
3
22
2 2 2 2
33
2
9 2 ( 2) 7 2 5 ( 1) 0
5 6 ( 1)( 5 6)
0
9 2 ( 2)
( 1) ( 1) 7 2 5 ( 7 2 5)
( 5 6). ( ) 0
y y y y y
y y y y y
yy
y y y y y y
y y h x




Vì
2 2 2 2
33
11
(x) 0
9 2 ( 2)
( 1) ( 1) 7 2 5 ( 7 2 5)
y
h
yy
y y y y y y




vi
2
9
y
nên
2
2
5 6 0
3
y
yy
y
-Khi
23yx
(th u kin (*))
-Khi
38yx
(th u kin (*))
Vy nghim ca h 
38
;
23
xx
yy





Bài 17. Gii h 
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 56
2 2 2
2 2 2 2
32
5 16.4 5 16 .7 (1)
17 10 17 2 4 4 11 (2)
x y x y y x
x x y x y
Li gii
t
2
2t x y
ng
2
5 16.4 5 16 .7
t t t
22
22
5 4 5 4
(3)
77
tt
tt

Xét hàm s
14
5.
77
xx
fx

()fx
là hàm s nghch bin trên R
ng
2
( 2) (2 ) 2 2 2 2 2f t f t t t t x y
ng
3 2 2 2
5 17 7 2 4 2 7x x x x x
32
2 2 2 2
2 2 2 2 7 2 7 2 7 2 7x x x x x x x
Xét hàm s
32
()f t t t t
trên khong
0;
2
'( ) 3 2 1 0, 0f t t t t
f(t) là hàm s ng bin trên khong
0;
ng
2
2 2 7f x f x
2
1
2 2 7
3
x
xx
x
Suy ra : H p nghim (x;y) là:
17
1; , 3;
22
.
Bài 18. Gii h 
2 2 2
3 2 4 2 3 2
4 1 2 1 3 2 1 2 1
2 2 4 1
x y x x y x
x y x x x x y y
Li gii
u kin :
11x
Ta thy
( ; ) (0; ),x y a a R
là nghim ca h 
Khi
0x
, ta có :
3 2 4 2 3 2 2
2
1 1 1
2 2 4 1 2 2 4 1 1x y x x x x y y y y y
x x x
(*)
Xét hàm s :
2
( ) 1f t t t t
2
2
2
'( ) 1 1 0,
1
t
f t t t
t
.
Hàm s f(t) ng bin
  
11
(*) 2 2f y f y
xx



th     i ca h ta có :
2
4 1 1 3 2 1 1x x x x
t
10
10
ax
bx
ta có :
22
3 1 2( 1) 1 2 1x x x a b
 thành :
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 57
22
2
2 4 2 0 2 2 0
2
ab
a b ab a b a b a b
ab

Vi
2ab
, ta có :
35
2 1 1
56
x x x y
Vi
2ab
, ta có :
1 1 2 0x x x
(loi)
Vy nghim ca h 
35
( ; ) ; ; 0; |
56
x y a a R






Bài 19. Gii h 
4
4
22
3 2 5 (1)
2 ( 2) 8 4 0 (2)
x x y y
x x y y y
Li gii
u kin :
2x
Ta có :
4
4
(1) ( 2) 5 2 5 (1')x x y y
Xét hàm s
4
( ) 5f t t t
trên
0;
3
4
2
'( ) 1 0, 0
5
t
f t t
t
Hàm s f(t) ng bin trên
(0; )
  
4
44
2 ( ) 2 2f x f y x y x y
th      c :
2
4 7 4
74
0
4 2 4 0
2 4 0 (3)
y
y y y y y y y
y y y
Vi
02yx
(thu kin)
Gii (3): Xét hàm s
74
( ) 2 4g y y y y
trên
0;
63
'( ) 7 8 1 0, 0g y y y y
Hàm s g(y) ng bin trên
(0; )
Li có :
(3) ( ) (1) y 1 x 3g y g
(thu kin)
Vy nghim ca h 
23
;
01
xx
yy





Bài 20. Gii h 
2
20 6 17 5 3 6 3 5 0 (1)
2 2 5 3 3 2 11 6 13 (2)
x y x x y y
x y x y x x
Li gii
u kin :
6
5
(*)
2 5 0
3 2 11 0
x
y
xy
xy
(1) 20 3 6 17 3 5
3 6 2 6 3 5 2 5 3
x x y y
x x y y
Xét hàm s
32f t t t
trên tp
0;
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 58
32
' 3 0, 0
2
t
f t t t
t
Hàm s f(t) ng bin trên
0;

(3) 6 5 6 5 1f x f y x y y x
th   c :
2
2 3 4 3 5 9 6 13x x x x
u kin :
4
3
x 
)
2
2
2 3 4 2 3 5 9 3
2 1 3 1
3 4 2 5 9 3
23
1 1 0
3 4 2 5 9 3
x x x x x x
x x x x
xx
x x x x
xx
x x x x




1
0
x
x

(vì
23
11
3 4 2 5 9 3x x x x
vi mi
x
thu
Vi
01xy
(tha mãn h 
Vi
12xy
(tha mãn h 
Vy nghim ca h 
; 0; 1 ; 1; 2xy
Bài 21. Gii h 
2
2
1 3 (1)
1 3 (2)
y
x
xx
yy
Li gii
Tr theo v c :
2 2 2 2
1 1 3 3 1 3 1 3 (3)
y x x y
x x y y x x y y
Xét hàm s
2
( ) 1 3
t
f t t t
trên R
2
'( ) 1 3 ln3 0,
1
t
t
f t t R
t
Hàm s f(t) ng bin trên R.

(3) ( ) ( )f x f y x y
th c :
22
1 3 1 3 1 (4)
xx
x x x x
Xét hàm s
2
( ) 3 1
x
g x x x
trên R
2
2
1
'( ) 3 1 ln3 0
1
x
g x x x
x



, do
2
10xx
và
2
11x 
Hàm s g(x) ng bin trên R.

(4) ( ) (0) x 0 y 0g x g
Vy h m duy nht :
0
0
x
y
Bài 22: Gi
2
3 2 6 3 12 0.x x x
Li gii
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 59
u kin:
2
6
3
x
Xét hàm s
2
3 2 6 3 12f x x x x
vi
2
;6
3
x



'
3 2 2
6 0, ;6
3
2 3 2 2 6
f x x x
xx




.
Suy ra hàm s
2
3 2 6 3 12f x x x x
ng bin trên khong
2
;6
3



Ta có:
2
2 3.2 2 6 2 3.2 12 2 2 12 12 0 2fx
là nghim duy nht c
T cách gii trên, ta nhn thtrình có mt nghim bng 2 nên có th  
cách gii sau.
Cách khác:
2
3 2 6 3 12 0x x x
2
3 2 6 3 2 6
3 4 0
3 2 6
x x x x
x
xx
42
3 2 2 0
3 2 6
x
xx
xx
4
2 3 2 0 2
3 2 6
x x x
xx



Bài 23: . Gi
2
4 4 2 16 10 0.x x x
Li gii
u kin:
4x
Xét hàm s
2
4 4 2 16 10f x x x x
vi
4x
2
1 1 2
0, 4
2 4 2 4
16
x
f x x
xx
x

Suy ra:
2
4 4 2 16 10f x x x x
ng bin trên
4;
2
5 5 4 5 4 2 5 16 10 3 1 2.3 10 0f
5x
là nghim duy nht c
Bài 24: . Gi
3
3
3 4 3 1 3 . *x x x x
Li gii
Xét
3
1 t tf t
vi t
t
R.
Có
2
3
1
( ) 1 0 1
3 ( 1)
f t t
t
ft
ng bin trên hai khong
( ; 1)
và
( 1; )
.
Ta có
* .( 3 )f x f x
Luôn có
3 0 1 3xx
nên:
- Nu
43 xx 
a
mà
ft
ng bin trên
( 1; )
thì:
(1)
33xx
2
3
30
1
1
7 6 0
16
x
x
x
x
xx
x


(tha mãn
a
).
- Nu
31x
3
4 0 4 0xx
.
* 1 * 0VT VT
(vô lí).
Vy
1x
là nghim c
Bài 25: Gi
2
9 28 21 1 *x x x
ng: Ta xây dng hàm
2
()f t mt nt
 ý rng hng t
1x
v phi có bc thp nh
ng vi
nt
trong
,ft

1n
. Ta nhìn nhn
2
9x
i
2
khía cnh
22
9 9.xx
thì
9m

nhìn nhn
22
9 (3 )xx
thì
1m
y m=9 hoc m=1.
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 60
Nu
9m
2
( ) 9f t t t
.
C
*
v dng:
2
9( ) 9( 1) 1x u x u x x
22
9 ( 18 8) 9 1x x u u u x
ng nht h s c:
2
10
18 28
9
9 21
{4; 3}
uu
u
uu
u



loi
Nu
1m
2
()f t t t
C
*
v dng
2
(3 ) 3 ( 1) 1x u x u x x
22
9 ( 6 2) 1 1x x u u u x
.
ng nht h s c
2
6 2 28
5
1 21
u
u
uu

    Bài  c gii quy        c:
*
2
9 30 25 3 5 1 1x x x x x
(3 5) ( 1)f x f x
**
vi
2
()f t t t
 rng
2
()f t t t
ch ng bin trên
1
( ; )
2

và nghch bin trên
1
( ; )
2

  a
1
10
2
x
y ta ch có
(3 5) ( 1)f x f x
3 5 1xx
khi
13
35
22
xx
Còn
3
1
2
x
thì sao? L ý rng hàm s b   
22
()tt
. trên , da vào
h s bc cao nht là
9
, ta ch mi xét
3t x u
nên bây gi ta s xét t=u-3x
C
*
v dng
2
( 3 ) 3 1 1u x u x x x
22
9 ( 6 4) 1 1x x u u u x
ng nht h s
2
6 4 28
4
1 21
u
u
uu

Kim tra li: Có
31
43
22
xx
n
4u
Bài mi thc s c gii quyt.
Li gii
u kin:
1x
Nu
31
35
22
xx
Ta có
*
2
(3 5) 3 5 1 1x x x x
(3 5) ( 1)f x f x
vi
2
()f t t t
3 5 1xx
((do
ft
ng bin trên
1
( ; )
2

)
2
5
3 5 0
3
2
13
(3 5) 1
{2; }
9
x
x
x
xx
x


(th
Nu
31
1 4 3
22
xx
**
*
2
(4 3 ) 4 3 1 1x x x x
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 61
(4 3 ) ( 1)f x f x
vi
2
()f t t t
4 3 1xx
( do
ft
ng bin trên
1
( ; )
2

và
**
)
2
4 3 0
(4 3 ) 1
x
xx

4
3
25 13
{}
18
x
x
v
Vy
*
có tp nghim
25 13
{2; }
18
S
 gii Bài trên bt
1 3 5xy
  h i xng loi 2.
Bài 26: Gi
2
2
28
1 2 2
23
xx
xx
xx


.
Ln 3 THPT Phú Ring 2016
Li gii

2x 
Pt
2
2
2
2 4 1 2
41
23
22
23
22
1
x
x x x x
xx
xx
x
xx
x





(1)
2
4 2 2 1 2 3x x x x x
2
2
2 2 2 2 1 2 1 2x x x x







(2)
Xét pt
2
22tt
có pt
2
' 3 4 2 0f t t t t
Vng bin trên

2
1
3 13
2 1 2 1
2
3 1 0
x
f x f x x x x
xx
Vy pt có nghim: x = 2,
3 13
2
x
Bài 27: Tng các nghim c
3
3 2 2
4 5 6 7 9 4x x x x x
là:
A.
4
. B.
2
. C.
3
. D.
4
.
Li gii
A
t
3
2
7 9 4y x x
, ta có h :
32
3
3
23
4 5 6
11
7 9 4
x x x y
y y x x
x x y
Xét hàm s :
32
31f t t t f t t

T 
11f y f x y x



3
2
1 7 9 4x x x
32
4 6 5 0x x x
5
15
2
x
x

Vy tng các nghim c : 4
Bài 28: Nghim nh nht c
3
3
6 5 5 5x x x
có dng
2
a b c
vi
,ab

abc
là:
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 62
A.
5
. B.
20
. C.
21
. D.
23
.
Li gii
C
Ta có
33
33
6 5 5 5 6 5 6 5x x x x x x x
(*)
Xét hàm s
3
f t t t
trên . Ta có
2
3 1 0,f t t t
. Suy ra
3
f t t t
ng bin trên .
T
*
3
65f x f x
3
65xx
3
6 5 0xx
2
1 5 0x x x
1
1 21
2
x
x

Vm là
1 21
1;
2
xx
.
m nh nht
1 21
2
x
1
1
21
a
b
c
21abc
Nhn xét: Có th gii Bài ng sau:
33
33
6 5 5 5 6 5 1 5 4x x x x x x
2
2
3
3
2
2
3
3
61
14
6 5 6 5 1
1
6
4
6 5 6 5 1
x
x x x
xx
x
xx
xx

V t ra là gii s rt phc tp.
Vì vy ta s u ca hàm s
Bài 29: Tng các c
32
3
3 2 1 2 1x x x x
là:
A.
3
. B.
3
. C.
5
. D.
23
.
Li gii
B
Cách 1:
Ta có
32
3
3 2 1 2 1x x x x
3
3
( 1) ( 1) (2 1) 2 1x x x x
Xét hàm
3
f x t t
trên .
2
3 1 0f x t
f t
ng bin trên
Ta có:
3
(21 1)xf x f
3
211x x
32
30x x x
2
3 1 0x x x
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 63
0
35
2
35
2
x
x
x
Vy tng các nghim c
3 5 3 5
03
22

Cách 2:
t
3
2 1 1xy
. Ta có h sau:
32
32
32
3 3 2
x x x y
y y y x
Ly 2 pt tr cho nhau ta có:
3 3 2 2
3( ) 4( ) 0x y x y x y
22
( )( 3 3 4) 0x y x xy y x y
22
33
( ) ( ) ( 1) 1 0
2 2 4
y
x y x y



xy
Vy :
3
2 1 1xx
32
30x x x
2
( 3 1) 0x x x
0
35
2
35
2
x
x
x

Vy tp nghim c
3 5 3 5
{}
2
0; ; .
2
S

Bài 30: Gii b
3
8 2 2 1 x x x x
có tp ngim
;S a b

ab
là:
A.
77
8

. B.
77
8

. C.
7 17
8

. D.
7 17
8

.
Li gii
D

1x 
.
3
2 2 1 1 1x x x x


3
2 2 1 1 1x x x x x
3
3
2 2 1 1x x x x
2 1 1f x f x

3
f t t t
.

3
f t t t
trên .
2
3 1 0, f t t t f t

2
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 64

1 , 2 2 1 2 1f x f x x x
hay
12xx
2
20
10
20
14
x
x
x
xx




1 17
1 0 0
8
xx
1 17
1
8
x
.

1 17
1;
8
S



7 17
8
ab

.
Bài 31: Gii b 
3
8 2 2 1 x x x x
có tp ngim
;c
a
S
b


vi
a
b
ti gin
,,abc

abc
là:
A.
10
. B.
9
. C.
8
. D.
11
.
Li gii
A

1
2
x
.

1 2 6 2 1 3 4 2x x x

2 1 3 0 5 2 :xx


5x
:

2 6 2 1 3f x x x x

5;
.
1 1 2 6
' 2 1 3 0; 5
2 2 2 6 2 1
xx
f x x x
x x x



fx

5;

74f
.

2 7 7f x f x
.

1
;7
2
S



.
Vy
1
2 10
7
a
b a b c
c
Bài tp luyn tp
1)
3
3
x 6 x 6
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 65
2)
2
5 x 3x 1 8x 16x 24
3)
33
2x 1 5x 2 5x 2 2x 1
4)
3 5 3
2 2 2
5
x 1 2x 2 x 2 x 3
5)
11
x 2x x
xx
6)
3
4x x x 1 2x 1 0
7)
3
x 2x 3 y 1 . 3y 1
2x 3 3y 2 2
8)
3
3y 2y 3x 2 x 8 2 x
5 4x 3y 1 3
9)
22
x x 2 x 4 y 1 y 3 y 5
x y x y 44
10)
33
23
x 12y x 2 8y 8y
x 8y 2y 5x
11)
3 2 3 2
2
x 3x 2 y 3y
3 x 2 y 8y
XI.     S DNG S    NG TRÒN
NG THNG
Bài 1u kin ca s thc  m phân bit:
2
2x x a x
. (2.4)
Li gii
u kin:
2
0 0 1.x x x
t
2
0.y x x
 thành:
2
2 2 2
2 (1)
2
11
0 (2)
24
0
0 (3)
x y a
x y a
x y x x y
y
y







Trong mt phng tng thng
:2x y a
, 
ng tròn có tâm
1
;0 ,
2
I



bán kính
1
2
R
, thuc phn
0.y
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 66
S nghim c m cng thng
và nng tròn
,IR
. Do
 m phân bing thng
ct nng tròn
,IR

2
1
1
11
, 2 0
25
2
2
24
5
2
22
2
a
d I a a
a
aa
a




.
Vm phân bit khi
25
2
2
a

.
Bài 2: Gii và bin lun theo
m

11 1m x m x
.
Nu
0m
m.
Nu
0m
m duy nht
0x
.
Nu
0m
.
t
0
0
u m x
v m x
.

1
22
2
,0
u v m
u v m
uv

2
.
Nghiêm ca h
2
m c ng thng
d
u v m
vi cung
AB
c ng
tròn
C
22
2u v m
.

2
có nghim
( ,( ))OH d O D R
) Vi
2Rm
là bán kính cng tròn
C
)
2
22
2 2 2
m m m
m m m
.
2
2 4 2 4m m m m
.

2
2
2u m u m
.
2 2 2 2
2 2 2 0 2 2 2 0u mu m m u mu m m
.
2
1,2
4
2
m m m
u


.
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 67
2
2
2
1,2 1,2
4
2
m m m
x u m m





.
Vy
2
1,2
4
2
m m m
x

.
Nu
0m

1
có nghim duy nht
0x
.
Nu
24m

1
có nghim
2
1,2
4
2
m m m
x

.
Nu
4
02
m
m


1
vô nghim.
Bài 3: Gii và bin lun theo
a
b
2a x a x
1
.
Li gii
Ta ch xét
0a
(vì nu
0a
thì biu thc
ax

t
u a x
v a x



22
2
12
,0
uv
u v a
uv

2
.
T     m
;M u v
tha mãn
2
;M u v
thuc ph ng tròn
22
:2C u v a
cha trong tam giác
OAB

u
2 2 2aa
: B
1
vô nghim.
u
2 2 0 1aa
: B
1
có nghim tha mãn
02u a x a
02a x a
2
0 xa
.
x
y
2a
2a
H
2
B
A
2
O
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 68
u
2 2 2a
12a
: B  
1
có nghim tha mãn
1
2
0
2
u a x u
u u a x a
.
(vi
1 2 1 2
; u u u u
là các nghim c
2
2
22u u a
 
v
)).
Gi
2
2
22u u a
Có
1
2
11
11
ua
ua
vì vy
1
2
0 1 1
1 1 2
a x u a
u a a x a
2
21
1 1 2
a x a a
u a a x a
21
2 1 2
a x a a
a a a x a
2
41a x a
.
Vy
0
2
a
a
: B
1
vô nghim.
01a
: B
1
có nghim
2
0 xa
12a
: B
1
có nghim
2
41a x a
Bài 4: Cho h 
x y a
x y xy a

1
vi
a
là tham s
nh
a
 h có nghim.
b)Gii và bin lun theo
a
.
Li gii
t
,0
,0
u x u
y y v



2
2 2 2 2
2
3
,0
,0
u v a
u v a
aa
u v uv a u v C
uv
uv



2
.
(vì
2
2 2 2 2 2
22
u v u v a u v
uv

).
x
y
a
0
( )
H
B
a
O
a
A
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 69
Vì vy h
1
có nghim
0
,
a
OH d O R
(vi
2
2
3
aa
R
là bán kính cng tròn
C
)
2
2
0
Ra
R
a

2 2 2
2
0
R a R
a

2 2 2
2 3 2 2
0
a a a a a
a
0
2 3 4 2
1
a
a a a
a

0
0
14
a
a
a

0
14
a
a

.
b) Theo kt qu câu (a)
0a
: H
2
có nghim duy nht
00
00
ux
vy





.
14a
: Ta có
2
2
2
2
3
aa
u a u

v
).
2 2 2
6 6 3 2 3u au a a a
22
3 3 0u au a a
2
1,2
3 12 3
6
a a a
u


và
1,2 1,2 2,1
v a u u
.
Vy khi
0a
h
1
có nghim duy nht
0
0
x
y
.
Khi
14a
h
1
có hai nghim
2
1,2
2
2,1
xu
yu
.
Khi
4
01
a
a

h
1
vô nghim.
Bài 5: nh
k
 h m duy nht
2
2
2
2
1 1
1 2
x y k
y x k
Li gii
Vi
0k
: D thy rng h  m, vì vy ta ch ng hp
0k
Xét trong mt
phng t
Oxy
.
nh hình tròng
1
C
tâm
0; 1I
có bán kính
1
Rk
nh hình tròn
2
C
tâm
1;0J
có bán kính
2
Rk
 m duy nht
1
C
và
2
C
tip xúc ngoài vi nhau
12
1
22
2
R R IJ k k
y
x
O
-1
J
-1
I
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 70
XII.  S DNG GIÁC HÓA
Bài 1. 
3
32x x x
Li gii
u kin
2x 
Nu
2x
ta có
32
3 4 2x x x x x x x

Nu
22x
t
2cos 0x

3
8cos 6cos 2cos 2
2cos3 2 cos
2

cos3 cos
2
4
5
4
7
k
k
k


Do
0


nên
4 4 4 4
0; ; 0; 2cos ; 2cos
5 7 5 7
x x x
Bài 2: nh
m
 bm
22
cos 2 cos cos . 2 cosx x x x m
.
Li gii:
t
2
2 cos
cos
xu
v x


22
(1) 2
12
u v uv m
uv
u

22
2
22
2
2
12
uv
u v u v
u v m
u


.
22
2
2
( ) 2
2
12
uv
uv
u v m
u



22
2
2
( ) 2( ) 2( 1) 0
12
uv
u v u v m
u


.
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 71
22
1
22
2
2( )
1 2 3
12
2( )
1 2 3
12
u v C
u v m D
u
u v C
u v m D
u




Rõ ràng
2D
không ct cung
ABC
.

1
có nghim
1D
ct cung
ABC
.
0 1 2 3 2m
.
1 2 3 3m
.
13m
.
XI. PHƯƠNG TRÌNH VÔ TỈ CÓ THAM SỐ
 
 
;0f x m


f x A m
.

fx
trên D.

y A m


y f x
.

f x A m

:

y f x

min max
D
D
f x A m f x
.
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 72


y A m

y f x


 
;0f x m

;0f x m


f x A m

f x A m
.
. L
fx
trên D.


f x A m


,y A m

max
D
A m f x
max
D
khi f x
.

f x A m


,y A m

min
D
A m f x
min
D
khi f x
.
 
f x A m

f x A m

xD
?

f x A m

min
D
x D f x A m
.

f x A m

max
D
x D f x A m
.
:





2. Các ví d
Bài 1:  m thc phân bit :
21x x m
Li gii
u kin:
1x 
i
21x x m
Xét hàm s
21f x x x
. Ta có
1 1 1
1
11
x
fx
xx


0 1 1 0 0f x x x
Bng bin thiên
Da vào bng bim thc phân bit khi
12m
.
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 73
Bài 2: Tìm
m
 
33
11x x m
có nghim.
Li gii
Xét hàm s
33
11f x x x
trên .
Ta có
22
33
11
,1
3 1 3 1
f x x
xx

22
33
11
0 0 0
3 1 3 1
f x x
xx

33
lim lim 1 1
xx
f x x x
 
33
lim 1 1
x
xx

22
3
2
33
2
lim 0
1 1 1
x
x x x



lim 0
x
fx

.
Bng bin thiên:
Vm khi và ch khi
02m
.
Bài 3: Chng minh rng
0m
       m thc phân bit:
2
2 8 ( 2)x x m x
(K B -2007)
Li gii
Do
0m
nên
2x
(1)
2
( 2)( 4) ( 2) ( 2)( 4) ( 2)x x m x x x m x
2
32
2
( 2) ( 2)( 4) 0
6 32 0(*)
x
x x x m
x x m


Yêu cu Bài quy v cht nghim trong
(2; )
Bii (*)
32
6 32m x x
.
Xét hàm s
32
( ) 6 32f x x x
vi
2x
.
Ta có
'2
( ) 3 12 0, 2f x x x x
và
lim ( )
x
fx


Bng bin thiên:
T bng bin thiên suy ra
0m
t nghim
2x
.
Vm thc phân bit
0m
.
+
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 74
Nhn xét: u kin
2x
vic kho sát hàm s
()fx
trên là rt d dàng ch yu là
ng bin ca hàm s
()fx
.
Bài 4:  m duy nht
2 3 2
3 1 2 2 1x x x m
trên
1
;1
2



Li gii
Xét hàm s
2 3 2
3 1 2 2 1f x x x x
trên
1
;1
2



.
Ta có
2
'
2 3 2 2 3 2
3 3 4 3 3 4
()
1 2 1 1 2 1
x x x x
f x x
x x x x x x



Xét hàm s
32
21g x x x
trên
1
;1
2



. Ta có
2
3 4 0 0g x x x x
Da vào bng bin thiên ta thy
1
( ) 1, ;1
2
g x x



và
1
;1
2
x



ta có
15
3( ) 4 3 4 3.1 4 3 4 7
22
xx
.
Suy ra
2 3 2
3 3 4 1
0, ;1
2
1 2 1
x
x
x x x




00f x x
Bng bin thiên:
Vm duy nht khi
3 3 22
4
2
m
hoc
1m
.
Nhn xét :
Vic s dng k i t
2
2 3 2 2 3 2
3 3 4 3 3 4
1 2 1 1 2 1
x x x x
x
x x x x x x



là khâu quyt
n vic xét du co hàm, m ng cho vic s dng tính cht ca hàm s .
Bài 5: Tìm
m
 m thc phân bit
44
2 2 2 6 2 6 2008
A
x x x x m K
.
Li gii
u kin
06x
Xét hàm s
44
2 2 2 6 2 6f x x x x x
trên
0;6
. Ta có
33
44
1 1 1 1 1
2
26
26
fx
xx
xx







3 3 2 2
4 4 4 4
1 1 1 1 1
2
2 6 2 6x x x x





Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 75
22
4 4 4 4 4 4
4
1 1 1 1 1 1 1
2 6 2 6 2 6
26
x x x x x x
xx




44
11
0 0 2
26
f x x
xx
Lp bng bin thiên:
vi
4
4
0 2 6 2 6; 2 6 3 2; 6 2 3 12f f f
T bng bin thiên suy ra giá tr cn tìm ca
m
là:
4
2 6 2 6 6 3 2m
.
i vi mt s Bài không s d trc tip mà phi sau quá trình bii
t n ph thích hp mi s d .Ta xét Bài sau :
Bài 6: Có bao nhiêu giá tr nguyên ca tham s
m
 
2 4 2
3 1 1x x m x x
có nghim

A.
1
. B.
8
. C.
15
. D.
27
.
Li gii
Chn A.
Tnh c
0;D 
.
Ta có:
2 4 2 2 2 2 2
3 1 1 2 1 1 1 1x x m x x x x x x m x x x x
22
22
11
2 1 1
11
x x x x
m
x x x x
t
2
22
1 2 2
11
1
11
1
x x x
t
x x x x
x
x


Do
0x
nên
2
2
11
1
1
2
x
xx
x
x



2
2
11
1
1; 3
2
13
1
1
x
xx
t
x
x





1
tr 
2
2
2 1 1
2 1 0 2 2
t
t mt m t
tt
 
2
có nghim thuc
1; 3
Xét hàm s:
1
2 ; 1; 3y t t
t
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 76
Vi
1 2 1 2
; 1; 3 ;t t t t

xét t s
21
2 1 2 1
2 1 1 2
2 1 2 1 1 2
11
2 2 2
.
1
20
.
tt
t t t t
t t t t
t t t t t t

Suy ra hàm s
1
2yt
t

ng bin trên na khong
1; 3
1 1 5 3
1 2 3 1 2
3
y t y t
tt
53
1
3
m
Do
m
là s nguyên nên có duy nht 1 giá tr ca
m
tha mãn yêu cu bài toán.
Bài 7: Tìm s các giai tr a tham s
m
 
2 3 2 3 2 2
( ) ( ) 6 1 4 6 4 0x m x x m x m x m x m
có nghim.
A.
0
. B.
1
. C.
2
. D.
3
.
Li gii
Chn B.
t:
2
2
0, 0
a x m x
ab
b x m x

2 2 2
22
2 ( ) 4 4
( )( )
a b x m a b x m
ab x m x x m x m
Kt hp vi
( ),
c h 
3 3 2
3 a 1 ( ) 6 0
ab m
a b b a b a b
32
( ) ( ) 3( ) 6 0
ab m
a b a b a b
2
2
2
2
2
ba
ab
a a m
a a m
ab m




Xét hàm
2
2y f a a a
vi
02a
có bng bin thiên
Vy
01m
suy ra
1m
.
Bài 8: Bit rng p
x a a x
có nghim khi và ch khi
m
a
n

vi
,mn
là các s nguyên

m
n
là phân s ti gin. Tính
T n m
.
A.
2T
. B.
5T
. C.
3T 
. D.
1T
Li gii
Chn B
u kin:
0
0
x
ax

.
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 77
t
0y a x
Suy ra:
0
x a y
x y x y
y a x


( ) ( 1) 0x y x y
x y x y
Nên
x x a
. ( D thy vi
0x
thì
0ax
).
t
0t x t
:
2
t t a
Xét hàm s
2
f t t t
vi
0t
có bng bin thiên:
Suy ra
1
4
a 
5T
.
Bài 9: 
2
4
1 3 1 2 1m x x x
, bit rng tp tt c các giá tr ca tham s m 
m là na khong
( ; ].ab
Tính giá tr biu thc
33
.S a b
A.
28
.
27
B.
26
.
27
C.
1.
D.
1.
Li gii
Chn B.
u kin
1x
, Chia hai v cho
1x
c pt:
4
11
32
11
xx
m
xx


t
44
12
1
11
x
t
xx

Do
22
1 2 1 0 1 1 0 1
11
xt
xx


2
3 2 (*)m t t
.
Bng bin thiên ca hàm
2
( ) 3 2f t t t
trên
[0;1)
Theo bng bin thiên thì (*) có nghim thuc [0; 1)
1 1/3m
.
Bài 10: 
2
2 1m x x m
bit rng tp hp các tham s th

;ab
. Tính giá tr
ab
A.
0
B.
2 2.
C.
2.
D.
2.
Li gii
Chn B.

D
.
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 78

2
2
1 2 ;
21
x
m x m x m f x x
x

.

22
2
22
22
' 2 1 ;
22
xx
f x x x
xx


.
Cho
2
22
2
2
22
' 0 0 2 2 2 4
2
2
x
x
f x x x
x
x


.
n thiên
x

2
2

'fx
0
0
fx

2
2


22m
.
Vy
0ab
XIV. TRẮC NGHIỆM PHƯƠNG TRÌNH VÔ TỈ
TN 1.1: Tng các nghim ca 
23
2( 6) 5 8x x x
là
A.
6
. B.
3
. C.
6
. D.
3
.
Phân tích. Khác vi hai ví d trên, biu thc là bc 3, ta vn gii theo công thc
,AB

c bi s h tr ca máy tính casio, ta s c thành tích s
dng bc 2 nhân bc 2.
Li gii

u kin:
32
8 0 ( 2)( 2 4) 0 2.x x x x x
23
2( 6) 5 8x x x
2 2 3 4 3 2
( 8.( 6) 25( 8) 8 41 104 96 88 0x x x x x x x
2
22
2
6 4 0
( 6 4)(8 18 28) 0 3 13.
8 18 28 0:
xx
x x x x x
x x VN
Kt lun: So vu kim là
3 13.x 
TN 1.2: S nghim c
2
2 6 1 4 5x x x
là
A.
1
. B.
3
. C.
2
. D.
0
.
Li gii

u kinh:
5
4
x 
.
Ta có:
2
22
2 6 1 4 5 2 6 1 4 5x x x x x x
4 3 2
6 8 2 1 0x x x x
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 79
Sử dụng máy tính Casio ta thu được:
1
2
3
4
2.414213562
0.414213562
3.732050808
0.2679491924
x
x
x
x

Tư duy Viet đảo:
1 2 1 2
2, 1x x x x
Nhân tử thu được:
2
2x 1x 
Vy:
22
2 1 4 1 0x x x x
ng hp 1: Vi
2
2 1 0 1 2x x x
.
Kt hu kin ta có
12x 
.
ng hp 2: Vi
2
4 1 0 2 3x x x
.
Kt hu kin ta có
23x 
.
Kết luận:  m phân bit
23x 
và
12x 
.
TN 1.3: Tm c
2
2 6 1 4 5x x x
là
A.
10 2 2 2 3
. B.
10 2 2 2 3
. C.
8 2 2 2 3
.
D.
12 2 2 2 3
Li gii
B
a sau khi s dc nhân t
2
2 1.xx
2
2 6 1 4 5x x x
22
2 2 4 3 2
2 6 1 0 2 6 1 0
(2 6 1) 4 5 6 8 2 1 0
x x x x
x x x x x x x






2
22
3 11 3 11
2 6 1 0 1 2
22
( 2 1)( 4 1) 0
23
1 2 2 3
x x x
xx
x x x x
x
xx




Kt lun: Tm là:
22
1 2 2 3 10 2 2 2 3
TN 1.4: Nghim nh nh 
23
2 5 1 7 1x x x
có dng
a b c
vi
,.a b c
  
abc
có kt qu là
A.
11
. B.
10
. C.
9
.
D.
12
.
Li gii
A
a sau khi s dc nhân t
2
8 10.xx
23
2 5 1 7 1x x x
2
2 2 3
2 5 1 0
(2 5 1) 49( 1)
xx
x x x
2
4 3 2
2 5 1 0
4 29 21 10 50 0
xx
x x x x
2
22
2 5 1 0 4 6
(4 3 5) ( 8 10) 0
46
x x x
x x x x
x

Kt lun: Nghim nh c
1
4 6 1 11
6
a
x b a b c
c
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 80
TN 1.5: Tng các nghim c  
2 2 2
2 3 1 2 3 4 1x x x x x x
có dng
a b c
vi
,.a b c

abc
có kt qu là
A.
2 33
3
. B.
2 33
4
. C.
1 33
4
.
D.
1 33
4
Li gii
D
u kin:
2
2
2
2 3 1 0
2
20
1
3 4 1 0
xx
x
xx
x
xx

2 2 2
( ) 3 2 1 2 ( 1) (2 1)( 2) 3 4 1x x x x x x x
2
22
10
( 1) (2 1)( 2) 1
( 1) (2 1)( 2) ( 1)
x
x x x x
x x x x

22
1
1
( 1) (2 3 3) 0
x
x
x x x
hoc
3 33
4
x


Kt lun: Tng các nghi
3 33 1 33
1
44

TN 1.6: Nghi
3 2 2
1 1 1x x x x
có dng
2
a b c
vi
,.a b c
 
abc
có kt qu là
A.
7
. B.
6
. C.
5
.
D.
8
.
Li gii
A
u kinh:
1x 
.
Ta có:
3 2 2
1 1 1x x x x
22
3 2 2 3 2 2
1 1 1 1 1 1x x x x x x x x
6 5 3 2 5 4 2
4 4 0 4 4 1 0x x x x x x x x x x
(*)
Sử dụng máy tính Casio ta thu được:
1
2
3
0.430159709
1.618033989
0.618033988
x
x
x


Tư duy Viet đảo:
2 3 2 3
1.0000000001 1,x 0.99999999989 1x x x
Nhân tử thu được:
2
1xx

2 3 2
1 2 3 1 0x x x x x x
(**)
u kin có nghim c
32
10xx
3 2 2
3 1 3 3 1
00
8 2 2 4 2
x x x x x x
Vì
32
1
0 2 3 1 0
2
x x x x

2
15
10
2
x x x
.
Kt hu kin ta thy ch có nghim
15
2
x
tha mãn.
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 81
Kết luận: m duy nht là
1
15
17
2
5
a
x b a b c
c
.
TN 1.7: T nghi
22
1 1 4x x x x x
gn nht vi giá tr

A.
0
. B.
1
. C.
3
.
D.
5
.
Li gii
A
u kin
4.x
i:
22
1 4 1x x x x x
2
2
4 1 0
4 2 4 1
x x x
x x x x
2
32
2 3 0
4 11 4 0
xx
x x x
2
31
0
4 11 4 0
x
x
xx
0
11 185
8
x
x
- Kt lun. Tm c
2
11 185
0.1057445
8




.
Nhn xét.
- ng hp:
1 3 2
a a a
(ví d 2) trong dng toán này vic s dng h u ki bii giúp chúng
ta va s dc phép bia s dc phép bii h qu.
- c thù ca dng toán này là viu kin
22
3 3 3 1 1 1
0a x b x c a x b x c
n. Nng hp vi u kin này là
c s dng phép bii h qu.
TN 1.8: Tp nghim ca b
11 4 2 1 x x x
có là
,S a b

ab
là
A.
6
. B.
2
. C.
7
.
D.
9
.
Li gii
D

11 0 11
4 0 4 4
2 1 0 0,5
xx
x x x
xx





.
11 4 2 1 x x x
11 3 5 2 4 2 1 4 2 1 8x x x x x x x
2
2
80
8
12 5
7 60 0
4 2 1 8
x
x
x
xx
x x x


.

4;5S
.
Vy
4
9
5
a
ab
b
TN 1.9: Tp nghim ca b
22
12 12
11 2 9
x x x x
xx


có là
,S a b c

abc
là
A.
1
. B.
2
. C.
0
.
D.
1
.
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 82
Li gii
D
2
2
2
12 0
11
12 0
12 0
11 2 9
11
0
11 2 9
xx
xx
xx
xx
xx






34
3
34
24
2
xx
x
x
x
x



.
Vy:
2
2,4 3 4 1
3
a
S b a b c
c


 
2
12 0,xx
  
sinh.
TN 2.1: 
2
1 2 6 7 7 12.x x x x x x
S nghim c
A.
0
. B.
2
. C.
1
.
D.
3
.
- Phân tích.
- c ht ta nhm duy nht
2.x
Nu ta s dp
m ng, dc các biu thc nhau nên có th dn vic phi kt hp vi
 tìm cách khc phc v này bng cách tìm nhóm các biu thc vi sao cho
 dng
2 . 0,x f x

0, 2.f x x
-  ý rng, vu kin:
2x 
  c du ca nh thc
1x
vì vy khi thc hin
phép nhân liên hi vi
1 2,xx
ta cn to ra nhân t:
2
12xx
hay ta cn tìm m, n sao cho:
20mx n x
khi
1; 2,xx
tc ta có h:
1
1
3
2 2 4
3
m
mn
mn
n



T  hai v ci 3 cho ta:
2
3 21 36 3 1 2 3 6 7 0x x x x x x
Tin hành vic nhóm nhân t cho biu thc
3 1 2,xx
ta s c:
2
1 4 3 2 2 16 32 3 6 7 0x x x x x x x
i vi
67xx
thì do
6 0, 2xx
nên ta s 
2
1 4 3 2 6 7 7 3 3 10 0x x x x x x x x
Li gii
C
u kin
2.x 
i:
2
1 4 3 2 6 7 7 3 3 10 0.x x x x x x x x
2
1 2 2
6 7. 2 5 0.
4 3 2 7 3
x x x
x x x x
x x x
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 83
2
1 6 7
2 5 0
4 3 2 7 3
x x x
xx
x x x




2.x
Do
2
1 6 7
5 0, 2.
4 3 2 7 3
x x x
xx
x x x
Vm duy nht
2.x
TN 2.2: 
22
2 3 21 17.x x x x x
S nghim c
A.
0
B.
2
C.
1
D.
3
- Phân tích.
Ta nhc rm
1; 2xx
. Do v có nhân t
2
1 2 3 2x x x x
nh s dng liên h giu quan tâm là cách
tách - 
Gi s ta s nhóm
2
1 1 2 2
2 3 21 17 .x x a x b a x b x
Thay các giá tr
1; 2xx
vào các
ng thc
2
11
22
2 3 0
,
21 17 0
x x a x b
a x b x
ta s  c
11
11
20
3 2 0
ab
ab
1
1
1
;
1
a
b
22
22
20
2 5 0
ab
ab
2
2
3
.
1
a
b

Li gii
B
u kin
17
.
21
x
i:
22
2 3 1 3 1 21 17 3 2 0.x x x x x x x
2
2
2
2
9 3 2
32
3 2 0.
3 1 21 17
2 3 1
xx
xx
xx
xx
x x x


2
2
19
3 2 1 0
3 1 21 17
2 3 1
xx
xx
x x x



2
3 2 0xx
1
2
x
x
Do
2
1 9 17
1 0, .
21
3 1 21 17
2 3 1
x
xx
x x x
Kt lun. Tp nghim c
1;2 .T
TN 2.3: 
2
1 1 2 2 1 1 .x x x x x x
Gi s 
dng
b
xa
c

  
a
,
b
,
c
là các s   
b
c
là phân s ti gin. Tính
S a b c
A.
49
. B.
47
. C.
30
. D.
15
.
Phân tích. Ta nhn thy
1 1 1 1 ,x x x
tuy nhiên kh s dng liên hp ta
ph ng hp
1 1 0 x
và
1 1 0.x
 tránh nhng v v phc t
ny sinh, ta có th x 
Li gii
A
u kin
0.x
i:
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 84
2
1 1 2 2 1 1 1 1 1 1 .x x x x x x x
2
2 2 1 1 1 1x x x x x
22
2 2 1 1 0x x x x x x
2
22
31
10
2 2 1
xx
xx
x x x x

22
11
10
2 2 1
x x x x
xx
x x x x
22
1
1 1 0
2 2 1
xx
xx
x x x x





22
1 0 1
2 2 1 1 0 2
xx
x x x x x x
Khi 
35
1.
2
x

22
2 2 2 1 1 0 *x x x x x x
Ta có:
22
22
2
2 2 1 1 1 1 1 1 1 1 0
0
x x x x x x x x x x
x x x x x

* 0.x
- Kt lun. Tp nghim c
35
;0 .
2
T





TN 2.4: 
2
1
2x x x
x
. Mt nghing
2
ab
x
.
Tính tng
2
S a b
.
A.
4S
. B.
5S
. C.
4S 
. D.
5S 
Li gii
C
u kin
1
.
10
x
x
c nhân t
2
1.xx
i:
2
1
1 1 0x x x
x




22
2
11
0
1
1
1
x x x x
xx
xx
x





2
2
11
10
1
1
1
xx
xx
xx
x












Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 85
2
2
10
1
1 1 0 1
xx
x x x x
x




ng hp.
2
10xx
15
.
2
x

ng hp.
2
1
1 1 0 * .x x x x
x




ng x lý 1. (S d qu)
Thay
2
1
11x x x
x
t  qu.
22
1 1 0x x x x x
2
2
2
1
10
1
x x x
xx
xx


2
22
1 1 0x x x x x
32
2 1 2 0x x x x
Vu kin
1
10
x
x
thì
3
2 1 0xx
 qu
32
2 1 2 0x x x x
vô nghim,
m.
ng x lý 2. (S dc ti
+ Nu
1,x
i
1 1 1 0 x x x x x a
.
Vi
1x
0,VT a
tc (a) vô nghim.
+ Nu
1 0,x
i
23
10x x x x x
2
23
1
1 0
xx
xb
x x x x
Vi
10x
0,VT b
tm.
T m.
Kt lum
15
.
2
x
TN 2.5: 
22
2 1 1.x x x x
S nghim c
A.
0
. B.
4
. C.
3
. D.
2
.
Li gii
D
- Phân tích. Nhn thy
2 2 2 2
2 1 2 1 2 1 1x x x x x x x x x x
t i gii sau:
u kin
1.x
i:
2 2 2
2 1 2 1 2 1x x x x x x x x x
22
2 1 2 1 1 0x x x x x x
2
2
2 1 0 1
2 1 1 0 2
x x x
x x x
2
10
1
20
x
xx

1x
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 86
2
2 2 2 1xx
42
2
4 4 8 0
x
xxx
32
2
2 2 4 0
x
x x x
2x
Do:
32
2 4 2 2 4 4 0, 2x x x
- Kt lun. Tp nghim c
1;2 .T
TN 2.6: 
33
1 2 3 3 2.x x x
Bit mt nghim c
b
xa
c

, trong

a
,
b
,
c
là các s nguyên và
b
c
là phân s ti gin. Tính tng
32S a b c
.
A.
10
. B.
7
. C.
7
. D.
10
.
Phân tích.
Nhn thy
1 2 3 3 2x x x
và không có giá tr nào ca
x
làm cho các biu thc
33
1, 2 3xx
ng thi bng 0. Nên ta có th thc hin phép nhân liên h xut hin nhân t
3 2 .x
Li gii
B
i:
22
33
3
32
3 2 0
1 1 2 3 2 3
x
x
x x x x
22
33
3
1
3 2 1 0
1 1 2 3 2 3
x
x x x x




3 2 0x
2
3
x
22
33
3
1
1 0,
1 1 2 3 2 3
Do x
x x x x
Kt luân. Nghim c
0
2
2 3 2 7.
3
3
a
x b a b c
c
TN 2.7: Gi
S
là tp nghim c
22
5 5 2 3 2x x x x x
. S phn t ca
S
là
A.
0
. B.
1
. C.
2
. D.
3
.
- Phân tích. Nhn thy
22
5 5 2 4 3 1 3x x x x x x x
và
2
3 2 1 2x x x x
ng thi:
2
5 5 2 0x x x
nên ta có th thc hin phép bi i:
2
2
2
43
5 5 2
5 5 2
xx
x x x
x x x

 làm xut hin nhân t
1.x
Li gii
B
u kin
55
.
2
x

      i:
22
5 5 2 3 2 0x x x x x
2
2
2
43
3 2 0
5 5 2
xx
xx
x x x

2
3
1 2 0
5 5 2
x
xx
x x x



10x
1x
2
3 5 5
2 0, x
2
5 5 2
x
Do x
x x x
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 87
Vm là
1.x 
TN 2.8: Gi
S
là tp nghim c
22
2 2 1 1.x x x x
S phn t ca
S
là
A.
0
. B.
2
. C.
1
. D.
3
.
- Phân tích. Nhn thy
2 2 2
2 2 2 1 vaø x 1 1 1 ,x x x x x x x x x
nh vy khi
chúng ta thc hin phép nhân liên hp s xut hin nhân t:
1.x
Tuy nhiên khi
1,x
biu thc
2
2 2 1 0x x x
   i
2
2
2
2 2 1
2 2 1
xx
x x x
x x x
là mt phép
bic khi thc hin phép nhân liên hp ta c n biu thc liên hp
      x lý các dng toán này ta có th    ng hp ca x làm cho
0f x g x
ng hp
0.f x g x
C th, vi bài toán này ta có th x 
Li gii
C
u kin
1.x
+ Nhn thy
1x
là mt nghim c
+ Vi
1x
i:
22
2 2 1 1 0x x x x
2
2
1 1 0
2 2 1
xx
xx
x x x
2
1 1 0 *
2 2 1
x
xx
x x x




Khi
1 x
thì
1 0 x
và
2
10
2 2 1
x
x
x x x
 m
1.x
- Kt lum duy nht
1.x
TN 2.9: Gi
22
1 2 3 1x x x x
c nghim có dng
x a b

a
,
b
là
các s nguyên. Tính tng
S a b
.
A.
0
. B.
1
. C.
2
. D.
3
.
Li gii
B
Vì
1x 
không là nghim c      
2
2
1
23
1
x
xx
x
2
2
1
2 3 1 1
1
x
x x x x
x
2
22
1
2 3 1
x
x x x

2
2 1 0xx
12x
1a
,
2b
. Vy
3S
.
Nhn xét:
V dt ra là làm sao nh n s
1x
vào hai v.
ng xut phát t vic tàm ra s
và
sao cho
2
2
1
23
1
x
x x x x
x
vi
0
.
2
22
2
2 3 1 1
1
23
x x x x x x
x
x x x


2 2 2
2
2
1 2 1 . 3
11
1
23
xx
xx
x
x x x


Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 88
 vi nh
,
sao cho:
2
2
11
2 2 .
31


1
,
1

.
TN 2.10: 
3
22
3
3 1 5 1 2 .x x x x x
S nghim c
A.
2
B.
0
C.
3
D.
4
- Phân tích. Nhn thy
22
3 1 5 1 2x x x x x
và không có giá tr nào ca
x
làm cho các biu
thc
3
2
3
3 1, 5 1x x x
ng thi bng 0. T   ng liên h xut hin nhân t
2
2.xx
Li gii
A
i:
3
22
3
3 1 5 1 2 0x x x x x
2
2
2
2
22
3
3
3
2
20
3 1 3 1 5 1 5 1
xx
xx
x x x x x x
2
20xx
0
2
x
x
Do:
2
2
22
3
3
3
1
1 0,
3 1 3 1 5 1 5 1
x
x x x x x x
- Kt lum
0; x 2.x 
TN 3.1: Tm c
22
5 2 2 5 10 0x x x x
là:
A.
13
. B.
5
. C.
10
. D.
25
.
Li gii
A
u kinh
2
5 10 0x x x
.
 thành:
22
5 10 2 5 10 8 0x x x x
2
2
5 10 2
5 10 4
xx
xx
1
22
2
3
5 10 2 5 6 0
2
x
x x x x
x


.
Vy
2 2 2 2
12
2 3 13xx
.
TN 3.2: Tích các nghim c
23
2 5 1 7 1x x x
bng
A.
10
. B.
6
. C.
10
. D.
6
.
Li gii
C
u kinh
1x
.
22
3 1 2 1 7 1 1pt x x x x x x
22
11
3. 7 2 0
11
xx
x x x x

2
1
2
1
x
xx


hoc
2
11
13
x
xx

Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 89
Vi
2
2
1
2 4 3 5 0
1
x
xx
xx

m.
Vi
2
11
13
x
xx

2
8 10 0xx
46x
.
Tích các nghim ca ng
10
.
TN 3.3: Bi
22
4
6
1
x x x x
x
có mt nghim dng
0
ab
x
c
vi
,,abc
là các
s 
a
c
là phân s ti ging
2 2 2
S a b c
bng:
A.
14
. B.
21
. C.
29
. D.
30
.
Li gii
D
u kinh:
23x
và
1x
.
2
4
pt 3 2 2 2
1
x x x x
x



.
23
3 2 1 2
1
x
x x x x
x
.
Chia hai v 
12xx
c:
2
1 3 1 3
. 2. . 1
1 2 2
1
xx
x x x
x


t
13
.
12
x
t
xx

 thành
2
2 1 0tt
1t
hoc
1
2
t
.
Vi
1
2
t
ta có
1 3 1
.
1 2 2
x
xx

3
21
2
x
x
x
2
13
3
4. 1
2
x
x
x
x


2x
Vi
1t 
ta có
13
.1
12
x
xx


3
1
2
x
x
x
2
21
3
1
2
x
x
x
x

1
15
2
x
x


0
15
2
x
và
1a
;
5b
;
2c
.
Vy
2 2 2
30S a b c
.
TN 3.4: Bi
22
4 2 3 4x x x x
có mt nghim là
0
ab
x
c

vi
,,abc
là các s

a
c
là phân s ti ging
S a b c
bng
A.
19
. B.
15
. C.
2
. D.
7
.
Li gii
A
u kinh:
22x
.
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 90
t
2
4t x x
thì
2
2
4
4
2
t
xx

.
2
2
3 2 8 0
4
3
t
pt t t
t

.
Vi
2t
suy ra
2
42xx
2
42xx
2
22
2
0
2 4 0
x
x
x
xx


.
Vi
4
3
t 
suy ra
2
4
4
3
xx
2
4
2
2 14
3
3
9 12 10 0
x
x
xx
.
2a
;
14b
;
3c
.

19S
.
TN 3.5: Bi
33
2
1 1 2 1x x x
có nghim duy nht
0
a
x
b
vi
,ab
là các
s  tng
22
S a b
bng:
A.
13
. B.
5
. C.
11
. D.
29
.
Li gii
A
u kinh:
11x
.
t
1
1
ax
bx


u kin
, 0;1ab
.
Ta có h
22
33
2
2
ab
a b ab

2
3
22
32
a b ab
a b ab a b ab
2
32
22
6 6 0
ab a b
a b a b a b
2
22
1
6
1
ab a b
ab
ab
ab

(Do
0ab
).
Vi
1
1
2
a b ab
  
a
;
b
là nghim c  
2
1
0
2
XX
13
1
2
ax
3
2
x
.

13S
.
Cách 2 : u ki nh:
11x
.
33
2
1 1 2 1x x x
22
1 1 2 1 2 1x x x x
1 1 1xx
1 1 2 1 1x x x
2(1 ) 2 1 1 0xx
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 91
13
1
3
2
2
13
1
2
x
x
x VN




.
TN 3.6: Tm c
1 4 ( 1)(4 ) 5x x x x
là
A.
6
. B.
3
. C.
9
. D.
27
.
Li gii
C
u kinh:
14x
.
t
14t x x

0t
)
2
5
( 1)(4 )
2
t
xx
PT(1) tr thành:
2
5
5
2
t
t

2
2 15 0tt
3
5 (l)
t
t

Vi
3t
1 4 3xx
5 2 ( 1)(4 ) 9xx
( 1)(4 ) 2xx
( 1)(4 ) 4xx
2
30xx
0
3
x
x
Vy tp nghim c
0;3S
.
TN 3.7: Tích các nghim c
22
1 3 1 1x x x x
là
A.
1
2
. B.
5
. C.
5
. D.
1
.
Li gii
B
t
2
3 1 0t x x
22
13x x t
.  thành
2
31tt
2
20tt
1( )
2( )
t tm
t loai

Vi
2
1: 1 4t x x
2
50xx
12
.5xx
TN 3.8: Tm c
2 2 2
2 2 2 1 7x x x x x x
là
A.
11
. B.
1
. C.
9
. D.
25
4
.
Li gii
A
2 2 2
2 2 2 1 7x x x x x x
2 2 2
2 2 ( 1 1) 7x x x x
22
2 2 ( 1 1) 7x x x x
22
2 2 1 8 0x x x x
t
2 2 2
1 0 2 2 2( 1)t x x x x t
 thành
2
2( )
2 6 0
3
()
2
t tm
tt
t loai

.
Vi
2
2: 1 4t x x
2
50xx
1
5
S
P


2 2 2
12
2 11x x S P
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 92
TN 3.9:  
2 f x f x
có tp nghim nghim
1;2;3A
  
3
2. 1 3. 2 2.g x g x g x
có tp nghim
0;3;4;5B
.Hi tp nghim c  
1 1 . 1f x g x f x g x f x g x
có bao nhiêu phn t ?
A.
1
. B.
4
. C.
6
. D.
7
.
Li gii
A
2
1
0
2 1 2
20
3
x
fx
f x f x f x x
f x f x
x
3
2 ( ) 1 3. ( ) 2 2. ( )g x g x g x
3
22
33
3
11
2 1 2 2 1 1 3 2 3 3 2 2 0
23
11
2 1 1 3 2 2 3 2 1 0
23
0
2 1 1 0
3
1
4
3 2 1 0
5
g x g x g x g x
g x g x g x
x
gx
x
gx
x
gx
x
1 1 . 1f x g x f x g x f x g x
1 1 1 1f x g x f x g x
1
1
1
fx
x
gx
.Vy tp nghim cn t.
TN 3.10:  
2 f x f x
có tp nghim nghim
1;2;3A
  
3
2. 1 3. 2 2.g x g x g x
có tp nghim
0;3;4;5B
.Hi tp nghim c  
.1f x g x f x g x
có bao nhiêu phn t ?
A.
3
. B.
4
. C.
6
. D.
7
.
Li gii
C
2
1
0
2 1 2
20
3
x
fx
f x f x f x x
f x f x
x
3
2 ( ) 1 3. ( ) 2 2. ( )g x g x g x
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 93
3
22
33
3
11
2 1 2 2 1 1 3 2 3 3 2 2 0
23
11
2 1 1 3 2 2 3 2 1 0
23
0
2 1 1 0
3
1
4
3 2 1 0
5
g x g x g x g x
g x g x g x
x
gx
x
gx
x
gx
x
. 1 1 1 0f x g x f x g x f x g x
0
1
1
2
3
1
4
5
x
x
fx
x
x
gx
x
x

.Vy tp nghim cn t.
TN 4.1: Bit nghim nh nht c  
2
32
3
16x 6x 2
3x 7x 6x 4 3
3

có dng
*
, , ,
a c a
abc
bb
ti gin. Tính giá tr ca biu thc
2 3 4
S a b c
.
A.
S 2428.
B.
S 2432.
C.
S 2418.
D.
S 2453.
Li gii
B
t
2
3
16x 6x 2
3
y

. Ta có h
2
3
32
16x 6x 2
1
3
3x 7x 6x 4
2
3
y
y

Cng (1) vi (2) theo v c
32
3
33
3x 9x 12x 6
11
3
y y y y x x
(3)
Xét hàm s
3
,f t t t t
, vì
'2
3 1 0,f t t t
nên hàm
f
ng bin trên .

3 1 1f y f x y x
c
3 2 2
1
27
3x 7x 3x 1 0 1 3x 4x 1 0
3
27
3
x
xx
x
Nghim nh nht c
27
x
3
suy ra
a 2, 3, 7bc
.
Vy
2 3 4 2 3 4
2 3 7 2432S a b c
.
i vi hc sinh lp 10, ta chng minh hàm
3
f t t t
ng bin trên 
Vi mi
1 2 1 2
,,t t t t
, ta có
2
3 3 2
12
22
1 1 2 2 2 2
1 1 2 2 1
1 2 1 2
3
1 1 0
24
f t f t
t t t t t t
t t t t t
t t t t




Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 94
Cách 2:
2
32
3
2
3 2 2 2
3
16x 6x 2
3x 7x 6x 4 3
3
16x 6x 2
3x 7x 6x 4 16x 6x 2 16x 6x 2 3
3


2
3 2 2
3
22
3
3
16x 6x 2
3 3x 4x 2 16x 6x 2 3
3
16x 6x 2 16x 6x 2
1 1 (*)
33
x
xx

Xét hàm s
3
,f t t t t
, vì
'2
3 1 0,f t t t
nên hàm
f
ng bin trên .

22
33
16x 6x 2 16x 6x 2
* 1 1
33
f x f x




3 2 2
1
27
3x 7x 3x 1 0 1 3x 4x 1 0
3
27
3
x
xx
x
TN 4.2: 
3
3
1 2 2 1xx
có ba nghim phân bim bé nhc biu th
i dng
ab
c
vi
,,abc
là các s nguyên,
0, 0, 3bac
. Tính giá tr ca biu thc
3 3 3
?P a b c
A.
134
. B.
132
. C.
116
. D.
118
.
Li gii
B
t
3
3
2 1 2 1t x t x
      u tr thành
3
3
3
2
2
33
12
12
12
13
( ) 2 0
2( )
24
xt
xt
xt
x t x t t
xt
x t t x











c
33
1
15
1 2 2 1 0
2
15
2
x
x x x x x
x


Nghim bé nht c
15
2
x


1; 5; 2a b c
và
132P
.
TN 4.3: Gi
0
x
là nghim âm c  
󰇛 󰇜
3
222
331.28137 xxxxxx
. Bit
0
x
có dng
ab
c
vi
,,abc
là các s t nhiên ,
a
là s
nguyên t. Hi tng
2T b a c
chia ht cho s 
A.
17
. B.
19
. C.
18
. D.
15
.
Li gii
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 95
B
D thy
0x
không là nghi  pt cho
3
x
c:
3
232
3
31
.2
8137
x
xxx
x
 dng:
3
3
33
22
2 2 1 3 1 3
1 2. 1 3 2. 3 *
x x x x x x




Xét hàm s
3
2f t t t
vi
t
ng bin trên .

3
2 3 2
1 3 2 8 13 3
* 3 1 2 0
x x x x x x
1
1
1
5 89
1 16
4
5 89
5 89
4
x
x
x
x
x






Vy
0
5 89
89 2.5 4 95 19
4
xT




TN 4.4: Cho hàm s
()fx
liên tc trên  th .
H
1 sin 1 cosf x f x
có tt c bao nhiêu nghim thuc
3;2
?
A.
0
. B.
1
. C.
2
. D. Vô s.
Li gii
B
1 sin 1 0 1 sin 2
3;2
1 cos 1
0 1 cos 2
xx
x
x
x

1 sin 1 cos 1 sin 1 cosf x f x x x
( Vì
()fx
ng bin trên
0; 2
sin cos 0 tan 1
4
x x x x k
Do
3;2
4
xx
thy có duy nht 1 nghim.
TN 4.5: Gi
0
x
là nghim thc c
2 2 4 2 2
5 1 6 1 2 2 1 1x x x x x x x
, bit bình
a nghim
0
x
có dng
2
0
ab
x
c
,,abc
,
b
a
ti gin .Tính
S a b c
A.
26S
. B.
25
. C.
24
. D.
22
.
Li gii
A
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 96
Vì :
2 2 4 2 2
5 1 6 1 2 2 1 1 0 0x x x x x x x
u kin :
0x
Chia
2
x
hai v :
2 2 2 4 2
1 1 2 1 1
5 6 2 1
x x x x x




t :
2
1
0t
x

2
5 6 2 2 1t t t t t
2
2
5 5 1 (1 ) 1 1t t t t
t
5 , 1u t v t
u kin:
5, 1uv

22
11u u v v
( ) ( )f u f v
Cách 1: 
2
( ) 1f t t t
u kin :
1t
2
'( ) 1 0
1
t
ft
t
hàm s ng bin trên
1; 
nên ta có u = v
 
22
11
51
xx
42
2 2 4 4 2
1 2 1 1 1
5 1 4 0 4 1 0xx
x x x x x
2
2
1 17
()
8
1 17
()
8
xn
xl
26S
Cách 2:
22
11u u v v
22
1 1 0u v u v
22
10
11
uv
uv
uv



uv

22
11
51
xx
42
2 2 4 4 2
1 2 1 1 1
5 1 4 0 4 1 0xx
x x x x x
2
2
1 17
()
8
1 17
()
8
xn
xl
26S
TN 4.6: Cho
32
3 6 1f x x x x

1 1 2f f x f x
có s nghim thc là
A.
4
. B.
6
. C.
7
. D.
9
.
Li gii
A
t
1t f x
263
23
xxxt
.

1 1 2f f x f x
tr thành:
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 97
11f t t
2
1
1 2 1
t
f t t t

32
1
4 8 1 0
t
t t t

1
2
3
1
2; 1
1;1
1;6
t
tt
tt
tt


2
3
1;1
5;6
tt
tt

.
(Vì
32
4 8 1g t t t t
;
27g
;
14g 
;
1 10g 
;
6 25g
).

263
23
xxxt
,  m c th hàm s
263
23
xxxy
ng thng
yt
. Ta có bng bin thiên.
Da vào bng bin thiên, ta có
+ Vi
2
1;1tt
, ta có d ct (C) tm phân bim.
+ Vi
3
5;6tt
, ta có d ct (C) tm.
Vm.
TN 4.7: T    m c  
4
2 2 2
1+ 2x -x + 1- 2x - x = 2 x -1 2x -4x +1 1
là
A.
9
. B.
5
. C.
4
. D. 8.
Li gii
C
2 2 4 2
1 1 1 1 1 1 1 2 1 2 1 1 2x x x x



22
1 1 0 1 1xx
.

2
1 0 0;1t x t

2
2 1 1 1 1 2 2 1 3t t t t

1
0;
2
t



3

0
3
0
VT
VP

1
0;
2
t


.

1
;1 ,
2
t




3

2
4
3 2 2 4 2 1t t t
2
3
11
2 2 1 4tt
t
t

0t
).

1t

4
.

11
ft
t
t


1
;1
2



.
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 98
2
1 1 1
' 0, ;1 :
2
2
f t t f t
t
t




1
;1
2



.

2
3
2 2 1g t t t

1
;1
2



.
2
23
1
' 6 2 1 4 2 1 0, ;1 :
2
g t t t t t t f t




1
;1
2



.

1t

2
0
4 1 1
2
x
tx
x
.
 
22
0 2 4
.
TN 4.8: Tng các nghim c
3
3
1 2 2 1 xx
là
A.
3
. B.
5
. C.
4
. D.
3
2
.
Li gii
A
3
3
2 2 1 2 2 1x x x x
3
3
33
2 2 1 2 2 1x x x x
3
2 1 1f x f x

3
2f t t t
 .
2
' 3 2 0, f t t t f t

2

33
1 , 2 2 1 2 1f x f x x x
3
2 1xx
2
1 1 0x x x
15
1
2
xx

.
Vy tng các nghim c
TN 4.9: S nghim c
32
3
8 36 53 25 3 5 x x x x
là
A.
0
. B.
1
. C.
3
. D.
2
.
Li gii
C
3
3
33
2 3 2 3 3 5 3 5x x x x
3
2 3 3 5 1f x f x

3
f t t t
.

3
f t t t
 .
2
' 3 1 0,f t t t t t

2

33
1 , 2 2 3 3 5 2 3 3 5f x f x x x
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 99
32
8 36 51 22 0x x x
2
53
2 8 20 11 0 2
4
x x x x x
.

f g x f h x
 
3
f t mt nt
 
3
33
3 5 3 5m x n x


1n
.

3
3
33
3 5 3 5m px u px u m x x


3
3
28xx
nên
3
8mp

1, 2
8, 1
mp
mp


.

1, 2mp

3
f t t t

3
3
33
3 5 3 5m px u px u m x x
3
3
2 2 3 5 3 5x u x u x x
3 2 2 3
3
8 12 6 1 5 3 5x u x u x u u x

2
3
12 36
6 1 53 3
5 15
u
uu
uu

.
 
1, 2mp
 
8, 1mp


TN 4.10: Nghim nh nht c
32
3
15 78 141 5 2 9 x x x x
có dng
2
a b c
vi
,,abc

abc
là
A.
17
. B.
11
. C.
13
. D.
15
.
Li gii
C
3
3
33
5 5 5 2 9 5 2 9x x x x
3
5 2 9 1f x f x

3
5f t t t
.

3
5f t t t
trên ,
2
' 3 5 0,f t t t
ft

2

33
1 , 2 5 2 9 5 2 9f x f x x x
32
15 75 125 2 9x x x x
32
15 73 116 0x x x
2
11 5
4 11 29 0 4
2
x x x x x
.
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 100
Vy nghim nh nht là:
11
11 5
1 17
2
5
a
x b a b c
c
            
 
3
3
33
5 2 9 5 2 9 1m px u px u m x x

3
5f t mt t
.
Do sau khi khai trin
3
m px u
 
3 3 3
mp x x
trong
3
1mp

1mp


3
3
1 5 2 9 5 2 9 2x u x u x x

3
xu

22
3 15u x x
5u
.

3
3
33
2 5 5 5 2 9 5 2 9 3x x x x
Khai trin
3


1mp

TN 5.1:
3 2 2
2 7 11 25 12 6 1 x x x x x
. Tính tm
c
A. 50. B. 100. C. 53. D. 80.
Li gii
A
22
2 7 4 3 6 1 1x x x x x

2
4
: 3 0,
7
x do x x x
.

22
2 7 4 3 6 1VT x x x x x VP
.

""

22
7 4 3 8 7 0 1 7x x x x x x x
.

1 7xx
.
TN 5.2: Tính tích các nghim c
11
1 1xx
xx
A. -2. B.
15
2
. C.
15
2
. D. 2.
Li gii
B

1x
.
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 101

1
1
11
1.
11
2
1 2
1
1
11
1 1
2
Cauchy
Cauchy
x
x
xx
xx
xx
xx
x
x
x
xx









1 , 2

""
trong
2

2
1
1
1 5 1 5
1 0
1
22
1
x
x
x x x x
x
x



.

15
2
x
.
TN 5.3:
2
4 4 1 2 2 3 4 14x x x x x x
. Tính tích các nghim c
trình?
A. 3. B. 5. C. 2. D. -9.
Li gii
C
1 2 2 3 4 14 1 2 2 3 4 14 8 1VP x x x x x x x x

""

2x
.
2
8 2 8 2VT x

""

2x
.

1 , 2

2x
.
TN 5.4:
5 2 7
4 3 2 1 1
1
x
x
có bao nhiêu nghim thc?
A. 1. B. 2. C. 3. D. 4.
Li gii
A

1x 
.
5 2 7
1 4 1 3 2 3 2
1
x
x
 
5 2 7 5 2 7
, , 4 1
4 1 4 1
x
xx



3
5 2 7 5 2 7 5 2 7 5 2 7
4 1 3 . .4 1
4 1 4 1 4 1 4 1
Cauchy
xx
x x x x
3
1 5 2 7 1 5 2 7
4 1 3. 5 2 7
2 1 2 1
x
xx


Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 102
3
3
5 2 7
4 1 3 2 1
1
x
x
5 2 7
4 1 3 2 3 3
1
x
x

2 , 3

""
trong
3

5 2 7
41
41
x
x
3
2
3
4 1 0
1
5 2 7
41
5 2 7
41
41
4 1 2 1
41
x
x
x
x
x
x
x








1
0
32
32
4
4 1 2 1
4
x
x
x
x
x





.

32
4
x

.
TN 5.5:
8 4 8 6 4
4 9 2 25 x x x x x

nghim th
A.
1
. B.
2
. C.
3
. D.
4
.
Li gii
A
0x
là 1 nghim c

4
2
; 2
; 3
ux
vx
.

u v u v

""

, uv

2
x=
3

.
TN 5.6:   
2 2 2 2
2 4 5 2 6 10 29 x y x y x y x y
. Cp
;xy
tha
 ca
5 100A x y
?
A.
1
. B.
0
. C.
100
. D.
25
.
Li gii
A

D
.
22
22
1 (2 ) 1 (3 ) 29x y x y
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 103

2
2
2
2
2
2
1 (2 )
1; 2
1 ; 3 1 (3 )
2;5
2 5 29
u x y
u x y
v x y v x y
uv
uv



.

u v u v

""

, uv

1
5 2 1 , 0
5
x y x y
.
TN 5.7:  
4 2 2 4 2
4 1 11 1x x x x x
     m
thc?
A.
1
. B.
0
. C.
2
. D.
3
.
Li gii
D
+
0x
là 1 nghim ca pt
+
0x

2
; 2x
1; x
ux
v

u v u v

""

, uv
 c
2x 
.
TN 5.8: 
4 2 4 2
8 32 6 18 5 2x x x x
. Tính tm ca

A.
48
7
. B.
48
5
. C.
48
15
. D.
15
7
.
Li gii
A

2
2
4; 4
3; 3
0; 0
Ax
Bx
O

42
42
8 32
6 18
52
OA x x
OB x x
AB
ta có
AO BO AB
Du bng xy ra khi
,,A B C
thng hàng
24
7
x
.
TN 5.9: 
2 2 2
1 1 2 1x x x x x x
có bao nhiêu nghim thc?
A.
1
. B.
2
. C.
3
. D.
4
.
Li gii
A

2
2
10
1 5 1 5
22
1 0,
xx
xx
x x x
.
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 104
BCS 
22
1; 1; 1; 1x x x x

2 2 2 2 2 2
1 1 1 1 1 1 2VT x x x x x x x x x


.
Hay
22
1 1 2 2x x x x x

2
2
2
2 2 2 1 1 0VT x x x x x x
Hay
2
2 2 3x x x

1 , 2 , 3
22
2
1 1 2
22
x x x x x
x x x

""
trong
2,3

22
11
1
11
x x x x
x
.

1x
.
TN 6.1: Tp hp tt c các giá tr ca tham s
2
x
 
12
2xx
có nghim là
A.
5m
. B.
8
3
m
. C.
8
5
3
m
. D.
8
5
3
m
.
Li gii
C
u kinh
11x
.
t
1 1 , 2 2t x x t
 thành
2
2 4 *t t m

*
  m ca parabol
2
: 2 4P y t t
ng thng
:d y m
i trc hoành.
 nghim ca pt
*
chính là s m ca
P
và
d
.
Phát ha
P
và
d
lên cùng h trc, ta thm khi
26m
.
TN 6.2: Có bao nhiêu giá tr nguyên ca tham s
2018;2018m
  
2
2
3
2 5 3 6 0
x
x mx x
x
có nghim.
A.
2017
. B.
2018
. C.
2019
. D.
2020
.
Li gii
C
Tnh:
3;0 3;D



O
2
2
2
6
y
x
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 105
Ta có:
2
2
3
2 5 3 6 0
x
x mx x
x
2
2
3
2 3 3 5
x
x x mx
x
22
33
2 3 5 1
xx
m
xx

t
2
3
0
x
tt
x


1
tr thành:
2
2 3 5 2t t m
 
1
có nghing trình
2
có nghi
Do
2
0 2 3 0 0t t t m
Do
2018;2018m
m

nên có
2019
giá tr nguyên ca
m
tha mãn yêu cu bài toán.
TN 6.3: Có bao nhiêu giá tr nguyên ca tham s
m
 
2 4 2
3 1 1x x m x x
có nghim

A.
1
. B.
8
. C.
15
. D.
27
.
Li gii
A
Tnh c
0;D 
.
Ta có:
2 4 2 2 2 2 2
3 1 1 2 1 1 1 1x x m x x x x x x m x x x x
22
22
11
2 1 1
11
x x x x
m
x x x x
t
2
22
1 2 2
11
1
11
1
x x x
t
x x x x
x
x


Do
0x
nên
2
2
11
1
1
2
x
xx
x
x



2
2
11
1
1; 3
2
13
1
1
x
xx
t
x
x





1
tr 
2
2
2 1 1
2 1 0 2 2
t
t mt m t
tt
 
2
có nghim thuc
1; 3
Xét hàm s:
1
2 ; 1; 3y t t
t
Vi
1 2 1 2
; 1; 3 ;t t t t

xét t s
21
2 1 2 1
2 1 1 2
2 1 2 1 1 2
11
2 2 2
.
1
20
.
tt
t t t t
t t t t
t t t t t t

Suy ra hàm s
1
2yt
t

ng bin trên na khong
1; 3
1 1 5 3
1 2 3 1 2
3
y t y t
tt
53
1
3
m
Do
m
là s nguyên nên có duy nht 1 giá tr ca
m
tha mãn yêu cu bài toán.
TN 6.4: Tìm s các giai tr   a tham s
m
  
2 3 2 3 2 2
( ) ( ) 6 1 4 6 4 0x m x x m x m x m x m
có nghim.
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 106
A.
0
. B.
1
. C.
2
. D.
3
.
Li gii
B
t:
2
2
0, 0
a x m x
ab
b x m x

2 2 2
22
2 ( ) 4 4
( )( )
a b x m a b x m
ab x m x x m x m
Kt hp vi
( ),
c h 
3 3 2
3 a 1 ( ) 6 0
ab m
a b b a b a b
32
( ) ( ) 3( ) 6 0
ab m
a b a b a b
2
2
2
2
2
ba
ab
a a m
a a m
ab m




Xét hàm
2
2y f a a a
vi
02a
có bng bin thiên
Vy
01m
suy ra
1m
.
TN 6.5:  
2
4
1 3 1 2 1m x x x
, bit rng tp tt c các giá tr ca tham s m 
m là na khong
( ; ].ab
Tính giá tr biu thc
33
.S a b
A.
28
.
27
B.
26
.
27
C.
1.
D.
1.
Li gii
B
u kin
1x
, Chia hai v cho
1x
c pt:
4
11
32
11
xx
m
xx


t
44
12
1
11
x
t
xx

Do
22
1 2 1 0 1 1 0 1
11
xt
xx


2
3 2 (*)m t t
.
Bng bin thiên ca hàm
2
( ) 3 2f t t t
trên
[0;1)
Theo bng bin thiên thì (*) có nghim thuc [0; 1)
1 1/3m
.
TN 6.6: Bit rng tp hp các giá tr ca
m
 
( 2) 3 (2 1) 1 1 0m x m x m
có
nghin
;ab
.
Giá tr ca
2019 2020 172S b a
là :
A.
1918
. B.
1819
. C.
1981
. D.
2019
.
Li gii
C
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 107
+)
( 2) 3 (2 1) 1 1 0m x m x m
u kin
31x
t
3
1
ax
bx


,
0 , 2ab
+) Ta có :
22
4
( 2) (2 1) 1 0
ab
m a m b m

(I)``
+) Trong h t 
22
4ab
ng tròn tâm
O
bán kính
2R
, và

( 2) (2 1) 1 0m a m b m
ng thng
có h s góc
2
21
m
k
m
(vì vi
1
2
m
m).
+) Nhn xét thy
m
11
;
33
I




c nh.
+) H (I) có nghim

nm trong min góc nhn to bi
12
,dd
+)
71
;
33
IA


1
d
có h s góc
1
1
7
k
.
+)
17
;
33
IB


2
d
có h s góc
2
7k
.
+) Yêu cu bài toán
12
1 2 3 5
7
7 2 1 5 3
m
k k k m
m
3
5
5
3
a
b
2019 2020 172 1981.S b a
TN 6.7: Gi T là tp các giá tr nguyên c    
mxxmx 4184416
2
có 1
nghim.Tính tng các phn t ca T.
A.0. B.20. C.-20. D.10.
Li gii
C
t
416 , 0x m tt
. Ta có
2
16 4m t x
 thành
2 16 4 2
2 . 2 1 0
21
16 4 2 1
t x x m x
x t x t
tx
x m x

y
x
B
A
d
2
:
k
2
=7
:
k
=
2-m
2m-1
d
1
:
k
1
=
1
7
-1
3
-1
3
f
x
( )
=
4
x
2
2
2
O
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 108
5204
2
1
4164
0
2
2
xxm
x
xxm
x
T  th
1
nghim
20
44
m
m
Do
m
thuc
Z
nên
20;3;2;1;0;1;2;3 T
.
TN 6.8: Có bao nhiêu giá tr
m
 
m x m x m
có nghim
A.
2
B.
3
. C.
4
. D.
5
.
Li gii
C

2
0
0
0
0
0
0
0
0
mx
m
m
mx
x
xm
m
xm
x




.
+ Khi
0m
m duy nht
0x
.
+ Khi
0m

22
2m x m x m x m
2
2 2 2 2
2
22
20
2 2 2 2 *
42
mm
m m x m m x m m
m x m m

u kin
0m
nên
2 4 3 2
2
*
4 4 4
m
m x m m m
3
43
2
2
4
44
4
m
m
mm
x m m
x


.
u kin
2
0 xm
m khi:
3
2
3
2
2
2
4
0 4 2 4
4
20
4
4
m
m
mm
mm
m
mm
m




.
V m thì
0m
hoc
24m

4
giá tr nguyên ca
m
tha mãn bài
ra.
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 109
TN 6.9: Tìm giá tr nh nht ca
m
 
33
4 2 2
2 1 3 1 1 0x x x m
có nghim.
A.
3
.
4
m 
. B.
5
4
m 
. C.
7
4
m 
. D.
5
4
m
.
Li gii
B
t
33
2 2 4 2
1, 1 2 1t x t t x x

22
3 1 0 3 1t t m t t m
Xét hàm s
2
3 1, 1y t t t
Bng bin thiên
3
1
2
1
5
4
t
y

Da vào bng bim khi
5
4
m 
TN 6.10: Hi có bao nhiêu giá tr
m
        
222x x x m m
có các nghi
A.
2019
. B.
2018
. C.
2015
. D.
2014
.
Li gii
Chn C
Ta ch cng hp
0x
và
0m
u thc v nh.
t
22y x x m
và
2 , 0z x m y z
Ta có h 
2
2
2
x y m
x z y
x m z



Không mt tính tng quát, ta gi s
m y z
2 2 2x z x y x m
y m z m y z
Thay
m y z
vào h c:
2
2
4
2 4 4
4
mm
x m m x m m x
 có
2
0 4 0 4 5,6,7...,2019.x m m m m
y có tt c
2015
giá tr
m
tha mãn yêu cu c ra.
| 1/109
| | Tải xuống

Có thể bạn quan tâm:

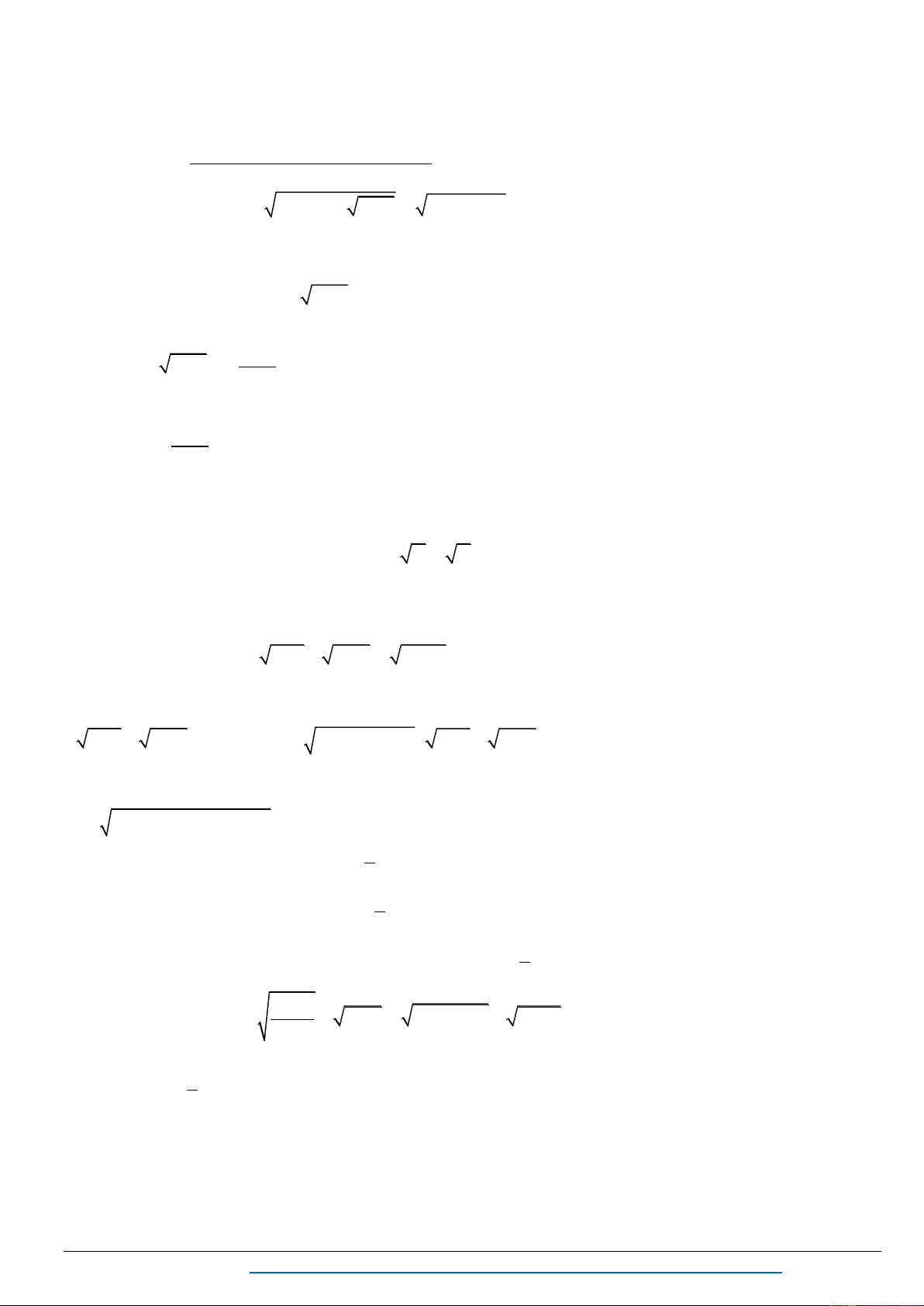
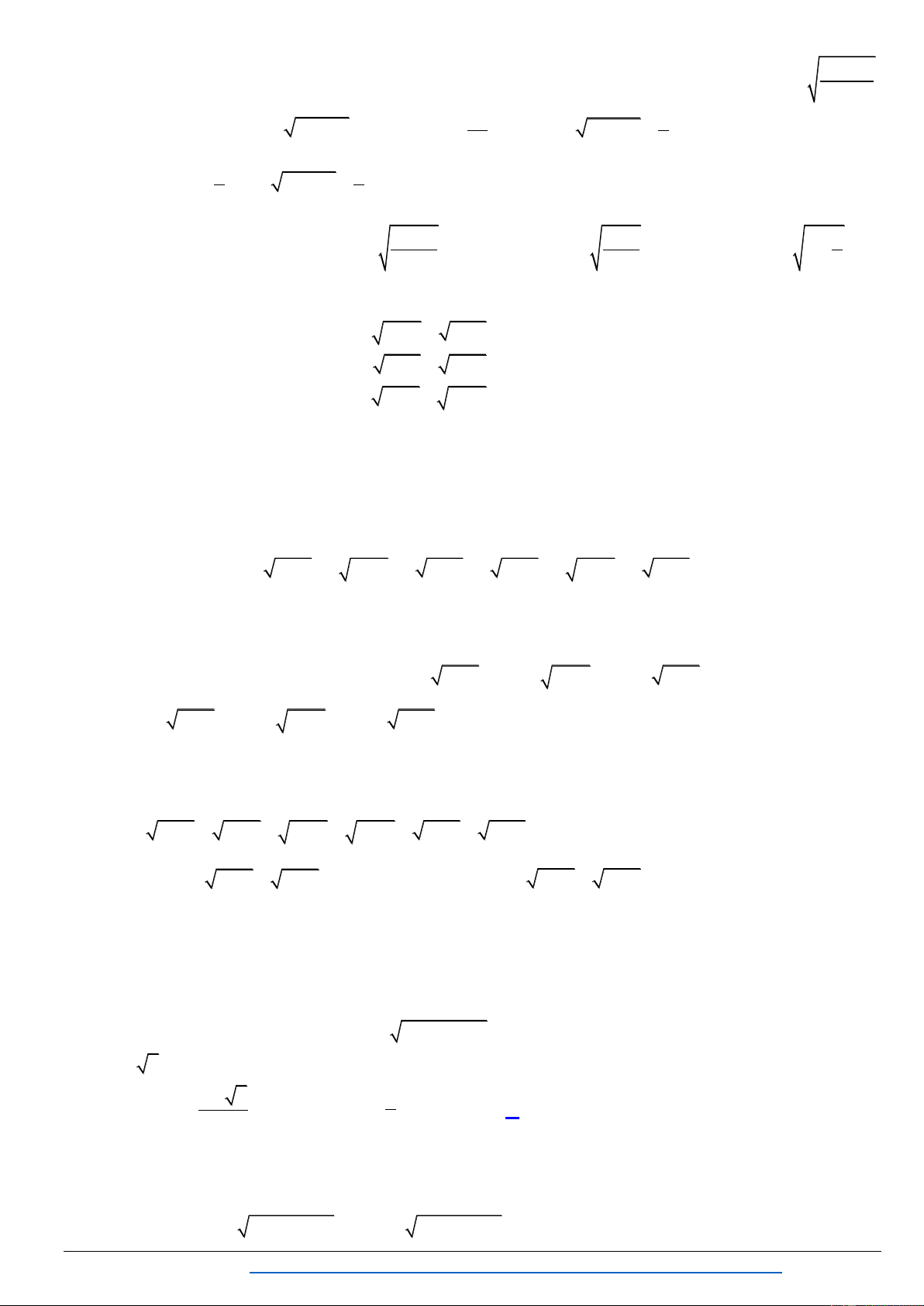
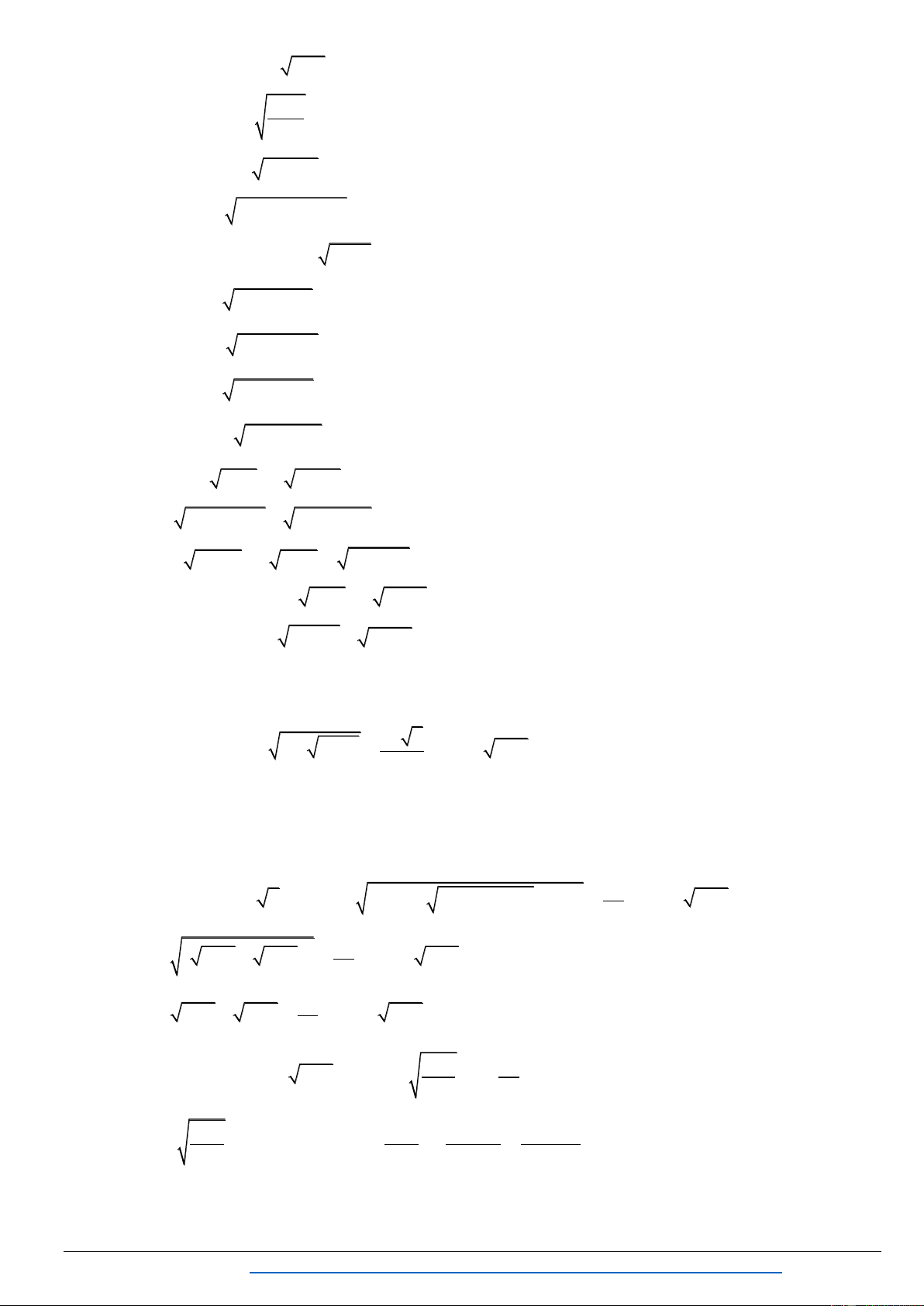
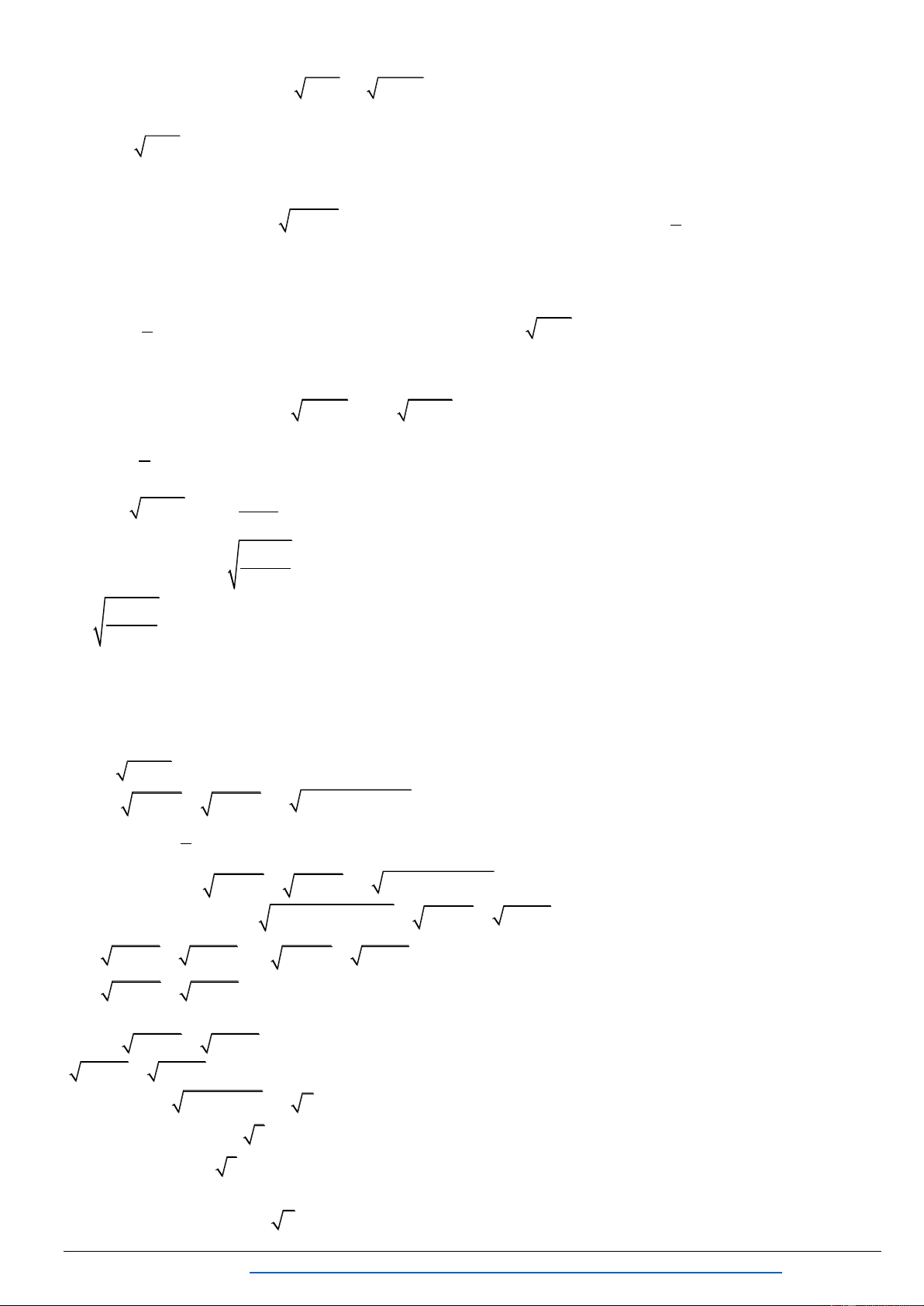
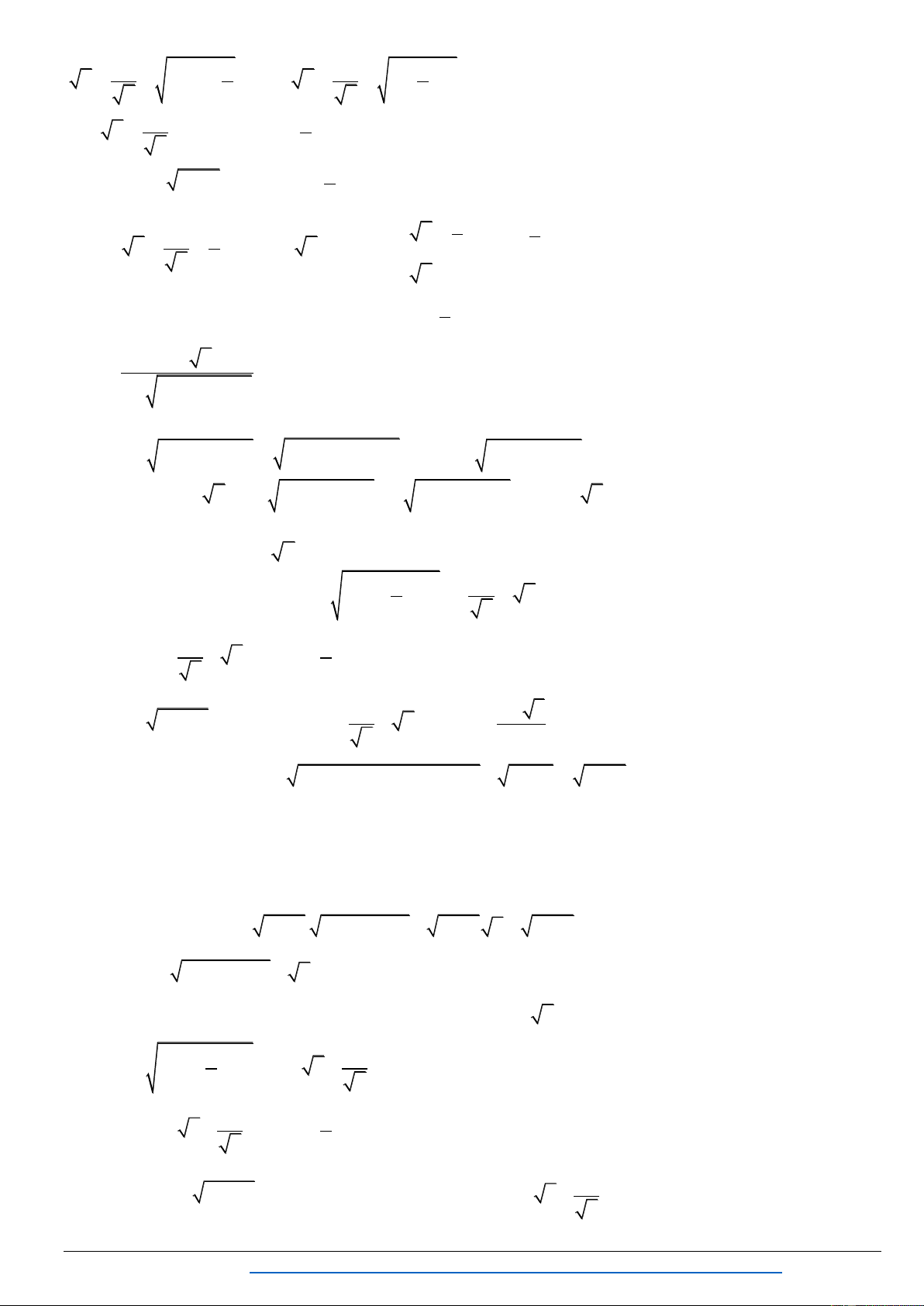
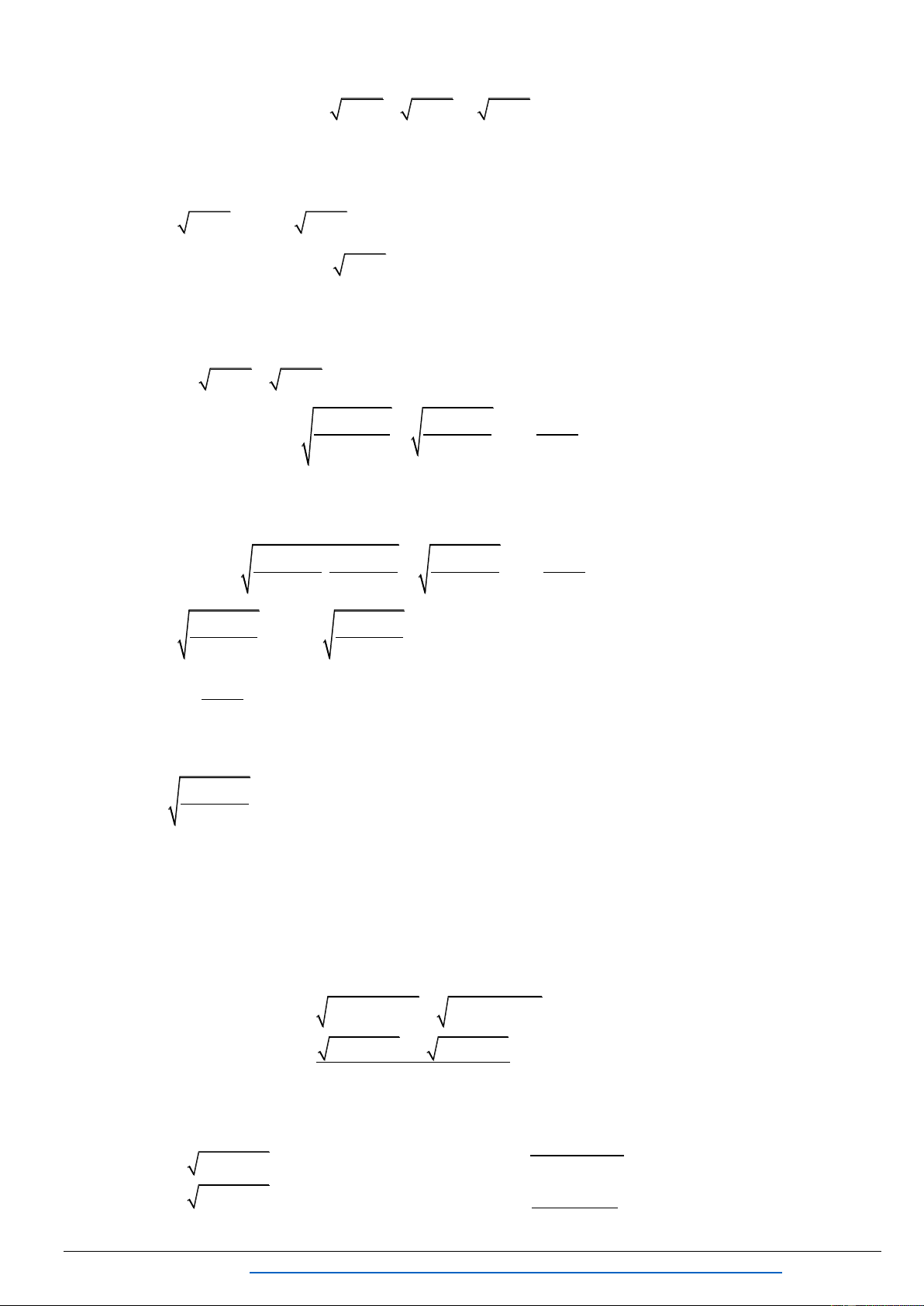
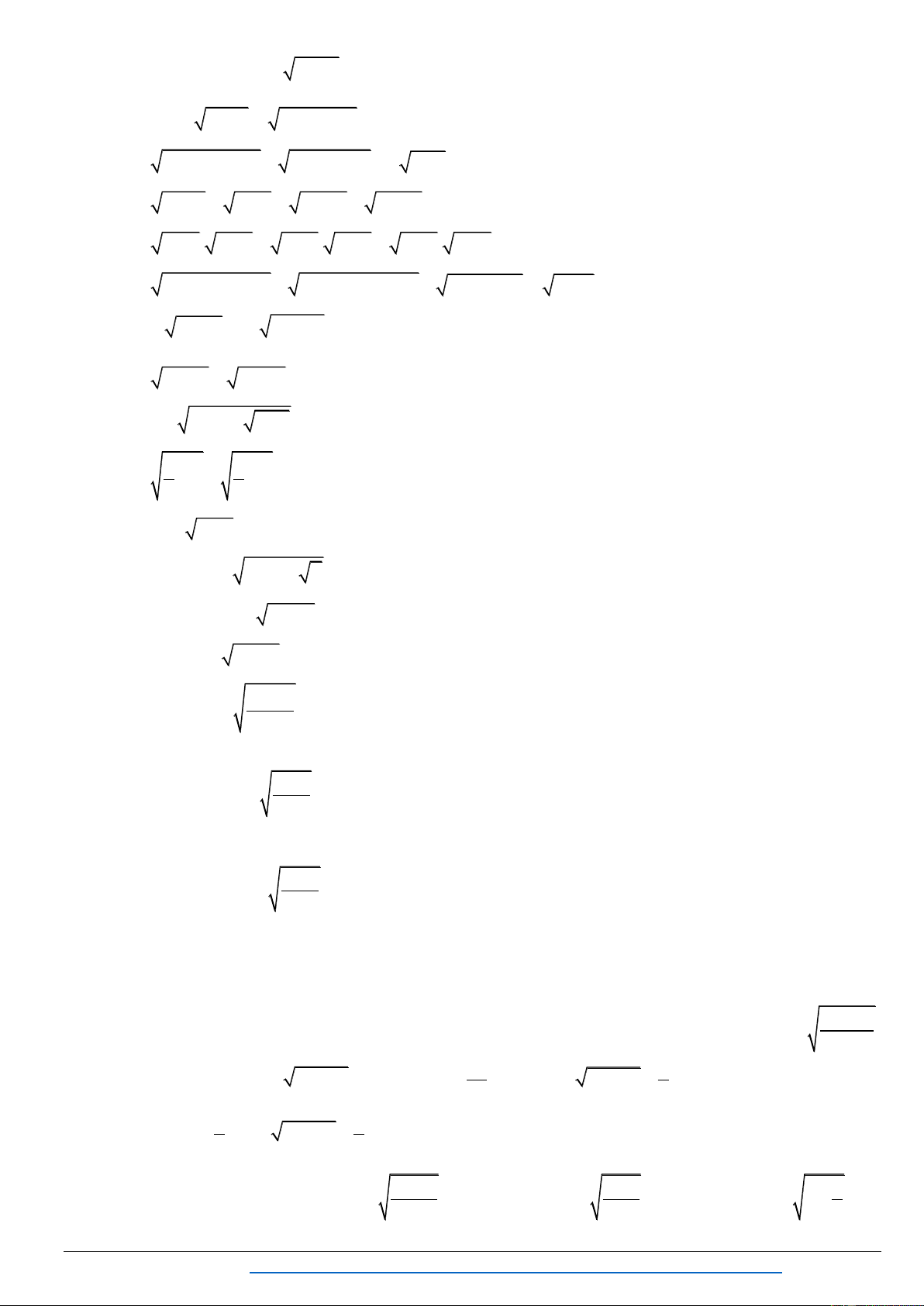
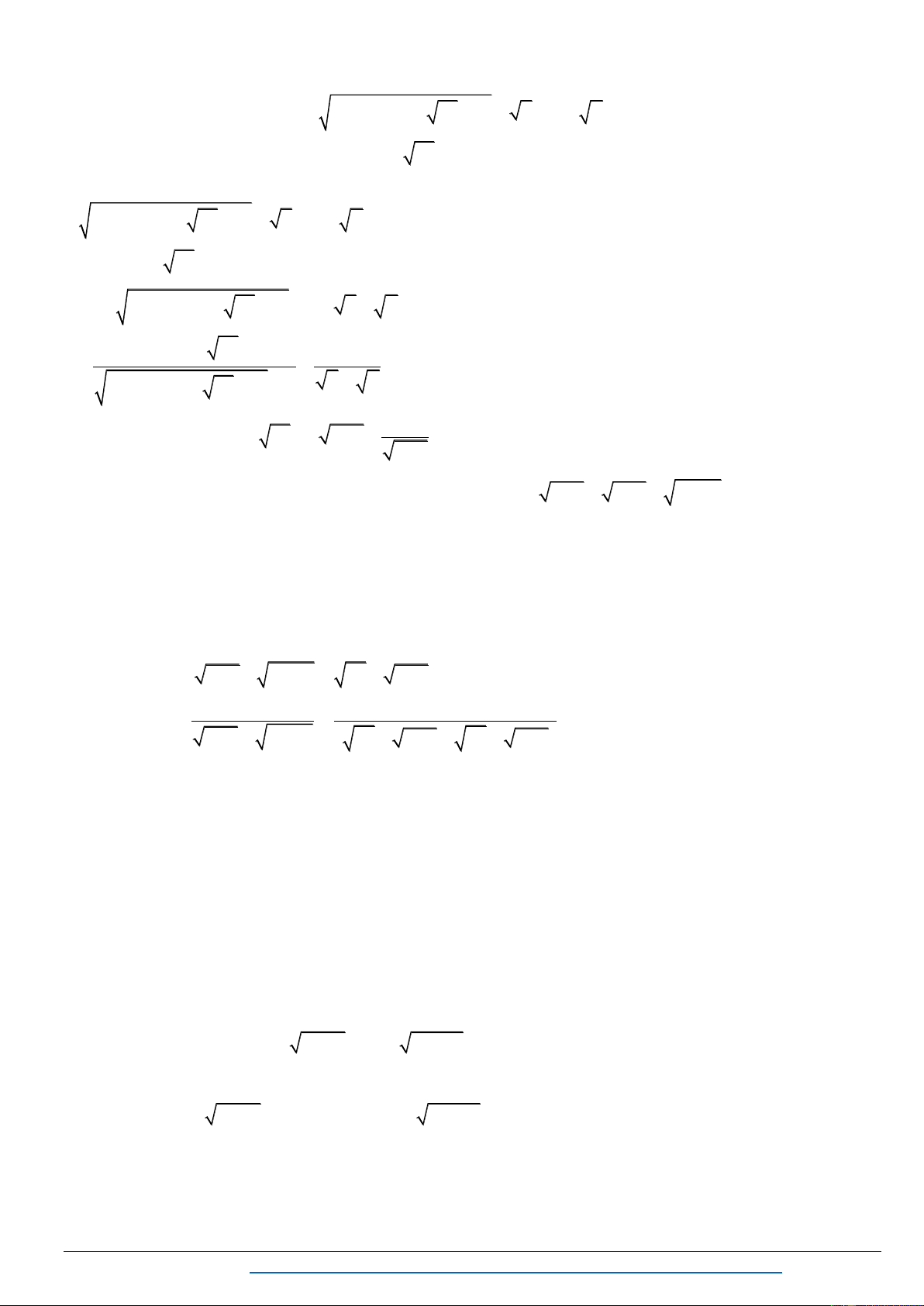
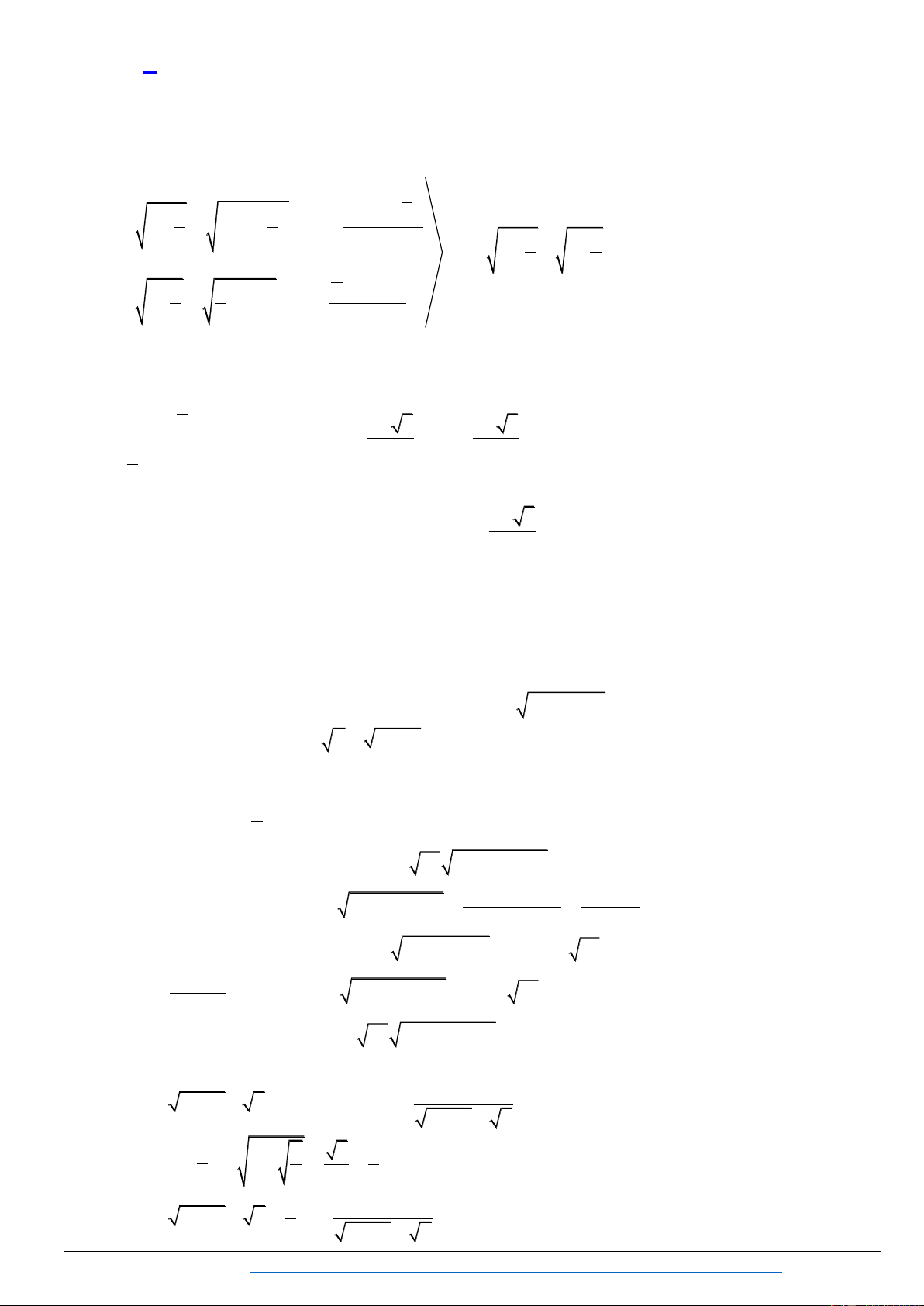
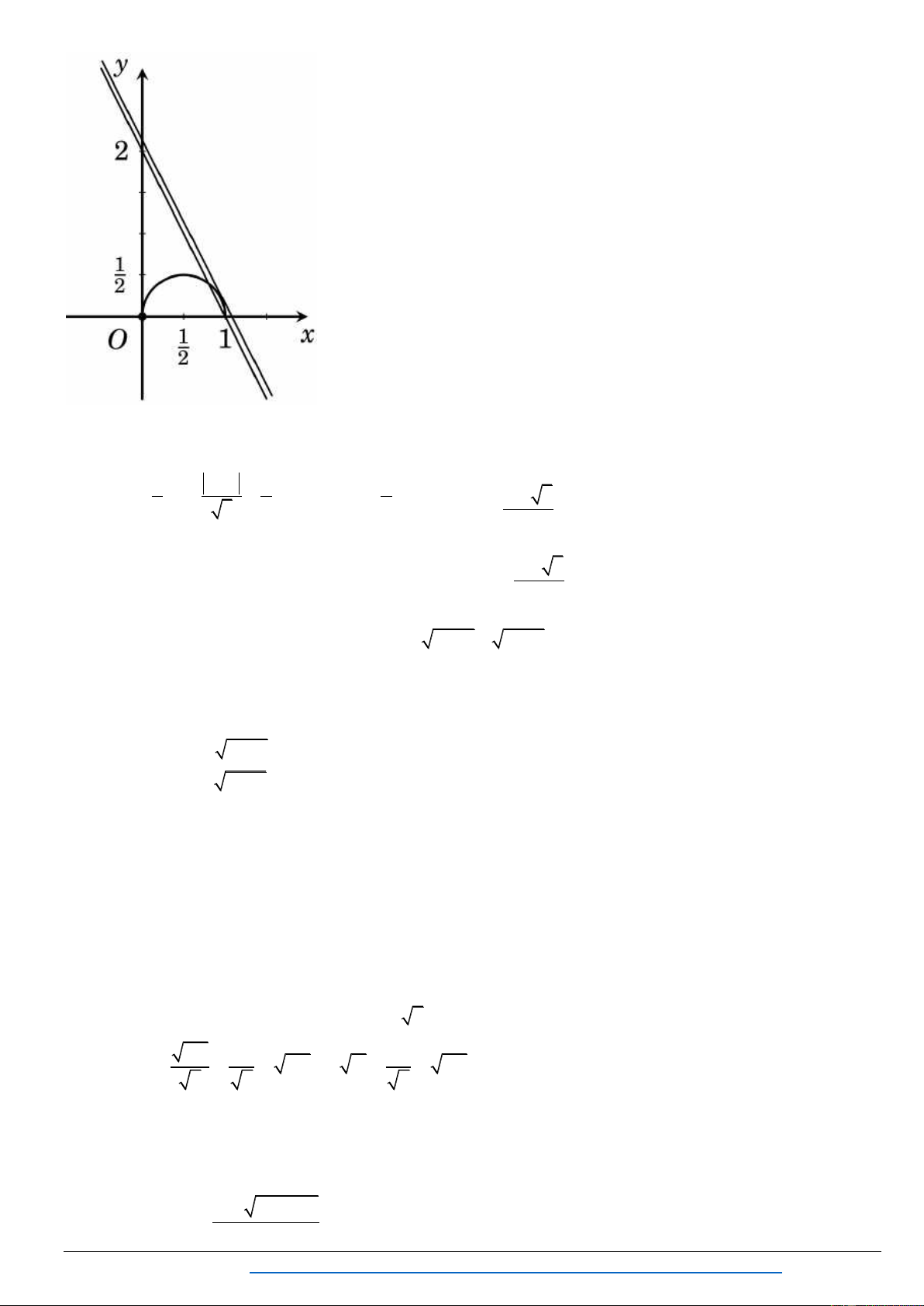
Preview text:

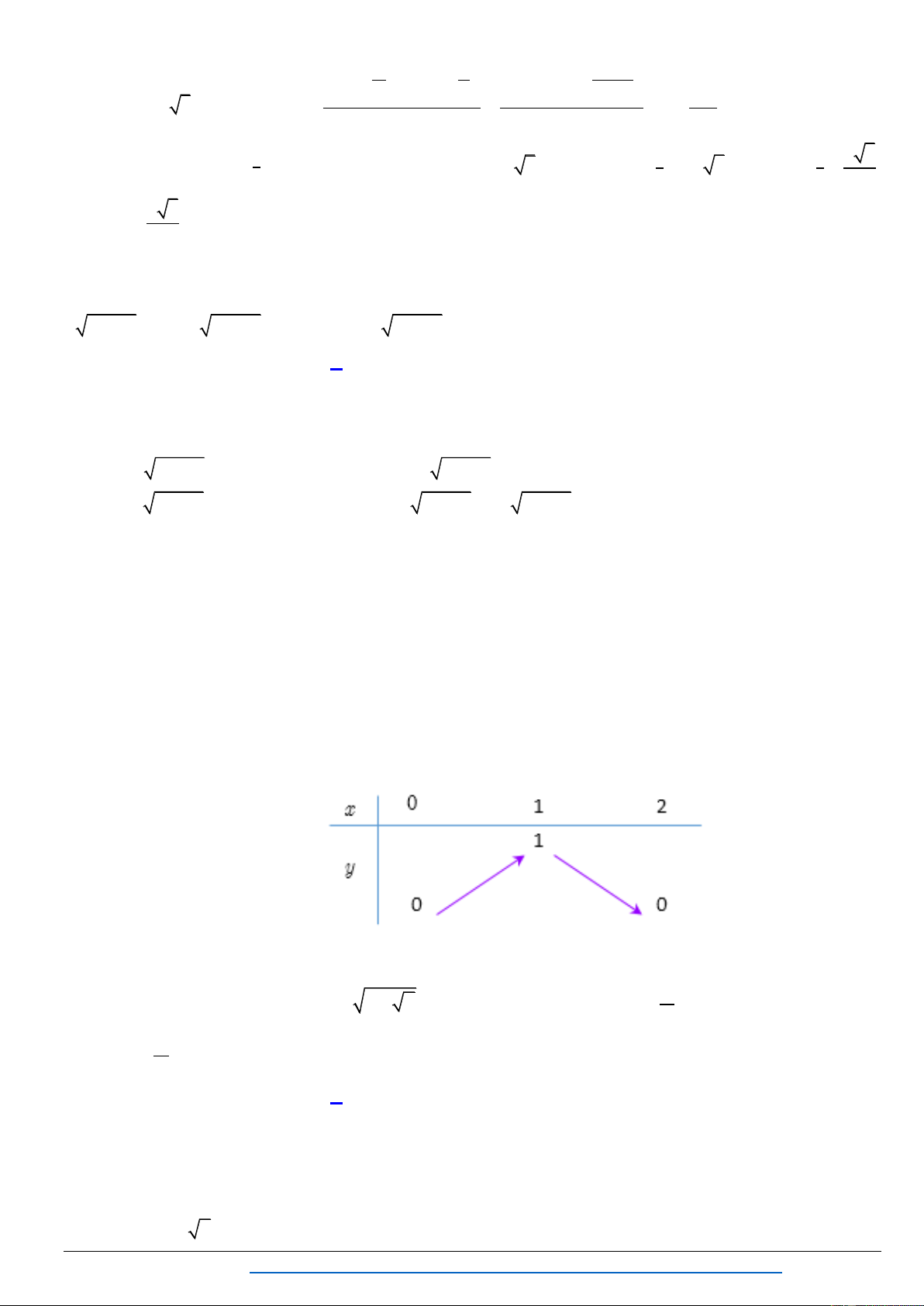
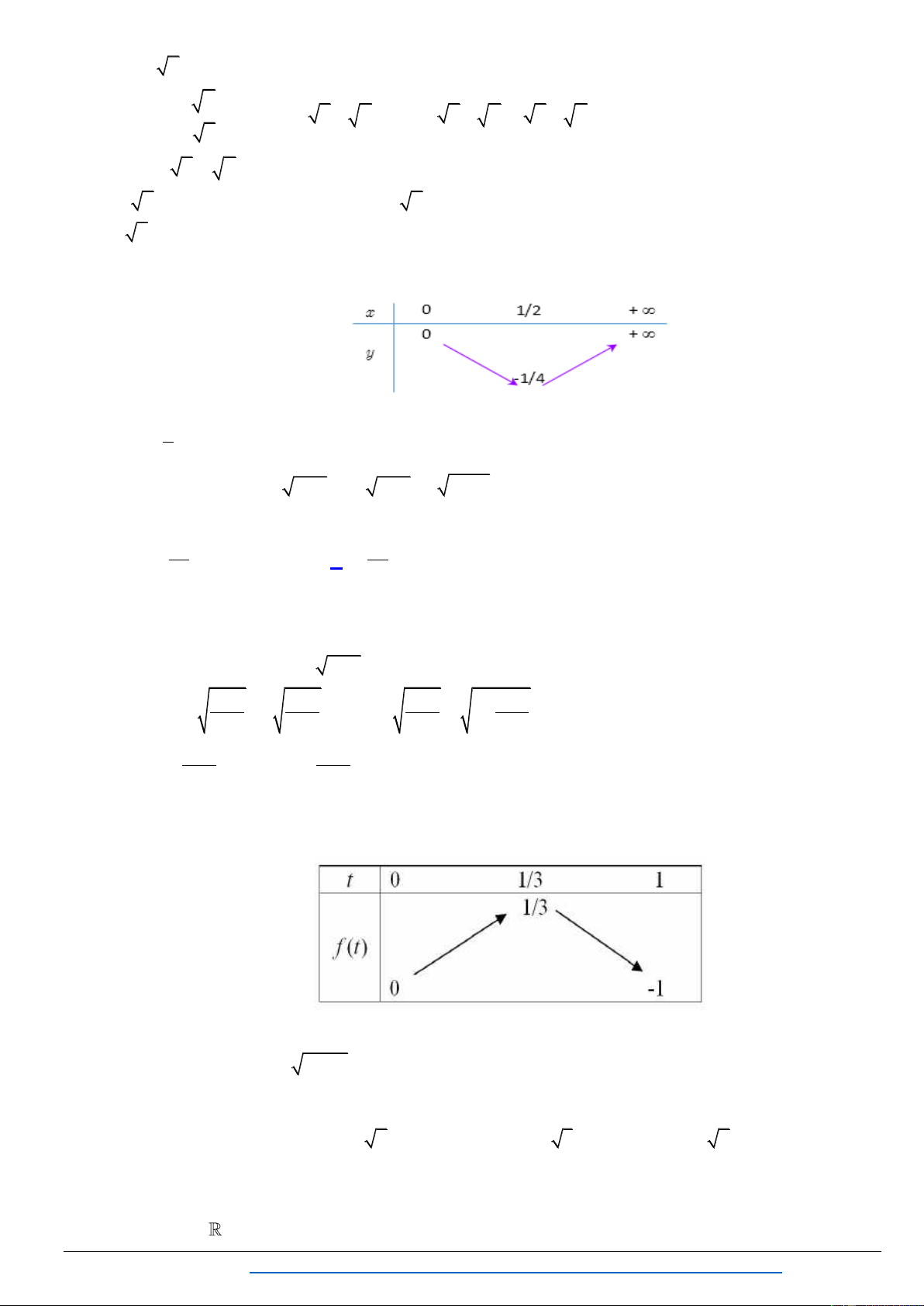
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE Contents
I. PHƯƠNG TRÌNH VÔ TỈ GIẢI BẰNG PHƯƠNG PHÁP BIẾN ĐỔI TƯƠNG ĐƯƠNG .......................... 1
II. PHƯƠNG TRÌNH VÔ TỈ THÊM BỚT THÀNH HẰNG ĐẲNG THỨC ................................................... 6
III.PHƯƠNG TRÌNH VÔ TỈ SỬ DỤNG PHƯƠNG PHÁP ĐẶT ẨN PHỤ .................................................. 11 1.
ĐẶT ẨN PHỤ HOÀN TOÀN .............................................................................................................. 11 2.
ĐẶT ẨN PHỤ KHÔNG HOÀN TOÀN .............................................................................................. 14 3.
ĐẶT ẨN PHỤ ĐƯA VỀ PHƯƠNG TRÌNH TÍCH ............................................................................. 14 4.
ĐẶT ẨN PHỤ ĐƯA VỀ HỆ ................................................................................................................ 15
IV. PHƯƠNG TRÌNH VÔ TỈ NHÂN LIÊN HỢP .......................................................................................... 19 1.
PHƯƠNG TRÌNH VÔ TỈ NHÂN LIÊN HỢP TRỰC TIẾP CÁC BIỂU THỨC CÓ SẴN TRONG
PHƯƠNG TRÌNH ....................................................................................................................................... 19 2.
PHƯƠNG TRÌNH VÔ TỈ NHÂN LIÊN HỢP THÊM BỚT HẰNG SỐ ............................................. 22 3.
PHƯƠNG TRÌNH VÔ TỈ NHÂN LIÊN HỢP THÊM BỚT BIỂU THỨC BẬC NHẤT .................... 25
V. PHƯƠNG TRÌNH VÔ TỈ GIẢI BẰNG PHƯƠNG PHÁP VECTƠ .......................................................... 26
VI. PHƯƠNG TRÌNH VÔ TỈ ĐƯA VỀ DẠNG f u  f v ...................................................................... 32
VII. PHƯƠNG TRÌNH VÔ TỈ SỬ DỤNG BĐT ĐỂ ĐÁNH GIÁ ................................................................. 38
VIII. PHƯƠNG TRÌNH VÔ TỈ SỬ DỤNG BĐT BUNHIACOPXKI ........................................................... 42
IX. PHƯƠNG TRÌNH VÔ TỈ SỬ DỤNG BĐT COSI ................................................................................... 46
X. PHƯƠNG TRÌNH VÔ TỈ SỬ DỤNG TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ ............................................... 50
XI. PHƯƠNG TRÌNH VÔ TỈ SỬ DỤNG SỰ TƯƠNG GIAO CỦA ĐƯỜNG TRÒN ĐƯỜNG THẲNG .. 65
XII. PHƯƠNG TRÌNH VÔ TỈ SỬ DỤNG PHƯƠNG PHÁP LƯỢNG GIÁC HÓA .................................... 70
XI. PHƯƠNG TRÌNH VÔ TỈ CÓ THAM SỐ ................................................................................................ 71
XIV. TRẮC NGHIỆM PHƯƠNG TRÌNH VÔ TỈ .......................................................................................... 78
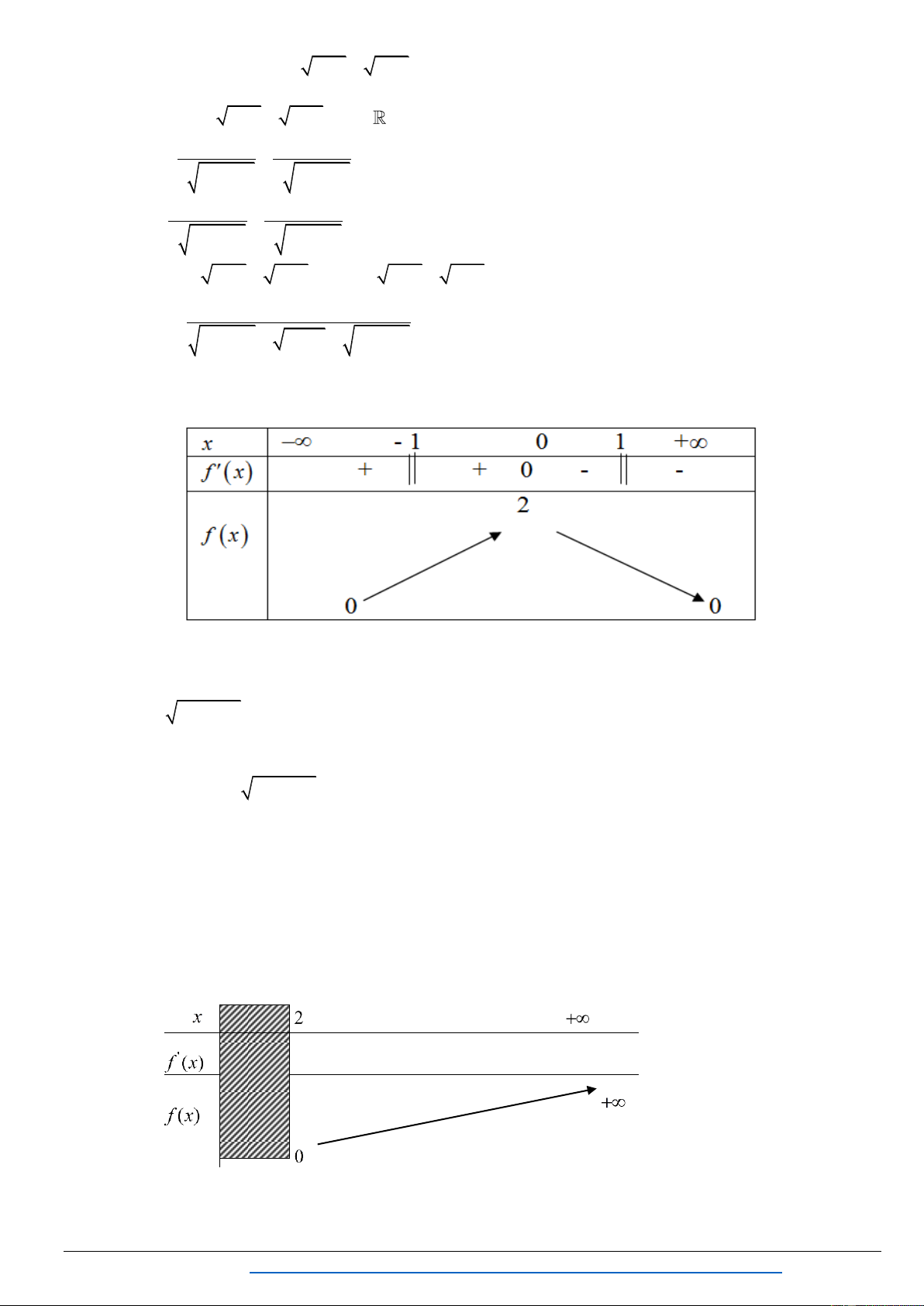
I. PHƯƠNG TRÌNH VÔ TỈ GIẢI BẰNG PHƯƠNG PHÁP BIẾN ĐỔI TƯƠNG ĐƯƠNG 1. Phƣơng pháp chungB  0  A B   . 2 A B    B 0 A B   . A B A  0  B  0  A B   . B  0  2 A B
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 1
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE B  0  
A B  A  0 .  2 A B    B 0 A B   . A B L Đố ớ , ứ ẩ , ệ ớ  B ớ . Đ ề ệ ứ .
 B ớ . C ể ế ế ề .
 B ớ . B ế ể ử ứ . Bài 1: Gi 2
2x 1  x  3x 1  0   1 ( Khối D – 2006) Lời giải X là ng A  . B 2
x  3x 1 0 2 (1) 
2x 1  x  3x 1   2 2
2x 1 (x  3x 1) 2 2
x  3x 1 0
x  3x 1 0 x 1        4 3 2 2 2
x  6x 11x 8x  2  0
(x 1) (x  4x  2)  0 x  2  2
Kết luậ P ã ệm x  1, x  2  2.
Nhận xét: P ng tổng quát: 2
mx n ax bx  , c ( ,
m a  0) ều gi ợc theo d ng A  .
B Nế lũ ừ ợc nghiệm h u tỷ thì sẽ tiế à H ể phân tích thành tích
số ( ầ i, nhân tới, cộng chéo). Còn nếu ra nghiệm vô tỷ ta sẽ tiến hành sử dụng chứ l ủa máy
tính bỏ ú ể l ợng nhân tử chung bậ , ứ ể ề d ng tích số bậc hai nhân bậc
hai mà dễ à ợc nghiệm. Bài 2: Gi trình: 3 2
x x x  5   x  4 x  2 2 Lời giải
Đ ều kiệ x ịnh: x  2  . 2 2 Ta có: 3 2
x x x  5   x  4 x  2   3 2
x x x  5  x  4 x  2 6 5 4 3 2
x  2x x  9x x  22x  7  0 Vậy:  2
x x   4 3 2 3
1 x x  3x x  7  0 Vì 4 3 2 2
x x x x   x  2
x x     2 3 7 1
2x x  7  0 x   . D (*) 2
x  3x 1  0 3  13 Với 2
x  3x 1  0  x  . 2 3  13
Thử l i nghiệ ợc x
là nghiệm duy nh t thỏa mãn. 2 3  13
Kết luận: P ệm duy nh t x  . 2
Nhận xét: ể phân tích ta dùng máy tính casio
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 2
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE
Sử dụng máy tính Casio ta thu được: x  3.302775638, x  0  .3027756377 1 2
Tư duy Viet đảo: x x  3, x x  1  1 2 1 2
Nhân tử thu được: 2 x  3x 1 6 5 4 3 2
x  2x x  9x x  22x  7 Nhập máy tính: 2 x  3x  Calc 100 1 Bài 3: Gi 2 2
7  x x x  5  3  2x x Lời giải 2 3
  2x x  0 P ( )    2 2
7  x x x  5  3 2x x  3   x 1   
x  2 (do x  0 không là nghiệm củ ) x  5    x  3   x 1  3   x 1  2   x  0  x  2      0   2   x  0  x  1   x  1. x    3 2 
x x 16x 16  0 x  4  2 2 2
x (x  5)  (x  2)
Kết luậ P ã ệm duy nh t x  1. 
A  0 hay B  0
Nhận xét: P n: A B   , ọn A B
A  0 hay B  0. D à ểm của bài toán, ta nên chọ à n nh t, tức chọn 2
B  3  2x x  0 Bài 4: Gi 3 3 3 x 1  x  2  2x  3. Lời giải P ã ới:
x  x 3 3 3 1 2  2x 3 
x x 3 3 3 3 1 2
x 1  x  2   0  x 1  3  3 x  
1  x  22x  3  0  x  2   3 x   2 3
Thử l i ta th y các giá trị x  1; x  2; x  ều thỏ ã ã . 2  
- Kết luận. Tập nghiệm củ ã là 3 T  1  ;2; .  2  3 x  8 Bài 5. Gi 2
x  2  x - 2x  4  2x 1. 2x 1 Lời giải 1
Đ ều kiện x   . P ã ới: 2
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 3
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE 3 x  8 2
 2x 1  x  2x  4  x  2 2x 1 3 x  8 3 
 2 x  8  2x   1   2
x  2x  4  2  x  2 2
x  2x  4   x  2 3 2
x  5x  7x  3  0 2x 1 x 1  x 3
Thử l i ta th y nghiệm củ ã ỉ có giá trị x  1. 3 x 1
Bài 6. Tổng các nghiệm củ 2
x  3  x x 1  x 1 là x  3 A. 0 . B. 2 . C. 2  . D. 1. Lời giải Đáp án: B
Đ ều kiện x  1.  P ã ới: 2 3  x 1     x  3     
x x1 x12 2 x 3   3 x 1 3 
 2 x 1  x  3   2 x x   1  2  x   1  2 x x   1   x   1 x  3 3 x 1 2 2 
x x 1  x  2x  2  0  x  1 3. x  3
- Tập nghiệm củ ã là T  1 3;1 3. „
Vậy tổng các nghiệm là: 1 3 1 3  2 Bài 7: C 3 2 x x x   2 27 18 9
27x  2x   1
2x 1 125  0 . Gi sử nghiệm củ a b a trình có d ng x
với a, b, c là các số à tối gi n. Tính c c
S a b c .
A. S  46 . B. S  47 .
C. S  48 . D. S  49 . Lời giải Đáp án: B Ta có: 3 2 x x x   2 27 18 9
27x  2x   1 2x 1 125  0
  x   x3 2 1 3  1  25
 2x 1  3x  5 16  22  x  9
Suy ra: a  16, b  22, c  9 Vậy S  47 Bài 8: Biết rằ 3 x x   2
x x x    2 4 4 2 2020
2 1009  3x  có một nghiệ b   c d
nh t d ng x  a
a, b, d  , ,
c e là các số nguyên tố. K a b c d e e bằng:
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 4
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE A. 901. B. 902 . C. 903 . D. 904 . Lời giải Đáp án: C 3 x x   2
x x x    2 4 4 2 2020 2 1009  3x
 x  4  x  2 1 1  2019  2019
 x  4  x  2 1
  x  2   x  2 1 1 1 1 2019 1  2019  4 4 2 2      x  2 1   x  2 1 1 1  2019       2   2   x  2 1   x  2 1 1 1  2019  2 2
 x  4  x  2 1 1  2018  0     x  2 1 3 897 1  2  1   3 897 x  1  2   1   3 897 x  1  2
Vậy a  1, b  1, c  3, d  897, e  2  a b c d e  904. Bài 9: Gi sử 2
2x 1  x  3x 1  0 có một nghiêm có d ng x a b c * a, , b c
. K a b c có kết qu là A. 5. B. 1. C. 0 . D. 4 . Lời giải 1
Đ ều kiện x  . P ã ới: 2 2
x 3x 1 0   2 x  3x  
1  2x 1  x 3x  2 2 1  2x 1. 2  2
x  3x 1  0
x 3x 1 0      4 3 2
x  6x 11x 8x  2  0  2x 2x 
1 2x 4x2  0 3 5 3  5   x   2 2 x 1      x  1  x  2  2.  x  2 2
Vậy a  2, b  1, c  2  a b c  5. Bài 10: C 1 1 1 1 1 1 1 1 2 2 2 2 3 2 8 x   x    x   x x
 4x  5x  5x 1 (1) 16 2 16 2 16 2 2 16 2018 can Tổ ệm củ ằng
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 5
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE 25  8 5 25  8 5 49 A. . B. . C. . D. 3. 16 16 16 Lời giải Chọn B 1 Từ ( ) 3 2
4x  5x  5x 1  4x   1  2 x x   1  0  x   4 Ta có 2 1 1 1 1 1 1  1  2 2 2 3 2 (1)  8 x   x    x   x
 4x  5x  5x 1   16 2 16 2 16 2  4  2018 can 1 1 1 1 1 1 2 2 2 3 2  8 x   x    x x
 4x  5x  5x 1 16 2 16 2 2 16 2017 can 1 1   2 3 2  1 8 x x
 4x  5x  5x 1  8 x   4x   1  2 x x    1 2 16  4   1 x      x   2 x x   4 4 1 1  0   5 1 x   2  D ổ ệ 25 8 5 m bằng 16
II. PHƢƠNG TRÌNH VÔ TỈ THÊM BỚT THÀNH HẰNG ĐẲNG THỨC Bài 1: Gi 2
4x 14x 1  4 6x 10 Lời gi i 2
4x 14x 1  4 6x 10 2
 4x  20x  25  6x 10  4 6x 10  4
 2x  5   6x 10  22 2
 2x  5  6x 10  2 x  7 Bài 2. 2
3x  6x  3  3 Lời giải 2 x  7 3
 x  6x 3  t
Cách 1: Đ t t
t  0 ta có:  . 3 2 3
 t  7  x 2 3
 y  6  t
Đ t y x 1 hệ ở thành  . 2 3
 t  6  y
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 6
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE 3x  21 Cách 2: P ã ớ 2
x  6x  3  9 2  49 1
9x 18x  9  3x  21 2
 9x  21x
 3x  21 3x  21  4 4 2 2  7   1   3x   3x  21       2   2  4x  9 x  3 4 Bài tậ : 1) 2 7x  7x  . 2) 2 2x  4x  . 3) 2 27x 18x x  . 28 2 3 Bài 3.
[phƣơng pháp nhóm thành hằng đẳng thức] 2
x y  2  4  z y  5z 11  G ệ 2
y z  2  4  x z  5x 11  2 z
x  2  4  y x  5 y 11  Lời giải ĐK 2  x  4
Cách 1: Nhân 2 vế của mỗ ới 2 và cộng với vế theo vé, ta có
2x  2 y  2z  2 x  2  2 y  2  2 z  2  2 4  x  2 4  y  2 4  z 2 2 2
 2x  2y  2z 10x 10y 10z  66
[Dạng toán hoặc dạng phƣơng pháp đã ghi chú bằng mực đỏ]
 2x 3  2 y 3  2z 3   x 2  2
1   y  2  2
1   z  2  2 2 2 2 1   4 x  2
1   4  y  2
1   4  z  2 1  0
x y z  3.
Cách 2: Đánh giá bằng bất đẳng thức 2 2 2
x  2  4  x
y  2  4  y
z  2  4  z x  6x 11 y  6 y 11 z  6z 11* 2
Ta có:  x  2  4  x   2x  2  4  x  4  x  2  4  x  2 Suy ra VT  
*  6 , d u "  " x y ra khi x y z  3 . M t khác, VP  
*  6 , d “=” x y ra khi x y z  3 .
Vậy x y z  3 . Bài 4: Biế 2 2
8x  8x  3  8x 2x  3x 1 có 3 nghiệm x , x , x (x x x ) Tính 1 2 3 1 2 3
T x  ( 7 1)x x ? 1 2 3 5  7 3 A. T  . B. T .
C. T  3 .
D. T  8. 4 2 Lời giải Đáp án: C Đ ều kiện : 2
2x  3x 1  0 2 2 2 2 2
Pt  8x  8x  3  8x 2x  3x 1  4(x  2x  3x 1)  (2x 1)
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 7
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE  3  3    2 x
2 2x  3x 1  1 4     2
2 2x 3x 1  4x 1  7 1  x   4 3  3 7 1 3  3 Vậy T    7   1   3 4 4 4
Bài 5: Nghiệm nhỏ nh t của 2
(x  3) x  8x  48  x  24 có d ng x m n p (với , m n
và p là số nguyên tố). Tính giá trị T m n p . A. T  25 . B. T  27 . C. T  3. D. T  7 . Lời giải Đáp án: A Đ ều kiện: 1  2  x  4. P ã ới  x   2 2 3
x 8x  48  2x  24   2
x x    x   2 x x    2 6 9 2 3 8 48
x 8x  48  9 x  2 2 3 x 8x 48         9    x 3 2
 x 8x  48  3   1  x3 2
 x 8x  48  3   2 x  0   x  0  1      x  2   2 7  x  2   2 7 (thỏa mãn). 2  2
x 8x  48  0 
x  22 7 x  6    x  6   2      x  5   31  x  5   31 (thỏa mãn). 2  2
x  20x 12  0 
x  5 31
Nghiệm nhỏ nh t sẽ là x  5
  31 . D m n p  5 1 31  25 .
[Các Bài phân tích hằng đẳng thức] Bài 6. 2
2 x  3  9x x  4 . HD: PT  x  
x    x   x   2 2 2 3 2 3 1 9 3 1  9x . Bài 7. 2
x  9x  20  2 3x 10 . HD: PT 2
 3x 10  2 3x 10 1 x  6x  9  0. Bài 8. 2
2x 1  x  3x 1. HD: PT   x   2 4 2
1  4 2x 1 1  4x  4x 1. Bài 9. 2
x x 10 1 80x  10 . HD: PT 2
 4x  4x  40 1 80x  40 2 2  4x  2.2 .
x 19 19  1 80x  40 1 80x  400
  x      x  2 2 2 19 1 80 20 . 4x  9 Bài 10. 2 7x  7x  . 28 HD: PT 2 2
 196x 196x  28. 4x  9 196x 196x  2. 28x  63
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 8
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE 2
 196x  224x  64  28x  63 2. 28x  63 1
  x     x   2 2 14 8 28 63 1 . Bài 11.
4  3 10  3x x  2 . x  2  HD: PT   . 4  3 10 3x   x 22 * +   2 2 *  3
 10  3x x  4x  12 
10  3x  4x 16x    x 2 4 10 3
12 10  3x  9  4x  28x  49  
x  2   x  2 2 10 3 3 2 7 . Bài 12. x   2 2 4 1
x 1  2x  2x 1 .
HD: PT   x   2 2 8 4 1
x 1  16x 16x  8
  x  2   x   2 x    2x   2 4 1 8 4 1 1 16
1  16x  24x  9
  x   x  2   x  2 2 4 1 4 1 4 3 . Bài 13. Giải phƣơng trình 2 2
x x x 1  2 3x 1  x x  3   1 . Lời giải   2 2
1  2x x x 1  4 3x 1  2x  2x  6 2 2 2
x  2x x x 1  x x 1 3x 12 3x 1  1  0
 x x x  2  x   2 2 1 3 1 1  0 2
x x x 1  0 1   x  0 x 1       . 3  x     x 1 1 x  0 3 1 1 0 Vậy ã ệm.
Hệ thống bài tập tƣơng tự: 1. 2
2 2x 1  x  2x . 2. 2
x 1  x  4x  5 . 3. 2 x  2  x  2 . 4. 2
x x 12 x 1  36 . 5. 2
2x  2x 1  4x 1 . 6. 2 3x  2  4
x  21x  22 . 7. 4 2
x x  3  3. 8. 2
1 x 1  x .
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 9
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE 9. 2
x  5x  4  2 x 1 .  3 10. 2 8  4  x x x . 2 11. 2 2
x 1  2x x  2x .
12.  x  3 4  x12  x  28  x . 13. 2
x x    x   2 3 1 3 x 1 . 14.  x   2 2 1
x  3x  3  x  2x  3 . 15.  x   2 2 2
x  2x  2  x x 1 . 16.  x   2 2 1
x  2x  3  x 1. 17.   x 2 2 2 1
x  2x 1  x  2x 1.
18. x  4 x  3  2 3  2x  11. 19. 2 2
2x x  9  2x x 1  x  4 . 20. 2
2 2x  4  4 2  x  9x 16 . 21. 2
4x  3x  3  4x x  3  2 2x 1 . 22. 2 2
1 x  2x  4 4x 1  2x 1 . 27 2
Bài 14: G x x 1  x 2 2 1 x 1 8 Lời giải
Ý tƣởng: Sử dụng phương pháp phân tích hằng đẳng thức + đặt ẩn phụ.
Đ ều kiện: x 1. 27
Nhân 2 vế với 2, ợc x 1 2  x   1  x   1  x 1  x  2 1 x 1 4
  x   x  2 27 1 1  x  2 1 x 1 4 27
x 1  x 1  x  2 1 x 1 (1) 4 x 1 27
Chia c hai vế cho x 1 , ợc 1  x  2 1 x  (2). 1 4 2 x 1 2 x 1 Đ 1 t
t t  0 2    t 1   . x 1 x 1 4 t  2 2 1
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 10
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE   27 2  t 1   t  2 4 3 2
t  3t  4t  6t 13  0 2   2t  1 5
t  2  x  . 3 5 Vậy S    . 3
III.PHƢƠNG TRÌNH VÔ TỈ SỬ DỤNG PHƢƠNG PHÁP ĐẶT ẨN PHỤ Phƣơng pháp chung
a. Đƣa phƣơng trình vô tỷ về dạng phƣơng trình một ẩn 2
at bt c  0a  0 .
b. Đƣa phƣơng trình vô tỷ về phƣơng trình nhiều ẩn phụ. Dạng 1. . .n a f x b f x c 0 Dạng 2. . a f x . b g x 2a . b f x .g x h x Dạng 3. n m a f x b f x c Dạng 4. n 2 n n 2 a A b . A B c B 0 Dạng 5. . a f x . b g x
c. f x .g x Dạng 6. 2 2 . a f x . b g x c. d. f x . e g x n Dạng 7. n f x b x a x a x f x b x n Dạng 8. .n ax b p cx d . q x r Dạng 9. 2 2 x 2a x b a b x 2a x b a b cx d
Dạng 10. Đ t ẩn phụ không hoàn toàn
1. ĐẶT ẨN PHỤ HOÀN TOÀN Bài 1: Gi i : 2 2
x  4x  2  2 x  4x  5 . S  2  2 2 x   3   53 3   85 
Bài 2: Gi i :  x   x     x   2 5 2 4 5  3  0 S   ;  x  . 5  2 2   Bài 3: Gi i : 2
7x  7  7x  6  2 49x  7x  42  18114x .
Đ t t  7x  7  7x  6
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 11
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE
Bài 4. Gi i b x  1  2 2x  3  2x  2 1 ĐK x  1
Đ t t x   x  2 1
t  1 t  0 t  0 2  2t t 0 2 2     T ợ 1
c b 2 2t  1  2t t      t  4 3 2 
4t  4t  7t  4  0    2  4 4t  3 4t  2 7t  4   0 2
+Với t  0 . Kết hợ ều kiện thì t  0 không thỏa mãn (2)
+Với t  1 thì (2)  t   3 t  2 2 4
4t t  2  0  t  2  x 1  2  x  3TMDK 2
Tập nghiệm của b là S    3;  2
Bài 5: Gi i b 3 7x  8  1   2x 1   1  1 ĐK x  12 2 t  Đ 1
t t  2x  1  x  t  0 2 2 7t  K ( ) ở 9 2 thành 3  1  t   1 2 2 7t  
9  t 2t  7t 9  2t 2t3 2 2 2 3 2
 t  t   4t  3t  2 1 3 2 4
2t  4t  3  0
Ta có t t t t   t t2 4 2 2 2 2 4 2 4 3 2
 4t  3  0, t   0 .
Từ ( )  t  
1 t  3  0  1  t  3
 1  2x 1  3  1  x  5 . Bài 6: 2
7 x  7  7 x  6  2 49x  7x  42  181 14x (1) Đ ề 6 u kiện: x  , 7 2
(1)  14x 181  7 x  7  7 x  6  2 49x  7x  42  0
 7x  7  7x  6  2 7x  77x  6  7 x  7  7x  6 182  0
  x   x  2 7 7 7 6
 7 x  7  7x  6 182  0 .
Đ t 7x  7  7x  6  t  0 , 2
t t  182  0  14 
t  13  0  t  13 .
Suy ra 7x  7  7x  6 13  0 vì hàm số vế ồng biến nên ta có
7x  7  7x  6 13  0  x  6 . Bài 7: 2 x  1 
x  4x  1  3 x (1) . 0  x  2  3 Đ ều kiện:  . x  2  3
Nhận xét: x  0 là một nghiệm.
Với x  0 , chia hai vế cho x , ợc
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 12
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE 1 1 1 1 x
x  4   3  x
x   4  3 (2) . x x x x Đ 1 1 t 2 x
t (t  2)  x   t  2 . x x 5 Từ (2), ta có 2
t  6  3  t t  . 2  1  1 1 5 x x   Suy ra x 2x 5 x 2 0 2          4 . x 2    x  2 x  4  1 
Vậy b ã ập nghiệm là 0;    4;  .  4 x x Bài 8:  . 1  2 1 (1) 2 x x   1
Đ ều kiện: x  0 . 2 Nhận xét:
 2x x    x  2  x      2 2 1 1 1 1 1
2 x x   1  0 .
D , ( )  x x  
 2x x     2 1 2 1
2 x x   1  1  x x (2).
Ta có x  0 không ph i là nghiệm của b .
Với x  0 , chia hai vế cho x ợc  1   1  2 x   2   x 1     (3)  x   x  Đ 1 1 t 2
x t x   t  2 . K ( ) ở thành x x  2
2t  2  t 1  t  1 3 5 1 
x 1 x x 2 Bài 9: G 4 3 2 3 2
2x  6x 10x  6x  8  x x
x 1  x  2   1 Lời giải 4 3 2
2x  6x 10x  6x 8  0  2  x   1  2
2x  6x  8  0 Đ ều kiện:     x  0 . 3
x x  0 x  0 K ( ) 2 2 2 2
x 1. 2x  6x  8  x 1 x x 1x  2  0 2
 2x  6x  8  x x  2  0 2
Nhận xét x  0 không ph i là nghiệm nên chia cho x , ta có:  4   2  2 x   6 1 x   0     3  x   x  Đ 2 4 t 2 x
t x   t  4 x x t   1  Ta có 2
2t  2  t 1    t  2 1  x   1  x  4. 2 t   2t 1 0 x
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 13
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE
2. ĐẶT ẨN PHỤ KHÔNG HOÀN TOÀN Bài 1: Gi i : 2
2012x  4x  3  2011x 4x  3 . x t
Đ t t  4x  3 2 2
 2012x  2011xt t  0   t  x   2012
Bài 2: Gi i :  x   2 2 1
x  2x  3  x  1. Đ t 2 t
x  2x  3   x   2 1 t x  1 2
x  2x  3  x  
1 t  2 x   1  0 t  2
t   x  
1 t  2 x   1  2
0  t x  2
3. ĐẶT ẨN PHỤ ĐƯA VỀ PHƯƠNG TRÌNH TÍCH
Bài 1: [Đặt ẩn phụ đƣa về phƣơng trình tích] G x  
x    x 2 2010 1 1 .
Đ ều kiện: x  0 .
Đ t t  1 x 0  t   1
x  t x   t 2 2 2 1 1 . T à ầ ợc  t 2 
t  t2 2 2 1 2011 1   t2  2 2 1
t t 1005  0   t2 1
 0 (Vì 0  t 1 nên 2
t t 1005  0 )
Bài 2: [Phƣơng trình tích] G  2 x   3 2 2  5 x 1 Đ t 2 u x 1; v x x 1   2 2
2 u v   5uv  u  2v2u v  0 .
Bài 3: [Phƣơng trình tích] G 3 3 2 3 2
7x 1  x x  8  x  8x 1  2 . Đ 3 3 2 3 2
a  7x 1; b   x x  8; c x  8x 1
a b c   a b c3 2  8 Và 3 3 3
a b c  8
 a b c3 3 3 3
a b c  0
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 14
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE
 3a bb cc a  0
Bài 4: Giải bất phƣơng trình  2 2 x    x  4 2 2 2 1 1
 1 x  3x 1   1 Lời giải Đ ều kiện 1   x 1. Đ t 2 2
x 1  a  0, 1 x b  0 Suy ra 2 2 2 4
3x 1  2a b ; 1 x ab .
Ta có:  a b 2 2 2 2
ab  2a b  2a ba b  2  0 .
Vì a b  0  2a b  0 . D a b  2  0 Suy ra 2 2
1 x  1 x  2  x  0 . 4 2 2 2 x x 1 x x 1 x 1
Bài 5: Giải bất phƣơng trình    x  2 1 2 x   2   1 x 1 x Lời giải Đ ều kiện x  0 2 2 2 2
x x 1 x x 1 x x 1 x 1 Ta có   1  .   2  2 2 2 2   x 1 x x 1 x 2 2     Đ x x 1 x x 1 t  a  0,  b  0, 2 2 x 1 x 1 2  K x 1 2  b 1 2 x   2
2  ab a 1 b  b  
1 a b   1  0  b  1 2 x x 1  1 x  2 1  0 ( ú ) x
Vậy nghiệm của b là 0;  .
4. ĐẶT ẨN PHỤ ĐƢA VỀ HỆ Bài 1.
Đặt ẩn phụ đƣa về hệ bậc nhất hai ẩn
 xy  3   xy  3 2 1 2 5 1  Gi i hệ .
x  2 y 1  2 2x y 1 
 9x  2y  21  5x 11 Lời giải 2 2  a  2b 11  2 x
 x  2y 1  a  0 x  2y 1 a  Đ 5 t        1 2 2 2
 2x y 1  b  0  
2x y 1  b  2a b  3 y   5
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 15
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE 2 2 2 2
 5x 11  a  2b ; 9x  2y  21  a  4b . 3 3 a  4b 1 3 3 a  4b 1   K ệ ã ở thành  2 a  2b   2 2  a  4b
a  2b a  4b a  2b   2 2   2 2  2 2  a  2ba  0    b a  2b 0 3 3
a  4b    2 2
a  4b  2 2
a  2b   aba ba  2b  0   . a b  a  2b 3  111 2
2x  2y 1  0 x  3 1   6 2
TH1: a  0  b    1   . 3 3 4
2x y  5    8 2 1 3  2 2 y   3  6 2  5 x  
2x  2y 1 1  3
TH2: b  0  a  1     .
2x y  5  0 5 y   3 3  1  3 11 5
2x  2 y 1   x  3 3 1  5  TH3: 6 5 a b      . 3 5 1   4
2x y  5  y  3  5  3 3  2  4 11 12
2x  2 y 1   x  3 3 2  12  6 12
TH4: a  2b      . 3 3 12 1   1 4 12
2x y  5   3 y  12  3 Bài 2.
Đặt ẩn phụ đƣa về hệ bậc nhất hai ẩn   x y   2 2 2
x  7  y 2 y 1  xy  2 y G ệ  2 2x x  7   x y 2 2
2 y 1  3xy x Lời giải 2
 x 7  u Đ t  . 2
 2y 1  v  K ệ ã ở thành 2 2 2
x  7  4yx  9     x y   2
u yv xy  2 y u   2y 2  2 2 2
x  7  2y 2y 1  xy  4 x  3             . 2xu   x y 2
v  3xy xv  x 2      x  0 x  0 y  2 2 y 1 x   y  0 y  0 Bài 19.
[Đặt hai ẩn] G 3 24  x  12  x  6 .
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 16
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE u   v  6 Đ 3 u
24  x; v  12  x   . 2 2 u   v  36 Đ ố S   8  8; 2  4;  3 . Bài 20.
[Đƣa về hệ đối xứng loại 2] G 3 3
x 1  2 2x 1 . 3
x 1 2t Đ 3 t  2x 1   . 3 t  1  2x     Đ ố 1 5 S  1  ;  .  2   Bài 21.
[Đƣa về hệ đối xứng loại 2] G 2
x  2  2 2x 1 . 2
x  2x  2 y    1
Đ y 1  2x 1   . 2
y  2y  2  x   1
Đ ố S  2 2 . Bài 22.
Bài tập tự luyện
1)  x   x   2 1
4  5 x  5x  28 . 2) 
  x  x 2 4 4 2
x  2x 12 . 5 1 3). 5 x   2x   4 2 x 2x 4). 2
3x  2  x 1  4x  9  2 3x  5x  2 . x 5).
x x  x  1 3 1 4 3  3  0 x . 3 6). 2 x   2  x   2 3
2 x  1 2 x  2 . 7). 2
x x 12 x 1  36. 8).   x 2 2 2 1
x  2x 1  x  2x 1. 9).
x  5 x 1  0 . 10). 2 3 9 x x   2 4 . 11). x x   3 2
5  3 x  5x  2  4 . 4 12). 2 2
x x 1  x x 1  2 . 2 2 13).
4x  5x 1  2 x x 1  9x  3 .
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 17
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE 2 3 14).
2x 3x  2  3 x 8 . 15). 2 2 4 2
x  3 x 1  x x 1 . 16). 2 2
5x 14x  9  x x  20  5 x 1 . 17). 3 3 3 3
3x 1  5 x  2x  9  4x 3  0 . 18).
2  x. 3 x  3 x. 5 x  5 x. 2  x . 3 2 3 2 3 3 19).
3x x  2011  3x  7x  2012  6x  2013  2012 . 3 3 20). x. 25  x  3
x  25  x   30. 21). 4 4
57  x x  40  5. 22).
x  2011 x 1  2012 . 1 1 23). 3  x   x  1 2 2 . 24). 2
x x  5  5 . 25).
x  2011 2011 x . 2 26).
2x  6x 1  4x  5 . 27). 3 3
x  2  3 3x  2 . x 28). 2 4 9 7x 7x    8 . x  7 Bài 14. 2
3x  6x  3  3 Lời giải 2 x  7 3
 x  6x 3  t
Cách 1: Đ t t
t  0 ta có:  . 3 2 3
 t  7  x 2 3
 y  6  t
Đ t y x 1 hệ ở thành  . 2 3
 t  6  y 3x  21 Cách 2: P ã ớ 2
x  6x  3  9 2  49 1
9x 18x  9  3x  21 2
 9x  21x
 3x  21 3x  21  4 4 2 2  7   1   3x   3x  21       2   2  4x  9 x  3 4 Bài tậ : 1) 2 7x  7x  . 2) 2 2x  4x  . 3) 2 27x 18x x  . 28 2 3
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 18
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE
IV. PHƢƠNG TRÌNH VÔ TỈ NHÂN LIÊN HỢP
1. PHƢƠNG TRÌNH VÔ TỈ NHÂN LIÊN HỢP TRỰC TIẾP CÁC BIỂU THỨC CÓ SẴN TRONG PHƢƠNG TRÌNH Bài 1. Gi 2 2 2 2 2x 1 
x  3x  2 
2x  2x  3  x x  2 Hƣớng dẫn giải 2 2x 1 0 T ều kiệ x ịnh:  . 2
x 3x  2  0 K 2 2 2 2 2x 1 
x  3x  2 
2x  2x  3  x x  2   2 2
2x 1  2x  2x  3    2 2
x  3x  2  x x  2   0 2  x  4 2  x  4    0 2 2 2 2
2x 1  2x  2x  3
x  3x  2  x x  2      x   1 1 2 4     0 2 2 2 2
 2x 1  2x  2x  3
x  3x  2  x x  2   2
x  4  0  x  2  .
Kết hợp vớ ều kiện và thử l ợc nghiệm củ là x  2  . Bài 2. Gi 2 2
2x 16x 18 
x 1  2x  4 Hƣớng dẫn giải 2
2x 16x 18  0 T ều kiệ x ịnh:  2 x 1 0 K 2 2
2x 16x 18 
x 1  2x  4 2 2
x 1  2x  4  2x 16x 18   1 2  2 x 1 2   x 1  2
2x  4  2x 16x 18 2  x 1  0 2   2 2
2 x 1  2x  4  2x 16x 18  3 Gi i (2): 2
x 1  0  x  1  . 4x  8  0  Cộng (1) vớ ( ) ợc 2
3 x 1  4x  8  9  x   1  4x  82 2 x  2       32   3 57 x 2 x  32   3 57      x  . 2 7
7x  64x  73  0  7  32   3 57 x   7 3  2  3 57
Kết hợp vớ ều kiện và thử à ợc các nghiệm là x  1  và x  . 7
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 19
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE Bài 3. Gi  x   x   2 3 1 2
3x  7x  2  4  4x  2 Hƣớng dẫn giải T ề 1
u kiệ x ịnh: x   3
 3x1 x2 2
3x  7x  2  4  4x  2  2x   1  2
3x  7x  2  4  4x  2 3x 1  x  2 2x  2 1  3x 7x 2 4 2  3x 1 x 2            0   K  1 x   2    2x  
1  3x 1  2 x  2  2  0  x 1  x  2   1 Vậ ệm x
, x 1và x  2 . 2 1 1 x 1 Bài 4. Gi   4 4 4 2x 1 x  2 x Hƣớng dẫn giải
T ều kiệ x ịnh: x  0 . K ới: 4 4
x  2  2x 1 x 1  2x   1  x  2 4 4 x 1 x x 1   4 2  
1   2    2    2 2   1    22   1  2   1  4 3 2 2 3 4 4 4 4 x x x x x x x x x        x 1 1 1     0 4  2   1   2 
  2   2 2  1  22  1  2  1  4 3 2 2 3 4 4 4 4 x x x x x x x x x    x 1. Vậy ệm x 1. Bài 5: Gi 3 3 2x 2 5x 14 3x 16 x 2 Đ ều kiện x 2
H ớng dẫn nhân chia liên hợp vế trái xu t hiện nhân tử chung 3x 16 16 Gi i ra nghiệm x 3 1 1 1 x Bài 6: Gi x 2 2x 1 2 2 x x x 0
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 20
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE 1 1 2x 1 x 2 2 x x
H ớng dẫn nhân chia liên hợp xu t hiện nhân tử chung x 1 Đ ố x 1 Bài 7: Gi x 2 3x 5 2x 3
H ớng dẫn nhân chia liên hợp vt xu t hiện nhân tử chung 2x 3 Đ ố 3 x 2 2 2x Bài 8: Gi x 21 (1) 2 3 9 2x x 3 9 2x H ớng dẫn th y thay vào (1) 3 9 2x 2 Đ ố 9 7 : ; 0 0 ; 2 2
Bài 9: Cho x ;y thỏa mãn : 2 2 x x 2011 y y 2011 2011 Tính x y ? Ta có: 2 2 x x 2011 y 2011 y 2 2 y y 2011 x 2011 x
Cộng vế với vế ta có x y 0 . Luyện tập : Gi 1) 2 x 2 2x 1 21 x 2 2 2) 2x 5 3 x x 5x 8 3)2 3 8x 6x 4x 1 4) 10x 1 3x 5 9x 4 2x 2 2 2 2 5)1 x 4x x 3x 3 2x x 2 2 2 6) x 15 3x 2 x 8 2 7) x 5 x 2 1 x 7x 10 3 2 2 2 2 8) 3x 7x 3 x 2 3x 5x 1 x 3x 4 2 2 2 2 9) 2x x 1 3x x 1 x 4x 3 2x 4x 3 2 x 10) x 4 2 2 1 1 x 11) 1 x 1 x x 2 1 1 4x 12) 3 x
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 21
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE
xy xy xy 2  x y  y
Bài 10: Gi x 1yxy x1x 4    Ta có:
xy xy xy 2  x y  y
x 1yxy x1x 4    (1) 
xy   x y xy  2  y x y  0
x yy xy 2 x    y
 0  x y   x     2  y xy x y xy y  2 
Với x y .Từ ( ) y xy x 1     x  2 1  2  2  x 1   4 4
x 1  x 1  y  2  y   1 Bài 11.
[phƣơng pháp liên hợp] G ệ  2 x  2x   y   2
1  y  6x 1  0 2 Lời giải
   y  x y  2 2 4 1  y  0   4 4 4 4 1  x 1  y  2  y x 1 4 4
x 1 y  2 y x 1   4 x 1  y  2
 4y x1 4 4 4 y x 1 4 4
y x 1  0  x y 1  y
 4y   y y2 0 4   7 4
y  2y y  4
Nếu 0  y  1 thì 7 4
y  2 y y  4 . S ệm Nếu y  1 thì 7 4
y  2 y y  4 . S ệm
2. PHƢƠNG TRÌNH VÔ TỈ NHÂN LIÊN HỢP THÊM BỚT HẰNG SỐ Bài 1. G 2 2
x  5  3x x 12  5 . Lời giải Ta có:  2
x      x     2 5 3 3 6 4  x 12   0 Bài 2. Gi i hệ
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 22
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE 2 9
x 9xy 5x  4y 9 y  7    1 
x y  2 1  9 
x y2  7x 7y 2 Lời giải
Đ ều kiện: y  0; x y  0.
Đ t: x y t  0 . Từ   2
2  t  2 1  9t  7t 2 3t 1 2    9t 1
 0  t  0 (sử dụng nhân liên hợp). 7t t  2 1 1
x y   y x  .Thế vào   1 ta có: 3 3  1   1  1 2 9x  9x x
 5x  4 x   9 x   7      3   3  3
xx   2 2 9 4 
9x  4 9x 3  1  0 3     x   2 3 9 4  2x     0.  3   9x  3 1  4 1    x
y  . Vậy hệ có nghiệm: x y 4 1 ;  ; .   9 9  9 9  Bài 3.
Giải phƣơng trình bằng phƣơng pháp liên hợp Gi 2
6  x  2x  6  6x  5  x  2x  5 . Lời giải Đ ề 5 u kiện  x  6 . 6 P ã
 x   x   x   2 6 1 2 6 4 6
5 5  x  2x 15 5  x 2x 10 6x  30   
 x  3x  5 6  x 1 2x  6  4 6x  5  5      x 1 2 6 5    x  3  0   *  6  x 1 2x  6  4 6x  5  5  5 2 6 2 6 Với  x  6 ta có  
 3     3  0 . 6 2x  6  4 6x  5  5 4 5 D   *  x  5.
Vậ ệm duy nh t x  5. Bài 4: Gi 2
3x 1  6  x  3x 14x  8  0 (4)
(trích đề thi đại học khối B-2010) Lời giải 1
Đ ều kiện:   x  6 3 P (4)   x      x 2 3 1 4 1 6  3x  1  4x 5  0
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 23
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE 3 x  5 x  5    3x   1  x  5  0 3x 1  4 6  x 1 x  5  3 1  3x 1  0    3x 1  4 6  x 1 Ta th 3 1 
 3x 1  0 vô nghiệm vì 3x 1  4 6  x 1 3 1  1  
 3x 1 0, x    ;6   3x 1  4 6  x 1  3  Vậ ệm duy nh t x=5
Bài 5: Gi i b ập số th c:  x  2
1  x 1  x  2  0 Lời giải
Đ ều kiệ x ịnh: x 1. Ta có:  x  2
1  x 1  x  2  0   x  2 2
1  2 x 1  2 x  2  0   2
2x  5x  2  2 x 1  
1  x  2  2 x  2  0  x
x  22x   2 2 1 
x  2  x  2  2  0 x 1 1  x x x
x  22x   2 2 2  2 1    0 x 1 1 x  2  2      x   2 x 2 2  2x 1    0   . x 1 1 x  2  2   2 x  2 Vì: 2x 1   0, x
 1. D 1 x  2. x 1 1 x  2  2
Kết luận: Tập nghiệm của b S  1; 2 . Bài 6: C 3 2 2 2
3 x x  8  2 
x 15 . Gọi S là tổ ệm th c của . Tí S . A. S  0 . B. S  1. C. S  2 . D. S  4 . Lời giải Đáp án: C
Ta d ợc nghiệm x  1  , và ta viết l
3 2x   2x    2 3 1 8 3 x 15  4 3 2 x   2 2 1 x 1 x 1    3 4 3 2 2 2 x x 1 x  8  3 x 15  4 2  x  1   1   3 1 1    2 3 4 3 2 2 2
 x x 1 x  8  3 x 15  4 P   1  x  1  . 3 Gi 2 . Vì  0; 3 4 3 2 x x 1
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 24
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE 1 1 2 2 2 2 x 15  x  8  x 15  4  x  8  3   2 2 x 15  4 x  8  3 N 2 vô nghiệm.
Vậ ệm x  1, x  1
 . Suy ra S    2 2 1 1  2 .
Bài 7: Gi i b ập số th c: 3 x  2  3x  4  3 2x 1  x  3
Đ ợc tập nghiệm là S  a;b. K . a b có kết qu là. A. 3 . B. 3  . C. 12 . D. 12 . Lời giải Đáp án: C
Đ ều kiệ x ịnh: x  3.
Ta có: 3 x  2  3x  4  3 2x 1  x  3
 3x  4  3x 4 43 2x 13 x3   1  0      x   3 x 4 6 x 4 x 4 3 4     0 3x  4  4 2x 1  3 x  3 1     x   3 6 1 4 3     0    3x  4  4 2x 1  3 x  3 1     x   3 6 1 4  2  1  0    3x  4  4 2x 1  3 x  3 1       x   3 2 2x 1 x 3 4      0    3  x  4. 3x  4  4 2x 1  3 x  3 1  
Kết luận: Tập nghiệm của b S  3; 4 .
3. PHƯƠNG TRÌNH VÔ TỈ NHÂN LIÊN HỢP THÊM BỚT BIỂU THỨC BẬC NHẤT
Bài 1: Gi i b ập số th c: 3 2 2
x  3x x  2  2x
x  4  2x 11 Lời giải
Đ ều kiệ x ịnh: x  4  . Ta có: 3 2 2
x  3x x  2  2x
x  4  2x 11 3 2 2
x  3x x  2  2x x  4  2x 11  0 2
x x 32 x  4x 2 2x11  0
x 32  4x  4 x  22  2x 11 2    x   0
x  3  2 x  4
x  2  2x 11 2 2 x  2x  7 x  2x  7 2  x   0
x  3  2 x  4
x  2  2x 11   x
x  2x  7 2 1 2     0 .
x  3 2 x  4 x  2  2x 11  x  4  x  4 
Đ ều kiện có nghiệm:     x  3  . 3 2
x  3x x  2  0 3 2
x  3x x  3  0
x 3 2 x  4  2  0 Vì x  3
  x2 2x11 1 5 0
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 25
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE 2 x 1    0
x  3  2 x  4
x  2  2x 11 2
x  2x  7  0 D 
x  1 2 2 . x  3 
Kết luận: Tập nghiệm của b S   1   2 2;  .
Nhận xét: Sử dụ TABLE à SOLVE ợc: x 1.828427124 .
2 x  4  4.828427125  x  3 T à ức tìm nhân tử:  .
 2x 11  3.828427125  x  2 Bài 2: Gi 2 2
2x x  3  x x  21x 17 ợc 2 nghiệm x , x (x x ) . K 1 2 1 2 2 2 x x có kết qu là: 2 1 A. 3 . B. 4 . C. 2 . D. 8 . Lời giải Đáp án: A Đ ề 17 u kiện x  . P ã ới: 21
 2x x x  x  x  2 2 3 1 3 1 21
17  x  3x  2  0.   9 x x  2 2 x  3x  2 3 2  2  
x 3x  2  0. 2
2x x  3  x 1
3x 1 21x 17   1 9  2
x  3x  2  1  0 2
 2x x  3  x 1 3x 1 21x 17  x  2
x  3x  2  1 0  x  2 1 9 17 Do  1  0, x   . 2
2x x  3  x 1
3x 1 21x 17 21 - Vậy: 2 2 2 1
x x  2 1  3 2 1
Nhận xét: Ta nhậ ợc rằ ệm x  1; x  2 . Do vậ à ẽ có
nhân tử  x   x   2 1
2  x  3x  2 ịnh sử dụ l ợng liên hợ ể gi à . Đ ều quan tâm
là cách tách - l ợng có tron . Gi sử ta sẽ nhóm  2
2x x  3  a x b
a x b  21x 17 . Thay các giá trị x  1; x  2 vào các 1 1   2 2  2
 2x x 3 a x b  0
2  a b  0
a  1 a b  2  0 1 1  ẳng thức  , ta sẽ ợc 1 1  1   ; 2 2          
a x b  21x 17  0  3 2a b 0  b 1  2a b 5 0  1 1 1 2 2 2 2  a  3 2   . b  1   2
V. PHƯƠNG TRÌNH VÔ TỈ GIẢI BẰNG PHƯƠNG PHÁP VECTƠ 2 2
 x 9  y 9 10
Bài 1: G ệ xy 8
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 26
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE Lời giải Cách 1:
Trừ 2 vế  x y  8 thế vào 2 2 2
x  9  y  9 10 3 .
Đ t t x  4 ( t ẩn phụ khéo léo)  x  4  t và y  4  t thế vào 3 ta có 2 2
t  8t  25  t  8t  25  10 4  t  2 2 2 2 2 25
 64t  25  t , t  25. 4 2 2 2 4
t  50t  625  64t  625  50t t t  0  x y  4 . Cách 2: P é 2 2
 x 9  y 9 10
Ta có xy 8
Đ t u   x;3 v   y;3  u v  8;6 2 2 u x  9 v y  9 Áp dụ BĐT 2 2
u v u v x  9  y  9  10 x yx  4
D u bằng x y ra  u ; v ù ức là    . x y  8 y  4
CÁC BÀI TẬP GIẢI VECTO NHƢ TRÊN
 3x  3y  6
 x 1 y 1 4
 x y 10 1)  2)  3) 
 3x  7  3y  7  8 
x  6  y  4  6 
x  24  y  24 14  Bài 2: G 2 2
x  2x  5 
x  2x 10  29   1 . Lời giải u
  x 1;2
Trong m t phẳng tọ ộ Oxy , xé é  . v    1   ; x 3 2 |
u | x  2x  5  K 2 |
v | x  2x 10 . u v    2  ;5 |
u v | 29  2 |
u | x  2x  5  2 |
v | x  2x 10
u v  ( 2  ;5) |
u v | 29  Suy ra   1 |  u v | |
u |  | v | .
u  v u k.v k  0 .  2   2   k  2 k
x 1  k 1 x       k   3     3 3   . 2  k.3 2  1 x 1   1   x         3x 3 2x 2 x  3  5
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 27
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE Bài 3: G 2 2 2
x  2x  2  4x 12x  26  9x 12x  29 . Lời giải: u
  x 1  ;1
Trong m t phẳng tọ ộ Oxy , xé é  . v   2x 3;4 2
u x  2x  2   
u v  3x  2;5 thì 2
v  4x 12x  25  2
u v  9x 12x  29 
x 1 k 2x  3 S  
1  u v u v
u kvk  0  1k.4  1  1 k    1   k  4    k     4 4   . 1   7 x 1  2x 3        4x 4 2x 3 x  4  2 7 Vậ  
1 có nghiệm duy nh t x  . 2 Bài 4:
Gi i b x   x   x  2 1 3 2 3  2x  2   1 (Bộ ề Tuyển sinh) Lời giải Đ ều kiện x 1
u  x 32    u    xx  x 1 3; 1 
Xét trong m t phẳng tọ ộ Oxy    v  2 . v   1  ;1   . u v
x 1  x  3  2
x  6x  9  x 1 Suy ra b   1  . u v u v
u  v x  3  x 1  x 3 x  2 2
x  7x 10  0   
 x  5  x  5. x  3  x  3
Vậy x  5 là nghiệm duy nh t củ   1 .
x y xy  3   1 Bài 5.
x 1 y 1  4  2 Lời giải
ĐK xy  0 ; x  1  ; y  1  Cách 1
Từ 2 ta có : x y  2  2 x y xy 1  16 3 Từ  
1 ta có : x y xy  3  x y  3  xy t xy t t  0  x y  3  tx y  6 Thế vào 3 ta có 2
2 t t  4  11 t t  3  
x y  3. xy  9
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 28
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE Cách 2
Dễ th y x  0 ; y  0 x y
Áp dụ BĐT x y xy  3 
 3  x y  6 2
Từ 2 ta có : 4  x 1  y 1  2   x    1   y   1   4  x y  6  Đ BĐT  
x y  3 .
x 1  y 1  Các Bài tƣơng tự 3
 x 3y 2 xy  8 
 2x 3 4x 12y 3 4y 1  2 2x 32y 3 1)  2) 
x  7  y  7  6 
x y  4xy
x  2y  3z  4  3
x  2y  6y  2 3)  4)  2 2 2
 4  x  1 y  25  9z  4 3  3
y  x  3x  4 Bài 6. G : x x    x   2 3 2 4 2 x   1  x  3   2.1 . Lời giải Đ 2 iều kiện:   x  4 . 3
Đ t u   x
;1 và v  3x  2; 4  x   0 . Khi , .
u v x 3x  2  4  x u v   2 . 2 x   1  x  3 Suy ra, ph ng trình   2.1 trở thành .
u v u . v k
  0:u k.v .
x k 3x  2  
x 4  x  3x  2 1
  k 4  xx  0  x  0     2 x  4  x 3 2  3x  2
x  4x  3x  2  0 x  0  x  2     . x   2;1 2;1 2  x 1 2
Vậy tập nghiệm của ph ng trình là S  2;1 2. 45 Bài 7. Gi 2 2 2
x  2x  5 
x  4x  40  x  5x  (2.2) 4 Lời giải P x ịnh x   .
Đ t u   x 1;2 và v  2  ; x 6
K u v  3;4  u v  5
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 29
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE u
x  2  2 2 1 2
x  2x  5 v    x2 2 2 2
 6  x  4x  40 2 2
u v u v
x  2x  5 
x  4x  40  5 Để ( . ) ệm thì: 2 45  5  5 2 x  5x   5  x   0  x     4  2  2 5 Thay x   à ( . ) y thỏa mãn. 2 5
Vậ ( . ) ệm duy nh t x   . 2 2
Bài 8. Giải phương trình: 4  x     6 6 3 1 2sin 2 2 40 4 sin x  o
c s x 1  5 11   1  . Lời giải Đ t T   x     x c x 2 4 6 6 3 1 2sin 2 2 40 4 sin os 1 . 3   Ta có:  6 6 x c x    2 2 x c x 2 2  x x  2 2 4 sin os 1 4 sin os 3sin cos sin x  o c s x 1   2 2   x x    2  x 2 4 12sin cos 1 3 1 sin 2  3cos 2x . K 4 4 4 4 4 T
9  18sin 2x  160  36 cos 2x
9  9sin 2x  9sin 2x  144 16  36 cos 2x Xé u   2 2
3;3sin 2x;3sin 2x và v   2 12; 4;6 o c s 2x . 4 4 u
9  9 sin 2x  9 sin 2x ; 4
v  144  16  36 o c s 2x .
T u v u v T    x  2   x x2 2 2 2 225 3sin 2 4 3sin 2 6 cos 2 .
M t khác theo b ẳng thức Bunhiacopski ta có:   x  2   x
x2      x   x x2 2 2 2 2 2 2 2 2 3sin 2 4 3sin 2 6 cos 2 1 1 3sin 2 4 3sin 2 6 cos 2  100   2 2   Suy ra:  2 x     2 2 3sin 2 4
3sin 2x  6 cos 2x  50 T  5 11   . 2 2  3 3sin 2x 3sin 2x    P  
1 có nghiệm khi và chỉ khi: 2 1  2 4 6 o c s 2x  2 2 2 3
 sin 2x  4  3sin 2x  6cos 2x 2 4 1 1 k 2  os c 2x   1 os c 4x   os c 4x
x   arccos  , k  . 3 3 3 3 2 1 k Vậ  
1 có nghiệm là: x   arccos  , k  . 3 2 Bài 9.
Giải bất phƣơng trình 2
x 1  x  3  2x 10x 16 *. Lời giải x 1 Đ ều kiện   x  1. 2
2x 10x 16  0
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 30
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE
Xét u x 1 ; x 3 và u 1;  1  0 . Ta có . u v
x 1  3 , u v
x    x  2 2 . 1
3 . 2  2x 10x 16 . B * trở thành: .
u v u . v , m t khác .
u v u . v nên ta có .
u v u . v  k  0 : u kv . K
 x 1  k
x 1  x  3
x 3  kx  3 x  3  0    
 x   x  (thỏ ã ều kiện). x 1   x 3 2 5 2  x  5
Vậy b ã ệm duy nh t là x  5. 2009 1 x 1 x ... 1 x 2008 1 2 2008 2008 Bài 10: Gi i hệ: 1 2007 1 x 1 x ... 1 x 2008 1 2 2008 2008 Lời giải Đ ều kiện: x 1, i 1,2008 i
Trong m t phẳng tọ ộ Oxy , xé ai 1
x ; 1 x ,i 1,2008 . i i K 2008 a 2, i 1,2008 a 2008 2 i i i 1 2008 2008 2008 a 1 x ; 1 x i 1 1 i 1 i 1 i 1 2 2 2008 2008 2008 a 1 x 1 x i i i i 1 i 1 i 1 2008.2009 2008.2007 2008 2 2008 2008 a a a a . , i j 1,2008. i i i j i 1 i 1 H a: a a 2, , i j 1,2008 i j Nên a a , , i j 1,2008 x x , , i j 1,2008 i j i j 2009 2009 1 x , i 1,2008 1 x , i 1,2008 i 2008 i 2008
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 31
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE 1 x , i 1,2008 i 2008 1
Vậy hệ ã ệm duy nh t là x x ... x 1 2 2008 2008 2 x y 1 x y 3 x y 2 x y 1
Bài 11: Gi i hệ x y 2 1 x y 2 1 Lời giải a x y;1
Trong không gian Oxy xé b 1 x y; 3 x y (Vớ ều kiện 1 x y 3 ) 2 a x y 1 b 2 . a b x y 1 x y 3 x y . a b a . b a b 1 x y x y 3 x y x y 2 theo gt 3 2 x y 3 x y x y 1 0 x y 2 2 x y 1 x y 2 x y 1 0 x y 2 1 x 2 Kết hợp với x y 2 1 ta gi ợc . y 1
VI. PHƢƠNG TRÌNH VÔ TỈ ĐƢA VỀ DẠNG f u  f v 3 3 2
x y  3y  3x  2  0   1
Bài 1: T ể hệ ệm:  có nghiệm. 2 2 2
x  1 x  3 2y y m  0  2 Hƣớng dẫn giải Đ ều kiệ x ịnh: 1
  x 1,0  y  2 . 3 Ta có:   3
1  x  3x   y   1  3 y  
1 . Xét hàm số f t  3
t  3t nghịch biến trên kho ng  1   ;1 .
K ( ) ng f x  f y  
1  x y 1  y x 1 . T à ( ) ợc 2 2 2 2
x  2 1 x m  0  x  2 1 x m 3 .
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 32
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE
Hệ có nghiệ ( ) ệ n  1  ;  1 .
Xét hàm số g x 2 2
 x  2 1 x n  1  ;  1 . Ta có: 2  x   2 1 1 2 x x
g x  2  x  
gx  0  x  0 2 2 1 x 1 x Ta có b ng biến thiên:
Từ b ng biến thiên suy ra yêu cầu Bài thỏa mãn khi 1   m  2 .
17  3x 5 x 3y   4 4  y  0  1 Bài 2: Gi i hệ b :  . 2
2 2x y  5  3 3x  2y 1  x  6x 13   2 Lời giải.   1  3
 5 x  2 5 x  3  
 4  y  2 4  y  .
Đ t f t   3t  2 t , ta có f t ồng biến
 5  x  4  y y x 1 thay vào 2 2
 2 3x  4  3 5x  9  x  6x 13   x
 x     x   x   2 2 3 4 2 2 3 5 9 3
3   x x      
xx   2 3 1  1  0  
 3x  4  x  2
5x  9  x  3  xx   1  0   2 3   1  0
 3x  4  x  2
5x  9  x  3 x  0    x 0    x 1  0 x  1  Hệ ệm: 0;   1 ; 1  ; 2  4 4
x 1  x 1  y  2  y  1
Bài 3. [Hàm số] G ệ  2 x  2x   y   2
1  y  6 y 1  0 2 Lời giải
P     x y  2 2 1
 4y y  0 . P   4
x   x    4 y   4 1 1 1 1 1   4 y   4
1 1  x y 1 . 2 Suy ra  4
y y  y y 7 4 4
y  2y y  4  0 .
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 33
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE
 Với y  0  x  1  Với 7 4
y  2 y y  4  0 , hàm số ồng biến  có duy nh t nghiệm y  1 .
Bài 4. Phƣơng trình vô tỉ dạng: 2
ax bx c k dx e đƣa về dạng: 2
u ku dx e k dx e Bài56: Gi 2
x  3x 1  2 x 1 Lời giải 2 2
x  3x 1  2 x 1  (x  2)  2(x  2)  x 1 2 x 1 u   v
Đ t u x  2;v x 1 ợc: 2 2
u  2u v  2v   từ x u   v   2 Bài 5: Gi 2
2x  2x 1  4x 1 Lời giải 2 2 2
2x  2x 1  4x 1  4x  4x  2  2 4x 1  (2x 1)  2(2x 1)  4x 1 2 4x 1 u   v
Đ t u  2x 1;v  4x 1 ợc: 2 2
u  2u v  2v   từ x u   v   2 Bài 6: Gi 2
x x 1  8x 1 Lời giải 2 2 2
x x 1  8x 1  4x  4x  4  4 8x 1  (2x 1)  4(2x 1)  8x 1 4 8x 1 u   v
Đ t u  2x 1;v  8x 1 ợc: 2 2
u  4u v  4v   từ x u   v   4 Bài 7: Gi 2 4
x  21x  22  3x  2 Lời giải 2 2 2 4
x  21x  22  3x  2  4x  21x  22  3x  2  (2x  4) (2x  4)  3x  2  3x  2 u   v
Đ t u  2x  4;v  3x  2 ợc: 2 2
u u v v   từ x u  1 v 4 Bài 8: Gi 2 27x 18x x  3 Lời giải 4 2 2 2 27x 18x x
 81x  54x  9x 12  (9x  3)  (9x  3)  9x 12  9x 12 3 Bài61: Gi 4 2
x x  3  3 Lời giải
x x    x 2 4 2 2 2 2 2 3 3
x x  3 x  3 ...
Bài 9. [Dạng toán đƣa về 3 3
u ku v kv ] Gi 3 2 3
8x  36x  53x  25  3x  5 . Lời giải
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 34
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE 3 2 3
8x  36x  53x  25  3x  5   x  3 3 2
3  2x  3  3x  5  3x  5 .
Đ t u  2x 3; 3
v  3x  5 . 3 3
u u v v  u v 2 2
u uv v  
1  0  u v . x  2 3  
2x  3  3x  5 3 2
 8x  36x  51x  22  0  5  3  . x   4
Bài 10. [Dạng toán đƣa về 3 3
u ku v kv ] Gi 3 2 3
4x  6x  4x 1  2x 1 . Lời giải 3 2 3 3
4x  6x  4x 1 
2x 1   x     x   3 2 1 2 2
1  2x 1 2 2x 1 .
Đ t u  2x 1, 3 v  2x 1 . 3 3
u  2u v  2v  u v 2 2
u uv v  2  0  u v .  x  0  3
 2x 1  2x 1 3 2
 8x 12x  4x  0  x  1  .  1 x    2
Bài 11. [Dạng toán đƣa về 3 3
u ku v kv ] 20 Gi 3 2 3 9x  9x
x 1  1 2x . 3 Lời giải 20 3 2 3 3 9x  9x
x 1  1 2x   x     x   3 3 1 3 3
1  1 2x  3 1 2x . 3
Đ t u  3x 1, 3 v  1 2x . 3 3
u  3u v  3v  u v 2 2
u uv v  3  0  u v . 3
 3x 1  1 2x 3 2
 27x  27x 11x  0  x  0.
Bài 12. [Dạng toán đƣa về 3 3
u ku v kv ] Gi 3 2 3
4x 18x  30x 17  2x 1 . Lời giải 3 2 3 3
4x 18x  30x 17 
2x 1    x    x 3 3 2 2 3 2
 2x 1 2 2x 1 .
Đ t u  3 2x , 3 v  2x 1 . 3 3
u  2u v  2v  u v 2 2
u uv v  2  0  u v . 3
 3 2x  2x -1 3 2
 8x  36x  56x  28  0  x 1.
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 35
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE
Bài 13. [Đặt ẩn phụ đƣa dạng toán 2
ax bx c k dx e về dạng 2 2
u au v av ] 2
x  3x 1  2 x 1 Lời giải Đ ều kiện: x  1  .
Đ t y x 1, y  0 . 2
x  3x 1 2y P ã ở thành hệ  . 2
x 1 y Cộng hai vế củ , ợc y  x 2 2
x  2x y  2y   x y x y  2  0   . y x  2
Thay lầ l ợt các giá trị y vừ ợ à ầu, ta nhận hai nghiệm 5  13 1 5 x  và x  . 2 2
Bài 14. [Đặt ẩn phụ đƣa dạng toán 2
ax bx c k dx e về dạng 2 2
u au v av ] 2
x x 1  8x 1 Lời giải Đ ề 1 u kiện: x   . 8
Đ t y  8x 1, y  0 . 2 2
x x 1 y
4x  4x  4  4y P ã ở thành hệ    . 2 2 8
 x 1 y 8
 x 1 y Cộng hai vế củ , ợc y x
4x  4x  3  y  4y  2x  2 1   y  22 2 1 2 2   . y  2  x  3
Thay lầ l ợt các giá trị y vừ ợ à ầu, ta nhận nghiệm x  3 . Bài 15. [Đặt
ẩn phụ đƣa dạng toán 2
ax bx c k dx e về dạng 2 2
u au v av ] 4 2 27x 18x x  3 Lời giải Đ ề 4 u kiện: x   . 3 Đ 4 t y x  , y  0 . 3 2
27x 18x y 2  8
 1x  54x  3y P ã ở thành hệ  4   . 2 2 x   y  9
 y 12  9y  3 Cộng hai vế củ , ợc
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 36
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE x x
y y   x  2  x    y2 2 2 81 63 12 9 3 9 3 9 3 3  3y
y  3x 1   .
 9x  3  3y9x  3y  4  0  4  y  3  x   3
Thay lầ l ợt các giá trị y vừ ợ à ầu, ta nhận hai nghiệm 7   33 5   37 x  và x  . 18 8 Bài 16. [Đặt
ẩn phụ đƣa dạng toán 2
ax bx c k dx e về dạng 2 2
u au v av ] 3 2 3
8x  36x  53x  25  3x  5 Lời giải Đ t 3
y  3x  5 . 3 2 8
 x 36x  53x  25  y P ã ở thành hệ  . 3 3
 x  5  y Cộng hai vế củ , ợc
8x  36x  56x  30  y y  2x  33 3 2 3 3
 2x  3  y y
 2x  3 y2x  32  y2x  3 2  y 1  0  
y  2x  3
 2x32  y2x3 2  y 1  0 2
Dễ th y  x    yx   2 2 3 2 3  y 1  0 . 5  3
Thay y  2x  3 à ầu, ta nhận hai nghiệm x  2 và x  . 4 3 8
 x  4x 1 y Bài 17: 3 3
8x  4x 1  6x 1 , ta có  3
6x 1 y Lời giải Cộng vế : 3 3
 8x  2x y y
  x y 2 2 2
4x  2xy 1 y   0  y  2x  D 3 3 3 2x
6x 1  8x  6x 1  0  4x  3x  os c . 3  5 7
x  cos , x  cos , x  cos . 9 9 9
BTLT : Giải phƣơng trình : 1) 2
x  4  2 2x  4 2x 1 2) 2 5x 1  2  5 5 3) 2
4x  4x 1  2 4x  2 4) 2
49x  65x 17  3 2x 1 5) 2
75x  79x  28  2 3x  4
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 37
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE 6) 3 2 3
x  6x 10x 13  2 4x 1 7) 3 2 3
8x 12x  7x  5  2 3x  2 8) 3 2 3
128x  288x  218x  61  x  2 .
VII. PHƢƠNG TRÌNH VÔ TỈ SỬ DỤNG BĐT ĐỂ ĐÁNH GIÁ Bài 1: 2 2 2
x x  9  7x  22x  28  13x  43x  37  3 3  x  3 Lời giải. 2  1  75 5 3 Ta có 2
x x  9  x       2  4 2 x x
  x  2  x  2  x  2 2 7 22 28 2 1 3 3 3 3  3 x  3 2 2 2  1   7   7   7  2
13x  43x  37  x   3 2x   3 2x   3 2x           2   2   2   2   1 x   0  2  2x 1  0 1
Cộng từng vế ợc VT VP    x   x  3  0 2   7 2x   0  2
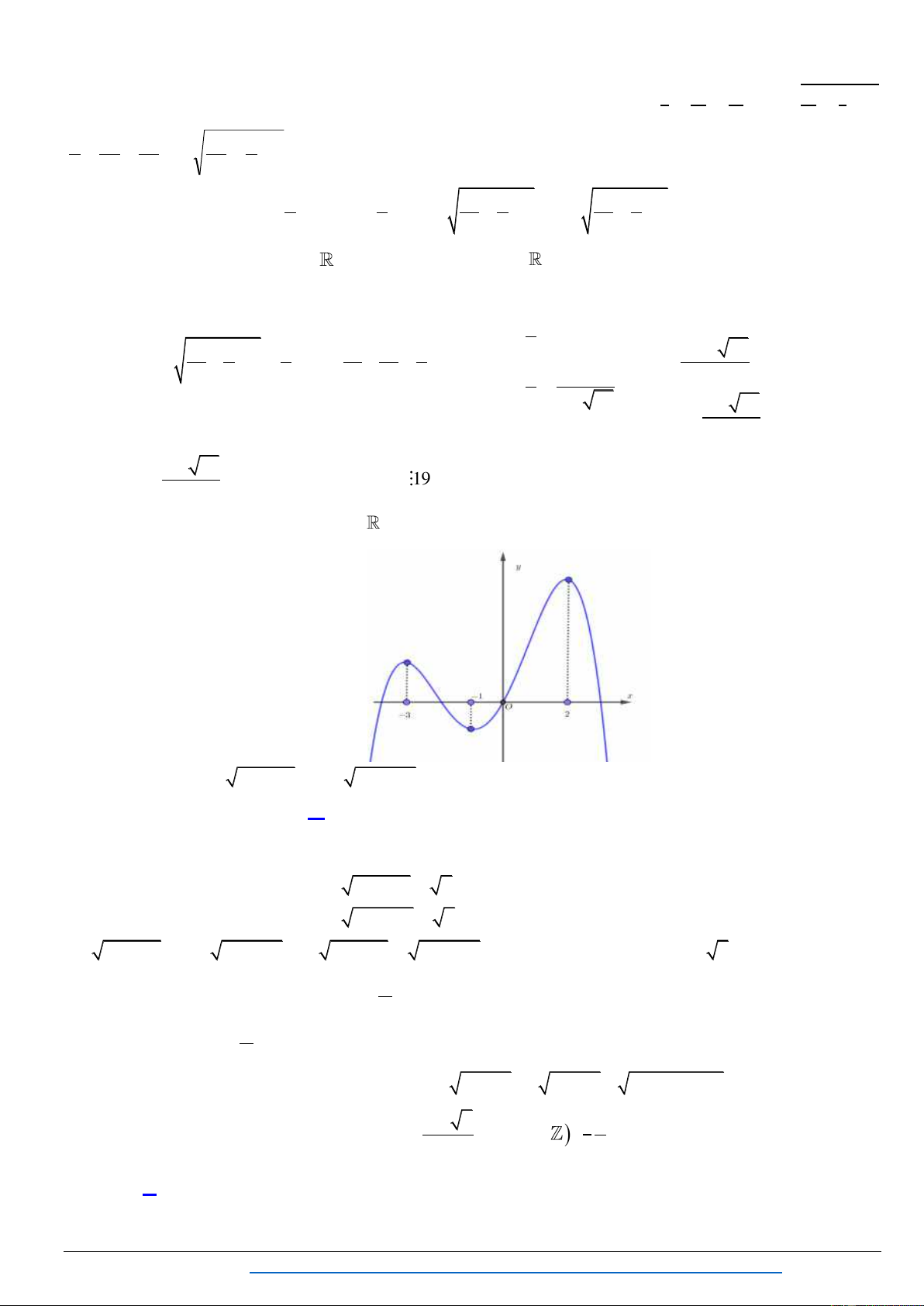
Bài 2: Gi  x   x    2
x   x     x 2 6 1 1 2 1 3 x  2
Dễ th y x 1 không là nghiệm củ N ã 6 x   1 x 1   2
x  2x x 1  3  6x   1
x 1   x  2 x 1  22 2
xx133 x1 2 2 2 2
x  2  2 x 1  0  x  2  2 x 1
Nhận xét:   2x 2xx13 2
 6 x 1 x 1   2
x  2x x 1  3  6x   1 x 1 Vậ ã ệm
x  6 xy y  6   6  3 3 x y
Bài 3: Gi x   2 2 2 x y  3 2 2  
x xy y
Nhận xét: x  0, y  0 không ph i là nghiệm
Nếu x  0, y  0 thì vế trái củ ( ) ỏa mãn
x, y  0 .
Vì 2 xy x y nên  
1  6  x  6 xy y x  3 x y  y  4x  2 y  2x y  3 3 .
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 38
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE  3 2 2 2 2 x y 3 3 3 x y  2  3 3 x y x y 2 2  M t khác xy
x xy y    4 2 2 2 2   2 2
x y xy x  . y 2  3 3 x y  Ta chứng minh  2 2 2 x y 5 2 2    x  . y Ta có        3 3 3 2 2 5 2 x y x y 6 6 3 3 4 2 2 4
x y  4x y  3x y  3x y . 6 3 3 3 3 4 2
x x y x y  3x y Dễ th y  5 . 6 3 3 3 3 2 4
y x y x y  3x y Kết hợp với 2 và  2 2
2 x y   x y ta có 6  3 3 x y  3  x   2 2 2 x y 2 2 
x xy yx   2 2
2 x y   x   x y  2x y 6 . x 1
Từ 3 và 6  2x y  3 và x y   . y 1 2 2 2 2
 5x  2xy  2y  2x 2xy 5y  3x y  1 Bài 4. G ệ  . 3
 2x y 1  7x 12y  8  2xy y  5  2 Lời giải 2 2 2 2 Ta có: 2 2 2 2
5x  2xy  2 y  2x  2xy  5 y  2x y   x y   x  2 y   x y
 2x y x  2y  3x  3y  3x y . x y  0   
1  2x y  0  x y  0 .
x  2y  0  Thế vào (2) ta có: 3 2
3x 1  2 19x  8  2x x  5 2
x x  x    x     x   3 2 2 1 3 1 2
2  19x  8  0    x x x x x
 2x x 2 4 2 2 2    x   2 1  3x 1
x  2 x  2 19x 8  19x82 2 3 3
x  0  y  0 2
x x  0  
TM . Vậy hệ ệm.
x 1 y 1  1 1
x   y   3 4 4   1 1 Bài 5.
[Đặt ẩn phụ, đánh giá khó] Gi i hệ y   z   3 16 16   9 9  z   x   3  16 16 
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 39
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE Lời giải 9
Đ ều kiện: x, y, z  . 16 9 7 13
Đ t: a x  ;b y  ; c z  . Ta có: 12 12 12  4 1
a   b   3 3 3   25 49  b   c   3 48 48   25 49  c   a   3  48 48  4 1 25 49 Do   3;   3 nên: 3 3 48 48
 Nếu a  0,b  4 1 0 thì a
b   3  Vô nghiệm. 3 3
 Nếu a  0,b  4 1 0 thì a
b   3  Vô nghiệm. 3 3 Vậy . a b  0 . T . b c  0; .
a c  0 . Suy ra 2 2 2
a .b .c  0  abc  0 .
Dễ th y nếu một số bằng 0 thì hai số còn l ũ ằng 0  a b c  0.   Suy ra  x y z 19 7 13 ; ;  ; ;   . 12 12 12 
x x y y  2  1 Bài 6. Giải hệ  . 3 2 3
x  2y y  2  x 2 Lời giải
Đ ều kiện x  0, y  0 . B ế của   1 , ta có
x x y y2 3 3
 4  x  4  2xy xy y 3.
Thay 3 vào 2 ợc 3 2 3
4  2xy xy y  2y y  2x 3 2
y xy xy x  2  y
y y x x y y 2
x  2  y . Từ   1 suy ra y y xx x y y 2 2     y 2
x y y x x y
x x x  2x Ta có  2 y y  2  y y       2 x y x
y y x y y x x y x x y do (4). D   x   2 1
1 y   2 x  2y 2
 2x  2y y x y y x y y x y y x x y do (4).
x x y y  2 .
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 40
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE
x x y y  2  x 1
Đẳng thức x y ra  x 1   .  y 1 2 y  1   2 4x  
 2x 1 1 2 3
x y  3y  2   1
Bài 7. x y  2 2 2 2
1  x  2y 2 Lời giải 2 2 Từ     2 2
x y   2 2 2
x y    y   1  0 2 2
 0  x y  1
x 1, y 1. x  0 Nếu 2
x 1 1  0  x  0 ta có y  1  hệ có nghiệm  . y 1 Nếu 2
x 1 1  0  x  0 , nhân 2 vế của   1 với 2 x 1 1 ta có   1  2 x  2 x    2  x  2 3 4 1 1
x y  3y  2
  2x    2 3 4
1 1  x y  3y  2 3 2 2 3
x 1 4 x 1  3  y  3y  2
  x     x      y   y  2 2 2 1 1 . 1 3 2 1 4 .
Với x  0 ; x  1; y  1; ta có 2 x 1 1  0 , 2
x 1  3  0 ,  y   y  2 1 1  0 nên 4 vô nghiệm. Bài 8. [Đánh giá] 3 3 2 2
x y x xy y   1  G ệ  13 3 2 2 4 4
 6x y x y
x y  2xy  2  4 4 Lời giải
Nhận xét: x y  0 không ph i là nghiệm của hệ nên 2 2
x xy y  0
x xy y 2 x y2 1 2 x y2 2 2
(1)  x y   3    3 . 2 2 2 2
x xy y
x xy y 3 3 2 2
x xy y    1 Từ (3) 
x y  3   * . 3 2 L i có 2 2 4 4 2 2
x y x y x y   2 2 6 4
x y   2 xy 4 13 3 Từ (2) và (4) 
x y 2xy   2 xy 5 4 4
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 41
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE
Nếu xy  0 thì từ (5) ta có : 13 x y 3 3 1  2xy   2
xy x y   (mâu thuẫn) 4 4 13 3
xy  0 . Từ (5) ta có: 13    x y  3 13 x y  3
 2xy   2xy
 4xy  x y2  x y2  x y2 4 4 4   
x y   1 3 x y   0   .  4  xy  0 1 1  3 Do x y
  x y  3. Đối chiếu với (*) ta th ẳng thức x y ra  x y
x y  . 3 4 2 x y  3 
VIII. PHƢƠNG TRÌNH VÔ TỈ SỬ DỤNG BĐT BUNHIACOPXKI Bài 1: G 2
x  4  6  x x 10x  27  Lời giải
Đ ề ệ 4  x  6.
 f x VT x 4  6 x Đ  . T g   x 2
VP x 10x  27
f x  x x   x  2 2 10 27 5  2  2  
1 . D "  " x  x  5 .   B.C.S   g x x    x
   x 2 2 2 1 4 1 6 1 1 4
  6 x  2 2   x  4 6  x D "  " x    x  5 . 1 1
 x  4  6 x  2 N ệ ủ ỏ ã  , là "  " trong   1 , 2 ồ ờ x 2
x 10x  27  2  x  5.
Kế ợ ớ ề ệ , ệ x  5.
Nhận x t D ế ậ lớ ế ề ử ụ ẳ ứ ể . N ậ
x x   x  2 2 10 27 5  2  2 ằ
ế ệ ụ ẳ ứ B.C.S ế à    x  4 
6 x  2 ế ổ ở ế . Bài 2: G 2 2 2 x x 1 
x x 1  x x  2   1 Lời giải 2
x x 1 0     Đ ề ệ 1 5 1 5   x   x  . 2
x x 1 0, x   2 2
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 42
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE Á ụ BĐT B.C.S ố 2 2 1; x x 1; 1;
x x 1 ợ 2 2 VT x x  
x x    2 2
  2x x   2 1 1 1 1 1 x x   1   2 x  . Hay 2 2 x x 1 
x x 1  2 x 2 T VT
x x x  
x   x     x  2 2 2 2 2 2 1 1  0 2 2
 x x 1 x x 1  2 x Hay 2
x x  2  2 x 3 Từ   1 ,2,3    D "  " trong 2
x x  2  2 x  2 2 x x 1 x x 1 2,3 ồ ờ x    x 1. 1 1
S ớ ề ệ , ệ x 1.
Nhận x t Để ằ VT A B ế ệ ụ ẳ ứ B.C.S ể ị
lớ . Rồ , ẽ ứ VP lớ ằ ị à . Bài 3. Gi i hệ 4  x 3 4 2  4 1 y  3 2  4  y 3 4 2  4 1 x  3 2 Lời giải 4 4 x y 3 3
Nếu x y thì 4 4 2  4  2  4 1 y  1
x y x  mâu thuẫn. 3 3 2 2
T với x y  ta có x y . 4 4 x 3 x 3 3 Ta có: 2 4  4 1 x  4.  4 1 x  2. x 2. 3 2 3 2 2
Theo b ẳng thức Bunhiacosky, ta có: 4 4 2 2 xx  6  6x 2 4.
 4    4  4 
 4  2x  4 3. 3  3  3  3 3 3
Từ 2;3  2x  4  1 x  2.
x   x  6 2 2 2
 0  x  6  x   6. 2 2
Vậy hệ có hai 4 nghiệm:  ;
x y là:  6; 6; 6; 6; 6; 6; 6; 6. Bài 4: G  2 2  x x  
x x   6 3 2 13 2 2 5 2 4 4
x x x x   1  0 Lời giải
Ý tƣởng: Đánh giá và dùng B.C.S 2 2  1   1  1 Nhận xét 6 3 2 3
x x x x 1  x   x    0      2   2  2 Nên b ã 2 2
 13  2x  2x  5  2x  4x  4  0
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 43
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE 2 2
 2x  2x  5  2x  4x  4  13   1 2 2 Dễ th y 2 2 2 2
a b c d  a c  b d  2 2    1   3  2 Nên 2 2
2x  2x  5  2x  4x  4  2  x        1 x 2 1    2   2     2 2  1   5   2   13     .  2   2  1 x  1 x 4 Vậy (1) x y ra 2    x  . 3 1 5 2 2
Bài 5: G x 1  x  3 
2  x  3  2 x   1  Lời giải
  x   x  
x    x 2 2 1 3 2 3 1   1 B.C.S T
x    x    
x    x 2 2 2 2 1. 1 1. 3 1 1 . 3 1
x   x  
x    x 2 2 1 3 2 3 1 2 x 1 x  3 x  3  0 D "  " x à ỉ    2 1 1
x 1  x  6x  9 x  3 x  3      x  5 3 . 2
x  7x 10  0
x  5 x  2 Từ  
1 ,2,3  ệ x  5. Bài 6: G 4 2 4 4 3
x  6x 8  x  2  4  x  6x 3x x  30   1 h n t D ể ứ 4 2 4
x  6x  8  4  xx  2 
4 xx  2 ú ế ệ ụ ẳ ứ C ợ a b ab  à 4 4
x  2  4  x
A B ụ ẳ 2
ứ B.C.S. C ệ là ệ é ể ụ
ẳ ứ C ể ứ 6x 3x ể ụ ợ ế 3
x   ( ể ứ ớ ụ ằ ố). Cụ ể ế ổ 3
6x 3x  2. 27.x . Lời giải
Đ ề ệ 2  x  4 . Á ụ ẳ ứ C ợ
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 44
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE
4  x x  2 4 2
x  6x 8 
4 xx  2      1 2 2 3 3
6x 3x  2. 27.x  27  x 3 Á ụ ẳ ứ B.C.S ợ B.C.S 4 4
x  2  4  x  1. x  2 1. 4  x   2 2
1 1  x  2  4  x  4 4
x  2  4  x  2 1. x  2 1. 4  x  2  2 2
1 1 x  2  4  x 4 4
x  2  4  x  2 4  2 4
L 2  3  4 4 2 4 4 3
 x  6x 8  x  2  4  x  6x 3x x  30 5 Từ  
1 ,5  Đẳ ứ x  "  " trong 2,3,4 ồ ờ x 
4  x x  2  3  27  xx  3.
x  2 4 x    1 1
Kế ợ ớ ề ệ , ệ ủ là x  3. Bài 7: Gi 2 4 2 4
13 2x x  9 2x x  32 Lời giải
Cách 1: Áp dụng b ẳng thức AM-GM Ta có: 2 2 13 13 8  3x 39x 2 4 2 2 13 2x x
x (8  4x )   26  (1) 2 2 2 4 2 2 3 3 8 13x 39x 2 4 2 2 9 2x x
9x (8  4x )   6  (2) 2 2 2 4 Từ (1) và (2) ta có 2 4 2 4
13 2x x  9 2x x  32 2 2
x  8 4x 2 10 Vậy 2 4 2 4 2
13 2x x  9 2x x  32  
 5x  8  x   2 2 9
 x  8 4x 5
Cách 2: Áp dụng b ẳng thức Bunhiacopxki Ta có   x x x x 2 2 2 4 2 4 32 13 2 9 2  x   x   x 2 2 2 2 . 13 26 13 3 3 6 3 2  x    2 2
. 13 27 26  6 13x  3x  2  x  2 16.5 . 16  5x
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 45
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE
5x 165x 2 2 2 2 16.  32 4
IX. PHƢƠNG TRÌNH VÔ TỈ SỬ DỤNG BĐT COSI Bài 1: Gi 2 4 2 4
13 2x x  9 2x x  32 Lời giải
Cách 1: Áp dụng b ẳng thức AM-GM Ta có: 2 2 13 13 8  3x 39x 2 4 2 2 13 2x x
x (8  4x )   26  (1) 2 2 2 4 2 2 3 3 8 13x 39x 2 4 2 2 9 2x x
9x (8  4x )   6  (2) 2 2 2 4 Từ (1) và (2) ta có 2 4 2 4
13 2x x  9 2x x  32 2 2
x  8 4x 2 10 Vậy 2 4 2 4 2
13 2x x  9 2x x  32  
 5x  8  x   2 2 9
 x  8 4x 5
Cách 2: Áp dụng b ẳng thức Bunhiacopxki Ta có   x x x x 2 2 2 4 2 4 32 13 2 9 2  x   x   x 2 2 2 2 . 13 26 13 3 3 6 3 2  x    2 2
. 13 27 26  6 13x  3x  2  x  2 16.5 . 16  5x
5x 165x 2 2 2 2 16.  32 4 Bài 2. Gi 3 2 4
4x  4x  5x  9  4 16x  8   1 Lời giải  Đ ề 1 u kiện: x  . 2 Ta có : 4 4
4 16x  8  4 2.2.2.2x  
1  2  2  2  2x   1  2x  7 . Đẳ 1
ng thức x y ra  2x 1  2  x  . 2 1
Từ (1)  4x  4x  5x  9  2x  7   x  22x  2 3 2 1  0  x  . 2 a b c Bài 3: Nghiệm củ 1 1 x x   1 có d ng với a, , b c   . K x x 2
2a  3b  4c có kết qu là
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 46
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE A. 25 . B. 7 . C. 10 . D. 20 . Lời giải Chọn A. Đ ề ệ x 1.   1  1 x     1  1 Cauchy   x
x   1. x      T xx  2 1 1 
  x   1  x 2  1 x xx Cauchy   1  1 1 1     1 x x   x x 2 Từ  
1 , 2  D "  " trong 2 x  1 1  x   x 1 5 1 5 2  
x x 1  0  x   x  . 1 2 2   x 1  x
Kế ợ ớ ề ệ , ệ ủ là 1 5 x  . 2 a 1  Vậy b
 1  2a  3b  4c  25 c  5  3 3 2 2
x y  7(x y)xy  8xy 2(x y ) (1) Bài 4.
G ệ  y  2x3 62x (2)  Lời giải 3
Đ ều kiện x  , y  0 2 Từ (1) 2 2 2 2
 (x y)(x y  6xy)  8 xy 2xy(x y ) 2 2 2    T BĐT C 2xy x y (x y) 2 2 0 
2xy(x y )   2 2 2 2 2 2
x y  6xy  4xy  (x y)  2 4xy(x y)  4(x y) xy 2 (x y) 2 2 2 2 
(x y 6xy) 
2xy(x y ) 4(x y) xy 2 2 2 2 2
 (x y)(x y  6xy)  8 xy 2xy(x y )
Đẳng thức x y ra  x y thế vào (2)  1 
 2x 3  x  2x  6  (x 3)  2  0  
 2x 3  x  3 Do x  3 6 1  x    2 2 2 2 1  1 
 2x 3  x    2  0   2
 2x 3  x
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 47
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE
x  3  0  x  3  y  3 3 3 2 2
x y xy 2(x y ) (1)  Bài 5. G ệ  2
4 x x 1  9(y 1) 2x  2 (2) Lời giải
Đ ều kiện: x 1 Từ (2)  y  1 Ta có x y
xy x y 0  xy  ; 0 
2xy x y  2 2 2 2 2 2 2 
x y  2 2 2
x y xy  2 2  xy  2 2
x y    x y 2 2 2
x y xy .
D     x y 2 2
x y xy   xy  2 2 1
2 x y   x y . Ta có 2
2 x 1 2 x 1  x 1  9 x   1 x 1  11   
x    x   x 5 2 1 9 11 x 1   9  x  3 2 3 8
 1x 279x 315x 125  0  1 1 2     1  2 2 1 2x 1 2 y 1 2xy
Bài 6 . G ệ  3 2   1
x  2 y  2 1 2x  1 2y  2  2 Lời giải   Đ ề 1 u kiện , x y  0;   *   .  2 1 1 2 1 1 2 Ta có 2 2 x  , y  suy ra    2  2  2xy 1 4 4 2 2 1 2xy   3 1 2x 1 2 y   M , 1  1 1 2 , a b  0;   thì . a b  1 *  * và ta có   3.  2  2 2 1 a 1 b 1 ab C ứ ( ) : Ta có 2    1 1  4 1 1 2 4 3           0 2 2 2 2 2 2    1 ab 1 a 1 b    1 1 1 1 . 1  ab a b a b 2 2 Theo B.C.S. ta có  2 1 a  2
1 b  1 ab   4  2   2   1 1 1  ab a b 1 1 2
a b2 ab   1 L     0 5 . 2 2 1 a 1 b 1 ab 1 ab 2 1 a  2 1 b   
Từ (4) à (5) ( ) ú , ẳ ứ x à ỉ a b .
Á ụ ( ) ớ a  2 ,
x b  2y ta có :
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 48
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE 1 1 2  
ẳ ứ x à ỉ x y . Thay vào (2) ta có 2 2 1 2x 1 2 y 1 2xy 2 1
 u x  0
x  1 2x
 2 x  2 1 2x  2 1. Đ t  ợc hệ 2
v  1 2x  0  1  2 2 1  1  9  4 2 u          u x x 2u  2v  2 1  2       6 4 36 ho c  suy ra  ho c  2 2
 2u v 1 2   2  4 1   9  4 2 v     y   v y 2    6  4  36
2 2x y   1 1
Bài 7. Gi i hệ  3 8x  3 y  3 3 
2  x y 1 2 x  0 ĐK y   0 x y 4 3 3 x y  x y3      3 x  3 3 y
Ta có thể chứng minh b ẳng thức 3 4
B ẳng thức x y ra  x y 2x y
Áp dụ BĐT ế trái củ ( ) ợc 3 8x  3 3 y  (*) 3 4  2 2 1 1 L i có 2 x
  y  1   0  2xy  2 x y    1 **  2  2 Từ (*) (**) ta có :  3x  3 3 4 8
y   2 x y   1  3 x  3 y  3 3 8
2  x y 1
Suy ra (2) vô nghiệm. Vậy hệ ệm.
 2x  3  y  2x   6 (1)
Bài 8. Gi i hệ  3x  3y 7xyxy 8xy 2 2x  2y  (2)  x  3 Đ ều kiện:  2 y   0 Áp dụ BĐT C ,
x y  7 x yxy  x y3  4x yxy  2 x y3 3 3
.4 x y.xy
 4x y2 xy  4 xy  2 x  2
y  2xy  4 xy.2  2 x  2
y .2xy  8xy 2 2 x  2   y
Đẳng thức x y ra  x y D ừ (2)  x y . Thay vào (1) ta có x
2x  3  x  2x  6  3
 2x  3  x  3 1  
 2  0  x  3 2x  3  x
 2x  3  x  1 1 (Vì x  3 nên  2   2  0 ) 2 2x  3  x 2x  3  x
Tập nghiệm của hệ S    3
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 49
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE
X. PHƢƠNG TRÌNH VÔ TỈ SỬ DỤNG TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ Bài 1.
[Tính đơn điệu của hàm số] 3 3 3 3
2  2  2  2  x
6  6  6  6  x . Đ x  2  Lời giải N ậ xé
Đ f x 
x g x 3 2 ;  6  x
f f f f x  g g g g x . 1 1
Do f  x 
 0; g x 
 0  f x, g x ồng biến trên  2;   . 2 2  x 3 6  x2 3
Với x  2 thì f x  g x  2
f f x  f g x  g g x  2
f f f x  f g g x  g g g x  2
f f f f x  f g g g x  g g g g x  2  VT VP Với 2
  x  2 thì f x  g x  2 lập luậ ta có VT VP .
Nhận th y x  2 là nghiệm củ .
x  2 là nghiệm duy nh t củ . Bài 2: 4 3
x  3  2x 1  4  x Lời giải Đ 1 x  2 P 4 3
x  3  2x 1  4  x  0
Dễ th y khi x VT VT là à ồng biến.
 Pt có nghiệm duy nh t x 1. Bài 3:
5 x  3x 1  4  2x 1 Lời giải
P 5 x  3x 1  4  2x 1  0
(  x 1 là nghiệm ) Bài 4: 5 5
2x 1  5x  2  5x  2  2x 1 Lời giải P 5 5
2x 1  2x 1  5x  2  5x  2 Xét   5
f t t t nhận th y khi t f t   f t  ồng biến.
 2x 1 5x  1 2  x  ( lo i )  vô nghiệm. 3 Bài 5:
2x  2x 1 
x  3  1 x  3 Lời giải Đ ề 1 u kiện: x   . 2 P 2x  
1  2x 1   x  3   1  1 x  3
Hàm số f t   t t ồng biến  2x 1  x  3 1  .......
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 50
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE Bài 6. G 2
x  2x  7  x  3  2 1 8x  1 1 8x Lời giải Đ ề 1 u kiện: x   8
P ới x    x      x2 2 3 3 1 1 8  1 1 8x Hàm số   2
f t t t ồng biến trên kho ng 0;  nên x  3  1 1 8x , gi
ợc x 1; x  3 t / m 3 3 3  3
x y y y x x   1 Bài 7. G ệ  5 5
 x y  2 2  Lời giải   3 3 3 3 1  x
x x y
y y . Hàm số   3 3
f t t t t ồng biến trên nên x y .
Thế x y vào 2 ợc x y  1 . 5 5 3  3
x y y x   1 Bài 8.
G ệ  x  y  2 1 3 2 3   Lời giải
Đ ều kiện: x 1   5 3 5 3 1  x x y y . Hàm số   5 3
f t t t ồng biến trên nên x y .
Thế x y vào 2 ợc x 1  3x  2  3 * . Vế trái của  
* là hàm số ồng biến trên kho ng 1; ệm duy nh t
x  2t / m  y  2 4  4
x y   y xxy  2   1 Bài 9. G ệ  2 2
 x y  2 2 Lời giải
Đ ều kiện: x  0; y  0 . Thế 2 2
2  x y vào   1 ợc 4 4 x
y   y x 2 2
xy x y  3 4 3 4     x x y y Hàm số   3 4
f t t t ồng biến trên nên x y .
Thế x y vào 2 ợc x y  1 (t/m) ho c x y  1( lo i). 3
x x  2 y   1 2 y 1   1 Bài 10.
G ệ  xy   2 2 2 1 1 0   Lời giải
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 51
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE Đ ề 1 u kiện: y   . 2   3
1  x x  2 y   1
2 y 1  2 y 1 . Hàm số   3
f t t t
ồng biến trên 0;   nên x  2 y 1 . Thế x
2 y 1 vào 2 ợc x  1 y  0t / m .  4 4
 x 1  x 1  y  2  y   1
Bài 11: Giải hệ phƣơng trình:  2 x   2x  y  2
1  y  6y 1  0 2 Lời giải
Điều kiện: x  1   1   4 x 14 4 4
 2  x 1  y  2  y Hàm số   4
f t  f  2  t đồng biến t  0 4 4
 x 1  y  x  y 1 và y  0
Thế vào 2  yy   1  6 5 3
y  y  3y  3y  9  0 0
 y  0 hoặc y  1 3
2y  y  2x 1 x  3 1x    1
Bài 12: Giải hệ phƣơng trình:  2
y  2y 1  4  x  4  2 Lời giải Điều kiện: 4   x  4 Đặt 2
1 x  t  1 x  t ; t  0 Khi đó: 3 2x 1 x  2t  2t   3 3 2
1  2y  y  2t  t  y  t  y  1  x  y  1  x;y  0
Thế vào 2 , ta có:
1 x  3  2x  4  x  4   32x  
3   1x 2  x  4   1  0
 x  3....  0  x  3  ... 3 2 3 2
x 3x  2  y 3y (1) Bài 13.
[pp hàm số] Gi i hệ  2 3
x  2  y  8y (2) 
*/ Cách thức mà trong thực tế bản thân đã làm:
 Hãy l a chọn biế ổ ệ về d ng f (x)  f (y) .
 Nhận xét gì về tập giá trị của (x - 1) và của y  3 ?
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 52
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE
 Hàm số ệu trên tậ ợc xét không ? Lời giải 3 2
y  3y  0  x  2 Đ ều kiện : 2
y  8y  0   (*)  y  0 x  2  0  Ta có :
x x y y   x
x    y  3 3 2 3 (1) 3 3 ( 1) 3( 1) 3  3 y 3 (1') 3
Xét hàm số f (t)  t  3t trên tập [1; ) 2
f '(t)  3t  3  0, t
 1  f(t) là hàm số ồng biến trên kho ng (1;) K
f x   f y    x   y   x  2 (1') ( 1) 3 1 3 1
y  3 kết hợp vớ ( ), ợc : 2 2
x  2x 1 y  3 
x  2x  2  y (1')    2 2 3
x  2  y  8y 9  
 (x  2)  y  8y (2') Thế ( ') à ( '), ợc :
9x 18   x  2x  22 2  8 2
x  2x  2 4 3 2
x  4x  8x 17x  6  0 3 2
 (x  3)(x x  5x  2)  0 x  3  0 x  3  
x  3  y 1(Tm)   3 2 2
x x  5x  2  0
x (x 1)  4x  (x  2)  0(VN) x  3
Vậy hệ có nghiệm duy nh t :  y 1   8x 3 3
2x 1  y  4 y  0 (1) Bài 14.
[pp hàm số] Gi i hệ  2 3 2
4x 8x  2y y  2y  3  0 (2) Lời giải 1
Đ ều kiện : x  2   x
  x   y y   x  3 3 3 (1) 4(2 1) 1 2 1 4 4 2 1
 2x 1  4y y (1') 3
Xét hàm số : f (t)  4t t trên tập [0; ) 2
f '(t)  12t 1  0, t
  0  Hàm số f(t) ồng biến trên kho ng (0;) K
f x   2 (1') 2
1  f ( y)  2x 1  y y 1  2x thế à ( ), ợc :
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 53
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE y  2 2 1  4 2 y   3 2
1  2 y y  2 y  3  0  y  0  y  1  4 3 2
y  2y y  2y  0  y(y 1)(y1)(y 2)  0  y  2    y 1 1
Khi y  0  x  (thỏ ã ều kiện) 2 Khi y  1
  x 1 (thỏ ã ều kiện) 5 Khi y  2
  x  (thỏ ã ều kiện) 2
Khi y  1  x  1 (thỏ ã ều kiện)   1   5 
Vậy tập nghiệm của hệ là ( ; x y)  (  1; 1  );(1; 1  ); ;0 ; ; 2        2   2  Bài 15.
[pp hàm số] Gi i hệ 2 2 2 2 3
 x  3y 8  (y x)(y xy x  6) (1) 
(x y 13)( 3y 14  x 1)  5 (2) 
*/ Cách thức mà trong thực tế bản thân đã làm:
 Hãy l a chọn biế ổ ệ về d ng f (x)  f (y) .
 Nhận xét gì về tập giá trị của (x + 1) và của (y - 1) ?
 Hàm số ệu trên tậ ợc xét không ? Lời giải x  1  x 1 0  Đ ều kiện :    14 (*) 3  y 14  0 y   3 3 3
Ta có : (1)   x   1  3 x   1   y   1  3 y   1 (1') 3 2
Xét hàm số f (t)  t  3t f '(t)  3t  3  0, t   R
 Hàm số f(t) ồng biến trên R
K (1')  f (x 1)  f ( y 1)  x 1  y 1  y x  2 thế à ( ), ợc :
(2x 11)( 3x  8  x 1)  5 (3) 5  11
3x  8  x 1   0 (4) x
không là nghiệm của (3) 2x  (Do 11 2 5 8 11 11 
Xét hàm số g(x) 
3x  8  x 1  D  ;  ;     2x  trên 11 3 2   2  3 1 10 g '(x)    2 3x  8 2 x 1 2x  2 11 6x 17 10  8 11 11     x        
2 (3x  8)(x 1)(3 x 1  3x  8) 2x   0, ; ; 2 11  3 2   2    8 11 11 
Hàm số g(x) ồng biến trên ;   và ;    3 2   2 
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 54
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE  8 11 - Khi x  ; 
 : (4)  g(x)  g(3)  x  3  y  5 (thỏ ã ều kiện (*))  3 2  11  -Khi x  ; 
 :(4)  g(x)  g(8)  x  8  y 10 (thỏ ã ều kiện (*))  2 
x  3 x  8 Vậy hệ ệm :  ; 
y  5 y 10  1 3x  4 2
x  3y 1  y   (1)  Bài 16.
[pp hàm số] Gi i hệ y x 1   3
9 y  2  7x  2 y  2  2 y  3 (2)  Lời giải x  1  x 1 0  Đ ều kiện :    2 (*) 9  y  2  0 y   9 1 1 Ta có : 2 (1)  y
 3y  (x 1)   3 x 1 (1') y x 1 1 2
Xét hàm số f (t)  t   3t trên kho ng (0; ) t 1 2t   1 t  2 1
f '(t)  2t   3   0, t  (0;) 2 2 t t
 Hàm số f(t) ồng biến trên (0;) K
f y f x   2 (1') ( ) 1  y
x 1  x 1  y thế à ( ), ợc : 2 3
9 y  2  7 y  2 y  5  2 y  3 2        3 9 y 2 ( y 2) 
7 y  2 y  5  ( y 1)  0     2 2 y  5 y  6
( y 1)( y  5 y  6)    0 2 2 2 2 3 3
9 y  2  ( y  2)
( y 1)  ( y 1) 7 y  2 y  5  ( 7 y  2 y  5) 2
 (y  5y  6).h(x)  0  1 y 1   Vì h(x)      0 với 2 2 2 2 3 3
 9y  2  (y  2) (y 1)  (y 1) 7y  2y  5  ( 7 y  2y  5)   2 y  2 y   nên 2
y  5y  6  0   9 y  3
-Khi y  2  x  3 (thỏ ã ều kiện (*))
-Khi y  3  x  8 (thỏ ã ều kiện (*)) x  3 x  8
Vậy nghiệm của hệ là  ;  y  2 y  3 Bài 17.
[pp hàm số] Gi i hệ
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 55
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE 2 5
 16.4x y    2
5 16x y  2 2 2 2 yx 2 .7 (1)  3
x 17x 10y 17  2 
 2x 4 4y 11 (2) Lời giải Đ 2
t t x  2 y ( ) ng 2t 2 5  4 5  4 t tt  2 5 16.4 5 16 .7 t       (3) 2t 2 7 7 t x x    
Xét hàm số f x 1 4  5.   
   f (x) là hàm số nghịch biến trên R  7   7  2
P ( ) ng f (t  2)  f (2t)  t  2  2t t  2  x  2 y  2 K ( ) ng 3 2 x x x    2 x   2 5 17 7 2 4 2x  7
 x  3  x  2  x     2 x   2 x    2 x   2 2 2 2 2 7 2 7 2 7  2x  7 3 2
Xét hàm số f (t)  t t t trên kho ng 0;   2
f '(t)  3t  2t 1  0, t
  0  f(t) là hàm số ồng biến trên kho ng 0; P ng x 1
f x    f  2 2 2x  7  2
x  2  2x  7  x3  1    7 
Suy ra : Hệ p nghiệm (x;y) là: 1; , 3;     .  2   2  Bài 18.
[pp hàm số] Gi i hệ 2 2 2
4 1 2x y 1 3x  2 1 2x y  1 x  3 2 4 2 3 2
2x y x x x  2x y 4y 1  Lời giải Đ ều kiện : 1   x 1 Ta th y ( ; x ) y  (0; )
a , a R là nghiệm của hệ ã . Khi x  0 , ta có : 1 1 1 3 2 4 2 3 2 2 2x y x
x x  2x y 4y  1  2y  2y 4y  1   1 (*) 2 x x x Xét hàm số : 2
f (t)  t t t  1 2 t 2
f '(t)  1  t  1   0, t
 .  Hàm số f(t) ồng biến 2 t  1   D  f y 1 1 (*) 2  f  2y   
thế à ò l i của hệ ta có :  x x 2
4 1  x 1  3x  2 1  x  1  x
a  1 x  0 Đ t  ta có : 2 2
3x x 1  2(x  1) 1  2a b 1
b  1 x  0 P ở thành :
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 56
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE 2a b 2 2
2a b ab  4a  2b  0  2a ba b  2  0  a b  2 3 5
Với 2a b , ta có : 2 1  x  1  x x    y   5 6
Với a b  2 , ta có : 1  x  1  x  2  x  0 (lo i)  3 5  
Vậy nghiệm của hệ là (x; y)    ; ; 
 0;a | aR   5 6    4 4
x  3  x  2  y  5  y (1) Bài 19.
[pp hàm số] Gi i hệ  2 2
x  2x(y  2)  y 8y  4  0 (2) Lời giải
Đ ều kiện : x  2 4 4 Ta có : (1)  (x  2)  5  x  2  y  5  y (1') Xét hàm số 4
f (t)  t t  5 trên 0; 3 2t f '(t) 1  0, t   0
 Hàm số f(t) ồng biến trên (0;) 4 t  5
K f  4 x  2 4 4
f (y)  x  2  y x y  2 thế à ( ), ợc :  y
4 y   y y2 0 4  y 7 4
y  2 y y  4  0   7 4
y  2y y  4  0 (3)
Với y  0  x  2 (thỏ ã ều kiện) 7 4
Gi i (3): Xét hàm số g ( y)  y  2 y y  4 trên 0; 6 3
g '( y)  7 y  8 y 1  0, y   0
 Hàm số g(y) ồng biến trên (0;)
L i có : (3)  g( y)  g(1)  y  1  x  3 (thỏ ã ều kiện) x  2 x  3
Vậy nghiệm của hệ là  ;  y  0 y 1 Bài 20.
[pp hàm số] Gi i hệ
20 6 x 17 5 y 3x 6 x 3y 5 y  0 (1)  2
2 2x y  5  3 3x  2y 11  x  6x 13 (2)  Lời giải x  6 y 5 Đ ều kiện :  (*)
2x y  5  0  3
 x  2y 11 0
(1)  20  3x 6  x  17  3y 5  y
 36  x  2 6  x  35 y  2 5 y 3
Xét hàm số f t   3t  2 t trên tập 0;
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 57
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE f t  3t 2 '  3 t   0, t
  0  Hàm số f(t) ồng biến trên 0; 2 t
K (3)  f 6  x  f 5  y  6  x  5  y y x 1 thế à ( ), ợc : 4 2
2 3x  4  3 5x  9  x  6x 13 (Đ ều kiện : x   ) 3
 2 3x  4 x  2  3 5x  9 x  3 2  x x 2
xx   1 3
xx   1 2    x x
3x  4   x  2
5x  9   x  3  
xx   2 3 1        x   x  
x    x    1 0 3 4 2 5 9 3  x  1  2 3   (vì 
11 với mọi x thuộ TXĐ) x  0
3x  4   x  2
5x  9   x  3
Với x  0  y  1  (thỏa mãn hệ ) Với x  1
  y  2 (thỏa mãn hệ )
Vậy nghiệm của hệ là  ; x y   0; 1; 1  ; 2   2
x x 1  3y (1) Bài 21.
[pp hàm số] Gi i hệ  2
y y 1  3x (2)  Lời giải
Trừ theo vế ( ) ( ), ợc :  2    2    y x 2 x 2 1 1  3  3   1  3   1  3y x x y y x x y y (3) Xét hàm số 2 ( )   1  3t f t t t trên R t f '(t)  1
 3t ln3  0, t
  R  Hàm số f(t) ồng biến trên R. 2 t 1
K (3)  f (x)  f ( y)  x y thế à ( ), ợc : 2 x x x x      2 1 3 1 3
x 1  x (4) Xét hàm số x g x   2 ( ) 3
x 1  x trên R   '( )  3x g x  1 2
x 1  xln3   0 , do 2
x 1  x  0 và 2 x 1  1 2  x 1 
 Hàm số g(x) ồng biến trên R.
K (4)  g(x)  g(0)  x  0  y  0 x  0 Vậy hệ ệm duy nh t :  y  0 Bài 22: Gi 2
3x  2  6  x  3x 12  0. Lời giải
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 58
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE Đ ề 2 u kiện:  x  6 3 2 
Xét hàm số f x 2
 3x  2  6  x  3x 12 với x ;6   3  3 2  2  ' f x    6x  0, x   ;6   . 2 3x  2 2 6  x  3   2 
Suy ra hàm số f x 2
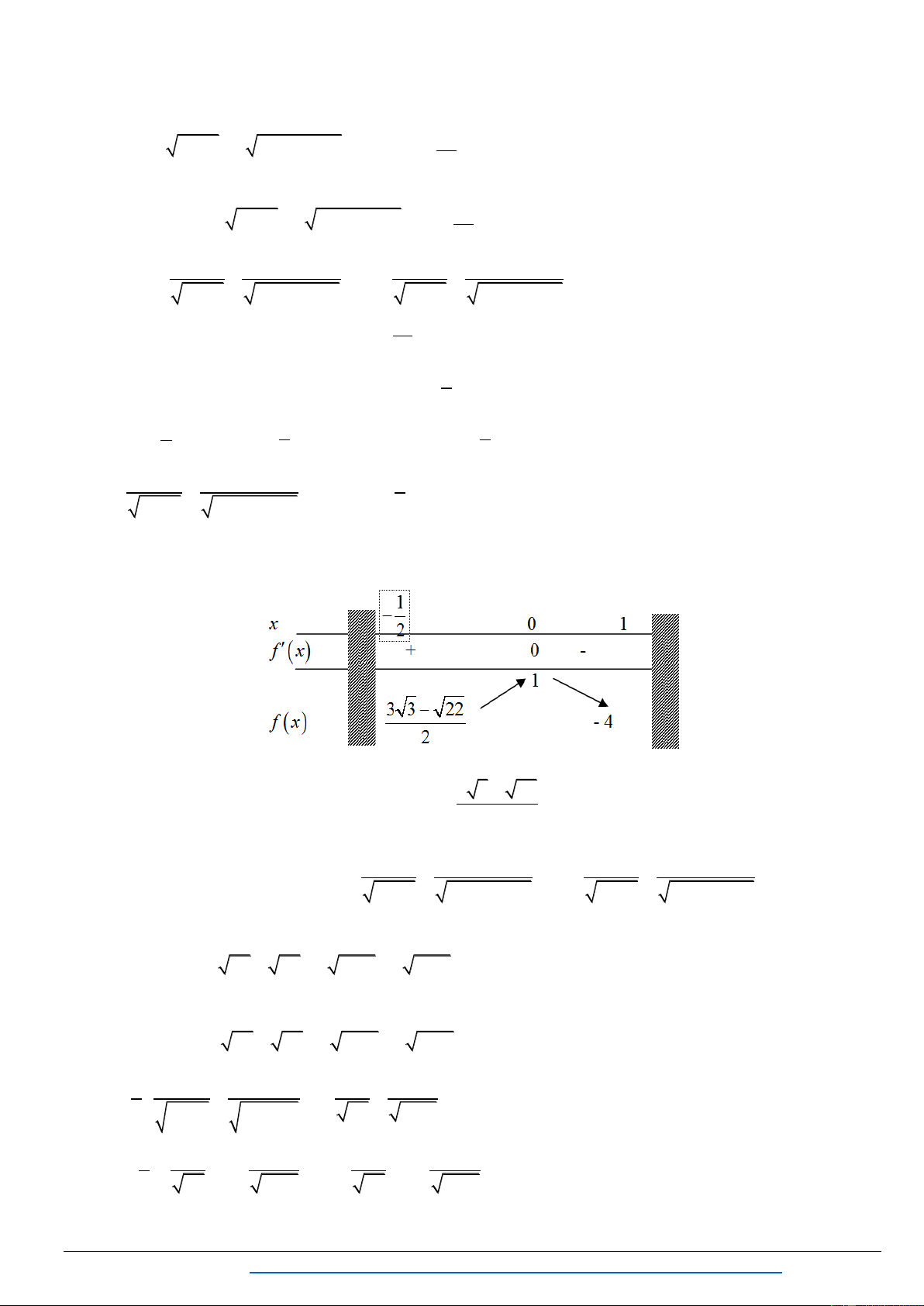
 3x  2  6  x  3x 12 ồng biến trên kho ng ; 6    3  Ta có: f   2
2  3.2  2  6  2  3.2 12  2  2 12 12  0  x  2 là nghiệm duy nh t củ
Từ cách gi i trên, ta nhận th trình có một nghiệm bằng 2 nên có thể ù í ể ề cách gi i sau.
 3x2 6x 3x2 6xCách khác: 2
3x  2  6  x  3x 12  0   3 2 x  4  0
3x  2  6  x 4 x  2     4
3 x  2 x  2  0   x  2  3 
x 2  0  x  2 
3x  2  6  x
 3x  2  6  xBài 23: . Gi 2
x  4  x  4  2 x 16 10  0. Lời giải
Đ ều kiện: x  4
Xét hàm số f x 2
x  4  x  4  2 x 16 10 với x  4   1 1 2x f x     0, x   4 2 2 x  4 2 x  4 x 16
Suy ra: f x 2
x  4  x  4  2 x 16 10 ồng biến trên 4; f   2
5  5  4  5  4  2 5 16 10  3 1 2.3 10  0
x  5 là nghiệm duy nh t củ Bài 24: . Gi 3 3
3  x  4  x  3  x  1 3  x .   * Lời giải Xét f t  3
t t 1 với t t  R. 1 Có f (  t) 1
0 t 1  f t ồng biến trên hai kho ng (;1) và (1; ) . 2 3 3 (t 1)
Ta có *  f  – x  f ( 3  x .
) Luôn có 3 x 0 1 x  3 nên:
- Nếu 3 – x   x  4 a mà f t  ồng biến trên (1;  ) thì: x 3 3   x 0 
(1)  3  x  3  x  
 x 1  x 1 (thỏa mãn a). 2
x  7x  6  0  x 16 - Nếu 3 x 1 3
 4  x0  4  x 0 . VT   *  1   VT   *  0 (vô lí).
Vậy x 1 là nghiệm củ . Bài 25: Gi 2
9x  28x  21  x 1 *
Ý tưởng: Ta xây d ng hàm 2
f (t)  mt nt Để ý rằng h ng tử x 1 ở vế ph i có bậc th p nh
ứng với nt trong f t, n 1 . Ta nhìn nhận 2 9x ới 2 khía c nh 2 2
9x  9.x thì m  9 nhìn nhận 2 2
9x  (3x) thì m 1 . N ậy m=9 ho c m=1.
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 59
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE Nếu m  9 2
f (t)  9t t . Cầ * về d ng: 2
9(x u)  x u  9(x 1)  x 1 2 2  9x  ( x 1
 8u 8)  u u  9  x 1  10  1
 8u u  2  8 u  
Đồng nh t hệ số ợc:    9  lo i 2 u   u  9  21 u  {4; 3  } Nếu m 1 2
f (t)  t t Cầ * về d ng 2
(3x u)  3x u  (x 1)  x 1 2 2  9x  ( x 6
u  2) u u 1 x 1 .  6  u  2  2  8
Đồng nh t hệ số ợc   u  5 2 u   u 1  21
Đế lẽ Bài ã ợc gi i quyế , ậ
“ ” ò ở í ớc: * 2
 9x  30x  25  3x  5  x 1 x 1
f (3x 5)  f ( x 1) ** với 2
f (t)  t t 1 1 Lƣu ý rằng 2
f (t)  t t
chỉ ồng biến trên ( ; ) và nghịch biến trên ( ;   ) , a 2 2 1 x 1  0   2 N ậ 1 3
y ta chỉ có f (3x  5)  f ( x 1)  3x  5 
x 1 khi 3x  5    x  2 2 3 Còn 1  x
thì sao? L ể ý rằng hàm số bậ ũ ủ , là 2 2 ( t
 )  t . Ở trên , d a vào 2
hệ số bậc cao nh t là 9 , ta chỉ mới xét
t  3x u nên bây giờ ta sẽ xét t=u-3x Cầ * về d ng 2 (u  3 ) x
u 3x x 1 x 1  6  u  4  2  8 2 2  9x  ( x 6
u  4)  u u 1 x 1 . Đồng nh t hệ số   u  4 2 u   u 1  21 3 1
Kiểm tra l i: Có x
 4  3x   ọn u  4 2 2
Đế Bài mới th c s ợc gi i quyết. Lời giải Đ ều kiện: x 1 3 1 Nếu x   3x  5   2 2 Ta có * 2
 (3x 5)  3x 5  x 1 x 1
f (3x 5)  f ( x 1) với 2
f (t)  t t  1 3x  5 
x 1 ((do f t  ồng biến trên ( ; ) ) 2  5 x  3  x  5  0  3    
x  2 (thỏ ĐKXĐ) 2
(3x  5)  x 1 13 x{2; }  9 3 1 Nếu 1  x
 4  3x   ** 2 2 * 2  (4 3 ) x
 4 3x x 1 x 1
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 60
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE f (4 3 )
x f ( x 1) với 2
f (t)  t t  1 4  3x
x 1 ( do f t  ồng biến trên ( ; ) và ** ) 2  4   x 4  3x  0    3    2
(4  3x)  x 1 25  13 x{ }  18 v 25  13 Vậy  
* có tập nghiệm S  {2; } 18
Lƣu ý: T ũ ể gi i Bài trên bằ t x 1  3y 5 ể ề hệ ối xứng lo i 2. 2 x  2x  8 Bài 26: Gi  x 1 x  2  2 2    x  2x . 3
Lần 3 – THPT Phú Riềng 2016 Lời giải ĐK x  2    
x   x  
x  x   x 2 2 4 1 2  Pt    x  4 x 1 2 x  2x  3 x  2  2   1 2  
 x  2x  3 x  2  2
(1)   x   x     x   2 4 2 2
1 x  2x   3    
x     x  2    (2) 
 x       x  2 2 2 2 2 1 2 1  2   
Xét pt  t   2
2 t  2 có pt f t 2 '
 3t  4t  2  0 t   Vậ f( ) ồng biến trên x 1 
D ( )  f x    f x   3 13 2 1 
x  2  x 1    x  2
x  3x 1  0 2 3  13
Vậy pt có nghiệm: x = 2, x  2
Bài 27: Tổng các nghiệm củ 3 2 3 2
x  4x  5x  6  7x  9x  4 là: A. 4 . B. 2 . C. 3 . D. 4  . Lời giải Đáp án: A 3 2
x  4x 5x  6  y Đ 3 t 3 2
y  7x  9x  4 , ta có hệ : 3 
y y  x   1   x   1 2 3
7x  9x  4  y
Xét hàm số : f t  3
t t f t 2
 3t 1 là à ệ .
Từ f y  f   x   
1   y x 1  x  5 D   x   3 2
1  7x  9x  4 3 2
x  4x  6x  5  0  1   5 x   2
Vậy tổng các nghiệm củ là : 4 a b c
Bài 28: Nghiệm nhỏ nh t củ 3 3
6x  5  x  5x  5 có d ng
với a,b   . K 2
a b c là:
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 61
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE A. 5 . B. 20 . C. 21 . D. 23. Lời giải Đáp án: C Ta có 3 3 3 3
6x  5  x  5x  5  6x  5  6x  5  x x (*) Xét hàm số   3
f t t t trên
. Ta có f t  2
 3t 1  0, t   . Suy ra   3
f t t t ồng biến trên .
Từ *  f  3 6x  5  f x 3
 6x  5  x 3
x  6x  5  0  x   2
1 x x  5  0 x  1    1 21 x   2 1 21 Vậ ệm là x  1  ; x  . 2 a 1   D ệ 1 21 m nhỏ nh t x   b   1
  a b c  21  2 c  21 
Nhận xét: Có thể gi i Bài à ớng sau: 3 3 3 3
6x  5  x  5x  5 
6x  5 1  x  5x  4 6 x   1   x   1  2 x x  4 3 6x  52 3  6x  5 1 x  1    6 2 
x x  4  3 6x 52 3  6x  5 1 
V ề t ra là gi ò l i sẽ r t phức t p.
Vì vậy ta sẽ ù í ệu của hàm số
Bài 29: Tổng các củ 3 2 3
x  3x  2x 1  2x 1 là: A. 3 . B. 3  . C. 5 . D. 23. Lời giải Đáp án: B Cách 1: Ta có 3 2 3
x  3x  2x 1  2x 1 3  x
x   x 3 ( 1) ( 1) (2 1)  2x 1 Xét hàm   3
f x t t trên . f  x 2
 3t 1  0  f t ồng biến trên
Ta có: f x   3
1  f ( 2x 1) 3
x 1  2x 1  3 2
x  3x x  0  x 2
x  3x   1  0
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 62
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE  x  0     3 5 x   2   3  5 x   2  
Vậy tổng các nghiệm củ là 3 5 3 5 0    3 2 2 Cách 2: 3 2
x 3x  2x y
Đ t 3 2x 1  y 1. Ta có hệ sau:  3 2
y 3y  3y  2x
L y 2 pt trừ cho nhau ta có: 3 3 2 2
x y  3(x y )  4(x y)  0 2 2
 (x y)(x xy y  3x  3y  4)  0  y 3 3  2
 (x y) (x   )  (y 1 2 ) 1  0    2 2 4   x y
Vậy : 3 2x 1  x 1 3 2
x  3x x  0 2
x(x  3x 1)  0  x  0   3  5  x   2   3  5 x   2   Vậy tập nghiệm củ là 3 5 3 5 S  {0; ; }. 2 2 Bài 30: Gi i b 3
8x  2x   x  2 x 1  có tập ngiệm S   ;
a b . K a b là: 7   7 7   7 7   17 7   17 A. . B. . C. . D. . 8 8 8 8 Lời giải Đáp án: D Đ ề ệ x  1  .    x3 2
 2x  x   1 1 x 1    x3 2
 2x  x   1
x 1  x 1
  x  x   x  3 3 2 2 1  x 1
f 2x  f x 1   1 ớ à là   3
f t t t . Xé à ố   3
f t t t trên . f t  2
 3t 1  0, t
   f t ồ ế 2
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 63
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE Từ  
1 ,2  f 2x  f x 1  2x x 1 hay x 1  2x x 1  0 2x  0     2 2x  0 x 1  4x 1 17  1
  x  0  0  x  8 1 17  1   x  . 8      Vậ ậ ệ ủ là 1 17 7 17 S   1  ;
  a b  . 8   8 a a Bài 31: Gi i b 3
8x  2x   x  2 x 1  có tập ngiệm S  ;c   tối gi n b  với b
a, ,bc  . K abc là: A. 10 . B. 9 . C. 8 . D. 11. Lời giải Đáp án: A 1 Đ ề ệ x  . 2 K ,  
1   x  2  x  6 2x 1 3  4 2
Vớ 2x 1  3  0  x  5  2 : l ú . Vớ x  5:
Xé à ố f x   x  2  x 6 2x 13 l ụ 5; .      f x 1 1     x    x 2 x 6 ' 2 1 3   0; x   5
 2 x  2 2 x  6  2x 1
f x l ồ ế 5; à f 7  4 .
D 2  f x  f 7  x  7 .  
Kế ợ ớ ề , ậ ệ là 1 S  ;7   . 2  a 1  Vậy b
  2  a b c  10 c  7 
Bài tập luyện tập 1) 3 3 x  6  x  6
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 64
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE 2) 2
 5x  3x 1  8x 16x 24 3 3
3) 2x 1  5x  2  5x  2  2x   1 4) 3 2 5 2 3 2 5
x 1  2x  2  x  2  x  3 1 1 5) x  2x   x  x x 6) 3 4x  x  x   1 2x  1  0 3 x  2x  3  y  1. 3y 1
7)  2x3 3y2 2  3 3
 y 2y 3x 2 x  8 2 x
8)  54x  3y1 3 
 x  x  2  x  4  y 1  y 3  y 5 9)  2 2
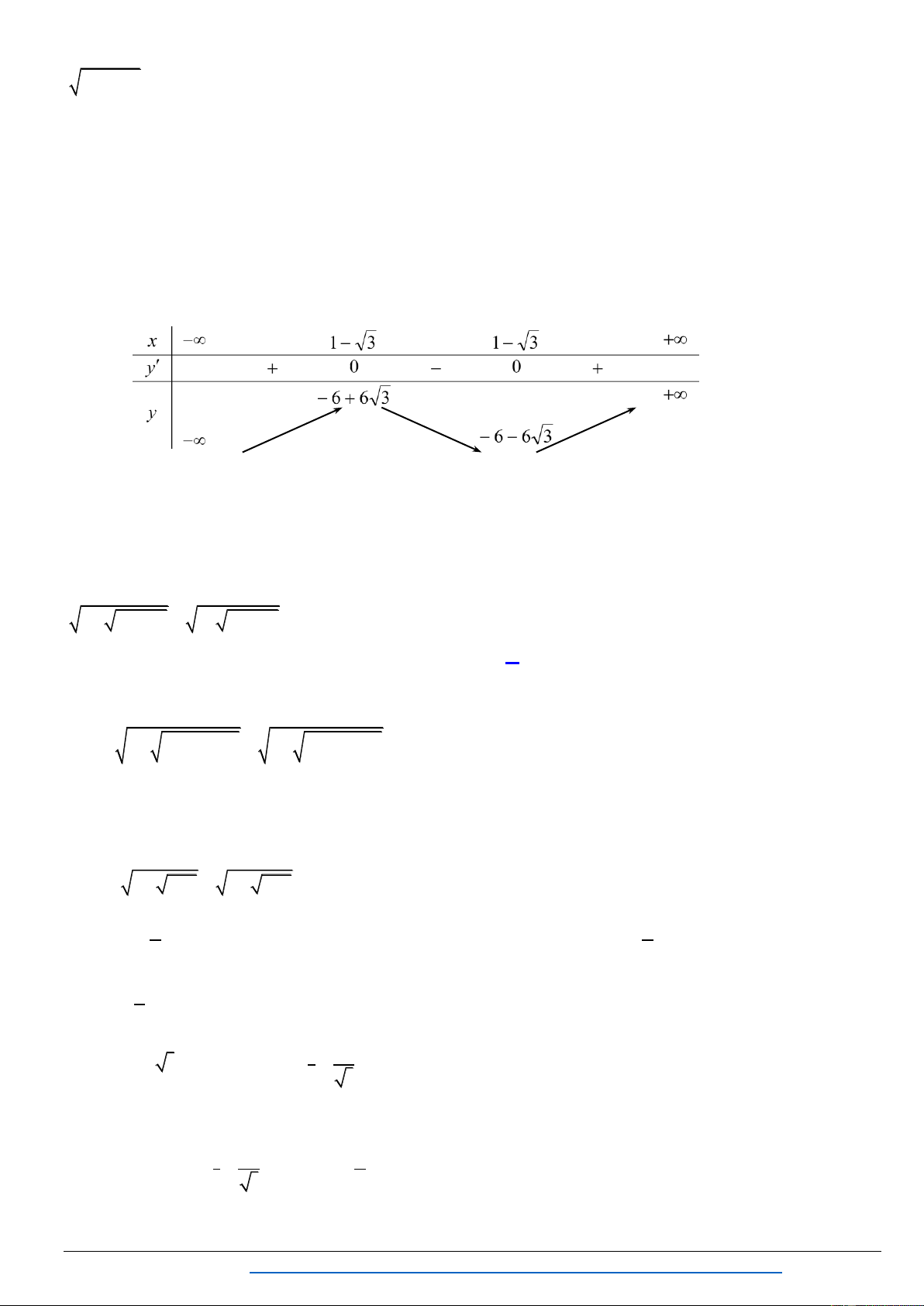
x  y  x  y  44 3 3
x 12y  x  2  8y 8y  10)  2 3  x 8y  2y  5x  3 2 3 2 x 3x 2  y 3y 11)  2 3  x  2  y  8y 
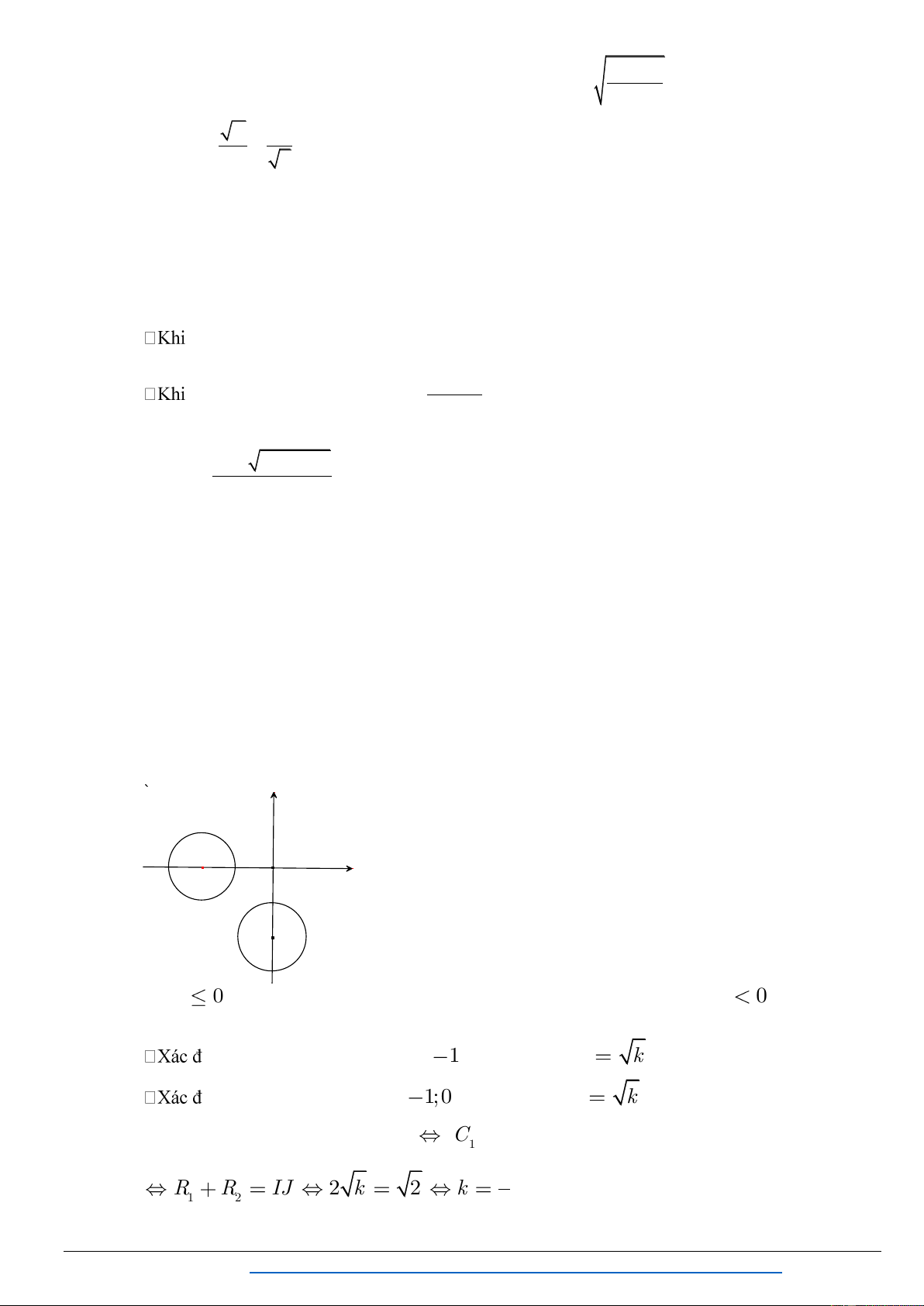
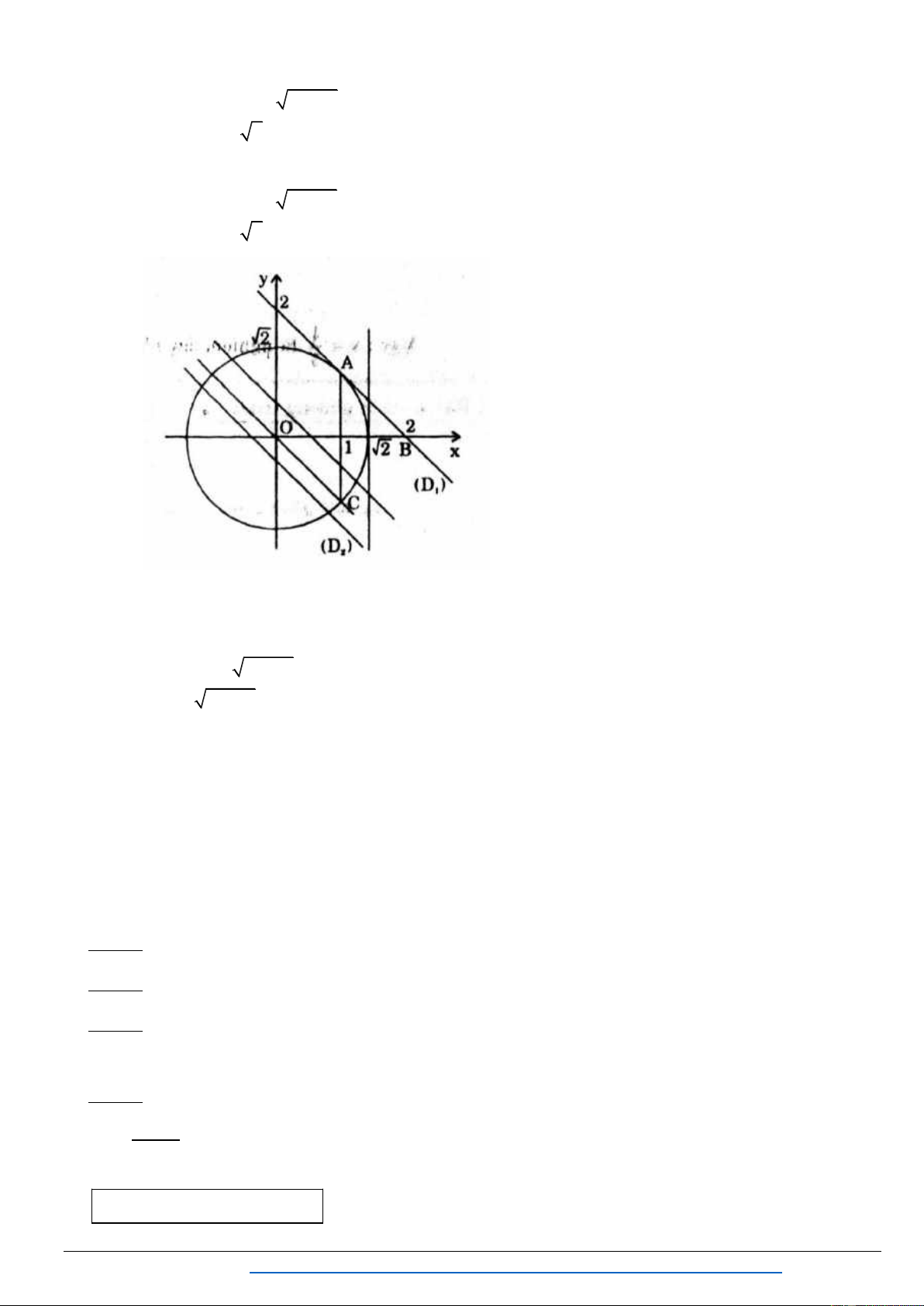
XI. PHƯƠNG TRÌNH VÔ TỈ SỬ DỤNG SỰ TƯƠNG GIAO CỦA ĐƯỜNG TRÒN ĐƯỜNG THẲNG
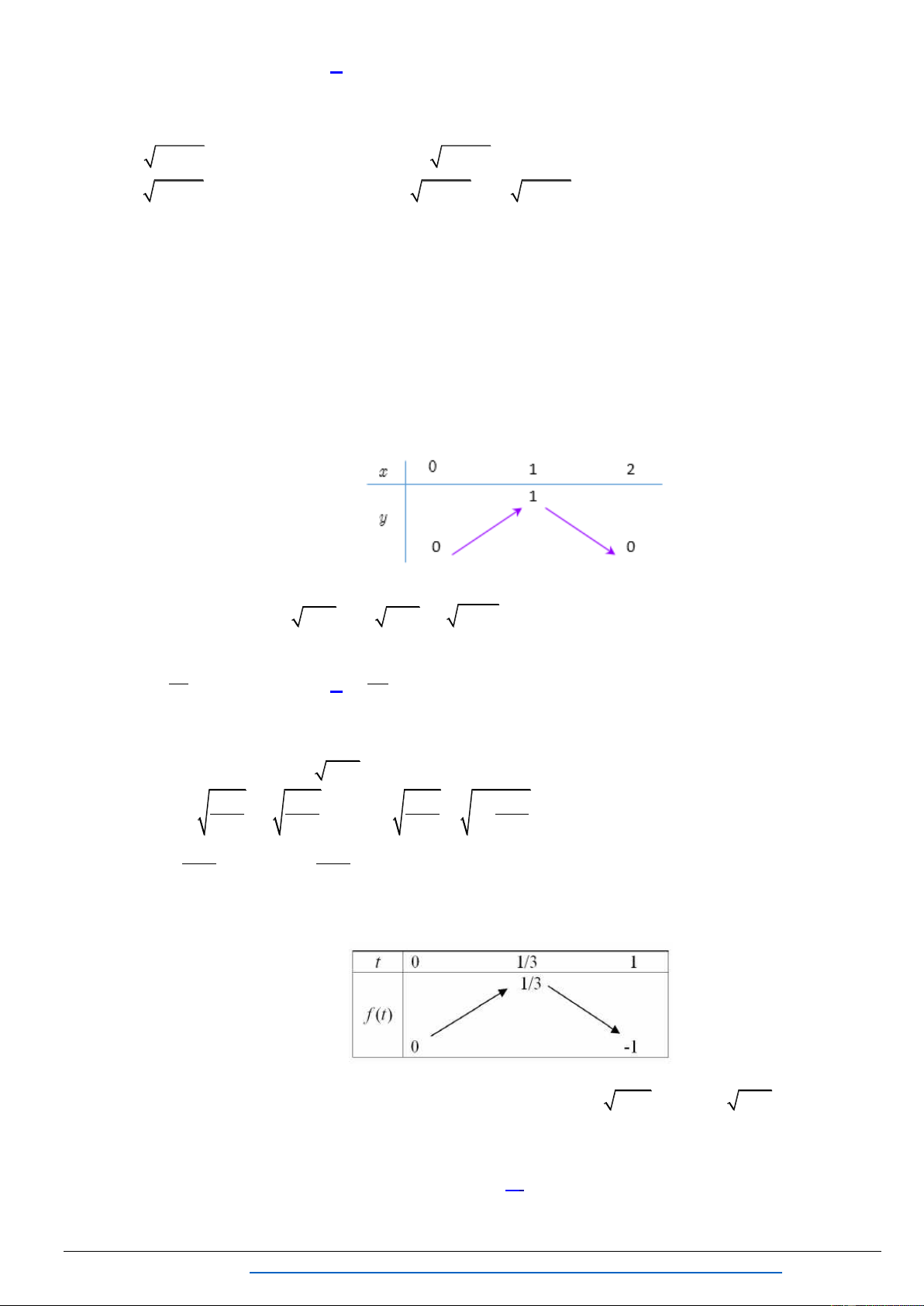
Bài 1. Tìm điều kiện của số thực a để phƣơng trình sau có hai nghiệm phân biệt: 2
x x a  2x . (2.4) Lời gi i Điều kiện: 2
x x  0  0  x  1. Đặt 2 y x x  0.
Phƣơng trình (2.4) trở thành:
2x y a (1)
2x y a  2   1  1 2 2 2
x y x  0   x   y  (2)     2   4 y  0  y  0 (3) 
Trong m t phẳng tọ ộ, ( ) là ờng thẳng  : 2x y a ,   ( ) à ( ) là ử ờ 1 1 ng tròn có tâm I ;0 , 
 bán kính R  , thuộc phần y  0.  2  2
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 65
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE
Số nghiệm củ ( .4) í là ố ểm củ ờng thẳng  và nử ờng tròn  I, R . Do
ể ( .4) ệm phân biệ ờng thẳng  cắt nử ờng tròn I, R . K      ad I ,  1 1 1 1 2   
a  2a   0 2  5  2   5 2   4  2  a  . 2 a  2   a  2 a  2 2  5
Vậ ( .4) ệm phân biệt khi 2  a  . 2
Bài 2: Gi i và biện luận theo m m x m x  11   1 . Nếu m  0 ệm.
Nếu m  0 ệm duy nh t x  0 . Nếu m  0 . u
  mx  0 Đ t  .
v m x  0 2 2 u   v  2m  K   1  u   v m 2 . u,v  0 
Nghiêm của hệ 2 í là ểm củ ờng thẳng d u v m với cung AB củ ờng tròn C 2 2
u v  2m . D 2 có nghiệm
OH d(O,(D))  R ) Với R  2m là bán kính củ ờng tròn C ) 2m m m    2m m   2m . 2 2 2 2
 2m m  4m  2  m  4.
Lú u  m u2 2  2m. 2 2 2 2
 2u  2mu m  2m  0  2u  2mu m  2m  0 . 2
m  4m mu  . 1,2 2
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 66
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE 2 2  m 4m m    2
x u m     m . 1,2 1,2  2    2
m 4m m Vậy x   . 1,2 2 Nếu m  0  
1 có nghiệm duy nh t x  0 . 2
m 4m m
Nếu 2  m  4   1 có nghiệm x   . 1,2 2 m  4 Nếu    1 vô nghiệm. 0  m  2
Bài 3: Gi i và biện luận theo a b
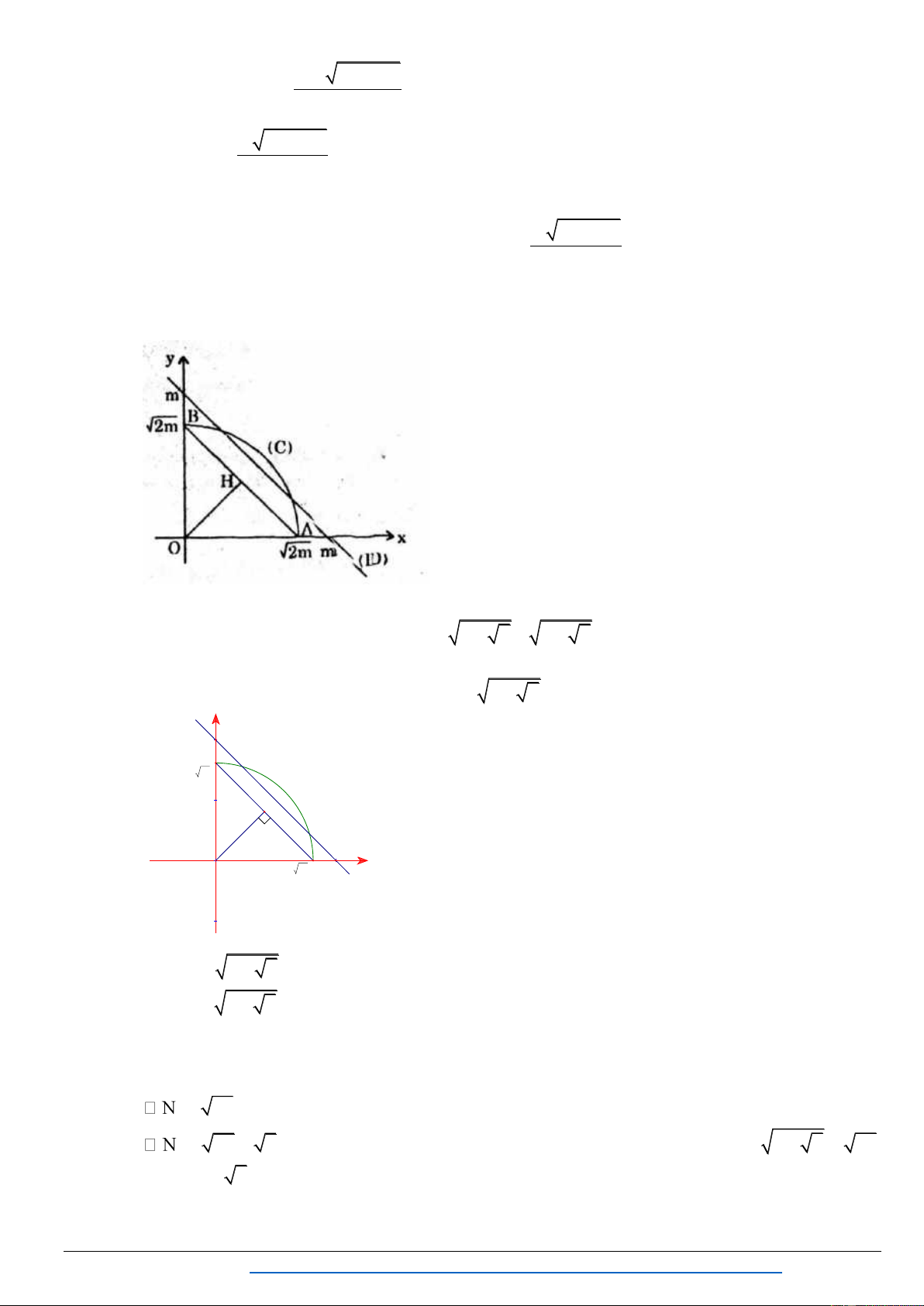
a x a x  2   1 . Lời giải
Ta chỉ xét a  0 (vì nếu a  0 thì biểu thức a x ) y 2 B 2a H x 2a A 2 Ou   v  2 u   a x  Đ t  PT   2 2 1  u
  v  2a 2 .
v a xu,v  0 
Từ ểm M u;v thỏa mãn 2  M u;v thuộc phầ ờng tròn C 2 2
: u v  2a chứa trong tam giác OAB . D
ếu 2a  2  a  2 : B   1 vô nghiệm.
ếu 2a  2  0  a  1: B  
1 có nghiệm thỏa mãn 0  u a x  2a
 0  a x  2a 2
 0  x a .
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 67
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE ếu 2  2a  2
1 a  2: B   1 có nghiệm thỏa mãn
0  u a x u1  .
u u a x  2a  2
(với u ;u u u
là các nghiệm củ u    u2 2 2
 2a . (Đã ử v )). 1 2  1 2
Gi u    u2 2 2  2a  
u  1 a 1 0  a
x u  1 a  1
a x a  2 a 1 Có 1  vì vậy 1   
u 1 a 1                2 u 1 a 1 a x 2au 1 a 1 a x 2a  2 2
a x a  2 a 1    a   2 4 1  x a .
a  2 a 1  a x  2a Vậy a  0  : B   1 vô nghiệm. a  2 0  a 1: B   1 có nghiệm 2 0  x a 1 a  2: B  
1 có nghiệm a   2 4 1  x a
 x y a Bài 4: Cho hệ 
 1 với a là tham số
x y xy a
)X ịnh a ể hệ có nghiệm.
b)Gi i và biện luận theo a . Lời giải u   v a  u   v au
  x,u  0 2    Đ 2a a t  ệ 2 2 2 2  u
  v uv a u   v  C 2 .
y y,v  0  3   u, v  0  u  ,v  0 
u v2  2 2 u v  2 a   2 2 u v  (vì uv   ). 2 2 y a B a ( ≥0) H Δ x O A a
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 68
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE a  0  2 2a a Vì vậy hệ   1 có nghiệm   (với R
là bán kính củ ờng tròn OH d
O,  R 3  R a 2 2 2      R 2 2 2
R a  2R
2a a  3a  22a a C  )   2 2      a  0 a  0 a  0 a  0 a  0      a 0
2  a  3a  4  2a  a  0    .      1 a 4 a 1  1   a  4 b) Theo kết qu câu (a) u   0 x  0
a  0 : Hệ 2 có nghiệm duy nh t    . v   0 y  0  1 a  4 2a a
: Ta có u  a u 2 2 2  (Đã ử v ). 3 2 2 2
 6u  6au  3a  2a  3a 2 2
 3u  3au a a  0 2
3a  12a  3au  và v
a u u . 1,2 6 1,2 1,2 2,1 x  0
Vậy khi a  0 hệ   1 có nghiệm duy nh t  .  y  0 2 x u  1,2
Khi 1 a  4 hệ   1 có hai nghiệm  . 2  y u  2,1 a  4 Khi  hệ   1 vô nghiệm. 0  a  1 x    y  2 2 1  k   1 Bài 5:
X ịnh k ể hệ ệm duy nh t y   x  2 2 1  k 2 Lời giải y -1 O J x -1 I Vớik
0 : Dễ th y rằng hệ ã ệm, vì vậy ta chỉ xé ờng hợp k 0 Xét trong m t phẳng tọ ộ Oxy . ịnh hình tròng C tâm I 0; 1 có bán kính R k 1 1 ịnh hình tròn C tâm J 1;0 có bán kính R k 2 2 D ệ ã ệm duy nh t C và C tiếp xúc ngoài với nhau 1 2 1 R R IJ 2 k 2 k 1 2 2
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 69
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE
XII. PHƢƠNG TRÌNH VÔ TỈ SỬ DỤNG PHƢƠNG PHÁP LƢỢNG GIÁC HÓA Bài 1.
[Lƣợng giác hóa] G 3 x  3x x  2 Lời giải
Đ ều kiện x  2  Nếu x  2 ta có 3
x x x x  2 3
x  4  x x  2 . S ệ . Nếu 2   x  2
Đ t x  2cos 0      . K 3
8cos   6 cos  2 cos  2   2cos3  2 cos 2   cos3  cos 2  k 4    5   k   k 4     7 4 4 4 4
Do 0     nên   0;   ; 
x  0; x  2cos ; x  2 cos 5 7 5 7
Bài 2: Định m ể b ệm 2 2
cos x  2  cos x  cos .
x 2  cos x m . Lời giải: 2    Đ u 2 cos x t  . K
v  cos x 2 2 u   v  2 u
  v uv m   
u v2  2 2 u v  2 2 (1)  u   v  2  u   v   m .  2  1   u  2 1   u  2  2 2 u   v  2  2 2 u   v  2 2  (u v)  2   u   v   m 2
 (u v)  2(u v)  2(m 1)  0 . 2  1   u  2 1   u  2 
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 70
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE 2 2  u
  v  2(C)   u   v  1
  2m  3 D1 1   u  2    2 2 u
  v  2(C)
uv 1 2m3D2 1   u  2 
Rõ ràng  D2 không cắt cung ABC . D   1 có nghiệm   1 D cắt cung ABC .  0  1
  2m  3  2 .
 1 2m  3  3 .  1   m  3.
XI. PHƯƠNG TRÌNH VÔ TỈ CÓ THAM SỐ 1. Phƣơng pháp chung
a. Bài toán 1. T ể f  ; x m  0 ệ D
 B ớ . Độ lậ ( ) ỏ ế ố x à ề f x  Am .
 B ớ . Lậ ế ủ à ố f x trên D.
 B ớ . D à ế x ị ị ủ ố ể ờ ẳ y Am ằ
ắ ồ ị à ố y f x .
 B ớ 4. Kế l ậ ị ầ ủ ể f x  Am ệ D. Lƣu ý:
 Nế à ố y f x GTLN à GTNN D ị ầ là ỏ ã
min f x  Am  max f x . D D
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 71
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE
 Nế à ầ ố ể ệ ệ , ỉ ầ à
ế ể x ị ờ ẳ y Am ằ ắ ồ ị à ố y f x ể ệ .
b. Bài toán 2. T ể f  ;
x m  0 f  ; x m  0 ệ D
 B ớ . Độ lậ ( ) ỏ ế ố x à ề f x  Amf x  Am.
 B ớ . Lậ ế ủ à ố f x trên D.
 B ớ . D à ế x ị ị ủ ố ể ệ
 Vớ f x  Am là ồ ầ ồ ị ằ ờ
ẳ y Am, ứ là Am  max f x khi max f x  . DD
 Vớ f x  Am là ồ ầ ồ ị ằ ớ ờ
ẳ y Am, ứ là Am  min f x khi min f x  . DD
c. Bài toán 3. T ố ể f x  Amf x  Am ệ ú x  D ?
 B f x  Am ệ ú x
  D  min f x  Am . D
 B f x  Am ệ ú x
  D  max f x  Am . D Lƣu ý:  C à l ệ , ệ   ầ ế ổ ể ề à .
 K ổ ế , ầ ế ề ệ ủ ế ớ . 2. Các ví dụ
Bài 1: T ể ệm th c phân biệt : 2 x 1  x m Lời giải Đ ều kiện: x  1 
P ã ới 2 x 1  x mx
Xét hàm số f x  2 x 1  x . Ta có f  x 1 1 1  1 x 1 x 1
f  x  0  1 x 1  0  x  0 B ng biến thiên
D a vào b ng biế ã ệm th c phân biệt khi 1 m  2 .
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 72
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE
Bài 2: Tìm m ể 3 3
1 x  1 x m có nghiệm. Lời giải
Xét hàm số f x 3 3
 1 x  1 x trên . 1 1
Ta có f  x   , x   1  3 1 x2 3 1 x2 3 3 f  x 1 1  0    0  x  0 3 1 x2 3 1 x2 3 3 f x  3 3 lim lim
1 x  1 x       3 3 lim 1 x x 1    x x x 2  lim  0 x
1 x2  x 1 x  2 3 2 3 3 1
T lim f x  0 . x B ng biến thiên:
Vậ ã ệm khi và chỉ khi 0  m  2 .
Bài 3: Chứng minh rằng m
  0 , l ệm th c phân biệt: 2
x  2x  8  ( m x  2) (K B -2007) Lời giải
Do m  0 nên x  2 (1)  x x   m x    x x  2 ( 2)( 4) ( 2) ( 2)( 4)  ( m x  2) x  2 2
 (x  2) (x  2)(x  4)  m  0     3 2
x  6x  32  m  0(*)
Yêu cầu Bài quy về chứ (*) ột nghiệm trong (2; ) Biế ổi (*) 3 2
m x  6x  32 . Xét hàm số 3 2
f (x)  x  6x  32 với x  2 . Ta có ' 2
f (x)  3x 12x  0, x
  2 và lim f (x)   x B ng biến thiên: +
Từ b ng biến thiên suy ra m
  0 (*) ú ột nghiệm x  2 .
Vậ ã ú ệm th c phân biệt m   0.
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 73
Chuyên đề : PT-BPT-HPT VÔ TỈ TOÁN THPT - MAKE THE MATH SHINE
Nhận xét: Sau khi tìm được điều kiện x  2 việc khảo sát hàm số f (x) ở trên là rất dễ dàng chủ yếu là
dùng đạo hàm tuy nhiên dùng định nghĩa cũng suy ra tính đồng biến của hàm số f (x) .
Bài 4: T ể ệm duy nh t   2 3 2 1
3 1 x  2 x  2x 1  m trên ;1    2  Lời giải  1  
Xét hàm số f x 2 3 2
 3 1 x  2 x  2x 1 trên ;1   .  2  2 3  x 3x  4x  3 3x  4  Ta có ' f (x)    x   2 3 2 2 3 2 1 x x  2x 1  1 x
x  2x 1   1  
Xét hàm số g x 3 2
x  2x 1 trên ;1 
 . Ta có gx 2
 3x  4x  0  x  0  2   1 
D a vào b ng biến thiên ta th y g(x)  1, x    ;1    2   1  1 5 và x    ;1 
 ta có 3( )  4  3x  4  3.1 4   3x  4  7 .  2  2 2 3 3x  4  1  Suy ra   0, x    ;1   2 3 2     2 1 x x 2x 1 
D f  x  0  x  0 B ng biến thiên: 3 3  22 Vậ ệm duy nh t khi 4   m  ho c m 1. 2 Nhận xét : 2 3  x 3x  4x  3 3x  4 
Việc sử dụng kỹ năng biến đổi từ   x   là khâu quyết 2 3 2 2 3 2 1 x x  2x 1  1 x
x  2x 1 
định đến việc xét dấu của đạo hàm, mở đường cho việc sử dụng tính chất của hàm số .
Bài 5: Tìm m ể ú ệm th c phân biệt 4 4
2x  2x  2 6  x  2 6  x mK  2008 . ALời giải
Đ ều kiện 0  x  6
Xét hàm số f  x 4 4
 2x  2x  2 6  x  2 6  x trên 0;6. Ta có     f  x 1 1 1 1 1         2   3   3  4 4  2x 6 2 6  x x x    3 3 2 2 1  1 1       1   1                4 4 4 4 2  2x   6  x     2x   6  x  
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 74
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE 2 2    1 1   1  1  1  1 1               4 4 4  2x
6  x   2x  2x 6  x 4 4 4 4  6  x  2x 6  x    f  x 1 1  0    0  x  2 4 4 2x 6  x Lập b ng biến thiên: với f   4
0  2 6  2 6; f 2  6  3 2; f 6 4  2 3  12
Từ b ng biến thiên suy ra giá trị cần tìm của m là: 4
2 6  2 6  m  6  3 2 .
Đối với một số Bài không sử dụng được phương pháp hàm số trực tiếp mà phải sau quá trình biến đổi
như đặt ẩn phụ thích hợp mới sử dụng được phương pháp hàm số .Ta xét Bài sau :
Bài 6: Có bao nhiêu giá trị nguyên của tham số m ể 2 4 2
x  3x 1  m x x 1 có nghiệm A. 1. B. 8 . C. 15 . D. 27 . Lời giải Chọn A.
Tậ x ịnh củ D  0;  . Ta có: 2 4 2
x x   m x x    2
x x     2
x x    m  2
x x   2 3 1 1 2 1 1
1 x x   1 2 2 x x 1 x x 1  2 1 m 1 2 2   x x 1 x x 1 2   Đ x x 1 2x 2 t t   1  1 2 2 x x 1 x x 1 1 x  1 x   2x 2x  1 1  1  1 2 x x 1 2   x x 1  Do x  0 nên       2 t 1; 3  1  1  3 x   2  1 xx  1  x 2  K   2t 1 1 1 trở à 2
2t mt 1  0  m   2t  2 t t
Để ã ệ 2 có nghiệm thuộc 1; 3 1
Xét hàm số: y  2t  ;t  1; 3 t
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 75
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE  1   1   t t
 2t     2t   2t t  2 1    2 1 2 1 t t t .t       1
Với t ;t  1; 3 ;t t 2 1 1 2   2   0 1 2  1 2  xét tỉ số t t t t t .t 2 1 2 1 1 2 1 1 1 5 3
Suy ra hàm số y  2t
ồng biến trên nửa kho ng 1; 3  y 1  2t   y 3 1 2t   t      t t 3 5 3 1 m  3
Do m là số nguyên nên có duy nh t 1 giá trị của m thỏa mãn yêu cầu bài toán.
Bài 7: Tìm số các giai trị ủa tham số m ể 2 3 2 3
x m x
x m x  m   2 2 ( ) ( ) 6 1
x m  4x  6  4m  0 có nghiệm. A. 0 . B. 1. C. 2 . D. 3 . Lời giải Chọn B. 2
a x m x 2 2 2
a b  2 x m  (a b)  4x  4m Đ t: 
a  0,b  0   2 b
  x m x 2 2
ab  ( x m x)( x m x)  m Kết hợp với ( )  , ợc hệ ab m   3 3 a b  
b  a b 2 3 a 1
 (a b)  6  0 ab m   3 2
(a b)  (a b)  3(a b)  6  0 a b  2 b   2  a  2         ab m    aa 2a m a 2  m
Xét hàm y f a 2
 a  2a với 0  a  2 có b ng biến thiên
Vậy 0  m 1 suy ra m 1 . m
Bài 8: Biết rằng p x a a x có nghiệm khi và chỉ khi a   với ,
m n là các số nguyên n m à
là phân số tối gi n. Tính T n m . n A. T  2 . B. T  5 . C. T  3  . D. T  1 Lời giải Chọn B x  0  Đ ều kiện:  .
a x  0
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 76
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE
Đ t y a x  0
x a y Suy ra: 
x y x y  0  ( x y)( x y 1)  0
y a x
x y x y
Nên x x a . ( Dễ th y với x  0 thì a x  0 ).
Đ t t x t  0 ề: 2
t t a Xét hàm số   2
f t t t với t  0 có b ng biến thiên: 1 Suy ra a   T  5. 4 Bài 9: C 4 2 m x 1  3
x 1  2 x 1 , biết rằng tập t t c các giá trị của tham số m ể ã ệm là nửa kho ng ( ;
a b]. Tính giá trị biểu thức 3 3
S a b . 28 26 A. . B.  . C. 1.  D. 1. 27 27 Lời giải Chọn B.
Đ ều kiện x 1, Chia hai vế cho x 1 ợc pt: x 1 x 1 x 1 2 4 m  3   2 . Đ t 4 4 t   1 x 1 x 1 x 1 x 1 2 2 Do x 1  2   1 0  1  1 0  t  1 x 1 x 1 T 2 m  3
t  2t (*) . B ng biến thiên của hàm 2 f (t)  3
t  2t trên [0;1)
Theo b ng biến thiên thì (*) có nghiệm thuộc [0; 1)  1   m 1/ 3. Bài 10: C 2
m x  2  x m  
1 biết rằng tập hợp các tham số th ể ú
ệ ệ là a;b. Tính giá trị a b A. 0 B. 2 2. C. 2  . D. 2. Lời giải Chọn B. Tậ x ị D  .
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 77
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE T   x 2
1  m x  2  m x m
f x; x   . 2 x  2 1   Tí x x
f ' x   x  2   2 2 2 2 2 1   ; x   . 2 2 x  2 x  2 2  x  2 x   2 Cho f ' x 2 2 2  0 
 0  x  2  2  x  2  4   . 2 x  2 x  2 B ến thiên x   2 2  f ' x  0  0   2 f x  2 
D à ế , ể à ố ệ ệ  2  m  2 .
Vậy a b  0
XIV. TRẮC NGHIỆM PHƯƠNG TRÌNH VÔ TỈ
TN 1.1: Tổng các nghiệm của 2 3
2(x x  6)  5 x  8 là A. 6  . B. 3 . C. 6 . D. 3  .
Phân tích. Khác với hai ví dụ trên, biểu thứ ức là bậc 3, ta vẫn gi i theo công thức A  , B ể
ợ ậc bố . Lú ới s hỗ trợ của máy tính casio, ta sẽ í ợc thành tích số d ng bậc 2 nhân bậc 2. Lời giải Đáp án: C Đ ều kiện: 3 2
x  8  0  (x  2)(x  2x  4)  0  x  2  . 2 3
2(x x  6)  5 x  8 2 2 3 4 3 2
( 8.(x x  6)  25(x  8)  8x  41x 104x  96x  88  0 2
x  6x  4  0 2 2
 (x  6x  4)(8x 18x  28)  0    x  3 13. 2 8
x 18x  28  0 :VN
Kết luận: So vớ ều kiệ , ã ệm là x  3  13.
TN 1.2: Số nghiệm củ 2
2x  6x 1  4x  5 là A. 1. B. 3 . C. 2 . D. 0 . Lời giải Đáp án: C Đ ề 5
u kiệ x ịnh: x   . 4
Ta có: x x   x
  x x  2 2 2 2 6 1 4 5 2 6 1  4x  5 4 3 2
x  6x  8x  2x 1  0
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 78
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE x  2.414213562 1  x  0.  414213562
Sử dụng máy tính Casio ta thu được: 2 x  3.732050808  3 x  0.2679491924  4
Tư duy Viet đảo: x x  2, x x  1  1 2 1 2
Nhân tử thu được: 2 x  2x 1 Vậy:  2
x x   2 2
1 x  4x   1  0
Trƣờng hợp 1: Với 2
x  2x 1  0  x 1 2 .
Kết hợ ều kiện ta có x  1 2 .
Trƣờng hợp 2: Với 2
x  4x 1  0  x  2  3 .
Kết hợ ều kiện ta có x  2  3 .
Kết luận: P ệm phân biệt x  2  3 và x 1 2 . TN 1.3: Tổ ệm củ 2
2x  6x 1  4x  5 là
A. 10  2 2  2 3 . B. 10  2 2  2 3 .
C. 8  2 2  2 3 .D. 12  2 2  2 3 Lời giải Đáp án: B
Lũ ừa sau khi sử dụ ợc nhân tử 2 x  2x 1. 2
2x  6x 1  4x  5 2 2
2x  6x 1 0
2x  6x 1 0     2 2 4 3 2
(2x  6x 1)  4x  5
x  6x 8x  2x 1 0    2 3 11 3 11
2x 6x 1 0 x   x  x 1 2     2 2    2 2
(x  2x 1)(x  4x 1)  0  x  2  3
x 1 2  x  2  3 2 2
Kết luận: Tổ ệm là: 1 2  2  3 10  2 2  2 3
TN 1.4: Nghiệm nhỏ nh 2 3
2x  5x 1  7 x 1 có d ng a b c với a, . b c  . K
a b c có kết qu là A. 11. B. 10 . C. 9 . D. 12 . Lời giải Đáp án: A
Lũ ừa sau khi sử dụ ợc nhân tử 2 x  8x 10. 2 3
2x  5x 1  7 x 1 2
2x  5x 1 0   2 2 3
(2x  5x 1)  49(x 1) 2
2x  5x 1 0   4 3 2
4x  29x  21x 10x  50  0 2
2x  5x 1 0 x  4  6      2 2
(4x  3x  5)(x 8x 10)  0 x  4  6 a 1 
Kết luận: Nghiệm nhỏ củ là x  4  6  b
 1  a b c 11 c  6 
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 79
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE
TN 1.5: Tổng các nghiệm củ 2 2 2
2x  3x 1  x x  2  3x  4x 1 có d ng a b c với a, . b c
. K a b c có kết qu là 2  33 2  33 1 33 1 33 A. . B. . C. . D. 3 4 4 4 Lời giải Đáp án: D 2
2x  3x 1 0  x  2  Đ ều kiện: 2
x x  2  0     x 1 2
3x  4x 1  0  2 2 2 ( )
  3x  2x 1 2 (x 1) (2x 1)(x  2)  3x  4x 1 1   x  0 2
 (x 1) (2x 1)(x  2) 1 x   2 2
(x 1) (2x 1)(x  2)  (x 1) x  1    3 33 
x  1 ho c x   2 2
(x 1) (2x  3x  3)  0 4   
Kết luận: Tổng các nghiệ là 3 33 1 33 1  4 4 a b c TN 1.6: Nghiệ 3 2
x x   2 x   1 x 1 1 có d ng với a, . b c
. K a b c 2 có kết qu là A. 7 . B. 6 . C. 5 . D. 8 . Lời giải Đáp án: A
Đ ều kiệ x ịnh: x  1  . Ta có: 3 2
x x   2 x   1 x 1 1
x x   x   x   x x  2  x  2 3 2 2 3 2 2 1 1 1 1 1  x   1 6 5 3 2
x x x x x   x 5 4 2 4 4 0
x x  4x  4x   1  0 (*) x  0  .430159709 1 
Sử dụng máy tính Casio ta thu được: x  1.618033989 2 x  0  .618033988  3
Tư duy Viet đảo: x x 1.0000000001 1, x x  0  .99999999989  1  2 3 2 3
Nhân tử thu được: 2 x x 1 D (*)  x 2
x x   3 2
1 x  2x  3x   1  0 (**)
Đ ều kiện có nghiệm củ 3  1  3 3  1 3 2
x x 1  0 3 2 2
x x   0  x x x   0  x     8  2  2 4  2 1 1 5 Vì 3 2 x
 0  x  2x  3x 1  0 . D (**) 2
x x 1 0  x  . 2 2 1 5
Kết hợ ều kiện ta th y chỉ có nghiệm x  thỏa mãn. 2
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 80
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE a 1 1 5 
Kết luận: P ệm duy nh t là x   b
 1  a b c  7 . 2 c  5 
TN 1.7: Tổ nghiệ 2 2
x x 1  x x 1  4  x gần nh t với giá trị à A. 0 . B. 1. C. 3 . D. 5 . Lời giải Đáp án: A
Đ ều kiện x  4. P ã ới: 2
 4  x x x 1  0  2
x  2x 3  0 2 2
x x 1  4  x x x 1    
4  x  2 4  x 2 x x   1 3 2      4x 11x 4x 0 3  x  1 x  0     x  0  11 185  x  2
4x 11x  4  0  8 2 11 185 
- Kết luận. Tổ ệm củ là    0.1057445   . 8   Nhận xét.
- T ờng hợp: a a a (ví dụ 2) ở trong d ng toán này việc sử dụng hệ ều kiệ ể biế ổi giúp chúng 1 3 2
ta vừa sử dụ ợc phép biế ổ ũ ừa sử dụ ợc phép biế ổi hệ qu .
- Đ c thù của d ng toán này là việ ều kiện 2 2
a x b x c a x b x c  0 ố n. Nế ờng hợp việ ều kiện này là 3 3 3 1 1 1
, ú ã ệc sử dụng phép biế ổi hệ qu .
TN 1.8: Tập nghiệm của b x 11 
x  4  2x 1 có là S  a,b. K a b là A. 6 . B. 2 . C. 7 . D. 9 . Lời giải Đáp án: D x 11 0 x  1  1  
Đ ề ệ x  4  0  x  4  x  4.   2x 1  0 x  0,5   x 11 
x  4  2x 1
x 11 3x  5  2 x  42x  
1   x  42x   1  8  xx 8  0  x  8        x  .  x  4  2x   1  8  x 12 5 2 2
x  7x  60  0
Kế ợ ớ ề ệ , ậ ệ ủ là S  4;5  . a  4 Vậy 
a b  9 b   5 2 2 12  x x 12  x x
TN 1.9: Tập nghiệm của b  
S a,b c . K x 11 2x  có là     9
a b c là A. 1. B. 2 . C. 0 . D. 1.
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 81
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE Lời giải Đáp án: D 2
 12  x x  0    1 1  2  2      
12  x x  0 12 x x 0   
x 11 2x  9    1 1    0
x 11 2x 9 x  3   x  4  x  3    3   x  4    .   2   x  4 x  2  a  2   Vậy: S   2  ,4  3  b
  4  a b c  1  c  3   Lƣu ý T ờ ờ ợ 2
12  x x  0, à là lầ ờ ủ ọ sinh.
TN 2.1: C  x   x    x   2 1 2 6
x  7  x  7x 12. Số nghiệm củ là A. 0 . B. 2 . C. 1. D. 3 . - Phân tích.
- T ớc hết ta nhậ ị ệm duy nh t x  2. Nếu ta sử dụ l ợp
mộ ờng, d ớc các biểu thứ là ợc nhau nên có thể dẫ ến việc ph i kết hợp với
. T ẽ tìm cách khắc phục v ề này bằng cách tìm nhóm các biểu thức với sao cho
ợ ề d ng  x  2. f x  0, f x  0, x   2  .
- Để ý rằng, vớ ều kiện: x  2
 ẳ ị ợc d u của nhị thức  x   1 vì vậy khi th c hiện 2
phép nhân liên hợ ối với  x   1
x  2, ta cần t o ra nhân tử:  x  
1  x  2 hay ta cần tìm m, n sao cho:  1 m
m n 1  3
mx n x  2  0 khi x  1; x  2, tức ta có hệ:   
2m n  2 4 n   3
Từ hai vế củ ới 3 cho ta: 2
3x  21x  36  3 x   1
x  2  3 x  6 x  7  0
Tiến hành việc nhóm nhân tử cho biểu thức 3 x   1 x  2, ta sẽ ợc:
x  x  x  2 1 4 3
2  2x 16x  32  3 x  6 x  7  0
Đối với  x  6 x  7 thì do x  6  0, x   2  nên ta sẽ
x x  x x  x  x   2 1 4 3 2 6 7 7
3  x  3x 10  0 Lời giải Đáp án: C
Đ ều kiện x  2.  P ã ới:
x x  x x  x  x   2 1 4 3 2 6 7 7
3  x  3x 10  0. x  2 1  x  2  x    x  6  2 x  7.
 x  2x  5  0.
x  4  3 x  2 x  7  3
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 82
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE 2       x   x  1 x 6 x 7 2  
 x  5  0  x  2.
x  4  3 x  2 x  7  3    x  2 1
x  6 x  7 Do 
 x  5  0, x   2. 
x  4  3 x  2 x  7  3
Vậ ã ệm duy nh t x  2. TN 2.2: C 2 2
2x x  3  x x  21x 17. Số nghiệm củ là A. 0 B. 2 C. 1 D. 3 - Phân tích.
Ta nhậ ợc rằ ệm x  1; x  2 . Do vậ à ẽ có nhân tử
x  x   2 1
2  x  3x  2 ịnh sử dụ l ợng liên hợ ể gi à . Đ ều quan tâm là cách tách - l ợ . Gi sử ta sẽ nhóm  2
2x x  3  a x b
a x b  21x 17 . Thay các giá trị x  1; x  2 vào các 1 1   2 2  2
 2x x 3 a x b  0
2  a b  0
a  1 a b  2  0 1 1  ẳng thức  , ta sẽ ợc 1 1  1   ; 2 2          
a x b  21x 17  0  3 2a b 0  b 1  2a b 5 0  1 1 1 2 2 2 2  a  3 2   . b  1   2 Lời giải Đáp án: B Đ ề 17 u kiện x  . P ã ới: 21
 2x x x  x  x  2 2 3 1 3 1 21
17  x  3x  2  0.   9 x x  2 2 x  3x  2 3 2  2  
x 3x  2  0. 2
2x x  3  x 1
3x 1 21x 17   1 9  2
x  3x  2  1  0 2
 2x x  3  x 1 3x 1 21x 17  x  2
x  3x  2  1 0  x  2 1 9 17 Do  1 0, x   . 2
2x x  3  x 1
3x 1 21x 17 21
Kết luận. Tập nghiệm củ ã là T  1;  2 . TN 2.3: C    x  2 1 1
2x  2x 1  x   1  x x. Gi sử b d ng x a
. a , b , c là các số à b là phân số tối gi n. Tính c c
S a b c A. 49 . B. 47 . C. 30 . D. 15 .
Phân tích. Ta nhận th y  1 x  
1  1 x 1  ,
x tuy nhiên kh sử dụ é l ợng liên hợp ta
ph à ờng hợp 1 x 1  0 và   
1 x 1 0. Để tránh nh ng v ề v ề phức t n y sinh, ta có thể xử l Lời giải Đáp án: A
Đ ều kiện x  0. P ã ới:
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 83
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE    x 2 1 1
2x  2x 1  x  
1  1 1 x  1 x   1 x. 2
 2x  2x 1  x 1   1 x   1 x   2 2
2x  2x 1  x x   x 1 x   0 2 x  3x 1 
x 1 x  0 2 2  
2x  2x 1  x x
x1 xx1 x 
x 1 x  0 2 2  
2x  2x 1  x x         x x 1 x x 1  1  0   2 2
 2x  2x 1  x x
x 1 x  0  1   2 2
 2x  2x 1  x x x 1 x  0  2 Khi   3  5 1  x  . 2
    2x x  x  2 2 2 2 1 1
x x x   0*
 2x 2x1 x1 x x 2 1
x 1  x  2 2 2 1  x  
1  1 x   x   1  0 Ta có:  2
 x x x x x  0 D   *  x  0.   
- Kết luận. Tập nghiệm củ ã là 3 5 T   ; 0.  2   1 a b TN 2.4: C 2 x x x
 2 . Một nghiệ ủ ng x  . x 2 Tính tổng 2
S a b . A. S  4 . B. S  5. C. S  4  . D. S  5  Lời giải Đáp án: C x 1 B ớ . Đ ều kiện .   1   x  0
B ớ . T ợc nhân tử  2 x x   1 . P ã ới:   1  2 2     2 x x 1 x x 1 x x   1   x  1  0      0 x   2 x x 1  1  x x  1 x          1 1  2 x x   1   0   2 x x 1  1   x x  1    x    
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 84
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE 2
x x 1  0     1  2 x x
1  x x 1 0   1    x     B ớ . T ờng hợp. 2 x x 1  1 5 0  x  . 2   B ớ 4. T ờ 1 ng hợp. 2 x x
1  x x 1 0 *.   x  
H ớng xử lý 1. (Sử dụng phƣơng trình hệ quả) 1 Thay 2 x
1  x x 1 từ ầ à (*) ệ qu . x x  2 x x   1 x  2
x x     2 1 x x   1  0 
  2x x 1  0 2  x x 1
xx x   x x  2 2 2 1 1  0 3 2
x  2x 1 2 x x  0 x 1 Vớ ều kiện  thì 3
x  2x 1  0 ệ qu 3 2
x  2x 1 2 x x  0 vô nghiệm,  1   x  0 (*) ệm.
H ớng xử lý 2. (Sử dụng đánh giá trực tiếp trên phƣơng trình)
+ Nếu x  1, (*) ới x x   1  x 1 x x   1  0 a .
Với x 1  VT a  0, tức (a) vô nghiệm.
+ Nếu 1  x  0, (*) ới 2  x 1 x x     2 3 1
x x x x   0  x     1   0 b 2 3
x x x x Với 1
  x  0 VT b  0, tứ ( ) ệm. Từ (*) ệm. 1 5
Kết luậ . P ã ệm x  . 2 TN 2.5: C 2 2
x x  2  x 1  x 1. Số nghiệm củ là. A. 0 . B. 4 . C. 3 . D. 2 . Lời giải Đáp án: D - Phân tích. Nhận th y
 2x x  x  2x x  x  2x x x  2 2 1 2 1 2 1  x 1 từ lời gi i sau:
Đ ều kiện x 1. P ã ới: 2
x x   x    2
x x   x   2 2 1 2 1
x x  2  x 1 2
x x  2  x 1  0   1
  2x x   x   2 2 1
x x  2  x 1   1  0   2
x x  2  x 11 0  2   x 1 0 1    x 1 2
x x  2  0
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 85
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE    x  2 2
2  x  2  2 x 1   4 2
x  4x  4x 8  0 x  2     x  2 x  2     3 2
x  2x  4  0 Do: 3 2
x  2x  4  2 2  4  4  0, x   2
- Kết luận. Tập nghiệm củ ã là T  1;  2 . TN 2.6: C 3 3
x 1  2x  3  3x  2. Biết một nghiệm củ là b x a  , trong c b
a , b , c là các số nguyên và là phân số tối gi n. Tính tổng S  3a  2b c . c A. 10 . B. 7 . C. 7  . D. 10  . Phân tích.
Nhận th y  x  
1  2x  3  3x  2 và không có giá trị nào của x làm cho các biểu thức 3 3
x 1, 2x  3 ồng thời bằng 0. Nên ta có thể th c hiện phép nhân liên hợ ể xu t hiện nhân tử 3x  2. Lời giải Đáp án: B P ã ới: 3x  2  3x  2  0 x  2 3 1  x  
1 2x  3  2x  32 3 3       x   1 3 2 1  0    2    3x 2 0 x   x  2 3 1  x  
1 2x  3  2x  32 3 3 3   1 Do 1  0, x   x  2 3 1  x  
1 2x  3  2x  32 3 3 a  0 2 
Kết luân. Nghiệm củ ã là x   b
  2  3a  2b c  7. 3 c  3 
TN 2.7: Gọi S là tập nghiệm củ 2 2
x  5x  5  x
x  2  3x  2 . Số phần tử của S là A. 0 . B. 1. C. 2 . D. 3 .
- Phân tích. Nhận th y  2
x x     x   2 5 5
2  x  4x  3   x   1  x   3 và 2
x  3x  2   x   1  x  2 ồng thời: 2
x  5x  5  x  2  0 nên ta có thể th c hiện phép biế ổi: 2 x  4x  3 2
x  5x  5  x  2 
ể làm xu t hiện nhân tử  x   1 . 2
x  5x  5  x  2 Lời giải Đáp án: B   Đ ề 5 5 u kiện x  . P ã ới:  2
x x   x   2 5 5
2  x  3x  2  0 2 2 x  4x  3  x  3  2 
x  3x  2  0  x   1   x  2  0  x 1 0 2
x  5x  5  x  2 2
x  5x  5  x  2      x 3 5 5 x  1  Do
x  2  0,x  2     2 x 5x 5 x 2
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 86
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE
Vậ ã ệm là x  1. 
TN 2.8: Gọi S là tập nghiệm củ 2 2
x x  2  x  2 x  
1 1. Số phần tử của S là A. 0 . B. 2 . C. 1. D. 3 .
- Phân tích. Nhận th y  2
x x    x   2
x x x x   2 2 2 2
1 vaø x 1   x1  x1 , nh vậy khi
chúng ta th c hiện phép nhân liên hợp sẽ xu t hiện nhân tử:  x  
1 . Tuy nhiên khi x  1, biểu thức 2 x x 2
x x  2  2x   1  0 ế ổi 2
x x  2  2 x   1  là một phép 2
x x  2  2 x   1
biế ổ . V ậ ớc khi th c hiện phép nhân liên hợp ta cầ ú ến biểu thức liên hợp
ã 0 . Để xử lý các d ng toán này ta có thể ờng hợp của x làm cho
f x  g x  0 à ờng hợp f x  g x  0. Cụ thể, với bài toán này ta có thể xử l Lời giải Đáp án: C
Đ ều kiện x 1.
+ Nhận th y x 1 là một nghiệm củ ã .
+ Với x 1, ã ới: 2 x x 2 x x   x  2 2 2 1  x 1  0   x   1  x   1  0 2
x x  2  2  x   1       x x 1 
x 1  0  * 2
x x  2  2x   1    x
Khi x 1 thì x 1  0 và
x 1  0 (*) ệm x 1. 2
x x  2  2  x   1
- Kết luậ . P ã ệm duy nh t x  1.
TN 2.9: Gi  x   2 2 1
x  2x  3  x 1 ợc nghiệm có d ng x a b a , b là
các số nguyên. Tính tổng S a b . A. 0 . B. 1. C. 2 . D. 3 . Lời giải Đáp án: B 2 x 1 Vì x  1  không là nghiệm củ 2
x  2x  3  x 1 x   2 2
x  2x  3   x   2 1 2 1   x   1   2
x  2x 1  0  x 1 2 x 1  2      1 2 3 1 x x x x
a 1, b  2 . Vậy S  3. Nhận xét:
V ề dắt ra là làm sao nhậ ợ ể ền số x 1 vào hai vế. 2  Ý ở x 1
ng xu t phát từ việc tàm ra số  và  sao cho 2
x  2x  3   x    
  x      . x  với 0 1
x  2x  3   x   2 2 2
x 1  x    x   1   2      x 1 x 2x 3 x  2 1  2
x  21.  x   2 3    1  2
x      x 1    2      x 1 x 2x 3 x
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 87
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE 2 1   1 
Đế , ỉ việ x ịnh  ,  sao cho: 2  2.       1,   1  .  2 3    1   TN 2.10: C 3 2 2 3
x  3x 1  x  5x 1  2 .
x Số nghiệm củ là A. 2 B. 0 C. 3 D. 4
- Phân tích. Nhận th y  2
x x     x   2 3 1 5
1  x  2x và không có giá trị nào của x  làm cho các biểu thức 3 2 3
x  3x 1, 5x 1 ồng thời bằng 0. Từ ể l ợng liên hợ ể xu t hiện nhân tử  2x 2x. Lời giải Đáp án: A P ã ới: 3 2 3
x  3x 1  5x 1   2
x  2x  0 2 x  2x    2
x  2x  0
3  x  3x  2 3 1
 x 3x   1 5x   1  5x  2 2 2 3 1 x  2  x  2x  0 0  x  2 1 Do: 1  0, x  
3  x  3x  2 3 1
 x  3x   1 5x   1  5x  2 2 2 3 1
- Kết luậ . P ã ệm x  0; x  2.
TN 3.1: Tổ ệm củ 2 2
x  5x  2  2 x  5x 10  0 là: A. 13 . B. 5 . C. 10 . D. 25 . Lời giải Đáp án: A Đ ều kiệ x ịnh 2
x  5x 10  0  x  . K ở thành: 2 2
x  5x 10  2 x  5x 10  8  0 2
x 5x 10  2      x 3 2 2 1
x  5x 10  2  x  5x  6  0   . 2   
x  5x 10  4  x 2  2 Vậy 2 2 2 2
x x  2  3 13. 1 2
TN 3.2: Tích các nghiệm củ 2 3
2x  5x 1  7 x 1 bằng A. 10  . B. 6  . C. 10 . D. 6 . Lời giải Đáp án: C
Đ ều kiệ x ịnh x 1.
pt   x     2
x x    x   2 3 1 2 1 7
1 x x   1 x 1 x 1    x 1 x 1 1 3.  7  2  0   2  2 2 x x 1 x x 1 2 x x  ho c 1 2 x x 1 3
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 88
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE x 1 Với 2
 2  4x  3x  5  0 , ệm. 2 x x 1 x 1 1 Với  2
x  8x 10  0  x  4  6 . 2 x x 1 3
K Tích các nghiệm của ằng 10. 4 a b TN 3.3: Biế 2 2
x x  6 
x x có một nghiệm d ng x
với a, b, c là các x 1 0 c
số à a là phân số tối gi . K ổng 2 2 2
S a b c bằng: c A. 14 . B. 21 . C. 29 . D. 30 . Lời giải Đáp án: D Đ ều kiệ x ịnh: 2
  x  3 và x 1.  
pt  3  x2  x 4 2 
 2  x x  2   .  x 1     x
3  x2  x 2 3    x   1  x  2 x  . 1 1 3  x 1 3  x
Chia hai vế  x   1  x  2 ợc: .  2.  x 1 x  2 x   . 1 2 1 x  2  Đ 1 3 x 1 t t  . ở thành 2
2t t 1  0  t  1  ho c t  . x 1 x  2 2 1   x  3 1 1 3  x 1 3  x  Với t  ta có .   2
x 1   3 xx  2 2 x 1 x  2 2 x  2 4.  x   2 1  x  2  2   x 1 x  1  1 3  x 3  x   Với t  1  ta có .  1  
1 x  3 x  1 5 x 1 x  2 x  2   1 x2    x x  2  2  K 1 5 x
và a 1 ; b  5 ; c  2 . 0 2 Vậy 2 2 2
S a b c  30 . a b TN 3.4: Biế 2 2
x  4  x  2  3x 4  x có một nghiệm là x  
với a, b, c là các số 0 c
à a là phân số tối gi . K ổng S a b c bằng c A. 19 . B. 15 . C. 2 . D. 7 . Lời giải Đáp án: A Đ ều kiệ x ịnh: 2   x  2.
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 89
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE 2  Đ t 4 t 2
t x  4  x thì 2 x 4  x  . 2 t  2 2 
pt  3t  2t  8  0  4  . t    3  2   x  2 x  2 Với t  2 suy ra 2
x  4  x  2 2
 4  x  2  x     . 2
2x  4x  0 x  0  4 4 4  2   x   2  14 Với t   suy ra 2
 4  x    x   3  x   . 3 3 3  2 9
x 12x 10  0
a  2; b 14; c  3. K S 19 . 3 3 a
TN 3.5: Biế   x    x 2 1 1
 2  1 x có nghiệm duy nh t x
với a, b là các 0 b số . K ị tổng 2 2
S a b bằng: A. 13 . B. 5 . C. 11. D. 29 . Lời giải Đáp án: A Đ ều kiệ x ịnh: 1   x 1.
a  1 x Đ t 
, ều kiện a,b 0;  1 . b   1 x 2 2  2 a b  2   a b    2ab  2 Ta có hệ    3 3
a b  2  ab   a b
3 3aba b  2 ab  
ab   a b2 2 2 2ab  2   a b2      
a b  1 (Do ab  0 ). 
a b   6  a b
3 a b2 6a b6  0 
a b 1 1 1 Với
a b  1  ab  . K a ;  b   là nghiệm củ 2 X X   0 2 2 1 3
a  1 x  3  x  . 2 2 K S 13.
Cách 2 : Đ ều kiệ x ịnh: 1   x 1.
  x3    x3 2 1 1
 2  1 x    x   x 2   x  2 1 1 2 1  2  1 x
 1 x  1 x 1  1 x 1 x  2 1 x 1  2(1 )
x  2 1 x 1  0
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 90
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE  1   3  1 x  2 3    x  .      x  VN  2 1 3 1  2
TN 3.6: Tổ ệm củ x 1  4  x  (x 1)(4  x)  5 là A. 6 . B. 3 . C. 9 . D. 27 . Lời giải Đáp án: C Đ ều kiệ x ịnh: 1   x  4. 2  Đ t 5 t t
x 1  4  x ( t  0 )  (x 1)(4  x)  2 2 t  5 t
PT(1) trở thành: t   5 2
t  2t 15  3 0   2 t  5  (l) Với t  3 
x 1  4  x  3  5  2 (x 1)(4  x)  9  (x 1)(4  x)  2    x
(x 1)(4  x)  4 2
 x  3x  0 0  x 3
Vậy tập nghiệm củ S  0;  3 .
TN 3.7: Tích các nghiệm củ 2 2
x x 1  3  x x 1  1 là 1 A. . B. 5  . C. 5 . D. 1. 2 Lời giải Đáp án: B Đ t 2
t  3  x x 1  0 2 2
x x 1  3t . P ã ở thành t   tm 2
3  t t  1 2
t t  2  1( ) 0  t  2  (loai) Với 2 t  1:
x x 1  4 2
x x  5  0  x .x  5  1 2 TN 3.8: Tổ ệm củ 2 2 2
2x  2x x x  2 x x 1  7 là 25 A. 11. B. 1. C. 9  . D. . 4 Lời giải Đáp án: A 2 2 2
2x  2x x x  2 x x 1  7 2 2 2
 2x  2x  ( x x 1 1)  7 2 2
 2x  2x  ( x x 1 1)  7 2 2
 2x  2x x x 1  8  0 Đ t 2 2 2 t
x x 1  0  2x  2x  2(t 1) . P ở thành t  2(tm) 2 2t t 6 0      3  . t   (loai)  2 S   Với 2 t  2 :
x x 1  4 2
x x  5  1 0   2 2 2
x x S  2P 11 P  5 1 2
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 91
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE TN 3.9: P
2  f x  f x có tập nghiệm nghiệm A  1; 2;  3 , g x 3 2.
1  3.g x  2  2.g x có tập nghiệm B  0;3;4;  5 .Hỏi tập nghiệm củ
f x 1  g x 1  f x  g x  f x.g x 1 có bao nhiêu phần tử ? A. 1. B. 4 . C. 6 . D. 7 . Lời giải Đáp án: A    f   xx 1  
f x  f x 0 2  
f x 1 x  2 2   f
x f x2  0 x  3  3
2  g(x) 1  3.g(x)  2  2.g(x) 1
  g x 
g x    1 2 1 2 2
1 1  3g x 3
 2  3 3g x  2  2  0 2 3 1
  g x  2 1 2
1 1   3g x  2  2 3g x  2  2 3 3 1  0 2 3 x  0  2g  x11 0      g xx 3 1   3  g xx 4 3  2 1  0   x  5
f x 1  g x 1  f x  g x  f x.g x 1
f x 1  g x 1  1
  f x 1
  g x      f   x 1  
  .Vậy tập nghiệm củ ần tử. g   xx 1 1 TN 3.10: P
2  f x  f x có tập nghiệm nghiệm A  1; 2;  3 , g x 3 2.
1  3.g x  2  2.g x có tập nghiệm B  0;3;4;  5 .Hỏi tập nghiệm củ
f x.g x 1 
f x  g x có bao nhiêu phần tử ? A. 3 . B. 4 . C. 6 . D. 7 . Lời giải Đáp án: C    f   xx 1  
f x  f x 0 2  
f x 1 x  2 2   f
x f x2  0 x  3  3
2  g(x) 1  3.g(x)  2  2.g(x)
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 92
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE 1
  g x 
g x    1 2 1 2 2
1 1  3g x 3
 2  3 3g x  2  2  0 2 3 1
  g x  2 1 2
1 1   3g x  2  2 3g x  2  2 3 3 1  0 2 3 x  0  2g  x11 0      g xx 3 1   3  g xx 4 3  2 1  0   x  5
f x.g x 1 
f x  g x   f x  
1  g x   1  0 x  0 x 1 
f x 1 x  2    
.Vậy tập nghiệm củ 6 ần tử. g   x 1 x  3  x  4  x  5 2 16x  6x  2
TN 4.1: Biết nghiệm nhỏ nh t củ 3 2 3 3x  7x  6x  4  3 có d ng 3 a ca * a, , b c
, tối gi n. Tính giá trị của biểu thức 2 3 4
S a b c . b b A. S  2428. B. S  2432. C. S  2418. D. S  2453. Lời giải Đáp án: B 2  16x  6x  2 3 y     2   1  Đ 16x 6x 2 3 t 3 y  . Ta có hệ  3 3 2  3x  7x  6x  4 y  2  3 3 2 3x  9x 12x  6 3
Cộng (1) với (2) theo vế ợc 3 3 y y
y y  x   1  x 1 (3) 3
Xét hàm số f t  3
t t,t  , vì ' f t  2
 3t 1 0, t
  nên hàm f ồng biến trên .
K 3  f y  f x  
1  y x 1 . T à ( ) ợc  x 1   2  7 3 2
3x  7x  3x 1  0   x   1  2 3x  4x   1  0  x   3   2  7 x   3  Nghiệm nhỏ nh t củ là 2 7 x 
suy ra a  2, b  3, c  7 . 3 Vậy 2 3 4 2 3 4
S a b c  2  3  7  2432 .
Đối với học sinh lớp 10, ta chứng minh hàm   3
f t t t đồng biến trên nhƣ sau: Với mọi
t ,t  , t t , ta có 1 2 1 2
f t   f t  2 3 3 2
t t t tt  3t 1 2 1 1 2 2 2 2 2 2 
t t t t 1  t   1  0 1 1 2 2  1  t t t t  2  4 1 2 1 2
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 93
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE Cách 2: 2 16x  6x  2 3 2 3 3x  7x  6x  4  3 3   
 3x  7x  6x  4  16x  6x  2  16x  6x  2 2 16x 6x 2 3 2 2 2 3  3 3  
 3x 3x  4x  2  16x  6x  2 2 16x 6x 2 3 2 2 3  3 3       x   2 2 3 16x 6x 2 16x 6x 2 3 1  x 1   (*) 3 3
Xét hàm số f t  3
t t,t  , vì ' f t  2
 3t 1 0, t  
nên hàm f ồng biến trên .       K  
*  f x   2 2 16x 6x 2 16x 6x 2 3 3 1  f    x 1   3  3    x 1   2  7 3 2
 3x  7x  3x 1  0  x   1  2 3x  4x   1  0  x   3   2  7 x   3 TN 4.2: C 3 3
x 1  2 2x 1 có ba nghiệm phân biệ ệm bé nh ợc biểu thị  ớ a b i d ng
với a, b, c là các số nguyên, b  0, a  0, c  3 . Tính giá trị của biểu thức 3 3 3
P a b c ? c A. 134 . B. 132 . C. 116 . D. 118 . Lời giải Đáp án: B Đ t 3 3 t
2x 1  t  2x 1 . K ầu trở thành 3 x 1  2t 3 3
x 1 2t  x 1  2t 2     1  3    3 3 2
x t  2(t x) (x t) 
x t t  2     0 x t  2  4     x 1     T ợ 1 5 c 3 3
x 1  2x x  2x 1  0  x   2   1   5 x   2   Nghiệm bé nh t củ là 1 5 x
, a  1;b  5;c  2 và P 132. 2 TN 4.3: Gọi x là nghiệm âm củ √ ( ) 0 ab 2 2 3
7x 13x  8  2x . x 2
1  3x  3x . Biết x có d ng 
với a, b, c là các số t nhiên , a là số 0 c
nguyên tố. Hỏi tổng T b  2a c chia hết cho số à A. 17 . B. 19 . C. 18 . D. 15 . Lời giải
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 94
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE Đáp án: B
Dễ th y x  0 không là nghiệ ế pt cho 3 x ợc: √ 7 13 8 1 3 3    . 2   3 2 3 2 x x x x x 3 3       Đ ề 2 2 1 3 1 3 d ng: 3 3 1  2. 1         3   2.   3 *  2  2    x   xx x x x  
Xét hàm số f t  3
t  2t với t  , à à ồng biến trên .  x 1 1  1     D   1 3 2 8 13 3 x 5 89 3 *    3  1     2  0    x  2 3 2 x x x x x x 1 16   4   x 5 89    5  89  x       4     5 89  Vậy x   
  T  89  2.5 4 95 19 0   4  
TN 4.4: Cho hàm số f (x) liên tục trên à ồ thị ẽ.
Hỏ f  1sin x   f  1 cos x  có t t c bao nhiêu nghiệm thuộc  3  ;2? A. 0 . B. 1. C. 2 . D. Vô số. Lời giải Đáp án: B        x   1 sin x 1 0 1 sin x 2 3; 2      1   cos x 1
0  1 cos x  2
f  1sin x   f  1 cos x   1sin x  1 cos x ( Vì f (x) ồng biến trên 0; 2 
 sin x  cos x  0  tan x  1  x    k 4  Do x   3
 ;2  x   thỏ . Vậy có duy nh t 1 nghiệm. 4
TN 4.5: Gọi x là nghiệm th c củ 2 2 4 2 2
x 5x 1  x 6x 1  2x  2x 1  x 1, biết bình 0  ủ a b a a nghiệm x có d ng 2 x
a, ,bc , tối gi n .Tính S abc 0 0 c b
A. S  26 . B. 25 . C. 24 . D. 22 . Lời giải Đáp án: A
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 95
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE Vì : x  2 2 x   x   4 2 2 5 1 6 1 
2x  2x 1  x 1  0  x  0
Đ ệu kiện : x  0  1 1  2 1 1 1 Chia 2 x hai vế :  5   6    2   1  Đ t : t   0 2 2  2 4 2 x x x x x   2 x 2
5  t  6  t  2  2t t 1 t
t   t 2   t   t2 5 5 1 (1 ) 1 1
Đ t u  5 t,v 1 t . Đ ều kiện: u  5,v 1 Lú 2 2
u u 1  v v 1  f (u)  f (v) Cách 1: Xé à 2
f (t)  t t 1 Đ ều kiện : t 1 t f '(t)  1
 0  hàm số ồng biến trên 1; nên ta có u = v 2 t 1  1 17 2 x  (n) K 1 1 1 2 1 1 1 8 5  1 4 2  5   1   
 4  0  4x x 1  0   2 2 x x 2 2 4 4 2 x x x x x  1 17 2  x  (l)  8  S  26 Cách 2: 2 2
u u 1  v v 1  u v   2 2
u 1  v 1  0      u vu v 1  
  0  u v 2 2 
u 1  v 1  K 1 1 5  1 2 2 x x  1 17 2 x  (n) 1 2 1 1 1 4 2  8 5   1   
 4  0  4x x 1  0    S  26 2 2 4 4 2 x x x x x  1 17 2  x  (l)  8
TN 4.6: Cho f x 3 2
x 3x  6x 1. P f f x 
1 1  f x  2 có số nghiệm th c là A. 4 . B. 6 . C. 7 . D. 9 . Lời giải Đáp án: A
Đ t t f x 1 3
t x  3 2
x  6x  2 .
K f f x  
1 1  f x  2 trở thành:
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 96
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE t   1   t   1 
f t  1  t 1      f  t 2
1  t  2t 1 3 2 t
  4t 8t 1  0 t   1 
t t  2  ; 1   t t  1  ;1 2   1       .
t t  1  ;1
t t  5;6  3   2  
t t  1;6  3   (Vì g t  3 2
t  4t 8t 1; g  2    7  ; g   1  4 ; g   1  1
 0 ; g 6  25 ). Xé 3 t x  3 2
x  6x  2 , là à ộ ểm củ ồ thị hàm số 3 y x  3 2
x  6x  2 à ờng thẳng y t . Ta có b ng biến thiên.
D a vào b ng biến thiên, ta có
+ Với t t  1
 ;1 , ta có d cắt (C) t ểm phân biệ , ệm. 2  
+ Với t t  5;6 , ta có d cắt (C) t ể , ệm. 3   Vậ ã 4 ệm. TN 4.7: Tổ ệm củ  4 2 2  2 1+ 2x - x + 1- 2x - x = 2 x -1 2x - 4x +  1   1 là A. 9 . B. 5 . C. 4 . D. 8. Lời giải Đáp án: C
    x  2   x  2  x  4  x  2 1 1 1 1 1 1 1 2 1 2 1 1 2  
Đ ề ệ  x  2   x  2 1 1 0 1 1.
Đ t  x  2 1
 0  t 0;  1 . Lú   2
2  1 1 t  1 1 t  2t 2t   1 3   VT   0   Vớ 1 t  0;   3   3 ệ ớ 1 t  0;   .  2  VP   0  2    Vớ 1 t  ;1 ,   ế 3 ợ 2      1 1 2
t t t  2 4 3 2 2 4 2 1 3  
 2t 2t   1
4 ( ế t  0). t t
N ậ t 1 là ộ ệ ủ 4 .   Xé à ố   1 1 f t   1 ;1   . t t 2 
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 97
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE     f t  1 1 1 '     0, t  
;1  f t : ị ế 1 ;1 . 2       t 2 t 2  2   
Xé à ố g t  t t  2 3 2 2 1 1 ;1   . 2     
g 't   6t 2t  2 1 2 3
1  4t 2t   1  0, t  
;1  f t  :   ồ ế 1 ;1 .    2  2  x
Vậ t 1 là ệ ủ    t  x  2 0 4 1 1  . x  2 Vậ ổ ệ 2 2 0  2  4 .
TN 4.8: Tổng các nghiệm củ 3 3
x 1  2 2x 1  là 3 A. 3 . B. 5 . C. 4 . D. . 2 Lời giải Đáp án: A  3 3
x  2x  2x 1 2 2x 1
x x   x  3 3 3 3 2 2 1  2 2x 1
f x  f 3 2x 1   1
Xé à ố f t 3
t  2t l ụ . f t  2 '
 3t  2  0, t
   f t ồ ế 2
Từ      f x  f  3 x   3 1 , 2 2
1  x  2x 1 3
x  2x 1  x   2
1 x x   1  0 1   5
x 1  x  . 2
Vậy tổng các nghiệm củ là .
TN 4.9: Số nghiệm củ 3 2 3
8x  36x  53x  25  3x  5  là A. 0 . B.1. C. 3 . D. 2 . Lời giải Đáp án: C
   x    x     x 3 3 3 3 2 3 2 3 3 5  3x  5
f x    f 3 2 3 3x  5    1 à à là   3
f t t t . Xé à ố   3
f t t t l ụ à x ị . f t  2 '
 3t 1 0, t
   t t ồ ế 2
Từ      f x    f  3 x   3 1 , 2 2 3 3
5  2x  3  3x  5
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 98
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE 3 2
 8x  36x  51x  22  0    x  2 5 3 2
8x  20x 1 
1  0  x  2  x  . 4
Nhận x t T ầ ế ề f g x  f hx     à   3
f t mt nt . T ầ ồ ể ứ ế mx  3 3 3 3 5
n 3x  5 à
ớ ế PT ọ n 1.
C ệ ò l là ử ở ế mpx u   px u  mx  3 3 3 3 3 5  3x  5 . Dễ
m 1, p  2  x3 3 2  8x nên 3 mp  8 ờ ợ x  .
m  8, p 1
Nế m  1, p  2   3
f t t t . D , ầ ế ề
mpx u   px u  mx  3 3 3 3 3 5  3x  5
  x u3  x u 3 2 2
 3x 5 3x 5 3
x   u 2 x   2 u   3 3 8 12 6
1 x u u  5  3x  5 12  u  36  
Đồ ệ ố ớ ế ủ , ợ ệ 2 6u 1  53  u  3  .  3
u u  5  15  
D ờ ợ m  1, p  2 ế xé ờ ợ ế ế m  8, p   1 . N lờ a b c
TN 4.10: Nghiệm nhỏ nh t củ 3 2 3
x 15x  78x 141  5 2x  9  có d ng với 2
a, ,bc . K abc là A. 17 . B.11. C.13 . D. 15 . Lời giải Đáp án: C
  x    x     x 3 3 3 3 5 5 5 2 9  5 2x 9
f x    f 3 5 2x  9    1
ớ à f t 3  t  5t .
Xé à ố f t 3
t  5t trên , f t  2 '
 3t  5  0, t
   f t ồ ế 2
Từ      f x    f  3 x   3 1 , 2 5 2
9  x  5  2x  9 3 2
x 15x  75x 125  2x  9 3 2
x 15x  73x 116  0    x  4 11 5 2
x 11x  29  0  x  4  x  . 2
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 99
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE a 11 11 5 
Vậy nghiệm nhỏ nh t là: x   b
 1  a b c 17 2 c  5  Nhận x t
N í ụ , ầ í  à
mpx u   px u  mx  3 3 3 3 5 2 9  5 2x 9  
1 ớ à f t  3  mt  5t . Do sau khi khai triển   3 m px u ử  3  3 3 mp x x trong  3
mp 1 ể ọ m p  1. Lú à
   x u3  xu 3 1 5
 2x 9  5 2x 9 2 T ễ   3 x u ử  u 2 2 3 x 1
 5x u  5  . 3
Lú à    x  3  x     3 x   3 2 5 5 5 2 9  5 2x 9 3
Khai triển 3 ợ  ị m p  1 là ú ớ . TN 5.1: C 3 2 2
2 7x 11x  25x 12  x  6x 1  . Tính tổ ệm củ A. 50. B. 100. C. 53. D. 80. Lời giải Đáp án: A
   x   2x x   2 2 7 4
3  x  6x 1   1 Đ ề ệ 4 x   2
do : x x  3  0, x   . 7 T VT
x   2x x   2 2 7 4
3  x  6x 1  VP .
D "  " x   x     2 x x   2 7 4
3  x  8x  7  0  x  1  x  7 .
Kế ợ ớ ề ệ , ệ ủ là x 1  x  7 . 1 1
TN 5.2: Tính tích các nghiệm củ x x   1   1 x x 1 5 1 5 A. -2. B. . C. . D. 2. 2 2 Lời giải Đáp án: B
Đ ề ệ x 1.
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 100
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE   1  1 x     1  1 Cauchy   x
x   1. x      T xx  2 1 1 
  x   1  x 2  1 x xx Cauchy   1  1 1 1     1 x x   x x 2 Từ  
1 ,2  D "  " trong 2 x  1 1  x   x 1 5 1 5 2  
x x 1  0  x   x  . 1 2 2   x 1  x
Kế ợ ớ ề ệ , ệ ủ là 1 5 x  . 2 TN 5.3: C 2
4  4x x x 1  x  2  2x  3  4x 14 . Tính tích các nghiệm củ trình? A. 3. B. 5. C. 2. D. -9. Lời giải Đáp án: C
VP x 1  x  2  2x  3  4x 14  x 1 x  2  2x  3  4x 14  8  
1 D "  " x x  2 .
VT    x  2 8 2  8 2 D "  " x x  2 . Từ  
1 ,2  P ệ x  2 . 5 2  7 TN 5.4: P
 4x  3 2 1  
1 có bao nhiêu nghiệm th c? x 1 A. 1. B. 2. C. 3. D. 4. Lời giải Đáp án: A Đ ề ệ x  1  .   5 2  7 1   4x   1  3 2  3 2 x 1   Sử ụ BĐT C ố 5 2 7 5 2 7   ợ x   ,
x  , 4x  1 4 1 4 1 5 2  7 5 2  7 Cauchy 5 2  7 5 2  7       x  
x   4x  3 1 3
x  . x  .4x  1 4 1 4 1 4 1 4 1 1 5 2  7 1 5 2  7    4x   3 1  3. 5 2  7 2 x 1 2 x 1
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 101
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE 5 2  7   4x   1  3  2  3 3 1 x 1 5 2  7   4x   1  3 2  3 3 x 1  Từ  5 2 7
2,3  "  " trong 3 x     x   4 x 1 4 1 4x   1  0 x  1  5 2  7            x   4  x  1 5 2 7 4 1                   x  4x  1 4  x  1  2 3 2 3 1 4 1 x  1  x  0   3   2      x    . 4   x   3 2 1  2 1 x  4  4   Kế ợ ớ ề ệ , ệ 3 2 x  . 4 TN 5.5: C 8 4 8 6 4 x  4  x  9 
x  2x x  25  . P nghiệm th A. 1. B. 2 . C. 3 . D. 4 . Lời giải Đáp án: A
x  0 là 1 nghiệm củ u     4x; 2 Đ  . v    2x; 3
M u v u v à "  " x  u, v ù 2  x=  . 3 TN 5.6: C 2 2 2 2
x y  2x  4 y  5 
x y  2x  6 y 10  29  . C p  ; x y thỏa
ã . Tí ị của A  5x 100 y ? A. 1. B. 0 . C. 100 . D. 25 . Lời giải Đáp án: A Tậ x ị D  .
  x  2   y  x  2 2 2 1 (2 ) 1  (3  y)  29
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 102
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE      u   x   yux 2 2 1 (2 y) 1; 2    Đ v   1   ;
x 3  y   v   1   x2 2  (3 y) .   u v    2  ;5 
u v   2  2 2  5  29 
M u v u v à "  " x  u, v ù 1
 5x  2y  1  x  , y  0 . 5 TN 5.7: C 4 2 2 4 2
x  4x  1 x
x 11x 1. P ệm th c? A. 1. B. 0 . C. 2 . D. 3 . Lời giải Đáp án: D
+ x  0 là 1 nghiệm của pt u     2x; 2x
+ x  0 , Đ v   1; x
M u v u v à "  " x  u, v ù ợc x   2 . TN 5.8: C 4 2 4 2
x  8x  32  x  6x 18  5 2 . Tính tổ ệm của 48 48 48 15 A. . B. . C. . D. . 7 5 15 7 Lời giải Đáp án: A
A 2x  4; 4   4 2      OA x 8x 32   C ọ B 2 x  3; 3 4 2  O
B x  6x 18   O  0; 0   AB 5 2 
ta có AO BO AB 24 D u bằng x y ra khi ,
A B, C thẳng hàng  x   . 7 TN 5.9: P 2 2 2 x x 1 
x x 1  x x  2  
1 có bao nhiêu nghiệm th c? A. 1. B. 2 . C. 3 . D. 4 . Lời giải Đáp án: A 2
x x 1 0     Đ ề ệ 1 5 1 5   x   x  . 2
x x 1 0, x   2 2
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 103
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE Á ụ BĐT BCS ố 2 2 1; x x 1; 1;
x x 1 ợ 2 2 VT x x  
x x    2 2
  2x x   2 1 1 1 1 1 x x   1   2 x  . Hay 2 2 x x 1 
x x 1  2 x 2 T VT
x x x  
x   x     x  2 2 2 2 2 2 1 1  0 Hay 2
x x  2  2 x 3 2 2
 x x 1 x x 1  2 x Từ   1 ,2,3  
 D "  " trong 2,3 ồ ờ x 2
x x  2  2 x 2 2 x x 1 x x 1    x 1. 1 1
S ớ ề ệ , ệ x 1.
TN 6.1: Tập hợp t t c các giá trị của tham số x ể x  2  x có nghiệm là 2 1 2 8 8 8 A. m  5 . B. m  . C. m  5 . D. m  5 . 3 3 3 Lời giải Đáp án: C Đ ều kiệ x ịnh 1   x 1.
Đ t t  1 x  1 x, 2  t  2 ở thành 2
2t t  4  m   *
P * í là à ộ ểm của parabol P 2
: y  2t t  4 à ờng thẳng
d : y m ù ới trục hoành.
D , ố nghiệm của pt * chính là số ểm của P và d  .
Phát họa  P và d  lên cùng hệ trục, ta th ã ệm khi 2  m  6 . y 6 2 x O 2 2
TN 6.2: Có bao nhiêu giá trị nguyên của tham số m  2  018;201  8 ể 2 x  3 2
2x  5mx  3x  6  0 có nghiệm. x A. 2017 . B. 2018 . C. 2019 . D. 2020 . Lời giải Đáp án: C
Tậ x ịnh: D   3;0  3;   
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 104
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE 2 x  3 x  3 Ta có: 2
2x  5mx  3x
 6  0  2x 3 2 2  3x  5mx x x 2 2 x  3 x  3  2  3  5m  1 x x 2  Đ x 3 t t
t  0  1 trở thành: 2
2t  3t  5m2 x Để  
1 có nghiệ ng trình 2 có nghiệ . Do 2
t  0  2t  3t  0  m  0 m 2  018;201  8 Do 
nên có 2019 giá trị nguyên của m thỏa mãn yêu cầu bài toán. m
TN 6.3: Có bao nhiêu giá trị nguyên của tham số m ể 2 4 2
x  3x 1  m x x 1 có nghiệm A. 1. B. 8 . C. 15 . D. 27 . Lời giải Đáp án: A
Tậ x ịnh củ D  0;  . Ta có: 2 4 2
x x   m x x    2
x x     2
x x    m  2
x x   2 3 1 1 2 1 1
1 x x   1 2 2 x x 1 x x 1  2 1 m 1 2 2   x x 1 x x 1 2   Đ x x 1 2x 2 t t   1  1 2 2 x x 1 x x 1 1 x  1 x   2x 2x  1 1  1  1 2 x x 1 2   x x 1  Do x  0 nên       2 t 1; 3  1  1  3 x   2  1 xx  1  x 2  K   2t 1 1 1 trở à 2
2t mt 1  0  m   2t  2 t t
Để ã ệ 2 có nghiệm thuộc 1; 3 1
Xét hàm số: y  2t  ;t  1; 3 t  1   1   t t
 2t     2t   2t t  2 1    2 1 2 1 t t t .t       1
Với t ;t  1; 3 ;t t 2 1 1 2   2   0 1 2  1 2  xét tỉ số t t t t t .t 2 1 2 1 1 2 1 1 1 5 3
Suy ra hàm số y  2t
ồng biến trên nửa kho ng 1; 3  y 1  2t   y 3 1 2t   t      t t 3 5 3 1 m  3
Do m là số nguyên nên có duy nh t 1 giá trị của m thỏa mãn yêu cầu bài toán. TN 6.4: Tìm số các giai trị ủa tham số m ể 2 3 2 3
x m x
x m x  m   2 2 ( ) ( ) 6 1
x m  4x  6  4m  0 có nghiệm.
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 105
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE A. 0 . B. 1. C. 2 . D. 3 . Lời giải Đáp án: B 2
a x m x 2 2 2
a b  2 x m  (a b)  4x  4m Đ t: 
a  0,b  0   2 b
  x m x 2 2
ab  ( x m x)( x m x)  m Kết hợp với ( )  , ợc hệ ab m   3 3 a b  
b  a b 2 3 a 1
 (a b)  6  0 ab m   3 2
(a b)  (a b)  3(a b)  6  0 a b  2 b   2  a  2         ab m    aa 2a m a 2  m
Xét hàm y f a 2
 a  2a với 0  a  2 có b ng biến thiên
Vậy 0  m 1 suy ra m 1 . TN 6.5: C 4 2 m x 1  3
x 1  2 x 1 , biết rằng tập t t c các giá trị của tham số m ể ã ệm là nửa kho ng ( ;
a b]. Tính giá trị biểu thức 3 3
S a b . 28 26 A. . B.  . C. 1.  D. 1. 27 27 Lời giải Đáp án: B
Đ ều kiện x 1, Chia hai vế cho x 1 ợc pt: x 1 x 1 x 1 2 4 m  3   2 . Đ t 4 4 t   1 x 1 x 1 x 1 x 1 2 2 Do x 1  2   1 0  1  1 0  t  1 x 1 x 1 T 2 m  3
t  2t (*) . B ng biến thiên của hàm 2 f (t)  3
t  2t trên [0;1)
Theo b ng biến thiên thì (*) có nghiệm thuộc [0; 1)  1   m 1/ 3.
TN 6.6: Biết rằng tập hợp các giá trị của m ể (m  2) x  3  (2m 1) 1 x m 1  0 có nghiệ là n  ; a b .
Giá trị của S  2019b  2020a 1  72 là : A.1918 . B.1819 . C.1981. D. 2019 . Lời giải Đáp án: C
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 106
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE
+) (m  2) x  3  (2m 1) 1 x m 1  0 , ều kiện 3   x 1
a x 3 +) Đ t 
, 0  a, b  2 b   1 x 2 2 a b  4 +) Ta có :  (I)``
(m  2)a  (2m 1)b m 1  0 +) Trong hệ tọ ộ O , 2 2
a b  4 là ờng tròn tâm O bán kính R  2 , và  2 m
(m  2)a  (2m 1)b m 1  0 là ờng thẳng  có hệ số góc k  (vì với 2m 1 1 m  ệm). 2 y d2: k2=7 f(x) = 4 x2 2 B 2-m : k = 2m-1 -1 1 d1: k1= 3 O A 7 2 x -1 3  1 1 
+) Nhận xét th y  ểm I  ;    cố ịnh.  3 3 
+) Hệ (I) có nghiệm   nằm trong miền góc nhọn t o bởi d , d 1 2  7 1  1 +) IA ;   
d có hệ số góc k  .  3 3  1 1 7  1 7  +) IB ;   
d có hệ số góc k  7 .  3 3  2 2  3 a   1 2  m 3 5  5
+) Yêu cầu bài toán  k k k  
 7   m    1 2 7 2m 1 5 3 5 b    3
S  2019b  2020a 172 1981.
TN 6.7: Gọi T là tập các giá trị nguyên củ ể 16x m  4  4x2 18x  4  m có 1
nghiệm.Tính tổng các phần tử của T. A.0. B.20. C.-20. D.10. Lời giải Đáp án: C
Đ t t  16x m  4,t  0 . Ta có 2
m t 16x  4 P ở thành         
x t   x t   t 2x 16x m 4 2x 2 . 2 1  0     t  2x 1
 16x m  4  2x 1
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 107
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE x  0  m  4 2 x 16x  4   1 x   2  m  4 2 x  20x  5  4  m  4
Từ ồ thị, 1 nghiệm  m  20
Do m thuộc Z nên T   ; 3  ; 2  ; 3 ; 2 ; 1 ; 0 ; 1   20 .
TN 6.8: Có bao nhiêu giá trị m ể m x m x m có nghiệm A. 2 B. 3 . C. 4 . D. 5 . Lời giải Đáp án: C m x  0  m  0     m  0 ĐKXĐ m x 0   x  0   . 2 m  0  0  x m   x mx  0
+ Khi m  0 ệm duy nh t x  0 . + Khi m  0 2 2
m x m x  2 m x m 2
m  2m  0  2 2 2 2
 2m  2 m x m  2 m x m  2m  4 * 2
m x   2
m  2m2   m  2 
D ều kiện m  0 nên   *  4   2 m x 4 3 2
m  4m  4mm  2 m  2  3     m 4  m . 4 3    4
x m  4mx   4 D ều kiện 2
0  x m ệm khi:  m  2   m  2 3
m 4  m    0  m  4  2  m  4. 4        m m m 2  2 3 0 4 2   m  4
Vậ ể ệm thì m  0 ho c 2  m  4 . D 4 giá trị nguyên của m thỏa mãn bài ra.
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 108
Chuyên đề : PT-BPT-HPT VÔ TỈ
TOÁN THPT - MAKE THE MATH SHINE
TN 6.9: Tìm giá trị nhỏ nh t của m ể 3 4 2 3 2
x  2x 1  3 x 1 1 m  0 có nghiệm. 3 5 7 5
A. m   . . B. m   . C. m   . D. m  . 4 4 4 4 Lời giải Đáp án: B Đ t 3 2 2 3 4 2 t
x 1, t  1  t x  2x 1 T ợ 2 2
t  3t 1 m  0  t  3t 1  m Xét hàm số 2
y t  3t 1,t  1 B ng biến thiên 3 t 1 2 1   y 5  4 5
D a vào b ng biế , ệm khi m   4
TN 6.10: Hỏi có bao nhiêu giá trị m à ỏ 0 0 ể
2 x  2 x  2 x m m có các nghiệ ề A. 2019 . B. 2018 . C. 2015 . D. 2014 . Lời giải Chọn C
Ta chỉ cầ xé ờng hợp x  0 và m  0 . K ểu thức vế ề x ịnh.
Đ t y  2 x  2 x m và z  2 x m y, z  0
2 x y m 
Ta có hệ 2 x z y
2 x m z 
Không m t tính tổng quát, ta gi sử m y z
 2 x z  2 x y  2 x m y m z m y z 2 m  4m
Thay m y z vào hệ ợc: 2
2 x m m  4x  4m m x  4 Để có 2
x  0  m  4m  0  m  4  m  5, 6, 7..., 2019.
N ậy có t t c 2015 giá trị m thỏa mãn yêu cầu củ ề ra.
Trần Mạnh Tường https://www.facebook.com/groups/TAILIEUDAYTHEMTOANTHPT/ 109