



















































































Preview text:
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng
PHƯƠNG PHÁP HÀM ĐẶC TRƯNG GIẢI PT, BPT MŨ – LÔGARIT
Dạng 1: Phương pháp hàm đặc trưng giải pt, bpt mũ không chứa tham số 2
Dạng 2: Phương pháp hàm đặc trưng giải pt, bpt mũ chứa tham số 18
Dạng 3: Phương pháp hàm đặc trưng giải pt, bpt lôgarit không chứa tham số 28
Dạng 4: Phương pháp hàm đặc trưng giải pt, bpt lôgarit chứa tham số 54
Dạng 5: Phương pháp hàm đặc trưng giải pt, bpt có tổ hợp mũ - lôgarit không chứa 73 tham số
Dạng 6: Phương pháp hàm đặc trưng giải pt, bpt có tổ hợp mũ - lôgarit chứa tham số 102
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 1
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng
PHƯƠNG PHÁP HÀM ĐẶC TRƯNG GIẢI PT, BPT MŨ - LÔGARIT
Phương pháp hàm số đặc trưng thường xuyên xuất hiện trong đề thi THPT Quốc Gia và đề thi
tốt nghiệp THPT, nó cũng là một trong những câu phân loại của đề:
-Câu 47 mã đề 101 – THPT QG năm 2017.
-Câu 35 đề tham khảo – BGD&ĐT năm 2018.
-Câu 46 mã đề 101 – THPT QG năm 2018.
-Câu 47 đề tham khảo – BGD&ĐT năm 2020.
-Câu 47 đề tham khảo – BGD&ĐT năm 2021. -……..
Sau đây, tôi xin trình bày cơ sở lý thuyết và giới thiệu một số bài toán áp dụng của nó:
I - CƠ SỞ LÝ THUYẾT
Cho hàm số đặc trưng y f t liên tục trên tập D .
+ Nếu hàm số f t đơn điệu một chiều (đồng biến hoặc nghịch biến) trên D và tồn tại
u , v D thì f u f v u v .
+ Nếu hàm số f t đồng biến trên D và tồn tại u , v D thì f u f v u v .
+ Nếu hàm số f t nghịch biến trên D và tồn tại u , v D thì f u f v u v . II - ÁP DỤNG
DẠNG 1: PHƯƠNG PHÁP HÀM ĐẶC TRƯNG GIẢI PT, BPT MŨ KHÔNG CHỨA THAM SỐ
1 - PT MŨ KHÔNG CHỨA THAM SỐ 2 2 Câu 1.
Gọi S là tập hợp mọi nghiệm thực của phương trình x 3x2 x x2 2 2
2x 4 . Số phần tử của S là A. 3. B. 2. C. 1. D. 4. Lời giải Chọn C 2 2 2 2
Ta có: x 3x2 x x2 2 2 2x 4 x 3x2 2 x x2 2 2
x 3x 2 2
x x 2 . Xét hàm số 2t f t t trên . Ta có: ' 2t f t
.ln2 1 0 , với mọi x .
Suy ra f t đồng biến trên . Nên f 2
x x f 2 3 2
x x 2 . 2 2
x 3x 2 x x 2 x 2 .
Suy ra phương trình đã cho có 1 nghiệm.
Suy ra số phần tử của S là 1. 3 2 Câu 2.
Tính tổng các nghiệm của phương trình
x 3x x x2 3 2 2019 2019
x 3x 2 0 . A. 3 . B. 2 . C. 2 . D. 3 . Lời giải Chọn D 3 2
x 3x x x2 3 2 2019 2019
x 3x 2 0 . 3 2
x 3x x 3 2 x2 2019
x 3x x 2019 x 2 (1). Xét hàm số:
2019t , ' 2019t f t t f t
ln2019 1 0,t f t đồng biến trên . x 1 (1) f 3 2
x 3x x f x 2 3 2 3 2
x 3x x x 2 x 3x 2 0 . x 1 3
Vậy tổng các nghiệm là 3 .
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 2
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng 2 2 Câu 3.
Phương trình x x 32 x 2 2 x3 2 9 6 4 3x x x
5x có số nghiệm là A. 1. B. 3. C. 2. D. 0. Lời giải 2 2
Phương trình đã cho tương đương với x x 32 x 2 2 x3 2 9 6 4 3x x x 5x 2 2 x x 2 x x 4 x6 64 2 3 2 4 6 3 x x x x (*) Xét hàm số 2t 3 t f t t
, ta ó ' 2t.ln2 1 3 t f t
.ln3 0 , t nên hàm số f t đồng biến trên . x 2 Khi đó * f 2
x x f 4x 6 2
x x 4x 6 . x 3 3 2 Câu 4. Phương trình 23x x x 3 2 2
.2 1024 23x 10x x có tổng các nghiệm gần nhất với số nào dưới đây. A. 0,35. B. 0, 40. C. 0, 50. D. 0, 45. Lời giải Chọn D 3 2 3 2 Ta có: 23x x x 3 2 23x x 3 10 x 2 2
.2 1024 23x 10x x 2
23x x 2 10x Hàm số
2t ' 2t f t t f t
ln2 1 0 đồng biến trên . 3 2 5 2 23x x 3 10 x 2 3 2 2
23x x 2
10x 23x x 10x x 0 hoặc x 23 10 Tổng các nghiệm bằng 0, 4347 . 23 a b 3 Câu 5. Gọi x là một nghiệm lớn hơn 1 của phương trình 0 c 1 1 x x 2x 3 1 2 1
2x 1 . Giá trị của P a b c là 3
A. P 6 .
B. P 0 .
C. P 2 .
D. P 4 . Lời giải Chọn D
Điều kiện xác định: x 0 . 1 1 x 1 x 1 x 1 x 1 2 3 1 2 x 2 2x 1 3 3 1 x 3 2x 1 1 x 1 2 3 x 3 x 1 1 . Xét hàm số 3t f t
t t 0 , ' 3t f t .ln3 1 0 2x 1 1 1 3 1 f f x 1
x 1 x
a 1, b 1, c 2 . Vậy P 4 . 2x 2x 2 Câu 6.
Có bao nhiêu cặp số nguyên x ; y thỏa mãn 1 x 2020 và 2 9y 3y x x ? A. 2020. B. 1010. C. 6. D. 7. Lời giải Chọn D Ta có y y y y x x x x 2 2 2 9 3 3 3 (1).
Xét hàm f t 2
t t , t 0 .
Ta có: f 't 1 2t 0 , t 0 f t là hàm đồng biến trên 0 ; .
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 3
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng Vì vậy, (1)
3y 3y f x f x . Theo giả thiết, 1 2020 1 3y x
2020 0 y log 2020 . 3
Vì y nguyên nên y 0 ;1 ; 2 ; 3 ; 4 ; 5 ;
6 x 1 ; 3 ; 9 ; 27 ; 81 ; 243 ; 72 9 .
Vậy có 7 cặp x ; y thỏa mãn. 2 Câu 7.
Có bao nhiêu số nguyên dương x thỏa mãn x 2 cos 2.2 sin 2 y x y ? A. 4. B. 3. C. 1. D. 0. Lời giải Chọn D 2 2 Có x 2 cos y x 1 cos y 2
2.2 x sin y 2 2 x 1 2 cos x (3). Đặt
2t ' 2t f t t f t
.ln2 1 0 , t 0 Hàm số y f t đồng biến trên 0 ;
Vì vậy phương trình (3) f x f 2 x 2 2 1 cos
x 1 cos x x s
in x x 0 .
Mà x là số nguyên dương. Vậy không có giá trị nào của x thỏa mãn. Câu 8.
Có bao nhiêu cặp số nguyên x ; y thỏa mãn 0 x 2020 và x 1 3 1 3y x y ? A. 2020 . B. 2021 . C. 2022 . D. 2023 . Lời giải Chọn B Ta có: x 1 3 1 3y x
y f x
1 f y Xét hàm số 3t f t t ' 3t f t
.ln3 1 0 , t R
Do đó f x
1 f y x 1 y x y 1
Vì 0 x 2020 0 y 1 2020 1 y 2021
Mà y nên y 1 ; 2 ; 3 ;.. ; 202 1
Vậy có 2021 cặp số nguyên x ; y thỏa mãn yêu cầu bài toán. Câu 9.
Có bao nhiêu cặp số nguyên dương x ; y là nghiệm của phương trình .3125x 1 5y x y
và thỏa mãn y 60 . A. 10 . B. 13 . C. 11. D. 12 . Lời giải Chọn D
Ta có .3125x 1 5y x y 5
.5 x 1 5y x y log 5 .5 x log 1 5y x y
5x log x log y 1 y 5 5 5 5
5x log 5x y 1 log y 1 . 5 5
Xét hàm số f t t log t , t 0 . 5 1
Ta có f 't 1
0, t 0 . Khi đó f 5x f y
1 5x y 1. t.ln5
Như vậy tương ứng với mỗi giá trị x nguyên dương ta đều có y nguyên dương mà y 60 61
suy ra 5x 61 x . 5
Mặt khác x nguyên dương nên x 1 ; 2 ; 3;..;1 2 .
Vậy có 12 cặp số x ; y nguyên dương thỏa mãn đề bài.
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 4
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng x22 1 3 1
Câu 10. Tổng các nghiệm của phương trình x6 x 1 9.3
x 4 2 x 2 x8 x 4 5 27 5.5 x bằng A. 37 . B. 6 . C. 3 . D. 3 . Lời giải Chọn D x22 1 3 1 Ta có: x6 x 1 9.3
x 4 2 x 2 x8 x 4 5 27 5.5 x 2 1 x 1 8 3 x 8
3x x x 4x 1 1 x8 4 1 2 2 x 4 x 1 5 5 1
Xét hàm số f t 3t t , 5t ln5
có: f 't
3t ln3 1 0,t nên hàm số y f t luôn nghịch biến 5t
Do đó, phương trình
1 có nghiệm f x f 2 8 x 4x 1 có nghiệm 3 37 x 2 2
x 8 x 4x 1 2
x 3x 7 0 3 37 x 2
Vậy tổng các nghiệm của phương trình trên là 3 .
Câu 11. Số nghiệm của phương trình x x x x x x 2 2 2 3 5 x 8 x3 5 2 8 3 .8 3 5 .8 là A. 4 . B. 3 . C. 1. D. 2 . Lời giải Đặt 2
u x 8x 3, v 3x 5 , phương trình đã cho viết lại là
.8v .8u 1 8v 8u u v u v u v 1 *
Ta thấy u 0 hoặc v 0 thỏa mãn phương trình * . 1 8v 8u 1
Với u 0 và v 0 ta có * ** v u Ta thấy: 8u 1 8u 1 Nếu u 0 thì
0 và nếu u 0 thì
0 . Do đó VP * * 0, u 0 . u u 1 8v 1 8v Nếu v 0 thì
0 và nếu v 0 thì
0 . Do đó VT * * 0, v 0 . v v Từ đó suy ra * * vô nghiệm.
Như vậy, phương trình đã cho tương đương với x 4 13 2 u 0
x 8x 3 0 x 4 13 . v 0 3x 5 0 5 x 3
Vậy, phương trình đã cho có 3 nghiệm.
Câu 12. Phương trình x 2 x 1 2 e e
1 x 2 2x 1 có nghiệm trong khoảng nào?
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 5
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng 5 3 3 1 A. 2; . B. ; 2 . C. 1; . D. ;1 . 2 2 2 2 Lời giải Chọn A 1 ĐK: x 2 x 2 x 1 2 e e
1 x 2 2x 1 x x e e
x x 2 2 2 1 1 2 1 1 2 x e x 2 2 x 1 1 e 2x 1 1 * 1 Xét hàm số t
f t e t 2 1 với t 2 1 1 ' t f
t e 2t
1 0 với mọi t . Suy ra hàm số đồng biến trên ; . 2 2
* f x f 2x 1 x 2x 1 x 0 x 0 x 0 x 1 2 . 2 2 x 2x 1
x 2x 1 0 x 1 2 x 1 2
Câu 13. Có bao nhiêu số nguyên
y 10 sao cho tồn tại số nguyên x thỏa mãn y y 2 x x x x 2 2 2 1 5 2 5 1 ? A. 10 B. 1 C. 5 D. Vô số Phân tích
Phương trình dạng f u f v .
Phương pháp: Chứng minh y f t đơn điệu trên a;b . Từ phương trình suy ra u v . Từ
đó tìm sự liên hệ giữa 2 biến , x y và chọn , x y thích hợp. Lời giải Chọn C y 2 y y y 2 2 Ta có: 2 x2 x x 1 x 2 x2 x x 1 2 5 2 5 1 5 2 x 1 5 x x Xét: 1 5t f t
t đồng biến trên . Do đó từ phương trình trên suy ra: y y y y
x x x x 2 2 2 2 2 1 1
2 2 x 1 2 . y
Do x nguyên nên ta có 2
2 và y 10 nên y 0; 2; 4; 6; 8 . 1 2
Câu 14. Có bao nhiêu số nguyên y sao cho tồn tại x ;3 3x xy 9 x thỏa mãn 27
1 xy 27 ?. 3 A. 10 . B. 12 . C. 11. D. 9 . Lời giải Chọn C 2
Viết lại phương trình thành 3x 9
27 x 1 27 x y xy 2 +) Ta có 2
1 3x 9x log
1 xy xy 3x 9x 1
log t t , với t 1 xy 0 . 27 27 31 1
+) Xét hàm số f x 2
3x 9x 1. Ta có
f x 1 x ;3 . 4 3
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 6
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng 1 1
+) Xét hàm số g t log t t, t 0. gt
1 ; gt 0 t 27 t ln 27 ln 27 1 2 31 1
t 8,07.10 ; 0,04 31 Ta có
f x 1, x ;3 suy ra
g t 1 4 3 4 t 1; 8, 4 1 2 1 8, 07.10 1 0, 04 y 12 8, 07.10
1 xy 0, 04 hay x x
1 1 xy 8, 4 7, 4 0 y x 1 3 y 1 3 , ( x ;3
, y nguyên). 3 0 y 22
+) Nhận thấy y 2; y 1 thỏa mãn đề. +) Với 2
0 y 22 , ta có
1 3x 9x 1 log
1 xy 1 xy 0 . 27 1
Nhập hàm, thay các giá trị nguyên của y, kiểm tra nghiệm x ;3
dẫn đến chọn 1 y 9 3 . Vậy y 2 ; 1 ;1; 2;...;
9 nên có 11 giá trị nguyên của y thỏa mãn đề.
Câu 15. Có bao nhiêu cặp số nguyên ;
x y thỏa mãn đồng thời 1 x 2022 và 2 x 2 x y 2 384.128
6.8 6 3y 7x 14x ? A. 674 . B. 1348. C. 1346 . D. 2022 . Lời giải Chọn B 2 2 x 2x y 2 7 x 1 2 + Ta có: y x x x 3 y 1 384.128 6.8 6 3 7 14 3.2 7 1 3.2 3y 1. + Xét hàm số 3.2t f t
t, t 0 có 3.2t f t
.ln 2 1 0 nên hàm số đồng biến trên 0; . 2
+ Do đó: x y 2 7 1 3 1
7 x 2x 6 3y . x 23
x 3n 2
+ Vì x, y nên 2
x 2x 3 , n x3 x 3n 1 2020 n 1
3n 2 2022 0 n 673 mà 3 3 1 x 2022 1 3n 2022 1 1 n 674 n 674 3
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 7
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng
hay có 1348 số nguyên n . Mỗi giá trị của n cho chúng ta một cặp số nguyên ; x y thỏa mãn
điều kiện của bài toán.
Vậy có 1348 cặp số nguyên ;
x y thỏa mãn điều kiện của bài toán.
Câu 16. Có bao nhiêu cặp số nguyên dương ;
x y thoả mãn 0 x 2020 và 3x 1 27y x y . A. 2020. B. 673 . C. 672 . D. 2019 . Lời giải Chọn B Ta có: 3x.
1 27 y. log 3 . x 1 log 27 y x y x .y 3 3 x log
x 1 3y log y x 1 log
x 1 3y log y log 3 3 3 3 3 3 x 1 log
x 1 3y log 3y . (*) 3 3
Xét hàm số f t t log t , với t 1; 202 1 . 3 1
f 't 1
0 , t 1; 202 1 . l t n3
Suy ra hàm số f t liên tục và đồng biến trên 0; 202 1 .
Mà (*) f x
1 f 3y x 1 3y x 3y 1. 1 2021
Vì 0 x 2020 0 3y 1 2020 1 3y 2021 y . 3 3 Do
y y 1; 2;3;..; 67
3 . Ứng với mỗi giá trị y cho ta một x nguyên dương. Vậy có 673 cặp ;
x y thỏa yêu cầu bài toán.
Câu 17. Cho hàm số f x x x 3 e e 2x .
x Phương trình f x x f x 1 4 2
x 3 0 có tập nghiệm là A. 0 . B. 1 . C. 0; 1 . D. 1 ; 3 . Lời giải Chọn A
Trước hết ta nhận thấy rằng: f x là hàm lẻ vì: f x x x 3 e
e 2x x f x
Đạo hàm: f x x x 2 ' e e
6x 1 0 Hàm số đơn điệu tăng.
Từ phương trình giả thiết: f x x f x 1 x f x x f x 1 4 2 3 0 4 2 x 3 x x 1 x x 1 4 2 3 4 2
3 4x 2.2x f x f x x x 3 0 2x 3 VN
tập nghiệm của phương trình đã cho là: 0 .
2x 1 x 0 x y xy xy 1
Câu 18. Cho các số thực x , y với x 0 thỏa mãn 3 1 e e
x y 1 1 1 e 3y . Gọi x3 e y
m là giá trị nhỏ nhất của biểu thức T x 2 y 1 . Mệnh đề nào sau đây là đúng?
A. m 2;3 .
B. m 1; 0 .
C. m 0; 1 .
D. m 1; 2 . Lời giải Chọn C x y xy xy 1 Từ giả thiết 3 1 e e
x y 1 1 1 e 3y x3 e y x y 1 xy 1 3 e x y xy (1). x y 3 1 e 1 3 xy 1 e e
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 8
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng t 1 t 1
Xét hàm số f t = e
t với t ta có f 't = e 1 0, t
f t là hàm et et
số đồng biến trên . x 1
Phương trình (1) có dạng f x 3y f xy
1 x 3y xy 1 y (x 0) . x 3 2 2x 2 4 x 6x 5
Khi đó T x 2 y 1 x 1 T ' 1 0, x 0 x 3 x 32 x 32 2.0 2 1 T 0 1 m . min 0 3 3 10 1 1 1
Câu 19. Có bao nhiêu cặp ;
x y thỏa mãn 10xy x y 10xy và *
x , y 0 . x y A. 14 . B. 7 . C. 21. D. 10 . Lời giải 10 1 10 1 1 x y xy x y xy x y 1 10 1 1 1 10 1 10 x y .10 10 .10xy
.10 x y 1 .10xy x y xy x y xy
Xét hàm số ( ) .10t f t t
trên khoảng 0; . (
) 10t .10t f t t ln10 0, t
0 nên hàm số ( ) .10t f t t
đồng biến trên khoảng 0; 10 1 1 10 1 10 1 Do đó:
.10x y 1 .10xy 1 x y xy x y xy 1 1 1
10 x y 1 10 y x . xy y x 1 1 Vì y 2, y 0 nên 2 x
8 x 8x 1 0 4 15 x 4 15 , * x y x
x A 1; 2;3; 4;5;6; 7 . 0 1
Với mỗi số a 0 phương trình 2 y
a y ay 1 0 (*) có S a 0 y P 1 0
Phương trình (*) luôn có hai nghiệm y 0 . Vậy có 14 cặp x; y thỏa mãn yêu cầu bài toán. Câu 20. Có bao nhiêu cặp số nguyên x ; y thỏa mãn 0 x 2020 và 2 x y 2
2.625 10.125 3y 4x 1 A. 2020 . B. 674 . C. 2021 . D. 1347 . Lời giải Chọn D Cách 1 Ta có 2 2 x y 2 4 x 3 y 1 2
2.625 10.125 3y 4x 11 2.5 2.5
3y 4x 1 2 4 x 2 3 y 1 2.5 4x 2.5 3y 1 * Xét hàm số 2.5t f t
t là hàm số đồng biến trên .
Ta có f 2
x f y 2 2 * 4 3
1 4x 3y 1 4x 1 3y 2x 1 2x 1 3y **
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 9
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng
Do x, y nguyên nên 2x 1 ; 2x 1 và 3 là số nguyên tố nên ** tương đương với hoặc 2x
1 3 hoặc 2x 1 3 Nếu 2x
1 3 2x 1mod3 2x 4mod3 x 2mod3 Nếu 2x 1 3 2x 1
mod3 2x 2mod3 x 1mod3
Ta có 2021 giá trị nguyên của x sao cho 0 x 2020 . Trong đó có 674 số chia hết cho 3.
Nên có 1347 số thỏa ** . Với mỗi giá trị nguyên của x thì ta tìm được một và chỉ một giá
trị y nguyên tương ứng. Vậy có 1347 cặp ;
x y nguyên thỏa mãn bài toán. Cách 2 Ta có 2 2 x y 2 4 x 3 y 1 2
2.625 10.125 3y 4x 11 2.5 2.5
3y 4x 1 2 4 x 2 3 y 1 2.5 4x 2.5 3y 1 * Xét hàm số 2.5t f t
t là hàm số đồng biến trên .
Ta có f 2
x f y 2 2 * 4 3
1 4x 3y 1 4x 1 3y ** x 3k
Ta thấy x x 3k 1 k .
x 3k 2
Với x 3k thì 2 2
4x 1 4.9k 1 không chia hết cho 3 nên trường hợp này loại. x 3k 1 Với 2
thì x 3m 1 m nên 2
4x 1 12m 3 chia hết cho 3. x 3k 2 x 3k 1 Vậy
mặt khác 0 x 2020 nên có 1347 số nguyên x thỏa ** . x 3k 2
Với mỗi giá trị nguyên của x thì ta tìm được một và chỉ một giá trị y nguyên tương ứng. Vậy
có 1347 cặp x ; y nguyên thỏa mãn bài toán. 2
Câu 21. Có bao nhiêu cặp số nguyên ; a b thỏa ab
abab 2 2 4.2 8
a b 3a b ab 2 0 ? A. 12. B. 10. C. 14. D. 9. Lời giải Chọn A 2 +) Ta có: ab
abab 2 2 4.2 8
a b 3a b ab 2 0 ab2 2 2 3ab3a3 2 2 2 b a b
3ab 3a 3b 1 . +) Xét hàm 2t f t
t trên , có ' 2t f t
.ln2 1 0, t
f t đồng biến và liên tục trên , nên:
f a b2 f ab a b a b2 1 2 3 3 3
2 3ab 3a 3b 2
a b 2
3 a b 3b 2 0 2 .
+) Xem (2) là phương trình bậc hai biến a và b là tham số. Tồn tại cặp số thực ; a b thỏa (2) khi và chỉ khi phương trình (2) có nghiệm 9 2 21 9 2 21
Δ 0 b 32 4 2
b 3b 2 2
0 3b 18b 1 0 b 3 3
Do b nguyên nên b 6, 5 , 4 , 3, 2, 1 , 0 .
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 10
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng a 4
+) Với b 6 : phương trình (2) thành 2
a 9a 20 0 . a 5 a 2
+) Với b 5 : phương trình (2) thành 2
a 8a 12 0 . a 6 a 1
+) Với b 4 : phương trình (2) thành 2
a 7a 6 0 . a 6
+) Với b 3 : phương trình (2) thành 2
a 6a 2 0 a 3 7 . a 0 +) Với b 2
:phương trình (2) thành 2
a 5a 0 . a 5 a 0
+) Với b 1: phương trình (2) thành 2
a 4a 0 . a 4 a 1
+) Với b 0 : phương trình (2) thành 2
a 3a 2 0 . a 2
Vậy có 12 cặp số nguyên a,b thỏa yêu cầu bài toán: 4 ; 6 , 6; 4 ,5; 2, 2 ; 5, 5
; 6,6; 5,1; 4,4;
1 , 0; 2,2;0,0; 1 ,1;0. 2 2 2
Câu 22. : Cho các số thực ,
x y thỏa mãn x 2 y xy 2 2 1 ( 1) xy y e e x xy y e
0 . Gọi M, m lần lượt 1
là GTLN, GTNN của biểu thức P
. Tính M m . 1 xy 1
A. M m 1 .
B. M m 2 .
C. M m .
D. M m 3 . 2 Lời giải Chọn A 2 2 2 2 2 2 Ta có x 2 y xy 2 2 1 ( 1) xy y e e x xy y e 0
x 2 y xy 2 2 1 ( 1) y e x xy y e 0 2 2 2
x xy 2 y 2 2 1 y 2 e
x xy 2 y e 1 y (1) Xét hàm ( ) t
f t e t,t . Ta có ( ) t
f t e 1 0 t
nên f (t) đồng biến trên . Do đó (1) 2 2 2 2 2 2 2 2
f (x xy 2y ) f (1 y ) x xy 2y 1 y x xy y 1 1
x y2 xy xy 1 Khi đó suy ra 1 xy . 1
x y2 3xy 3 xy 3 1 1 1 1 1 3 Do đó P P
. Vậy M m 1 11 1 xy 1 1 2 1 xy 2 3 2 2 2
Câu 23. Cho các số thực x , y thỏa mãn x 2 y x 2 y 2yx 2 5 16.4 5 16 .7
. Gọi M và m lần lượt
10x 6 y 26
là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P
. Tính T M m . 2x 2 y 5 21 19 A. T .
B. T 10 .
C. T 15 . D. T . 2 2 Lời giải Chọn D Đặt 2
t x 2y , khi đó giả thiết tương đương với
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 11
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng t 2 2t
5 16.4t 5 16t t 5 4 5 4 2 .7 .(1) t 2 2 7 7 t u u u u 1 4 1 1 4 4
Xét hàm số f u 5
trên . Ta có: f u 5 ln ln 0 , t 7 7 7 7 7 7
Suy ra f u là hàm số nghịch biến trên . Do đó
f t f t 2 2 (1) 2 2
t 2 2t t 2 x 2 y 2 2 y x 2 2
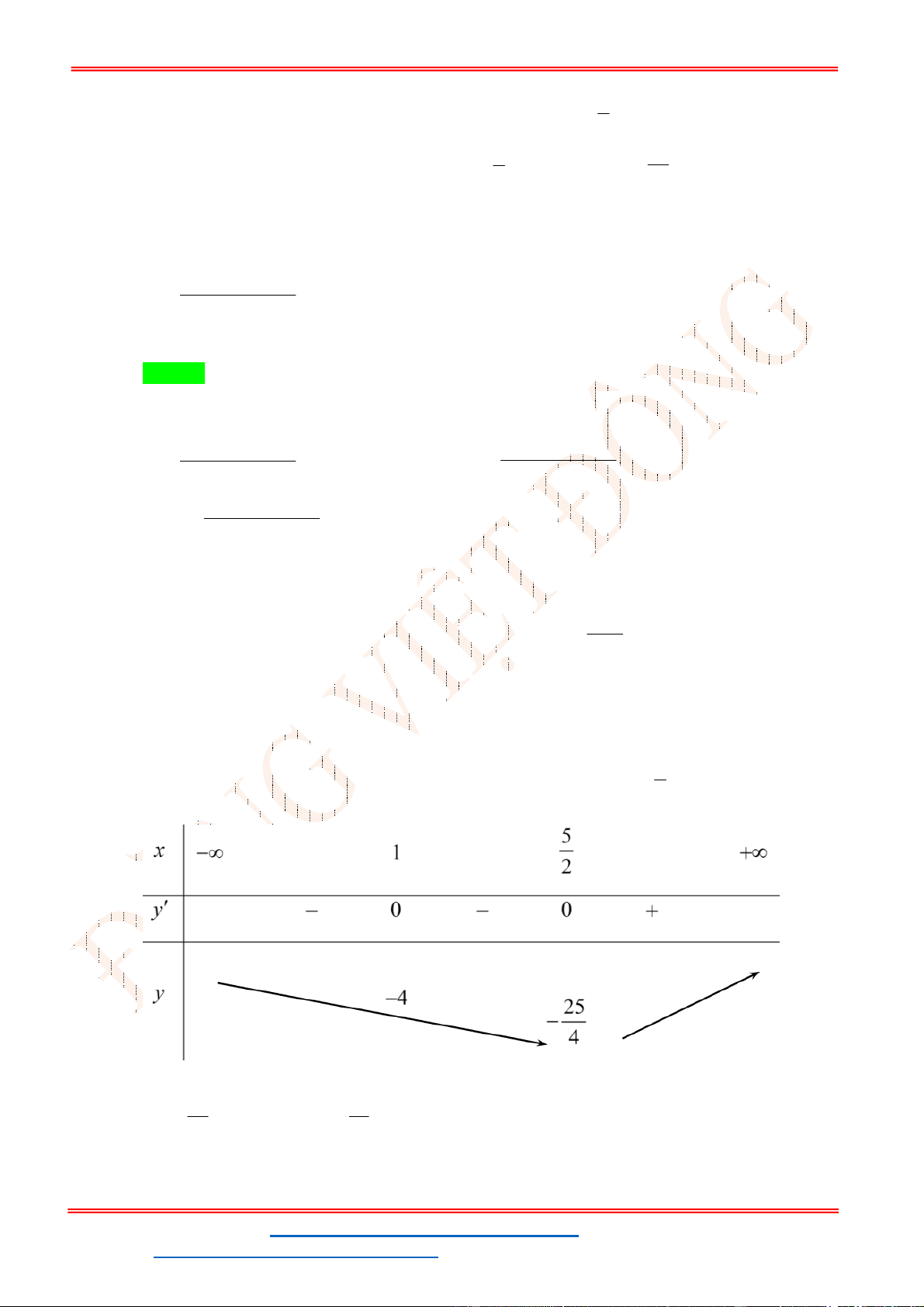
10x 6 y 26 3x 10x 20 Khi đó P 2 2x 2 y 5 x 2x 3 x 5 2
4x 22x 10 Ta có P 0
1 . Bảng biến thiên như sau: 2 32 2 x x x 2 5 5 19
Từ BBT, ta suy ra M 7 , m
. Vậy M m 7 . 2 2 2
Câu 24. Có bao nhiêu cặp số nguyên ; x y thỏa mãn 2xy 4 x y 7 4 7 2 1
2 2 7 y xy y x e e x y y e A. 8 . B. 5 . C. 6 . D. 7 . Lời giải Chọn C Ta có: 2xy 4 x y 7 4 7 2 1
2 2 7 y xy y x e e x y y e
x xy y 2xyy 4 x7 4 7 2 e e
2x2 y y 7 (vì y e 0 y )
x xy y 2xyy 4 x7 4 7 2 . e e
4x 7 2xy y
x xy y 2xyy e
xy y x 4x7 4 7 . 2 1 2 4 7 e 1
xy y 2xyy e
x 4x7 2 1 4 7 e 1 7 1
với x ; x ; y 0 2xy y 4x 7 4 2 xy y 1 x 1 2 4 7 e e . 2xy y 4x 7 t 1
Xét f t e t 0 t t 1
f t e 0 t
0 f t đồng biến trên các khoảng xác định 2 t
f 2xy y f 4x 7
2xy y.4x 7 0 TH1:
Giả sử 2xy y 0 và 4x 7 0 . Do x, y nên 2xy y 1 và 4x 7 1.
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 12
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng 1 f
2xy y f 1 1 1 e
. Do đó, f 2xy y f 4x 7 .
f 4x 7 f 1 e 1 1
2xy y.4x 7 0 TH2: 4x 7 9
f 2xy y f 4x 7 2xy y 4x 7 y 2 . 2x 1 2x 1
Theo bài, y nên 2x 11; 3 ;
9 x 4; 1;0;1; 2; 5 .
2 - BPT MŨ KHÔNG CHỨA THAM SỐ 2 2
Câu 25. Tìm số nghiệm nguyên của bất phương trình 2x 1 5 x 1 00 x 1 0 x50 2 2 2
x 25x 150 0 A. 6 . B. 4 . C. 5 . D. 3 . Lời giải Chọn B Đặt 2
a 2x 15x 100 ; 2
b x 10x 50 ta có bất phương trình:
2a 2b a b 0 2a 2b a
b a b (do hàm số 2x y
x là hàm số đồng biến trên ) Với a b 2 2
2x 15x 100 x 10x 50 2
x 25x 150 0
x 10;15 . Vậy bất phương trình có 4 nghiệm nguyên. 2 2
Câu 26. Số nghiệm nguyên của bất phương trình 2x 1 5 x 1 00 x 1 0 x50 2 2 2
x 25x 150 0 là A. 6 . B. 4 . C. 3 . D. 5 . Lời giải Chọn B ĐKXĐ: x . 2 2
Xét bất phương trình 2x 1 5 x 1 00 x 1 0 x50 2 2 2
x 25x 150 0 . 2 2 2 x 1 5 x 1 00 x 1 0 x50 2 x x 2 2 2 2 15 100
x 10x 50 0 . 2 x x
x x 2 2 15 100 2 x 1 0 x50 2 2 2 15 100 2
x 10x 50 1 Xét hàm số 2t f t
t với t . Ta có ' 2t f t
.ln2 1 0 với t . Suy ra hàm số f t đồng biến trên .
Mặt khác, f 2 x x f 2 1 2 15 100
x 10x 50 . Suy ra 2 2 2
2x 15x 100 x 10x 50 x 25x 150 0 1 5 x 1 0 .
Nghiệm nguyên của bất phương trình là x 14; 1 3; 12; 1 1 .
Vậy số nghiệm nguyên của bất phương trình là 4.
Câu 27. Tập nghiệm S của bất phương trình 2 x 1 x 1 2 3 3
x 2x là
A. S 0; .
B. S 0; 2 .
C. S 2; .
D. S 2; 0 . Lời giải Chọn D
Điều kiện : x 0. Ta có 2 x 1 x 1 2 3 3
x 2x 2 x 1 x 1 2 3 2x 3 x 1
Xét hàm f t t 1 2 3
t trên 0; . có f t t 1 ' 3 .ln3 2t
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 13
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng 2 có f t t 1 ' 3
.ln3 2 0,t 0; nên hàm số f t t 1 ' 3
.ln3 2t liên tục và đồng biến trên 0; .
t 0; f 't f '0 3.ln3 0 f t t 1 2 3
t liên tục và đồng biến trên 0;. x 0 x 0 Vậy
1 f 2x f x 2x x . 2 2x x x 2 2 2
Câu 28. Tìm số nghiệm nguyên của bất phương trình 2x 1 5 x 1 00 x 1 0 x50 2 2 2
x 25x 150 0 . A. 6 . B. 4 . C. 5 . D. 3 . Lời giải Chọn B 2
u 2x 15x 100 Đặt: 2
u v x 25x 150 . 2
v x 10x 50 2 2 2 x 1 5 x 1 00 x 1 0 x50 2 2 2
25 150 0 2u 2v x x
u v 0 2u 2v u v . Xét hàm 2t f t t có ' 2t f t
.ln2 1 0,t .
Suy ra hàm f t là hàm đồng biến trên .
Mà f u f v nên u v . Suy ra 2 2 2
2x 15x 100 x 10x 50 x 25x 150 0 10 x 15 .
Vì x x 11,12,13,1 4 .
Vậy bất phương trình đã cho có bốn nghiệm nguyên. 3 2 x 1
6 x 48 x36 2
Câu 29. Bất phương trình 1 2 3.2 x x x x
có bao nhiêu nghiệm nguyên? A. 8 . B. 10 . C. 9 . D. Vô số. Lời giải Chọn A x 1 Điều kiện: . x 0
Ta chỉ xét với các giá trị nguyên của x . Với x 1
thay vào bất phương trình không thỏa mãn.
Với x 2 , bất phương trình tương đương với: 2 2
16 x 48 x36 2 4 x6 x x 4x 6
2x x 1 4x 6 2 1 .2 x x 1.2 .2 x * x Xét hàm số 2 2t f t
.t trên khoảng 0; ta có: 2 2 t 2 ' 2 2 .2t f t t
ln2 0 , t 0 .
Vậy hàm số f t đồng biến trên khoảng 0; , khi đó: x 4x 6
f x 4 6 * 1 f x 1 x x 2
x x 2
1 16x 48x 36 3 2
x 15x 48x 36 0
x 6 2 5 1,1 01 x 3 2
x 12x 12 0 .
3 x 6 2 5 10,898
Vây bất phương trình có 8 nghiệm nguyên.
Câu 30. Tìm số nghiệm nguyên của bất phương trình
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 14
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng 2 2 2 x 4 x9 x 5 x 1 2021 2021 x
1 8 x 0 . A. 7 . B. 5 . C. 6 . D. 8 . Lời giải Chọn C 2 2 Ta có 2 x 4 x9 x 5 x 1 2021 2021 x 1 8 x 0 2 2 2 x 4 x9 x 5 x 1 2 2021 2021
x 9x 8 0 2 2 2 x 4 x9 2 x 5 x 1 2 2021
2x 4x 9 2021
x 5x 1 f 2
x x f 2 2 4 9 x 5x 1 , với 2021t f t t . ' 2021t f t
ln20211 0, t , suy ra hàm số f t đồng biến trên . Do vậy f 2
x x f 2 x x 2 2 2 4 9 5
1 2x 4x 9 x 5x 1 2
x 9x 8 0
1 x 8 . Vì x nguyên nên suy ra x 2, 3, 4, 5, 6, 7 .
Vậy bất phương trình có 6 nghiệm nguyên.
Câu 31. Có bao nhiêu cặp số nguyên dương ;
x y thỏa mãn 1 x 10 và 2 9y 3y x x A. 10 . B. 11. C. 9 . D. 8 . Lời giải Chọn A Ta có 2 y y 2 9 3 9y 3y x x x x .
Xét hàm số đặc trưng f t 2
t t với t 0 .
Ta có f 't 2t 1 0,t 0 suy ra f t là hàm số đồng biến trên t 0 . Suy ra 2
9y 3y
3y 3y x x f x f x .
Với giả thiết 1 x 10 ta có: 3y 10 y 2 . TH1: 1
y 1 3 x 10 x 3; 4;5;6;7;8;9;1 0 có 8 cặp nghiệm ; x y thỏa mãn. TH2: 2
y 2 3 9 x 10 x 9;1 0 có 2 cặp nghiệm ; x y thỏa mãn.
Vậy có tất cả 10 cặp nghiệm ; x y thỏa mãn. 2
Câu 32. Có bao nhiêu cặp số nguyên dương ; x y thỏa mãn x 2 cos 2.2 sin 2 y x y A. 1. B. 0 . C. 2 . D. 3 . Lời giải: Chọn B 2 2 Ta có x 2 cos y x 1 cos y 2
2.2 x sin y 2 2 x 1 2 cos y . (1) Đặt
2t ' 2t f t t f t
.ln2 1 0, t 0 .
Suy ra hàm số y f t là hàm số đồng biến trên 0; .
Suy ra f x f 2 y 2 2 1 1 cos
x 1 cos y x sin y x 0 vô lí.
Vậy không tồn tại cặp số nguyên dương ;
x y nào thỏa mãn đề bài.
Câu 33. Xét các số thực không âm x và y thoả mãn x y 1 2x . y 4
3 . Giá trị nhỏ nhất của biểu thức 2 2
P x y 4x 6 y bằng 65 33 57 49 A. . B. . C. . D. . 8 4 8 8 Lời giải Chọn A
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 15
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng Ta có: x y 1 2 x2 y2 2 y 32 2 .4 3 .2 3 2 2 .2 3 2 .2 x x y y x y x . 1 3
Nếu y 0 và x thì 1 luôn đúng. 2 2 3
Nếu y 0 và x , khi đó ta xét hàm số .2t f t t
với t 0 , ta có f t liên tục trên 2
0; và ' 2t .2t f t t
ln2 0, t 0 f t đồng biến trên nửa khoảng 0; . 3 Do đó
1 f 2 y f 3 2x 2x 2 y 3 x y 3 . 2 3
Gọi phương trình đường thẳng d : x y 0 . 2
Từ 2 và 3 suy ra tập hợp các điểm M ;
x y thỏa mãn đề là T , với T miền mặt phẳng
thuộc góc phần tư thứ nhất nằm phía trên đường thẳng d kể cả đường thẳng d . 2 2 Ta có 2 2
P x y 4x 6 y x 2 y 3 P 13 với P 13 vì tâm I 2 ; 3 3
không thỏa mãn x y . 2 tâm I 2 ; 3 2 2
Gọi C : x 2 y 3 P 13 là đường tròn có . R P 13
Khi T và C có điểm chung thì d I , d R 3 2 3 2 169 65
P 13 P 13 P . 2 8 8 65 5 1 Khi P
đường tròn C tiếp xúc đường thẳng d tại A ;
thỏa vì A thuộc T . 8 4 4 65 5 1
Vậy giá trị nhỏ nhất của biểu thức P là khi x và y . 8 4 4
Câu 34. Xét các số thực không âm x và y thỏa mãn x3 y4 x 3 . y 3
4 . Giá trị nhỏ nhất của biểu thức 2 2
P x y 5x 4y bằng 43 33 49 57 A. . B. . C. . D. . 8 4 8 8 Lời giải Chọn A Ta có x3 y 4 x 3 y 4 3 y 4 3 .3 4 3 .3 4 3 .3 4 3 x x y y x y x * Xét hàm số .3t f t t , t 0 , ta có 3t f t
1 t ln 3 0 , t 0 f t đồng biến trên 0; .
* f 3y f 4 x, x, y 0 3y 4 x x 4 3y , x, y 0 2 Xét biểu thức 2 2
P x y x y P y 2 5 4 4 3
y 54 3y 4y 43 2
P 10 y 35y 36 8 7 43 y 5 7 Vậy min P khi và chỉ khi 4 ; x y ; 8 4 4
x 4 3y
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 16
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng 2 2 2 2 x
Câu 35. Cho các số thực , x y thỏa mãn x 2 y x 2 y 2yx 2 5 16.4 5 16 .7 và
y 1. Gọi M và 2
m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức
10x 6 y 26 P
. Khi đó, giá trị của biểu thức T M m bằng 2x 2 y 5 21 19
A. T 10 . B. T . C. T .
D. T 15 . 2 2 Lời giải Chọn C Đặt 2 t x 2 . y t 2 2 t t t 5 4 5 4 t Ta có 5 16.4 2 5 4 2 .7 1 . t 2 2t 7 7 u u u u 5 4u 1 4 1 1 4 4
Xét hàm số f u 5
ta có f u 5 ln ln 0, u 7u 7 7 7 7 7 7
Suy ra hàm số f u luôn nghịch biến trên . Khi đó
1 f t 2 f 2t t 2 2t t 2. 2 x 2 x 2 Mặt khác 2
y 1 x 2 y 2 t 2. Suy ra t 2 y
. Thay vào P ta được 2 2 2 3x 10x 20 P 3 P 2
x 2 5 P x 20 3P 0 2 . 2 x 2x 3
Khi P 3, vì P xác định nên phương trình 2 có nghiệm. 2 Khi đó
P P P 2 0 5 3 20 3 0 2
P 19P 35 0 5 5 19
P 7. Vậy T M m 7 . 2 2 2 2 2 x y2 4x y 2
Câu 36. Xét các số thực dương , x y thỏa 2021
0. Tìm giá trị nhỏ nhất của biểu x 22
thức P 2y 4 . x 1 A. 2021 . B. 2020 . C. . D. 2 . 2 Lời giải Chọn D 2 2 x y2 4x y 2 4x y 2
Từ giả thiết, ta suy ra 2021
2 x y 2 log 1 . 2 2 2021 2 x 2 x 2
a 4x y 2 Đặt 2
b a x y 2 thì 1 trở thành b x 22 2
x 4x 4
2 b a log a log b log a 2a log b 2b 2 . 2021 2021 2021 2021 1
Xét hàm số f t log
t 2t trên 0; ta có f t 2 0, t 0 2021 t ln 2021
Suy ra hàm số f t luôn đồng biến trên khoảng 0; .
Khi đó f a f b a b x y x 2 2 2 4 2 2
y x 2.
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 17
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng Thay vào ,
P ta được P x x x 2 2 2 4 4 2 1 2 2. Vậy P
2 khi và chỉ khi x 1, y 3. min
DẠNG 2: PHƯƠNG PHÁP HÀM ĐẶC TRƯNG GIẢI PT, BPT MŨ CHỨA THAM SỐ
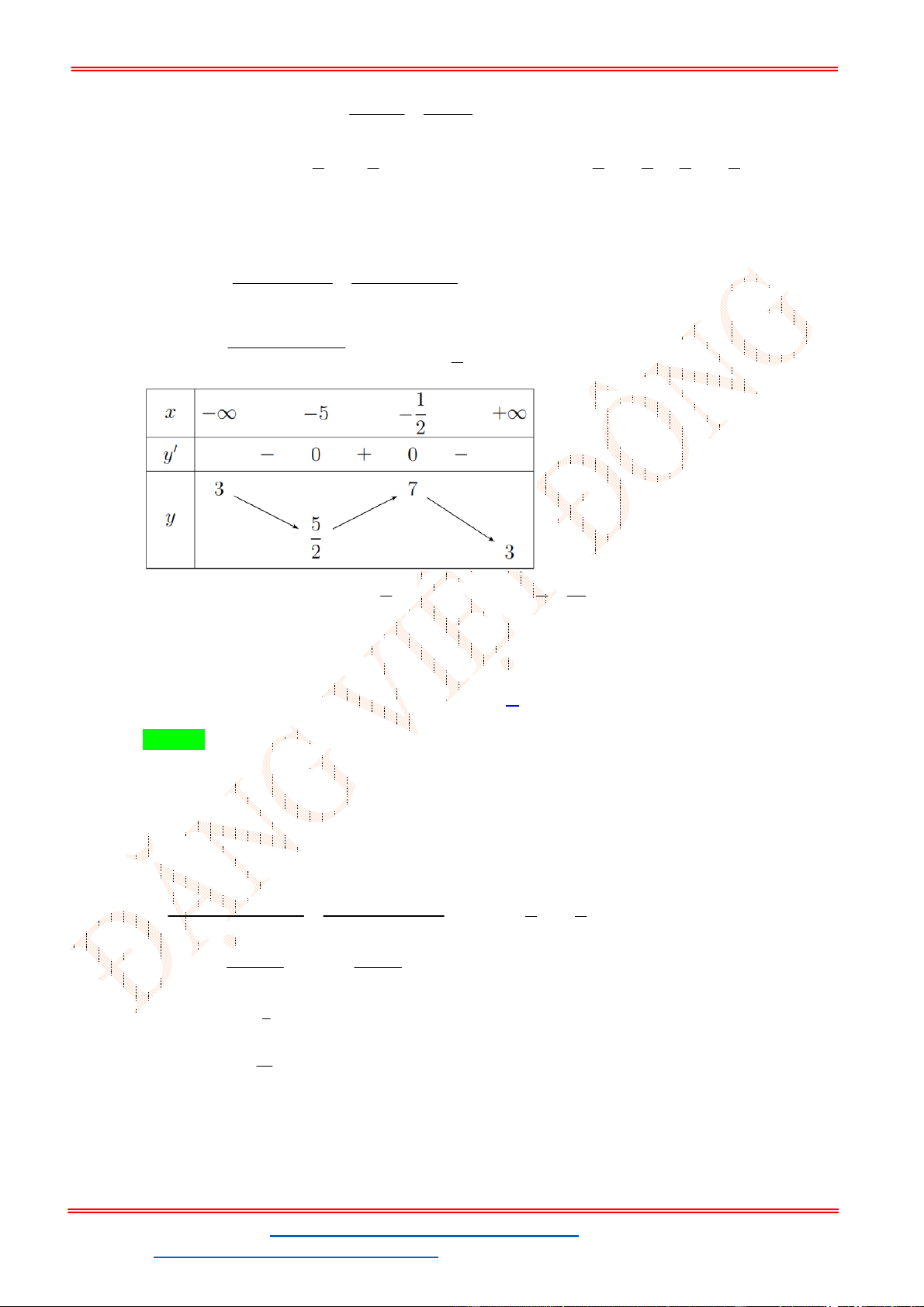
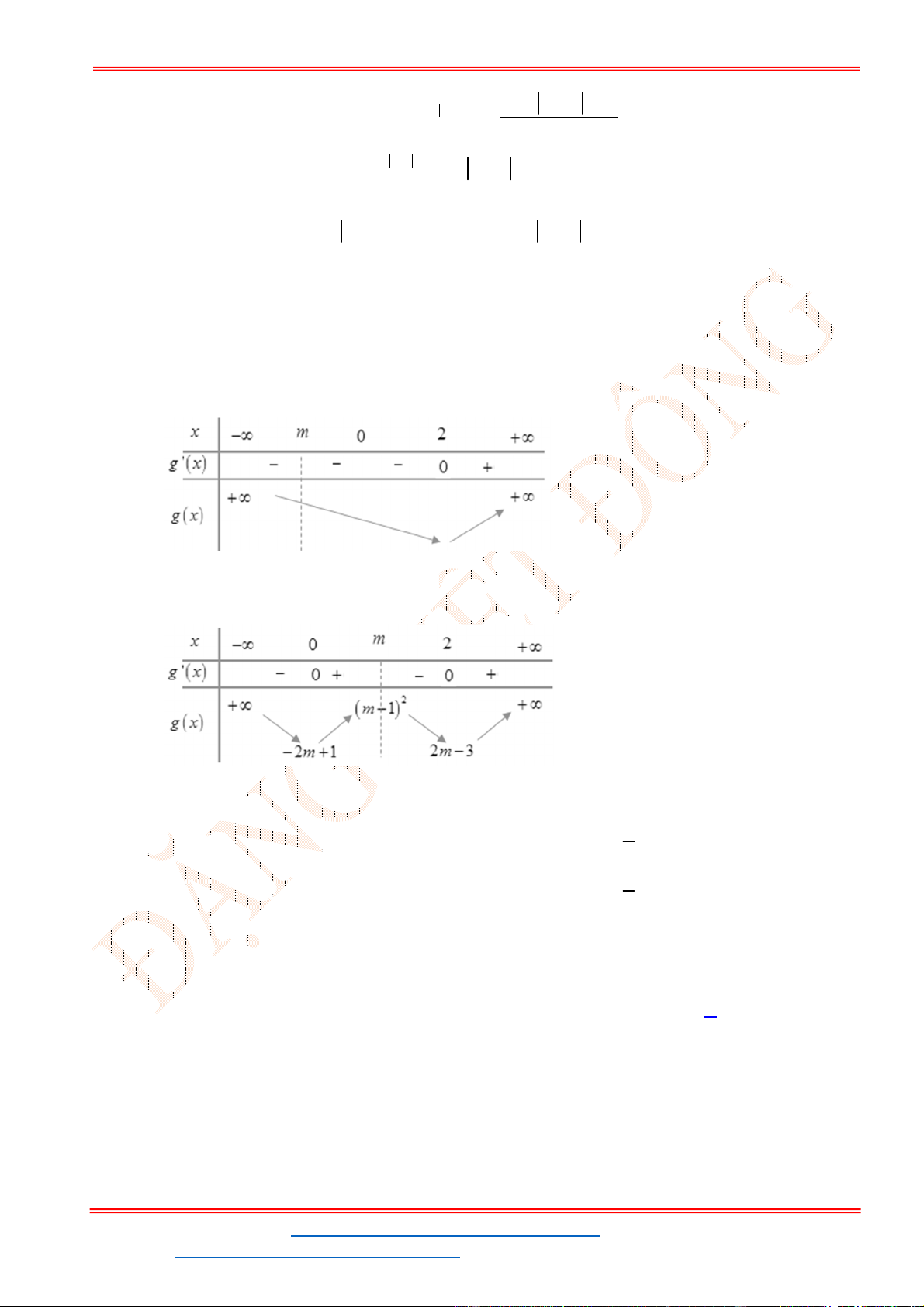
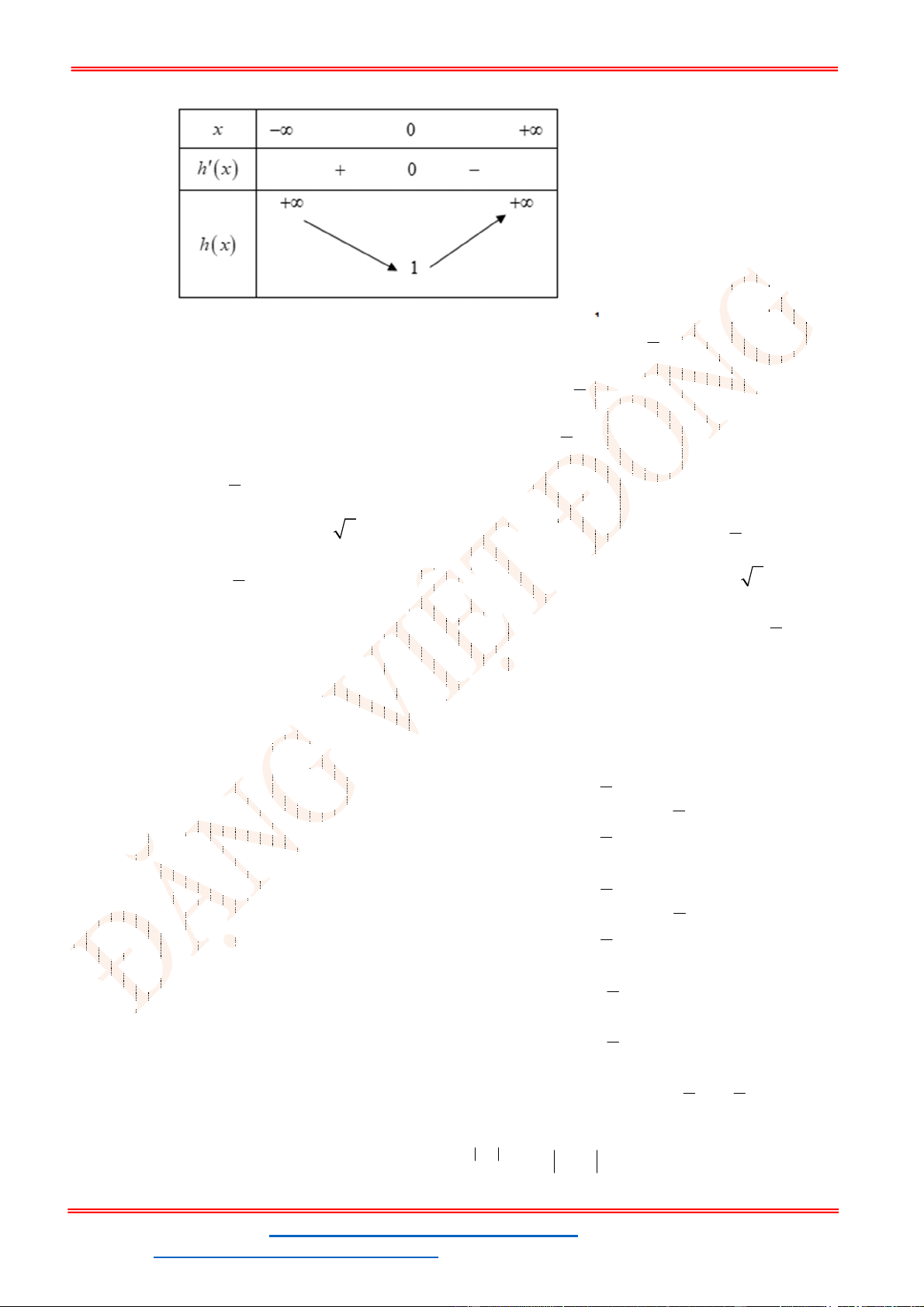
Câu 37. Có bao nhiêu giá trị nguyên dương của tham số m nhỏ hơn 2021 để phương trình x 2 2 2 x m m có nghiệm thực. A. 2020 . B. 2021 . C. 2022 . D. 2019 . Lời giải Chọn A Ta có x 2 x x x x 2 2 2 2 2 2 2 x m m m m 1 .
m 2x 0
Dễ thấy: khi m 0 2x 0
Xét hàm số f t 2 t t
Dễ thấy hàm số đồng biến trên khoảng 0; .
Do đó x x x 2 x 2 1 2 2 2 2 2 x 2x f m f m m
Đặt 2x a với a m g a 2 0
a a trên khoảng 0; 1
Phương trình có nghiệm khi và chỉ khi m . 4
Vậy có 2020 giá trị của m thỏa mãn điều kiện. 3 2 2
Câu 38. Cho phương trình x x 2xm x x 3 2 2
x 3x m 0 . Có bao nhiêu số nguyên m để phương
trình có ba nghiệm phân biệt? A. 5 . B. 1. C. 2 . D. 3 . Lời giải Chọn D Ta có: 3 2 2
x x 2 xm x x 3 2 2
x 3x m 0 3 2 2
x x 2 xm 3 2 x x 2 2
x x 2x m 2
x x * Xét 2t f t t Có ' 2t f t
.ln2 1 0 suy ra f t là hàm đồng biến trên Khi đó 3 2 2
* x x 2x m x x 3
x 3x m * * Xét h x 3
x x h x 2 3 ; '
3x 3; h ' x 0 x 1 h h h h CD 1 2; CT 1 2
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 18
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng
Phương trình có ba nghiệm phân biệt khi và chỉ khi 2 m 2 2 m 2
Mà m nguyên nên m 1;0; 1
Kết luận: Có ba số nguyên m để phương trình có ba nghiệm phân biệt. 2 2 3x 3mx4
2 x mx3m
Câu 39. Cho phương trình 2 3 3
x 2mx 3m 4
1 . Gọi S là tập hợp
tất cả các giá trị nguyên của tham số m thuộc khoảng 0; 2020 sao cho phương trình 1 có
hai nghiệm phân biệt. Số phần tử của tập S là A. 2020 . B. 2018 . C. 2019 . D. 2021 . Lời giải Chọn B 2 2
3x 3mx4 x mx m 2 3 2 3 3
x 2mx 3m 4 2 2 x mx x mx m
3 3 4 x mx 2 3 2 2 3 3 3 4 3
2x mx 3m 2 . t t
Xét hàm số f t 3 t trên tập . Ta có f 't 3 ln 3 1 0 , t suy ra hàm
số y f t đồng biến trên .
Khi đó, phương trình f 2
x mx f 2 2 3 3 4
2x mx 3m 2 2
3x 3mx 4 2x mx 3m 2
x 2mx 3m 4 0 3 . Phương trình
1 có hai nghiệm phân biệt khi và chỉ khi phương trình 3 có hai nghiệm phân m 1 biệt Δ ' 0 2
m 3m 4 0 . m 4
Mà m nguyên và thuộc khoảng 0; 2020 suy ra S 2;3; 4;..; 201 9 .
Vậy tập S có 2018 phần tử. 2
Câu 40. Cho phương trình s
m in 2 xcos2 x cos x2 2 e e 3cos x s
m in2x 1 ( m là tham số thực). Số giá trị
nguyên dương của m để phương trình đã cho vô nghiệm là A. 3 . B. 2 . C. Vô số. D. 1. Lời giải Chọn D Ta có 2 2 s
m in 2 xcos2 x cos x2 2 s
m in 2 xcos2 x cos x2 2 e e 3cos x s
m in2x 1 e s
m in2x cos2x e cos x 2 f m x x f 2 sin2 cos2 cos x 1 với t f t e t . Xét t f t
e t có ' t f t
e 1 0,t . Do đó ta có: f m x x f 2 x 2 sin2 cos2 cos
2 msin2x cos2x cos x 2 .
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 19
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng
2msin2x 3cos2x 5 vô nghiệm khi và chỉ khi:
m2 2 2 2 2 3
5 m 4 2 m 2 . Vì
m m 1.
Câu 41. Có bao nhiêu giá trị m nguyên để phương trình 2 2cos xcosx 2 c m os 256 8cos2 2 4 cos 2 x m x m x m 8
có đúng 2 nghiệm phân biệt thuộc ; . 2 2 A. 4 . B. 8 . C. 7 . D. 9 . Lời giải Chọn B Ta có: 2 2cos xcosx 2 c m os 256 8cos2 2 4 cos 2 x m x m x m 8 (1) 2
8 2cos xcosx 2 2 c m os 2 8 2cos 1 8cos 2 .cos 2 x m x x m x m 8 2
8 2cos xcosx 2 2 c m os 2 8 2cos cos 2 x m x x 2 .
m cosx m (2) Xét hàm đặc trưng 2t f t t có ' 2t f t
.ln2 1 0, t , suy ra hàm f t đồng biến trên .
Phương trình (2) f 2
8 2cos x cosx f 2 .
m cosx m 2
8 2cos x cosx 2 .
m cosx m 8cosx 2cosx
1 m 2cosx 1 0 1 cosx 2 2cosx
1 8cosx m 0 m cosx 8 1
Do phương trình cosx không có nghiệm trong ;
nên phương trình (1) có đúng 2 2 2 2 m
nghiệm phân biệt trong ; khi 0
1 0 m 8 . 2 2 8
Vì m nguyên nên m 0;1; 2;3; 4;5;6;
7 có 8 giá trị m thoả mãn.
Câu 42. Có tất cả bao nhiêu giá trị nguyên của tham số m để phương trình sau có nghiệm thực? 3
sinx2 m3sinx 3 2 x x x m sinx2 sinx 1 2 sin 6cos 9sin 6 2 2 1 A. 20 . B. 21 . C. 22 . D. 24 . Lời giải Chọn B
Chia cả hai vế phương trình cho sinx 2 2 ta được: 3 m3sinx 3 2 2sin 2 sin 6cos 9sin 6 8 2 x x x x m 3 m3sinx 3 2 2sin 2 sin 6sin 9sin 8 2 x x x x m 3 m3sinx 2sinx 2 3 2
m 3sinx 2
8 12sinx 6sin x sin x 3 3 m3sinx 2sin 2 3sin 2 x m x
2 sinx 1
Xét hàm f u u 3
2 u trên . Có f u u 2 '
2 .ln2 3u 0, u . Do đó hàm số f u đồng biến trên .
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 20
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng
Khi đó phương trình
1 f 3 m 3sinx f 2 sinx 3
m 3sinx 2 sinx m x x3 3sin 2 sin m x x3 3sin 2 sin 2
Đặt t sinx , 1 t
1 thì 2 trở thành: m t t 3 3 2 3 .
Xét hàm số g t t t 3 3 2 trên đoạn 1; 1 . t 1
Có g t t 2 ' 3 3 2
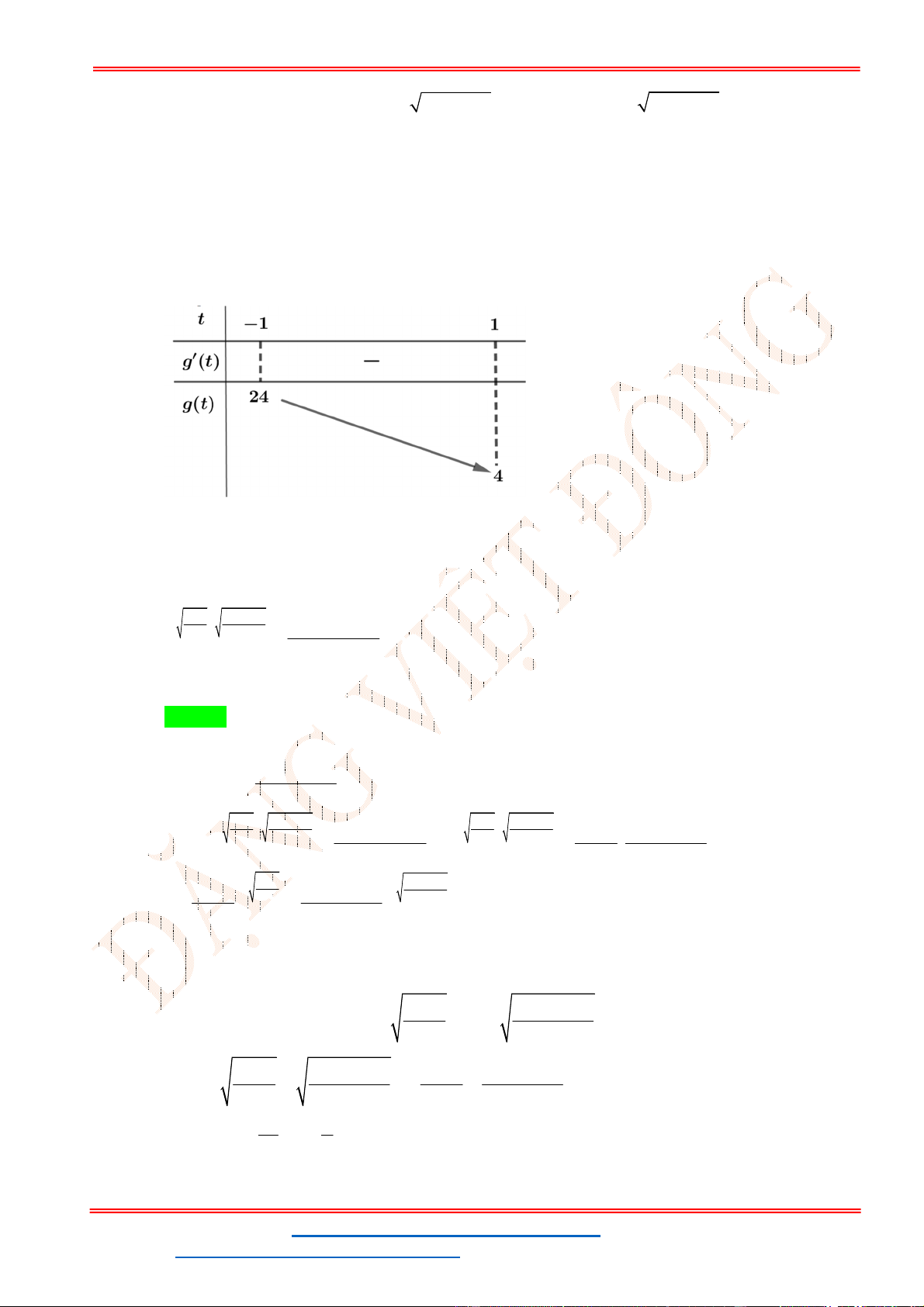
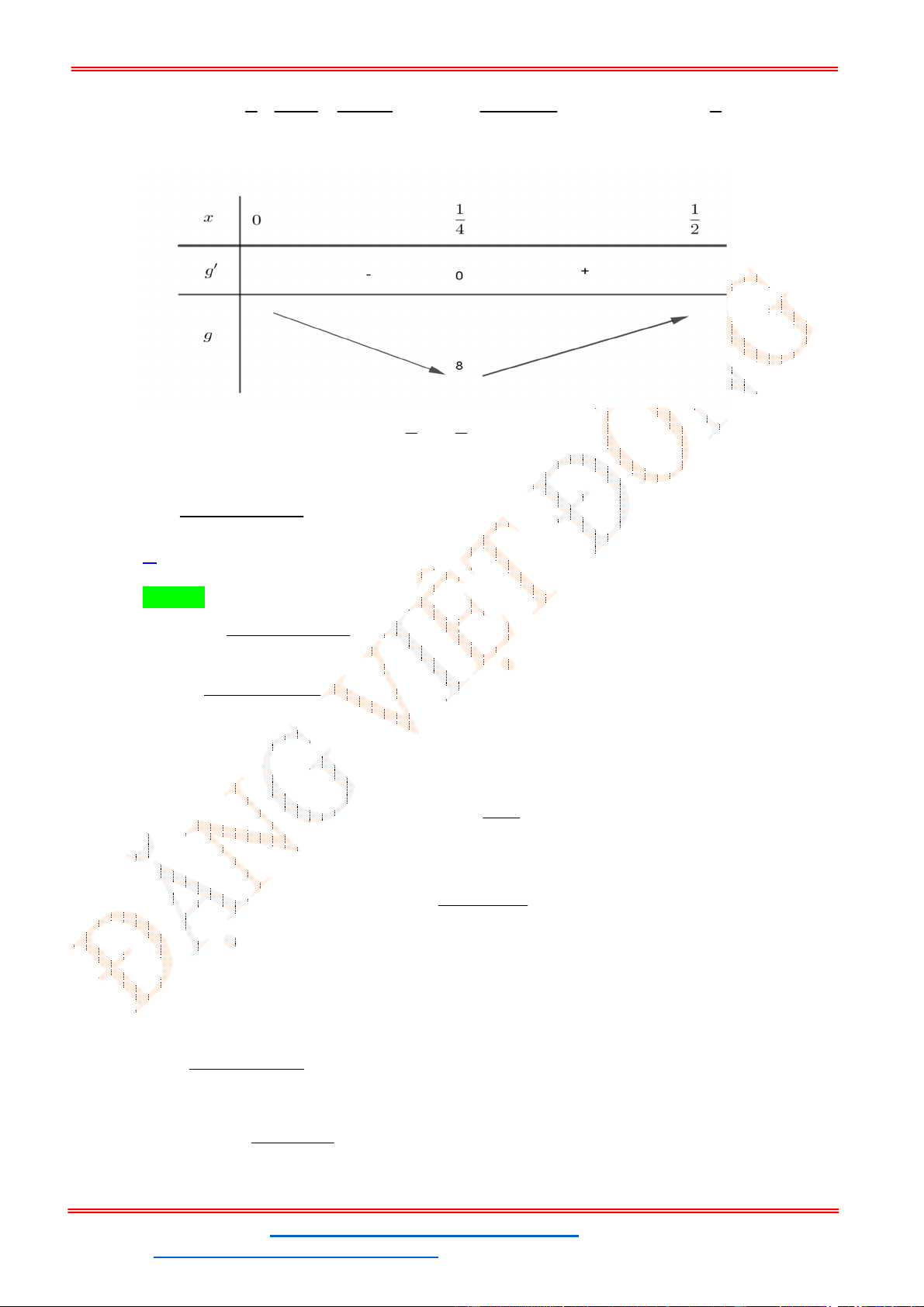
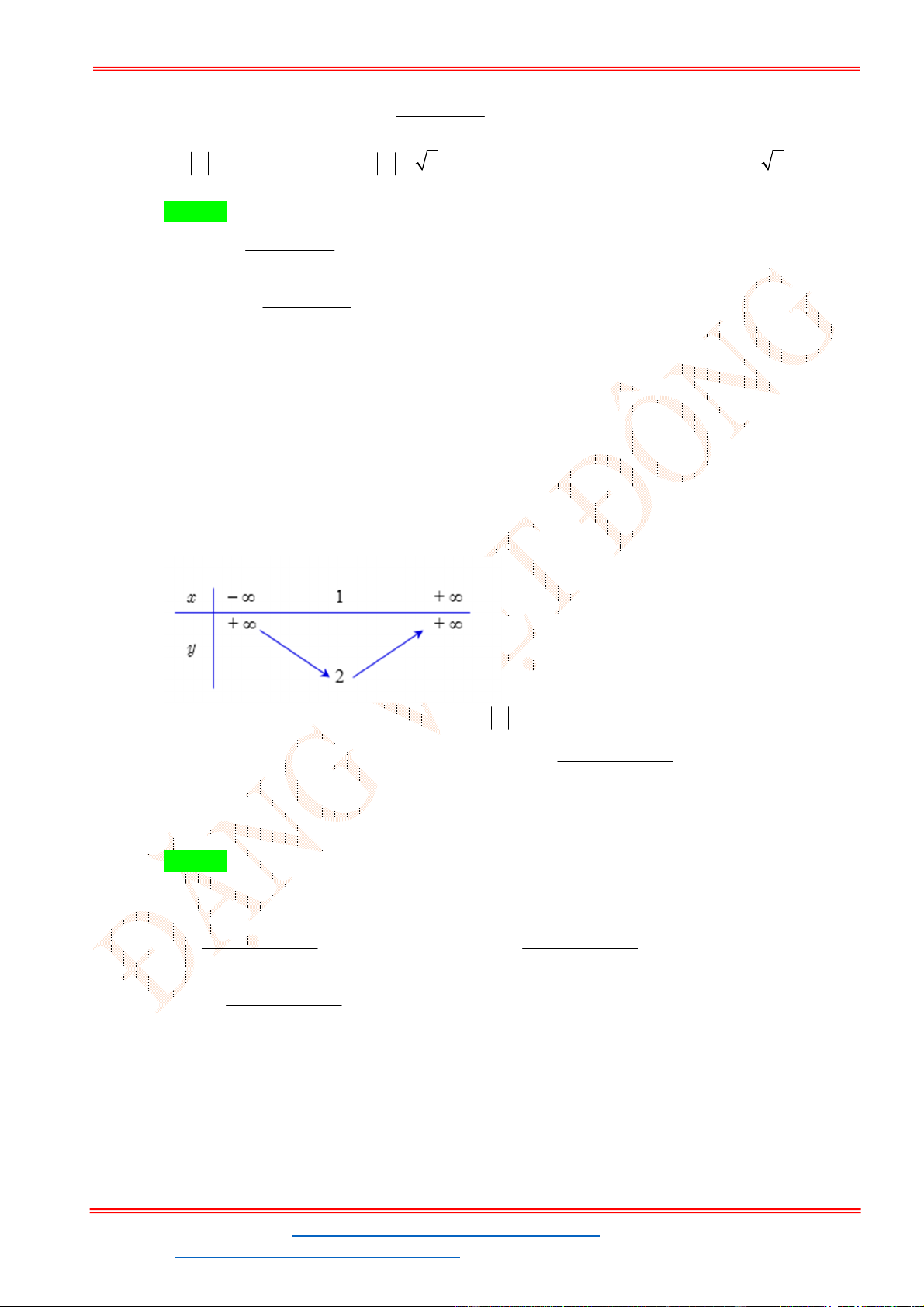
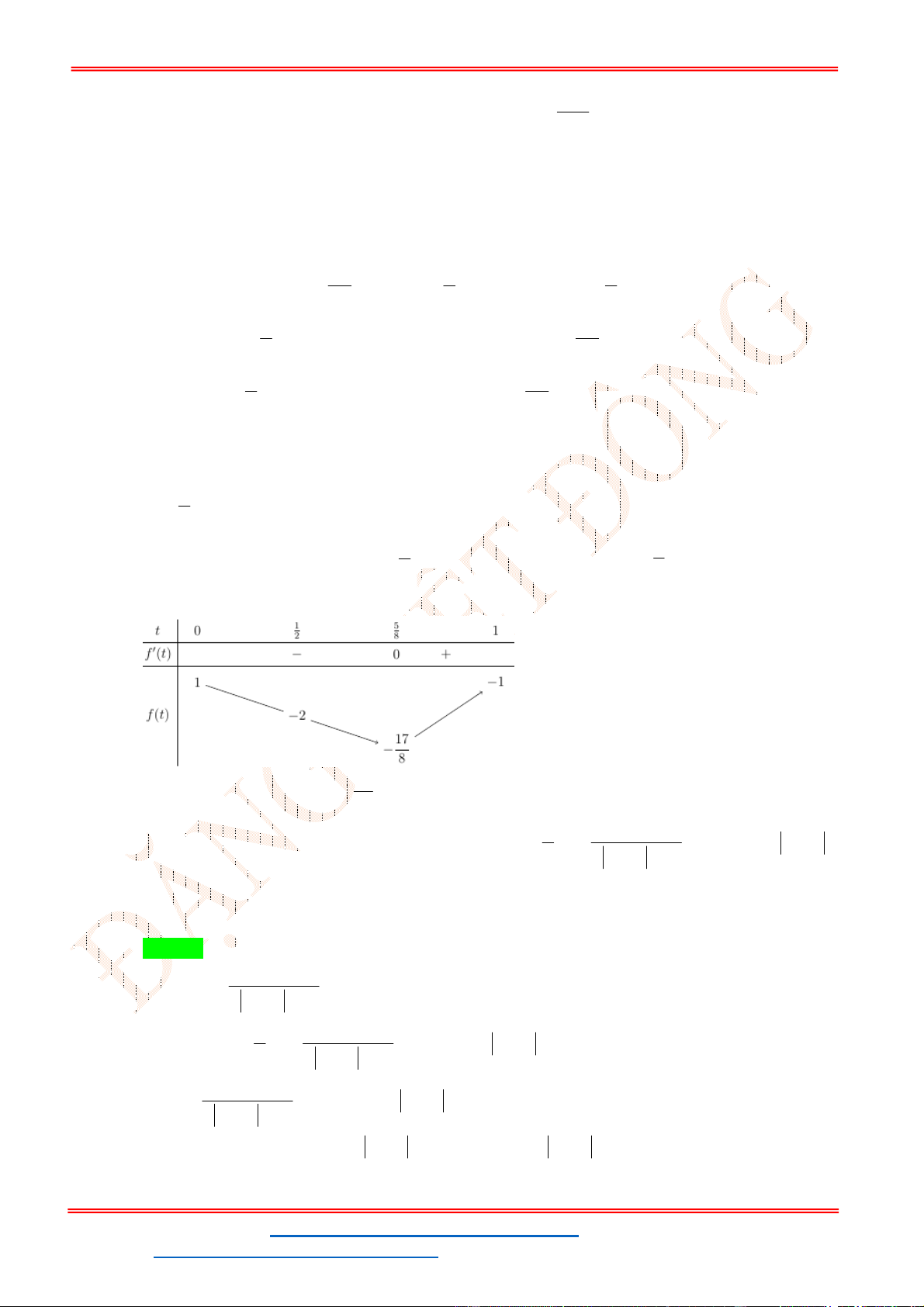
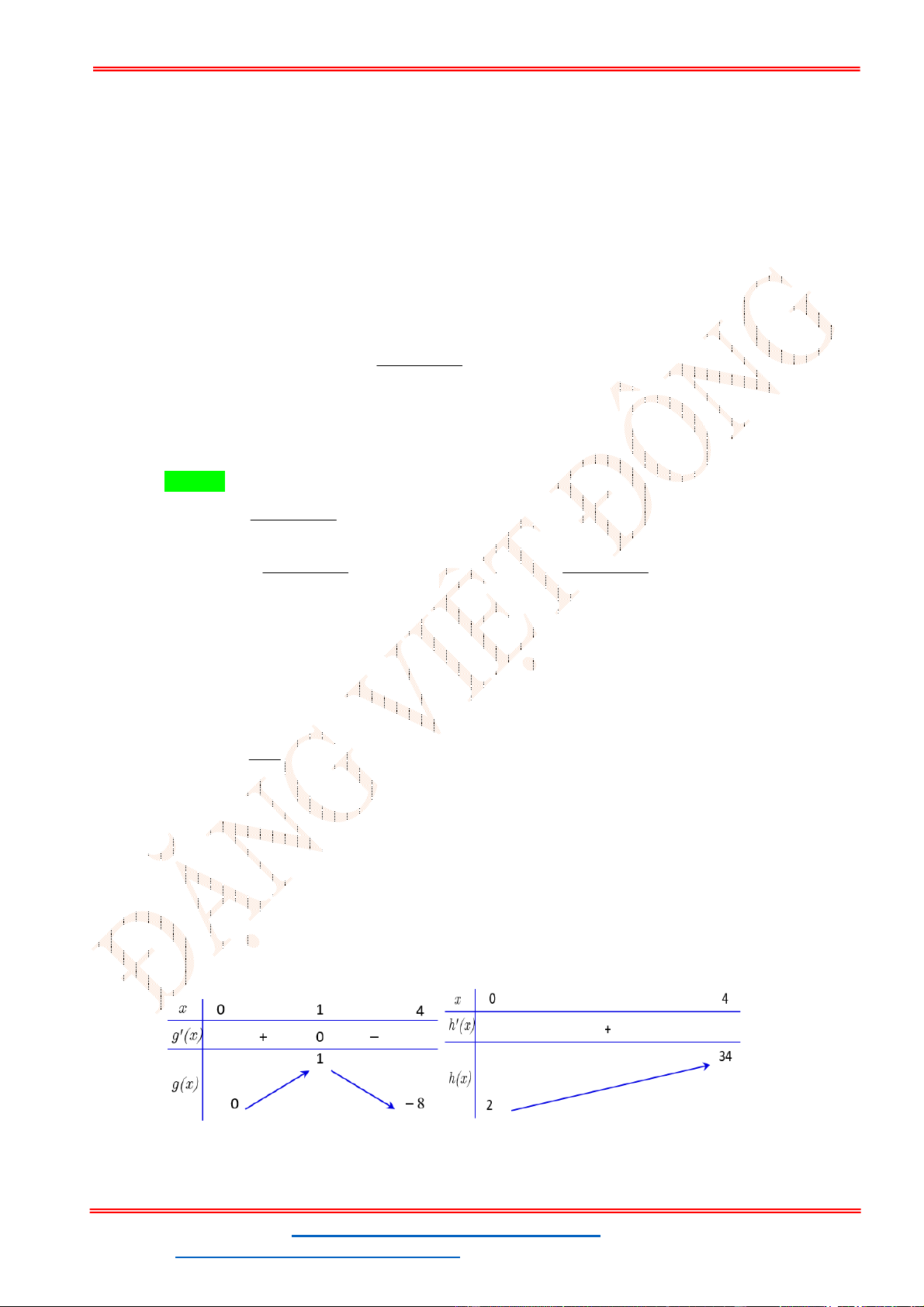
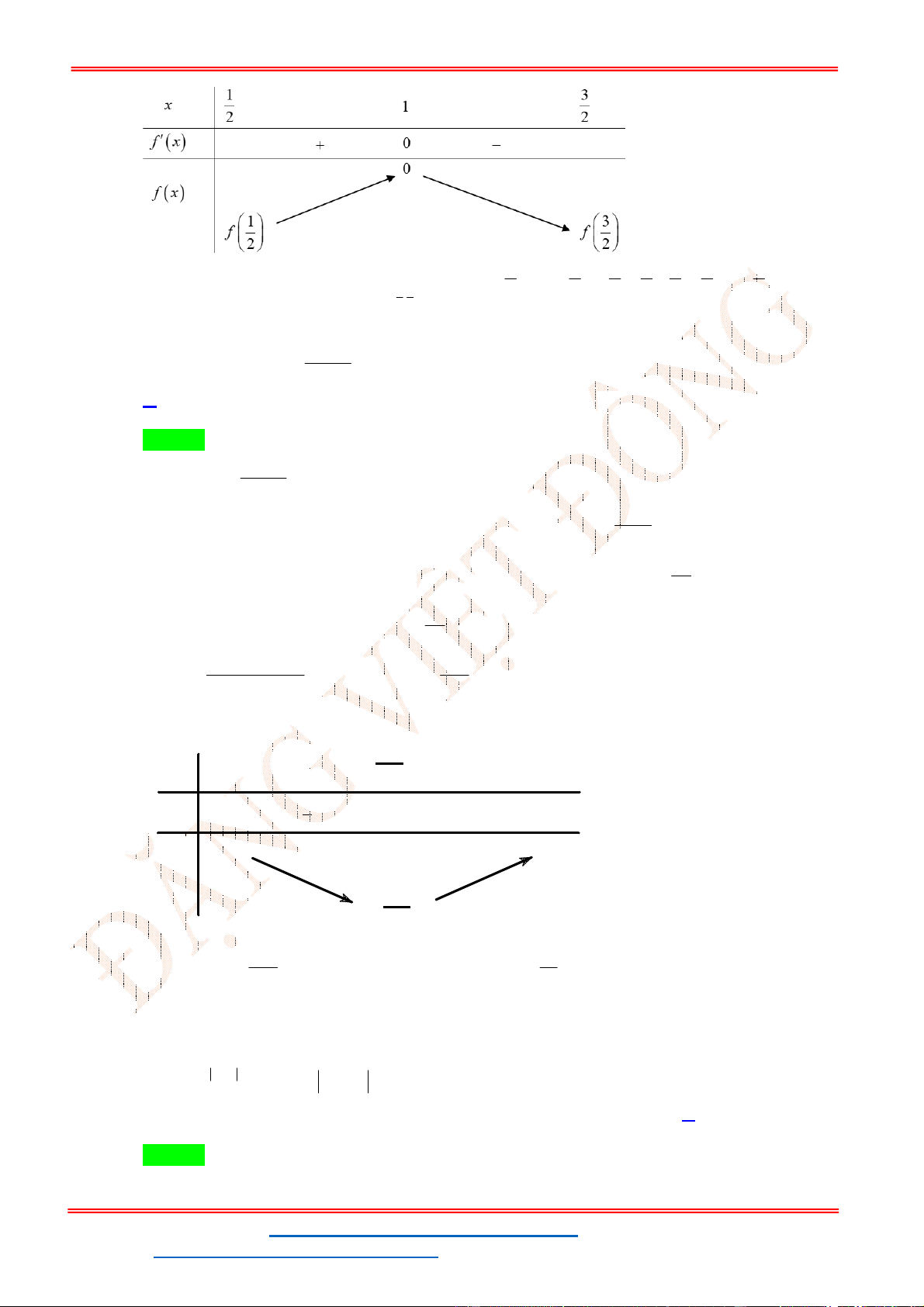
g 't 0 t 2 2 1 t 3 1 ;1 Bảng biến thiên:
Phương trình 3 có nghiệm trên đoạn 1;
1 khi và chỉ khi 4 m 24 .
Do m nguyên nên m 4;5;..; 2 4 .
Vậy có 21 giá trị nguyên của m thỏa mãn bài toán.
Câu 43. Có bao nhiêu giá trị nguyên dương của m nhỏ hơn 20 để phương trình 4 2 x 1 x mx 1 3 2 2
x mx x x x e
có nghiệm thực dương? 4 x 1 A. 19 . B. 16 . C. 18 . D. 17 . Lời giải Chọn A x 0 Điều kiện 2
x mx 1 . 0 x 4 2 4 2 x 1 x mx 1 x 1 x mx 1 3 2 2 2 2
x mx x 2 x x mx 1 Ta có x x e x x e . . 4 4 x 1 x 1 x 4 2 x 1 4 2 x mx 1 x 1 2 x mx 1 . x e . x e * 2 x x Xét hàm số 2 . t f t
t e , với t 0 . t 2 ' 2 . . t f t t e
t e 0, t 0 . Do đó hàm số y f t đồng biến trên 0 ; . 4 2 x 1 x mx 1
Phương trình * có dạng f f . 2 x x 4 2 4 2 x 1 x mx 1 x 1 x mx 1 Suy ra 4 3 2
x x x 1 mx . 2 2 x x x x 1 1 2 m x x ** . 2 x x
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 21
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng 1 1
Đặt a x
, x 0 a 2 và 2 2 x a 2 . x 2 x ** trở thành 2
m a a 2 *** .
* có ngiệm thực dương *** có nghiệm a 2 ; .
Xét hàm số g a 2
a a 2 trên 2 ; .
Có g 'a 2a 1 0, a 2 . Suy ra hàm g a đồng biến trên 2 ; .
Do đó g a g 2, a 2 ; g a 0, a 2 ; . m Vậy **
* có nghiệm a 2 ; m 0 . Mà
m 1 ; 2 ; 3 ;.. ;1 9 . 0 m 20
Có 19 giá trị của tham số m thỏa mãn bài toán.
Câu 44. Gọi S là tập hợp các giá trị của tham số m sao cho hai phương trình 2 2 1 3m x và x 2
m 3 2x x 1 có nghiệm chung. Tính tổng các phần tử của S . 5 A. 6 B. 3 . C. 1. D. . 2 Lời giải Chọn B
Vì hai phương trình đã cho có nghiệm chung nên hệ sau có nghiệm 2
2x 1 3m m log 2x 1 3 2 x log x x x x 2 2 2 1 3 2 1 3 2 x 2
m 3 2x x 1
m 3 2x x 1 2 x log 2 log x 3 2 1 2 2 1 2 1 3 3 log 2 2 1 3x x x x x x . 3 3 Xét hàm số 3t f t
t xác định trên ' 3t f t .ln3 1 0 suy ra hàm 3t f t t
đồng biến trên suy ra log 2 2 2 1 2 1 3x x x x . 3 Xét hàm số 2 2 1 3x g x x
xác định và liên tục trên .
Ta có g x x x g x x 2 g x x 3 ' 4 3 ln3 ' 4 3 ln 3 ' ' 3
ln 3 0 . Suy ra hàm số g' x
nghịch biến trên . Do đó g x 0 có nhiều nhất là 3 nghiệm. x 0 m 0 x
Ta lại có g 0 g
1 g 2 0 . Suy ra phương trình 2
2x 1 3 x 1 m 1 . x 2 m 2 Vậy S 3 .
Câu 45. Cho phương trình x 2 3 3 x
1 3x 2 3x 3 2 3x m m
m 3 , với m là tham số. Có
bao nhiêu giá trị nguyên âm của m để phương trình có nghiệm thực? A. 3. B. 6. C. 4. D. 5. Lời giải Chọn A x 2 3 3 x
1 3x 2 3x 3 2 3x m m m 3 x 2 3 3 x
1 3x 2 3x 3 2 3x m m m 3 3
3 x 3x 3x 3 3x 3 3x m m m 3
x x x 3 3 3 3 3 3 3x m m 3 .
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 22
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng
Xét hàm đặc trưng f t 3
t t có f t 2 '
3t 1 0, t . 3 Vậy 3
3 x 3x 3x 3 3x 3 3x 3x m m f f m 3 x x 2 3 3
3 3 x 3x m 3 m . (*) Đặt 3x u
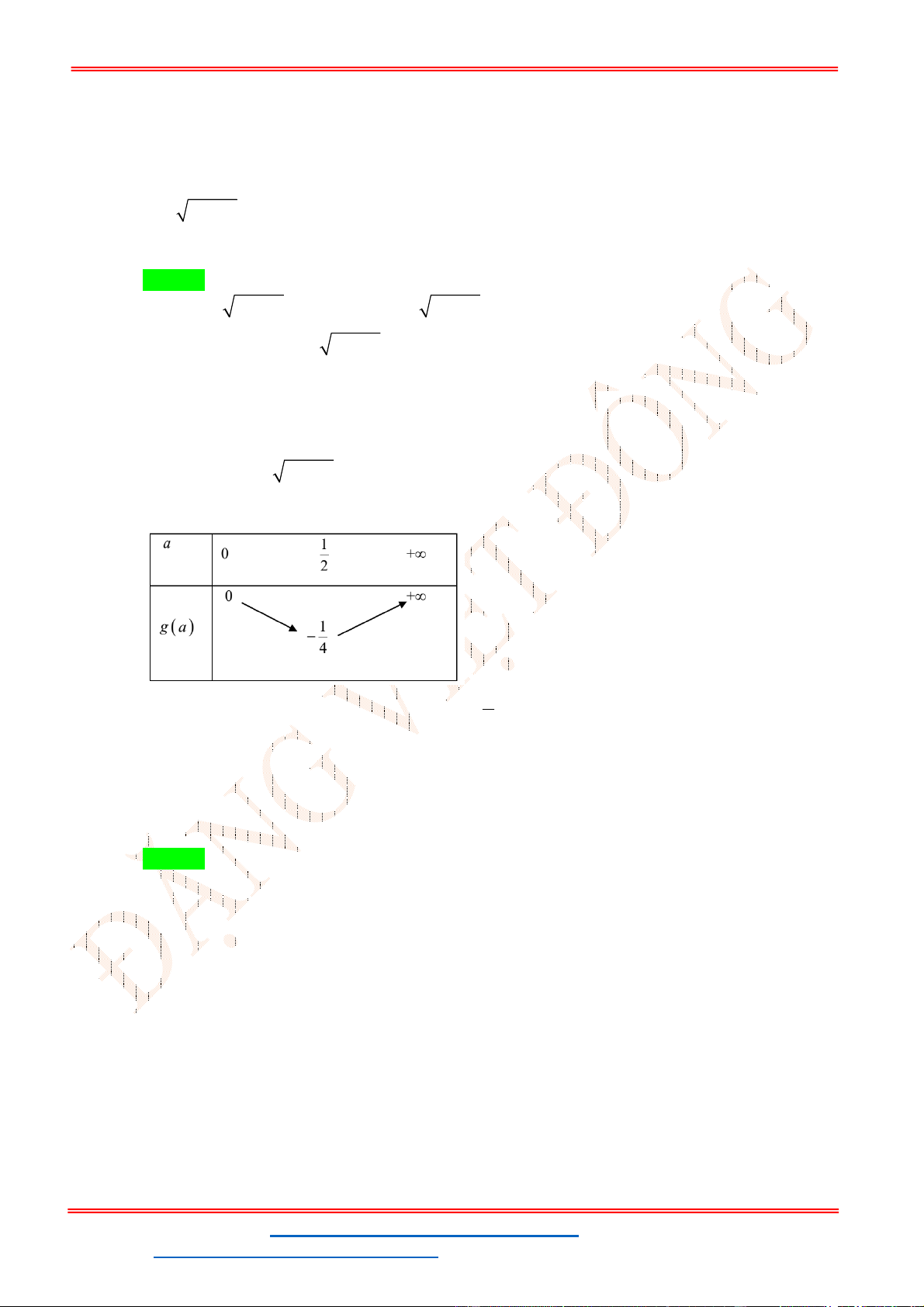
, với điều kiện u 0 và đặt g u 2
u u 3
Phương trình (*) g u m . 1
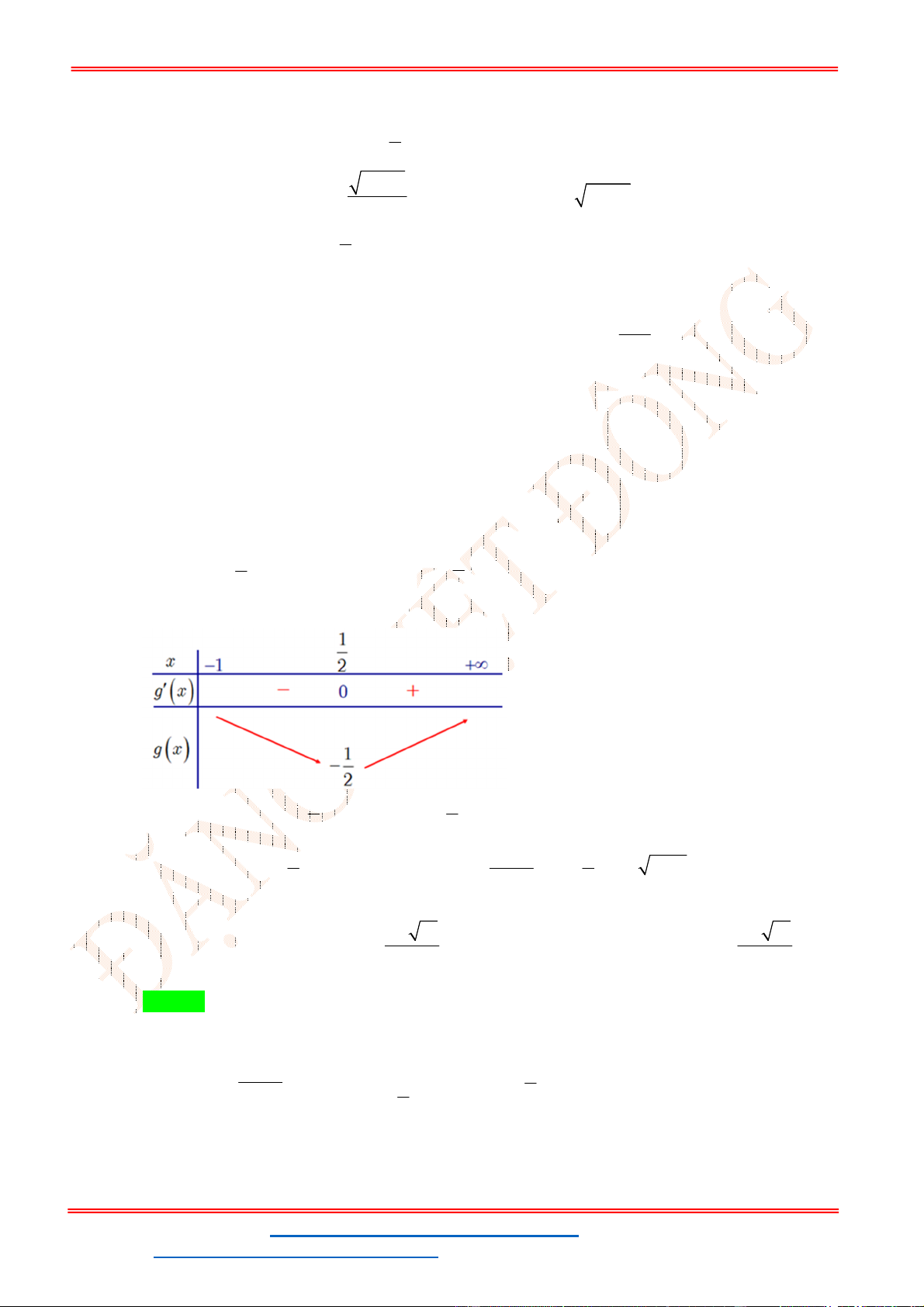
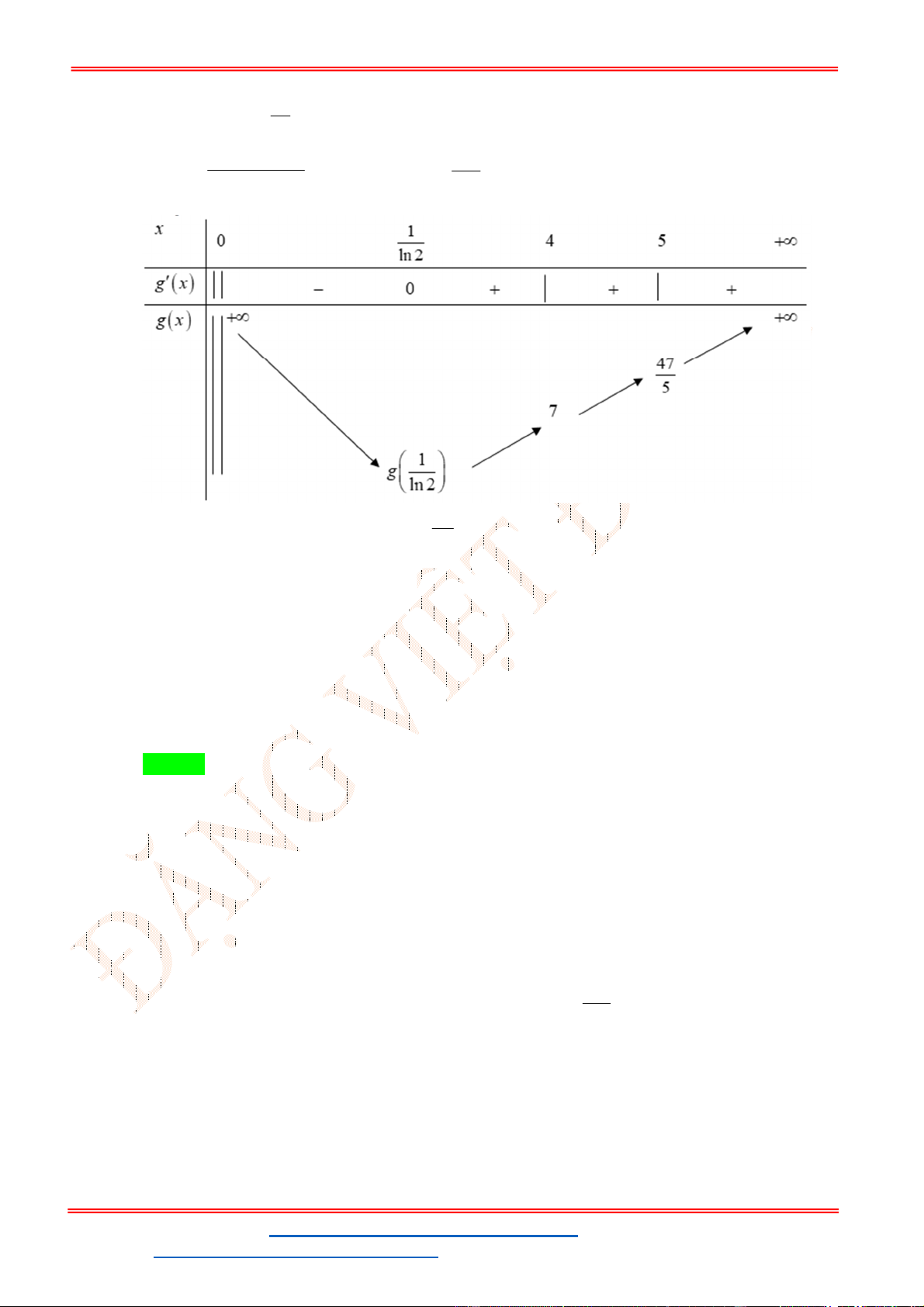
g 'u 2u 1, g 'u 0 u ta có bảng biến thiên của g u : 2 13
Từ bảng biến thiên ta thấy phương trình đã cho có nghiệm thực khi và chỉ khi m . 4
Vậy có tất cả 3 giá trị nguyên âm của m để phương trình có nghiệm thực là: -3; -2; -1.
Câu 46. Tìm tất cả các giá trị thực của tham số m để phương trình 2 x x
m x 2 5 12 16 2 x 2
có hai nghiệm thực phân biệt thỏa mãn điều kiện 2 x x 1 2 x 1 2017 2017
2018x 2018 .
A. m 2 6;3 3 .
B. m 2 6;3 3 . 11 11 C. m 3 3; 3 2 6. D. m 2 6; 3 . 3 3 Lời giải Chọn A Ta có 2 x x 1 2 x 1 2017 2017 2018x 2018 2 x x 1 x 2 x 1 2017 1009 2 1 2017
1009 2 x 1
f 2x x 1 f 2 x 1. Xét hàm số 2017u f u 1009u Ta có ' 2017u f t
ln2017 1009 0, u f u đồng biến.
Nên 2x x 1 2 x 1 1 x 1. 2 Ta lại có 2 x x
m x 2 5 12 16 2
x 2 x 2
x m x 2 3 2 2 2 2 x 2 2 x 2 x 2 3 2 . m . 2 2 x 2 x 2 x 2 2 2x Xét t
t ' x 0, x 1;1 3 2 x 2 2x 2 3 Nên t 3 . 3
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 23
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng 2
Khi đó phương trình trở thành 2
3t 2 mt 3t m . t 2 2 2 3t 2
Xét hàm số f t 3t . ta có f 't 3 . t 2 2 t t 6
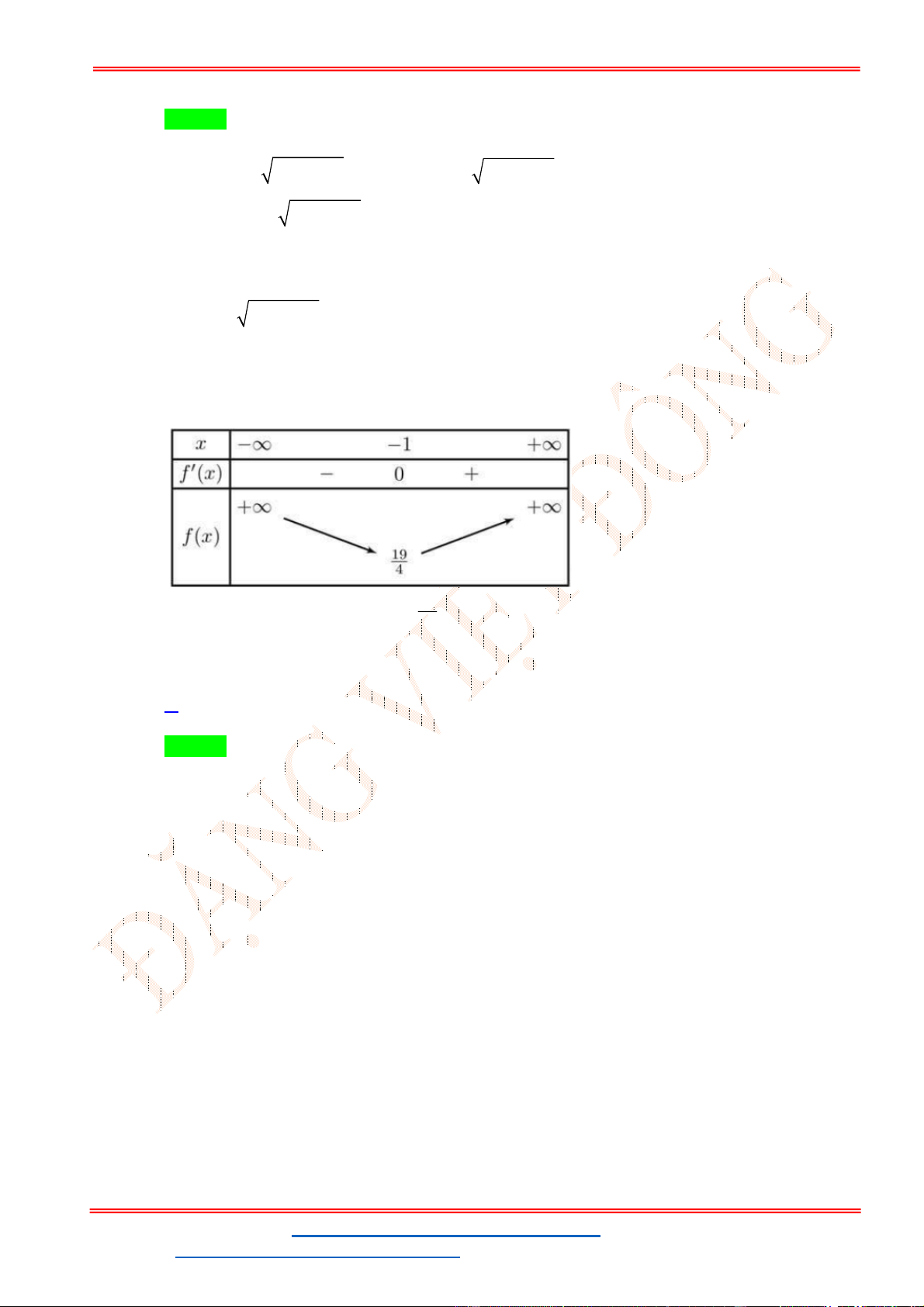
Cho f 't 0 t . 3 Bảng biến thiên
Dựa vào bảng biến thiên suy ra 2 6 m 3 3 .
Câu 47. Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn 2 021; 202 1 để phương trình 3
x2 m3x 3 2 x x x m x2 x 1 2 6 9 2 2
1 có một nghiệm duy nhất? A. 4038 . B. 3 . C. 2021. D. 4039 . Lời giải Chọn A
Chia cả hai vế của phương trình cho 2 2x ta được: 3 m3x 3 3 3 2 2 2 6 9 8 2 x x x x m m3 x 2 2 3 2 x m x 2 x * . Xét hàm đặc trưng: 3 2t f t t
Ta có f t t 2
2 ln 2 3t 0, t
nên f t đồng biến trên . * 3
m 3x 2 x 3 2
m x 6x 9x 8 .
Xét hàm số f x 3 2
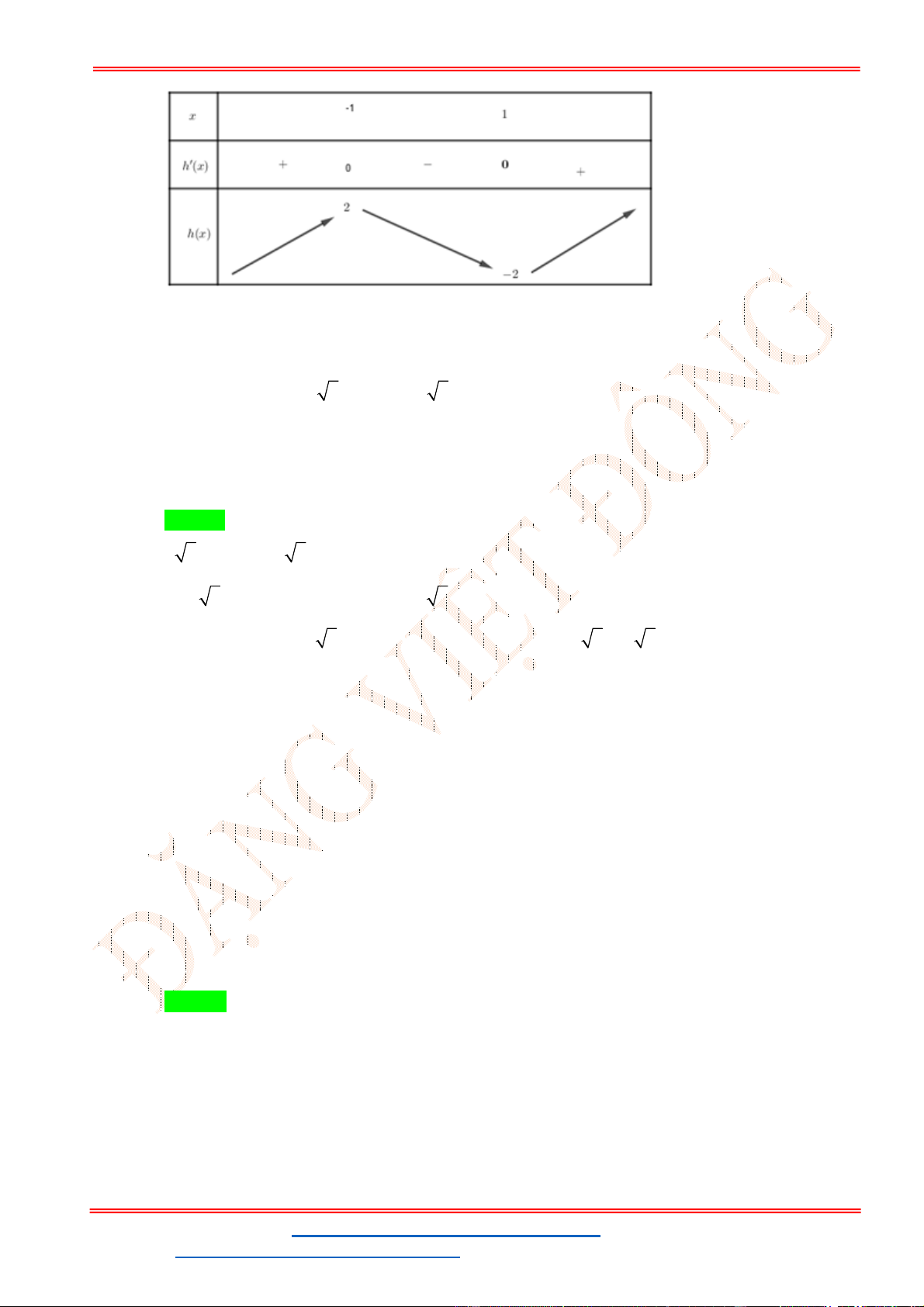
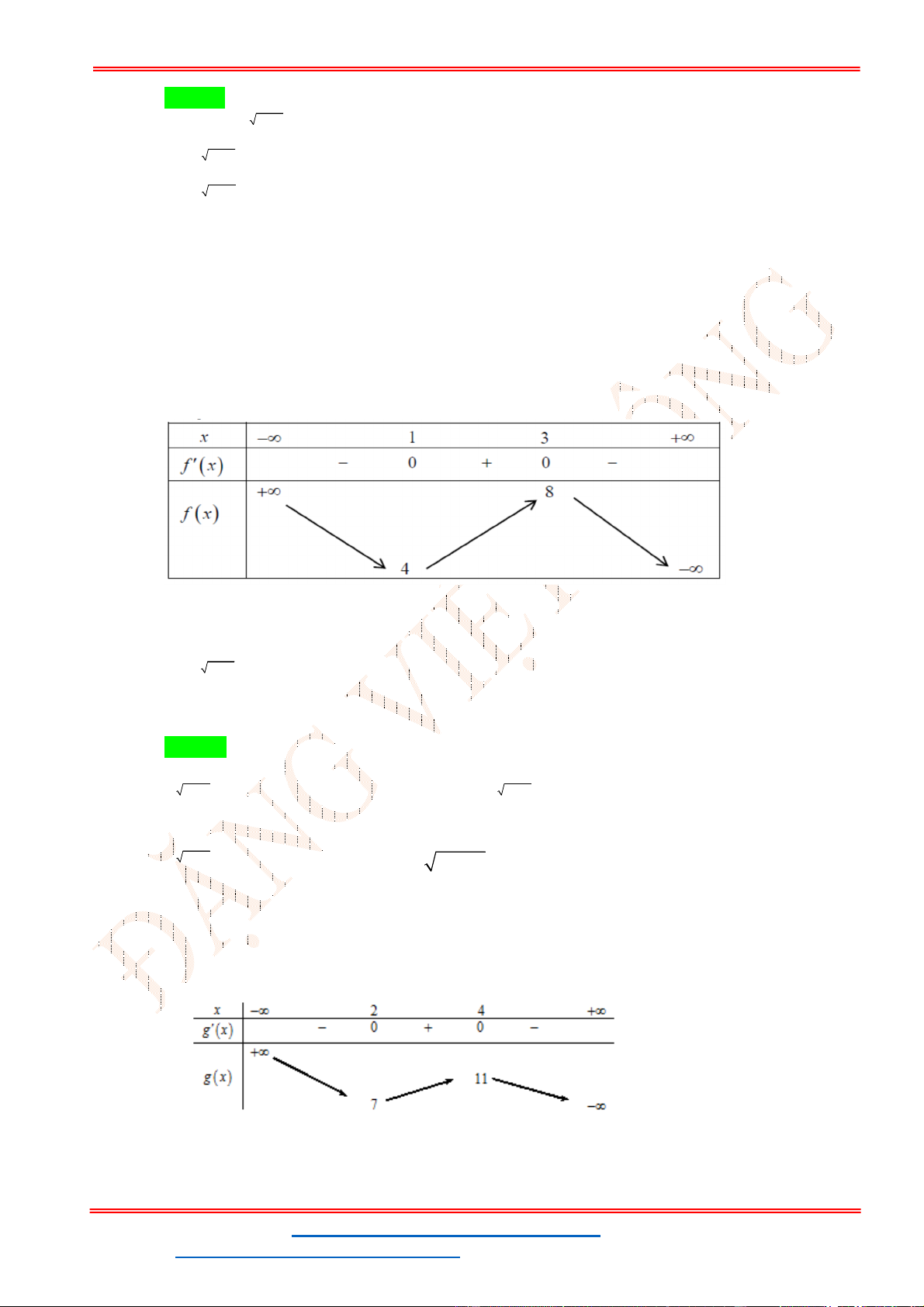
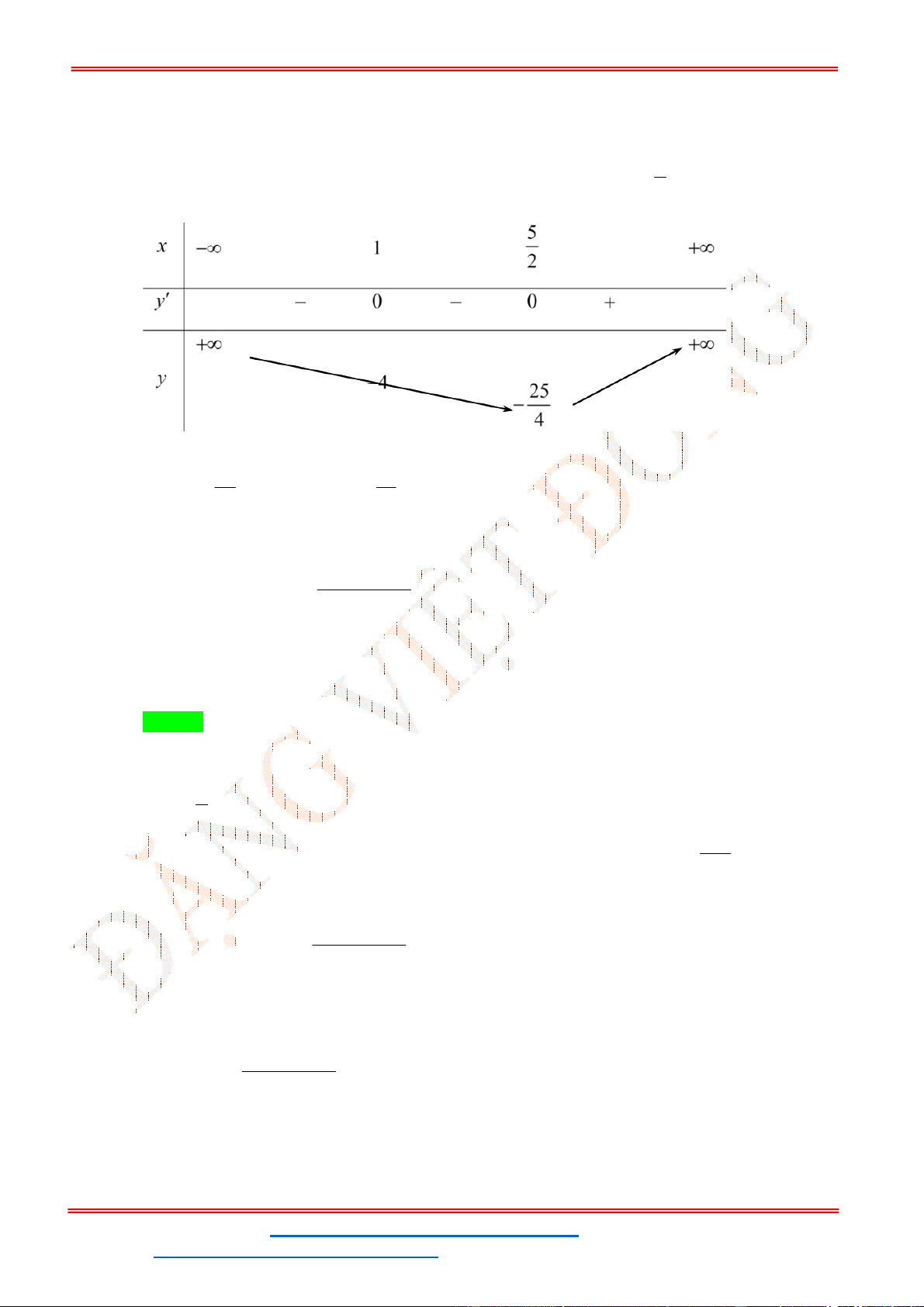
x 6x 9x 8 có bảng biến thiên như sau: x 1 3 f x 0 0 f x 8 4 m 8
Phương trình có nghiệm duy nhất khi và chỉ khi: . m 4 9 m 2021
Kết hợp với yêu cầu đề bài ta có:
. Vậy có tất cả 4038 số nguyên m thỏa mãn. 2 021 m 3 3
Câu 48. Phương trình x2 m3x 3 2 x x x m x2 x 1 2 6 9 2 2
1 có 3 nghiệm phân biệt khi và chỉ khi m ; a b đặt 2 2
T b a thì
A. T 36 .
B. T 48 .
C. T 64 . D. T 72 . Lời giải
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 24
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng Chọn B 3
Ta có x2 m3x 3 2 x x x m x2 x 1 2 6 9 2 2 1 3 m3x 3 2 3 2 2 6 9 2 2 x x x x m . 3 m x x m x x3 3 2 2 3 2 2 .
Xét hàm f t t 3
2 t trên . có f t t 2 '
2 .ln2 3t 0,t nên hàm số liên tục và đồng biến trên .
Do đó từ suy ra m x x3 3 2 2 3
m 8 9x 6x x .
Xét hàm số f x 3 2
x 6x 9x 8 trên . x 3 có f x 2 ' 3
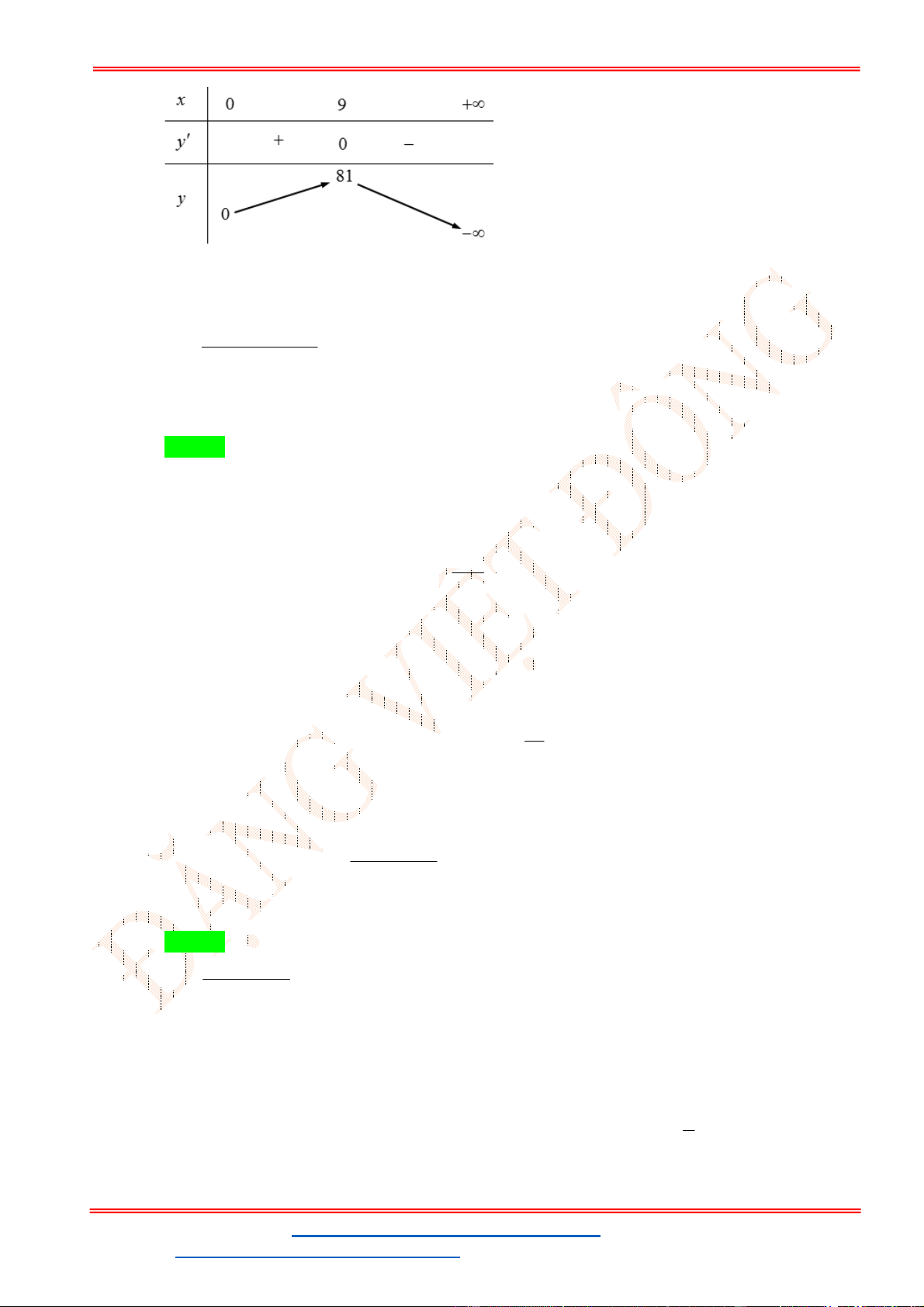
x 12x 9 ; f ' x 0 . x 1 Bảng biến thiên
Dựa vào bảng biến thiên ta có, phương trình có 3 nghiệm phân biệt khi 4 m 8 .
Suy ra a 4; b 8 2 2
T b a 48 . Câu 49. Tổng tất cả các giá trị nguyên của tham số m để phương trình 3
x3 m3x 3 2 x3 3 9 24 .3 3x x x x m
1 có ba nghiệm phân biệt bằng A. 45 . B. 38 . C. 34 . D. 27 . Lời giải Chọn D Phương trình tương đương với 3 m x 3 x m x x x x x m m x x3 3 3 2 3 3 3 3 9 24 27 3 3 3 3 3
Xét hàm đặc trưng: f t t 3
t f t t 2 3 '
3 ln3 3t 0; t . 3 m x x m x
x3 m x x m x3 3 3 3 3 3 3 3 3 3 3 3x 3 2
m x 9x 24x 27 . x 2
Đặt g x 3 2
x 9x 24x 27 g ' x 2 3
x 18x 24 0 . x 4 Ta có bảng biến thiên:
Để phương trình có 3 nghiệm phân biệt thì 7 m 11 m 8;9;1
0 . Vậy tổng các giá trị m bằng 27 .
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 25
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng
Câu 50. Tập hợp tất cả các giá trị thực của tham số
m để phương trình 3m m e e 2 x x 2 2 1
1 x 1 x có nghiệm là 1 1 1 1 A. 0; ln2 . B. ; ln2 . C. 0; . D. ln2; . 2 2 e 2 Lời giải Chọn B 1 t 2 Đặt 2
t x 1 x . 2 2
t 1 2x 1 x
Khi đó: 3m m t 2 e e t 1 3m m 3 e
e t t .
Xét hàm f u 3
u u f u 2 '
3u 1 0 Hàm số luôn đồng biến. 3m m 3 e
e t t em t m 1
Phương trình có nghiệm: e 2 m ln2 . 2
Câu 51. Tìm số giá trị nguyên của tham số thực m để tồn tại các số thực x ; y thỏa mãn 2 2
x y m
x y xym 2 2 e e
x y x y xy 2m 2 : A. 6 . B. 9 . C. 8 . D. 7 . Lời giải Chọn B 2 2
Ta có: x y m
x y xym 2 2 e e
x y x y xy 2m 2 2 2
x y m 2 2 e
1 exyxym x y m
x y xy m 1 0 1 Xét hàm số et f t t 1 trên et f t
1 , f t 0 et 1 0 t 0 Bảng biến thiên:
Từ bảng biến thiên suy ra f t 0 t . Do đó 1 f 2 2
x y m f x y xy m 0 2 2
x y m 0
x y 2 2xy m 0 2
x y xy m 0
x y xy m 0
x y S Đặt 2 S 4P xy P 2
S 2P m 0 2
S 2S 3m 2 trở thành 3
S P m 0
S P m
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 26
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng Xét phương trình 2
S 2S 3m 2
S 2S 3m 0 4 1
Hệ 3 có nghiệm 4 có nghiệm 1 3m 0 m 3 1 Do 2 S 4P nên 2 P S 4 3 1 Ta có: 2 2
S 2S 3m 3S 3P 3S S 2
S S 0 0 S 4 4 4 2
0 S 2S 24 0 3m 24 0 m 8
Do m nguyên nên m 0;1;...; 8 .
Vậy có 9 giá trị nguyên của tham số thực m thỏa mãn yêu cầu bài toán. 2 2
2 x 2 xm 2 10
Câu 52. Cho bất phương trình 2
x 2 xm 2 3 3
, với m là tham số thực. Có bao nhiêu giá 3
trị nguyên của m để bất phương trình đã cho nghiệm đúng với mọi x 0; 2 ? A. 9 . B. 11. C. 10 . D. 15 . Lời giải Chọn C 2 2
x 2x m 0
x 2x m 0 Điều kiện: . 2 2
x 2x m 2
x 2x m 4 2 2
x 2x m 2
2 x 2x m 1 2 Đặt: t
t 1, t 0 . 2 2 2 t
x 2x m 2 1 t 1 t 10 1 1
Khi đó bất phương trình trở thành: 3 3t 3t 3 . 3 3 3 1 Xét hàm số 3 t 3t f t . 1 t 1 Ta có ' 3 .ln3 .3t f t
.ln3 0, t 1, t 0 . 2 t
Nên f t nghịch biến trên các khoảng 1
; 0 và 0; . 10 + Trên khoảng 1
; 0 ta có f t f 1
nên bất phương trình vô nghiệm. 3 t 1 1 1
+ Trên khoảng 0; . Ta có 3t 3
f t f 1 t 1. 3 3 2
x 2x m 2 Hay 0 1 2 0
x 2x m 2 2 2
x x m
m x 2 2 4 2 16 5 1 17 m .
Bất phương trình đã cho nghiệm đúng với mọi x 0; 2 khi và chỉ khi x 2 1 17 m 1 17 m m 16
đúng với mọi x 0; 2 . x 2 1 5 0 5 m m 5 m
Do m nên m 6;7;8;9;10;11;12;13;14;1 5 .
Có 10 giá trị nguyên của m thỏa yêu cầu bài toán.
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 27
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng
Câu 53. Có bao nhiêu giá trị nguyên của tham số m 2
0; 20 để bất phương trình sau nghiệm đúng 2 2
vớimọi x 3;
5 : mx2xm
x xm 2 2
2x 2 m 1 ? A. 41. B. 32. C. 35. D. 38. Lời giải Ta có: m x 2 xm
x xm 2 2 2 2
2x 2 m
1 , x 3; 5
m xm 2 2 x mx
x m 2 1 1 1 2 2 1
, x 3; 5
m xm 2 2 x mx
x mx m x m 2 1 1 1 2 2 2 1 1 1
, x 3; 5
m xm 2 m x m 2 2 1 1 x mx 1 2 2 1 1 2 x mx
1 , x 3; 5 (*) Xét hàm số 2t f t t trên . ' 2t f t
.ln2 1 0 x 2 (*) f m x m f 2 1 1 x mx
1 , x 3; 5
m x m 2 2 1 1
x mx 1, x 3; 5
x m 2 1 0
, x 3; 5
x m 1, x 3; 5 m 1 3 m 4 m 1 5 m 4 2 0 m 4 Mặt khác m 2 0; 20 nên 4 m 20
Vì m nên có 32 số nguyên m thỏa mãn.
DẠNG 3: PHƯƠNG PHÁP HÀM ĐẶC TRƯNG GIẢI PT, BPT LÔGARIT KHÔNG CHỨA THAM SỐ
1 - PT LÔGARIT KHÔNG CHỨA THAM SỐ x 2
Câu 54. Gọi x , x là hai nghiệm thực của phương trình 2 log
x 7x 10 0 . Tính 1 2 3 2 x 4x 5
x x . 1 2 A. 5 . B. 3 . C. 5 . D. 3 . Lời giải Chọn C
+) Điều kiện: x 2 . 3 x 2 +) Khi đó phương trình 2 log
x 7x 11 0 3 2 x 4x 5
log 3x 6 log 2
x 4x 5 3x 6 2
x 4x 5 0 3 3
log 3x 6 3x 6 log 2
x 4x 5 2 x 4x 5 * 3 3
+) Xét hàm số f t log t t trên 0; 3 1
Ta có f 't
1 0, t 0 . t.ln3
Vậy hàm số y f t đồng biến trên 0; .
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 28
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng
Mà * có dạng f x f 2 3 6
x 4x 5 7 5 x tm 2 Nên phương trình 2
3x 6 x 4x 5 2
x 7x 11 0 7 5 x tm 2
x x 5 . 1 2 2x 1 a a
Câu 55. Phương trình 2 log
3x 8x 5 có hai nghiệm là a và
(với a , b * và là 3 2 (x 1) b b
phân số tối giản). Giá trị của b là A. 1. B. 4 . C. 2 . D. 3 . Lời giải Chọn D 1 2x 1 0 x Điều kiện 2 . x 1 0 x 1 2x 1 Ta có: 2 log
3x 8x 5 . 3 x 2 1 2x 1 2x 1 2 2 log
1 3x 8x 4 log
3 x 1 2x 1 . 3 2 3 x 2 1 3 x 1 log 2x 1 2x
1 log 3x 2
1 3x 2 1 1 . 3 3
Xét hàm số: f t log t t với t 0 . 3 1 f 't
1 0 t 0 . t.ln3
Suy ra hàm số f t đồng biến trên 0; . 2 Phương trình
1 f 2x
1 f 3x 1 x 2
x x 2 2 2 1 3 1
3x 8x 4 0 hay 2 . x 3 2
Vậy hai nghiệm của phương trình là 2 và suy ra b 3 . 3 2x 1 a
Câu 56. Phương trình 2 log
3x 8x 5 có hai nghiệm là a và
. Giá trị của b là 3 2 (x 1) b A. 1. B. 4 . C. 2 . D. 3 . Lời giải Chọn D 1 2x 1 0 x Điều kiện 2 . x 1 0 x 1 2x 1 Ta có: 2 log
3x 8x 5 . 3 x 2 1
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 29
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng 2x 1 2x 1 2 2 log
1 3x 8x 4 log
3 x 1 2x 1 . 3 2 3 x 2 1 3 x 1 log 2x 1 2x
1 log 3x 2
1 3x 2 1 1 . 3 3
Xét hàm số: f t log t t với t 0 . 3 1 f 't
1 0 t 0 . t.ln3
Suy ra hàm số f t đồng biến trên 0; . 2 Phương trình
1 f 2x
1 f 3x 1 . x 2
x x 2 2 2 1 3 1
3x 8x 4 0 hay 2 . x 3 2
Vậy hai nghiệm của phương trình là 2 và suy ra b 3 . 3 2 x 1 Câu 57. Biết x , x
x x là nghiệm của phương trình 2 log
x x 0 và 1 2 1 2 4 2x 3 1 2x 3x
a b với a,b là các số nguyên dương. Tính a b . 1 2 2
A. a b 4 .
B. a b 13 .
C. a b 8 .
D. a b 11. Lời giải Chọn C 2 x 1 3
Điều kiện của phương trình là:
0 2x 3 0 x
. Với điều kiện này thì 2x 3 2
phương trình đã cho tương đương: 2 2 1 x 1 x 1 2 2 log
x x 0 log
2x 2x 0 2 2 2 2x 3 2x 3 log 2 x 2 1 2x log
2x 3 2x 2 2 log 2 x 2 1 2x 3 log
2x 3 2x 3 2 2 log 2 x 2
1 1 2x 2 log
2x 3 2x 3 2 2 log 2 2x 2 2 2x 2 log
2x 3 2x 3 * . 2 2
Xét hàm số, g t log t t , chúng ta có thể dễ dàng thấy rằng khi t 0 thì hàm số g t liên 2
tục và luôn đồng biến. Hơn nửa, phương trình * chúng ta có thể viết lại 1 3 x g 2
x g x 2 2 2 2 2
3 2x 2 2x 3 . 1 3 x 2 1 3 1 3 1 1
Vậy 2x 3x 2. 3. 5 3
a b a 5, b 3 a b 8 . 1 2 2 2 2 2 2 x 3x 4
Câu 58. Phương trình 2 ln
x 4x 2 0 có hai nghiệm x , x . Khi đó x x bằng x 2 1 2 1 2
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 30
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng A. 4 . B. 2 . C. 4 . D. 2 . Lời giải Chọn A 2 x 3x 4
Với điều kiện x 2 ta có: 2 ln
x 4x 2 0 . x 2 2
x x 2 ln 3 4
x 3x 4 ln x 2 x 2 (1).
Xét hàm số f t t lnt,t 0; . 1
Ta có f 't 1 0,t 0; nên hàm số f t đồng biến trên khoảng 0; . t
Phương trình (1) có dạng f 2
x 3x 4 f x 2 nên ta có: x 2 2 2
x 3x 4 x 2 2 1
x 4x 2 0
(thỏa mãn điều kiện). x 2 2 2
Vậy ta có: x x 4 . 1 2 2
4x 4x 1
Câu 59. Biết x , x là hai nghiệm của phương trình 2 log
4x 1 6x và 1 2 7 2 x 1 x 2x
a b với a , b là hai số nguyên dương. Tính a b . 1 2 4
A. a b 13 .
B. a b 11.
C. a b 16 .
D. a b 14 . Lời giải Chọn D 1
Điều kiện: x 0, x . 2 2
4x 4x 1 Ta có: 2 log
4x 1 6x log 2
4x 4x 2
1 4x 4x 1 log 2x 2x . 7 7 7 2 x 1
Xét hàm số f t log t t có f 't
1 0 t 0 nên là hàm số đồng biến trên 7 l t n7 0; . 3 5 Do đó ta có 2 2
4x 4x 1 2x 4x 6x 1 0 x . 4 Khi đó 3 5 3 5 1 3 5 3 5 1 x 2x 2
9 5 hoặc x 2x 2 9 5 . 1 2 1 2 4 4 4 4 4 4 3 5 3 5 Vậy x ; x
. Do đó a 9;b 5 và a b 9 5 14 . 1 2 4 4 2 x 3x 2
Câu 60. Phương trình 2 log
x 4x 3 có các nghiệm x , x . Hãy tính giá trị của biểu 2 2 3x 5x 8 1 2 thức 2 2
A x x 3x x . 1 2 1 2 A. 31. B. 31. C. 1. D. 1 Lời giải Chọn C x 2 Ta có 2
3x 5x 8 0 x nên điều kiện của phương trình là: 2
x 3x 2 0 . x 1
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 31
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng 2 x 3x 2 Khi đó 2 log
x 4x 3 2 2 3x 5x 8 log 1 2
x 3x 2 log 2
3x 5x 8 2
3x 5x 8 2
x 3x 2 . 2 2 2 log 1 1 2
x 3x 2 2
x 3x 2 log 2
3x 5x 8 2
3x 5x 8 . 2 2 2 2 1 1 1
Xét hàm số f t log t t, (t 0) ; 'ft 0 t 0 . 2 2 l t n2 2
Nên hàm số f t đồng biến trên khoảng 0; .
Mà phương trình có dạng: f 2
x x f 2 3 2
3x 5x 8 .
Do đó phương trình đã cho tương đương với phương trình: x 1 2
x x 2 3 5 8
x 3x 2 2
2x 8x 6 0 T / m . x 3
Vậy A x x 3x x x x 2 2 2 2
5x .x 4 5.3 1. 1 2 1 2 1 2 1 2 2 x 1 x 1
Câu 61. Biết phương trình log 2log
có một nghiệm dạng x a b 2 trong 5 3 x 2 2 x
đó a,b là các số nguyên. Tính 2a b . A. 3 . B. 8 . C. 4 . D. 5 . Lời giải Chọn B 2 x 1 x 1 2 x 1 x 1 Ta có log 2log log 2log 1 . 5 3 5 3 x 2 2 x x 2 x ĐKXĐ: x 1 . 1 log
2 x 1 2log 2 x log x 2log x 1 * 5 3 5 3
Xét hàm số f t log t 2log t 1 , với t 1. 5 3 1 2 f 't
0 với mọi t 1, suy ra f t đồng biến trên khoảng 1; . t.ln5 t 1 ln3 Từ (*) ta có f 2 x
1 f x nên suy ra
x x x 2 2 1 2 x 1 0
x 1 2 (do x 1 ).
Suy ra x 3 2 2 a 3; b 2 2a b 8 . 2 x x 3
Câu 62. Tổng các nghiệm phương trình 2 log
x 3x 1 2log 2 có giá trị bằng 3 2 9 x 2x 2 A. 1. B. 2. C. 3 . D. 1 . Lời giải Chọn C 2 x x 3 Phương trình: 2 log
x 3x 1 2log 2 3 2 9 x 2x 2 2 x x 3 log
log 2 2x 4x 4 x x 3 2 2 2 3 3 x 2x 2
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 32
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng 2 x x 3 log 2
2x 4x 4 2 x x 3 3 2 2x 4x 4 log 2
x x 3 2
x x 3 log 2
2x 4x 4 2
2x 4x 4 . 3 3 1
Xét hàm số f t log t t , t 0 thì f 't
1 0 , t 0 . 3 t.ln3
Do đó f t đồng biến với mọi t 0 , nên phương trình f 2
x x f 2 3
2x 4x 4 2 2 2
x x 3 2x 4x 4 x 3x 1 0 . 3 5
Phương trình có 2 nghiệm x . 2
Vậy tổng các nghiệm của phương trình có giá trị là 3 . 2
4x 4x 1
Câu 63. Biết x , x
x x là hai nghiệm của phương trình 2 log
4x 1 6x và 1 2 1 2 7 2x 1 x 3x
a 2 b với a, b là các số nguyên dương. Tính a b 1 2 4
A. a b 14 .
B. a b 16 .
C. a b 17 .
D. a b 15 . Lời giải 1 4x 4x 1 x 2 2 2 1 x 0 0 2 . 2x 2x x 0 2
4x 4x 1 2 2 2 log
4x 1 6x log
2x 1 2x 1
log 2x 2x 7 7 2x 7
Xét hàm f t log t t t 0 . 7 1
Ta có f t 1 0 t
0 , vậy f t log t t t 0 là hàm đồng biến suy ra 7 t ln 7 log 2x 2 1 2x 2 1
log 2x 2x 2x 2 1 2x 2
4x 6x 1 0 7 7 3 5 x 2 2 4
4x 6x 1 0 . 3 5 x 1 4 1 x 3x 12 2 5 . 1 2 4
Câu 64. Tìm tổng các nghiệm của phương trình: log 3 x x 2 3
x 7x log x 2
1 4x 7 . 4 2 A. 17 . B. 2 . C. 9 . D. 11. Lời giải Chọn B 3
x x 2 0 Điều kiện x 1 0
Với điều kiện trên, ta có: log 3 x x 2 3
x 7x log x 2 1 4x 7 4 2 3 3 log
x x 2 x x 2 log 2x 2 2
4x 8x 4 2 2 log
x x 2 x x 2 log 2x 2 2x 22 3 3 * 2 2
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 33
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng
Đặt f t 2
log t t , t 0 2 1
Ta có f 't
2t 0, t 0 l t n2
Do đó hàm số f t đồng biến trên khoảng 0; .
Nên f 3
x x f x 3 * 2 2 2
x x 2 2x 2
x x x 2 3 3 2 2 2 2
x 4x 7x 6 0 x 2
Vậy tổng các nghiệm của phương trình là 2.
Câu 65. Cho phương trình
x x x x
x x 3 log 3 2 3 6 16 2log 4 2 3 có một nghiệm có a b dạng x
, trong đó a, b là hai số nguyên dương. Giá trị của biểu thức a b bằng 2 A. 9 . B. 10 . C. 14 . D. 5 . Lời giải Chọn C
Điều kiện x 4 . 1 Bất phương trình
log x 3 x x 3 3x 8 log x 4 x 33 2 1
log x 3 x 3 x 3 3 x 3 3 x 3 1 log x 4 x 4 3 1 2
x x 3
x x 3 log 3 3 1 log 4 4 1
f x 3 f x 4 *. 1
Với hàm số f t 3
logt t ; t 0 ,có đạo hàm: f 't 2
3t ; t 0 l t n10
Suy ra hàm số đơn điệu tăng. Từ (*) suy ra: x 4 x 4 a b f x 9 5
3 f x 4 x 3 x 4 x x 3 x 42 9 5 x 5 2 2 a 9 suy ra:
a b 14 . b 5 2 1 2x 1 1
Câu 66. phương trình log
x 2 x 3 log 1
2 x 2 , gọi S là tổng tất cả các 2 2 2 x x
nghiệm của nó. Khi đó, giá trị của S là 1 13 1 13 A. S .
B. S 2 . C. S . D. S 2 . 2 2 Lời giải Chọn C 1 2 x Điều kiện 2 . x 0 2 1 2x 1 1 Ta có : log
x 2 x 3 log 1 2 x 2 2 2 2 x x 2 2 1 1 log x 2 x 2 1 log 2 2 1 1 2 2 x x
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 34
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng
Xét hàm số f t log t t 2 1 , t 0 . 2 1 2
2ln2.t 2ln2.t 1
Ta có f t 2t 1 , t 0 . tln2 t.ln2 a 2ln2 0 Vì 2
2ln2.t 2ln2.t 1 có suy ra 2
2ln2.t 2ln2.t 1 0 . 2 ' ln 2 2ln2 0
Do đó f t 0;t 0 nên hàm số f t đồng biến trên khoảng 0; . 1 Vậy
1 f x 1 2 f 2
x 2 2 x x x 1 3 13 3 2
x 2x 4x 1 0 x 2 3 13 x 2 x 1 1 13
Kết hợp với điều kiện ta được 3 13 . Vậy S . x 2 2 4x 2019
Câu 67. Cho phương trình 2 log
x 6x 2016 . Tổng tất cả các nghiệm của phương trình 2 2 x 2x 3 là A. 2. B. 5. C. 6. D. 4. Lời giải Chọn C 4x 2019 2019 Điều kiện: 0 x 1 2 x 2x 3 4 Đây là một dạng cơ bản của phương trình hàm đặc trưng: u log
v u log u u log v v a a a v 4x 2019
Phương trình đã cho log 2
x 2x 3 4x 2019 2 2 x 2x 3
log 4x 2019 log 2
x 2x 3 2
x 2x 3 4x 2019 2 2
log 4x 2019 4x 2019 log 2
x 2x 3 2 x 2x 3 2 2 f x f 2 4 2019
x 2x 3 1
Với hàm số: f t t log t có đạo hàm: f 't 1 0 , t 0 . 2 l t n2
Suy ra hàm số đơn điệu trên tập xác định.
Suy ra: f x f 2 x x 2 2 4 2019 2
3 4x 2019 x 2x 3 x 6x 2016 0 x 48
. Vậy x x 6 . x 4 2 1 2
Câu 68. Có bao nhiêu giá trị nguyên của y thỏa mãn 5x log
x y y . Biết rằng y 2020 . 5 A. 1. B. 4 . C. 3 . D. 7 . Lời giải
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 35
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng Chọn A
Điều kiện x y 0 . Đặt log 5t x y t x y . 5 5
x t y Khi đó: t x
5 t 5 x . 5t x y Xét hàm số
5u ' 5u f u u f u
.ln5 1 0 hàm số đồng biến với u .
Ta có: f t f x t x . Khi đó: 5x 5x x y y x .
Đặt 5x ' 5 .x g x x g x
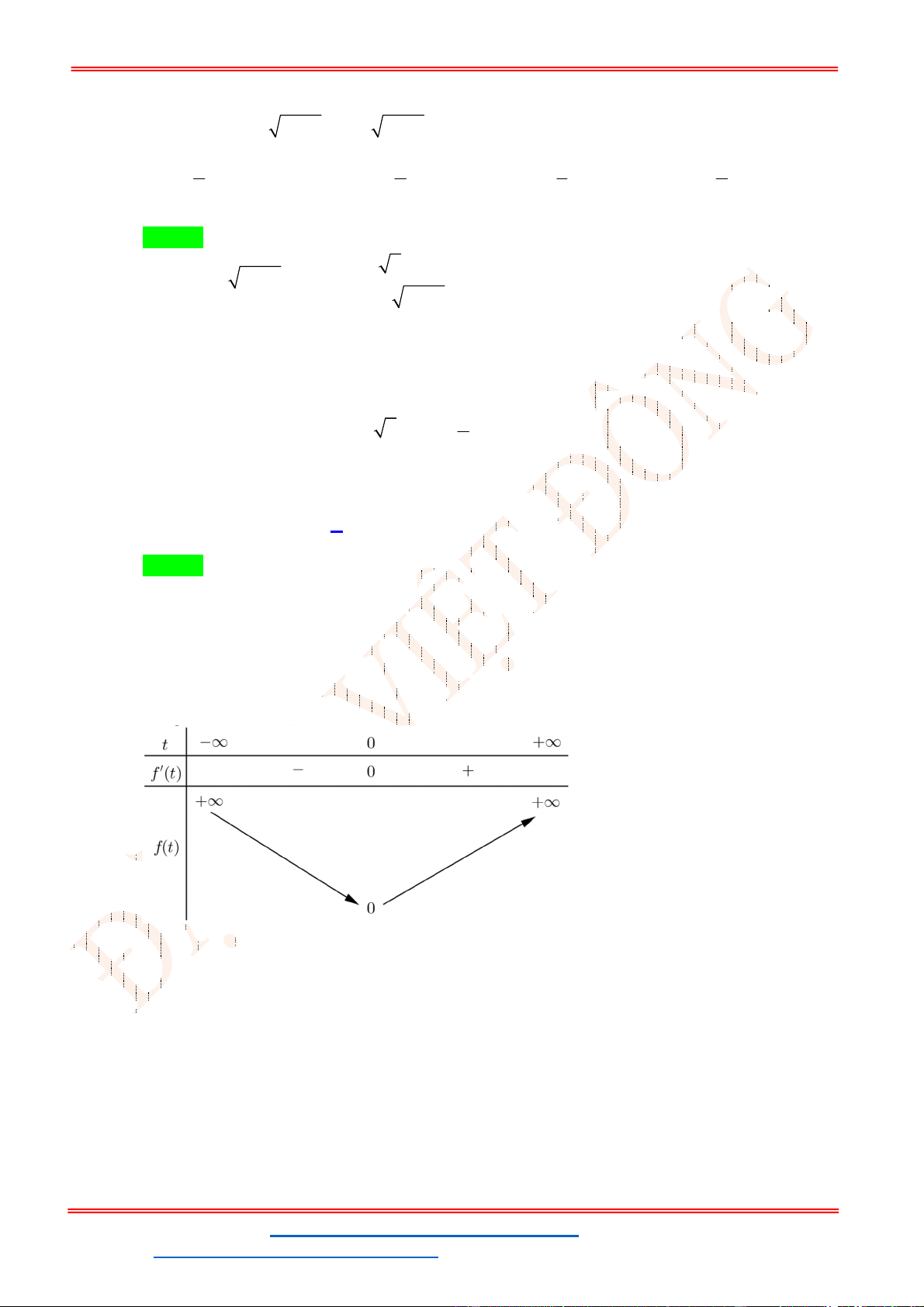
ln5 1 0 x log ln5 . 5 1
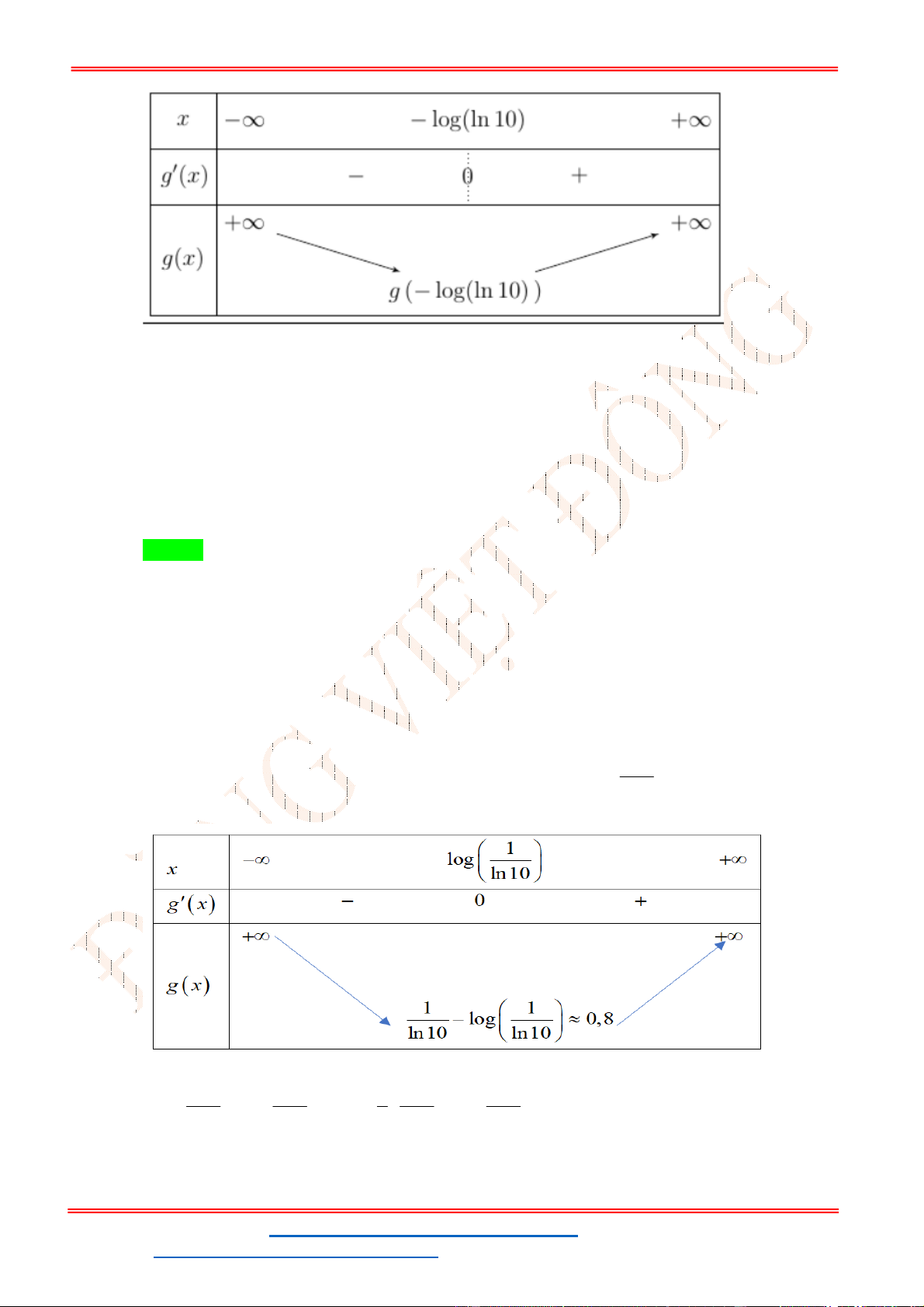
Để phương trình có nghiệm thì y log ln5 0,917 . 5 ln5
Mà y 2020 nên có đúng 2020 giá trị nguyên của y thỏa mãn yêu cầu đề bài.
Câu 69. Có bao nhiêu cặp số x ; y thuộc đoạn 1 ; 2020 thỏa mãn y là số nguyên và ln ey x x y ? A. 2021 . B. 2020 . C. 6 . D. 7 . Lời giải Chọn D Xét hàm số
et ' 1 et f t t f t
0,t f t đồng biến trên 1 . Theo đề ra: ln ey x x y
f lnx f y 2 . Từ
1 , 2 suy ra ln ey x y x
.Để 1 x 2020 thì 1 ey 2020 0 y ln2020 . y
y 1 ; 2 ;3 ; 4 ;5 ;6 ; 7 . 1 y 2020
Với mỗi giá trị y 1 ; 2 ;3 ; 4 ;5 ;6 ;
7 ta có một giá trị x tương ứng thuộc đoạn 1 ; 2020
Vậy có 7 cặp số x ; y thỏa mãn. Câu 70. Có bao nhiêu cặp số nguyên dương ; x y với x 2020 thỏa mãn log
1 2 2 1 4y x x y . 2 A. 5 . B. 1010 . C. 6 . D. 2020 . Lời giải Chọn A
Theo đề bài log
1 2 2 1 4y log 2 1 2 2 1 2 2 y x x y x x y 2 2 Đặt log 2 1 2 1 2t t x x . 2
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 36
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng Ta có t 2 2 2 y t 2 y 1 . Xét hàm số 2t f t t trên R ' 2t f t
.ln2 1 0 t R f t đồng biến trên R .
1 f t f 2 y t 2 y log 2 x 1 2 y 2 2 1 2 y x 2 y 1 x 2 1. 2 y 1 Mà 2 1 x 2020 2 1 2020 y 1 log 2019 . 2 2 Vì
y Z y 1; 2;3; 4; 5 .
Vậy có 5 cặp điểm cặp số nguyên dương ; x y .
Câu 71. Có bao nhiêu cặp số nguyên dương ;
x y thoả mãn 1 x 2020 và 2y y 2x log y 1 x 2 ? 2 A. 2021 . B. 10 . C. 2020 . D. 11. Lời giải Chọn D Theo đề bài, 2y y 2x log y 1 x 2 2 x y y y y 2 2y y y 2y 2 log 2 2x log x 2 2 log 2 2x 2 log 2 2 2 2 2 2 y y x x y y 2 2 2 2 2. 2 log 2 2 log 1 . 2 2 2 2
Xét hàm số f t 2t log t , t 0 . 2 1
Vì f 't 2
0 t 0 f t đồng biến trên 0; tln2 x x y 2 2y y 2 2y nên 1 f 2 y y y y 1 f 2
2.2 2x 2 2x 2 x 2 . 2 2
Do 1 x 2020 nên 0 y 1 log 2020 1 y 11,98 . 2 Do *
y nên y 1 ; 2;3;..;1
1 , với mỗi giá trị y cho ta 1 giá trị x thoả đề.
Vậy có 11 cặp số nguyên ;
x y thoả mãn đề bài.
Câu 72. Có bao nhiêu cặp số nguyên x ; y thoả mãn 0 x 2020 và log 3 3 2 9y x x y ? 3 A. 2019 . B. 6 . C. 2020 . D. 4 . Lời giải Chọn D + Ta có: log 3 3
2 9y 1 log 1 2 9y x x y x x y 1 . 3 3 + Đặt t log
x 1 . Suy ra: 1 3t 3t x x 1. 3 Khi đó: t 2
1 3 2 3 y t y 2. Xét hàm số: 3h f h h , ta có: ' 1 3 . h f h
ln3 0 h nên hàm số f h đồng biến trên .
Do đó: 2 2 2 log 2 1 2 1 3 y 1 9y f t f y t y x y x x . 3
+ Do 0 x 2020 nên 1 1 2021 1 9y x
2021 0 y log 2021 3, 46 . 9
Do y nên y 0;1 ; 2;
3 , với mỗi giá trị y cho ta 1 giá trị x thoả đề.
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 37
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng
Vậy có 4 cặp số nguyên x ; y thoả đề.
Câu 73. Cho 0 x 2021 và log
1 3 1 27y x x y
. Có bao nhiêu cặp số x ; y nguyên thỏa 3 mãn điều kiện trên? A. 2021 . B. 2020 . C. 4 . D. 3 . Lời giải Chọn D Ta có: log
1 3 1 27y log 1 1 27y x x y x x 3y 3 3 log x 3 1 3 log 3 1 3 y x
3y * . 3 Xét hàm đặc trưng 3t f t t . Ta có ' 3t f t
.ln3 1 0, t nên hàm số 3t f t
t đồng biến trên .
Khi đó, từ phương trình * ta có: log 1 3 log 1 3 1 27 y 27 y f x f y x y x x 1 . 3 3
Mà 0 x 2021 0 27 y 1 2021 0 y log 2022 2, 31 . 27
Vì y nên y 0 ;1 ;
2 x 0 ; 26 ; 72 8 .
Do đó có 3 cặp số nguyên x ; y 0 ; 0 ; 26 ; 1
; 728 ; 2 thỏa mãn phương trình đã cho.
Câu 74. Cho 1 x 2022 và log 4 2 2 4y x x y
. Hỏi có bao nhiêu cặp số nguyên x ; y 2
nguyên thỏa mãn các điều kiện trên? A. 1. B. 4 . C. 5 . D. 2 . Lời giải Chọn C Ta có: log 4
2 2 4y log 2 2 4y x x y x x 2 y 2 2
log x 2 x 2 2
2 y 2 y t log t 2 t 2 y 2 2
f x 2 f t 2
3 x 2 t 2 y 2024 log 3 2 y log 2024 2 2 log 3 log 2024 t 2 2 0,8 y
5,5 1 y 5 . 2 2
Vậy có đúng 5 giá trị nguyên của y thỏa mãn ứng với 5 cặp x ; y nguyên thỏa mãn.
Câu 75. Có bao nhiêu cặp số nguyên dương ;
x y thỏa mãn đồng thời hai điều kiện: 6 1 x 10 và
x x 2 2 y 2 2 log 10 20 20 10
y x 2x 1? A. 4 . B. 2 . C. 3 . D. 1. Lời giải Chọn D Điều kiện: 2
10x 20x 20 0 , đúng x . Ta có
x x 2 2 y 2 2 log 10 20
20 10 y x 2x 1
x x
x x 2 2 2 y 2 2 1 log 10 2 2 10 y
x x
x x 2 2 2 y 2 2 1 log10 log 2 2 10 y
x x
x x 2 2 2 y 2 2 2 log 2 2 10 y 2 x x
x x 2 log 2 2 2 y 2 10 log 2 2 10 y (*).
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 38
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng Xét hàm 10t f t t trên .
Ta có 10t f t
.ln10 1 0 , t . Do đó f t đồng biến trên . 2 Khi đó (*) f 2
x x f 2 log 2 2 y 2 x x 2 log 2 2 y 2 2 2 10y x x 2 2 1 1 10y x . 2 2 2 Vì 6
1 x 10 nên y x 6 1 1 1 10 10 1 1 y 2 2 6 0 log 10 1 1 . Vì
y nên y 1; 2; 3 . x 2 (ktm) + Với y 1 2
x 2x 2 10 2
x 2x 8 0 . x 4 (tm) + Với y 2 2 4
x 2x 2 10 2
x 2x 9998 0 (không có giá trị x nguyên nào thỏa mãn). + Với y 3 2 9
x 2x 2 10 2
x 2x 999999998 0 (không có giá trị x nguyên nào thỏa mãn).
Vậy có một cặp nguyên dương ; x y 4;
1 thỏa mãn yêu cầu bài toán.
Câu 76. Có bao nhiêu cặp số nguyên
x ; y thoả mãn x y 0; 2 0 x 20 và
log x 2 y 2 2
x 2 y 3xy x y 0 ? 2 A. 19. B. 6 C. 20. D. 41. Lời giải Chọn C
+ Điều kiện: x 2 y 0
+ Ta có: x y 0 nên
log x 2 y 2 2
x 2 y 3xy x y 0 2
x y x 2y 2 2 log
x 2 y 3xy x y 0 2 x y log 2 2
x 2 y 3xy log x y 2 2
x 2 y 3xy x y 0 2 2 log 2 2
x 2 y 3xy 2 2
x 2 y 3xy log
x y x y 1 2 2 1
Xét hàm số: f t log t t , ta có: f 'h
1 0 t 0 ; nên hàm số f t đồng 2 l t n2
biến trên 0 ; .
Do đó: f 2 2
x y xy f x y 2 2 1 2 3
x 2 y 3xy x y
x y x 2 y
1 0 x 1 2 y vì x y 0 1 9 21
+ Do 20 x 20 suy ra y 2 2
+ Do y nên y 9 ; 8 ;..; 9 ;1
0 , với mỗi giá trị y cho ta 1 giá trị x thoả đề.
Vậy có 20 cặp số nguyên x ; y thoả đề. 1 1 1
Câu 77. Phương trình x 9 log 2 x 1 x 9 9 2 x 1 x 9 có tất cả 3 2020 2020 2020
bao nhiêu nghiệm thực phân biệt? A. 4 . B. 1. C. 3 . D. 2 .
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 39
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng Lời giải Chọn C 1 x 9 log 1 1 2 x 1 x 9 9 2 x 1 x 9 (1) 3 2020 2020 2020 1 ĐKXĐ:
x 9 0 x 1 8180 . 2020 1
Chia hai vế của phương trình (1) cho
x 9 ta được: 2020 log 1 9 2 x 1 x 9 2 x 1 3 2020 1 x 9 2020 log 1 9 2 x 1 log x 9 2 x 1 2 3 3 2020 1 x 9 2020 log 1 9 2 x 1 log x 9 2 x 1 log 9 3 3 3 2020 1 x 9 2020 log 9 9 2 x 1 2 x 1 log (2) 3 3 1 1 x 9 x 9 2020 2020
Đặt f t log t t với t 0 , 3 1 f 't
1 0,t 0 . t.ln3
Suy ra hàm số đồng biến trên 0; . 9 9
Do đó, (2) f 2 x 2 1 f x 1 1 1 x 9 x 9 2020 2020 1 1 3 2 3 2 x 9x
x 0 x 18180x x 0 x 2
x 18180x 1 0 2020 2020
x 0TM 2
x 9090 9090 1 TM 2
x 9090 9090 1 TM
Vậy phương trình có 3 nghiệm thực phân biệt. 4 4 x 1
Câu 78. Có bao nhiêu số nguyên dương x thỏa mãn sin ycos y 2 log x 4 sin 2 y ? 2 2 A. Vô số. B. 3 . C. 1. D. 2 . Lời giải Chọn B Ta có: 4 4 x 1 log x 4 y
y sin 2 y log y y x 4 4 sin cos 2 sin cos 2 1 x 1 4 sin 2 y 2 2 2
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 40
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng 4 4 y y log x 2sin cos 2 2 1 x 1 2 4sin . y cos y 2 2 4 4 2 sin ycos y 2 log x 2 2 1 x 1 2 4sin . y cos y 2 2 2 sin y cos y 2 4 4 y y log x 2sin cos 1 x 1 2 2 4 4
sin y cos y (2). 2 Xét hàm số
2t ' 2t f t t f t
.ln2 1 0 , t 0 .
hàm số y f t đồng biến 0 ; . 4 4 2 sin ycos y
Vì vậy (2) f log x 1 f 2 4 4 sin y cos y x 1 2 . 2 1 1 Ta có: 4 4 2
sin y cos y 1 sin 2 y ;1 nên 4 4 1
2 sin y cos y 2 2 2
2 x 1 4 1 x 3 .
Mà x là số nguyên dương x 1 ; 2 ; 3 .
Vậy có 3 giá trị x thỏa mãn. Câu 79. Tính tổng tất cả các nghiệm của phương trình
1 log x 3 log x 2
1 x x 4 2 x 3 . 2 2 2
A. S 2 .
B. S 1. C. S 1 .
D. S 1 2 . Lời giải Chọn B Điều kiện: x 1 . Ta có:
1 log x 3 log x 2
1 x x 4 2 x 3 2 2 2 log
x 3 x 3 2 1 log x 2 1 x * 2 2
Xét hàm số f t log t t 2
1 trên khoảng 0; . 2 2 1 t 1
2t t 2ln 2. 1 ln 2 1 2 ln 2
f t t 2 2 1 0 t 0 . t ln 2 t ln 2 t ln 2
Vậy hàm số f t đồng biến trên khoảng 0; . Suy ra x 1 x 1
* f x 3 f x 1
x 3 x 1
x 1 x 1. 2
x x 2 0 x 2
Vậy tổng các nghiệm của phương trình bằng 1.
Câu 80. Số nghiệm của phương trình sin 2x cos x 1 log
sin x trên khoảng 0; là: 2 2 A. 4 . B. 3 . C. 2 . D. 1. Lời giải
Vì sin x 0 và cos x 0 , x 0;
nên phương trình đã cho tương đương 2
sin 2x cos x log cos x 1 log sin x log cos x 2 2 2
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 41
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng log
cos x cos x log
sin 2x sin 2x * 2 2 1
Xét hàm số f t log t t , với t 0;
1 ta có f t 1 0, t 0 ;1 . 2 t ln 2
Do đó, hàm số f t đồng biến trên khoảng 0; 1 . 1
Từ phương trình * , ta có f cos x f sin 2x cos x sin 2x sin x hay x . 2 6 2 x 1 x 1
Câu 81. Biết phương trình log 2 log
có một nghiệm dạng x a b 2 trong 5 3 x 2 2 x
đó a, b là các số nguyên. Tính 2a b . A. 3 . B. 8 . C. 4 . D. 5. Lời giải Chọn B Điều kiện: x 0 x 0 x 1 1 x 1 . 0 x 2 2 x x Ta có: 2 x 1 x1 log 2 log
log 2 x 1 log x 2 log x 1 2 log 2 x 5 3 5 5 3 3 x 2 x
log 2 x 1 2log 2 x log x 2log x 1 * 5 3 5 3
Xét hàm số: f t log t 1 2log t trên 2; 5 3 1 2
Ta có: f 't với mọi t 2; . t 0 1 ln 5 t.ln 3
Suy ra f t đồng biến trên 2; x
Từ đó ta có f
x f x 1 2 * 2
1 2 x x 1 x 2 x 1 0 x 1 2
Vậy x 1 2 x 3 2 2 a 3,b 2 2
Câu 82. Số nghiệm thực của phương trình x 1 2 log 2 1 4x x x log 3x . 2 2 A. 0 . B. 1. C. 2 . D. 3 . Lời giải Chọn B Đk: x 0 . 2 Ta có 2
x x 1 1, x 0 do đó x 1 2 log 2
x x 1 0, x 0 . 2 2 x 1 2 1 2 log
x x 1 0 2 Với 0 x thì
, do đó phương trình đã cho vô nghiệm. 3
4x log 3x 0 2 1 Với x . 3 2 x 1 2 2 log 2 1 4x x x log 3x x x 1 2 log 2 1 3 2 x x x log 3x .(*) 2 2 2 2
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 42
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng Xét hàm số 2t f t
log t , với t 1. 2 t 1
Có f t 2
ln 2 log t f t 0 ,t 1; . 2 t ln 2
Suy ra hàm số đồng biến trên khoảng 1; . 1 1 Do đó (*) f 2 x
x 1 f 3x 2 x
x 1 3x x ; . 3 3
Vậy phương trình đã cho có 1 nghiệm thực. 2 1 2x 1 1
Câu 83. Cho phương trình log
x 2 x 3 log 1
2 x 2 , gọi S là tổng tất cả 2 2 2 x x
các nghiệm của nó. Khi đó, giá trị của S là 1 13 1 13
A. S 2 . B. S .
C. S 2 . D. S . 2 2 Lời giải 1 2 x Điều kiện 2 . x 0
Xét hàm số f t log t t 2 1 , t 0 . 2 1 2
2 ln 2.t 2 ln 2.t 1
Ta có f t 2 t 1
0 , t 0 , do đó hàm số f t đồng t ln 2 t.ln 2
biến trên khoảng 0; . Mặt khác ta có: 2 1 2x 1 1 log
x 2 x 3 log 1 2 x 2 2 2 2 x x 2 2 1 1 log x 2 x 2 1 log 2 2 1
f x 1 2 f 2 2 2 x x x x 1 1 3 13 x 2 2 3 2
x 2x 4x 1 0 x x 2 3 13 x 2 x 1 1 13
Kết hợp với điều kiện ta được 3 13 . Vậy S . x 2 2 2 y 1
Câu 84. Cho x , y là hai số thỏa mãn 2
x 2x y 1 log
. Tính giá trị nhỏ nhất của biểu 2 x 1 thức 2 x 1 2 P e
4x 2 y 1. 1 1 A. . B. . C. 1. D. 1 . 2 2 Lời giải
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 43
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng x 1 2 y 1 0 Điều kiện: 1 . x 1 0 y 2 2 y 1 2 Ta có 2
x 2x y 1 log x 1 y log 2 y 1 log x 1 2 2 2 x 1 1 x 2 1 log x 1 log 2 y 1 y 2 2 2 2 x 2 1 log 2 x 2 1 2 y 1 log 2 y 1 . 1 2 2 1
Xét hàm số f t t log t trên khoảng 0; có f 't 1
0, t 0; . Suy ra 2 l t n2
hàm số f t t log t đồng biến trên khoảng 0; . 2
Khi đó ta có x 2 1 2 1 2 y 1 2
2 y 2x 4x 1. Suy ra 2 x 1 2 2 x 1 2 P e
4x 2 y 1 e 2x 4x .
Xét hàm số g x 2 x 1 2 e
2x 4x trên khoảng 1 ; . Có g x 2 x 1 ' 2e
4x 4 , g x 2 x 1 ' 4e
4 0 x . Suy ra g x 2 x 1 ' 2e 4x 4 đồng
biến, do đó g ' x 0 có nhiều nhất một nghiệm. 1 1 Ta thấy g ' 0
nên g ' x 0 x 1 ; . 2 2
Bảng biến thiên hàm số y g x 1 1
Suy ra min g x . Vậy min P . 1 ; 2 2 2 1 2x 1 1
Câu 85. Cho phương trình log
x 2 x 3 log 1
2 x 2 . Gọi S là tổng tất 2 2 2 x x
cả các nghiệm của nó. Khi đó, giá trị của S là 1 13 1 13
A. S 2 . B. S .
C. S 2 . D. S . 2 2 Lời giải Chọn D x 2 x 2 0 x 0 x 0 Điều kiện: 2x 1 1 . 0 1 2 x x x 2 2
Khi đó phương trình đã cho
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 44
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng 2 1 1 log
x 2 x 2 2 x 2 1 log 2 2 1 2 2 x x 2 x x 2 1 1 log 2 2 1 log 2 2 1 (*) 2 2 x x
Xét hàm số f t log t t 2
1 , với t 0; . 2 2 1
t ln4 tln4 1
Có f 't 2t 2 . l t n2 l t n2 Xét tam thức bậc hai 2 t ln4 l t n4 1. Ta có 2 Δ ln4 4ln4 0 nên 2
t ln4 tln4 1 0, t .
Do đó f 't 0, t 0 .
Suy ra hàm số f t log t t 2
1 luôn đồng biến trên khoảng 0; . 2 Khi đó 2 1 2x 1 4x 4x 1 * 3 2 x 2 2 x 2 x 2
x 2x 4x 1 0 2 x x x x 1 3 13 x 2 3 13 x 2 3 13
Đối chiếu điều kiện, phương trình đã cho có nghiệm x 1, x . 2 3 13 1 13
Vậy tổng tất cả các nghiệm là S 1 . 2 2 1 2x
Câu 86. Xét các số thực dương x và y thỏa mãn ln
3x y 1. Giá x y 1 2
trị nhỏ nhất của biểu thức g(x) bằng x x y 1 1 A. . B. 8 . C. . D. 4 . 8 4 Lời giải Chọn B 1
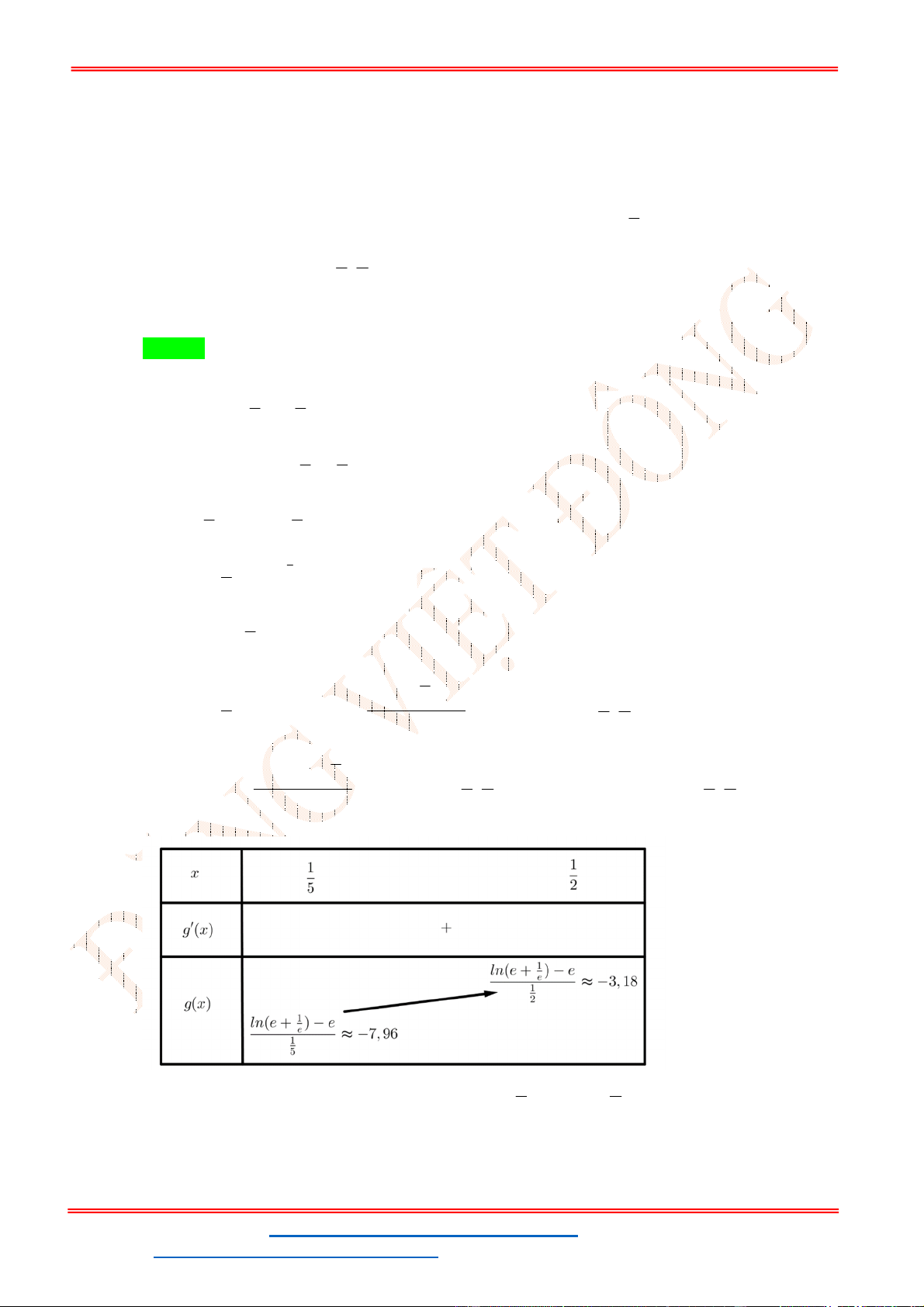
Điều kiện 0 x . 2 1 2x Ta có từ giả thiết: ln
3x y 1 ln
1 2x 1 2x ln x y x y (1) x y . 1
Xét hàm số f t ln t t trên khoảng 0; . Ta có f t 1 0 với mọi t 0 t
Do đó hàm số f t luôn đồng biến trên khoảng 0; .
Vậy (1) 1 2x x y y 1 3x
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 45
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng 1 2 1 4x 1 1 Ta có g(x) g x
g x 0 x . 2 2 x 1 2x x 2x 2 x x 4 2 Khi đó ta có BBT 1 1 Vậy GTNN của g( )
x là 8 khi x , y . 4 4 Câu 87. Có bao nhiêu cặp số nguyên dương ; x y thỏa mãn: 3 2 2x 3x 1 log
14x 3y 7 2
x 1 đồng thời 1 x 2022 ? 7
6xy 1 2x 3y A. 1347 . B. 1348 . C. 674 . D. 673 . Lời giải Chọn A 3 2 2x 3x 1 Ta có log
14x 3y 7 2 x 1 7
6xy 1 2x 3y x 2 1 2x 1 log
14x 3y 7 2 x 1 log x 1 log
3y 1 3y 7 x 1 7 2 7 2 7 3y 1 2x 1 log x 2 1 7 x 2 1 log 3y 1 3y 7 7
log 7 x 2 1 7 x 2 1 log
3y 1 3y 1 (*). 7 7 1
Xét hàm số f t log t t . Ta có f t 1 0 , t
0 nên f t đồng biến trên 7 t ln 7 khoảng 0; . x 2 7 1 1
Do đó, (*) x 2 7 1
3y 1 y . 3
y nguyên dương khi x 2 7
1 13 x chia hết cho 3 hoặc x chia 3 dư 2.
Do đó x 2;3;...; 202 1 \ 4;7;10;....; 202
0 . Vậy có 2020 673 1347 cặp ; x y thỏa mãn.
Câu 88. Lần lượt cho hai số thực dương ,
x y thỏa mãn phương trình sau đây: 3x 3y 2 2 log
x y xy 6 x y 2 . Gọi giá trị lớn nhất và giá trị nhỏ nhất 2 2 2
x y xy 3 của 2x 3y 2 biểu thức P
lần lượt là M và m . Giá trị của biểu thức M m bằng x y 1
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 46
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng 60 26 40 A. . B. 12 . C. . D. . 13 5 13 Lời giải Chọn A 3x 3y Ta có: 2 2 log
x y xy 6 x y 2 2 2 2
x y xy 3 3x 3y 2 2 1 log
x y xy 6 x y 3 2 2 2
x y xy 3 6 x y 2 2 log
x y xy 6 x y 3 2 2 2
x y xy 3 log 2 2
x y xy 3 2 2
x y xy 3 log 6 x y 6 x y 2 2 1
Xét hàm đặc trưng y f t log t t f t 1 0 t 0 . 2 tln2
Suy ra hàm số f t đồng biến trên 2 2 0;
x y xy 3 6 x y
x a b 2 2 Đặt:
a b a b a ba b 3 6a b 6a b
y a b
a 3 cos t 2 a 2 2 2 3 2
b 9 3 . Đặt: b 3sin t Suy ra biểu thức 2x 3y 2
a b a b 5 5a b 2
3cost 23sint 2 2 3 2 P x y 1
a b a b 1 2a 1
2 3 cost 2 1
5 3 cos t 3sin t 12
2 3P 5 3cost 3sin t 12 5P 2 3 cos t 5 2 2 30 2 30 30 2 30
Điều kiện có nghiệm 2 3P 5 3 9 12 5P P 13 13 30 2 30 P M max 13 60 Như vậy suy ra: M m 13 30 2 30 P m min 13
Câu 89. Có bao nhiêu cặp số ,
x y là các số nguyên không âm thỏa mãn:
21 x 2y 2 log x 2y 2log x y 2xy x 2x y2 2 2
4x 4y 2 2 A. 2. B. 3. C. 4. D. 5. Lời giải Chọn B 2 2
Ta có 21 x 2y log x 2y 2log 2 2
x y 2xy x 2 x y 4x 4y 2 2 1 1 2 x 2 y x 2 y
log x 2 y log x y 2 x
x y2 2x 2 y 2 2 2 1 log x 2 y 2 x 2 y
log x y2 x
x y2 x 2 2
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 47
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng log 2 x 2 y 2 x 2 y
log x y2 x x y2 x (1) 2 2 1
Xét hàm số g t log t t với t 0 , có gt 1 0, t 0 . 2 t.ln 2
Suy ra hàm số y g t log t t đồng biến trên khoảng 0; . 2 2 2 Từ
1 g 2 x 2y g x y x 2 x 2y x y x x y
x y x y2 2 2 2
2 x y (2) Xét hàm số 2
h u u u với u 0 , có hu 2u 1 0, u 0 . Suy ra hàm số 2 y
h u u u đồng biến trên khoảng 0; .
Từ h x y h x y x y x y x y x y2 2 2 2 2 2 2 2
x xy y x y y x 2 2 2 2
1 y x x 0 (3)
Ta coi phương trình (3) là phương trình bậc hai ẩn y , khi đó: Phương trình (3) có nghiệm
x 2 2 0 1
x x 0 x 1 0 x 1. y
Do x là số nguyên không âm nên x 0 hoặc x 1 . y 0
+) Với x 0 , suy ra 3 2
y 2 y 0 (thoả mãn). y 2
+) Với x 1 , suy ra 2
3 y 0 y 0 (thoả mãn). Vậy có 3 cặp ;
x y thoả mãn là 0;0,0; 2,1;0 . 8
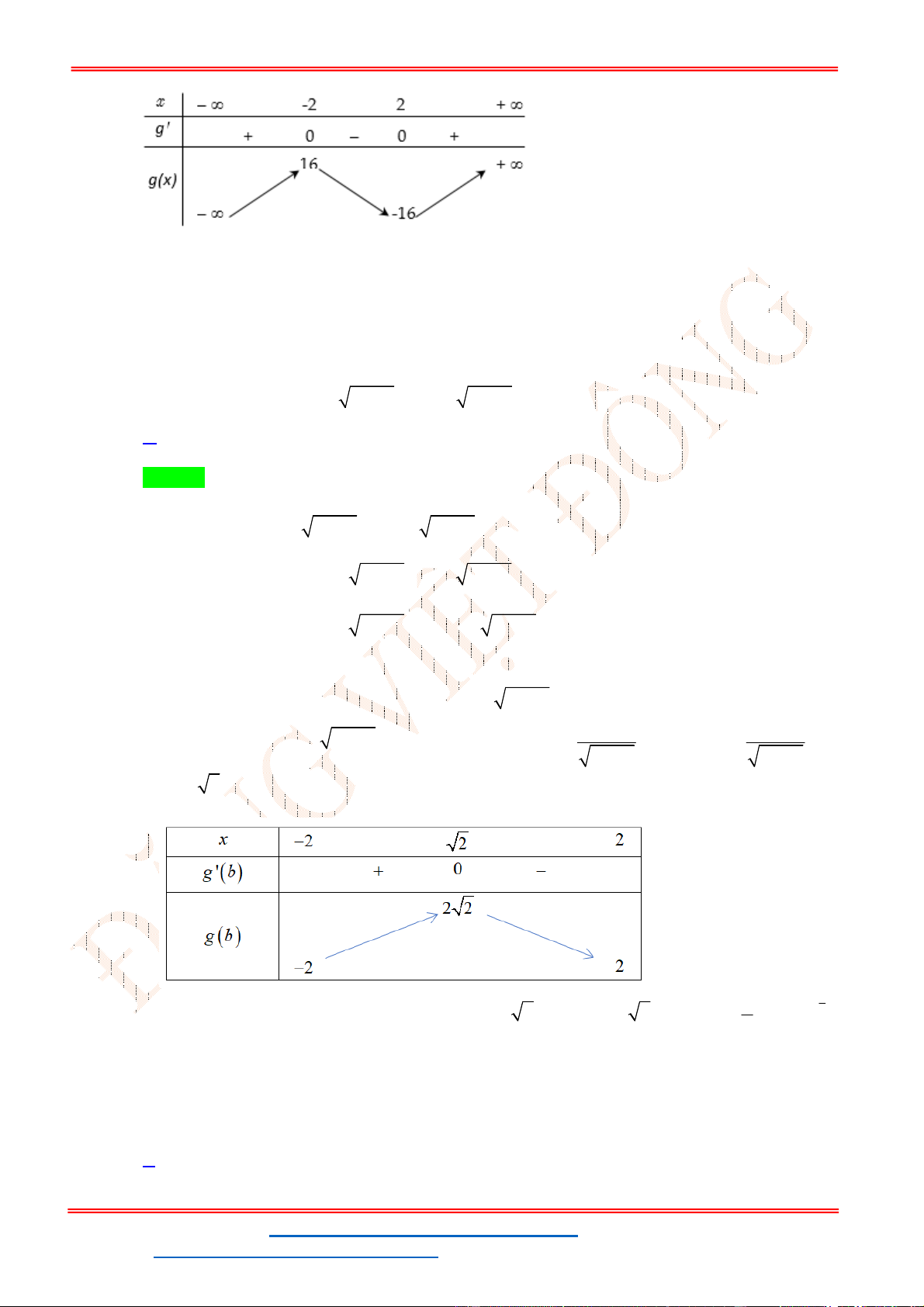
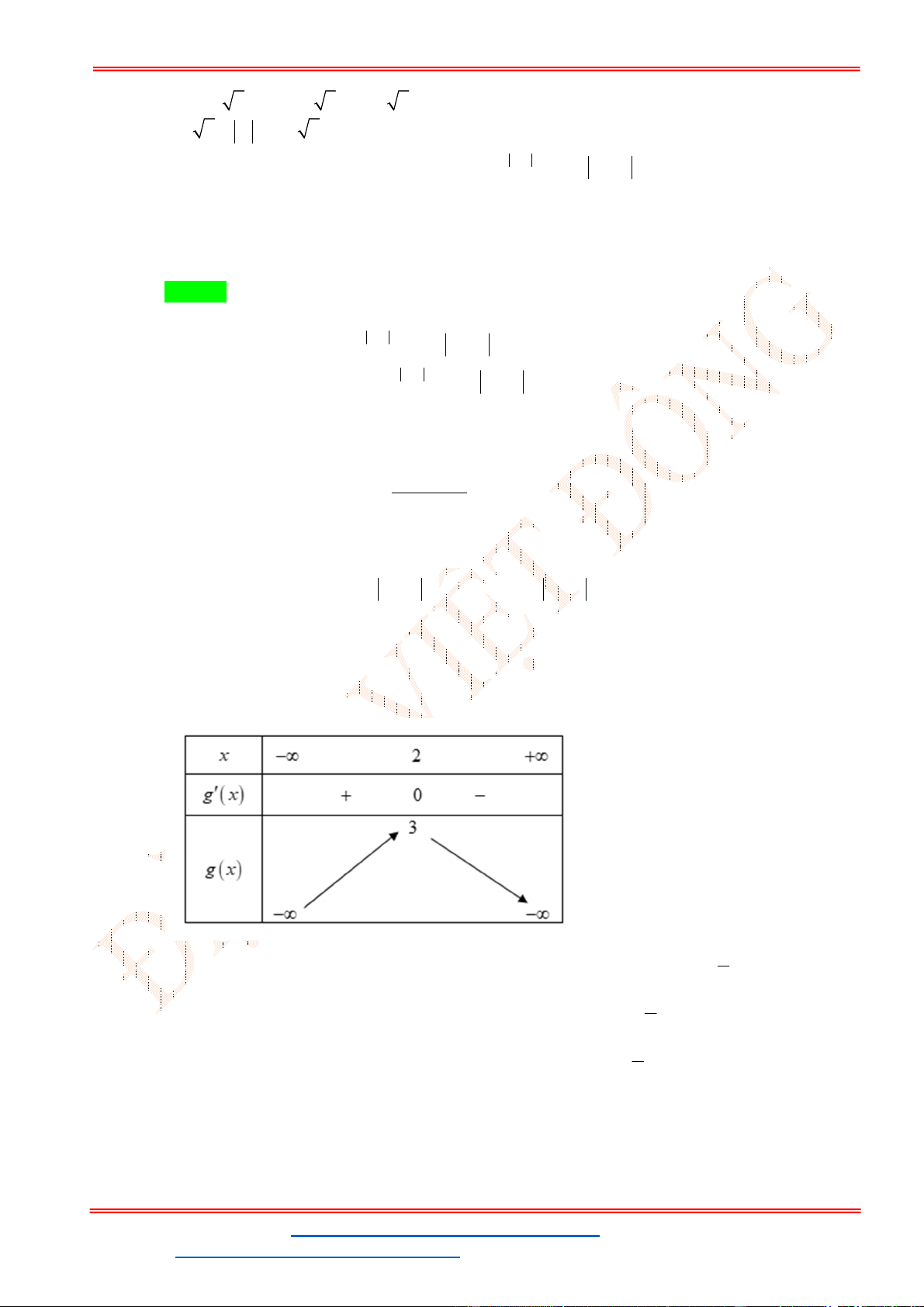
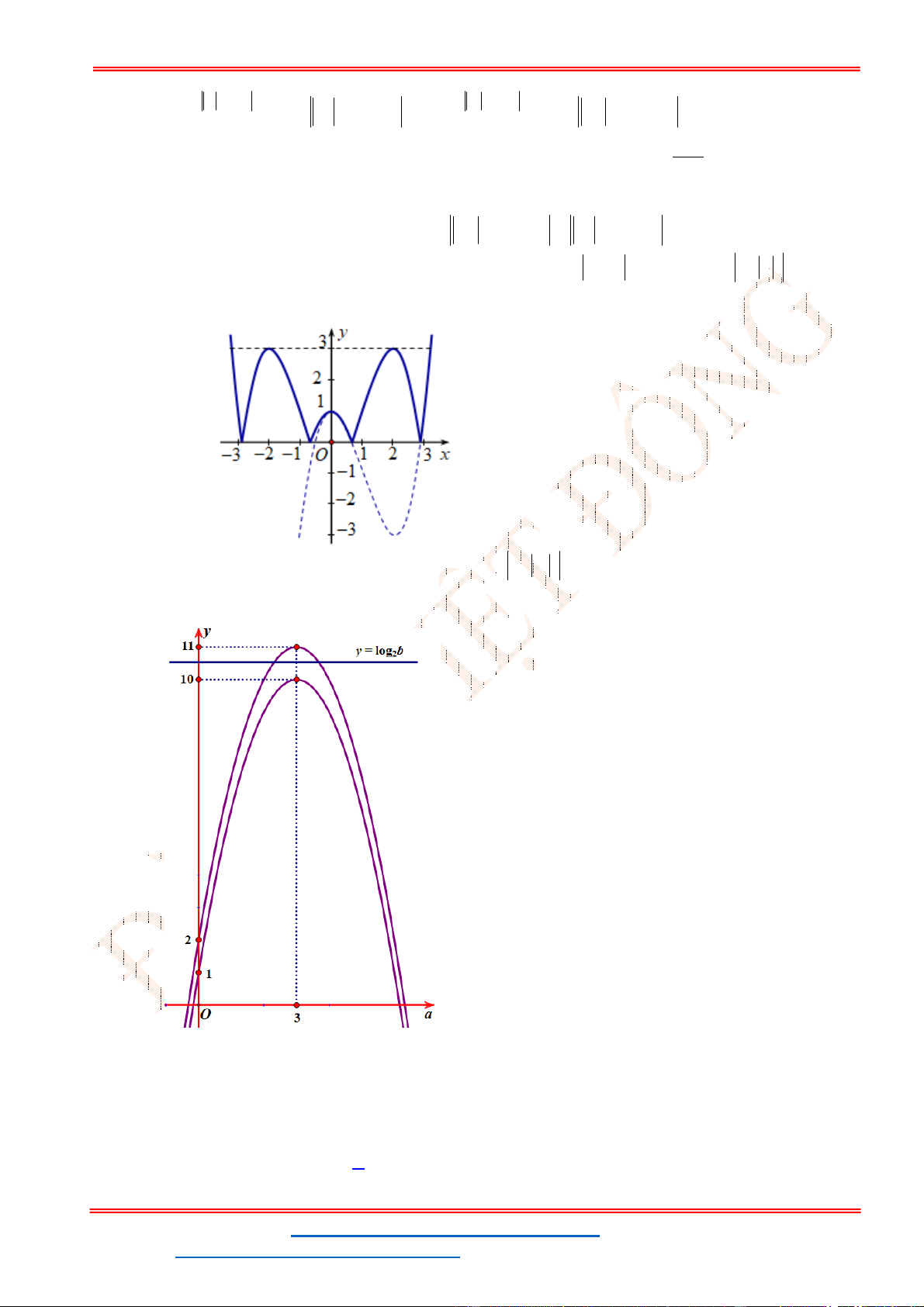
Câu 90. Cho các số thực a, b, c lớn hơn 1 thỏa log abc 1
4ab . Khi ấy, giá trị nhỏ nhất của 2 c 1 1 1 biểu thức T log 2 log 2 log 2 bằng 2 3 6 2a 2b 2 2 3 6 c 1 1 3 A. . B. . C. 6 2 . D. . 2 4 2 Lời giải Chọn A 8 8 8 Đầu tiên, ta có: log abc 1 4ab log
4ab 4ab log 2 2 2 c
c c 1
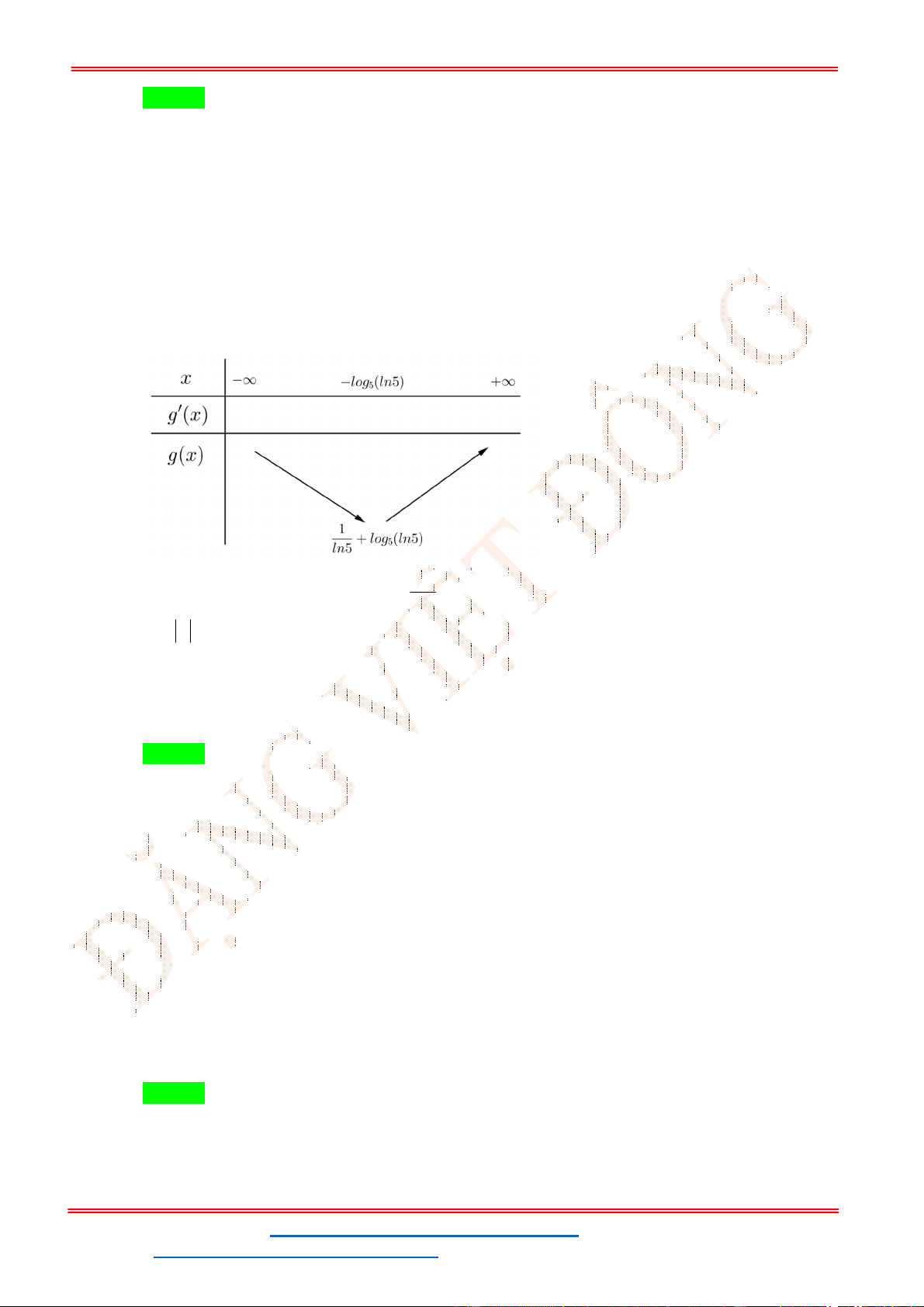
Xét hàm số y f t log t t, f t 1 0, t
R f t đồng biến trên R 2 t ln 2 8 8
f 4ab f 4ab
abc 2 log a log b log c 1 2 2 2 c c Đặt x log ; a y log ;
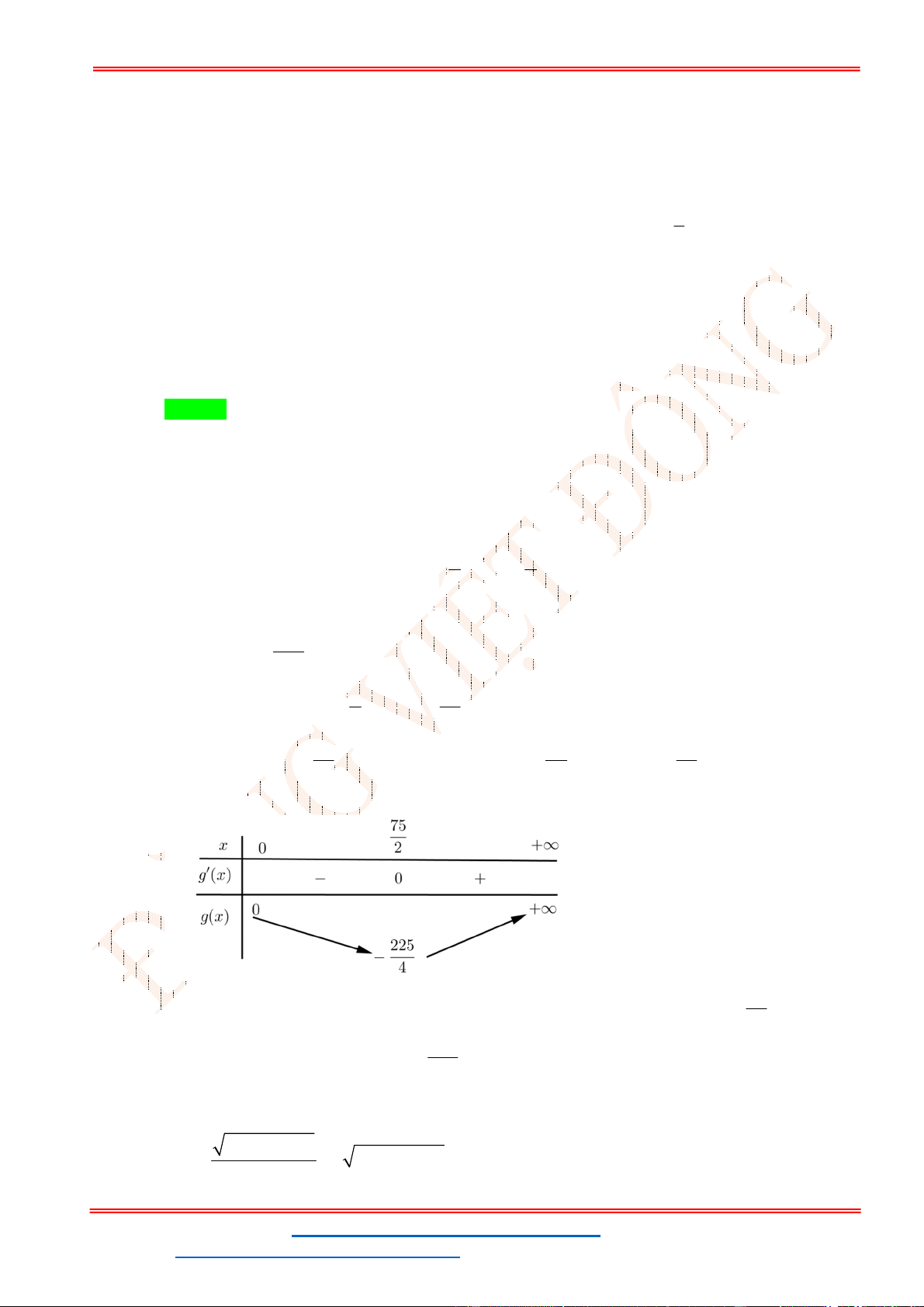
b z log c x y z 1 2 2 2 1 1 1 1 1 1 1 1 1 Ta có: T log 2 log 2 log 2 . . 2 3 6 2a 2b 2c 2 3 6 2 3 6 2 log 2a 3 log 2b 6 log 2c 2 2 2 1 1 1 1 1 1 2 4 log a 3 9 log b 6 36 log c 2 4x 3 9 y 6 36z 2 2 2
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 48
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng 1 2 4x 1 3 9 y 1
6 36z 2 4x 3 9 y 6 36z 2 4x 16 3 9 y 36 6 36z 144 16 36 144 1 2 4x 1 3 9 y 1 6 36z 2 4x 3 9 y 6 36z 2 . 2. . 2. . 2 4x 16 3 9 y 36 6 36z 144 16 36 144 1 1 1 2 4x 3 9 y 6 36z 3
x y z 3 1 1 2 3 6 16 36 144 4 4 4 4 2 1 1 1 1 Vậy T
khi và chỉ khi x ; y ; z a; ; b c 3 6 2; 2; 2 min 2 2 3 6
2 - BPT LÔGARIT KHÔNG CHỨA THAM SỐ
Câu 91. Tính tổng tất cả các nghiệm nguyên của bất phương trình log 2 x 3 2
log x x 4x 1 0 2 2 . A. 4 . B. 6 . C. 5 . D. 3 . Lời giải Chọn B
Điều kiện: x 0 . Ta có log 2 x 3 2
log x x 4x 1 0 log 2 x 3 2
x 3 log 4x 4x * . 2 2 2 2 1
Xét hàm số f t log t t trên D 0; . Ta có f 't
1 0 t D hàm số f 2 l t n2
đồng biến trên D .
Suy ra f 2
x f x 2 * 3 4
x 3 4x 1 x 3 .
Vậy tập hợp các nghiệm nguyên của bất phương trình là 1; 2; 3 . 2 3x x 1
Câu 92. Số nghiệm nguyên của bất phương trình 2 log
x x 2 0 là 3 2 2x 2x 3 A. 4 . B. 1. C. 3 . D. 2 . Lời giải Chọn A 2
3x x 1 0 Điều kiện: 2 2
2x 2x 3
3x x 1 0 x . 2
2x 2x 3 0 Ta có 2 3x x 1 2 log
x x 2 0 log 3x x 1 log
2x 2x 3 x x 2 0 2 2 2 2 3 3 3 2x 2x 3 log 2 3x x 2
1 3x x 1 log 2
2x 2x 3 2
2x 2x 3 * . 3 3 1
Xét hàm số f t log t t với t 0 . Ta có f 't
1 0 t 0 . 3 l t n3
Vậy hàm số đã cho đồng biến với t 0 . Khi đó 2 2 2
* 3x x 1 2x 2x 3 x x 2 0 1 x 2 .
Do x x 1;0;1;
2 . Vậy phương trình đã cho có 4 nghiệm nguyên.
Câu 93. Biết tập nghiệm của bất phương trình 2
x 6x 2 log 2 x 2x log
x 1 0 là khoảng 2 1 2
2;a b với ,ab , giá trị của a b bằng A. 10 . B. 22 . C. 8 . D. 4 .
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 49
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng Lời giải Chọn C 2
x 2x 0 Điều kiện x 2 . x 1 0 Ta có 2
x 6x 2 log 2 x 2x log x 1 0 2
x 6x 2 log 2 x 2x log x 1 0 2 2 2 1 2 2
x 2x log 2
x 2x 4 x 1 2 log x 1 2 2 2
x 2x log 2
x 2x 4 x 1 log 4 x 1 2 2 1
Xét f u u log u f ' u 1 0u 0 2 l u n2
Hàm y f u đồng biến trên 0; (*). Từ (*) ta có 2
x 2x log 2
x 2x 4 x
1 log 4 x 2
1 x 2x 4 x 1 x 2 2 2 2
x 6x 4 0, x 2 3 5 x 3 5, x 2 .
Đối chiếu với điều kiện ta có tập nghiệm là S 2;3 5
Vậy a 3;b 5 a b 8 .
Câu 94. Có bao nhiêu cặp số nguyên dương ;
x y thỏa mãn điều kiện x 2020 và
39y 2y x log x 3 1 2 ? 3 A. 4 . B. 2 . C. 3772 . D. 3774 . Lời giải: Chọn D 3
Ta có 39y 2 log 1 2 3.9y y x x
6 y x 3log x 1 2 3 3 2 y 1 3 32 y 1 x 1 3log x 1 . (*) 3 Xét hàm số 3t f t 3t có ' 3t f t
.ln3 3 0, t . Suy ra hàm số 3t f t
3t đồng biến trên . Do đó * f 2 y 1 f log x 1 2 y 1 log x 2 y 1 1 3 1 x . 3 3 log 20211
Vì x 2020 nên 2 y 1 3 3 1 2020 y 2,9 . 2
Với giả thiết y nguyên dương suy ra y 1; 2 .
Với y 1 có 26 x 2020 suy ra có 1995 cặp số ; x y thỏa mãn.
Với y 2 có 242 x 2020 suy ra có 1779 cặp số ; x y thỏa mãn.
Vậy có tất cả 3774 cặp số ;
x y thỏa mãn đề bài.
Câu 95. Biết tập nghiệm của bất phương trình 2
x 6x 2 log 2 x 2x log
x 1 0 là khoảng 2 1 2
2;a b , với a,b là các số tự nhiên. Giá trị của a b bằng A. 10 . B. 22 . C. 8 . D. 4 . Lời giải Chọn C
Điều kiện xác định: x 2 (*).
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 50
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng Ta có: Bpt 2
x 2x log 2 x 2x log
x 1 4x 2 2 2 2
x 2x log 2
x 2x 4x 4 log 4x 4 , (1). 2 2
Xét hàm đặc trưng: f t t log t liên tục và đồng biến trên 0; . 2
Do đó: f 2
x x f x 2 1 2 4
4 x 2x 4x 4 2
x 6x 4 0 3 5 x 3 5 .
Giao với điều kiện (*) ta được: 2 x 3 5 . Vậy S 2;3 5 .
Như vậy a 3;b 5 a b 8 .
Câu 96. Tập nghiệm của bất phương trình log 2 2
x x 2 4 x 2
2x x 2 1 là a; b . 2 Khi đó . a b bằng: 15 12 16 5 A. . B. . C. . D. . 16 5 15 12 Lời giải Chọn C 2x Ta có: 2 2
x x 2 x x 2
x 2 x . 2 x 2 x Ta có: log 2 2
x x 2 4 x 2
2x x 2 1 2 log x 2
x 2 x 4 2
2x x 2 1 2 2 2x
2 3x 2 x 2 2 log 2
4 2x x 2 1 log 2x x 2 1, 1 2 2 2 x 2 x 2 x 2 x Ta có 2
x 2 x 0 , x . x 0 8 Điều kiện: 2
3x 2 x 2 0 2
2 x 2 3x x 0 x , * 5 2 2 4x 8 9 x
Với điều kiện * , ta có 1 log 2
3x 2 x 2 2
3x 2 x 2 log 2 x 2 x 2
x 2 x, 2 2 2 1
Xét hàm số f t log t t với t 0 . Có f 't
1 0 , t 0; . 2 t.ln2 Hàm số
f t log t t đồng biến trên 0; , 2
3x 2 x 2 0; và 2
2x 2 x0; Nên f 2 x
x f 2 2 3 2 2
x 2 x 2 x 0 x 0 2 2
3x 2 x 2 x 2 x 2
x 2 2x 2 2 x 2 4 2 x 3x 2 2 x . 3
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 51
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng 8 2 16
Kết hợp với ĐK ta có tập nghiệm bất phương trình là ; hay . a b . 5 3 15 Câu 97. Cho x , y là các số thực dương thỏa mãn bất đẳng thức x 1 4 3 2 2 2 log
9 y 6 y x y 2 y x
1 . Biết y 1000 , hỏi có bao nhiêu cặp số nguyên 3y 1
dương x ; y thỏa mãn bất đẳng thức 1 ? A. 1501100 . B. 1501300 . C. 1501400 . D. 1501500 . Lời giải Chọn D Ta có x 1 xy y 4 3 2 2 2 log
9 y 6 y x y 2 y x log 4 3 2
9 y 6 y y 2 2 2 x y 2x . y y y 2 3y 1 3y y 2
xy y
y y y y xy y2 2 2 log log 3 3 2
xy y xy y2 2
y y 2 log log 3
3y y *
Xét hàm f t 2
logt t với t 0 ; 1 f 't
2t 0 , t 0 ; . Suy ra f t là hàm đồng biến trên t 0 ; . l t n10
f xy y f 2 * 3y y 2
xy y 3y y x 3y .
Vì y 2020 nên ta có các trường hợp sau
y 1 x 1 ; 2 ; 3 .
y 2 x 1 ; 2 ; 3 ; 4 ; 5 ; 6 . ........................
y 1000 x 1 ; 2 ;.... ; 300 0 .
Vậy số cặp nghiệm thỏa mãn điều kiện đề bài là: 3 6 9 .. 3000 1501500 .
Câu 98. Tập nghiệm của bất phương trình log 2 2
x x 2 4 x 2
2x x 2 1 là a; b . Khi đó ab bằng 2 12 5 15 16 A. . B. . C. . D. . 5 12 16 15 Lời giải Chọn D Điều kiện: 2 2
x x 2 4 x 0 .
Bất phương trình trở thành: log x x x x x 2 2 2 4 2 2 1 2 2x x 2 log 2
4 2x x 2 1 1 log
2 2x x 2 1 2 2 2 x 2 x 2 x 2 x x 2 3x 2 x 2 2 log 2
2 2x x 2 0 log 2x x 2 0 2 2 2 x 2 x 2 x 2 x log 2
3x 2 x 2 log 2 x x 2 2
2x x 2 0 2 2
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 52
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng log 2
3x 2 x 2 2
3x 2 x 2 log 2 x x 2 2
x x 2 * 2 2 2 3
x 2 x 2 0 Điều kiện: ** . 2 x x 2 0
Xét hàm số f t t log t , với t 0 . 2 1
Ta có f t 1
0,t 0 . Do đó hàm f t là hàm đồng biến trên 0; . t ln 2 Bất phương trình * trở thành f 2 x
x f 2 x x 2 2 3 2 2
2 3x 2 x 2 x x 2 . 2
3x 2 x 2 0 1
Kết hợp với điều kiện * * tức là ta đi giải: 2 2 3
x 2 x 2 x x 2 2 +) Giải 1 3 x 0 x 0 2 2 x x x x 3x 0 3 2 2 0 2 2 3 x 0 4 2 x 2 3 x2 2 8 5 x x 0 x 0 x 0 8 8 x 8 8 x 0 5 x 5 5 5 8
Do đó tập nghiệm của 1 là S ; . 1 5 +) Giải 2 x 0 2 2x 0 x 2 2 2 2
3x 2 x 2 x x 2
x 2 2x x . 2 2 3 x 2 4 x 3 2 x 3 2
Do đó tập nghiệm của 2 là S ; . 2 3 8 2
Vậy tập nghiệm của bất phương trình đã cho là S S S ; . 1 1 5 3 8 2 16 Từ đó ab . . 5 3 15
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 53
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng
DẠNG 4: PHƯƠNG PHÁP HÀM ĐẶC TRƯNG GIẢI PT, BPT LÔGARIT CHỨA THAM SỐ
1 - PT LÔGARIT CHỨA THAM SỐ 2 x m Câu 1. Cho phương trình: 2 ln
x m 3 . Có bao nhiêu giá trị nguyên dương m không vượt 2 2x 3
quá 20 để phương trình có 2 nghiệm phân biệt. A. 14. B. 15 . C. 16 . D. 17 . Lời giải Chọn D
Do m nguyên dương nên 2
x m 0,x . 2 x m Phương trình 2 ln
x m 3 2
x m 2 x 2 x 2 ln ln 2 3 2 3 x m 2 2x 3 2
x m 2
x m 2 x 2 ln ln 2 3 2x 3 (1).
Xét hàm số f t lnt t với t 0 . 1 Có '
f t 1 0,t 0 . Do đó hàm số đồng biến trên 0; . t
Mà phương trình (1) có dạng f 2
x m f 2 2x 3 . Do đó suy ra 2 2 2
x m 2x 3 x m 3 (2).
Phương trình (1) có 2 nghiệm phân biệt khi và chỉ khi phương trình (2) có hai nghiệm phân
biệt m 3 0 m 3 . m Lại do
nên ta được 17 giá trị của m thỏa mãn. m 20 Câu 2. Có bao nhiêu số nguyên dương của tham số m để phương trình log 2
x 2x m 2
log x 72x 2 4m 4x có nghiệm? 4 4 A. 80. B. 82. C. 81. D. 83. Lời giải Chọn C x 0 Điều kiện: . 2
x 2x m 0 Ta có log 2
x 2x m 2
log x 72x 2 4m 4x 4 4 log 2
x 2x m 4 2
x 2x m log 16x 4.16x (*) 4 4
Xét hàm số f t log t 4t với t 0 4 1
Ta có f 't
t 0 với mọi t 0 f t là hàm đồng biến l t n4
Do đó, (*) f 2
x x m f x 2 2 16
x 2x m 16x 2
m x 18x (1)
Phương trình (*) có nghiệm khi phương trình (1) có nghiệm x 0 . Ta có BBT của hàm số 2
y x 18x trên 0; như sau:
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 54
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng
Dựa vào BBT ta thấy, phương trình (1) có nghiệm x 0 khi m 81 . Vì
m nên m 1; 2;3;..;8 1 . Câu 3.
Có bao nhiêu giá trị nguyên của tham số m để phương trình 2
3x 3x m 1 2 log
x 5x 2 m 2 2 2x x 1
có hai nghiệm phân biệt lớn hơn 1? A. 5 . B. 2 . C. 4 . D. 3 . Lời giải Chọn B Điều kiện : 2
3x 3x m 1 0 * .
Biến đổi phương trình sang dạng log 2
3x 3x m 2
1 3x 3x m 1 log 2. 2 2x x 1 2. 2
2x x 1 , ** 2 2 1
Xét hàm số y log t t, t 0 y ' 1 0 2 l t n2
Từ phương trình ** ta có : y 2
x x m y 2 3 3 1 2x x 1 2
x x m 2 3 3 1
2 2x x 1 2
x 5x 1 m 0, 1
Để phương trình có hai nghiệm phân biệt lớn hơn 1
1 có hai nghiệm phân biệt lớn hơn 1 Δ 0 21 4m 0 21
x x 2 0 5 2 0 m 3 1 2 4 x 1 x 1 0 1 m 5 1 0 1 2 Vậy có hai giá trị. Câu 4. Cho ,
x y là hai số thực dương thỏa mãn 5x y 4 . Tổng tất cả giá trị nguyên của tham số 2
x 2 y m
m để phương trình 2 log
x 3x y m 1 0 có nghiệm là 3 x y A. 10. B. 5. C. 9. D. 2. Lời giải Chọn B 2
x 2 y m 2 log
x 3x y m 1 0 3 x y log 2
x 2 y m 2
x 2 y m log 3 x y 3 x y 1 3 3 Vì ,
x y 0 nên x y 0 . Xét hàm số f t log t t là hàm số đồng biến trên 0; . 3 Khi đó 1 2 2
x 2 y m 3x 3y x 3x y m 0* 4
Kết hợp với điều kiện 5x y 4 y 4 5x . Vì ,
x y 0 0 x . 5
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 55
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng 4 Ta có * 2 2
x 2x m 4 0 m x 2x 4,x 0; . 5 4 44 Hàm số 2
y x 2x 4 nghịch biến trên 0 ; (do 1 0 ) nên 2
x 2x 4 4 . 5 25 Do vậy m 2;
3 là các giá trị cần tìm.
Vậy tổng tất cả các giá trị m thỏa ycbt là 5. Câu 5.
Có bao nhiêu số nguyên m để phương trình: 2
3x 3x m 1 2 log
x 5x 2 m có hai nghiệm phân biệt lớn hơn 1? 2 2 2x x 1 A. 3 . B. vô số. C. 4 . D. 2. Lời giải Chọn D Điều kiện: 2
3x 3x m 1 0 . Ta có: 2
3x 3x m 1 2
3x 3x m 1 2 log
x 5x 2 m 2 log
1 x 5x 1 m 2 2 2x x 1 2 2 2x x 1 2
3x 3x m 1 2 log
x 5x 1 m 2 2 4x 2x 2 log 2
3x 3x m 1 log 2
4x 2x 2 2
4x 2x 2 2
3x 3x m 1 2 2 log 2
3x 3x m 1 2
3x 3x m 1 log 2
4x 2x 2 2
4x 2x 2 1 2 2 1
Xét hàm số: f t t log t trên 0; , ta có f 't 1
0 , t 0; . 2 t.ln2
Do đó hàm số f t đồng biến trên 0; .
Suy ra: f 2
x x f 2 1 4 2 2
3x 3x m 1 2 2
4x 2x 2 3x 3x m 1 2
x 5x m 1 2 . Điều này đúng với mọi x . 5
Xét hàm số: g x 2
x 5x trên , ta có g ' x 2x 5 0 x . 2 Bảng biến thiên:
Theo bảng biến thiên ta thấy: phương trình 2 có hai nghiệm phân biệt lớn hơn 1 khi và chỉ 25 21 khi m 1 4 m 3 . 4 4
Do m nên m 5 ; 4 .
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 56
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng 2
3x 2x 3 Câu 6.
Tìm m để phương trình 2 2 log
x 2x 2m 2 luôn có nghiệm. 2 2 2 x m
A. m 1. B. m 2 .
C. m 1. D. m 2 . Lời giải Chọn A 2 3x 2x 3 x 0 Điều kiện 0 . 2 2 x m m 0 2
3x 2x 3 Ta có: 2 2 log
x 2x 2m 2 2 2 2 x m log 2
3x 2x 3 og l 2 2 2
x m 2 2 2
x m 2 3x 2x 3 2 2 log 2
3x 2x 3 2
3x 2x 3 og l 2 2 2
x m 2 2 2 x m . 2 2 1
Xét hàm số f t log t t t 0 có f 't
1 0, t 0. 2 l t n2
Suy ra hàm số y f t đồng biến trên 0; . Ta được f 2
x x f 2 2 x m 2
x x 2 2 x m 2 2 3 2 3 2 3 2 3 2
x 2x 3 2m . Xét parabol 2
y x 2x 3 có bảng biến thiên như sau:
Để phương trình có nghiệm thì 2
2m 2 m 1. 2
3x 3x m 1 Câu 7.
Có bao nhiêu số nguyên m để phương trình 2 log
x 5x 2 m có hai 2 2 2x x 1
nghiệm phân biệt lớn hơn 1. A. 3 . B. Vô số. C. 2 . D. 4 . Lời giải Chọn C Điều kiện: 2
3x 3x m 1 0 . Ta có: 2
3x 3x m 1 2
3x 3x m 1 2 log
x 5x 2 m 2 log
1 x 5x 1 m 2 2 2x x 1 2 2 2x x 1 2
3x 3x m 1 2 log
x 5x 1 m 2 2 4x 2x 2 log 2
3x 3x m 1 log 2
4x 2x 2 2
4x 2x 2 2
3x 3x m 1 2 2 log 2
3x 3x m 1 2
3x 3x m 1 log 2
4x 2x 2 2
4x 2x 2 1 2 2 1
Xét hàm số: f t t log t trên 0; , ta có f 't 1
0 , t 0; . 2 t.ln2
Do đó hàm số f t đồng biến trên 0; .
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 57
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng
Suy ra: f 2
x x f 2 1 4 2 2
3x 3x m 1 2 2
4x 2x 2 3x 3x m 1 2
x 5x m 1 2 . 5
Xét hàm số: g x 2
x 5x trên , ta có g ' x 2x 5 0 x . 2 Bảng biến thiên:
- Theo bảng biến thiên ta thấy: phương trình 2 có hai nghiệm phân biệt lớn hơn 1 khi và 25 21 chỉ khi m 1 4 m 3 . 4 4
Do m nên m 5 ; 4 .
Vậy có 2 giá trị nguyên của m thỏa mãn yêu cầu bài toán. 4x 1 Câu 8. Cho phương trình 2 log
x 2 m 2 x 5 . Hỏi có tất cả bao nhiêu giá trị thực 2 2 x 2mx 4
của tham số m để phương trình đã cho có hai nghiệm thực phân biệt nằm trong đoạn 2;6
và thỏa mãn 100m là số nguyên? A. 40 . B. 2 . C. 1. D. 3 . Lời giải Chọn B
Đây là một dạng cơ bản sử dụng phương trình đặc trưng.
Với trường hợp u,v 0 ta có: u log
v u log u u log v v f u f v u v v u . a a a
0 v 1
Hàm số f t log t t là một hàm đơn điệu có đạo hàm đương f 't 1 0 t 0 a l t na .
Ta biến đổi phương trình ban đầu như sau: 4x 1
Điều kiện xác định: 0 . 2 x 2mx 4 Vì yêu cầu bài toán cho biết có hai nghiệm 4x 1 0 x 2;6 2
x 2mx 4 0 2
x 2mx 4 0 4x 1 Ta có 2 log
x 2 m 2 x 5 2 2 x 2mx 4 log 4x 1 log 2
x 2mx 4 2
x 2mx 4 4x 1 . 2 2 log 4x 1 4x 1 log 2
x 2mx 4 2
x 2mx 4 . 2 2
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 58
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng
f x f 2 4 1
x 2mx 4 (1) Áp dụng tính chất của hàm đơn điệu suy ra 2 2
4x 1 x 2mx 4 x 2m 2 x 5 0 m 2 5
Điều kiện có hai nghiệm phân biệt Δ' m 22 2
5 m 4m 1 0 (*) m 2 5
Suy ra nghiệm x m 2
2 m 4m 1 m 0 1 m 2 2 m 2 m 4m 1 2 m m 4m 1 4 1 YCBT 0 m 2 2 m 4 4
m 2 m 4m 1 6
m 4m 1 4 m 17 m 12 (**) 1
Kết hợp (*) và (**) suy ra 2 5 m 2 3, 6 2
00 100 5 100m 25 có hai 4 24 25
giá trị thực của m thỏa mãn điều kiện bài toán là m ; . 100 100 3
x 9x 2m Câu 9. Cho phương trình 2 3 log
1 3x 9x x 2m , với m là tham số. Hỏi có tất cả 2 2 3x 1
bao nhiêu giá trị nguyên của tham số m để phương trình đã cho có ba nghiệm phân biệt. A. 14. B. 15 . C. 16 . D. 17 . Lời giải Chọn B 2 3 x 1 0
Điều kiện xác định: 3
x 9x 2m 0 .(*) 3
x 9x 2m 0 u
Ta sẽ đưa phương trình về dạng log
v u .. u . v a v 3
x 9x 2m Ta có 2 3 log
1 3x 9x x 2m 2 2 3x 1 log 3
x 9x 2m log 2 3x 1 2 3x 1 3
x 9x 2m . 2 2 log 3
x 9x 2m 3
x 9x 2m log 2 3x 1 2 3x 1 . 2 2 f 3
x x m f 2 9 2 3x 1 (1)
Với hàm số f t log t t đơn điệu tăng trên miền t 0 . 2
Từ (1) suy ra f 3
x x m f 2 9 2 3x 1 3 2
x 9x 2m 3x 1 3 2
x 3x 9x 1 2m (2)
Tất cả các nghiệm phương trình (2) luôn thỏa mãn điệu kiên (*) vì: 3 2
x 9x 2m 3x 1 0
Để (2) có hai nghiệm phân biệt y x x x m y x x x CT 3 2 CD 3 2 29 3 9 1 2 3 9 5
2 m 14 . Suy ra có 15 giá trị nguyên của m thỏa mãn bài toán.
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 59
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng 2
x mx m
Câu 10. Cho phương trình 2 log
x 2mx 2m . Gọi S là tập chứa tất cả các giá trị 2 2 3x 1
nguyên của tham số m thuộc đoạn 2 022; 202
2 để phương trình đã cho có hai nghiệm thực
phân biệt. Số phần tử của tập S là A. 3 . B. 4042 . C. 4043 . D. 4041 . Lời giải Chọn B
Đây là dạng phát triển từ dạng cơ bản, chúng ta phải biến đổi khéo léo:
Với trường hợp u,v 0 ta có: k u a .u u log
v u log v k a .u log v k
a .u k . a a a v v v 2
x mx m
Với phương trình đã cho 2 log
x 2mx 2m (1) 2 2 3x 1 2 3 x 1 0
Điều kiện xác định: 2
x mx m 0 .(2) 2
x mx m 0 Có (1) 2 2
x mx m
2x 2mx 2m 2 2 1 log
x 2mx 2m 1 log
x 2mx 2m 1. 2 2 2 2 3x 1 3x 1 2
2x 2mx 2m
Dễ dàng tách được tiếp log 2 3x 1 2
2x 2mx 2m 2 2 3x 1 log 2
2x 2mx 2m 2
2x 2mx 2m log 2 3x 1 2 3x 1 (3) 2 2 1
Xét hàm đặc trưng f t log t t f ' t 1 0 t
0 hàm đơn điệu tăng. 2 l t n2
Từ (3) f 2
x mx m f 2 x 2 2 2 2 2 3
1 2x 2mx 2m 3x 1 (4) 2
x 2mx 2m 1 0 . Dễ thấy hệ thức (4) thỏa mãn điều kiện (2)
Để phương trình có hai nghiệm thực phân biệt thì phương trình 2
x 2mx 2m 1 0 có hai m 1 2
nghiệm thực phân biệt. Suy ra 2
Δ' m 2m 1 0 m 1 2 2 022 m 3 Suy ra
có 4042 giá trị m nguyên thỏa mãn. 1 m 2022 3 2
x 3x 3x 3m 8
Câu 11. Cho phương trình 3 log
x 3x 3m 2 . Gọi S là tập chứa tất cả các 2 2 x 2x 3
giá trị nguyên của tham số m để phương trình đã cho có đúng hai nghiệm. Số phần tử của S là: A. 1. B. 2 . C. 3 . D. 0 . Lời giải Chọn A 3 2
x 3x 3x 3m 8
Điều kiện xác định: 3 2
0 x 3x 3x 3m 8 0 . 2 x 2x 3 3 2
x 3x 3x 3m 8
Phương trình đã cho biến đổi thành 3 log
1 x 3x 3m 1 2 2 x 2x 3 3 2
x 3x 3x 3m 8 log 3 2
x 3x 3x 3m 8 2 3x 6x 9 2 2 x 2x 3
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 60
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng log 3 2
x 3x 3x 3m 8 3 2
x 3x 3x 3m 8 log 2
3x 6x 9 2 3x 6x 9 2 2 . (*)
Xét hàm đặc trưng f t log t t là đơn điệu trên khoảng 0; . Nên từ (*) suy ra: 2 3 2 2
x 3x 3x 3m 8 3x 6x 9 0 (TM điều kiện) 1
3m 1 2 m 3
x 3x 3m 1 có hai nghiệm khi và chỉ khi 3 3m 1 2 m 1
Suy ra có duy nhất một giá trị nguyên m thỏa mãn. Câu 12. Có bao nhiêu giá trị nguyên của tham số m để phương trình
log 3x m 2
2log x x 75x 25m 2 có hai nghiệm thực phân biệt? 5 5 A. 57 . B. 58 . C. 55 . D. 56 . Lời giải Chọn D 3
x m 0 Điều kiện . x 0
log 3x m 2
2log x x 75x 25m 2 5 5
log 3x m 2 2
log x x 25 3x m log 25 5 5 5 2 2 x x log
3x m 25 3x m log 25 * 5 5 5 5
Xét hàm số f t log t 25t , với t 0 . 5 1
Ta có f 't
25 0 , t 0 f t là hàm số đồng biến trên khoảng 0 ; . l t n5 2 2 x x
Khi đó * 3x m m 3 x . 5 25 2 x 2x 75
Xét hàm số g x
3x , x 0 . Ta có g ' x 3 0 x . 25 25 2
Bảng biến thiên của g x 2 x
Phương trình đầu có 2 nghiệm phân biệt khi và chỉ khi phương trình m 3x có hai 25 225
nghiệm phân biệt dương m ; 0 . Vì m m 5 6 ; 5 5 ; 5 4 ;.. ; 2 ; 1 có 4
56 giá trị của m thỏa mãn.
Câu 13. Có bao nhiêu giá trị nguyên dương của tham số
m để phương trình 2 2x mx 1 2 log
2x mx 1 x 2 có hai nghiệm thực phân biệt? 2 x 2
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 61
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng A. 3 . B. 4 . C. 2 . D. 1. Lời giải Chọn B x 2 0 Điều kiện: . 2
2x mx 1 0 2 2x mx 1 Ta có 2 log
2x mx 1 x 2 2 x 2 2 2 log
2x mx 1 2x mx 1 log
x 2 x 2 2 2 f 2
2x mx 1 f x 2 1 1
Xét hàm số f t log t t với t 0; có f 't
1 0 , t 0; 2 l t n2
f t đồng biến trên 0; nên 1 2
2x mx 1 x 2 . x 2 x 2 Từ đó .
2x mx 1 x 22 2 2
x m 4 x 3 0 2
YCBT 2 có hai nghiệm phân biệt x , x lớn hơn 2 1 2
m 42 12 0 m m
x 2 x 2 0 x x 4 0
4 m 4 0 1 2 1 2
x 2 x 2 0
x x 2 x x 4 0 3
2 4 m 4 0 1 2 1 2 1 2 m 8 9 * 9 m
mà m m 1; 2;3; 4 . m 2 2 ----------HẾT----------
Câu 14. Có bao nhiêu số nguyên m để phương trình ln m 2sinx ln m 3sinx sinx có nghiệm thực? A. 5 . B. 4 . C. 3 . D. 6 . Lời giải Chọn B
m 2sinx ln m 3sinx 0 Điều kiện: .
m 3sinx 0
Phương trình đã cho tương đương: sin 2sin ln 3sin x m x m x e . sin 3sin ln 3sin x m x m x e sinx .
lnm3sinx sin ln 3sin x e m x e sinx , 1 . Xét t f t
e t , t . Ta có ' t f t
e 1 0 , t . Nên hàm số f t đồng biến trên . Vậy
1 f ln m 3sinx f sinx
ln m 3sinx sinx .
Đặt a sinx , a 1 ; 1
. Phương trình trở thành: ln m 3a a a m e 3a . Xét a g a
e 3a , a 1 ; 1 , ' a g a
e 3 0 , a 1 ; 1 .
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 62
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng 1
Vậy để phương trình có nghiệm thực thì g
1 m g
1 e 3 m 3 . e
Vậy có 4 giá trị nguyên của tham số m là: 0 ; 1; 2 ; 3 .
Câu 15. Tìm giá trị lớn nhất của tham số m để phương trình ln m ln m cosx cos x có nghiệm thực? e 1 A. .
B. e 1. C. e . D. 1. 2 Lời giải Chọn B
Đặt v ln m cosx v
e m cosx v m e cosx .
Phương trình trở thành ln m v cosx cos x m v e cos x m e v . Do đó v cos cos x e x e v v cos x e v e cosx (1). Xét hàm số u f u e u . ' u f u
e 1 0 với u .
Vậy (1) f v f cosx v cosx cosx e
cosx m (2). Đặt t g t
e t , với t cosx , t 1 ; 1 . ' t g t e 1 '
g t 0 t 0 . Bảng biến thiên
Để phương trình (2) có nghiệm thì 1 m e 1.
Vậy giá trị lớn nhất của m thỏa mãn yêu cầu bài toán là e 1. Câu 16. Tìm tất cả các giá trị của tham số thực m để phương trình 2sinx m 1 2
8sin x 10sinx 2 m log
có đúng bốn nghiệm phân biệt thuộc đoạn 2 2sinx 2 1 5 0; 6 17 17 17 A. m ; 2 . B. m ; 2 . C. m ; 1 . D. m . 8 8 8 Lời giải Chọn A
2sinx m 1 0 Điều kiện (a). 2sinx 1 0
Phương trình đã cho viết lại thành 2 2sinx 2
1 2sinx m log 2sinx m
1 log 2sinx 2 1 2 2 2 2sinx 2
1 log 2sinx 2
1 1 2sinx m 1 log 2sinx m 1 2 2 2 2sinx 2 1 log 2 2sinx 2 1
2sinx m 1 log
2sinx m 1 1 2 2
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 63
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng 1
Xét hàm số f t t log t , t 0; , có f 't 1
0,t 0; nên f t đồng 2 l t n2
biến trên 0; .
Phương trình (1) được viết lại thành
f 22sinx 2
1 f 2sinx m
1 2 2sinx 2 1
2sinx m 1 2
8sin x 10sinx 1 m 2 5 1 1
Đặt t sinx , với x 0; và sinx
ta được t 0; 1 \ . 6 2 2 1 5 Với mỗi t 0;
1 chỉ thu được 1 giá trị của x 0; . 2 6 1 5 Với mỗi t ;1
ta thu được 2 giá trị của x 0; . 2 6
Phương trình 2 trở thành: 2
8t 10t 1 m 3 .
Phương trình đã cho có 4 nghiệm phân biệt khi và chỉ khi 3 có hai nghiệm phân biệt 1 t ;1 2 1 5 Xét f t 2
8t 10t 1, t 0;
1 \ , có f 't 16t 10 0 t . 2 8
Bảng biến thiên của f t 17
Từ bảng biến thiên suy ra m 2 . 8 2 1 2x 4x 6
Câu 17. Tổng tất cả các giá trị của tham số m để phương trình 2 log
x 2 x x m 2 2 x m 1
có đúng ba nghiệm phân biệt là A. 2 . B. 3 . C. 1. D. 0 . Lời giải Chọn B 2 2x 4x 6 Điều kiện:
0 x . x m 1 2 1 2x 4x 6 Phương trình: 2 log
x 2 x x m * 2 2 x m 1 2 2x 4x 6 2 log
2x 4 x x m 2 x m 1 log 2
2x 4x 6 log x m 2
1 2x 4x 4 x m 2 2
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 64
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng log 2
2x 4x 6 2
2x 4x 6 log
x m 1 2 4 x m 4 2 2 log 2
2x 4x 6 2
2x 4x 6 log
4 x m 4 4 x m 4 1 2 2
Xét hàm f t log t t trên khoảng 0 ; . 2 1 có ' f t
1 0, t 0 suy ra f t đồng biến trên khoảng 0 ; . tln2 Khi đó 1 f 2
2x 4x 6 f 4 x m 4 2
2x 4x 6 4 x m 4 2
2 x m x 2x 1 2
2x 2m x 2x 1 (do 2 2
x 2x 1 (x 1) 0,x )
2x 2m 2 x 2x 1 2
2m x 4x 1 2 2 2m x 1
Vẽ đồ thị hai hàm số g x 2
x 4x 1 và h x 2
x 1 trên cùng hệ trục tọa độ Oxy
(Chú ý: Hai đồ thị hàm số y g x và y h x tiếp xúc với nhau tại điểm A1 ; 2 ) Để phương trình
* có đúng ba nghiệm phân biệt thì 2 phải có đúng ba nghiệm phân biệt
đường thẳng y 2m và hai đồ thị trên có đúng ba điểm chung phân biệt. 1 m 2m 1 2
2m 2 m 1 . 2m 3 3 m 2
Vậy tổng tất cả các giá trị của m bằng 3.
Câu 18. Có bao nhiêu số nguyên của m để phương trình log 2x m 2
2log x x 4x 2m 1 có 2 2
hai nghiệm thực phân biệt? A. 2 . B. 3 . C. 1. D. 4. Lời giải Chọn C
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 65
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng x 0 Điều kiện m x 2
log 2x m 2
2log x x 4x 2m 1 2 2
log 2x m 2
2log x x 2 x 2m 1 2 2
log 2x m 2 x 2m 2 2
1 log x x 2 2
log 22x m 2 x 2m 2 2
log x x (1) 2 2
Xét f u log u u, u 0 2 1 ' f u
1 0 , do đó hàm số đồng biến trên 0; . l u n2
Khi đó (1) f x m f 2
x x m 2 2 2 2 2 2
x x 4x 2m
Xét hàm số g x 2
x 4x, x 0
Phương trình có 2 nghiệm dương khi 4 2m 0 2 m 0 suy ra có 1 giá trị nguyên.
Câu 19. Cho phương trình 3log x log 3x m 3
2x 6x 2m 0 , với m là tham số. Có bao nhiêu 3 3
giá trị nguyên của tham số m để phương trình đã cho có hai nghiệm thực phân biệt? A. 1. B. 3 . C. 4 . D. vô số. Lời giải Chọn A x 0 Điều kiện: . 3x m 0
Ta có 3log x log 3x m 3
2x 6x 2m 0 3 3 3
log x log 3x m 3
2x 6x 2m 0 3 3 3 3
log x 2x log 3x m 6x 2m 3 3 3 3
log x 2x log 3x m 2 3x m 1 3 3 1
Xét hàm số f t log t 2t trên 0; ta có f 't
2 0 , với mọi t 0; . 3 t ln 3
Do đó f t đồng biến trên 0; . Từ (1) ta có f 3
x f x m 3 3 3
x 3x m m x 3x (2)
Xét hàm số g x 3
x 3x trên khoảng 0; , ta có bảng biến thiên
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 66
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng Phương trình
1 có 2 nghiệm phân biệt phương trình 2 có 2 nghiệm phân biệt thuộc
khoảng 0; 2 m 0 .
Mặt khác, do m nguyên nên m 1.
Câu 20. Có bao nhiêu giá trị nguyên của m trên đoạn 2 021; 202 1 để phương trình ln 2 x 2
x 4x 5 2 2
2x 3x m 1 2x 3x m 3 2
x 6x 13x 10 2
2x 3x m 2 1
2x 3x m có nghiệm thực A. 2020. B. 2019. C. 2021. D. 2023. Lời giải Chọn A
Ta có pt đã cho tương đương với: 2 3 x 2 x 4x 5 ln
x 2 x 23 2
2x 3x m x x m 2 2 3 2 2
2x 3x m 1 2x 3x m ln x 2 x 22 1
x 2 x 23
ln 2x 3x m x x m x x m x x m
2 3 2 1 2 3 2 3 3 2 2 2 2 1
Xét hàm số: f t 2 t t 3 ln
1 t t , t 1 Suy ra: ' f t 2 1
3t 0 t f t đồng biến trên . 2 t 1
Suy ra: f x f 2 1 2
2x 3x m . 2
2x 3x m x 2 x 2 0 x 2
2x 3x m x 22 2 2
x x 4 m 2
Để phương trình đã cho có nghiệm tương đương với 2 có nghiệm x 2; .
Xét hàm số: g x 2
x x 4, x 2;. Ta có bảng biến thiên:
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 67
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng x 2 +∞ -∞ +∞ f(x) 2
Từ bảng biến thiên ta có ycbt m 2 suy ra có 2020 giá trị m thỏa mãn.
Câu 21. Tìm số giá trị nguyên của m thuộc 2
0 ; 20 để phương trình log 2 2
x m x x 4 2m 9 x 1 1 2m 2
x 4 có nghiệm? 2 A. 12. B. 23. C. 25. D. 10. Lời giải Chọn B Điều kiện xác định: 2 2
x m x x 4 0 . log 2 2
x m x x 4 2m 9 x 1 1 2m 2 x 4 2 log x 2
x 4 x m 2 2
2mx 9x 1
x 4 2m x 4 2 4x 2 2 log
m 2mx 9x 1 x 4 2m x 4 2 2 x 4 x 2 4x m x 4 mx 2 2 log
2mx 9x 1
x 4 2m x 4 2 2 x 4 x log 2
4x m x 4 mx 2
8x 2m x 4 2mx 1 log 2
x 4 x 2 x 4 x 2 2 log 2
8x 2m x 4 2mx 2
8x 2m x 4 2mx log 2
x 4 x 2
x 4 x 1 2 2
Xét hàm số f t log t t , t 0; . 2 1 f 't
1 0, t 0 ; nên hàm số luôn đồng biến trên 0; . l t n2 Khi đó 1 2 2
8x 2m x 4 2mx x 4 x 8x m 2
x x 2 2 4
x 4 x 8x 2m 1 2 x 4 x x 2 8 x 4 x 2m 1
m x 2 2 1 2
x 4 x 4 1 2m 2 2
x x 4 x . 2
Xét hàm số g x 2 2
x x 4 x với x ; .
x 4 x2 2
Ta có g ' x 0, x . 2 x 4
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 68
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng 4 4 g x x x x lim x lim 2 ; x x 2 lim lim 4 x 2
x 4 x x 4 1 1 2 x 4 lim g x 2 lim x 1 1 . 2 x x x
Ta có bảng biến thiên của g x 1 2m 5
Để phương trình có nghiệm thì 2 m . 2 2
Do m nguyên thuộc 2
0 ; 20 nên số giá trị m là 23. 2 x 1 x 1
Câu 22. Cho biết phương trình log 2 log
có nghiệm duy nhất x a b 2 . 5 3 x 2 2 x mx a 2
Hỏi m thuộc khoảng nào dưới đây để hàm số y
có giá trị lớn nhất trên đoạn x m 1; 2 bằng 2 .
A. m 7; 9 .
B. m 6; 7 .
C. m 2; 4 .
D. m 4; 6 . Lời giải
+ Điều kiện: x 1 . 2 x 1 x 1 2 x 1 x 1 Ta có: log 2 log log 2 log 5 3 x 2 5 3 2 x x 2 x log 2 x
1 log x log x 1 log 2 x 2 2 5 5 3 3 log 2 x
1 log 2 x 2 log x log x 2 1 (*). 5 3 5 3
Xét hàm số f t log t log t 2 1 , với t 1 5 3 1 2
có f t 0, t 1 t.ln 5 t 1 .ln 3
nên f t đồng biến do đó (*) x 2 x 1 x 1 2 (vì x 1 )
x 3 2 2 . Vậy a 3 . mx 1
+ Với a 3 , ta xét hàm số y x m
TXĐ: D \ m 2 m 1 y '
0 do đó hàm số luôn nghịch biến. x m2
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 69
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng m 1; 2
Khi đó hàm số có giá trị lớn nhất trên đoạn 1; 2 bằng 2 y 1 2 m 1; 2 m 3 m 1 . 2 1 m
Câu 23. Cho x, y là hai số thực dương thỏa mãn 5x y 4 . Tổng tất cả giá trị nguyên của tham số 2
x 2 y m
m để phương trình 2 log
x 3x y m 1 0 có nghiệm là 3 x y A. 10. B. 5. C. 9. D. 2. Lời giải Chọn B 2
x 2 y m 2 log
x 3x y m 1 0 3 x y log 2
x 2 y m 2
x 2 y m log 3 x y 3 x y 1 3 3
Vì x, y 0 nên x y 0 . Xét hàm số f t log t t là hàm số đồng biến trên 0; . 3 Khi đó 1 2 2
x 2 y m 3x 3y x 3x y m 0 * 4
Kết hợp với điều kiện 5x y 4 y 4 5x . Vì x, y 0 0 x . 5 4 Ta có * 2 2
x 2x m 4 0 m x 2x 4, x 0; . 5 4 44 Hàm số 2
y x 2x 4 nghịch biến trên 0; (do 1 0 ) nên 2
x 2x 4 4 . 5 25 Do vậy m 2;
3 là các giá trị cần tìm.
Vậy tổng tất cả các giá trị m thỏa ycbt là 5.
2 - BPT LÔGARIT CHỨA THAM SỐ 2
x 3x m m
Câu 24. Với giá trị nào của m thì bất phương trình 2 log
x 4x 2 có nghiệm thỏa 2 2 3x 5x 4 2
x R .
A. m . B. m 2 . C. m 4 . D. m 2 . Lời giải Chọn A Vì 2
3x 5x 4 0 x R nên điều kiện: 2
x 3x m 0 x . R Ta có: 2
x 3x m m 2 log
x 4x 2 2 2 3x 5x 4 2 log 1 2
x 3x m log 2
3x 5x 4 2
3x 5x 4 2
x 3x m 2 2 2 log 1 1 2
x 3x m 2
x 3x m log 2
3x 5x 4 2
3x 5x 4 (1) 2 2 2 2 Xét hàm số: 1 1 1
f t log t t trên khoảng 0; f 't 0;t 0 . 2 2 tln2 2
Nên hàm số f t đồng biến trên khoảng 0; .
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 70
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng (1) f 2
x x m f 2 3
3x 5x 4 2 2
x 3x m 3x 5x 4 x R 2
m 2x 8x 4 x R Kết hợp điều kiện: 2
2x 8x 4 m 0 x R 2
x 3x m 0 8 2m 0 9 4m 0 m . 2
x 2x m
Câu 25. Cho bất phương trình 2 log
x 4x 3 m ( m là tham số). Có bao nhiêu giá 2 2 x x 1
trị nguyên của m để bất phương trình đã cho nghiệm đúng với mọi x 0; 4 ? A. 4 . B. 1. C. 0 . D. 2 . Lời giải Chọn B 2
x 2x m Điều kiện: 0 2
x 2x m 0 1 2 x x 1 2
x 2x m 2
x 2x m Ta có: 2 log
x 4x 3 m 2 log
1 x 4x 2 m 2 2 x x 1 2 2 x x 1 log 2
x 2x m log 2
2x 2x 2 2
x 4x 2 m 2 2 log 2
x 2x m log 2
2x 2x 2 2
2x 2x 2 2
x 2x m 2 2 log 2
x 2x m 2
x 2x m log 2
2x 2x 2 2 2x 2x 2 2 2
Đặt f t log t t với t 0; 2 1
f 't
1 0, t 0; tln2
Hàm số f t đồng biến trên khoảng 0; . Mà f 2
x x m f 2 2
2x 2x 2 2 2
x 2x m 2x 2x 2 2
x 4x 2 m 0 2 2
m x 2x g x Từ 1 và 2 ta có: , x 0; 4 2
m x 4x 2 h x Bảng biến thiên m 1
Từ bảng biến thiên ta suy ra 1 m 2 m 2
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 71
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng
Vậy m 2 thỏa yêu cầu bài toán. Câu 26. Tìm tất cả các giá trị của m để bất phương trình 2log 2 sinx m 2
4log sinx 2sinx cos2x 2m 1 0 có nghiệm. 3 3 1
A. m 2; 2 . B. m .
C. m .
D. m 0 . 4 Lời giải Chọn D si nx 0
Ta có điều kiện của bất phương trình sinx 0 . 2 sinx m 0 Khi đó 2log 2 sinx m 2
4log sinx 2sinx cos2x 2m 1 0 1 3 3 2log 2
sinx m 2 2 sinx m
4log sinx 1 cos2x 3 3 2log 2
sinx m 2 2 sinx m 2
4log sinx 2sin x 3 3 log 2 sinx m 2 2
sinx m 2log sinx sin x 3 3 log 2 sinx m 2 2 2
sinx m log sin x sin x 2 . 3 3
Xét hàm số f t log t t với t 0. 3 1
Ta có f 't
1 0, t 0 nên hàm f t đồng biến trên 0; . t.ln3
Do đó bất phương trình (2) tương đương với 2 2 2 2
sinx m sin x m sin x sinx .
Suy ra bất phương trình (1) có nghiệm khi 2 m 2
max sin x sinx trên miền sinx 0 . 1
Xét hàm số g t 2
t t, với t 0;
1 . g 't 2t 1; g 't 0 t . 2 1 1 1 Vì g 1 0; g ;
g 0 0 nên max g t 0; min g t . 2 4 0; 1 0; 1 4
Vậy bất phương trình (*) có nghiệm khi 2
m 0 m 0. 3 2 2
x 2x 2m 2
Câu 27. Cho bất phương trình: 3 2 log
2x 2 m x x 1 . Có bao nhiêu giá 4 2 4x 4x 2
trị nguyên của m 0;15 để bất phương trình (1) nghiệm đúng với mọi số thực x 1; 2 ? A. 6 . B. 8 . C. 7 . D. 5 . Lời giải Chọn D Điều kiện 3 2
x x m
m g x 3 2 2 2 2 2 0 2
2x 2x 2 - Bất phương trình (1) log 2
4x 4x 2 2
4x 4x 2 log 3 2
2x 2x 2m 2 3 2
2x 2x 2m 2 2 2 1
Xét hàm số: f t t log t với t 0 , có f 't 1 0 , t 0 . 2 tln2
Nên bất phương trình (2) f 2
x x f 3 2
x x m 2 3 2 4 4 2 2 2 2
2 4x 4x 2 2x 2x 2m 2 h x 3 2
x x 2x 2 m .
- Xét hàm số: h x 3 2
x x 2x 2 với x 1;2 , có h 2
' x 3x 2x 2 0 với x 1;2 .
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 72
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng
Suy ra hàm số h x đồng biến trên đoạn 1; 2 max h x h 2 10 . 1;2
x 0 1; 2
- Xét hàm số: g x 3 2
2x 2x 2 với x 1;2 , có g' x 2 6x 4x 0 2 x 3 2 46 Ta có g
1 2; g 2 10; g
max g x g 2 10 3 27 1;2 Bất phương trình (1) nghiệm đúng với mọi số thực x 1;2
m max g x
2m g x , x 1; 2 2 1;2 m 10 . m
h x,x 1; 2 m max h x 1;2
Do m nguyên và m 0,15 m 10,11,12,13,1 4
- Vậy có 5 giá trị nguyên của m thỏa mãn yêu cầu của đề bài.
Câu 28. Có bao nhiêu giá trị nguyên dương của tham số m để bất phương trình 2 2x mx 1 2 log
2 x 2x mx 1 nghiệm đúng với x 0; 1 ? 2 x 2 A. 10 . B. 5 . C. 1. D. 6 . Lời giải Chọn D x 2 0 Điều kiện: . 2
2x mx 1 0 2 2x mx 1 Ta có 2 log
2x mx 1 x 2 2 x 2 2 2 log
2x mx 1 2x mx 1 log x 2 x 2 f 2
2x mx 1 f x 2 1 2 2 1
Xét hàm số f t log t t với t 0; có f 't
1 0 , t 0; 2 tln2
f t đồng biến trên 0; nên 2
1 2x mx 1 x 2 . 0 x 1 0 x 1 3 Từ đó
m 4 x .
2x mx 1 x 22 2 2
x m 4 x 3 0 2 x
YCBT m 4 2 m 6 .
DẠNG 5: PHƯƠNG PHÁP HÀM ĐẶC TRƯNG GIẢI PT, BPT CÓ TỔ HỢP MŨ -
LÔGARIT KHÔNG CHỨA THAM SỐ
Câu 29. Có bao nhiêu cặp số x; y thuộc đoạn 1; 2020 thỏa mãn y là số nguyên và ln y x
x y e ? A. 6 . B. 7 . C. 2021 . D. 2020 . Lời giải Chọn B Ta có: ln y ln y ln y x x y e x x e e . 1
Xét hàm số f t t ln t trên 0; , ta có f t 1 0, t
0 f t đồng biến trên t
0; y f x f e y x e .
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 73
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng
Do x 1; 2020 nên 1 y
e 2020 0 y ln 2020 .
Mà y và y 1; 2020 nên y 1; 2;3; 4;5; 6; 7 .
Vậy có 7 cặp số x; y thỏa mãn bài toán.
Câu 30. Có bao nhiêu cặp số nguyên x; y thoả mãn x 2; 4374 và 2.3y log y 1 x 3 3x y 3 ? A. 7. B. 8. C. 6. D. 9. Lời giải Chọn A Đặt y 1 3 3y t
3t y log 3t . 3
Phương trình đã cho tương đương với: 6t log
x t 3x log 3t 3 3
6t log 3t 3x log x t 3 3
9t log 3t 3 x t log x t * 3 3 1
Xét hàm số: f u 3u log u liên tục trên 0; , có f u 3 0, u 0; 3 u ln 3 .
Suy ra: hàm số y f u đồng biến trên 0; 1
* f 3t f x t 2 Từ 1 và 1 2 3 2 2.3y t x t t x x .
Ta có: 2 x 4374 , suy ra: y 1 2 2.3
4374 log 2 log 2 y 1 log 4374 3 3 3
1 y 1 log 4374 log 2 1 y 8 . Vì y nguyên, nên y 1; 2;3; 4;5;6;7 . 3 3
Dễ thấy, ứng mỗi giá trị của y , ta tìm được một giá trị nguyên của x .
Vậy có 7 cặp số nguyên x; y thoả mãn yêu cầu bài toán.
5x 3x
Câu 31. Tính tổng S tất cả các nghiệm của phương trình: x 1 ln
5 5.3x 30x 10 0 . 6x 2
A. S 1 .
B. S 2 .
C. S 1 . D. S 3 Lời giải 1
Điều kiện x . 3
Phương trình tương đương
ln 5x 3x ln 6 2 55x 3x x
56x 2 0
ln 5x 3x 55x 3x ln 6x 2 56x 2 (1). 1
Xét hàm sô f t ln t 5t,t 0 . Có f 't 5 0 , t 0 nên f t đồng biến. Từ 1 t suy ra 5x 3x f
f 6x 2 5x 3x 6x 2 5x 3x 6x 2 0
Xét 5x 3x g x
6x 2 , ' 5x ln 5 3x g x ln 3 6 1 x 2 x g x 2 ' 5 ln 5 3 ln 3 0 x . 3
Nên g ' x 0 có không quá 1 nghiệm suy ra g x 0 có không quá 2 nghiệm trên 1 ; . 3
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 74
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng
Mà g 0 g
1 0 . Vậy phương trình có nghiệm 0,1 . Do đó S 1. 1 11 x 1 2 2x 11
Câu 32. Số nghiệm nguyên thuộc khoảng 0;12 của bất phương trình 3 x 3 x log2 2 x x 1 là: A. 7 . B. 8 . C. 5 . D. 11. Lời giải Chọn C 11
Điều kiện x và x 0 . 2 1 11 1 11 x 1 2 2x 11 x 1 2 1 2x 11
Khi đó 3 x 3 x log
3 x 3 x log 2 2 x x 1 2 2 2
x x 1 11 1 11 2 1 11 x 1 2 x 1 2 1 1 1 1 11
3 x 3 x log x 3 x log x 1 3 x log 2 . 2 2 2 2 1 2 x 2 x x 1 x t 1 t 1
Xét hàm số f t 3 log t với t 0 . Khi đó f t 3 ln 3 0, t 0 nên hàm 2 2 2t ln 2
số đã cho đồng biến trên 0; . Do đó 2 1 11 1 11 x 3x 10 11 f x 1 f 2 x 1 2 0 x ; 2 0;5. x x x x x 2
Vậy trên khoảng 0;12 có 5 nghiệm nguyên thỏa yêu cầu bài toán.
Câu 33. Có bao nhiêu cặp số nguyên x; y thỏa mãn đồng thời 2x y log x y và x , y thuộc 2 đoạn 2 ;10? A. 6. B. 7. C. 5. D. 8. Lời giải Chọn A 2x y log
x y 2x x log
x y x y 2x x log x y 2 x y * . 2 log2 2 2 Xét hàm số 2t f t
t có ' 2t f t
ln 2 1 0,t .
Hàm số đồng biến trên , do đó:
* x log x y 2x 2x x y y x * * . 2 Xét hàm số 2x g x x trên đoạn 2 ;10. Ta có: ' 1 2x g x ln 2
g ' x 0 x log log e . 2 2 x 2 log log e 10 2 2 log e Kết hợp * * và BBT t g a ' có: x 2 2 y log . 0 2 e
Do y nên y 2 hoặc y 1. log e 2 log 2
Với y 2 ta có: g xgx 2 . Do e
9 x nên x 1 ;0;1;
2 . Trường hợp này có 4 cặp số
x; y thỏa mãn. 4 1014
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 75
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng
Với y 1 ta có: g x 1
. Do x nên x 0;1 . Trường hợp này có 2 cặp số x; y thỏa mãn.
Vậy có tất cả 6 cặp số x; y thỏa mãn yêu cầu bài toán.
Câu 34. Có bao nhiêu số nguyên x thoả mãn 2 x x 1 3 4.3 27 . log
x 1 x 3 0 ? 3 A. 2 . B. 4 . C. 1. D. 3 . Lời giải Chọn D
Điều kiện: x 1 0 x 1 . 2 x x 1 3 4.3 27 0 1 log
x 1 x 3 0 3 Ta có 2 x x 1 3 4.3 27 . log
x 1 x 3 0 3 2 x x 1 3 4.3 27 0 2
log x 1 x 3 0 3 2 x x 1 3 4.3 27 0 Giải hệ 1 ta có . log
x 1 x 3 0 3 3x 9 x 2
+) 3 x 4.3x 27 0 3x 2 2 1
12.3x 27 0 . 3x 3 x 1
Suy ra tập nghiệm S ; 1 2; . 1 +) log
x 1 x 3 0 log
x 1 x 1 4 3 3 3 1
Xét hàm số f t log t t f t 1 0, t
0 nên hàm số f t log t t đồng 3 t.ln 3 3
biến trên khoảng 0; .
Từ 3 f x
1 f 3 x 1 3 x 2 nên tập nghiệm S 1 ; 2 . 2
Do đó tập nghiệm của hệ
1 là S S S 1 ;1 2 . 1 2 2 x x 1 3 4.3 27 0 Giải hệ 2 ta có . log
x 1 x 3 0 3 +) x x x 2 2 1 3 4.3 27 0 3
12.3x 27 0 3 3x 9 1 x 2 .
Suy ra tập nghiệm S 1; 2 3 +) log
x 1 x 3 0 log
x 1 x 1 4 4 3 3 1
Xét hàm số f t log t t f t 1 0, t
0 nên hàm số f t log t t đồng 3 t.ln 3 3
biến trên khoảng 0; .
Từ 4 f x
1 f 3 x 1 3 x 2 nên tập nghiệm S 2; . 4
Do đó tập nghiệm của hệ 2 là S S S 2 . 3 4
Kết luận: Bất phương trình có tập nghiệm S 1 ; 1 2 .
Vậy bất phương trình có 3 nghiệm nguyên. Câu 35. Tổng
S của tất cả các nghiệm thuộc khoảng (0; 4 ) của phương trình 2 2 sin x cos 2022 2022
x 2ln(cot x ) là
A. S 18 .
B. S 8 .
C. S 7 .
D. S 16 .
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 76
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng Lời giải.
Điều kiện cot x 0 . Ta có 2 2 2 2 sin x cos x sin x cos 2022 2022
2 ln(cot x) 2022 2022 x ln 2 cos x ln 2 sin x 2 sin 2022 x ln 2 sin x 2 cos 2022 x ln 2 cos x
Xét hàm số ( ) 2022t f t
ln t với t 0 t 1 f (
t) 2022 ln 2022 0, t
0 hàm số f (t) đồng biến trên khoảng (0; ) . t k Khi đó f 2 x f 2 x 2 2 (1) sin cos
sin x cos x cos 2x 0 x , k . 4 2
Do cot x 0 nên x
k , k . 4
5 9 13
Mà x (0; 4 ) suy ra x ; ; :
. Suy ra S 7 . 4 4 4 4
Câu 36. Có bao nhiêu cặp số nguyên (x; y) thỏa mãn đồng thời các điều kiện 2 x 2022 , y 3 1 y 2022 và x y2 4 log 4 2 ? 2 2x 1 A. 1011. B. 1010. C. 1009. D. 1012. Lời giải 1 y 3 y x y 3 Ta có: 2 2 x2 y 4 log 4 2 log 2 2 2 2 4 2x 1 2x 1 y 4 2 x2
log ( y 3) 2 log (2x 1) 2 (1) 2 2 Xét hàm số: t 1 f (t) log t 2 t [4; ) 2 t 1 1 t 2 ln 2 ln 2 f (t) 0 t [4; ) t ln 2
Suy ra: (1) y 3 2x 1 y 2x 2 3 Do 1 y 2022
x 1012 x {2;3;,1012} 2
Do đó: (x; y) {(2; 2); (3; 4);; (1012; 2022)} có 1011 cặp thỏa mãn ycbt
Câu 37. Có bao nhiêu cặp số ;
x y nguyên thoả mãn 0 x 2022 và log 2 2 3 8y x x y ? 2 A. 2018 . B. 1. C. 4 . D. 2019 . Lời giải Chọn C
Đặt log 2 2 2 2 2t x t x . 2 Khi đó ta được phương trình 2t 2 y t 1 3 y t 1 3 3 8 2 1 3 2 2 1 2 y t y t y t 3y * . 2
Xét hàm sô 2a f a a trên có 2a f a ln 2 1 0 a . Khi đó hàm số đồng biến trên nên phương trình
* f t
1 f 3y t 1 3y t 3y 1 hay log
2x 2 3 y 1 . 2 log 2 1 log 4046 1
Do 0 x 2022 nên 2 2
log 2 1 3 y log 4046 1 y 2 2 3 3
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 77
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng
Và y y 0;1; 2; 3 . 3x 1
Câu 38. Có bao nhiêu cặp số nguyên ;
x y thỏa mãn 0 y 2022 và log 1 3x y ? 2 y A. 7 . B. 6 . C. 2022 . D. 2021 . Lời giải Chọn B
ĐK: 3x 1 x 0 3x 1 log
1 3x log 3x 1 3x y
1 log y y (*) 2 2 2 y
Xét hàm số f t log t t với t 0 2 1
f t 1 0, t
0 f t đồng biến trên khoảng 0; suy ra t ln 2
* 3x 1 y , vì 0 2022 0 3x y
1 2022 0 x log 2023 3
Mà x nguyên nên x 1;2;3;4;5;
6 . Vì ứng với mỗi gia trị x x có duy nhất 1 giá trị 0 3 ox y
1 do đó có 6 cặp cặp số nguyên ; x y thỏa mãn.
Câu 39. Cho 0 x 2020 và log
2 2 3 8y x x y
. Có bao nhiêu cặp số x; y nguyên thỏa mãn 2 các điều kiện trên? A. 1. B. 2019 . C. 4 . D. 2018 . Lời giải Chọn C
Đặt log 2x 2 u 1 u x 2 1 2
Khi đó phương trình đã cho trở thành: u 1 2 1 3 8y u y u 1 3 2 1 2 y u 3y . Xét hàm đặc trưng 2t f t
t, có 2t f t ln 2 1 0, t
f t là hàm số đồng biến trên . Ta có: u 1 3 2 1 2 y u
3y f u 1 f 3y 3 1 3 2 y u y x 1. y log 2021 Theo bài ra: 3 2 0 2
1 2020 0 y 3, 7 . 3 Vậy có 4 cặp ;
x y thỏa mãn là 0;0, 7;
1 , 63; 2, 511;3 . Câu 40. Giả sử ;
x y là cặp số nguyên thỏa mãn đồng thời 8 x 2022 và 2y log y 1 x 2
2x y . Tổng các giá trị của y bằng 2 A. 60 . B. 63 . C. 2022 . D. 49 . Lời giải Chọn D + Ta có: 2y log y 1 2 2 2.2y
1 2 2y log 2 2y x x y y x x 2 2 y 1 y 1 2 log 2 2 2y log 2 2y x x * 2 2
+ Xét hàm số f t t log t , t 0 là hàm số đồng biến trên 0; nên 2 y 1 y y 1 * 2 2x 2 x 2 + ta có: y 1 8 x 2022 8 2
2022 4 y log 2024 4 y 10 2
Suy ra y 4;5;6;7;8;9;1 0 .
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 78
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng
Câu 41. Có bao nhiêu cặp số ; x y (trong đó ,
x y nguyên dương thuộc đoạn 0;2022 thỏa mãn điều kiện 2x log 2 y 615 2
y x 615 2 A. 1. B. 3 . C. 4 . D. 2 . Lời giải Chọn A
2x x 2
y 615 log 2 y 615 . 2
Đặt log 2 615 2 615 2t t y y
. Khi đó ta có 2x 2t x t . 2 Xét hàm số 2x f x
x, x , ta có 2x f x
ln 2 1 0,x nên hàm số f x đồng biến trên . Do vậy 2x 2t log 2 615 2 2x x t x t x y y 615 . 2 Theo bài ra 2 2 x 2
0 y 2022 0 y 2022 0 2 615 2022 log 615 x log 2 2022 615 2 2
9, 3 x 21, 9 .
Khi x chạy từ 10 tới 21, ta thấy x 12 y 59 . Vậy có 1 cặp số ;
x y thỏa mãn yêu cầu bài toán.
Câu 42. Có bao nhiêu cặp số nguyên x; y thoả mãn 2 x 2021 và 2y log y 1 x 2
2x y 2 A. 2020 . B. 10 . C. 9 . D. 2021 . Lời giải Chọn B y y t 2y Đặt log 1 2 1 2 2
2t 2 2y 2.2t 2 2.2t 2y x t x x x x 2 2
Phương trình đã cho trở thành: 2y 2.2t 2 y 2.2y 2.2t t y y t *
Xét hàm số: ( ) 2.2u f u
u . Tập xác định D . Ta có: ( ) 2.2u f u .ln 2 1 0 u
. Suy ra hàm số ( ) 2.2u f u
u đồng biến trên
Do đó phương trình * có một nghiệm duy nhất:
2 2.2 y 2y 2 2 y y t x x y log 2x 2
Do 2 x 2021 log 4 y log 4042 2 y log 4042 11, 98 2 2 2
Lại có y là số nguyên nên: y 2;3.;...;1 1
Với mỗi giá trị của y ta tìm được duy nhất một giá trị của x. Vậy có 10 cặp số nguyên x; y
để thoả mãn điều kiện bài toán.
Câu 43. Có bao nhiêu cặp số nguyên x; y thỏa mãn 0 y 2022 và x 3
3 3x 6 9 y log y . 3 A. 2022 . B. 9 . C. 8 . D. 7 . Lời giải Chọn D Đặt log 3t t y y . 3 Phương trình trở thành x t x t 2
3 3x 6 9.3 3t 3 3x 3 3t 2 Xét hàm số
3a 3 3a f a a f a
ln 3 3 0, a , tức là f a đồng biến trên .
Suy ra x t 2 x log y 2 . 3
Để x thì log y 3
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 79
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng Mà y y 2 3 6 0 2022 1;3;3 ;3 ;....;3
Suy ra có 7 cặp số nguyên x; y thỏa mãn yêu cầu bài toán.
Câu 44. Trong mặt phẳng với hệ tọa độ Oxy , điểm M x ; y biểu diễn nghiệm của phương trình log 9 18 3y x x y
. Có bao nhiêu điểm M có tọa độ nguyên thuộc hình tròn tâm O 3
bán kính R 7 ? A. 7 . B. 2 . C. 3 . D. 49 . Lời giải Chọn B
Điều kiện: x 2 Ta có log 9 18 3y log
2 2 3y x x y x x y 3 3 Đặt log 2 2 3t t x x
ta được 3t 3y t y 3 Xét hàm số 3u f u
u thì f u là hàm đồng biến, vậy y t log x 2 3
Do M có tọa độ nguyên và nằm trên hình tròn tâm O bán kính bằng R 7 nên: 2 2 x y 49 2 x 7
M có tọa độ nguyên nên x log x 2 3 TH1: x 1
y 0 ( thỏa mãn)
TH2: x 1 y 1( thỏa mãn)
TH3: x 7 y 2 ( loại)
Vậy có 2 điểm thỏa mãn yêu cầu là 1 ;0,1; 1 Câu 45. Có bao nhiêu cặp số nguyên dương x, y thoả mãn 2 4 x 1 2 x x y 2 x4 3 log 4 4 2 3
log 2x y 1 đồng thời , x y 2021 A. 15 . B. 28 . C. 22 . D. 35 . Lời giải Chọn C 2 4 x 1 2 x x y 2 x4 3 log 4 4 2 3
log 2x y 1 2 4 x 4 x2 2 x x 2 x y 1 3 log 4 4 2 3
log 2x y 1 1 Xét 3t f t
.log t ( t 2 ). 3t t t 1
f t 3 ln 3.log t 3 ln 3.log t 0 , t 2 . t.ln10 t.ln10 Do đó 2 2
1 4x 4x 2 2x y 1 y 4x 2x 3 1 3 897 1 3 897 2
y 2021 4x 2x 3 2021 x 4 4 Vì x
0; 2022 nên x 1; 2;3;...; 21; 2 2 .
Vì mỗi giá trị của x có đúng một giá trị của y nên có 22 cặp số nguyên dương x, y thoả mãn.
Câu 46. Có bao nhiêu số nguyên y thuộc đoạn 2 021; 202
1 sao cho ứng với mỗi y tồn tại số thực x thỏa mãn log 5 2x y y 5 2x ? 2 A. 2017 . B. 2016 . C. 4041 . D. 2021 .
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 80
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng Lời giải Chọn A Ta có log 5 2x y y 5 2x x 2 5 2 5 2 x y y 2 x x 2 2 5
2 5 2 x 2x y y 1 .
Xét hàm số g t 2
t t , t 0 .
Có gt 2t 1 0, t 0 . Do đó, hàm số g t đồng biến trên khoảng 0; . 1
2x 5 2x g y g x 2 2 5 2 x y 2 2 x 2x y 5 . Xét hàm số 2 2 x 2x f x 5 . Có 2
2.ln 2.2 x ln 2.2x f x
, f x 0 x 1 Ta có BBT 19 Vì y 2 021; 202 1 , y nên y 2021. 4
Vậy có 2017 giá trị cần tìm của y .
Câu 47. Có bao nhiêu cặp số nguyên ;
x y thỏa mãn 0 y 2020 và log 4 4 1 2x y x y ? 2 A. 11. B. 1 2 . C. 2 0 2 1 . D. 10 . Lời giải Chọn A
Điều kiện: 4 y 4 0 y 1. Ta có: log 4 4 1 2x y x y 2
log 4 y 1 x 1 2x y 2 log
y 1 x 1 2x y 2 2 log
y 1 y 1 x 2x log y 1 2 y x 2x 2 2 log 1 2 Xét hàm đặc trưng 2t f t t ta có ' 1 2t f t ln 2 0
Hàm số y f t đồng biến trên R, do đó ta có log 1 1 2x y x y 2
Theo đề bài ta có: 0 y 2020
0 2x 1 2020 1 2x 2021 0 x log 2021 10, 98 2
Mà y Z y 0, 1; 2; 3; 4; 5; 6; 7; 8; 9;1 0
Ứng với mỗi giá trị của y cho 1 giá trị x tương ứng.
Vậy có 11 cặp số nguyên ;
x y thỏa yêu cầu bài toán. Câu 48. Cho ,
x y là các số thực thoả mãn log 3 6 2 3.9y x x y
. Biết 5 x 2021, tìm số cặp 3 ,
x y nguyên thoả mãn đẳng thức trên. A. 5 B. 2 C. 4 D. 3 Lời giải
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 81
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng Chọn B
Ta có: log 3x 6 x 2y 3.9y log x 2 2 y 1 x 2 3 2 y 1 3 3 log x 2 2 y 1 2 y 1 x 2 3 log 3 (1) 3 3
Xét hàm số f t log t t,t 0 3 1
Ta có: f 't
1 0, t 0 f t là hàm số đồng biến trên tập xác định t.ln 3 Từ (1) suy ra 2 y 1 2 y 1 x 2 3 x 3 2 y log 7 1 log 2023 1
Do 5 x 2021 nên 2 1 3 3 5 3 2 2021 y 2 2 y 1 x 25 Mà y nguyên nên y 2 x 241 Câu 49. Có bao nhiêu cặp số nguyên dương ; x y với x 2020 thỏa mãn
2 3 31 9y x y
log 2x 1 3 A. 1010 . B. 2020 . C. 3 . D. 4 . Lời giải Chọn C Đặt log 2 1 2 3t x t x 1, ta được 3 t 2 y t 2 3 3 1 2 3 1 3
3.3 3.3 y y t t 2 y (*). Xét hàm số
3.3u 3.3u f u u f u ln 3 1 0, u
f u đồng biến trên .
Do đó (*) t 2y , vậy nên 2
2 3 y 1 9y x 2x 1. Vì 2020 9y x
4039 y log 4039 . Vì y nguyên dương nên y 1; 2; 3 . Ta thấy với 9
mỗi giá trị nguyên của y thì tìm được 1 giá trị nguyên của x . Vậy có 3 cặp ; x y thỏa mãn.
Câu 50. Có bao nhiêu cặp số nguyên x; y thỏa mãn 0 y 2020 và x 3
3 3x 6 9 y log y . 3 A. 2020 B. 9. C. 7 . D. 8 . Lời giải Chọn C Ta có: x 3 3 3 6 9 log 3x 3 2 9 3 log 3x x y y x y y 3 x 2 3 y 3log y * 3 3 2 log3 3 . Xét hàm số: 3t f t 3t 2 .
Ta có: 3t f t .ln 3 3 0, t
. Suy ra hàm số y f t đồng biến trên . Khi đó: * 2 log 2 2 log 3x f x f y x y y . 3 3 Do 0 y 2020 và x, y nguyên nên: x2 1 3
2020 2 x 2 log 2020 x 2;3; 4;5; 6; 7;8 . 3
Ứng với mỗi giá trị x có một giá trị của y nên có 7 cặp số x; y nguyên thỏa mãn yêu cầu bài toán. Câu 51. Có bao nhiêu cặp số nguyên x; y thỏa mãn 0 x 4000 và
525y 2y x log x 5 1 4 ? 5 A. 3 . B. 2 . C. 4 . D. 5 . Lời giải
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 82
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng Chọn A Đặt log 1 5t x t x 1. 5 Phương trình trở thành: 2y y t 2 y t 1 5 5 2 5 1 5t 4 5 2 y 5 t 1 . Xét hàm số
5u 5u f u u f u
.ln 5 1 0 nên hàm số luôn đồng biến.
Vậy để f 2 y f t
1 2 y t 1 2 y 1 t log x 1 5
0 2 y 1 log 4001 0 2 y 1 5 y 0;1; 2 5
Với mỗi nghiệm y ta tìm được một nghiệm x tương ứng.
Câu 52. Có bao nhiêu cặp số nguyên x; y thỏa mãn 0 y 2021 và x 3
3 3x 6 9 y log y ? 3 A. 2021 . B. 7 . C. 9 . D. 2020 . Lời giải Chọn B x 1 3 x 1 3 y log 3 y 3 Đặt x 1
3 u x 1 log u , u 0 , suy ra: u log u 3y log 3y . * 3 3 3
Xét hàm số f t t log t trên 0; . 3 1
Ta có: f t 1
0 , t 0 nên từ * suy ra: t ln 3
* f u f 3y u 3y Khi đó ta có: x 1 x2 3y 3 y 3 ** y Theo giả thiết:
1 y 2021 , suy ra: 0 y 2021 x x x2 1 3 2021
0 x 2 log 2021 6, 928 3 x x
x 2;3; 4;5;6;7; 8 (có 7 số) 0 x 2 6 2 x 8
Từ ** ta có, ứng với mỗi giá trị của x , cho duy nhất một giá trị của y nên có 7 cặp.
Câu 53. Có bao nhiêu cặp số nguyên ;
x y thỏa mãn 2 x 2021 và 2y log y 1 x 2
2x y ? 2 A. 2020 . B. 9 . C. 2019 . D. 10 . Lời giải Chọn D Đặt log 1 2y x t . Suy ra y 1 2 2t x , t y 1 x 2 2 . 2
Phương trình đã cho trở thành: y t y 1 2 2 2 2
2.2y 2.2t t y y t . Xét hàm số 2.2x g x
x có 2.2x g x ln 2 1 0, x
nên hàm số y g x luôn đồng biến. Khi đó 2.2y 2.2t y
t y t hay log 1 2y y x . 2 Suy ra y 1 y y y 1 y 1 x 2 2 x 2 2 2 .
Mà 2 x 2021 nên y 1 2 2
2021 1 y 1 log 2021 hay 2 y log 2021 1. 2 2
Lại có y là số nguyên nên y 2,3,...,1
1 tức 10 giá trị thỏa mãn.
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 83
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng Xét biểu thức 1 2y x
, mỗi giá trị nguyên của y cho tương ứng 1 giá trị nguyên của x nên
có 10 cặp số nguyên ,
x y thỏa mãn yêu cầu đề bài. 2x 1
Câu 54. Có bao nhiêu cặp số nguyên ;
x y thỏa mãn 0 y 2020 và log 1 2x y ? 3 y A. 2019 . B. 11. C. 2020 . D. 4 . Lời giải Chọn B y 0 2x 1 Từ giả thiết ta có: x
0 2 1 x 0 y y 0 Ta có: PT log
2x 1 2x 1 log y y (*) 3 3
Xét hàm số f t log t t trên 0; 3 1
Khi đó f t
1 0 do đó hàm số f t log t t đồng biến trên 0; t ln 3 3 (*) có dạng 2x 1 2x f f y y 1 Vì 0
2020 0 2x 1 2020 1 2x y
2021 0 x log 2021 2 0 x log 2021 2
x 0;1; 2;3; 4;5;6;7;8;9;1
0 . Vậy có 11 cặp x; y thỏa mãn. x
Câu 55. Có bao nhiêu cặp số nguyên x ; y thỏa mãn 0 x 2020 và log 3 3 2 9y x x y ? 3 A. 2019 . B. 6 . C. 2020 . D. 4 . Lời giải Chọn D Cách 1:
Ta có: log 3 3 2 9y log 2
1 1 2 3 y x x y x x y . 1 3 3 Đặt log
1 1 3t x t x . 3 Phương trình 1 trở thành: t 2 3 2 3 y t y 2 Xét hàm số 3u f u u trên . 1 3u f u
ln 3 0, u nên hàm số f u đồng biến trên .
Do đó 2 f t f 2y t 2y log
1 2 1 9y 9y x y x x 1 3 Vì 0
2020 0 9 y 1 2020 1 9 y x
2021 0 y log 2021 9 log 2021 3,464 3
Do y y 0;1; 2;
3 , có 4 giá trị của y nên cũng có 4 giá trị của x
Vậy có 4 cặp số nguyên x; y . Cách 2:
Ta có: log 3 3 2 9y log 2
1 1 2 3 y x x y x x y 3 3
Xét hàm số f x log x 1 x 1 với x 0; 2020. 3
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 84
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng 1
Ta có f x
1 0,x x 0; 2020 Hàm số f x đồng biến trên đoạn x 1 ln 3 0;2020 .
Suy ra f 0 f x log x 1 x 1 f 2020 1 f x log 2021 2021 3 2 1 2 9y y log 2021 2021 2028 3 Nếu y y 0
y 0 2 y 9 9 9 1 y 0
Khi đó 2 9y 2 9y 2027 9y y y y
2027 2 y 2027
y log 2027 3, 465 y 3 0 y 3 9 y 0;1; 2;
3 . Do f x là hàm số luôn đồng biến nên với mỗi giá trị của y chỉ cho 1 giá trị của x . +) y 0 log
x 1 x 1 1 x 0 3 +) y 1 log
x 1 x 1 11 log
x 1 x 10 x 8 3 3 +) y 2 log
x 1 x 1 85 log
x 1 x 84 x 80 3 3 +) y 3 log
x 1 x 1 735 log
x 1 x 734 x 729 3 3
Vậy có 4 cặp số nguyên x; y .
Câu 56. Có bao nhiêu cặp số nguyên dương
x; y thoả mãn 1 x 2020 và 2y y 2x log y 1 x 2 2 A. 2021 . B. 10 . C. 2020 . D. 11. Lời giải Chọn D Theo đề bài, 2y y 2x log y 1 x 2 2 x y y y y 2 2y y y 2y 2 log 2 2x log x 2 2 log 2 2x 2 log 2 2 2 2 2 2 y y x x y y 2 2 2 2 2. 2 log 2 2 log 1 . 2 2 2 2
Xét hàm số f t 2t log t , t 0 . 2 1
Vì f t 2 0 t
0 f t đồng biến trên 0; t ln 2 x x y 2 2 y y 2 2 y nên 1 f 2 y y y y 1 f 2
2.2 2 x 2 2 x 2 x 2 . 2 2
Do 1 x 2020 nên 0 y 1 log 2020 1 y 11,98 . 2 Do *
y nên y 1; 2;3;...;1
1 , với mỗi giá trị y cho ta 1 giá trị x thoả đề.
Vậy có 11 cặp số nguyên x; y thoả mãn đề bài.
Câu 57. Cho phương trình log 3x 6x 6 2 2 y 2 2
3 y x 2x 1. Hỏi có bao nhiêu cặp số ; x y 3
và 0 x 2020 ; y thỏa mãn phương trình đã cho? A. 5 . B. 6 . C. 7 . D. 4 . Lời giải Chọn D
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 85
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng
log 3x 6x 6 2
3y y x 2x 1 log 3 x 2x 2 2 2 2 2 2 y 2 2
3 y x 2x 1. 3 3
1 log x 2x 2 2 2 y 2 2
3 y x 2x 1. 3 log 2 2 2 2 2 2 2 2 3y x x x x y (1). 3
Đặt log 2 2 2 2 2 2 3z x x z x x thì (1) trở thành: 3 2 z y 2
3 z 3 y (2). Xét hàm số
3t 3t f t t f t ln 3 1 0, t .
Suy ra hàm số f t đồng biến trên . (2) 2 2 f z f y z y .
Thay trở lại cách đặt ta có: log 2 2 2 2 2 2 2 2 3y x x y x x . 3
Xét hàm số: g x 2
x 2x 2, x 0; 2020 g x 2x 2 .
g x 0 x 1. Bảng biến thiên: Suy ra:
1 g x 2 y 2 4076362 1 3
4076362 0 y log 4076362 . 3
g x 1
g x 3
Do y 0 y log 4076362 3, 7 y 0;1; 2; 3 . . 3 g x 4 3 g x 9 3
Dựa vào bảng biến thiên của hàm số g x ta thấy mỗi phương trình trên có một nghiệm 0 x 2020 . Vậy có 4 cặp số ;
x y thỏa mãn đề bài.
Câu 58. Có bao nhiêu cặp số nguyên ,
x y với 1 x 2020 thỏa mãn 2y 1 2 log x x y x ? 2 A. 4 . B. 9 . C. 10 . D. 11. Lời giải
Ta có 2y 1 2 log x log 2y x y x x x x
y 1 2 . Đặt log 2t t x x . Khi đó 2 2 2 t t y y 1t y 1 2 . 2 2 1 2 2 1 2 2 2 t t y t y y 1 t 1 1 1 log log 1 2 y y t t x x y x 2 2 Vì 1 1 2020 1 2 y x
2020 0 1 y log 2020 1 log 2020 y 1 2 2 Khi đó 1 9;...;1 , 2 y y x
11.1 11 cặp số nguyên thỏa mãn
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 86
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng x y 1
Câu 59. Có bao nhiêu số nguyên y sao cho bất phương trình log3 3 5 9x log y nghiệm 3 125
đúng với mọi x 3 ? A. 19683 . B. 243. C. 242 . D. 19682 . Lời giải
Điều kiện: y 0 . x y 1 log 3 log y 3x log y 3 3 3 3 5 9 log 5 9 5 3log 5 3log 5 x x y x y y 3.3 x 3 3 3 125 Xét hàm số 5 t f t 3t . Ta có ' 5 t f t
.ln5 3 0,t 9 nên hàm số y f t nghịch biến. Từ giả thiết: log 3 log 3 0 27x f y f x y x y (*) 3 3
Bất phương trình (*) nghiệm đúng với mọi x 3 khi 3
0 y 27 19683 .
Vì y nguyên nên y 1; 2;3;...1968 2 .
Vậy có 19682 số nguyên y thỏa mãn đề bài.
Câu 60. Có bao nhiêu cặp số nguyên x ; y thỏa mãn điều kiện log 2 2002 1002 2y x x y 2
và 1002 x 2021? A. 10 . B. 11. C. 12 . D. 18 . Lời giải
Phương trình trở thành log 1001 1001 2y x x y 2 1
Hàm số f t log t t f' t
1 0 t 0 ; 2 tln2
Hàm số f t đồng biến trên 0 ; . Vậy 1001 2y x
1002 2y 1001 2021 0 y log 1020 . 2
Do mỗi y cho ta một x và y nguyên nên y 0 ;1 ; 2 ;...; 9
Vậy có 10 cặp x ; y thỏa mãn. Câu 61. Có bao nhiêu cặp số nguyên ; x y thỏa mãn 0 x 2020 và x x 2 2 ln
1 x 1 y e y ? A. 0 . B. 7 . C. 1. D. 8 . Lời giải Chọn C 2 2 Ta có x x 2 2 ln
1 x 1 y e y y y ln x 1 x 1 lne e * .
Xét hàm số f t lnt t trên 0; . 1
Ta có f 't 1 0 với mọi t 0; . t
Suy ra hàm số f t lnt t đồng biến trên 0; . Do đó * 2 1 e y x y x 2 ln 1 .
Vì x nguyên nên e y nguyên mà e y nguyên khi và chỉ khi y 0 .
Thử lại ta thấy y 0 thì x 0 .
Vậy có duy nhất một cặp số nguyên ;
x y thỏa mãn yêu cầu bài toán.
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 87
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng
Câu 62. Xét cặp số nguyên dương x ; y thỏa log 7 7 3 343y x y
x và 0 x 2020 . Giá trị 7 0 0
x 42 y bằng 0 0 A. 300 . B. 0 . C. 400 . D. 2020 . Lời giải Chọn A
Ta có log 7 7 3 343y 1 log 3 1 3 7 y x y x x y x 7 7 1 log 3 1 7 y x x 3y . 7
Xét hàm số f t t log t,t 1; 2021 . 7 1
f 't 1
0, t 1; 202
1 hàm số f t đồng biến trên khoảng 1; 202 1 . tln7 log x 1 3 y 7 Mà 3 1 7 y f x f
, Suy ra x 1 7 y . 3
0 x 2020 1 x 1 2021 0 log
x 1 log 2021 3.9 7 7
Mà y suy ra log
x 1 và phải chia hết cho 3 log
x 1 3 x 342 y 1 7 7 .
Vậy x 42 y 300 . 0 0
Câu 63. Có bao nhiêu giá trị nguyên của x 1 5 thỏa mãn x 9log 3x 3 2.3 3
.3x 9.3x 9x 45 log
2 x 1 0 . 3 4 A. 12. B. 13. C. 15. D. 14. Lời giải
Điều kiện: x 2 . x Đặt 9log 3x 3 2.3 3 .3x 9.3x g x 9x 45 log 2 x 1 . 3 4 • Xét log
2 x 1 0 x 2 N . 4 x
• Xét 9log 3x 3 2.3 3
.3x 9.3x 9x 45 0 3 x 9log 3x 3 2.3 3
.3x 9.3x 9x 45 3 x log 3x 3 2.3 x 2 3
.3 .3 3x x 5 3 x log 3x 3 x 2.3 x2 3 3 3
2.3x x 2 3 log 3x 3 x 3 3 log 3x 3 2.3 x2 3
2.3x x 2. 3 Xét hàm số
3t ' 3t f t t f t
ln3 1 0 Hàm số f t đồng biến.
f log 3x 3 f 2.3x x 2 3
log 3x 3 2.3x x 2 3 log 3x 3 x x x 1
3 3 3.3 x 1 3 x 1 3 log 3x 3 3 3 log 3x 3 x 1 3 x 1 3 Xét hàm số
3u ' 3u f u u f u
ln3 1 0 Hàm số f u đồng biến.
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 88
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng
f log 3x 3 f x 1 3
log 3x 3 x 1 3 x x 1 3 3 3 2.3x 3 3 x log N 3 2
Ta có bảng xét dấu g x : x 1 4, 1 3, 1 2,......, 2 ,
1 . Vậy có 14 giá trị nguyên x thỏa mãn. 2 x 2 x 2020 x
Câu 64. Số nghiệm của phương trình e 2 2 ln x 2
x 2018 là 2 A. 4 . B. 2 . C. 0 . D. 3 . Lời giải Chọn A x 2
Điều kiện của phương trình: . x 2 2 x 2 x 2020 x Ta có: e 2 2 ln x 2 x 2018 2 2 x 2 x 2020 x e x 2 x 2 2 2020 ln 2 x 2 2 2 x 2 x 2020 x ln 2 x 2 e x e 2 2 2020 ln x 2 1 . 2
Xét hàm số t f t
e t , t . ' t f t
e 1 0,t f t đồng biến trên . 2 2 x x 1 f x f 2 x x 2 2020 ln 2 2020 ln x 2 2 2 2 x x 2
2020 ln x 2 0 2 . 2 2 x
Xét hàm số g x x 2
ln x 2 2020 . 2 3 2 2x
x x 4x 2
g ' x x 1 . 2 2 x 2 x 2 x 2 , 34 1 g ' x 3 2
0 x x 4x 2 0 x 0 , 47 . 2 x 1,81 3
Bảng biến thiên của g x :
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 89
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng
Ta có: g x 2
020,85 0 , g x 2
016,8 0 nên 2 có 4 nghiệm phân biệt thuộc 3 1 ;
2 2; .
Vậy phương trình đã cho có 4 nghiệm. y 2
Câu 65. Cho hai số dương x, y thỏa mãn log
4x y 2xy 2 8 2x 2
y 2 . Giá trị nhỏ 2
nhất của P 2x y là số có dạng M a b c với a, b , a 2 . Khi đó S a b c bằng
A. S 17.
B. S 7.
C. S 19.
D. S 3. Lời giải Chọn D y 2
Với hai số dương x, y thỏa mãn log
4x y 2xy 2 8 2x 2 y 2 . 2
y 2log 4x y 2xy 2 8 2x 2 y 2 2
y 2 log 2x 1 y 2 8 2x 1 y 2 3 y 2 2 8 Ta có log 2x 1 log y 2 2x 1 3 2 2 y 2 8 8 log
2x 1 2x 1 log 1 2 2 y 2 y 2 1
Xét hàm đặc trưng f t log t t trên 0; có f't
1 0, t 0 nên hàm số 2 tln2
f t đồng biến trên 0; 2 . 8 8 8
Từ (1) và (2) suy ra f 2x 1 f 2x 1 y 2 . y 2 y 2 2x 1 8 8 AM GM
P 2x y 2x 2 2x 1 3 4 2 3. 2x 1 2x 1 8 1 2 2
Dấu bằng xảy ra khi 2x 1 2x 2 1 8 x . 2x 1 2
Vậy S a b c 3.
Câu 66. Có bao nhiêu cặp số nguyên ;
x y thỏa mãn 0 x 2020 và log 3 3 2 9y x x y ? 3 A. 2019 . B. 6 . C. 2020 . D. 4 . Lời giải Chọn D ĐK: x 1 . Ta có log 3 3 2 9y x x y 3 3log 3x 3 log 3x3 3 3 32 y 2 y 1 1 3 * 3
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 90
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng Xét hàm số 3 3t f t t trên , vì ' 3 3t f t
.ln3 0, t 0 nên hàm số f t đồng biến trên . Từ đó
* f log 3x 3 f 2 y 1 log 3x 3 2y 1. 3 3
Mặt khác 0 x 2020 log 3x 3 1 ; log
6063 2 y 1 1 ; log 6063 3 3 3 1
2 y 1 log 6063 3
0 y 3 . Vậy có 4 . cặp ; x y thỏa mãn. y Z 2x 1
Câu 67. Có bao nhiêu cặp số nguyên ;
x y thỏa mãn 0 y 2020 và log 1 2x y ? 3 y A. 2019 . B. 11. C. 2020 . D. 4 . Lời giải Chọn B y 0 2x 1 Từ giả thiết ta có: x
0 2 1 x 0 y y 0 Ta có: PT log
2x 1 2x 1 log y y * 3 3
Xét hàm số f t log t t trên 0; . 3 1
Khi đó f 't
1 0 do đó hàm số f t log t t đồng biến trên 0; tln3 3 (*) có dạng 2x 1 2x f f y y 1 Vì 0
2020 0 2x 1 2020 1 2x y
2021 0 x log 2021 2 0 x log 2021 2
x 0;1; 2;3; 4;5;6;7;8;9;1 0 . Vậy có 11 cặp ; x y thỏa mãn. x
Câu 68. Số nghiệm thực của phương trình 6x 3log
5x 1 2x 1 là 6 A. 0 . B. 2 . C. 1. D. 3 . Lời giải Chọn B 1
Điều kiện: x . 5 PT: 6x 3 3log 5 1 5 1 6x x x x 3x 6 x 3log 5x 1 1 . 6 log 5 1 6 6 Xét hàm số 6t f t 3t , vì ' 6t f t
.ln6 3 0,t nên f t đồng biến trên . Khi đó
1 f x f log 5x 1 x log 5x 1 log 5x 1 x 0 6 6 6 1
Xét hàm số h x log 5x 1 x trên ; , ta có 6 5 5 h ' x 1 5x 1 ln6 25 1
h ' x 0, x
và lim h ' x ;
lim h ' x 1 5x 2 1 ln6 5 1 x x 5 Bảng biến thiên:
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 91
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng 1
Từ BBT suy ra phương trình h x 0 có nhiều nhất 2 nghiệm thuộc khoảng ; 5
Mà h 0 0, h 1 0 .
Vậy phương trình đã cho có đúng hai nghiệm x 0, x 1.
Câu 69. Cho 0 x 2020 và log
2 2 3 8y x x y
. Có bao nhiêu cặp số x ; y nguyên thỏa mãn 2 các điều kiện trên? A. 2019. B. 2018. C. 1. D. 4. Lời giải Chọn D
Do 0 x 2020 nên log
2x 2 luôn có nghĩa. 2 Ta có log
2 2 3 8y x x y 2 log 3
1 1 3 2 y x x y log 1 2 x 3 2 y x y 1 2 log 1 2 3 2 Xét hàm số 2t f t t .
Tập xác định D và ' 1 2t f t
ln2 f 't 0 t .
Suy ra hàm số f t đồng biến trên . Do đó 1 log x 1 3y 3 1 2 y x 2 y log x 1 . 8
Ta có 0 x 2020 nên 1 x 1 2021 suy ra 0 log x 1 log 2021. 8 8
Lại có log 2021 3, 66 nên nếu y thì y 0 ;1 ; 2 ; 3 . 8
Vậy có 4 cặp số x ; y nguyên thỏa yêu cầu bài toán là các cặp 0 ;0 , 7 ; 1 , 63 ; 2 , 511 ;3 .
5x 3x
Câu 70. Tính tổng S tất cả các nghiệm của phương trình x 1 ln
5 5.3x 30x 10 0 . 6x 2
A. S 1.
B. S 2 .
C. S 1.
D. S 3. Lời giải Chọn A 1
Điều kiện x . 3
Phương trình tương đương
ln 5x 3x ln 6 2 55x 3x x
56x 2 0
ln 5x 3x 55x 3x ln 6x 2 56x 2 (1).
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 92
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng 1
Xét hàm số f t lnt 5t, t 0 . Có f't 5 0 , t 0 nên f t đồng biến trên t 0; . Từ 1 suy ra 5x 3x f
f 6x 2 . 5x 3x 6x 2 5x 3x 6x 2 0
Xét 5x 3x g x
6x 2 , ' 5x ln5 3x g x ln3 6 1 x 2 x g x 2 ' 5 ln5 3 ln3 0 , x . 3 Nên '
g x 0 có không quá 1 nghiệm suy ra g x 0 có không quá 2 nghiệm trên 1 ;
. Mà g 0 g
1 0 . Vậy phương trình có tập nghiệm là 0, 1 . Do đó S 1. 3 2 x 80
Câu 71. Số nghiệm của phương trình x 1 2 ln 2.3
2 x 80 ln3 là 3x A. 2 . B. 3 . C. 1. D. 0 . Lời giải Chọn C PT 2 2 x 1 x 1 ln x 80 2 x 80 ln3 2.3 1 1
Xét hàm số f t lnt 2t,t 0 ; Ta có: f 't 2 0,t 0 Hàm số f t đồng t
biến trên 0; . Từ (1) suy ra f 2 x
f x 1 2 x 1 2 x 1 x 1 2 80 3 x 80 3 x 80 9 9 x 80 0
Xét hàm số g x x 1 2 9
x 80 trên . Ta có: g ' x x 1 2.9 ln3 2x
g ' x 4.9x ln32 1 2
g ' x 0 x x log 2
2ln 3 1 g ' x ' g log 2 2ln 3 1 3, 7 0 0 9 0 9
lim g ' x ;
lim g ' x x x Bảng biến thiên:
Dựa vào bảng biến thiên ta có '
g x 0,x hàm số g x đồng biến trên
phương trình g x 0 có nhiều nhất một nghiệm. Mà g 1 0
Do đó phương trình đã cho có duy nhất 1 nghiệm.
Câu 72. Có bao nhiêu cặp số nguyên dương
x ; y thoả mãn 1 x 2020 và 2y y 2x log y 1 x 2 2
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 93
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng A. 2021. B. 10 . C. 2020 . D. 11. Lời giải Chọn D Theo đề bài, 2y y 2x log y 1 x 2 2 y y 2y 2 log 2 2x log x 2 2 2 x y y y y 2 2y 2 2 log 2 2x 2 log 2 2 2 y y x x y y 2 2 2 2 2. 2 log 2 2 log 1 . 2 2 2 2
Xét hàm số f t 2t log t , t 0 . 2 1
Vì f 't 2
0 t 0 f t đồng biến trên 0 ; tln2 x x y 2 2y y 2 2y nên 1 f 2 y y y y 1 f 2
2.2 2x 2 2x 2 x 2 . 2 2
Do 1 x 2020 nên 0 y 1 log 2020 1 y 11,98 . 2 Do *
y nên y 1 ; 2; 3;...;1
1 , với mỗi giá trị y cho ta 1 giá trị x thoả đề.
Vậy có 11 cặp số nguyên x ; y thoả mãn đề bài.
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 94
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng Câu 73. Có bao nhiêu cặp số nguyên ; x y và 0 x 2020 thỏa mãn 2x 6 8 log
y 2 2y ? 2 x 1 x 1 A. 2018 . B. 2 . C. 2020 . D. 1. Lời giải Chọn D
Điều kiện của x : x ; 3
1; . Nên ta chỉ kiểm tra 2 x 2020 2x 6 8 x y 2 6 8 Ta có: log
y 2 2 log 2 y 2y 2 2 x 1 x 1 x 1 x 1 2 x6 log2 2x 6 2x 6 x y 2 6 x 1 log y 2 log 2
y 2y 1 2 2 x 1 x 1 x 1 Đặt 2t f t t .
Ta có: ' 1 2t f t
.ln2 0 t f t luôn đồng biến. 2x 6 2x 6 2x 6 Do đó:
1 f y f log y log 2y 2 2 x 1 x 1 x 1 2x 6 8 Đặt u u' 0 x ; 3 1; 2 x 1 x 1 2x 6 4046
Do 2 x 2020 và u
luôn nghịch biến trên 2; 2020 nên u ;10 x 1 2019 Mà: 2y u
và y nên u 4; 8
4 2y y 2
*Với u 4 2x 6
4 2x 6 4x 4 x 5 x 1 8
2y y 3
*Với u 8 2x 6 7 (loại)
8 2x 6 8x 8 x x 1 3
Vậy, phương trình có một cặp nghiệm thỏa bài toán: 5; 2 .
Câu 74. Có tất cả bao nhiêu cặp số a, b với a, b là các sổ nguyên dương thỏa mãn
log a b 3
(a b) 3 2 2 a b
3ab a b 1 1? 3 A. 2 B. 3 C. 1 D. Vô số Lời giải Chọn A
Với a, b là các số nguyên dương, ta có 3
log (a b) (a b) 3 2 2 a b
3ab(a b 1) 1 3 3 3 a b 3 3 log
a b 3ab(a b) 3 2 2
a b ab 3ab(a b) 1 3 2 2
a b ab log 3 3 a b 3 3
a b log 3 2 2
a b ab 3 2 2
a b ab 3 3
Xét hàm số f t log t t trên 0; 3 1
f t
1 0,t 0 nên hàm số f t đồng biển trên 0; l t n3
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 95
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng
Khi đó, phương trình (1) trở thành f 3 3
a b f 3 2 2
a b ab 3 3
a b 3 2 2
a b ab 2 2
a b aba b 3 0 2 2
a b ab 0 *
a b 3 0 Do *
a,b nên phưong trinh
* vô nghiệm. Suy ra a b 3 Mà a, b là các sổ nguyên 0 a 3 a 2 0 b 3 b 1 dương nên a b 3 b 1 * a,b b 2
Vậy có hai cặp số a, b thỏa mãn yêu càu bài toán.
Câu 75. Có bao nhiêu cặp số nguyên dương ,
x y thỏa 1 x 100 và log y x y .log 2 2 ? 2 x A. 99 . B. 98 . C. 10 . D. 90 . Lời giải Chọn A 2 Ta có log y
x y .log 2 2 log y x y 2 x 2 log 2x
log y x y 2log x log y x y 2 log x 2 2 2 2 2 y x y x x y 2
x y x x 1 .
Xét hàm số f t 2
t t, t 1. Ta có f 't 2t 1 0,t 1.
Do đó hàm số f t đồng biến trên 1, . Khi đó,
f x y f x 2 2 1
x y x x y x y x x .
Dễ thấy ứng với mỗi số nguyên dương 1 x 100 ta có 1 số nguyên dương y thỏa 2
y x x .
Vậy có tổng cộng 100 2 1 99 cặp số nguyên dương ,
x y thỏa yêu cầu đề bài.
Câu 76. Tìm số nghiệm x thuộc 0;100 của phương trình sau 1 cos x 1 2
cos x log 3cos x 1 . 4 2 A. 51. B. 49. C. 50 . D. 52 . Lời giải Chọn A x 1 1 Ta có cos 1 2
cos x log 3cos x 1 ; ĐK : cos x . 4 2 3 cos
2 x 1 2cos x log 3cos x 1 . 2 cos x 2
cos x 3cos x 1 log 3cos x 1 2 cos x 2 log cosx 2
3cos x 1 log 3cos x 1 , 1 2 2
Xét hàm số: f t t log t;t 0 . 2
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 96
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng 1
f 't 1
0,t 0 . Nên hàm số f t đồng biến trên 0; . t ln2
Phương trình f cosx 1 2
f 3cos x 1 . cos x 2 3cos x 1 1 Đặt a cos ; x a ;1 a . Phương trình trở thành:
2 3a 1 0,2 . Xét 3 a 1 g a
2 3a 1; a ;1 . 3 1 a 1
g 'a 2 ln2 3 0,a ;1
. Vậy hàm số g a nghịch biến trên ;1 . 3 3
Do đó nếu phương trình 2 có nghiệm thì có nhiều nhất một nghiệm, ta thấy g 1 0 , Suy ra phương trình
có nghiệm duy nhất: a 1 cos x 1 x k 2 , k .
x 2k , mà x 0;10
0 . Suy ra x 0; 2; 4; ; 100 .
Vậy có tất cả 51 giá trị x thỏa yêu cầu bài toán. Câu 77. Có bao nhiêu cặp số nguyên x ; y thoả mãn 0 x 2020 và 2 2 ln 1 1 y x x x y e ? A. 0 . B. 7 . C. 1. D. 8 . Lời giải Chọn C Ta có: 2 2 ln 1 1 y 2ln 2ln x 1 1 y x x x y e x e y e 1 . Xét hàm số: t f t t e , ta có: ' 1 t f t
e 0 nên hàm số f t đồng biến trên . Do đó:
1 f 2ln x
1 f y y 2ln x 1 .
+ Do 0 x 2020 nên 1 x 1 2021 0 y 2ln2021 15, 22 .
Do y nên y 0;1 ; 2;..;14;1 5 . y Có y x 2 2ln 1 x e 1.
Với y 0;1 ; 2;..;14;1
5 thì chỉ có y 0 thì x .
Vậy có duy nhất 1 cặp số nguyên x ; y thoả mãn đề bài.
Câu 78. Có bao nhiêu cặp số nguyên dương ;
x y thỏa mãn đồng thời hai điều kiện: 6 1 x 10 và
x x 2 2 y 2 2 log 10 20
20 10 y x 2x 1? A. 4 . B. 2 . C. 3 . D. 1. Lời giải Chọn D Điều kiện: 2
10x 20x 20 0, đúng x . Ta có
x x 2 2 y 2 2 log 10 20 20 10
y x 2x 1 2 2 2 2 2 1 log 10 2 2 10 y x x x x y 2 2 2 2 2 1 log10 log 2 2 10y x x x x y 2 2 2 2 2 2 log 2 2 10 y x x x x y
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 97
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng 2 x x
x x 2 log 2 2 2 y 2 10 log 2 2 10 y (*). Xét hàm 10t f t t trên .
Ta có 10t f t
.ln10 1 0 , t . Do đó f t đồng biến trên . 2 Khi đó (*) f 2
x x f 2 log 2 2 y 2 x x 2 log 2 2 y 2 2 2 10y x x 2 2 1 1 10y x . 2 2 Vì 6 2
1 x 10 nên y x 6 1 1 1 10 10 1 1 y 2 2 6 0 log 10 1 1 . Vì y
nên y 1;2; 3 . x 2 (ktm) + Với y 1 2
x 2x 2 10 2
x 2x 8 0 . x 4 (tm) + Với y 2 2 4
x 2x 2 10 2
x 2x 9998 0 (không có giá trị x nguyên nào thỏa mãn). + Với y 3 2 9
x 2x 2 10 2
x 2x 999999998 0 (không có giá trị x nguyên nào thỏa mãn).
Vậy có một cặp nguyên dương ; x y 4;
1 thỏa mãn yêu cầu bài toán. 6x
Câu 79. Cho phương trình 2 log
2 2x 1 y 2
3 y 2x 0 .Với các cặp số ; x y 3 2x 1 1 1 7
thoả mãn phương trình trên, giá trị nhỏ nhất của 2 1 2 4 2 2 2.3 y T x x x thuộc 3 3 khoảng nào sau đây? A. 4 ; 2 . B. 1 1; 9 , 5 . C. 6 ; 4 . D. 9 ,5; 8 . Lời giải Chọn B
Điều kiện x 0 . 6x Ta có 2 log
2 2x 1 y 2
3 y 2x 0 3 2x 1 1
2 log 3 2 1 1 2 2 2 1 2 3 y x x y 2x 0 3
2 2 log 2 1 2 1 2 2 1 2 3 y x x y 2x 0 3 2 log 2 1 2 2
1 2 2 2 2 1 2 3 y x x x y 3 2 log 2 1 2 1 2 1 2 2 y 2 1 log 3 3 y x x (1) 3 3 1
Xét hàm số y f t log t t f t 1 0, t 0 . 3 t ln 3
Suy ra hàm số y f t đồng biến trên khoảng 0; . 2 2 Từ
2 y 2 1 2 1 1 3 2 1 1 3 y f x f x . 1 7 Do đó 2 1 2 4 2 2 2.3 y T x x x
x x x x 2 1 7 2 1 2 4 2 2. 2 1 1 . 3 3 3 3
Đặt t 2x 1 1 2
2x t 1.
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 98
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng 1 7 1 2 Suy ra T
t t 1 4 t 1 2t 2 2 2 3 2 1
t t 3t . 3 3 3 3 t 1 Có 2
T t 2t 3 T 0 . t 3 Bảng biến thiên 29
Từ bảng biến thiên suy ra minT 9 , 67 1 1; 9 ,5 . 3 x y ln
Câu 80. Cho hai số thực dương ,
x y thỏa mãn 2 ln x y ln 5 2 .5 2
. Giá trị nhỏ nhất của biểu thức 1 3 1 3
P (x 1)ln x (y 1)ln y với x và y
là m , khi đó m thuộc khoảng nào 2 2 2 2 sau đây 1 A. m ;0 .
B. m 0; 1 .
C. m 1; 2 .
D. m 2; 4 . 2 Lời giải Chọn A x y ln Ta có: 2 ln( x y ) ln 5
ln( x y )ln 2 ln( x y ) ln 5 ln( x y ) ln( x y ) ln 5 ln 2 2 .5 2 2 .5 2 2 .5 2 .2 ln(x y) ln10 10 2 ln10 ln( ) ln10.log 2 ln( ) log 2 ln( ) ln10.log 2 x y x y x y e e log 2
x y 10
x y 2 . Do đó
P (x 1) ln x ( y 1) ln y x
1 ln x 3 x ln 2 x . Xét hàm số f ( )
x (x 1)ln x (3 ) x ln(2 ) x x 1 3 x x 2 2x Ta có: f (
x) ln x ln(2 x) ln . x 2 x 2 x x(2 x) 2 2 x 2x 4x 4 4 x 2 2 1 1 3
Lại có: f x . 0, x ; 2 x2 x 2x x 2 2x x 2 2 2 2 2 1 3
Do đó f x 0 có nhiều nhất một nghiệm trên ; . 2 2
Mà x 1 là một nghiệm của pt f x 0 nên phương trình f x 0 có nghiệm duy nhất là
x 1 . Từ đó ta có bảng biến thiên như sau:
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 99
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng 1 3 3 1 5 3 1
Dựa vào BBT, ta suy ra min P min f x f f ln ln ; 0 . 1 3 ; 2 2 2 2 2 2 2 2 2
Câu 81. Có bao nhiêu số nguyên dương b sao cho ứng với mỗi b , có đúng 3 giá trị nguyên dương 2a a
của a thỏa mãn log
2a a b 1 ? 2 ab A. 1. B. 2. C. 3. D. 0. Lời giải Chọn A 2a a * Ta có log
2a a b 1 log
2a a 2a a log ab ab (1) 2 2 2 ab 1
* Xét hàm số f t log t t trên khoảng 0; , vì f t 1 0, t 0; 2 t ln 2 a 2a
nên f t đồng biến trên khoảng 0; . Do đó (1) 2 a ab 1 b . a 2a * Xét hàm số g a 1 trên khoảng 0; , ta thấy a 2a.ln 2. 2a a 1 ga
; g a 0 a . 2 a ln 2
Bảng biến thiên của hàm số g a : 1 a 0 +∞ ln2 g'(a) 0 + +∞ +∞ g(a) 1 g( ) ln2 1 11 Mặt khác: g 2, 9 ; g
1 3; g 2 3; g 3
3, 7; g 4 5 . ln 2 3
Do đó chỉ khi b 4 thì có đúng 3 giá trị nguyên dương của a thỏa mãn bất phương trình đã
cho. Vậy có đúng một số nguyên b thỏa mãn.
Câu 82. Có bao nhiêu số nguyên x sao cho ứng với mỗi số nguyên x có đúng 5 số nguyên y thỏa 2 mãn y x2 3 y log
x 2 y 3 ? 2 y 3 A. 13 . B. 11. C. 12 . D. 10 . Lời giải Chọn D
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 100
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng 2 y 3 2 x y
y x y 3 ln 2 3 2 + Ta có: 3 log
x 2 y 3 2 y 3 x2 y 3 3 ln 2 y 3 2 y 3 2 3 .ln y 3 x2 y 3 3
.ln x 2y 3 + Xét hàm số 3t f t
.ln t (với t 3 ) có t 3t
f t 3 .ln 3.ln t
0 nên hàm số đồng biến trên 3; . t 2
+ Do đó: y x2y 2 2 3 log
x 2 y 3 y 3 x 2 y 3 y x 2 y (*) 2 y 3
TH1: x 2 y thì 2
* x y 2 y . Xét hàm số g y 2
y 2 y có bảng biến thiên
Để có 5 giá trị nguyên của y thỏa mãn bài toán thì điều kiện là g
1 x g 2 3 x 8.
TH2: x 2 y thì 2
* x y 2 y . Xét hàm số h y 2
y 2 y có bảng biến thiên
Để có 5 giá trị nguyên của
y thỏa mãn bài toán thì điều kiện là
h 4 x h3 8 x 3 .
Vậy có 10 giá trị nguyên của x thỏa mãn điều kiện của bài toán.
Câu 83. Có bao nhiêu số nguyên dương y sao cho ứng với mỗi y , có đúng bốn số nguyên dương x 2x 3x thỏa mãn ln
2x x 3 y 0? xy A. 4. B. 1. C. 3. D. 2. Lời giải Chọn C Với x
, y 0; ta có 2x 3x ln
2x x 3 y 0 ln 2x 3 ln 2x x xy
3x xy 0 xy
ln 2x 3 2x x
3x ln xy xy * .
Xét hàm f t ln t t với t 0; . 1
f t 1 0 , t 0; . Suy ra f t là hàm đồng biến trên 0; . t x x 2x 3 2x * 2x f
3x f xy 2 3x xy y y 3. x x
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 101
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng 2x
Xét hàm g x
3 với x 0; . x
2x x ln 2 1 1 g ' x
; g ' x 0 x . 2 x ln 2 Bảng biến thiên: 47
Yêu cầu bài toán thoả mãn 7 y . 5
Mà y nguyên dương nên y 7;8; 9 .
DẠNG 6: PHƯƠNG PHÁP HÀM ĐẶC TRƯNG GIẢI PT, BPT CÓ TỔ HỢP MŨ - LÔGARIT CHỨA THAM SỐ
Câu 84. Cho phương trình 5x m log
x m với m là tham số. Có bao nhiêu giá trị nguyên của 5 m 2
0; 20 để phương trình đã cho có nghiệm? A. 19 B. 9 C. 21 D. 20 Lời giải Chọn A
Điều kiện: x m
x m 5t Đặt: t log x m
5x x 5t t 1 . 5 5x m t Xét hàm số
5u 5u f u u f u ln 5 1 0, u . Do đó: 1 5x 5x x t x m m x . Xét hàm số 5x f x x , x m
Do: 5x 0 m x , suy ra phương trình có nghiệm luôn thỏa điều kiện. x 1 1 5x f x
ln 5 , f x 0 1 5 ln 5 0 x log . 5 ln 5 Bảng biến thiên:
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 102
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng x ∞ ≈ 0,295 +∞ y' + 0 ≈ 0,917 y ∞ ∞
Dựa vào bảng biến thiên m 20;20
m 0,917 m 19 ; 18;...; 1 .
Vậy có 19 giá trị nguyên của m thỏa ycbt.
Câu 85. Cho phương trình 3x m log ( x m) với m là tham số. Có bao nhiêu giá trị nguyên của 3 m 1
5;15 để phương trình đã cho có nghiệm? A. 15 B. 16 C. 9 D. 14 Lời giải Chọn D
Ta có: 3x m log
x m 3x x log ( x m) x m (*) . 3 3 Xét hàm số ( ) 3t f t
t , với t . Có ( ) 3t f' t
ln 3 1 0, t nên hàm số f t đồng
biến trên tập xác định. Mặt khác phương trình (*) có dạng: f (x) f log (x m) . Do đó ta 3
có f (x) f log (x m) x log (x m) 3x x m 3x x m 3 3 1 Xét hàm số 3x g x
x , với x . Có ( ) 3x g' x
ln 3 1, g'(x) 0 x log3 ln 3 Bảng biến thiên
Từ bảng biến thiên ta thấy các giá trị của tham số để phương trình có nghiệm là: 1
m ; g log
. Vậy số giá trị nguyên của m 1
5;15 để phương trình đã cho 3 ln 3 có nghiệm là:14 .
Câu 86. Cho phương trình 7x m log
x m với m là tham số. Có bao nhiêu giá trị nguyên của 7 m 2
5; 25 để phương trình đã cho có nghiệm? A. 9 B. 25 C. 24 D. 26 Lời giải Chọn C
ĐK: x m x 7 m t Đặt t log x m ta có 7x 7t x t 1 7 7t m x Do hàm số 7u f u
u đồng biến trên , nên ta có
1 t x . Khi đó:
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 103
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng 7x 7x m x m x .
Xét hàm số 7x g x x
1 7x g x
ln 7 0 x log ln 7 . 7 Bảng biến thiên:
Từ đó phương trình đã cho có nghiệm khi và chỉ khi m g log ln 7 0 ,856 7
(cácnghiệm này đều thỏa mãn điều kiện vì 7x x m 0 )
Do m nguyên thuộc khoảng 2
5; 25 , nên m 2 4; 1 6;...; 1 .
Câu 87. Cho phương trình log 2 4x x m
m với m là tham số thực. Có bao nhiêu giá trị nguyên 2 của m 2
7; 27 sao cho phương trình trên có nghiệm? A. 10 . B. 26 . C. 1. D. 53 . Lời giải Chọn B
Điều kiện: 2x m 0 . Ta có log 2 4x x m m 2 log 2 x log 2 xm 2 2 4 2 2 log 2 2 2 x x m x m x x m 2x (1). 2 2 Xét hàm số 2t f t
t,t . Có 2t f t ln 2 1 0, t
. Suy ra hàm f t đồng biến trên .
Từ (1) ta được f log 2x m f 2x log 2x m 2x 2 2 4x 2 4x x m
2x m (2).
Xét hàm 4x g x 2x .
Ta có 4x ln 4 2 4 .x g x 2 ln 2 2 . 1
Có g x 0 x x log . 0 4 ln 2
Bảng biến thiên của hàm g x như sau x x 0 g x 0 g x g x0
Từ bảng biến thiên suy ra phương trình (2) có nghiệm 1
m g x m g x g log 0 , 914 . 0 0 4 ln 2
Do m và m 2
7; 27 nên ta đươc m 2 6; 2 5;...; 1 .
Vậy có 26 giá trị của m thỏa mãn yêu cầu bài toán.
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 104
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng
Câu 88. Cho phương trình 5x m log
x m 0 với m là tham số. Có bao nhiêu giá trị nguyên 1 5
của tham số m 2
0; 20 để phương trình đã cho có nghiệm thực? A. 20 . B. 21 . C. 18 . D. 19 . Lời giải Ta có: 5x log 0 5x m x m log
x m m 0 1 . 1 5 5
ĐKXĐ: x m . Đặt t log
x m , ta có 5t x m . 5 t
x m 5t x m 5 *
Khi đó ta có hệ phương trình . t m 5x
5x x 5t t 2 Xét hàm số 5u f u u , u . . + 5u f u ln 5 1 0, u suy ra hàm số 5u f u
u đồng biến trên .
Do đó 2 f x f t x t .
Thay vào phương trình * ta có 5x m x 3 . Ta có 5x x m
0 , do đó phương trình
1 có nghiệm phương trình 3 có nghiệm x . x 1
Xét hàm số 5x g x x
, x , có g x 1 5 ln 5, g x 0 x log . 5 ln 5
+ lim x 5x ;
lim x 5x . x x BBT 1 x log 5 ln 5 g x 0 1 log g x 5 e ln 5 1
Từ bảng biến thiên ta thấy phương trình có nghiệm m log 0,91. 5 e ln 5 Vì m 2
0; 20 và là số nguyên, suy ra m 2 0; 1 9;...; 1
Vậy có 19 giá trị của m .
Câu 89. Cho phương trình 2x m log
x m với m là tham số. Có bao nhiêu giá trị nguyên của 2 m 1
8;18 để phương trình đã cho có nghiệm? A. 9 B. 19 C. 17 D. 18 Lời giải Chọn C
ĐK: x m x 2 m t Đặt t log x m ta có 2x 2t x t 1 2 2t m x Do hàm số 2u f u
u đồng biến trên , nên ta có
1 t x . Khi đó:
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 105
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng 2x 2x m x m x .
Xét hàm số 2x g x x
g x 1 2x ln 2 0 x log ln 2 . 2 Bảng biến thiên:
Từ đó phương trình đã cho có nghiệm khi và chỉ khi m g log ln 2 0,914 (các 2
nghiệm này đều thỏa mãn điều kiện vì 2x x m 0 )
Do m nguyên thuộc khoảng 1
8;18 , nên m 1 7; 1 6;...; 1 .
Câu 90. Cho phương trình 5x m log
x m . Có bao nhiêu giá trị m nguyên trong khoảng 5 2
0; 20 để phương trình trên có nghiệm? A. 15 . B. 19 . C. 14. D. 17 . Lời giải Chọn B
Ta có phương trình 5x m log
x m (1) với điều kiện x m 0 . 5 Đặt log
x m t 5t x m
(*) thay vào phương trình (1) ta có 5x m t 5
x m 5t 5x t m
(**) . Từ (*) và (**) ta có hệ phương trình
. Từ hệ phương trình ta t m 5x
suy ra 5t 5x x t
5x 5t x t . Xét hàm số 5x f x x trên , ta có 1 5x f x .ln 5 0 x nên hàm số 5x f x x
luôn đồng biến trên , do đó ta có 5x 5t x t
f x f t x t thay
vào phương trình (**) ta có 5x x m 5x x m . Đặt 5x g x x ta có 1 x 1
1 5 .x g x
ln 5 . Ta có 0 1 5 .x g x ln 5 0 5 x log . ln 5 5 ln 5 1 1 1 Ta có BBT với g log log . 5 5 ln 5 ln 5 ln 5
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 106
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng
Từ bảng biến thiên ta thấy phương trình 5x x
m có nghiệm khi m hay 1 1 m log
. Ta suy ra có 19 giá trị nguyên của m thỏa mãn. 5 ln 5 ln 5
Câu 91. Có bao nhiêu giá trị nguyên của tham số m thuộc 2
020; 2020 để phương trình x
e ln x 2m 2m có nghiệm? A. 2019 . B. 2020 . C. 2021 . D. 4039 . Lời giải Chọn A Ta có x
e ln x 2m 2m x
e x ln x 2m x 2m x ln x2m
e x e
ln x 2m (*). Xét hàm số t
f t e t với t t f
t e 1 0, t
. Suy ra hàm số f t đồng biến trên . Do đó *
ln 2 ln 2 2 x 2 x f x f x m x x m x m e
m e x . Xét hàm số x x g x e x
g x e 1 g x 0 x 0 . Bảng biên thiên 1
Từ bảng biên thiên suy ra phương trình có nghiệm khi và chỉ khi 2m 1 m . 2
Mà m , m 2
020; 2020 nên m 1; 2;3;...; 201 9 .
Vậy có 2019 giá trị nguyên của tham số m thuộc 2
020; 2020 để phương trình x
e ln x 2m 2m có nghiệm.
Câu 92. Cho phương trình ln x x
m e m 0 , với m là tham số thực. Có bao nhiêu giá trị nguyên m 2 021; 202
1 để phương trình đã cho có nghiệm? A. 2022 . B. 4042 . C. 2019 . D. 2021 . Lời giải Chọn D
Điều kiện: x m 0 . t
x m e Đặt ln t t
x m x m e , ta có hệ phương trình sau: . x t m e Suy ra t x x t
x t e e e x e t * . Xét hàm số x
f x e x , có x f
x e 1 0, x
f x luôn đồng biến trên khoảng ; .
Ta thấy * có dạng f x f t x t .
Khi đó ta có phương trình x x
x m e m e x Xét hàm số x
g x e x , có x 1; 0 x g x e g x
e 1 x 0 . Bảng biến thiên
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 107
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng
Dựa vào bảng biến thiên ta thấy phương trình đã cho có nghiệm khi m 1 .
m 2021; 202 1 Mà
nên ta có m 1; 2;...; 2020; 202
1 . Tức là có 2021 số nguyên m thỏa m mãn đề bài.
Câu 93. Có bao nhiêu số nguyên dương m để phương trình x
e 1 m ln mx 1 có hai nghiệm phân biệt trên đoạn 1 0;1 0 ? A. 2201 . B. 2020 . C. 2021 . D. 2202 . Lời giải Chọn A
Điều kiện mx 1 0 . Ta có x
e 1 m ln mx 1 x
e mx mx 1 m ln mx 1 x ln mx 1
e mx e
m ln mx 1 (1). Xét hàm số t
f t e mt, t . Có t f
t e m 0, t
, m 0 . Suy ra hàm f t đồng biến trên . Từ (1) ta được ln 1 ln 1 x f x f mx x mx
e mx 1 (2).
Ta thấy (2) luôn có một nghiệm x 0 1
0;10. Do đó ta cần tìm các giá trị của m để (2)
có đúng một nghiệm x 0, x 1 0;10 . x e 1
Với x 0 thì (2) m . x x e 1
Xét hàm g x , x 10 ;10 \ 0 . x x x xe e 1
Ta có g x . 2 x Đặt x x
h x xe e 1, x . Có x
h x xe , h x 0 x 0 .
Ta thấy lim h x ,
lim h x 1, h0 0 . x x
Bảng biến thiên của hàm h x như sau
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 108
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng x 0 h x 0 1 h x 0
Từ bảng biến thiên suy ra h x 0, x
g x 0, x 0 .
Ta có lim g x 1, lim g x 1. x 0 x 0
Bảng biến thiên của hàm y g x với x 1 0;1 0 \ 0 như sau x 1 0 0 10 y ' 10 e 1 y 10 1 1 10 1 e 10
Từ bảng biến thiên suy ra (2) có đúng một nghiệm
x 0, x 1 0;10 1 0 10 1 e e 1 m , \ 1 . 10 10
Do m nguyên dương nên m 2,3, 4,..., 220
2 . Vậy có 2201 giá trị của m thỏa mãn yêu cầu bài toán.
Câu 94. Có bao nhiêu số nguyên dương m nhỏ hơn 20 thỏa mãn phương trình log log m 10x mx m
có đúng hai nghiệm thực x phân biệt. A. 13 . B. 12 . C. 10 . D. 11. Lời giải Chọn A m m 0 m 0 Điều kiện: . m x log m m 0
x log m 0 Đặt 10x t
0 x log t . Ta có: log log
m 10x log log log log log 10t mx m m t m m t m t m m 10t 10t t log
log t log m
log t log m
log t log m 10 m log m 10 m log t t log 10 log 10 m t
t log m * . Xét hàm số log 10 t f t
t với t 0 .
Ta có: 10t f t
ln10 1 0 t . Suy ra hàm số log 10 t f t
t đồng biến với t 0 .
Vậy * log t t log m hay 10x log log 10x x m m x .
Xét hàm số 10x g x x .
Ta có: 10x g x ln10 1.
Khi đó 0 10x g x
ln10 1 0 x log ln10 . Bảng biến thiên
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 109
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng
Vậy phương trình đã cho có hai nghiệm log m g log ln10
g logln10 m 10 6, 3 . m Do
m 7;8;9;;1
9 . Suy ra có 13 giá trị m thỏa mãn yêu cầu bài toán. m 20
Câu 95. Có bao nhiêu giá trị nguyên của tham số m thuộc khoảng 2 021; 202 1 để phương trình
10x log x 3m 3m có nghiệm? A. 2021. B. 2020 . C. 2010 . D. 4040 . Lời giải Chọn B
Ta có: 10x log x 3m 3m
10x x log x 3m x 3m 10x x log x 3m log 3 10 x m (1) Xét hàm số: 10t f t
t;t . ' 10t f t
ln10 1 0;t nên hàm số f t đồng biến trên .
Do đó phương trình (1)
log 3 3 10x 10x x x m x m
x 3m (2). x x 1
Đặt g x 10 x g ' x 10 ln10 1; g ' x 0 x log . ln10 Ta có bảng biến thiên:
Từ bảng biến thiên ta thấy: để phương trình (2) có nghiệm thì: 1 1 1 1 1 3m log m log 0,3 . ln10 ln10 3 ln10 ln10 Vì m 2 021; 202
1 nên m 1; 2;3;....; 2020 .
Vậy có 2020 giá trị nguyên của tham số m thỏa yêu cầu đề.
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 110
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng
Câu 96. Có bao nhiêu giá trị nguyên của tham số m 2
0; 20 để phương trình:
8x 2x 12m 3log
2x x 3m có đúng hai nghiệm thực phân biệt. 2 3 A. 19 . B. 18 . C. 20 . D. 21 . Lời giải Chọn C Ta có:
8x 2x 12m
8x 2x 12m 2x x m x 3 3log
2 x 3m 3log y (đặt) 2 2 3 3 3 8
x 2x 12m 3.2y 1
x 2x 3m 3 y 8
x 2x 12m 3.2y
4x 4.2x 12m 12 y
12x 3.2x 3.2y 12 y
f x f y, Với 12 3.2t f t t
là hàm số luôn đồng biến trên x y Khi đó:
1 8x 2x 12m 3.2x
8x 4.2x 12m
2x 2.2x 3m
f x 2x 2.2x x 2
Xét hàm số: f x 2 2 .ln2 'f x 0 x log 2 ln2
Khi đó lập BBT và được: m 0,17 m Z
m 19; 18;..;0} m 20;20
Câu 97. Có bao nhiêu số nguyên dương a sao cho tồn tại số thực x thỏa mãn phương trình sau 3 3 log x 1 x 3logx x a 1 3 2021 2020 a 2020 A. 9 . B. 5 . C. 8 . D. 12 . Lời giải Chọn A ĐK: x 1 . Phương trình 3 3 log x 1 x 3logx x a 1 3 2021 2020 a 2020 x 3 lo g x 1 3 3lo g x x a 1 3 2021 2020 2021 a 2020 (1)
Xét hàm số 2021t f t
t 2020,t 1.
20202021t ln 2021 2021t f t t 0, t 1.
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 111
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng 3log 3 x 1
Hàm số f t đồng biến trên 1
; , nên từ (1) x a . (*)
TH1: 1 x 0 không tồn tại a thỏa mãn (*). log x
TH2: x 0 (*) log x log x a a a 1 log 1 10 log x 1
Vì a nguyên dương a 1;2;3;...; 9 . 2 2
Câu 98. Tgất cả các giá trị của tham số m để phương trình x 4x5m 2 2 log m 1 có đúng 1 2 x 4 x6 nghiệm là A. 2 . B. 1. C. 4 . D. 0 . Lời giải Chọn D Đặt 2
t x 4x 5 , khi đó t 1.
Thế vào phương trình đã cho ta được phương trình sau t 2 m t 2 m 2 2 2 2 ln 1 2 ln
1 t m x 4 x 5 m (Do hàm đặc trưng 2u f u ln u 1 có 2u 2u f u ln u
1 .ln 2 0, u 0 f u đồng biến trên 0; ) u 1 2 2
Vậy x 4x5m 2 2 log
m 1 có đúng 1 nghiệm 2 x 4 x6 2 2
x 4x 5 m 0 có đúng 1 nghiệm 2
m 1 0 m 1
Tổng tất cả các giá trị m bằng 0 .
Câu 99. Có bao nhiêu giá trị nguyên dương của tham số m để tồn tại cặp số ,
x y thỏa mãn 2 x3 y y 1 e e
1 2x 2 y đồng thời thỏa mãn 2
log 5x 2y 1 m 2 2
log x m 1 0 ? 3 3 A. 1. B. 0 . C. 6 . D. 7 . Lời giải Chọn B Ta có 2x3y y 1 e e
1 2x 2 y 2 x3 y y 1 e 2x 3y e y 1 * . Xét hàm số et f t t trên . ' et f t
1 0 , t hàm số f t đồng biến trên . Từ đó
* f 2x 3y f y
1 2x 3y y 1 2y 1 2x .
Thay vào bất phương trình 2
log 5x 2y 1 m 2 2
log x m 1 0 ta được: 3 3 2
log 3x m 2 2
log x m 1 0 2 2
log x mlog x m 2 0 3 3 3 3 2 2 m 3m log x 2 0 (Vô lý). 3 2 4
Vậy không có giá trị nào của tham số m để tồn tại cặp ,
x y thỏa mãn yêu cầu bài toán. 2
Câu 100. Tổng tất cả các giá trị của tham số x 2 x 1 2 xm
m để phương trình 3 log 2 x m 2 2 x 2 x3
có đúng ba nghiệm phân biệt là: A. 2 . B. 3 . C. 1. D. 0 . Lời giải Chọn B
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 112
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng 2
ln 2 x m 2
x 2 x3(2 xm 2)
Phương trình tương đương 3 ln 2
x 2x 3 2 x 2 x3 2 3
.ln x 2x 3 2 xm 2 3
.ln 2 x m 2 (*). Xét hàm đặc trưng 3t f t
.ln t, t 2 là hàm số đồng biến nên từ phương trình (*) suy ra 2
x 2x 3 2 x m 2 g x 2
x 2x 2 x m 1 0 . 2
x 4x 2m 1 khi x m
2x 4 khi x m
Có g x
g ' x 2 x 2m 1 khi x m 2x khi x m
x 2 khi x m
và g ' x 0 .
x 0 khi x m
Xét các trường hợp sau:
TH1: m 0 ta có bảng biến thiên của g x như sau:
Phương trình chỉ có tối đa 2 nghiệm nên không có m thoả mãn.
TH2: m 2 tương tự.
TH3: 0 m 2 , bảng biến thiên g x như sau: m 2 m 1 1 0 1
Phương trình có 3 nghiệm khi 2m 1 0 2m 3 m . 2 2
m 1 0 2m 3 3 m 2
Cả 3 giá trị trên đều thoả mãn, nên tổng của chúng bằng 3.
Câu 101. Có bao nhiêu số nguyên dương a để phương trình sau đây có ít nhất một nghiệm thực. x loga log log 1 x a a 2x 2 A. 8 B. 1 C. 0 D. 9 Lời giải
Điều kiện x 0 . log a x 1 t Vì log x log a a x nên đặt loga x 1 t ta có log a log x 2 a x t 2t . log a t
t 2x 1 Vì log 1 log 0 ( ) a a a f x x
2x đồng biến trên (0; ) . Vì vậy f (x) f (t) x t .
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 113
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng Hay loga x x 1.
Nếu a 1 thay lại vào phương trình ta có x x 1 x 2 . Vậy a 1 thỏa mãn. ln(x 1) ln x Nếu log 1 a a
x t x
1 2 . Vậy log a 1 . ln x ln x
Do vậy a (0;10) . Mà a nguyên dương và lớn hơn 1 nên a {2, 3, 4,, 9}
Vậy có 9 giá trị của a thỏa mãn điều kiện đầu bài. 2
Câu 102. Tổng tất cả các giá trị của tham số m để phương trình x 2x 1 2 3 xm log 2 x m 2 2 x 2 x3
có đúng ba nghiệm phân biệt là A. 3 . B. 2 . C. 3 . D. 2 . Lời giải Chọn C Ta có 2 x 2 x3 2
ln 2 x m 2 x 2 x 1 2 xm 3 3 log
2 x m 2 2 x 2 x3 2 xm 2 3 ln 2
x 2x 3 ln 2
x 2x 3 2x2x3 .3
ln 2 x m 2 2 xm 2 .3 t 1 Xét
ln .3 , 2; ' 3t ln 3t f t t t f t t
ln 3 0,t 2 t
Vậy hàm số f t đồng biến. f 2
x 2x 3 f 2 x m 2 2
x 2x 3 2 x m 2 2 x 1 2m 1 2
x 2x 1 2 x m 2 x 4x 1 2m 2
Điều kiện cần để phương trình có 3 nghiệm là: 1 Th1:
1 có nghiệm kép m
thử lại ta thấy thỏa mãn 2 3
Th2: 2 có nghiệm kép m
thử lại ta thấy thỏa mãn 2 Th3:
1 và 2 có nghiệm chung x m .Thế 1 vào ta có m 1 1 3 Ta có 1 3 2 2
Bình luận: Bài toán là sự giao thoa giữa phương pháp sử dụng tính đơn điệu hàm số với biện luận nghiệm.
Câu 103. Tìm các giá trị m để phương trình sin x 5cosx m 5 3 log
m 5 có nghiệm. sinx 5cosx 1 0
A. 6 m 6 . B. 5
m 5 .
C. 5 6 m 5 6 . D.
6 m 5 . Lời giải Chọn C Ta có:
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 114
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng
sin x 5cosx m 5 3 log m 5 sinx 5cosx 1 0 sin x 5cosx 1 0 3 ln m 5 m 5 3
ln sin x 5cosx 10 sin x 5cosx 1 0 3
.ln sin x 5cosx 10 m 5 3 .ln m 5 t 1 Xét
ln .3 , 5; ' 3t ln 3t f t t t f t t
ln 3 0,t 5 t
Vậy hàm số f t đồng biến.
f sin x 5cosx 10 f m 5 sin x 5cosx 10 m 5
sin x 5cosx 5 m
Mà 6 sin x 5cosx 6
Vậy để phương trình có nghiệm ta phải có 5 6 m 5 6
Câu 104. Có bao nhiêu giá trị nguyên của tham số m thuộc khoảng 1 00 ;1 00 để phương trình
ex m ln x m có hai nghiệm phân biệt? A. 100. B. 99. C. 98. D. 97. Lời giải Chọn C
Ta có ex m ln x m 1 Đặt :
et et t ln x m x m m x *
1 ex et ex et x t x t 2 Xét hàm số eu f u u . TXĐ: D ' eu f u
1 0 , u
y f u đồng biến trên 3
2 f x f t 4
Từ 3 và 4 x t . Thay vào * ta được:
ex x m
Xét hàm số: ex g x
x , D ' ex g x
1, ' 0 ex g x
1 0 x 0 .
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 115
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng
Yêu cầu bài toán được thỏa khi và chỉ khi đường thẳng : y m cắt đồ thị : ex C y x
tại 2 điểm phân biệt. Dựa vào BBT m 1. Do m 1 00 ;1
00 , m m 2 ; 3 ;.. ; 9 9
Vậy số giá trị nguyên của tham số m là: 99 2 1 98 . m x m x 1
Câu 105. Số giá trị nguyên của m để phương trình ln 2 1 1 mx e e e m x e có e 1 1 nghiệm nằm trong đoạn ; 5 2 A. 3 . B. 5 . C. 6 . D. 4 . Lời giải Chọn D
Phương trình tương đương m x 1 1 1 ln e e mx e m 1 x 1 e e e 1 1
m x 1 ln e
mx m x 1 mx e e e e 1 1 e ln e
mx e mx e e e e 1 ln 1 e ln e e
mx e mx e e e e 1 f ln e t f mx
e với f t e t đồng biến trên e 1 ln e e 1 e 1 1 ln e
mx e m
g x với x ; e x 5 2 1 e ln e e 1 1 1 1
Ta có g ' x
0, x x ;
g x đồng biến trên ; 2 x 5 2 5 2 Ta có BBT: 1 1
Do đó phương trình có nghiệm khi và chỉ khi: g m g 7 , 96 m 3 ,18 5 2
Mà m m 7 ; 6 ; 5 ; 4 .
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 116
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng
Câu 106. Có bao nhiêu giá trị nguyên dương của tham số m để tồn tại các số thực , x y thoả mãn 3x5 y 1 0 x3 y9 e e
1 2x 2y và 2
log 3x 2y 4 m 6 log x 5 2
m 9 0 ? 5 5 A. 4 . B. 3 . C. 6 . D. 5 . Lời giải Chọn A Ta có 3x5y 1 0 x3 y9 3x5 y 1 0 x3 y9 e e
1 2x 2y e
3x 5y 10 e
x 3y 9 .
f 3x 5y 10 f x 3y 9 1 (với t
f t e t ). Xét t
f t e t t f
t e 1 0 t
1 3x 5y 10 x 3y 9 2x 2 y 1 0 Khi đó 2
log 3x 2y 4 m 6 log x 5 2 m 9 0 5 5 2
log x 5 m 6 log x 5 2 m 9 0 * 5 5 Đặt t log x 5 5 2
t m 2 *
6 t m 9 02
Phương trình * có nghiệm phương trình 2 có nghiệm
m 2 2 m 2 6 4
9 0 3m 12m 0 0 m 4 . Vì m
nên m 1; 2;3; 4 . 2
Câu 107. Có bao nhiêu số thực x, y thỏa mãn hệ thức 2 2 y x log
x . Hỏi có tất cả bao nhiêu giá trị 2 y 1
nguyên của m 2022; 2022 để tồn tại duy nhất một số thực x thỏa mãn hệ thức 2 2
4 y 10x mx 1? A. 2036 . B. 2033 . C. 2034 . D. 2035 . Lời giải Chọn D 2 Vì 2
2 y x 0 nên log
x 0 . Mà 2 y 1 1 nên log
x 0 x 1 . 2 y 1 2 y 1 2 2 y 1 log x 2 2 2 y x 2 y x 2 2 2 log x 2.2 2 log x 2 2 y 1 2 y 1 2x log 2 y 1 2 2 y .log 2 2 2 1 1 2x y .log 2 x * 2 2 Đặt 2
u 2 y 1, v x u 1, v
1 . Khi đó * 2u.log 2 . v u log v . 2 2 t t 2t
Xét hàm đặc trưng f t 2 .log t t 1 f t 2 ln 2.log t 0, t 1. 2 2 t ln 2 Vậy hàm số 2t f t
.log t đồng biến trên khoảng 1; . 2 Ta có 2u.log 2v u
.log v f u f v 2
u v 2 y 1 x . 2 2 Khi đó: 2 2 4 2 2 3
4 y 10x mx 1 x 2x 1 10x mx 1 x 12x m g x m .
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 117
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng
m g 1 m 1 1
Phương trình g x m có nghiệm duy nhất x 1 .
m g 2 m 1 6
Mà m 2022; 2022 nên m 16; 11; 10; 9;...; 202 2 .
Vậy có 2035 giá trị nguyên của m 2022; 2022 .
Câu 108. Có bao nhiêu giá trị nguyên dương a sao cho ứng với mỗi a , tồn tại ít nhất số thực b thỏa mãn log 8 log 5a 5 5 a 2 b b 2 2 4
6 2b 4 b ? A. 11. B. 10 . C. 9 . D. 2002 . Lời giải Chọn A
PT đã cho tương đương với log5 a log5 a 2 b b 2 8 2.2 4
4 2b 4 b 2 2 3 log 5 a log5 a 2 b b 2 2 2.2 4
b 4 b 2 3 3 log5 a log5 a 2 b b 2 2 2.2 4
2 b 4 b .
Xét hàm số f t 3
t 2t f t 2
3t 2 0, t
nên hàm số đồng biến trên .
Do đó PT đã cho tương đương với: log5 a 2 2
b 4 b 1 . b b
Xét hàm số g b 2
b 4 b , b 2
; 2 gb 1
gb 1 0 2 4 b 2 4 b b 2 .
Ta có bảng biến thiên như sau: 3 a a 3
PT (1) có nghiệm b khi và chỉ khi log5 log5 2 2 2 2 2 2 2 2 log a a 5 . 5 2
Mà a là số nguyên dương nên a 1; 2;...;1 1 .
Câu 109. Tìm số giá trị nguyên của tham số thực m để tồn tại các số thực x, y thỏa mãn 2 2
x y m
x y xy m 2 2 e e
x y x y xy 2m 2 . A. 6. B. 9. C. 8.
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 118
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng D. 7. Lời giải Xét hàm số ( ) t 1, . ( ) t f t e t t
f t e 1 và f (
t) 0 t 0 . Ta thấy f (
t) đổi dấu từ "- " sang "+" khi qua t 0 nên f (t) f (0) 0, t . 2 2
x y m e 2 2
x y m 1 0, x , y Do đó:
. Dấu "=" xảy ra khi và chỉ khi
x y xym e
(x y xy m) 1 0, x , y 2 2
x y m .
x y xy m 2 2 2 2
x y m
Hay x y m
x y xym 2 2 e e
x y x y xy 2m 2
x y xy m 2
S 2P m
Đặt S x y, P . x y , ta có: 2
S S 3P 0 . Vì 2
S 4P S [0; 4]
S P m
Lấy (1)+2.(2) vế theo vế ta được: 2
S 2S 3m(3) . Xét hàm số 2
f (S ) S 2S, S [0; 4] , có f (
S) 2S 2 0, S [0; 4].
Yêu cầu bài toán (3) có nghiệm
f (0) 3m f (4) 0 m 8 . Vậy, có 9 giá trị nguyên của tham số m thỏa mãn.
Câu 110. Có bao nhiêu giá trị nguyên y sao cho tồn tại số (THPT Lê Thánh Tông - HCM-2022) Có
tất cả bao nhiêu số b nguyên dương sao cho tồn tại đúng hai số thực a thỏa mãn đẳng thức 2 2 a 6 a 1 2 2a 1 2 a 1 . b 2 b .2 3 7 log 2
a 6a log b ? 2 2 A. 1024 . B. 1023 . C. 2047 . D. 2048 . Lời giải Chọn B 2
x a 6a
Đặt y log b 0 b 2y . 2 x y 0 Ta được y x 1 2 y 2 x 1 2 .2 2 .2 3 7 log 2x y x y
2 x y 14 log
x y 6 0 . 2 2 2 Xét hàm số 2 2 t 2t f t
14 log t 6 , t 0 . 2 t t 14 t t 14
f t 4 ln 4 2 ln 2
f t 2 2 4 ln 4 2 ln 2 0 t 0 2 t.ln 2 t ln 2
f t 0 có nhiều nhất hai nghiệm dương. Ta thấy f
1 f 2 0 . 2 t 1
x y 1
log b 1 6a a
Do vậy, ta được f t 2 0 . 2 t 2 x y 2
log b 2 6a a 2
Câu 111. Có tất cả bao nhiêu giá trị nguyên của tham số
m để phương trình log 2 2x m x m
3x 1 có nghiệm thuộc 0; 3 ? 2 A. 2 . B. 5 . C. 7 . D. 3 . Lời giải Chọn C
Điều kiện: m x 0 Ta có log 2 2x m x m 3x 1 2 log 2 2 2 2 2x m x m x x 2
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 119
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng log 2 2
2 2 log 2x 2x m x m x (*). 2 2
Xét hàm số f t log t t trên 0; . 2 1
Ta có: f 't 1 0, t 0 . t.ln2
Suy ra hàm số f t liên tục và đồng biến trên 0; . Do đó (*)
2 2 2x 2 2 2x 2 2x f m x f m x m 2x . Đặt 2x g x 2x . Vì ' 2 .x g x
ln2 2 0, x 0; 3 nên ta có BBT 1
Do đó ycbt 1 2m 14 m 7 . 2
Vì m nên m 1; 2;3; 4;5;6; 7 .
Vậy có 7 giá trị m cần tìm. Câu 112. Số giá trị m nguyên thuộc khoảng 2
019; 2020 để phương trình log 3x 3
x 3m 3 3m .3x 9x có đúng hai nghiệm là 3 A. 2018 . B. 4036 . C. 2019 . D. 2020 . Lời giải Chọn A 3x x m x x m m x x 3 3 1 Ta có log 3 3 3 3 3 .3 9 log
3.3x 3x 3x 3m . 3 3 x 3
log 3x 3x 3m 1 x 3.3x 3x 3x 3m 3
log 3x 3x 3m 1 3x 3x 3m 1 3.3x x 1 3 log
3x 3x 3m 1 3x 3x 3m x 1 x 1 1 log 3 3 1 . 3 3 1
Xét hàm số f t log t t trên 0; có f 't
1 0 t 0 nên hàm số 3 t.ln3
f t log t t đồng biến trên 0; . 3 Do đó
x x m x 1 x x m x 1 2 1 3 3 3 1 3 3 3 3 1 3
3 x 3m 3.3x f f 1 0 . Đặt 3x t
, t 0 . Phương trình trên trở thành 2 3m t
3t 1 0 2 .
Phương trình ban đầu có hai nghiệm khi và chỉ khi phương trình 2 có hai nghiệm t , t thỏa 1 2 Δ 0
mãn 0 t t t t 0 . 1 2 1 2 t .t 0 1 2
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 120
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng m 2 3 5 m log 5
+) Δ 0 3m 3 3 4 0 . m * 3 1 m 0 0 3 3m t t 0
+) Khi đó theo định lý Viet ta có 1 2 m 1 * * . t .t 0 1 0 1 2 Kết hợp
* và ** ta được: m 0 .
Do m nguyên thuộc khoảng 2
019; 2020 nên m 2 018; 2 017;..; 1 .
Vậy có 2018 giá trị nguyên của m thỏa mãn.
Câu 113. Có bao nhiêu giá trị nguyên của tham số m để tồn tại cặp số ; x y thỏa mãn 3x5 y x3 y 1 e e
1 2x 2 y , đồng thời thỏa mãn 2
log 3x 2y 1 m 6 2
log x m 9 0 3 3 ? A. 6 . B. 5 . C. 8 . D. 7 . Lời giải Chọn B
Ta có 3x5y x3 y 1 e e
1 2x 2 y 3x5 y x y x3 y 1 e 3 5 e
x 3y 1 (1) Xét hàm số et f t
t trên . Ta có ' et f t
1 0 nên hàm số đồng biến trên .
Khi đó (1) f 3x 5y f x 3y
1 3x 5 y x 3y 1 2 y 1 2x .
Thế vào phương trình còn lại ta được 2
log x m 6 2
log x m 9 0 (2) 3 3
Đặt t log x . Số nghiệm của phương trình (2) chính là số nghiệm của phương trình 3 2
t m 2
6 t m 9 0 (3)
Phương trình (3) có nghiệm khi 0 2
3m 12m 0 0 m 4 .
Do đó có 5 số nguyên m thỏa mãn.
Câu 114. Có bao nhiêu giá trị nguyên của tham số m để tồn tại cặp số ;
x y thỏa mãn điều kiện 5 x7 y 3x5 y2 3 3
2 x y
1 0 , đồng thời thỏa mãn
2 x y m 2 ln 4 3 3
2 lnx m 1 0 có nghiệm? A. 2019 . B. 6 . C. 2020 . D. 4 . Lời giải Chọn D 5 x7 y 3x5 y2 3 3
2 x y 1 0 5 x7 y 3x5 y2 3
5x 7 y 3
3x 5 y 2 Xét hàm số 3t f t t ' 3t f t
ln3 1 0, t . Suy ra hàm số 3t f t
t đồng biến trên .
Nên f 5x 7 y f 3x 5y 2 5x 7 y 3x 5y 2 y 1 x 1 Thế 1 vào phương trình
2 x y m 2 ln 4 3 3
2 lnx m 1 0 ta được
2 x m 2 ln
2 lnx m 1 0 .
Đặt t lnx , phương trình có dạng: 2
t m 2
2 t m 1 0 . Để phương trình có nghiệm thì 0 2
3m 4m 8 0 2 2 7 2 2 7 1 , 09 m 2, 43 . 3 3
Vì m nên m 1 ; 0;1; 2
Do đó có 4 số nguyên m thỏa mãn.
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 121
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng
Câu 115. Có bao nhiêu giá trị nguyên dương của tham số m để tồn tại các số thực x , y thỏa mãn đồng thời 3x5y 1 0 x3 y9 e e
1 2x 2 y và 2
log 3x 2y 4 m 6 log x 5 2
m 9 0 ? 5 5 A. 3 . B. 5 . C. 4 . D. 6 . Lời giải Chọn C
Theo bài 3x5y 1 0 x3 y9 e e
1 2x 2 y 3x5 y 1 0 x3 y9 e e
x 3y 9 3x 5y 10 3x5 y 1 0 x3 y9 e
3x 5y 10 e
x 3y 9 Xét hàm số t f t
e t, t . Ta có: ' t f t
e 1 0, t .
Suy ra hàm số luôn đồng biến trên .
Khi đó phương trình f t 0 có nghiệm là duy nhất. Tức là:
3x 5 y 10 x 3y 9 2 y 1 2x .
Thay vào phương trình thứ 2, ta được: 2
log 3x 2y 4 m 6 log x 5 2 m 9 0 5 5 2
log x 5 m 6 log x 5 2 m 9 0 1 . 5 5 Đặt log
x 5 t t , x 5
. Khi đó phương trình trở thành 5 2
t m 2
6 t m 9 0 * .
Tồn tại x , y thỏa mãn yêu cầu bài toán khi và chỉ khi phương trình * có nghiệm, tức là:
m 2 2 Δ 6 4 m 9 0 2
3m 12m 0 0 m 4 .
Vậy có 4 giá trị nguyên dương của m thỏa mãn yêu cầu bài toán.
Câu 116. Tìm các giá trị m để phương trình sin x 5cosx m 5 3 log
m 5 có nghiệm. sinx 5cosx 1 0
A. 6 m 6 . B. 5
m 5 .
C. 5 6 m 5 6 . D.
6 m 5 . Lời giải Chọn C Ta có
sin x 5cosx m 5 3 log m 5 sinx 5cosx 1 0 sin x 5cosx 1 0 3 ln m 5 m 5 3
ln sin x 5cosx 10 sin x 5cosx 1 0 3
.ln sin x 5cosx 10 m 5 3 .ln m 5 (1) 1 Xét
ln .3t f t t ,t 5 , vì
' 3t ln 3t f t t
ln 3 0,t 5 nên hàm số f t đồng t
biến trên 5; . Khi đó
1 f sin x 5cosx 10 f m 5
sin x 5cosx 10 m 5
sin x 5cosx 5 m
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 122
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng Mà
6 sin x 5cosx 6 nên để phương trình có nghiệm ta phải có
5 6 m 5 6. 2
Câu 117. Cho phương trình x 1 2 .log 2
x 2x 3 4 xm log
2 x m 2 với m là tham số thực. 2 2
Có bao nhiêu giá trị nguyên của m trên đoạn 2
019 ; 2019 để phương trình có đúng 2 nghiệm phân biệt. A. 4036 . B. 4034 . C. 4038 . D. 4040 . Lời giải Chọn C
Điều kiện: x . x 2 1 2 .log 2
x 2x 3 4 xm log 2 x m 2 2 2 x 2 1 2 .log x 1 2 2 xm log
2 x m 2 1 2 2 2 2 Xét hàm số 2t y .log
t 2 với t 0 . 2 Hàm số 2t y .log
t 2 xác định và liên tục trên 0 ; . 2 t 2t Ta có y ' 2 .log t 2 .ln2 0, t 0 . 2 t 2ln2 Vậy hàm số 2t y .log
t 2 đồng biến trên 0 ; . 2 x 2 1 2 x m 2 2 Từ
1 f x
1 f 2 x m x 1
2 x m x 2 1
2 x m 2
2m x 4x 1 1 * . 2
2m x 1 2 Xét phương trình 2
2m x 4x 1. Ta có bảng biến thiên của hàm số g x 2
x 4x 1 3 Phương trình 2
2m x 4x 1 có 2 nghiệm phân biệt khi 2m 3 m . 2 3 Phương trình 2
2m x 4x 1 có 1 nghiệm khi 2m 3 m . 2 3 Phương trình 2
2m x 4x 1 vô nghiệm khi 2m 3 m . 2 Xét phương trình 2
2m x 1. Ta có bảng biến thiên của hàm số h x 2 x 1
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 123
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng 1 Phương trình 2
2m x 1 có 2 nghiệm phân biệt khi 2m 1 m . 2 1 Phương trình 2
2m x 1 có 1 nghiệm khi 2m 1 m . 2 1 Phương trình 2
2m x 1 vô nghiệm khi 2m 1 m . 2 3 Khi m : phương trình 2
2m x 4x 1 có nghiệm x 2 , phương trình 2
2m x 1 có 2 3
2 nghiệm phân biệt x 2 . Vậy
* có 3 nghiệm phân biệt, suy ra loại m . 2 1 Khi m : phương trình 2
2m x 4x 1 có 2 nghiệm phân biệt x 2 2 , phương 2 1 trình 2
2m x 1 có nghiệm x 0 . Vậy
* có 3 nghiệm phân biệt, suy ra loại m . 2 Xét phương trình 2 2 2
x 4x 1 x 1 2x 4x 2 0 x 1 suy ra không tồn tại m để phương trình
1 và 2 có cùng tập nghiệm gồm 2 phần tử. Vậy không tồn tại m để * có 2 nghiệm phân biệt.
Yêu cầu bài toán
* có 2 nghiệm phân biệt. 3 m 2 1 TH1:
1 có 2 nghiệm phân biệt và 2 vô nghiệm m . 1 2 m 2 1 m 2 3
TH2: 2 có 2 nghiệm phân biệt và 1 vô nghiệm m . 3 2 m 2 3 m 2 TH3:
1 có nghiệm x 2 và 2 có nghiệm x 0 m . 1 m 2 1 3
Kết hợp với điều kiện m thuộc đoạn 2
019 ; 2019 ta có m 2 019 ; ; 2019 . 2 2
Vì m nguyên nên nên ta có 4038 giá trị của m . 2
Câu 118. Cho phương trình x 1 3 log 2
x 2x 3 9 xm log
2 x m 2 0 1 3 3
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 124
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng
Gọi S là tập tất cả các giá trị m để phương trình
1 có đúng 3 nghiệm thực phân biệt. Khi
đó tổng các phần tử của S bằng A. 3 . B. 2 . C. 0 . D. 3 . Lời giải Chọn A x 2 1 3 log 2
x 2x 3 9 xm log
2 x m 2 0 3 3 x 2 1 3 log x 1 2
3 xm log 2 x m 2 2 3 2 2 3 Xét hàm: 3t f t
.log t 2 trên khoảng 0; 3 t 1 ' 3 .ln3.log 2 .3t f t t 3 t 2ln3 t 1 3 .ln 2 .3t t
0,t 0; t 2ln3
f t là hàm đồng biến trên 0; f x 2
f x m x 2 2 1 2 1 2 x m
x 4 x m2 1 4 2
x m 2 2
1 x 4x 1 2m 0 2
x 2m 1 0 3 2
x 4x 1 2m 0 4 Phương trình
1 có đúng 3 nghiệm thực phân biệt, ta xét các trường hợp sau: 1
TH1. Phương trình 3 có nghiệm kép m 2 1 x 2 2 Thay m vào 4 ta được 2
x 4x 2 0 2 x 2 2 1 m
là một giá trị cần tìm. 2 3
TH2. Phương trình 4 có nghiệm kép 4 1 2m 0 m 2 3 Thay m vào 3 ta được 2
x 2 0 x 2 2 3 m
là một giá trị cần tìm. 2
TH3.Phương trình (3) và phương trình (4) mỗi phương trình có hai nghiệm phân biệt trong đó có một nghiệm chung
Gọi a là nghiệm chung. Khi đó ta có 2
a 2m 1 0 (*) 2
a 4a 1 2m 0
a m thế vào (*) ta được m 1 Thay m 1 vào (3) ta được 2
x 1 x 1 x 1 Thay m 1 vào (4) ta được 2
x 4x 3 0 x 3
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 125
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng Vậy m 1
là một giá trị cần tìm 1 3
Do đó tổng các phần tử của S là 1 3 . 2 2 Câu 119. 2
Cho phương trình 4 xm.log 2 2 3 2 2 x x x x .log
2 x m 2 0 với m là tham số. 1 2 2
Tổng tất cả các giá trị của tham số m để phương trình đã cho có ba nghiệm phân biệt là A. 4 . B. 1. C. 2 . D. 3 . Lời giải Chọn D
Phương trình đã cho tương đương với phương trình
2 xm .log 2 3 2 2 1 2 2 2 x x x x .log
2 x m 2 0 2 2
2 xm .log 2 3 2 2 1 2 2 2 x x x x .log 2 x m 2 2 2 2 x 2 2 . x log 2
x 2x 3 2 xm .log
2 x m 2 . 2 2 1 2
Xét hàm số f t t 3
2 .log t với t 2 . Do t 2 suy ra log t 1. 2 2 t 1 f't 3 t 3 2 .
2 .ln2.log t 0 . 2 t.ln2
Do đó hàm f t đồng biến trên 2; mà f 2
x 2x 3 f 2 x m 2 suy ra 2 x 1 m 2x 2 x 1 2 2 2
x 2x 3 2 x m 2 x m x * . 2 2 2 x 1 m 2 2 2 x 1 2 x 1
Vẽ đồ thị các hàm số y 2x và y
trên cùng một hệ trục tọa độ. 2 2 2 2 2 x 1
Đồ thị hai hàm số tiếp xúc với nhau tại điểm 1;
1 . Điểm cực trị của đồ thị hàm số y 2 2 1 2 x 1 3 là 0;
, điểm cực trị của đồ thị hàm số y 2x là 2; . 2 2 2 2
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 126
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng 1 3
Dựa vào đồ thị, để
* có ba nghiệm phân biệt thì m ;1; . 2 2 1 3
Tổng tất cả các giá trị của tham số m thỏa mãn là 1 3 . 2 2
Câu 120. Có bao nhiêu giá trị thực của tham số a để phương trình 4 xa log 2 3 2 2 x 2 2 x x x log
2 x a 2 0 có 3 nghiệm thực phân biệt? 1 2 2 A. 0 . B. 2 . C. 1. D. 3 . Lời giải Chọn D 1 1
PT đã cho tương đương với 2 log
x 2x 3 log x a . 2 2 0 1 2 xa 2 1 x 2 x 2 2 2 2 2 2 log x x x a xa 1 2 2 3 log 2 2 2 2 2 2 x 2 2 2 x 2 x 2 x 1 2 log 2
x 2x 3 2 xa log 2 x a 2 2 2 2 2 x 2 x3 2 log 2
x 2x 3 2 xa log
2 x a 2 1 2 2 2 2 t 2t Xét hàm số 2t f t
.log t,t 2 ; Ta có: f 't 2 lnt
0, t 2 Hàm số f t 2 tln2
đồng biến trên 2; . Từ (1) suy ra f 2
x x f x a 2 2 3 2
2 x 2x 3 2 x a 2 2
x 2x 1 2 x a (*) 2
x 2x 1 2 x a 2
x 4x 2a 1 0 2 2
x 2x 1 2 x a 2
x 2a 13
Phương trình (*) có 3 nghiệm phân biệt nếu xảy ra một trong các trường hợp sau:
* TH1: (2) có hai nghiệm phân biệt và (3) có nghiệm kép khác hai nghiệm của (2): 3 Δ ' 0 a a 2 3 2 0 2 1 a Δ ' 0 2a 1 0 1 2 3 a 2
* TH2: (3) có hai nghiệm phân biệt và (2) có nghiệm kép khác hai nghiệm của (3): 3 Δ ' 0 a a 2 3 2 0 2 3 a Δ ' 0 2a 1 0 1 2 3 a 2
* TH3: (2) và (3) đều có hai nghiệm phân biệt, trong đó có một nghiệm chung: 2
x 4x 2a 1 0
Điều này xảy ra khi hệ có nghiệm 2 x 2a 1 2
x 4x 2a 1 0 x a x 1 2 x 2a 1 a 1 a 1 x 1
Khi a 1 ta có: 2 trở thành 2
x 4x 3 0 x 3
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 127
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng x 1 3 trở thành 2 x 1 x 1
Khi đó: PT đã cho có 3 nghiệm. 1 3
Vậy a ;1; . 2 2 BỔ SUNG CÁCH 2: Xét phương trình 2
x 2x 1 2 x a * Vẽ đồ thị hàm số 2
y x 2x 1
1 ; y 2 x a 2 trên cùng một hệ trục tọa độ ta được:
nh¸nh bªntr¸icña 2 tiÕpxócvíi 1 Nhận xét
* có 3 nghiệm phân biệt nh¸nh bªnph¶icña 2 tiÕpxócvíi 1
1 vµ 2 cïng trïng cùc trÞ t¹i1 1 a 2
x x a x 2 2 1 2 cãnghiÖmkÐp 3 2 x 2x 1
2 x a cãnghiÖmkÐp a 2 a 1 a 1
Vậy có 3 giá trị của a thỏa mãn bài toán.
Câu 121. Cho phương trình 3 2 m m
x x 2 .log x 3x 1 2 3 2 3 1 3 1 2 1 3 2 2 .log 0 81 3 3 2 m 3m 1 2
Gọi S là tập hợp tất cả các giá trị m nguyên để phương trình đã cho có số nghiệm thuộc đoạn 6;
8 . Tính tổng bình phương tất cả các phần tử của tập S . A. 20 . B. 28 . C. 14 . D. 10 . Lời giải Chọn A 3 2 3 2 m 3m 1 x 3x 1 2 1 Ta có 2 .log 3 2 x 3x 1 2 2 .log 0 81 3 3 2 m 3m 1 2
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 128
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng 3 2 x x m m 2
.log x 3x 1 2 3 2 3 1 2 3 1 2 3 2 2 .log 3 2
m 3m 1 2 . 3 3 t t 1 Xét hàm số 2t f t
.log t với t 2 ; Ta có f 't 2 ln2.log t 2 . 0t 2 . 3 3 tln3
Suy ra hàm số f t đồng biến trên 2; .
Do đó phương trình tương đương với 3 2 3 2
m 3m 1 x 3x 1 1 .
Vẽ đồ thị hàm số g x 3 2
x 3x 1 từ đó suy ra đồ thị g x và đồ thị của g x như hình vẽ.
Từ đồ thị suy ra
1 có 6, 7, 8 nghiệm 0 g m 3 .
Từ đồ thị suy ra các giá trị nguyên của m là 3 , 1, 0 , 1, 3 . Vậy S 20 . Từ đồ thị, ta có: 10 11
10 log b 11 2 b 2 2
Vậy có 1023 số nguyên dương b thỏa mãn.
Câu 122. Có bao nhiêu số nguyên a a 3 sao cho tồn tại số thực x thỏa mãn a log x a 3log2021 2021 x 3 ? A. 2019 . B. 2018 . C. 2020 . D. 2003. Lời giải
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 129
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng Chọn B
ĐK có nghiệm là x 3. log a log a Ta có: log x 2021 a 3 2021 log a log a log a 2021 x 3 2021 x 3 2021 x 3 2021 x x 1
Xét hàm số f t log a 2021 t
t trên 0; f t log a 1 2021 t .log a 1 0 t
0 vµ a 3 Hàm số f t đồng biến trên 0; 2021 Do đó
1 f log a log a log a 2021 x
3 f x 2021 x 3 x 2021 x x 3 log a 2021 log x log x 3 log a log x log x 3 2021 2021 2021 2021 2021 log x 3 2021 log a 2021 log x 2021 log x 3 2021 Mà log x 3 log x x 3 và log
x 0 x 3 nên 1 x 3 2021 2021 2021 log x 2021 log x 3 2021
Lại có: Hàm số g x
liên tục trên 3; log x 2021
và lim g x 1; lim g x x x 3 log x 3 2021
Do đó tập giá trị của hàm số g x là ; 1 log x 2021
Khi đó phương trình đã cho có nghiệm thì log
a 1 a 2021 2021
Lại có a nguyên và a 3 nên a 3; 4;...; 202 0 .
Vậy có 2018 số nguyên a a 3 thỏa mãn yêu cầu bài toán.
Câu 123. Có bao nhiêu số nguyên a a 2 sao cho tồn tại số thực x thỏa mãn x ln 4 2 ln 2 log x log a 4 x a 4 ? log a A. 2 . B. 3 . C. 1. D. 9 . Lời giải Chọn A Ta có: x x ln 4 2 ln 2 ln 2 log x log a 4 x a 4 ln 4logx 2log a 4 x a 4 log a log a x 2 ln ln 2 2log x a 2 log a log t 2 2log x Đặt a 2 t log .
a 2 log x log t 2 log a 2 log x
ln t.ln t 2 ln .
x ln x 2
Xét hàm f u ln u.ln u 2 ln u 2 ln u
f u 0 u u 2 Do 2log x 2log 2 t 2 a 2 1 2log x 2log a 2log 2 2 a u x a x x x x x 2 log a 1. 1 log a
a 10 a 2; 3 2
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 130
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng a
Câu 124. Có bao nhiêu số nguyên a a 2 sao cho tồn tại số thực x thỏa mãn: x a log log 2 x 2 ? A. 8. B. 9. C. 1. D. Vô số. Lời giải Chọn A a a Xét phương trình x a log log 2 x 2 a x log log 2 x 2 . a Vì a x log log 2
0 nên suy ra x 2 . a log a Ta có: a x log log 2
x 2 loga loga log 2 2 a x x x x . Xét hàm số log a f t t
t có f t log a 1 log . a t
1 0 , t 2 . Do đó f t là hàm số
đồng biến trên 2; . Mà loga f x
2 f x log a x 2 x log a x x 2 .
Trường hợp 1: log a 1 a 10 . y y = xlog a y = x 2 0 x 1 2
Dễ thấy hai đồ thị của hai hàm số log a y x
và y x 2 không có điểm chung, vậy a 10
không thỏa mãn yêu cầu bài toán.
Trường hợp 1: log a 1 a 10 .
Dễ thấy phương trình loga x
x 2 luôn có nghiệm duy nhất. y y = x 2 y = xlog a 0 x 1 2
Vậy a 2;3;...;
9 có 8 giá trị của a thỏa mãn. Câu 125. Có bao nhiêu số tự nhiên a sao cho tồn tại số thực x thoả 3 3log x 1 x a 3 x 3log x 1 2021 2020 a 2020 A. 9. B. 8. C. 5. D. 12 Lời giải
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 131
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay
ST&BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phương pháp hàm đặc trưng Chọn A 3log x 1 3 3log x 1 a x a 2020 Xét phương trình: 2021
, điều kiện: x 1 , 3 x 2020 3 3log x 1 3log x 3 x a log a 2020 log x 2020 2021 1 2021 3 3 x log x 2020 x a log x a 2020 2021 3log 1 3log 20 1 2 1 Xét hàm số 3
f (t) t log
t 2020 , trên 0; 21 3 20 2 3t 2
f '(t) 3t 0, t
0 nên hàm số f (t) đồng biến trên 0;
3t 2020ln 2021 a
Do đó trở thành: log x 1 x a
x x log 1 log x log . a log(x 1) log x log a 1, x 1
nên a 10 a 1, 2,3, 4,5,6,7,8, 9 log x 1
ĐT: 0978064165 - Email: dangvietdong.ninhbinh.vn@gmail.com Trang 132
Facebook: https://www.facebook.com/dongpay - Kênh Youtube: Thầy Đặng Việt Đông ID TikTok: dongpay




