Phương pháp hàm số đặc trưng – Nguyễn Văn Rin

Tài liệu gồm 43 trang được tổng hợp và biên soạn bởi thầy giáo Nguyễn Văn Rin, trình bày cơ sở lý thuyết và giới thiệu một số ví dụ áp dụng của phương pháp hàm số đặc trưng trong các đề thi thử THPT Quốc Gia môn Toán cũng như đề chính thức của Bộ Giáo dục và Đào tạo qua các năm.

22 11 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu ôn thi THPTQG môn Toán

Môn: Toán

Thông tin:

43 trang 6 tháng trước

Tác giả:

Profile Nguyễn Vân
ThS. Nguyeãn Vaên Rin – HBT Trang 1/43
TT LTĐH CAO THẮNG – HUẾ PHƯƠNG PHÁP
ThS. Nguyeãn Vaên Rin – HBT HÀM SỐ ĐẶC TRƯNG
SÑT: 089.8228222
Họ và tên: …………………………………….................….……; Trường:……………………..………; Lớp: ……………………….....
Phương pháp hàm số đặc trưng thường xuyên xuất hiện trong đề thi THPT Quốc Gia và nó cũng là một trong
những câu phân loại của đề:
- Câu 47 mã đề 101 – THPT QG năm 2017.
- Câu 35 đề tham khảo – BGD&ĐT năm 2018.
- Câu 46 mã đề 101 – THPT QG năm 2018.
- Câu 47 đề tham khảo – BGD&ĐT năm 2020.
Sau đây, tôi xin trình bày cơ sở lý thuyết và giới thiệu một số ví dụ áp dụng của nó trong các đề thi thử THPT
Quốc Gia cũng như đề chính thức của BGD&ĐT qua các năm.
I. Cơ sở lý thuyết: Cho hàm số
y f x
liên tục trên tập
D
.
Nếu hàm số
f x
đơn điệu (đồng biến hoặc nghịch biến) trên
D
thì
, ,
u v D f u f v u v
.
Nếu hàm số
f x
đồng biến trên
D
thì
, ,
u v D f u f v u v
.
Nếu hàm số
f x
nghịch biến trên
D
thì
, ,
u v D f u f v u v
.
II. Áp dụng
1. Giải phương trình, bất phương trình mũ và logarit
Câu 1. (Chuyên Thái Bình 18) Tính tổng tất cả các nghiệm của phương trình
3 2
3
2
2
3 3 5
log 1 6 7
1
x x x
x x x
x
.
A.
2 3
. B.
2
. C.
0
. D.
2 3
.
Lời giải
Chọn C.
Điều kiện
3 2
2
3 3 5
x x x
3 2
3 3 5 0
x x x
.
Với điều kiện trên, phương trình đã cho tương đương
3 2
3
2
2
3 3 5
log 1 6 7
1
x x x
x x x
x
3
3 2 2 2
log 3 3 5 log 1 6 7 1
x x x x x x x
3 2 3 2 2 2
log 3 3 5 3 3 5 log 1 1 *
x x x x x x x x
.
Xét hàm số
log
y f t t t
trên khoảng
0;
.
Ta có:
1
1 0, 0
ln10
f t t
t
.
Suy ra hàm số
f t
đồng biến trên khoảng
0;
.
3 2 2 3 2 2
* 3 3 5 1 3 3 5 1
f x x x f x x x x x
3 2
2 3 6 0
x x x
2
3
3
x
x
x
.
Đối chiếu điều kiện, ta được
3
x
thỏa mãn.
Vậy
3 3 0
S
.
Câu 2. (SGD Bắc Ninh 18) Cho phương trình
2
2 2
1 2 1 1
log 2 3 log 1 2 2
2
x
x x x
x x
, gọi
S
là tổng tất cả các nghiệm của nó. Khi đó, giá trị của
S
là
A.
2
S
. B.
1 13
2
S
. C.
2
S
. D.
1 13
2
S
.
ThS. Nguyeãn Vaên Rin – HBT Trang 2/43
Lời giải
Chọn D.
Điều kiện
1
2
2
0
x
x
.
Với điều kiện trên, phương trình đã cho tương đương
2
2
2 2
1 1
log 2 2 1 log 2 2 1 *
x x
x x
.
Xét hàm số
2
2
log 1
y f t t t
trên khoảng
0;
.
Ta có
1
2 1
ln 2
f t t
t
2
2ln 2. 2ln 2. 1
0
.ln 2
t t
t
,
0
t
.
Suy ra hàm số
f t
đồng biến trên khoảng
0;

.
Do đó
1
* 2 2f x f
x
1
2 2x
x
3 2
2 4 1 0
x x x
1
3 13
2
3 13
2
x
x
x
.
Kết hợp với điều kiện ta được
1
3 13
2
x
x
.
Vậy
1 13
2
S
.
Câu 3. (Nguyễn Trãi - Đà Nẵng 18) Gọi
0
3a b
x
c
là một nghiệm lớn hơn
1
của phương trình
1
1
2
1
2 3 1 2 1
3
x
x
x x
. Giá trị của
P a b c
là
A.
6
P
. B.
0
P
. C.
2P
. D.
4P
.
Lời giải
Chọn D.
Với
1x
ta có
1
1
1
2 3 1
3
x
x
x
2
2 1
x
1
1
2
1
3 3 1
2
x
x
x
x
1
1
2
1
3 3 1
2
x
x
x
x
1
.
Xét hàm số
3
t
f t t
trên khoảng
0;
.
Ta có
3 .ln3 1 0
t
f t
, 0t
.
1
1 1
2
f f x
x
1
1
2
x
x
1 3
2
x
1a
,
1b
,
2
c
.
Vậy
4P
.
Câu 4. (THTT 18) Biết
1
x
,
2
x
là hai nghiệm của phương trình
2
2
7
4 4 1
log 4 1 6
2
x x
x x
x
và
1 2
1
2
4
x x a b
với
a
,
b
là hai số nguyên dương. Tính
.a b
A.
16
a b
. B.
11
a b
. C.
14
a b
. D.
13.
a b
Lời giải
ThS. Nguyeãn Vaên Rin – HBT Trang 3/43
Chọn C.
Điều kiện
0
1
2
x
x
Ta có
2
2
2 2
7 7
2 1
4 4 1
log 4 1 6 log 4 4 1 2
2 2
x
x x
x x x x x
x x
2 2
7 7
log 2 1 2 1 log 2 2 1x x x x
Xét hàm số
7
1
log 1 0
ln 7
f t t t f t
t
với
0t
Vậy hàm số đồng biến
Phương trình
1
trở thành
2 2
3 5
4
2 1 2 2 1 2
3 5
4
x
f x f x x x
x
Vậy
1 2
9 5
4
2 9; 5 9 5 14.
9 5
4
l
x x a b a b
tm
Câu 5. (Lương Thế Vinh 19) Phương trình
2
3
2
2 1
log 3 8 5
( 1)
x
x x
x
có hai nghiệm là
a
và
a
b
(với
a
,
*
b
và
a
b
là phân số tối giản). Giá trị của
b
là
A.
1
. B.
4
. C.
2
. D.
3
.
Lời giải
Chọn D
Điều kiện
1
2 1 0
2
1 0
1
x
x
x
x
.
Ta có:
2
3
2
2 1
log 3 8 5
1
x
x x
x
2
3
2
2 1
log 1 3 8 4
1
x
x x
x
2
3
2
2 1
log 3 1 2 1
3 1
x
x x
x
2 2
3 3
log 2 1 2 1 log 3 1 3 1
x x x x
1
.
Xét hàm số
3
log
f t t t
trên khoảng
0;
.
Ta có
1
1 0
.ln 3
f t
t
, 0t
.
Suy ra hàm số
f t
đồng biến trên
0;

.
2
1 2 1 3 1
f x f x
.
2
2
2 1 3 1 3 8 4 0
x x x x
hay
2
2
3
x
x
.
Vậy hai nghiệm của phương trình là
2
và
2
3
suy ra
3
b
.
Câu 6. (Lê Xoay - Vĩnh phúc 18) Số nghiệm của phương trình trên khoảng
là
2
sin 2 cos 1 log sinx x x
0;
2
ThS. Nguyeãn Vaên Rin – HBT Trang 4/43
A. . B. . C. . D. .
Lời giải
Chọn D
Vì và nên phương trình đã cho tương đương
Xét hàm số , với ta có .
Do đó hàm số đồng biến trên khoảng .
*
hay .
Câu 7. (Cổ Loa - Hà Nội 19) Cho hàm số
2
ln 1
x x
f x x x e e
. Hỏi phương trình
3 2 1 0
x
f f x
có bao nhiêu nghiệm thực?
A.
3
. B.
0
. C.
2
. D.
1
.
Lời giải
Chọn D
Ta có
2 2
1 0,x x x x x x x x x
.
2
2
1
ln 1 ln
1
x x x x
f x x x e e e e
x x
2
ln 1
x x
x x e e
f x
.
Suy ra
f x
là hàm số lẻ.
Mà
2
2
2
1
2 1
1
x x
x
x
f x e e
x x
2
2
2 2
1
1
1
0
1 1
x x x x
x x
x
e e e e
x x x
,
x
Suy ra
f x
đồng biến trên
.
Do đó
3 2 1 0
x
f f x
3 2 1
x
f f x
3 1 2
x
f f x
3 1 2
x
x
3 2 1 0 *
x
x
.
Xét hàm số
3 2 1
x
g x x
trên
.
3 ln3 2 0,
x
g x x
.
Suy ra
g x
đồng biến trên
nên (*) nếu có nghiệm thì có nghiệm duy nhất.
Mà
0x
là một nghiệm của phương trình (*).
Vậy tập nghiệm của phương trình (*) là
0S
.
Câu 8. (TƯ NGHĨA 19) Cho hàm số
y f x
liên tục trên
R
và có đồ thị như hình vẽ dưới đây .
Số nghiệm của phương trình
3 2
3 4 2
3 2
3 1
f x f x f x
f x
f x
là
A.
6
. B.
9
. C.
7
. D.
8
.
Lời giải
4
3
2
1
sin 0
x
cos 0
x
, 0;
2
x
2 2 2
sin 2 cos log cos 1 log sin log cosx x x x x
2 2
log cos cos log sin 2 sin 2 *
x x x x
2
log
f t t t
0;1
t
1
1 0, 0;1
ln 2
f t t
t
f t
0;1
cos sin 2 cos sin 2f x f x x x
1
sin
2
x
6
x
ThS. Nguyeãn Vaên Rin – HBT Trang 5/43
Chọn B
Vì
1
4
f x
nên
3 1 0,f x x
.
Đặt
t f x
ta được
3 2
3
3
3 4 2
3 2 1 1 3 1 3 1 *
3 1
t t t
t t t t t
t
Xét hàm đặc trưng
3
g u u u
trên
.
Ta có
2
3 1 0,g u u u
.
Do đó
* 1 3 1 1 3 1g t g t t t
2
0 1
1
0
1
2 1 3 1
1 2
f x
t
t
t
t t t
f x
.
Dựa vào đồ thị phương trình (1) có
3
nghiệm phân biệt và phương trình (2) có
6
nghiệm phân biệt
(không trùng nhau).
Vậy phương trình đã cho có
9
nghiệm phân biệt.
Câu 9. (Nguyễn Du - DakLak 19) Cho hàm số
3 2
y f x ax bx cx d
(với
, , , , 0
a b c d a
). Biết
đồ thị hàm số
y f x
có hai điểm cực trị là
0;1
A
và
2; 3
B
. Hỏi tập nghiệm của phương trình
3
3
2 0
f x f x f x
có bao nhiêu phần tử?
A.
2019
. B.
2018
. C.
9
. D.
8
.
Lời giải
Chọn D
Ta có
3 2
f x ax bx cx d
2
3 2
f x ax bx c
.
Theo giả thiết ta có hệ
3 2
0 0
0 1
3 1
2
0 1
1 3
1 4 0 0
8 4 1 3
2 0
3
1
2
c a
d b
a b c
a b d
f
f
f x x x
f
f
.
+ Xét phương trình:
3
3
2 0
f x f x f x
3
3
3 3
2. 2. *
f x f x f x f x
.
Xét hàm số đặc trưng
3 2
2 3 2 0, h t t t h t t t
.
3
3
*
f x f x f x f x
3 2
3 2
3 2
3 1 0 1
0
1 3 0 2
1
3 2 0 3
x x
f x
f x x x
f x
x x
Bấm máy, phương trình (1) có 3 nghiệm phân biệt, phương trình (2) có 2 nghiệm phân biệt, phương
trình (3) có 3 nghiệm phân biệt (không trùng nhau).
Vậy phương trình đã cho có
8
nghiệm phân biệt.
2. Tìm điều kiện để phương trình, bất phương trình có nghiệm
Câu 10. (Đề Chính Thức 18 - Mã 103) Cho phương trình với là tham số. Có bao
nhiêu giá trị nguyên của để phương trình đã cho có nghiệm ?
A. . B. . C. . D. .
Hướng dẫn giải
Chọn C
ĐK:
0
x m
(a).
Đặt ta có hệ .
Do hàm số đồng biến trên , nên ta có .
Khi đó: (thỏa điều kiện a).
7
7 log
x
m x m
m
25;25
m
9
25
24
26
7
log
t x m
7
7
x
t
m t
m x
7 7
x t
x t
1
7
u
f u u
1
t x
7 7
x x
m x m x
ThS. Nguyeãn Vaên Rin – HBT Trang 6/43
Xét hàm số .
Bảng biến thiên:
Từ đó phương trình đã cho có nghiệm khi và chỉ khi .
Do nguyên thuộc khoảng , nên .
Câu 11. (Đề tham khảo BGD 18) Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
3
3
3 3sin sinm m x x
có nghiệm thực?
A.
5
. B.
7
. C.
3
. D.
2
.
Lời giải
Chọn A
Ta có
33
3 3
3 3sin sin 3 3sin sinm m x x m x x m
.
Đặt
3
3
sin 1 1
3sin 3sin 3
u x u
v m x v m x m u
.
Ta có hệ
3
3 3
3
3
3 3 *
3
v u m
u u v v
v m u
.
Xét hàm số
3
3y f t t t
trên
.
2
3 1 0,f t t t
nên hàm số
f t
đồng biến trên
.
* f u f v u v
.
Suy ra
3 3
3 3 1u m u m u u
.
Xét hàm số
3
3g u u u
trên đoạn
1;1
.
Ta có
2
3 3 0 1
g u u u
.
1 2; 1 2g g
.
Suy ra
1;1
1;1
max 2;min 2g u g u
.
Do đó phương trình (1) có nghiệm khi và chỉ khi
2 2
m
.
Vì
m
nên
0; 1; 2m
.
Câu 12. Có bao nhiêu giá trị nguyên dương nhỏ hơn
2018
của tham số
m
để phương trình
2
log 2 2
x
m m x
có nghiệm thực?
A.
2017
. B.
2016
. C.
1005
. D.
1004
.
Lời giải
Chọn A
Điều kiện:
2 0
2 0
x
x
m a
m m b
.
Ta có
2 2
2
log 2 2 2 2 2 2 2 2 *
x x x x x x x
m m x m m m m
.
Xét hàm số
2
f t t t
trên khoảng
0;
.
Vì
2 1 0, 0f t t t
nên hàm số
f t
đồng biến trên khoảng
0;
.
7
x
g x x
1 7 ln7 0
x
g x
7
log ln 7
x
7
log ln 7 0,856
m g
m
25;25
24; 16;...; 1
m
ThS. Nguyeãn Vaên Rin – HBT Trang 7/43
Do đó
* 2 2 2 2 4 2
x x x x x x
f m f m m
.
Xét hàm số
4 2
x x
g x
trên
.
2
1
4 ln 4 2 ln 2 0 2. 2 2 0 2 1
2
x x x x x
g x x
.
Bảng biến thiên
YCBT
1
4
m
.
Vậy
1;2;...;2017m
.
Câu 13. (KHTN Hà Nội 19) Có bao nhiêu giá trị nguyên của tham số để phương trình
có nghiệm ?
A. . B. . C. . D. .
Lời giải
Chọn A
ĐK:
Ta có
Đặt ta có
Do hàm số đồng biến trên , nên ta có . Khi đó:
.
Xét hàm số .
Bảng biến thiên:
Từ đó phương trình đã cho có nghiệm khi và chỉ khi
(các nghiệm này đều thỏa mãn điều kiện vì )
Do nguyên và , nên .
Câu 14. Cho hàm số
3 3 2
1 3 4 2f x m x x m x
với
m
là tham số. Có bao nhiêu số nguyên
2018;2018m
sao cho
0f x
với mọi giá trị
2;4x
.
A.
4037
. B.
2021
. C.
2019
. D.
2020
.
Lời giải
Chọn D
Ta có
0f x
3 3 2
1 3 4 2 0m x x m x
(1).
Xét hàm số
3
g t t t
trên
, có
2
3 1 0g t t
,
t
.
m
10
m
1
4
2 log 2
x
x m m
9
10
5
4
2 0
x m
1
4
2 log 2
x
x m m
2
2 log 2 2
x
x m m
2
log 2
t x m
2 2
2 2
x
t
t m
x m
2 2
x t
x t
1
2
u
f u u
1
t x
2 2 2 2
x x
x m m x
2
x
g x x
g x
2 ln 2 1 0
x
2
log ln 2
x
2
2
log ln 2
2 log ln 2
2
g
m g m
0,457
2 2 0
x
x m
m
10
m
1, 2,3,4,5,6,7,8,9
m
3 3
1 1
x x mx mx
–
ThS. Nguyeãn Vaên Rin – HBT Trang 8/43
Do đó hàm số
g t
đồng biến trên
.
1 1g x g mx
1x mx
1x
m
x
,
2;4x
.
Vì hàm số
1x
h x
x
nghịch biến trên đoạn
2;4
nên
2;4
5
min 4
4
h x h
.
YCBT
2;4
minm h x
5
4
m
.
Vì
m
nguyên thuộc đoạn
2018;2018
nên có
2020
giá trị của
m
thỏa mãn.
Câu 15. (Chuyên Vĩnh Phúc 18) Tìm tất cả các giá trị của tham số để phương trình
có nhiều nghiệm nhất.
A. . B. . C. . D. .
Lời giải
Chọn B
Điều kiện
0
ln 0
m x a
m m x b
.
Phương trình đã cho tương đương với
ln
x
m m x e
(thỏa điều kiện b).
Đặt
y
m x e
(thỏa điều kiện a) .
Ta có hệ
*
.
Vì hàm số đồng biến trên nên
* f x f y
x x
m x e m e x
.
Xét hàm số ; ; .
BBT
Suy ra phương trình có nhiều nhất là hai nghiệm .
Câu 16. (SỞ CÀ MAU 19) Gọi
S
là tập tất cả các giá trị nguyên của tham số để bất
phương trình đúng
với mọi . Số phần tử của tập là
A. 4038. B.
2021
. C. 2022. D. 2020.
Lời giải
Chọn B
.
Xét: , ta có .
Hàm số luôn đồng biến trên .
* 2 1 2 1f x f m x x m x
2
1
x
m
x
.
YCBT
1;3
2 5
min
1 4
x
m m
x
.
Vì
m
nên
2019; 2018;...;1m
.
Vậy có giá trị cần tìm.
m
ln ln
m m x x
0
m
1
m
em
1
m
ln
m x y
e
y
m x
e
e e e e
e
x
x y x y
y
m y
y x x y
m x
e
t
f t t
x y
e
x
g x x
e 1
x
g x
0 0
g x x
1
m
2019;2019
m
3 3 3 2 3 3
1 3 2 13 3 10 0
m x m x m m x m m
1;3
x
S
3 3 3 2 3 3
1 3 2 13 3 10 0, 1;3
m x m x m m x m m x
3
3
2 2 1 1 , 1;3 . *
x x m x m x x
3
,f t t t t
2
3 1 0,f t t t
f t
2021
ThS. Nguyeãn Vaên Rin – HBT Trang 9/43
Câu 17. (ĐỀ 17 VTED 19) Có bao nhiêu số nguyên
m
để bất phương trình
6 4 3 2 2
6 15 3 6 10 0
x x mx m x mx
nghiệm đúng với mọi số thực
x
.
A.
4
. B.
3
. C. Vô số. D.
5
.
Lời giải
Chọn B
Ta có:
6 4 3 2 2 6 4 2 3 3 2 2
6 15 3 6 10 0 6 15 10 3 6x x mx m x mx x x x m x m x mx
3
3
2 2 2
2 3 2 1 3 1 2 1
x x mx mx f x f mx
Trong đó
3
3f x t t
đồng biến trên
.
2 2 2 2
2 1 2 1 1 0, 4 0 2 2
f x f mx x mx x mx x m m
.
Câu 18. (SỞ QUẢNG BÌNH 19) Gọi là tập hợp tất cả các giá trị nguyên dương của tham số để bất
phương trình sau nghiệm đúng với mọi . Tổng tất cả các
phần tử của bằng
A. . B.
2
. C.
1
. D.
4
.
Lời giải
Chọn A
Ta có:
Xét hàm đặc trưng
Bài toán trở thành tìm để bất phương trình nghiệm đúng với mọi
YCBT
2
m
.
Vì
m
nên
1;2 1 2 3
m S
.
Câu 19. (Chuyên Thái Bình 19) Có bao nhiêu giá trị nguyên của tham số để phương trình
có nghiệm biết .
A. 16. B. 15. C. 17. D. 18.
Lời giải
Chọn A
Đặt . Ta được hệ phương trình sau:
.
Vì nên hàm số đồng biến trên
. Do đó: .
Khi đó ta được: .
Dễ thấy đồng biến trên nên phương trình (**) có nghiệm trên đoạn khi
và chỉ khi:
Vì thuộc số nguyên nên có 16 số thỏa mãn bài toán.
S
m
6 4 3 3 2
3 4 2 0
x x m x x mx
1;3
x
S
3
6 4 3 3 2 6 4 2 3 3
3 4 2 0 3 4 2
x x m x x mx x x x m x mx
3
3
2 2
1 1 1
x x mx mx
3 2
' 3 1 0
f t t t f t t
2 2
1 1 1
f x f mx x mx
m
2
1
x mx
1;3
x
2
2
1
1 , 1;3
x
x mx m g x x
x
2
1;3
1
' 1 0 1;3 1 2
x
g x x Min g x g
x
m
3
3
( )
f f x m x m
1;2
x
5 3
( ) 3 4f x x x m
3
3
( ) ( )
t f x m t f x m
3 3 3
3
3 3
( ) ( ) ( ) (*)
( )
( )
( ) ( )
f t x m f t t f x x
f t x m
t f x m
f x t m f x t m
5 3 4 2
( ) 3 4 , '( ) 5 9 0,f x x x m f x x x x
3
( ) ( )
h x f x x
(*)
x t
3 5 3 5 3 5 3
1 2
( ) 3 4 2 3 ( ) (**)
3 3
f x x m x x m x x m g x x x m
5 3
1 2
( )
3 3
g x x x
1;2
1;2
(1) (2) 1 16.
g m g m
m
ThS. Nguyeãn Vaên Rin – HBT Trang 10/43
Câu 20. (Tập huấn Bắc Ninh 19) Cho phương trình
3 6 4 2
2 . 6 4 . 3 2 1 8 20 10 1
x x m x m x x x
. Biết
;
a
b
(với
,a b
là các số nguyên dương và phân số
a
b
tối giản) là tập tất cả các giá trị của tham số
m
để phương trình đã cho có hai nghiệm dương phân biệt. Tính
2 2
S a b
.
A.
17
. B.
5
. C.
25
. D.
10
.
Lời giải
Chọn C
Với
0
x
phương trình đã cho tương đương với
3
3
10 1
6 4 . 6 4 2 8 20x m x m x x
x x
3
3
1 1
6 4 2 6 4 2 2 2 *
x m x m x x
x x
.
Xét hàm số
3
2f t t t
trên
.
Ta có
2
3 2 0,f t t t
nên hàm số đồng biến trên
.
Do đó
2
1 1 1
* 6 4 2 6 4 2 4 2 6f x m f x x m x m x x
x x x
.
Xét hàm số
2
1
2 6g x x x
x
trên khoảng
0;
.
2 2
4 3
2 2
1
1 1 2 1 2 1
2 2 2 6 0 . 3 4 1 3
0,57... 0
x
x x
g x x x x
x
x x x x
.
Bảng biến thiên
YCBT
3
4
m
2 2
3 4 25
S
.
Câu 21. (TRẦN NHÂN TÔNG - QUẢNG NINH 18) Phương trình
3
2 3 3 2 2 1
2 6 9 2 2 1
x m x x x
x x x m
có
3
nghiệm phân biệt khi và chỉ khi
( ; )m a b
. Tính
2 2
T b a
.
A.
36
T
. B.
48
T
. C.
64
T
. D.
72
T
.
Hướng dẫn giải
Chọn B
Ta có
3
2 3 3 2 2 1
2 6 9 2 2 1
x m x x x
x x x m
3
3
3 3 2
2 2 8 3 2 2
m x x
x m x
3
3
3 2
2 3 2 2
m x x
m x x
*
.
Xét hàm số
3
2
t
g t t
trên
.
2
2 .ln 2 3 0,
t
g t t t
nên hàm số
g t
đồng biến trên
.
Do đó
3 3
* 3 2 3 2
g m x g x m x x
3
3 2
m x x
2 3
8 9 6
m x x x
.
Xét hàm số
3 2
6 9 8f x x x x
trên
.
có
2
3 12 9f x x x
;
3
0
1
x
f x
x
.
Bảng biến thiên
–
ThS. Nguyeãn Vaên Rin – HBT Trang 11/43
Dựa vào bảng biến thiên ta có, phương trình có 3 nghiệm phân biệt khi
4 8
m
.
Suy ra
4; 8
a b
2 2
48
T b a
.
Câu 22. (SGD Bà Rịa Vũng Tàu 18) Có bao nhiêu giá trị nguyên của tham số
m
để tồn tại cặp số
;x y
thỏa
3 5 3 1
e e 1 2 2
x y x y
x y
và
2 2
3 3
log 3 2 1 6 log 9 0
x y m x m
.
A.
6
. B.
5
. C.
8
. D.
7
.
Lời giải
Chọn B
Điều kiện
0
3 2 1 0
x
x y
.
Ta có:
3 5 3 1
e e 1 2 2
x y x y
x y
3 5 3 1
e 3 5 e 3 1
x y x y
x y x y
*
.
Xét hàm số
e
t
f t t
trên
.
Ta có
e 1 0
t
f t
nên hàm số đồng biến trên
.
Do đó
*
3 5 3 1
f x y f x y
3 5 3 1x y x y
2 1 2y x
.
Thế vào phương trình còn lại ta được
2 2
3 3
log 6 log 9 0
x m x m
.
Đặt
3
logt x
, phương trình trở thành
2 2
6 9 0
t m t m
1
.
Phương trình
1
có nghiệm
0
2
3 12 0
m m
0 4
m
.
Do đó có
5
số nguyên
m
thỏa mãn.
Câu 23. (SỞ BÀ RỊA VŨNG TÀU 19) Cho phương trình
3 2 2
2 5 3
3 3 3 5 0
x x x m x x
x x m
. Gọi
S
là
tập hợp các giá trị nguyên của tham số
m
để phương trình trên có ba nghiệm phân biệt. Số phần tử
của
S
là
A.
2
. B.
4
. C.
3
. D.
1
.
Lời giải
Chọn C
Phương trình đã cho trở thành
3 2 2
2 3 2 5 2
3 2 3 5
x x x m x x
x x x m x x
. (1)
Xét hàm số
3
t
f t t
,
t
có
3 .ln3 1 0
t
f t
,
t
f t
luôn đồng biến trên
.
Do đó phương trình
3 2 2 3
(1) 2 5 3 5
x x x m x x m x x
. (2)
Xét hàm số
3 2
3 5 3 3; 0 1
g x x x g x x g x x
.
Ta có bảng biến thiên
x
1
1
g x
0
0
g x
7
3
Từ bảng biến thiên ta thấy, phương trình đã cho có ba nghiệm phân biệt
(2)
có ba nghiệm phân biệt
3 7
m
. Vì
m
nên
4;5;6
m
. Vậy có 3 giá trị
m
nguyên.
Câu 24. Cho phương trình
2 1 sin
cos sin
e e 2 sin cos
x
m x x
x m x
với
m
là tham số thực. Gọi
S
là tập tất cả
các giá trị của
m
để phương trình có nghiệm. Khi đó
S
có dạng
; ;a b
 
. Tính
10 20T a b
.
A.
10 3
T . B.
0
T
. C.
1T
. D.
3 10
T .
Lời giải
Chọn A
ThS. Nguyeãn Vaên Rin – HBT Trang 12/43
Ta có
2 1 sin
cos sin
e e 2 sin cos
x
m x x
x m x
2 1 sin
cos sin
e cos sin e 2 1 sin
x
m x x
m x x x
Xét hàm số
e
t
f t t
t
,
e 1 0
t
f t
f t
đồng biến trên
.
Suy ra
2 1 sin
cos sin
e cos sin e 2 1 sin cos sin 2 1 sin
x
m x x
m x x x m x x x
cos sin 2
m x x
.
Phương trình có nghiệm khi
2 2
1 4 3
m m
.
; 3 3;S
 
. Vậy
10 20T a b
10 3
.
Câu 25. (Chuyên Lương Thế Vinh – Đồng Nai 18) Có bao nhiêu số nguyên
m
để phương trình
2
2
2
2
3 3 1
log 5 2
2 1
x x m
x x m
x x
có hai nghiệm phân biệt lớn hơn
1
.
A.
3
. B. Vô số. C.
2
. D.
4
.
Lời giải
Chọn C
Điều kiện:
2
3 3 1 0
x x m
(a).
Ta có:
2
2
2
2
3 3 1
log 5 2
2 1
x x m
x x m
x x
2
2
2
2
3 3 1
log 1 5 1
2 1
x x m
x x m
x x
2
2
2
2
3 3 1
log 5 1
4 2 2
x x m
x x m
x x
2 2 2 2
2 2
log 3 3 1 log 4 2 2 4 2 2 3 3 1
x x m x x x x x x m
2 2 2 2
2 2
log 3 3 1 3 3 1 log 4 2 2 4 2 2
x x m x x m x x x x
1
Xét hàm số:
2
logf t t t
trên
0;

, ta có
1
f t
,
0;t

.
Do đó hàm số
f t
đồng biến trên
0;

.
Suy ra:
2 2
1 4 2 2 3 3 1
f x x f x x m
2 2
4 2 2 3 3 1
x x x x m
(thỏa điều kiện a)
2
5 1
x x m
2
. Điều này đúng với mọi
x
.
Xét hàm số:
2
5g x x x
trên
, ta có
5
2 5 0
2
g x x x
.
Bảng biến thiên:
Theo bảng biến thiên ta thấy: phương trình
2
có hai nghiệm phân biệt lớn hơn
1
khi và chỉ khi
25
1 4
4
m
21
3
4
m
.
Do
m
nên
5; 4
m
.
Vậy có
2
giá trị nguyên của
m
thỏa mãn yêu cầu bài toán.
ThS. Nguyeãn Vaên Rin – HBT Trang 13/43
Câu 26. (SGD Phú Thọ 18) Có bao nhiêu giá trị nguyên dương của tham số
m
để phương trình
2
2
2
2 1
log 2 1 2
2
x mx
x mx x
x
có hai nghiệm thực phân biệt?
A.
3
. B.
4
. C.
2
. D.
1
.
Lời giải
Chọn B
Điều kiện:
2
2 0
2 1 0
x
x mx
.
Ta có
2
2
2
2 1
log 2 1 2
2
x mx
x mx x
x
2 2
2 2
log 2 1 2 1 log 2 2x mx x mx x x
2
2 1 2
f x mx f x
1
Xét hàm số
2
log
f t t t
với
0;t

có
1
1 0
ln 2
f t
t
,
0;t

.
f t
đồng biến trên
0;

nên
1
2
2 1 2
x mx x
.
Từ đó
2
2
2
2
2
4 3 0 2
2 1 2
x
x
x m x
x mx x
.
YCBT
2
có hai nghiệm phân biệt
1
x
,
2
x
lớn hơn
2
2
1 2
1 2
4 12 0
2 2 0
2 2 0
m
x x
x x
1 2
1 2 1 2
4 0
2 4 0
m
x x
x x x x
4 4 0
3 2 4 4 0
m
m
m
8
9
9
2
2
m
m
m
mà
*
1;2;3;4
m m
.
Câu 27. (SGD Bắc Ninh 18) Tập hợp tất cả các giá trị thực của tham số
m
để phương trình
3 2 2
2 1 1 1
m m
e e x x x x
có nghiệm là
A.
1
0; ln 2
2
. B.
1
; ln 2
2

. C.
1
0;
e
. D.
1
ln 2;
2

.
Lời giải
Chọn B
Đặt
2
2 2 2 2
1
1 1 2 1 1
2
t
t x x t x x x x
.
2
2 2
1
1
1 1
x x x
t
x x
;
2
2 2
0 1
2
0 1
2
1
x
t x x x
x x
.
2
1 1; 1 1; 2 1 2
2
t t t t
.
Phương trình trở thành
2
3 3 3
1
2 . 1 *
2
m m m m
t
e e t e e t t
.
Xét hàm
3
f u u u
trên
.
2
3 1 0,f u u u
nên hàm số
f u
đồng biến trên
.
*
m m
f e f t e t
.
ThS. Nguyeãn Vaên Rin – HBT Trang 14/43
Phương trình có nghiệm
1
1 2 ln 2
2
m
e m
.
Câu 28. (SỞ NAM ĐỊNH 19) Cho hàm số
2019 2019
x x
f x
. Tìm số nguyên
m
lớn nhất để
2 2019 0
f m f m
A.
673
. B.
674
. C.
673
. D.
674
.
Lời giải
Chọn B
Hàm số
2019 2019
x x
f x
xác định trên
.
Ta có:
2019 2019 2019 2019
x x x x
f x f x f x
là hàm lẻ trên
.
Mà
2019 ln 2019 2019 ln 2019 0,
x x
f x x
nên hàm số
f x
đồng biến trên
.
Do vậy:
2 2019 0 2 2019
f m f m f m f m
2 2019 2 2019 673
f m f m m m m
Do đó giá trị
m
nguyên lớn nhất thỏa mãn là
674
.
Câu 29. (Đặng Thành Nam 19) Cho hàm số
2
ln 1
f x x x
. Có tất cả bao nhiêu số nguyên
m
thỏa
mãn bất phương trình
1
log log 0
2019
m
f m f
A.
65
. B.
66
. C.
64
. D.
63
.
Lời giải
Chọn C
Điều kiện:
1
m
.
Hàm số
2
ln 1
f x x x
có TXĐ
D
.
Ta có
2 2
2
1
ln 1 ln ln 1
1
f x x x x x f x
x x
,
x
.
Mặt khác
2
1
' 0,
1
f x x
x
, nên
f x
đồng biến trên
.
Khi đó ta có
log 2019
1 1 1
log log 0 log log log log
2019 2019 2019
1 log 2019
log log log 10 65,77.
2019 log
m m m
m
f m f f m f f m f
m m m
m
Suy ra
2;3;...;65
m
. Vậy có tất cả 64 số nguyên
m
thỏa mãn.
Câu 30. (Đặng Thành Nam 19) Cho hàm số
2
1
( ) e e e
x x x
f x
. Có bao nhiêu số nguyên dương
m
thỏa
mãn bất phương trình
12
7 0
1
f m f
m
?
A.
4
. B.
6
. C.
3
. D.
5
.
Lời giải
Chọn D
Tập xác định
D
.
Ta có
2
1x x x
f x e e e f x
.
Suy ra
f x
là hàm số lẻ.
2 2
1 1x x x x
f x e e
2 2
1 1
2 2
'( ) 1 e 1 e 0,
1 1
x x x x
x x
f x x
x x
.
f x
đồng biến trên
.
ThS. Nguyeãn Vaên Rin – HBT Trang 15/43
12
( 7) 0
1
f m f
m
12 12
( 7)
1 1
f m f f
m m
.
1 5
12
7 .
1
1
m
m
m
m
Vì
m
là số nguyên dương nên
1,2,3,4,5 .
m
Câu 31. (ĐỀ 08 VTED 19)
Cho hàm số
2 2
x x
f x
. Có bao nhiêu số nguyên
m
để bất phương trình
3 2 2
2 3 2 5 0
f x x x m f x x
có nghiệm đúng với mọi
0;1
x
.
A.
7
. B.
3
. C.
9
. D.
8
.
Lời giải
Chọn D
Ta có
2 2
x x
f x f x
và
2 ln 2 2 ln 2 0,
x x
f x x
.
Suy ra
3 2 2
2 3 2 5 0
f x x x m f x x
3 2 2
2 3 2 5
f x x x m f x x
3 2 2
2 3 2 5x x x m x x
3 2 2 3 2
3 2 2 3 2
2 3 2 5 3 5 5
2 3 2 5 5
x x x m x x x x x m
x x x m x x x x x m
Xét hàm số
3 2
3 5 5, 0;1
g x x x x x
có
0;1
max 2
g x
3 2
5, 0;1
h x x x x x
có
0;1
min 5
h x
Do đó
3 2
3 2
3 5 5
5
x x x m
x x x m
,
0;1
x
2
5
m
m
.
Vậy có
8
nguyên thỏa mãn.
Câu 32. Cho hàm số
2
1
y f x x x
. Tìm các giá trị của
m
để bất phương trình
3
3
2019
0
2019
x x
x m f x m
f x x
nghiệm đúng với mọi
x
4;16
.
A.
35228
m
. B.
36416
m
. C.
38421
m
. D.
34662
m
.
Lời giải
Chọn B
Xét
2
2
2
1 1
1 1
1
f x x x x x
f x
x x
Ta có
3
3
2019
0
2019
x x
x m f x m
f x x
3
3
2019
2019
x x
x m f x m
f x x
3 3
2019 2019 1
x m f x m x x f x x
(Vì
1
f x
f x
).
Xét hàm số
2
. 1
g t t f t t t t
trên .
2 2
2 2 2
2 2
1 2 2 1 . 2 2 2
1 1
AM GM
t t
g t t t t t t t
t t
2 2 0g t t t
.
Vậy hàm số
g t
luôn đồng biến trên
.
3 3 3
1 2019 2019 2020g x m g x x x m x x m x x
.
1
nghiệm đúng với mọi
x
3
4;16
2020 36416
m Max x x
.
4;16
ThS. Nguyeãn Vaên Rin – HBT Trang 16/43
Câu 33. (Yên Mô A – Ninh Bình 19) Tổng tất cả các giá trị nguyên của tham số
m
để phương trình
3
3 3 3 2 3
3 9 24 .3 3 1
x m x x x
x x x m
có ba nghiệm phân biệt bằng
A.
45
. B.
38
. C.
34
. D.
27
.
Lời giải
Chọn D
Phương trình tương đương với
3 3
3
3 3 3 2 3 3 3
3 9 24 .3 3 1 3 3 3 3 *
x m x x x m x x
x x x m m x x
.
Xét hàm đặc trưng
3
3
t
f t t
trên
.
2
3 ln3 3 0,
t
f t t t
nên hàm số
f t
đồng biến trên
.
3
3 3
* 3 3 3 3 3 3f m x f x m x x m x x
3 2
9 24 27
m x x x
.
Đặt
3 2
9 24 27
g x x x x
2
2
3 18 24 0
4
x
g x x x
x
.
Ta có bảng biến thiên:
Phương trình có
3
nghiệm phân biệt
7 11
m
.
Vì
8;9;10 8 9 10 27
m m S
.
Câu 34. (YÊN LẠC 19) Cho phương trình
2 3 3
27 3 .9 3 1 3 1 1
x x x
x x m x m x
,
m
là tham số.
Biết rằng giá trị
m
nhỏ nhất để phương trình đã cho có nghiệm trên
0;
là
elna b
, với
,a b
là
các số nguyên. Giá trị của biểu thức
17 3a b
bằng
A.
26
. B.
54
. C.
48
. D.
18
.
Lời giải
Chọn A
Phương trình đã cho tương đương
2 3
3
3 2
3 3 3 . 3 3 3
x x x x
x x x x mx mx
3
3
3 3
x x
x x mx mx
(*).
Xét hàm số
3
f t t t
có
2
3 1 0,
f t t t f t
là hàm đồng biến trên
.
Do đó từ
*
suy ra
3
x
x mx
. Vì
0
x
suy ra
3
1
x
m
x
.
Xét hàm số
3
( ) 1
x
f x
x
trên
0;
.
Ta có
3
2
3 ln 3 3
1
0 3 ln 3 1 0 log e
ln3
x x
x
x
f x x x
x
.
Dấu của
f x
cũng là dấu của nhị thức bậc nhất
ln 3 1
x
, do đó ta có bảng biến thiên:
ThS. Nguyeãn Vaên Rin – HBT Trang 17/43
Từ bảng biến thiên suy ra giá trị nhỏ nhất của
m
để phương trình có nghiệm là
1 eln3
m
.
Suy ra
1, 3 17 3 17 9 26
a b a b
.
Câu 35. (Sơn Tây Hà Nội 19) Cho phương trình
2
1
2
2 2
2 .log 2 3 4 log 2 2
x mx
x x x m
với
m
là
tham số thực. Có bao nhiêu giá trị nguyên của
m
trên đoạn
2019;2019
để phương trình có đúng 2
nghiệm phân biệt.
A.
4036
. B.
4034
. C.
4038
. D.
4040
.
Lời giải
Chọn C
Điều kiện:
x
.
2
1
2
2 2
2 .log 2 3 4 log 2 2
x mx
x x x m
1
.
Xét hàm số
2
2 .log 2
t
y t
với
0t
.
Ta có
2
2
2 .log 2 .ln 2 0, 0
2 ln 2
t
t
y t t
t
.
Vậy hàm số
2
2 .log 2
t
y t
đồng biến trên
0;
.
Từ
2
2 2
2
1 2
1 1 2 1 2
1 2
x x m
f x f x m x x m
x x m
2
2
2 4 1 1
2 1 2
m x x
m x
*
.
TH1:
1
có 2 nghiệm phân biệt và
2
vô nghiệm
3
1
2
1
2
2
m
m
m
.
TH2:
2
có 2 nghiệm phân biệt và
1
vô nghiệm
1
3
2
3
2
2
m
m
m
.
TH3:
1
có nghiệm
2
x
và
2
có nghiệm
0
x
3
2
1
2
m
m
m
.
Kết hợp với điều kiện
m
thuộc đoạn
2019;2019
ta có
1 3
2019; ;2019
2 2
m
.
Vì
m
nguyên nên nên ta có 4038 giá trị của
m
.
Câu 36. (Thanh Chương Nghệ An 19) Gọi
S
là tập hợp tất cả các giá trị nguyên của tham số
m
thuộc đoạn
10;10
để bất phương trình
2
2
3
2
2 1
log 2 4 5 2
1
x x m
x x m
x x
có nghiệm. Số phần tử của tập
hợp
S
bằng
A. 20. B. 10. C. 15. D. 5.
Lời giải
+
∞
+
∞
0
x
f'
f
log
3
e
+
+
0
∞
1+e.ln3
2
2
21
2 2
2 .log 1 2 2 log 2 2
x mx
x x m
ThS. Nguyeãn Vaên Rin – HBT Trang 18/43
Chọn B
Điều kiện xác định:
2
2
2 1
0
1
x x m
x x
2
2 1 0x x m
(vì
2
1x x
2
1 3
0
2 4
x
với mọi
x
). (*)
Khi đó:
2
2
3
2
2 1
log 2 4 5 2
1
x x m
x x m
x x
2
2
3
2
2 1
log 1 2 4 4 2
1
x x m
x x m
x x
2
2
3
2
2 1
log 2 4 4 2
3 1
x x m
x x m
x x
2 2
3 3
log 2 1 log 3 1x x m x x
2 2
2 2 1 6 1x x m x x
2
3
log 2 1x x m
2
2 2 1x x m
2
3
log 3 1x x
2
6 1x x
. (1)
Xét hàm số
3
log 2f t t t
với
0t
.
Ta có:
1
2 0, 0
.ln3
f t t
t
.
Suy ra hàm số
f t
đồng biến trên khoảng
0;
.
Do đó (1)
2
2 1f x x m
2
3 1f x x
2
2 1x x m
2
3 1x x
(thỏa mãn (*))
2
2 2x x m
.
BPT
2
2 2x x m
có nghiệm
minm g x
với
2
2 2g x x x
.
Xét hàm số
2
2 2g x x x
với
x
có
2 2g x x
.
0
g x
2 2 0x 1x
.
Bảng biến thiên
Từ bảng biến thiên suy ra
min 1g x
. Do đó
1m
.
Vì
10;10
m
nên tập
1;2;...;10
S
. Vây
S
có 10 phần tử.
Câu 37. (PHỤ DỰC – THÁI BÌNH 19) Tìm số giá trị nguyên của
m
thuộc
20;20
để phương trình
2 2 2
2
log ( 4) (2 9) 1 (1 2 ) 4x m x x m x m x
có nghiệm?
A. 12. B. 23. C. 25. D. 10.
Lời giải
Chọn B
Điều kiện xác định:
2 2
4 0x m x x
.
2 2 2
2
log 4 2 9 1 1 2 4x m x x m x m x
2 2 2
2
log 4 2 9 1 4 2 4x x x m mx x x m x
2 2
2
2
4
log 2 9 1 4 2 4
4
x
m mx x x m x
x x
2
2 2
2
2
4 4
log 2 9 1 4 2 4
4
x m x mx
mx x x m x
x x
ThS. Nguyeãn Vaên Rin – HBT Trang 19/43
2 2 2 2
2 2
log 4 4 8 2 4 2 1 log 4 4x m x mx x m x mx x x x x
2 2 2 2
2 2
log 8 2 4 2 8 2 4 2 log 4 4 1
x m x mx x m x mx x x x x
Xét
hàm số
2
logf t t t
,
0;t 
.
1
1 0, 0;
ln 2
f t t
t
nên hàm số luôn đồng biến trên khoảng
0;
.
Khi đó
1
2 2
8 2 4 2 4x m x mx x x
2 2
2 4 4 8m x x x x x
2
8
2 1
4
x
m
x x
2
8 4
2 1
4
x x x
m
2 2 2
1 2
2 1 2 4 4
2
m
m x x x x x x
.
Xét hàm số
2 2
4g x x x x
với
;x 
.
Ta có
2
2
2
4
( ) 0,
4
x x
g x x
x
.
2
lim lim 4
x x
g x x x x
 
2
4
lim
4
x
x
x x

2
4
lim 2
4
1 1
x
x

;
2
2
4
lim lim 1 1
x x
g x x
x
 

.
Ta có bảng biến thiên của
( )g x
Để phương trình có nghiệm thì
1 2 5
2
2 2
m
m
.
Do
m
nguyên thuộc
20;20
nên số giá trị
m
là 23.
Câu 38. (CHUYÊN THÁI NGUYÊN 19) Gọi
S
là tập hợp các giá trị nguyên dương của
m
để phương trình
3
cos 2 3cos 3 2 cos 2 cos 1
2 cos 6sin 9cos 6 2 2 1
x m x x x
x x x m
có nghiệm thực . Khi đó tổng của
hai phần tử lớn nhất và nhỏ nhất của tập
S
bằng
A.
28
. B.
21
. C.
24
. D.
4
.
Lời giải
Chọn A
Ta có
3
3
cos 2 3cos cos 2
2 cos 2 3cos 2 1
x m x x
x m x
3
3
3
3cos 2 cos
3
2 3cos 2 2 cos
m x x
m x x
*
.
Xét hàm số đặc trưng
3
2
u
f u u
trên
.
2
2 ln 2 3 0,
u
f u u u
nên hàm số đồng biến trên
.
3
* 3cos 2 cosf m x f x
3
3cos 2 cosm x x
3 2
cos 6cos 9cos 8x x x m
.
ThS. Nguyeãn Vaên Rin – HBT Trang 20/43
Đặt cos x t với điều kiện
1;1t
, suy ra
3 2
6 9 8f t t t t m
.
Dễ thấy
1;1
min 4
t
f t
và
1;1
max 24
t
f t
nên phương trình đã cho có nghiệm khi và chỉ khi
4;24m
. Suy ra
4;5;...;24S
nên tổng của hai phần tử lớn nhất và nhỏ nhất của
S
bằng 28 .
Câu 39. (Thuận Thành 2 Bắc Ninh 19) Gọi
S
là tập chứa các giá trị nguyên của
m
để phương trình
3 3
3 18 30 6 10 2
1
x x m x x m m
e e e
có 3 nghiệm thực phân biệt. Tính tổng các phần tử của tập
S
.
A.
110
. B.
106
. C.
126
. D.
24
.
Lời giải
Chọn A
Đặt
3
6 10t x x
.
Ta có phương trình
3 2 3 3
1 (1)
t m t m m t t m m
e e e e e e e
.
Xét hàm số
3
( )
x x
f x e e xác định trên
.
Ta có
3
( ) 3 0,
x x
f x e e x
.
Suy ra
( )f x
đồng biến trên
.
Từ
1
, ta có
( ) ( )f t f m
, suy ra t m hay
3
6 10 (2)x x m .
Phương trình
3 3
3 18 30 6 10 2
1
x x m x x m m
e e e
có
3
nghiệm thực phân biệt khi phương trình
(2)
có
3
nghiệm thực phân biệt.
Xét hàm số
3
( ) 6 10g x x x với
x
.
2 2
( ) 3 6 3 2 ; ( ) 0 2g x x x g x x
.
Ta có bảng biến thiên của
( )g x
Dựa vào bảng biến thiên, phương trình
(2)
có
3
nghiệm thực phân biệt khi và chỉ khi
10 4 2 10 4 2m
.
Ta có
10 4 2 4,34
và
10 4 2 15,66
. Suy ra
{5;6;7;8;9;10;11;12;13;14;15}S
.
Tổng các phần tử của
S
là
11
5 15 110
2
.
Câu 40. (CHUYÊN THÁI NGUYÊN 19) Tìm tất cả các giá trị thực của tham số
m
để phương trình
2 2
5 12 16 2 2
x x m x x
có hai nghiệm thực phân biệt thoả mãn
2 1 2 1
2018 2018 2019 2019
x x x
x
.
A.
11 3
2 6 ;
3
m
. B.
2 6 ;3 3m
.
C. 2 6 ;3 3m
. D.
11 3
3 3; 2 6
3
m
.
Lời giải
Chọn B
Xét bất phương trình
2 1 2 1
2018 2018 2019 2019 (1)
x x x
x
. Điều kiện:
1x
.
Đặt
2 1
2( 1) 1
2
2 1
a x x
a b
a b x x
b x
.
ThS. Nguyeãn Vaên Rin – HBT Trang 21/43
(1)
trở thành
2018 2018 2019 0 2(2018) 2019 2(2018) 2019 (2)
2
a b a b
a b
a b
.
Xét hàm số ( ) 2(2018) 2019
t
f t t liên tục trên
.
( ) 2.2018 ln 2018 2019 0,
t
f t t
nên
( )f t
đồng biến trên
.
Bất phương trình
(2) ( ) ( ) 2 1 2 1 1 1f a f b a b x x x x
.
Với
1 1x
, ta có:
2 2
5 12 16 2 2
x x m x x
2
2 2
3 2 2 2 2 2 x x m x x
2
2
2 2
3 2 (3)
2
2
x x
m
x
x
.
Đặt
2
2
2
x
t
x
với
1;1x
.
3
2
2 2
0, 1;1
2
x
t x
x
nên hàm t đồng biến trên
1;1
, suy ra
1
3
3
t .
Do hàm t đơn điệu trên
1;1
nên ứng với mỗi giá trị của
1
; 3
3
t
ta tìm được đúng một giá trị
của
1;1
x
và ngược lại.
Viết lại phương trình (3) theo ẩn t :
2
3 4 t m
t
với
1
3
3
t .
(3)
có 2 nghiệm thực phân biệt
1;1x
(4)
có 2 nghiệm thực phân biệt
1
; 3
3
t
(*)
.
Xét hàm số
2
( ) 3g t t
t
liên tục trên
1
; 3
3
.
2
2
( ) 3
g t
t
. Cho
2
2 2 1
( ) 0 ; 3
3 3
3
g t t t
.
Bảng biến thiên:
Dựa vào bảng biến thiên, ta có
(*)
2 6 ;3 3m
Vậy
2 6 ;3 3m
thoả yêu cầu bài toán.
Câu 41. (KIM LIÊN - HÀ NỘI 19) Cho bất phương trình . Tìm tất
cả các giá trị thực của tham số để bất phương trình nghiệm đúng với mọi .
A. . B. . C. . D.
.
Lời giải
Chọn D
Ta có:
(1)
3 3
4 2 2 2 2
2 1 1 1
x x m x x x m
m
1x
1
2
m
1
m
1
2
m
1
m
3 3
4 2 2 2 2
2 1 1 1
x x m x x x m
3 3
4 2 4 2 2 2
2 1 2 1 0
x x m x x m x x
3 3
4 2 4 2 2 2
2 1 2 1
x x m x x m x x
ThS. Nguyeãn Vaên Rin – HBT Trang 22/43
Xét hàm số , .
Có nên hàm số đồng biến trên .
Bất phương trình (1) có dạng
.
Xét hàm số với .
Bất phương trình đã cho nghiệm đúng với mọi , .
.
Bảng biến thiên:
Tập giá trị của hàm số trên là .
Vậy , .
Câu 42. (Nguyễn Du 19) Cho hàm số
f x
liên tục trên
có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên
của
n
để phương trình sau có nghiệm
x
.
2
16sin 6sin 2 8 1f x x f n n
A. 10. B. 6. C. 4. D. 8.
Lời giải
Chọn B
Nhìn vào đồ thị ta thấy hàm số
f x
luôn đồng biến trên
, do đó
2 2
16sin 6sin 2 8 1 16sin 6sin 2 8 1f x x f n n x x n n
Ta xét
2
16sin 6sin 2 8 1
8 1 cos 2 6sin 2 8 1 0
8cos 2 6sin 2 1 0
x x n n
x x n n
x x n n
Để phương trình có nghiệm
x
thì
2 2
2 2 2 2 2
8 6 100 10 10n n n n n n
2
1 41 1 41
10
2 2
n n n
(do
2
10,n n n ).
Vì
n
nguyên nên
3; 2; 1;0;1;2
n
.
Câu 43. (Ngô Quyền - Hà Nội 19) Tập hợp tất cả các giá trị của tham số
m
để phương trình
1 1 sin sinm m x x
có nghiệm là đoạn
;a b
. Khi đó giá trị của biểu thức
1
4 2
T a
b
bằng
A.
4
. B.
5
. C.
3
. D.
3
.
Lời giải
3
f t t t
t
2
3 1 0, f t t t
f t
3 3 3 34 2 2 4 2 2
2 1 2 1
f x x m f x x x m x
4 2 2
2 1
x x m x
4 2
1
m x x
4 2
1
g x x x
1;x

1x
m g x
1x
3 2
4 2 2 2 1 0, 1g x x x x x x
g x
1;

;1
m g x
1x
1
m
ThS. Nguyeãn Vaên Rin – HBT Trang 23/43
Chọn A
Ta có
1 sin 1 0 1 sin 2 0 1 sin 2,x x x x
.
Đặt
1 sint x
. Ta có
0 2t
và
2
sin 1x t
.
Khi đó phương trình có dạng:
2 2
1 1 1 1m m t t m t m t t t
*
.
Xét hàm số
2
, 0f t t t t
.
Ta có
2 1 0, 0f t t t
.
Do đó hàm số
2
f t t t
luôn đồng biến trên
0;
.
Vì thế
2
* 1 1t m t m t t
**
Xét hàm số
2
1, 0; 2g t t t t
.
2 1g t t
;
1
0 2 1 0
2
g t t t
.
Bảng biến thiên của hàm số
2
1, 0; 2g t t t t
Phương trình đề bài có nghiệm
**
có nghiệm
5
0; 2 1 2
4
t m
.
Vậy
5
;1 2
4
m
nên
5
; 1 2 4
4
a b T
.
Câu 44. (TT Thanh Tường - Nghệ An 19) Cho hàm số
3 3
7 3 7 3 2019f x x x x
. Gọi
S
là tập hợp
các giá trị nguyên của m thỏa mãn điều kiện
3 2 2
2 3 2 2 5 0, 0;1f x x x m f x x x .
Số phần tử của
S
là
A.
7
. B.
3
. C.
9
. D.
5
.
Lời giải
Chọn C
Vì
3 3
7 3 7 3 2019f x x x x
là hàm số lẻ và đồng biến trên
nên ta có
3 2 2
2 3 2 2 5f x x x m f x x
3 2 2
2 3 2 2 5f x x x m f x x
3 2 2
3 2 2
3 2 2
2 3 2 2 5
2 3 2 2 5
2 3 2 2 5
x x x m x x
x x x m x x
x x x m x x
3 2
3
4 5 5
5
x x x m
x x m
.
Xét
3 2
4 5 5
g x x x x
và
3
5
h x x x
trên
0;1
có bảng biến thiên là
ThS. Nguyeãn Vaên Rin – HBT Trang 24/43
Từ bảng biến thiên suy ra
3 2 2
2 3 2 2 5 0, 0;1f x x x m f x x x khi và chỉ khi
3
3 5
5
m
m
m
.
Câu 45. (Thị Xã Quảng Trị 19) Cho hàm số
y f x
liên tục trên
và có đồ thị như hình vẽ bên. Tìm giá
trị của tham số
m
để phương trình
3
2
2
2
1
m m
f x
f x
có đúng ba nghiệm thực phân biệt.
A.
2m
. B. 26m . C. 10m . D.
1m
.
Lời giải
Chọn B
Phương trình tương đương
3
3 2 2
1 1 (*)m m f x f x
Xét hàm số
3
f t t t
trên
có
2
3 1 0f t t t
nên hàm số đồng biến trên
.
Từ phương trình
2
(*) 1m f x
( Đk
1m
). Khi đó phương trình
2
2 2 2
2
1 (1)
1 1
1 (2)
f x m
m f x f x m
f x m
Nếu
1m
ta có
0f x
phương trình có 2 nghiệm nên
1m
(loại).
Nếu
1m
phương trình
(2)
có đúng một nghiệm. Như vậy để phương trình đã cho có ba nghiệm phân
biệt thì phương trình
(1)
có đúng hai nghiệm phân biệt suy ra
2
26
1 5
26
m
m
m
, do
1m
nên ta chọn 26m .
Câu 46.
(Yên Phong 19) Cho hàm số
y f x
liên tục trên
và có đồ thị như hình vẽ. Có bao nhiêu giá trị
của tham số
m
để phương trình sau có
3
nghiệm phân biệt
3
2
2
4
3
2 5
m m
f x
f x
.
A.
0
. B.
1
. C.
2
D.
3
.
Lời giải
Chọn B
Phương trình đã cho tương đương
3 2 2
4 3 2 5m m f x f x
1
2
3
6
1
O
1
4
y
x
ThS. Nguyeãn Vaên Rin – HBT Trang 25/43
3 2 2
8 2 2 5 1 2 5m m f x f x
3
3
2 2
2 2 2 5 2 5m m f x f x .
Xét hàm số
3
g a a a
,
a
. Ta có
2
3 1 0g a a
,
a
.
Do đó,
g a
đồng biến trên
. Mặt khác,
2
2 2 5g m g f x
2
2 2 5m f x .
2 2
0
2 4 5
m
f x m
2
2
0
4 5 0
4 5
2
m
m
m
f x
2
5
2
4 5
2
m
m
f x
.
Phương trình đã cho có ba nghiệm phân biệt khi và chỉ khi đường thẳng
2
4 5
2
m
y
cắt đồ thị hàm
số
y f x
tại ba điểm phân biệt.
Từ đó,
2
4 5
4
2
m
2
4 5 32m
37
2
m
.
Đối chiếu với điều kiện, ta thu được
37
2
m
.
Vậy có đúng
1
giá trị của tham số
m
thỏa mãn yêu cầu bài toán.
Câu 47. (ĐỀ 16 VTED 19) Cho hàm đa thức bậc ba
y f x
có đồ thị của các hàm số
y f x
;
y f x
như hình vẽ bên. Gọi
S
là tập hợp tất cả các giá trị nguyên của
m
để phương trình
2 3f f x m f x x m
có đúng
3
nghiệm thực. Tổng các phần tử của
S
bằng
A.
0
. B.
6
. C.
7
. D.
5
.
Lời giải
Chọn C
2 3f f x m f x x m
. (1)
Xét hàm
3g t f t t
trên
.
Ta có
3
g t f t
.
3 3f f x m f x m f x x
1
2
3
6
1
O
1
4
y
x
ThS. Nguyeãn Vaên Rin – HBT Trang 26/43
Từ đồ thị hàm số
y f x
ta suy ra
3f x
x
. Dấu “
” chỉ xảy ra khi
1x
.
Do đó
3 0
g t f t
t
. Dấu “
” chỉ xảy ra khi
1t
.
Vậy hàm
3g t f t t
đồng biến trên
.
Ta có (1)
g f x m g x
f x m x
(Vì hàm
3g t f t t
đồng biến trên
)
f x x m
. (*)
Ta có
3 2
f x ax bx cx d
2
3 2f x ax bx c
.
Từ đồ thị hàm số ta có
1 0
0 0
2 0
1 3
f
f
f
f
0
0
12 4 0
3 2 3
a b c d
c
a b c
a b c
1
3
0
2
a
b
c
d
3 2
3 2f x x x
.
Vậy (*)
3 2
3 2
m x x x h x
.
Ta có
2
3 6 1 0h x x x
3 2 3
3
3 2 3
3
x
x
.
Bảng biến thiên
Phương trình có ba nghiệm phân biệt
h m h
4; ;2m
. Tổng các phần tử của
S
bằng
2
4
7m
.
3. Tìm GTLN, GTNN của hàm số
Câu 48. (MĐ 102 - BGD&ĐT 17) Xét các số thực dương thỏa mãn . Tìm giá
trị nhỏ nhất của .
A. . B. . C. . D. .
Lời giải
Chọn A
Điều kiện: .
Ta có .
Xét hàm số trên khoảng .
Ta có . Suy ra hàm số đồng biến trên khoảng .
Do đó .
Do nên .
, a b
2
1
log 2 3
ab
ab a b
a b
min
P
2P a b
min
2 10 3
2
P
min
3 10 7
2
P
min
2 10 1
2
P
min
2 10 5
2
P
1ab
2 2 2
1
log 2 3 log 2 1 2 1 log *
ab
ab a b ab ab a b a b
a b
2
log
y f t t t
0;
1
1 0, 0
.ln 2
f t t
t
f t
0;
2
* 2 1 2 1 2 1 2
2 1
b
f ab f a b ab a b a b b a
b
0, 0
a b
2
0 0 2
2 1
b
b
b
ThS. Nguyeãn Vaên Rin – HBT Trang 27/43
Khi đó: . Xét hàm số trên khoảng .
Lập bảng biến thiên
Vậy .
Câu 49. (Chuyên Vĩnh Phúc 18) Xét các số thực dương
x
,
y
thỏa mãn
1 2
ln 3 1
x
x y
x y
. Tìm giá trị
nhỏ nhất
min
P của
1 1
P
x
xy
.
A.
min
8P . B.
min
4P . C.
min
2P . D.
min
16P .
Lời giải
Chọn A
Điều kiện
1
0
2
x
.
Từ giả thiết
1 2
ln 3 1
x
x y
x y
ln 1 2 1 2 ln x x x y x y
1
Xét hàm số
ln f t t t
trên
0;
có
1
1 0
f t
t
,
0 t
do đó hàm
f t
đơn điệu.
Vậy
1 1 2 3 1 x x y x y
2
Có
1 1 1 2 1 2
1 2
P
x x x y x x
xy
Đặt
1 2
1 2
g x
x x
, ta có
2
2
1 4
1 2
g x
x
x
suy ra
1
0
4
g x x
.
Do đó
1
0;
2
min 8
g x . Vậy
min
8P .
Câu 50. (Lê Văn Thịnh - Bắc Ninh 18) Cho
0 ; 1x y
thỏa mãn
2
1
2
2018
2017
2 2019
x y
x
y y
. Gọi
M
,
m
lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức
2 2
4 3 4 3 25S x y y x xy
. Khi đó
M m
bằng bao nhiêu?
A.
136
3
. B.
391
16
. C.
383
16
. D.
25
2
.
Lời giải
Chọn B
Ta có
2
1
2
2018
2017
2 2019
x y
x
y y
1 2
2
2017 2018
2017
1 2018
y
x
x
y
2
2 2
2 1
b
P a b b
b
2
( ) 2
2 1
b
g b b
b
0;2
2
2
2 10
0;2
5 5
4
2 0 2 1
2
2 1
2 10
0;2
4
b
g b b
b
b
min
10 2 2 10 3
4 2
P g
ThS. Nguyeãn Vaên Rin – HBT Trang 28/43
2
1 2
2017 1 2018 2017 2018
y x
y x
Xét hàm số
2
2017 2018
t
f t t
, với
0 1t
.
2 2
2018 .2017 .ln 2017 2 .2017 2017 2018 .ln 2017 2 0
t t t
f t t t t t
Hàm số
f t
đồng biến trên
0 1t
1
y x
1y x
Theo giả thiết
2 2
4 3 4 3 25S x y y x xy
2
2
2 2
4 3 2 3 2 2 2
4 3 2
4 3 1 . 4 1 3 25 1
4 3 3 4 5 4 25 1
16 20 16 12 15 12 12 15 12 25 25
16 32 18 2 12
x x x x x x
x x x x x x
x x x x x x x x x x
x x x x
Xét hàm số
4 3 2
16 32 18 2 12
S x x x x x
, với
0 1x
.
3 2
64 96 36 2S x x x x
. Cho
0
S x
2 3
4
1
2
x
x
Bảng biến thiên
Từ bảng biến thiên, ta có
0;1
0;1
25
max
2
191
min
16
M S x
m S x
.
Vậy
25 191 391
2 16 16
M m
.
Câu 51. (Trần Phú – Đà Nẵng 18) Cho hai số thực
x
,
y
thỏa mãn:
3 2
2 7 2 1 3 1 3 2 1
y y x x x y
. Tìm giá trị lớn nhất của biểu thức
2P x y
.
A.
10
P
. B.
4P
. C.
6
P
. D.
8
P
.
Lời giải
Chọn B
3 2
2 7 2 1 3 1 3 2 1
y y x x x y
3 2
2 3 3 1 1 2 1 1 3 1 2 1
y y y y x x x x
.
3
3
2 1 1 2 1 1 1
y y x x .
Xét hàm số
3
2
f t t t
trên
0;
.
Ta có:
2
6 1
f t t
0
với
0
t
f t
luôn đồng biến trên
0;
.
Vậy
1 1 1
y x
1 1
y x
.
2 2 2 1
P x y x x
với
1
x
.
Xét hàm số
2 2 1
g x x x
trên
;1
.
191
16
12
+ 0
2- 3
4
+
191
16
1
0
12
2+ 3
4
y
y'
x
1
2
0
0
25
2
ThS. Nguyeãn Vaên Rin – HBT Trang 29/43
Ta có:
1
1
1
g x
x
1 1
1
x
x
.
0 0
g x x
.
Bảng biến thiên
g x
:
Từ bảng biến thiên của hàm số
g x
suy ra giá trị lớn nhất của
P
là:
;1
max 4
g x

.
Câu 52. (TRẦN NHÂN TÔNG - QUẢNG NINH 18) Cho hai số thực
,x y
thỏa mãn:
3
9 2 3 5 3 5 0
x y xy x xy
.
Tìm giá trị nhỏ nhất của
3 3 2
6 3 3 1 2
xy x x y
P x y
.
A.
296 15 18
9
. B.
36 296 15
9
. C.
36 4 6
9
. D.
4 6 18
9
.
Hướng dẫn giải
Chọn B.
Ta có
3
9 2 3 5 3 5 0
x y xy x xy
3
27 6 3 5 3 5 2 3 5
x x xy xy xy
.
Xét hàm
3
2f t t t
với
0;t

có
2
' 3 2 0 0;f t t t

nên hàm số liên tục và đồng biến trên
0;

.
Khi đó ta có
3 3 5
x xy
0
x
và
2
9 3 5x xy
.
Với
0
x
thì
0 5 l
.
với
0
x
thì
3 3 2
6 3 3 1 2
xy x x y
P x y
3 3 2
6 9 3 2
xy x x y
x y
3 3
6 3 2 2
xy xy x yx y
3 3 2 2
3 3 2 4
x y xy x yx y
3
2 4
x y x y
Mà
2
9 5 5 5 4 5
4 2 4 .
3 3 3
3
x
x y x x x
x x x
. Đặt
t x y
thì
4 5
3
t .
Xét
3
2 4f t t t
với
4 5
3
t . Khi đó
2
3 2 0
f t t
với
4 5
3
t .
Do đó
4 5 36 296 15
9
3
f t f
Suy ra
36 296 15
9
P
. Vậy GTNN của
P
là
36 296 15
9
.
Câu 53. (Đô Lương 4 - Nghệ An 18) Xét các số thực dương
, x y
thỏa mãn
2 2
3
log 3 3
2
x y
x x y y xy
x y xy
. Tìm giá trị lớn nhất của
3 2 1
6
x y
P
x y
.
A.
2
. B.
1
. C.
3
. D.
4
.
Lời giải
Chọn B
Ta có
2 2
3
log 3 3
2
x y
x x y y xy
x y xy
4
ThS. Nguyeãn Vaên Rin – HBT Trang 30/43
2 2 2 2
3 3
log 3 2 log 2 2
x y x y x y xy x y xy
2 2 2 2
3 3 3
log 3 log 3 log 2 2
x y x y x y xy x y xy
2 2 2 2
3 3
log 3 3 log 2 2
x y x y x y xy x y xy
*
.
Xét hàm số
3
log
f t t t
, với
0t
.
có
1
1 0
.ln 3
f t
t
,
0
t
.
Vậy hàm số
f t
liên tục và đồng biến trên khoảng
0;

.
Do đó:
2 2 2 2
3 2 3 2
f x y f x y xy x y x y xy
1
.
Từ
1
2
3 2
xy x y x y
.
Ta có
2
1
1
2
x y
x x xy xy x y xy xy
.
Đẳng thức xảy ra khi và chỉ khi
1 x y
.
Do đó từ
1
, suy ra:
2
2
1
3 2
4
x y
x x y x y .
Đặt
t x y
,
0t
.
Suy ra:
2
2
2
1
2 1 3 2
2 1
3 22 3
4
6 6 4 6
t
t t t
x y x
t t
P f t
x y t t
.
Ta có:
2
2
3 36 135
0 3
4 6
t t
f t t
t
(nhận).
Bảng biến thiên
Dựa vào BBT, ta có
0;
max max 3 1

P f t f
khi và chỉ khi
x y x
x y y
.
Câu 54. (SỞ HÀ TĨNH 19) Cho các số thực
, ,x y z
thỏa mãn
16
2 2 2
log 2 2 2
2 2 2 1
x y z
x x y y z z
x y z
. Tổng giá trị lớn nhất và nhỏ nhất của biểu
thức
x y z
F
x y z
bằng
A.
1
3
. B.
1
3
. C.
2
3
. D.
2
3
.
Lời giải
Chọn C
• Ta có:
16
2 2 2
log 2 2 2
2 2 2 1
x y z
x x y y z z
x y z
2 2 2 2 2 2
4 4
1 1
log log 2 2 2 1 2
2 2
x y z x y z x y z x y z
2 2 2 2 2 2
4 4 4
log log 2 2 2 1 log 4 2 2 2 1 4
x y z x y z x y z x y z
2 2 2 2 2 2
4 4
2 2 2 1 log 2 2 2 1 4 log 4 *
x y z x y z x y z x y z

3
0
t
f t
f t
0
ThS. Nguyeãn Vaên Rin – HBT Trang 31/43
• Xét hàm số
4
logf t t t
trên
0;
1
' 1 0, 0;
.ln 4
f t t
t
f t
đồng biến trên
0;
.
Khi đó: (*)
2 2 2
2 2 2 1 4
x y z x y z
2 2 2
1
2 2 2 0
2
x y z x y z
S
S
là mặt cầu tâm
1;1;1
I
và bán kính
10
2
R
.
• Ta có:
x y z
F
x y z
1 1 1 0
F x F y F z P
• Điều kiện tương giao của mặt phẳng
P
và măt cầu
S
:
;
d I P R
2 2 2
1 3
10
2
1 1 1
F
F F F
2
2 6 10 3 2 3
F F F
2
6 4 26 0
F F
1 2 10 1 2 10
3 3
F
.
max min
1 2 10 1 2 10
,
3 3
F F
.
max min
1 2 10 1 2 10 2
3 3 3
F F
.
Câu 55. (Chuyên Lam Sơn - Thanh Hóa 18) Cho
x
,
y
là các số thực dương thỏa mãn
2 2
3 5
5 1 3 ( 2)
3 5
xy
x y x y
xy
x y x . Tìm giá trị nhỏ nhất của biểu thức
T x y
.
A.
min
2 3 2
T
. B.
min
3 2 3
T
. C.
min
1 5
T
. D.
min
5 3 2
T
.
Lời giải
Chọn B.
Theo đề ra ta có
2 2
2 1
2 1
3 5
5 1 3 ( 2)
3 5
1 1
5 2 5 1
3 3
xy
x y x y
xy
x y xy
x y xy
x y x
x y xy
Xét
1
5
3
t
t
f t t
.
5 ln 5 3 ln3 1 0
t t
f t
1
2 1
2
x
x y xy y
x
.
Vì
0
y
nên
2
x
.
Ta có:
2
1 1
2 2
x x x
T x y x
x x
2
2
2 3 2;
4 1
0
2
2 3 2;
x
x x
T
x
x


Lập bảng biến thiên ta được
min
3 2 3
T
tại
2 3
x .
ThS. Nguyeãn Vaên Rin – HBT Trang 32/43
Câu 56. (THTT 18) Xét các số thực dương
,x y
thỏa mãn
2 2
3
log 3 3 .
2
x y
x x y y xy
x y xy
Tìm giá trị lớn nhất
max
P
của biểu thức
3 2 1
.
6
x y
P
x y
A.
3
. B.
2
. C.
1
. D.
4
.
Lời giải
Chọn C
Ta có:
2 2
3
log 3 3
2
x y
x x y y xy
x y xy
2 2 2 2
3 3
log 3 3 log 2 2
x y x y x y xy x y xy
.
Xét hàm số
3
log
f t t t
,
0t
có
1
1 0, 0
ln 3
f t t
t
. Vậy hàm số
f t
luôn đồng
biến và liên tục trên khoảng
0;

.
Do đó:
2 2 2 2
3 2 3 2
f x y f x y xy x y x y xy
1
Từ
1
2
3 2
xy x y x y
.
Ta có
2
1
1
2
x y
x x xy xy x y xy xy
Đẳng thức xảy ra khi và chỉ khi
1 x y
.
Do đó từ
1
, suy ra:
2
2
1
3 2
4
x y
x x y x y .
Đặt
t x y
,
0t
.
Suy ra:
2
2
2
1
2 1 3 2
2 1
3 22 3
4
6 6 4 6
t
t t t
x y x
t t
P f t
x y t t
.
Ta có:
2
2
3 36 135
0 3
4 6
t t
f t t
t
(nhận)
Bảng biến thiên
Dựa vào BBT, ta có
0;
max max 3 1

P f t f
khi và chỉ khi
x y x
x y y
.
Câu 57. (Trần Hưng Đạo - TP HCM 18) Xét các số thực dương
x
,
y
thỏa mãn
2
2 1
2
2
2018
1
x y
x y
x
. Tìm
giá trị nhỏ nhất
min
P
của
2 3P y x
.
A.
min
1
2
P
. B.
min
7
8
P
. C.
min
3
4
P
. D.
min
5
6
P
.
Lời giải
Chọn B
Ta có
2
2 1
2
2
2018
1
x y
x y
x
2
2018
2
2
2 1 log
1
x y
x y
x
2 2
2018 2018
2 1 2 2 log 2 log 1
x x y x y x

3
0
t
f t
f t
0
ThS. Nguyeãn Vaên Rin – HBT Trang 33/43
2 2
2018 2018
2 1 log 1 2 2 log 2
x x x y x y
Có dạng
2
1 2
f x f x y
với
2018
2 log
f t t t
,
0
t
.
Xét hàm số
2018
2 log
f t t t
,
0
t
, ta có
1
2 0
.ln 2018
f t
t
0
t
nên hàm số
f t
đồng biến trên khoảng
0;
. Khi đó
2
1 2
f x f x y
2
1 2
x x y
2
1
y x
.
Ta có
2 2
2 3 2 1 3 2 3 2
P y x x x x x
.
Bảng biến thiên
x

3
4
P
7
8
Vậy
min
7
8
P
khi
3
4
x
.
Câu 58. (Mộ Đức - Quãng Ngãi 18) Cho hai số thực dương
x
,
y
thay đổi thỏa mãn đẳng thức
2
2 1 2
1 .2 .2 .
xy x y
xy x y
Tìm giá trị nhỏ nhất
min
y
của
y
.
A.
min
3
y
. B.
min
2
y
. C.
min
1
y
. D.
min
3
y
.
Lời giải
Chọn B.
Ta có
2
2 1 2
1 2 2
xy x y
xy x y
2
2 1 2 1
2 1 1 2 2 1
xy x y
xy x y
Xét hàm
1 .2
t
f t t
với
1t
.
Khi đó
2 1 .2 .ln 2 0
t t
f t t
với
1t
.
Từ
2
1 2 1 1xy x y
2
2
2 1
x
y
x
2
2
2 2 4
0
2 1
x x
y
x
2
2 2 4 0
x x
2
1
x
x
Loại
1
x
vì điều kiện của
t
nên
2 2
f
.
Câu 59. (Chuyên Thái Bình 18) Cho
2
số thực dương
,x y
thỏa mãn
1
3
log 1 1 9 1 1
y
x y x y
. Giá trị nhỏ nhất của biểu thức
2P x y
là
A.
min
11
2
P
. B.
min
27
5
P
. C.
min
5 6 3
P
. D.
min
3 6 2
P
.
Lời giải
Chọn D
Ta có
1
3
log 1 1 9 1 1
y
x y x y
3 3
1 log 1 log 1 1 1 9
y x y x y
3 3
1 log 1 log 1 1 9
y x y x
3 3
9
log 1 1 log 1
1
x x y
y
3 3
9 9
log 1 1 2 2 log
1 1
x x
y y
(*).
Xét hàm số
3
log 2f t t t
với
0t
có
1
1 0
ln3
f t
t
với mọi
0t
nên hàm số
f t
luôn
đồng biến và liên tục trên
0;

.
ThS. Nguyeãn Vaên Rin – HBT Trang 34/43
Từ (*) suy ra
9
1
1
x
y
9 8
1
1 1
y
x
y y
, do
0
x
nên
0;8
y
.
Vậy
8 9 9
2 2 2 1 2 1 3 3 6 2
1 1 1
y
P x y y y y
y y y
.
Vậy
min
3 6 2
P
khi
9 3
2 1 1
1
2
y y
y
.
Câu 60. (Thăng Long - Hà Nội 18) Cho
a
,
b
là hai số thực dương thỏa mãn
5
4 2 5
log 3 4
a b
a b
a b
.
Tìm giá trị nhỏ nhất của biểu thức
2 2
T a b
A.
1
2
. B.
5
2
. C.
3
2
. D.
1
.
Lời giải
Chọn B
5 5 5
4 2 5
log 3 4 log 4 2 5 log 5 5 4 2 5
a b
a b a b a b a b a b
a b
5 5
log 4 2 5 4 2 5 log 5 5
a b a b a b a b
(*)
Hàm số
5
log 0
f t t t t
có
'
1
1 0
ln5
f t
t
f t
đồng biến nên (*)
4 2 5 5 4 2 5 5
f a b f a b a b a b
.
4 2 5 5 5 3a b a b a b
2 2
T a b
2
2
2 2
3 5 5
5 3 10 30 25 10
2 2 2
T b b b b b
.
Vậy GTNN
5
2
T
.
Câu 61. (Chuyên Bắc Ninh 18) Cho
x
,
y
là các số thực dương thỏa mãn
3
2 1
log 2
x y
x y
x y
. Tìm giá trị
nhỏ nhất của biểu thức
1 2
T
x
y
.
A.
3 3
. B.
4
. C.
3 2 3
. D.
6
.
Lời giải
Chọn D
Ta có
3
2 1
log 2
x y
x y
x y
3 3
log 2 1 log 2x y x y x y
3 3
log 2 1 log 3 3 2 1x y x y x y
3 3
log 2 1 2 1 log 3 3 3 3x y x y x y x y
(*)
Xét hàm số
3
log
f t t t
với
0t
.
Khi đó
1
1 0, 0
ln 3
f t t
t
, suy ra hàm số
f t
liên tục và đồng biến trên
0;

.
Do đó
* 2 1 3 3 2 1 1 2x y x y x y x y
.
Vì
, 0 0
x y y
.
Xét
1 2 1 2 1 1 1
1 2 1 2
T
x y y
y y y y
Áp dụng bất đẳng thức Cô si ta có
3
3 3
1 2
3. 3. 3. 8 6
1 2 2 1 2
T
y y y y
.
ThS. Nguyeãn Vaên Rin – HBT Trang 35/43
Dấu
" "
xảy ra
1
1 2
2
1 2
1
2 1 2
4
x y
x
y y
y
y y
.
Câu 62. (Chuyên Nguyễn Du - Đăk Lăk 19) Cho các số dương
,x y
thỏa mãn
5
1
log 3 2 4
2 3
x y
x y
x y
.
Giá trị nhỏ nhất của biểu thức
4 9
6 2A x y
x y
bằng
A.
31 6
.
4
B.
11 3.
C.
27 2
.
2
D.
19.
Lời giải
Chọn D
Điều kiện:
1
0
2 3
1
, 0
x y
x y
x y
x y
.
Ta có:
5
1
log 3 2 4
2 3
x y
x y
x y
5 5
5 5
log 1 1 5 1 log 2 3 2 3
log 5 1 5 1 log 2 3 2 3 * .
x y x y x y x y
x y x y x y x y
Xét hàm số
5
( ) log
f t t t
trên
0;
ta có
1
( ) 1 0, 0; .
ln5
f t t
t
Hàm số
5
( ) log
f t t t
đồng biến trên
0; .
* 5 1 2 3 3 2 5
x y x y x y
.
Mặt khác, ta có:
4 9 4 9
6 2 9 4 3 2 2.6 2.6 5 19
A x y x y x y
x y x y
Vậy GTNN của
19
A
, dấu “ = ” xảy ra
4
9
2
9
3
4
3
2
3 2 5
x
x
x
y N
y
y
x y
.
Câu 63. (Ba Đình 19) Xét các số thực dương
,x y
thỏa mãn
2
2 1
2
2
2019
( 1)
x y
x y
x
. Giá trị nhỏ nhất
min
P
của
biểu thức
2
P y x
bằng
A.
min
1
4
P
. B.
min
1
2
P
. C.
min
7
8
P
. D.
min
15
8
P
.
Lời giải
Chọn D
Ta có:
2
2 1
2
2
2019
( 1)
x y
x y
x
2
2 1
2
2
1 .2019 2 .2019
x
y
x x y
2
2
2 1 4
2
1 .2019 2 .2019
x x
y
x x y
2
2
2 1 2 2
1 .2019 2 .2019
x x y
x x y
. (1)
Đặt
2
1 , 2 , 0, 0 ,
u x v x y u v
khi đó (1) trở thành
2 2
.2019 .2019 .
u v
u v
(2)
Xét hàm đặc trưng
2
.2019 , 0 ,
t
f t t t
ta có
ThS. Nguyeãn Vaên Rin – HBT Trang 36/43
2 2
' 2019 2 .2019 .ln 2019 0, 0:
t t
f t t t

Hàm
f t
đồng biến trên
(0; ).
Phương trình
2
2
2 1 2 1.
f u f v u v x x y y x
Suy ra
2
2 2 2P y x x x
.
Do
P
là hàm bậc hai có hệ số
2 0
a
nên
1 1 1 15
min 2. 2 .
2 4 16 4 8
b
P P P
a
Câu 64. (Lý Nhân Tông 19) Cho hai số thực
,x y
thỏa mãn
2 2
3
log 3 3 .
2
x y
x x y y xy
x y xy
Tìm giá trị lớn nhất của biểu thức
2 3
.
6
x y
P
x y
A.
43 3 249
.
94
B.
37 249
.
94
C.
69 249
.
94
D.
69 249
.
94
Lời giải
Chọn D
Điều kiện
2 2
0 0.
2
x y
x y
x y xy
2 2
3
log 3 3
2
x y
x x y y xy
x y xy
2 2 2 2
3 3
2log 2log 2 3 3x y x y xy x y xy x y
2 2 2 2
3 3
2log 2 2log 2 2 3 3x y x y xy x y xy x y
2 2 2 2
3 3
2log 3 3 3 3 2log 2 2
x y x y x y xy x y xy
Xét hàm đặc trưng
3
2log , 0; ,
f t t t t

ta có
2
1 0, 0; .
.ln 3
f t t
t

Suy ra hàm
f t
đồng biến trên khoảng
0;

.
Phương trình
2 2 2 2
3 3 2 2 3 3f x y f x y xy x y xy x y
Đặt
,
2
.
2
x y
a
x a b
y a b x y
b
Khi đó
3 3
2 6
a b
P
a
và
2
là:
2
2
3 1 1.
a b
Đặt
3 1 cos ,
0;2
sin ,
a t
t
b t
, khi đó
3cos 3sin 6 3
2 3 .cos 3 sin 6 3 8 3
2cos 8 3
t t
P P t t P
t
Do phương trình luôn có nghiệm
t
nên ta có
2
2
2
69 249 69 249
2 3 3 6 3 8 3 47 69 24 0 .
94 94
P P P P P
Vậy giá trị lớn nhất của
P
là
69 249
.
94
Câu 65. (Chuyên Thái Nguyên 19) Xét các số thực dương
,x y
thỏa mãn
3
1
log 3 3 4
3
y
xy x y
x xy
. Tìm
giá trị nhỏ nhất
min
P
của
P x y
.
A.
min
4 3 4
3
P
. B.
min
4 3 4
3
P
. C.
min
4 3 4
9
P
. D.
min
4 3 4
9
P
.
Lời giải
Chọn A
ThS. Nguyeãn Vaên Rin – HBT Trang 37/43
Để
1
0
3
y
x xy
mà từ giả thiết
, 0
x y
suy ra
1 0 1y y
.
Vậy ĐKXĐ:
0;0 1x y
.
Ta có :
3
1
log 3 3 4
3
y
xy x y
x xy
3 3 4
1
3
3
xy x y
y
x xy
3 3 3
3 1
3
3
xy x y
y
x xy
3
3 3
3 1
3
3 3
xy x
y
y
x xy
3 3 3
3 3 .3 3 .3 (*)
y xy x
y xy x
Xét
.3
t
f t t
với
0t
. Ta có
3 .3 .ln3 0
t t
f t t
với
0
t
, suy ra
f t
đồng biến trên khoảng
0;

. Từ
(*)
ta có
3 3 3
f y f xy x
với
3 3 0,3 0
y xy x
nên
3
3 3 3
3( 1)
x
y xy x y
x
.
Ta có
3 3 1 4
1
3 1 3 1 3 3
x x
P x y x x
x x
4 4 4 4 4 3 4
1 2 1 .
3 1 3 3 1 3 3
P x x
x x
.
Vậy
min
4
1
3 1
2 3 3
4 3 4 3
3
3 3 1
2 3 1
0;0 1
3
x
x
x
x
P y
x
y
x y
.
Câu 66. (CHUYÊN LÊ THÁNH TÔNG - QUẢNG NAM 19) Cho hai số dương
x
;
y
thỏa
2
2
log 4 2 2 8 2 2 2
y
x y xy x y
. Giá trị nhỏ nhất của
2
P x y
là số có dạng
M a b c
với
, , 2
a b a
. Tính
S a b c
.
A.
17
S
. B.
7
S
. C.
19
S
. D.
3
S
.
Lời giải
Chọn D
Với hai số dương
x
;
y
thỏa
2
2
log 4 2 2 8 2 2 2
y
x y xy x y
Ta có
2
2 log 4 2 2 8 2 2 2
y x y xy x y
2
2 log 2 1 2 8 2 1 2 3 2
y x y x y y
2 2
8
log 2 1 log 2 2 1 3
2
x y x
y
2 2
8 8
log 2 1 2 1 log
2 2
x x
y y
.
Xét hàm đặc trưng
2
log
f t t t
trên
0;

có
1
1 0, 0
ln 2
f t t
t
nên hàm số
f t
đồng
biến trên
0;

.
8 8 8
2 1 2 1 2
2 2 2 1
f x f x y
y y x
.
8 8
P 2 2 2 2 1 3 4 2 3
2 1 2 1
AM GM
x y x x
x x
.
Dấu bằng xảy ra khi
2
8 1 2 2
2 1 2 1 8
2 1 2
x x x
x
.
Vậy
3
S a b c
.
ThS. Nguyeãn Vaên Rin – HBT Trang 38/43
Câu 67. (Gia Lộc - Hải Dương 19) Cho
, 0
x y
thỏa mãn
3
log 3
x y
xy x y
xy
. Tìm giá trị nhỏ nhất
của biểu thức
2 2
9
1 3 1
x y
P
y x
.
A.
10
. B.
71
7
. C.
72
7
. D.
73
7
.
Lời giải
Chọn C
Ta có
3
log 3
x y
xy x y
xy
log 3 log 3x y xy xy x y
.
log 3 3 log 1
x y x y xy xy
.
Xét hàm số
log
f t t t
trên khoảng
0;
;
1
1 0, 0
.ln10
f t t
t
.
Suy ra hàm số
f t
đồng biến trên
0;

.
Phương trình
1
tương đương
3 3
f x y f xy x y xy
.
Theo bất đẳng thức Schwarz ta có
2 2
2 2 2
3 3
9
2
1 3 1 1 3 1 2 3
y x y
x y x
P
y x y x x y
.
Theo bất đẳng thức Cô-si cho 2 số dương ta có
2
3 2 .3 12 0 12 0
xy x y x y xy xy xy xy
.
Vì
0
xy
nên
12 3 12
xy x y
.
Đặt
3 12
u x y u
.
Từ
2
ta có
2
, 12
2
u
P f u u
u
2
2
0
4
0
4
2
u
u u
f u f u
u
u
(không thỏa mãn).
Min
72
12
7
f u f
.
Vậy
72
7
P
Min
72
7
P
khi
2
2
3 12
3 12
6
12
3
2
3 12 3 12 3 9
1 3 1
x y
x y
x
u
x y
y
y y y y
y x
.
Câu 68. (CỤM TRẦN KIM HƯNG - HƯNG YÊN 19) Cho
, ,a b c
là các số thực thỏa mãn
2
2 2 2
log ( 2) ( 2) ( 2).
1
a b c
a a b b c c
a b c
Tìm giá trị lớn nhất của biểu thức
3 2
.
a b c
P
a b c
A.
6 2 3
.
3
B.
8 2 2
3
. C.
6 2 3
3
. D.
4 2 2
3
.
Lời giải
Chọn C
Ta có:
2
2 2 2
log 2 2 2
1
a b c
a a b b c c
a b c
ThS. Nguyeãn Vaên Rin – HBT Trang 39/43
2 2 2 2 2 2
2 2
log 2 1 log 1 1
a b c a b c a b c a b c
2 2 2 2 2 2
2 2
log 2 2 2 2 2 2 log 1 1
a b c a b c a b c a b c
(*)
Xét hàm
2
log
f t t t
với
0t
,
Ta có,
1
' 1 0, 0;
ln 2
f t t
t

nên hàm số
f t
đồng biến trên
0;

.
Khi đó,
2 2 2
* 2 2 2 1
f a b c f a b c
2 2 2
2 2 2 1
a b c a b c
2 2 2
1 1 1 2
a b c
Ta lại có,
3 2
3 1 2 1 1 1 6 3
a b c
P P a P b P c P
a b c
(**)
Áp dụng bất đẳng thức Bunhiacopxki ta có:
2
2 2 2 2
6 3 3 1 2 1 1 1 2. 3 2 1
P P a P b P c P P P
2
6 2 3 6 2 3
3 12 8 0
3 3
P P P
Vậy,
max
6 2 3
3
P
khi
3 1 1 1 3
, ,
3 3 3
a b c
.
Câu 69. (Hội các trường chuyên 19) Cho
, 0;2
x y
thỏa mãn
3 8 11
x x ey ey
. Giá trị lớn nhất
của
ln 1 lnP x y
bằng
A.
1 ln 3 ln 2
. B.
2 ln 3 ln 2
. C.
1 ln 3 ln 2
. D.
1 ln 2
.
Lời giải
Chọn B
Điều kiện:
1
1,x y
e
.
Ta có :
3 8 11
x x ey ey
2 2 2
5 24 11x x e y ey
2 2 2
11 5 24 0
e y ey x x
(*), có
2
2 5 0
x
, 1x
.
Do đó (*)
11 2 5
8
8
2
3 3
11 2 5
2
x
x
y
ey
ey x
e
ey x x
x
y
ey
e
.
+) Do
8 9
2
x
y
e e
nên loại
8
x
y
e
.
+) Với
3
x
y
e
,
1 2
x
:
Khi đó, ta được:
ln ln 3
P x x
trên
1;2
.
Ta có
1 1
2 ln
2 3 ln 3
P
x x
x x
1 1
0 0
2 ln
2 3 ln 3
P
x x
x x
3 ln 3 ln 0
x x x x
3 ln 3 lnx x x x
(**)
Xét hàm
lnf t t t
trên
1;

, có
1
ln 0, 1;
2 ln
f t t t
t

.
Khi đó (**)
3
3 3
2
f x f x x x x
.
Bảng biến thiên:
ThS. Nguyeãn Vaên Rin – HBT Trang 40/43
Từ đó
max
2 ln3 ln 2P
tại
3
2
x
,
3
2
y
e
.
Câu 70. (THTT 19) Cho hai số thực dương
,x y
thỏa mãn
2 2
log log 6 6x x x y y x
. Giá trị nhỏ
nhất của biểu thức
6 8
3 2P x y
x y
bằng
A.
59
3
. B.
19
. C.
53
3
. D.
8 6 2
.
Lời giải
Chọn B
Điều kiện:
0
0 6
x
y
.
Từ giả thiết ta có:
2 2
2 2 2 2
log log 6 6 log log 6 6x x x y y x x x x y x y
(*)
Xét hàm số
2
logf t t t
với
0t
, Ta có
1
' 1 0, 0
ln 2
f t t
t
nên hàm số
2
logf t t t
đồng biến trên khoảng
0;

.
Do đó
2 2
* 6 6 6 6 **f x f x y x x y x y x y
( do
0x
)
Áp dụng Bất đẳng thức Cô si cho các cặp số dương và bất đẳng thức
**
, ta có:
6 8 3 3 6 8 3 3 6 8
3 2 .6 2 . 2 . 19
2 2 2 2 2 2
x y x y
P x y x y
x y x y x y
.
Đẳng thức xảy ra khi và chỉ khi
6
2
3 6
4
2
8
2
x y
x
x
y
x
y
y
. Vậy giá trị nhỏ nhất của
P
bằng 19.
Câu 71. (Sở Quảng Nam 19) Cho hai số thực dương
x
,
y
thỏa mãn
1
2
2 2 log 2
y y
y x x
. Giá trị nhỏ
nhất của biểu thức
x
P
y
bằng
A.
ln 2
2
e
. B.
ln 2
2
e
. C.
ln 2
2
e
. D.
2ln 2
e
.
Lời giải
Chọn C
Có
1
2
2 2 log 2
y y
y x x
2
2 2 log 2 2 1
y y
y x x
.
1
Đặt
2
log 2 2
y
t x
2 2 2
y t
x 2 2 2
t y
x
.
1
trở thành :
2 2 2 1
y t y
y t
1
2 1 2
y t
y t
.
2
Xét hàm số
2 ,
x
f x x x
2 ln 2 1 0,
x
f x x
nên hàm số
2
x
f x x
luôn
đồng biến trên
. Kết hợp với
2
ta có:
1t y
2
log 2 2 1
y
x y
1
2 2 2
y y
x
1
2
y
x
.
ThS. Nguyeãn Vaên Rin – HBT Trang 41/43
Khi đó
x
P
y
1
2
y
y
1 1
2
2 ln 2 2
y y
y
P
y
.
Cho
0 ln 2 1 0P y
1
ln 2
y
.
Bảng biến thiên:
Vậy
min
ln 2
2
e
P
khi
2
e
x
và
1
ln 2
y
.
Câu 72. (Chuyên Lam Sơn 19) Cho
,x y
thỏa mãn
3
2 2
log ( 9) ( 9)
2
x y
x x y y xy
x y xy
Tìm giá trị
lớn nhất của biểu thức
3 2 9
10
x y
P
x y
khi
,x y
thay đổi.
A. 2. B. 3. C. 1. D. 0.
Lời giải
Chọn C
Điều kiện xác định;
2 2
0 ( ) 0
2
x y
x y
x y xy
.
Vì
2 2 2 2
3
2 ( ) 2 0
2 4
y
x y xy x y
với
,x y
.
Ta có
3
2 2
log ( 9) ( 9)
2
x y
x x y y xy
x y xy
.
2 2 2 2
3 3
log ( ) log ( 2) 9( )x y x y xy x y xy x y
.
2 2 2 2
3 3
2 log ( ) 9( ) log ( 2) 2x y x y x y xy x y xy
.
2 2 2 2
3 3
log 9( ) 9( ) log ( 2) 2x y x y x y xy x y xy
(1)
.
Đặt
3
( ) logf t t t
( 0)t
.
Có
1
'( ) 1 0
.ln 3
f t
t
với
( 0)t
f
là hàm đồng biến với
( 0)t
. Khi đó:
2 2 2 2
(9( )) ( 2) 9( ) 2f x y f x y xy x y x y xy .
2 2
2 9 9 0x y xy x y .
2 2
4 4 4 8 36 36 0x y xy x y .
2 2
(2 ) 18(2 ) 3( 3) 19 0x y x y y .
Mà
2 2
3( 3) 0 (2 ) 18(2 ) 19 0y x y x y
1 2 19x y
.
Mặt khác
2 19
1 0 1
10
x y
P P
x y
Dấu bằng xảy ra khi
2 19 8
3 0 3
x y x
y y
.
Câu 73. (Hải Hậu 19) Cho hai số thực dương
x, y
thỏa mãn
3
9
3 2
1
x
y
y
x
. Giá trị lớn nhất của biểu thức
6S x y
là
A.
89
.
12
B.
11
.
3
C.
17
.
12
D.
82
.
3
Lời giải
Chọn B
Theo giả thiết
0y
nên ta có:
ThS. Nguyeãn Vaên Rin – HBT Trang 42/43
3
3
3
3
9
3 2 9 3 2 1 3 3 3 2 3 2
1
x
y x x y y x x y y
y
x
3 3 2
f x f y
với
3
f t t t
.
Ta có
2
3 1 0,f t t t
nên hàm số
f t
đồng biến trên
, suy ra
3 3 2
x y
hay
2
2
3
3
y x
. Do
0
y
và
3 3 2
x y
nên
2
3
x
.
Khi đó
2
2 2
2 2 11 11
6 6 3 3 6 3 1
3 3 3 3
S x y x x x x x
.
Do đó
11
max
3
S
khi
1x
.
4. Tìm nghiệm nguyên của phương trình
Câu 74. (ĐỀ THAM KHẢO – BGD&ĐT 20) Có bao nhiêu cặp số nguyên
;x y
thỏa mãn
0 2020
x
và
3
log 3 3 2 9
y
x x y
?
A.
2019
. B.
6
. C.
2020
. D.
4
.
Lời giải
Chọn D
Đặt
1
3
log 3 3 3 3 3 3 1
t t
t x x x
.
Phương trình trở thành
1 2
1 3 2 3 *
t y
t y
.
Xét hàm số
3
u
y f u u
trên
.
Ta có
1 3 ln3 0,
u
f u u
nên hàm số
f u
đồng biến trên
.
Do đó
2
* 1 2 1 2 3 1 9 1
y y
f t f y t y x
.
Vì
0 2020
x
nên
9
0 9 1 2020 0 log 2021
y
y
.
0;1;2;3
y y
.
Vậy có
4
cặp số nguyên
;x y
thỏa YCBT.
Câu 75. (CHUYÊN LÊ HỒNG PHONG – NAM ĐỊNH 19) Cho
0 2020
x
và
2
log (2 2) 3 8
y
x x y
.
Có bao nhiêu cặp số
( ; )x y
nguyên thỏa mãn các điều kiện trên?
A. 2019. B. 2018. C. 1. D. 4.
Lời giải
Chọn D
Do
0 2020
x
nên
2
log (2 2)
x
luôn có nghĩa .
Ta có
2
log (2 2) 3 8
y
x x y
3
2
log ( 1) 1 3 2
y
x x y
2
log ( 1)
3
2
log ( 1) 2 3 2
x
y
x y
(1)
Xét hàm số
( ) 2
t
f t t
.
Tập xác định
D
và
( ) 1 2 ln 2
t
f t
( ) 0
f t
t
.
Suy ra hàm số
( )f t
đồng biến trên
. Do đó
2
(1) log ( 1) 3x y
3
1 2
y
x
8
log ( 1)
y x
.
Ta có
0 2020
x
nên
1 1 2021
x
suy ra
8 8
0 log ( 1) log 2021
x .
Lại có
8
log 2021 3,66
nên nếu
y
thì
0;1;2;3
y
.
Vậy có 4 cặp số
( ; )x y
nguyên thỏa yêu cầu bài toán là các cặp
(0;0)
,
(7;1)
,
(63;2)
,
(511;3)
.
Câu 76. Có bao nhiêu cặp số nguyên
;x y
thỏa
0 2017
y
và
2
2
2
2
2 3
log 8 2 2
5 2 3
x x y
x x y
x x
.
A.
44
. B.
22
. C.
42
. D.
21
.
Lời giải
Chọn C
ThS. Nguyeãn Vaên Rin – HBT Trang 43/43
Đặt
2
2
2
2 3
, 0 8 2 2 2 1
5 2 3
a x x y
a b x x y b a
b x x
.
Phương trình đã cho trở thành
2 2 2 2
log log 2 1 2 log 2 log *a b b a a a b b
.
Xét hàm số
2
logy f t t t
trên khoảng
0;
.
Ta có
1
1 0, 0
ln 2
f t t
t
nên hàm số đồng biến trên khoảng
0;
.
2 2
* 2 2 2 2 3 5 2 3f a f b a b x x y x x
2
2 8 3y x x
.
2
2
8 3
2
2
2
8 3 0 49 8
0 2 8 3 2034 42GTN
0 41
8 1014 0
x x
y
x x x
y x x
x
x x
.
5. Tính tích phân
Câu 77. Cho hàm số
y f x
xác định và liên tục trên khoảng
0;
thỏa mãn
1 2
f
và
3
2 3
3 3 4
2 1 , 0;f x f x x
x x x
. Tính
3
2
dx
I f x
.
A.
3
3ln5 2ln7
2
I
. B.
5
3ln3 2ln2
2
I
.
C.
15
2ln7 3ln5
2
I
. D.
13
I
.
Lời giải
Chọn B
Ta có
3 3
3
2 3
3 3 4
2 1 3 1 3 1 *
f x f x xf x xf x x x
x x x
.
Xét hàm số
3
3g t t t
trên
.
Vì
2
3 3 0,g t t t
nên hàm số đồng biến trên
.
1
* 1 1 1g xf x g x xf x x f x
x
1
1 dx ln
f x x x C
x
.
Do
1 2
f
nên
1 2 1
C C
.
Vậy
3
3
2
2
2
5
1 ln dx ln 1 3ln 3 2ln 2
2 2
x
I x x x x x
.
--- HẾT ---
Facebook: Nguyeãn Vaên Rin
…
Ñöøng bao giôø ñeå ñeán ngaøy mai nhöõng vieäc baïn coù theå laøm ngaøy hoâm nay!
Benjamin Franklin
CHÚC CÁC BẠN HỌC TỐT!
| 1/43
| | Tải xuống

Có thể bạn quan tâm:

Preview text:


TT LTĐH CAO THẮNG – HUẾ PHƯƠNG PHÁP
ThS. Nguyeãn Vaên Rin – HBT
HÀM SỐ ĐẶC TRƯNG SÑT: 089.8228222
Họ và tên: …………………………………….................….……; Trường:……………………..………; Lớp: ……………………….....
Phương pháp hàm số đặc trưng thường xuyên xuất hiện trong đề thi THPT Quốc Gia và nó cũng là một trong
những câu phân loại của đề:
- Câu 47 mã đề 101 – THPT QG năm 2017.
- Câu 35 đề tham khảo – BGD&ĐT năm 2018.
- Câu 46 mã đề 101 – THPT QG năm 2018.
- Câu 47 đề tham khảo – BGD&ĐT năm 2020.
Sau đây, tôi xin trình bày cơ sở lý thuyết và giới thiệu một số ví dụ áp dụng của nó trong các đề thi thử THPT
Quốc Gia cũng như đề chính thức của BGD&ĐT qua các năm.
I. Cơ sở lý thuyết: Cho hàm số y f x liên tục trên tập D .
 Nếu hàm số f x đơn điệu (đồng biến hoặc nghịch biến) trên D thì u  , v  ,
D f u  f v  u v .
 Nếu hàm số f x đồng biến trên D thì u  , v  ,
D f u  f v  u v .
 Nếu hàm số f x nghịch biến trên D thì u  , v  ,
D f u  f v  u v . II. Áp dụng
1. Giải phương trình, bất phương trình mũ và logarit Câu 1.
(Chuyên Thái Bình 18) Tính tổng tất cả các nghiệm của phương trình 3 2
x  3x  3x  5 log   x  3 2 1
x  6x  7 . 2 x 1 A. 2  3 . B. 2 . C. 0 . D. 2  3 . Lời giải Chọn C. 3 2
x  3x  3x  5 Điều kiện  0  3 2
x  3x  3x  5  0 . 2 x 1 3 2
x  3x  3x  5 3
Với điều kiện trên, phương trình đã cho tương đương log   x   2 1
x  6x  7 2 x 1 
x x x   
x    x x  x  3 3 2 2 2 log 3 3 5 log 1 6 7 1   3 2
x x x   3 2
x x x    2 x   2 log 3 3 5 3 3 5 log 1  x 1 * .
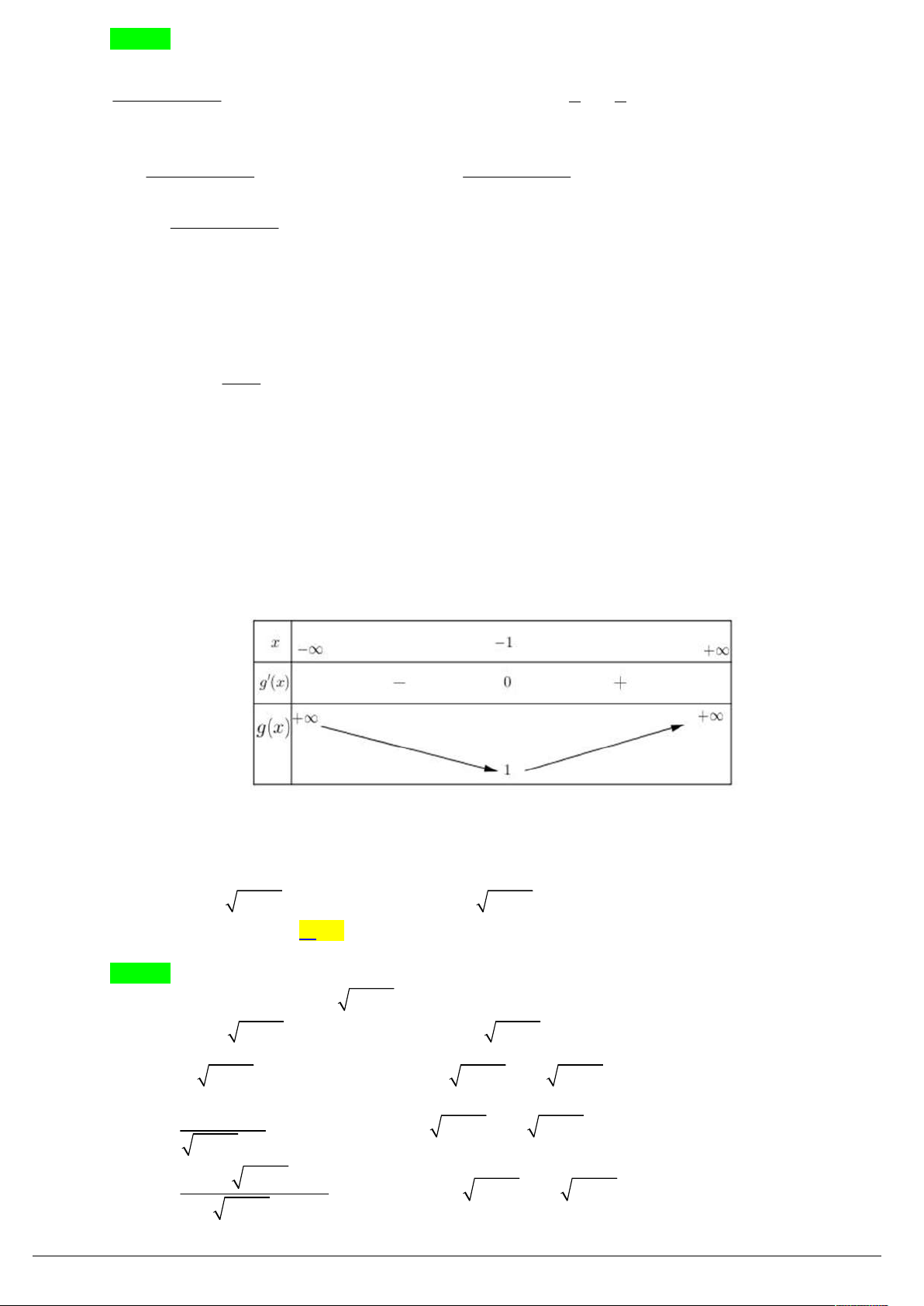
Xét hàm số y f t   log t t trên khoảng 0;   . 1
Ta có: f t   1  0, t   0 . t ln10
Suy ra hàm số f t  đồng biến trên khoảng 0;   .    f  3 2
x x x    f  2 x   3 2 2 * 3 3 5
1  x  3x  3x  5  x 1 x  2   3 2
x  2x  3x  6  0  x   3  . x  3 
Đối chiếu điều kiện, ta được x   3 thỏa mãn.
Vậy S  3   3  0 . 2 1 2x 1  1  Câu 2.
(SGD Bắc Ninh 18) Cho phương trình log
x  2  x  3  log  1
 2 x  2 , gọi S 2   2   2 xx
là tổng tất cả các nghiệm của nó. Khi đó, giá trị của S là 1 13 1 13 A. S  2  . B. S  . C. S  2 . D. S  . 2 2
ThS. Nguyeãn Vaên Rin – HBT Trang 1/43 Lời giải Chọn D.  1 2  x   Điều kiện  2 . x  0 
Với điều kiện trên, phương trình đã cho tương đương 2      x    x   2 1 1 log 2 2 1  log 2   2  1 * . 2 2         x   x  
Xét hàm số y f t   log t  t  2
1 trên khoảng 0;   . 2 1 2
2 ln 2.t  2 ln 2.t 1
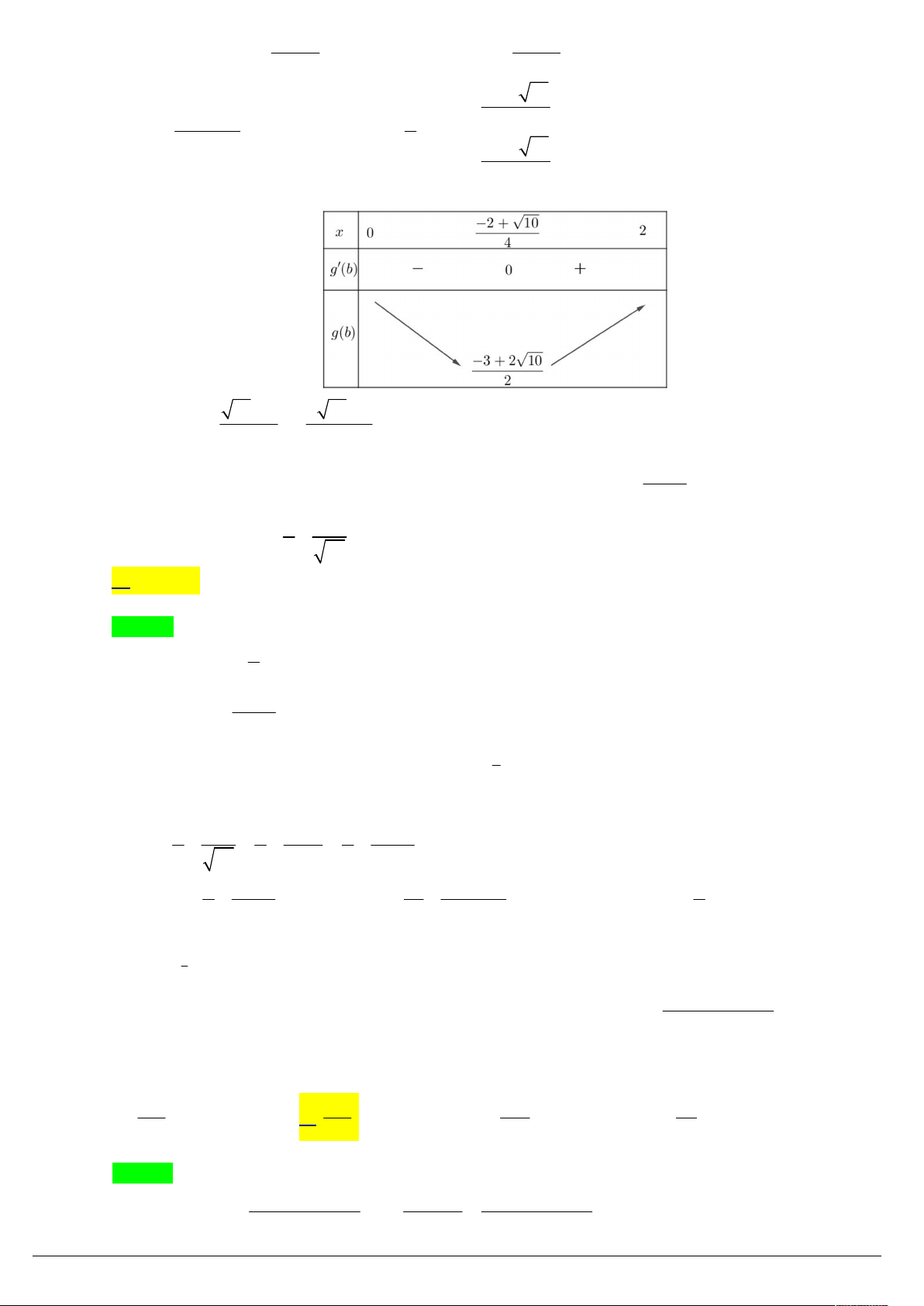
Ta có f  t    2 t   1   0 , t   0 . t ln 2 t.ln 2
Suy ra hàm số f t  đồng biến trên khoảng 0;  .   1
Do đó     f x   1 * 2  f 2     x  2  2   x x  x  1   3  13  3 2
x  2x  4x 1  0  x  .  2   3  13 x   2 x  1
Kết hợp với điều kiện ta được  3  13 . x   2 1 13 Vậy S  . 2 a b 3 Câu 3.
(Nguyễn Trãi - Đà Nẵng 18) Gọi x
là một nghiệm lớn hơn 1 của phương trình 0 c 1 1 x     2x  3 1 x 2  1  
  2x 1. Giá trị của P a b c là   3    A. P  6 . B. P  0 . C. P  2 . D. P  4 . Lời giải Chọn D. Với x  1 ta có 1 1 x   1 1 1 x 1 2 1 x 1     1  2 3 x x  1 2 x 2 x     2x 1  3  3 1  x   3   3  x 1   1 .   3    2x 2x Xét hàm số    3t f t
t trên khoảng 0;   .
Ta có    3t f t
.ln 3 1  0 , t  0 .  1 1 1  3    1  ff x     1 
x 1  x
a  1, b  1, c  2 .  2x  2x 2 Vậy P  4 . 2
 4x  4x 1  Câu 4.
(THTT 18) Biết x , x là hai nghiệm của phương trình 2 log
 4x 1  6x và 1 2 7   2x   1 x  2x
a b với a , b là hai số nguyên dương. Tính a  . b 1 2   4
A. a b  16 .
B. a b  11.
C. a b  14 .
D. a b  13. Lời giải
ThS. Nguyeãn Vaên Rin – HBT Trang 2/43 Chọn C.x  0  Điều kiện  1 x    2
 4x  4x 1   2x 1   2  2 2 Ta có 2 log
 4x 1  6x  log 
  4x  4x 1  2x 7   7 2x  2x       log 2x  2 1  2x  2 1
 log 2x  2x 1 7 7   1
Xét hàm số f t   log t t f t
1  0 với t  0 7   tln7
Vậy hàm số đồng biến  3  5  x  2 2 4 Phương trình  
1 trở thành f 2x  
1   f 2x  2x   1  2x    3  5  x   4  9  5  l  4
Vậy x  2x  
a  9;b  5  a b  9  5  14. 1 2  9  5  tm  4 2x 1 a Câu 5.
(Lương Thế Vinh 19) Phương trình 2 log
 3x  8x  5 có hai nghiệm là a và (với a , 3 2 (x 1) b a b   * và
là phân số tối giản). Giá trị của b là b A. 1 . B. 4 . C. 2 . D. 3 . Lời giải Chọn D  1 2x 1  0 x  Điều kiện    2 . x 1  0  x  1  2x 1 2x 1 Ta có: 2 log
 3x  8x  5 2  log
1  3x  8x  4 3  3 2 x  2 1  x   1 2x 1  log  3 x  2
1  2x 1  log 2x 1  2x 1  log 3 x 1  3 x 1   1 . 3     3   2   2 3 2   3 x   1
Xét hàm số f t   log t t trên khoảng 0;   . 3   1
Ta có f t  
1  0 , t  0 . t.ln 3
Suy ra hàm số f t  đồng biến trên 0;  .
   f x    f  x  2 1 2 1 3 1  .  x  2
x    x  2 2 2 1 3 1
 3x  8x  4  0 hay  2 .  x   3 2
Vậy hai nghiệm của phương trình là 2 và suy ra b  3 . 3 Câu 6.
(Lê Xoay - Vĩnh phúc 18) Số nghiệm của phương trình sin 2x  cos x  1 log sin x 2   trên khoảng    0; là    2 
ThS. Nguyeãn Vaên Rin – HBT Trang 3/43 A. 4 . B. 3 . C. 2 . D. 1 . Lời giải Chọn D   
Vì sin x  0 và cos x  0 , x   0;
nên phương trình đã cho tương đương    2 
sin 2x  cos x  log cos x  1 log sin x  log cos x 2   2   2    log
cos x  cos x  log
sin 2x  sin 2x * 2   2     1
Xét hàm số f t   log t t , với t 0 
;1 ta có f t   1  0, t   0  ;1 . 2 t ln 2
Do đó hàm số f t  đồng biến trên khoảng 0  ;1 . 1 
*  f cos x  f sin 2x  cos x  sin 2x  sin x  hay x  . 2 6 Câu 7.
(Cổ Loa - Hà Nội 19) Cho hàm số    2 ln 1  x x f x x x e e      . Hỏi phương trình 3x f
  f 2x  
1  0 có bao nhiêu nghiệm thực? A. 3. B. 0 . C. 2 . D. 1 . Lời giải Chọn D Ta có 2 2 x 1  x
x x x x  x x  0, x    .    x x 1
   ln  2 1     ln  x x f x x x e e 2 x x    ee
ln  x 1 xe e      
  f x . 2  x 1  x
Suy ra f x là hàm số lẻ. 2 x 2 x x 1 1 2 2 x 1 2 x 1 xx 1
Mà f  xxx   e e xx   e e   e e  0 , x   2 x 1  x 2 2 x 1  x x 1
Suy ra f x đồng biến trên  . Do đó 3x f
  f 2x   1  0  3x f
   f 2x   1  3x f
  f 12x  3x 1 2x
 3x  2x 1  0* .
Xét hàm số    3x g x
 2x 1 trên  .    3x g x ln 3  2  0, x    .
Suy ra g x đồng biến trên  nên (*) nếu có nghiệm thì có nghiệm duy nhất.
Mà x  0 là một nghiệm của phương trình (*).
Vậy tập nghiệm của phương trình (*) là S    0 . Câu 8.
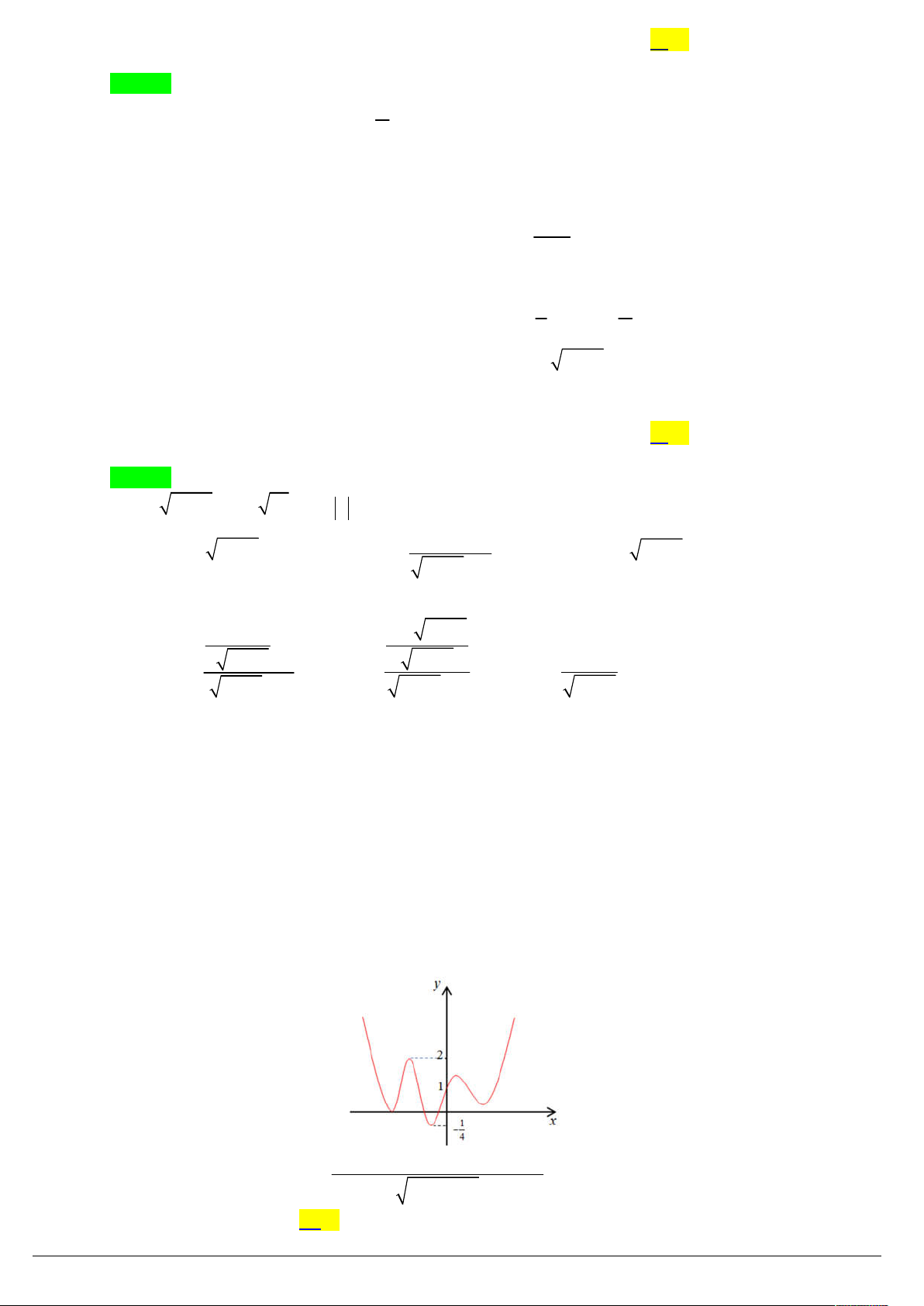
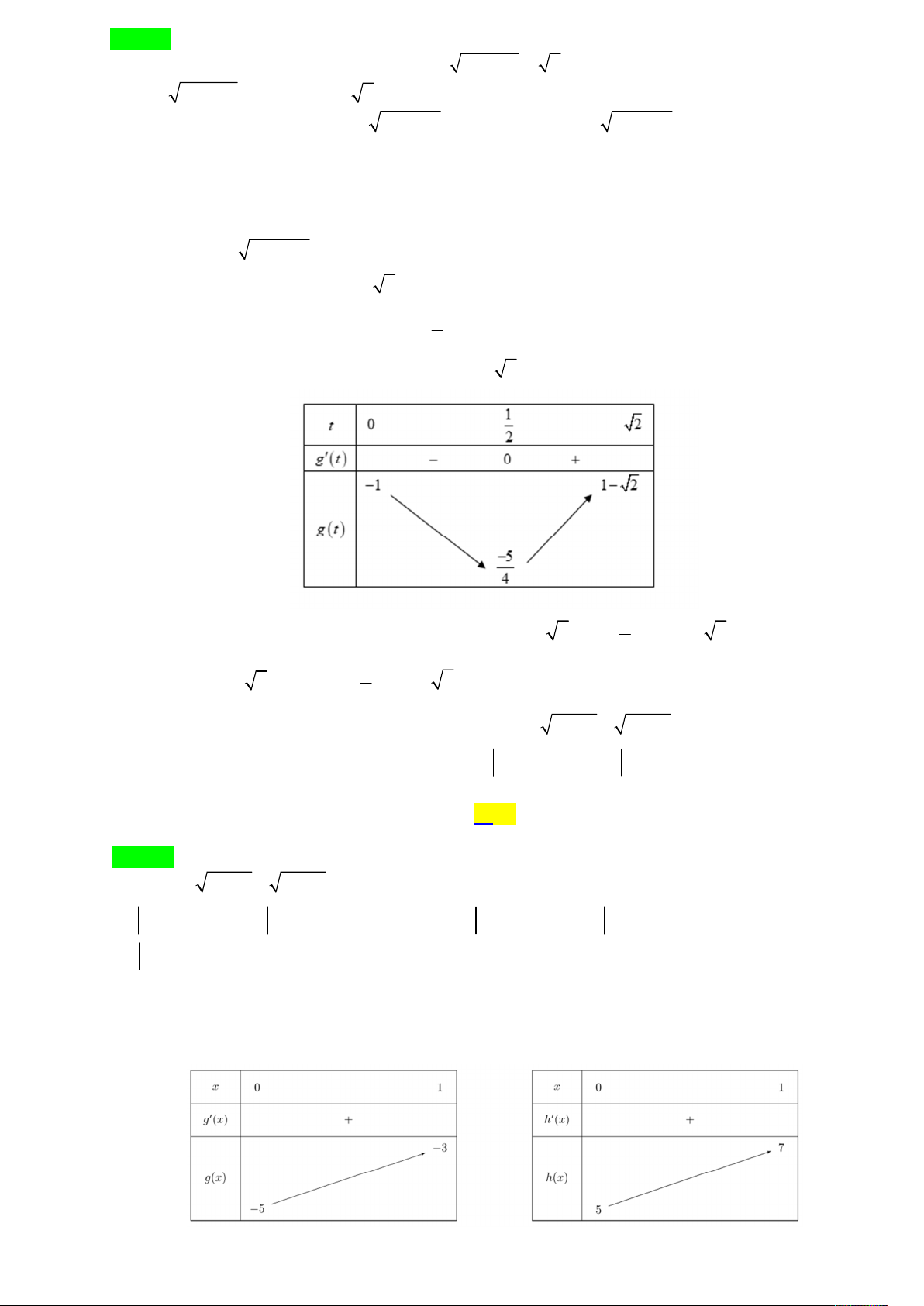
(TƯ NGHĨA 19) Cho hàm số y f x liên tục trên R và có đồ thị như hình vẽ dưới đây . 3 f x 2
 3 f x  4 f x  2
Số nghiệm của phương trình
 3 f x  2 là
3 f x 1 A. 6 . B. 9 . C. 7 . D. 8 . Lời giải
ThS. Nguyeãn Vaên Rin – HBT Trang 4/43 Chọn B 1
Vì f x   nên 3 f x 1  0, x    . 4 3 2 3
t  3t  4t  2 3
Đặt t f x ta được
 3t  2  t   1  t  
1   3t 1  3t 1 * 3t 1
Xét hàm đặc trưng   3
g u u u trên  .
Ta có gu 2
 3u 1  0, u    . t   1  t  0
f x  0   1
Do đó *  g t  
1  g  3t 1  t 1  3t 1       . 2
t  2t 1  3t 1 t  1  
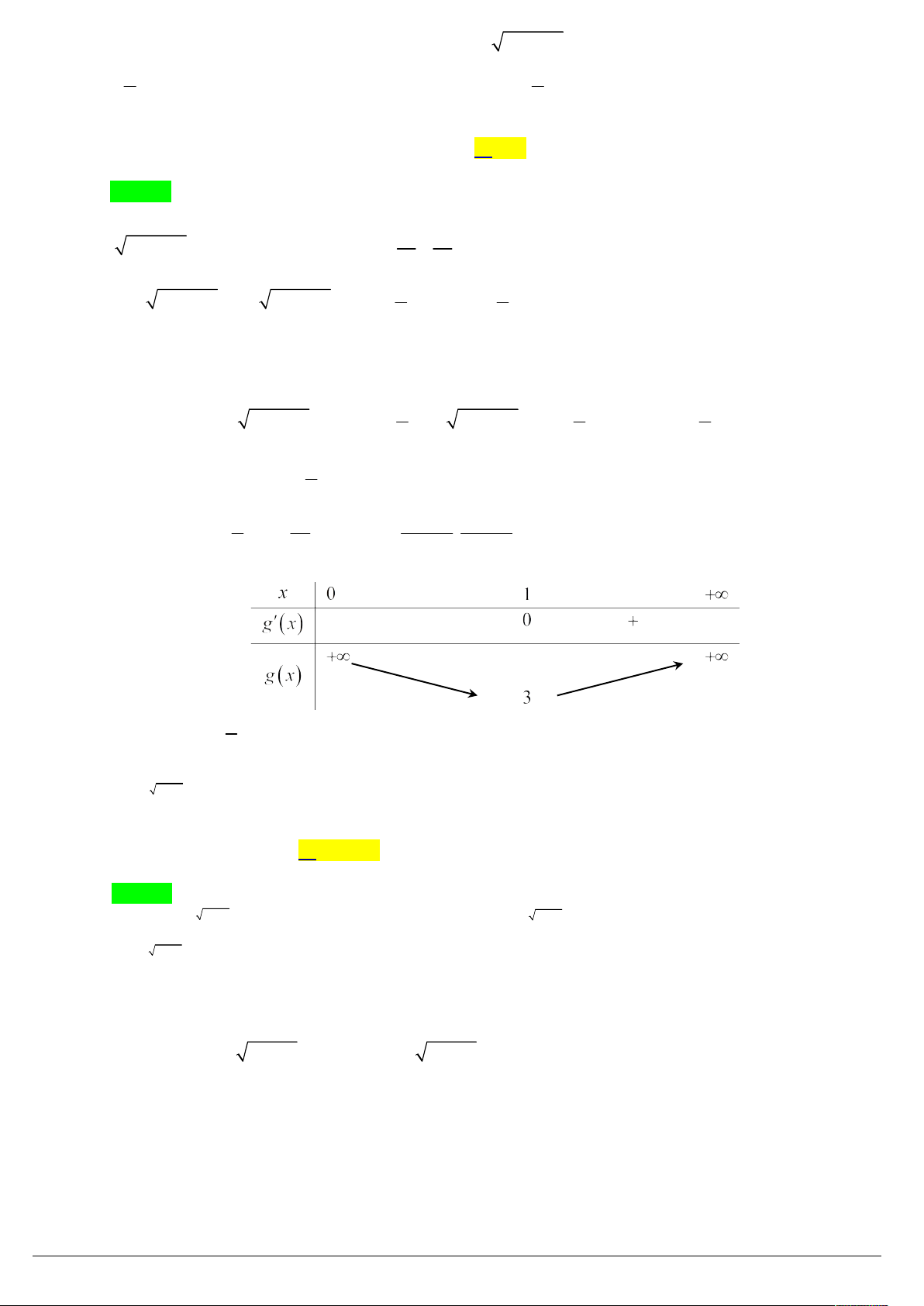
f x  1  2 
Dựa vào đồ thị phương trình (1) có 3 nghiệm phân biệt và phương trình (2) có 6 nghiệm phân biệt (không trùng nhau).
Vậy phương trình đã cho có 9 nghiệm phân biệt. Câu 9.
(Nguyễn Du - DakLak 19) Cho hàm số    3 2 y
f x ax bx cx d (với 
a, b, c, d  , a  0 ). Biết
đồ thị hàm số y f x có hai điểm cực trị là A0;  1 và B 2; 3
  . Hỏi tập nghiệm của phương trình 3
f x  f x 3  2
f x  0 có bao nhiêu phần tử? A. 2019 . B. 2018 . C. 9 . D. 8 . Lời giải Chọn D Ta có   3 2
f x ax bx cx d f  x 2
 3ax  2bx c .  f 0  0 c  0 a  1  f  0  1   d  1 b   3
Theo giả thiết ta có hệ       f x 3 2
x  3x 1. f  2  0 12a  4b  0 c  0    f   8
a  4b 1  3  3  d  1 2     + Xét phương trình: 3 3
f x  f x 3  2
f x  0 3
f x 
f x   3 f x 3 2.
 2. f x   * .
Xét hàm số đặc trưng h t 3
t t ht 2 2
 3t  2  0, t   .  f x 3 2  0
x  3x 1  0   1           3 3 * f x
f x f x  f x  f   x 3 2
 1  x  3x  0 2   f x 3 2  1 
x  3x  2  0   3 
Bấm máy, phương trình (1) có 3 nghiệm phân biệt, phương trình (2) có 2 nghiệm phân biệt, phương
trình (3) có 3 nghiệm phân biệt (không trùng nhau).
Vậy phương trình đã cho có 8 nghiệm phân biệt.
2. Tìm điều kiện để phương trình, bất phương trình có nghiệm
Câu 10. (Đề Chính Thức 18 - Mã 103) Cho phương trình 7x m  log x m m 7   với là tham số. Có bao
nhiêu giá trị nguyên của m  2
 5; 25 để phương trình đã cho có nghiệm ? A. 9 . B. 25 . C. 24 . D. 26 . Hướng dẫn giải Chọn C
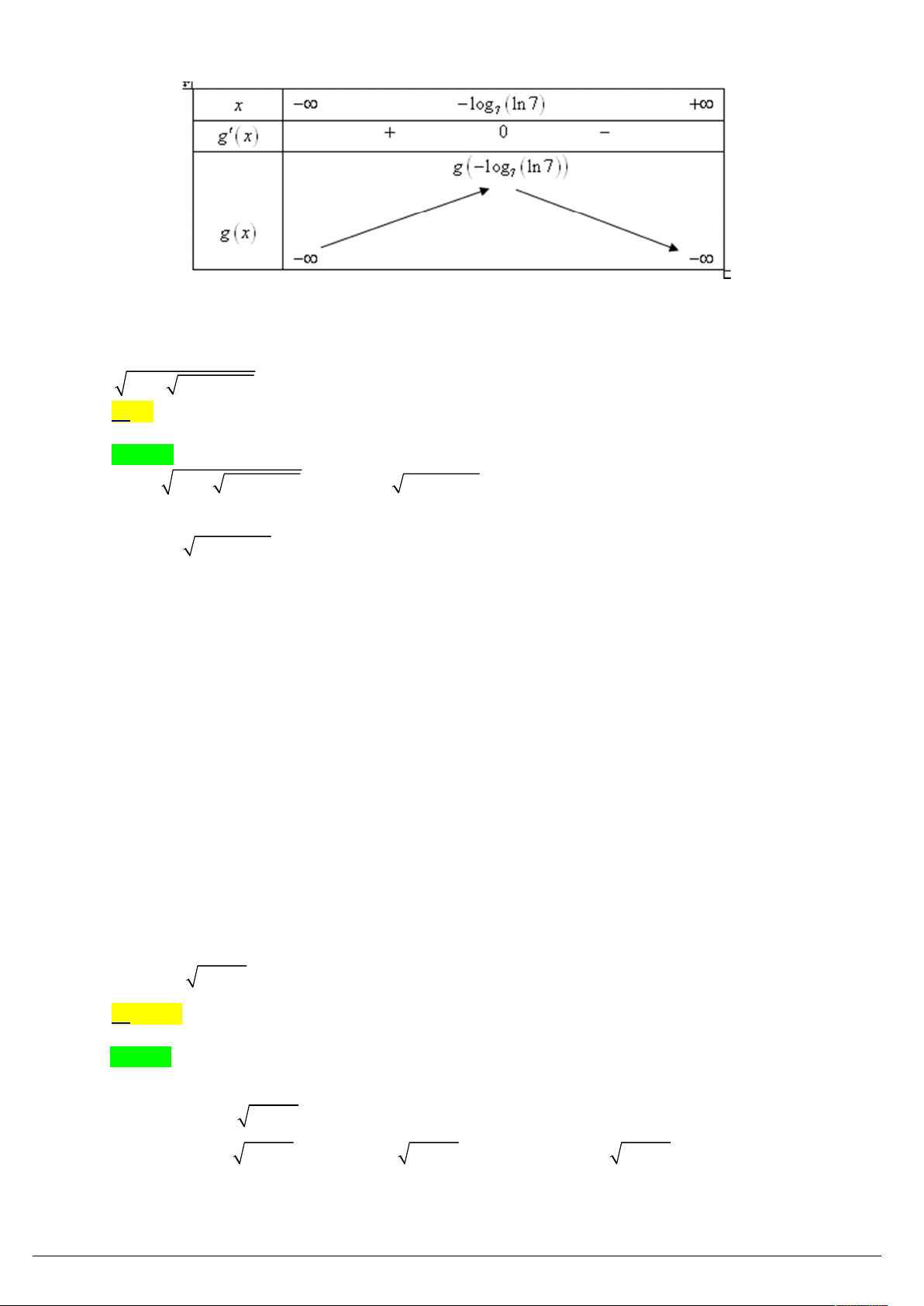
ĐK: x m  0 (a).  x 7  m t Đặt t  log x m  7x   7t xt   1 7   ta có hệ  . 7t m   x Do hàm số    7u f u
u đồng biến trên  , nên ta có   1  t x . Khi đó: 7x      7x m x m x (thỏa điều kiện a).
ThS. Nguyeãn Vaên Rin – HBT Trang 5/43
Xét hàm số     7x g x x
    1 7x g x
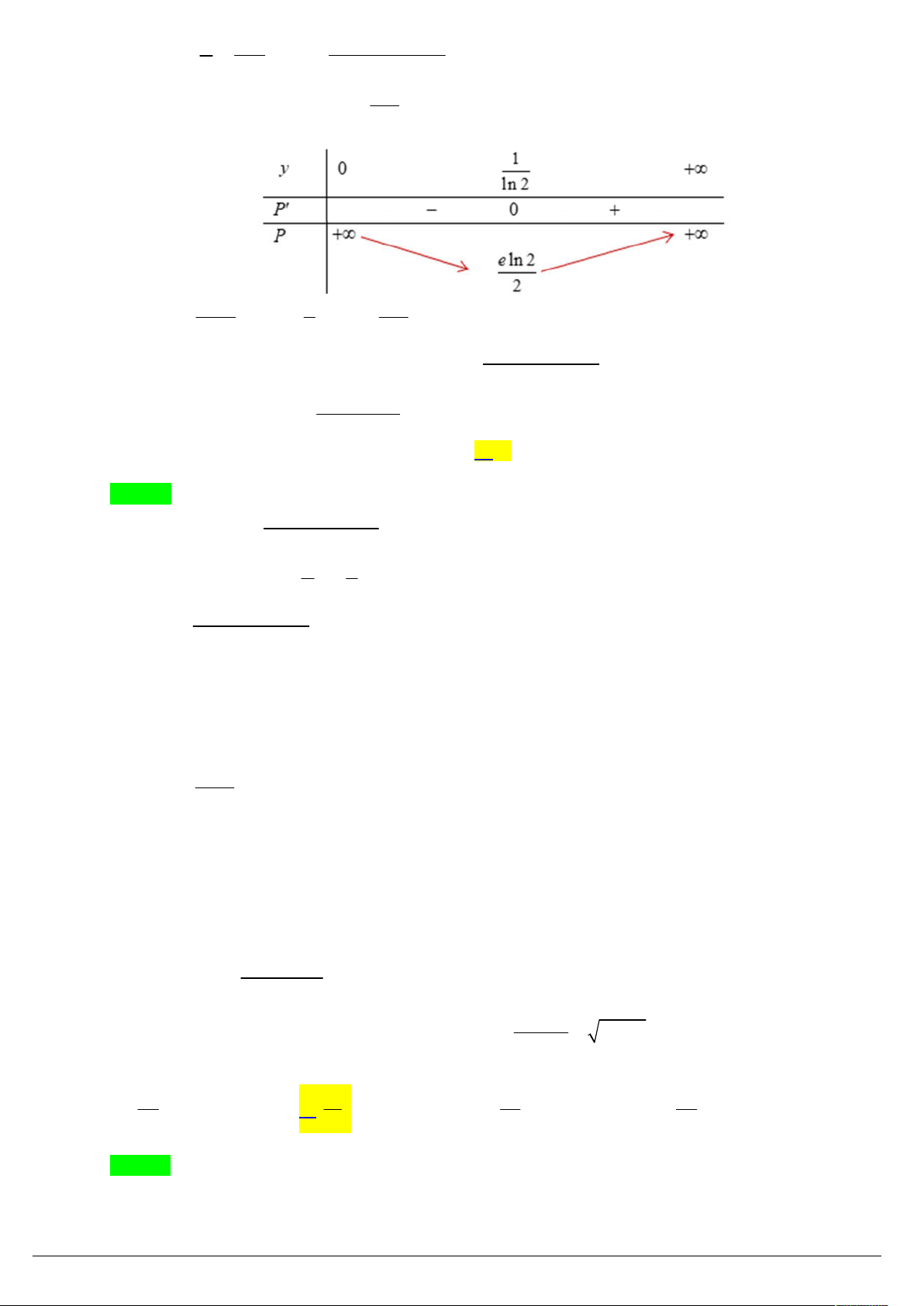
ln 7  0  x   log ln 7 7   . Bảng biến thiên:
Từ đó phương trình đã cho có nghiệm khi và chỉ khi m g  log ln 7  0  ,856 7   .
Do m nguyên thuộc khoảng  2
 5; 25 , nên m  2  4; 1  6;...;   1 .
Câu 11. (Đề tham khảo BGD 18) Có bao nhiêu giá trị nguyên của tham số m để phương trình 3 3
m  3 m  3sin x  sin x có nghiệm thực? A. 5 . B. 7 . C. 3 . D. 2 . Lời giải Chọn A Ta có 3 3 3 3
m  3 m  3sin x  sin x  3 m  3sin x  sin x m . u   sin x   1   u   1 Đặt  . 3 3 v
m  3sin x v m  3sin x m  3u  3 3 
v u m Ta có hệ 3 3 
u  3u v  3v * . 3
v m  3u
Xét hàm số y f t  3
t  3t trên  . f t  2
 3t 1  0, t
   nên hàm số f t  đồng biến trên  .  
*  f u  f v  u v . Suy ra 3 3
u m  3u m u  3u   1 .
Xét hàm số g u 3
u  3u trên đoạn  1   ;1 .
Ta có gu 2
 3u  3  0  u  1  . g   1  2; g   1  2  .
Suy ra max g u   2; min g u   2 . 1;  1 1;  1
Do đó phương trình (1) có nghiệm khi và chỉ khi 2   m  2 .
Vì m   nên m 0; 1  ;   2 .
Câu 12. Có bao nhiêu giá trị nguyên dương nhỏ hơn 2018 của tham số m để phương trình log   2x m m
 2x có nghiệm thực? 2   A. 2017 . B. 2016 . C. 1005 . D. 1004 . Lời giải Chọn A
m  2x  0 a  Điều kiện:  .
m m  2x  0 b  2 2 Ta có log   2x  2    2x  2x   2x   2x  2x  2x m m x m m m m * . 2         Xét hàm số   2
f t t t trên khoảng 0;   .
Vì f t   2t 1  0, t
  0 nên hàm số f t  đồng biến trên khoảng 0;   .
ThS. Nguyeãn Vaên Rin – HBT Trang 6/43 Do đó * 
  2x   2x   2x  2x   4x 2x f m f m m .
Xét hàm số   4x 2x g x   trên  . g xx x      x 2 x x 1 4 ln 4 2 ln 2 0 2. 2  2  0  2   x  1 . 2 Bảng biến thiên – 1 YCBT  m   . 4
Vậy m 1; 2;...; 20  17 .
Câu 13. (KHTN Hà Nội 19) Có bao nhiêu giá trị nguyên của tham số mm  10 để phương trình x 1 2   log
x  2m m 4   có nghiệm ? A. 9 . B. 10 . C. 5 . D. 4 . Lời giải Chọn A
ĐK: x  2m  0 Ta có x 1 2   log
x  2m m  2x  log
x  2m  2m 2   4    x
2  t  2m Đặt t  log x  2m
 2x   2t xt   1 2   ta có 
2t x  2  m Do hàm số    2u f u
u đồng biến trên  , nên ta có  
1  t x . Khi đó: 2x   2  2  2x x m mx .
Xét hàm số    2x g x
x g x  2x ln 2 1  0  x  log ln 2 2   . Bảng biến thiên: g  log ln 2 2  
Từ đó phương trình đã cho có nghiệm khi và chỉ khi 2m g  log ln 2  m  2   2
 0, 457 (các nghiệm này đều thỏa mãn điều kiện vì  2  2x x m  0 )
Do m nguyên và m  10 , nên m 1, 2,3, 4,5, 6, 7,8,  9 .
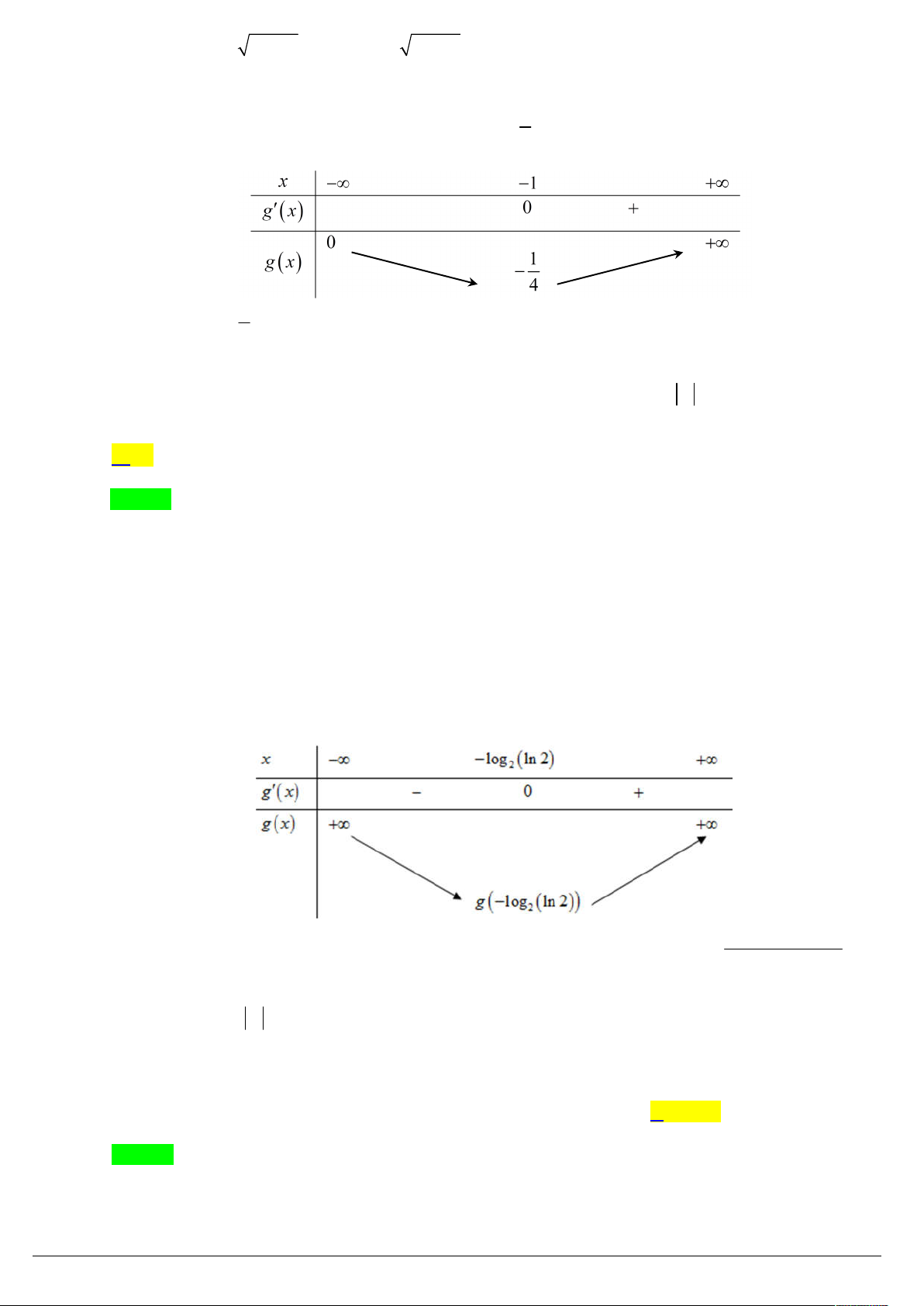
Câu 14. Cho hàm số f x   3  m  3 2 1
x  3x  4  mx  2 với m là tham số. Có bao nhiêu số nguyên m  2  018; 201 
8 sao cho f x  0 với mọi giá trị x 2; 4. A. 4037 . B. 2021 . C. 2019 . D. 2020 . Lời giải Chọn D 3 3
Ta có f x  0   3  m  3 2 1
x  3x  4  mx  2  0   x   1   x  
1  mx  mx (1). Xét hàm số   3
g t t t trên  , có gt  2
 3t 1  0 , t    .
ThS. Nguyeãn Vaên Rin – HBT Trang 7/43
Do đó hàm số g t  đồng biến trên  . x 1   
1  g x  
1  g mx  x 1  mx m  , x  2; 4 . x x 1 5
Vì hàm số h x 
nghịch biến trên đoạn 2; 4 nên min h x  h 4  . x 2;4 4 5
YCBT  m  min h x  m  . 2;4 4
Vì m nguyên thuộc đoạn  2  018; 201 
8 nên có 2020 giá trị của m thỏa mãn.
Câu 15. (Chuyên Vĩnh Phúc 18) Tìm tất cả các giá trị của tham số m để phương trình ln m  ln m x  x có nhiều nghiệm nhất. A. m  0 . B. m  1 . C. m  e . D. m  1  . Lời giải Chọn B
m x  0  a Điều kiện  . m  ln 
m x  0 b 
Phương trình đã cho tương đương với  ln    x m m
x e (thỏa điều kiện b).
Đặt ln m x  y y
m x e (thỏa điều kiện a)  ey m x . 
ex m y Ta có hệ 
 ex  ey y x  ex x  ey y * .
ey m x  Vì hàm số    et f t
t đồng biến trên  nên  
*  f x  f y  x y x x
m x e m e x .
Xét hàm số    ex g x
x ;    ex g x
1 ; g x  0  x  0 . BBT
Suy ra phương trình có nhiều nhất là hai nghiệm  m  1 .
Câu 16. (SỞ CÀ MAU 19) Gọi S là tập tất cả các giá trị nguyên của tham số m  20  19; 2019 để bất phương trình  3  m  3 x   3  m  2 x   3  m m  3 1 3 2 13 3
x 10  m m  0 đúng
với mọi x 1; 
3 . Số phần tử của tập S là A. 4038. B. 2021 . C. 2022. D. 2020. Lời giải Chọn B  3  m  3 x   3  m  2 x   3  m m  3 1 3 2 13 3
x 10  m m  0, x  1;  3 .   x  3 2
x  2  m x   3
1   m x   1 , x  1;  3 .   *   Xét: f t  3
t t, t
   , ta có f t  2
 3t 1  0, t    .
Hàm số f t  luôn đồng biến trên  .  x  2
*  f x  2  f mx  
1   x  2  mx   1  m  . x 1 x  2 5 YCBT  m  min  m  . 1;  3 x 1 4
Vì m   nên m  2  019;  2018;..  .;1 .
Vậy có 2021 giá trị cần tìm.
ThS. Nguyeãn Vaên Rin – HBT Trang 8/43 Câu 17. (ĐỀ 17 VTED 19) Có bao nhiêu số nguyên m để bất phương trình 6 4 3
x x mx   2  m  2 6 15 3
x  6mx 10  0 nghiệm đúng với mọi số thực x . A. 4 . B. 3 . C. Vô số. D. 5 . Lời giải Chọn B Ta có: 6 4 3
x x mx   2  m  2 6 4 2 3 3 2 2 6 15 3
x  6mx 10  0  x  6x 15x 10  m x  3m x  6mx
  x  3   x    mx  3 2 2
 mx    f  2 2 3 2 1 3 1
x  2  f mx   1
Trong đó f x 3
t  3t đồng biến trên  . f  2
x    f mx   2 2 2 2
1  x  2  mx 1  x mx 1  0, x
    m  4  0  2   m  2 .
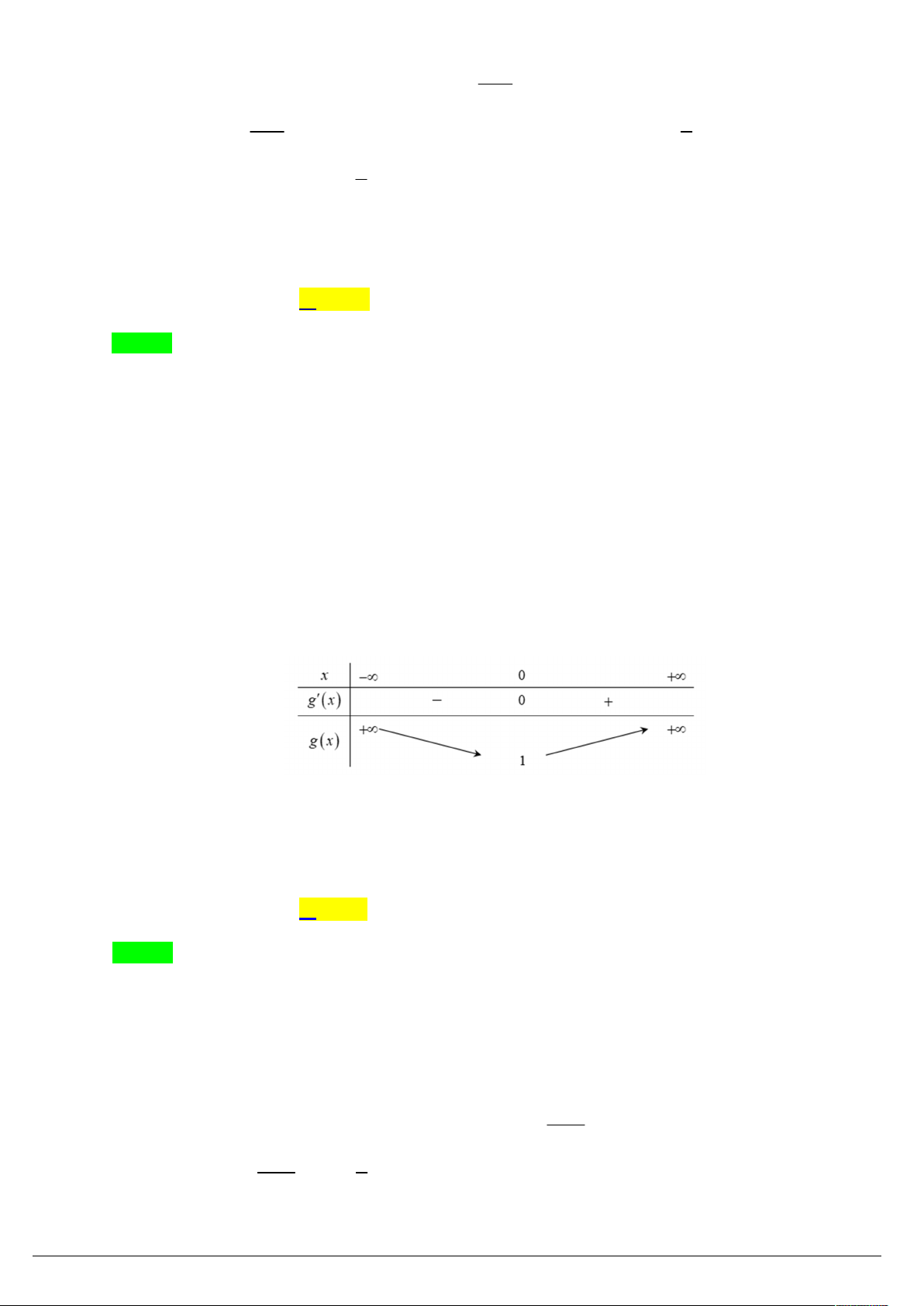
Câu 18. (SỞ QUẢNG BÌNH 19) Gọi S là tập hợp tất cả các giá trị nguyên dương của tham số m để bất phương trình sau 6 4 3 3 2
x  3x m x  4x mx  2  0 nghiệm đúng với mọi x 1;3. Tổng tất cả các
phần tử của S bằng A. 3 . B. 2 . C. 1. D. 4 . Lời giải Chọn A Ta có: 6 4 3 3 2 6 4 2 3 3
x  3x m x  4x mx  2  0  x  3x  4x  2  m x mx
  x  3   x    mx3 2 2 1 1  mx   1
Xét hàm đặc trưng f t  3
t t f t  2 '  3t  1  0    f  2
x    f mx 2 1 1
x 1  mx
Bài toán trở thành tìm m để bất phương trình 2
x 1  mx nghiệm đúng với mọi x 1;3 2 x 1 2
x 1  mx m
g x , x  1;  3 x 1
g ' x  1  0 x
  1;3  Min g x g 1  2 2       x 1;3   x  YCBT  m  2 . Vì m
  nên m 1; 
2  S  1 2  3.
Câu 19. (Chuyên Thái Bình 19) Có bao nhiêu giá trị nguyên của tham số m để phương trình f
f x m x m có nghiệm x 1;2 biết 5 3
f ( x)  x  3x  4m .   3 3 ( ) A. 16. B. 15. C. 17. D. 18. Lời giải Chọn A Đặt 3 3 t
f ( x)  m t f ( x)  m . Ta được hệ phương trình sau: 3 3 3 3
f (t)  x m
f (t)  x m
f (t)  t f ( x)  x (*)      . 3 3
t f ( x)  m
f (x)  t m   f ( x)  t m  Vì 5 3 4 2
f (x)  x  3x  4m, f '( x)  5x  9x  0, x    nên hàm số 3
h( x)  f ( x)  x đồng biến trên 
. Do đó: (*)  x t . 1 2 Khi đó ta được: 3 5 3 5 3 5 3
f (x)  x m x  3x  4m x  2x  3m g(x)  x x m(**) . 3 3 1 2 Dễ thấy 5 3 g(x)  x
x đồng biến trên 1;2 nên phương trình (**) có nghiệm trên đoạn 1;2 khi 3 3
và chỉ khi: g(1)  m g(2)  1  m  16.
Vì m thuộc số nguyên nên có 16 số thỏa mãn bài toán.
ThS. Nguyeãn Vaên Rin – HBT Trang 9/43
Câu 20. (Tập huấn Bắc Ninh 19) Cho phương trình 3 x
x m x m   6 4 2 2 . 6 4 . 3 2
1  8x  20x 10x 1. Biết  aa ;   
 (với a, b là các số nguyên dương và phân số
tối giản) là tập tất cả các giá trị của tham số  bb
m để phương trình đã cho có hai nghiệm dương phân biệt. Tính 2 2
S a b . A. 17 . B. 5 . C. 25 . D. 10 . Lời giải Chọn C
Với x  0 phương trình đã cho tương đương với 10 1
6x  4m.6x  4m  2 3
 8x  20x   3 x x 3       x m 3 1 1 6 4
 2 6x  4m  2x   2 2x      * .  x   x
Xét hàm số f t  3
t  2t trên  .
Ta có f t  2
 3t  2  0, t
   nên hàm số đồng biến trên  . 2  1  1  1 
Do đó *  f  6x  4m   f 2x  
6x  4m  2x
 4m  2x   6x     .  x xx  2  1 
Xét hàm số g x  2x   6x  
trên khoảng 0;   .  x  2 2  1   1  2x 1 2x 1  x  1 g x 4 3  2 2x  2   6  0  .
 3  4x 1  3x     . 2  2   x   x x x x  0  ,57...  0  Bảng biến thiên – 3 YCBT  m  2 2
S  3  4  25 . 4 Câu 21. (TRẦN NHÂN TÔNG - QUẢNG NINH 18) Phương trình 3
x2 m3x  3 2 x x x mx2 x 1 2 6 9 2 2      
1 có 3 nghiệm phân biệt khi và chỉ khi m  (a;b) . Tính 2 2
T b a . A. T  36 . B. T  48 . C. T  64 . D. T  72 . Hướng dẫn giải Chọn B 3 3 3
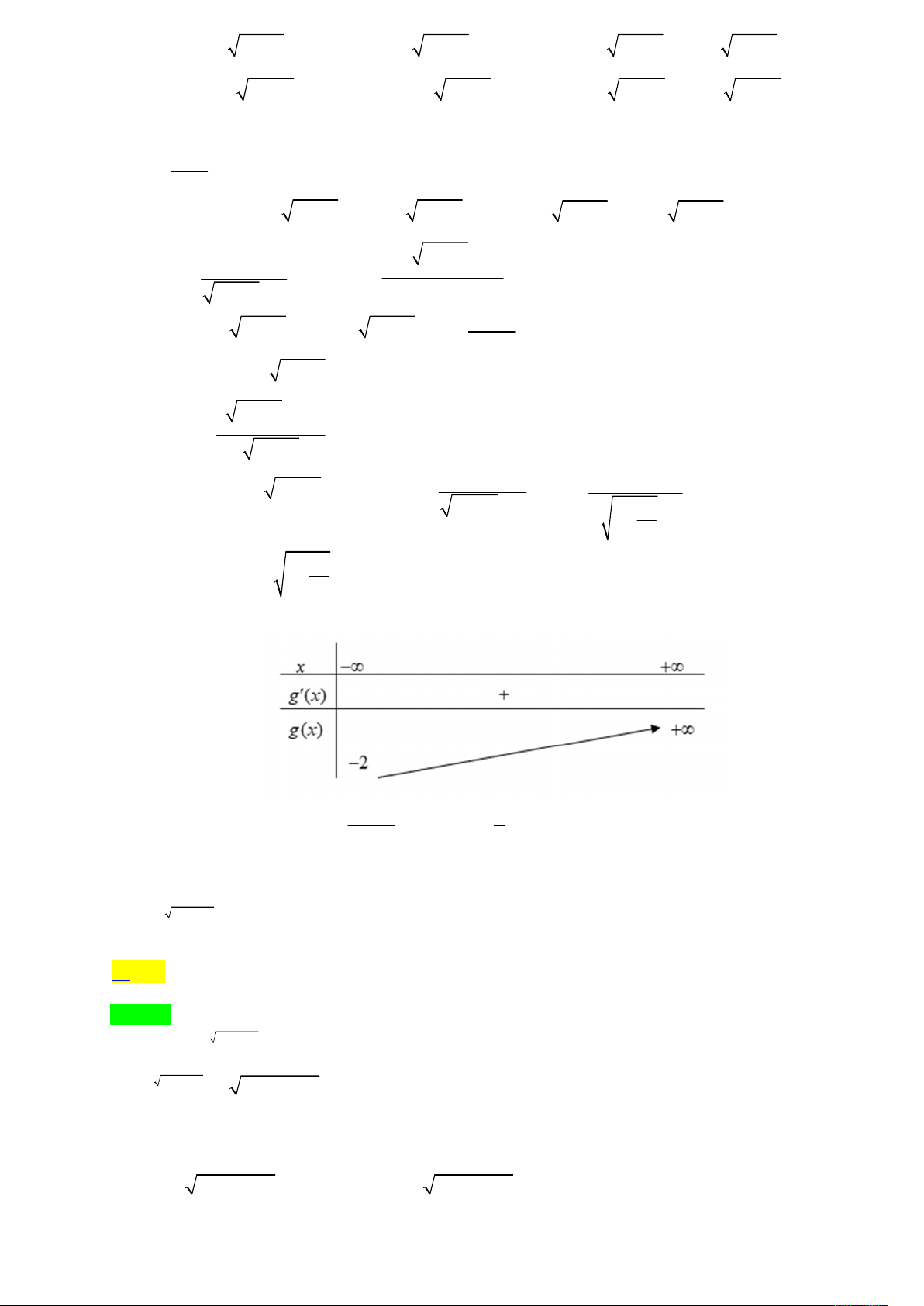
Ta có x2 m3x  3 2 x x x mx2 x 1 2 6 9 2 2       1 m3 x      3 2 2 2  8   3  2  2 x x m x 3 mxx   m x     x3 3 2 2 3 2 2 * . Xét hàm số   3  2t g tt trên  . gt t 2
 2 .ln 2  3t  0, t
   nên hàm số g t  đồng biến trên  .
Do đó    g  3 m x   g   x 3 * 3 2 
m  3x  2  x m x    x3 3 2 2 3
m  8  9x  6x x .
Xét hàm số f x 3 2
 x  6x  9x  8 trên  . x  3
có f  x 2  3
x 12x  9 ; f  x  0   . x  1  Bảng biến thiên
ThS. Nguyeãn Vaên Rin – HBT Trang 10/43
Dựa vào bảng biến thiên ta có, phương trình có 3 nghiệm phân biệt khi 4  m  8 .
Suy ra a  4; b  8 2 2
T b a  48 .
Câu 22. (SGD Bà Rịa Vũng Tàu 18) Có bao nhiêu giá trị nguyên của tham số m để tồn tại cặp số  ; x y thỏa 3x5 y x3 y 1 e e  
 1 2x  2 y và 2
log 3x  2y   1  m  6 2
log x m  9  0 . 3 3 A. 6 . B. 5 . C. 8 . D. 7 . Lời giải Chọn Bx  0 Điều kiện  .
3x  2 y 1  0  Ta có: 3x5y x3 y 1 e e  
 1 2x  2 y 3x5 yx yx3 y 1 e 3 5 e     
  x  3y   1 * . Xét hàm số    et f tt trên  .
Ta có    et f t
1  0 nên hàm số đồng biến trên  .
Do đó *  f 3x  5y  f x  3y  
1  3x  5 y x  3y 1  2 y  1 2x .
Thế vào phương trình còn lại ta được 2
log x  m  6 2
log x m  9  0 . 3 3
Đặt t  log x , phương trình trở thành 2
t  m   2
6 t m  9  0   1 . 3 Phương trình  
1 có nghiệm    0  2
3m 12m  0  0  m  4 .
Do đó có 5 số nguyên m thỏa mãn. 3 2 2
Câu 23. (SỞ BÀ RỊA VŨNG TÀU 19) Cho phương trình x x 2xm x x5 3 3  3
x  3x m  5  0 . Gọi S là
tập hợp các giá trị nguyên của tham số m để phương trình trên có ba nghiệm phân biệt. Số phần tử của S là A. 2 . B. 4 . C. 3 . D. 1. Lời giải Chọn C 3 2 2
Phương trình đã cho trở thành x x 2xm   3 2
x x x m x x 5    2 3 2 3
x x  5 . (1) Xét hàm số    3t f t
t , t   có    3t f t
.ln 3 1  0 , t    f t  luôn đồng biến trên  . Do đó phương trình 3 2 2 3
(1)  x x  2x m x x  5  m  x  3x  5 . (2)
Xét hàm số g x 3
 x x   g x 2 3 5
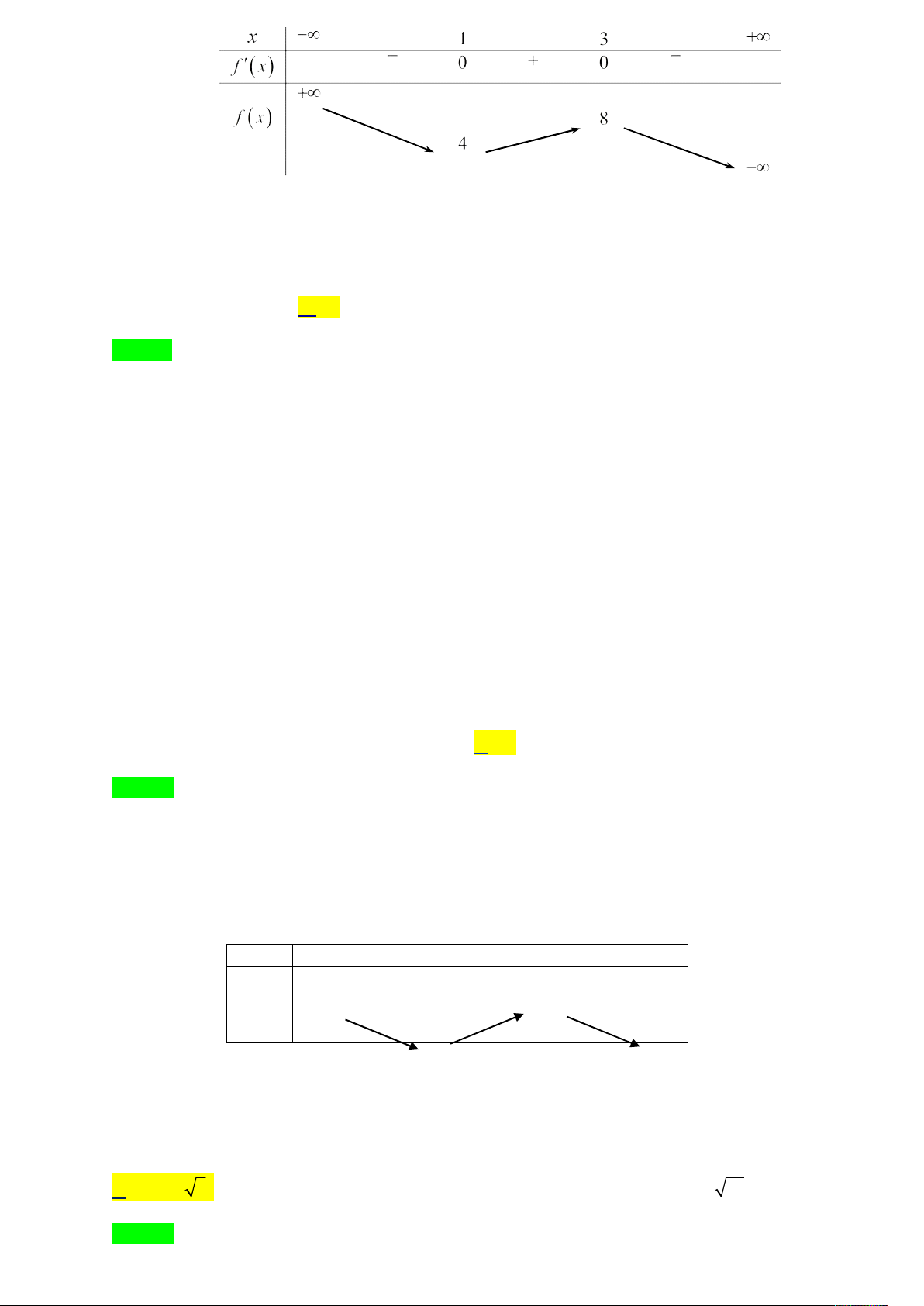
 3x  3; g x  0  x  1  . Ta có bảng biến thiên x  1 1  g x  0  0   7 g x 3 
Từ bảng biến thiên ta thấy, phương trình đã cho có ba nghiệm phân biệt  (2) có ba nghiệm phân biệt
 3  m  7 . Vì m   nên m  4 ;5; 6 . Vậy có 3 giá trị m nguyên.
Câu 24. Cho phương trình mcosxsin x  2 1sin x e  e
 2  sin x m cos x với m là tham số thực. Gọi S là tập tất cả
các giá trị của m để phương trình có nghiệm. Khi đó S có dạng  ;  a ; b  . Tính
T  10a  20b . A. T  10 3 . B. T  0 . C. T  1 .
D. T  3 10 . Lời giải Chọn A
ThS. Nguyeãn Vaên Rin – HBT Trang 11/43
Ta có mcosxsin x  2 1sin x e  e
 2  sin x m cos x
m cos xsin x 21sin x  e
m cos x  sin x  e  21 sin x Xét hàm số    et f t
t t   ,    et f t
1  0  f t  đồng biến trên  .
Suy ra mcosxsin x 21sin x e
m cos x  sin x  e
 2 1 sin x  m cos x  sin x  21 sin x
m cos x  sin x  2 .
Phương trình có nghiệm khi 2 2
m 1  4  m  3 .  S   ;
  3   3;  . Vậy T  10a  20b  10 3 .   
Câu 25. (Chuyên Lương Thế Vinh – Đồng Nai 18) Có bao nhiêu số nguyên m để phương trình 2
3x  3x m 1 2 log
x  5x  2  m có hai nghiệm phân biệt lớn hơn 1. 2 2 2x x 1 A. 3 . B. Vô số. C. 2 . D. 4 . Lời giải Chọn C Điều kiện: 2
3x  3x m  1  0 (a). Ta có: 2
3x  3x m 1 2
 3x  3x m 1  2 log
x  5x  2  m 2  log
1  x  5x 1 m 2 2   2x x 1 2 2 2x x 1   2
3x  3x m 1 2  log
x  5x 1 m 2 2 4x  2x  2  log  2
3x  3x m   1  log  2
4x  2x  2   2
4x  2x  2   2
3x  3x m 1 2 2   log  2
3x  3x m   1   2
3x  3x m   1  log  2
4x  2x  2   2 4x  2x  2   1 2 2  1
Xét hàm số: f t   t  log t trên 0;  , ta có f t   1  0 , t   0;  . 2 t.ln 2
Do đó hàm số f t  đồng biến trên 0;  .
Suy ra:    f  2
x x    f  2 1 4 2 2
3x  3x m   1 2 2
 4x  2x  2  3x  3x m 1 (thỏa điều kiện a) 2
x  5x m 1 2 . Điều này đúng với mọi x   . 5
Xét hàm số: g x 2
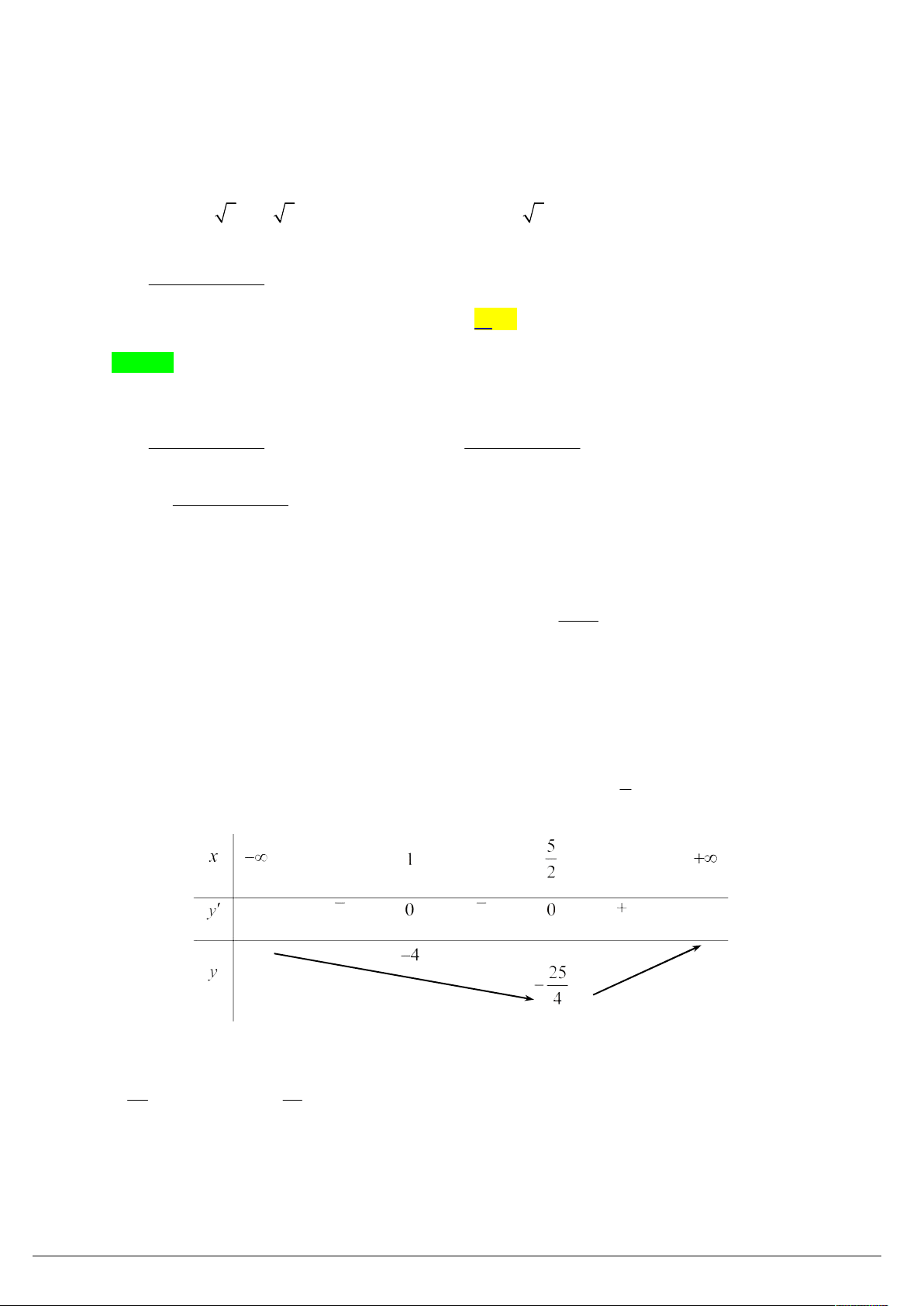
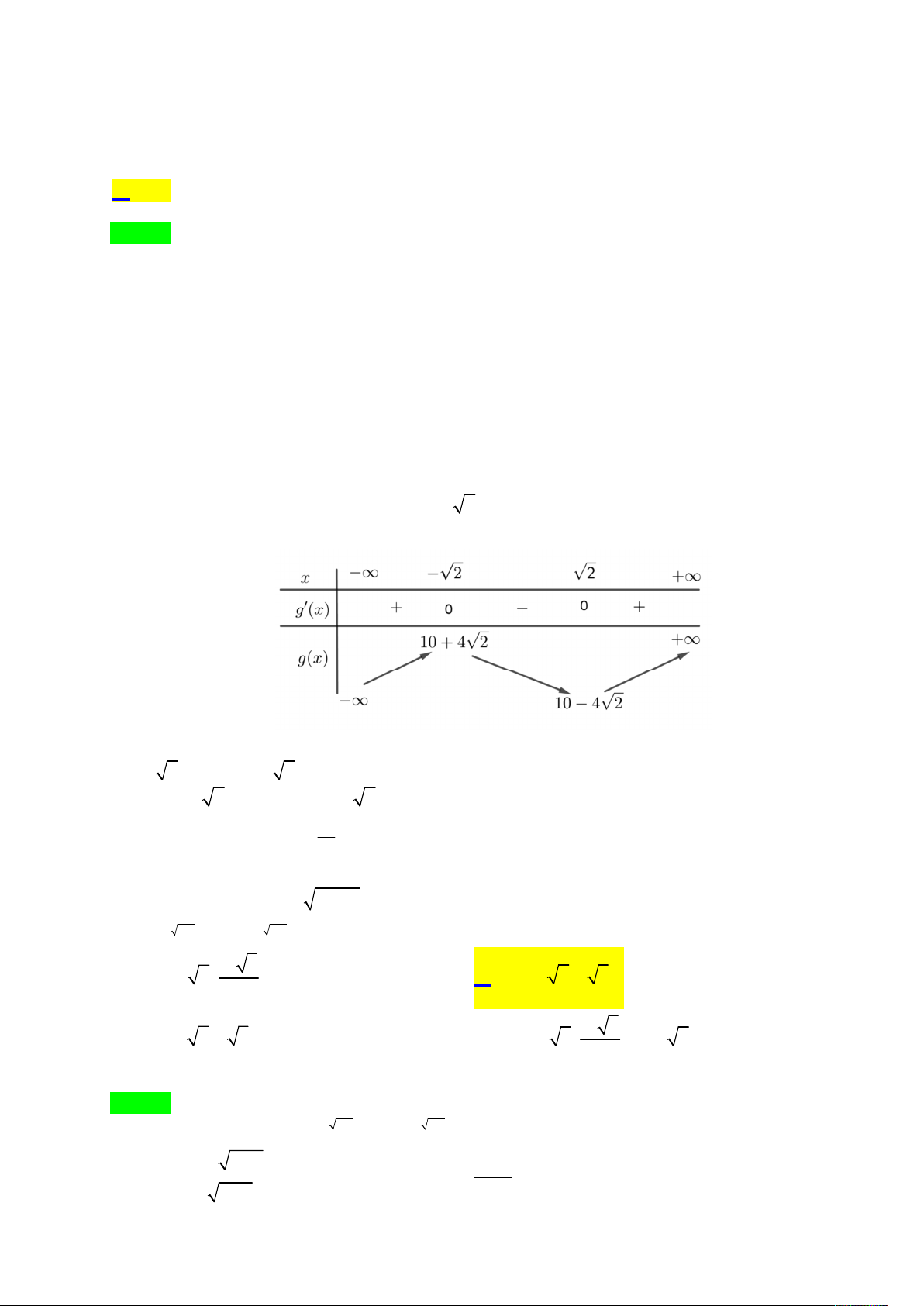
x  5x trên  , ta có g x  2x  5  0  x  . 2 Bảng biến thiên:
Theo bảng biến thiên ta thấy: phương trình 2 có hai nghiệm phân biệt lớn hơn 1 khi và chỉ khi 25 21 
m 1  4    m  3  . 4 4
Do m   nên m  5  ;   4 .
Vậy có 2 giá trị nguyên của m thỏa mãn yêu cầu bài toán.
ThS. Nguyeãn Vaên Rin – HBT Trang 12/43
Câu 26. (SGD Phú Thọ 18) Có bao nhiêu giá trị nguyên dương của tham số m để phương trình 2  2x mx 1    2 log 
  2x mx 1  x  2 có hai nghiệm thực phân biệt? 2  x  2    A. 3 . B. 4 . C. 2 . D. 1. Lời giải Chọn Bx  2  0 Điều kiện:  . 2
2x mx 1  0  2  2x mx 1    Ta có 2 log 
  2x mx 1  x  2 2  x  2    2 2  log
2x mx 1  2x mx 1  log
x  2  x  2 2 2    f  2
2x mx 1  f x  2   1 1
Xét hàm số f t   log t t với t 0;  có f t   1  0 , t   0;  . 2 t ln 2
f t  đồng biến trên 0;  nên   1 2 
2x mx 1  x  2 . x  2  x  2   Từ đó    . 2
2x mx 1    x  22 2 x  
m  4 x  3  0 2  
YCBT  2 có hai nghiệm phân biệt x , x lớn hơn 2 1 2
  m  42 12  0 m   m       
  x  2  x  2  0  x x  4  0
 4  m  4  0 1   2  1 2     x  2 x  2  0
x x  2 x x  4  0 
3  2 4  m  4  0 1 2  1 2  1  2     m  8  9  *  9  m
mà m    m 1; 2;3;  4 . m  2   2
Câu 27. (SGD Bắc Ninh 18) Tập hợp tất cả các giá trị thực của tham số m để phương trình 3m m e e   2 x   x  2 2 1
1 x 1 x  có nghiệm là  1   1   1   1  A. 0; ln 2   . B. ;  ln 2   . C. 0;   . D. ln 2;    .  2   2   e   2  Lời giải Chọn B 2 t 1 Đặt 2 2 2 2
t x  1 x t  1 2x 1 x x 1 x  . 2 2 x 1 x x 0  x  1 2 t  1  ; 2
t  0  1 x x    x  . 2 2 2 2 1 x 1 x 1 x x 2   2  t   1  1;t   1  1;t    2  1  t  2 .  2    2  t   m m 1 Phương trình trở thành 3 3m m 3 e
e  2t. 1  e
e t t     * . 2   Xét hàm   3
f u u u trên  . f u 2
 3u 1  0, u
   nên hàm số f u đồng biến trên  .
*   m     m f e
f t e t .
ThS. Nguyeãn Vaên Rin – HBT Trang 13/43 m 1
Phương trình có nghiệm  1  e  2  m  ln 2 . 2
Câu 28. (SỞ NAM ĐỊNH 19) Cho hàm số
  2019x 2019 x f x   
. Tìm số nguyên m lớn nhất để
f m  f 2m  2019  0 A. 6  73 . B. 674 . C. 673 . D. 674 . Lời giải Chọn B Hàm số
  2019x 2019 x f x    xác định trên  . Ta có:
   2019x  2019x  2019x  2019x f x
   f x  f x là hàm lẻ trên  .
Mà    2019x ln 2019  2019x f x ln 2019  0, x
   nên hàm số f x đồng biến trên  .
Do vậy: f m  f 2m  2019  0  f 2m  2019   f m
f 2m  2019  f m  2m  2019  m m  67  3
Do đó giá trị m nguyên lớn nhất thỏa mãn là 674 .
Câu 29. (Đặng Thành Nam 19) Cho hàm số f x   2 ln x
x 1 . Có tất cả bao nhiêu số nguyên m thỏa  1 
mãn bất phương trình f log m  f log  0  m   2019  A. 65 . B. 66 . C. 64 . D. 63 . Lời giải Chọn C
Điều kiện: m  1.
Hàm số f x   2 ln x
x 1 có TXĐ D   . 1
Ta có f x  ln  2 x x 1  ln   ln  2 x
x 1   f x , x   . 2    x x 1 1
Mặt khác f ' x   0, x
 , nên f x đồng biến trên  . 2 x 1 Khi đó ta có  1   1   1 
f log m  f log  0  f m   ff m f   m  log  log  m  log  log    2019   2019 m   2019  1 log 2019 log 2019  log m   log  log m   m  10  65, 77. m 2019 log m
Suy ra m 2;3;...; 
65 . Vậy có tất cả 64 số nguyên m thỏa mãn. 2
Câu 30. (Đặng Thành Nam 19) Cho hàm số x 1 ( ) e ex e x f x    
. Có bao nhiêu số nguyên dương m thỏa  12 
mãn bất phương trình f m  7  f  0   ? m  1  A. 4 . B. 6 . C. 3. D. 5 . Lời giải Chọn D
Tập xác định D   . 2 Ta có   x 1    x x f x e e
e    f x .
Suy ra f x là hàm số lẻ.   2   2 x   x f x 2 2 xx 1   xx 1 e e     x x 1  xx 1 f '(x)  1 e  1 e   0, x      . 2 2  x 1   x 1 
f x đồng biến trên  .
ThS. Nguyeãn Vaên Rin – HBT Trang 14/43  12   12   12 
f (m  7)  f  0  
f (m  7)   ff      .  m 1   m 1   m  1  12 1   m  5  m  7    .  m 1 m  1  
Vì m là số nguyên dương nên m 1, 2,3, 4,  5 . Cho hàm số   2x 2 x f x   
. Có bao nhiêu số nguyên m để bất phương trình
Câu 31. (ĐỀ 08 VTED 19) f  3 2
x x x m   f  2 2 3
2x x  5  0 có nghiệm đúng với mọi x0;  1 . A. 7 . B. 3 . C. 9. D. 8. Lời giải Chọn D Ta có
   2x  2x f x
  f x và    2x ln 2  2x f x ln 2  0, x    . Suy ra f  3 2
x x x m   f  2 2 3
2x x  5  0  f  3 2
x x x m   f  2 2 3
x  2x  5 3 2 2
x  2x  3x m x  2x  5 3 2 2 3 2 
x  2x  3x m x  2x  5 
x  3x  5x  5  m     3 2 2 3 2
x  2x  3x m  x  2x  5 
x x x  5  m
Xét hàm số g x 3 2
x  3x  5x  5, x 0; 
1 có max g x  2 0;  1 hx 3 2
x x x  5, x 0; 
1 có min h x  5 0;  1 3 2 
x  3x  5x  5  m  2   m Do đó  , x  0;  1   . 3 2
x x x  5  m  5  m
Vậy có 8 nguyên thỏa mãn. Câu 32. Cho hàm số
y f x 2
 1 x x . Tìm các giá trị của m để bất phương trình 3 x  2019x
x mf x m 
 0 nghiệm đúng với mọi x  4;16 . f  3 x  2019x
A. m  35228 .
B. m  36416 .
C. m  38421.
D. m  34662 . Lời giải Chọn B 2 1 1
Xét f x  1 x  x 2
 1 x x   2 1 f    x x x  3 x  2019x 3 x  2019x
Ta có  x mf x m 
 0   x mf x m   f  3 x  2019xf  3 x  2019x 1
  x mf x m   3 x xf  3 2019
x  2019x 
1 (Vì f x  ). f x
Xét hàm số g t   t f t   t  2 .
1 t t  trên  . 2 2 AM GM t t gt  2 2 2  1 t   2t  2 1 t .
 2t  2 t  2t 2 2 1 t 1 t
gt   2 t  2t  0 .
Vậy hàm số g t  luôn đồng biến trên  .
   g x m  g  3 x x 3 3 1 2019
x m  x  2019x m x  2020x .  
1 nghiệm đúng với mọi x  4;16  m Max  3
x  2020x   36416 . 4;16
ThS. Nguyeãn Vaên Rin – HBT Trang 15/43
Câu 33. (Yên Mô A – Ninh Bình 19) Tổng tất cả các giá trị nguyên của tham số m để phương trình 3
x3 m3x   3 2     x3 3 9 24 .3  3x x x x m
1 có ba nghiệm phân biệt bằng A. 45 . B. 38 . C. 34 . D. 27 . Lời giải Chọn D
Phương trình tương đương với 3
x  mx       3 xx mx        x x x x m m x     x3 3 3 3 2 3 3 3 3 9 24 .3 3 1 3 3 3 3   * . Xét hàm đặc trưng   3  3t f tt trên  . f t t 2
 3 ln 3  3t  0, t
   nên hàm số f t  đồng biến trên  .
   f m x   f   x  m x   x m    x3 3 3 * 3 3 3 3 3  3x 3 2
m   x  9x  24x  27 . x  2
Đặt g x 3 2
 x  9x  24x  27  g x 2  3
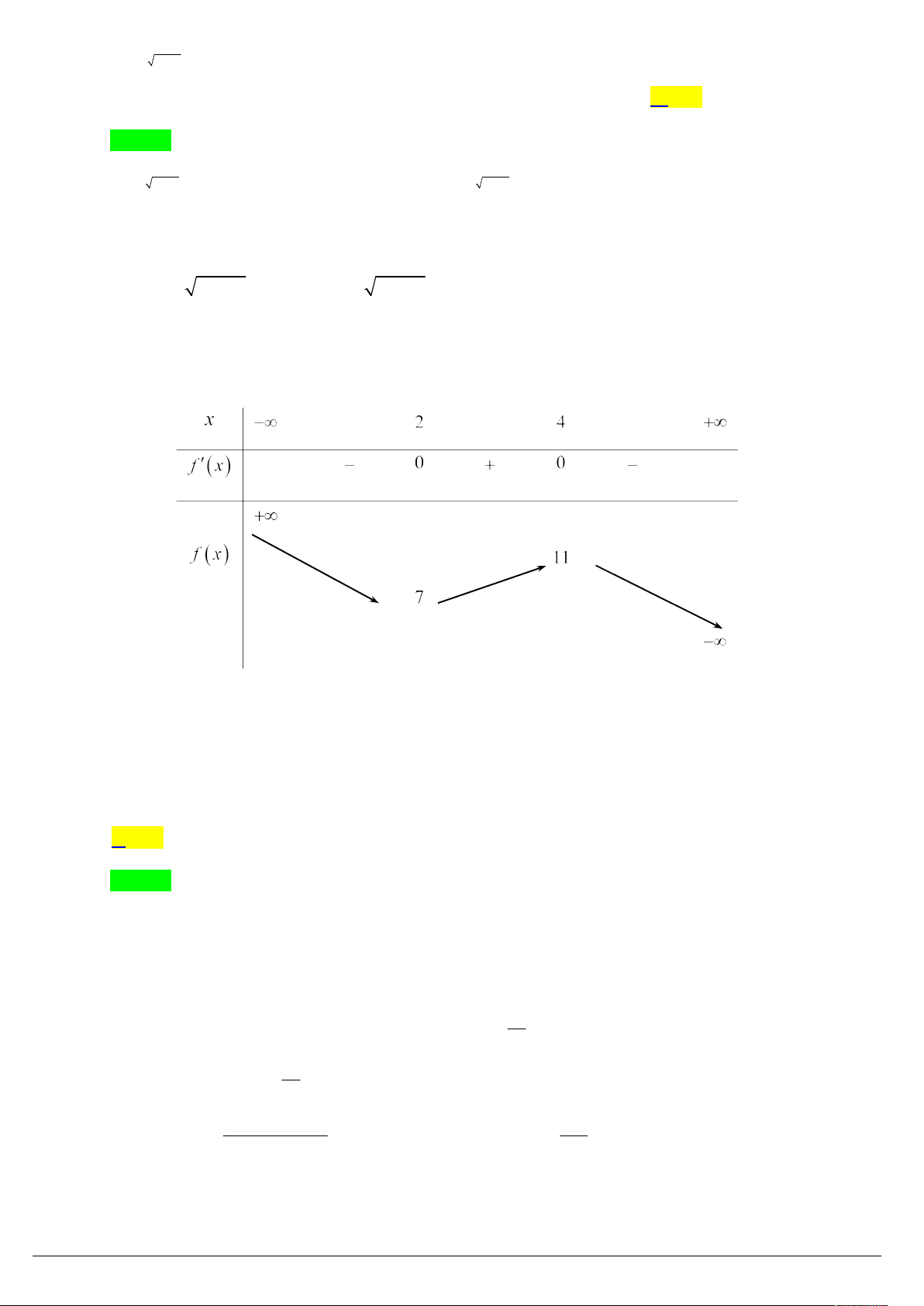
x 18x  24  0   . x  4  Ta có bảng biến thiên:
Phương trình có 3 nghiệm phân biệt  7  m  11.
Vì m    m 8;9;1 
0  S  8  9 10  27 .
Câu 34. (YÊN LẠC 19) Cho phương trình x x    2   x x x   3 m   3 27 3 .9 3 1 3
1 x  m  
1 x , m là tham số.
Biết rằng giá trị m nhỏ nhất để phương trình đã cho có nghiệm trên 0;  là a  e ln b , với a, b là
các số nguyên. Giá trị của biểu thức 17a  3b bằng A. 26 . B. 54 . C. 48 . D. 18 . Lời giải Chọn A 2 3 3
Phương trình đã cho tương đương 3 2
 3 3x  3 .3x   3x    3x x x x x
 mx  mx   x  3 x xx   mx3 3 3  mx (*). Xét hàm số   3
f t t t có f t  2
 3t 1  0, t
    f t  là hàm đồng biến trên  . 3x Do đó từ   * suy ra  3x x
mx . Vì x  0 suy ra 1  m . x 3x
Xét hàm số f (x)  1 trên 0;  . x
3x ln3 x 3x x 1
Ta có f  x   0  3
x ln 3 1  0  x   log e . 2   3 x ln 3
Dấu của f  x cũng là dấu của nhị thức bậc nhất x ln 3 1, do đó ta có bảng biến thiên:
ThS. Nguyeãn Vaên Rin – HBT Trang 16/43 x 0 log3e + ∞ f' 0 + + ∞ + ∞ f 1+e.ln3
Từ bảng biến thiên suy ra giá trị nhỏ nhất của m để phương trình có nghiệm là m  1 e ln 3 .
Suy ra a  1, b  3  17a  3b  17  9  26 . 2
Câu 35. (Sơn Tây Hà Nội 19) Cho phương trình x  1 2 .log  2
x  2x  3  4 xm log
2 x m  2 với m là 2  2  
tham số thực. Có bao nhiêu giá trị nguyên của m trên đoạn  2  019; 201 
9 để phương trình có đúng 2 nghiệm phân biệt. A. 4036 . B. 4034 . C. 4038 . D. 4040 . Lời giải Chọn C
Điều kiện: x   .  x 2 1 2 .log  2
x  2x  3  4 xm log 2 x m  2 2  2    x 2 1 2 .log  x 1 2     2 xm log 2 x m  2 2  2 2 2     1 .   Xét hàm số  2t y
.log t  2 với t  0 . 2   t 2t Ta có y  2 .log t  2 .ln 2   0, t   0 . 2   t  2ln 2 Vậy hàm số  2t y
.log t  2 đồng biến trên 0;  . 2    x  2 1  2 x m 2 2   Từ  
1  f  x  
1   f 2 x m    x   1
 2 x m    x  2 1
 2  x m  2
2m  x  4x 1   1   * . 2 2m x 1 2   3 m    2 1 TH1:  
1 có 2 nghiệm phân biệt và   2 vô nghiệm    m  . 1 2 m    2  1 m    2 3 TH2:  
2 có 2 nghiệm phân biệt và   1 vô nghiệm    m  . 3 2 m    2  3 m    2 TH3:  
1 có nghiệm x  2 và  
2 có nghiệm x  0    m   . 1 m    2  1   3 
Kết hợp với điều kiện m thuộc đoạn  2  019; 201  9 ta có m  2019;  ; 2019    . 2 2     
Vì m nguyên nên nên ta có 4038 giá trị của m .
Câu 36. (Thanh Chương Nghệ An 19) Gọi S là tập hợp tất cả các giá trị nguyên của tham số m thuộc đoạn 2 
2x x m 1 1
 0;10 để bất phương trình 2 log
 2x  4x  5  2m có nghiệm. Số phần tử của tập 3 2 x x 1 hợp S bằng A. 20. B. 10. C. 15. D. 5. Lời giải
ThS. Nguyeãn Vaên Rin – HBT Trang 17/43 Chọn B
Điều kiện xác định: 2 2
2x x m 1  1  3  0 2
 2x x m 1  0 (vì 2
x x 1  x  
 0 với mọi x ). (*) 2   x x 1  2  4 Khi đó: 2
2x x m 1 2
2x x m 1 2 log
 2x  4x  5  2m 2  log
1  2x  4x  4  2m 3 2 x x 1 3 2 x x 1 2
2x x m 1 2  log
 2x  4x  4  2m 3 3 2 x x   1  log  2
2x x m   1  log 3 2
x x 1    2
x x m     2 2 2 1
6 x x   1 3 3   log  2
2x x m 1   2
2 2x x m   1  log 3 2
x x 1   2
6 x x   1 . (1) 3  3 
Xét hàm số f t   log t  2t với t  0 . 3 1
Ta có: f t    2  0, t   0 . t.ln 3
Suy ra hàm số f t  đồng biến trên khoảng 0;   . Do đó (1)  f  2
2x x m   1  f   2
3 x x   1  2
 2x x m 1   2
3 x x   1 (thỏa mãn (*)) 2
x  2x  2  m . BPT 2
x  2x  2  m có nghiệm  m  min g x với g x 2
x  2x  2 .
Xét hàm số g x 2
x  2x  2 với x   có g x  2x  2 .
g x  0  2x  2  0  x  1  . Bảng biến thiên
Từ bảng biến thiên suy ra min g x  1. Do đó m 1. Vì m  1
 0;10 nên tập S  1; 2;...;1 
0 . Vây S có 10 phần tử.
Câu 37. (PHỤ DỰC – THÁI BÌNH 19) Tìm số giá trị nguyên của m thuộc  2
 0; 20 để phương trình 2 2 2
log (x m x x  4)  (2m  9)x 1 (1 2m) x  4 có nghiệm? 2 A. 12. B. 23. C. 25. D. 10. Lời giải Chọn B Điều kiện xác định: 2 2
x m x x  4  0 . log  2 2
x m x x  4   2m  9 x 1 1 2m 2 x  4 2  log x 2
x  4  x  m 2 2
 2mx  9x 1
x  4  2m x  4 2  4x  2 2  log 
m   2mx  9x 1 x  4  2m x  4 2 2  x  4  x  2  4x m x 4 mx     2 2  log 
  2mx  9x 1 x  4  2m x  4 2  2 x 4 x     
ThS. Nguyeãn Vaên Rin – HBT Trang 18/43  log  2
4x m x  4  mx  2
8x  2m x  4  2mx 1 log  2
x  4  x  2 x  4  x 2 2   log  2
8x  2m x  4  2mx   2
8x  2m x  4  2mx  log  2
x  4  x   2
x  4  x 1 Xét 2 2   
hàm số f t   log t t , t 0;  . 2 1
f t  
 1  0, t  0;   nên hàm số luôn đồng biến trên khoảng 0;   . t ln 2 Khi đó   1 2 2
 8x  2m x  4  2mx
x  4  x m  2 x   x   2 2 4
x  4  x 8x x  2 8 x  4  x 8x  2m  1  2m  1 2 x  4  x 4  m
 2m  1 2x  1 2 2
x  4  x  2 2
x x  4  x  . 2
Xét hàm số g x 2 2
x x  4  x với x  ;    .
x  4  x2 2 Ta có g (  x)   0, x   . 2 x  4  4  4 g x  x      lim x    lim  2 ;     2 lim lim x 4 x x x    x 2 
x  4  x x 4  1   1 2 x   4  lim g x 2  lim x  1 1   . 2 x x  x    
Ta có bảng biến thiên của g(x) 1  2m 5
Để phương trình có nghiệm thì  2  m  . 2 2
Do m nguyên thuộc  2
 0; 20 nên số giá trị m là 23.
Câu 38. (CHUYÊN THÁI NGUYÊN 19) Gọi S là tập hợp các giá trị nguyên dương của m để phương trình 3
cos x2 m3cos x  3 2 x x x m  cosx2 cos x 1 2 cos 6sin 9 cos 6 2 2       
1 có nghiệm thực . Khi đó tổng của
hai phần tử lớn nhất và nhỏ nhất của tập S bằng A. 28 . B. 21. C. 24 . D. 4 . Lời giải Chọn A 3 3
Ta có cosx2 m3cosx  x  cos x2 2 cos 2 m 3cos x     2  1   3 3 3 
m3cos x   3 2  3 cos  2cos  2 x m x
 2  cos x * . Xét hàm số đặc trưng   3  2u f uu trên  . f uu 2
 2 ln 2  3u  0, u
   nên hàm số đồng biến trên  .    f  3 *
m  3cos x   f 2  cos x  3 m  3cos x  2  cos x  3 2
 cos x  6 cos x  9 cos x  8  m .
ThS. Nguyeãn Vaên Rin – HBT Trang 19/43
Đặt cos x t với điều kiện t  1  
;1 , suy ra f t  3 2  t
  6t  9t  8  m .
Dễ thấy min f t   4 và max f t   24 nên phương trình đã cho có nghiệm khi và chỉ khi t   1;  1 t   1;  1
m 4; 24 . Suy ra S  4;5;...; 2 
4 nên tổng của hai phần tử lớn nhất và nhỏ nhất của S bằng 28 .
Câu 39. (Thuận Thành 2 Bắc Ninh 19) Gọi S là tập chứa các giá trị nguyên của m để phương trình 3 3 3x 18  x30m x 6 x 10  m 2m eee
 1 có 3 nghiệm thực phân biệt. Tính tổng các phần tử của tập S . A. 110 . B. 106 . C. 126 . D. 24 . Lời giải Chọn A Đặt 3
t x  6x 10 .
Ta có phương trình 3tm t m 2m 3t t 3    1 m m e e e
e e ee (1) . Xét hàm số 3 ( ) x x
f x e e xác định trên  . Ta có 3 (  )  3 x x f x
e e  0, x    .
Suy ra f (x) đồng biến trên  . Từ  
1 , ta có f (t)  f ( )
m , suy ra t m hay 3
x  6x 10  m (2) . 3 3 Phương trình 3x 18  x30m x 6 x 10  m 2m eee
 1 có 3 nghiệm thực phân biệt khi phương trình (2) có 3 nghiệm thực phân biệt. Xét hàm số 3
g(x)  x  6x 10 với x   . 2
gx x    2 ( ) 3 6
3 x  2; g (x)  0  x   2 .
Ta có bảng biến thiên của g( ) x
Dựa vào bảng biến thiên, phương trình (2) có 3 nghiệm thực phân biệt khi và chỉ khi
10  4 2  m  10  4 2 .
Ta có 10  4 2  4,34 và 10  4 2  15, 66 . Suy ra S  {5;6; 7;8;9;10;11;12;13;14;15} . 11
Tổng các phần tử của S là 5 15 110. 2
Câu 40. (CHUYÊN THÁI NGUYÊN 19) Tìm tất cả các giá trị thực của tham số m để phương trình 2 x x
m x   2 5 12 16 2 x  2 có hai nghiệm thực phân biệt thoả mãn 2 xx 1  2 x 1 2018 2018    2019x  2019 .  11 3 
A. m   2 6 ;  .
B. m  2 6 ;3 3 .  3      11 3 
C. m  2 6 ;3 3  .
D. m   3 3 ;   .   2 6   3   Lời giải Chọn B Xét bất phương trình 2 xx 1  2 x 1 2018 2018    2019x  2019
(1) . Điều kiện: x  1  . 
a  2x x 1 a b Đặt 
a b  2(x 1)  x 1  . 2 b   2  x 1 
ThS. Nguyeãn Vaên Rin – HBT Trang 20/43 a b
(1) trở thành 2018a  2018b  2019
 0  2(2018)a  2019a  2(2018)b  2019b (2) . 2
Xét hàm số ( )  2(2018)t f t
 2019t liên tục trên  . (  )  2.2018t f t
ln 2018  2019  0, t
   nên f (t) đồng biến trên  .
Bất phương trình (2)  f (a)  f (b)  a b  2x x 1  2 
x 1  1  x  1 . Với 1
  x  1, ta có: 2 x x
m x   2 5 12 16 2 x  2 2 x  2 x  2
  x  2   2
x    mx   2 3 2 2 2 2 x  2  3  2  m (3) . 2 x  2 x  2 x  2 Đặt t  với x  1  ;  1 . 2 x  2 2  2x 1 t   0, x   1
 ;1 nên hàm t đồng biến trên 1  ;1 , suy ra  t  3 . 3    2x 2 3  1 
Do hàm t đơn điệu trên 1 
;1 nên ứng với mỗi giá trị của t  ; 3 
 ta tìm được đúng một giá trị  3  của x  1  ;  1 và ngược lại. 2 1
Viết lại phương trình (3) theo ẩn t : 3t   m 4 với  t  3 . t 3  1 
(3) có 2 nghiệm thực phân biệt x  1  ; 
1  (4) có 2 nghiệm thực phân biệt t  ; 3   (*) .  3  2  1 
Xét hàm số g(t)  3t  liên tục trên ; 3 . t    3  2 2 2  1  g (  t)  3  . Cho 2 g (
t)  0  t   t   ; 3 . 2 t 3 3    3  Bảng biến thiên:
Dựa vào bảng biến thiên, ta có (*)  m  2 6 ;3 3 
Vậy m  2 6 ;3 3 thoả yêu cầu bài toán. 
Câu 41. (KIM LIÊN - HÀ NỘI 19) Cho bất phương trình 3 4 2 3 2 2
x x m
x   x  2 2 1 x  
1  1 m . Tìm tất
cả các giá trị thực của tham số m để bất phương trình nghiệm đúng với mọi x  1 . 1 1 A. m  . B. m  1 . C. m  . D. m 1 . 2 2 Lời giải Chọn D Ta có: 3 4 2 3 2 2
x x m
x   x  2 2 1 x   1  1 m   4 2
x x m 3 4 2 3 2
x x m x    2 2 1 2x   1  0   4 2
x x m 3 4 2 3 2 
x x m x    2 2 1 2x   1 (1)
ThS. Nguyeãn Vaên Rin – HBT Trang 21/43 Xét hàm số   3
f t t t , t   .
Có f t  2
 3t 1  0, t
   nên hàm số f t  đồng biến trên  .
Bất phương trình (1) có dạng 3 4 2 3 2 3 4 2 3 2 f
x x m f 2x 1 
x x m  2x 1     4 2 2
x x m  2x 1 4 2
m  x x 1 .
Xét hàm số g x 4 2
 x x 1 với x 1;  .
Bất phương trình đã cho nghiệm đúng với mọi x  1  m g x , x   1 . g x 3
  x x   x  2 4 2 2 2x   1  0, x   1 . Bảng biến thiên:
Tập giá trị của hàm số g x trên 1;  là  ;   1 .
Vậy m g x , x  1  m  1 .
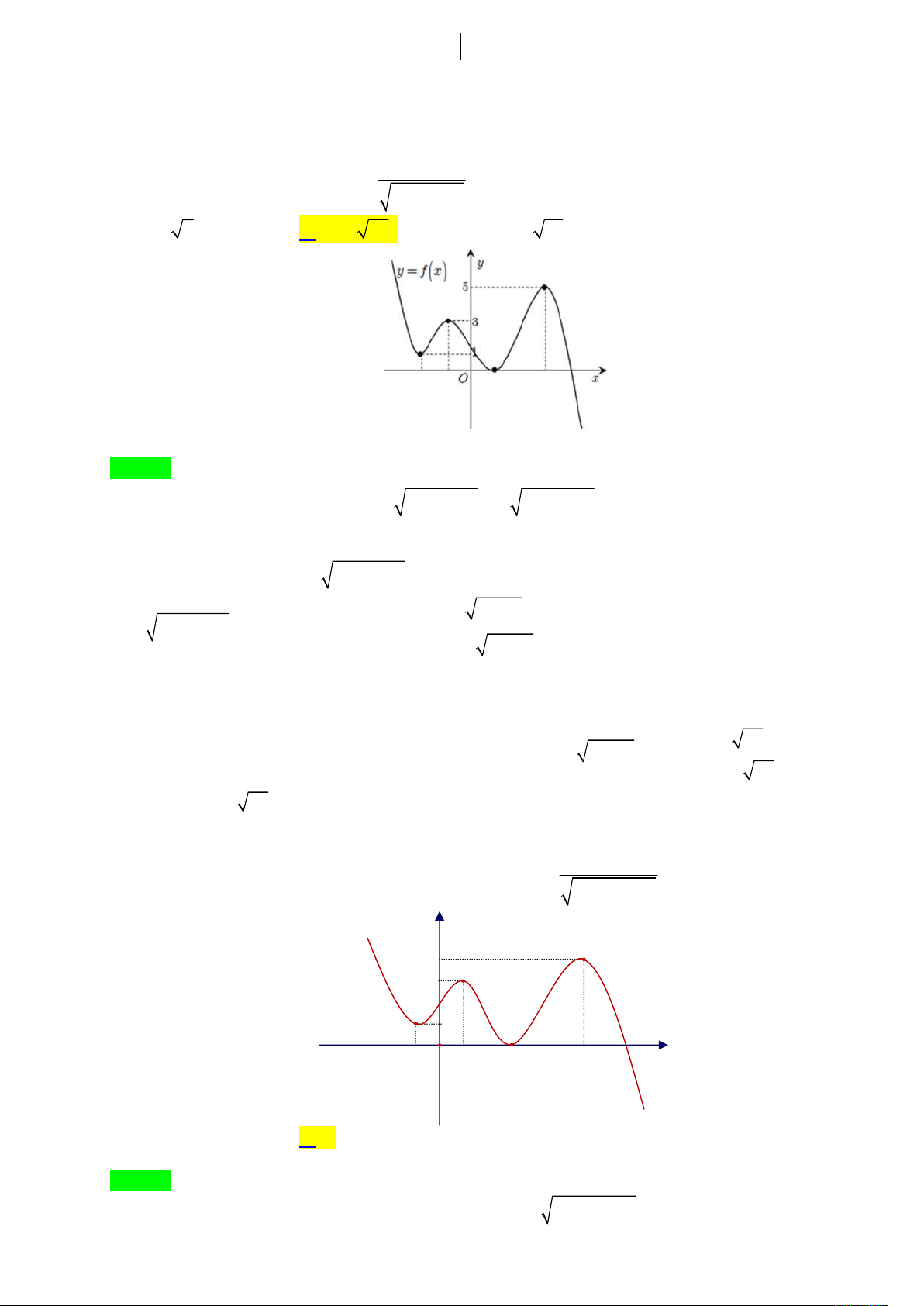
Câu 42. (Nguyễn Du 19) Cho hàm số f x liên tục trên  có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên
của n để phương trình sau có nghiệm x   . f  2 16 
sin x  6 sin 2x  8  f nn   1  A. 10. B. 6. C. 4. D. 8. Lời giải Chọn B
Nhìn vào đồ thị ta thấy hàm số f x luôn đồng biến trên  , do đó f  2  x
x    f nn   2 16sin 6sin 2 8 1  16 
sin x  6sin 2x  8  n n   1 Ta xét 2 1
 6sin x  6sin 2x  8  n n   1  8
 1 cos 2x  6sin 2x  8  nn   1  0
 8cos 2x  6sin 2x n n   1  0 2 2
Để phương trình có nghiệm x   thì 2 2    2
n n   2 n n 2 8 6
 100  10  n n  10 1 41 1 41 2
n n  10   n  (do 2 n n  1  0, n  ). 2 2
Vì n nguyên nên n  3  ; 2  ; 1  ;0;1;  2 .
Câu 43. (Ngô Quyền - Hà Nội 19) Tập hợp tất cả các giá trị của tham số m để phương trình 1
m m 1 1 sin x  sin x có nghiệm là đoạn a ;b . Khi đó giá trị của biểu thức T  4a   2 b bằng A. 4  . B. 5  . C. 3  . D. 3 . Lời giải
ThS. Nguyeãn Vaên Rin – HBT Trang 22/43 Chọn A
Ta có 1  sin x  1  0  1 sin x  2  0  1 sin x  2, x    .
Đặt t  1 sin x . Ta có 0  t  2 và 2
sin x t 1.
Khi đó phương trình có dạng: 2 2
m m 1 t t 1  m 1 t m 1 t t t * .
Xét hàm số f t  2
t t, t  0 .
Ta có f t   2t 1  0, t   0 . Do đó hàm số   2
f t t t luôn đồng biến trên 0;   . Vì thế   2
*  t m 1 t m t t 1 *  *
Xét hàm số g t  2
t t 1, t  0 ; 2  .   1
gt   2t 1; gt   0  2t 1  0  t  . 2
Bảng biến thiên của hàm số g t  2
t t 1, t  0 ; 2    5
Phương trình đề bài có nghiệm  * 
* có nghiệm t  0; 2     m  1 2 .   4  5  5 Vậy m   ;1 2 
nên a   ;b  1 2  T  4  . 4    4
Câu 44. (TT Thanh Tường - Nghệ An 19) Cho hàm số f x 3 3
 7  3x  7  3x  2019x . Gọi S là tập hợp
các giá trị nguyên của m thỏa mãn điều kiện f  3 2
x x x m   f  2 2 3
2x  2x  5  0, x   0  ;1 .
Số phần tử của S là A. 7 . B. 3 . C. 9 . D. 5 . Lời giải Chọn C Vì f x 3 3
 7  3x  7  3x  2019x là hàm số lẻ và đồng biến trên  nên ta có f  3 2
x x x m    f  2 2 3
2x  2x  5  f  3 2
x x x m   f  2 2 3
2x  2x  5 3 2 2
x  2x  3x m  2x  2x  5 3 2
x  4x  5x  5  m 3 2 2
x  2x  3x m  2x  2x  5   . 3  
x x  5  m  3 2 2
x  2x  3x m  2
x  2x  5  Xét g x 3 2
x  4x  5x  5 và h x 3
x x  5 trên 0; 
1 có bảng biến thiên là
ThS. Nguyeãn Vaên Rin – HBT Trang 23/43
Từ bảng biến thiên suy ra f  3 2
x x x m   f  2 2 3
2x  2x  5  0, x   0  ;1 khi và chỉ khi m  3    3  m  5 . m  5 
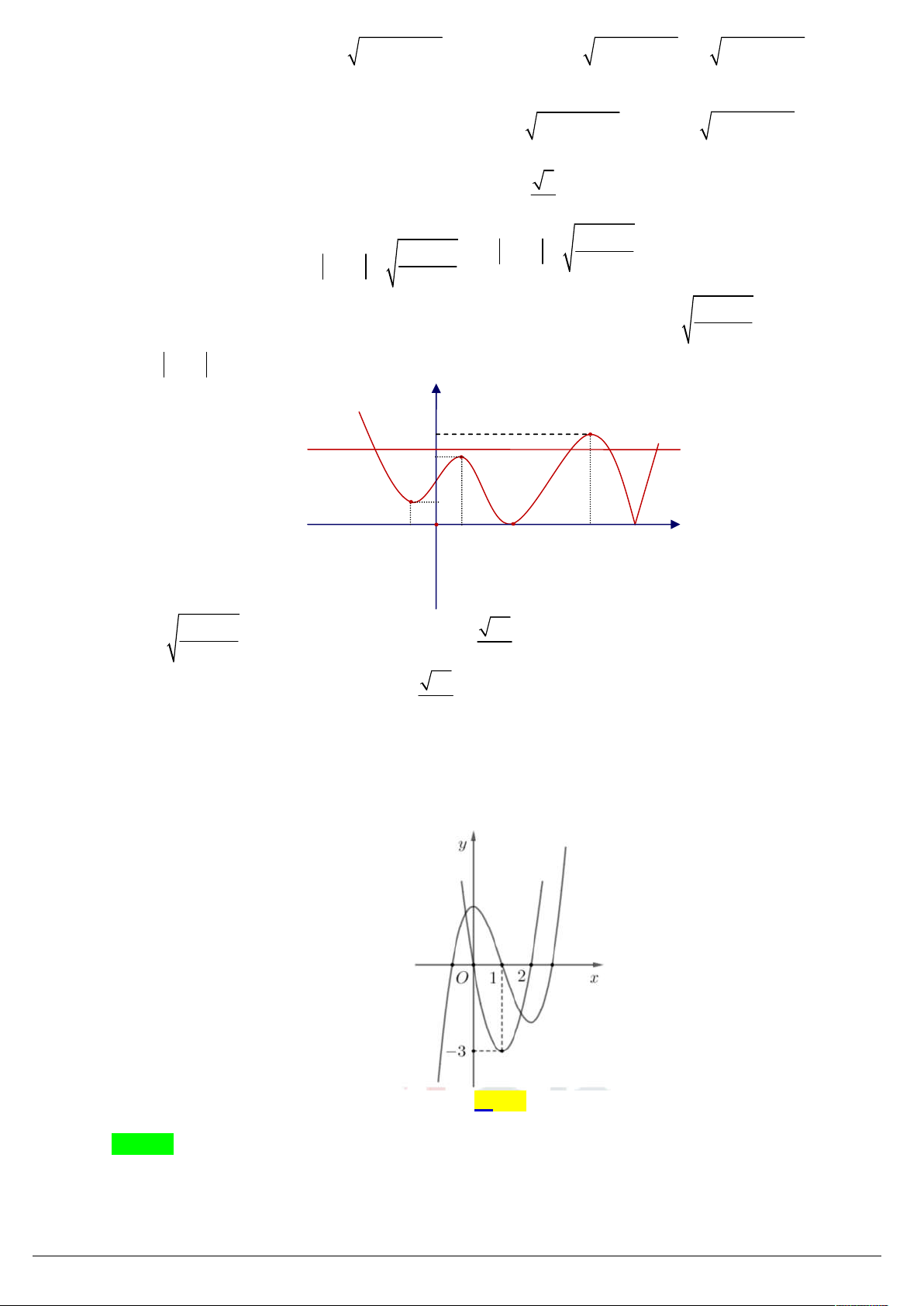
Câu 45. (Thị Xã Quảng Trị 19) Cho hàm số y f x liên tục trên và có đồ thị như hình vẽ bên. Tìm giá 3 m m
trị của tham số m để phương trình 2
f x  2 có đúng ba nghiệm thực phân biệt. 2 f x 1 A. m  2 . B. m  26 .
C. m  10 . D. m  1 . Lời giải Chọn B 3
Phương trình tương đương 3 m m   2
f x   2 1 
f x  1 (*) Xét hàm số   3
f t t t trên  có f t 2  3t  1  0 t
  nên hàm số đồng biến trên . Từ phương trình 2 (*)  m
f x  1 ( Đk m  1 ). Khi đó phương trình  f x 2  m  1 (1) 2 m f x 2
 1  f x 2  m  1    f x 2   m  1 (2) 
Nếu m  1 ta có f x  0 phương trình có 2 nghiệm nên m  1 (loại).
Nếu m  1 phương trình (2) có đúng một nghiệm. Như vậy để phương trình đã cho có ba nghiệm phân m  26
biệt thì phương trình (1) có đúng hai nghiệm phân biệt suy ra 2 m  1  5   , do m  1 m   26  nên ta chọn m  26 .
(Yên Phong 19) Cho hàm số y f x liên tục trên  và có đồ thị như hình vẽ. Có bao nhiêu giá trị Câu 46. 3 4m m
của tham số m để phương trình sau có 3 nghiệm phân biệt 2
f x  3 . 2
2 f x  5 y 4 3 2 1 1 O 1 6 x A. 0 . B. 1. C. 2 D. 3 . Lời giải Chọn B
Phương trình đã cho tương đương 3 2
m m   f x 2 4
 3 2 f x  5  
ThS. Nguyeãn Vaên Rin – HBT Trang 24/43 3 3 2 3
m m   f x 2 8 2 2
 5 1 2 f x  5 2 2  
 2m  2m   2 f x  5  2 f x  5 . Xét hàm số   3
g a a a , a   . Ta có ga 2
 3a 1  0 , a    .
Do đó, g a đồng biến trên  . Mặt khác, g m  g  2 2
2 f x  5  2
 2m  2 f x  5 .    m  0 5 m  m  0     2  2   4m  5  0   . 2 2 f   x 2  4m  5 2    4m  5 2 4m  5  f x  f x    2   2 2 4m  5
Phương trình đã cho có ba nghiệm phân biệt khi và chỉ khi đường thẳng y  cắt đồ thị hàm 2
số y f x tại ba điểm phân biệt. y 4 3 2 1 1 O 1 6 x 2 4m  5 37 Từ đó,  4 2
 4m  5  32  m   . 2 2 37
Đối chiếu với điều kiện, ta thu được m  . 2
Vậy có đúng 1 giá trị của tham số m thỏa mãn yêu cầu bài toán.
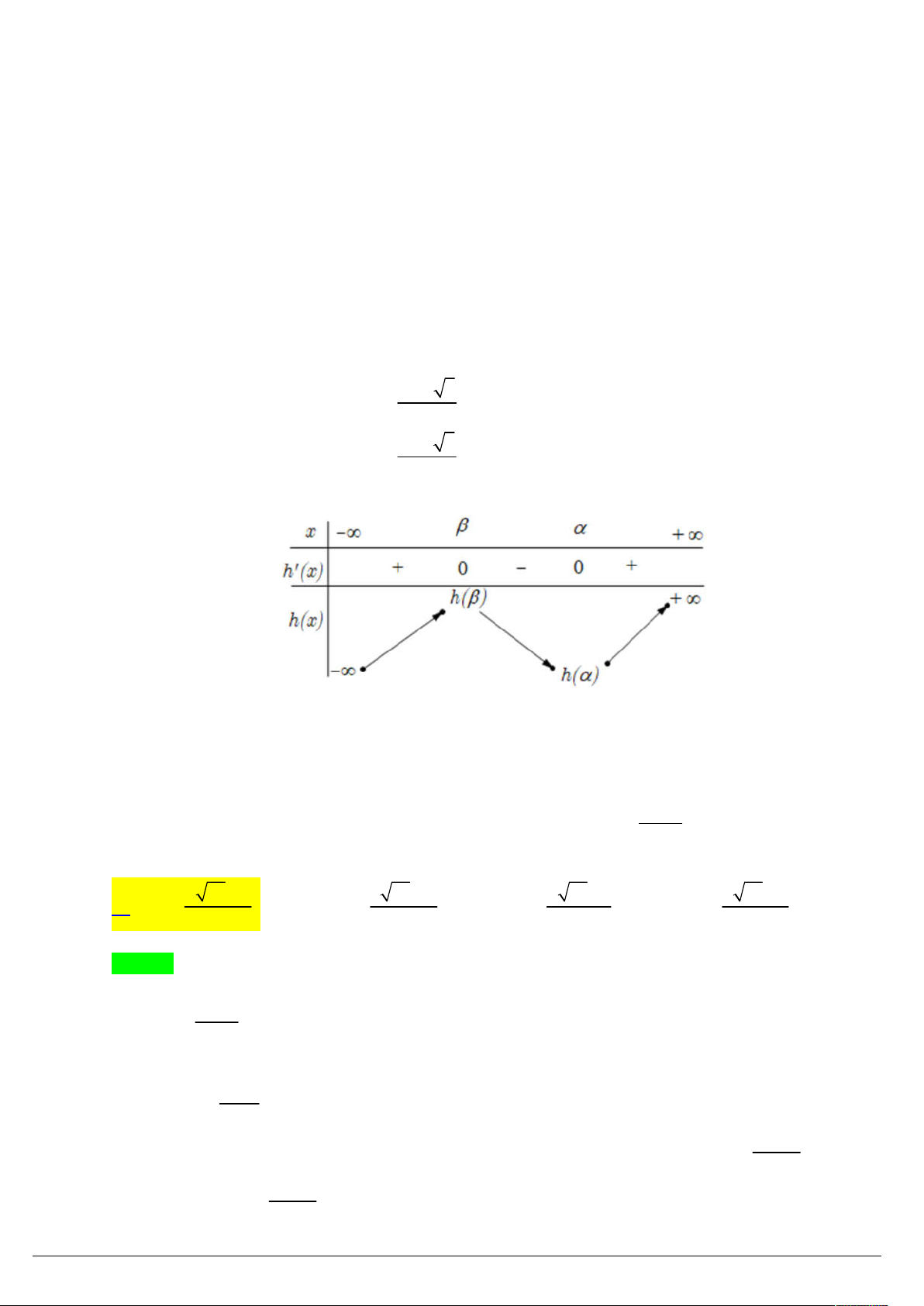
Câu 47. (ĐỀ 16 VTED 19) Cho hàm đa thức bậc ba y f x có đồ thị của các hàm số y f x ; y f  x
như hình vẽ bên. Gọi S là tập hợp tất cả các giá trị nguyên của m để phương trình
f f x  m  2 f x  3 x m có đúng 3 nghiệm thực. Tổng các phần tử của S bằng A. 0 . B. 6  . C. 7  . D. 5  . Lời giải Chọn C
f f x  m  2 f x  3 x m  f f x  m  3 f x  m  f x  3x . (1)
Xét hàm g t   f t   3t trên  .
Ta có g t   f t   3 .
ThS. Nguyeãn Vaên Rin – HBT Trang 25/43
Từ đồ thị hàm số y f  x ta suy ra f  x  3  x
   . Dấu “  ” chỉ xảy ra khi x  1 .
Do đó gt   f t   3  0 t
   . Dấu “  ” chỉ xảy ra khi t  1.
Vậy hàm g t   f t   3t đồng biến trên  .
Ta có (1)  g f x  m  g x  f x  m x (Vì hàm g t   f t   3t đồng biến trên  )
f x  x m . (*) Ta có   3 2
f x ax bx cx d f  x 2
 3ax  2bx c .  f   1  0
a b c d  0 a  1  f     0  0 c  0 b   3
Từ đồ thị hàm số ta có       f x 3 2
x  3x  2 . f   2  0
12a  4b c  0  c  0   f   1  3  3
a  2b c  3  d  2    Vậy (*) 3 2
m x  3x x  2  h x .  3  2 3 x     3
Ta có h x 2
 3x  6x 1  0   .  3  2 3  x     3 Bảng biến thiên
Phương trình có ba nghiệm phân biệt  h    m h    m  4  ;; 
2 . Tổng các phần tử của S 2 bằng m  7   . 4 
3. Tìm GTLN, GTNN của hàm số 1 ab
Câu 48. (MĐ 102 - BGD&ĐT 17) Xét các số thực dương a, b thỏa mãn log
 2ab a b  3 . Tìm giá 2 a b trị nhỏ nhất P
P a  2b min của . 2 10  3 3 10  7 2 10 1 2 10  5 A. P  . B. P  . C. P  . D. P  . min 2 min 2 min 2 min 2 Lời giải Chọn A
Điều kiện: ab  1. 1 ab Ta có log
 2ab a b  3  log 2 1 ab   2 1 ab  log
a b a b * 2 2       2       . a b
Xét hàm số y f t   log t t trên khoảng 0;  . 2 1
Ta có f t   1  0, t
  0 . Suy ra hàm số f t đồng biến trên khoảng 0; . t.ln 2 b   2
Do đó *  f 21 ab  f a b  21 ab  a b a 2b  
1  2  b a  .   2b 1 b   2
Do a  0, b  0 nên
 0  0  b  2 . 2b 1
ThS. Nguyeãn Vaên Rin – HBT Trang 26/43 b   2 b   2
Khi đó: P a  2b
 2b . Xét hàm số g(b) 
 2b trên khoảng 0;2 . 2b 1 2b 1  2   10 b    0;2 5  5 gb 4   2  0  2b 1    2  2 2b   1 2  2   10 b   0; 2  4 Lập bảng biến thiên  10  2  2 10  3 Vậy Pg    . min  4  2    1 2x
Câu 49. (Chuyên Vĩnh Phúc 18) Xét các số thực dương x , y thỏa mãn ln
 3x y 1   . Tìm giá trị x   y  1 1 nhỏ nhất P của P   . min x xy A. P  8 . B. P  4 . C. P  2 . D. P  16 . min min min min Lời giải Chọn A 1
Điều kiện 0  x  . 2  1 2x  Từ giả thiết ln
 3x y 1  
 ln 1 2x  1 2x  ln  x y   x y   1 x   y  1
Xét hàm số f t   ln t t trên 0;  có f t   1  0 , t  0 do đó hàm f t  đơn điệu. t Vậy  
1  1 2x x y  3x y  1 2 1 1 1 2 1 2 Có P       x xy x x y x 1 2x 1 2 1 4 1
Đặt g x  
, ta có g x   
suy ra g x  0  x  . x 1 2x 2 x 1 2x2 4
Do đó min g x  8 . Vậy P  8 . min  1  0;    2  2    x x y 2018
Câu 50. (Lê Văn Thịnh - Bắc Ninh 18) Cho 0  ; x y  1 thỏa mãn 1 2017  . Gọi M , m 2
y  2 y  2019
lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức S   2 x y  2 4 3
4 y  3x  25xy . Khi đó
M m bằng bao nhiêu? 136 391 383 25 A. . B. . C. . D. . 3 16 16 2 Lời giải Chọn B 2  1 y 2 2017 x  2018   x x y 2018 Ta có 1 2017    2
y  2 y  2019 2017x 1 y2  2018
ThS. Nguyeãn Vaên Rin – HBT Trang 27/43 2  1 y   x y      2 2017 1 2018 2017 x  2018   Xét hàm số   t f t   2
2017 t  2018 , với 0  t  1.      2   t t t f t tt   2 2018 .2017 .ln 2017 2 .2017 2017
t  2018.ln 2017  2t  0  
 Hàm số f t  đồng biến trên 0  t  1
 1 y x y  1 x
Theo giả thiết S   2 x y  2 4 3
4 y  3x  25xy
 4x  31 x.41 x2 2
 3x  25x 1 x       2
4x  3x  3 2
4x  5x  4  25x1 x 4 3 2 3 2 2 2
 16x  20x 16x 12x 15x 12x 12x 15x 12  25x  25x 4 3 2
 16x  32x 18x  2x 12
Xét hàm số S x 4 3 2
 16x  32x 18x  2x 12 , với 0  x  1.  2  3 x    S x 3 2
 64x  96x  36x  2 . Cho S x  0  4   1 x   2 Bảng biến thiên 2- 3 1 2+ 3 x 0 4 2 4 1 y' 0 + 0 0 + 12 25 12 y 2 191 191 16 16  25
M  max S x    0;  1 2
Từ bảng biến thiên, ta có  . 191
m  min S x   0;  1  16 25 191 391
Vậy M m    . 2 16 16 Câu 51. (Trần Phú – Đà Nẵng 18) Cho hai số thực x , y thỏa mãn: 3
y y xx   x   2 2 7 2 1 3 1 3 2 y  
1 . Tìm giá trị lớn nhất của biểu thức P x  2 y . A. P  10 . B. P  4 . C. P  6 . D. P  8 . Lời giải Chọn B 3
y y xx   x   2 2 7 2 1 3 1 3 2 y   1   3 2
2 y  3y  3y   1   y  
1  2 1 x 1 x  3 1 x  2 1 x . 3   y  3 2 1   y  
1  2  1 x   1 x   1 .
Xét hàm số f t  3
 2t t trên 0;  .
Ta có: f t  2
 6t 1  0 với t
  0  f t  luôn đồng biến trên 0;  . Vậy  
1  y 1  1 x y  1 1 x .
P x  2 y x  2  2 1 x với  x   1 .
Xét hàm số g x  2  x  2 1 x trên   ;1 .
ThS. Nguyeãn Vaên Rin – HBT Trang 28/43 1 1 x 1
Ta có: g x  1 
. g x  0  x  0 . 1 x 1 x
Bảng biến thiên g x : 4
Từ bảng biến thiên của hàm số g x suy ra giá trị lớn nhất của P là: max g x  4 . ;  1
Câu 52. (TRẦN NHÂN TÔNG - QUẢNG NINH 18) Cho hai số thực
x, y thỏa mãn: 3
9x  2  y 3xy  5 x  3xy 5  0 .
Tìm giá trị nhỏ nhất của 3 3
P x y xy   2 6 3 3x  
1  x y  2 . 296 15 18 36  296 15 36  4 6 4 6 18 A. . B. . C. . D. . 9 9 9 9 Hướng dẫn giải Chọn B. Ta có 3
9x  2  y 3xy  5 x  3xy  5  0 3
 27x  6x  3xy  5 3xy  5  2 3xy  5 .
Xét hàm f t  3
t  2t với t  0;  có f t  2 '
 3t  2  0 t
  0;  nên hàm số liên tục và đồng biến trên 0;  .
Khi đó ta có 3x  3xy  5  x  0 và 2
9x  3xy  5 .
Với x  0 thì 0  5  l  . với x  0 thì 3 3
P x y xy   2 6 3 3x  
1  x y  2 3 3
x y xy   2 6
9x  3 x y  2 3 3
x y  6xy  3xy  2 x y  2 3 3 2 2
x y  3x y  3xy  2 x y  4
  x y3  2  x y  4 2 9x  5 5 5 4 5 4 5
Mà x y x   4x   2 4 . x
. Đặt t x y thì t  . 3x 3x 3x 3 3 4 5 4 5 Xét f t  3
t  2t  4 với t
. Khi đó f t  2
 3t  2  0 với t   . 3 3  4 5  36  296 15
Do đó f t   f     3  9   36  296 15 36  296 15 Suy ra P
. Vậy GTNN của P là . 9 9 Câu 53. (Đô Lương 4 - Nghệ An 18) Xét các số thực dương x, y thỏa mãn x y 3x  2 y 1 log
x x  3  y y  3  xy . Tìm giá trị lớn nhất của P  . 3 2 2    
x y xy  2 x y  6 A. 2 . B. 1. C. 3 . D. 4 . Lời giải Chọn B x y Ta có log
x x  3  y y  3  xy 3 2 2    
x y xy  2
ThS. Nguyeãn Vaên Rin – HBT Trang 29/43  log
x y  3 x y  2  log  2 2
x y xy  2   2 2
x y xy  2 3 3   log
x y  3 x y  log 3  log  2 2
x y xy  2   2 2
x y xy  2 3 3 3   log
3 x y  3 x y  log    2 2
x y xy  2   2 2
x y xy  2 * . 3 3 
Xét hàm số f t   log t t , với t  0 . 3 1
có f t   1  0 , t   0 . t.ln 3
Vậy hàm số f t  liên tục và đồng biến trên khoảng 0;  .
Do đó: f   x y  f  2 2
x y xy     x y 2 2 3 2 3
x y xy  2   1 . 2 Từ  
1  xy   x y  3 x y  2 . 2
x y 1 
Ta có x x xy xy x y   1  xy     xy .  2 
Đẳng thức xảy ra khi và chỉ khi x y 1.
x y  2 1 2 Do đó từ   1 , suy ra: x
  x y  3 x y  2 . 4
Đặt t x y , t  0 . t  2 1 2 2 x y 2t 1
t  3t  2 2 1 x 3
t  22t  3 Suy ra: 4 P   
f t  . x y  6 t  6 4t  6 2
3t  36t 135
Ta có: f t  
 0  t  3 (nhận). 4t  62 Bảng biến thiên t 0 3  f t   0  f t  x y 1 x  2
Dựa vào BBT, ta có max P  max f t   f 3  1 khi và chỉ khi    . 0; x y  3 y  1   Câu 54. (SỞ HÀ TĨNH 19) Cho các số thực x, y, z thỏa mãn 
x y z  log
x x  2  y y  2  z z  2 . Tổng giá trị lớn nhất và nhỏ nhất của biểu 16  2 2 2       
2x  2 y  2z 1  
x y z thức F  bằng
x y z 1 1 2 2 A. . B.  . C. . D.  . 3 3 3 3 Lời giải Chọn C
x y z  • Ta có: log
x x  2  y y  2  z z  2 16  2 2 2       
2x  2 y  2z 1   1 1 
log  x y z   log  2 2 2
2x  2 y  2z   1   2 2 2
x y z
 2 x y z 4 4    2 2
 log  x y z   log  2 2 2
2x  2 y  2z   1  log 4   2 2 2
2x  2 y  2z 1  4 x y z 4 4 4      2 2 2
2x  2 y  2z   1  log  2 2 2
2x  2 y  2z 1  4 x y z  log 4 x y z * 4    4   
ThS. Nguyeãn Vaên Rin – HBT Trang 30/43 1
• Xét hàm số f t   t  log t trên 0;    f 't   1  0, t   0;   4 t.ln 4
f t  đồng biến trên 0;   . Khi đó: (*) 2 2 2
 2x  2 y  2z 1  4 x y z 1 2 2 2
x y z  2x  2 y  2z   0 S  2 10
 S  là mặt cầu tâm I 1;1  ;1 và bán kính R  . 2
x y z • Ta có: F
x y z
 1 F x  1 F y  1 F z  0  P
• Điều kiện tương giao của mặt phẳng  P và măt cầu S  : 1 3F 10
d I; P  R  
  F 2    F 2    F 2 2 1 1 1   F   2 2 6
10 3F  2F  3 2
 6F  4F  26  0 1 2 10 1 2 10   F  . 3 3 1 2 10 1 2 10  F  , F  . max min 3 3 1 2 10 1 2 10 2  FF    . max min 3 3 3
Câu 55. (Chuyên Lam Sơn - Thanh Hóa 18) Cho x , y là các số thực dương thỏa mãn xy xy 3 5 2  x2 5   x 1   3
y y(x  2) . Tìm giá trị nhỏ nhất của biểu thức T x y . 3xy 5 A. T  2  3 2 . B. T  3  2 3 . C. T  1 5 . D. T  5  3 2 . min min min min Lời giải Chọn B. Theo đề ra ta có xy xy 3 5 2  x2 5   x 1   3
y y(x  2) 3xy 5 xy 1 xy 1 2 1  5 
x  2 y  5   xy 1 x2 y xy 1 3 3  t 1
Xét f t   5   t . 
   5t ln 5  3  t f t ln 3 1  0 3t x 1
x  2 y xy 1  y  . x  2
Vì y  0 nên x  2 . 2 x 1 x x 1
Ta có: T x y x   x  2 x  2 2 x  2  3 x x  2; 4 1     T    0    x  22
x  2  3 2;  
Lập bảng biến thiên ta được T
 3  2 3 tại x  2  3 . min
ThS. Nguyeãn Vaên Rin – HBT Trang 31/43 x y
Câu 56. (THTT 18) Xét các số thực dương x, y thỏa mãn log
x x  3  y y  3  . xy 3 2 2
x y xy  2 3x  2 y 1
Tìm giá trị lớn nhất P
của biểu thức P  . max x y  6 A. 3 . B. 2 . C. 1. D. 4 . Lời giải Chọn C Ta có: x y log
x x  3  y y  3  xy 3 2 2
x y xy  2  log
3 x y  3 x y  log  2 2
x y xy  2 2 2
x y xy  2 . 3 3 1
Xét hàm số f t   log t t , t  0 có f t  
1  0, t  0 . Vậy hàm số f t  luôn đồng 3 t ln 3
biến và liên tục trên khoảng 0;  .
Do đó: f   x y  f  2 2
x y xy     x y 2 2 3 2 3
x y xy  2   1 2 Từ  
1  xy   x y  3 x y  2 . 2
x y 1 
Ta có x x xy xy x y   1  xy     xy  2 
Đẳng thức xảy ra khi và chỉ khi x y 1.
x y  2 1 2 Do đó từ   1 , suy ra: x
  x y  3 x y  2 . 4
Đặt t x y , t  0 . t  2 1 2 2 x y 2t 1
t  3t  2 2 1 x 3
t  22t  3 Suy ra: 4 P   
f t  . x y  6 t  6 4t  6 2
3t  36t 135
Ta có: f t  
 0  t  3 (nhận) 4t  62 Bảng biến thiên t 0 3  f t   0  f t  x y 1 x  2
Dựa vào BBT, ta có max P  max f t   f 3  1 khi và chỉ khi    . 0; x y  3 y  1    2 2 x y  1 2x y
Câu 57. (Trần Hưng Đạo - TP HCM 18) Xét các số thực dương x , y thỏa mãn 2018  . Tìm  x  2 1
giá trị nhỏ nhất P
của P  2 y  3x . min 1 7 3 5 A. P  . B. P  . C. P  . D. P  . min 2 min 8 min 4 min 6 Lời giải Chọn B  2 2 x y  1 2x y 2x y Ta có 2018   2  2 x y   1  log  2018 2 x  2 1  x   1  2  x  2 1
 2 2x y  log
2x y  log  x  2 1 2018 2018
ThS. Nguyeãn Vaên Rin – HBT Trang 32/43  2  x  2 1  log  x  2 1
 2 2x y  log 2x y 2018   2018   2
Có dạng f  x  1  
f 2x y với f t   2t  log t ,  t   0 .   2018 1
Xét hàm số f t   2t  log t ,  t
  0 , ta có f t   2   0  t
  0 nên hàm số f t  2018 t.ln 2018 2
đồng biến trên khoảng 0;   . Khi đó f  x  1  
f 2x y   x  2 1  2x y 2
y x 1.  
Ta có P y x   2 x   2 2 3 2
1  3x  2x  3x  2 . Bảng biến thiên 3 x   4   P 7 8 7 3 Vậy P  khi x  . min 8 4
Câu 58. (Mộ Đức - Quãng Ngãi 18) Cho hai số thực dương x , y thay đổi thỏa mãn đẳng thức
   xy     2 2 1 2 1 .2 .2x y xy x y
. Tìm giá trị nhỏ nhất y của y . min A. y  3 . B. y  2 . C. y  1. D. y  3 . min min min min Lời giải Chọn B. 2 Ta có    xy     2 2 1 2 1 2 2x y xy x yxy  2xy 1  2 x
yx y 1 2 1 1 2 2         1 Xét hàm       1 .2t f t t với t  1.
Khi đó    2t     1 .2t f t t .ln 2  0 với t   1. 2 x  2 Từ   2
1  2xy 1  x y 1  y  2x 1 2 2x  2x  4  x  2 y   0 2
 2x  2x  4  0   2x  2 1 x  1   Loại x  1
 vì điều kiện của t nên f 2  2 . Câu 59. (Chuyên Thái Bình 18) Cho 2 số thực dương x, y thỏa mãn y  log  x   1  y   1 1 
 9  x 1 y 1
P x y là 3     
. Giá trị nhỏ nhất của biểu thức 2 11 27 A. P  . B. P  . C. P  5   6 3 . D. P  3   6 2 . min 2 min 5 min min Lời giải Chọn D y 1 
Ta có log  x 1 y 1 
 9  x 1 y 1 3           y   1 log x 1  log
y 1   x 1 y 1  9  3   3         y   1 log x 1  log
y 1  x 1  9  3   3    9  log
x 1  x 1   log y 1 3   3   y 1 9 9  log
x 1  x 1 2   2  log (*). 3   3 y 1 y 1 1
Xét hàm số f t   log t t  2 với t  0 có f t  
1  0 với mọi t  0 nên hàm số f t  luôn 3 t ln 3
đồng biến và liên tục trên 0;  .
ThS. Nguyeãn Vaên Rin – HBT Trang 33/43 9 9 8  y
Từ (*) suy ra x 1   x  1 
, do x  0 nên y  0;8 . y 1 y 1 y 1 8  y 9 9
Vậy P x  2 y
 2 y  2 y 1  2 y   1   3  3  6 2 . y 1 y 1 y 1 9 3 Vậy P  3
  6 2 khi 2 y   1   y  1. min y 1 2
 4a  2b  5 
Câu 60. (Thăng Long - Hà Nội 18) Cho a , b là hai số thực dương thỏa mãn log
a  3b  4 . 5    a b
Tìm giá trị nhỏ nhất của biểu thức 2 2
T a b 1 5 3 A. . B. . C. . D. 1. 2 2 2 Lời giải Chọn B
 4a  2b  5  log
a  3b  4  log
4a  2b  5  log 5 a b  5 a b  4a  2b  5 5   5   5        a b   log
4a  2b  5  4a  2b  5  log 5 a b  5 a b (*) 5     5     1
Hàm số f t   log t t t  0 có ' f t   1  0 5   t ln 5
f t  đồng biến nên (*)  f 4a  2b  5  f 5a b  4a  2b  5  5a b .
4a  2b  5  5a b  a  5  3b 2  3  5 5 2 2 2
T a b T  5  3b 2 2
b  10b  30b  25  10 b      .  2  2 2 5 Vậy GTNN T  . 2 2x y 1
Câu 61. (Chuyên Bắc Ninh 18) Cho x , y là các số thực dương thỏa mãn log
x  2 y . Tìm giá trị 3 x y 1 2
nhỏ nhất của biểu thức T   . x y A. 3  3 . B. 4 . C. 3  2 3 . D. 6 . Lời giải Chọn D 2x y 1 Ta có log
x  2 y  log
2x y 1  log
x y x  2 y 3   3   3 x y  log
2x y 1  log 3x  3y x  2 y 1 3   3    log
2x y 1  2x y 1  log 3x  3y  3x  3y (*) 3   3  
Xét hàm số f t   log t t với t  0 . 3 1
Khi đó f t  
1  0, t  0 , suy ra hàm số f t  liên tục và đồng biến trên 0;  . t ln 3
Do đó *  2x y 1  3x  3y x  2y  1  x  1 2y . 1
Vì x, y  0  0  y  . 2 1 2 1 2 1 1 1 Xét T        x y 1 2 y y 1 2 y y y 1 2
Áp dụng bất đẳng thức Cô si ta có 3 T  3.3  3.3  3. 8  6 . y 1 2 y
2 y 1 2 y
ThS. Nguyeãn Vaên Rin – HBT Trang 34/43     1 x 1 2 y x     2 Dấu "  " xảy ra  1   2 y y   . 1 2y 1 2yy     4
x y 1 
Câu 62. (Chuyên Nguyễn Du - Đăk Lăk 19) Cho các số dương x, y thỏa mãn log
 3x  2 y  4 . 5   2x  3y   4 9
Giá trị nhỏ nhất của biểu thức A  6x  2 y   bằng x y 31 6 27 2 A. . B. 11 3. C. . D. 19. 4 2 Lời giải Chọn D
x y 1  0 
Điều kiện: 2x  3y
x y  1.  x, y  0 
x y 1  Ta có: log
 3x  2 y  4 5   2x  3y  
 log x y 1 1  5 x y 1  log 2x  3y  2x  3y 5      5  
 log 5 x y 1   5 x y 1  log
2x  3y  2x  3y * . 5       5    
Xét hàm số f (t)  log t t trên 0;  ta có 5   1 f (  t)  1  0, t   0;  . t ln 5
 Hàm số f (t)  log t t đồng biến trên 0; . 5  
*  5 x y  
1  2x  3y  3x  2 y  5 . Mặt khác, ta có: 4 9  4   9 
A  6x  2 y    9x   4 y     
 3x  2 y  2.6  2.6  5  19 x yx y    4 9x   x  2  x  9    3
Vậy GTNN của A  19 , dấu “ = ” xảy ra  4 y     N  . y 3   y 3
x  2 y  5   2    2 2 x y  1 2x y
Câu 63. (Ba Đình 19) Xét các số thực dương , x y thỏa mãn 2019 
. Giá trị nhỏ nhất P của 2 (x 1) min
biểu thức P  2y x bằng 1 1 7 15 A. P  . B. P  . C. P  . D. P  . min 4 min 2 min 8 min 8 Lời giải Chọn D  2
2 x y   1 2x y 2 2 2 x 1  Ta có: 2019            2 1 .2019 2 .2019 y x x y 2 (x 1) 2 2 2    2 2 x  1 4 x     2 1 .2019 2 .2019 y x x y   x   2 x  1 1 .2019
 2x y 22 xy .2019 . (1) 2
Đặt u   x  
1 , v  2x y, u  0,v  0, khi đó (1) trở thành 2u 2 .2019  .2019 . v u v (2) Xét hàm đặc trưng   2  .2019 t f t t
, t  0, ta có
ThS. Nguyeãn Vaên Rin – HBT Trang 35/43   2t 2 '  2019  2 .2019 t f t t .ln 2019  0, t
 0 :   Hàm f t  đồng biến trên (0; ).
Phương trình    f u   f v  u v   x  2 2 2 1
 2x y y x 1. Suy ra 2
P  2 y x  2x x  2 .  b   1  1 1 15
Do P là hàm bậc hai có hệ số a  2  0 nên min P P   P  2.   2  .      2a   4  16 4 8 x y
Câu 64. (Lý Nhân Tông 19) Cho hai số thực x, y thỏa mãn log
x x  3  y y  3  . xy 3 2 2
x y xy  2 x  2 y  3
Tìm giá trị lớn nhất của biểu thức P  . x y  6 43  3 249 37  249 69  249 69  249 A. . B. . C. . D. . 94 94 94 94 Lời giải Chọn D x y Điều kiện
 0  x y  0. 2 2
x y xy  2 x y log
x x  3  y y  3  xy 3 2 2
x y xy  2
 2 log  x y  2 log  2 2
x y xy  2 2 2
x y xy  3x  3y 3 3
 2 log  x y  2  2 log  2 2
x y xy  2 2 2
x y xy  2  3x  3y 3 3
 2 log 3x  3y  3x  3y  2 log  2 2
x y xy  2 2 2
x y xy  2 3 3 2
Xét hàm đặc trưng f t   2log t t, t  0;  , ta có f t   1  0, t   0; . 3   t.ln 3
Suy ra hàm f t  đồng biến trên khoảng 0;  .
Phương trình  f x y  f  2 2
x y xy   2 2 3 3
2  x y xy  2  3x  3y x y a  ,
x a b   2 3a b  3 Đặt    Khi đó P
và 2 là: a  2 2 3 1  b  1.
y a b x y   2a  6 b  .   2   3 a   1  cos t, Đặt 
t 0;2  , khi đó  b  sin t, 
3cos t  3 sin t  6 3 P
 2P  3.cos t  3 sin t  6 3  8 3P 2 cos t  8 3
Do phương trình luôn có nghiệm t nên ta có 69  249 69  249
2P  3  3  6 3 8 3P2 2 2
 47P  69P  24  0   P  . 94 94 69  249
Vậy giá trị lớn nhất của P là . 94 1 y
Câu 65. (Chuyên Thái Nguyên 19) Xét các số thực dương x, y thỏa mãn log
 3xy x  3y  4 . Tìm 3 x  3xy
giá trị nhỏ nhất P
của P x y . min 4 3  4 4 3  4 4 3  4 4 3  4 A. P  . B. P  . C. P  . D. P  . min 3 min 3 min 9 min 9 Lời giải Chọn A
ThS. Nguyeãn Vaên Rin – HBT Trang 36/43 1 y Để  0 mà từ giả thiết ,
x y  0 suy ra 1 y  0  y  1. x  3xy
Vậy ĐKXĐ: x  0; 0  y  1. 1 y 1 y 31 y Ta có : log
 3xy x  3y  4
3xy x3 y4   3
3xyx3 y3   3 3 x  3xy x  3xy x  3xy 31 y 3 3 xyx       33y     3 3 3 .3 3 .3 xyx y xy x (*) 33 x  3xy 3 y Xét    .3t f t t
với t  0 . Ta có    3t  .3t f t t .ln 3  0 với t
  0 , suy ra f t  đồng biến trên khoảng 0; . Từ (*) ta có
f 3  3y  f 3xy x với
3  3y  0,3xy x  0 nên 3  x
3  3y  3xy x y  . 3(x 1) 3  x  3  x 1  4
Ta có P x y x    x   1      3 x  1  3x  1 3    3   4 4 4 4 4 3  4
P   x   1    2  x   1 .   . 3 x   1 3 3 x   1 3 3  4 x 1   3 x   1  2 3  3  x   4 3  4  3  x  3 Vậy P    y   . min  3 3 x   1   2 3 1 y   x 0;0 y 1      3  
Câu 66. (CHUYÊN LÊ THÁNH TÔNG - QUẢNG NAM 19) Cho hai số dương x ; y thỏa y
log 4x y  2xy  2 2  8  2x  2 y  2 . Giá trị nhỏ nhất của P  2x y là số có dạng 2   
M a b c với a,b  , a  2 . Tính S a b c .
A. S 17 .
B. S  7 . C. S  19 . D. S  3. Lời giải Chọn D y 2
Với hai số dương x ; y thỏa log
4x y  2xy  2  8  2x  2 y  2 2     
Ta có  y  2 log 4x y  2xy  2  8  2x  2 y  2 2     
  y  2 log 2x 1 y  2  8  2x 1 y  2  3 y  2 2         8  log 2x 1  log y  2   2x 1  3 2   2     y  2  8  8  log
2x 1  2x 1  log  . 2     2   y  2 y  2   1
Xét hàm đặc trưng f t   log t t trên 0;  có f t   1  0, t
  0 nên hàm số f t  đồng 2 t ln 2
biến trên 0;  .  8  8 8 f 2x   1  f  2x 1   y   2   . y  2 y  2 2x 1   8  8 AM GM
P  2x y  2x   2  2x   1   3  4 2  3   . 2x 1  2x 1  8 1 2 2
Dấu bằng xảy ra khi 2x 1   2x  2 1  8  x  . 2x 1 2
Vậy S a b c  3.
ThS. Nguyeãn Vaên Rin – HBT Trang 37/43 x  3y
Câu 67. (Gia Lộc - Hải Dương 19) Cho ,
x y  0 thỏa mãn log
xy x  3y  
. Tìm giá trị nhỏ nhất xy   2 2 x 9 y
của biểu thức P   . 1 3y 1 x 71 72 73 A. 10 . B. . C. . D. . 7 7 7 Lời giải Chọn C x  3y  Ta có log
xy x  3y  
 log  x  3y  log  xy  xy   x  3y . xy  
 log x 3y  x 3y  log xy  xy   1 . 1
Xét hàm số f t   log t t trên khoảng 0;   ; f t   1  0, t   0 . t.ln10
Suy ra hàm số f t  đồng biến trên 0;  . Phương trình  
1 tương đương f x  3y  f xy  x  3y xy .
Theo bất đẳng thức Schwarz ta có x 9 y xy2  x y2 2 2 2 3 3 P      2 . 1 3y 1 x 1 3y 1 x
2   x  3y
Theo bất đẳng thức Cô-si cho 2 số dương ta có
xy x y
x y   xy2 3 2 .3
12xy  0  xy xy 12  0 .
Vì xy  0 nên xy  12  x  3y  12 .
Đặt u x  3y u  12 . 2 u
Từ 2 ta có P f u  , u  12 u  2 2 u  4uu  0 f u 
f u  0  (không thỏa mãn). 2    u  2 u  4  72
 Min f u   f 12  . 7 72 72 Vậy P   Min P  khi 7 7
x  3y  12 x  3  y 12   x  6
u  12   x 3y     .    3  y 12  2 2
 3y 12  3y  9 y y  2  1 3y 1 x    
Câu 68. (CỤM TRẦN KIM HƯNG - HƯNG YÊN 19) Cho a, b, c là các số thực thỏa mãn 
a b c  log
a(a  2)  b(b  2)  c(c  2). Tìm giá trị lớn nhất của biểu thức 2  2 2 2 
a b c 1
3a  2b c P  .
a b c 6  2 3 8  2 2 6  2 3 4  2 2 A. . B. . C. . D. . 3 3 3 3 Lời giải Chọn C Ta có:
a b c log
a a  2  b b  2  c c  2 2 2 2 2      
a b c 1
ThS. Nguyeãn Vaên Rin – HBT Trang 38/43
 log a b c  2a b c 1  log  2 2 2
a b c   2 2 2
1  a b c 1 2 2
 log 2a  2b  2c  2a  2b  2c  log  2 2 2
a b c   2 2 2
1  a b c 1 (*) 2 2
Xét hàm f t   log t t với t  0 , 2 1
Ta có, f 't   1  0, t
 0; nên hàm số f t đồng biến trên 0; . t ln 2
Khi đó,    f a b c  f  2 2 2 * 2 2 2
a b c   1 2 2 2 2 2 2
 2a  2b  2c a b c 1  a   1  b   1  c   1  2
3a  2b c Ta lại có, P
  P  3a  
1   P  2b   1   P   1 c   1  6  3P (**)
a b c
Áp dụng bất đẳng thức Bunhiacopxki ta có:  P2 P a  P b   P c 2 P 2 P 2  P 2 6 3 3 1 2 1 1 1 2. 3 2 1                    6  2 3 6  2 3 2
 3P 12P  8  0   P  3 3 6  2 3 3 1 1 1 3 Vậy, P  khi a  , b  , c  . max 3 3 3 3
Câu 69. (Hội các trường chuyên 19) Cho ,
x y 0; 2 thỏa mãn  x  3 x  8  ey ey 1  1 . Giá trị lớn nhất
của P  ln x  1 ln y bằng
A. 1 ln 3  ln 2 .
B. 2 ln 3  ln 2 .
C. 1 ln 3  ln 2 . D. 1 ln 2 . Lời giải Chọn B 1
Điều kiện: x  1, y  . e
Ta có :  x  3 x  8  ey ey 1  1 2 2 2
x  5x  24  e y 11ey 2 2  e y ey   2 11
x  5x  24  0 (*), có    x  2 2 5  0 , x   1.  11 2x  5  x  8 ey y  
ey x  8 2  e Do đó (*)       .  11 2x  5 ey  3  x 3  x   ey y    2  e x  8 9 x  8 +) Do y    2 nên loại y  . e e e 3  x +) Với y  , 1  x  2 : e
Khi đó, ta được: P  ln x  ln 3  x trên 1; 2 . 1 1 Ta có P   2x ln x
23  x ln 3  x 1 1 P  0    0 2x ln x
2 3  x ln 3  x
 3  x ln 3  x  x ln x  0  3  x ln 3  x  x ln x (**) 1
Xét hàm f t   t ln t trên 1;  , có f t   ln t   0, t   1;  . 2 ln t 3
Khi đó (**)  f 3  x  f x  3  x x x  . 2 Bảng biến thiên:
ThS. Nguyeãn Vaên Rin – HBT Trang 39/43 3 3 Từ đó P
 2 ln 3  ln 2 tại x  , y  . max 2 2e
Câu 70. (THTT 19) Cho hai số thực dương x, y thỏa mãn log x x x y  log
6  y  6x . Giá trị nhỏ 2   2   6 8
nhất của biểu thức P  3x  2 y   bằng x y 59 53 A. . B. 19 . C. . D. 8  6 2 . 3 3 Lời giải Chọn Bx  0 Điều kiện:  . 0  y  6 
Từ giả thiết ta có: log x x x y  log 6  y 2 2
 6x  log x x  log  x 6  y   x 6  y 2 2 2 2       (*) 1
Xét hàm số f t   log t t với t  0 , Ta có f 't  
1  0 , t  0 nên hàm số f t   log t t 2 t ln 2 2
đồng biến trên khoảng 0;  .
Do đó    f  2
x   f x   y 2 * 6
  x x 6  y  x  6  y x y  6**   ( do x  0 )
Áp dụng Bất đẳng thức Cô si cho các cặp số dương và bất đẳng thức *  * , ta có: 6 8 3  3x 6   y 8  3 3x 6 y 8
P  3x  2 y   
x y      .6  2 .  2 .  19     . x y 2  2 x  2 y 2 2 x 2 y    x y  6  3x 6 x  2
Đẳng thức xảy ra khi và chỉ khi    
. Vậy giá trị nhỏ nhất của P bằng 19. 2 x y  4    y 8   2 y
Câu 71. (Sở Quảng Nam 19) Cho hai số thực dương x , y thỏa mãn 2y y 2x log  y 1 x 2      . Giá trị nhỏ 2  x
nhất của biểu thức P  bằng y e  ln 2 e  ln 2 e ln 2 e A. . B. . C. . D. . 2 2 2 2 ln 2 Lời giải Chọn C Có 2y y 2x log  y 1 x 2       2y   2  log 2  2 y y x x 1 .   1 2   2  Đặt  log 2  2y t x
 2  2y  2t x
 2  2t  2y x . 2    
1 trở thành : 2 y   2t  2 y yt 1 y 1 2     1  2t yt . 2 Xét hàm số    2x f x
x , x       2x f x ln 2 1  0 , x    nên hàm số    2x f xx luôn
đồng biến trên  . Kết hợp với 2 ta có: t y 1  log 2  2y xy 1 y y 1 2x 2 2     2   1 2y x    .
ThS. Nguyeãn Vaên Rin – HBT Trang 40/43 x 1 2yy 1  y 1 2 y ln 2 2   Khi đó P    P  . y y 2 y 1
Cho P  0  y ln 2 1  0  y  . ln 2 Bảng biến thiên: e ln 2 e 1 Vậy P  khi x  và y  . min 2 2 ln 2 x y
Câu 72. (Chuyên Lam Sơn 19) Cho x, y thỏa mãn log
x(x  9)  y( y  9)  xy Tìm giá trị 3 2 2
x y xy  2 3x  2 y  9
lớn nhất của biểu thức P
khi x, y thay đổi. x y  10 A. 2. B. 3. C. 1. D. 0. Lời giải Chọn C x y Điều kiện xác định;
 0  (x y)  0 . 2 2
x y xy  2 y 3 Vì 2 2 2 2
x y xy  2  (x  ) 
y  2  0 với x  , y   . 2 4 x y Ta có log
x(x  9)  y( y  9)  xy . 3 2 2
x y xy  2 2 2 2 2
 log ( x y)  log ( x y xy  2)  x y xy  9( x y) . 3 3 2 2 2 2
 2  log ( x y)  9(x y)  log (x y xy  2)  x y xy  2 . 3 3 2 2 2 2
 log 9( x y)  9(x y)  log ( x y xy  2)  x y xy  2 (1) . 3 3
Đặt f (t)  log t t ( t   0) . 3 1 Có f '(t)  1  0 với ( t
  0)  f là hàm đồng biến với ( t   0) . Khi đó: t.ln 3 2 2 2 2
f (9(x y))  f (x y xy  2)  9(x y)  x y xy  2 . 2 2
x y xy  2  9x  9 y  0 . 2 2
 4x  4 y  4xy  8  36x  36 y  0 . 2 2
 (2x y) 18(2x y)  3( y  3) 19  0 . Mà 2 2
 3( y  3)  0  (2x y) 18(2x y) 19  0  1
  2x y  19 . 2x y 19
2x y  19 x  8 Mặt khác P 1 
 0  P  1 Dấu bằng xảy ra khi    . x y 10 y  3  0 y  3   3 9x x
Câu 73. (Hải Hậu 19) Cho hai số thực dương x, y thỏa mãn
 3y  2 . Giá trị lớn nhất của biểu thức y 1
S  6x y là 89 11 17 82 A. . B. . C. . D. . 12 3 12 3 Lời giải Chọn B
Theo giả thiết y  0 nên ta có:
ThS. Nguyeãn Vaên Rin – HBT Trang 41/43 3 9x x 3y 2 9x x 3y 2  y  1 3x3 3x  3y 23 3 3y 2                 y 1      
f 3x  f  3y  2  với   3
f t t t .
Ta có f t  2
 3t 1  0, t
  nên hàm số f t đồng biến trên  , suy ra 3x  3y  2 2 2 hay 2 y  3x
. Do y  0 và 3x  3y  2 nên x  . 3 3 2 2 11 11
Khi đó S  6x y  6x  3x   3  x  6x   3   x  2 2 2 1   . 3 3 3 3 11 Do đó max S  khi x  1 . 3
4. Tìm nghiệm nguyên của phương trình
Câu 74. (ĐỀ THAM KHẢO – BGD&ĐT 20) Có bao nhiêu cặp số nguyên  x; y thỏa mãn 0  x  2020 và
log 3  3   2  9y x x y ? 3   A. 2019 . B. 6 . C. 2020 . D. 4 . Lời giải Chọn D Đặt t log 3x 3 t t 1 3x 3 3 x 3         1. 3
Phương trình trở thành    t 1  2 1  3  2  3 y t y   * . Xét hàm số      3u y f u u trên  .
Ta có    1 3u f u ln 3  0, u
   nên hàm số f u đồng biến trên  . Do đó          2 * 1 2  1  2 
 3 y 1  9y f t f y t y x 1. Vì 0  x  2020 y
nên 0  9 1  2020  0  y  log 2021. 9
y    y 0;1; 2;  3 .
Vậy có 4 cặp số nguyên  ; x y thỏa YCBT.
Câu 75. (CHUYÊN LÊ HỒNG PHONG – NAM ĐỊNH 19) Cho 0  x  2020 và log (2  2)   3  8y x x y . 2
Có bao nhiêu cặp số (x ; y) nguyên thỏa mãn các điều kiện trên? A. 2019. B. 2018. C. 1. D. 4. Lời giải Chọn D
Do 0  x  2020 nên log (2x  2) luôn có nghĩa . 2
Ta có log (2  2)   3  8y x x y 2 3
 log ( 1)  1  3  2 y x x y 2 log ( x 1  ) 2 3  log ( 1)  2  3  2 y x y (1) 2
Xét hàm số ( )   2t f t t .
Tập xác định D   và (  )  1 2t f t ln 2  f (  t)  0 t    .
Suy ra hàm số f (t) đồng biến trên  . Do đó (1)  log (x 1)  3y 3  1  2 y x 2
y  log (x 1) . 8
Ta có 0  x  2020 nên 1  x 1  2021 suy ra 0  log (x 1)  log 2021. 8 8
Lại có log 2021  3, 66 nên nếu y   thì y 0;1; 2;  3 . 8
Vậy có 4 cặp số (x ; y) nguyên thỏa yêu cầu bài toán là các cặp (0;0) , (7 ;1) , (63; 2) , (511; 3) . 2
2x  3x y
Câu 76. Có bao nhiêu cặp số nguyên  ;
x y  thỏa 0  y  2017 và 2 log
x  8x  2  2 y . 2 2 5x  2x  3 A. 44 . B. 22 . C. 42 . D. 21 . Lời giải Chọn C
ThS. Nguyeãn Vaên Rin – HBT Trang 42/43 2 
a  2x  3x y Đặt  a,b  0 2
x  8x  2  2 y b  2a 1 . 2 b
  5x  2x  3 
Phương trình đã cho trở thành log a  log b b  2a 1  2a  log
2a b  log b * . 2 2 2   2  
Xét hàm số y f t   t  log t trên khoảng 0;   . 2 1
Ta có f t   1  0, t
  0 nên hàm số đồng biến trên khoảng 0;   . t ln 2
   f a  f b  a b   2
x x y  2 * 2 2 2 2 3
 5x  2x  3 2
 2 y x  8x  3 . 2 2 x 8 x3 
x  8x  3  0 49  x  8 y 2 2
0  2 y x  8x  3  2034     42 GTN . 2 
x  8x 1014  0 0  x  41   5. Tính tích phân
Câu 77. Cho hàm số y f x xác định và liên tục trên khoảng 0;   thỏa mãn f   1  2 và 3 3 4 3
f  x 3  
f x  2  1  , x   0;     I f x dx 2     . Tính   3    . x x x 2 3 5 A. I   3ln 5  2ln 7 . B. I   3ln 3 2ln 2 . 2 2 15 13 C. I   2ln 7  3ln 5 . D. I   2ln 3 3ln 2 . 2 2 Lời giải Chọn B 3 3 3 4 3 3
Ta có  f  x 
f x  2  1 
  xf x   3 xf x   x 1  3 x 1 *   2     3          x x x     .
Xét hàm số g t  3
t  3t trên  . Vì gt  2
 3t  3  0, t
   nên hàm số đồng biến trên  . 1
*  g xf  x  g x  
1  xf  x  x 1  f  x  1   x  1 
f x  1
dx  x  ln x C   .  x  Do f  
1  2 nên 1 C  2  C  1. 3 3 2  x  5
Vậy I   x 1 ln x dx 
x x ln x   1  3ln 3  2 ln 2     . 2 2 2   2 --- HẾT ---
Facebook: Nguyeãn Vaên Rin …
Ñöøng bao giôø ñeå ñeán ngaøy mai nhöõng vieäc baïn coù theå laøm ngaøy hoâm nay! Benjamin Franklin CHÚC CÁC BẠN HỌC TỐT!
ThS. Nguyeãn Vaên Rin – HBT Trang 43/43