


NGUY
˜
ÊN H
˜
U
,
U ÐIÊ
,
N
PHU
,
O
,
NG PH
´
AP
QUY N
.
AP TO
´
AN H
.
OC
(T ´ai b
,
an lâ
`
n th
´
u
,
hai)
NH
`
A XU
´
ÂT B
,
AN GI
´
AO D
.
UC

c
Ebook 1.0 c
,
ua cuô
´
n s
´
ach nguyên gô
´
c t
`
u
,
b
,
an in, c
´
ac b
.
an tham
kh
,
ao, cho
´
y kiê
´
n sai s
´
ot v
`
a l
`
o
,
i khuyên t
´
ai b
,
an. M
.
oi liên h
.
ê
T
´
ac gi
,
a: Nguy
˜
ên H
˜
u
,
u Ðiê
,
n
Ði
.
ên tho
.
ai: 0989061951
Email: huudien@vnu.edu.vn
Web: http://nhdien.wordpress.com
Ch
.
iu tr ´ach nhi
.
êm xuâ
´
t b
,
an:
Gi
´
am
¯
dô
´
c Ngô Trâ
`
n
´
ai
Tô
,
ng biên t
.
âp V
˜
u Du
,
o
,
ng Th
.
uy
Biên t
.
âp n
.
ôi dung:
Ngô Long H
.
âu
Biên t
.
âp t ´ai b
,
an:
Tru
,
o
,
ng Công Th
`
anh
Tr`ınh b `ay b`ıa:
T
.
a Tr
.
ong Tr
´
ı
Chê
´
b
,
an:
Ngu
˜
ên H
˜
u
,
u Ðiê
,
n
51
GD −00
05/796-00 M
˜
a sô
´
: 8H663M0

L
`
O
,
I N
´
OI Ð
`
ÂU
M
.
ôt phu
,
o
,
ng ph
´
ap râ
´
t m
.
anh trong to
´
an h
.
oc d
`
ung nghiên c
´
u
,
u
v
`
a ch
´
u
,
ng minh c
´
ac gi
,
a thuyê
´
t l
`
a nguyên l
´
y quy n
.
ap to
´
an h
.
oc. C
´
o
vô sô
´
c
´
ac v
´
ı d
.
u trong c
´
ac môn h
.
oc
,
o
,
chu
,
o
,
ng tr
`
ınh phô
,
thông d
`
ung
nguyên l
´
y n
`
ay
¯
dê
,
di
˜
ên gi
,
ai v
`
a mô t
,
a. Nhu
,
ng
¯
dê
,
hiê
,
u thâ
´
u
¯
d
´
ao vê
`
k
˜
y thu
.
ât
´
ap d
.
ung trong h
.
oc t
.
âp, s
´
ang t
.
ao râ
´
t
´
ıt s
´
ach
¯
du
,
.
o
,
c b
`
an t
´
o
,
i.
T
`
ai li
.
êu nu
,
´
o
,
c ngo
`
ai c
˜
ung
¯
d
˜
a c
´
o m
.
ôt sô
´
s
´
ach n
´
oi riêng vê
`
vâ
´
n
¯
dê
`
n
`
ay, theo tôi c
˜
ung chu
,
a
¯
dâ
`
y
¯
d
,
u v
`
a râ
´
t nhiê
`
u ngu
,
`
o
,
i kh
´
o tiê
´
p x
´
uc
¯
du
,
.
o
,
c v
´
o
,
i t
`
ai li
.
êu n
`
ay. Tôi m
.
anh d
.
an thu th
.
âp v
`
a kh
,
ao s
´
at nguyên
l
´
y quy n
.
ap to
´
an h
.
oc theo m
.
oi kh
´
ıa c
.
anh v
`
a minh h
.
oa b
`
˘
ang c
´
ac
b
`
ai t
.
âp trong chu
,
o
,
ng tr
`
ınh phô
,
thông. Ðây l
`
a lo
.
ai s
´
ach cung câ
´
p
v
`
a th
,
ao lu
.
ân nh
˜
u
,
ng phu
,
o
,
ng ph
´
ap h
.
oc t
.
âp v
`
a gi
,
ai b
`
ai t
.
âp cho c
´
ac
b
.
an yêu th
´
ıch to
´
an h
.
oc, c
´
ac thâ
`
y cô gi
´
ao, sinh viên c
´
ac tru
,
`
o
,
ng su
,
ph
.
am v
`
a c
´
ac b
.
an
,
o
,
l
´
o
,
p h
.
oc sinh gi
,
oi l
`
am t
`
ai li
.
êu tiê
´
p t
.
uc ph
´
at
triê
,
n. Chu
,
o
,
ng
¯
dâ
`
u xem x
´
et c
´
ac kh
´
ıa c
.
anh c
,
ua nguyên l
´
y quy n
.
ap
to
´
an h
.
oc. Do khuôn khô
,
c
,
ua cuô
´
n s
´
ach ch
´
ung tôi
¯
d
˜
a không ch
´
u
,
ng
minh c
.
˘
an k
˜
e s
.
u
,
tu
,
o
,
ng
¯
du
,
o
,
ng c
,
ua nguyên l
´
y quy n
.
ap to
´
an h
.
oc v
`
a
tiên
¯
dê
`
th
´
u
,
t
.
u
,
; s
.
u
,
tu
,
o
,
ng
¯
du
,
o
,
ng c
,
ua c
´
ac d
.
ang nguyên l
´
y quy n
.
ap
to
´
an h
.
oc..v.v. Chu
,
o
,
ng hai kh
,
ao s
´
at c
´
ac kh
´
ıa c
.
anh k
˜
y thu
.
ât c
,
ua
nguyên l
´
y n
`
ay. T
`
u
,
chu
,
o
,
ng ba m
˜
ôi chu
,
o
,
ng d
`
ung kh
,
ao s
´
at c
´
ac b
`
ai
t
.
âp vê
`
m
.
ôt lo
.
ai ch
,
u
¯
dê
`
ch
,
ı
´
ap d
.
ung phu
,
o
,
ng ph
´
ap quy n
.
ap to
´
an
h
.
oc nhu
,
: Sô
´
h
.
oc, D
˜
ay sô
´
, H
`
ınh h
.
oc, Ða th
´
u
,
c, Tô
,
h
.
o
,
p, Liên phân
sô
´
...
T
`
ai li
.
êu ch
´
ung tôi tham kh
,
ao c
´
o h
.
an v
`
a ch
´
˘
ac c
`
on nhiê
`
u b
`
ai
t
.
âp hay chu
,
a n
´
oi t
´
o
,
i, ho
.
˘
ac c
´
o sai s
´
ot trong thê
,
hi
.
ên
´
y tu
,
,
o
,
ng mong
b
.
an
¯
d
.
oc cho
´
y kiê
´
n s
,
u
,
a
¯
dô
,
i v
`
a bô
,
sung. M
.
oi liên h
.
ê g
,
u
,
i vê
`
¯
d
.
ia ch
,
ı:
Nh
`
a xuâ
´
t b
,
an Gi
´
ao d
.
uc, 81 Trâ
`
n Hu
,
ng Ð
.
ao, H
`
a N
.
ôi.
H
`
a N
.
ôi, th
´
ang 5 n
˘
am 2000
T
´
ac gi
,
a
3

CHU
,
O
,
NG 1
NGUYÊN L
´
Y QUY N
.
AP TO
´
AN H
.
OC
1.1. Suy di
˜
ên v
`
a quy n
.
ap . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
1.2. Nguyên l
´
y quy n
.
ap to
´
an h
.
oc . . . . . . . . . . . . . . . . . . . . . . . . . . 6
1.3. Giai
¯
do
.
an quy n
.
ap v
`
a gi
,
a thiê
´
t quy n
.
ap . . . . . . . . . . . . . . 8
1.4. Hai bu
,
´
o
,
c c
,
ua nguyên l
´
y quy n
.
ap to
´
an h
.
oc . . . . . . . . . 14
1.5. Khi n
`
ao d
`
ung phu
,
o
,
ng ph
´
ap quy n
.
ap . . . . . . . . . . . . . . . . 19
1.6. B
`
ai t
.
âp. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
1.1. Suy di
˜
ên v
`
a quy n
.
ap
Ðê
,
minh h
.
oa hai kh
´
ai ni
.
êm râ
´
t hay g
.
˘
ap trong th
.
u
,
c tê
´
l
`
a suy
di
˜
ên v
`
a quy n
.
ap, ta lâ
´
y câu ca dao Vi
.
êt Nam ai c
˜
ung biê
´
t:
¨Sô
´
cô c´o m
.
e c´o cha
M
.
e cô
¯
d `an b `a cha cô
¯
d `an ông
Sô
´
cô c´o v
.
o
,
c´o chô
`
ng
Sinh con
¯
dâ
`
u l`ong ch
,
˘ang g ´ai th`ı trai.¨
Ðây l
`
a câu
¯
do
´
an c
,
ua ông thâ
`
y b
´
oi, ta
¯
d
˜
a biê
´
t thâ
`
y b
´
oi ch
,
ı
¯
do
´
an m
`
o thôi, nhu
,
ng ông thâ
`
y b
´
oi trong câu ca dao n
`
ay râ
´
t khôn
l
`
a d
`
ung m
.
ôt kh
,
˘
ang
¯
d
.
inh luôn luôn
¯
d
´
ung ¨ai c ˜ung c´o m
.
e, c´o cha¨.
T
`
u
,
¯
d
´
o d
`
u
´
ap d
.
ung cho ngu
,
`
o
,
i
¯
dê
´
n b
´
oi c
.
u thê
,
n
`
ao c
˜
ung
¯
d
´
ung luôn,
ngh
˜
ıa l
`
a kh
,
˘
ang
¯
d
.
inh riêng c
˜
ung
¯
d
´
ung. Bu
,
´
o
,
c suy lu
.
ân t
`
u
,
kh
,
˘
ang
¯
d
.
inh chung
´
ap d
.
ung cho nh
˜
u
,
ng kh
,
˘
ang
¯
d
.
inh riêng bi
.
êt g
.
oi l
`
a ph´ep
suy di
˜
ên. Ph
´
ep suy di
˜
ên
,
o
,
v
´
ı d
.
u trên l
`
a luôn
¯
d
´
ung v
´
o
,
i hai câu
¯
dâ
`
u,

1.1. Suy di
˜
ên v
`
a quy n
.
ap 5
nhu
,
ng c
´
o thê
,
sai
,
o
,
hai câu sau. Trong to
´
an h
.
oc râ
´
t hay d
`
ung ph
´
ep
suy di
˜
ên, ch
,
˘
ang h
.
an, nê
´
u hai g
´
oc trong c
,
ua m
.
ôt tam gi
´
ac
¯
d
˜
a cho
l
`
a 30
0
v
`
a 70
0
, th
`
ı
¯
diê
`
u kh
,
˘
ang
¯
d
.
inh sau
¯
d
´
ung: ¨ G
´
oc th
´
u
,
ba c
,
ua
tam gi
´
ac
¯
d
˜
a cho l
`
a 80
0
¨. M
.
ênh
¯
dê
`
chung
,
o
,
¯
dây l
`
a: ¨Tô
,
ng c
´
ac g
´
oc
trong c
,
ua m
.
ôt tam gi
´
ac l
`
a 180
0
¨.
Bây gi
`
o
,
ta
¯
d
.
oc l
.
ai chuy
.
ên cu
,
`
o
,
i dân gian Vi
.
êt nam:
¨Bô
´
n ông thâ
`
y b
´
oi r
,
u nhau
¯
di xem voi. T
´
o
,
i ch
˜
ô voi
¯
d
´
u
,
ng, bô
´
n
thâ
`
y b
´
oi chen v
`
ao, s
`
o
,
t
.
ân tay xem con voi n
´
o thê
´
n
`
ao. Vê
`
t
´
o
,
i ch
.
o
,
,
bô
´
n thâ
`
y h
.
op nhau b
`
ınh phâ
,
m.
Thâ
`
y s
`
o
,
¯
du
,
.
o
,
c c
´
ai v
`
oi voi n
´
oi:
- Tu
,
,
o
,
ng voi l
.
a l
´
˘
am, t
´
e ra ch
,
ı giô
´
ng con
¯
d
,
ıa c
.
u
,
c l
´
o
,
n. Tôi s
`
o
,
v
`
ao
n
´
o uô
´
n cong ngu
,
`
o
,
i l
.
ai.
Thâ
`
y ôm ph
,
ai c
´
ai chân, v
.
ôi c
˜
ai:
- Voi ch
,
ı h
.
êt nhu
,
c
´
ai c
.
ôt nh
`
a thôi. Tôi ôm v
`
ao v
`
u
,
a tay c
´
ai c
.
ôt
c
´
ai.
Thâ
`
y n
´
˘
am ph
,
ai c
´
ai tai voi, chê:
- C
´
ac b
´
ac ch
,
ı n
´
oi m
`
o. Con voi th
.
ât ra t
.
u
,
a nhu
,
c
´
ai qu
.
at to
tu
,
´
o
,
ng.
Thâ
`
y t
´
um ph
,
ai c
´
ai
¯
duôi voi, cu
,
`
o
,
i khâ
,
y:
- Ba b
´
ac n
´
oi sai c
,
a. Tôi
¯
d
˜
a t
´
um n
´
o trong tay, th
`
ı
¯
d
´
ung l
`
a m
.
ôt
c
´
ai chô
,
i xê
,
¯
d
.
ai.
Không ai ch
.
iu ai, bô
´
n thâ
`
y to tiê
´
ng c
˜
ai nhau ô
`
n
`
ao m
.
ôt g
´
oc
ch
.
o
,
... ¨
M
˜
ôi ông thâ
`
y b
´
oi
¯
dê
`
u d
`
ung kh
,
˘
ang
¯
d
.
inh riêng c
,
ua m
`
ınh
¯
dê
,
¯
do
´
an, ph
´
at biê
,
u kh
,
˘
ang
¯
d
.
inh chung. Bu
,
´
o
,
c suy lu
.
ân t
`
u
,
kh
,
˘
ang
¯
d
.
inh
riêng tiê
´
n t
´
o
,
i ph
´
at biê
,
u kh
,
˘
ang
¯
d
.
inh chung
¯
du
,
.
o
,
c g
.
oi l
`
a ph´ep quy

6 Chu
,
o
,
ng 1. Nguyên l
´
y quy n
.
ap to
´
an h
.
oc
n
.
ap. Kh
,
˘
ang
¯
d
.
inh chung
,
o
,
¯
dây l
`
a ¨con v
.
ât
¯
d
´
o l
`
a con voi¨. Nhu
,
v
.
ây
4 ông thâ
`
y b
´
oi
¯
dê
`
u ph
´
at biê
,
u kh
,
˘
ang
¯
d
.
inh chung sai. Ch
´
˘
ac c
´
o m
.
ôt
ông n
`
ao
¯
d
´
o s
´
ang m
´
˘
at th
`
ı s
˜
e
¯
d
´
ung. Ta thâ
´
y r
`
˘
ang phu
,
o
,
ng ph
´
ap quy
n
.
ap c
´
o thê
,
¯
du
,
a
¯
dê
´
n kê
´
t qu
,
a nh
.
ân
¯
d
.
inh sai. Phu
,
o
,
ng ph
´
ap quy n
.
ap
râ
´
t hay
¯
du
,
.
o
,
c d
`
ung trong nghiên c
´
u
,
u khoa h
.
oc, nhâ
´
t l
`
a to
´
an h
.
oc.
Nhu
,
v
.
ây ch
´
ung ta ph
,
ai hiê
,
u phu
,
o
,
ng ph
´
ap quy n
.
ap thê
´
n
`
ao
¯
dây
v
`
a
´
ap d
.
ung thê
´
n
`
ao
¯
dê
,
nh
.
ân
¯
du
,
.
o
,
c m
.
ênh
¯
dê
`
kh
,
˘
ang
¯
d
.
inh
¯
d
´
ung.
1.2. Nguyên l
´
y quy n
.
ap to
´
an h
.
oc
Ðê
,
ng
´
˘
an g
.
on ta k
´
y hi
.
êu m
.
ôt kh
,
˘
ang
¯
d
.
inh to
´
an h
.
oc l
`
a P(x),
,
o
,
¯
dây x l
`
a m
.
ôt biê
´
n sô
´
. Ngu
,
`
o
,
i ta thu
,
`
o
,
ng
¯
du
,
a vê
`
d
.
ang m
.
ênh
¯
dê
`
¨
V
´
o
,
i m
.
oi x (trong m
.
ôt t
.
âp S n
`
ao
¯
d
´
o), P(x)¨. Trong cuô
´
n s
´
ach n
`
ay
ta lâ
´
y x = n l
`
a nh
˜
u
,
ng sô
´
t
.
u
,
nhiên
1
, S l
`
a t
.
âp c
´
ac sô
´
t
.
u
,
nhiên (bao
gô
`
m to
`
an b
.
ô c
´
ac sô
´
nguyên du
,
o
,
ng). Ta s
,
u
,
d
.
ung m
.
ôt t
´
ınh châ
´
t râ
´
t
quan tr
.
ong c
,
ua t
.
âp sô
´
t
.
u
,
nhiên, thu
,
`
o
,
ng ngu
,
`
o
,
i ta công nh
.
ân nhu
,
m
.
ôt tiên
¯
dê
`
(
¯
du
,
.
o
,
c g
.
oi l
`
a tiên
¯
dê
`
th
´
u
,
t
.
u
,
).
Tiên
¯
dê
`
: Trong m
˜
ôi t
.
âp h
.
o
,
p kh´ac r
˜
ông c
,
ua nh
˜
u
,
ng sô
´
t
.
u
,
nhiên c´o
m
.
ôt phâ
`
n t
,
u
,
nh
,
o nhâ
´
t.
Cho m
˜
ôi sô
´
t
.
u
,
nhiên n
´
u
,
ng v
´
o
,
i m
.
ôt kh
,
˘
ang
¯
d
.
inh P(n). V
´
ı d
.
u,
v
´
o
,
i 1 ta cho tu
,
o
,
ng
´
u
,
ng v
´
o
,
i kh
,
˘
ang
¯
d
.
inh P(1): ¨sô
´
1 l
`
a m
.
ôt sô
´
l
,
e¨,
sô
´
2 cho tu
,
o
,
ng t
´
u
,
ng v
´
o
,
i P(2): ¨ sô
´
2 l
`
a m
.
ôt sô
´
ch
˜
˘
an¨; ... B
`
˘
ang
phu
,
o
,
ng ph
´
ap nhu
,
v
.
ây ch
´
ung ta t
.
ao ra d
˜
ay kh
,
˘
ang
¯
d
.
inh riêng
P(1), P(2), . . . , P(n), . . . . Nguyên l
´
y quy n
.
ap to
´
an h
.
oc cho ta m
.
ôt
phu
,
o
,
ng ph
´
ap kiê
,
m tra kh
,
˘
ang
¯
d
.
inh P(n)
¯
d
´
ung ho
.
˘
ac sai v
´
o
,
i m
.
oi n.
Nguyên l
´
y quy n
.
ap to
´
an h
.
oc
¯
du
,
.
o
,
c thê
,
hi
.
ên qua
¯
d
.
inh l
´
ı sau:
1
Trong s
´
ach n
`
ay khi n
´
oi
¯
dê
´
n sô
´
t
.
u
,
nhiên, ta hiê
,
u
¯
d
´
o l
`
a sô
´
t
.
u
,
nhiên kh
´
ac sô
´
0.

1.2. Nguyên l
´
y quy n
.
ap to
´
an h
.
oc 7
Ð
.
inh l
´
y 1.1. Cho n
0
l `a m
.
ôt sô
´
nguyên du
,
o
,
ng v`a P(n) l `a m
.
ênh
¯
dê
`
c´o ngh˜ıa v
´
o
,
i m
.
oi sô
´
t
.
u
,
nhiên n ≥ n
0
. Nê
´
u
A) P(n
0
) l`a
¯
d ´ung v `a
B) Nê
´
u P(k)
¯
d ´ung, th`ı P(k + 1) c ˜ung
¯
d ´ung v
´
o
,
i m
˜
ôi sô
´
t
.
u
,
nhiên
k ≥ n
0
,
khi
¯
d´o m
.
ênh
¯
dê
`
P(n)
¯
d ´ung v
´
o
,
i m
.
oi sô
´
t
.
u
,
nhiên n ≥ n
0
.
Ch
´
u
,
ng minh. Ta s
˜
e ch
´
u
,
ng minh b
`
˘
ang ph
,
an ch
´
u
,
ng. Gi
,
a s
,
u
,
ngu
,
.
o
,
c
l
.
ai, m
.
ênh
¯
dê
`
kh
,
˘
ang
¯
d
.
inh P(n) trong Ð
.
inh l
´
ı 1.1 không
¯
d
´
ung v
´
o
,
i
m
.
ôt sô
´
t
.
u
,
nhiên n ≥ n
0
n
`
ao
¯
d
´
o. Ngh
˜
ıa l
`
a tô
`
n t
.
ai m
.
ôt sô
´
t
.
u
,
nhiên
m ≥ n
0
, m
`
a P(m) không
¯
d
´
ung. Ta lâ
´
y sô
´
t
.
u
,
nhiên m nh
,
o nhâ
´
t
m
`
a P(m) không
¯
d
´
ung (
¯
diê
`
u n
`
ay th
.
u
,
c hi
.
ên
¯
du
,
.
o
,
c do tiên
¯
dê
`
th
´
u
,
t
.
u
,
). Theo
¯
diê
`
u ki
.
ên A), ta c
´
o bâ
´
t
¯
d
,
˘
ang th
´
u
,
c m > n
0
, t
`
u
,
¯
d
´
o suy ra
m −1 ≥ n
0
. T
`
u
,
bâ
´
t
¯
d
,
˘
ang th
´
u
,
c v
`
u
,
a l
.
âp v
`
a c
´
ach ch
.
on sô
´
t
.
u
,
nhiên
m suy ra P( m −1) l
`
a
¯
d
´
ung, nhu
,
ng n
´
o không k
´
eo theo
¯
du
,
.
o
,
c P(m)
¯
d
´
ung cho sô
´
tiê
´
p theo m = (m −1) + 1. Ðiê
`
u n
`
ay tr
´
ai v
´
o
,
i gi
,
a thiê
´
t
B).
J
Xuâ
´
t ph
´
at t
`
u
,
m
.
ênh
¯
dê
`
kh
,
˘
ang
¯
d
.
inh v
´
o
,
i c
´
ac tru
,
`
o
,
ng h
.
o
,
p riêng,
ch
,
˘
ang h
.
an nhu
,
c
´
ac sô
´
1, 2, ho
.
˘
ac 3 c
´
o thê
,
nâ
,
y sinh gi
,
a thiê
´
t m
.
ênh
¯
dê
`
¯
d
´
ung v
´
o
,
i m
.
oi sô
´
t
.
u
,
nhiên. Sau
¯
d
´
o
¯
dê
,
ch
´
u
,
ng minh gi
,
a thiê
´
t c
,
ua
ta v
`
u
,
a xây d
.
u
,
ng ngu
,
`
o
,
i ta l
´
y lu
.
ân theo nguyên l
´
y quy n
.
ap to
´
an
h
.
oc. Phu
,
o
,
ng ph
´
ap ch
´
u
,
ng minh nhu
,
v
.
ây g
.
oi l
`
a phu
,
o
,
ng ph ´ap quy
n
.
ap to ´an h
.
oc. Theo
¯
d
.
inh l
´
ı trên phu
,
o
,
ng ph
´
ap n
`
ay gô
`
m hai bu
,
´
o
,
c,
th
´
u
,
nhâ
´
t ta kiê
,
m tra kh
,
˘
ang
¯
d
.
inh m
.
ôt t
´
ınh châ
´
t v
´
o
,
i n = n
0
, g
.
oi
l
`
a Bu
,
´
o
,
c co
,
s
,
o
,
; sau
¯
d
´
o ch
´
u
,
ng minh r
`
˘
ang nê
´
u v
´
o
,
i m
˜
ôi k ≥ n
0
, P(k)
tho
,
a m
˜
an t
´
ınh châ
´
t
¯
d
˜
a biê
´
t, th
`
ı suy ra P(k + 1) c
˜
ung c
´
o t
´
ınh châ
´
t
â
´
y, g
.
oi l
`
a Bu
,
´
o
,
c quy n
.
ap. Kê
´
t lu
.
ân l
`
a P(n) c
´
o t
´
ınh châ
´
t
¯
d
˜
a cho v
´
o
,
i
m
.
oi n ≥ n
0
. C
´
ach ch
´
u
,
ng minh theo quy n
.
ap to
´
an h
.
oc l
`
a tr
´
anh

8 Chu
,
o
,
ng 1. Nguyên l
´
y quy n
.
ap to
´
an h
.
oc
cho ta ph
,
ai kiê
,
m tra vô h
.
an bu
,
´
o
,
c c
´
ac kh
,
˘
ang
¯
d
.
inh c
,
ua m
.
ênh
¯
dê
`
.
1.3. Giai
¯
do
.
an quy n
.
ap v
`
a gi
,
a thiê
´
t quy n
.
ap
Phu
,
o
,
ng ph
´
ap quy n
.
ap to
´
an h
.
oc râ
´
t hay
¯
du
,
.
o
,
c
´
ap d
.
ung trong
nghiên c
´
u
,
u v
`
a t
`
ım t
`
oi trong to
´
an h
.
oc, c
´
ac ng
`
anh khoa h
.
oc kh
´
ac.
Ðê
,
hiê
,
u c
´
ach
´
ap d
.
ung phu
,
o
,
ng ph
´
ap quy n
.
ap cho
¯
dâ
`
y
¯
d
,
u, ta xem
x
´
et m
.
ôt sô
´
v
´
ı d
.
u sau
¯
dây nhu
,
m
.
ôt ph
´
ep ¨suy lu
.
ân c´o l´y¨ m
`
a G.
Polya
¯
d
˜
a
¯
dê
`
c
.
âp.
V
´
ı d
.
u 1.1. Cho tru
,
´
o
,
c m
.
ôt sô
´
t
.
u
,
nhiên n. H ˜ay t`ım tô
,
ng c ´ac sô
´
t
.
u
,
nhiên 1, 2, . . . , n.
L
`
o
,
i gi
,
ai. Ta k
´
y hi
.
êu S
n
l
`
a tô
,
ng ph
,
ai t
`
ım, ngh
˜
ıa l
`
a
S
n
= 1 + 2 + ··· + n. (1.1)
Ta hy v
.
ong l
`
a t
`
ım ra công th
´
u
,
c ng
´
˘
an g
.
on
¯
dê
,
t
´
ınh tô
,
ng trên, công
th
´
u
,
c
¯
d
´
o gi
´
up ta t
´
ınh nhanh, g
.
on ho
,
n l
`
a ph
,
ai th
.
u
,
c hi
.
ên lâ
`
n lu
,
.
o
,
t
c
´
ac ph
´
ep c
.
ông trong tô
,
ng. Ta c
˜
ung biê
´
t
¯
dây l
`
a câ
´
p sô
´
c
.
ông, nê
´
u
b
.
an
¯
d
.
oc
¯
d
˜
a biê
´
t vê
`
câ
´
p sô
´
n
`
ay, th
`
ı ta c
´
o thê
,
c
´
o ngay công th
´
u
,
c t
´
ınh
tô
,
ng. Nhu
,
ng
,
o
,
¯
dây ta muô
´
n minh h
.
oa qu
´
a tr
`
ınh
´
ap d
.
ung nguyên
l
´
y quy n
.
ap to
´
an h
.
oc nên nh
˜
u
,
ng
¯
diê
`
u
¯
d
˜
a biê
´
t vê
`
câ
´
p sô
´
c
.
ông ta b
,
o
qua, coi nhu
,
chu
,
a biê
´
t.
Ta t
´
ınh tô
,
ng S
n
t
`
u
,
¯
d
,
˘
ang th
´
u
,
c (1.1) v
´
o
,
i m
.
ôt v
`
ai sô
´
t
.
u
,
nhiên
liên tiê
´
p, ch
,
˘
ang h
.
an b
´
˘
at
¯
dâ
`
u t
`
u
,
1. Nh
˜
u
,
ng kê
´
t qu
,
a t
´
ınh to
´
an c
´
ac
tru
,
`
o
,
ng h
.
o
,
p riêng ta xê
´
p v
`
ao b
,
ang
n 1 2 3 4 5 6
S
n
1 3 6 10 15 21
M
.
uc
¯
d
´
ıch c
,
ua ta l
`
a t
`
ım
¯
du
,
.
o
,
c quy lu
.
ât chung (kh
,
˘
ang
¯
d
.
inh chung),
v
´
o
,
i b
,
ang trên, m
˜
ôi sô
´
t
.
u
,
nhiên
,
o
,
h
`
ang trên trong b
,
ang cho tu
,
o
,
ng

1.3. Giai
¯
do
.
an quy n
.
ap v
`
a gi
,
a thiê
´
t quy n
.
ap 9
´
u
,
ng v
´
o
,
i c
´
ac sô
´
,
o
,
h
`
ang du
,
´
o
,
i. T
`
ım ra quy lu
.
ât c
,
ua m
.
ôt b
`
ai to
´
an ph
.
u
thu
.
ôc v
`
ao râ
´
t nhiê
`
u yê
´
u tô
´
: s
.
u
,
kh
´
eo l
´
eo trong quan s
´
at; s
.
u
,
nh
.
ay
c
,
am d
.
u
,
¯
do
´
an v
`
a kiê
,
m tra c
,
ua ta; t
`
u
,
c
´
ac kinh nghi
.
êm
¯
d
˜
a tr
,
ai qua
trong t
´
ınh to
´
an c
´
ac b
`
ai to
´
an tu
,
o
,
ng t
.
u
,
, t
`
u
,
kh
,
a n
˘
ang liên h
.
ê b
`
ai
to
´
an tu
,
o
,
ng t
.
u
,
v
´
o
,
i
¯
diê
`
u ki
.
ên m
´
o
,
i, v.v...
Trên b
,
ang trên ta d
˜
ê thâ
´
y quy lu
.
ât: T
´
ıch c
,
ua hai sô
´
liên tiê
´
p
,
o
,
h
`
ang trên b
`
˘
ang 2 lâ
`
n sô
´
¯
dâ
`
u tiên tu
,
o
,
ng
´
u
,
ng
,
o
,
h
`
ang du
,
´
o
,
i. Th
.
ât
v
.
ây, 1.2=2.1, 2.3=2.3, 3.4=2.6, 4.5=2.10, 5.6=2.15. Nhu
,
v
.
ây giai
¯
do
.
an quy n
.
ap c
,
ua ch
´
ung ta
¯
d
˜
a th
`
anh công: T
`
ım ra quy lu
.
ât v
´
o
,
i
c
´
ac tru
,
`
o
,
ng h
.
o
,
p riêng n = 1, 2, 3, 4, 5, 6.
Tiê
´
p t
.
uc m
.
ôt c
´
ach t
.
u
,
nhiên l
`
a m
,
o
,
r
.
ông quy lu
.
ât trên cho b
,
ang
sô
´
v
´
o
,
i c
´
ac sô
´
t
.
u
,
nhiên bâ
´
t k
`
y. Ta
¯
du
,
a ra gi
,
a thiê
´
t th
´
ıch h
.
o
,
p v
´
o
,
i
quy lu
.
ât v
`
u
,
a t
`
ım
¯
du
,
.
o
,
c. Ð
.
˘
at
1 + 2 + ··· + n =
n(n + 1)
2
. (1.2)
M
.
ôt gi
,
a thiê
´
t ta
¯
d
˜
a l
`
am nhu
,
v
.
ây
¯
du
,
.
o
,
c g
.
oi l
`
a gi
,
a thiê
´
t quy n
.
ap.
Nhu
,
ng câu h
,
oi
¯
d
.
˘
at ra l
`
a
¯
d
,
˘
ang th
´
u
,
c (1.2) c
´
o
¯
d
´
ung v
´
o
,
i m
.
oi n =
1, 2, . . . hay không? R
˜
o r
`
ang nê
´
u (1.2)
¯
d
´
ung v
´
o
,
i m
.
oi sô
´
t
.
u
,
nhiên
th
`
ı b
`
˘
ang c
´
ach thay n b
`
˘
ang n + 1 ch
´
ung ta s
˜
e c
´
o
¯
d
,
˘
ang th
´
u
,
c
1 + 2 + ··· + n + (n + 1) =
( n + 1)(n + 2)
2
. (1.3)
Tr
´
ai l
.
ai, gi
,
a thiê
´
t (1.2) l
`
a
¯
d
´
ung v
´
o
,
i m
.
oi n = 1, 2, . . ., nê
´
u 1) n
´
o
¯
d
´
ung v
´
o
,
i n = 1 v
`
a 2) n
´
o
¯
d
´
ung v
´
o
,
i m
˜
ôi sô
´
k suy ra c
˜
ung
¯
d
´
ung
v
´
o
,
i c
,
a k + 1. Ðiê
`
u n
`
ay không c
´
o c
´
ach n
`
ao kh
´
ac l
`
a ph
,
ai
´
ap d
.
ung
nguyên l
´
y quy n
.
ap to
´
an h
.
oc. Ngh
˜
ıa l
`
a ch
´
ung ta ph
,
ai kiê
,
m tra
nh
˜
u
,
ng
¯
diê
`
u ki
.
ên A) v
`
a B) c
,
ua
¯
d
.
inh l
´
ı 1.1.
Bu
,
´
o
,
c co
,
s
,
o
,
: v
´
o
,
i n = 1, công th
´
u
,
c (1.2)
¯
d
´
ung (n
´
o c
`
on
¯
d
´
ung cho c
,
a
n = 2, 3, 4, 5, 6).

10 Chu
,
o
,
ng 1. Nguyên l
´
y quy n
.
ap to
´
an h
.
oc
Bu
,
´
o
,
c quy n
.
ap: Bây gi
`
o
,
ch
´
ung ta ch
´
u
,
ng minh công th
´
u
,
c (1.2)
¯
d
´
ung
cho c
,
a
¯
diê
`
u ki
.
ên B). V
´
o
,
i m
.
uc
¯
d
´
ıch
¯
d
´
o ta gi
,
a thiê
´
t công th
´
u
,
c (1.2)
¯
d
´
ung v
´
o
,
i m
.
ôt sô
´
n = k ≥ 1 n
`
ao
¯
d
´
o v
`
a s
˜
e ch
´
u
,
ng minh
¯
d
,
˘
ang th
´
u
,
c
(1.2)
¯
d
´
ung v
´
o
,
i n = k + 1. Ta biê
´
n
¯
dô
,
i
1 + 2 + ··· + k + (k + 1) =
k(k + 1)
2
+ (k + 1 ) =
( k + 1)(k + 2)
2
.
Kê
´
t qu
,
a l
`
a (1.2)
¯
d
´
ung v
´
o
,
i n = k + 1. Theo nguyên l
´
y quy n
.
ap to
´
an
h
.
oc công th
´
u
,
c (1.2)
¯
d
´
ung v
´
o
,
i m
.
oi n = 1, 2, . . .
J
T
´
om l
.
ai, qua v
´
ı d
.
u
¯
do
,
n gi
,
an trên ta thâ
´
y c
´
ac bu
,
´
o
,
c qu
´
a tr
`
ınh
t
`
ım t
`
oi v
`
a ch
´
u
,
ng minh nguyên l
´
y quy n
.
ap to
´
an h
.
oc.
V
´
ı d
.
u 1.2. T´ınh tô
,
ng
S
n
=
1
a(a + 1)
+
1
(a + 1)(a + 2)
+ ··· +
1
(a + (n −1))(a + n)
v
´
o
,
i a 6= 0, −1, −2, . . . ; n = 1, 2, . . .
L
`
o
,
i gi
,
ai. Vi
.
êc tru
,
´
o
,
c tiên ta ph
,
ai t
`
ım ra công th
´
u
,
c gi
,
a thiê
´
t quy
n
.
ap cho tô
,
ng trên. Ta t
´
ınh
S
1
=
1
a(a + 1)
,
S
2
= S
1
+
1
(a + 1)(a + 2)
=
1
a(a + 1)
+
1
(a + 1)(a + 2)
=
2
a(a + 2)
,
S
3
= S
2
+
1
(a + 2)(a + 3)
=
3
a(a + 3)
,
S
4
= S
3
+
1
(a + 3)(a + 4)
=
4
a(a + 4)
.
Ch
´
ung ta c
´
o thê
,
¯
du
,
a ra gi
,
a thiê
´
t r
`
˘
ang
S
n
=
n
a(a + n)
. (1.4)

1.3. Giai
¯
do
.
an quy n
.
ap v
`
a gi
,
a thiê
´
t quy n
.
ap 11
Bu
,
´
o
,
c co
,
s
,
o
,
: Nhu
,
¯
d
˜
a kiê
,
m tra
,
o
,
trên.
Bu
,
´
o
,
c quy n
.
ap: Gi
,
a thiê
´
t (1.4)
¯
d
´
ung v
´
o
,
i sô
´
t
.
u
,
nhiên n = k n
`
ao
¯
d
´
o.
Khi
¯
d
´
o
S
k+1
= S
k
+
1
(a + k)(a + k + 1)
=
k
a(a + k)
+
1
(a + k)(a + k + 1)
=
1
a + k
.
k
2
+ (a + 1)k + a
a(a + k + 1)
.
Nhu
,
ng k
2
+ (a + 1)k + a = (a + k)(k + 1) , suy ra
S
k+1
=
1
a + k
.
(a + k)(k + 1)
a(a + k + 1)
=
k + 1
a(a + k + 1)
.
T
`
u
,
kê
´
t qu
,
a v
`
u
,
a t
´
ınh v
`
a bu
,
´
o
,
c co
,
s
,
o
,
suy ra gi
,
a thiê
´
t quy n
.
ap (1.4)
l
`
a
¯
d
´
ung v
´
o
,
i m
.
oi sô
´
t
.
u
,
nhiên n ≥ 1.
J
V
´
ı d
.
u 1.3. T´ınh tô
,
ng
S
n
=
2
1 − a
2
+
2
1 + a
2
+
4
1 + a
4
+ ··· +
2
n
1 + a
2
n
v
´
o
,
i n = 1, 2, . . . ; |a| 6= 1.
L
`
o
,
i gi
,
ai. Ta phân t
´
ıch: Sô
´
lu
,
.
o
,
ng sô
´
h
.
ang c
,
ua tô
,
ng l
`
a n + 1;
tr
`
u
,
sô
´
h
.
ang
¯
dâ
`
u tiên, c
`
on l
.
ai c
´
ac sô
´
h
.
ang kh
´
ac
¯
dê
`
u c
´
o d
.
ang
2
k
1 + a
2
k
( k = 1, 2, . . . , n). Ta t
´
ınh
S
1
=
2
1 − a
2
+
2
1 + a
2
=
4
1 − a
4
,
S
2
= S
1
+
4
1 + a
4
=
4
1 − a
4
+
4
1 + a
4
=
8
1 − a
8
,
S
3
= S
2
+
8
1 + a
8
=
8
1 − a
8
+
8
1 + a
8
=
16
1 − a
16
.
Do 4 = 2
2
, 8 = 2
3
v
`
a 16 = 2
4
t
`
u
,
c
´
ac biê
,
u th
´
u
,
c c
,
ua S
1
, S
2
v
`
a S
3
c
´
o
thê
,
¯
du
,
a ra gi
,
a thiê
´
t:
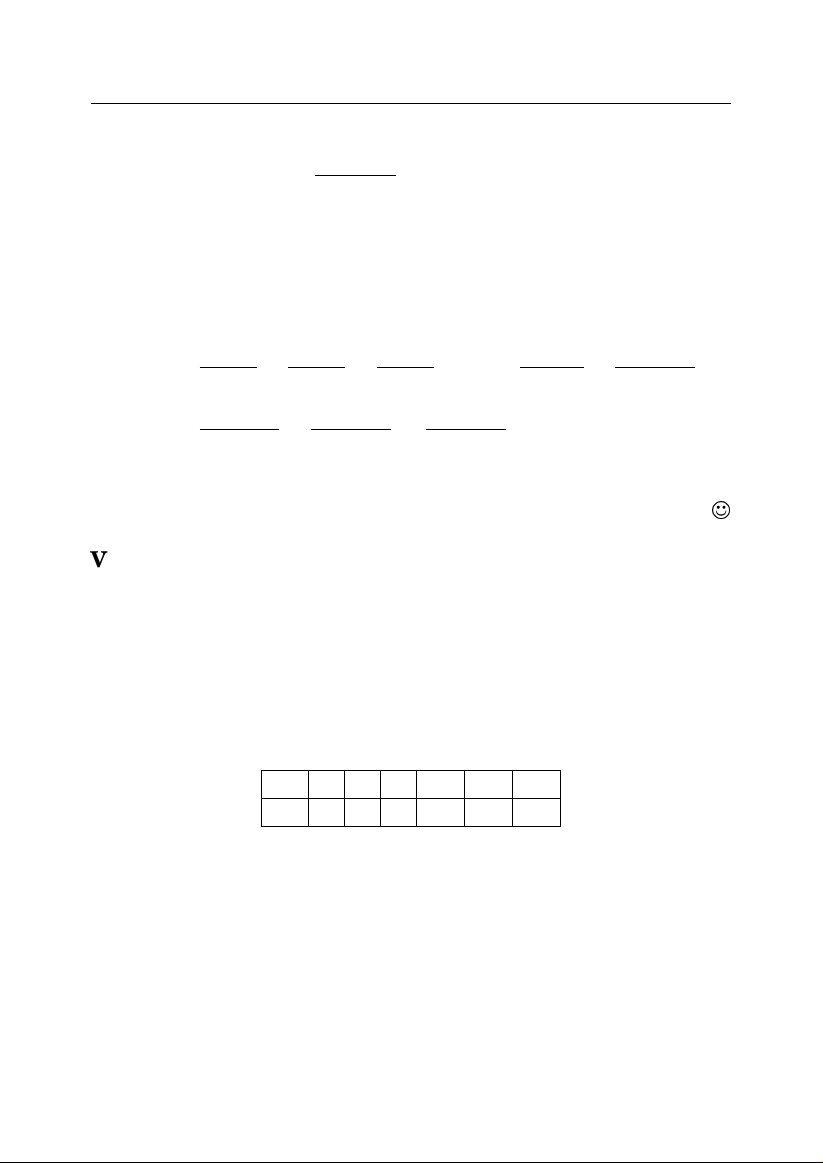
12 Chu
,
o
,
ng 1. Nguyên l
´
y quy n
.
ap to
´
an h
.
oc
S
n
=
2
n+1
1 − a
2
n+1
, ( n = 1, 2, . . .). (1.5)
Bu
,
´
o
,
c co
,
s
,
o
,
: V
´
o
,
i n = 1, công th
´
u
,
c (1.5)
¯
d
´
ung nhu
,
¯
d
˜
a kiê
,
m tra
,
o
,
trên.
Bu
,
´
o
,
c quy n
.
ap: Gi
,
a s
,
u
,
(1.5)
¯
d
´
ung v
´
o
,
i sô
´
t
.
u
,
nhiên n = k n
`
ao
¯
d
´
o.
Khi
¯
d
´
o
S
k+1
=
2
1 − a
2
+
2
1 + a
2
+
4
1 + a
4
+ ··· +
2
k
1 + a
2
k
+
2
k+1
1 + a
2
k+ 1
=
2
k+1
1 − a
2
k+ 1
+
2
k+1
1 + a
2
k+ 1
=
2
k+2
1 − a
2
k+ 2
.
Ð
,
˘
ang th
´
u
,
c (1.5) c
˜
ung
¯
d
´
ung v
´
o
,
i n = k + 1. Nhu
,
v
.
ây, t
`
u
,
nguyên l
´
y
quy n
.
ap to
´
an h
.
oc
¯
d
,
˘
ang th
´
u
,
c (1.5)
¯
d
´
ung v
´
o
,
i m
.
oi n ≥ 1.
J
V
´
ı d
.
u 1.4. T´ınh tô
,
ng c
,
ua n sô
´
l
,
e t
.
u
,
nhiên
¯
dâ
`
u tiên.
L
`
o
,
i gi
,
ai. Ta k
´
y hi
.
êu tô
,
ng ph
,
ai t
`
ım l
`
a S
n
:
S
n
= 1 + 3 + 5 + ··· + (2n − 1).
Ðê
,
xây d
.
u
,
ng gi
,
a thiê
´
t quy n
.
ap to
´
an h
.
oc ta t
´
ınh tô
,
ng
,
o
,
m
.
ôt sô
´
gi
´
a
tr
.
i
¯
du
,
.
o
,
c li
.
êt kê trong b
,
ang sau:
n 1 2 3 4 5 6
S
n
1 4 9 16 25 36
Bây gi
`
o
,
ph
.
u thu
.
ôc v
`
ao s
.
u
,
quan s
´
at c
,
ua ta v
`
a kinh nghi
.
êm trên
kê
´
t qu
,
a riêng
¯
dê
,
d
.
u
,
¯
do
´
an m
.
ênh
¯
dê
`
tô
,
ng qu
´
at chung. D
˜
ê thâ
´
y
c
´
ac sô
´
,
o
,
h
`
ang S
n
¯
dê
`
u l
`
a sô
´
ch
´
ınh phu
,
o
,
ng: S
1
= 1
2
, S
2
= 2
2
, S
3
=
3
2
, S
4
= 4
2
, S
5
= 5
2
, S
6
= 6
2
. Nhu
,
v
.
ây ta c
´
o thê
,
¯
du
,
a ra gi
,
a thiê
´
t
chung l
`
a
S
n
= n
2
. (1.6)
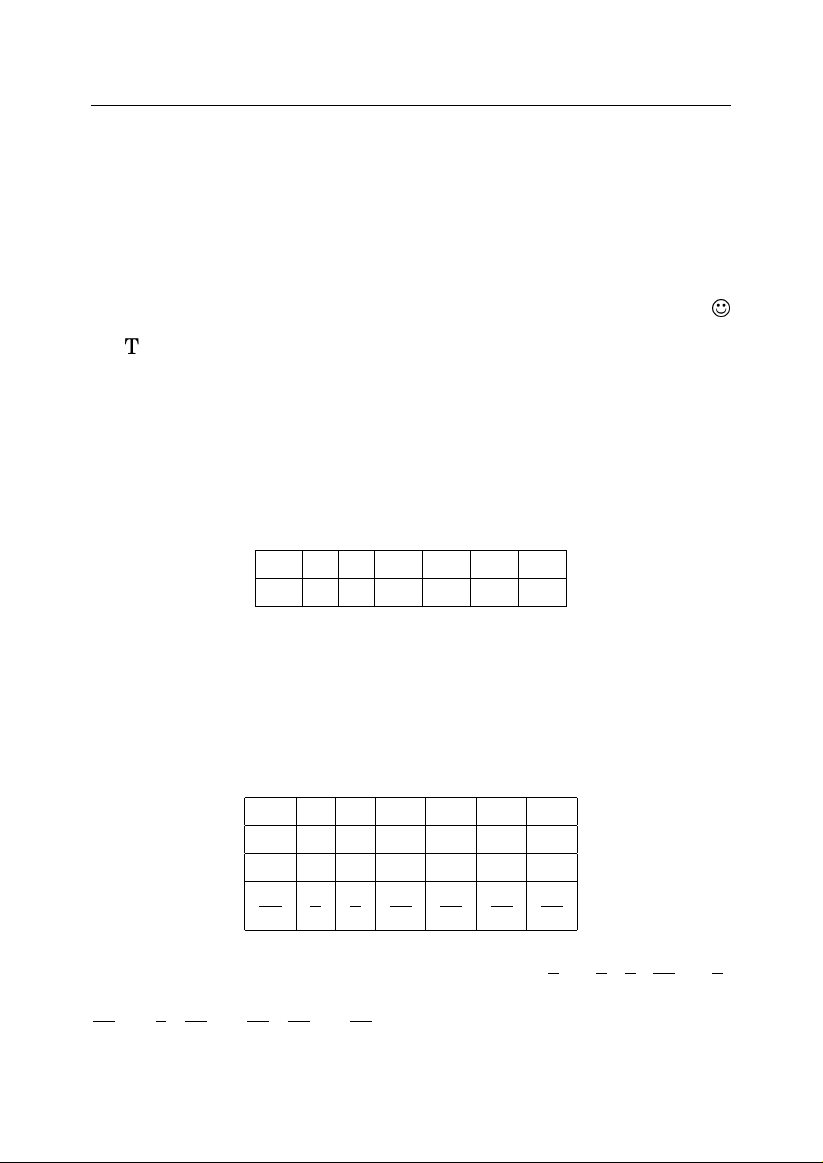
1.3. Giai
¯
do
.
an quy n
.
ap v
`
a gi
,
a thiê
´
t quy n
.
ap 13
Ta s
˜
e ch
´
u
,
ng minh (1.6)
¯
d
´
ung v
´
o
,
i m
.
oi sô
´
t
.
u
,
nhiên n.
Bu
,
´
o
,
c co
,
s
,
o
,
: V
´
o
,
i n = 1, tô
,
ng ch
,
ı c
´
o m
.
ôt sô
´
h
.
ang S
n
= 1; biê
,
u th
´
u
,
c
n
2
= 1 v
´
o
,
i n = 1, nhu
,
v
.
ây (1.6)
¯
d
´
ung.
Bu
,
´
o
,
c quy n
.
ap: Gi
,
a s
,
u
,
(1.6)
¯
d
´
ung v
´
o
,
i n = k, (S
k
= k
2
). ta s
˜
e
ch
´
u
,
ng minh (1.6)
¯
d
´
ung v
´
o
,
i n = k + 1: S
k+1
= ( k + 1)
2
. Th
.
ât v
.
ây,
S
k+1
= S
k
+ ( 2k + 1) = k
2
+ ( 2k + 1) = (k + 1)
2
.
J
Ta x
´
et thêm m
.
ôt v
´
ı d
.
u n
˜
u
,
a theo c
´
ach l
`
am c
,
ua G. Polya.
V
´
ı d
.
u 1.5. T´ınh tô
,
ng b`ınh phu
,
o
,
ng c
,
ua n sô
´
t
.
u
,
nhiên
¯
dâ
`
u tiên.
L
`
o
,
i gi
,
ai. Ta tiê
´
n h
`
anh t
`
ım công th
´
u
,
c cho gi
,
a thiê
´
t quy n
.
ap. Ð
.
˘
at
T
n
= 1
2
+ 2
2
+ ··· + n
2
.
Ta h
˜
ay t
`
ım m
.
ôt sô
´
gi
´
a tr
.
i c
,
ua tô
,
ng khi cho n = 1, 2, . . . , 6.
n 1 2 3 4 5 6
T
n
1 5 14 30 55 91
Nh
`
ın v
`
ao b
,
ang trên ta kh
´
o c
´
o thê
,
t
`
ım ra quy lu
.
ât chung cho T
n
.
V
´
o
,
i thông tin
´
ıt
,
oi nhu
,
v
.
ây không cho kê
´
t qu
,
a g
`
ı, nhu
,
ng v
´
o
,
i kinh
nghi
.
êm ta c
´
o thê
,
liên h
.
ê v
´
o
,
i c
´
ac v
´
ı d
.
u
¯
d
˜
a gi
,
ai v
`
a so s
´
anh nh
˜
u
,
ng
d
˜
ay sô
´
trong v
´
ı d
.
u 1.1 v
`
a ch
`
ıa kho
´
a t
`
ım ra quy lu
.
ât chung trong
b
,
ang sau:
n 1 2 3 4 5 6
T
n
1 5 14 30 55 91
S
n
1 3 6 10 15 21
T
n
S
n
1
1
5
3
14
6
30
10
55
15
91
21
D
`
ong cuô
´
i c
`
ung trong b
,
ang ta c
´
o thê
,
viê
´
t l
.
ai:
1
1
=
3
3
,
5
3
,
14
6
=
7
3
,
30
10
=
9
3
,
55
15
=
11
3
,
91
21
=
13
3
. Bây gi
`
o
,
ta c
´
o thê
,
¯
du
,
a ra gi
,
a thiê
´
t

14 Chu
,
o
,
ng 1. Nguyên l
´
y quy n
.
ap to
´
an h
.
oc
r
`
˘
ang
T
n
S
n
=
2n + 1
3
. T
`
u
,
kê
´
t qu
,
a v
´
ı d
.
u 1.1 ta c
´
o
T
n
=
2n + 1
3
.
n(n + 1)
2
ho
.
˘
ac l
`
a
1
2
+ 2
2
+ ··· + n
2
=
n(n + 1)(2n + 1)
6
. (1.7)
Ta ch
´
u
,
ng minh b
`
˘
ang quy n
.
ap to
´
an h
.
oc cho công th
´
u
,
c (1.7)
¯
d
´
ung v
´
o
,
i m
.
oi sô
´
t
.
u
,
nhiên n.
Bu
,
´
o
,
c co
,
s
,
o
,
: B
`
˘
ang c
´
ach xây d
.
u
,
ng trên,
¯
d
,
˘
ang th
´
u
,
c (1.7)
¯
d
´
ung v
´
o
,
i
n = 1.
Bu
,
´
o
,
c quy n
.
ap: Gi
,
a s
,
u
,
(1.7)
¯
d
´
ung v
´
o
,
i sô
´
t
.
u
,
nhiên n = k n
`
ao
¯
d
´
o. Ta
s
˜
e ch
´
u
,
ng minh r
`
˘
ang n
´
o c
˜
ung
¯
d
´
ung v
´
o
,
i n = k + 1, ngh
˜
ıa l
`
a
1
2
+ 2
2
+ ··· + k
2
+ (k + 1 )
2
=
( k + 1)(k + 2)(2k + 3)
6
.
Th
.
ât v
.
ây,
T
k+1
= T
k
+ (k + 1 )
2
=
k(k + 1)(2k + 1)
6
+ (k + 1 )
2
= (k + 1)
k(2k + 1) + 6(k + 1)
6
=
( k + 1)(k + 2)(2k + 3)
6
.
Nhu
,
v
.
ây b
`
ai to
´
an
¯
d
˜
a gi
,
ai xong.
J
1.4. Hai bu
,
´
o
,
c c
,
ua nguyên l
´
y quy n
.
ap to
´
an h
.
oc
Nhu
,
ta
¯
d
˜
a biê
´
t nguyên l
´
y quy n
.
ap to
´
an h
.
oc gô
`
m hai phâ
`
n,
vi
.
êc kiê
,
m tra c
,
a hai câ
`
n
¯
du
,
.
o
,
c tôn tr
.
ong khi
´
ap d
.
ung nguyên l
´
y.
Nê
´
u ta b
,
o
¯
di m
.
ôt trong hai
¯
diê
`
u ki
.
ên kiê
,
m tra
¯
d
´
o, th
`
ı ta s
˜
e nh
.
ân
¯
du
,
.
o
,
c nh
˜
u
,
ng kê
´
t lu
.
ân sai. Thông qua c
´
ac v
´
ı d
.
u sau
¯
dê
,
minh h
.
oa
v
`
a hiê
,
u
¯
diê
`
u n
`
ay ho
,
n.
V
´
ı d
.
u 1.6. Ch
´
u
,
ng minh r
`
˘ang m
.
oi sô
´
t
.
u
,
nhiên
¯
dê
`
u b
`
˘ang sô
´
t
.
u
,
nhiên liê
`
n sau.

1.4. Hai bu
,
´
o
,
c c
,
ua nguyên l
´
y quy n
.
ap to
´
an h
.
oc 15
L
`
o
,
i gi
,
ai. Ta ch
´
u
,
ng minh theo phu
,
o
,
ng ph
´
ap quy n
.
ap to
´
an h
.
oc.
Gi
,
a thiê
´
t r
`
˘
ang m
.
ênh
¯
dê
`
kh
,
˘
ang
¯
d
.
inh
¯
d
´
ung v
´
o
,
i sô
´
t
.
u
,
nhiên n = k
n
`
ao
¯
d
´
o, ngh
˜
ıa l
`
a
k = (k + 1). (1.8)
Ch
´
ung ta s
˜
e ch
´
u
,
ng minh
¯
d
,
˘
ang th
´
u
,
c sau
¯
d
´
ung
( k + 1) = (k + 2) . (1.9)
Th
.
ât v
.
ây, Theo gi
,
a thiê
´
t quy n
.
ap (1.8) c
.
ông hai vê
´
¯
d
,
˘
ang th
´
u
,
c v
´
o
,
i
1, ta nh
.
ân
¯
du
,
.
o
,
c
k + 1 = (k + 1) + 1 = k + 2.
Nhu
,
v
.
ây, kh
,
˘
ang
¯
d
.
inh
¯
d
´
ung v
´
o
,
i n = k th
`
ı n
´
o
¯
d
´
ung v
´
o
,
i n = k + 1,
do
¯
d
´
o m
.
ênh
¯
dê
`
b
`
ai to
´
an
¯
d
´
ung v
´
o
,
i m
.
oi n.
J
H
.
ê qu
,
a c
,
ua b
`
ai to
´
an n
`
ay l
`
a tâ
´
t c
,
a c
´
ac sô
´
t
.
u
,
nhiên
¯
dê
`
u b
`
˘
ang
nhau. Ðiê
`
u n
`
ay th
.
ât vô l
´
y, v
.
ây c
´
ach ch
´
u
,
ng minh sai
,
o
,
¯
dâu? D
˜
ê
d
`
ang thâ
´
y ngay trong ch
´
u
,
ng minh
´
ap d
.
ung nguyên l
´
y quy n
.
ap
to
´
an h
.
oc nhu
,
ng b
,
o qua kiê
,
m tra tru
,
`
o
,
ng h
.
o
,
p n = 1.
Ðiê
`
u ki
.
ên A) v
`
a B) trong Ð
.
inh l
´
ı 1.1 c
´
o m
.
ôt
´
y ngh
˜
ıa
¯
d
.
˘
ac bi
.
êt:
Ðiê
`
u ki
.
ên A) t
.
ao ra co
,
s
,
o
,
¯
dê
,
th
.
u
,
c hi
.
ên quy n
.
ap.
Ðiê
`
u ki
.
ên B)
¯
du
,
a ra nguyên t
´
˘
ac cho vi
.
êc m
,
o
,
r
.
ông t
.
u
,
¯
d
.
ông vô
h
.
an trên co
,
s
,
o
,
¯
diê
`
u ki
.
ên A); nguyên t
´
˘
ac
¯
di t
`
u
,
tru
,
`
o
,
ng h
.
o
,
p riêng
n
`
ay sang tru
,
`
o
,
ng h
.
o
,
p riêng kh
´
ac; t
`
u
,
k
¯
dê
´
n k + 1.
,
O
,
v
´
ı d
.
u .1.6 ta không kiê
,
m tra
¯
diê
`
u ki
.
ên A) c
,
ua Ð
.
inh l
´
ı 1.1,
nên không t
.
ao ra co
,
s
,
o
,
¯
dê
,
th
.
u
,
c hi
.
ên quy n
.
ap, v
`
ı v
.
ây không c
´
o
ngh
˜
ıa g
`
ı khi th
.
u
,
c hi
.
ên kiê
,
m tra
¯
diê
`
u ki
.
ên B) c
,
ua Ð
.
inh l
´
ı 1.1,
th
.
u
,
c châ
´
t l
`
a không c
´
o g
`
ı
¯
dê
,
m
,
o
,
r
.
ông c
,
a. Ta x
´
et thêm v
´
ı d
.
u:
V
´
ı d
.
u 1.7. Ch
´
u
,
ng minh r
`
˘ang v
´
o
,
i m
.
oi sô
´
t
.
u
,
nhiên n bâ
´
t
¯
d
,
˘ang th
´
u
,
c
sau
¯
d ´ung
2
n
> 2n + 1. (1.10)

16 Chu
,
o
,
ng 1. Nguyên l
´
y quy n
.
ap to
´
an h
.
oc
L
`
o
,
i gi
,
ai. Gi
,
a thiê
´
t bâ
´
t
¯
d
,
˘
ang th
´
u
,
c (1.10)
¯
d
´
ung v
´
o
,
i n = k, v
´
o
,
i k l
`
a
m
.
ôt sô
´
t
.
u
,
nhiên n
`
ao
¯
d
´
o, ngh
˜
ıa l
`
a ta c
´
o
2
k
> 2k + 1. (1.11)
Ta s
˜
e ch
´
u
,
ng minh bâ
´
t
¯
d
,
˘
ang th
´
u
,
c (1.10)
¯
d
´
ung v
´
o
,
i n = k + 1
2
k+1
> 2(k + 1) + 1. (1.12)
Th
.
ât v
.
ây, 2
k
l
`
a m
.
ôt sô
´
không nh
,
o ho
,
n 2 v
´
o
,
i m
.
oi sô
´
t
.
u
,
nhiên kh
´
ac
không. Ta c
.
ông vê
´
tr
´
ai c
,
ua (1.11) v
´
o
,
i 2
k
v
`
a c
.
ông vê
´
ph
,
ai c
,
ua (1.11)
v
´
o
,
i 2. Ta nh
.
ân
¯
du
,
.
o
,
c
2
k
+ 2
k
> 2k + 1 + 2.
Ngh
˜
ıa l
`
a
2
k+1
> 2(k + 1) + 1.
B
`
ai to
´
an
¯
d
˜
a gi
,
ai xong.
J
Tâ
´
t nhiên v
´
ı d
.
u n
`
ay c
˜
ung m
´
˘
ac sai lâ
`
m nhu
,
v
´
ı d
.
u tru
,
´
o
,
c không
kiê
,
m tra Bu
,
´
o
,
c co
,
s
,
o
,
. Th
.
u
,
c châ
´
t c
,
ua c
´
ach ch
´
u
,
ng minh trên l
`
a bâ
´
t
¯
d
,
˘
ang th
´
u
,
c (1.10)
¯
d
´
ung v
´
o
,
i n = k + 1, nê
´
u n
´
o
¯
d
´
ung v
´
o
,
i n = k. Ðiê
`
u
n
`
ay không suy ra bâ
´
t
¯
d
,
˘
ang th
´
u
,
c
¯
d
´
ung v
´
o
,
i
´
ıt nhâ
´
t m
.
ôt gi
´
a tr
.
i c
,
ua
n, ch
´
u
,
chu
,
a n
´
oi t
´
o
,
i v
´
o
,
i m
.
oi sô
´
t
.
u
,
nhiên n.
Nhu
,
ng ta c
´
o thê
,
th
,
u
,
v
´
o
,
i n = 1 ho
.
˘
ac n = 2 bâ
´
t
¯
d
,
˘
ang th
´
u
,
c (1.10)
sai. V
´
o
,
i n ≥ 3 bâ
´
t
¯
d
,
˘
ang th
´
u
,
c (1.10)
¯
d
´
ung. Gi
´
a tr
.
i sô
´
t
.
u
,
nhiên nh
,
o
nhâ
´
t n = 3 bâ
´
t
¯
d
,
˘
ang th
´
u
,
c (1.10)
¯
d
´
ung (
¯
diê
`
u ki
.
ên A) v
´
o
,
i n
0
= 3 v
`
a
l
.
˘
ap l
.
ai c
´
ach ch
´
u
,
ng minh
,
o
,
trên t
`
u
,
gi
,
a thiê
´
t (1.10)
¯
d
´
ung v
´
o
,
i n = k
suy ra n
´
o
¯
d
´
ung v
´
o
,
i n = k + 1 (
¯
diê
`
u ki
.
ên B). V
`
ı v
.
ây theo nguyên l
´
y
quy n
.
ap to
´
an h
.
oc ta c
´
o kê
´
t lu
.
ân: Bâ
´
t
¯
d
,
˘
ang th
´
u
,
c (1.10)
¯
d
´
ung v
´
o
,
i
m
.
oi sô
´
t
.
u
,
nhiên n ≥ 3 (ch
´
u
,
không ph
,
ai v
´
o
,
i m
.
oi sô
´
t
.
u
,
nhiên nhu
,
¯
dê
`
b
`
ai ra).
Trong vi
.
êc
´
ap d
.
ung phu
,
o
,
ng ph
´
ap quy n
.
ap to
´
an h
.
oc m
`
a ch
,
ı
ch
´
u
,
ng minh
¯
diê
`
u ki
.
ên A) c
,
ua Ð
.
inh l
´
ı 1.1 th
`
ı m
´
o
,
i ch
,
ı
¯
du
,
a ra
¯
du
,
.
o
,
c

1.4. Hai bu
,
´
o
,
c c
,
ua nguyên l
´
y quy n
.
ap to
´
an h
.
oc 17
co
,
s
,
o
,
¯
dê
,
quy n
.
ap ch
´
u
,
không c
´
o nguyên t
´
˘
ac n
`
ao
¯
dê
,
m
,
o
,
r
.
ông co
,
s
,
o
,
¯
d
´
o (nhu
,
¯
d
.
inh l
´
ı l
´
o
,
n Fermat). Ta x
´
et m
.
ôt sô
´
v
´
ı d
.
u:
V
´
ı d
.
u 1.8. Ch
´
u
,
ng minh r
`
˘ang nh
˜
u
,
ng gi ´a tr
.
i c
,
ua h `am sô
´
f (n) =
n
2
−n + 41 v
´
o
,
i n = 0, 1, . . . l `a nh
˜
u
,
ng sô
´
nguyên tô
´
.
L
`
o
,
i gi
,
ai. Ta t
´
ınh f (0) = 1, f (1) = 41, f (2) = 43, f (3) = 47,
f (4) = 53, f ( 5) = 61, f (6) = 71, f (7) = 83, f (8) = 97, f (9) = 113.
Ta c
´
o thê
,
t
´
ınh to
´
an tiê
´
p t
.
uc gi
´
a tr
.
i c
,
ua f (n) cho t
´
o
,
i n = 40, tâ
´
t c
,
a
gi
´
a tr
.
i n
`
ay
¯
dê
`
u l
`
a sô
´
nguyên tô
´
. Nhu
,
ng v
´
o
,
i n = 41 ta c
´
o f (41) =
41
2
− 41 + 41 = 41
2
. Kê
´
t qu
,
a f (41) không ph
,
ai l
`
a sô
´
nguyên tô
´
,
nên kê
´
t lu
.
ân c
,
ua b
`
ai to
´
an l
`
a không
¯
d
´
ung.
J
Nhu
,
v
.
ây ta thâ
´
y m
.
ôt m
.
ênh
¯
dê
`
c
´
o thê
,
¯
d
´
ung v
´
o
,
i 40 tru
,
`
o
,
ng h
.
o
,
p
riêng, nhu
,
ng không
¯
d
´
ung v
´
o
,
i m
.
oi tru
,
`
o
,
ng h
.
o
,
p n
´
oi chung.
V
´
ı d
.
u 1.9. Ða th
´
u
,
c x
n
− 1, v
´
o
,
i n l `a sô
´
t
.
u
,
nhiên du
,
o
,
ng. Ða th
´
u
,
c
n `ay liên quan
¯
dê
´
n b `ai to ´an h`ınh h
.
oc chia
¯
du
,
`
o
,
ng tr`on ra n phâ
`
n
b
`
˘ang nhau, nên
¯
da th
´
u
,
c n `ay
¯
du
,
.
o
,
c râ
´
t nhiê
`
u l˜ınh v
.
u
,
c to ´an h
.
oc
nghiên c
´
u
,
u v `a
¯
dê
`
c
.
âp
¯
dê
´
n. Ð
.
˘ac bi
.
êt c ´ac nh `a to ´an h
.
oc quan tâm
t
´
o
,
i vâ
´
n
¯
dê
`
phân t´ıch
¯
da th
´
u
,
c n `ay ra c´ac th
`
u
,
a sô
´
l `a c ´ac
¯
da th
´
u
,
c
v
´
o
,
i h
.
ê sô
´
nguyên ±1, li
.
êu
¯
diê
`
u
¯
d´o c`on
¯
d ´ung v
´
o
,
i m
.
oi n?
L
`
o
,
i gi
,
ai. B
`
˘
ang c
´
ach khai triê
,
n c
´
ac tru
,
`
o
,
ng h
.
o
,
p riêng, c
´
ac nh
`
a
to
´
an h
.
oc nh
.
ân thâ
´
y r
`
˘
ang tâ
´
t c
,
a c
´
ac h
.
ê sô
´
trong c
´
ac th
`
u
,
a sô
´
¯
du
,
.
o
,
c
khai triê
,
n c
´
o gi
´
a tr
.
i tuy
.
êt
¯
dô
´
i không qu
´
a 1. Ch
,
˘
ang h
.
an,
x − 1 = x −1,
x
2
−1 = (x −1)(x + 1),
x
3
−1 = (x −1)(x
2
+ x + 1),
x
4
−1 = (x −1)(x + 1)(x
2
+ 1) ,

18 Chu
,
o
,
ng 1. Nguyên l
´
y quy n
.
ap to
´
an h
.
oc
x
5
−1 = (x −1)(x
4
+ x
3
+ x
2
+ x + 1),
x
6
−1 = (x −1)(x + 1)(x
2
+ x + 1)(x
2
− x + 1).
Nh
˜
u
,
ng cô
´
g
´
˘
ang ch
´
u
,
ng minh
¯
diê
`
u nghi ng
`
o
,
¯
d
´
ung v
´
o
,
i m
.
oi n c
,
ua
c
´
ac nh
`
a to
´
an h
.
oc không th
`
anh công. M
.
ôt th
`
o
,
i gian sau, nh
`
a to
´
an
h
.
oc Nga V. Ivanov (n
˘
am 1941) ch
,
ı ra r
`
˘
ang v
´
o
,
i
¯
da th
´
u
,
c x
n
− 1,
¯
diê
`
u nghi ng
`
o
,
ch
,
ı
¯
d
´
ung v
´
o
,
i c
´
ac tru
,
`
o
,
ng h
.
o
,
p nh
,
o ho
,
n 105. Nhu
,
ng
v
´
o
,
i n = 105, m
.
ôt th
`
u
,
a sô
´
c
,
ua x
105
−1 l
`
a
x
48
+ x
47
+ x
46
− x
43
− x
42
−2x
41
− x
40
− x
39
+ x
36
+
+x
35
+ x
34
+ x
33
+ x
32
+ x
31
− x
28
− x
26
− x
24
− x
22
− x
20
+ x
17
+x
16
+ x
15
+ x
14
+ x
13
+ x
12
− x
9
− x
8
−2x
7
− x
6
+ x
5
+ x
2
+ x + 1.
Th
`
u
,
a sô
´
n
`
ay không c
´
o t
´
ınh châ
´
t c
,
ua c
´
ac
¯
da th
´
u
,
c m
`
a c
´
ac nh
`
a to
´
an
h
.
oc muô
´
n.
J
V
´
ı d
.
u 1.10. Ch
´
u
,
ng minh r
`
˘ang v
´
o
,
i m
.
oi sô
´
n m
.
ênh
¯
dê
`
sau
¯
dây
¯
d ´ung: ¨Nê
´
u a v`a b l `a nh
˜
u
,
ng sô
´
t
.
u
,
nhiên du
,
o
,
ng, m`a max(a, b) = n,
th`ı a = b ¨.
L
`
o
,
i gi
,
ai. Bu
,
´
o
,
c co
,
s
,
o
,
: V
´
o
,
i m
˜
ôi n k
´
y hi
.
êu A
n
l
`
a m
.
ênh
¯
dê
`
c
,
ua b
`
ai
to
´
an
¯
d
˜
a cho. R
˜
o r
`
ang A
1
l
`
a
¯
d
´
ung, v
`
ı nê
´
u max(a, b) = 1, th
`
ı hai sô
´
a v
`
a b ph
,
ai tr
`
ung nhau v
`
a b
`
˘
ang 1 (do a v
`
a b l
`
a sô
´
t
.
u
,
nhiên).
Bu
,
´
o
,
c quy n
.
ap: Gi
,
a s
,
u
,
A
k
l
`
a
¯
d
´
ung. Nê
´
u a v
`
a b l
`
a nh
˜
u
,
ng sô
´
t
.
u
,
nhiên
sao cho max(a, b) = k + 1. Ta x
´
et hai sô
´
a
1
= a −1 v
`
a b
1
= b − 1,
khi
¯
d
´
o max(a
1
, b
1
) = k, t
`
u
,
¯
d
´
o suy ra a
1
= b
1
, v
`
ı gi
,
a thiê
´
t A
k
l
`
a
¯
d
´
ung, do
¯
d
´
o a = b, ngh
˜
ıa l
`
a A
k+1
c
˜
ung
¯
d
´
ung. Theo nguyên l
´
y quy
n
.
ap to
´
an h
.
oc A
n
¯
d
´
ung v
´
o
,
i m
.
oi sô
´
t
.
u
,
nhiên n.
H
.
ê qu
,
a: Cho a v
`
a b l
`
a hai sô
´
t
.
u
,
nhiên bâ
´
t k
`
y. Ta t
´
ınh
¯
du
,
.
o
,
c
max(a, b) = k, m
`
a k l
`
a m
.
ôt sô
´
t
.
u
,
nhiên. Theo v
´
ı d
.
u trên A
n
¯
d
´
ung

1.5. Khi n
`
ao d
`
ung phu
,
o
,
ng ph
´
ap quy n
.
ap 19
v
´
o
,
i m
.
oi n, th
`
ı n
´
o c
˜
ung
¯
d
´
ung v
´
o
,
i A
k
. T
`
u
,
¯
d
´
o suy ra a = b. Ngh
˜
ıa l
`
a
tâ
´
t c
,
a c
´
ac sô
´
t
.
u
,
nhiên
¯
dê
`
u b
`
˘
ang nhau. Th
.
ât vô l
´
y!
Trong v
´
ı d
.
u trên c
´
ach ch
´
u
,
ng minh sai
,
o
,
¯
dâu? Ta xem l
.
ai to
`
an
b
.
ô c
´
ach ch
´
u
,
ng minh v
`
a nguyên l
´
y quy n
.
ap to
´
an h
.
oc. Bu
,
´
o
,
c quy
n
.
ap trong ch
´
u
,
ng minh không nh
´
˘
ac t
´
o
,
i
¯
diê
`
u k ≥ 1, khi bu
,
´
o
,
c quy
n
.
ap chuyê
,
n tiê
´
p t
`
u
,
A
k
sang A
k+1
. Th
.
u
,
c tê
´
trong t
´
ınh to
´
an ch
´
u
,
ng
minh không
¯
d
,
am b
,
ao k ≥ 1.
J
1.5. Khi n
`
ao d
`
ung phu
,
o
,
ng ph
´
ap quy n
.
ap
Phu
,
o
,
ng ph
´
ap quy n
.
ap to
´
an h
.
oc râ
´
t c
´
o t
´
ac d
.
ung trong nghiên
c
´
u
,
u, d
.
u
,
¯
do
´
an kê
´
t qu
,
a v
`
a ch
´
u
,
ng minh kiê
,
m nghi
.
êm kê
´
t qu
,
a.
Nhu
,
ng nhiê
`
u khi ch
´
ınh phu
,
o
,
ng ph
´
ap quy n
.
ap to
´
an h
.
oc l
`
am vi
.
êc
ch
´
u
,
ng minh d
`
ai d
`
ong, biê
´
n
¯
dô
,
i ph
´
u
,
c t
.
ap gây râ
´
t nhiê
`
u kh
´
o kh
˘
an
trong ch
´
u
,
ng minh. Nhiê
`
u b
`
ai to
´
an gi
,
ai b
`
˘
ang phu
,
o
,
ng ph
´
ap quy
n
.
ap c
´
o thê
,
gi
,
ai b
`
˘
ang m
.
ôt phu
,
o
,
ng ph
´
ap kh
´
ac. Ch
´
ınh G. Polya c
´
o
n
´
oi: ¨Nhiê
`
u b
`
ai to
´
an ch
´
u
,
ng minh b
`
˘
ang quy n
.
ap to
´
an h
.
oc c
´
o thê
,
ch
´
u
,
ng minh b
`
˘
ang c
´
ach kh
´
ac, c
´
ach kh
´
ac
¯
d
´
o n
`
˘
am trong ch
´
ınh c
´
ach
ch
´
u
,
ng minh quy n
.
ap to
´
an h
.
oc khi ta phân t
´
ıch k
˜
y n
.
ôi dung ch
´
u
,
ng
minh¨.
Trong to
´
an h
.
oc ngu
,
`
o
,
i ta hay d
`
ung k
´
y hi
.
êu
∑
l
`
a m
.
ôt tô
,
ng.
Thu
,
`
o
,
ng tô
,
ng c
´
o d
.
ang A
α
+ A
α+1
+ ··· + A
β
(α v
`
a β l
`
a nh
˜
u
,
ng sô
´
nguyên)v
`
a
¯
du
,
.
o
,
c viê
´
t
β
∑
k=α
A
k
(
¯
d
.
oc l
`
a tô
,
ng c
,
ua A
k
, k ch
.
ay t
`
u
,
α
¯
dê
´
n
β). Nhu
,
v
.
ây
A
α
+ A
α+1
+ ··· + A
β
=
β
∑
k=α
A
k
k g
.
oi l
`
a ch
,
ı sô
´
c
,
ua tô
,
ng, c
`
on α v
`
a β l
`
a gi
´
a tr
.
i
¯
dâ
`
u v
`
a gi
´
a tr
.
i cuô
´
i
c
,
ua ch
,
ı sô
´
k. M
˜
ôi sô
´
h
.
ang bên tr
´
ai c
,
ua
¯
d
,
˘
ang th
´
u
,
c l
`
a
¯
d
´
ung v
´
o
,
i m
.
ôt

20 Chu
,
o
,
ng 1. Nguyên l
´
y quy n
.
ap to
´
an h
.
oc
gi
´
a tr
.
i k (k = α, α + 1, . . . , β). V
´
ı d
.
u
n
∑
k=1
k
2
= 1
2
+ 2
2
+ ··· + n
2
, ( n ≥ 1),
n+1
∑
k=−1
10
2k
= 10
−2
+ 10
0
+ 10
2
+ ··· + 10
2(n+1)
, (n ≥ −2).
Ph
´
ep lâ
´
y tô
,
ng c
´
o nh
˜
u
,
ng t
´
ınh châ
´
t sau: Nê
´
u cho a v
`
a b l
`
a nh
˜
u
,
ng
sô
´
, ta c
´
o c
´
ac
¯
d
,
˘
ang th
´
u
,
c
β
∑
k=α
aA
k
= a
β
∑
k=α
A
k
,
β
∑
k=α
(aA
k
+ bB
k
) = a
β
∑
k=α
A
k
+ b
β
∑
k=α
B
k
.
K
´
y hi
.
êu tô
,
ng không ph
.
u thu
.
ôc v
`
ao ch
,
ı sô
´
, nhu
,
ng ph
.
u thu
.
ôc v
`
ao
gi
´
a tr
.
i ban
¯
dâ
`
u v
`
a gi
´
a tr
.
i cuô
´
i c
`
ung
β
∑
k=α
A
k
=
β
∑
i =α
A
i
=
β−α
∑
i =0
A
α+i
Tr
,
o
,
l
.
ai nh
˜
u
,
ng v
´
ı d
.
u
,
o
,
phâ
`
n tru
,
´
o
,
c, trong qu
´
a tr
`
ınh t
´
ınh to
´
an
quy n
.
ap t
´
ınh tô
,
ng
1
2
+ 2
2
+ ··· + n
2
=
n
∑
k=1
k
2
B
`
˘
ang c
´
ach
´
ap d
.
ung t
´
ınh châ
´
t c
,
ua k
´
y hi
.
êu tô
,
ng v
`
a công th
´
u
,
c tô
,
ng
c
´
ac sô
´
t
.
u
,
nhiên
n
∑
k=1
k =
n(n + 1)
2
, ( n ≥ 1). Th
.
ât v
.
ây, d
˜
ê thâ
´
y
n
∑
k=0
( k + 1)
3
−
n
∑
k=0
k
3
= (n + 1)
3
.

1.5. Khi n
`
ao d
`
ung phu
,
o
,
ng ph
´
ap quy n
.
ap 21
Vê
´
tr
´
ai c
,
ua
¯
d
,
˘
ang th
´
u
,
c trên c
´
o thê
,
biê
,
n
¯
dô
,
i
n
∑
k=0
( k + 1)
3
−
n
∑
k=0
k
3
=
n
∑
k=0
[(k + 1)
3
−k
3
] =
n
∑
k=0
(3 k
2
+ 3k + 1)
= 3
n
∑
k=1
k
2
+ 3
n
∑
k=1
k +
n
∑
k=0
1.
Nhu
,
v
.
ây t
`
u
,
c
´
ac
¯
d
,
˘
ang th
´
u
,
c trên r
´
ut ra
( n + 1)
3
= 3
n
∑
k=1
k
2
+ 3
n(n + 1)
2
+ (n + 1),
Chuyê
,
n vê
´
v
`
a t
´
ınh to
´
an ta c
´
o
n
∑
k=1
k
2
=
1
3
[(n + 1)
3
−3
n(n + 1)
2
−(n + 1)] =
1
6
n(n + 1)(2n + 1).
T
´
ınh tô
,
ng sau
¯
dây (b
`
ai . 1.2)
n
∑
k=1
1
(a + k −1)(a + k)
, n = 1, 2, ..; a 6= 0, −1, −2, . . .
Ta s
,
u
,
d
.
ung
¯
d
,
˘
ang th
´
u
,
c sau
1
(a + k −1)(a + k)
=
1
a + k −1
−
1
a + k
.
Ð
.
˘
at b
k
=
1
a + k
, nhu
,
v
.
ây
n
∑
k=1
1
(a + k −1)(a + k)
=
n
∑
k=1
( b
k−1
−b
k
) = b
0
−b
n
=
1
a
−
1
a + n
=
n
a(a + n)
.
Cuô
´
i c
`
ung ta nh
.
ân
¯
du
,
.
o
,
c
n
∑
k=1
1
(a + k −1)(a + k)
=
n
a(a + n)
.
Vâ
´
n
¯
dê
`
c
,
ua phâ
`
n n
`
ay ta c
`
on
¯
dê
`
c
.
âp tiê
´
p
,
o
,
Chu
,
o
,
ng 3.
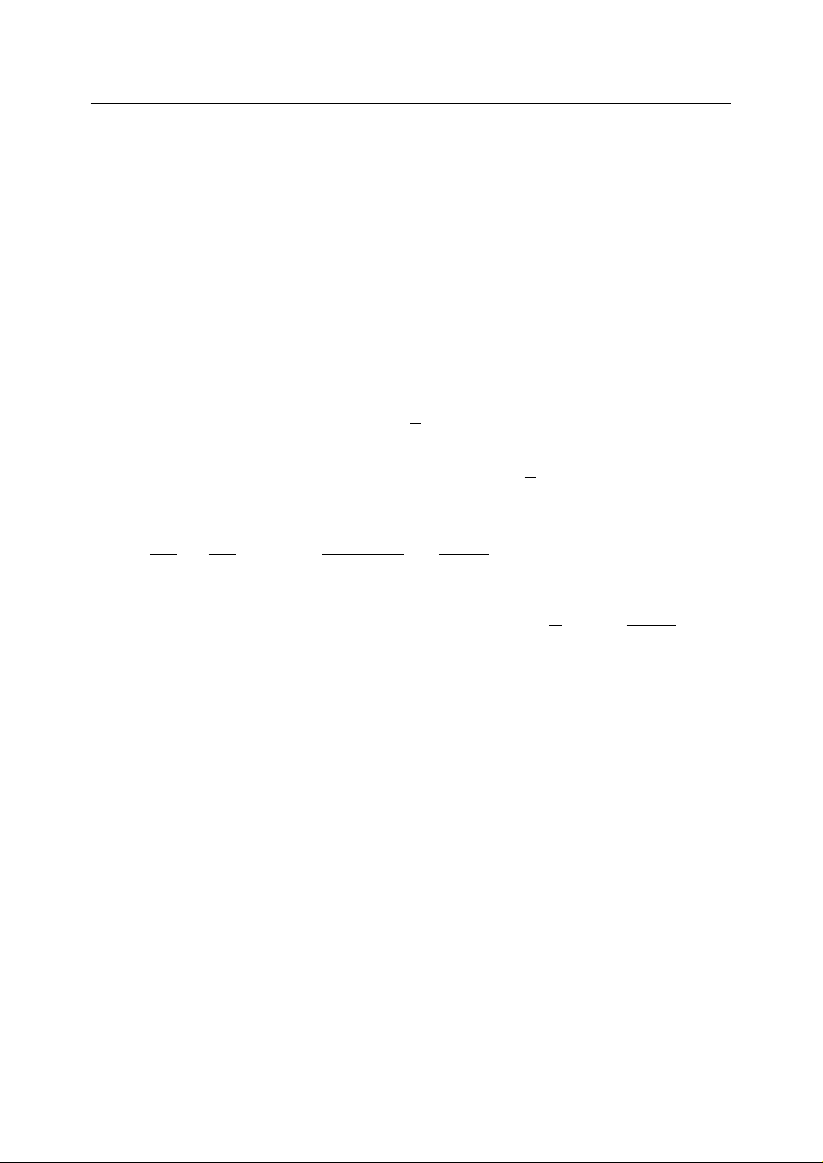
22 Chu
,
o
,
ng 1. Nguyên l
´
y quy n
.
ap to
´
an h
.
oc
1.6. B
`
ai t
.
âp
.
.
. 1.11. T
´
ınh tô
,
ng b
`
˘
ang c
´
ach xây d
.
u
,
ng gi
,
a thiê
´
t v
`
a ch
´
u
,
ng minh
b
`
˘
ang quy n
.
ap to
´
an h
.
oc c
´
ac tô
,
ng sau:
a) S
n
= 1
2
−2
2
+ ··· + (−1)
n−1
n
2
;
b) S
n
= 1
3
+ 2
3
+ ··· + n
3
;
c) S
n
= 1.1! + 2.2! + ··· + n.n!.
.
.
. 1.12. Ch
´
u
,
ng minh
´
ıt nhâ
´
t b
`
˘
ang hai c
´
ach c
´
ac công th
´
u
,
c sau:
a) 1
2
+ 3
2
+ ···+ (2n −1)
2
=
1
3
n(2n −1)(2n + 1), n = 1, 2, . . .
b) 1.2.3 + 2.3.4 + ···+ n(n + 1)(n + 2) =
1
4
n(n + 1)(n + 2)(n +
3) , n = 1, 2, . . .
c)
1
1.2
+
1
2.3
+ ··· +
1
n(n + 1)
=
n
n + 1
, n = 1, 2, . . .
.
.
. 1.13. Cho n > 1 l
`
a sô
´
t
.
u
,
nhiên. Ta
¯
d
.
˘
at x
0
=
1
n
; x
k
=
1
n − k
(x
0
+
x
1
+ ··· + x
k−1
), k = 1, 2, . . . , n −1. H
˜
ay t
´
ınh tô
,
ng x
0
+ x
1
+ ··· +
x
n−1
.

CHU
,
O
,
NG 2
K
˜
Y THU
.
ÂT D
`
UNG PHU
,
O
,
NG PH
´
AP
QUY N
.
AP TO
´
AN H
.
OC
2.1. M
.
ôt sô
´
d
.
ang nguyên l
´
y quy n
.
ap to
´
an h
.
oc. . . . . . . . . . . 23
2.2. M
.
ênh
¯
dê
`
trong nguyên l
´
y quy n
.
ap to
´
an h
.
oc . . . . . . . . 31
2.3. Bu
,
´
o
,
c quy n
.
ap
¯
du
,
.
o
,
c xây d
.
u
,
ng trên P(k) . . . . . . . . . . . . . 36
2.4. Bu
,
´
o
,
c quy n
.
ap
¯
du
,
.
o
,
c xây d
.
u
,
ng trên P(k + 1) . . . . . . . . . 40
2.5. Quy n
.
ap to
´
an h
.
oc v
`
a ph
´
ep truy hô
`
i . . . . . . . . . . . . . . . . . 43
2.6. Quy n
.
ap to
´
an h
.
oc v
`
a tô
,
ng qu
´
at ho
´
a . . . . . . . . . . . . . . . . 51
2.7. B
`
ai t
.
âp. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 55
2.1. M
.
ôt sô
´
d
.
ang nguyên l
´
y quy n
.
ap to
´
an h
.
oc
Ðiê
`
u ki
.
ên A) trong Ð
.
inh l
´
ı 1.1 cho ta co
,
s
,
o
,
m
,
o
,
r
.
ông b
´
˘
at
¯
dâ
`
u
t
`
u
,
gi
´
a tr
.
i n
0
. Ðiê
`
u ki
.
ên B) c
,
ua Ð
.
inh l
´
ı 1.1 cho ta m
.
ênh
¯
dê
`
kh
,
˘
ang
¯
d
.
inh P(n)
¯
d
´
ung v
´
o
,
i n
0
+ 1, n
0
+ 2, . . .. Th
.
u
,
c tê
´
nhiê
`
u khi trong
bu
,
´
o
,
c quy n
.
ap ph
,
ai
¯
d
`
oi h
,
oi hai gi
´
a tr
.
i n = k − 1 v
`
a n = k c
,
ua
m
.
ênh
¯
dê
`
,
¯
dê
,
suy ra m
.
ênh
¯
dê
`
¯
d
´
ung v
´
o
,
i n = k + 1. Trong tru
,
`
o
,
ng
h
.
o
,
p n
`
ay bu
,
´
o
,
c co
,
s
,
o
,
ph
,
ai kiê
,
m tra không nh
˜
u
,
ng ch
,
ı v
´
o
,
i n
0
, m
`
a c
,
a
v
´
o
,
i n
0
+ 1. Tô
,
ng qu
´
at ho
,
n ta c
´
o thê
,
ph
´
at biê
,
u l
.
ai
¯
d
.
inh l
´
ı
,
o
,
phâ
`
n
tru
,
´
o
,
c nhu
,
sau:
Ð
.
inh l
´
y 2.1. Cho p l `a sô
´
nguyên du
,
o
,
ng v `a d ˜ay c ´ac m
.
ênh
¯
dê
`
P(1), P(2), . . . , P(n), . . .

24 Chu
,
o
,
ng 2. K
˜
y thu
.
ât d
`
ung phu
,
o
,
ng ph
´
ap quy n
.
ap to
´
an h
.
oc
nê
´
u
A) P(1), P(2), . . . , P(p) l `a nh
˜
u
,
ng m
.
ênh
¯
dê
`
¯
d ´ung v `a
B) V
´
o
,
i m
˜
ôi sô
´
t
.
u
,
nhiên k ≥ p c ´ac m
.
ênh
¯
dê
`
P(k − p + 1), P(k − p +
2) , . . . , P(k)
¯
d ´ung, suy ra m
.
ênh
¯
dê
`
P(k+1) c ˜ung
¯
d ´ung,
th`ı m
.
ênh
¯
dê
`
P(n)
¯
d ´ung v
´
o
,
i m
.
oi sô
´
nguyên du
,
o
,
ng n.
Ch
´
u
,
ng minh
¯
d
.
inh l
´
ı n
`
ay ho
`
an to
`
an l
.
˘
ap l
.
ai nhu
,
¯
d
.
inh l
´
ı 1.1.
Sau
¯
dây ta x
´
et m
.
ôt sô
´
v
´
ı d
.
u s
,
u
,
d
.
ung d
.
ang
¯
d
.
inh l
´
ı 2.1.
V
´
ı d
.
u 2.1. Cho v
0
= 2, v
1
= 3 v `a v
´
o
,
i m
˜
ôi sô
´
t
.
u
,
nhiên k c´o
¯
d
,
˘ang
th
´
u
,
c sau: v
k+1
= 3v
k
−2v
k−1
. Ch
´
u
,
ng minh r
`
˘ang v
n
= 2
n
+ 1.
L
`
o
,
i gi
,
ai. Bu
,
´
o
,
c co
,
s
,
o
,
: V
´
o
,
i n = 0 v
`
a n = 1 kê
´
t lu
.
ân b
`
ai to
´
an
¯
d
´
ung,
do
¯
diê
`
u ki
.
ên b
`
ai
¯
d
˜
a cho.
Bu
,
´
o
,
c quy n
.
ap: Gi
,
a s
,
u
,
r
`
˘
ang v
k−1
= 2
k−1
+ 1; v
k
= 2
k
+ 1, khi
¯
d
´
o
v
k+1
= 3(2
k
+ 1) −2(2
k−1
+ 1) = 2
k+1
+ 1.
Theo nguyên l
´
y quy n
.
ap to
´
an h
.
oc d
.
ang
¯
d
.
inh l
´
ı 2.1, suy ra v
n
=
2
n
+ 1
¯
d
´
ung v
´
o
,
i m
.
oi sô
´
t
.
u
,
nhiên n.
J
V
´
ı d
.
u 2.2. Cho x
1
v `a x
2
l `a nghi
.
êm c
,
ua phu
,
o
,
ng tr`ınh x
2
−27x +
14 = 0; n l `a m
.
ôt sô
´
t
.
u
,
nhiên bâ
´
t k`y. Ch
´
u
,
ng minh r
`
˘ang tô
,
ng S
n
=
x
n
1
+ x
n
2
không chia hê
´
t cho 715.
L
`
o
,
i gi
,
ai. Theo công th
´
u
,
c Viet x
1
+ x
2
= 27; x
1
x
2
= 14.
Bu
,
´
o
,
c co
,
s
,
o
,
: C
´
ac sô
´
S
1
= 27; S
2
= (x
1
+ x
2
)
2
−2x
1
x
2
= 701 v
`
a
S
3
= (x
1
+ x
2
)[(x
1
+ x
2
)
2
− 3x
1
x
2
] = 27 · 687
¯
dê
`
u không chia hê
´
t
cho 715. Suy ra m
.
ênh
¯
dê
`
c
,
ua b
`
ai to
´
an
¯
d
´
ung v
´
o
,
i n = 1, 2, 3.
Bu
,
´
o
,
c quy n
.
ap: Gi
,
a s
,
u
,
m
.
ênh
¯
dê
`
¯
d
´
ung v
´
o
,
i n = k − 2, n = k −

2.1. M
.
ôt sô
´
d
.
ang nguyên l
´
y quy n
.
ap to
´
an h
.
oc 25
1, n = k, ta t
´
ınh
x
k+1
1
+ x
k+1
2
= (x
1
+ x
2
)(x
k
1
+ x
k
2
) − x
1
x
2
(x
k−1
1
+ x
k−1
2
)
= (x
1
+ x
2
)[(x
1
+ x
2
)(x
k−1
1
+ x
k−1
2
) −
− x
1
x
2
(x
k−2
1
− x
k−2
2
)] − x
1
x
2
(x
k−1
1
+ x
k−1
2
)
= 715(x
k−1
1
+ x
k−1
2
) −378 (x
k−2
1
+ x
k−2
2
).
Do
¯
d
´
o x
k+1
1
+ x
k+1
2
không chia hê
´
t cho 715, v
`
ı 378 không chia hê
´
t
cho 715, n
´
oi c
´
ach kh
´
ac m
.
ênh
¯
dê
`
¯
d
´
ung v
´
o
,
i n = k + 1.
J
V
´
ı d
.
u 2.3. Ch
´
u
,
ng minh v
´
o
,
i m
.
oi sô
´
th
.
u
,
c x > 0 v `a m
.
oi sô
´
t
.
u
,
nhiên
n bâ
´
t
¯
d
,
˘ang th
´
u
,
c sau
¯
d ´ung
x
n
+ x
n−2
+ x
n−4
+ ··· +
1
x
n−4
+
1
x
n−2
+
1
x
n
≥ n + 1. (2.1)
L
`
o
,
i gi
,
ai. 1a) V
´
o
,
i n = 1 bâ
´
t
¯
d
,
˘
ang th
´
u
,
c (2.1) c
´
o d
.
ang
x +
1
x
≥ 2. (2.2)
Bâ
´
t
¯
d
,
˘
ang th
´
u
,
c (2.2) suy ra t
`
u
,
bâ
´
t
¯
d
,
˘
ang th
´
u
,
c hiê
,
n nhiên: (x −
1)
2
≥ 0.
1b) V
´
o
,
i n = 2 bâ
´
t
¯
d
,
˘
ang th
´
u
,
c (2.1) c
´
o d
.
ang
x
2
+ 1 +
1
x
2
≥ 3. (2.3)
Bâ
´
t
¯
d
,
˘
ang th
´
u
,
c (2.2)
¯
d
´
ung v
´
o
,
i m
.
oi x > 0, v
.
ây n
´
o c
˜
ung
¯
d
´
ung v
´
o
,
i x
2
,
x
2
+
1
x
2
≥ 2.
C
.
ông hai vê
´
c
,
ua bâ
´
t
¯
d
,
˘
ang th
´
u
,
c sau c
`
ung v
´
o
,
i 1, ta nh
.
ân
¯
du
,
.
o
,
c (2.3).
2) Gi
,
a s
,
u
,
bâ
´
t
¯
d
,
˘
ang th
´
u
,
c (2.1)
¯
d
´
ung v
´
o
,
i n = k, m
`
a k l
`
a m
.
ôt sô
´
t
.
u
,
nhiên n
`
ao
¯
d
´
o
x
k
+ x
k−2
+ x
k−4
+ ··· +
1
x
k−4
+
1
x
k−2
+
1
x
k
≥ k + 1, (2.4)

26 Chu
,
o
,
ng 2. K
˜
y thu
.
ât d
`
ung phu
,
o
,
ng ph
´
ap quy n
.
ap to
´
an h
.
oc
ta s
˜
e ch
´
u
,
ng minh khi
¯
d
´
o bâ
´
t
¯
d
,
˘
ang th
´
u
,
c (2.1)
¯
d
´
ung v
´
o
,
i n = k + 2,
hay l
`
a
x
k+2
+ x
k
+ x
k−2
+ ··· +
1
x
k−2
+
1
x
k
+
1
x
k+2
≥ k + 3. (2.5)
Th
.
ât v
.
ây, trong (2.2) thê
´
x b
,
o
,
i x
k+2
, ta nh
.
ân
¯
du
,
.
o
,
c
x
k+2
+
1
x
k+2
≥ 2. (2.6)
C
.
ông vê
´
tu
,
o
,
ng
´
u
,
ng c
,
ua c
´
ac bâ
´
t
¯
d
,
˘
ang th
´
u
,
c (2.4) v
`
a (2.6), ta s
˜
e c
´
o
(2.5).
T
´
om l
.
ai: Bu
,
´
o
,
c co
,
s
,
o
,
: Trong 1a) v
`
a 1b) ta
¯
d
˜
a ch
´
u
,
ng minh bâ
´
t
¯
d
,
˘
ang th
´
u
,
c
¯
d
´
ung cho n = 1 v
`
a n = 2.
Bu
,
´
o
,
c quy n
.
ap: Trong 2) ta
¯
d
˜
a ch
´
u
,
ng minh t
`
u
,
gi
,
a thiê
´
t
¯
d
´
ung
c
,
ua (2.1) v
´
o
,
i n = k suy ra n
´
o
¯
d
´
ung v
´
o
,
i n = k + 2. Kê
´
t qu
,
a l
`
a
+ T
`
u
,
1a) v
`
a 2) cho ta kh
,
˘
ang
¯
d
.
inh l
`
a bâ
´
t
¯
d
,
˘
ang th
´
u
,
c (2.1)
¯
d
´
ung
v
´
o
,
i m
.
oi sô
´
l
,
e n.
+ T
`
u
,
1b) v
`
a 2) cho ta kh
,
˘
ang
¯
d
.
inh l
`
a bâ
´
t
¯
d
,
˘
ang th
´
u
,
c (2.1)
¯
d
´
ung
v
´
o
,
i m
.
oi sô
´
ch
˜
˘
an n.
Nhu
,
v
.
ây, bâ
´
t
¯
d
,
˘
ang th
´
u
,
c (2.1)
¯
d
´
ung v
´
o
,
i m
.
oi sô
´
t
.
u
,
nhiên n.
J
V
´
ı d
.
u 2.4. Ch
´
u
,
ng minh r
`
˘ang v
´
o
,
i m
.
oi sô
´
t
.
u
,
nhiên n
¯
d
,
˘ang th
´
u
,
c
sau
¯
d ´ung:
a)
12
7
.2
n
−
17
7
.2
n−1
= 2
n−1
;
b)
17
7
.2
n
−
12
7
.2
n−2
= 2
n+1
,
,
o
,
¯
dây [a] l `a sô
´
nguyên l
´
o
,
n nhâ
´
t nh
,
o ho
,
n a.
L
`
o
,
i gi
,
ai. Bu
,
´
o
,
c co
,
s
,
o
,
: V
´
o
,
i n = 1, 2, 3 nh
˜
u
,
ng
¯
d
,
˘
ang th
´
u
,
c trên
¯
d
´
ung
b
`
˘
ang c
´
ach kiê
,
m tra tr
.
u
,
c tiê
´
p.

2.1. M
.
ôt sô
´
d
.
ang nguyên l
´
y quy n
.
ap to
´
an h
.
oc 27
Bu
,
´
o
,
c quy n
.
ap: Gi
,
a thiê
´
t r
`
˘
ang hai
¯
d
,
˘
ang th
´
u
,
c
¯
d
´
ung v
´
o
,
i ba sô
´
t
.
u
,
nhiên liên tiê
´
p k, k + 1, k + 2. Ta s
˜
e ch
´
u
,
ng minh c
´
ac
¯
d
,
˘
ang th
´
u
,
c
trên
¯
d
´
ung v
´
o
,
i n = k + 3.
2a) T
`
u
,
12
7
.2
k+3
=
12
7
(1 + 7 )2
k
= 12.2
k
+
12
7
.2
k
;
17
7
.2
k+2
=
17
7
(1 + 7 )2
k−1
= 17.2
k−1
+
17
7
.2
k−1
,
suy ra
12
7
.2
k+3
−
17
7
.2
k+2
= 12.2
k
−17.2
k−1
+
12
7
2
k
−
17
7
2
k−1
.
Nhu
,
ng v
`
ı a)
¯
d
´
ung v
´
o
,
i n = k
12
7
.2
k+3
−
17
7
.2
k+2
= 12.2
k
−17.2
k−1
+ 2
k−1
= 2
k+2
.
V
.
ây
¯
d
,
˘
ang th
´
u
,
c a)
¯
d
´
ung v
´
o
,
i n = k + 3.
2b) T
`
u
,
17
7
.2
k+3
= 17.2
k
+
17
7
.2
k
,
12
7
.2
k+1
= 12.2
k−2
+
12
7
.2
k−2
,
suy ra
17
7
.2
k+3
−
12
7
.2
k+1
= 17.2
k
−12.2
k−2
+
17
7
2
k
−
12
7
.2
k−2
.
Nhu
,
ng v
`
ı b) v
´
o
,
i n = k , ta c
´
o
17
7
.2
k+3
−
12
7
.2
k+1
= 17.2
k
−12.2
k−2
+ 2
k+1
= 2
k+4
.
V
.
ây
¯
d
,
˘
ang th
´
u
,
c b)
¯
d
´
ung v
´
o
,
i n = k + 3.
Theo nguyên l
´
y quy n
.
ap to
´
an h
.
oc a), b)
¯
d
´
ung v
´
o
,
i m
.
oi sô
´
t
.
u
,
nhiên
n.
J
V
´
ı d
.
u 2.5. Ch
´
u
,
ng minh r
`
˘ang
u
n
=
α
n+1
− β
n+1
α − β
, (2.7)
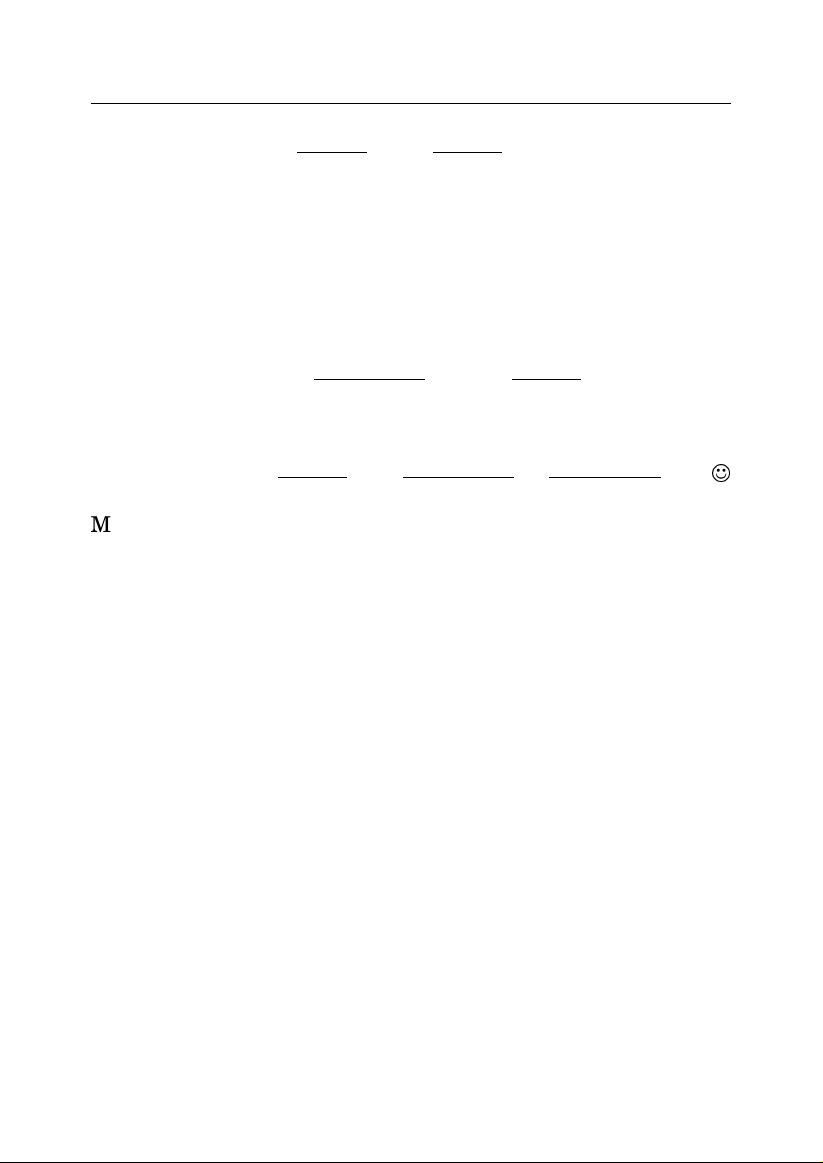
28 Chu
,
o
,
ng 2. K
˜
y thu
.
ât d
`
ung phu
,
o
,
ng ph
´
ap quy n
.
ap to
´
an h
.
oc
nê
´
u
u
1
=
α
2
− β
2
α − β
, u
2
=
α
3
− β
3
α − β
( α 6= β)
v `a v
´
o
,
i m
˜
ôi sô
´
t
.
u
,
nhiên k > 2 c´o
¯
d
,
˘ang th
´
u
,
c sau:
u
k
= (α + β)u
k−1
−αβu
k−2
.
L
`
o
,
i gi
,
ai. 1) V
´
o
,
i n = 1 v
`
a n = 2, (2.7)
¯
d
´
ung do
¯
diê
`
u ki
.
ên
¯
d
˜
a cho.
2) Gi
,
a s
,
u
,
¯
d
,
˘
ang th
´
u
,
c
¯
d
´
ung v
´
o
,
i n = k −1 v
`
a n = k −2
u
k−2
=
α
k−1
− β
k−1
α − β
, u
k−1
=
α
k
− β
k
α − β
khi
¯
d
´
o
u
k
= (α + β)
α
k
− β
k
α − β
−αβ
α
k−1
− β
k−1
α − β
=
α
k+1
− β
k+1
α − β
.
J
M
.
ôt d
.
ang nguyên l
´
y quy n
.
ap m
.
anh ho
,
n nguyên l
´
y quy n
.
ap ta
¯
d
˜
a
biê
´
t c
˜
ung râ
´
t
¯
du
,
.
o
,
c hay d
`
ung.
Ð
.
inh l
´
ı 2.2 Cho m
.
ôt d ˜ay m
.
ênh
¯
dê
`
P(1), P(2), . . . , P(n), . . .
Nê
´
u
A) P(1) l `a kh
,
˘ang
¯
d
.
inh
¯
d ´ung, v `a
B) v
´
o
,
i m
˜
ôi sô
´
t
.
u
,
nhiên k ≥ 1, nh
˜
u
,
ng kh
,
˘ang
¯
d
.
inh
P(1), P(2), . . . , P(k)
¯
d ´ung suy ra kh
,
˘ang
¯
d
.
inh P(k + 1) c ˜ung
¯
d ´ung,
th`ı P(n)
¯
d ´ung v
´
o
,
i tâ
´
t c
,
a sô
´
t
.
u
,
nhiên n ≥ 1.
D
.
ang n
`
ay kh
´
ac v
´
o
,
i c
´
ac d
.
ang tru
,
´
o
,
c l
`
a gi
,
a thiê
´
t m
.
anh ho
,
n
,
o
,
bu
,
´
o
,
c quy n
.
ap. Ta gi
,
a thiê
´
t tâ
´
t c
,
a kh
,
˘
ang
¯
d
.
inh P(1), P(2), . . . , P(k)
¯
d
´
ung suy ra P(k + 1) c
˜
ung
¯
d
´
ung. D
˜
ê d
`
ang ch
´
u
,
ng minh hai c
´
ach
ph
´
at biê
,
u
¯
d
.
inh l
´
ı 1.1. v
`
a
¯
d
.
inh l
´
ı 2.2 tu
,
o
,
ng
¯
du
,
o
,
ng nhau. Nhu
,
ng
trong th
.
u
,
c tê
´
´
ap d
.
ung v
`
ao b
`
ai to
´
an c
.
u thê
,
d
`
ung
¯
d
.
inh l
´
ı 2.2 d
˜
ê gi
,
ai
ho
,
n.

2.1. M
.
ôt sô
´
d
.
ang nguyên l
´
y quy n
.
ap to
´
an h
.
oc 29
V
´
ı d
.
u 2.6. Ch
´
u
,
ng minh r
`
˘ang nê
´
u x +
1
x
l `a sô
´
nguyên th`ı x
n
+
1
x
n
c ˜ung l `a sô
´
nguyên v
´
o
,
i m
.
oi sô
´
t
.
u
,
nhiên du
,
o
,
ng n.
L
`
o
,
i gi
,
ai. Bu
,
´
o
,
c co
,
s
,
o
,
: Khi n = 1 m
.
ênh
¯
dê
`
hiê
,
n nhiên
¯
d
´
ung.
Bu
,
´
o
,
c quy n
.
ap: Gi
,
a s
,
u
,
v
´
o
,
i m
.
oi sô
´
t
.
u
,
nhiên t
`
u
,
1
¯
dê
´
n k, x
k
+
1
x
k
l
`
a
nh
˜
u
,
ng sô
´
nguyên. Ta câ
`
n ch
´
u
,
ng minh r
`
˘
ang x
k+1
+
1
x
k+1
c
˜
ung l
`
a
sô
´
nguyên.
Th
.
ât v
.
ây, x
k+1
+
1
x
k+1
= (x +
1
x
)(x
k
+
1
x
k
) − (x
k−1
+
1
x
k−1
).
Theo gi
,
a thiê
´
t c
,
a 3 biê
,
u th
´
u
,
c x +
1
x
, x
k
+
1
x
k
, x
k−1
+
1
x
k−1
¯
dê
`
u biê
,
u
di
˜
ên c
´
ac sô
´
nguyên. V
.
ây x
k+1
+
1
x
k+1
c
˜
ung l
`
a m
.
ôt sô
´
nguyên.
J
V
´
ı d
.
u 2.7. Ch
´
u
,
ng minh r
`
˘ang m
.
oi sô
´
t
.
u
,
nhiên l
´
o
,
n ho
,
n 1 c´o thê
,
biê
,
u di
˜
ên du
,
´
o
,
i d
.
ang t´ıch c
,
ua nh
˜
u
,
ng sô
´
nguyên tô
´
.
L
`
o
,
i gi
,
ai. Bu
,
´
o
,
c co
,
s
,
o
,
: Hiê
,
n nhiên m
.
ênh
¯
dê
`
¯
d
´
ung v
´
o
,
i m
.
oi sô
´
nguyên tô
´
, tru
,
`
o
,
ng h
.
o
,
p
¯
d
.
˘
ac bi
.
êt n = 2.
Bu
,
´
o
,
c quy n
.
ap: Gi
,
a s
,
u
,
m
.
ênh
¯
dê
`
¯
d
´
ung v
´
o
,
i m
.
oi sô
´
t
.
u
,
nhiên k,
m
`
a 2 ≤ k < n. Ngh
˜
ıa l
`
a m
.
oi sô
´
2 ≤ k < n
¯
dê
`
u biê
,
u di
˜
ên du
,
´
o
,
i d
.
ang
t
´
ıch c
´
ac th
`
u
,
a sô
´
nguyên tô
´
. Ta x
´
et hai tru
,
`
o
,
ng h
.
o
,
p
1) Nê
´
u n l
`
a sô
´
nguyên tô
´
th
`
ı m
.
ênh
¯
dê
`
¯
d
´
ung.
2) Nê
´
u n l
`
a h
.
o
,
p sô
´
th
`
ı theo
¯
d
.
inh ngh
˜
ıa h
.
o
,
p sô
´
tô
`
n t
.
ai hai sô
´
nguyên n
1
< n v
`
a n
2
< n sao cho n = n
1
n
2
. Theo gi
,
a thiê
´
t quy
n
.
ap n
1
v
`
a n
2
¯
dê
`
u biê
,
u di
˜
ên
¯
du
,
.
o
,
c th
`
anh t
´
ıch c
´
ac sô
´
nguyên tô
´
. Do
¯
d
´
o suy ra n c
˜
ung biê
,
u di
˜
ên
¯
du
,
.
o
,
c th
`
anh t
´
ıch c
´
ac sô
´
nguyên tô
´
.
J
Ch
´
u
´
y: Ta c
˜
ung c
´
o thê
,
ch
´
u
,
ng minh s
.
u
,
biê
,
u di
˜
ên trong b
`
ai n
`
ay
cho m
.
oi sô
´
t
.
u
,
nhiên l
`
a duy nhâ
´
t.

30 Chu
,
o
,
ng 2. K
˜
y thu
.
ât d
`
ung phu
,
o
,
ng ph
´
ap quy n
.
ap to
´
an h
.
oc
V
´
ı d
.
u 2.8. Ch
´
u
,
ng minh r
`
˘ang m
˜
ôi c
.
˘ap sô
´
nguyên n ≥ 1 v `a b > 1
tô
`
n t
.
ai biê
,
u di
˜
ên du
,
´
o
,
i d
.
ang
n = c
s
b
s
+ c
s−1
b
s−1
+ ··· + c
1
b + c
0
, (2.8)
,
o
,
¯
dây s ≥ 0 l `a m
.
ôt sô
´
nguyên, v `a 0 ≤ c
i
≤ b − 1 v
´
o
,
i m
.
oi i =
0, 1, . . . , s −1 v `a 0 < c
s
≤ b −1.
L
`
o
,
i gi
,
ai. Ta lâ
´
y sô
´
bâ
´
t k
`
y b > 1 v
`
a
´
ap d
.
ung phu
,
o
,
ng ph
´
ap ch
´
u
,
ng
minh quy n
.
ap to
´
an h
.
oc.
Bu
,
´
o
,
c co
,
s
,
o
,
: V
´
o
,
i n = 1, ta lâ
´
y s = 0, c
0
= 1 ≤ b − 1. Ta nh
.
ân
¯
du
,
.
o
,
c d
.
ang
¯
d
,
˘
ang th
´
u
,
c (2.8) d
.
ang 1 = c
0
.
Bu
,
´
o
,
c quy n
.
ap: Gi
,
a s
,
u
,
biê
,
u di
˜
ên (2.8)
¯
d
´
ung v
´
o
,
i m
.
oi sô
´
t
.
u
,
nhiên
k nh
,
o ho
,
n n. Theo
¯
d
.
inh l
´
ı co
,
b
,
an c
,
ua sô
´
h
.
oc v
´
o
,
i n v
`
a b c
´
o thê
,
t
`
ım
¯
du
,
.
o
,
c sô
´
nguyên không âm n
1
v
`
a r, sao cho
n = bn
1
+ r, 0 ≤ r ≤ b −1.
D
˜
ê thâ
´
y n
1
< n. th
.
ât v
.
ây, nê
´
u ta c
´
o n
1
≥ n, th
`
ı v
`
ı b > 1, r ≥ 0 ta
c
´
o n = bn
1
+ r > n, vô l
´
y.
Ta x
´
et hai tru
,
`
o
,
ng h
.
o
,
p
1) Nê
´
u n
1
= 0, th
`
ı n = r, th
`
ı (2.8) tu
,
o
,
ng
´
u
,
ng v
´
o
,
i biê
,
u di
˜
ên v
´
o
,
i
s = 0, c
0
= r.
2) Nê
´
u n
1
≥ 1, th
`
ı 1 ≤ n
1
< n, theo gi
,
a thiê
´
t quy n
.
ap biê
,
u
di
˜
ên (2.8)
¯
d
´
ung v
´
o
,
i m
.
oi sô
´
t
.
u
,
nhiên k ≤ n . Ngh
˜
ıa l
`
a v
´
o
,
i n
1
ta c
´
o
n
1
= r
t
b
t
+ r
t−1
b
t−1
+ ··· + r
0
v
´
o
,
i m
.
ôt sô
´
n
`
ao
¯
dâ
´
y t v
`
a 0 ≤ r
i
≤ b −1 (i = 0, 1, .., t), r
t
> 0. Khi
¯
d
´
o
n = bn
1
+ r = r
t
b
t+1
+ r
t−1
b
t
+ ··· + r
0
b + r,
ngh
˜
ıa l
`
a, biê
,
u di
˜
ên (2.8) tu
,
o
,
ng
´
u
,
ng v
´
o
,
i s = t + 1, c
s
= r
t
, . . . , c
1
=
r
0
, c
0
= r.
J

2.2. M
.
ênh
¯
dê
`
trong nguyên l
´
y quy n
.
ap to
´
an h
.
oc 31
Ch
´
u
´
y: Ta c
˜
ung c
´
o thê
,
ch
´
u
,
ng minh s
.
u
,
biê
,
u di
˜
ên trong b
`
ai n
`
ay
cho m
.
oi sô
´
t
.
u
,
nhiên l
`
a duy nhâ
´
t. Ðây l
`
a
¯
d
.
inh l
´
ı vê
`
s
.
u
,
biê
,
u di
˜
ên
m
.
ôt sô
´
t
.
u
,
nhiên n theo co
,
sô
´
b.
C
`
on m
.
ôt sô
´
d
.
ang kh
´
ac n
˜
u
,
a c
,
ua nguyên l
´
y quy n
.
ap to
´
an h
.
oc
ch
´
ung ta s
˜
e x
´
et sau.
2.2. M
.
ênh
¯
dê
`
trong nguyên l
´
y quy n
.
ap to
´
an
h
.
oc
Trong c
´
ac v
´
ı d
.
u tru
,
´
o
,
c ta thâ
´
y r
`
˘
ang
¯
da sô
´
vi
.
êc
´
ap d
.
ung nguyên
l
´
y quy n
.
ap to
´
an h
.
oc l
`
a s
.
u
,
biê
´
n
¯
dô
,
i công th
´
u
,
c ho
.
˘
ac biê
,
u th
´
u
,
c to
´
an
h
.
oc. Trong m
.
uc nh
,
o n
`
ay ch
´
ung tôi nhâ
´
n m
.
anh
¯
dê
´
n vi
.
êc
´
ap d
.
ung
nguyên l
´
y quy n
.
ap trên c
´
ac m
.
ênh
¯
dê
`
không ph
,
ai l
`
a công th
´
u
,
c
ho
.
˘
ac biê
,
u th
´
u
,
c to
´
an h
.
oc. Trong tru
,
`
o
,
ng h
.
o
,
p nhu
,
v
.
ây c
´
ac bu
,
´
o
,
c
P(k) c
,
ua m
.
ênh
¯
dê
`
kh
,
˘
ang
¯
d
.
inh
¯
du
,
.
o
,
c x
´
ac
¯
d
.
inh mê
`
m d
,
eo ho
,
n thông
qua c
´
ac v
´
ı d
.
u sau:
V
´
ı d
.
u 2.9. Ch
´
u
,
ng minh r
`
˘ang tô
,
ng l
.
âp phu
,
o
,
ng c
,
ua ba sô
´
t
.
u
,
nhiên
liên tiê
´
p chia hê
´
t cho 9.
L
`
o
,
i gi
,
ai. Bu
,
´
o
,
c co
,
s
,
o
,
: Tô
,
ng 1
3
+ 2
3
+ 3
3
chia hê
´
t cho 9. Ngh
˜
ıa l
`
a
m
.
ênh
¯
dê
`
c
,
ua b
`
ai to
´
an l
`
a
¯
d
´
ung, khi sô
´
¯
dâ
`
u tiên c
,
ua 3 sô
´
liên tiê
´
p
l
`
a 1.
Bu
,
´
o
,
c quy n
.
ap: Gi
,
a s
,
u
,
m
.
ênh
¯
dê
`
kh
,
˘
ang
¯
d
.
inh c
,
ua b
`
ai to
´
an
¯
d
´
ung
v
´
o
,
i k, ngh
˜
ıa l
`
a k
3
+ (k + 1)
3
+ (k + 2)
3
chia hê
´
t cho 9. Ta s
˜
e ch
´
u
,
ng
minh r
`
˘
ang v
´
o
,
i ba sô
´
t
.
u
,
nhiên liên tiê
´
p b
´
˘
at
¯
dâ
`
u t
`
u
,
( k + 1) kh
,
˘
ang
¯
d
.
inh c
,
ua b
`
ai to
´
an c
˜
ung
¯
d
´
ung, n
´
oi c
´
ach kh
´
ac (k + 1)
3
+ (k + 2 )
3
+
( k + 3)
3
s
˜
e chia hê
´
t cho 9. Th
.
ât v
.
ây,
( k + 1)
3
+ (k + 2)
3
+ (k + 3)
3
= (k
3
+ (k + 1)
3
+ (k + 2)
3
) + 9(k
2
+
3k + 3).

32 Chu
,
o
,
ng 2. K
˜
y thu
.
ât d
`
ung phu
,
o
,
ng ph
´
ap quy n
.
ap to
´
an h
.
oc
Tô
,
ng ba sô
´
liên tiê
´
p b
´
˘
at
¯
dâ
`
u t
`
u
,
k + 1 biê
,
u di
˜
ên nhu
,
tô
,
ng c
,
ua hai
sô
´
h
.
ang
¯
dê
`
u chia hê
´
t cho 9, th
`
ı tô
,
ng n
`
ay c
˜
ung chia hê
´
t cho 9.
J
V
´
ı d
.
u 2.10. Ch
´
u
,
ng minh r
`
˘ang m
.
oi sô
´
nguyên
¯
dô
`
ng (tiê
`
n Vi
.
êt
Nam
1
) l
´
o
,
n ho
,
n 6 c´o thê
,
¯
dô
,
i ra tiê
`
n l
,
e không du
,
b
`
˘ang nh
˜
u
,
ng
¯
dô
`
ng
tiê
`
n gô
`
m nh
˜
u
,
ng t
`
o
,
2
¯
dô
`
ng v `a 5
¯
dô
`
ng.
L
`
o
,
i gi
,
ai. Bu
,
´
o
,
c co
,
s
,
o
,
: V
´
o
,
i sô
´
tiê
`
n 7
¯
dô
`
ng, m
.
ênh
¯
dê
`
kh
,
˘
ang
¯
d
.
inh
¯
d
´
ung: 7=5+2.
Bu
,
´
o
,
c quy n
.
ap: Gi
,
a s
,
u
,
kh
,
˘
ang
¯
d
.
inh
¯
d
´
ung v
´
o
,
i sô
´
k ≥ 7
¯
dô
`
ng. Ðê
,
ch
´
u
,
ng minh
¯
diê
`
u kh
,
˘
ang
¯
d
.
inh c
˜
ung
¯
d
´
ung v
´
o
,
i sô
´
k + 1
¯
dô
`
ng. Ta x
´
et
hai kh
,
a n
˘
ang:
1) k
¯
du
,
.
o
,
c
¯
dô
,
i ch
,
ı b
`
˘
ang m
.
ôt lo
.
ai tiê
`
n t
`
o
,
2
¯
dô
`
ng.
2) k
¯
du
,
.
o
,
c
¯
dô
,
i b
`
˘
ang c
´
ac lo
.
ai tiê
`
n,
´
ıt nhâ
´
t c
´
o m
.
ôt t
`
o
,
lo
.
ai 5
¯
dô
`
ng.
Ta ph
,
ai ch
´
u
,
ng minh k + 1
¯
dô
`
ng c
˜
ung
¯
dô
,
i
¯
du
,
.
o
,
c b
`
˘
ang c
´
ac lo
.
ai
tiê
`
n
¯
d
˜
a cho. V
´
o
,
i sô
´
( k + 1)
¯
dô
`
ng th
`
ı ta
¯
dô
,
i nhu
,
sau:
- Nê
´
u k
¯
dô
`
ng
,
o
,
tru
,
`
o
,
ng h
.
o
,
p 1), th
`
ı
´
ıt nhâ
´
t ph
,
ai c
´
o 4 t
`
o
,
2
¯
dô
`
ng,
v
`
ı k > 6. Ðê
,
¯
dô
,
i k + 1
¯
dô
`
ng, ta lâ
´
y 2 t
`
o
,
lo
.
ai 2
¯
dô
`
ng
¯
dô
,
i th
`
anh 1 t
`
o
,
lo
.
ai 5
¯
dô
`
ng.
- Nê
´
u k
¯
dô
`
ng trong tru
,
`
o
,
ng h
.
o
,
p 2), th
`
ı
¯
dê
,
¯
dô
,
i k + 1
¯
dô
`
ng, ta lâ
´
y
m
.
ôt t
`
o
,
lo
.
ai 5
¯
dô
`
ng
¯
dô
,
i lâ
´
y 3 t
`
o
,
lo
.
ai 2
¯
dô
`
ng.
Theo nguyên l
´
y quy n
.
ap to
´
an h
.
oc kh
,
˘
ang
¯
d
.
inh
¯
d
´
ung v
´
o
,
i m
.
oi
sô
´
n
¯
dô
`
ng v
´
o
,
i n > 6.
J
V
´
ı d
.
u 2.11. Ch
´
u
,
ng minh r
`
˘ang n
¯
du
,
`
o
,
ng th
,
˘ang kh ´ac nhau trên
m
.
ôt m
.
˘at ph
,
˘ang
¯
di qua m
.
ôt
¯
diê
,
m chia m
.
˘at ph
,
˘ang ra 2n phâ
`
n.
L
`
o
,
i gi
,
ai. Bu
,
´
o
,
c co
,
s
,
o
,
: V
´
o
,
i n = 1 m
.
ênh
¯
dê
`
kh
,
˘
ang
¯
d
.
inh l
`
a
¯
d
´
ung, v
`
ı
m
.
ôt
¯
du
,
`
o
,
ng th
,
˘
ang chia m
.
˘
at ph
,
˘
ang ra hai phâ
`
n.
1
1
¯
dô
`
ng
,
o
,
¯
dây ta hiê
,
u l
`
a 1000
¯
dô
`
ng trên th
.
u
,
c tê
´
.

2.2. M
.
ênh
¯
dê
`
trong nguyên l
´
y quy n
.
ap to
´
an h
.
oc 33
Bu
,
´
o
,
c quy n
.
ap: Gi
,
a s
,
u
,
m
.
ênh
¯
dê
`
¯
d
´
ung v
´
o
,
i sô
´
n n
`
ao
¯
d
´
o, ngh
˜
ıa l
`
a
n
¯
du
,
`
o
,
ng th
,
˘
ang kh
´
ac nhau
¯
di qua m
.
ôt
¯
diê
,
m chia m
.
˘
at ph
,
˘
ang ra 2n
phâ
`
n. Ðê
,
ch
´
u
,
ng minh m
.
ênh
¯
dê
`
kh
,
˘
ang
¯
d
.
inh c
˜
ung
¯
d
´
ung v
´
o
,
i n + 1
¯
du
,
`
o
,
ng th
,
˘
ang, ta ch
´
u
´
y r
`
˘
ang nê
´
u d
.
u
,
ng
¯
du
,
`
o
,
ng th
,
˘
ang
¯
di qua
¯
diê
,
m
¯
d
˜
a cho v
`
a không tr
`
ung v
´
o
,
i
¯
du
,
`
o
,
ng th
,
˘
ang n
`
ao trong sô
´
c
´
ac
¯
du
,
`
o
,
ng
th
,
˘
ang c
`
on l
.
ai, th
`
ı ch
´
ung ta s
˜
e nh
.
ân thêm 2 phâ
`
n n
˜
u
,
a c
,
ua m
.
˘
at
ph
,
˘
ang. Nhu
,
v
.
ây sô
´
phâ
`
n c
,
ua m
.
˘
at ph
,
˘
ang
¯
d
˜
a c
´
o l
`
a 2n c
.
ông v
´
o
,
i 2,
ho
.
˘
ac l
`
a 2(n + 1).
J
V
´
ı d
.
u 2.12. Trong th `anh phô
´
c´o n nh `a. T`ım sô
´
l
´
o
,
n nhâ
´
t nh
˜
u
,
ng
h `ang r`ao kh´ep k´ın không c
´
˘at nhau c´o thê
,
xây d
.
u
,
ng
¯
du
,
.
o
,
c trong
th `anh phô
´
, nê
´
u m
˜
ôi h `ang r `ao vây quanh ´ıt nhâ
´
t m
.
ôt nh `a v `a
không c´o hai h `ang r `ao n `ao vây quanh m
.
ôt c
.
um nh `a.
L
`
o
,
i gi
,
ai. Bu
,
´
o
,
c co
,
s
,
o
,
: Khi n = 1 sô
´
h
`
ang r
`
ao câ
`
n t
´
ınh l
`
a X
1
= 1.
Khi n = 2 ta c
´
o thê
,
quây m
˜
ôi nh
`
a m
.
ôt h
`
ang r
`
ao sau
¯
d
´
o l
.
ai
d
.
u
,
ng m
.
ôt h
`
ang r
`
ao quây c
,
a hai nh
`
a. Nhu
,
v
.
ây sô
´
h
`
ang r
`
ao X
2
= 3.
Khi n = 3 ta c
´
o thê
,
quây m
˜
ôi nh
`
a m
.
ôt h
`
ang r
`
ao, sau
¯
d
´
o quây
hai nh
`
a bâ
´
t k
`
y b
`
˘
ang m
.
ôt h
`
ang r
`
ao v
`
a sau c
`
ung l
`
a m
.
ôt h
`
ang r
`
ao
quây c
,
a ba nh
`
a. Ta c
´
o X
3
= 5.
Do
¯
d
´
o gi
,
a thiê
´
t quy n
.
ap: X
n
= 2n −1. Ðê
,
ch
´
u
,
ng minh công
th
´
u
,
c l
`
a
¯
d
´
ung, ta c
´
o nh
.
ân x
´
et sau: Ðô
´
i v
´
o
,
i m
.
ôt th
`
anh phô
´
n nh
`
a
theo c
´
ac
¯
diê
`
u ki
.
ên
¯
dâ
`
u b
`
ai, luôn xây d
.
u
,
ng
¯
du
,
.
o
,
c
¯
d
´
ung n h
`
ang r
`
ao
¨riêng¨ c
,
ua m
˜
ôi nh
`
a v
`
a ch
,
ı c
´
o m
.
ôt h
`
ang r
`
ao ¨chung¨ cho c
,
a th
`
anh
phô
´
.
Bu
,
´
o
,
c quy n
.
ap: Gi
,
a s
,
u
,
công th
´
u
,
c X
n
= 2n − 1
¯
d
´
ung v
´
o
,
i m
.
oi
n ≤ k v
`
a ta câ
`
n ch
´
u
,
ng minh n
´
o c
˜
ung
¯
d
´
ung v
´
o
,
i n = k + 1.
Ta x
´
et h
.
ê thô
´
ng h
`
ang r
`
ao v
´
o
,
i sô
´
h
`
ang r
`
ao l
´
o
,
n nhâ
´
t c
´
o thê
,
d
.
u
,
ng
¯
du
,
.
o
,
c trong m
.
ôt th
`
anh phô
´
c
´
o k + 1 nh
`
a v
`
a tho
,
a m
˜
an c
´
ac

34 Chu
,
o
,
ng 2. K
˜
y thu
.
ât d
`
ung phu
,
o
,
ng ph
´
ap quy n
.
ap to
´
an h
.
oc
¯
diê
`
u ki
.
ên c
,
ua
¯
dâ
`
u b
`
ai. Theo nh
.
ân x
´
et trong h
.
ê thô
´
ng
¯
d
´
o luôn c
´
o
1 (v
`
a ch
,
ı 1) h
`
ang r
`
ao l
´
o
,
n quây c
,
a th
`
anh phô
´
. Gi
,
a s
,
u
,
h
`
ang r
`
ao
¯
d
´
o b
.
i b
,
o
¯
di th
`
ı l
´
uc
¯
d
´
o th
`
anh phô
´
¯
du
,
.
o
,
c quây th
`
anh 2 khu b
`
˘
ang 2
h
`
ang r
`
ao. Khu th
´
u
,
nhâ
´
t ch
,
˘
ang h
.
an l
`
a m nh
`
a, khu th
´
u
,
hai c
´
o l
nh
`
a: m ≥ 1; l ≥ 1; m + l = k + 1.
H
.
ê thô
´
ng h
`
ang r
`
ao quây khu th
´
u
,
nhâ
´
t c
˜
ung l
`
a l
´
o
,
n nhâ
´
t t
´
u
,
c l
`
a
c
´
o tâ
´
t c
,
a 2m −1 h
`
ang r
`
ao, v
`
a quây khu th
´
u
,
hai c
´
o 2l −1 h
`
ang r
`
ao
(theo gi
,
a thiê
´
t quy n
.
ap). Không thê
,
c
´
o h
`
ang r
`
ao n
`
ao c
´
o thê
,
quây
¯
dô
`
ng th
`
o
,
i nh
˜
u
,
ng ngôi nh
`
a t
`
u
,
2 khu
¯
dang x
´
et
¯
d
´
o. Do
¯
d
´
o ch
,
ı c
`
on
l
.
ai m
.
ôt h
`
ang r
`
ao duy nhâ
´
t. Ð
´
o l
`
a h
`
ang r
`
ao chung quây c
,
a th
`
anh
phô
´
. Nhu
,
v
.
ây ta c
´
o
X
k+1
= (2m −1) + (2l −1) + 1 = 2(m + l) −1
= 2(k + 1) −1.
J
V
´
ı d
.
u 2.13. T
`
u
,
2n sô
´
1, 2, 3, . . . , 2n ta lâ
´
y ra m
.
ôt c ´ach bâ
´
t k`y n + 1
sô
´
. Ch
´
u
,
ng minh r
`
˘ang trong sô
´
c ´ac sô
´
lâ
´
y ra
¯
d´o c´o ´ıt nhâ
´
t m
.
ôt sô
´
chia hê
´
t cho m
.
ôt sô
´
kh ´ac.
L
`
o
,
i gi
,
ai. (Phu
,
o
,
ng ph
´
ap gi
,
ai sau
¯
dây l
`
a c
,
ua M. Fritman).
2
Khi
n = 1 m
.
ênh
¯
dê
`
¯
d
´
ung l
`
a hiê
,
n nhiên.
Gi
,
a s
,
u
,
m
.
ênh
¯
dê
`
¯
d
´
ung v
´
o
,
i n − 1 ngh
˜
ıa l
`
a t
`
u
,
2(n − 1) sô
´
1, 2, . . . , 2(n −1) (
,
o
,
¯
dây n ≥ 2) c
´
o thê
,
ch
.
on ra
¯
du
,
.
o
,
c n sô
´
sao cho
trong
¯
d
´
o c
´
o
´
ıt nhâ
´
t m
.
ôt sô
´
chia hê
´
t cho m
.
ôt sô
´
kh
´
ac.
Ta ch
´
u
,
ng minh m
.
ênh
¯
dê
`
¯
d
´
ung v
´
o
,
i n. Gi
,
a s
,
u
,
t
`
u
,
2n sô
´
1, 2, . . . , 2n
ta c
´
o thê
,
ch
.
on
¯
du
,
.
o
,
c n + 1 sô
´
sao cho trong
¯
d
´
o không c
´
o sô
´
n
`
ao l
`
a
b
.
ôi sô
´
c
,
ua sô
´
kh
´
ac. Ta k
´
y hi
.
êu t
.
âp tâ
´
t c
,
a n + 1 sô
´
¯
d
´
o l
`
a X
n+1
. Ðô
´
i
v
´
o
,
i t
.
âp X
n+1
x
,
ay ra 4 tru
,
`
o
,
ng h
.
o
,
p.
2
B
`
ai n
`
ay c
˜
ung c
´
o thê
,
gi
,
ai b
`
˘
ang phu
,
o
,
ng ph
´
ap Ðirichlet trong [1]

2.2. M
.
ênh
¯
dê
`
trong nguyên l
´
y quy n
.
ap to
´
an h
.
oc 35
1. X
n+1
không ch
´
u
,
a c
,
a 2n −1 v
`
a 2n,
2. X
n+1
ch
´
u
,
a 2n −1 v
`
a không ch
´
u
,
a 2n,
3. X
n+1
không ch
´
u
,
a 2n −1 v
`
a ch
´
u
,
a 2n,
4. X
n+1
ch
´
u
,
a c
,
a 2n −1 v
`
a 2n.
Tru
,
`
o
,
ng h
.
o
,
p 1: Ta b
,
o
¯
di t
`
u
,
X
n+1
m
.
ôt sô
´
bâ
´
t k
`
y, c
`
on l
.
ai n sô
´
m
`
a
m
˜
ôi sô
´
¯
dê
`
u không l
´
o
,
n ho
,
n 2n −2 v
`
a trong sô
´
¯
d
´
o không c
´
o sô
´
n
`
ao
l
`
a b
.
ôi c
,
ua m
.
ôt sô
´
kh
´
ac.
Tru
,
`
o
,
ng h
.
o
,
p 2: Ta b
,
o t
`
u
,
X
n+1
sô
´
2n −1, c
`
on l
.
ai l
`
a n sô
´
m
`
a m
.
oi
sô
´
¯
dê
`
u không l
´
o
,
n ho
,
n 2n −2 v
`
a không c
´
o sô
´
n
`
ao l
`
a b
.
ôi c
,
ua m
.
ôt sô
´
kh
´
ac.
Tru
,
`
o
,
ng h
.
o
,
p 3: Ta b
,
o t
`
u
,
X
n+1
sô
´
2n, c
`
on l
.
ai l
`
a n sô
´
m
`
a m
.
oi sô
´
¯
dê
`
u không l
´
o
,
n ho
,
n 2n − 2 v
`
a không c
´
o sô
´
n
`
ao l
`
a b
.
ôi c
,
ua m
.
ôt sô
´
kh
´
ac.
Tru
,
`
o
,
ng h
.
o
,
p 4: Tru
,
´
o
,
c hê
´
t ta thâ
´
y trong X
n+1
không ch
´
u
,
a sô
´
n do
¯
d
´
o trong tru
,
`
o
,
ng h
.
o
,
p n
`
ay ta b
,
o t
`
u
,
X
n+1
hai sô
´
2n − 1 v
`
a 2n
thêm v
`
ao sô
´
n ta c
˜
ung nh
.
ân
¯
du
,
.
o
,
c n sô
´
m
`
a m
.
oi sô
´
¯
dê
`
u không l
´
o
,
n
ho
,
n 2n −2. Ta s
˜
e ch
´
u
,
ng minh r
`
˘
ang trong n sô
´
¯
d
´
o không c
´
o sô
´
n
`
ao
chia hê
´
t cho sô
´
kh
´
ac. Ðê
,
ch
´
u
,
ng minh
¯
diê
`
u n
`
ay ta ch
,
ı câ
`
n ch
´
u
,
ng
minh:
1) Trong sô
´
¯
d
´
o tr
`
u
,
sô
´
n không c
´
o sô
´
n
`
ao chia hê
´
t cho n v
`
a
2) Sô
´
n không chia hê
´
t cho sô
´
n
`
ao kh
´
ac, ngo
`
ai n.
Ðiê
`
u th
´
u
,
nhâ
´
t l
`
a hiê
,
n nhiên v
`
ı tâ
´
t c
,
a c
´
ac sô
´
¯
d
´
o
¯
dê
`
u không l
´
o
,
n
ho
,
n 2n −2.
Ðiê
`
u th
´
u
,
hai c
˜
ung l
`
a hiê
,
n nhiên v
`
ı trong X
n+1
sô
´
2n không
chia hê
´
t cho m
.
ôt sô
´
n
`
ao kh
´
ac.
V
.
ây nê
´
u m
.
ênh
¯
dê
`
không
¯
d
´
ung cho 2n sô
´
th
`
ı c
˜
ung
¯
d
´
ung cho

36 Chu
,
o
,
ng 2. K
˜
y thu
.
ât d
`
ung phu
,
o
,
ng ph
´
ap quy n
.
ap to
´
an h
.
oc
2(n −1) sô
´
. Ðiê
`
u n
`
ay mâu thu
˜
ân v
´
o
,
i gi
,
a thiê
´
t quy n
.
ap. V
.
ây m
.
ênh
¯
dê
`
¯
d
˜
a cho
¯
d
´
ung v
´
o
,
i 2n sô
´
1, 2, . . . , 2n v
´
o
,
i n l
`
a sô
´
t
.
u
,
nhiên bâ
´
t k
`
y.
J
2.3. Bu
,
´
o
,
c quy n
.
ap
¯
du
,
.
o
,
c xây d
.
u
,
ng trên P(k)
Trong ch
´
u
,
ng minh b
`
˘
ang phu
,
o
,
ng ph
´
ap quy n
.
ap to
´
an h
.
oc, kh
´
o
kh
˘
an nhâ
´
t l
`
a bu
,
´
o
,
c quy n
.
ap chuyê
,
n t
`
u
,
m
.
ênh
¯
dê
`
P(k) sang m
.
ênh
¯
dê
`
P(k + 1). Trong phâ
`
n n
`
ay c
˜
ung nhu
,
c
´
ac v
´
ı d
.
u
,
o
,
m
.
uc sau ta
xem x
´
et k
˜
y c
´
ac kh
,
a n
˘
ang biê
´
n
¯
dô
,
i quy n
.
ap tr
.
u
,
c tiê
´
p t
`
u
,
kh
,
˘
ang
¯
d
.
inh
¯
d
´
ung c
,
ua P(k) sang kh
,
˘
ang
¯
d
.
inh
¯
d
´
ung c
,
ua P(k + 1).
V
´
ı d
.
u 2.14. Ch
´
u
,
ng minh r
`
˘ang
2
n−1
(a
n
+ b
n
) > (a + b)
n
, (2.9)
,
o
,
¯
dây a + b > 0, a 6= b, n > 1.
L
`
o
,
i gi
,
ai. Bu
,
´
o
,
c co
,
s
,
o
,
: V
´
o
,
i n = 2
¯
d
,
˘
ang th
´
u
,
c (2.9) c
´
o d
.
ang
2(a
2
+ b
2
) > (a + b)
2
. (2.10)
V
`
ı a 6= b ta c
´
o bâ
´
t
¯
d
,
˘
ang th
´
u
,
c
¯
d
´
ung (a − b)
2
> 0, c
.
ông hai vê
´
bâ
´
t
¯
d
,
˘
ang th
´
u
,
c n
`
ay v
´
o
,
i (a + b)
2
, ta c
´
o (2.10).
Bu
,
´
o
,
c quy n
.
ap: Gi
,
a s
,
u
,
(2.9)
¯
d
´
ung v
´
o
,
i sô
´
n = k n
`
ao
¯
d
´
o,
2
k−1
(a
k
+ b
k
) > (a + b)
k
. (2.11)
Ðê
,
ch
´
u
,
ng minh (2.9) c
˜
ung
¯
d
´
ung cho n = k + 1, ta nhân hai vê
´
(2.11) v
´
o
,
i a + b v
`
ı a + b > 0 ta nh
.
ân bâ
´
t
¯
d
,
˘
ang th
´
u
,
c
¯
d
´
ung
2
k−1
(a
k
+ b
k
)(a + b) > (a + b)
k+1
. (2.12)
Nhu
,
v
.
ây
¯
dê
,
ch
´
u
,
ng minh (2.9)
¯
d
´
ung v
´
o
,
i n = k + 1 bây gi
`
o
,
ta ch
,
ı
câ
`
n ch
´
u
,
ng minh
2
k
(a
k+1
+ b
k+1
) > 2
k−1
(a
k
+ b
k
)(a + b). (2.13)

2.3. Bu
,
´
o
,
c quy n
.
ap
¯
du
,
.
o
,
c xây d
.
u
,
ng trên P(k) 37
Sau khi biê
´
n
¯
dô
,
i v
`
a
¯
do
,
n gi
,
an hai vê
´
ta
¯
du
,
.
o
,
c bâ
´
t
¯
d
,
˘
ang th
´
u
,
c tu
,
o
,
ng
¯
du
,
o
,
ng a
k+1
+ b
k+1
> a
k
b + b
k
a, t
`
u
,
¯
d
´
o suy ra
(a
k
−b
k
)(a −b) > 0. (2.14)
X
´
et hai tru
,
`
o
,
ng h
.
o
,
p:
1) Nê
´
u a > b, v
`
a
¯
diê
`
u ki
.
ên
¯
d
˜
a cho l
`
a a > −b, suy ra a > |b|.
V
`
ı v
.
ây a
k
> b
k
. Do
¯
d
´
o bâ
´
t phu
,
o
,
ng tr
`
ınh (2.14)
¯
d
´
ung.
2) Nê
´
u a < b, l
´
y lu
.
ân tu
,
o
,
ng t
.
u
,
phâ
`
n trên ta c
´
o a
k
< b
k
, trong
tru
,
`
o
,
ng h
.
o
,
p n
`
ay (2.14) c
˜
ung
¯
d
´
ung. T
´
om l
.
ai, (2.14)
¯
d
´
ung v
´
o
,
i m
.
oi
a 6= b, do
¯
d
´
o (2.9)
¯
d
´
ung v
´
o
,
i n = k + 1.
J
V
´
ı d
.
u 2.15. Cho d ˜ay sô
´
0 < a
1
< a
2
< ··· < a
n
, v `a e
i
= ±1, i =
1, 2, . . . Ch
´
u
,
ng minh r
`
˘ang
n
∑
i =1
e
i
a
i
nh
.
ân ´ıt nhâ
´
t C
2
n+1
gi ´a tr
.
i kh ´ac
nhau khi e
i
thay
¯
dô
,
i dâ
´
u trong tô
,
h
.
o
,
p 2
n
kh
,
a n ˘ang xâ
,
y ra.
L
`
o
,
i gi
,
ai. Bu
,
´
o
,
c co
,
s
,
o
,
: Khi n = 1, tô
`
n tai
¯
d
´
ung 2 gi
´
a tr
.
i kh
´
ac nhau
c
,
ua tô
,
ng ( a v
`
a −a) v
`
a C
2
2
= 1, nhu
,
v
.
ây m
.
ênh
¯
dê
`
¯
d
´
ung.
Bu
,
´
o
,
c quy n
.
ap: Gi
,
a s
,
u
,
m
.
ênh
¯
dê
`
¯
d
´
ung v
´
o
,
i n = k; ngh
˜
ıa l
`
a
k
∑
i =1
e
i
a
i
nh
.
ân
´
ıt nhâ
´
t C
2
k+1
gi
´
a tr
.
i kh
´
ac nhau. Gi
,
a s
,
u
,
thêm m
.
ôt phâ
`
n t
,
u
,
a
k+1
, m
`
a a
k+1
> a
k
. Ta câ
`
n ph
,
ai ch
,
ı ra r
`
˘
ang tô
,
ng s
˜
e c
´
o C
2
k+2
gi
´
a
tr
.
i. Theo gi
,
a thiê
´
t quy n
.
ap
¯
d
˜
a c
´
o s
˜
˘
an C
2
k+1
gi
´
a tr
.
i c
,
ua tô
,
ng kh
´
ac
nhau sinh b
,
o
,
i a
1
, a
2
, . . . , a
k
; ta câ
`
n t
`
ım nh
˜
u
,
ng gi
´
a tr
.
i kh
´
ac nhau
c
,
ua tô
,
ng, c
´
o sô
´
lu
,
.
o
,
ng l
`
a C
2
k+2
− C
2
k+1
= k + 1. T
`
ım c
´
ac tô
,
ng
¯
d
´
o
b
`
˘
ang c
´
ach sau
¯
dây: Ð
.
˘
at S =
k
∑
i =1
a
i
(nhu
,
v
.
ây th
`
ı S ≥
k
∑
i =1
e
i
a
i
v
´
o
,
i m
.
oi
s
.
u
,
l
.
u
,
a ch
.
on e
i
), v
`
a ch
´
u
´
y r
`
˘
ang c
´
ac tô
,
ng sau S + a
k+1
, S + (a
k+1
−
a
k
), S + (a
k+1
− a
k−1
), . . . , S + (a
k+1
− a
1
) c
´
o gi
´
a tr
.
i kh
´
ac nhau v
`
a

38 Chu
,
o
,
ng 2. K
˜
y thu
.
ât d
`
ung phu
,
o
,
ng ph
´
ap quy n
.
ap to
´
an h
.
oc
l
´
o
,
n ho
,
n th
.
u
,
c s
.
u
,
S. Nhu
,
v
.
ây tô
`
n t
.
ai k + 1 gi
´
a tr
.
i kh
´
ac nhau n
˜
u
,
a
c
,
ua tô
,
ng
¯
d
˜
a cho.
J
V
´
ı d
.
u 2.16. Nê
´
u a > 0 v `a b > 0, th`ı (n −1)a
n
+ b
n
≥ na
n−1
b, v
´
o
,
i
n l `a sô
´
nguyên du
,
o
,
ng;
¯
d
,
˘ang th
´
u
,
c xâ
,
y ra khi v `a ch
,
ı khi a = b.
L
`
o
,
i gi
,
ai. M
.
ênh
¯
dê
`
¯
d
´
ung v
´
o
,
i n = 1. Gi
,
a s
,
u
,
m
.
ênh
¯
dê
`
¯
d
´
ung v
´
o
,
i
n = k,
( k −1)a
k
+ b
k
≥ ka
k−1
b
Ðê
,
xây d
.
u
,
ng m
.
ênh
¯
dê
`
v
´
o
,
i n = k + 1, ta tiê
´
n h
`
anh c
´
ac bu
,
´
o
,
c
1) Nhân hai vê
´
bâ
´
t
¯
d
,
˘
ang th
´
u
,
c v
´
o
,
i a
( k −1)a
k+1
+ b
k
a ≥ ka
k
b.
2) C
.
ông thêm a
k+1
v
`
ao bâ
´
t
¯
d
,
˘
ang th
´
u
,
c trên
ka
k+1
+ b
k
a ≥ ka
k
b + a
k+1
.
3) Chuyê
,
n b
k
a sang vê
´
ph
,
ai ta c
´
o
ka
k+1
≥ ka
k
b + a
k+1
−b
k
a.
4) C
.
ông thêm b
k+1
v
`
ao hai vê
´
c
,
ua bâ
´
t
¯
d
,
˘
ang th
´
u
,
c n
`
ay
ka
k+1
+ b
k+1
≥ ka
k
b + a
k+1
−b
k
a + b
k+1
.
Theo gi
,
a thiê
´
t quy n
.
ap th
`
ı bâ
´
t
¯
d
,
˘
ang th
´
u
,
c trên tr
,
o
,
th
`
anh
¯
d
,
˘
ang
th
´
u
,
c khi v
`
a ch
,
ı khi a = b. Ðê
,
ch
´
u
,
ng minh P(k + 1)
¯
d
´
ung, ta ch
,
ı
ra vê
´
ph
,
ai c
,
ua bâ
´
t
¯
d
,
˘
ang th
´
u
,
c sau c
`
ung th
,
oa m
˜
an
ka
k
b + a
k+1
−b
k
a + b
k+1
≥ (k + 1)a
k
b
v
`
a bâ
´
t
¯
d
,
˘
ang th
´
u
,
c tr
,
o
,
th
`
anh
¯
d
,
˘
ang th
´
u
,
c khi v
`
a ch
,
ı khi a = b. Th
.
ât

2.3. Bu
,
´
o
,
c quy n
.
ap
¯
du
,
.
o
,
c xây d
.
u
,
ng trên P(k) 39
v
.
ây, ta biê
´
n
¯
dô
,
i t
`
u
,
du
,
´
o
,
i lên
ka
k
b + a
k+1
−b
k
a + b
k+1
≥ (k + 1)a
k
b,
−a
k
b + a
k+1
−b
k
a + b
k+1
≥ 0,
a
k
(a − b) + b
k
( b − a) ≥ 0,
(a
k
−b
k
)(a −b) ≥ 0.
Bâ
´
t
¯
d
,
˘
ang th
´
u
,
c n
`
ay
¯
d
´
ung (do a − b v
`
a a
k
− b
k
c
´
o c
`
ung dâ
´
u), suy
ngu
,
.
o
,
c l
.
ai bâ
´
t
¯
d
,
˘
ang th
´
u
,
c ta câ
`
n ch
´
u
,
ng minh l
`
a
¯
d
´
ung v
`
a
¯
d
,
˘
ang th
´
u
,
c
xâ
,
y ra khi v
`
a ch
,
ı khi a = b.
J
V
´
ı d
.
u 2.17. Ch
´
u
,
ng minh r
`
˘ang
S
n
= 1 −2 + 3 −4 + ··· + (−1)
n−1
.n = (−1)
n−1
n + 1
2
,
o
,
¯
dây [x] l `a sô
´
nguyên l
´
o
,
n nhâ
´
t nh
,
o ho
,
n x, n l `a sô
´
nguyên du
,
o
,
ng.
L
`
o
,
i gi
,
ai. Ðê
,
ch
´
u
,
ng minh
¯
du
,
.
o
,
c b
`
ai to
´
an, ta ch
´
u
,
ng minh công
th
´
u
,
c sau
h
n
2
i
+
n + 1
2
= n
v
´
o
,
i m
.
oi n. Th
.
ât v
.
ây,
a) v
´
o
,
i n = 2m l
`
a sô
´
ch
˜
˘
an, ta c
´
o
h
n
2
i
+
n + 1
2
= [m] +
m +
1
2
= m + m = n.
b) v
´
o
,
i n = 2m + 1 l
`
a sô
´
l
,
e
h
n
2
i
+
n + 1
2
=
m +
1
2
+ [m + 1] = m + m + 1 = n.
Bu
,
´
o
,
c co
,
s
,
o
,
: S
1
= 1 = (−1)
0
1 + 1
2
, m
.
ênh
¯
dê
`
¯
d
´
ung v
´
o
,
i n = 1

40 Chu
,
o
,
ng 2. K
˜
y thu
.
ât d
`
ung phu
,
o
,
ng ph
´
ap quy n
.
ap to
´
an h
.
oc
Bu
,
´
o
,
c quy n
.
ap: Gi
,
a s
,
u
,
¯
d
,
˘
ang th
´
u
,
c
¯
d
´
ung v
´
o
,
i n = k , ngh
˜
ıa l
`
a
S
k
= 1 −2 + 3 −4 + ··· + (−1)
k−1
.k = (−1)
k−1
k + 1
2
.
Khi
¯
d
´
o
S
k+1
= S
k
+ (−1)
k
( k + 1) = (−1)
k−1
k + 1
2
+ (−1)
k
( k + 1)
= (−1)
k
k + 1 −
k + 1
2
= (−1)
k
.
k + 2
2
.
Ð
,
˘
ang th
´
u
,
c sau c
`
ung suy ra t
`
u
,
¯
d
,
˘
ang th
´
u
,
c
,
o
,
phâ
`
n trên. Ð
,
˘
ang th
´
u
,
c
c
,
ua
¯
dê
`
ra
¯
d
´
ung v
´
o
,
i n = k + 1.
J
2.4. Bu
,
´
o
,
c quy n
.
ap
¯
du
,
.
o
,
c xây d
.
u
,
ng trên P(k + 1)
Bu
,
´
o
,
c quy n
.
ap trong nguyên l
´
y quy n
.
ap to
´
an h
.
oc câ
`
n kh
,
˘
ang
¯
d
.
inh P(k + 1) suy t
`
u
,
P(k). Nhu
,
ng nhiê
`
u khi vi
.
êc biê
´
n
¯
dô
,
i tr
.
u
,
c
tiê
´
p t
`
u
,
P(k) sang P(k + 1) g
.
˘
ap râ
´
t nhiê
`
u kh
´
o kh
˘
an ho
.
˘
ac không
c
´
o hu
,
´
o
,
ng ch
´
ınh x
´
ac. Khi
¯
d
´
o ta ph
,
ai l
`
am ngu
,
.
o
,
c l
.
ai
¯
dê
,
biê
,
u di
˜
ên
P(k + 1) ra m
.
ênh
¯
dê
`
c
,
ua P(k) v
`
a tiê
´
n h
`
anh quy n
.
ap. Phâ
`
n n
`
ay
v
`
a phâ
`
n tru
,
´
o
,
c liên quan m
.
ât thiê
´
t v
`
a tu
,
o
,
ng
¯
du
,
o
,
ng nhau.
V
´
ı d
.
u 2.18. Ch
´
u
,
ng minh r
`
˘ang sô
´
z
n
= 3
2n+1
+ 40n −67 chia hê
´
t
cho 64 v
´
o
,
i m
.
oi sô
´
t
.
u
,
nhiên n.
L
`
o
,
i gi
,
ai. Bu
,
´
o
,
c co
,
s
,
o
,
: z
1
= 3
3
+ 40 −67 = 0 chia hê
´
t cho 64. m
.
ênh
¯
dê
`
¯
d
´
ung v
´
o
,
i n = 1
Bu
,
´
o
,
c quy n
.
ap: Gi
,
a s
,
u
,
z
n
chia hê
´
t cho 64. Khi
¯
d
´
o
z
n+1
= 3
2n+3
+ 40n −27
= 9(3
2n+1
+ 40n −67) −320n + 576 = 9.z
n
−64( 5n −9)
c
˜
ung chia hê
´
t cho 64. B
`
ai to
´
an
¯
d
´
ung v
´
o
,
i m
.
oi n.
J

2.4. Bu
,
´
o
,
c quy n
.
ap
¯
du
,
.
o
,
c xây d
.
u
,
ng trên P(k + 1) 41
V
´
ı d
.
u 2.19. K´y hi
.
êu R
n
=
r
2 +
q
2 +
p
2 + ··· +
√
2 c ˘an b
.
âc hai
n lâ
`
n. Ch
´
u
,
ng minh r
`
˘ang cos
π
2
n
=
1
2
R
n−1
, sin
π
2
n
=
1
2
√
2 − R
n−2
v
´
o
,
i m
.
oi n ≥ 3.
L
`
o
,
i gi
,
ai. Bu
,
´
o
,
c co
,
s
,
o
,
: cos
π
4
= sin
π
4
=
√
2
2
, m
.
ênh
¯
dê
`
¯
d
´
ung v
´
o
,
i
n = 3 v
`
ı
cos
π
2
3
= cos
π
8
=
v
u
u
t
1 + cos
π
4
2
=
p
2 +
√
2
2
=
R
2
2
,
sin
π
2
3
= sin
π
8
=
v
u
u
t
1 −cos
π
4
2
=
p
2 −
√
2
2
=
√
2 − R
1
2
.
Bu
,
´
o
,
c quy n
.
ap: Gi
,
a s
,
u
,
m
.
ênh
¯
dê
`
¯
d
´
ung v
´
o
,
i sô
´
t
.
u
,
nhiên k ≥ 3. Khi
¯
d
´
o
cos
π
2
k+1
=
v
u
u
t
1 + cos
π
2
k
2
=
√
2 + R
k−1
2
=
R
k
2
,
sin
π
2
k+1
=
v
u
u
t
1 −cos
π
2
k
2
=
√
2 − R
k−1
2
.
Nhu
,
v
.
ây, m
.
ênh
¯
dê
`
¯
d
´
ung v
´
o
,
i n = k + 1. Theo nguyên l
´
y quy n
.
ap
to
´
an h
.
oc c
´
ac công th
´
u
,
c
¯
d
´
ung v
´
o
,
i m
.
oi n ≥ 3.
J
V
´
ı d
.
u 2.20. Ch
´
u
,
ng minh r
`
˘ang
n
5
5
+
n
4
2
+
n
3
3
−
n
30
l `a sô
´
nguyên
v
´
o
,
i n = 0, 1, 2, ...
L
`
o
,
i gi
,
ai. Bu
,
´
o
,
c co
,
s
,
o
,
: M
.
ênh
¯
dê
`
¯
d
´
ung v
´
o
,
i n = 0.

42 Chu
,
o
,
ng 2. K
˜
y thu
.
ât d
`
ung phu
,
o
,
ng ph
´
ap quy n
.
ap to
´
an h
.
oc
Bu
,
´
o
,
c quy n
.
ap: Gi
,
a s
,
u
,
m
.
ênh
¯
dê
`
¯
d
´
ung v
´
o
,
i n = k. Ta câ
`
n ph
,
ai ch
´
u
,
ng
minh
( k + 1)
5
5
+
( k + 1)
4
2
+
( k + 1)
3
3
−
k + 1
30
l
`
a sô
´
nguyên. Ta khai triê
,
n biê
,
u th
´
u
,
c trên
k
5
+ 5k
4
+ 10k
3
+ 10k
2
+ 5k+
5
+
k
4
+ 4k
3
+ 6k
2
+ 4k + 1
2
+
+
k
3
+ 3k
2
+ 3k + 1
3
−
k + 1
30
.
Nh
´
om l
.
ai
¯
dê
,
xuâ
´
t hi
.
ên P(k)
(
k
5
5
+
k
4
2
+
k
3
3
−
k
30
) + ( (k
4
+ 2k
3
+ 2k
2
+ k) + (2k
3
+ 3k
2
+ 2k) + (k
2
+ k) + 1)
Nhu
,
v
.
ây nh
´
om th
´
u
,
nhâ
´
t theo gi
,
a thiê
´
t l
`
a sô
´
nguyên v
`
a c
´
ac nh
´
om
sau c
˜
ung l
`
a sô
´
nguyên, suy ra tô
,
ng c
,
ua ch
´
ung l
`
a sô
´
nguyên v
`
a
¯
d
´
o
c
˜
ung l
`
a m
.
ênh
¯
dê
`
b
`
ai to
´
an v
´
o
,
i n = k + 1.
J
V
´
ı d
.
u 2.21. Ch
´
u
,
ng minh r
`
˘ang v
´
o
,
i m
.
oi sô
´
nguyên n ≥ 2 v `a |x| < 1
th`ı bâ
´
t
¯
d
,
˘ang th
´
u
,
c sau luôn
¯
d ´ung:
(1 − x)
n
+ ( 1 + x)
n
< 2
n
.
L
`
o
,
i gi
,
ai. Bu
,
´
o
,
c co
,
s
,
o
,
: Khi n = 2 bâ
´
t
¯
d
,
˘
ang th
´
u
,
c
¯
d
´
ung hiê
,
n nhiên.
Bu
,
´
o
,
c quy n
.
ap: Gi
,
a s
,
u
,
bâ
´
t
¯
d
,
˘
ang th
´
u
,
c
¯
d
´
ung v
´
o
,
i n = k. Ta ph
,
ai
ch
´
u
,
ng minh bâ
´
t
¯
d
,
˘
ang th
´
u
,
c c
˜
ung
¯
d
´
ung v
´
o
,
i n = k + 1; do gi
,
a thiê
´
t
¯
dâ
`
u b
`
ai v
`
a gi
,
a thiê
´
t quy n
.
ap ta c
´
o
(1 − x)
k+1
+ ( 1 + x)
k+1
< [(1 − x)
k
+ ( 1 + x)
k
][(1 − x) + (1 + x)]
< 2
k
.2 = 2
k+1
.
Nhu
,
v
.
ây bâ
´
t
¯
d
,
˘
ang th
´
u
,
c
¯
du
,
.
o
,
c ch
´
u
,
ng minh v
´
o
,
i n = k + 1.
J
V
´
ı d
.
u 2.22. V
´
o
,
i m
.
oi x trong 0 ≤ x ≤ π, ch
´
u
,
ng minh r
`
˘ang
|sin nx| ≤ n sin x,
,
o
,
¯
dây n l `a sô
´
nguyên không âm.

2.5. Quy n
.
ap to
´
an h
.
oc v
`
a ph
´
ep truy hô
`
i 43
L
`
o
,
i gi
,
ai. Bu
,
´
o
,
c co
,
s
,
o
,
: V
´
o
,
i n = 1 bâ
´
t
¯
d
,
˘
ang th
´
u
,
c
¯
d
´
ung l
`
a tâ
´
t nhiên.
Bu
,
´
o
,
c quy n
.
ap: Gi
,
a s
,
u
,
bâ
´
t
¯
d
,
˘
ang th
´
u
,
c
¯
d
´
ung v
´
o
,
i n = k: |sin kx| ≤
k sin x. Ta câ
`
n ch
´
u
,
ng minh bâ
´
t
¯
d
,
˘
ang th
´
u
,
c c
˜
ung
¯
d
´
ung v
´
o
,
i n = k + 1.
Ta x
´
et
|sin(k + 1)x| = |sin(kx + x)| = |sin(kx) cos x + cos(kx) sin x|
= |sin(kx) cos x|+ |cos(kx) sin x|
= |sin(kx)||cos x|+ |cos(kx)||sin x|
≤ |k sin x|+ |sin x| ≤ (k + 1) sin x.
Nh
˜
u
,
ng bâ
´
t
¯
d
,
˘
ang th
´
u
,
c trên
¯
du
,
.
o
,
c suy ra b
,
o
,
i 0 ≤ x ≤ π nên sin x ≥
0 v
`
a |cos kx| ≤ 1. Nhu
,
v
.
ây ta
¯
d
˜
a ch
´
u
,
ng minh bâ
´
t
¯
d
,
˘
ang th
´
u
,
c
¯
d
´
ung
cho n = k + 1. Suy ra n
´
o
¯
d
´
ung v
´
o
,
i m
.
oi n ≥ 1.
J
2.5. Quy n
.
ap to
´
an h
.
oc v
`
a ph
´
ep truy hô
`
i
Nhiê
`
u b
`
ai to
´
an ta
¯
d
˜
a x
´
et c
´
o liên quan
¯
dê
´
n d
˜
ay sô
´
nhu
,
câ
´
p sô
´
c
.
ông, câ
´
p sô
´
nhân, ... m
˜
ôi sô
´
h
.
ang c
,
ua ch
´
ung
¯
du
,
.
o
,
c biê
,
u di
˜
ên b
`
˘
ang
c
´
ach lâ
´
y nh
˜
u
,
ng gi
´
a tr
.
i c
,
ua sô
´
h
.
ang tru
,
´
o
,
c n
´
o, ngo
`
ai nh
˜
u
,
ng sô
´
h
.
ang
kh
,
o
,
i
¯
dâ
`
u c
,
ua d
˜
ay. Nh
˜
u
,
ng công th
´
u
,
c sô
´
h
.
ang chung c
,
ua d
˜
ay nhu
,
v
.
ây
¯
du
,
.
o
,
c
¯
du
,
a ra v
`
a coi nhu
,
l
`
a
¯
d
.
inh ngh
˜
ıa m
.
ôt d
˜
ay. Phu
,
o
,
ng ph
´
ap
cho m
.
ôt d
˜
ay nhu
,
v
.
ây râ
´
t giô
´
ng v
´
o
,
i nguyên l
´
y quy n
.
ap to
´
an h
.
oc.
Ta c
´
o thê
,
d
`
ung quy n
.
ap
¯
dê
,
¯
d
.
inh ngh
˜
ıa m
.
ôt kh
´
ai ni
.
êm m
´
o
,
i. Nh
˜
u
,
ng
nh
`
a to
´
an h
.
oc g
.
oi n
´
o l
`
a lo
.
ai
¯
d
.
inh ngh˜ıa quy n
.
ap, nhu
,
ng c
´
ac nh
`
a
khoa h
.
oc m
´
ay t
´
ınh g
.
oi n
´
o l
`
a
¯
d
.
inh ngh˜ıa hô
`
i quy. Ðê
,
hiê
,
u vâ
´
n
¯
dê
`
n
`
ay ta x
´
et m
.
ôt v
´
ı d
.
u. Ð
.
inh ngh
˜
ıa giai th
`
u
,
a c
,
ua m
.
ôt sô
´
nguyên,
k
´
y hi
.
êu l
`
a P(n) = n!, nhu
,
sau: nê
´
u n = 0 ta g
´
an P(n) = 1 v
`
a nê
´
u
v
´
o
,
i m
˜
ôi n > 0 g
´
an gi
´
a tr
.
i P(n) = n ·(n −1) ·. . . ·2 ·1 ngh
˜
ıa l
`
a t
´
ıch

44 Chu
,
o
,
ng 2. K
˜
y thu
.
ât d
`
ung phu
,
o
,
ng ph
´
ap quy n
.
ap to
´
an h
.
oc
n sô
´
nguyên du
,
o
,
ng
¯
dâ
`
u tiên. Ta t
´
ınh m
.
ôt sô
´
gi
´
a tr
.
i
¯
dâ
`
u
0! = 1,
1! = 1 = 1 ·0!,
2! = 2 · 1 = 2 ·1! = 2,
3! = 3 · 2 · 1 = 3 ·2! = 6.
Nhu
,
v
.
ây v
´
o
,
i m
.
oi sô
´
t
.
u
,
nhiên n, ho
.
˘
ac l
`
a n = 0 c
´
o P(n)=1; ho
.
˘
ac l
`
a
n > 0 c
´
o P(n) = n · (n − 1)!. Ðiê
`
u n
`
ay g
.
o
,
i
´
y ta
¯
d
.
inh ngh
˜
ıa theo
quy n
.
ap c
,
ua P(n) nhu
,
sau:
Bu
,
´
o
,
c co
,
s
,
o
,
: Nê
´
u n = 0, th
`
ı n! = 1 v
`
a
Bu
,
´
o
,
c quy n
.
ap: Nê
´
u n!
¯
d
˜
a x
´
ac
¯
d
.
inh, th
`
ı ta c
´
o thê
,
x
´
ac
¯
d
.
inh
( n + 1)! b
`
˘
ang (n + 1) ·n!.
Bu
,
´
o
,
c quy n
.
ap trong
¯
d
.
inh ngh
˜
ıa trên trong tin h
.
oc ngu
,
`
o
,
i ta
thu
,
`
o
,
ng g
.
oi l
`
a Bu
,
´
o
,
c hô
`
i quy v
`
a g
.
oi
¯
d
.
inh ngh
˜
ıa kiê
,
u nhu
,
trên l
`
a
¯
d
.
inh ngh
˜
ıa theo hô
`
i quy. Ta thâ
´
y r
`
˘
ang
¯
d
.
inh ngh
˜
ıa hô
`
i quy
,
o
,
trên
ho
`
an to
`
an nhu
,
nguyên l
´
y quy n
.
ap to
´
an h
.
oc. Bu
,
´
o
,
c co
,
s
,
o
,
cho ta gi
´
a
tr
.
i t
.
ai sô
´
t
.
u
,
nhiên ban
¯
dâ
`
u 0. Bu
,
´
o
,
c hô
`
i quy cho ta biê
´
t nê
´
u ta
¯
d
˜
a
biê
´
t
¯
d
.
inh ngh
˜
ıa t
.
ai n th
`
ı ta c
´
o thê
,
¯
d
.
inh ngh
˜
ıa
¯
du
,
.
o
,
c t
.
ai n + 1 (bu
,
´
o
,
c
tiê
´
p theo). Nhu
,
v
.
ây
¯
d
.
inh ngh
˜
ıa
¯
dâ
`
y
¯
d
,
u cho m
.
oi sô
´
t
.
u
,
nhiên n.
Ð
.
inh ngh
˜
ıa xuâ
´
t ph
´
at t
`
u
,
0 v
`
a t
`
u
,
ng bu
,
´
o
,
c liên tiê
´
p
¯
d
.
inh ngh
˜
ıa
P(n) cho nh
˜
u
,
ng sô
´
t
.
u
,
nhiên c
`
ang ng
`
ay c
`
ang l
´
o
,
n. Nhu
,
ng
¯
dê
,
t
´
ınh
to
´
an P(n) ta
¯
di ngu
,
.
o
,
c l
.
ai, t
`
u
,
m
.
ênh
¯
dê
`
l
´
o
,
n nhâ
´
t
¯
dê
´
n m
.
ênh
¯
dê
`
nh
,
o
nhâ
´
t. V
´
ı d
.
u ta t
´
ınh
3! = 3 · 2! = 3 · 2 · 1! = 3 · 2 ·1 ·0! = 3 ·2 ·1 ·1 = 6
Theo
¯
d
.
inh ngh
˜
ıa muô
´
n t
´
ınh gi
´
a tr
.
i P(n) ta kiê
,
m tra xem nê
´
u
n = 0 th
`
ı
´
ap d
.
ung bu
,
´
o
,
c co
,
s
,
o
,
c
,
ua
¯
d
.
inh ngh
˜
ıa; ngu
,
.
o
,
c l
.
ai ta tr
`
u
,
n
¯
di 1
¯
dê
,
¯
du
,
a b
`
ai to
´
an vê
`
sô
´
nguyên nh
,
o ho
,
n, nhu
,
v
.
ây bu
,
´
o
,
c hô
`
i quy
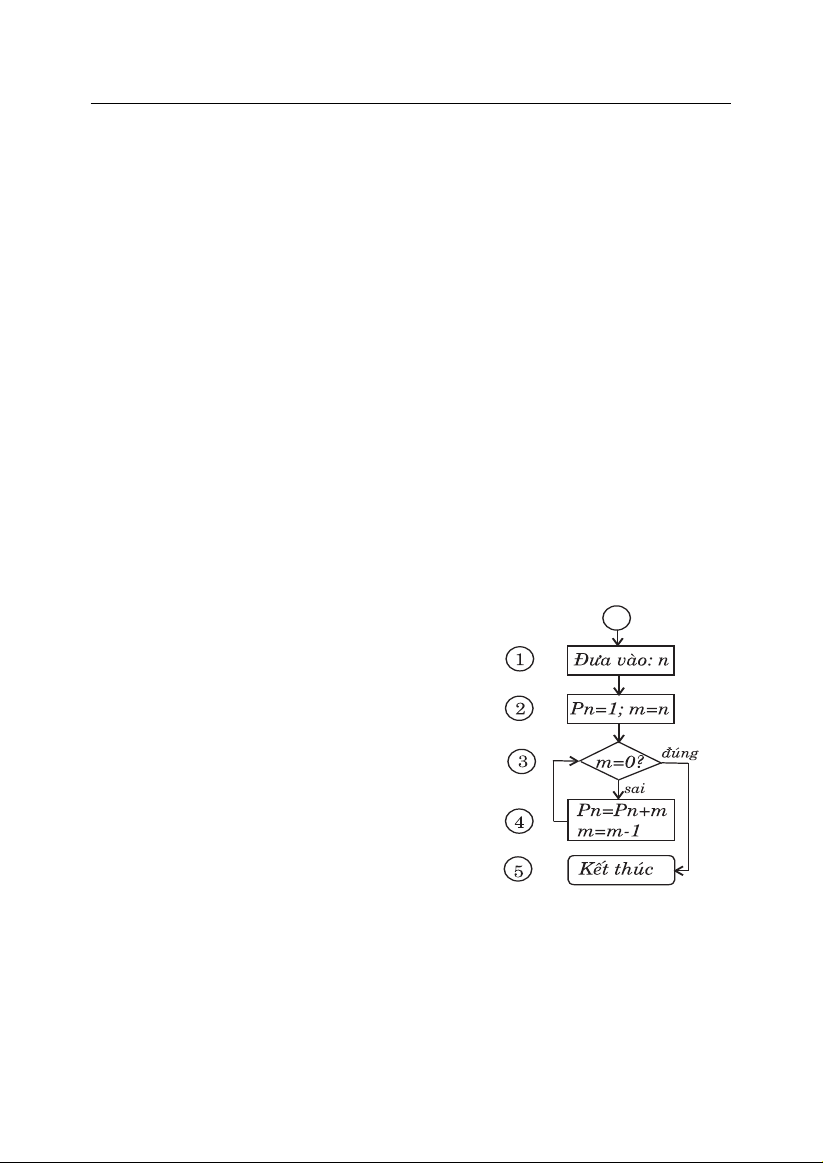
2.5. Quy n
.
ap to
´
an h
.
oc v
`
a ph
´
ep truy hô
`
i 45
gi
,
am b
.
âc c
,
ua b
`
ai to
´
an
¯
dê
´
n khi vê
`
bu
,
´
o
,
c co
,
s
,
o
,
v
`
a t
´
ınh to
´
an xong
ho
`
an to
`
an.
Râ
´
t nhiê
`
u ngôn ng
˜
u
,
l
.
âp tr
`
ınh c
˜
ung cho ta t
´
ınh to
´
an
¯
du
,
.
o
,
c công
th
´
u
,
c theo
¯
d
.
inh ngh
˜
ıa hô
`
i quy, ch
,
˘
ang h
.
an nhu
,
câu l
.
ênh sau trong
ngôn ng
˜
u
,
l
.
âp tr
`
ınh Pascal:
if n = 0 then Pn : = 1 else Pn := n ·(n −1)! ;
D
`
ong l
.
ênh trên n
´
oi v
´
o
,
i chu
,
o
,
ng tr
`
ınh biên d
.
ich r
`
˘
ang:
1. Kiê
,
m tra xem n = 0 c
´
o
¯
d
´
ung không ?
2. Nê
´
u tr
,
a l
`
o
,
i l
`
a Ð
´
ung, th
`
ı g
´
an P(n) = 1;
3. Nê
´
u tr
,
a l
`
o
,
i l
`
a Sai, th
`
ı g
´
an P(n) := n ·(n − 1)!;
Ðê
,
t
´
ınh tiê
´
p t
.
uc m
´
ay ph
,
ai g
.
oi d
`
ong l
.
ênh lâ
`
n n
˜
u
,
a
¯
dê
,
t
´
ınh ( n −
1)! v
`
a c
´
u
,
tiê
´
p t
.
uc nhu
,
v
.
ây t
´
o
,
i khi n = 0. M
.
ôt câu l
.
ênh không thê
,
hi
.
ên hê
´
t vi
.
êc t
´
ınh to
´
an hô
`
i quy.
Trong to
´
an h
.
oc v
`
a tin h
.
oc ngu
,
`
o
,
i
H
`
ınh 2.1:
ta t
.
ao ra c
´
ac thu
.
ât to
´
an thê
,
hi
.
ên chu
tr
`
ınh t
´
ınh to
´
an. C
´
o nhiê
`
u c
´
ach mô
t
,
a thu
.
ât to
´
an nhu
,
li
.
êt kê t
`
u
,
ng bu
,
´
o
,
c
th
.
u
,
c hi
.
ên ho
.
˘
ac b
`
˘
ang so
,
¯
dô
`
khô
´
i (biê
,
u
¯
dô
`
). Nhu
,
ch
´
ung ta
¯
d
˜
a thâ
´
y thu
.
ât
to
´
an c
˜
ung l
`
a m
.
ôt công c
.
u mô t
,
a vi
.
êc
th
.
u
,
c hi
.
ên nguyên l
´
y quy n
.
ap to
´
an
h
.
oc, nhâ
´
t l
`
a c
´
ac biê
,
u
¯
dô
`
thu
.
ât to
´
an
hô
`
i quy. Ta lâ
´
y v
´
ı d
.
u t
`
ım thu
.
ât to
´
an
t
´
ınh giai th
`
u
,
a c
,
ua sô
´
t
.
u
,
nhiên cho
tru
,
´
o
,
c ?
1. Cho gi
´
a tr
.
i sô
´
t
.
u
,
nhiên n;
2. Ð
.
˘
at kê
´
t qu
,
a Pn := 1 v
`
a biê
´
n
¯
dê
´
m m := n;

46 Chu
,
o
,
ng 2. K
˜
y thu
.
ât d
`
ung phu
,
o
,
ng ph
´
ap quy n
.
ap to
´
an h
.
oc
3. Kiê
,
m tra m = 0? nê
´
u
¯
d
´
ung
¯
di
¯
dê
´
n bu
,
´
o
,
c 5; nê
´
u sai
¯
dê
´
n bu
,
´
o
,
c 4;
4. T
´
ınh Pn := Pn ∗ m v
`
a m := m −1;
¯
di
¯
dê
´
n bu
,
´
o
,
c 3;
5. Kê
´
t th
´
uc.
So
,
¯
dô
`
khô
´
i thê
,
hi
.
ên qua h
`
ınh 1.
Nhu
,
v
.
ây vi
.
êc chuyê
,
n t
`
u
,
công th
´
u
,
c hô
`
i quy ho
.
˘
ac c
´
ac m
.
ênh
¯
dê
`
hô
`
i quy sang thu
.
ât to
´
an v
`
a biê
,
u
¯
dô
`
thê
,
hi
.
ên qu
´
a tr
`
ınh t
´
ınh to
´
an
t
`
u
,
nh
.
âp d
˜
u
,
li
.
êu v
`
ao v
`
a lâ
´
y kê
´
t qu
,
a ra, c
˜
ung nhu
,
c
´
ac bu
,
´
o
,
c t
´
ınh
to
´
an
¯
d
`
oi h
,
oi ta ph
,
ai hiê
,
u thâ
´
u
¯
d
´
ao phu
,
o
,
ng ph
´
ap quy n
.
ap to
´
an
h
.
oc. Trong cuô
´
n s
´
ach n
`
ay ta s
˜
e
¯
dê
`
c
.
âp
¯
dê
´
n m
.
ôt sô
´
b
`
ai t
.
âp vê
`
thu
.
ât to
´
an v
`
a biê
,
u
¯
dô
`
¯
dê
,
minh ho
.
a.
Ta
¯
du
,
a v
`
ao
¯
d
.
inh ngh
˜
ıa h
.
ê sô
´
Newton
3
C
k
n
=
n!
k!(n − k)!
, ( n = 0, 1, . . . ; k = 0, 1, . . . , n). (2.15)
D
`
ung
¯
d
.
inh ngh
˜
ıa giai th
`
u
,
a v
`
a gi
,
an u
,
´
o
,
c th
`
u
,
a sô
´
chung, ta nh
.
ân
¯
du
,
.
o
,
c
C
k
n
=
n(n − 1) . . . (n −k + 1)
k!
, ( n = 0, 1, . . . ; k = 0, 1, . . . , n)
(2.16)
Ch
´
ung ta thiê
´
t l
.
âp tam gi ´ac Pascal theo nguyên t
´
˘
ac: C
.
ôt
¯
dâ
`
u tiên
v
`
a ¨c
.
anh huyê
`
n¨ ch
,
ı gô
`
m to
`
an sô
´
m
.
ôt; sô
´
¯
d
´
u
,
ng
,
o
,
h
`
ang th
´
u
,
n v
`
a
c
.
ôt k, l
`
a tô
,
ng c
,
ua hai sô
´
,
o
,
h
`
ang n −1, t
.
ai c
.
ôt th
´
u
,
k − 1 v
`
a k.
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
. . . . . . . . . . . . . . .
3
K
´
y hi
.
êu tu
,
o
,
ng
¯
du
,
o
,
ng C
k
n
≡ C
k
n
.

2.5. Quy n
.
ap to
´
an h
.
oc v
`
a ph
´
ep truy hô
`
i 47
V
´
ı d
.
u 2.23. Ch
´
u
,
ng minh r
`
˘ang nh
˜
u
,
ng sô
´
trong b
,
ang trên l `a
nh
˜
u
,
ng h
.
ê sô
´
Newton: m
˜
ôi sô
´
¯
d
´
u
,
ng
,
o
,
h `ang th
´
u
,
n v `a c
.
ôt th
´
u
,
k
l `a C
k
n
.
L
`
o
,
i gi
,
ai. Ch
´
u
,
ng minh b
`
˘
ang quy n
.
ap, v
´
o
,
i n = 0 m
.
ênh
¯
dê
`
¯
d
´
ung.
Gi
,
a s
,
u
,
h
`
ang th
´
u
,
n
¯
du
,
.
o
,
c t
.
ao b
,
o
,
i c
´
ac sô
´
C
0
n
, C
1
n
, . . . , C
k
n
v
`
a k
´
y
hi
.
êu β
n+1,0
, β
n+1,1
, . . . , β
n+1,n+1
l
`
a nh
˜
u
,
ng sô
´
,
o
,
h
`
ang th
´
u
,
n + 1. Ta
s
˜
e ch
´
u
,
ng minh r
`
˘
ang β
n+1,k
= C
k
n+1
. Th
.
ât v
.
ây,
´
ap d
.
ung nguyên t
´
˘
ac
t
.
ao b
,
ang sô
´
v
`
a gi
,
a thiê
´
t quy n
.
ap, ta c
´
o
β
n+1,k
= C
k−1
n
+ C
k
n
=
n!
( k −1)!(n − k + 1)!
+
n!
k!(n − k)!
=
n!
( k −1)!(n − k)!
(
1
n − k + 1
+
1
k
) =
( n + 1)!
k!(n − k + 1)!
.
Th
.
u
,
c tê
´
ta
¯
d
˜
a ch
´
u
,
ng minh công th
´
u
,
c
C
k−1
n
+ C
k
n
= C
k
n+1
. (2.17)
V
´
ı d
.
u 2.24. H ˜ay viê
´
t thu
.
ât to ´an v `a v˜e so
,
¯
dô
`
khô
´
i tu
,
o
,
ng
´
u
,
ng
¯
dê
,
t´ınh h
.
ê sô
´
Newton C
k
n
khi cho n, k(1 ≤ k ≤ n).
L
`
o
,
i gi
,
ai. H
`
ınh 2 thê
,
hi
.
ên biê
,
u
¯
dô
`
c
,
ua thu
.
ât to
´
an.
1. Nh
.
âp thông sô
´
n v
`
a k;
2.T
´
ınh t := k! theo thu
.
ât to
´
an v
`
a so
,
¯
dô
`
¯
d
˜
a biê
´
t;
3. Chuâ
,
n b
.
i t
´
ınh n (n −1) . . . (n − k + 1), biê
´
n i nh
.
ân gi
´
a tr
.
i
¯
dâ
`
u
l
`
a n;
4. Ðu
,
a v
`
ao biê
´
n m ch
´
u
,
a gi
´
a tr
.
i c
,
ua m
˜
âu sô
´
, kh
,
o
,
i
¯
dâ
`
u l
`
a 1;
5. B
´
˘
at
¯
dâ
`
u t
´
ınh m
˜
âu sô
´
k bu
,
´
o
,
c v
´
o
,
i gi
´
a tr
.
i n(n −1) . . . (i + 1), i < n
nhân v
´
o
,
i i v
`
a nh
.
ân gi
´
a tr
.
i m = n(n −1) . . . i.
6. Gi
´
a tr
.
i c
,
ua ch
,
ı sô
´
gi
,
am
¯
di 1.
7. Kiê
,
m tra ch
,
ı sô
´
c
´
o nh
,
o ho
,
n sô
´
h
.
ang sau c
`
ung n −k + 1 không
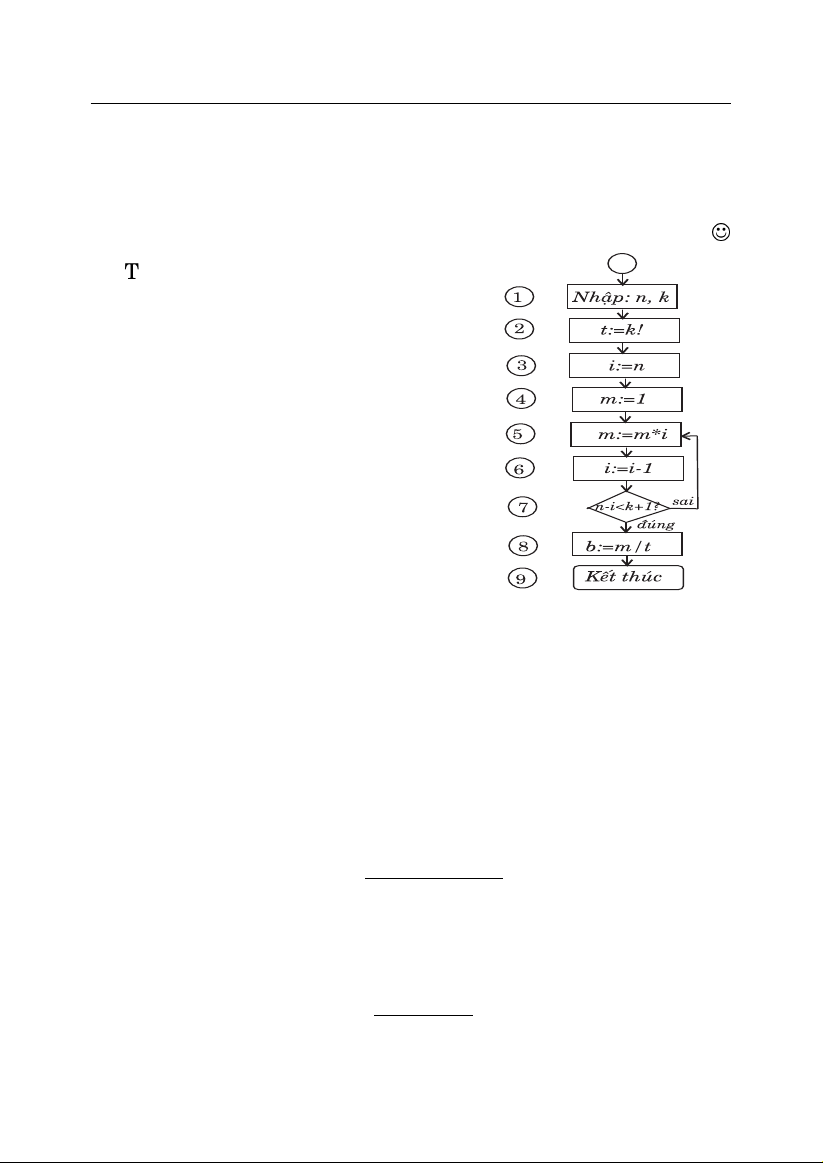
48 Chu
,
o
,
ng 2. K
˜
y thu
.
ât d
`
ung phu
,
o
,
ng ph
´
ap quy n
.
ap to
´
an h
.
oc
? nê
´
u không
¯
d
´
ung quay vê
`
bu
,
´
o
,
c 5; nê
´
u
¯
d
´
ung
¯
di tiê
´
p bu
,
´
o
,
c 8.
8. G
´
an biê
´
n b ch
´
u
,
a gi
´
a tr
.
i thu
,
o
,
ng c
,
ua m = n(n −1) . . . (n −k + 1)
v
`
a t = 1, 2, . . . , k.
9. Kê
´
t th
´
uc: kê
´
t qu
,
a c = C
k
n
.
J
Trong th
.
u
,
c tê
´
nhiê
`
u b
`
ai to
´
an cho
H
`
ınh 2.2:
d
˜
ay sô
´
a
1
, a
2
, . . . , a
n
, . . .
x
´
ac
¯
d
.
inh b
`
˘
ang công th
´
u
,
c hô
`
i quy
a
n
= f (a
n−1
, a
n−2
, . . . , a
n−k
) v
´
o
,
i
1 ≤ k ≤ n − 1 v
`
a f l
`
a m
.
ôt h
`
am
¯
d
˜
a
biê
´
t. C
˜
ung nhu
,
¯
d
.
inh ngh
˜
ıa
,
o
,
trên khi
cho m
.
ôt sô
´
sô
´
h
.
ang ban
¯
dâ
`
u v
`
a h
`
am
f th
`
ı c
´
ac sô
´
h
.
ang c
,
ua d
˜
ay
¯
dê
`
u t
´
ınh
¯
du
,
.
o
,
c. D
˜
ây sô
´
nhu
,
v
.
ây
¯
dê
`
u g
.
oi l
`
a d
˜
ay
hô
`
i quy.
V
´
ı d
.
u 2.25. Cho d˜ay sô
´
a
1
, a
2
, . . . , a
n
, . . .
¯
du
,
.
o
,
c
¯
d
.
inh ngh˜ıa theo
công th
´
u
,
c sau:
( n + 2)(n + 1)a
n+2
−n
2
a
n
= 0, (n = 1, 2, . . .) (2.18)
v `a a
1
= 0, a
2
= 1. H ˜ay t`ım a
n
?
L
`
o
,
i gi
,
ai. Ta viê
´
t l
.
ai công th
´
u
,
c (2.18 )
a
n+2
=
n
2
( n + 1)(n + 2)
a
n
. (2.19)
D
˜
ê thâ
´
y r
`
˘
ang nh
˜
u
,
ng sô
´
h
.
ang mang ch
,
ı sô
´
l
,
e b
`
˘
ang 0. Th
.
ât v
.
ây,
¯
d
.
˘
at n = 2k −1, khi
¯
d
´
o v
´
o
,
i k = 1, 2, . . . ta c
´
o
a
2k+1
=
(2 k −1)
2
2k(2k + 1)
a
2k−1
. (2.20)

2.5. Quy n
.
ap to
´
an h
.
oc v
`
a ph
´
ep truy hô
`
i 49
V
`
ı a
1
= 0, t
`
u
,
(2.20) theo quy n
.
ap suy ra a
3
= 0, a
5
= 0, . . .. Khi ta
¯
d
.
˘
at n = 2k, th
`
ı nh
˜
u
,
ng sô
´
h
.
ang ch
˜
˘
an c
´
o công th
´
u
,
c
a
2k+2
=
2k
2
( k + 1)(2k + 1)
a
2k
. (2.21)
V
´
o
,
i k = 1, 2, 3 t
`
u
,
(2.21) ta t
´
ınh
¯
du
,
.
o
,
c
a
4
=
2
2.3
.a
2
=
1
1.3
.1 =
1
3
,
a
6
=
2.2
2
3.5
.a
4
=
2.4
3.5
.
1
3
,
a
8
=
2.3
2
4.7
.a
6
=
2.4.6
3.5.7
.
1
4
.
Ta so s
´
anh m
˜
ôi sô
´
h
.
ang v
´
o
,
i ch
,
ı sô
´
v
`
a
¯
du
,
a ra gi
,
a thiê
´
t
a
2k
=
2.4.6 . . . (2k −2)
1.3.5 . . . (2k −1)
1
k
. (2.22)
T
`
u
,
(2.22) v
´
o
,
i k = 2, 3, 4 nh
.
ân
¯
du
,
.
o
,
c a
2
, a
4
v
`
a a
8
,
o
,
trên. Gi
,
a s
,
u
,
(2.22)
¯
d
´
ung v
´
o
,
i sô
´
k n
`
ao
¯
d
´
o, ta s
˜
e ch
´
u
,
ng minh n
´
o c
˜
ung
¯
d
´
ung v
´
o
,
i
k + 1:
a
2k+2
=
2.4.6 . . . 2k
1.3.5 . . . (2k + 1)
1
k + 1
. (2.23)
Th
.
ât v
.
ây, do (2.21) v
`
a gi
,
a thiê
´
t quy n
.
ap ta c
´
o
a
2(k+1)
=
2k
2
( k + 1)(2k + 1)
.
2.4 . . . (2k −2)
1.3 . . . (2k −1)
.
1
k
=
2.4 . . . (2k −2)2k
1.3 . . . (2k −1)(2k + 1)
.
1
k + 1
.
Nhu
,
v
.
ây, công th
´
u
,
c (2.22)
¯
du
,
.
o
,
c ch
´
u
,
ng minh. T
´
om l
.
ai,
a
n
=
0 n = 2k −1 (k = 1, 2, . . .)
2.4 . . . (2k −2)
1.3 . . . (2k −1)
.
1
k
n = 2k.

50 Chu
,
o
,
ng 2. K
˜
y thu
.
ât d
`
ung phu
,
o
,
ng ph
´
ap quy n
.
ap to
´
an h
.
oc
V
´
ı d
.
u 2.26. Chia m
.
˘at ph
,
˘ang th `anh bao nhiêu phâ
`
n t
`
u
,
n
¯
du
,
`
o
,
ng
th
,
˘ang,
¯
dôi m
.
ôt c
´
˘at nhau v `a không c´o ba
¯
du
,
`
o
,
ng th
,
˘ang n `ao
¯
dô
`
ng
quy?
L
`
o
,
i gi
,
ai. Ta
¯
d
.
˘
at F(n) l
`
a sô
´
phâ
`
n m
.
˘
at ph
,
˘
ang do n
¯
du
,
`
o
,
ng th
,
˘
ang
t
.
ao ra. Ta x
´
et n + 1
¯
du
,
`
o
,
ng th
,
˘
ang bâ
´
t k
`
y theo gi
,
a thiê
´
t b
`
ai ra. n
¯
du
,
`
o
,
ng th
,
˘
ang
¯
dâ
`
u chia m
.
˘
at ph
,
˘
ang ra F(n) phâ
`
n; c
`
on
¯
du
,
`
o
,
ng th
,
˘
ang
th
´
u
,
n + 1, g b
.
i c
´
˘
at t
.
ai n
¯
diê
,
m kh
´
ac nhau v
´
o
,
i n
¯
du
,
`
o
,
ng th
,
˘
ang
¯
dâ
`
u,
nhu
,
v
.
ây
¯
du
,
`
o
,
ng th
,
˘
ang g
¯
du
,
.
o
,
c chia ra n + 1 phâ
`
n. Suy ra
¯
du
,
`
o
,
ng
th
,
˘
ang g
¯
di qua n + 1 phâ
`
n
¯
d
˜
a cho, m
˜
ôi phâ
`
n
¯
du
,
.
o
,
c chia l
`
am
¯
dôi,
do
¯
d
´
o g t
.
ao thêm ra n + 1 phâ
`
n m
´
o
,
i, ngh
˜
ıa l
`
a
F(n + 1) = F(n) + n + 1.
Thay n trong
¯
d
,
˘
ang th
´
u
,
c trên b
`
˘
ang n −1, n − 2, . . . , 2, 1 ta c
´
o
F(n) = F(n −1) + n,
F(n −1) = F(n −2 ) + n −1,
. . . . . .
F(3) = F(2 ) + 3,
F(2) = F(1 ) + 2.
Do F(1) = 2 v
`
a c
.
ông c
´
ac
¯
d
,
˘
ang th
´
u
,
c trên ta nh
.
ân
¯
du
,
.
o
,
c
F(n) = 1 + (1 + 2 + ···+ n) = 1 +
n(n + 1)
2
.
Ho
.
˘
ac l
`
a
F(n) =
n
2
+ n + 2
2
.
J
V
´
ı d
.
u 2.27. (B `ai to ´an th ´ap H `a n
.
ôi). Cho ba chiê
´
c c
.
oc. C
.
oc th
´
u
,
nhâ
´
t xâu n c ´ai
¯
d˜ıa c´o
¯
du
,
`
o
,
ng k´ınh kh ´ac nhau sao cho c ´ac
¯
d˜ıa c´o
¯
du
,
`
o
,
ng k´ınh l
´
o
,
n ho
,
n
,
o
,
du
,
´
o
,
i. Ch ´ung ta muô
´
n chuyê
,
n tâ
´
t c
,
a c´ac
¯
d˜ıa,

2.6. Quy n
.
ap to
´
an h
.
oc v
`
a tô
,
ng qu
´
at ho
´
a 51
m
˜
ôi lâ
`
n m
.
ôt chiê
´
c, sang c
.
oc th
´
u
,
hai m`a c´ac
¯
d˜ıa v
˜
ân xê
´
p th
´
u
,
t
.
u
,
t
`
u
,
l
´
o
,
n lên
¯
dê
´
n nh
,
o. Trong th
`
o
,
i gian chuyê
,
n qua c ´ac c
.
oc không
¯
du
,
.
o
,
c
¯
d
.
˘at
¯
d˜ıa l
´
o
,
n lên
¯
d˜ıa nh
,
o (
¯
dê
`
u n `ay câ
`
n thiê
´
t c´o c
.
oc th
´
u
,
ba). Sô
´
lâ
`
n
´ıt nhâ
´
t
¯
dê
,
chuyê
,
n to`an b
.
ô
¯
d˜ıa trong c
.
oc m
.
ôt sang c
.
oc hai l `a bao
nhiêu?
L
`
o
,
i gi
,
ai. K
´
y hi
.
êu M
n
l
`
a sô
´
lâ
`
n nh
,
o nhâ
´
t chuyê
,
n xong n
¯
d
˜
ıa t
`
u
,
c
.
oc m
.
ôt sang c
.
oc hai. R
˜
o r
`
ang M
1
= 1, nhu
,
v
.
ây ta gi
,
a s
,
u
,
n > 1.
Ðê
,
chuyê
,
n
¯
du
,
.
o
,
c
¯
d
˜
ıa du
,
´
o
,
i c
`
ung sang c
.
ôt hai, ta ph
,
ai chuyê
,
n n −1
¯
d
˜
ıa
,
o
,
trên sang c
.
ôt ba. Nhu
,
v
.
ây ta c
´
o sô
´
lâ
`
n chuyê
,
n
´
ıt nhâ
´
t l
`
a
M
n−1
. M
.
ôt lâ
`
n chuyê
,
n
¯
d
˜
ıa to nhâ
´
t sang c
.
ôt th
´
u
,
hai, v
`
a l
.
ai ph
,
ai
th
.
u
,
c hi
.
ên M
n−1
lâ
`
n chuyê
,
n sô
´
n − 1
¯
d
˜
ıa t
`
u
,
c
.
ôt th
´
u
,
ba vê
`
c
.
ôt th
´
u
,
hai. Nhu
,
v
.
ây,
M
n
= 2M
n−1
+ 1, M
1
= 1.
D
˜
ê d
`
ang b
`
˘
ang quy n
.
ap ta ch
´
u
,
ng minh
¯
du
,
.
o
,
c M
n
= 2
n
− 1. Th
.
ât
v
.
ây, v
´
o
,
i n = 1 công th
´
u
,
c
¯
d
´
ung. Gi
,
a s
,
u
,
công th
´
u
,
c
¯
d
´
ung v
´
o
,
i sô
´
n = k,
M
k
= 2
k
−1. Ta x
´
et M
k+1
= 2M
k
+ 1 = 2(2
k
−1) + 1 = 2
k+1
−1,
do
¯
d
´
o công th
´
u
,
c
¯
d
´
ung v
´
o
,
i n = k + 1.
J
2.6. Quy n
.
ap to
´
an h
.
oc v
`
a tô
,
ng qu
´
at ho
´
a
Râ
´
t nhiê
`
u b
`
ai to
´
an d
˜
ê gi
,
ai ho
,
n
,
o
,
d
.
ang tô
,
ng qu
´
at. Nhâ
´
t
l
`
a ch
´
u
,
ng minh b
`
˘
ang phu
,
o
,
ng ph
´
ap quy n
.
ap khi d
.
u
,
¯
do
´
an gi
,
a
thiê
´
t quy n
.
ap. Ch
,
˘
ang h
.
an nhu
,
ta ph
,
ai ch
´
u
,
ng minh d
˜
ay m
.
ênh
¯
dê
`
P(1), P(2), . . . không c
´
o
¯
d
,
u thông tin
¯
dê
,
th
.
u
,
c hi
.
ên bu
,
´
o
,
c quy
n
.
ap. Trong tru
,
`
o
,
ng h
.
o
,
p
¯
d
´
o ta x
´
et d
˜
ay m
.
ênh
¯
dê
`
tô
,
ng qu
´
at ho
,
n
Q(1), Q(2), . . . m
`
a v
´
o
,
i m
˜
ôi n m
.
ênh
¯
dê
`
Q(n) k
´
eo theo P(n), v
`
a sau
¯
d
´
o ta l
.
ai
´
ap d
.
ung phu
,
o
,
ng ph
´
ap quy n
.
ap cho Q(1) , Q(2), Q(3) , . . .
Trong m
.
uc n
`
ay ta x
´
et m
.
ôt sô
´
v
´
ı d
.
u nhu
,
v
.
ây:

52 Chu
,
o
,
ng 2. K
˜
y thu
.
ât d
`
ung phu
,
o
,
ng ph
´
ap quy n
.
ap to
´
an h
.
oc
V
´
ı d
.
u 2.28. T´ınh tô
,
ng
S
n
=
1
2
+
2
2
2
+ ··· +
n
2
n
. (2.24)
L
`
o
,
i gi
,
ai. Ta nh
.
ân x
´
et tô
,
ng trên c
´
o thê
,
viê
´
t l
.
ai l
`
a
S
n
(x) = 1x + 2x
2
+ ··· + nx
n
. (2.25)
Tô
,
ng ta câ
`
n t
´
ınh ch
,
ı l
`
a tru
,
`
o
,
ng h
.
o
,
p riêng c
,
ua (2.25) S
n
(
1
2
). Ta c
´
o
thê
,
d
`
ung k
˜
y thu
.
ât t
´
ınh tô
,
ng
,
o
,
cuô
´
i Chu
,
o
,
ng 1
¯
dê
,
c
´
o công th
´
u
,
c t
´
ınh
tô
,
ng (2.25)(b
.
an
¯
d
.
oc th
.
u
,
c hi
.
ên nhu
,
m
.
ôt b
`
ai t
.
âp). Ta
¯
du
,
a ra công
th
´
u
,
c
,
o
,
¯
dây v
`
a ch
´
u
,
ng minh b
`
˘
ang quy n
.
ap to
´
an h
.
oc:
S(x) =
x − (n + 1 )x
n+1
+ nx
n+2
(1 − x)
2
, (2.26)
v
´
o
,
i x 6= 1.
V
´
o
,
i n = 1
¯
d
,
˘
ang th
´
u
,
c (2.26) c
´
o d
.
ang x =
x − 2x
2
+ x
3
(1 − x)
2
hiê
,
n nhiên
¯
d
´
ung.
Gi
,
a s
,
u
,
(2.26)
¯
d
´
ung v
´
o
,
i sô
´
t
.
u
,
nhiên n. Khi
¯
d
´
o
S
n+1
= x + 2x
2
+ 3x
3
+ ··· + nx
n
+ (n + 1)x
n+1
=
x − (n + 1 )x
n+1
+ nx
n+2
(1 − x)
2
+ (n + 1)x
n+1
=
x − (n + 1 )x
n+1
+ nx
n+2
+ (n + 1)x
n+1
−2(n + 1)x
n+2
+ (n + 1)x
n+3
(1 − x)
2
=
x − (n + 2 )x
n+2
+ (n + 1)x
n+3
(1 − x)
2
.
Nhu
,
v
.
ây (2.26)
¯
d
´
ung v
´
o
,
i n + 1.
Áp d
.
ung (2.26) t
.
ai gi
´
a tr
.
i x =
1
2
ta c
´
o
S
n
(
1
2
) =
1
2
−(n + 1)
1
2
n+1
+ n
1
2
n+2
1
2
2
= 2 −
n + 2
2
n
.
J

2.6. Quy n
.
ap to
´
an h
.
oc v
`
a tô
,
ng qu
´
at ho
´
a 53
V
´
ı d
.
u 2.29. Ch
´
u
,
ng minh r
`
˘ang nê
´
u A
1
+ ··· + A
n
= π, 0 < A
i
≤
π, i = 1, 2, . . . , n, th`ı
sin A
1
+ sin A
2
+ ··· + sin A
n
≤ n sin
π
n
.
L
`
o
,
i gi
,
ai. Ch
´
u
,
ng minh b
`
˘
ang quy n
.
ap to
´
an h
.
oc
¯
dê
´
n bu
,
´
o
,
c quy n
.
ap
k, m
.
ênh
¯
dê
`
P(k)
¯
d
´
ung c
´
o d
.
ang nê
´
u A
1
+ ··· + A
k
= π, 0 < A
i
≤
π, i = 1, 2, . . . , k, th
`
ı
sin A
1
+ ··· + sin A
k
≤ k sin
π
k
.
Ðê
,
ch
´
u
,
ng minh m
.
ênh
¯
dê
`
P(k + 1)
¯
d
´
ung ta cho tru
,
´
o
,
c A
1
+ ··· +
A
k
+ A
k+1
= π, 0 < A
i
≤ π, i = 1, . . . , k + 1 ph
,
ai ch
´
u
,
ng minh
sin A
1
+ ··· + sin A
k
+ sin A
k+1
≤ (k + 1) sin
π
k + 1
.
Nê
´
u ta d
`
ung gi
,
a thiê
´
t quy n
.
ap th
`
ı
sin A
1
+ ··· + sin A
k−1
+ sin(A
k
+ A
k+1
) ≤ k sin
π
k
không thê
,
suy ra
¯
du
,
.
o
,
c bu
,
´
o
,
c tiê
´
p theo. Do vi
.
êc tô
,
ng c
,
ua c
´
ac A
i
b
`
˘
ang π d
˜
ân
¯
dê
´
n h
.
an chê
´
râ
´
t nhiê
`
u khi ch
´
u
,
ng minh. Bây gi
`
o
,
ta
x
´
et m
.
ênh
¯
dê
`
r
.
ông ho
,
n Q(n) :
Nê
´
u 0 < A
i
≤ π, i = 1, . . . , n, khi
¯
d
´
o
sin A
1
+ ··· + sin A
n
≤ n sin
A
1
+ ··· + A
n
n
.
Ta thâ
´
y r
`
˘
ang Q(n) suy ra P(n). r
˜
o r
`
ang Q(1)
¯
d
´
ung. Gi
,
a s
,
u
,
Q(k)

54 Chu
,
o
,
ng 2. K
˜
y thu
.
ât d
`
ung phu
,
o
,
ng ph
´
ap quy n
.
ap to
´
an h
.
oc
¯
d
´
ung, v
`
a gi
,
a s
,
u
,
c
´
o 0 < A
i
≤ π, i = 1, . . . , k + 1, khi
¯
d
´
o
sin A
1
+ ··· + sin A
k
+ sin A
k+1
≤ k sin(
A
1
+ ··· + A
k
k
) + sin A
k+1
= (k + 1)[
k
k + 1
sin(
A
1
+ ··· + A
k
k
) +
1
k + 1
sin A
k+1
]
≤ (k + 1)[sin(
k
k + 1
(
A
1
+ ··· + A
k
k
) +
1
k + 1
A
k+1
)]
≤ (k + 1) sin(
A
1
+ ··· + A
k
+ A
k+1
k + 1
).
Trong biê
´
n
¯
dô
,
i hai bâ
´
t
¯
d
,
˘
ang th
´
u
,
c sau c
`
ung câ
`
n ph
,
ai ch
´
u
,
ng minh
cho hai g
´
oc c
´
o
¯
d
´
anh gi
´
a nhu
,
trên c
´
o thê
,
ch
´
u
,
ng minh
¯
du
,
.
o
,
c (b
.
an
¯
d
.
oc h
˜
ay kiê
,
m tra l
.
ai). Nhu
,
v
.
ây t
`
u
,
s
.
u
,
¯
d
´
ung
¯
d
´
˘
an c
,
ua m
.
ênh
¯
dê
`
Q(k + 1) suy ra P(k + 1) c
˜
ung
¯
d
´
ung.
J
V
´
ı d
.
u 2.30. Cho u
i
l `a sô
´
h
.
ang th
´
u
,
i c
,
ua d ˜ay Fibonacci. Ch
´
u
,
ng
minh r
`
˘ang
u
2
n+1
+ u
2
n
= u
2n+1
.
L
`
o
,
i gi
,
ai. Kh
,
˘
ang
¯
d
.
inh
¯
d
´
ung v
´
o
,
i n = 1. Gi
,
a s
,
u
,
m
.
ênh
¯
dê
`
¯
d
´
ung v
´
o
,
i
n = k. Khi
¯
d
´
o
u
2
k+2
+ u
2
k+1
= (u
k+1
+ u
k
)
2
+ u
2
k+1
= u
2
k+1
+ 2u
k+1
u
k
+ u
2
k
+ u
2
k+1
= (u
2
k+1
+ u
2
k
) + (2u
k+1
u
k
+ u
2
k+1
)
= u
2k+1
+ ( 2u
k+1
u
k
+ u
2
k+1
).
Theo công th
´
u
,
c d
˜
ay Fibonacci th
`
ı bu
,
´
o
,
c quy n
.
ap
¯
du
,
.
o
,
c ch
´
u
,
ng minh
ho
`
an to
`
an nê
´
u ta ch
,
ı ra r
`
˘
ang 2u
k+1
u
k
+ u
2
k+1
= u
2k+2
. Do c
´
o công
th
´
u
,
c
¯
d
´
o nên u
2k+1
+ (2u
k+1
u
k
+ u
2
k+1
) = u
2k+1
+ u
2k+2
= u
2k+3
.
Bây gi
`
o
,
ch
,
ı c
`
on ch
´
u
,
ng minh 2u
k+1
u
k
+ u
2
k+1
= u
2k+2
. Ta c
˜
ung tiê
´
n

2.7. B
`
ai t
.
âp 55
h
`
anh theo quy n
.
ap, v
´
o
,
i n = 1 công th
´
u
,
c
¯
d
´
ung hiê
,
n nhiên, gi
,
a s
,
u
,
¯
d
´
ung v
´
o
,
i n = k ta c
´
o
2u
k+2
u
k+1
+ u
2
k+2
= 2(u
k+1
+ u
k
) u
k+1
+ u
2
k+2
= 2u
2
k+1
+ 2u
k
u
k+1
+ u
2
k+2
= (2u
k+1
u
k
+ u
2
k+1
) + (u
2
k+1
+ u
2
k+2
)
= u
2k+2
+ (u
2
k+1
+ u
2
k+2
).
Ch
´
ung ta l
.
ai vu
,
´
o
,
ng ph
,
ai b
`
ai to
´
an ban
¯
dâ
`
u, nê
´
u
¯
d
,
˘
ang th
´
u
,
c sau
¯
d
´
ung u
2
k+1
+ u
2
k+2
= u
2k+3
. Nê
´
u c
´
o v
.
ây th
`
ı u
2k+2
+ (u
2
k+1
+ u
2
k+2
) =
u
2k+2
+ u
2k+3
= u
2k+4
v
`
a bu
,
´
o
,
c quy n
.
ap phâ
`
n n
`
ay ho
`
an to
`
an xong.
Kê
´
t qu
,
a l
`
a nê
´
u
¯
d
´
ung m
.
ênh
¯
dê
`
th
´
u
,
nhâ
´
t th
`
ı
¯
d
´
ung m
.
ênh
¯
dê
`
th
´
u
,
hai v
`
a ngu
,
.
o
,
c l
.
ai. Th
.
u
,
c ra b
`
ai to
´
an x
´
et hai d
˜
ay m
.
ênh
¯
dê
`
P(n) : u
2
n+1
+ u
2
n+1
= u
2n+1
,
Q(n) : 2u
n+2
u
n+1
+ u
2
n+2
= u
2n+2
.
P(1) v
`
a Q(1)
¯
dê
`
u
¯
d
´
ung. Theo l
´
y lu
.
ân c
,
ua phâ
`
n trên thâ
´
y r
`
˘
ang
P(k) v
`
a Q(k)
¯
d
´
ung suy ra P(k + 1)
¯
d
´
ung, v
`
a v
´
o
,
i P( k + 1) v
`
a Q(k)
l
.
ai suy ra Q(k + 1)
¯
d
´
ung. Nhu
,
v
.
ây t
`
u
,
P(k) v
`
a Q(k) suy ra P(k + 1)
v
`
a Q(k + 1)
¯
dê
`
u
¯
d
´
ung.
J
2.7. B
`
ai t
.
âp
.
.
. 2.31. Cho x
1
< x
2
< . . . < x
n
l
`
a nh
˜
u
,
ng sô
´
nguyên du
,
o
,
ng.
Ch
´
u
,
ng minh bâ
´
t
¯
d
,
˘
ang th
´
u
,
c
(x
5
1
+ x
5
2
+ ···+ x
5
n
) + (x
7
1
+ x
7
2
+ ···+ x
7
n
) ≥ 2(x
3
1
+ x
3
2
+ ···+ x
3
n
)
2
.
(2.27)
Ch
´
u
,
ng minh r
`
˘
ang
¯
d
,
˘
ang th
´
u
,
c ch
,
ı xâ
,
y ra khi v
`
a ch
,
ı khi x
k
= k
( k = 1, 2, . . . , n).

56 Chu
,
o
,
ng 2. K
˜
y thu
.
ât d
`
ung phu
,
o
,
ng ph
´
ap quy n
.
ap to
´
an h
.
oc
.
.
. 2.32. Ch
´
u
,
ng minh bâ
´
t
¯
d
,
˘
ang th
´
u
,
c
(a
1
+ a
2
+ ··· + a
k
)
2
≤ k(a
2
1
+ a
2
2
+ ··· + a
2
k
), (2.28)
,
o
,
¯
dây k ≥ 1 l
`
a sô
´
t
.
u
,
nhiên v
`
a a
1
, a
2
, . . . , a
k
l
`
a nh
˜
u
,
ng sô
´
th
.
u
,
c bâ
´
t
k
`
y.
.
.
. 2.33. Cho f (x) = (x
2
−1)
1/2
, x > 1. Ch
´
u
,
ng minh r
`
˘
ang f
(n)
(x) >
0 v
´
o
,
i n l
,
e v
`
a f
(n)
(x) < 0 v
´
o
,
i n ch
˜
˘
an.
.
.
. 2.34. Ch
´
u
,
ng minh r
`
˘
ang phu
,
o
,
ng tr
`
ınh x
2
+ y
2
= z
n
c
´
o nghi
.
êm
nguyên (x, y, z) v
´
o
,
i m
.
oi n = 1, 2, 3, . . .

CHU
,
O
,
NG 3
T
`
IM CÔNG TH
´
U
,
C TÔ
,
NG QU
´
AT
3.1. Câ
´
p sô
´
c
.
ông v
`
a câ
´
p sô
´
nhân . . . . . . . . . . . . . . . . . . . . . . . . 57
3.2. T
´
ınh tô
,
ng v
`
a sô
´
h
.
ang tô
,
ng qu
´
at . . . . . . . . . . . . . . . . . . . . . . 66
3.3. Phu
,
o
,
ng tr
`
ınh truy hô
`
i tuyê
´
n t
´
ınh . . . . . . . . . . . . . . . . . . . . . . 71
3.4. Tô
,
ng c
,
ua nh
˜
u
,
ng l
˜
uy th
`
u
,
a c
`
ung b
.
âc c
´
ac sô
´
t
.
u
,
nhiên 84
3.5. B
`
ai t
.
âp. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 87
Phu
,
o
,
ng ph
´
ap quy n
.
ap to
´
an h
.
oc gô
`
m hai bu
,
´
o
,
c nhu
,
hai chu
,
o
,
ng
tru
,
´
o
,
c ta
¯
d
˜
a kh
,
ao s
´
at. Bu
,
´
o
,
c co
,
s
,
o
,
chuyê
,
n sang bu
,
´
o
,
c gi
,
a thiê
´
t quy
n
.
ap l
`
a râ
´
t quan tr
.
ong, n
´
o
¯
d
`
oi h
,
oi nhiê
`
u kinh nghi
.
êm gi
,
ai to
´
an,
ph
´
an
¯
do
´
an
¯
d
´
ung,
¯
du
,
a ra kh
,
˘
ang
¯
d
.
inh chung ch
´
ınh x
´
ac v
`
a c
´
o l
´
y.
Chu
,
o
,
ng n
`
ay ta d
`
u
,
ng l
.
ai vi
.
êc thiê
´
t l
.
âp m
.
ôt sô
´
c
´
ach t
`
ım công th
´
u
,
c
tô
,
ng qu
´
at cho c
´
ac m
.
ênh
¯
dê
`
kh
,
˘
ang
¯
d
.
inh l
`
a d
˜
ay sô
´
. Sau khi t
`
ım ra
tô
,
ng ta c
´
o thê
,
ch
´
u
,
ng minh b
`
˘
ang quy n
.
ap to
´
an h
.
oc.
3.1. Câ
´
p sô
´
c
.
ông v
`
a câ
´
p sô
´
nhân
Trong c
´
ac chu
,
o
,
ng tr
`
ınh phô
,
thông ta
¯
d
˜
a h
.
oc câ
´
p sô
´
c
.
ông v
`
a
câ
´
p sô
´
nhân,
,
o
,
¯
dây ta nh
´
˘
ac l
.
ai hai công th
´
u
,
c t
´
ınh tô
,
ng nhu
,
ng
¯
du
,
.
o
,
c ch
´
u
,
ng minh b
`
˘
ang quy n
.
ap.
V
´
ı d
.
u 3.1. Ch
´
u
,
ng minh
¯
d
,
˘ang th
´
u
,
c sau:
1 + q + q
2
+ ··· + q
n
=
1 −q
n+1
1 −q
, (3.1)

58 Chu
,
o
,
ng 3. T
`
ım công th
´
u
,
c tô
,
ng qu
´
at
v
´
o
,
i m
.
oi q 6= 1 v`a v
´
o
,
i m
.
oi n = 0, 1, 2, . . . (câ
´
p sô
´
nhân).
L
`
o
,
i gi
,
ai. Gi
,
a thiê
´
t quy n
.
ap c
´
o ngay trong
¯
dâ
`
u b
`
ai.
Ð
.
˘
at S
n
= 1 + q + ··· + q
n
. V
´
o
,
i n = 0, S
0
= 1 công th
´
u
,
c (3.1)
¯
d
´
ung.
Gi
,
a s
,
u
,
v
´
o
,
i sô
´
t
.
u
,
nhiên n = k n
`
ao
¯
d
´
o ta c
´
o
¯
d
,
˘
ang th
´
u
,
c
S
k
=
1 −q
k+1
1 −q
.
Ta s
˜
e ch
´
u
,
ng minh
¯
d
,
˘
ang th
´
u
,
c
¯
d
´
ung v
´
o
,
i sô
´
t
.
u
,
nhiên tiê
´
p theo,
ngh
˜
ıa l
`
a
S
k+1
=
1 −q
k+2
1 −q
.
Th
.
ât v
.
ây,
S
k+1
= S
k
+ q
k+1
=
1 −q
k+1
1 −q
+ q
k+1
=
1 −q
k+2
1 −q
.
J
V
´
ı d
.
u 3.2. Cho b v `a d l `a hai sô
´
. T`ım sô
´
h
.
ang tô
,
ng qu ´at a
n
c
,
ua
d ˜ay,
¯
du
,
.
o
,
c x ´ac
¯
d
.
inh theo công th
´
u
,
c sau (câ
´
p sô
´
c
.
ông):
a
1
= b, a
n
= a
n−1
+ d (n = 2, 3, . . .).
L
`
o
,
i gi
,
ai. Ta câ
`
n t
`
ım sô
´
h
.
ang a
n
theo nh
˜
u
,
ng sô
´
¯
d
˜
a cho b v
`
a d, c
˜
ung
nhu
,
ch
,
ı sô
´
n
¯
d
˜
a cho. Ta t
´
ınh m
.
ôt sô
´
gi
´
a tr
.
i: a
1
= b, a
2
= a
1
+ d =
b + d, a
3
= a
2
+ d = (b + d) + d = b + 2d, a
4
= a
3
+ d = b + 3d. D
˜
ê
d
`
ang
¯
du
,
a ra gi
,
a thiê
´
t quy n
.
ap
a
n
= b + (n −1).d. (3.2)
Ta s
˜
e ch
´
u
,
ng minh (3.2)
¯
d
´
ung v
´
o
,
i m
.
oi sô
´
t
.
u
,
nhiên n. Th
.
ât v
.
ây,
Bu
,
´
o
,
c co
,
s
,
o
,
: V
´
o
,
i n = 1, (3.2)
¯
d
´
ung v
´
o
,
i c
´
ach t
´
ınh phâ
`
n trên.

3.1. Câ
´
p sô
´
c
.
ông v
`
a câ
´
p sô
´
nhân 59
Bu
,
´
o
,
c quy n
.
ap: Gi
,
a s
,
u
,
(3.2)
¯
d
´
ung v
´
o
,
i sô
´
t
.
u
,
nhiên n n
`
ao
¯
d
´
o. Khi
¯
d
´
o, t
`
u
,
(3.2) cho ta kê
´
t qu
,
a
a
n+1
= a
n
+ d = [b + (n −1)d] + d = b + nd.
Nhu
,
v
.
ây (3.2)
¯
d
´
ung v
´
o
,
i m
.
oi sô
´
t
.
u
,
nhiên n.
J
Bây gi
`
o
,
ta x
´
et câ
´
p sô
´
c
.
ông v
`
a câ
´
p sô
´
nhân m
`
a công sai v
`
a công
b
.
ôi c
,
ua ch
´
ung không l
`
a h
`
˘
ang sô
´
, ch
´
ung biê
´
n
¯
dô
,
i nhu
,
sô
´
h
.
ang tô
,
ng
qu
´
at c
,
ua câ
´
p sô
´
c
.
ông ho
.
˘
ac câ
´
p sô
´
nhân.
V
´
ı d
.
u 3.3. Cho m
.
ôt d ˜ay sô
´
n sô
´
h
.
ang
a
1
= a
1
, a
2
= a
1
+ d
1
, a
3
= a
2
+ d
2
, . . . , a
n
= a
n−1
+ d
n−1
, (3.3)
,
o
,
¯
dây d ˜ay sô
´
d
1
, d
2
, . . . , d
n−1
l `a m
.
ôt câ
´
p sô
´
c
.
ông v
´
o
,
i công sai d 6= 0
(câ
´
p sô
´
c
.
ông-c
.
ông) . Ch
´
u
,
ng minh r
`
˘ang
a
k
= a
1
+ (k −1 )d
1
+
1
2
( k −1)(k −2)d , (3.4)
S
n
= n(a
1
+ d −d
1
) +
n(n − 1)(2d
1
−3d)
4
+
n(n + 1)(2n + 1)d
12
.
(3.5)
L
`
o
,
i gi
,
ai. Công th
´
u
,
c trên c
´
o thê
,
ch
´
u
,
ng minh b
`
˘
ang phu
,
o
,
ng ph
´
ap
quy n
.
ap nhu
,
ng
¯
dê
,
ng
´
˘
an g
.
on ta ch
,
ı d
`
ung phu
,
o
,
ng ph
´
ap t
´
ınh to
´
an
v
`
a biê
´
n
¯
dô
,
i. D
˜
ay sô
´
(3.3) g
.
oi l
`
a câ
´
p sô
´
c
.
ông-c
.
ông v
´
o
,
i sô
´
h
.
ang th
´
u
,
k, a
k
, công sai th
´
u
,
k, d
k
v
`
a công sai d. D
˜
ê d
`
ang c
´
o a
k
= a
1
+ d
1
+
d
2
+ ··· + d
k−1
. V
´
o
,
i d
˜
ay sô
´
l
`
a c
´
ac sô
´
gia c
,
ua (3.3) ta c
´
o
d
k
= d
1
+ (k −1 )d,
d
1
+ d
2
+ ··· + d
k
=
d
1
+ d
k
2
k =
2d
1
+ (k −1 )d
2
k.
V
.
ây
a
k
= a
1
+ (k −1 )d
1
+
1
2
( k −1)(k −2)d .

60 Chu
,
o
,
ng 3. T
`
ım công th
´
u
,
c tô
,
ng qu
´
at
Tô
,
ng c
,
ua nh
˜
u
,
ng sô
´
h
.
ang câ
´
p sô
´
c
.
ông-c
.
ông t
´
ınh
¯
du
,
.
o
,
c nhu
,
sau:
S
n
=
n
∑
k=1
a
k
=
n
∑
k=1
[(a
1
+ d −d
1
) + (d
1
−
3
2
d)k +
d
2
k
2
]
= n(a
1
+ d −d
1
) + (d
1
−
3
2
d)
n
∑
k=1
k +
d
2
n
∑
k=1
k
2
,
T
`
u
,
¯
dây suy ra công th
´
u
,
c (3.5).
J
V
´
ı d
.
u 3.4. Cho m
.
ôt d ˜ay sô
´
n sô
´
h
.
ang
a
1
= a
1
, a
2
= a
1
+ d
1
, a
3
= a
2
+ d
2
, . . . , a
n
= a
n−1
+ d
n−1
,
,
o
,
¯
dây d ˜ay sô
´
d
1
, d
2
, . . . , d
n−1
l `a m
.
ôt câ
´
p sô
´
nhân v
´
o
,
i công b
.
ôi q 6= 1
(câ
´
p sô
´
c
.
ông-nhân). Ch
´
u
,
ng minh r
`
˘ang
a
k
= a
1
+
d
1
( q
k−1
−1)
q −1
(3.6)
S
n
= n(a
1
+
d
1
1 −q
) +
d
1
( q
n
−1)
( q −1)
2
. (3.7)
L
`
o
,
i gi
,
ai. T
`
u
,
gi
,
a thiê
´
t c
,
ua b
`
ai to
´
an v
`
a công th
´
u
,
c cho câ
´
p sô
´
c
.
ông
v
`
a câ
´
p sô
´
nhân ta c
´
o công th
´
u
,
c
d
k
= d
1
q
k−1
, d
1
+ d
2
+ ··· + d
k
=
d
1
( q
k
−1)
q −1
.
Ta d
˜
ê d
`
ang t
´
ınh
¯
du
,
.
o
,
c
a
k
= a
1
+ d
1
+ d
2
+ ··· + d
k−1
= a
1
+
d
1
( q
k−1
−1)
q −1
.
T
`
u
,
¯
d
,
˘
ang th
´
u
,
c sau c
`
ung suy ra
S
n
=
n
∑
k=1
a
k
=
n
∑
k=1
[(a
1
+
d
1
1 −q
) +
d
1
q −1
q
k−1
]
= n(a
1
+
d
1
1 −q
) +
d
1
( q
n
−1)
( q −1)
2
.
J

3.1. Câ
´
p sô
´
c
.
ông v
`
a câ
´
p sô
´
nhân 61
V
´
ı d
.
u 3.5. Cho d ˜ay h
˜
u
,
u h
.
an n sô
´
a
1
= a
1
, a
2
= a
1
q
1
, a
3
= a
2
q
2
, . . . , a
n
= a
n−1
q
n−1
, (3.8)
,
o
,
¯
dây d˜ay sô
´
q
1
, q
2
, . . . , q
n−1
l `a câ
´
p sô
´
c
.
ông v
´
o
,
i công sai d 6= 0. D ˜ay
sô
´
(3.8) g
.
oi l `a câ
´
p sô
´
nhân-c
.
ông v
´
o
,
i sô
´
h
.
ang th
´
u
,
k, a
k
, công b
.
ôi
th
´
u
,
k, q
k
v `a công sai d. H˜ay l
.
âp công th
´
u
,
c t´ınh sô
´
h
.
ang tô
,
ng qu ´at
c
,
ua câ
´
p sô
´
nhân-c
.
ông v `a tô
,
ng nh
˜
u
,
ng sô
´
h
.
ang
¯
dâ
`
u c
,
ua n´o.
L
`
o
,
i gi
,
ai. V
`
ı q
k
= q
1
+ (k −1 )d, th
`
ı ta c
´
o
a
k
= a
1
q
1
q
2
. . . q
k−1
= a
1
k−1
∏
l=1
q
l
= a
1
k−1
∏
l=1
[q
1
+ (l −1)d]
= a
1
[q
k−1
1
+ S
k−2
1
dq
k−2
1
+ S
k−2
2
d
2
q
k−3
1
+ ··· + S
k−2
k−3
d
k−3
q
2
1
+ S
k−2
k−2
d
k−2
q
1
]
ho
.
˘
ac l
`
a
a
k
=
a
1
k−2
∑
l=0
S
k−2
l
d
l
q
k−l−1
1
, v
´
o
,
i k=2, 3, . . . , n ;
a
1
v
´
o
,
i k=1 ,
,
o
,
¯
dây S
n
0
= 1 v
´
o
,
i n = 0, 1, 2, . . ., c
`
on S
n
i
v
´
o
,
i 0 < i ≤ n v
`
a i nguyên,
l
`
a tô
,
ng c
,
ua tâ
´
t c
,
a c
´
ac t
´
ıch d
.
ang p
1
p
2
..p
i
, Nh
˜
u
,
ng th
`
u
,
a sô
´
c
,
ua m
˜
ôi
t
´
ıch l
`
a i sô
´
, ho
`
an to
`
an kh
´
ac nhau v
`
a nh
.
ân gi
´
a tr
.
i nguyên t
`
u
,
1
¯
dê
´
n
n. Nê
´
u trong tô
,
ng S
n
i
ta nh
´
om nh
˜
u
,
ng sô
´
h
.
ang không ch
´
u
,
a sô
´
n
nhu
,
m
.
ôt sô
´
h
.
ang, v
`
a c
´
ac sô
´
h
.
ang c
´
o ch
´
u
,
a n nhu
,
m
.
ôt th
`
u
,
a sô
´
, v
`
a
sau
¯
d
´
o
,
o
,
nh
´
om th
´
u
,
hai ta
¯
du
,
a n ra ngo
`
ai ngo
.
˘
ac, ta s
˜
e nh
.
ân
¯
du
,
.
o
,
c
S
n
i
= S
n−1
i
+ nS
n−1
i −1
. (3.9)
Ta d
`
ung (3.9) viê
´
t c
´
ac gi
´
a tr
.
i S
n
i
v
`
ao b
,
ang tam gi
´
ac m
,
o
,
r
.
ông
¯
dê
´
n
vô c
`
ung nhu
,
sau
62 Chu
,
o
,
ng 3. T
`
ım công th
´
u
,
c tô
,
ng qu
´
at
t 0 1 2 3 4 5 6 7 . . .
0 1 . . .
1 1 1 . . .
2 1 3 2 . . .
3 1 6 11 6 . . .
4 1 10 35 50 24 . . .
5 1 15 85 225 274 120 . . .
6 1 21 175 735 1624 1764 720 . . .
7 1 28 322 1960 6769 13132 13068 5040 . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. . . .
B
,
ang trên c
´
o nhiê
`
u t
´
ınh châ
´
t râ
´
t hay, v
´
ı d
.
u
¯
du
,
`
o
,
ng ch
´
eo l
`
a
a
n
= n!, n = 0, 1, 2, . . ., nhu
,
ng ta không nghiên c
´
u
,
u
,
o
,
¯
dây.
Bây gi
`
o
,
ta t
`
ım công th
´
u
,
c tô
,
ng S
n
c
,
ua câ
´
p sô
´
nhân-c
.
ông. T
`
u
,
(3.9) ta c
´
o
¯
d
,
˘
ang th
´
u
,
c
a
1
= a
1
,
a
2
= a
1
S
0
0
q
1
,
a
3
= a
1
( S
1
0
.q
2
1
+ S
1
1
.d.q
1
)
...............................
a
k
= a
1
( S
k−2
0
q
k−1
1
+ S
k−2
1
dq
k−2
1
+ ··· + S
k−2
k−2
d
k−2
q
1
)
C
.
ông theo vê
´
c
,
ua c
´
ac
¯
d
,
˘
ang th
´
u
,
c trên v
`
a s
´
˘
ap xê
´
p theo sô
´
m
˜
u
t
˘
ang dâ
`
n c
,
ua q
1
ta nh
.
ân
¯
du
,
.
o
,
c
S
k
= a
1
[1 + q
1
1
(1 + S
1
1
d
1
+ S
2
2
d
2
+ ··· + S
k−2
k−1
d
k−2
)
+ q
2
1
(1 + S
2
1
d
1
+ S
3
2
d
2
+ ··· + S
k−2
k−3
d
k−3
) + ···
+ q
k−2
1
(1 + S
k−2
1
d) + q
k−1
1
],
ho
.
˘
ac l
`
a
S
n
= a
1
[1 +
n−1
∑
i =1
(
n−i−1
∑
k=0
S
i +k−1
k
d
k
) q
i
1
].
J

3.1. Câ
´
p sô
´
c
.
ông v
`
a câ
´
p sô
´
nhân 63
V
´
ı d
.
u 3.6. Cho d ˜ay h
˜
u
,
u h
.
an n sô
´
a
1
= a
1
, a
2
= a
1
q
1
, a
3
= a
2
q
2
, . . . , a
n
= a
n−1
q
n−1
, (3.10)
,
o
,
¯
dây d ˜ay sô
´
q
1
, q
2
, .., q
n−1
l `a câ
´
p sô
´
nhân v
´
o
,
i công b
.
ôi q 6= 1. D ˜ay
sô
´
h
˜
u
,
u h
.
an trên g
.
oi l `a câ
´
p sô
´
nhân-nhân v
´
o
,
i th
`
u
,
a sô
´
th
´
u
,
k l `a a
k
,
k-công b
.
ôi l `a q
k
v `a công b
.
ôi q. H ˜ay l
.
âp công th
´
u
,
c t´ınh sô
´
h
.
ang
tô
,
ng qu´at v`a tô
,
ng n sô
´
h
.
ang
¯
dâ
`
u tiên c
,
ua d˜ay câ
´
p sô
´
nhân-nhân.
L
`
o
,
i gi
,
ai. Ta
¯
d
˜
a biê
´
t q
k
= q
1
q
k−1
, khi
¯
d
´
o
a
k
= a
1
q
1
q
2
. . . q
k−1
= a
1
q
k−1
1
q
1+2+3+···+(k−2)
hay l
`
a
a
k
= a
1
q
k−1
1
q
( k −2)(k −1)
2
,
S
n
=
n
∑
k=1
a
k
= a
1
q
n
∑
k=1
q
k−1
1
q
k(k −3)
2
.
Nh
˜
u
,
ng d
˜
ay sô
´
,
o
,
c
´
ac b
`
ai t
.
âp trên g
.
oi l
`
a c
´
ac d
˜
ay c
.
˘
ap
¯
dôi. Ðê
,
m
,
o
,
r
.
ông ho
,
n n
˜
u
,
a d
.
u
,
a trên co
,
s
,
o
,
c
,
ua câ
´
p sô
´
c
.
ông v
`
a câ
´
p sô
´
nhân
ngu
,
`
o
,
i ta l
.
ai gh
´
ep thêm c
´
ac câ
´
p sô
´
c
.
˘
ap
¯
dôi m
.
ôt lâ
`
n n
˜
u
,
a, ta lâ
´
y v
´
ı
d
.
u sau: Ta x
´
et d
˜
ay h
˜
u
,
u h
.
an t
`
u
,
n sô
´
b
1
, b
2
= b
1
+ a
1
, b
3
= b
2
+ a
2
, . . . , b
n
= b
n−1
+ a
n−1
,
o
,
¯
dây d
˜
ay sô
´
a
1
, a
2
, . . . , a
n−1
l
`
a câ
´
p sô
´
c
.
ông-c
.
ông v
´
o
,
i công sai d v
`
a
công sai th
´
u
,
k l
`
a d
k
. Khi
¯
d
´
o v
`
ı b
k
= b
1
+ a
1
+ a
2
+ ··· + a
k−1
v
`
a v
`
ı
(3.4) ta t
`
ım
¯
du
,
.
o
,
c sô
´
h
.
ang th
´
u
,
k c
,
ua câ
´
p sô
´
c
.
˘
ap ba
b
k
= b
1
+ (k −1)(a
1
+ d −d
1
) +
( k −1)k(2d
1
−3d)
4
+
( k −1)k(2k − 1)d
12
.
(3.11)

64 Chu
,
o
,
ng 3. T
`
ım công th
´
u
,
c tô
,
ng qu
´
at
Tô
,
ng nh
˜
u
,
ng sô
´
h
.
ang c
,
ua d
˜
ay ta t
`
ım
¯
du
,
.
o
,
c
S
n
=
n
∑
k=1
b
k
=
n
∑
k=1
[(b
1
+ d
1
− a
1
−d)
+ k(a
1
−
3
2
d
1
+
11
6
d) + k
2
(
d
1
2
−d) + k
2
d
6
].
Ta nh
.
ân
¯
du
,
.
o
,
c
S
n
= n(b
1
+ d
1
− a
1
−d) +
n(n + 1)(6a
1
−9d
1
+ 11d)
12
(3.12)
+
n(n + 1)(2n + 1)(d
1
−2d)
12
+
n
2
( n + 1)
2
d
24
.
J
Ðê
,
minh h
.
oa
´
ap d
.
ung công th
´
u
,
c trên ta x
´
et b
`
ai t
.
âp:
V
´
ı d
.
u 3.7. T`ım sô
´
h
.
ang tô
,
ng qu ´at c
,
ua d ˜ay câ
´
p sô
´
c
.
˘ap ba sau
¯
dây
2, 5, 9, 17, 32, 57, 95, . . . (3.13)
v `a t´ınh tô
,
ng n sô
´
h
.
ang
¯
dâ
`
u tiên.
L
`
o
,
i gi
,
ai. D
˜
ay t
.
ao ra b
,
o
,
i nh
˜
u
,
ng hi
.
êu liên tiê
´
p c
,
ua d
˜
ay
¯
d
˜
a cho l
`
a
3, 4, 8, 15, 25, 38, . . .
Tiê
´
p t
.
uc t
.
ao ra d
˜
ay gô
`
m nh
˜
u
,
ng hi
.
êu c
,
ua c
´
ac phâ
`
n t
,
u
,
l
`
a
1, 4, 7, 10, 13, . . . (3.14)
¯
dây l
`
a câ
´
p sô
´
c
.
ông c
´
o sô
´
h
.
ang
¯
dâ
`
u tiên l
`
a d
1
= 1 v
`
a công sai d = 3.
V
`
ı b
1
= 2, a
1
= 3, theo công th
´
u
,
c (3.11) sô
´
h
.
ang tô
,
ng qu
´
at cho d
˜
ay
(3.13) l
`
a
b
n
=
1
2
( n
3
−5n
2
+ 14n −6).
Vê
`
tô
,
ng c
,
ua n sô
´
h
.
ang
¯
dâ
`
u theo công th
´
u
,
c (3.12) ta c
´
o
S
n
=
1
24
n(3n
3
−14n
2
+ 57n + 2).
J

3.1. Câ
´
p sô
´
c
.
ông v
`
a câ
´
p sô
´
nhân 65
V
´
ı d
.
u 3.8. T`ım công th
´
u
,
c t´ınh tô
,
ng
S
n
= 3.2 + 5.5 + 7.8 + ··· + (2n + 1)(3n −1).
L
`
o
,
i gi
,
ai. Nê
´
u ch
´
ung ta l
.
ai l
.
˘
ap l
.
ai c
´
ach th
,
u
,
mâ
´
y gi
´
a tr
.
i ban
¯
dâ
`
u
v
`
a mâ
`
y m
`
o t
`
ım kê
´
t qu
,
a th
`
ı kh
´
a vâ
´
t v
,
a. Ta h
˜
ay nh
`
ın k
˜
y v
`
ao
¯
dê
`
b
`
ai v
`
a
¯
d
.
˘
at sô
´
h
.
ang tô
,
ng qu
´
at a
n
= (2n + 1)(3n −1). Ta thâ
´
y r
`
˘
ang
th
`
u
,
a sô
´
th
´
u
,
nhâ
´
t l
`
a câ
´
p sô
´
c
.
ông v
`
a th
`
u
,
a sô
´
th
´
u
,
hai c
˜
ung l
`
a câ
´
p sô
´
c
.
ông. Câu h
,
oi
¯
d
.
˘
at ra l
`
a d
.
u
,
a v
`
ao công th
´
u
,
c
¯
d
˜
a c
´
o c
,
ua câ
´
p sô
´
c
.
ông
c
´
o t
´
ınh
¯
du
,
.
o
,
c tô
,
ng S
n
,
o
,
trên không? B
`
ai to
´
an c
´
o thê
,
ph
,
ai
¯
du
,
a vê
`
tru
,
`
o
,
ng h
.
o
,
p tô
,
ng qu
´
at ho
,
n:
T
´
ınh tô
,
ng S
n
= a
1
b
1
+ a
2
b
2
+ ···+ a
n
b
n
v
´
o
,
i a
1
, a
2
, . . . , a
n
l
`
a câ
´
p
sô
´
c
.
ông c
´
o công sai d
a
v
`
a b
1
, b
2
, . . . , b
n
l
`
a câ
´
p sô
´
c
.
ông c
´
o công sai
d
b
. Ta c
´
o
S
n
=
n
∑
k=1
a
k
b
k
=
n
∑
k=1
[a
1
+ (k −1 )d
a
].b
k
=
n
∑
k=1
[(a
1
−d
a
) + kd
a
].b
k
= (a
1
−d
a
)
n
∑
k=1
b
k
+ d
a
n
∑
k=1
k.b
k
= (a
1
−d
a
)
2b
1
+ (n −1)d
b
2
n + d
a
n
∑
k=1
k.[(b
1
−d
b
) + kd
b
]
= (a
1
−d
a
)
2b
1
+ (n −1)d
b
2
n + d
a
( b
n
∑
k=1
k + d
a
d
b
n
∑
k=1
k
2
= (a
1
−d
a
)(b
1
−d
b
) n +
1
2
[d
a
( b
1
−d
b
) + d
b
(a
1
−d
a
)]n(n + 1)+
+
1
6
d
a
d
b
n(n + 1)(2n + 1).
Ho
.
˘
ac l
`
a
S
n
=
1
3
d
a
d
b
n
3
+
1
2
( d
a
b
1
+ d
b
a
1
−d
a
d
b
) n
2
+
1
6
(6a
1
b
1
−3d
b
a
1
−3d
a
b
1
+ d
a
d
b
) n. (3.15)

66 Chu
,
o
,
ng 3. T
`
ım công th
´
u
,
c tô
,
ng qu
´
at
Áp d
.
ung công th
´
u
,
c (3.15) v
`
ao v
´
ı d
.
u trên v
´
o
,
i a
1
= 3, d
a
= 2, b
1
=
2, d
b
= 3. Ta c
´
o kê
´
t qu
,
a
S
n
=
1
2
n(4n
2
+ 7n + 1).
Công th
´
u
,
c tô
,
ng qu
´
at trên
¯
d
˜
a t
´
ınh
¯
du
,
.
o
,
c qua tr
.
u
,
c tiê
´
p biê
´
n
¯
dô
,
i. V
´
o
,
i
công th
´
u
,
c n
`
ay ta c
˜
ung c
´
o thê
,
ch
´
u
,
ng minh b
`
˘
ang quy n
.
ap to
´
an h
.
oc
(d
`
anh cho b
.
an
¯
d
.
oc). Nhu
,
ng nhiê
`
u khi ch
´
u
,
ng minh b
`
˘
ang quy n
.
ap
to
´
an h
.
oc d
˜
ân
¯
dê
´
n biê
´
n
¯
dô
,
i biê
,
u th
´
u
,
c vô c
`
ung ph
´
u
,
c t
.
ap l
`
am n
,
an
l
`
ong ch
´
ung ta. M
˜
ôi phu
,
o
,
ng ph
´
ap ch
,
ı m
.
anh v
´
o
,
i m
.
ôt l
´
o
,
p b
`
ai to
´
an
n
`
ao
¯
d
´
o thôi.
3.2. T
´
ınh tô
,
ng v
`
a sô
´
h
.
ang tô
,
ng qu
´
at
Chu
,
o
,
ng tru
,
´
o
,
c ta
¯
d
˜
a quan s
´
at c
´
ac phu
,
o
,
ng
´
an kh
´
ac nhau c
,
ua
phu
,
o
,
ng ph
´
ap quy n
.
ap, nhiê
`
u khi
¯
di t
`
ım m
.
ôt sô
´
h
.
ang tô
,
ng qu
´
at
ho
.
˘
ac m
.
ôt tô
,
ng c
,
ua m
.
ôt d
˜
ay ngu
,
`
o
,
i ta
´
ap d
.
ung phu
,
o
,
ng ph
´
ap quy
n
.
ap to
´
an h
.
oc m
.
ôt c
´
ach hiê
,
n nhiên do c
´
ac bu
,
´
o
,
c hô
`
i quy liên tiê
´
p
m
`
a ta t
`
ım
¯
du
,
.
o
,
c công th
´
u
,
c tô
,
ng qu
´
at. Nh
˜
u
,
ng v
´
ı d
.
u sau
¯
dây minh
h
.
oa phu
,
o
,
ng ph
´
ap quy n
.
ap n
`
ay.
V
´
ı d
.
u 3.9. D
˜
ây sô
´
a
0
, a
1
, a
2
, . . .
¯
du
,
.
o
,
c xây d
.
u
,
ng theo c ´ach sau: Hai
sô
´
¯
dâ
`
u a
0
v `a a
1
l `a nh
˜
u
,
ng sô
´
¯
d ˜a cho, m
˜
ôi sô
´
sau
¯
d´o l `a trung b`ınh
c
.
ông c
,
ua hai sô
´
tru
,
´
o
,
c
¯
d´o. H ˜ay biê
,
u di
˜
ên a
n
theo a
0
, a
1
v `a n.
L
`
o
,
i gi
,
ai. Ta c
´
o
a
2
=
a
0
+ a
1
2
, a
3
=
a
1
+ a
2
2
, a
4
=
a
2
+ a
3
2
, a
5
=
a
3
+ a
4
2
, . . .
t
`
u
,
¯
d
´
o suy ra
a
2
− a
1
=
a
0
− a
1
2
, a
3
− a
2
=
a
1
− a
2
2
, a
4
− a
3
=
a
2
− a
3
2
, . . .

3.2. T
´
ınh tô
,
ng v
`
a sô
´
h
.
ang tô
,
ng qu
´
at 67
Suy ra
a
2
− a
1
= −
a
1
− a
0
2
a
3
− a
2
= −
a
2
− a
1
2
=
a
1
− a
0
2
2
a
4
− a
3
= −
a
3
− a
2
2
= −
a
1
− a
0
2
3
................
D
˜
ê thâ
´
y r
`
˘
ang (phu
,
o
,
ng ph
´
ap quy n
.
ap to
´
an h
.
oc
¯
du
,
.
o
,
c
´
ap d
.
ung
,
o
,
¯
dây)
a
n
− a
n−1
= (−1)
n−1
a
1
− a
0
2
n−1
.
C
.
ông theo vê
´
c
,
ua c
´
ac
¯
d
,
˘
ang th
´
u
,
c trên, ta c
´
o
a
n
− a
1
= −
a
1
− a
0
2
+
a
1
− a
0
2
2
−
a
1
− a
0
2
3
+ ··· + (−1)
n−1
a
1
− a
0
2
n−1
= −
a
1
− a
0
2
(1 −
1
2
+
1
2
2
+ ··· + (−1)
n−2
1
2
n−2
)
=
a
1
− a
0
3
{(−1)
n−1
1
2
n−1
−1}.
T
`
u
,
¯
d
´
o suy ra
a
n
=
2a
1
+ a
0
3
+ (−1)
n−1
a
1
− a
0
3.2
n−1
.
J
V
´
ı d
.
u 3.10. D ˜ay sô
´
a
1
, a
2
, a
3
, . . .
¯
du
,
.
o
,
c x ´ac
¯
d
.
inh theo công th
´
u
,
c
a
1
= 2 v `a a
n
= 3a
n−1
+ 1.
H ˜ay t´ınh a
1
+ a
2
+ ··· + a
n
.
L
`
o
,
i gi
,
ai. Ta x
´
et
¯
d
,
˘
ang th
´
u
,
c a
k
= 3a
k−1
+ 1. Cho k gi
´
a tr
.
i
2, 3, 4, . . . , n v
`
a c
.
ông l
.
ai ta nh
.
ân
¯
du
,
.
o
,
c
n
∑
k=2
a
k
= 3
n
∑
k=2
a
k−1
+ n −1. Ta
¯
d
.
˘
at a
1
+ a
2
+ ···+ a
n
= S. Khi
¯
d
´
o ta c
´
o S − a
1
= 3(S −a
n
) + n −1.
Suy ra
S =
1
2
{3a
n
− a
1
−n + 1}.

68 Chu
,
o
,
ng 3. T
`
ım công th
´
u
,
c tô
,
ng qu
´
at
Ta ch
,
ı c
`
on biê
,
u di
˜
ên a
n
qua a
1
. Ta c
´
o
a
n
= 3a
n−1
+ 1, a
n−1
= 3a
n−2
+ 1.
T
`
u
,
¯
d
´
o suy ra a
n
− a
n−1
= 3(a
n−1
− a
n−2
). V
`
ı thê
´
a
n
− a
n−1
= 3(a
n−1
− a
n−2
) = 3
2
(a
n−2
− a
n−3
) =
= 3
3
(a
n−3
− a
n−4
) = ··· = 3
n−2
(a
2
− a
1
).
Nhu
,
ng a
2
= 3a
1
+ 1 = 7, v
`
ı v
.
ây a
n
− a
n−1
= 5.3
n−2
(quy n
.
ap to
´
an
h
.
oc
¯
d
˜
a d
`
ung
,
o
,
¯
dây). V
´
o
,
i c
´
ac gi
´
a tr
.
i n b
`
˘
ang 2, 3, 4, . . . , n ta c
´
o
a
2
− a
1
= 5.1,
a
3
− a
2
= 5.3,
a
4
− a
3
= 5.3
2
,
. . . . . . . . . . . .
a
n
− a
n−1
= 5.3
n−2
.
C
.
ông theo c
´
ac vê
´
c
,
ua
¯
d
,
˘
ang th
´
u
,
c, ta t
´
ınh
¯
du
,
.
o
,
c
a
n
− a
1
= 5(1 + 3 + 3
2
+ ··· + 3
n−2
) =
5
2
(3
n−1
−1) .
T
`
u
,
biê
,
u th
´
u
,
c c
,
ua S ta c
´
o
S =
1
2
{3(a
n
− a
1
) + 2a
1
−n + 1} =
=
1
2
{
15
2
(3
n−1
−1) + 4 − n + 1} =
1
4
{5(3
n
−1) −2n}.
J
V
´
ı d
.
u 3.11. D ˜ay sô
´
a
1
, a
2
, . . . x ´ac
¯
d
.
inh theo công th
´
u
,
c
a
n
= ka
n−1
+ l (n = 2, 3, . . .). H ˜ay biê
,
u di
˜
ên a
n
theo a
1
, k, l v `a n.
L
`
o
,
i gi
,
ai. Ta c
´
o a
n
= ka
n−1
+ l, a
n−1
= ka
n−2
+ l. Suy ra
a
n
−a
n−1
= k(a
n−1
−a
n−2
) = k
2
(a
n−2
−a
n−3)
= . . . = k
n−2
(a
2
−a
1
),

3.2. T
´
ınh tô
,
ng v
`
a sô
´
h
.
ang tô
,
ng qu
´
at 69
t
`
u
,
¯
d
´
o suy ra
a
2
− a
1
= (a
2
− a
1
),
a
3
− a
2
= k(a
2
− a
1
),
a
4
− a
3
= k
2
(a
2
− a
1
),
. . . . . . . . .
a
n
− a
n−1
= k
n−2
(a
2
− a
1
).
C
.
ông l
.
ai c
´
ac
¯
d
,
˘
ang th
´
u
,
c trên ta c
´
o
a
n
= k
n−1
a
1
+
k
n−1
−1
k − 1
l.
J
V
´
ı d
.
u 3.12. Cho d ˜ay a
1
, a
2
, . . . tho
,
a m ˜an
¯
d
,
˘ang th
´
u
,
c sau:
a
n+1
−2a
n
+ a
n−1
= 1. H ˜ay biê
,
u di
˜
ên a
n
theo a
1
, a
2
v `a n.
L
`
o
,
i gi
,
ai. Ta viê
´
t l
.
ai
¯
d
,
˘
ang th
´
u
,
c du
,
´
o
,
i d
.
ang sau:
a
n+1
− a
n
−(a
n
− a
n−1
) = 1.
Ta
¯
d
.
˘
at a
n
− a
n−1
= x
n
, (n = 2, 3, . . .). Khi
¯
d
´
o ta c
´
o x
n+1
− x
n
= 1.
Thay v
`
ao
¯
d
,
˘
ang th
´
u
,
c sau c
`
ung gi
´
a tr
.
i n b
`
˘
ang 2, 3, . . . , n −1 v
`
a c
.
ông
l
.
ai, ta nh
.
ân
¯
du
,
.
o
,
c x
n
− x
2
= n −2.
Ta l
.
ai thay n = 3, 4, . . . , n v
`
ao a
n
− a
n−1
= x
n
v
`
a c
.
ông l
.
ai ta
nh
.
ân
¯
du
,
.
o
,
c
a
n
− a
2
= x
3
+ x
4
+ ··· + x
n
.
Hay l
`
a
a
n
= a
2
+ x
3
+ x
4
+ ··· + x
n
.
Nhu
,
ng
n
∑
k=3
x
k
=
n
∑
k=3
(x
2
+ k −2)
= (n −2)x
2
+ (n −2) + (n −3) + ··· + 1
= (n −2)x
2
+
( n −1)(n −2)
2
.

70 Chu
,
o
,
ng 3. T
`
ım công th
´
u
,
c tô
,
ng qu
´
at
T
`
u
,
¯
d
´
o suy ra
a
n
= a
2
+ (n −2)x
2
+
( n −1)(n −2)
2
= a
2
+ (n −2)(a
2
− a
1
) +
( n −1)(n −2)
2
=
( n −1)(n −2)
2
+ (n −1)a
2
−(n −2)a
1
.
J
V
´
ı d
.
u 3.13. Cho hai d ˜ay sô
´
a
1
, a
2
, a
3
, . . .
b
1
, b
2
, b
3
, . . .
¯
du
,
.
o
,
c x ´ac
¯
d
.
inh theo công th
´
u
,
c sau:
a
n+1
=
a
n
+ b
n
2
; b
n+1
=
2a
n
b
n
a
n
+ b
n
,
o
,
¯
dây a
0
v `a b
0
l `a nh
˜
u
,
ng sô
´
¯
d ˜a cho a
0
> b
0
> 0. T´ınh a
n
v `a b
n
theo
a
0
, b
0
v `a n.
L
`
o
,
i gi
,
ai. D
˜
ê thâ
´
y r
`
˘
ang a
n+1
b
n+1
= a
n
b
n
, v
`
a suy ra a
n
b
n
= a
0
b
0
v
´
o
,
i m
.
oi sô
´
nguyên n. Nhu
,
ng
√
a
n
−
√
b
n
√
a
n
+
√
b
n
=
a
n
−
√
a
n
b
n
a
n
+
√
a
n
b
n
=
a
n
−
p
a
n−1
b
n−1
a
n
+
p
a
n−1
b
n−1
=
a
n−1
+ b
n−1
2
−
p
a
n−1
b
n−1
a
n−1
+b
n−1
2
+
p
a
n−1
b
n−1
=
√
a
n−1
−
p
b
n−1
√
a
n−1
+
p
b
n−1
!
2
.
Ta
¯
d
.
˘
at
√
a
n
−
√
b
n
√
a
n
+
√
b
n
= u
n
. Khi
¯
d
´
o ta c
´
o
u
n−1
= u
2
n−2
,
u
n−2
= u
2
n−3
,
. . . . . .

3.3. Phu
,
o
,
ng tr
`
ınh truy hô
`
i tuyê
´
n t
´
ınh 71
u
2
= u
2
1
,
u
1
= u
2
0
.
Nâng b
.
âc l
˜
uy th
`
u
,
a c
,
ua c
´
ac
¯
d
,
˘
ang th
´
u
,
c lâ
`
n lu
,
.
o
,
t v
´
o
,
i
1, 2, 2
2
, . . . , 2
n−2
. Ta t
´
ınh
¯
du
,
.
o
,
c u
n−1
= u
2
n−1
0
. Nhu
,
ng
u
n−1
=
√
a
n−1
−
p
b
n−1
√
a
n−1
+
p
b
n−1
=
a
n−1
−
√
a
0
b
0
a
n−1
+
√
a
0
b
0
,
u
0
=
√
a
0
−
√
b
0
√
a
0
+
√
b
0
=
a
0
−
√
a
0
b
0
a
0
+
√
a
0
b
0
.
Nhu
,
v
.
ây ta c
´
o
a
n−1
−
√
a
0
b
0
a
n−1
+
√
a
0
b
0
=
a
0
−
√
a
0
b
0
a
0
+
√
a
0
b
0
2
n−1
.
J
3.3. Phu
,
o
,
ng tr
`
ınh truy hô
`
i tuyê
´
n t
´
ınh
M
.
uc tru
,
´
o
,
c ta thâ
´
y c
´
ac b
`
ai to
´
an
¯
dê
`
u cho d
˜
ay sô
´
v
`
a c
´
ac sô
´
h
.
ang
¯
du
,
.
o
,
c liên h
.
ê v
´
o
,
i nhau b
`
˘
ang công th
´
u
,
c truy hô
`
i. C
´
ach gi
,
ai
¯
dê
`
u t
`
ım
trong công th
´
u
,
c truy hô
`
i mô
´
i liên h
.
ê
¯
dê
,
t
´
ınh
¯
du
,
.
o
,
c sô
´
h
.
ang tô
,
ng
qu
´
at v
`
a tô
,
ng n sô
´
h
.
ang
¯
dâ
`
u tiên. Không ph
,
ai l
´
uc n
`
ao ta c
˜
ung
c
´
o c
´
ac phu
,
o
,
ng tr
`
ınh truy hô
`
i
¯
d
.
ep
¯
d
˜
e nhu
,
c
´
ac b
`
ai t
.
âp phâ
`
n tru
,
´
o
,
c.
M
.
uc n
`
ay ta ch
,
ı ra m
.
ôt c
´
ach tô
,
ng qu
´
at t
´
ınh sô
´
h
.
ang tô
,
ng qu
´
at v
`
a
tô
,
ng nh
˜
u
,
ng d
˜
ay tho
,
a m
˜
an phu
,
o
,
ng tr
`
ınh truy hô
`
i.
Cho k sô
´
h
.
ang
¯
dâ
`
u c
,
ua d
˜
ay sô
´
x
1
, x
2
, x
3
, . . . , x
n
, . . . (3.16)
l
`
a x
1
= u
1
, x
2
= u
2
, . . . , x
k
= u
k
. M
˜
ôi sô
´
h
.
ang th
´
u
,
k + 1 c
,
ua d
˜
ay
(3.16) tô
`
n t
.
ai mô
´
i liên h
.
ê
x
k+n
+ a
1
x
n+k−1
+ a
2
x
n+k−2
+ ··· + a
k
x
n
= b
n
, (3.17)
,
o
,
¯
dây a
1
, a
2
, . . . , a
k
l
`
a nh
˜
u
,
ng sô
´
¯
d
˜
a cho, c
`
on b
1
, b
2
, . . . , b
n
, . . . l
`
a d
˜
ay
¯
d
˜
a cho. Khi
¯
d
´
o (3.17) cho ph
´
ep ta t
´
ınh
¯
du
,
.
o
,
c m
.
oi phâ
`
n t
,
u
,
liên tiê
´
p

72 Chu
,
o
,
ng 3. T
`
ım công th
´
u
,
c tô
,
ng qu
´
at
c
,
ua d
˜
ay (3.16) v
`
a sau
¯
d
´
o ta cô
´
g
´
˘
ang biê
,
u di
˜
ên sô
´
h
.
ang tô
,
ng qu
´
at
c
,
ua ch
´
ung. X
´
et v
´
ı d
.
u
V
´
ı d
.
u 3.14. T`ım công th
´
u
,
c tô
,
ng qu´at c
,
ua d˜ay x´ac
¯
d
.
inh nhu
,
sau:
x
1
= 5, x
2
= 19, x
n
−5x
n−1
+ 6x
n−2
= 0.
L
`
o
,
i gi
,
ai. T
`
u
,
mô
´
i liên h
.
ê hô
`
i quy x
n
= 5x
n−1
−6x
n−1
, ta t
`
ım
¯
du
,
.
o
,
c
x
1
= 5 = 3
2
−2
2
, x
2
= 19 = 3
3
−2
3
,
x
3
= 5x
2
−6x
1
= 65 = 3
4
−2
4
, x
4
= 5x
3
−6x
2
= 211 = 3
5
−2
5
,
x
5
= 5x
4
−6x
3
= 665 = 3
5
−2
5
, x
6
= 5x
5
−6x
4
= 2059 = 3
6
−2
6
.
Ta gi
,
a thiê
´
t r
`
˘
ang sô
´
h
.
ang tô
,
ng qu
´
at c
,
ua d
˜
ay c
´
o d
.
ang
x
n
= 3
n+1
−2
n+1
. (3.18)
Gi
,
a thiê
´
t
¯
du
,
.
o
,
c ch
´
u
,
ng minh b
`
˘
ang phu
,
o
,
ng ph
´
ap quy n
.
ap.
1) Ta
¯
d
˜
a kiê
,
m tra (3.18)
¯
d
´
ung v
´
o
,
i n = 1 v
`
a n = 2.
2) Ta gi
,
a thiê
´
t (3.18)
¯
d
´
ung v
´
o
,
i n = k v
`
a n = k + 1, ngh
˜
ıa l
`
a
x
k
= 3
k+1
−2
k+1
v
`
a x
k+1
= 3
k+2
−2
k+2
. Khi
¯
d
´
o ta t
`
ım
¯
du
,
.
o
,
c
x
k+2
= 5x
k+1
−6x
k
= 5(3
k+2
−2
k+2
) −6 (3
k+1
−2
k+1
)
= (15 − 6)3
k+1
−( 10 − 6)2
k+1
= 3
k+3
−2
k+3
.
Nhu
,
v
.
ây (3.18)
¯
d
´
ung v
´
o
,
i n = k + 2. Theo nguyên l
´
y quy n
.
ap to
´
an
h
.
oc suy ra (3.18)
¯
d
´
ung v
´
o
,
i m
.
oi n.
J
Phu
,
o
,
ng tr
`
ınh (3.17) g
.
oi phu
,
o
,
ng tr`ınh hô
`
i quy tuyê
´
n t´ınh b
.
âc
k. Nh
˜
u
,
ng sô
´
a
1
, a
2
, a
3
, . . . , a
k
g
.
oi l
`
a nh
˜
u
,
ng h
.
ê sô
´
, c
`
on b
n
g
.
oi l
`
a sô
´
h
.
ang t
.
u
,
do. Khi v
´
o
,
i m
.
oi n, b
n
= 0 phu
,
o
,
ng tr
`
ınh g
.
oi l
`
a thuâ
`
n
nhâ
´
t. B
`
ai to
´
an
¯
d
.
˘
at ra l
`
a t
`
ım c
´
ach biê
,
u di
˜
ên sô
´
h
.
ang tô
,
ng qu
´
at
x
n
qua c
´
ac
¯
d
.
ai lu
,
.
o
,
ng ban
¯
dâ
`
u
¯
d
˜
a cho. Trong m
.
uc n
`
ay ta ch
,
ı x
´
et
phu
,
o
,
ng tr
`
ınh truy hô
`
i b
.
âc hai.

3.3. Phu
,
o
,
ng tr
`
ınh truy hô
`
i tuyê
´
n t
´
ınh 73
V
´
ı d
.
u 3.15. T`ım sô
´
h
.
ang tô
,
ng qu´at x
n
cho phu
,
o
,
ng tr`ınh truy hô
`
i
thuâ
`
n nhâ
´
t b
.
âc hai:
a
0
x
n+2
+ a
1
x
n+1
+ a
2
x
n
= 0. (3.19)
L
`
o
,
i gi
,
ai. Ta g
.
oi t
1
v
`
a t
2
l
`
a nghi
.
êm c
,
ua phu
,
o
,
ng tr
`
ınh b
.
âc hai
a
0
t
2
+ a
1
t + a
2
= 0 (a
0
6= 0, a
2
6= 0).
Khi
¯
d
´
o theo công th
´
u
,
c Viet a
0
( t
1
+ t
2
) = −a
1
, a
0
t
1
t
2
= a
2
.
Phu
,
o
,
ng tr
`
ınh (3.19) c
´
o thê
,
viê
´
t du
,
´
o
,
i d
.
ang
x
n+2
−(t
1
+ t
2
)x
n+1
+ t
1
t
2
x
n
= 0. (3.20)
Sô
´
h
.
ang tô
,
ng qu
´
at c
,
ua d
˜
ay
¯
d
˜
a cho ph
.
u thu
.
ôc v
`
ao hai gi
´
a tr
.
i t
1
v
`
a
t
2
kh
´
ac nhau ho
.
˘
ac b
`
˘
ang nhau:
1) Tru
,
`
o
,
ng h
.
o
,
p t
1
6= t
2
:
Thay n b
`
˘
ang n −2 v
`
ao (3.20) ta nh
.
ân
¯
du
,
.
o
,
c
x
n
−(t
1
+ t
2
)x
n−1
+ t
1
t
2
x
n−2
= 0. (3.21)
Ta viê
´
t l
.
ai
x
n
−t
2
x
n−1
= t
1
(x
n−1
−t
2
x
n−2
). (3.22)
Thay n b
`
˘
ang c
´
ac gi
´
a tr
.
i n − 1, n − 2, . . . , 4, 3 v
`
ao (3.22) ta nh
.
ân
¯
du
,
.
o
,
c
x
n−1
−t
2
x
n−2
= t
1
(x
n−2
−t
2
x
n−3
)
x
n−2
−t
2
x
n−3
= t
1
(x
n−3
−t
2
x
n−4
)
. . . . . .
x
4
−t
2
x
3
= t
1
(x
3
−t
2
x
2
)
x
3
−t
2
x
2
= t
1
(x
2
−t
2
x
1
).
(3.23)
Nhân c
´
ac vê
´
tu
,
o
,
ng
´
u
,
ng c
,
ua (3.22) v
`
a (3.23), gi
,
an u
,
´
o
,
c th
`
u
,
a sô
´
chung, ta nh
.
ân
¯
du
,
.
o
,
c
x
n
−t
2
x
n−1
= t
n−2
1
(x
2
−t
2
x
1
). (3.24)

74 Chu
,
o
,
ng 3. T
`
ım công th
´
u
,
c tô
,
ng qu
´
at
Tu
,
o
,
ng t
.
u
,
viê
´
t (3.21) du
,
´
o
,
i d
.
ang
x
n
−t
1
x
n−1
= t
2
(x
n−1
−t
2
x
n−2
)
v
`
a sau
¯
d
´
o thay n b
`
˘
ang c
´
ac gi
´
a tr
.
i n −1, n −2, . . . , 4, 3, c
˜
ung t
´
ınh
¯
du
,
.
o
,
c
x
n
−t
1
x
n−1
= t
n−2
2
(x
2
−t
1
x
1
). (3.25)
T
`
u
,
(3.24) v
`
a (3.25) ta c
´
o
t
1
x
n
−t
2
x
n
= t
n−1
1
(x
2
−t
2
x
1
) − t
n−1
2
(x
2
−t
1
x
1
).
Ho
.
˘
ac l
`
a nghi
.
êm c
,
ua (3.19) c
´
o d
.
ang
x
n
= C
1
t
n
1
+ C
2
t
n
2
, (3.26)
,
o
,
¯
dây
C
1
=
x
2
−t
2
x
1
t
1
( t
1
−t
2
)
, C
2
=
t
1
x
1
− x
2
t
2
( t
1
−t
2
)
. (3.27)
Ngu
,
.
o
,
c l
.
ai, C
1
v
`
a C
2
l
`
a nh
˜
u
,
ng h
`
˘
ang sô
´
bâ
´
t k
`
y, kiê
,
m tra tr
.
u
,
c tiê
´
p
d
˜
ay v
´
o
,
i sô
´
h
.
ang tô
,
ng qu
´
at (3.26) l
`
a nghi
.
êm c
,
ua phu
,
o
,
ng tr
`
ınh â
,
n
(3.19). Gi
´
a tr
.
i duy nhâ
´
t c
,
ua d
˜
ay {x
n
}
¯
du
,
.
o
,
c x
´
ac
¯
d
.
inh, nê
´
u cho hai
gi
´
a tr
.
i ban
¯
dâ
`
u c
,
ua d
˜
ay. Khi
¯
d
´
o C
1
v
`
a C
2
x
´
ac
¯
d
.
inh theo công th
´
u
,
c
(3.27).
Tr
,
o
,
l
.
ai v
´
ı d
.
u trên th
`
ı t
1
= 3, t
2
= 2 l
`
a nghi
.
êm c
,
ua phu
,
o
,
ng
tr
`
ınh b
.
âc hai t
2
−5t + 6 = 0. Khi
¯
d
´
o nê
´
u C
1
v
`
a C
2
l
`
a nh
˜
u
,
ng h
`
˘
ang
sô
´
bâ
´
t k
`
y, th
`
ı d
˜
ay v
´
o
,
i sô
´
h
.
ang tô
,
ng qu
´
at
x
n
= C
1
.3
n
+ C
2
.2
n
l
`
a nghi
.
êm c
,
ua phu
,
o
,
ng tr
`
ınh truy hô
`
i x
n
−5x
n−1
+ 6x
n−2
= 0. V
´
o
,
i
x
1
= 5, x
2
= 19, ta x
´
ac
¯
d
.
inh
¯
du
,
.
o
,
c C
1
= 3, C
2
= −2 v
`
a nhu
,
v
.
ây sô
´
h
.
ang tô
,
ng qu
´
at c
,
ua d
˜
ay l
`
a x
n
= 3
n+1
−2
n+1
.
Trong tru
,
`
o
,
ng h
.
o
,
p nghi
.
êm t
1
, t
2
l
`
a nh
˜
u
,
ng sô
´
ph
´
u
,
c., ngh
˜
ıa
l
`
a t
1
= ρ(cos α + i sin α), t
2
= ρ(cos α − i sin α), theo công th
´
u
,
c
Moivre ta c
´
o
t
n
1
= ρ
n
(cos nα + i sin nα), t
n
2
= ρ
n
(cos nα −i sin nα)

3.3. Phu
,
o
,
ng tr
`
ınh truy hô
`
i tuyê
´
n t
´
ınh 75
v
`
a nghi
.
êm tô
,
ng qu
´
at (3.26) tr
,
o
,
th
`
anh
x
n
= P
1
ρ
n
cos nα + P
2
ρ
n
sin nα, (3.28)
,
o
,
¯
dây P
1
v
`
a P
2
l
`
a h
`
˘
ang sô
´
bâ
´
t k
`
y. Ðê
,
x
´
ac
¯
d
.
inh h
`
˘
ang P
1
v
`
a P
2
trong
(3.28) khi cho hai gi
´
a tr
.
i
¯
dâ
`
u x
1
v
`
a x
2
, ta c
´
o
P
1
= C
1
+ C
2
=
( t
1
+ t
2
)x
1
− x
2
t
1
t
2
,
P
2
= i( C
1
−C
2
) = i
( t
1
+ t
2
)x
2
−(t
2
1
+ t
2
2
)x
1
t
1
t
2
( t
1
−t
2
)
,
ho
.
˘
ac l
`
a
P
1
=
2
ρ
cos α.x
1
−
1
ρ
2
.x
2
, P
2
=
cotgα
ρ
2
x
2
−
cos 2α
ρ sin α
.x
1
. (3.29)
2) Tru
,
`
o
,
ng h
.
o
,
p t
1
= t
2
: Nhu
,
trong tru
,
`
o
,
ng h
.
o
,
p tru
,
´
o
,
c ch
´
ung ta
suy ra t
`
u
,
(3.24) v
`
a (3.25) v
´
o
,
i t
1
= t
2
x
n
−t
1
x
n−1
= t
n−2
1
(x
2
−t
1
x
1
). (3.30)
Ðê
,
x
´
ac
¯
d
.
inh
¯
du
,
.
o
,
c x
n
câ
`
n t
`
ım m
.
ôt phu
,
o
,
ng tr
`
ınh n
˜
u
,
a cho x
n
v
`
a
x
n−1
. T
`
u
,
phu
,
o
,
ng tr
`
ınh x
n
−2t
1
x
n−1
+ t
2
1
x
n−2
= 0 c
´
o thê
,
viê
´
t du
,
´
o
,
i
d
.
ang
( n −2)x
n
−2(n −2)t
1
x
n−1
+ (n −2)t
2
1
.x
n−2
= 0
ho
.
˘
ac l
`
a
( n −2)x
n
−(n −1)t
1
x
n−1
= t
1
[(n − 3)x
n−1
−(n −2)t
1
x
n−2
].
(3.31)
Sau khi thê
´
n tu
,
o
,
ng
´
u
,
ng b
`
˘
ang n −1, n − 2, . . . , 4, 3 v
`
ao (3.31) ta

76 Chu
,
o
,
ng 3. T
`
ım công th
´
u
,
c tô
,
ng qu
´
at
nh
.
ân
¯
du
,
.
o
,
c
( n −3)x
n−1
−(n −2)t
1
x
n−2
= t
1
[(n − 4)x
n−2
−(n −3)t
1
x
n−3
],
( n −4)x
n−2
−(n −3)t
1
x
n−3
= t
1
[(n − 5)x
n−3
−(n −4)t
1
x
n−4
],
. . . . . .
2x
4
−3t
1
x
3
= t
1
(x
3
−2t
1
x
2
),
x
3
−2t
1
x
2
= −t
2
1
x
1
.
(3.32)
Lâ
`
n lu
,
.
o
,
t thê
´
c
´
ac vê
´
tu
,
o
,
ng
´
u
,
ng c
,
ua (3.32) v
`
ao (3.31) ta nh
.
ân
¯
du
,
.
o
,
c
( n −2)x
n
−(n −1)t
1
x
n−1
= −t
n−1
1
.x
1
. (3.33)
T
`
u
,
(3.30) v
`
a (3.33) ta t
`
ım
¯
du
,
.
o
,
c
( n −1)x
n
−(n −2)x
n
= (n −1)t
n−2
1
(x
2
−t
1
x
1
) + t
n−1
1
x
1
,
ho
.
˘
ac l
`
a
x
n
= (C
1
+ C
2
.n)t
n
1
, (3.34)
,
o
,
¯
dây
C
1
=
2t
1
x
1
− x
2
t
2
1
, C
2
=
x
2
−t
1
x
1
t
2
1
.
B
.
an
¯
d
.
oc c
´
o thê
,
kiê
,
m tra d
˜
ê d
`
ang (3.34) l
`
a kê
´
t qu
,
a c
,
ua (3.26) khi
ta cho t
2
= t
1
.
J
V
´
ı d
.
u 3.16. T`ım sô
´
h
.
ang tô
,
ng qu ´at c
,
ua d ˜ay x ´ac
¯
d
.
inh theo công
th
´
u
,
c sau:
x
1
= 10, x
2
= −12, x
n
+ 4x
n−2
= 0.
L
`
o
,
i gi
,
ai. T
`
u
,
phu
,
o
,
ng tr
`
ınh t
2
+ 4 = 0 ta t
´
ınh
¯
du
,
.
o
,
c t
1
= 2i =
2( cos
π
2
+ i sin
π
2
), t
2
= −2i = 2(cos
π
2
− i sin
π
2
) hay l
`
a ρ = 2, α =
π
2
. Khi
¯
d
´
o nghi
.
êm c
,
ua phu
,
o
,
ng tr
`
ınh truy hô
`
i l
`
a
x
n
= (P
1
cos
nπ
2
+ P
2
sin
nπ
2
)2
n
.

3.3. Phu
,
o
,
ng tr
`
ınh truy hô
`
i tuyê
´
n t
´
ınh 77
T
`
u
,
(3.39) suy ra P
1
= 3, P
2
= 5, do
¯
d
´
o sô
´
h
.
ang tô
,
ng qu
´
at ph
,
ai t
`
ım
l
`
a
x
n
= (3 cos
nπ
2
+ 5 sin
nπ
2
)2
n
.
ho
.
˘
ac l
`
a
x
n
=
3.2
n
v
´
o
,
i n = 4k
5.2
n
v
´
o
,
i n = 4k + 1
−3.2
n
v
´
o
,
i n = 4k + 2
−5.2
n
v
´
o
,
i n = 4k + 3
V
´
ı d
.
u 3.17. Bây gi
`
o
,
ta quan tâm câu h
,
oi t`ım nghi
.
êm riêng c
,
ua
phu
,
o
,
ng tr`ınh truy hô
`
i không thuâ
`
n nhâ
´
t b
.
âc hai v
´
o
,
i h
.
ê sô
´
h
`
˘ang
sô
´
a
0
x
n+2
+ a
1
x
n+1
+ a
2
x
n
= b
n
(a
0
6= 0, a
2
6= 0). (3.35)
L
`
o
,
i gi
,
ai. Ta c
˜
ung x
´
et nghi
.
êm t
1
, t
2
c
,
ua phu
,
o
,
ng tr
`
ınh a
0
t
2
+ a
1
t +
a
2
= 0.
1) Tru
,
`
o
,
ng h
.
o
,
p t
1
6= t
2
: Khi
¯
d
´
o theo phâ
`
n trên t
n
1
v
`
a t
n
2
l
`
a nh
˜
u
,
ng
nghi
.
êm riêng c
,
ua phu
,
o
,
ng tr
`
ınh thuâ
`
n nhâ
´
t (3.17) v
`
a c
´
o nghi
.
êm
theo công th
´
u
,
c (3.26).
Nghi
.
êm riêng c
,
ua phu
,
o
,
ng tr
`
ınh (3.35) ta s
˜
e t
`
ım theo phu
,
o
,
ng
ph
´
ap biê
´
n
¯
dô
,
i h
`
˘
ang sô
´
nhu
,
sau: Ta ph
,
ai t
`
ım nghi
.
êm riêng ξ
n
c
´
o
d
.
ang
ξ
n
= α
n
t
n
1
+ β
n
t
n
2
, (3.36)
n
´
o ch
,
ı kh
´
ac (3.26) l
`
a h
.
ê sô
´
α
n
v
`
a β
n
c
´
o thê
,
ph
.
u thu
.
ôc v
`
ao n. Ta c
´
o
ξ
n+1
= α
n+1
t
n+1
1
+ β
n+1
t
n+1
2
= α
n
t
n+1
1
+ β
n
t
n+1
2
+ (α
n+1
−α
n
) t
n+1
1
+ (β
n+1
− β
n
) t
n+1
2
.
Bây gi
`
o
,
ta
¯
d
.
˘
at
¯
diê
`
u ki
.
ên cho c
´
ac d
˜
ay {α
n
} v
`
a {β
n
} tho
,
a m
˜
an
∆αt
n+1
1
+ ∆βt
n+1
2
= 0, (3.37)

78 Chu
,
o
,
ng 3. T
`
ım công th
´
u
,
c tô
,
ng qu
´
at
,
o
,
¯
dây ∆α = α
n+1
−α
n
, ∆β = β
n+1
− β
n
. Khi
¯
d
´
o
ξ
n+1
= α
n
t
n+1
1
+ β
n
t
n+1
2
ξ
n+2
= α
n+1
t
n+2
1
+ β
n+1
t
n+2
2
= α
n
t
n+2
1
+ β
n
t
n+2
2
+ ∆αt
n+2
1
+ ∆βt
n+2
2
.
Ta thê
´
biê
,
u th
´
u
,
c ξ
n
, ξ
n+1
, ξ
n+2
v
`
ao (3.35), ta nh
.
ân
¯
du
,
.
o
,
c
(a
0
t
n+2
1
+ a
1
t
n+1
1
+ a
2
t
n
1
). α
n
+ (a
0
t
n+2
2
+ a
1
t
n+1
2
+ a
2
t
n
2
).β
n
+
+ a
0
( ∆αt
n+2
1
+ ∆βt
n+2
2
) = b
n
.
Do (a
0
t
n+2
1
+ a
1
t
n+1
1
+ a
2
t
n
1
). α
n
= 0 v
`
a (a
0
t
n+2
2
+ a
1
t
n+1
2
+ a
2
t
n
2
).β
n
=
0 suy ra
∆αt
n+2
1
+ ∆βt
n+2
2
=
b
n
a
0
. (3.38)
T
`
u
,
(3.38) v
`
a (3.17) ta t
`
ım
¯
du
,
.
o
,
c
∆α = α
n+1
−α
n
=
b
n
a
0
.
1
t
n+1
1
( t
1
−t
2
)
∆β = β
n+1
− β
n
=
b
n
a
0
.
1
t
n+1
1
( t
2
−t
1
)
.
(3.39)
Sau khi thê
´
lâ
`
n lu
,
.
o
,
t n b
`
˘
ang c
´
ac gi
´
a tr
.
i tu
,
o
,
ng
´
u
,
ng n − 1, n −
2, . . . , 2, 1, 0 v
`
ao (3.39) ta nh
.
ân
¯
du
,
.
o
,
c
α
n
−α
n−1
=
b
n−1
a
0
.
1
t
n
1
( t
1
−t
2
)
,
α
n−1
−α
n−2
=
b
n−2
a
0
.
1
t
n−1
1
( t
1
−t
2
)
,
. . . . . .
α
3
−α
2
=
b
2
a
0
.
1
t
3
1
( t
1
−t
2
)
,
α
2
−α
1
=
b
1
a
0
.
1
t
2
1
( t
1
−t
2
)
,

3.3. Phu
,
o
,
ng tr
`
ınh truy hô
`
i tuyê
´
n t
´
ınh 79
α
1
−α
0
=
b
0
a
0
.
1
t
1
( t
1
−t
2
)
.
Ta c
.
ông theo vê
´
c
,
ua c
´
ac
¯
d
,
˘
ang th
´
u
,
c trên v
`
a ch
´
u
´
y α
0
6= 0 ta t
`
ım
¯
du
,
.
o
,
c
α
n
=
1
a
0
t
n
1
( t
1
−t
2
)
( b
0
t
n−1
1
+ b
1
t
n−2
1
+ ··· + b
n−2
t
1
+ b
n−1
).
Tu
,
o
,
ng t
.
u
,
ta c
˜
ung t
`
ım
¯
du
,
.
o
,
c
β
n
=
1
a
0
t
n
2
( t
2
−t
1
)
( b
0
t
n−1
2
+ b
1
t
n−2
2
+ ··· + b
n−2
t
2
+ b
n−1
).
Nhu
,
v
.
ây t
`
u
,
công th
´
u
,
c (3.36) ta c
´
o
ξ
n
=
f (t
1
) − f (t
2
)
a
0
( t
1
−t
2
)
, (3.40)
,
o
,
¯
dây
f (t) = b
0
t
n−1
+ b
1
t
n−2
+ ··· + b
n−2
t + b
n−1
.
2) Tru
,
`
o
,
ng h
.
o
,
p t
1
= t
2
: Tu
,
o
,
ng t
.
u
,
c
´
ach l
`
am trên ta c
˜
ung t
`
ım
¯
du
,
.
o
,
c ξ
n
d
.
ang ξ
n
= (α
n
+ nβ
n
) t
n
1
, v
`
a ta c
˜
ung nh
.
ân
¯
du
,
.
o
,
c
ξ
n
=
f
0
( t
1
)
a
0
.
Trên
¯
dây ta
¯
d
˜
a kh
,
ao s
´
at phu
,
o
,
ng tr
`
ınh truy hô
`
i b
.
âc hai.
Phu
,
o
,
ng tr
`
ınh b
.
âc cao ho
,
n ta c
˜
ung c
´
o thê
,
l
`
am tu
,
o
,
ng t
.
u
,
. Ta c
˜
ung
th
`
anh l
.
âp phu
,
o
,
ng tr
`
ınh
t
k
+ a
1
t
k−1
+ a
2
t
k−2
+ ··· + a
k−1
t + a
k
= 0 (3.41)
g
.
oi l
`
a phu
,
o
,
ng tr
`
ınh
¯
d
.
˘
ac tru
,
ng c
,
ua (3.17). Phu
,
o
,
ng tr
`
ınh sau
¯
dây
g
.
oi l
`
a phu
,
o
,
ng tr
`
ınh truy hô
`
i tuyê
´
n t
´
ınh thuâ
`
n nhâ
´
t
x
n+k
+ a
1
x
n+k+1
+ ··· + a
k
x
k
= 0. (3.42)
Ta không ch
´
u
,
ng minh
¯
d
.
inh l
´
ı sau

80 Chu
,
o
,
ng 3. T
`
ım công th
´
u
,
c tô
,
ng qu
´
at
Ð
.
inh l
´
ı 3.1: Nê
´
u t
1
nghi
.
êm b
.
ôi s lâ
`
n c
,
ua (3.41), th`ı s d ˜ay sô
´
v
´
o
,
i sô
´
h
.
ang tô
,
ng qu ´at
t
n
1
, nt
n
1
, n
2
t
n
1
, . . . , n
s−1
t
n
1
l `a nghi
.
êm riêng c
,
ua phu
,
o
,
ng tr`ınh thuâ
`
n nhâ
´
t (3.42)
Nhu
,
v
.
ây tâ
´
t c
,
a c
´
ac nghi
.
êm c
,
ua phu
,
o
,
ng tr
`
ınh
¯
d
.
˘
ac tru
,
ng theo
¯
d
.
inh l
´
ı trên cho ta k nghi
.
êm riêng c
,
ua (3.42).
x
(1)
n
, x
(2)
n
, . . . , x
(k)
n
.
Ð
.
inh l
´
ı 3.2: Nghi
.
êm chung c
,
ua phu
,
o
,
ng tr`ınh thuâ
`
n nhâ
´
t
(3.42)
¯
du
,
.
o
,
c cho b
`
˘ang công th
´
u
,
c
x
n
= C
1
x
(1)
n
+ C
2
x
(2)
n
+ ··· + C
k
x
(k)
n
,
o
,
¯
dây C
1
, C
2
, . . . , C
k
l `a nh
˜
u
,
ng h `ang sô
´
bâ
´
t k`y.
Ð
.
inh l
´
ı 3.3: Nghi
.
êm chung c
,
ua phu
,
o
,
ng tr`ınh truy hô
`
i tuyê
´
n
t´ınh (3.17)
¯
du
,
.
o
,
c cho b
`
˘ang công th
´
u
,
c
x
n
= C
1
x
(1)
n
+ C
2
x
(2)
n
+ ··· + C
k
x
(k)
n
+ ξ
n
,
o
,
¯
dây C
1
, C
2
, . . . , C
k
l `a nh
˜
u
,
ng h`ang sô
´
bâ
´
t k`y v`a ξ
n
l `a m
.
ôt nghi
.
êm
riêng c
,
ua (3.17).
H
`
˘
ang sô
´
C
1
, C
2
, . . . , C
k
¯
du
,
.
o
,
c x
´
ac
¯
d
.
inh b
`
˘
ang gi
´
a tr
.
i k sô
´
h
.
ang
ban
¯
dâ
`
u c
,
ua d
˜
ay.
Nghi
.
êm riêng c
,
ua phu
,
o
,
ng tr
`
ınh (3.17)
¯
du
,
.
o
,
c t
`
ım b
`
˘
ang phu
,
o
,
ng
ph
´
ap biê
´
n
¯
dô
,
i h
`
˘
ang sô
´
c
´
o d
.
ang
ξ
n
= α
1n
x
(1)
n
+ α
2n
x
(2)
n
+ ··· + α
kn
x
(k)
n
.
Tru
,
`
o
,
ng h
.
o
,
p riêng
¯
d
.
inh l
´
ı sau râ
´
t hay
¯
du
,
.
o
,
c
´
ap d
.
ung
Ð
.
inh l
´
ı 3.4: Nê
´
u b
n
= q
n
.P
s
( n),
,
o
,
¯
dây P
s
( n) l `a
¯
da th
´
u
,
c c
,
ua n
b
.
âc s, c`on q l `a m-lâ
`
n nghi
.
êm l
.
˘ap c
,
ua (3.42), phu
,
o
,
ng tr`ınh (3.17)

3.3. Phu
,
o
,
ng tr
`
ınh truy hô
`
i tuyê
´
n t
´
ınh 81
c´o nghi
.
êm riêng d
.
ang ξ = q
n
Q
m+s
( n),
,
o
,
¯
dây Q
m+s
( n) l `a
¯
da th
´
u
,
c
c
,
ua n, b
.
âc m + s.
Sau
¯
dây l
`
a m
.
ôt sô
´
v
´
ı d
.
u
´
ap d
.
ung c
´
ac Ð
.
inh l
´
ı trên
V
´
ı d
.
u 3.18. Ch
´
u
,
ng minh r
`
˘ang v
´
o
,
i m
.
oi sô
´
t
.
u
,
nhiên n, sô
´
z
n
=
4
n+1
+ 6n + 5 chia hê
´
t cho 9.
L
`
o
,
i gi
,
ai. Nh
˜
u
,
ng sô
´
z
1
= 27, z
2
= 81 v
`
a z
3
= 279 chia hê
´
t cho 9.
C
`
on z
n
c
´
o thê
,
nh
.
ân
¯
du
,
.
o
,
c theo công th
´
u
,
c tô
,
ng qu
´
at
x
n
= C
1
.4
n
+ C
2
.n.1
n
+ C
3
.1
n
v
´
o
,
i C
1
= 4, C
2
= 6, C
3
= 5.
D
˜
ay v
´
o
,
i sô
´
h
.
ang tô
,
ng qu
´
at x
n
l
`
a nghi
.
êm chung c
,
ua phu
,
o
,
ng
tr
`
ınh thuâ
`
n nhâ
´
t tuyê
´
n t
´
ınh v
´
o
,
i h
.
ê sô
´
không
¯
dô
,
i, m
`
a nghi
.
êm
c
,
ua phu
,
o
,
ng tr
`
ınh thuâ
`
n nhâ
´
t c
´
o nghi
.
êm t
1
= 4 v
`
a nghi
.
êm l
.
˘
ap
t
2
= t
3
= 1. Suy ra phu
,
o
,
ng tr
`
ınh
¯
d
.
˘
ac tru
,
ng l
`
a (t − 4)(t − 1)
2
= 0
ho
.
˘
ac l
`
a t
3
−6t
2
+ 9t −4 = 0, v
`
a phu
,
o
,
ng tr
`
ınh truy hô
`
i l
`
a
x
n+3
−6x
n+2
+ 9x
n+1
−4x
n
= 0.
V
`
ı z
n
l
`
a nghi
.
êm riêng c
,
ua phu
,
o
,
ng tr
`
ınh truy hô
`
i, ta c
´
o
z
n+3
= 6z
n+2
−9z
n+1
+ 4z
n
.
T
`
u
,
¯
dây, nê
´
u gi
,
a s
,
u
,
nh
˜
u
,
ng sô
´
z
n
, z
n+1
v
`
a z
n+2
chia hê
´
t cho 9, th
`
ı
z
n+3
c
˜
ung chia hê
´
t cho 9. Nhu
,
v
.
ây theo nguyên l
´
y quy n
.
ap to
´
an
h
.
oc b
`
ai to
´
an
¯
d
˜
a
¯
du
,
.
o
,
c gi
,
ai
¯
dâ
`
y
¯
d
,
u.
J
V
´
ı d
.
u 3.19. T`ım công th
´
u
,
c tô
,
ng qu ´at cho tô
,
ng
x
n
= 1
5
+ 2
5
+ 3
5
+ ··· + n
5
.
L
`
o
,
i gi
,
ai. Ta c
´
o
x
1
= 1, x
n+1
− x
n
= (n + 1)
5
.

82 Chu
,
o
,
ng 3. T
`
ım công th
´
u
,
c tô
,
ng qu
´
at
Ta
¯
d
˜
a c
´
o phu
,
o
,
ng tr
`
ınh truy hô
`
i không thuâ
`
n nhâ
´
t b
.
âc m
.
ôt v
´
o
,
i h
.
ê
sô
´
không
¯
dô
,
i. Phu
,
o
,
ng tr
`
ınh
¯
d
.
˘
ac tru
,
ng t −1 = 0 c
´
o nghi
.
êm t
1
= 1.
Theo c
´
ac
¯
d
.
inh l
´
ı 3.1 -3.3 nghi
.
êm chung c
,
ua phu
,
o
,
ng tr
`
ınh n
`
ay l
`
a
x
n
= C
1
+ ξ
n
,
,
o
,
¯
dây ξ
n
l
`
a nghi
.
êm riêng c
,
ua phu
,
o
,
ng tr
`
ınh ta
¯
dang
x
´
et.
Nhu
,
ng v
`
ı b
n
= 1
n
.(n + 5)
5
v
`
a sô
´
1 l
`
a nghi
.
êm c
,
ua phu
,
o
,
ng tr
`
ınh
¯
d
.
˘
ac tru
,
ng, theo
¯
d
.
inh l
´
ı 3.4 (m = 1, s = 5) ξ
n
l
`
a
¯
da th
´
u
,
c b
.
âc s
´
au
c
,
ua n. Khi
¯
d
´
o
x
n
= B
0
+ B
1
n + B
2
n
2
+ B
3
n
3
+ B
4
n
4
+ B
5
n
5
+ B
6
n
6
.
Thay v
`
ao phu
,
o
,
ng tr
`
ınh ta thiê
´
t l
.
âp
,
o
,
phâ
`
n
¯
dâ
`
u, ta nh
.
ân
¯
du
,
.
o
,
c
B
1
( n + 1) + B
2
( n + 1)
2
+ B
3
( n + 1)
3
+ B
4
( n + 1)
4
+ B
5
( n + 1)
5
+B
6
( n + 1)
6
− B
1
n − B
2
n
2
− B
3
n
3
− B
4
n
4
−B
5
n
5
− B
6
n
6
= (n + 1)
5
.
Ðô
`
ng nhâ
´
t h
.
ê sô
´
tru
,
´
o
,
c
¯
dô
`
ng b
.
âc c
,
ua n c
,
ua hai vê
´
¯
d
,
˘
ang th
´
u
,
c, ta
c
´
o
6B
6
= 1, 5B
5
+ 15B
6
= 5, 4B
4
+ 10B
5
+ 20B
6
= 10,
3B
3
+ 6B
4
+ 10B
5
+ 16B
6
= 10,
2B
2
+ 3B
3
+ 4B
4
+ 5B
5
+ 6B
6
= 5,
B
1
+ B
2
+ B
3
+ B
4
+ B
5
+ B
6
= 1.
T
`
u
,
¯
d
´
o suy ra
B
6
=
1
6
, B
5
=
1
2
, B
4
=
5
12
, B
3
= 0, B
2
= −
1
12
, B
1
= 0.
Khi
¯
d
´
o
x
n
= B
0
−
1
12
n
2
+
5
12
n
4
+
1
2
n
5
+
1
6
n
6
.
T
`
u
,
¯
dây v
´
o
,
i n = 1 ta nh
.
ân
¯
du
,
.
o
,
c 1 = B
0
+ 1, ngh
˜
ıa l
`
a B
0
= 0 suy ra
1
5
+ 2
5
+ ··· + n
5
=
1
12
(2 n
6
+ 6n
5
+ 5n
4
−n
2
).
J
V
´
ı d
.
u 3.20. Gi
,
ai phu
,
o
,
ng tr`ınh
x
n+1
−nx
n
= n!n
5
(3.43)
v
´
o
,
i
¯
diê
`
u ki
.
ên ban
¯
dâ
`
u l `a x
1
= 1.
3.3. Phu
,
o
,
ng tr
`
ınh truy hô
`
i tuyê
´
n t
´
ınh 83
L
`
o
,
i gi
,
ai. Ta x
´
et phu
,
o
,
ng tr
`
ınh thuâ
`
n nhâ
´
t tu
,
o
,
ng
´
u
,
ng
y
n+1
−ny
n
= 0. (3.44)
Sau khi thay n b
,
o
,
i lâ
`
n lu
,
.
o
,
t gi
´
a tr
.
i n −1, n −2, . . . , 2, 1 v
`
ao (3.44)
ta c
´
o
y
n
= (n −1)y
n−1
y
n−1
= (n −2)y
n−2
. . . . . .
y
3
= 2y
2
y
2
= y
1
= C.
Nhân theo vê
´
c
´
ac
¯
d
,
˘
ang th
´
u
,
c trên ta t
`
ım
¯
du
,
.
o
,
c y
n
= C(n − 1)!.
Nghi
.
êm riêng ξ
n
c
,
ua (3.43) ta t
`
ım theo phu
,
o
,
ng ph
´
ap biê
´
n
¯
dô
,
i
h
`
˘
ang sô
´
d
.
ang ξ
n
= (n −1)!u
n
. Khi ta thê
´
v
`
ao (3.43), nh
.
ân
¯
du
,
.
o
,
c
n!u
n+1
− n!u
n
= n!n
5
, ho
.
˘
ac l
`
a u
n+1
− u
n
= n
5
. Ta nh
.
ân
¯
du
,
.
o
,
c
phu
,
o
,
ng tr
`
ınh truy hô
`
i c
´
o nghi
.
êm chung (kê
´
t qu
,
a b
`
ai t
.
âp tru
,
´
o
,
c)
u
n
= B
0
+
1
12
n
2
( n −1)
2
(2 n
2
−2n −1).
v
´
o
,
i B
0
= 0 ta c
´
o
ξ
n
=
1
12
n
2
( n −1)
2
(2 n
2
−2n −1)(n −1)!.
Suy ra nghi
.
êm chung c
,
ua b
`
ai to
´
an l
`
a
x
n
= y
n
+ ξ
n
= [C +
1
12
n
2
( n −1)
2
(2 n
2
−2n −1)](n − 1)!.
V
´
o
,
i n = 1 cho gi
´
a tr
.
i ban
¯
dâ
`
u ta nh
.
ân
¯
du
,
.
o
,
c C = 1 v
`
a suy ra d
˜
ay
ph
,
ai t
`
ım l
`
a:
x
n
= [
1
12
n
2
( n −1)
2
(2 n
2
−2n −1) + 1](n −1)!.
J

84 Chu
,
o
,
ng 3. T
`
ım công th
´
u
,
c tô
,
ng qu
´
at
3.4. Tô
,
ng c
,
ua nh
˜
u
,
ng l
˜
uy th
`
u
,
a c
`
ung b
.
âc c
´
ac sô
´
t
.
u
,
nhiên
Ta
¯
d
˜
a g
.
˘
ap m
.
ôt sô
´
b
`
ai vê
`
t
´
ınh tô
,
ng c
,
ua l
˜
uy th
`
u
,
c
`
ung b
.
âc c
´
ac sô
´
t
.
u
,
nhiên, nhu
,
v
´
o
,
i l
˜
uy th
`
u
,
a b
.
âc hai, b
.
âc ba. Phâ
`
n n
`
ay ta
´
ap d
.
ung
công th
´
u
,
c Newton
¯
dê
,
t
´
ınh
¯
du
,
.
o
,
c tô
,
ng c
,
ua m
.
ôt sô
´
m
˜
u n
`
ao
¯
d
´
o c
´
ac
sô
´
t
.
u
,
nhiên t
`
u
,
1
¯
dê
´
n n. Ðê
,
t
´
ınh tô
,
ng
S
k
= 1
k
+ 2
k
+ 3
k
+ ··· + n
k
(3.45)
v
´
o
,
i k l
`
a m
.
ôt sô
´
t
.
u
,
nhiên, ta
´
ap d
.
ung
¯
d
,
˘
ang th
´
u
,
c sau
(x + 1)
k+1
= x
k+1
+ C
1
k+1
x
k
+ C
2
k+1
x
k−1
+ ··· + C
k
k+1
x + 1.
Thay x lâ
`
n lu
,
.
o
,
t c
´
ac gi
´
a tr
.
i 1, 2, 3, . . . , n ta nh
.
ân
¯
du
,
.
o
,
c
2
k+1
= 1
k+1
+ C
1
k+1
1
k
+ C
2
k+1
1
k−1
+ ··· + C
k
k+1
1 + 1,
3
k+1
= 2
k+1
+ C
1
k+1
2
k
+ C
2
k+1
2
k−1
+ ··· + C
k
k+1
2 + 1,
4
k+1
= 3
k+1
+ C
1
k+1
3
k
+ C
2
k+1
3
k−1
+ ··· + C
k
k+1
3 + 1,
..............................................
n
k+1
= (n −1)
k+1
+ C
1
k+1
( n −1)
k
+ ··· + C
k
k+1
( n −1) + 1,
( n + 1)
k+1
= n
k+1
+ C
1
k+1
n
k
+ C
2
k+1
n
k−1
+ ··· + C
k
k+1
n + 1.
C
.
ông theo vê
´
c
,
ua c
´
ac
¯
d
,
˘
ang th
´
u
,
c v
`
a ta nh
.
ân
¯
du
,
.
o
,
c
( n + 1)
k+1
= C
1
k+1
S
k
+ C
2
k+1
S
k−1
+ ··· + C
k
k+1
S
1
+ n + 1
hay l
`
a
S
k
=
1
k + 1
[(n + 1)
k+1
−C
2
k+1
S
k−1
−··· − C
k
k+1
S
1
−n −1]. (3.46)
T
`
u
,
biê
,
u th
´
u
,
c (3.46) cho ph
´
ep ta t
´
ınh lâ
`
n lu
,
.
o
,
t tô
,
ng (3.45). V
´
ı d
.
u
v
´
o
,
i k = 1, 2, . . . t
`
u
,
(3.46) ta t
´
ınh
¯
du
,
.
o
,
c
S
1
=
1
2
[(n + 1)
2
−n −1] =
n(n + 1)
2
=
1
2
n
2
+
1
2
n,

3.4. Tô
,
ng c
,
ua nh
˜
u
,
ng l
˜
uy th
`
u
,
a c
`
ung b
.
âc c
´
ac sô
´
t
.
u
,
nhiên 85
S
2
=
1
3
[(n + 1)
3
−3S
1
−n −1] =
n(n + 1)(2n + 1)
6
=
1
3
n
3
+
1
2
n
2
+
1
6
n,
S
3
=
1
4
[(n + 1)
4
−6S
2
−4S
1
−n −1] = [
n(n + 1)
2
]
2
=
1
4
n
4
+
1
2
n
3
+
1
4
n
2
,
S
4
=
1
5
[(n + 1)
5
−10S
3
−10S
2
−5S
1
−n −1]
=
n(n + 1)(2n + 1)(3n
2
+ 3n + 1)
30
=
1
5
n
5
+
1
2
n
4
+
1
3
n
3
−
1
30
n,
S
5
=
1
6
[(n + 1)
6
−15S
4
−20S
3
−15S
2
−6S
1
−n −1]
=
1
12
n
2
( n + 1)
2
(2 n
2
+ 2n −1) =
1
6
n
6
+
1
2
n
5
+
5
12
n
4
−
1
12
n
2
,
S
6
=
1
42
n(n + 1)(2n + 1)(3n
4
+ 6n
3
−3n + 1)
=
1
7
n
7
+
1
2
n
6
+
1
2
n
5
−
1
6
n
3
+
1
12
n,
S
7
=
1
24
n
2
( n + 1)
2
(3 n
4
+ 6n
3
−n
2
−4n + 2)
=
1
8
n
8
+
1
2
n
7
+
7
12
n
6
−
7
24
n
4
+
1
12
n
2
.
Ta s˜e ch
´
u
,
ng minh r
`
˘ang tô
,
ng S
k
l `a m
.
ôt
¯
da th
´
u
,
c b
.
âc k + 1 c´o sô
´
h
.
ang t
.
u
,
do b
`
˘ang không, h
.
ê sô
´
tru
,
´
o
,
c n
k+1
b
`
˘ang
1
k + 1
, h
.
ê sô
´
tru
,
´
o
,
c
n
k
b
`
˘ang
1
2
, h
.
ê sô
´
tru
,
´
o
,
c n
k−1
b
`
˘ang
k
12
, h
.
ê sô
´
tru
,
´
o
,
c n
k−2
b
`
˘ang 0.
Th
.
ât v
.
ây, Gi
,
a thiê
´
t
¯
diê
`
u kh
,
˘
ang
¯
d
.
inh trên
¯
d
´
ung v
´
o
,
i nh
˜
u
,
ng
tô
,
ng S
1
, S
2
, . . . , S
k−1
. Ta câ
`
n kê
´
t lu
.
ân kh
,
˘
ang
¯
d
.
inh c
˜
ung
¯
d
´
ung v
´
o
,
i
tô
,
ng S
k
. Kh
,
˘
ang
¯
d
.
inh S
k
l
`
a m
.
ôt
¯
da th
´
u
,
c theo n v
`
a h
.
ê sô
´
t
.
u
,
do b
`
˘
ang
0, suy ra t
`
u
,
¯
d
,
˘
ang th
´
u
,
c (3.46). C
´
ac h
.
ê sô
´
a
k
, a
k−1
, a
k−2
tu
,
o
,
ng
´
u
,
ng

86 Chu
,
o
,
ng 3. T
`
ım công th
´
u
,
c tô
,
ng qu
´
at
tru
,
´
o
,
c n
k
, n
k−1
, n
k−2
trong S
k
c
˜
ung t
`
u
,
(3.17) ta t
`
ım
¯
du
,
.
o
,
c
a
k
=
1
k + 1
[C
1
k+1
−C
2
k+1
1
k
] =
1
2
,
a
k−1
=
1
k + 1
[C
2
k+1
−C
2
k+1
.
1
2
−C
3
k+1
1
k − 1
] =
k
12
,
a
k−2
=
1
k + 1
[C
3
k+1
−C
2
k+1
k − 1
12
−C
3
k+1
.
1
2
−C
4
k+1
1
k − 2
] = 0.
Nhu
,
v
.
ây trong tru
,
`
o
,
ng h
.
o
,
p chung ta c
´
o công th
´
u
,
c
n
∑
i =1
i
k
=
1
k + 1
.n
k+1
+
1
2
n
k
+
1
2
C
1
k
B
2
n
k−1
+
1
4
C
3
k
B
4
n
k−3
+
+
1
6
C
5
k
B
6
n
k−5
+
1
8
C
7
k
B
8
n
k−7
+ ···
(3.47)
sô
´
h
.
ang cuô
´
i c
`
ung l
`
a n ho
.
˘
ac n
2
. Trong (3.47) nh
˜
u
,
ng sô
´
B
2
, B
4
, B
6
, B
8
, . . . g
.
oi l
`
a nh
˜
u
,
ng sô
´
Bernoulli. M
.
ôt sô
´
sô
´
Bernoulli
¯
du
,
.
o
,
c li
.
êt kê trong b
,
ang
B
2
=
1
6
, B
4
= −
1
30
, B
6
=
1
42
, B
8
= −
1
30
, B
10
=
5
66
,
B
12
= −
691
2730
, B
14
= −
7
6
, B
16
=
3617
510
, B
18
= −
43867
798
,
B
20
= −
174611
330
, B
22
=
854513
123
, B
24
= −
236364091
2730
,
B
26
=
8553103
6
, B
28
= −
23749461029
870
, B
30
=
8615841276005
14322
,
B
32
= −
7709321041217
510
, B
34
=
2577867858367
6
.
Nh
˜
u
,
ng sô
´
n
`
ay
¯
d
,
u cho ta t
´
ınh
¯
du
,
.
o
,
c công th
´
u
,
c tô
,
ng l
˜
uy th
`
u
,
a
b
.
âc m
.
ôt, hai, ba, . . . , ba mu
,
o
,
i tu
,
c
,
ua n ch
˜
u
,
sô
´
t
.
u
,
nhiên
¯
dâ
`
u tiên.
Bây gi
`
o
,
không kh
´
o kh
˘
an g
`
ı t
´
ınh
¯
du
,
.
o
,
c công th
´
u
,
c d
.
ang
∑
n
t=1
[P(t)]
k
,
o
,
¯
dây P(t) l
`
a
¯
da th
´
u
,
c theo t. V
´
ı d
.
u ch
´
u
,
ng minh nh
˜
u
,
ng
¯
d
,
˘
ang th
´
u
,
c sau
¯
dây

3.5. B
`
ai t
.
âp 87
1) 1
2
+ 3
2
+ 5
2
+ ··· + (2n −1)
2
=
1
3
n(2n − 1)(2n + 1);
2) 1
2
+ 5
2
+ 9
2
+ ··· + (4n + 1)
2
=
1
3
( n + 1)(16n
2
+ 20n + 3).
Th
.
ât v
.
ây,
1)
n
∑
t=1
(2 t −1)
2
=
n
∑
t=1
(4 t
2
−4t + 1) = 4
n
∑
t=1
t
2
−4
n
∑
t=1
t + n
= 4.
n(n + 1)(2n + 1)
6
−4
n(n + 1)
2
+ n
=
1
3
n(2n − 1)(2n + 1).
2)
n
∑
t=1
(4 t + 1)
2
=
n
∑
t=1
(16 t
2
+ 8t + 1) = 16
n
∑
t=1
t
2
+ 8
n
∑
t=1
t + n
= 16.
n(n + 1)(2n + 1)
6
+ 8.
n(n + 1)
2
+ n + 1
=
( n + 1)(16n
2
+ 20n + 3)
3
.
B
.
an
¯
d
.
oc c
´
o thê
,
gi
,
ai nhiê
`
u b
`
ai to
´
an tu
,
o
,
ng t
.
u
,
nhu
,
v
.
ây.
3.5. B
`
ai t
.
âp
.
.
. 3.21. Ch
´
u
,
ng minh r
`
˘
ang
S
n
= a
1
b
1
+ a
2
b
2
+ ··· + a
n
b
n
=
a
1
b
1
−qa
n
b
n
1 −q
−dqb
1
q
n−1
−1
(1 − q)
2
.
v
´
o
,
i a
1
, a
2
, . . . , a
n
l
`
a câ
´
p sô
´
c
.
ông c
´
o công sai d v
`
a b
1
, b
2
, . . . , b
n
l
`
a câ
´
p
sô
´
nhân c
´
o b
.
ôi sô
´
q 6= 1.
.
.
. 3.22. T
`
ım sô
´
h
.
ang tô
,
ng qu
´
at c
,
ua câ
´
p sô
´
c
.
ông
2, 5, 10, 17, 26, 37, . . .
v
`
a t
´
ınh tô
,
ng n sô
´
h
.
ang
¯
dâ
`
u tiên c
,
ua n
´
o.

88 Chu
,
o
,
ng 3. T
`
ım công th
´
u
,
c tô
,
ng qu
´
at
.
.
. 3.23. H
˜
ay t
`
ım công th
´
u
,
c tô
,
ng
S
n
= 3.2 + 5.5 + 7.8 + ··· + (2n + 1)(3n −1).
.
.
. 3.24. H
˜
ay t
`
ım nghi
.
êm chung c
,
ua c
´
ac phu
,
o
,
ng tr
`
ınh sau:
a) x
n+1
+ x
n+1
+ x
n
= 0;
b) x
n+1
+ 2x
n+1
+ x
n
= 0;
c) x
n+2
− x
n
= 0;
d) x
n+3
−3x
n+2
+ 3x
n+1
− x
n
= 0.
.
.
. 3.25. T
`
ım công th
´
u
,
c tô
,
ng qu
´
at cho d
˜
ay x
´
ac
¯
d
.
inh theo công th
´
u
,
c
sau:
a) x
1
= 10, x
2
= 16, x
n+2
−4x
n+1
+ 3x
n
= 0;
b) x
1
= 1, x
2
= −3, x
3
= −29, x
n+3
−9x
n+2
+ 26x
n+1
−24x
n
= 0;
c) x
1
= 1, x
2
= −7, x
n+2
−6x
n+1
+ 9x
n
= −4.

CHU
,
O
,
NG 4
S
´
Ô H
.
OC
4.1. Ph
´
ep chia hê
´
t . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 89
4.2. Thu
.
ât to
´
an Euclide . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 94
4.3. Sô
´
ph
´
u
,
c .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 99
4.4. Nh
˜
u
,
ng v
´
ı d
.
u kh
´
ac . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 105
4.5. B
`
ai t
.
âp .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 108
4.1. Ph
´
ep chia hê
´
t
Trong sô
´
h
.
oc ph
´
ep chia cho ta râ
´
t nhiê
`
u t
´
ınh châ
´
t vê
`
nh
˜
u
,
ng
sô
´
nguyên. Nhiê
`
u b
`
ai to
´
an ph
´
at biê
,
u du
,
´
o
,
i d
.
ang c
´
ac ph
´
ep chia
nh
˜
u
,
ng sô
´
nguyên v
`
a kê
,
c
,
a c
´
ac thu
.
ât to
´
an t
´
ınh to
´
an. Ta nh
´
˘
ac l
.
ai
m
.
ôt sô
´
kh
´
ai ni
.
êm. Nê
´
u a v
`
a b l
`
a nh
˜
u
,
ng sô
´
nguyên, ta n
´
oi r
`
˘
ang
b chia hê
´
t cho a, k
´
y hi
.
êu l
`
a b
.
.
. a, khi tô
`
n t
.
ai m
.
ôt sô
´
nguyên c sao
cho b = ca. Sô
´
c g
.
oi l
`
a thu
,
o
,
ng c
,
ua ph
´
ep chia, a nhiê
`
u khi g
.
oi l
`
a
u
,
´
o
,
c sô
´
c
,
ua b, sô
´
b g
.
oi l
`
a b
.
ôi sô
´
c
,
ua a. Tru
,
`
o
,
ng h
.
o
,
p không tô
`
n t
.
ai c
theo
¯
d
.
inh ngh
˜
ıa trên ta n
´
oi r
`
˘
ang b không chia hê
´
t cho a, k
´
y hi
.
êu
b 6
.
.
. a. T
`
u
,
¯
d
.
inh ngh
˜
ıa
¯
do
,
n gi
,
an trên ta suy ra h
`
ang lo
.
at c
´
ac t
´
ınh
châ
´
t c
,
ua ph
´
ep chia,
,
o
,
¯
dây ta ch
,
ı lâ
´
y m
.
ôt v
´
ı d
.
u
¯
do
,
n gi
,
an: Nê
´
u b
.
.
. a
v
`
a c
.
.
. a, th
`
ı (ub + vc)
.
.
. a v
´
o
,
i m
.
oi sô
´
nguyên bâ
´
t k
`
y u v
`
a v. Hai kh
´
ai
ni
.
êm sau
¯
dây râ
´
t hay
¯
du
,
.
o
,
c d
`
ung.
M
.
ôt sô
´
d g
.
oi l
`
a u
,
´
o
,
c sô
´
chung l
´
o
,
n nhâ
´
t c
,
ua hai sô
´
nguyên a v
`
a

90 Chu
,
o
,
ng 4. Sô
´
h
.
oc
b, k
´
y hi
.
êu d=(a, b), khi
1) a v
`
a b
¯
dê
`
u chia hê
´
t cho d;
2) d chia hê
´
t cho m
.
oi u
,
´
o
,
c sô
´
chung kh
´
ac c
,
ua a v
`
a b.
M
.
ôt sô
´
m g
.
oi l
`
a b
.
ôi sô
´
chung nh
,
o nhâ
´
t c
,
ua hai sô
´
nguyên a v
`
a
b, k
´
y hi
.
êu m=[a, b], khi
1) m chia hê
´
t cho c
,
a a v
`
a b;
2) M
.
oi b
.
ôi sô
´
chung kh
´
ac c
,
ua a v
`
a b
¯
dê
`
u chia hê
´
t cho m.
Công th
´
u
,
c liên quan gi
˜
u
,
a hai kh
´
ai ni
.
êm trên l
`
a
[a, b] =
ab
(a, b)
.
V
´
ı d
.
u 4.1. Ch
´
u
,
ng minh r
`
˘ang v
´
o
,
i m
.
oi sô
´
nguyên n ≥ 0, sô
´
3
3n+3
−
26n −27 chia hê
´
t cho 169.
L
`
o
,
i gi
,
ai. Ta
¯
d
.
˘
at A
n
= 3
3n+3
−26n −27. Khi
¯
d
´
o A
0
= 3
3
−27 = 0
suy ra A
0
chia hê
´
t cho 169.
Gi
,
a s
,
u
,
A
n
chia hê
´
t cho 169 v
´
o
,
i n n
`
ao
¯
d
´
o. Ta biê
´
n
¯
dô
,
i A
n+1
nhu
,
sau
A
n+1
= 3
3(n+1)+3
−26(n + 1) −27
= A
n
+ 26.3
3n+3
−26 = A
n
+ 26[(3
3
)
n+1
−1]
= A
n
+ 26( 3
3
−1)(3
3n
+ ··· + 1) = A
n
+ 4.169.( 3
3n
+ ··· + 1).
T
`
u
,
¯
d
´
o suy ra A
n+1
chia hê
´
t cho 169.
J
V
´
ı d
.
u 4.2. Ch
´
u
,
ng minh r
`
˘ang v
´
o
,
i sô
´
n nguyên du
,
o
,
ng
1) C = 7
n
+ 3n −1 chia hê
´
t cho 9;
2) E = a
4n+1
− a chia hê
´
t cho 30, v
´
o
,
i a l `a sô
´
nguyên.
L
`
o
,
i gi
,
ai. 1) Nê
´
u n = 1, th
`
ı C
1
= 7 + 3 − 1 chia hê
´
t cho 9. Gi
,
a s
,
u
,
n = k ≥ 1 v
`
a C
k
= 7
k
+ 3k −1 chia hê
´
t cho 9. Khi
¯
d
´
o v
´
o
,
i n = k + 1

4.1. Ph
´
ep chia hê
´
t 91
sô
´
C
k+1
= 7
k+1
+ 3(k + 1 ) −1 = 7.7
k
+ 3k + 2
= 7.7
k
+ 21k −7 −18k + 9 = 7(7
k
+ 3k −1) − 9(2k −1)
= 7C
k
−9( 2k −1)
c
˜
ung chia hê
´
t cho 9. Theo phu
,
o
,
ng ph
´
ap quy n
.
ap to
´
an h
.
oc C chia
hê
´
t cho 9 v
´
o
,
i m
.
oi n nguyên du
,
o
,
ng.
2) Nê
´
u n = 1, th
`
ı
E
1
= a
5
− a = a(a
2
−1)(a
2
+ 1) = a(a −1 )(a + 1)[(a
2
−4) + 5]
= (a −2)(a − 1)a(a + 1)(a + 2) + 5( a −1)a(a + 1).
Th
`
u
,
a sô
´
th
´
u
,
nhâ
´
t chia hê
´
t cho 5! = 120 = 4.30, c
`
on th
`
u
,
a sô
´
th
´
u
,
hai chia hê
´
t cho 5.3! = 30. Suy ra E
1
chia hê
´
t cho 30.
Gi
,
a s
,
u
,
n = k ≥ 1 v
`
a E
k
= a
4k+1
−a chia hê
´
t cho 30. Khi
¯
d
´
o v
´
o
,
i
n = k + 1 sô
´
E
k+1
= a
4k+5
− a = a
4k+5
− a + a
4k+1
− a
4k+1
= (a
4k+1
− a) + (a
4k+5
− a
4k+1
) = E
k
+ a
4k
.E
1
c
˜
ung chia hê
´
t cho 30.
J
V
´
ı d
.
u 4.3. Ch
´
u
,
ng minh r
`
˘ang nê
´
u v
´
o
,
i nh
˜
u
,
ng sô
´
t
.
u
,
nhiên du
,
o
,
ng
a, b, c th
,
oa m˜an a
2
+ b
2
= c
2
, th`ı m
.
oi sô
´
c´o d
.
ang E
k
= a
2
k
+ b
2
k
+ c
2
k
v `a F
k
= (ab)
2
k
+ (bc)
2
k
+ (ca)
2
k
v
´
o
,
i k ≥ 2 chia hê
´
t cho sô
´
D =
1
2
(a
4
+ b
4
+ c
4
).
L
`
o
,
i gi
,
ai. Ta ch
´
u
,
ng minh
¯
dô
`
ng th
`
o
,
i sô
´
E
k
v
`
a F
k
chia hê
´
t cho D.
Tru
,
´
o
,
c tiên ta kh
,
˘
ang
¯
d
.
inh a
4
+ b
4
+ c
4
l
`
a sô
´
ch
˜
˘
an. Th
.
ât v
.
ây, nê
´
u
c = 2k, th
`
ı a v
`
a b l
`
a ho
.
˘
ac
¯
dô
`
ng th
`
o
,
i l
,
e ho
.
˘
ac
¯
dô
`
ng th
`
o
,
i ch
˜
˘
an v
`
a suy
ra a
4
+ b
4
+ c
4
l
`
a ch
˜
˘
an. Nê
´
u c = 2k + 1, th
`
ı a
2
+ b
2
l
`
a l
,
e v
`
a suy ra

92 Chu
,
o
,
ng 4. Sô
´
h
.
oc
a
4
+ b
4
= (a
2
+ b
2
)
2
−2a
2
b
2
c
˜
ung l
`
a l
,
e. Do c
4
= (2k + 1)
4
l
`
a l
,
e nên
(a
4
+ b
4
) + c
4
ch
˜
˘
an, v
`
ı l
`
a tô
,
ng hai sô
´
l
,
e.
Ta x
´
et sô
´
F
2
= (ab)
4
+ (bc)
4
+ (ca)
4
= a
4
b
4
+ c
4
(a
4
+ b
4
) = 2Dc
4
+ a
4
b
4
−c
8
= 2Dc
4
+ (a
2
b
2
−c
4
)(a
2
b
2
+ c
4
).
V
`
ı 2a
2
b
2
= c
4
− (a
4
+ b
4
), nên a
2
b
2
− c
4
=
c
4
−(a
4
+ b
4
)
2
− c
4
=
−D, T
`
u
,
¯
d
´
o suy ra F
2
chia hê
´
t cho D. C
˜
ung nhu
,
v
.
ây E
2
chia hê
´
t
cho D. M
.
ênh
¯
dê
`
c
,
ua b
`
ai to
´
an suy ra t
`
u
,
quy n
.
ap to
´
an h
.
oc v
´
o
,
i c
´
ac
¯
d
,
˘
ang th
´
u
,
c E
k+1
+ 2F
k
= E
2
k
v
`
a F
k+1
+ 2(a.b.c)
2
k
E
k
= F
2
k
.
J
V
´
ı d
.
u 4.4. Ch
´
u
,
ng minh r
`
˘ang v
´
o
,
i sô
´
t
.
u
,
nhiên du
,
o
,
ng bâ
´
t k`y n, sô
´
2
4
n
+ 5 chia hê
´
t cho 21.
Tô
,
ng qu ´at: V
´
o
,
i sô
´
t
.
u
,
nhiên bâ
´
t k`y a > 1, n ≥ 1, biê
,
u th
´
u
,
c
B
n
= a
4
n
+ a
3
− a −1 chia hê
´
t cho (a −1)(a + 1)(a
2
+ a + 1).
L
`
o
,
i gi
,
ai. Nê
´
u n = 1, th
`
ı B
1
= a
4
+ a
3
−a −1 = (a −1)(a + 1)(a
2
+
a + 1).
Gi
,
a s
,
u
,
n = k ≥ 1 v
`
a B
k
chia hê
´
t cho ( a −1)(a + 1)(a
2
+ a + 1).
Khi
¯
d
´
o v
´
o
,
i n = k + 1 ta nh
.
ân
¯
du
,
.
o
,
c
B
k+1
= a
4
k+ 1
+ a
3
− a −1 = (a
4
− a + a)
4
k
+ a
3
− a −1
= [a(a
3
−1) + a]
4
k
+ a
3
− a −1 = K(a −1)(a
2
+ a + 1)+
+ a
4
k
+ a
3
− a −1 = K(a −1)(a
2
+ a + 1) + B
k
.
M
.
˘
at kh
´
ac
B
k+1
= (a
4
+ a − a)
4
k
+ a
3
− a −1 = [a (a
3
+ 1) −a]
4
k
+ a
3
− a −1
= K(a + 1) + a
4
k
+ a
3
− a −1 = K(a + 1) + B
k
.

4.1. Ph
´
ep chia hê
´
t 93
(K
´
y hi
.
êu K(a + 1) l
`
a biê
,
u th
´
u
,
c lu
˜
y th
`
u
,
a c
,
ua a + 1.) V
`
ı c
´
ac sô
´
a −1, a + 1 v
`
a a
2
+ a + 1 nguyên tô
´
c
`
ung nhau, suy ra B
k+1
chia
hê
´
t cho t
´
ıch c
,
ua ch
´
ung. V
´
o
,
i a = 2, ta c
´
o B
n
= 2
4
n
+ 5.
J
V
´
ı d
.
u 4.5. 1) Ch
´
u
,
ng minh r
`
˘ang 3
2
n
−1 chia hê
´
t cho 2
n+2
v `a không
chia hê
´
t cho 2
n+3
v
´
o
,
i n nguyên du
,
o
,
ng.
2) Ch
´
u
,
ng minh r
`
˘ang 2
3
n
+ 1 chia hê
´
t cho 3
n+1
v `a không chia hê
´
t
cho 3
n+2
v
´
o
,
i n nguyên du
,
o
,
ng.
L
`
o
,
i gi
,
ai. 1) Ta c
´
o
A
n+1
= 3
2
n+1
−1 = (3
2
n
)
2
−1 = (3
2
n
−1)(3
2
n
+ 1) .
V
´
o
,
i n = 1 m
.
ênh
¯
dê
`
¯
d
´
ung. Gi
,
a s
,
u
,
A
n
= 3
2
n
−1 chia hê
´
t cho 2
n+2
.
V
`
ı 3
2
n
+ 1 chia hê
´
t cho 2, nên A
n+1
s
˜
e chia hê
´
t cho 2.2
n+2
= 2
n+3
.
M
.
˘
at kh
´
ac, ta gi
,
a s
,
u
,
A
n
= 3
2
n
− 1 không chia hê
´
t cho 2
n+3
.
Nhu
,
ng 3
2
n
+ 1 không chia hê
´
t cho 4, v
`
ı (3
2
n
+ 1) − 2 = 3
2
n
− 1
chia hê
´
t cho 4 (th
.
âm ch
´
ı chia hê
´
t cho 4.2
n
do phâ
`
n trên. V
`
ı v
.
ây
(3
2
n
+ 1) chia cho 4 du
,
2) t
`
u
,
¯
dây suy ra A
n+1
không chia hê
´
t cho
2
n+4
.
2) Ch
´
u
,
ng minh tu
,
o
,
ng t
.
u
,
nhu
,
phâ
`
n trên. Ta s
,
u
,
d
.
ung
2
3
n+1
+ 1 = (2
3
n
)
3
+ 1 = (2
3
n
+ 1)(2
2,3
n
−2
3
n
+ 1)
= (2
3
n
+ 1)[(2
3
n
+ 1)
2
−3.2
3
n
].
Sô
´
trong ngo
.
˘
ac vuông chia hê
´
t cho 3, không chia hê
´
t cho 9.
J
V
´
ı d
.
u 4.6. 1) Ch
´
u
,
ng minh r
`
˘ang nê
´
u p l `a sô
´
nguyên tô
´
, th`ı sô
´
a
p
− a chia hê
´
t cho p v
´
o
,
i m
.
oi a (a l `a sô
´
nguyên du
,
o
,
ng).
2) Ch
´
u
,
ng minh r
`
˘ang nê
´
u p l `a sô
´
nguyên tô
´
v `a a không chia hê
´
t
cho p, th`ı sô
´
a
p−1
−1 chia hê
´
t cho p (
¯
d
.
inh l´y Fermat).

94 Chu
,
o
,
ng 4. Sô
´
h
.
oc
L
`
o
,
i gi
,
ai. 1) V
´
o
,
i a = 1 m
.
ênh
¯
dê
`
l
`
a hiê
,
n nhiên, v
`
ı trong tru
,
`
o
,
ng
h
.
o
,
p n
`
ay a
p
− a = 1 −1 = 0.
Gi
,
a s
,
u
,
m
.
ênh
¯
dê
`
¯
d
´
ung v
´
o
,
i m
.
ôt sô
´
a n
`
ao
¯
dâ
´
y, ngh
˜
ıa l
`
a a
p
− a
chia hê
´
t cho p. Ta s
˜
e ch
´
u
,
ng minh m
.
ênh
¯
dê
`
c
˜
ung
¯
d
´
ung cho a + 1.
Th
.
ât v
.
ây,
´
ap d
.
ung phân t
´
ıch nh
.
i th
´
u
,
c Newton, ta nh
.
ân
¯
du
,
.
o
,
c
(a + 1)
p
−(a + 1) = a
p
+ p f (a) + 1 − a −1 = (a
p
− a) + p f (a).
,
O
,
¯
dây f (a) l
`
a
¯
da th
´
u
,
c b
.
âc p −1 theo a. Do
´
ap d
.
ung công th
´
u
,
c h
.
ê
sô
´
Newton v
`
a nh
´
om c
´
ac th
`
u
,
a sô
´
c
´
o p
¯
du
,
a ra ngo
`
ai l
.
âp ra f (a ).
M
.
ênh
¯
dê
`
¯
d
´
ung v
´
o
,
i a + 1, theo nguyên l
´
y quy n
.
ap to
´
an h
.
oc n
´
o
¯
d
´
ung v
´
o
,
i m
.
oi a ≥ 1.
2) T
`
u
,
phâ
`
n tru
,
´
o
,
c suy ra a
p
− a chia hê
´
t cho sô
´
nguyên tô
´
p.
Khi
¯
d
´
o t
`
u
,
¯
d
,
˘
ang th
´
u
,
c
a
p
− a = a(a
p−1
−1) .
Do
¯
diê
`
u ki
.
ên
¯
dâ
`
u b
`
ai a không chia hê
´
t p, nên a
p−1
− 1 chia hê
´
t
cho p.
Ch
´
u
´
y: Nê
´
u ta
¯
d
.
˘
at a = 2, 3, . . . , p −1, th
`
ı nhu
,
h
.
ê qu
,
a c
,
ua kê
´
t
lu
.
ân trên c
´
ac sô
´
2
p−1
−1, 3
p−1
−1, . . . , (p −1)
p−1
−1 chia hê
´
t cho
p ho
.
˘
ac l
`
a 2
p−1
, 3
p−1
, . . . , (p −1)
p−1
chia cho p du
,
1.
Trong tru
,
`
o
,
ng h
.
o
,
p n
`
ay tô
,
ng 2
p−1
+ 3
p−1
+ ···+ (p −1 )
p−1
chia
hê
´
t cho p, v
´
o
,
i p l
`
a sô
´
nguyên tô
´
.
J
4.2. Thu
.
ât to
´
an Euclide
Cho a > 0 v
`
a b > 0 l
`
a nh
˜
u
,
ng sô
´
nguyên. T
`
ım u
,
´
o
,
c sô
´
chung
l
´
o
,
n nhâ
´
t c
,
ua hai sô
´
¯
d
˜
a cho
¯
du
,
.
o
,
c t
`
ım theo thu
.
ât to
´
an c
,
ua Euclide
nhu
,
sau:
Ðê
,
cho ti
.
ên
¯
d
.
˘
at r
0
= a v
`
a r
1
= b. Chia sô
´
a cho sô
´
b
¯
du
,
.
o
,
c

4.2. Thu
.
ât to
´
an Euclide 95
thu
,
o
,
ng q
1
v
`
a sô
´
du
,
l
`
a r
2
. Ta c
´
o thê
,
viê
´
t
a = bq
1
+ r
2
, (0 ≤ r
2
< r
1
).
Nê
´
u b > a ta c
´
o q
1
= 0 v
`
a r
2
= a. Nê
´
u r
2
= 0, th
`
ı a chia hê
´
t cho
b; trong tru
,
`
o
,
ng h
.
o
,
p n
`
ay u
,
´
o
,
c sô
´
chung l
´
o
,
n nhâ
´
t l
`
a b. Nê
´
u r
2
6= 0,
ta tiê
´
n h
`
anh bu
,
´
o
,
c tiê
´
p theo: Lâ
´
y b chia cho r
2
, lâ
`
n n
`
ay k
´
y hi
.
êu
thu
,
o
,
ng v
`
a sô
´
du
,
l
`
a q
2
v
`
a r
3
, ta c
´
o
b = r
2
q
2
+ r
3
(0 ≤ r
3
< r
2
).
Nê
´
u r
3
= 0, th
`
ı thu
.
ât to
´
an d
`
u
,
ng. Tru
,
`
o
,
ng h
.
o
,
p ngu
,
.
o
,
c l
.
ai ta l
.
ai
lâ
´
y r
2
chia cho r
3
¯
du
,
.
o
,
c thu
,
o
,
ng q
3
v
`
a sô
´
du
,
r
4
, hay l
`
a r
2
= r
3
q
3
+
r
4
(0 ≤ r
3
< r
2
). C
´
u
,
tiê
´
p t
.
uc nhu
,
v
.
ây, v
`
ı c
´
ac sô
´
du
,
¯
dê
`
u thu
.
ôc
[0, b) v
`
a b > r
1
> r
2
> . . . ≥ 0 d
˜
ay sô
´
gi
,
am ng
.
˘
at ch
´
u
,
ng t
,
o sau
m
.
ôt sô
´
bu
,
´
o
,
c (sô
´
bu
,
´
o
,
c không l
´
o
,
n ho
,
n b) s
˜
e d
˜
ân t
´
o
,
i sô
´
du
,
b
`
˘
ang 0 v
`
a
thu
.
ât to
´
an s
˜
e d
`
u
,
ng. Kê
´
t qu
,
a ta nh
.
ân
¯
du
,
.
o
,
c d
˜
ay
r
0
= r
1
q
1
+ r
2
r
1
= r
2
q
2
+ r
3
r
2
= r
3
q
3
+ r
3
. . .
r
n−2
= r
n−1
q
n−1
+ r
n
r
n−1
= r
n
q
n
(0 ≤ r
i
< r
i −1
, i = 1, 2, . . . , n).
(4.1)
Trong công th
´
u
,
c trên r
n
l
`
a sô
´
du
,
cuô
´
i c
`
ung kh
´
ac 0.
V
´
ı d
.
u 4.7. Ta ch
´
u
,
ng minh r
`
˘ang r
n
l `a u
,
´
o
,
c sô
´
chung l
´
o
,
n nhâ
´
t c
,
ua
a v `a b.
L
`
o
,
i gi
,
ai. 1) Ta ch
,
ı ra r
`
˘
ang r
n
l
`
a u
,
´
o
,
c sô
´
chung c
,
ua a v
`
a b.
Do r
n−1
chia hê
´
t cho r
n
v
`
a công th
´
u
,
c hô
`
i quy
r
i −1
= r
i
q
i
+ r
i +1
(i = 1, 2, . . . , n; r
n+1
= 0). (4.2)

96 Chu
,
o
,
ng 4. Sô
´
h
.
oc
Ðê
,
¯
d
.
at m
.
uc
¯
d
´
ıch c
,
ua ta th
`
ı ph
,
ai ch
,
ı ra r
n
l
`
a u
,
´
o
,
c sô
´
chung c
,
ua
tâ
´
t c
,
a r
n−1
, r
n−2
, . . . , r
0
.
¯
d
,
˘
ang th
´
u
,
c cuô
´
i c
`
ung c
,
ua (4.1) cho ta thâ
´
y
r
n−2
chia hê
´
t cho r
n
(v
`
ı r
n−1
¯
d
˜
a chia hê
´
t cho r
n
). Gi
,
a s
,
u
,
v
´
o
,
i m
.
ôt
sô
´
n
`
ao
¯
d
´
o i(1 ≤ i ≤ n −1) nh
˜
u
,
ng sô
´
r
n−1
, r
n−2
, . . . , r
i
chia hê
´
t cho
r
n
. Khi
¯
d
´
o t
`
u
,
(4.2) suy ra r
i −1
chia hê
´
t cho r
n
. Nhu
,
v
.
ây b
`
˘
ang quy
n
.
ap ch
´
ung ta kê
´
t lu
.
ân r
1
= b c
˜
ung chia hê
´
t cho r
n
, c
`
on
¯
d
,
˘
ang th
´
u
,
c
¯
dâ
`
u tiên c
,
ua (4.1) cho ta r
n
l
`
a u
,
´
o
,
c sô
´
c
,
ua a.
2) Ta ch
´
u
,
ng minh r
n
l
`
a u
,
´
o
,
c sô
´
chung l
´
o
,
n nhâ
´
t c
,
ua a v
`
a b.
Th
.
ât v
.
ây, K
´
y hi
.
êu d l
`
a u
,
´
o
,
c sô
´
chung bâ
´
t k
`
y c
,
ua a v
`
a b (ngh
˜
ıa
l
`
a r
0
, r
1
c
´
o u
,
´
o
,
c sô
´
chung d). T
`
u
,
¯
d
,
˘
ang th
´
u
,
c
¯
dâ
`
u tiên c
,
ua (4.1) suy
ra r
2
chia hê
´
t cho d . V
`
ı thê
´
d c
˜
ung l
`
a u
,
´
o
,
c sô
´
chung c
,
ua r
1
v
`
a r
2
.
Gi
,
a s
,
u
,
d l
`
a u
,
´
o
,
c sô
´
chung c
,
ua r
i −1
, r
i
v
´
o
,
i sô
´
i(1 ≤ i ≤ n −1) n
`
ao
¯
d
´
o;
khi
¯
d
´
o t
`
u
,
(4.1) suy ra d l
`
a u
,
´
o
,
c sô
´
chung c
,
ua r
i +1
. Theo nguyên l
´
y
quy n
.
ap to
´
an h
.
oc, d l
`
a u
,
´
o
,
c sô
´
c
,
ua r
n
. B
`
˘
ang c
´
ach n
`
ay ta thâ
´
y r
`
˘
ang
m
.
oi u
,
´
o
,
c sô
´
chung c
,
ua a v
`
a b c
˜
ung l
`
a u
,
´
o
,
c sô
´
chung c
,
ua r
n
, suy ra
r
n
l
`
a u
,
´
o
,
c sô
´
chung l
´
o
,
n nhâ
´
t.
J
D
.
ang quy n
.
ap to
´
an h
.
oc
¯
di t
`
u
,
bu
,
´
o
,
c i + 1 v
`
a i
¯
dê
´
n bu
,
´
o
,
c i − 1
nhu
,
trên g
.
oi l
`
a ph´ep quy n
.
ap ngu
,
.
o
,
c.
Ngu
,
`
o
,
i ta c
´
o thê
,
biê
,
u di
˜
ên u
,
´
o
,
c sô
´
chung l
´
o
,
n nhâ
´
t b
`
˘
ang c
´
ac tô
,
h
.
o
,
p tuyê
´
n t
´
ınh c
,
ua hai sô
´
a v
`
a b thông qua b
`
ai t
.
âp sau.
V
´
ı d
.
u 4.8. Cho a v `a b l `a hai sô
´
nguyên du
,
o
,
ng. Khi
¯
d´o
(a, b) = s
n
a + t
n
b
v
´
o
,
i n = 0, 1, 2 . . ., s
n
v `a t
n
l `a nh
˜
u
,
ng sô
´
h
.
ang th
´
u
,
n c
,
ua d ˜ay {s
n
},
{t
n
} x ´ac
¯
d
.
inh b
,
o
,
i
s
0
= 1, t
0
= 0, s
1
= 0, t
1
= 1

4.2. Thu
.
ât to
´
an Euclide 97
v `a
s
i
= s
i −2
−q
i −1
s
i −1
,
t
i
= t
i −2
−q
i −2
t
i −1
,
v
´
o
,
i i = 2, 3, . . . , n,
,
o
,
¯
dây q
i
l `a thu
,
o
,
ng sô
´
th
´
u
,
i trong thu
.
ât to ´an
Euclide khi t`ım u
,
´
o
,
c sô
´
chung l
´
o
,
n nhâ
´
t.
L
`
o
,
i gi
,
ai. Ta s
˜
e ch
´
u
,
ng minh r
`
˘
ang
r
i
= s
i
a + t
i
b, (4.3)
v
´
o
,
i i = 0, 1, 2 . . . , n. V
`
ı (a, b) = r
n
nên t
`
u
,
(4.3) c
´
o thê
,
suy ra l
`
o
,
i
gi
,
ai.
D
`
ung phu
,
o
,
ng ph
´
ap quy n
.
ap to
´
an h
.
oc
¯
dê
,
ch
´
u
,
ng minh (4.3).
V
´
o
,
i i = 0, ta c
´
o a = r
0
= 1.a + 0.b = s
0
a + t
0
b. Do
¯
d
´
o (4.3)
¯
d
´
ung
v
´
o
,
i i = 0. M
.
˘
at kh
´
ac b = r
1
= 0.a + 1.b = s
1
a + t
1
b, nhu
,
v
.
ây
(4.3) c
˜
ung
¯
d
´
ung v
´
o
,
i i = 1. Gi
,
a thiê
´
t r
i
= s
i
a + t
i
b
¯
d
´
ung v
´
o
,
i m
.
oi
i = 1, 2, . . . , k − 1. Khi
¯
d
´
o, t
`
u
,
bu
,
´
o
,
c k trong thu
.
ât to
´
an Euclide ta
c
´
o
r
k
= r
k−2
−r
k−1
q
k−1
theo gi
,
a thiê
´
t quy n
.
ap suy ra
r
k
= (s
k−2
a + t
k−2
b) − (s
k−1
a + t
k−1
b)q
k−1
= (s
k−2
−s
k−1
q
k−1
)a + (t
k−2
−t
k−1
q
k−1
) b
= s
k
a + t
k
b.
J
V
´
ı d
.
u 4.9. Cho a l `a sô
´
t
.
u
,
nhiên, a > 1. H ˜ay t`ım (a
m
−1, a
n
−1),
,
o
,
¯
dây m v `a n l `a nh
˜
u
,
ng sô
´
t
.
u
,
nhiên.
L
`
o
,
i gi
,
ai. Ð
.
˘
at (n, m) = d. Ta ch
´
u
,
ng minh r
`
˘
ang (a
m
−1, a
n
−1) =
(a
d
−1). Không mâ
´
t t
´
ınh tô
,
ng qu
´
at ta c
´
o thê
,
gi
,
a thiê
´
t n ≥ m. Ta

98 Chu
,
o
,
ng 4. Sô
´
h
.
oc
ch
´
u
,
ng minh quy n
.
ap theo m. V
´
o
,
i m = 0,
¯
d
,
˘
ang th
´
u
,
c hiê
,
n nhiên.
Gi
,
a s
,
u
,
m > 0. Ta
¯
d
.
˘
at n = mq + r, 0 ≤ r < m. Ta c
´
o
a
n
−1 = a
mq
a
r
−1 = a
mq
a
r
− a
r
+ a
r
−1
= a
r
(a
mq
−1) + (a
r
−1) = A(a
m
−1) + (a
r
−1) ,
,
o
,
¯
dây A l
`
a sô
´
nguyên. T
`
u
,
nh
˜
u
,
ng
¯
d
,
˘
ang th
´
u
,
c n
`
ay suy ra
(a
n
−1, a
m
−1) = (a
m
−1, a
r
−1)
v
`
a theo gi
,
a thiê
´
t quy n
.
ap to
´
an h
.
oc ta c
´
o
(a
m
−1, a
r
−1) = a
(m,r)
−1 = a
d
−1.
J
V
´
ı d
.
u 4.10. Ch
´
u
,
ng minh r
`
˘ang b
.
ôi sô
´
chung nh
,
o nhâ
´
t (BSCN)
c
,
ua d ˜ay 1, 2, . . . , 2n b
`
˘ang b
.
ôi sô
´
chung nh
,
o nhâ
´
t c
,
ua n + 1, n +
2, . . . , 2n:
BSCN(1, 2, . . . , n) = BSCN(n + 1, n + 2, . . . , 2n).
L
`
o
,
i gi
,
ai. Ta
¯
d
.
˘
at [1, 2, . . . , 2n] = s v
`
a [n + 1, n + 2, . . . , 2n] = t. v
`
ı
s l
`
a m
.
ôt b
.
ôi sô
´
chung c
,
ua c
´
ac sô
´
n + 1, n + 2, . . . , 2n, c
`
on t l
`
a b
.
ôi
sô
´
nh
,
o nhâ
´
t nên s chia hê
´
t cho t. Ðê
,
ch
´
u
,
ng minh ngu
,
.
o
,
c l
.
ai t chia
hê
´
t s ta ph
,
ai ch
´
u
,
ng minh r
`
˘
ang m
˜
ôi sô
´
chia hê
´
t cho n + 1, n +
2, . . . , 2n c
˜
ung chia hê
´
t cho 1, 2, . . . , n. Ta s
˜
e ch
´
u
,
ng minh
¯
diê
`
u
¯
d
´
o
b
`
˘
ang phu
,
o
,
ng ph
´
ap quy n
.
ap theo n. V
´
o
,
i n = 1 kh
,
˘
ang
¯
d
.
inh l
`
a
hiê
,
n nhiên. Gi
,
a s
,
u
,
m
.
ênh
¯
dê
`
¯
d
´
ung v
´
o
,
i n , ta ch
´
u
,
ng minh n
´
o c
˜
ung
¯
d
´
ung v
´
o
,
i n + 1. Cho m l
`
a sô
´
chia hê
´
t cho (n + 1) + 1, (n + 1) +
2, . . . , 2(n + 1). T
`
u
,
m chia hê
´
t cho 2(n + 1) nên m chia hê
´
t cho
n + 1 v
`
a suy ra m chia hê
´
t cho n + 1, n + 2, . . . , 2n (ta ch
,
ı thêm
v
`
ao
¯
dâ
`
u d
˜
ay c
´
ac sô
´
m
`
a theo gi
,
a thiê
´
t m
¯
d
˜
a chia hê
´
t). Theo gi
,
a
thiê
´
t quy n
.
ap m chia hê
´
t cho 1, 2, . . . , n, c
`
on tru
,
´
o
,
c
¯
d
´
o ta
¯
d
˜
a c
´
o m
chia hê
´
t cho n + 1.
J

4.3. Sô
´
ph
´
u
,
c 99
V
´
ı d
.
u 4.11. Ch
´
u
,
ng minh r
`
˘ang tô
,
ng tâ
´
t c
,
a u
,
´
o
,
c sô
´
c
,
ua sô
´
t
.
u
,
nhiên
n > 2 nh
,
o ho
,
n n
√
n.
L
`
o
,
i gi
,
ai. Ta k
´
y hi
.
êu tô
,
ng c
,
ua tâ
´
t c
,
a u
,
´
o
,
c sô
´
c
,
ua sô
´
n b
`
˘
ang D(n).
Ta ph
,
ai ch
´
u
,
ng minh r
`
˘
ang D( n) < n
√
n v
´
o
,
i n ≥ 3. Ta ch
.
on tru
,
`
o
,
ng
h
.
o
,
p n = 2
α
(α l
`
a sô
´
nguyên, α ≥ 2). Khi
¯
d
´
o
D(n) = 1 + 2 + 2
2
+ ··· + 2
α
= 2
α+1
−1 < 2
α+
α
2
= n
√
n.
Gi
,
a thiê
´
t r
`
˘
ang n 6= 2
α
v
`
a D(k ) < k
√
k v
´
o
,
i m
.
oi 3 ≤ k < n v
`
a ch
´
ung
ta s
˜
e ch
´
u
,
ng minh D(n) < n
√
n. Do nh
˜
u
,
ng
¯
diê
`
u kê
,
trên, ta c
´
o thê
,
x
´
et n = mp,
,
o
,
¯
dây p l
`
a sô
´
nguyên tô
´
l
,
e. Ch
´
u
´
y r
`
˘
ang p ≥ 3, 1 + p <
p
√
p (th
.
ât v
.
ây, v
´
o
,
i p ≥ 4, 1 +
1
p
< 2 <
√
p; v
´
o
,
i p = 3, 1 + 3 <
3
√
3). V
`
ı thê
´
, nê
´
u m = 1, th
`
ı D(p) = 1 + p < p
√
p; tu
,
o
,
ng t
.
u
,
, nê
´
u
m = 2, th
`
ı D( n) = 1 + 2 + p + 2p = 3 + 3p < 2p
p
2p = n
√
n, nê
´
u
m ≥ 3, th
`
ı theo gi
,
a thiê
´
t quy n
.
ap D(m) < m
√
m. Nhu
,
v
.
ây m
˜
ôi
u
,
´
o
,
c sô
´
c
,
ua n c
´
o d
.
ang d ho
.
˘
ac dp ,
,
o
,
¯
dây d l
`
a u
,
´
o
,
c sô
´
c
,
ua m, nên
D(n) = D(m) + pD(m) = D(m)(1 + p)
< m
√
m.p
√
p = n
√
n.
J
4.3. Sô
´
ph
´
u
,
c
Ta nh
´
˘
ac l
.
ai kh
´
ai ni
.
êm co
,
b
,
an c
,
ua sô
´
ph
´
u
,
c. M
.
ôt sô
´
ph
´
u
,
c z c
´
o
d
.
ang
¯
d
.
ai sô
´
z = x + iy,
,
o
,
¯
dây x v
`
a y l
`
a nh
˜
u
,
ng sô
´
th
.
u
,
c, c
`
on i l
`
a
¯
do
,
n
v
.
i
,
ao c
´
o t
´
ınh châ
´
t i
2
= −1; sô
´
x g
.
oi l
`
a phâ
`
n th
.
u
,
c, c
`
on sô
´
y g
.
oi l
`
a
phâ
`
n
,
ao c
,
ua sô
´
ph
´
u
,
c z.
Hai sô
´
ph
´
u
,
c z
1
= x
1
+ iy
1
, z
2
= x
2
+ iy
2
l
`
a b
`
˘
ang nhau khi v
`
a
ch
,
ı khi x
1
= x
2
, y
1
= y
2
. Nê
´
u x = y = 0, th
`
ı z = 0 + i0 = 0. M
.
oi
sô
´
th
.
u
,
c c
´
o thê
,
coi nhu
,
l
`
a m
.
ôt sô
´
ph
´
u
,
c khi phâ
`
n
,
ao c
,
ua n
´
o b
`
˘
ang 0.
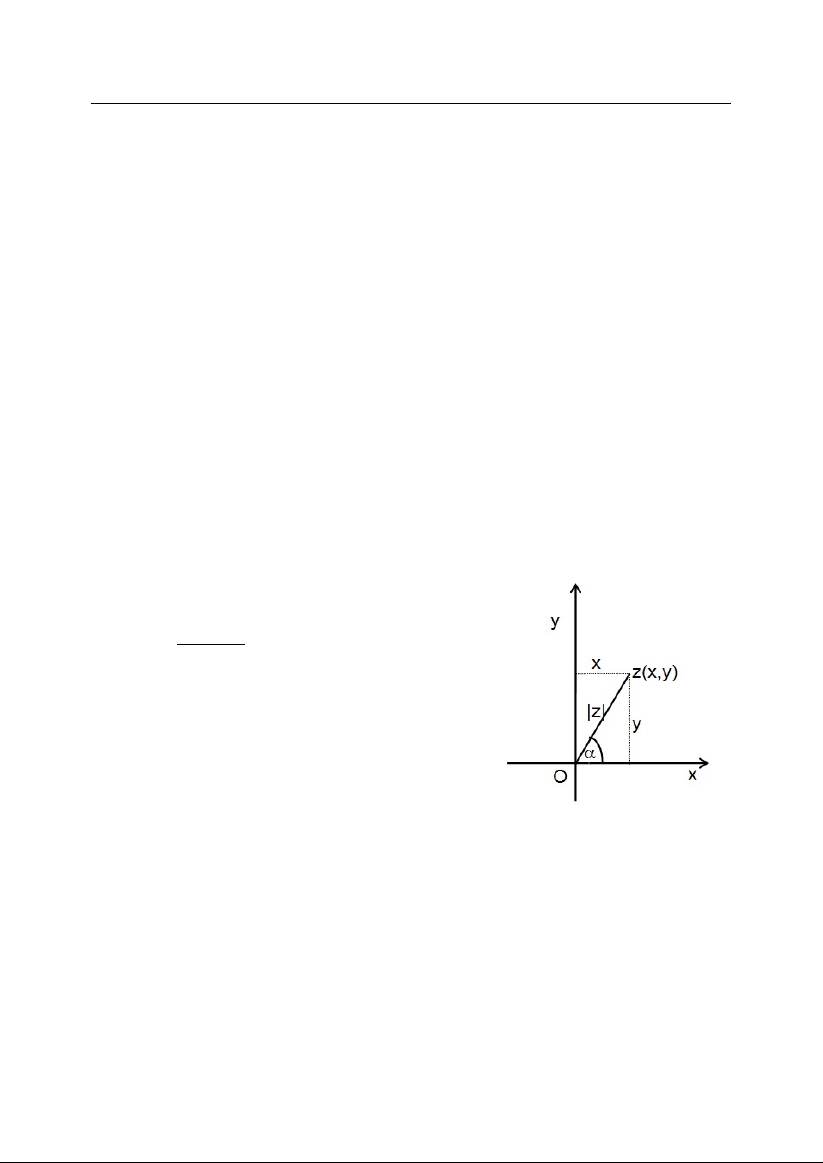
100 Chu
,
o
,
ng 4. Sô
´
h
.
oc
Nhu
,
v
.
ây t
.
âp sô
´
th
.
u
,
c ch
,
ı l
`
a t
.
âp con c
,
ua t
.
âp sô
´
ph
´
u
,
c. Nh
˜
u
,
ng ph
´
ep
to
´
an
¯
du
,
.
o
,
c
¯
d
.
inh ngh
˜
ıa trên t
.
âp sô
´
ph
´
u
,
c gô
`
m:
(x
1
+ iy
1
) + (x
2
+ iy
2
) = (x
1
+ x
2
) + i(y
1
+ y
2
),
(x
1
+ iy
1
) − (x
2
+ iy
2
) = (x
1
− x
2
) + i(y
1
−y
2
),
(x
1
+ iy
1
)(x
2
+ iy
2
) = (x
1
x
2
−y
1
y
2
) + i(x
1
y
2
+ x
2
y
1
).
Sô
´
¯
z = x −iy g
.
oi l
`
a sô
´
liên h
.
o
,
p c
,
ua z = x + iy. R
˜
o r
`
ang nê
´
u z
1
l
`
a liên h
.
o
,
p c
,
ua z
2
, th
`
ı z
2
c
˜
ung liên h
.
o
,
p c
,
ua z
1
.
Sô
´
ph
´
u
,
c c
´
o liên h
.
ê ch
.
˘
at ch
˜
e v
´
o
,
i h
.
ê t
.
oa
¯
d
.
ô vuông g
´
oc nhu
,
h
`
ınh
v
˜
e.
M
˜
ôi sô
´
ph
´
u
,
c z = x + iy biê
,
u di
˜
ên nhu
,
m
.
ôt
¯
diê
,
m (x, y) trong
h
.
ê t
.
oa
¯
d
.
ô vuông g
´
oc.
Ð
.
ô d
`
ai t
`
u
,
¯
diê
,
m gô
´
c t
.
oa
¯
d
.
ô
¯
dê
´
n
H
`
ınh 4.1:
¯
diê
,
m sô
´
ph
´
u
,
c g
.
oi l
`
a modun c
,
ua z v
`
a
¯
du
,
.
o
,
c k
´
y hi
.
êu |z|. T
`
u
,
h
`
ınh v
˜
e ta thâ
´
y
|z| =
p
x
2
+ y
2
≥ 0. G
´
oc gi
˜
u
,
a tr
.
uc
Ox v
`
a Oz
¯
do theo chiê
`
u ngu
,
.
o
,
c kim
¯
dô
`
ng hô
`
g
.
oi l
`
a argumen c
,
ua z; v
`
a k
´
y
hi
.
êu l
`
a argz. R
˜
o r
`
ang
(
x = |z|cos α,
y = |z|sin α,
,
o
,
¯
dây α = argz. Nhu
,
v
.
ây sô
´
ph
´
u
,
c z =
x + iy biê
,
u di
˜
ên qua d
.
ang lu
,
.
o
,
ng gi
´
ac
z = ρ(cos α + i sin α), ρ = |z|, α = argz.
,
o
,
d
.
ang lu
,
.
o
,
ng gi
´
ac sô
´
ph
´
u
,
c, c
´
o nhiê
`
u thu
.
ân l
.
o
,
i trong c
´
ac ph
´
ep
t
´
ınh. Ch
,
˘
ang h
.
an ta lâ
´
y ph
´
ep nhân hai sô
´
ph
´
u
,
c: z
1
= ρ
1
(cos α
1
+

4.3. Sô
´
ph
´
u
,
c 101
i sin α
1
), z
2
= ρ
2
(cos α
2
+ i sin α
2
). Khi
¯
d
´
o
z
1
z
2
=
= ρ
1
ρ
2
[(cos α
1
cos α
2
−sin α
1
sin α
2
) + i(cos α
1
sin α
2
+ cos α
2
sin α
1
)]
= ρ
1
ρ
2
[cos(α
1
+ α
2
) + i sin(α
1
+ α
2
)].
Công th
´
u
,
c nhân v
`
a chia sô
´
ph
´
u
,
c
,
o
,
d
.
ang n
`
ay kh
´
a
¯
d
.
ep. Kê
´
t qu
,
a
tô
,
ng qu
´
at:
V
´
ı d
.
u 4.12. Cho nh
˜
u
,
ng sô
´
ph
´
u
,
c
z
1
= ρ
1
(cos α
1
+ i sin α
1
),
z
2
= ρ
2
(cos α
2
+ i sin α
2
),
........................
z
n
= ρ
n
(cos α
n
+ i sin α
n
).
Khi
¯
d´o
z
1
z
2
. . . z
n
= ρ
1
ρ
2
. . . ρ
n
(cos (α
1
+ α
2
+ ··· + α
n
)+
i sin(α
1
+ α
2
+ ··· + α
n
)) (4.4)
v
´
o
,
i n = 2, 3, . . .
L
`
o
,
i gi
,
ai. Ch
´
u
,
ng minh
¯
d
,
˘
ang th
´
u
,
c trên b
`
˘
ang phu
,
o
,
ng ph
´
ap quy
n
.
ap to
´
an h
.
oc theo n. V
´
o
,
i n = 2, công th
´
u
,
c (4.4)
¯
d
´
ung theo ph
´
ep
nhân hai sô
´
ph
´
u
,
c. Gi
,
a s
,
u
,
¯
d
,
˘
ang th
´
u
,
c
¯
d
´
ung cho m
.
ôt sô
´
n n
`
ao
¯
d
´
o. Ta
s
˜
e ch
´
u
,
ng minh
¯
d
,
˘
ang th
´
u
,
c (4.4)
¯
d
´
ung cho n + 1. Th
.
ât v
.
ây, v
´
o
,
i n + 1
sô
´
ph
´
u
,
c z
µ
= ρ
µ
(cos α
µ
+ i sin α
µ
), µ = 1, 2, . . . , n + 1. S
,
u
,
d
.
ung gi
,
a
thiê
´
t quy n
.
ap
z
1
z
2
. . . z
n
z
n+1
= ρ
1
ρ
2
. . . ρ
n
[cos(α
1
+ α
2
+ ··· + α
n
)
+ i sin (α
1
+ α
2
+ ··· + α
n
)].ρ
n+1
(cos α
n+1
+ i sin α
n+1
)

102 Chu
,
o
,
ng 4. Sô
´
h
.
oc
= ρ
1
ρ
2
. . . ρ
n
ρ
n+1
[cos(α
1
+ α
2
+ ··· + α
n
) cos α
n+1
−sin(α
1
+ α
2
+ ··· + α
n
) sin α
n+1
+ i[cos(α
1
+ α
2
+ ··· + α
n
) sin α
n+1
+ sin(α
1
+ α
2
+ ··· + α
n
) cos α
n+1
]
= ρ
1
ρ
2
. . . ρ
n
ρ
n+1
[cos(α
1
+ α
2
+ ··· + α
n+1
)
+ i sin (α
1
+ α
2
+ ··· + α
n+1
)].
J
Tru
,
`
o
,
ng h
.
o
,
p riêng α
1
= α
2
= . . . = α
n
= α v
`
a ρ
1
= ρ
2
= . . . =
ρ
n
= ρ công th
´
u
,
c v
`
u
,
a ch
´
u
,
ng minh tr
,
o
,
th
`
anh
z
n
= ρ
n
(cos nα + i sin nα).
Nê
´
u
¯
diê
,
m z n
`
˘
am trên
¯
du
,
`
o
,
ng tr
`
on
¯
do
,
n v
.
i th
`
ı z = cos α + i sin α v
`
a
(cos α + i sin α)
n
= (cos nα + i sin nα).
Công th
´
u
,
c sau c
`
ung g
.
oi l
`
a công th
´
u
,
c Moivre. Công th
´
u
,
c Moivre
c
´
o nhiê
`
u
´
u
,
ng d
.
ung trong th
.
u
,
c tê
´
c
˜
ung nhu
,
gi
,
ai b
`
ai to
´
an liên quan
¯
dê
´
n sô
´
ph
´
u
,
c. Nhiê
`
u b
`
ai to
´
an râ
´
t hay nhu
,
ng không liên quan
¯
dê
´
n
phu
,
o
,
ng ph
´
ap quy n
.
ap to
´
an h
.
oc tôi không x
´
et
¯
dê
´
n
,
o
,
¯
dây
1
.
V
´
ı d
.
u 4.13. Ch
´
u
,
ng minh r
`
˘ang nê
´
u kê
´
t qu
,
a th
.
u
,
c hi
.
ên m
.
ôt sô
´
h
˜
u
,
u
h
.
an ph´ep t´ınh (ph´ep c
.
ông, ph´ep tr
`
u
,
, ph´ep nhân, ph´ep chia) trên
d ˜ay sô
´
x
1
, x
2
, . . . , x
n
l `a m
.
ôt sô
´
u, th`ı kê
´
t qu
,
a th
.
u
,
c hi
.
ên c ˜ung c´ac
ph´ep t´ınh
¯
d´o trên d ˜ay liên h
.
o
,
p
¯
x
1
,
¯
x
2
, . . . ,
¯
x
n
s˜e nh
.
ân
¯
du
,
.
o
,
c sô
´
¯
u
liên h
.
o
,
p c
,
ua u.
L
`
o
,
i gi
,
ai. Bu
,
´
o
,
c co
,
s
,
o
,
: Ðâ
`
u tiên ta s
˜
e ch
´
u
,
ng minh m
.
ênh
¯
dê
`
¯
d
´
ung
v
´
o
,
i t
`
u
,
ng ph
´
ep t
´
ınh trên hai sô
´
ph
´
u
,
c. Cho x
1
= a + ib, x
2
= c + id.
1
B
.
an
¯
d
.
oc c
´
o thê
,
t
`
ım thâ
´
y m
.
ôt sô
´
´
u
,
ng d
.
ung c
,
ua sô
´
ph
´
u
,
c trong [2].

4.3. Sô
´
ph
´
u
,
c 103
khi
¯
d
´
o
x
1
+ x
2
= (a + c) + (b + d)i = u,
¯
x
1
+
¯
x
2
= (a −ib) + (c −id) = (a + c) − (b + d)i =
¯
u.
B
`
˘
ang phu
,
o
,
ng ph
´
ap tu
,
o
,
ng t
.
u
,
ta kiê
,
m tra ph
´
ep tr
`
u
,
, nhân, chia hai
sô
´
ph
´
u
,
c, kh
,
˘
ang
¯
d
.
inh
¯
dê
`
u
¯
d
´
ung.
Bây gi
`
o
,
gi
,
a s
,
u
,
cho biê
,
u th
´
u
,
c h
˜
u
,
u h
.
an c
´
ac sô
´
ph
´
u
,
c x
1
, x
2
, . . . , x
n
.
Th
.
u
,
c hi
.
ên t
´
ınh to
´
an biê
,
u th
´
u
,
c nhu
,
v
.
ây l
`
a th
.
u
,
c hi
.
ên m
.
ôt d
˜
ay c
´
ac
ph
´
ep t
´
ınh trên hai sô
´
ph
´
u
,
c, vi
.
êc th
.
u
,
c hi
.
ên c
´
o thê
,
¯
d
´
anh sô
´
th
´
u
,
t
.
u
,
¯
du
,
.
o
,
c. Ch
,
˘
ang h
.
an biê
,
u th
´
u
,
c
u =
x
1
x
2
+ x
3
x
4
x
1
+ x
2
− x
3
.
Ðê
,
th
.
u
,
c hi
.
ên u ngu
,
`
o
,
i ta th
.
u
,
c hi
.
ên c
´
ac bu
,
´
o
,
c sau:
1)x
1
x
2
= u
1
, 4)u
3
− x
3
= u
4
,
2)x
3
x
4
= u
2
, 5)u
1
+ u
2
= u
5
,
3)x
1
+ x
2
= u
3
, 6)u
5
: u
4
= u.
Gi
,
a s
,
u
,
m
.
ênh
¯
dê
`
¯
d
´
ung v
´
o
,
i tâ
´
t c
,
a c
´
ac biê
,
u th
´
u
,
c m
`
a trong s
.
u
,
t
´
ınh
to
´
an
¯
d
`
oi h
,
oi không qu
´
a k bu
,
´
o
,
c th
.
u
,
c hi
.
ên, c
´
ac bu
,
´
o
,
c th
.
u
,
c hi
.
ên
,
o
,
¯
dây l
`
a: c
.
ông, tr
`
u
,
, nhân ho
.
˘
ac chia hai sô
´
ph
´
u
,
c. Ta s
˜
e ch
´
u
,
ng minh
m
.
ênh
¯
dê
`
¯
d
´
ung v
´
o
,
i c
´
ac biê
,
u th
´
u
,
c
¯
d
`
oi h
,
oi k + 1 bu
,
´
o
,
c th
.
u
,
c hi
.
ên.
Th
.
ât v
.
ây, bu
,
´
o
,
c th
.
u
,
c hi
.
ên cuô
´
i c
`
ung k + 1 trên hai sô
´
u
i
v
`
a u
j
, m
`
a
nh
˜
u
,
ng sô
´
n
`
ay l
`
a kê
´
t qu
,
a c
,
ua vi
.
êc th
.
u
,
c hi
.
ên không qu
´
a k ph
´
ep
t
´
ınh. Kê
´
t qu
,
a khi ta thay x
1
, x
2
, . . . , x
n
b
`
˘
ang c
´
ac sô
´
liên h
.
o
,
p c
,
ua
ch
´
ung th
`
ı theo gi
,
a thiê
´
t quy n
.
ap c
´
ac sô
´
u
i
v
`
a u
j
c
˜
ung thay b
`
˘
ang
c
´
ac sô
´
liên h
.
o
,
p c
,
ua ch
´
ung trong kê
´
t qu
,
a th
.
u
,
c hi
.
ên ph
´
ep t
´
ınh. Khi
¯
d
´
o u c
˜
ung thay b
`
˘
ang sô
´
liên h
.
o
,
p c
,
ua n
´
o
¯
u trong bu
,
´
o
,
c th
.
u
,
c hi
.
ên
th
´
u
,
k + 1.
J
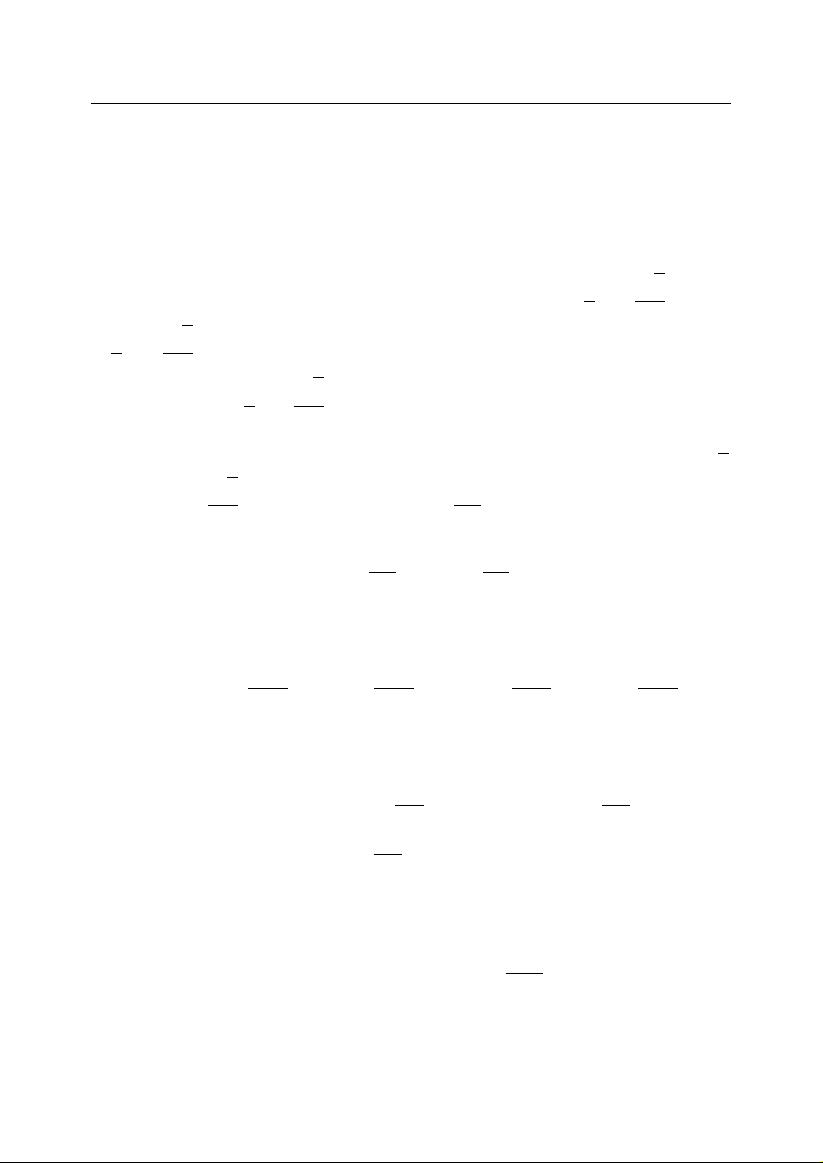
104 Chu
,
o
,
ng 4. Sô
´
h
.
oc
V
´
ı d
.
u 4.14. Cho z l `a nghi
.
êm c
,
ua phu
,
o
,
ng tr`ınh b
.
âc hai x
2
+ x +
1 = 0. Ch
´
u
,
ng minh r
`
˘ang v
´
o
,
i n = 0, 1, . . . ta c´o
1 + z
n
+ z
2n
=
(
0, nê
´
u n không chia hê
´
t cho 3,
3, nê
´
u n chia hê
´
t cho 3.
L
`
o
,
i gi
,
ai. Nghi
.
êm c
,
ua phu
,
o
,
ng tr
`
ınh l
`
a b
1
= −
1
2
+ i
√
3
2
, b
2
=
−
1
2
− i
√
3
2
. Ta k
´
y hi
.
êu z l
`
a nghi
.
êm bâ
´
t k
`
y c
,
ua phu
,
o
,
ng tr
`
ınh,
ngh
˜
ıa l
`
a z = −
1
2
+ i
√
3
2
µ,
,
o
,
¯
dây µ = 1 khi z = b
1
v
`
a µ = −1 khi
z = b
2
. Ð
.
˘
at α = arg z(π ≤ α ≤ π); b
,
o
,
i v
`
ı |z| = 1 nên cos α = −
1
2
v
`
a sin α =
√
3
2
µ, t
`
u
,
¯
dây ta c
´
o α =
2π
3
µ. Suy ra z c
´
o biê
,
u di
˜
ên
lu
,
.
o
,
ng gi
´
ac sau
z = cos
2π
3
µ + i sin
2π
3
µ.
Áp d
.
ung công th
´
u
,
c Moivre
δ
n
= 1 + z
n
+ z
2n
= 1 + (cos
2nπ
3
µ + i sin
2nπ
3
µ) + (cos
4nπ
3
µ + i sin
4nπ
3
µ).
Áp d
.
ung công th
´
u
,
c biê
´
n
¯
dô
,
i lu
,
.
o
,
ng gi
´
ac cho tô
,
ng cos v
`
a sin ta
nh
.
ân
¯
du
,
.
o
,
c
δ
n
= 1 + 2 cos nπµ cos
nπ
3
µ + 2i sin nπµ cos
nπ
3
µ
= 1 + (−1)
n
2 cos
nπ
3
.
Ta ch
´
u
´
y cos nπµ = cos nπ = (−1)
n
, sin nπµ = 0. Cho n chia hê
´
t
cho 3. Khi
¯
d
´
o n = 3k (k l
`
a sô
´
t
.
u
,
nhiên) v
`
a
δ
n
= δ
3k
= 1 + (−1)
3k
.2 cos
3kπ
3
= 1 + (−1)
k
.2(−1)
k
= 1 + 2 = 3.

4.4. Nh
˜
u
,
ng v
´
ı d
.
u kh
´
ac 105
Ngu
,
.
o
,
c l
.
ai n c
´
o d
.
ang n = 3k + s ( s = 1 v
`
a s = 2) v
`
a
δ
n
= δ
3k+s
= 1 + (−1)
3k+s
.2 cos
(3 k + s)π
3
= 1 + (−1)
k+s
.2(−1)
k
. cos
sπ
3
= 1 + (−1)
k+s
.2.(−1)
k
.(−1)
s+1
.
1
2
= 0.
V
.
ây b
`
ai to
´
an c
´
o thê
,
viê
´
t l
.
ai du
,
´
o
,
i d
.
ang
δ
3k+s
= 1 + z
3k+s
+ z
6k+2s
=
(
0, s 6= 0, (k = 0, 1, . . . ; s = 1, 2)
3, s = 0,
(4.5)
V
`
ı 1 + z + z
2
= 0, nên 0 = (1 − z)(1 + z + z
2
) = 1 − z
3
suy
ra z
3
= 1. V
´
o
,
i k = 0 ta c
´
o δ
s
= 1 + z
s
+ z
2s
( s = 0, 1, 2); δ
0
=
1 + 1 + 1 = 3, δ
1
= 1 + z + z
2
= 0, δ
2
= 1 + z
2
+ z
4
= 1 + z
2
(1 + z
2
,
,
o
,
¯
dây
¯
d
˜
a
´
ap d
.
ung 1 + z
2
= −z. V
`
a nhu
,
v
.
ây v
´
o
,
i k = 0, (4.5)
¯
d
´
ung.
Gi
,
a s
,
u
,
bây gi
`
o
,
(4.5)
¯
d
´
ung v
´
o
,
i k ≥ 0 n
`
ao
¯
d
´
o, ta s
˜
e ch
´
u
,
ng minh
r
`
˘
ang n
´
o c
˜
ung
¯
d
´
ung cho k + 1. Th
.
ât v
.
ây,
δ
3(k+1)+s
= 1 + z
3k+s+3
+ z
6k+2s+6
= 1 + z
3k+s
z
3
+ z
6k+2s
z
6
= 1 + z
3k+s
+ z
6k+2s
= δ
3k+s
,
,
o
,
¯
dây ta
¯
d
˜
a s
,
u
,
d
.
ung z
3
= 1, z
6
= (z
3
)
2
= 1.
J
4.4. Nh
˜
u
,
ng v
´
ı d
.
u kh
´
ac
V
´
ı d
.
u 4.15. Cho n v `a k l `a nh
˜
u
,
ng sô
´
t
.
u
,
nhiên, k ≥ 2. Ch
´
u
,
ng minh
r
`
˘ang tô
`
n t
.
ai n sô
´
t
.
u
,
nhiên liên tiê
´
p, m
˜
ôi sô
´
trong ch ´ung phân t´ıch
ra t´ıch ´ıt nhâ
´
t k th
`
u
,
a sô
´
nguyên tô
´
.
L
`
o
,
i gi
,
ai. V
´
o
,
i k = 2 kh
,
˘
ang
¯
d
.
inh c
,
ua b
`
ai to
´
an c
´
o ngh
˜
ıa l
`
a tô
`
n t
.
ai n
liên tiê
´
p nh
˜
u
,
ng h
.
o
,
p sô
´
. D
˜
ay nhu
,
v
.
ây v
´
ı d
.
u nhu
,
( n + 1)! + 2, (n +

106 Chu
,
o
,
ng 4. Sô
´
h
.
oc
1)! + 3, . . . , (n + 1)! + (n + 1). Gi
,
a thiê
´
t v
´
o
,
i sô
´
k n
`
ao
¯
d
´
o ta
¯
d
˜
a t
`
ım
¯
du
,
.
o
,
c n sô
´
t
.
u
,
nhiên liên tiê
´
p
N, N + 1, . . . , N + n − 1
m
˜
ôi sô
´
n
`
ay phân t
´
ıch ra t
´
ıch
´
ıt nhâ
´
t k th
`
u
,
a sô
´
nguyên tô
´
. Khi
¯
d
´
o
m
˜
ôi sô
´
trong nh
˜
u
,
ng sô
´
sau
(N + n −1)! + N, (N + n −1)! + N + 1, . . . , (N + n −1)! + N + n −1
phân t
´
ıch
¯
du
,
.
o
,
c ra
´
ıt nhâ
´
t k + 1 th
`
u
,
a sô
´
nguyên tô
´
. Th
.
ât v
.
ây, m
˜
ôi
sô
´
trong c
´
ac sô
´
(N + n −1)! + N + i (i = 0, 1, . . . , n −1) chia hê
´
t
cho N + i, m
`
a theo gi
,
a thiê
´
t quy n
.
ap nh
˜
u
,
ng sô
´
n
`
ay phân t
´
ıch
¯
du
,
.
o
,
c
ra t
´
ıch
´
ıt nhâ
´
t k th
`
u
,
sô
´
nguyên tô
´
, c
`
on sô
´
(N + n −1)! + N + i
N + i
hiê
,
n nhiên l
`
a kh
´
ac 1.
J
V
´
ı d
.
u 4.16. Cho m v`a n l`a nh
˜
u
,
ng sô
´
t
.
u
,
nhiên. Ch
´
u
,
ng minh r
`
˘ang
´ıt nhâ
´
t m
.
ôt trong c ´ac sô
´
n
√
m,
m
√
n không vu
,
.
o
,
t qu ´a
3
√
3.
L
`
o
,
i gi
,
ai. Ta s
˜
e ch
´
u
,
ng minh v
´
o
,
i m
.
oi sô
´
t
.
u
,
nhiên n c
´
o bâ
´
t
¯
d
,
˘
ang
th
´
u
,
c sau 3
n
≥ n
3
. Ch
´
u
,
ng minh theo quy n
.
ap to
´
an h
.
oc. V
´
o
,
i n =
1, 2, 3, 4 ta c
´
o 3
1
≥ 1
3
, 3
2
≥ 2
3
, 3
3
≥ 3
3
, 3
4
≥ 4
3
. Gi
,
a s
,
u
,
kh
,
˘
ang
¯
d
.
inh
¯
d
´
ung v
´
o
,
i n = k , (k ≥ 4). Khi
¯
d
´
o theo gi
,
a thiê
´
t quy n
.
ap
3
k+1
= 3.3
k
≥ 3.k
3
= k
3
+ 3k
2
+ 3k + (k −3)k
2
+ (k
2
−3)k > (k + 1)
3
.
V
`
ı k > 3, (k −3)k
2
≥ 1, (k
2
−3)k > 1. Nhu
,
v
.
ây v
´
o
,
i m
.
oi sô
´
t
.
u
,
nhiên
n, ta c
´
o 3
n
≥ n
3
ho
.
˘
ac l
`
a
3
√
3 ≥
n
√
n.
Cho m v
`
a n sô
´
t
.
u
,
nhiên v
`
a n ≥ m. Khi
¯
d
´
o
n
√
m ≤
n
√
n ≤
3
√
3.
J
V
´
ı d
.
u 4.17. B
.
ô ba Pythagore l`a m
.
ôt b
.
ô ba sô
´
t
.
u
,
nhiên (x, y, z),
sao cho x < y < z v `a x
2
+ y
2
= z
2
. Ch
´
u
,
ng minh r
`
˘ang v
´
o
,
i sô
´

4.4. Nh
˜
u
,
ng v
´
ı d
.
u kh
´
ac 107
t
.
u
,
nhiên bâ
´
t k`y n, sô
´
2
n+1
c´o m
.
˘at trong n b
.
ô ba Pythagore kh ´ac
nhau.
L
`
o
,
i gi
,
ai. Ch
´
u
,
ng minh b
`
˘
ang quy n
.
ap to
´
an h
.
oc theo n,
1) V
´
o
,
i n = 1 kê
´
t lu
.
ân hiê
,
n nhiên: Sô
´
4 g
.
˘
ap 1 lâ
`
n trong c
´
ac b
.
ô.
2) Gi
,
a s
,
u
,
m
.
ênh
¯
dê
`
¯
d
´
ung v
´
o
,
i bâ
´
t k
`
y k ≤ n. Khi
¯
d
´
o nê
´
u b
.
ô
ba Pythagore (x, y, z) c
´
o ch
´
u
,
a sô
´
2
n+2
, v
`
a nh
˜
u
,
ng sô
´
x, y, z không
nguyên tô
´
c
`
ung nhau, th
`
ı nh
˜
u
,
ng sô
´
n
`
ay c
´
o th
`
u
,
a sô
´
chung 2 v
`
a
(
x
2
,
y
2
,
z
2
) l
`
a b
.
ô ba Pythagore trong
¯
d
´
o ch
´
u
,
a sô
´
2
n+1
. Theo gi
,
a thiê
´
t
quy n
.
ap nh
˜
u
,
ng b
.
ô ba nhu
,
v
.
ây c
´
o sô
´
lu
,
.
o
,
ng n. Gi
,
a s
,
u
,
(x, y, z) b
.
ô ba
Pythagore , m
`
a c
´
ac sô
´
c
,
ua ch
´
ung x, y, z nguyên tô
´
c
`
ung nhau, v
`
a
m
.
ôt trong ch
´
ung b
`
˘
ang 2
n+2
.
Theo
¯
diê
`
u ki
.
ên x
2
+ y
2
= z
2
. V
`
ı thê
´
nê
´
u z l
`
a sô
´
ch
˜
˘
an th
`
ı x v
`
a y
không ch
˜
˘
an (do ch
´
ung nguyên tô
´
c
`
ung nhau). V
`
a suy ra x
2
v
`
a y
2
khi chia cho 4 cho du
,
1. Khi
¯
d
´
o x
2
+ y
2
khi chia cho 4 cho sô
´
du
,
2,
nhu
,
ng trong khi
¯
d
´
o z
2
chia hê
´
t cho 4. D
˜
ân
¯
dê
´
n vô l
´
y. Suy ra z l
`
a
sô
´
l
,
e v
`
a tru
,
`
o
,
ng h
.
o
,
p riêng z 6= 2
n+2
.
Nhu
,
ng x
2
= (z − y)(z + y), v
`
a nê
´
u x = 2
n+2
, th
`
ı
x
2
= 2
2n+4
= (z − y)(z + y), t
`
u
,
¯
d
´
o z − y = 2
k
, z + y =
2
2n+4−k
(0 ≤ k ≤ 2 n + 4 ). Suy ra z =
1
2
(2
k
+ 2
2n+4−k
).
Nhu
,
v
.
ây z l
`
a l
,
e, th
`
ı ho
.
˘
ac l
`
a k = 1, ho
.
˘
ac l
`
a k = 2n + 3.
Trong tru
,
`
o
,
ng h
.
o
,
p th
´
u
,
nhâ
´
t z = 1 + 2
2n+2
, y = 2
2n+2
− 1,
x = 2
n+2
v
`
a nhu
,
v
.
ây 0 < 2
n+2
< 2
2n+2
−1 < 2
2n+2
+ 1 v
´
o
,
i n ≥ 1,
th
`
ı (2
n+2
, 2
2n+2
− 1, 2
2n+2
+ 1 ) b
.
ô ba Pythagore . Trong tru
,
`
o
,
ng
h
.
o
,
p th
´
u
,
hai z = 1 + 2
2n+2
, y = 1 − 2
2n+2
. Nhu
,
v
.
ây trong tru
,
`
o
,
ng
h
.
o
,
p cuô
´
i c
`
ung y < 0, th
`
ı tô
`
n t
.
ai m
.
ôt b
.
ô ba (x , y, z) sao cho x, y, z
nguyên tô
´
c
`
ung nhau v
`
a x = 2
n+2
.

108 Chu
,
o
,
ng 4. Sô
´
h
.
oc
Cuô
´
i c
`
ung cho y = 2
n+2
, khi
¯
d
´
o l
´
y lu
.
ân tu
,
o
,
ng t
.
u
,
nhu
,
phâ
`
n
trên ta nh
.
ân
¯
du
,
.
o
,
c z = 2
n+2
+ 1 v
`
a ho
.
˘
ac l
`
a x = 2
2n+2
−1, ho
.
˘
ac l
`
a
x = 1 −2
2n+2
. Nhu
,
ng v
´
o
,
i n ≥ 1 trong tru
,
`
o
,
ng h
.
o
,
p th
´
u
,
nhâ
´
t x > y,
c
`
on tru
,
`
o
,
ng h
.
o
,
p th
´
u
,
hai −x < 0.
Nhu
,
v
.
ây, tô
`
n t
.
ai m
.
ôt b
.
ô ba sô
´
Pythagore (x, y, z) sao cho x, y, z
nguyên tô
´
c
`
ung nhau v
`
a c
´
o m
.
ôt sô
´
l
`
a 2
n+2
. V
`
ı thê
´
tâ
´
t c
,
a c
.
˘
ap b
.
ô
ba trong n
´
o ch
´
u
,
a 2
n+2
, b
`
˘
ang n + 1.
J
V
´
ı d
.
u 4.18. Ch
´
u
,
ng minh r
`
˘ang nê
´
u a ≡ b (mod m), th`ı a
m
k
≡ b
m
k
(mod m
k+1
),
,
o
,
¯
dây k = 0, 1, 2, . . .
L
`
o
,
i gi
,
ai. Ta ch
´
u
,
ng minh b
`
˘
ang quy n
.
ap theo k. V
´
o
,
i k = 0 th
`
ı
m
.
ênh
¯
dê
`
¯
d
´
ung hiê
,
n nhiên. Gi
,
a s
,
u
,
v
´
o
,
i m
.
ôt k n
`
ao
¯
d
´
o, ta c
´
o a
m
k
≡
b
m
k
(mod m
k+1
). Ta
¯
d
.
˘
at l = m
k
. Ta c
´
o
a
m
k+ 1
−b
m
k+ 1
= (a
l
−b
l
)(a
l(m−l)
+ a
l(m−2)
b
l
+ ··· + b
l(m−1)
).
V
`
ı theo gi
,
a thiê
´
t quy n
.
ap, th
`
u
,
a sô
´
th
´
u
,
nhâ
´
t chia hê
´
t cho m
k+1
,
v
.
ây ch
,
ı c
`
on ch
´
u
,
ng minh th
`
u
,
a sô
´
th
´
u
,
hai chia hê
´
t cho m. Nhu
,
ng
a ≡ b (mod m), t
`
u
,
¯
d
´
o a
l
≡ b
l
(mod m) v
`
a a
l(m−1)
+ a
l(m−2)
b
l
+
··· + b
l(m−1)
≡ a
l(m−1)
+ a
l(m−1)
+ ··· + a
l(m−1)
≡ ma
l(m−1)
≡ 0
(mod m).
J
4.5. B
`
ai t
.
âp
.
.
. 4.19. Ch
´
u
,
ng minh r
`
˘
ang v
´
o
,
i m
.
oi sô
´
nguyên du
,
o
,
ng n, 11
n+1
+
12
2n−1
chia hê
´
t cho 133.
.
.
. 4.20. Ch
´
u
,
ng minh r
`
˘
ang v
´
o
,
i sô
´
n nguyên du
,
o
,
ng
1) A = n
7
+ 6n chia hê
´
t cho 7;
2) B = 2
6n+1
+ 3
2n+2
chia hê
´
t cho 11;
3) D = 2
2n+1
−9n
2
+ 3n −2 chia hê
´
t cho 54.

4.5. B
`
ai t
.
âp 109
.
.
. 4.21. Ch
´
u
,
ng minh r
`
˘
ang v
´
o
,
i n nguyên du
,
o
,
ng, sô
´
2
3n+3
−7n + 41
chia hê
´
t cho 49. Tô
,
ng qu
´
at: V
´
o
,
i a, n l
`
a nh
˜
u
,
ng sô
´
nguyên du
,
o
,
ng,
biê
,
u th
´
u
,
c A
n
= (a + 1)
n
− an − 1 chia hê
´
t cho a
2
.
.
.
. 4.22. Ch
´
u
,
ng minh r
`
˘
ang m
.
ôt sô
´
c
´
o sô
´
ch
˜
˘
an ch
˜
u
,
sô
´
, ch
˜
u
,
sô
´
¯
dâ
`
u
tiên v
`
a ch
˜
u
,
sô
´
cuô
´
i c
`
ung l
`
a 1, c
´
ac sô
´
c
`
on l
.
ai l
`
a 0, th
`
ı n
´
o chia hê
´
t
cho 11.
.
.
. 4.23. Ch
´
u
,
ng minh r
`
˘
ang m
.
ôt sô
´
t
.
ao b
,
o
,
i 3
n
ch
˜
u
,
sô
´
1, chia hê
´
t cho
3
n
.
.
.
. 4.24. Ch
´
u
,
ng minh r
`
˘
ang v
´
o
,
i sô
´
t
.
u
,
nhiên n ≥ 2, nh
˜
u
,
ng sô
´
c
´
o
d
.
ang N = 2
2
n
+ 1 c
´
o ch
˜
u
,
sô
´
cuô
´
i c
`
ung l
`
a ch
˜
u
,
sô
´
7 (Sô
´
Fermat).
.
.
. 4.25. Cho d
˜
ay sô
´
a
1
, a
2
, a
3
, . . . sao cho a
1
= a
2
= 1 v
`
a a
n+2
=
a
n
+ a
n+1
. Ch
´
u
,
ng minh r
`
˘
ang a
5n
chia hê
´
t cho 5 v
´
o
,
i n = 1, 2, . . ..

CHU
,
O
,
NG 5
D
˜
AY S
´
Ô
5.1. D
˜
ay sô
´
t
.
u
,
nhiên . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 110
5.2. D
˜
ay tr
.
ôi ho
,
n.. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 117
5.3. Nh
˜
u
,
ng bâ
´
t
¯
d
,
˘
ang th
´
u
,
c nô
,
i tiê
´
ng . . . . . . . . . . . . . . . . . . . . . 121
5.4. D
˜
ay
¯
do
,
n
¯
di
.
êu . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 128
5.5. Sô
´
e . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 131
5.6. D
˜
ay sô
´
Fibonacci . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 134
5.7. B
`
ai t
.
âp .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 139
Phu
,
o
,
ng ph
´
ap quy n
.
ap to
´
an h
.
oc
¯
du
,
.
o
,
c
´
ap d
.
ung cho râ
´
t nhiê
`
u
b
`
ai to
´
an vê
`
d
˜
ay sô
´
. Kê
´
t h
.
o
,
p v
´
o
,
i c
´
ac t
´
ınh châ
´
t c
,
ua bâ
´
t
¯
d
,
˘
ang th
´
u
,
c
v
`
a
¯
d
,
˘
ang th
´
u
,
c th
`
ı ch
´
u
,
ng minh b
`
˘
ang phu
,
o
,
ng ph
´
ap n
`
ay râ
´
t ng
´
˘
an
g
.
on v
`
a d
˜
ê hiê
,
u.
5.1. D
˜
ay sô
´
t
.
u
,
nhiên
V
´
ı d
.
u 5.1. Cho d˜ay vô h
.
an sô
´
t
.
u
,
nhiên a
1
= 1, a
2
, a
3
, . . . , a
n
, . . . v`a
tho
,
a m ˜an bâ
´
t
¯
d
,
˘ang th
´
u
,
c sau
a
n
≤ 1 + a
1
+ a
2
+ ··· + a
n−1
v
´
o
,
i m
.
oi sô
´
t
.
u
,
nhiên n ≥ 2. Ch
´
u
,
ng minh r
`
˘ang v
´
o
,
i m
.
oi sô
´
t
.
u
,
nhiên
du
,
o
,
ng c´o thê
,
biê
,
u di
˜
ên nhu
,
tô
,
ng c
,
ua m
.
ôt v `ai sô
´
¯
du
,
.
o
,
c ch
.
on trong
d ˜ay.
L
`
o
,
i gi
,
ai. Ta s
˜
e ch
´
u
,
ng minh r
`
˘
ang m
.
oi sô
´
t
.
u
,
nhiên N tho
,
a m
˜
an

5.1. D
˜
ay sô
´
t
.
u
,
nhiên 111
bâ
´
t
¯
d
,
˘
ang th
´
u
,
c 0 < N < 1 + a
1
+ a
2
+ ··· + a
n
, c
´
o thê
,
biê
,
u di
˜
ên
nhu
,
m
.
ôt tô
,
ng c
,
ua m
.
ôt v
`
ai sô
´
trong d
˜
ay a
1
, a
2
, . . . , a
n
.
V
´
o
,
i n = 1 m
.
ênh
¯
dê
`
¯
d
´
ung v
`
ı a
1
= 1, khi
¯
d
´
o 0 < N < 1 + 1 ch
,
ı
l
`
a N = 1 = a
1
.
Gi
,
a s
,
u
,
m
.
ênh
¯
dê
`
¯
d
´
ung v
´
o
,
i sô
´
t
.
u
,
nhiên n = k ≥ 1, ngh
˜
ıa l
`
a m
.
oi
sô
´
t
.
u
,
nhiên N tho
,
a m
˜
an bâ
´
t
¯
d
,
˘
ang th
´
u
,
c 0 < N < 1 + a
1
+ a
2
+
··· + a
k
, c
´
o thê
,
biê
,
u di
˜
ên nhu
,
m
.
ôt tô
,
ng c
,
ua m
.
ôt v
`
ai sô
´
trong d
˜
ay
a
1
, a
2
, . . . , a
k
. Ta s
˜
e ch
´
u
,
ng minh r
`
˘
ang n
´
o c
˜
ung
¯
d
´
ung v
´
o
,
i n = k + 1.
Ta ch
,
ı x
´
et tru
,
`
o
,
ng h
.
o
,
p sau
¯
dây l
`
a
¯
d
,
u
1 + a
1
+ ··· + a
k
≤ N < 1 + a
1
+ ··· + a
k
+ a
k+1
v
`
ı nê
´
u 0 < N < 1 + a
1
+ ···+ a
k
, th
`
ı m
.
ênh
¯
dê
`
¯
d
´
ung suy ra t
`
u
,
gi
,
ai
thiê
´
t quy n
.
ap.
Do
¯
diê
`
u ki
.
ên
¯
dâ
`
u b
`
ai, ta nh
.
ân
¯
du
,
.
o
,
c
0 ≤ 1 + a
1
+ ··· + a
k
− a
k+1
≤ N − a
k+1
< 1 + a
1
+ ··· + a
k
.
Nê
´
u N − a
k+1
= 0, th
`
ı m
.
ênh
¯
dê
`
¯
d
´
ung v
´
o
,
i n = k + 1; nê
´
u N −
a
k+1
> 0, th
`
ı theo gi
,
a thiê
´
t quy n
.
ap N − a
k+1
c
´
o thê
,
biê
,
u di
˜
ên
nhu
,
tô
,
ng c
,
ua m
.
ôt v
`
ai sô
´
trong a
1
, a
2
, . . . , a
k
v
`
a khi
¯
d
´
o N biê
,
u
¯
di
˜
ên
nhu
,
tô
,
ng trên v
`
a thêm v
`
ao a
k+1
.
J
V
´
ı d
.
u 5.2. Cho p
1
< p
2
< . . . < p
n
< . . . l `a d˜ay sô
´
nguyên tô
´
.
Ch
´
u
,
ng minh r
`
˘ang gi
˜
u
,
a hai sô
´
p
1
+ p
2
+ ···+ p
n
v `a p
1
+ p
2
+ ···+
p
n+1
luôn luôn c´o m
.
ôt sô
´
ch´ınh phu
,
o
,
ng.
L
`
o
,
i gi
,
ai. Gi
,
a s
,
u
,
2 = p
1
< p
2
< p
3
. . . d
˜
ay sô
´
nguyên tô
´
.
1) Ta ch
´
u
,
ng minh r
`
˘
ang v
´
o
,
i n ≥ 7, p
n
> 2n + 1: Ta ch
´
u
,
ng minh
b
`
˘
ang phu
,
o
,
ng ph
´
ap quy n
.
ap. V
´
o
,
i n = 7, ta c
´
o p
7
= 17 > 15, m
.
ênh
¯
dê
`
¯
d
´
ung. Gi
,
a s
,
u
,
m
.
ênh
¯
dê
`
¯
d
´
ung cho n = k, p
k
> 2k + 1. Ta ch
´
u
,
ng

112 Chu
,
o
,
ng 5. D
˜
ay sô
´
minh m
.
ênh
¯
dê
`
c
˜
ung
¯
d
´
ung v
´
o
,
i n = k + 1, th
.
ât v
.
ây, do p
n
l
`
a sô
´
l
,
e v
´
o
,
i m
.
oi n > 1, nên p
k+1
− p
k
≥ 2, ngh
˜
ıa l
`
a p
k+1
≥ p
k
+ 2 >
2k + 1 + 2 = 2(k + 1) + 1. Nhu
,
v
.
ây ta
¯
d
˜
a ch
´
u
,
ng minh
¯
d
´
ung cho
m
.
oi n ≥ 7, p
n
> 2n + 1.
2) Ta ch
´
u
,
ng minh v
´
o
,
i m
.
oi n, y
n
≥ n
2
: K
´
y hi
.
êu y
n
l
`
a tô
,
ng
y
n
= p
1
+ p
2
+ ··· + p
n
.
Ta c
´
o y
1
= 2 > 1
2
, y
2
= 5 > 2
2
, y
3
= 10 > 3
3
, y
4
= 17 > 4
2
, y
5
=
28 > 5
2
, y
6
= 41 > 6
6
v
`
a y
7
= 2 + 3 + 5 + 7 + 11 + 13 + 17 =
58 > 49 = 7
2
. Ta s
˜
e ch
´
u
,
ng minh quy n
.
ap theo n, v
´
o
,
i n ≥ 7 ta c
´
o
y
n
> n
2
.
Th
.
ât v
.
ây, Gi
,
a s
,
u
,
v
´
o
,
i n = k, ta c
´
o y
k
> k
2
. V
´
o
,
i n = k + 1 ta t
´
ınh
y
k+1
= y
k
+ p
k+1
> k
2
+ (2k + 1) = (k + 1)
2
, ta
¯
d
˜
a s
,
u
,
d
.
ung kê
´
t
qu
,
a phâ
`
n trên v
`
a gi
,
a thiê
´
t quy n
.
ap. Ngh
˜
ıa l
`
a ta
¯
d
˜
a ch
´
u
,
ng minh
v
´
o
,
i m
.
oi n, y
n
≥ n
2
.
Lâ
´
y m
2
l
`
a sô
´
ch
´
ınh phu
,
o
,
ng l
´
o
,
n nhâ
´
t không l
´
o
,
n ho
,
n y
n
(c
´
o thê
,
lâ
´
y
¯
du
,
.
o
,
c theo ch
´
u
,
ng minh trên v
`
a tiên
¯
dê
`
th
´
u
,
t
.
u
,
). Khi
¯
d
´
o theo
ch
´
u
,
ng minh trên m ≥ n ho
.
˘
ac l
`
a m = n + k, k ≥ 0. Nhu
,
v
.
ây, v
´
o
,
i
m
.
oi n ≥ 1 tô
`
n t
.
ai sô
´
k ≥ 0 sao cho
( n + k)
2
≤ y
n
≤ (n + k + 1)
2
.
Ta s
˜
e ch
´
u
,
ng minh p
n+1
> 2(n + k) + 1. Gi
,
a s
,
u
,
ngu
,
.
o
,
c l
.
ai, ta c
´
o
p
n+1
≤ 2(n + k) + 1. Nhu
,
ng v
´
o
,
i n ≥ 2, p
n+1
≥ p
n
+ 2. Suy ra
p
n
≤ 2(n + k) + 1 −2 = 2(n + k) − 1,
p
n−1
≤ 2(n + k) + 1 −4 = 2(n + k) − 3,
...............................
p
n−j
≤ 2(n + k) + 1 −2(j + 1) = 2(n + k) − (2j + 1),
...............................

5.1. D
˜
ay sô
´
t
.
u
,
nhiên 113
3 = p
2
≤ 2(n + k) + 1 −2(n −1) = 2(n + k) −(2n − 3),
2 = p
1
≤ 2(n + k) + 1 −2n = 2(n + k) − (2n −1).
C
.
ông t
`
u
,
ng vê
´
c
´
ac bâ
´
t
¯
d
,
˘
ang th
´
u
,
c trên, ta c
´
o
y
n
= p
1
+ p
2
+ ··· + p
n
≤ 2n(n + k) − (1 + 3 + ··· + (2n −1))
= 2n(n + k) − n
2
= n
2
+ 2nk + 1 −1 = (n + k)
2
−1.
Ngh
˜
ıa l
`
a y
n
≤ (n + k)
2
−1. Nhu
,
ng theo gi
,
a thiê
´
t y
n
≥ (n + k)
2
v
`
a
y
n
l
`
a sô
´
nguyên. D
˜
ân
¯
dê
´
n vô l
´
y. Suy ra p
n+1
> 2(n + k) + 1. Khi
¯
d
´
o
y
n+1
= y
n
+ p
n
> (n + k)
2
+ 2(n + k) + 1 = (n + k + 1)
2
> y
n
,
ngh
˜
ıa l
`
a
y
n
< (n + k + 1)
2
< y
n+1
.
Suy ra (n + k + 1)
2
n
`
˘
am gi
˜
u
,
a y
n
v
`
a y
n+1
.
J
V
´
ı d
.
u 5.3. Cho d ˜ay sô
´
chia th `anh t
`
u
,
ng nh´om nhu
,
sau:
(1 ), (2, 3), (4, 5, 6), (7, 8, 9, 10), (11, 12, 13, 14, 15), . . . T´ınh tô
,
ng S
1
+
S
3
+ S
5
+ ··· + S
2n−1
,
,
o
,
¯
dây S
k
l `a tô
,
ng nh
˜
u
,
ng sô
´
c
,
ua nh´om th
´
u
,
k.
L
`
o
,
i gi
,
ai. Sô
´
¯
dâ
`
u tiên c
,
ua nh
´
om th
´
u
,
k b
`
˘
ang
(1 + 2 + ··· + ( k −1)) + 1 =
k(k −1)
2
+ 1.
C
`
on tô
,
ng c
,
ua k sô
´
,
o
,
nh
´
om th
´
u
,
k l
`
a
S
k
=
k(
k(k −1)
2
+ 1 +
( k + 1)k
2
)
2
=
k
3
+ k
2
.
B
`
˘
ang quy n
.
ap to
´
an h
.
oc theo n, ta ch
´
u
,
ng minh r
`
˘
ang
S
1
+ S
3
+ ··· + S
2n−1
= n
4
. (5.1)
1) V
´
o
,
i n = 1, ta c
´
o S
1
= 1 = 1
4
.

114 Chu
,
o
,
ng 5. D
˜
ay sô
´
2) Gi
,
a s
,
u
,
(5.1)
¯
d
´
ung v
´
o
,
i n n
`
ao
¯
dâ
´
y, ta ch
´
u
,
ng minh cho n + 1.
S
1
+ S
2
+ ··· + S
2(n+1)−1
= (S
1
+ S
2
+ ··· + S
(2n−1)
) + S
2n+1
= n
4
+
(2 n + 1)
3
+ ( 2n + 1)
2
= n
4
+ ( 2n + 1)(2 n
2
+ 2n + 1)
= n
4
+ 4n
3
+ 6n
2
+ 4n + 1 = (n + 1)
4
.
Ð
,
˘
ang th
´
u
,
c (5.1)
¯
d
´
ung v
´
o
,
i m
.
oi n nguyên du
,
o
,
ng.
J
V
´
ı d
.
u 5.4. Cho d ˜ay sô
´
F
1
, F
2
, F
3
, . . . , F
n
, . . .
¯
du
,
.
o
,
c x ´ac
¯
d
.
inh theo công
th
´
u
,
c sau: F
1
= −1, F
2
= −1, F
n
= −F
n−1
−2F
n−2
v
´
o
,
i n ≥ 3. Ch
´
u
,
ng
minh r
`
˘ang v
´
o
,
i n ≥ 2 sô
´
2
n+1
−7F
2
n−1
l `a sô
´
ch´ınh phu
,
o
,
ng.
L
`
o
,
i gi
,
ai. Ch
´
u
,
ng minh b
`
˘
ang quy n
.
ap to
´
an h
.
oc theo n, m
.
ênh
¯
dê
`
sau: V
´
o
,
i n ≥ 2,
2
n+1
−7F
2
n−1
= (2F
n
+ F
n−1
)
2
.
Th
.
ât v
.
ây, n = 2 ta c
´
o 2
3
−7 = (−2 + 1)
2
. Gi
,
a s
,
u
,
m
.
ênh
¯
dê
`
¯
d
´
ung
v
´
o
,
i m
.
oi k ≤ n ,
,
o
,
¯
dây n ≥ 2. Khi
¯
d
´
o
(2F
n+1
+ F
n
)
2
= (−2F
n
−4F
n−1
+ F
n
)
2
= (−F
n
−4F
n−1
)
2
= F
2
n
+ 8F
n
F
n−1
+ 16F
2
n−1
= 2(4F
2
n
+ 4F
n
F
n−1
+ F
2
n−1
) + 14F
2
n−1
−7F
2
n
= 2(2F
n
+ F
n−1
)
2
+ 14F
2
n−1
−7F
2
n
= 2(2
n+1
−7F
2
n−1
) + 14F
2
n−1
−7F
2
n
= 2
n+2
−7F
2
n
.
Nhu
,
v
.
ây m
.
ênh
¯
dê
`
¯
d
´
ung v
´
o
,
i k = n + 1.
J
V
´
ı d
.
u 5.5. Cho n ≥ 1 l `a m
.
ôt sô
´
t
.
u
,
nhiên. Ð
.
inh ngh˜ıa d ˜ay sô
´
x
1
, x
2
, . . . v `a y
1
, y
2
, . . . theo c ´ach sau:
x
1
= n, y
1
= 1, x
i +1
= [
x
i
+ y
i
2
], y
i +1
= [
n
x
i +1
] (i = 1, 2, . . .),

5.1. D
˜
ay sô
´
t
.
u
,
nhiên 115
[x] sô
´
nguyên l
´
o
,
n nhâ
´
t không l
´
o
,
n ho
,
n x .
Ch
´
u
,
ng minh r
`
˘ang min{x
1
, x
2
, . . . , x
n
} = [
√
n].
L
`
o
,
i gi
,
ai. Ta s
˜
e ch
´
u
,
ng minh v
´
o
,
i m
˜
ôi i (i = 1, 2, . . .), x
i
≥ [
√
n].
Bâ
´
t
¯
d
,
˘
ang th
´
u
,
c
¯
d
´
ung v
´
o
,
i i = 1. Gi
,
a s
,
u
,
bâ
´
t
¯
d
,
˘
ang th
´
u
,
c
¯
d
´
ung v
´
o
,
i
i = k. Khi
¯
d
´
o x
k
= [
√
n] + t, t ≥ 0,
y
k
= [
n
[
√
n] + t
] ≥ [
[
√
n]
2
[
√
n] + t
] ≥ [
[
√
n]
2
−t
2
[
√
n] + t
] = [
√
n] − t
suy ra
x
k+1
= [
x
k
+ y
k
2
] ≥ [
[
√
n] + t + [
√
n] − t
2
] = [
√
n].
Khi
¯
d
´
o theo nguyên l
´
y quy n
.
ap to
´
an h
.
oc bâ
´
t
¯
d
,
˘
ang th
´
u
,
c câ
`
n ch
´
u
,
ng
minh
¯
d
´
ung v
´
o
,
i m
.
oi i = 1, 2, . . ..
Gi
,
a s
,
u
,
v
´
o
,
i m
.
ôt sô
´
s n
`
ao
¯
d
´
o c
´
o x
s
= [
√
n] + t,
,
o
,
¯
dây t ≥ 1
(
¯
diê
`
u n
`
ay c
´
o thê
,
¯
du
,
.
o
,
c, ch
,
˘
ang h
.
an lâ
´
y s = 1). Ngo
`
ai ra nê
´
u lâ
´
y
n = [
√
n]
2
+ p,
,
o
,
¯
dây sô
´
p tho
,
a m
˜
an 0 ≤ p ≤ 2[
√
n] (ta c
˜
ung lâ
´
y
¯
du
,
.
o
,
c do p l
`
a sô
´
t
.
u
,
nhiên v
`
a p tho
,
a m
˜
an nhu
,
v
.
ây v
`
ı nê
´
u ngu
,
.
o
,
c l
.
ai
th
`
ı d
˜
ân t
´
o
,
i
¯
diê
`
u vô l
´
y n ≥ ([
√
n + 1]
2
).
Khi
¯
d
´
o
y
s
= [
n
[
√
n] + t
] = [
[
√
n]
2
+ p
[
√
n] + t
] ≥ [
[
√
n]
2
+ 2[
√
n]
[
√
n] + 1
] = [
√
n]
v
`
ı
[
√
n] < [
[
√
n]
2
+ 2[
√
n]
[
√
n] + 1
] < [
√
n + 1].
T
`
u
,
y
s
≤ [
√
n] < [
√
n] + t = x
s
ta nh
.
ân
¯
du
,
.
o
,
c y
s
≤ x
s
−1 suy ra
x
s+1
= [
x
s
+ y
s
2
≤ [
2x
s
−1
2
] = x
s
−1 < x
s
.

116 Chu
,
o
,
ng 5. D
˜
ay sô
´
Ðiê
`
u n
`
ay ngh
˜
ıa l
`
a khi x
s
> [
√
n] v
´
o
,
i s = 1, 2, . . . d
˜
ay x
1
, x
2
, . . . s
˜
e
gi
,
am th
.
u
,
c s
.
u
,
v
`
a v
´
o
,
i s
¯
d
,
u l
´
o
,
n (nhu
,
ng nh
,
o ho
,
n n, v
`
ı x
1
= n) th
`
ı s
˜
e
c
´
o
¯
d
,
˘
ang th
´
u
,
c x
s
= [
√
n].
J
V
´
ı d
.
u 5.6. Cho d˜ay sô
´
a
1
, a
2
, . . . , a
n
¯
du
,
.
o
,
c
¯
d
.
inh ngh˜ıa theo
¯
d
,
˘ang
th
´
u
,
c sau: a
k
= k −1 v
´
o
,
i k = 1, 2, 3, 4 v `a a
2n−1
= a
2n−2
+ 2
n−2
, a
2n
=
a
2n−5
+ 2
n
v
´
o
,
i m
.
oi n ≥ 3. Ch
´
u
,
ng minh r
`
˘ang v
´
o
,
i m
.
oi sô
´
t
.
u
,
nhiên n
kh ´ac không
¯
d
,
˘ang th
´
u
,
c sau
¯
d ´ung:
a) 1 + a
2n−1
=
12
7
.2
n−1
; b) 1 + a
2n
=
17
7
.2
n−1
.
L
`
o
,
i gi
,
ai. V
´
o
,
i n = 1 v
`
a n = 2
¯
d
,
˘
ang th
´
u
,
c
¯
d
´
ung v
´
o
,
i b
`
˘
ang c
´
ach kiê
,
m
tra tr
.
u
,
c tiê
´
p. Gi
,
a s
,
u
,
hai
¯
d
,
˘
ang th
´
u
,
c trên
¯
d
´
ung v
´
o
,
i hai sô
´
t
.
u
,
nhiên
liên tiê
´
p n −1 v
`
a n. Ta s
˜
e ch
´
u
,
ng minh hai
¯
d
,
˘
ang th
´
u
,
c
¯
d
´
ung cho
gi
´
a tr
.
i tiê
´
p theo n + 1.
T
`
u
,
¯
d
.
inh ngh
˜
ıa c
,
ua d
˜
ay 1 + a
2n+1
= 1 + a
2n
+ 2
n−1
. Ch
´
u
´
y t
´
o
,
i
¯
d
,
˘
ang th
´
u
,
c b) cho gi
´
a tr
.
i n, ta c
´
o 1 + a
2n+1
=
17
7
.2
n−1
+ 2
n−1
. V
`
ı
¯
d
,
˘
ang th
´
u
,
c a) trong b
`
ai .2.4 nên c
´
o 1 + a
2n+1
=
12
7
.2
n
suy ra
¯
d
,
˘
ang th
´
u
,
c a) c
,
ua b
`
ai to
´
an v
´
o
,
i gi
´
a tr
.
i n + 1.
T
`
u
,
¯
d
.
inh ngh
˜
ıa c
,
ua d
˜
ay 1 + a
2n+2
= 1 + a
2n−3
+ 2
n+1
. Ch
´
u
´
y t
´
o
,
i
¯
d
,
˘
ang th
´
u
,
c a) cho gi
´
a tr
.
i n −1, ta c
´
o 1 + a
2n+2
=
12
7
.2
n−2
+ 2
n+1
.
V
`
ı
¯
d
,
˘
ang th
´
u
,
c b) trong b
`
ai .2.4 nên c
´
o 1 + a
2n+2
=
17
7
.2
n
suy ra
¯
d
,
˘
ang th
´
u
,
c b) c
,
ua b
`
ai to
´
an v
´
o
,
i gi
´
a tr
.
i n + 1.
J

5.2. D
˜
ay tr
.
ôi ho
,
n 117
5.2. D
˜
ay tr
.
ôi ho
,
n
Cho hai d
˜
ay
a
1
, a
2
, a
3
, . . . (5.2)
b
1
, b
2
, b
3
, . . . (5.3)
Ta g
.
oi d
˜
ay (5.2) tr
.
ôi ho
,
n d
˜
ay (5.3) nê
´
u ch
´
ung tho
,
a m
˜
an bâ
´
t
¯
d
,
˘
ang
th
´
u
,
c:
b
n
≤ a
n
, ( n = 1, 2, . . .) (5.4)
Trong to
´
an h
.
oc thu
,
`
o
,
ng d
`
ung lo
.
ai bâ
´
t
¯
d
,
˘
ang th
´
u
,
c n
`
ay,
¯
d
.
˘
ac bi
.
êt c
´
ac
b
`
ai to
´
an vê
`
¯
d
´
anh gi
´
a m
.
ôt qu
´
a tr
`
ınh, t
`
ım gi
´
o
,
i h
.
an, ...
V
´
ı d
.
u 5.7. Ch
´
u
,
ng minh bâ
´
t
¯
d
,
˘ang th
´
u
,
c
4
n
n + 1
<
(2 n)!
( n!)
2
, ( n = 2, 3, . . .). (5.5)
L
`
o
,
i gi
,
ai. Ch
´
u
,
ng minh quy n
.
ap theo n. Bâ
´
t
¯
d
,
˘
ang th
´
u
,
c (5.5)
¯
d
´
ung
v
´
o
,
i n = 2 suy ra t
`
u
,
4
2
2 + 1
−
(2.2 )!
(2!)
2
=
16
3
−6 < 0.
Gi
,
a s
,
u
,
(5.5)
¯
d
´
ung v
´
o
,
i m
.
ôt sô
´
n n
`
ao
¯
d
´
o. Ta s
˜
e ch
´
u
,
ng minh r
`
˘
ang n
´
o
c
˜
ung
¯
d
´
ung cho n + 1,
4
n+1
n + 2
<
(2 n + 2)!
((n + 1)!)
2
. (5.6)
Th
.
ât v
.
ây, ta viê
´
t vê
´
tr
´
ai c
,
ua (5.6) du
,
´
o
,
i d
.
ang
4
n+1
n + 2
=
4
n
n + 1
4(n + 1)
n + 2
·
T
`
u
,
gi
,
a thiê
´
t quy n
.
ap ta c
´
o
4
n+1
n + 2
=
4
n
n + 1
4(n + 1)
n + 2
<
(2 n + 2)!
((n + 1)!)
2
.
2(n + 1)
2
(2 n + 1)(n + 2)
,

118 Chu
,
o
,
ng 5. D
˜
ay sô
´
m
.
˘
at kh
´
ac
0 <
2(n + 1)
2
(2 n + 1)(n + 2)
=
2n
2
+ 4n + 2
2n
2
+ 5n + 2
=
=
(2 n
2
+ 5n + 2) −n
2n
2
+ 5n + 2
= 1 −
n
2n
2
+ 5n + 2
< 1
v
´
o
,
i n = 1, 2, . . . v
`
a suy ra
4
n+1
n + 2
<
(2 n + 2)!
((n + 1)!)
2
.
2(n + 1)
2
(2 n + 1)(n + 2)
<
(2 n + 2)!
((n + 1)!)
2
.
J
V
´
ı d
.
u 5.8. Ch
´
u
,
ng minh bâ
´
t
¯
d
,
˘ang th
´
u
,
c
1 +
1
√
2
+ ··· +
1
√
n
>
√
n, (n = 2, 3, . . .). (5.7)
L
`
o
,
i gi
,
ai. V
´
o
,
i n = 2 ta c
´
o bâ
´
t
¯
d
,
˘
ang th
´
u
,
c 1 +
1
√
2
>
√
2, bâ
´
t
¯
d
,
˘
ang
th
´
u
,
c n
`
ay
¯
d
´
ung qua kiê
,
m tra tr
.
u
,
c tiê
´
p. Gi
,
a s
,
u
,
(5.7)
¯
d
´
ung v
´
o
,
i m
.
ôt
gi
´
a tr
.
i n n
`
ao
¯
d
´
o v
`
a ta s
˜
e ch
´
u
,
ng minh bâ
´
t
¯
d
,
˘
ang th
´
u
,
c c
˜
ung
¯
d
´
ung
v
´
o
,
i n + 1, ho
.
˘
ac l
`
a
1 +
1
√
2
+ ··· +
1
√
n + 1
>
√
n + 1, (n = 2, 3, . . .). (5.8)
Th
.
ât v
.
ây, c
.
ông hai vê
´
bâ
´
t
¯
d
,
˘
ang th
´
u
,
c (5.7) v
´
o
,
i sô
´
h
.
ang
1
√
n + 1
, ta
c
´
o
1 +
1
√
2
+ ··· +
1
√
n
+
1
√
n + 1
>
√
n +
1
√
n + 1
. (5.9)
Nhu
,
ng
√
n +
1
√
n + 1
=
√
n
2
+ n + 1
√
n + 1
>
√
n
2
+ 1
√
n + 1
=
√
n + 1.
T
`
u
,
¯
dây v
`
a (5.9) suy ra (5.8).
J

5.2. D
˜
ay tr
.
ôi ho
,
n 119
V
´
ı d
.
u 5.9. Ch
´
u
,
ng minh r
`
˘ang
a
1
b
1
a
1
+ b
1
+
a
2
b
2
a
2
+ b
2
+ ···+
a
n
b
n
a
n
+ b
n
≤
(a
1
+ ··· + a
n
)(b
1
+ ··· + b
n
)
(a
1
+ ··· + a
n
) + (b
1
+ ··· + b
n
)
,
(5.10)
,
o
,
¯
dây a
1
, a
2
, . . . , a
n
, b
1
, b
2
, . . . , b
n
l `a nh
˜
u
,
ng sô
´
du
,
o
,
ng.
L
`
o
,
i gi
,
ai. V
´
o
,
i n = 1 bâ
´
t
¯
d
,
˘
ang th
´
u
,
c
¯
d
´
ung. V
´
o
,
i n = 2 ta c
´
o d
.
ang
a
1
b
1
a
1
+ b
1
+
a
2
b
2
a
2
+ b
2
≤
(a
1
+ a
2
)(b
1
+ b
2
)
(a
1
+ a
2
) + (b
1
+ b
2
)
(5.11)
ho
.
˘
ac l
`
a
(a
1
+ a
2
)(b
1
+ b
2
)(a
1
+ b
1
)(a
2
+ b
2
) − a
1
b
1
(a
2
+ b
2
)(a
1
+ a
2
+ b
1
+ b
2
) −
−a
2
b
2
(a
1
+ b
1
)(a
1
+ a
2
+ b
1
+ b
2
) ≥ 0
ho
.
˘
ac l
`
a (a
1
b
2
− a
2
b
1
)
2
≥ 0 bâ
´
t
¯
d
,
˘
ang th
´
u
,
c n
`
ay hiê
,
n nhiên
¯
d
´
ung.
Gi
,
a s
,
u
,
(5.10)
¯
d
´
ung v
´
o
,
i sô
´
t
.
u
,
nhiên n ≥ 2 n
`
ao
¯
d
´
o. Ta s
˜
e ch
´
u
,
ng
minh n
´
o
¯
d
´
ung v
´
o
,
i n + 1. S
,
u
,
d
.
ung (5.10) v
`
a (5.11) ta c
´
o
a
1
b
1
a
1
+ b
1
+
a
2
b
2
a
2
+ b
2
+ ··· +
a
n
b
n
a
n
+ b
n
+
a
n+1
.b
n+1
a
n+1
+ b
n+1
≤
≤
(a
1
+ ··· + a
n
)(b
1
+ ··· + b
n
)
(a
1
+ ··· + a
n
) + (b
1
+ ··· + b
n
)
+
a
n+1
.b
n+1
a
n+1
+ b
n+1
≤
(a
1
+ ··· + a
n
+ a
n+1
)(b
1
+ ··· + b
n
+ b
n+1
)
(a
1
+ ··· + a
n
+ a
n+1
) + (b
1
+ ··· + b
n
+ b
n+1
)
.
J
V
´
ı d
.
u 5.10. Cho 0 < x
1
≤ x
2
≤ . . . ≤ x
n
. Ch
´
u
,
ng minh r
`
˘ang
x
1
x
2
+
x
2
x
3
+ ··· +
x
n−1
x
n
+
x
n
x
1
≥
x
2
x
1
+
x
3
x
2
+ ··· +
x
n
x
n−1
+
x
1
x
n
.
L
`
o
,
i gi
,
ai. V
´
o
,
i n = 2 bâ
´
t
¯
d
,
˘
ang th
´
u
,
c
¯
d
´
ung. V
´
o
,
i n = 3 ta c
´
o
x
1
x
2
+
x
2
x
3
+
x
3
x
1
−
x
2
x
1
−
x
3
x
2
−
x
1
x
3
=
(x
3
− x
2
)(x
3
− x
1
)(x
2
− x
x
1
x
2
x
3
≥ 0

120 Chu
,
o
,
ng 5. D
˜
ay sô
´
bâ
´
t
¯
d
,
˘
ang th
´
u
,
c
¯
d
´
ung. Gi
,
a s
,
u
,
bâ
´
t
¯
d
,
˘
ang th
´
u
,
c
¯
d
´
ung v
´
o
,
i n = k −1,
x
1
x
2
+
x
2
x
3
+ ··· +
x
k−1
x
1
≥
x
2
x
1
+
x
3
x
2
+ ··· +
x
1
x
k−1
.
Do ch
´
u
,
ng minh v
´
o
,
i tru
,
`
o
,
ng h
.
o
,
p n = 3 nên ta c
´
o
x
1
x
k−1
+
x
k−1
x
k
+
x
k
x
1
≥
x
k−1
x
1
+
x
k
x
k−1
+
x
1
x
k
.
C
.
ông hai bâ
´
t
¯
d
,
˘
ang th
´
u
,
c sau c
`
ung ta nh
.
ân
¯
du
,
.
o
,
c bâ
´
t
¯
d
,
˘
ang th
´
u
,
c
ph
,
ai ch
´
u
,
ng minh cho n = k.
J
V
´
ı d
.
u 5.11. Ch
´
u
,
ng minh r
`
˘ang nê
´
u t´ıch n sô
´
th
.
u
,
c du
,
o
,
ng
b
`
˘ang 1, th`ı tô
,
ng c
,
ua ch ´ung không nh
,
o ho
,
n n. N´oi c ´ach kh ´ac,
cho x
1
, x
2
, . . . , x
n
l `a nh
˜
u
,
ng sô
´
du
,
o
,
ng, ch
´
u
,
ng minh r
`
˘ang nê
´
u
x
1
x
2
. . . x
n
= 1 suy ra x
1
+ x
2
+ ··· + x
n
≥ n v
´
o
,
i m
.
oi n = 1, 2, . . .
L
`
o
,
i gi
,
ai. V
´
o
,
i n = 2, ta câ
`
n ph
,
ai ch
´
u
,
ng minh t
`
u
,
x
1
x
2
= 1 suy ra
x
1
+ x
2
> 2. Th
.
ât v
.
ây, t
`
u
,
bâ
´
t
¯
d
,
˘
ang th
´
u
,
c hiê
,
n nhiên (x
1
−1)
2
≥ 0,
suy ra x
2
1
+ 1 ≥ 2x
1
, chia hai vê
´
cho x
1
ta nh
.
ân
¯
du
,
.
o
,
c x
1
+
1
x
1
≥ 2,
ngh
˜
ıa l
`
a x
1
+ x
2
≥ 2,
¯
d
,
˘
ang th
´
u
,
c xâ
,
y ra khi x
1
= 1, do
¯
d
´
o x
1
=
x
2
= 1.
Gi
,
a s
,
u
,
m
.
ênh
¯
dê
`
¯
d
˜
a ch
´
u
,
ng minh
¯
d
´
ung cho n ≥ 2. Ta s
˜
e ch
´
u
,
ng
minh
¯
d
´
ung cho n + 1, ngh
˜
ıa l
`
a s
˜
e ch
´
u
,
ng minh t
`
u
,
x
1
x
2
. . . x
n
x
n+1
= 1 (5.12)
suy ra bâ
´
t
¯
d
,
˘
ang th
´
u
,
c
x
1
+ x
2
+ ··· + x
n
+ x
n+1
≥ n + 1. (5.13)
Ð
,
˘
ang th
´
u
,
c (5.12) ch
,
ı xâ
,
y ra hai tru
,
`
o
,
ng h
.
o
,
p sau:
I. Tâ
´
t c
,
a c
´
ac th
`
u
,
a sô
´
b
`
˘
ang nhau x
1
= x
2
= . . . = x
n+1
= 1.
II. Không ph
,
ai c
´
ac sô
´
¯
dê
`
u b
`
˘
ang nhau.

5.3. Nh
˜
u
,
ng bâ
´
t
¯
d
,
˘
ang th
´
u
,
c nô
,
i tiê
´
ng 121
Trong tru
,
`
o
,
ng h
.
o
,
p I. Ta c
´
o x
1
+ x
2
+ ··· + x
n+1
= n + 1.
Tru
,
`
o
,
ng h
.
o
,
p II. Trong c
´
ac th
`
u
,
a sô
´
c
´
o th
`
u
,
a sô
´
l
´
o
,
n ho
,
n 1 th
`
ı c
˜
ung
c
´
o th
`
u
,
a sô
´
nh
,
o ho
,
n 1. Nê
´
u không c
´
o
¯
dô
`
ng th
`
o
,
i hai sô
´
c
´
o t
´
ınh châ
´
t
trên th
`
ı t
´
ıch c
,
ua ch
´
ung s
˜
e kh
´
ac 1. Ch
,
˘
ang h
.
an x
1
< 1, x
n+1
> 1.
Khi
¯
d
´
o ta c
´
o y
1
x
2
x
3
. . . x
n
= 1,
,
o
,
¯
dây ta
¯
d
.
˘
at y
1
= x
1
x
n+1
. Do gi
,
a
thiê
´
t quy n
.
ap
¯
d
´
ung v
´
o
,
i n, nên ta c
´
o y
1
+ x
2
+ ···+ x
n
≥ n. Khi
¯
d
´
o
x
1
+ ··· + x
n+1
= (y
1
+ x
2
+ ··· + x
n
) + x
n+1
−y
1
+ x
1
≥ n + x
n+1
−y
1
+ x
1
= (n + 1) + x
n+1
−y
1
+ x
1
−1
= (n + 1) + x
n+1
− x
1
x
n+1
+ x
1
−1
= (n + 1) + (x
n+1
−1)(1 − x
1
).
Do ta c
´
o x
n+1
> 1 v
`
a x
1
< 1 suy ra
¯
diê
`
u câ
`
n ch
´
u
,
ng minh.
J
5.3. Nh
˜
u
,
ng bâ
´
t
¯
d
,
˘
ang th
´
u
,
c nô
,
i tiê
´
ng
B
`
ai t
.
âp vê
`
bâ
´
t
¯
d
,
˘
ang th
´
u
,
c vô c
`
ung phong ph
´
u v
`
a ch
,
ung lo
.
ai
kh
´
ac nhau,
¯
d
˜
a c
´
o nhiê
`
u s
´
ach
¯
dê
`
c
.
âp
¯
dê
´
n vâ
´
n
¯
dê
`
n
`
ay. Trong m
.
uc
n
`
ay ch
´
ung tôi ch
,
ı li
.
êt kê nh
˜
u
,
ng bâ
´
t
¯
d
,
˘
ang th
´
u
,
c co
,
b
,
an, tâ
´
t c
,
a
¯
dê
`
u
¯
du
,
.
o
,
c ch
´
u
,
ng minh b
`
˘
ang phu
,
o
,
ng ph
´
ap quy n
.
ap.
V
´
ı d
.
u 5.12. (Bâ
´
t
¯
d
,
˘ang th
´
u
,
c Cauchy). Cho d˜ay sô
´
du
,
o
,
ng bâ
´
t k`y
x
1
, x
2
, . . . , x
n
ch
´
u
,
ng minh r
`
˘ang
x
1
+ x
2
+ ··· + x
n
n
≥
n
√
x
1
x
2
. . . x
n
. (5.14)
Ð
,
˘ang th
´
u
,
c xâ
,
y ra khi v `a chi khi x
1
= x
2
= . . . = x
n
.
L
`
o
,
i gi
,
ai. C ´ach ch
´
u
,
ng minh th
´
u
,
nhâ
´
t: Ta
¯
d
.
˘
at a =
x
1
+ x
2
+ ··· + x
n
n
v
`
a
¯
d
.
˘
at g =
n
√
x
1
x
2
. . . x
n
. Khi
¯
d
´
o
¯
d
,
˘
ang th
´
u
,
c
(5.14) ch
,
ı l
`
a h
.
ê qu
,
a c
,
ua b
`
ai .5.11. Th
.
ât v
.
ây, g
n
= x
1
x
2
. . . x
n

122 Chu
,
o
,
ng 5. D
˜
ay sô
´
suy ra
x
1
g
.
x
2
g
. . .
x
n
g
= 1. Do kê
´
t qu
,
a b
`
ai to
´
an tru
,
´
o
,
c ta s
´
o
x
1
g
+
x
2
g
+ ··· +
x
n
g
≥ n. T
`
u
,
¯
d
´
o suy ra (5.14). Ð
,
˘
ang th
´
u
,
c ch
,
ı xâ
,
y ra khi
x
1
g
=
x
2
g
= . . . =
x
n
g
, ngh
˜
ıa l
`
a x
1
= x
2
= ... = x
n
.
C ´ach ch
´
u
,
ng minh th
´
u
,
hai: Phu
,
o
,
ng ph
´
ap ch
´
u
,
ng minh theo
quy n
.
ap d
.
ang kh
´
ac v
´
o
,
i b
`
ınh thu
,
`
o
,
ng do ch
´
ınh Cauchy
¯
du
,
a ra. C
´
o
thê
,
n
´
oi
¯
dây l
`
a c
´
ach ch
´
u
,
ng minh quy n
.
ap cho t
`
u
,
ng
¯
do
.
an ch
´
u
,
a c
´
ac
sô
´
t
.
u
,
nhiên.
V
´
o
,
i n = 1 = 2
0
bâ
´
t
¯
d
,
˘
ang th
´
u
,
c (5.14)
¯
d
´
ung. V
´
o
,
i n = 2 = 2
1
,
(5.14) suy ra t
`
u
,
(
√
x
1
−
√
x
2
)
2
≥ 0 v
`
a dâ
´
u
¯
d
,
˘
ang th
´
u
,
c x
,
ay ra khi
v
`
a ch
,
ı khi x
1
= x
2
. Gi
,
a s
,
u
,
(5.14)
¯
d
´
ung v
´
o
,
i sô
´
n. Khi
¯
d
´
o
x
1
+ x
2
+ ··· + x
2n
2n
=
x
1
+ x
2
2
+
x
3
+ x
4
2
+ ··· +
x
2n−1
+ x
2n
2
n
≥
n
r
x
1
+ x
2
2
.
x
3
+ x
4
2
. . .
x
2n−1
+ x
2n
2
≥
n
q
√
x
1
x
2
√
x
3
x
4
. . .
√
x
2n−1
x
2n
=
2n
√
x
1
x
2
. . . x
2n
.
Bâ
´
t
¯
d
,
˘
ang th
´
u
,
c (5.14)
¯
d
´
ung v
´
o
,
i 2n. Suy ra n
´
o
¯
d
´
ung v
´
o
,
i tâ
´
t c
,
a c
´
ac
sô
´
c
´
o d
.
ang 2
n−1
v
´
o
,
i m
.
oi sô
´
t
.
u
,
nhiên n.
V
´
o
,
i m l
`
a sô
´
t
.
u
,
nhiên. Nê
´
u m c
´
o d
.
ang 2
n
v
´
o
,
i n l
`
a m
.
ôt sô
´
n
`
ao
¯
d
´
o, th
`
ı (5.14)
¯
d
´
ung. V
`
ı v
.
ây ch
,
ı c
`
on kiê
,
m tra m n
`
˘
am trong kho
,
ang
gi
˜
u
,
a 2
n−1
v
`
a 2
n
. ngh
˜
ıa l
`
a 2
n−1
< m < 2
n
. Ta
¯
d
.
˘
at m + q = 2
n
. Khi
¯
d
´
o
x
1
+ x
2
+ ··· + x
m+q
m + q
≥
m+p
√
x
1
x
2
. . . x
m+q
.
Bây gi
`
o
,
ta
¯
d
.
˘
at x
m+1
= x
m+2
= . . . = x
m+q
=
x
1
+ x
2
+ ··· + x
m
m
,

5.3. Nh
˜
u
,
ng bâ
´
t
¯
d
,
˘
ang th
´
u
,
c nô
,
i tiê
´
ng 123
khi
¯
d
´
o
x
1
+ x
2
+ ··· + x
m
m
=
x
1
+ x
2
+ ··· + x
m+q
+ q
x
1
+ x
2
+ ··· + x
m
m
m + q
≥
m+q
r
x
1
x
2
. . . x
m
(
x
1
+ x
2
+ ··· + x
m
m
)
q
ho
.
˘
ac l
`
a
x
1
+ x
2
+ ··· + x
m
m
m+q
≥ x
1
x
2
. . . x
m
x
1
+ x
2
+ ··· + x
m
m
q
,
x
1
+ x
2
+ ··· + x
m
m
m
≥ x
1
x
2
. . . x
m
.
T
`
u
,
¯
dây suy ra (4.13)
¯
d
´
ung. Nhu
,
v
.
ây n
´
o
¯
d
´
ung v
´
o
,
i m
.
oi sô
´
t
.
u
,
nhiên
n.
Bây gi
`
o
,
ta ch
´
u
,
ng minh (5.14) xâ
,
y ra
¯
d
,
˘
ang th
´
u
,
c ch
,
ı khi x
1
=
x
2
= . . . = x
n
, th
.
ât v
.
ây, gi
,
a s
,
u
,
´
ıt nhâ
´
t c
´
o hai sô
´
trong x
1
, x
2
, . . . , x
n
,
ch
,
˘
ang h
.
an x
1
v
`
a x
2
không b
`
˘
ang nhau. Khi
¯
d
´
o
x
1
+ x
2
+ ··· + x
n
n
=
x
1
+ x
2
2
+
x
1
+ x
2
2
+ x
3
+ ··· + x
n
n
≥
n
s
x
1
+ x
2
2
2
x
3
x
4
. . . x
n
.
Nhu
,
ng t
`
u
,
x
1
6= x
2
suy ra
x
1
+ x
2
2
>
√
x
1
x
2
T
`
u
,
hai bâ
´
t
¯
d
,
˘
ang th
´
u
,
c trên ta suy ra
(
x
1
+ x
2
+ ··· + x
n
n
) >
n
√
x
1
x
2
. . . x
n
.
Nhu
,
v
.
ây m
.
ênh
¯
dê
`
¯
du
,
.
o
,
c ch
´
u
,
ng minh.
J

124 Chu
,
o
,
ng 5. D
˜
ay sô
´
Ch
´
u
´
y: sô
´
x
1
+ x
2
+ ··· + x
n
n
g
.
oi l
`
a trung b`ınh c
.
ông c
,
ua c
´
ac sô
´
x
1
, x
2
, . . . , x
n
. C
`
on sô
´
n
√
x
1
x
2
. . . x
n
g
.
oi l
`
a trung b`ınh nhân c
,
ua c
´
ac
sô
´
¯
d
˜
a cho.
V
´
ı d
.
u 5.13. (Bâ
´
t
¯
d
,
˘ang th
´
u
,
c Bernoulli). Ch
´
u
,
ng minh r
`
˘ang v
´
o
,
i
m
.
oi x > −1, x 6= 0 v `a v
´
o
,
i m
.
oi sô
´
t
.
u
,
nhiên n ≥ 2 bâ
´
t
¯
d
,
˘ang th
´
u
,
c
sau
¯
d ´ung
(1 + x)
n
> 1 + nx. (5.15)
L
`
o
,
i gi
,
ai. V
´
o
,
i n = 2 bâ
´
t
¯
d
,
˘
ang th
´
u
,
c (5.15) c
´
o d
.
ang 1 + 2x + x
2
>
1 + 2x v
`
a
¯
d
´
ung l
`
a hiê
,
n nhiên. Gi
,
a s
,
u
,
(5.15)
¯
d
´
ung v
´
o
,
i m
.
ôt sô
´
n ≥ 2.
Ta s
˜
e ch
´
u
,
ng minh n
´
o
¯
d
´
ung cho n + 1, ngh
˜
ıa l
`
a ph
,
ai ch
´
u
,
ng minh
(1 + x)
n+1
> 1 + (n + 1)x.
Th
.
ât v
.
ây, ta c
´
o
(1 + x)
n+1
> (1 + nx)(1 + x) = 1 + (n + 1 )x + nx
2
,
do nx
2
> 0 suy ra
¯
diê
`
u câ
`
n ch
´
u
,
ng minh.
J
Ch
´
u
´
y: Bâ
´
t
¯
d
,
˘
ang th
´
u
,
c Bernoulli c
`
on
¯
d
´
ung cho m
.
oi sô
´
th
.
u
,
c:
(1 + x)
α
> 1 + αx, x ≥ −1, α > 1,
,
o
,
¯
dây α l
`
a m
.
ôt sô
´
th
.
u
,
c l
´
o
,
n ho
,
n 1.
V
´
ı d
.
u 5.14. (Bâ
´
t
¯
d
,
˘ang th
´
u
,
c Cauchy-Bunyakovski). Ch
´
u
,
ng minh
r
`
˘ang
(x
2
1
+ x
2
2
+ ···+ x
2
n
)(y
2
1
+ y
2
2
+ ···+ y
2
n
) ≥ (x
1
y
1
+ x
2
y
2
+ ···+ x
n
y
n
)
2
(5.16)
v
´
o
,
i x
1
, x
2
, . . . , y
1
, y
2
, . . . l `a nh
˜
u
,
ng sô
´
th
.
u
,
c v `a n = 1, 2, 3, . . .
L
`
o
,
i gi
,
ai. V
´
o
,
i n = 1, (5.16)
¯
d
´
ung hiê
,
n nhiên. V
´
o
,
i n = 2, ta c
´
o
(x
1
y
1
+ x
2
y
2
)
2
= (x
2
1
+ x
2
2
)(y
2
1
+ y
2
2
) − (x
1
y
2
− x
2
y
1
)
2

5.3. Nh
˜
u
,
ng bâ
´
t
¯
d
,
˘
ang th
´
u
,
c nô
,
i tiê
´
ng 125
t
`
u
,
¯
dây suy ra bâ
´
t
¯
d
,
˘
ang th
´
u
,
c (5.16)
¯
d
´
ung v
´
o
,
i n = 2. Gi
,
a s
,
u
,
bâ
´
t
d
,
˘
ang th
´
u
,
c
¯
d
´
ung v
´
o
,
i n = k, ta ph
,
ai ch
´
u
,
ng minh n
´
o c
˜
ung
¯
d
´
ung v
´
o
,
i
n = k + 1. Th
.
ât v
.
ây, do bâ
´
t
¯
d
,
˘
ang th
´
u
,
c
¯
d
´
ung v
´
o
,
i n = 2 v
`
a gi
,
a thiê
´
t
quy n
.
ap ta c
´
o
(x
2
1
+ x
2
2
+ ··· + x
2
k+1
)(y
2
1
+ y
2
2
+ ··· + y
2
k+1
)
≥ (
q
x
2
1
+ x
2
2
+ ··· + x
2
k
q
y
2
1
+ y
2
2
+ ··· + y
2
k
+ x
k+1
y
k+1
)
2
≥ (x
1
y
1
+ x
2
y
2
+ ··· + x
k
y
k
+ x
k+1
y
k+1
)
2
.
J
V
´
ı d
.
u 5.15. (Bâ
´
t
¯
d
,
˘ang th
´
u
,
c Chebychev). Cho d ˜ay sô
´
x
1
, x
2
, ..., x
n
v `a y
1
, y
2
, ..., y
n
l `a 2n sô
´
, sao cho tho
,
a m ˜an
x
1
≤ x
2
≤ . . . ≤ x
n
y
1
≤ y
2
≤ . . . ≤ y
n
.
(5.17)
Ch
´
u
,
ng minh r
`
˘ang t´ıch c
,
ua trung b`ınh c
.
ông c´ac sô
´
x
1
, x
2
, . . . , x
n
v
´
o
,
i trung b`ınh c
.
ông c
,
ua c´ac sô
´
y
1
, y
2
, . . . , y
n
không vu
,
.
o
,
t qu´a trung
b`ınh c
.
ông c
,
ua c ´ac sô
´
x
1
y
1
, x
2
y
2
, . . . , x
n
y
n
, ho
.
˘ac l `a
x
1
+ x
2
+ ··· + x
n
n
.
y
1
+ y
2
+ ··· + y
n
n
≤
x
1
y
1
+ x
2
y
2
+ ··· + x
n
y
n
n
.
(5.18)
L
`
o
,
i gi
,
ai. Ta
¯
d
.
˘
at
A
n
= x
1
+ x
2
+ ··· + x
n
,
B
n
= y
1
+ y
2
+ ··· + y
n
,
C
n
= x
1
y
1
+ x
2
y
2
+ ··· + x
n
y
n
,
D
n
= nC
n
− A
n
B
n
.
(5.19)
Khi
¯
d
´
o bâ
´
t
¯
d
,
˘
ang th
´
u
,
c (5.18) c
´
o thê
,
viê
´
t l
.
ai
D
n
≥ 0 v
´
o
,
i n = 1, 2, . . . (5.20)

126 Chu
,
o
,
ng 5. D
˜
ay sô
´
Ta ch
´
u
,
ng minh b
`
˘
ang phu
,
o
,
ng ph
´
ap quy n
.
ap. V
´
o
,
i n = 1. Khi
¯
d
´
o
D
1
= 1C
1
− A
1
B
1
= x
1
y
1
− x
1
y
1
= 0.
Nhu
,
v
.
ây (5.20)
¯
d
´
ung v
´
o
,
i n = 1. Ta kiê
,
m tra v
´
o
,
i n = 2,
D
2
= 2C
2
− A
2
B
2
= 2(x
1
y
1
+ x
2
y
2
) − (x
1
+ x
2
)(y
1
+ y
2
)
= x
1
y
1
+ x
2
y
2
− x
1
y
2
− x
2
y
1
= (x
2
− x
1
)(y
2
−y
1
) ≥ 0,
v
`
ı x
2
− x
1
≥ 0 v
`
a y
2
−y
1
≥ 0 theo (5.17).
Nhu
,
v
.
ây nâ
,
y ra câu h
,
oi l
`
a biê
,
u di
˜
ên D
n
theo c
´
ac sô
´
x
1
, x
2
, . . . , x
n
v
`
a y
1
, y
2
, . . . , y
n
nhu
,
thê
´
n
`
ao? Ta ph
,
ai l
`
am thêm
tru
,
`
o
,
ng h
.
o
,
p riêng n
˜
u
,
a v
´
o
,
i n = 3. Ta c
´
o
D
3
= 3C
3
− A
3
B
3
= 3(x
1
y
1
+ x
2
y
2
+ x
3
y
3
) − (x
1
+ x
2
+ x
3
)(y
1
+ y
2
+ y
3
)
= (2x
1
y
1
− x
1
y
2
− x
1
y
3
) + (2x
2
y
2
− x
2
y
1
− x
2
y
3
)
+ ( 2x
3
y
3
− x
3
y
1
− x
3
y
2
)
= x
1
( y
1
−y
2
) + x
1
( y
1
−y
3
) + x
2
( y
2
−y
1
) + x
2
( y
2
−y
3
)+
+ x
3
( y
3
−y
1
) + x
3
( y
3
−y
2
).
T
`
u
,
¯
dây ta nh
.
ân
¯
du
,
.
o
,
c
D
3
= (x
2
− x
1
)(y
2
−y
1
) + (x
3
− x
1
)(y
3
−y
1
) + (x
3
− x
2
)(y
3
−y
2
).
So s
´
anh hai tru
,
`
o
,
ng h
.
o
,
p n = 2, 3 ta c
´
o thê
,
gi
,
a thiê
´
t r
`
˘
ang
D
n
= D
n−1
+ (x
n
− x
n−1
)(y
n
−y
n−1
) + ···+ (x
n
− x
1
)(y
n
−y
1
).
(5.21)
Ta ch
´
u
,
ng minh công th
´
u
,
c n
`
ay b
`
˘
ang quy n
.
ap to
´
an h
.
oc. V
´
o
,
i n = 2, 3
công th
´
u
,
c (5.21)
¯
d
´
ung. Gi
,
a s
,
u
,
n
´
o
¯
d
´
ung v
´
o
,
i m
.
ôt sô
´
n n
`
ao
¯
d
´
o. Ta

5.3. Nh
˜
u
,
ng bâ
´
t
¯
d
,
˘
ang th
´
u
,
c nô
,
i tiê
´
ng 127
t
´
ınh D
n+1
D
n+1
= (n + 1)C
n+1
− A
n+1
B
n+1
= (n + 1)(C
n
+ x
n+1
y
n+1
) − (A
n
+ x
n+1)
)(B
n
+ y
n+1
)
= (n C
n
− A
n
B
n
) + (C
n
− B
n
x
n+1
) + (nx
n+1
y
n+1
− A
n
y
n+1
).
Nhu
,
ng nC
n
− A
n
B
n
= D
n
m
.
˘
at kh
´
ac
C
n
− B
n
x
n+1
=
= x
1
y
1
+ ··· + x
n
y
n
−y
1
x
n+1
−y
2
x
n+1
−··· − y
n
x
n+1
= −y
1
(x
n+1
− x
1
) − y
2
(x
n+1
− x
2
) − ···− y
n
(x
n+1
− x
n
)
v
`
a
nx
n+1
y
n+1
− A
n
y
n+1
= nx
n+1
y
n+1
− x
1
y
n+1
−··· − x
n
y
n+1
= (x
n+1
− x
1
) y
n+1
+ (x
n+1
− x
2
) y
n+1
+ ··· + (x
n+1
− x
n
) y
n+1
.
V
`
a nhu
,
v
.
ây ta nh
.
ân
¯
du
,
.
o
,
c
D
n+1
= D
n
+ [−y
1
(x
n+1
− x
1
) − y
2
(x
n+1
− x
2
) − ···− y
n
(x
n+1
− x
n
)]
+ [y
n+1
(x
n+1
− x
1
) − y
n+1
(x
n+1
− x
2
) − ···− y
n+1
(x
n+1
− x
n
)]
= D
n
+ (x
n+1
− x
n
)(y
n+1
−y
n
) + ···+ (x
n+1
− x
1
)(y
n+1
−y
1
).
Nhu
,
v
.
ây, b
`
˘
ang quy n
.
ap ta kê
´
t lu
.
ân r
`
˘
ang
¯
d
,
˘
ang th
´
u
,
c (5.21)
¯
d
´
ung
v
´
o
,
i m
.
oi n = 2, 3, . . .
Ch
´
u
´
y r
`
˘
ang
¯
diê
`
u ki
.
ên (5.17) suy ra bâ
´
t
¯
d
,
˘
ang th
´
u
,
c
(x
n+1
− x
n
)(y
n+1
−y
n
) + ···+ (x
n+1
− x
1
)(y
n+1
−y
1
) ≥ 0
v
´
o
,
i m
.
oi sô
´
t
.
u
,
nhiên n > 1. T
`
u
,
¯
dây v
`
a (5.21) ta nh
.
ân
¯
du
,
.
o
,
c bâ
´
t
¯
d
,
˘
ang th
´
u
,
c
D
n
≥ D
n−1
, ( n = 2, 3, . . .). (5.22)
Bây gi
`
o
,
(5.20) suy ra t
`
u
,
(5.22) v
`
a tru
,
`
o
,
ng h
.
o
,
p n = 1.
J

128 Chu
,
o
,
ng 5. D
˜
ay sô
´
5.4. D
˜
ay
¯
do
,
n
¯
di
.
êu
Cho d
˜
ay sô
´
a
1
, a
2
, . . . , a
n
, . . . (5.23)
Ta g
.
oi d
˜
ay (5.23) b
.
i ch
.
˘an bên ph
,
ai, khi tô
`
n t
.
ai h
`
˘
ang sô
´
a sao cho
a
n
≤ a, (n = 1, 2, . . . ). Tu
,
o
,
ng t
.
u
,
ta c
˜
ung
¯
d
.
inh ngh
˜
ıa b
.
i ch
.
˘
an tr
´
ai
(khi
¯
d
´
o a
n
≥ a). Nê
´
u m
.
ôt d
˜
ay b
.
i ch
.
˘
an c
,
a tr
´
ai l
˜
ân ph
,
ai g
.
oi l
`
a d ˜ay
b
.
i ch
.
˘an. Suy ra m
.
ôt d
˜
ay b
.
i ch
.
˘
an khi v
`
a ch
,
ı khi tô
`
n t
.
ai h
`
˘
ang sô
´
K > 0 sao cho |a
n
| ≤ K, (n = 1, 2, . . .). D
˜
ay (5.23) g
.
oi l
`
a d ˜ay t ˘ang,
khi
a
1
≤ a
2
≤ . . . (5.24)
v
`
a l
`
a d
˜
ay gi
,
am khi
a
1
≥ a
2
≥ . . . (5.25)
M
.
ôt d
˜
ay m
`
a n
´
o c
´
o t
´
ınh châ
´
t (5.24) ho
.
˘
ac (5.25) g
.
oi l
`
a d ˜ay
¯
do
,
n
¯
di
.
êu.
Ta biê
´
t r
`
˘
ang m
.
ôt d
˜
ay g
.
oi l
`
a h
.
ôi t
.
u khi n tiê
´
n t
´
o
,
i vô c
`
ung th
`
ı d
˜
ay
¯
d
´
o tiê
´
n t
´
o
,
i m
.
ôt gi
´
a tr
.
i h
˜
u
,
u h
.
an. Ta c
´
o thê
,
ph
´
at biê
,
u m
.
ôt m
.
ôt
¯
d
.
inh
l
´
y co
,
b
,
an:
Ð
.
inh l
´
ı 5.1: Nê
´
u m
.
ôt d ˜ay
¯
d ˜a cho l `a t ˘ang (gi
,
am) v `a b
.
i ch
.
˘an bên
ph
,
ai (b
.
i ch
.
˘an bên tr ´ai), th`ı n´o h
.
ôi t
.
u.
Theo
¯
d
.
inh l
´
y trên nê
´
u c
´
ac
¯
diê
`
u ki
.
ên c
,
ua
¯
d
.
inh l
´
y tho
,
a m
˜
an
th
`
ı tô
`
n t
.
ai lim
n→∞
a
n
. Theo
¯
d
.
inh l
´
y trên th
`
ı nh
˜
u
,
ng sô
´
h
.
ang c
,
ua d
˜
ay
không tho
,
a m
˜
an t
´
ınh châ
´
t b
.
i ch
.
˘
an, th
`
ı lim
n→∞
a
n
= ∞ v
´
o
,
i d
˜
ay t
˘
ang
v
`
a lim
n→∞
a
n
= −∞ v
´
o
,
i d
˜
ay gi
,
am.
Nh
˜
u
,
ng b
`
ai to
´
an ch
´
u
,
ng minh tô
`
n t
.
ai gi
´
o
,
i h
.
an c
,
ua m
.
ôt d
˜
ay,
t
´
ınh gi
´
o
,
i h
.
an c
,
ua d
˜
ay c
´
o thê
,
d
`
ung nh
˜
u
,
ng quy t
´
˘
ac
¯
d
˜
a biê
´
t
¯
dê
,
t
´
ınh.
Nhiê
`
u khi ta ph
,
ai
´
ap d
.
ung
¯
d
.
inh l
´
y co
,
b
,
an trên nhu
,
ng ph
,
ai ch
´
u
,
ng
minh d
˜
ay ta x
´
et l
`
a
¯
do
,
n
¯
di
.
êu v
`
a b
.
i ch
.
˘
an. Ðê
,
gi
,
ai nh
˜
u
,
ng b
`
ai to
´
an
vê
`
d
˜
ay
¯
do
,
n
¯
di
.
êu thu
,
`
o
,
ng
´
ap d
.
ung tr
.
u
,
c tiê
´
p phu
,
o
,
ng ph
´
ap quy n
.
ap
to
´
an h
.
oc.

5.4. D
˜
ay
¯
do
,
n
¯
di
.
êu 129
V
´
ı d
.
u 5.16. D ˜ay sô
´
a
1
, a
2
, . . .
¯
du
,
.
o
,
c x ´ac
¯
d
.
inh theo công th
´
u
,
c
a
n+1
= a
n
(2 − αa
n
), (5.26)
,
o
,
¯
dây α l `a m
.
ôt sô
´
du
,
o
,
ng, c`on a
1
l `a m
.
ôt sô
´
bâ
´
t k`y trong (0,
1
α
). H ˜ay
t´ınh lim
n→∞
a
n
.
L
`
o
,
i gi
,
ai. 1) D
˜
ay
¯
d
˜
a cho l
`
a b
.
i ch
.
˘
an: T
`
u
,
(5.26) ta viê
´
t l
.
ai
a
n+1
=
1
α
[1 − (αa
n
−1)
2
]. (5.27)
B
,
o
,
i v
`
ı α > 0 v
`
a 0 < a
1
<
1
α
, th
`
ı (αa
1
− 1)
2
< 1 v
`
a t
`
u
,
(5.27) suy
ra (v
´
o
,
i n = 1) 0 < a
2
<
1
α
. C
˜
ung b
`
˘
ang phu
,
o
,
ng ph
´
ap nhu
,
v
.
ây
ch
´
u
,
ng minh r
`
˘
ang nê
´
u a
n
trong
¯
do
.
an (0,
1
α
), th
`
ı a
n+1
c
˜
ung n
`
˘
am
trong
¯
do
.
an n
`
ay. Theo nguyên l
´
y quy n
.
ap to
´
an h
.
oc tâ
´
t c
,
a phâ
`
n t
,
u
,
c
,
ua d
˜
ay sô
´
¯
dê
`
u n
`
˘
am trong
¯
do
.
an (0,
1
α
). Suy ra d
˜
ay
¯
d
˜
a cho l
`
a b
.
i
ch
.
˘
an.
2) T
´
ınh
¯
do
,
n
¯
di
.
êu: Ta l
.
ai c
´
o
a
n+1
− a
n
= a
n
(2 − αa
n
) − a
n
= a
n
(1 − αa
n
) > 0,
v
`
ı 0 < a
n
<
1
α
. Nhu
,
v
.
ây d
˜
ay
¯
do
,
n
¯
di
.
êu t
˘
ang v
`
a ta c
´
o thê
,
´
ap d
.
ung
¯
d
.
inh l
´
y co
,
b
,
an, d
˜
ay
¯
d
˜
a cho h
.
ôi t
.
u ngh
˜
ıa l
`
a c
´
o gi
´
o
,
i h
.
an.
3) T
`
ım gi
´
o
,
i h
.
an: Do nh
˜
u
,
ng l
´
y lu
.
ân phâ
`
n trên ta g
.
oi lim
n→∞
a
n
= l
´
ap d
.
ung v
`
ao (5.26) lim
n→∞
a
n+1
= ( lim
n→∞
a
n
). (2 − α lim
n→∞
a
n
).
Ta nh
.
ân
¯
du
,
.
o
,
c l = l(2 − αl). Nghi
.
êm c
,
ua phu
,
o
,
ng tr
`
ınh n
`
ay l
`
a
l = 0 ho
.
˘
ac l
`
a l =
1
α
. Nhu
,
ng d
˜
ay sô
´
l
`
a t
˘
ang nên ta ch
,
ı c
´
o thê
,
lâ
´
y
l =
1
α
.
J
V
´
ı d
.
u 5.17. D ˜ay sô
´
a
1
, a
2
, . . .
¯
du
,
.
o
,
c x ´ac
¯
d
.
inh theo công th
´
u
,
c
a
n+1
=
1
2
(a
n
+
α
a
n
), (5.28)

130 Chu
,
o
,
ng 5. D
˜
ay sô
´
,
o
,
¯
dây α l `a m
.
ôt sô
´
du
,
o
,
ng, c`on a
1
l `a m
.
ôt sô
´
du
,
o
,
ng bâ
´
t k`y. H˜ay t´ınh
lim
n→∞
a
n
.
L
`
o
,
i gi
,
ai. 1) D
˜
ay
¯
d
˜
a cho b
.
i ch
.
˘
an du
,
´
o
,
i: T
`
u
,
bâ
´
t
¯
d
,
˘
ang th
´
u
,
c α >
0, a
1
> 0 v
`
a (5.28) v
´
o
,
i n = 1 suy ra a
2
> 0. Gi
,
a thiê
´
t v
´
o
,
i m
.
ôt n
n
`
ao
¯
d
´
o a
n
> 0; khi
¯
d
´
o t
`
u
,
α > 0 v
`
a (5.28) suy ra a
n+1
> 0. Nhu
,
v
.
ây theo nguyên l
´
y quy n
.
ap to
´
an h
.
oc bâ
´
t
¯
d
,
˘
ang th
´
u
,
c a
n
> 0 v
´
o
,
i
n = 1, 2, . . .
2) D
˜
ay
¯
d
˜
a cho l
`
a
¯
do
,
n
¯
di
.
êu gi
,
am: T
`
u
,
(5.28) v
`
a bâ
´
t
¯
d
,
˘
ang th
´
u
,
c
trung b
`
ınh c
.
ông v
`
a trung b
`
ınh nhân ta c
´
o
a
n+1
=
a
n
+
α
a
n
2
≥
r
a
n
.
α
a
n
=
√
α.
Ðiê
`
u n
`
ay ch
´
u
,
ng t
,
o r
`
˘
ang tâ
´
t c
,
a c
´
ac sô
´
h
.
ang không nh
,
o ho
,
n
√
α.
M
.
˘
at kh
´
ac ta c
´
o
a
n+1
− a
n
=
1
2
(a
n
+
α
a
n
) − a
n
=
α − a
2
n
2a
n
,
a
n
> 0(n = 1, 2, . . .) v
`
a α −a
2
n
< 0 (
´
ıt nhâ
´
t v
´
o
,
i n = 2, 3, . . .) suy ra
a
n+1
< a
n
. Ngh
˜
ıa l
`
a d
˜
ay gi
,
am.
3) T
´
ınh gi
´
o
,
i h
.
an: C
˜
ung nhu
,
b
`
ai tru
,
´
o
,
c cho gi
´
o
,
i h
.
an trong (5.28)
ta nh
.
ân
¯
du
,
.
o
,
c phu
,
o
,
ng tr
`
ınh
l =
1
2
( l +
α
l
),
t
`
u
,
¯
d
´
o t
`
ım
¯
du
,
.
o
,
c gi
´
o
,
i h
.
an l =
√
α ( c
`
on tru
,
`
o
,
ng h
.
o
,
p l = −
√
α không
¯
du
,
.
o
,
c).
J

5.5. Sô
´
e 131
5.5. Sô
´
e
M
.
ôt h
`
˘
ang sô
´
to
´
an h
.
oc râ
´
t quan tr
.
ong sau sô
´
π l
`
a sô
´
e. Sô
´
e
¯
du
,
.
o
,
c
¯
d
.
inh ngh
˜
ıa nhu
,
l
`
a gi
´
o
,
i h
.
an c
,
ua d
˜
ay
a
n
= (1 +
1
n
)
n
, n = 1, 2, . . . (5.29)
ho
.
˘
ac l
`
a
e = lim
n→∞
(1 +
1
n
)
n
. (5.30)
V
´
ı d
.
u 5.18. D ˜ay (5.29) l `a d ˜ay t ˘ang.
L
`
o
,
i gi
,
ai. Ðiê
`
u kh
,
˘
ang
¯
d
.
inh không ph
,
ai ng
˜
âu nhiên: Khi n t
˘
ang
sô
´
m
˜
u trong (5.29) c
˜
ung t
˘
ang, nhu
,
ng phâ
`
n co
,
sô
´
gi
,
am (n
´
o tiê
´
n t
´
o
,
i
1 v
`
a c
´
o gi
´
a tr
.
i l
´
o
,
n ho
,
n 1). Ðê
,
thu
.
ân ti
.
ên t
´
ınh to
´
an ta
¯
du
,
a v
`
ao sô
´
p
n,k
= (1 −
1
n
)(1 −
2
n
) . . . (1 −
k − 1
n
), (5.31)
v
´
o
,
i n = 2, 3, . . . ; k = 2, 3, . . . , n.
V
´
o
,
i (0 < α < n) ta c
´
o bâ
´
t
¯
d
,
˘
ang th
´
u
,
c 0 < 1 −
α
n
< 1 −
α
n + 1
< 1
t
`
u
,
¯
d
´
o suy ra
0 < p
n,k
< p
n+1,k
< 1, (n = 2, 3, . . . ; k = 2, 3, . . . , n). (5.32)
Khai triê
,
n theo nh
.
i th
´
u
,
c Newton ta c
´
o
a
n
= (1 +
1
n
)
n
= 1 + C
1
n
1
n
+ ··· + C
k
n
1
n
k
+ ··· +
1
n
n
= 2 +
n
∑
k=2
n(n − 1) . . . (n −k + 1)
n
k
.
1
k!
, ( n = 2, 3, ...).
Ho
.
˘
ac khi ta d
`
ung (5.31), (1 +
1
n
)
n
= 2 +
n
∑
k=2
p
n,k
k!
. Khi
¯
d
´
o ta c
´
o thê
,
viê
´
t (5.29) du
,
´
o
,
i d
.
ang
a
n
= 2 +
n
∑
k=2
p
n,k
k!
( n = 1, 2, . . . ; k = 2, 3, . . . , n). (5.33)

132 Chu
,
o
,
ng 5. D
˜
ay sô
´
Ta c
´
o hi
.
êu a
n+1
− a
n
theo (5.33)
a
n+1
− a
n
= (2 +
n+1
∑
k=2
p
n+1,k
k!
) − (2 +
n
∑
k=2
p
n,k
k!
)
=
n
∑
k=2
p
n+1,k
− p
n,k
k!
+
p
n+1,n+1
( n + 1)!
v
`
a theo (5.32) ta c
´
o
a
n+1
− a
n
>
p
n+1,n+1
( n + 1)!
> 0.
J
Bây gi
`
o
,
, ta
¯
d
.
inh ngh
˜
ıa d
˜
ay e
1
, e
2
, . . . theo phu
,
o
,
ng ph
´
ap sau:
e
1
= 2, e
n
= 2 +
n
∑
k=2
1
k!
, ( n = 2, 3, . . .). (5.34)
D
˜
ê thâ
´
y r
`
˘
ang d
˜
ay n
`
ay l
`
a t
˘
ang. T
`
u
,
(5.32) v
`
a (5.33) suy ra bâ
´
t
¯
d
,
˘
ang
th
´
u
,
c
a
n
< e
n
. (5.35)
B
`
ai t
.
âp tiê
´
p sau ch
,
ı ra d
˜
ay e
1
, e
2
, . . . l
`
a b
.
i ch
.
˘
an v
`
a suy ra n
´
o h
.
ôi
t
.
u. T
`
u
,
¯
dây v
`
a (5.35) suy ra a
1
, a
2
, . . . c
˜
ung b
.
i ch
.
˘
an. B
`
˘
ang c
´
ach n
`
ay
ta ch
´
u
,
ng minh
¯
du
,
.
o
,
c s
.
u
,
tô
`
n t
.
ai gi
´
o
,
i h
.
an c
,
ua d
˜
ay (5.30).
V
´
ı d
.
u 5.19. Ch
´
u
,
ng minh r
`
˘ang nh
˜
u
,
ng sô
´
h
.
ang c
,
ua d˜ay (5.34)
tho
,
a m ˜an
e
n
< 3 −
1
2
n−1
, (n = 3, 4, . . .). (5.36)
L
`
o
,
i gi
,
ai. V
´
o
,
i n = 3 ta c
´
o e
3
< 2, 67 < 3 −
1
2
3−1
= 2, 75. Gi
,
a s
,
u
,
(5.36) tho
,
a m
˜
an v
´
o
,
i sô
´
n n
`
ao
¯
dâ
´
y. Ta s
,
u
,
d
.
ung bâ
´
t
¯
d
,
˘
ang th
´
u
,
c hiê
,
n
nhiên (n + 1)! > 2
n
v
´
o
,
i n > 1 v
`
a gi
,
a thiê
´
t quy n
.
ap ta nh
.
ân
¯
du
,
.
o
,
c
e
n+1
=e
n
+
1
( n + 1)!
< (3 −
1
2
n−1
) +
1
( n + 1)!
< 3 −
1
2
n−1
+
1
2
n
= 3 −
1
2
n
.
J

5.5. Sô
´
e 133
V
´
ı d
.
u 5.20. Gi
´
o
,
i h
.
an c
,
ua d ˜ay (5.34) l `a sô
´
e.
L
`
o
,
i gi
,
ai. Ta
¯
d
˜
a ch
´
u
,
ng minh
¯
du
,
.
o
,
c r
`
˘
ang d
˜
ay a
1
, a
2
, . . . v
`
a e
1
, e
2
, . . .
l
`
a h
.
ôi t
.
u. Ð
.
˘
at e
∗
= lim
n→∞
e
n
. T
`
u
,
(5.30) v
`
a (5.35) suy ra
e ≤ e
∗
. (5.37)
Ta s
˜
e ch
´
u
,
ng minh c
`
ung v
´
o
,
i (5.37) c
˜
ung c
´
o
e
∗
≤ e,
Th
.
ât v
.
ây, ta ch
.
on sô
´
t
.
u
,
nhiên s trong kho
,
ang (1, n). Nê
´
u bên ph
,
ai
c
,
ua (5.33) ta b
,
o
¯
di
p
n,s+1
( s + 1)!
, . . . ,
p
n,n
n!
, ta s
˜
e nh
.
ân
¯
du
,
.
o
,
c m
.
ôt sô
´
nh
,
o
ho
,
n a
n
, ngh
˜
ıa l
`
a
2 +
s
∑
k=2
p
n,k
k!
< a
n
, ( n = 3, 4, . . . ; s = 2, 3, . . . , n −1). (5.38)
Ta x
´
et
¯
d
,
˘
ang th
´
u
,
c (5.31). Khi n tiê
´
n t
´
o
,
i vô c
`
ung, c
`
on k cô
´
¯
d
.
inh, m
˜
ôi
th
`
u
,
a sô
´
tiê
´
n t
´
o
,
i 1. V
`
ı thê
´
lim
n→∞
p
n,k
= 1. Nê
´
u ta cho n tiê
´
n t
´
o
,
i vô
c
`
ung trong (5.38) ta s
˜
e nh
.
ân
¯
du
,
.
o
,
c
e
s
= 2 +
s
∑
k=2
1
k!
≤ e ( s = 2, 3, . . .).
Nhu
,
v
.
ây d
˜
ay t
˘
ang e
1
, e
2
, . . . . b
.
i ch
.
˘
an t
`
u
,
ph
´
ıa ph
,
ai sô
´
e, t
`
u
,
¯
d
´
o suy
ra bâ
´
t
¯
d
,
˘
ang th
´
u
,
c (5.38). Kh
,
˘
ang
¯
d
.
inh suy ra t
`
u
,
(5.36) v
`
a (5.37).
J
Nhu
,
v
.
ây sô
´
e c
´
o thê
,
t
´
ınh to
´
an
¯
dê
´
n
¯
d
.
ô ch
´
ınh x
´
ac n
`
ao
¯
dâ
´
y theo
công th
´
u
,
c trên
e
n
= 2 +
1
2!
+
1
3!
+ ··· +
1
n!
, ( n = 2, 3, . . .).
T
`
u
,
bâ
´
t
¯
d
,
˘
ang th
´
u
,
c a
n
< e
n
< e ta thâ
´
y r
`
˘
ang v
´
o
,
i m
˜
ôi n cô
´
¯
d
.
inh sô
´
e
n
gâ
`
n
¯
d
´
ung e. Sô
´
e
n
g
.
oi l
`
a xâ
´
p x
,
ı th
´
u
,
n c
,
ua e, c
`
on hi
.
êu
δ
n
= e −e
n
(5.39)

134 Chu
,
o
,
ng 5. D
˜
ay sô
´
g
.
oi l
`
a sai sô
´
c
,
ua e.
V
´
ı d
.
u 5.21. Ch
´
u
,
ng minh nh
˜
u
,
ng bâ
´
t
¯
d
,
˘ang th
´
u
,
c sau
e
i
−e
n
≤
2
( n + 1)!
.( 1 −
1
2
i −n
), n = 2, 3, . . . . ; i = n, n + 1, . . .
(5.40)
L
`
o
,
i gi
,
ai. Ta s
˜
e ch
´
u
,
ng minh (5.40) b
`
˘
ang quy n
.
ap
¯
dô
´
i vo
,
i i. V
´
o
,
i
i = n th
`
ı 0 ≤ 0 (5.40)
¯
d
´
ung. Gi
,
a s
,
u
,
(5.40)
¯
d
´
ung v
´
o
,
i sô
´
i n
`
ao
¯
d
´
o, ta
câ
`
n ph
,
ai ch
´
u
,
ng minh n
´
o c
˜
ung
¯
d
´
ung v
´
o
,
i n = i + 1. Th
.
ât v
.
ây,
e
i +1
−e
n
=
e
i
+
1
(i + 1)!
−e
n
= (e
i
−e
n
) +
1
(i + 1)!
≤
2
( n + 1)!
1 −
1
2
i −n
+
1
(i + 1)!
=
2
( n + 1)!
1 −
1
2
i −n
+
1
2
.
1
( n + 2)(n + 3) . . . (i + 1)
.
T
´
ıch (n + 2)(n + 3) . . . (i + 1) c
´
o i −n th
`
u
,
a sô
´
, m
˜
ôi th
`
u
,
a sô
´
l
´
o
,
n ho
,
n
2. Khi
¯
d
´
o 2(n + 2)(n + 3) . . . (i + 1) > 2
i −n+1
,
,
o
,
¯
dây e
i +1
− e
n
<
2
( n + 1)!
(1 −
1
2
i −n
+
1
2
i −n+1
) =
2
( n + 1)!
(1 −
1
2
(i+1)−n
). Nhu
,
v
.
ây,
(5.40)
¯
d
´
ung v
´
o
,
i m
.
oi i = n, n + 1, . . .
J
5.6. D
˜
ay sô
´
Fibonacci
M
.
ôt d
˜
ay sô
´
u
1
, u
2
, . . .
¯
du
,
.
o
,
c
¯
d
.
inh ngh
˜
ıa b
`
˘
ang công th
´
u
,
c
u
n+2
= u
n+1
+ u
n
, ( n = 1, 2, . . .) (5.41)
v
`
a
u
1
= 1, u
2
= 1. (5.42)
Nh
˜
u
,
ng sô
´
u
1
, u
2
, u
3
, . . . g
.
oi l
`
a sô
´
Fibonacci. D
˜
ay sô
´
n
`
ay c
´
o râ
´
t
nhiê
`
u
´
u
,
ng d
.
ung trong b
`
ai to
´
an th
.
u
,
c tê
´
. Theo
¯
d
,
˘
ang th
´
u
,
c (5.41)

5.6. D
˜
ay sô
´
Fibonacci 135
m
.
oi sô
´
kê
,
t
`
u
,
sô
´
th
´
u
,
ba
¯
dê
`
u l
`
a tô
,
ng c
,
ua hai sô
´
tru
,
´
o
,
c
¯
d
´
o.
Nh
˜
u
,
ng sô
´
¯
dâ
`
u tiên l
`
a 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89,
144, 233, 377. Nh
˜
u
,
ng b
`
ai t
.
âp sau liên quan
¯
dê
´
n c
´
ac t
´
ınh
châ
´
t c
,
ua d
˜
ay sô
´
n
`
ay c
´
o ch
´
u
,
ng minh b
`
˘
ang quy n
.
ap to
´
an h
.
oc,
c
`
on c
´
ac t
´
ınh châ
´
t kh
´
ac c
,
ua d
˜
ay sô
´
n
`
ay th
`
ı râ
´
t nhiê
`
u v
`
a ch
´
u
,
ng
minh b
`
˘
ang c
´
ac c
´
ach kh
´
ac nhau.
V
´
ı d
.
u 5.22. Tô
,
ng c
,
ua n sô
´
¯
dâ
`
u tiên b
`
˘ang sô
´
th
´
u
,
n + 2 tr
`
u
,
¯
di 1,
ho
.
˘ac l `a
u
1
+ u
2
+ ··· + u
n
= u
n+2
−1 (n > 1). (5.43)
L
`
o
,
i gi
,
ai. V
´
o
,
i n = 2
¯
d
,
˘
ang th
´
u
,
c
¯
d
´
ung v
`
ı theo (5.41) v
`
a (5.42) ta c
´
o
u
1
+ u
2
= 1 + 1 = 3 −1 = u
4
−1.
Gi
,
a s
,
u
,
(5.43)
¯
d
´
ung v
´
o
,
i sô
´
t
.
u
,
nhiên n n
`
ao
¯
d
´
o. T
`
u
,
gi
,
a thiê
´
t quy n
.
ap
v
`
a công th
´
u
,
c (5.41) v
´
o
,
i tô
,
ng c
,
ua n + 1 sô
´
Fibonacci ta c
´
o :
u
1
+ u
2
+ ··· + u
n+1
= (u
1
+ u
2
+ ··· + u
n
) + u
n+1
= (u
n+2
−1) + u
n+1
= u
n+1
+ u
n+2
−1 = u
n+3
−1.
Theo nguyên l
´
y quy n
.
ap to
´
an h
.
oc
¯
d
,
˘
ang th
´
u
,
c
¯
d
´
ung v
´
o
,
i m
.
oi n ≥ 2.
J
V
´
ı d
.
u 5.23. Ch
´
u
,
ng minh r
`
˘ang
¯
d
,
˘ang th
´
u
,
c
u
n+m
= u
n−1
u
m
+ u
n
u
m+1
(5.44)
¯
d ´ung v
´
o
,
i sô
´
t
.
u
,
nhiên bâ
´
t k`y n > 1 v `a v
´
o
,
i m
.
oi m = 1, 2, . . .
L
`
o
,
i gi
,
ai. Ta ch
´
u
,
ng minh b
`
˘
ang phu
,
o
,
ng ph
´
ap quy n
.
ap to
´
an theo
m. V
´
o
,
i m = 1 ta c
´
o
u
n−1
u
1
+ u
n
u
2
= u
n−1
+ u
n
= u
n+1
,

136 Chu
,
o
,
ng 5. D
˜
ay sô
´
v
`
a v
´
o
,
i m = 2:
u
n−1
u
2
+ u
n
u
3
= u
n−1
+ 2u
n
= (u
n−1
+ u
n
) + u
n
= u
n+1
+ u
n
= u
n+2
,
¯
d
,
˘
ang th
´
u
,
c (5.44)
¯
dê
`
u
¯
d
´
ung. Gi
,
a s
,
u
,
v
´
o
,
i sô
´
m n
`
ao
¯
d
´
o c
´
ac
¯
d
,
˘
ang th
´
u
,
c
sau
¯
d
´
ung
u
n+m
= u
n−1
u
m
+ u
n
u
m+1
(5.45)
u
n+m+1
= u
n−1
u
m+1
+ u
n
u
m+2
Ta s
˜
e ch
´
u
,
ng minh
¯
d
,
˘
ang th
´
u
,
c sau
¯
d
´
ung
u
n+m+2
= u
n−1
u
m+2
+ u
n
u
m+3
. (5.46)
Th
.
ât v
.
ây, c
.
ông t
`
u
,
ng vê
´
c
,
ua hai
¯
d
,
˘
ang th
´
u
,
c trong (5.45) ta nh
.
ân
¯
du
,
.
o
,
c
u
n+m+1
+ u
n+m
= u
n−1
( u
m+1
+ u
m
) + u
n
( u
m+2
+ u
m+1
)
¯
dây ch
´
ınh l
`
a
¯
d
,
˘
ang th
´
u
,
c (5.46) khi ta biê
´
n
¯
dô
,
i v
`
a
´
ap d
.
ung (5.41).
J
V
´
ı d
.
u 5.24. Ch
´
u
,
ng minh r
`
˘ang m
.
oi sô
´
Fibonacci c´o thê
,
biê
,
u di
˜
ên
du
,
´
o
,
i d
.
ang
u
n
=
1 +
√
5
2
!
n
−
1 −
√
5
2
!
n
√
5
, ( n = 1, 2, . . .) (5.47)
L
`
o
,
i gi
,
ai. V
´
o
,
i n = 1 v
`
a n = 2 ta nh
.
ân
¯
du
,
.
o
,
c u
1
= 1 v
`
a u
2
= 1. Gi
,
a
s
,
u
,
v
´
o
,
i m
.
ôt sô
´
n n
`
ao
¯
d
´
o c
´
o u
n
v
`
a u
n+1
theo công th
´
u
,
c (5.47) l
`
a sô
´
h
.
ang th
´
u
,
n v
`
a n + 1 c
,
ua d
˜
ay Fibonacci. Ta s
˜
e ch
´
u
,
ng minh r
`
˘
ang

5.6. D
˜
ay sô
´
Fibonacci 137
sô
´
h
.
ang th
´
u
,
n + 2 c
,
ua d
˜
ay c
˜
ung biê
,
u di
˜
ên theo công th
´
u
,
c (5.47).
Ðê
,
cho g
.
on ta k
´
y hi
.
êu
α =
1 +
√
5
2
, β =
1 −
√
5
2
.
Khi
¯
d
´
o u
n
=
α
n
− β
n
√
5
, u
n+1
=
α
n+1
− β
n+1
√
5
. Do c
´
ach
¯
d
.
˘
at ta c
´
o
α + β = 1 v
`
a αβ = −1. Suy ra α v
`
a β l
`
a nghi
.
êm c
,
ua phu
,
o
,
ng tr
`
ınh
x
2
− x −1 = 0. Khi
¯
d
´
o α
2
= α + 1, β
2
= β + 1. Nhu
,
v
.
ây ta c
´
o
u
n+2
= u
n+1
+ u
n
=
α
n+1
− β
n+1
√
5
+
α
n
− β
n
√
5
=
α
n
( α + 1) − β
n
(β + 1)
√
5
=
α
n
α
2
− β
n
β
2
√
5
=
α
n+2
− β
n+2
√
5
.
Theo quy n
.
ap to
´
an h
.
oc biê
,
u di
˜
ên u
n
b
`
˘
ang (5.47)
¯
d
´
ung v
´
o
,
i m
.
oi n.
J
V
´
ı d
.
u 5.25. Ch
´
u
,
ng minh r
`
˘ang
α
n
= u
n
α + u
n−1
v
´
o
,
i m
.
oi sô
´
t
.
u
,
nhiên n ≥ 2. α nhu
,
,
o
,
b `ai t
.
âp tru
,
´
o
,
c.
L
`
o
,
i gi
,
ai. V
´
o
,
i n = 2, 3
¯
d
,
˘
ang th
´
u
,
c
¯
d
´
ung. Gi
,
a s
,
u
,
¯
d
,
˘
ang th
´
u
,
c
¯
d
´
ung
v
´
o
,
i n = k v
`
a n = k + 1, ngh
˜
ıa l
`
a
α
k
= u
k
α + u
k−1
,
α
k+1
= u
k+1
α + u
k
.
Ta c
.
ông hai
¯
d
,
˘
ang th
´
u
,
c l
.
ai kê
´
t qu
,
a nh
.
ân
¯
du
,
.
o
,
c
α
k
+ α
k+1
= (u
k
+ u
k+1
) α + (u
k−1
+ u
k
),
ho
.
˘
ac l
`
a
α
k+2
= u
k+2
α + u
k+1
.

138 Chu
,
o
,
ng 5. D
˜
ay sô
´
Theo nguyên l
´
y quy n
.
ap to
´
an h
.
oc
¯
d
,
˘
ang th
´
u
,
c trong b
`
ai cho l
`
a
¯
d
˜
a
¯
d
´
ung.
J
Ho
`
an to
`
an tu
,
o
,
ng t
.
u
,
ta c
˜
ung c
´
o
β
n
= u
n
β + u
n−1
.
V
´
ı d
.
u 5.26. Ch
´
u
,
ng minh r
`
˘ang u
2
n
−u
n−1
u
n+1
= (−1)
n+1
v
´
o
,
i n >
1.
L
`
o
,
i gi
,
ai. V
´
o
,
i n = 2, ta c
´
o u
2
2
= u
1
u
3
−1
¯
d
,
˘
ang th
´
u
,
c
¯
d
´
ung.
Gi
,
a s
,
u
,
r
`
˘
ang u
2
k
− u
k−1
u
k+1
= (−1)
k
, ta câ
`
n ch
´
u
,
ng minh
¯
d
,
˘
ang
th
´
u
,
c trên c
˜
ung
¯
d
´
ung cho n = k + 1, ngh
˜
ıa l
`
a u
2
k+1
− u
k
u
k+2
=
( −1)
k+2
. Th
.
ât v
.
ây,
u
2
k+1
−u
k
u
k+2
= u
2
k+1
−u
k
( u
k+1
+ u
k
)
= u
k+1
( u
k+1
−u
k
) − u
2
k
= u
k+1
u
k−1
−u
2
k
= −(u
2
k
−u
k+1
u
k−1
) = −(−1)
k+1
= (−1)
k+2
.
J
V
´
ı d
.
u 5.27. Ch
´
u
,
ng minh r
`
˘ang nê
´
u n chia hê
´
t cho m , th`ı u
n
chia
hê
´
t cho u
m
.
L
`
o
,
i gi
,
ai. V
`
ı n chia hê
´
t cho m, nên ta c
´
o thê
,
viê
´
t n = mk. Ta s
˜
e
ch
´
u
,
ng minh quy n
.
ap theo k.
V
´
o
,
i k = 1, khi
¯
d
´
o n = m nhu
,
v
.
ây u
n
chia hê
´
t cho u
m
l
`
a
hiê
,
n nhiên. Gi
,
a s
,
u
,
u
mk
chia hê
´
t cho u
m
, ta x
´
et u
m(k+1)
. Nhu
,
ng
u
m(k+1)
= u
mk+m
v
`
a theo công th
´
u
,
c (5.44) ta c
´
o
u
m(k+1)
= u
mk−1
u
m
+ u
mk
u
m+1
.
Sô
´
h
.
ang th
´
u
,
nhâ
´
t c
´
o ch
´
u
,
a u
m
nên n
´
o chia hê
´
t cho u
m
, c
`
on sô
´
h
.
ang
th
´
u
,
hai theo gi
,
a thiê
´
t quy n
.
ap u
mk
chia hê
´
t cho u
m
. Nhu
,
v
.
ây tô
,
ng
c
,
ua hai sô
´
h
.
ang chia hê
´
t cho u
m
, suy ra u
m(k+1)
chia hê
´
t cho u
m
.
J

5.7. B
`
ai t
.
âp 139
5.7. B
`
ai t
.
âp
.
.
. 5.28. H
˜
ay t
`
ım u
,
´
o
,
c sô
´
chung l
´
o
,
n nhâ
´
t c
,
ua c
´
ac sô
´
2
2
2
+ 2
2
1
+ 1; 2
2
3
+ 2
2
2
+ 1; . . . ; 2
2
n+1
+ 2
2
n
+ 1; . . .
.
.
. 5.29. Ch
´
u
,
ng minh r
`
˘
ang nê
´
u p
n
l
`
a sô
´
nguyên tô
´
th
´
u
,
n, th
`
ı p
n
<
2
2
n
.
.
.
. 5.30. Ch
´
u
,
ng minh r
`
˘
ang nê
´
u 0 ≤ α
1
≤ β
1
≤ α
2
≤ . . . ≤ α
n
≤
β
n
≤
π
2
, th
`
ı
n
∑
i =1
(sin β
i
−sin α
i
) ≤ sin(
n
∑
i =1
(β
i
−α
i
)).
.
.
. 5.31. Ch
´
u
,
ng minh bâ
´
t
¯
d
,
˘
ang th
´
u
,
c
n
∑
i =1
1
n + i
>
13
24
, n = 2, 3, . . .
.
.
. 5.32. T
`
ım gi
´
o
,
i h
.
an c
,
ua d
˜
ay
a
1
=
√
c, a
2
=
q
c +
√
c, a
3
=
r
c +
q
c +
√
c, . . .
,
o
,
¯
dây c l
`
a h
`
˘
ang sô
´
du
,
o
,
ng.

CHU
,
O
,
NG 6
H
`
INH H
.
OC
6.1. V
´
ı d
.
u quy n
.
ap to
´
an h
.
oc cho h
`
ınh h
.
oc . . . . . . . . . . . . . . 140
6.2. B
`
ai t
.
âp .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 154
Phu
,
o
,
ng ph
´
ap quy n
.
ap to
´
an h
.
oc
´
ap d
.
ung râ
´
t nhiê
`
u trong c
´
ac
b
`
ai t
.
âp h
`
ınh h
.
oc. B
.
an
¯
d
.
oc c
´
o thê
,
t
`
ım thâ
´
y trong [7] nh
˜
u
,
ng kh
´
ıa
c
.
anh câ
`
n thiê
´
t cho phu
,
o
,
ng ph
´
ap n
`
ay trong h
`
ınh h
.
oc. Ta ch
,
ı li
.
êt
kê du
,
´
o
,
i
¯
dây m
.
ôt sô
´
b
`
ai râ
´
t
¯
diê
,
n h
`
ınh.
6.1. V
´
ı d
.
u quy n
.
ap to
´
an h
.
oc cho h
`
ınh h
.
oc
V
´
ı d
.
u 6.1. Trong m
.
˘at ph
,
˘ang cho n h`ınh lô
`
i ( n > 3 ), m
˜
ôi c
.
˘ap ba
trong ch ´ung c´o
¯
diê
,
m chung. Ch
´
u
,
ng minh r
`
˘ang tô
`
n t
.
ai
¯
diê
,
m, m `a
n´o n
`
˘am trên tâ
´
t c
,
a c ´ac h`ınh.
L
`
o
,
i gi
,
ai. 1. V
´
o
,
i n = 4, ta k
´
y hi
.
êu nh
˜
u
,
ng h
`
ınh b
`
˘
ang C
1
, C
2
, C
3
, C
4
.
Cho C
1
∩ C
2
∩ C
3
= A
4
, C
1
∩ C
2
∩ C
4
= A
3
, C
1
∩ C
3
∩ C
4
= A
2
,
C
2
∩C
3
∩C
4
= A
1
.
a. Nê
´
u A
4
n
`
˘
am trong tam gi
´
ac A
1
A
2
A
3
, th
`
ı b
,
o
,
i v
`
ı A
1
A
2
A
3
⊂ C
4
, ta c
´
o A
4
∈ C
4
v
`
a suy ra A
4
∈ C,
,
o
,
¯
dây C k
´
y hi
.
êu l
`
a giao c
,
ua
c
´
ac h
`
ınh C
1
, C
2
, C
3
, C
4
.
b. Nê
´
u A
1
A
2
A
3
A
4
l
`
a t
´
u
,
gi
´
ac lô
`
i v
`
a A l
`
a
¯
diê
,
m c
´
˘
at c
,
ua c
´
ac
¯
du
,
`
o
,
ng
ch
´
eo c
,
ua ch
´
ung, th
`
ı d
˜
ê thâ
´
y r
`
˘
ang A ∈ C.
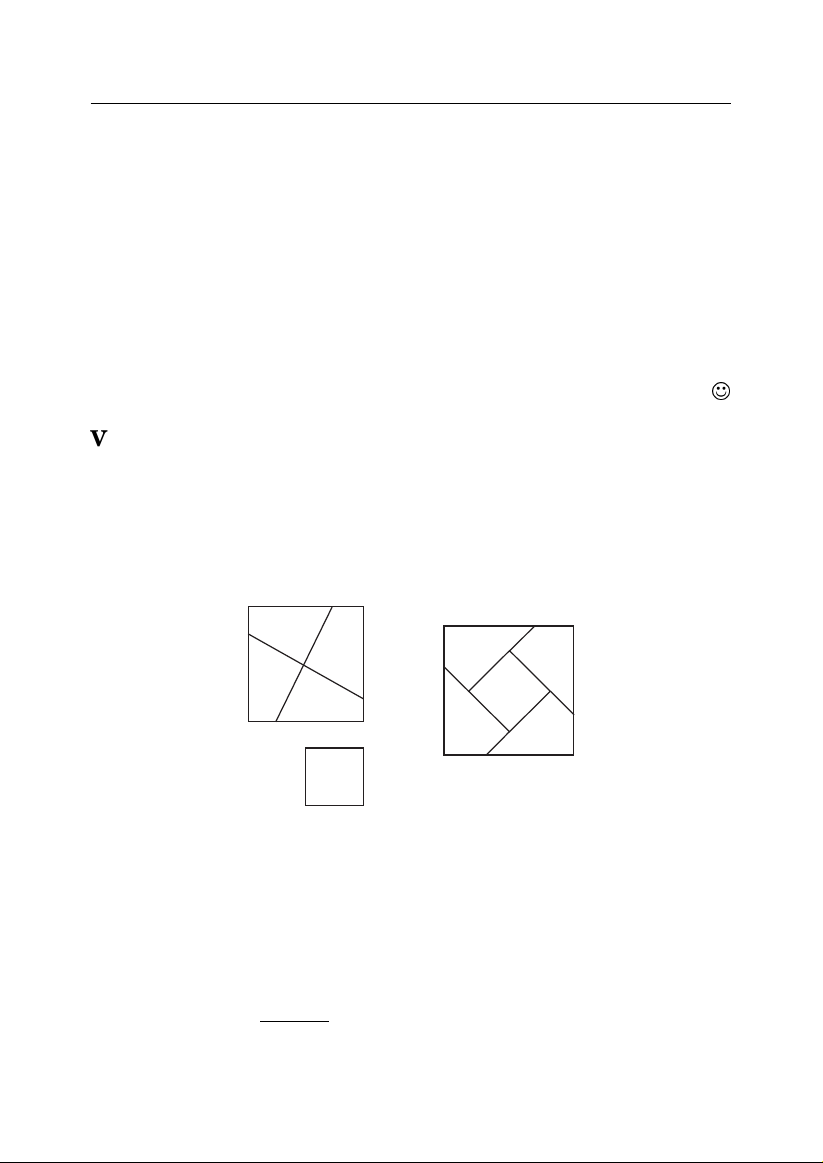
6.1. V
´
ı d
.
u quy n
.
ap to
´
an h
.
oc cho h
`
ınh h
.
oc 141
2. Gi
,
a s
,
u
,
¯
d
˜
a ch
´
u
,
ng minh cho kh
,
˘
ang
¯
d
.
inh
¯
d
´
ung v
´
o
,
i n − 1.
Ta x
´
et n h
`
ınh C
1
, C
2
, . . . , C
n
. Lâ
´
y C = C
n−1
∩ C
n
. Ta x
´
et d
˜
ay
C
1
, C
2
, . . . , C
n−1
, C. Ta s
˜
e ch
´
u
,
ng minh m
.
oi c
.
˘
ap ba c
´
ac h
`
ınh n
`
ay
¯
dê
`
u c
´
˘
at nhau. Th
.
ât v
.
ây, nê
´
u gi
˜
u
,
a ba h
`
ınh c
´
˘
at nhau không l
`
a C,
th
`
ı
¯
diê
`
u kê
´
t lu
.
ân trên hiê
,
n nhiên
¯
d
´
ung. Nê
´
u C n
`
˘
am trong sô
´
ba
h
`
ınh v
`
a v
´
ı d
.
u nhu
,
C
1
, C
2
, C, th
`
ı v
`
ı thê
´
nh
˜
u
,
ng h
`
ınh C
1
, C
2
, C
n−1
, C
n
c
´
o
¯
diê
,
m chung X (theo ch
´
u
,
ng minh t
.
ai
¯
diê
,
m 1.). Suy ra X ∈
C
n−1
∩C
n
= C. T
`
u
,
¯
dây kh
,
˘
ang
¯
d
.
inh c
,
ua b
`
ai to
´
an suy ra b
`
˘
ang quy
n
.
ap.
J
V
´
ı d
.
u 6.2. Cho n h`ınh vuông bâ
´
t k`y. Ch
´
u
,
ng minh r
`
˘ang ta c´o thê
,
c
´
˘at ch ´ung ra th`anh m
.
ôt sô
´
phâ
`
n
¯
dê
,
t
`
u
,
c ´ac phâ
`
n
¯
d´o ta c´o thê
,
gh´ep
l
.
ai th `anh m
.
ôt h`ınh vuông m
´
o
,
i.
L
`
o
,
i gi
,
ai. Khi n = 1,
¯
diê
`
u kh
,
˘
ang
¯
d
.
inh l
`
a hiê
,
n nhiên.
A B
C
D
1
1
1
1
M
P
N
Q
A B
C
D
2
2
2
2
A
B
C
D
N
P
Q
A
B
C
D
2
2
2
2
O
H
`
ınh 6.1:
Ta ch
´
u
,
ng minh r
`
˘
ang khi n = 2,
¯
diê
`
u kh
,
˘
ang
¯
d
.
inh
¯
d
´
o c
˜
ung
¯
d
´
ung. G
.
oi
¯
d
.
ô d
`
ai c
´
ac c
.
anh c
,
ua hai h
`
ınh vuông A
1
B
1
C
1
D
1
v
`
a
A
2
B
2
C
2
D
2
tu
,
o
,
ng
´
u
,
ng l
`
a x
1
v
`
a x
2
. Gi
,
a s
,
u
,
x
1
≥ x
2
. Trên c
´
ac c
.
anh
c
,
ua h
`
ınh A
1
B
1
C
1
D
1
v
´
o
,
i c
.
anh x
1
ta
¯
d
.
˘
at c
´
ac
¯
do
.
an A
1
M = B
1
N =
C
1
P = D
1
Q =
x
1
+ x
2
2
v
`
a c
´
˘
at h
`
ınh vuông
¯
d
´
o theo c
´
ac
¯
du
,
`
o
,
ng

142 Chu
,
o
,
ng 6. H
`
ınh h
.
oc
MP v
`
a NQ, r
˜
o r
`
ang MP v
`
a NQ c
´
˘
at nhau t
.
ai O c
,
ua h
`
ınh vuông
v
`
a t
.
ao v
´
o
,
i nhau m
.
ôt g
´
oc vuông. C
´
ac
¯
du
,
`
o
,
ng
¯
d
´
o chia h
`
ınh vuông
th
`
anh 4 phâ
`
n b
`
˘
ang nhau nh
˜
u
,
ng h
`
ınh
¯
d
´
o gh
´
ep v
`
ao h
`
ınh vuông
A
2
B
2
C
2
D
2
nhu
,
h
`
ınh bên. H
`
ınh nh
.
ân
¯
du
,
.
o
,
c s
˜
e l
`
a h
`
ınh vuông v
`
ı
c
´
ac gi
´
a tr
.
i g
´
oc M, N, P, Q b
`
u nhau, c
´
ac g
´
oc A, B, C, D l
`
a vuông v
`
a
AB = BC = CD = DA.
Gi
,
a s
,
u
,
m
.
ênh
¯
dê
`
¯
d
˜
a
¯
du
,
.
o
,
c ch
´
u
,
ng minh
¯
dô
´
i v
´
o
,
i n h
`
ınh vuông v
`
a
gi
,
a s
,
u
,
ta c
´
o n + 1 h
`
ınh vuông V
1
, V
2
, . . . , V
n
, V
n+1
. Ta lâ
´
y ra bâ
´
t
k
`
y hai h
`
ınh vuông, ch
,
˘
ang h
.
an V
n
v
`
a V
n+1
nhu
,
¯
d
˜
a ch
´
u
,
ng minh
,
o
,
trên sau khi
¯
d
˜
a c
´
˘
at m
.
ôt h
`
ınh vuông v
`
a gh
´
ep v
`
ao h
`
ınh vuông th
´
u
,
hai ta
¯
du
,
.
o
,
c m
.
ôt h
`
ınh vuông m
´
o
,
i V
0
. Do v
.
ây ta c
´
o n h
`
ınh vuông
V
1
, V
2
, . . . , V
n−1
, V
0
theo gi
,
a thiê
´
t quy n
.
ap c
´
o thê
,
c
´
˘
at ra
¯
du
,
.
o
,
c c
´
ac
phâ
`
n v
`
a t
`
u
,
c
´
ac phâ
`
n
¯
d
´
o c
´
o thê
,
gh
´
ep l
.
ai th
`
anh m
.
ôt h
`
ınh vuông
m
´
o
,
i.
J
V
´
ı d
.
u 6.3. Trong m
.
˘at ph
,
˘ang cho n ≥ 3
¯
diê
,
m, tâ
´
t c
,
a không n
`
˘am
trên
¯
du
,
`
o
,
ng th
,
˘ang. Ch
´
u
,
ng minh r
`
˘ang tâ
´
t c
,
a c ´ac
¯
du
,
`
o
,
ng th
,
˘ang nô
´
i
hai
¯
diê
,
m trong c´ac
¯
diê
,
m
¯
d ˜a cho t
.
ao ra sô
´
¯
du
,
`
o
,
ng th
,
˘ang kh´ac nhau
không nh
,
o ho
,
n n.
L
`
o
,
i gi
,
ai. V
´
o
,
i n = 3
¯
diê
,
m, m
.
ênh
¯
dê
`
hiê
,
n nhiên
¯
d
´
ung: Ba
¯
diê
,
m
không n
`
˘
am trên m
.
ôt
¯
du
,
`
o
,
ng th
,
˘
ang nô
´
i t
`
u
,
ng
¯
dôi v
´
o
,
i nhau t
.
ao ra
ba
¯
du
,
`
o
,
ng th
,
˘
ang kh
´
ac nhau.
Gi
,
a s
,
u
,
m
.
ênh
¯
dê
`
¯
d
´
ung v
´
o
,
i n ≥ 3
¯
diê
,
m. Ta ch
´
u
,
ng minh n
´
o
c
˜
ung
¯
d
´
ung v
´
o
,
i n + 1
¯
diê
,
m. Ta c
´
o thê
,
ch
´
u
,
ng minh r
`
˘
ang tô
`
n
t
.
ai
´
ıt nhâ
´
t m
.
ôt
¯
du
,
`
o
,
ng th
,
˘
ang ch
,
ı ch
´
u
,
a hai
¯
diê
,
m. Ta k
´
y hi
.
êu
¯
du
,
`
o
,
ng th
,
˘
ang
¯
di qua hai
¯
diê
,
m A
n
v
`
a A
n+1
l
`
a A
n
A
n+1
. Nê
´
u nh
˜
u
,
ng
¯
diê
,
m A
1
, A
2
, . . . , A
n
n
`
˘
am trên m
.
ôt
¯
du
,
`
o
,
ng th
,
˘
ang, th
`
ı sô
´
lu
,
.
o
,
ng c
´
ac
¯
du
,
`
o
,
ng th
,
˘
ang s
˜
e
¯
d
´
ung l
`
a n + 1: Gô
`
m n
¯
du
,
`
o
,
ng th
,
˘
ang nô
´
i A
n+1
v
´
o
,
i

6.1. V
´
ı d
.
u quy n
.
ap to
´
an h
.
oc cho h
`
ınh h
.
oc 143
c
´
ac
¯
diê
,
m A
1
, A
2
, . . . , A
n
v
`
a
¯
du
,
`
o
,
ng th
,
˘
ang ch
´
ung nô
´
i chung. Nê
´
u
A
1
, A
2
, . . . , A
n
không n
`
˘
am trên m
.
ôt
¯
du
,
`
o
,
ng th
,
˘
ang, th
`
ı theo gi
,
a
thiê
´
t quy n
.
ap c
´
o n
¯
du
,
`
o
,
ng th
,
˘
ang kh
´
ac nhau. Bây gi
`
o
,
ta thêm
c
´
ac
¯
du
,
`
o
,
ng th
,
˘
ang nô
´
i A
n+1
v
´
o
,
i c
´
ac
¯
diê
,
m A
1
, A
2
, . . . , A
n
. V
`
ı
¯
du
,
`
o
,
ng
th
,
˘
ang A
n
A
n+1
không ch
´
u
,
a m
.
ôt
¯
diê
,
m n
`
ao trong A
1
, A
2
, . . . , A
n−1
,
th
`
ı
¯
du
,
`
o
,
ng th
,
˘
ang n
`
ay kh
´
ac ho
`
an to
`
an v
´
o
,
i n
¯
du
,
`
o
,
ng th
,
˘
ang t
.
ao ra
b
,
o
,
i A
1
, A
2
, . . . , A
n
. Nhu
,
v
.
ây sô
´
¯
du
,
`
o
,
ng th
,
˘
ang t
.
ao ra c
˜
ung không
nh
,
o ho
,
n n + 1.
J
V
´
ı d
.
u 6.4. Trong m
.
˘at ph
,
˘ang cho n ≥ 3
¯
diê
,
m. Ðu
,
`
o
,
ng k´ınh c
,
ua
m
.
ôt h
.
ê thô
´
ng
¯
diê
,
m l`a
¯
do
.
an th
,
˘ang nô
´
i hai
¯
diê
,
m trong h
.
ê thô
´
ng v`a
¯
d
.
ô d `ai d c
,
ua
¯
do
.
an n `ay l`a l
´
o
,
n nhâ
´
t. Ch
´
u
,
ng minh r
`
˘ang sô
´
¯
du
,
`
o
,
ng
k´ınh không vu
,
.
o
,
t qu ´a n.
L
`
o
,
i gi
,
ai. Nê
´
u xuâ
´
t ph
´
at t
`
u
,
m
.
ôt
¯
diê
,
m A c
,
ua h
.
ê
¯
d
˜
a cho, ta c
´
o ba
¯
du
,
`
o
,
ng k
´
ınh AB, AC v
`
a AD. Khi
¯
d
´
o d
˜
ê thâ
´
y ba
¯
diê
,
m B, C v
`
a D s
˜
e
n
`
˘
am trên
¯
du
,
`
o
,
ng tr
`
on k
1
(A, d). Tâ
´
t c
,
a nh
˜
u
,
ng
¯
diê
,
m c
`
on l
.
ai c
,
ua h
.
ê
thô
´
ng s
˜
e n
`
˘
am ho
.
˘
ac trên k
1
ho
.
˘
ac bên trong n
´
o. b
,
o
,
i v
`
ı m
˜
ôi
¯
do
.
an
th
,
˘
ang BC, BD v
`
a CD không l
´
o
,
n ho
,
n d, th
`
ı nh
˜
u
,
ng
¯
diê
,
m B , C v
`
a D
s
˜
e n
`
˘
am trên cung c
,
ua k
1
, tu
,
o
,
ng
´
u
,
ng g
´
oc không l
´
o
,
n ho
,
n 60
0
. G
.
oi
¯
diê
,
m C bên trong cung
_
BD, v
´
o
,
i n
´
o
_
BD≤ 60
0
.Ta v
˜
e
¯
du
,
`
o
,
ng tr
`
on
k
2
(C, d); Nh
˜
u
,
ng
¯
diê
,
m cuô
´
i c
,
ua tâ
´
t c
,
a
¯
du
,
`
o
,
ng k
´
ınh c
,
ua h
.
ê
¯
d
˜
a cho
xuâ
´
t ph
´
at t
`
u
,
C, ph
,
ai n
`
˘
am trên cung
_
MN c
,
ua k
2
(M, N l
`
a giao
¯
diê
,
m c
,
ua k
1
v
`
a k
2
) v
`
a n
`
˘
am trong h
`
ınh tr
`
on k
1
. Nhu
,
ng m
˜
ôi
¯
diê
,
m
c
,
ua cung
_
MN, ngo
`
ai A,
¯
d
´
u
,
ng c
´
ach xa nh
˜
u
,
ng
¯
diê
,
m B ho
.
˘
ac D m
.
ôt
kho
,
ang c
´
ach l
´
o
,
n ho
,
n d, t
`
u
,
¯
d
´
o suy ra CA l
`
a
¯
du
,
`
o
,
ng k
´
ınh duy nhâ
´
t,
xuâ
´
t ph
´
at t
`
u
,
C.
Nhu
,
v
.
ây ta kê
´
t lu
.
ân r
`
˘
ang v
´
o
,
i m
.
ôt h
.
ê
¯
d
˜
a cho n
¯
diê
,
m, tô
`
n t
.
ai
hai kh
,
a n
˘
ang: ho
.
˘
ac l
`
a trong h
.
ê c
´
o m
.
ôt
¯
diê
,
m, t
`
u
,
n
´
o xuâ
´
t ph
´
at

144 Chu
,
o
,
ng 6. H
`
ınh h
.
oc
không qu
´
a m
.
ôt
¯
du
,
`
o
,
ng k
´
ınh, ho
.
˘
ac l
`
a t
`
u
,
m
˜
ôi
¯
diê
,
m
¯
dê
`
u xu
´
at ph
´
at
¯
d
´
ung hai
¯
du
,
`
o
,
ng k
´
ınh.
Kh
,
˘
ang
¯
d
.
inh c
,
ua b
`
ai to
´
an ch
´
u
,
ng minh b
`
˘
ang quy n
.
ap theo n.
V
´
o
,
i n = 3 kh
,
˘
ang
¯
d
.
inh hiê
,
n nhiên
¯
d
´
ung. Gi
,
a s
,
u
,
n
´
o
¯
d
´
ung v
´
o
,
i n =
k ≥ 3. Ta s
˜
e ch
´
u
,
ng minh n
´
o c
`
on
¯
d
´
ung c
,
a v
´
o
,
i h
.
ê c
´
o n = k + 1
¯
diê
,
m.
Th
.
ât v
.
ây, nê
´
u trong h
.
ê c
´
o k + 1
¯
diê
,
m: A
1
, A
2
, . . . , A
k+1
c
´
o
¯
diê
,
m,
v
´
ı d
.
u A
1
, t
`
u
,
n
´
o không xuâ
´
t ph
´
at
¯
du
,
`
o
,
ng k
´
ınh ho
.
˘
ac t
`
u
,
n
´
o xuâ
´
t
ph
´
at ch
,
ı m
.
ôt
¯
du
,
`
o
,
ng k
´
ınh, th
`
ı sô
´
lu
,
.
o
,
ng nh
˜
u
,
ng
¯
du
,
`
o
,
ng k
´
ınh c
,
ua
h
.
ê n
`
ay nhiê
`
u ho
,
n sô
´
lu
,
.
o
,
ng
¯
du
,
`
o
,
ng k
´
ınh c
,
ua h
.
ê A
2
, A
3
, . . . , A
k+1
nhiê
`
u nhâ
´
t l
`
a 1, ngh
˜
ıa l
`
a sô
´
lu
,
.
o
,
ng
¯
du
,
`
o
,
ng k
´
ınh c
,
ua h
.
ê ta
¯
dang x
´
et
không l
´
o
,
n ho
,
n k + 1. Nê
´
u m
.
ôt
¯
diê
,
m nhu
,
v
.
ây không tô
`
n t
.
ai, th
`
ı t
`
u
,
m
˜
ôi
¯
diê
,
m A
i
xuâ
´
t ph
´
at
¯
d
´
ung hai
¯
du
,
`
o
,
ng k
´
ınh v
`
a t
`
u
,
¯
d
´
o suy ra sô
´
lu
,
.
o
,
ng
¯
du
,
`
o
,
ng k
´
ınh b
`
˘
ang
2(k + 1)
2
= k + 1, Nhu
,
v
.
ây kê
´
t lu
.
ân c
,
ua
b
`
ai to
´
an
¯
d
´
ung v
´
o
,
i m
.
oi n.
J
V
´
ı d
.
u 6.5. Ch
´
u
,
ng minh r
`
˘ang n
¯
du
,
`
o
,
ng th
,
˘ang trong m
.
ôt m
.
˘at
ph
,
˘ang chia m
.
˘at ph
,
˘ang ra nh
˜
u
,
ng miê
`
n kh ´ac nhau, c´o thê
,
tô m `au
tr
´
˘ang ho
.
˘ac
¯
den cho m
˜
ôi miê
`
m sao cho nh
˜
u
,
ng miê
`
n c
.
anh nhau
kh ´ac m `au nhau.
L
`
o
,
i gi
,
ai. 1) Ðu
,
`
o
,
ng th
,
˘
ang AB chia m
.
˘
at ph
,
˘
ang P ra hai n
,
u
,
a m
.
˘
at
ph
,
˘
ang P
1
v
`
a P
2
. Tô P
1
m
`
au tr
´
˘
ang, P
2
m
`
au
¯
den v
`
a nhu
,
v
.
ây tho
,
a
m
˜
an
¯
d
`
oi h
,
oi b
`
ai to
´
an. V
´
o
,
i n = 1 m
.
ênh
¯
dê
`
¯
du
,
.
o
,
c ch
´
u
,
ng minh.
2) Gi
,
a s
,
u
,
m
.
ênh
¯
dê
`
¯
d
´
ung v
´
o
,
i n = k v
`
a m
.
˘
at ph
,
˘
ang P
¯
du
,
.
o
,
c tô
m
`
au nhu
,
yêu câ
`
u b
`
ai to
´
an. Ðu
,
`
o
,
ng th
,
˘
ang th
´
u
,
k + 1, CD chia m
.
˘
at
ph
,
˘
ang P ra hai n
,
u
,
a Q
1
v
`
a Q
2
. Tâ
´
t c
,
a c
´
ac phâ
`
n trong Q
1
ta gi
˜
u
,
nguyên m
`
au
¯
d
˜
a tô, c
`
on trong n
,
u
,
a Q
2
m
˜
ôi phâ
`
n ta thay tr
´
˘
ang
th
`
anh
¯
den v
`
a
¯
den th
`
anh tr
´
˘
ang.
Gi
,
a s
,
u
,
O
1
v
`
a O
2
l
`
a hai phâ
`
n bâ
´
t k
`
y c
.
anh nhau, sau khi k
,
e

6.1. V
´
ı d
.
u quy n
.
ap to
´
an h
.
oc cho h
`
ınh h
.
oc 145
¯
du
,
`
o
,
ng CD. Ch
,
ı c
´
o m
.
ôt trong hai kh
,
a n
˘
ang sau xâ
,
y ra:
a) O
1
v
`
a O
2
n
`
˘
am trên phâ
`
n kh
´
ac nhau c
,
ua CD,
b) O
1
v
`
a O
2
n
`
˘
am trên c
`
ung m
.
ôt ph
´
ıa c
,
ua CD.
Tru
,
`
o
,
ng h
.
o
,
p a) O
1
v
`
a O
2
sau khi k
,
e k
¯
du
,
`
o
,
ng th
,
˘
ang
¯
dâ
`
u tiên,
nhu
,
ng CD chu
,
a k
,
e th
`
ı ch
´
ung l
`
a m
.
ôt miê
`
n v
`
a
¯
du
,
.
o
,
c tô c
`
ung m
.
ôt
m
`
au. Nhu
,
ng sau khi k
,
e CD th
`
ı m
.
ôt miê
`
n Q
1
gi
˜
u
,
nguyên m
`
au ,
c
`
on phâ
`
n kia O
2
¯
du
,
.
o
,
c
¯
dô
,
i m
`
au theo c
´
ach d
.
u
,
ng. Ngh
˜
ıa l
`
a O
1
v
`
a O
2
kh
´
ac m
`
au nhau.
Tru
,
`
o
,
ng h
.
o
,
p b) Sau khi v
˜
e k
¯
du
,
`
o
,
ng th
,
˘
ang, m
`
a CD c
`
on chu
,
a
k
,
e , khi
¯
d
´
o O
1
v
`
a O
2
l
`
a hai miê
`
n c
.
anh nhau do k
¯
du
,
`
o
,
ng th
,
˘
ang
t
.
ao ra, theo gi
,
a thiê
´
t quy n
.
ap ch
´
ung kh
´
ac m
`
au nhau. Sau khi k
,
e
¯
du
,
`
o
,
ng th
,
˘
ang CD, nê
´
u O
1
v
`
a O
2
n
`
˘
am c
`
ung ph
´
ıa v
´
o
,
i Q
1
, th
`
ı m
`
au
c
,
ua ch
´
ung không
¯
dô
,
i, v
˜
ân kh
´
ac m
`
au nhau. Nê
´
u ch
´
ung n
`
˘
am c
`
ung
ph
´
ıa v
´
o
,
i Q
2
, th
`
ı m
`
au c
,
ua m
˜
ôi miê
`
n
¯
dê
`
u
¯
dô
,
i. Nhu
,
v
.
ây m
.
oi tru
,
`
o
,
ng
h
.
o
,
p O
1
v
`
a O
2
¯
dê
`
u c
´
o hai m
`
au kh
´
ac nhau.
J
V
´
ı d
.
u 6.6. Ch
´
u
,
ng minh r
`
˘ang nê
´
u n m
.
˘at ph
,
˘ang
¯
di qua m
.
ôt
¯
diê
,
m
sao cho không c´o ba m
.
˘at ph
,
˘ang n `ao c´o chung m
.
ôt
¯
du
,
`
o
,
ng th
,
˘ang,
th`ı ch ´ung chia không gian ra A
n
= n(n −1) + 2 phâ
`
n.
L
`
o
,
i gi
,
ai. 1) M
.
ôt m
.
˘
at ph
,
˘
ang chia không gian l
`
am hai phâ
`
n v
`
a
A
1
= 2. V
´
o
,
i n = 1 m
.
ênh
¯
dê
`
¯
d
´
ung.
2) Gi
,
a s
,
u
,
m
.
ênh
¯
dê
`
¯
d
´
ung v
´
o
,
i n = k, ho
.
˘
ac l
`
a k m
.
˘
at ph
,
˘
ang chia
không gian ra k (k − 1 ) + 2 phâ
`
n. Ta s
˜
e ch
´
u
,
ng minh k + 1 chia
không gian ra k(k + 1) + 2 phâ
`
n.
Th
.
ât v
.
ây, Gi
,
a s
,
u
,
P l
`
a m
.
˘
at ph
,
˘
ang th
´
u
,
k + 1. M
˜
ôi m
.
˘
at ph
,
˘
ang
trong k m
.
˘
at ph
,
˘
ang c
´
˘
at m
.
˘
at ph
,
˘
ang P m
.
ôt
¯
du
,
`
o
,
ng th
,
˘
ang n
`
ao
¯
d
´
o sao
cho m
.
˘
at ph
,
˘
ang P b
.
i chia ra nh
˜
u
,
ng phâ
`
n t
`
u
,
k
¯
du
,
`
o
,
ng th
,
˘
ang kh
´
ac

146 Chu
,
o
,
ng 6. H
`
ınh h
.
oc
nhau
¯
di qua c
`
ung m
.
ôt
¯
diê
,
m. Theo b
`
ai tru
,
´
o
,
c m
.
˘
at ph
,
˘
ang P
¯
du
,
.
o
,
c
chia ra 2k phâ
`
n, m
˜
ôi phâ
`
n l
`
a g
´
oc trong m
.
˘
at ph
,
˘
ang v
´
o
,
i
¯
d
,
ınh l
`
a
¯
diê
,
m
¯
d
˜
a cho.
k m
.
˘
at ph
,
˘
ang
¯
dâ
`
u tiên chia không gian th
`
anh m
.
ôt sô
´
g
´
oc
¯
da
di
.
ên. M
.
ôt sô
´
g
´
oc n
`
ay b
.
i chia ra l
`
am hai phâ
`
n b
,
o
,
i m
.
˘
at ph
,
˘
ang P.
V
´
o
,
i m
.
˘
at chung c
,
ua hai phâ
`
n c
´
o phâ
`
n c
,
ua m
.
˘
at ph
,
˘
ang gi
´
o
,
i h
.
an
b
,
o
,
i hai tia m
`
a theo n
´
o P c
´
˘
at nh
˜
u
,
ng m
.
˘
at c
,
ua g
´
oc
¯
da di
.
ên m
.
ôt trong
2k g
´
oc m
.
˘
at ph
,
˘
ang, m
`
a n
´
o chia ra b
,
o
,
i m
.
˘
at ph
,
˘
ang P.
Ðiê
`
u n
`
ay c
´
o ngh
˜
ıa l
`
a sô
´
g
´
oc
¯
da di
.
ên, m
`
a b
.
i chia l
`
am hai phâ
`
n
b
,
o
,
i P, không thê
,
l
´
o
,
n ho
,
n 2k.
M
.
˘
at kh
´
ac, m
˜
ôi phâ
`
n trong 2k phâ
`
n, m
`
a n
´
o b
.
i chia do P c
´
˘
at k
m
.
˘
at ph
,
˘
ang
¯
dâ
`
u tiên, l
`
a m
.
˘
at chung c
,
ua hai g
´
oc
¯
da di
.
ên v
`
a ngh
˜
ıa
l
`
a chia g
´
oc
¯
da di
.
ên t
.
ao b
,
o
,
i k m
.
˘
at ph
,
˘
ang ra l
`
am hai phâ
`
n.
Ðiê
`
u n
`
ay c
´
o ngh
˜
ıa sô
´
lu
,
.
o
,
ng nh
˜
u
,
ng g
´
oc
¯
da di
.
ên, m
`
a n
´
o b
.
i chia
ra l
`
am hai phâ
`
n b
,
o
,
i P, không thê
,
nh
,
o ho
,
n 2k.
V
`
ı m
.
˘
at ph
,
˘
ang P chia
¯
d
´
ung 2k phâ
`
n c
,
ua không gian t
.
ao b
,
o
,
i
k m
.
˘
at ph
,
˘
ang. V
`
ı thê
´
nê
´
u k m
.
˘
at ph
,
˘
ang chia không gian ra k(k −
1) + 2 phâ
`
n, th
`
ı k + 1 m
.
˘
at ph
,
˘
ang s
˜
e chia n
´
o ra
[k(k −1) + 2] + 2k = k(k + 1) + 2
phâ
`
n.
J
V
´
ı d
.
u 6.7. 8n −4
¯
diê
,
m n
`
˘am
,
o
,
d
.
ang ch
˜
u
,
th
.
âp (h`ınh v˜e v
´
o
,
i n = 4).
C´o bao nhiêu kh
,
a n ˘ang
¯
dê
,
ch
.
on bô
´
n
¯
diê
,
m trong ch ´ung
¯
dê
,
t
.
ao
th `anh
¯
d
,
ınh h`ınh vuông ?
L
`
o
,
i gi
,
ai. Ta ch
´
u
,
ng minh sô
´
lu
,
.
o
,
ng h
`
ınh vuông câ
`
n t
`
ım l
`
a 10n −9.
1) V
´
o
,
i n = 1, hiê
,
n nhiên
¯
d
´
ung v
`
ı ta c
´
o 1 = 10.1 −9 h
`
ınh vuông.
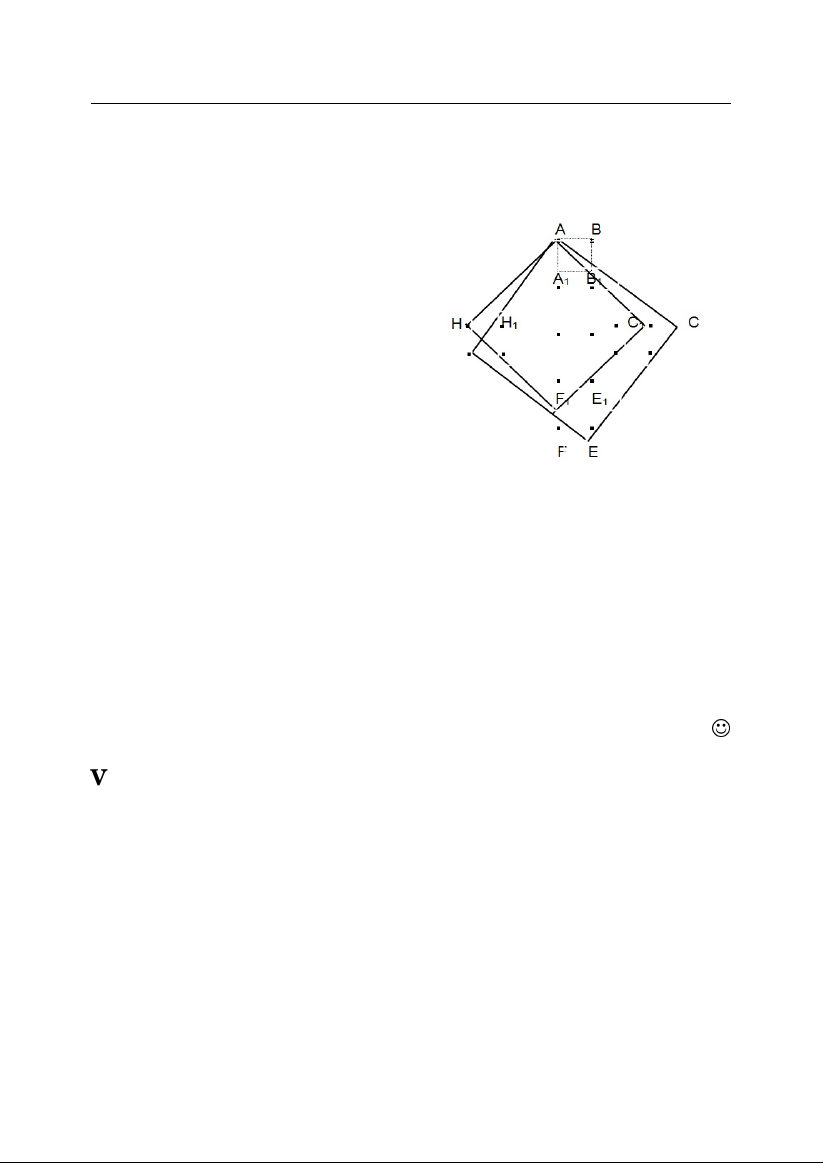
6.1. V
´
ı d
.
u quy n
.
ap to
´
an h
.
oc cho h
`
ınh h
.
oc 147
2) Không kh
´
o kh
˘
an l
´
˘
am v
´
o
,
i n = 2, ta c
´
o thê
,
ch
.
on
¯
du
,
.
o
,
c 11 =
10.2 −9 h
`
ınh vuông.
3) Gi
,
a s
,
u
,
m
.
ênh
¯
dê
`
¯
d
´
ung v
´
o
,
i
H
`
ınh 6.2:
n = k, m
`
a k ≥ 2.
Ta x
´
et h
`
ınh gô
`
m 8(k + 1) −
4
¯
diê
,
m (trong h
`
ınh v
´
o
,
i k = 3)
(h
`
ınh 5)
Theo gi
,
a thiê
´
t quy n
.
ap
ta c
´
o thê
,
ch
.
on
¯
du
,
.
o
,
c 10k −
9 h
`
ınh vuông, không c
´
o m
.
ôt
h
`
ınh vuông n
`
ao trong ch
´
ung c
´
o
m
.
ôt
¯
d
,
ınh tr
`
ung v
´
o
,
i c
´
ac
¯
diê
,
m
A, B, C, D, E, F, G, H. Bây gi
`
o
,
ta x
´
et nh
˜
u
,
ng h
`
ınh vuông c
´
o
¯
diê
,
m
tr
`
ung v
´
o
,
i A. Không kh
´
o kh
˘
an ta ch
,
ı t
`
ım
¯
du
,
.
o
,
c 3 h
`
ınh vuông
ABB
1
A
1
, ACED, AC
1
F
1
H. Nhu
,
v
.
ây, ch
,
ı c
´
o 10 h
`
ınh vuông kh
´
ac
nhau khi ta thay
¯
dô
,
i
¯
d
,
ınh A v
´
o
,
i c
´
ac
¯
diê
,
m B, C, . . . , H: 4 h
`
ınh
vuông d
.
ang AC
1
F
1
H, 4 h
`
ınh vuông d
.
ang ABB
1
A
1
v
`
a hai h
`
ınh
vuông ACEF, BDFH. Tô
,
ng c
.
ông tâ
´
t c
,
a l
`
a 10k −9 + 10 = 10(k +
1) −9 h
`
ınh vuông.
J
V
´
ı d
.
u 6.8. Ch
´
u
,
ng minh r
`
˘ang v
´
o
,
i m
.
oi sô
´
nguyên n ≥ 0 tô
`
n t
.
ai
m
.
ôt
¯
du
,
`
o
,
ng tr`on trên m
.
˘at ph
,
˘ang ch
´
u
,
a trong n´o n
¯
diê
,
m v
´
o
,
i t
.
oa
¯
d
.
ô
nguyên.
L
`
o
,
i gi
,
ai. Ch
´
u
,
ng minh quy n
.
ap theo n. Nê
´
u n = 0, th
`
ı th
.
u
,
c
châ
´
t
¯
du
,
`
o
,
ng tr
`
on K
0
không ch
´
u
,
a trong n
´
o m
.
ôt
¯
diê
,
m n
`
ao c
´
o t
.
oa
¯
d
.
ô nguyên,
¯
dê
,
c
´
o
¯
diê
`
u
¯
d
´
o ta lâ
´
y
¯
du
,
`
o
,
ng tr
`
on bâ
´
t k
`
y v
´
o
,
i tâm
O(x
0
, y
0
),
,
o
,
¯
dây ta ch
.
on m
.
ôt trong x
0
, y
0
không ph
,
ai l
`
a sô
´
nguyên
v
`
a b
´
an k
´
ınh r th
´
ıch h
.
o
,
p. Nê
´
u, v
´
ı d
.
u nhu
,
x
0
không nguyên, th
`
ı
148 Chu
,
o
,
ng 6. H
`
ınh h
.
oc
c
´
o thê
,
ch
.
on r l
`
a sô
´
nh
,
o nhâ
´
t trong {x
0
} v
`
a 1 − {x
0
}. Th
.
ât v
.
ây,
nê
´
u M(x, y)
¯
diê
,
m bâ
´
t k
`
y trong
¯
du
,
`
o
,
ng tr
`
on v
`
u
,
a d
.
u
,
ng K
0
, th
`
ı
x ≤ x
0
+ |OM| < x
0
+ r ≤ x
0
+ 1 − {x
0
} = [x
0
] + 1 v
`
a x ≥
x
0
− |OM| > x
0
−r ≥ x
0
− {x
0
} = [x
0
] hay l
`
a [x
0
] < x < [x
0
] + 1
v
`
a v
`
ı thê
´
x không l
`
a sô
´
nguyên.
Gi
,
a s
,
u
,
ch
´
ung ta
¯
d
˜
a xây
H
`
ınh 6.3:
d
.
u
,
ng
¯
du
,
.
o
,
c
¯
du
,
`
o
,
ng tr
`
on K
n
v
´
o
,
i
tâm O
n
, ch
´
u
,
a trong n
´
o n
¯
diê
,
m
v
´
o
,
i t
.
oa
¯
d
.
ô nguyên. Ta s
˜
e t
˘
ang
b
´
an k
´
ınh
¯
du
,
`
o
,
ng tr
`
on
¯
d
´
o lên v
`
a
gi
˜
u
,
nguyên tâm, t
˘
ang
¯
du
,
`
o
,
ng
tr
`
on
¯
dê
´
n m
´
u
,
c không ch
´
u
,
a
¯
diê
,
m c
´
o t
.
oa
¯
d
.
ô nguyên bên
trong ngo
`
ai K
n
. Ta nh
.
ân
¯
du
,
.
o
,
c
v
`
ong tr
`
on L
1
¯
dô
`
ng tâm v
´
o
,
i K
n
,
ch
´
u
,
a n
¯
diê
,
m c
´
o t
.
oa
¯
d
.
ô nguyên trong
¯
du
,
`
o
,
ng tr
`
on K
n
v
`
a
´
ıt nhâ
´
t
m
.
ôt
¯
diê
,
m c
´
o t
.
oa
¯
d
.
ô nguyên A trên
¯
du
,
`
o
,
ng tr
`
on.
Gi
,
a s
,
u
,
P v
`
a Q l
`
a
¯
diê
,
m c
´
˘
at (O
n
A) v
´
o
,
i
¯
du
,
`
o
,
ng tr
`
on K
n
, ho
,
n n
˜
u
,
a
O
n
n
`
˘
am gi
˜
u
,
a P v
`
a A. Ta d
.
u
,
ng
¯
du
,
`
o
,
ng tr
`
on L
2
v
´
o
,
i
¯
du
,
`
o
,
ng k
´
ınh [PA].
Khi
¯
d
´
o L
2
ch
´
u
,
a
¯
d
´
ung n + 1
¯
diê
,
m v
´
o
,
i t
.
oa
¯
d
.
ô nguyên: n
¯
diê
,
m bên
trong v
`
a m
.
ôt
¯
diê
,
m trên biên. Ta c
´
o thê
,
t
˘
ang không nhiê
`
u b
´
an
k
´
ınh
¯
du
,
`
o
,
ng tr
`
on L
2
¯
dê
,
¯
du
,
.
o
,
c
¯
du
,
`
o
,
ng tr
`
on K
n+1
¯
dô
`
ng tâm v
´
o
,
i L
2
,
m
`
a n
´
o ch
´
u
,
a n + 1
¯
diê
,
m c
´
o t
.
oa
¯
d
.
ô nguyên v
`
a không ch
´
u
,
a t
.
oa
¯
d
.
ô c
´
o
sô
´
nguyên n
`
ao kh
´
ac.
J
V
´
ı d
.
u 6.9. H
.
o
,
p c
,
ua m
.
ôt sô
´
h`ınh tr`on c´o di
.
ên t´ıch 1. Ch
´
u
,
ng minh
r
`
˘ang t
`
u
,
trong ch ´ung c´o thê
,
ch
.
on
¯
du
,
.
o
,
c m
.
ôt sô
´
h`ınh tr`on, t
`
u
,
ng
¯
dôi
m
.
ôt không c
´
˘at nhau, m `a di
.
ên t´ıch chung không nh
,
o ho
,
n
1
9
.

6.1. V
´
ı d
.
u quy n
.
ap to
´
an h
.
oc cho h
`
ınh h
.
oc 149
L
`
o
,
i gi
,
ai. B
`
ai to
´
an
¯
du
,
.
o
,
c suy ra t
`
u
,
m
.
ênh
¯
dê
`
sau:
Bô
,
¯
dê
`
: Trong m
.
˘at ph
,
˘ang cho n
¯
du
,
`
o
,
ng tr`on, ch ´ung ph
,
u m
.
˘at
ph
,
˘ang v
´
o
,
i di
.
ên t´ıch S. Khi
¯
d´o c´o thê
,
ch
.
on
¯
du
,
.
o
,
c m
.
ôt ho
.
˘ac m
.
ôt
sô
´
h`ınh tr`on
¯
dôi m
.
ôt không c
´
˘at nhau, tô
,
ng di
.
ên t´ıch c
,
ua ch ´ung
không nh
,
o ho
,
n
S
9
.
Ch
´
u
,
ng minh. Ta s
,
u
,
d
.
ung phu
,
o
,
ng ph
´
ap quy n
.
ap theo n . V
´
o
,
i
n = 1 kh
,
˘
ang
¯
d
.
inh
¯
d
´
ung hiê
,
n nhiên. Ta gi
,
a thiê
´
t r
`
˘
ang bô
,
¯
dê
`
¯
d
´
ung
v
´
o
,
i m
.
oi k < n. Ta x
´
et t
.
âp h
.
o
,
p R gô
`
m n h
`
ınh tr
`
on, m
`
a n
´
o ph
,
u m
.
˘
at
ph
,
˘
ang v
´
o
,
i di
.
ên t
´
ıch S v
`
a ta k
´
y hi
.
êu K l
`
a
¯
du
,
`
o
,
ng tr
`
on c
´
o b
´
an k
´
ınh
l
´
o
,
n nhâ
´
t r. G
.
oi S(K) l
`
a di
.
ên t
´
ıch
¯
du
,
`
o
,
ng tr
`
on n
`
ay. Nê
´
u S(K) ≥
S
9
,
th
`
ı h
`
ınh tr
`
on K th
,
ao m
˜
an kê
´
t lu
.
ân c
,
ua bô
,
¯
dê
`
. V
`
ı v
.
ây v
´
o
,
i S(K) <
S
9
. M
˜
ôi m
.
ôt h
`
ınh tr
`
on t
`
u
,
R c
´
o b
´
an k
´
ınh không l
´
o
,
n ho
,
n r, v
`
a suy
ra, nê
´
u n
´
o c
´
o
¯
diê
,
m chung v
´
o
,
i K, th
`
ı n
´
o ph
,
ai n
`
˘
am trong
¯
du
,
`
o
,
ng
tr
`
on
¯
dô
`
ng tâm v
´
o
,
i K c
´
o b
´
an k
´
ınh 3r. V
`
ı di
.
ên t
´
ıch c
,
ua
¯
du
,
`
o
,
ng tr
`
on
l
´
o
,
n n
`
ay l
`
a 9S(K), t
.
âp h
.
o
,
p R
1
c
,
ua tâ
´
t c
,
a h
`
ınh tr
`
on m
`
a c
´
o
¯
diê
,
m
chung v
´
o
,
i K, ph
,
u m
.
ôt phâ
`
n c
,
ua m
.
˘
at ph
,
˘
ang v
´
o
,
i di
.
ên t
´
ıch không
l
´
o
,
n ho
,
n 9S(K), suy ra nh
,
o ho
,
n S, v
`
ı 9S(K) < S. Khi
¯
d
´
o c
´
o
¯
du
,
`
o
,
ng
tr
`
on trong R không c
´
o
¯
diê
,
m chung v
´
o
,
i K. Tâ
´
t c
,
a nh
˜
u
,
ng
¯
du
,
`
o
,
ng
tr
`
on nhu
,
v
.
ây t
.
ao th
`
anh m
.
ôt t
.
âp kh
´
ac r
˜
ông R
2
= R \ R
1
v
`
a ph
,
u
m
.
ôt phâ
`
n m
.
˘
at ph
,
˘
ang v
´
o
,
i di
.
ên t
´
ıch S
2
≥ S − 9 S(K); V
´
o
,
i nh
˜
u
,
ng
¯
du
,
`
o
,
ng tr
`
on nhu
,
v
.
ây t
`
u
,
R
2
sô
´
lu
,
.
o
,
ng nh
,
o ho
,
n n. Theo gi
,
a thiê
´
t
quy n
.
ap t
`
u
,
t
.
âp h
.
o
,
p R
2
c
´
o thê
,
ch
.
on
¯
du
,
.
o
,
c m
.
ôt ho
.
˘
ac m
.
ôt sô
´
h
`
ınh
tr
`
on
¯
dôi m
.
ôt không giao nhau, tô
,
ng di
.
ên t
´
ıch c
,
ua ch
´
ung không
nh
,
o ho
,
n
S
2
9
, suy ra không nh
,
o ho
,
n
1
9
( S − 9S(K)) =
S
9
− S(K).
H
`
ınh tr
`
on K không c
´
o nh
˜
u
,
ng
¯
diê
,
m chung v
´
o
,
i bâ
´
t c
´
u
,
m
.
ôt
¯
du
,
`
o
,
ng
tr
`
on n
`
ao trong nh
˜
u
,
ng
¯
du
,
`
o
,
ng tr
`
on ta
¯
dang x
´
et. Thêm v
`
ao t
.
âp h
.
o
,
p

150 Chu
,
o
,
ng 6. H
`
ınh h
.
oc
nh
˜
u
,
ng
¯
du
,
`
o
,
ng tr
`
on
¯
dang x
´
et
¯
du
,
`
o
,
ng tr
`
on K, ta s
˜
e nh
.
ân
¯
du
,
.
o
,
c t
.
âp
h
.
o
,
p nh
˜
u
,
ng
¯
du
,
`
o
,
ng tr
`
on
¯
dôi m
.
ôt không giao nhau, m
`
a tô
,
ng di
.
ên
t
´
ıch c
,
ua ch
´
ung không nh
,
o ho
,
n
S
9
.
J
V
´
ı d
.
u 6.10. D ˜ay nh
˜
u
,
ng sô
´
t
.
u
,
nhiên a
1
, a
2
, . . . , a
n
, . . . x ´ac
¯
d
.
inh theo
¯
d
,
˘ang th
´
u
,
c
a
1
= 2, a
n+1
= (n + 1)a
n
+ 1, n = 1, 2, . . .
Trong m
.
ôt m
.
˘at ph
,
˘ang cho a
n
+ 1
¯
diê
,
m kh ´ac nhau, không c´o ba
¯
diê
,
m n `ao n
`
˘am trên m
.
ôt
¯
du
,
`
o
,
ng th
,
˘ang. Tâ
´
t c
,
a c ´ac
¯
do
.
an th
,
˘ang nô
´
i
nh
˜
u
,
ng
¯
diê
,
m n `ay
¯
du
,
.
o
,
c tô b
`
˘ang m
.
ôt trong n m `au
¯
d ˜a cho. Ch
´
u
,
ng
minh r
`
˘ang v
´
o
,
i m
.
oi n = 1, 2, . . . tô
`
n t
.
ai tam gi ´ac v
´
o
,
i nh
˜
u
,
ng
¯
d
,
ınh
trong c ´ac
¯
diê
,
m
¯
d ˜a cho, m `a nh
˜
u
,
ng c
.
anh c
,
ua n´o
¯
dê
`
u
¯
du
,
.
o
,
c tô c `ung
m
.
ôt m `au.
L
`
o
,
i gi
,
ai. Ch
´
u
,
ng minh quy n
.
ap theo n. V
´
o
,
i n = 1 kh
,
˘
ang
¯
d
.
inh
¯
d
´
ung hiê
,
n nhiên. Ta gi
,
a thiê
´
t r
`
˘
ang n
´
o c
˜
ung
¯
d
´
ung v
´
o
,
i n = k. Cho
a
k+1
+ 1
¯
diê
,
m th
,
oa m
˜
an
¯
diê
`
u ki
.
ên b
`
ai to
´
an v
`
a O l
`
a m
.
ôt trong
nh
˜
u
,
ng
¯
diê
,
m
¯
d
´
o. Tâ
´
t c
,
a
¯
do
.
an th
,
˘
ang nô
´
i O v
´
o
,
i m
˜
ôi
¯
diê
,
m c
`
on l
.
ai
t
`
u
,
a
k+1
¯
diê
,
m, l
`
a a
k+1
= (k + 1)a
k
+ 1. Nh
˜
u
,
ng
¯
do
.
an n
`
ay
¯
du
,
.
o
,
c tô
nhiê
`
u nhâ
´
t b
`
˘
ang k + 1 m
`
au kh
´
ac nhau. Suy ra t
`
u
,
nh
˜
u
,
ng
¯
do
.
an
th
,
˘
ang xuâ
´
t ph
´
at t
`
u
,
O, c
´
o
´
ıt nhâ
´
t a
k
+ 1
¯
do
.
an th
,
˘
ang tô c
`
ung m
.
ôt
m
`
au (nguyên l
´
y Dirichlet), lâ
´
y
¯
d
´
o l
`
a m
`
au
¯
d
,
o. Ta x
´
et nh
˜
u
,
ng
¯
diê
,
m
A
1
, A
2
, . . . , A
a
k
+1
, m
`
a ch
´
ung nô
´
i v
´
o
,
i O b
`
˘
ang
¯
do
.
an th
,
˘
ang m
`
au
¯
d
,
o.
Nê
´
u gi
˜
u
,
a ch
´
ung c
´
o hai A
i
v
`
a A
j
c
˜
ung nô
´
i b
`
˘
ang
¯
do
.
an th
,
˘
ang m
`
au
¯
d
,
o, th
`
ı tam gi
´
ac OA
i
A
j
l
`
a c
`
ung m
.
ôt m
`
au. Nê
´
u m
.
oi c
.
˘
ap hai
¯
diê
,
m
c
,
ua A
1
, A
2
, . . . , A
a
k
+1
¯
du
,
.
o
,
c nô
´
i b
`
˘
ang
¯
do
.
an th
,
˘
ang không ph
,
ai m
`
au
¯
d
,
o, ta c
´
o a
k
+ 1
¯
diê
,
m, nh
˜
u
,
ng
¯
do
.
an th
,
˘
ang gi
˜
u
,
a ch
´
ung
¯
du
,
.
o
,
c tô b
`
˘
ang
k m
`
au. Theo gi
,
a thiê
´
t quy n
.
ap ba
¯
do
.
an n
`
ao
¯
d
´
o trong ch
´
ung l
`
a
¯
d
,
ınh c
,
ua m
.
ôt tam gi
´
ac c
`
ung m
`
au.
J

6.1. V
´
ı d
.
u quy n
.
ap to
´
an h
.
oc cho h
`
ınh h
.
oc 151
V
´
ı d
.
u 6.11. Trong m
.
ôt m
.
˘at ph
,
˘ang cho 2000
¯
diê
,
m, không c´o ba
¯
diê
,
m n `ao n
`
˘am trên m
.
ôt
¯
du
,
`
o
,
ng th
,
˘ang. M
.
ôt sô
´
trong ch ´ung
¯
du
,
.
o
,
c
nô
´
i th`anh
¯
do
.
an th
,
˘ang theo nguyên t
´
˘ac sau: Nê
´
u
¯
diê
,
m A
¯
du
,
.
o
,
c nô
´
i
v
´
o
,
i
¯
diê
,
m B v `a
¯
diê
,
m B
¯
du
,
.
o
,
c nô
´
i v
´
o
,
i
¯
diê
,
m C, th`ı A không
¯
du
,
.
o
,
c
nô
´
i v
´
o
,
i
¯
diê
,
m C. Ch
´
u
,
ng minh r
`
˘ang v
´
o
,
i c ´ach nô
´
i trên ta thu
¯
du
,
.
o
,
c
không qu ´a 1 000 000
¯
do
.
an th
,
˘ang.
L
`
o
,
i gi
,
ai. B
`
˘
ang quy n
.
ap theo n ta s
˜
e ch
´
u
,
ng minh r
`
˘
ang
nê
´
u trong m
.
˘
at ph
,
˘
ang cho 2n
¯
diê
,
m th
,
oa m
˜
an
¯
diê
`
u ki
.
ên
¯
dâ
`
u b
`
ai, th
`
ı nh
˜
u
,
ng
¯
do
.
an th
,
˘
ang k
,
e
¯
du
,
.
o
,
c không qu
´
a n
2
( n =
2, 3, . . .). V
´
o
,
i n = 2 kh
,
˘
ang
¯
d
.
inh l
`
a hiê
,
n nhiên. Gi
,
a thiê
´
t
r
`
˘
ang kh
,
˘
ang
¯
d
.
inh
¯
d
´
ung v
´
o
,
i 2n
¯
diê
,
m, v
`
a ta x
´
et 2n + 2
¯
diê
,
m.
Lâ
´
y hai
¯
diê
,
m A v
`
a B t
`
u
,
nh
˜
u
,
ng
¯
diê
,
m nô
´
i
¯
du
,
.
o
,
c b
`
˘
ang
¯
do
.
an th
,
˘
ang.
C
`
on l
.
ai 2n
¯
diê
,
m, theo gi
,
a thiê
´
t quy n
.
ap nh
˜
u
,
ng
¯
do
.
an th
,
˘
ang k
,
e
¯
du
,
.
o
,
c gi
˜
u
,
a 2n
¯
diê
,
m n
`
ay không l
´
o
,
n ho
,
n n
2
. Nh
˜
u
,
ng
¯
do
.
an th
,
˘
ang k
,
e
t
`
u
,
A v
`
a B t
´
o
,
i 2n
¯
diê
,
m c
`
on l
.
ai, không qu
´
a 2n (v
`
ı nê
´
u m
.
ôt
¯
diê
,
m
¯
du
,
.
o
,
c nô
´
i v
´
o
,
i A, n
´
o s
˜
e không
¯
du
,
.
o
,
c nô
´
i v
´
o
,
i B v
`
a ngu
,
.
o
,
c l
.
ai). Ch
,
ı c
`
on
thêm m
.
ôt
¯
do
.
an nô
´
i A v
`
a B. Nhu
,
v
.
ây tâ
´
t c
,
a c
´
ac
¯
do
.
an th
,
˘
ang k
,
e
¯
du
,
.
o
,
c không qu
´
a n
2
+ 2n + 1 = (n + 1)
2
.
J
V
´
ı d
.
u 6.12. a) Ðiê
,
m O n
`
˘am trong phâ
`
n trong c
,
ua
¯
da gi ´ac lô
`
i
A
1
A
2
. . . A
n
. Ta x´et tâ
´
t c
,
a c ´ac g´oc A
i
OA
j
,
,
o
,
¯
dây i v `a j l `a nh
˜
u
,
ng
sô
´
t
.
u
,
nhiên kh ´ac nhau gi
˜
u
,
a c ´ac sô
´
1, 2, . . . , n. Ch
´
u
,
ng minh r
`
˘ang
gi
˜
u
,
a nh
˜
u
,
ng g´oc n `ay c´o ´ıt nhâ
´
t n −1 g´oc ph
,
ai l `a g´oc nh
.
on (ngh˜ıa
l `a ho
.
˘ac l `a g´oc vuông, g´oc t `u ho
.
˘ac l `a g´oc b
.
et).
b) C `ung b `ai to ´an cho
¯
da di
.
ên v
´
o
,
i n
¯
d
,
ınh.
L
`
o
,
i gi
,
ai. Ta ch
´
u
,
ng minh b
`
˘
ang quy n
.
ap theo n. V
´
o
,
i n = 3 kh
,
˘
ang
¯
d
.
inh
¯
du
,
.
o
,
c ch
´
u
,
ng minh d
˜
ê d
`
ang. Ta gi
,
a thiê
´
t r
`
˘
ang n
´
o
¯
d
´
ung v
´
o
,
i
n = k,
,
o
,
¯
dây k l
`
a m
.
ôt sô
´
t
.
u
,
nhiên n
`
ao
¯
d
´
o v
`
a ta x
´
et
¯
da gi
´
ac lô
`
i c
´
o
152 Chu
,
o
,
ng 6. H
`
ınh h
.
oc
sô
´
c
.
anh k + 1, A
1
A
2
. . . A
k+1
. Ta k
,
e
¯
du
,
`
o
,
ng th
,
˘
ang l
¯
di qua O vuông
g
´
oc v
´
o
,
i OA
k+1
(h
`
ınh 7).
´
It nhâ
´
t m
.
ôt trong nh
˜
u
,
ng
¯
d
,
ınh
H
`
ınh 6.4:
c
,
ua (k + 1)-
¯
da gi
´
ac n
`
˘
am trong n
,
u
,
a
m
.
˘
at ph
,
˘
ang kh
´
ac ph
´
ıa v
´
o
,
i A
k+1
ng
˘
an
b
,
o
,
i
¯
du
,
`
o
,
ng th
,
˘
ang l. Cho
¯
d
´
o l
`
a
¯
d
,
ınh
A
2
. Khi
¯
d
´
o g
´
oc A
2
OA
k+1
l
`
a t
`
u.
Theo gi
,
a thiê
´
t quy n
.
ap k-
¯
da gi
´
ac
lô
`
i A
1
A
2
. . . A
k
c
´
o
´
ıt nhâ
´
t k − 1 g
´
oc
không nh
.
on d
.
ang A
i
OA
j
v
`
a ch
´
ung
kh
´
ac v
´
o
,
i g
´
oc A
2
OA
k+1
. B
`
˘
ang c
´
ach
¯
d
´
o
ch
´
u
,
ng minh
¯
du
,
.
o
,
c r
`
˘
ang sô
´
lu
,
.
o
,
ng nh
˜
u
,
ng g
´
oc A
i
OA
j
không nh
.
on
trong (k + 1)−
¯
da gi
´
ac A
2
. . . A
k+1
´
ıt nhâ
´
t l
`
a k.
J
V
´
ı d
.
u 6.13. a) Ch
´
u
,
ng minh r
`
˘ang trong m
.
oi n− gi ´ac (n ≥ 4) c´o ´ıt
nhâ
´
t m
.
ôt
¯
du
,
`
o
,
ng ch´eo n
`
˘am tr
.
on v
.
en bên trong
¯
da gi ´ac.
b) Sô
´
nh
,
o nhâ
´
t c´ac
¯
du
,
`
o
,
ng ch´eo nhu
,
v
.
ây trong n− gi ´ac l `a bao
nhiêu?
L
`
o
,
i gi
,
ai. a) Nê
´
u
¯
da gi
´
ac l
`
a lô
`
i th
`
ı b
`
ai to
´
an l
`
a hiê
,
n nhiên. Bây gi
`
o
,
gi
,
a s
,
u
,
g
´
oc trong c
,
ua
¯
da gi
´
ac t
.
ai
¯
d
,
ınh A l
´
o
,
n ho
,
n 180
0
. B
,
o
,
i g
´
oc nh
`
ın
tr
.
on v
.
en m
.
ôt c
.
anh c
,
ua
¯
da gi
´
ac t
`
u
,
¯
d
,
ınh A luôn du
,
´
o
,
i m
.
ôt g
´
oc nh
,
o
ho
,
n 180
0
, cho nên t
`
u
,
¯
d
,
ınh A s
˜
e nh
`
ın
¯
du
,
.
o
,
c tr
.
on v
.
en
´
ıt nhâ
´
t hai
c
.
anh. Do
¯
d
´
o tô
`
n t
.
ai tia xuâ
´
t ph
´
at t
`
u
,
¯
diê
,
m A m
`
a trên
¯
d
´
o xâ
,
y ra
vi
.
êc
¯
dô
,
i (c
´
ac phâ
`
n) c
´
ac c
.
anh
¯
du
,
.
o
,
c nh
`
ın t
`
u
,
¯
diê
,
m A (h
`
ınh 9). M
˜
ôi
tia
¯
d
´
o cho m
.
ôt
¯
du
,
`
o
,
ng ch
´
eo n
`
˘
am tr
.
on v
.
en bên trong
¯
da gi
´
ac.
b) T
`
u
,
h
`
ınh 8 ta thâ
´
y c
´
ach d
.
u
,
ng m
.
ôt n− gi
´
ac c
´
o
¯
d
´
ung n − 3
¯
du
,
`
o
,
ng ch
´
eo n
`
˘
am tr
.
on v
.
en trong n
´
o. C
`
on l
.
ai ta ph
,
ai ch
´
u
,
ng minh
r
`
˘
ang trong m
.
oi n− gi
´
ac c
´
o
´
ıt nhâ
´
t n − 3
¯
du
,
`
o
,
ng ch
´
eo n
`
˘
am bên

6.1. V
´
ı d
.
u quy n
.
ap to
´
an h
.
oc cho h
`
ınh h
.
oc 153
H
`
ınh 6.5: H
`
ınh 6.6:
trong. V
´
o
,
i n = 3 m
.
ênh
¯
dê
`
¯
d
´
o d
´
ung. Gi
,
a s
,
u
,
m
.
ênh
¯
dê
`
¯
d
´
o
¯
d
´
ung
cho tâ
´
t c
,
a c
´
ac k− gi
´
ac, v
´
o
,
i k < n, ta ph
,
ai ch
´
u
,
ng minh n
´
o cho
n−gi
´
ac. Theo kê
´
t qu
,
a b
`
ai trên, n− gi
´
ac c
´
o thê
,
¯
du
,
.
o
,
c chia b
,
o
,
i m
.
ôt
¯
du
,
`
o
,
ng ch
´
eo n
`
˘
am tr
.
on v
.
en bên trong th
`
anh hai
¯
da gi
´
ac ( k + 1)−
gi
´
ac v
`
a ( n − k + 1)− gi
´
ac, v
´
o
,
i k + 1 < n v
`
a n −k + 1 < n. Trong
c
´
ac
¯
da gi
´
ac
¯
d
´
o c
´
o
´
ıt nhâ
´
t (k + 1) − 3 v
`
a (n − k + 1) − 3
¯
du
,
`
o
,
ng
ch
´
eo n
`
˘
am bên trong tu
,
o
,
ng
´
u
,
ng. Do
¯
d
´
o trong n−gi
´
ac c
´
o
´
ıt nhâ
´
t
1 + (k −2 ) + (n −k −2) = n −3
¯
du
,
`
o
,
ng ch
´
eo n
`
˘
am bên trong.
J
V
´
ı d
.
u 6.14. Ch
´
u
,
ng minh r
`
˘ang m
.
oi n−gi´ac c´o thê
,
c
´
˘at ra th `anh
c ´ac tam gi ´ac b
`
˘ang c ´ac
¯
du
,
`
o
,
ng ch´eo không c
´
˘at nhau.
L
`
o
,
i gi
,
ai. Ta ch
´
u
,
ng minh m
.
ênh
¯
dê
`
n
`
ay b
`
˘
ang quy n
.
ap theo n. V
´
o
,
i
n = 3 m
.
ênh
¯
dê
`
¯
d
´
ung. Gi
,
a s
,
u
,
m
.
ênh
¯
dê
`
¯
d
´
ung cho tâ
´
t c
,
a k−gi
´
ac, v
´
o
,
i
k < n, ta câ
`
n ch
´
u
,
ng minh n
´
o cho m
.
oi n− gi
´
ac. M
.
ôt n− gi
´
ac bâ
´
t
k
`
y c
´
o thê
,
¯
du
,
.
o
,
c chia b
,
o
,
i m
.
ôt
¯
du
,
`
o
,
ng ch
´
eo ra th
`
anh hai
¯
da gi
´
ac (b
`
ai
tru
,
´
o
,
c), trong
¯
dos m
˜
ôi
¯
da gi
´
ac c
´
o sô
´
c
.
anh nh
,
o ho
,
n n, t
´
u
,
c l
`
a ch
´
ung
c
´
o thê
,
¯
du
,
.
o
,
c chia ra th
`
anh c
´
ac tam gi
´
ac theo gi
,
a thiê
´
t quy n
.
ap.
J
V
´
ı d
.
u 6.15. Ch
´
u
,
ng minh r
`
˘ang tô
,
ng c ´ac g´oc trong c
,
ua m
.
ôt n−gi ´ac
bâ
´
t k`y b
`
˘ang (n −2)180
0
.

154 Chu
,
o
,
ng 6. H
`
ınh h
.
oc
L
`
o
,
i gi
,
ai. Ta ch
´
u
,
ng minh m
.
ênh
¯
dê
`
b
`
˘
ang quy n
.
ap. V
´
o
,
i n = 3 m
.
ênh
¯
dê
`
¯
d
´
ung l
`
a hiê
,
n nhiên. Gi
,
a s
,
u
,
m
.
ênh
¯
dê
`
¯
d
˜
a
¯
du
,
.
o
,
c ch
´
u
,
ng minh cho
tâ
´
t c
,
a c
´
ac k−gi
´
ac, v
´
o
,
i k < n, ta ph
,
ai ch
´
u
,
ng minh n
´
o cho m
.
oi n−
gi
´
ac. M
.
ôt n− gi
´
ac bâ
´
t k
`
y c
´
o thê
,
¯
du
,
.
o
,
c chia b
,
o
,
i m
.
ôt
¯
du
,
`
o
,
ng ch
´
eo ra
l
`
am 2
¯
da gi
´
ac (Xem b
`
ai tru
,
´
o
,
c). Nê
´
u sô
´
c
.
anh c
,
ua m
.
ôt
¯
da gi
´
ac
¯
d
´
o
b
`
˘
ang k + 1, th
`
ı sô
´
c
.
anh c
,
ua
¯
da gi
´
ac kia b
`
˘
ang n − k + 1, ho
,
n n
˜
u
,
a
c
,
a hai sô
´
¯
d
´
o
¯
dê
`
u nh
,
o ho
,
n n. Do
¯
d
´
o tô
,
ng c
´
ac g
´
oc c
,
ua c
´
ac
¯
da gi
´
ac
¯
d
´
o tu
,
o
,
ng
´
u
,
ng b
`
˘
ang (k − 1)180
0
v
`
a (n − k − 1)180
0
. C
˜
ung r
˜
o r
`
ang
r
`
˘
ang tô
,
ng c
´
ac g
´
oc c
,
ua n−gi
´
ac b
`
˘
ang tô
,
ng c
´
ac g
´
oc c
,
ua c
´
ac
¯
da gi
´
ac
¯
d
´
o, t
´
u
,
c l
`
a b
`
˘
ang (k −1 + n − k −1)180
0
= (n −2)180
0
.
J
V
´
ı d
.
u 6.16. Ch
´
u
,
ng minh r
`
˘ang m
.
oi n−gi ´ac lô
`
i v
´
o
,
i n ≥ 5
¯
dê
`
u c´o
thê
,
c
´
˘at ra th `anh ng ˜u gi ´ac lô
`
i.
L
`
o
,
i gi
,
ai. Ta ch
´
u
,
ng minh b
`
˘
ang quy n
.
ap r
`
˘
ang m
.
oi n− gi
´
ac lô
`
i v
´
o
,
i
n ≥ 5
¯
dê
`
u c
´
o thê
,
c
´
˘
at ra th
`
anh c
´
ac ng
˜
u gi
´
ac lô
`
i. V
´
o
,
i n = 5
¯
diê
`
u
¯
d
´
o
l
`
a hiê
,
n nhiên, c
`
on v
´
o
,
i n = 6 v
`
a 7 c
´
o thê
,
xem h
`
ınh 10 v
`
a 11.
Bây gi
`
o
,
gi
,
a s
,
u
,
r
`
˘
ang n ≥ 8 v
`
a m
.
oi m− gi
´
ac lô
`
i v
´
o
,
i 5 ≤ m < n
¯
dê
`
u c
´
o thê
,
c
´
˘
at ra th
`
anh c
´
ac ng
˜
u gi
´
ac. T
`
u
,
n− gi
´
ac c
´
o thê
,
c
´
˘
at ra
m
.
ôt ng
˜
u gi
´
ac t
.
ao b
,
o
,
i 5
¯
d
,
ınh liên tiê
´
p. Khi
¯
d
´
o c
`
on l
.
ai (n −3)− gi
´
ac.
B
,
o
,
i v
`
ı 5 ≤ n −3 < n, nên (n −3)− gi
´
ac l
.
ai c
´
o thê
,
c
´
˘
at ra th
`
anh
c
´
ac ng
˜
u gi
´
ac theo gi
,
a thiê
´
t quy n
.
ap to
´
an h
.
oc.
J
6.2. B
`
ai t
.
âp
.
.
. 6.17. Trong m
.
˘
at ph
,
˘
ang cho n ≥ 3
¯
diê
,
m. Ch
´
u
,
ng minh r
`
˘
ang m
˜
ôi
¯
diê
,
m c
´
o thê
,
nô
´
i v
´
o
,
i m
.
ôt sô
´
¯
diê
,
m c
`
on l
.
ai sao cho nh
˜
u
,
ng
¯
do
.
an th
,
˘
ang
nh
.
ân
¯
du
,
.
o
,
c không t
.
u
,
c
´
˘
at nhau v
`
a t
.
ao th
`
anh m
.
ôt
¯
da gi
´
ac lô
`
i g
´
ep
b
,
o
,
i nh
˜
u
,
ng tam gi
´
ac.
.
.
. 6.18. Ð
.
ô d
`
ai c
,
ua m
˜
ôi
¯
do
.
an th
,
˘
ang trong n ≥ 3
¯
do
.
an th
,
˘
ang
¯
d
˜
a
6.2. B
`
ai t
.
âp 155
H
`
ınh 6.7: H
`
ınh 6.8:
cho l
´
o
,
n ho
,
n 1. Biê
´
t r
`
˘
ang không c
´
o k ( k = 3, 4, . . . , n ) sô
´
¯
do
.
an c
´
o
thê
,
t
.
ao ra c
´
ac c
.
anh m
.
ôt
¯
da gi
´
ac. Ch
´
u
,
ng minh r
`
˘
ang tô
,
ng
¯
d
.
ô d
`
ai
c
,
ua c
´
ac
¯
do
.
an l
´
o
,
n ho
,
n 2
n−1
.
.
.
. 6.19. Trên m
.
˘
at ph
,
˘
ang b
.
i chia b
,
o
,
i n
¯
du
,
`
o
,
ng tr
`
on ra c
´
ac m
,
anh
kh
´
ac nhau. Ch
´
u
,
ng minh r
`
˘
ang m
.
˘
at ph
,
˘
ang c
´
o thê
,
tô b
`
˘
ang hai m
`
au
sao cho m
˜
ôi m
,
anh tô m
.
ôt m
`
au duy nhâ
´
t v
`
a hai m
,
anh liê
`
n nhau
c
´
o m
`
au kh
´
ac nhau.
.
.
. 6.20.
,
O
,
¯
dâ
`
u
¯
du
,
`
o
,
ng k
´
ınh m
.
ôt
¯
du
,
`
o
,
ng tr
`
on ta viê
´
t sô
´
1. M
˜
ôi n
,
u
,
a
¯
du
,
`
o
,
ng tr
`
on l
.
ai chia
¯
dôi v
`
a
,
o
,
¯
diê
,
m gi
˜
u
,
a ta viê
´
t tô
,
ng nh
˜
u
,
ng sô
´
,
o
,
hai
¯
dâ
`
u cung. Sau
¯
d
´
o m
˜
ôi phâ
`
n tu
,
cung ta l
.
ai chia l
`
am
¯
dôi v
`
a
,
o
,
¯
diê
,
m gi
˜
u
,
a viê
´
t sô
´
tô
,
ng
,
o
,
hai
¯
dâ
`
u cung. C
´
ach l
`
am n
`
ay l
.
˘
ap l
.
ai n
lâ
`
n. H
˜
ay t
´
ınh tô
,
ng c
´
ac sô
´
¯
d
˜
a viê
´
t ra.

CHU
,
O
,
NG 7
ÐA TH
´
U
,
C
7.1. Phân t
´
ıch
¯
da th
´
u
,
c ra th
`
u
,
a sô
´
. . . . . . . . . . . . . . . . . . . . . . . . 156
7.2. Nguyên l
´
y so s
´
anh c
´
ac h
.
ê sô
´
. . . . . . . . . . . . . . . . . . . . . . . 160
7.3. Ð
.
ao h
`
am c
,
ua
¯
da th
´
u
,
c. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 169
7.4. Ða th
´
u
,
c Chebychev . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 172
7.5. B
`
aii t
.
âp. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 174
7.1. Phân t
´
ıch
¯
da th
´
u
,
c ra th
`
u
,
a sô
´
Ða th
´
u
,
c b
.
âc n g
.
oi l
`
a h
`
am sô
´
c
´
o d
.
ang
P(x) = a
0
x
n
+ a
1
x
n−1
+ ··· + a
n
, (a
0
6= 0) (7.1)
,
o
,
¯
dây a
0
, a
1
, . . . , a
n
l
`
a nh
˜
u
,
ng h
`
˘
ang sô
´
(h
.
ê sô
´
¯
da th
´
u
,
c), c
`
on n ≥ 0
l
`
a m
.
ôt sô
´
nguyên (b
.
âc c
,
ua
¯
da th
´
u
,
c). Ða th
´
u
,
c l
`
a m
.
ôt l
´
o
,
p h
`
am
¯
do
,
n
gi
,
an, nhu
,
ng c
´
o râ
´
t nhiê
`
u
´
u
,
ng d
.
ung trong to
´
an h
.
oc. V
´
o
,
i n = 0
¯
da
th
´
u
,
c (7.1) l
`
a h
`
˘
ang sô
´
a
0
, v
´
o
,
i n = 1, P( x) tr
,
o
,
th
`
anh h
`
am tuyê
´
n
t
´
ınh P(x) = a
0
x + a
1
, c
`
on v
´
o
,
i n = 2, P l
`
a tam th
´
u
,
c b
.
âc hai P( x) =
a
0
x
2
+ a
1
x + a
2
. Ðê
,
¯
da th
´
u
,
c c
´
o b
.
âc l
`
a n th
`
ı luôn c
´
o
¯
diê
`
u ki
.
ên a
0
6= 0.
Trong tru
,
`
o
,
ng h
.
o
,
p ngu
,
.
o
,
c l
.
ai th
`
ı b
.
âc cao nhâ
´
t c
,
ua
¯
da th
´
u
,
c P l
`
a n.
Nê
´
u P(x) v
`
a Q(x) l
`
a nh
˜
u
,
ng
¯
da th
´
u
,
c, th
`
ı P(x) + Q(x), P(x) −
Q(x) v
`
a P(x).Q(x) c
˜
ung l
`
a
¯
da th
´
u
,
c, nhu
,
ng ph
´
ep chia hai
¯
da th
´
u
,
c
cho nhau không luôn luôn l
`
a m
.
ôt
¯
da th
´
u
,
c.
Sô
´
α g
.
oi l
`
a nghi
.
êm c
,
ua
¯
da th
´
u
,
c P(x), nê
´
u P(α) = 0. Nhu
,

7.1. Phân t
´
ıch
¯
da th
´
u
,
c ra th
`
u
,
a sô
´
157
v
.
ây, Nê
´
u tam th
´
u
,
c b
.
âc hai P(x) = ax
2
+ bx + c, m
`
a b
2
−4ac ≥ 0
th
`
ı hai nghi
.
êm c
,
ua tam th
´
u
,
c n
`
ay x
1
, x
2
¯
du
,
a ta
¯
dê
´
n phân t
´
ıch
P(x) = a(x − x
1
)(x − x
2
). Tô
,
ng qu
´
at ho
,
n ta c
´
o
V
´
ı d
.
u 7.1. Nê
´
u P(x) l `a m
.
ôt
¯
da th
´
u
,
c b
.
âc n ≥ 1 v `a α l `a m
.
ôt sô
´
th
.
u
,
c, th`ı α l `a nghi
.
êm c
,
ua P(x) khi v `a ch
,
ı khi tô
`
n t
.
ai m
.
ôt
¯
da th
´
u
,
c
Q(x) b
.
âc n −1, m `a n´o tho
,
a m ˜an
¯
d
,
˘ang th
´
u
,
c sau
P(x) = (x −α)Q(x) (7.2)
v
´
o
,
i m
.
oi x.
L
`
o
,
i gi
,
ai. Ðiê
`
u ki
.
ên
¯
d
,
u l
`
a tâ
´
t nhiên
¯
d
´
ung. Ta ch
´
u
,
ng minh
¯
diê
`
u
ki
.
ên câ
`
n, nê
´
u P(x) l
`
a
¯
da th
´
u
,
c b
.
âc n
P(x) =
n
∑
i =0
a
n−i
x
i
(7.3)
v
`
a P(α) = 0, ngh
˜
ıa l
`
a
P(α) =
n
∑
i =0
a
n−i
α
i
= 0. (7.4)
Ta s
,
u
,
d
.
ung
¯
d
,
˘
ang th
´
u
,
c a
n
− b
n
= (a − b)(a
n−1
+ a
n−2
b + ··· +
b
n−1
), t
`
u
,
(7.3) v
`
a (7.4) ta nh
.
ân
¯
du
,
.
o
,
c
P(x) = P(x) − P(α) =
n
∑
i =0
a
n−i
(x
i
−α
i
) =
= (x −α)
n
∑
i =1
a
n−i
(x
i −1
+ x
i −2
α + ··· + α
n−1
) = (x −α) Q(x),
,
o
,
¯
dây Q(x ) =
n
∑
i =1
a
n−i
(x
i −1
+ x
i −2
α + ··· + α
n−1
) hiê
,
n nhiên l
`
a
¯
da
th
´
u
,
c b
.
âc n −1 (v
`
ı a
0
6= 0).
J
V
´
ı d
.
u 7.2. Không c´o m
.
ôt
¯
da th
´
u
,
c b
.
âc n c´o nhiê
`
u ho
,
n n nghi
.
êm
sô
´
kh ´ac nhau.

158 Chu
,
o
,
ng 7. Ða th
´
u
,
c
L
`
o
,
i gi
,
ai. Ch
´
u
,
ng minh b
`
˘
ang phu
,
o
,
ng ph
´
ap quy n
.
ap theo n. Gi
,
a
s
,
u
,
P l
`
a m
.
ôt
¯
da th
´
u
,
c b
.
âc n v
`
a α
1
, α
2
, . . . l
`
a nghi
.
êm c
,
ua n
´
o ( α
i
6= α
j
v
´
o
,
i i 6= j). V
´
o
,
i n = 1, P(x ) = a
0
x + a
1
(a
0
6= 0) c
´
o m
.
ôt nghi
.
êm
duy nhâ
´
t α
1
= −
a
1
a
0
. Gi
,
a s
,
u
,
m
.
ênh
¯
dê
`
¯
d
´
ung v
´
o
,
i sô
´
n. Ta s
˜
e ch
´
u
,
ng
minh n
´
o c
˜
ung
¯
d
´
ung v
´
o
,
i n + 1. V
´
o
,
i m
.
uc
¯
d
´
ıch n
`
ay ta gi
,
a s
,
u
,
tô
`
n
t
.
ai m
.
ôt
¯
da th
´
u
,
c Q b
.
âc n + 1, m
`
a n
´
o c
´
o n + 2 nghi
.
êm kh
´
ac nhau
α
1
, α
2
, . . . , α
n+2
. Khi
¯
d
´
o Q c
´
o thê
,
biê
,
u di
˜
ên du
,
´
o
,
i d
.
ang (do .7.1)
Q(x) = (x −α
n+2
)Q
1
(x)
,
o
,
¯
dây Q
1
l
`
a
¯
da th
´
u
,
c b
.
âc n. V
`
ı th
`
u
,
a sô
´
x −α
n+2
không c
´
o nghi
.
êm
l
`
a m
.
ôt trong c
´
ac sô
´
α
1
, α
2
, . . . , α
n+1
, th
`
ı ch
´
ung l
`
a nghi
.
êm c
,
ua Q
1
.
Nhu
,
ng
¯
diê
`
u n
`
ay c
´
o ngh
˜
ıa l
`
a m
.
ôt
¯
da th
´
u
,
c b
.
âc n c
´
o n + 1 nghi
.
êm
ho
`
an to
`
an kh
´
ac nhau, tr
´
ai v
´
o
,
i gi
,
a thiê
´
t quy n
.
ap.
J
V
´
ı d
.
u 7.3. Ch
´
u
,
ng minh r
`
˘ang m
˜
ôi
¯
da th
´
u
,
c
P(x) = a
0
x
n
+ a
1
x
n−1
+ ··· + a
n
, (a
0
6= 0)
c´o thê
,
biê
,
u di
˜
ên du
,
´
o
,
i d
.
ang
P(x) = a
0
(x − α
1
)(x −α
2
) . . . (x −α
n
),
,
o
,
¯
dây α
1
, α
2
, . . . , α
n
l `a nghi
.
êm c
,
ua
¯
da th
´
u
,
c.
L
`
o
,
i gi
,
ai. Ta ch
´
u
,
ng minh b
`
˘
ang quy n
.
ap theo n. Nê
´
u n = 1, th
`
ı
P(x) = a
0
x + a
1
c
´
o m
.
ôt nghi
.
êm duy nhâ
´
t α
1
= −
a
1
a
0
v
`
a hiê
,
n nhiên
P(x) = a
0
(x +
a
1
a
0
) = a
0
(x − α
1
).
Gi
,
a s
,
u
,
m
.
ênh
¯
dê
`
kh
,
˘
ang
¯
d
.
inh
¯
d
´
ung v
´
o
,
i
¯
da th
´
u
,
c b
.
âc n −1 v
`
a cho
deg P(x) = n. Ta biê
´
t r
`
˘
ang P(x) tô
`
n t
.
ai nghi
.
êm nhu
,
c
´
ac b
`
ai t
.
âp
trên
¯
d
˜
a ch
´
u
,
ng minh, lâ
´
y α
1
l
`
a nghi
.
êm c
,
ua P(x). Khi
¯
d
´
o P(x) =
(x − α
1
)Q(x), d
˜
ê thâ
´
y deg Q(x) = n − 1 v
`
a h
.
ê sô
´
tru
,
´
o
,
c b
.
âc cao

7.1. Phân t
´
ıch
¯
da th
´
u
,
c ra th
`
u
,
a sô
´
159
nhâ
´
t c
,
ua
¯
da th
´
u
,
c n
`
ay tr
`
ung v
´
o
,
i a
0
c
,
ua P(x). T
`
u
,
¯
d
´
o suy ra nh
˜
u
,
ng
nghi
.
êm c
,
ua P(x) l
`
a α
1
v
`
a nh
˜
u
,
ng nghi
.
êm c
,
ua Q(x). Theo gi
,
a thiê
´
t
quy n
.
ap
Q(x) = a
0
(x − α
2
)(x −α
3
) . . . (x −α
n
),
,
o
,
¯
dây α
2
, α
3
, . . . , α
n
l
`
a tâ
´
t c
,
a nghi
.
êm c
,
ua Q(x). Khi
¯
d
´
o tâ
´
t c
,
a
nghi
.
êm c
,
ua P(x) l
`
a α
1
, α
2
, . . . , α
n
v
`
a
P(x) = (x −α
1
)Q(x) = a
0
(x − α
1
)(x −α
2
) . . . (x −α
n
).
J
K
´
y hi
.
êu F l
`
a m
.
ôt t
.
âp sô
´
: t
.
âp h
.
o
,
p sô
´
ph
´
u
,
c, t
.
âp h
.
o
,
p sô
´
th
.
u
,
c v
`
a
t
.
âp h
.
o
,
p sô
´
h
˜
u
,
u t
,
y. Nh
˜
u
,
ng
¯
da th
´
u
,
c không ph
,
ai h
`
˘
ang sô
´
P(x) v
´
o
,
i
h
.
ê sô
´
trong t
.
âp h
.
o
,
p F g
.
oi l
`
a không phân t´ıch
¯
du
,
.
o
,
c trên F, nê
´
u n
´
o
không thê
,
biê
,
u di
˜
ên
¯
du
,
.
o
,
c nhu
,
t
´
ıch c
,
ua hai
¯
da th
´
u
,
c (không ph
,
ai
¯
da th
´
u
,
c h
`
˘
ang sô
´
) c
´
o h
.
ê sô
´
thu
.
ôc F, c
´
o b
.
âc th
.
u
,
c s
.
u
,
nh
,
o ho
,
n b
.
âc
c
,
ua P(x).
V
´
ı d
.
u 7.4. Ch
´
u
,
ng minh r
`
˘ang m
.
oi
¯
da th
´
u
,
c th
.
u
,
c s
.
u
,
v
´
o
,
i h
.
ê
sô
´
thu
.
ôc F c´o thê
,
biê
,
u di
˜
ên nhu
,
t´ıch c
,
ua nh
˜
u
,
ng th
`
u
,
a sô
´
không phân t´ıch
¯
du
,
.
o
,
c trên F. S
.
u
,
biê
,
u di
˜
ên n `ay l `a duy
nhâ
´
t theo ngh˜ıa d ˜ay c
,
ua c´ac th
`
u
,
a sô
´
c´o thê
,
kh ´ac nhau
tu
,
o
,
ng
´
u
,
ng v
´
o
,
i h
`
˘ang sô
´
kh ´ac không c
,
ua F, n´oi c´ac kh´ac,
nê
´
u
P(x) = P
1
(x).P
2
(x) . . . , P
r
(x) = Q
1
(x).Q
2
(x) . . . Q
s
(x)
l `a hai biê
,
u di
˜
ên c
,
ua P(x) nhu
,
t´ıch c ´ac th
`
u
,
a sô
´
không phân t´ıch
¯
du
,
.
o
,
c trên F, th`ı r = s v `a P
i
(x) = α
i
Q
k
i
(x),
,
o
,
¯
dây 0 6= α
i
∈ F v `a
k
1
, k
2
, . . . , k
r
l `a nh
˜
u
,
ng sô
´
n `ao
¯
d´o xê
´
p th
´
u
,
t
.
u
,
theo 1, 2, . . . , r.
L
`
o
,
i gi
,
ai. Cho P(x) không ph
,
ai l
`
a
¯
da th
´
u
,
c h
`
˘
ang trong t
.
âp h
.
o
,
p F
v
`
a n = deg P(x). Nê
´
u n = 1, th
`
ı P(x) = a
0
x + a
1
l
`
a không phân
t
´
ıch
¯
du
,
.
o
,
c v
`
a n
´
o biê
,
u di
˜
ên nhu
,
t
´
ıch duy nhâ
´
t th
`
u
,
a sô
´
không phân
t
´
ıch
¯
du
,
.
o
,
c.

160 Chu
,
o
,
ng 7. Ða th
´
u
,
c
Cho n l
`
a sô
´
t
.
u
,
nhiên bâ
´
t k
`
y v
`
a gi
,
a thiê
´
t r
`
˘
ang m
.
oi
¯
da th
´
u
,
c b
.
âc
nh
,
o ho
,
n n c
´
o thê
,
biê
,
u di
˜
ên nhu
,
t
´
ıch c
´
ac th
`
u
,
a sô
´
không phân t
´
ıch
¯
du
,
.
o
,
c trên F.
Nê
´
u
¯
da th
´
u
,
c
¯
d
˜
a cho P(x ) l
`
a không phân t
´
ıch
¯
du
,
.
o
,
c trên F, th
`
ı
c
´
o thê
,
công nh
.
ân n
´
o biê
,
u di
˜
ên nhu
,
t
´
ıch c
,
ua m
.
ôt
¯
da th
´
u
,
c không
phân t
´
ıch
¯
du
,
.
o
,
c.
Nê
´
u
¯
da th
´
u
,
c phân t
´
ıch
¯
du
,
.
o
,
c, th
`
ı n
´
o c
´
o d
.
ang
P(x) = Q(x).H(x),
,
o
,
¯
dây Q(x) v
`
a H(x) l
`
a nh
˜
u
,
ng
¯
da th
´
u
,
c v
´
o
,
i h
.
ê sô
´
trong F v
`
a
deg Q(x) < n v
`
a deg H(x) < n. Nhu
,
ng khi
¯
d
´
o theo gi
,
a thiê
´
t quy
n
.
ap Q(x) v
`
a H(x) biê
,
u di
˜
ên nhu
,
t
´
ıch c
,
ua c
´
ac th
`
u
,
a sô
´
¯
da th
´
u
,
c
trên F. Suy ra c
˜
ung
¯
d
´
ung cho P(x). Ngh
˜
ıa l
`
a m
.
oi
¯
da th
´
u
,
c trên F
c
´
o thê
,
biê
,
u di
˜
ên nhu
,
t
´
ıch c
´
ac th
`
u
,
a sô
´
không phân t
´
ıch
¯
du
,
.
o
,
c c
´
o h
.
ê
sô
´
trong F. Ch
´
u
,
ng minh duy nhâ
´
t d
`
anh cho b
.
an
¯
d
.
oc.
J
7.2. Nguyên l
´
y so s
´
anh c
´
ac h
.
ê sô
´
Cho hai h
`
am sô
´
P
1
(x) v
`
a P
2
(x) x
´
ac
¯
d
.
inh trên m
.
ôt t
.
âp con D
c
,
ua sô
´
th
.
u
,
c. Ch
´
ung ta n
´
oi r
`
˘
ang P
1
(x) v
`
a P
2
(x) tr
`
ung nhau trong
D, nê
´
u
¯
d
,
˘
ang th
´
u
,
c P
1
(x) = P
2
(x)
¯
d
´
ung v
´
o
,
i m
.
oi x ∈ D. T
.
âp h
.
o
,
p c
´
ac
¯
da th
´
u
,
c l
`
a m
.
ôt l
´
o
,
p h
`
am
¯
d
.
˘
ac bi
.
êt. Miê
`
n x
´
ac
¯
d
.
inh c
,
ua m
˜
ôi
¯
da th
´
u
,
c
l
`
a t
.
âp h
.
o
,
p con c
,
ua sô
´
th
.
u
,
c. Nhu
,
v
.
ây hai
¯
da th
´
u
,
c P(x ) v
`
a Q(x)
tr
`
ung nhau, nê
´
u P(x) = Q(x)
¯
d
´
ung v
´
o
,
i m
.
oi x sô
´
th
.
u
,
c. L
´
o
,
p c
´
ac
¯
da
th
´
u
,
c c
´
o m
.
ôt t
´
ınh châ
´
t râ
´
t
¯
d
.
˘
ac bi
.
êt l
`
a
¯
dê
,
cho hai
¯
da th
´
u
,
c P(x) v
`
a
Q(x) tr
`
ung nhau ch
,
ı câ
`
n thiê
´
t kiê
,
m tra P(x) = Q(x)
¯
d
´
ung v
´
o
,
i
m
.
ôt sô
´
h
˜
u
,
u h
.
an gi
´
a tr
.
i c
,
ua x.
V
´
ı d
.
u 7.5. Cho
P(x) = a
0
x
n
+ a
1
x
n−1
+ ··· + a
n

7.2. Nguyên l
´
y so s
´
anh c
´
ac h
.
ê sô
´
161
v `a
Q(x) = b
0
x
m
+ b
1
x
m−1
+ ··· + b
m
l `a hai
¯
da th
´
u
,
c v `a n ≥ m. Ch
´
u
,
ng minh r
`
˘ang nê
´
u tô
`
n t
.
ai n + 1
nh
˜
u
,
ng sô
´
t
`
u
,
ng
¯
dôi m
.
ôt kh ´ac nhau α
1
, α
2
, . . . , α
n+1
( α
i
6= α
j
v
´
o
,
i i 6=
j) sao cho P(α
i
) = Q(α
i
), i = 1, 2, . . . , n + 1, th`ı n = m v `a a
0
=
b
0
, a
1
= b
1
, . . . , a
n
= b
n
.
L
`
o
,
i gi
,
ai. Do không c
´
o
¯
d
`
oi h
,
oi g
`
ı vê
`
b
0
6= 0 v
`
a l
.
ai c
´
o n ≥ m, ta c
´
o
thê
,
gi
,
a thiê
´
t (b
`
˘
ang c
´
ach
¯
d
´
anh sô
´
l
.
ai c
´
ac h
.
ê sô
´
)
Q(x) = b
0
x
n
+ b
1
x
n−1
+ ··· + b
n
Bu
,
´
o
,
c co
,
s
,
o
,
: nê
´
u n = 1, th
`
ı P (x) = a
0
x + a
1
, Q(x) = b
0
x + b
1
v
`
a
tho
,
a m
˜
an c
´
ac
¯
d
,
˘
ang th
´
u
,
c sau
a
0
α
1
+ a
1
= b
0
α
1
+ b
1
a
0
α
2
+ a
1
= b
0
α
2
+ b
1
Tr
`
u
,
theo vê
´
ta nh
.
ân
¯
du
,
.
o
,
c
a
0
( α
1
−α
2
) = b
0
( α
1
−α
2
)
Nhu
,
ng theo
¯
diê
`
u ki
.
ên α
1
6= α
2
ta c
´
o thê
,
gi
,
an u
,
´
o
,
c cho α
1
−α
2
6= 0.
Ta nh
.
ân
¯
du
,
.
o
,
c a
0
= b
0
, t
`
u
,
¯
d
´
o c
˜
ung suy ra a
1
= b
1
.
Bu
,
´
o
,
c quy n
.
ap: Gi
,
a s
,
u
,
m
.
ênh
¯
dê
`
¯
d
´
ung v
´
o
,
i n −1. Ta c
´
o
P(x)−P(α
n+1
) =
n
∑
i =0
a
i
x
n−i
−
n
∑
i =0
a
i
α
n−i
n+1
= a
0
(x
n
−α
n
n+1
) + a
1
(x
n−1
−α
n−1
n+1
) + ···+ a
n−1
(x − α
n+1
)
= (x −α
n+1
)(a
0
x
n−1
+ a
0
1
x
n−2
+ ··· + a
0
n−1
) = (x −α
n+1
)P
1
(x)
,
o
,
¯
dây P
1
(x) = a
0
x
n−1
+ a
0
1
x
n−2
+ ··· + a
0
n−1
Tu
,
o
,
ng t
.
u
,
Q(x) − Q(α
n+1
) = (x − α
n+1
)Q
1
(x),
,
o
,
¯
dây Q
1
(x) =
b
0
x
n−1
+ b
0
1
x
n−2
+ ··· + b
0
n−1
. Khi
¯
d
´
o v
´
o
,
i i = 1, 2, . . . , n ta nh
.
ân

162 Chu
,
o
,
ng 7. Ða th
´
u
,
c
¯
du
,
.
o
,
c
P
1
( α
i
) =
P(α
i
) − P(α
n+1
)
α
i
−α
n+1
=
Q(α
i
) − Q(α
n+1
)
α
i
−α
n+1
= Q
1
( α
i
)
v
`
a theo gi
,
a thiê
´
t quy n
.
ap a
0
= b
0
, a
0
1
= b
0
1
, . . . , a
0
n−1
= b
0
n−1
. Ta
¯
d
.
˘
at
P
2
(x) = a
1
x
n−1
+ a
2
x
n−2
+ ··· + a
n
Q
2
(x) = b
1
x
n−1
+ b
2
x
n−2
+ ··· + b
n
v
´
o
,
i i = 1, 2, . . . , n, n + 1 s
˜
e tho
,
a m
˜
an
P
2
( α
i
) = P(α
i
) − a
0
α
n
i
= Q(α
i
) − b
0
α
n
i
= Q
2
( α
i
)
L
.
ai
´
ap d
.
ung gi
,
a thiê
´
t quy n
.
ap ta c
´
o a
1
= b
1
, a
2
= b
2
, . . . , a
n
= b
n
.
J
V
´
ı d
.
u 7.6. T`ım tâ
´
t c
,
a c ´ac
¯
da th
´
u
,
c P(x) tho
,
a m ˜an
¯
d
,
˘ang th
´
u
,
c
P(x) = P(x + 1).
L
`
o
,
i gi
,
ai. D
˜
ê thâ
´
y, nê
´
u P(x) l
`
a
¯
da th
´
u
,
c h
`
˘
ang
sô
´
, th
`
ı n
´
o tho
,
a m
˜
an
¯
d
,
˘
ang th
´
u
,
c trên. Ta gi
,
a s
,
u
,
deg P(x) ≥ 1 v
`
a cho P(x) = a
0
x
n
+ a
1
x
n−1
+ ··· + a
n
,
a
0
6= 0 v
`
a P(x) tho
,
a m
˜
an
¯
d
,
˘
ang th
´
u
,
c P(x) = P(x + 1). Khi
¯
d
´
o
a
0
(x + 1)
n
+ a
1
(x + 1)
n−1
+ ··· + a
n
= a
0
x
n
+ a
1
x
n−1
+ ··· + a
n
t
`
u
,
¯
dây so s
´
anh h
.
ê sô
´
tru
,
´
o
,
c x
n−1
, ta nh
.
ân
¯
du
,
.
o
,
c na
0
+ a
1
= a
1
, t
´
u
,
c
l
`
a a
0
= 0 n
´
o vô l
´
y v
´
o
,
i gi
,
a thiê
´
t. Suy ra ch
,
ı c
´
o nh
˜
u
,
ng
¯
da th
´
u
,
c h
`
˘
ang
sô
´
l
`
a tho
,
a m
˜
an
¯
diê
`
u ki
.
ên
¯
dâ
`
u b
`
ai ra.
J
V
´
ı d
.
u 7.7. Ch
´
u
,
ng minh r
`
˘ang v
´
o
,
i m
.
oi sô
´
t
.
u
,
nhiên k tô
`
n t
.
ai duy
nhâ
´
t m
.
ôt
¯
da th
´
u
,
c P
k
(x) b
.
âc k + 1 sao cho P
k
(0 ) = 0 v `a x
k
=
P
k
(x + 1) − P
k
(x).

7.2. Nguyên l
´
y so s
´
anh c
´
ac h
.
ê sô
´
163
L
`
o
,
i gi
,
ai. Vi
.
êc tô
`
n t
.
ai
¯
da th
´
u
,
c P
k
(x) ta s
˜
e ch
´
u
,
ng minh quy n
.
ap
theo k. V
´
o
,
i k = 0 v
`
a k = 1 ta c
´
o
x
0
= 1 = (x + 1) − x;
x = (
1
2
(x + 1)
2
−
1
2
(x + 1)) −(
1
2
x
2
−
1
2
x)
Ngh
˜
ıa l
`
a P
0
(x) = x, P
1
(x) =
1
2
x
2
−
1
2
x.
Gi
,
a thiê
´
t v
´
o
,
i m
˜
ôi l ≤ k tô
`
n t
.
ai
¯
da th
´
u
,
c P
l
(x), v
´
o
,
i n
´
o P
l
(0 ) = 0
v
`
a x
l
= P
l
(x + 1) − P
l
(x). Ta c
´
o
x
k+1
= x. x
k
= xP
k
(x + 1) − xP
k
(x),
t
`
u
,
¯
d
´
o c
´
o
x
k+1
+ P
k
(x + 1) = (x + 1)P
k
(x + 1) − xP
k
(x).
Cho thêm
P
k
(x + 1) = a
k+1
x
k+1
+ a
k
x
k
+ ··· + a
1
x + a
0
.
Khi
¯
d
´
o
(1 +a
k+1
)x
k+1
= (x + 1)P
k
(x + 1) − xP
k
(x) −
k
∑
i =0
a
l
P
l
(x + 1) −
k
∑
l=1
a
l
P
l
(x)
= ((x + 1)P
k
(x + 1) −
k
∑
l=0
a
l
P
l
(x + 1)) −(xP
k
(x) −
k
∑
l=0
a
l
P
l
(x)).
V
´
o
,
i b
.
âc c
,
ua
¯
da th
´
u
,
c H(x) = xP
k
(x) −
k
∑
l=0
a
l
P
l
(x) cao nhâ
´
t ch
,
ı l
`
a
k + 1 v
`
a d
˜
ê thâ
´
y r
`
˘
ang h
.
ê sô
´
tru
,
´
o
,
c x
k+1
trong d
.
ang chuâ
,
n t
´
˘
ac c
,
ua
H(x)
¯
d
´
ung l
`
a a
k+1
. Nê
´
u gi
,
a s
,
u
,
r
`
˘
ang 1 + a
k+1
= 0, ta nh
.
ân
¯
du
,
.
o
,
c
H(x + 1) = H(x) v
`
a khi
¯
d
´
o ta c
´
o H(x) l
`
a h
`
˘
ang sô
´
(b
`
ai trên), n
´
o
tr
´
ai v
´
o
,
i a
k+1
6= 0. Suy ra 1 + a
k+1
6= 0 v
`
a nê
´
u ta
¯
d
.
˘
at
P
k+1
(x) =
1
1 + a
k+1
(xP
k
(x) −
k
∑
l=0
a
l
P
l
(x)),

164 Chu
,
o
,
ng 7. Ða th
´
u
,
c
Ta nh
.
ân
¯
du
,
.
o
,
c
x
k+1
= P
k+1
(x + 1) − P
k+1
(x).
Ch
´
u
,
ng minh duy nhâ
´
t d
`
anh cho b
.
an
¯
d
.
oc.
J
V
´
ı d
.
u 7.8. H ˜ay t`ım tâ
´
t c
,
a
¯
da th
´
u
,
c P(x) tho
,
a m ˜an
¯
diê
`
u ki
.
ên
P(x
2
−2) = (P(x ))
2
−2.
L
`
o
,
i gi
,
ai. Ta ch
´
u
´
y nhu
,
b
`
ai tru
,
´
o
,
c v
´
o
,
i m
.
oi sô
´
t
.
u
,
nhiên n tô
`
n t
.
ai
nhiê
`
u nhâ
´
t m
.
ôt
¯
da th
´
u
,
c P
n
(x) b
.
âc n tho
,
a m
˜
an
P
n
(x
2
−2) = (P
n
(x))
2
−2. (7.5)
V
´
o
,
i vi
.
êc so s
´
anh h
.
ê sô
´
tru
,
´
o
,
c sô
´
m
˜
u c
`
ung b
.
âc c
,
ua x trong phu
,
o
,
ng
tr
`
ınh trên ta t
`
ım
¯
du
,
.
o
,
c
P
1
(x) = x, P
2
(x) = x
2
−2, P
3
(x) = x
3
−3x,
P
4
(x) = x
4
−4x
2
+ 2, P
5
(x) = x
5
−5x
3
+ 5x.
Ngo
`
ai ra không kh
´
o kh
˘
an g
`
ı thiê
´
t l
.
âp
¯
du
,
.
o
,
c quan h
.
ê
P
3
(x) = xP
2
(x) − P
1
(x);
P
4
(x) = xP
3
(x) − P
2
(x);
P
5
(x) = xP
4
(x) − P
3
(x).
Ðiê
`
u n
`
ay g
.
o
,
i
´
y cho ta
¯
du
,
a ra m
.
ôt gi
,
a thiê
´
t sau
¯
dây:
M
.
oi
¯
da th
´
u
,
c trong d ˜ay
P
1
(x), P
2
(x), P
3
(x), . . . , P
n
(x), . . .
¯
du
,
.
o
,
c x ´ac
¯
d
.
inh theo c ´ac
¯
d
,
˘ang th
´
u
,
c sau
P
1
(x) = x, P
2
(x) = x
2
−2, . . . , P
n+1
(x) = xP
n
(x) − P
n−1
(x)
tho
,
a m ˜an
¯
diê
`
u ki
.
ên (7.5).

7.2. Nguyên l
´
y so s
´
anh c
´
ac h
.
ê sô
´
165
V
`
ı
¯
da th
´
u
,
c P
n
(x) b
.
âc n, theo b
`
ai t
.
âp tru
,
´
o
,
c, nê
´
u gi
,
a thiê
´
t trên
l
`
a
¯
d
´
ung th
`
ı ch
´
ung l
`
a tâ
´
t c
,
a c
´
ac
¯
da th
´
u
,
c tho
,
a m
˜
an
¯
diê
`
u ki
.
ên b
`
ai
to
´
an.
Bây gi
`
o
,
ta ch
´
u
,
ng minh gi
,
a thiê
´
t b
`
˘
ang quy n
.
ap to
´
an h
.
oc theo
n. V
´
o
,
i n = 1 v
`
a n = 2 gi
,
a thiê
´
t
¯
d
´
ung. Gi
,
a s
,
u
,
v
´
o
,
i n n
`
ao
¯
d
´
o
¯
da th
´
u
,
c
P
n
(x) v
`
a P
n+1
(x) tho
,
a m
˜
an
¯
diê
`
u ki
.
ên (7.5). Khi
¯
d
´
o
¯
dô
´
i v
´
o
,
i P
n+2
(x)
ta c
´
o
P
n+2
(x
2
−2) −(P
n+2
(x))
2
+ 2 =
= (x
2
−2)P
n+1
(x
2
−2) −P
n
(x
2
−2) −(xP
n+1
(x) − P
n
(x))
2
+ 2
= (x
2
−2)((P
n+1
(x))
2
−2) −((P
n
(x))
2
−2) −x
2
(P
n+1
(x))
2
+
+ 2xP
n+1
(x).P
n
(x) −(P
n
(x))
2
+ 2
= −2(P
n+1
(x))
2
−2(P(x))
2
+ 2xP
n+1
(x).P
n
(x) −2x
2
+ 8
= −2H
n
(x),
,
o
,
¯
dây ta
¯
d
.
˘
at
H
n
(x) = (P
n+1
(x))
2
+ (P
n
(x))
2
− xP
n+1
(x).P
n
(x) + x
2
−4.
M
.
˘
at kh
´
ac
H
n
(x) = (xP
n
(x) − P
n−1
(x))
2
+ (P
n
(x))
2
− x(xP
n
(x)
− P
n−1
(x)).P
n
(x) + x
2
−4
= (P
n
(x))
2
+ (P
n−1
(x))
2
− xP
n
(x).P
n−1
(x) + x
2
−4
= H
n−1
(x) = H
n−2
(x) = . . . = H
1
(x)
= (P
2
(x))
2
+ P
1
(x))
2
− xP
2
(x).P
1
(x) + x
2
−4
= (x
2
−2)
2
+ x
2
− x(x
2
−2)x + x
2
−4.
Suy ra P
n+2
(x
2
−2) = (P
n+2
(x))
2
−2.
J
V
´
ı d
.
u 7.9. Cho P(x) l`a
¯
da th
´
u
,
c v
´
o
,
i h
.
ê sô
´
th
.
u
,
c nh
.
ân gi´a tr
.
i sô
´
h
˜
u
,
u

166 Chu
,
o
,
ng 7. Ða th
´
u
,
c
t
,
y v
´
o
,
i m
.
oi sô
´
x h
˜
u
,
u t
,
y v`a gi ´a tr
.
i sô
´
vô t
,
y v
´
o
,
i m
.
oi sô
´
x vô t
,
y. Ch
´
u
,
ng
minh r
`
˘ang P(x) l `a
¯
da th
´
u
,
c tuyê
´
n t´ınh v
´
o
,
i h
.
ê sô
´
h
˜
u
,
u t
,
y.
L
`
o
,
i gi
,
ai. 1) Ta s
˜
e ch
´
u
,
ng minh r
`
˘
ang c
´
ac h
.
ê sô
´
c
,
ua P(x) l
`
a h
˜
u
,
u
t
,
y. Ch
´
u
,
ng minh b
`
˘
ang quy n
.
ap theo b
.
âc n c
,
ua P(x). Th
.
ât v
.
ây, v
´
o
,
i
n = 0, P(x) l
`
a h
`
˘
ang sô
´
v
`
a n
´
o l
`
a m
.
ôt sô
´
h
˜
u
,
u t
,
y (v
`
ı b
`
˘
ang v
´
ı d
.
u nhu
,
P(0)). Gi
,
a thiê
´
t kh
,
˘
ang
¯
d
.
inh
¯
d
´
ung v
´
o
,
i tâ
´
t c
,
a c
´
ac
¯
da th
´
u
,
c b
.
âc nh
,
o
ho
,
n sô
´
t
.
u
,
nhiên n (tâ
´
t nhiên tho
,
a m
˜
an
¯
diê
`
u ki
.
ên
¯
dâ
`
u b
`
ai) v
`
a cho
P(x) = a
0
x
n
+ a
1
x
n−1
+ ··· + a
n−1
x + a
n
. D
˜
ê thâ
´
y a
n
= P(0) l
`
a sô
´
h
˜
u
,
u t
,
y v
`
a nê
´
u ta
¯
d
.
˘
at
Q(x) = a
0
x
n−1
+ a
1
x
n−2
+ ··· + a
n−1
=
P(x) −a
n
x
,
th
`
ı Q(x ) s
˜
e nh
.
ân gi
´
a tr
.
i h
˜
u
,
u t
,
y v
´
o
,
i biê
´
n h
˜
u
,
u t
,
y x. Theo gi
,
a thiê
´
t
quy n
.
ap khi
¯
d
´
o nh
˜
u
,
ng sô
´
a
0
, a
1
, . . . , a
n−1
l
`
a h
˜
u
,
u t
,
y.
Nhu
,
v
.
ây h
.
ê sô
´
c
,
ua P(x) l
`
a h
˜
u
,
u t
,
y. V
´
o
,
i
¯
diê
`
u
¯
d
´
o P(x) không l
`
a
h
`
˘
ang sô
´
, v
`
ı trong tru
,
`
o
,
ng h
.
o
,
p ngu
,
.
o
,
c l
.
ai P(x) s
˜
e l
`
a h
˜
u
,
u t
,
y v
´
o
,
i m
.
oi
x. Cho P(x) = a
0
x
n
+ a
1
x
n−1
+ ··· + a
n
, n > 0. Không mâ
´
t t
´
ınh
tô
,
ng qu
´
at c
´
o thê
,
cho r
`
˘
ang a
i
l
`
a nguyên. Ngo
`
ai ra
¯
da th
´
u
,
c
Q(x) = a
n−1
0
.(P(x) − a
n
)
= (a
0
x)
n
+ a
1
(a
0
x)
n−1
+ ··· + a
n−1
a
n−2
0
(a
0
x).
Ngh
˜
ıa l
`
a
¯
da th
´
u
,
c
H(y) = y
n
+ a
1
y
n−1
+ ··· + a
n−1
a
n−2
0
y
tho
,
a m
˜
an
¯
diê
`
u ki
.
ên
¯
dâ
`
u b
`
ai.
Ta s
˜
e ch
´
u
,
ng minh r
`
˘
ang v
´
o
,
i m
.
oi sô
´
nguyên
¯
d
,
u l
´
o
,
n m phu
,
o
,
ng
tr
`
ınh H(y) = m c
´
o nghi
.
êm. Th
.
ât v
.
ây, lâ
´
y m > H(0) v
`
a ϕ(y) =
H(y) − m. Khi
¯
d
´
o ϕ(0) < 0 v
`
a lim
y→∞
ϕ(y) = +∞, v
`
ı thê
´
phu
,
o
,
ng
tr
`
ınh H(y) = m c
´
o nghi
.
êm du
,
o
,
ng y
m
. Lâ
´
y m = p l
`
a sô
´
nguyên tô
´

7.2. Nguyên l
´
y so s
´
anh c
´
ac h
.
ê sô
´
167
¯
d
,
u l
´
o
,
n. Ta c
´
o H(y
p
) = p. T
`
u
,
¯
diê
`
u ki
.
ên suy ra y
p
l
`
a sô
´
h
˜
u
,
u t
,
y v
`
a
v
`
ı h
.
ê sô
´
b
.
âc cao nhâ
´
t c
,
ua H(y) l
`
a 1, th
`
ı y
p
l
`
a nguyên v
`
a ngo
`
ai ra
y
p
¯
du
,
.
o
,
c chia hê
´
t b
,
o
,
i sô
´
h
.
ang t
.
u
,
do c
,
ua ϕ(y), ho
.
˘
ac l
`
a y
p
l
`
a u
,
´
o
,
c sô
´
c
,
ua p. Ngh
˜
ıa l
`
a y
p
= 1 ho
.
˘
ac l
`
a y
p
= p. Nhu
,
ng
¯
d
,
˘
ang th
´
u
,
c y
p
= 1
ch
,
ı c
´
o kh
,
a n
˘
ang nhiê
`
u nhâ
´
t v
´
o
,
i m
.
ôt p. Ngh
˜
ıa l
`
a y
p
= p cho tâ
´
t c
,
a
sô
´
nguyên tô
´
¯
d
,
u l
´
o
,
n p. N
´
oi c
´
ach kh
´
ac, ta
¯
d
˜
a nh
.
ân
¯
du
,
.
o
,
c H(p) = p
v
´
o
,
i tâ
´
t c
,
a sô
´
nguyên tô
´
¯
d
,
u l
´
o
,
n. T
`
u
,
nguyên l
´
y so s
´
anh c
´
ac h
.
ê sô
´
suy ra khi
¯
d
´
o H(y) = y v
`
a ngh
˜
ıa l
`
a P(x) = a
0
x + a
1
.
J
V
´
ı d
.
u 7.10. Cho P(x) l `a
¯
da th
´
u
,
c v
´
o
,
i h
.
ê sô
´
nguyên, v
´
o
,
i n´o P(0) =
P(1) = 1. v `a a
0
l `a sô
´
nguyên bâ
´
t k`y. Ta
¯
d
.
inh ngh˜ıa a
n+1
= P(a
n
)
v
´
o
,
i n ≥ 0. H ˜ay ch
´
u
,
ng minh r
`
˘ang v
´
o
,
i m 6= n c´o
¯
d
,
˘ang th
´
u
,
c sau
(a
m
, a
n
) = 1.
L
`
o
,
i gi
,
ai. Ta chia
¯
da th
´
u
,
c P(x) cho x(x −1). Lâ
´
y
P(x) = x(x −1)Q(x) + ax + b,
T
`
u
,
qu
´
a tr
`
ınh chia
¯
da th
´
u
,
c suy ra Q(x) l
`
a
¯
da th
´
u
,
c v
´
o
,
i h
.
ê sô
´
nguyên. Trong
¯
d
,
˘
ang th
´
u
,
c trên ta cho x = 0 v
`
a x = 1 v
`
a ch
´
u
´
y r
`
˘
ang P(0) = P(1) = 1,
¯
dô
´
i v
´
o
,
i a v
`
a b ta nh
.
ân
¯
du
,
.
o
,
c h
.
ê phu
,
o
,
ng
tr
`
ınh b = 1, a + b = 1, t
`
u
,
¯
dây suy ra b = 1 v
`
a a = 0, v
`
a nhu
,
v
.
ây
ta c
´
o P(x) = x(x − 1)Q(x) + 1,
,
o
,
¯
dây Q(x ) l
`
a
¯
da th
´
u
,
c v
´
o
,
i h
.
ê sô
´
nguyên.
Ta s
˜
e ch
´
u
,
ng minh b
`
˘
ang quy n
.
ap theo n,
¯
d
,
˘
ang th
´
u
,
c
a
n
≡ 1 (mod a
0
a
1
. . . a
n−1
),
t
`
u
,
¯
dây suy ra kê
´
t lu
.
ân c
,
ua b
`
ai to
´
an. Th
.
ât v
.
ây, cho m < n v
`
a
(a
m
, a
n
) = d, Khi
¯
d
´
o a
0
a
1
. . . a
n−1
chia hê
´
t cho d v
`
a suy ra a
n
− 1
chia hê
´
t cho d. Nhu
,
ng a
n
chia hê
´
t cho d, t
`
u
,
¯
dây a
n
−1 − a
n
chia
hê
´
t cho d hay l
`
a 1 chia hê
´
t cho d ho
.
˘
ac l
`
a d = 1.

168 Chu
,
o
,
ng 7. Ða th
´
u
,
c
Ch
,
ı c
`
on ch
´
u
,
ng minh r
`
˘
ang a
n
≡ 1 ( mod a
0
a
1
a
2
. . . a
n−1
) v
´
o
,
i m
.
oi
n. V
´
o
,
i n = 1 ta c
´
o a
1
= a
0
(a
0
− 1)Q(a
0
) + 1 v
`
a suy ra a
1
≡ 1
(mod a
0
). Gi
,
a thiê
´
t
¯
d
´
ung v
´
o
,
i n n
`
ao
¯
d
´
o a
n
≡ 1 (mod a
0
a
1
. . . a
n−1
)
ho
.
˘
ac l
`
a a
n
= 1 + ka
0
a
1
. . . a
n−1
,
,
o
,
¯
dây k l
`
a nguyên. V
´
o
,
i a
n+1
ta t
`
ım
¯
du
,
.
o
,
c
a
n+1
= a
n
(a
n
−1)Q(a
n
) + 1 = ka
0
a
1
. . . a
n−1
a
n
Q(a
n
) + 1,
t
`
u
,
¯
dây ta c
´
o a
n+1
≡ 1 ( mod a
0
a
1
. . . a
n−1
a
n
).
J
V
´
ı d
.
u 7.11. Cho d ˜ay c ´ac
¯
da th
´
u
,
c P
0
(x), P
1
(x), . . . , P
n
(x), . . . trong
¯
d´o P
0
(x) = 2, P
1
(x) = x v `a v
´
o
,
i m
.
oi n ≥ 1 th`ı
P
n+1
(x) + P
n−1
(x) = xP
n
(x).
Ch
´
u
,
ng minh r
`
˘ang tô
`
n t
.
ai ba sô
´
a, b v `a c sao cho v
´
o
,
i m
.
oi n ≥ 1 ta
¯
dê
`
u c´o
(x
2
−4)[P
2
n
(x) −4] = [aP
n+1
(x) + bP
n
(x) + cP
n−1
(x)]
2
. (7.6)
L
`
o
,
i gi
,
ai. Gi
,
a s
,
u
,
tô
`
n t
.
ai a, b, c
¯
dê
,
(7.6)
¯
d
´
ung v
´
o
,
i m
.
oi n. Khi
¯
d
´
o
(7.6)
¯
d
´
ung v
´
o
,
i n = 1. Thay n = 1 v
`
ao (7.6) suy ra
(x
2
−4)(x
2
−4) = [a(x
2
−2) + bx + 2c]
2
.
Ta nh
.
ân thâ
´
y nê
´
u ch
.
on a = 1, b = 0 v
`
a c = −1 th
`
ı
¯
d
,
˘
ang th
´
u
,
c trên
¯
du
,
.
o
,
c tho
,
a m
˜
an.
Bây gi
`
o
,
ta ch
´
u
,
ng minh: nê
´
u ch
.
on a = 1, b = 0, c = −1 th
`
ı (7.6)
¯
d
´
ung v
´
o
,
i m
.
oi n ≥ 2, t
´
u
,
c l
`
a ta ph
,
ai ch
´
u
,
ng minh
(x
2
−4)(P
2
n
(x) −4) = (P
n+1
(x) − P
n−1
(x))
2
. (7.6´)
V
`
ı P
n+1
(x) = xP
n
(x) − P
n−1
(x) nên (7.6´) tu
,
o
,
ng
¯
du
,
o
,
ng v
´
o
,
i
x
2
P
2
n
(x) −4P
2
n
(x) −4x
2
+ 16 = (xP
n
(x) −2P
n−1
(x))
2
= x
2
P
2
n
(x) −4xP
n
(x)P
n−1
(x) + 4P
2
n−1
(x).

7.3. Ð
.
ao h
`
am c
,
ua
¯
da th
´
u
,
c 169
Tu
,
o
,
ng
¯
du
,
o
,
ng v
´
o
,
i
P
2
n
(x) + x
2
−4 = P
n−1
(x)(xP
n
(x) − P
n−1
(x)) = P
n−1
(x)P
n+1
(x).
(7.7)
Ta s
˜
e ch
´
u
,
ng minh (7.7) b
`
˘
ang phu
,
o
,
ng ph
´
ap quy n
.
ap. V
´
o
,
i n = 1 th
`
ı
P
2
(x) = x
2
− 2, nên d
˜
ê d
`
ang thâ
´
y (7.7)
¯
d
´
ung. Gi
,
a s
,
u
,
(7.7)
¯
d
´
ung
v
´
o
,
i n = k , t
´
u
,
c l
`
a
P
2
k
(x) + x
2
−4 = P
k−1
(x)P
k+1
(x). (7.8)
Ta ph
,
ai ch
´
u
,
ng minh (7.7)
¯
d
´
ung v
´
o
,
i n = k + 1. Ta c
´
o
xP
k+1
(x)P
k
(x) = xP
k
(x)P
k+1
(x) ⇔
⇔(P
k+2
(x) + P
k
(x))P
k
(x) = (P
k+1
(x) + P
k−1
(x))P
k+1
(x)
⇔P
2
k
(x) + P
k
(x)P
k+2
(x) = P
2
k+1
(x) + P
k−1
(x)P
k+1
(x)
⇔P
2
k+1
(x) = P
2
k
(x) − P
k−1
(x)P
k+1
(x)) + P
k
(x)P
k+2
(x).
T
`
u
,
(7.8) suy ra
P
2
k+1
(x) = −(x
2
+ 4) −P
k
(x)P
k+2
(x).
¯
d
´
o l
`
a
¯
diê
`
u câ
`
n ch
´
u
,
ng minh.
J
7.3. Ð
.
ao h
`
am c
,
ua
¯
da th
´
u
,
c
Cho
¯
da th
´
u
,
c
P(x) = a
0
x
n
+ a
1
x
n−1
+ ··· + a
n
, (a
0
6= 0).
Ða th
´
u
,
c
P
0
(x) = na
0
x
n−1
+ (n −1)a
1
x
n−2
+ ··· + 2a
n−2
x + a
n−1
, (a
0
6= 0)
g
.
oi l
`
a
¯
d
.
ao h`am b
.
âc nhâ
´
t c
,
ua
¯
da th
´
u
,
c P(x). Ð
.
ao h
`
am c
,
ua
¯
d
.
ao
h
`
am b
.
âc nhâ
´
t P
0
(x) g
.
oi l
`
a
¯
d
.
ao h
`
am b
.
âc hai c
,
ua P(x) v
`
a k
´
y hi
.
êu
l
`
a P
00
(x). Ta c
´
o thê
,
¯
d
.
inh ngh
˜
ıa theo quy n
.
ap:
¯
d
.
ao h
`
am b
.
âc k c
,
ua

170 Chu
,
o
,
ng 7. Ða th
´
u
,
c
¯
da th
´
u
,
c P(x) l
`
a
¯
d
.
ao h
`
am c
,
ua
¯
d
.
ao h
`
am b
.
âc k −1 c
,
ua h
`
am P(x) v
`
a
k
´
y hi
.
êu l
`
a P
(k)
(x). Ho
.
˘
ac l
`
a, P
(k)
(x) = (P
(k−1)
(x))
0
.
T
`
u
,
¯
d
.
inh ngh
˜
ıa
¯
d
.
ao h
`
am c
,
ua
¯
da th
´
u
,
c ta d
˜
ê thâ
´
y c
´
ac t
´
ınh châ
´
t
sau
¯
d
´
ung:
1. Nê
´
u b
.
âc c
,
ua P(x) l
`
a n, th
`
ı b
.
âc c
,
ua P
0
(x) l
`
a n − 1 v
`
a
P
(n+1)
(x) = 0.
2. C
´
ac ph
´
ep t
´
ınh
¯
dô
´
i v
´
o
,
i
¯
d
.
ao h
`
am: nê
´
u P(x) v
`
a Q(x) l
`
a nh
˜
u
,
ng
¯
da th
´
u
,
c bâ
´
t k
`
y, c
`
on α l
`
a m
.
ôt sô
´
bâ
´
t k
`
y, th
`
ı
a) (P(x) ± Q(x))
0
= P
0
(x) ± Q
0
(x); (αP(x))
0
= αP
0
(x);
b) (P(x). Q(x))
0
= P
0
(x)Q(x) + P(x)Q
0
(x).
V
´
ı d
.
u 7.12. Ch
´
u
,
ng minh r
`
˘ang ((P(x))
n
)
0
= n(P(x ))
n−1
.P
0
(x).
L
`
o
,
i gi
,
ai. 1) Nê
´
u n = 1 th
`
ı P
0
(x) = P
0
(x).(P(x))
0
.
2) Gi
,
a s
,
u
,
((P(x))
n−1
)
0
= (n −1)(P(x))
n−2
.P
0
(x).
Khi
¯
d
´
o theo t
´
ınh châ
´
t b) ta c
´
o
((P(x))
n
)
0
= (P(x))
n−1
.P
0
(x) + (n −1)(P(x ))
n−2
.P
0
(x).P(x)
= n(P(x ))
n−1
.P
0
(x).
J
V
´
ı d
.
u 7.13. Ch
´
u
,
ng minh r
`
˘ang nê
´
u P(x) l `a
¯
da th
´
u
,
c bâ
´
t k`y b
.
âc n,
c`on a l `a m
.
ôt sô
´
bâ
´
t k`y, th`ı
P(x) = P(a) +
P
0
(a)
1!
(x −a) +
P
00
(a)
2!
(x −a)
2
+ ···+
P
(n)
(a)
n!
(x −a)
n
.
(Công th
´
u
,
c Taylor).
L
`
o
,
i gi
,
ai. Ch
´
u
,
ng minh b
`
˘
ang quy n
.
ap theo n b
.
âc c
,
ua
¯
da th
´
u
,
c P(x).

7.3. Ð
.
ao h
`
am c
,
ua
¯
da th
´
u
,
c 171
1) Nê
´
u n = 1, gi
,
a s
,
u
,
P(x) = A
0
+ A
1
(x − a). Khi
¯
d
´
o P
0
(x) =
A
1
(x − a)
0
= A
1
v
`
a nhu
,
v
.
ây P(a) = A
0
v
`
a P
0
(a) = A
1
, suy công
th
´
u
,
c Taylor
¯
d
´
ung cho
¯
da th
´
u
,
c b
.
âc nhâ
´
t. Gi
,
a s
,
u
,
công th
´
u
,
c
¯
d
´
ung
cho
¯
da th
´
u
,
c b
.
âc n −1. Nê
´
u P(x) l
`
a
¯
da th
´
u
,
c b
.
âc n v
`
a nê
´
u
P(x) = A
0
+ A
1
(x − a) + ··· + A
n−1
(x − a)
n−1
+ A
n
(x − a)
n
.
Khi
¯
d
´
o Q(x) = A
0
+ A
1
(x − a) + ··· + A
n−1
(x − a)
n−1
l
`
a
¯
da th
´
u
,
c
b
.
âc n −1 v
`
a theo gi
,
a thiê
´
t quy n
.
ap
A
0
= Q(a), A
1
=
Q
0
(a)
1!
, . . . , A
n−1
=
Q
(n−1)
(a)
( n −1)!
.
Ngo
`
ai ra ta c
`
on c
´
o
P
(i)
(x) = Q
(i)
(x) + n(n −1) . . . (n −i + 1)A
n
(x − a)
n−i
t
`
u
,
¯
d
´
o suy ra v
´
o
,
i i < n: P
(i)
(a) = Q
(i)
(a) v
`
a P
(n)
(a) = n!A
n
. Cuô
´
i
c
`
ung ch
´
ung ta nh
.
ân
¯
du
,
.
o
,
c:
A
0
= P(a), A
1
=
P
0
(a)
1!
, . . . , A
n−1
=
P
(n−1)
(a)
( n −1)!
A
n
=
P
(n)
(a)
n!
.
Suy ra công th
´
u
,
c Taylor
¯
d
´
ung v
´
o
,
i m
.
oi gi
´
a tr
.
i n.
J
V
´
ı d
.
u 7.14. Ch
´
u
,
ng minh r
`
˘ang nê
´
u P(x) v `a Q(x) l `a nh
˜
u
,
ng
¯
da
th
´
u
,
c bâ
´
t k`y v `a k l `a m
.
ôt sô
´
t
.
u
,
nhiên, th`ı
(P(x).Q(x))
(k)
= C
0
k
P
(k)
(x).Q(x) + C
1
k
P
(k−1)
(x)Q
0
(x)+
··· + C
k
k
P(x)Q
(k)
(x).
(Công th
´
u
,
c Leibniz).
L
`
o
,
i gi
,
ai. Ch
´
u
,
ng minh b
`
˘
ang phu
,
o
,
ng ph
´
ap quy n
.
ap theo k.
1) V
´
o
,
i k = 1 ta c
´
o
(P.Q)
0
= P
0
.Q + PQ
0
= C
0
1
P
0
Q + C
1
1
P.Q
0
.
Công th
´
u
,
c
¯
d
´
ung v
´
o
,
i k = 1.

172 Chu
,
o
,
ng 7. Ða th
´
u
,
c
2) Gi
,
a s
,
u
,
công th
´
u
,
c
¯
d
´
ung v
´
o
,
i sô
´
t
.
u
,
nhiên k. Khi
¯
d
´
o v
´
o
,
i k + 1
ta nh
.
ân
¯
du
,
.
o
,
c
(P.Q)
(k+1)
= ((P.Q )
(k)
)
0
= (C
0
k
P
(k)
.Q + ···+ C
s
k
P
(k−s)
.Q
(s)
+ ···)
0
= C
0
k
(P
(k+1)
.Q + P
k
Q
0
) + C
1
k
(P
(k)
.Q
0
+ P
(k−1)
.Q
00
) + ···
+ C
s
k
(P
k−s+1
Q(s) + P
(k−s)
Q
(s+1)
) + ···+ C
k
k
(P
0
Q
(k)
+ PQ
(k+1)
= C
0
k
P
(k+1)
.g + (C
0
k
+ C
1
k
)P
(k)
.Q
0
+ . . .
+ (C
s−1
k
+ C
s
k
)P
(k+1−s
.Q
(s)
+ ··· + C
k
k
P.Q
(k+1)
= C
0
k+1
P
(k+1)
.g + C
1
k+1
P
(k)
.Q
0
+ ···
+ C
s
k+1
P
(k+1−s)
.Q
(s)
+ ··· + C
k+1
k+1
PQ
(k+1)
.
Nhu
,
v
.
ây công th
´
u
,
c
¯
d
´
ung v
´
o
,
i m
.
oi sô
´
t
.
u
,
nhiên k.
J
7.4. Ða th
´
u
,
c Chebychev
Trong phâ
`
n n
`
ay ta x
´
et m
.
ôt d
.
ang
¯
d
.
˘
ac bi
.
êt c
,
ua
¯
da th
´
u
,
c gi
˜
u
,
vai
tr
`
o râ
´
t quan tr
.
ong trong nhiê
`
u b
`
ai to
´
an vê
`
l
´
y thuyê
´
t c
˜
ung nhu
,
k
˜
y thu
.
ât.
V
´
ı d
.
u 7.15. H `am sô
´
cos nθ, (n ∈ N) v
´
o
,
i thê
,
biê
,
u di
˜
ên nhu
,
¯
da th
´
u
,
c
b
.
âc n c
,
ua cos θ. Ngh˜ıa l `a,
cos nθ =
n
∑
i =0
a
n−i
cos
i
θ, a
0
6= 0. (7.9)
L
`
o
,
i gi
,
ai. 1) n = 0 v
`
a n = 2 m
.
ênh
¯
dê
`
hiê
,
n nhiên
¯
d
´
ung. V
´
o
,
i n = 2
v
`
a n = 3 ta nh
.
ân
¯
du
,
.
o
,
c
¯
da th
´
u
,
c tu
,
o
,
ng
´
u
,
ng b
.
âc hai, b
.
âc ba theo
công th
´
u
,
c lu
,
.
o
,
ng gi
´
ac.
cos 2θ = 2 cos
2
θ −1,
cos 3θ = 4 cos
3
θ −3 cos θ.

7.4. Ða th
´
u
,
c Chebychev 173
2) Gi
,
a s
,
u
,
m
.
ênh
¯
dê
`
¯
d
´
ung v
´
o
,
i n −1 v
`
a n, ngh
˜
ıa l
`
a
cos(n −1)θ =
n−1
∑
i =0
b
n−1−i
cos
i
θ, b
0
6= 0. (7.10)
cos nθ =
n
∑
i =0
c
n−i
cos
i
θ, c
0
6= 0.
Ta s
˜
e ch
´
u
,
ng minh trong tru
,
`
o
,
ng h
.
o
,
p
¯
d
´
o cos(n + 1)θ c
˜
ung c
´
o thê
,
biê
,
u di
˜
ên nhu
,
¯
da th
´
u
,
c c
,
ua cos θ c
´
o b
.
âc n + 1.
cos(n + 1)θ =
n+1
∑
i =0
d
n+1−i
cos
i
θ, d
0
6= 0. (7.11)
Ta
´
ap d
.
ung công th
´
u
,
c
cos nθ = 2 cos θ cos(n −1)θ −cos(n −2)θ,
¯
d
´
ung v
´
o
,
i m
.
oi n v
`
a θ. T
`
u
,
(7.11 ) v
`
a (7.10) suy ra
cos(n + 1)θ = 2 cos θ cos nθ − cos(n −1 )θ
= 2 cos θ
n
∑
i =0
c
n−i
cos
i
θ −
n−1
∑
i =0
b
n−1−i
cos
i
θ
= d
0
cos
n+1
θ + d
1
cos
n
θ + ···
Ta nh
.
ân thâ
´
y ngay
¯
dây l
`
a
¯
da th
´
u
,
c b
.
âc n + 1 c
,
ua cosθ, V
`
ı d
0
2c
0
6= 0
theo gi
,
a thiê
´
t quy n
.
ap.
Trong
¯
da th
´
u
,
c (7.9) c
,
ua cosθ, ta c
´
o thê
,
¯
du
,
a vê
`
d
.
ang m
.
ôt
¯
da
th
´
u
,
c chuâ
,
n t
´
˘
ac b
`
˘
ang c
´
ach
¯
d
.
˘
at x = cosθ v
`
a ta k
´
y hi
.
êu
¯
da th
´
u
,
c n
`
ay
l
`
a T
n
(x). Theo c
´
ach n
`
ay
T
n
(x) =
n
∑
i =0
a
n−i
x
i
. (7.12)
Ða th
´
u
,
c (7.12) g
.
oi l
`
a
¯
da th
´
u
,
c th
´
u
,
n-c
,
ua Chebychev. Nhu
,
v
.
ây do

174 Chu
,
o
,
ng 7. Ða th
´
u
,
c
công th
´
u
,
c (7.9) th
`
ı
¯
da th
´
u
,
c th
´
u
,
n c
,
ua Chebychev T
n
ta c
´
o:
T
0
(x) = 1, T
1
(x),
T
n
(x) = 2xT
n−1
(x) − T
n−2
(x), (n = 2, 3, . . .).
T
`
u
,
¯
d
,
˘
ang th
´
u
,
c trên ta t
`
ım
¯
du
,
.
o
,
c lâ
`
n lu
,
.
o
,
t c
´
ac
¯
da th
´
u
,
c c
,
ua Cheby-
chev v
´
o
,
i n = 2, 3, . . ..
T
0
(x) = 1,
T
1
(x) = x,
T
2
(x) = 2x
2
−1,
T
3
(x) = 4x
3
−3x,
T
4
(x) = 8x
4
−8x
2
+ 1,
T
5
(x) = 16x
5
−20x
3
+ 5x,
. . . . . .
V
´
ı d
.
u 7.16. Cho T
n
l `a
¯
da th
´
u
,
c th
´
u
,
n c
,
ua Chebychev. Ch
´
u
,
ng minh
m
.
ênh
¯
dê
`
sau: H
.
ê sô
´
,
o
,
¯
dô
´
i sô
´
c´o sô
´
m ˜u cao nhâ
´
t l `a 2
n−1
( n > 0).
L
`
o
,
i gi
,
ai. T
`
u
,
c
´
ac
¯
d
,
˘
ang th
´
u
,
c
,
o
,
b
`
ai tru
,
´
o
,
c m
.
ênh
¯
dê
`
¯
d
´
ung v
´
o
,
i n =
1, 2, 3, 4, 5. Gi
,
a s
,
u
,
m
.
ênh
¯
dê
`
¯
d
´
ung v
´
o
,
i sô
´
n n
`
ao
¯
d
´
o. Ta ch
´
u
,
ng minh
¯
d
´
ung cho n + 1 b
`
˘
ang c
´
ach suy ra t
`
u
,
công th
´
u
,
c
T
n+1
(x) = 2xT
(
x) − T
n−1
(x)
v
`
a nguyên l
´
y so s
´
anh c
´
ac h
.
ê sô
´
c
,
ua
¯
da th
´
u
,
c.
J
7.5. B
`
aii t
.
âp
.
.
. 7.17. Cho n l
`
a sô
´
t
.
u
,
nhiên v
`
a P(x) l
`
a
¯
da th
´
u
,
c b
.
âc nh
,
o ho
,
n n.
Ch
´
u
,
ng minh r
`
˘
ang tô
`
n t
.
ai m
.
ôt h
`
am h
˜
u
,
u t
,
y R(x) sao cho
P(x) = x(x + 1) . . . (x + n)(R(x + 1) − R(x)).

7.5. B
`
aii t
.
âp 175
.
.
. 7.18. K
´
y hi
.
êu P
0
(x), P
1
(x), P
2
(x), . . . , P
n
(x) l
`
a nh
˜
u
,
ng
¯
da th
´
u
,
c
P
0
(x) = 1, P
1
(x) = x, P
2
(x) =
x(x −1)
1.2
, . . .
P
n
(x) =
x(x −1)(x −2) . . . (x −n + 1)
1.2.3 . . . n
.
Ch
´
u
,
ng minh r
`
˘
ang m
.
oi
¯
da th
´
u
,
c P(x) b
.
âc n c
´
o thê
,
biê
,
u di
˜
ên du
,
´
o
,
i
d
.
ang
P(x) = b
0
P
0
(x) + b
1
P
1
(x) + ··· + b
n
P
n
(x),
,
o
,
¯
dây b
0
, b
1
, . . . , b
n
l
`
a nh
˜
u
,
ng sô
´
n
`
ao
¯
d
´
o.
.
.
. 7.19. Cho d
˜
ay sô
´
Fibonacci u
1
= 1, u
2
= 1, u
i +2
= u
i +1
+ u
i
,
¯
d
.
˘
at
F
n
(x) =
n
∑
i =1
u
i
x
i
. Ch
´
u
,
ng minh r
`
˘
ang
F
n
(x) =
u
n
x
n+2
+ u
n+1
x
n+1
− x
x
2
+ x −1
, (x
2
+ x −1 6= 0)
.
.
. 7.20. Ch
´
u
,
ng minh r
`
˘
ang h
`
am
sin(n + 1)θ
sin θ
c
´
o thê
,
biê
,
u di
˜
ên nhu
,
¯
da th
´
u
,
c U
n
b
.
âc n c
,
ua cos θ (g
.
oi l
`
a
¯
da th
´
u
,
c lo
.
ai hai b
.
âc th
´
u
,
n c
,
ua
Chebychev).
.
.
. 7.21. Ch
´
u
,
ng minh r
`
˘
ang nh
˜
u
,
ng
¯
da th
´
u
,
c lo
.
ai hai Chebychev
tho
,
a m
˜
an nh
˜
u
,
ng
¯
d
,
˘
ang th
´
u
,
c sau:
U
0
(x) = 1, U
1
(x) = 2x, U
n+1
(x) = 2xU
n
(x) −U
n−1
(x).
.
.
. 7.22. Cho
¯
da th
´
u
,
c P(x) = a
0
+ a
1
x + ··· + a
n
x
n
b
.
âc n v
´
o
,
i h
.
ê
sô
´
th
.
u
,
c v
`
a a ≥ 3 l
`
a m
.
ôt sô
´
th
.
u
,
c. Ch
´
u
,
ng minh r
`
˘
ang
´
ıt nhâ
´
t m
.
ôt
trong c
´
ac sô
´
|1 −P(0)|, |a −P(1)|, |a
2
−P(2)|, . . . , |a
n+1
−P(n + 1)|
không nh
,
o ho
,
n 1.
.
.
. 7.23. Ch
´
u
,
ng minh r
`
˘
ang v
´
o
,
i
¯
da th
´
u
,
c P
n
(x) = x
n
+ x
n−2
+ x
n−4
+
··· Bâ
´
t
¯
d
,
˘
ang th
´
u
,
c sau
¯
d
´
ung v
´
o
,
i m
.
oi x > 0 v
`
a n = 1, 2, . . .
P
n
(x) + P
n
(
1
x
) ≥ n + 1 +
1
2
(1 + (−1)
n
).

CHU
,
O
,
NG 8
TÔ
,
H
.
O
,
P V
`
A Ð
,
˘
ANG TH
´
U
,
C
8.1. M
.
ôt sô
´
công th
´
u
,
c tô
,
h
.
o
,
p . . . . . . . . . . . . . . . . . . . . . . . . . . . . 176
8.2. M
.
ôt sô
´
¯
d
,
˘
ang th
´
u
,
c.. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 186
8.3. B
`
ai t
.
âp .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 193
Trong chu
,
o
,
ng n
`
ay ta ch
´
u
,
ng minh m
.
ôt sô
´
¯
d
,
˘
ang th
´
u
,
c v
`
a
¯
d
.
inh
l
´
y liên quan
¯
dê
´
n
¯
d
,
˘
ang th
´
u
,
c, cô
´
g
´
˘
ang ch
´
u
,
ng minh b
`
˘
ang phu
,
o
,
ng
ph
´
ap quy n
.
ap to
´
an h
.
oc. Ðê
,
ng
´
˘
an g
.
on khi
´
ap d
.
ung nguyên l
´
y quy
n
.
ap to
´
an h
.
oc ta tr
`
ınh b
`
ay lâ
`
n lu
,
.
o
,
t c
´
ac bu
,
´
o
,
c m
.
ôt c
´
ach t
.
u
,
nhiên,
không nhâ
´
n m
.
anh nhu
,
c
´
ac chu
,
o
,
ng tru
,
´
o
,
c n
˜
u
,
a.
8.1. M
.
ôt sô
´
công th
´
u
,
c tô
,
h
.
o
,
p
Trong m
.
uc n
`
ay ta quan tâm t
´
o
,
i t
.
âp h
.
o
,
p gô
`
m h
˜
u
,
u h
.
an
c
´
ac phâ
`
n t
,
u
,
, v
´
ı d
.
u nhu
,
t
.
âp gô
`
m n phâ
`
n t
,
u
,
k
´
y hi
.
êu X =
{a
1
, a
2
, . . . , a
n
}. Khi xem x
´
et c
´
ac t
.
âp n
`
ay ch
´
ung ta quan tâm t
´
o
,
i
v
.
i tr
´
ı s
´
˘
ap xê
´
p c
,
ua c
´
ac phâ
`
n t
,
u
,
. Khi
¯
d
´
o ta n
´
oi t
.
âp X l
`
a t
.
âp
¯
du
,
.
o
,
c
s
´
˘
ap. Nh
˜
u
,
ng b
`
ai to
´
an tô
,
h
.
o
,
p quan tâm t
´
o
,
i sô
´
lu
,
.
o
,
ng c
´
ach s
´
˘
ap xê
´
p
nh
˜
u
,
ng phâ
`
n t
,
u
,
trong m
.
ôt t
.
âp h
.
o
,
p h
˜
u
,
u h
.
an. Ch
´
ung ta quan tâm
t
´
o
,
i nh
˜
u
,
ng d
.
ang co
,
b
,
an c
,
ua b
`
ai to
´
an tô
,
h
.
o
,
p nhu
,
sau:
M
.
ôt d
˜
ay n phâ
`
n t
,
u
,
kh
´
ac nhau c
,
ua t
.
âp h
.
o
,
p X s
´
˘
ap xê
´
p theo
m
.
ôt th
´
u
,
t
.
u
,
nhâ
´
t
¯
d
.
inh
¯
du
,
.
o
,
c g
.
oi l
`
a m
.
ôt ho ´an v
.
i c
,
ua X.
G
.
oi P
n
l
`
a sô
´
ho
´
an v
.
i c
,
ua n phâ
`
n t
,
u
,
. Ta c
´
o thê
,
x
´
et m
.
ôt sô
´
tru
,
`
o
,
ng

8.1. M
.
ôt sô
´
công th
´
u
,
c tô
,
h
.
o
,
p 177
h
.
o
,
p c
.
u thê
,
sau
n T
.
âp X C
´
ac ho
´
an v
.
i c
,
ua X Sô
´
ho
´
an v
.
i
0 ∅ ∅ 1 = 0!
1 {a } (a) 1 = 1!
2 {a
1
, a
2
} (a
1
, a
2
); (a
2
, a
1
) 2 = 2!
3 {a
1
, a
2
, a
3
} (a
1
, a
2
, a
3
); (a
1
, a
3
, a
2
); 6 = 3!
(a
2
, a
1
, a
3
); (a
2
, a
3
, a
1
);
(a
3
, a
1
, a
2
); (a
3
, a
2
, a
1
);
. . . . . . . . . . . .
V
´
o
,
i phu
,
o
,
ng ph
´
ap quy n
.
ap to
´
an h
.
oc ta d
.
u
,
¯
do
´
an v
`
a ch
´
u
,
ng minh
V
´
ı d
.
u 8.1. Sô
´
lu
,
.
o
,
ng ho´an v
.
i c
,
ua n phâ
`
n t
,
u
,
c´o thê
,
t´ınh b
`
˘ang công
th
´
u
,
c
P
n
= n!. (8.1)
L
`
o
,
i gi
,
ai. Ta ch
´
u
,
ng minh công th
´
u
,
c (8.1) b
`
˘
ang phu
,
o
,
ng ph
´
ap quy
n
.
ap to
´
an h
.
oc:
1) Theo b
,
ang trên công th
´
u
,
c (8.1)
¯
d
´
ung v
´
o
,
i n = 1.
2) Gi
,
a s
,
u
,
(8.1)
¯
d
´
ung v
´
o
,
i n = k ≥ 1. Ho
´
an v
.
i c
,
ua k + 1 phâ
`
n
t
,
u
,
c
´
o thê
,
l
.
âp nhu
,
sau: cô
´
¯
d
.
inh v
.
i tr
´
ı th
´
u
,
nhâ
´
t cho m
˜
ôi phâ
`
n t
,
u
,
(ngh
˜
ıa l
`
a c
´
o k + 1 c
´
ach) rô
`
i s
´
˘
ap k phâ
`
n t
,
u
,
c
`
on l
.
ai v
`
ao c
´
ac v
.
i tr
´
ı
tiê
´
p theo (theo gi
,
a thiê
´
t c
´
o P
k
c
´
ach). Do
¯
d
´
o
P
k+1
= (k + 1)P
k
= (k + 1)k! = (k + 1)!
Nhu
,
v
.
ây công th
´
u
,
c (8.1)
¯
d
´
ung v
´
o
,
i n = k + 1.
J
M
.
ôt d
˜
ay m phâ
`
n t
,
u
,
kh
´
ac nhau (m ≤ n) c
,
ua t
.
âp h
.
o
,
p X s
´
˘
ap
xê
´
p theo m
.
ôt th
´
u
,
t
.
u
,
x
´
ac
¯
d
.
inh
¯
du
,
.
o
,
c g
.
oi l
`
a m
.
ôt ch
,
ınh h
.
o
,
p ch
.
âp
m c
,
ua n phâ
`
n t
,
u
,
trong X.
K
´
y hi
.
êu A
m
n
l
`
a sô
´
lu
,
.
o
,
ng c
´
ac ch
,
ınh h
.
o
,
p ch
.
âp m c
,
ua n phâ
`
n t
,
u
,
.
Ta x
´
et m
.
ôt sô
´
v
´
ı d
.
u sau
178 Chu
,
o
,
ng 8. Tô
,
h
.
o
,
p v
`
a
¯
d
,
˘
ang th
´
u
,
c
m C
´
ac ch
,
ınh h
.
o
,
p c
,
ua X = {a
1
, a
2
, a
3
, a
4
} Sô
´
ch
,
ınh h
.
o
,
p
1 (a
1
); (a
2
); (a
3
); (a
4
); 4 = 4
2 (a
1
, a
2
); (a
2
, a
1
); (a
1
, a
3
); (a
3
, a
1
); 12 = 4.3
(a
1
, a
4
); (a
4
, a
1
); (a
2
, a
3
); (a
3
, a
2
);
(a
2
, a
4
); (a
4
, a
2
); (a
3
, a
4
); (a
4
, a
3
);
3 (a
1
, a
2
, a
3
); (a
1
, a
2
, a
4
); (a
2
, a
1
, a
4
) 24 = 4.3.2
(a
1
, a
3
, a
4
); (a
2
, a
3
, a
4
); (a
3
, a
1
, a
4
)
. . . . . . . . .
Ta ch
´
u
,
ng minh công th
´
u
,
c sau:
V
´
ı d
.
u 8.2. Sô
´
lu
,
.
o
,
ng ch
,
ınh h
.
o
,
p ch
.
âp m c
,
ua n phâ
`
n t
,
u
,
¯
du
,
.
o
,
c t´ınh
theo công th
´
u
,
c sau:
A
m
n
= n(n −1) . . . (n −m + 1). (8.2)
L
`
o
,
i gi
,
ai. Ch
´
u
,
ng minh b
`
˘
ang quy n
.
ap to
´
an h
.
oc
1) V
´
o
,
i m = 1 ta c
´
o A
1
n
= n, suy ra công th
´
u
,
c (8.2)
¯
d
´
ung v
´
o
,
i
m = 1.
2) Gi
,
a s
,
u
,
(8.2)
¯
d
´
ung v
´
o
,
i m = k ≥ 1, ngh
˜
ıa l
`
a
A
k
n
= n(n −1) . . . (n −k + 1)
C
´
ac ch
,
ınh h
.
o
,
p ch
.
âp k + 1 nh
.
ân
¯
du
,
.
o
,
c t
`
u
,
nh
˜
u
,
ng ch
,
ınh h
.
o
,
p ch
.
âp
k b
`
˘
ang c
´
ach thêm v
`
ao cuô
´
i d
˜
ay m
.
ôt trong n − k phâ
`
n t
,
u
,
c
`
on l
.
ai.
Nhu
,
v
.
ây m
.
ôt ch
,
ınh h
.
o
,
p ch
.
âp k s
˜
e cho n −k ch
,
ınh h
.
o
,
p ch
.
âp k + 1.
Do
¯
d
´
o
A
k+1
n
= (n − k)A
k
n
= n(n −1)(n −2) . . . (n −k + 1)(n −k)
Suy ra (8.2)
¯
d
´
ung v
´
o
,
i m = k + 1.
J
Ch
´
u
´
y: C
´
o thê
,
viê
´
t công th
´
u
,
c (8.2) du
,
´
o
,
i d
.
ang kh
´
ac
A
m
n
=
n!
( n −m)!
. (8.3)
8.1. M
.
ôt sô
´
công th
´
u
,
c tô
,
h
.
o
,
p 179
M
˜
ôi t
.
âp con m phâ
`
n t
,
u
,
kh
´
ac nhau c
,
ua t
.
âp X(m ≤ n)
¯
du
,
.
o
,
c g
.
oi
l
`
a tô
,
h
.
o
,
p ch
.
âp m c
,
ua n phâ
`
n t
,
u
,
c
,
ua X.
G
.
oi C
m
n
(ho
.
˘
ac nhu
,
c
´
ac phâ
`
n tru
,
´
o
,
c
¯
d
˜
a k
´
y hi
.
êu l
`
a C
m
n
). Ta x
´
et
m
.
ôt sô
´
v
´
ı d
.
u sau
m C
´
ac tô
,
h
.
o
,
p c
,
ua X = {a
1
, a
2
, a
3
, a
4
} Sô
´
tô
,
h
.
o
,
p
1 (a
1
); (a
2
); (a
3
); (a
4
); 4
2 (a
1
, a
2
); (a
1
, a
3
); (a
1
, a
4
); 6
(a
2
, a
3
); (a
2
, a
4
); (a
3
, a
4
);
3 (a
1
, a
2
, a
3
); (a
1
, a
2
, a
4
); 4
(a
1
, a
3
, a
4
); (a
2
, a
3
, a
4
);
4 (a
1
, a
2
, a
3
, a
4
); 1
. . . . . . . . .
Ch
´
ung ta nh
.
ân ra ngay l
`
a c
´
ac ch
,
ınh h
.
o
,
p ch
.
âp m c
,
ua n phâ
`
n t
,
u
,
nh
.
ân
¯
du
,
.
o
,
c t
`
u
,
c
´
ac tô
,
h
.
o
,
p ch
.
âp m b
`
˘
ang c
´
ach ho
´
an v
.
i m phâ
`
n t
,
u
,
n
`
ay. V
`
ı v
.
ây ta c
´
o liên h
.
ê sau
A
m
n
= C
m
n
.P
m
.
T
`
u
,
¯
d
´
o suy ra
C
m
n
=
A
m
n
P
m
=
n!
m!(n −m)!
.
Ðê
,
ch
´
u
,
ng minh theo phu
,
o
,
ng ph
´
ap quy n
.
ap ta ch
´
u
,
ng minh
V
´
ı d
.
u 8.3. Sô
´
lu
,
.
o
,
ng tô
,
h
.
o
,
p ch
.
âp m c
,
ua n
¯
du
,
.
o
,
c t´ınh theo công
th
´
u
,
c sau
C
m
n
=
n(n − 1) . . . (n −m + 1 )
1.2 . . . m
. (8.4)
L
`
o
,
i gi
,
ai. 1) Ta ch
´
u
´
y r
`
˘
ang C
1
n
= n, ngh
˜
ıa l
`
a v
´
o
,
i m = 1 công th
´
u
,
c
¯
d
´
ung.
2) Gi
,
a s
,
u
,
ta c
´
o
C
k
n
=
n(n − 1) . . . (n −k + 1)
1.2 . . . k
.

180 Chu
,
o
,
ng 8. Tô
,
h
.
o
,
p v
`
a
¯
d
,
˘
ang th
´
u
,
c
Ta s
˜
e ch
´
u
,
ng minh r
`
˘
ang
C
k+1
n
=
n(n − 1) . . . (n −k + 1)(n − k)
1.2 . . . k(k + 1)
.
Ðê
,
nh
.
ân tâ
´
t c
,
a tô
,
h
.
o
,
p k + 1 phâ
`
n t
,
u
,
trong n phâ
`
n t
,
u
,
:
¯
dâ
`
u tiên
ngu
,
`
o
,
i ta viê
´
t tâ
´
t c
,
a c
´
ac tô
,
h
.
o
,
p ch
.
âp k c
,
ua n phâ
`
n t
,
u
,
v
`
a thêm
v
`
ao m
˜
ôi tô
,
h
.
o
,
p n
`
ay m
.
ôt phâ
`
n t
,
u
,
th
´
u
,
k + 1 b
,
o
,
i m
.
ôt trong n − k
phâ
`
n t
,
u
,
c
`
on l
.
ai. Nhu
,
v
.
ây ta nh
.
ân
¯
du
,
.
o
,
c tâ
´
t c
,
a tô
,
h
.
o
,
p ch
.
âp k + 1
c
,
ua n phâ
`
n t
,
u
,
, nhu
,
ng s
˜
e nh
.
ân
¯
du
,
.
o
,
c b
.
ôi k + 1 lâ
`
n. Th
.
ât v
.
ây,
tô
,
h
.
o
,
p a
1
, a
2
, . . . , a
k
, a
k+1
s
˜
e c
`
ung nh
.
ân
¯
du
,
.
o
,
c theo c
´
ach; khi tô
,
h
.
o
,
p a
2
, a
3
, . . . , a
k
, a
k+1
thêm v
`
ao phâ
`
n t
,
u
,
a
1
; c
˜
ung nhu
,
khi tô
,
h
.
o
,
p
a
1
, a
3
, . . . , a
k
, a
k+1
thêm v
`
ao phâ
`
n t
,
u
,
a
2
; . . . ; cuô
´
i c
`
ung khi tô
,
h
.
o
,
p
a
1
, a
2
, a
3
, . . . , a
k
thêm v
`
ao a
k+1
. Ngh
˜
ıa l
`
a
C
k
n
= C
k
n
m − k
k + 1
=
n(n − 1) . . . (n −k + 1)(n − k)
1.2 . . . k(k + 1)
.
J
V
´
ı d
.
u 8.4. Ch
´
u
,
ng minh r
`
˘ang h
.
ê sô
´
Newton C
k
n
l `a nh
˜
u
,
ng sô
´
l
,
e khi
v `a ch
,
ı khi n = 2
s
−1.
L
`
o
,
i gi
,
ai. V
´
o
,
i n ≤ 8 m
.
ênh
¯
dê
`
khiê
,
m tra tr
.
u
,
c tiê
´
p
¯
d
´
ung. Gi
,
a s
,
u
,
n l
`
a sô
´
t
.
u
,
nhiên bâ
´
t k
`
y v
`
a gi
,
a s
,
u
,
m
.
ênh
¯
dê
`
kh
,
˘
ang
¯
d
.
inh
¯
d
´
ung v
´
o
,
i
m
.
oi sô
´
t
.
u
,
nhiên nh
,
o ho
,
n n. D
˜
ê thâ
´
y h
.
ê sô
´
¯
da th
´
u
,
c l
`
a
n
1
,
n(n − 1)
1.2
,
n(n − 1)(n −2)
1.2.3
, . . . ,
n(n − 1)(n −2) . . . 3.2
1.2.3 . . . (n −1)
,
tâ
´
t c
,
a l
`
a sô
´
l
,
e khi v
`
a ch
,
ı khi h
.
ê sô
´
¯
da th
´
u
,
c ngo
`
ai c
`
ung (m
`
a n
´
o
b
`
˘
ang n) l
`
a sô
´
l
,
e v
`
a nh
˜
u
,
ng sô
´
nh
.
ân
¯
du
,
.
o
,
c t
`
u
,
c
´
ac h
.
ê sô
´
¯
da th
´
u
,
c c
`
on
l
.
ai b
`
˘
ang c
´
ach b
,
o
¯
di c
´
ac th
`
u
,
a sô
´
l
,
e
,
o
,
m
˜
âu sô
´
v
`
a t
,
u
,
sô
´
, c
˜
ung l
`
a l
,
e. Ta
¯
d
.
˘
at n = 2m + 1. Trong tru
,
`
o
,
ng h
.
o
,
p nhu
,
v
.
ây h
.
ê sô
´
¯
da th
´
u
,
c không
c
´
o sô
´
cuô
´
i biê
,
u di
˜
ên b
`
˘
ang c
´
ac sô
´
trong d
˜
ay
m
1
,
m(m − 1)
1.2
,
m(m − 1)(m −2)
1.2.3
, . . . ,
m(m − 1)(m −2) . . . 3.2
1.2.3 . . . (m −1)
.

8.1. M
.
ôt sô
´
công th
´
u
,
c tô
,
h
.
o
,
p 181
T
`
u
,
¯
dây theo gi
,
a thiê
´
t quy n
.
ap to
´
an h
.
oc nh
˜
u
,
ng h
.
ê sô
´
¯
da th
´
u
,
c cuô
´
i
c
`
ung, c
`
on suy ra tâ
´
t c
,
a h
.
ê sô
´
¯
da th
´
u
,
c s
˜
e l
`
a l
,
e khi v
`
a ch
,
ı khi m c
´
o
d
.
ang 2
k
−1 ngh
˜
ıa l
`
a khi
¯
d
´
o n2(2
k
−1) + 1 = 2
k+1
−1.
J
V
´
ı d
.
u 8.5. Ch
´
u
,
ng minh r
`
˘ang t
`
u
,
c ´ac ch
˜
u
,
sô
´
1 v `a 2 ta c´o thê
,
l
.
âp
2
n+1
sô
´
m `a m
˜
ôi sô
´
¯
dê
`
u c´o 2
n
ch
˜
u
,
sô
´
v `a c
´
u
,
hai sô
´
m
.
ôt th`ı c ´ac ch
˜
u
,
sô
´
,
o
,
h `ang tu
,
o
,
ng
´
u
,
ng (v
.
i tr´ı tu
,
o
,
ng
´
u
,
ng) kh ´ac nhau không ´ıt ho
,
n
2
n−1
.
L
`
o
,
i gi
,
ai. Ta ch
´
u
,
ng minh b
`
˘
ang quy n
.
ap theo n. V
´
o
,
i n = 1 ta
¯
du
,
.
o
,
c
bô
´
n sô
´
11; 21; 12; v
`
a 22 tho
,
a m
˜
an m
.
ênh
¯
dê
`
.
G
.
oi a
0
l
`
a sô
´
c
´
o
¯
du
,
.
o
,
c khi thay trong a ch
˜
u
,
sô
´
1 b
`
˘
ang ch
˜
u
,
sô
´
2 v
`
a
thay 2 b
`
˘
ang 1 v
`
a
ab l
`
a sô
´
t
.
ao th
`
anh khi viê
´
t b c
.
anh a. Gi
,
a s
,
u
,
¯
d
˜
a
xây d
.
u
,
ng
¯
du
,
.
o
,
c t
.
âp h
.
o
,
p A
n
t
`
u
,
2
n+1
sô
´
, m
˜
ôi sô
´
c
´
o 2
n
ch
˜
u
,
sô
´
, ngo
`
ai
ra c
´
u
,
hai sô
´
m
.
ôt kh
´
ac nhau không
´
ıt ho
,
n 2
n−1
v
.
i tr
´
ı h
`
ang sô
´
.
X
´
et t
.
âp h
.
o
,
p A
n+1
gô
`
m c
´
ac sô
´
aa v
`
a aa
0
trong
¯
d
´
o a ∈ A
n
. Tâ
´
t c
,
a
nh
˜
u
,
ng sô
´
n
`
ay c
´
o 2
n+1
ch
˜
u
,
sô
´
v
`
a tâ
´
t c
,
a c
´
o 2
n+2
sô
´
. Ngo
`
ai ra bâ
´
t c
´
u
,
hai sô
´
n
`
ao
¯
dê
`
u kh
´
ac nhau không
´
ıt ho
,
n 2
n
h
`
ang sô
´
. Th
.
ât v
.
ây, c
´
ac
sô
´
aa v
`
a aa
0
, c
˜
ung nhu
,
c
´
ac sô
´
aa v
`
a bb
0
v
´
o
,
i m
.
oi a, b
¯
dê
`
u kh
´
ac nhau
¯
d
´
ung 2
n
h
`
ang sô
´
(trong c
´
ac h
`
ang sô
´
n
`
ay a v
`
a b kh
´
ac nhau, a
0
v
`
a
b
0
tr
`
ung nhau, v
`
a ngu
,
.
o
,
c l
.
ai). C
´
ac sô
´
aa v
`
a bb theo gi
,
a thiê
´
t quy
n
.
ap kh
´
ac nhau không
´
ıt ho
,
n 2
n
h
`
˘
ang sô
´
.
J
V
´
ı d
.
u 8.6. V
´
o
,
i c ´ac sô
´
nguyên m, n (0 ≤ m ≤ n) xây d
.
u
,
ng c ´ac sô
´
d(n, m) theo công th
´
u
,
c sau:
1) d(n, 0) = d(n, m) = 1, v
´
o
,
i m
.
oi n ≥ 0;
2) m.d(n, m) = m.d(n − 1, m) + (2n − m).d(n − 1, m −1), v
´
o
,
i m
.
oi
0 < m < n.
Ch
´
u
,
ng minh r
`
˘ang tâ
´
t c
,
a c ´ac sô
´
d(n, m)
¯
dê
`
u nguyên.

182 Chu
,
o
,
ng 8. Tô
,
h
.
o
,
p v
`
a
¯
d
,
˘
ang th
´
u
,
c
L
`
o
,
i gi
,
ai. Ta s
˜
e ch
´
u
,
ng minh b
`
˘
ang quy n
.
ap r
`
˘
ang d(n , m) = (C
m
n
)
2
.
Th
.
ât v
.
ây, v
´
o
,
i n = 1 th
`
ı
d(1, 0) = 1 =
C
0
1
2
; d(1, 1) = 1 =
C
0
1
2
.
Gi
,
a s
,
u
,
b
`
ai to
´
an
¯
d
´
ung v
´
o
,
i n = k: d(k, m) = (C
m
k
)
2
, v
´
o
,
i m
.
oi 0 ≤ m ≤
k. Khi
¯
d
´
o v
´
o
,
i n = k + 1, ta c
´
o
1) Nê
´
u 0 < m < k + 1 th
`
ı
m.d(k + 1,m) = m.d(k, m) + [2(k + 1) −m]d(k, m −1)
= m.
(
C
m
k
)
2
+ ( 2k + 2 − m)
C
m−1
k
2
=
k!
m!(k + 1 − m)!
2
[m(k + 1 − m)
2
+ ( 2k + 2 − m)m
= m.
C
m
k+1
2
.
2) Nê
´
u m = 0 ho
.
˘
ac k + 1, th
`
ı d(k + 1, 0) = 1 = (C
0
k+1
)
2
v
`
a
d(k + 1, k + 1) = 1 = (C
k+1
k+1
)
2
. V
.
ây theo nguyên l
´
y quy n
.
ap to
´
an
h
.
oc, ta c
´
o
d(n, m) =
(
C
m
n
)
2
, ∀0 ≤ m ≤ n.
J
V
´
ı d
.
u 8.7. Cho sô
´
lu
,
.
o
,
ng 3
n
¯
dô
`
ng xu ( n ≥ 1 ), m
.
ôt
¯
dô
`
ng xu trong
¯
d´o l `a gi
,
a v `a nh
.
e ho
,
n sô
´
c`on l
.
ai. Cho m
.
ôt chiê
´
c cân
¯
d˜ıa không c´o
qu
,
a cân. Ch
´
u
,
ng minh r
`
˘ang b
`
˘ang n lâ
`
n cân c´o thê
,
ph ´at hi
.
ên ra
¯
dô
`
ng tiê
`
n gi
,
a. C´o thê
,
b
`
˘ang n lâ
`
n cân luôn luôn ph ´at hi
.
ên ra
¯
dô
`
ng
tiê
`
n gi
,
a hay không, nê
´
u sô
´
lu
,
.
o
,
ng
¯
dô
`
ng xu không nh
,
o ho
,
n 3
n
+ 1?
L
`
o
,
i gi
,
ai. X
´
et tru
,
`
o
,
ng h
.
o
,
p n = 1. Ta
¯
d
.
˘
at hai
¯
dô
`
ng xu lên m
˜
ôi bên
m
.
ôt
¯
d
˜
ıa cân. Nê
´
u cân th
˘
ang b
`
˘
ang, th
`
ı
¯
dô
`
ng xu gi
,
a l
`
a
¯
dô
`
ng xu c
`
on
l
.
a
,
o
,
ngo
`
ai cân, c
`
on trên cân không cân b
`
˘
ang,
¯
dô
`
ng tiê
`
n gi
,
a n
`
˘
am
,
o
,
bên n
`
ao nh
.
e ho
,
n.
8.1. M
.
ôt sô
´
công th
´
u
,
c tô
,
h
.
o
,
p 183
Ta gi
,
a s
,
u
,
kh
,
˘
ang
¯
d
.
inh c
,
ua b
`
ai to
´
an
¯
d
´
ung v
´
o
,
i n −1. Bây gi
`
o
,
ta
c
´
o 3
n
. Ta chia ch
´
ung ra l
`
am ba nh
´
om theo 3
n−1
¯
dô
`
ng xu v
`
a
¯
d
.
˘
at
hai nh
´
om lên t
`
u
,
ng
¯
d
˜
ıa cân. Nê
´
u cân cân b
`
˘
ang, th
`
ı
¯
dô
`
ng xu gi
,
a
,
o
,
nh
´
om th
´
u
,
3, c
`
on ngu
,
.
o
,
c l
.
ai th
`
ı
,
o
,
nh
´
om trên
¯
d
˜
ıa cân nh
.
e ho
,
n. V
`
a
c
,
a hai tru
,
`
o
,
ng h
.
o
,
p kh
,
˘
ang
¯
d
.
inh c
,
ua b
`
ai to
´
an suy ra theo quy n
.
ap.
Ta s
˜
e ch
´
u
,
ng minh r
`
˘
ang nê
´
u sô
´
lu
,
.
o
,
ng
¯
dô
`
ng xu l
´
o
,
n ho
,
n 3
n
, th
`
ı
không ph
,
ai l
´
uc n
`
ao c
˜
ung ph
´
at hi
.
ên ra
¯
dô
`
ng xu gi
,
a b
`
˘
ang n lâ
`
n cân
v
`
a th
.
âm tr
´
ı trong tru
,
`
o
,
ng h
.
o
,
p
¯
d
˜
a biê
´
t m
.
ôt sô
´
¯
dô
`
ng xu th
.
ât rô
`
i.
Tru
,
`
o
,
ng h
.
o
,
p n = 1, kh
,
˘
ang
¯
d
.
inh trên
¯
d
´
ung hiê
,
n nhiên. Gi
,
a
s
,
u
,
kh
,
˘
ang
¯
d
.
inh
¯
d
´
ung v
´
o
,
i tâ
´
t c
,
a sô
´
t
.
u
,
nhiên k(k ≤ n − 1) v
`
a x
´
et
tru
,
`
o
,
ng h
.
o
,
p k = n . Ta k
´
y hi
.
êu F t
.
âp h
.
o
,
p tâ
´
t c
,
a c
´
ac
¯
dô
`
ng xu
¯
d
˜
a
cho, c
`
on J t
.
âp h
.
o
,
p tâ
´
t c
,
a c
´
ac
¯
dô
`
ng xu th
.
ât. Ch
´
u
´
y r
`
˘
ang sô
´
lu
,
.
o
,
ng
¯
dô
`
ng xu trong F l
´
o
,
n ho
,
n 3
n
, c
`
on sô
´
lu
,
.
o
,
ng trong J l
`
a bâ
´
t k
`
y, c
´
o
thê
,
l
`
a 0. D
˜
ê thâ
´
y r
`
˘
ang trên hai
¯
d
˜
ıa cân ph
,
ai
¯
d
.
˘
at sô
´
¯
dô
`
ng xu b
`
˘
ang
nhau. B
`
˘
ang c
´
ach nhu
,
v
.
ây trên m
.
ôt
¯
d
˜
ıa cân ho
.
˘
ac ngo
`
ai hai
¯
d
˜
ıa
cân c
´
o m
.
ôt nh
´
om nhiê
`
u ho
,
n 3
n−1
¯
dô
`
ng xu t
`
u
,
F. Ta k
´
y hi
.
êu nh
´
om
¯
d
´
o b
`
˘
ang N.
Nê
´
u N ngo
`
ai hai
¯
d
˜
ıa cân, th
`
ı theo
¯
diê
`
u kiên hai
¯
d
˜
ıa cân cân
b
`
˘
ang,
¯
dô
`
ng xu gi
,
a
,
o
,
nh
´
om N v
`
a theo gi
,
a thiê
´
t quy n
.
ap n
´
o không
thê
,
t
´
ach
¯
dô
`
ng tiê
`
n gi
,
a
¯
du
,
.
o
,
c b
`
˘
ang n −1 lâ
`
n cân.
Nê
´
u nh
´
om N l
`
a m
.
ôt trong hai
¯
d
˜
ıa cân v
`
a
¯
d
´
o l
`
a
¯
d
˜
ıa cân nh
.
e
ho
,
n, th
`
ı
¯
dô
`
ng xu gi
,
a n
`
˘
am trong n
´
o, khi
¯
d
´
o theo gi
,
a thiê
´
t quy n
.
ap
c
˜
ung không t
´
ach
¯
du
,
.
o
,
c
¯
dô
`
ng xu gi
,
a.
J
V
´
ı d
.
u 8.8. Cho b
,
ang h`ınh vuông c ´ac sô
´
a
11
a
12
. . . a
1n
a
21
a
22
. . . a
2n
.
.
.
.
.
. . . .
.
.
.
a
n1
a
n2
. . . a
nn
.

184 Chu
,
o
,
ng 8. Tô
,
h
.
o
,
p v
`
a
¯
d
,
˘
ang th
´
u
,
c
Ch
´
u
,
ng minh r
`
˘ang nê
´
u M l `a m
.
ôt h
`
˘ang sô
´
sao cho
n
∑
j=1
|x
1
a
j1
+ x
2
a
j2
+ ··· + x
n
a
jn
| ≤ M
v
´
o
,
i m
.
oi c ´ach ch
.
on nh
˜
u
,
ng sô
´
x
i
= ±1, th`ı
|a
11
|+ |a
22
|+ ···+ |a
nn
| ≤ M.
L
`
o
,
i gi
,
ai. Ta ch
´
u
,
ng minh m
.
ênh
¯
dê
`
b
`
˘
ang quy n
.
ap theo n. V
´
o
,
i
n = 1 m
.
ênh
¯
dê
`
¯
d
´
ung. Gi
,
a s
,
u
,
m
.
ênh
¯
dê
`
¯
d
´
ung v
´
o
,
i n − 1. Cho
x
1
, x
2
, . . . , x
n−1
l
`
a m
.
ôt c
´
ach ch
.
on bâ
´
t k
`
y c
,
ua ±1. Khi
¯
d
´
o ta d
`
ung
bâ
´
t
¯
d
,
˘
ang th
´
u
,
c sau
2|α| = |2α| = |(α + β) + (α − β)| ≤ |α + β| + |α − β|,
ta nh
.
ân
¯
du
,
.
o
,
c
2
n−1
∑
j=1
|x
1
a
j1
+ ··· + x
n−1
a
j,n−1
|+ 2|a
nn
|
≤
n−1
∑
j=1
|x
1
a
j1
+ ··· + x
n−1
a
j,n−1
+ a
nn
|+
+
n−1
∑
j=1
|x
1
a
j1
+ ··· + x
n−1
a
j,n−1
− a
nn
|+
+ |a
nn
+ x
1
a
j1
+ ··· + x
n−1
a
j,n−1
|+
+ |a
nn
− x
1
a
j1
−··· − x
n−1
a
j,n−1
|
=
n−1
∑
j=1
|x
1
a
j1
+ ··· + x
n−1
a
j,n−1
+ a
nn
|+
+
n−1
∑
j=1
|x
1
a
j1
+ ··· + x
n−1
a
j,n−1
− a
nn
| ≤ 2M.

8.1. M
.
ôt sô
´
công th
´
u
,
c tô
,
h
.
o
,
p 185
T
´
u
,
c l
`
a
n−1
∑
j=1
|x
1
a
j1
+ ··· + x
n−1
a
j,n−1
| ≤ M − |a
nn
|,
t
`
u
,
¯
dây theo gi
,
a thiê
´
t quy n
.
ap suy ra
|a
11
|+ |a
22
|+ ···+ |a
n−1,n−1
| ≤ M − |a
nn
|,
ngh
˜
ıa l
`
a |a
11
|+ |a
22
|+ ···+ |a
nn
| ≤ M.
J
V
´
ı d
.
u 8.9. Cho c ´ac sô
´
t
.
u
,
nhiên a
1
, a
2
, . . . , a
n
( n > 1), sao cho a
k
≤
k, (k = 1, 2, . . . , n) v `a tô
,
ng a
1
+ a
2
+ ··· + a
n
l `a ch
˜
˘an. Ch
´
u
,
ng minh
r
`
˘ang m
.
ôt trong c ´ac tô
,
ng
¯
d
.
ai sô
´
a
1
± a
2
± a
3
. . . ± a
n
b
`
˘ang 0.
L
`
o
,
i gi
,
ai. Ta ch
´
u
,
ng minh b
`
˘
ang quy n
.
ap theo n. Khi n = 2, ta d
˜
ê
thâ
´
y a
1
= a
2
= 1. Do
¯
d
´
o a
1
− a
2
= 0. Ðô
´
i v
´
o
,
i n + 1 sô
´
t
.
u
,
nhiên
a
1
, a
2
, . . . , a
n+1
( n ≥ 2) tho
,
a m
˜
an c
´
ac
¯
diê
`
u ki
.
ên c
,
ua b
`
ai to
´
an, ta
x
´
et hai tru
,
`
o
,
ng h
.
o
,
p sau:
1. a
n
6= a
n+1
. Ð
.
˘
at a
0
n
= |a
n
− a
n+1
|, khi
¯
d
´
o do 1 ≤ a
n
≤ n v
`
a
1 ≤ a
n+1
≤ n + 1 nên 1 ≤ a
0
n
≤ (n + 1) − 1 = n. M
.
˘
at kh
´
ac, tô
,
ng
a
1
+ a
2
+ ··· + a
n
+ a
n+1
ch
˜
˘
an, riêng a
n
+ a
n+1
c
´
o c
`
ung t
´
ınh ch
˜
˘
an
l
,
e v
´
o
,
i a
0
= |a
n
− a
n+1
|, do
¯
d
´
o tô
,
ng a
1
+ a
2
+ ··· + a
n−1
+ a
0
n
c
˜
ung
tho
,
a m
˜
an c
´
ac
¯
diê
`
u ki
.
ên c
,
ua b
`
ai to
´
an. Theo gi
,
a thiê
´
t quy n
.
ap ta
c
´
o m
.
ôt trong c
´
ac tô
,
ng a
1
± a
2
± . . . ± a
n−1
± a
0
n
= a
1
± a
2
± . . . ±
a
n−1
±|a
n
− a
n+1
| b
`
˘
ang 0. T
`
u
,
¯
d
´
o suy ra
¯
diê
`
u ph
,
ai ch
´
u
,
ng minh.
2. a
n
= a
n+1
. L
´
uc n
`
ay do a
1
+ a
2
+ ··· + a
n
+ a
n+1
ch
˜
˘
an v
`
a
a
n
+ a
n+1
= 2a
n
ch
˜
˘
an nên a
1
+ a
2
+ . . . + a
n−1
c
˜
ung ch
˜
˘
an. V
.
ây
n −1 sô
´
a
1
, a
2
, . . . , a
n−1
c
˜
ung tho
,
a m
˜
an c
´
ac
¯
diê
`
u ki
.
ên b
`
ai to
´
an nê
´
u
ch
,
ı câ
`
n n −1 > 1 hay n ≥ 3. Nhu
,
ng
¯
diê
`
u n
`
ay l
`
a hiê
,
n nhiên v
`
ı nê
´
u
n = 2, (r
˜
o r
`
ang ch
,
ı câ
`
n ch
´
u
´
y tru
,
`
o
,
ng h
.
o
,
p n
`
ay m
`
a thôi v
`
ı n ≥ 2),
th
`
ı t
`
u
,
gi
,
a thiê
´
t a
1
≤ 1, a
2
≤ 2 v
`
a a
3
≤ 3 v
`
a tô
,
ng a
1
+ a
2
+ a
3
ch
˜
˘
an,
ta suy ra a
1
= 1 v
`
a a
2
6= a
3
t
´
u
,
c l
`
a ro
,
i v
`
ao tru
,
`
o
,
ng h
.
o
,
p 1.
¯
d
˜
a x
´
et. Do

186 Chu
,
o
,
ng 8. Tô
,
h
.
o
,
p v
`
a
¯
d
,
˘
ang th
´
u
,
c
¯
d
´
o c
´
o thê
,
s
,
u
,
d
.
ung gi
,
a thiê
´
t quy n
.
ap
¯
dê
,
suy ra r
`
˘
ang
´
ıt nhâ
´
t m
.
ôt
trong c
´
ac biê
,
u th
´
u
,
c a
1
±a
2
±. . . ±a
n−1
b
`
˘
ang 0 v
`
a do
¯
d
´
o m
.
ôt trong
c
´
ac tô
,
ng a
1
± a
2
±. . . ± a
n−1
+ a
n
− a
n+1
c
˜
ung b
`
˘
ang 0.
J
8.2. M
.
ôt sô
´
¯
d
,
˘
ang th
´
u
,
c
Phâ
`
n n
`
ay ta ch
´
u
,
ng minh m
.
ôt sô
´
h
`
˘
ang
¯
d
,
˘
ang th
´
u
,
c
¯
d
´
ang nh
´
o
,
.
V
´
ı d
.
u 8.10. Ch
´
u
,
ng minh nh
.
i th
´
u
,
c Newton
(a + b)
n
=
n
∑
i =0
C
i
n
a
i
b
n−i
, (8.5)
,
o
,
¯
dây n l `a sô
´
nguyên du
,
o
,
ng.
L
`
o
,
i gi
,
ai. Bu
,
´
o
,
c co
,
s
,
o
,
: D
˜
ê thâ
´
y (8.5)
¯
d
´
ung v
´
o
,
i n = 1.
Bu
,
´
o
,
c quy n
.
ap: Gi
,
a s
,
u
,
¯
d
,
˘
ang th
´
u
,
c (8.5)
¯
d
´
ung v
´
o
,
i n, ta s
˜
e ch
´
u
,
ng
minh n
´
o c
˜
ung
¯
d
´
ung cho n + 1. Th
.
ât v
.
ây,
(a + b)
n+1
= (a + b)
n
(a + b) =
= [a
n
+ C
1
n
a
n−1
b + ··· + C
k
n
a
n−k
b
k
+ ··· + b
n
](a + b)
= a
n+1
+ C
1
n
a
n
b + ··· + C
k
n
a
n+1−k
b
k
+ ··· + ab
n
+
+ a
n
b + C
1
n
a
n−1
b
2
+ ··· + C
k
n
a
n−k
b
k+1
+ ··· + b
n+1
.
Suy ra
(a + b)
n+1
= a
n+1
+
h
1 + C
1
n
i
a
n
b +
h
C
1
n
+ C
2
n
i
a
n−1
b
2
+ ···
··· +
h
C
k−1
n
+ C
k
n
i
a
n+1−k
b
k
+ ··· + b
n+1
.
Nh
˜
u
,
ng h
.
ê sô
´
trong công th
´
u
,
c trên r
´
ut g
.
on theo công th
´
u
,
c (2.8)
v
`
a ta c
´
o
(a + b)
n+1
=
n+1
∑
i =0
C
i
n+1
a
n+1−i
b
i
.
V
.
ây
¯
d
,
˘
ang th
´
u
,
c (8.5)
¯
d
´
ung v
´
o
,
i n + 1.
J

8.2. M
.
ôt sô
´
¯
d
,
˘
ang th
´
u
,
c 187
V
´
ı d
.
u 8.11. V
´
o
,
i a
1
, a
2
, . . . , a
n
l `a nh
˜
u
,
ng sô
´
th
.
u
,
c, ch
´
u
,
ng minh r
`
˘ang
(a
1
+ a
2
+ ···+ a
n
)
2
= a
2
1
+ a
2
2
+ ···+ a
2
n
+ 2(a
1
a
2
+ a
1
a
3
+ ···+ a
n−1
a
n
)
(8.6)
v
´
o
,
i m
.
oi sô
´
t
.
u
,
nhiên n ≥ 2.
L
`
o
,
i gi
,
ai. V
´
o
,
i n = 2 công th
´
u
,
c (8.6) l
`
a h
`
˘
ang
¯
d
,
˘
ang th
´
u
,
¯
d
´
ang nh
´
o
,
.
Gi
,
a s
,
u
,
công th
´
u
,
c (8.6)
¯
d
´
ung v
´
o
,
i n = k −1, ngh
˜
ıa l
`
a
(a
1
+ a
2
+ ··· + a
k−1
)
2
= a
2
1
+ a
2
2
+ ··· + a
2
k−1
+ 2S
,
o
,
¯
dây S l
`
a tô
,
ng tâ
´
t c
,
a c
´
ac kh
,
a n
˘
ang t
`
u
,
ng
¯
dôi c
,
ua d
˜
ay
a
1
, a
2
, . . . , a
k−1
. Ta s
˜
e ch
´
u
,
ng minh
(a
1
+ a
2
+ ··· + a
k
)
2
= a
2
1
+ a
2
2
+ ··· + a
2
k
+ 2S
1
,
o
,
¯
dây S
1
= S + (a
1
+ a
2
+ ··· + a
k−1
)a
k
. Th
.
ât v
.
ây,
(a
1
+ a
2
+ ··· + a
k
)
2
= [(a
1
+ a
2
+ ··· + a
k−1
) + a
k
]
2
= (a
1
+ a
2
+ ··· + a
k−1
)
2
+ 2(a
1
+ ··· + a
k−1
)a
k
+ a
2
k
= (a
2
1
+ a
2
2
+ ··· + a
2
k−1
) + 2 S + 2(a
1
+ ··· + a
k−1
)a
k
+ a
2
k
= (a
2
1
+ a
2
2
+ ··· + a
2
k−1
) + 2 S
1
.
J
V
´
ı d
.
u 8.12. Cho sô
´
nguyên du
,
o
,
ng n v `a sô
´
th
.
u
,
c x, ch
´
u
,
ng minh
r
`
˘ang
[x] + [x +
1
n
] + [x +
2
n
] + ···+ [x +
n −1
n
] = [nx].
L
`
o
,
i gi
,
ai. B
`
ai ra không r
˜
o cho ta ph
,
ai quy n
.
ap theo thông sô
´
n
`
ao.
´
y tu
,
,
o
,
ng
¯
dê
,
ch
´
u
,
ng minh l
`
a ch
,
ı lâ
´
y gi
´
a tr
.
i x trong kho
,
ang nh
,
o
[
k
n
,
k + 1
n
) v
´
o
,
i k = 0, ±1, ±2, . . .
Ðâ
`
u tiên gi
,
a s
,
u
,
x n
`
˘
am trong kho
,
ang con [0,
1
n
). Khi
¯
d
´
o [x +
i
n
] = 0 v
´
o
,
i i = 0, 1, 2, . . . , n −1, nhu
,
v
.
ây
n−1
∑
i =0
[x +
i
n
] = 0. C
˜
ung c
´
o

188 Chu
,
o
,
ng 8. Tô
,
h
.
o
,
p v
`
a
¯
d
,
˘
ang th
´
u
,
c
[nx] = 0, nhu
,
v
.
ây ta
¯
d
˜
a ch
´
u
,
ng minh kê
´
t qu
,
a
¯
d
´
ung cho kho
,
ang
con
¯
dâ
`
u tiên.
Bây gi
`
o
,
ta gi
,
a s
,
u
,
kh
,
˘
ang
¯
d
.
inh
¯
d
´
ung cho kho
,
ang [
k − 1
n
,
k
n
),
,
o
,
¯
dây k l
`
a sô
´
nguyên du
,
o
,
ng, v
`
a cho x sô
´
th
.
u
,
c bâ
´
t k
`
y trong kho
,
ang
n
`
ay. Khi
¯
d
´
o
[x] + [x +
1
n
] + [x +
2
n
] + ···+ [x +
n −1
n
] = [nx].
C
.
ông thêm
1
n
v
`
ao x (ta l
`
am
¯
du
,
.
o
,
c v
`
ı b
`
˘
ang c
´
ach n
`
ay ta nh
.
ân
¯
du
,
.
o
,
c
sô
´
bâ
´
t k
`
y trong [
k
n
,
k + 1
n
)), m
˜
ôi sô
´
h
.
ang
,
o
,
bên tr
´
ai ngo
`
ai sô
´
h
.
ang
cuô
´
i c
`
ung,
¯
dê
`
u chuyê
,
n sang sô
´
h
.
ang bên ph
,
ai n
´
o, v
`
a sô
´
h
.
ang cuô
´
i
c
`
ung l
`
a [x +
n −1
n
] t
´
u
,
c l
`
a [x + 1] th
.
u
,
c châ
´
t c
.
ông 1 v
`
ao [x]. Nhu
,
v
.
ây thay x b
`
˘
ang x +
1
n
v
`
ao vê
´
tr
´
ai,
¯
d
,
˘
ang th
´
u
,
c trên t
˘
ang lên 1.
Ðô
`
ng th
`
o
,
i khi
¯
d
´
o khi x
,
o
,
[nx] thay b
`
˘
ang x +
1
n
, gi
´
a tr
.
i c
,
ua n
´
o
c
˜
ung t
˘
ang lên 1. Do m
˜
ôi bên c
,
ua
¯
d
,
˘
ang th
´
u
,
c
¯
dê
`
u t
˘
ang lên 1 khi
thay x b
`
˘
ang x +
1
n
, kê
´
t qu
,
a v
˜
ân c
`
on
¯
d
´
ung cho tâ
´
t c
,
a c
´
ac sô
´
trong
kho
,
ang [
k
n
,
k + 1
n
).
Theo gi
,
a thiê
´
t quy n
.
ap kê
´
t qu
,
a c
`
on
¯
d
´
ung cho tâ
´
t c
,
a gi
´
a tr
.
i
du
,
o
,
ng c
,
ua x. Ho
`
an to
`
an tu
,
o
,
ng t
.
u
,
c
˜
ung
¯
d
´
ung cho tâ
´
t c
,
a c
´
ac gi
´
a tr
.
i
âm c
,
ua x.
J
V
´
ı d
.
u 8.13. Ch
´
u
,
ng minh r
`
˘ang v
´
o
,
i m
.
oi sô
´
t
.
u
,
nhiên n ≥ 1
( n + 1)(n + 2) . . . (n + n) = 2
n
.1.3.5 . . . (2n −1).
L
`
o
,
i gi
,
ai. K
´
y hi
.
êu t
´
ıch
,
o
,
vê
´
tr
´
ai l
`
a T
n
. D
`
ung phu
,
o
,
ng ph
´
ap quy n
.
ap
to
´
an h
.
oc theo n. V
´
o
,
i n = 1 công th
´
u
,
c
¯
d
´
ung v
`
ı T
1
= (1 + 1) = 2
1
.

8.2. M
.
ôt sô
´
¯
d
,
˘
ang th
´
u
,
c 189
Gi
,
a s
,
u
,
công th
´
u
,
c
¯
d
´
ung v
´
o
,
i n = k . Ta c
´
o
T
k
= (k + 1)(k + 2) . . . (k + k) = 2
k
.1.3.5 . . . (2k −1).
Ta câ
`
n ch
´
u
,
ng minh
[(k + 1) + 1][(k + 1) + 2] . . . [(k + 1) + k][(k + 1) + (k + 1)] = 2
k+1
.1.3.5 . . . (2k + 1).
Ho
.
˘
ac l
`
a
( k + 2)(k + 3) . . . (k + 1 + k)(2k + 2 ) = 2
k+1
.1.3.5 . . . (2k + 1).
Th
.
ât v
.
ây,
T
k+1
= (k + 2)(k + 3) . . . (k + 1 + k)(2k + 2)
=
( k + 1)(k + 2)(k + 3)(k + k)
( k + 1)
.(k + 1 + k)(2k + 2)
= T
k
(2 k + 1).2(k + 1)
k + 1
.
J
V
´
ı d
.
u 8.14. Ch
´
u
,
ng minh
¯
d
,
˘ang th
´
u
,
c v
´
o
,
i m
.
oi sô
´
nguyên n ≥ 0
cos α cos 2α cos 4α . . . cos 2
n
α =
sin 2
n+1
α
2
n+1
sin α
.
L
`
o
,
i gi
,
ai. 1) V
´
o
,
i n = 0
¯
d
,
˘
ang th
´
u
,
c
¯
d
´
ung, v
`
ı cos α =
sin 2α
2 sin α
.
2) Gi
,
a s
,
u
,
¯
d
,
˘
ang th
´
u
,
c
¯
d
´
ung v
´
o
,
i n = k , t
´
u
,
c l
`
a
cos α cos 2α cos 4α . . . cos 2
k
α =
sin 2
k+1
α
2
k+1
sin α
.
Khi
¯
d
´
o n
´
o c
˜
ung
¯
d
´
ung v
´
o
,
i n = k + 1. Th
.
ât v
.
ây,
cos α cos 2α cos 4α . . . cos 2
k
α cos 2
k+1
α =
sin 2
k+1
α cos 2
k+1
α
2
k+1
sin α
=
sin 2
k+2
α
2
k+2
sin α
.
J
V
´
ı d
.
u 8.15. Ch
´
u
,
ng minh r
`
˘ang v
´
o
,
i m
.
oi sô
´
t
.
u
,
nhiên n ≥ 1
sin x + sin 2x + ··· + sin nx =
sin
n + 1
2
x
sin
x
2
sin
nx
2
.

190 Chu
,
o
,
ng 8. Tô
,
h
.
o
,
p v
`
a
¯
d
,
˘
ang th
´
u
,
c
L
`
o
,
i gi
,
ai. 1) V
´
o
,
i n = 1 kh
,
˘
ang
¯
d
.
inh trên l
`
a
¯
d
´
ung.
2) Cho
sin x + sin 2x + ··· + sin kx =
sin
k + 1
2
x
sin
x
2
sin
kx
2
.
Khi
¯
d
´
o
sin x + sin 2x + ··· + sin kx + sin(k + 1)x =
=
sin
k + 1
2
x
sin
x
2
sin
kx
2
+ sin(k + 1 )x =
=
sin
k + 1
2
x
sin
x
2
sin
kx
2
+ 2 sin
k + 1
2
x cos
k + 1
2
x
=
sin
k + 2
2
x
sin
x
2
sin
k + 1
2
x,
v
`
ı
2 cos
k + 1
2
x sin
x
2
= sin
k + 2
2
x − sin
kx
2
.
J
V
´
ı d
.
u 8.16. Ch
´
u
,
ng minh r
`
˘ang v
´
o
,
i m
.
oi sô
´
t
.
u
,
nhiên n ≥ 1
sin x + 2 sin 2x + 3 sin 3x + ···+ n sin nx =
( n + 1) sin nx −n sin(n + 1)x
4 sin
2
x
2
.
L
`
o
,
i gi
,
ai. 1) V
´
o
,
i n = 1 kh
,
˘
ang
¯
d
.
inh
¯
d
´
ung, v
`
ı
2 sin x −sin 2x
4 sin
2
x
2
=
2 sin x(1 −cos x)
4 sin
2
x
2
= sin x.

8.2. M
.
ôt sô
´
¯
d
,
˘
ang th
´
u
,
c 191
2) gi
,
a s
,
u
,
kh
,
˘
ang
¯
d
.
inh
¯
d
´
ung v
´
o
,
i n = k t
´
u
,
c l
`
a
sin x + 2 sin 2x + 3 sin 3x + ···+ k sin kx =
( k + 1) sin kx −k sin(k + 1)x
4 sin
2
x
2
.
Khi
¯
d
´
o
sin x + 2 sin 2x + 3 sin 3x + ··· + k sin kx + (k + 1) sin(k + 1)x =
=
( k + 1) sin kx −k sin(k + 1)x
4 sin
2
x
2
+ (k + 1 ) sin(k + 1)x
=
( k + 1) sin kx −k sin(k + 1)x + 2 (k + 1) sin(k + 1)x(1 − cos x)
4 sin
2
x
2
=
( k + 2) sin(k + 1)x + (k + 1) sin kx
4 sin
2
x
2
−
2(k + 1) cos x sin (k + 1)x
4 sin
2
x
2
=
( k + 2) sin(k + 1)x + (k + 1) sin kx
4 sin
2
x
2
−
( k + 1)[sin(k + 2)x + sin kx]
4 sin
2
x
2
=
( k + 2) sin(k + 1)x − (k + 1) sin(k + 2)x
4 sin
2
x
2
.
J
V
´
ı d
.
u 8.17. Ch
´
u
,
ng minh r
`
˘ang
1
2
tg
x
2
+
1
2
2
tg
x
2
2
+ ··· +
1
2
n
tg
x
2
n
=
1
2
n
cotg
x
2
n
−cotg x
v
´
o
,
i x 6= mπ.
L
`
o
,
i gi
,
ai. 1) V
´
o
,
i n = 1 kh
,
˘
ang
¯
d
.
inh
¯
d
´
ung, v
`
ı
1
2
cotg
x
2
−cotg x =
1
2
cotg
x
2
−
1 −tg
2
x
2
2 tg
x
2
=
tg
2
x
2
2 tg
x
2
=
1
2
tg
x
2
.

192 Chu
,
o
,
ng 8. Tô
,
h
.
o
,
p v
`
a
¯
d
,
˘
ang th
´
u
,
c
2) Gi
,
a s
,
u
,
kh
,
˘
ang
¯
d
.
inh
¯
d
´
ung v
´
o
,
i n = k , t
´
u
,
c l
`
a
1
2
tg
x
2
+
1
2
2
tg
x
2
2
+ ··· +
1
2
k
tg
x
2
k
=
1
2
k
cotg
x
2
k
−cotg x.
Khi
¯
d
´
o
1
2
tg
x
2
+
1
2
2
tg
x
2
2
+ ··· +
1
2
k
tg
x
2
k
+
1
2
k+1
tg
x
2
k+1
=
=
1
2
k
cotg
x
2
k
−cotg x +
1
2
k+1
tg
x
2
k+1
=
1
2
k+1
cotg
2
x
2
k+1
−1
cotg
x
2
k+1
+
1
2
k+1
cotg
x
2
k+1
−cotg x
=
1
2
k+1
cotg
x
2
k+1
−cotg x.
J
V
´
ı d
.
u 8.18. Cho a v `a A > 0 l `a nh
˜
u
,
ng sô
´
bâ
´
t k`y v `a
¯
d
.
˘at
a
1
=
1
2
(a +
A
a
), a
2
=
1
2
(a
1
+
A
a
1
), . . . , a
n
=
1
2
(a
n−1
+
A
a
n−1
).
Ch
´
u
,
ng minh r
`
˘ang
a
n
−
√
A
a
n
+
√
A
=
a
1
−
√
A
a
1
+
√
A
!
2
n−1
,
v
´
o
,
i m
.
oi sô
´
nguyên n ≥ 1.
L
`
o
,
i gi
,
ai. 1) Bu
,
´
o
,
c co
,
s
,
o
,
: D
˜
ê thâ
´
y
¯
d
,
˘
ang th
´
u
,
c
¯
d
´
ung v
´
o
,
i n = 1.
2) Bu
,
´
o
,
c quy n
.
ap: Gi
,
a thiê
´
t
¯
d
,
˘
ang th
´
u
,
c
¯
d
´
ung v
´
o
,
i n . Ta câ
`
n
ch
´
u
,
ng minh n
´
o c
˜
ung
¯
d
´
ung v
´
o
,
i n + 1. Th
.
ât v
.
ây
a
n+1
−
√
A
a
n+1
+
√
A
=
1
2
(a
n
+
A
a
n
) −
√
A
1
2
(a
n
+
A
a
n
) +
√
A
=
a
2
n
−2
√
Aa
n
+ A
a
2
n
+ 2
√
Aa
n
+ A
= (
a
n
−
√
A
a
n
+
√
A
)
2
.
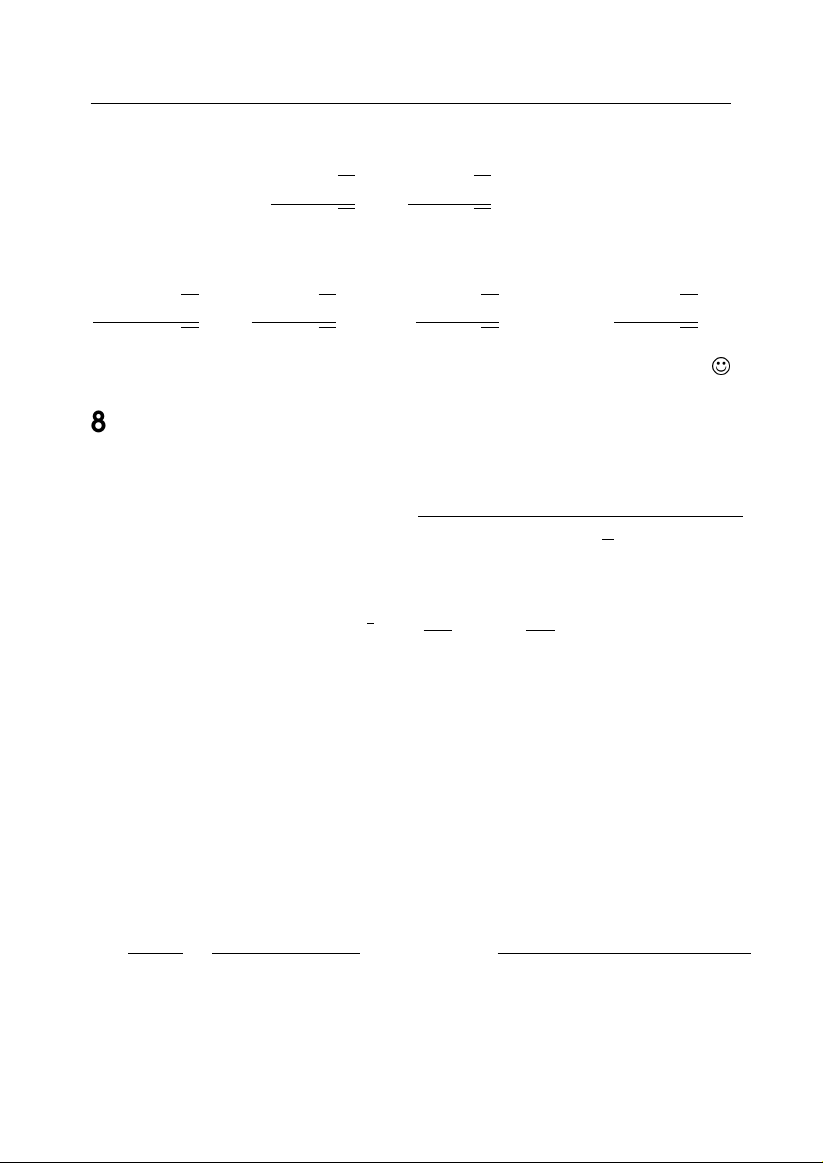
8.3. B
`
ai t
.
âp 193
Nhu
,
ng theo gi
,
a thiê
´
t quy n
.
ap
a
n
−
√
A
a
n
+
√
A
=
a
1
−
√
A
a
1
+
√
A
!
2
n−1
.
V
`
ı v
.
ây
a
n+1
−
√
A
a
n+1
+
√
A
=
a
n
−
√
A
a
n
+
√
A
!
2
=
a
1
−
√
A
a
1
+
√
A
!
2.2
n−1
=
a
1
−
√
A
a
1
+
√
A
!
2
n
J
8.3. B
`
ai t
.
âp
.
.
. 8.19. Ch
´
u
,
ng minh r
`
˘
ang
cos x + 2 cos 2x + ···+ n cos nx =
( n + 1) cos nx −n cos(n + 1)x −1
4 sin
2
x
2
.
.
.
. 8.20. Ch
´
u
,
ng minh r
`
˘
ang
(1 + i)
n
= 2
n
2
(cos
nπ
4
+ i sin
nπ
4
).
.
.
. 8.21. Cho hai d
˜
ay sô
´
a
1
, a
2
, . . . v
`
a b
1
, b
2
, . . . Ch
´
u
,
ng minh
¯
d
,
˘
ang
th
´
u
,
c
n
∑
µ=1
a
µ
b
µ
= a
n
B
n
−
n−1
∑
µ=1
(a
µ+1
− a
µ
)B
µ
, (n = 2, 3, . . .),
,
o
,
¯
dây B
k
=
k
∑
j=1
b
j
, k = 1, 2, . . . , n.
.
.
. 8.22. H
˜
ay t
`
ım tô
,
ng
1 −
k
m + 1
+
k(k −1)
( m + 1)(m + 2)
−···+ (−1)
k
k(k −1) . . . 2.1
( m + 1)(m + 2) . . . (m + k)
,
,
o
,
¯
dây m l
`
a sô
´
t
.
u
,
nhiên cô
´
¯
d
.
inh, k l
`
a sô
´
t
.
u
,
nhiên bâ
´
t k
`
y.

CHU
,
O
,
NG 9
LIÊN PHÂN S
´
Ô
9.1. Kh
´
ai ni
.
êm liên phân sô
´
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 194
9.2. Phân t
´
ıch sô
´
h
˜
u
,
u t
,
y th
`
anh liên phân sô
´
. . . . . . . . . . . . . 196
9.3. Phân sô
´
xâ
´
p x
,
ı . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 198
9.4. Liên phân sô
´
vô h
.
an . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 203
9.5. V
´
ı d
.
u . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 204
9.6. B
`
ai t
.
âp . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 210
9.1. Kh
´
ai ni
.
êm liên phân sô
´
M
.
ôt biê
,
u th
´
u
,
c c
´
o d
.
ang
q
0
+
1
q
1
+
1
q
2
+
.
.
.
+
1
q
n
(9.1)
trong
¯
d
´
o q
1
, q
2
, . . . , q
n
l
`
a sô
´
du
,
o
,
ng, c
`
on q
0
l
`
a sô
´
không âm, g
.
oi l
`
a
liên phân sô
´
. Nh
˜
u
,
ng sô
´
q
0
, q
1
, . . . , q
n
g
.
oi l
`
a phâ
`
n thu
,
o
,
ng không
¯
dâ
`
y
¯
d
,
u (phâ
`
n t
,
u
,
), c
`
on liên phân sô
´

9.1. Kh
´
ai ni
.
êm liên phân sô
´
195
q
0
+
1
q
1
+
1
q
2
+
.
.
.
+
1
q
n
(9.2)
g
.
oi l
`
a thu
,
o
,
ng
¯
dâ
`
y
¯
d
,
u c
,
ua phân sô
´
(9.1).
Ðê
,
thu
.
ân ti
.
ên liên phân sô
´
(9.1)
¯
du
,
.
o
,
c viê
´
t theo c
´
ach sau:
( q
0
, q
1
, . . . , q
n
). (9.3)
D
˜
ê thâ
´
y r
`
˘
ang v
´
o
,
i n ≥ 1 liên phân sô
´
(9.3) biê
,
u di
˜
ên m
.
ôt sô
´
du
,
o
,
ng
n
`
ao
¯
d
´
o ω, g
.
oi l
`
a gi
´
a tr
.
i c
,
ua n
´
o. Ta k
´
y hi
.
êu
ω = (q
0
, q
1
, . . . , q
n
).
Cho m
.
ôt liên phân sô
´
( ngh
˜
ıa l
`
a cho c
´
ac phâ
`
n t
,
u
,
c
,
ua n
´
o
q
0
, q
1
, . . . , q
n
) v
´
o
,
i gi
´
a tr
.
i ω. Ta k
´
y hi
.
êu ω
k
(0 ≤ k ≤ n) phâ
`
n
¯
dâ
`
y
¯
d
,
u
c
,
ua (9.2). Khi
¯
d
´
o
ω
k
= q
k
+
1
q
k+1
+
1
q
k+2
+
.
.
.
+
1
q
n
Ta thâ
´
y r
`
˘
ang ω
k
c
´
o thê
,
gi
˜
u
,
vai tr
`
o nhu
,
phâ
`
n không
¯
dâ
`
y
¯
d
,
u cuô
´
i
c
`
ung (th
´
u
,
k). B
,
o
,
i v
.
ây ta c
´
o thê
,
ch
´
u
´
y
¯
dê
´
n c
´
ach viê
´
t sau:
( q
0
, q
1
, . . . , q
k−1
, q
k
, . . . , q
n
) = (q
0
, q
1
, . . . , q
k−1
, ω
k
); (9.4)
ω
k
= (q
k
, q
k+1
, . . . , q
n
), k = 0, 1, . . . , n.
D
˜
ê thâ
´
y v
´
o
,
i k = 0 phâ
`
n
¯
dâ
`
y
¯
d
,
u c
,
ua (9.2) tr
`
ung v
´
o
,
i liên phân sô
´
¯
d
˜
a cho, v
´
o
,
i k = n l
`
a phâ
`
n không
¯
dâ
`
y
¯
d
,
u cuô
´
i c
`
ung q
n
, ngh
˜
ıa l
`
a
ω
0
= ω, ω
n
= q
n
.

196 Chu
,
o
,
ng 9. Liên phân sô
´
V
´
ı d
.
u: a) Sô
´
ω = (1, 2, 2) biê
,
u di
˜
ên nhu
,
phân sô
´
b
`
ınh thu
,
`
o
,
ng.
Th
.
ât v
.
ây
ω = 1 +
1
2 +
1
2
= 1 +
1
5
2
= 1 +
2
5
=
7
5
.
b) Sô
´
88
67
c
´
o thê
,
biê
,
u di
˜
ên nhu
,
liên phân sô
´
v
´
o
,
i nh
˜
u
,
ng phâ
`
n t
,
u
,
nguyên. Th
.
ât v
.
ây
88
67
= 1 +
21
67
, ( q
0
= 1),
67
21
= 3 +
4
21
, ( q
1
= 3),
21
4
= 5 +
1
4
, ( q
3
= 5, q
4
= 4).
V
.
ây ta c
´
o thê
,
viê
´
t
88
67
= (1, 3, 5, 4).
9.2. Phân t
´
ıch sô
´
h
˜
u
,
u t
,
y th
`
anh liên phân sô
´
Theo
¯
d
.
inh ngh
˜
ıa phâ
`
n tru
,
´
o
,
c nê
´
u sô
´
phâ
`
n t
,
u
,
c
,
ua liên phân sô
´
l
`
a h
˜
u
,
u h
.
an th
`
ı ta c
´
o thê
,
chuyê
,
n liên phân sô
´
th
`
anh m
.
ôt phân
sô
´
b
`
ınh thu
,
`
o
,
ng. Ngu
,
.
o
,
c l
.
ai, m
.
ôt phân sô
´
b
`
ınh thu
,
`
o
,
ng c
´
o thê
,
biê
,
u
di
˜
ên du
,
´
o
,
i d
.
ang liên phân sô
´
.
V
´
ı d
.
u 9.1. Ch
´
u
,
ng minh r
`
˘ang m
.
oi sô
´
h
˜
u
,
u t
,
y du
,
o
,
ng
¯
dê
`
u c´o thê
,
phân t´ıch th`anh liên phân sô
´
.
L
`
o
,
i gi
,
ai. Cho ω =
a
b
,
,
o
,
¯
dây a v
`
a b l
`
a sô
´
t
.
u
,
nhiên nguyên tô
´
c
`
ung
nhau. Theo thu
.
ât to
´
an Euclide chu
,
o
,
ng tru
,
´
o
,
c ta c
´
o

9.2. Phân t
´
ıch sô
´
h
˜
u
,
u t
,
y th
`
anh liên phân sô
´
197
a = bq
0
+ r
1
b = r
1
q
1
+ r
2
. . . . . .
r
n−2
= r
n−1
q
n−1
+ r
n
,
r
n−1
= r
n
q
n
,
(9.5)
,
o
,
¯
dây b > r
1
> r
2
> . . . > r
n−1
> r
n
= 1. T
`
u
,
¯
dây v
`
a nh
˜
u
,
ng
¯
d
,
˘
ang
th
´
u
,
c (9.5) suy ra q
n
≥ 2. Ta s
˜
e ch
´
u
,
ng minh r
`
˘
ang ω phân t
´
ıch
¯
du
,
.
o
,
c
th
`
anh liên phân sô
´
ω = (q
0
, q
1
, . . . , q
n
). (9.6)
Muô
´
n v
.
ây ta
¯
d
.
˘
at r
0
= b, ω
i
=
r
i −1
r
i
, (i = 1, 2, . . . , n).
Ð
,
˘
ang th
´
u
,
c
¯
dâ
`
u tiên c
,
ua (9.5) cho ta
ω =
a
b
= q
0
+
r
1
r
0
= q
0
+
1
ω
1
= (q
0
, ω
1
).
Tu
,
o
,
ng t
.
u
,
t
`
u
,
¯
d
,
˘
ang th
´
u
,
c th
´
u
,
hai ta t
`
ım
¯
du
,
.
o
,
c ω = (q
0
, q
1
, ω
2
). Ta
ch
´
u
,
ng minh r
`
˘
ang
ω = (q
0
, q
1
, . . . , q
i −1
, ω
i
), i = 1, 2, . . . , n. (9.7)
Th
.
ât v
.
ây, gi
,
a s
,
u
,
¯
d
,
˘
ang th
´
u
,
c (9.7)
¯
d
´
ung v
´
o
,
i sô
´
i n
`
ao
¯
d
´
o (1 ≤ i ≤
n −1). Ta s
˜
e ch
´
u
,
ng minh khi
¯
d
´
o n
´
o c
˜
ung
¯
d
´
ung c
,
a cho i + 1. Th
.
ât
v
.
ây, ta chia
¯
d
,
˘
ang th
´
u
,
c r
i −1
= r
i
q
i
+ r
i +1
v
´
o
,
i r
i
, ta nh
.
ân
¯
du
,
.
o
,
c
r
i −1
r
i
=
q
i
+
r
i +1
r
i
, theo
¯
d
.
inh ngh
˜
ıa c
,
ua ω
i
l
`
a ω
i
= q
i
+
1
ω
i +1
= (q
i
, ω
i +1
).
Suy ra ω = (q
0
, q
1
, . . . , q
i −1
, ω
i
) = (q
0
, q
1
, . . . , q
i −1
, q
i
, ω
i +1
), nhu
,
v
.
ây (9.7)
¯
d
˜
a ch
´
u
,
ng minh. T
`
u
,
(9.7) suy ra (9.6) v
´
o
,
i i = n.
V
´
ı d
.
u 9.2. Ch
´
u
,
ng minh r
`
˘ang s
.
u
,
phân t´ıch th `anh liên phân sô
´
c
,
ua m
˜
ôi sô
´
h
˜
u
,
u t
,
y l `a duy nhâ
´
t.

198 Chu
,
o
,
ng 9. Liên phân sô
´
L
`
o
,
i gi
,
ai. Gi
,
a s
,
u
,
c
`
ung v
´
o
,
i s
.
u
,
khai triê
,
n (9.6) ω c
`
on c
´
o biê
,
u di
˜
ên
kh
´
ac
ω = (q
0
0
, q
0
1
, . . . , q
0
m
), q
0
m
> 1. (9.8)
Ta cho r
`
˘
ang m ≥ n. Cho ω
0
i
l
`
a phâ
`
n
¯
dâ
`
y
¯
d
,
u
ω
0
i
= (q
0
i
, q
0
i +1
, . . . , q
0
m
), (i = 1, 2, . . . , m).
Hiê
,
n nhiên ta c
´
o
ω = q
0
+
1
ω
1
= q
0
0
+
1
ω
0
1
,
t
`
u
,
¯
dây suy ra r
`
˘
ang ch
´
ung b
`
˘
ang nhau phâ
`
n nguyên c
˜
ung nhu
,
phâ
`
n phân sô
´
,
o
,
hai vê
´
c
,
ua
¯
d
,
˘
ang th
´
u
,
c. Ngh
˜
ıa l
`
a q
0
= q
0
0
, ω
1
= ω
0
1
.
Ð
,
˘
ang th
´
u
,
c sau c
˜
ung c
´
o thê
,
viê
´
t:
q
1
+
1
ω
2
= q
0
1
+
1
ω
0
2
,
t
`
u
,
¯
d
´
o suy ra q
1
= q
0
1
, ω
2
= ω
0
2
. Theo c
´
ach n
`
ay (phu
,
o
,
ng ph
´
ap quy
n
.
ap to
´
an h
.
oc) ta s
˜
e d
˜
ân
¯
dê
´
n
¯
d
,
˘
ang th
´
u
,
c q
n−1
= q
0
n−1
v
`
a
ω
n
= ω
0
n
, (9.9)
,
o
,
¯
dây ω
n
= q
n
. Ta gi
,
a thiê
´
t r
`
˘
ang m > n. Khi
¯
d
´
o ω
0
n
= q
0
n
+
1
ω
0
n+1
,
,
o
,
¯
dây ω
0
n+1
> 1 v
`
a (9.9) suy ra
q
n
= q
0
n
+
1
ω
0
n+1
.
Nhu
,
ng
¯
d
,
˘
ang th
´
u
,
c
¯
d
´
o không thê
,
xâ
,
y ra, v
`
ı vê
´
ph
,
ai không ph
,
ai l
`
a
m
.
ôt sô
´
nguyên. Ðiê
`
u vô l
´
y
¯
d
´
o suy ra m = n, ω
0
n
= q
0
n
= q
n
.
J
9.3. Phân sô
´
xâ
´
p x
,
ı
Cho liên phân sô
´
( q
0
, q
1
, q
2
, . . . , q
n
). Ta x
´
et d
˜
ay liên phân sô
´
α
0
= (q
0
), α
1
= (q
0
, q
1
), . . . , α
n
= (q
0
, q
1
, . . . , q
n
). (9.10)

9.3. Phân sô
´
xâ
´
p x
,
ı 199
Ta biê
´
t r
`
˘
ang sô
´
α
i
l
`
a sô
´
h
˜
u
,
u t
,
y. V
`
ı thê
´
ch
´
ung c
´
o thê
,
biê
,
u di
˜
ên
nhu
,
nh
˜
u
,
ng phân sô
´
tô
´
i gi
,
an (D(a, b) l
`
a u
,
´
o
,
c sô
´
chung l
´
o
,
n nhâ
´
t c
,
ua
a v
`
a b)
α
i
= (q
0
, q
1
, . . . , q
i
) =
P
i
Q
i
, (D(P
i
, Q
i
) = 1; i = 0, 1, 2, ..., n). (9.11)
Phân sô
´
P
i
Q
i
g
.
oi l
`
a i-phân sô
´
xâ
´
p x
,
ı c
,
ua liên phân sô
´
( q
0
, q
1
, . . . , q
n
).
Phân sô
´
xâ
´
p x
,
ı gi
˜
u
,
vai tr
`
o quan trong trong l
´
y thuyê
´
t liên phân
sô
´
. Nh
˜
u
,
ng v
´
ı d
.
u sau
¯
dây ch
,
ı ra m
.
ôt sô
´
t
´
ınh châ
´
t c
,
ua ch
´
ung:
V
´
ı d
.
u 9.3. Ch
´
u
,
ng minh r
`
˘ang v
´
o
,
i m
.
oi liên phân sô
´
ta
¯
dê
`
u c´o
P
i +1
= P
i
q
i +1
+ P
i −1
, (9.12)
Q
i +1
= Q
i
q
i +1
+ Q
i −1
, (9.13)
P
i +1
Q
i
− P
i
Q
i +1
= (−1)
i
, (9.14)
v
´
o
,
i (i = 1, 2, . . . , n −1).
L
`
o
,
i gi
,
ai. Ta ch
´
u
,
ng minh quy n
.
ap theo i. V
´
o
,
i i = 1, ta t
´
ınh P
i
v
`
a
Q
i
v
´
o
,
i i = 1, 2. T
`
u
,
(9.11) ta t
`
ım
¯
du
,
.
o
,
c q
0
=
P
0
Q
0
=
q
0
1
v
`
a v
`
ı phân sô
´
P
0
Q
0
tô
´
i gi
,
an (theo
¯
d
.
inh ngh
˜
ıa), nên
P
0
= q
0
, Q
0
= 1. (9.15)
V
´
o
,
i i = 1 ta c
´
o (q
0
, q
1
) = q
0
+
1
q
1
=
q
0
q
1
+ 1
q
1
. Sô
´
q
0
q
1
+ 1 v
`
a q
1
nguyên tô
´
c
`
ung nhau. Ta
¯
d
˜
ê ch
´
u
,
ng minh
D(a + c, b) = D(a, b) (9.16)
v
´
o
,
i
¯
diê
`
u ki
.
ên c chia hê
´
t cho b. Áp d
.
ung (9.16) cho c = q
0
q
1
, b =
q
1
, a = 1, ta s
˜
e nh
.
ân
¯
du
,
.
o
,
c D(q
0
q
1
+ 1, q
1
) = D(q
1
, 1) = 1. bây gi
`
o
,

200 Chu
,
o
,
ng 9. Liên phân sô
´
t
`
u
,
(9.11) ta c
´
o
q
0
q
1
+ 1
q
1
=
P
1
Q
1
v
`
a
P
1
= q
0
q
1
+ 1, Q
1
= q
1
. (9.17)
V
´
o
,
i i = 2 ta c
´
o (q
0
, q
1
, q
2
) =
q
0
( q
1
q
2
+ 1) + q
2
q
1
q
2
+ 1
=
P
2
Q
2
.
Ð
,
˘
ang th
´
u
,
c sau c
`
ung l
`
a
¯
d
,
˘
ang th
´
u
,
c gi
˜
u
,
a c
´
ac phân sô
´
tô
´
i gi
,
an.
Th
.
ât v
.
ây
P
2
Q
2
tô
´
i gi
,
an theo
¯
d
.
inh ngh
˜
ıa, c
`
on bên vê
´
tr
´
ai ta s
˜
e
´
ap
d
.
ung hai lâ
`
n (9.16)
D(q
0
( q
1
q
2
+ 1) + q
2
, q
1
q
2
+ 1) = D(q
1
q
2
+ 1, q
2
) = D(q
2
, 1) = 1.
Suy ra
P
2
= q
0
( q
1
q
2
+ 1) + q
2
, Q
2
= q
1
q
2
+ 1. (9.18)
S
,
u
,
d
.
ung (9.17) v
`
a (9.18) v
´
o
,
i s
.
u
,
kiê
,
m tra tr
.
u
,
c tiê
´
p suy ra (9.12),
(9.13) v
`
a (9.14) v
´
o
,
i i = 1.
Gi
,
a s
,
u
,
kh
,
˘
ang
¯
d
.
inh
¯
d
´
ung v
´
o
,
i sô
´
i n
`
ao
¯
d
´
o ( (1 ≤ i ≤ n − 2) .
Ta s
˜
e ch
´
u
,
ng minh r
`
˘
ang ch
´
ung c
˜
ung
¯
d
´
ung v
´
o
,
i i + 1 ngh
˜
ıa l
`
a tho
,
a
m
˜
an nh
˜
u
,
ng
¯
d
,
˘
ang th
´
u
,
c sau
P
i +2
= P
i +1
q
i +2
+ P
i
, (9.12a)
Q
i +2
= Q
i +1
q
i +2
+ Q
i
, (9.13a)
P
i +2
Q
i +1
− P
i +1
Q
i +2
= (−1)
i +1
, (9.14a)
T
`
u
,
¯
d
.
inh ngh
˜
ıa (9.11) v
`
a theo (9.4) ta c
´
o
P
i +2
Q
i +2
= (q
0
, . . . , q
i
, q
i +1
, q
i +2
) = (q
0
, . . . , q
i
, q
∗
i +1
), (9.19)
,
o
,
¯
dây
q
∗
i +1
= q
i +1
+
1
q
i +2
. (9.20)
Ta so s
´
anh (9.19) v
´
o
,
i (9.11),
¯
du
,
a
¯
dê
´
n
¯
d
,
˘
ang th
´
u
,
c
P
i +2
Q
i +2
= (
P
i +1
Q
i +1
)
∗
, (9.21)

9.3. Phân sô
´
xâ
´
p x
,
ı 201
,
o
,
¯
dây dâ
´
u * ch
,
ı ra r
`
˘
ang thu
,
o
,
ng không
¯
dâ
`
y
¯
d
,
u cuô
´
i c
`
ung q
i +1
c
,
ua
phân sô
´
trong ngo
.
˘
ac câ
`
n
¯
du
,
.
o
,
c thê
´
b
`
˘
ang q
∗
i +1
t
`
u
,
(9.20). Theo gi
,
a
thiê
´
t quy n
.
ap, ngh
˜
ıa l
`
a t
`
u
,
(9.12) v
`
a (9.13), suy ra
P
i +1
Q
i +1
=
P
i
q
i +1
+ P
i −1
Q
i
q
i +1
+ Q
i −1
. (9.22)
T
`
u
,
(9.11) thâ
´
y r
`
˘
ang P
i −1
, Q
i −1
, P
i
v
`
a Q
i
không ph
.
u thu
.
ôc v
`
ao q
i +1
.
Khi
¯
d
´
o
´
ap d
.
ung trên (9.22) to
´
an t
,
u
,
*, ta nh
.
ân
¯
du
,
.
o
,
c
P
i +1
Q
i +1
∗
=
P
i
q
i +1
+ P
i −1
Q
i
q
i +1
+ Q
i −1
∗
=
P
i
( q
i +1
+
1
q
i +2
) + P
i −1
Q
i
( q
i +1
+
1
q
i +2
)
+ Q
i −1
=
q
i +2
(P
i
q
i +1
+ P
i −1
) + P
i
q
i +2
(Q
i
q
i +1
+ Q
i −1
) + Q
i
.
T
`
u
,
kê
´
t qu
,
a n
`
ay c
`
ung v
´
o
,
i (9.12), (9.13) v
`
a (3.21) cho ta
P
i +2
Q
i +2
=
P
i +1
q
i +2
+ P
i
Q
i +1
q
i +2
+ Q
i
. (9.23)
V
`
ı
P
i +2
Q
i +2
l
`
a phân sô
´
tô
´
i gi
,
an theo
¯
d
.
inh ngh
˜
ıa, Ðê
,
ch
´
u
,
ng minh
(9.12a) v
`
a (9.13a) ch
,
ı c
`
on kh
,
˘
ang
¯
d
.
inh vê
´
ph
,
ai (9.23) c
˜
ung l
`
a phân
sô
´
tô
´
i gi
,
an. Gi
,
a s
,
u
,
ngu
,
.
o
,
c l
.
ai, khi
¯
d
´
o P
i +1
q
i +2
+ P
i
v
`
a Q
i +1
q
i +2
+ Q
i
c
´
o u
,
´
o
,
c sô
´
chung d > 1. D
˜
ê thâ
´
y d c
˜
ung l
`
a u
,
´
o
,
c sô
´
chung c
,
ua c
,
a sô
´
P
i +1
(Q
i +1
q
i +2
+ Q
i
) − Q
i +1
(P
i +1
q
i +2
+ P
i
) = P
i +1
Q
i
− Q
i +1
P
i
.
Nhu
,
ng theo gi
,
a thiê
´
t quy n
.
ap hi
.
êu sau c
`
ung l
`
a (−1)
i
v
`
a không
chia hê
´
t cho d, tr
´
ai v
´
o
,
i
¯
diê
`
u gi
,
a s
,
u
,
ngu
,
.
o
,
c l
.
ai. Nhu
,
v
.
ây phân sô
´
,
o
,
vê
´
ph
,
ai c
,
ua (9.23) c
˜
ung l
`
a tô
´
i gi
,
an, suy ra (9.12a) v
`
a (9.13a)
¯
d
˜
a
ch
´
u
,
ng minh.

202 Chu
,
o
,
ng 9. Liên phân sô
´
Ta d
`
ung c
´
ac kê
´
t qu
,
a nh
.
ân
¯
du
,
.
o
,
c
¯
dê
,
ch
´
u
,
ng minh (9.14a). Ta c
´
o
P
i +2
Q
i +1
− P
i +1
Q
i +2
= (P
i +1
q
i +2
+ P
i
)Q
i +1
− P
i +1
(Q
i +1
q
i +2
+ Q
i
)
= −(P
i +1
Q
i
− P
i
Q
i +1
) = −(−1)
i
= (−1)
i +1
,
,
o
,
¯
dây ta
¯
d
˜
a d
`
ung (9.14) nhu
,
gi
,
a thiê
´
t quy n
.
ap.
J
V
´
ı d
.
u 9.4. Ch
´
u
,
ng minh nh
˜
u
,
ng
¯
d
,
˘ang th
´
u
,
c sau
a)
P
i −1
Q
i −1
−
P
i
Q
i
= (−1)
i
.
1
Q
i
Q
i −1
, (i ≥ 1);
b) Q
i
P
i −2
− P
i
Q
i −2
= (−1)
i −1
.q
i
, (i ≥ 2);
c)
P
i −2
Q
i −2
−
P
i
Q
i
= (−1)
i −1
.
q
i
Q
i
Q
i −2
, (i ≥ 2);
d)
Q
i
Q
i
−1
= (q
i
, q
i −1
, . . . , q
1
), (i ≥ 1).
L
`
o
,
i gi
,
ai. a) Suy ra t
`
u
,
¯
d
,
˘
ang th
´
u
,
c
P
i −1
Q
i −1
−
P
i
Q
i
=
P
i −1
Q
i
− P
i
Q
i −1
Q
i
Q
i −1
,
v
´
o
,
i t
,
u
,
sô
´
,
o
,
vê
´
ph
,
ai d
`
ung (9.14).
b) Theo (9.12) ta c
´
o P
i −2
= P
i
− q
i
P
i −1
, Q
i −2
= Q
i
−
q
i
Q
i −1
.Khi
¯
d
´
o Q
i
P
i −2
− P
i
Q
i −2
= Q
i
(P
i
− q
i
P
i −1
) − P
i
(Q
i
−
q
i
Q
i −1
) = q
i
(P
i
Q
i −1
−Q
i
P
i −1
) = (−1)
i −1
q
i
,
,
o
,
¯
dây ta
¯
d
˜
a d
`
ung (3.5).
c) Áp d
.
ung phâ
`
n b).
d) V
´
o
,
i i = 1
¯
d
,
˘
ang th
´
u
,
c
¯
d
˜
a cho c
´
o d
.
ang
Q
1
Q
0
= (q
1
),
¯
diê
`
u n
`
ay
¯
d
´
ung v
`
ı Q
0
= 1, Q
1
= q
1
, ( q
1
) = q
1
. Gi
,
a s
,
u
,
kh
,
˘
ang
¯
d
.
inh
¯
d
´
ung v
´
o
,
i
i(1 ≤ i ≤ n −1). Ta s
˜
e ch
,
ı ra r
`
˘
ang khi
¯
d
´
o n
´
o c
˜
ung
¯
d
´
ung v
´
o
,
i i + 1
hay l
`
a
Q
i +1
Q
i
= (q
i +1
, q
i
, . . . , q
1
).

9.4. Liên phân sô
´
vô h
.
an 203
Th
.
ât v
.
ây, t
`
u
,
(9.13) ta nh
.
ân
¯
du
,
.
o
,
c
Q
i +1
Q
i
= q
i +1
+
Q
i −1
Q
i
= q
i +1
+
1
Q
i
Q
i −1
= (q
i +1
,
Q
i
Q
i −1
).
J
9.4. Liên phân sô
´
vô h
.
an
Cho d
˜
ay sô
´
nh
˜
u
,
ng sô
´
th
.
u
,
c a
0
, a
1
, . . . k
´
y hi
.
êu
a
0
+
1
a
1
+
1
a
2
+
.
.
.
(9.24)
g
.
oi l
`
a liên phân sô
´
vô h
.
an, c
`
on sô
´
a
0
, a
1
, . . . g
.
oi l
`
a phâ
`
n thu
,
o
,
ng
không
¯
dâ
`
y
¯
d
,
u c
,
ua (9.24). Ðê
,
thu
.
ân ti
.
ên ch
´
ung ta viê
´
t (9.24) du
,
´
o
,
i
d
.
ang
(a
0
, a
1
, . . .). (9.25)
Nhu
,
ta
¯
d
˜
a biê
´
t, m
.
oi liên phân sô
´
h
˜
u
,
u h
.
an
¯
dê
`
u biê
,
u di
˜
ên m
.
ôt sô
´
(gi
´
a tr
.
i phân sô
´
), gi
´
a tr
.
i n
`
ay nh
.
ân
¯
du
,
.
o
,
c qua h
˜
u
,
u h
.
an bu
,
´
o
,
c th
.
u
,
c
hi
.
ên t
´
ınh to
´
an h
˜
u
,
u t
,
ı trên phâ
`
n thu
,
o
,
ng không
¯
dâ
`
y
¯
d
,
u. Nhu
,
ng
liên phân sô
´
vô h
.
an không c
´
o
¯
diê
`
u
¯
d
´
o.
Tu
,
o
,
ng t
.
u
,
nhu
,
phân sô
´
h
˜
u
,
u h
.
an
α
i
= (a
0
, a
1
, . . . , a
i
) (9.26)
g
.
oi l
`
a phân sô
´
xâ
´
p x
,
ı th
´
u
,
i, c
`
on m
˜
ôi liên phân sô
´
vô h
.
an
(a
k
, a
k+1
, . . .) (k = 0, 1, . . .)
g
.
oi l
`
a phâ
`
n du
,
c
,
ua (9.24). Sô
´
(9.26) x
´
ac
¯
d
.
inh theo công th
´
u
,
c (9.11)
α
i
=
P
i
Q
i
. Theo c
´
ach n
`
ay m
.
oi phân sô
´
vô h
.
an (9.24) tô
`
n t
.
ai d
˜
ay
phân sô
´
xâ
´
p x
,
ı
P
0
Q
0
,
P
1
Q
1
, . . . ,
P
n
Q
n
, . . . (9.27)

204 Chu
,
o
,
ng 9. Liên phân sô
´
M
˜
ôi m
.
ôt phân sô
´
xâ
´
p x
,
ı l
`
a m
.
ôt sô
´
th
.
u
,
c. Nê
´
u d
˜
ay (9.27) h
.
ôi t
.
u v
`
a
gi
´
o
,
i h
.
an c
,
ua n
´
o l
`
a m
.
ôt sô
´
ω th
`
ı phân sô
´
(9.24) g
.
oi l
`
a h
.
ôi t
.
u, c
`
on
ω l
`
a gi
´
a tr
.
i c
,
ua liên phân sô
´
vô h
.
an. Ta c
´
o thê
,
viê
´
t
ω = (a
0
, a
1
, . . .)
Trong tru
,
`
o
,
ng h
.
o
,
p ngu
,
.
o
,
c l
.
ai, liên phân sô
´
(9.24) g
.
oi l
`
a phân k
`
y.
9.5. V
´
ı d
.
u
V
´
ı d
.
u 9.5. Cho liên phân sô
´
b
0
+
a
1
b
1
+
a
2
b
2
+
.
.
.
+
a
n
b
n
Ta
¯
d
.
˘at
P
0
= b
0
, Q
0
= 1, P
1
= b
0
b
1
+ a
1
, Q
1
= b
1
, . . .
v `a công th
´
u
,
c chung
P
k+1
= b
k+1
P
k
+ a
k+1
P
k−1
,
Q
k+1
= b
k+1
Q
k
+ a
k+1
Q
k−1
.
Ch
´
u
,
ng minh r
`
˘ang
P
n
Q
n
= b
0
+
a
1
b
1
+
a
2
b
2
+
.
.
.
+
a
n
b
n
L
`
o
,
i gi
,
ai. D
˜
ê thâ
´
y r
`
˘
ang v
´
o
,
i k = 0, 1 công th
´
u
,
c
¯
d
´
ung. Gi
,
a thiê
´
t
n
´
o
¯
d
´
ung v
´
o
,
i k = n −1, ta s
˜
e ch
´
u
,
ng minh r
`
˘
ang n
´
o c
˜
ung
¯
d
´
ung cho

9.5. V
´
ı d
.
u 205
k = n. Nhu
,
v
.
ây gi
,
a thiê
´
t c
´
o
b
0
+
a
1
b
1
+
a
2
b
2
+
.
.
.
+
a
n−1
b
n−1
=
P
n−1
Q
n−1
Nhu
,
ng t
`
u
,
công th
´
u
,
c cho P
k
v
`
a Q
k
ta c
´
o
P
n−1
Q
n−1
=
b
n−1
P
n−2
+ a
n−1
P
n−3
b
n−1
Q
n−2
+ a
n−1
Q
n−3
,
o
,
¯
dây P
n−2
, P
n−3
, Q
n−2
, Q
n−3
không ph
.
u thu
.
ôc v
`
ao a
n−1
v
`
a b
n−1
.
M
.
˘
at kh
´
ac, d
`
ung gi
,
a thiê
´
t quy n
.
ap ta nh
.
ân
¯
du
,
.
o
,
c
b
0
+
a
1
b
1
+
a
2
b
2
+
.
.
.
+
a
n−1
b
n−1
+
a
n
b
n
=
( b
n−1
+
a
n
b
n
)P
n−2
+ a
n−1
P
n−3
( b
n−1
+
a
n
b
n
)Q
n−2
+ a
n−1
Q
n−3
=
P
n−1
+
a
n
b
n
P
n−2
Q
n−1
+
a
n
b
n
Q
n−2
=
b
n
P
n−1
+ a
n
P
n−2
b
n
Q
n−1
+ a
n
Q
n−2
=
P
n
Q
n
.
V
´
ı d
.
u 9.6. Ch
´
u
,
ng minh r
`
˘ang (sô
´
m
˜
âu sô
´
trong liên phân sô
´
b
`
˘ang
n).
r
r + 1 −
r
r + 1 −
.
.
.
−
r
r + 1
=
r
n+1
−r
r
r+1
−1

206 Chu
,
o
,
ng 9. Liên phân sô
´
L
`
o
,
i gi
,
ai. Ta k
´
y hi
.
êu liên phân sô
´
theo
P
n
Q
n
. Ta c
´
o
P
1
= r; Q
1
= r + 1;
P
2
= r(r + 1); Q
2
= r
2
+ r + 1;
Ta ch
´
u
,
ng minh b
`
˘
ang phu
,
o
,
ng ph
´
ap quy n
.
ap
P
n
= r
r
n
−1
r − 1
; Q
n
=
r
n+1
−1
r − 1
.
V
´
o
,
i n = 1 công th
´
u
,
c n
`
ay
¯
d
´
ung. Gi
,
ai thiê
´
t n
´
o
¯
d
´
ung v
´
o
,
i n = m, ta
s
˜
e ch
´
u
,
ng minh n
´
o
¯
d
´
ung v
´
o
,
i n = m + 1. Ta c
´
o (theo v
´
ı d
.
u trên)
P
m+1
= b
m+1
P
m
+ a
m+1
P
m−1
.
Trong tru
,
`
o
,
ng h
.
o
,
p c
,
ua ch
´
ung ta th
`
ı
P
m+1
= (r + 1)r
r
m−1
−1
r − 1
−r
2
r
m−1
−1
r − 1
= r
r
m−1
−1
r − 1
.
Tu
,
o
,
ng t
.
u
,
ta c
˜
ung c
´
o Q
m+1
=
r
m+2
−1
r − 1
.
J
V
´
ı d
.
u 9.7. Ch
´
u
,
ng minh r
`
˘ang
1
u
1
+
1
u
2
+ ··· +
1
u
n
=
1
u
1
−
u
2
1
u
1
+ u
2
−
u
2
2
u
2
+ u
3
−
.
.
.
−
u
2
n−1
u
n−1
+ u
n
.
L
`
o
,
i gi
,
ai. Ta
¯
d
.
˘
at
1
u
r
+
1
u
r+1
=
1
u
r
+ x
r
. Khi
¯
d
´
o ta t
`
ım
¯
du
,
.
o
,
c x
r
=
−
u
2
r
u
r
+ u
r+1
. V
`
ı thê
´
1
u
1
+
1
u
2
=
1
u
1
−
u
2
1
u
1
+ u
2
. Ho
,
n n
˜
u
,
a,
1
u
1
+
1
u
2
+
1
u
3
=
1
u
1
+
1
u
2
+ x
2
=
1
u
1
+ x
0
2
,

9.5. V
´
ı d
.
u 207
,
o
,
¯
dây x
0
2
= −
u
2
1
u
1
+ u
2
+ x
2
. Nhu
,
v
.
ây
1
u
1
+
1
u
2
+
1
u
3
=
1
u
1
−
u
2
1
u
1
+ u
2
+ x
2
=
1
u
1
−
u
2
1
u
1
+ u
2
−
u
2
2
u
2
+ u
3
.
Tu
,
o
,
ng t
.
u
,
b
`
˘
ang phu
,
o
,
ng ph
´
ap quy n
.
ap ta c
´
o thê
,
ch
´
u
,
ng minh công
th
´
u
,
c chung.
J
V
´
ı d
.
u 9.8. H ˜ay ch
´
u
,
ng minh
¯
d
,
˘ang th
´
u
,
c sau
a
1
b
1
+
a
2
b
2
+
.
.
.
+
a
n
b
n
=
a
1
c
1
b
1
c
1
+
a
2
c
1
c
2
b
2
c
2
+
.
.
.
+
a
n
c
n
c
n−1
b
n
c
n
,
,
o
,
¯
dây c
1
, c
2
, c
2
, . . . , c
n
l `a nh
˜
u
,
ng sô
´
bâ
´
t k`y kh ´ac 0.
L
`
o
,
i gi
,
ai. Ta k
´
y hi
.
êu bên tr
´
ai b
`
˘
ang phân sô
´
P
n
Q
n
, bên ph
,
ai b
`
˘
ang
phân sô
´
P
0
n
Q
0
n
. Ta ph
,
ai ch
´
u
,
ng minh
P
n
Q
n
=
P
0
n
Q
0
n
v
´
o
,
i m
.
oi sô
´
nguyên
du
,
o
,
ng n. Ta c
´
o
P
1
Q
1
=
a
1
b
1
;
P
2
Q
2
=
a
1
b
2
b
1
b
2
+ a
2
; ···
P
0
1
Q
0
1
=
c
1
a
1
c
1
b
1
;
P
0
2
Q
0
2
=
c
1
c
2
a
1
b
2
c
1
c
2
( b
1
b
2
+ a
2
)
; ···
Ta c
´
o thê
,
¯
d
.
˘
at P
1
= a
1
; Q
1
= b
1
; P
2
= a
1
b
2
; Q
2
= b
1
b
2
+ a
2
v
`
a khi
¯
d
´
o ta c
´
o c
´
ac
¯
d
,
˘
ang th
´
u
,
c sau (do b
`
ai 9.6)
P
n+1
= b
n+1
P
n
+ a
n+1
P
n−1
, Q
n+1
= b
n+1
Q
n
+ a
n+1
Q
n−1
.
Ta l
.
ai
¯
d
.
˘
at
P
0
1
= c
1
a
1
; P
0
2
= c
1
c
2
a
1
b
2
; Q
0
1
= c
1
b
1
; Q
0
2
= c
1
c
2
( b
1
b
2
+ a
2
).

208 Chu
,
o
,
ng 9. Liên phân sô
´
Ta s
˜
e ch
´
u
,
ng minh r
`
˘
ang v
´
o
,
i m
.
oi n c
´
ac
¯
d
,
˘
ang th
´
u
,
c sau
¯
d
´
ung
P
0
n
= c
1
c
2
. . . c
n
P
n
; Q
0
n
= c
1
c
2
. . . c
n
Q
n
.
Th
.
ât v
.
ây, ta ch
´
u
,
ng minh b
`
˘
ang quy n
.
ap, gi
,
a thiê
´
t c
´
ac
¯
d
,
˘
ang th
´
u
,
c
¯
d
´
ung v
´
o
,
i m
.
oi sô
´
nh
,
o ho
,
n hay b
`
˘
ang n, ta s
˜
e ch
´
u
,
ng minh n
´
o c
˜
ung
¯
d
´
ung v
´
o
,
i n + 1. Ta c
´
o
P
0
n+1
= c
n+1
b
n+1
P
0
n
+ c
n
c
n+1
a
n+1
P
0
n−1
,
Q
0
n+1
= c
n+1
b
n+1
Q
0
n
+ c
n
c
n+1
a
n+1
Q
0
n−1
.
T
`
u
,
¯
d
´
o suy ra
P
0
n+1
= c
n+1
b
n+1
c
1
c
2
. . . c
n
P
n
+ c
n
c
n+1
a
n+1
c
1
c
2
. . . c
n−1
P
n−1
= c
1
c
2
. . . c
n+1
( b
n+1
P
n
+ a
n+1
P
n−1
) = c
1
c
2
. . . c
n+1
P
n+1
.
Tu
,
o
,
ng t
.
u
,
ta c
˜
ung ch
´
u
,
ng minh
¯
du
,
.
o
,
c Q
0
n+1
= c
1
c
2
. . . c
n+1
Q
n+1
.
J
V
´
ı d
.
u 9.9. Ch
´
u
,
ng minh c ´ac
¯
d
,
˘ang th
´
u
,
c sau
1)
sin(n + 1)x
sin nx
= 2 cos x −
1
2 cos x −
1
2 cos x +
.
.
.
+
1
2 cos x
liên phân sô
´
b
.
âc n.
2) 1 + b
2
+ b
2
b
3
+ ··· + b
2
b
3
. . . b
n
=
1
1 −
b
2
b
2
+ 1 −
b
3
b
3
+ 1 −
.
.
.
+
b
n
b
n
+ 1
L
`
o
,
i gi
,
ai. 1) Ta
¯
d
.
˘
at liên phân sô
´
bên ph
,
ai b
`
˘
ang
P
n
Q
n
. D
˜
ê thâ
´
y

9.5. V
´
ı d
.
u 209
P
1
Q
1
= 2 cos x . V
`
ı thê
´
ta c
´
o thê
,
¯
d
.
˘
at P
1
=
sin 2x
sin x
; Q
1
=
sin x
sin x
. V
´
o
,
i
n=2, th
`
ı
P
2
Q
2
= 2 cos x −
1
2 cos x
=
4 cos
2
x − 1
2 cos x
.
Suy ra c
´
o thê
,
¯
d
.
˘
at
P
2
=
sin 3x
sin x
; Q
2
=
sin 2x
sin x
.
Ta s
˜
e ch
´
u
,
ng minh r
`
˘
ang P
n
=
sin(n + 1)x
sin x
; Q
n
=
sin nx
sin x
v
´
o
,
i m
.
oi
x. Th
.
ât v
.
ây, gi
,
a thiê
´
t công th
´
u
,
c
¯
d
´
ung v
´
o
,
i n, ta s
˜
e ch
´
u
,
ng minh n
´
o
¯
d
´
ung v
´
o
,
i n + 1. Ta c
´
o (theo b
`
ai .9.5 )
P
n+1
= 2 cos x
sin(n + 1)x
sin x
−
sin nx
sin x
=
1
sin x
sin(n + 2)x.
Ho
`
an to
`
an tu
,
o
,
ng t
.
u
,
ta ch
´
u
,
ng minh cho Q
n+1
=
sin(n + 1)x
sin x
, v
`
ı
thê
´
ta c
´
o công th
´
u
,
c
P
n
Q
n
=
sin(n + 1)x
sin nx
v
´
o
,
i m
.
oi sô
´
nguyên du
,
o
,
ng n.
2) Ta k
´
y hi
.
êu
P
n
Q
n
cho vê
´
ph
,
ai c
,
ua
¯
d
,
˘
ang th
´
u
,
c. Ta câ
`
n ph
,
ai
ch
´
u
,
ng minh
P
n
Q
n
= 1 + b
2
+ b
2
b
3
+ ··· + b
2
b
3
. . . b
n
v
´
o
,
i m
.
oi n nguyên du
,
o
,
ng.
Th
.
ât v
.
ây,
P
1
Q
1
=
1
1
;
P
2
Q
2
=
b
2
+ 1
1
v
`
ı thê
´
P
1
= 1, Q
1
= 1, P
2
= b
2
+ 1, Q
2
= 1. Khi
¯
d
´
o b
`
˘
ang quy n
.
ap

210 Chu
,
o
,
ng 9. Liên phân sô
´
ta c
´
o thê
,
ch
´
u
,
ng minh
¯
du
,
.
o
,
c
P
n
= 1 + b
2
+ b
2
b
3
+ ··· + b
2
b
3
. . . b
n
Q
n
= 1.
Suy ra
¯
d
,
˘
ang th
´
u
,
c câ
`
n ch
´
u
,
ng minh l
`
a
¯
d
´
ung.
J
V
´
ı d
.
u 9.10. Ch
´
u
,
ng minh r
`
˘ang nê
´
u m
.
ôt liên phân sô
´
c´o n phâ
`
n
t
,
u
,
b
`
˘ang 1, th`ı gi ´a tr
.
i phân sô
´
n `ay b
`
˘ang
u
n+1
u
n
,
,
o
,
¯
dây u
1
= u
2
=
1, u
3
= 2, . . . l `a nh
˜
u
,
ng sô
´
Fibonacci.
L
`
o
,
i gi
,
ai. Ta s
,
u
,
d
.
ung quy n
.
ap theo n. V
´
o
,
i n = 1 v
`
a n = 2 kh
,
˘
ang
¯
d
.
inh
¯
d
´
ung:
ω
1
= (1) = 1 =
1
1
=
u
2
u
1
, ω
2
= (1, 1) = 1 +
1
1
=
2
1
=
u
3
u
2
.
Gi
,
a thiê
´
t kh
,
˘
ang
¯
d
.
inh
¯
d
´
ung v
´
o
,
i n n
`
ao
¯
d
´
o, ngh
˜
ıa l
`
a ω
n
=
(1, 1, . . . , 1)
| {z }
n
=
u
n+1
u
n
. Ta s
˜
e ch
´
u
,
ng minh trong tru
,
`
o
,
ng h
.
o
,
p nhu
,
v
.
ây
n
´
o c
˜
ung
¯
d
´
ung cho n + 1. Th
.
ât v
.
ây,
ω
n+1
= (1, 1, . . . , 1)
| {z }
n+1
= (1, ω
n
)
= 1 +
1
ω
n
=
u
n
+ u
n+1
u
n+1
=
u
n+2
u
n+1
.
J
9.6. B
`
ai t
.
âp
.
.
. 9.11. Cho liên phân sô
´
vô h
.
an (q
0
, q
1
, . . .),
,
o
,
¯
dây q
0
≥ q
1
> 0, . . .
l
`
a nh
˜
u
,
ng sô
´
t
.
u
,
nhiên. H
˜
ay ch
´
u
,
ng minh nh
˜
u
,
ng kh
,
˘
ang
¯
d
.
inh sau:
a) D
˜
ay
P
0
Q
0
,
P
2
Q
2
, . . . , l
`
a d
˜
ay t
˘
ang.
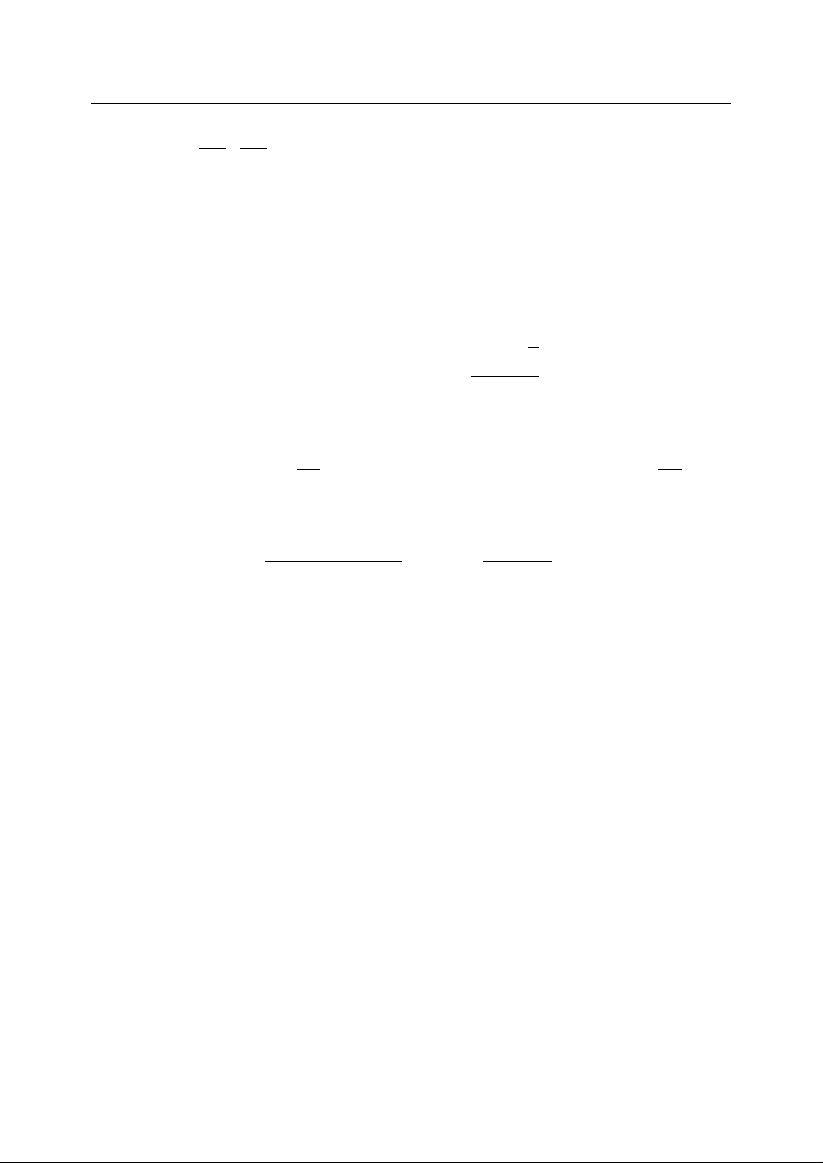
9.6. B
`
ai t
.
âp 211
b) D
˜
ay
P
1
Q
1
,
P
3
Q
3
, . . . , l
`
a d
˜
ay gi
,
am.
.
.
. 9.12. Cho (q
0
, q
1
, . . .) l
`
a liên phân sô
´
,
o
,
b
`
ai trên. Ch
´
u
,
ng minh
m
.
ênh
¯
dê
`
sau
a) (q
0
, q
1
, . . .) h
.
ôi t
.
u.
b) Sô
´
ω = (q
0
, q
1
, . . .) l
`
a sô
´
vô t
,
ı.
.
.
. 9.13. Ch
´
u
,
ng minh r
`
˘
ang ( 1, 1, . . .) =
1 +
√
5
2
.
.
.
. 9.14. Cho ω = (q
0
, q
1
, . . . , q
n
). Ch
´
u
,
ng minh r
`
˘
ang nê
´
u ta lâ
´
y
phân sô
´
xâ
´
p x
,
ı th
´
u
,
i
P
i
Q
i
¯
dô
´
i v
´
o
,
i ω, th
`
ı v
´
o
,
i sai sô
´
δ
i
= |ω −
P
i
Q
i
|(i =
0, 1, . . . , n −1) tho
,
a m
˜
an
¯
d
´
anh gi
´
a sau
1
Q
i
(Q
i
+ Q
i +1
)
< δ
i
<
1
Q
i
Q
i +1
.

CHU
,
O
,
NG 10
M
.
ÔT S
´
Ô Ð
`
Ê THI VÔ Ð
.
ICH
Râ
´
t nhiê
`
u nu
,
´
o
,
c h
`
ang n
˘
am
¯
dê
`
u tô
,
ch
´
u
,
c thi vô
¯
d
.
ich quô
´
c gia vê
`
môn to
´
an cho c
´
ac h
.
oc sinh tru
,
`
o
,
ng phô
,
thông. Nh
˜
u
,
ng k
`
y thi
¯
d
´
o
c
´
o râ
´
t nhiê
`
u b
`
ai gi
,
ai b
`
˘
ang phu
,
o
,
ng ph
´
ap quy n
.
ap. Sau
¯
dây ch
,
ı l
`
a
m
.
ôt sô
´
nh
,
o c
´
ac
¯
dê
`
¯
d
˜
a c
´
o, bên c
.
anh sô
´
b
`
ai l
`
a tên nu
,
´
o
,
c v
`
a n
˘
am ra
¯
dê
`
thi.
V
´
ı d
.
u 10.1. (Hungari 1932). Ch
´
u
,
ng minh r
`
˘ang nê
´
u a, b v `a n l `a
nh
˜
u
,
ng sô
´
t
.
u
,
nhiên v `a b chia hê
´
t cho a
n
, th`ı sô
´
(a + 1)
b
−1 chia hê
´
t
cho a
n+1
.
L
`
o
,
i gi
,
ai. Ta ch
´
u
,
ng minh b
`
˘
ang phu
,
o
,
ng ph
´
ap quy n
.
ap theo n. V
´
o
,
i
n = 0 m
.
ênh
¯
dê
`
kh
,
˘
ang
¯
d
.
inh
¯
d
´
ung, v
`
ı (a + 1)
b
−1 chia hê
´
t cho a.
Gi
,
a s
,
u
,
kh
,
˘
ang
¯
d
.
inh
¯
d
´
ung v
´
o
,
i sô
´
k n
`
ao
¯
d
´
o, ngh
˜
ıa l
`
a ta gi
,
a thiê
´
t nê
´
u
b
.
.
. a
k
, th
`
ı ((a + 1)
b
− 1)
.
.
. a
k+1
. Cho b
0
l
`
a sô
´
t
.
u
,
nhiên chia hê
´
t cho
a
k+1
. Ta
¯
d
.
˘
at b =
b
0
a
. Khi
¯
d
´
o b
.
.
. a
k
v
`
a v
`
ı
(a + 1)
b
0
= (a + 1)
ab
−1 = [(a + 1)
b
]
a
−1 =
= [(a + 1)
b
−1][(a + 1)
(a−1)b
+ (a + 1)
(a−2)b
+ ··· + (a + 1)
b
+ 1],
nên (a + 1)
b
0
− 1 chia hê
´
t cho a
k+2
. Th
.
ât v
.
ây, theo gi
,
a thiê
´
t quy
n
.
ap th
`
u
,
a sô
´
th
´
u
,
nhâ
´
t trong biê
,
u th
´
u
,
c sau c
`
ung chia hê
´
t cho a
k+1
,
c
`
on th
`
u
,
a sô
´
th
´
u
,
hai biê
,
u di
˜
ên du
,
´
o
,
i d
.
ang
[(a + 1)
(a−1)b
−1] + [(a + 1)
(a−2)b
−1] + ··· + [(a + 1)
b
−1] + a
212
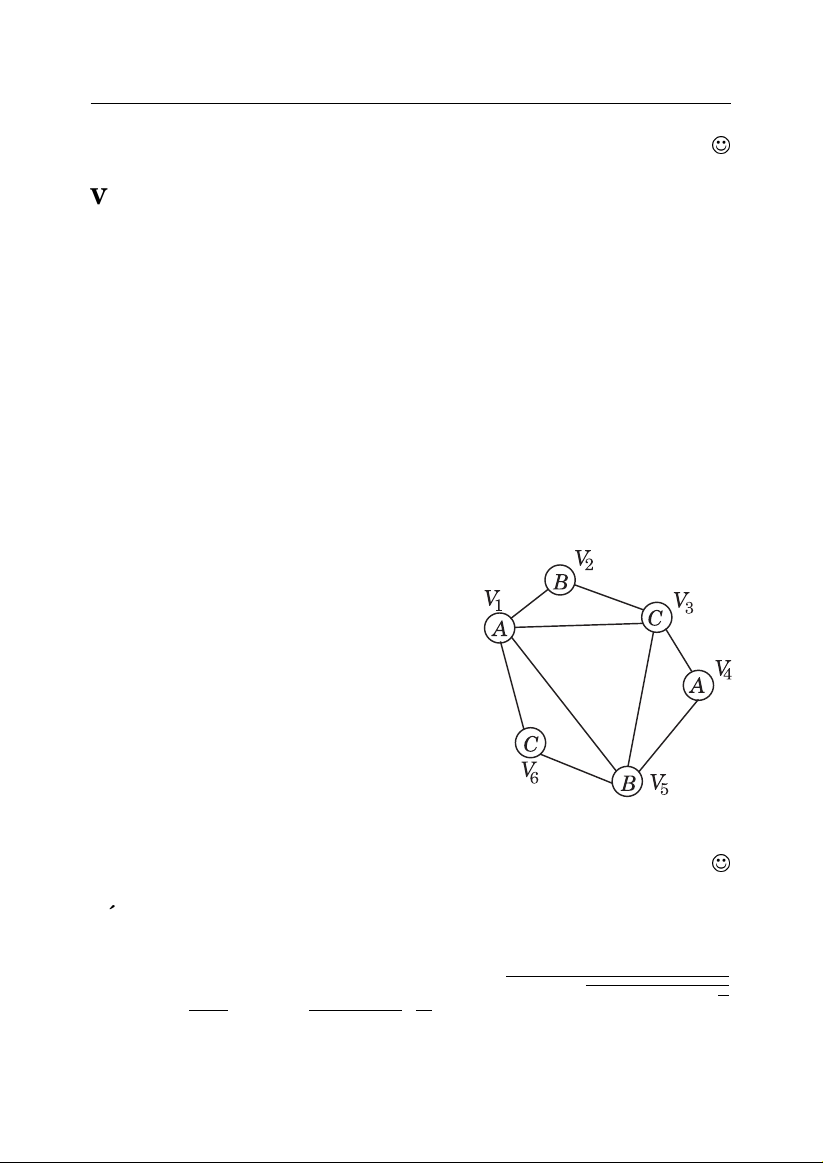
213
t
`
u
,
¯
d
´
o
¯
d
˜
ê thâ
´
y n
´
o chia hê
´
t cho a. Suy ra ((a + 1)
b
0
−1)
.
.
. a
k+2
.
J
V
´
ı d
.
u 10.2. (Hungari 1979). Nh
˜
u
,
ng
¯
d
,
ınh c
,
ua m
.
ôt
¯
da gi ´ac lô
`
i c´o
sô
´
c
.
anh l`a sô
´
l
,
e
¯
du
,
.
o
,
c tô m`au sao cho m
.
oi c
.
˘ap hai
¯
diê
,
m c
.
anh nhau
c´o m`au kh ´ac nhau. Ch
´
u
,
ng minh r
`
˘ang b
`
˘ang m
.
ôt sô
´
¯
du
,
`
o
,
ng ch´eo
không c
´
˘at nhau c
,
ua
¯
da gi ´ac n `ay c´o thê
,
c
´
˘at th `anh nh
˜
u
,
ng h`ınh
tam gi ´ac, m `a nh
˜
u
,
ng
¯
d
,
ınh c
,
ua m
˜
ôi tam gi ´ac
¯
du
,
.
o
,
c tô v
´
o
,
i nh
˜
u
,
ng
m `au kh ´ac nhau.
L
`
o
,
i gi
,
ai. Ch
´
u
,
ng minh b
`
˘
ang phu
,
o
,
ng ph
´
ap quy n
.
ap
¯
dô
´
i v
´
o
,
i sô
´
c
.
anh n c
,
ua
¯
da gi
´
ac. V
´
o
,
i n = 3 kh
,
˘
ang
¯
d
.
inh c
,
ua b
`
ai to
´
an l
`
a hiê
,
n
nhiên. cho n > 3. D
˜
ê thâ
´
y tô
`
n t
.
ai ba
¯
d
,
ınh kê
`
nhau V
1
, V
2
v
`
a V
3
c
,
ua
¯
da gi
´
ac
¯
du
,
.
o
,
c tô tu
,
o
,
ng
´
u
,
ng ba m
`
au kh
´
ac nhau A, B v
`
a C.
Nê
´
u V
4
không tô m
`
au A; ho
.
˘
ac l
`
a
nê
´
u V
4
tô m
`
au A, c
`
on V
5
không tô
m
`
au B; ho
.
˘
ac l
`
a nê
´
u V
4
c
´
o m
`
au A,
V
5
c
´
o m
`
au B, c
`
on V
6
không ph
,
ai
m
`
au C, c
`
on l
.
ai ta
´
ap d
.
ung gi
,
a
thiê
´
t quy n
.
ap . Nê
´
u V
4
c
´
o m
`
au
A, V
5
c
´
o m
`
au B v
`
a V
6
c
´
o m
`
au C,
h
`
ınh l
.
uc gi
´
ac V
1
V
2
V
3
V
4
V
5
V
6
ta c
´
o
thê
,
chia ra nhu
,
h
`
ınh v
˜
e (h
`
ınh 12),
phâ
`
n c
`
on l
.
ai c
,
ua
¯
da gi
´
ac ta
´
ap
d
.
ung gi
,
a thiê
´
t quy n
.
ap.
J
V
´
ı d
.
u 10.3. (Moscow 1945). M
.
ôt sô
´
trong c ´ac sô
´
a
1
, a
2
, . . . , a
n
b
`
˘ang
+1, sô
´
c`on l
.
ai b
`
˘ang -1. Ch
´
u
,
ng minh r
`
˘ang
2 sin(a
1
+
a
1
a
2
2
+ ···+
a
1
a
2
. . . a
n
2
n−1
)
π
4
= a
1
r
2 + a
2
q
2 + ··· + a
n
√
2.

214 Chu
,
o
,
ng 10. M
.
ôt sô
´
¯
dê
`
thi vô
¯
d
.
ich
L
`
o
,
i gi
,
ai. Ch
´
u
,
ng minh b
`
˘
ang phu
,
o
,
ng ph
´
ap quy n
.
ap to
´
an h
.
oc. V
´
o
,
i
n = 1 ta câ
`
n kiê
,
m tra công th
´
u
,
c 2 sin a
1
π
4
= a
1
√
2, hiê
,
n nhiên
¯
d
´
ung. Gi
,
a s
,
u
,
công th
´
u
,
c sau
¯
d
´
ung v
´
o
,
i sô
´
k n
`
ao
¯
d
´
o
2 sin(a
1
+
a
1
a
2
2
+ ···+
a
1
a
2
. . . a
k
2
k−1
)
π
4
= a
1
r
2 + a
2
q
2 + ··· + a
k
√
2.
Khi
¯
d
´
o
2 + a
1
r
2 + a
2
q
2 + ··· + a
k
√
2 =
= 2 + 2 sin(a
1
+
a
1
a
2
2
+
a
1
a
2
a
3
4
+ ··· +
a
1
a
2
. . . a
k
2
k−1
)
π
4
= 2 −2 cos(
π
2
+ (a
1
+ +
a
1
a
2
2
+
a
1
a
2
a
3
4
+ ··· +
a
1
a
2
. . . a
k
2
k−1
)
π
4
)
= 2(1 − cos2(1 +
a
1
2
+ +
a
1
a
2
4
+
a
1
a
2
a
3
8
+ ··· +
a
1
a
2
. . . a
k
2
k
)
π
4
)
= 4 sin
2
(1 +
a
1
2
+
a
1
a
2
4
+
a
1
a
2
a
3
8
+ ··· +
a
1
a
2
. . . a
k
2
k
)
π
4
.
V
`
ı 0 < 1 +
a
1
2
+
a
1
a
2
4
+ ···+
a
1
a
2
. . . a
k
2
k
< 2, t
`
u
,
bâ
´
t
¯
d
,
˘
ang th
´
u
,
c trên
suy ra
r
2 + a
1
q
2 + ··· + a
k
√
2 = 2 sin(1 +
a
1
2
+
a
1
a
2
4
+ ···+
a
1
a
2
. . . a
k
2
k
)
π
4
.
B
,
o
,
i v
`
ı h
`
am sin l
`
a h
`
am l
,
e, v
´
o
,
i a
0
= ±1, ta nhân v
`
ao hai vê
´
c
,
ua
¯
d
,
˘
ang th
´
u
,
c trên v
`
a biê
´
n
¯
dô
,
i
a
0
r
2 + a
1
q
2 + ··· + a
k
√
2 =
= a
0
2 sin(1 +
a
1
2
+
a
1
a
2
4
+
a
1
a
2
a
3
8
+ ··· +
a
1
a
2
. . . a
k
2
k
)
π
4
=
= 2 sin(a
0
+
a
0
a
1
2
+
a
0
a
1
a
2
4
+
a
0
a
1
a
2
a
3
8
+ ··· +
a
0
a
1
a
2
. . . a
k
2
k
)
π
4
.
¯
diê
`
u
¯
d
´
o ch
,
ı ra r
`
˘
ang công th
´
u
,
c
¯
du
,
.
o
,
c ch
´
u
,
ng minh
¯
d
´
ung v
´
o
,
i n =
k + 1. Theo nguyên l
´
y quy n
.
ap công th
´
u
,
c
¯
d
´
ung v
´
o
,
i m
.
oi n.
J

215
V
´
ı d
.
u 10.4. (Moscow 1984). Cho X = (x
1
, x
2
, . . . , x
n
) l `a d ˜ay n,
n ≥ 4, nh
˜
u
,
ng sô
´
không âm, tô
,
ng c
,
ua ch ´ung b
`
˘ang 1.
a) Ch
´
u
,
ng minh r
`
˘ang
x
1
x
2
+ x
2
x
3
+ ··· + x
n
x
1
≤
1
4
.
b) Ch
´
u
,
ng minh r
`
˘ang tô
`
n t
.
ai m
.
ôt tô
,
h
.
o
,
p Y = (y
1
, y
2
, . . . , y
n
) c
,
ua
X, sao cho
y
1
y
2
+ y
2
y
3
+ ··· + y
n
y
1
≤
1
n
.
L
`
o
,
i gi
,
ai. a) Áp d
.
ung phu
,
o
,
ng ph
´
ap quy n
.
ap
¯
dô
´
i v
´
o
,
i n, ta ch
´
u
,
ng
minh
(x
1
+ x
2
+ ··· + x
n
)
2
≥ 4(x
1
x
2
+ x
2
x
3
+ ··· + x
n
x
1
), (10.1)
,
o
,
¯
dây x
i
≥ 0 v
`
a n ≥ 4. T
`
u
,
¯
d
´
o v
´
o
,
i
n
∑
i =1
x
i
= 1 ta nh
.
ân
¯
du
,
.
o
,
c kê
´
t qu
,
a.
Nê
´
u n = 4, bâ
´
t
¯
d
,
˘
ang th
´
u
,
c (10.1) tu
,
o
,
ng
¯
du
,
o
,
ng v
´
o
,
i bâ
´
t
¯
d
,
˘
ang
th
´
u
,
c
(x
1
− x
2
+ x
3
− x
4
)
2
≥ 0
Ta ch
´
u
´
y
¯
d
,
˘
ang th
´
u
,
c x
,
ay ra khi v
`
a ch
,
ı khi x
1
+ x
3
= x
2
+ x
4
.
Bây gi
`
o
,
bâ
´
t
¯
d
,
˘
ang th
´
u
,
c (10.1)
¯
d
´
ung v
´
o
,
i m
.
ôt sô
´
cô
´
¯
d
.
inh bâ
´
t k
`
y
n
`
ao
¯
d
´
o n = k ≥ 4. Ta câ
`
n ch
´
u
,
ng minh
(x
1
+ x
2
+ ···+ x
k
+ x
k+1
)
2
≥ 4(x
1
x
2
+ x
2
x
3
+ ···+ x
k
x
k+1
+ x
k+1
x
1
).
(10.2)
V
`
ı tô
,
ng hai vê
´
c
,
ua bâ
´
t
¯
d
,
˘
ang th
´
u
,
c (10.2) l
`
a v
`
ong tr
`
on theo ch
,
ı
sô
´
, ta c
´
o thê
,
gi
,
a thiê
´
t x
k+1
≤ x
i
v
´
o
,
i i = 1, 2, . . . , k. Khi
¯
d
´
o t
`
u
,
gi
,
a
thiê
´
t quy n
.
ap suy ra
(x
1
+ x
2
+ ··· + x
k−1
+ (x
k
+ x
k+1
))
2
≥
≥ 4(x
1
x
2
+ x
2
x
3
+ ··· + x
k−1
(x
k
+ x
k+1
) + (x
k
+ x
k+1
)x
1
). (10.3)

216 Chu
,
o
,
ng 10. M
.
ôt sô
´
¯
dê
`
thi vô
¯
d
.
ich
B
,
o
,
i v
`
ı
(x
1
x
2
+ x
2
x
3
+ ··· + x
k−1
(x
k
+ x
k+1
) + (x
k
+ x
k+1
)x
1
) =
(x
1
x
2
+ x
2
x
3
+ ··· + x
k
x
k+1
+ x
k+1
x
1
) + x
k−1
x
k+1
+ x
k
(x
1
− x
k+1
))
v
`
a x
1
− x
k+1
≥ 0, th
`
ı t
`
u
,
(10.3) suy ra (10.2).
b) V
´
o
,
i tô
,
h
.
o
,
p bâ
´
t k
`
y Y = (y
1
, y
2
, . . . , y
n
) c
,
ua X ta
¯
d
.
˘
at
S
Y
= y
1
y
2
+ y
2
y
3
+ ··· + y
n
y
1
.
Ta k
´
y hi
.
êu
∑
S
Y
= S (tô
,
ng t
´
ınh theo tâ
´
t c
,
a n! ho
´
an v
.
i c
,
ua X). V
´
o
,
i
s
.
u
,
cô
´
¯
d
.
inh i v
`
a j, i 6= j sô
´
lu
,
.
o
,
ng c
,
ua nh
˜
u
,
ng tô
,
h
.
o
,
p c
,
ua X, trong
¯
d
´
o
x
i
¯
d
´
u
,
ng tru
,
´
o
,
c x
j
(xê
´
p theo v
`
ong l
.
˘
ap!), l
`
a n(n −2)!. T
`
u
,
¯
dây
S = n(n − 2)!
n
∑
i,j=1,i6=j
x
i
x
j
= n(n −2)!(1 −
n
∑
i =1
x
2
k
≤
≤ n(n −2)!(1 −
1
n
(
n
∑
k=1
x
k
)
2
) = n( n −2)!(1 −
1
n
) = (n −1)!.
Suy ra sô
´
nh
,
o nhâ
´
t trong S
Y
không vu
,
.
o
,
t qu
´
a
S
n!
≤
( n −1)!
n!
=
1
n
.
J
V
´
ı d
.
u 10.5. (Ba lan 1952-1953). Ch
´
u
,
ng minh r
`
˘ang nê
´
u n l `a m
.
ôt
sô
´
t
.
u
,
nhiên, th`ı
(
√
2 −1)
n
=
√
m −
√
m −1
v
´
o
,
i m
.
ôt sô
´
t
.
u
,
nhiên th´ıch h
.
o
,
p n `ao
¯
d´o m.
L
`
o
,
i gi
,
ai. Ta s
˜
e ch
´
u
,
ng minh b
`
˘
ang quy n
.
ap to
´
an h
.
oc kh
,
˘
ang
¯
d
.
inh
sau, v
´
o
,
i m
.
oi sô
´
t
.
u
,
nhiên n tô
`
n t
.
ai nh
˜
u
,
ng sô
´
t
.
u
,
nhiên a
n
v
`
a b
n
sao
cho
(
(1 −
√
2)
n
= a
n
−b
n
√
2
a
2
n
−2b
2
n
= (−1)
n
.
(10.4)

217
Th
.
ât v
.
ây, m
.
ênh
¯
dê
`
¯
d
´
ung v
´
o
,
i n = 1, v
`
ı trong tru
,
`
o
,
ng h
.
o
,
p n
`
ay
a
1
= b
1
= 1
¯
du
,
a c
´
ac vê
´
c
,
ua
¯
d
,
˘
ang th
´
u
,
c trên b
`
˘
ang nhau. Ta gi
,
a
thiê
´
t r
`
˘
ang v
´
o
,
i n cô
´
¯
d
.
inh bâ
´
t k
`
y ta c
´
o nh
˜
u
,
ng sô
´
th
´
ıch h
.
o
,
p a
n
v
`
a b
n
,
v
´
o
,
i ch
´
ung (10.4)
¯
d
´
ung. Khi
¯
d
´
o nh
˜
u
,
ng
¯
d
,
˘
ang th
´
u
,
c
(1 −
√
2)
n+1
= (1 −
√
2)
n
(1 −
√
2)
= (a
n
−b
n
√
2)(1 −
√
2)
= (a
n
+ 2b
n
) − (a
n
+ b
n
)
√
2,
suy ra s
.
u
,
tô
`
n t
.
ai c
,
ua nh
˜
u
,
ng sô
´
tu
,
o
,
ng
´
u
,
ng
a
n+1
= a
n
+ 2b
n
v
`
a b
n+1
= a
n
+ b
n
,
t
.
ai v
`
ı
a
2
n+1
−2b
2
n+1
= (a
n
+ 2b
n
)
2
−2(a
n
+ b
n
)
2
= −(a
2
n
−2b
2
n
) = (−1)
n+1
.
Nhu
,
v
.
ây
¯
diê
`
u kh
,
˘
ang
¯
d
.
inh
¯
d
´
ung v
´
o
,
i m
.
oi n.
Ta ch
,
ı c
`
on
¯
d
.
˘
at m = a
2
v
´
o
,
i n l
`
a sô
´
ch
˜
˘
an, v
`
a m = 2b
2
n
v
´
o
,
i n l
`
a sô
´
l
,
e,
¯
dê
,
nh
.
ân
¯
du
,
.
o
,
c l
`
o
,
i gi
,
ai b
`
ai to
´
an.
J
V
´
ı d
.
u 10.6. (Liên xô 1976). Cho x
0
v `a x
1
l `a nh
˜
u
,
ng sô
´
t
.
u
,
nhiên
nh
,
o ho
,
n 1000, v `a
¯
d
.
˘at
x
2
= |x
0
− x
1
|, x
3
= |x
1
− x
2
|, x
4
= |x
2
− x
3
|, . . .
Ch
´
u
,
ng minh r
`
˘ang ´ıt nhâ
´
t m
.
ôt trong nh
˜
u
,
ng sô
´
x
2
, x
3
, . . . , x
1500
b
`
˘ang 0.
L
`
o
,
i gi
,
ai. Ch
´
u
,
ng minh b
`
˘
ang quy n
.
ap theo n kê
´
t qu
,
a m
.
anh ho
,
n
¯
dê
`
ra: Nê
´
u trong d ˜ay sô
´
nhu
,
¯
dê
`
ra sô
´
x
0
v `a x
1
nh
,
o ho
,
n 2n, th`ı ´ıt
nhâ
´
t m
.
ôt trong nh
˜
u
,
ng sô
´
x
1
, x
2
, . . . , x
3n
b
`
˘ang 0.
Gi
,
a s
,
u
,
m
.
ênh
¯
dê
`
¯
d
˜
a
¯
du
,
.
o
,
c ch
´
u
,
ng minh v
´
o
,
i m
.
oi sô
´
nguyên nh
,
o
ho
,
n n. Nê
´
u trong d
˜
ay th
.
u
,
c s
.
u
,
c
´
o bâ
´
t
¯
d
,
˘
ang th
´
u
,
c x
3
< 2n −2, x
4
<
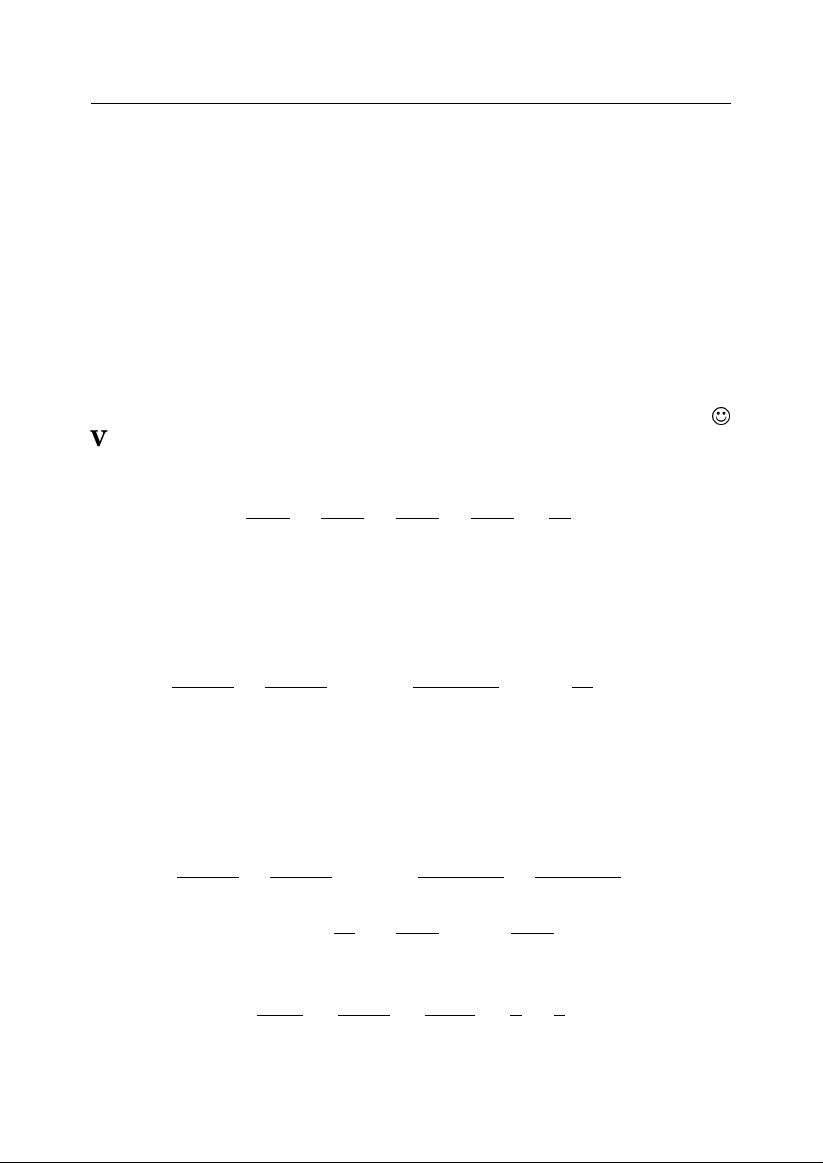
218 Chu
,
o
,
ng 10. M
.
ôt sô
´
¯
dê
`
thi vô
¯
d
.
ich
2n −2, th
`
ı t
`
u
,
gi
,
a thiê
´
t quy n
.
ap suy ra kê
´
t qu
,
a m
.
ênh
¯
dê
`
câ
`
n ch
´
u
,
ng
minh.
B
,
o
,
i v
`
ı theo
¯
diê
`
u ki
.
ên c
´
o x
0
≤ 2n −1, x
1
≤ 2n −1, th
`
ı v
´
o
,
i x
2
≥ 1
ta c
´
o x
3
≤ 2n −2, x
4
≤ 2n −3.
Nê
´
u x
3
6= 2n − 2, th
`
ı l
.
ai
¯
du
,
a vê
`
gi
,
a thiê
´
t quy n
.
ap. Nê
´
u x
3
=
2n − 2, th
`
ı x
2
= 1, x
1
= 2n − 1, x
0
= 2n − 2. Ta s
˜
e ch
´
u
,
ng minh
kh
,
˘
ang
¯
d
.
inh trong tru
,
`
o
,
ng h
.
o
,
p n
`
ay. Ta c
´
o
x
3
= 2n −2, x
4
= 2n −3, x
5
= 1, x
6
= 2n −4, x
7
= 2n −5,
x
8
= 1, . . . , x
3k
= 2n −2k, . . . , x
3n
= 0.
J
V
´
ı d
.
u 10.7. (Canada 1979). Cho a, b, c, d v`a e l `a nh
˜
u
,
ng sô
´
nguyên
th
,
oa m ˜an
¯
diê
`
u ki
.
ên 1 ≤ a < b < c < d < e. Ch
´
u
,
ng minh r
`
˘ang
1
[a, b]
+
1
[b, c]
+
1
[c, d]
+
1
[d, e]
≤
15
16
,
,
o
,
¯
dây [m, n] k´y hi
.
êu l `a b
.
ôi sô
´
chung nh
,
o nhâ
´
t c
,
ua m v `a n.
L
`
o
,
i gi
,
ai. Ta ch
´
u
,
ng minh theo quy n
.
ap bâ
´
t
¯
d
,
˘
ang th
´
u
,
c tô
,
ng qu
´
at
ho
,
n.
1
[a
0
, a
1
]
+
1
[a
1
, a
2
]
+ ··· +
1
[a
n−1
, a
n
]
≤ 1 −
1
2
n
(10.5)
,
o
,
¯
dây 0 < a
0
< a
1
< . . . < a
n
l
`
a nh
˜
u
,
ng sô
´
t
.
u
,
nhiên. V
´
o
,
i n = 1 th
`
ı
(10.5)
¯
d
´
ung hiê
,
n nhiên. Ta gi
,
a s
,
u
,
r
`
˘
ang (10.5)
¯
d
´
ung v
´
o
,
i n n
`
ao
¯
d
´
o,
v
`
a ta x
´
et nh
˜
u
,
ng sô
´
t
.
u
,
nhiên bâ
´
t k
`
y 0 < a
0
< a
1
< . . . < a
n
< a
n+1
.
Nê
´
u a
n+1
≥ 2
n+1
, th
`
ı [a
n
, a
n+1
] ≥ 2
n+1
v
`
a t
`
u
,
(10.5) suy ra
1
[a
0
, a
1
]
+
1
[a
1
, a
2
]
+ ··· +
1
[a
n−1
, a
n
]
+
1
[a
n
, a
n+1
]
≤
≤ (1 −
1
2
n
) +
1
2
n+1
= 1 −
1
2
n+1
.
Bây gi
`
o
,
cho a
n+1
< 2
n+1
. Ta ch
´
u
´
y r
`
˘
ang v
´
o
,
i nh
˜
u
,
ng sô
´
t
.
u
,
nhiên bâ
´
t
k
`
y p v
`
a q, p < q, ta c
´
o
1
[p, q]
=
(p, q)
pq
≤
q − p
pq
=
1
p
−
1
q

219
(Ta
¯
d
˜
a
´
ap d
.
ung
¯
d
,
˘
ang th
´
u
,
c [p, q](p, q) = p q v
`
a q − p chia hê
´
t cho
(p, q)). Suy ra
1
[a
0
, a
1
]
+
1
[a
1
, a
2
]
+ ··· +
1
[a
n−1
, a
n
]
+
1
[a
n
, a
n+1
]
≤
(
1
a
0
−
1
a
1
) + (
1
a
1
−
1
a
2
) + ···+ (
1
a
n
−
1
a
n+1
) =
=
1
a
0
−
1
a
n+1
< 1 −
1
2
n+1
,
Bâ
´
t
¯
d
,
˘
ang th
´
u
,
c (10.5) tr
,
o
,
th
`
anh
¯
d
,
˘
ang th
´
u
,
c v
´
o
,
i a
i
= 2
i
, i =
0, 1, . . . , n.
J
V
´
ı d
.
u 10.8. (Canada 1982). Cho a, b v `a c l`a nh
˜
u
,
ng nghi
.
êm c
,
ua
phu
,
o
,
ng tr`ınh
x
3
− x
2
− x −1 = 0.
Ch
´
u
,
ng minh r
`
˘ang sô
´
b
1982
−c
1982
b − c
+
c
1982
− a
1982
c − a
+
a
1982
−b
1982
a − b
l `a m
.
ôt sô
´
nguyên.
L
`
o
,
i gi
,
ai. Ta
¯
d
.
˘
at
r
n
=
b
n
−c
n
b − c
, s
n
=
c
n
− a
n
c − a
, t
n
=
a
n
−b
n
a − b
v
´
o
,
i n = 1, 2, . . .
Ta s
˜
e ch
´
u
,
ng minh r
`
˘
ang
r
n+3
= r
n+2
+ r
n+1
+ r
n
, n ≥ 1.
V
`
ı nh
˜
u
,
ng nghi
.
êm b v
`
a c th
,
oa m
˜
an
¯
d
,
˘
ang th
´
u
,
c
b
3
= b
2
+ b + 1, c
3
= c
2
+ c + 1,
nên
r
n+3
=
b
n+3
−c
n+3
b − c
=
b
n
( b
2
+ b + 1) −c
n
( c
2
+ c + 1)
b − c
=
b
n+2
−c
n+2
b − c
+
b
n+1
−c
n+1
b − c
+
b
n
−c
n
b − c
= r
n+2
+ r
n+1
+ r
n
.

220 Chu
,
o
,
ng 10. M
.
ôt sô
´
¯
dê
`
thi vô
¯
d
.
ich
Theo c
`
ung phu
,
o
,
ng ph
´
ap nhu
,
v
.
ây ta nh
.
ân
¯
du
,
.
o
,
c
s
n+3
= s
n+2
+ s
n+1
+ s
n
, t
n+3
= t
n+2
+ t
n+1
+ t
n
, n ≥ 1.
Ta s
˜
e ch
´
u
,
ng minh b
`
˘
ang phu
,
o
,
ng ph
´
ap quy n
.
ap to
´
an h
.
oc
¯
dô
´
i v
´
o
,
i n,
sao cho r
n
+ s
n
+ t
n
l
`
a sô
´
nguyên v
´
o
,
i m
.
oi n ≥ 1. V
`
ı
r
1
+ s
1
+ t
1
= 3,
r
2
+ s
2
+ t
2
= 2(a + b + c) = 2,
r
3
+ s
3
+ t
3
= 2(a + b + c)
2
−3(bc + ca + ab) = 5.
Kh
,
˘
ang
¯
d
.
inh
¯
d
´
ung v
´
o
,
i n = 1, 2, 3. Ta gi
,
a s
,
u
,
r
`
˘
ang kh
,
˘
ang
¯
d
.
inh
c
˜
ung
¯
d
´
ung v
´
o
,
i n = 1, 2, . . . , k + 2, k ≥ 1. Khi
¯
d
´
o
r
k+3
+ s
k+3
+ t
k+3
= (r
k+2
+ s
k+2
+ t
k+2
) + (r
k+1
+ s
k+1
+ t
k+1
) + (r
k
+ s
k
+ t
k
).
Theo gi
,
a thiê
´
t quy n
.
ap n
´
o l
`
a tô
,
ng c
,
ua ba sô
´
nguyên v
`
a suy ra
tô
,
ng
,
o
,
¯
dê
`
b
`
ai l
`
a sô
´
nguyên.
J
V
´
ı d
.
u 10.9. (CHLB Ð
´
u
,
c 1981). D ˜ay a
1
, a
2
, a
3
, . . .
¯
du
,
.
o
,
c cho nhu
,
sau: a
1
l `a sô
´
t
.
u
,
nhiên, a
n+1
= [1, 5a
n
] + 1 v
´
o
,
i m
.
oi n = 1, 2, . . .. C´o
thê
,
ch
.
on a
1
nhu
,
thê
´
n `ao
¯
dê
,
cho 100 000 sô
´
h
.
ang
¯
dâ
`
u tiên c
,
ua d˜ay
trên l `a nh
˜
u
,
ng sô
´
ch
˜
˘an, c`on sô
´
h
.
ang th
´
u
,
100 001 l `a m
.
ôt sô
´
l
,
e ?
L
`
o
,
i gi
,
ai. C
´
o thê
,
ch
.
on
¯
du
,
.
o
,
c m
.
ôt sô
´
nhu
,
¯
dâ
`
u b
`
ai
¯
d
.
˘
at ra l
`
a a
1
=
2
100001
− 2. B
`
˘
ang quy n
.
ap theo n ta s
˜
e ch
´
u
,
ng minh v
´
o
,
i m
.
oi n =
1, 2, . . . , 100001
¯
d
,
˘
ang th
´
u
,
c sau
¯
d
´
ung
a
n
= 3
n−1
.2
100001−n
. (10.6)
Th
.
ât v
.
ây, v
´
o
,
i n = 1 ta c
´
o 3
1−1
.2
100001−n
−2 = 2
100001
−2 = a
1
. Nê
´
u
ta gi
,
a thiê
´
t (10.6)
¯
d
´
ung v
´
o
,
i n n
`
ao
¯
d
´
o n ≤ 100000, th
`
ı
a
n+1
= [1, 5a
n
] + 1 = [1, 5(3
n−1
.2
100001−n
−2)] + 1
= [3
n
.2
100000−n
−3] + 1 = 3
n
2
100000−n
−2.

221
Khi
¯
d
´
o v
´
o
,
i n = 1, 2, . . . , 100000 sô
´
2
100001−n
l
`
a sô
´
ch
˜
˘
an,
c
`
on 2
100001−100001
= 1 l
`
a m
.
ôt sô
´
l
,
e. D
˜
ê thâ
´
y nh
˜
u
,
ng sô
´
a
1
, a
2
, . . . , a
100000
l
`
a sô
´
ch
˜
˘
an, c
`
on a
100001
l
`
a sô
´
l
,
e.
J
V
´
ı d
.
u 10.10. (A´o-Balan 1980). Ch
´
u
,
ng minh r
`
˘ang
∑
1
i
1
i
2
. . . i
k
= n,
,
o
,
¯
dây tô
,
ng th
.
u
,
c hi
.
ên theo tâ
´
t c
,
a t
.
âp h
.
o
,
p con kh ´ac r
˜
ông
{i
1
, i
2
, . . . , i
k
} c
,
ua {1, 2, . . . , n}
L
`
o
,
i gi
,
ai. Ta
´
ap d
.
ung phu
,
o
,
ng ph
´
ap quy n
.
ap theo n. V
´
o
,
i n = 1 ta
c
´
o
1
1
= 1,
¯
diê
`
u hiê
,
n nhiên
¯
d
´
ung. Ta gi
,
a thiê
´
t
¯
d
,
˘
ang th
´
u
,
c theo
¯
diê
`
u
ki
.
ên b
`
ai to
´
an
¯
d
´
ung v
´
o
,
i sô
´
n ≥ 1 n
`
ao
¯
d
´
o. M
˜
ôi t
.
âp con kh
´
ac r
˜
ông
c
,
ua t
.
âp h
.
o
,
p {1, 2, . . . , n, n + 1} l
`
a m
.
ôt trong nh
˜
u
,
ng d
.
ang sau
¯
dây:
a) T
.
âp h
.
o
,
p con c
,
ua t
.
âp h
.
o
,
p {1, 2, . . . , n};
b) T
.
âp h
.
o
,
p con c
,
ua t
.
âp h
.
o
,
p {1, 2, . . . , n} v
`
a sô
´
n + 1;
c) T
.
âp h
.
o
,
p m
.
ôt phâ
`
n t
,
u
,
{n + 1}.
Khi
¯
d
´
o v
´
o
,
i tô
,
ng theo
¯
diê
`
u ki
.
ên c
,
ua b
`
ai to
´
an trong tru
,
`
o
,
ng h
.
o
,
p
n + 1 ta nh
.
ân
¯
du
,
.
o
,
c
n + 1
1
n + 1
.n +
1
n + 1
= n + 1.
Nhu
,
v
.
ây ch
´
u
,
ng minh theo quy n
.
ap
¯
d
˜
a xong v
`
a b
`
ai to
´
an
¯
d
˜
a
¯
du
,
.
o
,
c
gi
,
ai.
J
V
´
ı d
.
u 10.11. (Balan 1981). Cho c ´ac d ˜ay sô
´
x
1
, x
2
, . . . ; y
1
, y
2
, . . .
tho
,
a m ˜an c ´ac
¯
diê
`
u ki
.
ên x
n+1
= x
3
n
−3x
n
; y
n+1
= y
3
n
−3y
n
v
´
o
,
i m
.
oi
n ≥ 1 v `a x
2
1
= y
1
+ 2. Ch
´
u
,
ng minh r
`
˘ang x
2
n
= y
n
+ 2 v
´
o
,
i m
.
oi
n ≥ 1.

222 Chu
,
o
,
ng 10. M
.
ôt sô
´
¯
dê
`
thi vô
¯
d
.
ich
L
`
o
,
i gi
,
ai. Ta ch
´
u
,
ng minh b
`
˘
ang quy n
.
ap theo n. V
´
o
,
i n = 1, công
th
´
u
,
c
¯
d
´
ung theo gi
,
a thiê
´
t. Gi
,
a s
,
u
,
n
´
o
¯
d
´
ung v
´
o
,
i n = k, t
´
u
,
c l
`
a x
2
k
=
y
k
+ 2 ( k ≥ 2). Ta ph
,
ai ch
´
u
,
ng minh b
`
ai to
´
an
¯
d
´
ung v
´
o
,
i n =
k + 1, t
´
u
,
c l
`
a x
2
k+1
= y
k+1
+ 1. Th
.
ât v
.
ây,
x
2
k+1
= (x
3
k
−3x
k
)
2
= x
6
k
−6x
4
k
+ 9x
2
k
= (y
k
+ 2)
3
−6(y
k
+ 2)
2
+ 9(y
k
+ 2)
= y
3
k
−3y
k
+ 2 = y
k+1
+ 2
t
´
u
,
c l
`
a x
2
k+1
= y
k+1
+ 2.
J
V
´
ı d
.
u 10.12. (Balan 1982). Cho q l `a m
.
ôt sô
´
t
.
u
,
nhiên ch
˜
˘an th
.
u
,
c s
.
u
,
l
´
o
,
n ho
,
n 0. Ch
´
u
,
ng minh r
`
˘ang v
´
o
,
i m
˜
ôi sô
´
t
.
u
,
nhiên n, sô
´
q
(q+1)
n
+ 1
chia hê
´
t cho (q + 1)
n+1
v `a không chia hê
´
t cho (q + 1)
n+2
.
L
`
o
,
i gi
,
ai. Ta ch
´
u
,
ng minh b
`
˘
ang quy n
.
ap theo theo n. V
´
o
,
i n = 0,
q
(q+1)
0
+ 1 = q + 1 không chia hê
´
t cho (q + 1)
0+2
. B
`
ai to
´
an
¯
d
´
ung
v
´
o
,
i n = 0.
Gi
,
a s
,
u
,
b
`
ai to
´
an
¯
d
´
ung v
´
o
,
i n(n > 0), t
´
u
,
c l
`
a q
(q+1)
n
+ 1 chia hê
´
t
cho (q + 1)
n+1
v
`
a không chia hê
´
t cho (q + 1)
n+2
. N
´
oi c
´
ach kh
´
ac
q
(q+1)
n
+ 1 = (q + 1)
n+1
s chia hê
´
t cho q + 1. Ta ph
,
ai ch
´
u
,
ng minh
b
`
ai to
´
an
¯
d
´
ung v
´
o
,
i c
,
a n + 1. Th
.
ât v
.
ây
q
(q+1)
n+1
+ 1 = ((q
(q+1)
n
+ 1) −1)
q+1
+ 1 = ((q + 1)
n+1
s −1)
q+1
+ 1
=
q+1
∑
j=0
C
j
q+1
( q + 1)
(n+1)j
.s
j
.(−1)
q+1−j
+ 1
=
q+1
∑
j=1
C
j
q+1
( q + 1)
(n+1)j
.s
j
.(−1)
q+1−j
= (q + 1)(q + 1)
n+1
s−
−C
2
q+1
( q + 1)
2(n+1)
s
2
+ ··· + (q + 1)
(q+1)(n +1)
s
q+1
=
= (q + 1)
n+2
( s −C
2
q+1
( q + 1)
n
s
2
+ ··· + (q + 1)
qn+q−1
s
q+1
).

223
Th
`
u
,
a sô
´
th
´
u
,
hai chia hê
´
t cho (q + 1). Do
¯
d
´
o q
(q+1)
n+1
+ 1 chia hê
´
t
cho (q + 1)
n+2
v
`
a không chia hê
´
t cho (q + 1)
n+3
.
J
V
´
ı d
.
u 10.13. (Anh 1978). Ch
´
u
,
ng minh r
`
˘ang v
´
o
,
i m
.
oi n ≥ 1, n ∈ N
th`ı 2 cos nθ l `a m
.
ôt
¯
da th
´
u
,
c b
.
âc n c
,
ua 2 cos θ v
´
o
,
i h
.
ê sô
´
nguyên.
L
`
o
,
i gi
,
ai. Ta s
˜
e ch
´
u
,
ng minh b
`
˘
ang quy n
.
ap theo n. v
´
o
,
i n = 1,
m
.
ênh
¯
dê
`
¯
d
´
ung. V
´
o
,
i n = 2, 2 cos 2θ = 2(2 cos
2
θ −1) = (2 cos θ)
2
−
2, t
´
u
,
c l
`
a m
.
ênh
¯
dê
`
¯
d
´
ung. Gi
,
a s
,
u
,
m
.
ênh
¯
dê
`
¯
d
´
ung v
´
o
,
i m
.
oi n, n ≤
k(k ≥ 2). Ta ph
,
ai ch
´
u
,
ng minh m
.
ênh
¯
dê
`
¯
d
´
ung v
´
o
,
i n = k + 1. Ta c
´
o
2 cos(k + 1)θ + 2 cos(k −1)θ = 4 cos kθ. cos θ = (2 cos kθ)(2 cos θ).
Suy ra 2 cos(k + 1)θ = 2 cos θ(2 cos kθ) − 2 cos(k −1)θ. Vê
´
ph
,
ai r
˜
o
r
`
ang l
`
a m
.
ôt
¯
da th
´
u
,
c b
.
âc k + 1 c
,
ua 2 cos θ v
´
o
,
i h
.
ê sô
´
nguyên. T
`
u
,
¯
d
´
o
suy ra m
.
ênh
¯
dê
`
¯
d
´
ung v
´
o
,
i n = k + 1 v
`
a do
¯
d
´
o n
´
o
¯
d
´
ung v
´
o
,
i m
.
oi n.
J
V
´
ı d
.
u 10.14. (Ðê
`
thi Olympic To´an quô
´
c tê
´
lâ
`
n th
´
u
,
18, 1976).
D ˜ay u
0
, u
1
, u
2
, . . .
¯
du
,
.
o
,
c x ´ac
¯
d
.
inh theo c ´ach sau u
0
= 2; u
1
=
5
2
;
u
n+1
= u
n
( u
2
n−1
−2) −u
1
, ( n ≥ 1).
Ch
´
u
,
ng minh r
`
˘ang v
´
o
,
i n ≥ 1 [u
n
] = 2
2
n
−(−1)
n
3
,
,
o
,
¯
dây [x] l `a sô
´
nguyên l
´
o
,
n nhâ
´
t không l
´
o
,
n ho
,
n x .
L
`
o
,
i gi
,
ai. Ta
¯
d
.
˘
at α
k
=
2
k
−(−1)
k
3
, k ≥ 0. Ta s
˜
e ch
´
u
,
ng minh r
`
˘
ang
α
n+1
= 2α
n
+ (−1)
n
v
´
o
,
i m
.
oi sô
´
nguyên n ≥ 0. Th
.
ât v
.
ây
2α
n
+ (−1)
n
= 2
2
n
−(−1)
n
3
+ (−1)
n
=
2
n+1
−2(−1)
n
+ 3(−1)
n
3
=
2
n+1
+ (−1)
n
3
=
2
n+1
−(−1)
n+1
3
= α
n+1
.

224 Chu
,
o
,
ng 10. M
.
ôt sô
´
¯
dê
`
thi vô
¯
d
.
ich
V
`
ı α
0
= 0 v
`
a α
1
= 1 t
`
u
,
c
´
ac
¯
d
,
˘
ang th
´
u
,
c n
`
ay suy ra tâ
´
t c
,
a α
k
l
`
a
nguyên. Ta s
˜
e ch
´
u
,
ng minh r
`
˘
ang u
n
= 2
α
n
+ 2
−α
n
, n ≥ 0. V
´
o
,
i k =
0, 1
¯
diê
`
u n
`
ay d
˜
ê kiê
,
m tra. Gi
,
a s
,
u
,
n
´
o
¯
d
´
ung v
´
o
,
i k = n − 1 v
`
a k = n,
v
`
a s
,
u
,
d
.
ung mô
´
i liên quan gi
˜
u
,
a α
n
v
`
a α
n−1
, ta s
˜
e nh
.
ân
¯
du
,
.
o
,
c
u
n+1
= u
n
( u
2
n−1
−2) −
5
2
= (2
α
n
+ 2
−α
n
). [(2
α
n−1
+ 2
α
n−1
)
2
−2] −
5
2
= (2
α
n
+ 2
−α
n
). (2
2α
n−1
+ 2
2α
n−1
)
2
) −
5
2
= (2
α
n
+ 2
−α
n
). (2
α
n
−(−)
n−1
+ 2
(−1)
n−1
−α
n
)
2
) −
5
2
= 2
2α
n
+(−1)
n
+ 2
(−1)
n−1
+ 2
−(−1)
n−1
+ 2
−2α
n
−(−1)
n
−
5
2
= 2
α
n+1
+ 2
−α
n+1
,
v
`
ı 2
(−1)
k
+ 2
−(−1)
k
=
5
2
v
´
o
,
i m
˜
ôi k ≥ 1. B
`
ai to
´
an
¯
d
˜
a
¯
du
,
.
o
,
c gi
,
ai v
`
ı
[u
n
] = [2
α
n
+ 2
−α
n
] = 2
α
n
, do
1
2
α
n
< 1 v
´
o
,
i n ≥ 1.
J
V
´
ı d
.
u 10.15. (Ðê
`
thi Olympic To´an quô
´
c tê
´
lâ
`
n th
´
u
,
22, 1981).
Biê
´
t r
`
˘ang h `am sô
´
f (x, y) tho
,
a m ˜an nh
˜
u
,
ng
¯
diê
`
u ki
.
ên:
a) f (0, y) = y + 1;
b) f (x + 1, 0) = f (x, 1) ;
c) f (x + 1, y + 1) = f (x, f (x + 1, y )) v
´
o
,
i tâ
´
t c
,
a nh
˜
u
,
ng sô
´
nguyên
không âm x v `a y. H ˜ay t`ım f (4, 1981).
L
`
o
,
i gi
,
ai. Ta c
´
o f (1, 0) = f (0, 1) = 2, f ( 1, 1) = f (0, f (1, 0)) =
f (0, 2) = 3. Ta s
˜
e ch
´
u
,
ng minh b
`
˘
ang quy n
.
ap r
`
˘
ang f (1, y) = y + 2.
V
´
o
,
i y = 1, kh
,
˘
ang
¯
d
.
inh
¯
d
´
ung. gi
,
a s
,
u
,
v
´
o
,
i sô
´
t
.
u
,
nhiên k n
`
ao
¯
d
´
o ta c
´
o

225
f (1, k) = k + 2. Khi
¯
d
´
o
f (1, k + 1) = f (0, f (1, k)) = f (0, k + 2) = k + 3.
T
`
u
,
b) ta nh
.
ân
¯
du
,
.
o
,
c f (2, 0) = f (1, 1) = 3, c
`
on t
`
u
,
c) f (2, 1) =
f (1, f (2, 0)) = f (1, 3) = 5.
Bây gi
`
o
,
ta ch
´
u
,
ng minh r
`
˘
ang f (2, k) = 2 k + 3. Th
.
ât v
.
ây, cho v
´
o
,
i
k n
`
ao
¯
d
´
o ta c
´
o f (2, k) = 2k + 3. Khi
¯
d
´
o f (2, k + 1) = f (1, f (2, k)) =
f (1, 2k + 3) = 2k + 5.
Ta nh
.
ân
¯
du
,
.
o
,
c f (3, 0) = f (2, 1) = 5. Ngo
`
ai ra f (3, y + 1) =
f (2, f (3, y)) = 2 f (3, y) + 3, ho
.
˘
ac l
`
a v
´
o
,
i m
.
oi sô
´
t
.
u
,
nhiên y ta c
´
o
f (3, y + 1) = 2 f (3, y) + 3. Ta
´
ap d
.
ung
¯
d
,
˘
ang th
´
u
,
c k lâ
`
n, nh
.
ân
¯
du
,
.
o
,
c
f (3, y + 1) = 2
k+1
. f (3, y −k) + 3(2
k
+ 2
k−1
+ ··· + 2 + 1),
t
`
u
,
¯
dây v
´
o
,
i k = y ta nh
.
ân
¯
du
,
.
o
,
c f (3, y + 1) = 52
y+1
+ 3.(2
y+1
−1).
Suy ra f (3, y) = 2
y+3
− 3 v
´
o
,
i m
.
oi sô
´
t
.
u
,
nhiên y. T
`
u
,
¯
d
,
˘
ang th
´
u
,
c
cuô
´
i c
`
ung ta nh
.
ân
¯
du
,
.
o
,
c
f (4, y) = f (3, f (4, y −1)) = 2
f (4,y−1)+3
−3
= 2
2
f (4,y−2)+3
−3+3
−3 = 2
2
f (4,y−2)+3
−3
= 2
y−1
z}|{
2
2
.
.
.
2
13+3
−3 = 2
y+2
z}|{
2
2
.
.
.
2
−3
,
o
,
¯
dây ta
´
ap d
.
ung
¯
d
,
˘
ang th
´
u
,
c f ( 4, 0) = f (3, 1) = 2
4
−3 = 13. Thay
gi
´
a tr
.
i v
`
ao
¯
d
,
˘
ang th
´
u
,
c trên ta c
´
o
¯
du
,
.
o
,
c f (4, 1981).
J

CHU
,
O
,
NG 11
B
`
AI T
.
ÂP T
.
U
,
GI
,
AI
.
.
. 11.1. Ch
´
u
,
ng minh r
`
˘
ang
a) 1.2.3 . . . p + 2.3 . . . p.(p + 1) + ···+ n(n + 1) . . . (n + p −1) =
=
n(n + 1) . . . (n + p)
p + 1
.
b) 2.1
2
+ 3.2
2
+ ··· + (n + 1).n
2
=
n(n + 1)(n + 2)(3n + 1)
12
.
c) 1 −
1
2
+
1
3
−
1
4
+ ···+
1
2n −1
−
1
2n
=
1
n + 1
+
1
n + 2
+ ···+
1
2n
.
d) 1
2
−2
2
+ 3
2
−4
2
+ ··· + (−1)
n−1
.n
2
= (−1)
n−1
n(n + 1)
2
.
.
.
. 11.2. Ch
´
u
,
ng minh c
´
ac
¯
d
,
˘
ang th
´
u
,
c sau
a + 1
2
+
a + 3
4
+
a + 7
8
+ ··· +
a + 2
n
−1
2
n
=
(a −1)(2
n
−1)
2
n
+ n.
.
.
. 11.3. Ch
´
u
,
ng minh r
`
˘
ang v
´
o
,
i m
.
oi sô
´
t
.
u
,
nhiên n
a) 6
2n
−1 chia hê
´
t cho 35;
b) n
6
−3n
5
+ 6n
4
−7n
3
+ 5n
2
−2n chia hê
´
t cho 24;
c) 2
n+2
.3
n
+ 5n −4 chia hê
´
t cho 25;
d) 5
2n+1
+ 2
n+4
+ 2
n+1
chia hê
´
t cho 23.
.
.
. 11.4. Ch
´
u
,
ng minh r
`
˘
ang
226

227
a)
√
n < 1 +
1
√
2
+
1
√
3
+ ··· +
1
√
n
< 2
√
n v
´
o
,
i n ≥ 2.
b) 2
1
2
n(n−1)
> n! v
´
o
,
i n ≥ 3.
.
.
. 11.5. Ch
´
u
,
ng minh bâ
´
t
¯
d
,
˘
ang th
´
u
,
c
log(n + 1) >
log1 + log2 + ··· + logn
n
.
.
.
. 11.6. Ch
´
u
,
ng minh
¯
d
,
˘
ang th
´
u
,
c
(1 + x)(1 + x
2
)(1 + x
4
) . . . (1 + x
2
n−1
) =
= 1 + x + x
2
+ x
3
+ ··· + x
2
n
−1
.
.
.
. 11.7. Ch
´
u
,
ng minh
¯
d
,
˘
ang th
´
u
,
c sau
1 +
1
a
+
a + 1
ab
+
(a + 1)(b + 1)
abc
+ ···
··· +
(a + 1)(b + 1) . . . (s + 1)(l + 1)
abc . . . skl
=
=
(a + 1)(b + 1) . . . (k + 1)(l + 1)
abc . . . kl
.
.
.
. 11.8. Ch
´
u
,
ng minh r
`
˘
ang
n
∑
k=1
(1 − a
n
)(1 − a
n−1
) . . . (1 − a
n−k+1
)
1 − a
k
= n.
.
.
. 11.9. H
˜
ay t
´
ınh tô
,
ng
S
n
=
a
b
+
a(a −1)
b(b − 1)
+
a(a −1)(a − 2)
b(b − 1)(b −2)
+
a(a −1) . . . (a − n + 1)
b(b − 1) . . . (b −n + 1 )
.
( b không b
`
˘
ang m
.
ôt trong c
´
ac sô
´
0, 1, 2, . . . , n −1)
.
.
. 11.10. Cho
S
n
= a
1
+ (a
1
+ 1)a
2
+(a
1
+ 1)(a
2
+ 1)a
3
+ ···
··· + (a
1
+ 1)(a
2
+ 1) . . . (a
n−1
+ 1)a
n
.

228 Chu
,
o
,
ng 11. B
`
ai t
.
âp t
.
u
,
gi
,
ai
Ch
´
u
,
ng minh r
`
˘
ang
S
n
= (a
1
+ 1)(a
2
+ 1) . . . (a
n
+ 1) −1.
.
.
. 11.11. Cho {u
n
} l
`
a d
˜
ay Fibonacci, ch
´
u
,
ng minh r
`
˘
ang
u
n
=
[
n −1
2
]
∑
k=0
C
k
n−k−1
.
.
.
. 11.12. H
˜
ay t
`
ım tâ
´
t c
,
a nghi
.
êm nguyên du
,
o
,
ng c
,
ua phu
,
o
,
ng tr
`
ınh
x
1
+ x
2
+ ··· + x
n
= m (m l
`
a sô
´
nguyên du
,
o
,
ng).
.
.
. 11.13. Ch
´
u
,
ng minh r
`
˘
ang sô
´
nghi
.
êm chung nguyên du
,
o
,
ng c
,
ua
nh
˜
u
,
ng phu
,
o
,
ng tr
`
ınh x + 2y = n; 2x + 3y = n − 1; . . . ; nx + (n +
1)y = 1; (n + 1)x + (n + 2)y = 0; b
`
˘
ang n + 1.
.
.
. 11.14. Ch
´
u
,
ng minh r
`
˘
ang sô
´
nghi
.
êm chung nguyên không âm
c
,
ua nh
˜
u
,
ng phu
,
o
,
ng tr
`
ınh sau x + 4y = 3n − 1; 4x + 9y = 5n − 4;
9x + 16y = 7n −9, . . . , n
2
x + (n + 1 )
2
y = n(n + 1); b
`
˘
ang n.
.
.
. 11.15. Ch
´
u
,
ng minh r
`
˘
ang v
´
o
,
i gi
´
a tr
.
i tu
`
y
´
y α ≤ 1 v
`
a c
´
ac sô
´
tu
`
y
´
y
x
1
, . . . , x
n
tho
,
a m
˜
an c
´
ac
¯
diê
`
u ki
.
ên 1 ≥ x
1
≥ x
2
≥ . . . ≥ x
n
> 0, ta
c
´
o bâ
´
t
¯
d
,
˘
ang th
´
u
,
c
(1 + x
1
+ x
2
+ ··· + x
n
)
α
≤ 1 + 1
α−1
x
α−1
1
+ 2
α−1
x
α
2
+ ··· + n
α−1
x
α
n
.
.
.
. 11.16. Ch
´
u
,
ng minh r
`
˘
ang v
´
o
,
i c
´
ac gi
´
a tr
.
i tu
`
y
´
y m, n ∈ N v
`
a c
´
ac
sô
´
tu
`
y
´
y x
1
, x
2
, . . . , x
n
, y
1
. . . , y
n
∈ [0, 1] tho
,
a m
˜
an c
´
ac
¯
diê
`
u ki
.
ên
x
i
+ y
i
= 1 v
´
o
,
i i = 1, 2, . . . , n, ta c
´
o bâ
´
t
¯
d
,
˘
ang th
´
u
,
c
(1 − x
1
· x
2
·. . . · x
n
)
m
+ ( 1 − y
m
1
) · . . . · (1 −y
m
n
) ≥ 1.
.
.
. 11.17. V
´
o
,
i m
˜
ôi gi
´
a tr
.
i n ∈ N h
˜
ay t
`
ım gi
´
a tr
.
i l
´
o
,
n nhâ
´
t k ∈ Z
+
¯
dê
,
sô
´
[(3 +
√
11)
2n−1
] chia hê
´
t cho 2
k
.

229
.
.
. 11.18. Ngu
,
`
o
,
i ta tô m
`
au c
´
ac
¯
d
,
ınh c
,
ua m
.
ôt
¯
da gi
´
ac lô
`
i c
´
o sô
´
c
.
anh
l
,
e, sao cho bâ
´
t k
`
y 2
¯
d
,
ınh lân c
.
ân
¯
du
,
.
o
,
c tô b
`
˘
ang 2 m
`
au kh
´
ac nhau.
Ch
´
u
,
ng minh r
`
˘
ang v
´
o
,
i m
.
oi c
´
ach tô m
`
au tho
,
a m
˜
an
¯
diê
`
u ki
.
ên trên
¯
da gi
´
ac c
´
o thê
,
chia th
`
anh c
´
ac tam gi
´
ac b
,
o
,
i c
´
ac
¯
du
,
`
o
,
ng ch
´
eo không
c
´
˘
at nhau, m
`
a hai
¯
dâ
`
u m
˜
ôi
¯
du
,
`
o
,
ng ch
´
eo, c
´
o hai m
`
au kh
´
ac nhau.
.
.
. 11.19. D
˜
ay sô
´
du
,
o
,
ng a
,
a
2
, ..., a
n
tho
,
a m
˜
an bâ
´
t
¯
d
,
˘
ang th
´
u
,
c a
2
n
≤
a
n
− a
n+1
v
´
o
,
i n ∈ N. Ch
´
u
,
ng minh r
`
˘
ang v
´
o
,
i bâ
´
t k
`
y gi
´
a tr
.
i n ∈ N
c
´
o
¯
d
´
anh gi
´
a a
n
<
1
n
.
.
.
. 11.20. Cho d
˜
ay sô
´
{a
n
} tho
,
a m
˜
an bâ
´
t
¯
d
,
˘
ang th
´
u
,
c {a
k+m
− a
k
−
a
m
} ≤ 1, v
´
o
,
i k, m ∈ N. Ch
´
u
,
ng minh r
`
˘
ang v
´
o
,
i bâ
´
t k
`
y p, q ∈ N c
´
o
bâ
´
t
¯
d
,
˘
ang th
´
u
,
c
a
p
p
−
a
q
q
<
1
p
+
1
q
.
.
.
. 11.21. Ch
´
u
,
ng minh r
`
˘
ang m
˜
ôi sô
´
h
.
ang c
,
ua d
˜
ay sô
´
3 +
√
5
2
!
n
+
3 −
√
5
2
!
n
−2, (n ∈ N)
l
`
a sô
´
t
.
u
,
nhiên v
`
a biê
,
u di
˜
ên du
,
´
o
,
i d
.
ang 5m
2
ho
.
˘
ac m
2
( m ∈ N) v
´
o
,
i n
tu
,
o
,
ng
´
u
,
ng ch
˜
˘
an ho
.
˘
ac l
,
e.
.
.
. 11.22. Ch
´
u
,
ng minh r
`
˘
ang tô
`
n t
.
ai
¯
d
´
ung m
.
ôt d
˜
ay sô
´
nguyên
a
1
, a
2
, . . . tho
,
a m
˜
an
¯
diê
`
u ki
.
ên a
1
= 1, a
2
> 1, a
3
n+1
+ 1 = a
n
a
n+2
v
´
o
,
i n ∈ N.
.
.
. 11.23. Ch
´
u
,
ng minh r
`
˘
ang v
´
o
,
i c
´
ac sô
´
tu
`
y
´
y m, n ∈ N, sô
´
S
m,n
= 1 +
m
∑
k=1
( −1)
k
( n + k + 1)!
n!(n + k)
chia hê
´
t cho m!, nhu
,
ng v
´
o
,
i m
.
ôt sô
´
gi
´
a tr
.
i m, n ∈ N sô
´
S
m,n
không
chia hê
´
t cho m!(n + 1).

230 Chu
,
o
,
ng 11. B
`
ai t
.
âp t
.
u
,
gi
,
ai
.
.
. 11.24. Trên m
.
˘
at ph
,
˘
ang c
´
o n
¯
du
,
`
o
,
ng tr
`
on kh
´
ac nhau c
´
o b
´
an k
´
ınh
¯
dê
`
u b
`
˘
ang 1
¯
du
,
.
o
,
c s
´
˘
ap xê
´
p kh
´
ac nhau. Ch
´
u
,
ng minh r
`
˘
ang ch
,
ı c
´
o m
.
ôt
trong sô
´
¯
d
´
o ch
´
u
,
a m
.
ôt cung, không c
´
˘
at m
.
ôt
¯
du
,
`
o
,
ng tr
`
on trong sô
´
nh
˜
u
,
ng
¯
du
,
`
o
,
ng tr
`
on c
`
on l
.
ai v
`
a c
´
o
¯
d
.
ô d
`
ai không nh
,
o ho
,
n
2P
n
.
.
.
. 11.25. C
´
o thê
,
chia m
.
ôt
¯
da gi
´
ac
¯
dê
`
u 2n− gi
´
ac bâ
´
t k
`
y th
`
anh c
´
ac
h
`
ınh thoi hay không?
.
.
. 11.26. Ch
´
u
,
ng minh r
`
˘
ang v
´
o
,
i m
.
oi a ∈ N, a > 2 tô
`
n t
.
ai vô sô
´
c
´
ac
sô
´
n ∈ N
¯
dê
,
sô
´
a
n
−1 chia hê
´
t cho n. Kh
,
˘
ang
¯
d
.
inh
¯
d
´
ung v
´
o
,
i a = 2
không?
.
.
. 11.27. Ch
´
u
,
ng minh r
`
˘
ang v
´
o
,
i sô
´
n ∈ N tu
`
y
´
y phu
,
o
,
ng tr
`
ınh
x
2
1
+ x
2
2
+ ··· + x
2
n
= y
2
c
´
o nghi
.
êm sô
´
t
.
u
,
nhiên.
.
.
. 11.28. D
˜
ay a
1
, a
2
, . . . , a
n
, . . . nh
˜
u
,
ng sô
´
t
.
u
,
nhiên
¯
du
,
.
o
,
c t
.
ao th
`
anh
theo c
´
ach sau: Ch
.
on m
.
ôt sô
´
c
´
o ba ch
˜
u
,
sô
´
bâ
´
t k
`
y a
1
, c
`
on a
2
l
`
a
tô
,
ng c
,
ua c
´
ac b
`
ınh phu
,
o
,
ng c
,
ua c
´
ac ch
˜
u
,
sô
´
a
1
, a
3
l
`
a tô
,
ng c
´
ac b
`
ınh
phu
,
o
,
ng c
´
ac ch
˜
u
,
sô
´
c
,
ua a
2
v
`
a tiê
´
p t
.
uc qu
´
a tr
`
ınh nhu
,
v
.
ây. Ch
´
u
,
ng
minh r
`
˘
ang trong d
˜
ay a
1
, a
2
, a
3
, . . . b
´
˘
at g
.
˘
ap ho
.
˘
ac l
`
a sô
´
1, ho
.
˘
ac sô
´
4.
.
.
. 11.29. Ch
´
u
,
ng minh r
`
˘
ang không tô
`
n t
.
ai d
˜
ay vô h
.
an c
´
ac sô
´
t
.
u
,
nhiên n
1
, n
2
, . . . th
,
oa m
˜
an hai
¯
diê
`
u ki
.
ên sau
¯
dây:
a) n
k
< n
k+1
v
´
o
,
i k = 1, 2, . . .
b) n
k
l
= n
k
+ n
l
v
´
o
,
i m
.
oi k = 1, 2, . . . v
`
a l = 1, 2, . . .
.
.
. 11.30. Ch
´
u
,
ng minh r
`
˘
ang v
´
o
,
i m
.
oi gi
´
a tr
.
i sô
´
t
.
u
,
nhiên bâ
´
t
¯
d
,
˘
ang
th
´
u
,
c sau
¯
d
´
ung
2
n
> n
2
.

CHU
,
O
,
NG 12
L
`
o
,
i gi
,
ai v
`
a g
.
o
,
i
´
y b
`
ai t
.
âp
12.1. L
`
o
,
i gi
,
ai v
`
a g
.
o
,
i
´
y b
`
ai t
.
âp chu
,
o
,
ng 1 . . . . . . . . . . . . . . . . . 231
12.2. L
`
o
,
i gi
,
ai v
`
a g
.
o
,
i
´
y b
`
ai t
.
âp chu
,
o
,
ng 2 . . . . . . . . . . . . . . . . . 233
12.3. L
`
o
,
i gi
,
ai v
`
a g
.
o
,
i
´
y b
`
ai t
.
âp chu
,
o
,
ng 3 . . . . . . . . . . . . . . . . . 236
12.4. L
`
o
,
i gi
,
ai v
`
a g
.
o
,
i
´
y b
`
ai t
.
âp chu
,
o
,
ng 4 . . . . . . . . . . . . . . . . . 236
12.5. L
`
o
,
i gi
,
ai v
`
a g
.
o
,
i
´
y b
`
ai t
.
âp chu
,
o
,
ng 5 . . . . . . . . . . . . . . . . . 237
12.6. L
`
o
,
i gi
,
ai v
`
a g
.
o
,
i
´
y b
`
ai t
.
âp chu
,
o
,
ng 6 . . . . . . . . . . . . . . . . . 240
12.7. L
`
o
,
i gi
,
ai v
`
a g
.
o
,
i
´
y b
`
ai t
.
âp chu
,
o
,
ng 7 . . . . . . . . . . . . . . . . . 240
12.8. L
`
o
,
i gi
,
ai v
`
a g
.
o
,
i
´
y b
`
ai t
.
âp chu
,
o
,
ng 8 . . . . . . . . . . . . . . . . . 244
12.9. L
`
o
,
i gi
,
ai v
`
a g
.
o
,
i
´
y b
`
ai t
.
âp chu
,
o
,
ng 9 . . . . . . . . . . . . . . . . . 247
M
.
uc l
.
uc . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 250
12.1. L
`
o
,
i gi
,
ai v
`
a g
.
o
,
i
´
y b
`
ai t
.
âp chu
,
o
,
ng 1
.
.
. 1.11. a) L
`
o
,
i gi
,
ai: Ta thiê
´
t l
.
âp b
,
ang cho m
.
ôt sô
´
gi
´
a tr
.
i c
,
ua n.
n = 1 2 3 4 5
S
n
= 1 -3 6 -10 15
Ta so s
´
anh v
´
o
,
i b
,
ang sô
´
,
o
,
b
`
ai
¯
dâ
`
u tiên d
˜
ê
¯
du
,
a
¯
dê
´
n gi
,
ai thiê
´
t
S
n
= (−1)
n−1
.
n(n + 1)
2
.
231
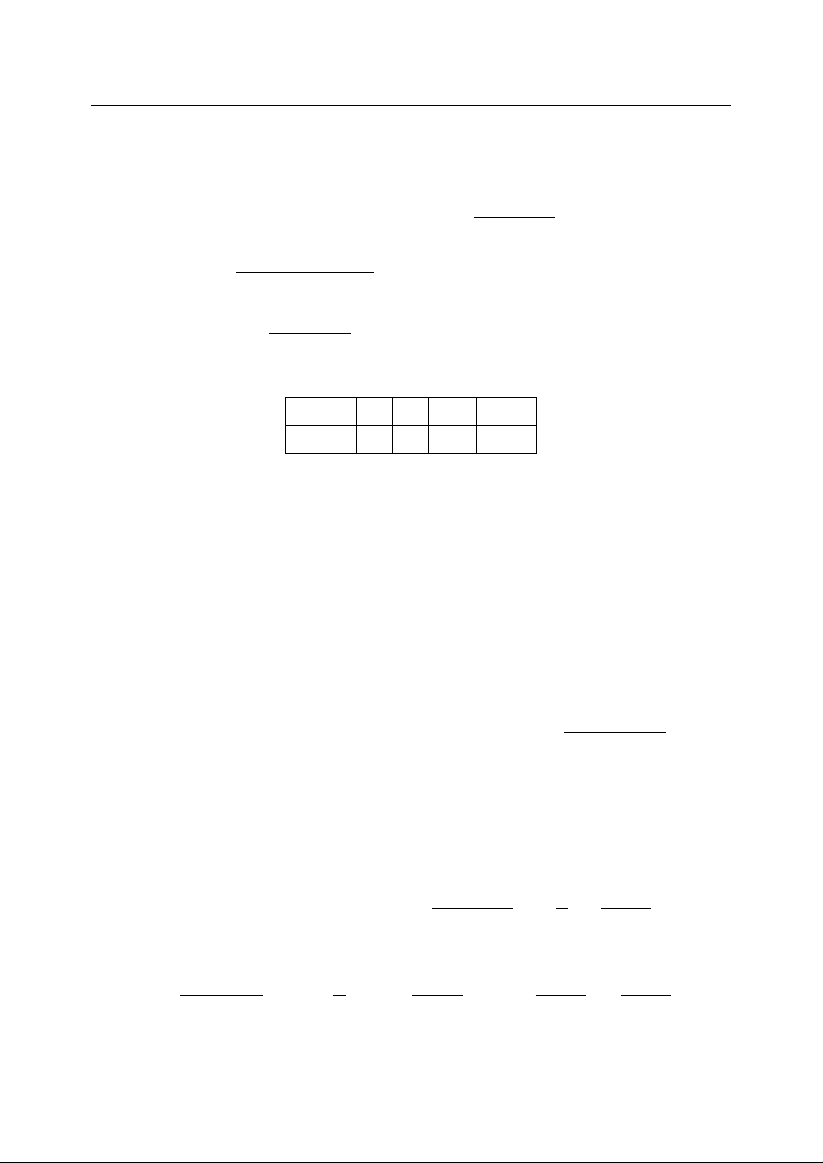
232 Chu
,
o
,
ng 12. L
`
o
,
i gi
,
ai v
`
a g
.
o
,
i
´
y b
`
ai t
.
âp
Gi
,
a s
,
u
,
¯
d
´
ung v
´
o
,
i n n
`
ao
¯
d
´
o, ta s
˜
e ch
´
u
,
ng minh
¯
d
,
˘
ang th
´
u
,
c
¯
d
´
o c
˜
ung
¯
d
´
ung cho n + 1. Ta c
´
o
S
n+1
= S
n
+ (−1)
n
( n + 1)
2
= (−1)
n−1
n(n + 1)
2
+ (−1)
n
( n + 1)
2
= (−1)
n
( n + 1)(n + 2)
2
.
b) Tr
,
a l
`
o
,
i: S
n
= [
n(n + 1)
2
]
2
.
c) L
`
o
,
i gi
,
ai: Ta l
.
âp b
,
ang m
.
ôt sô
´
gi
´
a tr
.
i ban
¯
dâ
`
u
n = 1 2 3 4
S
n
= 1 5 23 119
T
.
ai v
`
ı 1! = 1, 2! = 2, 3! = 6, 4! = 24, 5! = 120, ta c
´
o thê
,
l
`
am gi
,
ai
thiê
´
t S
n
= (n + 1)! − 1. V
´
o
,
i S
n+1
ta nh
.
ân
¯
du
,
.
o
,
c
S
n+1
= (1.1! + 2.2! + ··· + n.n!) + ( n + 1).(n + 1)!
= (n + 1)! − 1 + (n + 1).(n + 1)!
= (n + 1)!(1 + n + 1) − 1 = (n + 2)! −1.
.
.
. 1.12. a) L
`
o
,
i gi
,
ai: Ta
´
ap d
.
ung t
´
ınh châ
´
t c
,
ua tô
,
ng
n
∑
µ=1
(2 µ −1)
2
= 4
n
∑
µ=1
µ
2
−4
n
∑
µ=1
µ +
n
∑
µ=1
1 =
n(4n
2
−1)
3
.
,
o
,
¯
dây ta
´
ap d
.
ung công th
´
u
,
c t
´
ınh tô
,
ng lu
˜
y th
`
u
,
a c
,
ua c
´
ac sô
´
t
.
u
,
nhiên.
b) G
.
o
,
i
´
y: Tu
,
o
,
ng t
.
u
,
phâ
`
n a).
c) G
.
o
,
i
´
y: Ta
´
ap d
.
ung công th
´
u
,
c
1
x(x + 1)
=
1
x
−
1
x + 1
, ta t
`
ım
¯
du
,
.
o
,
c
n
∑
µ=1
1
µ(µ + 1)
=
n
∑
µ=1
1
µ
−
n
∑
µ=1
1
µ + 1
= 1 −
1
n + 1
=
n
n + 1
.

12.2. L
`
o
,
i gi
,
ai v
`
a g
.
o
,
i
´
y b
`
ai t
.
âp chu
,
o
,
ng 2 233
.
.
. 1.13. L
`
o
,
i gi
,
ai: Ch
´
u
,
ng minh b
`
˘
ang quy n
.
ap to
´
an h
.
oc theo k
¯
d
,
˘
ang th
´
u
,
c sau
x
0
+ x
1
+ ··· + x
k
=
1
n − k
v
´
o
,
i 0 ≤ k ≤ n −1.
V
´
o
,
i k = 0, kh
,
˘
ang
¯
d
.
inh
¯
d
´
ung hiê
,
n nhiên. Gi
,
a s
,
u
,
n
´
o
¯
d
´
ung v
´
o
,
i m
.
oi
n ≤ k. Khi
¯
d
´
o
x
0
+ x
1
+ ··· + x
k
+ x
k+1
=
1
n − k
+ x
k+1
=
1
n − k −1
(x
0
+ x
1
+ ··· + x
k
) +
1
n − k
=
1
( n + k − 1)(n − k)
+
1
n − k
=
1
n − k −1
.
Suy ra m
.
ênh
¯
dê
`
c
˜
ung
¯
d
´
ung v
´
o
,
i k + 1. Tru
,
`
o
,
ng h
.
o
,
p riêng, v
´
o
,
i k =
n −1 ta nh
.
ân
¯
du
,
.
o
,
c x
0
+ x
1
+ ··· + x
n−1
= 1.
12.2. L
`
o
,
i gi
,
ai v
`
a g
.
o
,
i
´
y b
`
ai t
.
âp chu
,
o
,
ng 2
.
.
. 2.31. L
`
o
,
i gi
,
ai: Ta k
´
y hi
.
êu bâ
´
t
¯
d
,
˘
ang th
´
u
,
c
¯
dê
`
ra l
`
a (2.27). Ch
´
u
,
ng
minh quy n
.
ap theo n. V
´
o
,
i n = 1, t
`
u
,
(2.27) ta c
´
o x
5
1
+ x
7
1
≥ 2x
6
1
, n
´
o
tu
,
o
,
ng
¯
du
,
o
,
ng v
´
o
,
i (1 − x
1
)
2
≥ 0, nhu
,
v
.
ây trong tru
,
`
o
,
ng h
.
o
,
p n
`
ay bâ
´
t
¯
d
,
˘
ang th
´
u
,
c
¯
d
´
ung.
Gi
,
a s
,
u
,
bâ
´
t
¯
d
,
˘
ang th
´
u
,
c
¯
d
´
ung v
´
o
,
i sô
´
n ≥ 1 n
`
ao
¯
d
´
o. Ta s
˜
e ch
´
u
,
ng
minh n
´
o c
˜
ung
¯
d
´
ung v
´
o
,
i n + 1. Cho x
1
< x
2
< . . . < x
n
< x
n+1
v
´
o
,
i
nh
˜
u
,
ng sô
´
nguyên du
,
o
,
ng. Theo gi
,
a thiê
´
t quy n
.
ap ta c
´
o (2.27) v
`
a
trong n
´
o c
´
o
¯
d
,
˘
ang th
´
u
,
c khi v
`
a ch
,
ı khi x
k
= k, k = 1, 2, . . . , n. Ngo
`
ai
ra bâ
´
t
¯
d
,
˘
ang th
´
u
,
c sau
¯
d
´
ung (ch
´
u
,
ng minh sau)
x
5
n+1
+ x
7
n+1
≥ 2[2(x
3
1
+ x
3
2
+ ··· + x
3
n
)x
3
n+1
+ (x
3
n+1
)
2
] (12.1)
v
`
a
¯
d
,
˘
ang x
,
ay ra ch
,
ı khi x
k
= k, k = 1, 2, . . . , n + 1 . C
.
ông theo vê
´

234 Chu
,
o
,
ng 12. L
`
o
,
i gi
,
ai v
`
a g
.
o
,
i
´
y b
`
ai t
.
âp
c
,
ua (2.27) v
`
a (12.1) ta nh
.
ân
¯
du
,
.
o
,
c
x
5
1
+ x
5
2
+ ··· + x
5
n
+ x
5
n+1
+ x
7
1
+ x
7
2
+ ··· + x
7
n
+ x
7
n+1
≥
≥ 2(x
3
1
+ x
3
2
+ ··· + x
3
n
+ x
3
n+1
)
2
v
`
a
¯
d
,
˘
ang th
´
u
,
c ch
,
ı xâ
,
y ra khi v
`
a ch
,
ı khi c
´
o
¯
d
,
˘
ang th
´
u
,
c trong (2.27)
v
`
a (12.1), ngh
˜
ıa l
`
a x
k
= k , k = 1, 2, . . . , n, n + 1. Nhu
,
v
.
ây kh
,
˘
ang
¯
d
.
inh
¯
d
´
ung v
´
o
,
i n + 1.
Ta ch
,
ı c
`
on ch
´
u
,
ng minh (12.1). Bâ
´
t
¯
d
,
˘
ang th
´
u
,
c (12.1) tu
,
o
,
ng
¯
du
,
o
,
ng v
´
o
,
i
x
5
n+1
(x
n+1
−1)
2
4
≥ x
3
1
+ x
3
2
+ ··· + x
3
n
. (12.2)
Bâ
´
t
¯
d
,
˘
ang th
´
u
,
c (12.2)
¯
du
,
.
o
,
c suy ra t
`
u
,
nh
˜
u
,
ng bâ
´
t
¯
d
,
˘
ang th
´
u
,
c v
`
a
¯
d
,
˘
ang th
´
u
,
c sau
x
3
1
+ x
3
2
+ ··· + x
3
n
≤ 1
3
+ 2
3
+ ··· + x
3
n
, (12.3)
1
3
+ 2
3
+ ··· + x
3
n
=
x
2
n
(x
n
+ 1)
2
4
,
x
n
≤ x
n+1
−1, (12.4)
x
2
n
(x
n
+ 1)
2
4
≤
(x
n+1
−1)
2
x
2
n+1
4
.
Ð
,
˘
ang th
´
u
,
c trong (12.2) khi v
`
a ch
,
ı khi c
´
o
¯
d
,
˘
ang th
´
u
,
c trong (12.3)
v
`
a (12.4), hay l
`
a x
k
= k, k = 1, 2, . . . , n + 1.
J
.
.
. 2.32. L
`
o
,
i gi
,
ai: V
´
o
,
i k = 1 bâ
´
t
¯
d
,
˘
ang th
´
u
,
c
¯
d
˜
a cho hiê
,
n nhiên
¯
d
´
ung
v
`
a tr
,
o
,
th
`
anh
¯
d
,
˘
ang th
´
u
,
c. Gi
,
a s
,
u
,
(2.28)
¯
d
´
ung v
´
o
,
i sô
´
nguyên k ≥ 1.
Ta
¯
d
.
˘
at
N = (a
1
+ a
2
+ ··· + a
k
+ a
k+1
)
2
= (a
1
+ a
2
+ .. + a
k
)
2
+ a
2
k+1
+ 2a
k+1
(a
1
+ a
2
+ ··· + a
k
).

12.2. L
`
o
,
i gi
,
ai v
`
a g
.
o
,
i
´
y b
`
ai t
.
âp chu
,
o
,
ng 2 235
Ta thê
´
th
`
u
,
a sô
´
th
´
u
,
nhâ
´
t
,
o
,
bên ph
,
ai phu
,
o
,
ng tr
`
ınh trên b
`
˘
ang biê
,
u
th
´
u
,
c l
´
o
,
n ho
,
n n
´
o trong (2.28), ta nh
.
ân
¯
du
,
.
o
,
c
N ≤ k(a
2
1
+ a
2
2
+ ··· + a
2
k
) + a
2
k+1
+ 2a
k+1
(a
1
+ a
2
+ ··· + a
k
)
= (k + 1)(a
2
1
+ a
2
2
+ ··· + a
2
k
+ a
2
k+1
) − a
2
1
− a
2
2
−··· − a
2
k
−ka
2
k+1
+
+ 2a
1
a
k+1
+ 2a
2
a
k+1
+ ··· + 2a
k
a
k+1
=
= (k + 1)(a
2
1
+ a
2
2
+ ··· + a
2
k+1
) − (a
1
− a
k+1
)
2
−(a
2
− a
k+1
)
2
−···
··· −(a
k
− a
k+1
)
2
.
T
`
u
,
¯
dây suy ra bâ
´
t
¯
d
,
˘
ang th
´
u
,
c (2.28) v
´
o
,
i k + 1, hay l
`
a
N ≤ (k + 1)(a
2
1
+ a
2
2
+ ··· + a
2
k+1
).
J
.
.
. 2.33. G
.
o
,
i
´
y: Ta biê
,
u di
˜
ên f
(k+1)
(x) theo f
(k)
(x) b
`
˘
ang m
.
ôt sô
´
gi
´
a
tr
.
i
f
0
(x) =
x
(x
2
−1)
1/2
, f
00
(x) = −
1
(x
2
−1)
3/2
f
000
(x) =
3x
(x
2
−1)
5/2
, f
(iv)
(x) = −
12x
2
+ 1
(x
2
−1)
7/2
f
(v)
(x) =
60x
3
+ 31x
(x
2
−1)
9/2
, f
(vi)
(x) = −
522x
4
+ 266x
2
+ 31
(x
2
−1)
11/2
.
Bây gi
`
o
,
ta ph
´
at biê
,
u l
.
ai b
`
ai to
´
an: nê
´
u f (x) = (x
2
−1)
1/2
, x > 1,
khi
¯
d
´
o
f
(n)
(x) =
g
n
(x)
(x
2
−1)
(2n−1)/2
,
o
,
¯
dây g
n
(x) l
`
a
¯
da th
´
u
,
c b
.
âc n −2, v
`
a
g
n
(x) l
`
a
(
h
`
am ch
˜
˘
an v
´
o
,
i tâ
´
t c
,
a c
´
ac h
.
ê sô
´
không âm, nê
´
u n ch
˜
˘
an
h
`
am l
,
e v
´
o
,
i tâ
´
t c
,
a c
´
ac h
.
ê sô
´
không du
,
o
,
ng, nê
´
u n l
,
e.
M
.
ênh
¯
dê
`
n
`
ay c
´
o thê
,
ch
´
u
,
ng minh b
`
˘
ang quy n
.
ap.
.
.
. 2.34. G
.
o
,
i
´
y: Chia hai tru
,
`
o
,
ng h
.
o
,
p n ch
˜
˘
an v
`
a l
,
e.

236 Chu
,
o
,
ng 12. L
`
o
,
i gi
,
ai v
`
a g
.
o
,
i
´
y b
`
ai t
.
âp
12.3. L
`
o
,
i gi
,
ai v
`
a g
.
o
,
i
´
y b
`
ai t
.
âp chu
,
o
,
ng 3
.
.
. 3.21. L
`
o
,
i gi
,
ai: Ta c
´
o
S
n
=
n
∑
k=1
a
k
b
k
= a
1
b
1
+
n−1
∑
k=1
a
k+1
b
k+1
= a
1
b
1
+
n−1
∑
k=1
(a
k
+ d)qb
k
= a
1
b
1
+ q
n−1
∑
k=1
a
k
b
k
+ dq
n
∑
k=1
b
k
= a
1
b
1
+ q(S
n
− a
n
b
n
) + dqb
1
q
n−1
−1
q −1
.
T
`
u
,
¯
d
´
o suy ra công th
´
u
,
c b
`
ai to
´
an.
.
.
. 3.22. Tr
,
a l
`
o
,
i: b
n
= n
2
+ 1, S
n
=
1
6
n(2n
2
+ 3n + 7).
.
.
. 3.23. Tr
,
a l
`
o
,
i: S
n
=
1
2
n(4n
2
+ 7n + 1).
.
.
. 3.24. Tr
,
a l
`
o
,
i:
a) x
n
= C
1
cos
2πn
3
+ C
2
sin
2πn
3
;
b) x
n
= (C
1
+ C
2
.n)(−1)
n
;
c) x
n
= C
1
+ C
2
( −1)
n
;
d) x
n
= C
1
+ C
2
n + C
3
n
2
.
.
.
. 3.25. Tr
,
a l
`
o
,
i:
a) x
n
= 7 + 3
n
; b) x
n
= 2
n
+ 3
n
−4
n
; c) x
n
= 2(3 −2n).3
n−1
−1.
12.4. L
`
o
,
i gi
,
ai v
`
a g
.
o
,
i
´
y b
`
ai t
.
âp chu
,
o
,
ng 4
.
.
. 4.19. L
`
o
,
i gi
,
ai: Khi n = 1, th
`
ı 11
2
+ 12 = 133, m
.
ênh
¯
dê
`
¯
d
´
ung
v
´
o
,
i n = 1. Gi
,
a s
,
u
,
11
k+1
+ 12
2k−1
chia hê
´
t cho 133. Ta s
˜
e ch
´
u
,
ng

12.5. L
`
o
,
i gi
,
ai v
`
a g
.
o
,
i
´
y b
`
ai t
.
âp chu
,
o
,
ng 5 237
minh 11
k+2
+ 12
2k+1
c
˜
ung chi hê
´
t cho 133. Th
.
ât v
.
ây,
11
k+2
+ 12
2k+1
= 11.11
k+1
+ 12
2
.12
2k−1
= 11.(11
k+1
+ 12
2k−1
) + 133.12
2k−1
.
Tô
,
ng thu
¯
du
,
.
o
,
c chia hê
´
t cho 133. V
.
ây m
.
ênh
¯
dê
`
¯
d
´
ung v
´
o
,
i m
.
oi n ≥ 1.
J
.
.
. 4.20. G
.
o
,
i
´
y: Tiê
´
n h
`
anh nhu
,
b
`
ai 4.2 phâ
`
n 1).
.
.
. 4.21. G
.
o
,
i
´
y: Tiê
´
n h
`
anh nhu
,
b
`
ai 4.2 phâ
`
n 2).
.
.
. 4.22. G
.
o
,
i
´
y: B
`
ai to
´
an
¯
du
,
a vê
`
ch
´
u
,
ng minh công th
´
u
,
c 10
2n−1
+ 1
chia hê
´
t cho 11 v
´
o
,
i m
.
oi n ≥ 1.
12.5. L
`
o
,
i gi
,
ai v
`
a g
.
o
,
i
´
y b
`
ai t
.
âp chu
,
o
,
ng 5
.
.
. 5.28. L
`
o
,
i gi
,
ai: Ta k
´
y hi
.
êu a
n
= 2
2
n+1
+ 2
2
n
+ 1.
1) V
´
o
,
i n = 1, a
1
= 2
2
1+1
+ 2
2
1
+ 1 = 21.
2) V
´
o
,
i n = 2, a
2
= 2
2
2+1
+ 2
2
2
+ 1 = 2
8
+ 2
4
+ 1 = 256 + 16 + 1 =
273 = 21.13 , nhu
,
v
.
ây, a
2
chia hê
´
t 21.
3) Ta s
˜
e ch
´
u
,
ng minh a
n
chia hê
´
t cho 21 v
´
o
,
i m
.
oi sô
´
t
.
u
,
nhiên n.
V
´
o
,
i n = 1 v
`
a n = 2 ta
¯
d
˜
a kiê
,
m tra.
Gi
,
a s
,
u
,
a
k
= 2
2
k+ 1
+ 2
2
k
+ 1 = 21m. Ta x
´
et a
k+1
= 2
2
k+ 2
+ 2
2
k+ 1
+
1. Nhu
,
ng 2
2
k+ 1
= a
k
− 2
2
k
− 1 = 21m − 2
2
k
− 1, nhu
,
v
.
ây a
k+1
=
2
2
k+ 2
+ (21m − 2
2
k
− 1) + 1 = 2
2
k.4
− 2
2
k
+ 21m = 2
2
k
(2
2
k.3
− 1) +
21m,
a
k+1
= 2
2
k
[(2
6
)
2
k−1
−1] + 21m = 2
2
k
[(64)
2
k−1
−1] + 21m.
Nhu
,
ng ( 64)
2
k−1
−1 chia hê
´
t cho 64 −1 = 63 = 21.3 v
`
a suy ra
a
k+1
chia hê
´
t cho 21. Nhu
,
v
.
ây a
n
chia hê
´
t cho 21 v
´
o
,
i m
.
oi n v
`
a v
`
ı

238 Chu
,
o
,
ng 12. L
`
o
,
i gi
,
ai v
`
a g
.
o
,
i
´
y b
`
ai t
.
âp
a
1
= 21 l
`
a sô
´
nh
,
o nhâ
´
t trong tâ
´
t c
,
a c
´
ac sô
´
, th
`
ı u
,
´
o
,
c sô
´
chung l
´
o
,
n
nhâ
´
t c
,
ua tâ
´
t c
,
a a
n
, n = 1, 2, . . . l
`
a 21.
J
.
.
. 5.29. L
`
o
,
i gi
,
ai: Nh
´
˘
ac l
.
ai c
´
ach ch
´
u
,
ng minh c
,
ua Euclide vê
`
tô
`
n
t
.
ai vô h
.
an sô
´
nguyên tô
´
. Nê
´
u p
1
p
2
. . . p
n
+ 1 l
`
a nh
˜
u
,
ng sô
´
nguyên tô
´
bâ
´
t k
`
y, sô
´
P = p
1
p
2
. . . p
n
+ 1 kh
´
ac 1 v
`
a suy ra n
´
o chia hê
´
t cho m
.
ôt
u
,
´
o
,
c sô
´
nguyên tô
´
n
`
ao
¯
d
´
o, tâ
´
t nhiên n
´
o ph
,
ai kh
´
ac p
1
, p
2
, . . . , p
n
.
Nhu
,
v
.
ây theo c
´
ach n
`
ay ta t
`
ım
¯
du
,
.
o
,
c m
.
ôt sô
´
nguyên tô
´
m
´
o
,
i. Nê
´
u
p
1
, p
2
, . . . , p
n
l
`
a n sô
´
nguyên tô
´
¯
dâ
`
u tiên. Trong tru
,
`
o
,
ng h
.
o
,
p
¯
d
´
o
u
,
´
o
,
c sô
´
trên s
˜
e l
`
a sô
´
nguyên tô
´
th
´
u
,
n + 1 : p
n+1
. Do
¯
d
´
o p
n+1
≤
p
1
p
2
. . . p
n
+ 1. Bây gi
`
o
,
bâ
´
t
¯
d
,
˘
ang th
´
u
,
c p
n
< 2
2
n
ch
´
u
,
ng minh theo
phu
,
o
,
ng ph
´
ap quy n
.
ap to
´
an h
.
oc. V
´
o
,
i n = 1 ta c
´
o p
1
= 2 bâ
´
t
¯
d
,
˘
ang
th
´
u
,
c l
`
a hiê
,
n nhiên. Gi
,
a s
,
u
,
bâ
´
t
¯
d
,
˘
ang th
´
u
,
c
¯
d
´
ung v
´
o
,
i m
.
oi gi
´
a tr
.
i
nh
,
o ho
,
n n. Ta s
˜
e ch
´
u
,
ng minh n
´
o
¯
d
´
ung cho n + 1. Th
.
ât v
.
ây,
p
n+1
≤ p
1
p
2
. . . p
n
+ 1 < 2
2
.2
2
2
. . . 2
2
n
+ 1 = 2
2
n+1−2
+ 1 < 2
2
n+1
.
J
.
.
. 5.30. L
`
o
,
i gi
,
ai: 1) V
´
o
,
i n = 1 ta c
´
o
sin β
1
−sin α
1
= 2 sin
β
1
−α
1
2
cos
β
1
+ α
1
2
≤ 2 sin
β
1
−α
1
2
cos
β
1
−α
1
2
= sin(β
1
−α
1
)
(v
`
ı 0 ≤
β
1
−α
1
2
≤
β
1
+ α
1
2
≤
π
2
)
2) Gi
,
a s
,
u
,
bâ
´
t
¯
d
,
˘
ang th
´
u
,
c
¯
d
˜
a cho
¯
d
´
ung v
´
o
,
i n −1. Khi
¯
d
´
o
n
∑
i =1
(sin β
i
−sin α
i
) =
n−1
∑
i =1
(sin β
i
−sin α
i
) + sin β
n
−sin α
n
=
n−1
∑
i =1
(sin β
i
−sin α
i
) + 2 sin
β
n
−α
n
2
cos
β
n
+ α
n
2

12.5. L
`
o
,
i gi
,
ai v
`
a g
.
o
,
i
´
y b
`
ai t
.
âp chu
,
o
,
ng 5 239
≤ sin(
n−1
∑
i =1
β
i
−
n−1
∑
i =1
α
i
) + 2 sin
β
n
−α
n
2
cos(
n−1
∑
i =1
(β
i
−α
i
) +
β
n
−α
n
2
)
= sin(
n−1
∑
i =1
(β
i
−α
i
)) + sin(
n
∑
i =1
(β
i
−α
i
)) + sin(−
n−1
∑
i =1
(β
i
−α
i
))
= sin(
n
∑
i =1
(β
i
−α
i
).
V
`
ı c
.
ông c
´
ac bâ
´
t phu
,
o
,
ng tr
`
ınh α
1
≥ 0, α
2
≥ β
1
, α
3
≥ β
2
, . . . , α
n
≥
β
n−1
ta nh
.
ân
¯
du
,
.
o
,
c α
1
+ α
1
+ ··· + α
n
≥ β
1
+ β
2
+ ··· + β
n−1
t
`
u
,
¯
d
´
o
suy ra
0 ≤
n−1
∑
i =1
(β
i
−α
i
) +
β
n
−α
n
2
≤
β
n
+ α
n
2
≤
π
2
.
J
.
.
. 5.31. L
`
o
,
i gi
,
ai: Ta
¯
d
.
˘
at S
n
=
n
∑
i =1
1
n + i
. V
´
o
,
i n = 2 ta c
´
o S
2
=
1
2 + 1
+
1
2 + 2
=
14
24
>
13
24
. Ta gi
,
a thiê
´
t r
`
˘
ang S
n
>
13
24
, v
´
o
,
i sô
´
n n
`
ao
¯
dâ
´
y. Ta s
˜
e ch
´
u
,
ng minh khi
¯
d
´
o c
˜
ung c
´
o bâ
´
t
¯
d
,
˘
ang th
´
u
,
c cho S
n+1
>
13
24
. Ta s
˜
e ch
´
u
,
ng minh bâ
´
t
¯
d
,
˘
ang th
´
u
,
c sau l
`
a
¯
d
,
u S
n+1
− S
n
> 0.
Th
.
ât v
.
ây,
S
n+1
−S
n
=
n+1
∑
i =1
1
n + i + 1
−
n
∑
i =1
1
n + i
=
1
2n + 1
+
1
2n + 2
−
1
n + 1
=
1
2(n + 1)(2n + 1)
> 0.
.
.
. 5.32. L
`
o
,
i gi
,
ai: D
˜
ay
¯
d
˜
a cho tho
,
a m
˜
an phu
,
o
,
ng tr
`
ınh truy hô
`
i
a
n
=
√
c + a
n−1
. Gi
,
a s
,
u
,
gi
´
o
,
i h
.
an l = lim
n→∞
a
n
tô
`
n t
.
ai. Khi
¯
d
´
o
lim
n→∞
a
n
= lim
n→∞
√
c + a
n−1
=
q
c + lim
n→∞
a
n−1
ho
.
˘
ac l
`
a l =
√
c + l,
t
`
u
,
¯
dây v
´
o
,
i ch
´
u
´
y l > 0, ta t
`
ım
¯
du
,
.
o
,
c l =
1
2
(1 +
√
4c + 1). Ta câ
`
n

240 Chu
,
o
,
ng 12. L
`
o
,
i gi
,
ai v
`
a g
.
o
,
i
´
y b
`
ai t
.
âp
ph
,
ai ch
´
u
,
ng minh gi
´
o
,
i h
.
an tô
`
n t
.
ai. Ta ch
´
u
´
y r
`
˘
ang d
˜
ay a
1
, a
2
, . . .
t
˘
ang, suy ra ch
,
ı c
`
on kiê
,
m tra n
´
o l
`
a b
.
i ch
.
˘
an. Ch
´
ınh x
´
ac ho
,
n ta s
˜
e
ch
´
u
,
ng minh bâ
´
t
¯
d
,
˘
ang th
´
u
,
c
a
n
< 1 +
√
c, (n = 1, 2, 3, . . .).
Th
.
ât v
.
ây, v
´
o
,
i n = 1 (1) tho
,
a m
˜
an a
1
√
c < 1 +
√
c. Gi
,
a s
,
u
,
bâ
´
t
¯
d
,
˘
ang
th
´
u
,
c (1) tho
,
a m
˜
an v
´
o
,
i n n
`
ao
¯
d
´
o. Khi
¯
d
´
o
a
n+1
=
√
c + a
n
<
q
c + (1 +
√
c) < 1 +
√
c.
J
12.6. L
`
o
,
i gi
,
ai v
`
a g
.
o
,
i
´
y b
`
ai t
.
âp chu
,
o
,
ng 6
.
.
. 6.17. G
.
o
,
i
´
y: D
˜
ê d
`
ang ch
´
u
,
ng minh b
`
˘
ang quy n
.
ap theo n.
.
.
. 6.18. G
.
o
,
i
´
y: T
`
u
,
m
.
ôt sô
´
do
.
an th
,
˘
ang c
´
o thê
,
t
.
ao th
`
anh
¯
da gi
´
ac
khi v
`
a ch
,
ı khi
¯
do
.
an l
´
o
,
n nhâ
´
t trong ch
´
ung ph
,
ai nh
,
o ho
,
n tô
,
ng c
´
ac
¯
do
.
an c
`
on l
.
ai.
.
.
. 6.19. G
.
o
,
i
´
y: Nh
˜
u
,
ng m
,
anh do n
¯
du
,
`
o
,
ng tr
`
on c
´
˘
at ra
¯
d
˜
a
¯
du
,
.
o
,
c tô
so
,
n theo gi
,
a thiê
´
t quy n
.
ap. Ta v
˜
e thêm m
.
ôt
¯
du
,
`
o
,
ng tr
`
on th
´
u
,
n + 1
, khi
¯
d
´
o ta
¯
dô
,
i m
`
au tâ
´
t c
,
a c
´
ac m
,
anh n
`
˘
am trong du
,
`
o
,
ng tr
`
on th
´
u
,
n + 1. Nhu
,
v
.
ây ta c
´
o m
.
˘
at ph
,
˘
ang ph
,
ai t
`
ım.
.
.
. 6.20. G
.
o
,
i
´
y: Tô
,
ng c
´
ac sô
´
l
`
a 2.3
n
.
12.7. L
`
o
,
i gi
,
ai v
`
a g
.
o
,
i
´
y b
`
ai t
.
âp chu
,
o
,
ng 7
.
.
. 7.17. L
`
o
,
i gi
,
ai: Ta ch
´
u
,
ng minh b
`
˘
ang quy n
.
ap theo n. V
´
o
,
i n = 1
m
.
ênh
¯
dê
`
¯
d
´
ung, v
`
ı
a
x(x + 1)
=
a
x
−
a
x + 1
= (−
a
x + 1
) − (−
a
x
).

12.7. L
`
o
,
i gi
,
ai v
`
a g
.
o
,
i
´
y b
`
ai t
.
âp chu
,
o
,
ng 7 241
Cho n > 1. Ta biê
,
u di
˜
ên
¯
da th
´
u
,
c P(x) du
,
´
o
,
i d
.
ang
P(x) = c + (x + n)P
1
(x),
,
o
,
¯
dây c l
`
a h
`
˘
ang sô
´
, c
`
on b
.
âc c
,
ua P
1
(x) nh
,
o ho
,
n n − 1. Theo gi
,
a
thiê
´
t quy n
.
ap
P
1
(x) = x(x + 1) . . . (x + n −1)(R
1
(x + 1) − R
1
(x)).
,
o
,
¯
dây R
1
(x) l
`
a m
.
ôt h
`
am h
˜
u
,
u t
,
y n
`
ao
¯
d
´
o v
`
a khi
¯
d
´
o
P(x) = x(x + 1) . . . (x + n)(R(x + 1) − R(x)).
,
o
,
¯
dây
R(x) = R
1
(x) −
c
n
.
1
x(x + 1) . . . (x + n −1)
.
Ch
´
u
´
y: Nê
´
u b
.
âc c
,
ua P(x) l
`
a n,
¯
diê
`
u kh
,
˘
ang
¯
d
.
inh trên l
`
a không
¯
d
´
ung, ta h
˜
ay xem ph
,
an v
´
ı d
.
u sau
P(x) = x(x + 1) . . . (x + n −1).
J
.
.
. 7.18. L
`
o
,
i gi
,
ai: Ch
´
u
,
ng minh b
`
˘
ang quy n
.
ap theo n. Nê
´
u n = 0,
P(x) = a m
.
ôt h
`
˘
ang sô
´
v
`
a khi
¯
d
´
o P(x) = a.P
0
(x). Gi
,
a thiê
´
t kh
,
˘
ang
¯
d
.
inh
¯
d
´
ung v
´
o
,
i tâ
´
t c
,
a
¯
da th
´
u
,
c b
.
âc nh
,
o ho
,
n n v
`
a P(x) = a
n
x
n
+ ···.
Ta
¯
d
.
˘
at b
n
= n!a
n
. Ða th
´
u
,
c P(x) −b
n
P
n
(x) s
˜
e c
´
o b
.
âc không l
´
o
,
n ho
,
n
n − 1 v
`
a c
´
o ngh
˜
ıa l
`
a theo gi
,
a thiê
´
t quy n
.
ap c
´
o sô
´
b
0
, b
1
, . . . , b
n−1
sao cho
P(x) −b
n
P
n
(x) = b
n−1
P
n−1
+ ··· + b
0
P
0
(x).
Suy ra kh
,
˘
ang
¯
d
.
inh
¯
d
´
ung cho c
,
a
¯
da th
´
u
,
c P(x).
J
.
.
. 7.19. L
`
o
,
i gi
,
ai: 1) V
´
o
,
i n = 1
¯
d
,
˘
ang th
´
u
,
c c
´
o d
.
ang u
1
x =
u
1
x
3
+ u
2
x
2
− x
x
2
+ x −1
ho
.
˘
ac l
`
a x =
x
3
+ x
2
− x
x
2
+ x −1
,
¯
d
,
˘
ang th
´
u
,
c n
`
ay
¯
d
´
ung.

242 Chu
,
o
,
ng 12. L
`
o
,
i gi
,
ai v
`
a g
.
o
,
i
´
y b
`
ai t
.
âp
2) Ch
´
u
,
ng minh r
`
˘
ang
¯
d
,
˘
ang th
´
u
,
c
¯
d
´
ung v
´
o
,
i sô
´
n n
`
ao
¯
d
´
o. Ta s
˜
e
ch
´
u
,
ng minh
¯
d
,
˘
ang th
´
u
,
c c
˜
ung
¯
d
´
ung cho n + 1. Th
.
ât v
.
ây, ta biê
´
n
¯
dô
,
i
F
n+1
(x) =
n+1
∑
i =1
u
i
n
= F
n
(x) + u
n+1
x
n+1
=
u
n
x
n+2
+ u
n+1
x
n+1
− x
x
2
+ x −1
+ u
n+1
x
n+1
.
Biê
´
n
¯
dô
,
i d
.
u
,
a v
`
ao công th
´
u
,
c u
n+2
= u
n
+ u
n+1
ta nh
.
ân
¯
du
,
.
o
,
c
F
n+1
(x) =
u
n+1
x
n+3
+ u
n+2
x
n+2
− x
x
2
+ x −1
, (x
2
+ x −1 6= 0)
.
.
. 7.20. G
.
o
,
i
´
y: Tiê
´
n h
`
anh nhu
,
7.16
.
.
. 7.21. G
.
o
,
i
´
y: Tiê
´
n h
`
anh nhu
,
7.16
.
.
. 7.22. L
`
o
,
i gi
,
ai: Ch
´
u
,
ng minh b
`
˘
ang quy n
.
ap theo n.
1) n = 0, Khi
¯
d
´
o P(x) = a
0
. Nê
´
u |1 − a
0
| < 1 v
`
a |a − a
0
| < 1.
Khi
¯
d
´
o |a −1| = |a − a
0
+ a
0
−1| ≤ |a − a
0
| + |a
0
−1| < 2, nhu
,
ng
a ≥ 3 d
˜
ân
¯
dê
´
n vô l
´
y!.
2) Gi
,
a s
,
u
,
m
.
ênh
¯
dê
`
¯
d
´
ung v
´
o
,
i k ≤ n −1. Ta x
´
et
¯
da th
´
u
,
c
Q(x) =
P(x + 1) − P(x)
a −1
.
D
˜
ê d
`
ang thâ
´
y r
`
˘
ang Q(x) l
`
a
¯
da th
´
u
,
c b
.
âc n −1. Theo gi
,
a thiê
´
t quy
n
.
ap tô
`
n t
.
ai sô
´
i(0 ≤ i ≤ n −1) sao cho
1 ≤ |a
i
− Q(i)| = |a
i
−
P(i + 1) − P(i)
a −1
|
=
|a
i +1
− P(i + 1) −a
i
+ P(i)|
a −1
≤
|a
i +1
− P(i + 1)|
a −1
+
|a
i
− P(i)|
a −1
.

12.7. L
`
o
,
i gi
,
ai v
`
a g
.
o
,
i
´
y b
`
ai t
.
âp chu
,
o
,
ng 7 243
C
´
o
´
ıt nhâ
´
t m
.
ôt trong c
´
ac sô
´
h
.
ang không nh
,
o ho
,
n
1
2
. Gi
,
a s
,
u
,
¯
d
´
o l
`
a
biê
,
u th
´
u
,
c th
´
u
,
nhâ
´
t, th
`
ı v
`
ı
a −1
2
≥ 1 do a ≥ 3, |a
i +1
− P(i + 1)| ≥
a −1
2
≥ 1.
Tu
,
o
,
ng t
.
u
,
, nê
´
u biê
,
u th
´
u
,
c th
´
u
,
hai không nh
,
o ho
,
n
1
2
, th
`
ı |a
i
−
P(i)| ≥ 1.
J
.
.
. 7.23. L
`
o
,
i gi
,
ai: 1) V
´
o
,
i n = 1. Khi
¯
d
´
o P
1
(x) + P
1
(
1
x
) = x +
1
x
v
`
a
bâ
´
t
¯
d
,
˘
ang th
´
u
,
c nh
.
ân
¯
du
,
.
o
,
c c
´
o d
.
ang
x +
1
x
≥ 2, (x > 0). (12.5)
V
`
ı x > 0, nên bâ
´
t
¯
d
,
˘
ang th
´
u
,
c vu
`
˘
a nh
.
ân
¯
du
,
.
o
,
c tu
,
o
,
ng
¯
du
,
o
,
ng v
´
o
,
i
(x − 1)
2
≥ 0 v
`
a suy ra m
.
ênh
¯
dê
`
¯
d
´
ung.
V
´
o
,
i n = 2 ta c
´
o P
2
(x) + P
2
(
1
x
) = (x
2
+ 1) + (
1
x
2
+ 1) = x
2
+
2 +
1
x
2
. Câ
`
n ph
,
ai ch
´
u
,
ng minh r
`
˘
ang P
2
(x) + P
2
(
1
x
) ≥ 2 + 1 +
1
2
(1 +
( −1)
2
) = 4 ho
.
˘
ac l
`
a x
2
+
1
x
2
≥ 2;
¯
diê
`
u n
`
ay suy ra t
`
u
,
(12.5). Gi
,
a s
,
u
,
m
.
ênh
¯
dê
`
¯
d
´
ung v
´
o
,
i n. Ta c
´
o bâ
´
t
¯
d
,
˘
ang th
´
u
,
c sau
¯
d
´
ung
P
n
(x) + P
n
(
1
x
) ≥ n + 1 +
1
2
(1 + (−1)
n
).
Ta s
˜
e ch
´
u
,
ng minh tru
,
´
o
,
c tiên bâ
´
t
¯
d
,
˘
ang th
´
u
,
c
¯
d
´
ung cho n + 2
P
n+2
(x) + P
n+2
(
1
x
) ≥ n + 3 +
1
2
(1 + (−1)
n+2
).
Ch
´
u
´
y P
n
tho
,
a m
˜
an
¯
d
,
˘
ang th
´
u
,
c P
n+2
(x) = x
n+2
+ P
n
(x). Suy ra
P
n+2
(x) + P
n+2
(
1
x
) = [P
n
(x) + P
n
(
1
x
)] + [x
n+2
+
1
x
n+2
]

244 Chu
,
o
,
ng 12. L
`
o
,
i gi
,
ai v
`
a g
.
o
,
i
´
y b
`
ai t
.
âp
Theo (*) bâ
´
t
¯
d
,
˘
ang th
´
u
,
c sau
¯
d
´
ung x
n+2
+
1
x
n+2
≥ 2. T
`
u
,
c
´
ac
¯
d
,
˘
ang
th
´
u
,
c v
`
a bâ
´
t
¯
d
,
˘
ang th
´
u
,
c sau c
`
ung v
`
a gi
,
a thiê
´
t quy n
.
ap ta c
´
o:
P
n+2
(x) + P
n+2
(
1
x
) ≥ n + 1 +
1
2
(1 + (−1)
n
) + 2.
= (n + 2) + 1 +
1
2
(1 + (−1)
n+2
).
Ta ch
´
u
´
y r
`
˘
ang (−1)
n
= (−1)
n+2
. Theo nguyên l
´
y quy n
.
ap m
.
ênh
¯
dê
`
¯
d
´
ung v
´
o
,
i m
.
oi sô
´
l
,
e n (v
`
ı n
´
o
¯
d
´
ung v
´
o
,
i n = 1) v
`
a
¯
d
´
ung v
´
o
,
i m
.
oi
n ch
˜
˘
an (v
`
ı n
´
o
¯
d
´
ung v
´
o
,
i n = 2). Nhu
,
v
.
ây bâ
´
t d
,
˘
ang th
´
u
,
c
¯
d
´
ung v
´
o
,
i
m
.
oi n ≥ 1.
J
12.8. L
`
o
,
i gi
,
ai v
`
a g
.
o
,
i
´
y b
`
ai t
.
âp chu
,
o
,
ng 8
.
.
. 8.19. L
`
o
,
i gi
,
ai: 1) v
´
o
,
i n = 1 kh
,
˘
ang
¯
d
.
inh
¯
d
´
ung, v
`
ı
2 cos x −cos 2x −1
4 sin
2
x
2
=
2 cos x −2 cos
2
x
4 sin
2
x
2
=
cos x(1 − cos x)
2 sin
2
x
2
= cos x.
2) Cho
cos x + 2 cos 2x + ···+ k cos kx =
( k + 1) cos kx −k cos(k + 1)x −1
4 sin
2
x
2
.
Khi
¯
d
´
o
cos x + 2 cos 2x + ··· + k cos kx + (k + 1) cos(k + 1)x =
=
( k + 1) cos kx −k cos(k + 1)x −1
4 sin
2
x
2
+ (k + 1 ) cos(k + 1)x
=
( k + 1) cos kx −k cos(k + 1)x −1
4 sin
2
x
2
+
2( 1 − cos x)(k + 1) cos(k + 1)x
4 sin
2
x
2
=
( k + 2) cos(k + 1)x + (k + 1) cos kx
4 sin
2
x
2
−
2(k + 1) cos x cos(k + 1)x + 1
4 sin
2
x
2

12.8. L
`
o
,
i gi
,
ai v
`
a g
.
o
,
i
´
y b
`
ai t
.
âp chu
,
o
,
ng 8 245
=
( k + 2) cos(k + 1)x + (k + 1) cos kx
4 sin
2
x
2
−
−
( k + 1)[cos(k + 2)x + cos kx] + 1
4 sin
2
x
2
=
( k + 2) cos(k + 1)x − (k + 1) cos(k + 2)x −1
4 sin
2
x
2
.
J
.
.
. 8.20. L
`
o
,
i gi
,
ai: 1) V
´
o
,
i n = 1 kh
,
˘
ang
¯
d
.
inh
¯
d
´
ung, v
`
ı
1 + i = 2
1
2
(cos
π
4
+ i sin
π
4
).
2) Gi
,
a s
,
u
,
¯
d
´
ung v
´
o
,
i n = k , t
´
u
,
c l
`
a
(1 + i)
k
= 2
k
2
(cos
kπ
4
+ i sin
kπ
4
).
Khi
¯
d
´
o
(1 + i)
k+1
= 2
k
2
(cos
kπ
4
+ i sin
kπ
4
).2
1
2
(cos
π
4
+ i sin
π
4
).
.2
k+ 1
2
(cos
( k + 1)π
4
+ i sin
( k + 1)π
4
).
J
.
.
. 8.21. L
`
o
,
i gi
,
ai: V
´
o
,
i n = 2
¯
d
,
˘
ang th
´
u
,
c
¯
d
´
ung: a
1
b
1
+ a
2
b
2
=
a
2
( b
1
+ b
2
) −(a
2
− a
1
) b
1
= a
2
B
2
− (a
2
− a
1
)B
1
. Ta s
˜
e ch
´
u
,
ng minh
nê
´
u kh
,
˘
ang
¯
d
.
inh
¯
d
´
ung v
´
o
,
i n n
`
ao
¯
d
´
o, th
`
ı n
´
o c
˜
ung
¯
d
´
ung v
´
o
,
i n + 1.
Ta c
´
o
n+1
∑
µ=1
a
µ
b
µ
=
n
∑
µ=1
a
µ
b
µ
+ a
n+1
b
n+1
= [a
n
B
n
−
n−1
∑
µ=1
(a
µ+1
− a
µ
)B
µ
] + a
n+1
b
n+1
.
(12.6)

246 Chu
,
o
,
ng 12. L
`
o
,
i gi
,
ai v
`
a g
.
o
,
i
´
y b
`
ai t
.
âp
Nhu
,
ng b
n+1
= B
n+1
− B
n
,
o
,
¯
dây a
n
B
n
+ a
n+1
b
n+1
= a
n
B
n
+
a
n+1
(B
n+1
− B
n
). T
`
u
,
kê
´
t qu
,
a cuô
´
i c
`
ung v
`
a (12.6) ta nh
.
ân
¯
du
,
.
o
,
c
n+1
∑
µ=1
a
µ
b
µ
= a
n+1
b
n+1
−(a
n+1
− a
n
)B
n
−
n−1
∑
µ=1
(a
µ+1
− a
µ
)B
µ
= a
n+1
b
n+1
−
n
∑
µ=1
(a
µ+1
− a
µ
)B
µ
.
.
.
. 8.22. L
`
o
,
i gi
,
ai: Ta ch
´
u
,
ng minh b
`
˘
ang quy n
.
ap theo k. V
´
o
,
i k = 1
tô
,
ng n
`
ay b
`
˘
ang
1 −
1
m + 1
=
m
m + 1
. (12.7)
V
´
o
,
i k = 2 ta t
´
ınh
¯
du
,
.
o
,
c
1 −
2
m + 1
+
2.1
( m + 1)(m + 2)
=
m
m + 2
. (12.8)
T
`
u
,
¯
d
,
˘
ang th
´
u
,
c (12.7) v
`
a (12.8)
¯
du
,
a
¯
dê
´
n gi
,
ai thiê
´
t tô
,
ng (12.6) b
`
˘
ang
m
m + k
. Ta s
˜
e ch
´
u
,
ng minh r
`
˘
ang
1 −
k + 1
n + 1
+
( k + 1)k
( m + 1)(m + 2)
−··· + (−1)
k+1
( k + 1)k . . . 2.1
( m + 1)(m + 2) . . . (m + k + 1)
=
m
m + k + 1
. (12.9)
Ta
¯
du
,
a v
`
ao
¯
d
.
inh ngh
˜
ıa sau
Q
i
( k) =
0, nê
´
u ho
.
˘
ac i < 0, ho
.
˘
ac i > k ;
( −1)
i
.
k(k −1) . . . (k −i + 1)
( m + 1) . . . (m + i)
, nê
´
u 0 ≤ i ≤ k
Khi
¯
d
´
o (12.9) c
´
o thê
,
viê
´
t
k+1
∑
i =0
Q
i
( k + 1) =
k+1
∑
i =0
[Q
i
( k) −
i
m + i
Q
i −1
( k)] =
=
k+1
∑
i =0
Q
i
( k) −
k+1
∑
i =0
i
m + i
Q
i −1
( k) =

12.9. L
`
o
,
i gi
,
ai v
`
a g
.
o
,
i
´
y b
`
ai t
.
âp chu
,
o
,
ng 9 247
=
k
∑
i =0
Q
i
( k) −
k
∑
i =0
i + 1
m + i + 1
Q
i
( k)
=
k
∑
i =0
m
m + i + 1
Q
i
( k)
=
k
∑
i =0
m
m + i + 1
.
m
m + k + 1
.
m + k + 1
m
Q
i
( k)
=
m
m + k + 1
k
∑
i =0
m + k + 1
m + i + 1
Q
i
( k)
=
m
m + k + 1
k
∑
i =0
m + k + 1 + i −i
m + i + 1
Q
i
( k)
=
m
m + k + 1
[
k
∑
i =0
Q
i
( k) +
k
∑
i =0
k − i
m + i + 1
Q
i
( k)]
=
m
m + k + 1
[
k
∑
i =0
Q
i
( k) −
k
∑
i =0
Q
i +1
( k)] =
m
m + k + 1
.
J
12.9. L
`
o
,
i gi
,
ai v
`
a g
.
o
,
i
´
y b
`
ai t
.
âp chu
,
o
,
ng 9
.
.
. 9.11. G
.
o
,
i
´
y: a)
´
ap d
.
ung
¯
d
,
˘
ang th
´
u
,
c
,
o
,
b
`
ai 9.4 ta nh
.
ân
¯
du
,
.
o
,
c
P
2i
Q
2i
−
P
2i−2
Q
2i−2
= −(−1)
2i−1
.
q
2i
Q
2i
Q
2i−2
,
t
`
u
,
¯
d
´
o c
´
o
P
2i
Q
2i
>
P
2i−2
Q
2i−2
(i = 1, 2, . . .).
b) tu
,
o
,
ng t
.
u
,
nhu
,
phâ
`
n a).
.
.
. 9.12. L
`
o
,
i gi
,
ai: a) D
˜
ay
P
1
Q
1
,
P
3
Q
3
, . . . h
.
ôi t
.
u, b
,
o
,
i v
`
ı theo b
`
ai t
.
âp
trên th
`
ı d
˜
ay gi
,
am, m
.
˘
at kh
´
ac sô
´
h
.
ang c
,
ua n
´
o
¯
dê
`
u du
,
o
,
ng. Ta
¯
d
.
˘
at

248 Chu
,
o
,
ng 12. L
`
o
,
i gi
,
ai v
`
a g
.
o
,
i
´
y b
`
ai t
.
âp
ω
0
= lim
i →∞
P
2i+1
Q
2i+1
. Ta s
˜
e ch
,
ı ra r
`
˘
ang d
˜
ay
P
0
Q
0
,
P
2
Q
2
, . . . c
˜
ung h
.
ôi t
.
u;
¯
dê
,
ch
´
u
,
ng minh
¯
du
,
.
o
,
c
¯
diê
`
u
¯
d
´
o câ
`
n ch
,
ı ra n
´
o b
.
i ch
.
˘
an ph
,
ai, v
`
ı ta
¯
d
˜
a biê
´
t
nhu
,
b
`
ai t
.
âp trên n
´
o
¯
d
˜
a l
`
a d
˜
ay t
˘
ang. Th
.
ât v
.
ây, t
`
u
,
(9.13) ta c
´
o
P
2i+1
Q
2i
− P
2i
Q
2i+1
= (−1)
2i
= 1,
t
`
u
,
¯
dây
P
2i+1
Q
2i+1
−
P
2i
Q
2i
=
P
2i+1
Q
2i
− P
2i
Q
2i+1
Q
2i
Q
2i+1
=
1
Q
2i
Q
2i+1
> 0. (12.10)
Ta
¯
d
.
˘
at α
00
= lim
i →∞
P
2i
Q
2i
. B
,
o
,
i v
`
ı d
˜
ay phân sô
´
xâ
´
p x
,
ı v
´
o
,
i ch
,
ı sô
´
l
,
e
tr
.
ôi ho
,
n phân sô
´
v
´
o
,
i ch
,
ı sô
´
ch
˜
˘
an, th
`
ı ω
00
≤ ω
0
. M
.
˘
at kh
´
ac
P
2m
Q
2m
<
ω
00
, ( m = 0, 1, . . .) v
`
a ω
0
<
P
2n+1
Q
2n+1
, ( n = 0, 1, . . .). Suy ra bâ
´
t
¯
d
,
˘
ang
th
´
u
,
c
P
2m
Q
2m
< ω
00
≤ ω
0
<
P
2n+1
Q
2n+1
tho
,
a m
˜
an tâ
´
t c
,
a sô
´
t
.
u
,
nhiên m, n. Ta s
˜
e ch
´
u
,
ng minh r
`
˘
ang ω
0
=
ω
00
. Ðê
,
¯
d
.
at m
.
uc
¯
d
´
ıch n
`
ay ta ph
,
ai kê
´
t lu
.
ân
P
2i+1
Q
2i+1
−
P
2i
Q
2i
c
´
o thê
,
tr
,
o
,
th
`
anh râ
´
t nh
,
o khi i
¯
d
,
u l
´
o
,
n. Theo b
`
ai trên d
˜
ay Q
0
, Q
1
, . . .
¯
do
,
n
¯
di
.
êu
t
˘
ang suy ra Q
n
≥ n, (n = 0, 1, . . .). Khi
¯
d
´
o t
`
u
,
(12.10) ta nh
.
ân
¯
du
,
.
o
,
c
0 <
P
2i+1
Q
2i+1
−
P
2i
Q
2i
=
1
Q
2i
Q
2i+1
≤
1
2i(2i + 1)
,
t
`
u
,
¯
dây
lim
i →∞
(
P
2i+1
Q
2i+1
−
P
2i
Q
2i
) = lim
i →∞
P
2i+1
Q
2i+1
− lim
i →∞
P
2i
Q
2i
= ω
0
−ω
00
= 0.
Ta k
´
y hi
.
êu ω gi
´
a tr
.
i chung c
,
ua ω
0
v
`
a ω
00
c
´
o thê
,
viê
´
t ω = lim
n→∞
P
n
Q
n
.
Theo
¯
d
.
inh ngh
˜
ıa gi
´
o
,
i h
.
an n
`
ay l
`
a gi
´
a tr
.
i c
,
ua liên phân sô
´
. Ta
¯
da
ch
´
u
,
ng minh xong m
.
oi liên phân sô
´
v
´
o
,
i c
´
ac phâ
`
n t
,
u
,
nguyên l
`
a h
.
ôi
t
.
u.
J

12.9. L
`
o
,
i gi
,
ai v
`
a g
.
o
,
i
´
y b
`
ai t
.
âp chu
,
o
,
ng 9 249
.
.
. 9.13. G
.
o
,
i
´
y: Theo b
`
ai trên liên phân sô
´
¯
d
˜
a cho l
`
a h
.
ôi t
.
u, ta c
´
o
thê
,
viê
´
t
ω = (1, 1, . . .) = (1, ω) = 1 +
1
ω
,
Ta thâ
´
y r
`
˘
ang ω l
`
a nghi
.
êm c
,
ua phu
,
o
,
ng tr
`
ınh ω
2
− ω −1 = 0. V
`
ı
ω > 0, th
`
ı ω =
1 +
√
5
2
.
.
.
. 9.14. L
`
o
,
i gi
,
ai: T
`
u
,
nh
˜
u
,
ng t
´
ınh châ
´
t c
,
ua liên phân sô
´
ta nh
.
ân
¯
du
,
.
o
,
c
ω −
P
i
Q
i
=
P
i
ω
i +1
+ P
i −1
Q
i
ω
i +1
+ Q
i −1
−
P
i
Q
i
=
Q
i
P
i −1
− Q
i −1
P
i
Q
i
(Q
i
ω
i +1
+ Q
i −1
)
v
`
a theo (9.13) ta c
´
o
δ
i
= |ω −
P
i
Q
i
| =
1
Q
i
(Q
i
ω
i +1
+ Q
i −1
)
. (12.11)
V
`
ı
ω
i +1
> q
i +1
, (12.12)
th
`
ı Q
i
(Q
i
ω
i +1
+ Q
i −1
) > Q
i
(Q
i
q
i +1
+ Q
i −1
) = Q
i
Q
i +1
t
`
u
,
¯
dây
δ
i
<
1
Q
i
Q
i +1
. m
.
˘
at kh
´
ac Q
i
(Q
i
ω
i +1
+ Q
i −1
) = Q
i
(Q
i
( ω
i +1
−q
i +1
) +
Q
i
q
i +1
+ Q
i −1
) v
`
a d
`
ung bâ
´
t
¯
d
,
˘
ang th
´
u
,
c (12.12 ) ta nh
.
ân
¯
du
,
.
o
,
c
Q
i
(Q
i
ω
i +1
+ Q
i −1
) < Q
i
(Q
i
+ (Q
i
q
i +1
+ Q
i −1
)) = Q
i
(Q
i
+ Q
i +1
).
T
`
u
,
¯
dây v
`
a (12.11) ta t
`
ım
¯
du
,
.
o
,
c
δ
i
>
1
Q
i
(Q
i
+ Q
i +1
)
.
J

T
`
AI LI
.
ÊU THAM KH
,
AO
[1] Phu
,
o
,
ng ph ´ap Ðirichlê v`a
´
u
,
ng d
.
ung,
Nguy
˜
ên H
˜
u
,
u Ðiê
,
n, NXB KHKT, 1999.
[2] Phu
,
o
,
ng ph ´ap sô
´
ph
´
u
,
c v `a h`ınh h
.
oc ph
,
˘ang,
Nguy
˜
ên H
˜
u
,
u Ðiê
,
n, NXB ÐHQG, 2000.
[3] Metod matematiqeskonju indukcii,
I. S. Sominskinju, Moskva, 1961.
[4] Matematiqeska indukci,
L. Petruxev, Sofi, 1983.
[5] Problem-Solving through problems,
Loren C. Larson, Springer-Verlag, 1983.
[6] C ´ac
¯
dê
`
thi vô
¯
d
.
ich to´an c ´ac nu
,
´
o
,
c,
X.V. Cônhiagin, G.A. Tônôian, I.F. Saru
,
gin,... NXB GD,
1996.
[7] Ph´ep quy n
.
ap trong h`ınh h
.
oc,
L.I. Golovina, I.M. Yaglom NXB GD, 1997.
250

N
.
ÔI DUNG
L
`
o
,
i n
´
oi
¯
dâ
`
u . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
Chu
,
o
,
ng 1. Nguyên l
´
y quy n
.
ap to
´
an h
.
oc. . . . . . . . . . . . . . . . . 4
1.1. Suy di
˜
ên v
`
a quy n
.
ap . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
1.2. Nguyên l
´
y quy n
.
ap to
´
an h
.
oc . . . . . . . . . . . . . . . . . . . . . . . . . . 6
1.3. Giai
¯
do
.
an quy n
.
ap v
`
a gi
,
a thiê
´
t quy n
.
ap . . . . . . . . . . . . . . . 8
1.4. Hai bu
,
´
o
,
c c
,
ua nguyên l
´
y quy n
.
ap to
´
an h
.
oc . . . . . . . . . . . 14
1.5. Khi n
`
ao d
`
ung phu
,
o
,
ng ph
´
ap quy n
.
ap . . . . . . . . . . . . . . . . . 19
1.6. B
`
ai t
.
âp . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
Chu
,
o
,
ng 2. K
˜
y thu
.
ât d
`
ung phu
,
o
,
ng ph
´
ap quy n
.
ap to
´
an h
.
oc
23
2.1. M
.
ôt sô
´
d
.
ang nguyên l
´
y quy n
.
ap to
´
an h
.
oc . . . . . . . . . . . . 23
2.2. M
.
ênh
¯
dê
`
trong nguyên l
´
y quy n
.
ap to
´
an h
.
oc. . . . . . . . . . 31
2.3. Bu
,
´
o
,
c quy n
.
ap
¯
du
,
.
o
,
c xây d
.
u
,
ng trên P(k) . . . . . . . . . . . . . . 36
2.4. Bu
,
´
o
,
c quy n
.
ap
¯
du
,
.
o
,
c xây d
.
u
,
ng trên P(k + 1) . . . . . . . . . . 40
2.5. Quy n
.
ap to
´
an h
.
oc v
`
a ph
´
ep truy hô
`
i . . . . . . . . . . . . . . . . . . 43
2.6. Quy n
.
ap to
´
an h
.
oc v
`
a tô
,
ng qu
´
at ho
´
a . . . . . . . . . . . . . . . . . . 51
2.7. B
`
ai t
.
âp . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 55
Chu
,
o
,
ng 3. T
`
ım công th
´
u
,
c tô
,
ng qu
´
at . . . . . . . . . . . . . . . . . . . 57
3.1. Câ
´
p sô
´
c
.
ông v
`
a câ
´
p sô
´
nhân . . . . . . . . . . . . . . . . . . . . . . . . . . 57
3.2. T
´
ınh tô
,
ng v
`
a sô
´
h
.
ang tô
,
ng qu
´
at. . . . . . . . . . . . . . . . . . . . . . 66
3.3. Phu
,
o
,
ng tr
`
ınh truy hô
`
i tuyê
´
n t
´
ınh . . . . . . . . . . . . . . . . . . . 71
251

252 N
.
ÔI DUNG
3.4. Tô
,
ng c
,
ua nh
˜
u
,
ng l
˜
uy th
`
u
,
a c
`
ung b
.
âc c
´
ac sô
´
t
.
u
,
nhiên . 84
3.5. B
`
ai t
.
âp . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 87
Chu
,
o
,
ng 4. Sô
´
h
.
oc . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 89
4.1. Ph
´
ep chia hê
´
t . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 89
4.2. Thu
.
ât to
´
an Euclide . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 94
4.3. Sô
´
ph
´
u
,
c . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 99
4.4. Nh
˜
u
,
ng v
´
ı d
.
u kh
´
ac . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 105
4.5. B
`
ai t
.
âp. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 108
Chu
,
o
,
ng 5. D
˜
ay sô
´
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 110
5.1. D
˜
ay sô
´
t
.
u
,
nhiên. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 110
5.2. D
˜
ay tr
.
ôi ho
,
n . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 117
5.3. Nh
˜
u
,
ng bâ
´
t
¯
d
,
˘
ang th
´
u
,
c nô
,
i tiê
´
ng . . . . . . . . . . . . . . . . . . . . . 121
5.4. D
˜
ay
¯
do
,
n
¯
di
.
êu . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 128
5.5. Sô
´
e . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 131
5.6. D
˜
ay sô
´
Fibonacci. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 134
5.7. B
`
ai t
.
âp. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 139
Chu
,
o
,
ng 6. H
`
ınh h
.
oc . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 140
6.1. V
´
ı d
.
u quy n
.
ap to
´
an h
.
oc cho h
`
ınh h
.
oc .. . . . . . . . . . . . . . 140
6.2. B
`
ai t
.
âp. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 154
Chu
,
o
,
ng 7. Ða th
´
u
,
c. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 156
7.1. Phân t
´
ıch
¯
da th
´
u
,
c ra th
`
u
,
a sô
´
. . . . . . . . . . . . . . . . . . . . . . . 156
7.2. Nguyên l
´
y so s
´
anh c
´
ac h
.
ê sô
´
. . . . . . . . . . . . . . . . . . . . . . . . 160
7.3. Ð
.
ao h
`
am c
,
ua
¯
da th
´
u
,
c . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 169
7.4. Ða th
´
u
,
c Chebychev . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 172

N
.
ÔI DUNG 253
7.5. B
`
aii t
.
âp . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 174
Chu
,
o
,
ng 8. Tô
,
h
.
o
,
p v
`
a
¯
d
,
˘
ang th
´
u
,
c . . . . . . . . . . . . . . . . . . . . . . . 176
8.1. M
.
ôt sô
´
công th
´
u
,
c tô
,
h
.
o
,
p . . . . . . . . . . . . . . . . . . . . . . . . . . . . 176
8.2. M
.
ôt sô
´
¯
d
,
˘
ang th
´
u
,
c . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 186
8.3. B
`
ai t
.
âp. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 193
Chu
,
o
,
ng 9. Liên phân sô
´
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 194
9.1. Kh
´
ai ni
.
êm liên phân sô
´
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 194
9.2. Phân t
´
ıch sô
´
h
˜
u
,
u t
,
y th
`
anh liên phân sô
´
. . . . . . . . . . . . 196
9.3. Phân sô
´
xâ
´
p x
,
ı . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 198
9.4. Liên phân sô
´
vô h
.
an . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 203
9.5. V
´
ı d
.
u. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 204
9.6. B
`
ai t
.
âp . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 210
Chu
,
o
,
ng 10. M
.
ôt sô
´
¯
dê
`
thi vô
¯
d
.
ich . . . . . . . . . . . . . . . . . . . . . 212
Chu
,
o
,
ng 11. B
`
ai t
.
âp t
.
u
,
gi
,
ai . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 226
Chu
,
o
,
ng 12. L
`
o
,
i gi
,
ai v
`
a g
.
o
,
i
´
y b
`
ai t
.
âp . . . . . . . . . . . . . . . . . . 231
12.1. L
`
o
,
i gi
,
ai v
`
a g
.
o
,
i
´
y b
`
ai t
.
âp chu
,
o
,
ng 1 . . . . . . . . . . . . . . . . . 231
12.2. L
`
o
,
i gi
,
ai v
`
a g
.
o
,
i
´
y b
`
ai t
.
âp chu
,
o
,
ng 2 . . . . . . . . . . . . . . . . . 233
12.3. L
`
o
,
i gi
,
ai v
`
a g
.
o
,
i
´
y b
`
ai t
.
âp chu
,
o
,
ng 3 . . . . . . . . . . . . . . . . . 236
12.4. L
`
o
,
i gi
,
ai v
`
a g
.
o
,
i
´
y b
`
ai t
.
âp chu
,
o
,
ng 4 . . . . . . . . . . . . . . . . . 236
12.5. L
`
o
,
i gi
,
ai v
`
a g
.
o
,
i
´
y b
`
ai t
.
âp chu
,
o
,
ng 5 . . . . . . . . . . . . . . . . . 237
12.6. L
`
o
,
i gi
,
ai v
`
a g
.
o
,
i
´
y b
`
ai t
.
âp chu
,
o
,
ng 6 . . . . . . . . . . . . . . . . . 240
12.7. L
`
o
,
i gi
,
ai v
`
a g
.
o
,
i
´
y b
`
ai t
.
âp chu
,
o
,
ng 7 . . . . . . . . . . . . . . . . . 240
12.8. L
`
o
,
i gi
,
ai v
`
a g
.
o
,
i
´
y b
`
ai t
.
âp chu
,
o
,
ng 8 . . . . . . . . . . . . . . . . . 244
12.9. L
`
o
,
i gi
,
ai v
`
a g
.
o
,
i
´
y b
`
ai t
.
âp chu
,
o
,
ng 9 . . . . . . . . . . . . . . . . . 247

254 Th
.
u
,
c h
`
anh t
´
ınh to
´
an
M
.
uc l
.
uc .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 250
PHU
,
O
,
NG PH
´
AP QUY N
.
AP TO
´
AN H
.
OC
M
˜
a sô
´
: 8H663M0
In 3.000 b
,
an (21TK), khô
,
14, 3 × 20, 3 cm T
.
ai Công ty In Ba
Ð
`
ınh, Thanh H
´
oa Sô
´
in: 127; Sô
´
XB 05/796-00.
In xong v
`
a n
.
ôp lu
,
u chiê
,
u th
´
ang 8 n
˘
am 2000.
Bấm Tải xuống để xem toàn bộ.




