Phương pháp sử dụng khoảng cách để tính góc trong Hình không gian 11 (có đáp án)

ỨNG DỤNG KHOẢNG CÁCH
ĐỂ TÍNH GÓC TRONG HÌNH KHÔNG GIAN LỚP 11
Bài toán tính góc trong không gian là dạng bài quan trọng trong chương trình toán lớp 11.
Đây cũng là dạng toán thường xuất hiện trong kỳ thi THPT Quốc gia những năm gần đây.
Giữa hai bài toán tính góc và tính khoảng cách có mối liên hệ rất chặt chẽ. Bài viết này đề cập
đến một trong những ứng dụng của khoảng cách, đó là tính góc giữa đường thẳng và mặt
phẳng, tính góc giữa hai mặt phẳng trong không gian.
I. GÓC GIỮA ĐƯỜNG THẲNG VÀ MẶT PHẲNG 1. Lý thuyết
Trong không gian, cho đường thẳng d và mặt phẳng (P) không vuông góc và không song
song với nhau. Gọi j = (d,(P)). Ta biết rằng:
j = (d (P)) = (d d¢) ∑ , , = AIH
với d¢ là hình chiếu của d trên (P), AÎd và AÏ(P), I = d Ç(P), H là hình chiếu của A trên (P). A d H d' I (P) AH d ( , A (P)) Từ đó ta có: sinj = = . AI AI
Như vậy việc tính góc giữa đường thẳng d và mặt phẳng (P) có thể quy về việc tính khoảng
cách từ A tới (P) và tính độ dài AI . 2. Ví dụ minh họa
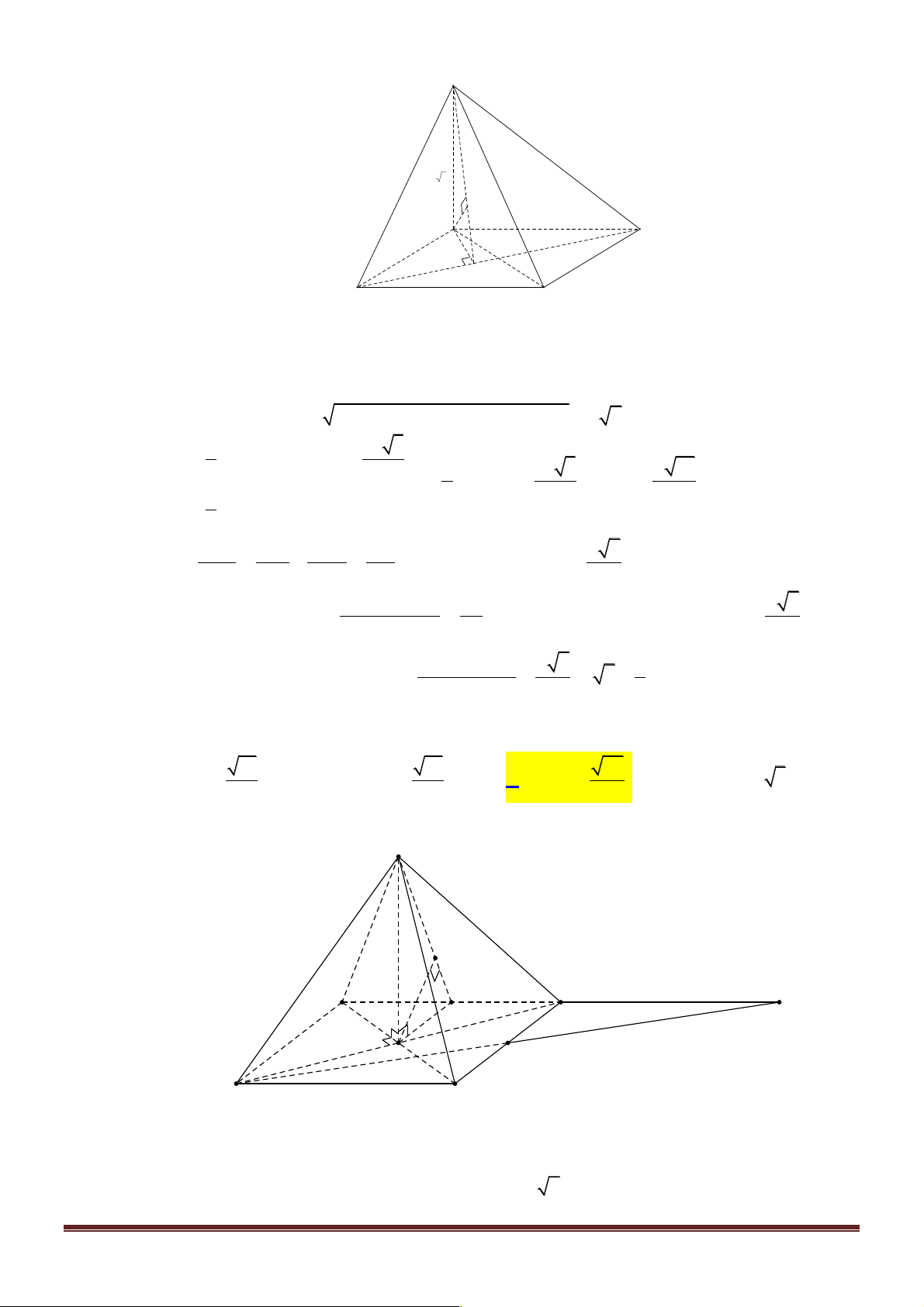
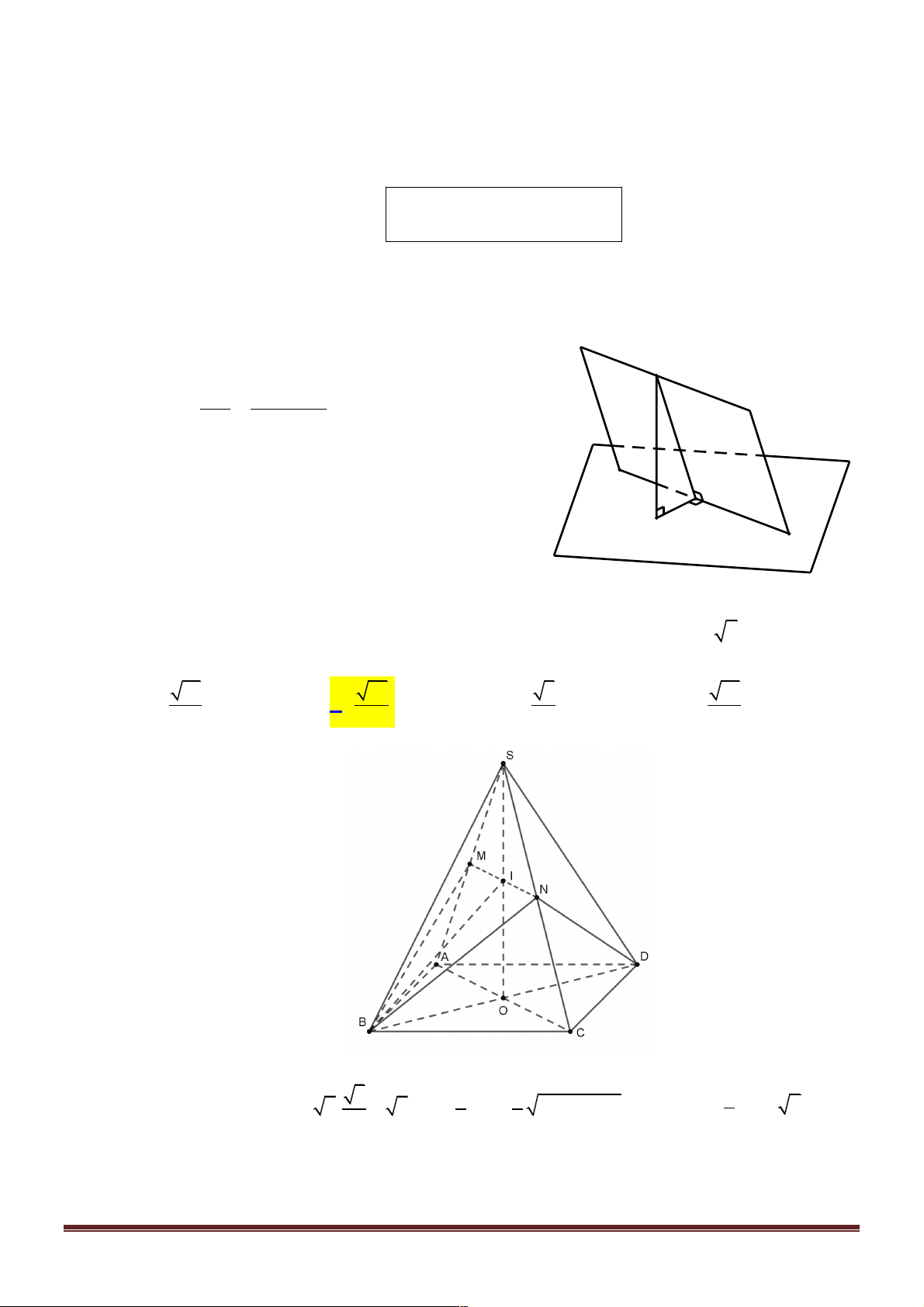
Câu 1. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, AB = 2a , BC = a , ∑ ABC =120°,
cạnh bên SD = a 3 , SD ^ ( ABCD). Gọi j là góc giữa đường thẳng SB và mặt phẳng
(SAC), tính sinj. 1 3 3 3 A. . B. . C. . D. . 4 4 4 7 Lời giải Trang 1 S a 3 K D C a H A 2a B
Trong mặt phẳng ( ABCD) kẻ DH ^ AC tại H .
Trong mặt phẳng (SDH ) dựng DK ^ SH tại K .
Chứng minh được DK ^ (SAC). Từ đó ta có: d ( ,
D (SAC)) = DK . Trong ACD D có 2 2
AC = AD + CD - 2 . AD C .
D cos120° = a 7. 1 ∑ 2 a 3 ü S = . AD DC.sinADC = ï 2 AD D C ï 1 a 3 a 21 2 2 ý Þ DH.AC = Þ DH = . 1 2 2 7 S DH.AC ï = AD D C 2 ïþ 1 1 1 8 a 6 Ta có: = + =
Þ d D, SAC = DK = 2 2 2 2 ( ( )) . DK SD DH 3a 4 d ( , B (SAC))
Gọi I = AC Ç BD . Ta có IB =
= Þ d (B SAC ) = d ( (SAC)) a 6 1 , D, = . d ( , D (SAC)) ( ) ID 4 d ( ,
B (SAC)) a 6 1 Gọi j = ( ,
SB (SAC)). Ta có sinj = = : a 6 = . BS 4 4
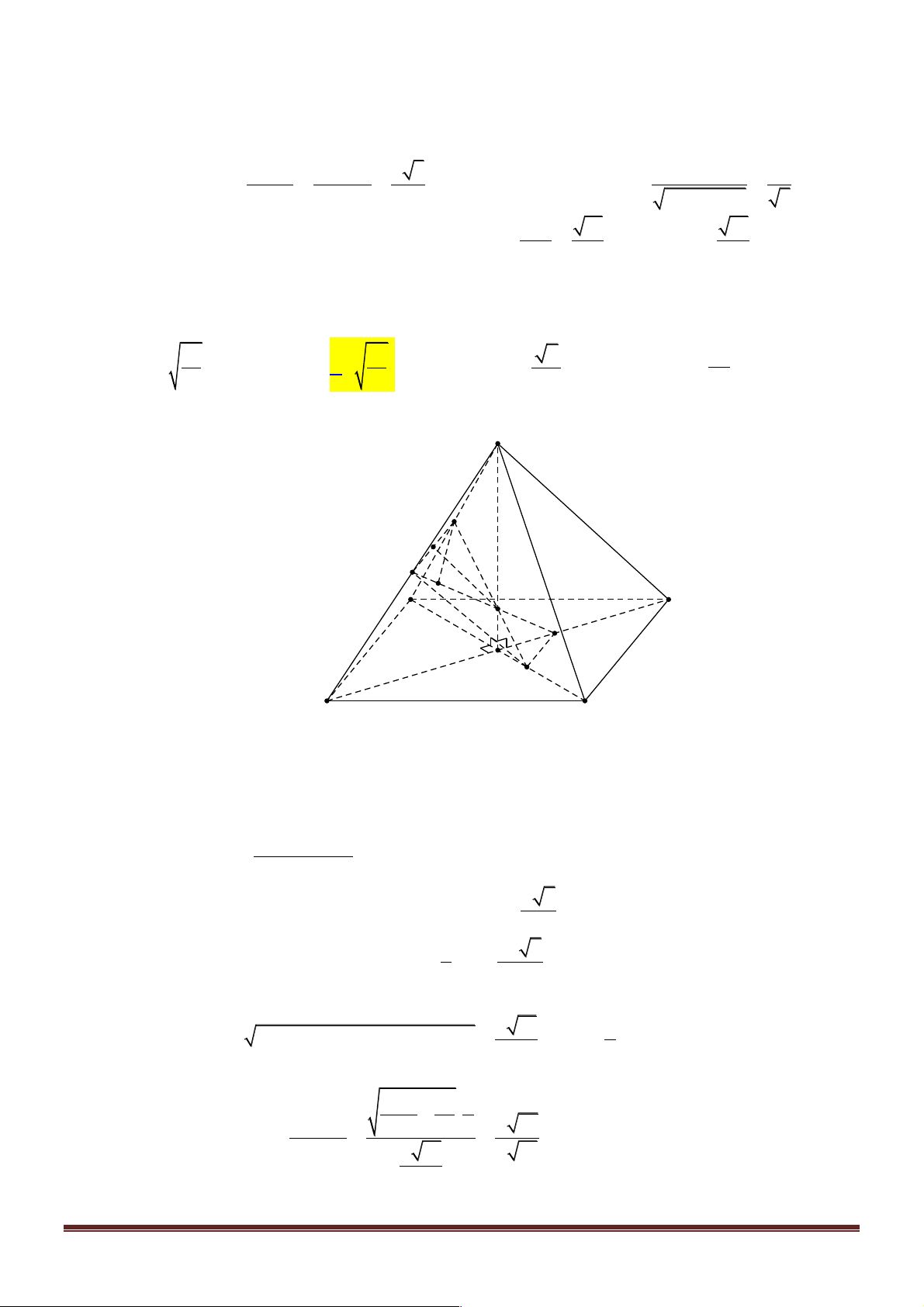
Câu 2. Cho hình chóp đều S.ABCD có SA = AB = a . Gọi M là trung điểm của cạnh BC . Tính tan
của góc giữa đường thẳng DM và mặt phẳng (SAB). 13 A. tana = 15 . B. tana = 26 . C. tana = . D. tana = 3 . 13 5 13 Lời giải S H A I B E O M D C
Gọi O = AC Ç BD , ta có O là trung điểm của AC, BD.
Vì S.ABCD là hình chóp đều nên SO^ ( ABCD).
ABCD là hình vuông cạnh AB = a Þ AC = BD = a 2. Trang 2 DSAC a 2
có SA = SC = a, AC =a 2 Þ SA
D C vuông cân tại S Þ SO = 2 d ( ; D (SAB))
Gọi E = DM Ç AB , a = (DM,(SAB)). Ta có sina = DE 2 Ta có æ a ö a 5 2 2 2
DM = MC + DC = + a =
Þ DE = 2DM = a 5 ç ÷ è 2 ø 2
Kẻ OI ^ AB tại I và OH ^ SI tại H . Ta chứng minh được: OH ^ (SAB). Khi đó: d ( ;
D (SAB)) DB = = 2 Þ d ( ; D SAB ) = 2d ( ;
O (SAB)) = 2OH d ( ; O (SAB)) ( ) OB S . O OI a 6 Xét SO D
I vuông tại O; OH là đường cao nên: OH = = . 2 2 SO + OI 6 ( a d D (SAB)) 6 ; 30 3 Þ sina = = = . DE a 5 15 195 Ta có: 2 2 sin a + cos a = 1Þ cosa = vì 0 0 a Îé0 ;90 ù. 15 ë û sina 26 Từ đó ta có: tana = = . cosa 13
Câu 3. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA ^ ( ABCD), SA = a , AB = a 3 , 3a AD =
. Gọi G là trọng tâm tam giác ACD , I là trung điểm của SB . Góc giữa đường 2
thẳng IG và mặt phẳng (SCD) bằng 3 3 3 3 A. arcsin . B. arcsin . C. arcsin . D. arcsin . 4 13 13 16 16 Lời giải
Ta có SB = 2a nên suy ra được tam giác SAI đều cạnh a . BI BG
Gọi H là trung điểm của SI thì = nên IG // HD. BH BD Do đó ( ,
IG (SCD)) = (H , D (SCD)). a 3 3a
Xét tam giác tam giác vuông AHD có AH = , AD =
suy ra HD = a 3 . 2 2 1 1 1 1
Vì HS = BS nên d (H,(SCD)) = d (B,(SCD)) = d ( ,
A (SCD)) = d 4 4 4 4 Trang 3 1 1 1 1 4 13 a a Mà = + = + = 3 Þ d =
Þ d (H (SCD)) 3 , = . 2 2 2 2 2 2 d SA AD a 9a 9a 13 4 13
d (H, SCD ) 3a 3
Suy ra sin (HD,(SCD)) ( ) = = = . HD 4 13.a 3 4 13
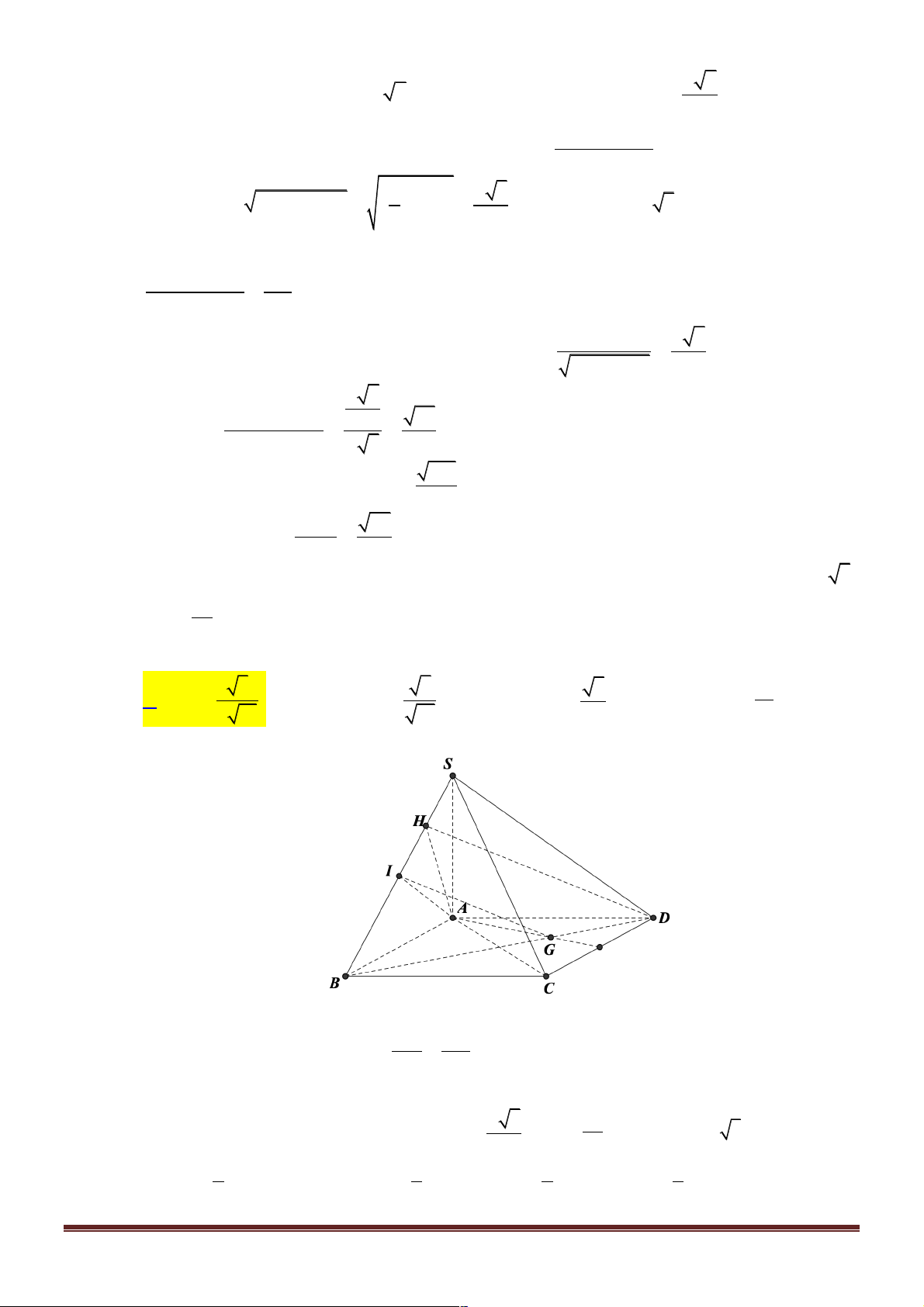
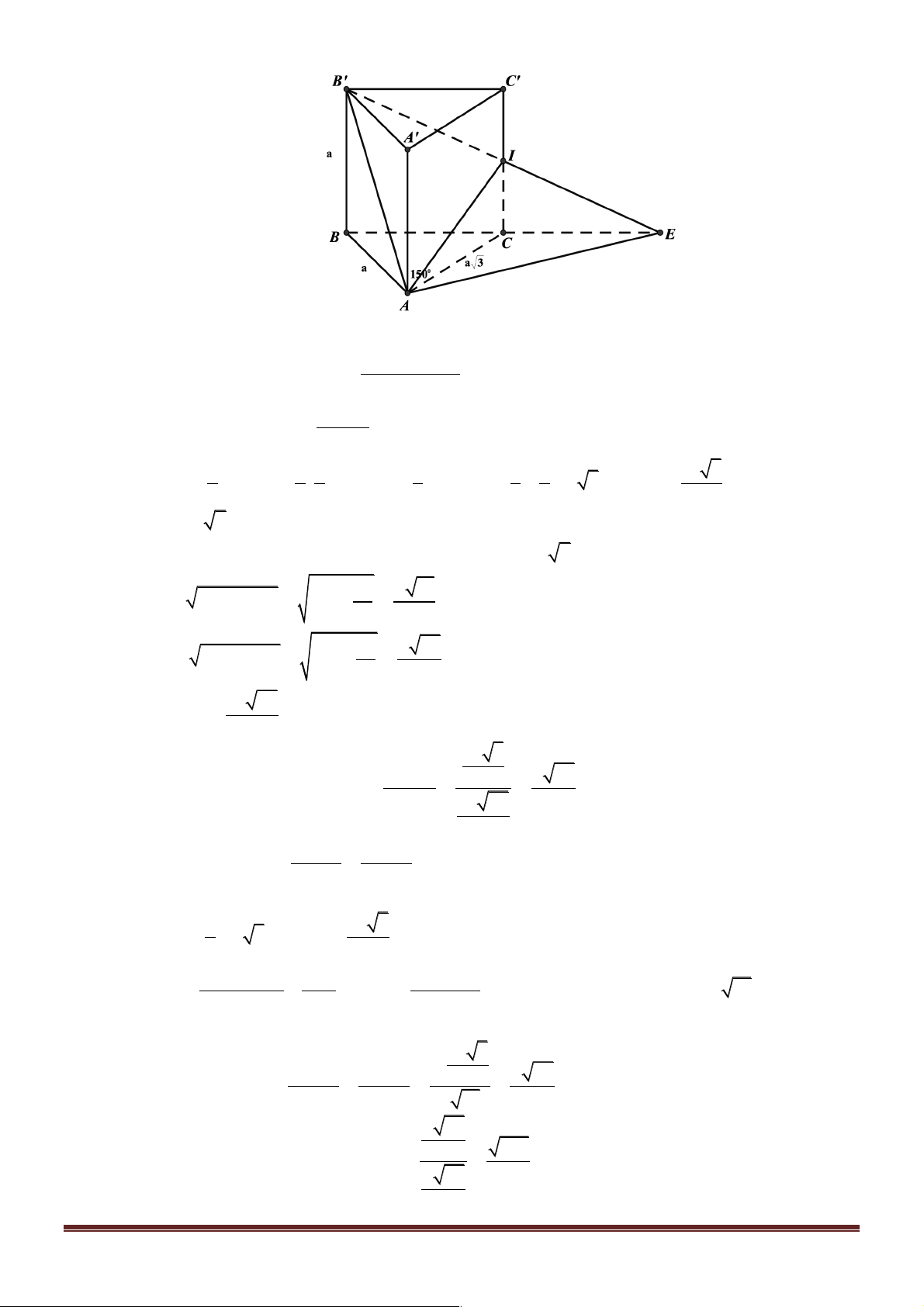
Câu 4. Cho hình hộp ABC . D A¢B C ¢ D
¢ ¢ có đáy ABCD là hình chữ nhật cạnh AB = a, AD = 2a , A B
¢ = a 3 . Gọi I là trọng tâm tam giác ( A C ¢ D
¢ ¢), j là góc giữa đường thẳng ID và mặt
phẳng (ICB). Giá trị của sinj bằng 9 6 6 23 A. . B. . C. . D. . 253 11 2 253 11 Lời giải
Gọi j là góc tạo bởi đường thẳng ID và mặt phẳng (ICB), H là trọng tâm tam giác ( ACD). d ( ;
D (ICB)) 3 d (H;(ICB)) Ta có: sinj = = . . ID 2 ID
Gọi E là hình chiếu của H lên CB , K là hình chiếu của H lên IE , ta chứng minh được
d (H;(ICB)) = HK . 2 2a 1 1 a 5 Ta có: 2 2 HE = DC = ; D I¢ = D B ¢ ¢ = 4 a + a = . 3 3 3 3 3 Mà 2 2 2 2 A A ¢ = A B
¢ - AB = 3a - a = a 2 Þ HI = a 2. 2 5a a 23 2 2 2
DI = DD¢ + D I¢ = 2 a + = 9 3 2a .a 2 Þ ( ( 9 ICB)) HE.HI 2 3 a d H; = HK = = = Þ sinj = . 2 2 2 HE + HI 22 a 11 253 9
Câu 5. Cho lăng trụ tam giác đều ABC.A¢B C
¢ ¢ , AA¢ = a, AB = 2a. Gọi I là trung điểm A¢B¢ , j là
góc tạo bởi AC¢ và (BIC¢). Tính cosj . 15 3 A. cosj = 10 . B. cosj = . C. cosj = 2 . D. cosj = 5 5 5 5 Lời giải Trang 4 d ( , A (BIC '))
Gọi K là trung điểm IB , j là góc giữa AC ' và (BIC '). Ta có: sinj = AC ' Ta có: (
ì BIC ') ^ ( ABB A
¢ ¢) (do C I¢ ^ ( ABB A ¢ ¢))
ï(ïíBIC')Ç(ABBA¢¢)= IB Þ B K ¢ ^ (BIC¢). ïB K ¢ ^ IB ïî
Mặt khác I là trung điểm A' B ' nên d ( A',(BIC ')) = d (B',(BIC ')) = B'K EA'
d ( A',(BIC '))
Gọi E là giao điểm của A' A và BI , ta có = EA d ( , A (BIC ')) EA' A' I 1 Mặt khác =
= (do AB // A'I ) EA AB 2 EA'
d ( A',(BIC ')) Suy ra 1 =
= Û d ( A BIC ) = d ( A (BIC )) a 2 , ' 2 ', ' = 2B ' K = 2. = a 2 EA d ( , A (BIC ')) ( ) 2 2 2 2 AC ' = A A ¢ + A C ¢ ¢ = a 5 d ( ,
A (BIC ')) a 2 10 Þ sinj = = = 15 Þ cosj = . AC ' a 5 5 5 Trang 5
II. GÓC GIỮA HAI MẶT PHẲNG 1. Lý thuyết
a) Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt vuông góc với hai mặt phẳng đó.
a ^ (a )üýÞ ((a),(b)) = (a, b) b ^ (b )þ
b) Trong trường hợp 2 mặt phẳng cắt nhau: “Góc giữa hai mặt phẳng là góc giữa hai đường
thẳng lần lượt nằm trong hai mặt phẳng và cùng vuông góc với giao tuyến tại một điểm”.
c) Ứng dụng khoảng cách để tính góc giữa hai mặt phẳng
Gọi j = ((a ),(b )) và c = (a )Ç(b ). Ta có: (α) A AA¢ d ( , A (b )) sinj = = AH d ( , A c)
Như vậy, bài toán tính góc giữa hai mặt phẳng có (β)
thể quy về bài toán tính khoảng cách từ một điểm c H
đến một mặt phẳng và tính khoảng cách từ một A'
điểm đến một đường thẳng. 2. Ví dụ minh họa
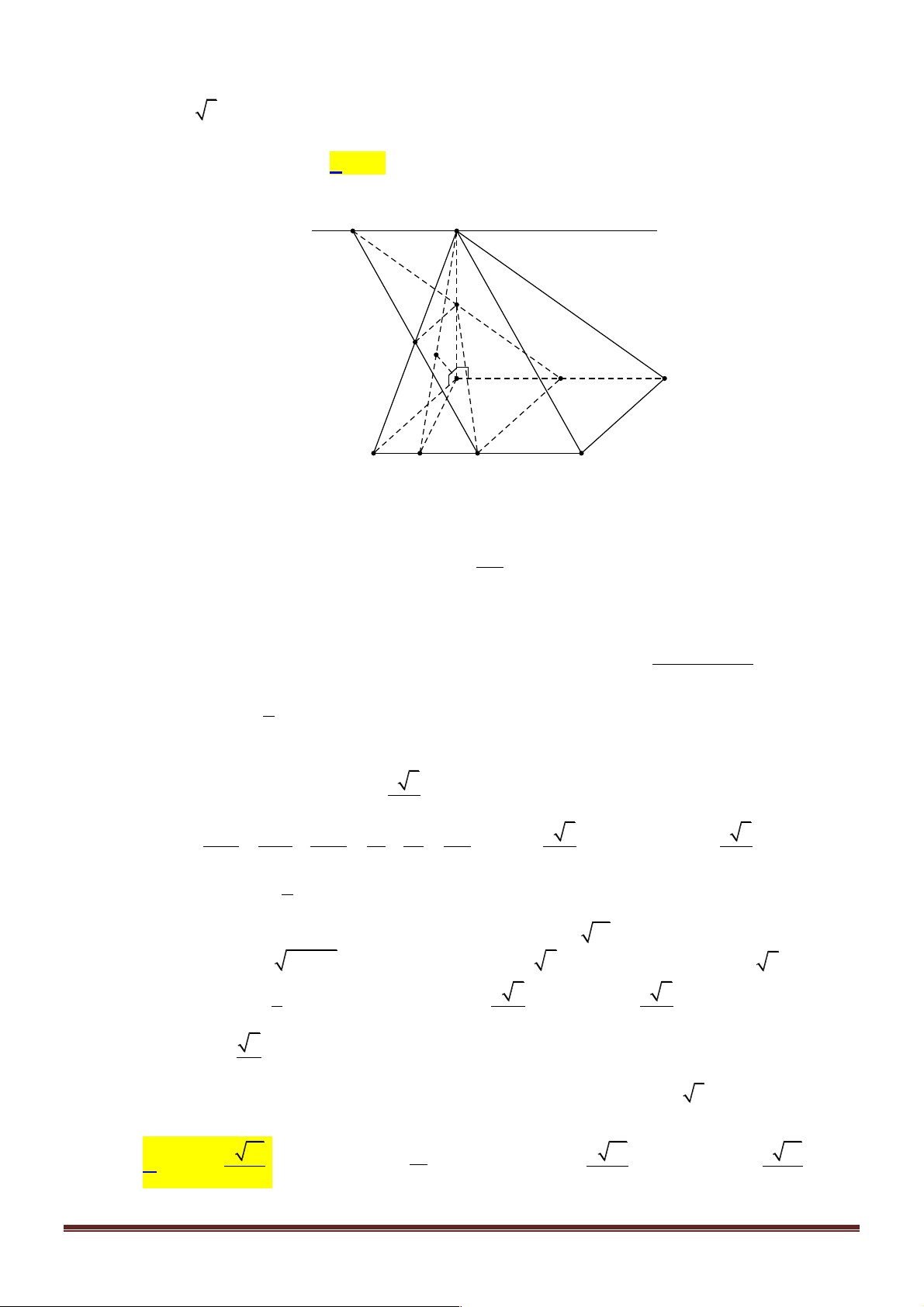
Câu 1. Cho hình chóp tứ giác đều S.ABCD có cạnh bên bằng cạnh đáy và bằng 2 2 . Gọi M , N lần
lượt là trung điểm của SA và SC . Côsin của góc giữa hai mặt phẳng (BMN )và (BDN ) bằng 13 10 3 15 A. . B. . C. . D. . 4 5 4 5 Lời giải
Gọi O = AC Ç BD, I = SO Ç MN . 3 1 1 1 Ta có: 2 2
AC = 4, BN = 2 2. = 6,OI = SO = SC - OC =
1 và ON = SA = 2 . 2 2 2 2
Gọi H , K lần lượt là hình chiếu vuông góc của D lên BN,(BMN ).
Khi đó: DH ^ BN, DK ^ (BMN) Þ DK ^ BN . Trang 6 ìBN ^ DH í Þ BN ^ HK . îBN ^ DK
Từ đó ta có: ((BMN) (BDN)) ∑ , = DHK =j. 2S B . D NO 4 3 OI.BO 4 Ta có: BDN DH = = =
và DK = 2d é ; O ë (BMN )ù = 2 = BN BN 3 û 2 2 OI + BO 5 DK 15 10
Suy ra: sinj = sin ((BMN ),(BDN )) ∑ ∑ = sin DHK = = Þ cosDHK = . DH 5 5
Câu 2. Cho hóp chóp đều S.ABCD có tất cả các cạnh bằng a . Gọi M , N lần lượt là trung điểm của
SA, SB và G là trọng tâm tam giác .
BCD Gọi a là góc giữa hai mặt phẳng (GMN ) và (SBD)
. Giá trị của sina bằng 2 34 2 2 A. . B. . C. . D. . 43 43 731 43 Lời giải S M I N J D A K E O G B C
Dựng đường cao SO của hình chóp.
Gọi K = SO Ç GM .
Ta có: (GMN) Ç (ABCD) = GE song song với CD, E ÎOD.
Khi đó: N, K, E thẳng hàng và NE = (BMN )Ç(SBD).
d(M ,(SBD)) Ta có: sina = . d(M , NE) a 2
Dễ thấy tam giác BSD vuâng cân tại S nên SO = . 2 Chứng minh được: 4 2a 2
KS = 4KO Þ SK = SO = . 5 5
Trong tam giác KMN dựng hai đường cao KI, MJ. a 17 a Ta có: 2 2
KN = SN + SK - 2SN.SK.cos 45° = , MN = . 10 2 Do đó: 2 2 17a a a - . ( KI MN a d M , NE ) . 100 16 2 43 = MJ = = = . KN a 17 4 17 10 Trang 7 d( , A (SBD)) a 2 34
d(M ,(SBD)) = = Þ sina = . 2 4 43 Trang 8
Câu 3. Cho khối chóp S.ABCD có đáy là hình bình hành, ∑
AB = 3, AD = 4, BAD =120°, cạnh bên
SA = 2 3 và vuông góc với mặt đáy. Gọi M , N, P lần lượt là trung điểm các cạnh ,
SA AD, BC . Tính góc giữa hai mặt phẳng (SBC) và (MNP). A. 30° . B. 45°. C. 60° . D. 90° . Lời giải J S x M I E N D A B K P C
Ta có: (SAD) Ç (SBC) = Sx //AD //BC .
ìMI //NP //AB ï
Gọi I là trung điểm của SB . Ta có: í NP . MI = ïî 2
Dễ dàng chứng minh được ,
IP MN, Sx đồng quy tại J . Như vậy I là trung điểm của JP , M
là trung điểm của JN .
d(M ,(SBC))
Gọi j là góc giữa hai mặt phẳng (SBC) và (MNP). Ta có: sinj = . d(M , IP) 1
d(M ,(SBC)) = d( , A (SBC)) 2
Hạ AK ^ BC, AE ^ SK Þ AE ^ (SBC) Þ d( ,
A (SBC)) = AE. ∑ 3 3 AK = .
AB sin ABK = 3.sin 60° = . 2 1 1 1 1 4 25 6 3 3 3 SA D K : = + = + = Þ AE =
Þ d(M ,(SBC)) = . 2 2 2 AE AS AK 12 27 108 5 5 1
Ta có d(M , PI ) = d(N, PI ) . 2 2 2 2 ABC D
: AC = AB + CB - 2 . AB C .
B cos60° =13 Þ AC = 13 .
JP = 2IP = SC = 13+12 = 5 , JN = 2MN = SD = 2 7 , PN = AB = 3 Þ S = 3 6. JPN 1 6 6 3 6 Mặt khác S
= d(N, JP).JP Þ d(N, JP) =
Þ d(M , IP) = . JPN 2 5 5 2 Vậy sinj = Þ j = 45° . 2
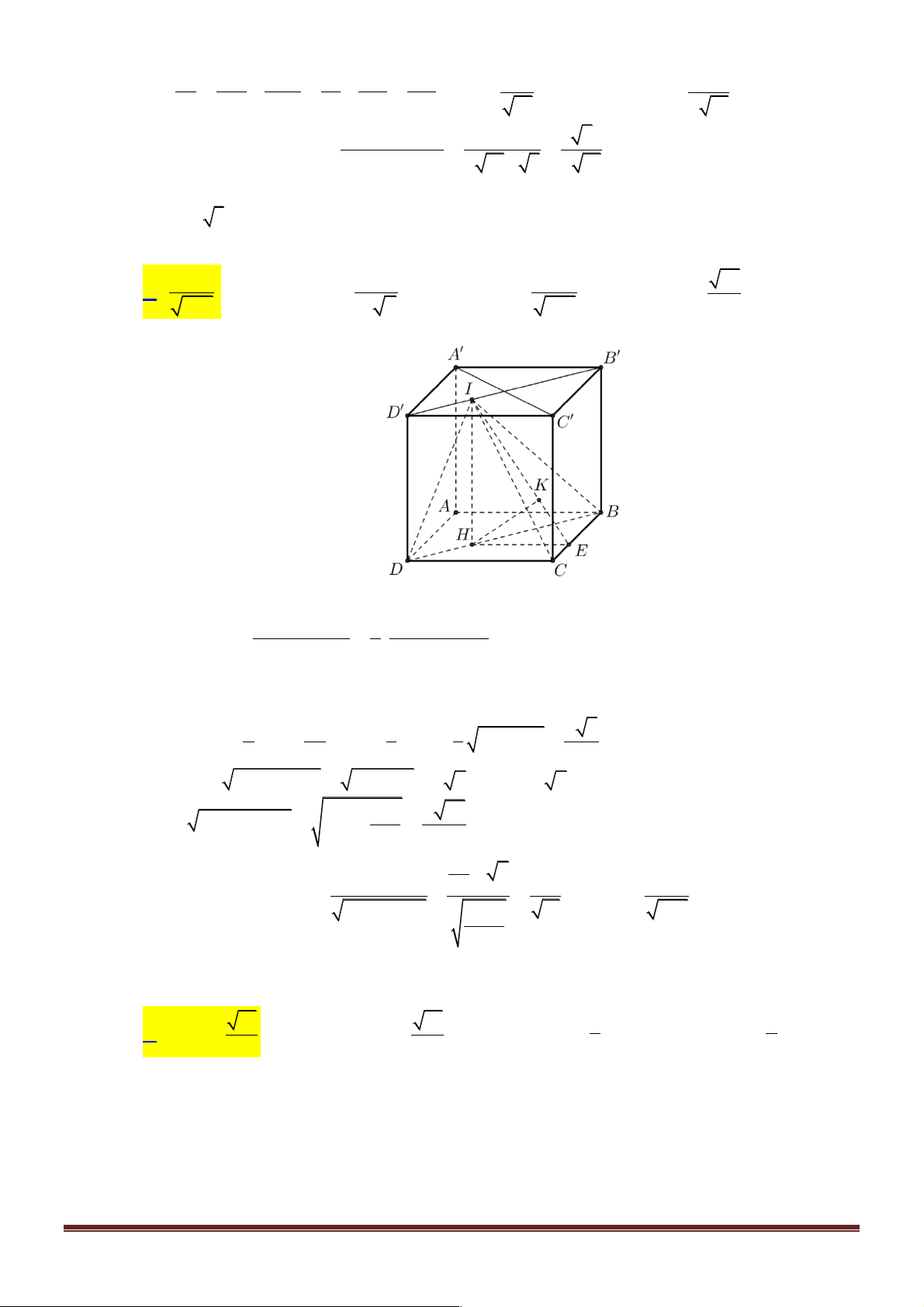
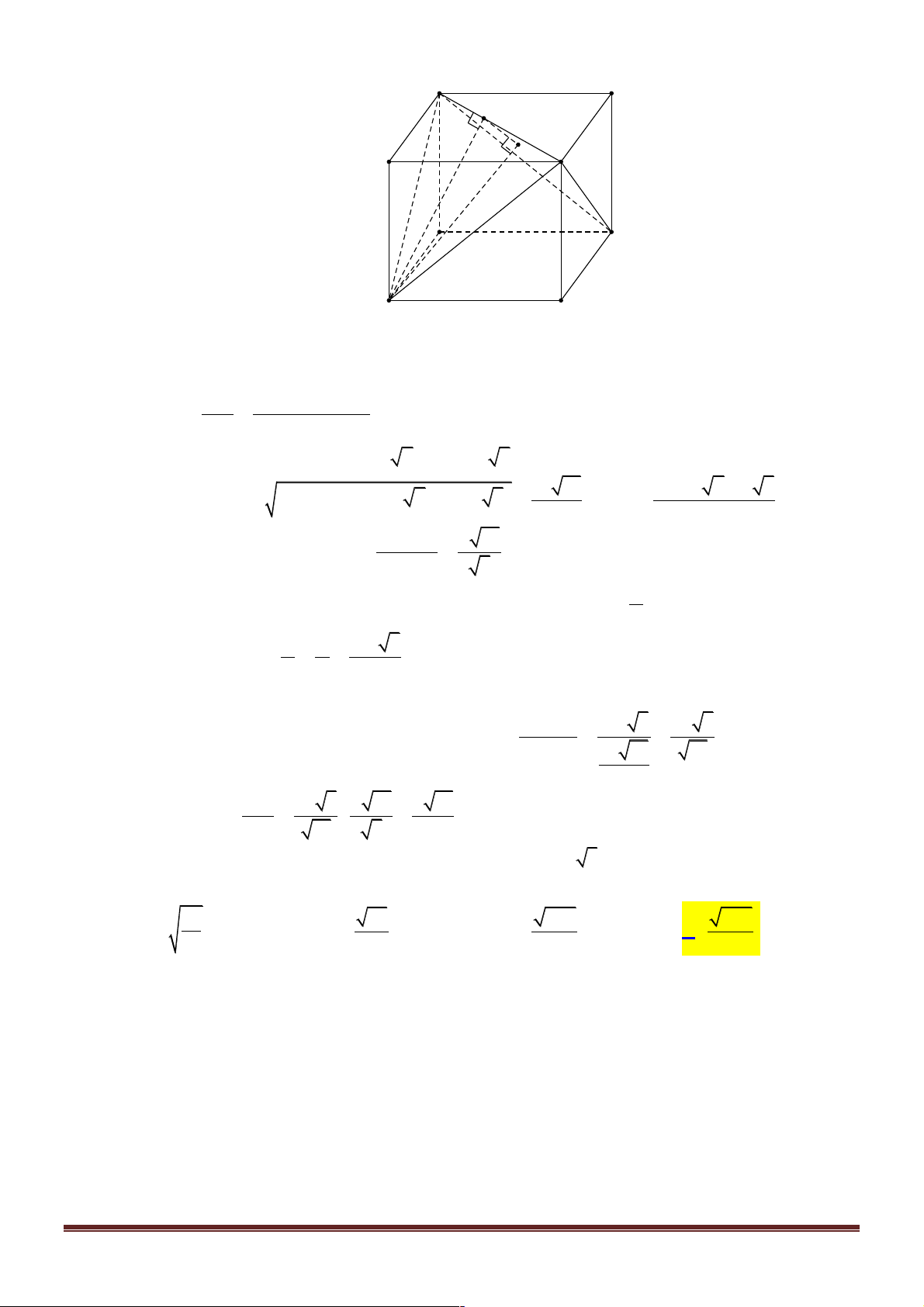
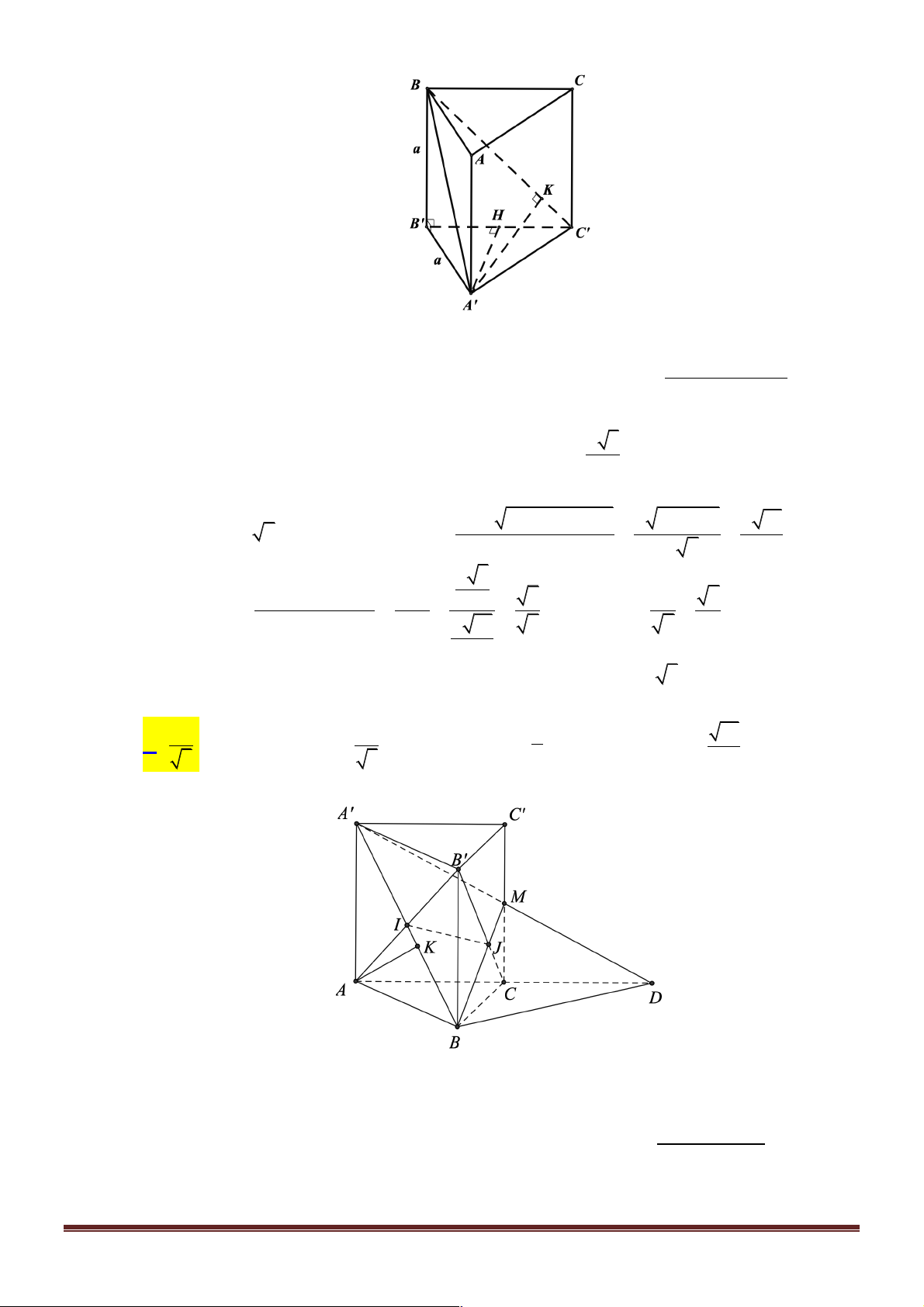
Câu 4. Cho hình hộp chữ nhật ABC . D A¢B C ¢ D
¢ ¢ có AB = 2a, AD = a, AA¢ = a 3. Gọi a là góc giữa hai mặt phẳng ( A C ¢ B ¢ ) và ( A C ¢ D ¢ ). Tính sina. 4 15 11 2 15 A. sina = . B. sina = . C. sina = 3 15 . D. sina = . 19 19 19 19 Lời giải Trang 9 A' B' I H D' C' B A D C
Gọi I là hình chiếu vuông góc của D lên A'C ' và H là hình chiếu vuông góc của D lên mp
(A'C'B). Khi đó: DH
d (D,( A'C 'B)) sina = = DI
d (D, A'C ')
Ta tính được A' D = 2 ;
a C ' D = a 7; A'C ' = a 5; a 19 a + a + a Ta có: S
= p p - 2a p - a 7 p - a 5 = 2 7 5 p = A D 'C 'D ( )( )( ) 2 với 2 2 2S a 19
Trong tam giác A'C ' D : A D 'C 'D DI = = A'C ' 5 V Đặt V = V ; ta có V =V =V =V =
ABCD.A'B'C 'D' A'.ABD C '.BCD
D.A'C 'D'
B.A'B'C ' 6 3 V V 2a 3 Þ V = V - 4. = = A'C 'BD 6 3 3 Do A
D 'C ' D = C
D ' A' B Þ S = S A D 'C'B A D 'C'D 3V 2a 3 4a 3
Trong tứ diện A'C ' BD : DH = d (D,( A'C 'B)) 3 A'C 'BD = = = 2 SD a A C B 19 19 ' ' 2 DH 4a 3 a 19 4 15 Vậy, sina = = : = . DI 19 5 19
Câu 5. Cho hình lăng trụ đứng ABC.A¢B C ¢ ¢ có ∑ AB = ,
a AC = a 3, BAC =150° , AA¢ = a . Gọi I là
trung điểm của CC¢ . Tính sin của góc giữa mặt phẳng ( AB I¢ ) và mặt phẳng ( ABC). 66 66 418 418 A. . B. . C. . D. . 57 57 11 22 Lời giải Trang 10
Gọi E = BC Ç B I¢ . Dễ thấy C là trung điểm của BE .
d (B, AB I¢ )
Ta có sin (( AB I¢ ),( ABC)) ( ) = * . d (B, AE) ( ) 3V
* Tính d (B,( AB I¢ )) . A BB I¢ = ( ) 1 S AB D I¢ 3 1 1 2 1 1 1 a 3 V = = = = ° = ¢ V ¢ ¢ . V ¢ ¢ ¢ V ¢ ¢ ¢ . a . a a 3.sin150 . A BB I . A BCC B ABC.A B C ABC. 2 2 3 3 A B C 3 2 12 AB¢ = a 2 2 2 2 2
BC = AB + AC - 2 .
AB AC sin150° = 7a Þ BC = a 7 2 a a 13 2 2 2
AI = AC + IC = 3a + = 4 2 2 a a 29 2 2 2
B I¢ = BC + IC = 7a + = 4 2 2 a 22 Þ S = AB D I¢ 4 2 a 3 3V ¢ a 66
Do đó từ suy ra d (B ( AB I¢ )) . A BB I 4 , = = = 2 SD ¢ a AB I 22 22 4 2S 4S
* Tính d (B, AE) ABE D ABC D = = (2) AE AE Ta có 2 1 a 3 S = . a a 3.sin150° = ABC D 2 4 2 2 2 2 2 AB + AE BE a + AE 2 2 2 2 2 AC = - Û 3a =
- 7a Û AE =19a Þ AE = a 19 2 4 2 2 a 3 4. 2S 4S a 57 Do đó d (B AE) ABE D ABC D 4 , = = = = AE AE a 19 19 a 66 418 Vậy từ suy ra
((AB I¢) (ABC)) 22 sin , = = . a 57 22 19 Trang 11
III. BÀI TẬP VẬN DỤNG a
Câu 1. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a , SO = với O là tâm của đáy. Gọi 2
E là trung điểm cạnh AD , j là góc giữa đường thẳng CD và mặt phẳng (SBE). Tính sinj . 1 2 A. sinj = 3 . B. sinj = . C. sinj = 1 . D. sinj = . 2 6 2 3 6 Lời giải S B C F K O P A E D I
Gọi F là trung điểm của AB . Do S.ABCD là hình chóp tứ giác đều nên SO ^ ( ABCD) và tứ
giác ABCD là hình vuông.
Trong ( ABCD), gọi I = BE ÇCD , P = AO Ç BE , K = FO Ç BE .
d (C,(SBE)) Ta có: sinj = (1) CI AB AE
Do AB // CD nên =
=1 Þ DI = AB = a Þ CI = ID + DC = 2a (2) DI ED 1
EO là đường trung bình của ABD D
Þ EO = AB và EO // AB. 2 EO PO 1 Suy ra = = 1 1
Þ PO = PA = OA. AB PA 2 2 3
d (C,(SBE)) CP =
= 4 Þ d (C,(SBE)) = 4d ( ,
O (SBE)) = 4d ( , O (SKE)). d ( ,
O (SBE)) OP
Ta có SOKE là tứ diện vuông nên 1 1 1 1 1 1 1 24 = + + = + + 1 1 1 = + + = 2 d ( , O (SBE)) 2 2 2 SO OE OK 2 2 2 2 SA - OA OE OK 2 2 2 æ a ö æ a ö æ a ö 2 a ç ÷ ç ÷ ç ÷ è 2 ø è 2 ø è 4 ø Þ ( a a d , O (SBE)) =
Þ d (C (SBE)) 2 , = (3). 2 6 6 2a 1
Thay (2), (3) vào (1) được sinj = : 2a = . 6 6 Trang 12
Câu 2. Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a , ∑
ABC = 60° và SB = a . Hình
chiếu vuông góc của điểm S lên mặt phẳng (ABC) trùng với trọng tâm của tam giác ABC .
Gọi j là góc giữa đường thẳng SB và mặt phẳng (SCD). Tính sinj . 3 1 A. sinj = . B. sinj = 1 . C. sinj = 2 . D. sinj = . 2 4 2 2 Lời giải S a A D P H B a C
Gọi H là trọng tâm của tam giác ABC . Theo giả thiết ta có SH ^ (ABC).
Gọi j là góc tạo bởi đường thẳng SB và mặt phẳng (SCD).
d(B,(SCD)) 3 d(H,(SCD)) Ta có sinj = = . SB 2 SB
Kẻ HP ^ SC tại P. +) ABC D
đều Þ CH ^ AB Þ CH ^ CD . CD ì ^ CH +) í
Þ CD ^ (SHC) Þ CD ^ HP. CD î ^ SH ìHP ^ SC +) í
Þ HP ^ (SCD) Þ HP = d(H,(SCD)) . îHP ^ CD
Do ABCD là hình thoi cạnh a và ∑
ABC = 60° nên tam giác ABC là tam giác đều a 3 2 3a a 6 Þ HB = 2 2 2
Þ SH = SB - BH = a - = . 3 9 3 SH × HC 2a 2a 2
Từ đó ta có: d(H ,(SCD)) = =
Þ d(B,(SCD)) = Þ sinj = . 2 2 SH + HC 3 2 2
Câu 3. Cho lăng trụ đều ABC.A¢B C
¢ ¢ có tất cả các cạnh bằng a . Tính côsin của góc giữa mặt phẳng (A B
¢ C )¢ và mặt phẳng (BCC'B'). 1 A. 7 . B. 42 . C. 42 . D. . 7 7 14 7 Lời giải Trang 13 Ta có (A B
¢ C )¢ Ç(BCC 'B') = BC¢.
d(A ;¢(BCC 'B')
Gọi a là góc giữa mặt phẳng (A B
¢ C )¢ và (BCC 'B'), khi đó sina = .
d(A ;¢ BC ) ¢
Gọi H là trung điểm của B C
¢ ¢. Ta có A¢H ^ B C
¢ ¢ mặt khác A¢H ^ BB¢. a Suy ra A H ¢ ^ (BB C ¢ C
¢ ). Do đó: d A¢ (BCC B ) 3 ( ; ' ' = A H ¢ = . 2
Trong mặt phẳng (A B
¢ C )¢ kẻ A¢K ^ BC¢. Tam giác A¢BC¢ cân tại B có 2 2 2 2
A¢C .¢ 4A¢B - A¢C¢ a 8a - a a 14
A¢B = BC¢ = a 2, A C
¢ ¢ = a suy ra A¢K = = = . 2BC¢ 2a 2 4 a 3
d(A ;¢(BCC ' B ') A H ¢ 6 1 7 Suy ra 2 sina = = = = . Vậy cosa = = .
d(A ;¢ BC ) ¢ A K ¢ a 14 7 7 7 4
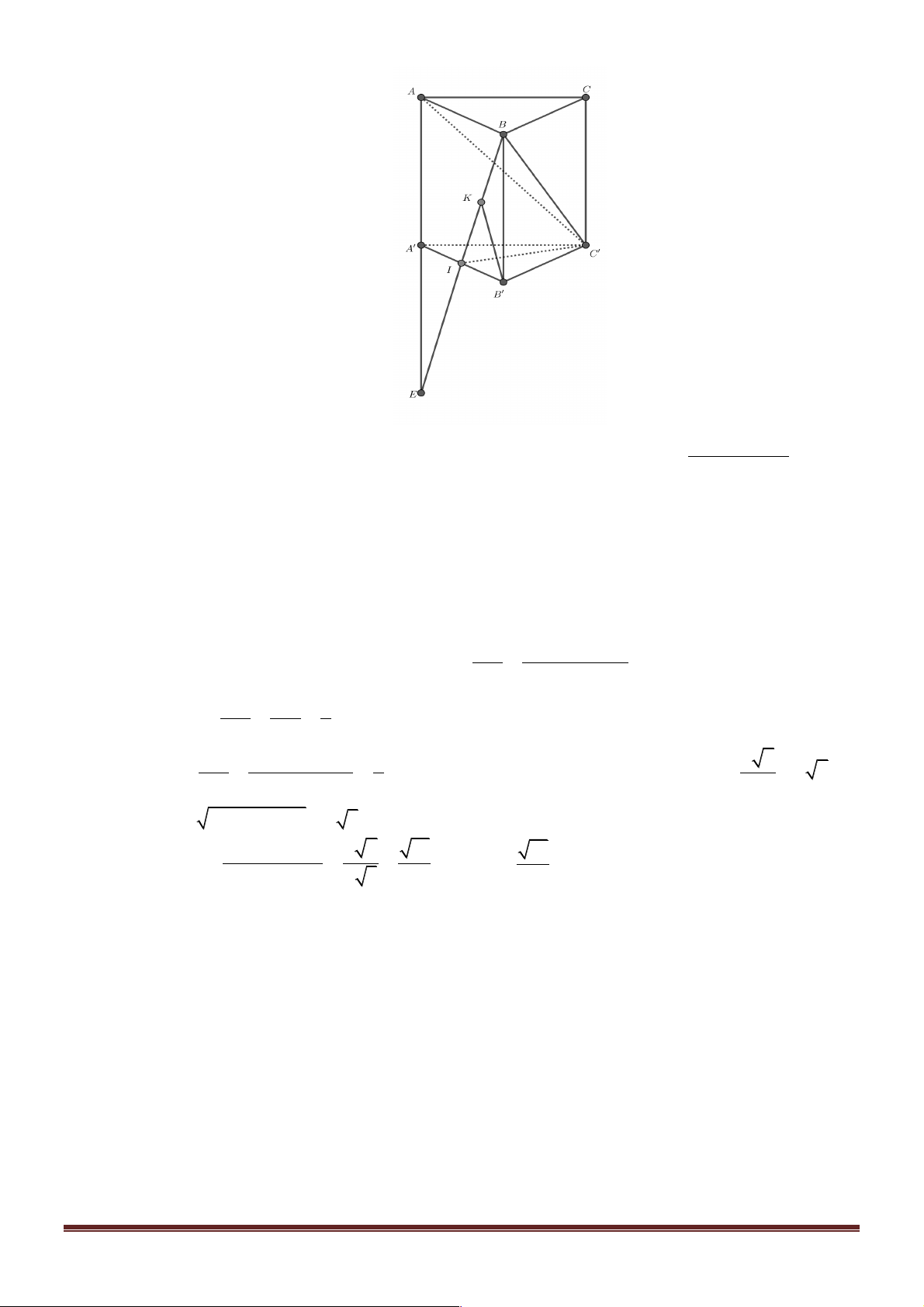
Câu 4. Cho lăng trụ đều ABC.A¢B C
¢ ¢ có cạnh đáy bằng 1, cạnh bên bằng 3 . Gọi M là trung điểm
của CC¢ . Tính sin của góc giữa hai mặt phẳng ( ACB¢) và (BMA¢). 2 1 2 21 A. . B. . C. . D. . 5 5 5 5 Lời giải
Gọi I là tâm hình chữ nhật ABB A
¢ ¢ và J là giao điểm của BM và B C ¢ .
Ta có IJ = ( ACB¢)Ç(BMA¢).
d ( A,(BMA¢))
Gọi j là góc giữa 2 mặt phẳng ( ACB¢) và (BMA¢). Khi đó: sinj = .
d ( A, IJ ) Trang 14 1
Gọi D = A¢M Ç AC , suy ra C là trung điểm của AD Þ BC = AD Þ ABD D vuông tại B 2 Þ BD ^ ( ABB A
¢ ¢) Þ (BDA¢) ^ ( ABB A ¢ ¢) ( ) 1 .
Dựng AK ^ A¢B (2). Từ ( )
1 và (2) suy ra AK ^ (BDA¢) Þ d ( A (BDA¢))) 3 , = AK = . 2 ì 15 ï S = DB A ¢ C ï Tam giác B AC ¢ có B A ¢ = B C ¢ = 2, AC =1 4 Þ í . ï ∑ 7 cos AB C ¢ = ïî 8 S ¢ ¢ B D I¢J B I B J 1 = 15 . = Þ S = . S ¢ ¢ B D I¢J 12 D ¢ B A B C 3 B AC 1 2
Ta có: B I¢ = B A ¢ = 2 4 ; 1 B J ¢ = B C ¢ = Þ 2 2 = ¢ + ¢ - ¢ ¢ ∑ IJ B I B J
2B I.B J.cos IB J ¢ = . 2 3 3 3 3 15 2
Þ d (( A IJ )) = d ((B¢ IJ )) 2SD ¢ 15 , , B IJ = = Þ sinj = : = . IJ 4 2 4 5 Trang 15