Preview text:
PHƯƠNG PHÁP TÌM GIAO ĐIỂM CỦA ĐƯỜNG THẲNG VÀ MẶT PHẲNG 1. Phương pháp
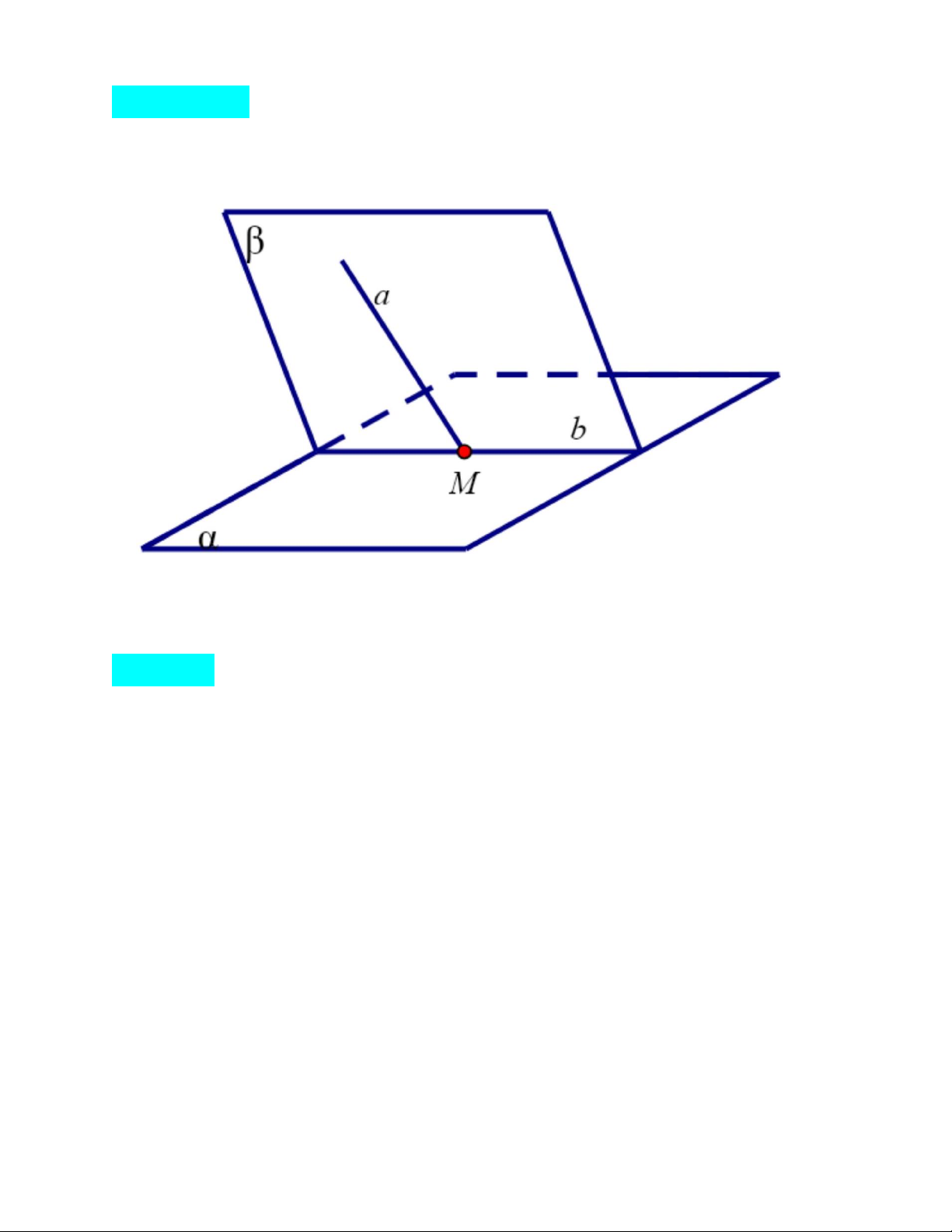
Muốn tìm giao điểm của một đường thẳng a và mặt (a)
phẳng , ta tìm giao điểm của a và một đường thẳng b nằm trong
• Bước 1: Xác định mp (b ) chứa a .
• Bước 2: Tìm giao tuyến b = (a )Ç(b ).
• Bước 3: Trong (b ): a Çb = M , mà b Ì (a ), suy ra M = a Ç(a ). 2. Các ví dụ
Ví dụ 1. Cho tứ giác ABCD (không có cặp cạnh đối nào song song) nằm trong mặt phẳng
(a). S là điểm không nằm trên (a).
a. Tìm giao tuyến của các cặp mặt phẳng: (SAC) và (SBD), (SAB) và (SCD).
b. Gọi M và N lần lượt là trung điểm của các cạnh SC và SD . Tìm giao điểm P của
đường thẳng BN với mặt phẳng (SAC).
c. Gọi Q và R lần lượt là trung điểm của SA và SB . Chứng minh rằng bốn điểm M, N,Q, R đồng phẳng.
Ví dụ 2. Trong mặt phẳng (a ), cho tứ giác ABCD . Gọi S là điểm không thuộc (a ),M
là điểm nằm trong tam giác SCD.
a. Xác định giao tuyến của hai mặt phẳng (SAM) và (SBD).
b. Xác định giao điểm của AM và mặt phẳng (SBD).
Ví dụ 3. Cho tứ diện SABC . Trên cạnh SA lấy điểm M , trên cạnh SC lấy điểm N , sao
cho MN không song song vói AC . Cho điểm O nằm trong tam giác ABC . Tìm giao
điểm của mặt phẳng (OMN) với các đường thẳng AC,BC và AB.
Ví dụ 4. Cho hình chóp S.ABCD có đáy là hình thang ABCD . Gọi E và F là hai điểm
lần lượt nằm trên hai cạnh SB và CD .
a. Tìm giao điểm của EF với mặt phẳng ( SAC) .
b. Tìm giao điểm của mặt phẳng (AEF) với các đường thẳng BC và SC . Trang 1




