Thông tin
Quiz

Phương trình, bất phương trình và hệ phương trình chứa tham số – Lê Bá Bảo

Tài liệu tóm tắt các dạng toán điển hình, các ví dụ mẫu có lời giải chi tiết và phần bài tập rèn luyện chủ đề phương trình, bất phương trình và hệ phương trình chứa tham số, do tác giả Lê Bá Bảo biên soạn.

Chủ đề:

Tài liệu chung Toán 10 394 tài liệu

Môn:

Toán 10 2.8 K tài liệu

Thông tin:

50 trang 1 năm trước

Tác giả:

Mai Nguyệt

docx.com.vn

Bình luận

Vui lòng đăng nhập hoặc đăng ký để gửi bình luận.

Phương trình, bất phương trình và hệ phương trình chứa tham số – Lê Bá Bảo

122 61 lượt tải Tải xuống

Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016

Giáo viên: LÊ BÁ BẢO...0935.785.115... -1- CLB Giáo viên trẻ TP Huế

CHUYÊN ĐỀ:

BÀI TOÁN THAM SỐ TRONG PHƢƠNG TRÌNH,

BẤT PHƢƠNG TRÌNH VÀ HỆ PHƢƠNG TRÌNH

I- LÝ THUYẾT: Một số dạng toán và phương pháp tương ứng:

Cho h¯m sè liªn tôc trªn tËp D.()y f x

Giả sử trên D tồn tại

   

x D x D

min max;f x f x



, nếu không

ta cần lập bảng biến thiên và đưa ra kết luận.

Dạng 1:

 

Ph¬ng tr×nh cã nghiÖm f x m x D

Phương pháp:

   

x D x D

ycbt min maxf x m f x



  

Dạng 2:

 

B©t ph¬ng tr×nh cã nghiÖm f x m x D

Phương pháp:

 

ycbt min f x m





Dạng 3:

 

B©t ph¬ng tr×nh nghiÖm ®óng f x m x D  

Phương pháp:

 

ycbt maxm f x





Dạng 4:

 

B©t ph¬ng tr×nh cã nghiÖm f x m x D

Phương pháp:

 

ycbt maxm f x





Dạng 5:

 

B©t ph¬ng tr×nh nghiÖm ®óng f x m x D  

Phương pháp:

 

ycbt min f x m





Dạng 6:

 

Cho h¯m sè ®¬n ®iÖu trªn tËp y f x D

Khi ®ã:

   

f u f v u v  

* THUẬT TOÁN: Để giải các bài toán tìm giá trị tham số m để phương trình (PT), bất phương

trình (BPT) có nghiệm ta có thể thực hiện theo các bước sau:

ThuËt to²n 1:

Đối với bài toán không cần đặt ẩn phụ

Bƣớc 1: Biến đổi đưa PT về dạng

   

f x g m

       

 

hoÆc hoÆc;f x g m f x g m

Bƣớc 2: Lập bảng biến thiên của hàm số

 

cã tËp x²c ®Þnh D,y f x

Suy ra:

   

x D x D

min max,.f x f x



(nếu có)

Bƣớc 3: Sử dụng các nhận xét và phương pháp đã nêu ở phần trên, đưa ra kết luận.

ThuËt to²n 2:

Đối với bài toán đặt ẩn phụ

Bƣớc 1: Đặt ẩn phụ

 

tx

. Từ điều kiện ràng buộc của

suy ra miền giá trị

 

tx

Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016

Giáo viên: LÊ BÁ BẢO...0935.785.115... -2- CLB Giáo viên trẻ TP Huế

Giả sử:

x D t X   

Bƣớc 1: Lúc này, biến đổi đưa PT về dạng

   

f t h m

       

 

hoÆc hoÆc ;f t h m f t h m

Lúc này biện luận điều kiện có nghiệm của PT

   

f t h m

với

tX

Các bước còn lại tương tự thuật toán 1.

* Với hệ phương trình có chứa tham số, tư duy, hoặc là dựa vào điều kiện có nghiệm của các

dạng hệ đặc thù, hoặc đưa về phương trình chứa 1 ẩn (có thể là ẩn phụ) vầ xét điều kiện có

nghiệm trên miền giá trị của ẩn (hoặc ẩn phụ) đó.

II- CÁC BÀI TẬP MINH HOẠ:

Bài tập 1:

T×m c²c gi² trÞ cña m ®Ó ph¬ng tr×nh: cã nghiÖm.

99x x x x m     

Bài giải:

§iÒu kiÖn: 09x

Pt (*)

9 2 (9 ) 9 9 2 (9 ) 9x x x x x x m x x x x m               

 

§Æt (9 ) 0 9t x x x   

* Tìm điều kiện của

Cách 1: Theo BDT Cauchy:

9 9 9

(9 ) 0

2 2 2

t x x t



      

Cách 2: Ta có



   



BBT:

Do ®ã:

t

Lóc ®ã ph¬ng tr×nh (*) trë th¯nh: (**)

9 2 2 9t t m t t m       

 

XÐt h¯m sè . Ta cã:

( ) 2 9 0 ( ) 2 2 0 1

f t t t t f t t t           

Lập bảng biến thiên:

Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016

Giáo viên: LÊ BÁ BẢO...0935.785.115... -3- CLB Giáo viên trẻ TP Huế

KÕt luËn: Ph¬ng tr×nh ®± cho cã nghiÖm khi chØ khi PT (**) cã nghiÖm

ycbt

0;9 0;

10.









   

Bài tập 1: Tìm

để phương trình sau có nghiệm

1x x m  

Bài giải: Điều kiện:

0x 

Xét hàm số

 

1f x x x  

trên











Ta có:

 

f x x x x

     



 

6 2 2 2

11x x x x     

(vô nghiệm)

Suy ra,

 

không đổi dấu trên

 

0; 

, mà

     

1 0 0, 0;

f f x x       

. Do đó

 

nghịch biến trên











Ta có BBT:

 

lim 0





Dựa vào BBT ta có yêu cầu bài toán

01m  

Bài tập 2: Tìm

để phương trình sau có nghiệm

11x x x x m     

Bài giải:

Xét hàm số

 

11f x x x x x     

trên



Ta có:

     

/ 2 2

2 1 2 1

0 2 1 1 2 1 1

2 1 2 1

f x x x x x x x

x x x x



          

   

  

   

  

2 1 2 1 0

1 3 1 3

2 1 2 1

2 4 2 4

x x x x





  







  



   



   





   











      



   

















   

   



   





vô nghiệm.

Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016

Giáo viên: LÊ BÁ BẢO...0935.785.115... -4- CLB Giáo viên trẻ TP Huế

Suy ra,

 

không đổi dấu trên

 

0; 

, mà

   

0 1 0 0,f f x x      

. Do đó

 

đồng biến trên



Ta có BBT:

   

lim 1; lim 1

f x f x

 

  

Dựa vào BBT ta có yêu cầu bài toán

01m  

Bài tập 3: Tìm

để phương trình sau có nghiệm

 

12 5 4x x x m x x     

Bài giải: Điều kiện:

0;4x









Phương trình

  

12 5 4

x x x

m m x x x x x



        

  

Xét hàm số

 

  

12 5 4 , 0;4f x x x x x x x



      





Ta có:

 

   

3 1 1 1

5 4 12 , 0;4

2 12 2 4 2 5

f x x x x x x x x

x x x













         





















  

Dễ thấy

     

5 4 , 0;4 0, 0;4x x x f x x        

. Do đó

 

đồng biến trên

0;4







. Suy ra phương trình

 

f x m

có nghiệm trên

0;4







   

 

0 4 2 3 5 2 12.f m f m      

Nhận xét: Ta có thể giải như sau:

Phương trình

x x x





  

. Ta có hàm số

 

12g x x x x  

đồng biến và

nhận giá trị dương trên

0;4







, hàm số

 

54h x x x   

nghịch biến và nhận giá trị

dương trên

0;4







. Suy ra

 

x x x





  

đồng biến trên

0;4







. Suy ra phương trình

 

f x m

có nghiệm trên

0;4







   

 

0 4 2 3 5 2 12.f m f m      

Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016

Giáo viên: LÊ BÁ BẢO...0935.785.115... -5- CLB Giáo viên trẻ TP Huế

Bài tập 4: Tìm

để phương trình sau có đúng 3 nghiệm phân biệt:

2m x x m  

Bài giải: Vì

2 0,xx    

nên phương trình

 

m x x m

     



2 1 0, .xx     

Xét hàm số

 

f x x







Ta có:

 

2 2 1









  





  



BBT:

   

lim 1; lim 1

f x f x

 

  

Yêu cầu bài toán

22m   

Bài tập 5: Tìm

để phương trình sau có nghiệm

 

3 4 1 1x x m x x     

Bài giải: Điều kiện:

1x 

Phương trình





  

1 1 0, 1x x x     

Xét hàm số

  

, 1;

f x x





  





  

Ta có:

 

   

 

1 1 3 3 3 4

2 2 1

x x x x x









       

















  

Với

1x 

thì

1 1 0xx   

3 3 0x 

3 4 0xx  

(xét biến thiên) và

2 2 1xx





. Suy ra

 

0, 1f x x  

. Do đó

 

đồng biến trên











BBT:

 

lim



 

Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016

Giáo viên: LÊ BÁ BẢO...0935.785.115... -6- CLB Giáo viên trẻ TP Huế

Yêu cầu bài toán

1m

Bài tập 6: Tìm

để bất phương trình sau có nghiệm

45x x m   

Bài giải: Điều kiện:

5; 4x









Xét hàm số

 

4 5, 5;4f x x x x



     





Ta có:

 

1 1 4 5

2 4 2 5 2 4 . 5

x x x x

   

   

   

 

5;4

x x x









       





  





BBT:

-5

-1

f'(x)

f(x)

Yêu cầu bài toán

32m

Bài tập 7: Tìm

để bất phương trình sau có nghiệm

31mx x m   

Bài giải: Điều kiện:

3x 

Bất phương trình







1 0, 3xx   

Xét hàm số

  

, 3;

f x x





  







Ta có:

 

0 3 5 4

2 1 3

f x x x x







  



        





  









BBT:

 

lim 0





Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016

Giáo viên: LÊ BÁ BẢO...0935.785.115... -7- CLB Giáo viên trẻ TP Huế

Yêu cầu bài toán

m

Đề 13: (Dự bị- 2004) Chứng minh rằng với mọi

0m 

thì phương trình sau luôn có nghiệm:

2 2 2 3

4 2 0

x m x m









     













Bài giải: TXĐ:

D  

Đặt

42xt  

Phương trình đã cho tương đương với:

2 2 3

4 2 0

t m t m









     













(1)

Xét hàm số

 

2 2 3

f t t m t m









     













, ta có

 

liên tục trên











và

 

lim



 

. Ta sẽ chứng minh

 

2 0, 0fm  

. Thật vậy:

 

f m m   

Xét hàm số

 

2 , 0

g m m m m    

. Ta có:

 

3 4 0

g m m m







    









BBT:

Dựa vào BBT, ta suy ra

   

2 0, 0f g m m   

. Suy ra điều phải chứng minh.

Bài tập 3: Tìm

để phương trình sau có nghiệm

  

3 6 3 6x x x x m      

Bài giải: Điều kiện:

3;6x









Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016

Giáo viên: LÊ BÁ BẢO...0935.785.115... -8- CLB Giáo viên trẻ TP Huế

Đặt

  

3 6 9 2 3 6 .t x x t x x        

Ta có:

1 1 6 3

2 3 2 6 2 6 3

x x x x

  

   

   

 

3;6

x x x









      





  





Suy ra:

   

3;6 3;6

max 3 2, min 3 6 3

t t t t t

   



   

   









     













hay

3;6 3;3 2xt



    





Lúc đó phương trình trở thành:

2 9 2

t m t t m



     

Xét hàm số

 

2 , 3;3 2 .f t t t t



  





Ta có:

 

2 2 0 1 3;3 2f t t t     

BBT:

18-6

f(t)

f'(t)

Dựa vào bảng biến thiên, yêu cầu bài toán

 

6 2 9

3 9 2 3 2 3.

f m f m



      

Bài tập 3: Tìm

để phương trình sau có nghiệm:

 

2 2 3 1 3 1 1 0x x m x x m          

Bài giải: Điều kiện:

3;1x









Đặt

  

3 1 4 2 3 1 .t x x t x x        

Ta có:

1 1 1 3

2 3 2 1 2 1 3

x x x x

  

   

   

 

3;1

1 3 1

x x x









       





  





Suy ra:

     

3;1 3;1

max 1 2 2, min 3 1 2t t t t t

   



   

   

      

hay

3;1 2;2 2xt



    





Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016

Giáo viên: LÊ BÁ BẢO...0935.785.115... -9- CLB Giáo viên trẻ TP Huế

Hoặc: Do

  

4 2 3 1 4 2t x x t      

và

   

3 1 2 3 1 2 2 2;2 2t x x x x t



          





Lúc đó phương trình trở thành:

 

1 3 0

t m t m m



      



1 0, 2;2 2tt



   





Xét hàm số

 

, 2;2 2 .

f t t













Ta có:

 

0, 2;2 2

f t t



   



BBT:

f'(t)

f(t)

+13

Dựa vào bảng biến thiên, yêu cầu bài toán

12 2 13



  

Bài tập 3: (CĐ 2011) Tìm

để phương trình sau có nghiệm:

  

 

6 2 4 2 2 4 4 2 2x x x m x x        

Bài giải: Điều kiện:

1;4x









Đặt

  

4 2 2 2 2 4 2 2 .t x x t x x x         

Ta có:

1 1 2 4 2 2

0 2 4 2 2

2 4 2 2 4 . 2 2

t x x

x x x x

   

       

   

 

1;4

4 4 2 2









  





  





Suy ra:

   

1;4 1;4

max 3 3, min 1 3t t t t

   

   

   

   

hay

1;4 3;3xt



   





Lúc đó phương trình trở thành:

44t t m  

Xét hàm số

 

4 4, 3;3 .f t t t t



   





Ta có:

 

2 4 0 2 2;2 2f t t t     

BBT:

Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016

Giáo viên: LÊ BÁ BẢO...0935.785.115... -10- CLB Giáo viên trẻ TP Huế

7-4

f(t)

f'(t)

Dựa vào bảng biến thiên, yêu cầu bài toán

0 1.m  

Bài tập 3: Tìm

để phương trình sau có nghiệm:

 

2 2 4 2 2

7 1 1 1 2x m x x x x m x x          

Bài giải: Điều kiện:

x  

Phương trình

  

 

2 2 2 2 2

1 1 1 1 2 7 0x x x x x m x x x x              

Đặt

2 2 /

2 1 2 1

t x x x x t

x x x x



        

   

Ta có:

   

/ 2 2

0 2 1 1 2 1 1t x x x x x x        

  

 

2 1 2 1 0

2 1 1 2 1 1

x x x x x x





  









      





  

2 2 2 2

2 1 2 1 0

1 1 3 1 1 3

2 2 4 2 2 4

x x x x





  







  



   



       





   

   

   





   

      

   

   



   

   





   

   



       

   



   





vô nghiệm.

Suy ra

 

không đổi dấu trên



, mà

 

0 1 0t 

suy ra

 

0,t x x   

vậy

 

đồng

biến trên



Ta có

   

lim 1; lim 1

t x t x

 

  

. Vậy

 

1;1t 

Lúc đó:

  

2 2 2 2

2 2 2 1 1t x x x x x      

nên phương trình trở thành:

 

2 12

2 7 0 2

m t m



      



 

2 0, 1;1tt    

Xét hàm số

   

, 1;1 .

f t t



  



Ta có:

 

4 12









  











Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016

Giáo viên: LÊ BÁ BẢO...0935.785.115... -11- CLB Giáo viên trẻ TP Huế

BBT:

-1

f'(t)

f(t)

Dựa vào bảng biến thiên, yêu cầu bài toán

13 13 13

2 13 .

3 2 6

mm        

Bài tập 3: Tìm

để phương trình sau có nghiệm

2 2 2 0x x x m x    

Bài giải: Điều kiện:

2x 

Phương trình



   

(do

2x 

)

Đặt





, khi đó

0 1 1, 1



      

(hoặc khảo sát

 





)

Phương trình trở thành:



2 0 2 , 0;1t t m m t t t



       





Xét hàm số

     

2 , 0;1 2 2 0 1 0;1f t t t t f t t t



         





BBT:

f(t)

f'(t)

-1

Dựa vào bảng biến thiên, yêu cầu bài toán

1 0 0 1mm       

Bài tập 3: Tìm

để phương trình sau có nghiệm:

 

2 2 4 2 2 4m x x x x      

Bài giải: Điều kiện:

2x 

+ Ta thấy

2x 

không phải là nghiệm của phương trình.

+ Xét

2x 

, phương trình













   

















(do

2x 

)

Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016

Giáo viên: LÊ BÁ BẢO...0935.785.115... -12- CLB Giáo viên trẻ TP Huế

Đặt







, khi đó

1 1, 2 1



      



(hoặc khảo sát

 







)

Phương trình trở thành:

 

2 2 , 1;

m t m t











      















Xét hàm số

     

 

2 2 2 2

, 1; 0, 1;

t t t t

f t t f t t

  

        



BBT:

 

lim



 

Dựa vào bảng biến thiên, yêu cầu bài toán

1 0 0 1mm       

Bài tập 3: Tìm

để phương trình sau có nghiệm

 

5 6 7 1 2x x m x x    

Bài giải: Điều kiện:

x  

Để ý rằng

 

5 6 7 3 1 2 2x x x x     

Phương trình

 

   

2 2 3 1 1 2x x m x x      

(*)

1x 

không là nghiệm của phương trình (*), nên (*) tương đương:

2 3.



  



Đặt







, khi đó

 



   



BBT:

   

lim 1; lim 1

t x t x

 

  

Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016

Giáo viên: LÊ BÁ BẢO...0935.785.115... -13- CLB Giáo viên trẻ TP Huế

Vậy









   















Phương trình trở thành:

3 , 1;

t m t









   













Xét hàm số

   

2 6 3 2

3 , 1; 0

f t t t f t





















       























BBT:

   

lim ; lim

f t f t





   

Dựa vào bảng biến thiên, yêu cầu bài toán

 

; 2 6 2 6;m



     





Bài tập 3: Tìm

để phương trình sau có nghiệm:

 

1 1 1

x x m x x x









     















Bài giải: Điều kiện:

1x 

Phương trình

  

 

1 1 1

x x x x m x x x









      



















 

m x x x x x

      



   

1 1 1 1

x x x m x m



          



Đặt





, khi đó

 

0;1t 

Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016

Giáo viên: LÊ BÁ BẢO...0935.785.115... -14- CLB Giáo viên trẻ TP Huế

Phương trình trở thành:

 

1 1, 0;1t m m t t

        

Xét hàm số

       

1, 0;1 1 0, 0;1f t t t f t t

          

BBT:

 

lim





 

Dựa vào bảng biến thiên, yêu cầu bài toán

1.m  

Bài tập 3: Tìm

để phương trình sau có nghiệm

 

18 1

  







  

Bài giải: Điều kiện:

x  

Phương trình

2 18













   



















(*)

Đặt







, khi đó

 

1 2 1



   



BBT:

   

lim 1; lim 1

t x t x

 

  

Vậy



1; 5xt



   







Phương trình trở thành:

 



1 , 1; 5

t m t



    







Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016

Giáo viên: LÊ BÁ BẢO...0935.785.115... -15- CLB Giáo viên trẻ TP Huế

Xét hàm số

   



   

 

18 18

1 , 1; 5 2 1 0 2

f t t t f t t t



           







BBT:

 

lim .





 

Dựa vào bảng biến thiên, yêu cầu bài toán

7m

Bài tập 3: Tìm

để phương trình sau có nghiệm:

 

tan cot tan cot 3 0x x m x x    

Bài giải: Điều kiện:





Đặt

tan cot tan tan 2

tan tan

t x x t x x

       

suy ra:

2 2 2

2 tan cott x x  

Phương trình trở thành:

1 0 , 2

t mt m t



      

Xét hàm số

   

, 2 0, 2

f t t f t t



      

BBT:

   

lim ; lim

f t f t

 

   

Dựa vào bảng biến thiên, yêu cầu bài toán

m  

hoặc

m 

Bài tập 3:

   

T×m ®Ó ph¬ng tr×nh 3 tan 1 sin 2 cos sin 3cosm x x x m x x   

(1) cã

Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016

Giáo viên: LÊ BÁ BẢO...0935.785.115... -16- CLB Giáo viên trẻ TP Huế

nghiÖm duy nhÊt 0; .

























Bài giải:

XÐt khi ®ã v¯ 0; , sin 0, cos 0, tan 0 sin 3 cos 0.

x x x x x x











     













 

PT (1) (2)

§Æt Lóc ®ã, PT (2) trë th¯nh: (3)

XÐt h¯m sè Ta cã:

(sin 2 cos ) tan 2

3 tan 1 3 tan 1

(sin 3 cos ) tan 3

tan 0 0; . 3 1

2 3 2 3

( ) 3 1 0 . ( ) .

x x x

x m x m

x x x

t x t x t m

t t t

f t t t f t





     





     



  

    





0, 0

( 3)

  



Lập bảng biến thiên:

 

lim



 

 

Ta cã, øng víi mçi tho° m±n PT (3), ta ®îc ®óng mét nghiÖm Do ®ã, PT (1)

cã nghiÖm duy nhÊt khi v¯ chØ khi PT (3) cã nghiÖm duy nhÊt Dùa v¯o BBT,

suy ra ycbt l¯

0 0; .

0; 0.









Bài tập 3: Tìm

để phương trình sau có đúng hai nghiệm phân biệt:

6 5 4 3 2

2 3 3 2 1 0x x x mx x x      

(1)

Bài giải:

+ Rõ ràng

0x 

không là nghiệm của phương trình (1).

+ Với

0x 

, phương trình (1)

1 1 1

2 3 0x x x m

     

  

  

  

       

  

  

  

  

  

     

(2)

Đặt

1 1 1

2 2.t x t x x t

x x x

         

Phương trình (2) trở thành:

   

2 2 3 2

3 2 2 3 0 2 6 4 0t t t t m t t t m           

(3)

Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016

Giáo viên: LÊ BÁ BẢO...0935.785.115... -17- CLB Giáo viên trẻ TP Huế

Từ phép đặt



, ta có với mỗi

2t 

cho ta 1 giá trị của

; với mỗi

thoả mãn

2t 

cho ta 2 giá trị

. Do đó, (1) có đúng hai nghiệm phân biệt



(3) chỉ có các nghiệm

2t 

và

2t 

, hoặc (3) có đúng 1 nghiệm

thoả mãn

2t 

. Ta xét hai trường hợp:

TH 1: (3) có đúng hai nghiệm

2t 

và

2t 





















không tồn tại

TH 2: (3) có đúng một nghiệm

và thoả mãn

2t 

Ta có (3)

2 6 4m t t t    

Xét hàm số

   

3 2 / 2

2 22

2 6 4, 2 3 4 6 0

2 22

f t t t t t f t t t











          













BBT:

   

lim ; lim

f t f t

 

   

Dựa vào bảng biến thiên, yêu cầu bài toán

 

2 22

16 44 22



























































Bài tập 3: (ĐH A - 2002) Tìm

để phương trình sau có nghiệm thuộc

1; 3







log log 1 2 1 0x x m    

Bài giải: Điều kiện:

0x 

Đặt

2 3 2

3 3 3

log 1 1;3 0 log 3 0 log 3t x x x x



          





1 log 1 4 1;2xt



     





Phương trình trở thành:

2 2 2 2, 1;2t t m m t t t



       





Xét hàm số

   

2, 1;2 2 1 0, 1;2f t t t t f t t t

   

         

   

   

Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016

Giáo viên: LÊ BÁ BẢO...0935.785.115... -18- CLB Giáo viên trẻ TP Huế

BBT:

Dựa vào bảng biến thiên, yêu cầu bài toán

0 2 4 0 2mm     

Bài tập 3: Tìm

để phương trình sau có nghiệm thuộc

0;1







 

1 1 2 2

4 4 1 2 2 2

x x x x

   

    

Bài giải: Điều kiện:

x  

Phương trình đã cho

 

4 4 4 4 1 2 2 2

x x x x



     

Đặt

 

   

0;1

min 0 0

2 2 , 0;1 2 2 ln 2 0, 0;1

max 1

x x x x

t x t

t x t x x

t x t























   

         



   

   









0;1 : 0;





   









Phương trình trở thành:

 

2 2 2 1 , 0;

2 2 1 2

m t t

t m t m t







      







Xét hàm số

 

, 0;

2 1 2

f t t















 

1 11

2 2 5

1 11 3















   



































BBT:

Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016

Giáo viên: LÊ BÁ BẢO...0935.785.115... -19- CLB Giáo viên trẻ TP Huế

Dựa vào bảng biến thiên, yêu cầu bài toán

2 11

2 2 11 4



       

Bài tập 3:

 

Cho ph¬ng tr×nh: (1)

2 1 2

log log 3 log 3x x m x   



T×m c²c gi² trÞ cña m ®Ó cã ph¬ng tr×nh nghiÖm .32;x



 





Bài giải:

 

Tõ ®iÒu kiÖn b¯i ra, ta thÊy log suy ra log nªn 5, 3 2 0.x x m   

 

   

     

 

PT (1)

(2)

§Æt PT (2) trë th¯nh: (3)

XÐt h¯m sè Ta cã:

2 2 2

log 2 log 3 log 3

log 5 . 2 3 3

5 . 0 5

x x m x

t x t t t m t m

f t t f t t

    



       





     



Lập bảng biến thiên:



Lóc ®ã, ph¬ng tr×nh (1) cã nghiÖm khi chØ khi PT (3) cã nghiÖm

ycbt KÕt hîp suy ra:

32; 5;

1 3. 0, 1 3.

m m m

  

   

  

  

     

Bài tập 3: Tìm

để phương trình sau có nghiệm:

   

4 3 3 3 4 1 1 0m x m x m       

(1)

Bài giải: Điều kiện:

3;1x









(1)

 

3 3 4 1 1

4 3 3 1 1 3 3 4 1 1

4 3 3 1 1

m x x x x m

   

           

   

Vì

   

3 1 4xx   

nên ta có thể đặt

3 2 sin

1 2 cos





















0; .















Khi đó ta có phương trình:

6 sin 8 cos 1

8 sin 6 cos 1









(2). Đặt

tan





, khi đó

0;1t









và

sin ; cos









, (2) trở thành:

7 12 9

5 16 7







0;1t









Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016

Giáo viên: LÊ BÁ BẢO...0935.785.115... -20- CLB Giáo viên trẻ TP Huế

Xét hàm số

   

 

7 12 9 52 8 60

, 0;1 0, 0;1

5 16 7

t t t t

f t t f t t

   

   

       

   

   



Do đó,

 

nghịch biến trên

0;1







BBT:

f(t)

f'(t)

Dựa vào bảng biến thiên, yêu cầu bài toán

m  

Nhận xét: Hoàn toàn ta có thể khảo sát trực tiếp hàm số

 

3 3 4 1 1

4 3 3 1 1

   



   

trên

3;1









để tìm điều kiện có nghiệm của phương trình.

Bài tập 3: Tìm

để phương trình sau có hai nghiệm phân biệt:

 

   

2 2 1 3 5 3 5 0

mm     

(1)

Bài giải: Điều kiện:

x  

(1)

 

3 5 3 5

2 2 1 0

   











    













   

Đặt

t t x













    

















Khi đó phương trình trở thành:

 

2 2 1 0 2 , 1

m m t m t



       



Với

1 : log

t t x t















    















. Do đó với

1t 

ta có duy nhất

0x 

, với

1t 

thì ta có 2 giá trị

Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016

Giáo viên: LÊ BÁ BẢO...0935.785.115... -21- CLB Giáo viên trẻ TP Huế

Xét hàm số

   

 

1 4 1

, 1 0, 1

t t t

f t t f t t

  

      



BBT:

Dựa vào bảng biến thiên, yêu cầu bài toán

2 0 0mm    

Bài tập 3: Tìm

để bất phương trình sau nghiệm đúng với mọi

thoả mãn

x 

   

2 2 2

9 2 1 6 1 4 0

x x x x x x

  

    

Bài giải: Điều kiện:

x  

Chia 2 vế của bất phương trình cho

xx

, ta được:

 

2 1 1 0

x x x x



   







    











   

Đặt

























. Ta có:

2 0 1

x x x t     

Bất phương trình trở thành:

  

2 1 1 0 , 1;

t m t m m t





        







Xét hàm số

    

 



2 1 2 2 4

, 1; 0 2 1;

t t t t

f t t f t t

   



         







BBT:

 

lim



 

Dựa vào bảng biến thiên, yêu cầu bài toán

3m

Bài tập 3: (Cao Đẳng - 2013) Tìm

để bất phương trình sau có nghiệm:

 

2 1 4x m x m    

Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016

Giáo viên: LÊ BÁ BẢO...0935.785.115... -22- CLB Giáo viên trẻ TP Huế

Bài giải: Điều kiện:

1x 

Đặt

1 1 0t x x t      

Bất phương trình trở thành:

 

1 4 , 0.

t m t m m t



      



Xét hàm số

   

 



1 2 5 5

, 0 0 1 0;

t t t

f t t f t t

  





        







BBT:

Dựa vào bảng biến thiên, yêu cầu bài toán

2m

Bài tập 3: Tìm

để bất phương trình sau nghiệm đúng với mọi

1;1x









1 12 1 16 3 1 2 15m x x x m x m       

Bài giải: Điều kiện:

1;1x









Bất phương trình

 

1 3 1 16 12 1 2 15m x x x x m        

      

 

2 9 1 6 1 1 1 3 1 1 2 5 0x x x x m x x



             





Đặt

   

3 1 1 0, 1;1

2 1 2 1

t x x t x x

          



suy ra

       

1;1 1;1

min 1 2; max 1 3 2

t x t t x t

   

   

   

   

     

1;1 2;3 2xt



      





Bất phương trình trở thành:

 

2 2 5 0 , 2 ; 3 2

t m t m t





       







Xét hàm số

   

 

2 5 2 8 5

, 2; 3 2 0, 2;3 2

t t t

f t t f t t

    

   

        

   

   



BBT:

Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016

Giáo viên: LÊ BÁ BẢO...0935.785.115... -23- CLB Giáo viên trẻ TP Huế

Dựa vào bảng biến thiên, yêu cầu bài toán

 

2;3 2

min 3 2

3 2 2

m f t f











   



Bài tập 3:

 

T×m ®Ó bÊt ph¬ng tr×nh: (1) cã

2 2 1 (2 ) 0m m x x x x     

nghiÖm 0;1 3 .x









Bài giải:

 

§Æt . Ta cã

2 2 0;1 3 0 1.

t x x x t x





        







Ta cã b°ng biÕn thiªn:

 

Tõ ®ã:

Víi ta biÕn ®æi:

BPT (1) trë th¯nh: (2)

XÐt h¯m sè Ta cã:

2 2 2 2

1 2.

1 2, 2 2 2 2 (2 ) 2.

( 1) 2

2 2 2

( ) 1 2 . ( ) 0, 1;2 .

( 1)

t t x x t x x x x t

m t t m

t t t

f t t f t t



             



    



  



      







y ra h¯m sè ®ång biÕn trªn

XÐt b°ng biÕn thiªn:

( ) 1;2 .ft







Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016

Giáo viên: LÊ BÁ BẢO...0935.785.115... -24- CLB Giáo viên trẻ TP Huế

Lóc ®ã, BPT (1) cã nghiÖm khi chØ khi BPT (2) cã nghiÖm

§iÒu n¯y x±y ra khi max

1;2

0;1 3 1;2 .

(2) .











  





  

Nhận xét: Nếu đề bài yêu cầu tìm

để bất phương trình đã cho nghiệm đúng

0;1 3x



  





thì yêu cầu bài toán

 

mf   

Bài tập 1: Tìm

để hệ phương trình sau có nghiệm:

1 2 1

x y xy

x y m





  







   





Bài giải: Điều kiện

1; .

xy

Hệ

  

(1)

(2)

4 1 2 1

1 2 1

x y x y

y y m

x y m











  





  

  

  

  

   

  













(do

0, 1;

x y x y    

)

Từ (1) ta thấy với mỗi

y 

sẽ cho ta một

1x 

. Vì vậy hệ đã cho có nghiệm



phương trình

(2) có nghiệm

y 

Xét hàm số

 

4 1 2 1, ;

f y y y y









     











Ta có:

 

2 1 3 1

4 1 2 1

f y y









      















BBT:

 

lim



 

Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016

Giáo viên: LÊ BÁ BẢO...0935.785.115... -25- CLB Giáo viên trẻ TP Huế

Dựa vào bảng biến thiên, yêu cầu bài toán

m

Bài tập 1: Tìm

để hệ phương trình sau có nghiệm:

(1)

(2)

x y m

y xy





  













Bài giải: Điều kiện

0xy 

Phương trình (2)

xy y









   













(do

0y 

không thoả mãn phương trình)

Thay vào phương trình (1) ta được:

4 4 4 4

0 , 2

y y y

y m m y

  

     

Xét hàm số

  

, ;2

f y y





  





Ta có:

    

0, ;2 \ 0f y y



    





BBT:

     

lim 4; lim ; lim

f y f y f y







    

Dựa vào bảng biến thiên, yêu cầu bài toán

4m

hoặc

2m 

Bài tập 1: Tìm

để hệ phương trình sau có 3 nghiệm phân biệt:

 

(1)

(2)

3 1 0

x y m

x xy





   













Bài giải: Điều kiện

0xy 

Phương trình (2)

xy x









   













(do

0x 

không thoả mãn phương trình)

Thay vào phương trình (1) ta được:

3 6 3

x x m



   

Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016

Giáo viên: LÊ BÁ BẢO...0935.785.115... -26- CLB Giáo viên trẻ TP Huế

Xét hàm số

  

3 6 , ;1

f x x x x





    





Ta có:

 

6 7 1 1 1

f x x x x



         

BBT:

     

lim ; lim ; lim

f x f x f x







     

Dựa vào bảng biến thiên, yêu cầu bài toán

11 20

3 9 12

27 15

7 3 4





    







        





Bài tập 1: Tìm

để hệ phương trình sau có nghiệm:

 

(1)

(2)

x y a





   







  





Bài giải: Điều kiện

1; 3.xy  

Đặt

1 0; 3 0u x v y      

Khi đó hệ trở thành:

 

u v a

























  













, suy ra

,uv

là nghiệm của phương

trình:

 

f t t at



   

Hệ đã cho có nghiệm

 

0ft

có nghiệm

,tt

thoả mãn:

 

0 1. 0 0 0 0;2

t t f a





       





Bài tập 1: Tìm m để hệ phương trình có nghiệm:

15 10

x y m





    







    





Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016

Giáo viên: LÊ BÁ BẢO...0935.785.115... -27- CLB Giáo viên trẻ TP Huế

Bài giải: Đặt

;u x v y

   

ta có

1 1 1 1

33x x x x u u

x x x

   





       







   

và

1 1 1 1 1

2 . 2 ; 2 . 2u x x x v y y

x x x y y

         

Khi đó hệ trở thành

 

3 15 10

uv m

u v u v m

















    











,uv

là nghiệm của phương trình bậc hai

 

58f t t t m   

Hệ có nghiệm

 

f t m

có 2 nghiệm

,tt

thỏa mãn

2; 2tt

Lập bảng biến thiên của hàm số

 

với

2t 



– 2

5/2



 



–

 



7/4



Nhìn bảng biến thiên ta có hệ có nghiệm

2 22

m    

Bài tập 1: Tìm m để hệ phương trình có nghiệm:

x x y y m













  





(I)

Bài giải:

§iÒu kiÖn: 0, 0.xy

 

§Æt

HÖ (I) trë th¯nh:

3 3 2 2 2 2

, 0, 0

1 1 1

1 3 ( )( ) 1 3 ( ) 1 3

1 3 1 3

( ) 3 1 3

u x v y u v

u v u v u v

u v m u v u uv v m u uv v m

uv m

u v uv m

   

  

  

     

  



  

  

           

  

  















  

   









(II)

Lóc ®ã: l¯ nghiÖm cña ph¬ng tr×nh: (*)

HÖ ®± cho cã nghiÖm ( HÖ (II) cã nghiÖm

Ph¬ng tr×nh (*) cã hai n

; ) 0, 0

uv m

u v X X m

x y u v





















  

  

 ghiÖm 0.X 

CáCách 1:

Sö dông HÖ thøc Viet: ycbt

0 ... 0 .









     











Cách 2:

Ph¬ng tr×nh (*)

X X m  

Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016

Giáo viên: LÊ BÁ BẢO...0935.785.115... -28- CLB Giáo viên trẻ TP Huế

 

XÐt h¯m sè . Ta cã:

( ) 0 ( ) 1 2 0 .

f X X X X f X X X       

Ta xÐt b°ng biÕn thiªn:

Dùa v¯o b°ng biÕn thiªn: ycbt

m  

Bài tập 1: Tìm

để hệ phương trình sau có nghiệm:

 

1 10 6

x y m















  

































   





















Bài giải: Điều kiện

0xy 

Hệ đã cho

10 6

x y m





   









    





(1). Đặt

; 2; 2.a x b y a b

      

Hệ (1) trở thành:

 

2 2 10 6

2 10 10

ab m

a b m

a b ab m



















  

  



    

   

  











Suy ra

,ab

là nghiệm của phương trình:

4 3 5 0 5 4 3, 2t t m m t t t        

(2)

Hệ có nghiệm



Phương trình (2) có hai nghiệm thoả mãn

2t 

Xét hàm số

 

4 3, 2f t t t t   

. Ta có:

 

2 4 0 2f t t t    

BBT:

   

lim ; lim .

f t f t

 

   

Dựa vào bảng biến thiên, yêu cầu bài toán

3 15 5mm   

Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016

Giáo viên: LÊ BÁ BẢO...0935.785.115... -29- CLB Giáo viên trẻ TP Huế

Bài tập 1: Tìm

để hệ phương trình sau có nghiệm:

 

3 2 2 15x y xy x y

x y m





    













Bài giải:

Đặt

,S x y P xy  

, khi đó hệ trở thành:

(1)

(2)

3 2 8 15 0 3 2 8 15 0

4 8 4 4 2 15 4

S S P S S P

S P m S S m





       









    





(I)

Hệ đã cho có nghiệm



Hệ (I) có nghiệm

,SP

thoả mãn:

4SP

Từ (1) ta có:

2 2 2

3 2 15 8 2 2 15 0 3;5S S P S S S S



          





Do đó, hệ có nghiệm



Phương trình (2) có nghiệm

3;5S









Xét hàm số

 

4 2 15, 3;5f S S S S



    





. Ta có:

 

2 2 0 1f S S S    

BBT:

   

lim ; lim .

f S f S

 

   

-1

f(S)

f'(S)

-3

Dựa vào bảng biến thiên, yêu cầu bài toán

7 25

14 4 50

mm     

Bài tập 2: Tìm

để hệ phương trình sau có nghiệm

 

;xy

với

0, 0xy

   

    

3 5 33 0

xy x y x y xy

x y xy m x y xy x y m





   







         





Bài giải:

Đặt

,S x y P xy  

, khi đó hệ trở thành:

 

(1)

(2)

5 33 0

SP S P

S P m S SP m













      





(I)

Hệ đã cho có nghiệm



Hệ (I) có nghiệm

,SP

thoả mãn:

0, 0SP

và

4SP

Từ (1) ta có:

2 2 2

3 2 15 8 2 2 15 0 3;5S S P S S S S



          





+ Ta thấy

1S 

không thoả mãn (1).

Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016

Giáo viên: LÊ BÁ BẢO...0935.785.115... -30- CLB Giáo viên trẻ TP Huế

+ Với

1S 

, từ (1) ta có:

 

2 3 2

3 4 12

S S S S S









    











(*)

Mặt khác:







  











(**)

Từ (*), (**) suy ra:



4;S



 





và hệ có nghiệm



Phương trình

2 33







có

nghiệm



4;S



 





Xét hàm số

  

2 33

, 4;

f S S





  







Ta có:

 



2 35

0 7 4;

f S S





     







BBT:

 

lim .



 

Dựa vào bảng biến thiên, yêu cầu bài toán

16m

Bài tập 1: Tìm

để hệ phương trình sau có nghiệm

 

;xy

với

0, 0xy

x y xy

x y xy m













  





Bài giải:

Đặt

,S x y P xy  

, khi đó hệ trở thành:

9 16 9

S P S P

S P m P P m















   





(I)

Theo định lí Viet, ta có

,xy

là hai nghiệm thuộc



0;1







của phương trình:

40t Pt P  

Trước hết ta tìm

để phương trình

40t Pt P  

có hai nghiệm thuộc



0;1







Yêu cầu tương đương tìm

để phương trình





có hai nghiệm thuộc



0;1







(vì

t 

không là nghiệm)

Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016

Giáo viên: LÊ BÁ BẢO...0935.785.115... -31- CLB Giáo viên trẻ TP Huế

Xét hàm số

  

, 0;1

f t t











. Ta có:

 

2 2 1









  











BBT:

   

lim ; lim

f t f t





   

Dựa vào bảng biến thiên, suy ra phương trình





có hai nghiệm thuộc



0;1







khi và chỉ

khi

P

+ Hệ phương trình (I) có nghiệm



Phương trình

16 9P P m

có nghiệm

;











Xét hàm số

 

16 9 , ;

g P P P P





  





. Ta có:

 

32 9 0

g P P P    

BBT:

-11

-81

-5

g'(P)

g(P)

Dựa vào bảng biến thiên, suy ra hệ phương trình đã cho có nghiệm thoả yêu cầu bài toán

81 11

64 9

m    

Bài tập 3: Tìm

để hệ phương trình sau có nghiệm:

5 4 8 0

3 16 0

x y x y

x mx x





    







  





Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016

Giáo viên: LÊ BÁ BẢO...0935.785.115... -32- CLB Giáo viên trẻ TP Huế

Bài giải: Điều kiện:

,xy

Phương trình thứ nhất của hệ

4 5 8 0y y x x     

Xem phương trình này là phương trình bậc hai theo ẩn

, khi đó phương trình có nghiệm

0 1;4x



    





Từ đó suy ra, hệ đã cho có nghiệm



Phương trình

3 16 0x mx x  

(1) có nghiệm

1;4x









Đặt

1;2t x t



  





, phương trình (1) trở thành:

3 16 0 3 , 1;4t mt m t t



      





Xét hàm số

   

16 48

3 , 1;4 3 0 2 1;4f t t t f t t

   

         

   

   

BBT:

f'(t)

f(t)

Dựa vào bảng biến thiên, hệ đã cho có nghiệm

8 19m  

Bài tập 3: (HSG Hà Tĩnh 2013) Tìm

để hệ phương trình sau có nghiệm:

 

x m y x my

x y xy





  













Bài giải: Điều kiện:

,xy

Hệ đã cho

(1)

(2)

my y m

x yx y





  









  





Xem phương trình (2) là phương trình bậc hai theo biến

, có

nghiệm

 

4 0 ; 4 0;y y y



          





Do đó, hệ đã cho có nghiệm



Phương trình (1) có nghiệm

 

; 4 0;y



    





Ta có (1)

 

, ; 4 0;



      







Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016

Giáo viên: LÊ BÁ BẢO...0935.785.115... -33- CLB Giáo viên trẻ TP Huế

Xét hàm số

   

, ; 4 0;

f y y



     







 

0 1 ; 4 0;

f y y





         







BBT:

   

lim 0; lim 0

f y f y

 



Dựa vào bảng biến thiên, hệ đã cho có nghiệm

17 2

m   

Bài tập 4: (HSG Nghệ An 2006) Tìm

để hệ phương trình sau có 3 nghiệm phân biệt:

   

x y m

y x xy m x













   





Bài giải: Điều kiện:

,xy

Hệ đã cho

(1)

(2)

y m x

x mx m















  





Vì

y m x

nên hệ có 3 nghiệm phân biệt



Phương trình (2) có 3 nghiệm phân biệt.

(2)

 

x m x m

    



(do

1; 1xx  

không thoả mãn (2))

Xét hàm số

 





trên tập xác định.

Ta có:

 

0 0 3 3 .

f x x x x



        



BBT:

       

lim ; lim ; lim ; lim

f x f x f x f x



 

 

       

   

lim ; lim

f x f x





   

Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016

Giáo viên: LÊ BÁ BẢO...0935.785.115... -34- CLB Giáo viên trẻ TP Huế

Dựa vào bảng biến thiên, hệ đã cho có nghiệm

m

hoặc

m 

Bài tập 4: Tìm

để hệ phương trình sau có nghiệm:

(1)

(2)

3 3 2

2 2 2

3 3 2 0

1 3 2 0

x y y x

x x y y m





    







     





Bài giải: Điều kiện:

1;1 ; 0;2xy

   

  

   

   

Phương trình (1)

   

1 3 1 3x x y y     

(3)

Vì

1;1 1 0;2xx

   

    

   

   

Xét hàm số

     

3 2 / 2

3 , 0;2 3 6 0, 0;2f t t t t f t t t t



        





 

ft

nghịch biến trên

0;2







. Phương trình (3) có dạng:

   

11f x f y y x    

Thay vào phương trình (2) ta được:

2 1 0, 1;1x x m x



     





(4)

Đặt

1 1;1 0;1u x x u

   

       

   

   

, phương trình (4) trở thành:

21u u m  

(5)

Hệ đã cho có nghiệm



Phương trình (5) có nghiệm

0;1u









Xét hàm số

   

2 1, 0;1 2 2 0, 0;1g u u u u g u u u

   

         

   

   

BBT:

g(u)

g'(u)

-1

Dựa vào bảng biến thiên, hệ đã cho có nghiệm

12m   

Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016

Giáo viên: LÊ BÁ BẢO...0935.785.115... -35- CLB Giáo viên trẻ TP Huế

Bài tập 5: Tìm

để hệ phương trình sau có nghiệm:

 

(1)

(2)

4 3 1 2 1

2 2 1 0

x x y y

x x y y m





   







     





Bài giải: Điều kiện:











Phương trình (1)

   

 

2 3 2 2 1 3 2 1x x y y       

(3)

Vì

;0 2 1 0;1





    









. Từ (2) suy ra

2 0 ;0 2 0;1

x x x x





       









Xét hàm số

     

3 / 2

3 , 0;1 3 3 0, 0;1f t t t t f t t t



        





 

ft

nghịch biến trên

0;1







. Phương trình (3) có dạng:

 

2 2 1 2 2 1f x f y x y      

Thay vào phương trình (2) ta được:

2 2 4 2

2 2 8 , ;0

x x x x m x





      





(4)

Hệ đã cho có nghiệm



Phương trình (4) có nghiệm











Ta thấy:

2 2 4

2 2 8 0, ;0

x x x x x









      

















 

2 2 4

2 2 8 0

x x x x







   



  















Vậy hệ đã cho có nghiệm

0.m

Nhận xét: Trong trường hợp VP (4) chưa biết dấu thì ta khảo sát

 

2 2 4

2 2 8f x x x x x   

trên











. Điều này, không hề đơn giản!

Bài tập 4: Tìm

để hệ phương trình sau có nghiệm:

   

(1)

(2)

2 2 2 2

x y y x m xy

x y y x x y x





   







    





Bài giải: Điều kiện:

0xy 

Phương trình (2)

 

2 2 2

1 1 1x x x y y     

(3)

Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016

Giáo viên: LÊ BÁ BẢO...0935.785.115... -36- CLB Giáo viên trẻ TP Huế

Ta thấy

0x 

không thoả mãn (3). Mặt khác, vì

10xx  

và

1 1 0y  

nên từ (3)

suy ra

0y 

. Kết hợp điều kiện suy ra

0x 

Khi đó (3)

1 1 1

11y y y

     

(4)

Xét hàm số

       

2 / 2

1 , 0; 1 1 0, 0;

f t t t t t f t t t

             



 

ft

nghịch biến trên

 

0; 

. Phương trình (4) có dạng:

 

1f f y y xy









    













Thay vào phương trình (1) ta được:

 

2 2 2

1 1 1

1 1 2x x m x m

x x x









       













Ta có

2, 0xx

   

suy ra hệ có nghiệm

2 2 4.mm    

Bài tập 4: Tìm

để hệ phương trình sau có nghiệm:

 

(1)

(2)

x y xy x y xy





   













Bài giải: Điều kiện:

0xy 

Ta có:

 

2 2 2

3 3 3 3 3 3

x y x xy y

m m m

x y x y x y

  



     

Thay (1) vào ta được:

 

x y xy











  













(3)

Đặt

t x y

, khi đó từ (1) ta có:

 

33xyt t xy xy t t    

và

0, 0,xy t

30t 

nên

 

2 2 2 2

3 4 4 3 4 3

t t t t t

t t t











       





  





Mặt khác:

3x y t

xy t





, phương trình (3) trở thành:

























Xét hàm số

 





trên

  

; 3 1;



   





    

0, ; 3 1;f t t





        





BBT:

Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016

Giáo viên: LÊ BÁ BẢO...0935.785.115... -37- CLB Giáo viên trẻ TP Huế

Dựa vào bảng biến thiên, hệ đã cho có nghiệm

 

2;2 \ 1, 0,1









    







  





Bài tập 4: Tìm

để hệ phương trình sau có nghiệm:

(1)

(2)

1 2 2 1

3 3 2

x y xy x

x x xy a





   







   





Bài giải: Điều kiện:

1y 

Đặt

10zy  

, hệ trở thành:

x z xz

x xz a













  





Ta thấy

0z 

không thoả mãn hệ.

Với

0z 

, đặt

x tz

hệ trở thành:

 

(1)

(2)

z t t

z t t a













  





0z 

nên từ (1) suy ra







  









Từ hệ (1), (2) ta có:

   

2 , ;0 2; .



     



Xét hàm số

     

, ;0 2; .

f t t



    



 

   

0 3 ;0 2;

f t t



        



BBT:

     

lim ; lim ; lim .

f x f x f x



 



     

Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016

Giáo viên: LÊ BÁ BẢO...0935.785.115... -38- CLB Giáo viên trẻ TP Huế

Dựa vào bảng biến thiên, hệ đã cho có nghiệm

2 6 4



  







   





Bài tập 4: Tìm

để hệ phương trình sau có nghiệm

 

;xy

thoả mãn

1; 1xy

 

(1)

(2)

x y xy

m x x y y x y







  







      





Bài giải: Điều kiện:

;xy 

1; 1xy

, ta có:

    

1 1 0 1 0x y xy x y       

Từ (1)

 

4 2 2 0 6.x y x y x y         

Mặt khác, từ (1):

     

4 2 4 0

x y xy x y x y x y          

4xy  

1; 1xy

. Vậy

4;6xy









Đặt

4;6t x y t



   





Khi đó, (2) trở thành:

   

2 1 2 1

m t t t t m      

, (do

1tt

>0,

4;6t









Xét hàm số

 

2 1 , 4;6 .

f t t t t



   





 

2 1 ln2 0, 4;6

f t t t t













       





















   

 

   

 

4;6

max 6 64 37 6

min 4 16 17 4

f t f





















  









  





Hệ có nghiệm

   

16 17 4 64 37 6m    

Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016

Giáo viên: LÊ BÁ BẢO...0935.785.115... -39- CLB Giáo viên trẻ TP Huế

III- MỘT SỐ ĐỀ THI ĐẠI HỌC - CAO ĐẲNG TỪ 2002 - 2016:

Đề 01: (D- 2004) Tìm

để hệ sau có nghiệm:

x x y y m













  





Bài giải: Điều kiện:



















Đặt

 

, 0, 0u x v y u v   

. Hệ trở thành

(*)

u v m













  





uv m





















là hai nghiệm của phương trình

(**)

0t t m  

Hệ đã cho có nghiệm

 

;xy



Hệ (*) có nghiệm

0, 0uv  

Phương trình (**) có hai

nghiệm không âm

1 4 0

1 0 0 .





   



     











Đề 02: (D- 2006) CMR:

0a

, hệ phương trình sau có duy nhất nghiệm:

   

ln 1 ln 1

e e x y

y x a





    













Bài giải: Điều kiện:



















Hệ đã cho tương đương với

   

(1)

(2)

ln 1 ln 1 0

x a x

e e x a x

y x a







      













Hệ đã cho có nghiệm duy nhất khi chỉ khi phương trình (1) có nghiệm duy nhất trên

 

1; 

Xét hàm số

       

ln 1 ln 1 1

x a x

f x e e x a x x



        

 

liên tục trên

 

1; 

và

   

lim , lim

f x f x







   

nên phương trình

 

0fx

có nghiệm trên

 

1; 

Mặt khác:

 

  

1 0, 1.

x a x x a

f x e e e e x

x a x



          

  

 

fx

đồng biến trên

 

1; 

. Suy ra

 

0fx

có nghiệm duy nhất trên

 

1; 

Kết luận: Vậy hệ đã cho có nghiệm duy nhất (đ.p.c.m).

Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016

Giáo viên: LÊ BÁ BẢO...0935.785.115... -40- CLB Giáo viên trẻ TP Huế

Đề 03: (D - 2007) Tìm các giá trị của tham số

để hệ phương trình sau có nghiệm thực:

15 10

x y m





   







    





Bài giải: Điều kiện:



















Đặt

 

; 2; 2u x v y u v

     

Hệ đã cho trở thành

 

3 15 10

uv m

u v u v m

















    









Suy ra

,uv

là nghiệm của phương trình

(1)

5 8 0 5 8t t m t t m       

Hệ đã cho có nghiệm



Phương trình (1) có hai nghiệm

,tt

thỏa mãn

2, 2tt

Xét hàm số

 

5 8 2f t t t t   

Xét bảng biến thiên:

Dựa vào bảng biến thiên, ta có giá trị cần tìm của

là



;2 22; .







  









Đề 04: (ĐH-D-2011) Tìm

để hệ phương trình sau có nghiệm:

 

x y x xy m

x x y m





   







   





Bài giải: Điều kiện:





















Hệ đã cho

 

2 1 2

x x x y m





  









    





. Đặt

; 2 .

u x x v x y     

Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016

Giáo viên: LÊ BÁ BẢO...0935.785.115... -41- CLB Giáo viên trẻ TP Huế

Hệ đã cho trở thành

 

(1)

2 1 0

uv m

u m u m

u v m

v m u







   









  

  









Hệ có nghiệm khi chỉ khi phương trình (1) có ít nhất 1 nghiệm

u 

Với

   

; 1 2 1

4 2 1

u m u u u m



        



Xét

 

2 1 4

f u u



  



. Ta có

 

2 2 1 1 3

; 0 .

f u f u u

   

    



Bảng biến thiên:

Suy ra giá trị cần tìm là





Đề 05: (Khối A- 2008) Tìm

để phương trình sau có hai nghiệm thực phân biệt:

2 2 2 6 2 6x x x x m     

Bài giải: TXĐ:

0;6D









Đặt vế trái của phương trình là

 

2 2 2 6 2 6 0;6f x x x x x x



      





Ta có:

 

1 1 1 1

2 2 2 6

   



   

 

;

1 1 1 1 1

0;6



















    



























Đặt

 

1 1 1 1

u x v x

   



Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016

Giáo viên: LÊ BÁ BẢO...0935.785.115... -42- CLB Giáo viên trẻ TP Huế

Ta thấy

     

2 2 0 2 0u v f   

. Hơn nữa

   

,u x v x

cùng dương trên

 

0;2

và cùng âm

trên khoảng

 

2;6

Ta có bảng biến thiên:

Suy ra các giá trị

cần tìm là:

2 6 2 6 3 2 6m   

Giải thích cụ thể hơn:

 

   

 

1 1 1 1 1

0;6

f x x



















    



























Đặt

  



, ta có

   

 

3 3 2 2 2 2

a b a b a b a ab b a b







        







 

   

4 4 4 4 4 4

1 1 1 1 1 1 1 1 1

2 6 2 6 2 6

x x x x x x

























      



















  

















Do đó ta chỉ cần xét dấu

26xx



Đề 06: (Dự bị- 2007) Tìm

để phương trình:

13 1 0x x m x    

có nghiệm.

Bài giải: Phương trình (1)

13 1x x m x    

 

4 6 9 1

13 1

x x x m

x x m x





















   

   











Ycbt  đường thẳng

1ym

cắt phần đồ thị

 

4 6 9f x x x x  

;

 

1x 

tại ít nhất một

giao điểm.

Ta có:

     

 

;

3 2 / 2 2

4 6 9 1 12 12 9 3 4 4 3f x x x x x f x x x x x          

Ta có:

 

f x x x     

Bảng biến thiên:

Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016

Giáo viên: LÊ BÁ BẢO...0935.785.115... -43- CLB Giáo viên trẻ TP Huế

Từ bảng biến thiên ta có, ycbt

mm     

Đề 07: (Dự bị- 2007) Tìm

để phương trình:

3 2 4 6 4 5x x x x m       

có

đúng 2 nghiệm.

Bài giải: TXĐ:



4;D



 





Phương trình cho

   

4 2 4 1 4 6 4 9x x x x m          

   

4 1 4 3 4 1 4 3x x m x x m             

(1)

Đặt:

40tx  

, (1) trở thành:

13t t m   

(2)

Phương trình cho có đúng 2 nghiệm  phương trình (2) có đúng 2 nghiệm

0.t 

Cách 1: Vẽ đồ thị của hàm số

   

1 3 0f t t t t    

Ta có

 

nÕu

4 2 0 1

2 1 3

2 4 3

f t t





  



  











Từ đồ thị ta có, ycbt

24m  

Cách 2:

 

1 3 0t t m t     

hay hay

0 1 1 3 3

4 2 2 2 4

t t t

m t m m t

  

  

    

  



  

  

    

  

  

hay hay

0 1 3

2 4 2





  















   

  

  



  













. Do đó, yêu cầu bài toán

24m  

(khi

24m

thì (2) có đúng 2 nghiệm

,tt

thỏa

01t

và

3t 

)

Đề 08: (Dự bị- 2007) Tìm

để phương trình:

1x x m  

có nghiệm.

Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016

Giáo viên: LÊ BÁ BẢO...0935.785.115... -44- CLB Giáo viên trẻ TP Huế

Bài giải: TXĐ:



0;D



 





Xét hàm số

 

1f x x x  

;



0;x



 





 



















   

























0x

. Vì

 

x x x

  



Ta có

 

nghịch biến trên











và

lim ( ) 0

 



nên ta có



0 ( ) 1, 0;f x x



    





Vậy, phương trình (1) có nghiệm 

thuộc miền giá trị của

 

trên đoạn













0 1.m

Đề 09: (Khối A- 2007) Tìm

để phương trình sau có nghiệm:

3 1 1 2 1x m x x    

Bài giải: TXĐ:



1;D



 





Ph¬ng tr×nh ®± cho (1)



   



§Æt khi ®ã (1) trë th¯nh: (2)

, 3 2

t t t m



   



V× v¯ nªn

1 1 0 1

t x t



     



(Hoặc sử dụng đạo hàm với

, 0, 1

t t x



  



)

   

H¯m sè cã b°ng biÕn thiªn:

3 2 0 1f t t t t    

Phương trình đã cho có nghiệm



Phương trình (2) có nghiệm



0;1t









Dựa vào bảng biến thiên ta có các giá trị

cần tìm là:

m  

Đề 10: (Khối B- 2007) Chứng minh rằng với mọi giá trị dương của tham số

, phương trình sau

luôn có hai nghiệm thực phân biệt:

 

2 8 2x x m x   

Bài giải: Theo giả thiết

0m 

, ta có điều kiện của phương trình là

2x 

Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016

Giáo viên: LÊ BÁ BẢO...0935.785.115... -45- CLB Giáo viên trẻ TP Huế

Phương trình đã cho tương đương với

 

2 6 32 0

6 32 0

x x x m

x x m







     



   





Ta chứng minh phương trình

6 32x x m  

(1) có một nghiệm thuộc

 

2; 

Xét hàm số

     

3 2 2

6 32 2 3 12 0 2f x x x x f x x x x         

Bảng biến thiên:

Dựa vào bảng biến thiên ta thấy, với

0m 

phương trình (1) luôn có nghiệm thuộc

 

2; 

nên

phương trình đã cho luôn có hai nghiệm thực phân biệt.

Đề 11: (Dự bị- 2007) Tìm

để phương trình:

 

2 2 1 (2 ) 0m x x x x     

có nghiệm

0;1 3x









Bài giải: TXĐ:

D  

. Đặt

2 2 2

2 2 0 2 2t x x t x x       

Bất phương trình 

 

1 2 , 0;1 3

m t x





    







Khảo sát

()







với

 

12t

Ta có:

 

( 1)







. Vậy

 

đồng biến trên

1;2







Do đó, yêu cầu bài toán



Bất phương trình







có nghiệm

1;2t









   

max

1;2

m g t g







   

Đề 12: (Khối B- 2006) Tìm

để phương trình sau có hai nghiệm thực phân biệt:

2 2 1x mx x   

(1)

Bài giải:

Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016

Giáo viên: LÊ BÁ BẢO...0935.785.115... -46- CLB Giáo viên trẻ TP Huế

Ta có:

 

(2)

2 2 1

3 4 1 0

2 2 1

x mx x

x m x

x mx x











     





   

   











Để phương trình (1) có 2 nghiệm phân biệt



Phương trình (2) có 2 nghiệm

,xx

thỏa mãn:

xx  

 

   

víi

4 12 0

4 1 9

2 6 2 2

1 3 4

1 0 3 4 1

2 4 2

f f x x m x





     







     



















        





















Cách khác: Để phương trình (1) có 2 nghiệm phân biệt



Phương trình (2) có 2 nghiệm

,xx

thỏa mãn:

xx  

Ta có:

   

3 1 1

3 1 4 4

x m x m g x x











        













Tiến hành khảo sát

 

y g x x









  













, dựa vào bảng biến thiên và đưa ra kết luận.

Đề 13: (Dự bị- 2004) Tìm

để phương trình sau có nghiệm:

2 2 2 2

4 2 0

x m x m









     













Bài giải: TXĐ:

D  

Đặt

42xt  

Phương trình đã cho tương đương với:

2 2 2

4 2 0

t m t m









     













 

2 2 2 2 2 2

3 5 6

3 3 5 6 3 0 3 5 6 3 1 3

t m t m t t m t m



            



Đặt

 

3 5 6

f t t







. Ta có

 

3 6 11

f t t

  

   



Suy ra

 

giảm và liên tục trên

  

2; , 2 4f



 





và

 

lim



 

Vậy phương trình có nghiệm khi và chỉ khi

3 4 .

mm  

Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016

Giáo viên: LÊ BÁ BẢO...0935.785.115... -47- CLB Giáo viên trẻ TP Huế

Đề 14: (Khối B- 2004) Tìm

để phương trình sau có nghiệm:

 

2 2 4 2 2

1 1 2 2 1 1 1m x x x x x         

Bài giải: TXĐ:

1;1D









Đặt

2 2 2 2

1 1 . 1 1 0; 0 0t x x x x t t x           

2 2 1 2 2, 2 1 1.t x t t x x           

Suy ra:

1;1 0; 2xt



    





liên tục trên

1;1









Phương trình đã cho trở thành

 

(*)

m t t t m

  

      



Xét

 

0; 2

f t t

  











. Ta có

 

liên tục trên

0; 2







Phương trình đã cho có nghiệm

x 

Phương trình (*) có nghiệm

0; 2t









   

min max

0; 2 0; 2

f t m f t

   

   

   

  

Ta có:

 

0 0; 2

f t t f t





    







nghịch biến trên

0; 2







Suy ra

 

   

min max

0; 2 0; 2

2 2 1; 0 1f t f f t f

   

   

   

    

Vậy các giá trị

cần tìm là:

2 1 1m  

III- BÀI TẬP TỰ LUYỆN:

Bài 1: Tìm

để phương trình sau có hai nghiệm phân biệt:

12m x x m   

Bài 2: Tìm

để phương trình sau có nghiệm:

12x x x x m     

Bài 3: Tìm

để phương trình sau có nghiệm:

 

2 . 3 2 2

x x m x x x









     















Bài 4: Tìm

để phương trình sau có 4nghiệm phân biệt thuộc

;













444

sin cos cos 4x x x m  

Bài 5: Tìm

để phương trình sau có nghiệm thuộc

 

0;1

 

4 log log 0x x m  

Bài 6: Tìm

để phương trình sau có nghiệm thuộc



32;









Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016

Giáo viên: LÊ BÁ BẢO...0935.785.115... -48- CLB Giáo viên trẻ TP Huế

 

2 1 2

log log 3 log 3x x m x   

Bài 7: Tìm

để phương trình sau có nghiệm thuộc

 

2;4

       

1 log 2 5 log 2 1 0m x m x m       

Bài 8: Tìm

để bất phương trình sau có nghiệm:

4 .2 3 2 0



   

Bài 9: Tìm

để phương trình sau có nghiệm:

 

4 6 3 2 2 3x x x m x x      

Bài 10: Tìm

để phương trình sau có nghiệm:

41x x x m   

Bài 11: Tìm m để pt sau có nghiệm trên







log 5 log 3 0x x m  

Bài 12: Tìm m để pt sau có nghiệm thực:

3 1 1 2 1x m x x    

Bài 13: Tìm m để pt sau có 4 nghiệm thực phân biệt :

2 2 1

4 2 0

x x x x

  

  

Bài 14: Cho bất hương trình:

14x x m   

(1)

a, Tìm m để bpt (1) có nghiệm

b, Tìm m để bất phương trình nghiệm đúng với mọi x



[1; 2].

Bài 15: Cho bất phương trình:

4 .2 0



  

. Tìm m để bất phương trình nghiệm đúng

với mọi

xR

Bài 16: Tìm m để bất phương trình nghiệm đúng với mọi x sao cho

x 

2 2 2

9 2( 1)6 ( 1)4 0

x x x x x x

  

    

Bài 17: Tìm a để pt sau có nghiệm:

1 3 ( 1)(3 ) 2x x x x a      

Bài 18: Tìm m để pt có đúng 2 nghiệm thực phân biệt:

2 2 2 6 2 6x x x x m     

Bài 19: Tìm m để pt sau có nghiệm:

4 4 2

sin cos cos2 sin 2 0

x x x x m    

Bài 20: Tìm m để pt sau có nghiệm

(0; )





Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016

Giáo viên: LÊ BÁ BẢO...0935.785.115... -49- CLB Giáo viên trẻ TP Huế

1 1 1

sin cos 1 (tan cot )

2 sin cos

x x x x m

      

Bài 21: Tìm m để pt sau có nghiệm thuộc (0; 1):

4 log log 0x x m  

Bài 22: Tìm m để bpt có nghiệm:

4 2 3 0

mm   

Bài 23: Tìm m để bpt sau nghiệm đúng với mọi x

R

sin cos sin cosx x x x m  

Bài 24: Tìm m để bpt nghiệm đúng với

4;6x



  





(4 )(6 ) 2x x x x m    

Bài 25: Tìm m để pt sau có hai nghiệm thực phân biệt:

2 2 1x mx x   

Bài 26: Chứng minh rằng với mọi giá trị của tham số

, phương trình sau luôn có hai nghiệm

thực phân biệt:

( 2) 2 8m x x x   

Bài 27: Tìm

để hệ phương trình sau có nghiệm:

x y m





   







  





Bài 28: Tìm

để hệ phương trình sau có nghiệm duy nhất:

x y m

x xy





  













Bài 29: Tìm m để hệ sau có nghiệm:

3 4 0

x x x m





  







  





V- TÀI LIỆU THAM KHẢO:

1) Tuyển tập đề thi ĐH - CĐ toàn quốc Bộ giáo dục và đào tạo

2) Phƣơng pháp hàm số trong giải toán TS. Lê Xuân Sơn - ThS. Lê Khánh Hưng

3) Tuyển tập đề thi thử ĐH trên toàn quốc

4) Tạp chí Toán học và Tuổi trẻ NXB Giáo dục Việt Nam

Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016

Giáo viên: LÊ BÁ BẢO...0935.785.115... -50- CLB Giáo viên trẻ TP Huế

P/S: Các bài tập trong tài liệu chưa nhận được sự cho phép của quí thầy cô và các cơ quan liên

quan, nhưng tài liệu biên soạn chỉ với mục đích chia sẽ cho đồng nghiệp và tặng cho các em học

sinh có nguồn tư liệu quí để phục vụ khả năng tự học nên chúng tôi xin phép các tác giả, xin cảm

ơn các tác giả!

Trong quá trình biên soạn không thể tránh khỏi sai sót, kính mong quí thầy cô và các em học

sinh đóng góp để các bản update tiếp theo được hoàn thiện hơn! Xin chân thành cám ơn!

CLB GIÁO VIÊN TRẺ TP HUẾ

Phụ trách chung: Giáo viên LÊ BÁ BẢO.

Đơn vị công tác: Trƣờng THPT Phong Điền, Thừa Thiên Huế.

Email: beckbo1210@yahoo.com Facebook: Lê Bá Bảo

Số điện thoại: 0935.785.115

Bấm Tải xuống để xem toàn bộ.

| 1/50

| | Tải xuống

Preview text:

Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016 CHUYÊN ĐỀ:
BÀI TOÁN THAM SỐ TRONG PHƢƠNG TRÌNH,
BẤT PHƢƠNG TRÌNH VÀ HỆ PHƢƠNG TRÌNH
I- LÝ THUYẾT: Một số dạng toán và phương pháp tương ứng:
Cho h¯m sè y  f (x
) liªn tôc trªn tËp D.Giả sử trên D tồn tại min f x; max f x, nếu không x D  x D 
ta cần lập bảng biến thiên và đưa ra kết luận. Dạng 1:
Ph¬ng tr×nh f x  m cã nghiÖm x  D
Phương pháp: ycbt  min f x  m  max f x x D  x D  Dạng 2:
B©t ph¬ng tr×nh f x  m cã nghiÖm x  D
Phương pháp: ycbt  min f x  m x D  Dạng 3:
B©t ph¬ng tr×nh f x  m nghiÖm ®óng x   D
Phương pháp: ycbt  m  max f x x D  Dạng 4:
B©t ph¬ng tr×nh f x  m cã nghiÖm x  D
Phương pháp: ycbt  m  max f x x D  Dạng 5:
B©t ph¬ng tr×nh f x  m nghiÖm ®óng x   D
Phương pháp: ycbt  min f x  m x D  Dạng 6:
Cho h¯m sè y  f x ®¬n ®iÖu trªn tËp D Khi ®ã:
f u  f v  u  v
* THUẬT TOÁN: Để giải các bài toán tìm giá trị tham số m để phương trình (PT), bất phương
trình (BPT) có nghiệm ta có thể thực hiện theo các bước sau:
ThuËt to²n 1: Đối với bài toán không cần đặt ẩn phụ
Bƣớc 1: Biến đổi đưa PT về dạng f x  g m hoÆc f x  g m; hoÆc f x  g m
Bƣớc 2: Lập bảng biến thiên của hàm số y  f x, cã tËp x²c ®Þnh D . f
Suy ra: min f x, max f x . (nếu có) x D  x D 
Bƣớc 3: Sử dụng các nhận xét và phương pháp đã nêu ở phần trên, đưa ra kết luận.
ThuËt to²n 2: Đối với bài toán đặt ẩn phụ
Bƣớc 1: Đặt ẩn phụ t  x. Từ điều kiện ràng buộc của x suy ra miền giá trị t  x.
Giáo viên: LÊ BÁ BẢO...0935.785.115... -1-
CLB Giáo viên trẻ TP Huế
Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016 Giả sử: x
  D  t  X . f
Bƣớc 1: Lúc này, biến đổi đưa PT về dạng f t  h m,
hoÆc f thm; hoÆc f thm .
Lúc này biện luận điều kiện có nghiệm của PT f t  h m với t  X .
Các bước còn lại tương tự thuật toán 1.
* Với hệ phương trình có chứa tham số, tư duy, hoặc là dựa vào điều kiện có nghiệm của các
dạng hệ đặc thù, hoặc đưa về phương trình chứa 1 ẩn (có thể là ẩn phụ) vầ xét điều kiện có
nghiệm trên miền giá trị của ẩn (hoặc ẩn phụ) đó.
II- CÁC BÀI TẬP MINH HOẠ:
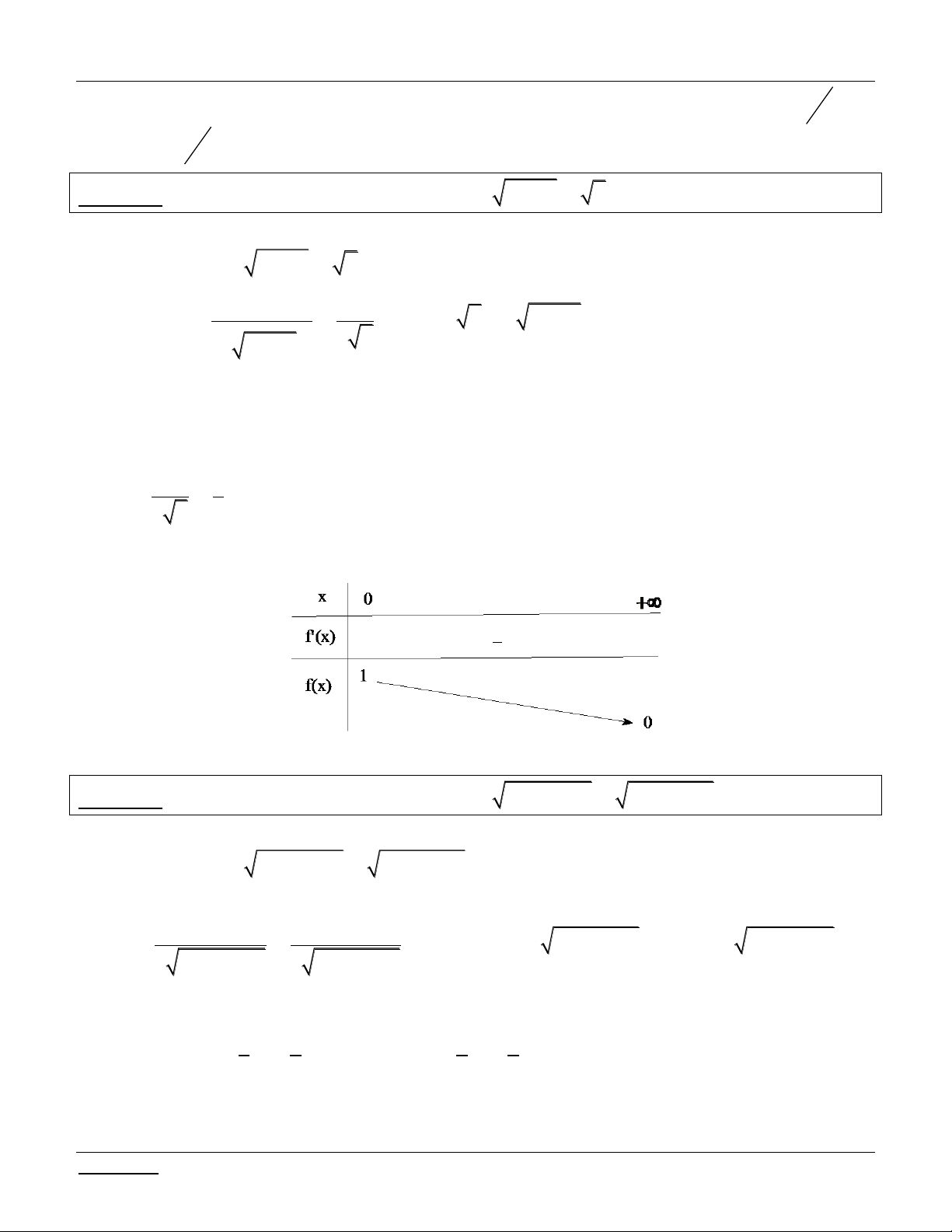
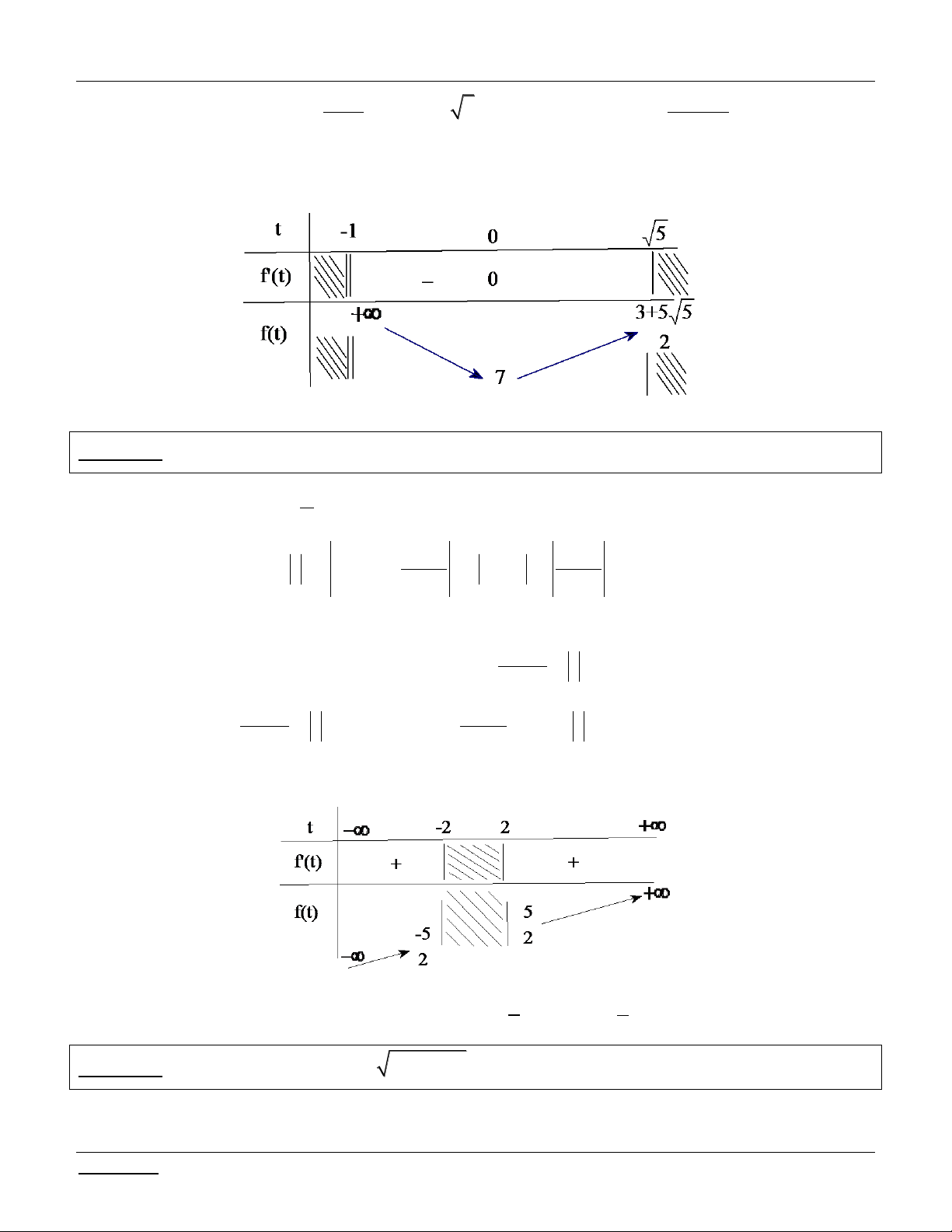
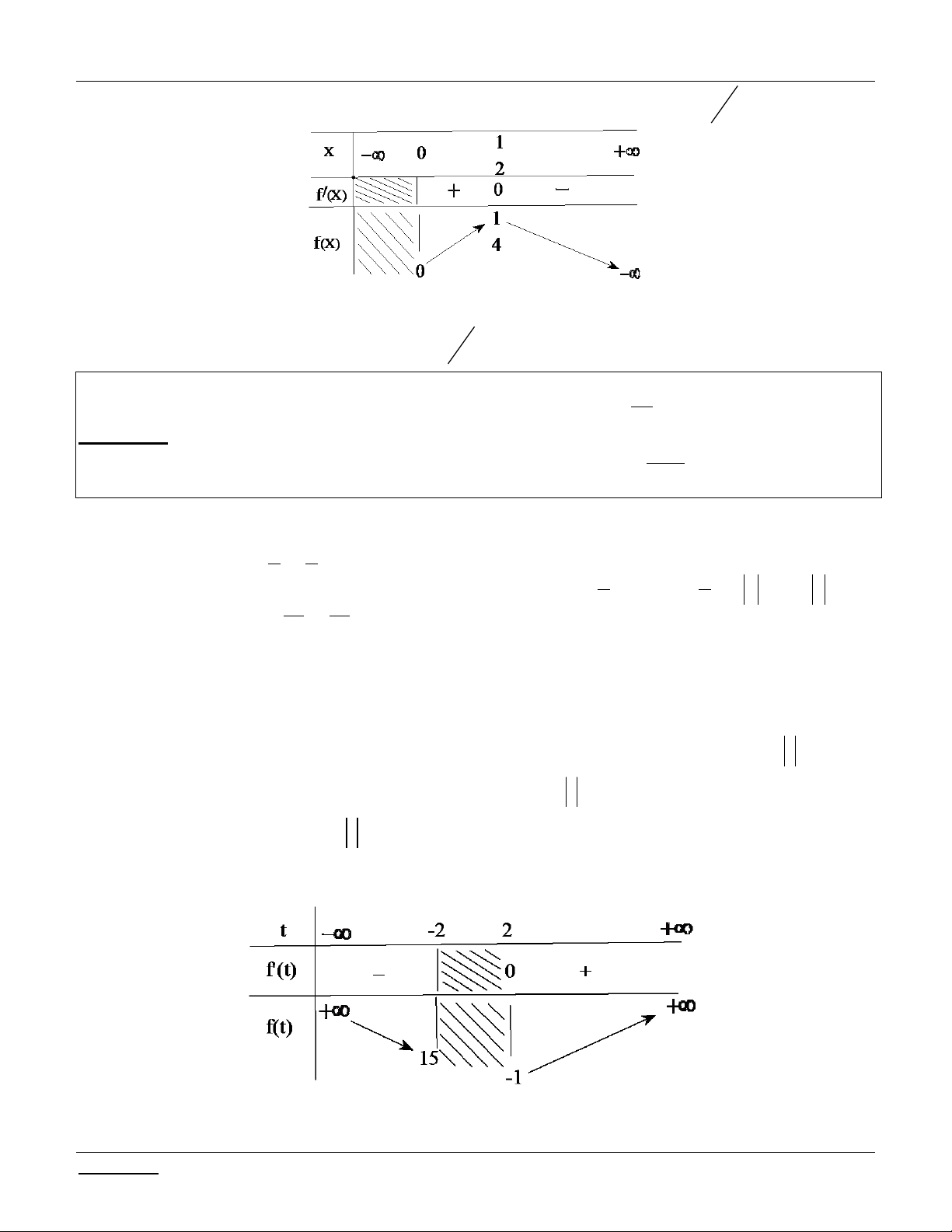
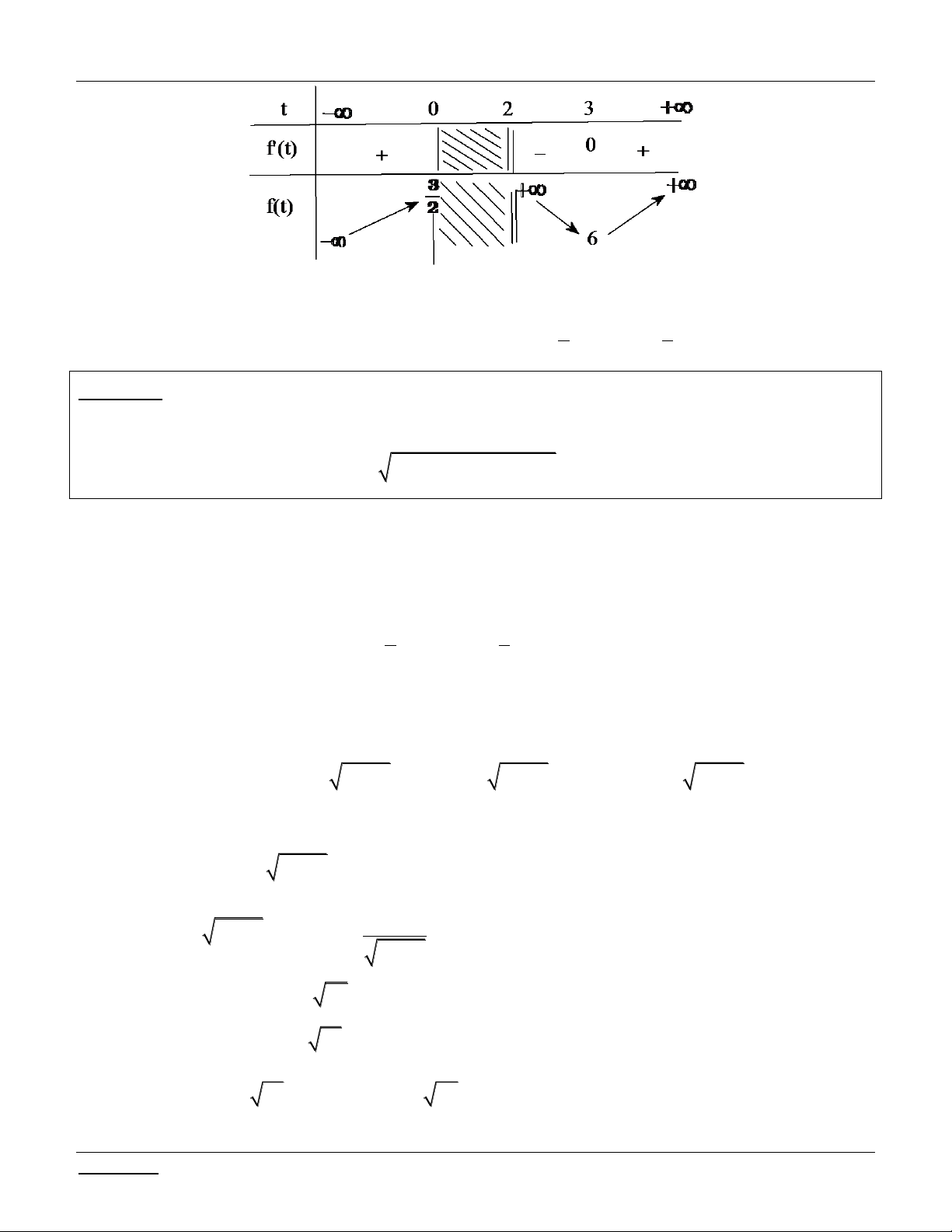
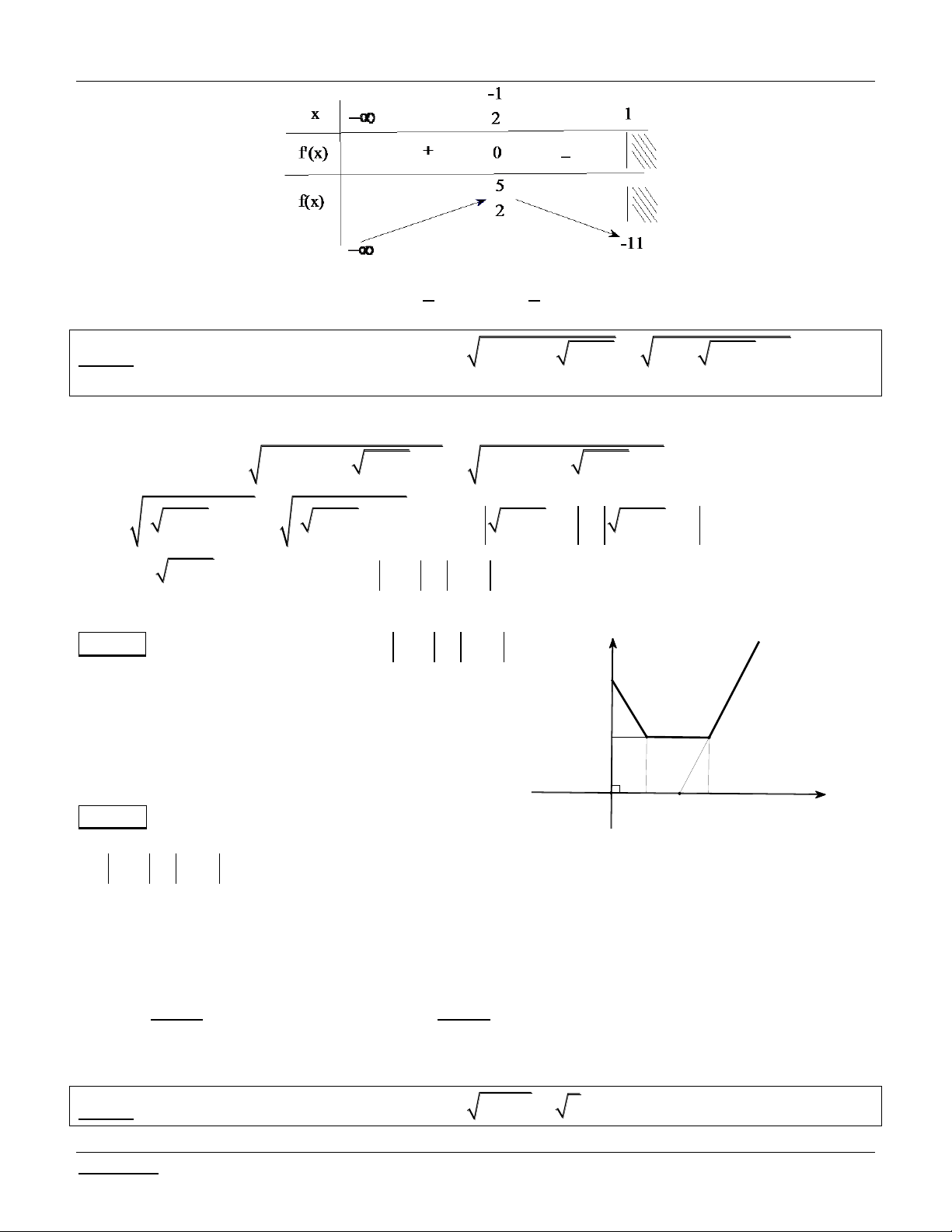
Bài tập 1: T×m c²c gi² trÞ cña m ®Ó ph¬ng tr×nh: 2 x  9 x  x
  9x  m cã nghiÖm.
Bài giải: §iÒu kiÖn: 0  x  9 Pt 2
 x  x 
x x  x   x  m 2 9 2 (9 ) 9
 9  2 x(9 x)  x
  9x  m (*) §Æt t 
x(9 x) 0  x   9
* Tìm điều kiện của t : x  9  x 9 9
Cách 1: Theo BDT Cauchy: t  x(9  x)    0  t  2 2 2 2  x  9
Cách 2: Ta có / 9 t   0  x  2 2 2 x   9x BBT: Do ®ã: 9 0  t  2
* Lóc ®ã ph¬ng tr×nh (*) trë th¯nh: 2 2
9  2t  t  m  t
  2t  9  m (**) XÐt h¯m sè 2 f t  t
  t    t  . Ta cã: / 9 ( ) 2 9 0 f (t)  2
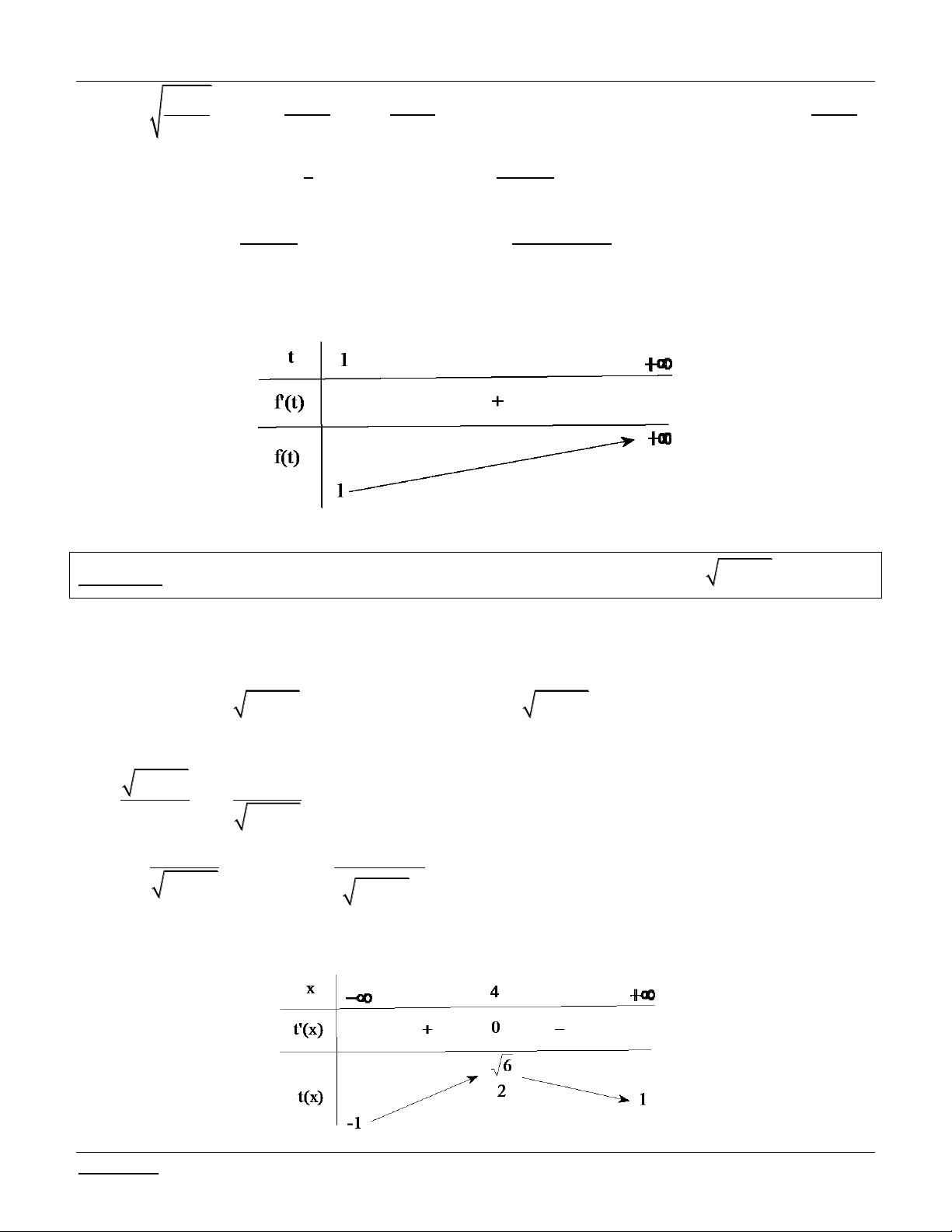
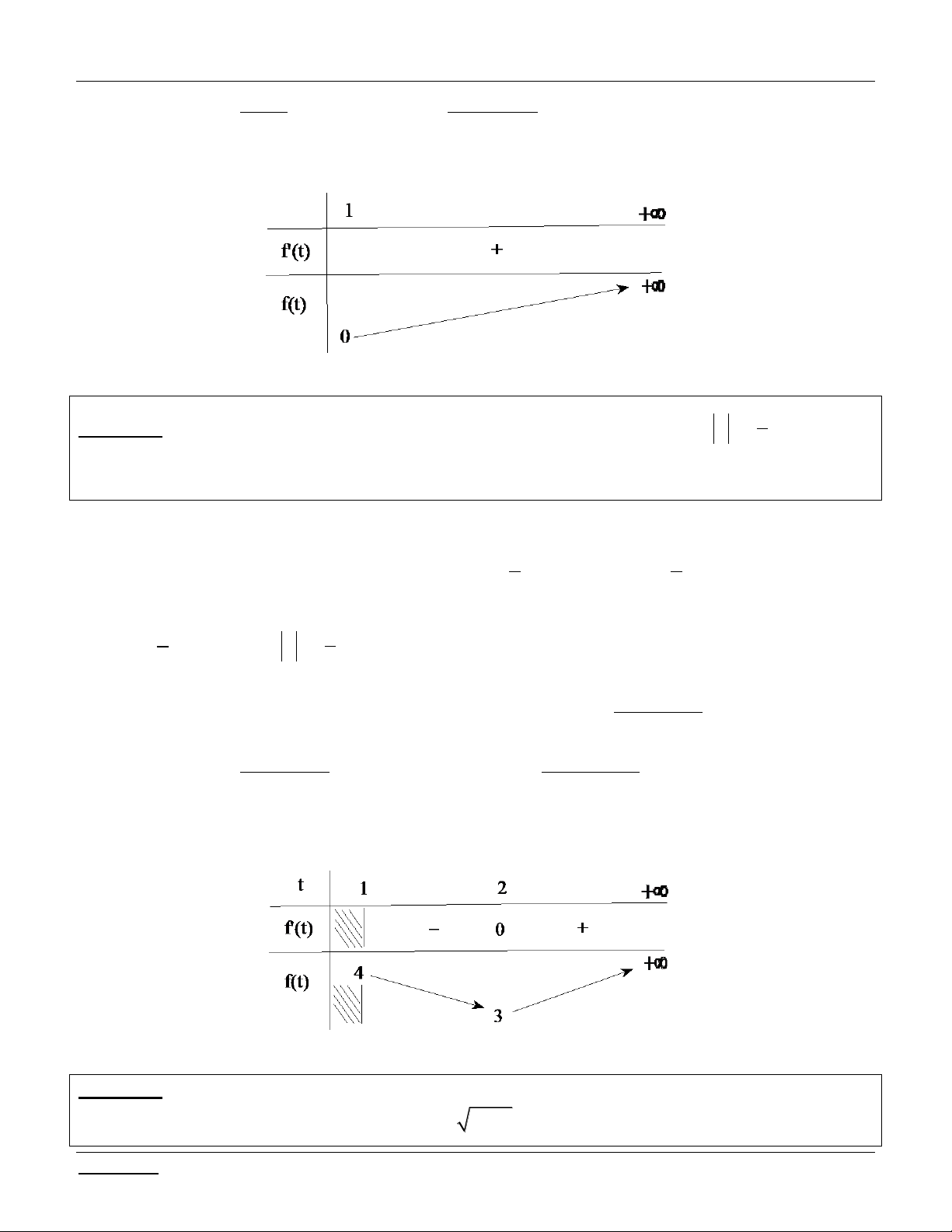
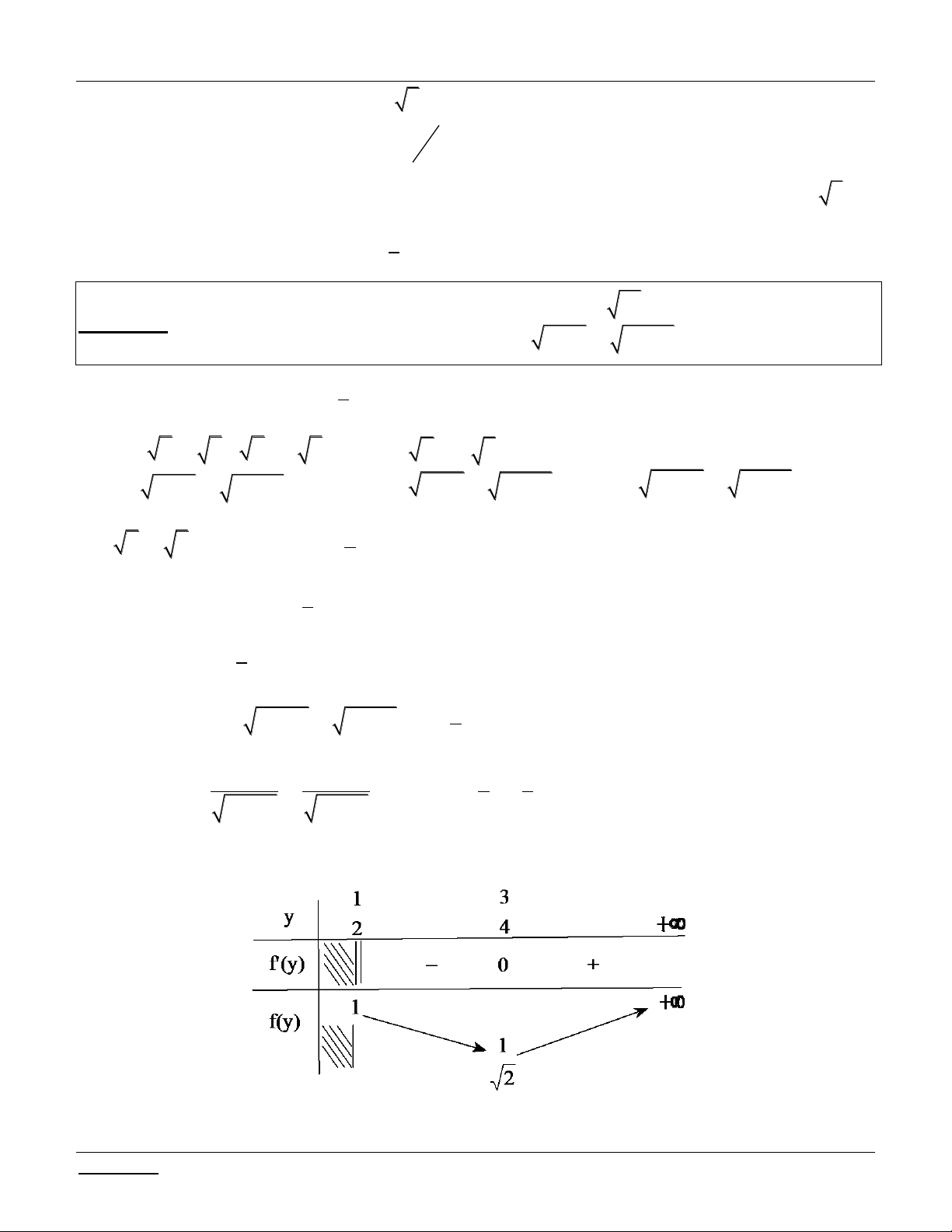
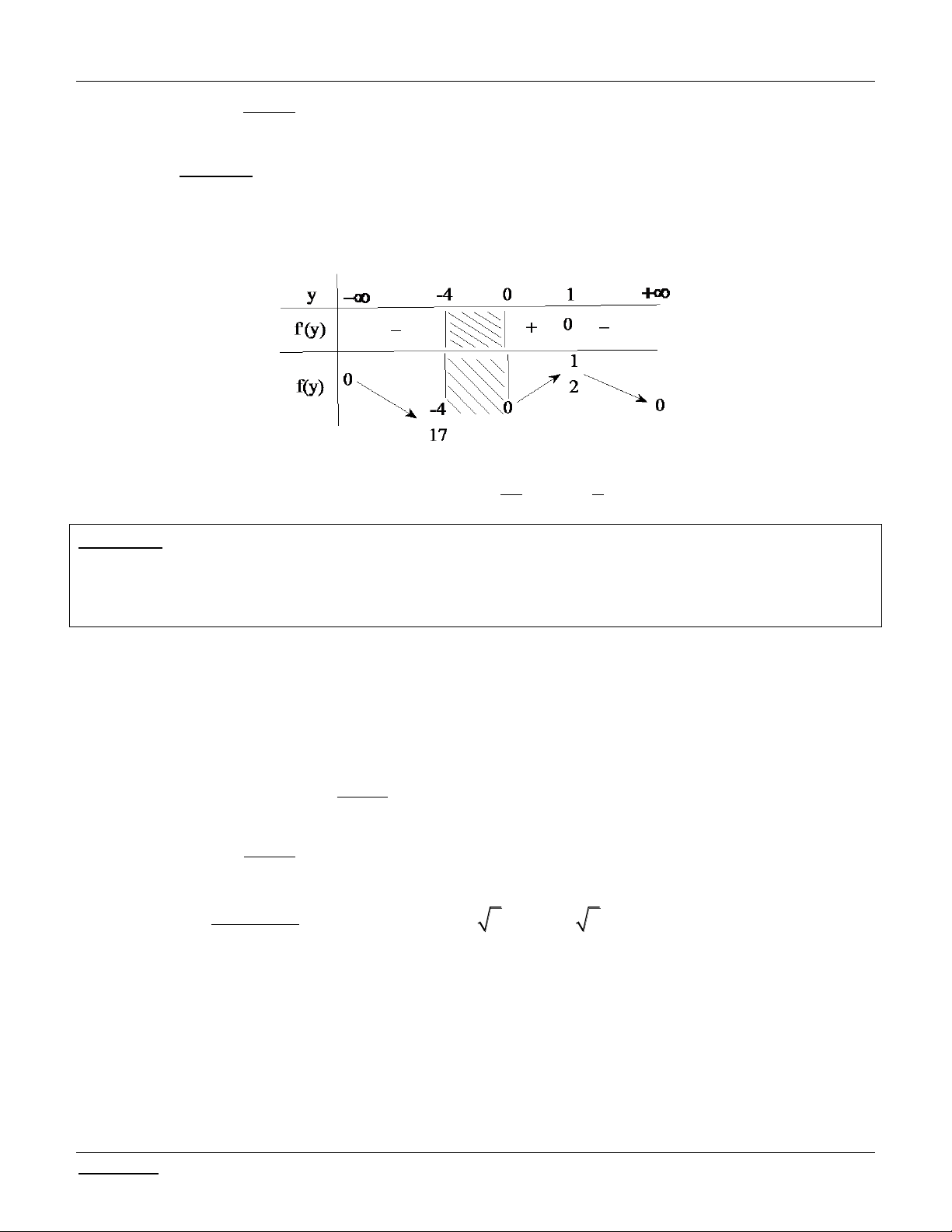
 t  2  0  t  1 2 Lập bảng biến thiên:
Giáo viên: LÊ BÁ BẢO...0935.785.115... -2- CLB Giáo viên trẻ TP Huế
Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016  
KÕt luËn: Ph¬ng tr×nh ®± cho cã nghiÖm x   
khi chØ khi PT (**) cã nghiÖm 9 0;9 t    0;   2  ycbt  9   m  10. 4
Bài tập 1: Tìm m để phương trình sau có nghiệm 4 2
x 1  x  m .
Bài giải: Điều kiện: x  0 .
Xét hàm số f x 4 2
 x 1  x trên 0;    . x 1
Ta có: f x   
 0  x x  4 x 1 3 3 / 2 4 2   2 2 1 x x
 x  x  3 6 2 2 2
1  x  x  1 (vô nghiệm) Suy ra, /
f x không đổi dấu trên 0;   , mà 1 1 / f   / 1 
  0  f x  0, x   0; 
 . Do đó f x nghịch biến trên 0;    4 2 8 2  .
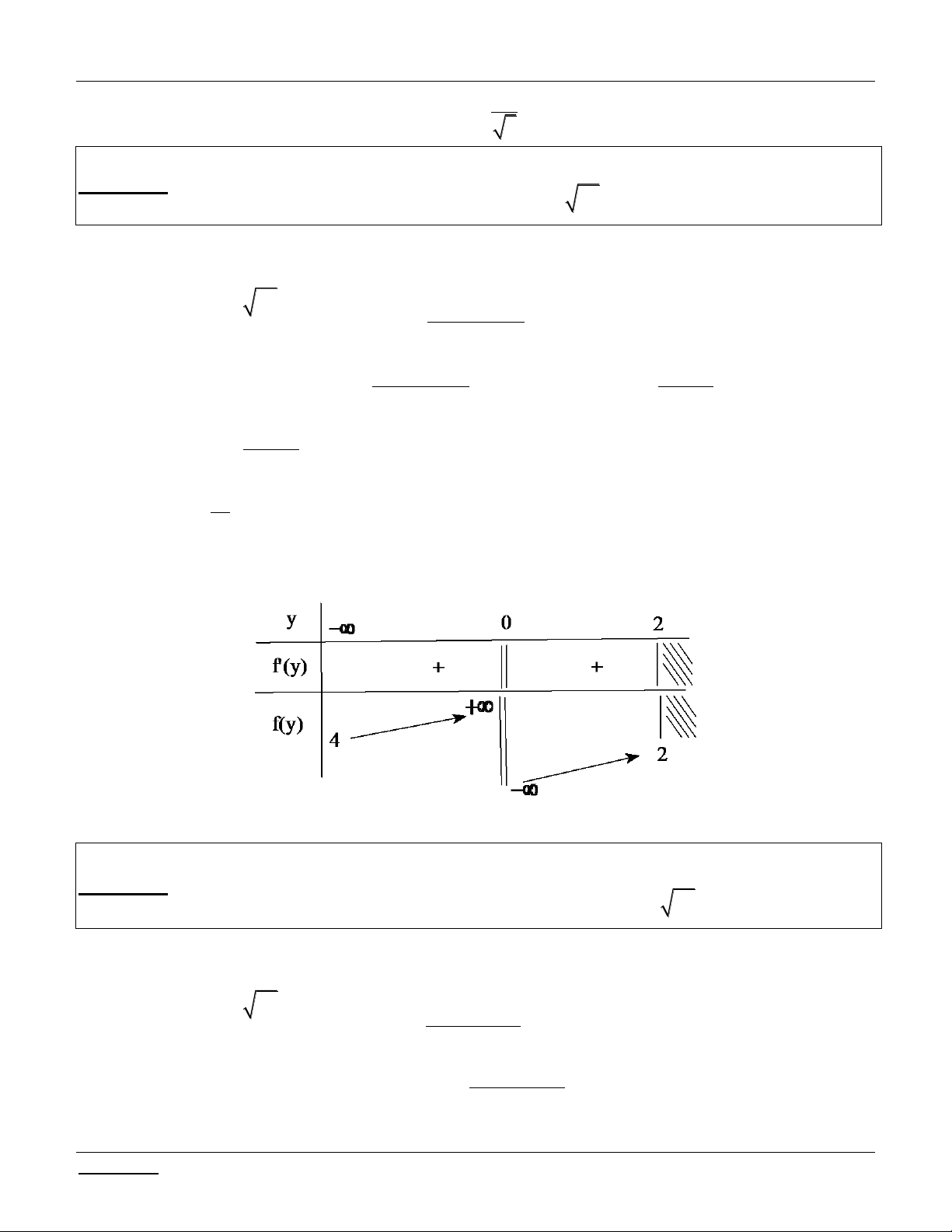
Ta có BBT: lim f x  0. x
Dựa vào BBT ta có yêu cầu bài toán  0  m  1.
Bài tập 2: Tìm m để phương trình sau có nghiệm 2 2
x  x 1  x x 1  m . Bài giải:
Xét hàm số f x 2 2
 x  x 1  x x  1 trên  . Ta có: 2x  1 2x 1 / f x  
 0  2x   2
1 x  x  1  2x   2 1 x  x  1 2 2 2 x  x  1 2 x  x  1 2x  
12x  1  0   
2x  1 2x 1  0   2   2                     vô nghiệm. 2x   2 1 3 1  x         2x  2 1 3 1  x     x   0        2 4    2 4       
Giáo viên: LÊ BÁ BẢO...0935.785.115... -3- CLB Giáo viên trẻ TP Huế
Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016 Suy ra, /
f x không đổi dấu trên 0;   , mà / f   /
0  1  0  f x  0, x    . Do đó
f x đồng biến trên  .
Ta có BBT: lim f x  1; lim f x  1  . x x
Dựa vào BBT ta có yêu cầu bài toán  0  m  1.
Bài tập 3: Tìm m để phương trình sau có nghiệm x x  x  12  m  5 x  4 x .
Bài giải: Điều kiện: x 0;4    . x x  x  12
Phương trình  m 
 m  x x  x 12 5x  4 x 
5  x  4  x
Xét hàm số f x
x x x 12 5 x 4 x, x 0;4          Ta có: 3 1    1 1  /
f x   x     
 5  x  4  x   x x  x  12    , x   0; 4 2         2 x  12  2 4 x 2 5  x   Dễ thấy x  x x     / 5 4 ,
0; 4  f x  0, x   0; 
4 . Do đó f x đồng biến trên 0;4    
 . Suy ra phương trình f x  m có nghiệm trên 0;4    f  
0  m  f 4  2 3  5   2  m  12.
Nhận xét: Ta có thể giải như sau: x x  x  12
Phương trình  m 
. Ta có hàm số g x  x x  x  12 đồng biến và
5  x  4  x
nhận giá trị dương trên 0; 4 
 , hàm số h x  5 x  4 x nghịch biến và nhận giá trị x x  x  dương trên 0; 4    
 . Suy ra f x 12  đồng biến trên 0; 4  
5  x  4  x  . Suy ra phương trình
f x  m có nghiệm trên 0;4    f  
0  m  f 4  2 3  5   2  m  12.
Giáo viên: LÊ BÁ BẢO...0935.785.115... -4- CLB Giáo viên trẻ TP Huế
Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016
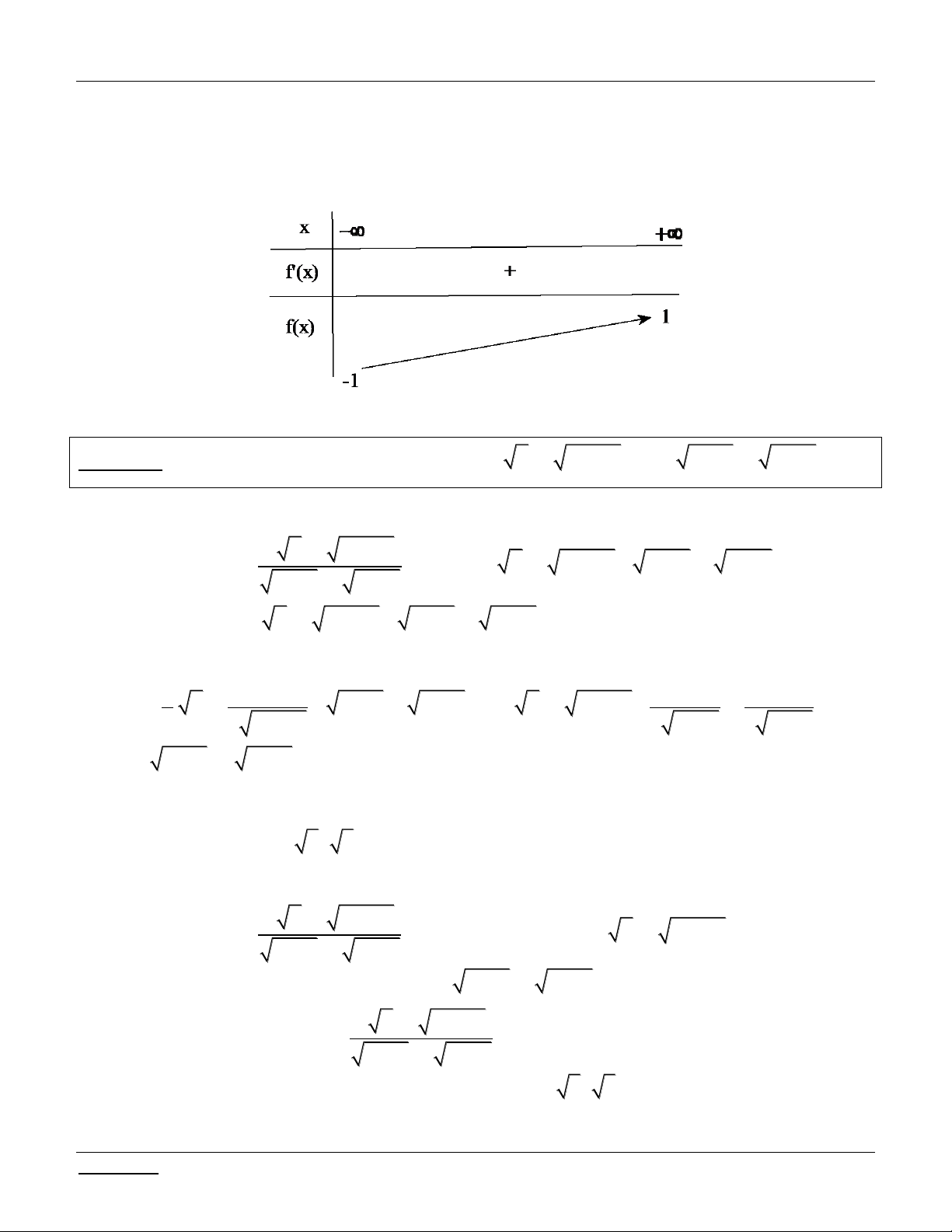
Bài tập 4: Tìm m để phương trình sau có đúng 3 nghiệm phân biệt: 2
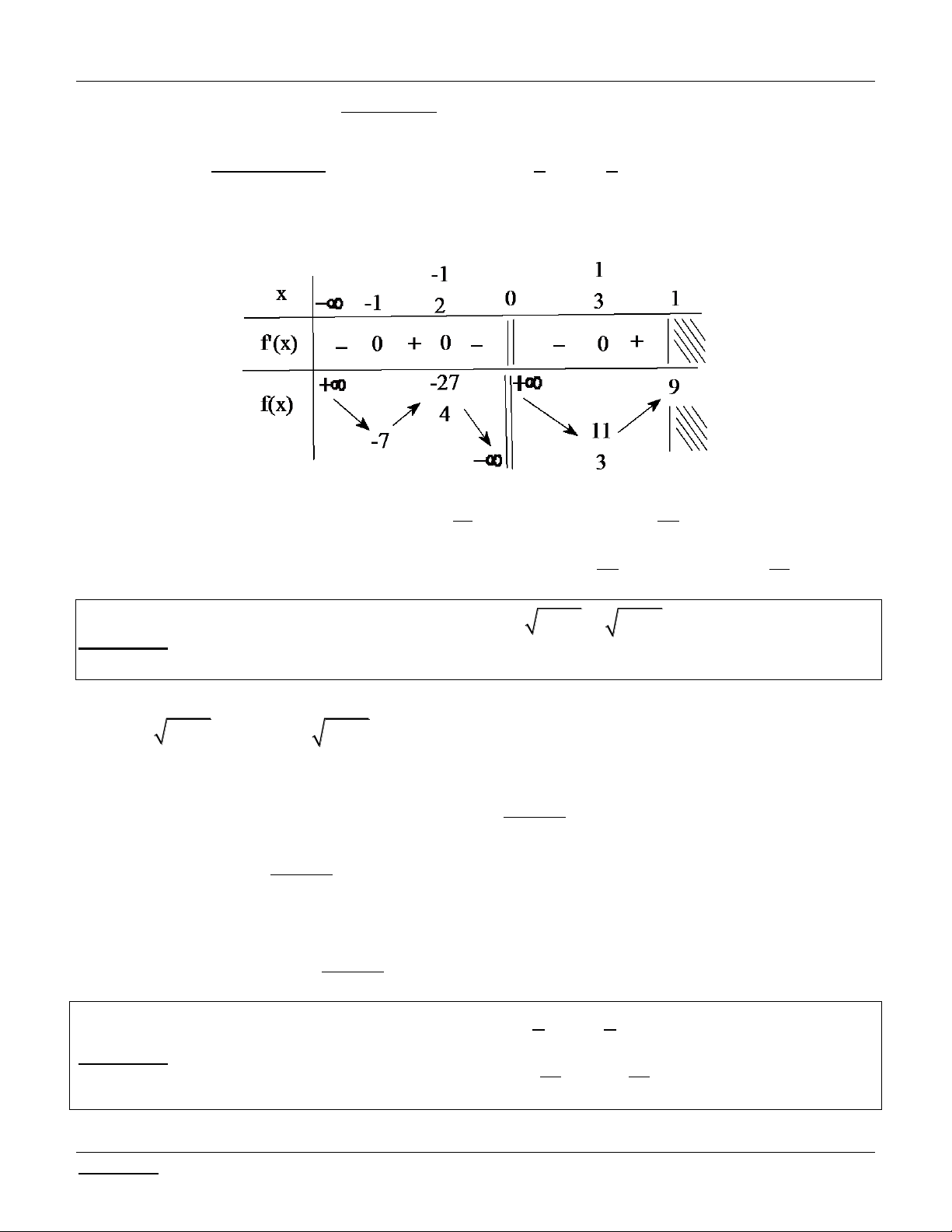
m x  2  x  m .
Bài giải: Vì 2 x  2  0, x
   nên phương trình  m  x 2 x  2  
1  x  m  do 2
x  2 1  0, x   .  2 x  2 1 x
Xét hàm số f x   , x   . 2 x  2 1  2 2  x  2 x  2  Ta có: / f x   0   . 
x   x   2 2 2 x   2 2 2 1 
BBT: lim f x  1; lim f x  1  . x x
Yêu cầu bài toán   2  m  2 .
Bài tập 5: Tìm m để phương trình sau có nghiệm 3
x  3x  4  m  x  x 1   1 .
Bài giải: Điều kiện: x  1. 3 x  3x  4
Phương trình  m 
do x  x 1  1  0, x   1.
x  x 1  1 3 x  3x  4
Xét hàm số f x  , x 1    ;    . x x 1 1       
x  x    2 x   3
x  x   1 1 1 1 3 3 3 4       
2 x 2 x 1 Ta có: / f x  .
 x  x 1 21
Với x  1 thì x  x 1  1  0 , 2 3x  3  0, 3
x  3x  4  0 (xét biến thiên) và 1 1   0 . Suy ra /
f x  0, x
  1. Do đó f x đồng biến trên 1;    2 x 2 x 1  .
BBT: lim f x   . x
Giáo viên: LÊ BÁ BẢO...0935.785.115... -5- CLB Giáo viên trẻ TP Huế
Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016
Yêu cầu bài toán  m  1.
Bài tập 6: Tìm m để bất phương trình sau có nghiệm 4  x  x  5  m .
Bài giải: Điều kiện: x  5;4     .
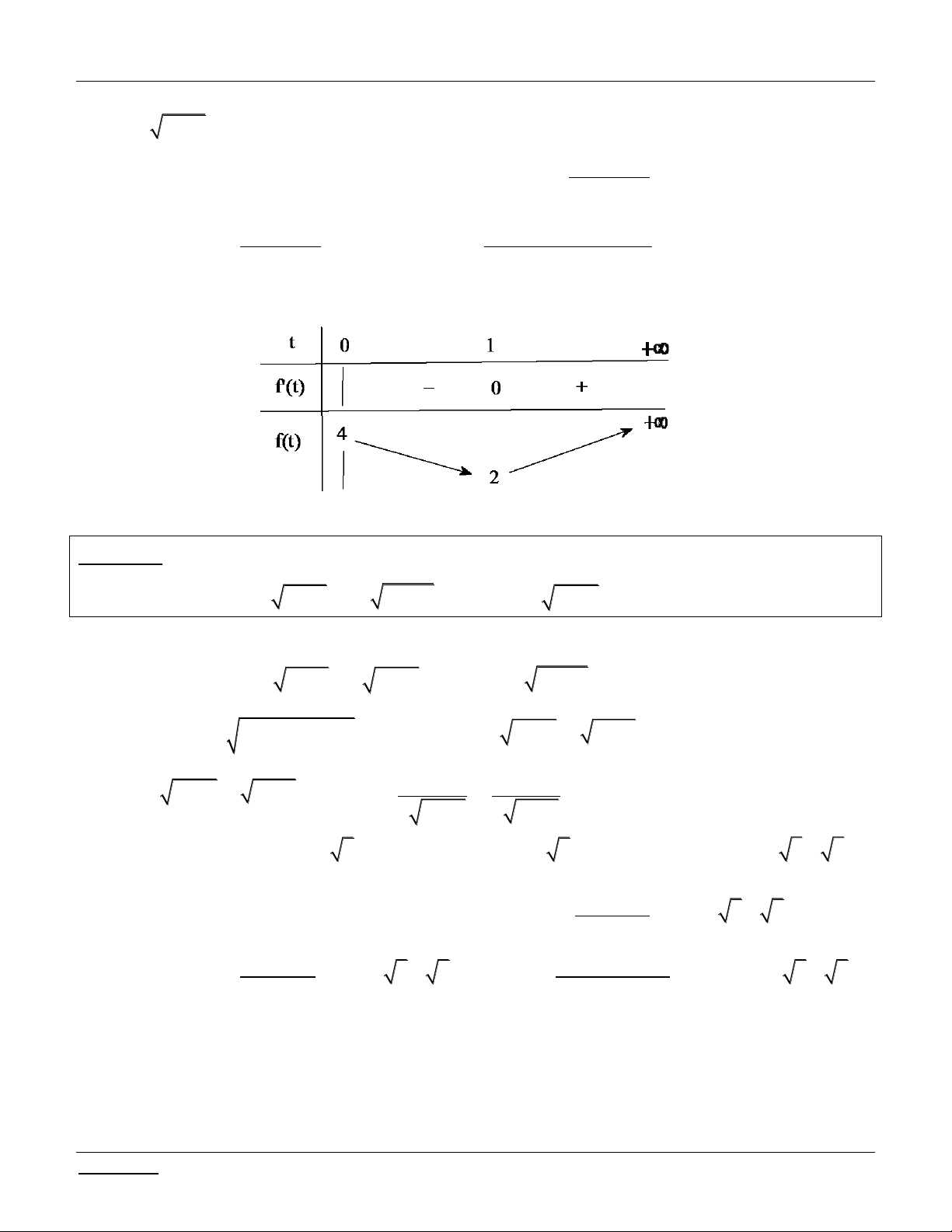
Xét hàm số f x 4 x x 5, x  5;4         . 1  1
4  x  x  5 Ta có: / f x     0 . 2 4  x 2 x  5
2 4  x . x  5 x     5  ; 4 1
 4  x  x  5    x   . 4
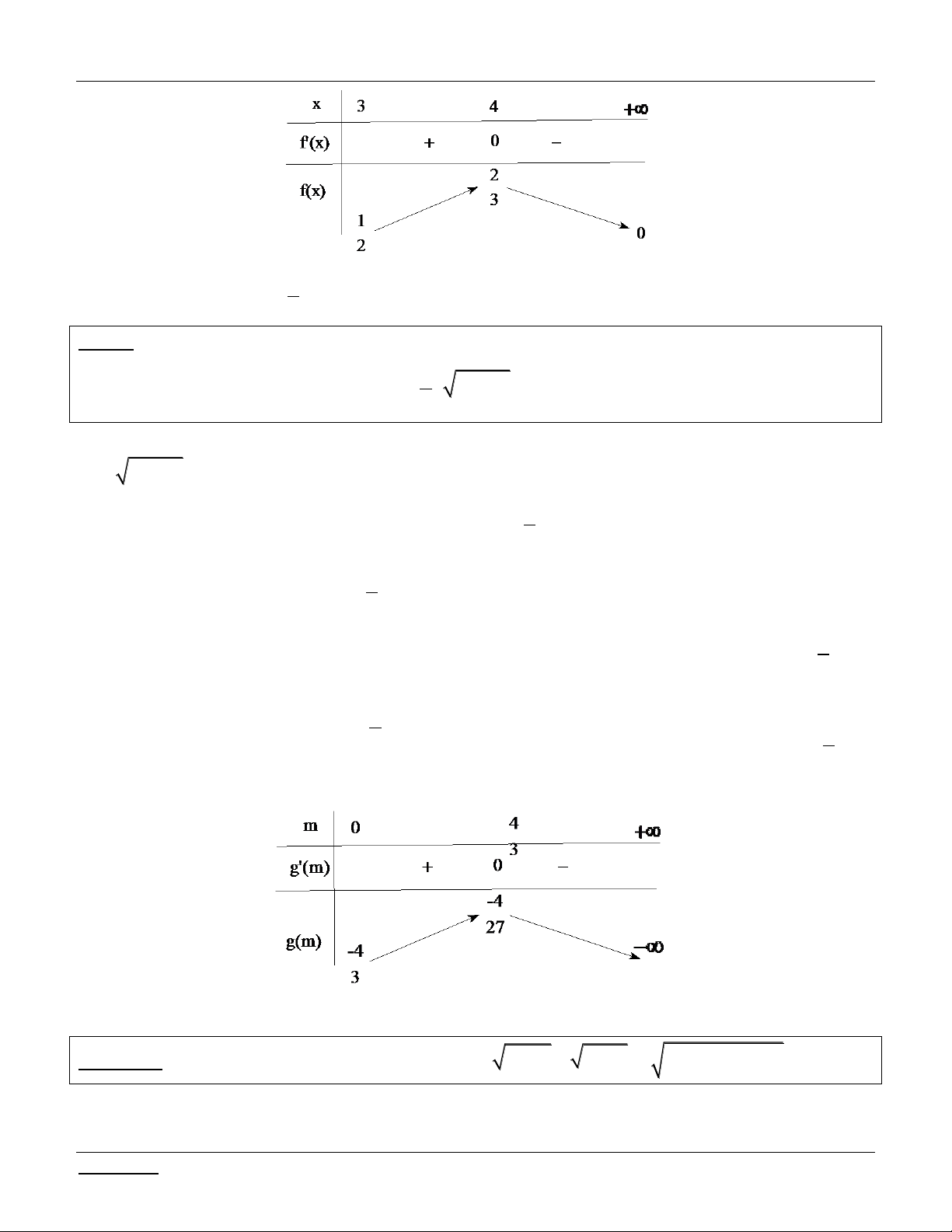
 x  x  5 2  BBT: -1 x -5 2 4 f'(x) + 0 _ 3 2 f(x) 3 3
Yêu cầu bài toán  m  3 2 .
Bài tập 7: Tìm m để bất phương trình sau có nghiệm mx  x  3  m  1.
Bài giải: Điều kiện: x  3 . x  3  1
Bất phương trình  m 
do x 1  0, x   3. x 1 x  3  1
Xét hàm số f x  , x    3;    . x 1   5  x  0
5  x  x  3  Ta có: / f x 
 0  x  3  5  x    x  4 .    x     3  5 2 1 3  x x x 2 2 
BBT: lim f x  0. x
Giáo viên: LÊ BÁ BẢO...0935.785.115... -6- CLB Giáo viên trẻ TP Huế
Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016 2
Yêu cầu bài toán  m  . 3
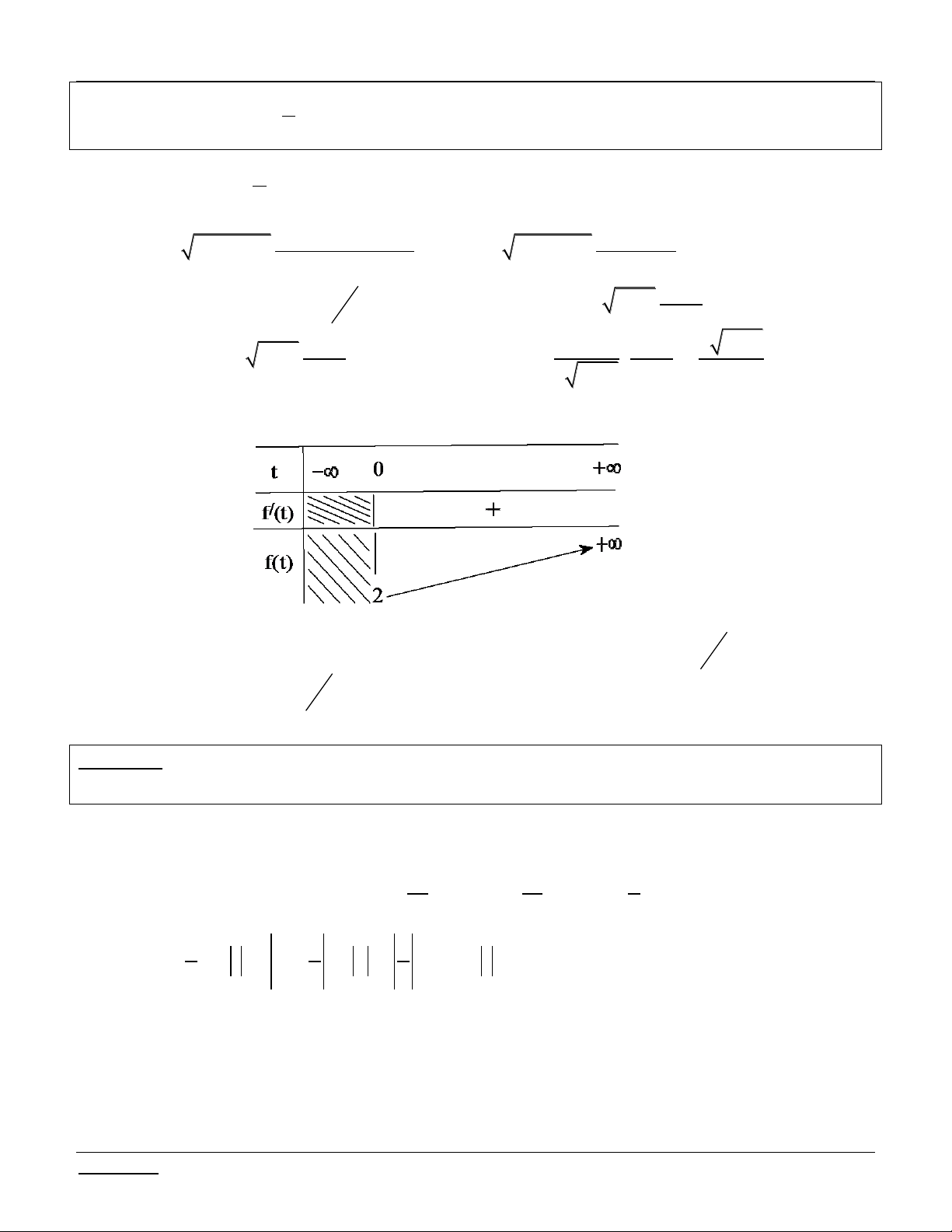
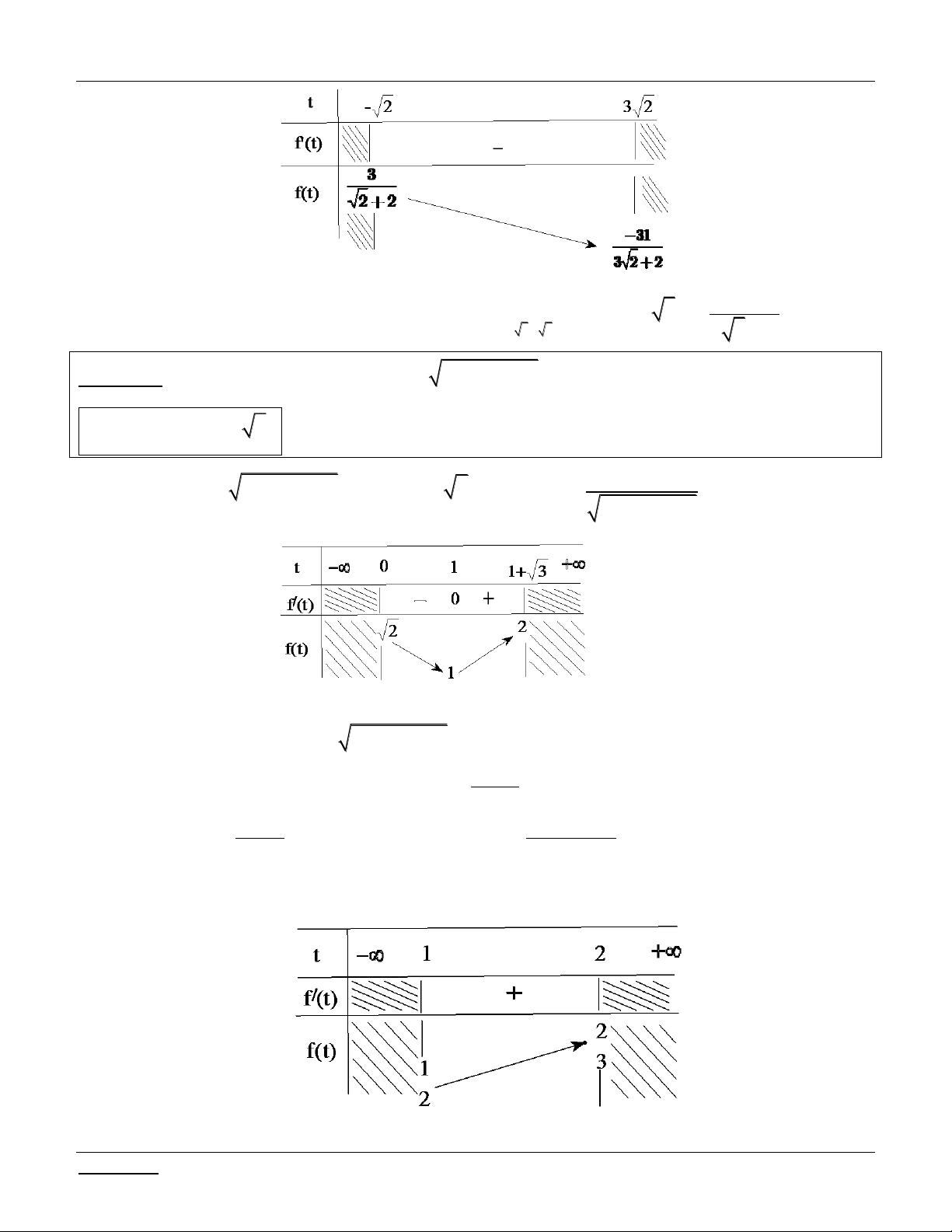
Đề 13: (Dự bị- 2004) Chứng minh rằng với mọi m  0 thì phương trình sau luôn có nghiệm:  5 2  2  2 3 x  m 
  x  4  2 m  0   3
Bài giải: TXĐ: D   . Đặt 2
x  4  t  2.  5
Phương trình đã cho tương đương vớ   i: 2 2 3 t  4  m 
 t  2 m  0  (1)  3  5  
Xét hàm số f t 2 2 3
 t  4  m 
 t  2 m  f t 2;   
, ta có   liên tục trên    3  và 4
lim f t  . Ta sẽ chứng minh f   2  0, m
  0 . Thật vậy: f   3 2 2  m   2m  . t 3 m   0 4 
Xét hàm số g m 3 2  m 
 2m  , m  0 . Ta có: / g m 2  3
 m  4m  0   . 3 4 m    3 BBT:
Dựa vào BBT, ta suy ra f  
2  g m  0, m
  0. Suy ra điều phải chứng minh.
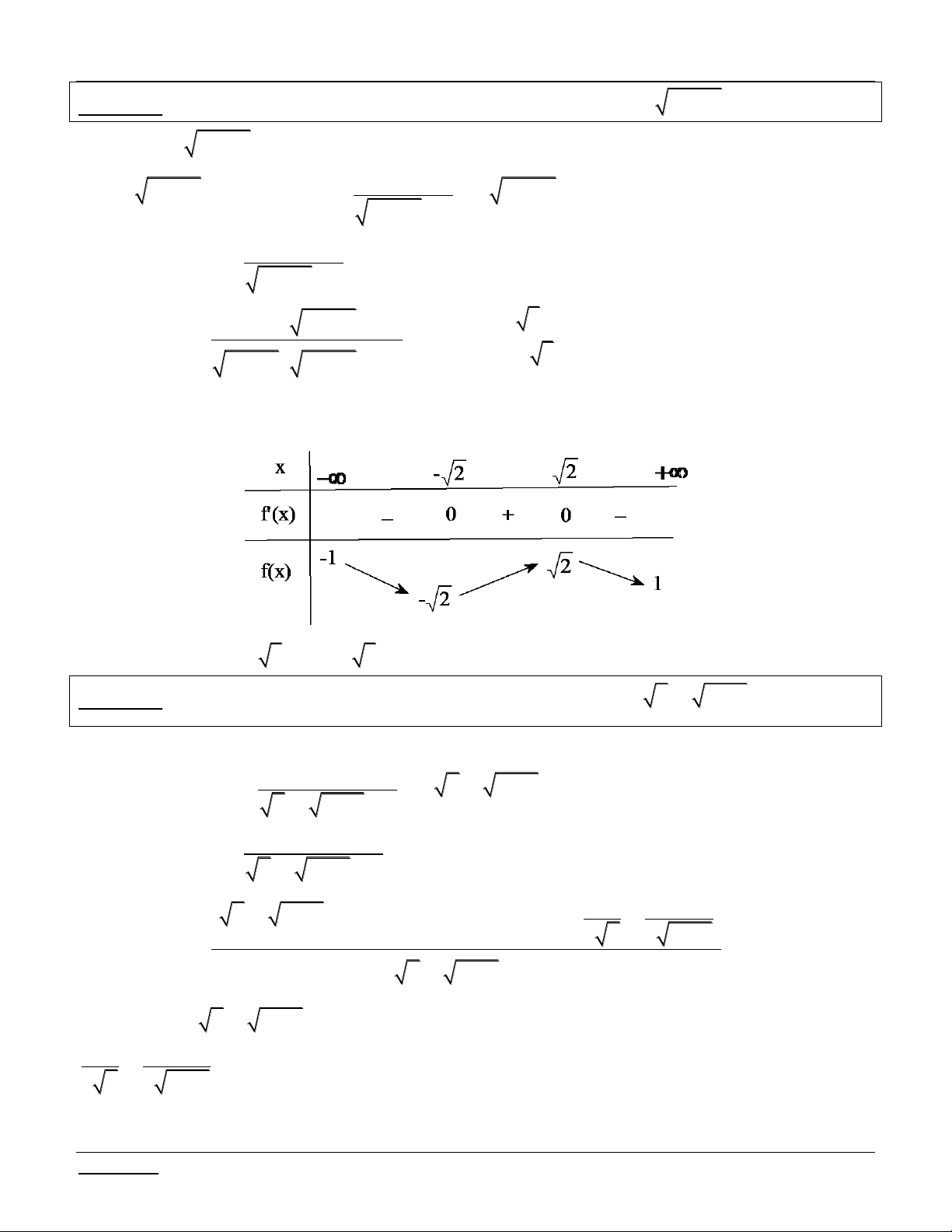
Bài tập 3: Tìm m để phương trình sau có nghiệm x  3  6  x  x  
3 6 x  m .
Bài giải: Điều kiện: x  3;6     .
Giáo viên: LÊ BÁ BẢO...0935.785.115... -7- CLB Giáo viên trẻ TP Huế
Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016 Đặt 2
t  x  3  6 x  t  9  2 x   3 6 x. 1 1
6  x  x  3 Ta có: / t     0 2 x  3 2 6  x 2 6  x x  3 x     3  ;  6 3
 6  x  x  3    x  . 6
 x  x  3 2  3     
Suy ra: max t  t    3 2, mint  t     3  t   6  3 hay x   3  ;6  t   3; 3 2      3;6    3;6    .   2         2 t  9
Lúc đó phương trình trở thành: 2 t 
 m  t  2t  9  2m . 2 
Xét hàm số f t 2
 t  2t, t   3;3 2 .   /
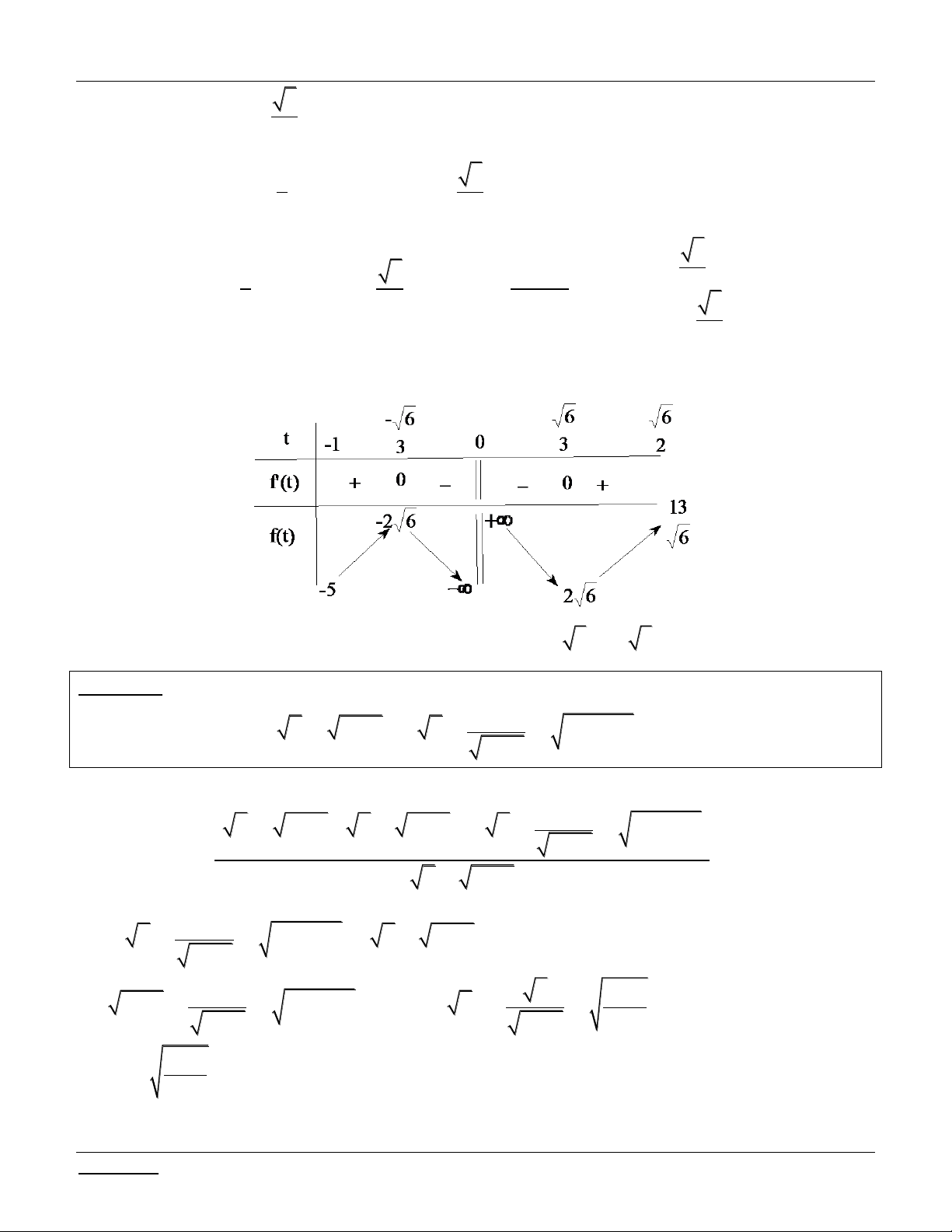
f t  2t  2  0  t  1  3; 3 2   Ta có:    . BBT: 3 2 t 3 f'(t) + 18-6 2 f(t) 3 
Dựa vào bảng biến thiên, yêu cầu bài toán  f     m  f   6 2 9 3 9 2 3 2   m  3. 2
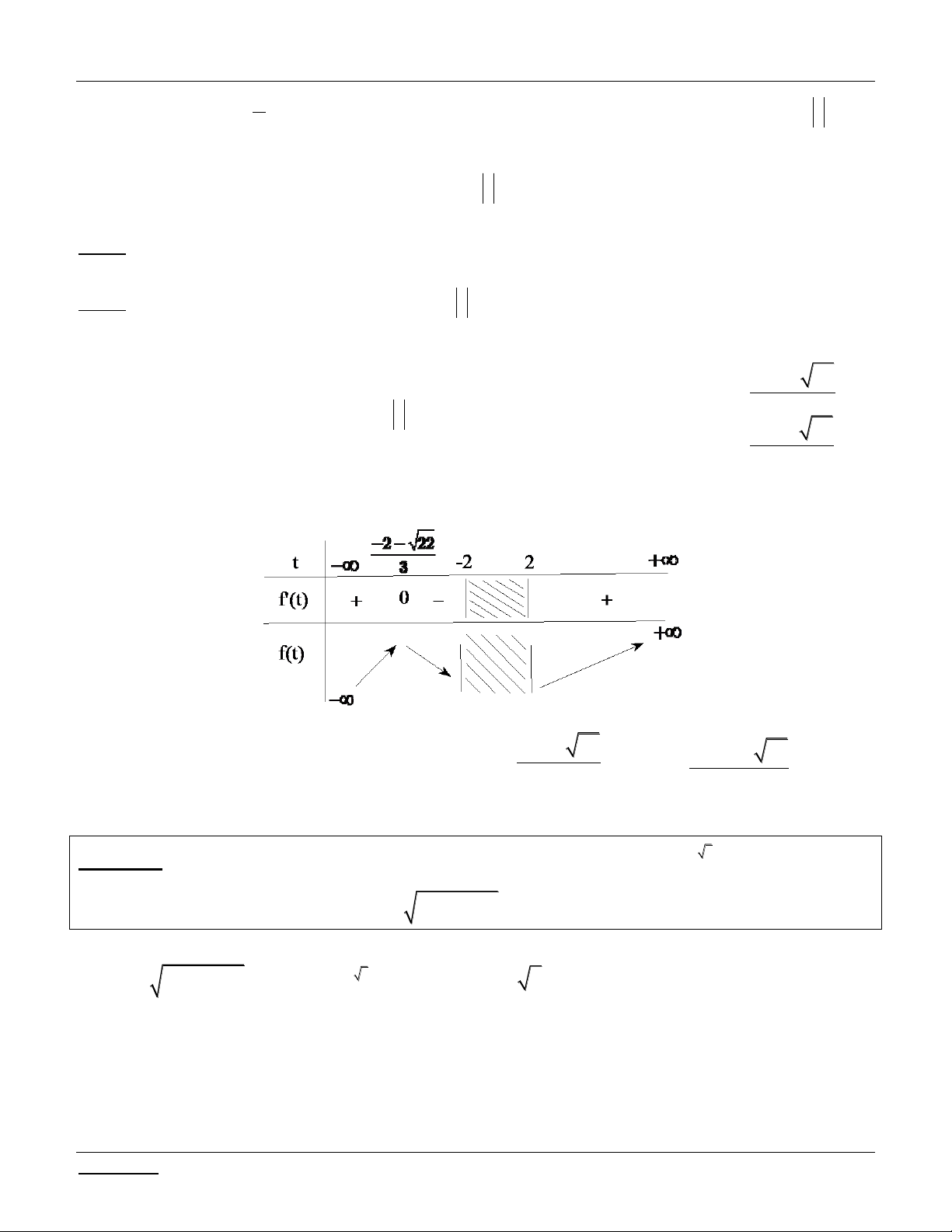
Bài tập 3: Tìm m để phương trình sau có nghiệm: 2 2 x
 2x  3 m  
1  x  3  1x m 1  0.
Bài giải: Điều kiện: x  3;1     . Đặt 2
t  x  3  1x  t  4  2 x   3 1x. 1 1
1 x  x  3 Ta có: / t     0 2 x  3 2 1  x 2 1  x x  3 x     3  ;  1
 1 x  x  3    x  1  . 1
 x  x  3     
Suy ra: max t  t  
1  2 2, mint  t   3  t   1  2 hay x   3  ;1  t  2;2 2      3;1  3;1       .    
Giáo viên: LÊ BÁ BẢO...0935.785.115... -8- CLB Giáo viên trẻ TP Huế
Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016 Hoặc: Do 2
t  4  2 x  
3 1x  4  t  2   và t 
x  3  1 x  2 x  
3  1x  2 2  t  2;2 2     . t  t  3
Lúc đó phương trình trở thành: t m   2 2
1 t  m  3  0  m  t 1  
do t 1  0, t   2;2 2     . 2 t  t  3   2 t  2t  2
Xét hàm số f t  , t  2;2 2 .   Ta có: / f t   0, t   2;2 2 . 2   t 1   t  1 BBT: t 2 2 2 f'(t) + 12 2+13 f(t) 7 3 12 2  13
Dựa vào bảng biến thiên, yêu cầu bài toán  3  m  . 7
Bài tập 3: (CĐ 2011) Tìm m để phương trình sau có nghiệm:
6  x  2 4 x2x  
2  m  4 4 x  2x 2.
Bài giải: Điều kiện: x 1  ;4    . Đặt 2
t  4 x  2x  2  t  2  x  2 4 x2x   2 . 1  1
2 4  x  2x  2 Ta có: / t   
 0  2 4  x  2x  2 2 4  x 2x  2
4  x . 2x  2 x    1;4   .      x x 3 4 4  2x  2    
Suy ra: max t  t  
3  3, mint  t   1  3 hay x   1; 4  t   3; 3     1  ;4 1  ;4     .    
Lúc đó phương trình trở thành: 2
t  4t  4  m . 
Xét hàm số f t 2
 t  4t  4, t   3; 3 .   /
f t  2t  4  0  t  2  2;2 2   Ta có:    . BBT:
Giáo viên: LÊ BÁ BẢO...0935.785.115... -9- CLB Giáo viên trẻ TP Huế
Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016 t 3 2 3 _ f'(t) 0 + 1 f(t) 7-4 3 0
Dựa vào bảng biến thiên, yêu cầu bài toán  0  m  1.
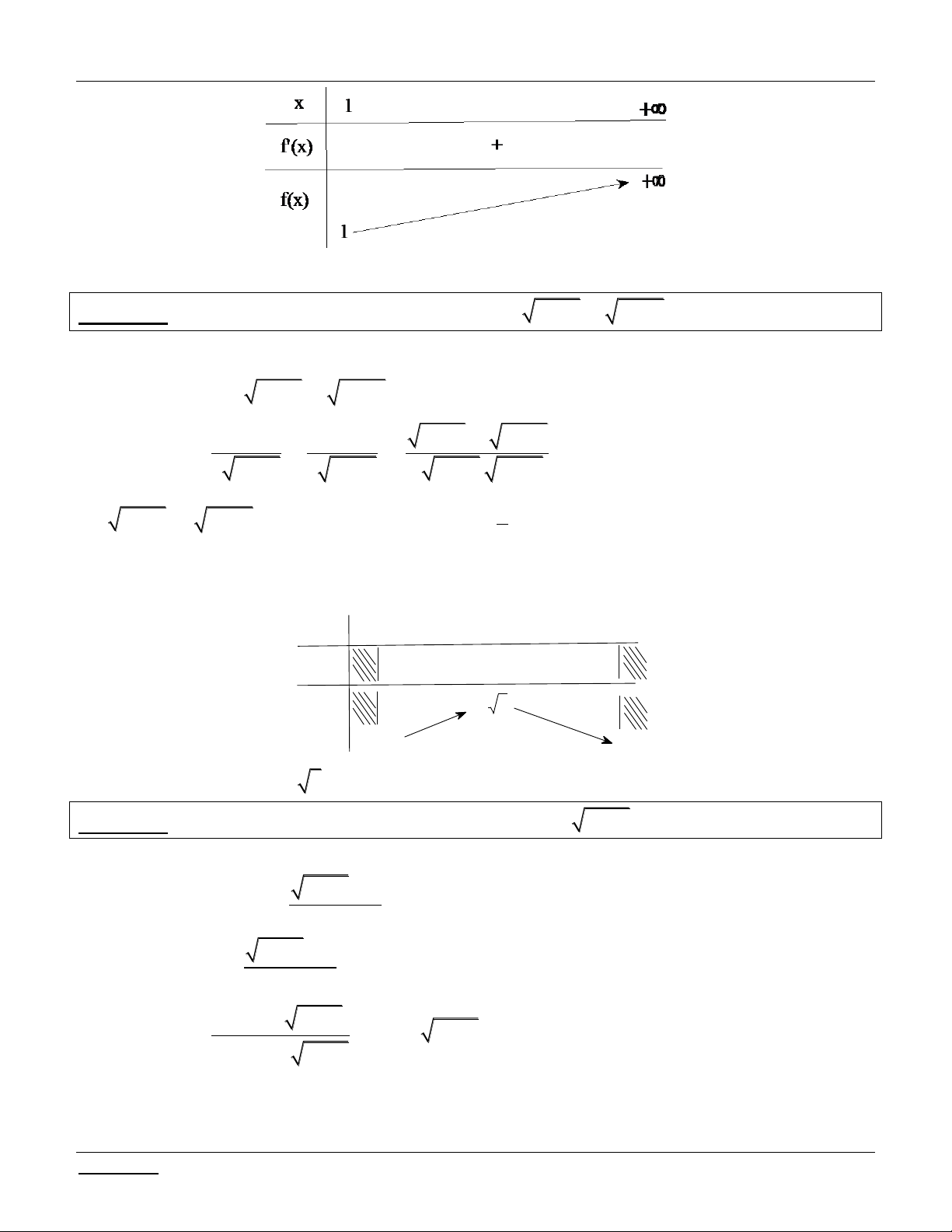
Bài tập 3: Tìm m để phương trình sau có nghiệm: 2 2 4 2
x   m x  x   x  x   m  2 7 1 1
x  x  1   2 .
Bài giải: Điều kiện: x   . Phương trình 2  x   2
x  x   2
x  x   m  2 2 1 1
x  x  1  x  x  1   2  7  0 2x  1 2x 1 Đặt 2 2 /
t  x  x  1  x  x  1  t   . 2 2 2 x  x  1 2 x  x  1 Ta có: /
t    x   2
x  x    x   2 0 2 1 1 2 1 x  x  1 2x  
12x  1  0     2x  2
1 x x   1  2x  2 2 1  2 x  x   1  2x  
12x  1  0   
2x  1 2x 1  0 2   2  2  2        1     1    3   1     1   3    vô nghiệm. x       x            x           x     x   0        2 2 4  2  2 4        Suy ra /
t x không đổi dấu trên  , mà / t   0  1  0 suy ra /
t x  0, x
   vậy t x đồng biến trên  .
Ta có lim t x  1; lim t x  1  . Vậy t   1  ;  1 . x x Lúc đó: 2 2 t  x  
 2x x   2 2 2 2
1 x  x  
1 nên phương trình trở thành: 2 t  
 m t   2 2 t 12 2  7  0  2  m 
do t  2  0, t    1  ;  1 . 2 t  2 2 t  12 2 t  4t 12 t  2 
Xét hàm số f t  , t   1  ;  1 . Ta có: / f t   0  . t  2   t  2 t  6 2  
Giáo viên: LÊ BÁ BẢO...0935.785.115... -10- CLB Giáo viên trẻ TP Huế
Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016 BBT: t -1 1 _ f'(t) 13 f(t) 13 3 13 13 13
Dựa vào bảng biến thiên, yêu cầu bài toán   2  m  13    m   . 3 2 6 4
Bài tập 3: Tìm m để phương trình sau có nghiệm 2
x 2 2 x 2x  m x  0 .
Bài giải: Điều kiện: x  2 . x  2 x  2 Phương trình 4   2
 m  0 (do x  2) x x x  2 x  2 2 x  Đặt 4 t  , khi đó 4 4 0  t   1  1, x
  1 (hoặc khảo sát u x 2  ) x x x x
Phương trình trở thành: 2 2 t 2t m 0 m t 2t, t          0;   1  .
Xét hàm số f t 2 t t t   / 2 , 0;1
f t 2t 2 0 t 1            0;    1  . BBT: t 0 1 f'(t) _ 0 f(t) -1
Dựa vào bảng biến thiên, yêu cầu bài toán  1   m
  0  0  m  1.
Bài tập 3: Tìm m để phương trình sau có nghiệm: m  4 2 x   x   4 2 2 2
4  x  2  2 x  4 .
Bài giải: Điều kiện: x  2 .
+ Ta thấy x  2 không phải là nghiệm của phương trình.  x 2    x  2
+ Xét x  2 , phương trình  4  4 m  2    2 x   (do 2)  x  2  x  2  
Giáo viên: LÊ BÁ BẢO...0935.785.115... -11- CLB Giáo viên trẻ TP Huế
Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016 x  2 x  2 4 x  Đặt 4 t  , khi đó  1   1, x
  2  t  1 (hoặc khảo sát u x 2  ) x  2 x  2 x  2 x  2 2 1    t  2t
Phương trình trở thành: m   2t  2  m  , t    1;    . t  2t  1 2 2 t  2t 2t  2t  2
Xét hàm số f t  , t  1;  /
  f t   0, t   1; . 2   2t  1 2t  1
BBT: lim f t  . t
Dựa vào bảng biến thiên, yêu cầu bài toán  1   m
  0  0  m  1.
Bài tập 3: Tìm m để phương trình sau có nghiệm 2
x  x   m x   2 5 6 7 1 x  2 .
Bài giải: Điều kiện: x   . 2 Để ý rằng 2
x  x   x     2 5 6 7 3 1 2 x   2 . 2 2 Phương trình   2
x    x    mx   2 2 2 3 1 1 x  2 (*) Do x  1
 không là nghiệm của phương trình (*), nên (*) tương đương: 2 x  2 x  1  2  3.  m 2 x  1 x  2 x  1 2  x Đặt t  , khi đó / t   0  x  2 . 2 x  2  x 23 2
BBT: lim t x  1; lim t x  1  . x x
Giáo viên: LÊ BÁ BẢO...0935.785.115... -12- CLB Giáo viên trẻ TP Huế
Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016  6   
Vậy x    t   1  ;  . 2    2  6   Phương trình trở  thành:  3t  , m t   1  ; . t  2     6    2 2  6 3  2 t t   
Xét hàm số f t   t / t    f   t 3 3 , 1;   0   . 2 t  2   t  6  t    3
BBT: lim f t   ;
 lim f t   . t 0 t 0    
Dựa vào bảng biến thiên, yêu cầu bài toán  m   ;  2  6  2 6;       .
Bài tập 3: Tìm m để phương trình sau có nghiệm:    x  x 1 1   4 m  x 
 x x   1   1    .  x 1 
Bài giải: Điều kiện: x  1.   
x  x 1 x  x 1 1   4 m  x 
 x x   1         Phương trình x 1    x  x   1 1 1 4  m x 
 x x  
1  x  x 1 x 1 1 x x 1 4  x 1 
 x x   1  1m 4 x    1m . x 1 x 1 x x 1 Đặt 4 t 
, khi đó t  0;  1 . x
Giáo viên: LÊ BÁ BẢO...0935.785.115... -13- CLB Giáo viên trẻ TP Huế
Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016 1 1 Phương trình trở thành:
 t  1m  m  
t  1, t  0;1 . 2 2   t t 1 2
Xét hàm số f t  
t  1, t  0;  / 1  f t  1  0, t   0;1 . 2   2   t t
BBT: lim f t   . t 0 
Dựa vào bảng biến thiên, yêu cầu bài toán  m  1. 
x 2 x 12 2 2 18 x  1
Bài tập 3: Tìm m để phương trình sau có nghiệm   m . 2 2 x  1
x  2  x  1
Bài giải: Điều kiện: x   . 2  x 2    18 Phương trình   1     m (*)  2    x  2  x  1   1 2 x  1 x  2 1  2x 1 Đặt t  , khi đó / t   0  x  . 2 x  1  x 13 2 2
BBT: lim t x  1; lim t x  1  . x x 
Vậy x    t   1  ; 5 . 2 18 Phương trình trở  thành: t   1   , m t   1  ; 5 . t  1 
Giáo viên: LÊ BÁ BẢO...0935.785.115... -14- CLB Giáo viên trẻ TP Huế
Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016 2 18  18
Xét hàm số f t  t   1  , t   / 1  ; 5  f 
t  2t  1  0  t  2 . t  1  t  2 1
BBT: lim f t   .  t 1 
Dựa vào bảng biến thiên, yêu cầu bài toán  m  7 .
Bài tập 3: Tìm m để phương trình sau có nghiệm: 2 2
tan x  cot x  m tanx  cotx 3  0 . 
Bài giải: Điều kiện: x  k . 2 1 1
Đặt t  tan x  cotx  t  tan x   tan x   2 tan x tan x suy ra: 2 2 2
t  2  tan x  cot x . 2 t  1
Phương trình trở thành: 2
t  mt  1  0  m   , t  2. t 2 2 t  1 t 1
Xét hàm số f t  , /
t  2  f t   0,  t  2. 2 t t
BBT: lim f t   ;
 lim f t  . t t 5 5
Dựa vào bảng biến thiên, yêu cầu bài toán  m   hoặc m  . 2 2
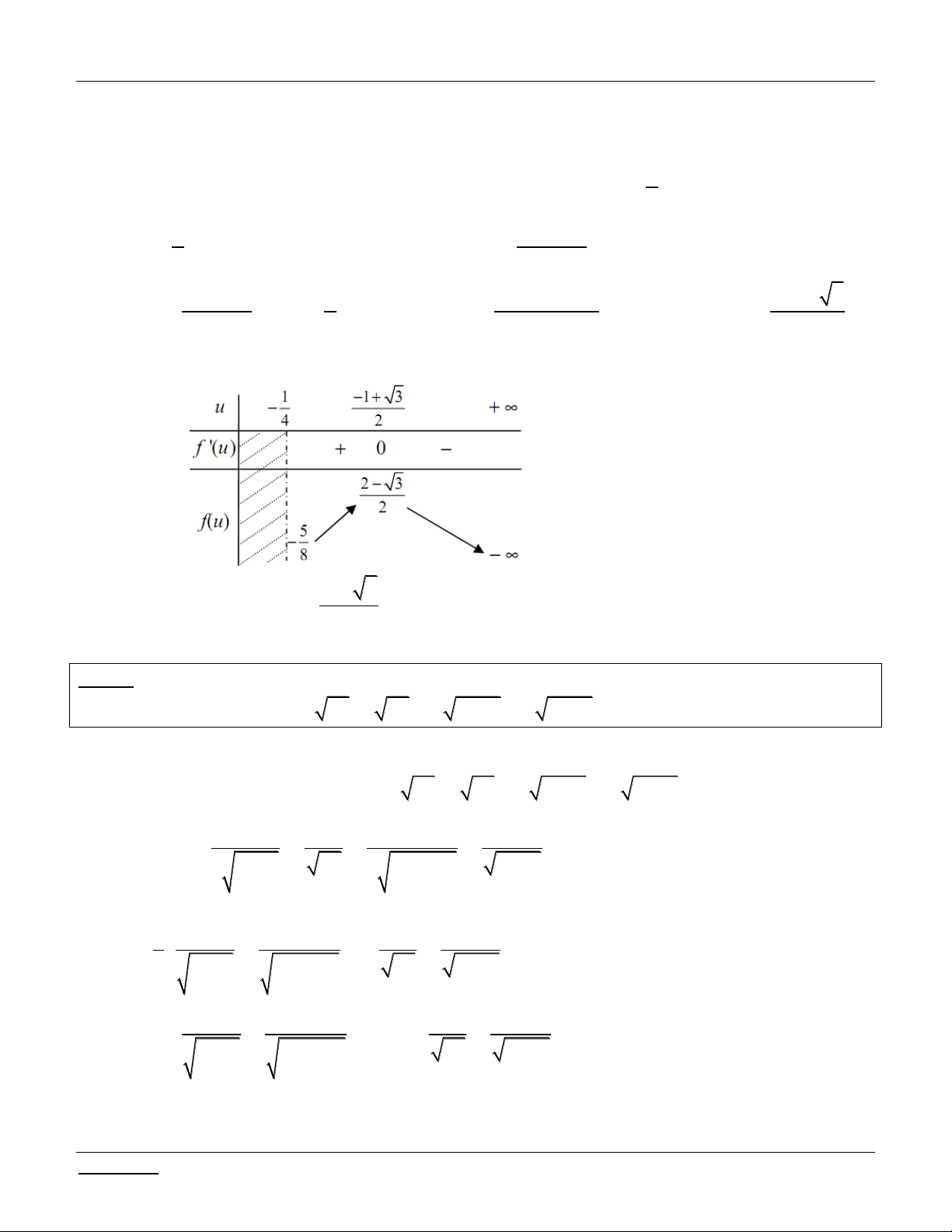
Bài tập 3: T×m m ®Ó ph¬ng tr×nh 3 tan x  1 sin x  2 cos x  m sin x  3 cos x  (1) cã
Giáo viên: LÊ BÁ BẢO...0935.785.115... -15- CLB Giáo viên trẻ TP Huế
Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016    
nghiÖm duy nhÊt x  0  ; .   2     
Bài giải: XÐt x  0
 ; , khi ®ã sin x  0, cos x  0, tan x  0 v¯ sin x  3 cos x  0.   2 
(sin x  2 cos x) tan x  2
PT (1)  3 tan x  1
 m  3 tan x  1  m (2)
(sin x  3 cos x ) tan x  3 t  2
§Æt t  tan x t  0 x  0;   t   m 2  Ló . c ®ã, PT (2) trë th¯nh: 3 1 (3) t  3 t  2 3 t  2 3 t  1
XÐt h¯m sè f (t)  3 t  1 t  0 T . a cã: / f (t)  .   0, t  0 t  3
2 t  1 t  3 2 (t  3)
Lập bảng biến thiên: lim f t  . t
Ta cã, øng víi mçi t  0 tho° m±n PT (3), ta ®îc ®óng mét nghiÖm x  0;   D . o ®ã, PT (1) 2
cã nghiÖm duy nhÊt x  0;   khi v¯ chØ khi PT (3) cã nghiÖm duy nhÊt t  0 D . ùa v¯o BBT, 2
suy ra ycbt l¯ m  2.
Bài tập 3: Tìm m để phương trình sau có đúng hai nghiệm phân biệt: 6 5 4 3 2
x  2x  3x mx  3x  2x 1  0 (1) Bài giải:
+ Rõ ràng x  0 không là nghiệm của phương trình (1).  1   1   1      
+ Với x  0, phương trình (1) 3 2  x     2 x    3 x   m  0  (2) 3     2  x   x     x  1 1 1
Đặt t  x   t  x   x   2  t  2. x x x
Phương trình (2) trở thành: t  2 t    2 t   3 2 3 2
2  3t m  0  t  2t  6t  4 m  0 (3)
Giáo viên: LÊ BÁ BẢO...0935.785.115... -16- CLB Giáo viên trẻ TP Huế
Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016 1
Từ phép đặt t  x 
, ta có với mỗi t  2
 cho ta 1 giá trị của x ; với mỗi t thoả mãn t  2 x
cho ta 2 giá trị x . Do đó, (1) có đúng hai nghiệm phân biệt  (3) chỉ có các nghiệm t  2 và 1 t  2
 , hoặc (3) có đúng 1 nghiệm t thoả mãn t  2 . Ta xét hai trường hợp: 2 8  m  0 
TH 1: (3) có đúng hai nghiệm t  2 và t  2   
không tồn tại m . 1 2 m   0 
TH 2: (3) có đúng một nghiệm t và thoả mãn t  2 . Ta có (3) 3 2
 m  t  2t  6t  4.  2   22 t  
Xét hàm số f t 3 2
 t  t  t  /
t   f t 2 3 2 6 4, 2
 3t  4t  6  0   . 2   22 t   3
BBT: lim f t   ;
 lim f t  . t t     2   22      16  44 22 m f       m  
Dựa vào bảng biến thiên, yêu cầu bài toán   3      27  . m   f   m   0 2    
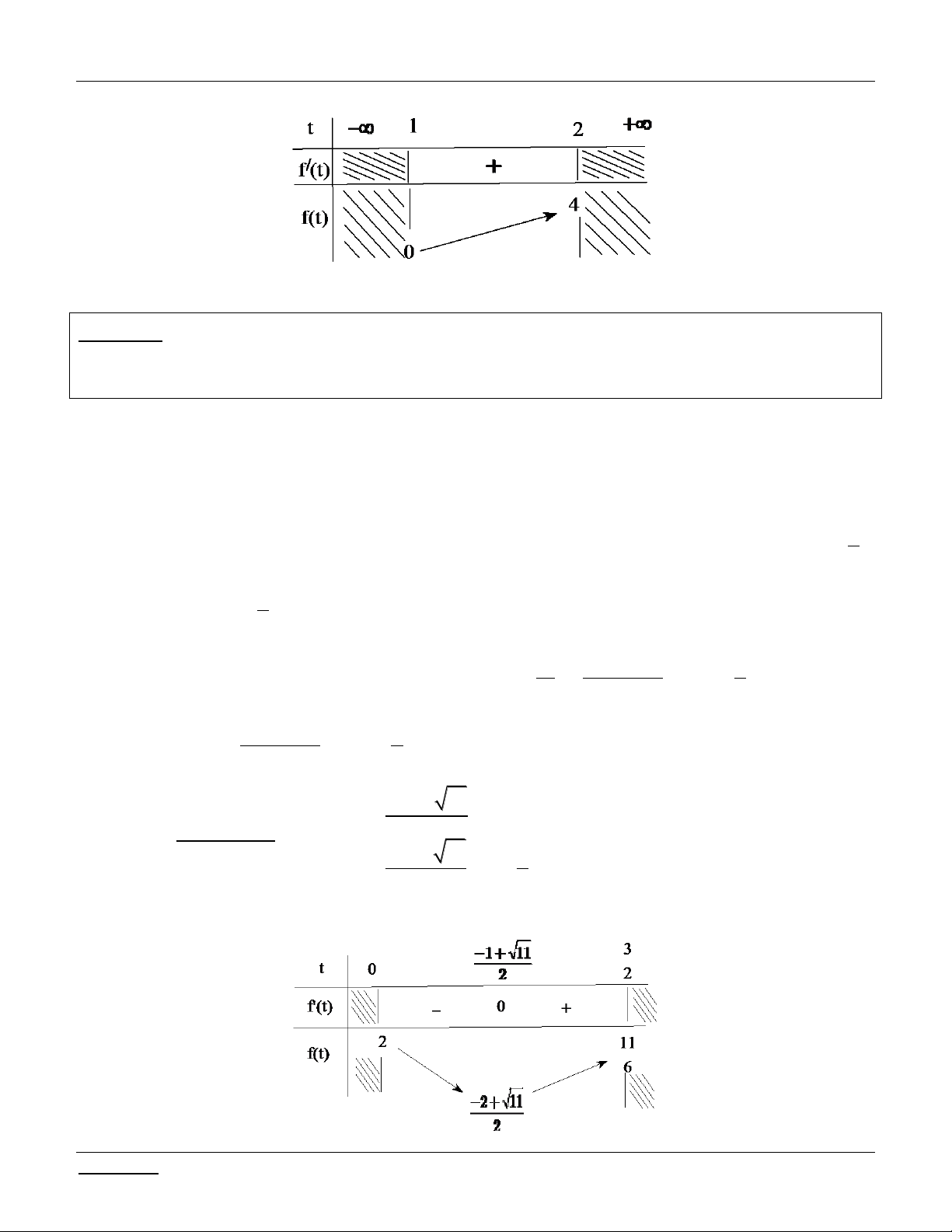
Bài tập 3: (ĐH A - 2002) Tìm m để phương trình sau có nghiệm thuộc 3 1; 3     : 2 2
log x  log x  1  2m 1  0 . 3 3
Bài giải: Điều kiện: x  0 . Đặ   t 2 3 2
t  log x 1  x   1;3
 0  log x  3  0  log x  3 3   3 3   2 1 log x 1 4 t 1  ;2       3   .
Phương trình trở thành: 2 2 t t 2 2m 2m t t 2, t 1  ;2           .
Xét hàm số f t 2 t t / 2, t 1  ;2
f t 2t 1 0, t 1  ;2               .
Giáo viên: LÊ BÁ BẢO...0935.785.115... -17- CLB Giáo viên trẻ TP Huế
Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016 BBT:
Dựa vào bảng biến thiên, yêu cầu bài toán  0  2m  4  0  m  2 .
Bài tập 3: Tìm m để phương trình sau có nghiệm thuộc 0;1   : 1 x  1 x    2 x 2 4 4 1 2 2 x m      2m.
Bài giải: Điều kiện: x   . Phương trình đã cho 44x 4 x   4  1 2x 2 x m       2m m  int 
x  t   0  0   0;1 Đặ          
t t  2x  2 x , / x  0;1  t   x  
2x 2 xln2  0, x  0;1       
t x  t   3 max 1   0;1      2  3  x 
 0;1 : t  0;     2   2 m t t 2  3  
Phương trình trở thành: 2 2 t   2  2m   1 t  m   , t  0;  . 2 2t 1  2    2 t t 2  3  
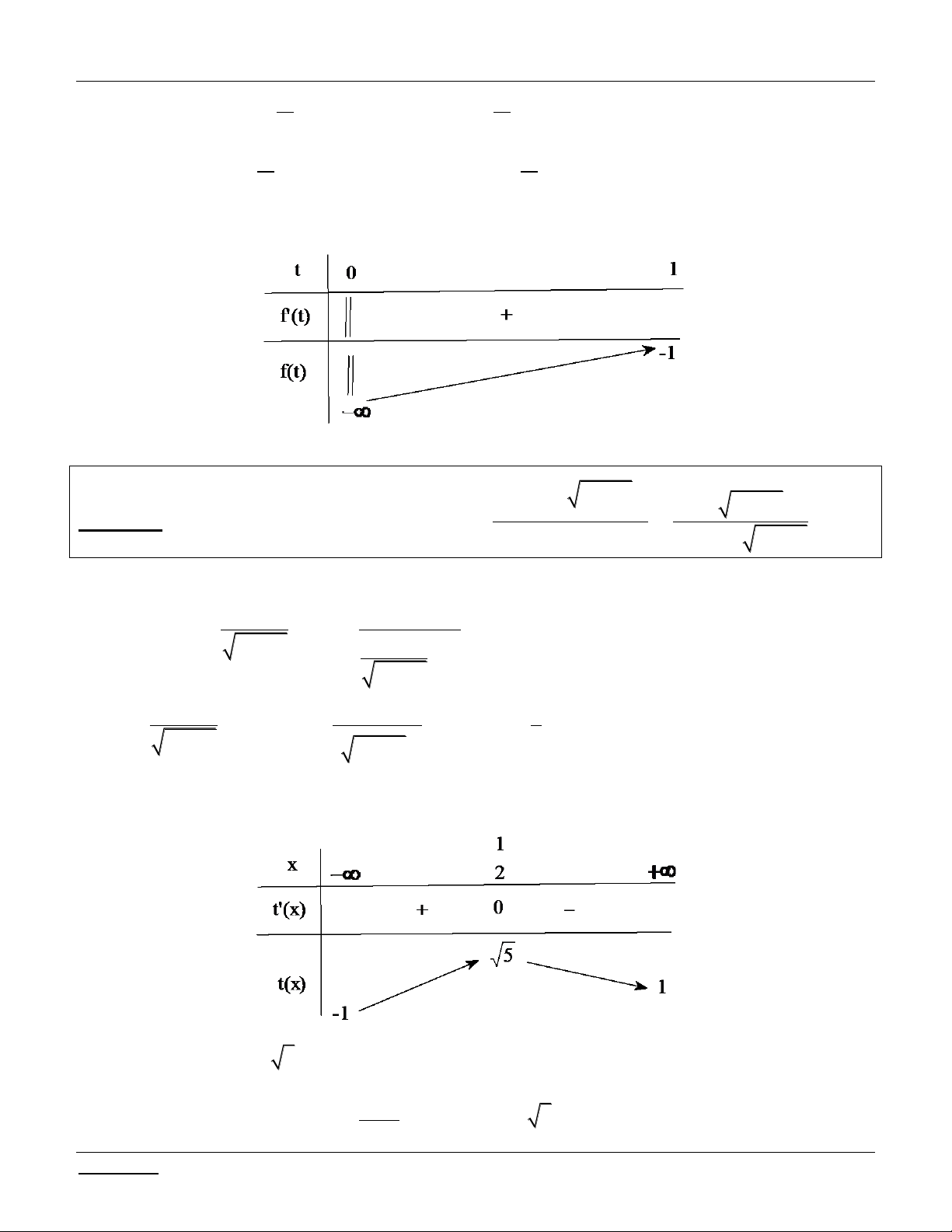
Xét hàm số f t  , t  0;  . 2t 1  2     1   11 t      f t 2 2t 2t 5 / 2   0       t  2 1   11 3 2 1 t    0;   2  2  BBT:
Giáo viên: LÊ BÁ BẢO...0935.785.115... -18- CLB Giáo viên trẻ TP Huế
Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016 2   11 m
Dựa vào bảng biến thiên, yêu cầu bài toán    2  2
  11  m  4 . 2 2
Bài tập 3: Cho ph¬ng tr×nh: 2 2
log x  log x  3  m log x  3 2 1  2  (1) 2
T×m c²c gi² trÞ cña m ®Ó cã ph¬ng tr×nh nghiÖm x   32;    . 
Bài giải: Tõ ®iÒu kiÖn b¯i ra, ta thÊy log x  5, suy ra log x  3  2 nªn m  0. 2  2  PT (1) 2
 log x  2 log x  3  m log x  3 2 2  2  2 2 2
 log x  2 log x  3  m log x  3 2 2  2  (2) 2 t  1
§Æt t  log x t  5 .
t  2t  3  m t  3  m  2   PT (2) trë th¯nh: 2 2   2 (3) t  3 t  1 4 
XÐt h¯m sè f t  t  5 T . a cã: / f t   0 t  5 t  3 t 32 Lập bảng biến thiên:
Lóc ®ã, ph¬ng tr×nh (1) cã nghiÖm x 32;
 khi chØ khi PT (3) cã nghiÖm t     5;      ycbt  2
1  m  3 .KÕt hîp m  0, suy ra: 1  m  3.
Bài tập 3: Tìm m để phương trình sau có nghiệm: 4m   3
x  3  3m  4 1x m 1  0 (1)
Bài giải: Điều kiện: x  3;1     . x    x 
(1)  m  x    x   3 3 4 1 1 4 3 3 1
1  3 x  3  4 1 x  1  m 
4 x  3  3 1 x  1  2 2
 x  3  2sin   
Vì  x  3  1x   4 nên ta có thể đặt       , 0; .
 1 x  2 cos  2    
6 sin   8 cos   1 
Khi đó ta có phương trình: m  (2). Đặt t  tan , khi đó t 0;1 
8 sin   6 cos   1 2   2 2t 1t 2 7t 12t  9 và sin   ; cos  
, (2) trở thành: m  , t 0;1  2 2   1  t 1  t 2 5t 16t  7  .
Giáo viên: LÊ BÁ BẢO...0935.785.115... -19- CLB Giáo viên trẻ TP Huế
Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016 2 2 7t 12t  9
52t  8t  60
Xét hàm số f t , / t 0;1 f t 0, t 0;1         . 2     5t 16t 7      
5t 16t  72 2
Do đó, f t nghịch biến trên 0;1   . BBT: t 0 1 f'(t) _ 9 f(t) 7 7 9 7 9
Dựa vào bảng biến thiên, yêu cầu bài toán   m  . 9 7 x    x 
Nhận xét: Hoàn toàn ta có thể khảo sát trực tiếp hàm số g x  3 3 4 1 1  trên
4 x  3  3 1  x  1  3;1  
 để tìm điều kiện có nghiệm của phương trình.
Bài tập 3: Tìm m để phương trình sau có hai nghiệm phân biệt: 3 2 3 2 x x 3 2 2 x m  2m  
1 3  5 3  5  0 (1)
Bài giải: Điều kiện: x   . 3 2 3 2 x x 3 5    3 5    
(1)  2m  2m   1             0 .  2     2    3 2 x 3 5    Đặt t       t  1, x     .  2    2 1 t 1
Khi đó phương trình trở thành: 2m  2m   1  t  0  2  m  , t  1 . t t  2 3 2 x 3 5    Với 3
t  1 : t       x   log
t . Do đó vớ t  x    i 1 ta có duy nhất 0, với 3 5  2    2
t  1 thì ta có 2 giá trị x .
Giáo viên: LÊ BÁ BẢO...0935.785.115... -20- CLB Giáo viên trẻ TP Huế
Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016 2 2 t 1 t  4t  1
Xét hàm số f t  , /
t  1  f t   0, t   1. t  2 t  2 2 BBT:
Dựa vào bảng biến thiên, yêu cầu bài toán  2
 m  0  m  0 . 1
Bài tập 3: Tìm m để bất phương trình sau nghiệm đúng với mọi x thoả mãn x  : 2 2 x x    2x x   2 2 2 2 9 2 1 6 1 4 x x m m       0 .
Bài giải: Điều kiện: x   . 2 2 2x x  2x x  9 3    
Chia 2 vế của bất phương trình cho 2 2 4 x x  , ta được:    2   m  1   m  1  0  4   2 2 2x x  3 1 Đặ   t t     x 
 2x  x  0  t  1  . Ta có: 2 . 2 2 2 t  2t  1
Bất phương trình trở thành: 2 t 2m 1t m 1 0 m , t 1          ;    . 2t 1   2 2 t  2t  1 2t  2t  4
Xét hàm số f t , t 1  ;  / f t 0 t 2 1           ;  . 2   2t 1    2t   1
BBT: lim f t  . t
Dựa vào bảng biến thiên, yêu cầu bài toán  m  3 .
Bài tập 3: (Cao Đẳng - 2013) Tìm m để bất phương trình sau có nghiệm:
x 2m x 1  m 4.
Giáo viên: LÊ BÁ BẢO...0935.785.115... -21- CLB Giáo viên trẻ TP Huế
Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016
Bài giải: Điều kiện: x  1.
Đặt t  x 1  x   1  t  0 3 t t  4
Bất phương trình trở thành:  2
t 1mt  m  4  m  , t  0. . t  1 t t  t  1 2 3 2t  5t  5 4 / 
Xét hàm số f t , t 0 f t 0 t 1          0; . 2   t 1    t   1 BBT:
Dựa vào bảng biến thiên, yêu cầu bài toán  m  2 .
Bài tập 3: Tìm m để bất phương trình sau nghiệm đúng với mọi x  1;1     2
m 1x 12 1x  16x  3m 1  x  2m 15 .
Bài giải: Điều kiện: x  1;1     .
Bất phương trình  m  x   x  2 1 3 1
 16x 12 1x  2m 15 .  
 2 91 x6 1x1  x 1x m 3 1x  1x   2  5  0   3 1 Đặt /
t  3 1  x  1 x  t x    0, x    1  ;  1 2 1  x 2 1 x   
suy ra min t x  t  
1   2; max t x  t   1  3 2  x   1  ;1  t    2; 3 2     x  1;1 x  1;1             2 2  t  5  
Bất phương trình trở thành: 2
2t  m t   2  5  0  m  , t   2; 3 2   . t  2   2 2 2  t  5   2
 t  8t  5  
Xét hàm số f t  , /
t   2; 3 2  f   t   0, t    2; 3 2   . t  2   t  2 2   BBT:
Giáo viên: LÊ BÁ BẢO...0935.785.115... -22- CLB Giáo viên trẻ TP Huế
Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016 31 
Dựa vào bảng biến thiên, yêu cầu bài toán  m 
min f t  f  .   3 2 t   2;3 2   3 2  2
Bài tập 3: T×m m ®Ó bÊt ph¬ng tr×nh: m  2
x  2x  2  
1  x(2 x)  0 (1) cã  nghiÖm x   0;1  3 .       x 1
Bài giải: §Æt 2
t  x  2x  2 x  0;1 3    . Ta cã / t 
 0  x  1. 2 x  2x  2 Ta cã b°ng biÕn thiªn: Tõ ®ã: 1  t  2.
Víi 1  t  2, ta biÕn ®æi: 2 2 2 2
t  x  2x  2  t  x  2x  2  x
 (2  x)  t  2. 2 t  2 BPT (1) trë th¯nh: 2
m(t  1)  t  2  m  (2) t  1 2 2 t  2 t  2t  2
XÐt h¯m sè f (t) 1 t 2 T . a cã: / f (t) 0, t 1  ;2        . 2 t 1 (t 1)    
Suy ra h¯m sè f (t ® ) ång biÕn trªn 1  ;2.   XÐt b°ng biÕn thiªn:
Giáo viên: LÊ BÁ BẢO...0935.785.115... -23- CLB Giáo viên trẻ TP Huế
Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016  
Lóc ®ã, BPT (1) cã nghiÖm x 0;1
3 khi chØ khi BPT (2) cã nghiÖm t 1  ;2    .       
§iÒu n¯y x±y ra khi m  max 2  f (2)  . t 1  ;2   3  
Nhận xét: Nếu đề bài yêu cầu tìm m để bất phương trình đã cho nghiệm đúng x    0;1  3    
thì yêu cầu bài toán  m  f   1 1   . 2 x
 2y  xy  0 
Bài tập 1: Tìm m để hệ phương trình sau có nghiệm:   .
 x 1  2y 1  m  1
Bài giải: Điều kiện x  1; y  . 2
 x  y 
 x 2 y 0  x  2 y x   4y (1)   Hệ       
 x 1  2y 1  m
 x 1  2y 1  m
 4y 1  2y 1  m (2)     1
(do x  y  0, x   1; y  ) 2 1
Từ (1) ta thấy với mỗi y 
sẽ cho ta một x  1. Vì vậy hệ đã cho có nghiệm  phương trình 2 1 (2) có nghiệm y  . 2 1 
Xét hàm số f y  4y 1  2y 1, y   ;    . 2   2 1 3 1    Ta có: / f y    0  y    ;    . 4y 1 2y 1 4 2 
BBT: lim f y  . y
Giáo viên: LÊ BÁ BẢO...0935.785.115... -24- CLB Giáo viên trẻ TP Huế
Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016 1
Dựa vào bảng biến thiên, yêu cầu bài toán  m  . 2 2
 x y  m  0 (1) 
Bài tập 1: Tìm m để hệ phương trình sau có nghiệm:  . y   xy  2 (2) 
Bài giải: Điều kiện xy  0 . y   2  Phương trình (2) 2
 xy  2 y  
y  4y  4 (do y  0 không thoả mãn phương trình) x    y  2 y  4y  4 4y  4
Thay vào phương trình (1) ta được:
y  m  0  m  , y  2 . y y 4y  4
Xét hàm số f y , y  ;2    y  . 4 Ta có: / f y 0, y ;2      \ 0 2     y  .
BBT: lim f y  4; lim f y   ;
 lim f y  . y y 0 y 0   
Dựa vào bảng biến thiên, yêu cầu bài toán  m  4 hoặc m  2 .
 x  2 3
1  y  m  0 (1)
Bài tập 1: Tìm m để hệ phương trình sau có 3 nghiệm phân biệt:  . x   xy  ( 1 2) 
Bài giải: Điều kiện xy  0 . x   1  Phương trình  (2) 2
 xy  1 x  
x  2x  1 (do x  0 không thoả mãn phương trình) y    x 2 x  2x  1
Thay vào phương trình (1) ta được: 2 3x  6x   m  3. x
Giáo viên: LÊ BÁ BẢO...0935.785.115... -25- CLB Giáo viên trẻ TP Huế
Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016 2 x  2x  1
Xét hàm số f x 2 3x 6x , x  ;1      x  . 6x  7x 1 1 1
Ta có: f x 3 2 /   0  x  1
  x    x  . 2 x 2 3
BBT: lim f x   ;
 lim f x   ;
 lim f x  . x x 0 x 0    11 20   m  3  9   m  12  
Dựa vào bảng biến thiên, yêu cầu bài toán 3 3    . 27    15 7   m  3   4   m    4    4
 x 1  y 3  a (1) 
Bài tập 1: Tìm a để hệ phương trình sau có nghiệm:  . x
  y  2a   1 (2) 
Bài giải: Điều kiện x  1  ; y  3..
Đặt u  x 1  0; v   y  3  0.  u
  v  a u   v  a  Khi đó hệ   trở thành:  , u v  , suy ra là nghiệm của phương       2   2 2 a  2 2 1 a u v a uv       2 a  2a
trình: f t 2 2  t at   0 . 2
Hệ đã cho có nghiệm  f t  0 có nghiệm t , t thoả mãn: 1 2  t f   2 a 2a t 0 1. 0 0 0 a 0;2         1 2 2   .  1 1 x    y   5  x y
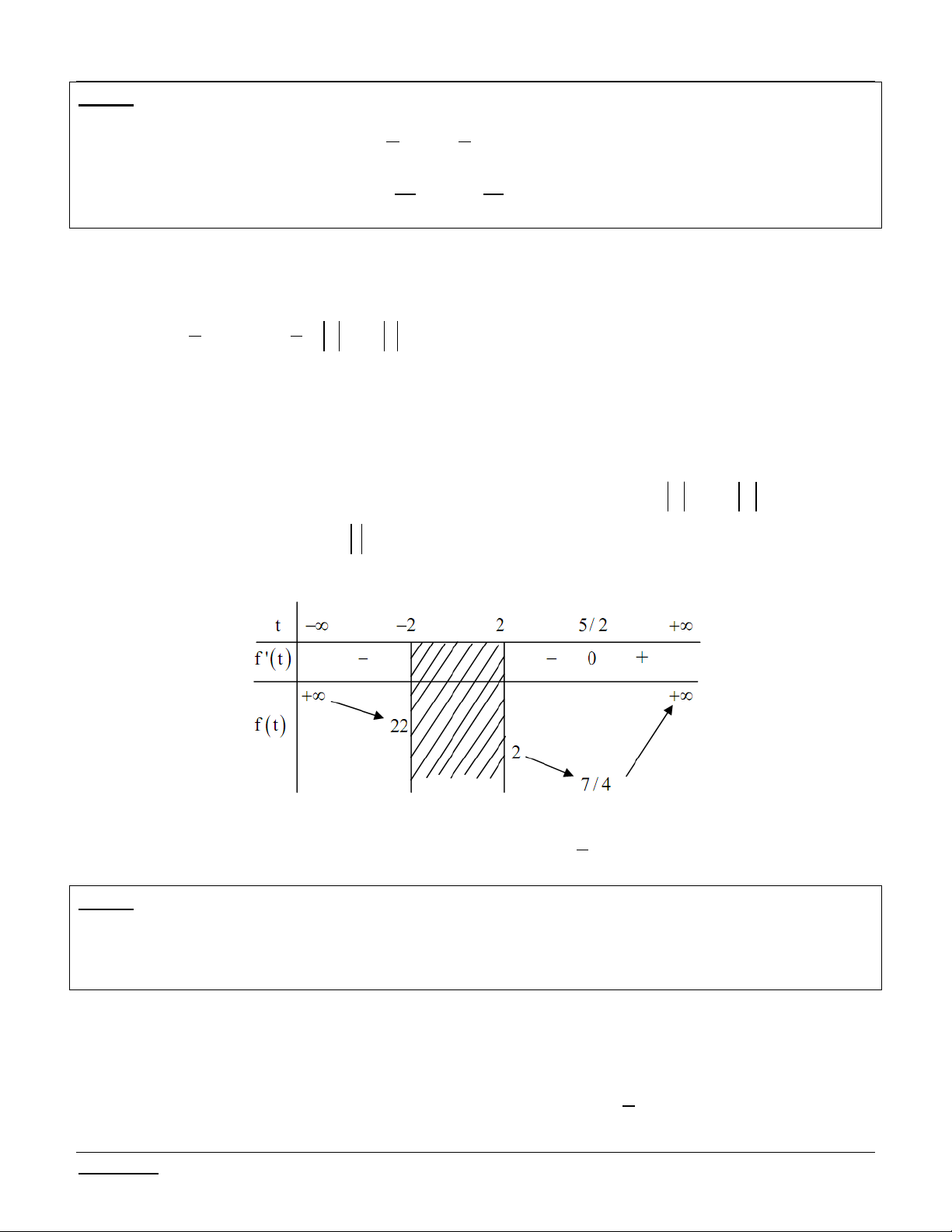
Bài tập 1: Tìm m để hệ phương trình có nghiệm:   3 1 3 1 x    y   15m 10  3 3  x y 
Giáo viên: LÊ BÁ BẢO...0935.785.115... -26- CLB Giáo viên trẻ TP Huế
Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016 3 1 1 1  1      1  1
Bài giải: Đặt u  x 
; v  y  ta có 3 x x    3x  x        u  3u x y 3 x x x x      1 1 1 1 1 và u  x   x   2 x .
 2 ; v  y   2 y .  2 x x x y y u  v  5 u  v  5 Khi đó hệ   trở thành    3 3 u 
 v  3u  v  15m 10 u  v  8 m      ,
u v là nghiệm của phương trình bậc hai f t 2
 t  5t  8  m
Hệ có nghiệm  f t  m có 2 nghiệm t , t thỏa mãn t  2; t  2 . 1 2 1 2
Lập bảng biến thiên của hàm số f t với t  2 t  – 2 2 5/2 +  f t – – 0 + +  +  f t 22 2 7/4 7
Nhìn bảng biến thiên ta có hệ có nghiệm 
 m  2  m  22 4
 x  y  1 
Bài tập 1: Tìm m để hệ phương trình có nghiệm:  (I) x
 x y y  1 3m 
Bài giải: §iÒu kiÖn: x  0, y  0. §Æt u 
x , v  y u  0, v  0 u   v  1 u   v  1 u   v  1    HÖ (I) trë th¯nh:      3 3 2 2 2 2 u 
 v  1 3m (
 u  v)(u uv  v )  1 3m (
 u  uv  v )  1 3m    u   v  1 u   v  1    u   v  1        2 (II) (
 u  v)  3uv  1 3m 1
  3uv  1 3m     uv m    Lóc ®ã: ,
u v l¯ nghiÖm cña ph¬ng tr×nh: 2
X  X  m  0 (*)
HÖ ®± cho cã nghiÖm (x;y)  HÖ (II) cã nghiÖm u  0, v  0
 Ph¬ng tr×nh (*) cã hai nghiÖm X  0.   0 
CáCách 1: Sö dông HÖ thøc Viet: ycbt 1  S
  0  ...  0  m  .  4 P   0 
Cách 2: Ph¬ng tr×nh (*)  2
X  X  m
Giáo viên: LÊ BÁ BẢO...0935.785.115... -27- CLB Giáo viên trẻ TP Huế
Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016 XÐt h¯m sè 2
f X  X  X X  . Ta cã: / 1 ( ) 0
f (X)  12X  0  X  . 2 Ta xÐt b°ng biÕn thiªn:
Dùa v¯o b°ng biÕn thiªn: ycbt  1 0  m  . 4     x y 1 1       4     xy 
Bài tập 1: Tìm m để hệ phương trình sau có nghiệm:  .   1   2 2
 x  y  1       10m  6   2 2    x y  
Bài giải: Điều kiện xy  0 .  1 1 x
 y    4  x y 1 1 Hệ đã cho  
a  x  ; b  y 
 a  2; b  2.  (1). Đặt 1 1 2 2 x   y    10m  6 x y  2 2  x y  a  b  4 a  b  4   a  b  4    Hệ (1) trở thành:      a
  2 b  2  10m  6 
a b2 2 2
 2ab  10m  10 a
 b  3  5m    Suy ra ,
a b là nghiệm của phương trình: 2 2
t  4t  3  5m  0  5m  t  4t  3, t  2 (2)
Hệ có nghiệm  Phương trình (2) có hai nghiệm thoả mãn t  2 .
Xét hàm số f t 2
 t  4t  3, t  2 . Ta có: /
f t  2t  4  0  t  2 .
BBT: lim f t   ;
 lim f t   .  t x
Dựa vào bảng biến thiên, yêu cầu bài toán  3m  15  m  5 .
Giáo viên: LÊ BÁ BẢO...0935.785.115... -28- CLB Giáo viên trẻ TP Huế
Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016 3   2 2
x  y 2xy 2x y  15
Bài tập 1: Tìm m để hệ phương trình sau có nghiệm:  . 2 2 x   y  m  Bài giải:
Đặt S  x  ,
y P  xy , khi đó hệ trở thành:  2   2
3S  2S  8P 15  0 3
 S 2S  8P 15  0 (1)      (I) 2 2 4
 S  8P  4m 4
 S  2S 15  4m (2)    
Hệ đã cho có nghiệm  Hệ (I) có nghiệm S, P thoả mãn: 2 S  4P . Từ (1) ta có: 2 2 2 3S 2S 15 8P 2S S 2S 15 0 S  3;5              .
Do đó, hệ có nghiệm  Phương trình (2) có nghiệm S  3;5     .
Xét hàm số f S  2 4S 2S 15, S  3;5      / 
 . Ta có: f S  2S 2  0  S  1.
BBT: lim f S    ;
 lim f S   .  S S S -3 -1 5 _ f'(S) 0 + 50 f(S) 18 14 7 25
Dựa vào bảng biến thiên, yêu cầu bài toán  14  4m  50   m  . 2 2
Bài tập 2: Tìm m để hệ phương trình sau có nghiệm x;y với x  0, y  0: xy
 x y  3x yxy  . 2 2 x
  y  3xy   m  
5 x  yxy x  y m  33  0  Bài giải:
Đặt S  x  ,
y P  xy , khi đó hệ trở thành: S
 P  3S  P (1)   (I) 2 S   P   m  
5 S SP  m  33  0 (2) 
Hệ đã cho có nghiệm  Hệ (I) có nghiệm S, P thoả mãn: S  0, P  0 và 2 S  4P . Từ (1) ta có: 2 2 2 3S 2S 15 8P 2S S 2S 15 0 S  3;5              .
+ Ta thấy S  1 không thoả mãn (1).
Giáo viên: LÊ BÁ BẢO...0935.785.115... -29- CLB Giáo viên trẻ TP Huế
Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016 2 3 2 3S S
S  4S 12S 0  S  1 
+ Với S  1, từ (1) ta có:  P     (*) S 1 4 4S   0 1 S   4  3S S   0  Mặt khác:  P  0  (**) S 1 S   1  2 S  2S  33
Từ (*), (**) suy ra: S   4;   
và hệ có nghiệm  Phương trình m  có S 1 nghiệm S   4;    . 2 S  2S  33
Xét hàm số f S  , S    4;    . S 1   2 S  2S  35 Ta có: / f S 0 S 7       4; . 2     S   1
BBT: lim f S    .  S
Dựa vào bảng biến thiên, yêu cầu bài toán  m  16.
Bài tập 1: Tìm m để hệ phương trình sau có nghiệm x;y với x  0, y  0: x
  y  4xy   . 2 2 x
  y  7xy  m  Bài giải:
Đặt S  x  ,
y P  xy , khi đó hệ trở thành: S   4P S   4P      (I) 2 2 S   9P  m 1
 6P  9P  m  
Theo định lí Viet, ta có x, y là hai nghiệm thuộc 0;1 của phương trình: 2t 4Pt P  0.
Trước hết ta tìm P để phương trình 2
t  4Pt  P  0 có hai nghiệm thuộc 0;1 . 2 t 1
Yêu cầu tương đương tìm P để phương trình P 
có hai nghiệm thuộc 0;1 t  4t 1  (vì 4 không là nghiệm)
Giáo viên: LÊ BÁ BẢO...0935.785.115... -30- CLB Giáo viên trẻ TP Huế
Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016   2 t 0 t 2t 2t 1  /  
Xét hàm số f t , t 0;1  
. Ta có: f t   0   . 4t 1    2 1 4 1 t t     2
BBT: lim f t   ;
 lim f t     1 1 t t 4 4 2 t
Dựa vào bảng biến thiên, suy ra phương trình P 
có hai nghiệm thuộc 0;1 4t 1  khi và chỉ 1 1 khi  P  . 4 3 1 1
+ Hệ phương trình (I) có nghiệm  Phương trình 2
16P  9P  m có nghiệm P   ;   . 4 3   1 1 9
Xét hàm số g P 2
 16P  9P, P   ;  / 
. Ta có: g P  32P  9  0  P  . 4 3   32 BBT: 1 9 1 P 4 32 3 g'(P) _ 0 + -5 -11 g(P) 4 9 -81 64
Dựa vào bảng biến thiên, suy ra hệ phương trình đã cho có nghiệm thoả yêu cầu bài toán 81 11    m   . 64 9  2 2 x
  y  5x  4y  8  0 
Bài tập 3: Tìm m để hệ phương trình sau có nghiệm:  2 3
 x mx x 16  0 
Giáo viên: LÊ BÁ BẢO...0935.785.115... -31- CLB Giáo viên trẻ TP Huế
Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016
Bài giải: Điều kiện: x  ,  y   .
Phương trình thứ nhất của hệ 2 2
 y  4y  x  5x  8  0 .
Xem phương trình này là phương trình bậc hai theo ẩn y , khi đó phương trình có nghiệm 0 x 1  ;4
       .
Từ đó suy ra, hệ đã cho có nghiệm  Phương trình 2
3x mx x 16  0 (1) có nghiệm x 1  ;4    . Đặt t x t 1  ;2 
    , phương trình (1) trở thành: 16 4 3 3t mt 16 0 m 3t , t 1  ;4        3 t   . 16 48
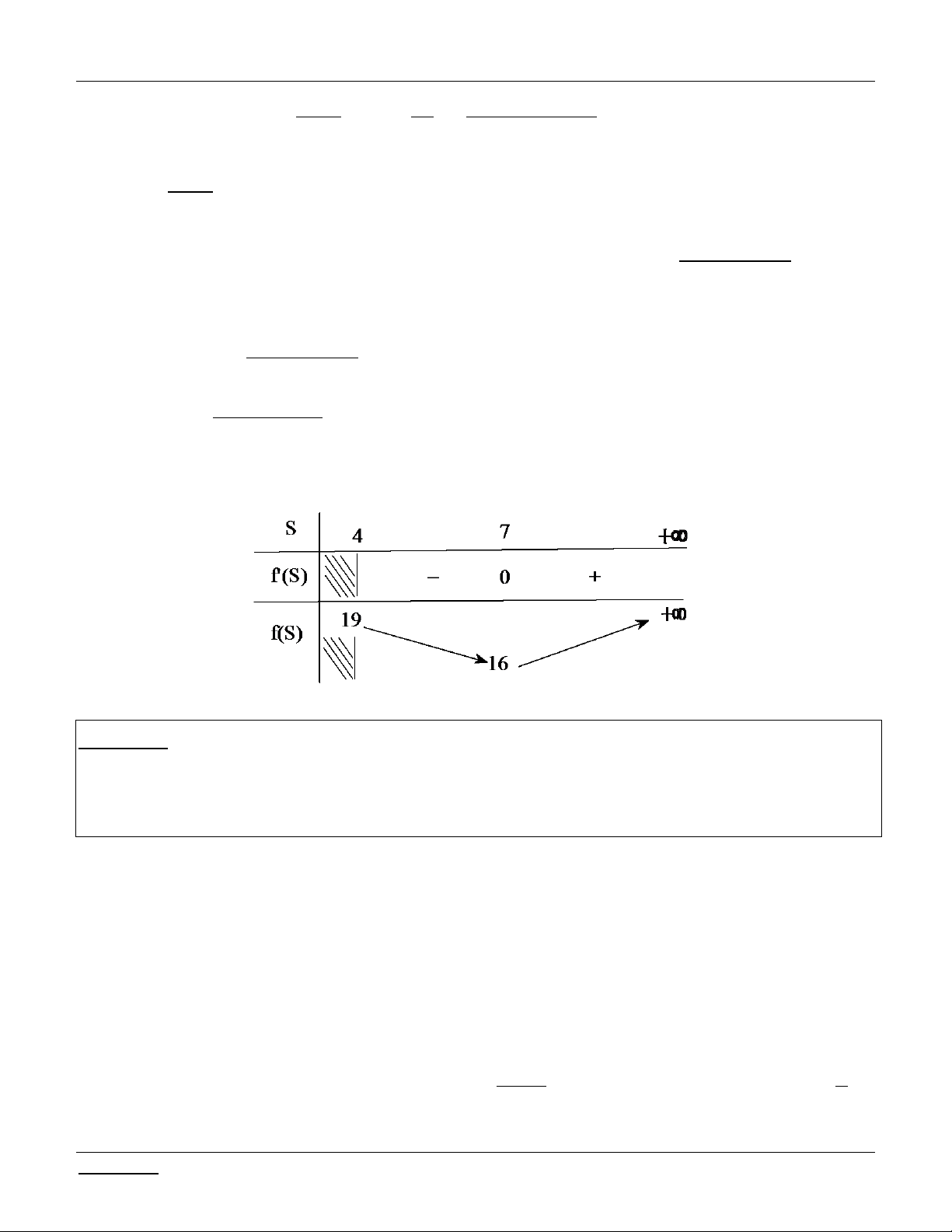
Xét hàm số f t 3t , / t 1  ;4 f t 3 0 t 2 1  ;4           3      4 t t   . BBT: t 1 2 f'(t) _ 0 19 f(t) 8
Dựa vào bảng biến thiên, hệ đã cho có nghiệm  8  m  19 .
Bài tập 3: (HSG Hà Tĩnh 2013) Tìm m để hệ phương trình sau có nghiệm:  2 x  m  y  x my  2 x  y  xy 
Bài giải: Điều kiện: x  ,  y   .  2 m
 y y  m  0 (1)  Hệ đã cho   . 2 x
 yx y  0 (2) 
Xem phương trình (2) là phương trình bậc hai theo biến x , có nghiệm 2 y 4y 0 y  ; 4     
      0;     .
Do đó, hệ đã cho có nghiệm  Phương trình (1) có nghiệm y  ; 4      0;      . y Ta có (1) m , y ; 4        0; . 2     y 1  
Giáo viên: LÊ BÁ BẢO...0935.785.115... -32- CLB Giáo viên trẻ TP Huế
Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016 y
Xét hàm số f y , y ; 4       0; 2     y 1    f y 2 1 y / 0 y 1 ; 4   
       0; . 2       2 y   1
BBT: lim f y  0; lim f y  0 y y 4 1
Dựa vào bảng biến thiên, hệ đã cho có nghiệm    m  . 17 2
Bài tập 4: (HSG Nghệ An 2006) Tìm m để hệ phương trình sau có 3 nghiệm phân biệt: x
 y  m  y   2
1 x  xy  m x   1 
Bài giải: Điều kiện: x  ,  y   . y
  m x (1)  Hệ đã cho   . 3 2 x
 mx  m  0 (2) 
Vì y  m x nên hệ có 3 nghiệm phân biệt  Phương trình (2) có 3 nghiệm phân biệt. x
(2)  x  m x   3 3 2 1  m 
(do x  1; x  1  không thoả mãn (2)) 2 x 1 x
Xét hàm số f x  3  trên tập xác định. 2 x 1 2 x  2 x  3 / 
Ta có: f x  
 0  x  0  x  3  x   3. x  2 2 1
BBT: lim f x   ;
 lim f x   ;
 lim f x   ;
 lim f x   x x x 1 x 1    
lim f x   ;
 lim f x  . x 1 x 1  
Giáo viên: LÊ BÁ BẢO...0935.785.115... -33- CLB Giáo viên trẻ TP Huế
Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016 3 3 3 3
Dựa vào bảng biến thiên, hệ đã cho có nghiệm  m  hoặc m   . 2 2  3 3 2 x
 y  3y  3x 2  0 (1) 
Bài tập 4: Tìm m để hệ phương trình sau có nghiệm:  2 2 2 x
  1x 3 2y y m  0 (2) 
Bài giải: Điều kiện: x  1;1; y 0;2        . 3 2
Phương trình (1)  x    x   3 2 1 3
1  y  3y (3) Vì x  1;1 x 1 0;2          .
Xét hàm số f t 3 2 t t / t       f t 2 3 , 0;2
 3t  6t  0, t     0;  2 
 f t nghịch biến trên 0;2 
 . Phương trình (3) có dạng: f x  
1  f y  y  x 1
Thay vào phương trình (2) ta được: 2 2 x 2 1 x m 0, x  1;1         (4) Đặt 2 u 1 x x  1;1 u 0;1          
  , phương trình (4) trở thành: 2
u  2u 1  m (5)
Hệ đã cho có nghiệm  Phương trình (5) có nghiệm u 0;1    .
Xét hàm số g u 2 u u / 2 1, u 0;1
g u 2u 2 0, u 0;1               . BBT: u 0 1 g'(u) + 2 g(u) -1
Dựa vào bảng biến thiên, hệ đã cho có nghiệm  1   m  2.
Giáo viên: LÊ BÁ BẢO...0935.785.115... -34- CLB Giáo viên trẻ TP Huế
Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016  3 4
 x 3x y   1 2y  1 (1) 
Bài tập 5: Tìm m để hệ phương trình sau có nghiệm:  2 2
 x x  y  2y   2 1  m  0 (2)   1 
Bài giải: Điều kiện: y   ; 0  . 2   
Phương trình (1)   x   x   y  3 3 2 3 2 2 1  3 2y  1 (3)  1   1 
Vì y   ; 0  2y  1   0;1          . Từ (2) suy ra 2 2x x 0 x ; 0  2  x  0;1 2          2  
Xét hàm số f t 3 t t / t       f t 2 3 , 0;1
 3t  3  0, t     0;  1 
 f t nghịch biến trên 0;1
  . Phương trình (3) có dạng: f  2
 x  f  2y 1  2
 x  2y 1  1 
Thay vào phương trình (2) ta được: 2 2 4 2
2x  x  2x  8x  m
 , x   ; 0  (4) 2     1 
Hệ đã cho có nghiệm  Phương trình (4) có nghiệm x   ; 0  . 2      1   2 2 4 2
 x  x  2x  8x  0, x    ; 0  Ta thấy:  2      2  m   0   2 2 4     x  x  x  x  x   4 2 2 8 0 0       m   0 m   0    
Vậy hệ đã cho có nghiệm  m  0.
Nhận xét: Trong trường hợp VP (4) chưa biết dấu thì ta khảo sát f x 2 2 4
 2x  x  2x  8x  1  trên  ; 0 
. Điều này, không hề đơn giản! 2     2 x   2 1  y  2  y  2
1  x   m xy (1)
Bài tập 4: Tìm m để hệ phương trình sau có nghiệm:  2 2 2 2 x
 y 1y  1x  x y x (2) 
Bài giải: Điều kiện: xy  0 . Phương trình (2) 2 2  x 
 x  x y  2 1 1 1  y  (3)
Giáo viên: LÊ BÁ BẢO...0935.785.115... -35- CLB Giáo viên trẻ TP Huế
Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016
Ta thấy x  0 không thoả mãn (3). Mặt khác, vì 2
x  1  x  0 và 2
1 1  y  0 nên từ (3)
suy ra y  0 . Kết hợp điều kiện suy ra x  0 . 1 1 1 Khi đó (3) 2   1 
 y y 1  y (4) 2 x x x Xét hàm số f t 2 t 2
 t t 1  t , t  0;  /
  f t 2  1
 1  t  0, t  0;   2 1  t 1   1
 f t nghịch biến trên 0; 
 . Phương trình (4) có dạng: f    f  
y   y  xy  1  x  x  1    1 1
Thay vào phương trình (1) ta được: 2 x 1        2 1  x  2  m  x   m  2 2 2 2  x  x x 1 Ta có 2 x   2, x
  0 suy ra hệ có nghiệm  m 2  2  m  4. 2 x x y   2 2
xy  x  y  xy (1) 
Bài tập 4: Tìm m để hệ phương trình sau có nghiệm:  1 1 2    m (2)  3 3 x y 
Bài giải: Điều kiện: xy  0 . 1 1 
x y 2 2 3 3
x  xy  y x y 2 2  Ta có: 2   m   m   m 3 3 3 3 3 3 x y x y x y x y2 2 xy x y Thay (1) vào ta đượ   c: 2 2  m     m (3) 3 3 x y  xy 
Đặt t  x  y , khi đó từ (1) ta có: 2
xyt  t  xy  xy t   2 3
3  t và xy  0, t  0, t x y2 2 2 2 2 t t t t 1 t  1 t  3  0  nên xy        0  . t  3 4 4 t  3 4 t  3 t  3   2 x  y t  3 t 3    Mặt khác: 
, phương trình (3) trở thành: 2    m . xy t  t  t 
Xét hàm số f t 3  trên  ;  3 1     ;    t  . 3  / f t 0, t ; 3 1   
      ; 2     t  BBT:
Giáo viên: LÊ BÁ BẢO...0935.785.115... -36- CLB Giáo viên trẻ TP Huế
Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016  2 0  m  1 
Dựa vào bảng biến thiên, hệ đã cho có nghiệm m  2;2     \ 1  , 0,1  . 2     1 m 4       2 x
 y 1 2xy 2x  1 (1) 
Bài tập 4: Tìm a để hệ phương trình sau có nghiệm:  3 x
  3x  3xy  a  2 (2) 
Bài giải: Điều kiện: y  1  .  2 2 x
 z 2xz  1 Đặ 
t z  y  1  0 , hệ trở thành:  3 2 x
  3xz  a  2 
Ta thấy z  0 không thoả mãn hệ.  3 z
  2t 2t  ( 1 1)
Với z  0 , đặt x  tz hệ trở thành:  3 z
  3t 3t  a 2 (2)  t  0 
Do z  0 nên từ (1) suy ra 2
t  2t  0  . t  2  2 t  3
Từ hệ (1), (2) ta có: a  2  , t   ;   0  2;   . t  2 2 t  3
Xét hàm số f t  , t   ;   0  2;   . t  2    f t 2 t 4t 3 / 
 0  t  3   ;  0  2; . 2     t   2
BBT: lim f x   ;
 lim f x   ;
 lim f x   .  t t t 2   
Giáo viên: LÊ BÁ BẢO...0935.785.115... -37- CLB Giáo viên trẻ TP Huế
Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016 a  2 6 a     4  
Dựa vào bảng biến thiên, hệ đã cho có nghiệm     . 3 1 a  2 a       2    2
Bài tập 4: Tìm m để hệ phương trình sau có nghiệm x;y thoả mãn x  1; y  1: x
  y  4  2xy (1)  2x y    m   2 2
x  x  y  y  5  x  y (2) 
Bài giải: Điều kiện: x; y   .
Do x  1; y  1, ta có: x   1 y  
1  0  xy x y1  0
Từ (1)  x  y  4  2x  y  2  0  x  y  6. 1 2 1 2
Mặt khác, từ (1): x  y  4  2xy 
x y  x y x y4  0 2 2
 x  y  4 do x  1; y  1. Vậy x y 4;6    . Đặt t x y t 4;6
      .
Khi đó, (2) trở thành: t   2    t m t t   2 2 1 2
t  1 t  m , (do 2t 1 t >0, t 4;6     ). Xét hàm số   t f t  2 2 t
1 t, t 4;6     .     t  1 / 
 f t  2  2t 1 t ln  2      0, t    4;6     2   t  1 m
 ax f t  f 6  64      37 6 t 4;6      m
 in f t  f 4  16      17 4 t 4;6     
Hệ có nghiệm  16 17  
4  m  64 37   6 .
Giáo viên: LÊ BÁ BẢO...0935.785.115... -38- CLB Giáo viên trẻ TP Huế
Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016
III- MỘT SỐ ĐỀ THI ĐẠI HỌC - CAO ĐẲNG TỪ 2002 - 2016:
 x  y  1 Đề 
01: (D- 2004) Tìm m để hệ sau có nghiệm: x
 x y y  1 3m  x   0 
Bài giải: Điều kiện:  y   0  u   v  1 Đặ  t u 
x, v  y u  0, v   0 . Hệ trở thành  (*) 3 3 u 
 v  1 3m  u   v  1     ,
u v là hai nghiệm của phương trình 2
t t  m  0 (**) u  v  m 
Hệ đã cho có nghiệm x;y  Hệ (*) có nghiệm u  0, v  0 Phương trình (**) có hai
  1 4m  0  1 
nghiệm không âm  S   1  0  0  m  .  4 P   m  0 
Đề 02: (D- 2006) CMR: a
  0 , hệ phương trình sau có duy nhất nghiệm:  x y e  e  ln 
1xln1y y  x  a  x   1 
Bài giải: Điều kiện:  y   1   x a  x e  e  ln 
1xln1a x  0 (1)
Hệ đã cho tương đương với  y
  x a (2) 
Hệ đã cho có nghiệm duy nhất khi chỉ khi phương trình (1) có nghiệm duy nhất trên  1  ;   . Xét hàm số   x a  x f x  e
e  ln1x ln1a x x    1 .
Do f x  liên tục trên  1  ; 
 và lim f x   ,
 lim f x   nên phương trình x 1  x
f x  0 có nghiệm trên  1  ;   . Mặt khác:  a x a x 1 1 / f x x  e e    e  a e   1       x a  x
 x a x 0, x 1. 1 1 1 1
 f x đồng biến trên  1  ; 
 . Suy ra f x  0 có nghiệm duy nhất trên  1  ;   .
Kết luận: Vậy hệ đã cho có nghiệm duy nhất (đ.p.c.m).
Giáo viên: LÊ BÁ BẢO...0935.785.115... -39- CLB Giáo viên trẻ TP Huế
Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016
Đề 03: (D - 2007) Tìm các giá trị của tham số m để hệ phương trình sau có nghiệm thực:  1 1 x
  y   5  x y  1 1 3 3 x    y   15m 10  3 3  x y  x   0 
Bài giải: Điều kiện:  y   0  1 1
Đặt u  x  ; v  y  u  2; v   2 . x y u  v  5 u  v  5   Hệ đã cho trở thành    . 3 3 u   v  3 
u v  15m 10 u  v  8 m     Suy ra ,
u v là nghiệm của phương trình 2 2
t  5t  8 m  0  t  5t  8  m (1) .
Hệ đã cho có nghiệm  Phương trình (1) có hai nghiệm t , t thỏa mãn t  2, t  2 . 1 2 1 2
Xét hàm số f t 2
 t  5t  8 t   2 . Xét bảng biến thiên: 7 
Dựa vào bảng biến thiên, ta có giá trị cần tìm của m là m   ;2  2  2;      . 4   
Đề 04: (ĐH-D-2011) Tìm m để hệ phương trình sau có nghiệm:  3 2  x   y   2
2 x  xy  m  2 x
  x y  1 2m  x    
Bài giải: Điều kiện:  y      2  x x 
2x y  m 1 Hệ đã cho  2 
. Đặt u  x  x   ; v  2x y. 2  x x 
2x y  12m 4 
Giáo viên: LÊ BÁ BẢO...0935.785.115... -40- CLB Giáo viên trẻ TP Huế
Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016   2 uv  m u    
2m  1u m  0 (1) Hệ đã cho trở thành    u
  v  1 2m v
  12m u   1
Hệ có nghiệm khi chỉ khi phương trình (1) có ít nhất 1 nghiệm u   . 4 2 1 u   u
Với u   ;  
1  m 2u   2 1  u
  u  m  . 4 2u  1 2 u   u 1 2 2u  2u 1 1   3
Xét f u  , u   . Ta có /
f u   ; /
f u  0  u  . 2   2u  1 4  u   2 2 1 Bảng biến thiên: 2  3
Suy ra giá trị cần tìm là m  . 2
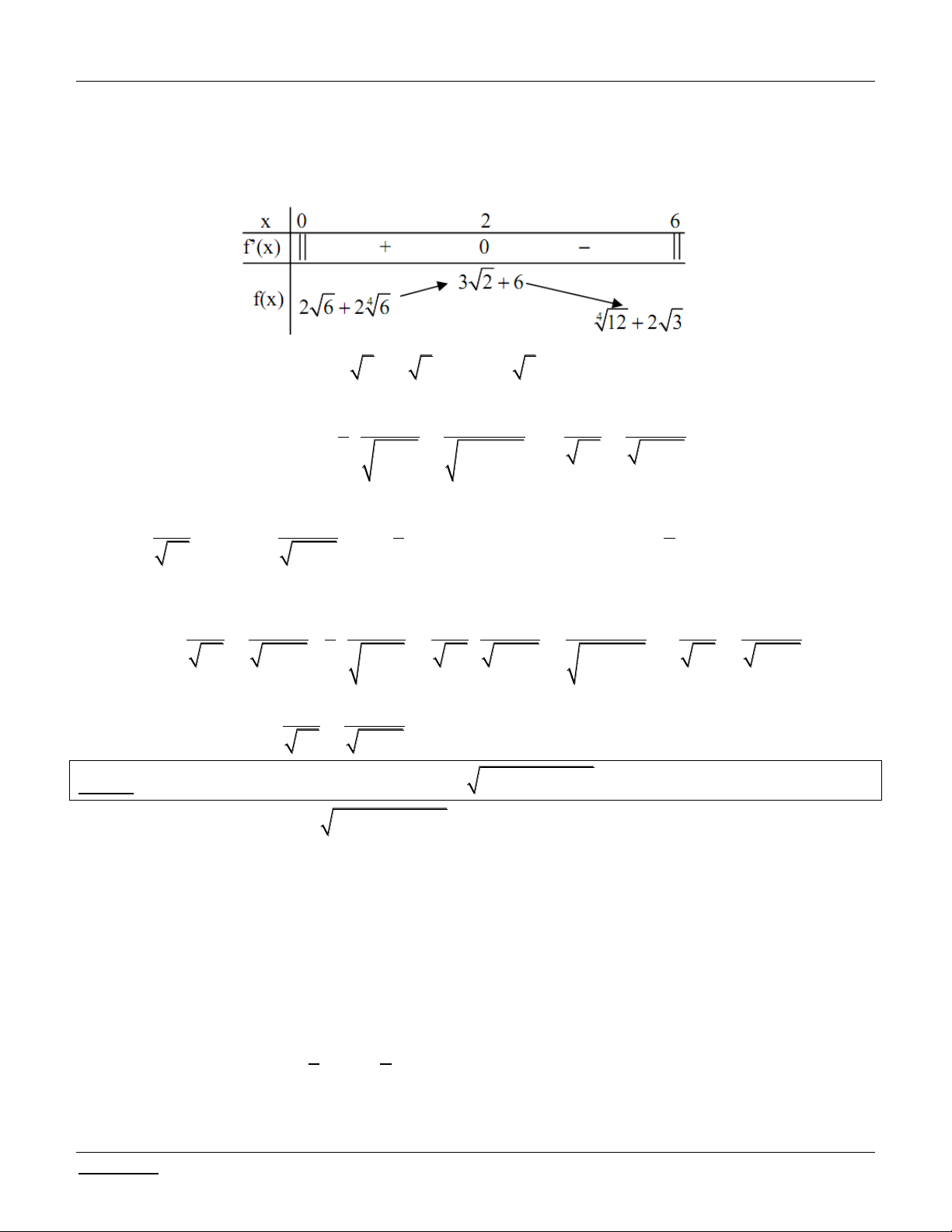
Đề 05: (Khối A- 2008) Tìm m để phương trình sau có hai nghiệm thực phân biệt: 4 4
2x  2x  2 6 x  2 6 x  m
Bài giải: TXĐ: D 0;6   
Đặt vế trái của phương trình là f x 4 4 2x 2x 2 6 x
2 6 x x 0;6          1 1 1 1 Ta có: / f x      3 2x   3 4 4 6 2 2 2 6  x x x     1  1 1     1 1             ;     x  0;  6
2   3   3       4 4 2x 6 2 6 x x x  1 1 1 1
Đặt u x   ; v x   .  3   3 4 4 2x 6 2 6  x x x
Giáo viên: LÊ BÁ BẢO...0935.785.115... -41- CLB Giáo viên trẻ TP Huế
Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016
Ta thấy u    v   / 2 2  0  f  
2  0 . Hơn nữa u x, v x cùng dương trên 0;2 và cùng âm trên khoảng 2;  6 . Ta có bảng biến thiên:
Suy ra các giá trị m cần tìm là: 4
2 6  2 6  m  3 2  6.     1  1 1     1 1       
Giải thích cụ thể hơn: / f x          x  0;  6
2   3   3       4 4 2x 6 2 6 x x x    1 1 1 1  Đặt a   0; b  , ta có  3 3
a b   2 2
a b   a b  2 2
a ab b  a b 4 4 2x 6  x 2 2 
  0            1 1   1  1 1 1 1    1 1  /
 f x       .              4 4  2x 6  x  2     4    2 4 4 2x 6 x 4   2 4 4 2x 6 2 6  x x x       1 1
Do đó ta chỉ cần xét dấu  . 4 4 2x 6  x
Đề 06: (Dự bị- 2007) Tìm m để phương trình: 4 4
x 13x  m  x 1  0 có nghiệm.
Bài giải: Phương trình (1) 4 4
 x 13x  m  1x x   1  x   1       x
 13x m  1x4 3 2 4 4
 x  6x  9x  1m   
Ycbt  đường thẳng y  1 m cắt phần đồ thị f x 3 2
 4x  6x  9x ; x   1 tại ít nhất một giao điểm.
Ta có: f x 3 2
 x  x  x ; x   /  f x 2 
x  x    2 4 6 9 1 12 12 9
3 4x  4x   3 1 3 Ta có: /
f x  0  x    x  . 2 2 Bảng biến thiên:
Giáo viên: LÊ BÁ BẢO...0935.785.115... -42- CLB Giáo viên trẻ TP Huế
Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016 5 3
Từ bảng biến thiên ta có, ycbt  1  m   m   . 2 2
Đề 07: (Dự bị- 2007) Tìm m để phương trình: x  3 2 x  4  x  6 x  4  5  m có đúng 2 nghiệm.
Bài giải: TXĐ: D   4;   
Phương trình cho  x  42 x  4 1  x  46 x  4  9  m 2 2   x 4  
1   x 4   3  m 
x  4 1  x  4  3  m (1)
Đặt: t  x  4  0 , (1) trở thành: t 1  t  3  m (2)
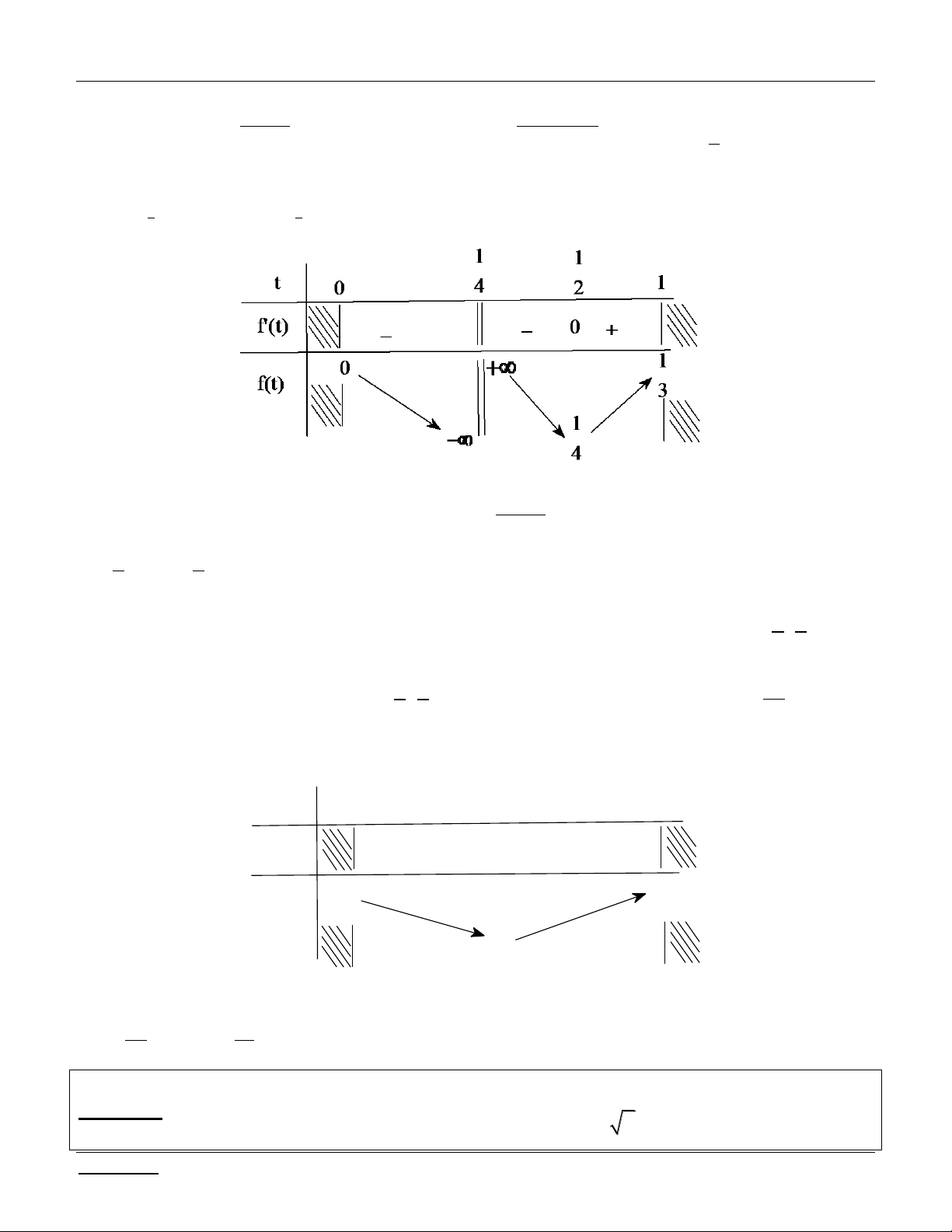
Phương trình cho có đúng 2 nghiệm  phương trình (2) có đúng 2 nghiệm t  0.
Cách 1: Vẽ đồ thị của hàm số f t  t 1  t  3 t   0 y 4  2t 4 nÕu 0  t  1 
Ta có f t  2  nÕu 1  t  3  2 2
 t  4 nÕu t  3 
Từ đồ thị ta có, ycbt  2  m  4 . t 1 O 2 3 Cách 2: 0   t  1 1   t  3 t   3
 t 1  t  3  m    t   0   hay  hay  m   4  2t m   2 m   2t  4        0   t  1 t   3  1   t  3  2  m 4      hay  hay m   2 . Do đó, yêu cầ   m   u bài toán 2 4 m   2   4  m   4  m t   t     2    2
(khi 2  m  4 thì (2) có đúng 2 nghiệm t , t thỏa 0  t  1 và t  3 ) 1 2 1 2
Đề 08: (Dự bị- 2007) Tìm m để phương trình: 4 2
x 1  x  m có nghiệm.
Giáo viên: LÊ BÁ BẢO...0935.785.115... -43- CLB Giáo viên trẻ TP Huế
Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016
Bài giải: TXĐ: D   0;   
Xét hàm số f x 4 2
 x 1  x ; x   0;    .     1  x 1  x x x 1     / f x    0 , x   0 . Vì    2  3 6  x x  2 4      3  2 4 1 x x    x   3 4 2 1 x
Ta có f x  nghịch biến trên 0;   
và lim f (x) 0 nên ta có 0 f (x) 1, x      0;    x    .
Vậy, phương trình (1) có nghiệm  m thuộc miền giá trị của f x  trên đoạn 0;     0  m  1.
Đề 09: (Khối A- 2007) Tìm m để phương trình sau có nghiệm: 4 2
3 x 1  m x 1  2 x 1 x 1 x 1
Bài giải: TXĐ: D 1   ;    . Ph¬ng tr×nh ®± cho 4  3   2  m (1) x  1 x  1 x 1 §Æt t  , khi ®ã (1) trë th¯nh: 2 4
 3t  2t  m (2) x  1 x 1 2 V× 4 4 t   1 v¯ x  1 nªn 0  t  1 x  1 x  1 x 1
(Hoặc sử dụng đạo hàm với 4 t 
, t  0, x  1) x  1
H¯m sè f t 2  3
 t  2t 0  t   1 cã b°ng biÕn thiªn:
Phương trình đã cho có nghiệm  Phương trình (2) có nghiệm t   0;  1  1
Dựa vào bảng biến thiên ta có các giá trị m cần tìm là: 1   m  . 3
Đề 10: (Khối B- 2007) Chứng minh rằng với mọi giá trị dương của tham số m , phương trình sau
luôn có hai nghiệm thực phân biệt: 2
x  2x  8  m x   2
Bài giải: Theo giả thiết m  0 , ta có điều kiện của phương trình là x  2 .
Giáo viên: LÊ BÁ BẢO...0935.785.115... -44- CLB Giáo viên trẻ TP Huế
Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016
Phương trình đã cho tương đương với    x  x 2  2 3 2 x 6x 32 m 0         . 3 2
x  6x  32 m  0 
Ta chứng minh phương trình 3 2
x  6x  32  m (1) có một nghiệm thuộc 2;   . /
Xét hàm số f x 3 2  x  x 
x    f x 2 6 32 2
 3x 12x  0 x   2 . Bảng biến thiên:
Dựa vào bảng biến thiên ta thấy, với m  0 phương trình (1) luôn có nghiệm thuộc 2;   nên
phương trình đã cho luôn có hai nghiệm thực phân biệt.
Đề 11: (Dự bị- 2007) Tìm m để phương trình: m  2
x  2x  2  
1  x(2  x)  0 có nghiệm x 0;1 3      
Bài giải: TXĐ: D   . Đặt 2 2 2
t  x 2x  2  0  t 2  x 2x 2 t  2  
Bất phương trình  m  1 t   2 , do x  0;1  3   t  1   2 t  2
Khảo sát g(t) 
với 1  t   2 t  1 t  2t  2
Ta có: g t 2 / 
 0 . Vậy g t đồng biến trên 1;2 2 (t  1)   . 2 t  2
Do đó, yêu cầu bài toán  Bất phương trình m  có nghiệm t 1  ;2  t  1   2
 m  max g t  g   2  . 1  ;2   3
Đề 12: (Khối B- 2006) Tìm m để phương trình sau có hai nghiệm thực phân biệt: 2
x  mx  2  2x 1 (1) Bài giải:
Giáo viên: LÊ BÁ BẢO...0935.785.115... -45- CLB Giáo viên trẻ TP Huế
Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016  1   1 x    x       Ta có: 2
x  mx  2  2x  1   2   2   x
 mx 2  2x  2 2 2 1 3  x  
m 4x 1  0 (2)  
Để phương trình (1) có 2 nghiệm phân biệt 1
 Phương trình (2) có 2 nghiệm x , x thỏa mãn:   x  x 1 2 1 2 2 
  m  42  12  0 m S m 4 1 9        m   2 6 2 2    1   3 m  4 f      1  0 víi f    x 2
 3x m  4x 1   2 4 2 
Cách khác: Để phương trình (1) có 2 nghiệm phân biệt 1
 Phương trình (2) có 2 nghiệm x , x thỏa mãn:   x  x 1 2 1 2 2 2 3x 1  1    Ta có: 2
3x 1  m  4x  m  4 
 g x x     x  2  1  
Tiến hành khảo sát y  g x  x     
, dựa vào bảng biến thiên và đưa ra kết luận.  2
Đề 13: (Dự bị- 2004) Tìm m để phương trình sau có nghiệm:  5 2  2  2 2 x  m 
  x  4  2 m  0   3
Bài giải: TXĐ: D   Đặt 2
x  4  t  2.  5
Phương trình đã cho tương đương vớ   i: 2 2 2 t  4  m 
 t  2 m  0   3 t  t 
 3t  3m  
5 t  6  3m  0  3t  5t  6  3m 1t 2 3 5 6 2 2 2 2 2 2  3m  1t 2 3t  5t  6 2 3
 t  6t 11
Đặt f t  , t  2 . Ta có / f t   0 t   2 . 1t 1t2
Suy ra f t giảm và liên tục trên 2  ;    , f   2  4 
và lim f t  . x 2
Vậy phương trình có nghiệm khi và chỉ khi 2
3m  4  m  . 3
Giáo viên: LÊ BÁ BẢO...0935.785.115... -46- CLB Giáo viên trẻ TP Huế
Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016
Đề 14: (Khối B- 2004) Tìm m để phương trình sau có nghiệm: m  2 2  x  x   4 2 2 1 1
2  2 1 x  1  x  1 x
Bài giải: TXĐ: D  1;1     Đặt 2 2 t   x  x Do 2 2 1 1 .
1  x  1x  t  0; t  0  x  0 . 2 4
t  2 2 1x  2  t  2, t  2  x  1 x  1  .    Suy ra: x   1  ;1  t   0; 2            liên tục trên 1;1   . 2 t   t  2
Phương trình đã cho trở thành m t   2 2  t
  t  2  m  (*) t  2 2 t   t  2    
Xét f t  t  0; 2 
 . Ta có f t liên tục trên 0; 2      t 2   .
Phương trình đã cho có nghiệ 
m x  Phương trình (*) có nghiệm t   0; 2    
 min f t  m  max f t 0; 2 0; 2         2 t   4t     Ta có: / f t   0 t   0; 2  f t   nghịch biến trên 0; 2 2      t  2      .
Suy ra min f t  f     .  
 2 2 1; maxf t f  0 1 0; 2 0; 2        
Vậy các giá trị m cần tìm là: 2 1  m  1.
III- BÀI TẬP TỰ LUYỆN:
Bài 1: Tìm m để phương trình sau có hai nghiệm phân biệt: 2
m x 1  x  2 m .
Bài 2: Tìm m để phương trình sau có nghiệm: 2
x x  x 1  2 x  m .
Bài 3: Tìm m để phương trình sau có nghiệm:    x  x  2 2  2  4 m  . x 
 3 x x   2   2    .  x  2    
Bài 4: Tìm m để phương trình sau có 4nghiệm phân biệt thuộc  ;   : 4 4    4 4 4
sin x  cos x  cos 4x  m .
Bài 5: Tìm m để phương trình sau có nghiệm thuộc 0; 
1 : 4log x 2 log x m  0. 2 1 2
Bài 6: Tìm m để phương trình sau có nghiệm thuộc 32;    :
Giáo viên: LÊ BÁ BẢO...0935.785.115... -47- CLB Giáo viên trẻ TP Huế
Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016 2 2
log x  log x  3  m log x  3 . 2 1  2  2
Bài 7: Tìm m để phương trình sau có nghiệm thuộc 2; 4: m   2
1 log x  2  m  5 log x 2  m 1  0 . 1     1   2 2
Bài 8: Tìm m để bất phương trình sau có nghiệm: x x 1 4 . m 2    3 2m  0 .
Bài 9: Tìm m để phương trình sau có nghiệm: 2
4 6  x  x  3x  m  x 2 2 3x .
Bài 10: Tìm m để phương trình sau có nghiệm: 3
x  4x  x 1  m . 1 
Bài 11: Tìm m để pt sau có nghiệm trên  ;2  : 2
log x  5 log x  3m  0 4  2 2  
Bài 12: Tìm m để pt sau có nghiệm thực: 4 2
3 x 1  m x 1  2 x 1 2 2
Bài 13: Tìm m để pt sau có 4 nghiệm thực phân biệt : x 2  x x 2  x 1 4 2   m  0
Bài 14: Cho bất hương trình: 2 2
x 1  4 x  m (1)
a, Tìm m để bpt (1) có nghiệm
b, Tìm m để bất phương trình nghiệm đúng với mọi x  [1; 2].
Bài 15: Cho bất phương trình: 2 2 x x 1 4 . m 2  
m  0 . Tìm m để bất phương trình nghiệm đúng
với mọi x  R 1
Bài 16: Tìm m để bất phương trình nghiệm đúng với mọi x sao cho x  2 2 2 2 2x x  2x x  2 9 2( 1)6 ( 1)4 x x m m       0
Bài 17: Tìm a để pt sau có nghiệm: x  1  3  x  (x  1)(3  x)  2a
Bài 18: Tìm m để pt có đúng 2 nghiệm thực phân biệt: 4 4
2x  2x  2 6 x  2 6 x  m 1
Bài 19: Tìm m để pt sau có nghiệm: 4 4 2
sin x  cos x  cos 2x  sin 2x  m  0 4 
Bài 20: Tìm m để pt sau có nghiệm x  (0; ) : 2
Giáo viên: LÊ BÁ BẢO...0935.785.115... -48- CLB Giáo viên trẻ TP Huế
Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016 1 1 1
sin x  cos x  1  (tan x  cot x   )  m 2 sin x cos x
Bài 21: Tìm m để pt sau có nghiệm thuộc (0; 1): 2 4 log
x  log x  m  0 2 1 2
Bài 22: Tìm m để bpt có nghiệm: 4x  2x m m  3  0.
Bài 23: Tìm m để bpt sau nghiệm đúng với mọi x  R : 6 6
sin x  cos x  sin x cosx  m
Bài 24: Tìm m để bpt nghiệm đúng với x  4;6      : 2
(4  x)(6 x)  x 2x  m
Bài 25: Tìm m để pt sau có hai nghiệm thực phân biệt: 2
x  mx  2  2x 1
Bài 26: Chứng minh rằng với mọi giá trị của tham số m , phương trình sau luôn có hai nghiệm thực phân biệt: 2 (
m x 2)  x  2x  8
 x 1  y 1  m 
Bài 27: Tìm m để hệ phương trình sau có nghiệm:  . x
  y  2m 1  2
 x y m  0 
Bài 28: Tìm m để hệ phương trình sau có nghiệm duy nhất:  . x   xy  1   2 x   3x  4  0 
Bài 29: Tìm m để hệ sau có nghiệm:  3 x
  3 x x m  0 
V- TÀI LIỆU THAM KHẢO:
1) Tuyển tập đề thi ĐH - CĐ toàn quốc
Bộ giáo dục và đào tạo
2) Phƣơng pháp hàm số trong giải toán
TS. Lê Xuân Sơn - ThS. Lê Khánh Hưng
3) Tuyển tập đề thi thử ĐH trên toàn quốc
4) Tạp chí Toán học và Tuổi trẻ
NXB Giáo dục Việt Nam
Giáo viên: LÊ BÁ BẢO...0935.785.115... -49- CLB Giáo viên trẻ TP Huế
Phương trình - Bất phương trình - Hệ phương trình chứa tham số Luyện thi THPT Quốc gia 2016
P/S: Các bài tập trong tài liệu chưa nhận được sự cho phép của quí thầy cô và các cơ quan liên
quan, nhưng tài liệu biên soạn chỉ với mục đích chia sẽ cho đồng nghiệp và tặng cho các em học
sinh có nguồn tư liệu quí để phục vụ khả năng tự học nên chúng tôi xin phép các tác giả, xin cảm ơn các tác giả!
Trong quá trình biên soạn không thể tránh khỏi sai sót, kính mong quí thầy cô và các em học
sinh đóng góp để các bản update tiếp theo được hoàn thiện hơn! Xin chân thành cám ơn!
CLB GIÁO VIÊN TRẺ TP HUẾ
Phụ trách chung: Giáo viên LÊ BÁ BẢO.
Đơn vị công tác: Trƣờng THPT Phong Điền, Thừa Thiên Huế.
Email: beckbo1210@yahoo.com
Facebook: Lê Bá Bảo
Số điện thoại: 0935.785.115
Giáo viên: LÊ BÁ BẢO...0935.785.115... -50- CLB Giáo viên trẻ TP Huế