Phương trình lôgarit chứa tham số

Tài liệu gồm 14 trang, được biên soạn bởi quý thầy, cô giáo Nhóm Toán VDC & HSG THPT, hướng dẫn phương pháp giải bài toán Phương trình lôgarit chứa tham số; đây là dạng toán thường gặp trong chương trình Toán 12 phần Giải tích chương 2.

25 13 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 6: Hàm số mũ và hàm số lôgarit (KNTT)

Môn: Toán 11

Thông tin:

29 trang 8 tháng trước

Tác giả:

Profile Kim Oanh
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 1
PHƯƠNG TRÌNH LÔGARIT CHỨA THAM SỐ
PHƯƠNG PHÁP
Tìm m để
, 0f x m
có nghiệm (hoặc có
k
nghiệm) trên D trong phương trình logarit chứa tham số:
Bước 1. Tách m ra khỏi biến số và đưa về dạng
f x A m
.
Bước 2. Khảo sát sự biến thiên của hàm số
f x
trên D.
Bước 3. Dựa vào bảng biến thiên để xác định giá trị của tham số
m
để đường thẳng
y A m
nằm ngang cắt đồ thị hàm số
y f x
.
Bước 4. Kết luận các giá trị cần tìm của m để phương trình
f x A m có nghiệm (hoặc có
k nghiệm) trên D.
Lưu ý
Nếu hàm số
y f x
có giá trị lớn nhất và giá trị nhỏ nhất trên D thì giá trị
A m
cần tìm là
những m thỏa mãn:
min max
x D
x D
f x A m f x
.
Nếu bài toán yêu cầu tìm tham số để phương trình có k nghiệm phân biệt, ta chỉ cần dựa vào bảng
biến thiên để xác định sao cho đường thẳng
y A m
nằm ngang cắt đồ thị hàm số
y f x
tại
k
điểm phân biệt.
Lưu ý quan trọng:
Các bước giải phương trình logarit có tham số cần chú ý:
 Bước 1. Đặt điều kiện (điều kiện đại số
điều kiện loga):
Đ
0 1
log
0
a
K
a
b
b

và
Đ
Đ
log 0
log 0
K
a
K
a
f x f x
f x f x


.
 Bước 2. Dùng các công thức và biến đổi đưa về các phương trình cơ bản rồi giải.
 Bước 3. So với điều kiện và kết luận giá trị tham số cần tìm.
Câu 1. Cho hàm số
2 2
8 1
2
3log 2 2 3 1 2 log 1 6 0x m x m x x m
. Số các giá trị nguyên
của m để phương trình đã cho có hai nghiệm phân biệt
1 2
,x x thỏa mãn
1 2
15x x
là:
A.
13
2
m
.
B.
2 3
2
m
. C.
13 2 3
2 2
m
. D.
3
4
m .
Lời giải
Chọn C
Ta có:
2 2
8 1
2
3log 2 2 3 1 2 log 1 6 0x m x m x x m
2 2
2 2
log 2 2 3 1 2 log 1 6x m x m x x m
2
2 2
1 6 0
2 2 3 1 2 1 6
x x m
x m x m x x m
mũ l
ẻ
mũ ch
n
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
Trang 2 TÀI LIỆU ÔN THI THPT QUỐC GIA
2
2
2
1 6 0 *
1 6 0
2
2 2 4 0 1
2
x x m
x x m
x m
x m x m
x
Phương trình đã cho có hai nghiệm phân biệt khi và chỉ khi phương trình (1) có hai nghiệm
phân biệt thỏa mãn (*)
2
2
2
4 2 1 6 0
4 8 1 0
2 3
2 2 1 6 0 .
2
3 6 0
2 2
m m m
m m
m m
m
m
Theo giả thiết
2
2
1 2
13 17
15 2 2 225 4 8 221 0
2 2
x x m m m m
.
Do đó
13 2 3
2 2
m
.
Câu 2. Cho phương trình
2
4 2 2
log log 5 1 log 0
x x m
(
m
là tham số thực). Có tất cả bao nhiêu
giá trị nguyên của
m
để phương trình đã cho có nghiệm?
A.
0
m
. B.
5
m
. C.
0 5
m
. D.
3
4
m
.
Lời giải
Chọn C
Điều kiện:
1
5
0
x
m
.
Xét phương trình:
2
4 2 2
log log 5 1 log
x x m
1
.
2 2 2 2 2
5 1 5 1 1
1 log log 5 1 log log log 5 2
x x
x x m m m m
x x x
.
Xét
1
5f x
x
trên khoảng
1
;
5
.
Có
2
1 1
0, ;
5
f x x
x
và
1
lim lim 5 5
x x
f x
x
 
.
Ta có bảng biến thiên của hàm số
f x
:
Phương trình
1
có nghiệm khi và chỉ phương trình
2
có nghiệm
1
5
x
.
Từ bảng biến thiên suy ra phương trình
1
có nghiệm khi và chỉ khi
0 5
m
.
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 3
Câu 3. Tìm tất cả các giá trị nguyên của tham số thực
m
để phương trình
2
3 1
3
4 log log 0
x x m
có hai nghiệm phân biệt thuộc khoảng
0;1
.
A.
0
B.
1
C.
2
D.
3
Lời giải
Chọn A
Ta có:
2 2
2
3 1 3 3 3 3
3
4 log log 0 2log log 0 log log 1
x x m x x m x x m
Đặt
3
log
t x
với
;0
t 
.
2
1
t t m
.
Xét
2
f t t t
.
' 2 1
1
' 0
2
f t t
f t t
Bảng biến thiên
Dựa vào bảng biến thiên
1 1
0 0
4 4
m m
.
Vậy không có giá trị nguyên
m
nào thỏa mãn yêu cầu bài toán.
Câu 4. Tìm các giá trị thực của tham số
m
để phương trình
2
3 3
log 3log 2 7 0
x x m
có hai nghiệm
thực
1 2
,
x x
thỏa mãn
1 2
3 3 72.
x x
A.
61
2
m
. B.
3
m
. C.
9
2
m
. D.
3
2
m
.
Lời giải
Chọn C
Tập xác định:
0; .
D

Đặt
3
log .
t x
Phương trình đã cho trở thành
2
3 2 7 0 * .
t t m
Để phương trình đã cho có hai nghiệm thì phương trình
*
có hai nghiệm
2
37
3 4 2 7 0 .
8
m m
Gọi
1 2
,
t t
là hai nghiệm của phương trình
* ,
ta có
1 2
1 2
3
.
2 7
t t
t t m
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
Trang 4 TÀI LIỆU ÔN THI THPT QUỐC GIA
Giả sử
1
2
1 3 1 1
2 3 2
2
log
3
.
log
3
t
t
t x
x
t x
x
Theo đề bài ta có
1 2
1 2
3 3 72 3 3 3 3 72
t t
x x
1 2 1 2 1 2
3 3.3 3.3 63 3 3 12
t t t t t t
1 1
1
2
1
2
1
1
2
1
2
1
3 12.3 27 0 .
2
2
1
t t
t
t
t
t
t
t
Mặt khác
1 2
9
2 7 2 2 7 .
2
t t m m m
Câu 5. Có tất cả bao nhiêu giá trị nguyên của tham số
m
để phương trình
3
3
log 3 log 9 16
x
x m
có hai nghiệm thỏa mãn
1 2
2 .
x x
A.
15
. B.
17
. C.
14
. D.
16
.
Lời giải
Chọn A
Tập xác định:
3; \ 2 .
D

Phương trình
3
3
4
log 3 16
log 3
m
x
x
.
Đặt
3
log 3 ,
t x
phương trình trở thành
2
4
16 16 4 0 * .
m
t t t m
t
Với
1 2
,
x x
là nghiệm của phương trình đã cho thỏa mãn
1 2 1 2 3 1 3 2
2 1 3 3 0 log 3 log 3 .
x x x x x x
Do đó, yêu cầu bài toán trở thành tìm
m
để phương trình
*
có hai nghiệm phân biệt thỏa mãn
2 1
64 4 0
0 16 0 0 16.
4 0
m
b
t t m
a
c
m
a
Mà
m
nên
1;2; ;15 .
m
Vậy có
15
giá trị nguyên của
m
thỏa mãn bài toán.
Câu 6. Cho hai số thực
, 1
a b
thỏa mãn
2021.
a b
Gọi
,
m n
là hai nghiệm của phương trình
log log 2log 2 0.
a b a
x x x
Giá trị nhỏ nhất của biểu thức
4
mn a
bằng
A.
8080
. B.
2032
. C.
1015
. D.
3626
.
Lời giải
Chọn A
Điều kiện:
0.
x
Ta có
2
log .log 2log 2 0 log .log 2log 2 0.
a b a b a a
x x x a x x
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 5
Đặt
log ,
a
t x
phương trình trở thành
2
log . 2 2 0 1 .
b
a t t
1 2log 1 2log 1 0
b b
a
nên
1
luôn có hai nghiệm
1 2
,t t
với
2
1 2
2
2log log .
log
a a
b
t t b b
a
Xét hai nghiệm m và n , ta có
2
1 2 1 2
log
2
a
b
t t t t
mn a a a a b
Do đó
2
2 2
4 4 2021 4 4.2021 2 8080 8080.mn a b b b b b
Dấu " " xảy ra khi và chỉ khi 2, 2019.b a
Câu 7. Có bao nhiêu số nguyên
20;20m
để phương trình
2 3
log log 2x m x
có nghiệm thực
A. 15 . B. 14. C. 24 . D. 21.
Lời giải
Chọn A
Điều kiện:
0x
m x
.
Đặt:
2 3
1
log log
4
x
t
m x
2
4.2
4
1
1
3
3
t
t
t
t
x
x
m x
m x
1
4.2
3
t
t
m t
.
Xét phương trình:
1
4.2
3
t
t
f t t
.
ln3
' 4.ln 2.2
3
t
t
f t ;
' 0f t
6
ln 3 1
log
4ln 2 2
t
.
Bảng biến thiên:
Từ bảng biến thiên ta thấy phương trình có nghiệm khi: 4,56m .
Mà
, 20;20 5;6;7;...;19m m m
.
Vậy có 15 số nguyên thỏa mãn yêu cầu bài toán.
Câu 8. Số các giá trị nguyên của tham số m để phương trình
2
2
log ( 1) log ( 8)x mx
có hai nghiệm
phân biệt là
A. 5 . B. Vô số. C. 4 . D. 3 .
Lời giải
Chọn D
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
Trang 6 TÀI LIỆU ÔN THI THPT QUỐC GIA
Điều kiện:
1
x
Ta có:
2 2
2 2 2
2
log ( 1) log ( 8) log ( 1) log ( 8) ( 1) 8
x mx x mx x mx
2
2 9
x x mx
.
Do
1
x
nên suy ra
2
2 9
.
x x
m
x
Xét hàm số
2
2 9
( )
x x
f x
x
trên khoảng
(1; ).

2
2
9
( )
x
f x
x
,
( ) 0 3.
f x x
Bảng biến thiên
Nhìn vào BBT ta thấy, từ yêu cầu của bài toán tìm được
4 8
m
.
Do
m
nguyên nên
5;6;7
m
.
Vậy có 3 giá trị của
m
thỏa mãn yêu cầu bài toán.
Câu 9. Có bao nhiêu giá trị nguyên của
m
để phương trình
3
3
log 3 log 9 16
x
x m
có hai nghiệm
thỏa mãn
1 2
2
x x
.
A.
17
. B.
16
. C.
14
. D.
15
.
Lời giải
Chọn D
Điều kiện xác định:
3
x
và
2
x
.
Biến đổi phương trình đã cho về phương trình sau:
3
3
log 3 4 log 3 16 0
x
x m
.
2
3 3
log 3 16log 3 4 0 (1)
x x m
.
Đặt
3
log 3
x t
, phương trình
1
trở thành:
2
16 4 0 2
t t m
.
Ta có:
3
log 3 3 3
t
x t x
.
Theo điều kiện đề bài thì
2
x
nên
3 3 2 0
t
t
.
Vậy để phương trình
3
3
log 3 log 9 16
x
x m
có hai nghiệm thỏa mãn
1 2
2
x x
thì phương trình
2
phải có hai nghiệm
t
dương phân biệt
1 2
1 2
0
64 4 0
16 0 0 16
4 0
. 4 0
m
t t m
m
t t m
.
Vậy có 15 giá trị nguyên
m
thỏa mãn.
Câu 10. Có bao nhiêu giá trị nguyên dương của tham số
m
nhỏ hơn
2022
để phương trình
5
log 5 2 0
x
m m x
có nghiệm thực?
A.
2022
. B.
2018
. C.
2021
. D.
1011
.
Lời giải
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 7
Chọn A
Phương trình đã cho tương đương với phương trình :
2
5 5
x x
m m
2
5 5 5 5
x x x x
m m
Ta có
5 0
x
m
,
5 0
x
Xét hàm đặc trưng
2
f t t t
trên
0;
.
2 1 0, 0;f t t t
f t
đồng biến trên khoảng
0;
do đó
1
5 5
x x
f m f
5 5
x x
m
2
5 5
x x
m
.
Đặt
5
x
a
,
0
a
. Ta có
2
m g a a a
.
Phương trình đã cho có nghiệm
1
4
m
mà
m
nguyên dương nhỏ hơn
2022
nên
1;2;3;...;2022
m
.
Vậy có 2022 giá trị
m
thỏa mãn yêu cầu bài toán.
Câu 11: Cho phương trình
2
2
1 1
2 2
1
1 log 1 4 5 log 4 4 0
1
m x m m
x
. Hỏi có bao nhiêu giá trị
m
nguyên âm để phương trình có nghiệm thực trong đoạn
1
;1
2
?
A. . B. . C. . D. .
Lời giải
Chọn D
Trên đoạn
1
;1
2
thì phương trình luôn xác định.
Với
m
nguyên âm ta có
1
m
, do đó phương trình đã cho trở thành
2
1 1
2 2
4 1 log 1 4 5 log 1 4 4 0
m x m x m
2
1 1
2 2
1 log 1 5 log 1 1 0
m x m x m
6
5
2
3
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
Trang 8 TÀI LIỆU ÔN THI THPT QUỐC GIA
Đặt
1
2
log 1
t x
, với
1
;1
2
x
thì
1 1
t
. Ta có phương trình
2 2 2
1 5 1 0 1 5 1
m t m t m m t t t t
2
2
5 1
1
t t
m
t t
*
Xét hàm số
2
2
5 1
1
t t
f t
t t
với
1 1
t
.
Ta có
2
2
2
4 4
1
t
f t
t t
;
0 1
f t t
.
7
1
3
f
,
1 3
f
Do đó
1;1
min 3
f t
và
1;1
7
max
3
f t
.
Phương trình đã cho có nghiệm thực trong đoạn
1
;1
2
khi và chỉ khi phương trình
*
có nghiệm
1;1
t
1;1
1;1
7
min max 3
3
f t m f t m
.
Do
m
nguyên âm nên
3; 2; 1
m
.
Câu 12. Có bao nhiêu giá trị nguyên của tham số
m
thuộc khoảng
10;10
để phương trình
1
27
3 log 3
x
x m m
có nghiệm?
A.
9
. B.
8
. C.
10
. D.
7
.
Lời giải
Chọn C
Điều kiện:
3 0
x m
Ta có
1
27 3
3 log 3 3 log 3 3
x x
x m m x m m
Đặt
3
log 3
t x m
, ta có ta có
3 3
3 3
3 3
x
x t
t
t m
x t
x m
Xét
3
u
f u u
có
3 ln 3 3 0
x
f u f u
đồng biến, ta có
3
3 3 log 3 3 3
x t x
x t f x f t x t x x m x m
*
Xét hàm số
3
x
g x x
có
3 ln 3 1
x
g x
;
3
1
0 log
ln3
g x x
.
Bảng biến thiên:
Phương trình
*
có nghiệm khi
3 3
1 1 1
3 log log 0;1;2...9
ln3 3 ln 3
m m m
.
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 9
Câu 13. Cho phương trình
1
2
2
log log 2 0
x m x
(1). Với
m
là giá trị của tập
| 49;S m m m
để phương trình
(1)
có nghiệm. Tính tổng lập phương tất cả các phần tử
của
S
A.
1382975
.
B.
1382976
. C.
1382977
. D.
1382978
.
Lời giải
Chọn A
Ta có:
1
2
2
log log 2 0
x m x
2 2
log log 2
x m x
2
2
2
x
m
x
.
Vì
2
x
nên
2
2 2
2
m
m
.
Kết hợp với
m
,
49
m
. Khi đó
2 49
m
.
Vì
m
nên
1;0;1...48
m
có 50 giá trị.
Vậy tổng
S
các giá trị của
m
để phương trình có nghiệm là:
2 2
3
3 3 3 3 3
48 .49
1 0 1 2 3 ... 28 1 1382975
4
S
.
Câu 14. Cho phương trình
5
2 2
1
2
2
1
log 2 3 1 log 1 3 0
5
x m x m x x m
. Số các giá trị nguyên của
m
để
phương trình đã cho có hai nghiệm phân biệt
1 2
,
x x
thỏa mãn
2 2
1 2
20
x x
là:
A.
13
B.
9
C.
14
D.
5
Lời giải
Chọn D
Ta có:
5
2 2
1
2
2
1
log 2 3 1 log 1 3 0
5
x m x m x x m
2 2
2 2
log 2 3 1 log 1 3
x m x m x x m
2
2 2
1 3 0
2 3 1 1 3
x x m
x m x m x x m
2
2
2
1 3 0 *
1 3 0 *
2 2 0 (1)
2
x x m
x x m
x m
x m x m
x
Phương trình đã cho có hai nghiệm phân biệt khi và chỉ khi phương trình (1) có hai nghiệm phân
biệt thỏa mãn (*)
2
2
2
1 3 0
4 1 0
2 1 1 3 0 2 3
4 3 0
2
m m m
m m
m m
m
m
.
Theo giả thiết
2 2 2 2
1 2
20 4 20 16 4 4
x x hay m m m
Do đó
4 2 3
m
. Vậy số các giá trị nguyên của
m
thỏa mãn là 5.
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
Trang 10 TÀI LIỆU ÔN THI THPT QUỐC GIA
Câu 15. Cho phương trình
ln ln cos cos (1)
x m m x
. Tìm tất cả các giá trị của
m
để phương trình
(1) có nghiệm.
A.
1
1 1
m e
B.
1 1
1 1
e m e
C.
1 1
m
D.
1 1
m e
Lời giải
Chọn D
Đặt
ln cos
u x m
ta được hệ phương trình:
cos
ln cos
cos
ln cos
u
x
u m x
e m x
m u x
e m u
Từ hệ phương trình ta suy ra:
cos
cos *
u x
e u e x
Xét hàm số
t
f t e t
có
' 1 0, .
t
f t e t
Hàm số
f t
đồng biến trên
;
 
* cos cos
f u f x u x
Khi đó ta được:
cos
ln cos cos cos **
x
m x x e x m
;
Đặt
cos , 1;1 .
z x z
Phương trình
**
trở thành:
**
z
e z m
Xét hàm số:
z
g z e z
trên
1;1 .
Hàm số
z
g z e z
liên tục trên
1;1
;
' 1;
z
g z e
' 0 1 0 0
z
g z e z
và có
Bảng biến thiên
Do đó
1;1
1;1
1 1,min 0 1
max g z g e g z g
Hệ phương trình ban đầu có nghiệm
phương trình
**
có nghiệm
1 1.
m e
Câu 16. Cho phương trình
2 1 sin 2
cos 2 sin 2
3 3 2 sin 2 cos 2
x
m x x
x m x
với
m
là tham số. Hỏi có
bao nhiêu giá trị
m
nguyên dương bé hơn
2021
để phương trình có nghiệm.
A.
2019
.
B.
2018
. C.
2020
. D.
2021
.
Lời giải
Chọn A
Ta có
2 1 sin 2
cos 2 sin 2
3 3 2 sin 2 cos 2
x
m x x
x m x
2 1 sin 2
cos 2 sin 2
3 cos 2 sin 2 3 2 1 sin 2
x
m x x
m x x x
Xét hàm số
3
t
f t t
t
,
3 ln 3 1 0
t
f t
f t
đồng biến trên
.
Suy ra
2 1 sin 2
cos 2 sin 2
3 cos 2 sin 2 3 2 1 sin 2
x
m x x
m x x x
cos 2 sin 2 2 1 sin 2
m x x x
cos 2 sin 2 2
m x x
. Phương trình có nghiệm khi
2 2
1 4 3
m m
.
; 3 3;m
 
. Do
, 2021
m m
nên có
2019
giá trị của tham số
m
.
Câu 17. Có bao nhiêu giá trị nguyên của tham số
m
thuộc khoảng
2022;2022
để phương trình
10 log 3 3
x
x m m
có nghiệm?
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 11
A.
2020
.
B.
4042
. C.
4040
. D.
2021
.
Lời giải
Chọn D
Ta có:
10 log 3 3
x
x m m
10 log 3 3
x
x x m x m
log 3
10 log 3 10
x m
x
x x m
(1)
Xét hàm số:
( ) 10 ;
t
f t t t
.
( ) 10 ln10 1 0;
t
f t t
nên hàm số
( )
f t
đồng biến trên
.
Do đó phương trình (1)
log 3 3 10 10 3
x x
x x m x m x m
(2).
Đặt
1
( ) 10 10 ln10 1; ( ) 0 log
ln10
x x
g x x g x g x x
.
Ta có bảng biến thiên:
Từ bảng biến thiên ta thấy: để phương trình (2) có nghiệm thì:
1 1 1 1 1
3 log log 0,3
ln10 ln10 3 ln10 ln10
m m
.
Vì
2022;2022
m
nên
1;2;3;....;2021
m
.
Vậy có
2021
giá trị nguyên của tham số
m
thỏa yêu cầu đề.
Câu 18. Cho phương trình
2
2 2 2
log 2 log log *
x x m x m
. Có bao nhiêu giá trị nguyên của tham
số
2021;2022
m
để phương trình (*) có nghiệm?
A.
2021
. B.
2022
. C.
4042
. D.
2024
.
Lời giải
Chọn D
Điều kiện:
2
0
log 0
x
m x
.
2 2
2 2 2 2 2 2
log 2log log 4 log 8log 4 log 4
x x m x m x x m x m
2
2 2 2 2
4log 4log 1 4 log 4 log 1
x x m x m x
2
2
2 2
2 2
2 2
2 log 1 2log 1
2log 1 2 log 1
2 log 1 2log 1
m x x
x m x
m x x
2 2
2 2
log log 1
log log
m x x
m x x
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
Trang 12 TÀI LIỆU ÔN THI THPT QUỐC GIA
* TH
1
:
2 2
log log
m x x
2
2
2
2 2
2 2
0 1
log 0
log log 0 1
log log
x
x
x x m
m x x
Đặt:
2
log 0
t x t
, phương trình
(1)
trở thành:
2 2
0 2
t t m t t m
Đặt:
2
( ) ( ;0
g t t t t 
.Bài toán trở thành: Tìm giá trị của tham số
m
để phương trình
2
có ít nhất 1 nghiệm
0
t
Ta có:
2
( ) ( ) 2 1 0 0
g t t t g t t t
Ta có BBT:
Dựa vào BBT, suy ra: để phương trình
2
có ít nhất 1 nghiệm
0
t
thì
0
m
(*)
* TH
2
:
2 2
log log 1
m x x
2
2
2 2 2
log 1
log log 2log 1
x
m x x x
2
2
2 2
log 1
log 3log 1 0 3
x
x x m
Đặt:
2
log 1
t x t
, phương trình
(1)
trở thành:
2 2
3 1 0 3 1 4
t t m m t t
Đặt:
2
( ) 1, 1;g t t t t
Ta có:
2
( ) 3 1 ( ) 2 3
g t t t g t t
3
( ) 0 2 3 0 1;
2
g t t t

Bài toán trở thành: Tìm giá trị của tham số
m
để phương trình
4
có ít nhất 1 nghiệm
1
t
Ta có BBT:
Dựa vào BBT, suy ra: để phương trình
4
có ít nhất 1 nghiệm
1
t
thì
5
4
m
(**)
Kết hợp (*) và (**),
2021;2022
m
1;0;1;2;...; 2022
m
Vậy có tất cả
2024
giá trị của
m
thỏa mãn.
Câu 19. Tìm tất cả các giá trị của
m
để phương trình
ln ln cos cos
m m x x
có nghiệm.
A.
1
1 1.
m e
e
B.
1 1.
m e
C.
1
1 1.
m
e
D.
1 1.
m e
Lời giải
Chọn B
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 13
Đặt
ln cos
u m x
ta được hệ phương trình:
cos
ln cos
cos
ln cos
u
x
u m x
e m x
m u x
e m u
Từ hệ phương trình ta suy ra:
cos
cos *
u x
e u e x
Xét hàm số
t
f t e t
có
' 1 0, .
t
f t e t
Hàm số
f t
đồng biến trên
.
* cos cos
f u f x u x
Khi đó ta được:
cos
ln cos cos cos **
x
m x x e x m
Đặt
cos , 1;1 .
z x z
Phương trình
**
trở thành:
**
z
e z m
Xét hàm số:
z
g z e z
trên
1;1 .
Hàm số
z
g z e z
liên tục trên
1;1
và có
1;1
1;1
1 1,min 0 1
max g z g e g z g
Ta có bảng biến thiên:
Hệ phương trình ban đầu có nghiệm
phương trình
**
có nghiệm
1 1.
m e
Câu 20. Giá trị nào của
m
để phương trình
2 2
3 3
log log 1 2 1 0
x x m
có ít nhất một nghiệm thuộc
đoạn
3
1; 3
.
A.
1 16
m
. B.
4 8
m
. C.
3 8
m
. D.
0 2
m
.
Lời giải
Chọn D
Điều kiện
0
x
. Đặt
2
3
log 1 1
t x
, ta được phương trình
2
2 2 0 *
t t m
.
Ta có
3
1; 3
x
3
0 log 3
x
2
3
1 log 1 2
t x
.
Phương trình đã cho có nghiệm thuộc
3
1; 3
x
*
có nghiệm
1; 2
t
.
Đặt
2
f t t t
, với
1; 2
t
.
Hàm số
f t
là hàm đồng biến trên đoạn
1; 2
. Ta có
1 2
f
và
2 6
f
.
Phương trình
2
2 2
t t m
2 2
f t m
có nghiệm
1; 2
t
1 2 2 2
f m f
1 2 2
2 2 2
f m
m f
2 2 2
2 2 6
m
m
0 2
m
.
Câu 21. Cho Có bao nhiêu giá trị nguyên của tham số
m
thuộc khoảng
2021;2021
để phương trình
10 log 3 3
x
x m m
có nghiệm?
A.
2021
. B.
2020
. C.
2010
. D.
4040
.
Lời giải
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
Trang 14 TÀI LIỆU ÔN THI THPT QUỐC GIA
Chọn B
Ta có:
10 log 3 3
x
x m m
10 log 3 3
x
x x m x m
log 3
10 log 3 10
x m
x
x x m
(1)
Xét hàm số:
( ) 10 ;
t
f t t t
.
( ) 10 ln10 1 0;
t
f t t
nên hàm số
( )
f t
đồng biến trên
.
Do đó phương trình (1)
log 3 3 10 10 3
x x
x x m x m x m
(2).
Đặt
1
( ) 10 10 ln10 1; ( ) 0 log
ln10
x x
g x x g x g x x
.
Ta có bảng biến thiên:
Từ bảng biến thiên ta thấy: để phương trình (2) có nghiệm thì:
1 1 1 1 1
3 log log 0,3
ln10 ln10 3 ln10 ln10
m m
.
Vì
2021;2021
m
nên
1;2;3;....; 2020
m
.
Vậy có
2020
giá trị nguyên của tham số
m
thỏa yêu cầu đề.
Câu 22. Có bao nhiêu giá trị
m
nguyên trong
2017;2017
để phương trình
log 2log 1
mx x
có
nghiệm duy nhất?
A.
2017
. B.
4014
. C.
2018
. D.
4015
.
Lời giải
Chọn C
Ta có
2
2 2
0 0
1
log 2log 1 1 0 1 0
2 1 1
log log 1 1
mx mx
x
mx x x x
mx x x
mx x mx x
Ta thấy
0
x
không là nghiệm của phương trình
1
.
Với
1 0
x
ta có phương trình
1
trở thành
1
2 2 .
m x
x
Xét hàm số
1
2 , 1; \ 0 .
f x x x
x

Ta có
2
1
1 0 1
f x x
x
Bảng biến thiên
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 15
Phương trình đã cho có nghiệm duy nhất khi phương trình
2
có nghiệm duy nhất trên
1; \ 0 .
Từ bảng biến thiên suy ra
0
.
4
m
m
Vì
1; 2;...; 2017
2017;2017
4
m
m
m
có
2018
giá trị
m
thỏa mãn.
Câu 23. Cho phương trình
2
2 2
1
2
2
4 .log 2 3 2 .log 2 2 0
x m
x x
x x x m
với m là tham số. Tổng tất cả các giá trị
của tham số m để phương trình đã cho có ba nghiệm phân biệt là
A. 3 . B. 2 . C. 4 . D. 1.
Lời giải
Chọn B
Ta có:
2
2 2
1
2
2
4 .log 2 3 2 .log 2 2 0
x m
x x
x x x m
2
1 1
2
2 2
2
2
4 .log 2 3 2 .log 2 2 0
x m
x x
x x x m
2
2 2
2 2
2.4 .log 2 3 2 .log 2 2 0
x m
x x
x x x m
2
2 2
2 2
2.4 .log 2 3 2 .log 2 2
x m
x x
x x x m
2
2
2
2
2
2.log 2 3
log 2 2
4
2
x m
x x
x x
x m
2
2
2 2
2 2
2.2 .log 2 3 2 .log 2 2
x m
x x
x x x m
2
2
3 2 2 2
2 2
2 .2 .log 2 3 2 .2 .log 2 2
x m
x x
x x x m
2
2 2
2 3 2
2 2
2 .log 2 3 2 .log 2 2
x m
x x
x x x m
(1)
Xét hàm số
2
2 .log
t
y f t t
với 2t , có
2
1
2 .ln 2.log 2 . 0, 2
ln 2
t t
f t t t
t
.
Suy ra hàm số
2
2 .log
t
y f t t
đồng biến trên nửa khoảng
2;
.
Khi đó
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
Trang 16 TÀI LIỆU ÔN THI THPT QUỐC GIA
2
2
2
2
2
2
1 2 3 2 2
2 3 2 2
2 1 2
2 1 2
2 2 3 2
2 1 3
f x x f x m
x x x m
x x x m
x x m x
x m
x m
Trường hợp 1: Phương trình (3) có 1 nghiệm kép và phương trình (2) có 2 nghiệm phân biệt
khác 0
1
2 1 0
1
2
2 3 0 3
2
2
m
m
m
m
m
.
Trường hợp 2: Phương trình (2) có 1 nghiệm kép và phương trình (3) có 2 nghiệm phân biệt
khác 2
1
2
2 1 0
5 3
2 1 4
2 2
2 3 0
3
2
m
m
m m m
m
m
.
Vậy tổng tất cả các giá trị của tham số
m
để phương trình đã cho có ba nghiệm phân biệt là
1 3
2
2 2
.
Câu 24. Cho phương trìn
2
2 2
1
2
2
4 log 2 3 2 log 2 2 0
x m
x x
x x x m
. Tìm tất cả các giá trị
của tham số m để phương trình trên có đúng hai nghiệm thực phân biệt.
A.
1
2
m
hoặc
3
2
m
. B.
1
2
m
. C.
3
2
m
. D.
3
2
m
hoặc
1
2
m
.
Lời giải
Chọn A
2
2 2
1
2
2
4 log 2 3 2 log 2 2 0
x m
x x
x x x m
2
2
2
2
1 2
2
2 2
2
2
3 2 2
3 2 3
log 2 3
log 2 2
2 log 2 3 2 log 2 2
2
2
x m
x x
x m
x x
x x
x m
x x x m
Xét hàm số
2 2
3
log 2 log
2 8
u
u
u u
f u
với
2
u
. Ta có
2
1 2
2 log .ln 2 0
8 .ln 2
u
u
f u u
u
2
u
. Suy ra hàm số
f u
đồng biến trên
2;

nên
2
2
2
2
4 1 2 0 1
2 3 2 2 1 2
1 2 0 2
x x m
f x x f x m x x m
x m
. phương trình
đã cho có đúng hai nghiệm phân biệt.
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 17
TH1: Phương trình (1) có nghiệm hai 2 nghiệm phân biệt, phương trình (2) vô nghiệm suy ra
3 2 0
1
2 1 0
2
m
m I
m
TH2: Phương trình (2) có nghiệm hai 2 nghiệm phân biệt, phương trình (1) vô nghiệm suy ra
3 2 0
3
2 1 0
2
m
m II
m
TH3: Phương trình (1) và (2) đều có hai nghiệm phân biệt và hai nghiệm này giống nhau
3 2 0
1 3
2 1 0
2 2
m
m III
m
Gọi
; ( )
a b b a
là hai nghiệm của phương trình (1), theo định lý viet ta có
4
. 2 1
a b
a b m
. Vì
;
a b
cung là nghiệm của phương trình (2) nên
0
. 2 1
a b
a b m
suy ra vô lý vậy
m
(III)
Vậy từ (I) ; (II) và (III) suy ra
1
2
m
hoặc
3
2
m
.
Câu 25. Cho phương trình
2
2
1 1
3 3
1
1 log 1 4 5 log 4 4 0 1
1
m x m m
x
. Hỏi có bao nhiêu
giá trị m nguyên
âm để phương trình (1) có nghiệm thực trên đoạn
2
;2
3
?
A.
6
. B.
5
. C.
2
. D.
3
.
Lời giải
Chọn D
Ta có
2
1 1
3 3
1 4 1 log 1 4 5 log 1 4 4 0
m x m x m
2
1 1
3 3
1 log 1 5 log 1 1 0
m x m x m
Đặt
1
3
log 1
t x
với
2
;2
3
x
thì
1 1
t
ta có phương trình:
2
2 2 2
2
5 1
1 5 1 0 1 5 1 2
1
t t
m t m t m m t t t t m
t t
Xét hàm số
2
2
5 1
1
t t
f t
t t
với
1 1
t
. Ta có
2
2
2
1
4 4
0
1
1
t
t
f t
t
t t
7
1 ; 1 3
3
f f
. Do đó
1;1 1;1
7
min 3;max
3
f t f t
Phương trình đã cho có nghiệm thực trong đoạn
2
;2
3
khi và chỉ khi phương trình (2) có
nghiệm
1;1 1;1
7
1;1 min max 3
3
t f t m f t m
Như vậy các giá trị nguyên âm của m cần tìm là
3; 2; 1
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
Trang 18 TÀI LIỆU ÔN THI THPT QUỐC GIA
Câu 26. Gọi
S
là tập chứa tất cả các giá trị thực của tham số
m
để tồn tại đúng
một bộ số thực
;
x y
thỏa mãn
2 2 2
2 2
log 4 log 15 3 0
x y m x y m
. Tính tổng bình
phương giá trị tất cả các phần tử của tập
S
đó
A.
144
289
B.
45
4
C.
225
256
D.
41
16
Lời giải
Chọn C
Áp dụng quy tắc cần và đủ, ta nhận thấy vai trò của hai ẩn
x
và
y
là như nhau. Nếu
;
x y
thỏa
mãn thì
;
y x
cũng thỏa mãn. Vì vậy, muốn bộ số
;
x y
thỏa mãn là duy nhất thì tất cả các biến
phải bằng nhau. Suy ra
x y
. Phương trình trở thành như sau:
2
2 2
2 2 2 2
2
2 2
log 2 4 log 2 15 3 0 1 log 4 1 2log 15 3 0
log 2 4 1 log 16 7 0
x m x m x m x m
x m x m
Để có duy nhất nghiệm thực
x
thì
2
1
4 1 16 7 0
15
16
m
m m
m
Ta thử lại:
Với
1
m
, ta có:
2 2 2
2 2
log 4log 12 0
x y x y
Dể thấy cho
2 2 2
2 2 2 2
0 log 4log 12 0 log 8log 12 0
y x x x x
Do phương trình trên có hai nghiệm nên suy ra trường hợp này loại
Với
15
16
m
, ta có:
2 2 2
2 2
15 285
log log 0
4 16
x y x y
Đánh giá thông qua bất đẳng thức Bunyakovsky, ta nhận thấy:
2
2 2 2 2
2 2 2 2
2
2
2 2 2 2
15 285 15 285
0 log log log log
4 16 4 2 16
15 225 15 15
0 log log log log
2 16 4 4
x y
x y x y x y
x y x y x y x y
Dấu bằng xảy ra khi và chỉ khi
15
4
4
4
1
1
2
16 2
8 2
x y
x y
x y
(thỏa mãn)
Suy ra
15
16
S
Tổng bình phương bằng:
225
256
Câu 27. Gọi
S
là tập chứa tất cả các giá trị thức của tham số
m
để tồn tại duy nhất bộ ba số thực
; ;
x y z
thỏa mãn điều kiện
2 2 2 2
2 2
log 2 2 log 4 2 2 0
x y z m x y z
. Tích tất cả các phần tử của
tập
S
tương ứng bằng:
A.
0
. B.
16
. C.
6
. D.
12
.
Lời giải
Chọn A
Điều kiện
2 0
x y z
.
Ta có
2 2 2
2 2 2 2 2
x y z x y z x y z
hay
2 2 2
4 2 2 4 2
x y z x y z
.
Dấu đẳng thức xảy ra
x y z
.
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 19
Khi đó
2 2 2
4 2 2 4 2
x y z x y z
2 2 2
2 2
1
log 4 2 2 2 log 2
2
x y z x y z
2 2 2
2 2
log 2 2 log 4 2 2 2
x y z x y z
.
2 2 2 2
2 2
log 2 2 log 4 2 2 0
x y z m x y z
2
2 2 2 2
2 2 2
2 log 4 2 2 log 2 4 log 4 2 2 2
m x y z x y z x y z
.
Đặt
2
log 4 2 2
t x y z
ta được
2
4 2 2
t mt
2
2 8 8 0
t m t
.
Yêu cầu bài toán
2
2 8 8 0
t m t
có đúng một giá trị
t
2
8 64 0
m
0
16
m
m
.
* Khi
0
m
thì
2
t
2
log 4 2 2 2
x y z
2 2
x y z
.
Mặt khác dấu đẳng thức xảy ra
x y z
nên
1
2
x y z
.
*
16
m
tương tự
1
32
x y z
. Vậy
0; 16
S
.
Câu 28. Cho hai số thực
,
x y
thỏa mãn hệ thức
2
2
2 1
2 log
y x
y
x
. Hỏi có tất cả bao nhiêu giá trị nguyên
40;40
m
để tồn tại duy nhất một số thực
x
thỏa mãn hệ thức
2 2
4 10 1 0
y x mx
?
A.
51
. B.
52
. C.
53
. D.
31
.
Lời giải
+) Vì
2
2
2 0, ;
y x
x y
nên với
0
y
thì
2 1
log 0 1
y
x x
.
Do đó điều kiện của bài toán là
1
0
x
y
.
+) Khi đó
2 2 2
2 2 2 1
2
2 1 2 1 2 1
2 log 2.2 2log 2 log
y x y x y x
y y y
x x x
2
2
2 1
2
2 1
2
2
2 2
2
log2
2 log 2 1 2 log
log 2 1
2
y
y
x
x
x
y x
y
.
Xét hàm đặc trưng
2
2 .log
t
f t t
trên
1;

, ta có
2
2
2 .ln 2.log 0, 1
ln 2
t
t
f t t t
t
.
Do đó hàm
f t
đồng biến trên
1;

.
Khi đó,
2
2 1
f y f x
2
2 2 2
2 1 4 1
y x y x
.
+) Ta có
2
2 2 2 2
4 10 1 0 1 10 1 0
y x mx x x mx
4 2
12 0
x x mx
3
12
x x m
(do
1
x
).
Xét hàm
3 2
12 3 12
g x x x g x x
,
0 2
g x x
.
Bảng biến thiên:
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
Trang 20 TÀI LIỆU ÔN THI THPT QUỐC GIA
Từ bảng biến thiên của hàm
g x
suy ra phương trình
2 2
4 10 1 0
y x mx
có duy nhất một
nghiệm khi và chỉ khi
11; 40
m
, do đó có tất cả
52
giá trị
m
thỏa mãn yêu cầu bài toán.
Câu 29. Cho các số thực
, ,
x y z
thỏa mãn
2 2 3 3
3 7
log 2 log 2 log
x y x y z
. Có bao giá trị nguyên của
z
để có đúng hai cặp
,
x y
thỏa mãn đẳng thức trên.
A.
2
. B.
211
. C.
99
. D.
4.
Lời giải
Chọn B
ĐK
2 2
0
0
0
0
x
x y
y
z
Ta có
2 2
2 2 3 3 3 3
3 7
2 3 1
log 2 log 2 log 2 7 2
10 3
t
t
t
x y
x y x y z t x y
z
.
+ Nếu
0
y
3
2 7
t
x
thay vào
1
ta được
3
2
3
3
49
2.7 3 log 2
t
t
t
do đó
3
3
49
log 2
10z
.
+ Nếu
0
y
Từ
1 & 2
suy ra
2
3
3
2
2 2
3 3
3 3
2
22 2
3 3
2
2
2 27
2
49 49
, *
27 27
2
2 49
2 1
t
t t
t
x
x y
y
x y
x y
x y
x
y
.
Đặt
3
, 2
x
u u
y
. Xét
2
3 3
3
3 4
2 2
0
2 6 2 4
0 2
2 1 2 1
4
u
u u u u
f u f u u
u u
u
.
Ta có bảng biến thiên
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 21
Nhận xét với mỗi giá trị
u
tương ứng với duy nhất 1 cặp
,
x y
thỏa mãn bài toán do đó
Yêu cầu bài toán tương đương
49 49
27 27
4 1
log log
33 8
4 49 1
10 10
33 27 8
t
z
.
Vì
z
là số nguyên nên có
211
giá trị thỏa mãn.
Câu 30. Cho phương trình sau:
2 2
2 4 2 2 4
2 2 2 4 1 2 1 0
x x m x mx
x mx x x m
. Hỏi có tất cả bao nhiêu giá trị thực
của tham số m để phương trình đã cho có 3 nghiệm thực x?
A. 4. B.
5
. C. 2. D. 3.
Lời giải
Chọn A
2 2
2 4 2 2 4
2 2 2 4 1 2 1 0
x x m x mx
x mx x x m
Nhân 2 vế với 2:
2 2
2 4 2 2 4
2 4 2 2 4 1 2 1 0
x x m x mx
x mx x x m
Đặt:
2
2 4
a x mx
,
2
4 1
b x x m
2 2
4 2 4
2 2 2 1 0 *
x x m x mx
a b
Nếu
0, 0
a b
thì
1 1
2 2 2 2
b a
b a
(vô lý).
Suy ra:
2
2
2
0
0 2 0
2
0
4 1 0
4 1 0 1
x
a x mx
tm x m
b
x x m
x x m
Để có 3 nghiệm thực phân biệt thì (1) có nghiệm:
0 1
x m
7 65
2
8
x m m
+ nghiệm kép
5
m
Câu 31. Tổng tất cả các số nguyên
a
để tồn tại số thực
b
thỏa mãn
4 2 2 3
b b
a a
A.
7
B.
0
C.
3
D.
2
Lời giải
Chọn C
Điều kiện
2
4 2
b
a
a
Đặt
2
2 , 0 2
a t t a t
, phương trình trở thành
2 2
2
2 2
9 4
4 9 2.3 .
3 . 0 1
4 3 4 3
2
3 0
3 0
b b
b b b
b
b b b b
b
b
t t t
t t
t t t t
t
t
Để phương trình (1) có nghiệm:
4 9
9 4
4 1 1
9 2 9 4 0 2.4 9 0 log 2
9 2 2
b
b b b b b
b log b
.
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
Trang 22 TÀI LIỆU ÔN THI THPT QUỐC GIA
Khi đó tổng hai nghiệm
1 2
3
b
t t
. Để có nghiệm
3
b
t
thì phương trình (1) phải có hai nghiệm không
âm
9 4 0
b b
0
b
Khi đó ta có hai trường hợp nghiệm của phương trình
Trường hợp 1:
3 2.4 9
2
b b b
t
. Ta có
2
3 2.4 9 3 2.4 9
2 2
2 2
b b b b b b
a a
Với
9
4
0 2
b log
ta thấy
2;1
a
mà
a
nguyên nên
1;0
a
.
Trường hợp 2:
3 2.4 9
2
b b b
t
. Ta có
2
3 2.4 9 3 2.4 9
2 2
2 2
b b b b b b
a a
Với
9
4
0 2
b log
ta thấy
2;0
a
mà
a
nguyên nên
1; 2
a
.
Vậy tổng tất cả số nguyên a thỏa mãn là
1 2 0 3
.
Câu 32. Cho phương trình
2
2
4 4 .2 log 2
x x
a x x b
. Có bao nhiêu bộ số
,
a b
thỏa mãn điều kiện
100 ,100 , 100 , 100
a b a b
sao cho phương trình có nghiệm
duy nhất
A.
15
B.
6
C.
3
D.
4
Lời giải
Chọn B
Ta có
2 2
2 2
4 4 .2 log 2 2 2 log 2
x x x x
a x x b a x x b
.
Ta nhận thấy
0
x x
là nghiệm thì
0
2
x x
cũng là nghiệm. Do đó để có nghiệm duy nhất thì
0
1
x
. Khi đó thay vào ta được:
4
2
4 log 1 2 1.
a
a b b
Đặt ,
100 100
p q
a b với ,p q
Khi đó:
400
2 1 1
100
p
q
b
. Chú ý
1
100
q
nên
400
p
. Ta có 2 tình huống:
Trường hợp 1:
400
1;2;4;5;8;10;16;20;25;40;50;80;100;200;4
00
p
p
.
Vì
400
2
2
400 400
2 1 101 log 101 60
log 101
p
b p
p
vậy
80;100;200;400
p
.
Khi đó ta có:
4
; ;31 ; 1;15 ; 2;3 ; 4;1
5
a b
. Với mỗi bộ số
;
a b
tương ứng đều có nghiệm
duy nhất bởi vì ta có đánh giá:
2
2 2
2 2
2 2 2 2 2 4 log 1 log 1 1
x x x x
a b a b x
.
Trường hợp 2: Nếu
400
p
khi đó vế trái có dạng phân số với mẫu số có dạng lũy thừa của 2.
Vì vậy vế phải cũng phải như vậy tức là
25
q
Lại có khi đó
400
1 2 1 1 0 100 0
100
p
q
b q
cho nên
25; 50; 75
q
.
Với
400
3
25 2
4
p
q p
(Loại).
Với
400
1 1
50 2 400 4,
2 2
p
q p a b
.
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 23
Khi đó:
2
2
1
2 2 4log 2
2
x x
x x
. Dùng TABLE ta thấy có duy nhất 1 nghiệm
1
x
Với
400
1 3
75 2 200 2,
4 4
p
q p a b
.
Khi đó:
2
2
3
2 2 2log 2
4
x x
x x
. Dùng TABLE ta thấy có duy nhất 1 nghiệm
1
x
Kết luận: Có tất cả 6 bộ số
;
a b
thỏa mãn điều kiện.
Câu 33. Cho phương trình sau:
2
2l g l g 1 l g
2 4 9 2 3 2 0
o x o x o x x x
m m
(với
m
là tham số thực). Gọi
S
là tập hợp tất cả các giá trị nguyên dương của
m
để phương trình đã cho có đúng hai nghiệm phân
biệt. Tổng của phần tử nhỏ nhất và phần tử lớn nhất của
S
bằng
A.
100
3 1
. B.
100
3 1
. C.
99
3
. D.
99
3 1
.
Lời giải
Chọn A
Điều kiện:
0
3
x
x
m
Phương trình đã cho tương đương với phương trình:
2
2l g l g 1 l g
2 4 3 2 3 0
o x o x o x x x
m
Ta có:
2
2lg lg 1 lg
2 4 3 2 3 0
x x x x x
m
2
2
2l g l g 1 l g
3
3
2log log 2 2log
2 4
x
x
o x o x o x
m
m
x x x
log 2
1
log
2
3
x
x
x
m
*
3
100
1
10
log ,
x
x
x m m
.
Trường hợp 1: Với
1
m
thì
3
log 0
x m
(loại). Do đó phương trình đã cho có 2 nghiệm phân
biệt
1
100,
10
x x
.
Trường hợp 2: Với
1
m
thì
3
log 0
x m
nên phương trình đã cho luôn nhận nghiệm
3
log
x m
Mà
1
100
10
nên phương trình đã cho có hai nghiệm phân biệt khi
1
100
10
3
1
log 100 3 3
10
m m
.
Do
m
nguyên dương,
1
m
nên
100
2;3;4;...,3 1
m
. Vậy
100
2;3;4;...,3 1
S
.
Suy ra tổng của phần nhỏ nhất và phần tử lớn nhất của
S
bằng
100
3 1
.
Câu 34. Cho hàm số
( )
2 1
x m
f x
x
. Gọi
S
là tập hợp các số nguyên dương
7
m
sao cho với mọi bộ số thực
, , 2;3
a b c thì
ln ( ) , ln ( ) , ln ( )
f a f b f c
là độ dài ba
cạnh của một tam giác. Tổng các phần tử của
S
là
A.
10
. B.
15
. C.
16
. D.
14
.
Lời giải
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
Trang 24 TÀI LIỆU ÔN THI THPT QUỐC GIA
Chọn C
Từ giả thiết ta có với
, 2;3
m S x thì
( ) 0
2 1
x m
f x
x
.
Xét hàm số
( ) ln ( ),
g x f x
ta có
( ) 1 2
( ) 0, , 2;3
( ) ( )(2 1)
f x m
g x m S x
f x x m x
do vậy
ta có bảng biến thiên của hàm số
( )
g x
như sau
TH1:
3
ln 0 4
7
m
m
, lúc này xét mọi bộ số thực
, , 2;3
a b c sao cho
ln ( ) ,
f a
ln ( ) ,
f b
ln ( )
f c
là độ dài ba cạnh của một tam giác khi đó ta cần có
2;3
2;3
2 min ( ) max ( )
x
x
g x g x
3 2
2ln ln
7 5
m m
2
3 2
7 5
m m
2
19 7 29
10
5 19 53 0
19 7 29
10
m
m m
m
,
kết hợp với
m S
ta có
6;7
m .
TH2:
2
ln 0 3
5
m
m
, lúc này xét mọi bộ số thực
, , 2;3
a b c
sao cho
ln ( ) ,
f a
ln ( ) ,
f b
ln ( )
f c
là độ dài ba cạnh của một tam giác khi đó ta cần có
2;3
2;3
2max ( ) min ( )
x
x
g x g x
3 2
ln 2ln
7 5
m m
2
2 3
5 7
m m
2
7 3 47 0
m m
3 5 53 3 5 53
14 14
m
, kết hợp với
m S
ta có
1;2
m .
TH3:
2
ln 0
5
3 4
3
ln 0
7
m
m
m
khi đó tồn tại
2;3
để
ln ( ) 0
f
khi đó chọn bất kỳ bộ
ba số
, ,
a b
với
, 2;3
a b
thì
ln ( ) ,
f a
ln ( ) ,
f b
ln ( )
f
không thể là độ dài của 3 cạnh
của một tam giác.
Từ 3 trường hợp trên ta có
1;2;6;7
S
do đó tổng các phần tử của
S
là
16
.
Câu 35. Cho hàm số
4
( ) log 2.log 2
x
f x x m
. Hỏi có bao nhiêu giá trị nguyên dương của tham số
m
để phương trình
2 0
f x x
có tổng tất cả các nghiệm bằng
2
.
A.
0
B.
1
C.
2
D.
3
Lời giải
Chọn D
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 25
+ Đặt
2
t x x
2;2
t
.
Giả sử
0
t
là nghiệm của phương trình
( ) 0
f t
khi đó:
0
2 *
x x t
.
Dễ thấy pt (*) chỉ có tối đa 2 nghiệm vì khi bình phương thoát hết căn chỉ ra phương trình bậc
hai.
+ Nếu
0
x
là một nghiệm của phương trình (*) thì
0
2
x
cũng là một nghiệm của
(*)
vì:
0 0 0 0 0 0
2 2 2 2
x x t x x t
.
Mà
0 0 0
2 2
x x x
nên suy ra
Để phương trình
2 0
f x x
có tổng các nghiệm bằng
2
Phương trình
( ) 0
f t
có duy nhất một nghiệm trên
2;2
.
+ Xét phương trình
( ) 0
f t
4
log 2.log 2 0
t
t m
ln 2
ln 2
.
ln 2ln 2
ln 2 2 ln
t
m
t
t m t
Vì
*
m
nên ta có:
ln 2 2 ln
t m t
2 2
2 2 0
m m
t t t t
.
+ Xét hàm số
2
( ) 2
m
g t t t
2 1
*
2;2
( ) 2 1 0
m
t
g t mt
m
Phương trình
( ) 0
g t
có nhiều nhất 1 nghiệm trên
2;2
Mặt khác
*
( ) 2 2 2 2 0
m
g t g m
Suy ra phương trình
( ) 0
g t
vô nghiệm.
Vậy không có giá trị nào của tham số
m
thỏa mãn yêu cầu bài toán.
Câu 36. Cho phương trình
2
2
3 3
log 3 log 2 2 1 0
3
x
m x m m
. Có bao
nhiêu giá trị nguyên của tham số
m
lớn hơn
2021
sao cho phương trình đã cho có hai nghiệm
phân biệt
1 2
,
x x
thoả
1 2
10
x x
?
A.
2020
. B.
2019
. C.
2020
. D.
2021
.
Lời giải
Chọn A
Điều kiện:
0
x
.
2
2
2 2
3 3 3 3
log 3 log 2 2 1 0 log 1 3 log 2 2 1 0
3
x
m x m m x m x m m
Đặt
3
log
t x
Phương trình trở thành
2
2 2 2
1 3 2 2 1 0 3 2 2 2 0
2 2
t m
t mt m m t m t m m
t m
2 2
3
3
m
m
x
x
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
Trang 26 TÀI LIỆU ÔN THI THPT QUỐC GIA
2 2
1 2
2
10 3 3 10
9.3 3 10 0 3 1
0 0
m m
m m m
x x
m m
Vì m
và
2021
m
nên
2020; 2019;...; 1
m
.
Câu 37. Hỏi có tất cả bao nhiêu giá trị nguyên của tham số
24;24
m
để ba
số hạng sau theo thứ tự tạo thành 1 cấp số cộng, với
1;2
x
:
3 2 1
9.2 1 ; ; 2 3.2
x x x
m
A.
2
. B.
1
. C.
17
. D.
7
.
Lời giải
Chọn A
Để ba số lập thành một cấp số cộng thì
3 2 1
9.2 1 2 3.2 2
x x x
m
3 2
2 6.2 9.2 2 1
x x x
m
.
Đặt
1 2
2 2 ;2 2;4
x
t
. Khi đó
3 2
6 9 2 1
f t t t t m
với
2;4
t
Suy ra
3 2 3 2
2;4
2;4
min 6 9 2 1 max 6 9
f t t t t m f t t t t
1 5
0 2 1 4 1;2
2 2
m m m
Câu 5. Hỏi có tất cả bao nhiêu giá trị nguyên của tham số
18;18
m
để
phương trình
2
2 1 .2 3 1 0
x x
m m
có hai nghiệm thỏa
1 2
0 1 3
x x
A.
8
. B.
18
. C.
11
. D.
12
.
Lời giải
Chọn D
Đặt
2 0
x
t
. Phương trình trở thành:
2
2
2 1
1 3 1 0
2 3
t t
t m t m m
t
Hai nghiệm thỏa mãn:
1 2
0 1 3
1 2 1 2
0 1 3 2 2 2 2 2
x x
x x t t
1 2
1 2 8
t t
Xét hàm số
2
2 1
2 3
t t
y f t
t
có bảng biến thiên như sau:
Suy ra
7 7 18
m m
tức có tất cả 12 giá trị nguyên
m
thỏa
Câu 38. Gọi
S
là tập hợp chứa tất cả các giá trị nguyên của
2022;2022
m
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 27
sao cho phương trình
2 2
2 2
log 2 1 log 2 3 0
x m x m
có hai nghiệm sao cho thỏa mãn
1 2
0 8
x x
. Số các phần tử của
S
là
A.
2021
. B.
2019
. C.
18
. D.
2023
.
Lời giải
Chọn A
Đặt
2
log
t x
. Phương trình trở thành:
2
2 2 1 2 3 0
f t t m t m
(1)
Hai nghiệm phân biệt thỏa mãn
1 2 1 2 2
0 8 log 8 3
x x t t
Ta xét phương trình (1) có:
2
2
2 1 2 3 4 6 2
m m m m
Khi
2
3 17
4
4 6 2 0
3 17
4
m
m m
m
thì phương trình (1) sẽ có hai nghiệm phân biệt là:
2
1
2
2
2 1 4 6 2
2 1 4 6 2
t m m m
t m m m
Đến đây ta chỉ cần điều kiện
2
2
2 1 4 6 2 3
t m m m
là bài toán được giải quyết
2 2
1
2 2 0
3
3
7
4 8 4 4 6 2
7
m
m
m
m
m m m m
Kết hợp với điều kiện
0
, suy ra:
; 2022;2022
3 17
4
2022 2
3 17 3
4 7
m Z m
m
m
m

Như vậy có tất cả
2021
giá trị nguyên
m
thỏa mãn
Câu 39. Hỏi có tất cả bao nhiêu giá trị nguyên của tham số
20;20
m để
phương trình sau có nghiệm
2 2 2
2
log 4 2 9 1 1 2 4
x m x x m x m x
A.
12
. B.
23
. C.
25
. D.
10
.
Lời giải
Chọn B
Phương trình tương đương với:
2 2 2
2
2 2 2
2
2
2 2
2
2
2
2
2
log 4 2 9 1 1 2 4
log 2 2 2 4 2 9 1 2 4
log 4 2 4 2 9 1 2 4
16
log 2 4 1 2 4 8
4
x m x x m x m x
x m x x m x m x
x x m m x m x
m m x x x
x x
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
Trang 28 TÀI LIỆU ÔN THI THPT QUỐC GIA
Đặt
2
4
t x x
, ta thấy
2
2 2
4
lim 4 0; lim 4 0; 2
x x
t
x x x x t x
t
 
 
Phương trình trở thành
2
2
2
2
4 4
16 2 4
log 1 2
t
m t
m t
t t
2
2
2 2
2 2
16 2 4
log 16 2 4 log
m t
t
m t t
t t
Xét hàm đặc trưng
2
( ) log
u
y f u u
t
có
1 1
0
ln 2
f u
u t
(xem như
t
là tham số)
Suy ra
( )
f u
luôn đồng biến
2 2 2 2 2
16
16 2 4 16 2 4
5 2
f m t f t m t t t
m
Do
0;t

nên suy ra
, 20;20
2
16 5
0 20 2
5 2 2
m Z m
t m m
m
Như vậy ta kết luận có tất cả 23 giá trị nguyên của tham số
m
. Chọn B
Câu 40. Cho hệ phương trình
2 2
2 2 2
1
2 1 2 .2 . 1
x y y
x y
x y
m y
,
m
là tham số.
Gọi
S
là tập các giá trị
m
nguyên để
1
có một nghiệm duy nhất. Tập
S
có bao nhiêu phần tử?
A.
0
. B.
1
. C.
3
. D.
2
.
Lời giải
Chọn B
Điều kiện
1 1;1
y y
.
Từ phương trình thứ nhất của hệ
1
ta có
2 2 2
x y y
x y y
.
Xét hàm số
2
t
y f t t
với t
.
Dễ thấy
2 .ln 2 1 0
t
y
với mọi t
nên hàm số
y f t
đồng biến trên
.
Do đó phương trình
2
tương đương với
2
x y y x y
.
Thay
2
x y
vào phương trình thứ hai của hệ
1
ta được
2 2
4 1 2 .2 . 1 3
y y
m y .
Để hệ đã cho có nghiệm duy nhất thì phương trình
3
phải có nghiệm duy nhất
1;1
y .
Giả sử
0
1;1
y
là một nghiệm của
3
thì
0 0
2 2
0
4 1 2 .2 . 1
y y
m y
.
Khi đó
0 0 0 0
2
2 2 2
0 0
4 1 2 .2 . 1 4 1 2 .2 . 1
y y y y
m y m y
nên
0
y
cũng là
nghiệm của
3
.
Suy ra
0 0 0
0
y y y
. Thay
0
y
vào
3
ta được
0
m
.
Thử lại: với
0
m
thì
3
viết thành
2 2
1
4 1 2.2 . 1 2 2 1 4
2
y y y
y
y y
.
Ta có
4 2
VT
, dấu bằng khi
1
2 0
2
y
y
y
;
4 2
VP
, dấu bằng khi
0
y
.
Suy ra phương trình
4
có nghiệm duy nhất là
0
y
.
Vậy
0
m
thỏa mãn (1 giá trị
m
thỏa).
_______________ TOANMATH.com _______________
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 29
| 1/29
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
PHƯƠNG TRÌNH LÔGARIT CHỨA THAM SỐ PHƯƠNG PHÁP
Tìm m để f  x, m  0 có nghiệm (hoặc có k nghiệm) trên D trong phương trình logarit chứa tham số:
Bước 1. Tách m ra khỏi biến số và đưa về dạng f  x  Am .
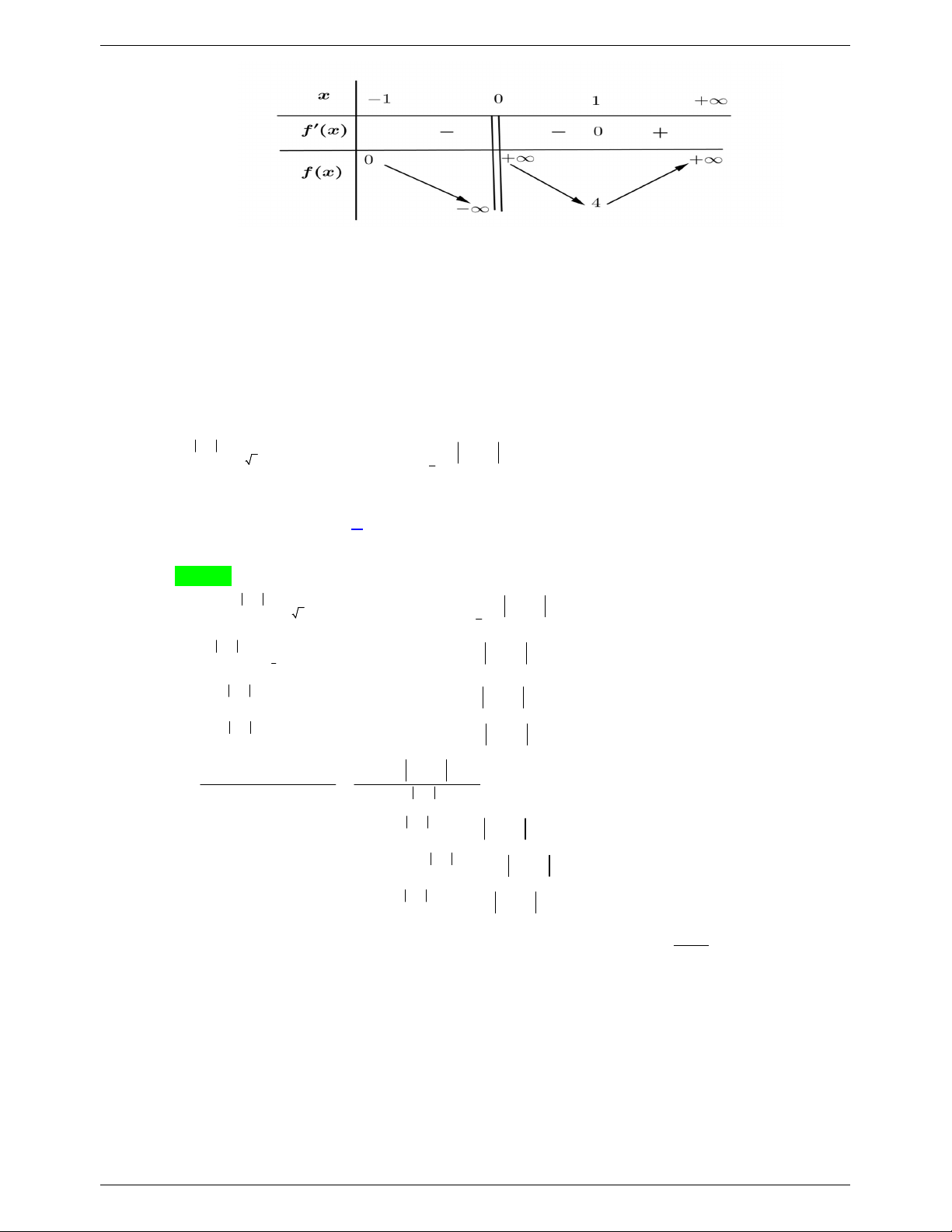
Bước 2. Khảo sát sự biến thiên của hàm số f  x trên D.
Bước 3. Dựa vào bảng biến thiên để xác định giá trị của tham số m để đường thẳng y  Am
nằm ngang cắt đồ thị hàm số y  f  x .
Bước 4. Kết luận các giá trị cần tìm của m để phương trình f  x  Am có nghiệm (hoặc có k nghiệm) trên D.  Lưu ý
Nếu hàm số y  f  x có giá trị lớn nhất và giá trị nhỏ nhất trên D thì giá trị Am cần tìm là
những m thỏa mãn: min f  x  Am  max f  x . x D  x D 
Nếu bài toán yêu cầu tìm tham số để phương trình có k nghiệm phân biệt, ta chỉ cần dựa vào bảng
biến thiên để xác định sao cho đường thẳng y  Am nằm ngang cắt đồ thị hàm số y  f  x tại k điểm phân biệt. Lưu ý quan trọng:
Các bước giải phương trình logarit có tham số cần chú ý:
 Bước 1. Đặt điều kiện (điều kiện đại số  điều kiện loga): 0  a  1 log K  f x   f x   a    Đ    0 Đ log K b  và mũ lẻ . a   b   0 log  f x   f x  a     Đ K    0 mũ chẵn
 Bước 2. Dùng các công thức và biến đổi đưa về các phương trình cơ bản rồi giải.
 Bước 3. So với điều kiện và kết luận giá trị tham số cần tìm. Câu 1. Cho hàm số 2 3log 2x  
2m  3 x 1 2m  log 
 2x  x16m  0. Số các giá trị nguyên 8 1  2
của m để phương trình đã cho có hai nghiệm phân biệt x , x thỏa mãn x  x  15 là: 1 2 1 2 1  3 2  3 13 2  3 3 A. m  . m  . C.  m  . D. m   . 2 B. 2 2 2 4 Lời giải Chọn C Ta có: 2
3log 2x  2m  3 x 1 2m  log    2x  x16m  0 8 1  2 2
 log 2x  2m  3 x 1 2m  log    2x  x16m 2 2  2 x  x 1 6m  0   2 2x   2m  3 2
x 1 2m  x  x 1 6m
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 1
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC 2 x  x 1 6m  0 * 2   x  x 1 6m  0     x  2m 2 x  
2m  2 x  4m  0   1  x  2
Phương trình đã cho có hai nghiệm phân biệt khi và chỉ khi phương trình (1) có hai nghiệm 2 4m  2m 1 6m  0 2  4m  8m 1  0 2  3 phân biệt thỏa mãn (*) 2
 2  2 1 6m  0    m  . 3    6m  0 2 2m  2  13 17
Theo giả thiết x  x  15  2m  22 2
 225  4m  8m  221  0   m  . 1 2 2 2 1  3 2  3 Do đó  m  . 2 2 Câu 2. Cho phương trình 2
log x  log 5x 1  log m  0 ( m là tham số thực). Có tất cả bao nhiêu 4 2   2
giá trị nguyên của m để phương trình đã cho có nghiệm? 3 A. m  0 . B. m  5 . C. 0  m  5. D. m   . 4 Lời giải Chọn C  1 x  Điều kiện:  5 . m   0 Xét phương trình: 2
log x  log 5x 1   log m   1 . 4 2   2   5x 1 5x 1 1
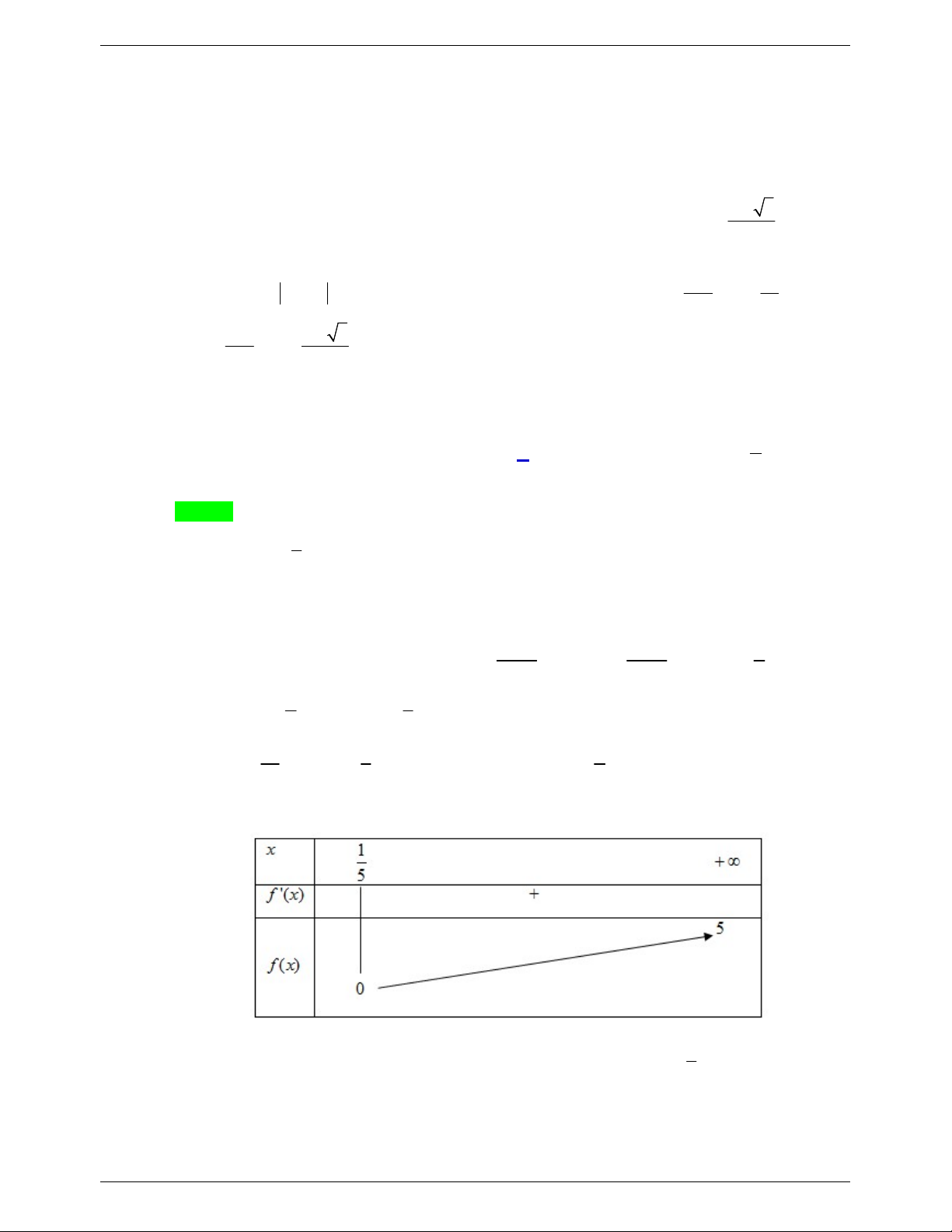
1  log x  log 5x 1   log m  log  log m   m  5   m 2 . 2 2   2 2 2   x x x  1  Xét f  x 1  5  trên khoảng ;     . x  5  1  1    Có f  x   0, x   ;   và f  x 1 lim  lim 5   5. 2     x  5  x x  x 
Ta có bảng biến thiên của hàm số f  x : 1 Phương trình  
1 có nghiệm khi và chỉ phương trình 2 có nghiệm x  . 5
Từ bảng biến thiên suy ra phương trình  
1 có nghiệm khi và chỉ khi 0  m  5. Trang 2
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
Câu 3. Tìm tất cả các giá trị nguyên của tham số thực m để phương trình 4log x 2  log x  m  0 3 1 3
có hai nghiệm phân biệt thuộc khoảng 0;  1 . A. 0 B. 1 C. 2 D. 3 Lời giải Chọn A Ta có:
4log x 2  log x  m  0  2log x 2  log x  m  0  log x2  log x  m 1 3 1 3 3 3 3   3
Đặt t  log x với t  ;0 . 3   2 1  t  t  m . Xét   2 f t  t  t . f 't  2t 1 f t 1 '  0  t   2 Bảng biến thiên 1 1
Dựa vào bảng biến thiên   m  0  0  m  . 4 4
Vậy không có giá trị nguyên m nào thỏa mãn yêu cầu bài toán.
Câu 4. Tìm các giá trị thực của tham số m để phương trình 2
log x  3log x  2m  7  0 có hai nghiệm 3 3
thực x , x thỏa mãn  x  3 x  3  72. 1  2  1 2 61 9 3 A. m  . B. m  3 . C. m  . D. m  . 2 2 2 Lời giải Chọn C
Tập xác định: D  0;. Đặt t  log .
x Phương trình đã cho trở thành 2
t  3t  2m  7  0 *. 3
Để phương trình đã cho có hai nghiệm thì phương trình * có hai nghiệm
    2   m   37 3 4 2 7  0  m  . 8 t   t  3
Gọi t ,t là hai nghiệm của phương trình *, ta có 1 2  . 1 2 t t  2m  7  1 2
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 3
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC 1 t   log x x  3t Giả sử 1 3 1 1    . 2 t  log t x    2 3 2 x 3  2
Theo đề bài ta có  x  3 x   3  72   1 3t  3 t2 3  3  72 1 2   1 t t2 1 t t2 1 t t2  3
 3.3  3.3  63  3  3 12  t   1 1  t  1 t  2 2t t 1  2 1 1  3 12.3  27  0   .  t 2    t   2 1 1   t  1  2 9
Mặt khác t t  2m  7  2  2m  7  m  . 1 2 2
Câu 5. Có tất cả bao nhiêu giá trị nguyên của tham số m để phương trình log x  3  m log 9  16 3   x3 có hai nghiệm thỏa mãn 2   x  x . 1 2 A. 15 . B. 17 . C. 14. D. 16 . Lời giải Chọn A
Tập xác định: D  3; \  2 . 4m
Phương trình  log x  3   16 . 3   log x3 3   4m
Đặt t  log x  3 , phương trình trở thành 2 t 
 16  t 16t  4m  0 *. 3   t Với x , x là nghiệm của phương trình đã cho thỏa mãn 1 2
2  x  x  1  x  3  x  3  0  log x  3  log x  3 . 1 2 1 2 3  1  3  2 
Do đó, yêu cầu bài toán trở thành tìm m để phương trình * có hai nghiệm phân biệt thỏa mãn    64  4m  0   b
t  t  0   16  0  0  m 16. 2 1 a   c  4m  0 a
Mà m   nên m 1; 2;;1  5 .
Vậy có 15 giá trị nguyên của m thỏa mãn bài toán.
Câu 6. Cho hai số thực a,b  1 thỏa mãn a  b  2021. Gọi ,
m n là hai nghiệm của phương trình
log x log x  2log x  2  0. Giá trị nhỏ nhất của biểu thức mn  4a bằng a b a A. 8080 . B. 2032 . C. 1015 . D. 3626 . Lời giải Chọn A Điều kiện: x  0. Ta có 2 log .
x log x  2log x  2  0  log .
a log x  2log x  2  0. a b a b a a Trang 4
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
Đặt t  log x, phương trình trở thành 2 log a.t  2t  2  0 b   1 . a
  1 2log a  1 2log 1  0 nên  
1 luôn có hai nghiệm t ,t với b b 1 2 2 2 t  t   2log b  log b . 1 2 log a a a b
Xét hai nghiệm m và n , ta có 2  1 t t2 1 t t2 log 2 a b mn  a a  a  a  b Do đó mn  a  b    b  b  b   b  2 2 2 4 4 2021 4 4.2021 2  8080  8080.
Dấu "  " xảy ra khi và chỉ khi b  2, a  2019.
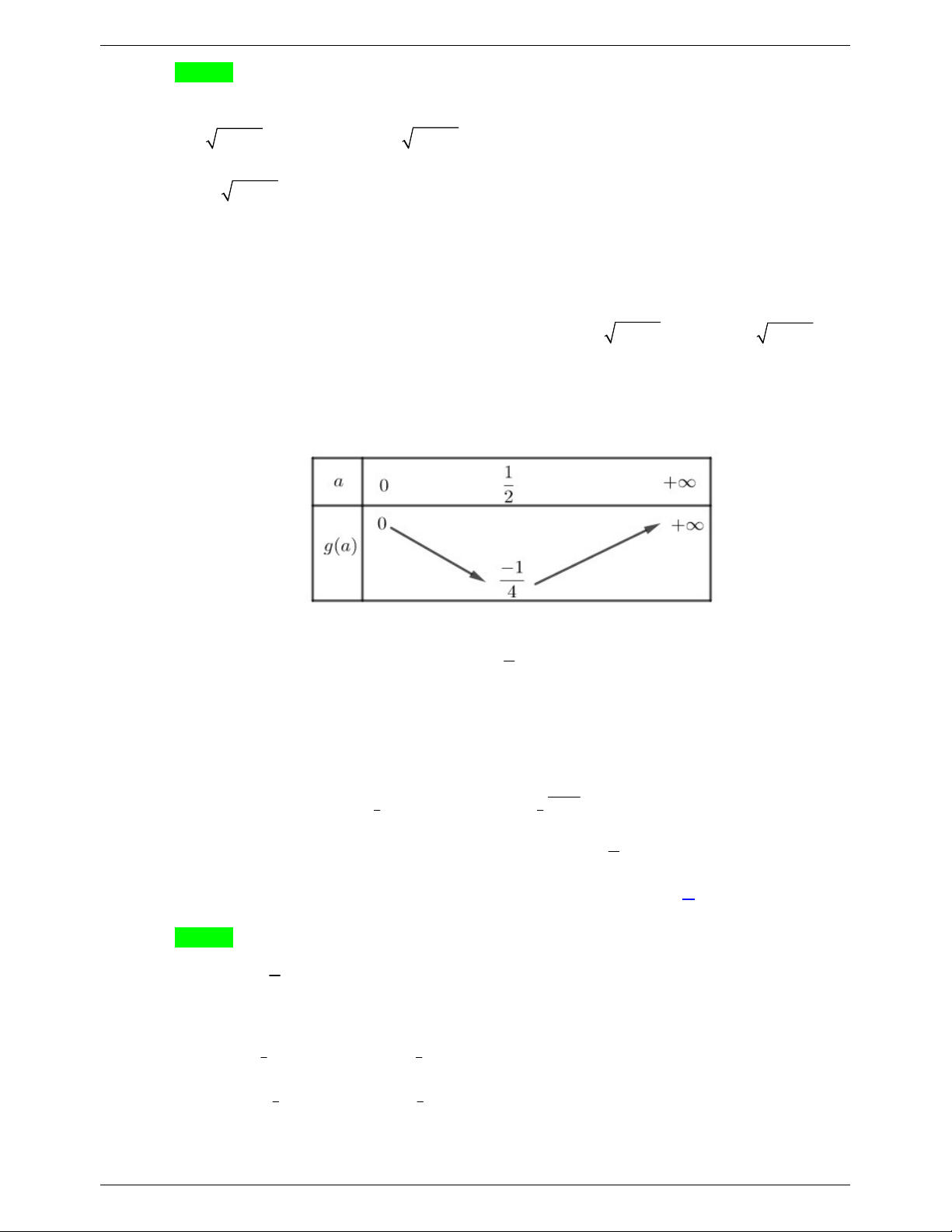
Câu 7. Có bao nhiêu số nguyên m  20;20 để phương trình log x  log m  x  2 có nghiệm thực 2 3   A. 15 . B. 14 . C. 24 . D. 21. Lời giải Chọn A x  0 Điều kiện:  . m  x  x   1  Đặt: t  log  log 2   3    4   m  x   x  2t x  4.2t 4   1    1  m   4.2t t   . t   1    3 3t m x    3t m  x 1
Xét phương trình: f t   4.2t t   . t   3 f t  ln 3 '    4.ln 2.2t ; 3t  ln 3  1 f 't  0  t  log   . 6    4ln 2  2 Bảng biến thiên:
Từ bảng biến thiên ta thấy phương trình có nghiệm khi: m  4,56 .
Mà m  , m 20;20  m 5;6;7;...;1  9 .
Vậy có 15 số nguyên thỏa mãn yêu cầu bài toán.
Câu 8. Số các giá trị nguyên của tham số m để phương trình log (x 1)  log (mx  8) có hai nghiệm 2 2 phân biệt là A. 5 . B. Vô số. C. 4 . D. 3 . Lời giải Chọn D
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 5
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC Điều kiện: x  1 Ta có: 2 2
log (x 1)  log (mx  8)  log (x 1)  log (mx  8)  (x 1)  mx  8 2 2 2 2 2  x  2x  9  mx . 2 x  2x  9 Do x  1 nên suy ra  . m x 2 x  2x  9 Xét hàm số f (x)  trên khoảng (1; ). x 2 x  9 f (  x)  , f (  x)  0  x  3. 2 x Bảng biến thiên
Nhìn vào BBT ta thấy, từ yêu cầu của bài toán tìm được 4  m  8 .
Do m nguyên nên m 5;6;  7 .
Vậy có 3 giá trị của m thỏa mãn yêu cầu bài toán.
Câu 9. Có bao nhiêu giá trị nguyên của m để phương trình log x  3  m log 9  16 có hai nghiệm 3   x3
thỏa mãn 2  x  x . 1 2 A. 17 . B. 16 . C. 14. D. 15 . Lời giải Chọn D
Điều kiện xác định: x  3 và x  2 .
Biến đổi phương trình đã cho về phương trình sau: log x  3  4m log 3 16  0 . 3   x3 2
 log x  3 16log x  3  4m  0 (1) . 3   3  
Đặt log x  3  t , phương trình   1 trở thành: 2
t 16t  4m  0 2 . 3   Ta có: log  3    3t x t x  3 . 3  
Theo điều kiện đề bài thì x  2 nên 3t  3  2  t  0 .
Vậy để phương trình log x  3  m log
9  16 có hai nghiệm thỏa mãn 2  x  x 3   x3 1 2
thì phương trình 2 phải có hai nghiệm t dương phân biệt   0  64  4m  0  t   t  16  0    0  m  16 . 1 2  4m  0 t .t  4m  0  1 2
Vậy có 15 giá trị nguyên m thỏa mãn.
Câu 10. Có bao nhiêu giá trị nguyên dương của tham số m nhỏ hơn 2022 để phương trình log   5x m m
 2x  0 có nghiệm thực? 5   A. 2022 . B. 2018 . C. 2021. D. 1011. Lời giải Trang 6
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC Chọn A
Phương trình đã cho tương đương với phương trình : x 2   5  5 x m m   x   x 2 5   5  5 x  5x m m Ta có 5x m   0 , 5x  0
Xét hàm đặc trưng   2
f t  t  t trên 0;   .
f t  2t 1  0,t0; 
 f t  đồng biến trên khoảng 0;  do đó   1    5x   5x f m f   5x  5x m 2   5 x  5x m . Đặt 5x a  , a  0 . Ta có     2 m g a  a  a . 1
Phương trình đã cho có nghiệm  m   mà m nguyên dương nhỏ hơn 2022 nên 4 m 1; 2;3;...;202  2 .
Vậy có 2022 giá trị m thỏa mãn yêu cầu bài toán. 1
Câu 11: Cho phương trình m   1 log  x  2 2 1  4 m  5 log
 4m  4  0 . Hỏi có bao nhiêu giá trị 1   1 x1 2 2  1 
m nguyên âm để phương trình có nghiệm thực trong đoạn  ;1  ? 2    A. 6 . B. 5 . C. 2 . D. 3 . Lời giải Chọn D  1  Trên đoạn  ;1 
thì phương trình luôn xác định. 2   
Với m nguyên âm ta có m  1, do đó phương trình đã cho trở thành 4m   2
1 log x 1  4 m  5 log x 1  4m  4  0 1     1   2 2  m   2
1 log x 1  m  5 log x 1  m 1  0 1     1   2 2
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 7
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC  1 
Đặt t  log x 1 , với x   ;1 thì 1  t  1. Ta có phương trình 1    2    2  2 t  5t 1 m   2
t  m  t  m    m 2t t   2 1 5 1 0 1  t  5t 1  m  * 2 t  t 1 2 t  5t 1 Xét hàm số f t   với 1  t  1. 2 t  t 1 2 4t  4 Ta có f t   
; f t   0  t  1. t  t  2 2 1 f   7 1  , f   1  3 3 7 Do đó min f t  3  và max f t  .  1  ;  1 1; 1 3  1 
Phương trình đã cho có nghiệm thực trong đoạn  ;1 
khi và chỉ khi phương trình * có nghiệm 2     7 t 1; 
1  min f t   m  max f t  3  m  .  1  ;  1 1; 1 3
Do m nguyên âm nên m 3;2;   1 .
Câu 12. Có bao nhiêu giá trị nguyên của tham số m thuộc khoảng 10;10 để phương trình x 1 3   log x  3m  m có nghiệm? 27   A. 9 . B. 8 . C. 10 . D. 7 . Lời giải Chọn C
Điều kiện: x  3m  0 Ta có x 1 3   log  3   3x x m m  log x  3m  3m 27   3   3x   t  3m
Đặt t  log x  3m , ta có ta có   3x  x  3t  t 3   3t   x  3m Xét    3u f u  u có    3x f u
ln 3  3  0  f u đồng biến, ta có
3x   3t            log  3  3x x t f x f t x t x x m  x  3m * 3   1 Xét hàm số    3x g x  x có    3x g x
ln 3 1; g x  0  x  log . 3 ln 3 Bảng biến thiên: 1 1 1
Phương trình * có nghiệm khi 3m  log  m  log  m 0;1; 2...9 . 3 3   ln 3 3 ln 3 Trang 8
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
Câu 13. Cho phương trình log  x  m  log
2  x  0 (1). Với m là giá trị của tập 2 1   2
S  m | m  49;m  
 để phương trình (1) có nghiệm. Tính tổng lập phương tất cả các phần tử của S A. 1382975 . B. 1382976 . C. 1382977 . D. 1382978 . Lời giải Chọn A x  2 
Ta có: log  x  m  log
2  x  0  log  x  m  log 2  x   . 2 2   2 1   2  m 2 x   2 2  m Vì x  2 nên  2  m   2 . 2
Kết hợp với m   , m  49 . Khi đó  2  m  49 .
Vì m   nên m  1;0;1...4  8 có 50 giá trị.
Vậy tổng S các giá trị của m để phương trình có nghiệm là: S   
1  0  1  2  3 ... 28  2 2 3 48 .49 3 3 3 3 3  1  1382975 . 4 Câu 14. Cho phương trình 1 log 2x   m  3 5 2 x 1 m  log
x  x 1 3m  0 . Số các giá trị nguyên của m để 2   2 1  5 2
phương trình đã cho có hai nghiệm phân biệt x , x thỏa mãn 2 2 x  x  20 là: 1 2 1 2 A. 13 B. 9 C. 14 D. 5 Lời giải Chọn D 1 Ta có: log 2x   m  3 5 2 x 1 m  log x  x 1 3m  0 2   2 1  5 2 2  log 2x  
m3 x 1m  log   2x  x13m 2 2  2 x  x 13m  0   2 2x   m  3 2
x 1 m  x  x 1 3m 2 x  x 1 3m  0 * 2 x  x 1 3m  0  *       x  m 2 x  
m  2 x  2m  0 (1)  x  2
Phương trình đã cho có hai nghiệm phân biệt khi và chỉ khi phương trình (1) có hai nghiệm phân 2 m  m 1 3m  0 2  m  4m 1  0 biệt thỏa mãn (*) 2
 2 11 3m  0    m  2  3 .  4  3m  0 m  2  Theo giả thiết 2 2 2 2
x  x  20 hay m  4  20  m  16  4   m  4 1 2
Do đó 4  m  2  3 . Vậy số các giá trị nguyên của m thỏa mãn là 5.
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 9
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
Câu 15. Cho phương trình ln ln
 cos x  m  m  cos x (1) 
. Tìm tất cả các giá trị của m để phương trình (1) có nghiệm. A. 1 1 m e   1   B. 1 1
e 1  m  e 1 C. 1  m  1 D. 1  m  e 1 Lời giải Chọn D u   ln  m  cos x u e  m  cos x
Đặt u  ln cos x  m ta được hệ phương trình:    ln  m  u cos  cos x x e  m  u
Từ hệ phương trình ta suy ra: u cos x e  u  e  cos x * Xét hàm số   t f t  e  t có '  t
f t  e 1  0,t  . 
Hàm số f t đồng biến trên ;
*  f u  f cos x  u  cos x Khi đó ta được:    cos ln cos  cos x m x x  e  cos x  m ** ;
Đặt z  cos x, z 1; 
1 . Phương trình ** trở thành: z e  z  m ** Xét hàm số:   z
g z  e  z trên 1;  1 . Hàm số   z
g z  e  z liên tục trên 1;  1 ; '  z g z  e 1; '   0 z g z
 e 1  0  z  0 và có Bảng biến thiên
Do đó max g  z  g  
1  e 1,min g z  g 0 1  1  ;  1  1  ;  1
Hệ phương trình ban đầu có nghiệm  phương trình ** có nghiệm  1  m  e 1.
Câu 16. Cho phương trình mcos2xsin2x 21sin 2x 3  3
 2  sin 2x  m cos 2x với m là tham số. Hỏi có
bao nhiêu giá trị m nguyên dương bé hơn 2021 để phương trình có nghiệm. A. 2019 . B. 2018 . C. 2020 . D. 2021. Lời giải Chọn A Ta có mcos2xsin2x 21sin 2 x 3  3  2  sin 2x  m cos 2x mcos 2 xsin 2 x 21sin 2 x  3  m cos 2x  sin 2x  3  21 sin 2x Xét hàm số    3t f t
 t t   ,    3t f t
ln 3 1  0  f t đồng biến trên  . Suy ra mcos2xsin2x 21sin 2x 3  m cos 2x  sin 2x  3  21 sin 2x
 m cos 2x  sin 2x  21 sin 2x
 m cos 2x  sin 2x  2 . Phương trình có nghiệm khi 2 2 m 1  4  m  3 .  m ;   3   3;   
. Do m ,m  2021 nên có 2019 giá trị của tham số m .
Câu 17. Có bao nhiêu giá trị nguyên của tham số m thuộc khoảng 2022;2022 để phương trình
10x  log  x  3m  3m có nghiệm? Trang 10
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC A. 2020 . B. 4042 . C. 4040 . D. 2021. Lời giải Chọn D
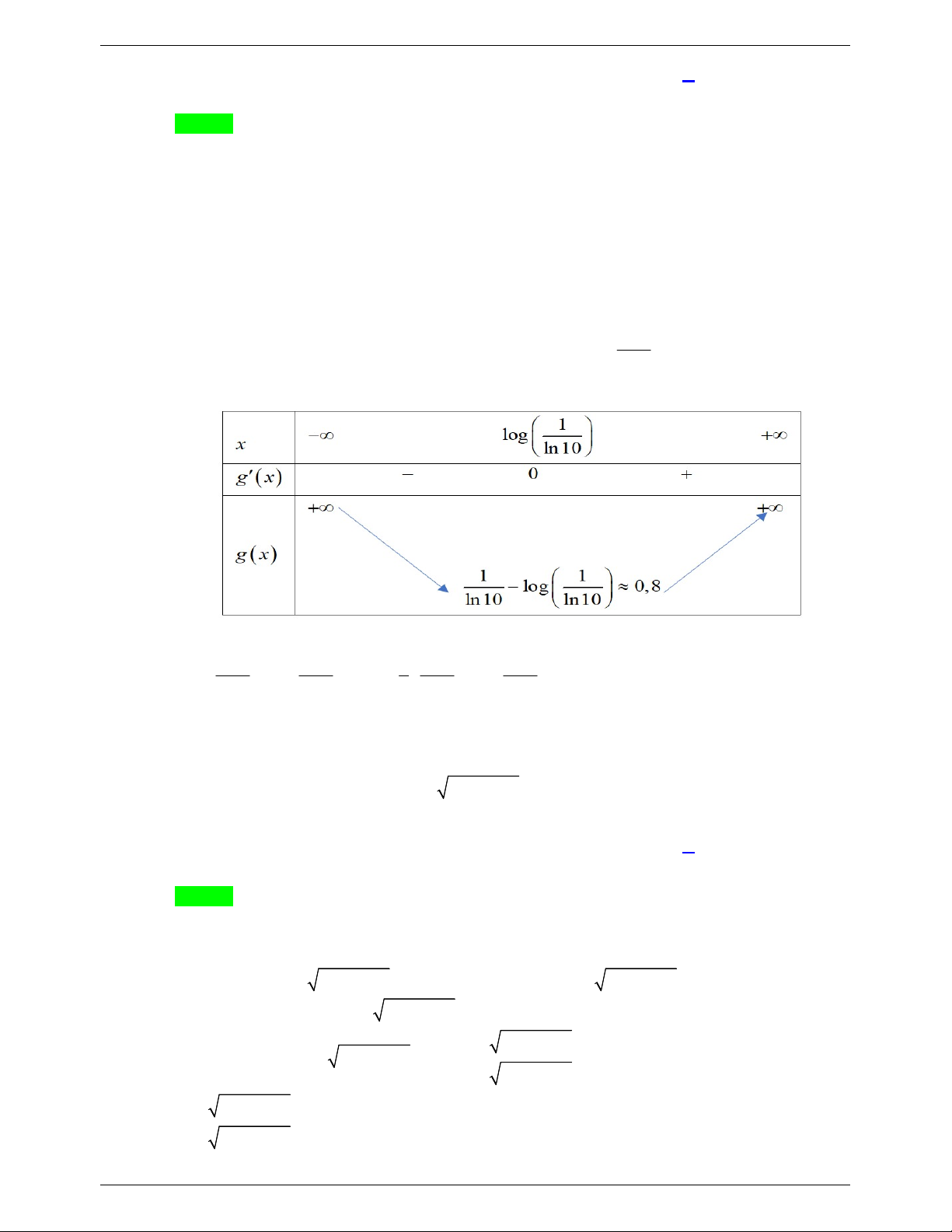
Ta có: 10x  log  x  3m  3m
 10x  x  log x  3m  x  3m
 10x  x  log  x  3m log 3  10 x m (1) Xét hàm số: ( )  10t f t  t; t    . (  ) 10t f t ln10 1  0; t
   nên hàm số f (t) đồng biến trên  .
Do đó phương trình (1)   log   3    3  10x  10x x x m x m  x  3m (2).   Đặt x g x   x  gx x 1 ( ) 10
10 ln10 1; g (x)  0  x  log   .  ln10  Ta có bảng biến thiên:
Từ bảng biến thiên ta thấy: để phương trình (2) có nghiệm thì: 1  1  1  1  1  3m   log  m   log  0,3      . ln10  ln10  3  ln10  ln10 
Vì m    2022;2022 nên m 1; 2;3;....;2021 .
Vậy có 2021 giá trị nguyên của tham số m thỏa yêu cầu đề. Câu 18. Cho phương trình 2
log x  2 log x  m  log x  m * . Có bao nhiêu giá trị nguyên của tham 2 2 2  
số m 2021; 2022 để phương trình (*) có nghiệm? A. 2021. B. 2022 . C. 4042 . D. 2024 . Lời giải Chọn D x  0 Điều kiện:  . m  log x  0  2 2 2
log x  2log x  m  log x  m  4 log x  8log x  4 m  log x  4m 2 2 2 2 2 2 2
 4log x  4log x 1  4 m  log x  4 m  log x 1 2 2 2  2     m  x   x  2log x  
1  2 m  log x  2 2 log 1 2log 1 2 2 2 1   2 2 2 m  log x 1  2  log x 1  2 2  m  log x  log x 1 2 2    m  log x  log x  2 2
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 11
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC log x  0 0  x 1 
* TH1: m  log x   log x 2    2 2  2 2 m  log x  log x 
log x  log x  m  0 1 2 2  2 2  
Đặt: t  log x t  0 , phương trình (1) trở thành: 2 2
t  t  m  0  t  t  m 2 2   Đặt: 2
g(t)  t  t(t   ;
 0.Bài toán trở thành: Tìm giá trị của tham số m để phương trình 2
có ít nhất 1 nghiệm t  0 Ta có: 2 g(t)  t  t  g (  t)  2t 1 0 t   0 Ta có BBT:
Dựa vào BBT, suy ra: để phương trình 2 có ít nhất 1 nghiệm t  0 thì m  0 (*) log x  1
* TH 2 : m  log x  log x 1 2  2 2  2
m  log x  log x  2log x 1  2 2 2 log x 1  2   2
log x  3log x 1 m  0 3  2 2  
Đặt: t  log x t  1 , phương trình (1) trở thành: 2 2
t  3t 1 m  0  m  t  3t 14 2   Đặt: 2
g(t)  t  t 1, t 1; Ta có: 2 g(t)  t  3t 1  g (  t)  2t  3 3 g (
 t)  0  2t  3  0  t  1; 2
Bài toán trở thành: Tìm giá trị của tham số m để phương trình 4 có ít nhất 1 nghiệm t  1 Ta có BBT: 5
Dựa vào BBT, suy ra: để phương trình 4 có ít nhất 1 nghiệm t  1 thì m   (**) 4
Kết hợp (*) và (**), m 2021;2022  m1;0;1;2;...; 202  2
Vậy có tất cả 2024 giá trị của m thỏa mãn.
Câu 19. Tìm tất cả các giá trị của m để phương trình ln m  ln m  cos x  cos x có nghiệm. 1 1 A. 1  m  e 1. B. 1  m  e 1. C. 1  m  1. D. 1  m  e 1. e e Lời giải Chọn B Trang 12
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC u   ln  m  cos x u e  m  cos x
Đặt u  ln m  cos x ta được hệ phương trình:    ln  m  u cos  cos x x e  m  u
Từ hệ phương trình ta suy ra: u cos x e  u  e  cos x * Xét hàm số   t f t  e  t có '  t
f t  e 1  0,t  .
 Hàm số f t đồng biến trên . 
*  f u  f cos x  u  cos x Khi đó ta được:    cos ln cos  cos x m x x  e  cos x  m **
Đặt z  cos x, z 1; 
1 . Phương trình ** trở thành: z e  z  m ** Xét hàm số:   z
g z  e  z trên 1;  1 . Hàm số   z
g z  e  z liên tục trên 1; 
1 và có max g  z  g  
1  e 1,min g z  g 0 1  1  ;  1  1  ;  1 Ta có bảng biến thiên:
Hệ phương trình ban đầu có nghiệm  phương trình ** có nghiệm  1  m  e 1.
Câu 20. Giá trị nào của m để phương trình 2 2
log x  log x 1  2m 1  0 có ít nhất một nghiệm thuộc 3 3 đoạn 3 1  ; 3    . A. 1  m  16 . B. 4  m  8. C. 3  m  8 . D. 0  m  2 . Lời giải Chọn D
Điều kiện x  0 . Đặt 2
t  log x 1  1, ta được phương trình 2
t  t  2m  2  0 * . 3 Ta có 3 x  1  ; 3     0  log x  3  2
1  t  log x 1  2 . 3 3
Phương trình đã cho có nghiệm thuộc 3 x  1  ; 3  
  * có nghiệm t 1; 2. Đặt   2
f t  t  t , với t 1; 2.
Hàm số f t  là hàm đồng biến trên đoạn 1; 2. Ta có f   1  2 và f 2  6 . Phương trình 2
t  t  2m  2  f t  2m  2 có nghiệm t 1; 2  f   1  2m  2  f 2  f    1  2m  2 2  2m  2      0  m  2 . 2m  2  f  2 2m  2  6
Câu 21. Cho Có bao nhiêu giá trị nguyên của tham số m thuộc khoảng 2021; 202  1 để phương trình
10x  log  x  3m  3m có nghiệm? A. 2021. B. 2020 . C. 2010 . D. 4040 . Lời giải
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 13
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC Chọn B
Ta có: 10x  log  x  3m  3m
 10x  x  log  x  3m  x  3m
 10x  x  log  x  3m log 3  10 x m (1) Xét hàm số: ( )  10t f t  t; t    . (  ) 10t f t ln10 1  0; t
   nên hàm số f (t) đồng biến trên  .
Do đó phương trình (1)   log   3    3  10x  10x x x m x m  x  3m (2).   Đặt x g x   x  gx x 1 ( ) 10
10 ln10 1; g (x)  0  x  log   .  ln10  Ta có bảng biến thiên:
Từ bảng biến thiên ta thấy: để phương trình (2) có nghiệm thì: 1  1  1  1  1  3m   log  m   log  0,3      . ln10  ln10  3  ln10  ln10 
Vì m    2021; 202 
1 nên m 1; 2;3;....;2020  .
Vậy có 2020 giá trị nguyên của tham số m thỏa yêu cầu đề.
Câu 22. Có bao nhiêu giá trị m nguyên trong 2017;2017 để phương trình log mx  2log  x   1 có nghiệm duy nhất? A. 2017 . B. 4014 . C. 2018 . D. 4015 . Lời giải Chọn C Ta có mx 0   mx  0        mx  x   x 1 log 2log 1  x 1  0  x 1  0   2   mx  x  2x 1    1 log  mx  logx  2 1 mx   x  2 1
Ta thấy x  0 không là nghiệm của phương trình   1 . 1
Với 1  x  0 ta có phương trình  
1 trở thành m  x   2 2. x 1
Xét hàm số f  x  x   2 , x  1  ; \  0 . x 1 Ta có f  x 1  0  x  1  2 x Bảng biến thiên Trang 14
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
Phương trình đã cho có nghiệm duy nhất khi phương trình 2 có nghiệm duy nhất trên 1; \  0 . m  0
Từ bảng biến thiên suy ra .  m   4 m 1  ; 2;...; 2  017 Vì m 2017;2017    
 có 2018 giá trị m thỏa mãn. m  4 Câu 23. Cho phương trình 4 xm.log  2  3  2 xx x x
.log 2 x  m  2  0 với m là tham số. Tổng tất cả các giá trị 2   2 2 2 1   2
của tham số m để phương trình đã cho có ba nghiệm phân biệt là A. 3 . B. 2 . C. 4 . D. 1. Lời giải Chọn B Ta có: 4 xm.log  2  3  2 xx x x .log 2 x  m  2  0 2   2 2 2 1   2
 4 xm.log  2  2  3 2 2  2 xx x x .log     2 x m 2 0 1 1 2   2 2
 2.4 xm.log   2  3 2 2 2  2 xx x x .log 2 x  m  2  0 2 2  
 2.4 xm.log   2  3 2 2 2  2 xx x x .log 2 x  m  2 2 2   2.log  2 x  2x  3 log 2 x  m  2 2  2     2 2 2 xx 4 xm 2 x 2  2.2 x.log  2
x  2x  3  2 xm.log 2 x  m  2 2  2 2   2 3 x 2  2 .2
x.log x  2x  3  2 .2 xm.log 2 x  m  2 2  2  2 2 2   2 x 2 x3  2 .log  2
x  2x  3  2 xm  .log 2 x  m  2 (1) 2  2 2 2   t t 1
Xét hàm số     2t y f t
.log t với t  2 , có f t   2 .ln 2.log t  2 .  0, t   2 . 2 2 t ln 2
Suy ra hàm số     2t y f t
.log t đồng biến trên nửa khoảng 2; . 2 Khi đó
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 15
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC   1  f  2
x  2x  3  f 2 x  m  2 2
 x  2x  3  2 x  m  2 2
x  2x 1  2x  m   2 x  2x 1  2  m  x x  22  2  m  3 2   2 x  2m 1  3
Trường hợp 1: Phương trình (3) có 1 nghiệm kép và phương trình (2) có 2 nghiệm phân biệt  1  2 1  0 m m  2 1 khác 0      m  .  2  m  3  0 3 2 m   2
Trường hợp 2: Phương trình (2) có 1 nghiệm kép và phương trình (3) có 2 nghiệm phân biệt  1 m   2 2m 1  0    5 3
khác 2  2m 1  4  m   m  . 2 2  2m 3 0       3 m   2
Vậy tổng tất cả các giá trị của tham số m để phương trình đã cho có ba nghiệm phân biệt là 1 3   2 . 2 2
Câu 24. Cho phương trìn 4 xm log  2  3  2x  x x x
log 2 x  m  2  0 . Tìm tất cả các giá trị 2   2 2 2 1   2
của tham số m để phương trình trên có đúng hai nghiệm thực phân biệt. 1 3 1 3 3 1 A. m  hoặc m  . B. m  . C. m  .
D. m   hoặc m   . 2 2 2 2 2 2 Lời giải Chọn A 4 xm log  2  3  2x  x x x log 2 x  m  2  0 2   2 2 2 1   2 2 log x  2x  3 log 2 x  m  2 12  2 xm log
x  2x  3  2x  x log 2 x  m  2   2  2  2 2 2   2   2   3 2 x 2 x  3 322 xm  2 2 log u 2u log u 1   u 2u Xét hàm số f u 2 2  
với u  2 . Ta có f u   2 log . u ln 2    0 3 2 u 8 2 8  u.ln 2 
u  2 . Suy ra hàm số f u đồng biến trên 2; nên 2      f  x 4x 1 2m 0 1 2
x  2x  3  f 2 x  m  2 2     x   1  2 x  m   . phương trình 2 x 1 2m  0  2
đã cho có đúng hai nghiệm phân biệt. Trang 16
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
TH1: Phương trình (1) có nghiệm hai 2 nghiệm phân biệt, phương trình (2) vô nghiệm suy ra 3   2m  0 1   m  I  2m 1  0 2
TH2: Phương trình (2) có nghiệm hai 2 nghiệm phân biệt, phương trình (1) vô nghiệm suy ra 3   2m  0 3   m  II  2m 1  0 2
TH3: Phương trình (1) và (2) đều có hai nghiệm phân biệt và hai nghiệm này giống nhau 3   2m  0 1 3    m  III  2m 1  0 2 2 a  b  4 Gọi ;
a b (b  a) là hai nghiệm của phương trình (1), theo định lý viet ta có  . Vì  . a b  2m 1 a  b  0
a;b cung là nghiệm của phương trình (2) nên 
suy ra vô lý vậy m   (III)  . a b  2  m 1 1 3
Vậy từ (I) ; (II) và (III) suy ra m  hoặc m  . 2 2 1
Câu 25. Cho phương trình m   1 log  x  2 2 1  4 m  5 log
 4m  4  0 1 . Hỏi có bao nhiêu 1   1   x 1 3 3 giá trị m nguyên  2 
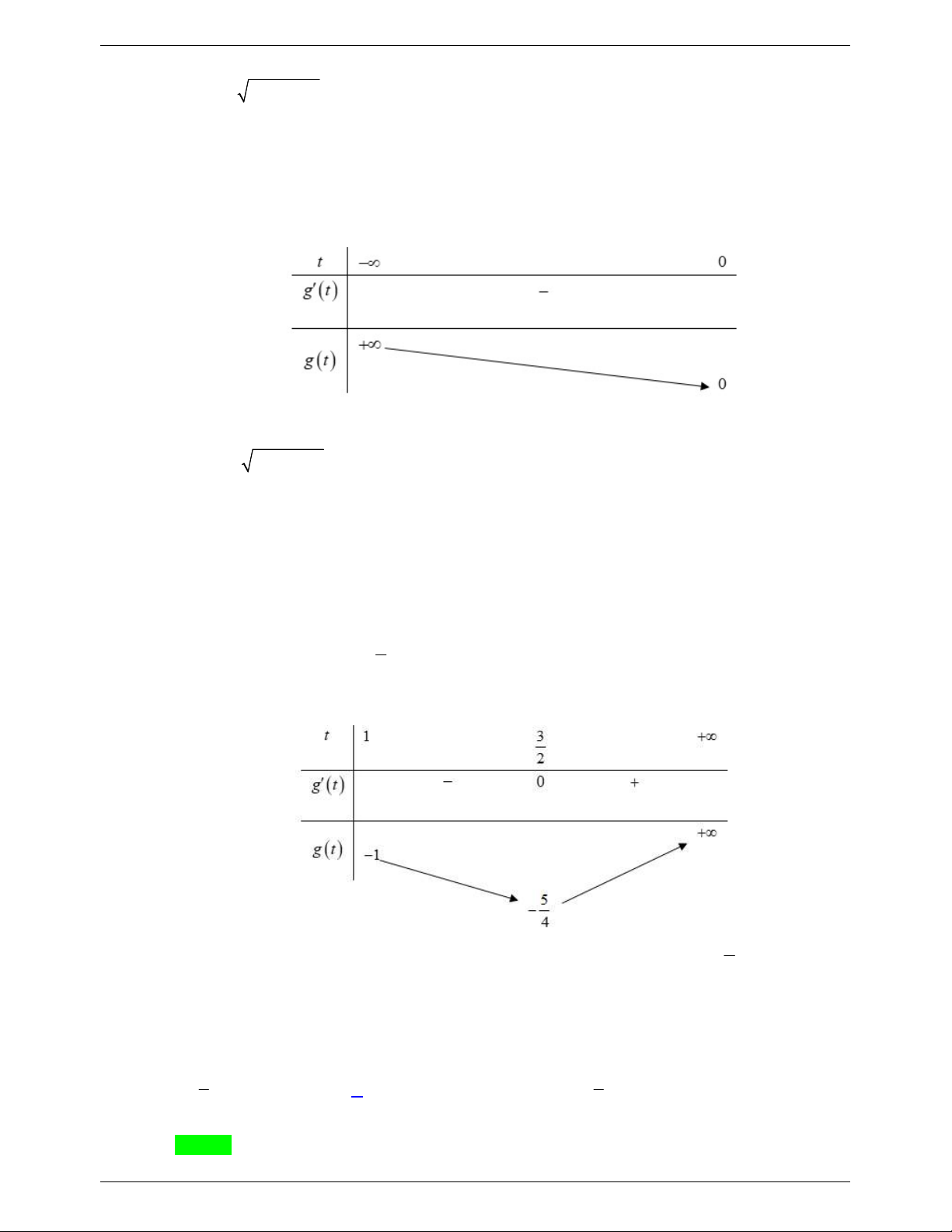
âm để phương trình (1) có nghiệm thực trên đoạn  ;2  ? 3    A. 6 . B. 5 . C. 2 . D. 3 . Lời giải Chọn D Ta có  1  4m   2 1 log
x 1  4 m  5 log x 1  4m  4  0 1     1   3 3  m   2 1 log
x 1  m  5 log x 1  m 1  0 1     1   3 3  2 
Đặt t  log x 1 với x   ;2 thì 1  t  1 ta có phương trình: 1    3    3 2    m   t 5t 1 2
1 t  m  5t  m 1  0  m 2t t   2 1  t  5t 1  m  2 2   t  t 1 2 t  5t 1 2 4t  4 t  1 Xét hàm số f t  
với 1  t  1. Ta có f t    0  2 t  t 1   t  t  2 2 t  1 1  7 f   7 1  ; f   1  3
 . Do đó min f t  3  ; max f t  3 1; 1 1; 1 3  2 
Phương trình đã cho có nghiệm thực trong đoạn  ;2 
khi và chỉ khi phương trình (2) có 3    7 nghiệm t 1; 
1  min f t   m  max f t   3  m  1; 1 1; 1 3
Như vậy các giá trị nguyên âm của m cần tìm là 3;2;  1
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 17
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
Câu 26. Gọi S là tập chứa tất cả các giá trị thực của tham số m để tồn tại đúng một bộ số thực  ; x y thỏa mãn 2
log  x  y  4m log  2 2
x  y 15  3m  0 . Tính tổng bình 2 2 
phương giá trị tất cả các phần tử của tập S đó 144 45 225 41 A. B. C. D. 289 4 256 16 Lời giải Chọn C
Áp dụng quy tắc cần và đủ, ta nhận thấy vai trò của hai ẩn x và y là như nhau. Nếu  ; x y thỏa
mãn thì  y; x cũng thỏa mãn. Vì vậy, muốn bộ số  ;
x y thỏa mãn là duy nhất thì tất cả các biến
phải bằng nhau. Suy ra x  y . Phương trình trở thành như sau:
 log 2x  4mlog 2x  153m  0  1 log x2 2 2
 4m 1 2log x 15  3m  0 2 2 2  2  2
 log x  2 4m 1 log x 16  7m  0 2     2 m  1
Để có duy nhất nghiệm thực x thì   4m  2 1  16  7m  0   1  5 m   16 Ta thử lại: Với m 1, ta có: 2
log  x  y  4log  2 2 x  y 12  0 2 2  Dể thấy cho 2
y  0  log  x  4log  2 x  2
12  0  log x  8log x 12  0 2 2 2   2  
Do phương trình trên có hai nghiệm nên suy ra trường hợp này loại 15 15 285 Với m  , ta có: 2 log  x  y  log  2 2 x  y   0 2 2  16 4 16
Đánh giá thông qua bất đẳng thức Bunyakovsky, ta nhận thấy: 2 15 285 15  x  y  285 2 0  log  x  y  log  2 2 x  y  2   log x  y  log    2 2 2     2 4 16 4  2  16   2 15 225  15 15 2  0  log x  y  log x  y   log x  y   log x  y   2   2    2    2   2 16  4  4 x  y  1
Dấu bằng xảy ra khi và chỉ khi 15  1  x  y  (thỏa mãn) 4 4 x  y  2  16 2  4  8 2 15 225 Suy ra S  
  Tổng bình phương bằng:  16  256
Câu 27. Gọi S là tập chứa tất cả các giá trị thức của tham số m để tồn tại duy nhất bộ ba số thực  x; y; z thỏa mãn điều kiện 2 log  2 2 2
2x  y  z  2m log 4x  2y  2z  0 . Tích tất cả các phần tử của 2  2   tập S tương ứng bằng: A. 0 . B. 16 . C. 6 . D. 12 . Lời giải Chọn A
Điều kiện 2x  y  z  0 . Ta có 2 2 2
2x  y  z  2 2x  y  z  2 2x  y  z hay 2 2 2
4x  2y  2z  4 2x  y  z .
Dấu đẳng thức xảy ra  x  y  z . Trang 18
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC 1 Khi đó 2 2 2
4x  2y  2z  4 2x  y  z  log 4x  2y  2z  2  log  2 2 2 2x  y  z 2 2  2  log  2 2 2
2x  y  z  2 log 4x  2y  2z  2 2   2   . 2 log  2 2 2
2x  y  z  2mlog 4x  2y  2z  0 2  2  
2m log 4x  2y  2z  log 2x  y  z   4 log  4x  2y  2z 2 2 2 2 2  2 2 2 2  .
Đặt t  log 4x  2 y  2z ta được t  2 4 2  2mt 2
 2t  m  8t  8  0 . 2   Yêu cầu bài toán  2
2t  m  8t  8  0 có đúng một giá trị t  m  2 8  64  0 m  0   . m  1  6
* Khi m  0 thì t  2  log 4x  2 y  2z  2  2x  y  z  2 . 2   1
Mặt khác dấu đẳng thức xảy ra  x  y  z nên x  y  z  . 2 1
* m  16 tương tự x  y  z  . Vậy S  0;1  6 . 32 2 Câu 28. Cho hai số thực , x y thỏa mãn hệ thức 2 2 y x  log
x . Hỏi có tất cả bao nhiêu giá trị nguyên 2 y 1 
m 40; 40 để tồn tại duy nhất một số thực x thỏa mãn hệ thức 2 2
4 y 10x  mx 1  0 ? A. 51. B. 52 . C. 53 . D. 31. Lời giải +) Vì 2 2
2 y x  0,x; y nên với y  0 thì log x  0  x  1. 2 y 1  x 1
Do đó điều kiện của bài toán là  . y  0 +) Khi đó 2 2 2 2 y x 2 y x 2 y 1  x 2 2  log x  2.2  2log x  2  log x 2 y 1  2 y 1  2 y 1  2 y 1  2 2 log x 2 2 y 1  x 2    y   x . 2x log 2 y   2 log 2 1 2 log 2   2 2 2 1 2 t 2t
Xét hàm đặc trưng    2t f t
.log t trên 1;  , ta có f t   2 .ln 2.log t   0,t  1. 2 2 t ln 2
Do đó hàm f t  đồng biến trên 1;  .
Khi đó, f  y    f  2 2 1
x   y   x  y  x  2 2 2 2 2 1 4 1 . +) Ta có y 
x  mx    x  2 2 2 2 2 4 10 1 0 1 10x  mx 1  0 4 2  x 12x  mx  0 3
 x 12x  m (do x  1). Xét hàm g  x 3  x  x  gx 2 12
 3x 12 , gx  0  x  2. Bảng biến thiên:
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 19
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
Từ bảng biến thiên của hàm g  x suy ra phương trình 2 2
4 y 10x  mx 1  0 có duy nhất một
nghiệm khi và chỉ khi m 11;40 , do đó có tất cả 52 giá trị m thỏa mãn yêu cầu bài toán.
Câu 29. Cho các số thực x, y, z thỏa mãn log  2 2 2x  y   log  3 3
x  2 y  log z . Có bao giá trị nguyên của z để có đúng hai cặp  x, y 3 7 
thỏa mãn đẳng thức trên. A. 2 . B. 211. C. 99 . D. 4. Lời giải Chọn B x  0  2 2 x  y  0 ĐK  y  0  z  0 2 2 2x  y  3t   1  Ta có log  2 2 2x  y   log  3 3 x  2y  3 3
 log z  t  x  2y  7t 2 . 3 7   z 10t  3  t 2t log 3 2 + Nếu y  0   3
2  x  7 thay vào   1 ta được 3 2.7  3t  t  log 2 do đó 3 49 z  10 . 3 3 49 + Nếu y  0 2 3  x       2  2 2 2x  y  3  27t    3 3 x  2 y 2  49 t    y      49 t Từ   1 & 2 suy ra      , * .       x  2y  2  49t  2 2 3 3 x  y 3 3   2  27     27 2  x   2  2 1   y          2 u 0 x  3u 2 6u  3 u  2u  4  Đặt 3
 u,u   2 . Xét f u 3   f  u   0  u   2  . y 2u  3   1 2u  4 2 2 1 u  4  Ta có bảng biến thiên Trang 20
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
Nhận xét với mỗi giá trị u tương ứng với duy nhất 1 cặp  x, y thỏa mãn bài toán do đó  4   1 t  log49 log   49 4  49  1  
Yêu cầu bài toán tương đương  33   8  27 27    10  z 10   . 33  27  8
Vì z là số nguyên nên có 211giá trị thỏa mãn.
Câu 30. Cho phương trình sau:  
 2x xm       2 2 4 2 2 x 4 2 2 2 4 1 2 mx x mx x x m  
1  0 . Hỏi có tất cả bao nhiêu giá trị thực
của tham số m để phương trình đã cho có 3 nghiệm thực x? A. 4. B. 5 . C. 2. D. 3. Lời giải Chọn A  
 2x xm       2 2 4 2 2 x 4 2 2 2 4 1 2 mx x mx x x m   1  0 Nhân 2 vế với 2:  
 2x xm       2 2 4 2 2 x 4 2 4 2 2 4 1 2 mx x mx x x m   1  0 Đặt: 2 a  2x  4mx , 2
b  x  4x  m 1   2x xm    2 4 2 x 4 2 2 2 mx a b   1  0 * b 1  a 1 2 2 2 2    Nếu a  0,b  0 thì  (vô lý). b a x  0 2 a  0 x  2mx  0  Suy ra:  tm    x  2m  2 b  0 x  4x  m 1  0  2 x  4x  m 1  0    1
Để có 3 nghiệm thực phân biệt thì (1) có nghiệm:  x  0  m  1 7  65  x  2m  m  8 + nghiệm kép  m  5
Câu 31. Tổng tất cả các số nguyên a để tồn tại số thực b thỏa mãn 4b   2   2  3b a a A. 7 B. 0 C. 3 D. 2 Lời giải Chọn C a  2  Điều kiện  4b  a  2 
Đặt a   t t   2 2 ,
0  a  t  2 , phương trình trở thành b b   b 2 b b 2 b 9 4 2
4  t  9  2.3 .t  t t  3 .t   0 1 b 2 b b 2 b  
4  t  t  3  4  t  3  t     2 3b  t  0 3  b   t  0
Để phương trình (1) có nghiệm:        4 b b b b b b  1 1 9 2 9
4  0  2.4  9  0    b  log  b  log 2   . 4 9  9  2 2 9 4
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 21
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
Khi đó tổng hai nghiệm   3b t t . Để có nghiệm 3b
t  thì phương trình (1) phải có hai nghiệm không 1 2 âm 9b 4b    0  b  0
Khi đó ta có hai trường hợp nghiệm của phương trình 2 3b  2.4b  9b 3b 2.4b 9b  3b 2.4b 9b      Trường hợp 1: t  . Ta có a  2   a     2 2 2  2   
Với 0  b  log 2 ta thấy a  2; 
1 mà a nguyên nên a 1;  0 . 9 4 2 3b  2.4b  9b 3b 2.4b 9b  3b 2.4b 9b      Trường hợp 2: t  . Ta có a  2   a     2 2 2  2   
Với 0  b  log 2 ta thấy a 2;0 mà a nguyên nên a 1;   2 . 9 4
Vậy tổng tất cả số nguyên a thỏa mãn là 1   2  0  3  .
Câu 32. Cho phương trình 4x  4  .2x a log  2
2x  x  b . Có bao nhiêu bộ số 2 
a,b thỏa mãn điều kiện 100a  ,  100b ,  1
 00  a,b 100 sao cho phương trình có nghiệm duy nhất A. 15 B. 6 C. 3 D. 4 Lời giải Chọn B
Ta có 4x  4  .2x log  2 2    x 2  2  2 x a x x b  a log x 2  x  b . 2 2    
Ta nhận thấy x  x là nghiệm thì x  2  x cũng là nghiệm. Do đó để có nghiệm duy nhất thì 0 0 4 p q
x  1. Khi đó thay vào ta được: 4  log 1  2a a b  b 1. Đặt a  ,b  với p, q  2   0 100 100 400 q q 400 Khi đó: 2 p  b 1  1. Chú ý 1 nên
  . Ta có 2 tình huống: 100 100 p 400 Trường hợp 1: 
  p 1;2;4;5;8;10;16;20;25;40;50;80;100;200;40  0 . p 400 p 400 400 Vì 2  b 1 101  log 101 p 
 60 vậy p 80;100;200;40  0 . 2 p log 101 2  4   Khi đó ta có:  ; a b ;31 ; 
 1;15;2;3;4; 
1  . Với mỗi bộ số  ;
a b tương ứng đều có nghiệm   5  
duy nhất bởi vì ta có đánh giá: 2x  2 x  2 2x2 x  4  a log b  
1  a log b 1x  2 2 2 1 . 2 2  400 Trường hợp 2: Nếu 
 khi đó vế trái có dạng phân số với mẫu số có dạng lũy thừa của 2. p
Vì vậy vế phải cũng phải như vậy tức là q25 400 q
Lại có khi đó 1  2 p  b 1  1  0  1
 00  q  0 cho nên q 25;50;7  5 . 100 400  p 3 Với q  25  2   p   (Loại). 4 400  p 1 1 Với q  5  0  2   p  4  00  a  4  ,b   . 2 2 Trang 22
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC x x  1  Khi đó: 2 2  2  4  log x 2  x 
. Dùng TABLE ta thấy có duy nhất 1 nghiệm x  1 2      2  400  p 1 3 Với q  7  5  2   p  2  00  a  2  ,b   . 4 4 x x  3  Khi đó: 2 2  2  2  log x 2  x 
. Dùng TABLE ta thấy có duy nhất 1 nghiệm x  1 2      4 
Kết luận: Có tất cả 6 bộ số a;b thỏa mãn điều kiện.
Câu 33. Cho phương trình sau:  2 2log xlog x 1log 2  4 x  9x 2  3x m
 2m  0 (với m là tham số thực). Gọi
S là tập hợp tất cả các giá trị nguyên dương của m để phương trình đã cho có đúng hai nghiệm phân
biệt. Tổng của phần tử nhỏ nhất và phần tử lớn nhất của S bằng A. 100 3 1. B. 100 3 1. C. 99 3 . D. 99 3 1. Lời giải Chọn A x  0 Điều kiện:  3x  m 
Phương trình đã cho tương đương với phương trình:  2 2log xlog x 1log 2  4
x  3x  23x  m  0 Ta có:  2 2lg xlg x 1lg 2
 4 x  3x  23x  m  0 log x  2 3x  m 3x  m   1     log x   2 2lo g xlog x 1lo g x 2 2  4
2log x  log x  2  2log x  2  3x  m x 100  1   x   . 10  * x  log , m m     3 
Trường hợp 1: Với m  1 thì x  log m  0 (loại). Do đó phương trình đã cho có 2 nghiệm phân 3 1 biệt x  100, x  . 10
Trường hợp 2: Với m  1 thì x  log m  0 nên phương trình đã cho luôn nhận nghiệm x  log m 3 3 1 Mà 100 
nên phương trình đã cho có hai nghiệm phân biệt khi 10 1 1 10 100  log m  100  3  m  3 . 3 10 Do m nguyên dương, m  1 100 100
nên m 2;3; 4;...,3  
1 . Vậy S  2;3;4;...,3   1 .
Suy ra tổng của phần nhỏ nhất và phần tử lớn nhất của S bằng 100 3 1. x  m
Câu 34. Cho hàm số f (x) 
. Gọi S là tập hợp các số nguyên dương 2x 1
m  7 sao cho với mọi bộ số thực a, , b c 2; 
3 thì ln f (a) , ln f (b) , ln f (c) là độ dài ba
cạnh của một tam giác. Tổng các phần tử của S là A. 10. B. 15. C. 16 . D. 14 . Lời giải
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 23
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC Chọn C x  m
Từ giả thiết ta có với m   S, x  2;  3 thì f (x)   0 . 2x 1 f (  x) 1 2m
Xét hàm số g(x)  ln f (x), ta có g (  x)    0,m S, x  2;  3 do vậy f (x) (x  m)(2x 1)
ta có bảng biến thiên của hàm số g(x) như sau m  3 TH1: ln
 0  m  4 , lúc này xét mọi bộ số thực a,b,c 2;  3 sao cho ln f (a) , 7
ln f (b) , ln f (c) là độ dài ba cạnh của một tam giác khi đó ta cần có 2 min g(x)  max g(x) x   2;  3 x   2;  3  19  7 29 m  m  3 m  2 2      m 3 m 2 2 ln  ln   10   2
 5m 19m  53  0   , 7 5  7  5  19  7 29 m   10
kết hợp với m S ta có m 6;  7 . m  2 TH2: ln
 0  m  3 , lúc này xét mọi bộ số thực a, , b c 2;  3 sao cho ln f (a) , 5
ln f (b) , ln f (c) là độ dài ba cạnh của một tam giác khi đó ta cần có 2  m  3 m  2  m  2  m  3
2 max g(x)   min g(x)  ln  2ln     2  7m  3m  47  0 x   2;  3 x   2;  3 7 5  5  7 3  5 53 3  5 53   m 
, kết hợp với m S ta có m 1;  2 . 14 14  m  2 ln  0  TH3: 5 
 3  m  4 khi đó tồn tại  2;3 để ln f ()  0 khi đó chọn bất kỳ bộ m  3 ln  0  7
ba số a,b, với a,b2; 
3 thì ln f (a) , ln f (b) , ln f ( ) không thể là độ dài của 3 cạnh của một tam giác.
Từ 3 trường hợp trên ta có S  1;2;6; 
7 do đó tổng các phần tử của S là 16.
Câu 35. Cho hàm số f (x)  log 2.log 2  x  m . Hỏi có bao nhiêu giá trị nguyên dương của tham số x 4  
m để phương trình f  x  2  x   0 có tổng tất cả các nghiệm bằng 2 . A. 0 B. 1 C. 2 D. 3 Lời giải Chọn D Trang 24
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
+ Đặt t  x  2  x  t   2; 2   .
Giả sử t là nghiệm của phương trình f (t)  0 khi đó: x  2  x  t * . 0   0
Dễ thấy pt (*) chỉ có tối đa 2 nghiệm vì khi bình phương thoát hết căn chỉ ra phương trình bậc hai.
+ Nếu x là một nghiệm của phương trình (*) thì 2  x cũng là một nghiệm của (*) vì: 0 0
2  x  2  2  x  t  x  2  x  t . 0  0  0 0 0 0
Mà x  2  x  2  x nên suy ra 0  0  0
 Để phương trình f  x  2  x  0 có tổng các nghiệm bằng 2
 Phương trình f (t)  0 có duy nhất một nghiệm trên  2;2   .
+ Xét phương trình f (t)  0  log 2.log 2  t  m  0 t 4   ln 2 ln 2  t  .  m ln t 2 ln 2
 ln 2  t  2mln t Vì *
m   nên ta có: ln 2  t  2m ln t  2m 2 2 m
 t  t  t  t  2  0 . + Xét hàm số 2 ( ) m g t  t  t  2 t   2;2 2m 1
 g (t)  2mt  1  0     * m   
 Phương trình g(t)  0 có nhiều nhất 1 nghiệm trên  2;2   Mặt khác g t  g   m * ( )
2  2  2  2  0  m 
Suy ra phương trình g(t)  0 vô nghiệm.
Vậy không có giá trị nào của tham số m thỏa mãn yêu cầu bài toán. 2   x  Câu 36. Cho phương trình 2 log
 3mlog x  2m  2m 1  0  . Có bao 3   3   3 
nhiêu giá trị nguyên của tham số m lớn hơn 2
 021 sao cho phương trình đã cho có hai nghiệm
phân biệt x , x thoả x  x 10 ? 1 2 1 2 A. 2020 . B. 2019 . C. 2020 . D. 2021. Lời giải Chọn A Điều kiện: x  0 . 2   x  log
 3mlog x  2m  2m 1  0     log x  2 2 2
1  3mlog x  2m  2m 1  0 3 3 3 3   3  Đặt t  log x 3 Phương trình trở thành     t  2 t m 2 2
 mt  m  m    t   m   2 1 3 2 2 1 0 3
2 t  2m  2m  0   t  2  m  2 x  3m   2m2 x  3
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 25
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC m 2m2 x  x  10  3  3  10 1 2 2
 9.3 m  3m 10  0  3m  1  m  0  m  0 Vì m và m  2
 021 nên m 2020;2019;...;  1 .
Câu 37. Hỏi có tất cả bao nhiêu giá trị nguyên của tham số m 24;24 để ba
số hạng sau theo thứ tự tạo thành 1 cấp số cộng, với x 1; 2 :  x  m  3x 2x 1 9.2 1 ; ; 2 3.2     A. 2 . B. 1. C. 17 . D. 7 . Lời giải Chọn A
Để ba số lập thành một cấp số cộng thì  x   3x 2x 1 9.2 1 2 3.2       2m 3x 2
 2  6.2 x  9.2x  2m 1. Đặt x 1 2 t  2  2 ;2     2;4. Khi đó f t  3 2
 t  6t  9t  2m 1 với t 2;4 Suy ra min  f t 3 2
 t  6t  9t  2m 1 max f t 3 2  t  6t  9t 2;4 2;4 1 5
 0  2m 1  4   m   m 1;  2 2 2
Câu 5. Hỏi có tất cả bao nhiêu giá trị nguyên của tham số m 18;18 để phương trình 2 2 x     1 .2x m
 3m 1  0 có hai nghiệm thỏa 0  x  1  3  x 1 2 A. 8 . B. 18. C. 11. D. 12. Lời giải Chọn D 2 t  2t 1 Đặt 2x t 
 0. Phương trình trở thành: 2 t  m  
1 t  3m 1  0  m  2t  3 Hai nghiệm thỏa mãn: 0 1 x 1 3 2 0   1  3 
 2  2   2  2  2x x x t  t 1 2 1 2  1  t  2  8  t 1 2 2 t  2t 1
Xét hàm số y  f t 
có bảng biến thiên như sau: 2t  3
Suy ra m  7  7  m  18 tức có tất cả 12 giá trị nguyên m thỏa
Câu 38. Gọi S là tập hợp chứa tất cả các giá trị nguyên của m 2022;2022 Trang 26
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC sao cho phương trình 2 log x  2m   1 log  2
x  2m  3  0 có hai nghiệm sao cho thỏa mãn 2 2 
0  x  x  8 . Số các phần tử của S là 1 2 A. 2021. B. 2019 . C. 18. D. 2023. Lời giải Chọn A
Đặt t  log x . Phương trình trở thành: f t  2  t  22m   1 t  2m  3  0 (1) 2
Hai nghiệm phân biệt thỏa mãn 0  x  x  8  t  t  log 8  3 1 2 1 2 2
Ta xét phương trình (1) có:    m  2 2 2
1  2m  3  4m  6m  2  3 17 m  Khi 2 4
  4m  6m  2  0  
thì phương trình (1) sẽ có hai nghiệm phân biệt là:  3   17 m   4 t  2m  2 1  4m  6m  2 1  t   2m   2 1  4m  6m  2 2
Đến đây ta chỉ cần điều kiện t  2m   2
1  4m  6m  2  3 là bài toán được giải quyết 2 m 1 2  2m  0  3     3  m  2 2
4m 8m  4  4m  6m  2 m  7  7  3   17 m 
Kết hợp với điều kiện   0 , suy ra: 4 m Z  ;m   2  022;2022    2  022  m  2 3 17 3   m   4 7
Như vậy có tất cả 2021 giá trị nguyên m thỏa mãn
Câu 39. Hỏi có tất cả bao nhiêu giá trị nguyên của tham số m  2  0;20 để
phương trình sau có nghiệm log  2 2
x  m  x x  4   2m 9 x 1 1 2m 2 x  4 2 A. 12 . B. 23. C. 25 . D.10 . Lời giải Chọn B
Phương trình tương đương với: log  2 2
x  m  x x  4   2m 9 x 11 2m 2x  4 2  log  2 2
2x  2m  2x x  4   2m 9 x 1 2m 2x  4 2  
 log x  x  42 2  2m  4 
 2m  9 x  1 2m 2 x  4 2      16  2  log  2m  4  1 2m x  4  x  8x 2      2 x  4  x2     
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 27
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC Đặt 2
t  x  4  x , ta thấy 2  2 2 x   x 
x   x    t   4 t lim 4 0; lim 4 0;  2x  x x t
16  2m  4 2t  4 2 4  t 
Phương trình trở thành log    1 2m t  2 2   t t    m  t t  log  2 2 16  2m  4 16 2 4 2 t      log  2t  2 2  t t u
Xét hàm đặc trưng y  f (u)  log u  có f u 1 1 
  0 (xem như t là tham số) 2 t u ln 2 t
Suy ra f (u) luôn đồng biến  f 16  2m  4 16 2
t   f  2t   16  2m  4 2 2 2 t  t  t  5  2m 16 5
Do t 0; nên suy ra 2 m Z  ,m   2  0;20 t 
 0  m    20  m  2 5  2m 2
Như vậy ta kết luận có tất cả 23 giá trị nguyên của tham số m . Chọn B 2xy  2y  x  2y 
Câu 40. Cho hệ phương trình  , m là tham số. 2x 1   m 2   1 2 y 2 .2 . 1 y
Gọi S là tập các giá trị m nguyên để  
1 có một nghiệm duy nhất. Tập S có bao nhiêu phần tử? A. 0 . B. 1. C. 3 . D. 2 . Lời giải Chọn B
Điều kiện y  1  y  1  ;  1 .
Từ phương trình thứ nhất của hệ  
1 ta có 2xy      2y x y  y 2 .
Xét hàm số     2t y f t  t với t  . Dễ thấy 2t
y  .ln 2 1  0 với mọi t  nên hàm số y  f t đồng biến trên  .
Do đó phương trình 2 tương đương với x  y  y  x  2 y .
Thay x  2 y vào phương trình thứ hai của hệ   1 ta được y    2 m   y 2 4 1 2 .2 . 1 y 3 .
Để hệ đã cho có nghiệm duy nhất thì phương trình 3 phải có nghiệm duy nhất y  1  ;  1 . Giả sử y  1
 ;1 là một nghiệm của 3 thì 0 4y 1   2 m  2 0y 2 .2 . 1 y . 0   0 Khi đó   2 0 4 y 1   2 m  2 0 .2 y . 1 y  0  4y 1  2 m  2 0y 2
.2 . 1 y nên  y cũng là 0 0 0 nghiệm của 3 .
Suy ra y   y  y  0 . Thay y  0 vào 3 ta được m  0. 0 0 0 y y y 1
Thử lại: với m  0 thì 3 viết thành 2 2
4 1  2.2 . 1 y  2   2 1 y . y 4 2 y 1
Ta có VT 4  2 , dấu bằng khi 2 
 y  0 ; VP4  2 , dấu bằng khi y  0. 2y
Suy ra phương trình 4 có nghiệm duy nhất là y  0.
Vậy m  0 thỏa mãn (1 giá trị m thỏa).
_______________ TOANMATH.com _______________ Trang 28
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 29