Phương trình logarit có chứa tham số

Tài liệu gồm 25 trang được biên soạn bởi tập thể quý thầy, cô giáo nhóm Nhóm Word Và Biên Soạn Tài Liệu Môn Toán THPT, hướng dẫn giải bài toán phương trình logarit có chứa tham số

46 23 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 6: Hàm số mũ và hàm số lôgarit (KNTT)

Môn: Toán 11

Thông tin:

25 trang 8 tháng trước

Tác giả:

Profile Kim Oanh
NHÓMWORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG:2019-2020
Trang 573
PHƯƠNG PHÁP GIẢI PHƯƠNG TRÌNH LOGARIT
Thường sử dụng các phương pháp sau:
1. Phương pháp đưa về cùng cơ số.
2. Phương pháp đặt ẩn phụ.
3. Phương pháp hàm số.
KIẾN THỨC CẦN NHỚ:
log . log log
a a a
b c b c
với , 0;0 1b c a .
log log
a
a
x x
với
0;0 1a
.
Nếu
1a
thì với
1 2 1 2 1 2
, 0 : log log
a a
x x x x x x
Nếu
0 1a
thì với
1 2 1 2 1 2
, 0 : log log
a a
x x x x x x
0
log log 0 1
a a
f x
f x g x a
f x g x
log 0 1
b
a
f x b f x a a
Phương trình bậc hai có hai nghiệm âm phân biệt
0
0
0
S
P
.
Phương trình bậc hai có hai nghiệm dương
0
0
0
S
P
.
Phương trình bậc hai có hai nghiệm trái dấu 0P .
PHƯƠNG TRÌNH LOGARIT CÓ CHỨA THAM SỐ
NHÓMWORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG:2019-2020
Trang 574
BÀI TẬP MẪU
Cho phương trình
2
2 2
log 2 2 log 2 0x m x m ( m là tham số thực). Tập hợp tất cả các giá trị của
m để phương trình đã cho có hai nghiệm phân biệt thuộc đoạn
1;2
là
A.
1;2 B.
1;2 C.
1; 2 D.
2;
Phân tích hướng dẫn giải
1. DẠNG TOÁN: Đây là dạng toán tìm điều kiện của tham số để phương trình logarit có nghiệm thỏa
mãn điều kiện cho trước.
2. HƯỚNG GIẢI:
B1:
Viết lại phương trình logarit về dạng phương trình bậc hai đối với 1 biểu thức logarit.
B2:
Đặt ẩn phụ là biểu thức logarit và tìm điều kiện cho ẩn phụ.
B2:
Tìm điều kiện cho phương trình ẩn phụ.
Từ đó, ta có thể giải bài toán cụ thể như sau:
Lời giải
Chọn C
Điều kiện :
0x
Ta có :
2
2
2 2 2 2
log 2 2 log 2 0 1 log 2 log 2 0 1x m x m x m x m
Đặt
2
logt x
, với
1;2x thì
0;1t , khi đó ta có phương trình:
2
2
1
1 2 2 0 1 0 2
1
t
t m t m t mt m
t m
Nhận thấy với mỗi số thực
0;1t
cho ta một số thực
1;2x
, do đó yêu cầu bài toán
2
có 2
nghiệm phân biệt thuộc
0;1
1 1
2
1 2
1 0;1
0 1 1
m
m
m
m
m
.
Vậy 1 2m .
Chú ý: Đối với phương trình bậc hai chứa tham số, nếu có dạng chính phương thì nên tìm cụ thể hai
nghiệm của phương trình.
Bài tập tương tự và phát triển:
Câu 43.1: Cho phương trình ( là tham số thực). Gọi là tập hợp
tất cả các số thực mà phương trình có hai nghiệm phân biệt thuộc đoạn . Số phần tử của
tập
là
A. . B. . C. . D. .
Lời giải
Chọn B
Điều kiện:
Phương trình:
2 2
3 3
log 3 log 3 2 2 1 0
x m x m m
m
S
m
S
2
0
1
3
0
x
2 2
3 3
log 3 log 3 2 2 1 0
x m x m m
2 2
3 3
log 3 log 2 1 0
x m x m m
NHÓMWORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG:2019-2020
Trang 575
Đặt , với thì
0;1t , khi đó ta có phương trình
Khi đó yêu cầu bài toán phương trình đã cho có hai nghiệm phân biệt thuộc đoạn
(Hệ vô nghiệm).
Vậy không có giá trị nào của thỏa mãn yêu cầu bài toán.
Câu 43.2: Cho phương trình
2
3 3
log 9 5 log 3 10 0x m x m (với m là tham số thực). Số giá trị
nguyên của tham số m để phương trình đã cho có hai nghiệm phân biệt thuộc
1;81
là
A.
2
. B.3 . C.
4
. D.5 .
Lời giải
Chọn C
Ta có:
2
3 3
log 9 5 log 3 10 0x m x m
.
Đặt
3
logt x
vì
1;81 0; 4x t .
Khi đó phương trình đã cho trở thành:
2
1 3 6 0t m t m
3
2
t
t m
.
ycbt
0 2 4 2 6
2 3 5
m m
m m
. Vậy có 4 số nguyên m thoả ycbt.
Câu 43.3: Cho phương trình ( là tham số thực ). Có bao nhiêu giá
trị nguyên của để phương trình đã cho có hai nghiệm thực phân biệt thuộc đoạn ?
A. . B. . C. . D. .
Lời giải
Chọn B
Ta có
Phương trình đã cho có hai nghiệm thực phân biệt thuộc đoạn khi và chỉ khi có một
nghiệm thuộc đoạn tức .
Vậy có giá trị nguyên của thỏa mãn bài toán.
3
log
t x
1;3
x
2 2
1
3 2 1 0
2 1
t m
t mt m m
t m
0;1
2 1
0 1 1
1
0 2 1 1 0
2
1 2 1
2
m
m
m m
m m
m
m
2
3 3
4log ( 3)log 2 0
x m x m
m
m
1;9
0
2
1
3
2
2
3 3 3 3
1
4 log ( 3) log 2 0 4 log ( 3)log 2 0
2
x m x m x m x m
2
3
3 3
3
3
3
log 1
log ( 3) log 2 0
log 2 1
log 2
x
x
x m x m
x m
x m
1;9
1
1;9 \ 3
0 2 2 0 2
2 1 1
m m
m m
2
m
NHÓMWORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG:2019-2020
Trang 576
Câu 43.4: Tìm tất cả các giá trị của tham số
m
để phương trình
2
3 3
log 3 log 1 0x x m
có đúng 2
nghiệm phân biệt thuộc khoảng
0;1
. Tìm tất cả các giá trị của tham số
m
để phương trình
2
3 3
log 3 log 1 0x x m có đúng 2 nghiệm phân biệt thuộc khoảng
0;1
A.
9
4
m
. B.
9
0
4
m
. C.
1
0
4
m
. D.
9
4
m
.
Lời giải
Chọn B
Ta có
2 2
3 3 3 3
log 3 log 1 0 log 3log 0 1x x m x x m
Đặt
3
logt x
với
0;1x
thì 0t , khi đó ta có phương trình
2
3 0 2t t m
Nhận thấy với mỗi số thực 0t cho ta một số thực
0;1x , do đó yêu cầu bài toán
Phương trình
2
có hai nghiệm âm phân biệt
2
3 4 0
0
3 9
0 0 0
2 4
0
0
m
S m
P
m
.
Câu 43.5: Cho phương trình
2
2
3 3
log 3 log (3 ) 2 2 1 0x m x m m
. Gọi
S
là tập tất cả các số tự nhiên m
mà phương trình có hai nghiệm phân biệt
1 2
,x x
thỏa mãn . Tính tổng các phần tử của
S
.
A.
6
. B. 1. C.
0
. D.
10
.
Lời giải
Chọn B
Với
m
2
2
3 3
PT log 3 1 log 2 2 1 0x m x m m
Đặt
3
log 3
t
t x x
Ta được phương trình:
2 2
3 2 1 0t mt m m
1
1 2
t m
t m
.
Phương trình có hai nghiệm phân biệt khi và chỉ khi
1 2 1 2.m m m
Khi đó
1 2 1 2
1 2
10 10
3 3 9.3 3 10 0
3 3
m m m m
x x
3 1 0 0.
m
m m
Câu 43.6: Tìm tất cả các giá trị của tham số thực m để phương trình
2
2 1
2
4 log log 0x x m có hai
nghiệm phân biệt thuộc khoảng
0;1
.
1 2
10
3
x x
NHÓMWORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG:2019-2020
Trang 577
A.
1
0
4
m . B.
1
0
4
m
. C.
1
4
m
. D.
1
0
4
m
.
Lời giải
Chọn A
Ta có
2
2
2 1 2 2
2
4 log log 0 log log 1x x m x x m
Đặt
2
logt x
với
0;1x thì
0t
, khi đó ta có phương trình .
Xét
2
f t t t
;0t 
. Có
1
' 2 1; ' 0
2
f t t f t t
Bảng biến thiên
Nhận thấy với mỗi số thực 0t cho ta một số thực
0;1x , do đó yêu cầu bài toán
có hai nghiệm phân biệt. Dựa vào bảng biến thiên suy ra
1 1
0 0
4 4
m m
Câu 43.7: Có bao nhiêu giá trị nguyên của tham số để phương trình có
nghiệm, trong đó có đúng một nghiệm thuộc đoạn ?
A. . B. . C. . D. .
Lời giải
Chọn D
Điều kiện: . Khi đó phương trình đã cho tương đương với
.
Đặt , với mỗi thì cho một giá trị .
Khi đó ta được phương trình .
Xét hàm số trên đoạn .
Ta có , .
Bảng biến thiên của
2
*
t t m
*
m
2 2
2 2
log 2 2log 1 0
x x m
1
;16
2
10
8
7
6
0
x
2
2 2
1 log 4log 1 0
x x m
2
2 2
log 2log
x x m
2
log
t x
1
;16
2
x
1;4
t
2
2
t t m
2
2
f t t t
1;4
2 2
f t t
0 1
f t t
f t
NHÓMWORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG:2019-2020
Trang 578
Từ bảng biến thiên suy ra thỏa mãn yêu cầu bài toán.
Vậy có tất cả 6 giá trị nguyên của thỏa mãn yêu cầu bài toán.
Câu 43.8: Tìm m để phương trình :
2
2
1 1
2 2
1
1 log 2 4 5 log 4 4 0
2
m x m m
x
có nghiệm thuộc đoạn
5
, 4
2
.
A.
m
. B.
7
3
3
m . C.
m
. D.
7
3
3
m .
Lời giải
Chọn D
Điều kiện: 2x . Khi đó phương trình đã cho tương đương với
2
2 2
1 2 log 2 4 5 log 2 4 4 0m x m x m
2
2 2
4 1 log 2 4 5 log 2 4 4 0m x m x m
2
2 2
1 log 2 5 log 2 1 0m x m x m
. (1)
Đặt
2
log 2t x
. Vì
5
;4 1;1
2
x t
.
Phương trình (1) trở thành
2
1 5 1 0m t m t m
.
2
2
5
1
2
1t t
m
t t
.
Xét hàm số
2
2
5 1
1
t t
f t
t t
, 1;1t
Ta có
2
2
2
2
4 4
' 0
2
1
t
t
f t
t
t t
.
Bảng biến thiên
Phương trình đã cho có nghiệm
5
;4
2
x
khi phương trình (2) có nghiệm
1;1t
.
1 3;8
m
m
NHÓMWORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG:2019-2020
Trang 579
Từ bảng biến thiên suy ra
7
3
3
m .
Câu 43.9: Tất cả các giá trị của tham số m để phương trình
3 3
log 2log 1mx x
có hai nghiệm phân
biệt là
A. 4m . B. 4m . C. 0m và 4m . D. 0m và 4m .
Lời giải
Chọn B
Ta có
23 3
2
1 0
1 0
log 2log 1 (*)
2 1
1
x
x
mx x
mx x x
mx x
.
Ta thấy
0x
không là nghiệm của (*).
Với
0x
:
1
(*)
1
2
x
m x
x
Xét hàm số
1
2f x x
x
với
1; \ 0x  .
Ta có
2
2 2
1 1
1
x
f x
x x
;
0 1f x x
(do
1; \ 0x 
).
Bảng biến thiên:
Dựa vào bảng biến thiên suy ra 4m là giá trị cần tìm.
Câu 43.10: Cho phương trình (với
m
là tham số thực). Có bao nhiêu
giá trị nguyên của m để phương trình đã cho có bốn nghiệm phân biệt.
A.
. B. . C. . D. .
Lời giải
Chọn B
Đặt (vì nên ), khi đó ta có phương trình
Nhận thấy: nếu thì ta có một giá trị . Nếu thì .
Xét hàm số với . Ta có bảng biến thiên :
2 2 2
ln 1 8ln 1 0
x x m
0
15
16
17
2
ln 1
t x
2
1 1
x
0
t
2
8 *
t t m
0
t
0
x
0
t
1
t
x e
2
8
f t t t
0
t
NHÓMWORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG:2019-2020
Trang 580
Yêu cầu bài toán có hai nghiệm dương phân biệt
Vậy có 15 giá trị nguyên của
m
thỏa mãn đề bài.
Câu 43.11: Cho phương trình
2
2 2 2
log 2 log 3 log 3x x m x
với
m
là tham số thực. Tìm tất cả
các giá trị của
m
để phương trình có nghiệm thuộc
16; .
A.
1 2m
. B.
1 5m
. C.
3
5
4
m
. D.
1 5m
.
Lời giải
Chọn B
Đặt
2
logt x
với
16;x
thì 4t , khi đó ta có phương trình
2
2 3 3 *t t m t
- Với
0m
thì phương trình vô nghiệm, do
2
2 3 0
, 4.
3 0
t t
t
t
- Với
0m
thì
2
2 2 2 2 2 2
* 2 3 3 1 2 3 1 3 1 3 0 1t t m t m t m t m
+
Nếu
1 3m t
: không thỏa mãn.
+ Nếu 1m thì
2
2
3
1
3 1
1
t loai
m
t
m
Do đó để phương trình đã cho có nghiệm
2
2
3 1
4 1 5
1
m
m
m
thoûa
.
Câu 43.12: Cho phương trình với là tham số thực. Tìm tất cả
các giá trị của để phương trình có nghiệm thuộc .
A. . B. . C. . D. .
Lời giải
Chọn D
Đặt với thì , khi đó ta có phương trình
Điều kiện xác định: .
- Với thì phương trình vô nghiệm, do
- Với
0m
thì
- Với
0m
thì
+
Nếu : không thỏa mãn.
+ Nếu
1m
thì (**)
*
16 0
m
2
3 3 3
log 4log 5 log 1
x x m x
m
m
27;
0 2
m
0 2
m
0 1
m
0 1
m
3
log
t x
27;x

3
t
2
4 5 1 *
t t m t
1
5
t
t
0
m
2
4 5 0
, 5.
1 0
t t
t
t
2
* 4 5 0
t t
1 ( )
.
5 ( )
t loaïi
t thoûa maõn
2
2 2
* 4 5 1
t t m t
2 2 2 2
1 2 4 5 0 **
m t m t m
1 1
m t
2 2
1 1 5 0
t m t m
2
2
1 ( )
5
1
t loaïi
m
t
m
NHÓMWORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG:2019-2020
Trang 581
Do đó để phương trình đã cho có nghiệm , kết hợp
suy ra .
Vậy với thì phương trình đã cho có nghiệm thuộc .
Câu 43.13: Tìm tất cả các giá trị thực của m để phương trình
2 2 2
log cos logcos 4 0x m x m
vô
nghiệm.
A.
2; 2m
. B.
2; 2m
. C.
2;2m
. D.
2; 2m
.
Lời giải
Chọn C
Ta có:
2 2 2
log cos logcos 4 0x m x m
2 2
log cos 2 log cos 4 0x m x m
(*)
Đặt
log cos x t
. Do cos 1x
0t
Khi đó phương trình (*) trở thành:
2 2
2 4 0.t mt m
(1)
Phương trình (*) vô nghiệm khi và chỉ khi phương trình (1) vô nghiệm hoặc có các nghiệm đều
dương. Điều này xảy ra khi và chỉ khi
1 2
1 2
0
0
0
. 0
t t
t t
2 2
2 2
2
1. 4 0
1. 4 0
2
0
1
4
0
1
m m
m m
m
m
2
2
2
2 4 0
2 2
2 4 0
2
2 0
2 2
4 0
m
m
m
m
m
m
m
2 2m
Câu 43.14: Cho hàm số
2 2
27 1
3
3log 2 3 1 log 1 3 0x m x m x x m
. Số các giá trị
nguyên của
m
để phương trình đã cho có hai nghiệm phân biệt
1 2
,x x
thỏa mãn
1 2
15x x
là:
A.
14
B.
11
C.
12
D.
13
Lời giải
Chọn D
Ta có:
2 2
27 1
3
3log 2 3 1 log 1 3 0x m x m x x m
2 2
3 3
log 2 3 1 log 1 3x m x m x x m
2
2 2
1 3 0
2 3 1 1 3
x x m
x m x m x x m
2
2
2
1 3 0 *
1 3 0 *
2 2 0 1
2
x x m
x x m
x m
x m x m
x
2 2
2 2
5 6
5 0 1 1
1 1
m m
m
m m
0
m
0 1
m
0 1
m
[27; )
NHÓMWORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG:2019-2020
Trang 582
Phương trình đã cho có hai nghiệm phân biệt khi và chỉ khi phương trình (1) có hai nghiệm
phân biệt thỏa mãn (*)
2
2
2
1 3 0
4 1 0
2 1 1 3 0 2 3
4 3 0
2
m m m
m m
m m
m
m
.
Theo giả thiết
2
2
1 2 1 2 1 2
15 4 225 4 221 0 13 17x x x x x x m m m
Do đó
13 2 3m
. Vậy số các giá trị nguyên của m thỏa mãn là 13.
Câu 43.15: Cho phương trình
2
9 3 3
log log 5 1 logx x m
( m
là tham số thực). Có tất cả bao nhiêu
giá trị nguyên của m
để phương trình đã cho có nghiệm?
A.
4.
B.
6.
C. Vô số. D.
5.
Lời giải
ChọnA
Phương trình
2
9 3 3
3 3
1 1
5 5
log log 5 1 log
5 1 1
log log 5 2
x x
x x m
x
m m
x x
Cách1..
Xét
1
5f x
x
trên khoảng
1
;
5
.
Có
2
1 1
0, ;
5
f x x
x
và
1
lim lim 5 5
x x
f x
x
 
.
Ta có bảng biến thiên của hàm số
f x :
Phương trình
1
có nghiệm phương trình
2
có nghiệm
1
5
x .
Từ bảng biến thiên suy ra phương trình
1
có nghiệm
0 5m
.
Mà
m
và
0m
nên
1; 2;3;4m .
Vậy có 4 giá trị nguyên của m để phương trình đã cho có nghiệm.
Cách 2.
2 5 1 3m x
Với
5m
, phương trình
3 thành
0. 1x
(vô nghiệm).
Với
5m
,
1
3
5
x
m
.
NHÓMWORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG:2019-2020
Trang 583
Xét
1
5
x
1 1
5 5
m
0
5. 5
m
m
0 5
m
.
Mà
m
và
0
m
nên
1;2;3;4
m .
Vậy có 4 giá trị nguyên của
m
để phương trình đã cho có nghiệm
Câu 43.16: Cho phương trình
2
5 5
2 log 3 log 1
x x m x x m
với
m
là tham số. Tất cả các
giá trị của
m
để phương trình đã cho có nghiệm thuộc khoảng
3;

là tập
;S a

. Đánh
giá nào sau đây đúng?
A.
3 1
a
. B.
1 1
a
. C.
1 2
a
. D.
2 5
a
.
Lời giải
Chọn A
Đặt
5
log
t x m
. Phương trình đã cho trở thành
2
1
2 3 1 3
1
2
t
x t x t x
t
x
+) Với
1 14
1 3
5 5
t x m m
.
+) Với
1 1
2 2
1
5 5
2
x x
t x m m x
x
Mà hàm số
1
2
x
f x x
đồng biến trên
3; 3 2.
m f

Kết hợp hai trường hợp trên ta được
2; 2
m a

.
Câu 43.17: Tổng tất cả các giá trị của tham số
m
sao cho phương trình
2
1
2
2 2
2 .log 2 3 4 .log 2 2
x mx
x x x m
có đúng ba nghiệm phân biệt là:
A. 2. B.
3
.
2
C. 0. D. 3.
Lời giải
Chọn D
Ta có:
2
1
2
2 2
2 .log 2 3 4 .log 2 2
x mx
x x x m
2
21
2
2 2
2 .log ( 1) 2 2 .log 2 2 (*)
x mx
x x m
Đặt
2
( ) 2 log ( 2), 0
t
f t t t
;
2
1
'( ) 2 ln 2.log ( 2) 2 0, 0
( 2)ln 2
t t
f t t t
t
.
hàm số
2
( ) 2 log ( 2)
t
f t t
đồng biến trên
(0; )

.
Khi đó (*)
2
2 2
2
2( ) ( 1)
( 1) 2 ( 1) 2
2( ) ( 1)
x m x
f x f x m x x m
x m x
NHÓMWORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG:2019-2020
Trang 584
2
2
4 1 2
1 2
x x m
I
x m
Vẽ đồ thị của hai hàm số
2
4 1f x x x và
2
1g x x trên cùng một hệ trục tọa độ.
Từ đồ thị suy ra
I có 3 nghiệm phân biệt
3
2 3
2
2 2 1
2 1 1
2
m
m
m m
m
m
Vậy tổng các giá trị của m là
Câu 43.18: Cho phương trình với m là tham số. Có bao nhiêu giá trị nguyên của
15;15 m
để phương trình đã cho có nghiệm?
A.
15
B. 16 C.
9
D. 14
Lời giải
Chọn D
Đặt
Ta có: .
Xét hàm số
( ) 3
t
f t t
, với t . Có
( ) 3 ln 3 1 0,
t
f' t t
nên hàm số
f t
đồng biến
trên tập xác định. Do đó
3
x
x m
3
x
x m
Xét hàm số
3
x
g x x
, với x . Có
( ) 3 ln3 1
x
g' x
, ( ) 0g' x
3
1
log
ln 3
x
Ta có bảng biến thiên
1 3
1 3.
2 2
3
3 log
x
m x m
3
log ( ) 3
a
x m a x m
3
3 log
x
m x m
3
3 log ( ) 3 3 (*)
x x a
x x m x m x a
(*)
( )
f x f a
3
log ( )
x a x x m
NHÓMWORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG:2019-2020
Trang 585
Từ bảng biến thiên ta thấy các giá trị của tham số để phương trình có nghiệm là
. Vậy số giá trị nguyên của
15;15 m để phương trình đã cho
có nghiệm là 14 .
Câu 43.19: Tìm tất cả các giá trị của m để phương trình
ln ln sin sinm m x x
có nghiệm.
A. . B. C. . D. .
Lời giải
Chọn B
Đặt ta được hệ phương trình:
sin
ln sin
sin
ln sin
u
x
u m x
e m x
m u x
e m u
Từ hệ phương trình ta suy ra:
sin
sin *
u x
e u e x
Xét hàm số
t
f t e t có Hàm số
f t đồng biến trên
.
Do đó
* sin sinf u f x u x
Khi đó ta được:
sin
ln sin sin sin **
x
m x x e x m
Đặt Phương trình
** trở thành:
Xét hàm số trên
1;1 .
Hàm số liên tục trên
1;1 và có
Hệ phương trình ban đầu có nghiệm
phương trình
** có nghiệm
1 1.m e
Câu 43.20: Cho phương trình . Tập tất cả các giá trị của
tham số để phương trình có hai nghiệm phân biệt thỏa mãn là khoảng
. Khi đó thuộc khoảng
A. . B. . C. . D. .
Lời giải
Chọn A
Theo đề ra ta chọn điều kiện của
là
TH1:
TH2: .
3
1
; log
ln 3
m g

1
1 1
m e
e
1 1
m e
.
1
1 1
m
e
1 1
m e
ln sin
u m x
' 1 0,
t
f t e t
sin , 1;1 .
a x a
**
a
e a m
a
g a e a
a
g a e a
1;11;1
1 1, min 0 1
max g a g e g a g
2
ln 1 2 ln 1 2 0 1
m x x m x x
m
1
1 2
0 2 4
x x
;a

a
3, 7;3,8
3, 6;3, 7
3,8;3,9
3,5;3,6
x
0 ln 1 0.
x x
0 1 ln 1 1
m x L
ln 1 1
0 1
2
ln 1
x L
m
x
x
m
ln 1
1
2
x
x m
NHÓMWORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG:2019-2020
Trang 586
Xét hàm số với .
Ta có:
Xét hàm số có
Hàm số nghịch biến trên có nhiều nhất một nghiệm trên
Mặt khác: và hàm số liên tục trên
Suy ra có ít nhất một nghiệm
Từ suy ra có một nghiệm duy nhất
có một nghiệm duy nhất .
Bảng biến thiên
Để có 2 nghiệm thỏa mãn thì
.
Câu 43.21: Giá trị thực của tham số
m
để phương trình
2
9 3
4log 3 2 3 log 2 1 0x m x m có hai
nghiệm thực
1
,x
2
x thỏa mãn
1 2
12x x thuộc khoảng nào sau đây?
A. 2 . B. 1. C.
3
. D. 4 .
Lời giải
Chọn B
Điều kiện 0x .
Ta có
2
3 3
1 log 2 3 log 2 1 0pt x m x m .
ln 1
2
x
f x
x
0
x
2
' 0 ln 1 0.
1
x
f x x
x
2
ln 1
1
x
g x x
x
2
1 1
' 0, 0
1
1
g x x
x
x
y g x
0;

0
g x
0; 2

4 5
2 3 ln 3 ln 4 0
3 4
g g
y g x
0;

0
g x
0
2;3 3 .
x
2 ; 3
0
g x
0
2;3
x
' 0
f x
0
2;3
x
1
1 2
0 2 4
x x
1 ln 5 6
0
6 ln 5
m
m
6
3, 728
ln 5
a
NHÓMWORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG:2019-2020
Trang 587
3
2
3 3
2
3
3
log 1
log (2 1) log 2 0
log 2
3
m
x
x
x m x m
x m
x
.
Theo đề, ta có:
2
1 2
12 3 3 12 1
m
x x m
.
Câu 43.22: Phương trình
2 2 2
2 3 2 2
3 9 3 3 .
x x m x x x x m
Có bao nhiêu giá trị nguyên của tham số
[ 2018;2018]
m
để phương trình đã cho có
4
nghiệm phân biệt ?
A.
2019
. B.
2018
. C.
2020
. D.
2021
.
Lời giải
Chọn C
Ta có:
2 2 2 2 2 2
2 3 2 2 2 3 2 2
3 9 3 3 3 3 3 9
x x m x x x x m x x m x x x x m
.
2 2 2 2 2
2 2 2
3 (3 9) 3 9 (3 1)(3 9) 0
x x x x m x x m x x x x m
.
2
2
2
2
2
2
1
0
3 1
0
2 2
3 9
2 2 0 (2)
x x
x x m
x
x x
x
x x m
x x m
.
Để phương trình đầu có 4 nghiệm phân biệt khi phương trình
2
có hai nghiệm phân biệt
1, 0
x x
.
Khi
' 0 3 0 3
2 2 2 2 3
3 3 3
m m
m m m m
m m m
.
Vì
[ 2018; 2018]
m
và m
nên có 2020 giá trị
m
cần tìm.
Câu 43.23: Tìm tập hợp tất cả các giá trị của tham số
m
để phương trình
2
3 1
3
4(log ) log 0
x x m
có
hai nghiệm thuộc
0;1
.
A.
1
0
5
m
. B.
1 1
6 4
m
. C.
1
1
4
m
. D.
1
0
4
m
.
Lời giải
Chọn D
Pt:
2 2
3 1 3 3
3
4(log ) log 0 log log
x x m x x m
(1)
Đặt
3
log
t x
, ta được phương trình
2
t t m
với
( ;0)
t

khi
0;1
x .
Để phương trình (1) có hai nghiệm
0;1
x khi phương trình
2
t t m
có hai nghiệm
( ;0)
t

.
Xét hàm số
2
y t t
trên
;0
 .
NHÓMWORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG:2019-2020
Trang 588
1 1
0 0
4 4
m m
.
Câu 43.24: Điều kiện cần và đủ của tham số để phương trình
2
5 5
log ( 1) log 4 0x m x m
có hai
nghiệm phân biệt thuộc
1; 25 là
A. . B. . C. . D. .
Lời giải
Chọn D
Pt:
2
5 5
log ( 1) log 4 0x m x m (1)
Đặt
5
logt x , với
0; 2t khi
1; 25x .
Ta được phương trình
2
2
4
( 1) 4 0 *
1
t t
t m t m m
t
Để phương trình (1) có hai nghiệm
1; 25x khi phương trình
* có hai nghiệm
0; 2t .
Xét hàm số
2
4
1
t t
y
t
trên
0; 2 .
Ta có
2
2
3
2 3
' 0
1
( 1)
t
t t
y
t
t
BBT.
10
3
3
m .
0
-
1
4
+∞
+∞
+∞
0
-
1
2
-∞
y
t
m
3 4
m
10
3
3
m
10
4
3
m
10
3
3
m
10
3
2
4
+∞
-∞
+
+
-
0
3
-
1
-3
y'
0
-∞
+∞
+∞
0
-1
-∞
y
t
NHÓMWORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG:2019-2020
Trang 589
Câu 43.25: Tìm tất cả các giá trị thực của tham số để phương trình
có hai nghiệm thỏa mãn
A.
2m
. B.
1m
. C.
1m
. D.
2m
.
Lời giải
Chọn C
Điều kiện 0x .
Đặt
3
logt x , ta có phương trình
2
( 2) 3 1 0t m t m .
GS :
1 3 1 2 3 2 1 2 3 1 3 2 3 1 2
log , log log log log 3t x t x t t x x x x .
Vậy để phương trình có hai nghiệm thỏa mãn yêu cầu đề bài khi và chỉ khi
2
1 2
0
8 8 0
1
3
2 3
m m
m
t t
m
.
Câu 43.26: Tổng tất cả các giá trị để phương trình
2
2 1 2
3 3
3 log ( 3 2 ) 9 log (2 2)
x m
x x
x x x m
có
đúng ba nghiệm phân biệt là
A. B. C. D.
Lời giải
Chọn D
Ta có
2
2 1 2
3 3
3 log ( 3 2 ) 9 log (2 2)
x m
x x
x x x m
1
2
2
21
3 3
3 .log 1 2 3 .log 2 2
x mx
x x m
2
Xét hàm số
3
3 .log 2 , 0.
t
f t t t
Vì
0, 0f t t
hàm số đồng biến trên
0;
.
Khi đó
2 2
2 1 2 1 2f x f x m x x m
.
2
2
4 1 2 0 3
2 1 4
x x m
x m
.
Phương trình
1 có đúng ba nghiệm phân biệt nếu xảy ra các trường hợp sau:
+) PT
3 có nghiệm kép khác hai nghiệm phân biệt của PT
4
3
2
m
, thay vào PT
4
thỏa mãn.
+) PT
4 có nghiệm kép khác hai nghiệm phân biệt của PT
3
1
2
m
, thay vào PT
3
thỏa mãn.
+) PT
4 có hai nghiệm phân biệt và PT
3 có hai nghiệm phân biệt, trong đó có một nghiệm
của hai PT trùng nhau
4 2 1x m ,với
1 3
.
2 2
m Thay vào PT
3 tìm được
1.m
KL:
1 3
;1; .
2 2
m
Cách 2:
Xem phương trình (3) và (4) là hai đường cong. Ta sẽ tìm điểm chung của hai đường cong đó.
m
2
3 3
log 2 log 3 1 0
x m x m
1 2
,
x x
1 2
. 27.
x x
m
4
2
0
3
NHÓMWORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG:2019-2020
Trang 590
Ta giải hệ:
2
2
4 1 2 0 1
1
2 1
x x m x
m
x m
.
Như vậy với 1m thì (3) và (4) có nghiệm chung là 1x .
Thay 1m vào lần lượt vào 2 phương trình ta được 3 nghiệm
1;3
. Vậy ta nhận 1m .
Xét 1m , phương trình có 3 nghiệm khi (3) có 2 nghiệm phân biệt và (4) có nghiệm kép hoặc
ngược lại. Như vậy ta có:
3 2 0
1
2 1 0
2
3
3 2 0
2
2 1 0
m
m
m
m
m
m
.
Từ đó ta có 3 giá trị của tham số
m
là
1 3
;1;
2 2
.
Câu 43.27: Tìm tất cả các giá trị của tham số
m
để phương trình
2
3
log 1
x m
x
có hai nghiệm phân biệt.
A. 01 m . B. 1m . C. Không tồn tại
m
. D. 1 0m .
Lời giải
Chọn B
Điều kiện:
1 0 1
1 1 0
x x
x x
Xét hàm số
2
2 2
3 3
; 1 0, 1;0 0 :
log 1 1 .ln 2.log 1
f x x f x x
x x x

Bảng biến thiên
Từ bảng biến thiên suy ra phương trình
2
3
log 1
x m
x
có hai nghiệm phân biệt khi và chỉ
khi 1m .
Câu 43.28: Có bao nhiêu giá trị thực của tham số để phương trình
2 2
3 2 4 6 3
.5 5 5
x x x x
m m
có đúng
nghiệm thực phân biệt.
A.
3
B. 2 C. 1 D. 4
Lời giải
Chọn A
Đặt
2
2
3 2
6 3
4
5
. 5
5
x x
x
x
u
u v
v
. Khi đó phương trình trở thành
1 1 0mu v uv m m u v u .
2
3 2
2
2
1
5 1
1 0
5
x x
x
u
u m v
v m
m
.
m
3
NHÓMWORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG:2019-2020
Trang 591
2
2
5
2
5
1
3 2 0
2
4 log
4 log
x
x x
x
x m
x m
.
Để phương trình có ba nghiệm thì:
+) TH1:
2
5
4 log
x m
có nghiệm kép
Tức
5
4 log 0 525
m m
.
+) TH2:
2
5
4 log
x m
có một nghiệm bằng
1
.
Tức
5
4 log 1 75
m m
.
+) TH3:
2
5
4 log
x m
có một nghiệm bằng
2
.
Tức
5
4 log 4 1
m m
.
Vậy có 3 giá trị của
m
cần tìm.
Câu 43.29: Với giá trị của tham số
m
thì phương trình
1 9 2 2 3 3 6 5 0
x x
m m m
có hai nghiệm
trái dấu?
A.
4 1.
m
B. Không tồn tại
m
. C.
3
1
2
m
. D.
5
1
6
m
.
Lời giải
Chọn A
Đặt
3 0
x
t
. Phương trình đã cho trở thành:
2
1 2 2 3 6 5 0.
f t
m t m t m

*
Yêu cầu bài toán
*
có hai nghiệm
,
t t
thỏa mãn
1 2
0 1
t t
.
1 0 1 0
1 1 0 1 3 12 0 4 1.
1 6 5 0 1 6 5 0
m m
m f m m m
m m m m
Câu 43.30: Cho phương trình
2 2
2 2 2 4 2
2
2 1 2 1 2 0
x mx x mx m
x mx m
. Tìm m để
phương trình có đúng 2 nghiệm thuộc
1
( ;2)
2
.
A.
1
0
8
m
B.
4
0
5
m
C.
1
1
8
m
D.
1
2
8
m
Lời giải
Chọn A
Ta có:
2 2
2 2 2 4 2
2
2 1 2 1 2 0
x mx x mx m
x mx m
.
2 2
2 2 2 4 2
2
2 1 2 1 2
x mx x mx m
x mx m
.
2 2
2 2 2 4 2
2 2
2 1 2 2 2 1 2 4 2
x mx x mx m
x mx x mx m
.
Xét hàm số :
( ) ( 2 1)
t
f t t
.
Ta có hàm số
( ) ( 2 1)
t
f t t
đồng biến trên
.
Khi đó phương trình có dạng
2 2
( 2 2) (2 4 2 )
f x mx f x mx m
.
2
2 2 2
2 2 2 4 2 2 0
2 1
x
x mx x mx m x mx m m
x
.
NHÓMWORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG:2019-2020
Trang 592
Để phương trình có đúng hai nghiệm thuộc khoảng
1
( ; 2)
2
khi và chỉ khi phương trình
2
2 1
x
m
x
có hai nghiệm thuộc
1
( ; 2)
2
.
Xét hàm số
2
2 1
x
y
x
trên khoảng
1
( ; 2)
2
.
Ta có
2
2
0
2 2
' 0
1(2 1)
x
x x
y
xx
1
0
8
m
.
Câu 43.31: Với những giá trị nào của m thì phương trình :
2
2
2 2 2
2 2 2
3 2 2 2
x x
x x
x x m
có nghiệm.
A.
8m
B.
7m
C.
6m
D.
5m
Lờigiải
Chọn A
Ta có:
2
2
2 2 2
2 2 2
3 2 2 2
x x
x x
x x m
.
2 2
2 2 2 2 2
3 4 2 2
x x x x
x x m
Đặt :
2
2 2 1t x x t
Khi đó phương trình trở thành
3 4
t t
t m
Ta có hàm số ( ) 3 4
t t
f t t
đồng biến trên
Để phương trình có nghiệm
1;
(3 4 ) m 8
t t
m Min t

.
Câu 43.32: Với những giá trị nào của m thì phương trình :
3 2 3 2
2 4
3 2
5 2 5 2 2 6 2
x mx x mx m
x mx m
có nghiệm duy nhất.
A.
1 1
, 0
2 2
m m
B.
1
2
m
C.
1 1
2 2
m
D.
1
4
m
Lời giải
Chọn C
Ta có:
3 2 3 2
2 4
3 2
5 2 5 2 2 6 2
x mx x mx m
x mx m
.
-
4
5
2
0
+∞
-∞
+
+
-
1
2
-
1
8
-
0
-1
y'
0
-∞
+∞
+∞
0
-
1
2
-∞
y
x
NHÓMWORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG:2019-2020
Trang 593
3 2 3 2
3 2 3 2
2 4
3 2
2 4
3 2 3 2
5 2 5 2 2 6 2
5 2 2(2 ) 5 2 2( 4 )
x mx x mx m
x mx x mx m
x mx m
x mx x mx m
Xét hàm số :
( ) ( 5 2)
t
f t t
Ta có hàm số
( ) ( 5 2)
t
f t t
nghịch biến trên
Khi đó phương trình có dạng
3 2 3 2
(2 ) ( 4 )
f x mx f x mx m
3 2 3 2 3 2
2 4 3 0
x mx x mx m x mx m
Xét hàm số
3 2 2
3 ' 3 6
y x mx m y x mx
0
' 0
2
x
y
x m
+)TH1 :
2
0 ' 3 0,m y x x
khi đó hàm số
3 2
3
y x mx m
đồng biến trên
.
Vậy khi đó phương trình có một nghiệm duy nhất.
+)TH1 :
3
0 (0) , (2 ) 4
m y m y m m m
. Khi đó để phương trình có một nghiệm duy
nhất khi
3
1 1
(0). (2 ) 0 ( 4 ) 0
2 2
y y m m m m m
.
Câu 43.33: Có bao nhiêu giá trị nguyên của m thì phương trình sau có nghiệm
2
1
sinx cos
2
2 3 7 4 3 os2 sinx
m x
m c x
A.
2
B.
1
C.
3
D.
4
Lời giải
Chọn D
Ta có:
2
1
sinx cos
2
2 3 7 4 3 os2 sinx
m x
m c x
.
2
sinx 2cos 1
sinx os2
2 3 2 3 os2 sinx
2 3 s inx 2 3 os2
m x
m c x
m c x
m c x
Xét hàm số :
( ) (2 3)
t
f t t
Ta có hàm số
( ) (2 3)
t
f t t
nghịch biến trên
Khi đó phương trình có dạng
(s inx ) (c os2x)
f m f
2
s inx os2x 2sin x-sinx 1
m c m
Đặt :
=sinx 1;1
t t
Khi đó phương trình trở thành
2
2 1
t t m
Để phương trình có nghiệm
2 2
1;1 1;1
9
( 2 1) Max( 2 1) 2 m
8
Min t t m t t
Câu 43.34: Giá trị thực của tham số
m
để phương trình
25 4( 1).5 5(4 1) 0
x x
m m
có hai nghiệm
thực
1
,
x
2
x
thỏa mãn
1 2
( 4)( 4) 30
x x
thuộc khoảng nào sau đây ?
A.
6; 7
B.
4;5
C.
3; 4
D.
2;3
NHÓMWORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG:2019-2020
Trang 594
Lời giải.
Chọn A
Đặt
5
x
t
, ta có phương trình
2
4( 1) 5(4 1) 0
t m t m
1
5 5 5
4 1
5 4 1(1)
5 4 1
x
x
x
x
t
t m
m
m
Ta có
1 2 2 2
( 4)( 4) 30 5.( 4) 30 2
x x x x
.Thay vào (1) ta được
2
26
5 4 1
4
m m
Câu 43.35: Giá trị thực của tham số
m
để phương trình
9 2(2 1).3 243 0
x x
m
có hai nghiệm thực
1
,
x
2
x
thỏa mãn
1 2
( 3)( 3) 30
x x
thuộc khoảng nào sau đây ?
A.
6; 7
B.
8;9
C.
7;8
D.
2;3
Lời giải
Chọn B
Đặt
3
x
t
, ta có phương trình
2
2(2 1) 243 0
t m t
GS: phương trình có nghiệm
1 2 1 2
5
1 2 1 2 1 2
3 , 3 . 3 243 3 5
x x x x
t t t t x x
Ta có
1 2 1 2 1 2 1 2
( 3)( 3) 30 3( ) 9 30 6
x x x x x x x x
Ta có
1 2 1 1
1 2
1 2 2 2
5 2 9
36
. 6 3 27
x x x t
t t
x x x t
Mà theo đề bài
1 2
34
4 2 36
4
t t m m
Câu 43.36: Giá trị thực của tham số
m
để phương trình
2
2 2
log 3.log 4 0
x x m
có hai nghiệm thực
1
,
x
2
x
thỏa mãn
1 2
( 4)( 4) 48
x x
thuộc khoảng nào sau đây ?
A.
1;2
B.
1;3
C.
0;1
D.
0; 2
Lời giải
Chọn B
Đặt
2
log
t x
, ta có phương trình
2
3 4 0
t t m
GS: phương trình có nghiệm
1 2 1 2 2 2 1 2 2 1 2 1 2
log , log log 3 8
t x t x t t x x x x
Ta có
1 2 1 2 1 2 1 2
( 4)( 4) 48 4( ) 16 48 6
x x x x x x x x
Ta có
1 2 1 1
1 2
1 2 2 2
6 2 1
. 2
. 8 4 2
x x x t
t t
x x x t
Mà theo đề bài
1 2
. 4 2 2
t t m m
Câu 43.37: Gọi
S
là tập hợp tất cả các giá trị thực của tham số
m
để tồn tại duy nhất cặp
( ; )
x y
thỏa mãn
đồng thời các điều kiện
2 2
3
log (2 6 5) 1
x y
x y
và
3 3 0.
x y m
Tổng các phần tử của
S
bằng
A.
3
B.
4
C.
5
D.
6
Lời giải
Chọn D
Ta có:
NHÓMWORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG:2019-2020
Trang 595
2 2
2 2
3
2 2
log (2 6 5) 1 3 2 6 5
2 6 2 0
x y
x y x y x y
x y x y
Ta thấy phương trình
2 2
2 6 2 0x y x y là phương trình đường tròn tâm
1; 3I bán
kính
12R
Để tồn tại duy nhất cặp số ( ; )x y thỏa mãn yêu cầu bài toán khi đường thẳng
: 3 3 0x y tiếp xúc với đường tròn
2 2
( ) : 2 6 2 0C x y x y
Khi và chỉ khi
3 3 3
( , ) 2 3
2
m
d I R
3 4 3
3 4 3
m
m
Câu 43.38: Tất cả các giá trị của tham số
m
để phương trình
5 5
log log 1mx x
có hai nghiệm
phân biệt là
A. 4m . B. 4m . C. 0m và 4m . D. 0m và 4m .
Lời giải
Chọn B
Ta có
2
1 0
1 0
log log 1 (*)
2 1
1
x
x
mx x
mx x x
mx x
.
Ta thấy 0x không là nghiệm của (*).
Với
0x
:
1
(*)
1
2
x
m x
x
Xét hàm số
1
2f x x
x
với
1; \ 0x .
Ta có
2
2 2
1 1
1
x
f x
x x
;
0 1f x x
(do
1; \ 0x  ).
Bảng biến thiên:
Dựa vào bảng biến thiên suy ra 4m là giá trị cần tìm.
NHÓMWORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG:2019-2020
Trang 596
Câu 43.39: Cho bất phương trình
2
2
1 1
2 2
1
1 log 2 4 5 log 4 4 0
2
m x m m
x
(
m
là tham số
thực). Tập hợp tất cả các giá trị của
m
để bất phương trình đã cho có nghiệm thuộc đoạn
5
,4
2
là
A.
3;

. B.
7
;
3

. C.
7
3;
3
. D.
7
;
3

.
Lời giải
Chọn A
Điều kiện:
2.
x
Ta có:
2
2
1 1
2 2
1
1 log 2 4 5 log 4 4 0
2
m x m m
x
2
2 2
4 1 log 2 4 5 log 2 4 4 0
m x m x m
Đặt
2
log 2
t x
, ta có phương trình trở thành:
2
1 5 1 0 *
m t m t m
Với
5
;4 ,
2
x
ta có:
1;1 .
t
2
2
5 1
*
1
t t
m
t t
,
1;1
t .
Để bất phương trình có nghiệm
1;1
t
Khi và chỉ khi
2
2
1;1
5 1
1
t t
m Min
t t
.
2
2
5 1
1
t t
f t
t t
. Ta có:
2
2
2
4 4
' 0, 1;1
1
t
f t t
t t
.
Suy ra:
1 1 , 1;1
f f t f t hay
7
3 , 1;1
3
f t t
.
Vậy
3
m
.
Câu 43.40: Cho bất phương trình
2
2 2
log 2 1 log 3 0
x m x m
(
m
là tham số thực). Tập hợp tất
cả các giá trị của
m
để bất phương trình nghiệm đúng với mọi
x
thuộc đoạn
4 ; 4 2
là
A.
7
2
m
. B.
9
2
m
. C.
m R
. D.
7
4
m
.
Lời giải
Chọn B
Điều kiện:
0
x
.
NHÓMWORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG:2019-2020
Trang 597
2
2
2 2 2 2
2
2 2
log 2 1 log 3 0 1 log 1 log 3 0
log 1 log 2 0
x m x m x m x m
x m x m
Với
5
4 ;4 2 1 ;
2
x t
, ta có bất phương trình bậc hai
2
(1 ) 2 0
t m t m
.
Bài toán trở thành tìm
m
để bất phương trình:
2
(1 ) 2 0
t m t m
,
5
2 ;
2
t
.
2
5 5
(1 ) 2 0, 2 ; 1 2 0, 2 ; *
2 2
t m t m t t t m t
Vì
5
1 0, 2 ;
2
t t
, nên
5 5 9
* 2 0, 2 ; 2 0
2 2 2
t m t m m
.
| 1/25
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

NHÓMWORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG:2019-2020
PHƯƠNG TRÌNH LOGARIT CÓ CHỨA THAM SỐ
PHƯƠNG PHÁP GIẢI PHƯƠNG TRÌNH LOGARIT
Thường sử dụng các phương pháp sau:
1. Phương pháp đưa về cùng cơ số.
2. Phương pháp đặt ẩn phụ.
3. Phương pháp hàm số.
KIẾN THỨC CẦN NHỚ: log  .
b c  log b  log c với ,
b c  0; 0  a  1. a a a log
với  0; 0  a  1. x log x a a
Nếu a  1 thì với x , x  0 : x x  log x  log x 1 2 1 2 a 1 a 2
Nếu 0  a  1 thì với x , x  0 : x x  log x  log x 1 2 1 2 a 1 a 2  f   x  0
log f x  log g x   0  a   1 a a f
  x  g x 
log f x  b f xbaa a 0  1   0 
Phương trình bậc hai có hai nghiệm âm phân biệt  S  0 . P  0    0 
Phương trình bậc hai có hai nghiệm dương  S  0 . P  0 
Phương trình bậc hai có hai nghiệm trái dấu  P  0 . Trang 573
NHÓMWORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG:2019-2020 BÀI TẬP MẪU Cho phương trình 2 log
2x m  2 log x m  2  0 ( m là tham số thực). Tập hợp tất cả các giá trị của 2     2
m để phương trình đã cho có hai nghiệm phân biệt thuộc đoạn 1; 2 là A. 1; 2 B. 1; 2 C. 1; 2 D. 2;
Phân tích hướng dẫn giải
1. DẠNG TOÁN: Đây là dạng toán tìm điều kiện của tham số để phương trình logarit có nghiệm thỏa
mãn điều kiện cho trước. 2. HƯỚNG GIẢI:
B1: Viết lại phương trình logarit về dạng phương trình bậc hai đối với 1 biểu thức logarit.
B2: Đặt ẩn phụ là biểu thức logarit và tìm điều kiện cho ẩn phụ.
B2: Tìm điều kiện cho phương trình ẩn phụ.
Từ đó, ta có thể giải bài toán cụ thể như sau: Lời giải Chọn C
Điều kiện : x  0 2 Ta có : 2 log
2x m  2 log x m  2  0  1 log x
m  2 log x m  2  0 1 2     2  2    2  
Đặt t  log x , với x 1;2 thì t 0; 
1 , khi đó ta có phương trình: 2 t   1
1 t 2  m  2 2
t m  2  0  t mt m 1  0   2 t m 1 
Nhận thấy với mỗi số thực t 0; 
1 cho ta một số thực x 1;2 , do đó yêu cầu bài toán  2 có 2 m 1  1  m  2
nghiệm phân biệt thuộc 0;  1      1  m  2 . m 1   0  ;1 0  m 1  1  Vậy 1  m  2 .
Chú ý: Đối với phương trình bậc hai chứa tham số, nếu  có dạng chính phương thì nên tìm cụ thể hai
nghiệm của phương trình.
Bài tập tương tự và phát triển:
Câu 43.1: Cho phương trình 2
log x  3mlog 3x  2m  2m 1  0 m S 3 3   2 (
là tham số thực). Gọi là tập hợp
tất cả các số thực m mà phương trình có hai nghiệm phân biệt thuộc đoạn 1;  3 . Số phần tử của tập S là A. 2 . B. 0 . C. 1. D. 3 . Lời giải Chọn B
Điều kiện: x  0 Phương trình: 2 2 2 2
log x  3mlog 3x  2m  2m 1  0  log x  3m log x  2m m 1  0 3 3   3 3 Trang 574
NHÓMWORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG:2019-2020
Đặt t  log x , với x 1;  3 thì t  3 0; 
1 , khi đó ta có phương trình
t  m 1 2 2
t  3mt  2m m 1  0   t  2  m 1 
Khi đó yêu cầu bài toán  phương trình đã cho có hai nghiệm phân biệt thuộc đoạn 0;  1  2   m  1
0  m 1  1    1
 0  2m 1  1  0  m  (Hệ vô nghiệm). 2  m 1 2m 1        m  2 
Vậy không có giá trị nào của m thỏa mãn yêu cầu bài toán.
Câu 43.2: Cho phương trình 2 log
9x m  5 log x  3m 10  0 (với m là tham số thực). Số giá trị 3     3
nguyên của tham số m để phương trình đã cho có hai nghiệm phân biệt thuộc 1;8  1 là A. 2 . B. 3 . C. 4 . D. 5 . Lời giải Chọn C Ta có: 2 log
9x m  5 log x  3m 10  0 . 3     3
Đặt t  log x vì x  1;8  1  t 0; 4. 3 t   3
Khi đó phương trình đã cho trở thành: 2
t  m 1t  3m  6  0   . t m  2  0  m  2  4 2  m  6 ycbt    
. Vậy có 4 số nguyên m thoả ycbt. m  2  3 m  5  
Câu 43.3: Cho phương trình 2 4log
x (m3)log x 2m  0 m 3 3 (
là tham số thực ). Có bao nhiêu giá
trị nguyên của m để phương trình đã cho có hai nghiệm thực phân biệt thuộc đoạn 1;9 ? A. 0 . B. 2 . C. 1. D. 3 . Lời giải Chọn B 2  1  Ta có 2 4 log
x  (m  3) log x  2  m  0  4 log x
 (m  3) log x  2  m  0 3 3  3  3  2   log x  1  x  3 2 3
 log x  (m  3) log x  2  m  0   3 3  
log x  2  m
log x  2  m 1  3  3  
Phương trình đã cho có hai nghiệm thực phân biệt thuộc đoạn 1;9 khi và chỉ khi   1 có một 0  2  m  2 0  m  2
nghiệm thuộc đoạn 1;9 \  3 tức    . 2  m  1 m  1  
Vậy có 2 giá trị nguyên của m thỏa mãn bài toán. Trang 575
NHÓMWORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG:2019-2020
Câu 43.4: Tìm tất cả các giá trị của tham số m để phương trình 2
log 3x  log x m  1  0 có đúng 2 3 3
nghiệm phân biệt thuộc khoảng 0; 
1 . Tìm tất cả các giá trị của tham số m để phương trình 2
log 3x  log x m  1  0 có đúng 2 nghiệm phân biệt thuộc khoảng 0;  1 3 3 9 9 1 9 A. m  . B. 0  m  . C. 0  m  . D. m   . 4 4 4 4 Lời giải Chọn B Ta có 2 2
log 3x  log x m 1  0  log x  3log x m  0 1 3 3 3 3  
Đặt t  log x với x  0; 
1 thì t  0 , khi đó ta có phương trình 2
t  3t m  0 2 3
Nhận thấy với mỗi số thực t  0 cho ta một số thực x  0; 
1 , do đó yêu cầu bài toán 2 3   4m  0   0    3 9
 Phương trình 2 có hai nghiệm âm phân biệt  S  0    0  0  m  . 2 4 P 0     m  0 
Câu 43.5: Cho phương trình log x2 2
3mlog (3x)2m 2m 1
 0 . Gọi S là tập tất cả các số tự nhiên m 3 3 10
mà phương trình có hai nghiệm phân biệt x , x thỏa mãn x x
. Tính tổng các phần tử của 1 2 1 2 3 S . A. 6 . B. 1. C. 0 . D. 10 . Lời giải Chọn B Với m  
PTlog x2 3m 1log x 2 2m 2m 1  0 3 3 Đặt log  3t t x x 3
t  1 m
Ta được phương trình: 2 2
t 3mt 2m m 1  0   . t  1 2m
Phương trình có hai nghiệm phân biệt khi và chỉ khi 1  2m  1  m m  2. 10 m m 10 Khi đó 1 2 1 2 3 3 9.3 m 3 m x x             10  0 1 2 3 3
 3m  1  m  0  m  0.
Câu 43.6: Tìm tất cả các giá trị của tham số thực m để phương trình 4 log
x 2  log x m  0 có hai 2 1 2
nghiệm phân biệt thuộc khoảng 0;  1 . Trang 576
NHÓMWORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG:2019-2020 1 1 1 1 A. 0  m  . B. 0  m  . C. m  . D.   m  0 . 4 4 4 4 Lời giải Chọn A 2 2 Ta có 4 log x
 log x m  0  log x
 log x  m 1 2  1  2  2   2
Đặt t  log x với x  0; 
1 thì t  0 , khi đó ta có phương trình 2
t t  m   * . 2 1 Xét   2
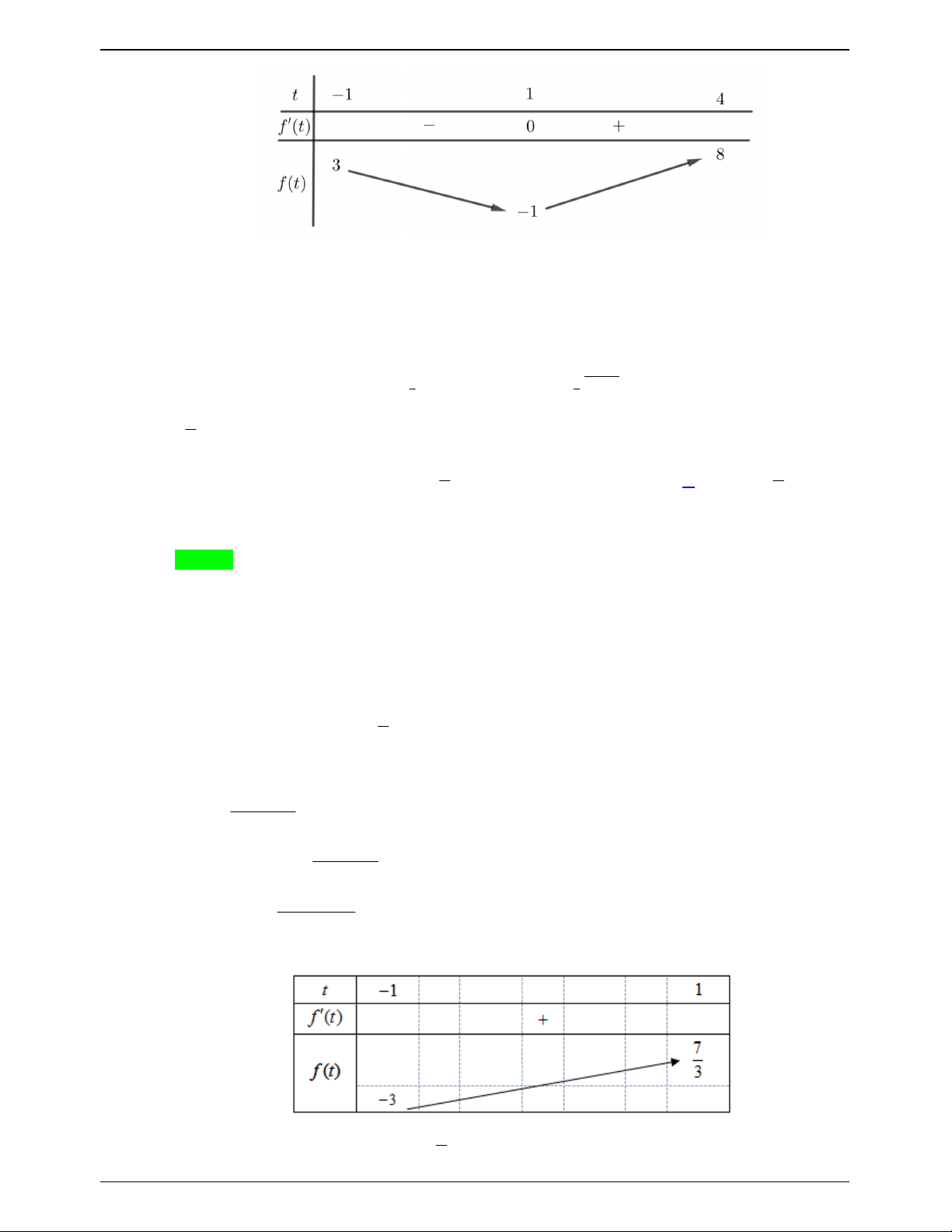
f t t t t  ;
 0 . Có f 't  2t 1; f 't   0  t   2 Bảng biến thiên
Nhận thấy với mỗi số thực t  0 cho ta một số thực x  0; 
1 , do đó yêu cầu bài toán  * 1 1
có hai nghiệm phân biệt. Dựa vào bảng biến thiên suy ra  
 m  0  0  m  4 4
Câu 43.7: Có bao nhiêu giá trị nguyên của tham số m để phương trình 2
log 2x  2log x m 1  0 2   2 có 2  1 
nghiệm, trong đó có đúng một nghiệm thuộc đoạn ;16 ?  2    A. 10 . B. 8 . C. 7 . D. 6 . Lời giải Chọn D
Điều kiện: x  0 . Khi đó phương trình đã cho tương đương với
1 log x  4log x m 1  0 2
 log x  2log x m 2 2 . 2 2 2 1
Đặt t  log x , với mỗi x   
;16 thì cho một giá trị t  1  ;  4 . 2  2   
Khi đó ta được phương trình 2
t  2t m .
Xét hàm số f t 2
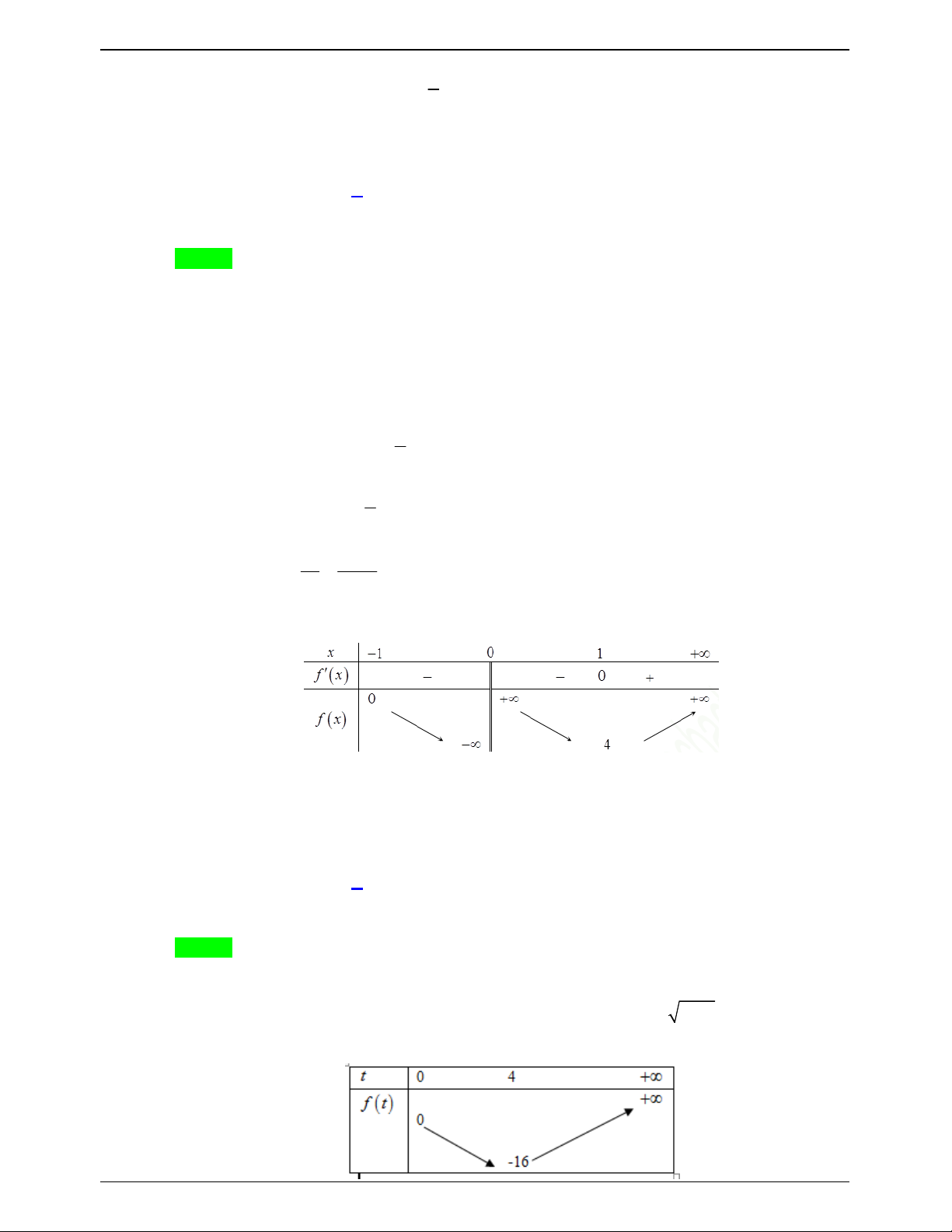
t  2t trên đoạn  1  ;4 .
Ta có f t   2t  2 , f t  0  t 1.
Bảng biến thiên của f t Trang 577
NHÓMWORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG:2019-2020
Từ bảng biến thiên suy ra m   1 3; 
8 thỏa mãn yêu cầu bài toán.
Vậy có tất cả 6 giá trị nguyên của m thỏa mãn yêu cầu bài toán. 2 1
Câu 43.8: Tìm m để phương trình :m   2 1 log x  2  4 m  5 log
 4m  4  0 có nghiệm thuộc đoạn 1     1 x  2 2 2  5  , 4  . 2    7 7 A. m   . B. 3   m  . C. m   .
D. 3  m  . 3 3 Lời giải Chọn D
Điều kiện: x  2 . Khi đó phương trình đã cho tương đương với  m   1  2
 log  x  2 2   4 m  5 log
x  2  4m  4  0  2    2    4m   2 1 log
x  2  4 m  5 log
x  2  4m  4  0 2     2    m   2 1 log
x  2  m  5 log
x  2  m 1  0 . (1) 2     2    5  Đặt t  log
x  2 . Vì x
; 4  t 1;  1 . 2    2   
Phương trình (1) trở thành m   2
1 t  m  5t m 1  0 . 2 t  5t 1  m  2 . 2 t t 1 2 t  5t 1
Xét hàm số f t   ,t 1;  1 2 t t 1 2 4  t  4 t  2
Ta có f 't   0   .
t t  2 2 t  2 1  Bảng biến thiên  5 
Phương trình đã cho có nghiệm x  ; 4 
 khi phương trình (2) có nghiệm t  1  ;  1 . 2    Trang 578
NHÓMWORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG:2019-2020 7
Từ bảng biến thiên suy ra 3  m  . 3
Câu 43.9: Tất cả các giá trị của tham số m để phương trình log mx  2 log
x 1 có hai nghiệm phân 3   3   biệt là A. m  4 . B. m  4 .
C. m  0 và m  4 .
D. m  0 và m  4 . Lời giải Chọn Bx 1  0  x 1  0 Ta có log mx  2 log x 1     (*) . 3   3   mx   x   2 2 1
mx x  2x  1  
Ta thấy x  0 không là nghiệm của (*). x  1 
Với x  0 : (*)   1
m x  2    x 1
Xét hàm số f x  x  2  với x 1;  \  0 . x 2 1 x 1
Ta có f  x 1 
; f   x  0  x  1 (do x 1; \   0 ). 2 2 x x Bảng biến thiên:
Dựa vào bảng biến thiên suy ra m  4 là giá trị cần tìm. Câu 43.10: Cho phương trình 2  2 x     2 ln 1 8ln x  
1  m  0 (với m là tham số thực). Có bao nhiêu
giá trị nguyên của m để phương trình đã cho có bốn nghiệm phân biệt. A. 0 . B. 15 . C. 16 . D. 17 . Lời giải Chọn B Đặt t   2 ln x   1 (vì 2
x 1  1 nên t  0), khi đó ta có phương trình 2
t  8t m *
Nhận thấy: nếu t  0 thì ta có một giá trị x  0 . Nếu t  0 thì t
x   e 1.
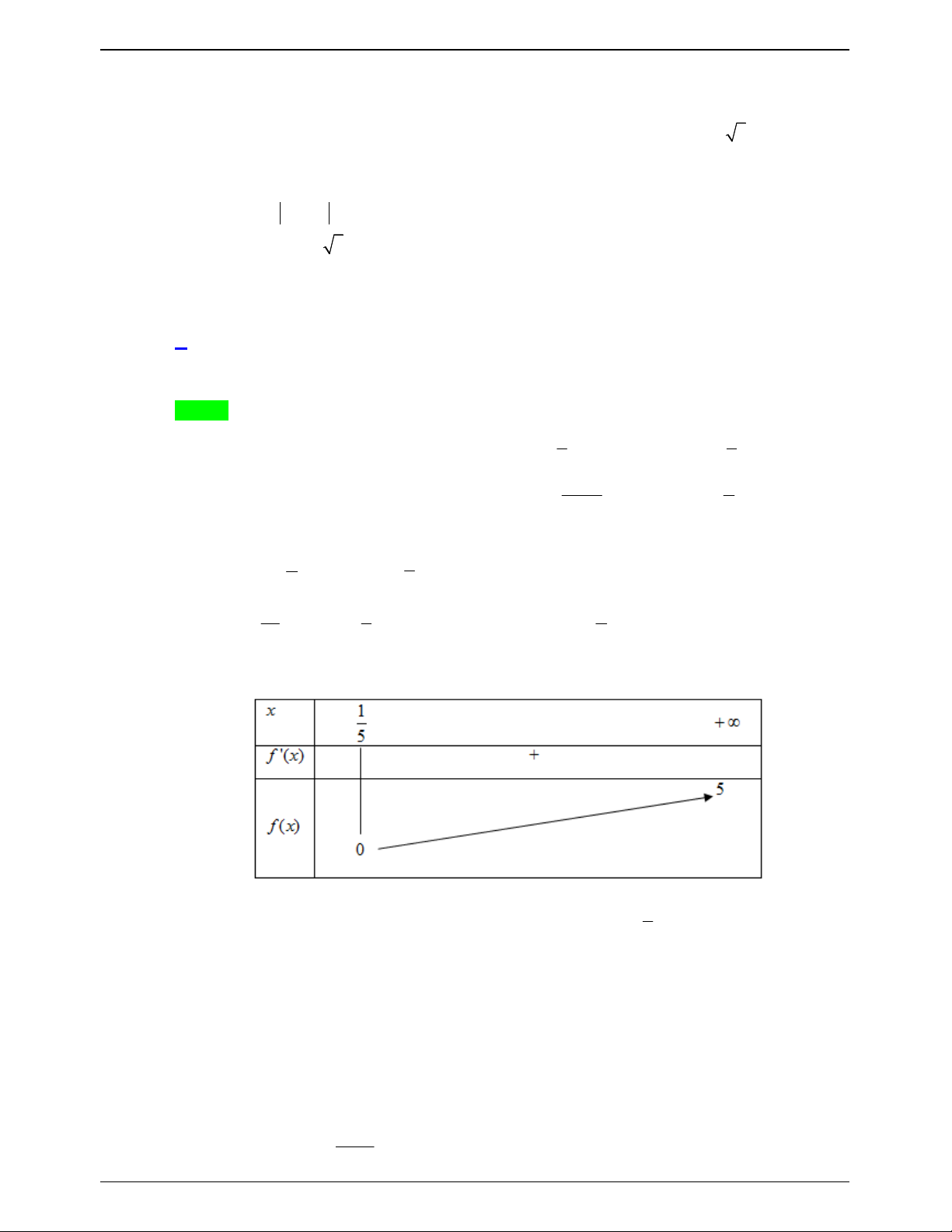
Xét hàm số f t  2
t  8t với t  0 . Ta có bảng biến thiên : Trang 579
NHÓMWORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG:2019-2020
Yêu cầu bài toán  * có hai nghiệm dương phân biệt  16  m  0
Vậy có 15 giá trị nguyên của m thỏa mãn đề bài. Câu 43.11: Cho phương trình 2
log x  2 log x  3  m log x  3 với m là tham số thực. Tìm tất cả 2 2  2 
các giá trị của m để phương trình có nghiệm thuộc 16; . 3
A. 1  m  2 .
B. 1  m  5 . C. m  5 . D. 1  m  5 . 4 Lời giải Chọn B
Đặt t  log x với x 16; thì t  4 , khi đó ta có phương trình 2
t  2t  3  m t  3* 2 2 
t  2t  3  0
- Với m  0 thì phương trình vô nghiệm, do  , t   4. t   3  0  2 - Với 2 2 2 2 2 2 m  0 thì  
*  t  2t  3  m t   3
 1 m t  23m  
1 t  31 3m   0  1
+ Nếu m  1  t  3 : không thỏa mãn.
t  3loai 
+ Nếu m  1 thì   2 1  3  m 1  t  2  1 m 2 3  m 1
Do đó để phương trình đã cho có nghiệm 
 4  1  m  5 thoûa . 2   1 m Câu 43.12: Cho phương trình 2
log x  4log x  5  m log x 1 m 3 3  3
 với là tham số thực. Tìm tất cả
các giá trị của m để phương trình có nghiệm thuộc 27; .
A. 0  m  2 .
B. 0  m  2 .
C. 0  m  1 .
D. 0  m  1 . Lời giải Chọn D
Đặt t  log x với x 27;  thì t  3 , khi đó ta có phương trình 2
t  4t  5  m t   1   * 3 t  1  Điều kiện xác định: . t  5  2 
t  4t  5  0
- Với m  0 thì phương trình vô nghiệm, do  , t   5. t  1  0 
t  1 (loaïi)
- Với m  0 thì   2
*  t  4t  5  0  . t   5 (thoûa maõn)
- Với m  0 thì    t t   m t  2 2 2 * 4 5 1   2  m  2 t   2 m   2 1 2
4 t  5  m  0 **
+ Nếu m  1  t  1 : không thỏa mãn.
t  1 (loaïi) + Nếu 
m  1 thì (**)  t    2   m  2 1 1
t m  5  0  2   m   5 t   1 2 m Trang 580
NHÓMWORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG:2019-2020 2 2 m  5 6m
Do đó để phương trình đã cho có nghiệm   5 
 0  1  m  1, kết hợp 2 2 1  m 1 m
m  0 suy ra 0  m  1 .
Vậy với 0  m  1 thì phương trình đã cho có nghiệm thuộc [27;  )  . Câu 43.13:
Tìm tất cả các giá trị thực của m để phương trình 2 2 2
log cos x mlog cos x m  4  0 vô nghiệm.
A. m   2; 2 .
B. m   2; 2  .
C. m   2;2 .
D. m  2; 2 . Lời giải Chọn C Ta có: 2 2 2
log cos x mlog cos x m  4  0 2 2
 log cos x  2mlog cos x m  4  0 (*)
Đặt log cos x t . Do cos x  1  t  0
Khi đó phương trình (*) trở thành: 2 2
t  2mt m  4  0. (1)
Phương trình (*) vô nghiệm khi và chỉ khi phương trình (1) vô nghiệm hoặc có các nghiệm đều
dương. Điều này xảy ra khi và chỉ khi 2 m 1. 2 m  4  0  2   0  2m  4  0  2 m 1. 2 m  4  0    2  m  2   0 2     2m  4  0          2  m  2   m  2 t  2m   t  0 2m  0 1 2   0    1   2   m  2   t  .t  0  2   1 2  m  4  0 2  m  4    0   1 Câu 43.14: Cho hàm số 2
3log 2x  m  3 x 1 m  log    2
x x 1 3m  0 . Số các giá trị 27 1  3
nguyên của m để phương trình đã cho có hai nghiệm phân biệt x , x thỏa mãn x x  15 là: 1 2 1 2 A. 14 B. 11 C. 12 D. 13 Lời giải Chọn D Ta có: 2
3log 2x  m  3 x 1 m  log    2
x x 1 3m  0 27 1  3 2
 log 2x  m  3 x 1 m  log    2
x x 1 3m 3 3  2
x x 1 3m  0    2 2x   m  3 2
x  1 m x x 1  3m  2
x x 1 3m  0 * 2  
x x 1 3m  0  *   
 x m 2 x  
m  2 x  2m  0  1  x  2  Trang 581
NHÓMWORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG:2019-2020
Phương trình đã cho có hai nghiệm phân biệt khi và chỉ khi phương trình (1) có hai nghiệm 2
m m 1 3m  0 2 
m  4m 1  0 phân biệt thỏa mãn (*) 2
 2 11 3m  0    m  2  3 . 4  3m  0 m  2  
Theo giả thiết x x  15   x x 2 2
 4x x  225  m  4m  221  0  1  3  m  17 1 2 1 2 1 2 Do đó 1
 3  m  2  3 . Vậy số các giá trị nguyên của m thỏa mãn là 13. Câu 43.15: Cho phương trình 2
log x  log 5x 1   log m ( m 9 3   3
là tham số thực). Có tất cả bao nhiêu
giá trị nguyên của m để phương trình đã cho có nghiệm? A. 4. B. 6. C. Vô số. D. 5. Lời giải ChọnA  1  1 x x   5    5 Phương trình 2
log x  log 5x 1   log m    9 3   3  5x 1 1 log log m 5     m 2 3 3     x   x Cách1.. 1  1 
Xét f x  5  trên khoảng ;    . x  5  1  1   1 
Có f  x   0, x  
;  và lim f x  lim 5   5 . 2     x  5  x x   x
Ta có bảng biến thiên của hàm số f x : 1 Phương trình  
1 có nghiệm  phương trình 2 có nghiệm x  . 5
Từ bảng biến thiên suy ra phương trình  
1 có nghiệm  0  m  5 .
Mà m   và m  0 nên m 1;2;3;  4 .
Vậy có 4 giá trị nguyên của m để phương trình đã cho có nghiệm. Cách 2.
2  5  mx  1 3
Với m  5 , phương trình  
3 thành 0.x  1 (vô nghiệm). 1
Với m  5 , 3  x  . 5  m Trang 582
NHÓMWORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG:2019-2020 1 1 1 m Xét x    
 0  0  m  5 . 5 5  m 5 5.5  m
Mà m   và m  0 nên m 1;2;3;  4 .
Vậy có 4 giá trị nguyên của m để phương trình đã cho có nghiệm Câu 43.16:
Cho phương trình  x  2 2 log
x m x  3 log
x m  1 với m là tham số. Tất cả các 5     5  
giá trị của m để phương trình đã cho có nghiệm thuộc khoảng 3; là tập S   ; a  . Đánh
giá nào sau đây đúng?
A. 3  a  1 .
B. 1  a  1.
C. 1  a  2 .
D. 2  a  5 . Lời giải Chọn A Đặt t  log
x m . Phương trình đã cho trở thành 5   t  1  x 2 2 tx 3t 1       1  x  3 t   x  2 1 14 +) Với t  1
  x m   3  m  . 5 5 1 1 1 +) Với x2 x2 t
x m  5
m x  5 x  2 1 Mà hàm số   2 5x f x x   
đồng biến trên 3;   m f 3  2.
Kết hợp hai trường hợp trên ta được m   2
 ;   a  2 . Câu 43.17: Tổng tất cả các giá trị của tham số
m sao cho phương trình x 2 1 2 .log  2
x  2x  3  4 xm.log
2 x m  2 có đúng ba nghiệm phân biệt là: 2  2   3 A. 2. B. . C. 0. D. 3. 2 Lời giải Chọn D 2 Ta có: x  1 2 .log  2
x  2x  3  4 xm.log 2 x m  2 2  2   x 2 1  2 .log  2
( x 1)  2  2 xm.log
2 x m  2 (*) 2  2 2   t t 1 Đặt ( )  2t f t
log (t  2), t  0 ; f '(t)  2 ln 2.log (t  2)  2  0, t   0 . 2 2 (t  2) ln 2  t
hàm số f (t)  2 log (t  2) đồng biến trên (0; ) . 2 2
2(x m)  (x 1) Khi đó (*) 2 2
f (x 1)   f 2 x m   (x 1)  2 x m       2
2( x m)  (x 1)  Trang 583
NHÓMWORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG:2019-2020 2
x  4x 1  2m    I  2
x 1  2m
Vẽ đồ thị của hai hàm số f x 2
 x  4x 1 và g x 2
x 1 trên cùng một hệ trục tọa độ.  3 m  2m  3  2 
Từ đồ thị suy ra  I  có 3 nghiệm phân biệt 
 2m  2  m  1   2m 1    1  m   2 1 3
Vậy tổng các giá trị của m là 1  3. 2 2 Câu 43.18:
Cho phương trình 3x m  log x m 3 
 với m là tham số. Có bao nhiêu giá trị nguyên của
m 15;15 để phương trình đã cho có nghiệm? A. 15 B. 16 C. 9 D. 14 Lời giải Chọn D Đặt log (  )     3a x m a x m 3
Ta có: 3x m  log
x m  3x   log (  )  
 3x   3a x x m x m xa (*) 3   . 3
Xét hàm số ( )  3t f t
t , với t   . Có ( )  3t f' t
ln 3 1  0,t  nên hàm số f t đồng biến
trên tập xác định. Do đó (*)  f (x)  f a  x a x  log (x  )
m  3x x m 3
 3x x  m  1 
Xét hàm số    3x g x
x , với x   . Có ( )  3x g' x
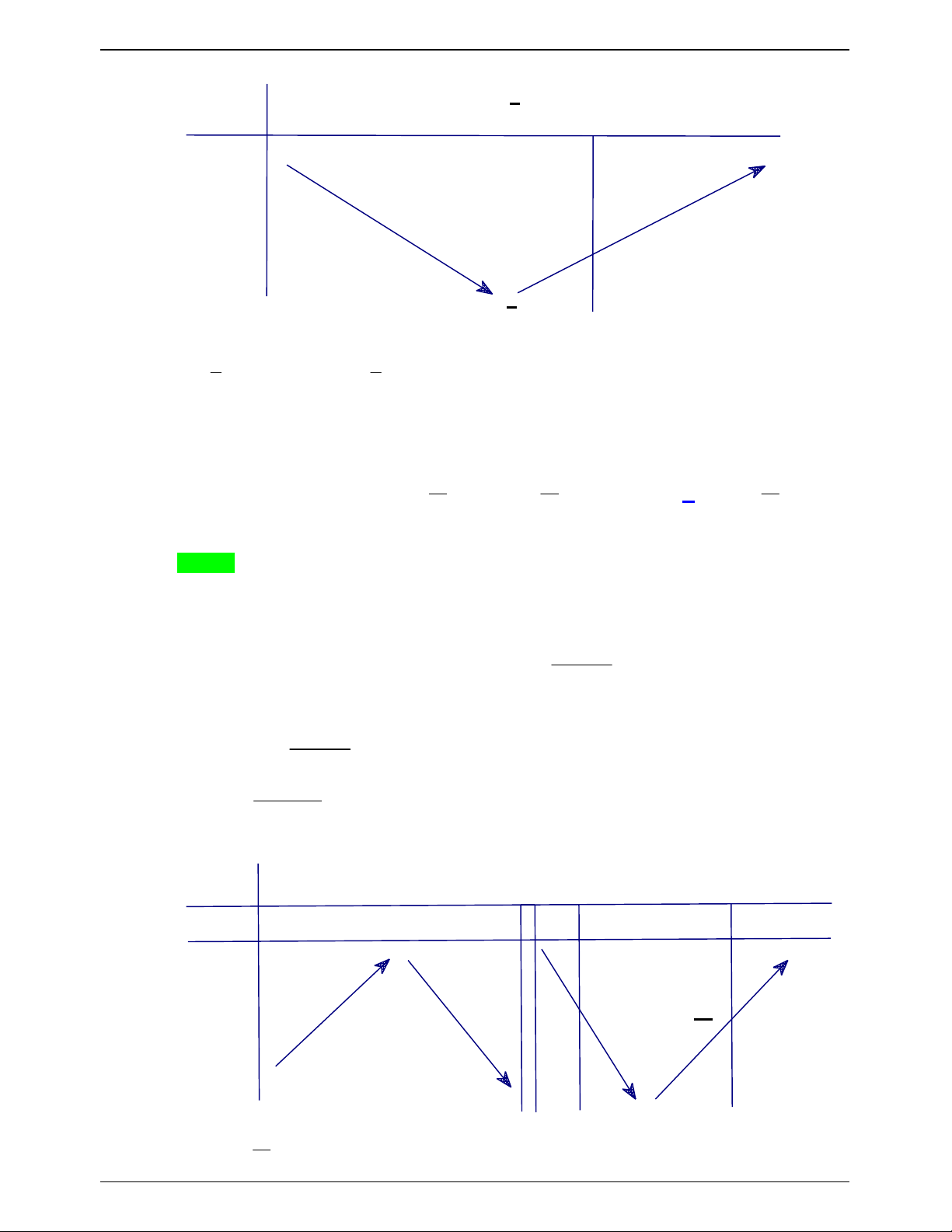
ln 3 1, g'(x)  0  x  log3    ln 3  Ta có bảng biến thiên Trang 584
NHÓMWORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG:2019-2020
Từ bảng biến thiên ta thấy các giá trị của tham số để phương trình có nghiệm là    1  
m  ; g log
. Vậy số giá trị nguyên của m    3   
15;15 để phương trình đã cho    ln 3   có nghiệm là 14 . Câu 43.19:
Tìm tất cả các giá trị của m để phương trình ln m  ln m  sin x  sin x có nghiệm. 1 1 A.
 1  m e 1.
B. 1  m e 1 . C. 1  m  1.
D. 1  m e 1. e e Lời giải Chọn B u   ln 
m  sin xu
e m  sin x
Đặt u  ln m  sin x ta được hệ phương trình:    ln  m u sin  sin x xem u  
Từ hệ phương trình ta suy ra: u sin x
e u e  sin x * Xét hàm số   t
f t e t có '  t f
t e 1  0, t
    Hàm số f t  đồng biến trên . 
Do đó *  f u  f sin x  u  sin x Khi đó ta được:    sin ln sin  sin x m x x e
 sin x m **
Đặt a  sin x, a  1  ; 
1 . Phương trình ** trở thành: a
e a m ** Xét hàm số   a
g a e a trên  1  ;  1 . Hàm số   a
g a e a liên tục trên 1; 
1 và có max g a  g  
1  e 1, min g a  g 0  1 1;  1 1;  1
Hệ phương trình ban đầu có nghiệm  phương trình ** có nghiệm  1  m e 1. Câu 43.20: Cho phương trình 2
m ln  x  
1   x  2  m ln  x  
1  x  2  0  
1 . Tập tất cả các giá trị của
tham số m để phương trình 1 có hai nghiệm phân biệt thỏa mãn 0  x  2  4  x là khoảng 1 2
a; . Khi đó a thuộc khoảng A. 3, 7;3,8 . B. 3, 6;3, 7 . C. 3,8;3,9. D. 3,5;3,6 . Lời giải Chọn A
Theo đề ra ta chọn điều kiện của x là x  0  ln  x   1  0. TH1: m  0   1  ln  x   1  1   L ln  x   1  1   L ln  x   1 1 TH2: m 0   1       . x  2 ln  x   1  x  2 m  m Trang 585
NHÓMWORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG:2019-2020 ln  x   1
Xét hàm số f x  với x  0 . x  2 x  2
Ta có: f ' x  0   ln  x   1  0. x 1 x  2 1 1
Xét hàm số g x   ln  x  
1 có g ' x    0, x   0 x 1  x  2 1 x 1
 Hàm số y g x nghịch biến trên 0;   g x  0 có nhiều nhất một nghiệm trên 0; 2  4   5 
Mặt khác: g 2 g 3   ln 3
 ln 4  0 và hàm số y g x liên tục trên     0;  3   4 
Suy ra g x  0 có ít nhất một nghiệm x  2;3 3 . 0    
Từ 2;3 suy ra g x  0 có một nghiệm duy nhất x  2;3 0  
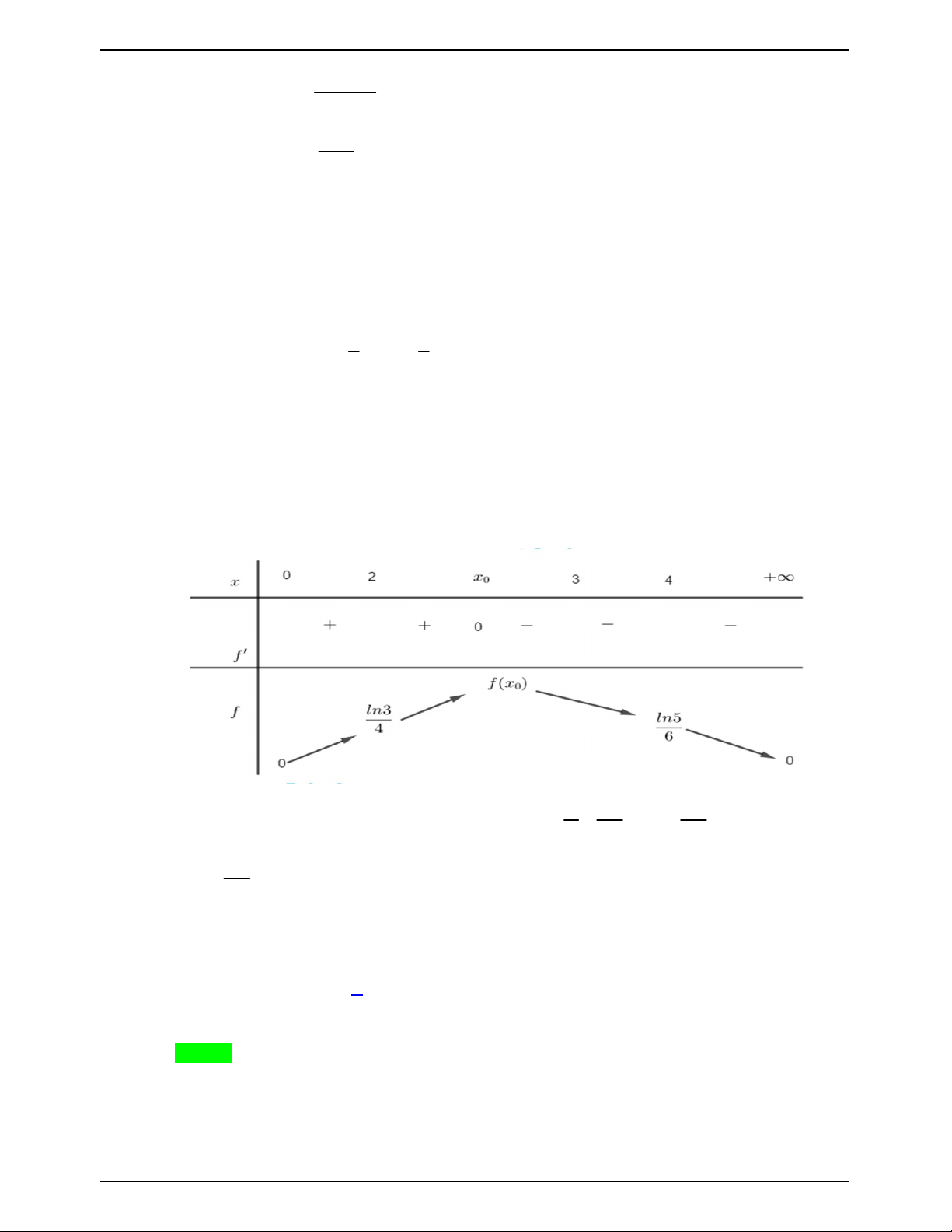
f ' x  0 có một nghiệm duy nhất x  2;3 0  . Bảng biến thiên 1 ln 5 6
Để 1 có 2 nghiệm thỏa mãn 0  x  2  4  x thì 0    m  1 2 m 6 ln 5 6  a   3, 728 . ln 5 Câu 43.21:
Giá trị thực của tham số m để phương trình 2 4 log
3x  2m  3 log x  2m 1  0 có hai 9     3
nghiệm thực x , x thỏa mãn x x  12 thuộc khoảng nào sau đây? 1 2 1 2 A. 2 . B. 1. C. 3 . D. 4 . Lời giải Chọn B
Điều kiện x  0 . 2
Ta có pt  1 log x  2m  3 log x  2m 1  0 . 3    3 Trang 586
NHÓMWORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG:2019-2020 log x  1 x  3 2 3
 log x  (2m 1) log x  2m  0   . 3 3   2 log x  2m x  3 m  3  Theo đề, ta có: 2   12  3  3 m x x  12  m  1. 1 2 2 2 2
Câu 43.22: Phương trình
2x 3xm x x2 x 2 3 9 3 3 x    .
m Có bao nhiêu giá trị nguyên của tham số
m [2018; 2018] để phương trình đã cho có 4 nghiệm phân biệt ? A. 2019 . B. 2018 . C. 2020 . D. 2021. Lời giải Chọn C 2 2 2 2 2 2
Ta có: 2x 3xm x x2
x 2 xm
2 x 3xm x x2 x 2 3  9  3  3  3  3  3 xm  9 . 2 2 2 2 2 x x
x 2xm
x 2xm x x x 2  3 (3  9)  3  9  (3 1)(3
xm  9)  0 . 2    x x x 1 2 3  1
x x  0      x  0  . 2 2 
x 2 xm
x  2x m  2 3  9  2 
x  2x m  2  0 (2) 
Để phương trình đầu có 4 nghiệm phân biệt khi phương trình 2 có hai nghiệm phân biệt
x  1, x  0 .  '  0 3   m  0 m  3   
Khi m  2  m  2
 m  2  2  m  3 . m 3 m 3    m  3    Vì m [ 2
 018; 2018] và m   nên có 2020 giá trị m cần tìm.
Câu 43.23: Tìm tập hợp tất cả các giá trị của tham số m để phương trình 2 4(log
x )  log x m  0 có 3 1 3 hai nghiệm thuộc 0;  1 . 1 1 1 1 1 A. 0  m  . B.m  . C. 1   m . D. 0  m  . 5 6 4 4 4 Lời giải Chọn D Pt: 2 2 4(log
x )  log x m  0  log x  log x  m (1) 3 1 3 3 3
Đặt t  log x , ta được phương trình 2
t t  m với t  ( ;
 0) khi x  0;  1 . 3
Để phương trình (1) có hai nghiệm x 0;  1 khi phương trình 2
t t  m có hai nghiệm t  (;0) . Xét hàm số 2
y t t trên ;0 . Trang 587
NHÓMWORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG:2019-2020 1 t - -∞ 0 2 +∞ +∞ y +∞ 0 1 - 4 1 1  
 m  0  0  m  . 4 4
Câu 43.24: Điều kiện cần và đủ của tham số m để phương trình 2 log
x  (m 1) log x  4  m  0 có hai 5 5
nghiệm phân biệt thuộc 1; 25 là 10 10 10
A. 3  m  4 . B. 3  m  . C.m  4 . D. 3  m  . 3 3 3 Lời giải Chọn D Pt: 2 log
x  (m 1) log x  4  m  0 (1) 5 5
Đặt t  log x , với t 0;2 khi x 1;2  5 . 5 2 t t  4 Ta được phương trình 2
t  (m 1)t  4  m  0  m    * t 1
Để phương trình (1) có hai nghiệm x 1;2  5 khi phương trình  
* có hai nghiệm t 0;2 . 2 t t  4 Xét hàm số y  trên 0; 2 . t 1 2 t  2t  3 t  3  Ta có y '   0  2  (t 1) t  1  BBT. t -∞ -3 -1 1 2 0 +∞ y' + 0 - - 0 + y +∞ +∞ 4 10 3 -∞ -∞ 3 10  3  m  . 3 Trang 588
NHÓMWORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG:2019-2020
Câu 43.25: Tìm tất cả các giá trị thực của tham số m để phương trình 2
log x m  2 log x  3m 1  0 3   3
có hai nghiệm x , x thỏa mãn x .x  27. 1 2 1 2 A. m  2  . B. m  1. C. m  1. D. m  2 . Lời giải Chọn C
Điều kiện x  0 .
Đặt t  log x , ta có phương trình 2
t  (m  2)t  3m 1  0 . 3
GS : t  log x , t  log x t t  log x  log x  log x x  3 . 1 3 1 2 3 2 1 2 3 1 3 2 3 1 2
Vậy để phương trình có hai nghiệm thỏa mãn yêu cầu đề bài khi và chỉ khi 2   0
m  8m  8  0   m  1   . t t  3 m  2  3  1 2  2
Câu 43.26: Tổng tất cả các giá trị m để phương trình x 2x 1  2 3
log (x  3  2x)  9 xm log (2 x m  2) có 3 3
đúng ba nghiệm phân biệt là A. 4 B. 2 C. 0 D. 3 Lời giải Chọn D 2 Ta có x 2x 1  2 3
log (x  3  2x)  9 xm log (2 x m  2)   1 3 3 x 2 1 3 .log  x 1 2     3 xm.log 2 x m  2 2 3  2 2 3     Xét hàm số    3t f t
.log t  2 ,t  0. 3  
Vì f t   0, t
  0  hàm số đồng biến trên 0; . 2 2 Khi đó 2
f  x 1   
f 2 x m    x 1  2 x m .   2
x  4x 1 2m  0 3   . 2 x  2m 1 4  Phương trình  
1 có đúng ba nghiệm phân biệt nếu xảy ra các trường hợp sau:
+) PT 3 có nghiệm kép khác hai nghiệm phân biệt của PT4 3  m
, thay vào PT 4 thỏa mãn. 2
+) PT 4 có nghiệm kép khác hai nghiệm phân biệt của PT 3 1  m
, thay vào PT 3 thỏa mãn. 2
+) PT 4 có hai nghiệm phân biệt và PT 3 có hai nghiệm phân biệt, trong đó có một nghiệm của hai PT trùng nhau 1 3
4  x   2m 1 ,với  m  . Thay vào PT 3 tìm được m 1. 2 2 1 3  KL: m   ;1; .  2 2  Cách 2:
Xem phương trình (3) và (4) là hai đường cong. Ta sẽ tìm điểm chung của hai đường cong đó. Trang 589
NHÓMWORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG:2019-2020 2 
x  4x 1 2m  0 x  1 Ta giải hệ:    . 2 x  2m 1 m  1  
Như vậy với m  1 thì (3) và (4) có nghiệm chung là x  1.
Thay m  1 vào lần lượt vào 2 phương trình ta được 3 nghiệm  1  ; 
3 . Vậy ta nhận m  1.
Xét m  1, phương trình có 3 nghiệm khi (3) có 2 nghiệm phân biệt và (4) có nghiệm kép hoặc
ngược lại. Như vậy ta có:
  3  2m  0  1  m  2m 1  0   2   .
  3  2m  0 3   m    2m 1  0  2   1 3 
Từ đó ta có 3 giá trị của tham số m là  ;1;  .  2 2  3
Câu 43.27: Tìm tất cả các giá trị của tham số m để phương trình x
m có hai nghiệm phân biệt. log x 1 2   A. 1   m  0 . B. m  1.
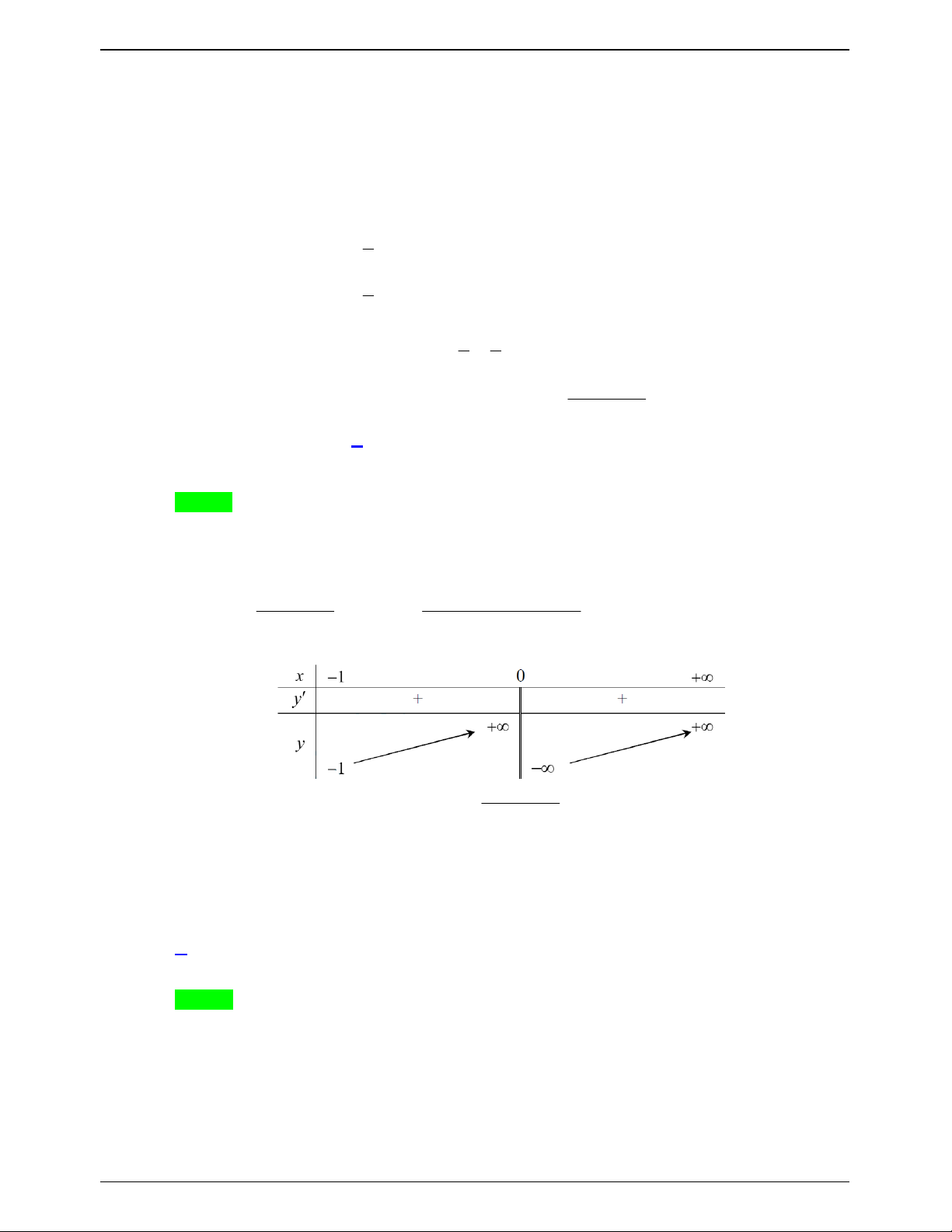
C. Không tồn tại m . D. 1   m  0 . Lời giải Chọn B x 1  0 x  1  Điều kiện:    x 1  1 x  0   Xét hàm số 3 3
f x  x
; f   x  1  0, x    1  ;0  0 :  log  x   1  x   2 1 .ln 2.log x 1 2 2   Bảng biến thiên 3
Từ bảng biến thiên suy ra phương trình x
m có hai nghiệm phân biệt khi và chỉ log x 1 2   khi m  1. 2 2
Câu 43.28: Có bao nhiêu giá trị thực của tham số m để phương trình x 3x2 4 x 63 .5  5  5 x mm có đúng
3 nghiệm thực phân biệt. A. 3 B. 2 C. 1 D. 4 Lời giải Chọn A 2 x 3x2 5    u Đặt 63   u.v  5
x . Khi đó phương trình trở thành 2 4 5 x   v
mu v uv m m u  
1  v u   1  0 . 2 x 3 x2 u  1 5    1  u  
1 m v  0     . 2 v m 2  5 x   m  Trang 590
NHÓMWORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG:2019-2020 x  1 2
x  3x  2  0     x  2 . 2 
4  x  log m  5 2
x  4  log m  5
Để phương trình có ba nghiệm thì: +) TH1: 2
x  4  log m có nghiệm kép 5
Tức 4  log m  0  m  525 . 5 +) TH2: 2
x  4  log m có một nghiệm bằng 1. 5
Tức 4  log m  1  m  75 . 5 +) TH3: 2
x  4  log m có một nghiệm bằng 2 . 5
Tức 4  log m  4  m  1. 5
Vậy có 3 giá trị của m cần tìm.
Câu 43.29: Với giá trị của tham số m thì phương trình   
1 9x  2 2  33x m m
 6m  5  0 có hai nghiệm trái dấu? 3 5 A. 4   m  1  .
B. Không tồn tại m . C. 1   m  . D. 1   m   . 2 6 Lời giải Chọn A
Đặt 3x t  0 . Phương trình đã cho trở thành: m   2
1 t  22m  3t  6m  5  0.
 * f t
Yêu cầu bài toán  * có hai nghiệm t , t thỏa mãn 0  t  1  t . 1 2 1 2 m 1  0 m 1  0    m   1 f   1  0  m  
1 3m 12  0  4  m  1.   m   1 6m  5  0 m   1 6m  5  0   2 2 x 2 mx2
2 x 4 mx2m Câu 43.30: Cho phương trình        2 2 1 2 1
x  2mx m  0 . Tìm m để 1
phương trình có đúng 2 nghiệm thuộc ( ; 2) . 2 1 4 1 1 A.   m  0 B.   m  0 C.   m  1 D.    m  2 8 5 8 8 Lời giải Chọn A 2 2 x 2 mx2
2 x 4 mx2m Ta có:        2 2 1 2 1
x  2mx m  0 . 2 2  
 x 2mx2  
 2x 4mx2m 2 2 1 2 1
x  2mx m . 2 2  x 2mx2     
x mx   
 2x 4mx 2 m 2 2 2 1 2 2 2 1
 2x  4mx  2  m .
Xét hàm số : ( )  ( 2 1)t f tt .
Ta có hàm số ( )  ( 2 1)t f t
t đồng biến trên  .
Khi đó phương trình có dạng 2 2
f (x  2mx  2)  f (2x  4mx  2  m) . 2 x 2 2 2
x  2mx  2  2x  4mx  2  m x  2mx m  0  m   . 2x 1 Trang 591
NHÓMWORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG:2019-2020 1
Để phương trình có đúng hai nghiệm thuộc khoảng ( ; 2) khi và chỉ khi phương trình 2 2 x 1 m  
có hai nghiệm thuộc ( ; 2) . 2x 1 2 2 x 1
Xét hàm số y   trên khoảng ( ; 2) . 2x 1 2 2 2x  2xx  0 Ta có y '    0  2  (2x 1) x  1   1 1 - x 2 -∞ -1 2 0 2 +∞ - y' 0 + + - 0 y +∞ +∞ 0 4 - 5 1 - 8 -∞ -∞ 1    m  0 . 8 x x  2 2 2 x 2x 2 2 2 
Câu 43.31: Với những giá trị nào của m thì phương trình : 2 3  2
x  2x m  2 có nghiệm. A. m  8 B. m  7 C. m  6 D. m  5 Lờigiải Chọn A x x  2 2 2 x 2x2 2 2  Ta có: 2 3  2
x  2x m  2 . 2 2 x 2x2 x 2 x2 2  3  4
x  2x  2  m Đặt : 2
t x  2x  2  t  1
Khi đó phương trình trở thành 3t  4t t m
Ta có hàm số ( )  3t  4t f t
t đồng biến trên 
Để phương trình có nghiệm   (3t  4t m Mint)  m  8 . 1; Câu 43.32:
Với những giá trị nào của m thì phương trình : 3 2 3 2
  2x mx   x 4mx m 3 2 5 2 5 2
 2x  6mx  2m có nghiệm duy nhất. 1 1 1 1 1 1 A.   m  , m  0 B. m   C.   m D. m   2 2 2 2 2 4 Lời giải Chọn C 3 2 3 2 2 x mx
x 4mx m Ta có:        3 2 5 2 5 2
 2x  6mx  2m . Trang 592
NHÓMWORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG:2019-2020 3 2 3 2   x mx
x mx m 5  22   5  2 4 3 2
 2x  6mx  2m 3 2 3 2   x mx
x mx m 5  22
 2(2x mx )   5  2 4 3 2 3 2
 2(x  4mx m)
Xét hàm số : ( )  ( 5  2)t f tt
Ta có hàm số ( )  ( 5  2)t f t
t nghịch biến trên 
Khi đó phương trình có dạng 3 2 3 2
f (2x mx )  f (x  4mx m) 3 2 3 2 3 2
 2x mx x  4mx m x  3mx m  0 Xét hàm số 3 2 2
y x  3mx m y '  3x  6mx x  0
y '  0  x  2m  +)TH1 : 2
m  0  y '  3x  0, x    khi đó hàm số 3 2
y x  3mx m đồng biến trên  .
Vậy khi đó phương trình có một nghiệm duy nhất. +)TH1 : 3
m  0  y(0)  m, y(2m)  4
m m . Khi đó để phương trình có một nghiệm duy 1 1 nhất khi 3
y(0).y(2m)  0  ( m 4
m m)  0    m  . 2 2 Câu 43.33:
Có bao nhiêu giá trị nguyên của m thì phương trình sau có nghiệm 2 1
  sinxm   cos x2 2 3 7 4 3  m  o c s2x  s inx A. 2 B. 1 C. 3 D. 4 Lời giải Chọn D 2 1 sinxm cos x Ta có:        2 2 3 7 4 3  m  o
c s2x  sinx . 2   m x
2  3 sinx  2  32cos 1  m cos2x  sinx   m c x
2  3 sinx  sinx  m  2  3 os2  cos2x
Xét hàm số : ( )  (2  3)t f tt
Ta có hàm số ( )  (2  3)t f t
t nghịch biến trên 
Khi đó phương trình có dạng f (s inx  m)  f (c os2x) 2  s inx  m  o c s2x  2
 s in x-sinx 1  m
Đặt : t=sinx  t  1  ;  1
Khi đó phương trình trở thành 2
2t t 1  m 9
Để phương trình có nghiệm 2 2  Min( 2
t t 1)  m  Max( 2
t t 1)  2   m   1  ;  1  1  ;  1 8 Câu 43.34:
Giá trị thực của tham số m để phương trình 25x  4( 1).5x m
 5(4m 1)  0 có hai nghiệm
thực x , x thỏa mãn (x  4)(x  4)  30 thuộc khoảng nào sau đây ? 1 2 1 2 A. 6; 7 B. 4;5  C. 3; 4  D. 2;3  Trang 593
NHÓMWORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG:2019-2020 Lời giải. Chọn A Đặt 5x t  , ta có phương trình 2
t  4(m 1)t  5(4m 1)  0 t  5 5x  5 x  1       t  4m 1  5x  4m 1
5x  4m 1(1)  
Ta có ( x  4)(x  4)  30  5.(x  4)  30  x  2 1 2 2 2 26 .Thay vào (1) ta được 2
5  4m 1  m  4 Câu 43.35:
Giá trị thực của tham số m để phương trình 9x  2(2  1).3x m
 243  0 có hai nghiệm thực x , 1
x thỏa mãn (x  3)(x  3)  30 thuộc khoảng nào sau đây ? 2 1 2 A. 6;7 B. 8;9  C. 7;8 D. 2;3 Lời giải Chọn B Đặt 3x t  , ta có phương trình 2
t  2(2m  1)t  243  0
GS: phương trình có nghiệm 1 x x2 1 x x2 5
t  3 , t  3  t .t  3
 243  3  x x  5 1 2 1 2 1 2
Ta có ( x  3)(x  3)  30  x x  3(x x )  9  30  x x  6 1 2 1 2 1 2 1 2 x x  5 x  2 t   9 Ta có 1 2 1 1     
t t  36 1 2 x .x  6 x  3 t  27  1 2  2  2 34
Mà theo đề bài t t  4m  2  36  m  1 2 4 Câu 43.36:
Giá trị thực của tham số m để phương trình 2 log
x  3.log x  4  m  0 có hai nghiệm thực 2 2
x , x thỏa mãn (x  4)(x  4)  48 thuộc khoảng nào sau đây ? 1 2 1 2 A. 1; 2  B. 1;3  C. 0;  1  D. 0; 2  Lời giải Chọn B
Đặt t  log x , ta có phương trình 2
t  3t  4  m  0 2
GS: phương trình có nghiệm t  log x ,t  log x t t  log x x  3  x x  8 1 2 1 2 2 2 1 2 2 1 2 1 2
Ta có ( x  4)(x  4)  48  x x  4(x x )  16  48  x x  6 1 2 1 2 1 2 1 2 x x  6 x  2 t   1 Ta có 1 2 1 1       t .t  2 1 2 x .x  8 x  4 t  2  1 2  2  2
Mà theo đề bài t .t  4  m  2  m  2 1 2 Câu 43.37:
Gọi S là tập hợp tất cả các giá trị thực của tham số m để tồn tại duy nhất cặp ( x; y) thỏa mãn
đồng thời các điều kiện log
(2x  6 y  5)  1 và 3x y  3  m  0. Tổng các phần tử của 2 2 x y 3 S bằng A. 3 B. 4  C. 5 D. 6  Lời giải Chọn D Ta có: Trang 594
NHÓMWORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG:2019-2020 2 2 log
(2x  6 y  5)  1  x y  3  2x  6 y  5 2 2 x y 3 2 2
x y  2x  6 y  2  0 Ta thấy phương trình 2 2
x y  2x  6 y  2  0 là phương trình đường tròn tâm I 1;  3 bán kính R  12
Để tồn tại duy nhất cặp số ( ;
x y) thỏa mãn yêu cầu bài toán khi đường thẳng
 : 3x y  3  0 tiếp xúc với đường tròn 2 2
(C) : x y  2x  6 y  2  0 3  3  m  3
Khi và chỉ khi d (I , )  R   2 3 2 m  3  4 3   m  3  4 3  Câu 43.38:
Tất cả các giá trị của tham số m để phương trình log mx  log
x 1 có hai nghiệm 5   5   phân biệt là A. m  4 . B. m  4 .
C. m  0 và m  4 .
D. m  0 và m  4 . Lời giải Chọn B x  1  0  x 1  0
Ta có log  mx   log x   1     (*) . 2
mx x 1
mx x  2x 1  
Ta thấy x  0 không là nghiệm của (*). x  1  
Với x  0 : (*)   1
m x  2    x 1
Xét hàm số f x  x  2  với x 1;  \  0 . x 2 1 x 1
Ta có f  x  1 
; f  x  0  x  1 (do x 1; \   0 ). 2 2 x x Bảng biến thiên:
Dựa vào bảng biến thiên suy ra m  4 là giá trị cần tìm. Trang 595
NHÓMWORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG:2019-2020 2 1 Câu 43.39:
Cho bất phương trình m   2 1 log x  2  4 m  5 log
 4m  4  0 ( m là tham số 1     1 x  2 2 2  5 
thực). Tập hợp tất cả các giá trị của m để bất phương trình đã cho có nghiệm thuộc đoạn , 4  2    là  7   7   7  A. 3;  . B. ;    . C. 3;   . D.  ;    .  3   3   3  Lời giải Chọn A
Điều kiện: x  2. 2 1 Ta có: m   2 1 log x  2  4 m  5 log  4m  4  0 1     1 x  2 2 2  4 m   2 1 log
x  2  4 m  5 log
x  2  4m  4  0 2     2   Đặt t  log
x  2 , ta có phương trình trở thành: m   2
1 t  m  5t m 1  0 * 2    5  Với x  ; 4 , 
ta có: t 1;  1 . 2    2 t  5t  1 *  m  , t 1;  1 . 2 t t  1
Để bất phương trình có nghiệm t 1;  1 2
t  5t 1 
Khi và chỉ khi m Min   .   2 1;1 t t 1   2 t  5t 1 2 4t  4 f t 
. Ta có: f 't    0, t   1  ;1 . 2   2 t t 1
 2t t   1 7 Suy ra: f  
1  f t   f   1 ,t 1;  1 hay 3
  f t   , t  1;  1 . 3 Vậy m  3  . Câu 43.40: Cho bất phương trình 2 log
2x m 1 log x m  3  0 ( m là tham số thực). Tập hợp tất 2     2
cả các giá trị của m để bất phương trình nghiệm đúng với mọi x thuộc đoạn 4 ; 4 2  là   7 9 7 A. m  . B. m  .
C. m R . D. m  . 2 2 4 Lời giải Chọn B
Điều kiện: x  0 . Trang 596
NHÓMWORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG:2019-2020
log 2x  m  
1 log x m  3  0  1 log x2 2
m 1 log x m  3  0 2 2 2   2 2
 log x  1 m log x m  2  0 2   2  5 
Với x  4 ; 4 2   t  1 ;
, ta có bất phương trình bậc hai 2
t  (1 m)t m  2  0 .     2   5 
Bài toán trở thành tìm m để bất phương trình: 2
t  (1 m)t m  2  0 , t   2 ;  . 2     5   5 2 
t  (1 m)t m  2  0, t   2 ;  t  
1 t  2  m  0, t   2 ; *  2   2       5   5  5 9
Vì t 1  0, t   2 ; 
, nên *  t  2  m  0, t   2 ; 
 2  m  0  m  . 2       2  2 2 Trang 597