Phương trình lôgarit không chứa tham số

Tài liệu gồm 24 trang, được biên soạn bởi quý thầy, cô giáo Nhóm Toán VDC & HSG THPT, hướng dẫn phương pháp giải bài toán Phương trình lôgarit không chứa tham số; đây là dạng toán thường gặp trong chương trình Toán 12 phần Giải tích chương 2.

29 15 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 6: Hàm số mũ và hàm số lôgarit (KNTT)

Môn: Toán 11

Thông tin:

24 trang 8 tháng trước

Tác giả:

Profile Kim Oanh
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 1
GIẢI PHƯƠNG TRÌNH LÔGARIT BẰNG PHƯƠNG PHÁP HÀM SỐ - ĐÁNH GIÁ
(KHÔNG CHỨA THAM SỐ)
PHƯƠNG PHÁP
Vận dụng các kết quả sau :
Kết quả 1 : Nếu
( )
fx
là hàm số đơn điệu trên
K
(với
K
là khoảng, đoạn hoặc nửa khoảng) thì
( )
0fx=
có tối đa một nghiệm trên
K
.
Kết quả 2 : Nếu
( )
fx
là hàm số liên tục trên đoạn
[ ]
;ab
và
( ) ( )
0
fafb<
thì phương trình
( )
0fx=
có nghiệm thuộc khoảng
( )
;ab
.
Kết quả 3 : Nếu
(
)
fx
là hàm đơn điệu trên
( ) ( )
,, ; .K abKfa fb ab∀ ∈ = ⇔=
Kết quả 4 : Nếu hàm
(
)
fx
tăng trong khoảng
và hàm
( )
gx
là hàm một hàm giảm trong
khoảng
thì phương trình
( ) ( )
f x gx=
có nhiều nhất một nghiệm trong khoảng
.
Các bước giải phương trình :
Bước 1 : Tìm điều kiện xác định của phương trình.
Bước 2 : Biến đổi phương trình sao cho một vế là hàm số đơn điệu, một vế là hằng số
hoặc một vế là hàm đồng biến và vế còn lại là hàm số nghịch biến.
Bước 3 : Nhẩm nghiệm của phương trình trên mỗi khoảng xác định (nếu có).
Bước 4 : Kết luận nghiệm của phương trình.
Câu 1. Tìm số nghiệm của phương trình
( )
2
2022 ln 2021 0x x xx
− −+ =
.
A.
1
. B.
2
. C.
3
. D.
4
.
Lời giải
Chọn B
Tập xác định
( )
0;D = +∞
.
Phương trình
( )
2
2022 ln 2021 0x x xx
− −+ =
(
)
2
2022 ln 2021x x xx
⇔− =−
2
2022 1
2021 ln
xx
xx
−
⇔=
−
1
0
ln 2021
x
x
xx
⇔ + −=
−
(NX:
1x =
và
2021x =
không là nghiệm của phương trình).
Xét hàm số
( )
1
ln 2021
x
fx x
xx
=+−
−
trên
( ) {
}
0; \ 1;2021+∞
.
Có
( )
( )
( ) { }
2
1 2021
1 0, 0; \ 1;2021
ln
2021
fx x
xx
x
′
=− − − < ∀ ∈ +∞
−
.
Bảng biến thiên:
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT VD_VDC
Trang 2 TÀI LIỆU ÔN THU THPT QUỐC GIA
Từ bảng biến thiên suy ra phương trình đã cho có
2
nghiệm.
Câu 2 . Có bao nhiêu cặp số
thuộc đoạn
[ ]
1;2020
thỏa mãn
y
là số nguyên và
ln
ln
xy
xe ye+=+
?
A.
6
. B.
7
. C.
2021
. D.
2020
.
Lời giải
Chọn B
Ta có:
ln
ln
xy
xe ye
+=+
Xét hàm số
( )
t
ft t e= +
có
( )
1 0,
t
ft e t
′
=+>∀
Suy ra hàm số
( )
ft
đồng biến trên
.
Do đó ta có:
( )
(ln ) lnf x fy x y= ⇔=
Ta có:
1 2020 0 ln ln 2020 0 ln 2020 0 7,61...xxyy≤≤ ⇔≤ ≤ ⇔≤≤ ⇔≤≤
Do
y
là số nguyên thuộc đoạn
[ ]
1;2020
nên
{ }
1; 2;3;4;5;6;7y ∈
.
Kết luận: có 7 cặp số
( )
;xy
thỏa yêu cầu bài toán.
Câu 3: Có bao nhiêu cặp số tự nhiên
( )
;xy
thỏa mãn đồng thời hai điều kiện:
( )
( )
23
log 2 log 2 4 1xy xy+ ≤ ++
và
( )
3
log 2xy y+ ≥−
?
A.
7
. B.
6
. C.
10
. D.
8
.
Lời giải
Chọn B
Đặt
2, 0t x yt=+>
, khi đó
( )
( )
23
log 2 log 2 4 1
xy xy
+ ≤ ++
trở thành
( )
23
log log 2 1tt
≤+
.
Dựa vào đồ thị ta thấy
( )
23
log log 2 1 0 4 0 2 4t t t xy≤ + ⇔<≤⇔< +≤
.
Kết hợp với điều kiện
( )
3
log 2xy y+ ≥−
ta có các cặp số tự nhiên
( ) ( ) ( ) ( ) ( ) ( )
( )
{ }
; 0;1,0;2,0;3,1;0,1;1,1;2
xy =
.
Câu 4: Có bao nhiêu cặp số nguyên
( )
;xy
thỏa mãn
0 2020y≤≤
và
3
21
log 1 2 ?
x
x
y
y

−
= +−


A.
2019
. B.
11
. C.
2020
. D.
4
.
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 3
Lời giải
Chọn B
Từ giả thiết ta có:
0
21
021 0
0
x
x
y
x
y
y
≠
−
> ⇔ >⇔ >
≥
.
Ta có phương trình
(
)
( )
33
log 2 1 2 1 log *
xx
yy⇔ − + −= +
Xét hàm số
( )
3
logft t t= +
trên
( )
0; +∞
.
Khi đó
( )
1
10
ln 3
ft
t
′
= +>
do đó hàm số
( )
3
logft t t= +
đồng biến trên khoảng
( )
0; +∞
(*) có dạng
(
)
(
)
21 21
xx
f fy y
−= ⇔= −
.
Vì
( )
2
0 2020 0 2 1 2020 1 2 2021 0 log 2021
xx
yx≤≤ ⇔≤ −≤ ⇔≤ ≤ ⇔≤≤
(
)
{ }
2
0 log 2021
0;1; 2;3;4;5;6;7;8;9;10
x
x
x
≤≤
⇔∈
∈
.
Vậy có
11
cặp
( )
;xy
thỏa mãn.
Câu 5: Phương trình
(
)
33
2
log 1 27 8 1
y
xy x− − = +−
có bao nhiêu nghiệm nguyên
( )
;xy
với
1992 2020
8 ;8x

∈

?
A. 26 B. 28 C. 24 D. 30
Lời giải
Chọn B
Ta có
( )
( )
3 3 3 33
22
log 1 27 8 1 log 1 1 27 2
yy
x y x xx y−− = +−⇔ −+−= +
Đặt
( )
2
log 1 1 2
t
t xx= − ⇔ −=
. Thay vào phương trình ta được
( ) ( )
3
33
2 3 21
ty
ty+= +
.
Xét hàm số
( )
3
2.
u
y fu u= = +
Ta có
(
)
2
3 2 ln 2 0,
u
fu u u
′
= + > ∀∈
. Do đó hàm số đồng biến trên
.
Khi đó
( ) ( )
( )
( )
2
1 3 3 log 1 3 8 1.
y
ft f y t y x y x⇔ = ⇔= ⇔ − = ⇔ = +
Do
1992 2020
8 ;8
x

∈

nên
1992 2020
8 8 1 8 1992 2019
y
y≤ +≤ ⇔ ≤ ≤
với
y ∈
.
Vậy có
28
giá trị nguyên của y nên phương trình có
28
nghiệm.
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 1
GIẢI PHƯƠNG TRÌNH LÔGARIT BẰNG PHƯƠNG PHÁP SỬ DỤNG HÀM ĐẶC TRƯNG
(KHÔNG CHỨA THAM SỐ)
PHƯƠNG PHÁP
Bước 1 : Đưa phương trình về dạng
( )
( )
( )
( )
f ux f vx=
.
Bước 2 : Xét hàm số
( )
y ft=
trên
D
.
Tính
( )
y ft
′′
=
.
Chứng minh hàm số
( )
y ft
′′
=
luôn đồng biến hoặc luôn nghịch biến trên
D
.
Suy ra
( )
( )
(
)
(
)
(
)
( )
f ux f vx ux vx= ⇔=
.
Câu 1. Biết rằng phương trình
2
2
2
2
log 4 9
25
x
xx
x

+
=−+ +

+

có hai nghiệm
x a bc= +
và
x a bc= −
với
,,abc
là các số nguyên dương. Tính tích
..abc
.
A.
8
. B.
8−
. C.
12−
. D.
12
.
Lời giải
Chọn D
Điều kiện xác định:
2
25
0
25 2
x
x
x
+−
>⇔>
+
2
2
2
2
log 4 9
25
x
xx
x

+
=−+ +

+

(
)
( )
22
22
log 2 log 2 5 4 9x x xx⇔ +− +=−+ +
(
)
( )
22
2 22
log 2 2 log 2 5 log 2 4 10xx x x⇔ + + += + + + +
( )
( )
22
22
log 2 2 log 4 10 4 10xx x x
⇔ + + += + + +
Xét hàm số:
(
)
2
log
ft t t
= +
trên
( )
0;
+∞
(
)
1
1 0, 0
ln 2
ft t
t
′
= + > ∀>
⇒
(
)
ft
đồng biến trên
( )
0; +∞
Đặt:
2
20
4 10 0
ux
vx
= +>
=+>
. Khi đó ta được
22
log loguu vv+= +
( ) ( )
fu fv⇔=
Do đó
( ) ( )
2
2 4 10
fu fv u v x x= ⇔=⇔ += +
2
2 23
4 80
2 23
x
xx
x
= +
⇔ − −=⇔
= −
(thỏa mãn điều kiện).
Vì
,,abc
là các số nguyên dương nên
2, 2, 3abc
= = =
. Vậy
. . 12abc=
.
Câu 2. Phương trình
2
2
2
2
32
log 4 3
3 58
xx
xx
xx
++
=−+
−+
có các nghiệm
12
;xx
. Hãy tính giá trị của biểu thức
22
1 2 12
3A x x xx=+−
.
A.
31
. B.
1−
. C.
1
. D.
31−
.
Lời giải
Chọn C
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
Trang 2 TÀI LIỆU ÔN THI THPT QUỐC GIA
Điều kiện:
2
2
32
0
3 58
xx
xx
++
>
−+
2
3 20
xx⇔ + +>
1
2
x
x
>−
⇔
<−
(do
2
2
5 71
3 5 83 0
6 12
xx x

− += − + >


)
Phương trình đã cho tương đương với:
2
2
2
2
32
log 4 3
3 58
xx
xx
xx
++
=−+
−+
( ) ( )
( ) ( )
[ ]
2 2 22
22
1
log 3 2 log 3 5 8 3 5 8 3 2
2
xx xx xx xx⇔ ++− −+= −+− ++
( )
( ) ( )
( )
( )
22 2 2
22
11
log 3 2 3 2 log 3 5 8 3 5 8 *
22
xx xx xx xx⇔ +++ ++= −++ −+
Xét hàm số
2
1
( ) log ,( 0)
2
ft t t t
=+>
;
11
'( ) 0 0
ln 2 2
ft t
t
= + > ∀>
.
Nên hàm số
()
ft
đồng biến trên
( )
0; +∞
.
Mà phương trình
( )
*
có dạng:
( ) ( )
22
32 3 58
fxx fxx++= −+
.
Nên phương trình đã cho tương đương với phương trình:
( ) ( )
22
3 58 32xx xx−+= ++
2
2 8 60xx⇔ − +=
1
3
x
x
=
⇔
=
(thỏa mãn điều kiện ban đầu)
Vậy
( )
2
22
1 2 12 1 2 1 2
3 5. 1A x x xx x x x x
=+− = + − =
.
Câu 3. Cho phương trình sau:
(
)
2
22
1 21 1
log 2 3 log 1 2 2
2
x
xx x
xx
+

+ ++= + + + +


.
Gọi
S
là tổng tất cả các nghiệm phương trình trên. Giá trị của
S
là:
A.
2S = −
. B.
1 13
2
S
−
=
. C.
2S
=
. D.
1 13
2
S
+
=
.
Lời giải
Chọn D
Điều kiện xác định:
1
2
2
0
x
x
− < <−
>
.
Phương trình đã cho tương đương
(
)
2
22
1 21 1
log 2 3 log 1 2 2
2
x
xx x
xx
+

+ ++= + + + +


( )
( )
2
2
22
11
log 2 2 1 log 2 2 1 *xx
xx


⇔ ++ +− = + + + −




Xét hàm số
(
) ( )
2
2
log 1ft t t= +−
,
0t >
.
Ta có:
( )
( )
1
21
ln 2
ft t
t
′
= +−
2
2ln 2. 2ln 2. 1
0
.ln 2
tt
t
−+
= >
,
0t∀>
. Do đó hàm số
(
)
ft
đồng biến
trên khoảng
(
)
0; +∞
.
Phương trình
( )
*
có dạng
( )
1
22fx f
x

+= +


1
22x
x
⇔ +=+
( )
( )
32 2
2
14
2 4 2 4 10 1 3 1 0x xxx x xx
xx
⇔+= ++⇔ − − −=⇔ + − − =
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 3
⇔
1
3 13
2
3 13
2
x
x
x
= −
−
=
+
=
. Kết hợp với điều kiện ta được
1
3 13
2
x
x
= −
+
=
. Vậy
1 13
2
S
+
=
.
Câu 4. Nghiệm nhỏ nhất của phương trình
2
42
5
1
2log 2 6 1 0
x
xx
x
+
+ − +=
có dạng
ab
c
+
, trong đó
,,,
b
ac b
a
∈∈
tối giản. Tính giá trị của biểu thức:
P abc=++
A.
6P =
. B.
4P =
. C.
8
P
=
. D.
5
P
=
.
Lời giải
Chọn A
Điều kiện:
0x >
Ta có:
2
42
5
1
2log 2 6 1 0
x
xx
x
+
+ − +=
( )
2 42
5
log 1 2 1x xx
⇔ ++ + +
2
5
1
log 5
2
xx= ++
( ) ( )
( ) ( )
( )
2
2
22
55
log 1 1 log 5 5 *x x xx⇔ ++ + = +
Xét hàm số
( )
2
5
logft t t= +
trên khoảng
(
)
0;
+∞
;
( ) ( )
1
2 0, 0;
ln 5
ft t t
t
′
= + > ∀ ∈ +∞
Hàm số
(
)
ft
đồng biến trên khoảng
( )
0;
+∞
.
Ta có:
( )
( )
( )
2 22
51
* 1 5 1 5 5 10
2
fx f x x x x x x
±
⇔ + = ⇔ += ⇔ − += ⇔ =
(thỏa mãn)
Nghiệm nhỏ nhất của phương trình là
51
2
x
−
=
. Vậy
152 6P
=−+ + =
.
Câu 5. Tất cả các nghiệm của phương trình
( )
2021
2021
2021 4041 2021 log 2021 2 1
x
xx=−+ +
thỏa mãn bất phương trình nào sau đây?
A.
2
10x
−>
. B.
2
30xx−<
. C.
2
0xx−≥
. D.
2
2 30xx+ −≤
.
Lời giải
Chọn C
Điều kiện ban đầu:
1
2
x >−
Ta có phương trình tương đương với
(
)
( )
2021
2021 2021
2021 4041 2021 log 2021 2 1 2021 4042 2021 2021.log 21
xx
xx x x=−+ +⇔=−+ +
( )
2021
2021 2021 2021 4042 2021 2021.log 2 1
x
xx x⇔ + −= ++ +
(
)
1
2021
2021 1 2 1 log 2 1
x
xx x
−
⇔ + −= ++ +
( ) ( )
( ) ( ) ( )
11
2021 2021
2021 log 2021 2 1 log 2 1 *
xx
xx
−−
⇔ + = ++ +
Xét hàm số
2021
( ) logft t t= +
trên khoảng
( )
0;
+∞
Ta có
( ) ( )
1
1 0, 0;
ln 2021
ft t
t
′
= + > ∀ ∈ +∞
⇒
Hàm số
( )
ft
đồng biến trên khoảng
( )
0; +∞
.
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
Trang 4 TÀI LIỆU ÔN THI THPT QUỐC GIA
Phương trình
( )
( )
( )
1 11
* 2021 2 1 2021 2 1 2021 2 1 0
x xx
f fx x x
− −−
⇔ = + ⇔ = +⇔ − −=
Xét hàm số
1
( ) 2021 2 1
x
gx x
−
= −−
trên
1
;
2

− +∞


.
Ta có:
(
)
1
2021 .ln 2021 2
x
gx
−
′
= −
;
( )
12
1
2021 .ln 2021 0, ;
2
x
gx x
−

′′
= > ∀ ∈ − +∞


Suy ra hàm số
(
)
gx
′
đồng biến trên
1
;
2

− +∞


⇒
Phương trình
( )
0gx
′
=
có tối đa một nghiệm
trên
1
;
2

− +∞


⇒
Hàm số
( )
gx
có tối đa một điểm cực trị
⇒
Phương trình
() 0gx=
có tối đa hai nghiệm phân biệt.
Ta có:
( )
3
2
1
2
lim 2021 0
x
gx
+
−

→−


= >
;
( )
2020
0
2021
g = −
( ) ( )
1
2
lim . 0 0
x
gxg
+

→−


<
nên phương trình
( )
0gx=
có ít nhất một nghiệm thuộc khoảng
1
;0
2

−


(
)
(
)
(
)
1 . 2 2 .2016 4032 0
gg
=− =−<
nên phương trình
( )
0gx=
có ít nhất một nghiệm thuộc
khoảng
(
)
1; 2
Do phương trình
( )
0gx=
có tối đa hai nghiệm nên phương trình
( )
0gx=
có đúng hai nghiệm
12
;xx
trong đó
1
1
;0
2
x

∈−


và
( )
2
1; 2x ∈
. Đến đây ta thử từng đáp án như sau:
Xét bất phương trình
2
1
10
1
x
x
x
>
−> ⇔
<−
⇒
Nghiệm
1
x
không thỏa mãn bất phương trình.
Xét bất phương trình
2
300 3xx x− <⇔<<
⇒
Nghiệm
1
x
không thỏa mãn bất phương trình.
Xét bất phương trình
2
1
0
0
x
xx
x
≥
−≥⇔
≤
⇒
Các nghiệm
12
;xx
thỏa mãn bất phương trình.
Xét bất phương trình
2
2 30 3 1xx x+ − ≤ ⇔− ≤ ≤
⇒
Nghiệm
2
x
không thỏa mãn bất phương
trình.
Câu 6. Cho phương trình sau:
( )
2 32
2
log 2 1 4 2 0xx xxx−−+−−−=
. Biết rằng phương trình trên có 1
nghiệm dương có dạng
o
x a bc= +
, trong đó
;ab∈
,
c
là số nguyên tố. Tính giá trị biểu thức
23T a bc= ++
A.
8T =
. B.
25
4
T =
. C.
17
2
T =
. D.
31
2
T =
.
Lời giải
Chọn A
Điều kiện ban đầu:
( )
2
2
12
2 1 1 20
12
x
xx x
x
>+
− −= − − > ⇔
<−
Do
o
x
là nghiệm dương nên ta xét phương trình trên khoảng
( )
1 2;+ +∞
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 5
Ta có:
( ) ( ) ( )
( )
2 32 2 2
22
log 21 420 log 21 21 1 1xx xxx xx xx x x
−−+−−−=⇔ −−+ −− +=+
( )
( )
( )
( ) ( ) ( )
22
22
log 2 1 1 2 1 1 log 1 1 *xx x xx x x x⇔ − − ++ − − += +++
Xét hàm số
( )
2
logft t t= +
trên khoảng
( )
0; +∞
,
( ) ( )
1
1 0, 0;
ln 2
ft t
t
′
= + > ∀ ∈ +∞
Hàm số
(
)
ft
đồng biến trên
(
)
0; +∞
Ta có:
( )
( )
( )
( )
( )
( )
( )
22
* 21 1 1 21 1 1fxx x fx xx x x⇔ − − + = +⇔ − − +=+
(
)
( )
2
2
13
2 20
1 220 13
10
1
x
xx
x xx x
x
x
= +
− −=
⇔+ −−=⇔ ⇔ =−
+=
= −
.
Đối chiếu với điều kiện, suy ra
13
x = +
. Vậy
2 3 2.1 3.1 3 8T a bc= + += + +=
.
Câu 7. Có bao nhiêu cặp số nguyên dương
(
)
;
xy
với
2020x ≤
thỏa mãn
(
)
(
)
( )
3
2 3 3 1 9 log 2 1
y
xy x
−= + − −
A.
3
. B.
1010
. C.
4
. D.
2020
.
Lời giải
Chọn A
Đặt
(
)
3
log 2 1 2 3 1
t
x tx−=⇒ =+
, ta được phương trình như sau:
( ) ( )
22
3 3 1 2 3 1 3 3.3 3.3 2
t y ty
y tt y+ − = + −⇔ += +
(*).
Xét hàm số
( ) ( )
3.3 3.3 ln3 1 0,
uu
fu u f u u
′
= + ⇒ = +> ∀∈
( )
fu⇒
đồng biến trên
.
Do đó (*)
2ty
⇔=
, vậy nên
2
2 3 19 21
yy
xx= +⇔ = −
.
Vì
9
2020 9 4039 log 4039
y
xy≤ ⇒ ≤ ⇔≤
. Vì
y
nguyên dương nên
{ }
1; 2; 3y ∈
.
Ta thấy với mỗi giá trị nguyên của
y
thì tìm được 1 giá trị nguyên của
x
. Vậy có 3 cặp
( )
;xy
thỏa mãn.
Câu 8. Có bao nhiêu cặp số
( )
;xy
là các số nguyên không âm thỏa mãn
2 22 2
22
2(1 2 ) log ( 2 ) 2log ( 2 ) 2( ) 4 4xy xy xy xyx xy xy
+ + + + = + + ++ + + +
?
A.
4
. B.
3
. C.
2
. D.
5
.
Lời giải
Chọn B
Từ
2 22 2
22
2(1 2 ) log ( 2 ) 2log ( 2 ) 2( ) 4 4xy xy xy xyx xy xy+ + + + = + + ++ + + +
Biến đổi về:
22
22
)2 2 log ( 2 ) log (2 [ ][ () *()]x y x y xy x xy x++ + = ++ +++
Xét hàm đặc trưng
2
( ) logft t t
= +
đồng biến trên
[0; )+∞
Có
22
(*) (2 2 ) (( ) ) 2 2 ( ) (**)f x y fxy x x y xy x⇔ + = ++⇔ +=++
Có
22
22()0()2222 22()x x y xy xy x y x yx xy= +−+≥⇔+≤ +≤ ++= +
Suy ra
4
()8()0 2xy xy xy+ ≤ + ⇒≤+≤
Với
0 ( 0; 0)xy x y+=⇔ = =
thỏa (**)
Với
1xy+=
. Ta được 2 cặp số
( )
;xy
:
( 0; 1)xy= =
không thỏa (**) và
( 1; 0)xy= =
thỏa (**)
Với
2xy+=
. Ta được 3 cặp số
( )
;
xy
:
( 0; 2)xy= =
thỏa (**);
( 2; 0)xy= =
không thỏa (**);
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
Trang 6 TÀI LIỆU ÔN THI THPT QUỐC GIA
( 1; 1)xy= =
không thỏa (**).
Vậy có tất cả 3 cặp số
( )
;xy
thỏa mãn yêu cầu bài toán.
Câu 9. Cho hàm số
3
3
( ) ln ln
fx x x
= +
. Biết rằng phương trình
( )
(
)
( )
3
3 23 2
33
22
3
log 2 9 7 6 log ln
3
x
f x xf x
x

−+ + + + =



có nghiệm
0
x
được viết dưới dạng
là:
0
3
a
x
bc
=
−
với
,,abc
nguyên dương. Từ đó giá trị của biểu thức
P abc=−+
là
A.
3
. B.
1
. C.
5
. D.
4
.
Lời giải
Chọn B
Điều kiện xác định
20
02
30
x
xx
x
−>
≠ ⇔>
>
.
Đầu tiên hàm số
3
3
( ) ln lnfx x x
= +
với
( )
2;x∀ ∈ +∞
có
( )
0fx
′
>
( )
2;x∀ ∈ +∞
Suy ra hàm số
( )
fx
đồng biến trên
( )
2; +∞
Ta có:
33
3 33
3
3
3
111
( ) ln ln ln ln ln ln ln lnfx x x f x x x x
xxx
  
= + ⇒ = + = +− = −
  
  
Suy ra
( )
( )
( )
( )
( )
3
3
3 3 3 2 3 23
3
ln ln
1 11
ln ln 2ln ln ln
2 1 ln 0
fx x x
f x x fx f x x f x fx
x xx
xx
= +
  
=−⇒ + == ⇒ = −
  
  
> >⇔ >
Từ đó ta có:
( )
(
)
( )
3
3 2 23 3
3
33 3
2 22
31
log 2 9 ln 7 6 log 7 6 log 3
33
x
f x x xf f x
xx

−+ = − + + = + +



33
22
3
33
2 22
3
1 ( 2) 1
log ( 2) 9 7 6 log 3 log 9 6 7
33
3
x
xx x x
xx
x
−
⇒ −+ =+ + ⇔ + − =
( ) ( )
22 2
33 3 3
( 2) 3 6 ( 2) ( 2)
log 7 log 3. log 2 3 2
33 3 3
xx x x
xx x x
−− − −

⇔ + = ⇔ + = +⋅


Xét hàm số
2
( ) log 3ft t t= +
với
0t >
.
Ta có
1
() 3 0
ln 2
ft
t
′
= +>
nên
()ft
đồng biến. Phương trình trên chính là
3
33
( 2) ( 2)
(2) 2 ( 2) 24
33
xx
f f xx
xx
−−

= ⇔ =⇔− =


32 3 3
3
3
2
6 12 8 0 2 ( 2) 2 2
21
xx x xx x x x⇔ − − −=⇔ = + ⇔ =+⇔ =
−
Dễ thấy nghiệm này thỏa mãn điều kiện xác định.
Vậy phương trình đã cho có nghiệm duy nhất là
3
2
21
x = ⇒
−
1P abc=−+=
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 7
Câu 10. Biết phương trình:
2
2
2
2
32
log 4 3
3 58
xx
xx
xx
++
=−+
−+
có nghiệm các nghiệm
12
;
xx
. Hãy tính giá trị
của biểu thức
22
1 2 12
3A x x xx=+−
.
A.
31
. B.
31
−
. C.
1
. D.
1−
.
Lời giải
Chọn C
+ Ta có :
2
3 5 8 0,x x xR− + > ∀∈
nên điều kiện của phương trình là:
2
2
3 20
1
x
xx
x
<−
+ +>⇔
>−
+
2
2
2
2
32
log 4 3
3 58
xx
xx
xx
++
=−+
−+
( ) ( )
( ) ( )
[ ]
2 2 22
22
1
log 3 2 log 3 5 8 3 5 8 3 2
2
xx xx xx xx⇔ ++− −+= −+− ++
.
( )
( ) ( ) ( )
22 2 2
22
11
log 3 2 3 2 log 3 5 8 3 5 8
22
xx xx xx xx⇔ +++ ++= −++ −+
.
+ Xét hàm số
( ) ( )
2
1
log , 0
2
ft t t t=+>
;
( )
11
' 0, 0
ln 2 2
ft t
t
= + > ∀>
.
Nên hàm số
( )
ft
đồng biến trên tập
( )
0; +∞
.
Mà phương trình có dạng :
( )
( )
22
32 3 58
fxx fxx++= −+
.
Vậy phương trình đã cho tương đương với phương trình:
( ) ( )
22
3 58 32xx xx−+= ++
2
2 8 60xx⇔ − +=
1
(/ )
3
x
tm
x
=
⇔
=
.
Vậy
22
1 2 12
31A x x xx=+− =
.
Câu 11. Có bao nhiêu cặp số
( )
;xy
nguyên thỏa mãn các điều kiện
0 2020x
≤≤
và
( )
2
log 2 2 3 8
y
x xy+ +− =
?
A.
2019
. B.
2018
. C.
1
. D.
4
.
Lời giải
Chọn D
Do
0 2020x≤≤
nên
( )
2
log 2 2
x +
luôn có nghĩa.
Ta có
( )
2
log 2 2 3 8
y
x xy+ +− =
( )
3
2
log 1 1 3 2
y
xx y⇔ + + += +
( )
( )
2
log 1
3
2
log 1 2 3 2
x
y
xy
+
⇔ ++ = +
( )
1
Xét hàm số
( )
2
t
ft t= +
.
Tập xác định
DR=
và
( )
1 2 ln 2
t
ft
′
= +
⇒
( )
0ft
′
>
,
tR
∀∈
.
Suy ra hàm số
( )
ft
đồng biến trên
R
.
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
Trang 8 TÀI LIỆU ÔN THI THPT QUỐC GIA
Do đó
( )
( )
2
1 log 1 3
xy⇔ +=
3
12
y
x
⇔ +=
( )
8
log 1yx⇔= +
.
Ta có
0 2020
x
≤≤
nên
1 1 2021x≤ +≤
suy ra
( )
88
0 log 1 log 2021x≤ +≤
.
Lại có
8
log 2021 3,66≈
và
yZ∈
nên
}
{
0;1;2;3
y ∈
.
Vậy có 4 cặp số
( )
;xy
nguyên thỏa yêu cầu bài toán là các cặp
( )
0;0
,
( )
7;1
,
( )
63; 2
,
( )
511;3
.
Câu 12. Biết phương trình
( )
2
3
2
21
log 3 8 5
1
x
xx
x
−
= −+
−
có hai nghiệm là
a
và
a
b
với
;ab
là các số nguyên
tố. Giá trị của
b
là:
A.
1
. B.
4
. C.
2
. D.
3
.
Lời giải
Chọn D
Điều kiện
1
2 10
2
10
1
x
x
x
x
−>
>
⇔

−≠
≠
.
Ta có:
( )
2
3
2
21
log 3 8 5
1
x
xx
x
−
= −+
−
.
( )
2
3
2
21
log 1 3 8 4
1
x
xx
x
−
⇔ −= − +
−
( )
( ) ( )
2
3
2
21
log 3 1 2 1
31
x
xx
x
−
⇔ = −− −
−
.
( )
(
) (
)
( )
(
)
22
33
log 2 1 2 1 log 3 1 3 1
xx x x⇔ −+ −= − + −
(
)
1
.
Xét hàm số:
( ) ( )
3
logft t t= +
với
0
t
>
.
( )
1
10
.ln 3
ft
t
′
= +>
,
0t∀>
.
Suy ra hàm số
( )
ft
đồng biến trên
( )
0; +∞
.
Phương trình
( )
(
) (
)
(
)
2
1 21 3 1
fx f x⇔ −= −
.
( )
2
2
2 13 1 3 8 40x x xx⇔ −= − ⇔ − + =
hay
2
2
3
x
x
=
=
.
Vậy hai nghiệm của phương trình là
2
và
2
3
suy ra
3b =
.
Câu 13. Tìm số nghiệm của phương trình
( )
22
31
3
log 1 log 1 2 2 1 1xx x x xx−++ − + =− −+
A.
2
. B.
1
. C.
3
. D.
4
.
Lời giải
Chọn B
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 9
Điều kiện:
1
2
x <
Ta có:
(
)
22
31
3
log 1 log 1 2 2 1 1
xx x x xx
−++ − + =− −+
( )
22
33
log 1 log 1 2 2 1 1xx x x xx
⇔ −+− − + =− −+
( ) ( )
22
33
log 1 1 log 1 2 1 2 *xx xx x x⇔ −++ −+= − +−
Xét hàm số
3
( ) log , 0f t t tt
= +>
. Dễ thấy
( )
1
1 0, 0
ln 3
ft t
t
′
= + > ∀>
.
Suy ra hàm số đồng biến trên
( )
0; +∞
.
Ta có
(
)
(
)
22
1 12 112fxx f x xx x−+ = − ⇔ −+=−
( )
2
2
2
12 0
112
1 12
x
xx x
xx x
−≥
⇔ −+=− ⇔
−+= −
2
1
0
2
0
x
x
xx
≤
⇔ ⇔=
−=
.
Vậy phương trình có một nghiệm là
0x =
.
Câu 14. Tổng tất cả các nghiệm của phương trình:
( ) ( )
32 3 2 2
2022 2022
log 10 2 3 9 45 27 log 2 5 7
xx x x x x x x−− ++ − − + = +−
là:
A.
3
. B.
6
. C.
36+
. D.
6
.
Lời giải
Chọn C
ĐKXĐ:
32
2
10 2 0
2 5 70
xx x
xx
− − +>
+ −>
.
Ta có:
( ) ( )
32 3 2 2
2022 2022
log 10 2 3 9 45 27 log 2 5 7xx x x x x x x−− ++ − − + = +−
⇔
( ) ( ) ( ) (
)
( )
32 32 2 2
2022 2022
log 10 2 3 10 2 log 2 5 7 3 2 5 7 1xx x xx x x x x x−− ++ −− += +−+ +−
.
Xét hàm số
( )
2022
log 3ft t t= +
trên
(
)
0;
+∞
.
( ) (
)
1
3 0, 0;
ln 2022
ft t
t
′
= + > ∀ ∈ +∞
⇒
Hàm số
( )
ft
đồng biến trên
( )
0;+∞
.
Do đó
( )
1
⇔
(
) ( )
32 2
10 2 2 5 7fx x x f x x−− += +−
⇔
32 2
10 2 2 5 7xx x x x− − += + −
⇔
32
3 15 9 0xx x− − +=
⇔
( )
( )
( )
3
36
36
x lo i
x th
x lo i
= −
= +
= −
¹
áa m·n
¹
.
Vậy phương trình đã cho có nghiệm duy nhất
36x = +
.
Câu 15. Phương trình
( )
( )
1
2
2
8084 8084
2021.log 3 2
2021.log 3 2
x
x
xx
e ee e
−
−
−
+= +
có bao nhiêu nghiệm?
A.
3
. B.
2
. C.
0
. D.
1
.
Lời giải
Chọn D
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
Trang 10 TÀI LIỆU ÔN THI THPT QUỐC GIA
ĐKXĐ:
2
3
x >
.
Ta có:
(
)
(
)
1
2
2
8084 8084
2021.log 3 2
2021.log 3 2
x
x
xx
e ee e
−
−
−
+= +
⇔
( ) ( )
( )
22
8084 8084
2021.log 3 2 2021.log 3 2
1
xx
xx
e e ee
−
−− −
−=−
Xét hàm số
(
)
tt
ft e e
−
= −
trên
R
.
( )
0,
tt
ft e e t R
−
′
= + > ∀∈
⇒
Hàm số
( )
ft
đồng biến trên
R
.
Do đó
(
)
1
⇔
( )
( )
2
8084
2021.log 3 2f xf
x

−=


⇔
( )
2
8084
2021.log 3 2x
x
−=
⇔
(
)
( )
2
4
log 3 2 0 2
x
x
− −=
Xét hàm số
( ) ( )
2
4
log 3 2gx x
x
= −−
trên
2
;
3

+∞


(
)
( )
2
34 2
0, ;
3 2 ln 2 3
gx x
xx

′
= + > ∀ ∈ +∞

−

⇒
Hàm số
( )
gx
đồng biến trên
2
;
3

+∞


.
Mà
( )
20g =
Do đó
( )
1
⇔
( ) ( )
2gx g=
⇔
2x =
.
Vậy phương trình đã cho có một nghiệm
2x =
.
Câu 16. Tìm số nghiệm của phương trình
(
)
( )
4
2
31log31
1
4 2 1 log
2
x
xx
x
x
++
− −=
A.
2
. B.
1
. C.
3
. D.
4
.
Lời giải
Chọn B
Với
0x >
, phương trình tương đương
( ) ( )
4 44 4
4 2 1 log 3 1 log log 3 1 log
x
xx xx
− −= + + + −


( ) ( )
4 4 44
4 log 3 1 log 3 1 log log 3 1
x
x xx x x⇔ + + = ++ + + +


Đặt
( )
4
log31 314
y
x yx+ = ⇔ +=
Phương trình trở thành:
( )
44
4 log 4 log 1
xy
xx yy⇔ ++ = ++
Xét hàm số
( )
4
4 log
t
ft t t
= ++
trên
( )
0;
+∞
.
Hàm số
( )
ft
đồng biến trên
( )
0; +∞
.
Phương trình
( ) ( ) ( )
1 fx fy x y⇔ = ⇔=
Trở lại phép đặt ta được:
4 3 1 4 3 10
xx
xx= +⇔ − −=
Xét hàm số
( )
431
x
gx x=−−
trên
R
.
Chứng minh được phương trình
( )
0gx=
có nhiều nhất hai nghiệm trên
R
.
Có
( ) (
)
0 10gg
= =
nên phương trình
( )
0gx=
có nghiệm
0; 1xx= =
.
Kết hợp điều kiện, phương trình có nghiệm
1x =
.
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 11
Câu 17. Phương trình
( )
2021 2021
2
1 76 5 1 1 22
log 1 log 4 1
2 93 3
xx x
x xx

+ + − = + − ++ +


có bao nhiêu
nghiệm?
A.
2
. B.
1
. C.
3
. D.
0
.
Lời giải
Chọn A
ĐKXĐ:
3
1
5
0
x
x
− < <−
>
.
Ta có:
( )
2021 2021
2
1 76 5 1 1 22
log 1 log 4 1
2 93 3
xx x
x xx

+ + − = + − ++ +


⇔
( )
( )
2
2
2021 2021
51 51
log 1 1 2 log 2 1
33
xx
xx

++ ++ = + + + +


.
Xét hàm số
( ) ( )
2
2021
log 2ft t t= ++
trên
( )
0;+∞
.
( )
(
) (
)
1
2 2 0, 0;
ln 2021
ft t t
t
′
= + + > ∀ ∈ +∞
⇒
Hàm số
( )
ft
đồng biến trên
( )
0;
+∞
.
Do đó
(
)
1
⇔
(
)
51
1
3
fx f
x

+= +


⇔
51
1
3
x
x
+= +
⇔
2
51
0
3
51
1
3
x
x
x
+≥

+= +


⇔
32
51
0
3
9 16 30 9 0
x
xx x
+≥
− − −=
⇔
51
0
3
3
11 13
18
11 13
18
x
x
x
x
+≥
=
−+
=
−−
=
đk
⇔
3
11 13
18
x
x
=
−−
=
.
Vậy phương trình đã cho có hai nghiệm phân biệt.
Câu 18. Số nghiệm dương của phương trình
2
2
33
1 log 1
11
22
2 1 log
22
x
xx
x
x

++


− −=
là
A.
0
. B.
3
. C.
2
. D.
1
.
Lời giải
Chọn D
Điều kiện
2
3
10
2
2
3
3
log 1
0
0
2
0
2
0
0
3
0
0
x
x
x
x
x
x
x
x
x
x
+>
−
>

+
>

>


>⇔ ⇔

<
−<<

≠

≠

.
Với
0x >
phương trình tương đương
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
Trang 12 TÀI LIỆU ÔN THI THPT QUỐC GIA
2 22 2
13 3
2 1 log 1 log log 1 log
22 2
x
x x xx

 
− −= + + + −
 

 

2 2 22
33 3
2 log 1 log 1 log log 1
22 2
x
x xx x x

 
⇔ + + = ++ + + +
 

 

.
Đặt
2
33
log 1 1 2
22
y
x yx

+ = ⇔ +=


.
Phương trình trở thành:
( )
22
2 log 2 log 1
xy
xx yy⇔ ++ = ++
Xét hàm số
( )
2
2 log
t
ft t t= ++
trên
( )
0; +∞
. Hàm số
( )
ft
đồng biến trên khoảng
(
)
0;
+∞
, (vì
là tổng của các hàm đồng biến).
Phương trình
( ) ( ) ( )
1 fx fy x y
⇔ = ⇔=
.
Khi đó
3
12
2
y
x += ⇔
33
12 2 10
22
xx
xx+= ⇔ − −=
.
Xét hàm số
( )
3
21
2
x
gx x=−−
trên
ta có
( )
3
2 ln 2
2
x
gx
′
= −
,
( )
0gx
′
=
có một nghiệm suy ra
( )
0gx=
có không quá
2
nghiệm
Mà
( ) ( )
0 20gg= =
.
Kết hợp điều kiện, phương trình có một nghiệm dương
2.x =
Câu 19. Tìm số nghiệm của phương trình
1
2021
73
log 7 7.3 56 14 0
82
xx
xx
x
x
+

+
+ + − −=

+

A.
0
. B.
2
. C.
1
. D.
3
.
Lời giải
Chọn B
Điều kiện
1
.
4
x >−
Phương trình đã cho tương đương
( )
( )
( )
( )
2021 2021
log 7 3 log 8 2 7 7 3 7 8 2 0
xx xx
xx+− ++ +− +=
( ) ( )
( ) ( )
2021 2021
log 7 3 7 7 3 log 8 2 7 8 2
xx xx
xx⇔ + + + = ++ +
(1).
Xét hàm số
(
)
2021
log 7ft t t= +
trên khoảng
( )
0; +∞
.
Ta có
( )
1
70
.ln 2021
ft
t
′
= +>
,
0t∀>
, do đó hàm số
( )
ft
đồng biến trên khoảng
( )
0; +∞
.
Từ
(
)
1
ta thấy
( )
( )
73 8 2
xx
f fx+= +
738 2
xx
x⇔+=+
7 3 8 20
xx
x⇔ + − −=
Xét
( )
738 2
xx
gx x=+−−
, ta có
( )
7 ln 7 3 ln 3 8
xx
gx
′
= +−
,
( ) ( ) ( )
22
7 ln 7 3 ln 3 0
xx
gx
′′
=+>
và
( )
gx
′
liên tục trên
.
Nên
( )
0gx
′
=
có không quá
1
nghiệm suy ra
( )
0gx=
có không quá
2
nghiệm.
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 13
Mà
( )
( )
0 10gg= =
.
Kết hợp với điều kiện suy ra phương trình có tập nghiệm là
{ }
0;1S =
.
Câu 20. Cho hàm số
(
)
2
( ) ln 1
xx
fx x x e e
−
= ++ + −
. Hỏi phương trình
(
)
2
22
11
log 2 3 log 1 2 2 0
2 21
x
f xx f x
xx


+ ++ + − + − + =



+


có bao nhiêu nghiệm thực?
A.
3
. B.
0
. C.
2
. D.
1
.
Lời giải
Chọn C
Xét hàm số
(
)
2
( ) ln 1
xx
fx x x e e
−
= ++ + −
Ta có:
2
1 0,x xx+ + > ∀∈
nên hàm số
( )
fx
xác định trên
.
Ta có:
( )
(
)
(
)
(
)
2
2
ln 1 ln 1
xx xx
fx x xe e x xe e
−−
− = − +− + − =− ++ + −
(
)
(
)
( )
2
ln 1
xx
x x e e fx
−
=− ++ + − =−
với
x
∀∈
. Suy ra
(
)
fx
là hàm số lẻ.
Mà
2
22
2 22
2x 1 x
1
1
21 1
( ) 0,
1 11
xx xx xx
x
xx
fx ee ee ee x
xx xx x
− −−
++
+
++
′
= ++ = ++ = ++ >∀∈
++ ++ +
Suy ra hàm số
( )
fx
đồng biến trên
.
Xét phương trình :
(
)
2
22
11
log 2 3 log 1 2 2 0
2 21
x
f xx f x
xx


+ ++ + − + − + =



+


.
Điều kiện:
( )
1
2; 0;
2
x

∈ − − ∪ +∞


.
Ta có :
( )
2
22
11
log 2 3 log 1 2 2 0
2 21
x
f xx f x
xx


+ ++ + − + − + =



+


( )
2
22
11
log 2 3 log 1 2 2
2 21
x
f xx f x
xx


⇔ + ++ =− − + − +



+


( )
2
22
1 21 1
log 2 3 log 1 2 2
2
x
f xx f x
xx

+

⇔ + ++ = + + + +





( )
2
22
1 21 1
log 2 3 log 1 2 2
2
x
xx x
xx
+

⇔ + ++= + + + +


.
( )
( )
( )
2
2
22
11
log 2 2 1 log 2 1 1xx
xx

⇔ + + +− = + + +


NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
Trang 14 TÀI LIỆU ÔN THI THPT QUỐC GIA
Với
1
2;
2
x

∈− −


ta thấy
( )
(
)
(
)
2
2
log 2 2 1fx x x
= + + +−
là hàm số đồng biến và
(
)
2
2
11
log 2 1gx
xx

= + ++


là hàm số nghịch biến. Do đó (1) có nhiều nhất một nghiệm
1
2;
2
x

∈− −


. Mà
(
) ( )
11
fg
−= −
nên
1x = −
là nghiệm duy nhất của (1) trong
1
2;
2

−−


Với
( )
0;x ∈ +∞
, xét hàm số
( ) ( )
2
2
log 1ht t t
= ++
có
( )
( )
1
2 0, 0
1 ln 2
ht t t
t
′
= + > ∀>
+
nên
( )
ht
là một hàm số đồng biến trên
( )
0; +∞
.
( )
( )
2
1 1 3 13
1 21 1 211 3 10
2
hx h x x x x
xx
+

⇔ + − = + ⇔ + −=+ ⇔ − −= ⇔ =


.
Vậy phương trình có 2 nghiệm.
Câu 21. Tính tổng
S
của tất cả các nghiệm của phương trình.
1
53
ln 5 5.3 30 10 0
62
xx
xx
x
x
+

+
+ + − −=

+

.
A.
1S =
. B.
2S =
. C.
1S = −
. D.
3
S =
.
Lời giải
Chọn A
Điều kiện:
( )
1
6 20 *
3
xx+ > ⇔ >−
.
Khi đó ta có:
( ) ( )
( ) ( ) ( )
1
53
ln 5 5.3 30 10 0 ln 5 3 5 5 3 ln 6 2 5 6 2 1
62
xx
x x xx xx
x xx
x
+

+
+ + − −=⇔ + + + = ++ +

+

Xét hàm số
( )
ln 5 , 0
y f t t tt= =+>
.
1
50 0yt
t
′
= + > ∀>
nên hàm số luôn đồng biến khi
0t >
,
do đó
( )
(
)
( ) ( )
1 53 6 2 53 6 2 2
xx xx
f fx x⇔ + = +⇔+=+
.
Với
[ ]
0;1x ∈
. Áp dụng bất đẳng thức Becnoulli ta có:
5 3 5 3 26 2
xx
xx xx x+ ≤ −+ −+= +
. Dấu
""=
xảy ra khi
1, 0xx= =
.
Với
0x ≤
hoặc
1
x ≥
. Áp dụng bất đẳng thức Becnoulli ta có:
5 3 5 3 26 2
xx
xx xx x+ ≥ −+ −+= +
. Dấu
""=
xảy ra khi
1, 0
xx= =
.
Vậy phương trình
( )
2
có nghiệm
1, 0xx= =
, suy ra
1S =
.
Cách giải khác: (Giải Phương trình (2)). Xét hàm số
( )
536 2
xx
fx x=+−−
có
( ) ( )
1 00ff= =
suy ra phương trình
( )
0fx=
có hai nghiệm
1, 0xx= =
.
Ta có
( ) ( ) ( ) ( )
22
5 ln 5 3 ln 3 6, 5 ln 5 3 ln 3 0,
xx x x
fx f x x
′ ′′
= + − = + >∀
nên
( )
0fx
′
=
có nhiều
nhất một nghiệm, suy ra
( )
0fx
′′
=
có nhiều nhất hai nghiệm. Vậy phương trình
( )
0fx=
có
hai nghiệm
1, 0xx= =
, suy ra
1S =
.
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 15
Câu 22. Cho phương trình
3 25
2 13 3
log log
21
xx
x
x

++ −

=



+


. Biết rằng phương trình trên có nghiệm
duy nhất có dạng là
x a bc
= +
(với
;;
abc∈
,
c
tối giản). Tính giá trị của
23
S ab c=++
.
A.
26
. B.
36
. C.
16
. D.
46
.
Lời giải
Chọn C
Điều kiện:
3x
>
.
Ta có:
3 25
2 13 3
log log
21
xx
x
x

++ −

=



+


35
2 13 3
log 2log
21
xx
x
x

++ −

⇔=



+


2
35
2 13 3
log log
21
xx
x
x

++ −

⇔=



+


( )
( ) ( )
2
3 5 35
log 2 1 3 log 2 1 log log 3x x xx⇔ ++ + + = + −
( )
1
Đặt
(
) ( )
2
213, 3 21 3yx y x y= ++ > ⇒ += −
.
Khi đó
( )
1
có dạng
( )
( )
22
35 35
log log 3 log log 3
yy xx+ −= + −
( )
2
Xét hàm số
( ) ( )
2
35
log log 3ft t t=+−
với
3t >
.
Ta có:
(
)
( )
12
0; 3
.ln 3 3 ln5
ft t
tt
′
= + > ∀>
−
.
Suy ra
( )
ft
là hàm số đồng biến trên
(
)
3; +∞
.
Khi đó:
( )
2
có dạng
(
) (
)
2 13
fy fx y x x x
= ⇔ = ⇔ ++=
( )
2
21 3xx⇔ += −
2
8 80xx⇔ − +=
4 22
4 22
x
x
= +
⇔
= −
Do
3x >
nên
4 22x
= +
. Khi đó:
4; 2; 2abc= = =
.
Vậy:
23 23
4 2 2 16S ab c=++=++=
.
Câu 23. Cho phương trình sau:
(
) (
)(
)
4
2
24 2 4 2 4
3
log 2 2 4 27 2 2 2
y
xy x y x y
+
++ + = + − +
. Khi
y
là số
nguyên thì phương trình trên có bao nhiêu nghiệm
x
là số nguyên?
A.
2
. B.
4
. C.
8
. D.
0
.
Lời giải
Chọn A
ĐK:
( )( )
24 2 4 2 4
2 24 0 2 1 2 0 ,xy x y x y xy++ + >⇔ + + >⇔∀
.
Ta có:
( ) ( )( )
4
2
24 2 4 2 4
3
log 2 2 4 27 2 2 2
y
xy x y x y
+
++ + = + − +
( ) ( )( ) ( )( ) ( )
4 24 24 4
3
2 log 2 1 2 27 2 1 2 3 2y xy xy y

⇔+ ++=−++++

NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
Trang 16 TÀI LIỆU ÔN THI THPT QUỐC GIA
( ) ( )
( )
24 2
33
4
27
log 2 1 log 2 2 1 3
2
xy x
y
⇔ ++ + = − ++
+
( ) (
)
(
)
22 4
33
4
27
log 2 1 2 1 log 2 3
2
xx y
y
⇔ ++ += − + +
+
( ) (
)
22
33
44
27 27
log 2 1 2 1 log
22
xx
yy
⇔ ++ += +
++
Xét hàm số
( ) ( )
3
1
log , 0 1 0, 0
ln 3
gt t tt g t t
t
′
= + > ⇒ = + > ∀>
.
Suy ra:
( )
y gt=
luôn đồng biến
0t∀>
.
Khi đó :
( )
(
)
22
44
27 27
* 21 21
22
gx g x
yy

⇔ + = ⇔ +=

++

.
Do
y
nguyên nên
x
nguyên khi và chỉ khi
4
2y +
là ước của 27, mà
4
22y +≥
nên
{ }
4
2 3; 9; 27 1yy+∈ ⇔ =±
. Suy ra
2x = ±
.
Câu 24. Tính tổng
S
của tất cả các nghiệm của phương trình
2
22
1 21 1
log ( 2) 3 log (l ) 2 2 0
2
x
xx x
xx
+
+ ++− −+ − + =
A.
1 13
2
S
+
=
. B.
3 13
2
S
+
=
. C.
3 13
2
S
−
=
. D.
1 13
2
S
−
=
.
Lời giải
Chọn A
Điều kiện:
( )
( )
( )
2;
1
( 2; ) 0;
1
2
( ; ) 0;
2
x
x
x
∈ − +∞
⇔ ∈ − − ∪ +∞
∈ −∞ − ∪ +∞
Khi đó phương trình được viết lại:
2
22
1 11
log 2 2( 2) 2 log (2 ) 2(2 ) (2 ) (1)x xx
x xx
+− +++= +− +++
Xét hàm số:
2
2
( ) log 2 , 0ft t t t t= − + ∀>
ta có :
'
1 12
() 2 22 .2 22 20, 0
ln 2 .ln 2 ln 2
ft t t t
tt
= + −≥ −= −> ∀>
nên
()ft
đồng biến trên khoảng
( )
0; +∞
.
(1)
11
( 2) (2 ) 2 2 (2)fx f x
xx
⇔ + = + ⇔ +=+
Bình phương hai vế phương trình (2) ta có:
32
2
1
41
24 2 4 10
3 13
2
x
x xxx
xx
x
= −
+ = + + ⇔ − − −= ⇔
±
=
thay vào phương trình ban đầu chỉ có
hai giá trị
3 13
1,
2
xx
+
=−=
thỏa mãn.
Vậy phương trình có hai nghiệm là
3 13
1,
2
xx
+
=−=
nên
1 13
2
S
+
=
.
Câu 25. Gọi
( )
12 1 2
, xx x x<
là các nghiệm của phương trình:
2
3
2
21
log 3 8 5.
( 1)
x
xx
x
−
= −+
−
Giá trị của
biểu thức
12
23Pxx= +
bằng:
A.
4P =
. B.
6P =
. C.
2P =
. D
6P = −
.
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 17
Lời giải
Chọn B
ĐK:
2
1
21
0
2
( 1)
1
x
x
x
x
>
−
>⇔
−
≠
Phương trình đã cho tương đương
22
33
log (2 1) log ( 1) 3( 1) (2 1) 1x xxx−− − = − − −+
22
33
log (2 1) (2 1) 3( 1) log 3( 1) (1)
xxx x⇔ −+ −= − + −
Xét
( )
3
logft t t= +
,với
0t >
có
( )
1
' 1 0, 0
ln3
ft t
t
= +> ∀>
suy ra
()ft
đồng biến trên
(0; )
+∞
. Từ đó ta có:
( ) ( )
2
(1) 2 1 3 1fx f x



⇔ −= −
(
)
2
2 13 1
xx
⇔ −= −
2
3 8 40xx⇔ − +=
2
2
3
x
x
=
⇔
=
Vậy tập nghiệm của phương trình là
2
2,
3
S

=


nên
6P =
.
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 1
GIẢI PT LÔGARIT BẰNG PHƯƠNG PHÁP ĐẶT ẨN PHỤ KHÔNG HOÀN TOÀN
(KHÔNG CHỨA THAM SỐ)
PHƯƠNG PHÁP
Phương pháp này thường được sử dụng đối với những phương trình khi lựa chọn ẩn phụ cho một biểu
thức thì các biểu thức còn lại không biểu diễn được triệt để qua ẩn phụ đó hoặc nếu biểu diễn được thì
công thức biểu diễn lại phức tạp.
Câu 1. Số nghiệm của phương trình
( )
2
22
lg lg .log 4 2log 0xx x x+ +=
là
A.
0
. B.
1
. C.
2
. D.
3
.
Lời giải
Chọn C
Điều kiện
0x >
( )
( )
22
22 2 2
lg lg .log 4 2 log 0 lg 2 log lg 2log 0x x x x x xx x+ +=⇔++ +=
(1)
Đặt
lgtx=
Khi đó phương trình (1) trở thành:
( )
2
22
2 log 2log 0
t xt x++ + =
(2)
Ta có:
( ) ( )
22
2 22
2 log 4.2log log 2
x xx∆= + − = −
.
Khi đó phương trình (2) có hai nghiệm phân biệt là:
22
2
22
2 log log 2
log
2
2 log log 2
2
2
xx
tx
xx
t
++−
= =
+−+
= =
.
Với
2 22
log lg log lg log 0
t xx xx x
= ⇔= ⇔− =
.
Đặt
( )
2
lg logfx x x= −
với
0x >
.
( )
1 1 11 1
0, 0
ln10 ln 2 ln10 ln 2
fx x
x xx

′
= − = − < ∀>


.
Suy ra hàm số
( )
2
lg logfx x x= −
luôn nghịch biến trên khoảng
( )
0; +∞
.
Mặt khác:
( )
10
f =
. Do đó phương trình
2
lg log 0xx−=
có nghiệm duy nhất là
1x =
( thoả điều kiện).
Với
2 lg 2 100t xx=⇔ =⇔=
(thoả điều kiện).
Vậy số nghiệm của phương trình là 2.
Cách 2 Điều kiện
0x >
( )
( )
2
22
2
22
2
2
lg lg .log 4 2log 0
lg 2 log lg 2log 0
lg lg
lg 2 lg 2 0
lg 2 lg 2
11
1 lg 2 lg 0
lg 2 lg 2
xx x x
x xx x
xx
xx
xx
+ +=
⇔ ++ + =

⇔ ++ + =



+ ++ =


(1)
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
Trang 2 TÀI LIỆU ÔN THI THPT QUỐC GIA
Đặt
lgtx=
. Phương trình trở thành
2
11
1 20
lg 2 lg 2
tt

+ ++ =


. Dễ thấy phương trình có hai
nghiệm
t
phân biệt nên phương trình đã cho coa 2 nghiệm phân biệt.
Câu 2. Số nghiệm thực của phương trình
2
22
log ( 1) log 2 6 0xx x x
+ − + −=
A.
0
. B.
1
. C.
2
. D.
3
.
Lời giải
Chọn C
Điều kiện:
0x >
Đặt
2
logtx=
. Khi đó phương trình trở thành:
2
( -1) 2 6 0t xt x+ + −=
.
Ta có
(
)
2
2
5
3
t
x
tx
= −
∆= − ⇒
= −
Với
3
tx= −
ta có
22
log 3 log 3 0x x xx=−⇔ +−=
(*)
Đặt
2
( ) log 3fx x x= +−
với
0x
>
, có
1
'( ) 1 0; 0
ln 2
fx x
x
= +> ∀>
Do đó hàm số f(x) đồng biến trên
(0; )+∞
mà
(2) 0 2fx=⇒=
là nghiệm duy nhất của hương
trình. Vậy phương trình đã cho có hai nghiệm thực.
Câu 3. Tổng các nghiệm thực của phương trình
( ) ( )
(
)
2
33
1 log 1 ( 2)log 1 3 0x xx x+ ++ − +−=
A.
1
. B.
2
. C.
2
3
−
. D.
4
3
.
Lời giải
Chọn D
Điều kiện :
1
x >−
Đặt :
( )
3
log 1tx= +
. Khi đó phương trình trở thành:
( )
2
1 ( 2) 3 0xtxt+ + − −=
.
Ta có:
( )
2
1
4
3
1
t
x
t
x
= −
∆= − ⇒
=
+
Với
1t = −
ta có
( )
3
12
log 1 1 1
33
x xx+ =−⇔ += ⇔ =−
(thỏa mãn điều kiện
1x >−
)
Với
3
1
t
x
=
+
ta có
( )
3
3
log 1
1
x
x
+=
+
(*)
Đặt
( ) (
)
3
log 1fx x= +
và
3
()
1
gx
x
=
+
với mọi
1x >−
, có
( )
1
'( ) 0;
1 ln 3
fx
x
= >
+
( )
2
3
() 0
1
gx
x
′
=−<
+
Do đó hàm số
(
)
fx
đồng biến trên
( 1; )− +∞
và hàm số
( )
gx
nghịch biến trên
( 1; )− +∞
2x⇒=
là nghiệm duy nhất của phương trình (*).
Vậy phương trình đã cho có hai nghiệm thực
12
2
;2
3
xx=−=
và
12
4
3
xx+=
.
Câu 4. Cho phương trình
( )
11
9 3 2 3 13
xx x x
mm
++
++= + +
. Hỏi có bao nhiêu giá trị của tham số thực
[ ]
20;20m ∈−
để phương trình trên có hai nghiệm phân biệt biết rằng
4m ∈
?
A.
79
. B.
82
. C.
81
. D.
80
.
Lời giải
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 3
Chọn D
Ta đặt
30
x
t= >
suy ra
( )
2
32 31
t t m t tm++ = + +
. Ta đặt
tm y+=
.
Khi đó:
( )
( )
22
2 31 0
y t ytt− + + +=
.
Ta có
( )
( )
2
31 1
4
1
31 1
12
4
tt
y
t tm
t
tt
t tm
y
++−
=
= +
∆= − ⇒ ⇔
+− −
+= +
=
.
Do đó:
( ) ( )
( ) ( )
2
2
444 0
4 21 0
m t t ft t
m t t gt t
= −= >
= − += >
và có đồ thị như hình bên.
Từ đây ta suy ra để có 2 nghiệm phân biệt thì điều kiện cần và đủ là
41
1 4 80
14 0
m
m
m
≥
⇒≤ ≤
−< <
Câu 5. Cho phương trình
(
)
22
2 2 22 2 1 2
2
log 48 log .log 256 .log 8 28 log2log 56log
x x x x x x xx x

−− − + +


=
.
Biết tổng các nghiệm của phương trình trên là một biểu thức có dạng:
4
62 2
ab cd
S
−−
+
= +
với
*
,,,abcd∈
. Khi đó biểu thức
T abcd=+++
có giá trị bằng
A.
40
. B.
40
. C.
50
. D.
30
.
Lời giải
Chọn A
Điều kiện:
12
2
22
22
0
0
1
16
48 log .log 256 0
2
48 8log log 0
x
x
x
xx
xx
>
>
⇔ ⇔ ≤≤

−≥
− −≥
.
Ta có
( )
22
2 2 22 2 1 2
2
log 48 log .log 256 .log 8 28 log2log 56logx x x x x x xx x

−− − + +


=
( )
( )
22
2 2 2 2 22 2
28 log 56 log 48 log .log 256 .log 8 0
2log log
x xx x x x x x x
+ − − −− − =
⇔
( )( ) ( )
2 2 2 22 2
2log log 28 2log 48 log .log 256 .log 8 0xx x x x x x x
⇔ − − −− − =
( )
(
)
2
2 2 2 22
2log log 28 48 8log log .log 8 0xx x x x x⇔ − −+ − − =
( )
( )
2
2
2 2 22
2log 0 1
log 28 48 8log log .log 8 0 2
xx
x xxx
−=
⇔
−+ − − =
.
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
Trang 4 TÀI LIỆU ÔN THI THPT QUỐC GIA
Xét hàm
(
)
2
12
1
2log , ; 16
2
f x x xx

= −∈


.
Ta có
( ) ( )
22
1, 0
ln 2 ln 2
fx fx x
x
′′
= − =⇔=
.
Bảng biến thiên của hàm số
( )
2
2log
fx x x= −
trên đoạn
12
1
; 16
2



như sau:
Từ bảng biến thiên ta thấy phương trình
( )
0fx=
có tối đa hai nghiệm. Mà
(
) (
)
2 40ff= =
nên phương trình
(
)
0
fx
=
có đúng 2 nghiệm
2, 4xx= =
.
Đặt
[
]
2
log , 12;4
t xt= ∈−
. Phương trình
( )
2
trở thành
(
)
2
28 3 48 8 0t t tt− ++ −− =
( )
( )
2 22
11
48 8 3 48 8 3 4 0
22
tt t tt t t⇔ −− −+ −−+ ++=
(
)
( )
2 22
11
48 8 3 48 8 3 4 0
22
tt t tt t t
⇔ −− −+ −−+ ++=
.
Đặt
2
48 8 , 0u tt u= −− ≥
.
Ta được phương trình ..
(
)
22
2 3 6 80u t ut t⇔ − + + + +=
(Chú ý
( )
( )
2
2
3 681t tt
′
∆= + − + + =
)
4
2
ut
ut
= +
⇔
= +
.
Với
4ut= +
ta được
2
48 8 4tt t
−−=+
( )
2
2
40
48 8 4
t
tt t
+≥
⇔
−−=+
2
40
8 16 0
t
tt
+≥
⇔
+− =
4 42t⇔=−+
. Khi đó
424
2x
−
=
.
Với
2ut= +
ta được
2
48 8 2tt t−−=+
( )
2
2
20
48 8 2
t
tt t
+≥
⇔
−−=+
2
40
6 22 0
t
tt
+≥
⇔
+− =
3 31t⇔ =−+
. Khi đó
31 3
2x
−
=
.
Vậy tổng các nghiệm của phương trình đã cho là
31 3 4 2 4
62 2S
−−
+
= +
. Suy ra
31, 3, 2, 4 40a bcd T= = = =⇒=
.
_______________ TOANMATH.com _______________
| 1/24
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT VD_VDC
GIẢI PHƯƠNG TRÌNH LÔGARIT BẰNG PHƯƠNG PHÁP HÀM SỐ - ĐÁNH GIÁ
(KHÔNG CHỨA THAM SỐ) PHƯƠNG PHÁP
Vận dụng các kết quả sau :
Kết quả 1 : Nếu f (x) là hàm số đơn điệu trên K (với K là khoảng, đoạn hoặc nửa khoảng) thì
f (x) = 0 có tối đa một nghiệm trên K .
Kết quả 2 : Nếu f (x) là hàm số liên tục trên đoạn [ ;
a b] và f (a) f (b) < 0 thì phương trình
f (x) = 0 có nghiệm thuộc khoảng ( ; a b).
Kết quả 3 : Nếu f (x) là hàm đơn điệu trên K, a
∀ ,b∈ K; f (a) = f (b) ⇔ a = . b
Kết quả 4 : Nếu hàm f (x) tăng trong khoảng (a;b) và hàm g (x) là hàm một hàm giảm trong
khoảng (a;b) thì phương trình f (x) = g (x) có nhiều nhất một nghiệm trong khoảng (a;b) .
Các bước giải phương trình :
Bước 1 : Tìm điều kiện xác định của phương trình.
Bước 2 : Biến đổi phương trình sao cho một vế là hàm số đơn điệu, một vế là hằng số
hoặc một vế là hàm đồng biến và vế còn lại là hàm số nghịch biến.
Bước 3 : Nhẩm nghiệm của phương trình trên mỗi khoảng xác định (nếu có).
Bước 4 : Kết luận nghiệm của phương trình.
Câu 1. Tìm số nghiệm của phương trình ( 2
x − 2022x)ln x − x + 2021= 0. A. 1. B. 2 . C. 3. D. 4 . Lời giải Chọn B
Tập xác định D = (0;+ ∞) . Phương trình ( 2
x − 2022x)ln x − x + 2021= 0 ⇔ ( 2
x − 2022x)ln x = x − 2021 2 x − 2022x 1 ⇔ = 1 x ⇔ + − x = 0 x − 2021 ln x ln x x − 2021
(NX: x =1 và x = 2021 không là nghiệm của phương trình). Xét hàm số ( ) 1 x f x = +
− x trên (0;+ ∞) \{1; } 2021 . ln x x − 2021 Có f ′(x) 1 2021 = − − −1< 0, x ∀ ∈ 0;+ ∞ \ 1;2021 . 2 ( ) { }
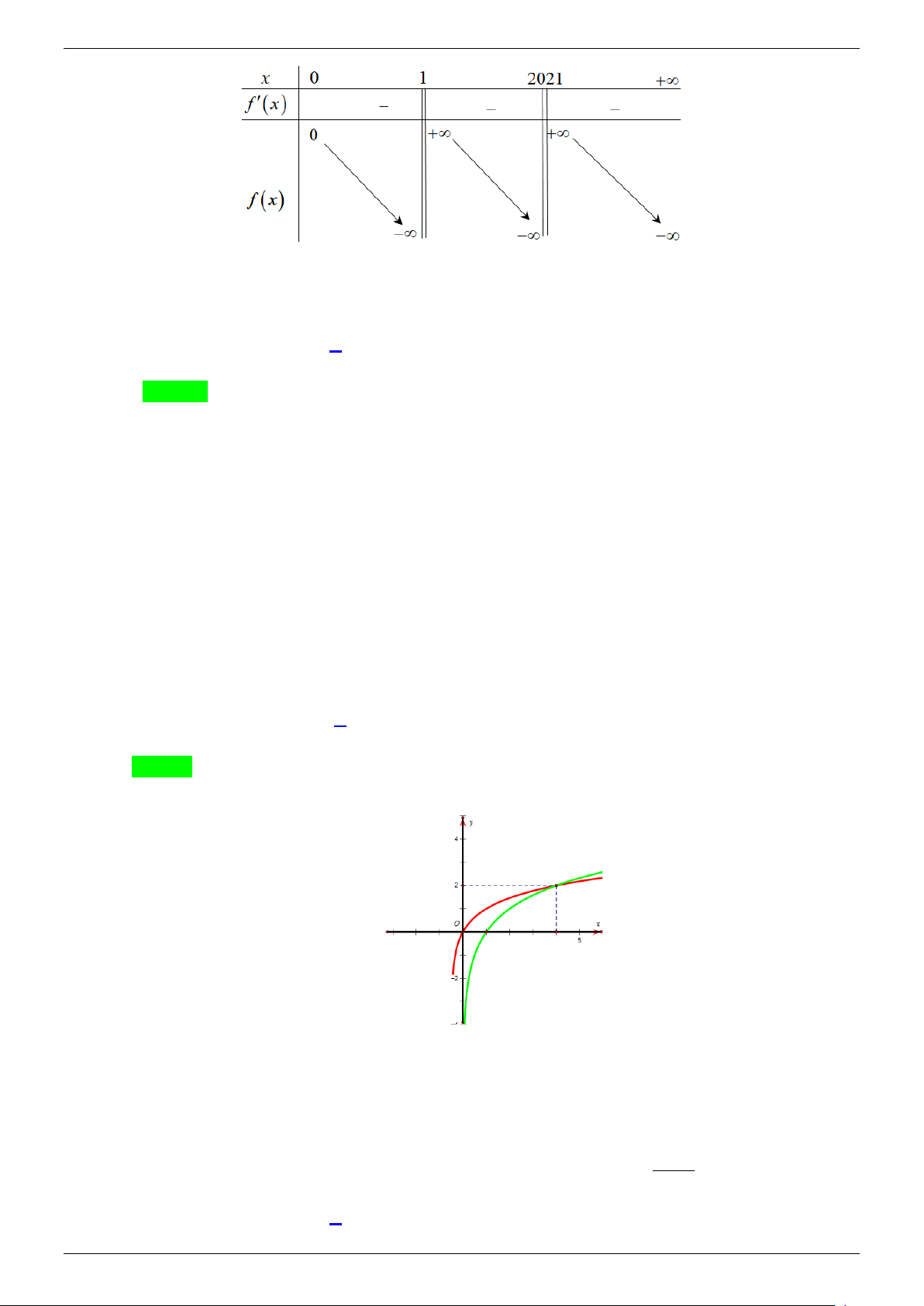
x ln x (x − ) 2021 Bảng biến thiên:
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 1
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT VD_VDC
Từ bảng biến thiên suy ra phương trình đã cho có 2 nghiệm.
Câu 2 . Có bao nhiêu cặp số ( ;
x y) thuộc đoạn [1;2020] thỏa mãn y là số nguyên và ln ln x y
x + e = y + e ? A. 6 . B. 7 . C. 2021. D. 2020 . Lời giải Chọn B Ta có: ln ln x y
x + e = y + e Xét hàm số ( ) t
f t = t + e có ′( ) =1 t f t + e > 0, t ∀
Suy ra hàm số f (t) đồng biến trên . 
Do đó ta có: f (ln x) = f ( y) ⇔ ln x = y
Ta có: 1≤ x ≤ 2020 ⇔ 0 ≤ ln x ≤ ln 2020 ⇔ 0 ≤ y ≤ ln 2020 ⇔ 0 ≤ y ≤ 7,61...
Do y là số nguyên thuộc đoạn [1;2020] nên y ∈{1;2;3;4;5;6; } 7 .
Kết luận: có 7 cặp số ( ;
x y)thỏa yêu cầu bài toán.
Câu 3: Có bao nhiêu cặp số tự nhiên ( ;
x y) thỏa mãn đồng thời hai điều kiện:
log x + 2y ≤ log 2x + 4y +1 và log x + y ≥ y − 2 ? 3 ( ) 2 ( ) 3 ( ) A. 7 . B. 6 . C. 10. D. 8 . Lời giải Chọn B
 Đặt t = x + 2y,t > 0 , khi đó log x + 2y ≤ log 2x + 4y +1 trở thành log t ≤ log 2t +1 . 2 3 ( ) 2 ( ) 3 ( )
 Dựa vào đồ thị ta thấy log t ≤ log 2t +1 ⇔ 0 < t ≤ 4 ⇔ 0 < 2x + y ≤ 4 . 2 3 ( )
 Kết hợp với điều kiện log x + y ≥ y − 2 ta có các cặp số tự nhiên 3 ( ) ( ; x y) = (
{ 0; )1,(0;2),(0;3),(1;0),(1; )1,(1;2)}. x  −  Câu 4: 2 1
Có bao nhiêu cặp số nguyên ( ;
x y) thỏa mãn 0 ≤ y ≤ 2020 và log   = +1− 2x y ? 3  y A. 2019 . B. 11. C. 2020 . D. 4 . Trang 2
TÀI LIỆU ÔN THU THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT VD_VDC Lời giải Chọn B y ≠ 0  x  − Từ giả thiết ta có: 2 1 
> 0 ⇔ 2x >1 ⇔ x > 0 . y  y ≥  0
Ta có phương trình ⇔ log 2x −1 + 2x −1 = log y + y * 3 ( ) 3 ( )
Xét hàm số f (t) = log t + t trên (0;+∞). 3
Khi đó f ′(t) 1 =
+1 > 0 do đó hàm số f (t) = log t + t đồng biến trên khoảng (0;+∞) t ln 3 3
(*) có dạng (2x − ) 1 = ( ) ⇔ = 2x f f y y −1.
Vì 0 ≤ ≤ 2020 ⇔ 0 ≤ 2x −1≤ 2020 ⇔ 1≤ 2x y
≤ 2021 ⇔ 0 ≤ x ≤ log 2021 2 ( )
0 ≤ x ≤ log 2021 2 ( ) 
⇔ x ∈{0;1;2;3;4;5;6;7;8;9;1 } 0 . x∈ Vậy có 11 cặp ( ; x y) thỏa mãn.
Câu 5: Phương trình 3 log ( − ) 3 1 − 27 = 8y x y
+1− x có bao nhiêu nghiệm nguyên ( ; x y) với 2 1992 2020 x∈ 8  ;8    ? A. 26 B. 28 C. 24 D. 30 Lời giải Chọn B Ta có 3 log ( − ) 3 y 3
1 − 27 = 8 +1− ⇔ log ( − ) 3 3 1 + −1 = 27 + 2 y x y x x x y 2 2 Đặt = log −1 ⇔ −1 = 2t t x x
. Thay vào phương trình ta được 3 t + = ( )3 3 2 3 + 2 y t y ( ) 1 . 2 ( ) Xét hàm số = ( ) 3 = + 2u y f u u . Ta có ′( ) 2 = 3 + 2u f u u ln 2 > 0, u
∀ ∈  . Do đó hàm số đồng biến trên  . Khi đó ( )
1 ⇔ ( ) = (3 ) ⇔ = 3 ⇔ log −1 = 3 ⇔ = 8y f t f y t y x y x +1. 2 ( ) Do 1992 2020 x ∈ 8  ;8  y   nên 1992 2020 8 ≤ 8 +1≤ 8
⇔ 1992 ≤ y ≤ 2019 với y ∈ .
Vậy có 28 giá trị nguyên của y nên phương trình có 28 nghiệm.
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 3
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
GIẢI PHƯƠNG TRÌNH LÔGARIT BẰNG PHƯƠNG PHÁP SỬ DỤNG HÀM ĐẶC TRƯNG
(KHÔNG CHỨA THAM SỐ) PHƯƠNG PHÁP
Bước 1 : Đưa phương trình về dạng f (u(x)) = f (v(x)).
Bước 2 : Xét hàm số y = f (t) trên D .
Tính y′ = f ′(t) .
Chứng minh hàm số y′ = f ′(t) luôn đồng biến hoặc luôn nghịch biến trên D .
Suy ra f (u(x)) = f (v(x)) ⇔ u(x) = v(x) . 2  + 
Câu 1. Biết rằng phương trình x 2 2 log 
 = −x + 4x + 9 có hai nghiệm x = a + b c và x = a − b c 2  2x + 5 
với a,b,c là các số nguyên dương. Tính tích . a . b c . A.8 . B. 8 − . C. 12 − . D. 12. Lời giải Chọn D 2 + −
Điều kiện xác định: x 2 5 > 0 ⇔ x > 2x + 5 2 2  x + 2  2 log 
 = −x + 4x + 9 ⇔ log x + 2 − log 2x + 5 = −x + 4x + 9 2 ( 2 ) 2 ( ) 2 2  2x + 5  ⇔ log ( 2 x + 2) 2
+ x + 2 = log 2x + 5 + log 2 + 4x +10 2 2 ( ) 2 ⇔ log ( 2 x + 2) 2
+ x + 2 = log 4x +10 + 4x +10 2 2 ( )
Xét hàm số: f (t) = log t + t trên (0;+∞) 2 f ′(t) 1 = +1 > 0, t
∀ > 0 ⇒ f (t) đồng biến trên (0;+∞) t ln 2 2  = + > Đặt: u x 2 0 
. Khi đó ta được log u + u = log v + v ⇔ f (u) = f (v) 2 2
v = 4x +10 > 0
Do đó f (u) = f (v) 2
⇔ u = v ⇔ x + 2 = 4x +10 x = 2 + 2 3 2
⇔ x − 4x −8 = 0 ⇔ 
(thỏa mãn điều kiện). x = 2 − 2 3
Vì a,b,c là các số nguyên dương nên a = 2,b = 2,c = 3. Vậy . a . b c =12 . 2 Câu 2. + + Phương trình x 3x 2 2 log
= x − 4x + 3 có các nghiệm x ; x . Hãy tính giá trị của biểu thức 2 2 3x − 5x + 8 1 2 2 2
A = x + x − 3x x . 1 2 1 2 A. 31. B. 1 − . C. 1. D. 31 − . Lời giải Chọn C
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 1
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC 2 + + x > 1 − 2
Điều kiện: x 3x 2 > 0 2
⇔ x + 3x + 2 > 0 ⇔ (do 2  5  71
3x − 5x + 8 = 3 x − + >   0 ) 2 3x − 5x + 8  x < 2 −  6  12 2 + +
Phương trình đã cho tương đương với: x 3x 2 2 log = x − 4x + 3 2 2 3x − 5x + 8 ⇔ ( 2 x + x + ) − ( 2 x − x + ) 1 log 3 2 log 3 5 8 = [( 2
3x − 5x + 8) − ( 2 x + 3x + 2)] 2 2 2 ⇔ ( 2 x + x + ) 1 + ( 2 x + x + ) = ( 2 x − x + ) 1 log 3 2 3 2 log 3 5 8 + ( 2
3x − 5x + 8) * 2 2 ( ) 2 2 Xét hàm số 1
f (t) = log t + t,(t > 0) ; 1 1 f '(t) = + > 0 t ∀ > 0 . 2 2 t ln 2 2
Nên hàm số f (t) đồng biến trên (0;+∞).
Mà phương trình (*) có dạng: f ( 2
x + x + ) = f ( 2 3 2
3x − 5x + 8) .
Nên phương trình đã cho tương đương với phương trình: ( x =1 2
x − x + ) = ( 2 3 5 8 x + 3x + 2) 2
⇔ 2x −8x + 6 = 0 ⇔ 
(thỏa mãn điều kiện ban đầu) x = 3 Vậy 2 2
A = x + x − 3x x = x + x − 5x .x =1. 1 2 1 2 ( 1 2)2 1 2
Câu 3. Cho phương trình sau: 2 1 2x +1  1 log x 2 x 3 log 1  + + + = + + + 2 x +   2 . 2 ( ) 2 2 xx
Gọi S là tổng tất cả các nghiệm phương trình trên. Giá trị của S là: A. 1 13 1 13 S = 2 − . B. S − = . C. S = 2 . D. S + = . 2 2 Lời giải Chọn D  1 2 − < x < −
Điều kiện xác định:  2 .  x > 0 2
Phương trình đã cho tương đương 1 2x +1  1 log x 2 x 3 log 1  + + + = + + + 2 x +   2 2 ( ) 2 2 xx  2 ⇔
x + + ( x + − )2  1   1   log 2 2 1 = log 2 + +  2 + −     1 * 2 2 ( )  x   x  
Xét hàm số f (t) = log t + (t − )2 1 , t > 0. 2 2 − +
Ta có: f ′ (t) 1 = + 2(t − ) 1 2ln 2.t 2ln 2.t 1 = > 0 , t
∀ > 0 . Do đó hàm số f (t) đồng biến t ln 2 t.ln 2 trên khoảng (0;+∞).
Phương trình (*) có dạng f ( x )  1 2 f 2  + = + 1  ⇔ x + 2 = 2 + x    x 1 4 3 2 ⇔ x + 2 =
+ + 4 ⇔ x − 2x − 4x −1 = 0 ⇔ (x + ) 1 ( 2
x − 3x −1 = 0 2 ) x x Trang 2
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC  x = 1 −  x = 1 −  − 1 13 ⇔ 3 13 x =  
. Kết hợp với điều kiện ta được . Vậy S + = . 2 3+  13 2  x =  2  3+ 13 x =  2 2 Câu 4. +
Nghiệm nhỏ nhất của phương trình x 1 4 2 2log
+ 2x − 6x +1 = 0 5 x a + b có dạng , trong đó , ∈ ,  ∈, b a c b
tối giản. Tính giá trị của biểu thức: P = a + b + c c a
A. P = 6 .
B. P = 4 .
C. P = 8.
D. P = 5. Lời giải Chọn A
Điều kiện: x > 0 2 + Ta có: x 1 4 2 1 2log
+ 2x − 6x +1 = 0 ⇔ log x +1 + x + 2x +1 2 = log x + + 5x 5 ( 2 ) 4 2 5 x 5 2 ⇔ log (x + ) 1 + (x + )2 2 2
1 = log x 5 + x 5 * 5 5 ( ) ( )2 ( )
Xét hàm số f (t) 2
= t + log t trên khoảng (0;+∞); f ′(t) 1 = 2t + > 0, t ∀ ∈(0;+∞) 5 t ln 5
Hàm số f (t) đồng biến trên khoảng (0;+∞). Ta có: ( ) f ( 2 x ) f ( x) 2 2 5 1 * 1 5 x 1 5x x 5x 1 0 x ± ⇔ + = ⇔ + = ⇔ − + = ⇔ = (thỏa mãn) 2 5 1
Nghiệm nhỏ nhất của phương trình là x − = . Vậy P = 1 − + 5 + 2 = 6 . 2
Câu 5. Tất cả các nghiệm của phương trình
2021x = 4041− 2021x + log 2021(2x + )2021 1
thỏa mãn bất phương trình nào sau đây? 2021 A. 2 x −1 > 0 . B. 2
x − 3x < 0 . C. 2
x − x ≥ 0. D. 2
x + 2x − 3 ≤ 0. Lời giải Chọn C Điều kiện ban đầu: 1 x > − 2
Ta có phương trình tương đương với
2021x = 4041− 2021 + log 2021(2 + )2021 1 ⇔ 2021x x x
= 4042 − 2021x + 2021.log 2x +1 2021 2021 ( )
⇔ 2021x + 2021x − 2021 = 4042x + 2021+ 2021.log 2x +1 2021 ( ) x 1 2021 − ⇔
+ x −1 = 2x +1+ log 2x +1 2021 ( ) ( x 1 2021 − ) log ( x 1 2021 − ⇔ + = 2x +1 + log 2x +1 * 2021 ) ( ) 2021 ( ) ( )
Xét hàm số f (t) = t + log
t trên khoảng (0;+∞) 2021 Ta có f ′(t) 1 =1+ > 0, t
∀ ∈(0;+∞) ⇒ Hàm số f (t) đồng biến trên khoảng (0;+∞). t ln 2021
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 3
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC Phương trình ( ) f ( x 1 − ) f ( x ) x 1 − x 1 * 2021 2 1 2021 2x 1 2021 − ⇔ = + ⇔ = + ⇔ − 2x −1 = 0  1 Xét hàm số x 1 g(x) 2021 − = − 2x −1 trên ;  − +∞  . 2    Ta có: g (x) x 1 2021 − ′ =
.ln 2021− 2 ; g (x) x 1 − 2  1 2021 .ln 2021 0, x ;  ′′ = > ∀ ∈ − +∞  2     1
Suy ra hàm số g′(x) đồng biến trên ;  − +∞ 
⇒ Phương trình g′(x) = 0 có tối đa một nghiệm 2     1 trên ;  − +∞  2   
⇒ Hàm số g (x) có tối đa một điểm cực trị
⇒ Phương trình g(x) = 0 có tối đa hai nghiệm phân biệt. 3 −
Ta có: lim g (x) 2 = 2021 > 0; g ( ) 2020 0 = −  1 + 2021 x  → −  2  
lim g (x).g (0) < 0  1
nên phương trình g (x) = 0 có ít nhất một nghiệm thuộc khoảng ;0 −    1 +  2 x  → −   2   g ( ) 1 .g (2) = ( 2 − ).2016 = 4032 −
< 0 nên phương trình g (x) = 0 có ít nhất một nghiệm thuộc khoảng (1;2)
Do phương trình g (x) = 0 có tối đa hai nghiệm nên phương trình g (x) = 0 có đúng hai nghiệm x 1
; x trong đó x  ;0 ∈ −
và x ∈ 1;2 . Đến đây ta thử từng đáp án như sau: 2 ( ) 1 2 1 2    x > 1 Xét bất phương trình 2 x −1 > 0 ⇔ 
⇒ Nghiệm x không thỏa mãn bất phương trình. x < 1 − 1 Xét bất phương trình 2
x − 3x < 0 ⇔ 0 < x < 3 ⇒ Nghiệm x không thỏa mãn bất phương trình. 1 x ≥1 Xét bất phương trình 2
x − x ≥ 0 ⇔ 
⇒ Các nghiệm x ; x thỏa mãn bất phương trình. x ≤ 0 1 2 Xét bất phương trình 2
x + 2x − 3 ≤ 0 ⇔ 3
− ≤ x ≤1 ⇒ Nghiệm x không thỏa mãn bất phương 2 trình.
Câu 6. Cho phương trình sau: log ( 2 x − 2x − ) 3 2
1 + x − x − 4x − 2 = 0 . Biết rằng phương trình trên có 1 2
nghiệm dương có dạng x = a + b c , trong đó a;b∈ o
 , c là số nguyên tố. Tính giá trị biểu thức
T = 2a + 3b + c
A. T = 8. B. 25 T = . C. 17 T = . D. 31 T = . 4 2 2 Lời giải Chọn A x >1+ 2 Điều kiện ban đầu: 2
x − 2x −1 = (x − )2 1 − 2 > 0 ⇔  x <1− 2
Do x là nghiệm dương nên ta xét phương trình trên khoảng (1+ 2;+∞) o Trang 4
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC Ta có: log ( 2 x − 2x − ) 3 2
1 + x − x − 4x − 2 = 0 ⇔ log ( 2 x − 2x − ) 1 + ( 2
x − 2x −1 x +1 = x +1 2 2 )( ) ⇔ log ( 2 x − 2x − ) 1 (x + ) 1 + ( 2
x − 2x −1 x +1 = log x +1 + x +1 * 2 )( ) 2 ( ) ( )
Xét hàm số f (t) = t + log t trên khoảng (0;+∞), f ′(t) 1 = 1+ > 0, t ∀ ∈(0;+∞) 2 t ln 2
Hàm số f (t) đồng biến trên (0;+∞)
Ta có: ( ) ⇔ f ( 2x − x − )(x + )) = f (x + ) ⇔ ( 2 * 2 1 1 1 x − 2x − ) 1 (x + ) 1 = x +1 x =1+ 3
x − 2x − 2 = 0  ⇔ (x + )
1 (x − 2x − 2) 2 2 = 0 ⇔  ⇔ x =1− 3 . x +1 = 0 x = 1 − 
Đối chiếu với điều kiện, suy ra x =1+ 3 . Vậy T = 2a + 3b + c = 2.1+ 3.1+ 3 = 8.
Câu 7. Có bao nhiêu cặp số nguyên dương ( ;
x y) với x ≤ 2020 thỏa mãn 2(3 − ) = 3(1+ 9y x y )−log 2x−1 3 ( ) A. 3. B. 1010. C. 4 . D. 2020 . Lời giải Chọn A
Đặt log 2 −1 = ⇒ 2 = 3t x t x
+1, ta được phương trình như sau: 3 ( )
( t + )− = ( 2y + ) t 2 3 3 1 2 3 1 3 − ⇔ 3.3 + = 3.3 y y t t + 2y (*).
Xét hàm số ( ) = 3.3u + ⇒ ′( ) = 3.3u f u u f u ln 3+1 > 0, u
∀ ∈  ⇒ f (u) đồng biến trên  .
Do đó (*) ⇔ t = 2y , vậy nên 2
2 = 3 y +1 ⇔ 9y x = 2x −1. Vì ≤ 2020 ⇒ 9y x
≤ 4039 ⇔ y ≤ log 4039. Vì y nguyên dương nên y ∈{1;2; } 3 . 9
Ta thấy với mỗi giá trị nguyên của y thì tìm được 1 giá trị nguyên của x . Vậy có 3 cặp ( ; x y) thỏa mãn.
Câu 8. Có bao nhiêu cặp số ( ;
x y) là các số nguyên không âm thỏa mãn 2 2 2 2
2(1+ x + 2y) + log (x + 2y) = 2log (x + y + 2xy + x) + 2(x + y) + 4x + 4y ? 2 2 A. 4 . B. 3. C. 2 . D. 5. Lời giải Chọn B Từ 2 2 2 2
2(1+ x + 2y) + log (x + 2y) = 2log (x + y + 2xy + x) + 2(x + y) + 4x + 4y 2 2 Biến đổi về: 2 2
2 x + 2y + log (2 x + 2y) = log ([x + y) + x]+[(x + y) + x] ( ) * 2 2
Xét hàm đặc trưng f (t) = log t + t đồng biến trên [0;+∞) 2 Có 2 2
(*) ⇔ f (2 x + 2y) = f ((x + y) + x) ⇔ 2 x + 2y = (x + y) + x (**) Có 2 2
x = 2 x + 2y − (x + y) ≥ 0 ⇔ (x + y) ≤ 2 x + 2y ≤ 2 x + 2y + x = 2 2(x + y) Suy ra 4
(x + y) ≤ 8(x + y) ⇒ 0 ≤ x + y ≤ 2
Với x + y = 0 ⇔ (x = 0; y = 0) thỏa (**)
Với x + y =1. Ta được 2 cặp số ( ;
x y): (x = 0; y =1) không thỏa (**) và (x =1; y = 0) thỏa (**)
Với x + y = 2 . Ta được 3 cặp số ( ;
x y): (x = 0; y = 2) thỏa (**); (x = 2; y = 0) không thỏa (**);
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 5
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
(x =1; y =1) không thỏa (**).
Vậy có tất cả 3 cặp số ( ;
x y) thỏa mãn yêu cầu bài toán. Câu 9. Cho hàm số 3 3
f (x) = ln x + ln x . Biết rằng phương trình   3 f ( (x − ) 3 2 + x ) 3 x 3 log 2 9 + f 7 + 6 + log  = ln   ( 2 3 3
x có nghiệm x được viết dưới dạng 2 2 ) 3 x 0   là: a x =
với a,b,c nguyên dương. Từ đó giá trị của biểu thức P = a − b + c là 0 3 b − c A. 3. B. 1. C. 5. D. 4 . Lời giải Chọn B x − 2 > 0
Điều kiện xác định x ≠ 0 ⇔ x > 2 . 3  x >  0 Đầu tiên hàm số 3 3
f (x) = ln x + ln x với x
∀ ∈(2;+∞) có f ′(x) > 0 x ∀ ∈(2;+∞)
Suy ra hàm số f (x) đồng biến trên (2;+∞) Ta có:  1   1   1  3 3 3 3 3 3 = + ⇒ = 3 f (x) ln x ln x f ln + 3 ln
= ln x + −ln x = ln x −       ln x x   x   x  3  f (x) 3 = ln x + ln x  Suy ra  3  1  3 3  f   x x f (x) 3  1 f    x ( 2x) 3  1 ln ln 2ln ln f  = − ⇒ + = = ⇒ =   ln ( 2 x ) 3 − f (x)   x   x   x
x > 2 >1⇔ ln x > 0  Từ đó ta có:     3
f (log (x −2) 3 2
+ 9x ) = ln( 2x) 3 x 3 3 1 3 −  + 3 + 3  =  + 3 f 7 6 log f 7 6 + log 3x 2 2 2   3 x   3x      3 2 1 x − 3 ( 2) 3 2 1 ⇒ − + = + 3 + ⇔ + − 3 log (x 2) 9x 7 6 log 3x log 9x 6 = 7 2 2 2 3 3x 3x 3x
(x − 2) 3x − 6 (x − 2) (x − 2) log 7 log 3.  ⇔ + = ⇔ + = log 2 + 3⋅ 2 2 2     2 ( ) ( ) 3 3 3 3 3x 3x  3x   3x
Xét hàm số f (t) = log t + 3t với t > 0. 2 Ta có 1 f (′t) =
+ 3 > 0 nên f (t) đồng biến. Phương trình trên chính là t ln 2  (x − 2)  (x − 2) 3 f = f (2) ⇔ = 2 ⇔ (x − 2) =   24x 3 3  3x  3x 3 2 3 3 3 2
⇔ x − 6x −12x −8 = 0 ⇔ 2x = (x + 2) ⇔ x 2 = x + 2 ⇔ x = 3 2 −1
Dễ thấy nghiệm này thỏa mãn điều kiện xác định.
Vậy phương trình đã cho có nghiệm duy nhất là 2 x =
⇒ P = a − b + c =1 3 2 −1 Trang 6
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC 2 Câu 10. + + Biết phương trình: x 3x 2 2 log
= x − 4x + 3 có nghiệm các nghiệm x ; x . Hãy tính giá trị 2 2 3x − 5x + 8 1 2 của biểu thức 2 2
A = x + x − 3x x . 1 2 1 2 A. 31. B. 31 − . C. 1. D. 1 − . Lời giải Chọn C x < 2 − + Ta có : 2
3x − 5x + 8 > 0, x
∀ ∈ R nên điều kiện của phương trình là: 2
x + 3x + 2 > 0 ⇔  x > 1 − 2 + + + x 3x 2 2 log = x − 4x + 3 2 2 3x − 5x + 8 ⇔ ( 2 x + x + ) − ( 2 x − x + ) 1 log 3 2 log 3 5 8 = [( 2
3x − 5x + 8) − ( 2 x + 3x + 2)] . 2 2 2 ⇔ ( 2 x + x + ) 1 + ( 2 x + x + ) = ( 2 x − x + ) 1 log 3 2 3 2 log 3 5 8 + ( 2 3x − 5x + 8) . 2 2 2 2 + Xét hàm số f (t) 1
= log t + t, t > 0 ; f (t) 1 1 ' = + > 0, t ∀ > 0 . 2 ( ) 2 t ln 2 2
Nên hàm số f (t) đồng biến trên tập (0;+∞).
Mà phương trình có dạng : f ( 2
x + x + ) = f ( 2 3 2
3x − 5x + 8) .
Vậy phương trình đã cho tương đương với phương trình: ( x =1 2
x − x + ) = ( 2 3 5 8 x + 3x + 2) 2
⇔ 2x −8x + 6 = 0 ⇔  (t/m). x = 3 Vậy 2 2
A = x + x − 3x x =1. 1 2 1 2
Câu 11. Có bao nhiêu cặp số (x; y) nguyên thỏa mãn các điều kiện 0 ≤ x ≤ 2020 và log 2 + 2 + − 3 = 8y x x y ? 2 ( ) A. 2019 . B. 2018 . C. 1. D. 4 . Lời giải Chọn D
Do 0 ≤ x ≤ 2020 nên log 2x + 2 luôn có nghĩa. 2 ( )
Ta có log 2 + 2 + − 3 = 8y x x y 2 ( ) ⇔ log ( + ) 3 1 + +1 = 3 + 2 y x x y 2 ⇔ log ( + ) log2(x+ ) 1 3 1 + 2 = 3 + 2 y x y ( ) 1 2
Xét hàm số ( ) = + 2t f t t .
Tập xác định D = R và ′( ) =1+ 2t f t
ln 2 ⇒ f ′(t) > 0 , t ∀ ∈ R .
Suy ra hàm số f (t) đồng biến trên R .
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 7
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC Do đó ( )
1 ⇔ log x +1 = 3y 3 ⇔ +1 = 2 y x
⇔ y = log x +1 . 8 ( ) 2 ( )
Ta có 0 ≤ x ≤ 2020 nên 1≤ x +1≤ 2021 suy ra 0 ≤ log x +1 ≤ log 2021. 8 ( ) 8
Lại có log 2021 ≈ 3,66 và y ∈ Z nên y ∈{0;1;2; } 3 . 8
Vậy có 4 cặp số (x; y) nguyên thỏa yêu cầu bài toán là các cặp (0;0) , (7 ) ;1 ,(63;2) ,(511;3). Câu 12. a Biết phương trình 2x −1 2 log
= 3x −8x + 5 có hai nghiệm là a và với ;
a b là các số nguyên 3 (x − )2 1 b
tố. Giá trị của b là: A. 1. B. 4 . C. 2 . D. 3. Lời giải Chọn D  1 2x −1 > 0 x > Điều kiện  ⇔  2 . x −1 ≠ 0 x ≠1 Ta có: 2x −1 2 log
= 3x −8x + 5 . 3 (x − )2 1 2x −1 2 − ⇔ log
−1 = 3x −8x + 4 2x 1 ⇔ log = 3(x − )2 1 − 2x −1 . 3 2 ( ) 3 (x − )2 1 3(x − ) 1 ⇔ log (2x − ) 1 + (2x − ) 1 = log (3(x − )2 1 )+3(x − )2 1 ( ) 1 . 3 3
Xét hàm số: f (t) = log t + t với . 3 ( ) t > 0 f ′(t) 1 = +1 > 0 , t ∀ > 0 . t.ln 3
Suy ra hàm số f (t) đồng biến trên (0;+∞).
Phương trình( ) ⇔ f ( x − ) = f ( (x − )2 1 2 1 3 1 ). x = 2
⇔ x − = (x − )2 2 2 1 3
1 ⇔ 3x −8x + 4 = 0 hay  2 . x =  3
Vậy hai nghiệm của phương trình là 2 và 2 suy ra b = 3 . 3
Câu 13. Tìm số nghiệm của phương trình 2
log x − x +1 + log (1− 2x) 2
+ 2x =1− x − x +1 3 1 3 A. 2 . B. 1. C. 3. D. 4 . Lời giải Chọn B Trang 8
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC Điều kiện: 1 x < 2 Ta có: 2
log x − x +1 + log (1− 2x) 2
+ 2x =1− x − x +1 3 1 3 2
⇔ log x − x +1 − log (1− 2x) 2
+ 2x =1− x − x +1 3 3 2 2
⇔ log x − x +1 + x − x +1 = log 1− 2x +1− 2x * 3 3 ( ) ( )
Xét hàm số f (t) = log t + t,t > 0 . Dễ thấy f ′(t) 1 = +1 > 0, t ∀ > 0. 3 t ln 3
Suy ra hàm số đồng biến trên (0;+∞).
Ta có f ( 2x − x + ) = f ( − x) 2 1
1 2 ⇔ x − x +1 =1− 2x 1  − 2x ≥ 0  1 x ≤ 2 x x 1 1 2x  ⇔ − + = − ⇔  ⇔  2 ⇔ x = 0 . 2 x − x +1 =  (1− 2x)2 2
x − x = 0
Vậy phương trình có một nghiệm là x = 0 .
Câu 14. Tổng tất cả các nghiệm của phương trình: log ( 3 2
x − x −10x + 2) 3 2
+ 3x − 9x − 45x + 27 = log ( 2
2x + 5x − 7 là: 2022 2022 ) A. 3. B. 6 . C. 3+ 6 . D. 6 . Lời giải Chọn C 3 2
x − x −10x + 2 > 0 ĐKXĐ:  . 2
2x + 5x − 7 > 0 Ta có: log ( 3 2
x − x −10x + 2) 3 2
+ 3x − 9x − 45x + 27 = log ( 2 2x + 5x − 7 2022 2022 ) ⇔ log ( 3 2
x − x −10x + 2) + 3( 3 2
x − x −10x + 2) = log ( 2
2x + 5x − 7) + 3( 2
2x + 5x − 7 1 . 2022 2022 ) ( )
Xét hàm số f (t) = log
t + 3t trên (0;+ ∞) . 2022 f ′(t) 1 = + 3 > 0, t
∀ ∈(0;+ ∞) ⇒ Hàm số f (t) đồng biến trên (0;+ ∞) . t ln 2022 Do đó ( ) 1 ⇔ f ( 3 2
x − x − x + ) = f ( 2 10 2
2x + 5x − 7) ⇔ 3 2 2
x − x −10x + 2 = 2x + 5x − 7 x = 3 − (lo¹i)  ⇔ 3 2
x − 3x −15x + 9 = 0 ⇔ x = 3+ 6 (tháa m·n ) .  x = 3 − 6  (lo¹i)
Vậy phương trình đã cho có nghiệm duy nhất x = 3+ 6 . 8084 2021.log 3x−2 8084 − 1 ( )
Câu 15. Phương trình 2021.log2(3x−2) x 2 x e + e = e + e
có bao nhiêu nghiệm? A. 3. B. 2 . C. 0 . D. 1. Lời giải Chọn D
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 9
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC ĐKXĐ: 2 x > . 3 Ta có: 8084 2021.log 3x−2 8084 8084 8084 − 1 ( ) 2021.log2(3x−2) x 2021.log 3x 2 2021.log 3x 2 2 x e + e = e + e ⇔ 2 ( ) 2 ( ) x x e e e e− − − − − = − ( )1 Xét hàm số ( ) t t f t e e− = − trên R . ′( ) t −t
f t = e + e > 0, t
∀ ∈ R ⇒ Hàm số f (t) đồng biến trên R .  8084 Do đó ( )
1 ⇔ f (2021.log 3x 2 f  − = 2 ( ))  x    8084 4 ⇔ 2021.log 3x − 2 =
⇔ log 3x − 2 − = 0 2 2 ( ) ( ) 2 ( ) x x  2
Xét hàm số g (x) 4
= log 3x − 2 − trên  ;  + ∞ 2 ( ) x 3    g (x) 3 4  2  ′ =   ( + > x ∀ ∈
+ ∞ ⇒ Hàm số g (x) đồng biến trên 2  ;+ ∞ . 3x 2) 0,  ; 2 ln 2 x 3  −     3  Mà g (2) = 0 Do đó ( )
1 ⇔ g (x) = g (2) ⇔ x = 2 .
Vậy phương trình đã cho có một nghiệm x = 2 .
Câu 16. Tìm số nghiệm của phương trình x + x + x 1 (3 ) 1 log 3 1 4 ( ) 4 − 2x −1 = log 2 2 x A. 2 . B. 1. C. 3. D. 4 . Lời giải Chọn B
Với x > 0 , phương trình tương đương
4x − 2x −1 = log 3x +1 + log log 3x +1  − log x 4 ( ) 4  4 ( ) 4
⇔ 4x + x + log x = 3x +1+ log 3x +1 + log log 3x +1  4 4 ( ) 4  4 ( )
Đặt log 3 +1 = ⇔ 3 +1 = 4y x y x 4 ( )
Phương trình trở thành: ⇔ 4x + + log = 4y x x + y + log y 1 4 4 ( ) Xét hàm số ( ) = 4t f t
+ t + log t trên (0;+∞). 4
Hàm số f (t) đồng biến trên (0;+∞). Phương trình ( )
1 ⇔ f (x) = f ( y) ⇔ x = y
Trở lại phép đặt ta được: 4x = 3 +1 ⇔ 4x x − 3x −1 = 0 Xét hàm số ( ) = 4x g x
− 3x −1 trên R .
Chứng minh được phương trình g (x) = 0 có nhiều nhất hai nghiệm trên R .
Có g (0) = g ( )
1 = 0 nên phương trình g (x) = 0 có nghiệm x = 0; x =1.
Kết hợp điều kiện, phương trình có nghiệm x =1. Trang 10
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
Câu 17. Phương trình 1 76  5 1  1 22 log x +1 + x − = log + −   4 x +1 + + có bao nhiêu 2021 ( ) 2021 2 2 9  3 x x 3x nghiệm? A. 2 . B. 1. C. 3. D. 0 . Lời giải Chọn A  3 1 − < x < − ĐKXĐ:  5 .  x > 0 Ta có: 1 76  5 1  1 22 log x +1 + x − = log + −   4 x +1 + + 2021 ( ) 2021 2 2 9  3 x x 3x 2 2 ⇔  5 1   5 1 log x 1 x 1 2 log 2 + + + + = + + + +     1 . 2021 ( ) 2021 ( )
 3 x   3 x
Xét hàm số f (t) = log
t + (t + 2)2 trên (0;+ ∞) . 2021 f ′(t) 1 =
+ 2(t + 2) > 0, t
∀ ∈(0;+ ∞) ⇒Hàm số f (t) đồng biến trên (0;+ ∞) . t ln 2021 Do đó ( ) 1 5 1 ⇔ f ( x )  5 1 1 f  + = +  ⇔ x +1 = + 3 x    3 x 5 1 + ≥ 0 3 x  5 1 + ≥ 0   5 1 x = 3 3 x  + ≥ 0 x = 3 đk ⇔   ⇔ ⇔  ⇔  . 2 3 x  11 − −  13   5 1  11 − + 13 x +1  = + x =   3 2 9
x −16x − 30x − 9 = 0  x =  18  3 x       18   11 − − 13  x =   18
Vậy phương trình đã cho có hai nghiệm phân biệt.  3   3
x 1 log  x 1 + +   2 
Câu 18. Số nghiệm dương của phương trình x 1 1  2   2 2 x 1 log  − − = là 2 2 2 x A. 0 . B. 3. C. 2 . D. 1. Lời giải Chọn D 3 x+1> 0 2  2  x − >  3    3 log  x +1   x > 0 2   2  x > 0 Điều kiện  0  > ⇔  ⇔  2 . x  x < 0 − < x < 0  3 x ≠ 0 x ≠ 0     
Với x > 0 phương trình tương đương
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 11
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC x 1  3    3  2 − x −1 = log x +1 + log log x +1 −     log x 2 2 2 2 2  2    2  x 3  3    3 
⇔ 2 + x + log x = x +1+ log x +1 + log log x +    1 . 2 2 2 2 2 2  2       3  3 Đặt log +1 = ⇔ +1 =   2y x y x . 2  2  2
Phương trình trở thành: ⇔ 2x + + log = 2y x x + y + log y 1 2 2 ( ) Xét hàm số ( ) = 2t f t
+ t + log t trên(0;+∞). Hàm số f (t) đồng biến trên khoảng(0;+∞), (vì 2
là tổng của các hàm đồng biến). Phương trình ( )
1 ⇔ f (x) = f ( y) ⇔ x = y . Khi đó 3 1 2y x + = ⇔ 3 x x 3
x +1 = 2 ⇔ 2 − x −1 = 0. 2 2 2
Xét hàm số g (x) x 3
= 2 − x −1 trên  ta có 2 g′(x) x 3
= 2 ln 2 − , g′(x) = 0 có một nghiệm suy ra g (x) = 0 có không quá 2 nghiệm 2
Mà g (0) = g (2) = 0 .
Kết hợp điều kiện, phương trình có một nghiệm dương x = 2. x x  + 
Câu 19. Tìm số nghiệm của phương trình 7 3 x 1 log 
 + 7 + + 7.3x − 56x −14 = 0 2021  8x + 2  A. 0 . B. 2 . C. 1. D. 3. Lời giải Chọn B Điều kiện 1 x > − . 4
Phương trình đã cho tương đương log 7x + 3x − log
8 + 2 + 7 7x + 3x x − 7 8x + 2 = 0 2021 ( ) 2021 ( ) ( ) ( ) ⇔ log
7x + 3x + 7 7x + 3x = log
8x + 2 + 7 8x + 2 (1). 2021 ( ) ( ) 2021 ( ) ( )
Xét hàm số f (t) = log t + 7t trên khoảng (0;+ ∞). 2021 Ta có f ′(t) 1 =
+ 7 > 0 , ∀t > 0 , do đó hàm số f (t) đồng biến trên khoảng (0;+ ∞). t.ln 2021 Từ ( )
1 ta thấy (7x + 3x f
) = f (8x+2) ⇔ 7x +3x =8x+2 ⇔ 7x +3x −8x−2 = 0
Xét ( ) = 7x + 3x g x −8x − 2 , ta có
′( ) = 7x ln 7 + 3x g x ln 3−8, ′ ( ) x = ( )2 x g x + ( )2 7 ln 7
3 ln 3 > 0 và g′( x) liên tục trên  .
Nên g′(x) = 0 có không quá 1 nghiệm suy ra g (x) = 0 có không quá 2 nghiệm. Trang 12
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
Mà g (0) = g ( ) 1 = 0.
Kết hợp với điều kiện suy ra phương trình có tập nghiệm là S = {0; } 1 . Câu 20. Cho hàm số ( 2 ( ) ln 1 ) x x f x x x e e− = + + + − . Hỏi phương trình 2  1   x  1 
f  log x 2 x 3 f log 1  + + + + − + − 
2 x + 2  = 0 có bao nhiêu nghiệm thực? 2 ( ) 2  2   2x +1  x     A. 3. B. 0 . C. 2 . D. 1. Lời giải Chọn C Xét hàm số ( 2 ( ) ln 1 ) x x f x x x e e− = + + + − Ta có: 2
x +1 + x > 0, x
∀ ∈  nên hàm số f (x) xác định trên  .
Ta có: (− ) = ( (− )2 + − ) −x x + − = − ( 2 ln 1 ln +1 + ) −x x f x x x e e x
x + e − e = −( ( 2 ln +1 + ) x −x x
x + e − e ) = − f (x) với x
∀ ∈  . Suy ra f (x) là hàm số lẻ. 2 2x x +1 + x +1 2 2 Mà 2 x +1 x − x x +1 x − x 1 f (′x) x − x = + e + e = + e + e =
+ e + e > 0, x ∀ ∈  2 2 2 x +1 + x x +1 + x x +1
Suy ra hàm số f (x) đồng biến trên  . 2   Xét phương trình :  1  x  1
f  log x 2 x 3 f log 1  + + + + − + −  2 x + 2  = 0 . 2 ( ) 2  2   2x +1  x     1
Điều kiện: x  2;  ∈ − − ∪(0;+∞   ) .  2  2   Ta có :  1  x  1
f  log x 2 x 3 f log 1  + + + + − + −  2 x + 2  = 0 2 ( ) 2  2   2x +1  x     2  1   x  1 
f  log x 2 x 3 f log 1  ⇔ + + + = − − + −  2 x + 2 2 ( ) 2   2   2x +1  x     2  1   2x +1  1 
f  log x 2 x 3 f log 1  ⇔ + + + = + + +  2 x + 2 2 ( ) 2  2  x x        2 1 2x +1  1 log x 2 x 3 log 1  ⇔ + + + = + + + 2 x +   2 . 2 ( ) 2 2 xx  ( x ) ( x ) 2 2  1   1 log 2 2 1 log 2 1  ⇔ + + + − = + + +     1 2 2 ( )  x   x
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 13
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC Với 1 x  2;  ∈ − − 
ta thấy f (x) = log
x + 2 + x + 2 −1 là hàm số đồng biến và 2 ( ) ( )2 2    2 g (x)  1   1 log 2  1  = + + +
là hàm số nghịch biến. Do đó (1) có nhiều nhất một nghiệm 2 x x      1 x  2;  ∈ − −  1   . Mà f (− ) 1 = g (− ) 1
x = − là nghiệm duy nhất của (1) trong  2; − − 2     nên 1  2 
Với x ∈(0;+∞) , xét hàm số h(t) = log (t + ) 2
1 + t có h′(t) 1 = + 2t > 0, t
∀ > 0 nên h(t) 2 (t + )1ln 2
là một hàm số đồng biến trên (0;+∞).
( ) ⇔ h( x+ − )  1  1 2 3+ 13 1 2 1 = h 1+ ⇔ 
x + 2 −1 =1+ ⇔ x − 3x −1 = 0 ⇔ x =  .  x x 2
Vậy phương trình có 2 nghiệm.
Câu 21. Tính tổng S của tất cả các nghiệm của phương trình.  5x + 3x x 1 ln 
 + 5 + + 5.3x − 30x −10 = 0 .  6x + 2  A. S =1. B. S = 2 . C. S = 1 − . D. S = 3. Lời giải Chọn A Điều kiện: 1
6x + 2 > 0 ⇔ x > − (*) . 3 Khi đó ta có:  5x + 3x x 1 ln 
 + 5 + + 5.3x − 30 −10 = 0 ⇔ ln (5x + 3x ) + 5(5x + 3x x
) = ln(6x+2)+5(6x+2) ( )1  6x + 2 
Xét hàm số y = f (t) = ln t + 5t, t > 0 . 1
y′ = + 5 > 0 t
∀ > 0 nên hàm số luôn đồng biến khi t > 0, t do đó ( )
1 ⇔ (5x + 3x ) = (6 + 2) ⇔ 5x + 3x f f x = 6x + 2 (2). Với x ∈[0; ]
1 . Áp dụng bất đẳng thức Becnoulli ta có: 5x + 3x ≤ 5x − x + 3x − x + 2 = 6x + 2. Dấu
" = "xảy ra khi x =1, x = 0 .
Với x ≤ 0 hoặc x ≥1. Áp dụng bất đẳng thức Becnoulli ta có:
5x + 3x ≥ 5x − x + 3x − x + 2 = 6x + 2. Dấu " = "xảy ra khi x =1, x = 0 .
Vậy phương trình (2) có nghiệm x =1, x = 0 , suy ra S =1.
Cách giải khác: (Giải Phương trình (2)). Xét hàm số ( ) = 5x + 3x f x
− 6x − 2 có f ( ) 1 = f (0) = 0
suy ra phương trình f (x) = 0 có hai nghiệm x =1, x = 0 . Ta có ′( ) x x = + − ′′( ) x = ( )2 x f x f x + ( )2 5 ln 5 3 ln 3 6, 5 ln 5 3 ln 3 > 0, x
∀ nên f ′(x) = 0 có nhiều
nhất một nghiệm, suy ra f ′′(x) = 0 có nhiều nhất hai nghiệm. Vậy phương trình f (x) = 0 có
hai nghiệm x =1, x = 0 , suy ra S =1. Trang 14
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC  + + 
Câu 22. Cho phương trình 2x 1 3  x − 3 log   log  =
. Biết rằng phương trình trên có nghiệm 3 25  x      2x +1 
duy nhất có dạng là x = a + b c (với a; ;
b c∈ , c tối giản). Tính giá trị của 2 3
S = a + b + c . A. 26 . B.36. C.16. D. 46 . Lời giải Chọn C
Điều kiện: x > 3.  + +   + +  Ta có: 2x 1 3  x − 3  − log 2x 1 3 x 3    log  = ⇔ log   = 2log 3 25  x   3 5        2x +1  x    2x +1  2  2x +1 + 3   x − 3 log   log  ⇔ = 3 5  x      2x +1 
⇔ log ( 2x +1+3)+ log (2x + )
1 = log x + log (x − 3)2 ( ) 1 3 5 3 5 Đặt y =
x + + ( y > ) ⇒ x + = ( y − )2 2 1 3, 3 2 1 3 . Khi đó ( )
1 có dạng log y + log ( y −3)2 = log x + log (x − 3)2 (2) 3 5 3 5
Xét hàm số f (t) = log t + log (t − 3)2 với t > 3 . 3 5 Ta có: f ′(t) 1 2 = + > ∀ > . t (t − ) 0; t 3 .ln 3 3 ln 5
Suy ra f (t) là hàm số đồng biến trên (3;+∞) .
Khi đó: (2) có dạng f ( y) = f (x) ⇔ y = x ⇔ 2x +1 + 3 = x x = 4 + 2 2
⇔ x + = (x − )2 2 1 3 2
⇔ x −8x + 8 = 0 ⇔  x = 4 − 2 2
Do x > 3 nên x = 4 + 2 2 . Khi đó: a = 4;b = 2;c = 2 . Vậy: 2 3 2 3
S = a + b + c = 4 + 2 + 2 =16 . 4
Câu 23. Cho phương trình sau: log (2x y + 2 + 4x + y )y +2 2 4 2 4 = 27 + ( 2 2 − 2x )( 4
y + 2 . Khi y là số 3 )
nguyên thì phương trình trên có bao nhiêu nghiệm x là số nguyên? A. 2 . B. 4 . C.8 . D. 0 . Lời giải Chọn A ĐK: 2 4 2 4
x y + + x + y > ⇔ ( 2 x + )( 4 2 2 4 0 2
1 y + 2) > 0 ⇔ x ∀ , y . 4
Ta có: log (2x y + 2 + 4x + y )y +2 2 4 2 4 = 27 + ( 2 2 − 2x )( 4 y + 2 3 ) ⇔ ( 4 y + 2)log ( 2 2x + ) 1 ( 4 y + 2) = 27 −  ( 2 2x + ) 1 ( 4 y + 2) + 3( 4 y + 2 3 )
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 15
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC ⇔ ( 2x + )+ ( 4y + ) 27 log 2 1 log 2 = − ( 2 2x +1 + 3 3 3 4 ) y + 2 ⇔
( 2x + )+( 2x + ) 27 log 2 1 2 1 = − log y + 2 + 3 4 ( 4 3 3 ) y + 2 ⇔ ( 2x + )+( 2 27 27 log 2 1 2x +1 = + log 3 ) 4 3 4 y + 2 y + 2
Xét hàm số g (t) 1
= log t + t ,t > 0 ⇒ g′ t = +1 > 0, t ∀ > 0. 3 ( ) tln3
Suy ra: y = g (t) luôn đồng biến t ∀ > 0 .  
Khi đó : ( ) ⇔ g ( 2 x + ) 27 2 27 * 2 1 = g ⇔  2x +1 =  . 4 4  y + 2  y + 2
Do y nguyên nên x nguyên khi và chỉ khi 4
y + 2 là ước của 27, mà 4 y + 2 ≥ 2 nên 4 y + 2∈{3;9;2 } 7 ⇔ y = 1 ± . Suy ra x = 2 ± . Câu 24. Tính tổng S của tất cả các nghiệm của phương trình 1 2x +1 1 2
log (x + 2) + x + 3− log
− (l+ ) − 2 x + 2 = 0 2 2 2 x x A. 1 13 S + = . B. 3 13 S + = . C. 3 13 S − = . D. 1 13 S − = . 2 2 2 2 Lời giải Chọn A x ∈( 2; − +∞) Điều kiện:  1  ⇔ x ∈( 2; − − ) ∪(0; 1 +∞) x ∈( ; −∞ − ) ∪(0;+∞) 2  2
Khi đó phương trình được viết lại: 1 1 1 2
log x + 2 − 2( x + 2) + x + 2 = log (2 + ) − 2(2 + ) + (2 + ) (1) 2 2 x x x Xét hàm số: 2
f (t) = log t − 2t + t , t ∀ > 0ta có : 2 ' 1 1 2 f (t) = + 2t − 2 ≥ 2 .2t − 2 = 2 − 2 > 0, t
∀ > 0 nên f (t) đồng biến trên khoảng t ln 2 t.ln 2 ln 2 (0;+∞). (1) 1 1
⇔ f ( x + 2) = f (2 + ) ⇔ x + 2 = 2 + (2) x x
Bình phương hai vế phương trình (2) ta có: x = 1 − 4 1 3 2 x 2 4
x 2x 4x 1 0  + = + + ⇔ − − − = ⇔
thay vào phương trình ban đầu chỉ có 2 3±  13 x x x =  2 3 13 hai giá trị x 1, x + = − = thỏa mãn. 2 3 13 1 13
Vậy phương trình có hai nghiệm là x 1, x + = − = nên S + = . 2 2 Câu 25. −
Gọi x , x x < x là các nghiệm của phương trình: 2x 1 2 log
= 3x −8x + 5. Giá trị của 1 2 ( 1 2 ) 3 2 (x −1)
biểu thức P = 2x + 3x bằng: 1 2
A. P = 4 .
B. P = 6 .
C. P = 2 . D P = 6 − . Trang 16
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC Lời giải Chọn B  1 x − x > ĐK: 2 1 > 0 ⇔  2 2 (x −1) x ≠1
Phương trình đã cho tương đương 2 2
log (2x −1) − log (x −1) = 3(x −1) − (2x −1) +1 3 3 2 2
⇔ log (2x −1) + (2x −1) = 3(x −1) + log 3(x −1) (1) 3 3
Xét f (t) = log t + t ,với t > 0 có f (t) 1 ' = +1> 0, t
∀ > 0 suy ra f (t) đồng biến trên 3 t ln3 (0;+∞). Từ đó ta có:
⇔ f ( x − ) = f  (x − )2 (1) 2 1 3 1    x = 2
⇔ x − = (x − )2 2 1 3 1 2
⇔ 3x −8x + 4 = 0  ⇔ 2 x =  3 2
Vậy tập nghiệm của phương trình là S 2,  =  nên P = 6 . 3  
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 17
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
GIẢI PT LÔGARIT BẰNG PHƯƠNG PHÁP ĐẶT ẨN PHỤ KHÔNG HOÀN TOÀN
(KHÔNG CHỨA THAM SỐ) PHƯƠNG PHÁP
Phương pháp này thường được sử dụng đối với những phương trình khi lựa chọn ẩn phụ cho một biểu
thức thì các biểu thức còn lại không biểu diễn được triệt để qua ẩn phụ đó hoặc nếu biểu diễn được thì
công thức biểu diễn lại phức tạp.
Câu 1. Số nghiệm của phương trình 2 lg x + lg .
x log 4x + 2log x = 0 là 2 ( ) 2 A. 0 . B. 1. C. 2 . D. 3. Lời giải Chọn C
Điều kiện x > 0 2 lg x + lg . x log (4x) 2
+ 2log x = 0 ⇔ lg x + 2 + log x lg x + 2log x = 0 (1) 2 2 ( 2 ) 2
Đặt t = lg x
Khi đó phương trình (1) trở thành: 2t + (2 + log x t + 2log x = 0 (2) 2 ) 2
Ta có: ∆ = (2 + log x)2 − 4.2log x = (log x − 2)2 . 2 2 2 
2 + log x + log x − 2 2 2 t = = log x  2
Khi đó phương trình (2) có hai nghiệm phân biệt là: 2  .
2 + log x − log x +  2 2 2 t = = 2  2
Với t = log x ⇔ lg x = log x ⇔ lg x − log x = 0 . 2 2 2
Đặt f (x) = lg x − log x với x > 0 . 2 f (x) 1 1 1  1 1  ′ = − = − < 0, x ∀ >   0 .
x ln10 x ln 2 x  ln10 ln 2 
Suy ra hàm số f (x) = lg x − log x luôn nghịch biến trên khoảng (0;+∞). 2 Mặt khác: f ( )
1 = 0. Do đó phương trình lg x − log x = 0 có nghiệm duy nhất là x =1 2 ( thoả điều kiện).
Với t = 2 ⇔ lg x = 2 ⇔ x =100 (thoả điều kiện).
Vậy số nghiệm của phương trình là 2.
Cách 2 Điều kiện x > 0 2 lg x + lg .
x log 4x + 2log x = 0 2 ( ) 2 2
⇔ lg x + (2 + log x lg x + 2log x = 0 2 ) 2   2 lg x lg ⇔ lg + 2 + lg + 2 x x x =   0 (1)  lg 2  lg 2  1    2 1 1+ lg x + 2 + lg x =     0  lg 2   lg 2 
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 1
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC    
Đặt t = lg x . Phương trình trở thành 1 2 1 1+ t + 2 + t =    
0 . Dễ thấy phương trình có hai  lg 2   lg 2 
nghiệm t phân biệt nên phương trình đã cho coa 2 nghiệm phân biệt.
Câu 2. Số nghiệm thực của phương trình 2
log x + (x −1)log x + 2x − 6 = 0 2 2 A. 0 . B. 1. C. 2 . D. 3. Lời giải Chọn C
Điều kiện: x > 0
Đặt t = log x . Khi đó phương trình trở thành: 2t + (x -1)t + 2x − 6 = 0 . 2 t = − Ta có ∆ = (x − )2 2
5 ⇒ t =3−x
Với t = 3− x ta có log x = 3− x ⇔ log x + x − 3 = 0 (*) 2 2
Đặt f (x) = log x + x − 3 với x > 0 , có 1 f '(x) = +1 > 0; x ∀ > 0 2 xln 2
Do đó hàm số f(x) đồng biến trên (0;+∞) mà f (2) = 0 ⇒ x = 2 là nghiệm duy nhất của hương
trình. Vậy phương trình đã cho có hai nghiệm thực.
Câu 3. Tổng các nghiệm thực của phương trình (x + ) 2
1 log x +1 + (x − 2)log x +1 − 3 = 0 3 ( ) 3 ( ) A. 1. B. 2 . C. 2 − . D. 4 . 3 3 Lời giải Chọn D
Điều kiện : x > 1 −
Đặt : t = log x +1 . Khi đó phương trình trở thành: (x + ) 2
1 t + (x − 2)t − 3 = 0 . 3 ( ) t = 1 − Ta có: (x 4)2  ∆ = − ⇒ 3  t =  x +1 Với t = 1 − ta có 1 2 log x +1 = 1
− ⇔ x +1 = ⇔ x = − (thỏa mãn điều kiện x > 1 − ) 3 ( ) 3 3 Với 3 t = ta có 3 log x +1 = (*) 3 ( ) x +1 x +1
Đặt f (x) = log x +1 và 3 g(x) = 3 ( ) x +1 với mọi 3 x > 1 − , có 1 f '(x) = ′ ( > g (x) = − < 0 x + ) 0; 1 ln 3 (x + )2 1
Do đó hàm số f (x) đồng biến trên ( 1;
− +∞) và hàm số g (x) nghịch biến trên ( 1; − +∞) ⇒ x = 2
là nghiệm duy nhất của phương trình (*).
Vậy phương trình đã cho có hai nghiệm thực 2
x = − ; x = 2 và 4 x + x = . 1 2 3 1 2 3
Câu 4. Cho phương trình x x 1 + ( x 1 9 3 2 3 + + + = + ) 1 3x m
+ m . Hỏi có bao nhiêu giá trị của tham số thực m∈[ 20
− ;20] để phương trình trên có hai nghiệm phân biệt biết rằng 4m∈ ? A. 79 . B. 82 . C. 81. D. 80 . Lời giải Trang 2
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC Chọn D
Ta đặt 3x = t > 0 suy ra 2t + 3t + 2m = (3t + )
1 t + m . Ta đặt t + m = y . Khi đó: 2
y − ( t + ) y + ( 2 2 3 1 t + t) = 0 .  3t +1+ t −1 y = 
t = t + m Ta có ∆ = (t − )2 4 1 ⇒  ⇔  . 
3t +1− (t − ) 1
t +1 = 2 t + m y =  4 2
4m = 4t − 4t = f (t) (t > 0) Do đó: 
và có đồ thị như hình bên. 2
4m = t − 2t +1 = g  (t) (t > 0) 4m ≥1
Từ đây ta suy ra để có 2 nghiệm phân biệt thì điều kiện cần và đủ là ⇒1≤ 4m ≤  80  1 − < 4m < 0
Câu 5. Cho phương trình   2 2log x −( 2 x − log x 48 − log .
x log 256x.log 8x + 28+ log xx = 56log x . 2 2 ) 2 2 2 1 2  2 
Biết tổng các nghiệm của phương trình trên là một biểu thức có dạng: a b 4 = 6 + 2 2 c d S − − + với *
a,b,c,d ∈ . Khi đó biểu thức T = a + b + c + d có giá trị bằng A. 40 . B. 40 . C. 50. D. 30. Lời giải Chọn A x > 0 x > 0 1  Điều kiện:  ⇔  ⇔ ≤ x ≤16 . 2 12 48 − log . x log 256x ≥ 0
48 −8log x − log x ≥ 0 2 2 2 2 2    Ta có 2 2log x −( 2 x − log x 48 − log .
x log 256x.log 8x + 28+ log xx = 56log x 2 2 ) 2 2 2 1 2  2  2
⇔ 2log x + (28− log x) x −56log x −( 2 x − log x 48 − log .
x log 256x.log 8x = 0 2 2 2 2 ) 2 2 2
⇔ (2log x − x log x − 28 − x − 2log x 48 − log .xlog 256x.log 8x = 0 2 )( 2 ) ( 2 ) 2 2 2
⇔ (2log x − x)( 2
log x − 28 + 48 −8log x − log x.log 8x = 0 2 2 2 2 2 )
2log x − x = 0 1 2 ( ) ⇔  . 2
log x − 28 + 48 −8log x − log x.log 8x = 0 2  2 2 2 2 ( )
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 3
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC 1 
 Xét hàm f ( x) = 2log x − x, x  ∈ ; 16 . 2  12 2    Ta có f ′(x) 2 = − f ′(x) 2 1, = 0 ⇔ x = . x ln 2 ln 2
Bảng biến thiên của hàm số f (x)  1
= 2log x − x trên đoạn ; 16 như sau: 2  12 2   
Từ bảng biến thiên ta thấy phương trình f (x) = 0 có tối đa hai nghiệm. Mà f (2) = f (4) = 0
nên phương trình f (x) = 0 có đúng 2 nghiệm x = 2, x = 4 .
 Đặt t = log x, t ∈ 12
− ;4 . Phương trình (2) trở thành t − + (t + ) 2 28
3 48 −8t − t = 0 2 [ ] 1 ⇔ ( 2
48 −8t − t ) −(t + 3) 2 1 2
48 −8t − t + t + 3t + 4 = 0 2 2 1 ⇔ ( 2
48 −8t − t ) −(t + 3) 2 1 2
48 −8t − t + t + 3t + 4 = 0 . 2 2 Đặt 2
u = 48 −8t − t , u ≥ 0 .
Ta được phương trình .. 2 ⇔ u − (t + ) 2 2
3 u + t + 6t + 8 = 0 (Chú ý ∆′ = (t + )2 − ( 2 3 t + 6t + 8) =1) u = t + 4 ⇔  . u = t + 2 t  + 4 ≥ 0 t  + 4 ≥ 0
Với u = t + 4 ta được 2
48 −8t − t = t + 4  ⇔  ⇔  2
48 − 8t − t = 2  (t + 4)2 t  + 8t −16 = 0 ⇔ t = 4 − + 4 2 . Khi đó 4 2−4 x = 2 . t  + 2 ≥ 0 t  + 4 ≥ 0
Với u = t + 2 ta được 2
48 −8t − t = t + 2  ⇔  ⇔  2
48 − 8t − t = 2  (t + 2)2 t  + 6t − 22 = 0 ⇔ t = 3 − + 31 . Khi đó 31−3 x = 2 .
 Vậy tổng các nghiệm của phương trình đã cho là 31−3 4 2−4 S = 6 + 2 + 2 . Suy ra
a = 31, b = 3, c = 2, d = 4 ⇒ T = 40 .
_______________ TOANMATH.com _______________ Trang 4
TÀI LIỆU ÔN THI THPT QUỐC GIA
Document Outline

  • Dạng-7-Giải-pt-logarit-bằng-phương-pháp-hàm-số-đánh-giá-(không-chứa-tham-số)-PB3
  • Dạng-8-Giải-pt-logarit-bằng-phương-pháp-hàm-đặc-trưng-(không-chứa-tham-số)-PB3
  • Dạng-9-Giải-pt-logarit-bằng-phương-pháp-đặt-ẩn-phụ-không-hoàn-toàn-(không-chứa-tham-số)-PB3