Thông tin
Quiz

Phương trình mũ chứa tham số

Tài liệu gồm 16 trang, được biên soạn bởi quý thầy, cô giáo Nhóm Toán VDC & HSG THPT, hướng dẫn phương pháp giải bài toán Phương trình mũ chứa tham số; đây là dạng toán thường gặp trong chương trình Toán 12 phần Giải tích chương 2.

Chủ đề:

Chương 6: Hàm số mũ và hàm số lôgarit (KNTT) 188 tài liệu

Môn:

Toán 11 3.2 K tài liệu

Thông tin:

16 trang 1 năm trước

Tác giả:

Kim Oanh

docx.com.vn

Bình luận

Vui lòng đăng nhập hoặc đăng ký để gửi bình luận.

Phương trình mũ chứa tham số

59 30 lượt tải Tải xuống

NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC

CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 1

PHƯƠNG TRÌNH MŨ CHỨA THAM SỐ

PHƯƠNG PHÁP

Phương trình một ẩn chứa tham số có dạng :









, 0 1

f x m 

, với

là tham số.

Phương pháp biện luận số nghiệm bằng bảng biến thiên (cô lập tham số):

 Bước 1 : Chúng ta tiến hành cô lập tham số

, nghĩa là chúng ta biến đổi phương

trình





về dạng phương trình













h m g x

, trong đó





h m

là biểu thức chỉ có

tham số

và





g x

là biểu thức chỉ có biến

 Bước 2 : Lập bảng biến thiến hàm

 Bước 3 : Biện luận số nghiệm phương trình và kết luận.

Phương pháp biện luận số nghiệm bằng tam thức bậc hai

 Bước 1 : Biến đổi phương trình





về phương trình bậc hai





. . 0 2

a t b t c  

 Bước 2 : Dựa vào định lý so sánh nghiệm với một số

 Bước 3 : Kết luận

Kiến thức bổ trợ :

Định lý so sánh nghiệm của phương trình bậc hai với một số

Xét





f x ax bx c

  

có hai nghiệm

1 2

x x

, khi đó :







1 2

. 0

x x a f

 

   







1 2

. 0

a f

x x S



 







   





 









1 2

. 0

a f

x x S



 







   





 



Hệ quả (so sánh nghiệm của phương trình bậc hai với hai số)

Xét





f x ax bx c

  

có hai nghiệm

1 2

x x

, khi đó :







 

1 2

. 0

2 2

a f

x x





 

 







   



 



 









 

1 2

. 0

a f

x x

a f



 









   









Câu 1. Có bao nhiêu giá trị nguyên của tham số

để phương trình

 

2 2

1 1 1 1

4 2 .2 2 1 0

x x

m m

   

    

có bốn nghiệm phân biệt?

. B.

. C.

. D.

Lời giải

Chọn A

Phương trình

   

2 2

1 1 1 1

4 2 .2 2 1 0 1

x x

m m

   

    

Điều kiện:

1 0 1 1

x x

     

Đặt

1 1

 



2 4

 

NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC

Trang 2 TÀI LIỆU ÔN THI THPT QUỐC GIA

Phương trình





trở thành:









2 2

2 2 1 0 2 2 1

t m t m m t t t

         

Ta thấy,



không thỏa mãn phương trình, suy ra



nên ta có

 

2 1

t t

 





Đặt

 

2 1

t t

g t

 





Để phương trình





có bốn nghiệm

1 2 3 4

, , ,

x x x x

phân biệt thì phương trình





có hai nghiệm

1 2

t t

sao cho

1 2

2 4

t t

  

. Do đó, dựa vào bảng biến thiên chúng ta được

 

Mà

 



không có giá trị của

thỏa mãn.

Câu 2. Có bao nhiêu số nguyên

để phương trình









1 .16 2 2 1 .4 6 1 0

x x

m m m

     

có hai

nghiệm phân biệt?

. B.

. C.

. D.

Lời giải

Chọn D

Phương trình:













1 .16 2 2 1 .4 6 1 0 1

x x

m m m     

Đặt





Phương trình





trở thành:

     

2 1

1 . 2 2 1 . 6 1 0 2

4 6

t t

m t m t m m

t t

 

       

 

Đặt

 

2 1

4 6

t t

f t

t t

 



 

NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC

CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 3

Để phương trình





có hai nghiệm

1 2

x x

phân biệt thì phương trình





có hai nghiệm

1 2

t t

sao cho

1 2

t t

 

. Do đó, dựa vào bảng biến thiên, chúng ta được

 

Vậy





2;3;4;5

m 

Câu 3. Có bao nhiêu giá trị nguyên của tham số

để phương trình









2 2

27 2 .18 1 .12 .8 0

x x x x

m m m m m

      

có ba nghiệm phân biệt.

. B.

. C.

. D.

Lời giải

Chọn A

Biến đổi phương trình như sau:













   

2 2

3 2 2 3

2 2

3 2

2 2

27 2 .18 1 .12 .8 0 1

3 2 .3 .2 1 .3 .2 .2 0

3 3 3

2 . 1 . 0

2 2 2

x x x x

x x x x x x

x x x

m m m m m

      

       

     

       

     

     

Đặt

 



 

 

, điều kiện



Khi đó phương trình trở thành





3 2 2 2

2 1 0

t mt m m t m m

      

t m







 



 



Với



thì

1 0 0

x x

 

    

 

 

. Suy ra phương trình





có ít nhất 1 nghiệm



Để phương trình





có ba nghiệm

1 2 3

, ,

x x x

phân biệt thì

1 1 2

1 2

1 1

m m

   



   

 

 



Vậy



Câu 4. Cho phương trình

     

5 .3 2 2 .2 . 3 1 .4 0

x x x x

m m m

     

, tập hợp tất cả các giá trị của

tham số

để phương trình có hai nghiệm phân biệt là khoảng





;

a b

. Tính

S a b

 



. B.



. C.



. D.



Lời giải

Chọn D

NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC

Trang 4 TÀI LIỆU ÔN THI THPT QUỐC GIA

Ta có

     

5 .3 2 2 .2 . 3 1 .4 0

x x x x

m m m     

 

   

3 3

5 . 2 2 . 1 0

4 2

m m m

 

      

 

 

Đặt

 



 

 

, điều kiện

0t 

Khi đó phương trình trở thành:

   

5 2 2 1 0m t m t m     

 

Do đó để phương trình

 

1 có hai nghiệm phân biệt thì phương trình

 

2 có hai nghiệm dương

phân biệt

 

2 4 3 0

0 3

2 2

3 5 3;5

0 1

1 5

m m

P m









 



  





  





 



       

  





 



  



  



 













Vậy

3a 

5b 

nên

8S a b  

Câu 5. Gọi

là tập hợp các giá trị nguyên của

sao cho phương trình

   

2 2

5 5

2 2

2 4

2 .3 2 1 .3 2 6 0

x x x x

m m m

   

     

có nghiệm. Tổng các phần tử của

bằng

. B.

. C.

. D.

Lời giải

Chọn A

   

2 2

5 5

2 2

2 4

2 .3 2 1 .3 2 6 0

x x x x

m m m

   

     

 

Đặt

3 3 3

x x

 

 

 

 

   .

Phương trình

 

1 trở thành

   

2 2 1 2 6 0m t m t m     

 

2 2

2 2 2 2 6m t t t t     

2 2 6

2 2

t t

 

 

 

 

(vì

2 2 0,t t t    ).

Phương trình

 

1 có nghiệm



 

2 có nghiệm

3t 



đường thẳng

y m

cắt đồ thị hàm số

 

2 2 6

2 2

t t

f t

t t

 



 

tại điểm có hoành độ

3t 

Xét hàm số

 

2 2 6

2 2

t t

f t

t t

 



 

với





3;t   

có:

 

6 4 16

2 2

t t

f t

t t

  



 

 

 

t L











 





Ta có bảng biến thiên:

NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC

CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 5

Từ bảng biến thiên suy ra





có nghiệm

2 6

  





3;4;5;6

S 

Tổng các phần tử của

bằng

3 4 5 6 18

   

Câu 6. Cho phương trình









9 2 2 1 3 3 4 1 0

x x

m m

    

có hai nghiệm thực

1 2

x x

thỏa mãn









1 2

2 2 12

x x

  

. Giá trị của

thuộc khoảng





 

. B.





3;9

. C.





2;0



. D.





1;3

Lời giải

Chọn D

Đặt





. Phương trình đã cho trở thành:









2 2 1 3 4 1 0

t m t m

    

(1)

Phương trình đã cho có hai nghiệm thực

1 2

x x

khi và chỉ khi phương trình (1) có hai nghiệm

dương phân biệt

 

4 8 4 0

0 2 2 1 0

3 4 1 0

m m

S m m









  



 









  

        

   



   





 











Khi đó phương trình (1) có hai nghiệm là

4 1

t m

 

và



Với

4 1

t m

 

thì





1 3

3 4 1 log 4 1

m x m

    

Với



thì

3 3 1

  

Ta có









1 2 1

2 2 12 2

x x x

    





log 4 1 2

  

 

(thỏa điều kiện).

Vậy



là giá trị cần tìm nên

thuộc khoảng





1;3

Câu 7. Phương trình





 





2 3 1 2 2 3 4 0

x x

     

có 2 nghiệm phân biệt

1 2

x x

thỏa mãn

1 2

2 3

log 3

x x



 

. Khi đó

thuộc khoảng

;

 

 

 

 

. B.





 

. C.

;

 

 

 

 

. D.

;

 

  

 

 

Lời giải

Chọn D

Đặt





2 3 , 0

t t

  

Phương trình trở thành

1 2

4 0 4 1 2 0

t t t a



       

(1)

Phương trình có 2 nghiệm phân biệt

1 2

x x

thỏa mãn





1 2

2 3

log 3 2 3 3

x x





    





 

   

1 2

2 3

3 2 3 3 2 3

2 3

x x



     



. Khi đó

1 2

t t



YCBT Phương trình (1) có 2 nghiệm dương phân biệt thỏa mãn

1 2

t t



NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC

Trang 6 TÀI LIỆU ÔN THI THPT QUỐC GIA

1 2

3 2 0

0; 0

4 1

. 1 2

1 2

t t

t t a

t t



 



 





 







 

  

       

  



  

 



 

 



 



Câu 8. Tìm số giá trị nguyên của tham số

 

10;10m  

để phương trình

   

2 2

10 1 10 1 2.3

x x



   

có đúng hai nghiệm phân biệt?

. B.

. C.

. D.

Lời giải

Chọn B

   

2 2

10 1 10 1

10 1 10 1 2.3 6

3 3

x x

m m



   

 

      

   

   

(1)

Đặt

2 2

10 1 10 1 1

, 1

3 3

x x

t t

   

 

   

   

   

. Khi đó (1) trở thành

. 6 6 0t m t t m

     

(2)

(1) có đúng hai nghiệm phân biệt khi và chỉ khi (2) có một nghiệm lớn hơn 1.

(2) 6m t t   

. Xét hàm số

( ) 6f t t t  

trên khoảng

(1; )

, ta có:

   

2 6; 0 3f t t f t t

 

     

Bảng biến thiên:

Dựa vào bảng biến thiên ta thấy

5m 

hoặc

9m 

là giá trị thỏa mãn yêu cầu bài toán.

 

10;10m  

nên

 

9; 8; 7; 6; 5; 4; 3; 2; 1;0;1;2;3;4;9m          

Suy ra có 15 giá trị

cần tìm.

Câu 9. Số các giá trị nguyên của tham số

để phương trình:

   

1 .16 2 2 3 .4 6 5 0

x x

m m m     

có hai nghiệm trái dấu là

. B.

. C.

. D.

Lời giải

Chọn D

Đặt 4 , 0

t t  , phương trình đã cho trở thành:

   

1 2 2 3 6 5 0m t m t m     

(*).

Đặt

     

1 2 2 3 6 5f x m t m t m     

Phương trình đã cho có hai nghiệm

1 2

,x x

trái dấu khi phương trình (*) có hai nghiệm

1 2

,t t

thỏa

mãn:

1 2

0 1t t  

NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC

CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 7

Điều đó xảy ra khi:

   

  

4 1

1 1 0 1 3 12 0

4 1

1 0 0 1 6 5 0

m f m m

   





    

 

   



      

  



    

 



 











Vậy có hai giá trị nguyên của tham số

thỏa mãn bài toán là



và



Câu 10. Có bao nhiêu giá trị nguyên của tham số

để phương trình













2 3 3

8 3 .4 3 1 .2 1 1

x x x

x x m x m x

       có đúng hai nghiệm phân biệt thuộc





0;10

101

. B.

100

. C.

102

. D.

103

Lời giải

Chọn A













2 3 3

8 3 .4 3 1 .2 1 1 (1)

x x x

x x m x m x      









   

2 2 2

x x

x x mx mx     

Xét hàm số





f t t t

 

Ta có 2

t x

 

mà

1 2 1024

0 10 1 2 1034 1 1034

0 10

x x t



 

         



 



Xét hàm số









, 1;1034 .

f t t t t  









3 1 0, 1;1034

f t t t



    

hay





f t t t

 

đồng biến trên





1;1034

Suy ra

 

2 2

x mx m



    

Xét hàm số

   

1, 0;10 .

g x x

  

 





2 2

2 .ln 2 1

.2 ln 2 2

x x

g x

x x





  

 

0 log

ln 2

g x x e



   

BBT

.ln 2 1 103,4

ycbt e m

   

mà

m Z



nên

3;103.

m 

Có tất cả 101 số nguyên

thoả mãn.

Câu 11. Tính tổng các giá trị nguyên của tham số

thuộc đoạn





5;5



để phương trình

9 2.3 2 1 0

x x



   

có duy nhất một nghiệm.



. B.



. C.

. D.

Lời giải

Chọn A

9 2.3 2 1 0

x x



   







9 6.3 2 1 0 1

x x

m   

Đặt





. Phương trình trở thành

6 1 2

t t m

   

Xét hàm số





6 1

g t t t

  





' 2 6

g t t

 





' 0 3

g t t

  

Bảng biến thiên

NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC

Trang 8 TÀI LIỆU ÔN THI THPT QUỐC GIA

Dựa vào bảng biến thiên suy ra phương trình đã cho có nghiệm duy nhất khi

2 10

2 1

  





  















Mà





5;5

m  

và





nên





5; 4; 3; 2; 1;0;5

m      

Vậy tổng các giá trị của

là

5 4 3 2 1 0 5 10

        

Câu 12. Gọi

là tập hợp các giá trị của tham số

sao cho hai phương trình

2 1 3

 

và

3 2 1

m x x

   

có nghiệm chung. Tính tổng các phần tử của

. B.

. C.

. D.

Lời giải

Chọn B

Vì hai phương trình đã cho có nghiệm chung nên hệ sau có nghiệm





 

2 2

log 2 1

2 1 3

log 2 1 3 2 1

3 2 1

m x

x x x

m x x



 



 



      

 

   







 





 

log 2 1

2 2 2

3 3

log 2 1 2 1 3 3 log 2 1 3

x x

x x x x x



          

Xét hàm số





f t t

 

xác định trên







' 3 .ln3 1 0

f t

   

suy ra hàm





f t t

 

đồng biến trên



suy ra





2 2

log 2 1 2 1 3

x x x

    

Xét hàm số





2 1 3

g x x

  

xác định và liên tục trên



Ta có













2 3

' 4 3 ln 3 '' 4 3 ln 3 ''' 3 ln 3 0

x x x

g x x g x g x

        

. Suy ra hàm số





g x

nghịch biến trên



. Do đó





g x



có nhiều nhất là 3 nghiệm.

Ta lại có













0 1 2 0

g g g

  

. Suy ra phương trình

0 0

2 1 3 1 1

2 2

x m

x x m

x m

  





     



 



Vậy



Câu 13. Tìm tất cả giá trị thực của tham số

để phương trình





1 2 3 4 0

m m

   

có nghiệm?

m



. B.



. C.

1 m

 

. D.











Lời giải

Chọn A

Ta có





1 2 4 3

m m

  

Trường hợp 1:

1 0

 

 

. Phương trình thành

0.2 1





phương trình vô nghiệm.

-10

-1

+ ∞

g (t)

g'(t)

NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC

CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 9

Trường hợp 2:

1 0 1

m m

   

. Ta có

4 3







Phương trình có nghiệm khi

4 3 4

0 1

1 3



   



Câu 14. Tìm tất cả giá trị nguyên của tham số

thuộc





10;10



để phương trình





9 4 3 3 2 5 3 0

x x

m m m

     

có hai nghiệm phân biệt?

. B.

. C.

. D.

Lời giải

Chọn C

Đặt

3 , 0

t t

 

. Khi đó ta có phương trình





2 2

4 3 2 5 3 0 (*)

t m t m m     

Phương trình đã cho có hai nghiệm phân biệt







có hai nghiệm phân biệt dương

4 4 0

3 4 0

2 5 3 0

m m



  



  





  

















 

  

 



 

























Vậy















thì phương trình có hai nghiệm phân biệt.

Nhận xét: phương trình





2 2

4 3 2 5 3 0

t m t m m

     

2 3

x m

 







 



Phương trình có hai nghiệm phân biệt dương

1 2 3 2

1 0 1

2 3 0 3

m m m

m m





   









 

     

  



  

 









Mà





và

thuộc





10;10



nên





3;4;5;6;7;8;9;10

m 

Câu 15. Tìm tất cả giá trị thực của tham số

để phương trình





6 3 3 9.2 9 27 0

x x x

m m

     

có

nghiệm thuộc khoảng





0;2

1 3

 

. B.

1 2

  

. C.

 



. D.

3 7

 

Lời giải

Chọn A

Ta có





6 3 3 9.2 9 27 0

x x x

m m

     









3 9 2 3 0

x x

    

3 9 0

2 3

2 3 0





 



 



 

  



Ta có

0 2 1 2 4

    

Để phương trình có nghiệm thuộc khoảng





0;2

thì

1 3 4 1 2

m m

      

NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC

Trang 10 TÀI LIỆU ÔN THI THPT QUỐC GIA

Câu 16. Cho phương trình









3 2 2

10 10 2 1 1 1

m m

x x x x

     

. Tìm tập hợp các giá trị của tham

số

để phương trình có nghiệm.

0; log 2

 

 

 

. B.

log 2;

 







 

. C.

 

 

 

. D.

; log 2

 







 

Lời giải

Chọn D

Điều kiện:





1;1

x  

Ta có

















3 2 2 2 2

10 10 2 1 1 1 1 2 2 1

m m

x x x x x x x x

          









3 2 2

10 10 1 1 1

m m

x x x x

 

       

 

 









3 2 2

10 10 1 1

m m

x x x x

       

(*)

Xét hàm









3 2

3 1 0,h t t t h t t t



       



nên từ phương trình (*) ta được:









2 2

1 10 1 10

m m

h x x h x x      

(**)

Xét

 

 

1 , 1;1

f x x x x     ta có

   

 

1 1

; 0 1;1

x x

f x f x x

 

 

     



Phương trình đã cho có nghiệm khi phương trình (**) có nghiệm

1 1

0 10 2 log 2 log 2

f m

 

      

 

 

Câu 17. Cho phương trình

3 2 2

2 3

3 0

x x x m x x

e e x x m

   

    

. Tập tất cả các giá trị thực của

để

phương trình có 3 nghiệm phân biệt có dạng





;

a b

. Tổng

a b



bằng

. B.

. C.



. D.

Lời giải

Chọn D

Ta có:

3 2 2

2 3

3 0

x x x m x x

e e x x m

   

    









3 2 2 3 2 2

2 3 2 3 2 2

3 0 2

x x x m x x x x x m x x

e e x x m e x x x m e x x

       

             

(1)

Xét hàm số





f t e t

 

với





Ta có





1 0

f t e t



    



nên hàm số





f t

đồng biến trên



Phương trình





có dạng









3 2 2

f x x x m f x x

    

Suy ra

3 2 2 3

2 3

x x x m x x m x x

        

(2)

Bài toán trở thành tìm tập các giá trị của

để phương trình





có 3 nghiệm phân biệt.

NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC

CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 11

Ta có bảng biến thiên của hàm số





g x x x

  

như sau

Từ bảng biến thiên suy ra





2; 2

m  

hay

2; 2

a b

  

. Vậy

2 2

a b

 

Câu 18. Tìm tất cả các giá trị nguyên của tham số

để phương trình

3 5 3 5

4 16.2 8

x x x x

     

  

có nghiệm.

. B.

. C.

. D.

Lời giải

Chọn A

Điều kiện

3 5

  

Đặt

3 5

t x x

   

Xét hàm số





3 5

f x x x

   

trên





3;5



Ta có

   

1 1

; 0 1

2 3 2 5

f x f x x

x x

 

    

 

Bảng biến thiên của hàm số





f x

trên





3;5



Từ đó suy ra

2 2;4

 



 

Khi đó ta có phương trình:

4 16.2 8

t t

  

Đặt



, do

2 2;4

 



 

nên

4 ;16

 



 

. Ta có phương trình

16 8

a a m

  

Xét hàm số





16 8

g a a a

  

với

4 ;16

 



 









2 16; 0 8

g a a g a a

 

    

Bảng biến thiên của hàm số





g a

với

4 ;16

 



 

Từ bảng biến thiên ta thấy để phương trình có nghiệm thì thì

56 8

  

NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC

Trang 12 TÀI LIỆU ÔN THI THPT QUỐC GIA

nguyên nên nên có

giá trị.

Câu 19. Điều kiện của tham số

để phương trình

 

2 2

1 1 1 1

4 2 2 2 1 0

x x

m m

   

    

có nghiệm là

đoạn





;

a b

. Giá trị của

b a



bằng



. C.

. D.



Lời giải

Chọn A

Điều kiện

1 1

  

Đặt

1 1

 



, khi





1;1

x  

ta có

 

1 1 1;2

x   .

Khi đó





2;4

t 

Bài toán trở thành: Tìm điều kiện của tham số

để phương trình





2 2 1 0

t m t m

    

có nghiệm trên





2;4





2 2 1

m t t t

     

có nghiệm trên





2;4

 

2 1

t t

m f t

  

 



có nghiệm trên





2;4

(do





2 0 2;4

t t   

Ta có

 

 

4 3

' 0 2;4

t t

f t t

  

   



Phương trình có nghiệm khi và chỉ khi

   

25 9

4 2

6 4

f m f m

      

Câu 20. Tìm tập hợp các giá trị của tham số

để phương trình

 

2 2

log log

3 2 3 .3 3 0

x x

m m

    

có hai nghiệm phân biệt

1 2

x x

thỏa mãn:

1 2

x x



m 

. B.



 









. C.

 

. D.

 

Lời giải

Chọn A

ĐK:



- Ta có:

 

2 2

log log

3 2 3 .3 3 0

x x

m m

    





2 2

2log log

3 2 3 .3 3 0

x x

m m

     

(1).

- Đặt

log

t  ,



. Ta được bất phương trình:





2 2

2 3 3 0

t m t m

    

(2).

Nhận thấy: (1) có hai nghiệm phân biệt khi và chỉ khi (2) có hai nghiệm phân biệt dương

 

1 2

2 3 0

3 0

t t m





 



    





  



 

3 ( 3) 0

3 0

m m



   







 





6 6 0 1

3 0 3

m m

   

 

    

 

   

 

(*)

Khi đó: (2) có hai nghiệm

thỏa mãn:

1 2

. 3

t t m

 

2 1 2 2

log log

3 .3 3

x x

  

2 1 2 2

log log

3 3

x x



  





2 1 2

log

3 3

x x

  

Từ









2 1 2

log

1 2 2 1 2

4 log 2 3 3

x x

x x x x

    

2 2

3 9 6

m m



 

     









Kết hợp điều kiện (*) ta được:

m  .

NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC

CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 13

Câu 21. Tập hợp tất cả các giá trị của tham số

để phương trình

2 2 2

sin cos cos

2019 2020 2021 .log

x x x

 

có nghiệm là

2020

2 2

m  . B.

2021

1 2

m  . C.

2021

0 2

m  . D.

2019

2 2

m  .

Lời giải

Chọn A

Ta có

2 2 2

sin cos cos

2019 2020 2021 .log

x x x

 

cos

1 cos

cos

2019 2020

log

2021



 

  

 

 

2 2

cos cos

1 2020

log 2019.

4080399 2021

x x

   

  

   

   





Đặt

cos

t x

 , với

0 1

 

ta có

 

1 2020

2019.

4080399 2021

t t

f t

   

 

   

   

nghịch biến trên đoạn





0;1

nên













1 0

f f t f 





0;1

t 







1 2020

f t 





0;1

t 

Phương trình





có nghiệm



1 log 2020

 



2020

2 2

m  .

Câu 22. Có tất cả bao nhiêu giá trị nguyên của tham số

để phương trình

 

2 3 2 1

m x

x m x



 

 

   

 

 

 

 

 

có hai nghiệm phân biệt

1 2

x x

thỏa mãn điều kiện

2 2

1 2

x x

 

Lời giải

Chọn C

Điều kiện xác định:



 

1 1

2 2

1 1 1

2 3 2 1 3 3 3 3 1

3 2 2

m x

x m x m

x x

x m x m x x m

x x



 

 

 

             

 

 

 

 

 

Xét hàm số









3 0

f t t t

  

. Ta có





3 .ln 3 1 0

f t t



   

Suy ra hàm số luôn đồng biến trên tập xác định.

Do đó

   

1 1

2 2 1 0 2

2 2

f f x m x m x mx

x x

 

        

 

 

Phương trình đã cho có hai nghiệm

1 2

x x

thỏa mãn điều kiện

2 2

1 2

x x

 

khi phương trình





có hai nghiệm phân biệt khác

và thỏa mãn điều kiện đã cho.

Khi đó

 

2 2

1 2 1 2

' 0

2 0

2.0 2 .0 1 0 2 0 2 2

2. 3

2 . 3

m m m

x x x x



 



 



 

          

 

 

  

 

 

 

  







nguyên nên





1;0;1

m  

Câu 23. Có bao nhiêu giá trị nguyên dương của tham số

nhỏ hơn 2021 để phương trình

2 4

x x

m m

  

có nghiệm thực?

NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC

Trang 14 TÀI LIỆU ÔN THI THPT QUỐC GIA

2018.

2019.

2020.

2021.

Lời giải

Chọn C

Ta có:

2 4 2 2 2 2

x x x x x x

m m m m

        

Ta thấy

2 0,2 0.

x x

  

Xét hàm





f t t t

 

trên





0; .



Ta có









' 2 1 0, 0;f t t t

     

Suy ra hàm số





f t

đồng biến trên nửa khoảng





0; .



Do đó









 

2 2 2 2 2 2 2

x x x x x x

f m f m m       

Đặt

2 , 0.

a a

 

Khi đó





có dạng

m a a

 

Bảng biến thiên hàm





g a a a

 

Phương trình đã cho có nghiệm khi

 

mà

nguyên dương nhỏ hơn 2021 nên





1;2;3;....., 2020 .

m 

Vậy có

2020

giá trị

thỏa mãn yêu cầu bài toán.

Câu 24. Cho phương trình

2 4 3

3 2 .

x mx m

x m

  



 



Có bao nhiêu số nguyên

để phương trình có

đúng hai nghiệm phân biệt thuộc đoạn





6;0



Lời giải

Chọn D

Điều kiện

x m

 

Với điều kiện trên

2 4 3

3 2

x mx m

x m

  



 



   

2 2

2 1

3 2

x m m

x m

   



  



Đặt

, 0

t x m t

  

ta được:

 

2 1

3 2

t m

  



 





Nhận thấy: Hàm số

 

2 1

3 2

t m

f t

  

 

đồng biến trên khoảng







Hàm số

 

g t



 nghịch biến trên khoảng







Và









2 2

f m g m

  

. Vậy





có nghiệm duy nhất

t m

 

Khi đó

2 2

x m m

x m

 



   



 



NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC

CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 15

Để phương trình có đúng hai nghiệm phân biệt thuộc đoạn

 

6;0

6 2 2 0

2 2 2 1 4

2 2

m m

   





    





 

 

   





  



Do m nguyên nên

 

1;3;4m  .

Câu 25. Tổng tất cả các giá trị nguyên của

để phương trình

 

3 3 3 2 3

3 9 24 .3 3 1

x m x x x

x x x m

   

     

có 3 nghiệm phân biệt là

27.

34.

38.

45.

Lời giải

Chọn A

 

   

 

3 3 3 2 3

3 3 3

3 3 3 3

3 9 24 .3 3 1

3 3 27 3 .3 3 1

3 3 3 27 3 3 1

3 ; 3

1 3 27 27 3 3 3 .

x m x x x

m x x

b a b a

x x x m

x m x

a x b m x

b a b a

   

 

     

 

       

 

       

   

         

Xét

   

3 2

3 3 .ln 3 3 0 ,

t t

f t t f t t t



       



     

3 2

3 3 3 3 9 24 27.f a f b a b x m x m x x m x x x                 

Xét hàm số

 

3 2

9 24 27f x x x x    

có

   

3 18 24 0 2 4.f x x x f x x x

 

         

Bảng biến thiên hàm số

 

3 2

9 24 27f x x x x    

Dựa vào BBT suy ra

 

7 11 8;9;10 .m m   

Vậy tổng các giá trị của

bằng

Câu 26. Gọi S là tập chứa tất cả các giá trị nguyên thuộc đoạn

 

40;40 của tham số m để phương

trình

2 2 4 3 2

2 2 4 2 4 0

x mx

x mx x mx

 

      có hai nghiệm phân biệt không âm. Số phần tử

của tập

là:

. B.

. C.

. D.

Lời giải

Chọn B

Ta có

2 2 4 3 2

2 2 4 2 4 0

x mx

x mx x mx

 

     

   

2 2 2 2 2 2

2 2 2 2 2 2 4 6 0

x mx

x x mx x mx x

 

          .

Đặt

2 2t x mx  

   

2 2 2 2

2 2 4 6 0 2 2 1 2 2 1 4 0

t t

x t t x t x x            

NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC

Trang 16 TÀI LIỆU ÔN THI THPT QUỐC GIA













2 4 2 2 1 0 *

t x     

TH1: Nếu



thì





luôn đúng.

TH2: Nếu

















2 2 4 0; 2 2 1 0 * *

t t x VT VP         .

TH3: Nếu

















2 2 4 0; 2 2 1 0 * *

t t x VT VP         .

Vậy

 

2 2

* 2 2 2 2 2 0

t x mx x mx

x m





         







Để phương trình có hai nghiệm phân biệt không âm thì

2 0 0

m m

  

Vì





40;40 ,m m

   



có 40 giá trị của

thỏa mãn.

_______________ TOANMATH.com _______________

Bấm Tải xuống để xem toàn bộ.

| 1/16

| | Tải xuống

Preview text:

NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
PHƯƠNG TRÌNH MŨ CHỨA THAM SỐ PHƯƠNG PHÁP
Phương trình một ẩn chứa tham số có dạng : f  x, m  0   1 , với m là tham số.
Phương pháp biện luận số nghiệm bằng bảng biến thiên (cô lập tham số):
 Bước 1 : Chúng ta tiến hành cô lập tham số m , nghĩa là chúng ta biến đổi phương trình  
1 về dạng phương trình h m  g  x 2 , trong đó hm là biểu thức chỉ có
tham số m và g  x là biểu thức chỉ có biến x .
 Bước 2 : Lập bảng biến thiến hàm g .
 Bước 3 : Biện luận số nghiệm phương trình và kết luận.
Phương pháp biện luận số nghiệm bằng tam thức bậc hai
 Bước 1 : Biến đổi phương trình  
1 về phương trình bậc hai 2 . a t  . b t  c  0 2.
 Bước 2 : Dựa vào định lý so sánh nghiệm với một số  Bước 3 : Kết luận Kiến thức bổ trợ :
Định lý so sánh nghiệm của phương trình bậc hai với một số Xét   2
f x  ax  bx  c có hai nghiệm x , x , khi đó : 1 2  x    x  . a f   0 . 1 2    . a f    0 
   x  x  S  2 . 1 2   0   . a f    0 
 x  x    S  2 . 1 2   0 
Hệ quả (so sánh nghiệm của phương trình bậc hai với hai số) Xét   2
f x  ax  bx  c có hai nghiệm x , x , khi đó : 1 2  . a f    0   . a f    0
   x  x    1 2 2  S  2    0  . a f    0
   x    x  1 2   . a f     0 Câu 1. Có bao nhiêu giá trị nguyên của tham số m để phương trình 2  x     2 1 1 1 1 4 2 .2 x m
 2m 1  0 có bốn nghiệm phân biệt? A. 0 . B. 2 . C. 3 . D. 4 . Lời giải Chọn A Phương trình 2  x     2 1 1 1 1 4 2 .2 x m  2m 1  0   1 Điều kiện: 2 1 x  0  1   x 1. Đặt 2 1 1 2 x t    , 2  t  4 .
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 1
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC Phương trình   1 trở thành: 2
t  m  t  m    mt   2 2 2 1 0 2  t  2t 1 2 t  2t 1
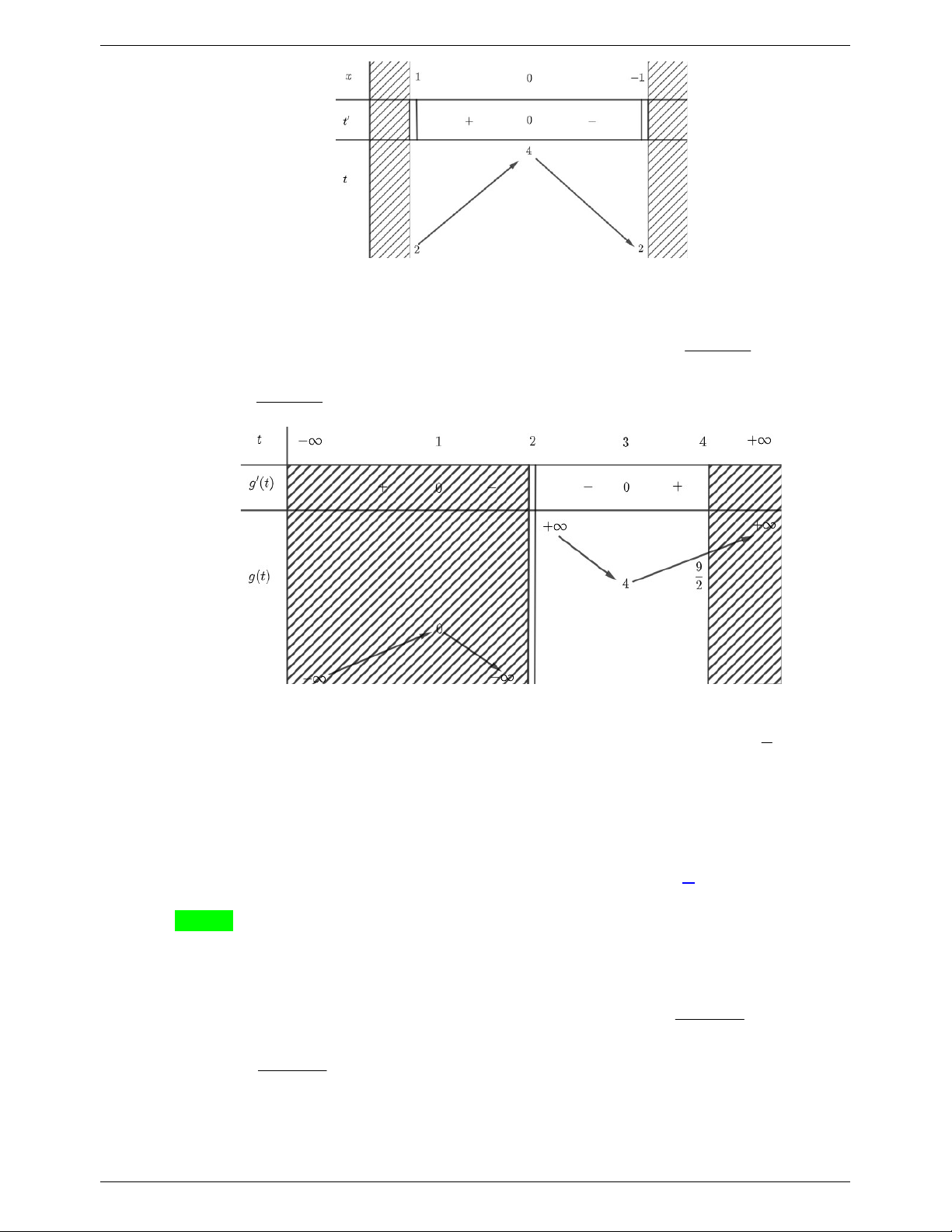
Ta thấy, t  2 không thỏa mãn phương trình, suy ra t  2 nên ta có m  2 t  2 2 t  2t 1 Đặt g t  . t  2 Để phương trình  
1 có bốn nghiệm x , x , x , x phân biệt thì phương trình 2 có hai nghiệm 1 2 3 4 9
t ,t sao cho 2  t  t  4 . Do đó, dựa vào bảng biến thiên chúng ta được 4  m  . 1 2 1 2 2
Mà m    không có giá trị của m thỏa mãn.
Câu 2. Có bao nhiêu số nguyên m để phương trình    1 .16x  22   1 .4x m m  6m 1  0 có hai nghiệm phân biệt? A. 1. B. 2 . C. 3 . D. 4 . Lời giải Chọn D Phương trình:    1 .16x  22   1 .4x m m  6m 1  0   1 . Đặt 4x t  , t  0 . 2 t  2t 1 Phương trình   1 trở thành: m   2 1 .t  22m  
1 .t  6m 1  0  m  2 . 2   t  4t  6 2 t  2t 1 Đặt f t  . 2 t  4t  6 Trang 2
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC Để phương trình  
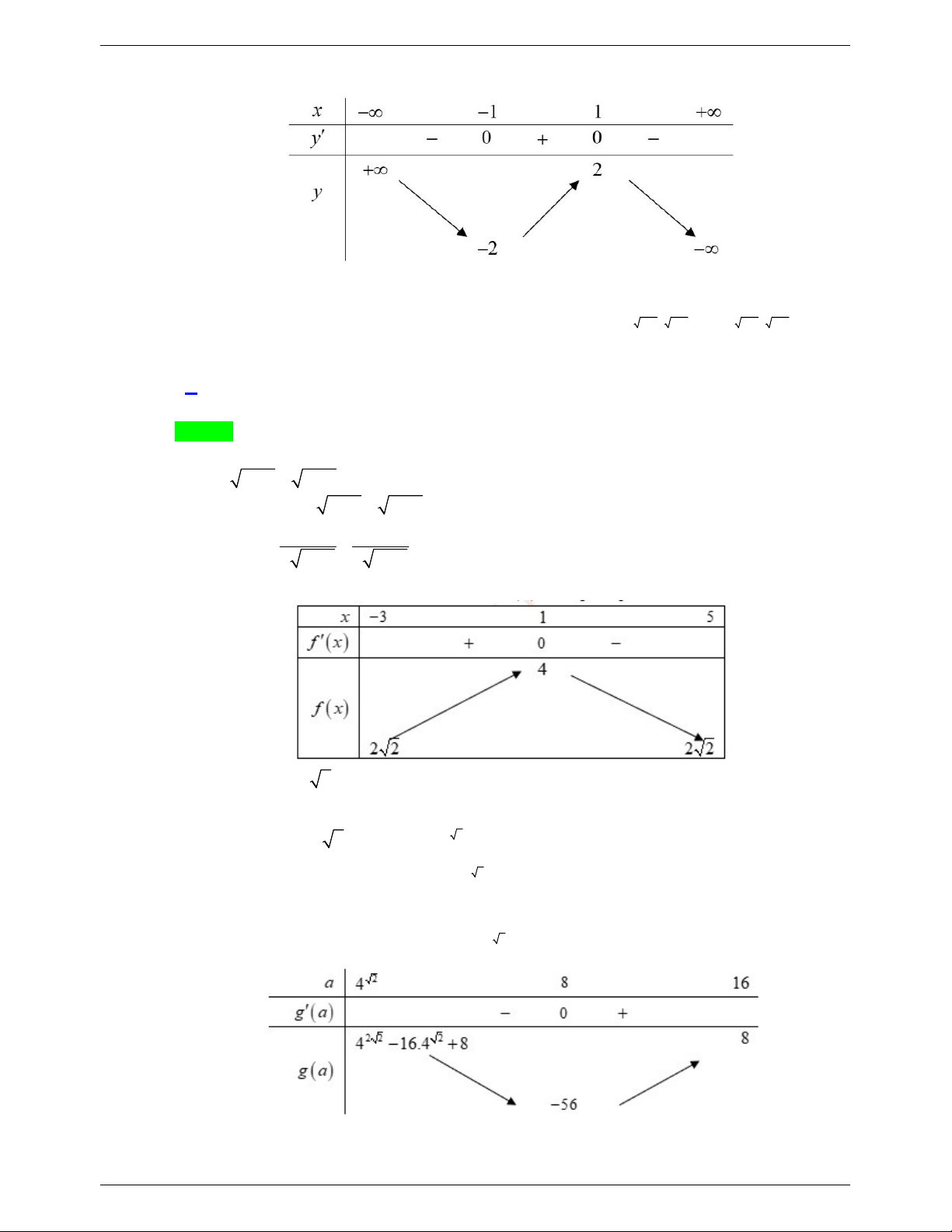
1 có hai nghiệm x , x phân biệt thì phương trình 2 có hai nghiệm t ,t 1 2 1 2 11
sao cho 0  t  t . Do đó, dựa vào bảng biến thiên, chúng ta được 1  m  . 1 2 2 Vậy m 2;3;4;  5 . Câu 3. Có bao nhiêu giá trị nguyên của tham số m để phương trình x x    2    x  2 27 2 .18 1 .12  .8x m m m m m
 0 có ba nghiệm phân biệt. A. 1. B. 2 . C. 3 . D. 4 . Lời giải Chọn A
Biến đổi phương trình như sau: 27 x  2 . m 18 x   2 m  m   1 .12 x   2 m  m .8x  0  1 3 x 2  3  2 . m 3 x.2 x   2 m  m   x 2 1 .3 .2 x   2 m  m  3 .2 x  0 3 x 2  3   3 x x      2 . m       3 2 m  m   1 .     2 m  m   0  2   2   2   3 x 
Đặt t    , điều kiện t  1.  2 
Khi đó phương trình trở thành t  1 3 2 t  mt   2 m  m   2 2 1 t  m  m  0   t  m  . t  m 1   3 x  Với t  1 thì 1  x  0  x  0  
. Suy ra phương trình  
1 có ít nhất 1 nghiệm x  0 .  2  m 1  1 m  2 Để phương trình  
1 có ba nghiệm x , x , x phân biệt thì     1  m  2 . 1 2 3 m  1  m  1 Vậy m  2 .
Câu 4. Cho phương trình   5.3x  2  2.2x. 3x  1 .4x m m m
 0 , tập hợp tất cả các giá trị của
tham số m để phương trình có hai nghiệm phân biệt là khoảng a;b . Tính S  a  b . A. S  4 . B. S  5 . C. S  6 . D. S  8 . Lời giải Chọn D
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 3
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
Ta có   5.3x  2  2.2x. 3x  1 .4x m m m  0   1 x x       m   3     m   3 5 . 2 2 .  1 m  0 . 4  2      x  3  Đặt t     , điều kiện t  0 . 2   
Khi đó phương trình trở thành: m   2
5 t  2m  2t 1 m  0 2 .
Do đó để phương trình  
1 có hai nghiệm phân biệt thì phương trình 2 có hai nghiệm dương m  5 a  0 2   2 m  4m  3 m  5  0     0  m  3 phân biệt    2  2m     3  m  5  m    3;5 0 . P  0 m  1   m  5  S  0 1 m 1   m  5   0 m  5
Vậy a  3 , b  5 nên S  a  b  8 .
Câu 5. Gọi S là tập hợp các giá trị nguyên của m sao cho phương trình 5 5      m   2 2x 2x x x 2  m   2 4 2 .3 2 1 .3
 2m  6  0 có nghiệm. Tổng các phần tử của S bằng A. 18 . B. 12. C. 20 . D. 14. Lời giải Chọn A 5 5      m   2 2x 2x x x 2  m   2 4 2 .3 2 1 .3  2m  6  0   1 . 2 5  1  2 x x x 1    Đặt 4  2 t 3 3     3. Phương trình   1 trở thành m   2 2 t  2m   1 t  2m  6  0 2  2t  2t  6 m 2t  t   2 2
2  2t  2t  6  m  2 (vì 2 t  2t  2  0, t  ). 2 t  2t  2 Phương trình  
1 có nghiệm  2 có nghiệm t  3  đường thẳng y  m cắt đồ thị hàm số 2   f t  2t 2t 6 
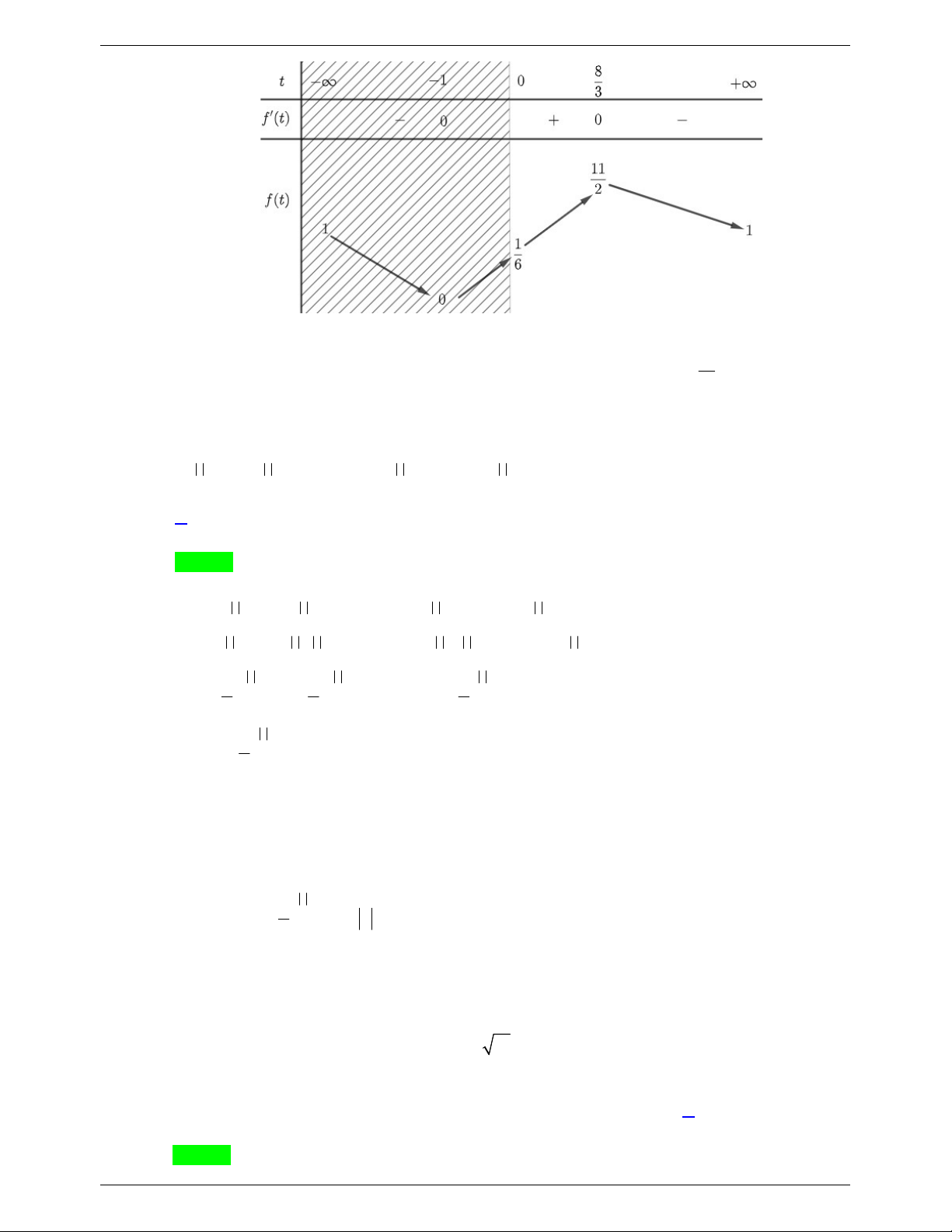
tại điểm có hoành độ t  3 . 2 t  2t  2  4 2 2t  2t  6 2 6t  4t 16 t  L Xét hàm số f t 
với t 3;  có: f t    0   3 . 2 t  2t  2 t 2t 22 2  t  2   L Ta có bảng biến thiên: Trang 4
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
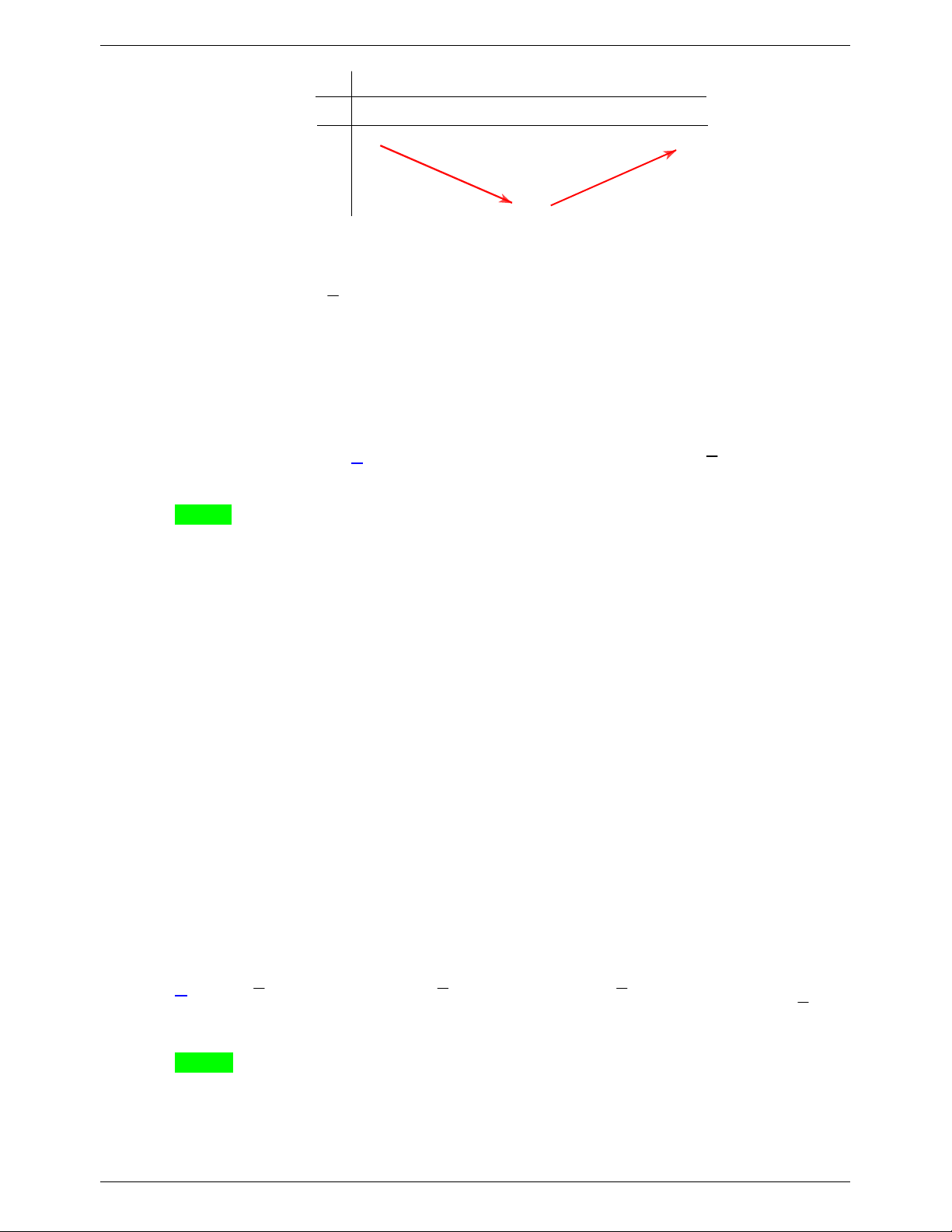
Từ bảng biến thiên suy ra  
1 có nghiệm  2  m  6  S  3;4;5;  6 .
Tổng các phần tử của S bằng 3  4  5  6  18 .
Câu 6. Cho phương trình 9x  22   1 3x m  34m  
1  0 có hai nghiệm thực x , x thỏa mãn 1 2
x  2 x  2 12 . Giá trị của m thuộc khoảng 1  2  A. 9;  . B. 3;9 . C. 2;0 . D. 1;3 . Lời giải Chọn D Đặt 3x t 
, t  0 . Phương trình đã cho trở thành: 2 t  22m   1 t  34m   1  0 (1)
Phương trình đã cho có hai nghiệm thực x , x khi và chỉ khi phương trình (1) có hai nghiệm 1 2 dương phân biệt   2 m  1   0 4m 8m  4  0  m  1    
 S     m   1 0 2 2 1  0  m     1 . m  P      3  4m   2 0 1  0  4  1 m   4
Khi đó phương trình (1) có hai nghiệm là t  4m 1 và t  3 . Với t  4m 1 thì 1
3x  4m 1  x  log 4m 1 . 1 3   Với t  3 thì 2 3x  3  x  1. 2
Ta có  x  2 x  2  12  x  2  log 4m 1  5
2  m  (thỏa điều kiện). 3   1  2  1 2 5
Vậy m  là giá trị cần tìm nên m thuộc khoảng 1;3 . 2 x x
Câu 7. Phương trình 2  3  1 2a2  3  4  0 có 2 nghiệm phân biệt x , x thỏa mãn 1 2 x  x  log
3. Khi đó a thuộc khoảng 1 2 2 3  3   3   3  A. ;    . B. 0;  . C. ;     . D.  ;    .  2   2   2  Lời giải Chọn D x
Đặt t  2  3 , t  0 1 2a Phương trình trở thành 2 t 
 4  0  t  4t 1 2a  0 (1) t x x
Phương trình có 2 nghiệm phân biệt x , x thỏa mãn x  x  log 3  2  3  3 1 2 2 3   1 2 1 2  x 2  3 1 x x   3  2  3
 3 2  3 . Khi đó t  3t . 1 2 2 x   1   2 2 3
YCBT Phương trình (1) có 2 nghiệm dương phân biệt thỏa mãn t  3t 1 2
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 5
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC   0 3    2a  0 t  0; t  0 1 2    3  t  3 a   1  t   t  4     2  a  1  . 1 2 t  1   2 t .t  1 2a a  1 1 2  t t 1 2a  1 2 t   3t  1 2 Câu 8. Tìm số giá trị nguyên của tham số
m  10;10 để phương trình   2x m  2x 2 x 1 10 1 10 1 2.3     
có đúng hai nghiệm phân biệt? A. 14. B. 15 . C. 13 . D. 16 . Lời giải Chọn B 2 2 x x  x x       10   2 1  m 10   2 2 x  10 1 10 1 1 1  2.3     m   6  (1) 3   3      2 2 x x  10 1  10 1 1 Đặt t    , t  1      . Khi đó (1) trở thành 3   3  t     1 2 t  .
m  6  t  6t  m  0 (2) t
(1) có đúng hai nghiệm phân biệt khi và chỉ khi (2) có một nghiệm lớn hơn 1. 2 (2)  m  t   6t . Xét hàm số 2 f (t)  t
  6t trên khoảng (1;) , ta có:
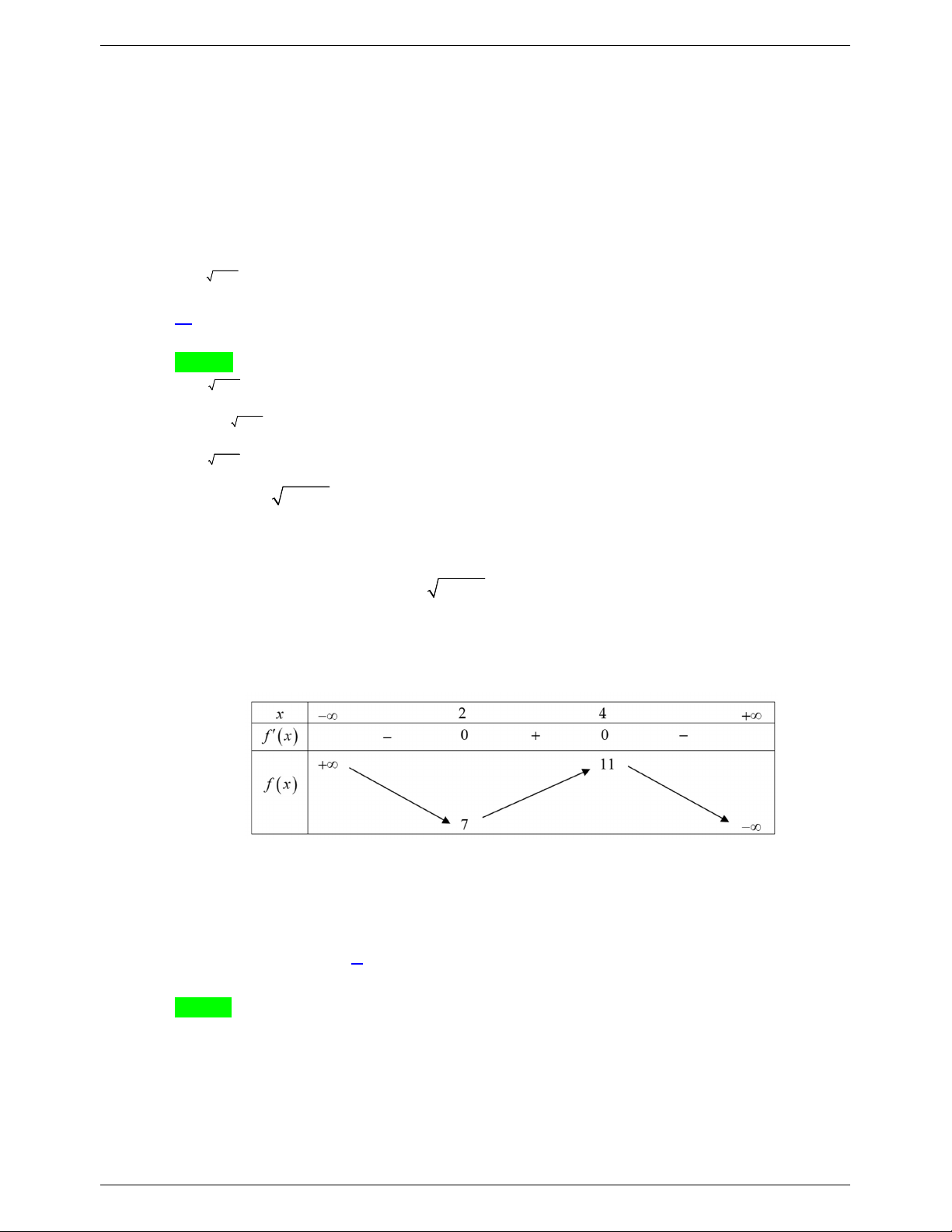
f t   2t  6; f t   0  t  3 . Bảng biến thiên:
Dựa vào bảng biến thiên ta thấy m  5 hoặc m  9 là giá trị thỏa mãn yêu cầu bài toán.
Do m  10;10 nên m  9;8;7;6;5;4;3;2;1;0;1; 2;3; 4;  9 .
Suy ra có 15 giá trị m cần tìm.
Câu 9. Số các giá trị nguyên của tham số m để phương trình:    1 .16x  22 3.4x m m  6m  5  0
có hai nghiệm trái dấu là A. 4 . B. 8 . C. 1. D. 2 . Lời giải Chọn D Đặt  4x t
,t  0 , phương trình đã cho trở thành: m   2
1 t  22m 3t  6m  5 0 (*).
Đặt f  x  m   2
1 t  2 2m 3t  6m  5 .
Phương trình đã cho có hai nghiệm x , x trái dấu khi phương trình (*) có hai nghiệm t ,t thỏa 1 2 1 2 mãn: 0 t 1 t . 1 2 Trang 6
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC 4 m  1   m   1 f   1 0   m   1 3m 12 0       m 1 
Điều đó xảy ra khi:           .  m   f     m   m  4 m 1 1 0 0 1 6 5 0        5 m   6
Vậy có hai giá trị nguyên của tham số m thỏa mãn bài toán là m   3 và m   2 . Câu 10. Có bao nhiêu giá trị nguyên của tham số m để phương trình x x    2   x x x   3 m   3 8 3 .4 3 1 .2 1 x  m  
1 x có đúng hai nghiệm phân biệt thuộc 0;10 A. 101. B. 100 . C. 102 . D. 103 . Lời giải Chọn A x x    2   x x x   3 m   3 8 3 .4 3 1 .2 1 x  m   1 x (1)   x  3   x x  x  mx3 2 2  mx 2 Xét hàm số   3 f t  t  t 1   2x 1024 Ta có  2x t  x mà 0  10   1  2x x
 x  1034 1  t 1034 0  x  10  Xét hàm số f t  3
 t  t,t 1;1034. f t 2  3t 1  0, t
 1;1034 hay   3
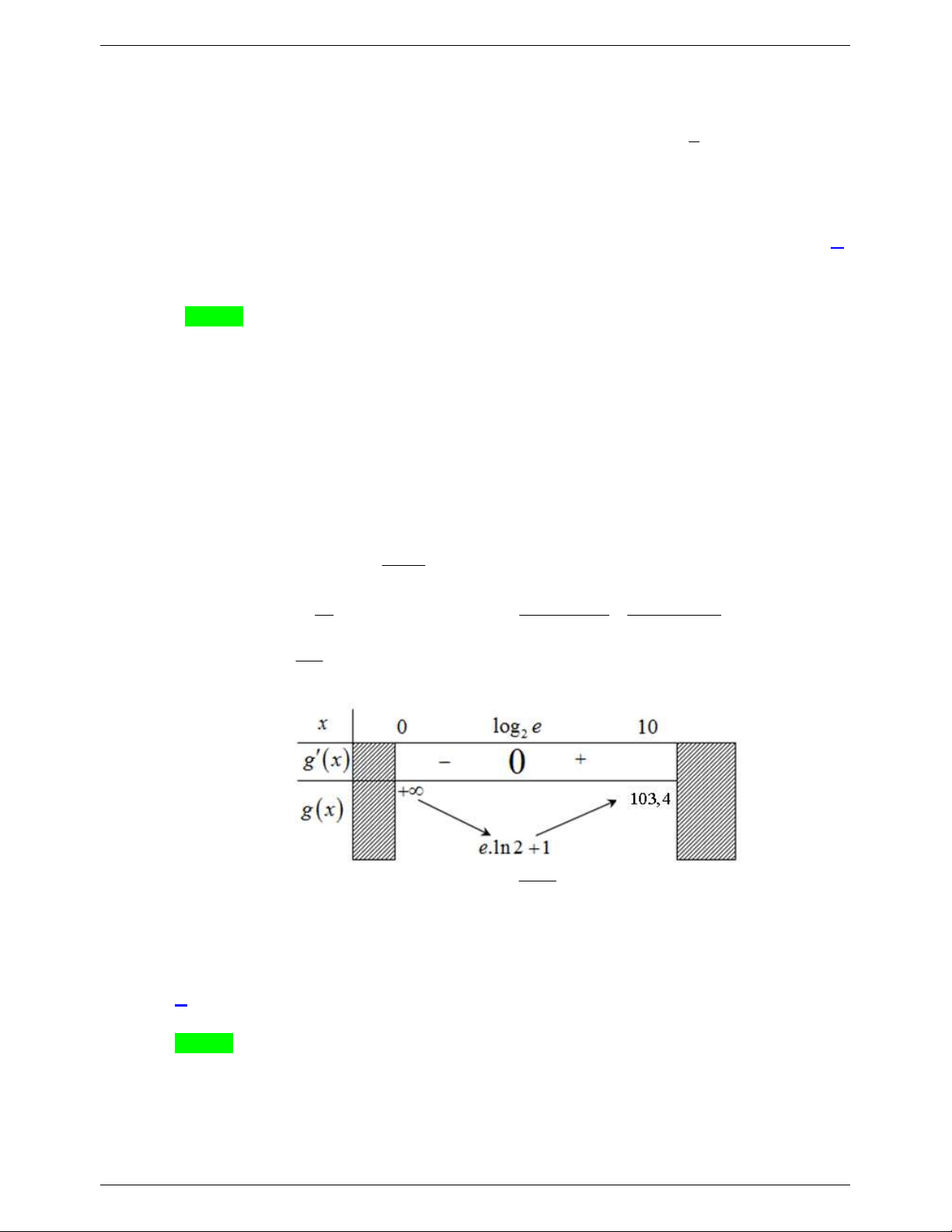
f t  t  t đồng biến trên 1;1034 x  x Suy ra   x 2 2  2  x  mx   m . x 2x . x 2x ln 2  2x 2x . x ln 2 1 Xét hàm số g  x 
1, x 0;10.  gx     x 2 2 x x g x 1  0  x   log e 2 ln 2 BBT ycbt  .
e ln 2 1  m  103, 4 mà m  Z nên m  3;103.
Có tất cả 101 số nguyên m thoả mãn.
Câu 11. Tính tổng các giá trị nguyên của tham số m thuộc đoạn 5;5 để phương trình x x 1 9 2.3  
 2m 1  0 có duy nhất một nghiệm. A. 10 . B. 15 . C. 0 . D. 7 . Lời giải Chọn A x x 1 9 2.3  
 2m 1  0 9x  6.3x  2m 1  0  1 Đặt 3x t 
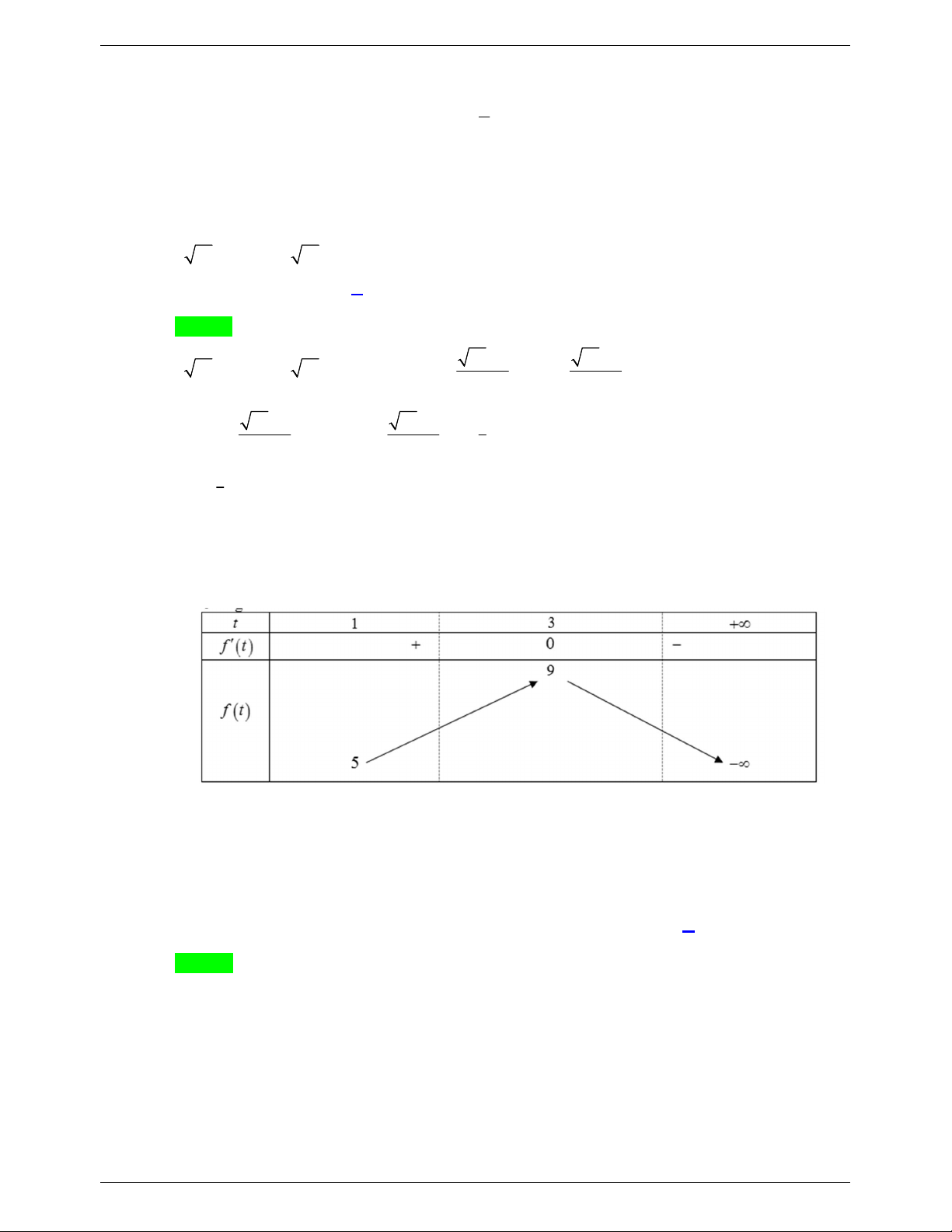
, t  0 . Phương trình trở thành 2 t  6t 1  2m . Xét hàm số g t 2
 t  6t 1, g 't  2t  6 g 't  0  t  3 Bảng biến thiên
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 7
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC t 0 3 + ∞ g'(t) - 0 + -1 + ∞ g (t) -10
Dựa vào bảng biến thiên suy ra phương trình đã cho có nghiệm duy nhất khi    m 5 2m  1  0    1   2m  1  m   2
Mà m 5;5 và m   nên m 5;4;3;2;1;0;  5
Vậy tổng các giá trị của m là 5  4  3  2 1 0  5  10 .
Câu 12. Gọi S là tập hợp các giá trị của tham số m sao cho hai phương trình 2 2 1 3m x   và x 2
m  3  2x  x 1 có nghiệm chung. Tính tổng các phần tử của S . 5 A. 6 . B. 3 . C. 1. D. . 2 Lời giải Chọn B
Vì hai phương trình đã cho có nghiệm chung nên hệ sau có nghiệm 2  2x 1  3m  m  log 2x 1 3  2    
 log 2x 1  3x  2x  x 1 x 2  2  2 3 x 2 m  3  2x  x 1 m   3  2x  x 1  log 2   log  2  3 2 x x 1 2 2 1  2 1  3   3  log  2 2 1  3x x x x x  x . 3 3  Xét hàm số    3t f t
 t xác định trên   '   3t f t
.ln 3 1  0 suy ra hàm    3t f t  t
đồng biến trên  suy ra log  2 2   2 1   2 1  3x x x x . 3 Xét hàm số   2  2 1 3x g x x
xác định và liên tục trên  . Ta có g  x x  x   g  x x 2    g  x x 3 ' 4 3 ln 3 ' 4 3 ln 3 ' '
 3 ln 3  0 . Suy ra hàm số g ' x
nghịch biến trên  . Do đó g  x  0 có nhiều nhất là 3 nghiệm. x  0 m  0 
Ta lại có g 0  g  
1  g 2  0 . Suy ra phương trình 2 2x 1 3x x 1       m 1   . x  2 m  2   Vậy S  3 .
Câu 13. Tìm tất cả giá trị thực của tham số m để phương trình    1 2x m
 3m  4  0 có nghiệm? m 1 4 4 4 A. 1  m  . B. m  . C. 1 m  . D.  4 . 3 3 3 m   3 Lời giải Chọn A Ta có    1 2x m  4  3m .
Trường hợp 1: m 1  0  m  1 . Phương trình thành 0.2x  1  phương trình vô nghiệm. Trang 8
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC  m x 4 3
Trường hợp 2: m 1  0  m  1 . Ta có 2  . m 1 4  3m 4
Phương trình có nghiệm khi  0  1 m  m 1 3
Câu 14. Tìm tất cả giá trị nguyên của tham số m thuộc 10;10 để phương trình x    m x 2 9 4 3
3  2m  5m  3  0 có hai nghiệm phân biệt? A. 20 . B. 21. C. 8 . D. 9 . Lời giải Chọn C Đặt  3x t
,t  0 . Khi đó ta có phương trình 2 t    m 2 4 3
t  2m  5m  3  0 (*) .
Phương trình đã cho có hai nghiệm phân biệt  pt * có hai nghiệm phân biệt dương      2  m 2 m  4m  4  0 m  2     4  3  m  4  0  m    3 .  3 m  2 2m  5m  3  0     2 m 1  3 m   2 m  2  Vậy 
3 thì phương trình có hai nghiệm phân biệt. m   2 x  m 1 Nhận xét: phương trình 2 t    m 2 4 3
t  2m  5m  3  0   . x  2m  3  m 1  2m  3 m  2 m  2   
Phương trình có hai nghiệm phân biệt dương  m 1  0  m 1   3 . m  2m 3 0  3      2 m   2
Mà m   và m thuộc 10;10 nên m 3;4;5;6;7;8;9;1  0 .
Câu 15. Tìm tất cả giá trị thực của tham số m để phương trình 6x    33x  9.2x m  9m  27  0 có
nghiệm thuộc khoảng 0;2 ? A. 1  m  3 . B. 1  m  2 . C. m   . D. 3  m  7 . Lời giải Chọn A
Ta có 6x    33x  9.2x m
 9m  27  0  3x 92x  m 3  0 3x  9  0 x  2     . 2x  m  3  0 2x  3 m
Ta có 0   2  1  2x x  4 .
Để phương trình có nghiệm thuộc khoảng 0;2 thì 1  3  m  4  1  m  2
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 9
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC Câu 16. Cho phương trình 3m m    2 x   x  2 10 10 2 1
1 x 1 x  . Tìm tập hợp các giá trị của tham
số m để phương trình có nghiệm.  1  1   1   1  A. 0; log 2   . B. log 2;    . C. 0;   . D.  ;  log 2  .  2   2   10  2    Lời giải Chọn D
Điều kiện: x 1;  1 Ta có 3m m    2 x   x  2  x  x    2 x   x  2 10 10 2 1 1 1 1 2  2x 1 x  m m       x 
 x x   x 2 3 2 2 10 10 1 1 1   m m    x   x 3 3 2   2 10 10 1 x  1 x  (*) Xét hàm h t  3  t  t  ht 2
 3t 1  0,t   nên từ phương trình (*) ta được:  2      m 2 1 10   1 10m h x x h x x (**) 2 1 x  x 1 Xét f  x 2
 x  1 x , x 1;  1 ta có f  x 
; f  x  0  x  1;  1 . 2 1 x 2 Phương trình đã cho có nghiệm khi phương trình (**) có nghiệm   m 1 1  0 10  f
 2  m  log 2  log 2   .  2  2 Câu 17. Cho phương trình 3 2 2 x x 2xm x x 3 e  e
 x  3x  m  0 . Tập tất cả các giá trị thực của m để
phương trình có 3 nghiệm phân biệt có dạng  ;
a b . Tổng a  2b bằng A. 1. B. 0 . C. 2 . D. 2 . Lời giải Chọn D Ta có: 3 2 2 x x 2xm x x 3 e  e  x  3x  m  0 3 2 2 3 2 x x  xm x  x x  x  xm              2 2 3 2 3 2 x x e e x x m e x x x m  e   2 3 0 2 x  x (1) Xét hàm số   t
f t  e  t với t   . Ta có   t
f t  e 1  0t   nên hàm số f t  đồng biến trên  . Phương trình   1 có dạng f  3 2
x  x  x  m  f  2 2 x  x Suy ra 3 2 2 3
x  x  2x  m  x  x  m  x  3x (2)
Bài toán trở thành tìm tập các giá trị của m để phương trình 2 có 3 nghiệm phân biệt. Trang 10
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
Ta có bảng biến thiên của hàm số g  x 3  x  3x như sau
Từ bảng biến thiên suy ra m 2;2 hay a  2
 ;b  2 . Vậy a  2b  2 .
Câu 18. Tìm tất cả các giá trị nguyên của tham số m để phương trình x3 5x x3 5 4 16.2 x  8  m có nghiệm. A. 65 . B. 64 . C. 11. D. 12. Lời giải Chọn A
Điều kiện 3  x  5
Đặt t  x  3  5  x .
Xét hàm số f  x  x  3  5  x trên 3;5. 1 1 Ta có f  x  
; f  x  0  x 1. 2 x  3 2 5  x
Bảng biến thiên của hàm số f x trên 3;5:
Từ đó suy ra t  2 2;4   .
Khi đó ta có phương trình: t t 4 16.2  8  m . Đặt 2t a  , do t  2 2; 4     nên 2 a 4 ;16   . Ta có phương trình 2 a 16a  8  m . Xét hàm số g a 2  a 16a  8 với 2 a  4 ;16   .
ga  2a 16; ga  0  a  8
Bảng biến thiên của hàm số g a với 2 a  4 ;16   .
Từ bảng biến thiên ta thấy để phương trình có nghiệm thì thì 56  m  8 .
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 11
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
Do m nguyên nên nên có 65 giá trị.
Câu 19. Điều kiện của tham số m để phương trình 2  x     2 1 1 1 1 4 2 2 x m
 2m 1  0 có nghiệm là
đoạn a;b . Giá trị của b  a bằng 23 23 35 35 A. .  . C. . D.  . 12 B. 12 12 12 Lời giải Chọn A
Điều kiện 1  x  1 Đặt 2 1 1 2 x t    , khi x  1  ;  1 ta có 2 1 1 x 1;2. Khi đó t 2;4 .
Bài toán trở thành: Tìm điều kiện của tham số m để phương trình 2
t  m  2t  2m 1  0 có nghiệm trên 2; 4  mt   2
2  t  2t 1 có nghiệm trên 2;4 2    m  f t  t 2t 1 
có nghiệm trên 2; 4 (do t  2  0t 2;4 ). t  2 2 t  4t  3 Ta có f 't   0t  2;4 . 2   t  2
Phương trình có nghiệm khi và chỉ khi f    m  f   25 9 4 2    m   . 6 4
Câu 20. Tìm tập hợp các giá trị của tham số m để phương trình 2 log2 x  m   log2 x 2 3 2 3 .3
 m  3  0 có hai nghiệm phân biệt x , x thỏa mãn: x x  4 . 1 2 1 2 m   6 A. m  6 . B.  . C. m   6 . D. m  1. m   6 Lời giải Chọn A ĐK: x  0 . - Ta có: 2 log2 x  m   log2 x 2 3 2 3 .3  m  3  0 2log2 x   m   log2 x 2 3 2 3 .3  m  3  0 (1). - Đặt log2 3 x t 
, t  0 . Ta được bất phương trình: 2 t  m   2 2 3 t  m  3  0 (2).
Nhận thấy: (1) có hai nghiệm phân biệt khi và chỉ khi (2) có hai nghiệm phân biệt dương   0    m  32 2    6m  6  0 m  1   (m 3) 0 t
  t  2 m  3  0       m  1  (*) 1 2     m  3  0 m  3  0 m  3  2 t t  m  3  0  1 2
Khi đó: (2) có hai nghiệm t , t thỏa mãn: 1 2 2 t .t  m  3 log  log2  1 x 2 x  2 1 x log2 2 x 2  3 .3  m  3 log x log x 2  3  m  3 2  3  m  3 . 1 2 2 1 2 2 m   6
Từ x x  4  log  x x  log2  1 x 2 x  2  2  3  3 2 2
 m  3  9  m  6   . 1 2 2 1 2 m   6
Kết hợp điều kiện (*) ta được: m  6 . Trang 12
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC Câu 21. Tập hợp tất cả các giá trị của tham số m để phương trình 2 2 2 sin x cos x cos 2019  2020  2021 .xlog m có nghiệm là 2 A. 2020 2  m  2 . B. 2021 1 m  2 . C. 2021 0  m  2 . D. 2019 2  m  2 . Lời giải Chọn A Ta có 2 2 2 sin x cos x cos 2019  2020  2021 .xlog m 2 2 2 cos 1cos 2019  2020 x x   log m   2 2   cos 2021 x  2021  2 2 cos x cos  1   2020 x   log m  2019.    1 . 2      4080399   2021  Đặt 2
t  cos x , với 0  t  1 t t     ta có f t  1 2020  2019.    
 nghịch biến trên đoạn 0;  1  4080399   2021  nên f  
1  f t  f 0 , t 0;  1
 1  f t  2020 , t 0;  1 . Phương trình  
1 có nghiệm  1 log m  2020  2020 2  m  2 . 2
Câu 22. Có tất cả bao nhiêu giá trị nguyên của tham số m để phương trình mx     2x  31 1 x 2   m  
  2x 1 có hai nghiệm phân biệt x , x thỏa mãn điều kiện   3  1 2   2 2 x  x  3. 1 2 A. 1. B. 2. C. 3. D. 4. Lời giải Chọn C
Điều kiện xác định: x  0. mx     2  31 1 1 1 x xm 1 1 2 2x 2       2 1  3  3     3 x x m x m x   3xm  x  m  1   3    2x 2x  Xét hàm số    3t f t
 t t  0 . Ta có    3t f t .ln 3 1  0 t 
Suy ra hàm số luôn đồng biến trên tập xác định.  1  1 Do đó f  f   x  m 2 
 x  m  2x  2mx 1  02  2x  2x
Phương trình đã cho có hai nghiệm x , x thỏa mãn điều kiện 2 2
x  x  3 khi phương trình 2 1 2 1 2
có hai nghiệm phân biệt khác 0 và thỏa mãn điều kiện đã cho.  2  '  0 m  2  0   Khi đó 2 2 2.0  2 . m 0 1  0    1
 m  2  0   2  m  2 2  m  2.   3       x  x  2  2x .x  3   2  1 2 1 2
Do m nguyên nên m 1;0;  1
Câu 23. Có bao nhiêu giá trị nguyên dương của tham số m nhỏ hơn 2021 để phương trình   2x  4x m m có nghiệm thực?
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 13
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC A. 2018. B. 2019. C. 2020. D. 2021. Lời giải Chọn C Ta có: x x x x 2   2  4   2   2  2 x  2x m m m m Ta thấy 2x 0, 2x m    0. Xét hàm   2
f t  t  t trên 0;.
Ta có f 't  2t 1  0,t 0;
Suy ra hàm số f t  đồng biến trên nửa khoảng 0;. Do đó  x     x  x x 2 2 2   2  2   2 x  2x f m f m m 2 Đặt  2x a
, a  0. Khi đó 2 có dạng 2 m  a  a
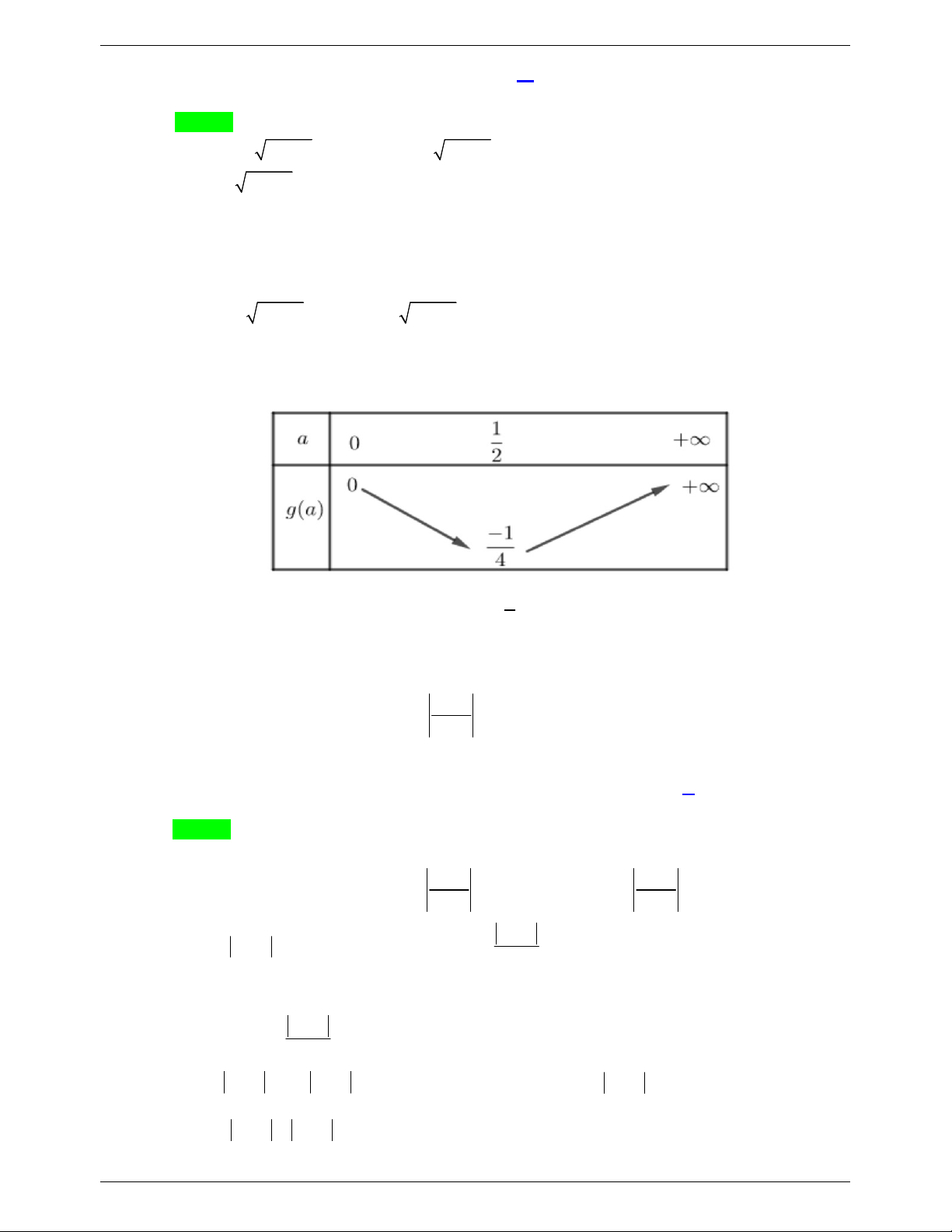
Bảng biến thiên hàm   2 g a  a  a 1
Phương trình đã cho có nghiệm khi m   , mà m nguyên dương nhỏ hơn 2021 nên 4 m 1;2;3;....., 202  0 .
Vậy có 2020 giá trị m thỏa mãn yêu cầu bài toán.    m  x mx m 2
Câu 24. Cho phương trình 2 2 4 3 3  2 
. Có bao nhiêu số nguyên m để phương trình có x  m
đúng hai nghiệm phân biệt thuộc đoạn 6;0? A. 0. B. 1. C. 2. D. 3. Lời giải Chọn D Điều kiện x  m    m      m  x mx m 2 2 2 Với điều kiện trên 2 2 4 3 3  2  x m m 2 1 2  3  2  . x  m x  m 2     m t m 2
Đặt t  x  m , t  0 ta được:  22 1 3  2  * . t 2
Nhận thấy: Hàm số f t t m22 1 3  
 2 đồng biến trên khoảng 0; . m  Hàm số g t 2 
nghịch biến trên khoảng 0; . t
Và f  m  2   g  m  2 . Vậy * có nghiệm duy nhất t  m  2 . x  2 
Khi đó x  m  m  2   . x  2  2m Trang 14
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
Để phương trình có đúng hai nghiệm phân biệt thuộc đoạn 6;0  6   2  2m  0  2  2m  2  1   m  4     . m  2   m  2 2 2m  m
Do m nguyên nên m 1;3;  4 .
Câu 25. Tổng tất cả các giá trị nguyên của m để phương trình 3 x3 m3x   3 2     x3 3 9 24 .3  3x x x x m
1 có 3 nghiệm phân biệt là A. 27. B. 34. C. 38. D. 45. Lời giải Chọn A 3 x3 m3 3 x   3 2
x  9x  24x  m x3 .3  3x 1 3
 3x  m x  x 33 3 3 x3  27  m  3x.3  3x 1   3
 3 m x   x  33 3 3 3
 m  3x  27  3  3 x   1 3 a  3  ; x b  m  3x   b 3 3 a b 3 a 3
1  3  27  b  a  27  3  3  b  3  a . Xét f t  t 3   t  f t t 2 3  3 .ln 3  3t  0 , t     f a  f b 3
 a  b  3 x  m  3x  m  3 x3 3 2
 3x  m  x  9x  24x  27. Xét hàm số f  x 3 2
 x  9x  24x  27 có f  x 2
 3x 18x  24  f x  0  x  2  x  4.
Bảng biến thiên hàm số f  x 3 2
 x  9x  24x  27
Dựa vào BBT suy ra 7  m  11  m  8;9;1 
0 . Vậy tổng các giá trị của m bằng 27
Câu 26. Gọi S là tập chứa tất cả các giá trị nguyên thuộc đoạn 40;40 của tham số m để phương trình 2x2mx2 4 3 2 2
 2x  4mx  x  2mx  4  0 có hai nghiệm phân biệt không âm. Số phần tử của tập S là: A. 25 . B. 40 . C. 60 . D. 30 . Lời giải Chọn B Ta có 2x2mx2 4 3 2 2
 2x  4mx  x  2mx  4  0 2 x 2mx2 2   x  2 x  mx     2 x  mx   2 2 2 2 2 2 2  4x  6  0 . Đặt 2 t  x  2mx  2 PT t 2 2 t
  x t  t  x     t  2 x     2 2 2 4 6 0 2 2 1 2 2x   1  4  0
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 15
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC t    t   2 2 4 2 2x   1  0   * .
TH1: Nếu t  2 thì * luôn đúng. TH2: Nếu t t     t   2 2 2 4 0; 2 2x   1  0 VT   *  VP *. TH3: Nếu t t     t   2 2 2 4 0; 2 2x   1  0 VT   *  VP * . x  0 Vậy * 2 2
 t  2  x  2mx  2  2  x  2mx  0   . x  2m
Để phương trình có hai nghiệm phân biệt không âm thì 2m  0  m  0 .
Vì m 40;40,m    có 40 giá trị của m thỏa mãn.
_______________ TOANMATH.com _______________ Trang 16
TÀI LIỆU ÔN THI THPT QUỐC GIA