



















Preview text:
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
GIẢI PHƯƠNG TRÌNH MŨ BẰNG PHƯƠNG PHÁP HÀM SỐ - ĐÁNH GIÁ
(KHÔNG CHỨA THAM SỐ) PHƯƠNG PHÁP
PHƯƠNG PHÁP HÀM SỐ
Tính chất 1: Nếu hàm số y = f ( x) liên tục và luôn đồng biến (hoặc luôn nghịch biến) trên ( ;
a b) thì phương trình f (x) = k có không quá một nghiệm trên ( ; a b)
Tính chất 2: Nếu hàm số y = f ( x) liên tục và luôn đồng biến (hoặc luôn nghịch biến);
hàm số y = g (x) liên tục và luôn nghịch biến (hoặc luôn đồng biến) trên (a;b) thì phương
trình: f (x) = g (x) có không quá một nghiệm trên (a;b).
Tính chất 3: Nếu y = f ( x) đồng biến hoặc nghịch biến trên ( ;
a b) thì f (u) = f (v)
⇔ u = v , u ∀ ,v ∈( ; a b) .
Tính chất 4: Nếu (n)
f (x) > 0 x ∀ ∈( ; a b) hoặc (n)
f (x) < 0 x
∀ ∈(a;b) thì phương trình
f (x) = 0 có nhiều nhất n nghiệm x∈(a;b) .
Tính chất 5: Cho hàm số y = f ( x) có đạo hàm đến cấp k liên tục trên (a;b). Nếu phương trình (k)
f (x) = 0 có đúng m nghiệm thì phương trình (k− )1 f
(x) = 0 có nhiều nhất là m +1 nghiệm.
Lưu ý: có thể thay ( ;
a b) bằng [a;b], ( ; a b], [ ; a b) .
PHƯƠNG PHÁP ĐÁNH GIÁ
• Quy tắc 1. Giải phương trình f (x) = g(x) .
Xác định x = x là một nghiệm của phương trình. 0 x > x
Chứng minh với mọi 0
thì phương trình vô nghiệm. x < x0
Kết luận x = x là nghiệm duy nhất. 0
• Quy tắc 2. Giải phương trình f (x) = g(x) . f (x) ≤ , m x ∀ ∈ D
Xét trên tập xác định D ta có
⇔ f (x) ≤ m ≤ g(x), x ∀ ∈ D . g(x) ≥ , m x ∀ ∈ D
Phương trình thỏa mãn khi f (x) = g(x) = m .
Hoặc đánh giá trực tiếp f (x) ≤ g(x) ; f (x) ≥ g(x) . Từ đó tìm dấu '' = '' xảy ra .
• Quy tắc 3. Sử dụng tính chất của hàm số lượng giác.
Ta có: sin x ∈[ 1 − ;1];cos x ∈[ 1 − ;1].
Điều kiện để hàm số lượng giác a cos x + bsin x = c có nghiệm là 2 2 2
a + b ≥ c .
Giá trị lượng giác của góc (cung) có liên quan đặc biệt.
Câu 1. Tính tổng tất cả các nghiệm của phương trình sau:
3x + 2x + 4 = 3(x + 2) . A. 1. B. 0 . C. 2 . D. 3. Lời giải Chọn A;
Ta có 3x + 2x + 4 = 3( + 2) ⇔ 3x + 2x x − 3x − 2 = 0
Xét hàm số ( ) = 3x + 2x f x
− 3x − 2 trên .
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 1
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
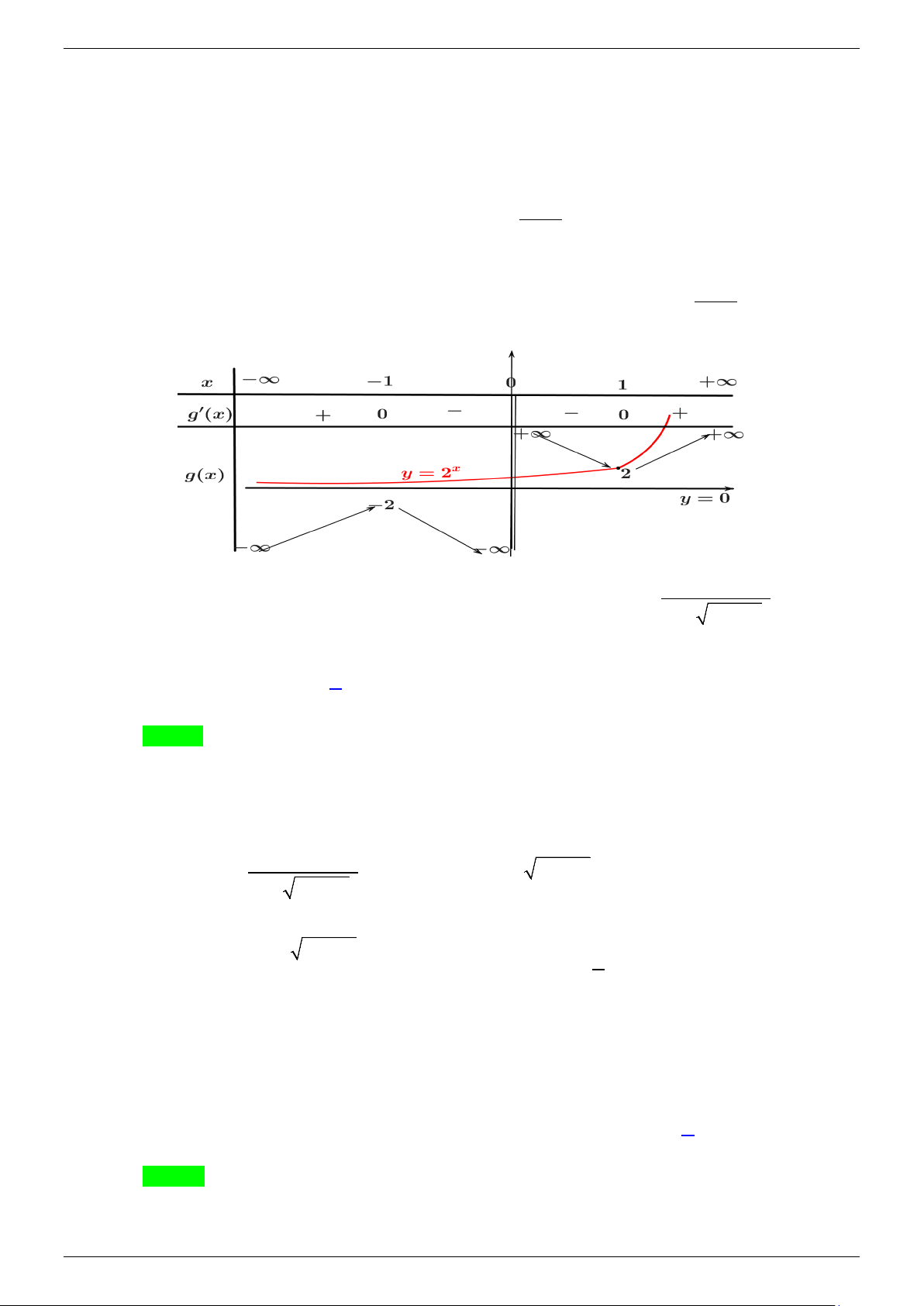
Ta có ′( ) = 3x ln3 + 2x f x ln 2 − 3 Khi đó ′ ( ) x = ( )2 x f x + ( )2 3 . ln3 2 . ln 2 > 0, x ∀ ∈ .
⇒ f ′(x) là hàm đồng biến, liên tục trên ⇒ f ′(x) = 0 có nhiều nhất một nghiệm trên .
Suy ra f (x) = 0 có nhiều nhất là hai nghiệm. Mà ta thấy f ( )
1 = f (0) = 0 ⇒ x = 0; x =1 là hai nghiệm của phương trình.
Vậy phương trình có tập nghiệm S = {0; }
1 . Do đó tổng các nghiệm là 1.
Câu 2. Gọi S là tập hợp mọi nghiệm của phương trình 2 2 x −3x+2 x −x−2 2 − 2
= 2x − 4 . Số phần tử của S là: A. 3. B. 2 . C. 1. D. 4 . Lời giải Chọn C Ta có x − = ( 2
x − x − ) −( 2 2 4 2 x − 3x + 2) .
Phương trình đã cho tương đương 2 2 x −3x+2 2 x −x−2 2 2
+ x − 3x + 2 = 2
+ x − x − 2 ( ) 1 Xét hàm số ( ) = 2t f t + t,( t ∀ ∈ ) . Ta có ′( ) = 2t f t ln 2 +1 > 0, t ∀ ∈ .
Suy ra f (t) là hàm số đồng biến trên tập . Do đó, từ ( ) 1 ta có 2 2
x − 3x + 2 = x − x − 2 ⇔ x = 2 .
Câu 3. Cho phương trình 9x + 9 = 6
− ⋅3x cos(π x), số nghiệm thực của phương trình là A. 1 B. 2 . C. 3. D. vô nghiệm. Lời giải Chọn A
Ta có phương trình x x x 9 9 + 9 = 6
− ⋅3 cos(π x) ⇔ 3 + = 6 − cos(π x) ( *) 3x Mà x 9 3 +
≥ 6; − 6cos(π x) ≤ 6, x ∀ ∈ R . 3x x 9 + = Phương trình 3 6
(*) có nghiệm khi và chỉ khi 3x ⇔ x =1. cosπ x = 1 − 3 cos x cos x
Câu 4. Số nghiệm của phương trình 1 1 − = cos3x trên [0; ] 2021 là? 16 8 A. 1932. B. 1930. C. 1925. D. 1927 . Lời giải Chọn B 3 4cos x 3cos x
Phương trình đã cho tương đương với: 1 1 3 − = 4cos x − 3cos x 2 2 3 4cos x 3cos 1 x 3 1 4cos ⇔ − x = − 3cos x ( ) 1 2 2 Trang 2
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC t t
Xét f (t) 1 = −
t , ta có f ′(t) 1 1
= ln −1< 0, t ∀ ∈ 2 2 2
Suy ra hàm số luôn nghịch biến trên R. Từ ( ) 1 : f ( 3
4cos x) = f (3cos x) π 3 3
⇔ 4cos x = 3cos x ⇔ 4cos x − 3cos x = 0 ⇔ cos3x = 0 ⇔ 3x = + kπ ,(k ∈) 2 π kπ ⇔ x = + ,(k ∈) 6 3 π kπ Theo bài ra ta có: 1 0 ≤ +
≤ 2021 ⇔ − ≤ k ≤1929,41284 . 6 3 2
Vì k ∈ nên có 1930 nghiệm. (x+2)2 1 3 1
Câu 5. Tổng các nghiệm của phương trình x+6 + + x +1 =
+ 9.3 + x + 4 2 − x bằng + 2 x 8 ( )( ) x +4 5 27 5.5 x A. 37 . B. 6 − . C. 3. D. 3 − . Lời giải Chọn D (x+2)2 1 3 1 Ta có: x+6 + + x +1 =
+ 9.3 + x + 4 2 − x + 2 x 8 ( )( ) x +4 5 27 5.5 x 2 2 − x−8 x+8 − x −4x 1 − x +4x 1 + 2 ⇔ 5 − 3 − x −8 = 5 − 3
− x − 4x −1.
Xét hàm số: ( ) = 5−t − 3t f t − t . Có: ( ) 5 t.ln 5 3t f t − ′ = −
− .ln 3−1< 0 với t ∀ ∈ .
Suy ra f (t) là hàm số nghịch biến trên .
Khi đó f ( x + ) = f ( 2 8 x + 4x + ) 1 2
⇔ x + 8 = x + 4x +1 2
⇔ x + 3x − 7 = 0 3 37 x − ± ⇔ = 2 ( hoặc . a c = 7
− < 0 suy ra phương trình có 2 nghiệm phân biệt trái dấu). b
Tổng 2 nghiệm x + x = − = 3 − . 1 2 a
Câu 6. Cho y = f (x) là hàm số chẵn xác định trên , sao cho f (0) ≠ 0 và phương trình
4x − 4−x = f (x) có đúng 10 nghiệm thực phân biệt. Số nghiệm thực của phương trình x − x 2 4 4 x f + = + 2 là 2 A. 10 B. 20 . C. 5. D. 15. Lời giải Chọn B
Từ giả thiết f (0) ≠ 0 ta suy ra x = 0 không phải là nghiệm của hai phương trình
4x − 4−x = f (x) và x − x 2 4 4 x f + = + 2 2
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 3
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC Ta có x − x 2 4 4 x f + = + 2 (*) 2 2x 2−x x f − = ( ) 1
⇔ (2x − 2−x )2 x 2 2 = f ⇔ 2 2x 2−x x f − = − (2) 2 Từ (2) 2−x 2x x f ⇔ − = − (3) 2
Xét phương trình (1) đặt x
t = . Khi đó ta có: 4t − 4−t = f (t ) (4) 2
Theo giả thiết phương trình 4x − 4−x = f (x) có 10 nghiệm phân biệt nên phương trình (4) có 10
nghiệm t . Suy ra phương trình (1) có 10 nghiệm x phân biệt. Giả sử 10 nghiệm đó là x ; x ;...; x 1 2 10
Chứng minh tương tự ta có phương trình (3) có 10 nghiệm phân biệt là −x ;−x ;...;−x 1 2 10
Dễ thấy số nghiệm của phương trình (*) bằng tổng số nghiệm phương trình ( ) 1 và (3) (nghiệm
trùng nhau tính 1 lần) . Vậy ta kết luận phương trình (*) có 20 nghiệm .
Câu 7. Cho tham số thực a . Biết phương trình x − x
e − e = 2cosax có 5 nghiệm
thực phân biệt. Hỏi phương trình x − x
e + e = 2cos ax + 4 có bao nhiêu nghiệm thực phân biệt? A. 10 B. 20 . C. 5. D. 15. Lời giải Chọn A 2 x x − Ta có x − x 2 2
e + e = 2cos ax + 4 ⇔ e − e = 2(cosax + ) 1 x x − ax 2 2
e − e = 2cos (1) 2 ⇔ x x − ax 2 2 e − e = 2 − cos (2) 2
Giả sử x là nghiệm của phương trình x − x
e − e = 2cosax (*), thì x ≠ 0 và 2x là nghiệm của 0 0 0 (1), 2
− x là nghiệm của (2); hoặc ngược lại. 0
Phương trình (*) có 5 nghiệm nên hai phương trình (1), (2) có 5 nghiệm phân biệt. Vậy phương trình x − x
e + e = 2cos ax + 4 có 10 nghiệm phân biệt. π sin x −
Câu 8. Tính tổng tất cả các nghiệm của phương trình 4 e
= tan x thuộc đoạn [0;50π ] ? π π π π A. 1853 . B. 2475 . C. 2671 . D. 2105 . 2 2 2 2 Lời giải Chọn B π
Điều kiện: x ≠ + kπ , k ∈ . 2 π sin x − Phương trình 4 e = tan x Trang 4
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
sin x − cos x
= ln sin x − ln cos x
2 ln cos x − cos x = 2 ln sin x −sin x ⇔ 2 ⇔ . tan x > 0 tan x > 0
+ Khi cos x < 0 và sin x < 0 , xét hàm số f (t) = 2 ln t − t , trên tập [ 1; − 0) . f ′(t) 2 =
−1 suy ra f ′(t) < 0 , t ∀ ∈[ 1; − 0) . t
Nên hàm số f (t) = 2 ln t − t nghịch biến trên [ 1; − 0) .
Mà phương trình 2 ln cos x − cos x = 2 ln sin x − sin x có dạng f (cos x) = f (sin x) .
Nên 2 ln cos x − cos x = 2 ln sin x − sin x ⇔ cos x = sin x ( )1
+ Khi cos x > 0 và sin x > 0, xét hàm số f (t) = 2 ln t − t , trên tập (0; ] 1 f ′(t) 2 =
−1 suy ra f ′(t) > 0 , t ∀ ∈(0; ] 1 . t
Nên hàm số f (t) = 2 ln t − t đồng biến trên (0; ] 1 .
Mà phương trình 2 ln cos x − cos x = 2 ln sin x − sin x có dạng f (cos x) = f (sin x) .
Nên 2 ln cos x − cos x = 2 ln sin x − sin x ⇔ cos x = sin x (2) π π Từ ( )
1 và (2) ta có cos x = sin x ⇔ sin x − =
0 ⇔ x = + kπ , k ∈ . 4 4 π
Do chỉ xét x ∈[0;50π ] nên 0 ≤ + kπ ≤ 50π 1 199 ⇔ − ≤ k ≤ . 4 4 4
Mà k ∈ ⇒ k ∈{0;1;2;3...; } 49 . π π π π
Vậy phương trình đã cho có các nghiệm ; +π; + 2π;...; + 49π . 4 4 4 4 π
Dãy số trên là 50 số hạng đầu liên tiếp của một cấp số cộng có số hạng đầu u = và công sai 1 4 π π
d = π nên tổng các nghiệm trên là 50 2475 S = 2. + 50 −1 π = . 50 ( ) 2 4 2
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 5
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
GIẢI PHƯƠNG TRÌNH MŨ BẰNG PHƯƠNG PHÁP HÀM ĐẶC TRƯNG
(KHÔNG CHỨA THAM SỐ) PHƯƠNG PHÁP
Nếu hàm số y = f (x) đơn điệu trên K thì với mọi u,v∈ K ta có f (u) = f (v) ⇔ u = v .
Nếu hàm số y = f (x) đơn điệu trên K thì trên K phương trình f (x) = 0 có tối đa một nghiệm.
Phương trình f (u) = f (v) .
Bước 1: Biến đổi phương trình về dạng f (u) = f (v) với u,v ∈ K , trong đó y = f (t)
là hàm số đơn điệu trên K )
Bước 2: Khảo sát hàm số y = f (t) để đưa ra tính đơn điệu của hàm số y = f (t) trên K .
Bước 3: Kết luận f (u) = f (v) ⇔ u = v .
Phương trình f (u) = 0 .
Bước 1: Biến đổi phương trình về dạng f (u) = 0 với u ∈ K , trong đó y = f (t) là
hàm số đơn điệu trên K )
Bước 2: Khảo sát hàm số y = f (t) để đưa ra tính đơn điệu của hàm số y = f (t) trên K .
Bước 3: Tìm giá trị u sao cho f (u = 0 . 0 ) 0
Bước 3: Kết luận phương trình f (u) = 0 ⇔ u = u 0
Câu 1. Tính tổng bình phương tất cả các nghiệm của phương trình phương trình 2 4 2 x − x −x − = + (x − )2 2 1 2 5 5 1 . A. 1. B. 5. C. 2 . D. 0 . Lời giải Chọn C 2 4 2 x − x −x − = + (x − )2 2 1 2 5 5 1 2 4 2 x −2 2 x −x 1 − 4 2 ⇔ 5 + x − 2 = 5
+ x − x −1(*). Xét hàm số ( ) = 5t f t
+ t ,t ∈ ⇒ ′( ) = 5t f t ln 5 +1 > 0, x ∀ ∈ .
⇒ y = f (t) là hàm số đồng biến trên . Ta có (*) ⇔ f ( 2
x − ) = f ( 4 2 2 x − x − ) 1 2 4 2
⇔ x − 2 = x − x −1 4 2
⇔ x − 2x +1 = 0 2 ⇔ x =1 ⇔ x = 1
± . Vậy tổng bình phương các nghiệm của phương trình là 2 .
Câu 2. Số nghiệm thực của phương trình 3.2x 4.3x 5.4x 6.5x + + = là A. 1. B. 5. C. 2 . D. 0 . Lời giải Chọn A x x x
Ta có 3.2x 4.3x 5.4x 6.5x + + = 2 3 4 3. 4. 5. ⇔ + + − 6 = 0 . 5 5 5 x x x
Xét hàm số f (x) 2 3 4 3. 4. 5. = + + − 6 5 5 5
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 1
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC x x x ⇒ f ′(x) 2 2 3 3 4 4
= 3. .ln + 4. .ln + 5. .ln < 0, x ∀ ∈ 5 3 5 5 5 5
⇒ hàm số y = f ′(x) nghịch biến trên .
⇒ phương trình f (x) = 0 có nhiều nhất 1 nghiệm trên . Mặt khác ta có hàm số 8 22
y = f (x) liên tục trên và f ( ) 1 = , f (2) = − ⇒ f ( ) 1 . f (2) < 0 . 5 25
Suy ra phương trình f (x) = 0 có nghiều nhất một nghiệm trên khoảng (1;2) .
Vậy phương trình đã cho có đúng 1 nghiệm.
Câu 3. Trên đoạn [ 2021 − ;2022], phương trình sin x 2 2020
= sin x + 2 − cos x có bao nhiêu nghiệm thực? A. 642 . B. 643. C. 1286. D. 1287 . Lời giải Chọn D Ta có sin x 2 2020
= sin x + 2 − cos x sin x 2 ⇔ 2020
= sin x + 1+ sin x (1)
Đặt t = sin x,t ∈[ 1 − ]
;1 , khi đó phương trình ( ) 1 trở thành t 2
2020 = t + 1+ t . Ta có 2 2
1+ t > t = t ≥ t − , t ∀ ∈[ 1; − ] 1 2
⇒ t + 1+ t > 0, t ∀ ∈[ 1; − ] 1 . Nên (2) ⇔ t = log t + 1+ t ⇔ log ( 2
t + 1+ t − t = 0 (2) 2020 ) 2020 ( ) 1
Xét hàm số f (t) = log ( 2
t + 1+ t − t ⇒ f ′(t) = −1< 0, t ∀ ∈[ 1; − ] 1 . 2020 ) 2 1+ t .ln 2020
⇒ Hàm số y = f (t) nghịch biến trên [ 1; − ] 1 . Do đó trên [ 1; − ]
1 phương trình f (t) = 0 có tối đa 1 nghiệm.
Mặt khác f (0) = 0 nên phương trình f (t) = 0 ⇔ t = 0 .
Nghĩa là (2) ⇔ t = 0 ⇒ sin x = 0 ⇔ x = kπ,k ∈ . Với 2021 2022 x ∈[ 2021 − ;2022] ta có 2021 −
≤ kπ ≤ 2022 ⇔ − ≤ k ≤ . π π
Mà k ∈ nên k ∈{ 643 − ; 642 − ;...; } 643 . Vậy trên [ 2021 −
;2022]phương trình có 1287 nghiệm thực.
Câu 4. Có bao nhiêu cặp số nguyên (x; y) thỏa mãn 1≤ x ≤ 2022 và 2 + − 25y = 5y x x . A. 1010. B. 2022 . C. 7 . D. 5. Lời giải Chọn D Theo bài: 2 y y 2 +
− 25 = 5 ⇔ + = 5y + 25y x x x x . Xét hàm f (t) 2
= t + t , (t > 0) .
Ta có: f ′(t) =1+ 2t > 0, t
∀ > 0 ⇒ f (t) là hàm đồng biến trên (0;+∞) .
Vì vậy, (1) ⇔ ( ) = (5y ) ⇔ = 5y f x f x .
Theo giả thiết, 1≤ ≤ 2022 ⇔ 1≤ 5y x
≤ 2022 ⇔ 0 ≤ y ≤ log 2022 . 5
y = 0 ⇒ x = 1
y =1⇒ x = 5
Vì y nguyên nên y = 2 ⇒ x = 25 . Vậy có tất cả 5cặp (x; y) thỏa mãn.
y = 3⇒ x =125
y = 4 ⇒ x = 625 Trang 2
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
Câu 5. Có bao nhiêu số nguyên x , x∈[ 10 − ;10] thỏa mãn 2 x sin 3.3 + 2 +1+ cos 2 = 3 y x y (*) ? A. 2 . B. 3. C. 1. D. 0 . Lời giải Chọn A Ta có: 2 x sin 3.3 + 2 +1+ cos 2 = 3 y x y 2 x 2 sin ⇔ 3.3 + 2 +1+1− 2sin = 3 y x y x+ ⇔ + (x + ) 2 1 sin y 2 3 2 1 = 3 + 2sin y .
Đặt ( ) = 3t + 2 ⇒ ′( ) = 3t f t t f t .ln 3+ 2 > 0, t
∀ ∈ ⇒ Hàm số đồng biến trên .
Vì vậy phương trình ( ) ⇔ f (x + ) = f ( 2 * 1 sin y) 2
⇔ x +1 = sin y 2
⇔ x = −cos y ⇔ 1 − ≤ x ≤ 0 .
Mà x nguyên, x ∈[ 10
− ;10] có 2 giá trị của x thỏa yêu cầu bài toán.
Câu 6. Có bao nhiêu cặp số nguyên (x; y) thỏa mãn x, y ∈[ 1; − 14] và
x + = ( y + )2 − (x + ) 2 1 2 1 2 2 + y + 2y . A. 8 . B. 4 . C. 1. D. 17 Lời giải Chọn B 2 + ≥
Điều kiện xác định y 2y 0 . x +1 ≥ 0
Theo bài x + = ( y + )2 − (x + ) 2 1 2 1 2 2 + y + 2y ⇔ x + = ( 2
y + y) + − (x + ) 2 1 2 2 2 2 2 + y + 2y ⇔ x + + (x + ) 2 = y + y + ( 2 1 2 1 2 2 y + 2y) (*) .
Xét hàm số f (t) = t + 2t trên khoảng (0;+∞) ta có: f ′(t) 1 = 2 + > 0, t
∀ > 0 ⇒ f (t) đồng biến trên (0;+∞) . 2 t
⇔ f (x + ) = f ( 2 y + y) 2 2 (*) 1
2 ⇔ x +1 = y + 2y ⇔ x = y + 2y −1. 5 − ≤ y ≤ 2 − Do x, y ∈[ 1; − 14] nên 2 1
− ≤ y + 2y −1≤14 ⇔ 1≤ ( y + )2 1 ≤16 ⇔ 0 ≤ y ≤ 3
Do y ∈ , y ∈[ 1; − 14] và 2
y + 2y ≥ 0 nên y ∈{0;1;2; } 3 .
Vậy có 4 cặp số nguyên (x; y) thoả bài toán là
Câu 7. Số nghiệm của phương trình sinx cos x 13 cosx sin 14 14 7 .2 x − = trong khoảng (0;3π ) là 2 A. 3. B. 4 . C. 2 . D. 5. Lời giải Chọn A Ta có: sinx cos x 13 cosx sin 14 14 7 .2 x − = 2 sin x cos 7 2 x 13 ⇔ − = sin x−cos x
−(sin x−cos x) 1 7 2 7 2− ⇔ − = − cos x sin 7 2 x 2
Xét hàm số ( ) = 7u − 2−u ⇒ ′( ) = 7u ln 7 + 2−u f u f u ln 2 > 0 u ∀ ∈ .
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 3
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
⇒ Hàm số f (u) đồng biến trên . ⇒ sinx−cosx
−(sin x−cos x) 1 7 2 7 2− − = −
có nghiệm khi và chỉ khi sin x − cosx =1. π π sin x sin ⇔ − = 4 4 π π x − = + k2π π 4 4 x = + k2π ⇔ ,k ∈ ⇔ 2 ,k ∈ π π
x − = π − + k2π = π + π x k2 4 4 π π
Suy ra tập các nghiệm thuộc (0;3π ) của phương trình là: 5 S ;π; = . 2 2
Vậy phương trình có 3 nghiệm thuộc (0;3π ) .
Câu 8. Cho phương trình ( 2x x − )( 2x x + ) = ( 4 2 2 2 2 2
3x − x − 2x).ln 2. Chọn mệnh đề đúng.
A. Phương trình có hai nghiệm trái dấu thuộc đoạn [ 1; − ] 1 .
B. Tổng các nghiệm thuộc đoạn [ 1; − ]
1 của phương trình bằng 1.
C. Tổng các nghiệm thuộc đoạn [ 1; − ]
1 của phương trình bằng 0 .
D. Phương trình vô nghiệm. Lời giải Chọn B Ta có: ( 2x x − )( 2x x + ) = ( 4 2 2 2 2 2
ln 2. 3x − x − 2x) 2 x x ⇔ − = ( 4 2 2 4 4
3x + 2x − 3x − 2x).ln 2 2 x ⇔ − ( 4 2 + ) x x x = − ( 2 4 3 2 ln 2 4 3x + 2x)ln 2 Xét hàm số ( ) u f u = − ( 2 4
3u + 2u)ln 2 ⇒ ′( ) = 4u f u ln 4 − ln 4(3u + ) 1 = ⇒ f ′(u) u u = ⇔ − ( u + ) 0 0 4 3 1 = 0 ⇔ u = 1
Lập BBT, ta dễ dàng suy ra hàm số f (u) đồng biến trên ( ;0
−∞ ) và (1;+∞); hàm số f (u) nghịch biến trên (0; ) 1 . x∈[0; ] 2 1 ⇒ x ∈ [0; ]1 Với khi đó hàm số = ( 2
y f x ) luôn đồng biến trên [ 1; − ] 1 ; hàm số x ∈ [ 1; − 0) 2 ⇒ x ∈[0; ] 1
y = f (x) đồng biến trên [0; ]
1 và nghịch biến trên [ 1; − 0) .
Suy ra phương trình 2x − ( 4 2 + ) x x x = − ( 2 4 ln 2. 3 2 4
ln 2. 3x + 2x) có tối đa 2 nghiệm. x = 0 Xét x ∈[0; ]
1 , phương trình có nghiệm khi và chỉ khi 2 x = x ⇔
là hai nghiệm phân biệt x = 1
của phương trình. Từ đó, x ∈[ 1;
− 0) thì phương trình vô nghiệm.
Vậy tổng các nghiệm của phương trình bằng 1.
Câu 9. Phương trình 2 ax +bx 6x e − e = ( −b) 2 6
x − ax có hai nghiệm phân biệt khi và chỉ khi
A. b ≠ 6 . B. a ∀ ,b∈ .
C. a ≠ 0 .
D. (a,b) ≠ (0;6) . Lời giải Trang 4
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC Chọn D Ta có: 2 ax +bx 6x e − e = ( −b) 2 6 x − ax 2 ax +bx 2 6x ⇔ e
+ ax + bx = e + 6x Xét hàm số ( ) u
f u = e + u ⇒ ′( ) u
f u = e +1 > 0 u ∀ ∈ .
⇒ Hàm số f (u) đồng biến trên . ⇒ 2 ax +bx 2 6x e
+ ax + bx = e + 6x có nghiệm khi và chỉ 2
ax + bx = 6x . x = 0 2
⇔ ax + (b − 6) x = 0 ⇔
ax + b − 6 = 0
⇒ Phương trình có hai nghiệm khi và chỉ khi a ≠ 0 và b ≠ 6 .
Câu 10. Có bao nhiêu số nguyên dương x thỏa mãn x + = ( 2 2 sin 2 2 .cos 2 y + ).2x y x . A. 2 . B. 1. C. 0 . D. 3. Lời giải Chọn B x +
y = ( 2 y + x) 2 2 2 sin x − x 2 sin y 1−x sin y 2 2 2 .cos 2 .2 ⇔ 2.2 + cos y = 2
+ x ⇔ 2 +1− x = 2 + sin y . (1) Xét hàm số ( ) = 2t f t
+ t . Ta có ′( ) = 2t f t
ln 2 +1 > 0 với mọi t .
Do đó hàm số f (t) đồng biến trên .
Khi đó (1) ⇔ f ( − x) = f ( 2 y) 2 1 sin
⇔ 1− x = sin y . Vì 2 sin y ∈[0 ]
;1 và x là số nguyên dương nên ta được x =1.
Câu 11. Có bao nhiêu cặp số nguyên dương ( ;
x y) thỏa mãn x ≤ 2022 và 4 3 y y 2
x − 2x − 2.3 = 9 − 3x + 2x . A. 19. B. 15. C. 13. D. 6 . Lời giải Chọn C 4 3 y y 2 4 3 2 2
− 2 − 2.3 = 9 − 3 + 2 ⇔ − 2 + 3 − 2 = 3 y + 2.3y x x x x x x x x
⇔ ( − )2 + ( − ) = ( y )2 2 2 2 3 + 2.3y x x x x . (1)
Vì x , y là các số nguyên dương do đó 2
x − x ≥ 0 và y > 0.
Xét hàm số f (t) 2
= t + 2t với t > 0 . Ta có f ′(t) = 2t + 2 > 0 với mọi t > 0.
Do đó hàm số f (t) đồng biến trên (0;+ ∞).
Khi đó (1) ⇔ ( 2 − ) = (3y ) 2 ⇔ − = 3y f x x f x x ⇔ y = log ( 2 x − x . 3 ) Điều kiện: 2
x − x > 0 . Suy ra x∈{2;3;...; } 2022 . Suy ra log ( 2
2 − 2) ≤ y ≤ log ( 2
2022 − 2022 ⇒1≤ y ≤13. 3 3 )
Với mỗi y ∈{1;2;...; }
13 ta có duy nhất x nguyên dương thỏa mãn.
Vậy có tất cả 13 cặp ( ;
x y) thỏa đề bài.
Câu 12. Có bao nhiêu cặp số nguyên dương ( ;
x y) thỏa mãn y ≤1994 và 2 3
x −x + y ( 3 x − y + ) 2 3 5 . 4 3 = 4 + 27x . A. 10. B. 13. C. 3. D. 9.
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 5
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC Lời giải Chọn A
Tập xác định D = . 3 2 x − y 3x 2 3
x −x + y ( 3 x − y + + + ) 2 2 3 x
x −x + y = + ⇔ ( 3x−y + ) 2 3 3 3 5 . 4 3 4 27 5 . 4 3 = 4 + 3 x 4 3 4 3 ⇔ = . (1) 3 2 x − y 3 5 5 x t + t
Xét hàm số f (t) 4 3 =
. Ta có f ′(t) 4 3 3 = − .ln 5 + .ln < 0 với mọi t . 5t 5t 5 5
Suy ra hàm số f (t) nghịch biến trên . Khi đó (1) ⇔ f ( 3
x − y) = f ( 2 x ) 3 2 3 2 3
⇔ x − y = 3x ⇔ y = x − 3x . (2)
Vì y > 0 và x là số nguyên dương nên x ≥ 4 .
y ≤1994 và từ (2) ta có: 3 2 3 2
x − 3x ≤1994 ⇔ x − 3x −1994 ≤ 0. (3) Hàm số g (x) 3 2
= x − 3x −1994 đồng biến trên [4;+ ∞) và g (13) < 0 , g (14) > 0.
Mặc khác x là số nguyên dương nên từ (3) ta có x ≤13. Suy ra x ∈{4;5;...; }
13 . Và với mỗi giá trị của x ta được duy nhất giá trị y thỏa mãn.
Vậy có tất cả 10 cặp ( ;
x y) thỏa đề bài.
Câu 13. Tính tổng các nghiệm của phương trình 2 2021x x 1 + x x 2 2021
+ 2021 .x = 2021 + 2021 .x . A. 2. B. 2021. C. 2022. D. 2023. Lời giải Chọn C
Điều kiện: x ∈
Chia 2 vế của phương trình cho 2021x > 0 , ta được: 2 2020x x −x 2 2021 + 2021x = 2021 + x 2 2020x x −x 2 ⇔ 2021 + 2020x = 2021 + x − x
Xét hàm số ( ) = 2021t f t + t trên ′( ) = 2021t f t .ln ( ) 2021 +1 > 0, t ∀
⇒ hàm số f (t) đồng biến trên mà f ( x) = f ( 2 2021 x − x) x = 0 Từ đó suy ra: 2
2021x = x − x ⇔ x = 2022
Vậy ta có: x + x = 2022. 1 2
Câu 14. Phương trình 6 4 x 3 + − + ( x − ) 2 6 8 15 3.4 − 6.2x x x x x
x +10 = 0 có bao nhiêu nghiệm? A. 1. B. 0. C. 2. D. 3. Lời giải Chọn A
Điều kiện: x ∈ Phương trình 6 4 2 x 3 x 2 ⇔ + 6 +15 +10 = 8 + 3.4 + 6.2x x x x x x x
⇔ ( + )3 + ( + )2 + ( + ) = ( x )3 + ( x )2 2 2 2 1 3 1 6 1 2 3. 2 + 6.(2x x x x x x x)
Xét hàm số f (t) 3 2
= t + 3t + 6t trên f ′(t) 2
= 3t + 6t + 6 = 3(t + )2 1 +1 > 0, t ∀ Trang 6
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
⇒ hàm số f (t) đồng biến trên mà ( 2 + ) 1 = (2x f x f x)
Từ đó suy ra: 2 +1 = .2x x x (2)
+ Xét x = 0 ⇒1 = 0 ( vô lý)⇒ x = 0 không là nghiệm của pt (2) . 2 + + Xét x x 1
≠ 0 , chia 2 vế của pt (2) cho x ta được: = 2x x = 2x y
Vậy số nghiệm của phương trình là số giao điểm của 2 đường 2 và bằng 1 (hiển
y = g ( x) x +1 = x
thị trong bảng biến thiên dưới đây) f (2.5x )
Câu 15. Cho hàm số ( ) 2022x 2022 x f x − = −
. Nghiệm x của phương trình = − thuộc 0 f ( x − + ) 1 3.5 1 khoảng nào dưới đây? A. ( 2; − − ) 1 . B. ( 1; − ) 1 . C. (1;5). D. (0;3). Lời giải Chọn B
Ta có: ′( ) = 2022x.ln (2022) + 2022−x f x .ln (2022) > 0, x ∀
⇒ hàm số f (x) đồng biến trên .
Ta lại có: (− ) = 2022−x − 2022x f x = − f (x) f (2.5x ) Phương trình ( x x = − ⇔ f = f + f − 3.5x +1) 1 (2.5 ) ( 3.5 1) x 5 =1⇒ x = 0
2.5x > 0, x ∀
Từ đó ta có: 2.5x = 3.5x +1 ⇔ ⇔ x 1
4.25x = 3.5x +1 5 = − (l) 4
Vậy nghiệm x = 0∈ 1; − 1 . 0 ( )
Câu 16. Gọi S là tập hợp gồm tất cả các nghiệm nguyên của phương trình 2 2 2 2 x −x 3−2x 2x−3 x−x 3 2 x −x 3−2x 2x−3 (2 + 9 − 4 − 3 ) + − 6 +11 − 6 = 2 + 9 − 4 − 3x−x x x x x . Tính tổng bình
phương các phần tử của S . A. 5. B. 25 . C. 13. D. 14. Lời giải Chọn D Phương trình 2 2 x −x 6−4x 4x−6 x−x 2 ⇔ (x −1)(2 + 3 − 2 − 3
) + (x −1)(x − 5x + 6) = 0
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 7
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC 2 2 x −x 6−4x 4x−6 x−x 2 ⇔ (x −1)(2 + 3 − 2 − 3
+ x − 5x + 6) = 0 x =1 ⇔ . 2 2
2x −x − 3x−x +
( 2x − x) 4x−6 6−4 = 2
− 3 x + (4x − 6) ( ) 1
Xét hàm số ( ) = 2t − 3−t f t + t trên tập .
Ta có ( ) 2t.ln 2 3 t f t − ′ = + .ln 3+1 > 0 , t
∀ ∈ suy ra hàmsố f (t) đồng biến trên . Do đó: x = 2 Phương trình ( ) 1 ⇔ f ( 2
x − x) = f (4x − 6) 2
⇔ x − x = 4x − 6 ⇔ . x = 3 Vậy tổng cần tìm là 2 2 2 1 + 2 + 3 =14 . 4 Câu 17. + Cho phương trình 2 sin x−sin x cos x 2022 2021 =
. Tổng các nghiệm thuộc [ 2021 − π;2021π ] 2
sin x − 2sin x + 2023 của phương trình là. π π A. 2021π . B. 2023 . C. 1010π . D. 2021 . 2 2 Lời giải Chọn D 2 2 Bất phương trình 2
1−sin x−cos x (cos x) + 2022 ⇔ 2021 = 2 (1− sin x) + 2022 ⇔ ( − )2 1−sin x + = ( 2 1 sin 2022 .2021 )2 2 + 2022.2021cos x x cos x ( ) 1 .
Xét hàm số ( ) = ( 2 + 2022)2021t f t t trên tập .
Ta có ′( ) = ( 2.ln 2021+ 2 + 2022.ln ) 2021 .2021t f t t t
Vì tam thức bậc hai 2t.ln 2021+ 2t + 2022.ln 2021 có 2
∆′ =1− 2022.ln 2021< 0 và ln 2021 > 0
Suy ra ′( ) = ( 2.ln 2021+ 2 + 2022.ln ) 2021 .2021t f t t t > 0 với t ∀ ∈
Hay hàm số f (t) đồng biến trên . Do đó:
Phương trình ( ) ⇔ f ( −
x) = f ( 2 x) 2 2 1 1 sin cos
⇔ 1− sin x = cos x ⇔ sin x − sin x = 0 sin = 0 x = k x π ⇔ ⇔ π , (k,m∈ ) . sin x = 1 x = + m2π 2
Xét các nghiệm thuộc [ 2021 − π;2021π ] ta có 2021 − π ≤ kπ ≤ 2021π 2021 − ≤ k ≤ 2021 +) ⇔ ⇒ k = 2021 − , 2020 − ,....,2020,2021. k ∈ k ∈ π 4043 4041 2021 −
π ≤ + m2π ≤ 2021π − ≤ m ≤ +) 2 ⇔ 4 4 ⇒ m = 1010 − , 1009 − ,...,1009,1010 . m∈Ζ m∈Ζ
Tổng cần tìm là S = [( 2021 − π ) + ( 2020 − π ) +...+ 2020π + 2021π ] π π π π π ( 1010π ) ( 1009π ) ... ( 1009π ) ( 1010π ) + − + − + + + + + 2021 = 2 2 2 2 2 Trang 8
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
Câu 18. Cho x ; y là hai số thực dương thỏa mãn ( − ) 4−2 1 .3 y xy
+ (x + 2y) x(1+3y) .3 = 0 . Giá trị nhỏ nhất
của biểu thức P = 3(x + y) bằng a b − c , với a ; b ; c là các số nguyên tố cùng nhau. Khi đó
a + b + c bằng A. 17 . B. 14. C. 16. D. 15. Lời giải Chọn C Ta có: ( − ) 4−2 1 .3 y xy
+ (x + 2y) x(1+3y) .3
= 0 ⇔ ( − ) 4−3xy + ( + ) x+2 1 .3 2 .3 y xy x y = 0 ⇔ ( −
) 3−3xy = ( + ) x+2 3 3 .3 2 .3 y xy x y ( ) 1
Xét hàm số ( ) = .3t f t t trên (0;+ ∞)
′( ) = 3t + .3t f t t .ln 3 > 0 t
∀ ∈(0;+ ∞) nên hàm số f (t) đồng biến trên (0;+ ∞) − x Do đó ( ) 3
1 ⇔ f (3− 3xy) = f (x + 2y) ⇔ 3− 3xy = x + 2y ⇔ y = ⇒ 0 < x < 3 3x + 2 − x
Khi đó P = (x + y) 3 11 3 = 3x + 3. = 3x + 2 + − 3 ≥ 2 11 − 3 3x + 2 3x + 2 11 − 2 x = Dấu bằng xảy ra ⇔ 3 11 −1 y = 3
Vậy min P = 2 11 − 3 ⇒ a = 2 ; b =11; c = 3 ⇒ a + b + c =16. 3 x −6x−4
Câu 19. Biết rằng phương trình 2 3 2 4 − 3 .2 x x x
− 24x = 32 có nghiệm là 3 3
x = a − b − c,(a,b,c∈) . Khi đó giá trị của 2abc bằng A. 28 . B. 24 . C. 54 D. 50. Lời giải Chọn A Điều kiện 3 x ≥ . 4 3 x −6x−4 24x 16 + 4x− + 12 3x 4 3x + 4 Phương trình 2 ⇔ 4x − 3.2 x = 8 ⇔ 4x − 3.( 4 2) 2 x = (4 2) x x + + − x ( x x x x + 4 ) 3 4 4 3. 2 ⇔ − = ( 4 2 ) 2 9 24 16 4 3 2 x x 2 + − x ( ) 3x + 4 x x 4 3. 2 ⇔ − = ( 2 ) 3 4 4 3 4 4 x (1) x t
Dễ thấy f (t) = t ( ) 2 4
. 2 đồng biến trên (0;+∞) x + x + Khi đó ( )
1 ⇔ f ( 4x −3) 3 4 3 4 3 2 = f ⇔ 4x − 3 =
⇔ 4x −12x − 24x −16 = 0 x x 3 2 3
⇔ x − x − x − = ⇔ x = (x + )3 3 2 6 12 8 0 3
2 ⇔ x 3 = x + 2 2 3 3 3 3 ⇔ x = = 1+ 3 + 9 =1− 3 − − 9
− ⇒ 2abc = 54 . 3 3 −1
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 9
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
Câu 20. Gọi a , b lần lượt là nghiệm âm lớn nhất và nghiệm dương nhỏ nhất của phương trình:
2sin x+3cos x + ( 2−cosx + − − ) cosx 5cos x 1−sin 2 2 sin cos 1 .2 = 4.2 + 2 x x x
. Tính 2a + 8b . A. π . B. 2π . C. 0 . D. π − . Lời giải Chọn A
2sin x+3cos x + ( 2−cosx + − − ) cosx 5cos x 1−sin 2 2 sin cos 1 .2 = 4.2 + 2 x x x 2sin x+2cos x 2 − cos x 4cos x 1−sin x−cos ⇔ 2 + 2 + sin − cos −1 = 4.2 + 2 x x x sin x+cos x 1−sin x−cos ⇔ 4 − 2
x + (sin x + cos x) 2cos x 1 + 1−(2cos x+ ) 1 = 4 − 2 + (2cos x + ) 1 (1) Xét hàm số ( ) t 1 = 4 − 2 −t f t + t trên . ( ) t 1 ' = 4 ln 4 + 2 −t f t ln 2 +1 > 0, t ∀ ∈ .
Hàm số f (t) đồng biến trên .
Khi đó (1) ⇔ f (sin x + cos x) = f (2cos x + )
1 ⇔ sin x − cos x =1 x = k2π π 1 3 − π π sin x ⇔ − = ⇔ π ⇒ a =
,b = ⇒ 2a + 8b = π . 4 2 x = + k2π 2 2 2 Câu 21. +
Phương trình 4−4x+2 8+x 3x+6 6x 21 2 − 4 = 3 x + 2 +
có bao nhiêu nghiệm dương?
3− 3x − 24 + 3x A. 0 . B. 1. C. 3. D. 2 . Lời giải Chọn B Điều kiện: 2 − ≤ x ≤1. 4−4x +2 8+x 3x+6 6x + 21 2 − 4 = 3 x + 2 +
3− 3x − 24 + 3x (6x + ) 21
3− 3x + 24 + 3x 2 1−x +2 8+x 3x+6 ( ) ⇔ 2 − 4
= 3. 3x + 6 + ( 3−3x − 24+3x)( 3−3x + 24+3x) (6x + ) 21
3− 3x + 24 + 3x 2 1−x +2 8+x 3x+6 ( ) ⇔ 2 − 4 = 3. 3x + 6 + 6 − x − 21 2( 1−x+ 8+x) 3x+6 ⇔ 2 − 4
= 3. 3x + 6 − ( 3−3x + 24+3x) 1−x + 8+x 3x+6 ⇔ 4 − 4
= 3. 3x + 6 − 3 ( 1− x + 8+ x) 1−x + 8+x ⇔ +
( −x + + x) 3x+6 4 3 1 8 = 4 + 3. 3x + 6 (1) Xét hàm số ( ) = 4t f t + 3 t , trên . Ta có : '( ) = 4t f t ln 4 + 3 > 0, t
∀ ∈ nên hàm số đồng biến trên Do đó
( )1 ⇔ f ( 1− x + 8+ x) = f ( 3x+6) ⇔ 1− x + 8+ x = 3x+6 Trang 10
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC ⇔ +
( − x)( + x) = x + ⇔ ( − x)2 9 2 1 8 3 6 3 1
+ 2 (1− x)(x + 8) = 0. = ⇔ − x ( − x + x + ) x 1 1 3 1 2 8 = 0 ⇔ .
3 1− x + 2 x + 8 = 0 (VN )
Vây phương trình có nghiệm duy nhất x =1. Câu 22. +
Phương trình 4−4x+2 8+x 3x+6 6x 21 2 − 4 = 3 x + 2 +
có bao nhiêu nghiệm dương?
3− 3x − 24 + 3x A. 1. B. 2 . C. 3. D. 0 . Lời giải Chọn A Điều kiện: 2 − ≤ x ≤1 (6x + ) 21
3− 3x + 24 + 3x 2 1−x +2 8+x 3x+6 ( ) PT 2 4 3. 3x 6 ( ⇔ − =
+ + 3 3x 24 3x)( 3 3x 24 3x) − − + − + + (6x + ) 21
3− 3x + 24 + 3x 2 1−x +2 8+x 3x+6 ( ) 2 4 3. 3x 6 ⇔ − = + + 6 − x − 21 2( 1−x+ 8+x) 3x+6 ⇔ 2 − 4
= 3. 3x + 6 − ( 3−3x + 24+3x) 1−x + 8+x 3x+6 ⇔ 4 − 4
= 3. 3x + 6 − 3 ( 1− x + 8+ x) 1−x + 8 ⇔ 4
+x + 3 ( − x + + x) 3x+6 1 8 = 4 + 3. 3x + 6 Xét hàm số ( ) = 4t f t
+ 3 t , với t ∈ 3;3 2 ; Ta có : '( ) = 4t f t
ln 4 + 3 ⇒ f '(t) > 0 với t ∈ 3;3 2 ⇒
hàm số đồng biến trên 3;3 2 ; Do đó :
f ( 1− x + 8+ x) = f ( 3x + 6) ⇔ 1− x + 8+ x = 3x + 6 ⇔ x =1
Vây phương trình có nghiệm duy nhất x =1 (x+2)2 Câu 23. 1 3 1
Gọi x , x là 2 nghiệm của phương trình x+6 + + x +1 =
+ 9.3 + x + 4 2 − x + 2 x 8 ( )( ) 1 2 x +4 5 27 5.5 x . Tìm
giá trị nhỏ nhất của biểu thức 2
P = a + (x + x a + 3x x 1 2 ) 1 2 A. 37 . B. 6 − . C. 3. D. 37 − . 4 Lời giải Chọn D Ta có: (x+2)2 1 3 1 x+6 + + x +1 =
+ 9.3 + x + 4 2 − x + 2 x 8 ( )( ) x +4 5 27 5.5 x
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 11
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC 1 2 x +4x 1 + 1 x+8 2 ⇔ + 3 + x +1 =
+ 3 − 2x − x + 8 + 2 x 8 x +4x 1 5 5 + 2 x +4x 1 + 1 2 x+8 1 ⇔ 3 −
+ x + 4x +1 = 3 − + x + 8 1 . 2 x +4x 1 + x+8 ( ) 5 5
Xét hàm số ( ) = 3t − 5−t f t
+ t trên tập D = .
Ta có ′( ) = 3t ln 3+ 5−t f t ln 5 +1 > 0 t ∀ ∈ .
Do đó hàm số f (t) luôn đồng biến trên tập D = .
Phương trình ( ) ⇔ f ( 2
x + x + ) = f (x + ) 2 1 4 1
8 ⇔ x + 4x +1 = x + 8 . 2
⇔ x + 3x − 7 = 0 . Theo định lý Viet ta có: 7 x x 3; x .x − + = − = 1 2 1 2 3 2
P = a + (x + x ) 2
a + 3x x = a − 3a − 7 1 2 1 2 3 37 P ' 2a 3 0 a P − = − = ⇔ = ⇔ = min 2 4 2 Câu 24. x − x+ 10 Biết rằng phương trình ( 2021 6 4) 2022 = −
4 có một nghiệm x = a + b . Khi đó 2 ab a x + 4 + x bằng A. 5. B. 11. C. 8 . D. 6 . Lời giải Chọn D 2 x − x+ 10 Từ giả thiết ( 2021 6 4) 2022 = 4 x + 4 + x ( ( 2021 x+2)2 2 2021 x −6x+4) 10 2 ⇔ 2022 x = 2021 x+2 10 − x 2022 10x 10 ⇔ 2022 x = ⇔ = ( ( ) x + 2)2 (x + 2)2 2021.10 2022 x (x + 2)2 ⇔ ( + ) (x+ )2 2 2021 2 2021.10 2 .2022 = 10 .2022 x x x ( ) 1 Xét hàm số ( ) 2021 = .2022 t f t t với t > 0 . Ta có ′( ) 2021t 2021 = 2022 + 2021 .2022 t f t t .ln 2022 > 0, t
∀ > 0. Suy ra hàm số f (t) đồng biến trên
(0;+∞). Khi đó ( ) ⇔ f ( x+ )2 1
2 ) = f (10x) ⇔ (x + )2 2 =10x x = 3− 5 2
⇔ x − 6x + 4 = 0 ⇔ . Khi đó tìm được 2
a = 3;b = 5 ⇔ ab − a = 6 . x = 3+ 5 − + Câu 25. a b Biết rằng phương trình 2 2 4x +5x 4x +5x 1 4 .3 x 4.3 − + + (4x + )2
1 = 9 có một nghiệm dương x = c , trong đó ; a ;
b c nguyên dương. Khi đó a + b − c bằng
A. a + b − c = 38 .
B. a + b − c =17 .
C. a + b − c =13 .
D. a + b − c = 28. Lời giải Chọn A Từ có 2 2 4x +5x 4x +5x 1 4 .3 x 4.3 − + + (4x + )2 1 = 9 2 ( x ) 2 4x +5x 1 4 3 1 .3 − ⇔ + + (4x + )2 1 = 9 ⇔ ( x + ) 2 4x +5x 1 − 1 9 3 1 .3 + 2x + = 2 4 Trang 12
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC ⇔ ( x + ) 2 4x +5x 1 − 2 1 9 3 1 .3
+ 4x + 2x + = ⇔ ( x + ) 2 4x +5x 1 − 2 3 1 .3 = 4
− x − 2x + 2 4 4 2 2 2 2 4x +5x 1 − 4 − x − 2x + 2 − − + ⇔ 3 = 3x 1 + −( 4 − x −2x+2) 4x 2x 2 ⇔ 3 = 3x +1 3x +1 3x 1 + 2 3 4 − x − 2x + 2 ⇔ =
⇔ ( x + ) x+ = (− x − x + ) 2 3 1 2 4 − x −2x+2 3 1 3 4 2 2 3 ( ) 1 2 4 − x −2x+2 3 3x +1
Do x > 0 nên 3x +1 > 0 , nếu 2 4
− x − 2x + 2 ≤ 0 thì phương trình ( ) 1 vô nghiệm
Từ đó ta xét hàm số ( ) = .3t f t t với t ∀ > 0
Ta có ′( ) = 3t + .3t f t
t .ln 3 > 0, t
∀ > 0 . Suy ra hàm số f (t) đồng biến trên (0;+∞) nên phương trình ( )
1 tương đương với f ( x + ) = f ( 2 3 1 4
− x − 2x + 2) 5 − − 41 x = 2
⇔ 4x + 5x −1 = 0 2
⇔ 4x + 5x −1 = 0 6 ⇔ . 5 − + 41 x = 8
Vì x > 0 nên ta lấy 5 41 x − + =
. Khi đó a = 5;b = 41;c = 8 ⇒ a + b − c = 38. 8
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 13
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC
GIẢI PHƯƠNG TRÌNH MŨ BẰNG PHƯƠNG PHÁP ĐẶT ẨN PHỤ KHÔNG HOÀN TOÀN
(KHÔNG CHỨA THAM SỐ) PHƯƠNG PHÁP Phương pháp :
+ Phương pháp đặt ẩn phụ không hoàn toàn là việc sử dụng một ẩn phụ chuyển phương trình ban
đầu thành một phương trình với một ẩn phụ nhưng các hệ số vẫn còn chứa x .
+ Phương pháp này thường được sử dụng đối với những phương trình khi lựa chọn ẩn phụ cho
một biểu thức thì các biểu thức còn lại không biểu diễn được triệt để qua ẩn phụ đó hoặc nếu biểu
diễn được thì công thức biểu diễn lại quá phức tạp. Sau khi biểu diễn ta thường được phương
trình bậc hai theo ẩn phụ (hoặc vẫn theo ẩn x ) có biệt số ∆ là một số chính phương.
+ Tìm mối liên hệ giữa ẩn phụ và x ; sau đó thế trở lại để tìm x . VÍ DỤ
Câu 1. Cho phương trình: 2 2 x 2 x 2
16 + (x − 3)4 − 2x + 2 = 0.
Tổng bình phương tất cả các nghiệm của của phương trình bằng A. 1. B. 0 . C. 1 . D. 2 . 2 Lời giải Chọn A Đặt 2 4x t =
, điều kiện t ≥1 (vì 2x 0 4 ≥ 4 =1).
Khi đó phương trình trở thành: 2 2 2
t + (x − 3)t − 2x + 2 = 0 . Ta có ∆ = x −
− − x + = (x + )2 2 2 2 2 ( 3) 4( 2 2) 1 > 0. (luôn đúng)
Phương trình có hai nghiệm 2
t = 2; t =1− x . Với 2 x 2 1 2
t = 2 ⇔ 4 = 2 ⇔ x = ⇔ x = ± . 2 2 Với 2 2 x 2
t =1− x ⇔ 4 =1− x , ta có đánh giá sau: 2 4x ≥1 2 x 2
⇒ 4 =1− x =1 ⇔ x = 0 . 2 1 − x ≤1 2 2 −
Vậy, phương trình đã cho có 3 nghiệm phân biệt và 2 2 2 + + 0 = 1 . 2 2
Câu 2. Tính tổng tất cả các nghiệm của phương trình sau
x−2 + ( x − ) x−2 3.25
3 10 5 + 3− x = 0 là: A. 4 − log 3. B. 2 − log 3. C. log 3 . 5 5 2 . D. 5 Lời giải Chọn A Đặt x 2
t = 5 − > 0 được phương trình
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 1
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC 1 t = 2 3.t
(3x 10)t 3 x 0 (3t ) 1 (t x 3) 0 + − + − = ⇔ − + − = ⇔ 3 t = 3 − x
Cách 2 chỗ này: Tính ∆ = ( x − )2 3 8 ≥ 0 * Với 1 t = ta có x 2 1
5 − = ⇔ x = 2 − log 3 3 5 3
* Với t = 3− x ta có x 2
5 − = 3− x . Nhận thấy 2 5 − = x y
là hàm số đồng biến trên và y = 3− x
là hàm số nghịch biến trên , mặt khác x = 2 thoả mãn phương trình nên x 2
5 − = 3− x có nghiệm duy nhất x = 2 .
Vậy phương trình đã cho có tập nghiệm {2 − log 3;2 và tổng các nghiệm là 5 } 2 − log 3+ 2 = 4 − log 3 5 5
Câu 3. Tổng tất cả các nghiệm của phương trình 9x + 2( − 2).3x x
+ 2x − 5 = 0 là: A. 5. B. 1. C. 1 − . D. 4 . Lời giải Chọn B Đặt = 3x t
> 0 được phương trình t = 1( − l) 2
t + 2(x − 2).t + 2x −5 = 0 ⇔ (t + )
1 (t + 2x −5) = 0 ⇔ t =5−2x
Cách 2 chỗ này: Tính ∆ = (x − )2 ' 3 ≥ 0
* Với t = 5 − 2x ta có 3x = 5 − 2x Nhận thấy = 3x y
là hàm số đồng biến trên và y = 5 − 2x là hàm số nghịch biến trên ,
mặt khác x =1 thoả mãn phương trình nên 3x = 5 − 2x có nghiệm duy nhất x =1.
Vậy phương trình đã cho có tập nghiệm { }
1 và tổng các nghiệm là 1.
Câu 4. Cho hàm số y = f (x) có đồ thị như hình vẽ
Gọi S là tập nghiệm của phương trình 2
f (x) f (x) 1− f (x) f (x) ⋅5 − ( 1 3
− 3⋅5 − ) f (x) f (x) 1 − f (x) + 2⋅5 − 3
= 0 . Tập S có bao nhiêu phần tử? A. 4 . B. 5. C. 7 . D.3. Lời giải Chọn A
Đặt t = f (x) phương trình đã cho trở thành: Trang 2
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC 2 t 1 − ( t t 1 − ) t 1 5 3 3 5 2 5 − ⋅ − − ⋅ + ⋅ − 3t t t = 0 t 2
⇔ 5 ⋅ − (5⋅3t −3⋅5t ) + 2⋅5t −5⋅3t t t
= 0 (*) (coi đây là phương trình bậc hai ẩn t ). Phương trình có: ( t t )2 t ( t t ) ( t t ∆ = ⋅ − ⋅ − ⋅ ⋅ − ⋅ = ⋅ − )2 5 3 3 5 4 5 2 5 5 3 5 3 5 ≥ 0 t = 1 − t = 1 − ⇒ 3 t ⇔
3 t t + 2 t = 2 − + = ( )1 5 5 5 t
Phương trình (1) có nghiệm t =1. Hàm số g (t) 3 =
nghịch biến trên còn hàm số 5
h(t) t + 2 =
đồng biến trên nên phương trình (1) có nghiệm duy nhất t =1. 5
Vậy phương trình (*) có nghiệm t = 1 − ,t =1. Với t = 1
− ⇒ f (x) = 1
− , dựa vào đồ thị hàm số suy ra phương trình f (x) = 1 − có 3 nghiệm phân biệt.
Với t =1⇒ f (x) =1, dựa vào đồ thị hàm số suy ra phương trình f (x) =1 có 1 nghiệm.
Vậy phương trình đã cho có 4 nghiệm.
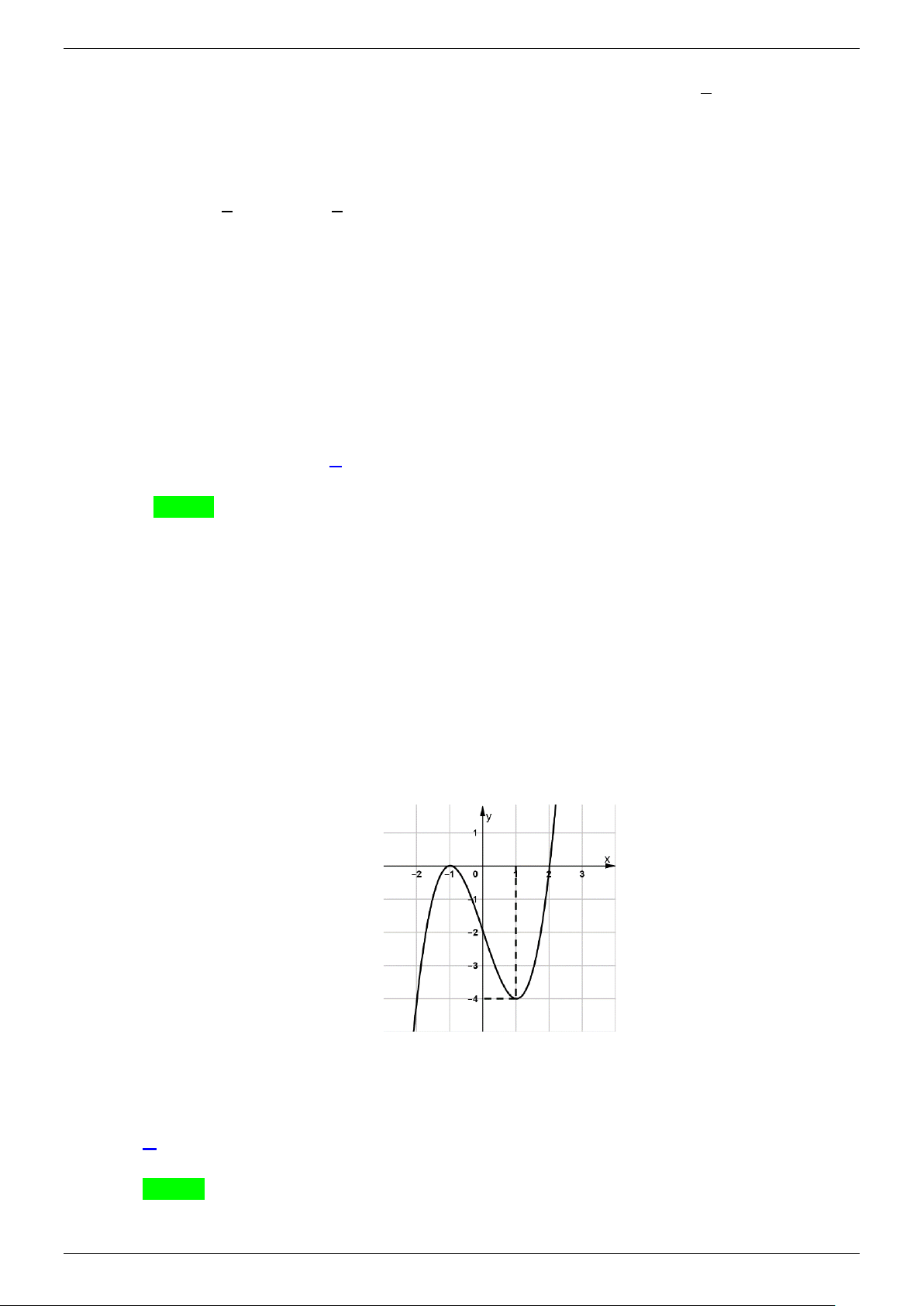
Câu 5. Cho hàm số y = f (x) có đồ thị như hình vẽ y 2 1 O 1 2 x
Phương trình 2f(x) + ( f (x) − ) 2 2 f (x) 2 4 7 2
+12 − 4 f (x) = 0 có bao nhiêu nghiệm? A. 6 . B. 8. C. 7 . D. 9. Lời giải Chọn B Đặt 2 f (x) t = 2
> 0 , phương trình đã cho trở thành 2 t + ( 2 f (x) − ) 2
7 t +12 − 4 f (x) = 0 2 7 − f (x) 2 + f (x) +1 t = = 4
∆ = ( f (x) − )2 − ( − f (x)) = ( f (x) + )2 2 2 2 2 7 4 12 4 1 ≥ 0 ⇒ 2 7 − f (x) 2 − f (x) −1 2 t = = 3− f (x) 2 Với 2 f (x) 2 t = 4 ⇒ 2
= 4 ⇔ f (x) = 2 ⇔ f (x) = ± 2 . Dựa vào đồ thị hàm số suy ra phương trình
f (x) = ± 2 có 4 nghiệm. (*)
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 3
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC 2 3 − f (x) > 0 f ( x)∈ − 3; 3 2 ( )
Vơt t = 3− f (x) > 0 ⇔ ⇔ 2 f (x) 2 2 = 3− f (x) 2 f (x) 2 2 + f (x) = 3 ( ) 1 Đặt 2
y = f (x), f (x)∈(− 3; 3) ⇒ y∈[0;3) . Khi đó phương trình ( )
1 trở thành: 2y + y = 3. Xét hàm số ( ) = 2y g y + y, y ∀ ∈[0;3) ′( ) = 2y g y
.ln 2 +1 > 0 ⇒ g ( y) đồng biến trên [0;3) ⇒ phương trình 2y + y = 3 nếu có nghiệm
thì nghiệm là duy nhất, suy ra phương trình 2y + y = 3 có nghiệm duy nhất y =1⇒ f (x) = 1 ± .
Dựa vào đồ thị hàm số suy ra phương trình f (x) = 1 ± có 4 nghiệm . (**)
Từ (*) và (**) suy ra phương trình đã cho có 8 nghiệm.
Câu 6. Cho hệ phương trình sau: 2x− y 1 + 2 − x+ y 1 + 2x− y 1 + 2 − x+ y 1 + 2x− y 1 + 2 − x+ y 1 2 2 3 3 5 5 + + + + = + ( ) 1 y ( 2
x + 3x − 3) + 2 = 0 (2)
Biết rằng hpt trên có nghiệm duy nhất ( x ; y x + y 0 0 ) , vậy giá trị
gần với giá trị nào sau đây: 0 0 A. 3, − 4. B. 3,4. C. 3, − 5 . D. 3,5 . Lời giải Chọn B
Đặt 2x − y = a , phương trình (1) của hệ trở thành
2(2a + 2−a ) + 3(3a + 3−a ) = 5(5a + 5−a )
Nếu a là nghiệm thì −a cũng là nghiệm nên chỉ cần xét a ≥ 0 . Xét hàm số ( ) t −t
f x = x + x , x >1 với số thực t dương tùy ý. Ta có: ( ) t 1 − = ( 2 ' 1 − t f x tx
− x ), do x >1 nên 2 1 t x− −
> 0 suy ra hàm số này đồng biến trên (1;+∞) .
Do đó, ta được bất đẳng thức sau: 2a + 2−a ≤ 3a + 3−a ≤ 5a + 5−a và dấu đẳng thức chỉ xảy ra khi a = 0 .
Suy ra 2(2a + 2−a ) + 3(3a + 3−a ) ≤ 5(5a + 5−a )
Đẳng thức phải xảy ra nên a = 0 hay 2x − y = 0 ⇔ 2x = y .
Thay vào phương trình (2) ta có: x( 2 x + x − ) 3 2 2 3
3 + 2 = 0 ⇔ x + 3x − 3x +1 = 0 3 3 2 3
⇔ 2x = x − 3x + 3x =1 ⇔ 2x = (x − )3 1 3 1
⇔ 2x = x −1 ⇔ x = 2
. Suy ra y = 2x = 3 1− 2 3 1− 2 1 1
Suy ra hệ phương trình có nghiệm là: ; = ( x ; y 0 0 ) 3 3 1− 2 1− 2 Trang 4
TÀI LIỆU ÔN THI THPT QUỐC GIA
NHÓM TOÁN VDC&HSG THPT MŨ - LOGARIT- VD_VDC 1 1
Như vậy, x + y = + ≈ 3, − 404 0 0 . 3 3 1− 2 1− 2
_______________ TOANMATH.com _______________
CHUYÊN ĐỀ VDC&HSG 12 NĂM 2021-2022 Trang 5
Document Outline
- Dạng-3-Giải-pt-mũ-bằng-phương-pháp-hàm-số-đánh-giá-(không-chứa-tham-số)-PB3
- Dạng-4-Giải-pt-mũ-bằng-phương-pháp-hàm-đặc-trưng-(không-chứa-tham-số)-PB3
- Dạng-5-Giải-pt-mũ-bằng-phương-pháp-đặt-ẩn-phụ-không-hoàn-toàn-(không-chứa-tham-số)-PB3




