Phương trình nghiệm nguyên liên quan đến mũ – logarit – Trần Trọng Trị

Tài liệu gồm 27 trang được biên soạn bởi tác giả Trần Trọng Trị (giáo viên Toán tiếp sức chinh phục kỳ thi tốt nghiệp THPT môn Toán năm học 2019 – 2020 trên kênh truyền hình Giáo dục Quốc gia VTV7)

35 18 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 6: Hàm số mũ và hàm số lôgarit (KNTT)

Môn: Toán 11

Thông tin:

27 trang 8 tháng trước

Tác giả:

Profile Kim Oanh
1
CHUYÊN ĐỀ
PHƯƠNG TRÌNH NGHIỆM NGUYÊN
LIÊN QUAN ĐẾN MŨ – LOGARIT
Tác giả: Trần Trọng Trị
Nhóm Giáo viên Toán tiếp sức Chinh phục kỳ thi THPT năm 2020
Tiếp nối chuyên đề Max – Min liên quan đến Mũ – Logarit, chuyên đề này kế
thừa các kĩ năng thu gọn mối quan hệ giữa các biến đã biết như:
( ) ( )
fu fv=
,
( ) ( )
fu fv≤
, với
f
là hàm số đơn điệu trên một khoảng cho trước; đánh giá
bằng các bất đẳng thức đơn giản; …. Từ đó sử dụng các kĩ thuật cơ bản liên quan
đến các biến nguyên để giải một bài toán phương trình nghiệm nguyên.
Thầy hy vọng với chuyên đề nhỏ này, sẽ giúp các em có cái nhìn rõ hơn về một
số dạng toán liên quan đến phương trình nghiệm nguyên.
1. Dạng 1: Có đúng một biến nguyên và rút được biến nguyên này theo biến
còn lại. Đến đây, ta xét hàm để tìm miền giá trị cho biến nguyên đó.
Ví dụ 1: (Đề 1 – VTV7) Có bao nhiêu số nguyên dương
x
sao cho tồn tại số
thực
y
lớn hơn
1
thỏa mãn
( )
2
23
2 1 log log
−+
+− − =
yx
xy x y y
x
?
A.
4.
B.
2.
C.
3.
D. Vô số.
Lời giải
Chọn B.
Điều kiện:
.
Ta có :
2
( )
2
23
2 1 log log
−+
+− − =
yx
xy x y y
x
( )
( )
2
2 3 log 2log log 2 3 log⇔ +− − + = −+ −xy x y y y y x x
(
)
( )
( )
22
2 3 log log 2 3 log⇔ +− − = −+ −
xy x y y y x xy
( )
1
+ Nếu
2
23xy y x> −+
thì
0
0
VT
VP
>
<
(do
log 0
y >
).
+ Nếu
2
23xy y x< −+
thì
0
0
VT
VP
<
>
(do
log 0
y >
).
Do đó, từ
( )
1
suy ra:
2
23
xy y x= −+
2
23
1
y
x
y
+
⇔=
+
.
Xét hàm
( )
2
23
1
y
fy
y
+
=
+
,
( )
1;y ∈ +∞
. Ta có:
( )
( )
2
2
2
2 62
0
1
yy
fy
y
− −+
′
= <
+
,
( )
1;
y∀ ∈ +∞
. Suy ra: Hàm số
( )
fy
nghịch biến trên
khoảng
( )
1; +∞
.
Suy ra:
( )
5
0;
2
x fy

= ∈


. Vì
*
x ∈
nên
{ }
1; 2x ∈
.
Vậy có
2
giá trị
x
thỏa yêu cầu bài toán.
2. Dạng 2: Khi phương trình rút gọn là phương trình bậc hai theo biến
không nguyên. Ta sử dụngđiều kiện có nghiệm của phương trình bậc hai để
tìm miền giá trị cho biến nguyên.
Ví dụ 2: Có bao nhiêu số nguyên
x
sao cho tồn tại số thực
y
thỏa mãn
22
43
++
=
xy x y
?
A.
4.
B.
2.
C.
3.
D. Vô số.
Lời giải
Chọn B.
( )
22
22 2 2
3 33
4 0l o g 4 0 2 l3 og 2 2 log 2
++
⇔+−+ =⇔ − − == +
xy x y
x y xy y y x x
.
(
)
*
3
Ta coi
( )
*
là phương trình bậc hai theo biến
y
. Phương trình
( )
*
có nghiệm
khi và chỉ khi
( )
( )
2
2
33
0 log 2 2 log 2 0 0,2 1,6xx x
′
∆ ≥ ⇔ − − ≥ ⇒− < <
.
Mà
x ∈
nên
{ }
0;1
x
∈
. Vậy có
2
giá trị
x
thỏa yêu cầu bài toán.
Chú ý:
Trong câu 1, ta có thể giải theo cách sử dụng điều kiện có nghiệm của
phương trình bậc hai như sau:
Từ
2
23xy y x= −+
2
2 30xy y x⇔ − +−=
(
)
*
.
Ta coi
( )
*
là phương trình bậc hai theo biến
y
. Phương trình
( )
*
có nghiệm
khi và chỉ khi
( )
2
3 13 3 13
1 3 3 10
23
xx x x x
−+
′
∆= − − =− + + ≥ ⇒ ≤ ≤
.
Vì
*
x ∈
nên
{
}
1; 2; 3x ∈
.
Với
1x =
, ta có :
2
2 20yy
− −=
có một nghiệm
1 31y =+>
(thỏa).
Với
2x =
, ta có :
2
2 2 10yy
− −=
có một nghiệm
13
1
2
y
+
= >
(thỏa).
Với
3x =
, ta có :
2
2
3 2 0 0;
3
yy y

− =⇔∈


(loại do
1y >
).
Vậy
{ }
1; 2x
∈
, tức là có
2
số nguyên dương
x
thỏa yêu cầu bài toán.
Với cách giải sử dụng điều kiện có nghiệm của phương trình bậc hai, ta
phải thử lại nghiệm, nên có hạn chế hơn so với phương pháp cô lập, xét
hàm. Do đó, trong một bài toán nếu có thể cô lập, xét hàm thì ta nên
chọn phương pháp này.
Ví dụ 3: (Đề tham khảo lần 2 năm 2020) Có bao nhiêu số nguyên
x
sao cho
tồn tại số thực
y
thỏa mãn
( )
( )
22
34
log logxy x y
+= +
?
A.
3.
B.
2.
C.
1.
D. Vô số.
Lời giải
Chọn B.
4
Điều kiện:
22
0
.
0
xy
xy
+>
+>
Điều kiện cần : Đặt
( )
(
)
22
34
22
3
log log
4
+=
= += + ⇔
+=
t
t
xy
t xy x y
xy
.
( )
2
2
2
3
2 2 .3 9 4 0
34
= −
⇔ ⇒ − +−=
+− =
t
ttt
tt
xy
yy
yy
( )
*
( )
*
có nghiệm
y
(
)
9
4
0 9 2 9 4 0 log 2 0,8548
′
⇔∆≥⇔ − − ≥⇔≤ ≈
t tt
t
.
Khi đó:
log 2
3
2
2
22
1
03
4 3, 27 0 .
1
x
x
xy x
x
x
= −
≤≤
+≤ ≈ ⇒ ⇒=
∈
=
Điều kiện đủ:
Với
( )
( )
2
2
4 10
0
31
1
9 2.3 2 4 0
41
41 31
t
t
tt t
t
tt
t
y
x
ft
y
−>
>
= +

=−⇒ ⇒ ⇒

= + +− =
= −
−= +
.
Khi
( )
0 0,8548 9 4 0
tt
t ft
<< ⇒ ≥ ⇒ >
nên loại
1= −x
.
Với
0=x
. Rõ ràng tồn tại
1y =
để
( )
(
)
22
34
log log
xy x y+= +
.
Với
1=x
. Rõ ràng tồn tại
0
y =
để
( )
( )
22
34
log logxy x y
+= +
.
Vậy có
2
số nguyên
x
thỏa yêu cầu bài toán là
0
x
=
,
1x =
.
Chú ý : Ngoài ra, ta có thể chặn điều kiện cho các biến bằng cách sử dụng các
bất đẳng thức cơ bản, điều kiện tương giao giữa đường thẳng và đường tròn
như sau :
( )
( )
22
3
4
+=
+=
t
t
xy d
xy C
. Do đó để
,xy
tồn tại thì đường thẳng
d
phải có điểm
chung với đường tròn
( )
C
( )
3
2
3
; 2 log 2 0,8548.
2
−
⇔ ≤ ⇔ ≤ ⇒≤ ≈
t
t
d Od R t
Hoặc
22
3
3
94
4
2
t
t
tt
t
xy
xy
xy
xy
+=
+=

⇔

−
+=
=
. Vì
( )
2
9
4
4 2.4 9 log 2
tt
x y xy t+ ≥ ⇔ ≥ ⇔≤
.
5
3. Dạng 3: Cả hai biến đều nguyên, trong đó có một biến nguyên thuộc tập K
cho trước, với K có thể là một khoảng, một đoạn. Khi đó, ta cũng rút biến
nguyên thuộc K theo biến còn lại để tìm miền giá trị cho biến đó.
Ví dụ 4: (Đề tham khảo lần 1 năm 2020) Có bao nhiêu cặp số nguyên
( )
;xy
thỏa mãn
0 2020x≤≤
và
( )
3
log 3 3 2 9+ += +
y
x xy
?
A.
2019
. B.
6
. C.
2020
. D.
4
.
Lời giải
Chọn D
Ta có:
(
)
( )
(
)
2
33
log 3 3 2 9 log 1 1 2 3
+ += + ⇔ ++ + = +
yy
x xy x x y
( ) ( )
12fx f y⇔ +=
, với
( )
3
t
ft t= +
,
t ∈
.
Ta có:
( )
1 3 ln3 0,
′
= + > ∀∈
t
ft t
nên hàm số
( )
ft
đồng biến trên
. Do đó:
( ) ( )
12fx f y+=
3
log ( 1) 2 9 1⇔ += ⇔= −
y
x yx
Vì
0 2020
x≤≤
nên
9
0 9 1 2020 0 log 2021≤ −≤ ⇔ ≤ ≤
y
y
.
Do
y
nguyên nên
{
}
0;1;2;3
y
∈
. Suy ra
( ) ( ) ( ) ( ) ( )
{ }
; 0;0 ; 8;1 ; 80;2 ; 728;3∈xy
.
Vậy có 4 cặp số nguyên
( )
;xy
thỏa đề.
4. Dạng 4: Cả hai biến đều nguyên, rút được biến này theo biến kia đưa về
bài toán tìm điểm nguyên trên các đường cong đơn giản
Ví dụ 5: Có bao nhiêu cặp số nguyên dương
(; )xy
thỏa mãn
1
2
log ( 1)( 1) 4 ( 1)( 1)
y
xy xy




?
A.
2
. B.
1
. C.
3
. D.
8
.
Lời giải
Chọn B
Từ giả thiết ta có
2
( 1) log ( 1)( 1) 4 ( 1)( 1)
y xy xy




2 22
44
log ( 1)( 1) ( 1) log 1 log 1 1
11
xy x x y x
yy

 



22
4
log ( 1) ( 1) log 1 2
1
xx y
y

22
44 4
log ( 1) ( 1) log 1
11 1
x x fx f
yy y




,
6
với
2
logft t t
,
0; .t 
Ta có
1
( ) 1 0, 0
ln 2
ft t
t

hàm số
ft
đồng biến trên
0; .

Do đó
44
11
11
fx f x
yy




4
1.
1
x
y

Vì
;xy
là số nguyên dương nên
4
1y
cũng là số nguyên dương
1 1; 2; 4 1; 3yy 
(loại
0
y =
).
Với
11yx
=⇒=
(nhận).
Với
30yx=⇒=
(loại).
Vậy có 1 cặp số nguyên dương
(; )xy
là
( )
1;1
.
5. Dạng 5: Đưa phương trình về tổng các bình phương của hai biến nguyên
Ví dụ 6: (Đề thi thử lần 2 – Sở GDĐT Hà Nội năm 2020) Cho các số thực
dương
,xy
thỏa mãn
log log log log 100+++ =
xyxy
và
log , log ,log ,log
xyxy
là các số nguyên dương.
Khi đó kết quả
xy
bằng
A.
164
10
. B.
144
10
. C.
100
10
. D.
200
10
.
Lời giải
Chọn A
Đặt
2
2
log
log
log
log
=
=
⇒

=
=
xa
xa
yb
yb
. Ta có:
11
log log log log log log log log 100
22
+++=+++=xyxyxyxy
22
11
100
22
⇔++ + =ab a b
( ) ( )
( ) ( )
22 22
22
1 1 202 1 1 9 11
⇔+ ++ = ⇔+ ++ =+ab ab
Mà
1+a
,
1+b
là các số nguyên dương nên suy ra
19
1 11
+=
+=
a
b
hoặc
1 11
19
+=
+=
a
b
.
7
Trường hợp 1:
64
64 100 164
100
1 9 8 logx 64
10
10 10
1 11 10 log 100
10
aa
x
xy
bb y
y
+
+= = =
=

⇔ ⇔ ⇔ ⇒= =

+= = =
=
Trường hợp 2:
100
100 64 164
64
1 11 10 logx 100
10
10 10
1 9 8 log 64
10
aa
x
xy
bb y
y
+
+= = =
=

⇔ ⇔ ⇔ ⇒= =

+= = =
=
.
Vậy
164
10xy =
.
6. Dạng 6: Đưa về phương trình tích của hai biến nguyên
Ví dụ 7: Có bao nhiêu số nguyên dương
x
sao cho tồn tại số nguyên dương
y
thỏa mãn điều kiện
( )( )
1
2
3
log 2 2 1 2 3.9 27 1
−
+
−+ + + = +


xy
xy
xy xy
?
A.
1
. B.
2
. C.
2020
. D.
2021
.
Lời giải
Chọn A
Điều kiện:
,
2 2 10
+
∈
− +>
xy
xy
.
Ta có:
( )( )
1
2
3
log 2 2 1 2 3.9 27 1
−
+
−+ + + = +


xy
xy
xy xy
( ) ( )
3
221
2
33 3
log 2 2 1 log 2 3 3 log 3
−+
+
⇔ − ++ + + = +
xy
xy
xy xy
(
) ( )
3
221
2
33
33
log 2 2 1 3 log 3 2 2 1
22
−+
+

⇔ −++ = + ⇔ −+=

++

xy
xy
xy fxy f
xy xy
,
với
(
)
3
log 3= +
t
ft t
,
( )
0;∈ +∞t
Ta có:
( )
1
2 ln 3 0, 0
ln3
′
= + > ∀>
t
ft t
t
nên hàm số
( )
ft
đồng biến trên khoảng
( )
0;+∞
.
8
Do đó
( )
3
221
2

− +=

+

fx y f
xy
3
221
2
⇔ − +=
+
xy
xy
( )( )
221 2 3⇔ −+ + =xy xy
.
( )
*
Vì
,xy
nguyên dương nên
( )
*
tương đương
2 2 11
23
2 2 13
21
− +=
+=
− +=
+=
xy
xy
xy
xy
( )
( )
01
23 1
11
21 0
−= =



+= =


⇔⇔

−= =



+= =



xy x
n
xy y
xy x
l
xy y
.
Vậy có
1
giá trị của
x
thỏa mãn bài toán.
7. Dạng 7: Sử dụng tính chất chia hết
Ví dụ 8: Có bao nhiêu số nguyên
x
thuộc đoạn
1;2020


sao cho tồn tại số
nguyên dương
y
thỏa mãn
( )
2
4 3 1 log
31
10
4
−+
+
=
xy x
y
?
A.
2020.
B.
1347.
C.
673.
D. Vô số.
Lời giải
Chọn B.
( )
( )
2
4 3 1 log
2
31 31
10 4 3 1 log log
44
−+
++

= ⇔ −+ =


xy x
yy
xy x
( )
( )
( )
2
4 3 1 2 log log 3 1 log 4⇔ − ++ = +−xy x y
( )
( )
2
4 3 1 log 2log log 4 log 3 1 0

⇔ − + + + − +=

xy x x y
( )
( )
( )
22
4 3 1 log log 4 log 3 1 0


⇔ − + + − +=


xy x x y
( )
1
+ Nếu
2
4 31>+xy
thì
( )
( )
2
log 4 log 3 1>+
xy
. Suy ra:
( )
10>VT
.
+ Nếu
2
4 31<+xy
thì
( )
( )
2
log 4 log 3 1<+xy
. Suy ra:
( )
10<VT
.
Do đó, từ
( )
1
suy ra:
2
4 31
= +xy
( )( )
2
2
11
41
33
xx
x
y yx
−+
−
⇔= ⇔= +
(
)
2
9
Với
31xk= +
,
32xk= +
,
k ∈
, từ
(
)
2
dễ dàng thấy
y
là số nguyên dương.
Xét
y
không là số nguyên dương. Từ
( )
2
, suy ra:
x
chia hết cho
3
.
Đặt
3xk=
,
*
k ∈
. Vì
1;2020x

∈∩

nên
*
1 3 2020,kk≤≤ ∈
1 673k⇒≤ ≤
,
*
k ∈
.
Do đó có
673
số nguyên
x
thuộc đoạn
1;2020


mà
y
không phải là số
nguyên dương.
Vậy có
2020 673 1347
−=
số nguyên
x
thỏa mãn yêu cầu bài toán.
8. Dạng 8: Đếm điểm nguyên trong các hình cơ bản
Ví dụ 9: Có bao nhiêu cặp số nguyên
( )
,ab
thỏa mãn đồng thời các điều kiện:
22
1ab+>
và
( )
22
22 2 2
22
22
44
3 lo g
2
ab
ba b a
ab
ab
+

+++

+ −≤

+

?
A.
10
. B.
6
. C.
7
. D.
8
.
Lời giải
Chọn D.
Ta có :
( )
( )( )
22 22
222 2 2 22
22 22
22 22
44 4
3 log 3 log
22
ab ab
bab a b ab
ab ab
ab ab
++

+++ + +

+ −≤ ⇔ + −≤

++

( ) (
)
22 22
22 2 2 2
3 log 4 log 2 1
ab ab
ab b a b
++
⇔ + −≤ + − + +
( )
(
) (
) ( )
22 22
22 22 2 2
2 log 2 4 log 4
ab ab
ab ab b b
++
⇔ + + + ≤ ++ +
.
Nếu
2 22
24+>+a bb
thì
( ) ( )
22 22
22 2
log 2 log 4
++
+> +
ab ab
ab b
. Suy ra:
( ) (
)
( ) ( )
22 22
22 22 2 2
2 log 2 4 log 4
++
+ + + > ++ +
ab ab
ab ab b b
(vô lí).
Do đó,
2 22 22
24 4a bb ab+ ≤+⇔+≤
.
Mà
22
1ab+>
,
,ab∈
nên nghiệm nguyên
( )
,ab
là các điểm nguyên trong
mặt phẳng tọa độ
( )
Oxy
nằm trong hình vành khăn, tạo bởi 2 đường tròn
đồng tâm
( )
0;0O
bán kính lần lượt là
1
và
2
(bỏ đi biên của hình tròn
( )
;1O
)
(Xem hình vẽ).
10
Suy ra:
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
{ }
, 2;0, 2;0,0;2,0; 2,1;1,1; 1, 1;1, 1;1ab ∈ − − −− −
.
Vậy có
8
cặp số nguyên
( )
,ab
.
Ví dụ 10: Có bao nhiêu cặp số nguyên
( )
,ab
thỏa mãn đồng thời các điều kiện:
22
0 16ab<+≤
và
2
16 64
log
2
b
ab
ab
+
+>
+
?
A.
10
. B.
6
. C.
7
. D.
8
.
Lời giải
Chọn D.
Từ điều kiện
22
0 16ab<+≤
, suy ra
a
,
b
không đồng thời bằng
0
nên
20ab+>
. Ta có:
( ) ( )
2 22
16 64
log 4 log 4 log 2
2
b
ab ab b a b
ab
+
+> ⇔+>+ +− +
+
( ) ( ) (
)
( )
22
log 2 2 log 4 4ab ab b b⇔ + ++ > +++
( )
( )
24fa b fb⇔ +>+
,
với là hàm số đồng biến trên khoảng
( )
0;+∞
.
Do đó,
( ) ( )
2 424 4fa b fb a b b a b+ > +⇔+ >+⇔+>
.
( )
2
logft t t= +
11
Kết hợp với điều kiện
22
0 16ab<+≤
,
,
ab∈
nên nghiệm nguyên
( )
,ab
là các
điểm nguyên trong mặt phẳng tọa độ
( )
Oxy
nằm trong hình tròn tâm
(
)
0;0O
,
bán kính bằng
4
(bỏ đi tâm
O
) và nằm ngoài hình vuông
4
xy
+=
.
(Xem hình vẽ).
Đếm trực tiếp trên hình, ta có
8
điểm nguyên thỏa mãn yêu cầu bài toán.
Vậy có
8
cặp số nguyên
( )
,ab
.
12
BÀI TẬP TỰ LUYỆN
Câu 1. Có bao nhiêu số thực
x
sao cho tồn tại số nguyên
y
thỏa mãn
( )
( )
2
2
22
3
3
log log 4 4 8
+ +−

−
− + +=


yx x x
x
xx
yy
?
A.
2.
B.
4.
C.
3.
D. Vô số.
Câu 2. Có bao nhiêu số nguyên
x
sao cho tồn tại số thực
y
thỏa mãn
( )
( )
22
34
log 2 2 log 4 2 4 2+ −= + −− +xy x y xy
?
A.
0
. B.
2
. C.
4
. D.
8
.
Câu 3. Có bao nhiêu số nguyên
y
để tồn tại số thực
x
thỏa mãn
( )
( )
22
72
log 4 3 log+= +xy xy
?
A.
1
. B.
2
. C.
0
. D.
3
.
Câu 4. Có bao nhiêu cặp số nguyên
( )
;xy
thỏa mãn
0 2020y<≤
và
2
31
log 2 2 3

−
= +−


x
x
y
y
?
A.
2019
. B.
7
. C.
2020
. D.
4
.
Câu 5. Có bao nhiêu cặp số nguyên
;xy
thỏa mãn
( )
31 1
3
1
5 5 1 15 3
5
+ + −−
+
+ + + += + −
x y xy xy
xy
xy y
?
A.
2
. B.
1
. C.
3
. D.
4
.
Câu 6. Có bao nhiêu cặp số nguyên dương
(
)
;xy
thỏa mãn
22
22
2
20
log 2 4 42
6
xy
xy x y
xy y



?
A.
1
. B.
2
. C.
3
. D.
4
.
Câu 7. (Chuyên ĐH Vinh – lần 2 – 2020) Có bao nhiêu cặp số thực dương
( )
;ab
thỏa mãn
2
log a
là số nguyên dương,
23
log 1 logab
= +
và
22 2
2020ab+<
?
A.
6.
B.
7.
C.
5.
D.
8.
Câu 8. Có bao nhiêu cặp số nguyên
( )
;xy
thỏa mãn
22
3 22
2.625 6250.125 9 4 5− =−+
xy
yx
?
A.
1
. B.
2
. C.
0
. D.
3
.
13
Câu 9. Có bao nhiêu bộ
( )
;xy
với
,
xy
là các số nguyên thỏa mãn
1 , 243≤≤xy
và
(
)
( )
2
3
9log 9 3 9=+−
xy
x xy x
?
A.
1
. B.
3
. C.
12
. D.
243
.
Câu 10. Có bao nhiêu cặp số nguyên
( )
,ab
thỏa mãn điều kiện:
( )
22 2
2 2 21
e e 1e 0
a b ab ab b
a ab b
+ ++
+ − + −− =
?
A.
4
. B.
2
. C.
9
. D.
6
.
Câu 11. Có bao nhiêu cặp số nguyên
( )
,xy
thỏa mãn điều kiện:
( )
( )
2
3
2
2
2 .8 32.2 2 3 5
yx
xx
xxy y x
+
+ −= +−+
?
A.
4
. B.
2
. C.
1
. D.
3
.
Câu 12. Có bao nhiêu cặp số nguyên không âm
( )
;xy
thỏa mãn điều kiện:
22
22
11
log 6 8 9 0
682
++
+ + − − +≤
++
xy
xy xy
xy
?
A.
45
. B.
49
. C.
48
. D.
47
.
Câu 13. Có bao nhiêu cặp số nguyên
( )
,ab
thỏa mãn điều kiện:
22
22
2
2 log 4 1
ab
ab
ab
ab
+
+
+
+ ≤+
+
?
A.
25
. B.
24
. C.
36
. D.
35
.
14
ĐÁP ÁN
Câu 1. Có bao nhiêu số thực
x
sao cho tồn tại số nguyên
y
thỏa mãn
( )
( )
2
2
22
3
3
log log 4 4 8
+ +−

−
− + +=


yx x x
x
xx
yy
?
A.
2.
B.
4.
C.
3.
D. Vô số.
Lời giải
Chọn B.
Điều kiện:
3
0
x
y
y
−
>
∈
. Ta có :
( )
( )
2
2
22
3
3
log log 4 4 8
+ +−

−
− + +=


yx x x
x
xx
yy
(
)
22
22
33
log log 2 2

−−
⇔ − ++ −= +−


xx
xx xx
yy
( ) ( )
( )
22 2
22
33 3
log log 2 2 2
 
−− −
⇔ + = ++ + ++ ⇔ = ++
 
 
xx x
xx xx f fxx
yy y
, với
( )
2
log= +ft t t
là hàm số đồng biến trên khoảng
( )
0;+∞
. Do đó:
( )
22
2
33 3
22
2

−− −
= ++ ⇔ = ++⇔ =

++

xx x
f fxx xx y
y y xx
.
Nhận xét : Nếu tồn tại cặp số
;xy
thì điều kiện
3
0
x
y
−
>
luôn thỏa mãn.
Cách 1: Xét hàm
2
3
2
x
y
xx

với
3
x ≠
, ta có :
2
2
2
65
2
xx
y
xx


;
2
0 6 5 0 3 14; 3 14y xx x
 
15
Bảng biến thiên
x

3 14
3
3 14

y
0
0
y
7 2 14
7

0
0
0
7 2 14
7

Dựa vào bảng biến thiên, suy ra :
7 2 14 7 2 14
; \0
77
y






.
Mà
y ∈
nên
{ }
2; 1y ∈− −
.
Mặt khác, dựa vào BBT, ứng với mỗi giá trị
{ }
2; 1y ∈− −
ta có
2
nghiệm
x
.
Vậy có
4
giá trị
x
thỏa yêu cầu bài toán.
Cách 2: Xét phương trình
( )
2
1 2 30+ − + +=yx y x y
*
Phương trình
*
có nghiệm khi và chỉ khi
2
1 42 3 0y yy
2
7 2 14 7 2 14
7 14 1 0
77
yy y


.
Vì
, 0 2; 1yy y

.
Với
2y = −
. Thay vào
*
, suy ra:
1
1;
2
x

∈−−


.
Với
1y
= −
. Thay vào
*
, suy ra:
{ }
1 2; 1 2
x ∈−− −+
.
Vậy có
4
giá trị
x
thỏa yêu cầu bài toán.
16
Câu 2. Có bao nhiêu số nguyên
x
sao cho tồn tại số thực
y
thỏa mãn
( )
( )
22
34
log 2 2 log 4 2 4 2
+ −= + −− +xy x y xy
?
A.
0
. B.
2
. C.
4
. D.
8
.
Lời giải
Chọn B
Ta có:
( )
( )
22
34
log 2 2 log 4 2 4 2+ −= + −− +xy x y xy
( ) ( ) ( )
22
34
log 2 2 log 1 2 1

⇔ + −= − + −

xy x y
.
Đặt
1, 2 1
ax b y
=−=−
. Phương trình trở thành
( )
( )
22
34
log log+= +ab a b
. Đây
chính là một câu trong đề tham khảo lần 2 năm 2019 – 2020.
Câu 3. Có bao nhiêu số nguyên
y
để tồn tại số thực
x
thỏa mãn
( )
( )
22
72
log 4 3 log+= +xy xy
?
A.
1
. B.
2
. C.
0
. D.
3
.
Lời giải
Chọn B
Điều kiện:
22
430
.
0
+>
+>
xy
xy
Điều kiện cần :
Đặt
( )
( )
22
72
22
437
log 4 3 log
2
+=
= += +⇔
+=
t
t
xy
t xy xy
xy
.
Để tồn tại
x
thì đường thẳng
:4 3 7 0
t
dx y+−=
và đường tròn
( )
C
tâm
( )
0;0O
,
( )
22
t
t
R = =
phải có điểm chung
(
)
;d Od R⇔≤
( )
7
2
77
2 5 log 5 1,006
5
2
t
t
t
t

⇔ ≤ ⇔ ≤ ⇒≤ ≈


.
Suy ra:
7
2
log 5
2
2 2 2,009
t
y ≤≤ ≈
, mà
y ∈
nên
{ }
1; 0;1y ∈−
.
Điều kiện đủ:
17
Với
( )
(
)
2
72
1 log 4 3 log 1=⇒ += +y xx
có nghiệm
1x =
nên nhận
1
y =
.
Với
(
)
2
2
47
49
0 7 16.2 16
2
2
=

=⇒ ⇒=⇒ =

=

t
t
tt
t
x
y
x
có nghiệm
t
nên tồn tại
x
.
Do đó nhận
0y =
.
Với
(
)
( )
2
72
1 log 4 3 log 1=−⇒ − = +y xx
.
Vì
(
)
2
2
log 1 0+≥x
nên
( )
7
log430431 1− ≥ ⇒ −≥⇒ ≥x xx
.
Xét hàm
(
)
( )
(
)
2
72
log 4 3 log 1= −− +fx x x
trên
)
1;
+∞
. Ta có :
(
)
(
)
(
)
( )
( )
( )
(
)
2
22
4ln 2 1 2ln 7 4 3
42
0
4 3 ln 7
1 ln 2 4 3 ln 7 1 ln 2
+− −
′
= −= =
−
+ −+
x xx
x
fx
x
x xx
( )
( )
0,196
1,108
xl
xn
≈−
⇔
≈
.
Lập bảng biên thiên, suy ra
( )
( )
1,108 0,975fx f
≤ ≈−
. Suy ra phương trình
( )
0fx=
vô nghiệm. Do đó, loại
1y = −
.
Vậy có
2
số nguyên
y
thỏa yêu cầu bài toán là
0
y =
,
1
y =
.
Câu 4. Có bao nhiêu cặp số nguyên
( )
;xy
thỏa mãn
0 2020y<≤
và
2
31
log 2 2 3 ?

−
= +−


x
x
y
y
A.
2019
. B.
7
. C.
2020
. D.
4
.
Lời giải
Chọn B
Từ giả thiết ta có:
31 0
31
0
0 2020
⇒ >⇒ >
−
>
<≤
x
x
y
x
y
. Khi đó, ta có:
18
2
31
log 2 2 3

−
= +−


x
x
y
y
(
)
( )
( ) ( )
22
log 3 1 3 1 log 2 2⇔ −+ −= +
xx
yy
( )
( )
31 2
⇔ −=
x
f fy
,
với
( )
2
log= +ft t t
là hàm số đồng biến trên khoảng
( )
0;+∞
. Do đó:
( )
(
)
31 2−=
x
f fy
31
2 31
2
−
⇔ = −⇔ =
x
x
yy
Vì
3
0 2020 0 3 1 2 2020 1 3 4041 0 log 4041 7,56<≤ ⇔< −≤× ⇔< ≤ ⇔<≤ ≈
xx
yx
.
Mà
x ∈
nên
{ }
1;2;3;4;5;6;7∈x
. Suy ra, có
7
cặp số nguyên
( )
,xy
Vậy có
7
cặp
( )
;xy
thỏa mãn.
Câu 5. Có bao nhiêu cặp số nguyên
;xy
thỏa mãn
(
)
31 1
3
1
5 5 1 15 3
5
+ + −−
+
+ + + += + −
x y xy xy
xy
xy y
?
A.
2
. B.
1
. C.
3
. D.
4
.
Lời giải
Chọn D
Ta có:
(
)
31 1
3
1
5 5 1 15 3
5
x y xy xy
xy
xy y
+ + −−
+
+ + + += + −
3 3 11
5 5 35 5 1
x y x y xy xy
x y xy
+ −− − − +
⇔ − ++ = − − −
.
Xét hàm số
( )
55 ,
−
=− +∈
tt
f t tt
. Ta có
( )
5 ln 5 5 ln5 1 0
tt
ft
−
′
= + +>
,
t∀∈
.
Suy ra : hàm số
( )
ft
đồng biến trên
.
Do đó:
( ) ( )
31+ = −−f x y f xy
31
x y xy⇔+ =− −
( )
31yxx⇔ + =−−
1
3
x
y
x
−−
⇔=
+
( Do
3= −x
không là nghiệm của phương trình)
2
1
3
⇔ =−+
+
y
x
.
Vì
,xy∈
nên
{ } { }
3 1;1;2;2 2;4;1;5+∈ − − ⇒∈−−−−xx
.
Vậy có
4
cặp số
;xy
thỏa yêu cầu bài toán.
19
Câu 6. Có bao nhiêu cặp số nguyên dương
(
)
;
xy
thỏa mãn
22
22
2
20
log 2 4 42
6
xy
xy x y
xy y



?
A.
1
. B.
2
. C.
3
. D.
4
.
Lời giải
Chọn B
Ta có:
22
22
2
20
log 2 4 42
6
xy
xy x y
xy y



22 22
22
log 2 20 2 20 log 6 6 *xy xy x y y x y y

 


Xét hàm số
2
log
ft t t
trên khoảng
0;

.
Ta có
1
1 0, 0
.ln 2
ft t
t

. Suy ra hàm số
ft
đồng biến trên
khoảng
0; 
.
Do đó,
22
* 2 20 6f x y fx y y



22
2 20 6xy x y y 
22
2 4 40⇔+−+ =xy xy
( ) ( )
22
1 2 45⇔− ++ =xy
( ) ( )
22
22
1 2 36⇔− ++ =+xy
.
Vì
,
xy
+
∈
nên
13
26
−=
+=
x
y
hoặc
16
23
−=
+=
x
y
( ) ( ) ( )
{ }
; 4;4,7;1xy⇒∈
.
Vậy có
2
cặp số nguyên dương
( )
;xy
.
Câu 7. (Chuyên ĐH Vinh – lần 2 – 2020) Có bao nhiêu cặp số thực dương
( )
;ab
thỏa mãn
2
log a
là số nguyên dương,
23
log 1 log
ab= +
và
22 2
2020ab+<
?
A.
6.
B.
7.
C.
5.
D.
8.
Lời giải
Chọn B
Đặt
2
log =an
(
*
∈n
) suy ra
2=
n
a
và
1
3
log 1 3
−
= −⇔ =
n
bn b
Ta có
2222222
2020 2 3 2020
−
+< ⇔ + <
nn
ab
(
)
1
20
( )
22 2 2
2
3 2020 2 2 log 2020 8
n
nn
−
⇒ < ⇒ −< ⇒<
, mà
*
7nn∈ ⇒≤
Xét hàm số
( )
2 32
23
tt
ft
−
= +
trên
. Ta có
( )
2 22
2.2 .ln2 2.3 .ln3 0,
−
′
= + > ∀∈
tt
ft t
. Suy ra hàm số
( )
ft
đồng biến trên
.
Vì
( )
(
)
2
7 2020fn f≤<
nên
7
n ≤
,
{
}
1;2;...;7
∈
n
.
Vậy có 7 cặp số thực dương
( )
;
ab
thỏa yêu cầu bài toán.
Chú ý: Khi có
7
n ≤
, thử với
7
n =
thấy thỏa thì ta có thể kết luận
{ }
1;2;...;7
∈n
.
Câu 8. Có bao nhiêu cặp số nguyên
( )
;xy
thỏa mãn
22
3 22
2.625 6250.125 9 4 5− =−+
xy
yx
?
A.
1
. B.
2
. C.
0
. D.
3
.
Lời giải
Chọn C
Ta có:
2 2 22
3 22 4 95 22
2.625 6250.125 9 4 5 2.5 2.5 9 4 5
+
− =−+⇔ − =−+
x y xy
yx yx
( ) ( ) ( )
22
4 2 95 2 2 2
2.5 4 2.5 9 5 4 9 5
+
⇔ + = + +⇔ = +
xy
x y fx fy
,
với
( )
2.5
t
ft t= +
là hàm số đồng biến trên
.
Do đó:
( ) (
)
( )( )
2 2 2 2 22
4 9549549523235= + ⇔ = +⇔ − =⇔ − + =fx fy x y x y xy x y
( )
*
.
Vì
,xy
là số nguyên nên
( )
*
tương đương
231
235
23 1
23 5
−=
+=
−=−
+=−
xy
xy
xy
xy
hoặc
235
231
23 5
23 1
−=
+=
−=−
+=−
xy
xy
xy
xy
.
Cả
4
trường hợp đều cho kết quả
,
xy∉
.
Vậy không tồn tại cặp số
( )
;xy
thỏa mãn bài toán.
21
Câu 9. Có bao nhiêu bộ
( )
;xy
với
,
xy
là các số nguyên thỏa mãn
1 , 243≤≤xy
và
( )
(
)
2
3
9log 9 3 9
=+−
xy
x xy x
?
A.
1
. B.
3
. C.
12
. D.
243
.
Lời giải
Chọn A
Ta có:
( )
(
)
2 22 2
33
9log 9 3 9 log 3 2
−
= + −⇔ += +−
xy xy
x x y x x x xy
22 2 2
33
log 3 log 3
−−
⇔ += +
xy xy
xx
( ) ( )
22
3
−
⇔=
xy
fx f
,
với
( )
3
log= +ft t t
là hàm số đồng biến trên khoảng
( )
0;+∞
.
Do đó:
( )
( )
2 222
33
−−
= ⇔=
xy xy
fx f x
( )
*
Ta có:
2 2 2 10
3 243 3 12 12
−
= ≤ = ⇒ ≤ ⇒≤
xy
x xy x
.
Mặt khác, vì
,
xy
+
∈
nên từ
( )
*
suy ra:
3
n
x =
, với
n
là số nguyên không âm.
Suy ra:
{ }
3 12 0;1; 2
n
xn= ≤ ⇒∈
.
Với
0n =
. Suy ra:
1x =
,
2
y =
.
Với
1n =
. Suy ra:
3
x =
,
32
4
39
3
y
y
−
=⇒=
(loại).
Với
2n =
. Suy ra:
9
x =
,
92
2
3 81
3
y
y
−
= ⇒=
(loại).
Vậy có
1
bộ
( )
,
xy
là
( )
1; 2
.
22
Câu 10. Có bao nhiêu cặp số nguyên
( )
,ab
thỏa mãn điều kiện:
( )
22 2
2 2 21
e e 1e 0
a b ab ab b
a ab b
+ ++
+ − + −− =
?
A.
4
. B.
2
. C.
9
. D.
6
.
Lời giải
Chọn D
Ta có:
(
)
22 2
2 2 21
e e 1e 0
+ ++
+ − + −− =
a b ab ab b
a ab b
22 2
2 2 21
e 1e 0
+− +
⇔ + − + −− =
a b ab b
a ab b
22 2
2 2 21 2
e 2e1
+− +
⇔ + − + = ++
a b ab b
a ab b b
( )
1
.
Xét hàm số đặc trưng:
(
)
e= +
t
ft t
với
.∈t
Ta có
( )
e 1 0,
′
= + > ∀∈
t
ft t
.
Suy ra hàm số
( )
ft
đồng biến trên
.
Do đó:
( )
( ) ( )
22 2
22 1⇔ +−= +f a b ab f b
22 2 2 2
21 1⇔+ −=+⇔−+=a b ab b a ab b
.
Cách 1:
22
10+=−−a ab b
, ta xem như là phương trình bậc hai theo biến
a
.
Phương trình có nghiệm
( )
22 2
4
4 10
3
bb b⇔∆= − − ≥ ⇔ ≤
.
Vì
b
∈
nên
{ }
1; 0;1b∈−
.
• Với
{ }
0 1;1ba= ⇒ ∈−
.
• Với
{
}
1 0;1
ba=−⇒ ∈
.
• Với
{ }
1 0; 1ba=⇒∈ −
.
Vậy có
6
cặp số nguyên
( )
,ab
.
Cách 2:
( )
2
2 2 22
12−+=⇔++− =a abb a b ab
( )
2
22
110⇔++− =++a b ab
Vì
,ab∈
nên
22
1
0
ab
ab
= =
−=
hoặc
( )
2
2
1
0
a ab
b
=−=
=
hoặc
( )
2
2
1
0
b ab
a
=−=
=
23
1
1
ab
ab
= =
⇔
= = −
hoặc
1, 0
1, 0
ab
ab
= =
⇔
=−=
hoặc
0, 1
0, 1
ab
ab
= =
⇔
= = −
Vậy có
6
cặp số nguyên
( )
,
ab
.
Câu 11. Có bao nhiêu cặp số nguyên
( )
,xy
thỏa mãn điều kiện:
( )
( )
2
3
2
2
2 .8 32.2 2 3 5
yx
xx
xxy y x
+
+ −= +−+
?
A.
4
. B.
2
. C.
1
. D.
3
.
Lời giải
Chọn B
Ta có:
( )
( )
( )
( )
( )
22
33
2 25
2 33 2
2 .8 32.2 2 3 5 2 3 2 2 5
yx yx
x x xx
x x y y x x x yx
+ ++
+
+ − = + − +⇔ + + = + + +
( ) ( )
( )
32
3 25f x x f yx⇔ + = ++
, với
( )
2
t
ft t= +
là hàm số đồng biến trên
.
Suy ra:
( )
3
32
22
35 5
3 25
22
xx x
x xyx y yx
xx
+− −
+ = + +⇔= ⇔=+
++
.
Cách 1:
Xét hàm
( )
2
5
2
x
gx
x
−
=
+
,
x
∈
. Ta có :
( )
( )
{
}
2
2
2
10 2
0 5 33;5 33
2
xx
gx x
x
−+ +
′
= =⇔∈ − +
+
.
Lập bảng biến thiên ta được
( )
5 33 5 33
;
44
gx

−− −+
∈



.
Vì
,xy∈
nên
( )
gx∈
. Suy ra
( ) { }
2; 1; 0gx∈− −
. Thử lại :
• Với
( )
2
5
2 21
2
x
gx x
x
−
=−⇒ =−⇒ =−
+
,
3y = −
.
• Với
( )
2
5 1 13 1 13
11 ;
22
2
x
gx x
x

− −− −+

=−⇒ =−⇒ ∈

+


(loại).
24
• Với
( )
2
5
0 05
2
x
gx x
x
−
=⇒ =⇒=
+
,
5
y =
.
Vậy có
2
cặp số nguyên
( )
;xy
là :
( )
1; 3−−
,
( )
5; 5
.
Cách 2:
Ta có:
2
5
2
x
yx
x
−
= +
+
. Vì
,xy∈
nên
2
5
2
x
x
−
∈
+
. Suy ra
2
5
2
x
k
x
−
= ∈
+
.
Ta có :
2
2
5
2 50
2
x
k kx x k
x
−
=⇔ −+ +=
+
( )
*
.
• Với
0 5; 5
k xy
=⇒= =
(nhận)
• Với
0k ≠
. Khi đó,
( )
*
có nghiệm khi và chỉ khi
( )
5 33 5 33
14 2 5 0 ;
44
kk k

−− −+
∆= − + ≥ ⇔ ∈



.
Vì
{ }
\0k
∈
nên
{ }
2; 1k ∈− −
. Thử lại ta nhận
2k = −
,
1x
= −
3
y = −
.
Vậy có
2
cặp số nguyên
( )
;xy
là :
( )
1; 3−−
,
( )
5; 5
.
Cách 3:
Ta có:
2
5
2
x
yx
x
−
= +
+
. Vì
,xy∈
nên
( )
( )
( )( )
( ) ( ) ( )
2 2 22
52 552 252xxxxxxx− +⇒− + +⇒ − + 
.
(
) ( ) ( )
22 2
2 27 2 27 2xx x
⇒ +− + ⇒ +
( )
{ } {
} { }
22
2 1; 3; 9; 27 1; 25 1;1; 5; 5x xx⇒ + ∈ ⇒ ∈ ⇒ ∈− −
. Thử lại:
• Với
13xy=−⇒ =−
(nhận).
• Với
1
1
3
xy=⇒=−
(loại).
• Với
145
5
27
xy=−⇒ =−
(loại).
• Với
55xy=⇒=
(nhận).
Vậy có
2
cặp số nguyên
( )
;xy
là :
( )
1; 3−−
,
( )
5; 5
.
25
Câu 12. Có bao nhiêu cặp số nguyên không âm
(
)
;
xy
thỏa mãn điều kiện:
22
22
11
log 6 8 9 0
682
++
+ + − − +≤
++
xy
xy xy
xy
?
A.
45
. B.
49
. C.
48
. D.
47
.
Lời giải
Chọn C.
Ta có:
log
22
22
11
6 8 90
682
++
+ + − − +≤
++
xy
xy xy
xy
( )
( )
22 22
log 11 11 log 6 8 2 6 8 2⇔ ++ +++≤ +++++xy xy xy xy
( )
1
Xét hàm số đặc trưng:
( )
log= +
ft t t
với
0>t
. Ta có:
(
)
1
1 0, 0
.ln10
′
= + > ∀> ⇒
ft t
t
Hàm số
( )
ft
đồng biến trên khoảng
( )
0;
+∞
.
Do đó
( )
( )
( )
22 22
1 11 6 8 2 11 6 8 2⇔ ++ ≤ ++⇔++≤++fxy fxy xy xy
( ) ( )
22
3 4 16⇔− +− ≤xy
.
26
Vì
,xy
là số nguyên không âm nên ta coi cặp số
(
)
,
xy
là các điểm nguyên
( )
,
xy
nằm trong hình tròn
( )
C
có tâm
( )
3; 4 , 4=IR
ở góc phần tư thứ nhất.
(Xem hình vẽ).
Vậy có
5752111 48×+×+++=
cặp số nguyên
( )
;xy
.
Chú ý: Ta cũng có tính tính trực tiếp như sau:
( ) ( ) ( ) ( )
22 2
*
16 1 73 4 16 3 ≤− +− ≤ ≤− ⇒− ≤⇒x xyx
.
Vì
x
là số nguyên không âm nên
{ }
0;1;2;3;4;5;6; 7x ∈
. Thay vào
(
)
*
ta cũng có
được
48
cặp số nguyên
( )
;xy
.
Câu 13. Có bao nhiêu cặp số nguyên
( )
,ab
thỏa mãn điều kiện:
22
22
2
2 log 4 1
ab
ab
ab
ab
+
+
+
+ ≤+
+
?
A.
25
. B.
24
. C.
36
. D.
35
.
Lời giải
Chọn B.
Điều kiện:
22
0
ab
ab
+
>⇔
+
a
,
b
không đồng thời bằng
0
. Khi đó, ta có:
( )
(
)
22 22
22
22
2 22
2 log 4 1 2 log 4 log 1
ab ab
ab ab
ab
ab ab
ab
++
++
+
+ ≤+⇔ + +≤+ ++
+
(
)
( )
(
)
22
2
22
22
2 log 2 log 2
ab
ab
ab ab
+
+

⇔ + +≤ + +

( )
( )
22
2fa b f a b

⇔ +≤ +

,
với
(
)
2
2 lo g
t
ft t= +
là hàm số đồng biến trên khoảng .
Do đó,
(
)
( )
(
)
( ) ( )
22
22 22
2 2 1 12fab f ab ab ab a b

+ ≤ + ⇔+≤ + ⇔ −+ − ≤

.
Kết hợp với điều kiện
,ab∈
,
a
,
b
không đồng thời bằng
0
nên nghiệm
nguyên
(
)
,ab
là các điểm nguyên trong mặt phẳng tọa độ
( )
Oxy
nằm trong
hình hoa, kể cả biên, bỏ đi điểm
( )
0;0O
(hình hoa là hình hợp bởi bốn hình
tròn bán kính
2
lần lượt có tâm
( )
1
1;1I
,
(
)
2
1; 1I
−
,
( )
3
1;1
I −
,
( )
4
1; 1I −−
)
(Xem hình vẽ).
( )
0;
+∞
27
Đếm trực tiếp, ta thấy đó là các điểm nguyên nằm trong hình vuông
ABCD
kích thước
44×
, bỏ đi điểm
( )
0;0
. Do đo, có
2
5 1 24−=
điểm nguyên.
Vậy có
24
cặp số nguyên
(
)
,
ab
.
| 1/27
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

CHUYÊN ĐỀ
PHƯƠNG TRÌNH NGHIỆM NGUYÊN
LIÊN QUAN ĐẾN MŨ – LOGARIT
Tác giả: Trần Trọng Trị
Nhóm Giáo viên Toán tiếp sức Chinh phục kỳ thi THPT năm 2020
Tiếp nối chuyên đề Max – Min liên quan đến Mũ – Logarit, chuyên đề này kế
thừa các kĩ năng thu gọn mối quan hệ giữa các biến đã biết như: f (u) = f (v) ,
f (u) ≤ f (v) , với f là hàm số đơn điệu trên một khoảng cho trước; đánh giá
bằng các bất đẳng thức đơn giản; …. Từ đó sử dụng các kĩ thuật cơ bản liên quan
đến các biến nguyên để giải một bài toán phương trình nghiệm nguyên.
Thầy hy vọng với chuyên đề nhỏ này, sẽ giúp các em có cái nhìn rõ hơn về một
số dạng toán liên quan đến phương trình nghiệm nguyên.
1. Dạng 1: Có đúng một biến nguyên và rút được biến nguyên này theo biến
còn lại. Đến đây, ta xét hàm để tìm miền giá trị cho biến nguyên đó.
Ví dụ 1: (Đề 1 – VTV7) Có bao nhiêu số nguyên dương x sao cho tồn tại số − + thực 2 3
y lớn hơn 1 thỏa mãn ( 2 + − 2 − ) 1 log = y x xy x y y log ? x A. 4. B. 2. C. 3. D. Vô số. Lời giải Chọn B.  y > 1 y > 1  Điều kiện: *  * x ∈  ⇔ x ∈ . 2y x 3  − +
2y − x + 3 > 0  > 0   x Ta có : 1 − + ( 2 3 2 + − 2 − ) 1 log = y x xy x y y log x ⇔ ( 2
xy + x − 2 y − 3)log y + 2log y = log(2y − x + 3) − log x ⇔ ( 2
xy + x − y − ) y =
( y − x + ) − ( 2 2 3 log log 2 3 log xy ) ( ) 1 VT  > 0 + Nếu 2
xy > 2y − x + 3 thì (do log y > 0). VP   < 0 VT  < 0 + Nếu 2
xy < 2y − x + 3 thì (do log y > 0). VP   > 0 2y + 3 Do đó, từ ( ) 1 suy ra: 2
xy = 2y − x + 3 ⇔ x = . 2 y +1 2y + 3
Xét hàm f (y) =
, y ∈(1;+∞). Ta có: 2 y +1 f ′(y) 2 2 − y − 6y + 2 = < 0 y ∀ ∈ 1;+∞ f y ( , (
). Suy ra: Hàm số ( ) nghịch biến trên y + )2 2 1 khoảng (1;+∞). Suy ra:   x = f (y) 5 ∈0; . Vì *
x ∈  nên x ∈{1; } 2 . 2   
Vậy có 2 giá trị x thỏa yêu cầu bài toán.
2. Dạng 2: Khi phương trình rút gọn là phương trình bậc hai theo biến
không nguyên. Ta sử dụngđiều kiện có nghiệm của phương trình bậc hai để
tìm miền giá trị cho biến nguyên.
Ví dụ 2: Có bao nhiêu số nguyên x sao cho tồn tại số thực y thỏa mãn 2 2 4x+ y 3x + = y ? A. 4. B. 2. C. 3. D. Vô số. Lời giải Chọn B. 2 2 x+ y x + y 2 2 4 = 3
⇔ x + y − (x + y) 2 2
log 4 = 0 ⇔ y − 2 y log 2 + x − 2x log 2 = 0 . (*) 3 3 3 2
Ta coi (*) là phương trình bậc hai theo biến y . Phương trình (*) có nghiệm
khi và chỉ khi ∆′ ≥ 0 ⇔ (log 2)2 −( 2
x − 2x log 2 ≥ 0 ⇒ 0
− ,2 < x < 1,6 . 3 3 )
Mà x ∈ nên x ∈{0; }
1 . Vậy có 2 giá trị x thỏa yêu cầu bài toán. Chú ý:
 Trong câu 1, ta có thể giải theo cách sử dụng điều kiện có nghiệm của
phương trình bậc hai như sau: Từ 2
xy = 2y − x + 3 2
⇔ xy − 2y + x − 3 = 0 (*) .
Ta coi (*) là phương trình bậc hai theo biến y . Phương trình (*) có nghiệm
khi và chỉ khi ∆′ = − x (x − ) 2 3 − 13 3 + 13 1
3 = −x + 3x +1 ≥ 0 ⇒ ≤ x ≤ . 2 3 Vì *
x ∈  nên x ∈{1;2; } 3 .
 Với x = 1, ta có : 2
y − 2y − 2 = 0 có một nghiệm y = 1+ 3 > 1 (thỏa).
 Với x = 2 , ta có : 2
2y − 2y −1 = 0 có một nghiệm 1 3 y + = > 1 (thỏa). 2  
 Với x = 3 , ta có : 2 2
3y − 2y = 0 ⇔ y ∈0; (loại do y >1). 3   Vậy x ∈{1; }
2 , tức là có 2 số nguyên dương x thỏa yêu cầu bài toán.
 Với cách giải sử dụng điều kiện có nghiệm của phương trình bậc hai, ta
phải thử lại nghiệm, nên có hạn chế hơn so với phương pháp cô lập, xét
hàm. Do đó, trong một bài toán nếu có thể cô lập, xét hàm thì ta nên chọn phương pháp này.
Ví dụ 3: (Đề tham khảo lần 2 năm 2020) Có bao nhiêu số nguyên x sao cho
tồn tại số thực y thỏa mãn log (x + y) = log ( 2 2 x + y ? 3 4 ) A. 3. B. 2. C. 1. D. Vô số. Lời giải Chọn B. 3 x + y > 0 Điều kiện:  . 2 2 x + y > 0
x + y = t
Điều kiện cần : Đặt t = log (x + y) = log ( 3 2 2 x + y ⇔  . 3 4 ) 2 2
x + y = 4tx = 3t −  y 2 ⇔  t t t y y (*) y + t t  ( ⇒ − + − = 3 − y ) 2 2 .3 9 4 0 2 2 = 4
(*) có nghiệm y ⇔ ∆′ ≥ 0 ⇔ 9t − 2(9t −4t ) ≥ 0 ⇔ t ≤ log 2 ≈ 0,8548. 9 4 x = 1 − log 2 3 2  ≤ ≤ Khi đó: 0 x 3 2  2 2 x + y ≤ 4 ≈ 3, 27 ⇒  ⇒ x = 0 .  x ∈ x =1  Điều kiện đủ:   4t t −1 > 0 y = 3 +1 t   > 0  Với  x = 1 − ⇒  ⇒  ⇒  . t t t
y = 4t −1 4t −1 =  (3t + )2 2 1  f
 (t) = 9 + 2.3 + 2 − 4 = 0
Khi 0 < < 0,8548 ⇒ 9t ≥ 4t t
⇒ f (t) > 0 nên loại x = 1 − .
 Với x = 0 . Rõ ràng tồn tại y = 1 để log (x + y) = log ( 2 2 x + y . 3 4 )
 Với x =1. Rõ ràng tồn tại y = 0 để log (x + y) = log ( 2 2 x + y . 3 4 )
Vậy có 2 số nguyên x thỏa yêu cầu bài toán là x = 0, x = 1.
Chú ý : Ngoài ra, ta có thể chặn điều kiện cho các biến bằng cách sử dụng các
bất đẳng thức cơ bản, điều kiện tương giao giữa đường thẳng và đường tròn như sau : x + y = 3  t (d) 
. Do đó để x, y tồn tại thì đường thẳng d phải có điểm 2 2 x + y = 4  t (C) 3 − t
chung với đường tròn (C) ⇔ ( ; ) ≤ ⇔ ≤ 2t d O d R ⇒ t ≤ log 2 ≈ 0,8548. 3 2 2
x + y = 3t t  + = Hoặc x y 3   ⇔ t t t t
− . Vì ( x + y)2 ≥ 4xy ⇔ 2.4 ≥ 9 ⇔ t ≤ log 2. 2 2 t 9 4  9 x + y = 4 xy =  4 2 4
3. Dạng 3: Cả hai biến đều nguyên, trong đó có một biến nguyên thuộc tập K
cho trước, với K có thể là một khoảng, một đoạn. Khi đó, ta cũng rút biến
nguyên thuộc K theo biến còn lại để tìm miền giá trị cho biến đó.
Ví dụ 4: (Đề tham khảo lần 1 năm 2020) Có bao nhiêu cặp số nguyên ( ; x y )
thỏa mãn 0 ≤ x ≤ 2020 và log 3 + 3 + = 2 + 9y x x y ? 3 ( ) A. 2019 . B. 6 . C. 2020 . D. 4 . Lời giải Chọn D
Ta có: log (3 + 3) + = 2 + 9y ⇔ log ( + ) 1 + ( + ) 2 1 = 2 + 3 y x x y x x y 3 3 ⇔ f (x + )
1 = f (2y) , với ( ) = + 3t f t t , t ∈ . Ta có: ′( ) =1+ 3t f t
ln 3 > 0, ∀t ∈  nên hàm số f (t) đồng biến trên  . Do đó: f (x + )
1 = f (2y) ⇔ log ( +1) = 2 ⇔ = 9y x y x −1 3
Vì 0 ≤ x ≤ 2020 nên 0 ≤ 9y −1≤ 2020 ⇔ 0 ≤ y ≤ log 2021. 9
Do y nguyên nên y ∈{0;1;2; } 3 . Suy ra ( ; x y ) ∈ (
{ 0;0);(8; )1;(80;2);(728;3)}.
Vậy có 4 cặp số nguyên ( ; x y ) thỏa đề.
4. Dạng 4: Cả hai biến đều nguyên, rút được biến này theo biến kia đưa về
bài toán tìm điểm nguyên trên các đường cong đơn giản
Ví dụ 5: Có bao nhiêu cặp số nguyên dương (x;y) thỏa mãn y 1  log (x 1)(y 1)  
 4  (x  1)(y  1) 2   ? A. 2 . B. 1 . C. 3 . D. 8 . Lời giải Chọn B
Từ giả thiết ta có (y 1)log (x 1)(y 1)   
 4  (x  1)(y  1) 2   4 4 log (x 1)(y 1)    
 (x  1)  log x  1  log y  1   x  1 2   2   2    y  1 y  1 4
 log (x  1)  (x  1)  log y  1  2  2 2   y  1 4 4  4 
 log (x  1)  (x  1)  log 
f x  1  f    , 2 2   y  1 y  1 y  1 5
với f t  t  log t , t  0;. 2 Ta có 1 f (  t)  1 
 0, t  0  hàm số f t đồng biến trên 0;. t ln 2   Do đó 4 f x   4   4 1  f    x  1    x  1  . y  1 y  1 y  1
Vì x;y là số nguyên dương nên 4 cũng là số nguyên dương y  1
y  1  1;2;4  y  1;  3 (loại y = 0 ).
 Với y = 1⇒ x = 1 (nhận).
 Với y = 3 ⇒ x = 0 (loại).
Vậy có 1 cặp số nguyên dương (x;y) là (1; ) 1 .
5. Dạng 5: Đưa phương trình về tổng các bình phương của hai biến nguyên
Ví dụ 6: (Đề thi thử lần 2 – Sở GDĐT Hà Nội năm 2020) Cho các số thực
dương x,y thỏa mãn log x + log y + log x + log y =100 và
log x , log y , log x , log
y là các số nguyên dương.
Khi đó kết quả xy bằng A. 164 10 . B. 144 10 . C. 100 10 . D. 200 10 . Lời giải Chọn A 2  x = ax = Đặt log log a  ⇒  . Ta có: 2  log y =  b log y = b 1 1
log x + log y + log x + log y = log x + log y + log x + log y = 100 2 2 1 1 2 2 ⇔ 2 2 2 2 a + b + a +
b = 100 ⇔ (a + ) + (b + ) =
⇔ (a + ) + (b + ) 2 2 1 1 202 1 1 = 9 +11 2 2 a + = a + =
Mà a +1, b +1 là các số nguyên dương nên suy ra 1 9  hoặc 1 11  . b +1 = 11 b +1 = 9 6 Trường hợp 1:  64 a +1 = 9 a = 8 logx = 64 x =10 64 1 + 00 164  ⇔  ⇔  ⇔  ⇒ xy = 10 = 10 100 b +1 = 11 b = 10   log y = 100  y =10 Trường hợp 2:  100 a +1 = 11
a =10 logx =100 x =10 100+64 164  ⇔  ⇔  ⇔  ⇒ xy = 10 = 10 . 64 b +1 = 9 b = 8   log y = 64  y =10 Vậy 164 xy = 10 .
6. Dạng 6: Đưa về phương trình tích của hai biến nguyên
Ví dụ 7: Có bao nhiêu số nguyên dương x sao cho tồn tại số nguyên dương y 1
thỏa mãn điều kiện log (2 − 2 + )1( + 2 ) − +2  + 3.9 = 27 +1 3  x y x y x y x y ? A.1. B. 2 . C. 2020 . D. 2021. Lời giải Chọn A + x y ∈ Điều kiện: ,   .
2x − 2y +1 > 0 Ta có: 1 log (2 − 2 + ) 1 ( + 2 ) − +2  + 3.9 = 27 +1 3  x y x y x y x y 3 ⇔ log (2 − 2 + ) 1 + log ( + 2 ) 2 x−2 y 1 + x+2 + 3 = 3 y x y x y + log 3 3 3 3 3   ⇔ log (2 − 2 + ) x− y+ 3 x+ 3 2 2 1 2 1 + 3 = log + 3 y x y
⇔ f 2x − 2y +1 = f , 3 3 ( )   x + 2 yx + 2y  với ( ) = log + 3t f t t , t ∈(0;+∞) 3 Ta có: ′( ) 1 = + 2t f t
ln 3 > 0, ∀t > 0 nên hàm số f (t ) đồng biến trên khoảng t ln 3 (0;+∞). 7 Do đó 3
f ( x − y + )  3  2 2 1 = f
 ⇔ 2x − 2y +1 =  x + 2y x + 2 y
⇔ (2x − 2y + )
1 ( x + 2 y) = 3 . (*)
2x − 2y +1 =1  x + y = Vì 2 3
x, y nguyên dương nên (*) tương đương 
2x − 2y +1 = 3 
x + 2y =1
x − y = 0 x =1   (n) x + 2y = 3 y =1 ⇔ ⇔  . x y 1  − = x =1   (l)
x + 2y =1 y = 0
Vậy có 1 giá trị của x thỏa mãn bài toán.
7. Dạng 7: Sử dụng tính chất chia hết
Ví dụ 8: Có bao nhiêu số nguyên x thuộc đoạn 1  ;2020   sao cho tồn tại số 2 x y x y + nguyên dương 4 −3 1 + log 3 1 y thỏa mãn ( ) 10 = ? 4 A. 2020. B. 1347. C. 673. D. Vô số. Lời giải Chọn B. ( 2 4 x −3 y+ ) 1 log x 3y +1  y +  10 = ⇔ ( 3 1 2 4x − 3y + ) 1 log x = log   4  4  ⇔ ( 2 4x − (3y + )
1 + 2)log x = log(3y + ) 1 − log 4 2
⇔ 4x − (3y + )
1  log x + 2 log x + log 4 − log (3y + ) 1 = 0   2
⇔  x − ( y + ) x +     ( 2 4 3 1 log
log 4x ) − log(3y + ) 1  = 0  ( ) 1 + Nếu 2
4x > 3y +1 thì ( 2
log 4x ) > log(3y + ) 1 . Suy ra: VT ( ) 1 > 0 . + Nếu 2
4x < 3y +1 thì ( 2
log 4x ) < log(3y + ) 1 . Suy ra: VT ( ) 1 < 0 . 2 4x −1 x −1 x +1 2 ( )( ) Do đó, từ ( ) 1 suy ra: 2
4x = 3y +1 ⇔ y = ⇔ y = x + (2) 3 3 8
Với x = 3k +1, x = 3k + 2 , k ∈ , từ (2) dễ dàng thấy y là số nguyên dương.
Xét y không là số nguyên dương. Từ (2) , suy ra: x chia hết cho 3. Đặt x = 3k , *
k ∈  . Vì x ∈ ∩ 1  ;2020   nên *
1 ≤ 3k ≤ 2020, k ∈  ⇒ 1 ≤ k ≤ 673 , * k ∈  .
Do đó có 673 số nguyên x thuộc đoạn 1  ;2020 
 mà y không phải là số nguyên dương.
Vậy có 2020 − 673 = 1347 số nguyên x thỏa mãn yêu cầu bài toán.
8. Dạng 8: Đếm điểm nguyên trong các hình cơ bản
Ví dụ 9: Có bao nhiêu cặp số nguyên ( ,ab) thỏa mãn đồng thời các điều kiện: 2
b a + b + 4 + 4a  2 2 ( 2 2 ) 2 2 2
a + b > 1 và a + b − 3 ≤ log   ? 2 2 a +b 2 2  a + 2b    A. 10. B. 6 . C. 7 . D. 8. Lời giải Chọn D. Ta có : 2  b ( 2 2 a + b + 4) 2 + 4a  ( 2b +4)( 2 2 a + b 2 2 2 2 )
a + b − 3 ≤ log 
 ⇔ a + b − 3 ≤ log 2 2 2 2 a +b 2 2 a +b 2 2  a + 2ba + 2b   2 2 2 2 2
⇔ a + b − 3 ≤ log b + 4 − log a + 2b +1 2 2 a +b ( ) 2 2 a +b ( ) ⇔ ( 2 2 a + b ) 2 2 2 2 2 + log a + 2b ≤ b + 4 + log b + 4 . 2 2 a +b ( ) ( ) 2 2 a +b ( ) Nếu 2 2 2
a + 2b > b + 4 thì 2 2 2 log a + 2b > log b + 4 . Suy ra: 2 2 a +b ( ) 2 2 a +b ( ) ( 2 2 a + b ) 2 2 2 2 2 + log a + 2b > b + 4 + log b + 4 (vô lí). 2 2 a +b ( ) ( ) 2 2 a +b ( ) Do đó, 2 2 2 2 2
a + 2b ≤ b + 4 ⇔ a + b ≤ 4 . Mà 2 2
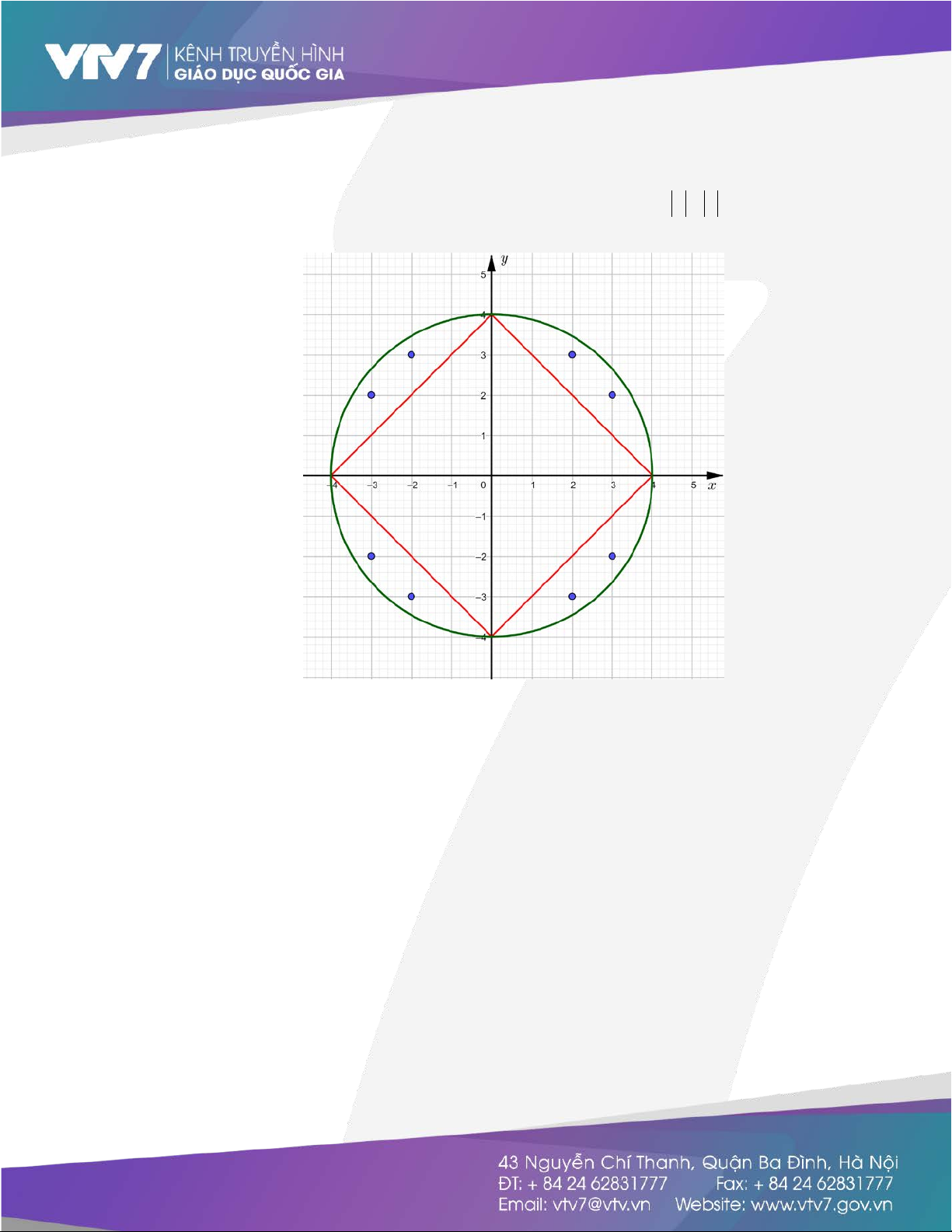
a + b > 1 , a,b ∈  nên nghiệm nguyên (a,b) là các điểm nguyên trong
mặt phẳng tọa độ (Oxy) nằm trong hình vành khăn, tạo bởi 2 đường tròn
đồng tâm O(0;0) bán kính lần lượt là 1 và 2 (bỏ đi biên của hình tròn ( ) ;1 O ) (Xem hình vẽ). 9 Suy ra: ( ,ab)∈ ( { 2;0),( 2 − ;0),(0;2),(0; 2 − ),(1; ) 1 ,(1;− ) 1 ,( 1 − ; ) 1 ,(−1; ) 1 } .
Vậy có 8 cặp số nguyên ( ,ab).
Ví dụ 10: Có bao nhiêu cặp số nguyên ( ,ab) thỏa mãn đồng thời các điều kiện: 16 b + 64 2 2
0 < a + b ≤ 16 và a + b > log ? 2 a + 2 b A. 10. B. 6 . C. 7 . D. 8. Lời giải Chọn D. Từ điều kiện 2 2
0 < a + b ≤ 16 , suy ra a , b không đồng thời bằng 0 nên
a + 2 b > 0 . Ta có: 16 b + 64 a + b > log
⇔ a + b > 4 + log b + 4 − log a + 2 b 2 2 ( ) 2 ( ) a + 2 b
⇔ log a + 2 b + a + 2 b > log b + 4 + b + 4 ⇔ f ( a + 2 b ) > f ( b + 4), 2 ( ) ( ) 2 ( ) ( )
với f (t) = t + log t
2 là hàm số đồng biến trên khoảng ( 0; +∞) .
Do đó, f ( a + 2 b ) > f ( b + 4) ⇔ a + 2 b > b + 4 ⇔ a + b > 4. 10
Kết hợp với điều kiện 2 2
0 < a + b ≤ 16 , ,
a b∈ nên nghiệm nguyên (a,b) là các
điểm nguyên trong mặt phẳng tọa độ (Oxy) nằm trong hình tròn tâm O(0;0),
bán kính bằng 4 (bỏ đi tâm O ) và nằm ngoài hình vuông x + y = 4 . (Xem hình vẽ).
Đếm trực tiếp trên hình, ta có 8 điểm nguyên thỏa mãn yêu cầu bài toán.
Vậy có 8 cặp số nguyên ( ,ab). 11
BÀI TẬP TỰ LUYỆN
Câu 1. Có bao nhiêu số thực x sao cho tồn tại số nguyên y thỏa mãn  −  y x + x + 3 3 − x x log
− log 4x + 4x + 8 = ? 2   2 ( ) ( 2 2 )  y y A. 2. B. 4. C. 3. D. Vô số.
Câu 2. Có bao nhiêu số nguyên x sao cho tồn tại số thực y thỏa mãn
log ( x + 2 y − 2) = log ( 2 2
x + 4 y − 2x − 4 y + 2 ? 3 4 ) A. 0 . B. 2 . C. 4 . D. 8 .
Câu 3. Có bao nhiêu số nguyên y để tồn tại số thực x thỏa mãn
log (4x + 3y) = log ( 2 2 x + y ? 7 2 ) A. 1. B. 2 . C. 0 . D. 3.
Câu 4. Có bao nhiêu cặp số nguyên ( ;
x y) thỏa mãn 0 < y ≤ 2020 và  3x −1 log   = 2 + 2 − 3x y ? 2  y A. 2019 . B. 7 . C. 2020 . D. 4 .
Câu 5. Có bao nhiêu cặp số nguyên
x;y thỏa mãn x+ y xy+ − xy− 1 3 1 5 + 5 + x( y + ) 1 1 +1 = 5 + − 3y ? x+3 5 y A. 2 . B. 1 . C. 3 . D. 4 .
Câu 6. Có bao nhiêu cặp số nguyên dương (x;y) thỏa mãn x y  20 2 2 log
x y  2x  4y  42 ? 2 2 2
x y  6y A. 1. B. 2 . C. 3 . D. 4 .
Câu 7. (Chuyên ĐH Vinh – lần 2 – 2020) Có bao nhiêu cặp số thực dương
(a;b) thỏa mãn log a là số nguyên dương, log a =1+ log b và 2 2 3 2 2 2
a + b < 2020 ? A. 6. B. 7. C. 5. D. 8.
Câu 8. Có bao nhiêu cặp số nguyên
(x; y) thỏa mãn 2 2 x 3 y 2 2 2.625 − 6250.125
= 9y − 4x + 5 ? A. 1. B. 2 . C. 0 . D. 3. 12
Câu 9. Có bao nhiêu bộ ( ;
x y ) với x, y là các số nguyên thỏa mãn
1 ≤ x, y ≤ 243 và 9 log ( 2 9 = 3xy x
+ 9x y − x ? 3 ) ( ) A. 1. B. 3. C. 12. D. 243.
Câu 10. Có bao nhiêu cặp số nguyên ( ,ab) thỏa mãn điều kiện: 2 2 a + b ab + ( − + − ) 2 2 2 2 1 e e 1 − e +ab+b a ab b = 0 ? A. 4 . B. 2 . C. 9. D. 6 .
Câu 11. Có bao nhiêu cặp số nguyên (x,y) thỏa mãn điều kiện:
2x .8x + x (x − y) y( 2 3 x +2 2 ) = 32.2
+ 2y − 3x + 5? A. 4 . B. 2 . C. 1. D. 3.
Câu 12. Có bao nhiêu cặp số nguyên không âm (x;y) thỏa mãn điều kiện: 2 2 x + y +11 2 2 log
+ x + y − 6x − 8y + 9 ≤ 0 ? 6x + 8 y + 2 A. 45 . B. 49 . C. 48 . D. 47 .
Câu 13. Có bao nhiêu cặp số nguyên ( ,ab) thỏa mãn điều kiện: 2 2 2 2
2a +b + log a + b ≤ 4a+b +1? 2 a + b A. 25 . B. 24 . C. 36. D. 35. 13 ĐÁP ÁN
Câu 1. Có bao nhiêu số thực x sao cho tồn tại số nguyên y thỏa mãn  −  y x + x + 3 3 − x x log
− log 4x + 4x + 8 = ? 2   2 ( ) ( 2 2 )  y y A. 2. B. 4. C. 3. D. Vô số. Lời giải Chọn B. x − 3  > 0 Điều kiện:  y . Ta có :  y ∈  −  y x + x + 3 3 − x x log
− log 4x + 4x + 8 = 2   2 ( ) ( 2 2 )  y yx − 3  x − ⇔ log − log   ( 3 2 x + x + 2) 2
− 2 = x + x − 2 2  y y
x − 3  x − 3  x −  ⇔ log + = log   ( 3 2 x + x + 2) + ( 2
x + x + 2) ⇔ f =   f ( 2 x + x + 2 2 2 )  y yy
, với f (t) = log t + t là hàm số đồng biến trên khoảng (0;+∞). Do đó: 2  x − 3  f = f ( x − 3 x − 3 2 x + x + 2) 2 ⇔
= x + x + 2 ⇔ y =   . 2  y y x + x + 2
Nhận xét : Nếu tồn tại cặp số  x −
x;y thì điều kiện 3 > 0 luôn thỏa mãn. y Cách 1: Xét hàm x  3 y
với x ≠ 3 , ta có : 2 x x  2 2 x   6x  5 y  ; 2 y  0  x
  6x  5  0  x  3  14;3  14
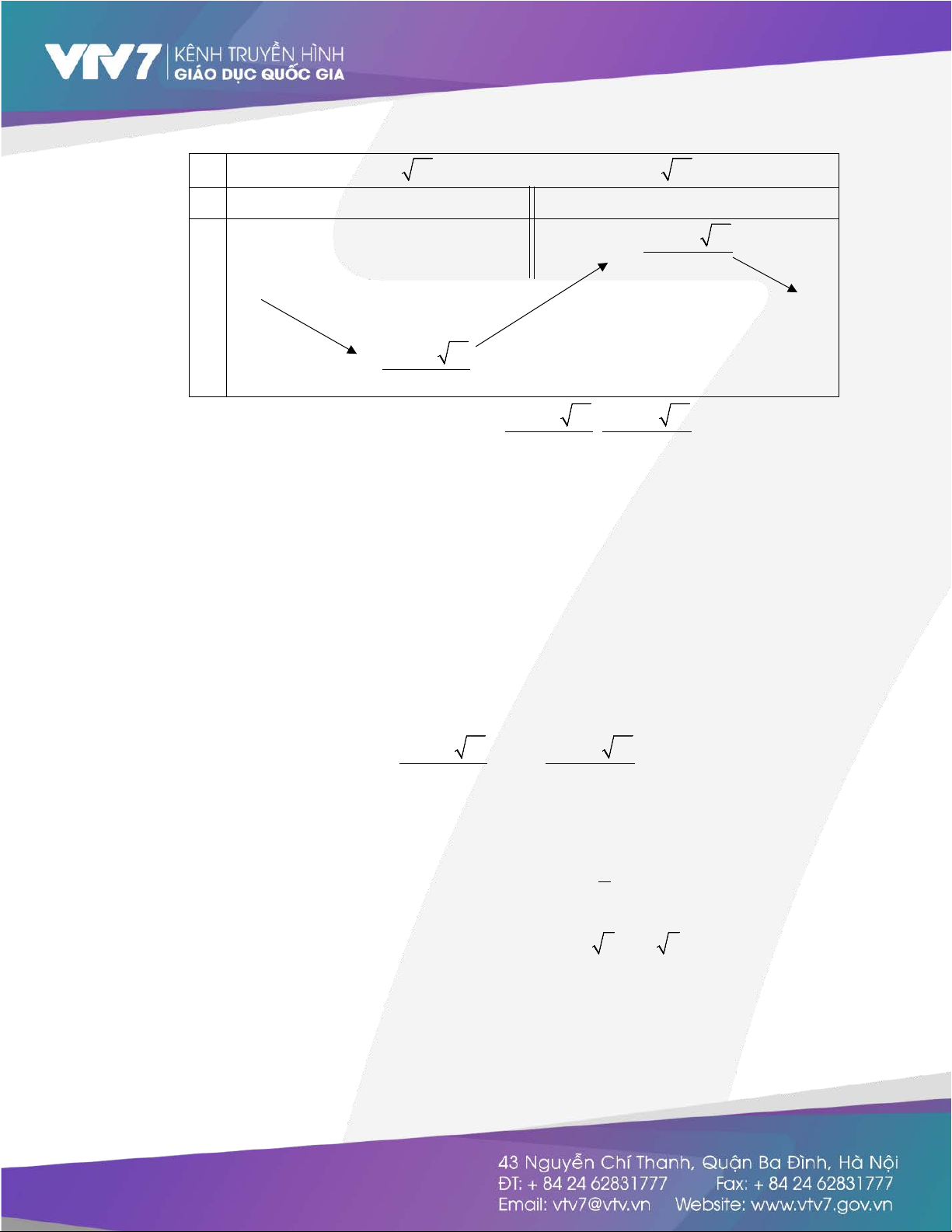
x x  2 2 2 14 Bảng biến thiên
x  3  14 3 3  14 
y  0   0  7  2 14 7 y 0 0 0 7  2 14 7  
Dựa vào bảng biến thiên, suy ra : 7  2 14 7  2 14 y  ;   \     0 .  7 7   
Mà y ∈ nên y ∈{ 2; − − } 1 .
Mặt khác, dựa vào BBT, ứng với mỗi giá trị y ∈{ 2; − − }
1 ta có 2 nghiệm x .
Vậy có 4 giá trị x thỏa yêu cầu bài toán.
Cách 2: Xét phương trình 2 yx + ( y − )
1 x + 2 y + 3 = 0   * Phương trình   2
* có nghiệm khi và chỉ khi   y  
1  4y 2y  3  0     2 7 2 14 7 2 14
 7y  14y  1  0   y  . 7 7 Vì y  ,
y  0  y  2;  1 .  Với   y = 2 − . Thay vào   * , suy ra: 1 x ∈  1; − − . 2    Với y = 1 − . Thay vào   * , suy ra: x ∈{ 1 − − 2; 1 − + 2}.
Vậy có 4 giá trị x thỏa yêu cầu bài toán. 15
Câu 2. Có bao nhiêu số nguyên x sao cho tồn tại số thực y thỏa mãn
log ( x + 2 y − 2) = log ( 2 2
x + 4 y − 2x − 4 y + 2 ? 3 4 ) A. 0 . B. 2 . C. 4 . D. 8 . Lời giải Chọn B
Ta có: log (x + 2y − 2) = log ( 2 2
x + 4 y − 2x − 4 y + 2 3 4 )
⇔ log (x + 2y − 2) = log (x − )2 1 + (2 y − )2 1  . 3 4  
Đặt a = x −1,b = 2y −1. Phương trình trở thành log (a + b) = log ( 2 2 a + b . Đây 3 4 )
chính là một câu trong đề tham khảo lần 2 năm 2019 – 2020.
Câu 3. Có bao nhiêu số nguyên y để tồn tại số thực x thỏa mãn
log (4x + 3y) = log ( 2 2 x + y ? 7 2 ) A. 1. B. 2 . C. 0 . D. 3. Lời giải Chọn B
4x + 3y > 0 Điều kiện:  . 2 2 x + y > 0 Điều kiện cần :
 x + y = t
Đặt t = log (4x + 3y) = log ( 4 3 7 2 2 x + y ⇔  . 7 2 ) 2 2
x + y = 2t
Để tồn tại x thì đường thẳng : 4 + 3 − 7t d x y
= 0 và đường tròn (C) tâm t O (0;0), 2t R =
= ( 2) phải có điểm chung ⇔ d ( ; O d ) ≤ R 7 ( )  7 t t t  ⇔ ≤ 2 ⇔ 
 ≤ 5 ⇒ t ≤ log 5 ≈ 1,006 . 7 5  2  2 log 7 5 Suy ra: 2 t 2 y ≤ 2 ≤ 2
≈ 2,009 , mà y ∈ nên y ∈{ 1; − 0; } 1 . Điều kiện đủ: 16
 Với y =1⇒ log (4x + 3) = log ( 2
x +1 có nghiệm x = 1 nên nhận y = 1. 7 2 )  x = t t  Với 4 7 y ⇒  ⇒
có nghiệm t nên tồn tại x . t ( t )2 t  49  = 0 7 = 16.2 ⇒ = 16   2 x = 2  2  Do đó nhận y = 0 .  Với y = 1
− ⇒ log (4x − 3) = log ( 2 x +1 . 7 2 ) Vì log ( 2 x +1 ≥ 0 nên log
4x − 3 ≥ 0 ⇒ 4x − 3 ≥ 1 ⇒ x ≥ 1. 7 ( ) 2 )
Xét hàm f (x) = log (4x −3) − log ( 2 x +1 trên 1;  +∞  ). Ta có : 7 2 ) 4 ln 2 x
( 2x + )1−2ln7(4x−3 4 2 ) x f ′( x) = ( − = = 4x − 3) ln 7 ( 0 2 x + ) 1 ln 2
(4x −3)ln7( 2x + )1ln 2 x ≈ 0 − ,196 (l) ⇔  . x ≈ 1,108  (n)
Lập bảng biên thiên, suy ra f (x) ≤ f (1,108) ≈ 0
− ,975 . Suy ra phương trình
f (x) = 0 vô nghiệm. Do đó, loại y = 1 − .
Vậy có 2 số nguyên y thỏa yêu cầu bài toán là y = 0 , y = 1.
Câu 4. Có bao nhiêu cặp số nguyên ( ;
x y) thỏa mãn 0 < y ≤ 2020 và  3x −1 log   = 2 + 2 − 3x y ? 2  y A. 2019 . B. 7 . C. 2020 . D. 4 . Lời giải Chọn B 0 < y ≤ 2020
Từ giả thiết ta có:  x 3x −1
⇒ 3 > 1⇒ x > 0 . Khi đó, ta có: > 0   y 17  3x −1 log   = 2 + 2 − 3x y
⇔ log 3x −1 + 3x −1 = log 2y + 2y 2 ( ) ( ) 2 ( ) ( ) 2  y  ⇔ (3x f − ) 1 = f (2 y) ,
với f (t) = log t + t là hàm số đồng biến trên khoảng (0;+∞). Do đó: 2 ( 3x x −1 3x f − )
1 = f (2 y) ⇔ 2 y = 3 −1 ⇔ y = 2
Vì 0 < ≤ 2020 ⇔ 0 < 3x −1≤ 2× 2020 ⇔ 1< 3x y
≤ 4041 ⇔ 0 < x ≤ log 4041 ≈ 7,56 . 3
Mà x ∈ nên x∈{1;2;3;4;5;6; }
7 . Suy ra, có 7 cặp số nguyên ( x, y) Vậy có 7 cặp ( ; x y ) thỏa mãn.
Câu 5. Có bao nhiêu cặp số nguyên
x;y thỏa mãn x+ y xy+ − xy− 1 3 1 5 + 5 + x( y + ) 1 1 +1 = 5 + − 3y ? x+3 5 y A. 2 . B. 1 . C. 3 . D. 4 . Lời giải Chọn D Ta có: x+ y xy+ − xy− 1 3 1 5 + 5 + x( y + ) 1 1 +1 = 5 + − 3y x+3 5 y x+3 y − x−3 y − xy 1 − xy 1 5 5 x 3y 5 5 + ⇔ − + + = − − xy −1.
Xét hàm số ( ) 5t 5− = − t f t
+ t,t ∈  . Ta có ( ) 5t ln5 5 t f t − ′ = + ln 5 +1 > 0 , t ∀ ∈  .
Suy ra : hàm số f (t) đồng biến trên  .
Do đó: f (x + 3y) = f (−xy − )
1 ⇔ x + 3y = −xy −1 ⇔ y (3 + x) = −x −1 −x −1 ⇔ y = ( Do x = 3
− không là nghiệm của phương trình) 2 ⇔ y = 1 − + . 3 + x x + 3
Vì x,y ∈ nên x + 3∈{1; 1 − ;2;− } 2 ⇒ x ∈{ 2 − ; 4 − ; 1 − ;− } 5 .
Vậy có 4 cặp số x;y thỏa yêu cầu bài toán. 18
Câu 6. Có bao nhiêu cặp số nguyên dương (x;y) thỏa mãn x y  20 2 2 log
x y  2x  4y  42 ? 2 2 2
x y  6y A. 1. B. 2 . C. 3 . D. 4 . Lời giải Chọn B Ta có: x y  20 2 2 log
x y  2x  4y  42 2 2 2
x y  6y log 2   x y 20     2  
x y  20  log  2 2
x y  6y   2 2
x y  6y * 2  2  
Xét hàm số f t log t t trên khoảng 0;   . 2
Ta có f t 1 
1 0,t  0 . Suy ra hàm số f t đồng biến trên t.ln 2 khoảng 0;   .
Do đó,   f  x y    f    2 2 * 2 20
x y  6 y  x y   2 2 2
20  x y  6y 2 2 ⇔ 2 2 2 2
x + y − 2x + 4 y = 40 ⇔ ( x − )
1 + ( y + 2) = 45 ⇔ ( x − ) + ( y + ) 2 2 1 2 = 3 + 6 . x − = x − = Vì x,y + ∈ nên 1 3  hoặc 1 6  ⇒ (x;y)∈ ( { 4;4),(7; )1}. y + 2 = 6 y + 2 = 3
Vậy có 2 cặp số nguyên dương (x;y) .
Câu 7. (Chuyên ĐH Vinh – lần 2 – 2020) Có bao nhiêu cặp số thực dương
(a;b) thỏa mãn log a là số nguyên dương, log a =1+ log b và 2 2 3 2 2 2
a + b < 2020 ? A. 6. B. 7. C. 5. D. 8. Lời giải Chọn B
Đặt log a = n ( *
n ∈  ) suy ra = 2n a và 1 log 1 3 − = − ⇔ = n b n b 2 3 Ta có 2 2 2 2n 2n−2 2
a + b < 2020 ⇔ 2 + 3 < 2020 ( ) 1 19 2n−2 2 ⇒ 3
< 2020 ⇒ 2n − 2 < log ( 2 2020 ⇒ n < 8, mà *
n∈  ⇒ n ≤ 7 2 )
Xét hàm số f (t) 2t 3t−2 = 2 + 3 trên  . Ta có f ′(t ) 2t 2t −2
= 2.2 .ln 2 + 2.3 .ln 3 > 0,∀t ∈  . Suy ra hàm số f (t) đồng biến trên  .
Vì f (n) ≤ f ( ) 2
7 < 2020 nên n ≤ 7 , n∈{1;2;...; } 7 .
Vậy có 7 cặp số thực dương ( ;
a b) thỏa yêu cầu bài toán.
Chú ý: Khi có n ≤ 7 , thử với n = 7 thấy thỏa thì ta có thể kết luận n∈{1;2;...; } 7 .
Câu 8. Có bao nhiêu cặp số nguyên (x; y) thỏa mãn 2 2 x 3 y 2 2 2.625 − 6250.125
= 9y − 4x + 5 ? A. 1. B. 2 . C. 0 . D. 3. Lời giải Chọn C Ta có: 2 2 2 2 x 3 y 2 2 4 x 9 y +5 2 2 2.625 − 6250.125
= 9y − 4x + 5 ⇔ 2.5 − 2.5 = 9y − 4x + 5 2 2 4 x 2 9 y +5 ⇔ + x = + ( 2 y + ) ⇔ f ( 2 x ) = f ( 2 2.5 4 2.5 9 5 4 9 y + 5) , với ( ) = 2.5t f t
+ t là hàm số đồng biến trên  . Do đó: f ( 2 x ) = f ( 2 y + ) 2 2 2 2 4 9
5 ⇔ 4x = 9 y + 5 ⇔ 4x − 9 y = 5 ⇔ (2x − 3y)(2x + 3y) = 5 (*) .
2x − 3y =1
2x − 3y = 5    x + y =  x + y = Vì 2 3 5 2 3 1
x, y là số nguyên nên (*) tương đương  hoặc . 2x − 3y = 1 −
 x − y = −  2 3 5  
2x + 3y = 5 −
2x + 3y = 1 −
Cả 4 trường hợp đều cho kết quả x,y ∉ .
Vậy không tồn tại cặp số (x;y) thỏa mãn bài toán. 20
Câu 9. Có bao nhiêu bộ ( ;
x y ) với x, y là các số nguyên thỏa mãn
1 ≤ x, y ≤ 243 và 9 log ( 2 9 = 3xy x
+ 9x y − x ? 3 ) ( ) A. 1. B. 3. C. 12. D. 243. Lời giải Chọn A Ta có: 9log ( 2
9x ) = 3xy + 9x ( y − x) 2 2 xy−2
⇔ log x + x = 3 + xy − 2 3 3 2 2 xy−2 xy−2
⇔ log x + x = 3 + log 3 ( 2) ( 2 3 − ⇔ = xy f x f ), 3 3
với f (t) = t + log t là hàm số đồng biến trên khoảng (0;+∞) . 3 Do đó: f ( 2
x ) = f ( xy−2 ) 2 xy−2 3 ⇔ x = 3 (*) Ta có: xy−2 2 2 10 3
= x ≤ 243 = 3 ⇒ xy ≤ 12 ⇒ x ≤ 12 .
Mặt khác, vì x,y + ∈ nên từ (*) suy ra: 3n
x = , với n là số nguyên không âm. Suy ra: = 3n x ≤ 12 ⇒ n∈{0;1; } 2 .
 Với n = 0 . Suy ra: x = 1, y = 2 .
 Với n = 1. Suy ra: x = 3 , 3y−2 4 3 = 9 ⇒ y = (loại). 3
 Với n = 2 . Suy ra: x = 9 , 9y−2 2 3 = 81⇒ y = (loại). 3
Vậy có 1 bộ (x,y) là (1;2) . 21
Câu 10. Có bao nhiêu cặp số nguyên ( ,ab) thỏa mãn điều kiện: 2 2 a + b ab + ( − + − ) 2 2 2 2 1 e e 1 − e +ab+b a ab b = 0 ? A. 4 . B. 2 . C. 9. D. 6 . Lời giải Chọn D Ta có: 2 2 a + b ab ( ) 2 2 2 2 1 e e 1 e +ab+ + − + − − b a ab b = 0 2 2 2
a +2b −ab 2 2 1 e 1 e + ⇔ + − + − − b a ab b = 0 2 2 2
a +2b −ab 2 2 1+b 2 ⇔ e
+ a − ab + 2b = e +1+ b ( )1.
Xét hàm số đặc trưng: ( ) = et f t
+ t với t ∈ .  Ta có ′( ) = et f t
+1 > 0,∀t ∈  .
Suy ra hàm số f (t) đồng biến trên .  Do đó: ( ) ⇔ f ( 2 2
a + b − ab) = f ( 2 2 2 1+ b ) 2 2 2 2 2
⇔ a + 2b − ab = 1+ b ⇔ a − ab + b =1. Cách 1: 2 2
a − ab + b −1 = 0 , ta xem như là phương trình bậc hai theo biến a . Phương trình có nghiệm 2 ⇔ ∆ = b − ( 2 b − ) 2 4 4 1 ≥ 0 ⇔ b ≤ . 3
Vì b∈ nên b∈{ 1; − 0; } 1 .
• Với b = 0 ⇒ a∈{ 1; − } 1 . • Với b = 1 − ⇒ a ∈{0; } 1 .
• Với b = 1⇒ a∈{0;− } 1 .
Vậy có 6 cặp số nguyên ( ,ab). Cách 2:
a − ab + b = ⇔ a + b + (a − b)2 2 2 2 2 1
= 2 ⇔ a + b + (a − b)2 2 2 = 1+1+ 0 2 2 
a = (a−b)2 2
b = (a−b)2 2 Vì , a ba = b = 1 = 1 = 1 ∈ nên  hoặc  hoặc 
a − b = 0 b = 0 a = 0 22 a = b = 1 a = 1,b = 0 a = 0,b = 1 ⇔  hoặc ⇔  hoặc ⇔  a = b = 1 − a = 1, − b = 0 a = 0,b = 1 −
Vậy có 6 cặp số nguyên ( ,ab).
Câu 11. Có bao nhiêu cặp số nguyên (x,y) thỏa mãn điều kiện:
2x .8x + x (x − y) y( 2 3 x +2 2 ) = 32.2
+ 2y − 3x + 5? A. 4 . B. 2 . C. 1. D. 3. Lời giải Chọn B Ta có: x x + ( − ) y( 2 x +2) x + x x x y = + y − x + ⇔
+ (x + x) y( 2 3 3 x +2)+5 2 3 3 = + y ( 2 2 .8 32.2 2 3 5 2 3 2 x + 2)+ 5 ⇔ f ( 3
x + x) = f (y( 2 3
x + 2)+ 5) , với ( ) = 2t f t
+ t là hàm số đồng biến trên  .
Suy ra: x + x = y(x + ) 3 3 2 x + 3x − 5 x − 5 3 2 + 5 ⇔ y = ⇔ y = x + . 2 2 x + 2 x + 2 Cách 1:
Xét hàm g(x) x − 5 = , x ∈ . Ta có : 2 x + 2 g′(x) 2 −x +10x + 2 =
= 0 ⇔ x ∈ 5 − 3 3;5 + 3 3 . 2 { } ( 2x +2)  
Lập bảng biến thiên ta được g(x) 5 − − 3 3 5 − + 3 3 ∈  ;  .  4 4  
Vì x,y ∈ nên g(x)∈ . Suy ra g(x)∈{ 2 − ; 1; − }0. Thử lại : x − 5
• Với g(x) = 2 − ⇒ = 2 − ⇒ x = 1 − , y = 3 − . 2 x + 2 x 5  1 13 1 13  − − − − + • 
Với g ( x) = 1 − ⇒ = 1 − ⇒ x ∈  ; (loại). 2 x 2 2 2  +   23 x − 5
• Với g(x) = 0 ⇒
= 0 ⇒ x = 5 , y = 5 . 2 x + 2
Vậy có 2 cặp số nguyên (x;y) là : ( 1; − 3 − ), (5;5). Cách 2: Ta có: x − 5 y x − 5 x − 5 = x +
. Vì x,y ∈ nên ∈. Suy ra = k ∈ . 2 x + 2 2 x + 2 2 x + 2 Ta có : x − 5 2
= k ⇔ kx − x + 2k + 5 = 0 (*) . 2 x + 2
• Với k = 0 ⇒ x = 5; y = 5 (nhận)
• Với k ≠ 0 . Khi đó, (*) có nghiệm khi và chỉ khi  
∆ = − k ( k + ) 5 − − 3 3 5 − + 3 3 1 4 2 5 ≥ 0 ⇔ k ∈  ;  .  4 4   Vì k ∈ \{ } 0 nên k ∈{ 2; − − }
1 . Thử lại ta nhận k = 2 − , x = 1 − y = 3 − .
Vậy có 2 cặp số nguyên (x;y) là : ( 1; − 3 − ), (5;5). Cách 3: Ta có: x − 5 y = x +
. Vì x,y ∈ nên 2 x + 2
(x − )( 2x + )⇒ (x − )(x + )( 2x + )⇒ ( 2x − )( 2 5 2 5 5 2 25 x + 2). ⇒ ( 2 x + − )( 2 x + ) ⇒ ( 2 2 27 2 27 x + 2) ⇒ ( 2 x + )∈{ } 2 2
1;3;9;27 ⇒ x ∈{1;2 } 5 ⇒ x ∈{ 1; − 1; 5 − ; } 5 . Thử lại: • Với x = 1 − ⇒ y = 3 − (nhận). • Với 1
x = 1⇒ y = − (loại). 3 • Với 145 x = 5 − ⇒ y = − (loại). 27
• Với x = 5 ⇒ y = 5 (nhận).
Vậy có 2 cặp số nguyên (x;y) là : ( 1; − 3 − ), (5;5). 24
Câu 12. Có bao nhiêu cặp số nguyên không âm (x;y) thỏa mãn điều kiện: 2 2 x + y +11 2 2 log
+ x + y − 6x − 8y + 9 ≤ 0 ? 6x + 8 y + 2 A. 45 . B. 49 . C. 48 . D. 47 . Lời giải Chọn C. Ta có: 2 2 log x + y +11 2 2
+ x + y − 6x − 8y + 9 ≤ 0 6x + 8 y + 2 ⇔ ( 2 2 x + y + ) 2 2 log
11 + x + y +11 ≤ log (6x + 8y + 2) + 6x + 8y + 2 ( )1
Xét hàm số đặc trưng: f (t) = t + logt với t > 0. Ta có: f ′(t ) 1 = 1+
> 0,∀t > 0 ⇒ Hàm số f (t) đồng biến trên khoảng (0;+∞). t.ln10 Do đó ( ) ⇔ f ( 2 2 x + y +
) ≤ f ( x+ y + ) 2 2 1 11 6 8
2 ⇔ x + y +11 ≤ 6x + 8 y + 2
⇔ (x − )2 + ( y − )2 3 4 ≤ 16 . 25
Vì x,y là số nguyên không âm nên ta coi cặp số (x,y) là các điểm nguyên
(x,y) nằm trong hình tròn (C) có tâm I (3;4),R = 4 ở góc phần tư thứ nhất. (Xem hình vẽ).
Vậy có 5× 7 + 5×2 +1+1+1 = 48 cặp số nguyên (x;y) .
Chú ý: Ta cũng có tính tính trực tiếp như sau:
(x −3)2 +( y − 4)2 ≤16 ( ) ⇒ (x −3)2 * ≤ 16 ⇒ 1 − ≤ x ≤ 7 .
Vì x là số nguyên không âm nên x ∈{0;1;2;3;4;5;6; }
7 . Thay vào (*) ta cũng có
được 48 cặp số nguyên (x;y) .
Câu 13. Có bao nhiêu cặp số nguyên ( ,ab) thỏa mãn điều kiện: 2 2 2 2
2a +b + log a + b ≤ 4a+b +1? 2 a + b A. 25 . B. 24 . C. 36. D. 35. Lời giải Chọn B. 2 2
Điều kiện: a + b > 0 ⇔ a , b không đồng thời bằng 0 . Khi đó, ta có: a + b 2 2 2 2 + a + b 2 2 2a b + log
≤ 4a+ b +1 ⇔ 2a +b + log ( 2 2
a + b ≤ 4a+b + log a + b +1 2 2 ) 2 ( ) a + b 2 2 ⇔ 2 + + log + ≤ 2 a+ b a b a b
+ log 2 a + b  ⇔ f ( 2 2
a + b ) ≤ f 2  ( a + b ) 2 ( ) 2 2 2 ( ) 2  ( )  , với ( ) = 2t f t
+ log t là hàm số đồng biến trên khoảng (0;+∞) . 2
Do đó, f (a + b ) ≤ f  ( a + b ) ⇔ a + b ≤ 
( a + b ) ⇔ ( a − )2 +( b − )2 2 2 2 2 2 2 1 1 ≤ 2 .
Kết hợp với điều kiện ,
a b∈ , a , b không đồng thời bằng 0 nên nghiệm
nguyên (a,b) là các điểm nguyên trong mặt phẳng tọa độ (Oxy) nằm trong
hình hoa, kể cả biên, bỏ đi điểm O(0;0) (hình hoa là hình hợp bởi bốn hình
tròn bán kính 2 lần lượt có tâm I 1;1 , I 1; 1 − , I 1; − 1 , I 1; − 1 − ) 4 ( ) 3 ( ) 2 ( ) 1 ( ) (Xem hình vẽ). 26
Đếm trực tiếp, ta thấy đó là các điểm nguyên nằm trong hình vuông ABCD
kích thước 4× 4, bỏ đi điểm (0;0). Do đo, có 2 5 −1 = 24 điểm nguyên.
Vậy có 24 cặp số nguyên ( ,ab). 27