Q là tập hợp số gì? Lý thuyết tập hợp Q các số hữu tỉ Toán lớp 7
1. Q là tập hợp số gì?
Q, viết tắt của "Q-rational," là một khái niệm vẫn đang là đề tài thú vị mà nhiều bạn đọc đam mê
toán học đang tìm hiểu để nắm bắt sự hiệu quả trong việc giải quyết các bài toán phức tạp. Q không
chỉ là một tập hợp các số hữu tỉ, mà còn đồng thời là một phần quan trọng của thế giới toán học.
Tập hợp số hữu tỉ Q, hay còn gọi là tập hợp các số hữu tỉ, đóng vai trò quan trọng trong cuộc sống
hàng ngày của chúng ta và có sự hiện diện mạnh mẽ trong nhiều khía cạnh khác nhau. Những con
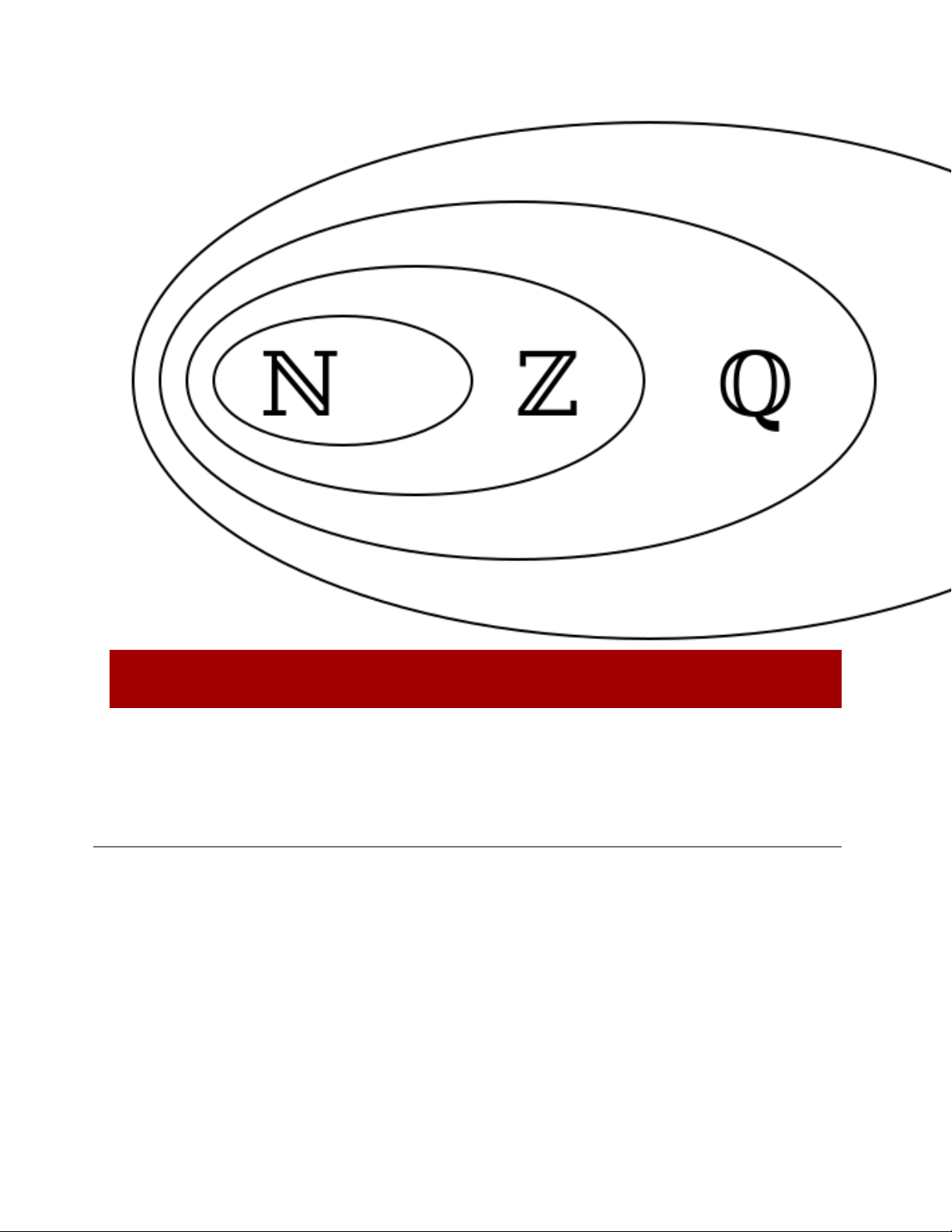
số này được biểu diễn dưới dạng phân số a/b, với a và b là các số nguyên thuộc tập hợp số nguyên
Z và điều quan trọng là b không thể bằng 0.
Những ví dụ đơn giản như 1, 3, 1/5, 3/7... đều thuộc tập hợp số hữu tỉ này. Chúng thường xuất
hiện trong các tình huống thường ngày, từ việc chia phần bánh ngọt thành nhiều phần bằng cách
sử dụng số 1/5 cho đến việc tính toán tỷ lệ lợi nhuận trong tài chính. Số hữu tỉ không chỉ đơn thuần
là một khái niệm trong toán học mà còn thể hiện sự hiện diện mạnh mẽ của chúng trong thế giới thực.    
Tập hợp số hữu tỉ Q không chỉ giúp chúng ta giải quyết các bài toán toán học phức tạp mà còn
phản ánh sự kết nối giữa toán học và cuộc sống hàng ngày. Việc hiểu biết và sử dụng hiệu quả tập
hợp này có thể giúp chúng ta trở nên thông thạo hơn trong việc giải quyết các vấn đề thực tiễn và
đưa ra các quyết định thông minh dựa trên sự hiểu biết về con số và tỷ lệ.
Số Q giống như một trục số vô hạn, bao gồm không chỉ các số hữu tỉ dương (các số lớn hơn 0) mà
còn cả các số hữu tỉ âm (các số nhỏ hơn 0). Trong thực tế, Q không có số nhỏ nhất và không có số
lớn nhất. Tập hợp các số hữu tỉ dương thường được ký hiệu là Q+, trong khi tập hợp các số hữu tỉ
âm là Q-. Số 0 là trường hợp đặc biệt, nó không thuộc số hữu tỉ âm và cũng không thuộc số hữu tỉ
dương; thay vào đó, nó chỉ thuộc tập hợp số Q.
Q không chỉ là một khái niệm trong toán học mà còn xuất hiện trong nhiều lĩnh vực khác, từ khoa
học tự nhiên đến kỹ thuật và kinh tế. Khám phá và hiểu sâu hơn về tập hợp số này sẽ giúp chúng
ta giải quyết nhiều vấn đề phức tạp trong cuộc sống hàng ngày.
2. Lý thuyết tập hợp Q các số hữu tỉ Toán lớp 7 1. Số hữu tỉ
- Các phân số bằng nhau là một khái niệm quan trọng trong toán học, nó thể hiện sự tương đương
giữa các biểu diễn khác nhau của cùng một số, và số này được gọi là số hữu tỉ.
Khi hai phân số có giá trị bằng nhau, điều này có nghĩa là chúng thể hiện cùng một lượng hay tỷ
lệ. Chẳng hạn, phân số 1/2 và 2/4 là các biểu diễn khác nhau của cùng một số, và số này là số hữu
tỉ. Các phân số bằng nhau còn gọi là tương đương, và quan hệ này thể hiện sự linh hoạt trong biểu
diễn của các số hữu tỉ.
Sự hiểu biết về khái niệm này không chỉ giúp chúng ta trong việc đơn giản hóa và tối ưu hóa các
phép tính số học mà còn hỗ trợ trong việc phân tích và so sánh các dữ liệu trong nhiều lĩnh vực, từ
khoa học đến tài chính và kỹ thuật. Các số hữu tỉ và tương đương của chúng chắc chắn đóng vai
trò quan trọng trong sự phát triển và áp dụng của toán học trong cuộc sống hàng ngày.
- Số hữu tỉ là số được viết dưới dạng phân số a/b với a, b ∈ Z và b ≠ 0
- Tập hợp các số hữu tỉ được kí hiệu là Q (x là số hữu tỉ thì ghi là x ∈ Q) Ví dụ 1: Ta có thể viết    
2. Biểu diễn các số hữu tỉ trên trục số
Để biểu diễn số hữu tỉ a/b (a,b ∈ Z; b > 0) trên trục số ta làm như sau:
Chia đoạn đơn vị [0;1] trên trục số thành b phần bằng nhau, mỗi phần là 1/b được gọi là đơn vị mới .
Nếu a > 0 thì phân số a/b được biểu diễn bằng một điểm nằm bên phải điểm O và cách điểm O
một đoạn bằng a lần đơn vị mới . L AK I M AR TS H O P
Nhanh chóng tiện lợi, không đun nước rườm rà TÌM HIỂU THÊM
Nếu a < 0 thì phân số a/b được biểu diễn bằng một điểm nằm bên trái điểm O và cách điểm O một
đoạn bằng |a| lần đơn vị mới .
3. So sánh hai số hữu tỉ
Để so sánh hai số hữu tỉ x, y ta thường làm như sau:
Viết x, y dưới dạng hai phân số có cùng mẫu dương x =
So sánh hai số nguyên a và b
+ Nếu a < b thì x < y + Nếu a = b thì x = y
+ Nếu a > b thì x > y
• Trên trục số nếu x < y thì điểm x nằm bên trái điểm y
• Số hữu tỉ lớn hơn 0 được gọi là số hữu tỉ dương.
• Số hữu tỉ nhỏ hơn 0 được gọc là số hữu tỉ âm.
• Số 0 không phải là số hữu tỉ dương cũng không phải là số hữu tỉ âm. Nhận xét:
+ Số hữu tỉ a/b là số hữu tỉ dương (a/b > 0) thì a, b cùng dấu.
+ Số hữu tỉ a/b là số hữu tỉ âm (a/b < 0) thì a, b trái dấu.
>> Tham khảo: Bài tập về số hữu tỉ minh họa
3. Tính chất của số hữu tỉ Q là gì?
Tập hợp số hữu tỉ Q có những tính chất đặc biệt và quan trọng trong toán học, và chúng ta cùng
điểm qua một số đặc điểm quan trọng của nó.
Trước hết, tập hợp Q là một tập hợp có thể đếm được, điều này có nghĩa là chúng ta có thể liệt kê
ra tất cả các số hữu tỉ một cách hệ thống. Phép nhân hai số hữu tỉ có dạng a/b * c/d = (a.c) / (b.d),
và phép chia là a/b : c/d = (a.d) / (b.c). Những quy tắc này giúp chúng ta thực hiện các phép tính
toán với các số hữu tỉ một cách dễ dàng.
Một tính chất thú vị khác của tập hợp số hữu tỉ là số đối của một số hữu tỉ dương sẽ là số hữu tỉ
âm, và ngược lại, số hữu tỉ âm sẽ có số đối là số hữu tỉ dương. Điều này dẫn đến việc tổng của một
số hữu tỉ và số đối của nó sẽ luôn bằng 0, một tính chất độc đáo trong toán học.
Quan trọng hơn, chúng ta cần phân biệt số hữu tỉ Q và số vô tỉ. Trong toán học, số vô tỉ là một loại
số viết biểu diễn dưới dạng số thập phân vô hạn không tuần hoàn, được ký hiệu là I. Ví dụ như
1.3333333, 0.999999999, 1.99999999, 5.9999999... là các con số vô tỉ. Số vô tỉ không thể biểu
diễn dưới dạng phân số a/b.
Trái lại, số hữu tỉ Q là những số thập phân vô hạn tuần hoàn, khác hoàn toàn với số vô tỉ. Các số
hữu tỉ có thể đếm được, và chúng được biểu diễn dưới dạng phân số a/b, trong đó a và b là các số
nguyên thuộc tập hợp số nguyên Z.
Tóm lại, tập hợp số hữu tỉ Q là một khía cạnh thú vị và quan trọng của toán học, và sự hiểu biết về
tính chất và sự khác biệt giữa số hữu tỉ và số vô tỉ giúp ta xây dựng nền tảng vững chắc trong lĩnh vực này.
Số hữu tỉ, như các dãy số khác trong toán học, cũng tuân theo các quy tắc cơ bản của phép cộng,
trừ, nhân, và chia. Cách tính các phép toán với số hữu tỉ Q rất đơn giản và dựa trên tính chất cơ bản của tập hợp này.
Trước hết, khi thực hiện phép nhân và chia với số hữu tỉ, chúng ta áp dụng theo quy tắc sau:
- Phép nhân: a/b * c/d = (a.c) / (b.d)
- Phép chia: a/b : c/d = (a.d) / (b.c)
Điều này có nghĩa rằng để nhân hai số hữu tỉ, chúng ta nhân tử số của chúng lại với nhau và mẫu
số của chúng lại với nhau. Còn để chia, chúng ta đảo ngược tử số và mẫu số của số bị chia và sau
đó nhân nó với số chia.
Khi thực hiện phép cộng và trừ với số hữu tỉ, nếu hai số hữu tỉ có cùng mẫu số, chúng ta chỉ cần
cộng hoặc trừ tử số của chúng lại với nhau. Nếu chúng không có cùng mẫu số, chúng ta sẽ quy đổi
cho cùng mẫu số rồi mới áp dụng cách tính cộng và trừ.
Dưới đây là một số ví dụ cụ thể:
1. Ví dụ về phép cộng: 4/5 + 7/5 = (4 + 7) / 5 = 11/5
2. Ví dụ về phép nhân: 4/5 * 6/9 = (4 * 6) / (5 * 9) = 24/45
3. Ví dụ về phép chia: 18/2 : 9/5 = (18 * 5) / (2 * 9) = 90/18
Những ví dụ này chỉ ra cách chúng ta có thể dễ dàng thực hiện các phép toán cơ bản với số hữu tỉ
Q bằng cách sử dụng tính chất cơ bản của chúng, làm cho việc làm toán với số hữu tỉ trở nên dễ dàng và tiện lợi.