Review for Midterm - Math for business | Trường Đại học Quốc tế, Đại học Quốc gia Thành phố HCM

REVIEW FOR MIDTERM CHAP 1
1. A specialist paint manufacturer receives $12 for each pot sold. The initial set-up cost for the
production run is $800 and the cost of making each tin of paint is $3.
a) Write down a formula for the total profi t, π, if the fi rm manufactures x pots of paint and sells y pots.
b) Use your formula to calculate the profi t when x = 1000 and y = 800.
c) State any restrictions on the variables in the mathematical formula in part (a)
d) Simplify the formula in the case when the firm sells all that it manufactures
2. The design costs of an advertisement in a glossy magazine are $9000 and the cost per cm2 of print is $50.
a) Write down an expression for the total cost of publishing an advert which covers x cm2.
b) The advertising budget is between $10 800 and $12 500. Write down and solve an inequality to
work out the minimum and maximum area that could be used.
3. A bonsai tree garden estimates that if it decreases the price of its tree by $5, it sells 30 more trees each month.
a) Assuming that monthly sales, Q, are related to prices, P , by a linear model,
Q = aP + b. State the value of the slope?
b) If the garden sells 120 trees in a month when the price of the tree is $90 work out the value of b .
c) Use this model to estimate monthly sales when the price is $75.
d) If the garden can only make 100 trees in a month w ork out the price that it needs to charge to sell them all.
4. Viettel post have three different prices of parcels: small – medium - large. Given that one consignment
has 6 small, 8 medium and 9 large parcels which cost $173.20 to post. Another consignment has 7
small, 13 medium and 17 large parcels with total postage $291.05. A large parcel costs twice as much
to post as a small one. Work out the totoal freight cost (shipping cost) if an accessories store want to
send 29 small parcels, 18 medium parcels and 6 large parcels to customers.
5. The supply and demand functions of a good are given by P = QS + 8 P = 23QD + 80
where P , QS and QD denote price, quantity supplied and quantity demanded respectively.
a) Find the equilibrium price and quantity.
b) Find the new equilibrium price and quantity if the government imposes a fixed tax of $36 on each good.
c) How much customer pay for tax? How much seller pay for tax?
d) Find the corresponding value of the government9s tax revenue. CHAP 2
1. A city centre tour guide currently charges $34 for a full day9s tour. The average number of customers
is 48. Market research suggests that for every $1 increase in tour price, the guide can expect to lose 2 customers per tour.
a) Show that if the price increase is $x then the expected revenue from each tour is 22x2 – 20x + 1632 P a g e 1 | 7
Compiled by Ngo Minh Tuyet Ngoc
b) The guide needs to ensure that the expected revenue is at least $1440. By solving a quadratic
inequality, find the range of prices that need to be charged.
c) What price should be charged to maximise expected revenue?
2. VieOn company sets a budget of $100000 on the Rap Viet All - star concert for rapper invitation and
other fees (venue rental, decoration, marketing,&). Assume that the fee to invite idol is approximately
$5000 for 1 idol and the others fee is $55000. Given that Pepsico sponsor for this concert $57000.
a) How many rapper could be invited?
b) VieOn charge the ticket price into 2 kinds: GA and VIP which cost $25 and $45, respectively.
Given that the stage capacity are 8000 for GA and 1000 for VIP. The GA ticket now is sold out.
Write down the profit quation of for this VieOn
plan. Which is the maximum profit.
* D¿ng toán với cái dữ kiện TR, TC, �㕅
3. If the demand function of a good is given by P = 80 2 3Q
a) Find the price when Q = 10, and deduce the total revenue.
b) If fixed costs are 100 and variable costs are 5 per unit find the total cost when Q = 10.
c) Use your answers to parts (a) and (b) to work out the corresponding profit.
4. The total cost, TC, of producing 100 units of a good is 600 and the total cost of producing 150 units is
850. Assuming that the total cost function is linear, find an expression for TC in terms of Q , the number of units produced.
5. Find an expression for the profi t function given the demand function 2Q + P = 25 and the average cost 32 function AC =
+ 5. Find the values of Q for which the firm � 㕄 a) breaks even b) makes a loss of 432 units c) maximises profit.
* Logarithms and exponential
6. Show that the production function is homogeneous and displays constant returns to scale.
7. The value of a second-hand car reduces exponentially with age, so that its value $ y after t years can
be modelled by the formula y = Ae-ax
If the car was $50 000 when new and was worth $38 000 after 2 years, fi nd the values
of A and a , correct to 3 decimal places. Use this model to predict the value of the car
a) when the car is 5 years old b) in the long run. CHAPTER 3 * Percentage
1. A shop sells books at 820% below the recommended retail price (r.r.p.)9. If it sells a book for $12.40 find a) the r.r.p.
b) the cost of the book after a further reduction of 15% in a sale P a g e 2 | 7
Compiled by Ngo Minh Tuyet Ngoc
c) the overall percentage discount obtained by buying the book from the shop in the sale compared
with the manufacturer9s r.r.p.
2. A TV costs $900 including 20% sales tax. Find the new price if tax is reduced to 15%.
3. An antiques dealer tries to sell a vase at 45% above the $18 000 which the dealer paid at auction.
a) What is the new sale price?
b) By what percentage can the dealer now reduce the price before making a loss?
* Index & Inflation
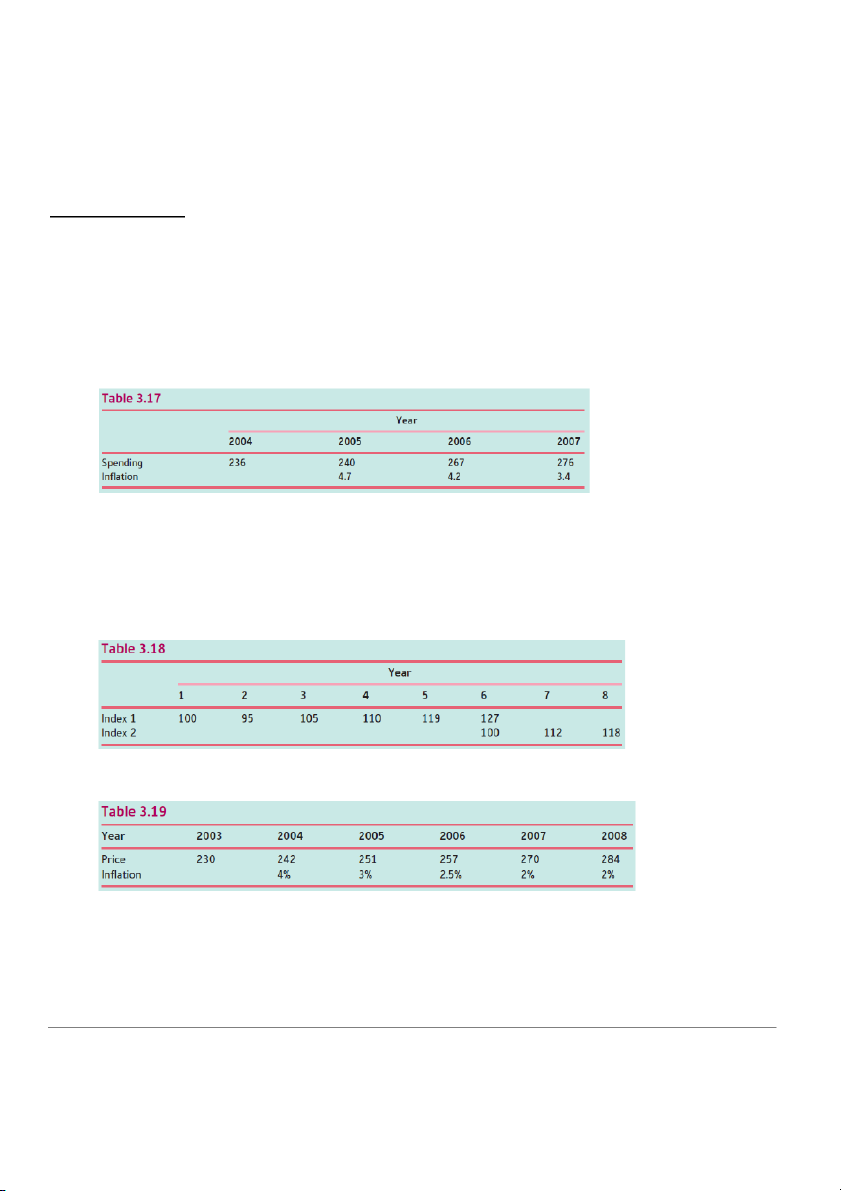
1. Table 3.17 shows government expenditure (in billions of dollars) on education for four consecutive
years, together with the rate of infl ation for each year.
a) Taking 2004 as the base year, work out the index numbers of the nominal data given in the third row of the table.
b) Find the values of expenditure at constant 2004 prices and hence recalculate the index numbers of real government expenditure.
c) Give an interpretation of the index numbers calculated in part (b).
2. Index numbers associated with the growth of unemployment during an 8-year period are shown in Table 3.18 .
a) What are the base years for the two indices?
b) If the government hadn9t switched to index 2, what would be the values of index 1 in years 7 & 8?
c) What values would index 2 have been in years 1, 2, 3, 4 and 5?
d) If unemployment was 1.2 million in year 4, how many people were unemployed in years 1 and 8?
3. The prices of a good at the end of each year between 2003 and 2008 are listed in Table 3.19 , which
also shows the annual rate of inflation.
a) Find the values of the prices adjusted to the end of year 2004, correct to 2 decimal places. Hence,
calculate the index numbers of the real data with 2004 as the base year. Give your answers correct to 1 decimal place. P a g e 3 | 7
Compiled by Ngo Minh Tuyet Ngoc
b) If the index number of the real price for 2009 is 109 and the rate of infl ation for that year is 2.5%,
work out the nominal value of the price in 2009. Give your answer rounded to the nearest whole number.
c) If the index number of the real data in 2002 is 95.6 and the nominal price is $215, find the rate of
inflation for 2002. Give your answer correct to 1 decimal place. * Interest
1. A principal, $30, is invested at 6% interest for 2 years. Determine the future value if the interest is compounded a) annually b) semi-annually c) quarterly d) monthly e) weekly f) daily
2. Use the formula S = Per%t
to determine the future value of $30 invested at 6% interest compounded continuously for 2 years.
3. A recent ANZ Bank ad offered the following nominal rates for a 3-year term deposit: Interest paid monthly: 4.00%
Interest paid quarterly: 4.05%
Interest paid annually: 4.10% a) Which is the best rate?
b) If another person want to borrow money from ANZ Bank. Which is the best rate?
4. Midwest Bank offers a return of 5% compounded annually for each and every year. The rival BFB
offers a return of 3% for the first year and 7% in the second and subsequent years (both compounded
annually). Which bank would you choose to invest in if you decided to invest a principal for (a) 2 years; (b) 3 years?
5. Determine the monthly repayments needed to repay a $100 000 loan which is paid back over 25
years when the interest rate is 8% compounded annually.
6. Ann borrow from ACB bank $150,000, which is paid back over 20 years when the interest rate is 9% compounded annually. a.
What is her monthly repayment? b.
Suppose that after 5 years, Ann plans to repay the loan by making an additional payment
each month along with her regular payment. How much must Ann pay each month if she wishes to pay off the loan in 10 years? 7. P a g e 4 | 7
Compiled by Ngo Minh Tuyet Ngoc
a) A person invests $5000 at the beginning of a year in a savings account that offers a return of 4.5%
compounded annually. At the beginning of each subsequent year an additional $1000 is invested
in the account. How much will there be in the account at the end of ten years?
b) A person invests $5000 at the beginning of a year in a savings account that offers a return of 4.5%
compounded annually. After 1 year, at the beginning of each month an additional $100 is invested
in the account. How much will there be in the account at the end of ten years? * Investment appraisal
1. An investor is given the opportunity to invest in one of two projects:
Project A costs $10 000 now and pays back $15 000 at the end of 4 years.
Project B costs $15 000 now and pays back $25 000 at the end of 5 years.
The current interest rate is 9%. By calculating the net present values, decide which, if either, of these
projects is to be recommended.
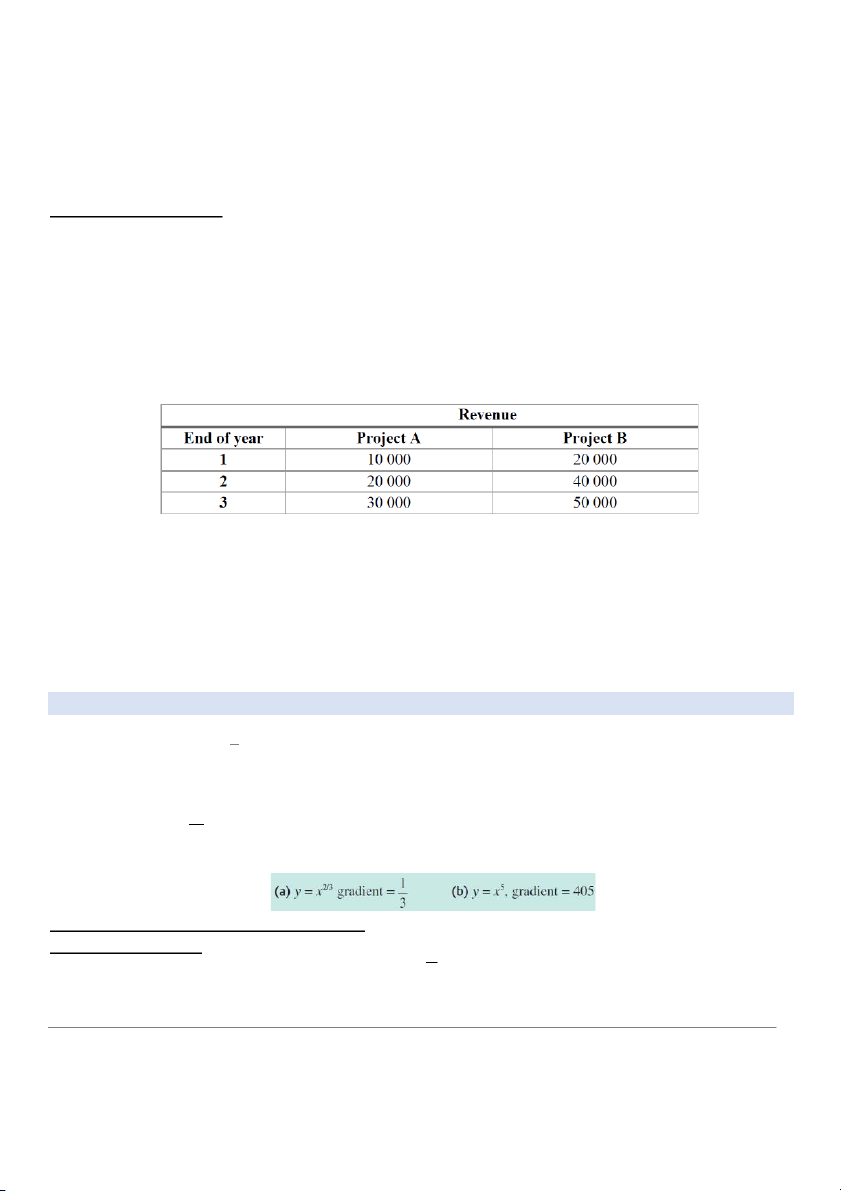
2. [Re: Quiz 2 Mr. Tri Anh sem 1 20 –
20-2021] An investor is given the opportunity to invest in one of
two projects. The following table show the revenue flows from the two projects during the nexr 3 years.
In condition, the project A requires an initial outlay of 50 000 when starting and project B needs to be
invested 30 000 at the beginning at each year. Given that the interest rate is 4% compounded
annually, by using NPV method or IRR method, what project should be advised?
3. A project requires an initial outlay of $80 000 and produces a return of $20 000 at the end of year 1,
$30 000 at the end of year 2, and $ R at the end of year 3. Determine the value of R if the internal rate of return is 10%. CHAPTER 4
1. Given the graph: y = √�㕥 . A is the point where x = 4, and B is the point where x = 4.1. In each case find
a) the y coordinates of A and B
b) the gradient of the chord AB �㕑þ c) the value of at A. �㕑ý
2. Find the coordinates of the point(s) at which the curve has the specified gradient.
* Rules of differentiation (tham kh¿o sách) * Marginal functions
1. A firm9s demand function is given by P = 100 2 4√�㕄 2 3Q P a g e 5 | 7
Compiled by Ngo Minh Tuyet Ngoc
a) Write down an expression for total revenue, TR, in terms of Q .
b) Find an expression for the marginal revenue, MR, and fi nd the value of MR when Q = 9.
c) Use the result of part (b) to e stimate the change in TR when Q increases by 0.25 units from its
current level of 9 units and compare this with the exact change in TR. 6
2. A fi rm9s average cost function takes the form AC = 4Q + a + �㕄
and it is known that MC = 35 when Q = 3. Find the value of AC when Q = 6.
3. If the consumption function is C = 0.02 Y2 + 0.1 Y + 25; find the value of Y when MPS = 0.38.
4. A firm9s production function is given by Q = 5L 2 0.1L
a) Find an expression for the marginal product of labour, MP L .
b) Solve the equation MP = 0 and briefly explain the signifi cance of this value of L . L
c) Show that the law of diminishing marginal productivity holds for this function. * Elasticity
1. The demand function of a good is given by
Calculate the price elasticity of demand at P = 5 and hence estimate the percentage
change in demand when P increases by 2%. 2.
a) Find the elasticity of demand in terms of Q for the demand function, P = 20 2 0.05Q .
b) For what value of Q is demand unit elastic?
c) Find an expression for MR and verify that MR = 0 when demand is unit elastic.
3. A supply function is given by Q = 40 + 0.1P2
a) Find the price elasticity of supply averaged along an arc between P = 11 and P = 13. Give your
answer correct to 3 decimal places.
b) Find an expression for price elasticity of supply at a general point, P . Hence:
Estimate the percentage change in supply when the price increases by 5% from its current level of
17. Give your answer correct to 1 decimal place.
Find the price at which supply is unit elastic. * Optimisation
1. The supply and demand equations of a good are given by 3P Q
– s = 3 and 2P + QD = 14, respectively.
The government decides to impose a tax, t , per unit. Find the value of t which maximises the
government9s total tax revenue on the assumption that equilibrium conditions prevail in the market.
2. A firm9s short-run production function is given by Q = 30L2 0.5L3. Find the value of wh L ich
maximises APL and verify that MPL = APL at this point. P a g e 6 | 7
Compiled by Ngo Minh Tuyet Ngoc
3. The demand and total cost functions of a good are P + Q 2 16 = 0 and , respectively.
a) Find expressions for TR, π, MR and MC in terms of Q . �㕑�㔋 b) Solve the equation
= 0, and hence determine the value of Q which maximises profi t. �㕑�㕄
c) Verify that, at the point of maximum profi t, MR = MC.
4. A manufacturer has fi xed costs of $200 each week, and the variable costs per unit can
be expressed by the function, VC = 2Q 2 36.
a) Find an expression for the total cost function and deduce that the average cost function is given by
b) Find the stationary point of this function and show that this is a minimum.
c) Verify that, at this stationary point, average cost is the same as marginal cost. (AC = MC)
5. The demand functions for a firm9s domestic and foreign markets are P1 = 50 2 5Q1 P2 = 30 2 4Q2
and the total cost function is TC = 10 + 10Q, where Q = Q1 + Q2. Determine the prices needed to maximise profit a) with price discrimination
b) without price discrimination.
Calculate the price elasticity of demand at point of maximum profit for each of the demand
functions with price discrimination. Vertify that the firm charges the higher price in the market with the lower value of |E|.
6. [4.8] The demand function of a good is given by Q = 4000e 0.01 P
a) Find an expression, in terms of P , for the elasticity of demand and hence determine the range of
values of P when the demand is inelastic.
b) Find the price which maximises total revenue. P a g e 7 | 7
Compiled by Ngo Minh Tuyet Ngoc