







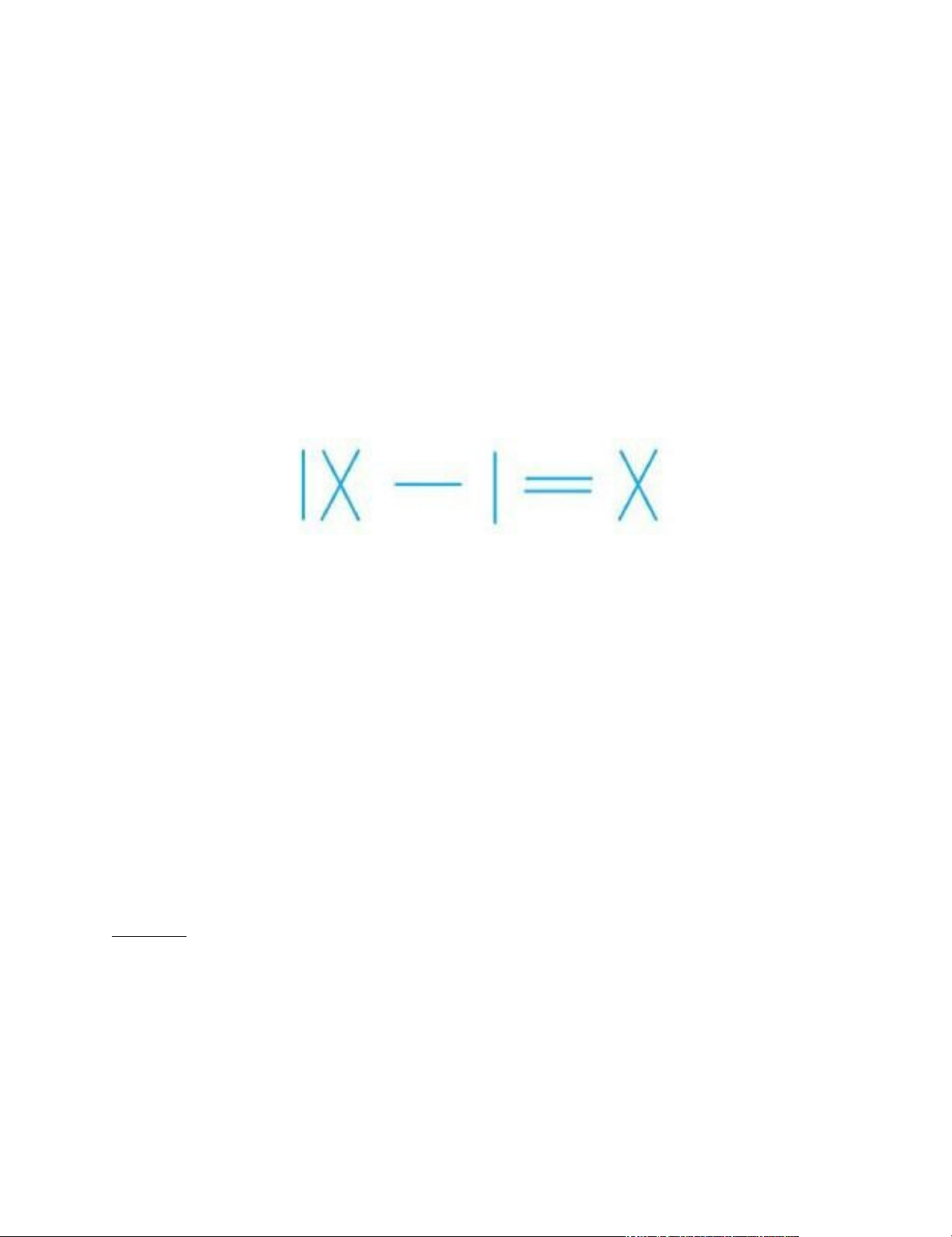






Preview text:
lOMoARcPSD|44744371
Phần SỐ VÀ ĐẠI SỐ
Chương 1. SỐ TỰ NHIÊN
Bài 1. TẬP HỢP – TẬP HỢP SỐ TỰ
NHIÊN A. MỘT SỐ DẠNG BÀI TẬP
DẠNG 1. Viết một tập hợp.
Phương pháp giải
Đọc và mô tả được nội dung của các dấu <, >, , . Hiểu được các từ “không nhỏ hơn,
không lớn hơn, không quá, …” để liệt kê đủ các phần tử (không thiếu, không thừa).
Nhớ quy tắc viết các phần tử của tập hợp.
VD1. Viết các tập hợp sau bằng cách liệt kê các phần tử:
Tập hợp A gồm các chữ cái tiếng Việt có mặt trong cụm từ “STRENGTH”.
Tập hợp B gồm các tháng trong quý ba trong năm.
Tập hợp C gồm các tháng có 30 ngày.
Tập hợp D gồm các số chẵn nhỏ hơn 10.
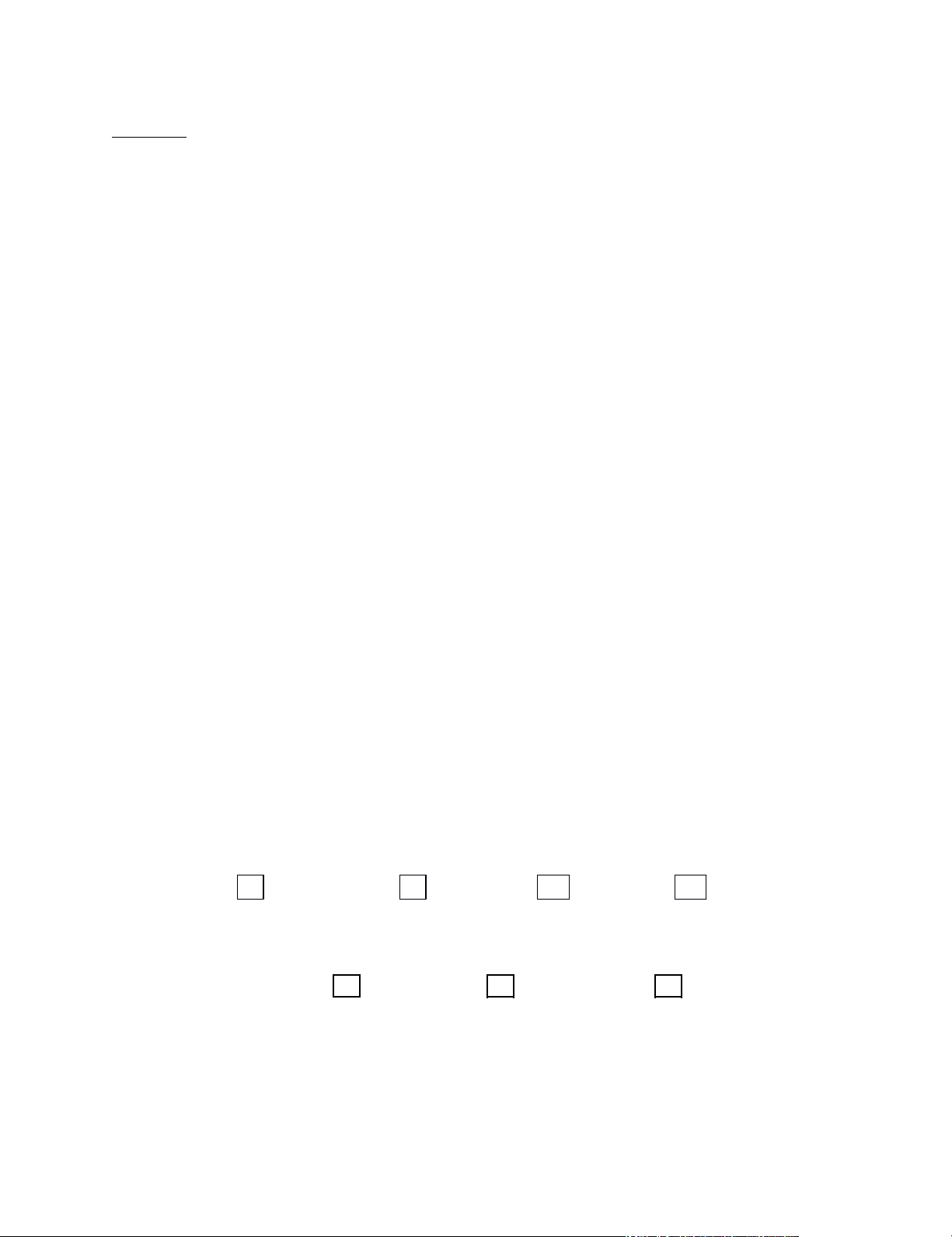
Tập hợp E gồm các số lẻ lớn hơn hoặc bằng 3 nhưng không quá 13. F = G =
Các tập hợp được biểu diễn dưới các hình vẽ sau:
VD2. Viết các tập hợp sau bằng cách chỉ ra tính chất đặc trưng của các phần tử: A = {0; 2; 4; 6; 8; 10} B = {3; 5; 7; 9; 11; 13} B = {3; 6; 9; 12; 15}
C = { 0; 5; 10; 15; 20; 25; 30}
D là tập hợp các số tự nhiên vừa lớn hơn 10 vừa nhỏ hơn 20. 1 lOMoARcPSD|44744371
DẠNG 2. Sử dụng các ký hiệu . Phương pháp giải
Giải thích được nội dung của các ký hiệu .
VD3. Cho X là tập hợp các số tự nhiên vừa lớn hơn 3 vừa nhỏ hơn 10.
Viết tập hợp X theo hai cách.
Trong các khẳng định sau, khẳng định nào đúnh, khẳng định nào sai? a. 1X; b. 5 X;c. 7 X; d. 10 X.
Trong các số 2; 4; 6; 8 10, số nào là phần tử thuộc tập hợp X, số nào không thuộc tập
hợp X? (Dùng ký hiệu để viết câu trả lời).
VD4. Cho 2 tập hợp E = {a; b; c; d} và F = {c; d; e; f}. Dùng các ký hiệu để ghi các phần tử. Thuộc E và thuộc F.
Thuộc E và không thuộc F.
Thuộc F và không thuộc E.
B. BÀI TẬP VẬN DỤNG
Bài 1. Viết tập hợp A và B gồm các chữ cái trong các cụm từ: 1) “HỌC SINH” 2) “BÀI TẬP”
Bài 2. Cho A là tập hợp các số tự nhiên nhỏ hơn 8 và B là tập hợp các số tự nhiên lẻ nhỏ hơn 7.
Viết tập hợp A và B bằng cách liệt kê các phần tử.
Dùng kí hiệu ; điền vào ô trống: 1 A ; 2 B ; 5 A; 3 B.
Bài 3. Cho hai tập hợp: A = {m, n, p}, B = {m, x, y}
Dùng kí hiệu ; điền vào ô trống: n A; p B; m .
Bài 4. Cho tập hợp U = chia hết cho 3}. Trong các số 3; 5; 6; 0; 7 số nào thuộc và số nào
không thuộc tập U? (Dùng ký hiệu để viết câu trả lời). 2 lOMoARcPSD|44744371
Bài 5. Hãy viết các tập hợp sau bằng cách liệt kê các phần tử:
Tập A gồm các ngày trong tuần.
Tập B gồm các tháng có 30 ngày.
Tập C gồm các số tự nhiên có 1 chữ số.
Tập D gồm các số thập phân có một chữ số sau dấu phẩy và có phần nguyên là 0.
Bài 6. Viết các tập hợp sau bằng cách liệt kê các phần tử: A = B = C = D = E =
F = là số chia hết cho 2 và không quá 10}
G = { là các số tự nhiên nhỏ hơn 20 và chia hết cho 5} H =
Bài 7. Viết mỗi tập hợp sau bằng cách chỉ ra tính chất đặc trưng cho các phần tử của tập hợp đó. A = {0; 3; 6; 9; 12; 15} B = {5; 10; 15; 20; 25; 30}
C = {10; 20; 30; 40; 50; 60; 70; 80; 90} D = {1; 5; 9; 13; 17} E = F =
Bài 8. Viết các tập hợp sau bằng hai cách:
Tập hợp A gồm các số tự nhiên lớn hơn 3 và nhỏ hơn hoặc bằng 9.
Tập hợp B gồm các số tự nhiên lớn hơn 2 và không quá 12.
Bài 9. Cho tập hợp L =
Nêu bốn số tự nhiên thuộc tập L và hai số tự nhiên không thuộc tập L.
Hãy mô tả tập L bằng cách nêu dấu hiệu đặc trưng theo một cách khác. 3 lOMoARcPSD|44744371
Bài 10. Cho tập hợp H = {2; 5; 6}. Viết tập hợp các số có 2 chữ số khác nhau lấy từ tập H.
Bài 11. Cho 2 tập hợp C = {3; 5; 7} và D = {1; 2}. Viết các tập hợp gồm 2 phần tử, trong
đó 1 phần tử C và 1 phần tử D.
Bài 12. Cho các tập hợp: A = {cam, táo}, B = {ổi, cam, chanh}
Dùng các kí hiệu. ; để ghi các phần tử: Thuộc A và thuộc B.
Thuộc A mà không thuộc B.
Bài 13. Cho 2 tập hợp V = {1; 3; 5}, S = {1; 2; 3}
Dùng các kí hiệu. ; để ghi các phần tử: Thuộc V và thuộc S
Thuộc V và không thuộc S.
Thuộc S và không thuộc V.
Bài 14. Cho tập hợp M = {mèo; chó; lợn; gà; thỏ} và N = {mèo; lợn; gà; vịt; ngỗng}.
Hãy viết các tập hợp sau:
Tập hợp E các phần tử của M mà không thuộc N.
Tập hợp F các phần tử của N mà không thuộc M.
Tập hợp G các phần tử vừa thuộc M vừa thuộc N.
Tập hợp H các phần tử thuộc ít nhất một trong hai tập hợp M và N.
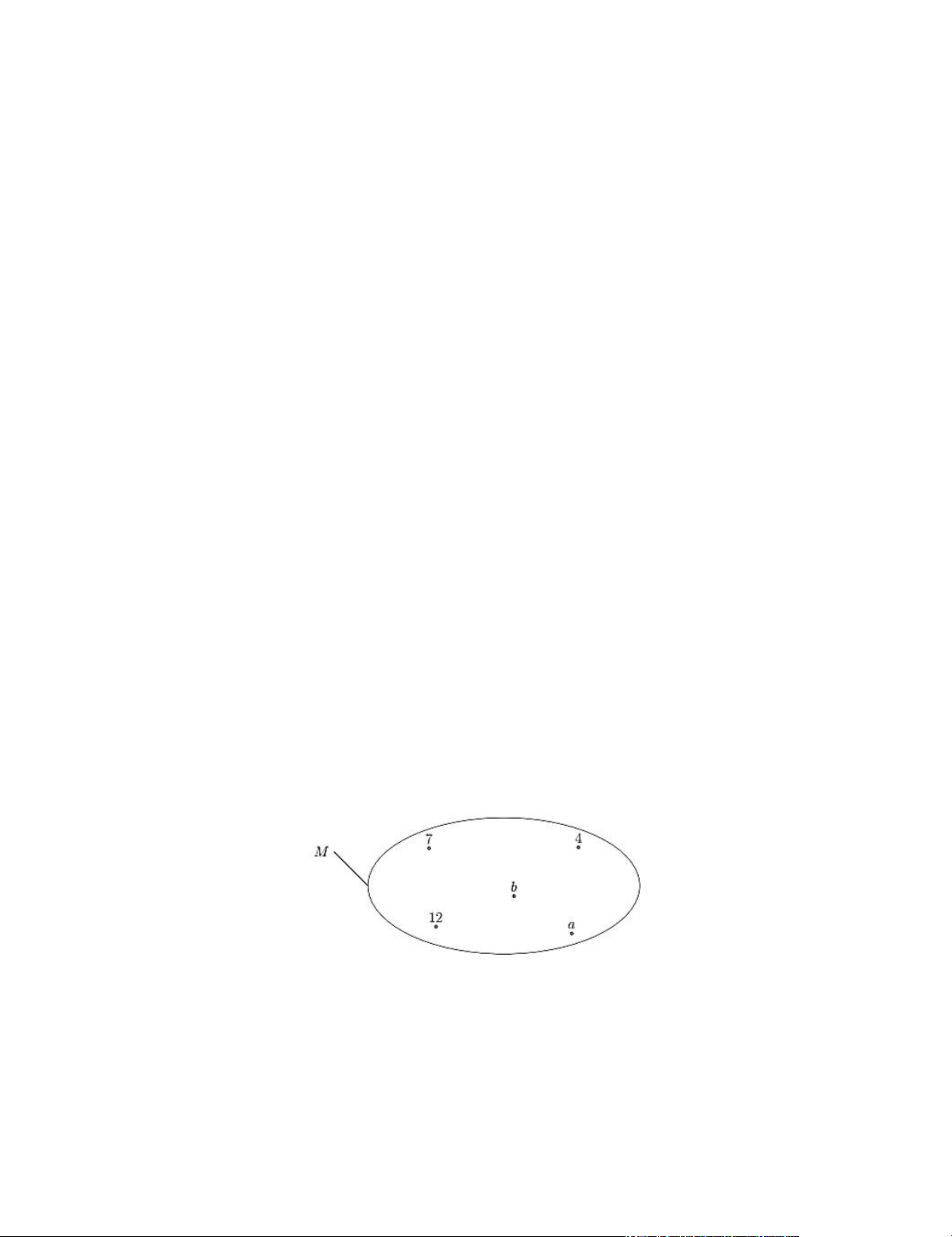
Bài 15. Viết tập hợp M được minh họa trong hình dưới đây
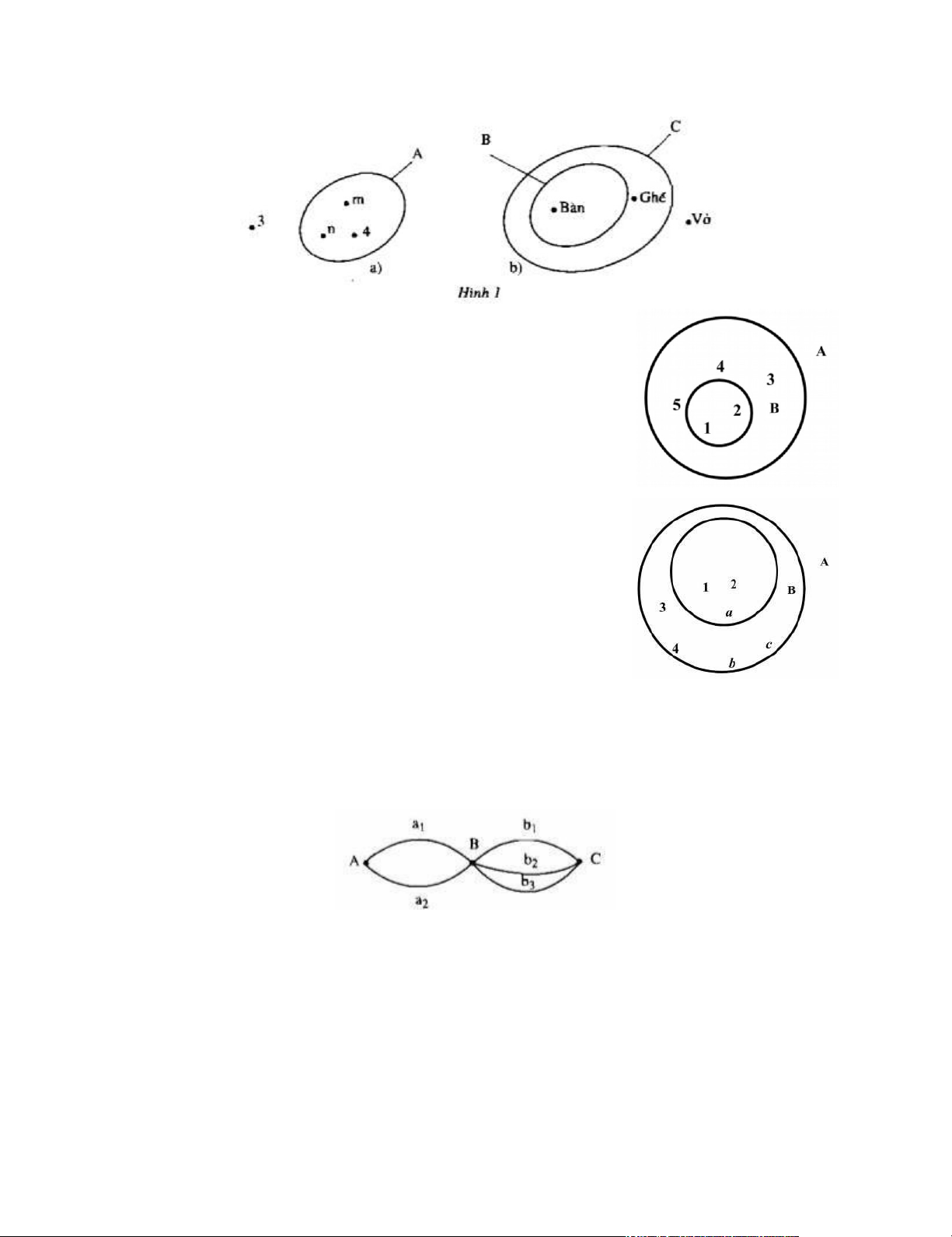
Bài 16. Nhìn các hình 1a, 1b. Hãy viết các tập hợp A, B, C. 4 lOMoARcPSD|44744371
Bài 17. Cho hình vẽ bên:
Bằng cách liệt kê các phần tử hãy viết tập A, B.
Bài 18. Cho hình vẽ bên:
Hãy viết tập hợp A, B bằng cách liệt kê.
Tìm các phần tử thuộc A mà không thuộc B.
Tìm các phần tử thuộc A và thuộc B.
Bài 19. Có hai con đường a1, a2 đi từ A đến B và có ba con đường b1, b2, b3 đi từ B đến C.
a1b1 là một trong các con đường đi từ A đến C qua B. Hãy viết tập hợp các con đường đi từ A đến C qua B. 5 lOMoARcPSD|44744371
Bài 2. SỐ PHẦN TỬ CỦA MỘT TẬP HỢP. TẬP HỢP
CON A. MỘT SỐ DẠNG BÀI TẬP
DẠNG 1. Tìm số phần tử của một tập hợp
VD1. Gọi A là tập hợp các tháng (dương lịch) có 30 ngày. Hỏi tập hợp A có bao nhiêu phần tử?
VD2. Tính số phần tử của các tập hợp sau: A = {15; 17; 19;…; 49; 51} B = {10; 12; 14;…; 76; 78}
VD3. Viết các tập hợp sau theo hai cách và tính số phần tử của mỗi tập hợp:
A là tập hợp các số lẻ không vượt quá 46.
B là tập hợp các số chẵn không vươt quá 46.
C là tập hợp các số tự nhiên lớn hơn 46.
D là tập hợp các số tự nhiên lớn hơn 46 nhưng nhỏ hơn 47.
DẠNG 2. Xác định xem tập hợp A có là con của tập hợp B không VD4.
Cho các tập hợp A = {1; 2; 3}, B = {2; 3; 4; 5}, M = {1; 2; 3; 4; 5}
Các tập hợp A và B có phải là tập con của tập hợp M không?
Tập hợp A có phải là tập hợp con của tập hợp B không? 6 lOMoARcPSD|44744371
VD5. Xem hình rồi cho biết các khẳng định sau là đúng hay sai? QM, QN,QP MP, NP N M
DẠNG 3. Viết các tập hợp con của một tập hợp cho trước.
VD6. Cho tập hợp A = {5; 6; 7}. Viết tất cả tập hợp con của tập hợp A.
VD7. Cho các tập hợp A = {10; 12; 14; 16; 18; 20; 22}, B = {. Hãy viết tập hợp M các số
chẵn có nhiều phần tử nhất sao cho M A và M B.
B. BÀI TẬP VẬN DỤNG
Bài 1. Cho A = {1; 3; a; b}; B = {3; b}
Điền các kí hiệu , , , , = thích hợp vào chỗ trống: 1…A; 3…A; 3…B; B…A 5…A; b…B; 1…B; x…A Bài 2.
Viết tập hợp A các số tự nhiên lớn hơn 10 và không vượt quá 19 bằng hai cách.
Điền các kí hiệu , , , , = thích hợp vào chỗ trống: 7…A; 18…A ;
{17; 18 ; 19}…A; {11; 12; 13; 14; 15; 16; 17; 18; 19}…A
Bài 3. Cho các tập hợp sau: A = {81; 92; a, b, e, d} K = {92; a, b, d} F = {1;8;9;2; a, b, e, d}
Điền kí hiệu thích hợp ( , , , , =) vào chỗ trống: 92…A; 1…K; F…A; K…A {1; 8}…F; {1; 2; d }…K; {92; a, b, d}…K
Bài 4. Xem hình bên hãy cho biết:
Tập hợp A có bao nhiêu phần tử?
Tập hợp B có bao nhiêu phần tử? 7 lOMoARcPSD|44744371
Bài 5. Mỗi tập hợp sau có bao nhiêu phần tử: A = {31; 33; 35;…; 77} B = {12; 14; 16;…; 98} C = {26; 29; 32;…; 83}
Bài 6. Viết tập hợp A các số tự nhiên nhỏ hơn 8, tập hợp B các số tự nhiên nhỏ hơn 4, tập
hợp C các số tự nhiên lớn hơn 4 nhưng nhỏ hơn 8. Dùng ký hiệu để thể hiện quan hệ giữa
tập hợp A với tập hợp B, tập hợp C.
Bài 7. Cho H = {x;y;z}. Viết tất cả các tập hợp con của tập hợp H.
Bài 8. Cho M = {a,b,c,d}. Viết các tập hợp con của tập hợp M sao cho mỗi tập hợp con đó có 2 phần tử.
Bài 9. Cho tập hợp C = {a; b; 3; 7}. Viết các tập hợp con của tập hợp C và mỗi tập con này đều có 2 phần tử.
Bài 10. Gọi P là tập hợp các số có bốn chữ số, trong đó hai chữ số tận cùng là 37. Hỏi tập
hợp P có bao nhiêu phần tử?
Bài 11. Cho A là tập hợp các số tự nhiên lẻ lớn hơn 5 và không lớn hơn 79.
Viết tập hợp A bằng cách chỉ ra tính chất đặc trưng của các phần tử.
Giả sử các phần tử của A được viết theo giá trị tăng dần. Tìm phần tử thứ 12 của A
Bài 12. Cần bao nhiêu số để đánh số trang (bắt đầu từ trang 1) của một cuốn sách có 1031 trang?
Bài 13. Tính số trang sách của một cuốn sách biết rằng để đánh số trang của cuốn sách đó
(bắt đầu từ trang 1) cần dung đúng 3897 chữ số. Bài 14. Tính nhanh: D=2+4+6+…+100 E=1+3+5+7+9+…+199 F=5+10+15+20+…+295 G=32+40+48+…+720 8 lOMoARcPSD|44744371
Bài 3. THỨ TỰ TRONG TẬP HỢP SỐ TỰ NHIÊN GHI SỐ TỰ NHIÊN
A. MỘT SỐ DẠNG BÀI TẬP
DẠNG 1. Viết số tự nhiên liền trước, số tự nhiên liền sau, các số tự nhiên liên tiếp. Phương pháp giải
Với số tự nhiên a 0 thì số liền trước là a – 1, số liền sau là a + 1.
VD1. Tìm số tự nhiên liền trước của 87.
VD2. Điền vào chỗ chấm các số tự nhiên thích hợp sao cho mỗi hàng là các số tự nhiên liên tiếp giảm dần:
……… ; 19 ; ……... 30 ; ……… ; ……… ……… ; ……… ; 52 ………. ; n ;……… n ;………..;………. ……….;……….; n ………. ; n ;……… n+1 ;………..;…….. .…….;……….; n+2 9 lOMoARcPSD|44744371
DẠNG 2. Phân biệt các chữ số hàng đơn vị, hàng chục, hàng trăm,…Tìm số chục, số
trăm,…của một số tự nhiên. Giá trị các chữ số của số tự nhiên.
Phương pháp giải
Nhớ tên các hàng đơn vị, hàng chục, hàng trăm, …
Phân biệt chữ số hàng chục và số chục (chẳng hạn như số 1532 có chữ số hàng chục là 3, số chục là 153).
VD3. Viết số tự nhiên có:
Chữ số hàng đơn vị là 4 và số chục là 13.
Số trăm là 128 và số đơn vị là 32.
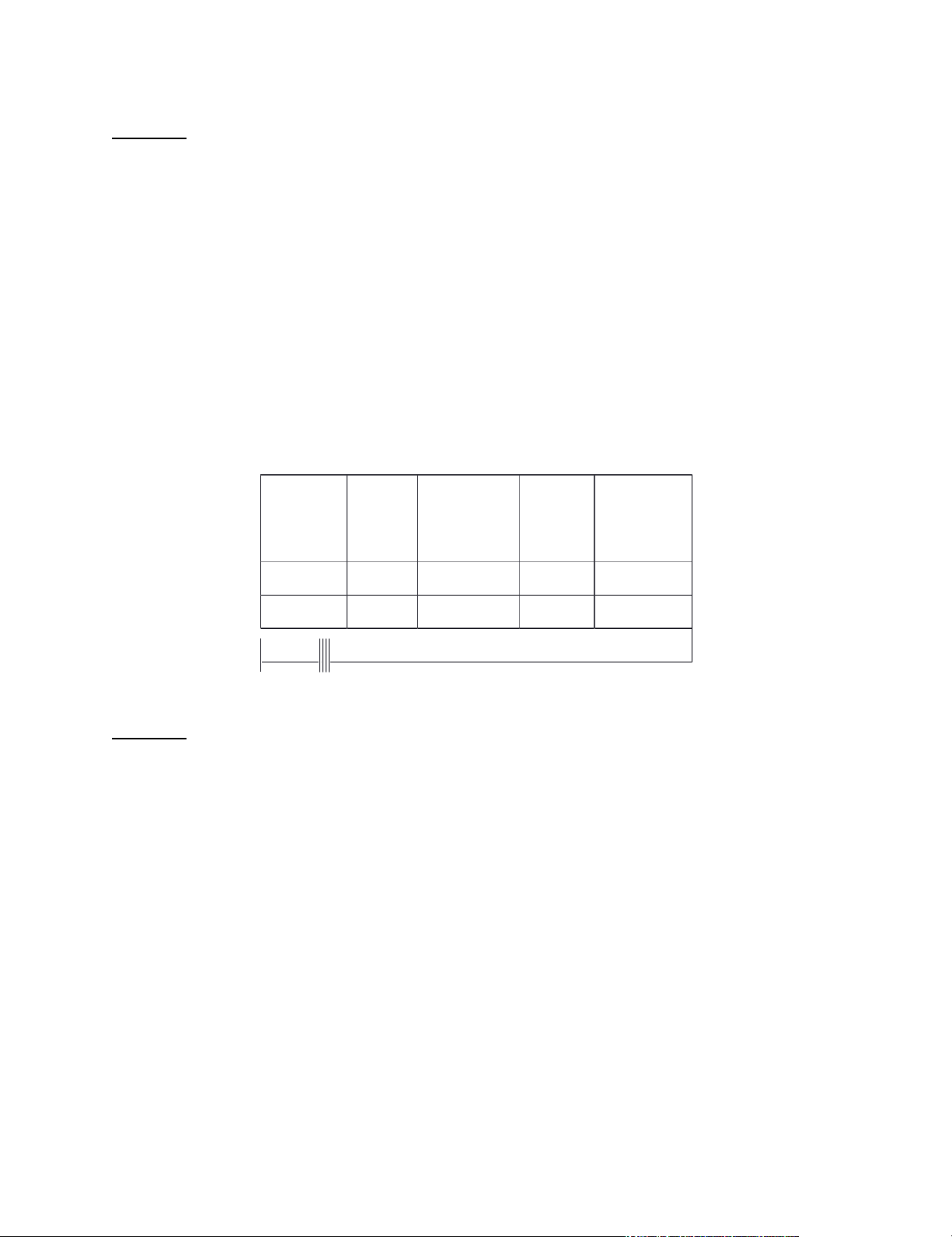
VD4. Điền vào bảng sau: Chữ số Số đã Số Chữ số Số hàng cho trăm hàng trăm chục chục 1328 2417
9568 VD5. Viết số 2 975 002 thành
tổng các giá trị chữ số của nó.
DẠNG 3. So sánh hai số tự nhiên. Tìm số tự nhiên nhỏ nhất, lớn nhất thảo mãn điều kiện cho trước.
Phương pháp giải
Số tự nhiên nhỏ nhất khi các chữ số hàng cao nhỏ nhất.
Số tự nhiên lớn nhất khi các chữ số hàng cao lớn nhất.
(Các chữ số từ trái sang phải là các chữ số từ hàng cao đến hàng thấp). VD6.
Viết số tự nhiên nhỏ nhất có hai chữ số.
Viết số tự nhiên lớn nhất có ba chữ số khác nhau.
VD7. Theo nguồn tính của CIA World Factbook, tính đến tháng 12 năm 2020, dân số
Trung Quốc là 1 441 457 889 người và dân số Ấn Độ là 1 386 638 130 người. 10 lOMoARcPSD|44744371
Hãy viết cách đọc các số chỉ dân số này.
Dân số nước nào lớn hơn?
DẠNG 4. Đọc và viết số La Mã.
VD8. Đọc các số La Mã sau: XIV, XVI, XIX và XXI.
VD9. Viết các số sau bằng số La Mã: 14, 24 và 26.
B. BÀI TẬP VẬN DỤNG Bài 1.
Viết số tự nhiên liền sau mỗi số: 99; x (với x ).
Viết số tự nhiên liền trước mỗi số: 200; y (với y ).
Bài 2. Tìm ba số tự nhiên liên tiếp, biết rằng tổng của chúng là 24. Bài 3.
Viết số tự nhiên có số chục là 215, chữ số hàng đơn vị là 3. Điền vào bảng: Chữ số Chữ số Chữ số Số Số hàng đơn hàng chục hàng trăm chục trăm vị 12 456 3 472
Bài 4. Đọc và viết:
Số tự nhiên lớn nhất có sáu chữ số khác nhau.
Số tự nhiên nhỏ nhất có bảy chữ số khác nhau.
Số tự nhiên chẵn lớn nhất có tám chữ số khác nhau.
Số tự nhiên lẻ nhỏ nhất có tám chữ số khác nhau.
Bài 5. Viết tập hợp các chữ số tự nhiên có hai chữ số, trong đó:
Chữ số hàng chục nhỏ hơn chữ số hàng đơn vị là 6.
Chữ số hàng chục gấp bốn lần chữ số hàng đơn vị.
Chữ số hàng chục nhỏ hơn chữ số hàng đơn vị, tổng hai chữ số bằng 15.
Bài 6. Viết dạng tổng quát củ một số tự nhiên: 11 lOMoARcPSD|44744371 Có hai chữ số. Có ba chữ số.
Có bốn chữ số, trong đó hai chữ số đầu giống nhau, hai chữ số cuối giống nhau.
Bài 7. Một số tự nhiên khác 0 thay đổi như thế nào nếu ta viết thêm:
Chữ số 0 vào cuối số đó?
Chữ số 5 vào cuối số đó?
Bài 8. Một số tự nhiên có ba chữ số thay đổi như thế nào nếu ta viết thêm chữ số 3 vào trước số đó? Bài 9. Cho số 7 531.
Viết thêm một chữ số 0 vào số đã cho để được số lớn nhất có thể có được.
Viết thêm một chữ số 4 xen vào giữa các chữ số của số đã cho để được số lớn nhất có thể có được.
Bài 10. Dùng ba chữ số 0, 3, 4 viết tất cả các số có ba chữ số khác nhau. Bài 11.
Dùng ba chữ số 3, 6, 8 viết tất cả các số tự nhiên có hai chữ số, mỗi chữ số viết một lần.
Dùng ba chữ số 3, 2, 0 viết tất cả các số tự nhiên có ba chữ số, mỗi chữ số viết một lần.
Bài 12. Dùng cả bốn chữ số 0, 3, 7, 6 viết số tự nhiên có bốn chữ số khác nhau và: Lớn nhất. Nhỏ nhất.
Bài 13. Cho là số tự nhiên có ba chữ số. Viết tập hợp các chữ số mà a có thể nhận để số này là số chẵn.
Bài 14. Tìm một số có hai chữ số biết rằng khi viết thêm chữ số 0 vào giữa hai số của số
đó thì được số mới gấp 7 lần số đã cho.
Bài 15. Tìm một số có ba chữ số biết rằng khi viết thêm chữ số 1 vào giữa hai số của số
đó thì được số mới gấp 9 lần số đã cho.
Bài 16. Tìm số tự nhiên có bốn chữ số có chữ số tận cùng là 5, nếu chuyển chữ số ở hàng
đơn vị lên đầu ta được số mới lớn hơn số phải tìm là 3249 đơn vị.
Bài 17. Biểu diễn các số 2571; 2024; theo mẫu: 12 lOMoARcPSD|44744371
1 983 = 1 x 1000 + 9 x 100 + 8 x 10 + 3
Bài 18. Bác Thoa đi chợ. Bác chỉ mang ba loại tiền: loại (có mệnh giá) 1 nghìn (1 000)
đồng, loại 10 nghìn (10 000) đồng và loại 100 nghìn (100 000) đồng. Tổng số tiền bác
phải trả là 695 nghìn đồng. Nếu mỗi loại tiền, bác mang theo không quá 9 tờ thì bác sẽ
phải trả bao nhiêu tờ tiền mỗi loại, mà người bán không phải trả lại tiền thừa? Bài 19.
Viết số La Mã của các số sau: 14; 18; 26.
Đọc các số La Mã sau: XXVI; XXIX; XIX.
Bài 20. Hãy thay đổi vị trí của một que tăm trong phép tính dưới đây để được phép tính đúng.
Bài 4. CÁC PHÉP TÍNH TRONG TẬP HỢP SỐ TỰ NHIÊN
A. MỘT SỐ DẠNG BÀI TẬP
DẠNG 1. Thực hiện phép tính. Áp dụng các tính chất để tính nhanh, tính nhẩm. Phương pháp giải
Để tính nhanh cần chú ý:
Giao hoán và kết hợp các số hạng của phép cộng khi chúng có tổng riêng là các số tròn trăm, tròn nghìn, …
Giao hoán và kết hợp các thừa số của phép nhân khi chúng có tích riêng là các số tròn trăm, tròn nghìn, … 13 lOMoARcPSD|44744371
Áp dụng tính chất phân phối của phép nhân đối với phép cộng khi có thừa số chung.
VD1. Thực hiện phép tính (tính nhanh nếu có thể). 1) 125:25+14–142:71 4) 36.68 + 5.14 + 68.64 2) 3+7+11+15+19+23+27 5) 79.12 + 12 – 60.12 3) 138 + 53 + 62 + 25.5.4.2 6) 25.15.4.6
VD2. Tính nhẩm 76.999. DẠNG 2. Tìm x. VD3. Tìm x, biết: 1) 3x + 1 503 935 = 3 294 470 4) (2x + 1). 2 907 = 8 721
2) 4x – 3 476 892 = 1 254 560 5) 24 : (x + 1) = 2 x : 144 – 23 = 121
DẠNG 3. Bài toán thực tế.
Phương pháp giải
Xét quan hệ trong bài để khẳng định đúng phép tính.
Nhiều bài toán cần phải đổi đơn vị, cần nắm vững cách đổi, chẳng hạn như: 1
tấn = 1 000 kg, 1 ha = 10 000 m2; …
VD4. Mẹ Lan mang 200 000 đồng vào siêu thị mua 2 kg khoai tây, 5 kg gạo và 2 nải
chuối chín. Giá mỗi kg khoai tây là 26 500 đồng, mỗi kg gạo là 18 000 đồng, mỗi nải
chuối là 15 000 đồng. Hỏi mẹ Lan còn bao nhiêu tiền? B. BÀI TẬP VẬN DỤNG
Bài 1. Thực hiện các phép tính: 1) 12.8 + 14.3 – 255 : 17 11) 18.3 – 182 + 3(51 : 17) 2) 68 + 42.5 – 625 : 25 12) (64 + 115 + 36) – 25.8 3) 25.8 – 12.5 + 272 : 17 – 8
13) 15.8 –(17–30+83)–144:6 4) 13.17–256:16+14:7–1 14) 250:50–(46–75+54):5 5) 289:17–324:18+18:3 15) 13(17–95+83):5–18:9 6) 19 + 19.99 – 25.8
16) 140 – 180(47 – 90 + 43) + 7 7) 63.26 + 63.58 + 84.37
17) 24(15 + 30 + 85 – 120) : 10 8) 57.143 – 57.47 + 96.43 18) 27 +73–30:(25–10) 9) 13 + 21.5 – (198 : 11 – 8)
19) 18 – 4(27 – 90 + 73) : 10
10) 15.24 – 14.5(145 : 5 – 27) 20) 15 – 25.8 : (100.2)
Bài 2. Tính bằng cách hợp lý: 1) 129 + 17 + 367 + 371 + 133 2) 237 + 868 + 763 + 132 + 29 3) 15+73+652+327+148 14 lOMoARcPSD|44744371 4) 5.4.25.47.2 9) (528 + 35) – 228 5) 53.64 + 53.36 10) 654 – (154 + 70) 6) 98.24 + 48 11) (2685 + 357) – 385 7) 545.2 12) 754 – (75 + 454) 375.4
Bài 3. Áp dụng các tính chất cơ bản của phép cộng và phép nhân để tính nhanh: 1) 81 + 243 + 19 4) 32.47 + 32.52 2) 168 + 79 + 132 5) 2.31.12 + 4.6.42 + 8.27.3 3) 5.25.2.16.4
6) 36.28 + 36.82 + 64.69 + 64.41
Bài 4. Tính nhanh bằng cách áp dụng tính chất kết hợp của phép cộng: 997 + 37; 49 + 194
Bài 5. Trong các tích sau, tìm các tích bằng nhau mà không tính kết quả của mỗi tích: 11.18; 15.45; 11.9.2;45.3.5; 6.3.11;9.5.15
Bài 6. Tính nhẩm bằng cách:
1) Áp dụng tính chất kết hợp của phép nhân: 17.4; 25.28.
2) Áp dụng tính chất phân phối của phép nhân đối với phép cộng: 13.12; 53.11; 39.101.
Bài 7. Tính nhẩm bằng cách áp dụng tính chất a(b – c) = ab – ac. 8.19; 65.98
Bài 8. Cho biết 37.3 = 111. Hãy tính nhanh: 37.12.
Bài 9. Tính nhẩm bằng cách thêm vào ở số hạng này, bớt đi ở số hạng kia cùng một số đơn vị: 57 + 39.
Bài 10. Tính nhẩm bằng cách thêm vào số bị trừ và số trừ cùng một số đơn vị: 213 – 98.
Bài 11. Tìm số tự nhiên x, biết: 1) x : 13 = 91 6) (x + 37) – 137 = 0 2) 5472 : x = 12 7) (235 – x) – 73 = 62 8) 235 – (x + 54) = 68 3) 5x : 11 = 0 9) (x – 315) + 247 = 926 4) 5x – 5 = 610 10) 124 + (118 – x) = 217 5) 0 : x = 0 15 lOMoARcPSD|44744371 11) 4221 : (x – 16) = 21 17) x – 36 : 18 = 12 12) 345 – (15x + 63) = 102 18) (x – 36) : 18 = 12
13) 732 : (57 – 135 : x) = 61 19) 3x + 4x = 7077 14) (17x + 23) : 12 = 9 20) 7x – 2x = 5135 15) (x – 45).27 = 0 21) 5(x – 7) = 0 16) 23(42 – x) = 23 22) 13(4x – 24) = 0 Bài 12.
Tìm số tự nhiên n, biết: 1 + 2 + 3 + 4 + … + n = 378
Tìm số tự nhiên x, biết: 2 + 4 + 6 + … + 2x = 110 Bài 13. Tìm n * 2 + 4 + 6 + … + 2n = 210
1 + 3 + 5 + … + (2n -1) = 225 Bài 14.
Có bao nhiêu số tự nhiên có 2 chữ số?
Tính tổng các số tự nhiên có hai chữ số. Bài 15.
Có bao nhiêu số lẻ có hai chữ số?
Tính tổng các số lẻ có hai chữ số?
Tính tổng các số chẵn có hai chữ số?
Tính tổng các số chia hết cho 3; mỗi số có hai chữ số. Bài 16. Tính tổng: A=2+4+6+…+98+100 B=1+3+5+…+2009+2011
C = (1 + 3 + 5 + 7 + … + 2021).(123123.456 – 123.456456) Bài 17. Tính nhanh: A=26+27+28+29+30+31+32+33
B=90–97+95–93+91–89+…+7–5+3–1
Bài 18. Nhà ga số 1 và nhà ga số 2 của một sân bay có thể tiếp nhận tương ứng khoảng 6
526 300 và 3 514 500 lượt hành khách mỗi năm. Nhờ đưa vào sử dụng nhà ga số 3 mà
mỗi năm sân bay có thể tiếp nhận được khoảng 22 851 200 lượt hành khách. Hãy tính số
lượt hành khách mà nhà ga số 3 có thể tiếp nhận mỗi năm. 16 lOMoARcPSD|44744371
Bài 19. Năm 2020 dân số Việt Nam ước tính khoảng 97 triệu người và dự kiến tới đầu
năm 2021 sẽ tăng thêm khoảng 830 nghìn người. Hãy ước tính dân số Việt Nam đầu năm 2021.
Bài 20. Một cơ thể trường thành khỏe mạnh cần nhiều nước. Lượng nước mà cơ thể một
người trưởng thành mất đi mỗi ngày khoảng: 450 ml qua da (mồ hôi), 550 ml qua hít thở,
150 ml qua đại tiện, 350 ml qua trao đổi chất, 1 500 ml qua tiểu tiện.
Lượng nước mà cơ thể một người trưởng thành mất đi trong một ngày khoảng bao nhiêu?
Qua việc ăn uống, mỗi ngày cơ thể hấp thụ được khoảng 1 000 ml nước. Một người
trường thành cần phải ăn uống thêm khoảng bao nhiêu nước để cân bằng lượng
nước đã mất trong ngày?
Bài 21. Dùng 21 000 đồng để mua vở. Vở loại I giá 2 000 đồng một cuốn, vở loại II
giá 1 500 đồng cuốn. Hỏi có thể mua nhiều nhất bao nhiêu cuốn vở nếu: Chỉ mua vở loại I. Chỉ mua vở loại II.
Bài 22. Một bệnh nhân bị sốt cao. Bác sĩ chỉ định uống 2 lít dung dịch Oresol để bù nước.
Biết mỗi gói Oresol pha với 200 ml nước. Bệnh nhân đó cần dùng bao nhiêu gói Oresol?
Bài 23. Một tàu hỏa cần chở 900 khách. Mỗi toa tàu chứa được 88 khách. Hỏi cần ít nhất
bao nhiêu toa để chở hết khách?
Bài 24. Một tàu hỏa cần chở 1 000 khách. Mỗi toa tàu có 13 khoang và mỗi khoang có 7
chỗ ngồi. Hỏi cần ít nhất mấy toa để chở hết khách?
Bài 25. Trường em có 50 phòng học, mỗi phòng học có 11 bộ bàn ghế, mỗi bộ bàn ghế
có thể xếp cho 4 học sinh ngồi. Trường có thể nhận nhiều nhất bao nhiêu học sinh để mọi
học sinh đều có chỗ ngồi.
Bài 26. Việt và Nam cùng đi từ Hà Nội đến Vinh. Tính xem ai đi lâu hơn và lâu hơn mấy giờ, biết rằng:
Việt khởi hành trước Nam 2 giờ và đến nơi trước Nam 3 giờ.
Việt khởi hành trước Nam 2 giờ và đến nơi sau Nam 1 giờ.
Bài 27. Bác Tâm từ Moskva về đến Hà Nội lúc 16 giờ ngày 10/5 (theo giờ Hà Nội).
Chuyến bay tổng cộng hết 14 giờ và giờ Moskva chậm hơn Hà Nội là 4 giờ (tức là lúc
đồng hồ ở Hà Nội chỉ 12 giờ thì đồng hồ ở Moskva chỉ 8 giờ). Hỏi bác Tâm khởi hành ở
Moskva lúc nào? (theo giờ Moskva).
Bài 28. Một phép trừ có tổng của số bị trừ, số trừ và hiệu bằng 1 062. Số trừ lớn hơn hiệu
là 279. Tìm số bị trừ và số trừ.
Bài 29. Cần bao nhiêu lượt chữ số để đánh số trang của một quyển sách dày 164 trang? 17 lOMoARcPSD|44744371
Bài 30. Để đánh số trang của một quyển sách người ta dùng tất cả 183 lượt chữ số. Hỏi
quyển sách đó có bao nhiêu trang?
Bài 31. Người ta xây một bức tường dạng tháp
(xem hình vẽ), bức tường có 40 tầng, tầng thứ
nhất có 40 viên gạch, tầng thứ hai có 39 viên
gạch, và cứ như thế lên một tầng thì số viên gạch
giảm đi 1 viên, đến tầng thứ 40 chỉ còn 1 viên
gạch. Hỏi để xây bức tường này thì cần bao nhiêu viên gạch?
Bài 32. Lớp 6A mỗi học sinh đều phải học tiếng
Anh hoặc tiếng Pháp. Biết rằng trong đó có 32 học sinh phải học tiếng Anh, 24 học sinh
học tiếng Pháp, 18 học sinh học cả 2 thứ tiếng. Hỏi lớp 6A có bao nhiêu học sinh?
Bài 5. LŨY THỪA VỚI SỐ MŨ TỰ
NHIÊN A. MỘT SỐ DẠNG BÀI TẬP
DẠNG 1. Tính giá trị của một lũy thừa. Viết gọn một số, một tích thành lũy
thừa. Phương pháp giải
Thuộc giá trị của một số lũy thừa nhỏ.
Phát biểu, giải thích được định nghĩa lũy thừa. 18 lOMoARcPSD|44744371
VD1. Viết các kết quả sau dưới dạng lũy thừa: 1) 62+82 2) 132 – 122 3)13+23+33+43
DẠNG 2. Nhân và chia hai lũy thừa cùng cơ số. Phương pháp giải
Nhân hai lũy thừa cùng cơ số:
Dùng công thức am.an = am + n.
Chú ý giữ nguyên cơ số, cộng các số mũ.
Chia hai lũy thừa cùng cơ số:
Dùng công thức am.an = am - n.
Chú ý giữ nguyên cơ số, trừ các số mũ.
VD2. Viết kết quả phép tính dưới dạng một lũy thừa: 1) 210.8 2) 35 : 27 3) a4.a.a2 4) a6 : a2 (a 0)
DẠNG 3. Tìm số mũ hoặc cơ số của một lũy thừa.
Phương pháp giải
Đưa về hai lũy thừa bằng nhau.
Trường hợp số mũ bằng nhau, chẳng hạn: an = bn thì a = b.
Trường hợp cơ số bằng nhau, chẳng hạn: am = an . Nếu a 0, a 1 thì m = n.
Nếu a = 0 thì m, n là số tự nhiên bất kỳ khác 0.
Nếu a = 1 thì m, n là số tự nhiên bất kỳ.
VD3. Tìm số tự nhiên x, biết rằng: 1) x5 = 32 2) 5x = 625
DẠNG 4. Biểu diễn một số dưới dạng lũy thừa của 10. Phương pháp giải
Viết thành a.103 + b.102 + c.101 + d.100.
VD4. Viết số 2 018 dưới dạng tổng các lũy thừa của 10.
VD5. Tính đến tháng 12 năm 2020 dân số Trung Quốc khoảng 1 442 458 000 người và
dân số Ấn Độ khoảng 1 386 640 000 người. Viết hai số chỉ số người này dưới dạng tích
của một số với một lũy thừa của 10.
DẠNG 5. Bài toán về số chính phương
Phương pháp giải 19 lOMoARcPSD|44744371
Số chính phương là bình phương của một số tự nhiên.
Số chính phương chỉ tận cùng bởi các chữ số 0, 1, 4, 5, 6, 9; không tận cùng bởi 2, 3, 7, 8.
VD6. Trong các số hoặc tổng sau, số hoặc tổng nào là số chính phương? 1) 640 000; 15 842; 46 517. 1+3+5+7+9+11+13. B. BÀI TẬP VẬN DỤNG
Bài 1. Viết gọn các tích sau bằng cách dùng lũy thừa: 1) 3.3.3.3.3 5) 25.5.4.2.10 2) 7.7.7.7 6) 2.10.10.3.5.10 3) 6.6.6.2.3 7) m.m.m 4) 3.5.15.15 8) (2x).(2x).(2x).(2x)
Bài 2. Viết gọn bằng cách dùng lũy thừa: 1) a.a.a.b.b 2) m.m.m.m + p.p
Bài 3. Viết thành dạng tích: 1) 25 4) 57 7) 45 2) 34 5) 74 8) 73 3) 43 6) 82 9) 105
Bài 4. Viết kết quả mỗi phép tính sau dưới dạng một lũy thừa: 1) 712 : 74 9) 57.27 2) x6 : x3 (x 0) 10) 23.24.22 3) x5 : x5 (x 0) 11) 102.107.103 4) 108 : 102 12) a3.a5.a2 5) a6 : a (a 0) 13) 62 – 32 6) (310.38) : 33 14) 252 - 242 7) 85.82 15) 13 + 23 8) 92.93 16) 13 +23+33 20



