















Preview text:
lOMoARcPSD|36442750 Ộ B KĨ K N G N Ă A+ A VẬT LÍ ĐẠI CƯƠNG 2
ĐẠI HỌC BÁCH KHOA HÀ NỘI
HANOI UNIVERSITY OF SCIENCE AND TECHNOLO GY
THẺ SINH VIÊN / Student ID card MSSV / ID No. IDOL HOBO + A SCAN ME
TÀI LIỆU ĐƯỢC TỔNG HỢP VÀ BIÊN SOẠN BỞI
CLB HỖ TRỢ HỌC TẬP BÁCH KHOA
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
BIÊN SOẠN BỞI CLB HỖ TRỢ HỌC TẬP BÁCH KHOA CLB.HTHT-WEBSITE.COM
Tài liệu là món quà nhân dịp năm mới Giáp Thìn 2024 của CLB Hỗ trợ Học tập dành cho các bạn sinh viên
Đại học Bách Khoa Hà Nội. CLB xin gửi lời cảm ơn chân thành nhất đến các bạn vì đã tin tưởng đồng hành
cùng CLB trong suốt thời gian vừa qua. Sự ủng hộ của các bạn chính là nguồn động lực lớn nhất để chúng
mình phấn đấu đưa CLB ngày một phát triển hơn. Cuối cùng, xin chúc các bạn một kỳ học tập hiệu quả và thành công.
Bản in lần thứ nhất, tháng 1 năm 2024
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 Mục lục 1
Form ôn tập trắc nghiệm theo chương . . . . . . . . . . . . . . . . . . . . . . . . . 4 2
Chương 1 - Điện trường tĩnh . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5 2.1
Tóm tắt lý thuyết . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5 2.2
Câu hỏi lý thuyết . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6 2.3
Bài tập . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13 3
Chương 2 - Vật dẫn . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21 3.1
Tóm tắt lý thuyết . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21 3.2
Câu hỏi lý thuyết . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22 3.3
Bài tập . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25 4
Chương 3 - Điện môi . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26 4.1
Tóm tắt lý thuyết . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26 4.2
Câu hỏi lý thuyết . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26 4.3
Bài tập . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28 5
Chương 4 - Từ trường . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30 5.1
Tóm tắt lý thuyết . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30 5.2
Câu hỏi lý thuyết . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31 5.3
Bài tập . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 38 6
Chương 5 - Cảm ứng điện từ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 43 6.1
Tóm tắt lý thuyết . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 43 6.2
Câu hỏi lý thuyết . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 43 6.3
Bài tập . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 45
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 3 7
Chương 6 - Vật liệu từ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 47 7.1
Tóm tắt lý thuyết . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 47 7.2
Câu hỏi lý thuyết . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 47 7.3
Bài tập . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 48 8
Chương 7 - Trường điện từ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 50 8.1
Tóm tắt lý thuyết . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 50 8.2
Câu hỏi lý thuyết . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 50 8.3
Bài tập . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 51 9
Chương 8 - Dao động điện từ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 53 9.1
Tóm tắt lý thuyết . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 53 9.2
Câu hỏi lý thuyết . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 54 9.3
Bài tập . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 55
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
1. Form ôn tập trắc nghiệm theo chương
Tài liệu ôn tập trắc nghiệm theo chương xem TẠI ĐÂY
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
2. Chương 1 - Điện trường tĩnh 2.1 Tóm tắt lý thuyết 1. Định luật Culomb ⃗ 1 q1q2 ⃗r F = 4πεε0 r2 r
2. ⃗E do q gây ra tại một điểm ⃗ ⃗ F q ⃗r E = = q0 4πεε0r2 r
3. ⃗E do các vật mang điện Z Z ⃗ dq ⃗r E = d⃗ E = 4πε0εr2 r tbv tbv
+ Vector cường độ điện trường gây ra bởi dây dẫn vô hạn tích điện đều |λ | E = 2πε0εr
+ Điện trường gây bởi đĩa tròn tích điện đều σ 1 Edia = 1 − 2εε q 0 1 + R2 h2
+ Điện trường gây bởi mặt phẳng tích điện đều σ E = 2εε0
4. Định lý Ostrograski - Gauox (O - G) I φ ⃗ e = Dd⃗S = ∑ qi i S
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 2.2 Câu hỏi lý thuyết 6
5. Điện thế của các vật mang điện: ∞ Z Z 1 dq Z V = dV = ; V ⃗ M = Ed⃗s 4πε0ε r M
6. Công dịch chuyển điện tích q trong điện trường: N Z A ⃗ MN = q0Ed⃗s; AMN = q0(VM −VN); dA = −q0dV M
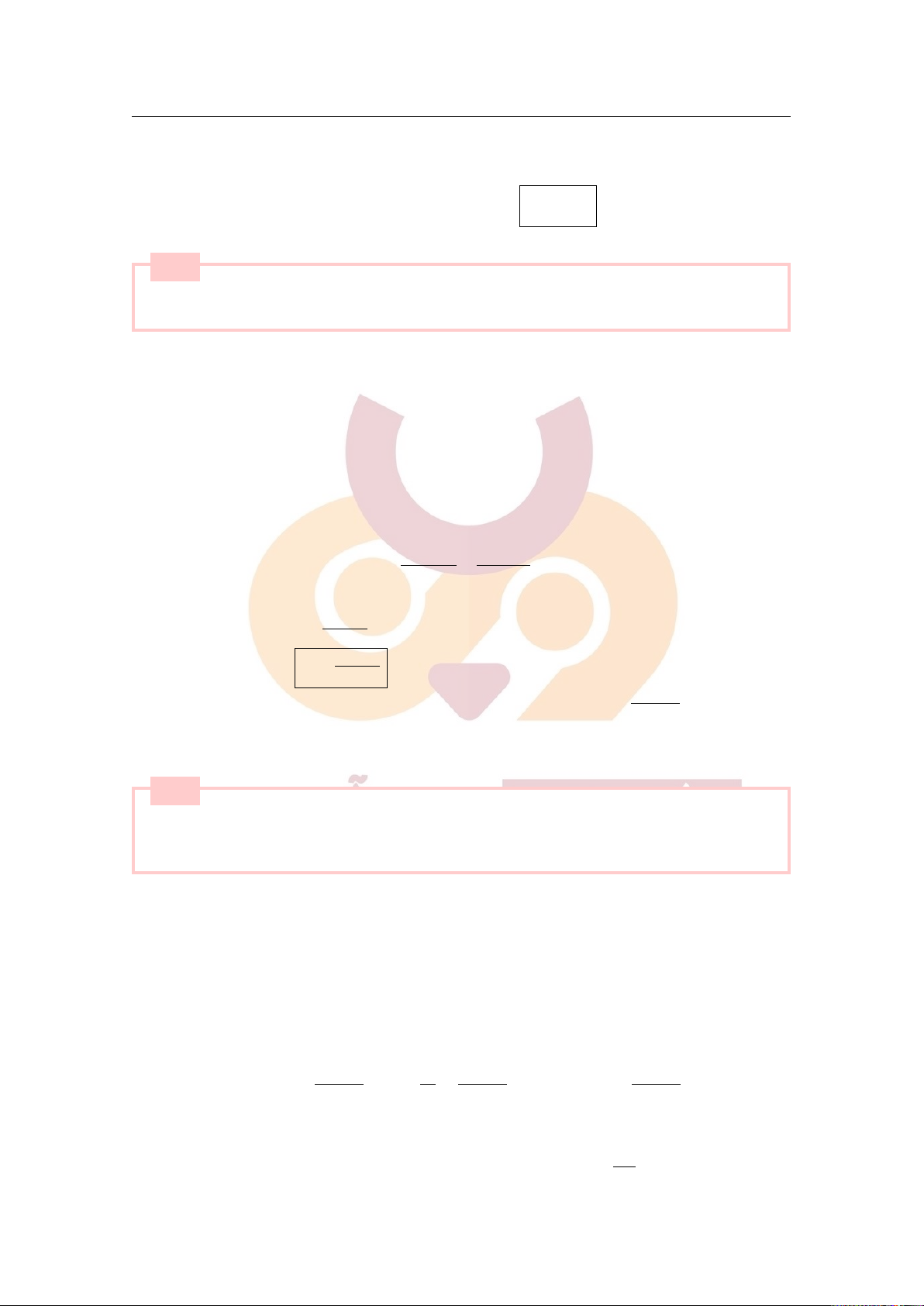
7. Hệ thức giữa cường độ điện trường và điện thế: dV E . s = − ds 2.2 Câu hỏi lý thuyết Câu 1
Trình bày khái niệm điện trường? Nêu định nghĩa và ý nghĩa của vectơ cường độ điện trường. Thiết lập
công thức xác định vectơ cường độ điện trường gây bởi điện tích điểm, hệ điện tích điểm và của một vật mang điện. ■ [Lời giải]
+ Khái niệm điện trường:
– Không gian bao quanh mỗi điện tích có xuất hiện một dạng đặc biệt của vật chất gọi là điện trường.
– Chính nhờ điện trường làm nhân tố trung gian, lực tương tác tĩnh điện được truyền đi với vận tốc hữu hạn.
– Mọi điện tích đặt trong điện trường đều bị điện trường đó tác dụng lực.
+ Vectơ cường độ điện trường:
– Vectơ cường độ điện trường tại một điểm là đại lượng có vectơ bằng lực tác dụng của điện trường
lên một đơn vị điện tích dương đặt tại điểm đó.
– Ý nghĩa: đặc trưng cho điện trường tại điểm đang xét về phương diện tác dụng lực.
+ Thiết lập công thức:
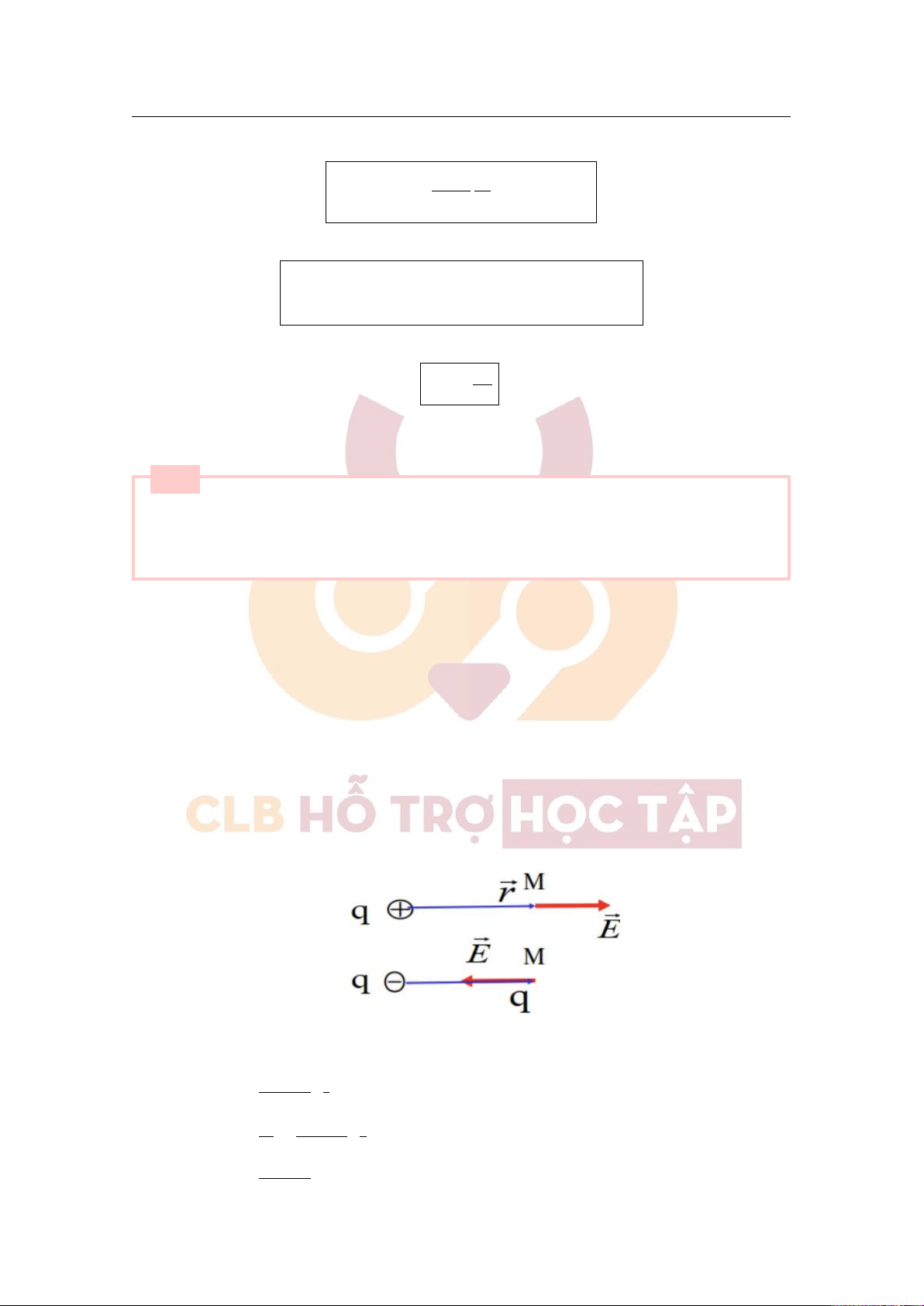
a, Xác định ⃗E do điện tích điểm q gây ra tại điểm M cách q một khoảng là r: ⃗ q · qo ⃗r F = · 4πεoεr2 r ⃗F q ⃗r ⇒ ⃗E = = · qo 4πεoεr2 r |q| ⇒ E = 4πεoεr2
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 2.2 Câu hỏi lý thuyết 7
(q > 0 : ⃗E hướng ra xa q; q < 0 : ⃗E hướng vào q).
b, Xét hệ điện tích điểm q1,q2,..qn. Xác định ⃗E tại M:
Đặt q tại M, lực tổng hợp tác dụng lên là: o qo
⃗F = ⃗F1 + ⃗F2 + ... + ⃗Fn ⃗ n ⃗ n Vectơ ⃗ F Fi
E tổng hợp tại M là: ⃗ E = = ∑ = ∑ ⃗Ei qo q i=1 o i=1
c, Xét một vật mang điện:
Chia vật mang điện thành nhiều phần nhỏ chứa điện tích dq. Vật mang điện được coi như một hệ vô số điện tích điểm. Z Z ⃗ dq ⃗r E = d⃗ E = · 4πεoεr2 r tbv tbv Z
- Với dây mật độ điện tích λ dl ⃗r λ (C/m): dq = λ dl; ⃗E = · 4πεoεr2 r tbv Z - Với mặt σ dS ⃗r σ (C/m2): dq = σ dS; ⃗E = · 4πεoεr2 r tbv Z - Với khối ρdV ⃗r ρ(C/m3): dq = ρdV ; ⃗E = · 4πεoεr2 r tbv Câu 2
Định nghĩa đường cảm ứng điện. Cho biết sự khác nhau cơ bản giữa phổ đường sức điện trường và phổ
đường cảm ứng điện. Viết công thức xác định thông lượng cảm ứng điện qua diện tích S. Tính điện
thông qua một mặt kín bao quanh một điện tích điểm. ■ [Lời giải]
+ Định nghĩa: Đường cảm ứng điện là đường cong mà tiếp tuyến tại mỗi điểm của nó trùng với phương
của véc tơ cảm ứng điện tại điểm đó. Chiều của đường cảm ứng điện là chiều của véc tơ cảm ứng điện ⃗D.
+ Sự khác nhau cơ bản: Phổ các đường sức điện trường bị gian đoạn khi đi qua mặt phân cách hai môi
trường, còn phổ các đường cảm ứng điện là liên tục.
+ Công thức xác định thông lượng:
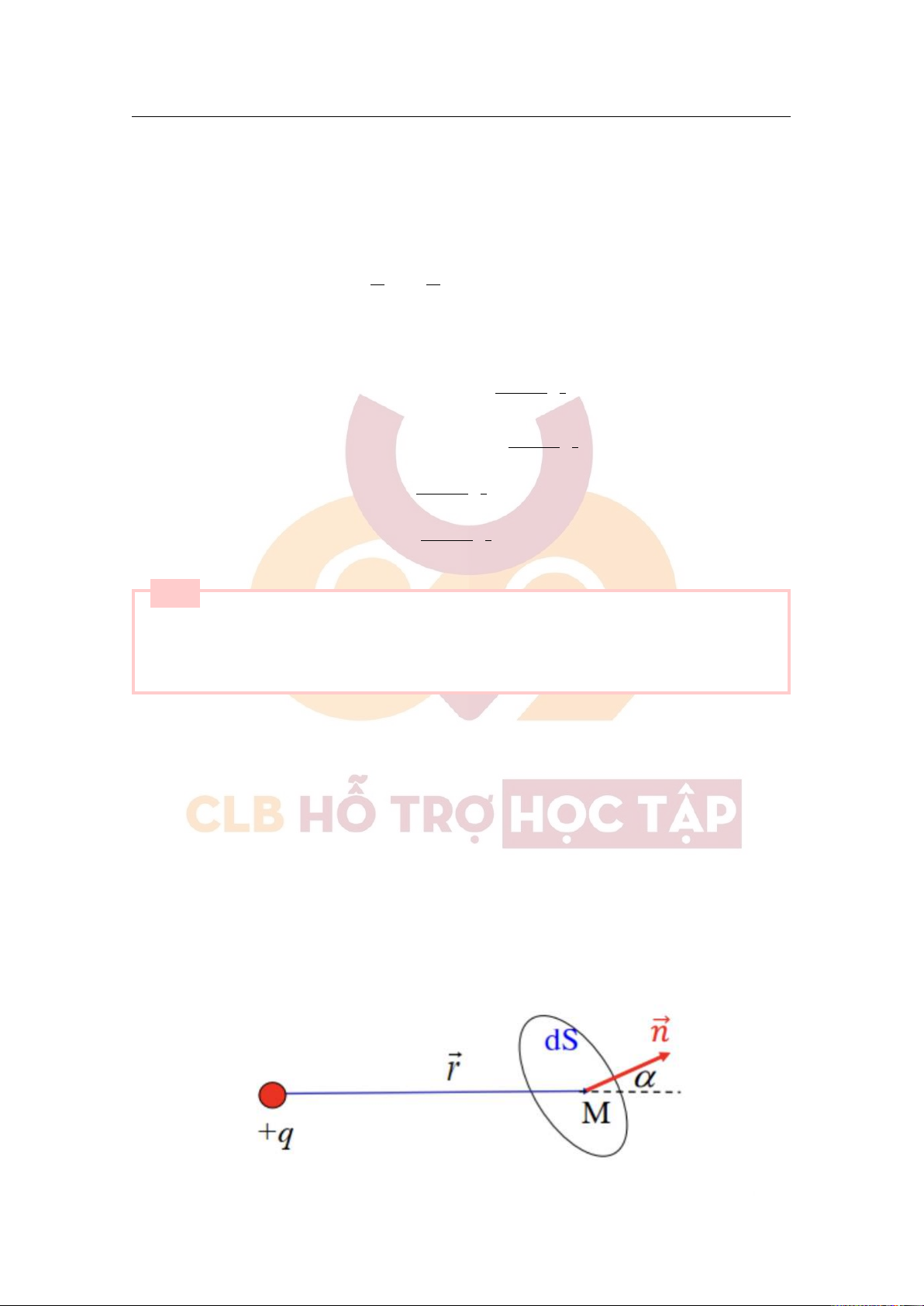
Thông lượng cảm ứng điện gửi qua diện tích dS bằng: dφe = ⃗Dd⃗S = D.dS.cosα.
Thông lượng cảm ứng điện gửi qua toàn bộ diện tích (S) bằng: Z Z φ ⃗ e = Dd⃗S = DdScosα .
+ Tính điện thông qua mặt kín bao quanh q:
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 2.2 Câu hỏi lý thuyết 8
- Thông lượng cảm ứng điện gửi qua diện tích dS bằng: q ⃗r q q dScosα q dφe = ⃗Dd⃗S = d⃗S = .⃗r.⃗n.dS = . = dΩ (Do⃗r.⃗n = rcosα) 4π r3 4πr3 4π r2 4π Với dScosα (dΩ =
là góc khối nhìn dS từ điểm O). r2
- Tích phân toàn bộ mặt kín S bao quanh q (với quy ước pháp tuyến dương hướng ra ngoài mặt S): I dΩ = 4π ⇒ φe = q S Câu 3
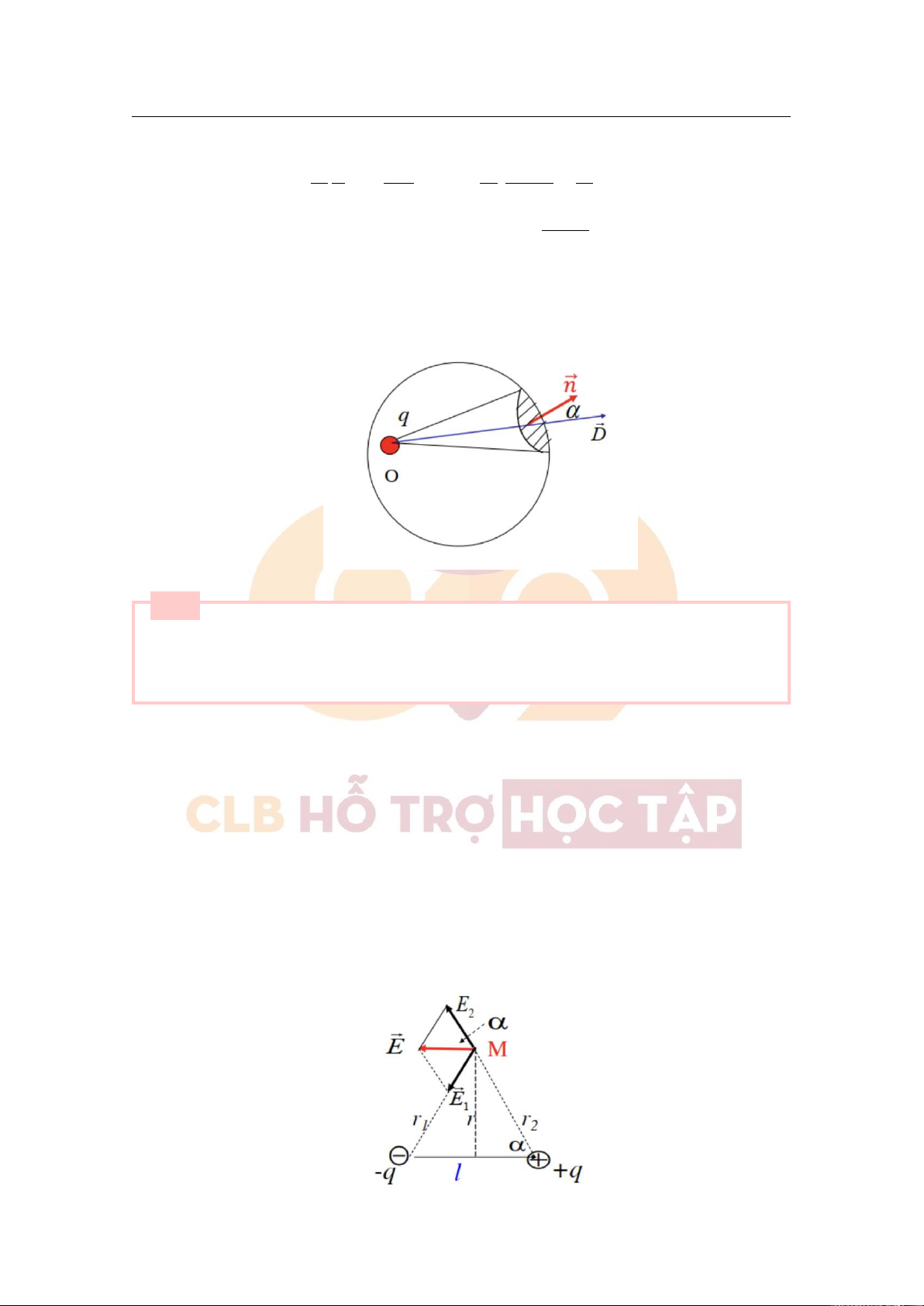
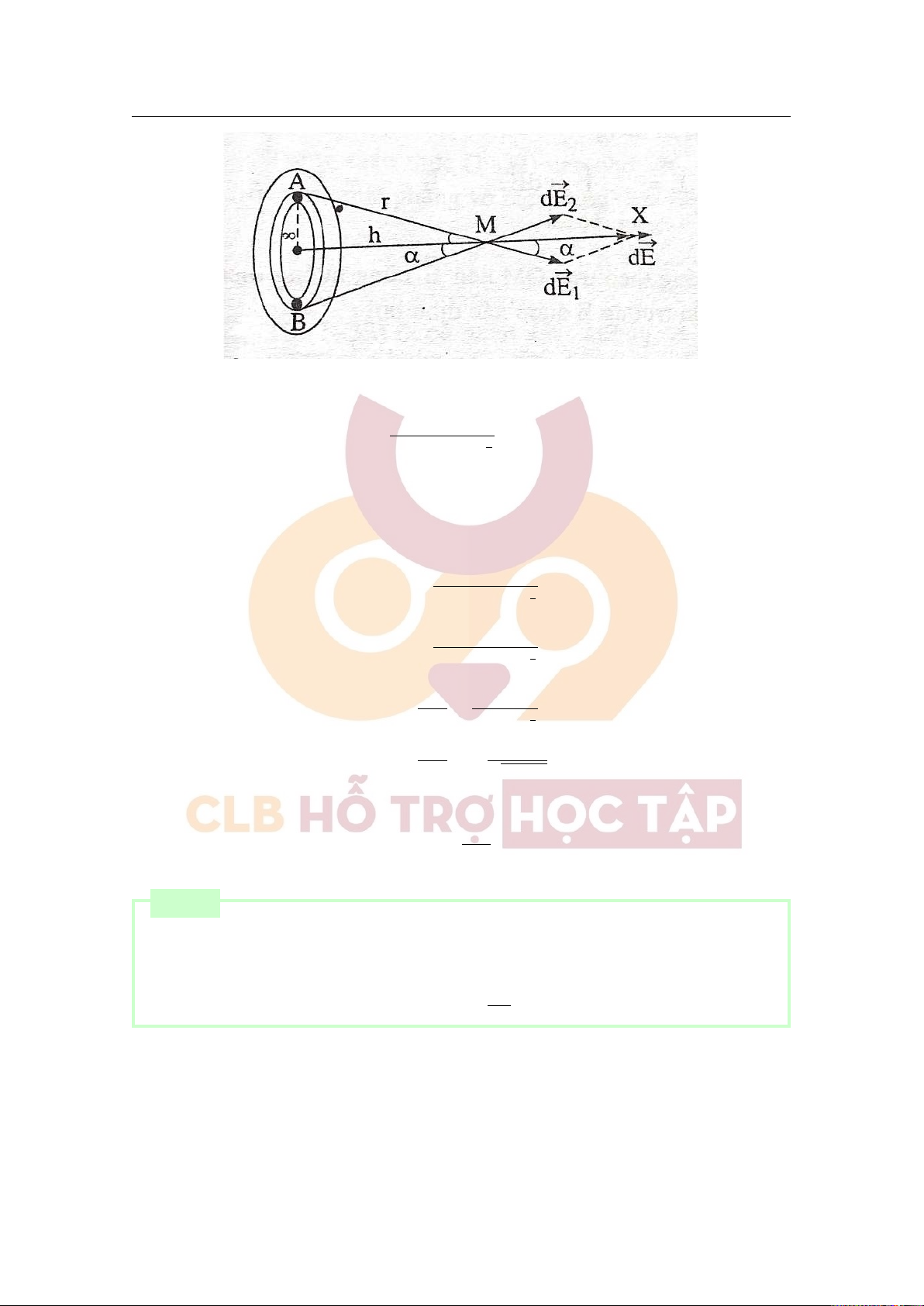
Nêu định nghĩa và ý nghĩa của mômen lưỡng cực điện. Xác định vectơ cường độ điện trường gây bởi
lưỡng cực điện tại điểm M nằm trên đường trung trực và cách tâm O của lưỡng cực một khoảng r khá
lớn so với khoảng cách giữa hai điện tích. ■ [Lời giải]
+ Định nghĩa: Lưỡng cực điện là một hệ 2 điện tích điểm có độ lớn bằng nhau nhưng trái dấu +q và -q
(q>0), cách nhau một đoạn l rất nhỏ so với khoảng cách từ lưỡng cực điện tới những điểm đang xét của
trường. Để đặc trưng cho tính chất điện của lưỡng cực người ta dùng đại lượng vectơ mômen lưỡng cực điện. ( Hướng từ -q đến +q.
+ Mômen lưỡng cực điện: ⃗pe = q⃗l
Độ lớn | pe |= ql, l là khoảng cách giữa +q và -q.
Ý nghĩa của mômen lưỡng cực điện: Biết vectơ ⃗p có thể tính được ⃗ e
E do lưỡng cực gây ra, vì thế ta nói
⃗p đặc trưng cho tính chất điện của lưỡng cực. e + Tính ⃗E:
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 2.2 Câu hỏi lý thuyết 9 Ta có: ⃗E = ⃗E1 + ⃗E2 r Vì q l2 r nên . Mà 1 = r2 E1 = E2 = r1 = r2 + ≈ r 4πεoεr2 4 1 E ql p ⇒ 1l e E = 2E1cosα = = = r1 4πεoεr3 4πε 1 oε r3 1 Vì ⃗ ⃗pe E ↑↓⃗l ⇒ ⃗ E . M = − 4πεoεr31 Câu 4
Phát biểu, viết biểu thức của định lý O-G trong điện trường. Áp dụng định lý O-G xác định cường độ
điện trường gây bởi mặt phẳng vô hạn tích điện đều với mật độ điện mặt σ. Từ kết quả trên suy ra
cường độ điện trường trong tụ điện phẳng tích điện. ■ [Lời giải]
+ Phát biểu: Điện thông qua một mặt kín S bằng tổng đại số các điện tích chứa trong mặt kín ấy. Biểu thức: I φ ⃗ e = Dd⃗S = ∑ qi i S
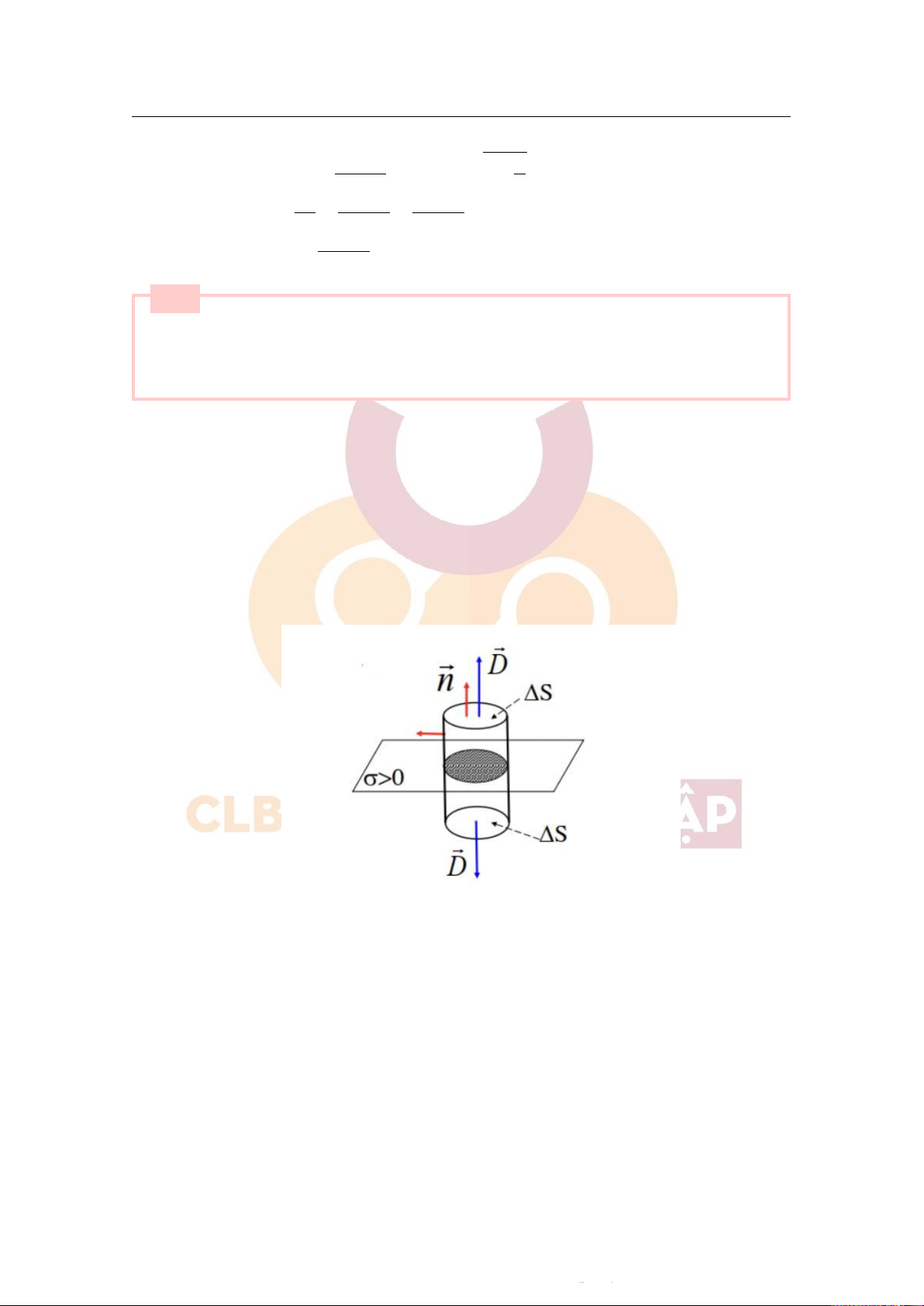
+ Điện trường gây bởi mặt phẳng vô hạn tích điện đều, mật độ điện mặt σ :
Xét điện trường tại điểm M.
- Vẽ qua M một mặt trụ có 2 đáy song song cách đều mặt phẳng.
- ⃗D có phương vuông góc với mặt phẳng.
- Tại mỗi điểm ở mặt bên: Dn = 0.
- Tại mỗi điểm trên 2 đáy: Dn = D = const.
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 2.2 Câu hỏi lý thuyết 10 Ta có: I I Z Z φ ⃗ e = Dd⃗S = DndS = DndS + DndS S S 2 đáy xq Z Z = DndS (Do DndS = 0) 2 đáy xq Z = D dS = 2D∆S 2 đáy = ∑ qi = σ dS (Theo định lý O-G) σ σ ⇒ D = ⇒ E = . 2 2εoε
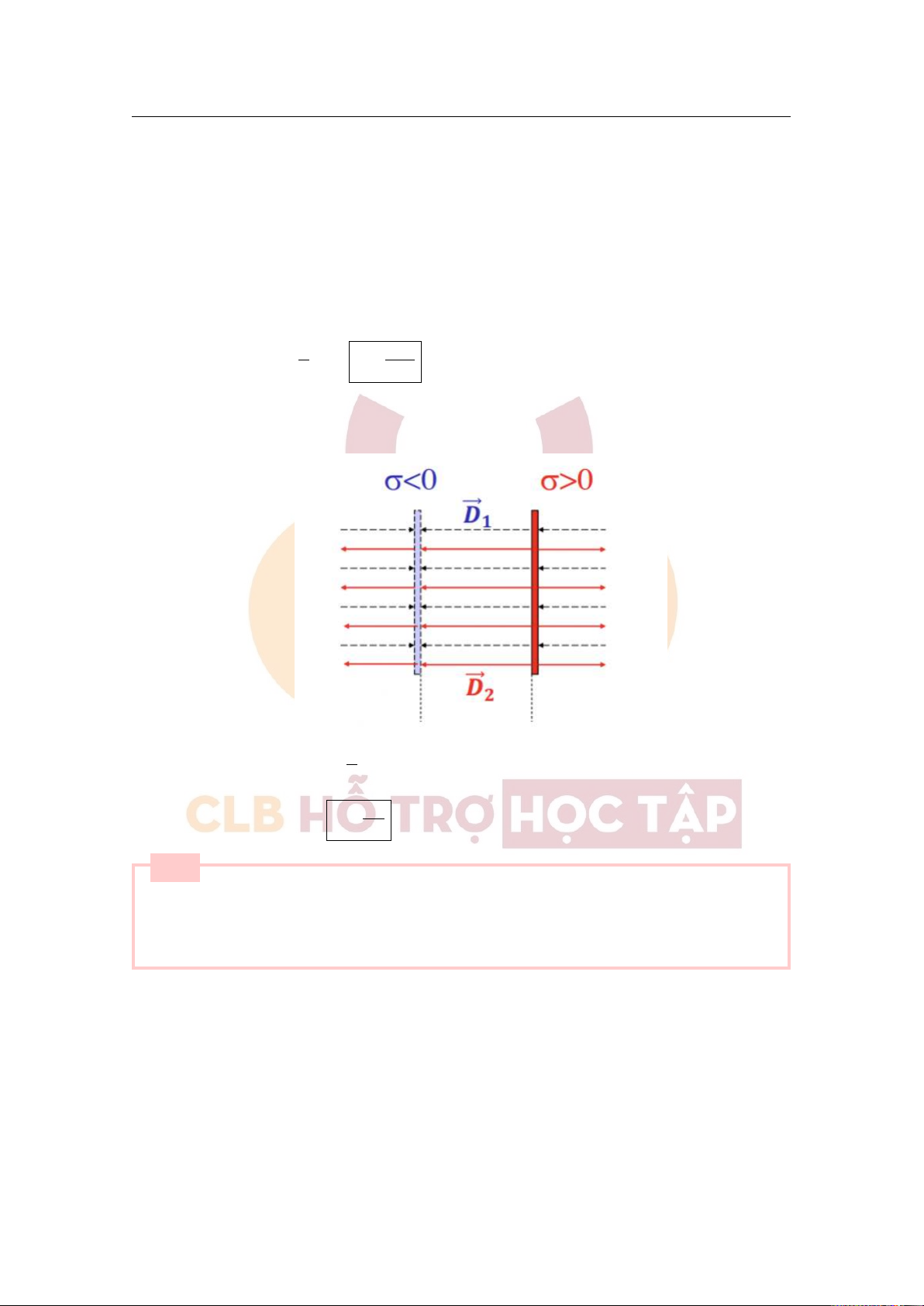
+ Cường độ điện trường trong tụ điện phẳng tích điện: ⃗ σ D = ⃗ D1 + ⃗ D2; D! = D2 = 2
Ở khoảng giữa 2 mặt phẳng: ⃗ D1 ↑↑ ⃗ D2 σ ⇒ D = D1 + D2 ⇒ E = . εoε Câu 5
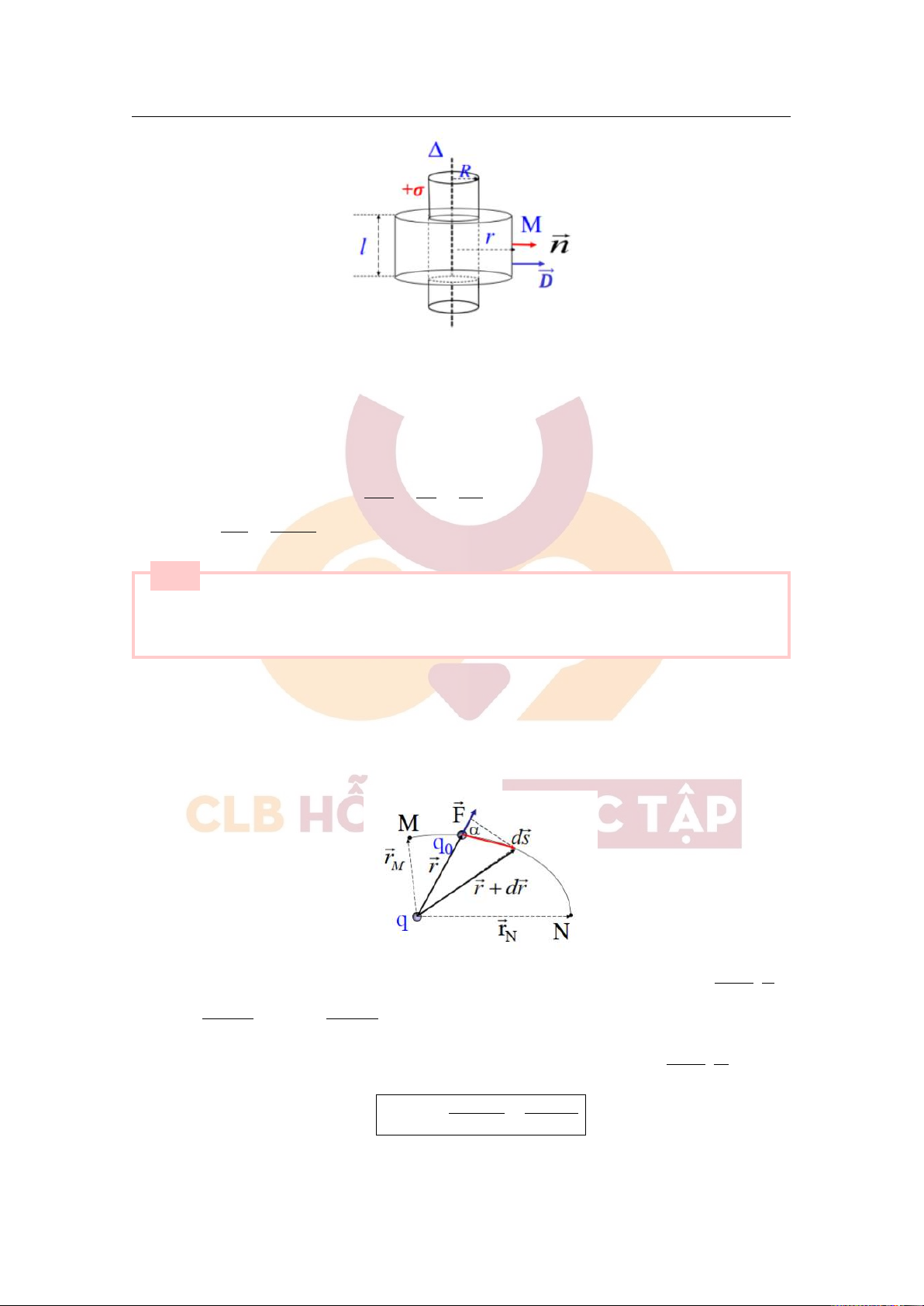
Phát biểu, viết biểu thức của định lý O - G trong điện trường. Áp dụng định lý O - G tính cường độ
điện trường gây bởi mặt trụ dài vô hạn, bán kính tiết diện ngang R, tích điện đều với mật độ điện mặt
σ , tại điểm M cách trục của trụ một khoảng r > R. ■ [Lời giải]
1.Phát biểu, viết biểu thức của định lý O - G trong điện trường.
+ Phát biểu: Điện thông qua một mặt kín S bằng tổng đại số các điện tích chứa trong mặt kín ấy. + Biểu thức: φ ⃗ e = H Dd⃗ S = ∑ qi. S i
2.Tính cường độ điện trường gây bởi mặt trụ dài vô hạn
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 2.2 Câu hỏi lý thuyết 11
- Vẽ qua M một mặt trụ đồng trục với mặt trụ mang điện, hai đáy cách nhau một khoảng l. I I Z Z - φ ⃗ e = Dd⃗S = DndS = DndS + DndS S S xq 2day Z Z Z Mà DndS = 0 → φe = DndS = D dS = D.2πrl 2day xq xq
- Theo định lý O - G, ta có: Q σ R λ
φe = Q = 2πRlσ = λ l → D = = = 2πrl r 2πr σ R λ ⇒ E = = ε0εr 2πεε0r Câu 6
Tính công của lực tính điện khi dịch chuyển điện tích điểm q trong điện trường của điện tích điểm 0 q.
Tại sao nói trường tĩnh điện là trường thế? ■ [Lời giải]
+ Giả sử dịch chuyển q trong điện trường 0
q từ điểm M đến N. Tính công của lực tĩnh điện trong dịch
chuyển đó. Xét q và q là các điện tích dương. Lực tác dụng lên là ⃗ ⃗ 0 q0
F = q0E (⃗E: điện trường do q gây ra tại vị trí q ) 0
+ Công của lực tĩnh điện trong chuyển dời vô cùng nhỏ q ⃗r d⃗s : dA = ⃗ Fd⃗s = q ⃗ 0E d⃗ s = q0. . d⃗s 4πεε0 r3 q q = 0qdr q0 .dscosα =
(ds cos α = dr: hình chiếu của ds lên⃗r) 4πεε0r2 4πεε0r2 N rN Z Z
+ Công của lực tĩnh điện trong chuyển dời q0q dr q từ M đến N: 0 AMN = dA = . 4πεε0 r2 M rM q q ⇒ 0q 0q AMN = − 4πεε0rM 4πεε0rN
→ Công của lực tĩnh điện trong sự dịch chuyển một điện tích điểm q trong một điện trường bất kỳ không 0
phụ thuộc vào một dạng đường cong dịch chuyển mà chỉ phụ thuộc vào điểm đầu và điểm cuối của chuyển dời.
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 2.2 Câu hỏi lý thuyết 12
Hay nếu dịch chuyển q theo một đường cong kín thì công của lực tĩnh điện trong dịch chuyển đó bằng không 0
→ Trường tĩnh điện là một trường thế. I I I A = ⃗Fd⃗s = q ⃗ ⃗ 0 Ed⃗s = 0 ⇒ Ed⃗s = 0 Câu 7
Trình bày về thế năng của một điện tích trong điện trường ■ [Lời giải]
+ Vì điện trường là một trường thế nên công của lực tĩnh điện trong dịch chuyển q bằng độ giảm thế 0
năng của điện tích đó trong điện trường: N Z A ⃗ MN = q0Ed⃗s = WM −WN M
+ Thế năng của q trong điện trường của một điện tích điểm 0 q :
Xét q dịch chuyển trong điện trường của 0 q. Khi đó: q0q q0q AMN = − = WM −WN 4πεε0rM 4πεε0rN
→ Biểu thức thế năng của q đặt trong điện trường của điện tích điểm 0
q và cách điện tích này một khoảng bằng q0q r là W =
+ C Quy ước chọn W của q khi nó ở xa 0 q vô cùng bằng không: 4πεε0r q0q
W∞ = 0 → C = 0 → W = 4πεε0r + Thế năng của q0qi
q trong điện trường của hệ điện tích điểm: 0 W = ∑Wi = ∑ 4πεε0ri Z ∞
+ Thế năng của q trong điện trường bất kỳ: ⃗ 0 WM = q0Ed⃗s M Câu 8
Định nghĩa và nêu ý nghĩa điện thế. Dẫn ra công thức tính điện thế tại một điểm trong điện trường của
một hệ các điện tích điểm phân bố rời rạc và tại một điểm của điện trường bất kỳ. ■ [Lời giải]
+ Định nghĩa: Tỷ số W/q không phụ thuộc vào điện tích
mà chỉ phụ thuộc vào các điện tích gây ra 0 q0
điện trường và vào vị trí điểm đang xét trong điện trường. Vậy ta có thể dùng tỷ số đó để đặc trưng cho
điện trường tại điểm đang xét. V = W/q được gọi là điện thế của điện trường tại điểm đang xét. 0
+ Ý nghĩa: Điện thế tại một điểm trong điện trường là một đại lượng về trị số bằng công của lực tĩnh
điện trong sự dịch chuyển một đơn vị điện tích dương từ điểm đó ra xa vô cùng.
+ Điện thế tại một điểm trong điện trường của một hệ các điện tích điểm phân bố rời rạc: q n n 0qi Wi qi qi Wi = → Vi = = → V = ∑ Vi = ∑ 4πε0εri q0 4πεε0ri 4πεε i=1 i=1 0ri ∞ ∞ Z Z
+ Điện thế tại điểm M trong điện trường bất kỳ: WM W ⃗ ⃗ M = q0Ed⃗s → VM = = Ed⃗s. q0 M M
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 2.3 Bài tập 13 2.3 Bài tập Bài tập 1
Đặt một tụ điện phẳng nằm ngang, các đường sức của điện trường bên trong tụ hướng thẳng đứng từ
trên xuống dưới. Khoảng cách giữa 2 bản tụ là d = 2 cm. Điện áp của tụ U = 10 V . Một hạt bụi nặng
m = 2.10−7g nằm cân bằng chính giữa, cách đều mỗi bản tụ 1cm. Lấy g = 10 m/s2.
a, Tính điện tích hạt bụi.
b, Điện áp của tụ đột ngột giảm một nửa. Hạt bụi sẽ chuyển động về phía nào, sau bao lâu tới bản cực
và khi chạm bản cực nó có vận tốc bằng bao nhiêu? ■ [Lời giải] a,
+ Vì tụ điện nằm ngang, hạt bụi nằm cân bằng chính giữa nên có lực tĩnh điện giữ cho hạt bụi cân bằng. Mà
các đường sức điện trường hướng từ trên xuống nên hạt bụi mang điện âm.
+ Điện tích của hạt bụi là: mgd 2.10−10.10.0, 02 | q |= = = 4.10−12C U 10 b,
+ Khi điện áp của tụ giảm một nửa, hạt bụi sẽ di chuyển dần với gia tốc a về bản cực âm. + Có: ⃗P + ⃗F = m⃗a qU ′ ⇒ ma = mg − d qU ′ ⇒ a = g − = 5(m/s2) md Lại có: d at2 = 2 2 r d
⇒ Thời gian tới bản cực là: t = ≈ 0,063(s) a
+ Khi chạm tới bản cực vận tốc hạt bụi là: v = at ≈ 0, 32(m/s) Bài tập 2
Từ bản dương của một tụ điện phẳng, một điện tử được tách ra với tốc độ ban đầu v dọc theo đường 0
sức điện trường. Biết tụ có hiệu điện thế U = 1,82V và khoảng cách giữa hai bản tụ là d = 4cm. Cho
me = 9, 1.10−31kg, | e |= 1, 6.10−19C. Bỏ qua tác dụng của trọng lực.
a) Tìm giá trị nhỏ nhất của v để điện tử có thể tới được bản âm của tụ điện. 0
b) Với v0 = 4.105m/s, điện tử có thể lại gần bản âm nhất một khoảng bao nhiêu? Sau thời gian bao lâu
kể từ lúc tách ra, điện từ lại quay lại bản dương của tụ điện?. ■ [Lời giải] a,
+ Để tới bản cực âm của tụ, động năng ban đầu phải thắng công cản hay: mv20 ≥ qU 2 r 2qU ⇒ v0 ≥ = 8.105(m/s) m
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 2.3 Bài tập 14 b,
+ Gia tốc của điện tử: | e | U a = − = −8.1012(m/s2) m.d Ta có: 02 − v20 = 2.a.S v2 (4.105)2 ⇒ S = − 0 = − = 0, 01(m) = 1(cm) 2a −2.8.1012
⇒ Điện từ lại gần bản âm nhất 1 khoảng d′ = 4 − 1 = 3(cm)
+ Thời gian điện tử quay lại bản dương: 2v0 t = = 10−7(s) | a | Bài tập 3
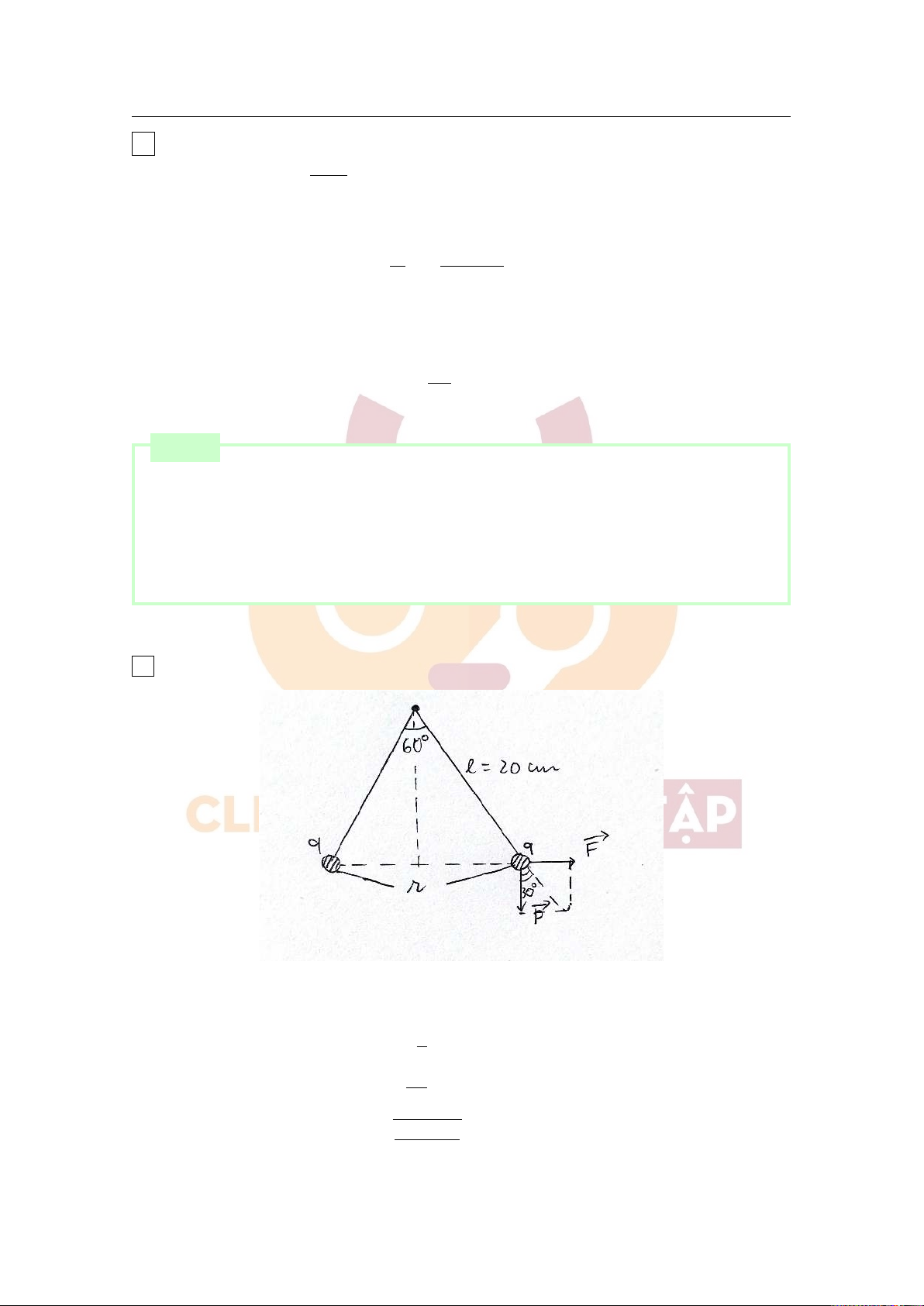
Ba con lắc đơn giống hệt nhau, mỗi con lắc gồm một quả cầu nhỏ có khối lượng m = 10g được buộc
vào sợi dây không co giãn có chiều dài l = 20cm. Lấy g = 10m/s2 và k = 9.109Nm2/C2.
a) Lúc đầu treo hai con lắc vào cùng một điểm O và tích điện q như nhau cho mỗi con lắc. Sau khi
được tích điện, góc giữa hai sợi dây treo là 60o. Tính điện tích q của mỗi con lắc.
b) Treo cả ba con lắc vào cùng điểm O và tích điện Q như nhau cho mỗi con lắc. Tương tác giữa các
quả cầu khiến chúng lập thành một tam giác đều cạnh a = 10cm. Tính điện tích Q của mỗi con lắc. ■ [Lời giải] a,
Vì góc giữa 2 sợi dây treo là 60o nên khoảng cách giữa 2 quả cầu là r = l = 20(cm).
Tại vị trí cân bằng của con lắc ta có: F = tan30o P kq2 ⇒ = mg.tan30o r2 r mg.tan30o
⇒ Điện tích của mỗi con lắc là: | q |= r = 5.10−7(C) k
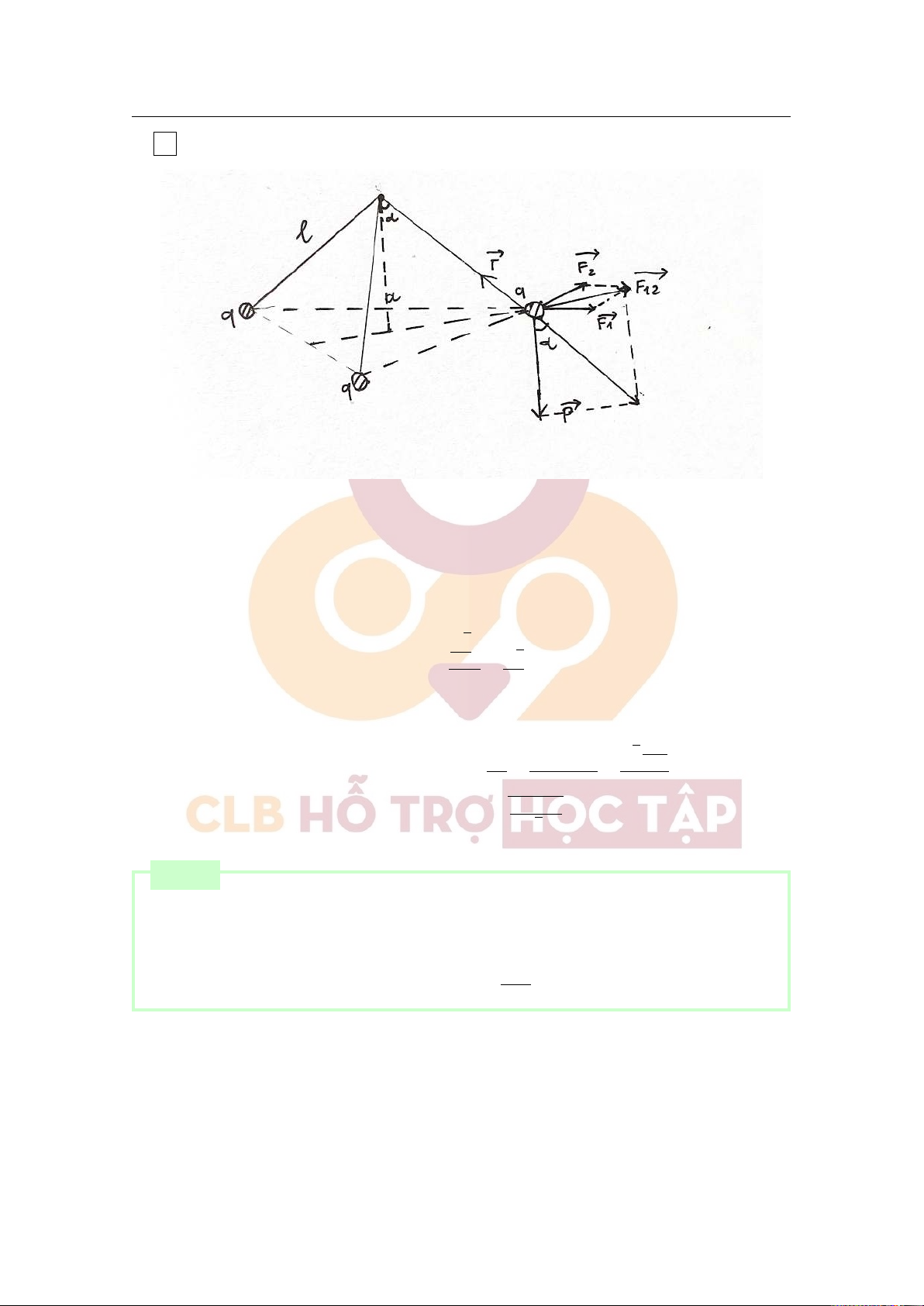
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 2.3 Bài tập 15 b,
Mỗi quả cầu của con lắc chịu tác dụng lực như nhau và gồm 4 lực: 2 lực tĩnh điện của 2 quả cầu còn lại, lực
căng dây ⃗T , trọng lực ⃗P.
Hợp lực của 2 lực tĩnh điện là: F12 = 2F1 cos 30o
Gọi α là góc giữa dây treo và phương thẳng đứng. Ta có: √3a √3 sin α = 3 = l 6
Tại vị trí quả cầu cân bằng ta có: √ kQ2 F 3 12 2F1 cos 30o tan α = = = a2 P mg mg r mg tan α
⇒ Điện tích mỗi con lắc: | Q | = a √ ≈ 1,39.10−7(C) 3k Bài tập 4
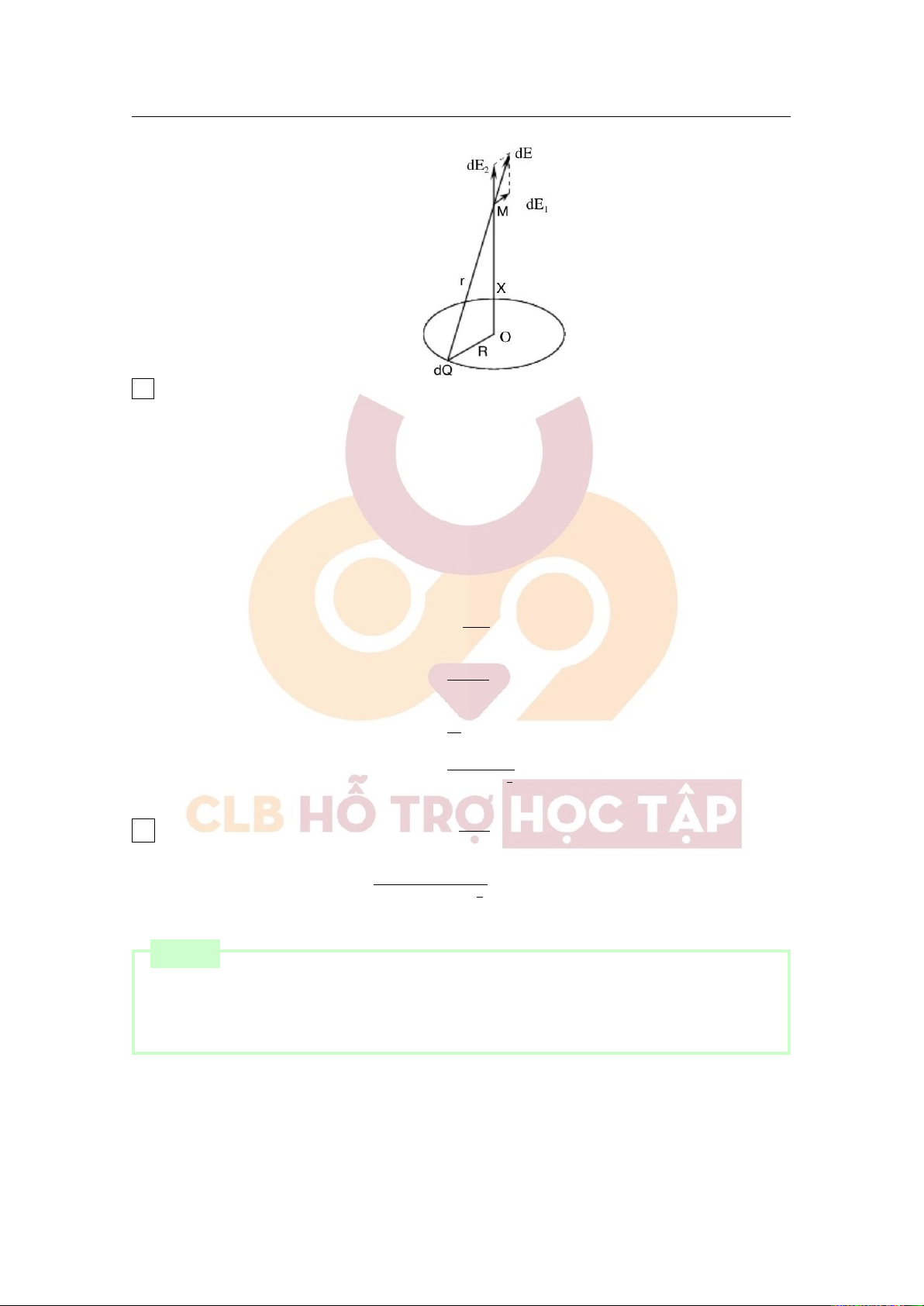
Một vòng dây dẫn tròn bán kính R, tích điện đều với điện tích dương Q trong chân không.
a) Xác định phương, chiều và độ lớn của cường độ điện trường tại điểm M nằm trên trục của vòng dây
và cách tâm vòng dây một khoảng x.
b) Áp dụng bằng số: R = 6 cm, x = 8 cm, Q = 2 nC, 1 k = = 9.109Nm2/C2. ■ 4πε0 [Lời giải]
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 2.3 Bài tập 16 a,
Chia vòng thành từng phần nhỏ tích điện dQ. Nó gây ra điện trường d⃗E tại M.
Chia d⃗E thành 2 thành phần d ⃗E và
. Do tính đối xứng của vòng dây nên tổng hợp các thành phần 1 d ⃗ E2 d ⃗ E1 tại M bằng 0.
⇒Vectơ cường độ điện trường tại M nằm trên trục vòng dây và có chiều hướng ra xa vòng dây.
Gọi α là góc giữa OM và d⃗E, khoảng cách từ dQ đến M là r. Ta có: Z E = dE2 vật Z = dE. cos α vật Z kdQ = . cos α r2 vật k cos α Z = dQ r2 vật kx = .Q r3 kQx = 3 (x2 + R2) 2
b, Áp dụng với R = 6 cm, x = 8 cm, Q = 2 nC, 1 k = = 9.109Nm2/C2. ta có: 4πε0 9.109.2.10−9.0, 08 E = = 1440(V /m) 3 (0, 082 + 0, 062) 2 Bài tập 5
Một đĩa tròn bán kính R, tích điện đều với mật độ điện mặt σ. Xác định phương, chiều và độ lớn của
vectơ cường độ điện trường tại điểm M nằm trên trục của đĩa và cách tâm đĩa một khoảng h. Suy ra
cường độ điện trường của mặt phẳng vô hạn mang điện đều. ■ [Lời giải]
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 2.3 Bài tập 17
Chia đĩa thành các hình vành khăn bán kính x, bề rộng dx. Mỗi phần vành khăn có: - Diện tích dS = 2πx.dx.
- Điện tích dq = σdS = σ.2πxdx. - Gây ra điện trường dq.h dE tại M với dE =
(Theo bài 4). Theo bài 4, vectơ cường độ điện 3 4πε0ε(x2 + h2) 2
trường tại M nằm trên trục của đĩa và hướng ra xa đĩa. Độ lớn cường độ điện trường tại M: R Z E = dE 0 R Z dq.h = 3 0 4πε0ε(x2 + h2) 2 R Z σ .2πxdx.h = 3 0 4πε0ε(x2 + h2) 2 R σ h Z x2 + h2 = . 4ε 3 0ε 0 (x2 + h2)2 σ h = 1 − √ 2ε0ε R2 + h2
Áp dụng cho mặt phẳng vô hạn tích điện đều (R → ∞): σ E = 2ε0ε Bài tập 6
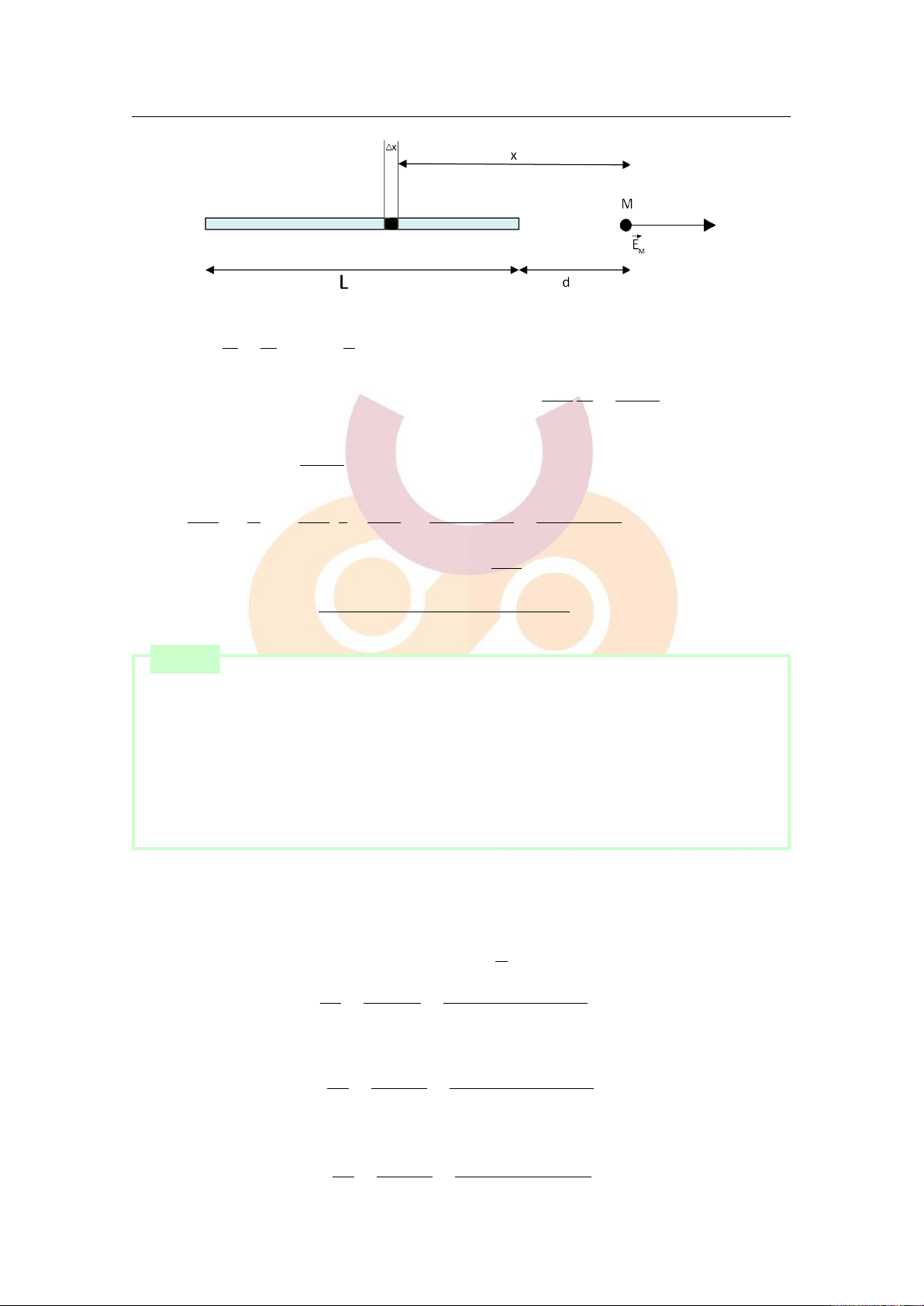
Một thanh chiều dài L tích điện đều với điện tích dương Q trong chân không
a) Xác định phương, chiều và độ lớn của vector cường độ điện trường tại điểm M trên đường thẳng
nằm dọc theo thanh, cách đầu gần hơn của thanh một khoảng d
b) Áp dụng bằng số: L = 8cm,d = 2cm,Q = 6nC,k = 1 = 9.109Nm2/C2 ■ 4πε0 [Lời giải]
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 2.3 Bài tập 18
1. Chia thanh dài L thành những đoạn dx rất nhỏ mang điện tích dq. Khi đó, dx dq Q = . Đặt λ =
: mật độ điện dài (C/m). L Q L → dq = λ dx.
Xét điện trường gây bởi phần tử 1 dq λ dx
dx tại điểm M, ta có: dE = = 4πε0 x2 4πε0x2
Suy ra điện trường do thanh L tác dụng lên điểm M: L+d Z Z λ dx E = dE = 4πε0x2 thanh L d L+d λ Z 1 λ 1 1 Lλ Q = dx = ( − ) = = 4πε0 x2 4πε0 d d + L 4πε0d(d + L) 4πε0d(d + L) d 2. Áp dụng hằng số: 1 L = 8cm, d = 2cm, Q = 6nC, k = = 9.109Nm2/C2 4πε0 6.10−9 E = = 27.103(V /m)
4π.8.86.10−12.2.10−2(8.10−2 + 2.10−2) Bài tập 7
Một mặt cầu kim loại có tâm O, bán kính b = 9cm, tích điện đều với điện tích Q1 = −4.10−9C. Bên
trong mặt cầu là một quả cầu rắn bán kính a = 5cm tích điện Q2 = 8.10−9C phân bổ đều theo thể tích
được đặt đồng tâm với mặt cầu kim loại. Điểm M cách tâm O một khoảng r. Dùng định lý O - G xác
định cường độ điện trường tại M trong các trường hợp sau: 1. r = r1 = 4cm 2. r = r2 = 6cm 3. r = r3 = 10cm ■ [Lời giải]
Với mỗi trường hợp r = r
ta chọn mặt Gau tương ứng- là mặt cầu tâm 1/r2/r3 O bán kính lần lượt là r = r
. Áp dụng định lý O-G ta có: 1/r2/r3
1. Trường hợp r = r1 < a: r1 3 D1.4πr21 = .Q2 a D Q 8.10−9.0, 04 ⇒ 1 2.r1 E1 = = = = 2, 3.104(V /m) ε0ε 4πε0ε.a3 4π.8, 86.10−12.1.0, 053
2. Trường hợp a < r = r2 < b: D2.4πr22 = Q2 D Q 8.10−9 ⇒ 2 2 E2 = = = = 2.104(V /m) ε0ε 4πε0ε.r2 4π.8, 86.10−12.1.0, 062 2
3. Trường hợp r = r3 > b: D3.4πr23 = Q1 + Q2 D Q 8.10−9 − 4.10−9 ⇒ 3 1 + Q2 E3 = = = = 3600(V /m) ε0ε 4πε0ε.r2 4π.8, 86.10−12.1.0, 12 3
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 2.3 Bài tập 19 Bài tập 8
Hai mặt cầu kim loại bán kính R1 = r và R2 = 10r được nối với nhau bằng một dây dẫn dài. Trước khi
nối dây, mặt cầu có bán kính lớn hơn điện tích dương Q, mặt cầu có bán kính nhỏ hơn chưa tích điện.
Tìm điện tích của mỗi quả cầu sau khi nối dây. ■ [Lời giải]
Khi nối dây, điện tích được truyền tới khi điện thế của 2 mặt cầu bằng nhau. Q1 Q2 V1 = V2 ⇐⇒ = 4πε0εR1 4πε0εR2 Q R r 1 ⇒ 1 = 1 = = Q2 R2 10r 10 Q Q1 = 11 Mặt khác, Q1 + Q2 = Q ⇒ 10Q Q2 = 11 Bài tập 9
Một mặt cầu kim loại cô lập tích điện đều điện tích Q trong chân không.
a) Dùng định lý O - G dẫn ra công thức xác định độ lớn của cường độ điện trường tại điểm A ở bên
ngoài mặt cầu, cách tâm mặt cầu một khoảng r . A
b) Xác định hiệu điện thế giữa hai điểm A và B lần lượt cách tâm mặt cầu các khoảng r và ( ). A rB rA < rB
Áp dụng bằng số (chỉ có ý b): 1 Q = 5nC, rB = 2rA = 10cm, k = = 9.109Nm2/C2. ■ 4πε0 [Lời giải] r O A A
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 2.3 Bài tập 20
1. Xét điểm A bên ngoài mặt cầu, cách O khoảng r . Dựng mặt Gauss bán kính bao quanh mặt cầu. A rA
Áp dụng định lý O-G, ta được: Q D.4πr2A = Q ⇒ D = 4πr2A D Q Q kQ ⇒ E = = = = (trong chân không ε = 1 ) ε0ε 4πε0εr2 4πε r2 A 0r2 A A
2. Xác định hiệu điện thế tại 2 điểm A,B cách mặt cầu rA,rB(rA < rB). Ta có: 1 Q −dV = Edr = . .dr 4πε0ε r2 VB rB rB Z Z Q Q Z dr kQ 1 1 ⇒ −dV = .dr = . ⇒ VA −VB = − 4πε0εr2 4πε0ε r2 ε rA rB VA rA rA
Áp dụng bằng số, ta được: 9.109.5.10−9 1 1 VAB = VA −VB = − = 450(V ) 1 0.05 0.1
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 3. Chương 2 - Vật dẫn 3.1 Tóm tắt lý thuyết
1. Đặc trưng của tụ điện Q U = V1 −V2 C = V1 −V2 Tụ điện phẳng σ d ε0εS U = Ed = C = ε0ε d Tụ điện cầu Q 1 1 4πε0εR1R2 U = V1 −V2 = − C = 4πε0ε R1 R2 R2 − R1 Tụ điện trụ λ R2 2πε0εl V1 −V2 = ln C = 2πε0ε R1 ln R2 R1
2. Năng lượng điện của một vật dẫn cô lập tích điện 1 1 Q2 W = QV = CV 2 = 2 2 2C 3. Năng lượng tụ điện 1 q2 1 W = qU = = CU2 2 2C 2
4. Mật độ năng lượng điện trường 1 1 we = ε0εE2 = DE 2 2
5. Năng lượng điện trường trong V 1 Z W = ε0εE2dV 2 V
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 3.2 Câu hỏi lý thuyết 22 3.2 Câu hỏi lý thuyết Câu 9 Trình bày:
1. Điều kiện cân bằng tĩnh điện của một vật dẫn mang điện
2. Các tính chất của vật dẫn tích điện cân bằng
3. Nêu ứng dụng về tính chất của vật dẫn tích điện cân bằng ■ [Lời giải]
+ Điều kiện cân bằng tĩnh điện:
- Vector cường độ điện trường tại mọi điểm bên trong vật dẫn bằng không: ⃗ Etr = 0
- Thành phần tiếp tuyến của vector cường độ điện trường tại mọi điểm trên mặt vật dẫn phải bằng không ⃗E . t = 0, ⃗ E = ⃗ En + Các tính chất:
- Tính chất 1: Vật dẫn là vật đẳng thế.
Xét 2 điểm M, N bất kỳ nằm trên vật dẫn. Hiệu điện thế giữa hai điểm đó là: N N Z Z V ⃗ M − VN = Ed⃗s = Esds M M (E là hình chiếu của ⃗ s
E trên phương chuyển dời) + Bên trong vật dẫn ⃗
Etr = 0 → V tại mọi điểm trong đều bằng nhau
+ Trên bề mặt vật dẫn ⃗Et = 0 → V tại mọi điểm trên mặt vật dẫn đều bằng nhau
+ Do V có tính chất liên tục nên điện thế tại mọi điểm của vật dẫn bằng nhau
- Tính chất 2: Khi vật dẫn ở trạng thái cân bằng tĩnh điện, điện tích chỉ phân bố trên bề mặt vật dẫn.
Bên trong vật dẫn, điện tích bằng 0.
Giả sử truyền cho vật dẫn một điện tích q nào đó. Tưởng tượng lấy một mặt kín (S) bất kỳ trong vật dẫn. Theo định lý O-G: I ∑q ⃗ i = Dd⃗S S
Bên trong vật dẫn: ⃗D = ε0ε⃗E = 0 → ∑qi = 0
- Tính chất 3: Sự phân bố của điện tích trên mặt vật dẫn phụ thuộc vào hình dạng của mặt đó. Điện
tích tập trung ở những chỗ có mũi nhọn và ngược lại, ở những chỗ lõm, điện tích rất ít, hầu như bằng 0. + Ứng dụng:
– Máy phát tĩnh điện VandaGraf
– Vật dẫn rỗng có tác dụng như 1 màn bảo vệ, gọi là màn điện
– Hiệu ứng mũi nhọn, gió điện: Giải phóng điện tích trên máy bay, phóng điện bảo vệ máy điện, cột thu lôi. Câu 10
Định nghĩa hiện tưởng điện hưởng. Thế nào là hai phần tử tương ứng? Phát biểu định lý các phần tử
tương ứng. Thế nào là hiện tượng điện hưởng một phần và điện hưởng toàn phần. ■ [Lời giải]
+ Định nghĩa: Hiện tưởng điện hưởng là hiện tượng khi đặt vật dẫn trung hoà trong điện trường ngoài ⃗
E thì hai phía của vật dẫn xuất hiện các điện tích trái dấu gọi là các điện tích cảm ứng. 0
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 3.2 Câu hỏi lý thuyết 23
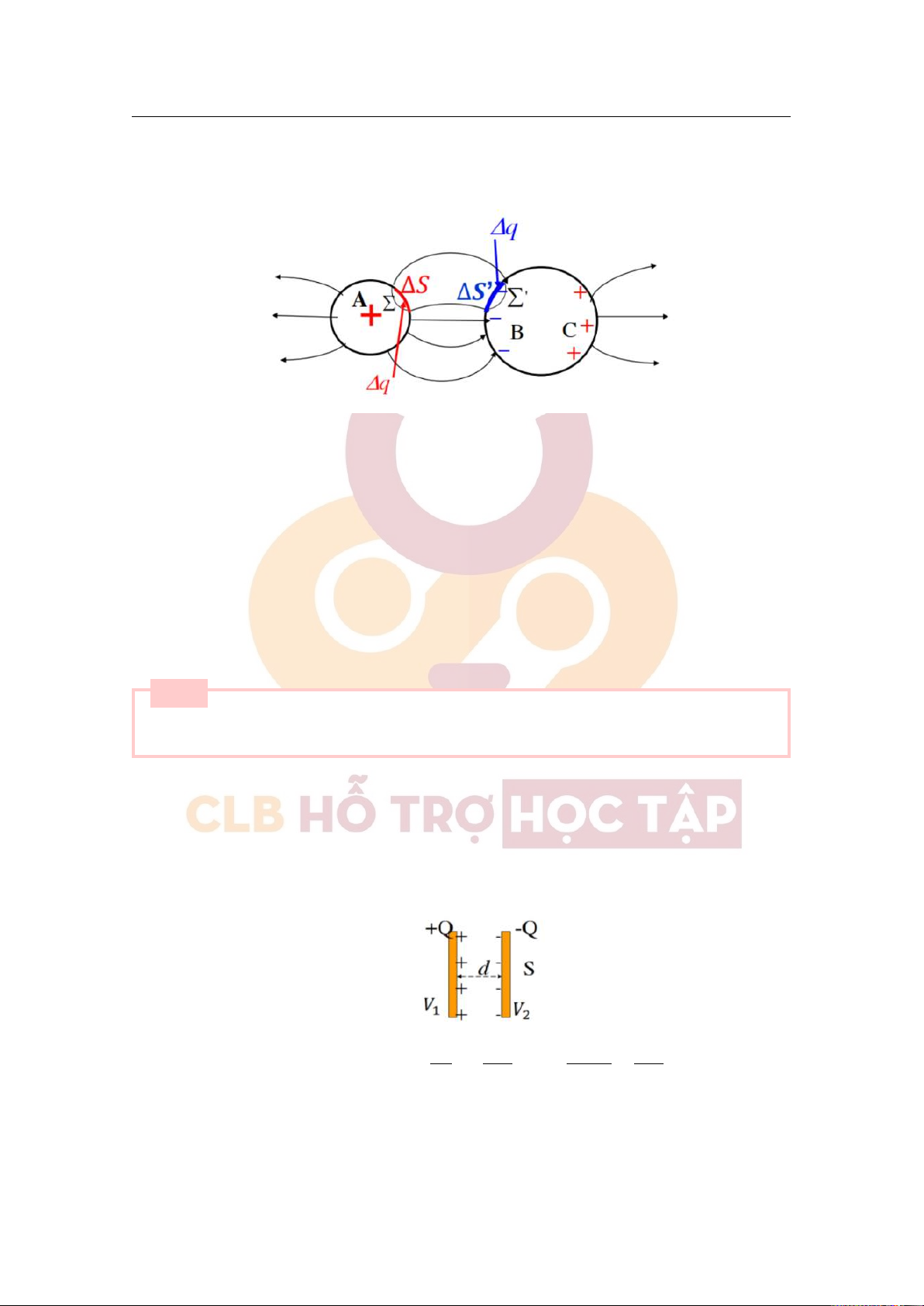
+ Xét một vật dẫn (BC) trung hoà đặt trong điện trường ngoài của một quả cầu kim loại (A) mang điện tích dương.
Xét tập hợp đường cảm ứng điện tựa trên chu vi của một phần tử diện tích δS trên vật mang điện A.
Giả sử tập hợp đường cảm ứng điện này tới tận cùng trên chu vi của phần tử diện tích δS′ trên vật dẫn
BC. Các phần tử diện tích ∆S và ∆S′ gọi là các phần tử tương ứng
+ Định lý về các phần tử tương ứng: Điện tích cảm ứng trên các phần tử tương ứng có độ lớn bằng nhau và trái dấu.
+ Điện hưởng một phần: Chỉ một phần số đường cảm ứng điện của vật mang điện gặp vật bị điện hưởng,
do đó độ lớn của điện tích cảm ứng nhỏ hơn của điện tích trên một vật mang điện (|q′| < |q|).
+ Điện hưởng toàn phần: Khi một vật dẫn (BC) bao bọc hoàn toàn vật mang điện A, toàn bộ đường cảm
ứng điện xuất phát từ A đến tận cùng trên vật dẫn (BC), ta có hiện tưởng điện hưởng toàn phần.
Áp dụng định lý về các phần tử tương ứng → độ lớn của điện tích cảm ứng bằng độ lớn của điện tích
trên vật mang điện: |q′| = |q|. Câu 11
Định nghĩa tụ điện. Thiết lập biểu thức điện dung của tụ điện phẳng và tụ điện cầu. ■ [Lời giải]
• Định nghĩa: Tụ điện là hệ 2 vật dẫn A và B cách nhau bởi 1 lớp điện môi ở trạng thái điện hưởng toàn phần.
• Thiết lập biểu thức điện dung: - Tụ phẳng: σ d Qd Q ε0εS U = V1 −V2 = Ed = d = → C = = ε0ε ε0εS V1 −V2 d - Tụ cầu:
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 3.2 Câu hỏi lý thuyết 24 Q 1 1 Q(R2 − R1) Q 4πε0εR1R2 U = V1 −V2 = − = → C = = 4πε0ε R1 R2 4πε0εR1R2 V1 −V2 R2 − R1 Nếu 4πε0εR2 ε0εS R 1
2 − R1 = d ≪ R1, có thể coi R2 ≈ R1 → C = = d d Câu 12
Trình bày năng lượng tương tác của hệ điện tích điểm, năng lượng của vật dẫn mang điện và năng lượng tụ điện ■ [Lời giải]
+ Năng lượng tương tác của một hệ điện tích điểm:
- Với hệ 2 điện tích điểm: Khi 1 q1q2
q đặt trong điện trường của , thế năng của là: 2 q1 q2 Wt = 4πε0ε r12 W cũng là thế năng của trong điện trường
là thế năng tương tác hay năng lượng tương t q1 q2. Ta nói Wt
tác điện của hệ 2 điện tích q và , ký hiệu là: 1 q2 1 q1q2 W12 = W21 = 4πε0ε r12 1 q 2 1 q1 W12 = W21 = q1 + q2 2 4πε0εr12 2 4πε0εr12 q2 = V
: Điện thế do q gây ra tại vị trí q 1 2 1 4π ε Lại có: 0ε r12 q 1 = V
: Điện thế do q gây ra tại vị trí q 2 1 2 4πε0εr12 Vậy: 1 W12 = W21 = (q1V1 + q2V2) 2
- Với hệ n điện tích điểm: 1 1 n W = q 1V1 + q2V2 + ... + qnVn = ∑ qiVi 2 2 i=1
+ Năng lượng của vật dẫn mang điện:
Chia vật dẫn thành những điện tích điểm dq Ta có: 1 Z 1 Z 1 1 1 q2 W = V dq = V dq = dV → W = qV = CV 2 = 2 2 2 2 2 2C
+ Năng lượng của tụ điện:
Hệ n vật dẫn có điện tích: q
và điện thế tương ứng: 1, q2, ..., qn V1,V2, ...,Vn n
Năng lượng của hệ vật dẫn là: 1 W = ∑ qiVi 2 i=1 Tụ điện: 1 1 1 W =
(q1V1 + q2V2). Do q1 = −q2 = q → W = q(V1 −V2) = qU 2 2 2 1 q2 1 ⇒ W = qU = = CU2 2 2C 2
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 3.3 Bài tập 25 3.3 Bài tập Bài tập 10
Một quả cầu cô lập tâm O bán kính a, tích điện dương Q phân bố đều theo thể tích.
a) Dùng định lý O-G dẫn ra công thức xác định độ lớn của cường độ điện tường tại điểm A ở bên ngoài
quả cầu, cách tâm O một khoảng r và tại điểm B ở bên trong quả cầu, cách tâm O một khoảng A rB. b) Áp dụng hằng số: 1
Q = 8nC, a = 2cm, rA = 3cm, rB = 1cm, k = = 9.109Nm2/C2. ■ 4πε0 [Lời giải]
a) Chọn mặt Gauss tâm O bán kính r : A I I Q = DdS = D dS = D.4πr2A 1 Q 1 Q kQ ⇒ D = . ⇒ EA = . = 4π r2 4πε r2 r2 A 0ε A A
Tại điểm B bên trong mặt cấu ⇒ Chọn mặt Gauss tâm O bán kính r , ta có: B I I q = Dds = D ds = D.4πr2B r 3 1 Q ⇒ B .Q = D.4πr2 . .rB a B ⇒ D = 4π a3 1 Q kQ ⇒ EB = . .rB = .rB 4πε0ε a3 a3 b) Thay số ta được: 9.109.8.10−9 EA = = 8.104(V /m) 0, 032 9.109.8.10−9 EB = .0.01 = 9.104(V /m) 0, 023 Bài tập 11
Một quả cầu kim loại bán kính R, tích điện Q.
a) Tính năng lượng điện trường của quả cầu. b) Áp dụng hằng số: 1 Q = 5nC, R = 10cm, k = = 9.109Nm2/C2. ■ 4πε0 [Lời giải]
1. Ta có: Điện trường gây bởi quả cầu: 1 Q E = . 4πε0ε r2
⇒ Mật độ năng lượng điện trường: 1 ω = ε0εE2 2
⇒ Năng lượng điện trường: ∞ Z Z Q2 dr 1 Q2 kQ2 W = ωdV = . = . = 8πε0ε r2 8πε0ε R 2R R 2. Thay số ta được: 9.109.(5.10−9)2 W = = 11, 25.10−7(J) 2.0, 1
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 4. Chương 3 - Điện môi 4.1 Tóm tắt lý thuyết
1. Vector phân cực điện môi:
⃗P = ε0χ⃗E = ε0(ε − 1)⃗E
2. Vector điện cảm trong điện môi: ⃗D = ε ⃗ 0E + ⃗ P
3. Mật độ điện mặt liên kết: σ ′ = P lk n = ε0(ε − 1)En
4. Mật độ năng lượng điện trường: 1 1 we = ε0εE2 = DE 2 2
5. Năng lượng điện trường trong V: 1 Z W = ε0εE2dV 2 V 4.2 Câu hỏi lý thuyết Câu 13
Thế nào là hiện tượng phân cực điện môi? Định nghĩa vector phân cực điện môi. Tìm mối liên hệ giữa
vector phân cực điện môi và mật độ điện tích liên kết trên bề mặt điện môi. ■ [Lời giải]
1. + Định nghĩa hiện tượng phân cực điện môi: là hiện tượng trên thanh điện môi đặt trong điện trường có xuất hiện điện tích.
+ Định nghĩa vector phân cực điện môi: là một đại lượng đo bằng tổng các mômen lưỡng cực điện của
các phân tử có trong một đơn vị thể tích của khối điện môi.
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 4.2 Câu hỏi lý thuyết 27 n ∑ ⃗pei ⃗ P i=1 e = ∆V
+ Liên hệ giữa vector phân cực điện môi và mật độ điện tích liên kết trên bề mặt điện môi
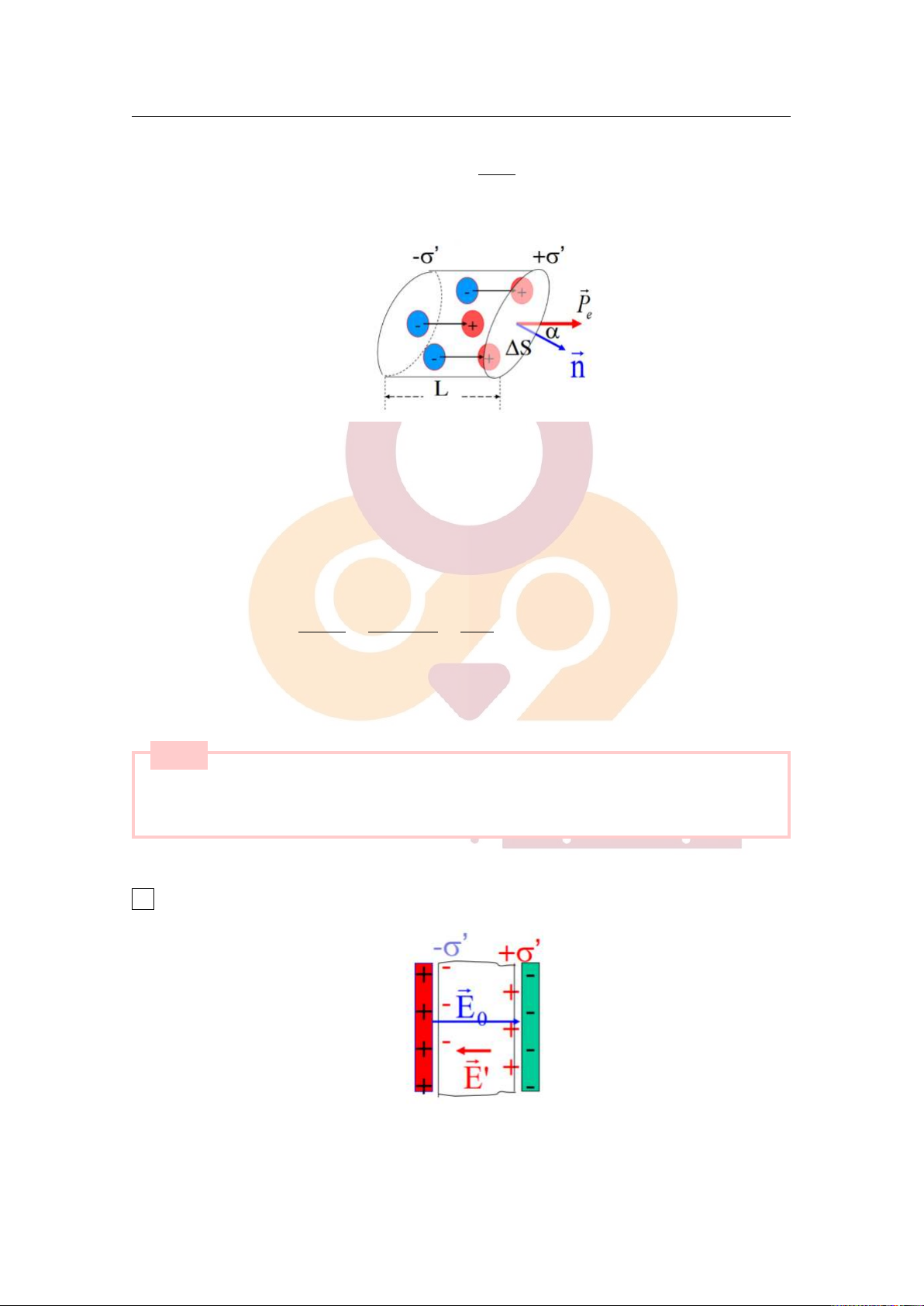
Tách ra trong điện môi một khối trụ xiên có:
– Đường sinh // ⃗E (tức là // ⃗P ), có chiều dài L. e
– Hai đáy //, mỗi đáy có diện tích ∆S.
– Mật độ điện mặt của mỗi đáy là +σ′,−σ′.
– Vector pháp tuyến ngoài của đáy mang điện tích dương là ⃗n.
– Có thể coi toàn bộ khối trụ như một lưỡng cực điện tạo ra bởi các điện tích liên kết −σ′∆S và
+σ ′∆S trên hai đáy cách nhau một đoạn L. Mômen điện của nó có độ lớn: σ ′.∆S.L n ∑ ⃗ p ei i=1 σ ′.∆S.L σ ′ ⇒ Pe = |⃗Pe| = = = ∆V ∆S.L. cos α cos α ⇒ σ′ = Pe cosα = Pen
+ Kết luận: Mật độ điện mặt σ′ của các điện tích liên kết xuất hiện trên mặt giới hạn của khối điện môi
có trị số bằng hình chiếu của vectơ phân cực diện môi trên pháp tuyến của mặt giới hạn đó. Câu 14
Xác định công thức tính cường độ điện trường tổng hợp trong chất điện môi đồng chất đẳng hướng.
Thế nào là hiệu ứng áp điện thuận và nghịch? ■ [Lời giải] 2.
+ Vector cường độ điện trường tổng hợp trong chất điện môi đồng chất đẳng hướng:
– Giả sử có một điện trường đều ⃗E giữa 2 mặt phẳng mang điện đều bằng nhau trái dấu. 0
– Chất điện môi lấp đầy khoảng không gian giữa hai mặt phẳng.
– Khối điện môi bị phân cực.
– Trên mặt điện môi xuất hiện các điện tích liên kết +σ′,−σ′.
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 4.3 Bài tập 28
– Các điện tích liên kết này gây ra điện trường phụ ⃗E′.
Khi đó, ta có điện trường tổng hợp trong điện môi là: ⃗E = ⃗E0 + ⃗E′
Vì ⃗E song song và ngược chiều với ⃗ 0
E′, nên ta có E = E0 − E′ σ ′ Ta có E′ = ε0
σ ′ = Pen = ε0χeEn = ε0χeE σ ′ ⇒ E′ = = χ ε eE 0
⇒ E = E0 − E′ = E0 − χeE E E ⇒ 0 0 E = =
, với ε = 1 + χ gọi là hằng số điện môi của môi trường e 1 + χe ε
– Nhận xét: Cường độ điện trường trong điện môi giảm đi ε lần so với cường độ điện trường trong chân không. + Hiệu ứng áp điện:
– Hiệu ứng áp điện thuận: Khi nén hoặc kéo giãn một số tinh thể điện môi, trên mặt giới hạn của
tinh thể xuất hiện điện tích trái dấu. Hiệu ứng áp điện thuận được ứng dụng rộng rãi trong kỹ
thuật để biến đổi những dao động cơ (âm) thành những dao động điện,...
– Hiệu ứng áp điện nghịch: Nếu đặt lên hai mặt của tinh thể một hiệu điện thế, nó sẽ bị giãn hoặc
nén. Hiệu ứng này được ứng dụng để chế tạo các nguồn phát siêu âm,... 4.3 Bài tập Bài tập 12
Một tụ điện phẳng có chứa điện môi (ε = 5), khoảng cách giữa 2 bản là d = 0,4 cm, hiệu điện thế giữa 2 bản là U = 1000V . Tính:
a) Cường độ điện trường trong chất điện môi.
b) Mật độ điện mặt trên hai bản tụ điện.
c) Mật độ điện mặt trên chất điện môi. ■ [Lời giải]
1. Cường độ điện trường trong chất điện môi là: U 1000 E = = = 2, 5.105(V /m) d 0, 4.10−2 2. Ta có công thức σ E =
, vì vậy mật độ điện mặt trên 2 bản tụ điện là: ε0ε
σ = ε0εE = 5.8, 86.10−12.2, 5.105 = 110, 75.10−7(C/m2)
3. Mật độ điện mặt trên chất điện môi là:
σ ′ = (ε − 1)ε0E = (5 − 1).8,86.10−12.2,5.105 = 8,86.10−6(C/m2) Bài tập 13
Giữa 2 bản của 1 tụ điện phẳng, có một bản thủy tinh (ε = 6). Diện tích mỗi bản tụ điện bằng 150 cm2.
Các bản tụ điện hút nhau với một lực bằng 6.10−3N. Tính mật độ điện tích liên kết trên mặt thủy tinh. ■ [Lời giải]
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 4.3 Bài tập 29
Gọi lực tương tác giữa 2 bản tụ điện là F. Ta thấy công dịch chuyển 2 bản tụ điện sát lại nhau có trị số bằng
năng lượng của tụ điện, nên ta có: Q2 σ 2S2 d Fd = = . 2C 2 εε0S r 2εε ⇒ σ = 0F S ( Mặt khác, ta có σ = εε0E σ ′ = (ε − 1)ε0E ε − 1 ε − 1 r 2εε ⇒ σ′ = σ = . 0F ε ε S s 5 2.6.8, 86.10−12.6.10−3 ⇒ σ′ = . ≈ 5,43.10−6 (C/m2) 6 0, 015
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 5. Chương 4 - Từ trường 5.1 Tóm tắt lý thuyết
1. Từ trường của các dòng điện
a. Từ trường của một dòng điện thẳng µ0µI I B = (cos θ1 − cosθ2), H = (cos θ1 − cosθ2) 4πR 4πR
Trường hợp dây AB dài vô hạn: µ0µI I B∞ = , H∞ = 2πR 2πR
b. Từ trường của dòng điện tròn ⃗ ⃗ µ0µ⃗Pm Pm B = , ⃗H = 2π(R2 + h2)3/2 2π(R2 + h2)3/2 Trường hợp tại tâm O: ⃗ µ0µI⃗S I⃗S B = , ⃗H = 2πR3 2πR3
2. Từ thông qua diện tích S Z Z Φ ⃗ m = Bd⃗S = BdS cos α S S
3. Định lý Ampe về dòng điện toàn phần I n Φ ⃗ m = Hd⃗l = ∑ Ii i=1 C 4. Lực Ampe d⃗ F = Id⃗l × ⃗B
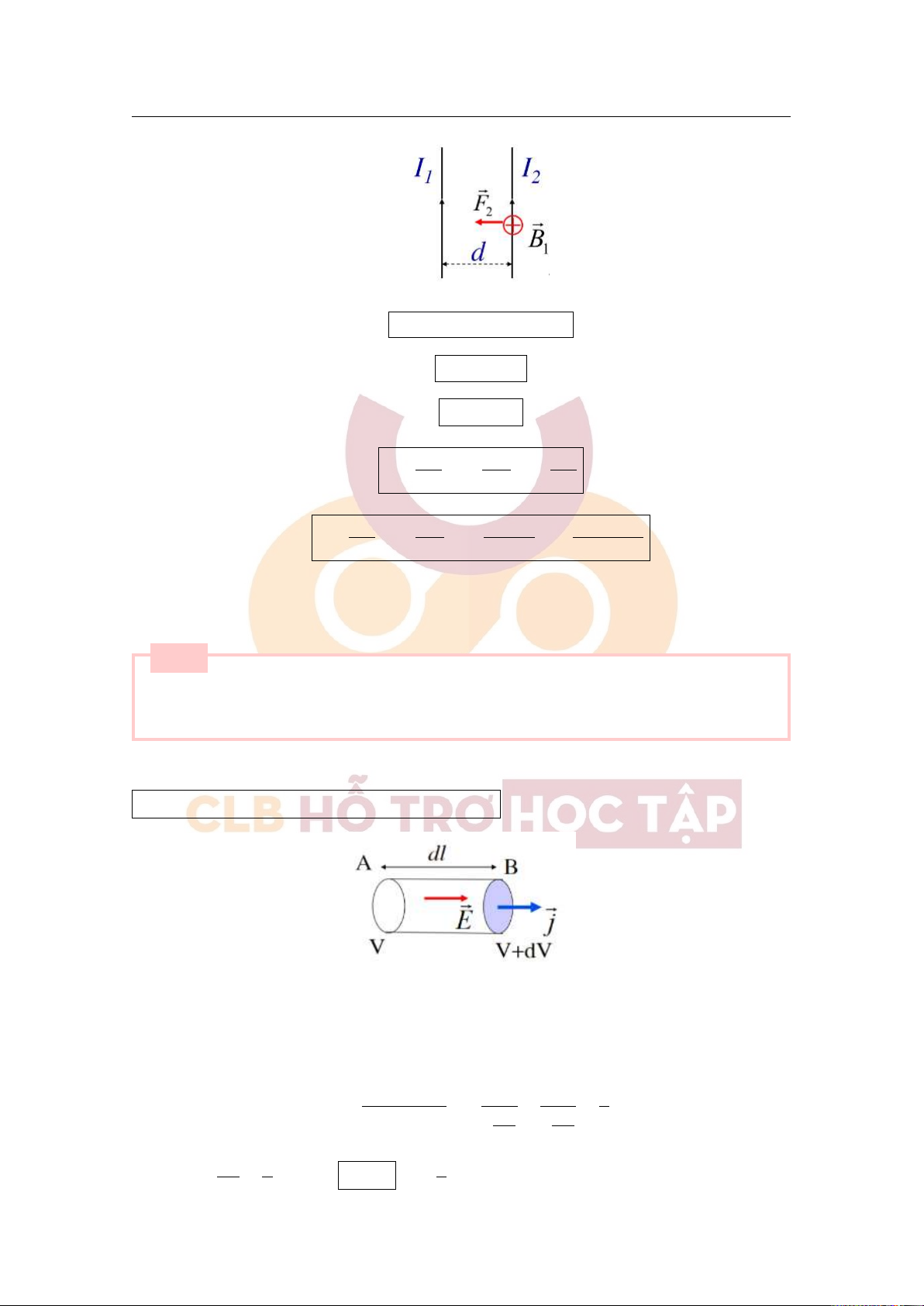
Tác dụng tương hỗ giữa 2 dòng điện thẳng dài vô hạn: µ0µI1I2l F2 = 2πd
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 5.2 Câu hỏi lý thuyết 31
5. Công của lực từ A = I△Φm = I(Φm − Φ ) 2 m1
Năng lượng của khung dây trong từ trường: Wm = −⃗Pm.⃗B 6. Lực Lorent ⃗FL = q⃗v ×⃗B
a.⃗v⊥⃗B : quỹ đạo tròn |q|B 2πm vm ω = , T = , R = m |q|B |q|B
b.⃗v theo hướng hợp với ⃗B một góc α : quỹ đạo là đường đinh ốc có bước h |q|B 2πm vm sin α 2πmv cos α ω = , T = , R = , h = m |q|B |q|B |q|B 5.2 Câu hỏi lý thuyết Câu 15
a. Thiết lập biểu thức của định luật Ohm dạng vi phân;
b. Trình bày khái niệm nguồn điện và thiết lập biểu thức suất điện động của nguồn điện. ■ [Lời giải]
a. Thiết lập biểu thức của định luật Ohm dạng vi phân
Xét một dòng điện chạy trong dây dẫn.
+ Chọn khối trụ trong dây dẫn chiều dài dl.
+ Hai đáy trụ là dS vuông góc với ⃗ n E.
+ Gọi V và dV là điện thế tại 2 đáy trụ: V − (V + dV ) dV Edl E dl = = − = = dSn R dl dl ρ ρ ρ dSn dSn dI E 1 ⇒ j = =
= σ E ⇒ ⃗j = σ⃗E (σ = : điện dẫn suất) dSn ρ ρ
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 5.2 Câu hỏi lý thuyết 32
b. Khái niệm nguồn điện và thiết lập biểu thức suất điện động của nguồn điện.
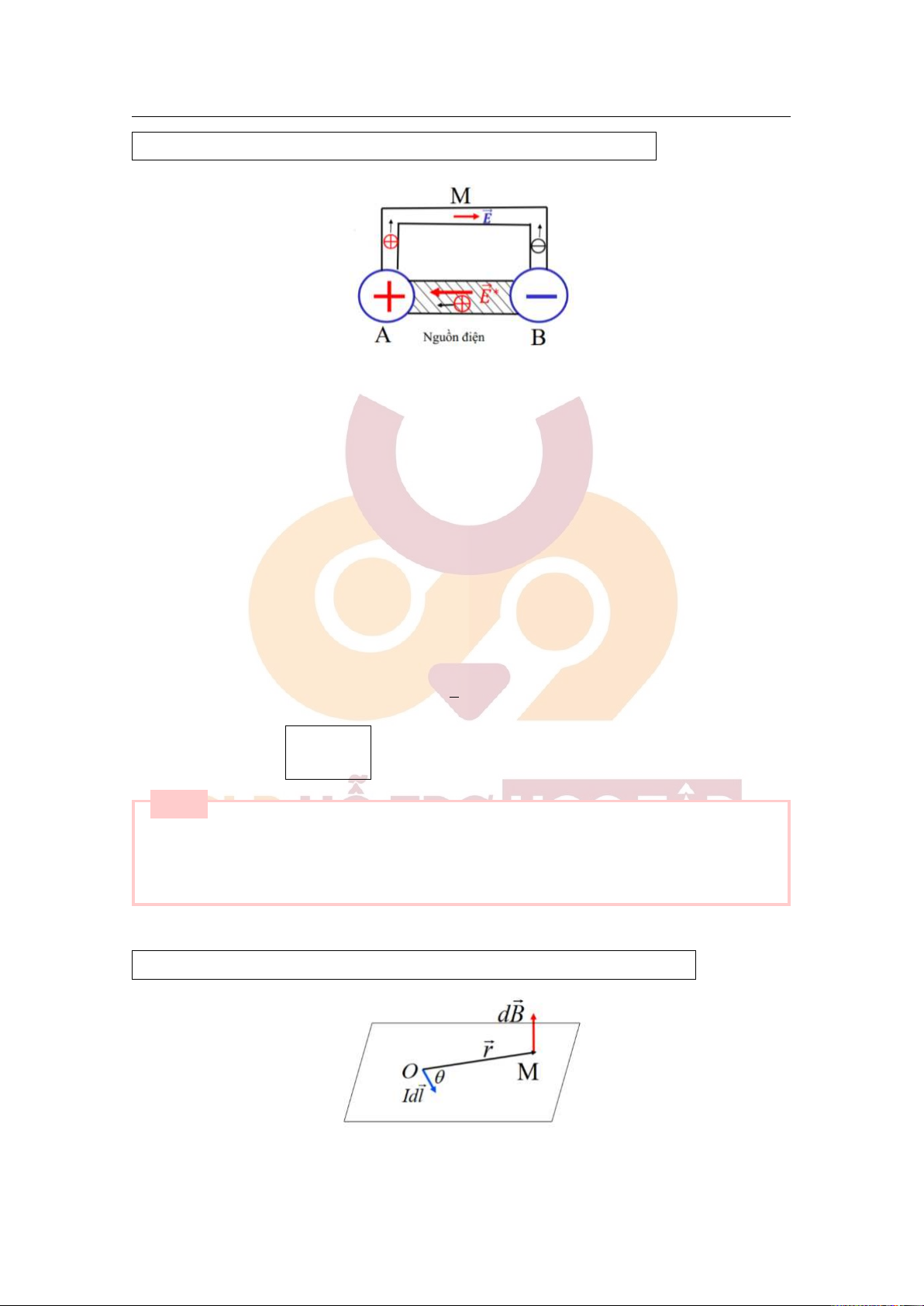
+ Xét hai vật dẫn A,B. Vật A mang điện dương, vật B mang điện âm → V . A > VB
Nối A với B bằng vật dẫn M:
– Các hạt điện dương chuyển động từ A → B.
– Các hạt điện âm chuyển động từ B → A.
Trong vật dẫn M xuất hiện dòng điện. – V giảm, tăng. Đến khi dòng điện ngừng. A VB VA = VB
+ Muốn duy trì dòng điện:
– Phải đưa các hạt điện dương từ B → A và các hạt điện âm từ A → B. Vì bị điện trường ngăn cản
nên các hạt điện không thể tự dịch chuyển;
– Phải tác dụng lên hạt điện dương một lực có khả năng đưa các hạt điện dương chạy ngược chiều
và hạt điện âm chạy cùng chiều điện trường tĩnh;
– Lực này về bản chất không phải là lực tĩnh điện nên được gọi là lực phi tĩnh điện hay lực lạ.
– Trường tạo ra lực lạ gọi là trường lạ. Nguồn tạo ra trường lạ gọi là nguồn điện.
+ Biểu thức suất điện động của nguồn điện:
Gọi ⃗E là vecto cường độ điện trường tĩnh và ⃗
E∗ là vecto cường độ điện trường lạ tại cùng một điểm trong mạch.
Công của lực điện trường tổng hợp trong dịch chuyển q một vòng quanh mạch kín: I A I I I A = q(⃗ E + ⃗ E∗)d⃗s ⇒ ξ = = (⃗E + ⃗ E∗)d⃗s = ⃗Ed⃗s + ⃗ E∗d⃗s q C C C C I I Mà
⃗Ed⃗s = 0 ⇒ ξ = ⃗E∗d⃗s C C Câu 16
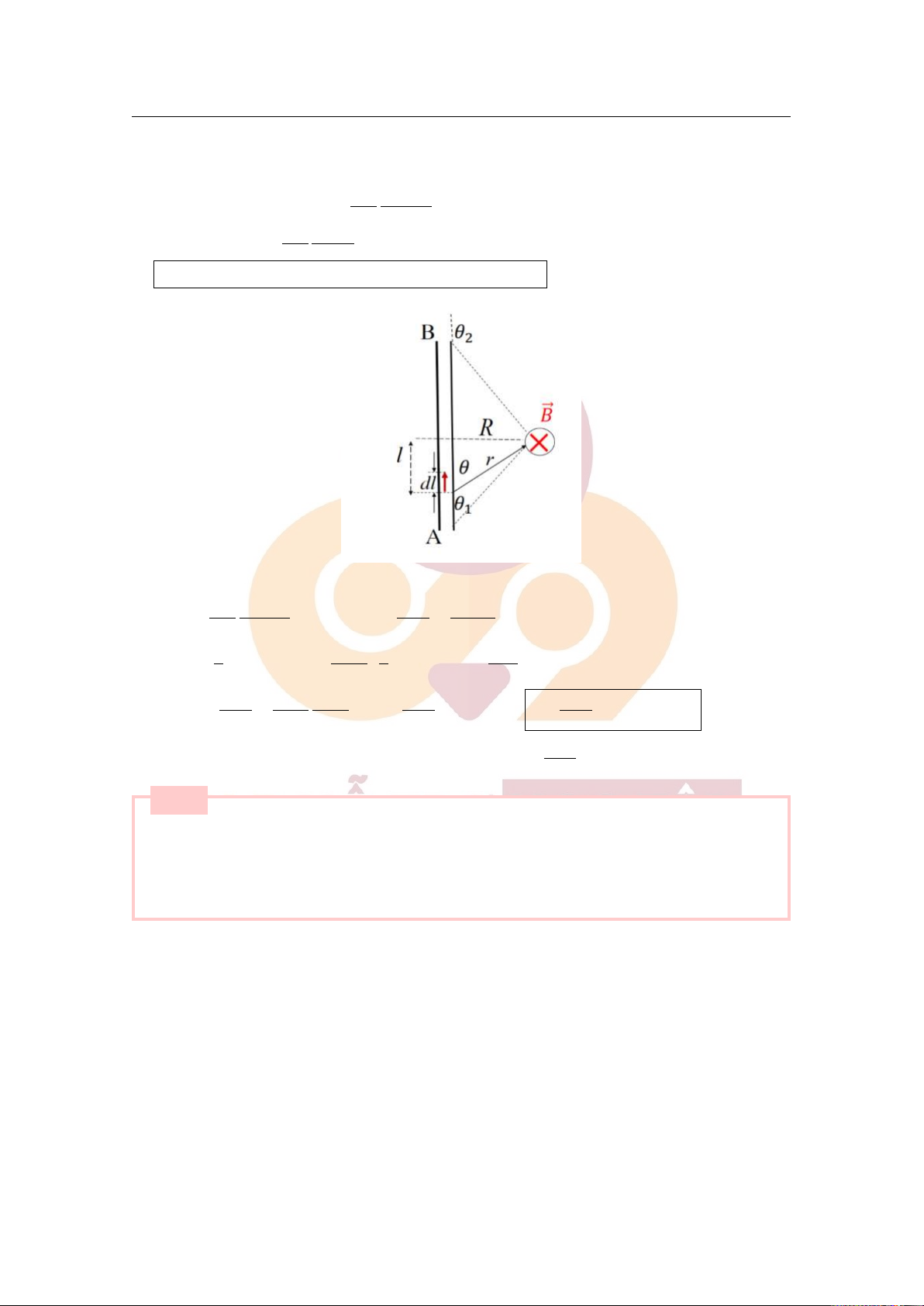
a. Phát biểu và viết biểu thức định luật Biot-Savart-Laplace, minh họa bằng hình vẽ;
b. Áp dụng định luật Biot-Savart-Laplace tìm cảm ứng từ gây bởi một đoạn dòng điện thẳng tại điểm M,
cách dòng điện một khoảng r, từ đó suy ra biểu thức cho trường hợp dòng điện thẳng dài vô hạn. ■ [Lời giải]
a. Phát biểu và viết biểu thức định luật Biot-Savart-Laplace, minh họa bằng hình vẽ.
+ Phát biểu: Vecto cảm ứng từ d⃗B do một phần tử dòng điện Id⃗l gây ra tại điểm M cách phần tử một
khoảng⃗r là một vecto có:
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 5.2 Câu hỏi lý thuyết 33 – Gốc tại điểm M.
– Phương vuông góc với mặt phẳng chứa Id⃗l và M.
– Chiều sao cho 3 vecto d⃗l,⃗r,d⃗B theo thứ tự đó tạo thành tam diện thuận. – Có độ lớn bằng: µ0µ Idl sin θ dB = . 4π r2 + Biểu thức: µ0µ Id⃗l ×⃗r d⃗ B = 4π r3
b. Áp dụng định luật Biot-Savart-Laplace tìm cảm ứng từ.
+ Xét phần tử dòng điện Idl gây ra tại điểm M vecto cảm ứng từ có độ lớn: µ Z Z 0 µ Idl sin θ µ0µI dl sin θ dB = → B = dB = 4π r2 4π r2 AB AB Ta có: l Rdθ R = cot θ → dl = ; R = sinθ → r = R sin2 θ r sin θ θ2 θ2 µ Z Rdθ sin2 θ µ Z µ ⇒ 0 µ I 0 µ I 0 µ I B = sin θ = sin θ dθ ⇒ B = (cos θ1 − cosθ2) 4π sin2 θ R2 4π 4π θ1 θ1
Trường hợp dây AB dài vô hạn: µ θ 0 µ I .
1 = 0, θ2 = π , ta có: B∞ = 2πR Câu 17
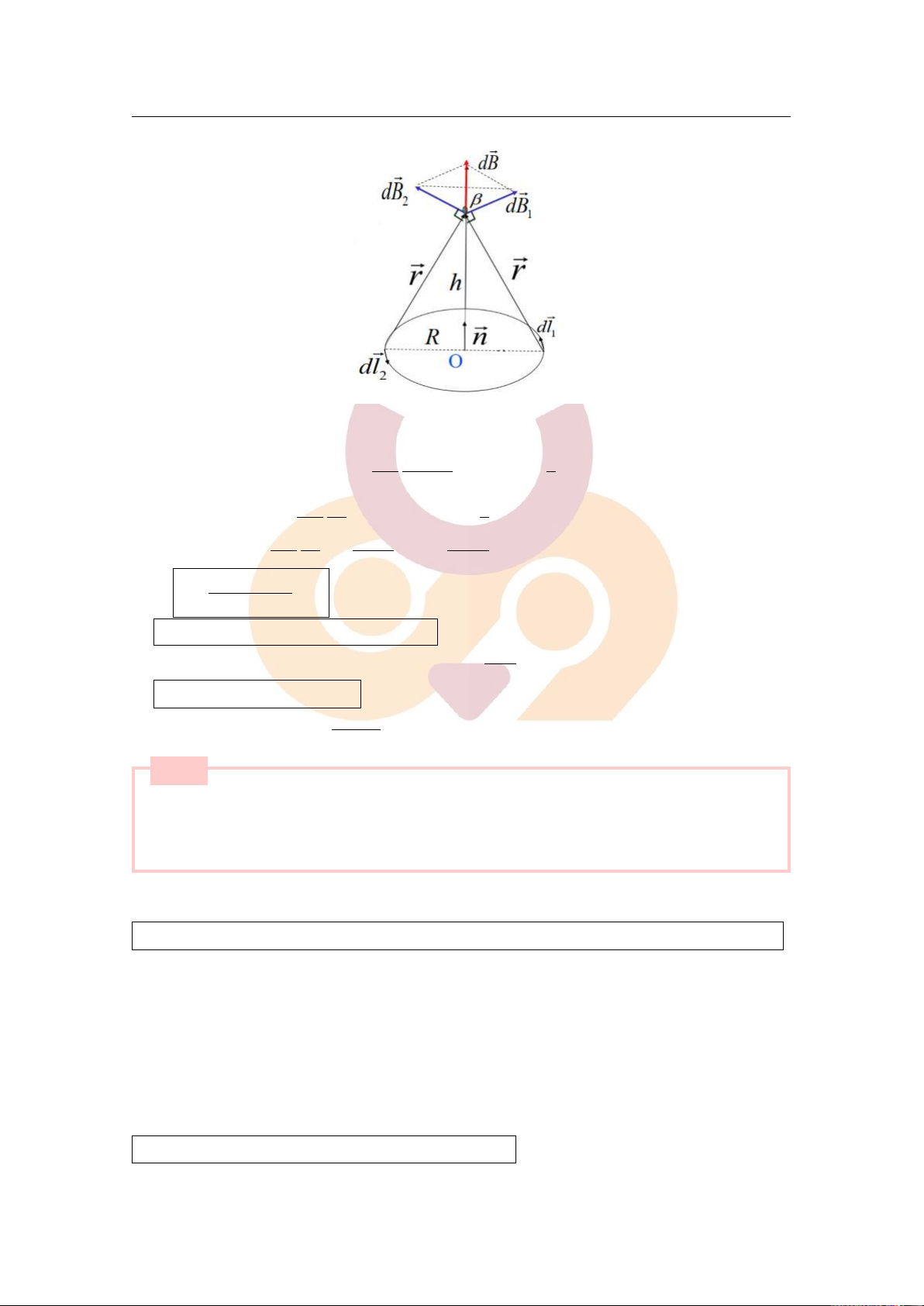
Xác định vecto cảm ứng từ gây bởi dòng điện tròn có cường độ I, bán kính R, tại điểm M nằm trên trục
của dòng điện, cách tâm O của dòng điện một khoảng h. Từ kết quả trên xét hai trường hợp giới hạn:
+ M trùng với tâm O của dòng điện (h = 0);
+ M ở rất xa dòng điện (h ≫ R). ■ [Lời giải]
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 5.2 Câu hỏi lý thuyết 34 Xét phần tử Idl và
cùng độ lớn, đối cứng qua tâm O, gây ra tại điểm M cảm ứng từ có độ lớn: 1 Idl2 µ0µ Idl sin θ π dB = (sin θ = sin = 1) 4π r2 2 µ Idl R → 0 µ dB = 2dB1 cos β = cos β Mà cosβ = 2π r2 r Z Z µ Idl µ Z µ → 0 µ 0 µ IR 0 µ IR B = dB = R = dl = πR 2π r3 2πr3 2πr3 µ ⇒ 0 µ IR2 B = (1) 2(R2 + h2)3/2
M trùng với tâm O của dòng điện (h = 0). + Với µ0µI
h = 0, áp dụng vào công thức (1), ta có: B . O = 2R
M ở rất xa dòng điện (h ≫ R). + Với µ ( 0 µ IR2 h ≫ R), ta có: B∞ = 2h3 Câu 18
Phát biểu, viết biểu thức và nêu ý nghĩa của định lý Ampe về lưu số của vecto cường độ từ trường. Áp
dụng định lý Ampe để xác định biểu thức cảm ứng từ trong lòng cuộn dây điện hình xuyến và trong
lòng ống dây điện thẳng dài vô hạn mang dòng điện I. ■ [Lời giải]
Phát biểu, viết biểu thức và nêu ý nghĩa của định lý Ampe về lưu số của vecto cường độ từ trường.
+ Phát biểu: Lưu số của vecto cường độ từ trường dọc theo đường cong kín (C) bất kỳ (1 vòng) bằng
tổng đại số cường độ của các dòng điện xuyên qua điện tích giới hạn bởi đường cong đó. I n + Biểu thức: ⃗
Hd⃗l = ∑ I . Trong đó: sẽ mang dấu dương nếu dòng điện thứ i Ii
i nhận chiều dịch chuyển i=1 C
trên đường cong làm chiều quay thuận xung quanh nó và I sẽ mang dấu âm trong trường hợp ngược i lại. I + Ý nghĩa: ⃗
Hd⃗l không cho ta công của lực từ và giá trị nói chung khác không; do đó, từ trường không C
phải là trường thế, mà là trường xoáy.
Áp dụng định lý Ampe để xác định biểu thức cảm ứng từ
+ Trong lòng cuộn dây hình xuyến:
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 5.2 Câu hỏi lý thuyết 35 ⃗
H tại mọi điểm trên đường tròn (C) có giá trị như nhau, có phương tiếp tuyến với (C). I I I ⃗ nI µ0µnI Hd⃗l = Hdl = H dl = H.2πR = nI → H = → B = 2πR 2πR C C C
+ Trong lòng ống dây điện thẳng dài vô hạn:
Ống dây thẳng dài vô hạn xem như một cuộn dây điện hình xuyến có R1 = R2 = ∞. nI n → H = = I = n
: số vòng dây trên một đơn vị chiều dài) 0I → B = µ0µ n0I (n0 2πR L Câu 19 Trình bày:
a. Khái niệm đường sức từ trường;
b. Định nghĩa từ thông qua diện tích S;
c. Phát biểu, viết biểu thức và nêu ý nghĩa của định lý O-G đối với từ trường. ■ [Lời giải]
a. Khái niệm đường sức từ trường.
+ Đường sức từ trường (đường cảm ứng từ) là đường cong vạch ra trong từ trường mà tiếp tuyến tại
mọi điểm của nó trùng với phương của vecto cảm ứng từ tại điểm đó, chiều của đường cảm ứng từ là
chiều của vecto cảm ứng từ.
b. Định nghĩa từ thông qua diện tích S.
+ Từ thông gửi qua diện tích dS là đại lượng có trị số bằng: dΦm = ⃗Bd⃗S = BdScosα.
|dS cosα| = dS : hình chiếu của n
dS lên mặt phẳng vuông góc với các đường cảm ứng từ. → |dΦm = BdSn|
+ Để tìm từ thông gửi qua diện tích S bất kỳ, ta phải chia (S) thành những diện tích nhỏ dS sao cho trên Z
mỗi phần tử ấy có thể coi ⃗B không đổi. → Φ ⃗ m = Bd⃗S. S
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 5.2 Câu hỏi lý thuyết 36
c. Định lý O-G đối với từ trường.
+ Phát biểu: Từ thông toàn phần gửi qua mặt kín bất kỳ thì bằng không. I
+ Biểu thức: ⃗Bd⃗S = 0. S
+ Ý nghĩa: Định lý O-G nói lên tính chất xoáy của từ trường, nghĩa là trong tự nhiên không tồn tại các hạt mang từ tính. Câu 20
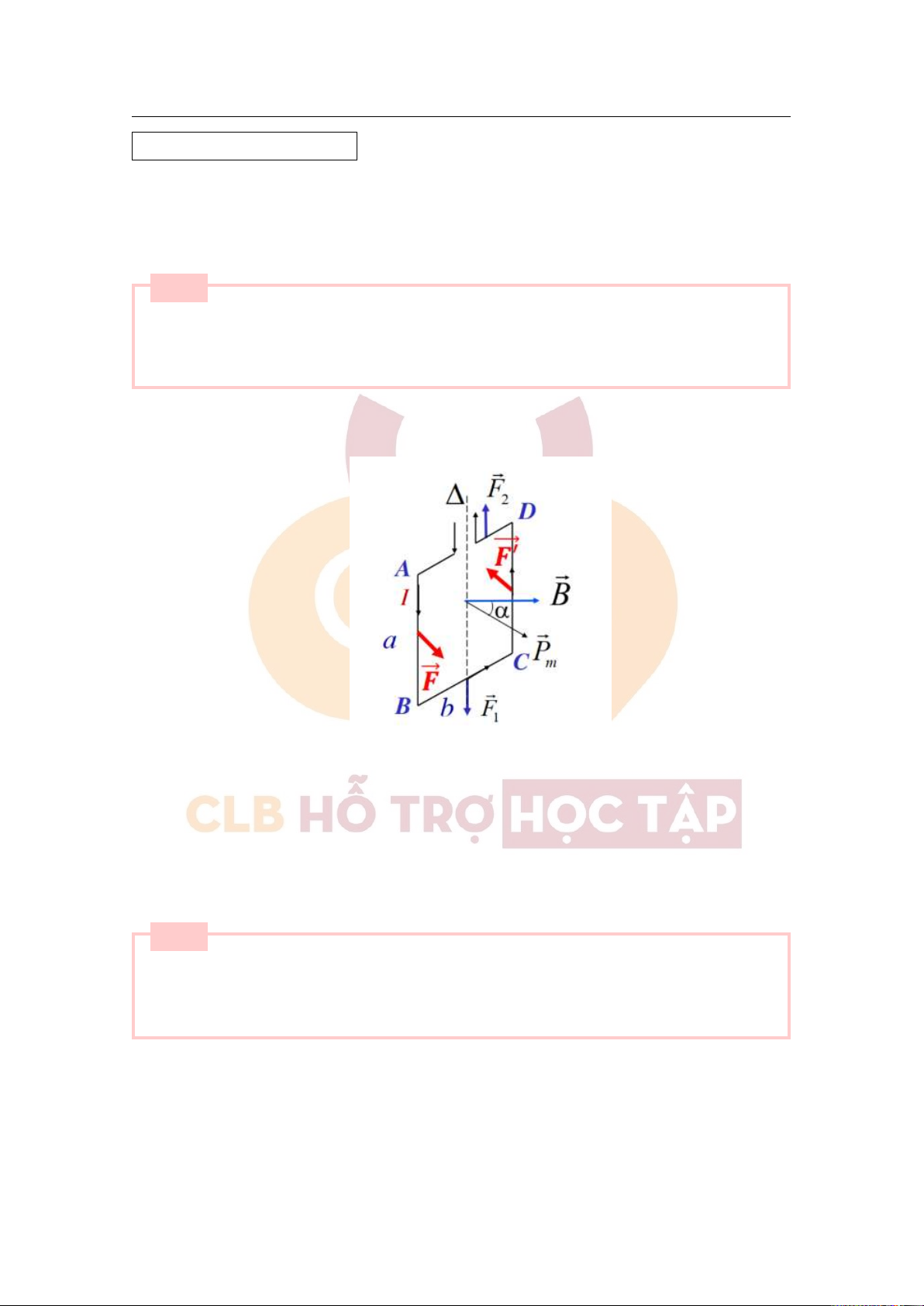
Trình bày tác dụng của từ trường đều lên một mạch điện kín (mạch điện kín là một khung dây dẫn cứng
hình chữ nhật có dòng điện cường độ I chạy qua) trong trường hợp cảm ứng ừng ⃗B hợp với vecto pháp
tuyến mặt phẳng khung một góc α. ■ [Lời giải]
+ Xét khung dây hình chữ nhật ABCD cạnh a,b có dòng điện I:
– Khung dây đặt trong từ trường đều ⃗B có phương vuông góc với AB,CD.
– Khung có thể quay quanh trục thẳng đứng ∆.
– Ban đầu mặt khung không vuông góc với từ trường.
+ Từ lực tác dụng lên khung: ⃗F1, ⃗F2,⃗F, ⃗F′. – ⃗F
. Chúng bị phản lực của khung triệt tiêu. 1 ↑↓ ⃗ F2, F1 = F2
– F = F′ = IaB. ⃗F và ⃗F′ tạo thành ngẫu lực làm khung quay quanh ∆ cho đến khi mặt phẳng của
khung vuông góc với từ trường. Khi đó vecto momen từ của khung dây sẽ cùng phương chiều với ⃗B.
– Khung quay theo chiều giảm của α. Câu 21
Trình bày về lực Lorent tác dụng lên hạt mang điện chuyển động trong từ trường có cảm ứng từ ⃗B.
Thành lập phương trình chuyển động của hạt mang điện q, khối lượng m, chuyển động vận tốc v dưới
tác dụng của từ trường đều ⃗B. ■ [Lời giải]
+ Xét hạt điện tích q chuyển động với vận tốc⃗v trong từ trường ⃗B:
– Hạt điện chuyển động này tương đương với phần tử dòng điện Id⃗l thỏa mãn điều kiện: Id⃗l = q⃗v.
– Từ lực tác dụng lên phần tử dòng điện là: d⃗F = Id⃗l ×⃗B.
– Từ lực tác dụng lên hạt chuyển động là: ⃗FL = q⃗v ×⃗B. Từ lực này được gọi là lực Lorent và có:
* Phương vuông góc với phương chuyển động của hạt điện và ⃗B.
* Chiều sao cho 2 vecto q⃗v,⃗B, ⃗F tạo thành tam diện thuận. L
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 5.2 Câu hỏi lý thuyết 37
* Độ lớn: FL = |q|vBsinα (với α là góc giữa⃗v và ⃗B).
+ Khảo sát chuyển động của hạt điện tích q (giả sử q > 0) trong từ trường đều ⃗B
– Chọn hệ Oxyz sao cho ⃗B ∥ Oz.
Tọa độ của ⃗B = (0,0,B)
– Tọa độ của hạt điện:⃗r = (x,y,z)
Tọa độ của vận tốc hạt điện:⃗v = (vx,vy,vz) ⃗ i ⃗j ⃗k → ⃗F L = q⃗ v × ⃗B = vx vy vz 0 0 B – Ta có: d⃗v FL = m⃗a = m = q⃗v × ⃗B (1) dt dvx m = qBv y (2) dt – Chiếu dv (1) lên 3 trục tọa độ: y m = −qBvx (3) dt dvz m = 0 → vz = const dt
– Giả sử tại t = 0,vOz = 0 → vz = vOz = 0. Khi đó hạt chỉ chuyển động trong một mặt phẳng
vuông góc với Oz (được chọn là mặt phẳng Oxy).
– Đặt qB = ω > 0 (vì q > 0. Nếu (q < 0 đặt |q|B = ω) m m dvx = ωvy Từ dt (2) và (3) suy ra: (4) dv y = −ωvx dt dvx dα ( = −vsinα – Gọi v dt dt α là góc tạo bởi ⃗ x = v cos α v và Oz, ta có: (5) → (6) vy = v sin α dv dα y = v cos α st dt – Kết hợp dα dα (4) và (6) ta có: −vsinα = ωvy = ωv sin α → = −ω dt dt → α = −ωt + α ( là giá trị của 0 α0 α khi t = 0) ( Thay vào v ( x = v cos (−ωt + α0) 5) → vy = v sin (−ωt + α0) dx ( vx = v cos ω t = – Giả sử tại vOx = v dt t = 0, v = vOx → → α0 = 0 → vOy = 0 dy v y = −v sin ωt = dt v x = sin ωt + x0 ω → v y = cos ωt + y ω 0 v x = sin ω Chọn ω v 2 x0 = 0, y0 = 0 → = R2 v → x2 + y2 = ω y = cos ω ω
Hạt chuyển động trên quỹ đạo tròn, trong mặt phẳng mv Oxy, tâm O, bán kính R = . qB
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 5.3 Bài tập 38 5.3 Bài tập Bài tập 14
Nối hai đầu một sợi dây dẫn bằng đồng có độ dài 3m , tiết diện tròn có đường kính d = 0.40mm với
một hiệu điện thế không đổi U = 8V . Xác định:
a) Cường độ dòng điện và mật độ dòng điện qua dây.
b) Số electron qua tiết diện của dây dẫn trong 1s.
c) Tốc độ trung bình của chuyển động định hướng của electron. Coi mật độ của electron tự do bằng mật
độ nguyên tử. Biết đồng có khối lượng mol nguyên tử là = 64g/mol, khối lượng riêng D = 8,9g/cm3,
điện trở suất ρ = 1,72.10−8Ωm, số Avogadro NA = 6,02.1023mol−1 và −e = −1,6.10−19C. ■ [Lời giải]
1. Điện trở của dây dẫn: ρ.l ρ.l R = = S π. d 2 2 Cường độ dòng điện: U U.π.d2 8.π.(0, 4.10−3)2 I = = = ≈ 19,48(A) R 4.l.ρ 4.3.1, 72.10−8
Mật độ dòng điện qua dây: I U 8 J = = = ≈ 1,55.108(A/m2) S l.ρ 3.1, 72.10−8
2. Số electron qua tiết diện dây dẫn trong I 1s là: Ne = ≈ 12,18.1019 e
3. Ta có công thức J = n0.e.v, vì vậy tốc độ trung bình của chuyển động định hướng của electron là: J J.µ v = = ≈ 1,16.102(m/s) n0.e NA.D.e Bài tập 15
Một dây dẫn dài vô hạn được uốn thành một góc vuông trên có dòng điện 15A chạy qua như hình vẽ. Tìm:
a) Cường độ từ trường tại A nằm trên một cạnh góc vuông cách O một đoạn OA = 3cm.
b) Cường độ từ trường tại B nằm trên phân giác của góc vuông cách O một đoạn OB = 15cm. ■ [Lời giải]
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 5.3 Bài tập 39 y + −→ HyB B + d −→ HxB O x I − → HA A
1. Theo nguyên lí chồng chất từ trường: −→ −→ −→ HA = HxA + HyA Dễ thấy − → −→
HyA = 0 do A ∈ Oy ⇒ HA = HxA ⇒ HA = HxA
Cường độ từ trường tại A là: I.(cos θ1 − cos θ2) 15.(cos π − cos π) H 2 A = = ≈ 39.8(A/m) 4.π.OA 4.π.0, 03
2. Theo nguyên lí chồng chất từ trường: −→ −→ −→ HB = HxB + HyB √ I.(cos θ1 − cos θ2) I.(cos π − cos π) I 2 H 4 xB = = = (1 + ) 4.π.d 4.π.d 4.π.d 2 √ I.(cos θ1 − cos θ2) I.(cos 0 − cos 3π ) I 2 H 4 yB = = = (1 + ) 4.π.d 4.π.d 4.π.d 2 Do −→ −→ H
cùng hướng, suy ra cường độ từ trường tại xA, HyA B là: √ √ I. 2 2 HB = HxB + HyB = 2 (1 + ) ≈ 38,42(A/m) 4π.OB 2 Bài tập 16
Hai vòng dây giống nhau bán kính R = 5cm được đặt song song trùng trục nhau và mặt phẳng của
chúng cách nhau một đoạn a = 20cm. Tìm cường độ từ trường tại tâm O
của mỗi vòng dây và tại 1, O2
điểm M nằm giữa đoạn O
trong trường hợp hai dòng điện 1O2
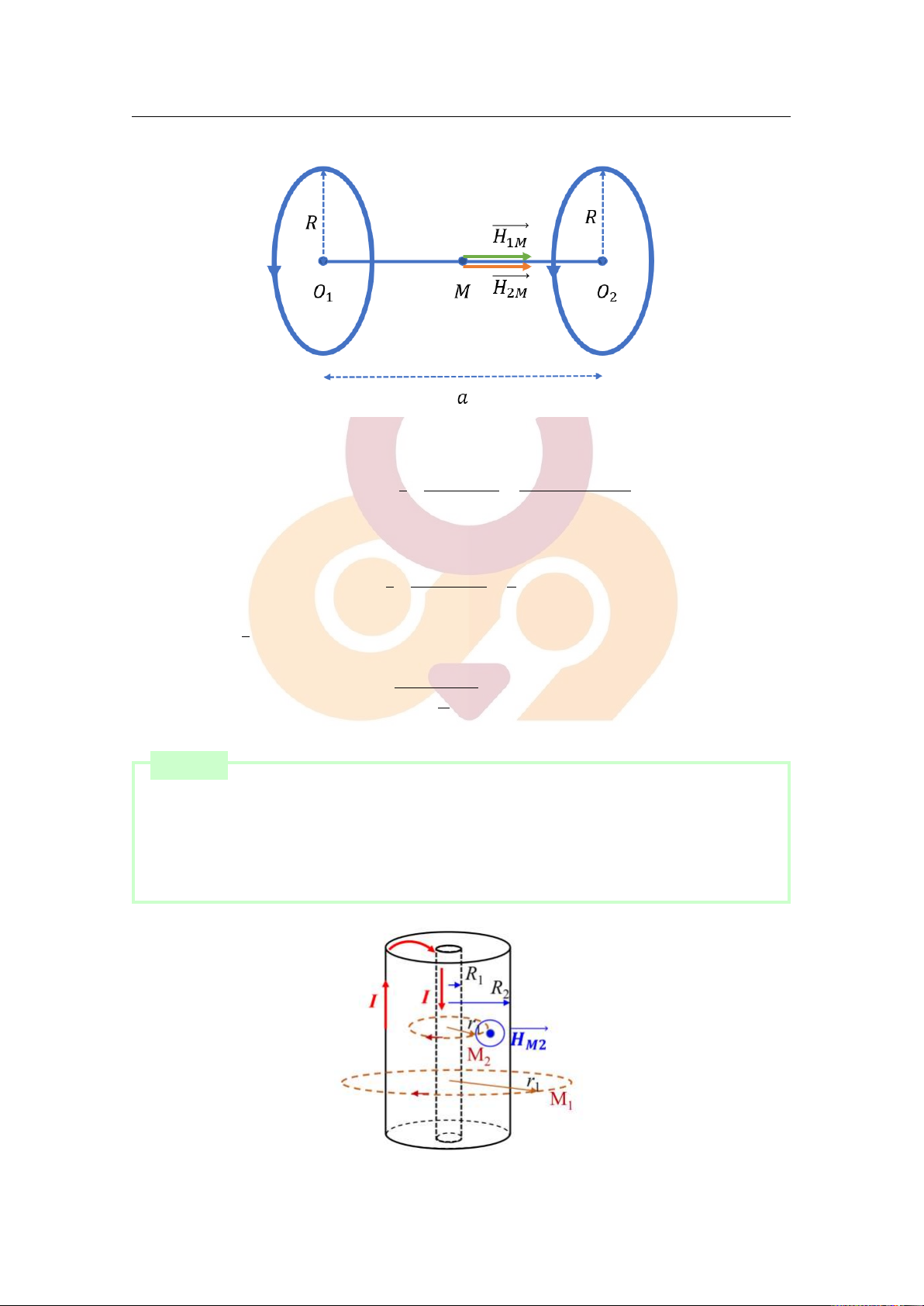
I1 = I2 = 3A và cùng chiều. ■ [Lời giải]
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 5.3 Bài tập 40
Cường độ từ trường tại một điểm bất kì cách O một khoảng 1 x là: I R2 R2 Hx = H1x + H2x = + 2 (R2 + x2)3/2 (R2 + (a − x)2)3/2 Tại tâm O là:
1 : x = 0, tâm O2 : x = a, suy ra cường độ từ trường tại tâm O1, O2 I R2 1 HO1 = HO = + ≈ 30,43(A/m) 2 2 (R2 + a2)3/2 R Tại điểm a M : x =
, suy ra cường độ từ trường tại điểm M là: 2 I.R2 HM = ≈ 5,37(A/m) 3/2 R2 + a2 4 Bài tập 17
Một dòng điện I = 10A chạy dọc theo thành của một ống mỏng hình trụ bán kính R2 = 8cm, sau đó
chạy ngược lại qua một dây dẫn đặc hình trụ bán kính R1 = 1mm đặt trùng với trục của ống. Tìm:
a) Cảm ứng từ tại các điểm cách trục của ống r1 = 9cm và r2 = 2cm.
b) Từ thông gây ra bỏi một đơn vị chiều dài của hệ thống. Coi toàn bộ hệ thống là dài vô hạn và bỏ qua
từ trường bên trong kim loại. ■ [Lời giải]
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 5.3 Bài tập 41 1. Vẽ đường tròn (C , đi qua 1): tâm O, bán kính r1 M1 I n
Theo định lý Ampere về dòng điện toàn phần: − →−→ H1dl1 = ∑ Ii i=1 (C1)
⇒ H12πr1 = I − I = 0 ⇒ H1 = 0 ⇒ B1 = 0(T ) Vẽ đường tròn (C , đi qua 2): tâm O, bán kính r2 M2 I n
Theo định lý Ampere về dòng điện toàn phần: − →−→ H2dl2 = ∑ Ii i=1 (C2) I µ 4.π.10−7.10 ⇒ 0I H22πr2 = I ⇒ H2 = ⇒ B2 = = = 10−4 (T ) 2πr2 2πr2 2.π.0, 02 Z 2. Do − → − →
B1 = 0 nên ở bên ngoài ống θ1 = B1.dS = 0
Từ thông gây ra bỏi hệ thống tập trung tại ống hình trụ là: Z − → − → Z µ R θ 0.I.l 2 2 = B2.dS = B2.dS = ln 2π R1
Từ thông do một đơn vị chiều dài hệ thống gây ra là: φ µ R φ = 2 = 0.I 2 ln ≈ 0,88.10−5 (W b) l 2π R1 Bài tập 18
Một electron chuyển động vào trong một từ trường đều có cảm ứng từ B = 3.10−3T với vận tốc
v = 19.106m/s theo phương hợp với đường sức từ một góc 30o. Quỹ đạo của electron là một đường đinh ốc. Xác định:
a) Bán kính của một vòng xoắn ốc.
b) Bước của đường đinh ốc đó. ■ [Lời giải]
1. Bán kính của một vòng xoắn ốc là: m.v. sin α 9, 1.10−31.19.1016. sin 30o R = = ≈ 18.10−3(m) e.B 1, 6.10−19.3.10−3
2. Bước của đường đinh ốc là: 2π.R h = v.T. cos α = ≈ 196.10−3(m) tan α Bài tập 19
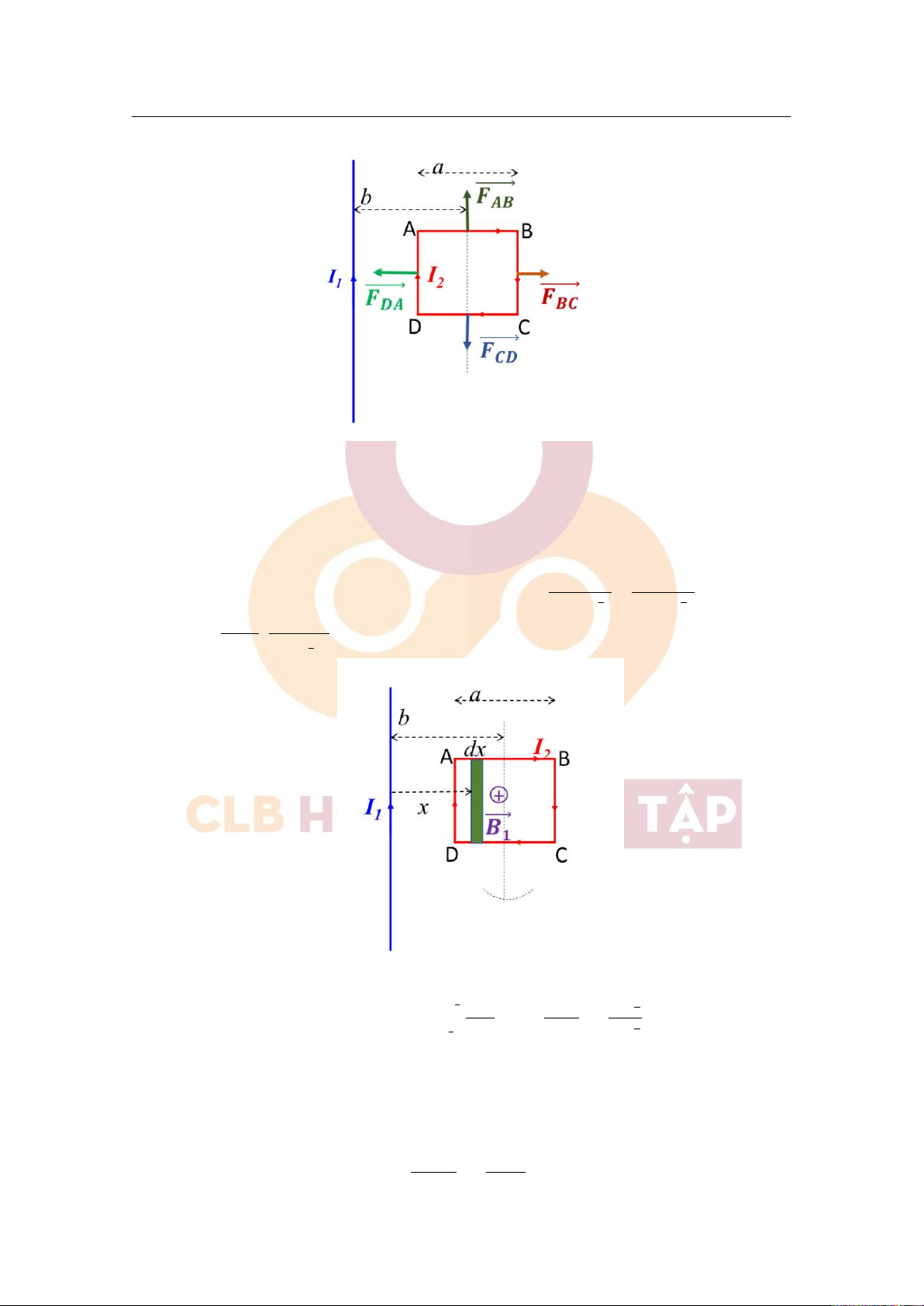
Cạnh của một dây dẫn thẳng dài. Trên có dòng điện cường độ I1 = 40A chạy qua, người ta đặt một
khung dây dẫn hình vuông ABCD có dòng điện cường độ I2 = 3A. Khung dây và dây dẫn nằm trong
cùng một mặt phẳng. Khung có thể quay xung quanh một trục song song với dây dẫn và đi qua điểm
giữa của hai cạnh đối diện của khung. Trục quay cách dây dẫn một đoạn d = 30mm. Mỗi cạnh của
khung có chiều dài a = 20mm. Tìm:
a) Lực F tác dụng lên khung dây.
b) Công cần thiết để quay khung một góc bằng π xung quanh trục của nó. ■
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 5.3 Bài tập 42 [Lời giải] 1. Lực tổng hợp − →
F tác dụng lên khung dây dẫn là: − → −→ −→ −−→ −→ F = FAB + FBC + FCD + FDA
Do dây dẫn dài vô hạn, nên vị trị tương đối của 2 cạnh AB, CD là như nhau −→ −−→ − → ⇒ FAB + FCD = 0 − → −→ −→ µ µ ⇒ 0I1 0I1
F = FBC + FDA ⇒ F = FDA − FBC = (BDA − BBC)I2a = − I2a 2π(b − a ) 2π(b + a ) 2 2 µ a2 ⇒ 0I1I2 F = , = 1, 2.10−5(N) 2π b2 − a 2 2
2. Từ thông của từ trường gửi qua khung dây là: Z − → − → Z b+ a 2 µ µ b + a φ 0I1 0I1a 2 0 = B .dS = a.dx = ln b− a 2π .x 2π b − a 2 2 khung
Độ biến thiên của từ thông qua khung khi quay một góc π quanh trục là:
∆φm = |(−φm) − φm| = 2φm
Công cần thiết để quay khung một góc π là: µ 0I1I2a 2b + a A = I2.∆φm = ln ≈ 6,65.10−7(J) π 2b − a
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
6. Chương 5 - Cảm ứng điện từ 6.1 Tóm tắt lý thuyết
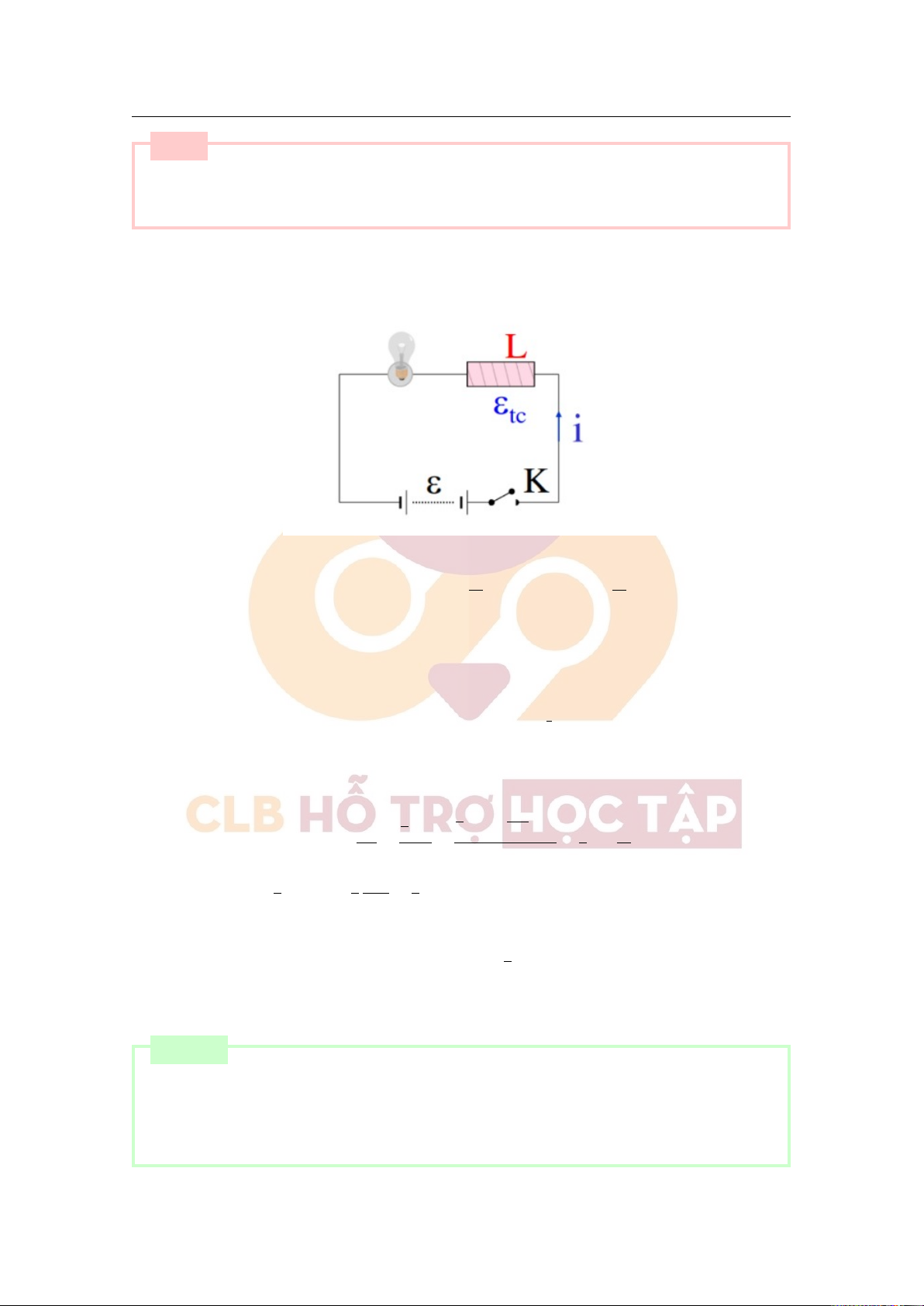
1. Biểu thức của suất điện động cảm ứng: dΦ ξc = − dt
2. Công thức tính suất điện động tự cảm: dI ξtc = −L dt
3. Công thức tính hệ số tự cảm của ống dây có chiều dài l, số vòng dây N: N2 L = µ0µ S l
4. Công thức tính năng lượng từ trường trong ống dây điện: LI2 W = 2
5. Công thức tính mật độ năng lượng từ trường trong ống dây điện: 1 W = µ0µn2I2 2 0
với n là số vòng trên 1 đơn vị dài của ống dây. 0 6.2 Câu hỏi lý thuyết Câu 22
Thế nào là hiện tượng cảm ứng điện từ? Phát biểu định luật Lenxơ về chiều của dòng điện cảm ứng.
Thiết lập biểu thức suất điện động cảm ứng. ■ [Lời giải]
+ Hiện tượng cảm ứng điện từ: Khi từ thông qua mạch kín thay đổi thì trong mạch xuất hiện một dòng
điện gọi là dòng điện cảm ứng. Hiện tượng đó được gọi là hiện tượng cảm ứng điện từ.
– Sự biến đổi của từ thông qua mạch kín là nguyên nhân sinh ra dòng cảm ứng.
– I chỉ tồn tại trong thời gian từ thông gửi qua mạch thay đổi. c
– Cường độ I tỷ lệ thuận với tốc độ biến thiên từ thông. c
– Chiều của I phụ thuộc vào từ thông qua mạch tăng hay giảm. c
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 6.2 Câu hỏi lý thuyết 44
+ Định luật Lenx: Dòng điện cảm ứng phải có chiều sao cho từ trường do nó sinh ra có tác dụng chống
lại nguyên nhân đã sinh ra nó.
+ Thiết lập biểu thức suất điện động cảm ứng:
– Dịch chuyển 1 vòng dây dẫn kim loại (C) trong từ trường để Φ qua m (C) thay đổi.
– Trong thời gian dt, từ trường qua (C) biến thiên một lượng dΦ . m
– Dòng cảm ứng xuất hiện trong vòng dây có cường độ I . c
Khi đó, công của từ lực tác dụng lên dòng cảm ứng: dA = IcdΦm
Theo định luật Lenx, từ lực tác dụng lên I phải ngăn cản sự dịch chuyển của vòng dây vì sự dịch c
chuyển này là nguyên nhân sinh ra Ic ⇒ Công của từ lực tác dụng lên dòng cảm ứng là công cản.
– Để dịch chuyển vòng dây ta phải tốn công dA′, về trị số bằng công cản đó.
Công để dịch chuyển vòng dây: dA′ = −dA = −I . cdΦm
Công dA′ này được chuyển thành năng lượng của dòng cảm ứng: dΦ ξ m
cIcdt = −IcdΦm ⇒ ξc = − dt Câu 23
Hiện tượng tự cảm là gì? Thiết lập biểu thức tính suất điện động tự cảm và biểu thức tính độ tự cảm
của một ống dây thẳng dài vô hạn. Nêu một ứng dụng của hiện tượng tự cảm và phân tích. ■ [Lời giải]
+ Hiện tượng tự cảm:
– Nếu ta làm thay đổi I trong môt mạch điện để từ thông do chính dông điện đó gửi qua diện tích
của mạch thay đổi thì trong mạch cũng xuất hiện I . c
– Vì dòng điện này do sự cảm ứng của dòng trong mạch sinh ra nên nó được gọi là dòng điện tự
cảm. Hiện tượng này được gọi là hiện tượng tự cảm.
+ Thiết lập biểu thức suất điện động tự cảm:
– Theo định luật cơ bản của hiện tượng cảm ứng điện từ, ta có: dΦ ξ m , trong đó: là từ tc = − Φm dt
thông do chính dòng điện trong mạch gửi qua diện tích của mạch đó.
– Vì Φ tỷ lệ thuận với tỷ lệ thuận với m
B và B tỷ lệ thuận với I nên Φm I.
⇒ Φm = LI, trong đó L là hệ số tự cảm. d(LI) dI ⇒ ξtc = − = −L dt dt
+ Tính độ tự cảm của một ống dây thẳng dài vô hạn:
– Từ trường bên trong ống dây là từ trường đều, cảm ứng từ tại mọi điểm bên trong ống là: n B = µ0µn0I = µ0µ I l – Lại có: n2S Φm = nBS = µ0µ I l Φ n2S ⇒ m L = = µ . 0 µ I l
+ Ứng dụng: Hiệu ứng bề mặt.
Khi dòng điện cao tần chạy qua 1 dây dẫn thì do hiện tượng tự cảm dòng điện ấy hầu như không chạy
trong lòng dây dẫn mà chỉ chạy ở mặt ngoài của nó.
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 6.3 Bài tập 45 Câu 24
Thiết lập biểu thức năng lượng từ trường của ống dây điện thẳng dài, từ đó suy ra năng lượng của từ trường bất kỳ. ■ [Lời giải]
+ Năng lượng từ trường của ống dây điện thẳng dài:
Áp dụng định luật Ôm trong quá trinh dòng điện được thiết lập: dI dI ξ + ξtc = RI → ξ − L = RI → ξ = RI + L dt dt ξ Idt
: Năng lượng do nguồn điện sinh ra trong dt
⇒ ξ Idt = RI2dt + LIdI với: RI2dt
: Nhiệt lượng tỏa ra trong thời gian dt LIdI
: Năng lượng từ trường (dWm = LIdI)
Vậy trong cả quá trình thành lập dòng điện, phần năng lượng của nguồn điện được tiềm tàng dưới dạng
năng lượng từ trường là: Wm = R Wm dW LIdI LI2 - 0 m = R I 0 ⇒ Wm = 12
+ Năng lượng của từ trường bất kỳ:
Từ trường của ống dây điện thẳng và dài là từ trường đều. Mật độ năng lượng từ trường của ống dây là:
(coi như từ trường chỉ tồn tại trong thể tích của ống dây đó) 1 1 n2S µ µ0 I2 W LI2 m 2 l 1 n2 w 2 m = = = = µ µ0 I2 V V Sl 2 l2 Lại có: n 1 B2 1 B = µ µ0 I → wm =
= BH Chia không gian thành dV rất nhỏ sao cho trong mỗi thể l 2 µ µ0 2
tích đó có thể coi từ trường là đều. Z 1 Z Wm = wmdV = BHdV V 2 V 6.3 Bài tập Bài tập 20
Một đĩa kim loại bán kính R = 20 cm quay quanh trục của nó với vận tôc góc 1500 vòng/phút. Tìm
hiệu điện thế xuất hiện giữa tâm đĩa và một điểm trên mép đĩa trong hai trường hợp:
a) Khi không có từ trường.
b) Khi đĩa đặt trong từ trường có càm ửng từ B = 5.10−2 T và đường sức từ vuông góc với đĩa. ■ [Lời giải]
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 6.3 Bài tập 46
1. Khí không có từ trường:
+ Khi đĩa quay, các electron bị văng ra mép đĩa, khi đó mép đĩa tích điện âm và tâm đĩa tích điện dương.
+ Lúc này các electron chuyển động đều dưới tác dụng của lực hướng tâm là lực điện: Fe = Fht = mw2r Z R Z R
Ta có công của lực điện: 1 A = −eU = − Fedr = − mw2rdr = − mw2R2 0 0 2 Từ đó, suy ra: mw2R2 U = = 2, 8.10−9(V ) 2e
2. Khi đĩa đặt trong từ trường có cảm ứng từ B: Đĩa chịu tác dụng của lực Lorentz F . L
Khí đó: Fht = Fe + FL = mw2R + ewrB Do F nên ta có e << FL Fht ≈ Fl = ewrB Z R Z R
Ta có công của lực điện: 1 A = −eU = − FLdr = − ewrBdr = − ewBR2 0 0 2 Từ đó, suy ra: wR2B U = = 15, 7.10−2(V ) 2 Bài tập 21
Một ống dây có đường kính D = 6 cm, độ tự cảm 0,001H, được quấn bởi loại dây có đường kính
d = 0, 4 mm. Các vòng đựọc quấn sát nhau, và chỉ quấn một lớp.
a) Tỉnh số vòng của ống dây.
b) Người ta giữ nguyên ống dây và đưa vào một lõi sắt có độ từ thẩm là µ = 400. Tìm độ tự cảm của
ống dây trong trường hợp này. ■ [Lời giải]
1. Hệ số tự cảm của ống dây được tính bởi công thức: µ0N2S L0 = (1) l
Ống dây có đường kính D = 6 cm D2 ⇒ S = π 4
Loại dây dùng để cuốn có đường kính d = 0,4 mm l ⇒ N = d Thay vào (1) ta được: πD2 µ0N L 4 0 = d Suy ra: 4L0d N = = 112(vòng) µ0πD2
2. Độ tự cảm của ống dây là: L = µL0 = 0, 4(H)
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
7. Chương 6 - Vật liệu từ 7.1 Tóm tắt lý thuyết
1. Công thức liên hệ giữa vecto từ độ ⃗J và vecto cường độ từ trường ⃗H: ⃗ J = χ ⃗ mH
với χ là hệ số từ hóa. m
2. Công thức liên hệ giữa cảm ứng từ ⃗B và cường độ từ trường ⃗H: ⃗B = µ0µ ⃗H
với µ = 1 + χ là độ từ thẩm. m 7.2 Câu hỏi lý thuyết Câu 25
a. Thế nào là chất thuận từ, nghịch từ, sắt từ?
b. Trình bày về vecto từ độ ⃗J. ■ [Lời giải]
a. Chất thuận từ, nghịch từ, sắt từ:
Mọi chất đặt trong từ trường đều bị từ hóa. Khi đó chúng trở thành có từ tính và sinh ra một từ trường phụ ⃗
B′. Từ trường tổng hợp ⃗
B trong chất bị từ hóa là: ⃗ B = ⃗ B
là vecto cảm ứng từ của từ trường ban đầu). 0 + ⃗ B′ (⃗ B0
+ Chất nghịch từ: ⃗B′ ↑↓ ⃗B0 → |⃗B| < |⃗B0|
+ Chất thuận từ: ⃗B′ ↑↑ ⃗B0 → |⃗B| > |⃗B0|
+ Chất sắt từ: ⃗B′ ↑↑ ⃗B0 → |⃗B| ≫ |⃗B0|
b. Vecto từ độ ⃗J:
Vecto từ độ là momen từ của một đơn vị thể tích của khối vật liệu từ. Gọi ∑⃗P là tổng các vecto momen mi
từ nguyên tử có trong thể tích ∆V của vật liệu. ∑⃗Pmi ⃗ ∆ J = V∆V
Nếu khối vật liệu bị từ hóa đồng đều thì |⃗J| = J là từ độ của vật liệu từ.
Thực nghiệm cho thấy: ⃗J tỷ lệ thuận với ⃗B của từ trường ngoài. 0
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 7.3 Bài tập 48 ⃗ χm J = ⃗B
(χ là độ từ hóa của vật liệu từ) µ 0 m 0 Lại có: ⃗B ⃗ ⃗ 0 = µ0H → ⃗ J = χmH. Câu 26
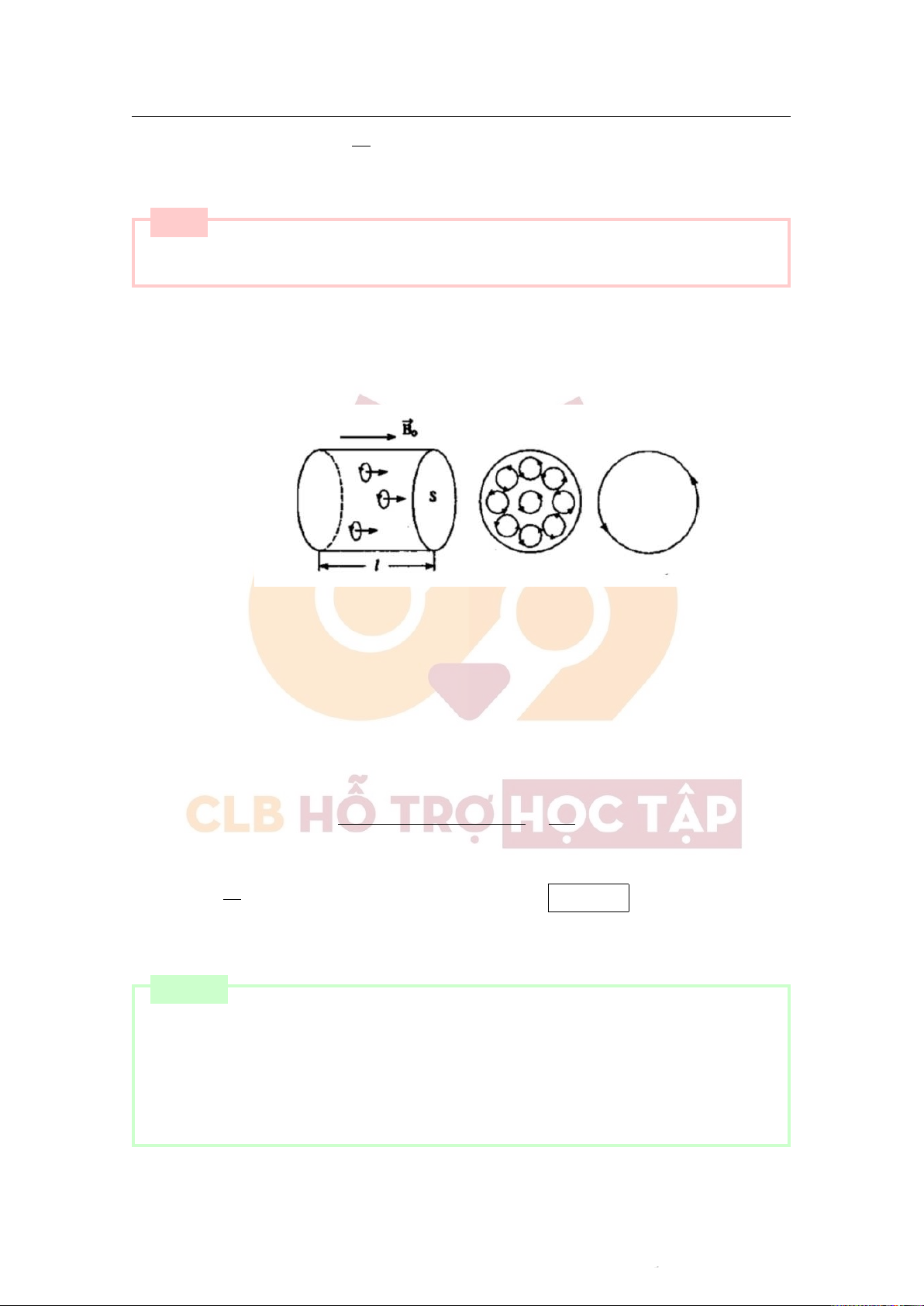
Xây dựng công thức tính cảm ứng từ tổng hợp trong chất thuận từ đồng chất và đẳng hướng. ■ [Lời giải]
+ Xét khối thuận từ đồng nhất hình trụ dài vô hạn, tiết diện thẳng S;
- Trụ đặt trong từ trường đều ⃗B có phương song song với đường sinh; 0
- Giả sử dưới tác động của từ trường ngoài, các momen từ nguyên tử ⃗P nằm dọc theo hướng ⃗ ; m B0
+ Xét các dòng điện nguyên tử trong một tiết diện thẳng của trụ:
- Bên trong tiết diện: các dòng điện nguyên tử từng cặp một ngược chiều nhau, chúng triệt tiêu lẫn nhau;
- Chỉ còn các dòng điện nằm dọc theo chu vi của tiết diện là cùng chiều và tạo thành một dòng
điện tròn chạy quanh chu vi của tiết diện.
+ Như vậy, xét toàn bộ hình trụ thì tất cả các dòng điện nguyên tử trong các tiết diện thẳng khác nhau sẽ
tương đương với một dòng điện duy nhất chạy quanh mặt ngoài của hình trụ giống như một ống dây
điện thẳng dài vô hạn.
+ Gọi n là số dòng điện tròn trên 1m dài của trụ và i là cường độ của các dòng điện đó. 0
Cảm ứng từ phụ ⃗B′ do chúng sinh ra trong trụ là: B′ = µ0n0i (1)
Mặt khác có thể tính từ độ J của khối thuận từ theo định nghĩa:
Momen từ của 1 đơn vị dài trụ n0iS J =
Thể tích 1 đơn vị dài trụ = = n0i (2) S.1 Từ (1) và (2) → B′ = µ ⃗ 0J. Vì ⃗
B′ ↑↑ ⃗J nên ⃗B′ = µ0J.
+ Từ trường tổng hợp trong hình trụ là ⃗B = ⃗B ⃗ 0 + ⃗ B′ = ⃗ B0 + µ0J Mà ⃗ χm J = ⃗B ⃗B µ 0
→ ⃗B = ⃗B0 + χm 0 = (1 + χm)⃗B0 = µ⃗B0 ⇒ ⃗B = µ0µ ⃗H 0 7.3 Bài tập Bài tập 22
Một dây dẫn thẳng dài l = 1m, có lõi sắt, tiết diện ngang S = 10cm2, hệ số tự cảm L = 0,44H. Từ
thông gửi qua tiết diện ngang của ống dây φ = 1,4.10−3Wb. Tìm:
a. Độ từ thẩm của lõi sắt;
b. Cường độ dòng điện chạy qua ống dây;
c. Năng lượng và mật độ năng lượng trong ống dây.
Đường cong từ hóa B = f (H) cho trên đồ thị sau: ■
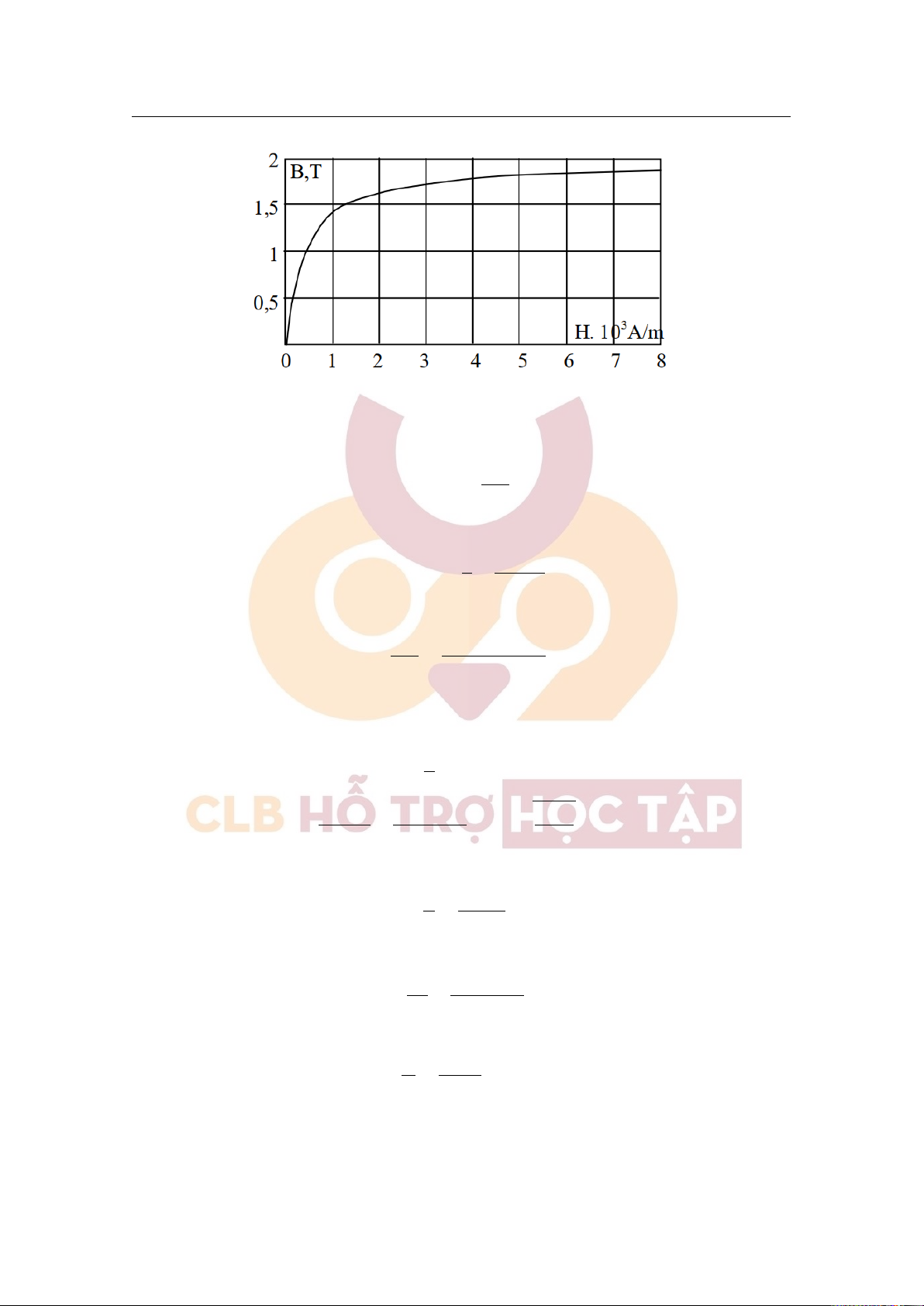
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 7.3 Bài tập 49 [Lời giải]
1. Độ từ thẩm của lõi sắt được xác định theo công thức: B µ = µ0H
Từ thông gửi qua tiết diện ngang của ống: φ 1, 4.103 φ = BS → B = = = 1, 4T S 10.10−4
Từ đồ thị trên, ta thấy ứng với B = 1,4T , cường độ từ trường sẽ có giá trị H = 0,8.103A/m. Do đó: B 1, 4 µ = = = 1400. µ0H 4π.10−7.0, 8.103
2. Trong ống dây thẳng, cường độ từ trường được tính bởi công thức: H = nI với N
n là số vòng dây trên đơn vị dài: n = l Mà: s µ0µN2S µ0µ(n/l)2S L L = = → n = = 500 vòng/m. l l µ0µSl
Vậy cường độ dòng điện chạy qua ống dây là: H 0, 8.103 I = = = 1, 6 A. n 500
3. Năng lượng từ trường trong ống dây: LI2 0, 44.(1, 6)2 W = = = 0, 56 J. 2 2
Mật độ năng lượng từ trường là: W 0, 56 w = = = 5, 6.102 J/m3. Sl 10−3.1
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
8. Chương 7 - Trường điện từ 8.1 Tóm tắt lý thuyết
1. Công thức tính mật độ dòng điện dịch: ⃗ ∂ ⃗D Jdịch = ∂t 2. Cảm ứng điện ⃗D: ⃗D = εoε⃗E
3. Mật độ dòng điện dẫn: ⃗jdẫn = σ⃗E 8.2 Câu hỏi lý thuyết Câu 27
Phát biểu luận điểm 1 của Maxwell. Phân biệt điện trường tĩnh và điện trường xoáy về nguồn gốc phát
sinh và tính chất cơ bản. Thiết lập phương trình Maxwell-Faraday dạng tích phân. ■ [Lời giải]
+ Phát biểu luận điểm 1 Maxwell:
Bất kì một từ trường nào biến đổi theo thời gian cũng sinh ra một điện trường xoáy.
+ Phân biệt điện trường tĩnh và điện trường xoáy: Điện trường tĩnh Điện trường xoáy
- Tồn tại xung quanh điện tích đứng yên
- Tồn tại xung quanh điện tích di chuyển
- Đường sức không khép kín - Đường sức khép kín
- Công của điện trường trong dịch chuyển
- Công của điện trường trong dịch chuyển I I
điện tích theo đường cong kín: q⃗ Ed⃗l = 0.
điện tích theo đường cong kín: q⃗ Ed⃗l ̸= 0. (C) (C)
Do đó điện trường tĩnh là trường thế.
Do đó điện trường xoáy không là trường thế.
+ Thiết lập phương trình Maxwell-Faraday: Z
- Suất điện động cảm ứng xuất hiện trong mạch: dΦ d ξ m ⃗ c = − = − Bd⃗S (1) dt dt S
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 8.3 Bài tập 51
- Mặt khác, suất điện động trong mạch có giá trị bằng lưu số của vectơ cường độ điện trường xoáy: I ξ ⃗ c = Ed⃗l (2) (C) I Z Từ (1) và (2) d ⇒ ⃗Ed⃗l = − ⃗Bd⃗S . dt S (C)
Lưu số của vectơ cường độ điện trường dọc theo một đường cong kín bất kì bằng về giá trị tuyệt đối
nhưng trái dấu với tốc độ biến thiên theo thời gian của từ thông qua diện tích giới hạn bởi đường cong đó. Câu 28
Phát biểu luận điểm 2 của Maxwell. Khái niệm dòng điện dịch. So sánh dòng điện dịch và dòng điện
dẫn. Thiết lập phương trình Maxwell-Ampe dạng tích phân. ■ [Lời giải]
+ Phát biểu luận điểm 2 Maxwell:
Bất kì một điện trường nào biến đổi theo thời gian cũng sinh ra một từ trường.
+ Khái niệm dòng điện dịch:
Dòng điện dịch là dòng điện tương đương với điện trường biến đổi theo thời gian về phương diện sinh ra từ trường.
+ So sánh dòng điện dịch và dòng diện dẫn Dòng điện dẫn Dòng điện dịch
- Là dòng chuyển dời có hướng của các hạt mang điện
- Là ⃗E biến thiên theo t
- Gây ra tỏa nhiệt Jun-Lenxơ
- Không gây ra tỏa nhiệt Jun-Lenxơ (trong chân không) - Gây ra từ trường ⃗B - Gây ra từ trường ⃗B
+ Thiết lập phương trình Maxwell-Ampe:
Xét một dường cong kín (C) nằm trong không gian có cả dòng diện dẫn và dòng diện dịch chạy qua. I Theo dịnh lý Ampe: ⃗ Hd⃗l = ∑ I . i = Idẫn + Idịch = Itp C ! Z Z Lại có: ∂ ⃗D I ⃗ ⃗ tp = Jtpd⃗S = J + d⃗S ∂ t S S ! I Z ∂ ⃗D ⇒ ⃗ Hd⃗l = ⃗ J + d⃗S ∂ t C S
Lưu số của vectơ cường độ từ trường dọc theo đường cong kín bất kì bằng cường độ dòng điện toàn
phần chạy qua diện tích giới hạn bởi đường cong đó. 8.3 Bài tập Bài tập 23
Một tụ điện phẳng có điện môi với hằng số điện môi giữa hai bản tụ ε = 5 được mắc vào điện áp
u = 200 cos 100πtV . Biết giá trị cực đại của mật độ dòng điện dịch là 0, 56.10−3A/m2. Tìm khoảng
cách giữa hai bản tụ. Cho biết ε0 = 8,86.10−12C2/Nm2 ■ [Lời giải]
+ Áp dụng công thức tính mật độ dòng điện dịch: ∂ D ∂ E |J d | = = ε0ε ∂ t ∂ t + Lại có: U U0 E = = cos ωt d d
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 8.3 Bài tập 52 + Suy ra: ε | 0εU0ω Jd|max = ⇒ d = ε0εU0ω = 5.10−3 m d |Jd|max Bài tập 24
Một trường điện từ có cường độ điện trường biến thiên theo thời gian theo quy luật E = E0 cosωt trong
dây dẫn kim loại có hằng số điện môi ε = 2, điện dẫn suất σ = 5,8.107Ω−1m−1. Biết tỉ số giữa giá trị
cực đại của mật độ dòng điện dịch và giá trị cực đại của mật độ dòng điện dẫn là 3,06.10−12. Tìm chu
kì biến đổi của dòng điện. Cho C2 ε0 = 8, 86.10−12 ■ Nm2 [Lời giải]
+ Mật độ dòng điện dịch: ∂ D ∂ E |J d | = = ε0ε = ε0ε ω E0 sin ωt ∂ t ∂ t
+ Mật độ dòng điện dẫn: |J| = σE = σE0 sinωt + Ta có tỉ số: |Jd|max ε0εω ε0ε2π ε0ε2π N = = = nên T = = 2π.10−7s |J|max σ σ T σ N
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
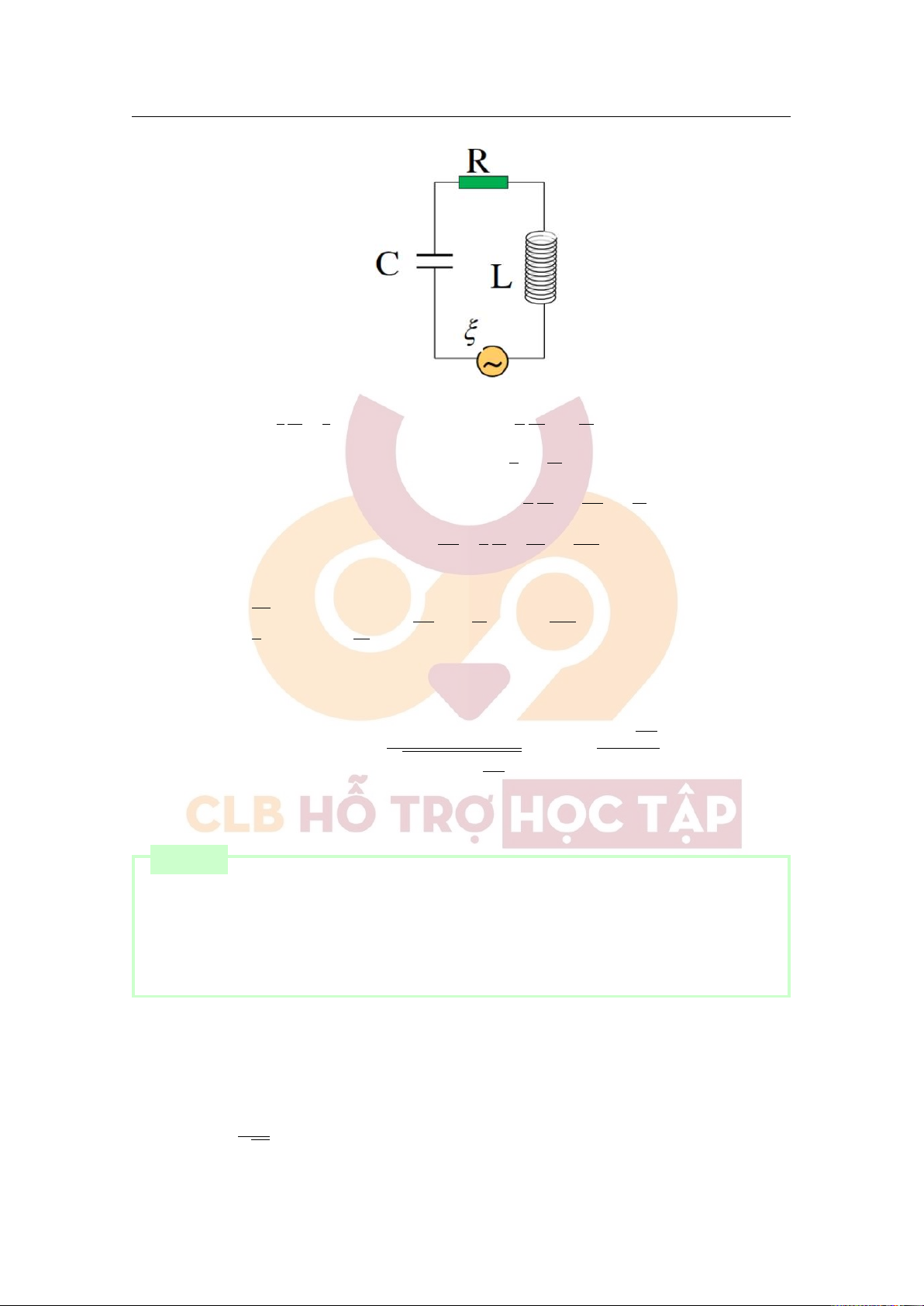
9. Chương 8 - Dao động điện từ 9.1 Tóm tắt lý thuyết
1. Dao động điện từ điều hòa: 1 q2 1 I = I 0 0 cos (ω0t + ϕ ), W = = LI2 = const 2 c 2 0 1 √ ω0 = √ , T = 2π LC LC
2. Dao động điện từ tắt dần: r
Chỉ có hiện tượng dao động tắt dần khi L R < 2 C 1 1
I = I0e−βt cos (ωt + ϕ), W = LI2 LI2e−2βt 2 max = 2 0 r 1 R 2 2π ω = − , T = LC 2L r 1 R 2 − LC 2L Giảm lượng loga: A(t) δ = ln = βt A(t + T )
3. Dao động điện từ cưỡng bức:
Nguồn ngoài có: ξ = ξ0 sinΩt I = I0 cos (Ωt + Φ) ξ0 I0 = r 1 2 R2 + ΩL − ΩC 1 ΩL − Ω cot Φ = − C R Cộng hưởng điện: 1 Ω = √ = ω0 LC
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 9.2 Câu hỏi lý thuyết 54 9.2 Câu hỏi lý thuyết Câu 29
Thiết lập phương trình dao động điện từ tắt dần. ■ [Lời giải]
+ Giả sử năng lượng của mạch giảm chỉ do tỏa nhiệt Jun-Lenx.
+ Giả sử trong khoảng thời gian dt, năng lượng dao động giảm một lượng −dW.
+ Nhiệt Jun-Lenx tỏa ra trên điện trở R là RI2dt. 1 q2 1 d 1 q2 1 −dW = RI2dt ⇒ −d + LI2 = RI2dt ⇒ + LI2 = −RI2 2 C 2 dt 2 C 2 q dq dI ⇒ + LI = −RI2 C dt dt q dI ⇒ + L + RI = 0 C dt 1 dq d2I dI ⇒ + L + R = 0 C dt dt2 dt d2I R dI 1 ⇒ + + I = 0 dt2 L dt LC 1 = ω2 Đặt LC d2I dI R R ⇒ + 2β + ω2I = 0 (∗) dt2 dt 0 = 2β → β = L 2L Với điều kiện R 2 ω , nghiệm của 0 > β hay 1 > (∗) có dạng: LC 2L q
I = I0eβt cos (ωt + ϕ), với ω = ω20 − β2 Câu 30
Thiết lập phương trình dao động điện từ cưỡng bức. ■ [Lời giải]
+ Xét thế điện động của nguồn ngoài là hàm sin của thời gian: ξ = ξ0 sinΩt
+ Trong khoảng thời gian dt, nguồn ngoài cung cấp năng lượng: ξ Idt.
+ Năng lượng này bằng độ tăng năng lượng điện từ của mạch và phần năng lượng biến thành nhiệt Jun-Lenx.
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 9.3 Bài tập 55 1 q2 1 q dq dI ξ Idt = d
+ LI2 + RI2dt ⇒ ξ0 sinΩtI = + LI + RI2 2 C 2 C dt dt q dI ⇒ ξ0 sinΩt = + L + RI C dt 1 dq d2I dI ⇒ ξ0ΩcosΩt = + L + R C dt dt2 dt d2I R dI 1 ξ ⇒ + + 0Ω I = cos Ωt dt2 L dt LC L 1 = ω2 Đặt ξ LC d2I dI 0Ω R R ⇒ + 2β + ω2 cos Ωt (1) dt2 dt 0 I = L = 2β → β = L 2L
⇒ I = I0e−βt cos(ωt + ϕ) + I0 cos(Ωt + Φ) (2)
Sau thời gian quá độ, số hạng thứ nhất trong (2) sẽ mất, dao động điện từ cưỡng bức ổn định với: 1 ξ ΩL − 0 Ω I = I ; C
0 cos (Ωt + Φ), trong đó: I0 = cot Φ = − r 1 2 R R2 + ΩL − ΩC 9.3 Bài tập Bài tập 25
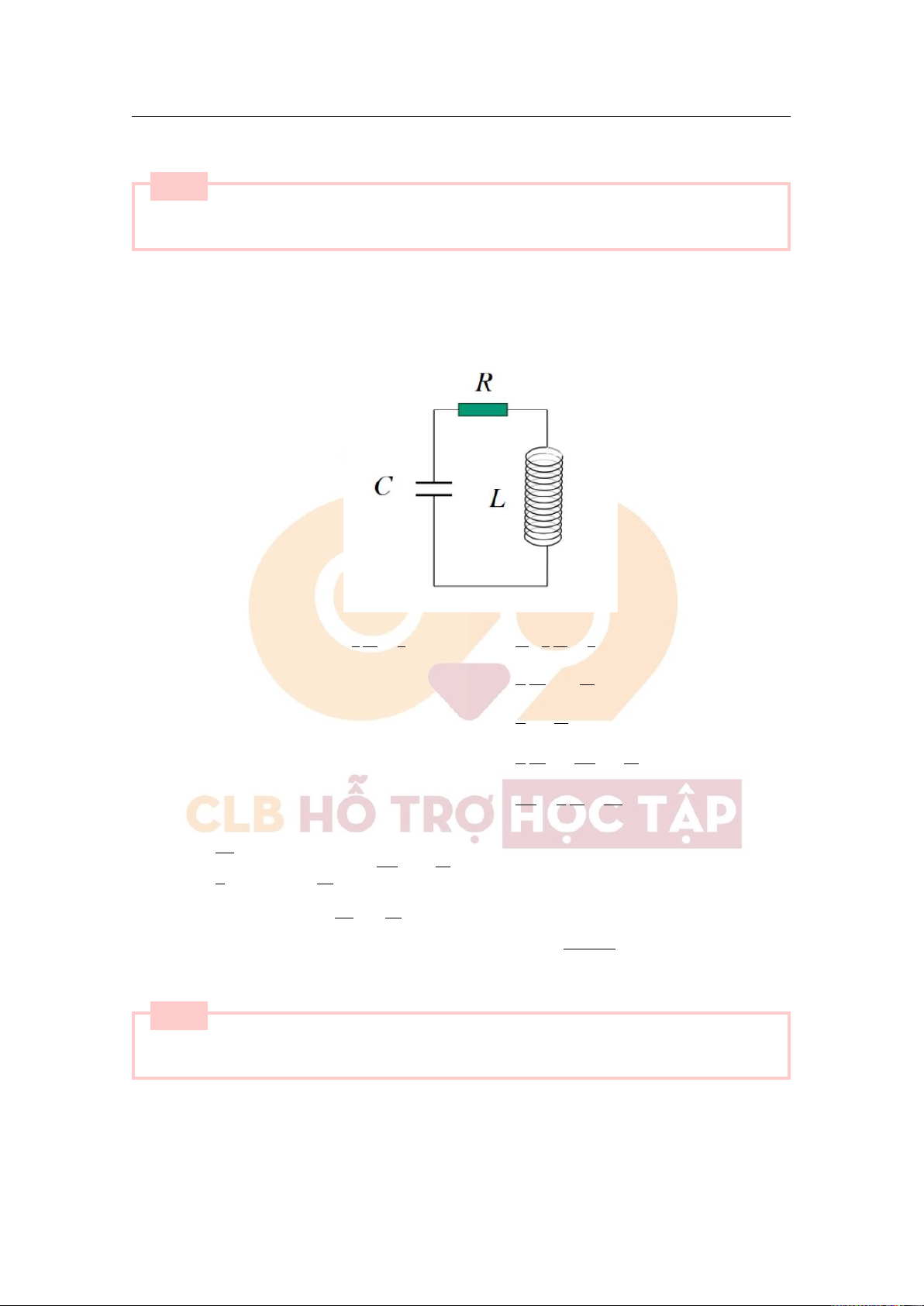
Một mạch dao động điện từ có điện dung C = 0,25µF, hệ số tự cảm L = 1,015H và điện trở r = 0.
Ban đầu hai cực của tụ điện được tích điện đến điện tích Q0 = 2,5.10−6C.
a. Viết phương trình dao động điện từ của mạch đối với điện tích q và dòng điện i.
b. Năng lượng điện từ của mạch.
c. Tần số dao động của mạch. ■ [Lời giải]
1. Phương trình dao động điện từ đối với điện tích q: q = Q0 cos (ω0t + ϕ) Với: 1 ω0 = √
= 1, 99.103 rad/s ≈ 2.103 rad/s LC (
Tại thời điểm ban đầu: t = 0 ⇒ cosϕ = 1 ⇒ ϕ = 0 q = Q0
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750 9.3 Bài tập 56
⇒ Phương trình: q = Q0 cos(ω0t + ϕ) = 2,5.10−6 cos(2.103t) Mà dq I =
= −ω0Q0 sinω0t = −5.10−3 sin(2.103t). dt
2. Năng lượng điện từ trường trong mạch: Q2 W = 0 = 12,5.10−6J 2C
3. Tần số dao động của mạch: 1 103 f = √ ≈ Hz 2π LC π Bài tập 26
Một mạch dao động có điện dung C = 35,4µF, hệ số tự cảm L = 0,7H và điện trở R = 100Ω. Đặt
vào mạch một nguồn điện xoay chiều có tần số 50Hz. Biên độ của suất điện động U0 = 220V. Tìm
biên độ cường độ dòng điện trong mạch. ■ [Lời giải]
Biên độ cường độ dòng điện trong mạch là: U0 U0 I = = r r 1 2 1 2 R2 + ΩL − R2 + 2π f L − ΩC 2π f C
Thay các giá trị: C = 35,4.10−6F, L = 0,7H, R = 100Ω, f = 50Hz, U0 = 220V, ta có: I ≈ 1, 34 A Bài tập 27
Hai tụ điện mỗi cái có điện dung C = 2mF, được mắc vào một mạch dao động gồm có cuộn cảm
L = 1mH, R = 5Ω. Hỏi những dao động điện từ xuất hiện trong mạch sẽ như thế nào nếu các tụ điện
được: a. Mắc song song b. Mắc nối tiếp ■ [Lời giải] r
Điều kiện để mạch dao động là: L R < 2 C r Nếu L R ≥ 2
thì trong mạch không có hiện tượng dao động. C 1. Hai tụ mắc song song: r L
Cbss = C1 +C2 ⇒ Cb = 2C ⇒ 2 = 3, 16 < R Cb
Vậy mạch không có hiện tượng dao động.
2. Hai tụ mắc nối tiếp: 1 1 1 C C r L = + ⇒ 1C2 Cbnt = = ⇒ 2 = 2 < R Cbnt C1 C2 C1 +C2 2 Cbnt
Vậy mạch không có hiện tượng dao động.
Downloaded by v?n ti?n Lê (vantienle525@gmail.com)

