









Preview text:
lOMoARcPSD|36442750 MÔN VẬT LÝ ĐẠI CƯƠNG VẬT L HOBO
TÀI LIỆU TỔNG HỢP VÀ BIÊN SOẠN BỞI CLB HỖ TRỢ HỌC TẬP
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
Bộ câu hỏi tự luận tham khảo - Vật lý đại cương 1 Học kỳ 2022.2
Lưu ý: Tài liệu chỉ sử dụng với mục đích ôn tập, sử dụng vào mục đích khác, CLB không chịu trách nhiệm.
Chương 2 - Động học chất điểm Câu 1
1. Định nghĩa vectơ gia tốc. Nêu đặc điểm và ý nghĩa của các vectơ gia tốc tiếp tuyến, gia tốc pháp tuyến.
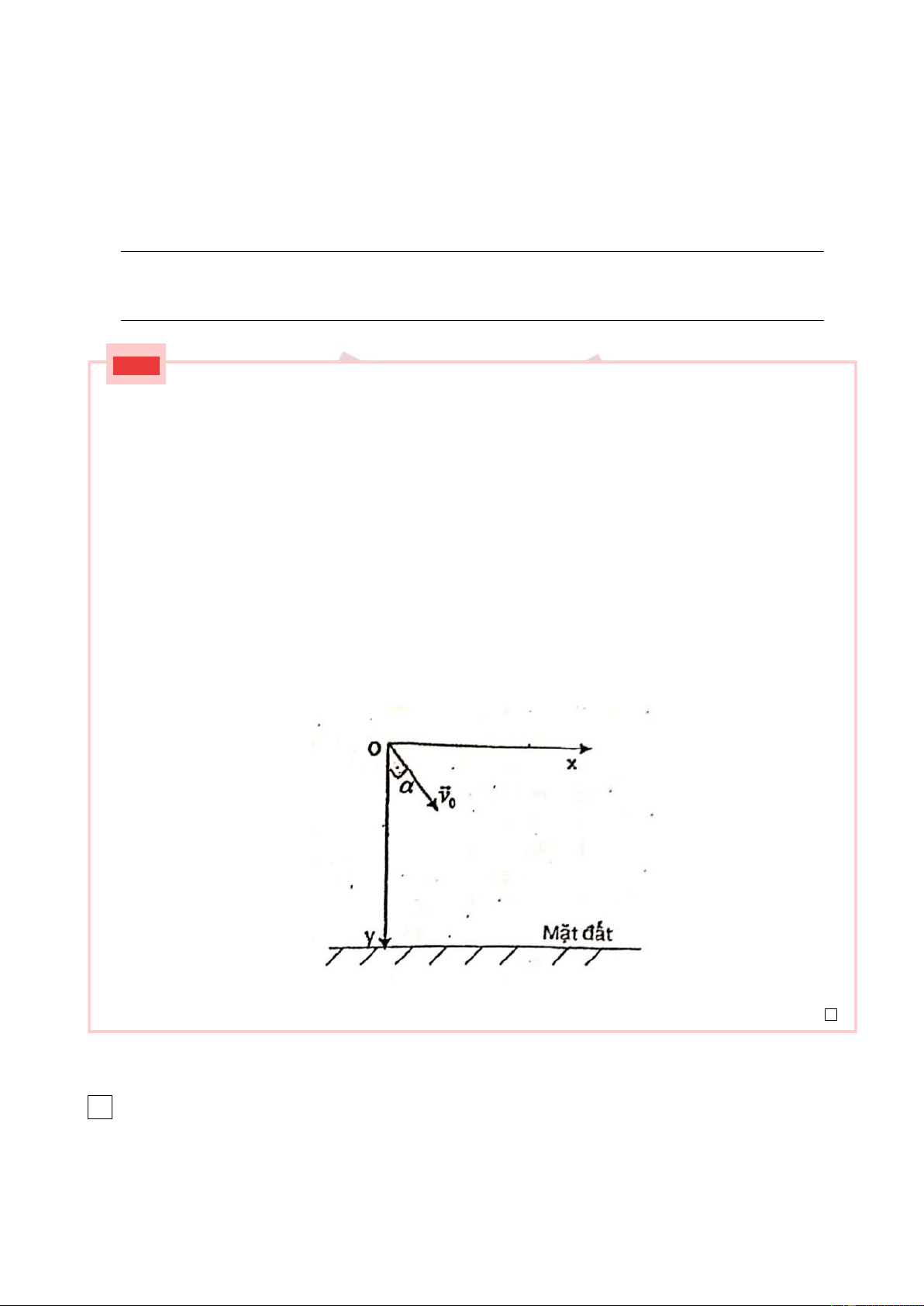
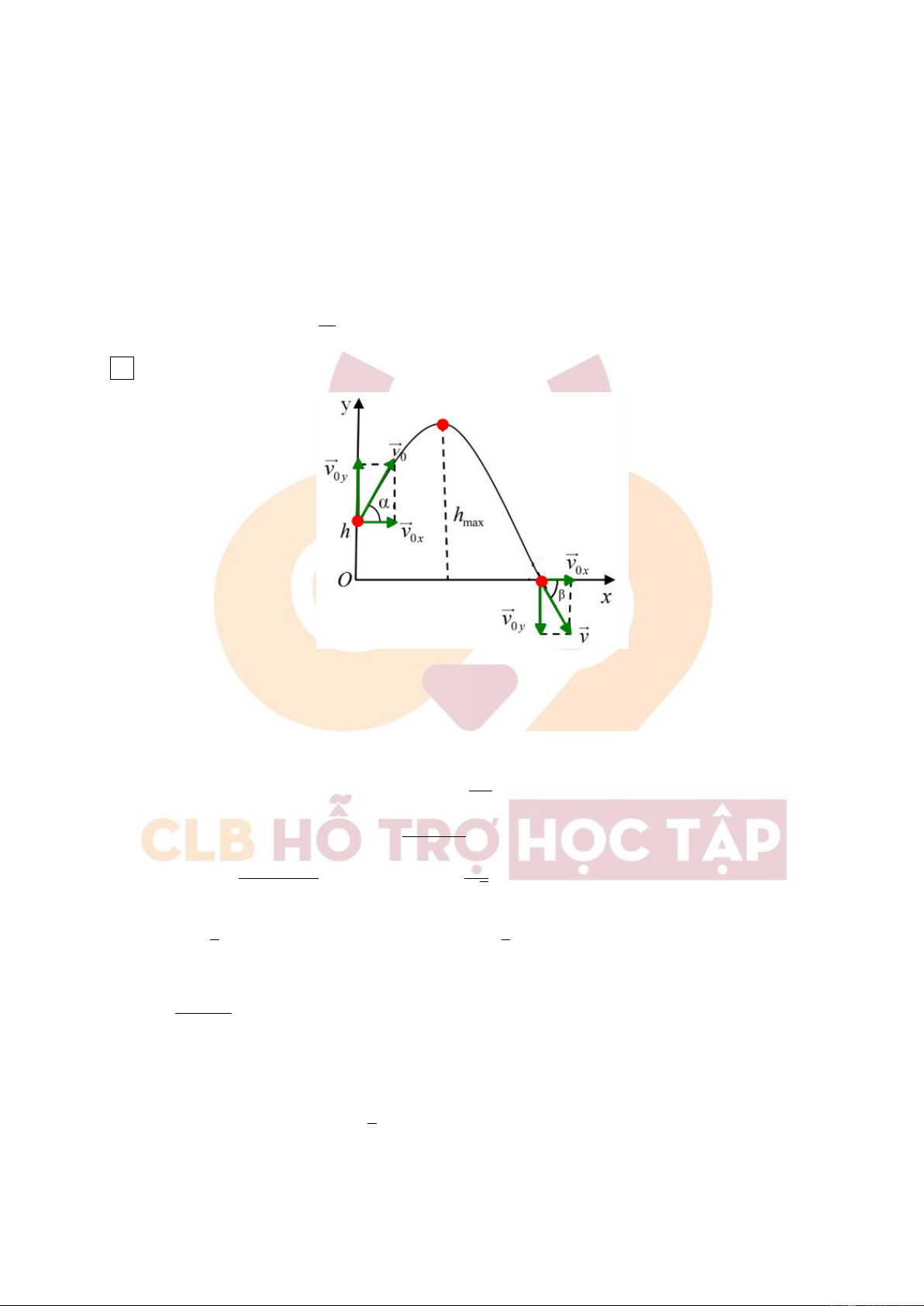
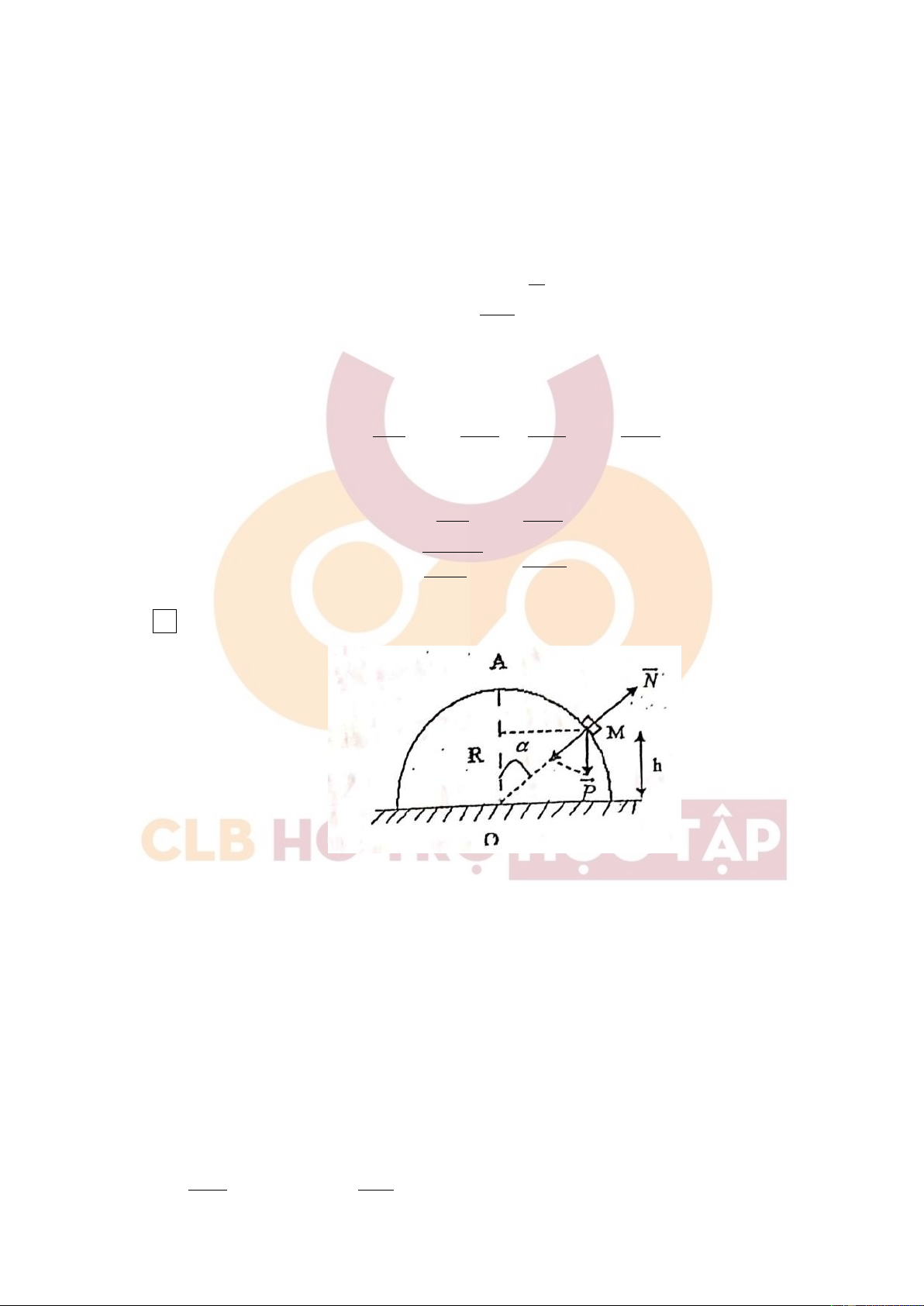
2. Từ đỉnh tháp có độ cao h,người ta ném một hòn đá xuống dưới đất với vận tốc ban đầu v0 theo
phương hợp với phương thẳng đứng 1 góc α (hình vẽ)
a) Viết phương trình chuyển động của hòn đá trong hệ toạ độ vuông góc, gốc toạ độ tại điểm bắt đầu ném (hình vẽ)
b) Cho h = 30m, v0 = 20m/s, α = 60o, g = 9, 8m/s2. Tìm thời gian bay và tốc độ của viên đạn khi chạm đất.
c) Tìm gia tốc pháp tuyển tại điểm chạm đất. Bỏ qua lực cản của không khí. [Lời giải] 1.
+ Định nghĩa vector gia tốc: Vecto gia tốc đặc trưng cho sự biến thiên của vector vận tốc, bằng đạo
hàm của vector vận tốc theo thời gian. 1
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
+ Gia tốc tiếp tuyến:
– Có phương trùng với phương tiếp tuyến của quỹ đạo.
– Có chiều là chiều chuyển động khi v tăng và ngược lại. – dv
Có độ lớn bằng đạo hàm của vecto vận tốc: at = dt
+ Gia tốc pháp tuyến:
– Có phương trùng với phương pháp tuyến của quỹ đạo
– Có chiều hướng về phía lõm của quỹ đạo – v2 Có độ lớn là an = R
+ Ý nghĩa của gia tốc tiếp tuyến và gia tốc pháp tuyến:
– Gia tốc tiếp tuyến: Đặc trưng cho sự biến thiên vận tốc về mặt giá trị.
– Gia tốc pháp tuyến: Đặc trưng cho sự biến thiên về phương của vecto vận tốc. 2.
a. Chọn trục Oxy như hình vẽ, gốc toạ độ là vị trí ném vật, gốc thời gian là lúc bắt đầu ném vật. v
Phương trình vận tốc là: x = v0. sin α vy = v0. cos α + gt x = v 0t. sin α
=⇒ Phương trình chuyển động là: gt2 y = v 0t. cos α + 2
b. Với h = 30m, v0 = 20m/s, α = 60o, g = 9, 8m/s2 √ √ vx = 10 3 x = 10 3 =⇒ =⇒ vy = 10 + 9, 8t y = 10t + 4, 9t2
Thời gian bay của hòn đá: y = h 2
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
=⇒ 4, 9t2 + 10t − 30 = 0 ⇐⇒ t = 1, 66s √ v 3m/s
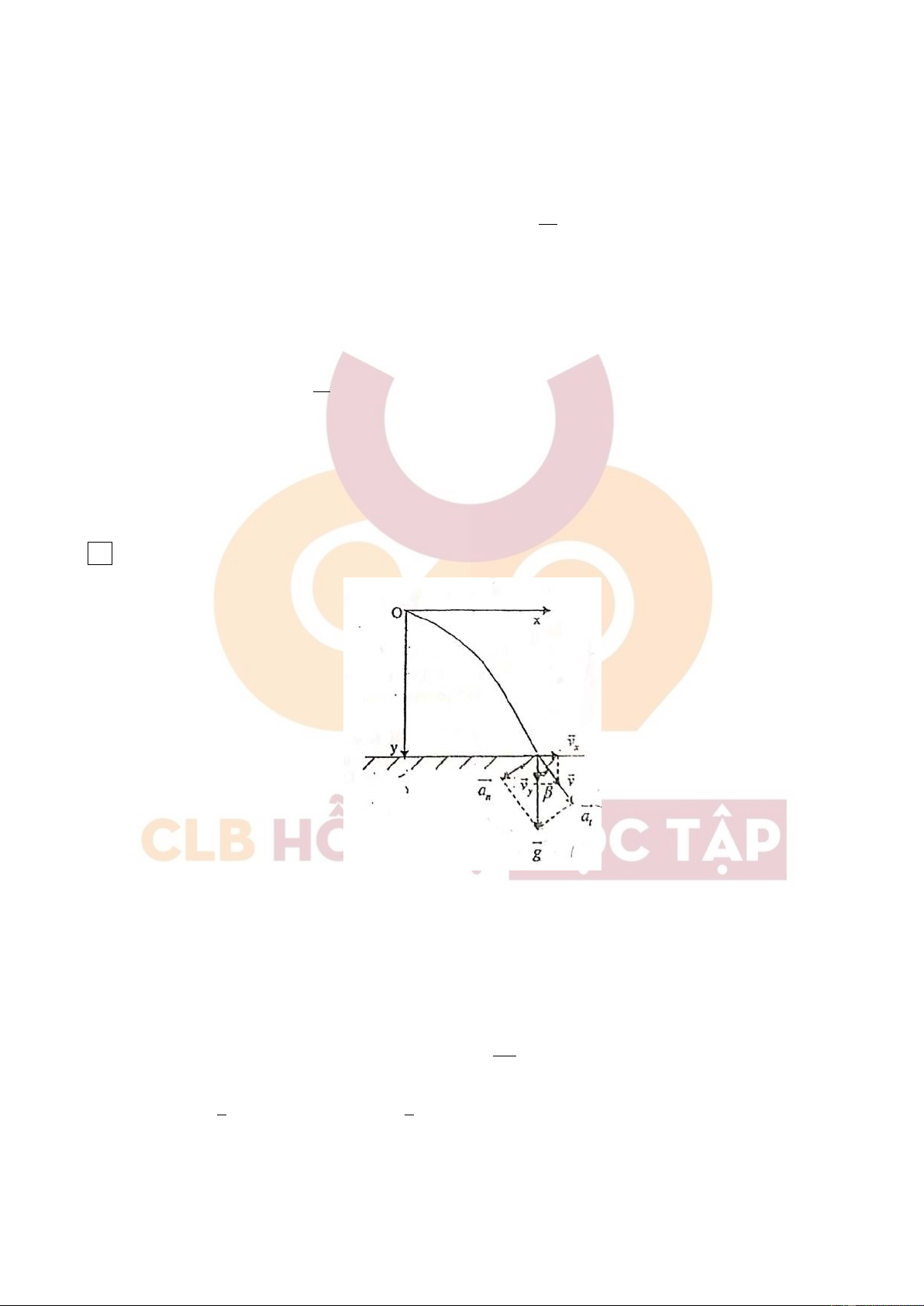
Tốc độ hòn đá khi chạm đất x = 10 =⇒ v = px2 + y2 = 31, 47m/s vy = 26, 27m/s c. Tại t = 1, 66s dv d
Gia tốc tiếp tuyến của hòn đá: a p t = =
300 + (10 + 9, 8t)2 = 8, 18m/s2 dt dt
Gia tốc pháp tuyến của hòn đá: an = pg2 − a2t = p9, 82 − 8, 182 = 5, 39m/s2 Câu 2
Viết biểu thức, nêu đặc điểm của vectơ vận tốc góc và vectơ gia tốc góc. [Lời giải]
+ Vectơ vận tốc góc: thể hiện tốc độ và hướng xoay của một vật thể khi nó di chuyển trên quỹ đạo
tròn hay quỹ đạo cong. Độ lớn của vectơ vận tốc góc xác định tại lúc t xác định bởi: ∆θ dθ | ⃗ω |= lim = ∆t→0 ∆t dt
+ Đặc điểm vectơ vận tốc góc:
– Độ lớn vectơ vận tốc góc thể hiện tốc độc xoay của vật thể, bằng đạo hàm của góc quay đối với thời gian.
– Phương: nằm trên trục của vòng tròn quỹ đạo.
– Chiều: thuận với chiều quay của chuyển động (tạo với vectơ vận tốc dài và vectơ bán kính một tam diện thuận).
– Mối liên hệ vectơ vận tốc góc và vectơ vận tốc dài: ⃗v = ⃗ω ∧ ⃗R ( ⃗R là vectơ bán kính).
+ Vectơ gia tốc góc: ⃗ d⃗ω β = dt
+ Đặc điểm vectơ gia tốc góc:
– Phương: nằm trên trục quỹ đạo tròn.
– Chiều: cùng chiều với ⃗ω khi β > 0 và ngược chiều ⃗ω khi < 0.
– Có giá trị bằng β (bằng đạo hàm của vận tốc góc đối với thời gian).
– Mối liên hệ gia tốc tiếp tuyến và gia tốc góc: ⃗at = ⃗β ∧ ⃗R . 3
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
Chương 3 - Động lực học chất điểm Câu 3
1. Trình bày các vấn đề sau:
a) Hệ quy chiếu quán tính và nguyên lý tương đối Galile
b) Hệ quy chiếu không quán tính và lực quán tính ly tâm
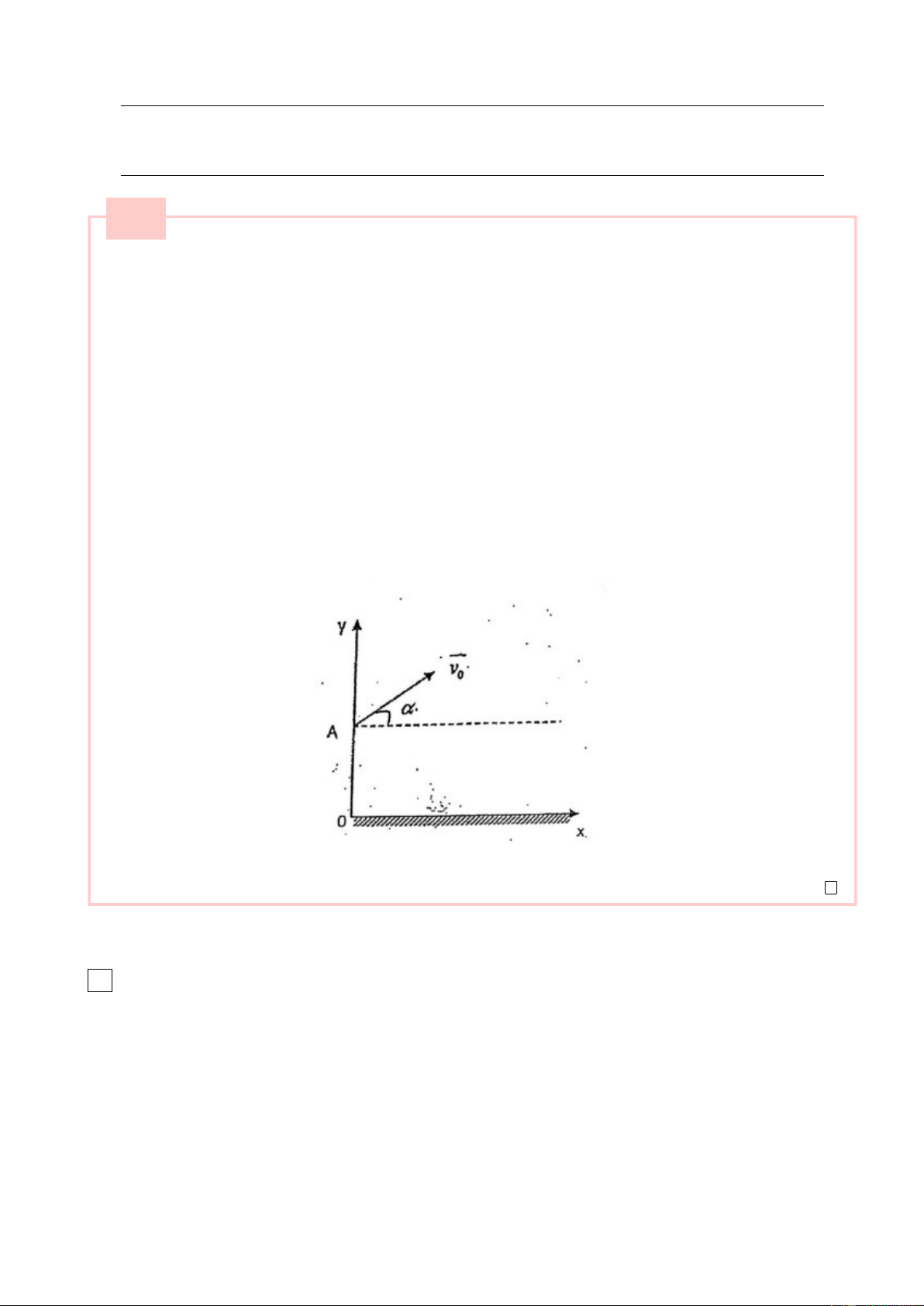
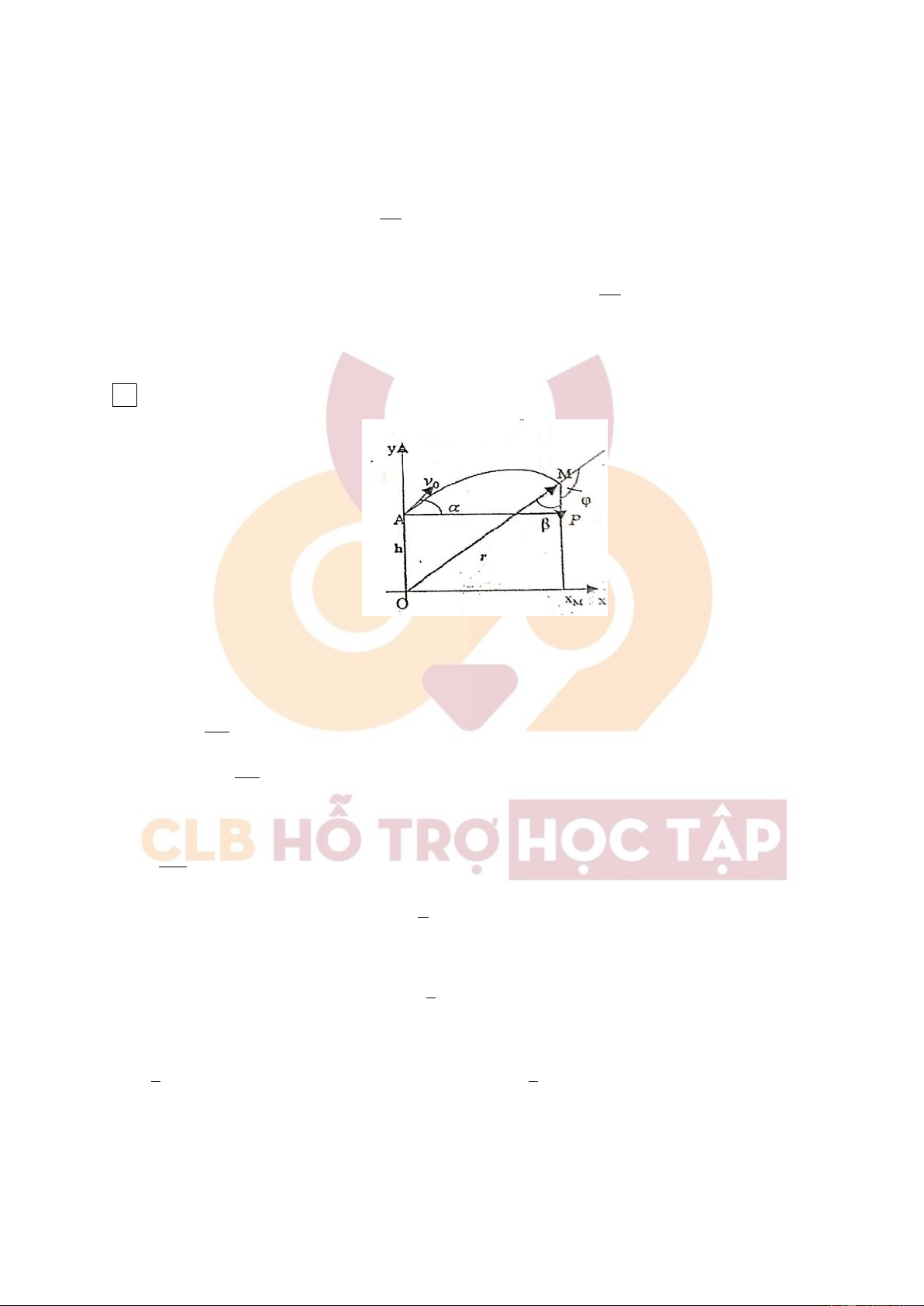
2. Từ một đỉnh tháp A cao h = 25m người ta ném một hòn đá lên phía trên theo phương hợp với
phương nằm ngang một góc α = 30o với tốc độ v0 = 15m/s (hình vẽ). Xác định:
a) Quỹ đạo của hòn đá, chọn gốc tọa độ ở chân tháp.
b) Tốc độ của hòn đá sau 2 giây kể từ khi ném.
c) Thời gian để hòn đá rơi xuống đất và tầm ném xa tính từ chân tháp. Lấy g = 9, 8m/s2 [Lời giải] 1.
+ Hệ quy chiếu quán tính: HQC mà trong đó các định luật quán tính của Newton được nghiệm đúng.
+ Nguyên lý tương đối Galileo: Mọi hệ qui chiếu chuyển động thẳng đều với một HQC quán tính
cũng là HQC quán tính. Hay các định luật Newton được nghiệm đúng trong hệ quy chiếu chuyển
động thẳng đều đối với hệ quy chiếu quán tính.
+ Hệ quy chiếu không quán tính: là HQC trong đó có xuất hiện gia tốc. Trong đó, các định luật 4
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
quán tính không được nghiệm đúng.
+ Lực quán tính ly tâm: Giả sử HQC không quán tính O1 chuyển động tròn quanh HQC quán tính
với gia tốc hướng tâm ⃗aht. Khi khảo sát chuyển động của vật trong HQC không quán tính O1, vật
chịu thêm tác dụng của lực ⃗
Fqtlt. Lực quán tính ly tâm ⃗ Fqtlt: – Là lực ảo – ⃗
Fqtlt ngược chiều với lực hướng tâm – v2 Độ lớn: |Fqtlt| = m R
2. Chọn trục Oxy như hình vẽ: v Phương trình vận tốc : x = v0. cos α vy = v0. sin α − gt x = v 0t. cos α
=⇒ Phương trình chuyển động: gt2 y = v + h 0t. sin α − 2 a. x
Từ phương trình chuyển động ta có t = , thay vào y: v0. cos α g 1 y = h + x. tan α −
.x2 ⇐⇒ y = 25 + √ x − 0, 029x2 2v2o. cos2 α 3
Vậy quỹ đạo là parabol. √ √ v 3 v 3m/s b. x = 7, 5 x = 7, 5 =⇒ Sau t = 2s, vy = 7, 5 − 9, 8t vy = −12, 1m/s =⇒ v = px2 + y2 = 17, 85m/s
c. Khi vật chạm đất, tức là y = 0
=⇒ −4, 9t2 + 7, 5t + 25 = 0 ⇐⇒ t = 3, 15(s) √
Tầm xa của vật: L = vx.t = 7, 5. 3.3, 15 = 40, 92(m) 5
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập Câu 4 1.
a) Nêu định nghĩa động lượng của một chất điểm và của một hệ chất điểm.
b) Trình bày các định lý về động lượng của chất điểm. Nêu ý nghĩa xung lượng của lực.
c) Trình bày định luật bảo toàn động lượng của hệ chất điểm cô lập và định luật bảo toàn động
lượng theo phương của hệ chất điểm. 2. Bài toán:
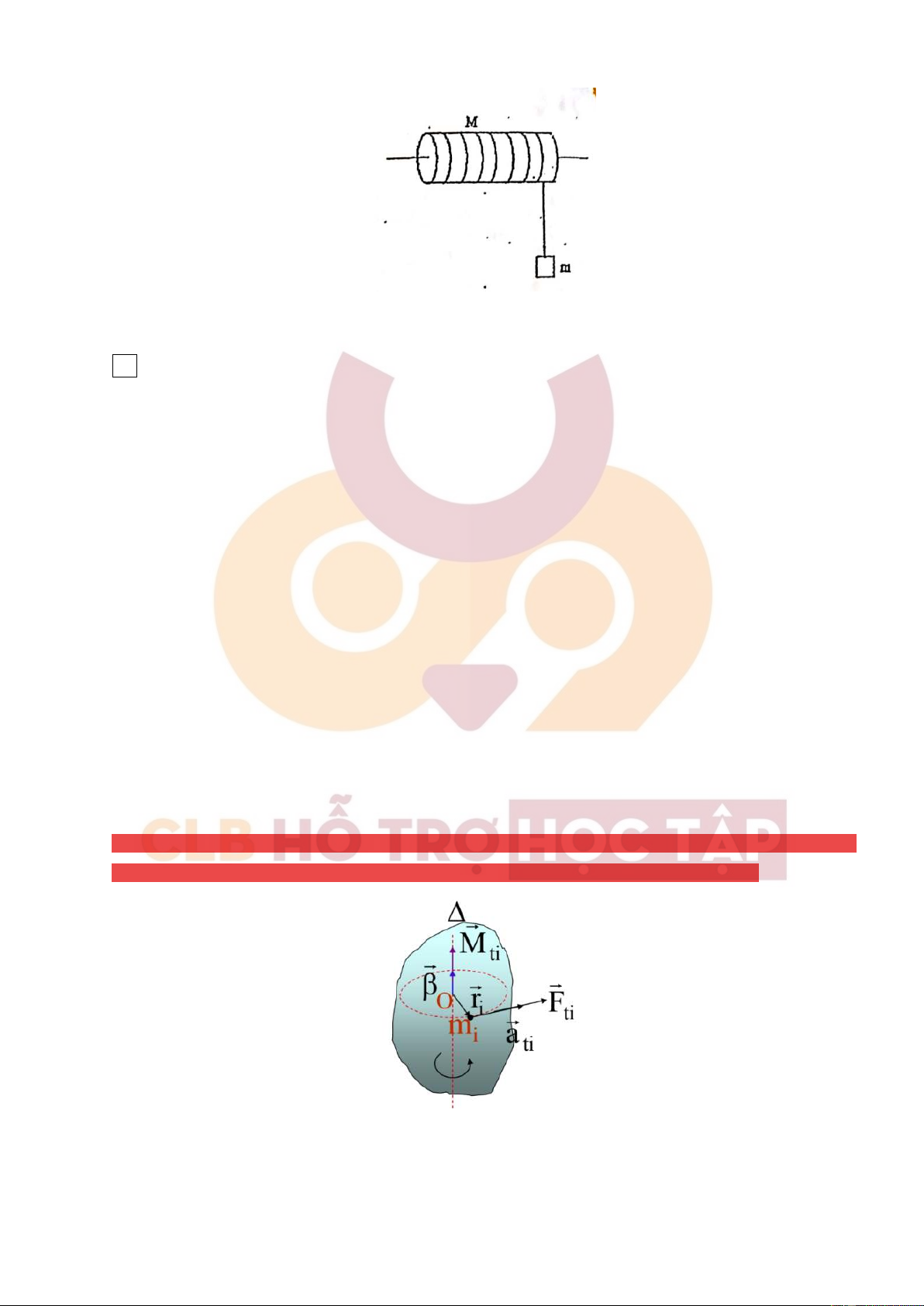
Một bì cát có khối lượng M được treo bằng một sợi dây mảnh không giãn. Bắn một viên đạn có
khối lượng m theo phương ngang và có tốc độ v vào bì cát. Viên đạn bị mắc vào đó và bì cát được
nâng lên đến độ cao h so với vị trí ban đầu. Tính tốc độ v theo các đại lượng m, M, h, g. [Lời giải] Giải 1.
a) Động lượng của 1 chất điểm là tích của khối lượng chất điểm đó nhân với vecto vận tốc.
Động lượng của 1 hệ chất điểm là tổng động lượng của các chất điểm. b)
+ Thiết lập định lý I: ⃗
F = −m⃗a = md⃗v = d(m⃗v). Gọi ⃗
K = m⃗v là vecto động lượng. dt dt ⃗ F = d ⃗K dt
Đạo hàm động lượng của một chất điểm đối với thời gian có giá trị bằng tổng hợp các lực tác
dụng lên chất điểm đó.
+ Thiết lập định lý II: ⃗ F = d ⃗K → ⃗ F dt = d ⃗ K dt
Tích phân 2 vế trong khoảng thời gian từ t1 đến t2 ứng với sự biến thiên động lượng từ ⃗ K1 đến ⃗ K2 K2 t2 t2 ˆ − → ˆ − → − → −→ −→ ˆ − → dK = F dt → ∆K = K2 − K1 = F dt K1 t1 t1 Nếu trong thời gian − → − → ∆t mà − →
F = const thì ∆K = F · ∆t
Độ biến thiên động lượng của một chất điểm trong khoảng thời gian nào đó có giá trị bằng xung
lượng của lực (hay tổng hợp lực) tác dụng lên chất điểm trong khoảng thời gian đó.
+ Ý nghĩa xung lượng của lực:
– Xung lượng của lực trong khoảng thời gian ∆t đặc trưng cho tác dụng của lực trong khoảng thời gian đó. 6
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
– Lực tuy lớn song thời gian tác dụng ngắn thì xung lượng của nó nhỏ và làm thay đổi trạng
thái chuyển động ít hơn so với cùng lực đó tác dụng trong thời gian dài;
– Tác dụng của lực không chỉ phụ thuộc vào cường độ mà còn phụ thuộc vào thời gian tác động. c)
+ Định luật bảo toàn động lượng của hệ chất điểm cô lập:
Xét hệ chất điểm cô lập thì − →
F = 0 và m1v1 + m2v2 + ... + mnvn = const
Vậy: Tổng động lượng của 1 hệ chất điểm cô lập là đại lượng bảo toàn.
+ Định luật bảo toàn động lượng theo một phương của hệ chất điểm:
Xét hệ chất điểm không cô lập − → F ̸= 0. d Nếu hình chiếu của − →
F lên phương x bằng không, chiếu phương trình (m dt 1v1 + m2v2 + ... + − → mnvn) = F lên phương x: d − → (m F dt 1v1 + m2v2 + ... + mnvn) = x = 0 → m −→ −→ −→
1v1x + m2v2x + ... + mnvnx = const
Vậy hình chiếu của tổng động lượng của hệ lên 1 phương x được bảo toàn. 2. Va chạm là va chạm mềm.
Gọi V là vận tốc của hệ viên đạn và bì cát sau va chạm.
Áp dụng định luật bảo toàn động lượng ta có: m mv = (M + m)V =⇒ V = v (1) m + M
Áp dụng định luật bảo toàn cơ năng ta có: 1
(M + m)gh = (M + m)V 2 =⇒ V = p2gh (2) 2 m √ M + m √ Từ (1) và (2) ta có: v = 2gh =⇒ v = 2gh M + m m 7
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập Câu 5
1. Nêu quan niệm về không gian và thời gian trong cơ học Newton. Phép biến đổi Galileo. Phát
biểu nguyên lý tương đối Galileo. 2. Bài toán:
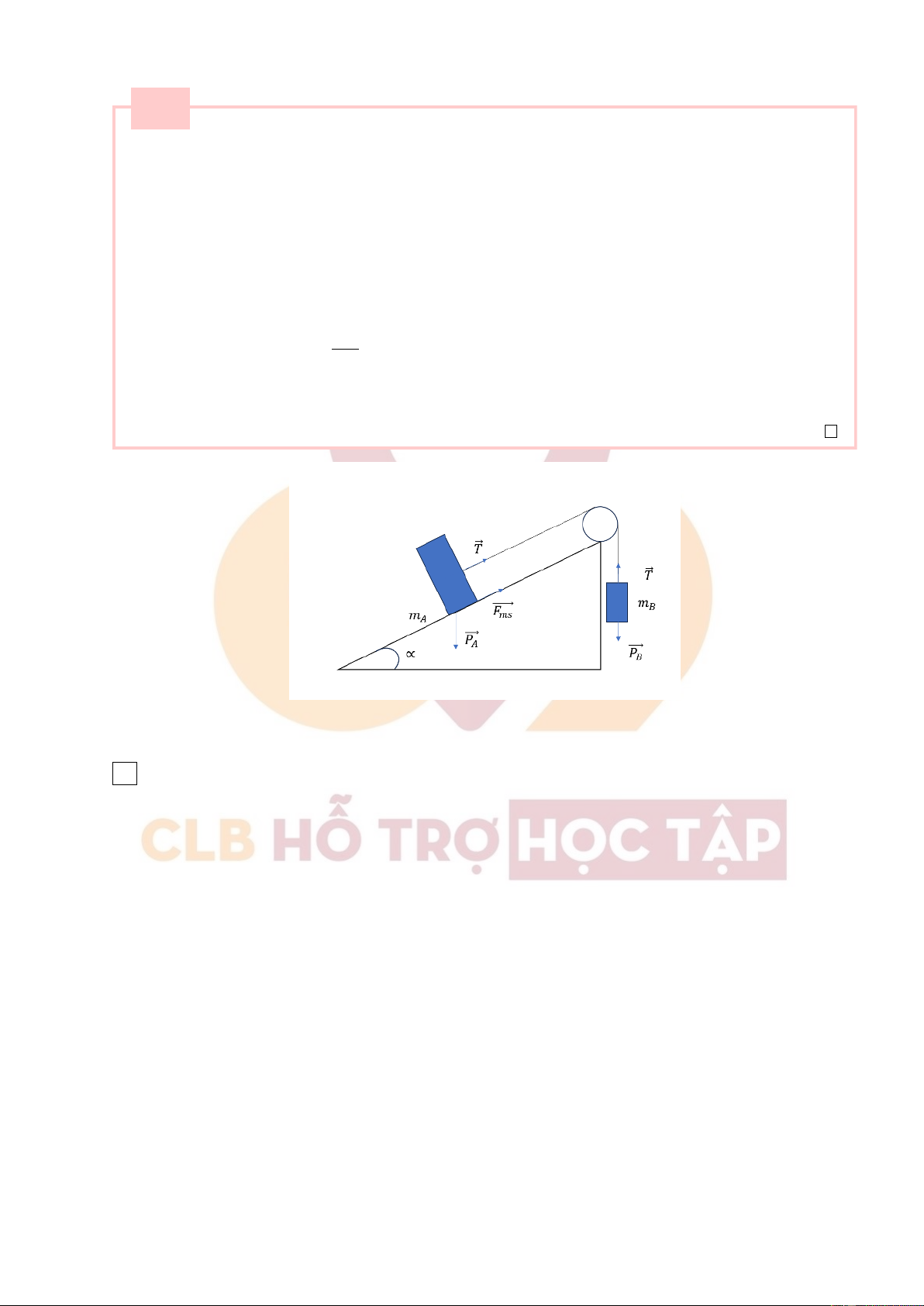
Một vật A có khối lượng mA đăt trên mặt phẳng nghiêng một góc α nối với vật B có khối lượng
mB bằng một sợi dây mảnh không giãn vắt qua ròng rọc có khối lượng không đáng kể (hình
vẽ).Hệ số ma sat giữa vật A và mặt phẳng nghiêng là k.Bỏ qua ma sát của ròng rọc. m
a) Tìm điều kiện của tỉ số B để vật B đi lên mA
b) Tìm gia tốc của các vật và lực căng dây khi đó. [Lời giải] 1.
+ Quan niệm về không gian và thời gian trong cơ học Newton:
– Thời gian có tính tuyệt đối, không phụ thuộc vào HQC
– Vị trí không gian có tính tương đối, phụ thuộc vào HQC
– Khoảng không gian có tính tuyệt đối, không phụ thuộc vào HQC
+ Phép biến đổi Galileo: Giả sử O′ chuyển động thẳng đều dọc theo Ox với vận tốc ⃗V . Nếu tại
t = 0, O′ trùng với O, ta có: ¯ OO′ = V t x = x′ + V t x′ = x − V t y = y′ y′ = y Ngược lại: z = z′ z′ = z t = t′ t′ = t 8
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
+ Nguyên lí tương đối Galileo: Mọi hệ quy chiếu chuyển động thẳng đều đối với 1 hệ quy chiếu
quán tính cũng là 1 hệ quy chiếu quán tính, hay là định luật Newton được nghiệm đúng trong hệ
quy chiếu chuyển động thẳng đều với hệ quy chiếu quán tính. 2. a)
Chọn chiều dương là chiều chuyển động của vật B đi lên (như hình vẽ).
Các lực phân tích như hình vẽ. m
Chiếu các lực lên trục (+) ta có:
A. sin α − k.mA.g. cos α − T = mA.a (1) T − mB.g = mB.a
→ mA(g. sin α − k.g. cos α) − mB.g = a(mA + mB) (2 )
Để B đi lên → a > 0 → mA(sin α − k. cos α) − mB > 0
→ mB < sin α − k. cos α mA mA sin α − k. cos α − mB a = .g b) Từ (1) và (2), ta có: mA + mB T = mB (a + g) 9
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập Câu 6 1.
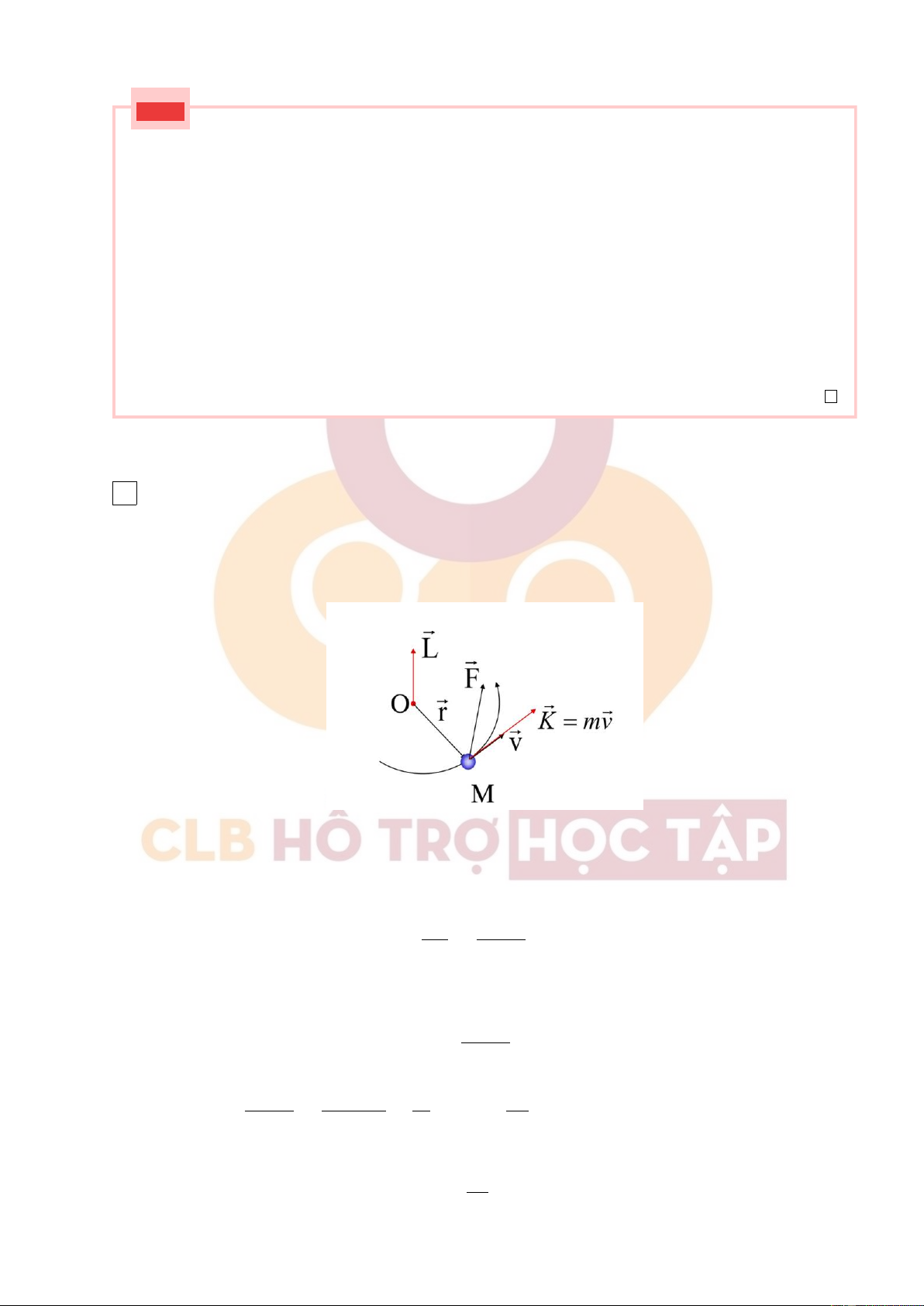
a) Định nghĩa mômen động lượng của một chất điểm đối với gốc O.
b) Trình bày định lý về mômen động lượng của một chất điểm và định luật bảo toàn mômen
động lượng của chất điểm. 2. Bài toán:
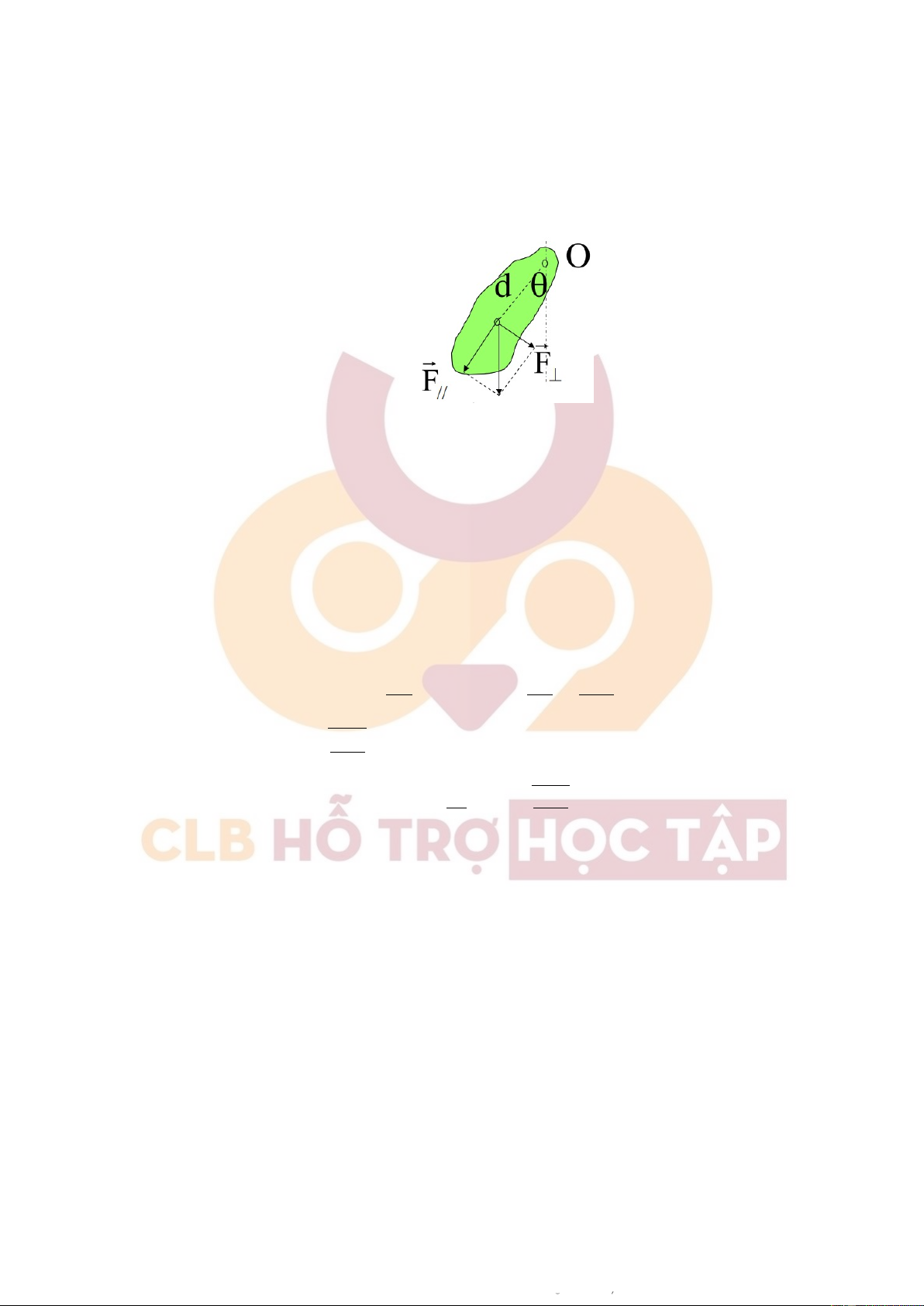
Từ một đỉnh tháp có độ cao h người ta ném một hòn đá có khối lượng m lên phia trên với vận tốc
v0 theo phương hợp với phương ngang một góc α.Tìm momen ngoại lực và momen động lương
của hòn đá đối với gôc O ở thời điểm t (gốc O chọn tại vị trí của chân tháp) [Lời giải] 1.
a) Momen động lượng của 1 chất điểm đối với gốc O: là đại lượng được xác định bằng tích có
hướng của vecto bán kính quỹ đạo với vecto động lượng ⃗ K. b)
+ Định lý về momen động lượng của một chất điểm đối với gốc toạ độ:
Xét chất điểm M chuyển động trên quỹ đạo cong dưới tác dụng của lực ⃗
F . Theo định lý về động lượng: d ⃗ K d(m⃗v) = = ⃗ F (∗) dt dt
Nhân có hướng hai về (*) với −−→ ⃗r = OM d(m⃗v) ⃗r × = ⃗r × ⃗ F dt d(m⃗v) d(⃗r d⃗r d⃗ L Vế trái: × ⃗v) ⃗r × = − × m⃗v = dt dt dt dt
Vế phải: ⃗r × ⃗F = ⃗µ/o( ⃗F ) mômen của lực ⃗F đối với O d⃗ L → = ⃗µ dt /o( ⃗ F ) 10
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
Đạo hàm theo thời gian của mômen động lượng của chất điểm đối với điểm O có giá trị bằng
mômen đối với O của tổng hợp lực tác dụng lên chất điểm.
+ Định luật bảo toàn mômen động lượng của chất điểm: – ⃗ d⃗ L F = 0 → ⃗µ/o( ⃗ F ) = 0 → = 0 → ⃗L = const dt
– Trong trường hợp chất điểm chuyển động luôn chịu tác dụng của 1 lực xuyên tâm (phương d⃗ L
của lực luôn đi qua điểm O cố định) thì ⃗µ/o( ⃗ F ) = 0 → = ⃗µ dt /o( ⃗
F ) = 0 → ⃗L = const
Vì ⃗L vuông góc với mặt phẳng chứa O và ⃗ K = m⃗v mà ⃗
L không đổi nên mặt phẳng này
cũng không đổi. Như vậy chất điểm luôn chuyển động trong mặt phẳng cố định.
2. Chọn gốc tọa độ O tại chân tháp, gốc thời gian là lúc bắt đầu ném. (Như hình vẽ) Ngoại lực tác dụng: − → − → F = P .
a. Độ lớn của momen ngoại lực: − → − →
M (P ) = P.r. sin( P , R ) = m.g.r. sin ϕ = m.g.r. sin β (1) x
Mà sin β = M , thay vào (1) ta được: r x M (P ) = m.g.r. M = m.g.x r M = (m.g.v0. cos α) t.
b. Độ lớn của momen động lượng. − → d L ˆ ˆ ˆ Ta có −−→ − → = M F ) =⇒ dL = M.dt =⇒ dL = M dt =⇒ L = M.dt + L dt /o( 0 π Trong đó: − → L0 = − → r . P = m.v0. sin α +
là momen động lượng tại A 2
=⇒ L0 = m.v0.r. cos α = h.m.v0. cos α ˆ ˆ 1 Lại có M dt = (mg.v0. cos α) tdt = mg.v 2 0. cos α.t2
=⇒ Độ lớn của momen động lượng của vật: 1 1 L = mg.v gt2 + h . 2
0. cos α.t2 + m.v0. cos α.h = m.v0. cos α. 2 11
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
Chương 4 - Cơ năng và trường lực thế Câu 7
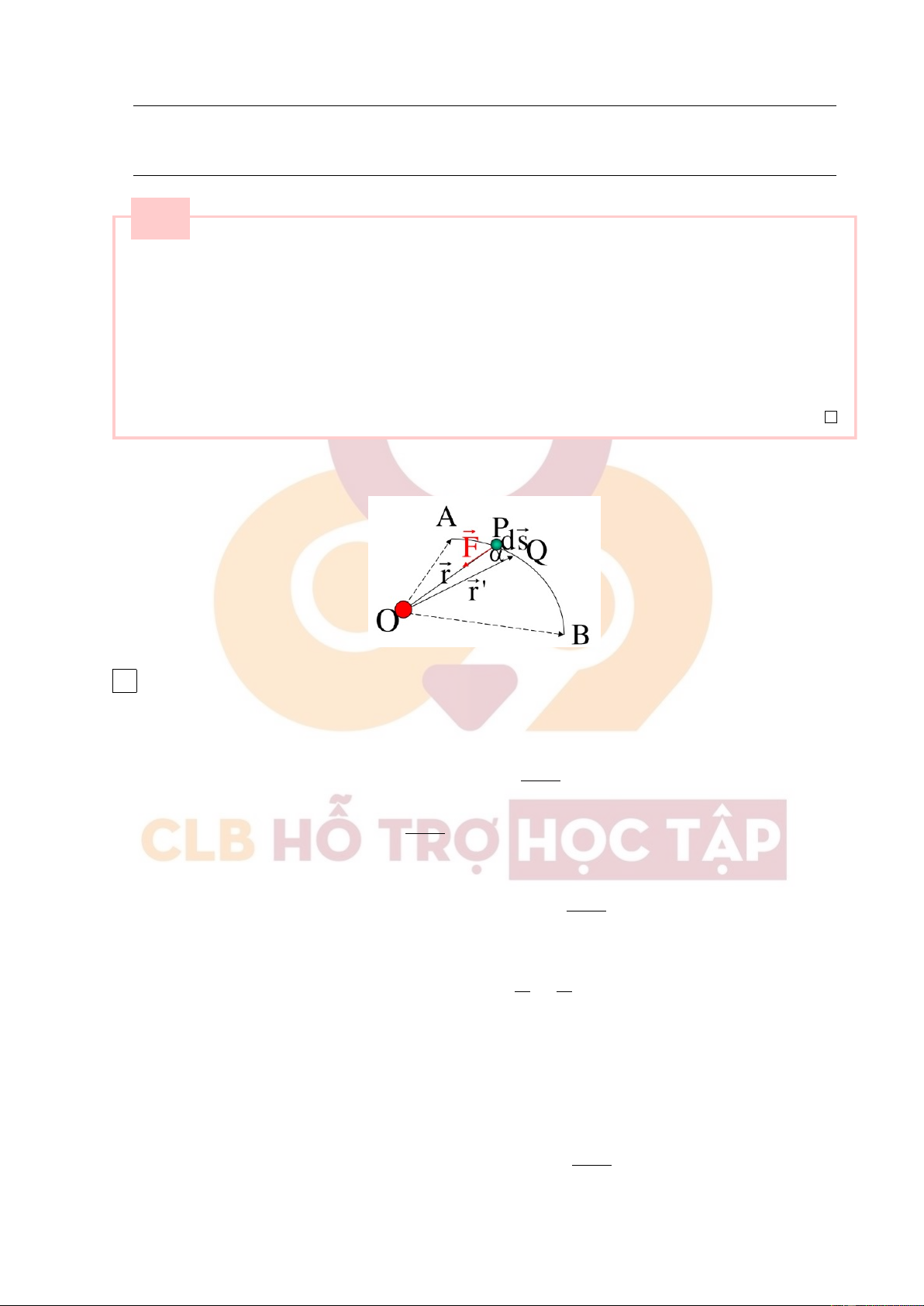
1. Tính công của lực hấp dẫn khi một vật có khối lượng m chuyển động trong trường hấp dẫn gây
bởi một vật có khối lượng M từ vị trí ⃗ r1 đến vị trí ⃗
r2. (Xem các vật như chất điểm, có vẽ hình).
Từ đó suy ra biểu thức tính thế năng của chất điểm trong trường hấp dẫn.
2. Bài toán: Tính thế năng hấp dẫn của một vật m cách Trái Đất (có khối lượng M) một khoảng
r tính từ tâm trái đất. Từ đó tính thế năng của vật có khối lượng m khi vật m cách bề mặt trái đất
một khoảng h«R, lấy mốc thế năng tại mặt đất. [Lời giải] 1.
+ Biểu thức tính của lực ⃗ F trên đoạn đường s: A = ⃗ F .⃗s = F s cos α M.m ⇒ dA = ⃗ F d⃗s = G .ds. cos α r2 M.m
Mà ds cos α = −dr ⇒ dA = −G dr r2 B r2 ˆ ˆ M.m ⇒ A = dA = −G dr r2 A r1 1 1 = G.M.m( − ) r2 r1
⇒ Công của lực hấp dẫn không phụ thuộc vào đường đi mà chỉ phụ thuộc vào vị trí điểm đầu và điểm cuối.
+ Biểu thức tính thế năng của chất điểm trong trường hấp dẫn: M.m A = W1 − W2 ⇒ W = −G + C r
với C là hằng số phụ thuộc vào gốc tính thế năng 12
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập 2.
+ Ta có biểu thức tính thế năng của chất điểm trong trường hấp dẫn là: M.m W (r) = −G + C r
+ Chọn mốc thế năng tại mặt đất, biểu thức tính thế năng của chất điểm trong trường hấp dẫn của trái đất là: M.m(r − R) W = G rR
+ Có r = R + h, khi h«R ta có r − R = h và rR ≈ R2 M.m GM ⇒ W = G h = mg
≈ 9, 8m/s2 là gia tốc trọng trường trên mặt đất. R2 0h với g0 = R2 Câu 8
1. Xét chuyển động của viên đạn trong trường hấp dẫn của Trái Đất. Tính vận tốc vũ trụ cấp I và cấp II
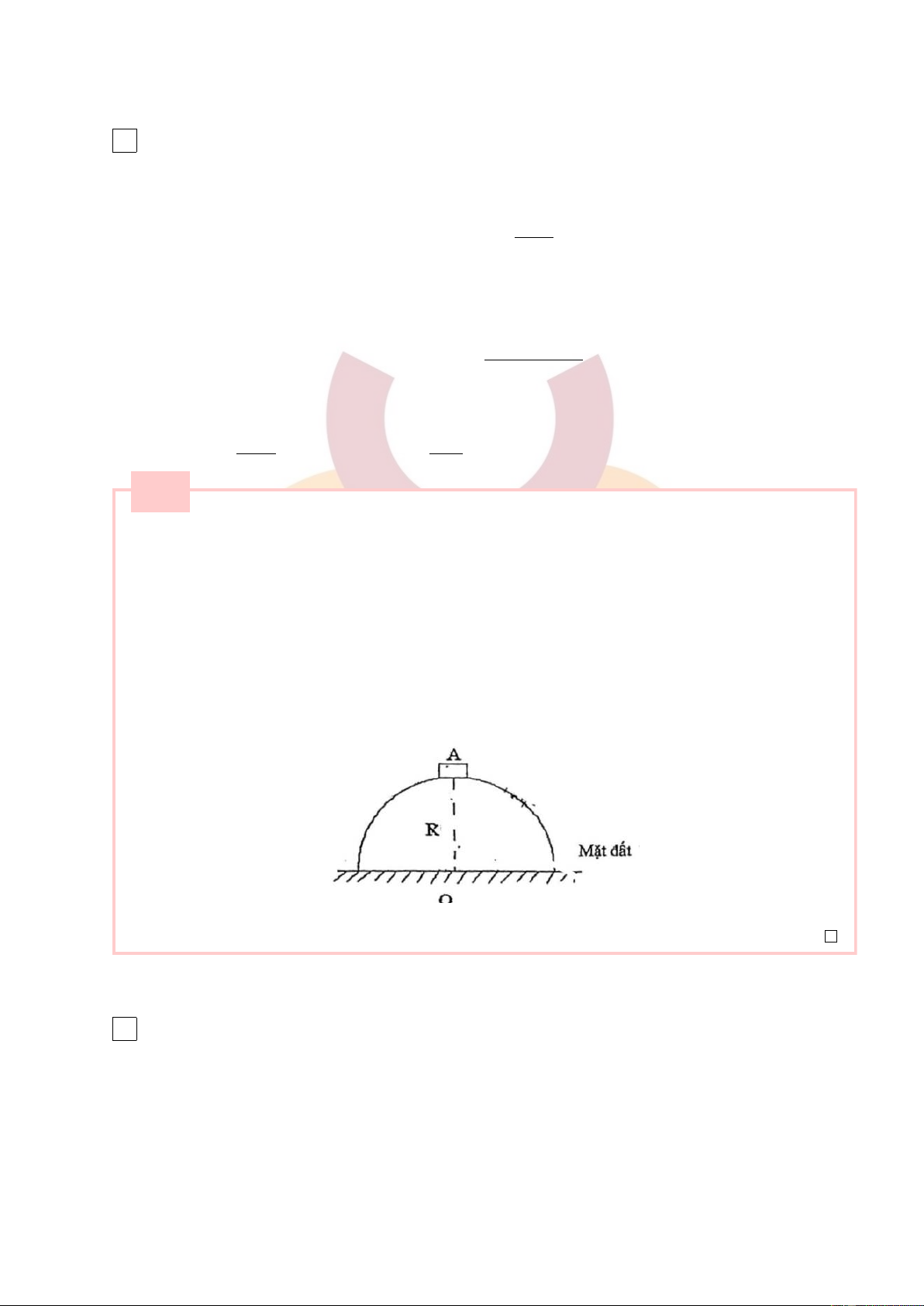
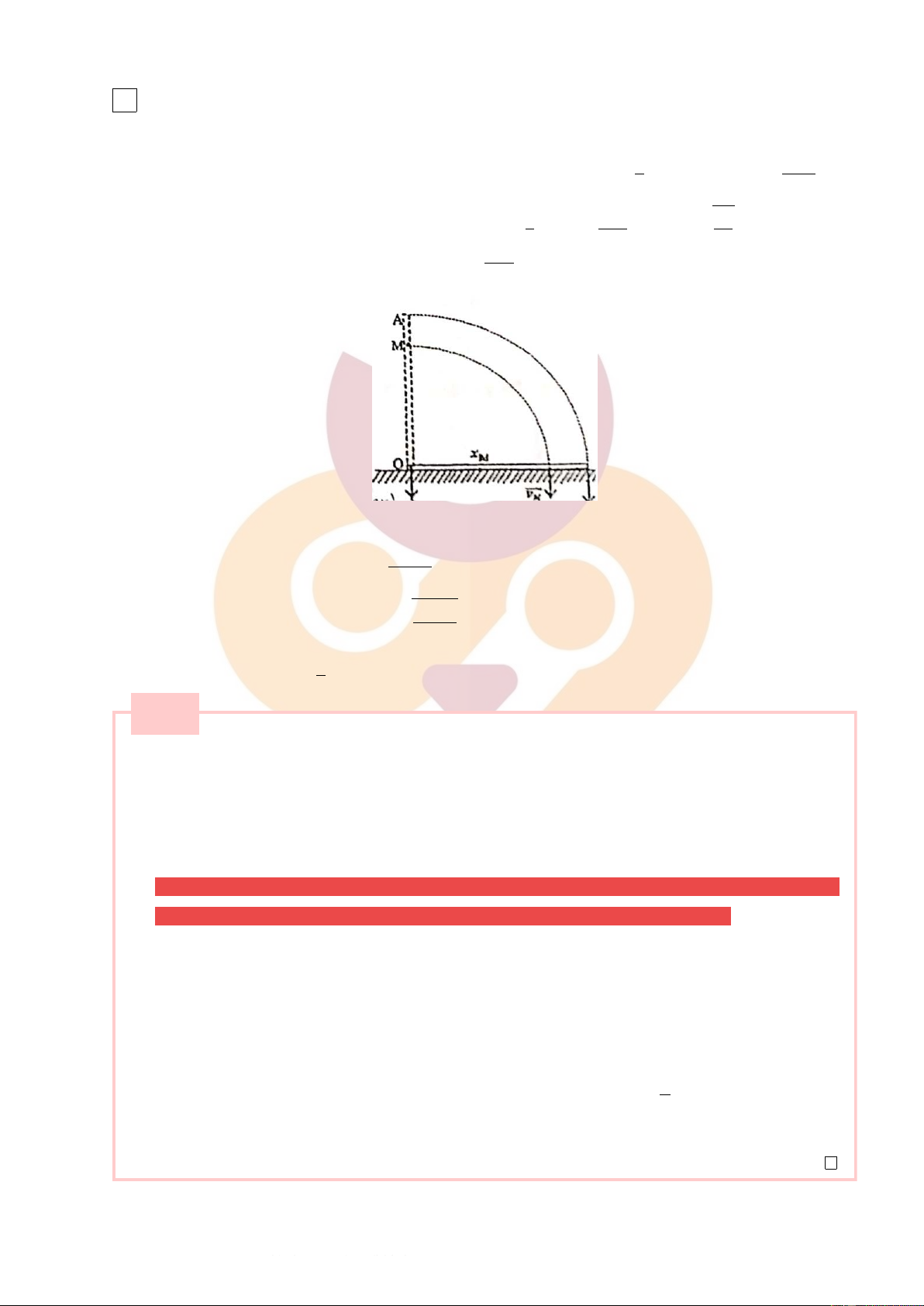
2. Bài toán: Một vật nhỏ trượt không ma sát từ đỉnh một bán cầu xuống dưới đất. Cho bán kính
R = 3m, g = 10m/s2. Bỏ qua lực cản của không khí.
(a) Từ độ cao nào so với mặt đất vật bắt đầu rời khỏi bán cầu.
(b) Tìm tốc độ của vật khi bắt đầu rời khỏi bán cầu và tại mặt đất. [Lời giải] 1.
+ Xét chuyển động của viên đạn khối lượng m trong trường hấp dẫn:
Từ một điểm A gần mặt đất, người ta bắn 1 viên đạn khối lượng m với vận tốc v. Có thể xảy ra các trường hợp sau:
v = v1 : Viên đạn bắt đầu chuyển động theo quỹ đạo tròn quanh Trái Đất. v = v2 : Viên đạn
thoát khỏi trường hấp dẫn của Trái Đất và chuyển động ra xa vô cùng. 13
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
v < v1 : Viên đạn chuyển động theo quỹ đạo là nhánh Parabol và rơi trở lại mặt đất.
v1 < v < v2 : Viên đạn chuyển động quanh Trái Đất theo quỹ đạo elip.
Khi đó: v1 được gọi là vận tốc vũ trụ cấp I và v2 được gọi là vận tốc vũ trụ cấp II.
+ Vận tốc vũ trụ cấp I: Vật chuyển động tròn quanh Trái Đất, coi quỹ đạo gần mặt đất.
⇒ aht = g0 với g0 là gia tốc trọng trường v2 ⇒ g 1 0 = R √ ⇒ v1 = g0.R ≈ 7, 9km/s
+ Vận tốc vũ trụ cấp II: Vật chuyển động ra xa vô cùng Theo định luật bảo toàn cơ năng: W0 = W∞ mv2 M.m mv2 M.m ⇒ 2 + −G = ∞ + −G 2 R 2 ∞
Điều kiện để vật chuyển động ra xa vô cùng: v∞ ≥ 0 mv2 M.m ⇒ 2 + −G ≥ 0 2 R r 2GM √ ⇒ v2 ≥ R = 2g R2 0.R ≈ 11, 2km/s 2. (a) Tìm độ cao h:
– Vật chịu tác dụng của trọng lực ⃗ P và phản lực ⃗
N . Theo định luật II Niuton: ⃗ F = ⃗ P + ⃗ N (1)
Chiếu (1) lên phương bán kính đi qua chất điểm, chiều dương hướng vào tâm bán cầu ta được: Fht = P cos α − N
– Vật rời khỏi mặt cầu tại điểm M khi NM = 0. Khi đó: mv2 mgh M = mg cos(α) = R R 14
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập ⇒ v2 = gh M
– Theo định luật bảo toàn cơ năng: mv2 2 mgR = mgh + M ⇒ h = R = 2(m) 2 3 (b)
– Tốc độ của vật khi rời khỏi mặt cầu: √ vM = pgh = 10.2 ≈ 4, 47(m/s)
– Tốc độ của vật khi chạm đất: Áp dụng định luật bảo toàn cơ năng: mv2 √ mgR = d ⇒ v 60 ≈ 7, 75(m/s) 2 d = p2gR = Câu 9
1. Trình bày các vấn đề sau:
a) Khái niệm động năng. Tìm biểu thức động năng của chất điểm.
b) Định lý về động năng của chất điểm
c) Định luật bảo toàn cơ năng của chất điểm trong trọng trường
2. Bài toán: Một vệ tinh có khối lượng m = 150kg chuyển động trên quỹ đạo tròn có bán kính
R = 7300km đối với tâm Trái Đất. Tính động năng, cơ năng và tốc độ của vệ tinh trên quỹ đạo.
Cho biết G = 6, 67.10−11Nm2/kg2. Khối lượng Trái Đất M = 5, 98.1024kg. Bỏ qua lực cản của không khí. [Lời giải] 1. (a)
+ Khái niệm: Động năng là phần năng lượng ứng với sự chuyển dời của vật. 15
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập (2) ˆ
+ Biểu thức động năng của chất điểm: Ta có: dA = ⃗ F d⃗s ⇒ A = ⃗ F d⃗s (1) d⃗v Mà ⃗ F = m⃗a = m dt (2) (2) v2 ˆ d⃗v ˆ ˆ mv2 mv2 mv2 ⇒ A 2 1 12 = m d⃗s = m⃗vd⃗v = d = − dt 2 2 2 (1) (1) v1 ⇒ A12 = W1 − W2 mv2
Vậy biểu thức động năng của chất điểm: Wđ = 2
(b) Định lý về động năng của chất điểm
Độ biến thiên động năng của chất điểm trong một quãng đường nào đó có giá trị bằng công của ngoại
lực tác dụng lên chất điểm trên quãng đường đó.
(c) Định luật bảo toàn cơ năng của chất điểm trong trọng trường
Chất điểm chuyển động trong trọng trường mà không chịu tác dụng của bất cứ lực nào khác thì cơ
năng của nó là một đại lượng bảo toàn. 2.
+ Thế năng của một vật trong trường hấp dẫn của trái đất là: M m U = −G
(lấy mốc thế năng tại vô cực) R mv2 M m mv2 GM m
Do vệ tinh chuyển động tròn nên FM = Fhd ⇒ = G ⇒ W = R R2 d = 2 2R 1 Vậy ta có: Wd = − U 2 + Thay số: M m 6, 67.1011.5, 98.1024.150 U = −G = − = −8, 2.109(J) R 7, 3.106 1 Wd = − U = 4, 1.109(J) 2 + Cơ năng của vệ tinh: 1
E = U + Wd = U = −4, 1.109(J) 2 + Tốc độ của vệ tinh: s r 2W 2.4, 1.109 v = d = ≈ 7, 4(km/s) m 1, 5.102 16
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
Chương 5 - Chuyển động quay của vật rắn Câu 10
1. Nêu các đặc điểm động học của chuyển động tịnh tiến và chuyển động quay quanh một trục
cố định của vật rắn.
2. Bài toán: Một cột đồng chất có chiều cao h = 5m đang dựng thẳng đứng thì bị đổ quay quanh
chân của nó xuống mặt phẳng nằm ngang. Xác định:
a) Vận tốc dài của đỉnh cột khi chạm đất.
b) Vị trí của điểm M trên cột sao cho khi M chạm đất thì vận tốc của nó đúng bằng vận tốc của
một vật thả tự do từ vị trí M (cho g = 9, 8 m/s2) [Lời giải] 1.
• Các đặc điểm động học của chuyển động tịnh tiến
+ Vật chuyển động tịnh tiến tức là mọi chất điểm của vật chuyển động với quỹ đạo giống hệt nhau.
+ Là chuyển động mà mọi chất điểm thuộc vật rắn cùng chuyển động với vận tốc và gia tốc như nhau.
• Các đặc điểm động học của chuyển động quanh quay một trục cố định
+ Khi vật chuyển động quay quanh một trục cố định thì mọi chất điểm của vật rắn đều chuyển
động tròn và có tâm quay nằm trên cùng một trục quay.
+ Vận tốc góc và gia tốc góc là như nhau với mọi chất điểm
+ Các chất điểm chuyển động tròn thỏa mãn: ⃗v = ⃗ w ∧ ⃗r ⃗a = ⃗ β ∧ ⃗r 17
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập 2. (a) 1 mh2
• Khi cột đổ xuống thế năng chuyển thành động năng quay: Wd = Iω2 trong đó I = . 2 3 1 Iω2 r 3g
Áp dụng định luật bảo toàn cơ năng: Wt = Wd = mgh = ⇒ ω = 2 2 h √
• Vận tốc đỉnh cột khi chạm đất: v = ω.h = 3gh ≈ 12(m/s) (b) Tại vị trí điểm M: √
- Vật rơi tự do có vận tốc: vM = 2gxM r 3gx
- Khi cột chạm đất: v′ = ω.x M M M = h 2 Do vM = v′ suy ra x h M M = ≈ 3, 33(m) 3 Câu 11
1. Trình bày các nội dung sau:
a) Tác dụng của lực trong chuyển động quay.
b) Mômen của lực đối với trục quay.
c) Thiết lập phương trình cơ bản của vật rắn quay xung quanh một trục cố định và giải thích các
đại lượng trong phương trình đó. Định nghĩa và ý nghĩa của mômen quán tính.
2. Bài toán: Một vật m = 1kg được nối với một cuộn dây cuốn vào 1 trụ đặc và được thả rơi
như hình vẽ. Trụ có bán kính R = 10cm và có khối lượng M = 6kg. Bỏ qua lực ma sát và khối lượng của dây.
(a) Tìm độ lớn gia tốc dài của vật m và lực căng dây. Cho g=10m/s2 π
(b) Tìm công thực hiện bởi lực căng dây khi trụ quay được một góc
(kể từ lúc bắt đầu thả 4 vật) 18
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập [Lời giải] 1.
(a) Tác dụng của lực trong chuyển động quay:
Trong chuyển động của vật rắn quanh một trục, chỉ các thành phần lực tiếp tuyến với quỹ đạo tại điểm
đặt mới thực sự gây ra tác dụng quay.
(b) Mômen của lực đối với trục quay:
Momen của lực tiếp tuyến ⃗
Ft với trục quay ∆ là một vecto ⃗
M được xác định bởi công thức: ⃗ M = ⃗r ∧ ⃗ Ft
Đặt tại tâm O của quỹ đạo
Có phương trùng với trục quay ∆ ⃗ M
Có chiều thuận đối với chiều quay từ ⃗ r sang ⃗ F t Độ lớn: M = r.Ft
Momen lực đối với trục quay là đại lượng đặc trưng cho tác dụng làm quay của lực đối với trục quay đó.
(c) Thiết lập phương trình cơ bản của vật rắn quay xung quanh một trục cố định và giải thích
các đại lượng trong phương trình đó. Định nghĩa và ý nghĩa của mômen quán tính.
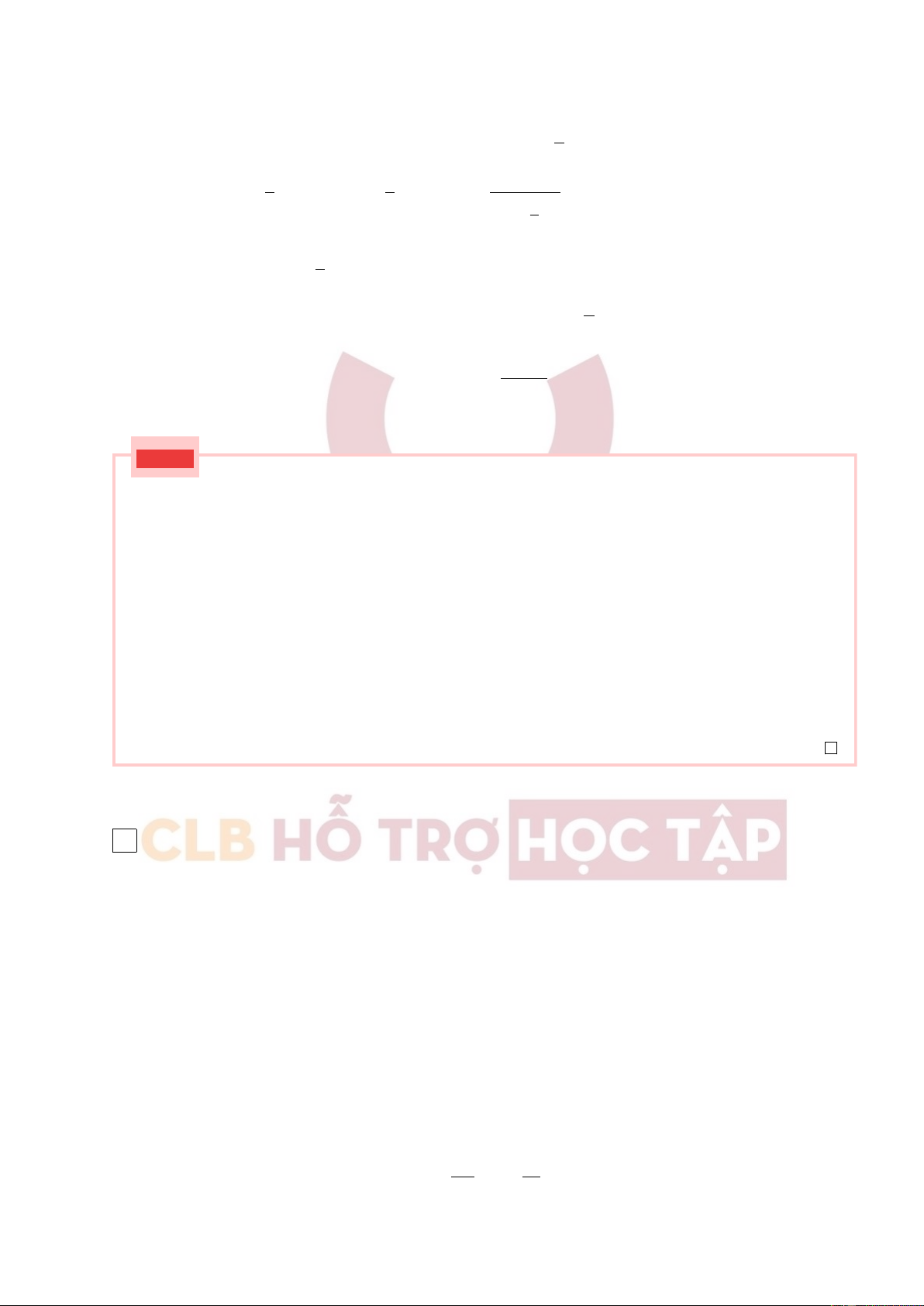
- Chất điểm thứ i chịu tác dụng của ngoại lực tiếp tuyến ⃗
Fti và chuyển động với gia tốc tiếp tuyến 19
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập ⃗
ati. Khi đó, momen của lực ⃗
Fti đối với trục quay là ⃗ Mi với: ⃗ Mi = ⃗ri ∧ ⃗ Fti = m⃗ri ∧ ⃗ ati Mà ⃗r ⃗ i ∧ ⃗
ati = ⃗ri ∧ (⃗β ∧ ⃗ri) = β.(⃗ri.⃗ri) − ⃗ri.(⃗ri.β) = mr2iβ Vậy ta có: m ⃗ ir2 i β = ⃗ Mi
Vật rắn gồm n chất điểm chịu tác dụng của các ngoại lực F1, F2, ..., Fn. Như vậy: X X ( m ⃗ i.r2 i ).⃗ β = Mi
- Phương trình cơ bản trong chuyển động quay của vật rấn quanh một trục cố định ⃗ M = I.⃗ β Trong đó: + ⃗ M = P ⃗
Mi là tổng các momen ngoại lực tác dụng lên vật
+ I = P mi.r2 là momen quán tính của vật đối với trục quay i ∆ + ⃗
β là gia tốc góc của vật rắn trong chuyển động quay quanh trục cố định, tỷ lệ thuận với tổng
hợp momen các ngoại lực đối với trục và tỉ lệ nghịch với momen quán tính của vật rắn đối với trục.
- Định nghĩa và ý nghĩa momen quán tính:
+ Là đại lượng vật lí đặc trưng cho tính bảo toàn trạng thái của vật trong chuyển động quay.
+ Momen quán tính cho biết mức quán tính của các vật trong chuyển động quay, tương tự như
khối lượng trong chuyển động tịnh tiến. 2.
(a) Chọn chiều dương của chuyển động hướng xuống dưới.
Các lực tác dụng biểu diển như trên hình.
+ Tính a và T. Có hệ phương trình: 20
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập P − T = ma a T .R = I β = I r 1 1 mg
Trong đó: I = MR2 ⇒ T = Ma ⇒ a = = 2, 5(m/s2) 2 2 1 m + M 2 1
+ Lực căng dây T: T = Ma = 7, 5(N) 2 π
(b) Công thực hiện bởi lực căng dây khi trụ quay được một góc : 4 0, 75π A = M.θ = T.R.θ = ≈ 0, 59(J) 4 Câu 12
1. Thiết lập biểu thức tính công và công suất của ngoại lực trong chuyển động quay của vật rắn
xung quanh một trục cố định. Suy ra định lý về động năng của vật rắn trong chuyển động quay.
2. Một vô lăng dạng đĩa tròn đồng tính có khối lượng m = 40kg, bán kính R = 0, 5m đang quay
xung quanh trục đi qua tâm và vuông góc với mặt đĩa với tốc độ góc ω = 240 vòng/phút. Tác
dụng lên vô lăng một lực hãm. Tìm độ lớn của mômen hãm trung bình trong các trường hợp:
a) Vô lăng dừng lại trong 40 s.
b) Vô lăng dừng lại sau khi quay được 5 vòng kể từ khi tác dụng lực hãm. [Lời giải] 1.
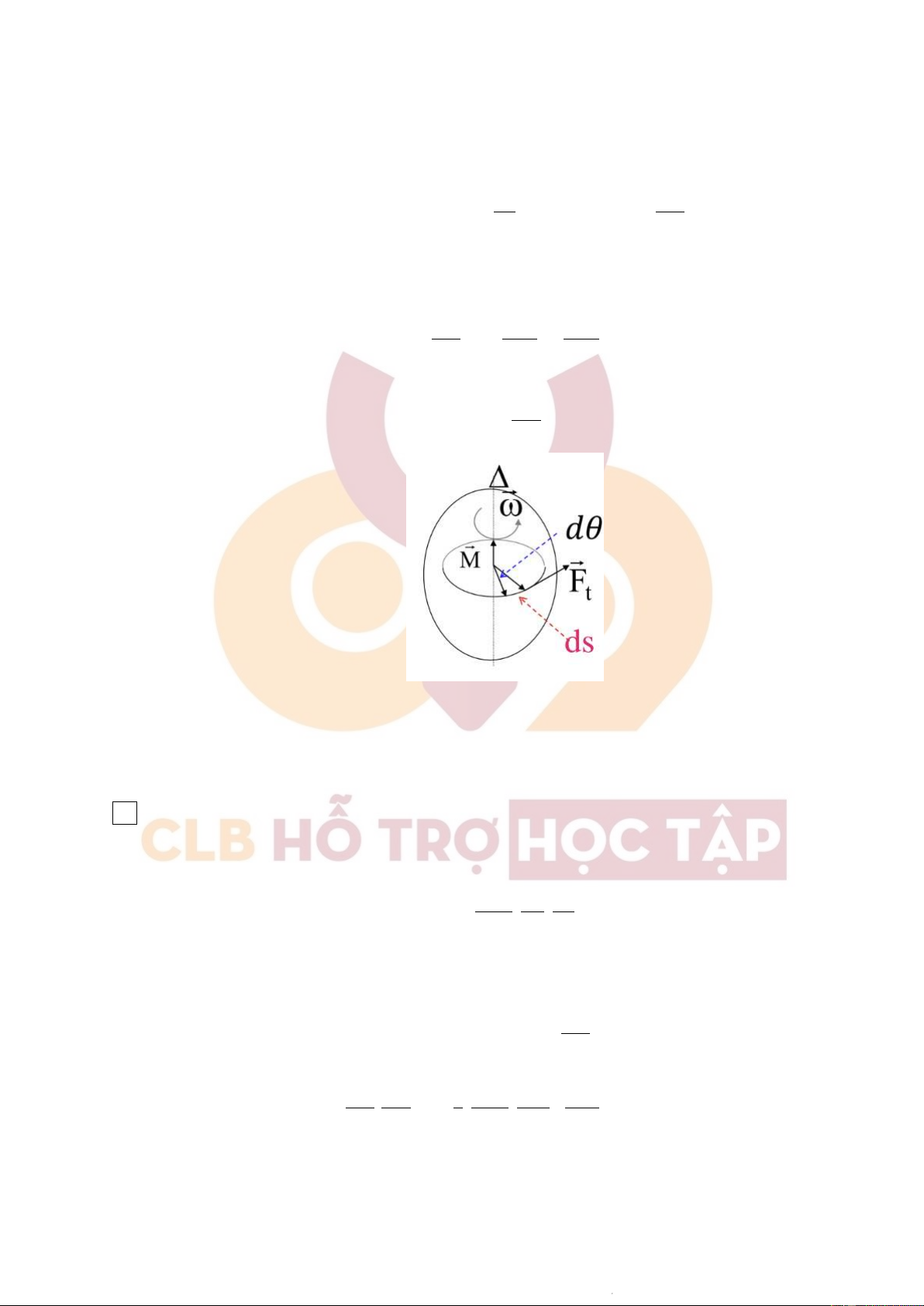
+ Thiết lập công thức tính công của ngoại lực trong chuyển động quay của vật rắn xung quanh 1 trục cố định: dA = ⃗ Ftd⃗s = Ftds = Ftrdθ dA = M dθ
Với M = rFt là mômen lực tiếp tuyến đối với ∆. Quy ước: M > 0 khi ⃗ Ft thuận theo chiều quay.
M < 0 với trường hợp ngược lại. + Công suất của lực: dA dθ P = = M = M ω dt dt 21
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập P = ⃗ M ⃗ω
+ Xét chuyển động quay của vật rắn quanh trục cố định: dω Iω2 dA = M dθ = Iβdθ = I dθ = Iωdω = d dt 2
Với chuyển dời bất kỳ, công của ngoại lực tác dụng: 2 ˆ Iω2 Iω 2 Iω 2 A = d = 2 − 1 = ∆W 2 2 2 d 1 Iω2 Wđ = . 2
+ Phát biểu định lý động năng của vật rắn quay: Động năng của vật rắn quây quanh một trục bằng
nửa tích số của momen quán tính vủa vật và bình phương vận tốc góc của vật đối với trục quay đó. 2.
a. Áp dụng định lý về mômen động lượng: mR2 πω 1 ∆L = Mh∆t → Mh = 0 − . . = −π = −3, 14(Nm) 2 60 ∆t
b. Áp dụng định lý động năng của vật rắn quay: Iω2 Ah = ∆Wd = 0 − 2 Iω2 1 1 mR2 2πω 2 1 Mh = . = − . . . = −16π(Nm) 2 πω1 2 2 60 2π.5 22
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập Câu 13
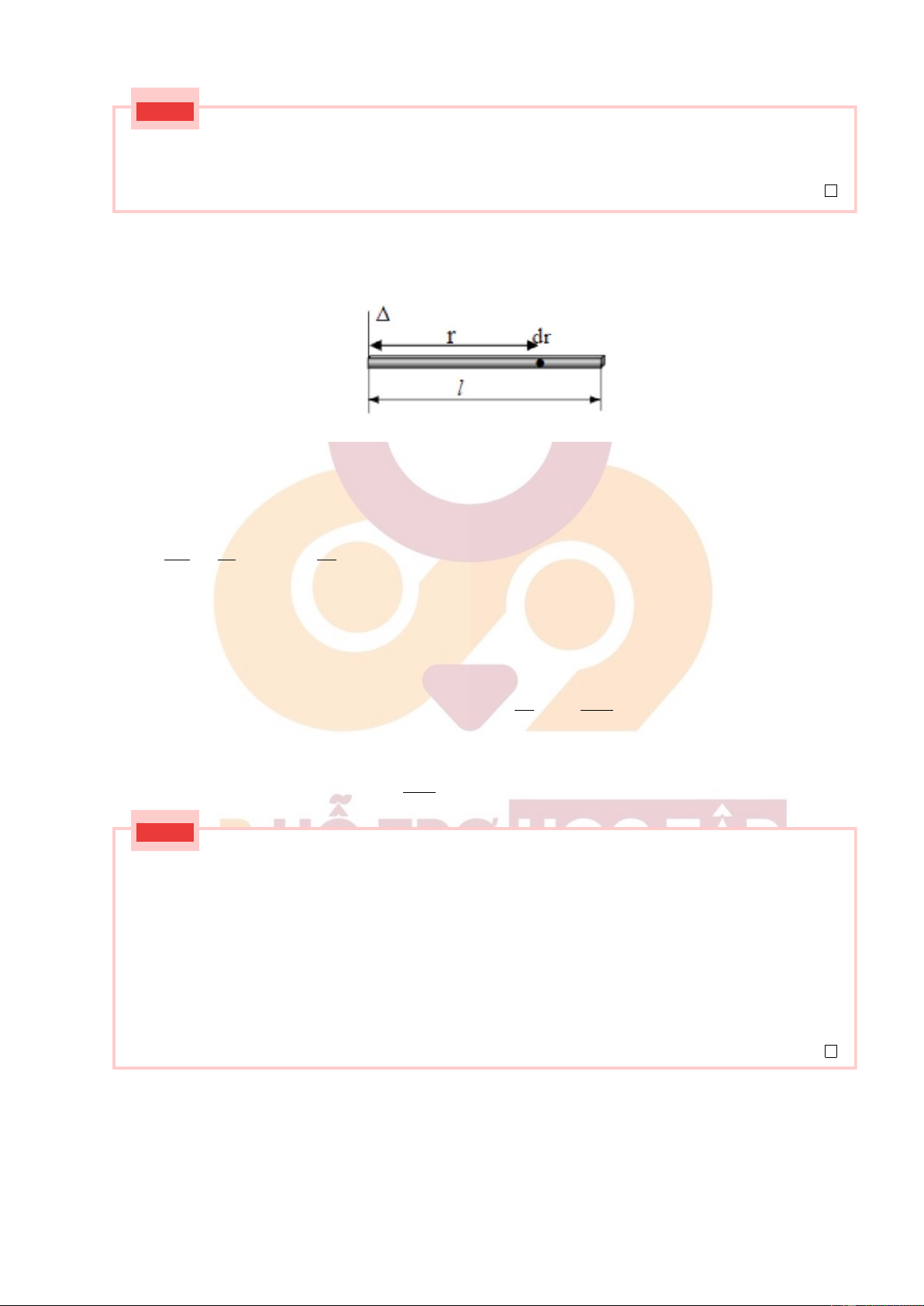
Tính mômen quán tính của một thanh đồng chất, chiều dài l, đối với trục ∆ đi qua một đầu của
thanh và vuông góc với thanh. (lưu ý: sinh viên không sử dụng định lý Steiner - Huygens) [Lời giải]
Xét thanh dài đồng chất dài l khối lượng M.
Xét một điểm trên thanh có khối lượng dm, cách trục ∆ một đoạn r và dài dr. dm dr M Ta có: = ⇒ dm = dr. M l l
Xét trục Ox có gốc O nằm tại trục quay, hướng dọc theo chiều dài của thanh. Mômen quán tính của thanh là: l l ˆ ˆ M M l2 I = r2dm = r2 dr = l 3 0 0 M l2
Vậy mômen quán tính của thanh dài là 3 Câu 14
(a) Viết biểu thức tính mômen động lượng của một chất điểm và của một hệ chất điểm đối với
gốc O. Từ đó suy ra biểu thức mômen động lượng của vật rắn quay xung quanh một trục cố định.
(b) Trình bày hai định lý về mômen động lượng và định luật bảo toàn mômen động lượng của hệ chất điểm. [Lời giải] 23
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập 1.
Mômen động lượng của một chất điểm đối với gốc O là: ⃗L = ⃗r × m⃗v
Mômen động lượng của hệ chất điểm đối với gốc O là: ⃗L = P ⃗ Li = P ⃗ri × mi⃗vi
Mômen động lượng của chất điểm quanh một trục có định là: ⃗ Li = Ii ⃗ ωi với Ii = mir2i
Mômen động lượng của hệ chất điểm quanh trục cố định là: ⃗L = P ⃗ Li = P Ii ⃗ ωi
Khi đó, mỗi chất điểm của vật rắn quay đều có cùng vận tốc góc ⃗ ω1 = ⃗ ω2 = ... = ⃗ ωn = ⃗ω
Mômen động lượng của vật rắn quay xung quanh một trục cố định là: ⃗ L = (P I I m i i).⃗
ω = I⃗ω với I = Pi i = Pi ir2i 2.
+ Định lý về mômen động lượng của hệ chất điểm đối với gốc O
Xét chất điểm thứ i của hệ: d ⃗ Li = ⃗µ dt /o( ⃗ Fi)(∗)
Cộng các phương trình (*) theo i: X d ⃗ Li X = ⃗µ dt /o( ⃗ Fi) i i X d ⃗ Li d X d⃗ L = ⃗ L
: Là đạo hàm theo thời gian của tổng mômen động lượng của hệ. dt dt i = dt i i X ⃗ µ/o( ⃗ Fi) = ⃗ M :
Là tổng mômen đối với O của các ngoại lực tác dụng lên hệ. i d⃗ L ⇒ = ⃗ M dt
Đạo hàm theo thời gian của mômen động lượng của một hệ chất điểm bằng tổng mômen các 24
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
ngoại lực tác dụng lên hệ (đối với một điểm gốc O bất kỳ)
+ Định luật bảo toàn mômen động lượng của hệ chất điểm:
Hệ chất điểm cô lập hoặc chịu tác dụng ngoại lực nhưng tổng mômen đối với gốc O bằng 0. Khi d⃗ L
đó theo định lý về mômen động lượng: = ⃗ M = 0 → ⃗L = const dt
Đối với hệ chất điểm cô lập, chịu tác dụng của các ngoại lực sao cho tổng mômen các ngoại
lực ấy đối với điểm gốc O bằng không thì tổng mômen động lượng của hệ là một đại lượng bảo toàn.
Chương 6 - Dao động và sóng cơ Câu 15
1. Thiết lập phương trình dao động tắt dần của con lắc lò xo dưới tác dụng của lực cản có độ lớn
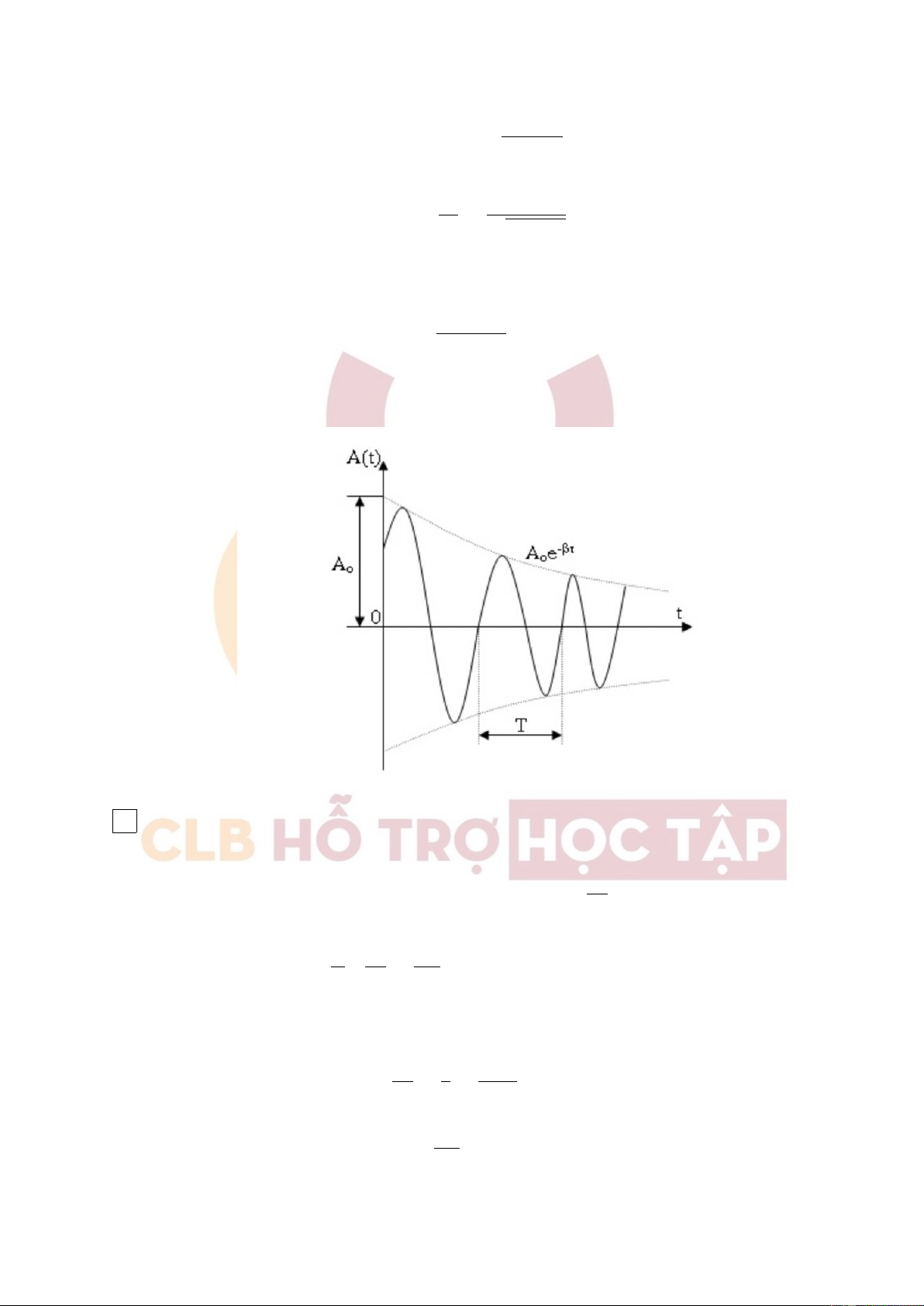
tỷ lệ với tốc độ. Vẽ đồ thị của dao động tắt dần. Tìm công thức tính giảm lượng loga của dao động tắt dần.
2. Một con lắc là xo dao động tắt dần với biên độ ban đầu A0 = 12cm. Sau 2,4 phút biên độ của nó giảm còn 6cm. a) Tìm hệ số tắt dần.
b) Sau bao lâu biên độ chỉ còn 2cm. [Lời giải] 1.
+ Thiết lập phương trình dao động tắt dần: d2x F + Fc = −kx − rv = m dt2 d2x r dx k + + + x = 0 dt2 m dt m Đặt k = ω2 = 2β
(β là hệ số tắt dần đặc trưng cho lực cản của môi trường.) m 0 ; r m d2x dx + 2β + ω2 dt2 dt 0 x = 0 (1)
Khi ω0 > β (1) có nghiệm: x = A0e−βtcos(ωt + φ) 25
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
Tần số góc và chu kỳ của dao động tắt dần: q ω = ω20 − β2 2π 2π T = = ≥ T ω p 0 ω20 − β2 + Giảm lượng loga: A = A0e−βt A(t) δ = ln = lneβT = βT A(t + T )
+ Đồ thị dao động tắt dần: 2. a) Biên độ dao động: A A 0
1 = A0e−βt1 ⇒ βt1 = ln A1 Suy ra: 1 A ln2 β = ln 0 =
= 0, 29(min−1) = 4, 8.10−3(s−1) t1 A1 2, 4
b) Khoảng thời gian để biên độ chỉ còn 2cm: A1 6 e−βt1 = = = eβ(t2−t1) A2 2 e−βt2 ln3 ⇒ t2 − t1 = = 3, 79(min) = 228, 9(s) β 26
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập Câu 16
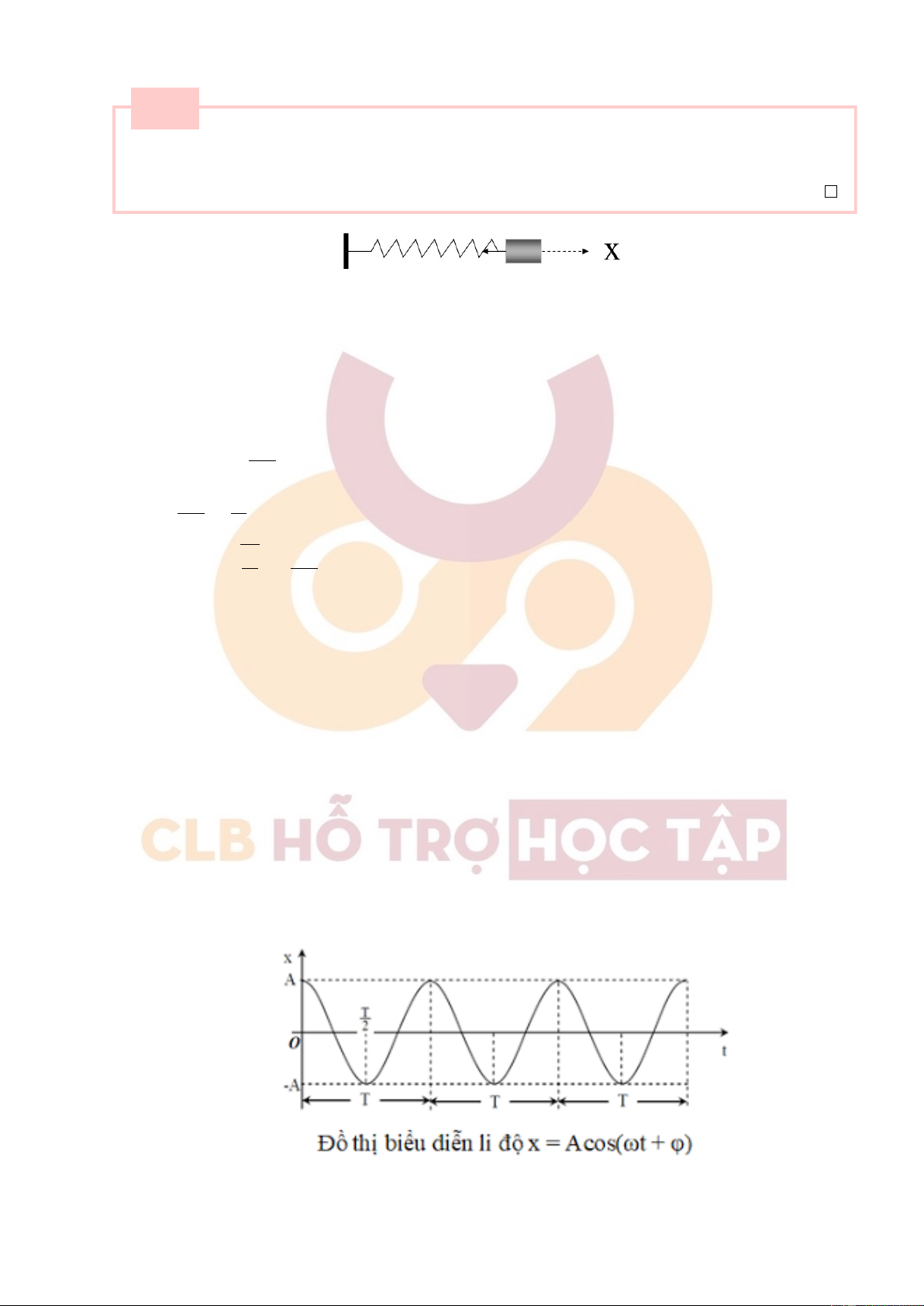
Thiết lập phương trình dao động điều hòa của con lắc lò xo. Vẽ đồ thị biểu diễn dao động điều
hòa của con lắc. Định nghĩa chu kỳ, tần số dao động. Xác định chu kỳ của con lắc vật lý. [Lời giải]
• Thiết lập phương trình dao động của con lắc lò xo:
Vật chịu tác dụng của lực đàn hồi F=-kx. Bỏ qua ma sát, vật dao động cơ điều hòa.
Theo định luật II Niuton: ⃗ F = m⃗a d2x ⇒ ma = m. = −kx dt2 d2x k ⇒ + x = 0 dt2 m r k d2x Đặt w = ⇒ + w2x = 0 (1) m dt2
x = Acos(wt + φ) là nghiệm của phương trình (1) và được gọi là phương trình dao động điều hòa của con lắc lò xo. Trong đó:
+ x : Li độ dao động của vật (đơn vị là m hoặc cm)
+ A : Biên độ của vật (giá trị lớn nhất của li độ) (đơn vị là m hoặc cm)
+ w : Tần số góc của dao động điều hòa
+ wt + φ : Pha dao động tại thời điểm t
+ φ : Pha ban đầu (pha dao động tại thời điểm ban đầu t=0)
• Đồ thị dao động điều hòa của con lắc 27
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
• Chu kì T: Thời gian vật thực hiện một dao động toàn phần hay thời gian ngắn nhất để trạng thái
dao động của vật lặp lại như cũ.
• Tần số f: Số dao động toàn phần vật thực hiện được trong 1s.
• Xác định chu kì của con lắc vật lí:
Con lắc vật lí chịu tác dụng của trọng lực ⃗ P . Phân tích ⃗
P thành các lực thành phần: ⃗ P = ⃗ F⊥ + ⃗ F// Chỉ ⃗
F gây ra tác dụng quay quanh trục O của con lắc: ⊥ | ⃗ F⊥| = mg sin θ ≈ mgθ
Phương trình cơ bản của vật rắn quay quanh trục O: M = Iβ = −F⊥.d d2θ d2θ mgd ⇒ I = −mgθd ⇒ + θ = 0 dt2 dt2 I r mgd Từ đó ta suy ra: w = I 2π r I
Vậy chu kì của con lắc vật lí là: T = = 2π w mgd 28
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
Chương 7 - Thuyết động học phân tử Câu 17 1. Trình bày:
a) Nội dung cơ bản của thuyết động học phân tử khí lý tưởng.
b) Viết phương trình cơ bản của thuyết động học phân tử và phương trình trạng thái của khí lý
tưởng. 2. Bài toán: Một bình dung tích V = 5l ở áp suất p = 8atm chứa 2 mol khí O2. Biết khối
lượng phân tử của O2 là µ = 32g/mol, tính:
a) Động năng chuyển động tịnh tiến trung bình của một phân tử khí O2.
b) Trung bình của bình phương vận tốc một phân tử khí O2.
Cho biết 1atm = 1, 013.105P a, NA = 6, 023.1023mol−1. [Lời giải] 1.
a) Nội dung của thuyết động học phân tử khí lý tưởng:
1. Các chất cấu tạo gián đoạn và gồm một số lớn các phần tử.
2. Các phần tử chuyển động hỗn loạn không ngừng.
3. Cường độ chuyển động phân tử biểu hiện nhiệt độ của hệ.
4. Kích thước phân tử rất nhỏ so với khoảng cách giữa chúng và có thể coi chúng là chất điểm.
5. Các phân tử không tương tác, trừ lúc va chạm với nhau.
1,2 đúng với mọi chất; 3,4,5 chỉ đúng với khi lý tưởng.
Khí lý tưởng là chất khí mà khi xét nó ta có thể bỏ qua lực tương tác giữa các phân tử khí và kích thước giữa chúng.
b) Phương trình cơ bản của thuyết động học phân tử: p = 2n 3 oWd
Phương trình trạng thái của khí lý tưởng: pV = m RT µ 2.
a) Từ phương trình thuyết động học phân tử chất khí có: 2 n.N p = A W 3 V d 29
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
Suy ra động năng chuyển động tịnh tiến trung bình của một phân tử khí O2: 3 pV Wd = . ≈ 5, 05.10−21(J) 2 n.NA
b) Do Wd = 1mv2 suy ra trung bình bình phương vận tốc của một phân tử khí O 2 2: 2W 2.N 3pV v2 = d = A W ≈ 1, 90.105(m/s) m µ d = nµ Câu 18 1.
a) Từ phương trình thuyết động học phân tử chất khí hãy dẫn ra biểu thức động năng chuyển
động và suy ra công thức tính vận tốc căn quân phương của các phân tử chất khí.
b) Nêu khái niệm bậc tự do, nội dung định luật phân bố đều theo các bậc tự do, từ đó suy ra biểu
thức nội năng cho một khối khí có khối lượng bất kì.
2. Bài toán: Một khối khí O2 đựng trong bình chứa hình lập phương có kích thước mỗi cạnh
bằng 0,10 m, ở áp suất 1, 013.105P a và nhiệt độ bằng 27oC, tính:
a) Động năng chuyển động tịnh tiến trung bình của một phần tử khí O2.
b) Số các phân tử khí O2 có trong bình khí nói trên.
(Cho biết k = 1, 38.10−23J/K, µ = 32g/mol). [Lời giải] 1.
a) Từ phương trình thuyết động học phân tử chất khí có: 2 3 p p = n 3 oWd ⇒ Wd = 2 no
Sử dụng phương trình trạng thái với một mol khí ta có: 3 RT 3 RT 3 Wd = = = kT 2 no.v 2 NA 2
Từ định nghĩa vận tốc căn quân phương: √ r s 3kT 3RT vc = v2 ⇒ vc = = m µ
b) Bậc tự do của một hạt là số toạ độ độc lập để xác định trạng thái động lực học của 1 phân tử. 30
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
Số bậc tự do của đơn nguyên tử i=3; lưỡng nguyên tử i=5; đa nguyên tử i=6.
Người ta chứng minh rằng biểu thức động năng trung bình của phân tử trong trường hợp tổng quát có dạng: i Wd = k 2 BT
Trong đó hệ số i gọi là số bậc tự do của phân tử.
Công thức tính nội năng của khí lí tưởng: m i U = RT µ 2 2.
a) Động năng chuyển động tịnh tiến trung bình của một phân tử khí O2 3 Wd = kT = 6, 21.10−21(J) 2
b) Số các phân tử khí có trong bình khí: p N = noV = V ≈ 2, 45.1022 kT Câu 19 1. Thiết lập:
a) Công thức khí áp cho một cột khí lí tưởng ở độ cao h so với mặt đất (có hình vẽ minh họa).
b) Biểu thức của định luật phân bố theo thế năng. 2. Bài toán:
Ở điều kiện áp suất bằng 1at và nhiệt độ 200C, một người trong trạng thái tĩnh, hít vào phổi một
lượng khí có thể tích bằng 0, 5l. Biết rằng trong không khí số phân tử ô-xy chiếm tỷ lệ 21% (coi
không khí là khí lý tưởng), tính số phân tử O2 trong mỗi lần hít vào, khi người đó ở: a) Trên mặt đất;
b) Trên một ngọn núi có độ cao h = 2000m và nhiệt độ cũng vẫn là 200C. Biết không khí có
µ = 29g/mol, R = 8, 31J/mol.K. [Lời giải] 1. a)
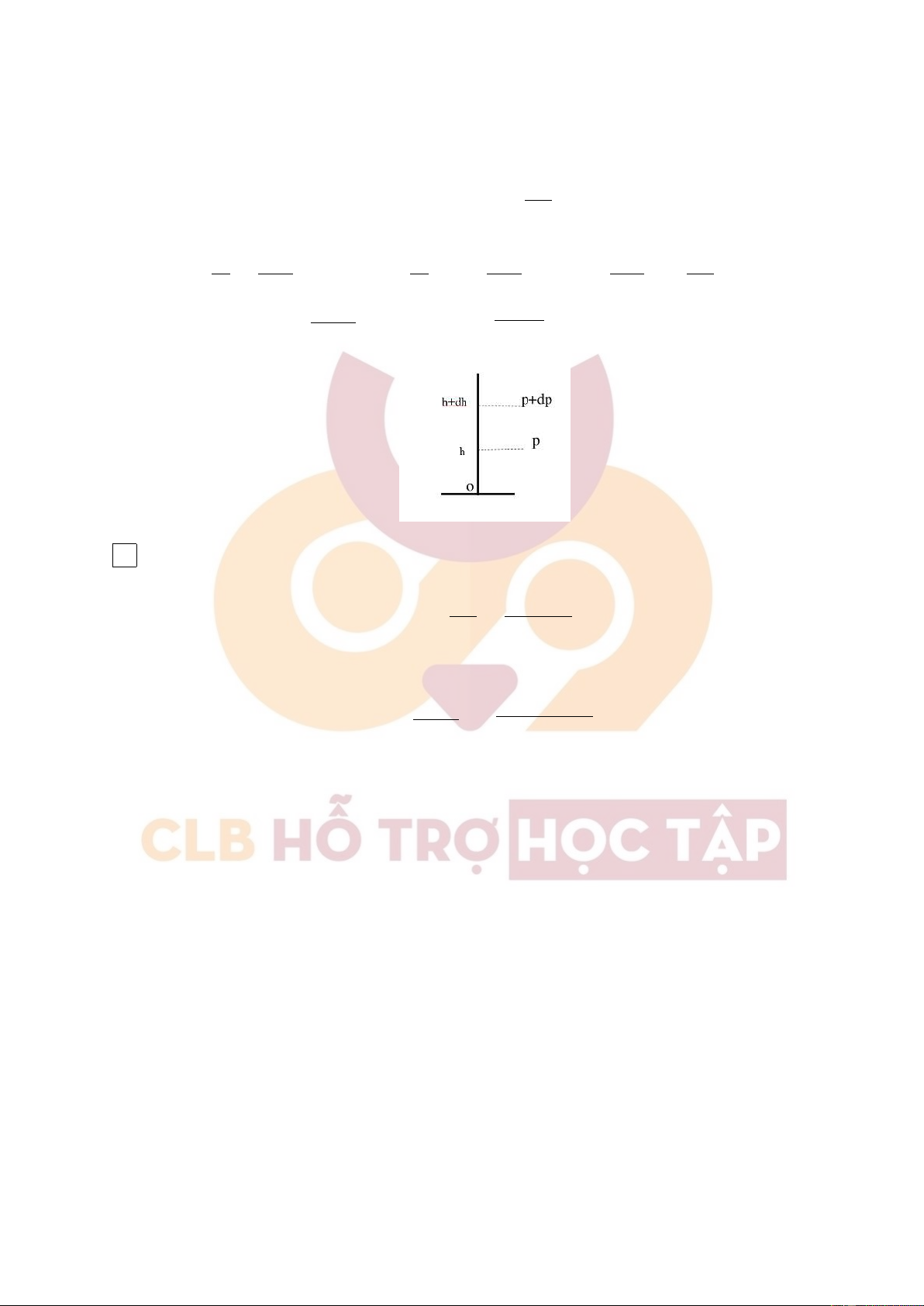
+ Xét 2 điểm có độ cao h và h + ∆h trên phương thẳng đứng có hiệu áp suất dp = −ρ.g.dh 31
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
- dp là trọng lượng của cột khí chiều cao dh và đáy là 1m2.
- dấu "-" do p và h biến thiên ngược chiều.
ρ là khối lượng riêng chất khí: pµ ρ = RT dp −µg ˆ p(h) dp ˆ h −µg p(h) µg ⇒ = dh ⇒ = dh ⇒ ln = − dh p RT p(0) p 0 RT p(0) RT −µgh −mgh
⇒ p(h) = p(0)e RT hay p(h) = p(0)e kBT 2.
a) Từ phương trình trạng thái khí lý tưởng pV 198.0, 5
⇒ Số mol không khí mỗi lần hít vào: n = = ≈ 0, 02(mol) RT 8, 31.293
Số phân tử O2 tương ứng: N = n.NA.21% = 2, 5.1021 (phân tử) −µgh −29.10.2000 b) Từ công thức khí áp: p(h) = p(0).e RT = e 8, 31.293 = 0, 8(at)
Số PTK tỷ lệ thuận với mật độ phân tử và áp suất
⇒ N(h) = 0, 8.N ≈ 2, 0.1021(phnt) 32
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
Chương 8 - Nguyên lý 1 Câu 20 1. Trình bày:
a) Khái niệm hệ nhiệt động và khí lý tưởng.
b) Thiết lập phương trình trạng thái khí lý tưởng cho 1 mol khí và một khối khí có khối lượng
bất kì. (Có hình vẽ minh họa)
2. Bài toán: Trong một ngày trời lạnh có nhiệt độ 15oC, thể tích và áp suất của khí bên trongmootj
lốp xe ô tô được lần lượt là 15dm3 và 1, 70atm. Sau đó, khi xe chạy trên đường cao tốc, nhiệt độ
khí vên trong lốp đo được là 45oC và thể tích cũng tăng lên thành 15, 9dm3. Coi khí bên trong
lốp xe lý tưởng, tính áp suất lốp xe khi đó. [Lời giải] 1. a)
+ Khái niệm hệ nhiệt động: Hệ nhiệt động là tập hợp các vật được xác định hoàn toàn bởi một
số các thông số vĩ mô, độc lập đối với nhau.
+ Khái niệm khí lý tưởng: Là khí tuân theo hoàn toàn chính xác hai định luật Boyle-Mariotte và Gay-Lussac.
b) Xét quá trình biến đổi của 1 khối khí xác định từ trạng thái p1, V1, T1 sang p2, V2, T2 thiết lập được phương trình: pV = const T
Suy ra phương trình trạng thái cho 1 mol khí: pv = RT
Phương trình trạng thái cho khối khí có khối lượng: pV = mRT µ 2.
Do lương khí bên trong lốp không đổi, áp dụng phương trình: p1V1 p = 2V2 T1 T2 T
Áp suất lốp khi xe đang chạy: p 2V1 2 = p1 ≈ 1, 77(atm) T1V2 33
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập Câu 21 1. Trình bày:
a) Khái niệm công và nhiệt trong một quá trình cân bằng.
b) Nội dung, biểu thức, ý nghĩa và hệ quả của nguyên lý I nhiệt động lực học. 2.Bài toán:
Một khối khí đựng trong một bình chứa có áp suất không đổi là 2, 3.105P a được nén từ thể tích
bằng 1, 7m3 xuống còn 1, 2m3. Khi đó, nội năng khối khí giảm đi một lượng bằng 1, 4.105J. Tính:
a) Công khối khí nhận được khi bị nén.
b) Nhiệt lượng khối khí sinh ra trong quá trình nén. [Lời giải] 1. a)
+ Công: Đại lượng đặc trưng cho mức độ trao đổi năng lượng thông qua chuyển động có hướng của hệ.
+ Nhiệt: Đại lượng đặc trưng cho mức trao đổi năng lượng thông qua chuyển động hỗn loạn của các phân tử. b)
+ Nội dung của nguyên lý I nhiệt động lực học: Trong một quá trình biến đổi, độ biến thiên nội
năng ∆U của hệ có giá trị bằng tổng công A và nhiệt Q mà hệ nhận được trong quá trình đó. ∆U = A + Q + Ý nghĩa:
– Nguyên lý 1 chính là định luật bảo toàn và chuyển hoá năng lượng áp dụng cho quá trình
biến đổi liên quan đến chuyển động nhiệt
– Bất kỳ máy nào hoạt động theo chu trinh thì A′ = Q nghĩa là không thể có động cơ nào
sinh công mà không nhận nhiệt từ bên ngoài hoặc sinh công lớn hơn nhiệt nhận từ ngoài vào
– Không tồn tại động cơ vĩnh cửu loại I + Hệ quả 1:
– Hệ cô lập có A = Q = 0 ⇒ δU = 0 (const)
⇒ Nội năng của hệ cô lập bảo toàn 34
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
– Nếu hệ cô lập chỉ có 2 vật trao đổi nhiệt cho nhau thì Q = Q1+Q2 = 0 có Q1 = −Q2 = Q′2
⇒ Nhiệt lượng do vật này tỏa ra bằng nhiệt lượng mà vật kia thu vào.
+ Hệ quả 2: Hệ biến đổi theo 1 chu trình (quá trình kín):
∆U = 0 ⇒ A = −Q ⇔ Q = −A
⇒ Trong một chu trình, công mà hệ nhận được có giá trị bằng nhiệt mà hệ nhận vào từ bên ngoài. 2.
a) Do quá trình là đẳng áp nên A = −p(V2 − V1)
⇒ A = −2, 3.105.(1, 2 − 1, 7) = 1, 15.105(J)
b) Từ nguyên lý I nhiệt động lực học: Q′ = −Q = −δU + A
⇒ Q′ = 1, 4.105 + 1, 15.105 = 2, 55.105(J) Câu 22
1. Xét một khối khí lý tưởng biến đổi theo quá trình cân bằng đẳng áp:
a) Viết phương trình và vẽ đồ thị của quá trình trong hệ 0pV .
b) Thiết lập biểu thức tính công và nhiệt trong quá trình biến đổi đó. 2. Bài toán:
Hơ nóng 10g khí Ô-xy ở nhiệt độ 100C tới thể tích 4l trong khi vẫn giữ nguyên áp suất ở 3at. Tính:
a) Công do khối khí thực hiện;
b) Nhiệt lượng mà khối khí nhận được. [Lời giải] 1. a)
+ Định nghĩa: Đẳng áp là quá trình biến đổi trong đó áp suất của hệ không đổi (p = const) V
+ Phương trình: V1 = 2 = const T1 T2 35
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
(1) → (2) : dãn đẳng áp + Quá trình:
(1) → (2′) : nén đẳng áp b) ˆ V2
+ Công nhận được: A = − pdV = p(V1 − V2) V1 ˆ m ˆ T2 m m m i + 2
+ Nhiệt hệ nhận được: Q = δQ = C dT = C C R∆T µ p p(T2−T1) = p∆T = T µ µ µ 2 1
(Cp là nhiệt dung đẳng áp) 2.
a) Từ phương trình trạng thái, thể tích khối khí trước khi hơ nóng là: m mRT 10.10−3.8, 31.283 Do pV 1 1 = RT = = 2, 5.10−3(m3) µ 1 ⇒ V1 = µp 29.3
Công mà khối khí đã thực hiện:
A′ = −A = p(V2 = V1) = 3, 98.(4 − 2, 5) = 441(J) V V V 4 b) Đẳng áp ⇒ 1 = 2 ⇒ T 2 = 283. = 453(K) T 2 = T1 1 T2 V1 2, 5 m i + 2
Nhiệt mà khối khí nhận được (do A > 0): Q = R∆T µ 2 10.10−3 ⇒ Q =
.2.8, 31.(453 − 283) ≈ 1545(J) 29 Câu 23
1. Xét một khối khí lý tưởng biến đổi theo quá trình cân bằng đoạn nhiệt:
a) Định nghĩa và thiết lập phương trình liên hệ giữa áp suất và thể tích của khối khí trong quá trình biến đổi đó.
b) Vẽ dạng đồ thị của quá trình trên trục tọa độ 0pV . Vì sao trên đồ thị 0pV đường đoạn nhiệt
dốc hơn đường đẳng nhiệt. 2. Bài toán:
Một khối khí đơn nguyên tử, ban đầu có áp suất bằng 1, 5.105P a và thể tích bằng 0, 08m3, được
nén đoạn nhiệt đến thể tích 0, 04m3. Tính:
a) Áp suất khối khí cuối quá trình nén;
b) Công khối khí nhận được trong quá trình. 36
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập [Lời giải] 1. a)
+ Định nghĩa: Đoạn nhiệt là quá trình biến đổi trong đó hệ không trao đổi nhiệt với môi trường. m i + Ta có: ∆U = A =
R∆T . Xét trong 1 quá trình biến đổi nhỏ: µ 2 m i δA = −pdV dU = δA = RdT . Mà µ 2 i CV = R 2 m m RT ⇒ −pdV = C µ V dT . Lại có: p = µ V dV dT R dV ⇒ −RT = C + = 0 V V dT hay T CV V R C Đặt: =
p − CV = γ − 1 ⇒ ln T + (γ − 1) ln V = const CV CV ⇒ ln T V γ−1 = const ⇒ T V γ−1 = const(1)
+ Từ phương trình trạng thái ⇒ pV γ = const. b)
(1) ⇒ (2) : nén đoạn nhiệt + Quá trình
(1) ⇒ (2′) : nén đẳng nhiệt
+ Giải thích tại sao đồ thị OpV đoạn nhiệt dốc hơn đẳng nhiệt:
– Trong quá trình đoạn nhiệt, độ biến thiên nội năng đúng bằng công mà khối khí nhận vào.
Khi nén đoạn nhiệt, δA > 0 ⇒ dU > 0 ⇒ dT > 0 (nhiệt độ khối khí tăng, đường đoạn nhiệt đi lên nhanh hơn).
– Tương tự, khi dãn đoạn nhiệt δA < 0 ⇒ dU < 0 ⇒ dT < 0
⇒ Nhiệt độ khối khí giảm ⇒ đường đoạn nhiệt dốc hơn so với đường đẳng nhiệt. 37
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập 2.
a) Từ phương trình liên hệ đoạn nhiệt: p1V γ1 = p2V γ2 V γ
⇒ Áp suất khối khí cuối quá trình nén: p 1 2 = p1 V2 i+2 3+2 V i 0, 08 3 ⇒ p 1 2 = p1 = 1, 5.105. = 4, 76.105(Pa) V2 0, 04
b) Công mà khối khí nhận được trong quá trình nén: p
4, 76.105.0, 04 − 1, 5.105.0, 08 A = 2V2 − p1V1 = = 1, 05.104(J) γ − 1 5 − 1 3 Câu 24
1. Định nghĩa trạng thái cân bằng và quá trình cân bằng. Một quá trình tiến hành như thế nào có
thể xem là một quá trình cân bằng.
2. Thiết lập biểu thức tính công của một khối khí nhận được trong quá trình biến đổi đẳng nhiệt. [Lời giải] 1.
+ Trạng thái cân bằng (TTCB): là trạng thái không đổi theo thời gian và tính bất biến đó không
phụ thuộc các quá trình của ngoại vật.
- Một TTCB được xác định bằng một số thông số nhiệt động nào đấy.
- Người ta biểu diễn TTCB của hệ trên đồ thị (P,V) bằng một điểm.
- Một hệ không tương tác với ngoại vật bao giờ cũng tự chuyển tới TTCB và trạng thái này tồn tại mãi.
- Để làm thay đổi trạng thái cân bằng của hệ, cần phải có ngoại vật ảnh hưởng lên hệ, dưới
dạng trao đổi công, trao đổi nhiệt hoặc đồng thời cả hai.
+ Quá trình cân bằng (QTCB): là quá trình biến đổi gồm một chuỗi liên tiếp các trạng thái cân bằng.
- Đây chỉ là một quá trình lý tưởng vì khi hệ chuyển từ TTCB này sang TTCB khác thì TTCB
trước cũng bị phá hủy, nó bị thay đổi theo thời gian;
- Trên đồ thi (P,V) QTCB được biểu diễn bằng một đường cong liên tục.
- Một quá trình biến đổi xảy ra vô cùng chậm sao cho tại mỗi thời điểm các thông số trạng
thái có giá trị giống nhau tại mọi điểm khác trong hệ thì quá trình biến đổi đó có thể coi là QTCB. 38
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập 2.
Thiết lập biểu thức tính công của một khối khí nhận được trong quá trình biến đổi đẳng nhiệt (1) → (2):
- Do là quá trình đẳng nhiệt, nên ta có PV = const ⇒ P1.V1 = P2.V2
- Công khối khí nhận được là: V2 V2 ˆ ˆ M.R.T.dV A = −P dV = − µ.V V1 V1 M V M P ⇒ A = .R.T. ln 1 = .R.T. ln 2 µ V2 µ P1
Chương 9 - Nguyên lý 2 Câu 25 1. Trình bày:
a) Nêu các hạn chế của nguyên lý 1
b) Phát biểu nguyên lý 2 nhiệt động lực học dưới dạng cổ điển của Clausius và Thompson và
nêu ý nghĩa của nguyên lý.
c) Thiết lập biểu thức định lượng của nguyên lý 2. 2. Bài toán:
Trong mỗi chu trình hoạt động, động cơ của một xe ô tô tải cần một nhiệt lượng bằng 104 J để
sinh công bằng 2.103 J. Tính:
a) Hiệu suất của động cơ.
b) Nhiệt lượng nhả cho nguồn lạnh trong mỗi chu trình [Lời giải] 1.
a) Nguyên lý 1 có những hạn chế:
- Nguyên lý 1 Không cho biết chiều diễn biến của quá trinh xảy ra trong thực tế; nhiệt truyền tự
nhiên từ vật nóng hơn sang vật lạnh hơn, không có quá trình tự nhiên ngược lại.
- Không nêu lên được sự khác nhau trong quá trinh chuyển hóa giữa công và nhiệt (A có thể
chuyển thành Q, nhưng Q không thể chuyển hóa hoàn tòan thành công được).
- Không đánh giá được chất lượng nhiệt. b)
+ Phát biểu của Clausius: Nhiệt không thể tự động truyền từ vật lạnh sang vật nóng hơn.
+ Phát biểu của Thompson: Không thể chế tạo được một máy hoạt động tuần hoàn biến đối liên 39
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
tục nhiệt thành công nhờ làm lạnh 1 vật mà môi trường xung quanh không chịu sự thay đổi nào.
Hay ta không thể chế tạo được động cơ vĩnh cửu loại 2.
+ Ý nghĩa: Nguyên lý thứ hai đã khắc phục những hạn chế của nguyên lý thứ nhất.
- Nguyên lý thứ 2 cho biết chiều diễn biến của các quá trình vĩ mô trong thực tế.
- Cho biết quy luật biến đối giữa nhiệt và công, có ý nghĩa quan trọng trong chế tạo các máy nhiệt.
- Cho biết cách xác định chất lượng nhiệt: nhiệt độ càng lớn, chất lượng càng cao.
c) Theo chu trình Carnot, hiệu suất của động cơ nhiệt thuận nghịch là: Q′ T
η = 1 − 2 , mà ta lại có η ≤ 1 − 2 Q1 T1 Q′ T Q′ T ⇒ 1 − 2 ≤ 1 − 2 ⇒ 2 ≥ 2 Q1 T1 Q1 T1 Q Q ⇒
1 + 2 ≤ 0, với Q′ là nhiệt lượng mà hệ nhả cho nguồn lạnh, Q là nhiệt mà hệ nhận T 2 2 = −Q′2 1 T2 của nguồn lạnh.
+ Trường hợp hệ biến đổi theo chu trình gồm vô số quá trình đẳng nhiệt tương ứng nhiệt độ:
T1, T2, ...Tn và đoạn nhiệt với nhiệt lượng Q1, Q2, ...Qn liên tiếp nhau: X Q ⇒ i ≤ 0 T i i
+ Nếu chu trình mà hệ trao đổi với vô số các nguồn nhiệt có nhiệt độ biến thiên liên tục thì biểu thức ˛ δQ
định lượng của nguyên lý thứ hai được viết là: ≤ 0 T
Dấu "=" xảy ra khi chu trình là thuận nghịch, ngược lại xảy ra khi chu trình không thuận nghịch. 2. A′ 2.103
a) Hiệu suất của động cơ là: η = 100% = .100% = 20% Q1 104
b) Nhiệt lượng động cơ nhả cho nguồn lạnh trong mỗi chu trình là:
Q′2 = Q1 − A′ = 104 − 2.103 = 8.103(J) 40
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập Câu 26
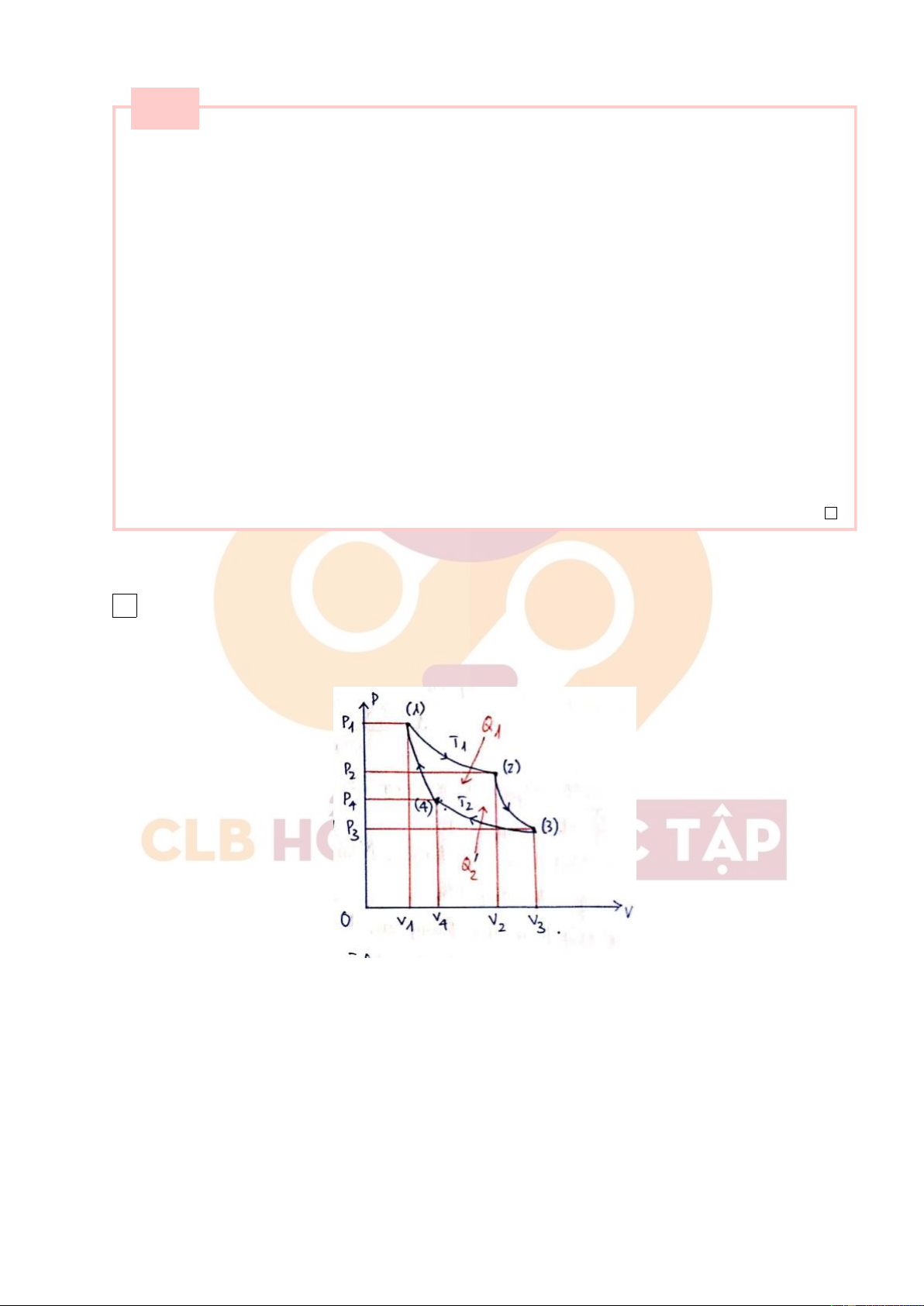
1. Xét chu trình Carnot thuận nghịch
a) Vẽ đồ thị chu trình trên trục tọa độ OPV và gọi tên các quá trình trong chu trình, chỉ rõ quá
trình nào hệ nhiệt động nhận nhiệt từ nguồn nóng và quá trình nào hệ nhả nhiệt cho nguồn lạnh.
b) Thiết lập biểu thức tính và nêu kết luận về hiệu suất động cơ nhiệt hoạt động theo chu trình.
c) Phát biểu định lý Cácnô, từ đó rút ra phương hướng thực tế để tăng hiệu suất của động cơ nhiệt.
2. Bài toán: Một động cơ nhiệt làm việc theo chu trình Carnot, trong mỗi chu trình nhận được
2000J nhiệt lượng từ nguồn nóng. Nhiệt độ của nguồn nóng là 227◦C, nhiệt độ của nguồn lạnh là 27◦C. Tính: a) Hiệu suất động cơ.
b) Công mà động cơ thực hiện trong mỗi chu trình. [Lời giải] 1.
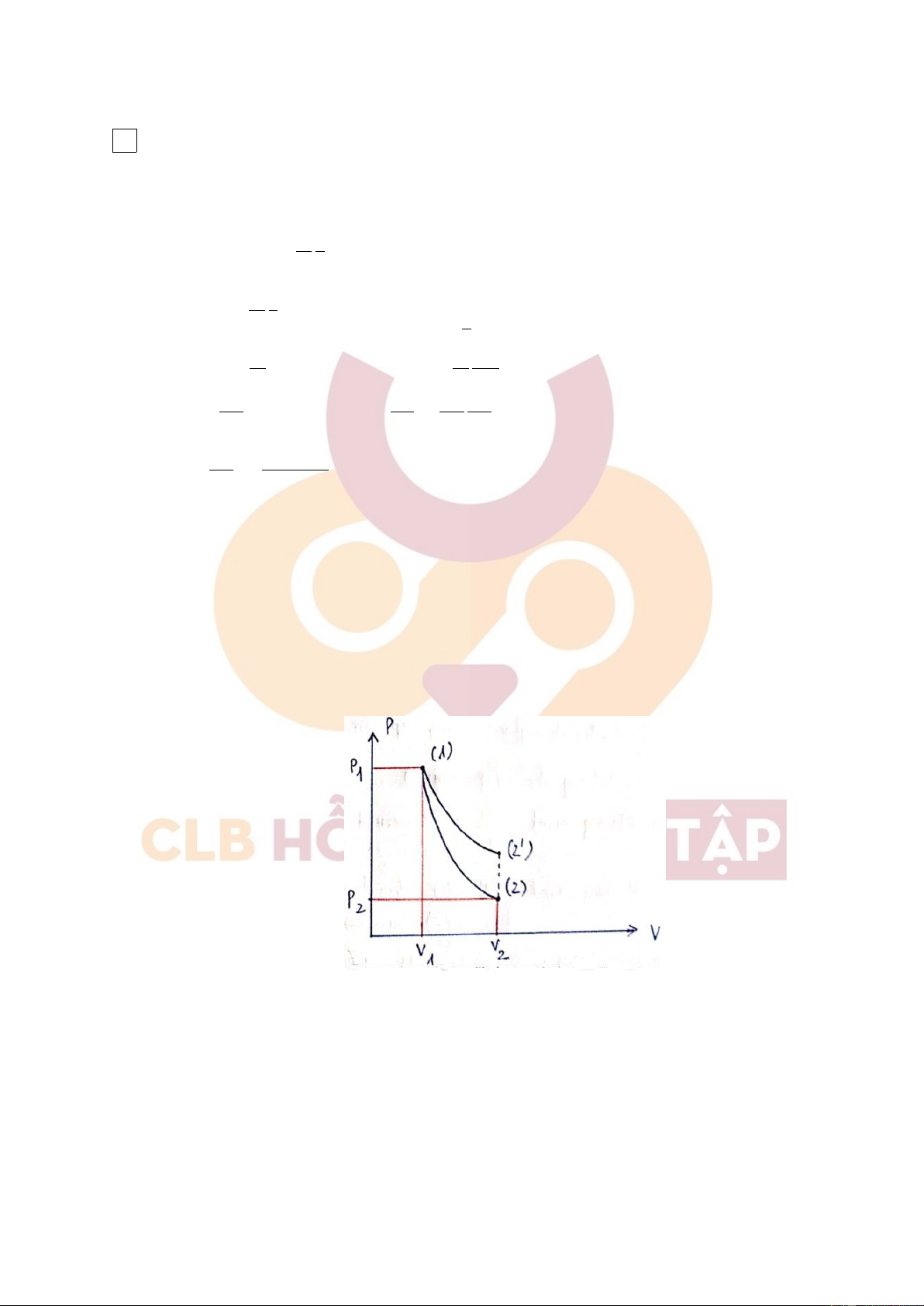
a) Định nghĩa: chu trình Carnot thuận nghịch là chu trình gồm 2 quá trình đẳng nhiệt thuận nghịch và
đoạn nhiệt thuận nghịch. Trong đó:
(1) → (2): giãn đẳng nhiệt ở nhiệt độ T1, nhận Q1 từ nguồn nóng.
(1) → (2): giãn đoạn nhiệt. Nhiệt độ giảm từ T1 → T2.
(3) → (4): nén đẳng nhiệt ở nhiệt độ T2, tác nhân tỏa nhiệt Q′ . 2
(4) → (1): nén đoạn nhiệt, nhiệt độ tăng từ T2 → T1
b) Xét 2 quá trình đẳng nhiệt (1)-> (2) và (3)->(4), ta có: 41
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập M V Q 2 1 = .R.T µ 1. ln V1 M V M V Q′ 4 3 2 = −Q′2 = − .R.T = .R.T µ 2. ln V 2. ln 3 µ V4 V T 3 2. ln V ⇒ η = 1 − 4 V T 2 1. ln V1
Xét 2 quá trình đoạn nhiệt còn lại, ta có: T1.V γ−1 2 = T2.V γ−1 3 T1.V γ−1 1 = T2.V γ−1 4 V V T ⇒ 2 = 3 ⇒ η = 1 − 2 V1 V4 T1 T ⇒ H = (1 − 2 ).100% T1
⇒ Hiệu suất chỉ phụ thuộc vào nguồn nóng, nguồn lạnh.
c) Định lý Carnot: Hiệu suất của tất cả động cơ thuận nghịch chạy theo chu trình Carnot với cùng
nguồn nóng và nguồn lạnh, đều bằng nhau và không phụ thuộc vào tác nhân cũng như cách chế tạo
máy. Hiệu suất của động cơ không thuận nghịch thì nhỏ hơn hiệu suất của động cơ thuận nghịch.
- Trong thực tế, để tăng hiệu suất của động cơ nhiệt, ta phải tăng nhiệt độ của nguồn nóng và giảm
nhiệt độ của nguồn lạnh; ngoài ra còn cần giảm bớt các mất mát về nhiệt để nó chạy theo chu trình
gần với chu trình thuận nghịch. 2. Bài toán T 300
a) Hiệu suất của động cơ là: η = 1 − 2 = 1 − = 40% T1 500 A′ b) Ta có η = Q1 T 500 − 300
⇒ Công mà động cơ thực hiện trong mỗi chu trình là: A′ = Q 1 − T2 1. = 2000. = T1 500 800(J) 42
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập Câu 27 1. Trình bày
a) Khái niệm và các tính chất hàm entropi của một hệ nhiệt động.
b) Biểu thức định lượng của nguyên lý 2 viết dưới dạng entropi.
c) Nội dung nguyên lý tăng entropi.
2. Bài toán: Tính độ biến thiên entropy khi cho dãn đẳng nhiệt 6g khí Hydro áp suất 100kPa đến áp suất 50kPa. [Lời giải] 1.
a) Khái niệm: hàm trạng thái S của hệ sao cho độ biến thiên của nó khi hệ biến đổi theo 1 quá trình
thuận nghịch bằng giá trị tích phân Clausius theo quá trình thuận nghịch đó, được gọi là hàm entropi của hệ. Tính chất hàm entropi:
+ S là một hàm trạng thái.
+ S là một đại lượng có tính cộng được. ˆ δQ
+ S được xác định sai khác nhau 1 hằng số cộng: S = S0 + T ˆ 2) δQ
b) Biểu thức định lương nguyên lý 2 dưới dạng hàm entropi: ∆S ≥ , dấu "=" xảy ra với (1) T
quá trình thuận nghịch, ngược lại dấu ">" khi quá trình không thuận nghịch.
c) Nội dung nguyên lý tăng entropi: Với quá trình nhiệt động thực tế xảy ra trong hệ cô lập, en-
tropi của hệ luôn tăng, nghĩa là một hệ cô lập không thể 2 lần đi qua cùng một trạng thái. Khi hệ đạt
trạng thái cân bằng thì quá trình không thuận nghịch sẽ kết thúc. Khi đó entropi đạt giá trị cực đại và bảo toàn. 2. Q M V
Độ biến thiên entropi trong quá trình đẳng nhiệt: ∆S = , với nhiệt lượng Q = .R.T. ln 2 Do T µ V1 V P
đây là quá trình đẳng nhiệt nên ta có: V 2 1 1.P1 = V2.P2 ⇒ = = 2 V1 P2 M V 6 Vậy ta có ∆S =
.R ln 2 = .8, 31. ln 2 ≈ 17.3(J/K) µ V1 2 43
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
Chương 10 - Khí thực Câu 28 1. Trình bày:
a) Những sự khác biệt trong mô hình khí lý tưởng và khí thực.
b) Khái niệm cộng tích, nội áp và thiết lập phương trình trạng thái cho khí thực trên cơ sở
phương trình trạng thái khí lý tưởng.
2. Bài toán: Tính nhiệt độ của 3,5g khí oxi chiếm thể tích 90cm3 ở áp suất 2,8 MPa nếu
được coi là khí lý tưởng và khí thực. Rút ra nhận xét về các kết quả nhận được. Cho biết
a = 1, 37.105Jm3/kmol2, b = 0, 03m3/kmol. [Lời giải] 1. a) Khí lý tưởng:
+ Phân tử khí có kích thước không đáng kể
+ Thể tích khối khí chính là thể tích dành cho chuyển động nhiệt tự do của phân tử khí.
+ Chỉ xét va chạm đàn hổi, bỏ qua tương tác hút/đẩy giữa các phân tử khí, nên áp suất trong không
khí gây bởi tổng hợp lực va chạm của các phân tử khí lên thành bình. Khí thực:
+ Khi nén hoặc hạ nhiệt độ, thể tích của khối khí giảm, lúc đó các phân tử lại gần nhau và không
thể bỏ qua lực tương tác giữa chúng.
+ Thể tích riêng của các phân tử cũng chiếm một phần đáng kể so với thể tích toàn bộ và không thể bỏ qua.
+ Các phân tử khí có tương tác với nhau nên áp suất của khối khí giảm đi do tương tác tĩnh điện
làm giảm lực tác dụng lên thành bình. b)
Cộng tích: Đối với khí thực, các phân tử có kích thước, vì vậy nếu gọi Vt là thể tích 1 kmol khí thực,
thì thể tích dành cho chuyển động tự do của các phân tử là: V = Vt − b, với b là số hạng bổ chính về
thể tích, được gọi là cộng tích. Đơn vị: m3/kmol
Nội áp: Đối với khí thực, do hút nhau nên lúc các phân tử tới va chạm vào thành bình, chúng bị 44
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
các phân tử bên trong kéo lại. Nếu gọi Pt là áp suất của khí thực thì P = Pt + Pi, với Pi là số hạng
bổ chính về áp suất, được gọi là nội áp.
Thiết lập phương trình Vandecvan: a
Thay V = Vt − b, P = Pt + Pi với Pi =
vào phương trình trạng thái khí lý tưởng (cho 1 kmol) V 2 t P V = RT , ta được: a Pt + .(V V 2 t − b) = R.T t
Đối với 1 khối khí thực M kg bất kỳ thì phương trình là: M 2.a M.b M.R.T Pt + .(V ) = µ2.V 2 t − t µ µ 2. M.R.T
+) Mô hình khí lý tưởng: Từ phương trình trạng thái khí lý tưởng: P.V = µ µ.P.V 32.2, 8.103.90.10−3 ⇒ T = = ≈ 277, 25(K) M.R 3, 5.8, 31 M 2.a M.b M.R.T
+) Mô hình khí thực: Từ phương trình trạng thái Pt + .(V ) = µ2.V 2 t − t µ µ µ M 2.a M.b ⇒ T = . P + . V − M.R µ2.V 2 µ 32 3, 52.10−6.1, 37.105 3, 5.10−3.0, 03 = . 2, 8.103 + . 90.10−3 − ≈ 277, 26(K) 3, 5.10−3.8, 31.103 322.902.10−6 32
+) Nhận xét: Ở áp suất nhỏ nhiệt độ khối khí tính được dựa trên 2 phương trình khác nhau xấp
xỉ nhau nên vẫn có thể áp dụng mô hình khí lý tưởng cho Oxi. Câu 29
1. Thiết lập phương trình trạng thái cho khí thực trên cơ sở phương trình trạng thái khí lý tưởng.
2. Vẽ đồ thị họ đường đẳng nhiệt Van-der-Waals. So sánh đường đẳng nhiệt Van-der-Waals và
đường đẳng nhiệt thực nghiệm. 1. Ta xét với 1 kmol khí.
Phương trình trạng thái của khí lý tưởng là: p.V = R.T (1)
Do trong khí lý tưởng các phân tử khí có thể coi như chất điểm còn đối với khí thực thì các phân tử
chiếm một thể tích nhất định. Do đó thể tích V dành cho chuyển động tự do của khí thực sẽ nhỏ hơn
thể tích của khí thực Vt:
V = V t − b (2) (b còn được gọi là cộng tích)
Trong khí lý tưởng các phân tử không tương tác với nhau nhưng trong khí thực do các phân tử hút 45
Downloaded by v?n ti?n Lê (vantienle525@gmail.com) lOMoARcPSD|36442750
Hỗ trợ Sinh viên Bách Khoa
CLB Hỗ Trợ Học Tập
nhau nên khi các phân tử tới va chạm vào thành bình sẽ bị các phân tử bên trong kéo lại. Nếu gọi Pt
là áp suất của khí thực thì: P = Pt + Pi (3)
(Trong đó Pi là số hạng hiệu chính về áp suất gọi là nội áp). Từ (1) + (2) + (3): (Pt + Pi)(Vt − b) = R.T (4)
Do lực hút gây ra áp suất Pi tỉ lệ với n2,
o no là mật độ phân tử. Mà mật độ phân tử khí tỉ lệ nghịch với thể tích khối khí: a Pi = (5) V 2 t Từ (4) + (5): a (Pt +
)(V t − b) = RT (6), là phương trình đúng với 1 kmol khí. V 2 t
Đối với 1 khối khí bất kì có khối lượng m: M Vt = V µ M Thay Pt = P, Vt = V vào (6): µ m2 a M M (P + )(V − b) = RT M 2 V 2 t µ µ 2. So sánh:
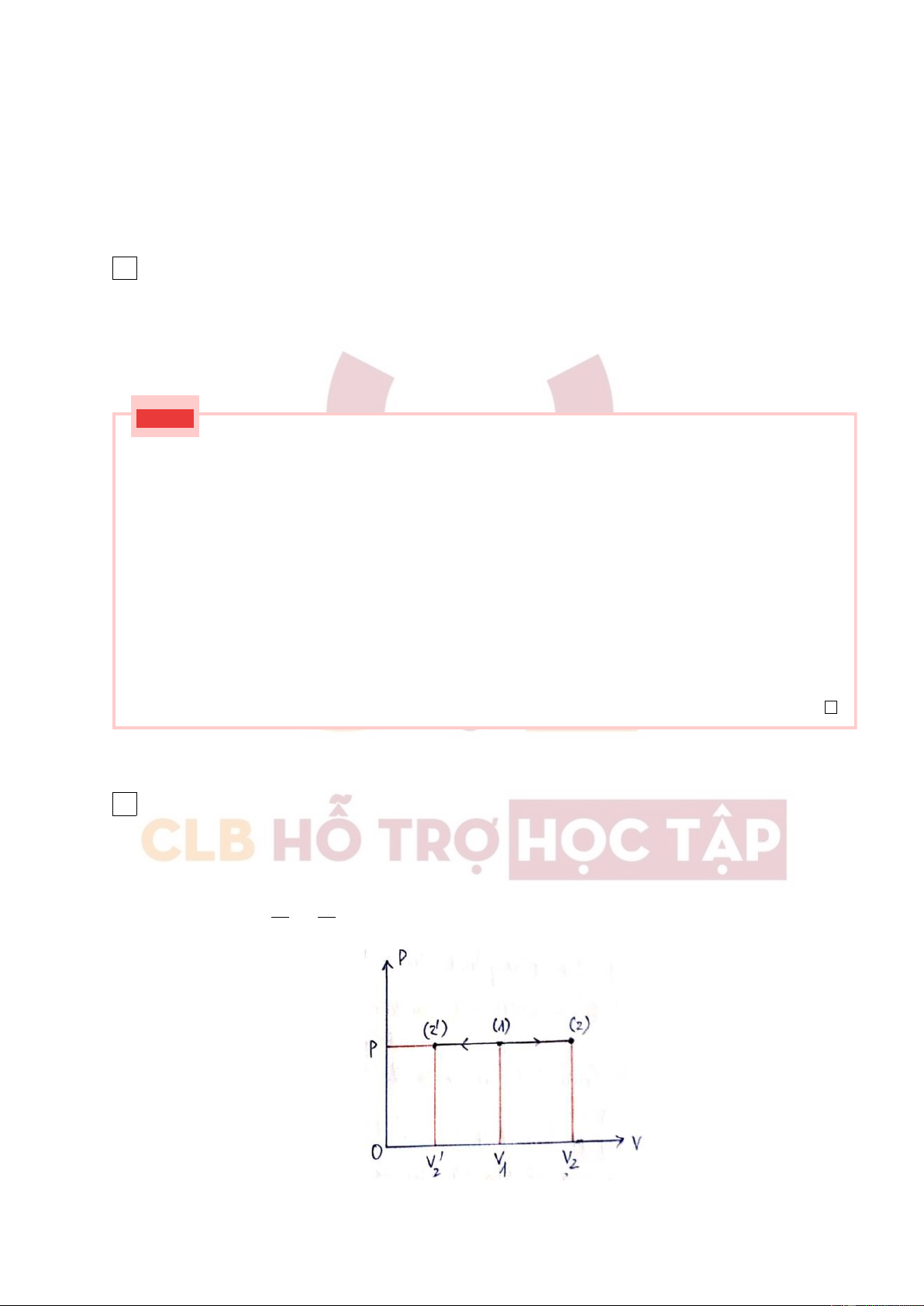
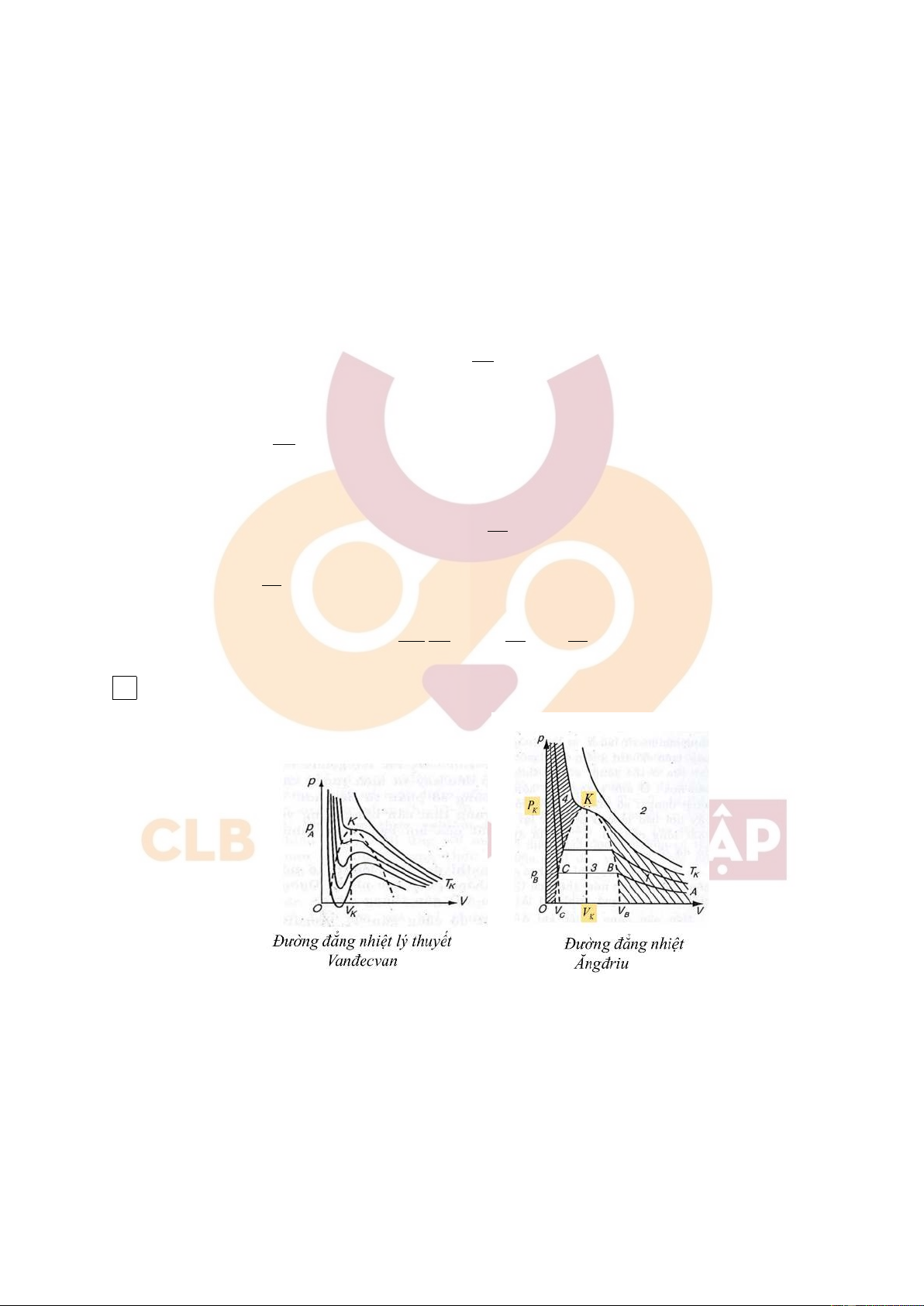
(a) Khi T ≥ Tk thì 2 đường đẳng nhiệt giống nhau.
(b) Tại T = Tk thì 2 đồ thị đều có một điểm uốn, nhiệt độ T = Tk đó được gọi là nhiệt độ tới hạn.
(c) Khi T < Tk thì ta thấy có sự khác nhau: đường đẳng nhiệt lý thuyết có những điểm lồi lõm
còn thực nghiệm lại là đoạn nằm ngang. Nguyên nhân gây ra sự khác nhau này là do khí thực
nghiệm không phải khí tinh khiết, nó có các tạp chất 46
Downloaded by v?n ti?n Lê (vantienle525@gmail.com)

