Slide Chương 4: Không gian vector | Môn Linear algebra and Algebraic structures - Đại học Sư phạm Kỹ thuật Thành phố Hồ Chí Minh

lOMoAR cPSD| 58759230 Chương 4. KHÔNG GIAN VECTƠ
4.1. Không gian vectơ và không gian con
4.2. Không gian hạch, không gian cột
và phép biến đổi tuyến tính 4.3. Tập
độc lập tuyến tính; Cơ sở lOMoAR cPSD| 58759230 4.4. Hệ tọa độ
4.5. Chiều của không gian vectơ 4.6. Hạng 4.7. Đổi cơ sở
4.1. Không gian vectơ và không gian con a/ Định nghĩa
V là tập hợp chứa tất cả các đoạn thẳng có hướng lOMoAR cPSD| 58759230 (8) c d .u c.u d.u (1) u+v V (2) u+v=v+u (9) c d. . u cd. (3) u+v+w=u+ . u v+w (10) 1.u u
(4) có 0 V : u+0=u (5) u V , có u V : u+ u =0
(6) c.u V (7) c. u v
c.u c.v lOMoAR cPSD| 58759230
4.1. Không gian vectơ và không gian con a/ Định nghĩa
V là tập hợp chứa tất V = Rn cả các (5) u V , có u đoạn V : thẳng có hướng (1) u+v V u+ u =0 (2) u+v=v+u
(6) c.u V (3) u+v+w=u+ (7) c. u v c.u c.v v+w
(4) có 0 V : u+0=u (8) c d .u c.u d.u lOMoAR cPSD| 58759230 (9) c d. . u cd. . u (10) 1.u u
4.1. Không gian vectơ và không gian con a/ Định nghĩa
V là tập hợp chứa tất
V là tập hợp chứa tất V =
cả các đa thức biến t, Rn bậc bé hơn hoặc cả các đoạn thẳng có bằng n hướng (1) u+v V (2) u+v=v+u lOMoAR cPSD| 58759230 (3) u+v+w=u+ (7) c. u v c.u v+w c.v
(4) có 0 V : u+0=u (8) c d .u c.u (5) u V , có u d.u V : (9) c d. . u cd. u+ u =0 . u
(6) c.u V (10) 1.u u lOMoAR cPSD| 58759230
4.1. Không gian vectơ và không gian con ĐỊNH NGHĨA
V là không gian vectơ và các phần tử của V gọi là các
vectơ nếu V và trên V có phép toán cộng, phép nhân vô
hướng thỏa các tiên đề sau u, v, w V c d; , : lOMoAR cPSD| 58759230
4.1. Không gian vectơ và không gian con ĐỊNH NGHĨA
V là không gian vectơ và các phần tử của V gọi là các
vectơ nếu V và trên V có phép toán cộng, phép nhân vô
hướng thỏa các tiên đề sau u, v, w V c d; , : lOMoAR cPSD| 58759230 (1) u+v V (7) c. u v c.u (2) u+v=v+u c.v (3) u+v+w=u+ v+w (8) c d .u c.u d.u
(4) có 0 V : u+0=u (9) (5) c d. . u cd. u V , có u V : u+ u =0 . u (10) 1.u u
(6) c.u V
4.1. Không gian vectơ và không gian con VÍ DỤ 1
Các không gian n, với n 1, là các không gian véctơ. lOMoAR cPSD| 58759230
4.1. Không gian vectơ và không gian con VÍ DỤ 1
Các không gian n, với n 1, là các không gian véctơ. VÍ DỤ 2
V là tập hợp các đoạn thẳng có hướng (cộng và nhân vô
hướng đã được học ở cấp 3) là một kgvt. lOMoAR cPSD| 58759230
4.1. Không gian vectơ và không gian con VÍ DỤ 1
Các không gian n, với n 1, là các không gian véctơ. VÍ DỤ 2
V là tập hợp các đoạn thẳng có hướng (cộng và nhân vô
hướng đã được học ở cấp 3) là một kgvt. VÍ DỤ 3
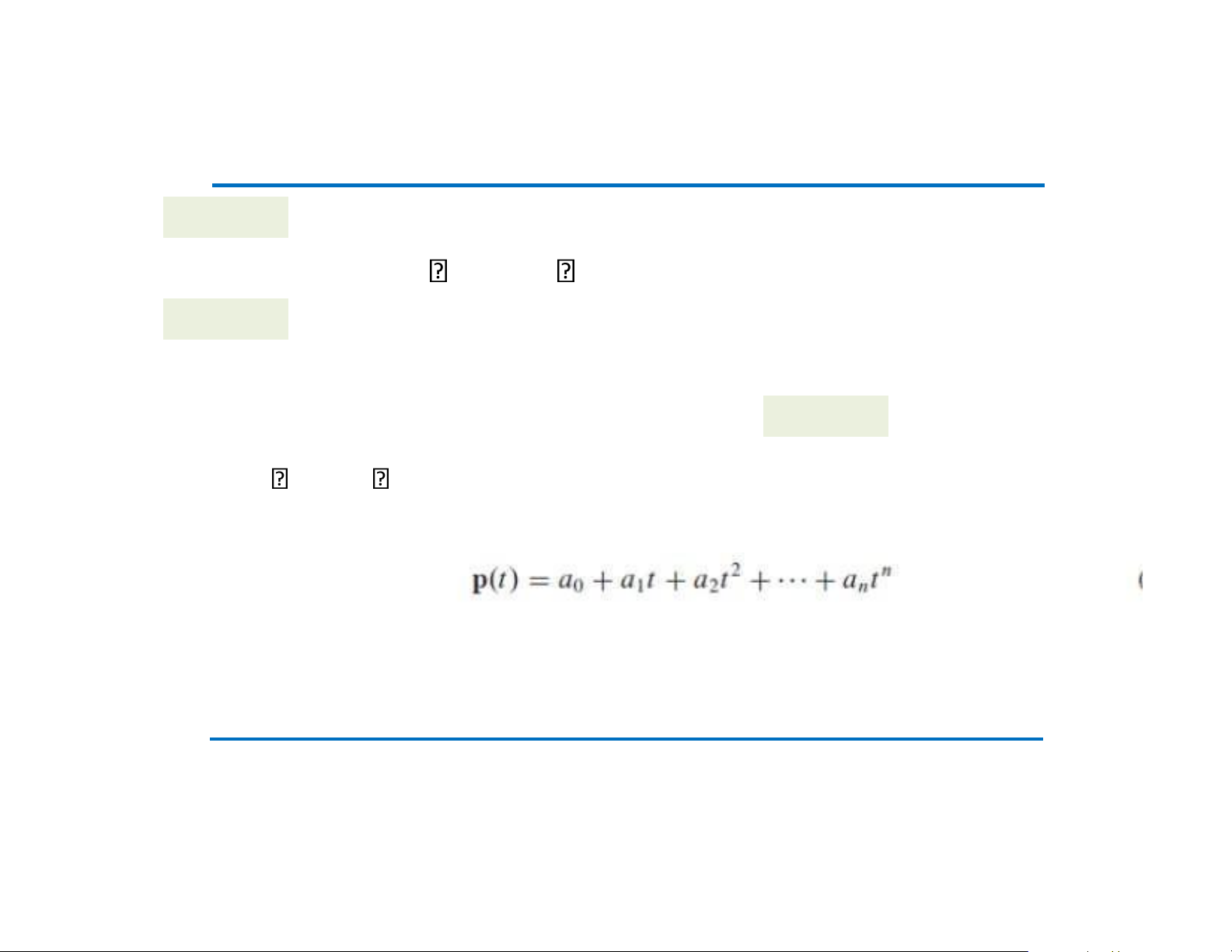
Với n 0, tập n các đa thức có bậc lớn nhất n bao gồm các đa thức dạng
với các hệ số a a a0, , ,1 ... n và biến t là các số thực.
4.1. Không gian vectơ và không gian con lOMoAR cPSD| 58759230 VÍ DỤ 4
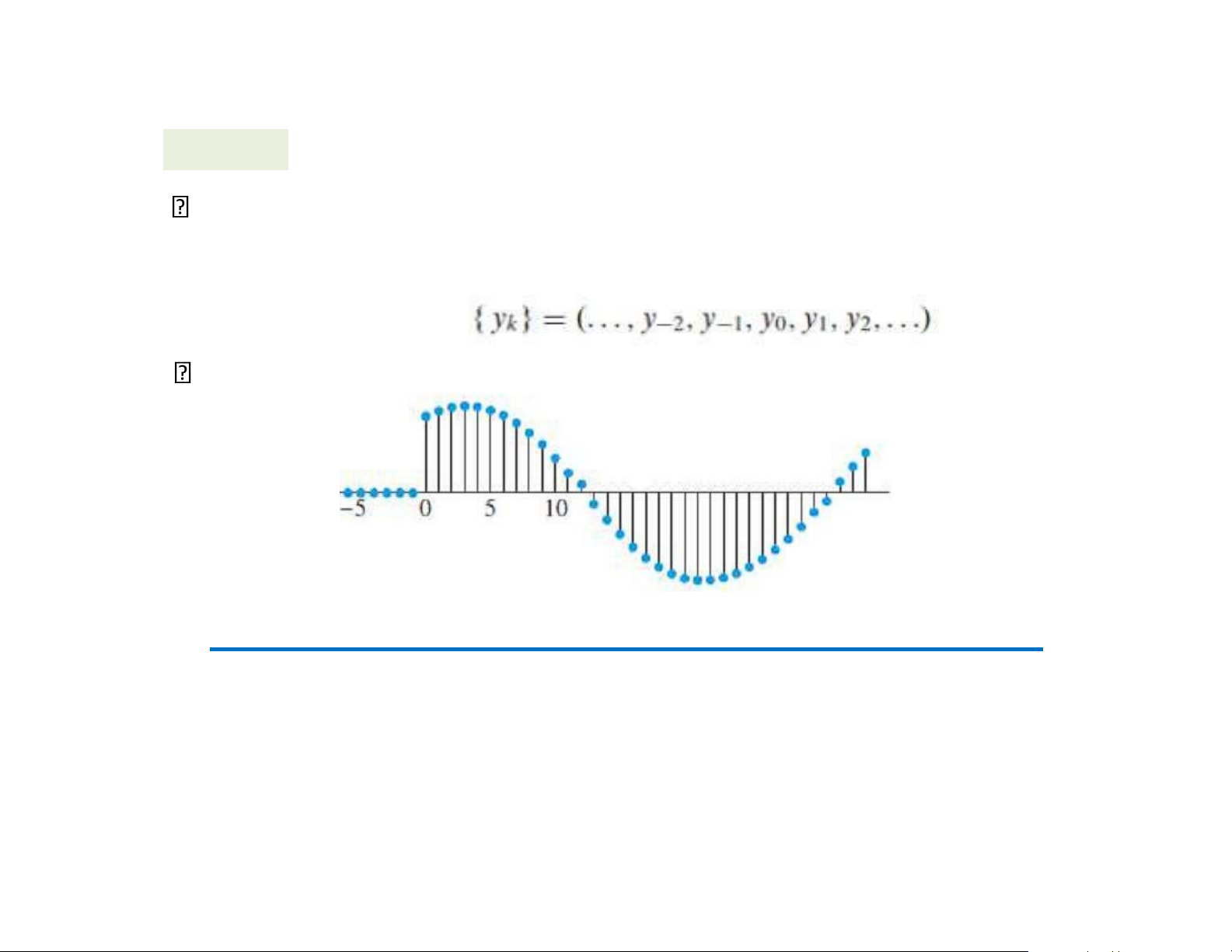
là tập tất cả các dãy vô hạn các số (thường được viết thành
một hàng thay vì một cột):
là không gian các tín hiệu.
4.1. Không gian vectơ và không gian con lOMoAR cPSD| 58759230 VÍ DỤ 4
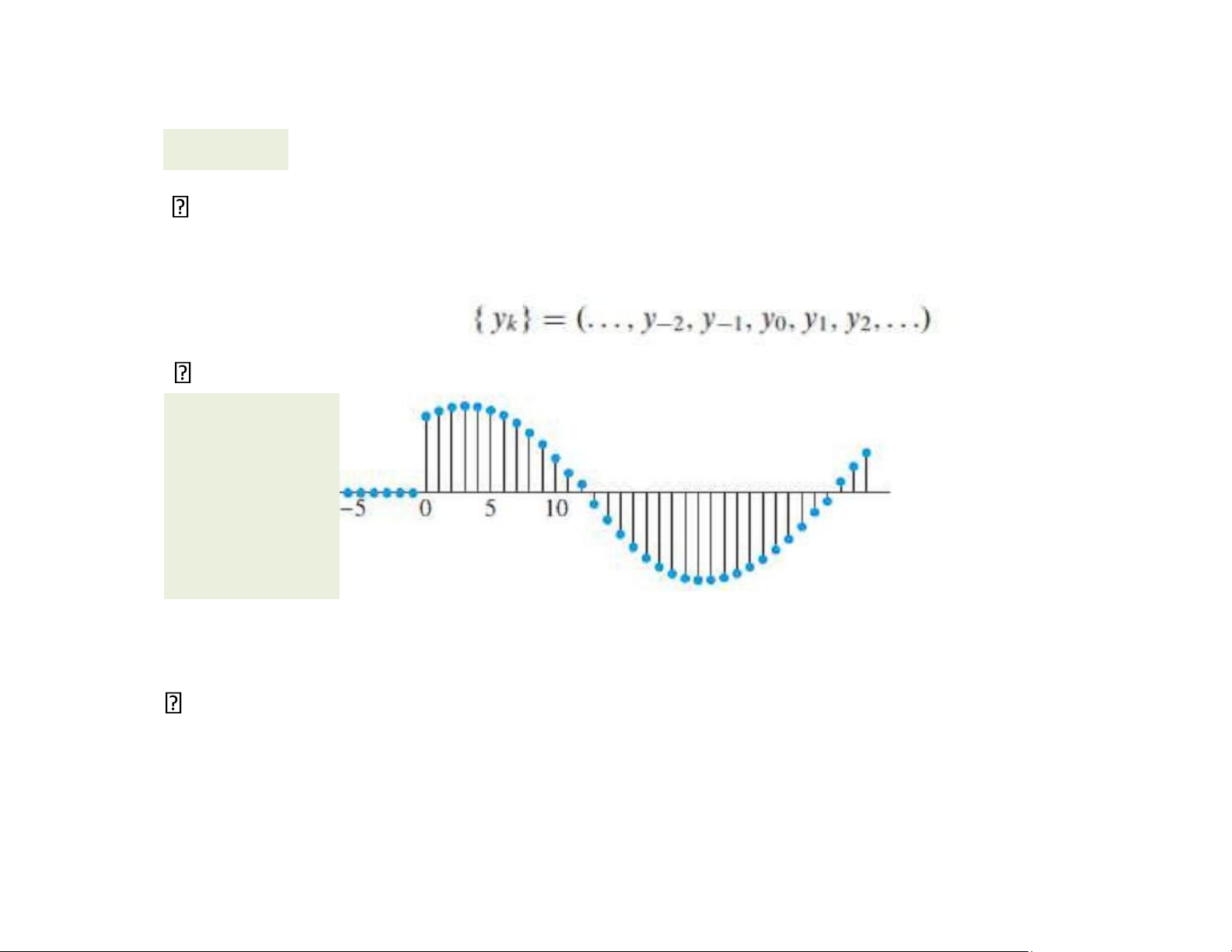
là tập tất cả các dãy vô hạn các số (thường được viết thành
một hàng thay vì một cột):
là không gian các tín hiệu. VÍ DỤ 5
V là tập tất cả các hàm giá trị thực được xác định trên một tập
là một không gian vectơ. lOMoAR cPSD| 58759230
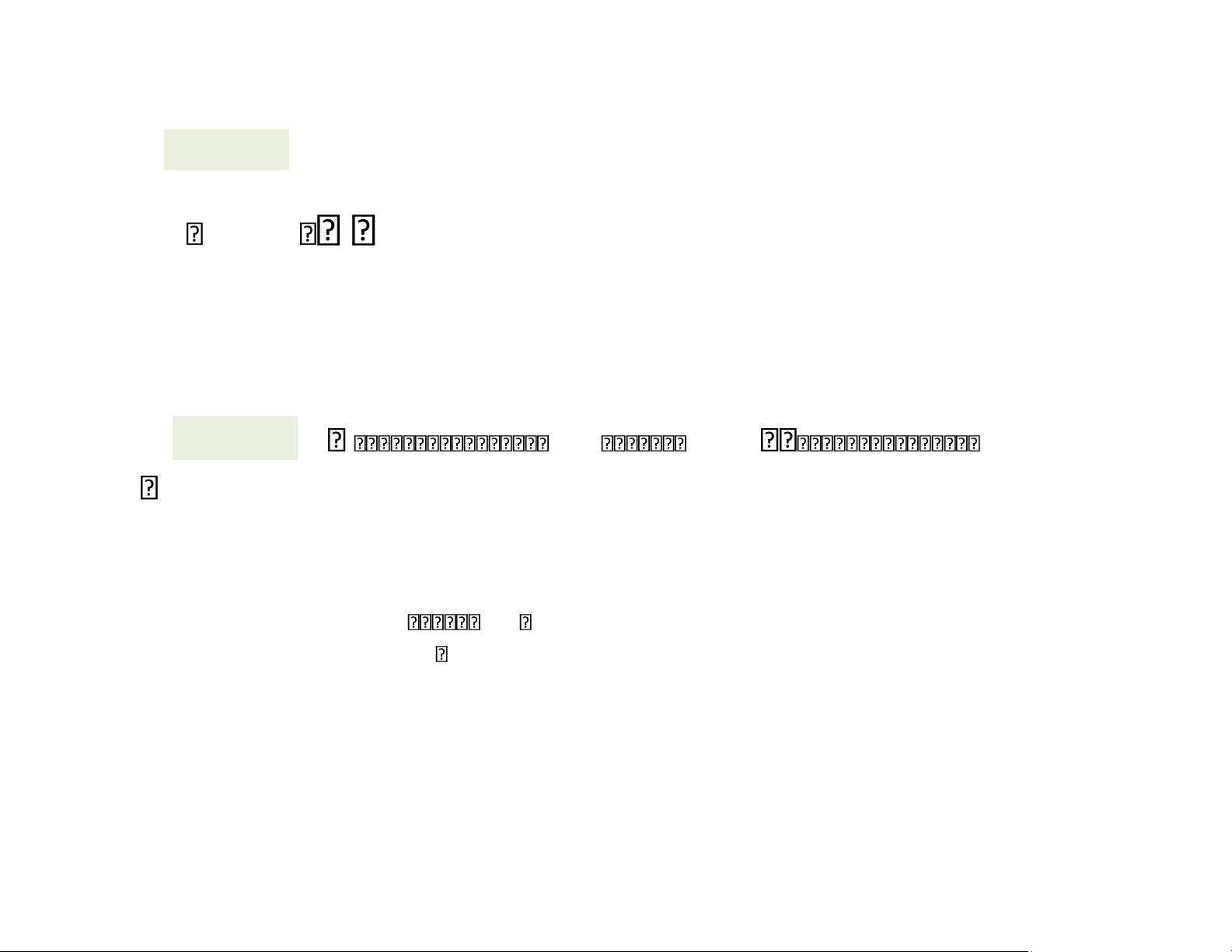
4.1. Không gian vectơ và không gian con b/ Không gian con ĐỊNH NGHĨA Cho kgvt V. H là kh.gian con của V khi
H V , 0 H u+v H c.u H uv, H c, lOMoAR cPSD| 58759230
4.1. Không gian vectơ và không gian con b/ Không gian con ĐỊNH NGHĨA Cho kgvt V. H là kh.gian con của V khi
H Vu+v , H0
uvH, H c, c.u H VÍ DỤ 6
0 V thì H
0 là một không gian con của V, gọi là không gian con không của V. lOMoAR cPSD| 58759230
4.1. Không gian vectơ và không gian con b/ Không gian con ĐỊNH NGHĨA Cho kgvt V.
H là kh.gian con của V khi
cH Vu+v.u H , H0 uvH, H c, lOMoAR cPSD| 58759230 VÍ DỤ 6
0 V thì H
0 là một không gian con của V, gọi là không gian con không của V. VÍ DỤ 7H s0t : s t, là không gian con của 3. lOMoAR cPSD| 58759230
4.1. Không gian vectơ và không gian con
c/ Không gian con sinh bởi tập hợp
ĐỊNH LÝ 1. Nếu v1, ,vp thuộc không gian véctơ V, thì
Span v1, ,vp là một không gian con của V. lOMoAR cPSD| 58759230
4.1. Không gian vectơ và không gian con
c/ Không gian con sinh bởi tập hợp
ĐỊNH LÝ 1. Nếu v1, ,vp thuộc không gian véctơ V, thì
Span v1, ,vp là một không gian con của V. Chú ý lOMoAR cPSD| 58759230
4.1. Không gian vectơ và không gian con
c/ Không gian con sinh bởi tập hợp
ĐỊNH LÝ 1. Nếu v1, ,vp thuộc không gian véctơ V, thì
Span v1, ,vp là một không gian con của V. Chú ý