Slide Chương 5: Giá trị riêng và vector riêng | Môn Linear algebra and Algebraic structures - Đại học Sư phạm Kỹ thuật Thành phố Hồ Chí Minh

lOMoAR cPSD| 58759230 Chương 5. GIÁ TRỊ RIÊNG VÀ VECTƠ RIÊNG 1
5.1. Giá trị riêng và vectơ riêng 5.2. Phương trình đặc trưng lOMoAR cPSD| 58759230 5.3. Chéo hóa 2
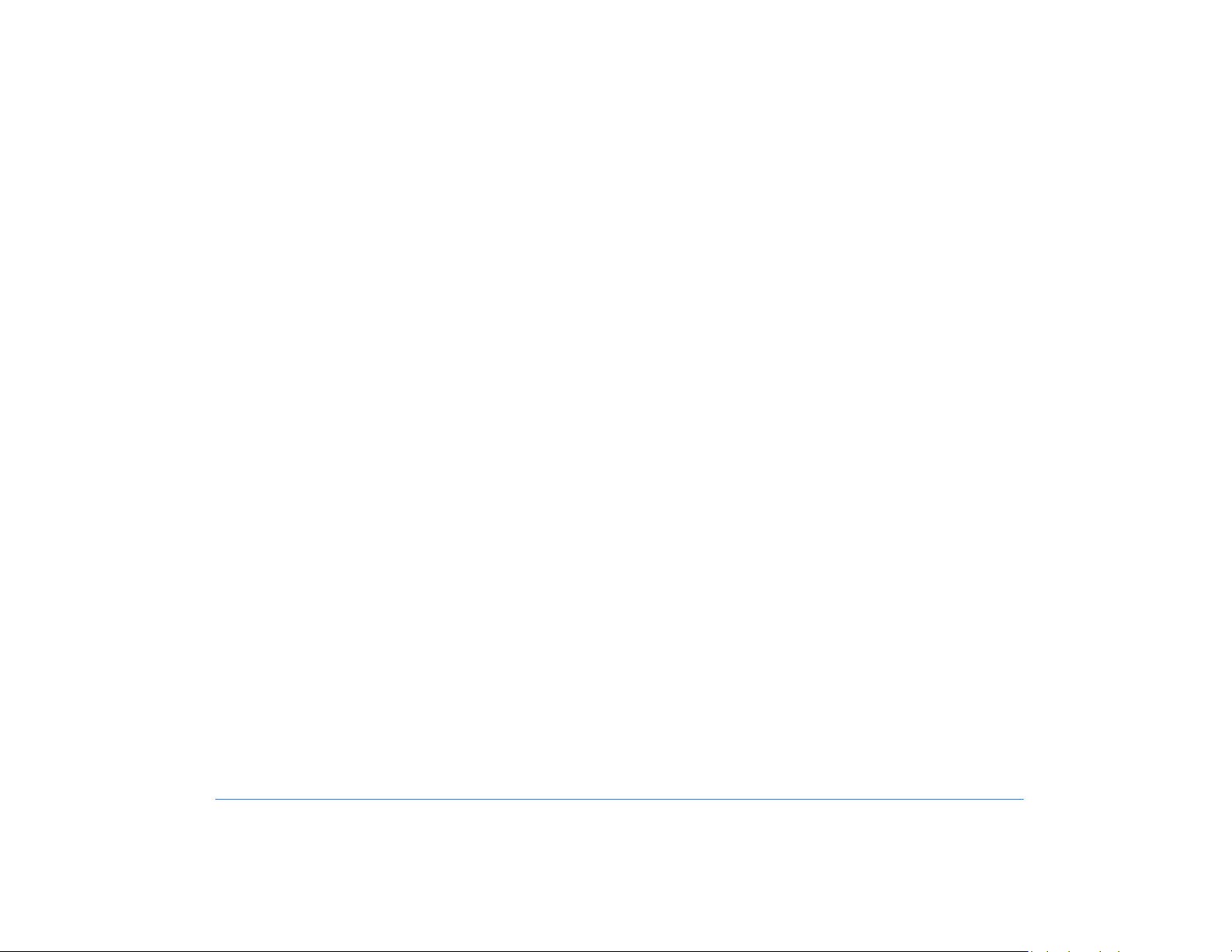
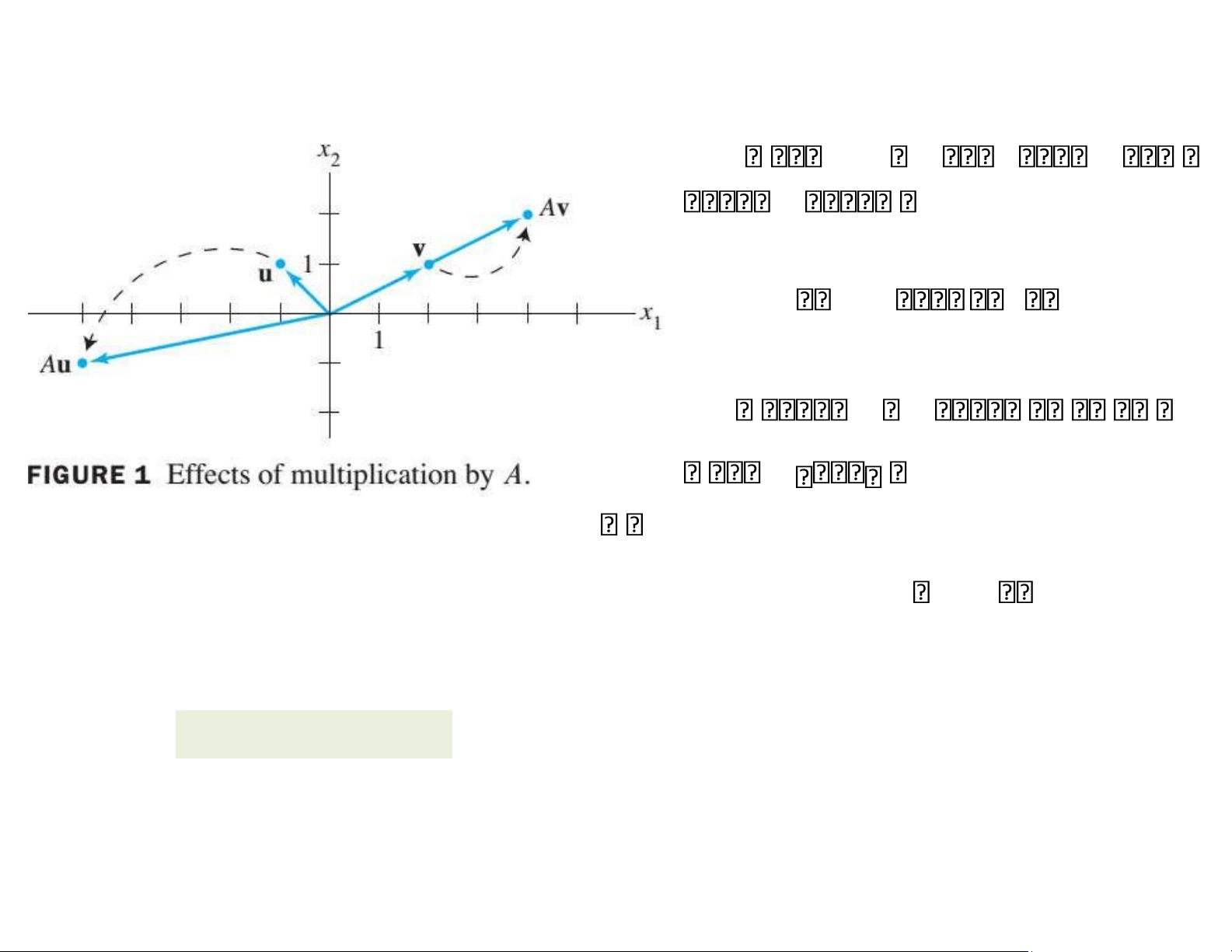
5.1+5.2. Giá trị riêng và vectơ riêng lOMoAR cPSD| 58759230 VÍ DỤ 1 Cho A 3 2 , u 11 , v 21 . Ảnh của u và v qua 1 0
phép nhân với A được chỉ ra ở hình 1. Thật sự, Av 2v. Vì
thế A chỉ kéo hoặc làm giãn v. lOMoAR cPSD| 58759230 A.u 13 02 . 11 51 k.u A.v 13 02 2 24 2.v . 1 3 ĐỊNH NGHĨA
Cho A là 1 ma trận cấp nxn. lOMoAR cPSD| 58759230
x là 1 vectơ riêng của A có số sao cho x x 1 0 . Ax x xn
Số là 1 giá trị riêng của A hệ Ax x có nghiệm
không tầm thường; nghiệm x≠0 là 1 VTR ứng với . Nul A I
được gọi là không gian riêng của A
ứng với giá trị riêng . lOMoAR cPSD| 58759230 4 ĐỊNH NGHĨA
Cho A là 1 ma trận cấp nxn. x
x là 1 vectơ riêng của A có số sao cho x x n1 0 . Ax x lOMoAR cPSD| 58759230
Số là 1 giá trị riêng của A hệ Ax x có nghiệm
không tầm thường; nghiệm x≠0 là 1 VTR ứng với . Nul A I
được gọi là không gian riêng của A
ứng với giá trị riêng .
Phương trình đặc trưng của A: det A I 0
Đa thức đặc trưng của A: det A I 5 CHÚ Ý
1. Giá trị riêng của A là nghiệm của phương trình det A I 0, với là ẩn. lOMoAR cPSD| 58759230
2. Vectơ riêng ứng với giá trị riêng là nghiệm không tầm thường của hệ A I x 0 .
3. Cho trước ma trận A và vectơ u. Kiểm tra u có là vectơ riêng của A bằng
cách kiểm tra A.u có là một bội của u không.
4. Không gian riêng ứng với giá trị riêng chứa vectơ không và tất cả các vectơ riêng ứng với .
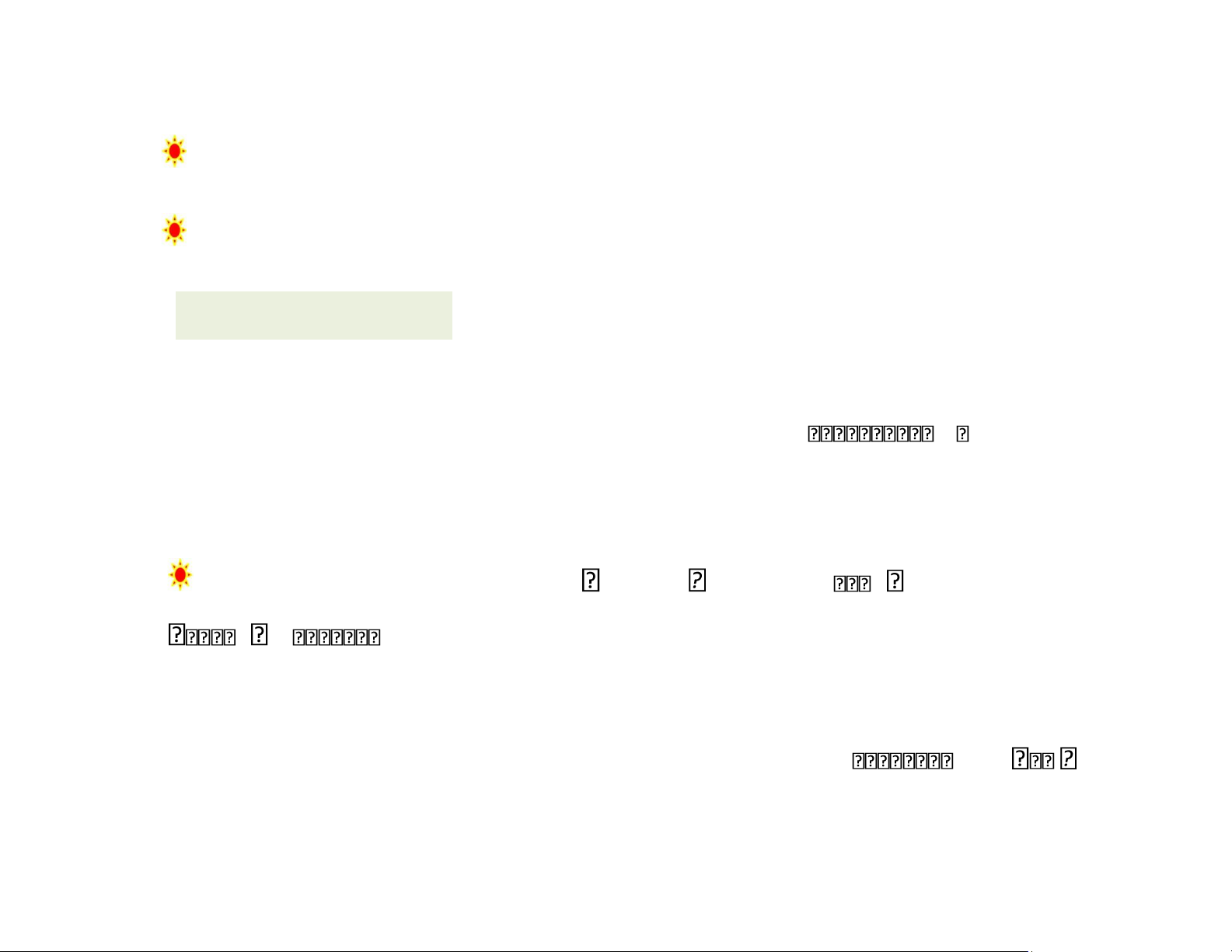
5. Các vectơ trong một cơ sở của không gian riêng gọi là các vectơ riêng cơ sở. 6 lOMoAR cPSD| 58759230 VÍ DỤ 2 Cho A 52 30 ,u 53 ,v 21 . Hỏi u và v có là những vectơ riêng của A không? lOMoAR cPSD| 58759230 7 VÍ DỤ 2 Cho A 2 3 ,u 53 ,v 21
. Hỏi u và v có là những 5 0 vectơ riêng của A không? u 0 v 0 , GIẢI A.u 5203 . 53 159 3.u lOMoAR cPSD| 58759230 2 3 A.v . 21 45 k.v 5 0
Như vậy u là vectơ riêng ứng với giá trị riêng 3, nhưng
v không là một vectơ riêng của A, vì Av
không là một bội của v. 8
VÍ DỤ 3 1 3 3 Cho A 3 5 3 . 6 6 4 a/ Chỉ ra
2 là một giá trị riêng của A,
và tìm một vectơ riêng tương ứng. lOMoAR cPSD| 58759230
b/Tìm một cơ sở của không gian riêng tương ứng với giá trị riêng 2.
c/ Tìm tất cả các giá trị riêng và vectơ riêng của A. 9
VÍ DỤ 3 1 3 3 Cho A 3 5 3 . 6 6 4 a/ Chỉ ra
2 là một giá trị riêng của A,
và tìm một vectơ riêng tương ứng. lOMoAR cPSD| 58759230
b/Tìm một cơ sở của không gian riêng tương ứng với giá trị riêng 2.
c/ Tìm tất cả các giá trị riêng và vectơ riêng của A. 10 GIẢI 3 3 3 3 3 3 0 2 a/ Vì det A 2 I 6 6 6, nên số là một giá trị riêng của A. lOMoAR cPSD| 58759230 GIẢI 3 3 3 3 3 3 0 2 a/ Vì det A 2 I 6 6 6, nên số
là một giá trị riêng của A. Giải hệ A 2 I
x 0. Ma trận bổ sung x1 x2 x3 3 3 3 0 3 3 3 0 1 1 1 0 A 2I 0 6 6 6 03 3 3 0 0 0 0 00 0 0 0 0 0 0 00 0 0 0 Hệ VSN. x x2 3, : tudo lOMoAR cPSD| 58759230 GIẢI 3 3 3 3 3 3 0 2 a/ Vì det A 2 I 6 6 6, nên số là một giá trị riêng của A. Giải hệ A 2 I
x 0. Ma trận bổ sung 3 3 3 0 3 3 3 0 1 1 1 0 A 2I 0 6 6 6 03 3 3 0 0 0 0 00 0 0 0 0 0 0 00 0 0 0 1 Hệ VSN.
xx x12 3, x:2tudox3 lOMoAR cPSD| 58759230
Do đó, một vectơ riêng ứng với 2 là u 1 . 0 GIẢI 3 3 3 3 3 3 0 2 a/ Vì det A 2 I 6 6 6, nên số là một giá trị riêng của A. Giải hệ A 2 I
x 0. Ma trận bổ sung 0 0 0 0 0 0 0 0Hệ VSN. A 2I 0 6 6 6 03 3 3 03 3 3 0 3 3 3 00 0 0 0 1 1 1 0
xx x12 3, x:2tudox3 lOMoAR cPSD| 58759230 0 0 0 0 1
Do đó, một vectơ riêng ứng với 2 là u 1 . 0
b/ CVậy cơ sở của không gian riêng ứng với ác vectơ riêng ứng với 2 là x x2 110 x3 101 , với x 2211 ,x 32 01 0. . 2 là lOMoAR cPSD| 58759230 0 1 c/ Tìm GTR: 1
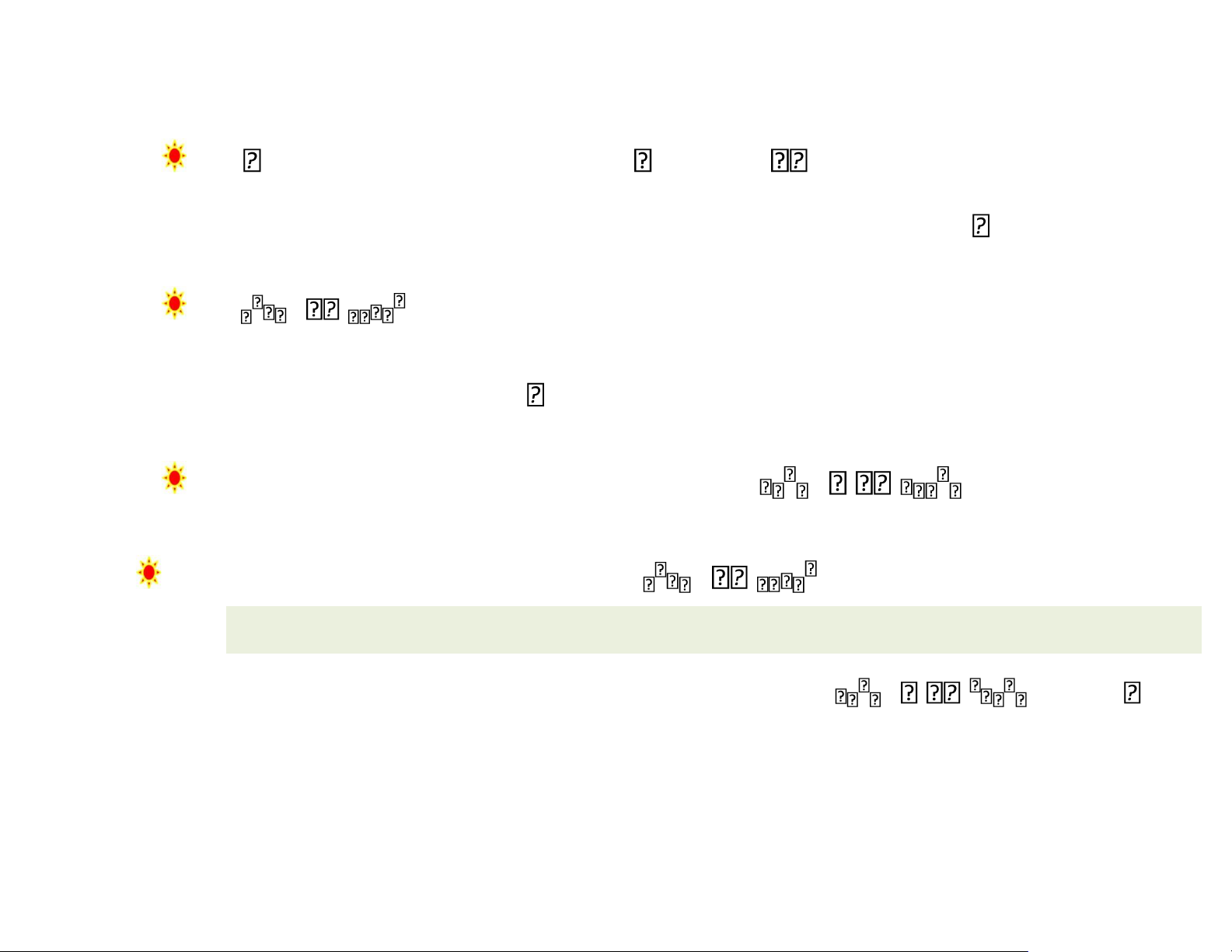
3 3 A I 3 5 3 6 6 4 lOMoAR cPSD| 58759230 15 c/ Tìm GTR: 1
3 3 A I 3 5 3 6 6 4 a a a11 12 13 CHÚ Ý 16 lOMoAR cPSD| 58759230 A a a a 21 22 23 a a a31 32 33 a23 detA a33 det A I 3 a11 a22 a33 2
aa11 1221 22aa aa1131 aa1333 aa2232 c/ Tìm GTR: