Slide về Cộng tham số Bzier - Đồ họa máy tính | Đại học Bách Khoa, Đại học Đà Nẵng
Slide về Cộng tham số Bzier - Đồ họa máy tính | Đại học Bách Khoa, Đại học Đà Nẵng giúp sinh viên tham khảo, ôn luyện và phục vụ nhu cầu học tập của mình cụ thể là có định hướng, ôn tập, nắm vững kiến thức môn học và làm bài tốt trong những bài kiểm tra, bài tiểu luận, bài tập kết thúc học phần, từ đó học tập tốt và có kết quả cao cũng như có thể vận dụng tốt những kiến thức mình đã học
Tài liệu liên quan:
Preview text:
TRƯỜNG ĐẠI HỌC BÁCH KHOA 2.1. Giới thiệu
KHOA CÔNG NGHỆ THÔNG TIN
• Đường cong tham số Bézier được sử dụng trong đồ
hoạ máy tính và nhiều lĩnh vực khác.
a. Phương trình tham số đoạn thẳng BÀI GIẢNG
• Xét một đoạn thẳng có điểm đầu P và điểm cuối P , 0 1
điểm C là một điểm bất kỳ nằm trên đoạn thẳng.
ĐƯỜNG VÀ MẶT CONG BÉZIER Nguyễn Tấn Khôi
• Phương trình tham số của đoạn thẳng:
C (u) = (1− u)P + uP 0 1 2/40 2.1. Giới thiệu 2.1. Giới thiệu B = 1− u • Đặt: 0
b. Phương trình tham số của đường cong bậc hai B = u 1 1
• Xét đa giác bao gồm các đỉnh P , P , P . 0 1 2
• Ta có: C (u ) = B P +B P = B P 0 0 1 1 i i i 0 =
>> Một điểm trên đường thẳng được xác định dựa vào
các hàm cơ sở và các điểm tương ứng.
• Chọn một tham số u ∈ [0, 1], điểm S ,S trên cạnh 0 1
P P được biểu diễn: 0 1 S ( ) u = (1 − ) u P + uP 0 0 1 S ( ) u = (1 − ) u P + uP 1 1 2 3/40 4/40 2.1. Giới thiệu 2.1. Giới thiệu
b. Phương trình tham số của đường cong bậc hai
c. Phương trình tham số của đường cong bậc hai
• Xét cạnh mới S S , điểm C trên cạnh này được xác • Triển khai: 0 1
định theo tham số u cũng là điểm nằm trên đường
C (u) = (1− u)((1− u )P + uP ) + u((1− u )P + uP ) 0 1 1 2
cong bậc hai có ba đỉnh điều khiển P , P , P . 0 1 2
C (u)= (1− u)(P − P u + Pu)+ u(P − Pu + P u) 0 0 1 1 1 2 2 2
C (u)= (1− u) P + (2u(1− u))P + u P 0 1 2
• Các hàm cơ sở: B = (1−u )2 0 2
B = 2u (1 u − )
C (u) = B P 1 i i
C (u) = (1− u)S + uS i 0 = 0 1 2 B = u 2 5/40 6/40 2.1. Giới thiệu
2.3. Đường cong tham số Bézier
b. Phương trình tham số của đường cong bậc ba
2.2.1. Phương trình đường cong
• Thực hiện tương tự quá trình trên, ta có phương trình n biểu diễn như sau: C( ) u = PB ( ) u 0 ≤ u ≤1 i , n i i 0 = 3 3 P ∈ ℝ
P (x , y , z ) x
∀ , y , z ∈ , ℝ i = 0…n C( ) u = B P i i i i i i i i i i i= 0 Trong đó: • Các hàm cơ sở: • {P}( i = 0...n i
) các đỉnh điều khiển của đường 2 B = 3 ( u 1 − ) u 1 cong; 2
B = 3u (1 − u) 2 3 B = u 3 7/40 8/40
2.3. Đường cong tham số Bézier
2.3. Đường cong tham số Bézier
2.2.1. Phương trình đường cong
Một điểm trên đường cong Bézier C(u) tại tham n số u có toạ độ:
C (u) = PB (u) 0 ≤ u ≤1 i n ,i i 0 = n = Trong đó: C (u) x B (u) x i n ,i i = 0
• Hàm trộn (blending funtion) hay còn gọi là đa n
C (u ) = C (u ) = y B (u)
thức Bernstein (Bernstein polynomial) có bậc n: y i , n i i= 0 n n!
C (u) = z B (u) B (u) i
u (1 u)n i− = − i = 0...n z i n ,i , n i i= 0 ! i (n − ) i ! 9/40 10/40
2.3. Đường cong tham số Bézier
2.3. Đường cong tham số Bézier
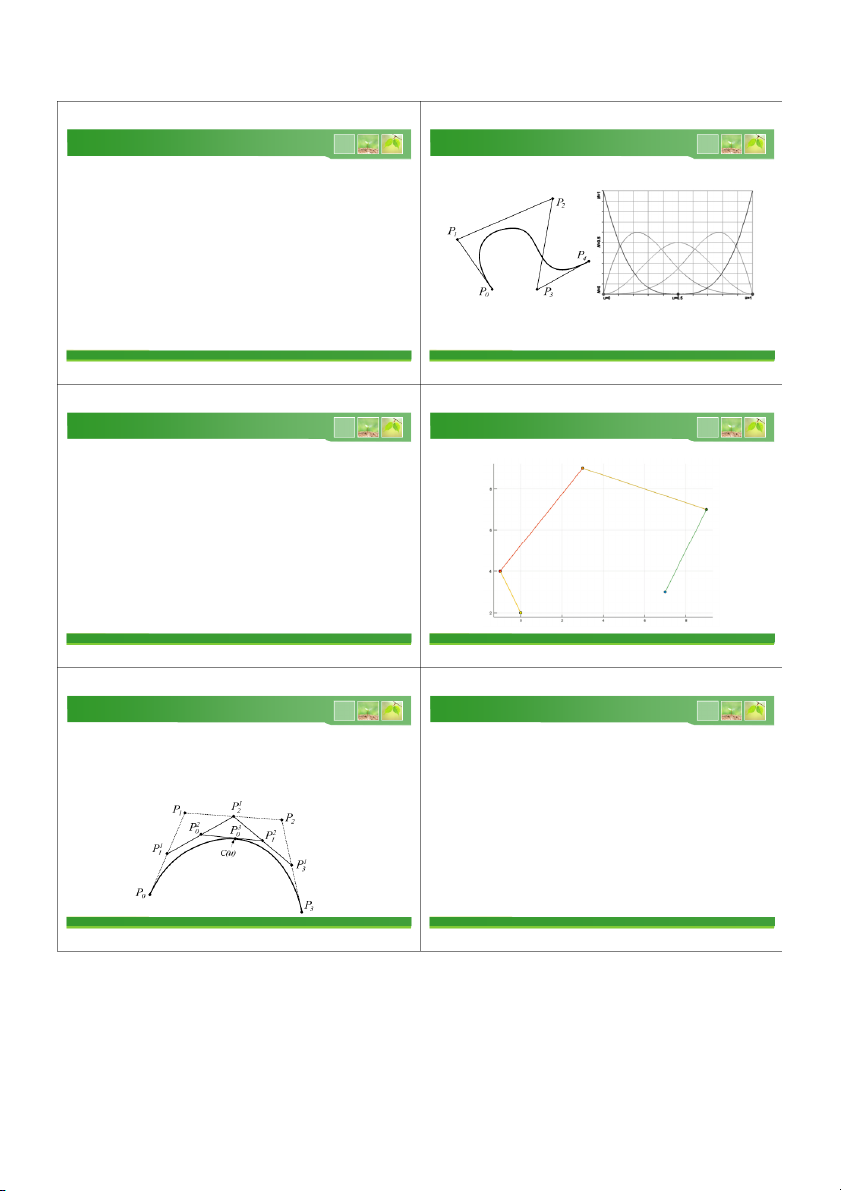
Ví dụ 2.1: Xét đường cong Bézier bậc hai (đường
Ví dụ 2.2: Xét đường cong Bézier bậc ba có (n + 1) = 4
parabola) có (n + 1) = 3 đỉnh điều khiển P , P , P : đỉ 0 1 2
nh điều khiển P , P , P , P . Phương trình của đường 0 1 2 3 cong như sau: 2 0 2 0 − 2 B (u) = u (1− u) = (1− u) 3 2 2 3
C (u ) = (1 u
− ) P + 3u (1 u
− ) P + 3u (1−u )P +u P 2, 0 0 1 2 3 0 C (u ) = ( 3 2 u − + 3u − 3u + ) 1 P + ( 3 2
3u − 6u + 3u )P + ( 3 2 3
− u +3u )P + u P 2 ( 3 0 1 ) 3 2 1 2 1 B (u) =
u (1 −u) − = 2u(1 − u) 3 2 2,1
C (u ) = ( P −
+ 3P −3P + P )u + (3P −6P +3P )u + ( 3
− P +3P )u + P 1 0 1 2 3 0 1 2 0 1 0
a = −P + 3P − 3 ( + 0 1 2 P 3 P ) 2 2 2 2 − 2 B ( )
u = u (1 − ) u = u 2, 2 2
b = 3P − 6P + 3 ( P 0 1 2 ) 3 2 ( C )
u = au + bu + cu + d, 2 2 c = ( 3 − P + 3 P 0 1 )
P(u) = (1−u) P + 2u(1−u )P + u P 0 1 2 d = (P0 ) 11/40 12/40
2.2.2. Tính chất của đường cong Bézier
2.3. Đường cong tham số Bézier
• Đường cong Bézier luôn luôn đi qua điểm đầu và điểm
Ví dụ 2.4: Đường cong Bézier và các hàm Bernstein
cuối của khung điều khiển: P 0 ( ) = P , P( ) 1 = P . tương ứng. 0 n B (u) ≡ 0 i ∀ ≠ 0,...,n, u ∈[0,1] i,n
• Các hàm Benstein có giá trị từ 0 đến 1.
• Đường cong Bézier có (n + 1) đỉnh điều khiển có bậc
p = n. Trong mỗi hàm trộn, tham số u có mũ i + (n − i)
= n. Do đó, bậc của đường cong Bézier là n. n
Tại tham số u = 0.5 ta có 5 hàm Bernstein. Để tính C(u) B ( ) u =1 i, n
với u xác định, ta tính các trọng số B (u) ứng với đỉnh i 0 = n,i
điều khiển P và sau đó tính tổng của chúng. i 13/40 14/40
2.2.3. Biễu biễn dạng ma trận
• Đường cong Bézier bậc p = 3 có 4 đỉnh điều khiển: 3 2 2 3 C(u) = (1 − ) u P + 3 ( u 1 − )
u P + 3u (1− u)P + u P 0 1 2 3 3 1 − 3 −3 1 u 2 3 − 6 3 0 u P P P P C( ) u = [ 0 1 2 3 ] 3 − 3 0 0 u 1 0 0 0 1 P M U C (u ) =[ ] P [ M][ ] U 15/40 16/40
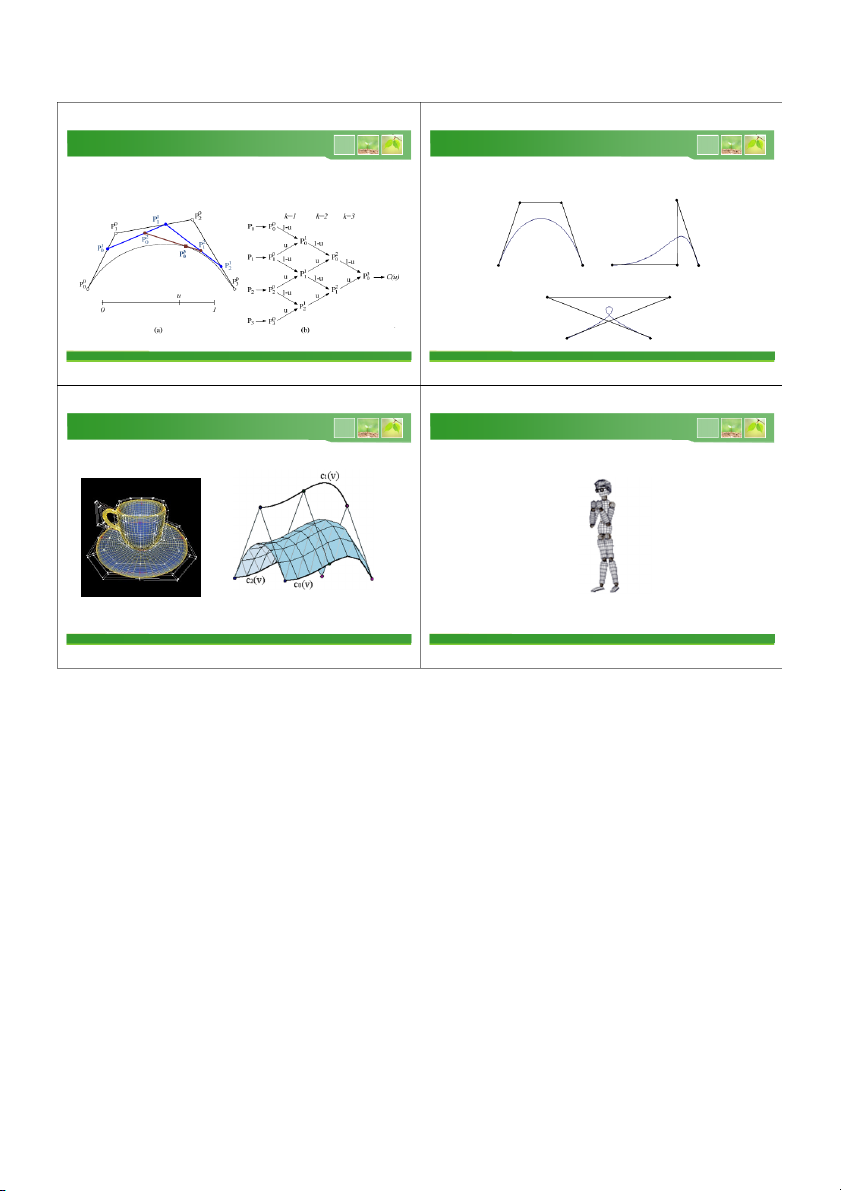
2.2.5. Thuật toán de Casteljau
2.2.5. Thuật toán de Casteljau
• Một đỉnh điều khiển của đường cong C(u) có thể được • j
P là các đỉnh điều khiển của đường cong Bézier bậc i
biểu diễn thông qua các đỉnh lân cận như sau:
n tại lần tính toán thứ j.
• Thuật toán de Casteljau: j j− 1 j− 1
P = (1− u )P + uP
i = 0,1, 2,…, n − j , j = 1, 2,…, n i i i 1 + 0
P = P, i = 0,…, p− 1 i i k k 1 − k 1 P = (1− ) u P
+ uP − , k = 1,…, ; p
i = 0,…, p − k i i i+1
• Tại bước k = p - 1 ta có n 1
P − là điểm trên đường cong 0
Bézier tại tham số u. 17/40 18/40
2.2.5. Thuật toán de Casteljau
2.2.6. Thay đổi hình dạng đường cong Bézier
• Tại bước k = p - 1 ta có n 1
P − là điểm trên đường cong 0
Bézier tại tham số u. 19/40 20/40 3. Mặt cong Bézier 21/40 22/40