Solution Tutorial 4 Time Value of Money SV - Quản lý tài chính | Trường Đại học Hà Nội

lOMoARcPSD|44744371 lOMoARcPSD|44744371
FIN5FMA - FINANCIAL MANAGEMENT
TUTORIAL 4 – TIME VALUE OF MONEY PART 1
1. What is the future value of $1,000 invested for 5 years at an interest rate of 5% p.a.?
FV  PV  (1  i)n = $1,000 * (1+5%)^5 = $1,276.28
2. If you deposit $1,000 in a bank that pays interest rate of 8% annually, how much will be in
your account after 6 years?
FV  PV  (1  i)n = $1,000*(1+8%)^6 = $1,586.88
3. What is the future value of $1,000 invested for 5 years at an interest rate of 5%,
compounded semi-annually?
FV  PV  (1  i)n = $1,000*(1+2.5%)^10 = $1,280.08
Note: in the formula, i represents periodic interest rate and n represents number of periods in which
interest is paid and reinvested. Since the interest is paid semi-annually or twice a year, each time,
interest is paid half (5%/2) of the annual rate (5%) and as such the interests are paid 10 times.
4. If you deposit $1,000 in a bank that pays interest rate of 8% p.a, compounded semi-annually,
how much will be in your account after 6 years?
FV  PV  (1  i)n = $1,000*(1+8%/2)^12 = $1,601.03
This exercise is similar to exercise #3
5. Suppose that bank A pays you 10% interest rate for $2,000 deposit and bank B pays you the
same 10% but compounded semi-annually. Which bank would you deposit your $2,000 for 5
years? Explain your choice using future value numbers.
Option 1: Bank A that pays 10% compounded once a year.
FV  PV  (1  i)n = $2,000*(1+10%)^5 = $3,221.02
Option 2: Bank B that pays 10% compounded semi-annually.
FV  PV  (1  i)n = $2,000*91+10%/2)^10 =$3,257.79
Obviously, after 5 years-period, the account in the bank B has higher value (3,257.79) than that
in the bank A. Therefore, holding all else constant (i.e. the risk of the two investments is the
same), you will be better off to deposit $2,000 at the bank B. lOMoARcPSD|44744371
6. What is the future value of $1000, continuously compounded at an interest rate of 4.5% for 7 years?
FV  PV  eAPRY = $1,000*e^(4.5%*7) = $1,370.26
7. How many years will it take for $12,000 to grow to be $23,605.82 if it is invested in an
account paying interest rate of 7%?
FV  PV  (1  i)n <> 23,605.82 = 12,000*(1+7%)^n Solving for n
n = ln(23,605.82/12,000)/ln(1+7%) = 10
8. How many months will it take for $10,000 to grow to be $20,969.06 if it is invested in an
account paying interest rate of 8%.
FV  PV  (1  i)n <> 20,969.06 =
10,000*(1+8%/12)^n Solving for n
n = ln(20,969.06/10,000)/ln(1+8%/12)
n = 111.44 or 112 months (round up)
9. What annual interest rate must $5,000 be invested so that it will grow to be $7,693.12 in 5 years?
FV  PV  (1  i)n <> 7,693.12 = 5,000*(1+i)^5 Solving for i
i = (7,693.12/5,000)^(1/5) – 1 = 9%
10. If you wish to accumulate $20,000 in 10 year, how much would you deposit today in an
account that pays an annual interest rate of 7%
FV  PV  (1  i)n <> FV PV 
(1  i)n Or
PV = $20,000/(1+7%)^10 = $10,166.99
11. What is the present value of $10,000 to be received in 5 years if the interest rate is 6%? PV FV 
= 10,000/(1+6%)^5 = $7,472.58
(1  i)n
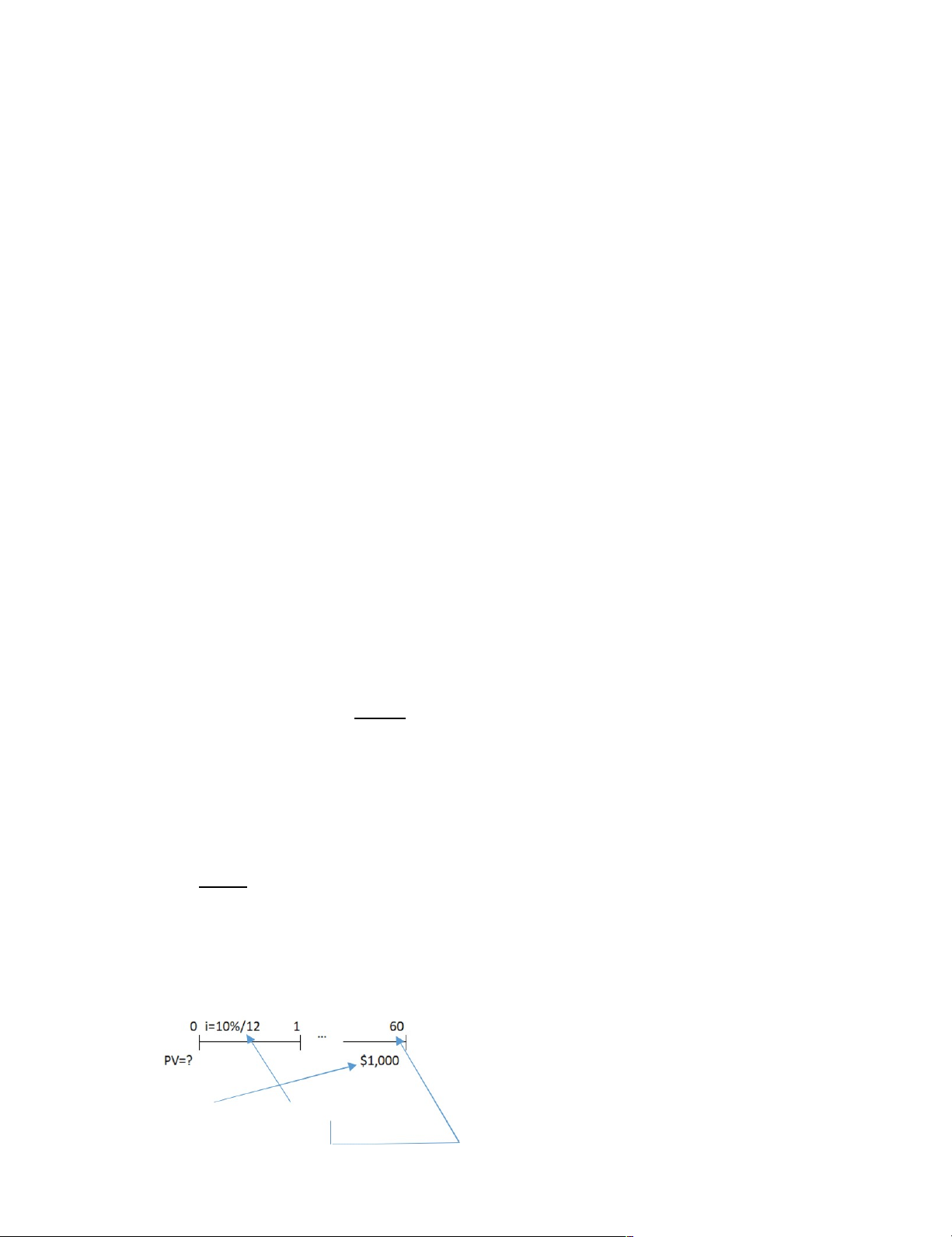
12. What is the present value of $1,000 to be received in 5 years if the interest rate is
10%, compounded monthly?
PV = $1,000/(1+10%/12)^60 = $607.79 lOMoARcPSD|44744371
13. What is the present value of $1,000 to be received in 5 years if the interest rate is 10%, compounded weekly? PV FV 
= $1,000/(1+10%/52)^260 = $606.82
(1  i)n
14. What is the effective annual rate for the investment with the annual interest rate of 10%, pay semi-annually?
*The annual interest rate is also called the annual percentage rate, quoted interest rate, and
nominal interest rate. In daily life and in this course, all interest rates are annual interest rates.
You will be instructed when the interest rate is not annual interest rate.
EAR  (1  APRm )m 1 = (1+10%/2)^2 = 10.25% *Note:
Consider the investment as below:
Bank offers a 1 year deposit rate of 10%, interest is paid TWO times per year. You are
interested in finding the total interest payment for your $100 deposit. -
After the first six month, you will receive the first interest payment which is half of the quoted annual rate.
Your account balance at this time: $100*(1+5%) =$105 -
Assuming that you will not withdraw any dollar from the account and your account
will be rolled over for another six months. -
At the end of the year, your account balance will be: $105*(1+5%) =$110.25 -
Effectively or actually, your return for one-year investment is: (110.25-100)/100 = 10.25%
As can be seen from the above example, the quoted rate is 10% might not be the “actual”
interest rate you will be received from the investment, but the effective annual rate will.
Quoted interest rate is always simple interest rate whereas the effective annual rate is with
annual interest rate considering the compounding effect.
15. You invest $1,000 for 5 years. The investment pays an annual interest rate of 12%,
compounded monthly. What is the effective annual rate for the investment?
EAR  (1  APRm )m 1 = (1+12%/12)^12 – 1 = 12.68%
16. You are offered an investment that pays $10,000 in year 1, $2,000 in year 2, $30,000 in
year 3, $15,000 in year 4. Another similar risk investment alternative offers 6% interest rate
with annually compounded. What is the value of that set of cash flows in today’s dollar? Timeline: lOMoARcPSD|44744371
? This question is quite challenging and different from all above exercises since we are provided
with more than one cash amount.
? We “discount” each cash amount back to the period 0 – find present value of each amount.
? Now cash flows are valued at the same point in time (period 0), we can compare them – we sum them up. Step 1: -
Assume that we deposit X dollar into an account paying 6%. For one year, we will
receive $10,000. The question is that how many dollars we have to deposit now?
PV= $10,000/(1+6%) = $9,433.96 -
Assume that we open another account that pays 6% p.a for two years. At the end of
second year, our account balance will be $2,000. Thus, to accumulate $2,000 in two
years, currently we have to deposit:
PV=$2,000/(1+6%)^2=$1,779.99 -
Assume that we open the third account that pays 6% p.a for three years. At the end of
the third year, our account balance will be $30,000. To accumulate $30,000, currently we need to deposit:
PV =$30,000/(1+6%)^3=$20,188.58 -
Assume that we open the fourth account that pays 6% p.a for four years. At the end of
the fourth year, our account balance will be $15,000. To accumulate $15,000, currently we need to deposit:
PV =$15,000/(1+6%)^4 =$11,881.40 Step 2:
Currently – at the time 0, we have four bank accounts; each is worth $9,433.96,
$1,779.99, $20,188.58, and $11,881.40. Totally, we have deposited $48,283.94.
17. You won a prize of $10,000. This will be paid to you into two equal amounts of $5,000 at the end
of year 1 and year 2. If you had the money now, you would deposit it in an account paying 12% with
monthly compounding. What is the present value of the stream of payment you will receive? Approach 1:
Assume that you open two accounts. The first account will be matured in one year for $5,000
and you earn interest of 12% with monthly compounding. The second account will be
matured in two years for $5,000 and you earn interest of 12% monthly compounding. lOMoARcPSD|44744371
For the first account, the amount that you have to deposit today is:
PV = $5,000/(1+1%)^12 = $4,437.25
For the second account, the amount that you have to deposit today is:
PV = $5,000/(1+1%)^24 = $3,937.83
The total amount that you have to deposit today is:
PV = $4,437.25 + $3,937.83 = $8,375.08.
Inference: if you are promised to be paid $5,000 in one year and another $5,000 in the second
year, the value of this “promise” is only $8,375.08 at the current time. Approach 2:
Since the cash flow occurs at the end of year 1 and year 2, but the interest is compounded every
month, the timing of cash flows and the compounding periods do not match. We, therefore, have to match them:
The interest is 12% per year and will be paid 12 times per year. Thus, effectively, for one
year investment, we accumulate the EAR of 12.6825% (= (1+12%/12)^12-1).
PV = $5,000/(1+12.6825%) + $5,000/(1+12.6825%)^2 = $8,375.08