Sử dụng chủ yếu suy luận trong giải toán trắc nghiệm – Trần Tuấn Anh

Tài liệu gồm 24 trang, được biên soạn bởi thầy Trần Tuấn Anh, hướng dẫn sử dụng chủ yếu suy luận trong giải toán trắc nghiệm, giúp học sinh ôn thi tốt nghiệp Trung học Phổ thông Quốc gia môn Toán.

24 12 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu ôn thi THPTQG môn Toán

Môn: Toán

Thông tin:

24 trang 6 tháng trước

Tác giả:

Profile Nguyễn Vân
SÖÛ DUÏNG CHUÛ YEÁU SUY LUAÄN TRONG GIẢI TOAÙN TRẮC NGHIỆM
Moät soá baøi toaùn coù daïng ñaëc bieät ñöôïc giaûi nhanh nhôø nhöõng suy luaän toaùn hoïc,
maø neáu chuùng ta giaûi baèng caùch thoâng thöôøng thì cho ta lôøi giaûi khaù daøi, do ñoù maát thôøi
gian. Ñaây thöôøng laø nhöõng baøi toaùn ôû möùc “ vaän duïng” vaø “ vaän duïng cao ”, do ñoù chuùng
ta caàn chuaån bò kieán thöùc saâu roäng ñeå linh hoaït trong vieäc giaûi quyeát baøi toaùn ñoù, khoâng
bò daäp theo moät khuoân maãu khoâ cöùng, thieáu saùng taïo.
Ví duï 1. Tìm giaù trò nhoû nhaát cuûa haøm soá
32
7 11 2= − + −y x x x
treân ñoaïn
[0;2]
.
A.
11=m
. B.
0=m
. C.
2=−m
. D.
3=m
.
(Caâu 23 - Maõ ñeà 101 – THPT QG - 2017)
Caùch giaûi thoâng thöôøng
Ta coù :
2
' 3 14 11= − +y x x
;
.
Xeùt caùc giaù trò:
( ) ( ) ( )
0 2; 1 3; 2 0= − = =y y y
.
Suy ra
( )
0;2
min 0 2= = −yy
.
Choïn ñaùp aùn C.
Caùch khaùc (duøng chuû yeáu suy luaän toaùn hoïc)
Xeùt
2m =−
laø giaù trò nhoû nhaát trong caùc giaù trò ôû 4 ñaùp aùn ñaõ cho.
Khi ñoù phöông trình
32
7 11 2 2− + − = −x x x
coù nghieäm
0 0;2=x
neân choïn ñaùp aùn C.
Ví duï 2. Tìm giaù trò thöïc cuûa tham soá m ñeå haøm soá
3 2 2
1
( 4) 3
3
y x mx m x= − + − +
ñaït cöïc
ñaïi taïi
3x =
.
A.
1m =
. B.
1m =−
. C.
5m =
. D.
7m =−
.
(Caâu 32 - Maõ ñeà 102 – THPT QG - 2017)
Caùch giaûi thoâng thöôøng
Ta coù
22
' 2 4= − + −y x mx m
.
Haøm soá ñaït cöïc ñaïi taïi
3x =
neân
( )
' 3 0=y
2
6 5 0 − + =mm
1
5
=
=
m
m
.
Laïi coù
( )
'' 2 2 '' 3 6 2= − = −y x m y m
.
Vôùi
1=m
thì
( )
'' 3 6 2 4 0= − = y
neân haøm soá ñaït cöïc tieåu taïi
3=x
.
Vôùi
5=m
thì
( )
'' 3 6 10 4 0= − = − y
neân haøm soá ñaït cöïc ñaïi taïi
3=x
.
Choïn ñaùp aùn C.
Caùch khaùc (duøng chuû yeáu suy luaän toaùn hoïc)
Ta coù
22
' 2 4= − + −y x mx m
;
22
' 0 2 4 0= − + − =y x mx m
( )
2
4 − =xm
2
2
−=
− = −
xm
xm
2
2
=+
=−
xm
xm
.
Do haøm soá
3 2 2
1
( 4) 3
3
y x mx m x= − + − +
coù heä soá
1
0
3
=a
neân
CÑ CT
xx
.
Suy ra
=−2
CÑ
xm
, maø
= 3
CÑ
x
neân ta ñöôïc
− = =2 3 5mm
.
Choïn ñaùp aùn C.
Ví duï 3. Heä thöùc lieân heä giöõa giaù trò cöïc ñaïi
CÑ
y
vaø giaù trò cöïc tieåu
CT
y
cuûa haøm soá
=−
3
2y x x
laø :
A.
+=0
CÑ CT
yy
. B.
=23
CÑ CT
yy
. C.
= 2
CT CÑ
yy
. D.
=
CT CÑ
yy
.
Caùch giaûi thoâng thöôøng
Ta coù
=−
2
' 3 2yx
;
= − =
2
' 0 3 2 0yx
=
2
32x
=
2
2
3
x
= − =
= = −
2 4 6
39
2 4 6
39
xy
xy
.
Vaäy
+=0
CÑ CT
yy
.
Choïn ñaùp aùn A.
Caùch giaûi khaùc (duøng chuû yeáu suy luaän toaùn hoïc)
Do haøm soá
=−
3
2y x x
laø haøm soá leû vaø coù taâm ñoái xöùng laø goác toïa ñoä
( )
0; 0O
neân
+=0
CÑ CT
yy
.
Choïn ñaùp aùn A.
Ví duï 4. Haøm soá
3 2 2
(2 1)
3
m
y x mx m x m= − + − +
nghòch bieán treân khi vaø chæ khi
A.
0m
hoaëc
1m
; B.
0m
; C.
01m
; D.
0m
.
Caùch giaûi thoâng thöôøng
Ta coù
2
' 2 2 1y mx mx m= − + −
.
TH1: Neáu
0m =
thì
' 1 0y = −
thoûa maõn baøi toaùn.
TH2: Neáu
0m
, ñeå thoûa maõn baøi toaùn ta caàn coù
( )
2
2
0
0
0
2 1 0
0
m
m
m
m m m
mm

− −
− +
Vaäy
0m
, choïn ñaùp aùn D.
Caùch giaûi khaùc 1 (choïn ñaïi dieän)
Neáu
3m =−
haøm soá trôû thaønh
32
3 7 9y x x x= − + − +
;
2
' 3 6 7 0,y x x x= − + −
(duøng maùy tính casio 570vn plus giaûi baát phöông trình
2
3 6 7 0xx− + −
seõ cho nghieäm
laø taäp )
Loaïi tröôøng hôïp B, C.
Neáu
3m =
haøm soá trôû thaønh
32
3 5 9y x x x= − + +
;
2
' 3 6 5 0y x x x= − +
Loaïi tröôøng hôïp A.
Vaäy choïn ñaùp aùn D.
Caùch giaûi khaùc 2 (duøng chuû yeáu suy luaän toaùn hoïc - phöông phaùp tam thöùc baäc hai)
Ta coù
2
' 2 2 1y mx mx m= − + −
laø tam thöùc baäc hai neân caàn xeùt
0m
hoaëc
0m =
.
Loaïi ba tröôøng hôïp A, B vaø C.
Choïn ñaùp aùn D.
Ví duï 5. Bieát ñöôøng thaúng
(3 1) 6 3= − + +y m x m
caét ñoà thò haøm soá
32
31= − +y x x
taïi ba ñieåm phaân bieät sao cho moät giao ñieåm caùch ñeàu hai giao ñieåm coøn laïi. Khi ñoù m
thuoäc khoaûng naøo döôùi ñaây ?
A.
( )
1;0−
. B.
( )
0;1
. C.
3
1;
2



. D.
3
;2
2



.
Caùch giaûi thoâng thöôøng
Yeâu caàu cuûa baøi toaùn töông ñöông vôùi phöông trình sau coù ba nghieäm phaân bieät laäp
thaønh caáp soá coäng
32
3 1 (3 1) 6 3− + = − + +x x m x m
32
3 (3 1) 6 2 0 − − − − − =x x m x m
. (*)
Goïi
1 2 3
,,x x x
laø ba nghieäm cuûa phöông trình treân, theo tính chaát caáp soá coäng ta coù :
13
2
2
+
=
xx
x
.
Maø theo ñònh lí Vi-eùt ta coù
1 2 3
3+ + =x x x
neân suy ra
22
3 3 1= =xx
.
Theá
1=x
vaøo phöông trình (*) ta ñöôïc
1
3
=−m
.
Khi
1
3
=−m
phöông trình (*) trôû thaønh :
32
0
3 2 0 1
2
=
− + = =
=
x
x x x x
x
thoûa maõn baøi
toaùn.
Maø
( )
1
1;0
3
= − −m
neân choïn ñaùp aùn A.
Caùch giaûi khaùc (duøng chuû yeáu suy luaän toaùn hoïc)
Nhaän xeùt raèng : neáu ñieåm uoán cuûa ñoà thò haøm soá
32
31= − +y x x
thuoäc ñöôøng
thaúng
(3 1) 6 3= − + +y m x m
thì thoûa maõn baøi toaùn.
Ta coù
2
' 3 6 ; '' 6 6 0 1= − = − = =y x x y x x
. Suy ra ñieåm
( )
1; 1−M
laø ñieåm uoán cuûa
ñoà thò haøm soá
32
31= − +y x x
.
Theá toïa ñoä cuûa M vaøo phöông trình
(3 1) 6 3= − + +y m x m
ta ñöôïc
( )
1
1;0
3
= − −m
.
Choïn ñaùp aùn A.
Ví duï 6. Cho haøm soá
1
1
+
=
−
x
y
x
coù ñoà thò
( )
C
. Giaù trò thöïc cuûa m thuoäc khoaûng naøo
trong caùc khoaûng cho döôùi ñaây, ñeå ñöôøng thaúng
( )
d
:
2=+y x m
caét ñoà thò
( )
C
taïi hai
ñieåm phaân bieät M, N sao cho tieáp tuyeán taïi M vaø N song song nhau laø :
A.
1
2;
2

−−


. B.
( )
0;2
. C.
( )
2;3
. D.
7
;5
2



.
Caùch giaûi thoâng thöôøng
Phöông trình hoaønh ñoä giao ñieåm laø :
1
2
1
+
=+
−
x
xm
x
( )( )
1 2 1 + = + −x x m x
2
1 2 2 + = − + −x x x mx m
( )
2
2 3 1 0 + − − − =x m x m
. (1)
Ñöôøng thaúng
( )
d
caét ñoà thò
( )
C
taïi hai ñieåm phaân bieät M, N khi phöông trình (1) coù
hai nghieäm phaân bieät khaùc 1
( )
0
10

g
(vôùi
( ) ( )
2
2 3 1= + − − −g x x m x m
)
( ) ( )
( )
2
3 8 1 0
2 3 1 0
− + +
+ − − −
mm
mm
2
2 17 0
20
+ +
−
mm
m
.
Goïi hai nghieäm cuûa phöông trình laø
12
,xx
( )
12
xx
, khi ñoù ta coù toïa ñoä giao ñieåm
( )
11
;2 +M x x m
;
( )
22
;2 +N x x m
.
Tieáp tuyeán taïi M vaø N song song vôùi nhau khi
( ) ( )
12
''=f x f x
(vôùi
( )
1
1
+
=
−
x
fx
x
)
( ) ( )
22
12
22
11
−−
=
−−xx
( ) ( )
22
12
11 − = −xx
( )
12
12
11
11
− = −
− = − −
xx
xx
=
+=
12
12
()
2
x x loaïi
xx
+ =
12
2xx
−
− =
3
2
2
m

= − − −


1
1 2;
2
m
.
Choïn ñaùp aùn A.
Caùch giaûi khaùc (duøng chuû yeáu suy luaän toaùn hoïc)
Nhaän xeùt raèng : Neáu hai ñieåm M, N treân ñoà thò
( )
C
cuûa haøm soá
+
=
+
ax b
y
cx d
maø tieáp
tuyeán cuûa
( )
C
taïi hai ñieåm M, N song song vôùi nhau thì ñöôøng thaúng MN ñi qua taâm
ñoái xöùng cuûa cuûa ñoà thò
( )
C
.
Taâm ñoái xöùng
I
cuûa ñoà thò
( )
C
laø giao ñieåm cuûa hai ñöôøng tieäm caän, ta coù
( )
1;1I
.
Ñöôøng thaúng
( )
d
:
2=+y x m
ñi qua
( )
1;1I
, suy ra
12=+m

= − − −


1
1 2;
2
m
.
Choïn ñaùp aùn A.
Ví duï 7. Giaù trò lôùn nhaát cuûa haøm soá
2
1
()
24
fx
xx
=
++
laø :
A.
3
. B.
1
3
. C.
1
4
. D.
4
.
Caùch giaûi thoâng thöôøng
Ñieàu kieän
2
2 4 0xx+ +
(luoân ñuùng). Taäp xaùc ñònh cuûa haøm soá laø .
Xeùt haøm soá
2
1
( ) ,
24
f x x
xx
=
++
.
( )
2
2
22
'( ) ; '( ) 0 2 2 0 1
24
x
f x f x x x
xx
+
= − = + = = −
++
.
Ta coù baûng bieán thieân
x
−
1−
+
'( )fx
+
0
-
()fx
1
3
0
0
Keát luaän:
( ) ( )
1
1
3
max f x f= − =
.
Choïn ñaùp aùn B.
Caùch giaûi khaùc (duøng chuû yeáu suy luaän toaùn hoïc)
Ta coù
( )
2
2
2 4 1 3 0,x x x x+ + = + +
.
Suy ra
( )
22
1 1 1 1
()
0 3 3
24
13
fx
xx
x
= = =
+
++
++
, vôùi
x
vaø
( )
1
1
3
f −=
.
Do ñoù, giaù trò lôùn nhaát cuûa
( )
fx
laø
1
3
.
Choïn ñaùp aùn B.
Ví duï 8. Tích phaân
1
2
1
1
−
=−
I x dx
baèng :
A.
2
. B.
3
2
. C.
2
. D.
.
Caùch giaûi thoâng thöôøng
Ñaët
sin=xt
,
;
22


−


t
cos .=dx t dt
.
Ñoåi caän :
1
2
= − = −xt
;
1
2
= =xt
.
Ta ñöôïc
2
2
2
1 sin .cos .
−
=−
I x t dt
2
2
cos cos .
−
=
t t dt
2
2
2
cos
−
=
tdx
2
2
1
(1 cos2 )
2
−
=+
t dx
11
2
sin2
2 2 2
2

= + =


−
xx
.
Choïn ñaùp aùn A.
Caùch khaùc (duøng chuû yeáu suy luaän toaùn hoïc)
Ta coù : , neân haøm soá coù ñoà
thò laø nöûa ñöôøng troøn phía treân truïc Ox (tính caû hai ñieåm ). Maø ñöôøng troøn
coù baùn kính , theo yù nghóa hình hoïc cuûa tích phaân ta suy ra:
. Vôùi S laø dieän tích hình troøn coù baùn kính baèng 1.
Choïn ñaùp aùn A.
Ví duï 9. Bieát raèng
( )
2
1
ln 2ln= + = −
e
I x x dx ae b
, vôùi
,ab
. Khi ñoù
=+S a b
baèng bao nhieâu ?
A.
0
. B.
3
2
. C.
1
. D.
2
.
Caùch giaûi thoâng thöôøng
Ta coù
( )
22
1 1 1
ln 2ln ln 2 ln= + = +
e e e
I x x dx xdx xdx
.
Xeùt tích phaân
2
1
ln=
e
J xdx
.
2 2 2 2
2
11
1
00
y x x y
yx
yy
2
1yx
( 1;0),(1;0)
22
1xy
1R
1
2
2
1
.1
1
2 2 2
S
x dx

−
− = = =
Ñaët
2
2
ln ln= =u x du xdx
x
;
= =dv dx v x
.
Ta ñöôïc
2
1
ln 2 ln
1
=−
e
e
J x x xdx
.
2
11
ln 2 ln 2 ln
1

= − +



ee
e
I x x xdx xdx
2
ln
1
=
e
xx
1. 0= = −ee
.
1; 0 1 = = = + =a b S a b
.
Choïn ñaùp aùn C.
Caùch khaùc (duøng chuû yeáu suy luaän toaùn hoïc)
Ta coù
( )
( ) ( )
2 2 2 2
ln 2ln '.ln . ln ' ln '+ = + =x x x x x x x x
neân suy ra :
( )
2
1
ln 2ln=+
e
I x x dx
( )
2
1
ln '=
e
x x dx
( ) ( )
22
1
ln ln
1
= = =
e
e
d x x x x e
.
Suy ra :
1= + =S a b
.
Choïn ñaùp aùn C.
Caâu 10. Trong , phöông trình
( )
( )
2
1 2 5 0− + + =z z z
coù nghieäm laø :
A.
1
12
=
= − +
z
zi
B.
12
12
= − −
= − +
zi
zi
C.
12
12
=−
=+
zi
zi
D.
12
12
1
= − −
= − +
=
zi
zi
z
.
Caùch giaûi thoâng thöôøng
Ta coù :
( )
( )
2
1 2 5 0− + + =z z z
2
1
2 5 0
=
+ + =
z
zz
1
12
12
=
= − −
= − +
z
zi
zi
.
Choïn ñaùp aùn D.
Caùch khaùc (duøng chuû yeáu suy luaän toaùn hoïc)
Do phöông trình
2
2 5 0+ + =zz
coù hai nghieäm neân phöông trình ñaõ cho coù ba nghieäm
khaùc nhau.
Choïn ñaùp aùn D.
Caâu 11. Xeùt số phốc
z
thoûa maõn
10
(1 2 ) 2 .i z i
z
+ = − +
Mốnh đố naøo sau ñaây ñuùng ?
A.
3
2.
2
z
B.
2.z
C.
1
2
z
D.
13
.
22
z
(Caâu 34 – Ñeà thöû nghieäm THPT QG naêm 2017)
Caùch giaûi thoâng thöôøng
Ñaët
=+z a bi
(vôùi
,ab
) vaø
22
0= = + k z a b
ta ñöôïc :
10
(1 2 ) 2+ = − +
+
i k i
a bi
( )
22
10
(1 2 ) 2
−
+ = − +
+
a bi
i k i
ab
22
10 10
(1 2 ) 2 + = − − +
ab
i k i i
kk
22
10 10
2 1 2 0
+ − + − + =
ab
k k i
kk
22
22
10 10
2 0 2
10 10
2 1 0 1 2

− + = + =





+ − = − =


aa
kk
kk
bb
kk
kk
.
Ñeå yù raèng
2 2 2 2 2
= + = +k a b k a b
, ta coù :
( ) ( )
( )
22
22
22
2 2 4 2
10
10 10 10
2 1 2
+
+ + − = + = =
ab
ab
kk
k k k k
.
( ) ( )
22
2
10
2 1 2 + + − =kk
k
42
5 5 10 0 + − =kk
2
2
1
2
k
k
=
=−
( )
1 ( )
1
k nhanä
k loaiï
=
=−
.
Vaäy
1==kz
töùc laø
13
.
22
z
Choïn ñaùp aùn D.
Caùch khaùc (duøng chuû yeáu suy luaän toaùn hoïc)
Vì caùc khoaûng
( )
3 1 1 3
;2 , 2; , ; , ;
2 2 2 2
+ −
ñoâi moät khoâng coù ñieåm chung vaø trong
boán ñaùp aùn thì coù moät ñaùp aùn ñuùng neân ta choïn ñaïi dieän.
Choïn
1=z
, ta coù :
10 10 3 10 10
(1 2 ) 2
3 10 10
+ = − + = = −
+
i i z i
zi
.
Khi ñoù
22
3 10 10 3 10 10
1
10 10 10 10
− = + =
i
. (thoûa maõn ñieàu kieän baøi toaùn)
Choïn ñaùp aùn D.
Caâu 12. Cho số phốc
z
thoûa maõn
3 4 4− + =zi
. Tìm giaù trò lôùn nhaát
max
P
cuûa bieåu
thöùc
=Pz
.
A.
max
12=P
. B.
max
5=P
. C.
max
9=P
. D.
max
3=P
.
Caùch giaûi thoâng thöôøng
Ñaët
=+z a bi
(vôùi
,ab
) ta ñöôïc
3 4 4+ − + =a bi i
( ) ( )
3 4 4 − + + =a b i
( ) ( )
22
3 4 16 − + + =ab
22
6 8 9 0 + − + + =a b a b
2 2 2 2
9 6 8 10. + + = − +a b a b a b
.
Suy ra
2
9 10+PP
2
10 9 0 1 9 − + P P P
.
Vaäy
max
9=P
.
Choïn ñaùp aùn C.
Caùch khaùc (duøng chuû yeáu suy luaän toaùn hoïc)
Số phốc
z
thoûa maõn
3 4 4− + =zi
neân ñieåm M bieåu dieãn cuûa soá phöùc
z
thuoäc ñöôøng
troøn taâm
( )
3; 4−I
, baùn kính
4=R
.
Suy ra,
=Pz
lôùn nhaát baèng
22
max
3 4 4 9= + = + + =P OI R
.
Choïn ñaùp aùn C.
Ví duï 13. Trong khoâng gian vôùi heä toïa ñoä
Oxyz
, cho maët caàu
( )
S
tieáp xuùc vôùi maët
phaúng
( )
Oxz
, coù baùn kính
3=R
vaø coù taâm naèm treân tia
Oy
. Maët cầu
( )
S
coù phöông
trình laø :
A.
( )
2 2 2
: 6 0+ + − =S x y z x
. B.
( )
2 2 2
: 6 0+ + − =S x y z y
.
C.
( )
2 2 2
: 6 0+ + − =S x y z z
. D.
( )
2 2 2
:9+ + =S x y z
.
Caùch giaûi thoâng thöôøng
Goïi
( )
0; ;0Ib
laø taâm cuûa maët caàu
( )
S
thì
0b
(do
I
naèm treân tia
Oy
).
Maët phaúng
( )
Oxz
coù phöông trình laø
0=y
.
Ta coù :
( )
,( ) =d I Oxz R
=
= =
=−
2
3 ( )
33
3 ( )
1
b
b nhaän
b
b loaïi
.
Vaäy
( ) ( )
2
2 2 2
: 3 3+ − + =S x y z
hay
( )
2 2 2
: 6 0+ + − =S x y z y
.
Choïn ñaùp aùn B.
Caùch giaûi khaùc 1 (duøng chuû yeáu suy luaän toaùn hoïc)
Do taâm maët caàu naèm treân tia
Oy
neân coù toïa ñoä daïng
( )
0; ;0Ib
. Suy ra, ta loaïi
ñaùp aùn A (taâm I coù hoaønh ñoä baèng 3), loaïi ñaùp aùn C (taâm I coù cao ñoä baèng 3), loaïi ñaùp
aùn D (taâm I truøng vôùi goác toïa ñoä neân khoâng tieáp xuùc vôùi maët phaúng
( )
Oxz
).
Choïn ñaùp aùn B.
Caùch giaûi khaùc 2 (duøng chuû yeáu suy luaän toaùn hoïc)
Do
( )
S
tieáp xuùc vôùi maët phaúng
( )
Oxz
, coù baùn kính
3=R
vaø coù taâm naèm treân
tia
Oy
neân
( )
0;3;0I
. Ñieåm
( )
0;6;0M
ñoái xöùng vôùi goác toïa ñoä qua taâm
( )
0;3;0I
thuoäc maët caàu neân ta loaïi ñöôïc caùc ñaùp aùn A, C, D.
Choïn ñaùp aùn B.
Ví duï 14. Trong khoâng gian vôùi heä toïa ñoä
Oxyz
, maët phaúng
( )
P
chöùa hai ñieåm
( )
1;0;1A
,
( )
1;2;2−B
vaø song song vôùi truïc
Ox
coù phöông trình laø :
A.
( )
: 2 3 0+ − =P x z
. B.
( )
: 2 2 0− + =P y z
.
C.
( )
:2 1 0− + =P y z
. D.
( )
:0+ − =P x y z
.
Caùch giaûi thoâng thöôøng
Caëp vectô chæ phöông cuûa maët phaúng
( )
P
laø :
( )
2;2;1=−AB
;
( )
1;0;0=i
.
Vectô phaùp tuyeán cuûa maët phaúng
( )
P
laø
( )
, 0;1; 2

= = −

n AB i
.
Maët phaúng
( )
P
ñi qua ñieåm
( )
1;0;1A
vaø coù vectô phaùp tuyeán
( )
0;1; 2=−n
laø
:
( ) ( ) ( )
0 1 1 0 2 1 0 2 2 0− + − − − = − + =x y z y z
.
Choïn ñaùp aùn B.
Caùch giaûi khaùc (duøng chuû yeáu suy luaän toaùn hoïc)
Maët phaúng song song vôùi truïc
Ox
coù daïng :
0+ + =By Cz D
, ta loaïi ñöôïc hai
ñaùp aùn A vaø D.
Laïi coù
( ) ( )
1;2;2 :2 1 0− − + =B P y z
neân loaïi ñaùp aùn C.
Choïn ñaùp aùn B.
Ví duï 15. Cho phöông trình
3 8 5xx+ + + =
. Trong caùc khaúng ñònh sau, khaúng
ñònh naøo ñuùng ?
A. Phöông trình coù moät nghieäm thuoäc khoaûng



17
;
35
vaø moät nghieäm thuoäc khoaûng
( )
+3:
.
B. Phöông trình coù ba nghieäm döông phaân bieät.
C. Phöông trình coù moät nghieäm baèng 1 vaø moät nghieäm nhoû hôn 1.
D. Phöông trình nghieäm duy nhaát
= 1x
.
Caùch giaûi thoâng thöôøng 1
Ñieàu kieän : .
Ta coù:
3 8 5xx+ + + =
3 2 ( 3)( 8) 8 25x x x x + + + + + + =

+ −
−

+ −

xx
x
xx
3 0 3
3
8 0 8
2 ( 3)( 8) 14 2x x x + + = −
( 3)( 8) 7x x x + + = −
22
11 24 49 14x x x x + + = − +
25 25 1xx = =
.
Vaäy phöông trình nghieäm duy nhaát
= 1x
.
Caùch giaûi thoâng thöôøng 2
Ñieàu kieän : .
Xeùt haøm , vôùi .
.
Ta coù baûng bieán thieân
x
- 3
y'
+
y
Töø baûng bieán thieân ta nhaän thaáy, ñöôøng thaúng neáu coù giao ñieåm vôùi ñoà thò
cuûa haøm soá thì coù toái ña moät giao ñieåm. Do ñoù, phöông trình
coù toái ña moät nghieäm. Maø
neân
laø nghieäm duy nhaát cuûa phöông trình ñaõ cho.
Choïn ñaùp aùn D.
Caùch giaûi khaùc (duøng chuû yeáu suy luaän toaùn hoïc)

+ −
−

+ −

xx
x
xx
3 0 3
3
8 0 8
( )
= + + +f x x x38
)
− +
;x 3
( ) ( )
= + − +
++
' , ;f x x
xx
11
03
2 3 2 8
−
+
+
5
=y 5
( )
= + + +f x x x38
+ + + =xx3 8 5
( )
= + + + =f 1 1 3 1 8 5
=x 1
Caùc haøm soá vaø ñoàng bieán treân R neân cuõng ñoàng bieán treân
vì coù heä soá goùc döông. Suy ra, caùc haøm soá vaø cuõng laø caùc haøm soá
ñoàng bieán treân . Do ñoù, haøm soá laø haøm soá ñoàng bieán
treân .
VT(1) laø haøm soá ñoàng bieán treân , VP(1) laø haøm haèng neân phöông trình (1)
neáu coù nghieäm thì coù nhieàu nhaát laø moät nghieäm.
Nhaän thaáy
neân laø nghieäm duy nhaát cuûa
phöông trình ñaõ cho.
Choïn ñaùp aùn D.
Ví duï 16. Cho phöông trình aån
x
sau ñaây :
24
20x x m− − =
, (
m
laø tham soá thöïc). Choïn
khaúng ñònh ñuùng ?
A. Phöông trình coù nghieäm thöïc duy nhaát khi
0m =
.
B. Phöông trình coù nghieäm thöïc duy nhaát khi
1m =
.
C. Phöông trình coù nghieäm thöïc duy nhaát khi
1m
.
D. Khoâng toàn taïi giaù trò thöïc cuûa
m
ñeå phöông trình coù nghieäm thöïc duy nhaát.
Caùch giaûi thoâng thöôøng
Ta coù
24
20x x m− − =
24
2x x m − =
.
Ñaët
( )
24
2f x x x=−
;
( )
32
' 4 4 4 1 0f x x x x x

= − = − =


0
1
1
x
x
x
=
= −
=
.
Baûng bieán thieân
x
−
1−
0
1
+
'y
+
0
-
0
+
0
-
y
1
1
=+yx3
=+yx8
)
− +
;3
=+yx3
=+yx8
)
− +
;3
= + + +y x x38
)
− +
;3
)
− +
;3
( )
= + + + =y 1 1 3 1 8 5
=x 1
−
0
−
Töø baûng bieán thieân suy ra, khoâng toàn taïi giaù trò cuûa tham soá m ñeå phöông trình ñaõ
cho coù nghieäm duy nhaát.
Vaäy choïn ñaùp aùn D.
Caùch giaûi khaùc (duøng chuû yeáu suy luaän toaùn hoïc – söû duïng tính chaát cuûa haøm soá chaün)
Nhaän xeùt raèng : neáu
0
x
laø moät nghieäm cuûa phöông trình ñaõ cho, suy ra
0
x−
cuõng
laø moät nghieäm cuûa phöông trình ñaõ cho. Vaäy ñeå phöông trình coù nghieäm duy nhaát thì
00
xx=−
2 0 0
00
xx = =
. Theá vaøo phöông trình ta ñöôïc
0m =
.
Ñaûo laïi, vôùi
0m =
thì phöông trình trôû thaønh :
24
20xx−=
22
20xx

− =


0
2
2
x
x
x
=
= −
=
.
Vaäy khoâng toàn taïi giaù trò cuûa tham soá m ñeå phöông trình ñaõ cho coù nghieäm duy nhaát.
Choïn ñaùp aùn D.
Ví duï 17. Giaù trò thöïc cuûa tham soá m ñeå phöông trình
2+ − =x x m
coù nghieäm
thöïc duy nhaát laø :
A.
1=m
. B.
0=m
. C.
2=m
. D.
m
.
Caùch giaûi thoâng thöôøng
Xeùt haøm soá
( )
2 , 0;2= + − f x x x x
;
( )
( )
1 1 2
'
2 2 2
22
−−
= − =
−
−
xx
fx
xx
xx
,
( )
0;2x
.
( )
'0=fx
20 − − =xx
2 − =xx
21 − = =x x x
.
Baûng bieán thieân
x
−
0
1
2
+
'y
+
0
-
y
2
2
2
Ñeå phöông trình ñaõ cho coù nghieäm duy nhất, ta caàn coù :
= 2m
.
Choïn ñaùp aùn C.
Caùch khaùc (duøng chuû yeáu suy luaän toaùn hoïc – söû duïng tính chaát cuûa haøm soá chaün)
Nhaän xeùt raèng : neáu
0
x
laø moät nghieäm cuûa phöông trình ñaõ cho, suy ra
−2
0
x
cuõng laø moät nghieäm cuûa phöông trình ñaõ cho. Vaäy ñeå phöông trình coù nghieäm duy nhaát
thì
=−2
00
xx
= =2 2 1
00
xx
. Theá vaøo phöông trình ta ñöôïc
= 2m
.
Ñaûo laïi, vôùi
= 2m
thì phöông trình trôû thaønh :
22+ − =xx
( )
+ − + − =2 2 2 4x x x x
( )
− =21xx
− + =
2
2 1 0xx
( )
− =
2
10x
=1x
.
Vaäy
= 2m
phöông trình ñaõ cho coù nghieäm duy nhaát.
Choïn ñaùp aùn C.
Ví duï 18. Tìm taát caû caùc giaù trò thöïc cuûa tham soá m ñeå phöông trình
1
4 2 0
xx
m
+
− + =
coù
hai nghieäm thöïc phaân bieät.
A.
( ;1)m −
. B.
(0; )m +
. C.
(0;1]m
. D.
(0;1)m
.
(Caâu 31 - Maõ ñeà 102 – THPT QG - 2017)
Caùch giaûi thoâng thöôøng
Ta coù
11
4 2 0 4 2
++
− + = − = −
x x x x
mm
.
Ñaët
( )
1
42
+
=−
xx
fx
;
( )
1
' 4 ln4 2 ln2
+
=−
xx
fx
;
( )
'0=fx
4 ln4 2.2 ln2=
xx
4 2 0 = =
xx
x
.
Baûng bieán thieân
x
−
0
+
'y
−
0
+
y
0
+
1−
Vaäy phöông trình coù hai nghieäm thöïc phaân bieät khi
11
01
00
− −


−

mm
m
mm
.
Choïn ñaùp aùn D.
Caùch khaùc (duøng chuû yeáu suy luaän toaùn hoïc)
Ta coù
1
4 2 0
xx
m
+
− + =
4 2.2 1 1 − + = −
xx
m
( )
2 1 1 − = −
x
m
.
Ñieàu kieän
1 0 1− mm
. (1)
Khi ñoù ta coù
2 1 1 2 1 1 0
2 1 1 2 1 1

− = − = + −

− = − − = − −


xx
xx
mm
mm
.
Ñeå thoûa maõn baøi toaùn ta caàn coù
1 1 0− − m
1 1 1 1 0 − − m m m
. (2)
Töø (1) vaø (2) suy ra :
01m
.
Choïn ñaùp aùn D.
Ví duï 19. Cho hai soá thöïc
0x
,
0y
thay ñoåi vaø thoûa maõn ñieàu kieän:
( )
+ = + −
22
x y xy x y x y
. Giaù trò lôùn nhaát M cuûa bieåu thöùc
=+
33
11
A
xy
laø :
A.
0=M
. B.
1=M
. C.
1
16
=M
. D.
16=M
.
Caùch giaûi thoâng thöôøng 1
Ta coù
+
= + =
33
3 3 3 3
11xy
A
x y x y
( )
( )
+ + −
=
22
33
x y x y xy
xy

+
=


2
xy
xy
. (*)
Neáu
+=0xy
thì
+ − = = =
22
00x y xy x y
. (traùi vôùi giaû thieát)
Vôùi
+0xy
thì:
( )
+−
+ = + − =
+
22
22
x y xy
x y xy x y xy xy
xy
, theá vaøo (*) ta ñöôïc:
( )

+

=

+−

2
2
22
xy
A
x y xy

=+

+−

2
22
3
1
xy
x y xy
.
Xeùt bieåu thöùc
==
+−

+−


2 2 2
3
3
1
x
xy
y
B
x y xy
xx
yy
; Ñaët
=0
x
t
y
ta ñöôïc
=
+−
2
3
1
t
B
tt
( )
− + + =
2
30Bt B t B
. (**)
Do (**) coù nghieäm neân
0
( )
+ −
2
2
3 4 0BB
− + +
2
3 6 9 0BB
− 13B
.
Suy ra
( )
+
2
1 16AB
.
Giaù trò lôùn nhaát cuûa A laø 16 khi
= = = =
1
31
2
B t x y
.
Choïn ñaùp aùn D.
Caùch giaûi thoâng thöôøng 2
Ta coù:
( )
+ = + − + = + −
22
22
1 1 1 1 1
x y xy x y xy
x y xy
xy
.
Ñaët
=
1
a
x
;
=
1
b
y
ta ñöôïc
+ = + −
22
a b a b ab
. (1)
=+
33
A a b
( )
( )
( )
= + + − = +
2
22
a b a b ab a b
.
Töø (1) suy ra
( ) ( ) ( )
+ = + − + − +
2 2 2
3
3
4
a b a b ab a b a b
. (vì

+


2
2
ab
ab
)
( ) ( )
+ − +
2
40a b a b
( )
+ 04ab
.
Suy ra:
( )
= + =
2
2
4 16A a b
.
Vaäy giaù trò lôùn nhaát cuûa A laø 16 khi
+=
=
4
4
ab
ab
= = = =
1
2
2
a b x y
.
Choïn ñaùp aùn D.
Caùch giaûi khaùc (duøng chuû yeáu suy luaän toaùn hoïc)
Do caùc bieåu thöùc
( )
22
;x y xy x y xy+ + −
vaø
33
11
xy
+
coù tính ñoái xöùng neân ta döï ñoaùn
bieåu thöùc A ñaït giaù trò lôùn nhaát khi
xy=
.
Maët khaùc, trong caùc giaù trò maø ñeà cho ôû ñaùp aùn thì
16=M
laø giaù trò lôùn nhaát.
Ta xeùt tröôøng hôïp naøy :
33
1
11
16
2
xy
xy
xy
=
= =
+=
, caùc giaù trò naøy thoûa maõn ñaúng
thöùc
( )
+ = + −
22
x y xy x y x y
.
Choïn ñaùp aùn D.
Caâu 20. Moät oâtoâ ñang döøng vaø baét ñaàu chuyeån ñoäng theo moät ñöôøng thaúng vôùi gia toác
( )
(
)
2
6 2 /a t t m s=−
, trong ñoù
t
laø khoaûng thôøi gian tính baèng giaây keå töø luùc oâtoâ baét
ñaàu chuyeån ñoäng. Hoûi quaõng ñöôøng oâ toâ ñi ñöôïc keå töø luùc baét ñaàu chuyeån ñoäng ñeán khi
vaän toác cuûa oâtoâ ñaït giaù trò lôùn nhaát laø bao nhieâu meùt ?
A.
18 meùt
. B.
45
2
meùt
.
C.
36 meùt
. D.
27
4
meùt
.
Höôùng daãn choïn ñaùp aùn
Ta coù
( ) ( ) ( )
2
6 2 6v t a t dt t dt t t C= = − = − +

.
Taïi thôøi ñieåm ban ñaàu
0t =
neân
( )
0 0 0vC= =
.
Ta ñöôïc
( ) ( )
2
2
6 3 9 9v t t t t= − = − − +
, töùc laø
max
9v =
khi
3t =
.
Quaõng ñöôøng caàn tìm laø :
( )
(
)
( )
3
33
22
00
3
6 3 18
3
0
t
s v t dt t t dt t meùt


= = − = − =



.
Choïn ñaùp aùn A.
Saøi Goøn, 17 - 7 - 2017
Traàn Tuaán Anh
Caùc phöông phaùp ñöôïc trình baøy ôû treân moät
caùch ñoäc laäp nhaèm ñem laïi cho ñoäc giaû caùi nhìn
chung, toång quaùt nhaát veà moãi phöông phaùp. Theá
nhöng, vieäc phaân ñònh raïch roøi caùc phöông phaùp
laø raát khoù khaên, coù nhieàu baøi toaùn chuùng ta phaûi
keát hôïp moät soá phöông phaùp ñeå choïn ñöôïc ñuùng
ñaùp aùn. ÔÛ trong phöông phaùp naøy laïi coù daáu veát
naøo ñoù cuûa phöông phaùp kia, khieán chuùng ta baên
khoaên trong vieäc choïn löïa phöông phaùp. Vì theá,
trong quaù trình giaûi toaùn, chuùng ta caàn linh hoaït
vaän duïng caùc phöông phaùp theo höôùng toång löïc
ñeå xöû lyù baøi toaùn traéc nghieäm. Taän duïng maët
maïnh, höõu duïng cuûa moãi phöông phaùp ñoái vôùi
caùc daïng baøi toaùn traéc nghieäm khaùc nhau. Khoâng
chæ tö duy treân neàn taûng moät phöông phaùp.
| 1/24
| | Tải xuống

Có thể bạn quan tâm:

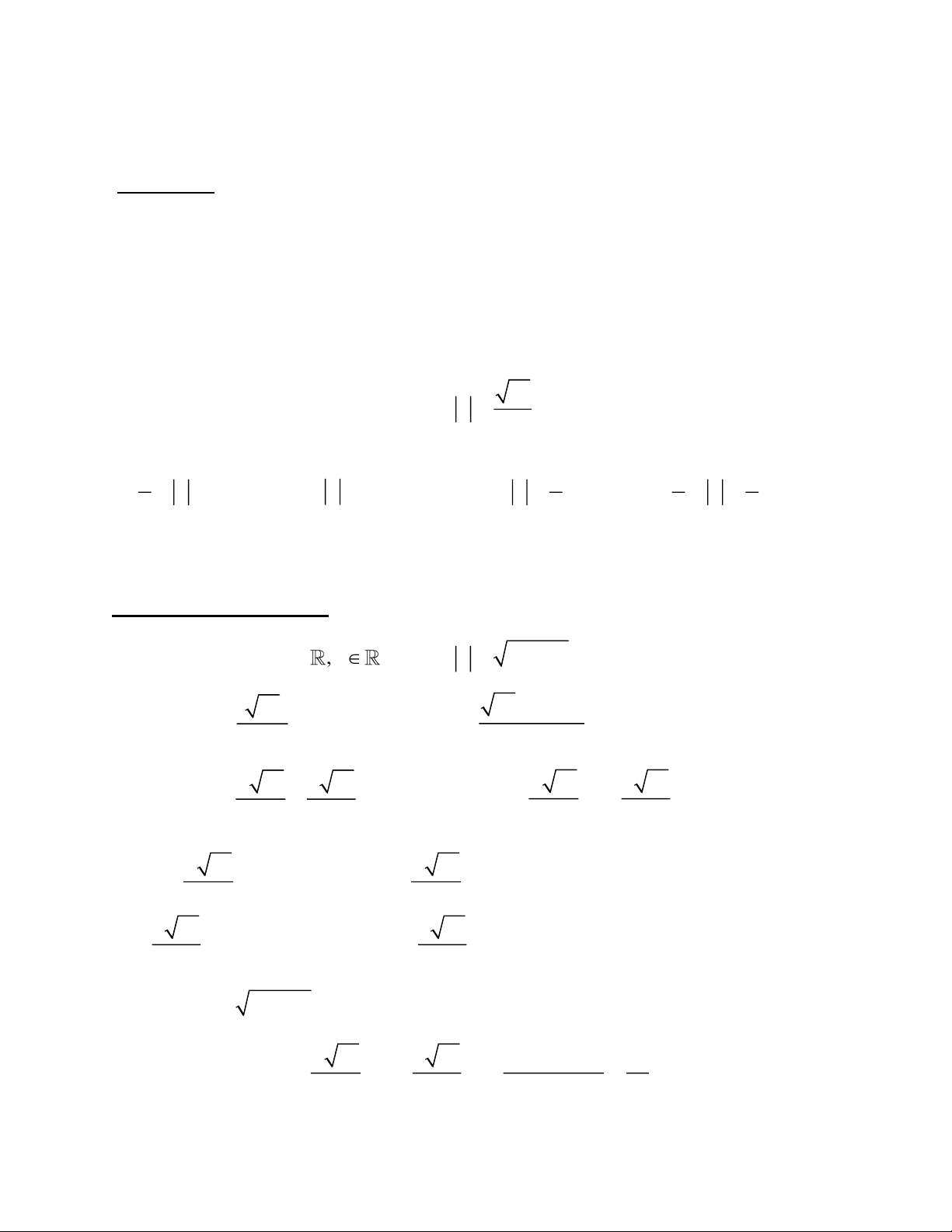
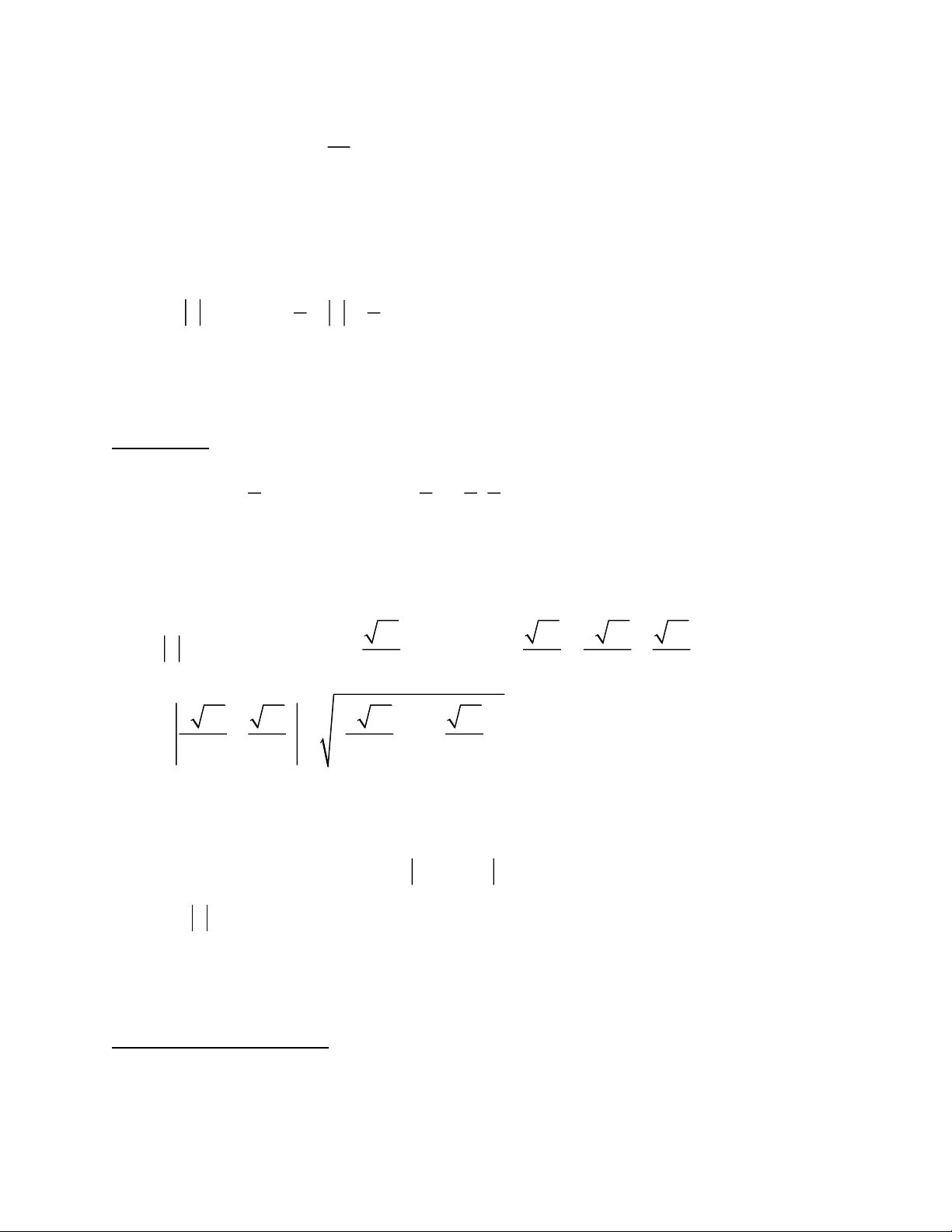
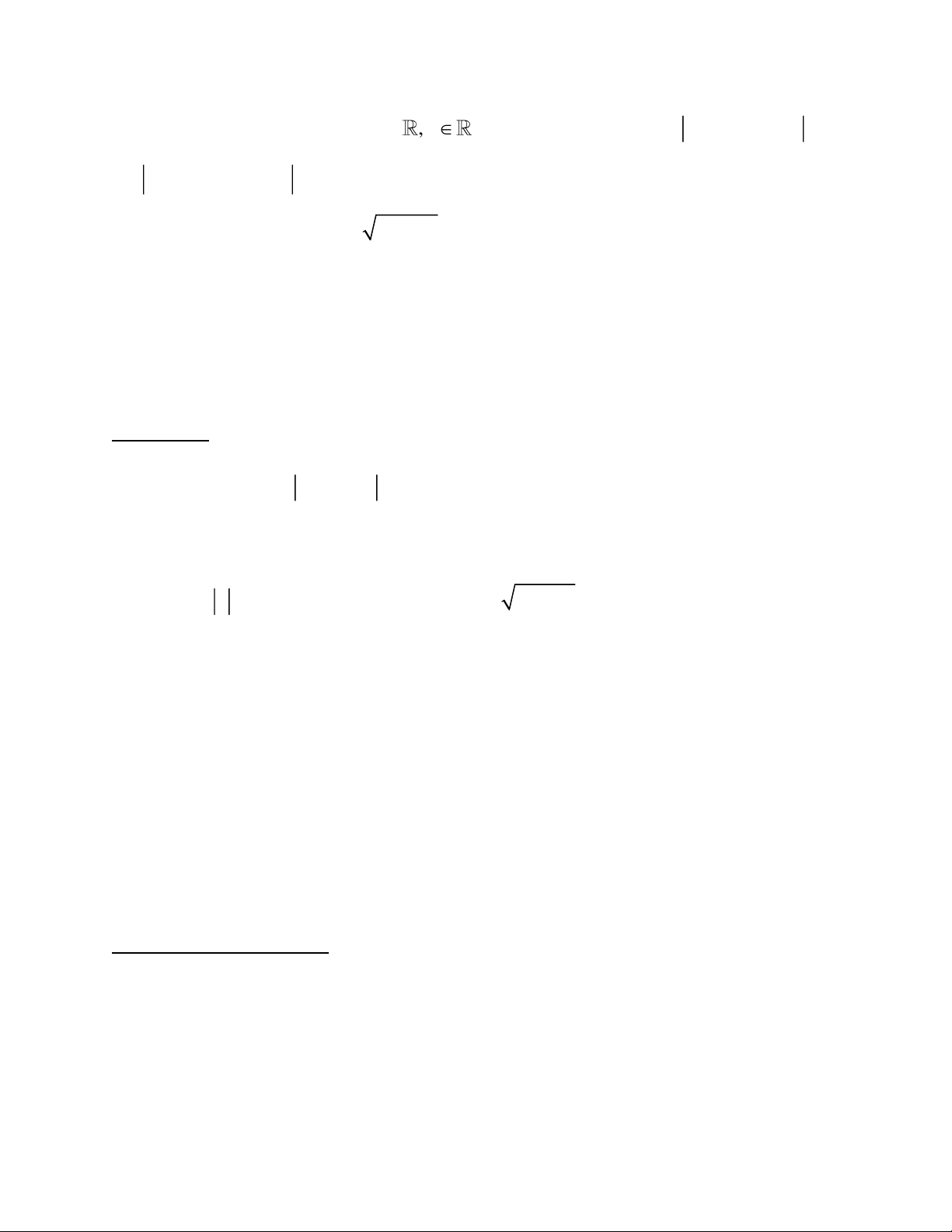
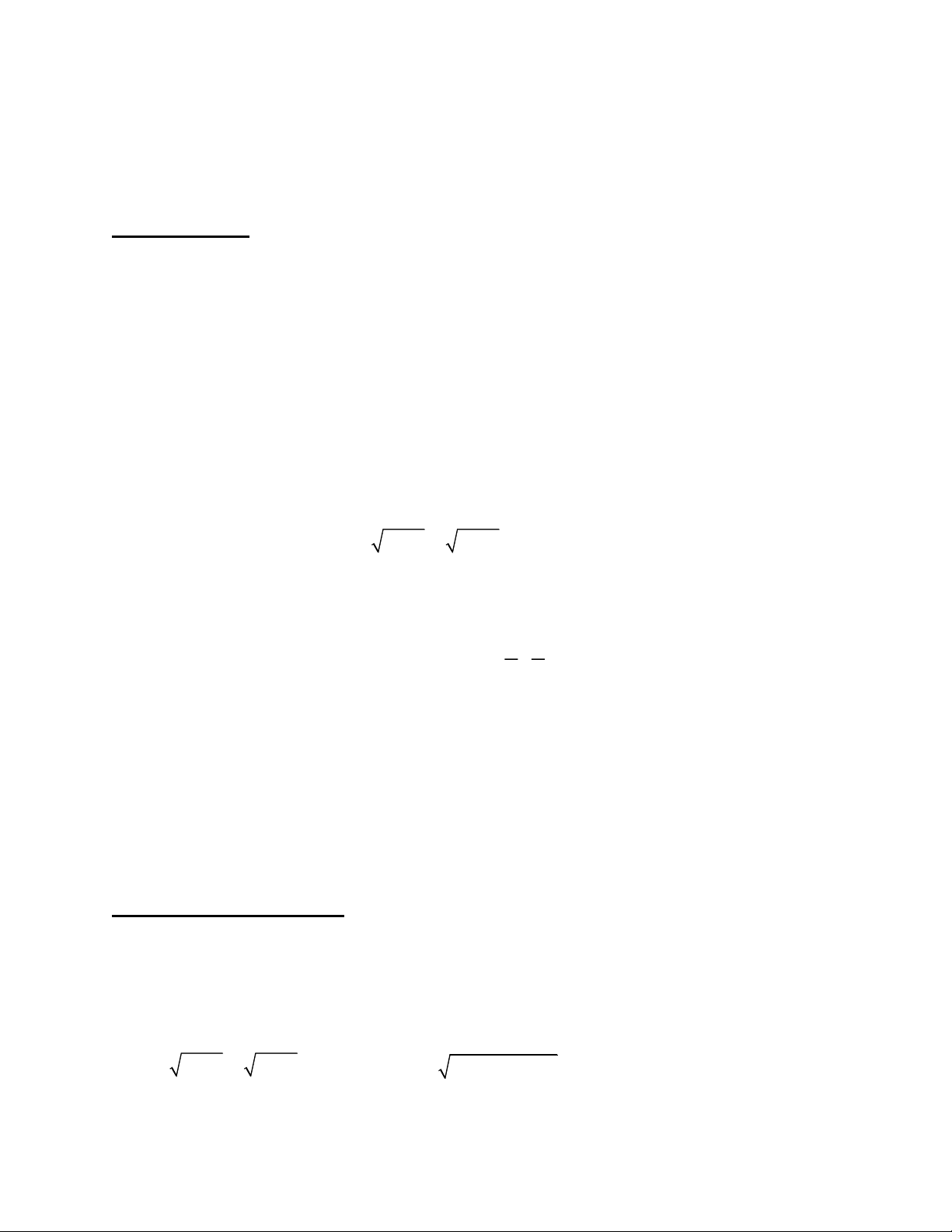
Preview text:

SÖÛ DUÏNG CHUÛ YEÁU SUY LUAÄN TRONG GIẢI TOAÙN TRẮC NGHIỆM
Moät soá baøi toaùn coù daïng ñaëc bieät ñöôïc giaûi nhanh nhôø nhöõng suy luaän toaùn hoïc,
maø neáu chuùng ta giaûi baèng caùch thoâng thöôøng thì cho ta lôøi giaûi khaù daøi, do ñoù maát thôøi
gian. Ñaây thöôøng laø nhöõng baøi toaùn ôû möùc “ vaän duïng” vaø “ vaän duïng cao ”, do ñoù chuùng
ta caàn chuaån bò kieán thöùc saâu roäng ñeå linh hoaït trong vieäc giaûi quyeát baøi toaùn ñoù, khoâng
bò daäp theo moät khuoân maãu khoâ cöùng, thieáu saùng taïo.
Ví duï 1. Tìm giaù trò nhoû nhaát cuûa haøm soá 3 2
y = x − 7x +11x − 2 treân ñoaïn [0; 2] .
A. m =11 . B. m = 0. C. m = 2 − . D. m = 3 .
(Caâu 23 - Maõ ñeà 101 – THPT QG - 2017)
Caùch giaûi thoâng thöôøng x =10;2 Ta coù : 2 
y ' = 3x −14x +11 ; 2
y ' = 0  3x −14x +11 = 0  11  . x = 0;2  3
Xeùt caùc giaù trò: y (0) = 2 − ; y ( ) 1 = 3 ; y (2) = 0 .
Suy ra min y = y (0) = 2 − . 0;2 Choïn ñaùp aùn C.
Caùch khaùc (duøng chuû yeáu suy luaän toaùn hoïc) Xeùt m = 2
− laø giaù trò nhoû nhaát trong caùc giaù trò ôû 4 ñaùp aùn ñaõ cho. Khi ñoù phöông trình 3 2
x − 7x +11x − 2 = 2
− coù nghieäm x = 00;2 neân choïn ñaùp aùn C.
Ví duï 2. Tìm giaù trò thöïc cuûa tham soá m ñeå haøm soá 1 3 2 2 y =
x − mx + (m − 4)x + 3 ñaït cöïc 3 ñaïi taïi x = 3.
A. m =1 . B. m = 1
− . C. m = 5. D. m = 7 − .
(Caâu 32 - Maõ ñeà 102 – THPT QG - 2017)
Caùch giaûi thoâng thöôøng Ta coù 2 2
y ' = x − 2mx + m − 4 . m = 1
Haøm soá ñaït cöïc ñaïi taïi x = 3 neân y '(3) = 0 2
m − 6m + 5 = 0   . m = 5
Laïi coù y ' = 2x − 2m y ' (3) = 6 − 2m .
Vôùi m =1 thì y ' (3) = 6 − 2 = 4  0 neân haøm soá ñaït cöïc tieåu taïi x = 3.
Vôùi m = 5 thì y ' (3) = 6 −10 = 4
−  0 neân haøm soá ñaït cöïc ñaïi taïi x = 3. Choïn ñaùp aùn C.
Caùch khaùc (duøng chuû yeáu suy luaän toaùn hoïc) Ta coù 2 2
y ' = x − 2mx + m − 4 ; x − m = 2 x = m + 2 2 2
y ' = 0  x − 2mx + m − 4 = 0  ( x − m)2 = 4     . x − m = 2 − x = m − 2 Do haøm soá 1 3 2 2 y =
x − mx + (m − 4)x + 3 coù heä soá 1 a =  0 neân xx . CÑ CT 3 3 Suy ra x
= m − 2, maø x
= 3 neân ta ñöôïc m − 2 = 3  m = 5 . CÑ CÑ Choïn ñaùp aùn C.
Ví duï 3. Heä thöùc lieân heä giöõa giaù trò cöïc ñaïi y vaø giaù trò cöïc tieåu y cuûa haøm soá CÑ CT y = 3
x − 2x laø : A. y + y = 0 2y
3y . C. y = 2y . D. y = y CÑ CT . B. = CÑ CT CT CÑ CT CÑ .
Caùch giaûi thoâng thöôøng Ta coù y = 2
' 3x − 2 ; y =  2 ' 0 3x − 2 = 0  2 3x = 2  2 2 x = 3  2 4 6 x = −  y =   3 9 .  2 4 6 x =  y = −  3 9 Vaäy y + y = 0. CÑ CT Choïn ñaùp aùn A.
Caùch giaûi khaùc (duøng chuû yeáu suy luaän toaùn hoïc) Do haøm soá y = 3
x − 2x laø haøm soá leû vaø coù taâm ñoái xöùng laø goác toïa ñoä O(0;0) neân y + y = 0. CÑ CT Choïn ñaùp aùn A. m Ví duï 4. Haøm soá 3 2 2 y =
x − mx + (2m −1)x + m nghòch bieán treân khi vaø chæ khi 3
A. m  0 hoaëc m 1 ; B. m  0 ; C. 0  m 1 ; D. m  0 .
Caùch giaûi thoâng thöôøng Ta coù 2
y ' = mx − 2mx + 2m −1 .
TH1: Neáu m = 0 thì y ' = 1
−  0 thoûa maõn baøi toaùn.
TH2: Neáu m  0 , ñeå thoûa maõn baøi toaùn ta caàn coù m  0  m  0     m  0 2 m − m  (2m − ) 2 1  0
−m + m  0
Vaäy m  0 , choïn ñaùp aùn D.
Caùch giaûi khaùc 1 (choïn ñaïi dieän) Neáu m = 3 − haøm soá trôû thaønh 3 2
y = −x + 3x − 7x + 9 ; 2 y ' = 3
− x + 6x − 7  0, x  
(duøng maùy tính casio 570vn plus giaûi baát phöông trình 2 3
− x + 6x − 7  0 seõ cho nghieäm laø taäp )
Loaïi tröôøng hôïp B, C.
Neáu m = 3 haøm soá trôû thaønh 3 2
y = x − 3x + 5x + 9 ; 2
y ' = 3x − 6x + 5  0  x 
Loaïi tröôøng hôïp A. Vaäy choïn ñaùp aùn D.
Caùch giaûi khaùc 2 (duøng chuû yeáu suy luaän toaùn hoïc - phöông phaùp tam thöùc baäc hai) Ta coù 2
y ' = mx − 2mx + 2m −1 laø tam thöùc baäc hai neân caàn xeùt m  0 hoaëc m = 0 .
Loaïi ba tröôøng hôïp A, B vaø C. Choïn ñaùp aùn D.
Ví duï 5. Bieát ñöôøng thaúng y = (3m −1)x + 6m + 3 caét ñoà thò haøm soá 3 2
y = x − 3x + 1
taïi ba ñieåm phaân bieät sao cho moät giao ñieåm caùch ñeàu hai giao ñieåm coøn laïi. Khi ñoù m
thuoäc khoaûng naøo döôùi ñaây ?  3   3  A. ( 1 − ;0). B. (0; ) 1 . C. 1;   . D. ;2   .  2   2 
Caùch giaûi thoâng thöôøng
Yeâu caàu cuûa baøi toaùn töông ñöông vôùi phöông trình sau coù ba nghieäm phaân bieät laäp thaønh caáp soá coäng 3 2
x − 3x + 1 = (3m −1)x + 6m + 3 3 2
x − 3x − (3m −1)x − 6m − 2 = 0. (*)
Goïi x , x , x laø ba nghieäm cuûa phöông trình treân, theo tính chaát caáp soá coäng ta coù : 1 2 3 + 1 3 = x x x . 2 2
Maø theo ñònh lí Vi-eùt ta coù x + x + x = 3 neân suy ra 3x = 3  x =1. 1 2 3 2 2 1
Theá x = 1 vaøo phöông trình (*) ta ñöôïc m = − . 3 x = 0 1 
Khi m = − phöông trình (*) trôû thaønh : 3 2
x − 3x + 2x = 0  x = 1 thoûa maõn baøi 3  x = 2  toaùn. 1 Maø m = − ( 1
− ;0) neân choïn ñaùp aùn A. 3
Caùch giaûi khaùc (duøng chuû yeáu suy luaän toaùn hoïc)
Nhaän xeùt raèng : neáu ñieåm uoán cuûa ñoà thò haøm soá 3 2
y = x − 3x + 1 thuoäc ñöôøng
thaúng y = (3m −1)x + 6m + 3 thì thoûa maõn baøi toaùn. Ta coù 2
y ' = 3x − 6x ; y ' = 6x − 6 = 0  x = 1. Suy ra ñieåm M (1; )1 − laø ñieåm uoán cuûa ñoà thò haøm soá 3 2
y = x − 3x + 1. 1
Theá toïa ñoä cuûa M vaøo phöông trình y = (3m −1)x + 6m + 3 ta ñöôïc m = − ( 1 − ;0) . 3 Choïn ñaùp aùn A. x + 1
Ví duï 6. Cho haøm soá y =
coù ñoà thò (C ). Giaù trò thöïc cuûa m thuoäc khoaûng naøo x −1
trong caùc khoaûng cho döôùi ñaây, ñeå ñöôøng thaúng (d ) : y = 2x + m caét ñoà thò (C ) taïi hai
ñieåm phaân bieät M, N sao cho tieáp tuyeán taïi M vaø N song song nhau laø :    7  A. 1 2; − − 
 . B. (0;2) . C. (2;3) . D. ;5   .  2   2 
Caùch giaûi thoâng thöôøng x + 1
Phöông trình hoaønh ñoä giao ñieåm laø :
= 2x + m x +1= (2x + m)(x − ) 1 x −1 2
x +1= 2x − 2x + mx − m 2
 2x + (m − 3) x − m −1= 0. (1)
Ñöôøng thaúng (d ) caét ñoà thò (C ) taïi hai ñieåm phaân bieät M, N khi phöông trình (1) coù   0
hai nghieäm phaân bieät khaùc 1   (vôùi g ( x) 2
= 2x + (m − 3) x − m −1) g ( ) 1  0 (  m − )2 3 + 8(m + ) 1  0 2 m + m +   2 17 0     m . 2 + 
(m − 3) − m −1 0  2 −  0
Goïi hai nghieäm cuûa phöông trình laø x , x ( x x , khi ñoù ta coù toïa ñoä giao ñieåm 1 2 ) 1 2
M ( x ;2x + m ; N ( x ;2x + m . 2 2 ) 1 1 ) x +
Tieáp tuyeán taïi M vaø N song song vôùi nhau khi f '( x = f ' x (vôùi f ( x) 1 = ) 1 ) ( 2) x −1 2 − 2 −
x −1= x −1  =  ( 1 2 x −1 = x −1   1 )2 ( 2 )2 (x − )2 1 (x − )2 1
x −1 = − x −1  1 ( 2 ) 1 2
x = x (loaï ) i m 3  1    1 2  x + x − = 2  −
= 2  m = −1  −2; −   . x + x = 1 2  2 2 2 1 2   Choïn ñaùp aùn A.
Caùch giaûi khaùc (duøng chuû yeáu suy luaän toaùn hoïc) ax + b
Nhaän xeùt raèng : Neáu hai ñieåm M, N treân ñoà thò (C ) cuûa haøm soá y = maø tieáp cx + d
tuyeán cuûa (C ) taïi hai ñieåm M, N song song vôùi nhau thì ñöôøng thaúng MN ñi qua taâm
ñoái xöùng cuûa cuûa ñoà thò (C ).
Taâm ñoái xöùng I cuûa ñoà thò (C ) laø giao ñieåm cuûa hai ñöôøng tieäm caän, ta coù I (1; ) 1 . Ñöôøng thaúng
(d) : y = 2x + m ñi qua I (1; )1, suy ra 1= 2 + m  1 
m = −1  −2; −   .  2  Choïn ñaùp aùn A. 1
Ví duï 7. Giaù trò lôùn nhaát cuûa haøm soá f (x) = laø : 2 x + 2x + 4 1 1 A. 3 . B. . C. . D. 4 3 4 .
Caùch giaûi thoâng thöôøng Ñieàu kieän 2
x + 2x + 4  0 (luoân ñuùng). Taäp xaùc ñònh cuûa haøm soá laø . 1
Xeùt haøm soá f (x) = , x  . 2 x + 2x + 4 2x + 2 f '(x) = −
; f '(x) = 0  2x + 2 = 0  x = 1 − . (x + 2x + 4)2 2 Ta coù baûng bieán thieân x − 1 − + f '(x) + 0 - f (x) 1 3 0 0
Keát luaän: max f (x) = f (− ) 1 1 = . 3 Choïn ñaùp aùn B.
Caùch giaûi khaùc (duøng chuû yeáu suy luaän toaùn hoïc)
Ta coù x + x + = (x + )2 2 2 4 1 + 3  0, x   . 1 1 1 1 Suy ra f (x) = =  = , vôùi x   vaø f (− ) 1 1 = . 2 x + 2x + 4 ( + x + 1)2 0 3 3 + 3 3
Do ñoù, giaù trò lôùn nhaát cuûa f (x) laø 1 . 3 Choïn ñaùp aùn B. 1
Ví duï 8. Tích phaân 2 I = 1 −  x dx baèng : 1 −  3 A. . B. . C. 2 . D.  . 2 2
Caùch giaûi thoâng thöôøng    
Ñaët x = sint , t  − ; 
  dx = cost.dt .  2 2    Ñoåi caän : x = 1
−  t = − ; x =1 t = . 2 2     2 2 2 2 1 Ta ñöôïc 2 I =
1 − sin x.cost.  dt = cos cos .  t t dt 2 = cos  tdx = (1 + cos 2 )  t dx    2  − − − − 2 2 2 2  1  1   2 = x + sin 2x =   . 2  2   2 − 2 Choïn ñaùp aùn A.
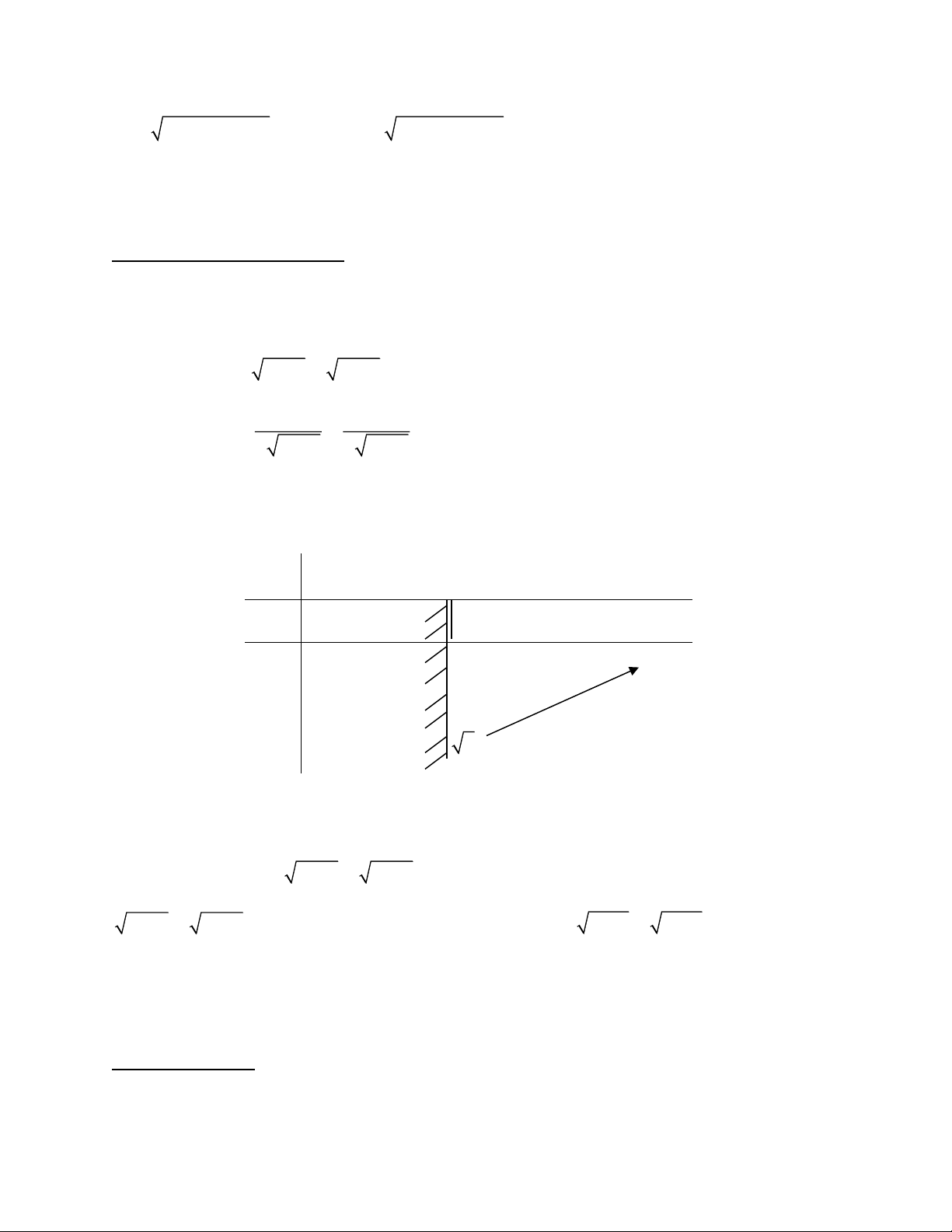
Caùch khaùc (duøng chuû yeáu suy luaän toaùn hoïc) 2 2 2 2 y 1 x x y 1 Ta coù : 2 y 1 x , neân haøm soá 2 y 1 x coù ñoà y 0 y 0
thò laø nöûa ñöôøng troøn phía treân truïc Ox (tính caû hai ñieåm ( 1; 0),(1; 0)). Maø ñöôøng troøn 2 2 x y 1 coù baùn kính R
1, theo yù nghóa hình hoïc cuûa tích phaân ta suy ra: 1 2 S .1  2 1− x dx = =
= . Vôùi S laø dieän tích hình troøn coù baùn kính baèng 1.  2 2 2 1 − Choïn ñaùp aùn A. e
Ví duï 9. Bieát raèng I = ( 2
ln x + 2ln x)dx = ae − 
b , vôùi a  , b  . Khi ñoù 1
S = a + b baèng bao nhieâu ? 3 A. 0 . B. . C. 1. D. 2 . 2
Caùch giaûi thoâng thöôøng e e e Ta coù I = ( 2 ln x + 2ln x) 2
dx = ln xdx + 2 ln   xdx. 1 1 1 e Xeùt tích phaân 2 J = ln  xdx. 1 2 Ñaët 2
u = ln x du =
ln xdx ; dv = dx v = x . x e e Ta ñöôïc 2
J = x ln x − 2 ln  xdx. 1 1  ee e 2
I =  xln x − 2 ln  xdx+ 2 ln  xdx 2 = e x ln x = e =1.e − 0. 1  1 1  1
a =1;b = 0  S = a + b =1. Choïn ñaùp aùn C.
Caùch khaùc (duøng chuû yeáu suy luaän toaùn hoïc) Ta coù 2 x + x = ( x)
2 x + x ( 2 x) = ( 2 ln 2ln '.ln . ln '
xln x)' neân suy ra : e e e e I = ( 2
ln x + 2ln x)dx = ( 2
x ln x)'dx = d ( 2 x ln x) = ( 2 x ln x) =  e . 1 1 1 1
Suy ra : S = a + b =1. Choïn ñaùp aùn C.
Caâu 10. Trong , phöông trình ( z − )( 2
1 z + 2z + 5) = 0 coù nghieäm laø : z = 1 − − 2iz =1 z = 1 − − 2iz =1− 2i  A.  B.  C.  D. z = 1 − + 2i . z = 1 − + 2iz = 1 − + 2iz =1+ 2i  z =1 
Caùch giaûi thoâng thöôøng z =1 z =1  Ta coù : ( z − )( 2
1 z + 2z + 5) = 0    z = 1 − − 2i . 2   z + 2z + 5 = 0 z = 1 − + 2  i Choïn ñaùp aùn D.
Caùch khaùc (duøng chuû yeáu suy luaän toaùn hoïc) Do phöông trình 2
z + 2z + 5 = 0 coù hai nghieäm neân phöông trình ñaõ cho coù ba nghieäm khaùc nhau. Choïn ñaùp aùn D. 10
Caâu 11. Xeùt số phốc z thoûa maõn (1 + 2i) z =
− 2 + .i Mốnh đố naøo sau ñaây ñuùng ? z 3 1 1 3
A.  z  2. B. z  2. C. z  D.  z  . 2 2 2 2
(Caâu 34 – Ñeà thöû nghieäm THPT QG naêm 2017)
Caùch giaûi thoâng thöôøng
Ñaët z = a + bi (vôùi a  ,b  ) vaø 2 2
k = z = a + b  0 ta ñöôïc : 10 10 (a − bi) (1+ 2i)k =
− 2 +  (1+ 2i)k = − 2 + i + i a bi 2 2 a + b a 10 b 10  a   b   10 10 (1 + 2i)k = −
i − 2 + i   k + 2 −  + 
−1+ 2k i = 0 2 2 k k 2 2  k   k   a 10  a 10 k − + 2 = 0 k + 2 = 2 2  k      k . b 10  b 10 + 2k −1 = 0 1 − 2k = 2 2    kk Ñeå yù raèng 2 2 2 2 2 k =
a + b k = a + b , ta coù : 2 2  a   b  10 10 10 ( 2 2 a + b 2 2 )
(k + ) + ( − k) 10 2 1 2 =   +   = = . 2 2 4 2  k   kk k 2  =  ( k 1
k + )2 + ( − k )2 10 2 1 2 = 4 2
 5k + 5k −10 = 0   2 k 2 k = 2 −
k = 1 (nhanä)   . k = 1 −  (loaiï) 1 3
Vaäy k = z =1 töùc laø  z  . 2 2 Choïn ñaùp aùn D.
Caùch khaùc (duøng chuû yeáu suy luaän toaùn hoïc)  3   1   1 3  Vì caùc khoaûng ;2 ,   (2;+), − ;  , ;   
 ñoâi moät khoâng coù ñieåm chung vaø trong  2   2   2 2 
boán ñaùp aùn thì coù moät ñaùp aùn ñuùng neân ta choïn ñaïi dieän. 10 10 3 10 10
Choïn z = 1, ta coù : (1+ 2i) =
− 2 + i z = = − i . z 3 + i 10 10 2 2 3 10 10  3 10   10  Khi ñoù − i =   + 
 =1. (thoûa maõn ñieàu kieän baøi toaùn) 10 10 10 10     Choïn ñaùp aùn D.
Caâu 12. Cho số phốc z thoûa maõn z − 3 + 4i = 4 . Tìm giaù trò lôùn nhaát P cuûa bieåu max thöùc P = z . A. P
=12. B. P = 5. C. P = 9. D. P = 3. max max max max
Caùch giaûi thoâng thöôøng Ñaët
z = a + bi (vôùi a  ,b  ) ta ñöôïc
a + bi − 3 + 4i = 4  ( 2 2
a − 3) + (b + 4)i = 4
 (a − 3) + (b + 4) =16 2 2
a + b − 6a + 8b + 9 = 0 2 2 2 2
a + b + 9 = 6a − 8b 10. a + b . Suy ra 2 P + 9 10P 2
P −10P + 9  0 1 P  9 . Vaäy P = 9 . max Choïn ñaùp aùn C.
Caùch khaùc (duøng chuû yeáu suy luaän toaùn hoïc)
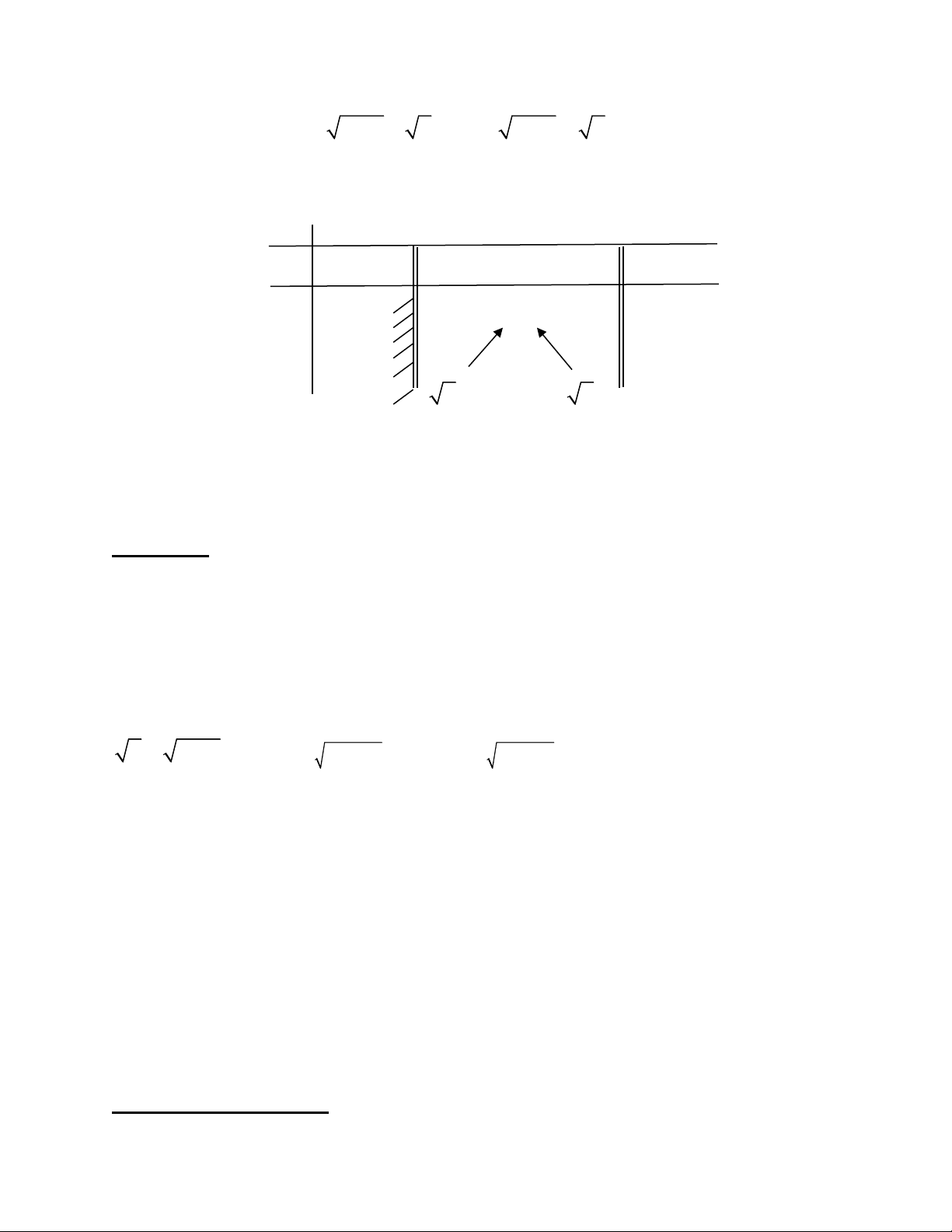
Số phốc z thoûa maõn z − 3 + 4i = 4 neân ñieåm M bieåu dieãn cuûa soá phöùc z thuoäc ñöôøng troøn taâm I (3; 4
− ) , baùn kính R = 4 .
Suy ra, P = z lôùn nhaát baèng 2 2 P
= OI + R = 3 + 4 + 4 = 9. max Choïn ñaùp aùn C.
Ví duï 13. Trong khoâng gian vôùi heä toïa ñoä Oxyz , cho maët caàu (S ) tieáp xuùc vôùi maët
phaúng (Oxz), coù baùn kính R = 3 vaø coù taâm naèm treân tia Oy . Maët cầu (S ) coù phöông trình laø : A. (S ) 2 2 2
: x + y + z − 6x = 0 . B. (S ) 2 2 2
: x + y + z − 6 y = 0 . C. (S ) 2 2 2
: x + y + z − 6z = 0 . D. (S ) 2 2 2
: x + y + z = 9 .
Caùch giaûi thoâng thöôøng Goïi I (0; ;
b 0) laø taâm cuûa maët caàu (S ) thì b  0 (do I naèm treân tia Oy ).
Maët phaúng (Oxz) coù phöông trình laø y = 0. bb = 3 (nhaä ) n
Ta coù : d (I,(Oxz)) = R  = 3  b = 3   . 2 1 b = −3 (loaï ) i
Vaäy (S ) x + ( y − )2 2 2 2 : 3
+ z = 3 hay (S ) 2 2 2
: x + y + z − 6 y = 0 . Choïn ñaùp aùn B.
Caùch giaûi khaùc 1 (duøng chuû yeáu suy luaän toaùn hoïc)
Do taâm maët caàu naèm treân tia Oy neân coù toïa ñoä daïng I (0; ;
b 0) . Suy ra, ta loaïi
ñaùp aùn A (taâm I coù hoaønh ñoä baèng 3), loaïi ñaùp aùn C (taâm I coù cao ñoä baèng 3), loaïi ñaùp
aùn D (taâm I truøng vôùi goác toïa ñoä neân khoâng tieáp xuùc vôùi maët phaúng (Oxz) ). Choïn ñaùp aùn B.
Caùch giaûi khaùc 2 (duøng chuû yeáu suy luaän toaùn hoïc)
Do (S ) tieáp xuùc vôùi maët phaúng (Oxz), coù baùn kính R = 3 vaø coù taâm naèm treân
tia Oy neân I (0;3;0). Ñieåm M (0;6;0) ñoái xöùng vôùi goác toïa ñoä qua taâm I (0;3;0)
thuoäc maët caàu neân ta loaïi ñöôïc caùc ñaùp aùn A, C, D. Choïn ñaùp aùn B.
Ví duï 14. Trong khoâng gian vôùi heä toïa ñoä Oxyz , maët phaúng ( P) chöùa hai ñieåm A(1;0; ) 1 , B ( 1
− ;2;2) vaø song song vôùi truïc Ox coù phöông trình laø :
A. (P) : x + 2z − 3 = 0. B. (P) : y − 2z + 2 = 0 .
C. (P) : 2y − z +1 = 0. D. (P) : x + y − z = 0 .
Caùch giaûi thoâng thöôøng
Caëp vectô chæ phöông cuûa maët phaúng ( P) laø : AB = ( 2 − ;2; ) 1 ; i = (1;0;0) .
Vectô phaùp tuyeán cuûa maët phaúng ( P) laø n =  AB,i = (0;1; 2 − )   .
Maët phaúng ( P) ñi qua ñieåm A(1;0; )
1 vaø coù vectô phaùp tuyeán n = (0;1; 2 − ) laø : 0( x − ) 1 + (
1 y − 0) − 2( z − )
1 = 0  y − 2z + 2 = 0 . Choïn ñaùp aùn B.
Caùch giaûi khaùc (duøng chuû yeáu suy luaän toaùn hoïc)
Maët phaúng song song vôùi truïc Ox coù daïng : By + Cz + D = 0, ta loaïi ñöôïc hai ñaùp aùn A vaø D. Laïi coù B( 1
− ;2;2)(P): 2y − z +1= 0 neân loaïi ñaùp aùn C. Choïn ñaùp aùn B.
Ví duï 15. Cho phöông trình x + 3 + x + 8 = 5 . Trong caùc khaúng ñònh sau, khaúng ñònh naøo ñuùng ?  1 7 
A. Phöông trình coù moät nghieäm thuoäc khoaûng  ;  vaø moät nghieäm thuoäc khoaûng  3 5  (3 : +).
B. Phöông trình coù ba nghieäm döông phaân bieät.
C. Phöông trình coù moät nghieäm baèng 1 vaø moät nghieäm nhoû hôn 1.
D. Phöông trình nghieäm duy nhaát x = 1.
Caùch giaûi thoâng thöôøng 1 x + 3  0 x  − Ñieàu kieän : 3     x  −3 . x + 8  0 x  −8
Ta coù: x + 3 + x + 8 = 5  x + 3 + 2 (x + 3)(x + 8) + x + 8 = 25
 2 (x + 3)(x + 8) = 14 − 2x  (x + 3)(x + 8) = 7 − x 2 2
x + 11x + 24 = 49 − 14x + x  25x = 25  x = 1.
Vaäy phöông trình nghieäm duy nhaát x = 1.
Caùch giaûi thoâng thöôøng 2 x + 3  0 x  − Ñieàu kieän : 3     x  −3 . x + 8  0 x  −8
Xeùt haøm f (x) = x + 3 + x + 8 , vôùi x  −3 +  ; ) . f '(x) = 1 + 1  , 0 x  (− ; 3 +) . 2 x + 3 2 x + 8 Ta coù baûng bieán thieân x − - 3 + y' + +  y 5
Töø baûng bieán thieân ta nhaän thaáy, ñöôøng thaúng y = 5 neáu coù giao ñieåm vôùi ñoà thò
cuûa haøm soá f (x) = x + 3 + x + 8 thì coù toái ña moät giao ñieåm. Do ñoù, phöông trình
x + 3 + x + 8 = 5 coù toái ña moät nghieäm. Maø f (1) = 1 + 3 + 1 + 8 = 5 neân x = 1
laø nghieäm duy nhaát cuûa phöông trình ñaõ cho. Choïn ñaùp aùn D.
Caùch giaûi khaùc (duøng chuû yeáu suy luaän toaùn hoïc)
Caùc haøm soá y = x + 3 vaø y = x + 8 ñoàng bieán treân R neân cuõng ñoàng bieán treân − +  ; 3 )
vì coù heä soá goùc döông. Suy ra, caùc haøm soá y = x + 3 vaø y = x + 8 cuõng laø caùc haøm soá
ñoàng bieán treân − +  ; 3
). Do ñoù, haøm soá y = x + 3 + x + 8 laø haøm soá ñoàng bieán treân − +  ; 3 ).
VT(1) laø haøm soá ñoàng bieán treân − +  ; 3
), VP(1) laø haøm haèng neân phöông trình (1)
neáu coù nghieäm thì coù nhieàu nhaát laø moät nghieäm.
Nhaän thaáy y(1) = 1 + 3 + 1 + 8 = 5 neân x = 1 laø nghieäm duy nhaát cuûa phöông trình ñaõ cho. Choïn ñaùp aùn D.
Ví duï 16. Cho phöông trình aån x sau ñaây : 2 4
2x − x − m = 0 , ( m laø tham soá thöïc). Choïn khaúng ñònh ñuùng ?
A. Phöông trình coù nghieäm thöïc duy nhaát khi m = 0 .
B. Phöông trình coù nghieäm thöïc duy nhaát khi m = 1.
C. Phöông trình coù nghieäm thöïc duy nhaát khi m  1.
D. Khoâng toàn taïi giaù trò thöïc cuûa m ñeå phöông trình coù nghieäm thöïc duy nhaát.
Caùch giaûi thoâng thöôøng Ta coù 2 4
2x − x − m = 0 2 4
 2x − x = m . x = 0 Ñaët    f (x) 2 4
= 2x − x ; f (x) 3 2 '
= 4x − 4x = 4x 1 − x  = 0  x = 1 − .    x = 1  Baûng bieán thieân x − 1 − 0 1 + y ' + 0 - 0 + 0 - y 1 1 − 0 −
Töø baûng bieán thieân suy ra, khoâng toàn taïi giaù trò cuûa tham soá m ñeå phöông trình ñaõ cho coù nghieäm duy nhaát. Vaäy choïn ñaùp aùn D.
Caùch giaûi khaùc (duøng chuû yeáu suy luaän toaùn hoïc – söû duïng tính chaát cuûa haøm soá chaün) Nhaän xeùt raèng : neáu − cuõng 0
x laø moät nghieäm cuûa phöông trình ñaõ cho, suy ra 0 x
laø moät nghieäm cuûa phöông trình ñaõ cho. Vaäy ñeå phöông trình coù nghieäm duy nhaát thì = −  = 
= . Theá vaøo phöông trình ta ñöôïc . 0 x 0 x 2x 0 x 0 0 0 m = 0
Ñaûo laïi, vôùi m = 0 thì phöông trình trôû thaønh : x = 0 2 4    2x − x = 0 2 2
x 2 − x  = 0  x = − 2 .    x = 2 
Vaäy khoâng toàn taïi giaù trò cuûa tham soá m ñeå phöông trình ñaõ cho coù nghieäm duy nhaát. Choïn ñaùp aùn D.
Ví duï 17. Giaù trò thöïc cuûa tham soá m ñeå phöông trình x + 2 − x = m coù nghieäm thöïc duy nhaát laø :
A. m =1 . B. m = 0. C. m = 2 . D. m .
Caùch giaûi thoâng thöôøng
Xeùt haøm soá f ( x) = x + 2 − x, x0;2 ; (x) 1 1 2 − x − x f ' = − = , x (0;2) . 2 x 2 2 − x 2 x(2 − x)
f '( x) = 0  2 − x − x = 0  2 − x = x  2 − x = x x =1. Baûng bieán thieân x − 0 1 2 + y ' + 0 - y 2 2 2
Ñeå phöông trình ñaõ cho coù nghieäm duy nhất, ta caàn coù : m = 2. Choïn ñaùp aùn C.
Caùch khaùc (duøng chuû yeáu suy luaän toaùn hoïc – söû duïng tính chaát cuûa haøm soá chaün) Nhaän xeùt raèng : neáu 0
x laø moät nghieäm cuûa phöông trình ñaõ cho, suy ra 2 − 0 x
cuõng laø moät nghieäm cuûa phöông trình ñaõ cho. Vaäy ñeå phöông trình coù nghieäm duy nhaát thì x = 2 −
. Theá vaøo phöông trình ta ñöôïc m = . 0 0
x  2x = 2  x = 1 0 0 2
Ñaûo laïi, vôùi m = 2 thì phöông trình trôû thaønh :
x + 2 − x = 2  2 2
x + 2 x (2 − x) + 2 − x = 4  x (2 − x) = 1  x − 2x + 1 = 0  (x − 1) = 0  x = 1 .
Vaäy m = 2 phöông trình ñaõ cho coù nghieäm duy nhaát. Choïn ñaùp aùn C.
Ví duï 18. Tìm taát caû caùc giaù trò thöïc cuûa tham soá m ñeå phöông trình x x 1 4 2 + − + m = 0 coù
hai nghieäm thöïc phaân bieät. A. m  (− ;1
 ) . B. m  (0;+) . C. m  (0;1]. D. m  (0;1) .
(Caâu 31 - Maõ ñeà 102 – THPT QG - 2017)
Caùch giaûi thoâng thöôøng Ta coù x x 1 + x x 1 4 2 m 0 4 2 + − + =  − = −m . Ñaët f (x) x x 1 4 2 + = − ; f (x) x x 1 ' 4 ln 4 2 + = − ln 2 ;
f '(x) = 0  4x ln 4 = 2.2x ln 2  4x = 2x x = 0 . Baûng bieán thieân x − 0 + y ' − 0 + 0 + y 1 − −m  1 − m 1
Vaäy phöông trình coù hai nghieäm thöïc phaân bieät khi     0  m  1. −m  0 m  0 Choïn ñaùp aùn D.
Caùch khaùc (duøng chuû yeáu suy luaän toaùn hoïc) Ta coù x x 1 4 2 + −
+ m = 0  4x − 2.2x +1 =1− m  (2x − ) 1 = 1− m .
Ñieàu kieän 1− m  0  m 1. (1)
2x −1 = 1− m
2x =1+ 1− m  0 Khi ñoù ta coù    .
2x −1 = − 1− m
2x =1− 1− m
Ñeå thoûa maõn baøi toaùn ta caàn coù 1− 1− m  0  1− m 11− m 1 m  0 . (2)
Töø (1) vaø (2) suy ra : 0  m 1. Choïn ñaùp aùn D.
Ví duï 19. Cho hai soá thöïc x  0, y  0 thay ñoåi vaø thoûa maõn ñieàu kieän: ( + ) = 2 + 2 1 1 x y xy x
y − xy . Giaù trò lôùn nhaát M cuûa bieåu thöùc A = + laø : 3 3 x y 1
A. M = 0. B. M =1. C. M = . D. M =16 . 16
Caùch giaûi thoâng thöôøng 1 2 2 2 3
(x + y)(x + y − xy) 1 1 x + 3  x + y  Ta coù = + = y A = =   . (*) 3 3 3 3 x y x y 3 3 x yxy
Neáu x + y = 0 thì 2 x + 2
y − xy = 0  x = y = 0 . (traùi vôùi giaû thieát) 2 2 x y xy Vôùi 2 2
x + y  0 thì: (x y) + − +
xy = x + y − xy xy =
, theá vaøo (*) ta ñöôïc: x + y  (x y)2 2 + 2    3xyA =  = 1 + . 2 2  2 x + 2 y −   x + y −  xy xy x 3 Xeùt bieåu thöùc = 3xy = y x 3t B ; Ñaët t =  0 ta ñöôïc B = 2 x + 2 y − xy  2 x 2 y t + 1 − t + x 1 −    y y  2
Bt − (B + 3) t + B = 0 . (**)
Do (**) coù nghieäm neân   2 0  (B + ) − 2 3 4B  0  − 2
3B + 6B + 9  0  −1  B  3 .
Suy ra A  ( + B)2 1  16 .
Giaù trò lôùn nhaát cuûa A laø 16 khi B =  t =  x = y = 1 3 1 . 2 Choïn ñaùp aùn D.
Caùch giaûi thoâng thöôøng 2 1 1 1 1 1
Ta coù: (x + y) xy = 2 x + 2 y − xy  + = + − . 2 2 x y x y xy Ñaët = 1 a ; = 1 b ta ñöôïc + = 2 + 2 a b a b − ab . (1) x y = 3 + 3 2 A a b = ( + )( 2 + 2 a b a
b − ab) = (a + b) . 2 2 2 2 3  a + b
Töø (1) suy ra a + b = (a + b) − 3ab  (a + b) − (a + b) . (vì ab    ) 4  2 
 (a + b)2 − 4(a + b)  0  0  (a + b)  4 . 2
Suy ra: A = (a + b)  2 4 = 16 . a + b =
Vaäy giaù trò lôùn nhaát cuûa A laø 16 khi 4 
a = b =  x = y = 1 2 . ab = 4 2 Choïn ñaùp aùn D.
Caùch giaûi khaùc (duøng chuû yeáu suy luaän toaùn hoïc) Do caùc bieåu thöùc ( 1 1 x + y) 2 2
xy ; x + y − xy vaø +
coù tính ñoái xöùng neân ta döï ñoaùn 3 3 x y
bieåu thöùc A ñaït giaù trò lôùn nhaát khi x = y .
Maët khaùc, trong caùc giaù trò maø ñeà cho ôû ñaùp aùn thì M =16 laø giaù trò lôùn nhaát. x = y
Ta xeùt tröôøng hôïp naøy : 1  1 1
x = y = , caùc giaù trò naøy thoûa maõn ñaúng + = 16 2  3 3  x y thöùc ( + ) = 2 + 2 x y xy x y − xy . Choïn ñaùp aùn D.
Caâu 20. Moät oâtoâ ñang döøng vaø baét ñaàu chuyeån ñoäng theo moät ñöôøng thaúng vôùi gia toác
a (t) = − t ( 2
6 2 m / s ), trong ñoù t laø khoaûng thôøi gian tính baèng giaây keå töø luùc oâtoâ baét
ñaàu chuyeån ñoäng. Hoûi quaõng ñöôøng oâ toâ ñi ñöôïc keå töø luùc baét ñaàu chuyeån ñoäng ñeán khi
vaän toác cuûa oâtoâ ñaït giaù trò lôùn nhaát laø bao nhieâu meùt ?
A. 18 meùt . B. 45 meùt. 2
C. 36 meùt . D. 27 meùt . 4
Höôùng daãn choïn ñaùp aùn
Ta coù v(t) = a
 (t)dt = ( − t) 2
6 2 dt = 6t − t + C .
Taïi thôøi ñieåm ban ñaàu t = 0 neân v(0) = 0  C = 0 .
Ta ñöôïc v(t) = t − t = − (t − )2 2 6 3 + 9  9 , töùc laø m
v ax = 9 khi t = 3.  3 t  3
Quaõng ñöôøng caàn tìm laø : 3 s = v  (t) 3 dt =
6t − t dt = 3t −  = 18 meùt . 0 0  ( 2 ) 2 ( )  3  0   Choïn ñaùp aùn A.
Caùc phöông phaùp ñöôïc trình baøy ôû treân moät
caùch ñoäc laäp nhaèm ñem laïi cho ñoäc giaû caùi nhìn
chung, toång quaùt nhaát veà moãi phöông phaùp. Theá
nhöng, vieäc phaân ñònh raïch roøi caùc phöông phaùp
laø raát khoù khaên, coù nhieàu baøi toaùn chuùng ta phaûi
keát hôïp moät soá phöông phaùp ñeå choïn ñöôïc ñuùng
ñaùp aùn. ÔÛ trong phöông phaùp naøy laïi coù daáu veát
naøo ñoù cuûa phöông phaùp kia, khieán chuùng ta baên
khoaên trong vieäc choïn löïa phöông phaùp. Vì theá,
trong quaù trình giaûi toaùn, chuùng ta caàn linh hoaït
vaän duïng caùc phöông phaùp theo höôùng toång löïc
ñeå xöû lyù baøi toaùn traéc nghieäm. Taän duïng maët
maïnh, höõu duïng cuûa moãi phöông phaùp ñoái vôùi
caùc daïng baøi toaùn traéc nghieäm khaùc nhau. Khoâng
chæ tö duy treân neàn taûng moät phöông phaùp.
Saøi Goøn, 17 - 7 - 2017 Traàn Tuaán Anh