Sử dụng hàm số chặn miền giá trị giải hệ chứa căn (hệ chứa căn phần 8) – Lương Tuấn Đức

T

À

I

L

I

Ệ

U

T

H

A

M

K

H

Ả

O

T

O

Á

N

H

Ọ

C

P

H

Ổ

T

H

Ô

N

G

_

x

 

 



-

C

H

U

Y

Ê

N

Đ

Ề

H

Ệ

P

H

Ư

Ơ

N

G

T

R

Ì

N

H

–

H

Ệ

B

Ấ

T

P

H

Ư

Ơ

N

G

T

R

Ì

N

H

–

H

Ệ

H

Ỗ

N

T

Ạ

P

T

R

U

N

G

Đ

O

À

N

H

O

À

N

G

S

A

–

Q

U

Â

N

Đ

O

À

N

T

Ă

N

G

T

H

I

Ế

T

G

I

Á

P

C

H

Ủ

Đ

Ạ

O

:

K

Ế

T

H

Ợ

P

S

Ử

D

Ụ

N

G

P

H

É

P

T

H

Ế

,

C

Ộ

N

G

Đ

Ạ

I

S

Ố

V

À

Ẩ

N

P

H

Ụ

(

T

I

Ế

P

T

H

E

O

)

G

I

Ả

I

H

Ệ

P

H

Ư

Ơ

N

G

T

R

Ì

N

H

C

H

Ứ

A

C

Ă

N

T

H

Ứ

C



P

H

Ố

I

H

Ợ

P

H

É

P

T

H

Ế

,

C

Ộ

N

G

Đ

Ạ

I

S

Ố

V

À

Ẩ

N

P

H

Ụ

.



S

Ử

D

Ụ

N

G

T

Í

N

H

C

H

Ấ

T

Đ

Ơ

N

Đ

I

Ệ

U

H

À

M

S

Ố

.



S

Ử

D

Ụ

N

G

K

Ế

T

H

Ợ

P

Đ

Á

N

H

G

I

Á

–

B

Ấ

T

Đ

Ẳ

N

G

T

H

Ứ

C

.



T

Ổ

N

G

H

Ợ

P

C

Á

C

P

H

É

P

G

I

Ả

I

P

H

Ư

Ơ

N

G

T

R

Ì

N

H

C

H

Ứ

A

C

Ă

N

.



B

À

I

T

O

Á

N

H

I

Ề

U

C

Á

C

H

G

I

Ả

I

.

C

R

E

A

T

E

D

B

Y

G

I

A

N

G

S

Ơ

N

(

F

A

C

E

B

O

K

)

;

G

A

C

M

A

1

4

3

1

9

8

@

G

M

A

I

L

.

C

O

M

(

G

M

A

I

L

)

T

H

Ủ

Đ

Ô

H

À

N

Ộ

I

–

M

Ù

A

X

U

Â

N

2

0

1

5

LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

2

“

N

o

n

s

ô

n

g

V

i

ệ

t

N

a

m

c

ó

t

r

ở

n

ê

n

t

ư

ơ

i

đ

ẹ

p

h

a

y

k

h

ô

n

g

,

d

â

n

t

ộ

c

V

i

ệ

t

N

a

m

c

ó

b

ư

ớ

c

t

ớ

i

đ

à

i

v

i

n

h

q

u

a

n

g

đ

ể

s

á

n

h

v

a

i

v

ớ

i

c

á

c

ư

ờ

n

g

q

u

ố

c

n

ă

m

c

h

â

u

đ

ư

ợ

c

h

a

y

k

h

ô

n

g

,

c

h

í

n

h

l

à

n

h

ờ

m

ộ

t

p

h

ầ

n

l

ớ

n

ở

c

ô

n

g

h

ọ

c

t

ậ

p

c

ủ

a

c

á

c

e

m

”

(

T

r

í

c

h

t

h

ư

C

h

ủ

t

ị

c

h

H

ồ

C

h

í

M

i

n

h

)

.

“

M

a

i

n

à

y

,

k

h

i

a

n

h

l

ấ

y

v

ợ

,

c

ó

q

u

a

n

t

â

m

e

m

g

á

i

n

à

y

s

u

ố

t

đ

ờ

i

đ

ư

ợ

c

k

h

ô

n

g

…

”

(

0

4

.

2

0

1

4

–

V

i

ệ

t

A

n

)

.

[

T

à

i

l

i

ệ

u

d

à

n

h

t

ặ

n

g

r

i

ê

n

g

e

m

,

V

i

ệ

t

A

n

y

ê

u

t

h

ư

ơ

n

g

c

ủ

a

n

h

,

n

h

â

n

d

ị

p

M

ù

a

t

h

i

2

0

1

5

]

LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

3

C

H

U

Y

Ê

N

Đ

Ề

H

Ệ

P

H

Ư

Ơ

N

G

T

R

Ì

N

H

–

H

Ệ

B

Ấ

T

P

H

Ư

Ơ

N

G

T

R

Ì

N

H

–

H

Ệ

H

Ỗ

N

T

Ạ

P

LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

T

R

U

N

G

Đ

O

À

N

H

O

À

N

G

S

A

–

Q

U

Â

N

Đ

O

À

N

T

Ă

N

G

T

H

I

Ế

T

G

I

Á

P

-------------------------------------------------------------------------------------------------------------------------------------------

Trong khuôn khổ Toán học sơ cấp nói chung và Đại số phổ thông nói riêng, hệ phương trình – hệ bất phương

trình – hệ hỗn tạp là dạng toán cơ bản nhưng thú vị, có phạm vi trải rộng, phong phú, liên hệ chặt chẽ với nhiều bộ

phận khác của toán học sơ cấp cũng như toán học hiện đại.

Tại Việt Nam, hệ phương trình, nội dung hệ phương trình – hệ bất phương trình – hệ hỗn tạp là một bộ phận

hữu cơ, quan trọng, được phổ biến giảng dạy chính thức trong chương trình sách giáo khoa Toán các lớp 9, 10, 11,

12 song song với các khối lượng kiến thức liên quan. Đây cũng là kiến thức phổ biến xuất hiện trong các kỳ thi

kiểm tra kiến thức thường niên, kỳ thi chọn học sinh giỏi toán các cấp trên toàn quốc, kỳ thi tuyển sinh lớp 10 hệ

THPT và trong kỳ thi tuyển sinh đại học – cao đẳng hàng năm, một kỳ thi đầy cam go, kịch tính và bất ngờ, nó lại

là một câu rất được quan tâm của các bạn học sinh, phụ huynh, các thầy cô, giới chuyên môn và đông đảo bạn đọc

yêu Toán.

Yêu cầu của dạng toán khá đa dạng, đa chiều, mục tiêu tìm các ẩn thỏa mãn một tính chất nào đó nên để thao

tác dạng toán này, các bạn học sinh cần liên kết, phối hợp, tổng hợp các kiến thức được học về phương trình, hệ

phương trình và bất phương trình, như vậy nó đòi hỏi năng lực tư duy của thí sinh rất cao. Tuy nhiên "Trăm hay

không hay bằng tay quen", các phương pháp cơ bản đã được được các thế hệ đi trước đúc kết và tận tụy cho thế hệ

tương lai, các bạn hoàn toàn đủ khả năng kế thừa, phát huy và sáng tạo không ngừng, chuẩn bị đủ hành trang nắm

bắt khoa học kỹ thuật, đưa đất nước ngày càng vững bền, phồn vinh, và hiển nhiên những bài toán trong các kỳ thi

nhất định không thể là rào cản, mà là cơ hội thử sức, cơ hội khẳng định kiến thức, minh chứng sáng ngời cho tinh

thần học tập, tinh thần ái quốc !

Các phương pháp giải và biện luận hệ phương trình – hệ bất phương trình – hệ hỗn tạp được luyện tập một

cách đều đặn, bài bản và hệ thống sẽ rất hữu ích, không chỉ trong bộ môn Toán mà còn phục vụ đắc lực cho các

môn khoa học tự nhiên khác như hóa học, vật lý, sinh học,...Tiếp theo các Lý thuyết giải hệ phương trình chứa căn

(Phần 1, 2, 3, 4, 5, 6, 7), tài liệu chủ yếu giới thiệu đến quý bạn đọc Lý thuyết giải hệ phương trình chứa căn ở cấp

độ cao, trình bày chi tiết các thí dụ điển hình về hệ giải được nhờ sử dụng tổng hợp các phép thế, phép cộng đại số,

đại lựợng liên hợp, sử dụng đồng bộ tính chất đơn điệu hàm số có chặn miền giá trị, các phép ước lượng – đánh giá

– bất đẳng thức phần tiếp theo. Đây là nội dung có mức độ khó tương đối, đòi hỏi các bạn độc giả cần có kiến thức

vững chắc về các phép giải phương trình chứa căn, kỹ năng biến đổi đại số và tư duy chiều sâu bất đẳng thức.

Các thao tác tính toán và kỹ năng trình bày cơ bản đối với phương trình, hệ phương trình xin không nhắc lại.

I

.

K

I

Ế

N

T

H

Ứ

C

H

U

Ẩ

N

B

Ị

1. Kỹ thuật nhân, chia đơn thức, đa thức, hằng đẳng thức.

2. Nắm vững các phương pháp phân tích đa thức thành nhân tử.

3. Nắm vững các phương pháp giải, biện luận phương trình bậc nhất, bậc hai, bậc cao.

4. Sử dụng thành thạo các ký hiệu toán học, logic (ký hiệu hội, tuyển, kéo theo, tương đương).

5. Kỹ năng giải hệ phương trình cơ bản và hệ phương trình đối xứng, hệ phương trình đồng bậc, hệ phương

trình chứa căn thông thường.

6. Kỹ thuật đặt ẩn phụ, sử dụng đại lượng liên hợp, biến đổi tương đương.

7. Kiến thức nền tảng về uớc lượng – đánh giá, hàm số - đồ thị, bất đẳng thức – cực trị.

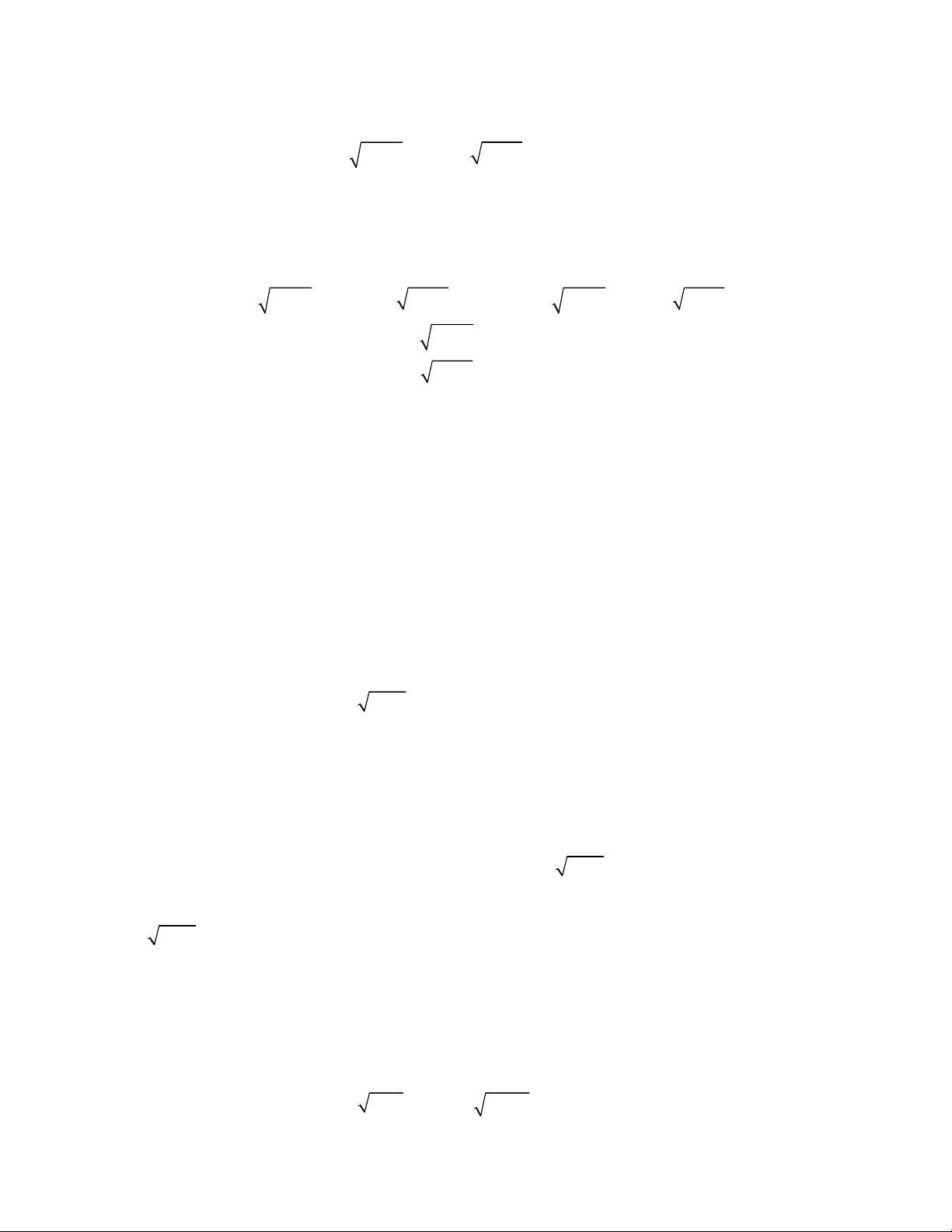
LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

4

I

.

M

Ộ

T

S

Ố

B

À

I

T

O

Á

N

Đ

I

Ể

N

H

Ì

N

H

V

À

K

I

N

H

N

G

H

I

Ệ

M

T

H

A

O

T

Á

C

B

à

i

t

o

á

n

1

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

   

 

2

3 3

1

,

;

1 1 1 1 0.

x y

x y y x



 







     







.

L

ờ

i

g

i

ả

i

.

Đ

i

ề

u

k

i

ệ

n

1; 1y x  

.

T

a

c

ó

 

2

1 1 1 1 0

1

1 1 1 0

1

x x x

x y

y y

y



     

 



     



 

    





 



.

V

ớ

i

đ

i

ề

u

k

i

ệ

n

t

r

ê

n

t

h

ì

       

3

3 3 3

1

1 0; 1 1 0 1 1 1 1 0

x

y y x x y y x



           

.

D

o

đ

ó

h

ệ

đ

ã

c

h

o

c

ó

n

g

h

i

ệ

m

k

h

i

v

à

c

h

ỉ

k

h

i

   

 

3

2

1

1 0 1

1

1 0 2

1

x y

y x

x y



  



  





 





R

õ

r

à

n

g

t

ừ

(

1

)

t

h

u

đ

ư

ợ

c

1

; 0 0; 1

x

y x y



     

,

đ

ề

u

k

h

ô

n

g

t

h

ỏ

a

m

ã

n

(

2

)

.

Kết luận hệ phương trình đã cho vô nghiệm.

N

h

ậ

n

x

é

t

.

M

ấ

u

c

h

ố

t

c

ủ

a

b

à

i

t

o

á

n

l

à

t

ì

m

r

a

đ

i

ề

u

k

i

ệ

n

(

*

)

.

T

ừ

đ

ó

d

ễ

d

à

n

g

q

u

a

n

s

á

t

đ

ư

ợ

c

đ

ặ

c

t

í

n

h

k

h

ô

n

g

â

m

c

ủ

a

v

ế

t

r

á

i

p

h

ư

ơ

n

g

t

r

ì

n

h

t

h

ứ

h

a

i

c

ủ

a

h

ệ

b

a

n

đ

ầ

u

.

C

á

c

b

ạ

n

c

h

ú

ý

đ

á

n

h

g

i

á

q

u

e

n

t

h

u

ộ

c

 

2

1

1 1 1 0

1

1 1 1 0

1

x x x

x y

y y

y



     

 





    



 

    





 



.

T

u

y

n

h

i

ê

n

c

á

c

d

ấ

u

đ

ẳ

n

g

t

h

ứ

c

k

h

ô

n

g

x

ả

y

r

a

,

n

ê

n

h

ệ

đ

ề

b

à

i

v

ô

n

g

h

i

ệ

m

.

B

à

i

t

o

á

n

2

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

  

 

2

4

1

1,

;

2 2 3 3 1 1

x y

x x y y



  







     







.

Lời giải.

Điều kiện

2

x



.

Từ phương trình thứ nhất của hệ ta có

 

2

1

1 1 1 1

1 1 1 2 0

1 1

x

x x

y y

y





     

 



 

  

      

 

 





Để ý rằng

 

  

4

1

1 2 1 2 2 1

2

0 3 3 1 0

x x x x

y y y



        



     

Do đó

    

4

2

2 3 3 1 1

x

x y y



    

.

Hệ có nghiệm khi và chỉ khi các dấu đẳng thức xảy ra, nghĩa là

1

x

y







 



Kết luận hệ ban đầu có nghiệm duy nhất

1; 1

x y

  

.

B

à

i

t

o

á

n

3

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

   

 

2

4 1,

;

2 1 2 1 2 0.

x y

x x y y



 







     







.

Lời giải.

LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

5

Điều kiện

1

;

2

x

y



 

. Từ

 

2

1

2

1 0

1

4

1

1 1

4 1

2

1 2 0

2

x

x x

x

x y

x

y

y y

  



  





  

    

  

  







 







Do đó

   

2 1 2 1 2 0

x x y y

     

. Dấu đẳng thức xảy ra khi

1

0

1

1 2 0

2

x

y

















 

 









Cặp giá trị này không thỏa mãn hệ ban đầu. Kết luận vô nghiệm.

B

à

i

t

o

á

n

4

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

   

 

2

3

1

1 1,

;

4 6 5 1 2.

x y

x x y y



   







     







.

Lời giải.

Điều kiện

4

; 1

x

y



 

.

Từ phương trình thứ nhất của hệ ta có

 

2

1 1

1 1 1 2 0

4

2

1

1 1 2 0

5

0

1

x

x x

x

y y

x y

y



 



      

 

 

 

  

   

      



 





 







Do đó

 

3

4

6 5 1 2

x

x y y



    

. Dấu đẳng thức xảy ra khi và chỉ khi

0

1

x

y







 



Kết luận hệ có nghiệm duy nhất

   

; 0; 1

x y

 

.

N

h

ậ

n

x

é

t

.

M

ở

đ

ầ

u

c

á

c

t

h

í

d

ụ

g

i

ớ

i

t

h

i

ệ

u

t

à

i

l

i

ệ

u

,

t

á

c

g

i

ả

s

ẽ

đ

à

o

s

â

u

c

á

c

b

à

i

t

o

á

n

ở

m

ứ

c

đ

ộ

đ

ơ

n

g

i

ả

n

h

ấ

t

v

ớ

i

h

ệ

h

a

i

p

h

ư

ơ

n

g

t

r

ì

n

h

,

t

r

o

n

g

đ

ó

m

ộ

t

p

h

ư

ơ

n

g

t

r

ì

n

h

c

ủ

a

h

ệ

c

ó

d

ạ

n

g

h

ữ

u

t

ỷ

,

k

h

u

y

n

h

ư

ớ

n

g

c

h

ủ

y

ế

u

t

ì

m

đ

i

ề

u

k

i

ệ

n

,

t

ì

m

i

ề

n

g

i

á

t

r

ị

c

á

c

ẩ

n

t

h

e

o

đ

i

ề

u

k

i

ệ

n

c

ó

n

g

h

i

ệ

m

c

ủ

a

p

h

ư

ơ

n

g

t

r

ì

n

h

b

ậ

c

h

a

i

h

a

y

p

h

â

n

t

í

c

h

ằ

n

g

đ

ẳ

n

g

t

h

ứ

c

.

P

h

ư

ơ

n

g

t

r

ì

n

h

c

h

ứ

a

c

ă

n

c

ò

n

l

ạ

i

c

ủ

a

h

ệ

r

ấ

t

đ

a

d

ạ

n

g

,

h

ì

n

h

t

h

ứ

c

à

n

g

p

h

ứ

c

t

ạ

p

b

a

o

n

h

i

ê

u

,

c

à

n

g

k

h

ó

q

u

a

n

s

á

t

đ

ể

đ

á

n

h

g

i

á

b

ấ

y

n

h

i

ê

u

,

t

r

ư

ớ

c

h

ế

t

x

i

n

đ

ề

c

ậ

p

đ

ế

n

c

á

c

ư

ớ

c

l

ư

ợ

n

g

t

h

u

ầ

n

t

ú

y

,

đ

á

n

h

g

i

á

đ

ơ

n

g

i

ả

n

,

c

h

ư

a

s

ử

d

ụ

n

g

c

á

c

t

í

n

h

c

h

ấ

t

h

à

m

s

ố

,

b

ấ

t

đ

ẳ

n

g

t

h

ứ

c

,

c

ự

c

t

r

ị

.

B

à

i

t

o

á

n

5

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

2

2 3 3

2

1 2 ,

;

1 4 3 0.

x x y y

x y

x x y y



   







    







.

Lời giải.

Điều kiện

3

4

x



. Phương trình thứ nhất của hệ tương đương với

   

 

2

1 1

1 1 1 2 0

1

1 1

1

1 1 0 2

1

x

x x

x y

y y

y



 

      





      

  



    



 





Phương trình thứ hai của hệ trở thành

 

     

2

3

1 4 1 2 2 1

x x y y      .

Rõ ràng với điều kiện trên thì

 

   

 

   

2

2 3 2 3

1 4 2; 1 2 0 1 4 1 2 2

x x y y x x y y

            

.

Khi đó (1) có nghiệm khi dấu đẳng thức xảy ra, nghĩa là

0

1

x

y











Thử lại, kết luận hệ phương trình đã cho có duy nhất nghiệm

   

;

0;1

x

y 

.

B

à

i

t

o

á

n

6

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

   

 

2

4

2

4

8 1 2 .

;

2 2 12 1 2 6 3.

x y y x

x y

y y x y x x



   







       







.

Lời giải.

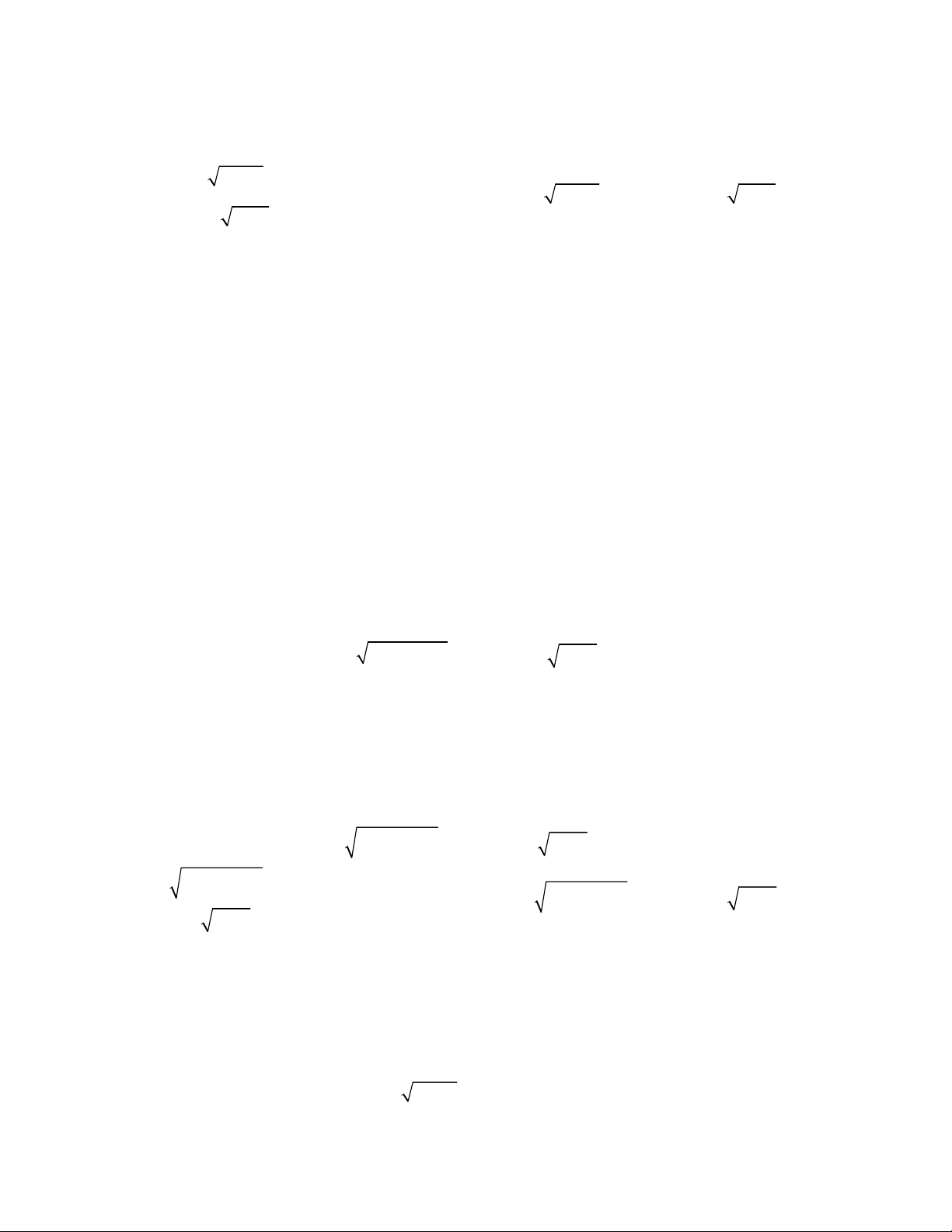
LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

6

Điều kiện

6

12

x



 

. Phương trình thứ nhất biến đổi về

   

 

2

1

4

2

1 2 1 3

1

4 1 4

1 1 1 2 0

4 1 4

x

x x

x y

y y

y



 



     





      

  

      

 

 





Khi đó

 

 

   

 

     

2

4

1 1 12 1.3 3, 1;3

1 1 12 1 2 6 3

1

2 6 0, 1;3

y x x

y x y x x

y x x x



 

       



 

 

        









      



.

Do đó phương trình thứ hai của hệ có nghiệm khi dấu đẳng thức xảy ra, nghĩa là

3

1

x

y







 



Thử lại vào hệ ban đầu, nghiệm đúng, kết luận nghiệm duy nhất

   

; 3; 1

x y

 

.

N

h

ậ

n

x

é

t

.

Đ

ố

i

v

ớ

i

b

à

i

t

o

á

n

6

,

đ

ể

c

h

ặ

n

m

i

ề

n

g

i

á

t

r

ị

c

ủ

a

c

á

c

b

i

ế

n

,

n

g

o

à

i

p

h

ư

ơ

n

g

c

á

c

h

s

ử

d

ụ

n

g

h

ằ

n

g

đ

ẳ

n

g

t

h

ứ

c

ó

t

h

ể

s

ử

d

ụ

n

g

đ

i

ề

u

k

i

ệ

n

c

ó

n

g

h

i

ệ

m

c

ủ

a

p

h

ư

ơ

n

g

t

r

ì

n

h

b

ậ

c

h

a

i

t

h

e

o

t

ừ

n

g

ẩ

n

x

h

o

ặ

c

y



T

ì

m

i

ề

n

g

i

á

t

r

ị

c

ủ

a

b

i

ế

n

y

t

h

ô

n

g

q

u

a

p

h

ư

ơ

n

g

t

r

ì

n

h

b

ậ

c

h

a

i

ẩ

n

x

:

 

2

2 4 8 1 0 1

x x y y    

.

B

i

ệ

t

h

ứ

c

 

2

1

4 8 1 4 2

y

y y y





      

.

Đ

i

ề

u

k

i

ệ

n

c

ó

n

g

h

i

ệ

m

x

l

à

   

0

4 2 0 4 2 0 2 0

y

y y y y





           

.



T

ì

m

i

ề

n

g

i

á

t

r

ị

c

ủ

a

b

i

ế

n

x

t

h

ô

n

g

q

u

a

p

h

ư

ơ

n

g

t

r

ì

n

h

b

ậ

c

h

a

i

ẩ

n

y

:

 

2

4

8 2 1 0 2

y

y x x    

.

B

i

ệ

t

h

ứ

c

 

  

2

16

4 2 1 4 8 12 4 1 3

x

x x x x x





           

.

Đ

i

ề

u

k

i

ệ

n

c

ó

n

g

h

i

ệ

m

y

l

à

     

0

4 1 3 0 4 1 3 0 1 3

x

x x x x





             

.

B

à

i

t

o

á

n

7

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

   

 

2

4

1 9 2 36,

;

3 4 5 17 4 2 1.

x y

x x x y x y



   







      







.

Lời giải.

Điều kiện

; 2

x y

 

.

Từ phương trình thứ nhất của hệ ta có

 

2

2 2

4

1 36 1 9

3

1 3 4 2

2 2 2 0 4

9 2 36 2 4

x x

y y

 

   



     



 

  

   

     

 

   

 

 

Vậy ta có

   

4

;2 , 2;4

x

y  

. Phương trình thứ hai của hệ tương đương với

       

2

3 2 1 17 4 2 1 1

x x y x y      

.

Rõ ràng

   

 

 

   

     

2

3 2 1 1.1 1, 4;2

3 2 1 17 4 2 1

17 4 2 0, 2;4 , 4;2

x x x

x x y x y

y x y y x



       



       





       



.

Do đó (1) có nghiệm khi dấu đẳng thức xảy ra, tức là

2

x

y











Thử lại trực tiếp, thỏa mãn hệ đề bài. Kết luận tập nghiệm

 

 

2;2

S 

.

B

à

i

t

o

á

n

8

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

2

4 2

2

9 3,

;

4 4 17 6 2 5 4.

x x y

x y

x x x y y



  







     







.

Lời giải.

Điều kiện

17

x



. Phương trình thứ nhất của hệ biến đổi trở thành

LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

7

 

2

1 2 3 1

1 4

1 9 4

2

2 2 2

9 4

3

3 3 3

x

x y

y y

x



     



 

  

     

  

     





 



 

Dễ thấy

 

2

4

4 2 2 2

4 4 2 1 2 4 2 1 1 2 1 1 1,x x x x x x x x x

                

.

Do đó

 

 

 

4

2

4 4 17 4, 3;1

4 4 17 6 2 5 4

2 2

6 2 5 0, ;

3 3

x x x x

x x x y y

y y y



      



      



 

    



 

 



.

Phương trình thứ hai của hệ có nghiệm khi và chỉ khi dấu đẳng thức xảy ra, hay

1

; 0

x

y



.

Cặp giá trị này thỏa mãn hệ ban đầu nên là nghiệm duy nhất của hệ.

B

à

i

t

o

á

n

9

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

2

2 2

4 5,

;

6 4 4 17 2 4 24.

x y x

x y

y x y x y



  







     







.

Lời giải.

Điều kiện

4

; 4

x

y





.

Phương trình thứ nhất của hệ biến đổi về

 

2

3

2 3 1 5

2

9

2 4 9

9

3 3

4

9

4 2 2

x

x y

y y

y

      

 



 

  

     

  



  







 

Vậy ta thu được điều kiện

 

3

4

;5 , ;

2 2

x

y







 









. Để ý rằng

 

 

 

 

2

3

0 4 4, ; ; 4 1, 4;5 6 4 4 24

2 2

3 3

17 2 4 0, 4;5 , ; 17 2 4 24 24

2

y y x x y x

y x y x y y x y

 

             

 

 

 

            

 

 

Do đó phương trình thứ hai của hệ có nghiệm khi các dấu đẳng thức xảy ra, tức là

0

5

y

x











Thử lại, kết luận hệ phương trình đã cho có duy nhất nghiệm

   

;

5;0

x

y 

.

B

à

i

t

o

á

n

1

0

.

T

r

í

c

h

l

ư

ợ

c

â

u

3

,

Đ

ề

t

h

i

t

u

y

ể

n

s

i

n

h

Đ

ạ

i

h

ọ

c

;

M

ô

n

T

o

á

n

;

K

h

ố

i

A

v

à

k

h

ố

i

A

1

;

Đ

ề

c

h

í

n

h

t

h

ứ

c

;

K

ỳ

t

h

i

t

u

y

ể

n

s

i

n

h

n

ă

m

2

0

1

2

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

3

2 3 2

2 2

3 9 9 22 3 9 ,

;

1

.

2

x x x x y y y

x y

x y x y



      







   







.

Lời giải.

Điều kiện

;x

y



. Hệ phương trình đã cho tương đương với

         

 

3

2 3 2

2 2

3 3

2 2

3 3 1 12 12 3 3 1 12 12

1 1

1

4 4

1 12 1 1 12 1 1

1 1

1 2

2 2

x x x x y y y y

x x y y

x y



          





     







      







   

   



   

   



LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

8

Chú ý rằng

 

2

1

1 3 3 1

1

1 1 1

2 2

2

2 2 2 2

2

1

3 1 1 3

1

1 1 1

1

2

2 2 2 2

2

x

x x x

y y y

y



 

  

   



          







  

     

    

    

 

    

          





 

 

  

 

  



 



Xét hàm số

 

3

12

; ;

2

f

t t t t







  









thì

 

2

3

4 0, ;

2

f

t t t









    









, hàm số liên tục, nghịch biến.

Khi đó

     

1

1 1 1 1 2

f

x f y x y x y



         

. Phương trình thứ hai của hệ trở thành

 

2

1

3 3 1 1 3

4

8 3 0 ; ; ; , ;

2

2 2 2 2 2

x

x x x y

     



       

 

   



    

.

Kết luận hệ phương trình đã cho có hai cặp nghiệm.

N

h

ậ

n

x

é

t

.

Đ

ể

g

i

ả

i

q

u

y

ế

t

b

à

i

t

o

á

n

t

r

ê

n

,

c

á

c

b

ạ

n

h

ọ

c

s

i

n

h

c

ầ

n

h

ậ

n

r

a

s

ự

đ

ồ

n

g

đ

i

ệ

u

g

i

ữ

a

h

a

i

ẩ

n

x

v

à

y

t

r

o

n

g

p

h

ư

ơ

n

g

t

r

ì

n

h

t

h

ứ

n

h

ấ

t

,

c

ố

g

ắ

n

g

t

h

ê

m

b

ớ

t

ạ

o

r

a

s

ự

t

ư

ơ

n

g

đ

ồ

n

g

h

à

m

s

ố

k

i

ể

u

   

f u f v u v  

.

T

u

y

n

h

i

ê

n

đ

ể

c

ó

đ

ư

ợ

c

đ

i

ề

u

n

à

y

t

h

ì

c

á

c

h

à

m

s

ố

c

ầ

n

đ

ơ

n

đ

i

ệ

u

(

c

ù

n

g

đ

ồ

n

g

b

i

ế

n

h

o

ặ

c

n

g

h

ị

c

h

b

i

ế

n

t

r

ê

n

m

ộ

t

m

i

ề

n

x

á

c

đ

ị

n

h

)

.

K

ế

t

q

u

ả

c

ủ

a

c

h

ú

n

g

t

a

t

h

u

đ

ư

ợ

c

h

à

m

s

ố

k

h

ô

n

g

c

h

o

p

h

é

p

đ

i

ề

u

đ

ó

 

3

12f

t t t





!

T

u

y

n

h

i

ê

n

ế

u

đ

ể

ý

m

ộ

t

c

h

ú

t

,

t

ừ

p

h

ư

ơ

n

g

t

r

ì

n

h

t

h

ứ

h

a

i

c

ủ

a

h

ệ

c

ó

t

h

ể

s

u

y

r

a

m

i

ề

n

g

i

á

t

r

ị

c

ủ

a

x

v

à

y

,

n

g

o

à

i

c

á

c

h

p

h

â

n

t

í

c

h

b

ì

n

h

p

h

ư

ơ

n

g

n

h

ư

l

ờ

i

g

i

ả

i

t

r

ê

n

đ

â

y

,

c

á

c

b

ạ

n

h

o

à

n

t

o

à

n

c

ó

t

h

ể

s

ử

d

ụ

n

g

đ

i

ề

u

k

i

ệ

n

c

ó

n

g

h

i

ệ

m

c

ủ

a

p

h

ư

ơ

n

g

t

r

ì

n

h

b

ậ

c

h

a

i

n

h

ư

s

a

u



V

i

ế

t

l

ạ

i

p

h

ư

ơ

n

g

t

r

ì

n

h

b

ậ

c

h

a

i

d

ạ

n

g

ẩ

n

x

,

t

h

a

m

s

ố

y

:

2

2 2

1

0 4 4 3

2

x x y y y y          

.

Đ

i

ề

u

k

i

ệ

n

c

ó

n

g

h

i

ệ

m

2

3 1

4

4 3 0 4 4 3 0

2

y

y y y y



          

.



V

i

ế

t

l

ạ

i

p

h

ư

ơ

n

g

t

r

ì

n

h

b

ậ

c

h

a

i

d

ạ

n

g

ẩ

n

y

,

t

h

a

m

s

ố

x

:

2

2 2

1

0

4 4 3

2

y

y x x x x



         

.

Đ

i

ề

u

k

i

ệ

n

c

ó

n

g

h

i

ệ

m

2

1

3

4 4 3 0 4 4 3 0

2

x x x x x

           

.

B

à

i

t

o

á

n

1

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

   

 

3

3 2 2

3 3 48 100,

;

2 2 2.

x y x y x y

x y

x x y y



     







   







.

Lời giải.

Điều kiện

;x

y



. Phương trình thứ hai của hệ biến đổi về

   

 

2

1

2

1

4

1 1 4

1

2

1

4

xx

x y

y



 





 

     

 







 





 

2 1 2 0 1 4

1; 1 4;4

2 1 2 4 1 0

x x

x y

y y

      

 

      

 

       

 

.

Phương trình thứ nhất của hệ trở thành

         

3

2 3 2

3 3

3

3 1 51 51 3 3 1 51 51

1

51 1 1 51 1 1

x x x x y y y y

x x y y



         



      

Xét hàm số

   

 

 

3

2 2

51 ; 3 51 3 17 0, 4; 4

f t t t t f t t t t



           

.

Hàm số trên liên tục và nghịch biến trên miền

 

4;4



nên

     

1 1 1 1 1 2

f x f y x y x y

          

.

Phương trình thứ hai trở thành

     

2 2 2

2

3

1 4 2 4 6 0 1 2

y

y y y y



          

(Vô nghiệm).

Kết luận hệ phương trình đã cho vô nghiệm.

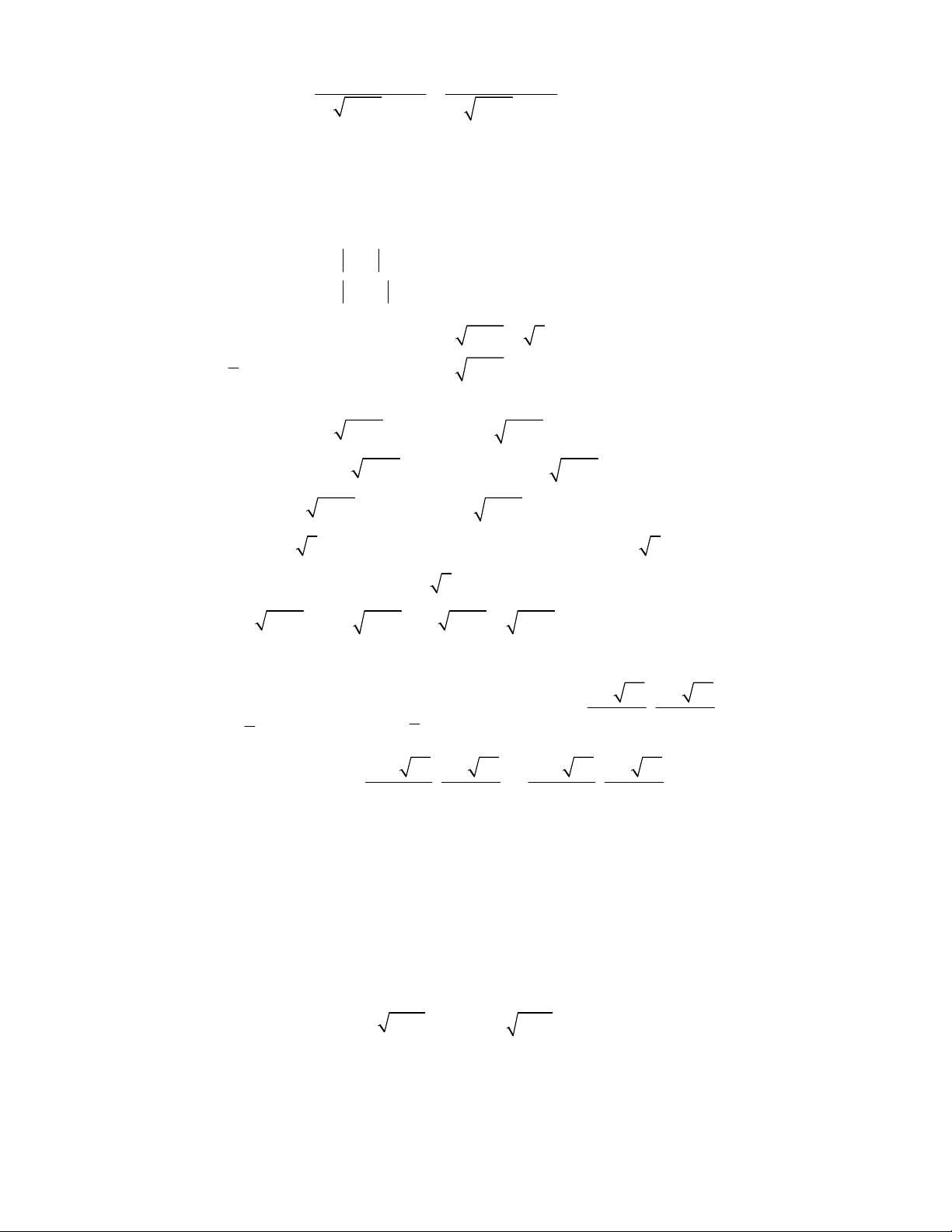
LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

9

B

à

i

t

o

á

n

1

2

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

     

 

2 2

2 14 3 13

,

2 4 3 4

;

9 2 3 1 .

x x y y

x y

x y x y

   





   







   





.

Lời giải.

Điều kiện

2

; 3

x

y



  

. Phương trình thứ hai của hệ biến đổi về

   

 

2

2 2 2 2

2

9

2 6 2 2 1 9 6 1 4 1 3 1 4

1

21 4

2 1 2 1 3

2 3 1 2 1 3 3

3 1 2

3 1 4

1 3

0 2 5

2 5

1

3 4

1

0 3 2

3

x y x y x x y y x y

xx

x x

y y

y

x

y



              



  

      

 

 

   

   

      

 

 

  





  



  

 



 

  

  

 

  

  







Phương trình thứ nhất của hệ tương đương với

 

       

 

   

3

2 2 4 3 3 4

2 2 4 2 3 3 4 3

2 4 2 3 4 3 1

x x y y

x x x y y y

x x y y

      

         

       

Xét hàm số

     

3

2 2

4 ; 0; 5 3 8 3 8 0, 0; 5

f t t t t f t t t t t t

   



          

   

.

Suy ra hàm số liên tục và nghịch biến trên miền

0; 5

 

 

. Khi đó

 

   

1 2 3 2 3 2 3 1

f x f y x y x y x y              

.

Thay thế vào phương trình thứ hai lại có

 

2

10

6 3 0

3 1 4

3

39 3 39

;

1

10 10

1

3

y y

y



  

  











  

  



  



 



  









.

Từ đây đi đến các nghiệm của hệ

 

13

39 3 39 13 39 3 39

; ; , ;

10 10 10 10

x y



  



  





  



  



  

.

N

h

ậ

n

x

é

t

.

B

à

i

t

o

á

n

s

ố

1

2

,

d

ạ

n

g

t

h

ứ

c

h

à

m

s

ố

c

ủ

a

p

h

ư

ơ

n

g

t

r

ì

n

h

c

ò

n

l

ạ

i

đ

ã

t

ă

n

g

c

ấ

p

s

o

v

ớ

i

m

o

t

i

p

h

ư

ơ

n

g

t

r

ì

n

h

đ

a

t

h

ứ

c

b

ậ

c

b

a

h

a

i

ẩ

n

c

ủ

a

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

c

â

u

3

,

Đ

ề

t

h

i

t

u

y

ể

n

s

i

n

h

đ

ạ

i

h

ọ

c

K

h

ố

i

A

v

à

k

h

ố

i

A

1

;

K

ỳ

t

h

i

t

u

y

ể

n

s

i

n

h

n

ă

m

2

0

1

2

.

C

á

c

ă

n

t

h

ứ

c

đ

ã

đ

ư

ợ

c

h

u

y

đ

ộ

n

g

v

à

b

ả

n

c

h

ấ

t

đ

ã

đ

ư

ợ

c

ẩ

n

g

i

ấ

u

đ

i

t

h

ô

n

g

q

u

a

c

á

c

p

h

é

p

b

i

ế

n

đ

ổ

i

đ

ạ

i

l

ư

ợ

n

g

l

i

ê

n

h

ợ

p

,

v

à

h

à

m

s

ố

c

ầ

n

x

é

t

đ

ơ

n

đ

i

ệ

u

n

g

h

ị

c

h

b

i

ế

n

t

r

ê

n

m

ộ

t

m

i

ề

n

h

ạ

n

h

ẹ

p

,

k

h

ô

n

g

n

h

ữ

n

g

đ

i

ề

u

k

i

ệ

n

t

ừ

p

h

ư

ơ

n

g

t

r

ì

n

h

t

h

ứ

h

a

i

,

m

à

c

ò

n

l

ồ

n

g

h

é

p

c

ả

đ

i

ề

u

k

i

ệ

n

k

h

ô

n

g

â

m

c

ủ

a

ẩ

n

h

à

m

c

ă

n

t

h

ứ

c

,

b

ắ

t

b

u

ộ

c

ầ

n

x

é

t

đ

i

ề

u

k

i

ệ

n

c

á

c

b

i

ế

n

d

ự

a

v

à

o

p

h

ư

ơ

n

g

t

r

ì

n

h

t

h

ứ

h

a

i

c

ủ

a

h

ệ

(

c

ó

t

h

ể

d

ự

a

v

à

o

p

h

â

n

t

í

c

h

ằ

n

g

đ

ẳ

n

g

t

h

ứ

c

h

o

ặ

c

đ

i

ề

u

k

i

ệ

n

c

ó

n

g

h

i

ệ

m

c

ủ

a

p

h

ư

ơ

n

g

t

r

ì

n

h

b

ậ

c

h

a

i

n

h

ư

đ

ã

đ

ề

c

ậ

p

)

,

t

á

c

g

i

ả

m

o

n

g

m

u

ố

n

c

á

c

b

ạ

n

đ

ộ

c

g

i

ả

h

ế

t

s

ứ

c

l

ư

u

ý

.

B

à

i

t

o

á

n

1

3

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

     

 

2 2

4

3 3 4 1 1 15 30,

;

2 2 3 4.

x x y y x y

x y

x y x y



       







    







.

Lời giải.

Điều kiện

3

; 1

x

y



  

. Phương trình thứ hai của hệ tương đương

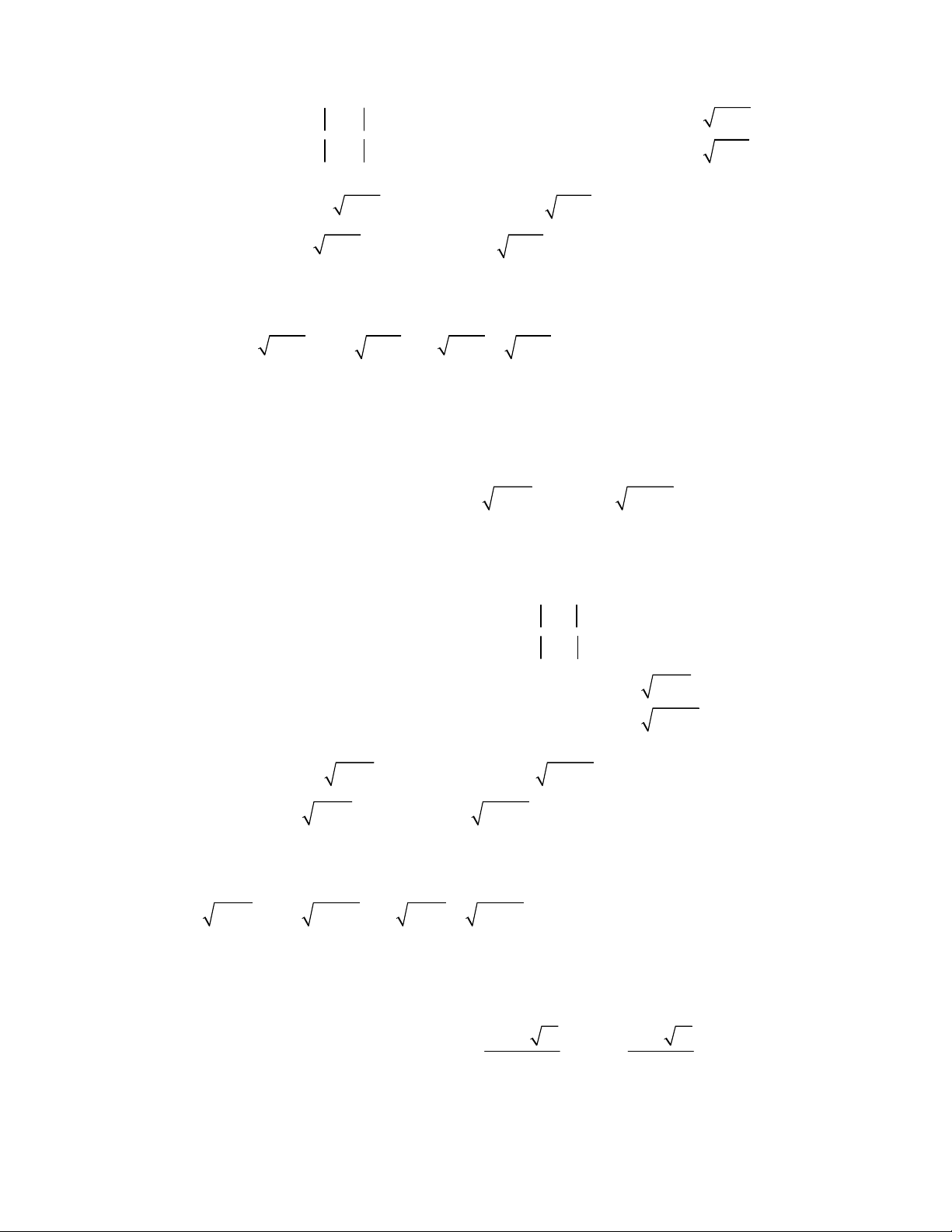
LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

10

   

 

2 2

2

4

4 6 9 9 2 3 9

2 32 9

0 3 2

3

2 3 5 1

3 3 3 6 0

3 3

0 1 1

3

9

x x y y x y

xx

x

x x

y y

y

          



   

  



     

 

  

    

    

      

 

  

 

  





Phương trình thứ hai của hệ trở thành

       

 

   

3 3

4

3 3 15 3 4 1 1 15 1

4

3 15 3 4 1 15 1 1

x

x x y y y

x x y y



       



      

Xét hàm số

 

 

   

 

3

2 2

4

15 ; 0;2 12 30 6 2 5 0, 0;2

f

t t t t f t t t t t t



          

.

Suy ra hàm số liên tục và nghịch biến trên miền

 

0

;2

. Khi đó

 

   

1 3 1 3 1 3 1 2

f x f y x y x y x y              

.

Thế vào phương trình thứ hai ta có

     

2

3 9 2 6 0 3 0 3;0

y y y y y y y           

.

Đối chiếu điều kiện thu được nghiệm

0

; 2

y

x



 

.

B

à

i

t

o

á

n

1

4

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

   

 

2

1 ,

;

10 5 30 3 2 3 6.

x y x y

x y

y x y x y x y y



   







       







.

Lời giải.

Điều kiện

;

2

y

x y



 

. Phương trình thứ nhất của hệ biến đổi về

 

   

 

2

2 2 2

2

2 2

2

2 2 1 2 1 4

1 21 4

2

1 2

1

1 4

2

1 2

1 4

0

2

3

1 1 3 4 4

3 1 9 3 3 3 3 6 9

0

3 6 3

x

y x y x x y y

xx

x

x y

y

y x

x x y x

y y y

y

          



   



  



 

       

  



  

 



  







  

          

  



   

   

         

  

  





Phương trình thứ hai của hệ tương đương với

       

 

   

3

5 3 2 3 6 5 3 6

5

3 6 5 3 6 1

y x y x y x y y y

y x x y y y

        



      

Xét hàm số

 

 

   

 

3

2 2

5

; 0;3 3 10 3 10 0, 0;3

f

t t t t f t t t t t t



          

.

Suy ra hàm số liên tục và nghịch biến trên miền

 

0

;3

. Do đó

   

3 6 3 6 3 6 2 6

f y x f y y x y y x y x y

              

.

Phương trình thứ nhất của hệ lại trở thành

       

2

2 2 2

2

6 1 1 4 2 5 1 4

2

5 22 22 0

11

11 8 2 11

5

2

y y y y

y y

y x

y

 

         

 



 

   

 

 



  

  

     



 



Đối chiếu điều kiện ta thu được nghiệm duy nhất.

N

h

ậ

n

x

é

t

.

B

à

i

t

o

á

n

s

ố

1

4

,

v

ẫ

n

x

o

a

y

q

u

a

n

h

m

o

t

i

p

t

ì

m

đ

i

ề

u

k

i

ệ

n

g

h

i

ệ

m

c

ủ

a

c

á

c

b

i

ế

n

x

v

à

y

t

ư

ơ

n

g

t

ự

c

á

c

b

à

i

t

o

á

n

m

ở

đ

ầ

u

t

à

i

l

i

ệ

u

.

K

h

ô

n

g

q

u

á

k

h

ó

c

á

c

b

ạ

n

đ

ề

u

b

i

ế

n

đ

ổ

i

q

u

y

v

ề

d

ạ

n

g

t

ư

ơ

n

g

đ

ồ

n

g

h

à

m

s

ố

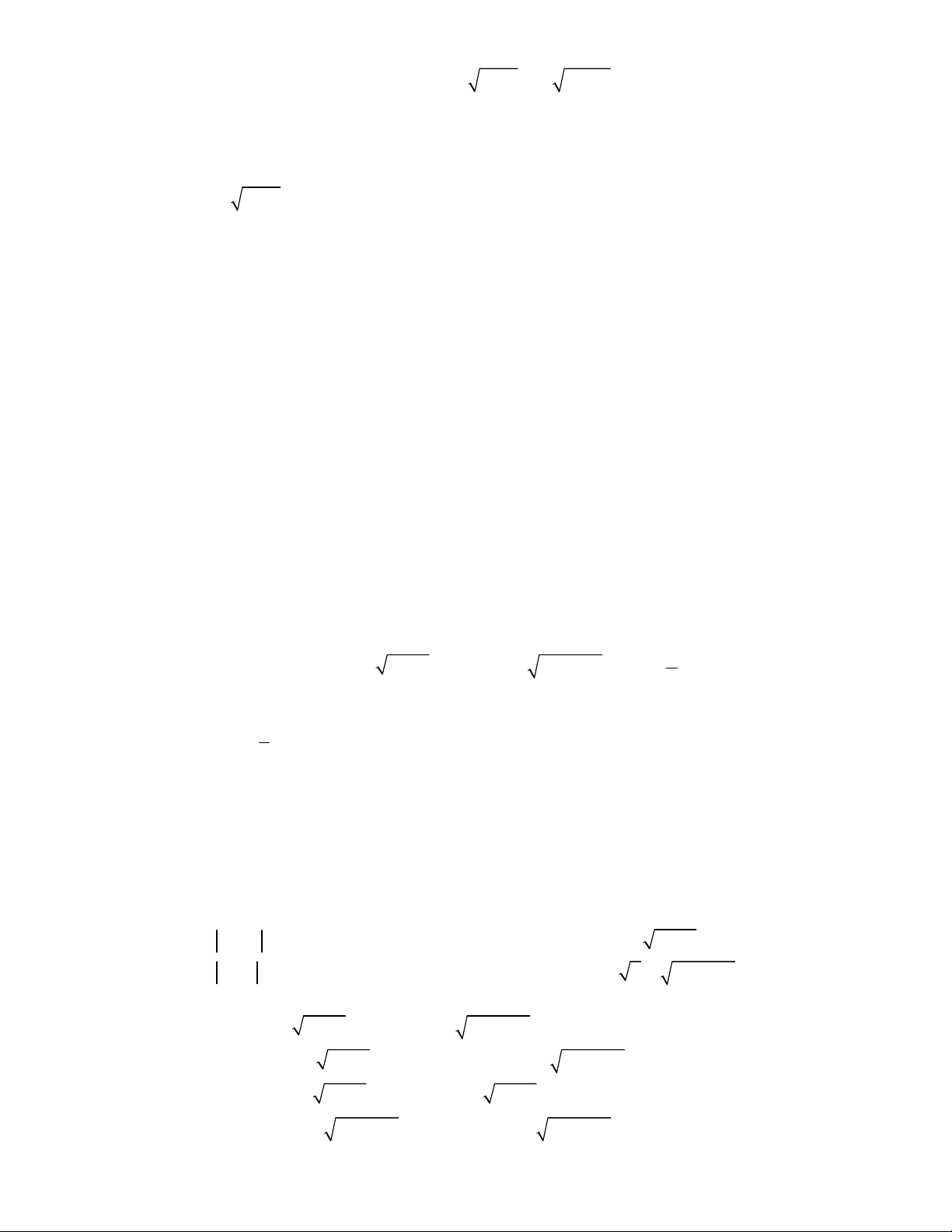
LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

11

   

; ; 3 6

f u f v u y x v y

    

.

T

u

y

n

h

i

ê

n

đ

ã

c

ó

s

ự

h

i

ệ

n

d

i

ệ

n

c

ủ

a

ẩ

n

h

à

m

c

ă

n

t

h

ứ

c

m

ứ

c

đ

ộ

p

h

ứ

c

t

ạ

p

h

ơ

n

,

n

ó

c

h

ứ

a

đ

ồ

n

g

t

h

ờ

i

h

a

i

ẩ

n

x

v

à

y

,

c

h

ắ

c

h

ắ

n

k

h

ô

n

g

í

t

b

ạ

n

h

ọ

c

s

i

n

h

t

ỏ

r

a

l

ú

n

g

t

ú

n

g

.

“

E

m

đ

i

x

a

q

u

á

,

e

m

đ

i

x

a

n

h

q

u

á

”

(

C

h

ắ

c

a

i

đ

ó

s

ẽ

v

ề

-

S

ơ

n

T

ù

n

g

M

T

P

)

Đ

ể

đ

á

n

h

g

i

á

ẩ

n

h

à

m

u y x 

c

ó

t

h

ể

d

i

ễ

n

đ

ạ

t

đ

ạ

i

k

h

á

i

,

h

i

ể

u

n

ô

m

n

a

k

i

ể

u

n

h

ư

m

ộ

t

n

g

ư

ờ

i

đ

ứ

n

g

i

m

,

m

ộ

t

n

g

ư

ờ

i

c

ứ

d

i

c

h

u

y

ể

n

r

a

x

a

(

h

o

ặ

c

h

a

i

n

g

ư

ờ

i

đ

i

v

ề

h

a

i

c

o

n

đ

ư

ờ

n

g

đ

ố

i

l

ậ

p

n

h

a

u

)

t

h

ì

k

h

o

ả

n

g

c

á

c

h

a

i

n

g

ư

ờ

i

n

g

à

y

c

à

n

g

l

ớ

n

,

c

ứ

c

ả

m

t

h

ấ

y

c

à

n

g

x

a

c

á

c

h

.

G

i

ả

d

ụ

x

é

t

đ

i

ề

u

k

i

ệ

n

0 2

0 4

0 2

x

x y

y

 



   



 



l

à

t

r

ư

ờ

n

g

h

ợ

p

đ

ơ

n

g

i

ả

n

k

h

i

h

a

i

b

i

ế

n

đ

ồ

n

g

b

ộ

đ

i

c

ù

n

g

h

ư

ớ

n

g

.

M

ộ

t

c

â

u

h

ỏ

i

đ

ặ

t

r

a

l

à

t

r

o

n

g

t

r

ư

ờ

n

g

h

ợ

p

đ

ó

t

h

ì

m

i

ề

n

g

i

á

t

r

ị

c

ủ

a

c

á

c

ẩ

n

h

à

m

đ

a

d

ạ

g

s

ẽ

n

h

ư

t

h

ế

n

à

,

t

h

í

d

ụ

2

; 2 ; ;3 2 1; 2; 3;...

x y x y y x x y x y y x        

K

h

i

m

à

h

a

i

b

i

ế

n

x

v

à

y

t

r

o

n

g

c

ă

n

t

h

ứ

c

h

i

a

r

ẽ

h

a

i

b

ê

n

c

h

i

ế

n

t

u

y

ế

n

?

K

h

á

đ

ơ

n

g

i

ả

n

,

c

h

ú

ý

t

h

ự

c

h

i

ệ

n

h

â

n

h

a

i

v

ế

b

ấ

t

p

h

ư

ơ

n

g

t

r

ì

n

h

v

ớ

i

m

ộ

t

s

ố

â

m

t

h

ì

b

ấ

t

p

h

ư

ơ

n

g

t

r

ì

n

h

đ

ổ

i

c

h

i

ề

u

o

0 2 2 0

2 2

0 2 0 2

x x

y x

y y

     

 

     

 

   

 

.

o

0 2 0 2 0 2

4 2 2

0 2 2 0 4 2 0

x x x

x y

y y y

     

  

      

  

         

  

.

V

à

n

h

i

ề

u

h

ơ

n

ữ

a

,

c

h

ú

n

g

t

a

c

ó

t

h

ể

t

h

ự

c

h

i

ệ

n

t

ă

n

g

c

ư

ờ

n

g

p

h

ứ

c

t

ạ

p

h

ó

a

ẩ

n

h

à

m

,

b

ằ

n

g

c

á

c

h

s

ử

d

ụ

n

g

c

á

c

p

h

é

p

b

i

ế

n

đ

ổ

i

l

i

ê

n

h

ợ

p

,

h

ằ

n

g

đ

ẳ

n

g

t

h

ứ

c

,

n

â

n

g

b

ậ

c

đ

a

t

h

ứ

c

p

h

í

a

t

r

o

n

g

c

ă

n

,

t

h

ậ

m

c

h

í

c

ó

t

h

ể

l

ồ

n

g

h

é

p

k

h

ả

o

s

á

t

h

à

m

s

ố

b

ắ

t

b

u

ộ

c

v

ớ

i

b

i

ể

u

t

h

ứ

c

d

ư

ớ

i

d

ấ

u

c

ă

n

t

r

o

n

g

m

ộ

t

s

ố

t

r

ư

ờ

n

g

h

ợ

p

k

h

ả

t

h

i

,

s

ẽ

t

h

u

đ

ư

ợ

c

n

h

ữ

n

g

b

à

i

t

o

á

n

t

h

ú

v

ị

.

B

à

i

t

o

á

n

1

5

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

   

2

2 2

5 2 2 ,

1

3 7 3 1 9 3 9 1 .

2

x x x y y x xy y

x x x y x y x y



     





 

         



 

 



Lời giải.

Điều kiện

1

3

0;

3

x

y x



   

. Phương trình thứ nhất của hệ tương đương với

 

2

2 2

1

1 5 2 4 0

5

2 4 0 1

x

x x xy x y

x xy x y

 



     



   



Loại trường hợp

1

x





. Ta nhận xét

     

 

2

2 2 2

2

2 1 1

1 4 4 1 2 1 2 1 1

1

2 1 1

1 3 1 2

1 2 1 1 0 1

1 1 2 3 4

1

2 3 2

x

x x x xy y x x y

x y

x

x x

x y x y

x y



 



            



 







  

  

     

 

 

   

   

       

 

   

 





Phương trình thứ hai của hệ tương đương với

   

     

2 3 7 3 1 2 9 3 18 9 18

2

3 7 3 1 27 9 2 9 3 9 9 27

2

3 1 3 1 9 3 1 12 3 1

2 3 3 9 3 12 3 2

x x x y x y x y

x x x x y x y x y

x x x x

x y x y x y x y

         



           



     

          

LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

12

Xét hàm số

 

 

    

 

3

2 2

2 9 12 ; 1;2 6 18 12 6 1 2 0, 1;2

f t t t t t f t t t t t t



             

.

Như vậy hàm số liên tục và nghịch biến trên miền

 

1

;2

nên

 

   

2 3 1 3 3 1 3 3 1 3 2 2f x f x y x x y x x y y x                 

.

Phương trình thứ (1) khi đó lại trở thành

   

2

2 2

2 2 2 2

5 2 4 0 5 2 2 2 4 2 2 0

8

2 3 8 2 3

5 4 4 4 4 8 4 0 13 16 4 0 ;

13 13

x xy x y x x x x x

x x x x x x x x x

          











             











Từ đây đi đến các nghiệm của hệ

 

8

2 3 10 4 3 8 2 3 10 4 3

; ; , ;

13 13 13 13

x y



  



  





  



  



  

.

N

h

ậ

n

x

é

t

.

Đ

ố

i

v

ớ

i

b

à

i

t

o

á

n

1

5

,

k

h

ô

n

g

q

u

á

k

h

ó

đ

ể

k

h

a

i

t

h

á

c

n

h

â

n

t

ử

p

h

ư

ơ

n

g

t

r

ì

n

h

t

h

ứ

n

h

ấ

t

c

ủ

a

h

ệ

,

c

á

c

b

ạ

n

l

ư

u

ý

p

h

ư

ơ

n

g

t

r

ì

n

h

a

i

ẩ

n

ế

u

c

ó

m

ộ

t

n

g

h

i

ệ

m

h

ằ

n

g

s

ố

c

ố

đ

ị

n

h

v

ớ

i

m

ộ

t

ẩ

n

,

g

i

ả

d

ụ

2

; 1; 1; 2;...

x

x y y



   

v

ớ

i

m

ọ

i

g

i

á

t

r

ị

c

ủ

a

ẩ

n

c

ò

n

l

ạ

i

,

c

h

ú

n

g

t

a

c

ó

t

h

ể

t

í

n

h

t

r

ự

c

t

i

ế

p

đ

ư

ợ

c

n

ó

b

ằ

n

g

c

á

c

h

g

á

n

g

i

á

t

r

ị

n

g

u

y

ê

n

b

ấ

t

k

ỳ

v

à

t

h

a

o

t

á

c

g

i

ả

i

p

h

ư

ơ

n

g

t

r

ì

n

h

.

P

h

ư

ơ

n

g

t

r

ì

n

h

t

h

ứ

n

h

ấ

t

c

ó

d

ạ

n

g

 

2

2 2

5

2 2

x

x x y y x xy y



    

.

C

ó

h

a

i

p

h

ư

ơ

n

g

á

n

g

h

i

ệ

m

c

ố

đ

ị

n

h



R

õ

r

à

n

g

t

ì

m

n

g

h

i

ệ

m

c

ố

đ

ị

n

h

ẩ

n

y

d

ễ

d

à

n

g

h

ơ

n

v

ì

c

h

ỉ

c

ầ

n

g

i

ả

i

p

h

ư

ơ

n

g

t

r

ì

n

h

b

ậ

c

h

a

i

ẩ

n

y

.

X

é

t

 

   

2

2 2

1

1 5 1 2 1. 2 2 4 2 0 2 1 0 1

x

y y y y y y y y



               

.

T

u

y

n

h

i

ê

n

k

h

i

đ

ó

v

ớ

i

n

g

h

i

ệ

m

c

ố

đ

ị

n

h

 

2

1 5 1 2 1 2

y x x x x x

      

(

L

o

ạ

i

)

.



C

h

u

y

ể

n

h

ư

ớ

n

g

t

ì

m

n

g

h

i

ệ

m

c

ố

đ

ị

n

h

ẩ

n

x

,

b

ắ

t

b

u

ộ

c

g

i

ả

i

p

h

ư

ơ

n

g

t

r

ì

n

h

b

ậ

c

b

a

ẩ

n

x

.

X

é

t

 

   

2

3 2

1

5 1 1 2 3 5 5 1 0

1

1 5 1 0 1;1;

5

y x x x x x x x x

x x x x



          

 

       

 

 

L

o

ạ

i

t

r

ư

ờ

n

g

h

ợ

p

1x 

đ

ã

x

é

t

ở

t

r

ê

n

.

V

ớ

i

 

2

1

1 5 1 2 2

x

y y y y



          

.

V

ớ

i

1

1 1 1 2 1

5.

2

5

5 25 5 5 5

x y y y



  



     



  



  

.

S

ử

d

ụ

n

g

c

h

i

ê

u

t

r

ò

n

à

y

c

á

c

b

ạ

n

c

ô

n

g

p

h

á

đ

ư

ợ

c

n

h

â

n

t

ử

p

h

ư

ơ

n

g

t

r

ì

n

h

t

h

ứ

n

h

ấ

t

,

t

u

y

n

h

i

ê

n

x

i

n

l

ư

u

ý

n

ó

c

h

ỉ

p

h

ù

h

ợ

p

k

h

i

c

ó

c

á

c

n

g

h

i

ệ

m

c

ố

đ

ị

n

h

ằ

n

g

s

ố

v

ớ

i

m

ộ

t

ẩ

n

(

t

r

ư

ờ

n

g

h

ợ

p

n

h

â

n

t

ử

n

h

ị

t

h

ứ

c

h

a

i

ẩ

n

k

h

ô

n

g

k

h

ả

t

h

i

)

.

T

a

c

ó

p

h

â

n

t

í

c

h

 

2

2 2

1

1 5 2 4 0

5

2 4 0 1

x

x x xy x y

x xy x y

 



     



   



T

r

ư

ờ

n

g

h

ợ

p

1

x





k

h

ô

n

g

t

h

ỏ

a

m

ã

n

đ

i

ề

u

k

i

ệ

n

x

á

c

đ

ị

n

h

n

ê

n

b

ị

l

o

ạ

i

n

g

a

y

l

ậ

p

t

ứ

c

.

T

h

ự

c

r

a

n

ó

l

à

m

ộ

t

ấ

m

n

h

i

ễ

u

đ

i

ề

u

p

h

ủ

l

ê

n

p

h

ư

ơ

n

g

t

r

ì

n

h

t

h

ứ

n

h

ấ

t

,

m

ụ

c

đ

í

c

h

ẩ

n

g

i

ấ

u

v

à

g

â

y

l

ạ

c

h

ư

ớ

n

g

v

à

t

ạ

o

r

a

s

ự

h

ư

n

g

p

h

ấ

n

h

ấ

t

h

ờ

i

c

h

o

c

á

c

b

ạ

n

h

ọ

c

s

i

n

h

c

ó

t

â

m

l

ý

n

ó

n

g

v

ộ

i

.

Đ

i

ể

m

ấ

u

c

h

ố

t

n

ằ

m

ở

p

h

ư

ơ

n

g

t

r

ì

n

h

(

1

)

h

ệ

q

u

ả

.

M

ộ

t

s

ố

b

ạ

n

đ

ọ

c

ó

x

u

h

ư

ớ

n

g

s

ử

d

ụ

n

g

p

h

ư

ơ

n

g

p

h

á

p

t

h

a

y

t

h

ế

v

ớ

i

p

h

ư

ơ

n

g

t

r

ì

n

h

(

1

)

n

h

ư

n

g

r

ấ

t

i

ế

c

đ

i

ề

u

n

à

y

q

u

á

p

h

ứ

c

t

ạ

p

,

c

h

ẳ

n

g

l

ẽ

t

h

ế

t

h

e

o

c

ô

n

g

t

h

ứ

c

n

g

h

i

ệ

m

c

ủ

a

p

h

ư

ơ

n

g

t

r

ì

n

h

b

ậ

c

h

a

i

ẩ

n

x

(

t

ư

ơ

n

g

ứ

n

g

y

)

,

c

h

ư

ớ

n

g

n

g

ạ

i

v

ậ

t

đ

ã

đ

ư

ợ

c

t

h

i

ế

t

l

ậ

p

n

h

ằ

m

c

h

ặ

n

đ

ứ

n

g

b

ư

ớ

c

đ

i

c

ủ

a

c

á

c

đ

ộ

i

q

u

â

n

v

ô

t

ổ

c

h

ứ

c

,

t

h

i

ế

u

t

i

n

h

t

h

ầ

n

.

V

ẫ

n

t

h

e

o

m

o

t

i

p

c

ũ

,

t

h

ự

c

h

i

ệ

n

c

h

ặ

n

m

i

ề

n

g

i

á

t

r

ị

c

ủ

a

c

á

c

ẩ

n

x

v

à

y

t

h

e

o

đ

i

ề

u

k

i

ệ

n

g

h

i

ệ

m

p

h

ư

ơ

n

g

t

r

ì

n

h

b

ậ

c

h

a

i

,

h

o

ặ

c

h

ằ

n

g

đ

ẳ

n

g

t

h

ứ

c

p

h

ư

ơ

n

g

t

r

ì

n

h

(

1

)

,

t

r

ư

ờ

n

g

h

ợ

p

n

à

y

c

ó

m

ộ

t

c

ấ

p

đ

ộ

k

h

á

c

v

ì

h

i

ệ

n

d

i

ệ

n

ẩ

n

h

à

m

h

a

i

b

i

ế

n

k

h

ó

c

h

ị

u

3

x

y





c

ố

t

h

ủ

t

ạ

i

p

h

ư

ơ

n

g

t

r

ì

n

h

t

h

ứ

h

a

i

,

n

ê

n

q

u

y

c

h

i

ế

u

t

h

e

o

h

ằ

n

g

đ

ẳ

n

g

t

h

ứ

c

s

ẽ

t

ỏ

r

a

t

ố

i

ư

u

h

ơ

n

     

 

2

2 2 2

2

1 1

1

4 4 1 2 1 2 1 1

1

x

x x xy y x x y

x y











           











LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

13

2 1 1

1 3 1 2

1 2 1 1 0 1

1 1 2 3 4

1

2 3 2

x

x x

x y x y

x y



  

  

     

 

 

   

   

       

 

   

 





S

ở

d

ĩ

c

ầ

n

t

h

ự

c

h

i

ệ

n

m

i

ề

n

g

i

á

t

r

ị

c

h

ặ

t

n

h

ư

v

ậ

y

v

ì

p

h

ư

ơ

n

g

t

r

ì

n

h

a

i

c

ó

d

ạ

n

g

h

à

m

s

ố

 

 

    

 

3

2 2

2

9 12 ; 1;2 6 18 12 6 1 2 0, 1;2

f

t t t t t f t t t t t t



             

.

T

h

a

o

t

á

c

q

u

y

v

ề

h

à

m

s

ố

t

á

c

g

i

ả

x

i

n

k

h

ô

n

g

n

h

ắ

c

l

ạ

i

.

V

ì

h

à

m

s

ố

n

g

h

ị

c

h

b

i

ế

n

t

r

ê

n

đ

o

ạ

n

 

1

;2

,

d

ễ

t

h

ấ

y

đ

a

p

h

ầ

n

c

á

c

ẩ

n

h

à

m

t

a

t

h

ư

ờ

n

g

l

à

m

c

h

o

n

ó

b

ị

c

h

ặ

n

t

r

ê

n

,

c

h

ặ

n

d

ư

ớ

i

,

h

o

ặ

c

b

ị

c

h

ặ

n

(

í

t

k

h

i

c

h

ạ

y

t

r

ê

n

h

a

i

k

h

o

ả

n

g

r

ờ

i

n

h

a

u

)

.

T

r

ư

ờ

n

g

h

ợ

p

đ

ơ

n

g

i

ả

n

l

à

c

á

c

b

i

ế

n

t

h

ỏ

a

m

ã

n

 

1 2

; 1;2

1 2

u

u v

v

 



 



 



.

D

o

đ

ó

c

h

ú

n

g

t

a

d

ự

đ

ị

n

h

c

h

ặ

n

m

i

ề

n

g

i

á

t

r

ị

c

á

c

ẩ

n

s

a

o

c

h

o

 

1 2

; 1;2

1 2

u

u v

m v n

 



 



   



.

Đ

ặ

c

b

i

ệ

t

c

ó

m

ộ

t

s

ố

t

ì

n

h

u

ố

n

g

x

ả

y

r

a

c

á

c

m

i

ề

n

 

; ;

;

m u n

p v q u v m q

m p n q

 





   





 



,

ở

đ

â

y

ẩ

n

h

à

m

u

v

à

v

t

ù

y

ý

.

S

a

u

k

h

i

đ

ã

t

i

ế

n

b

ư

ớ

c

v

ề

d

ạ

n

g

h

à

m

s

ố

,

n

ế

u

h

à

m

s

ố

đ

ó

k

h

ô

n

g

đ

ơ

n

đ

i

ệ

u

t

r

ê

n

t

ậ

p

s

ố

t

h

ự

c

h

a

y

m

i

ề

n

x

á

c

đ

ị

n

h

c

ơ

b

ả

n

(

m

i

ề

n

x

á

c

đ

ị

n

h

b

a

n

đ

ầ

u

)

t

h

ì

b

ắ

t

b

u

ộ

c

p

h

ả

i

l

i

ê

n

t

ư

ở

n

g

t

ớ

i

t

h

a

o

t

á

c

h

ặ

n

m

i

ề

n

g

i

á

t

r

ị

c

h

ặ

t

c

h

o

c

á

c

ẩ

n

h

à

m

,

s

ử

d

ụ

n

g

t

r

i

ệ

t

đ

ể

c

á

c

d

ữ

k

i

ệ

n

c

ủ

a

h

a

i

p

h

ư

ơ

n

g

t

r

ì

n

h

,

k

ế

t

h

ợ

p

t

ổ

n

g

h

ò

a

c

á

c

k

i

ế

n

t

h

ứ

c

đ

á

n

h

g

i

á

,

b

ấ

t

đ

ẳ

n

g

t

h

ứ

c

đ

ể

v

ư

ợ

t

q

u

a

c

a

o

đ

i

ể

m

q

u

y

ế

t

đ

ị

n

h

đ

ó

.

B

à

i

t

o

á

n

1

6

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

     

 

2

21 2 8 2 1 6 1 8,

;

2 2 2 1.

x y x y x y y y

x y

x y y xy x



         







    







.

Lời giải.

Điều kiện

2

1 0; 8 0

x

y y



   

.

Phương trình thứ hai của hệ tương đương với

 

   

 

2

2 2 2 2

2

2 2

2

4 4 2 4 4 2 4 4 2 2 1 2 1 4

2 1 22 1 4

2 2 1 2

2 1 1 4

2 1 2

1 2

1 4

x y y xy x x xy y x y y y

x yx y

x y

x y y

y

              



     

    



 

        

  

   

 



  





Suy ra nhận xét

 

0

2 1 2

0 2 1 4

2

1; 8 0;3

5 8 9

5 8 3

x y

x y y

y



   





     

 

  







.

Phương trình thứ hai của hệ tương đương với

     

       

 

3

2 3 2

21

2 8 2 1 6 1 8

2

1 2 1 3 2 1 9 2 1 8 8 3 8 9 8

2

1 3 2 1 9 2 1 8 3 8 9 8 1

x

y x y x y y y

x y x y x y x y y y y y

x y x y x y y y y

         

                

              

Xét hàm số

 

 

3

2

3 9 ; 0;3

f t t t t t   

ta có

    

 

2

3 6 9 3 1 3 0; 0;3

f t t t t t t



        

.

Hàm số đang xét liên tục và nghịch biến trên miền

 

0

;3

nên

 

   

1 2 1 8 2 1 8 2 1 8 2 2 7

f x y f y x y y x y y x y

                 

.

Khi đó

       

2

2 2 2

2

1 1 4 6 1 4 2 14 33 0; 0

x

y y y y y y



              

(Vô nghiệm).

Vậy hệ phương trình đề bài vô nghiệm.

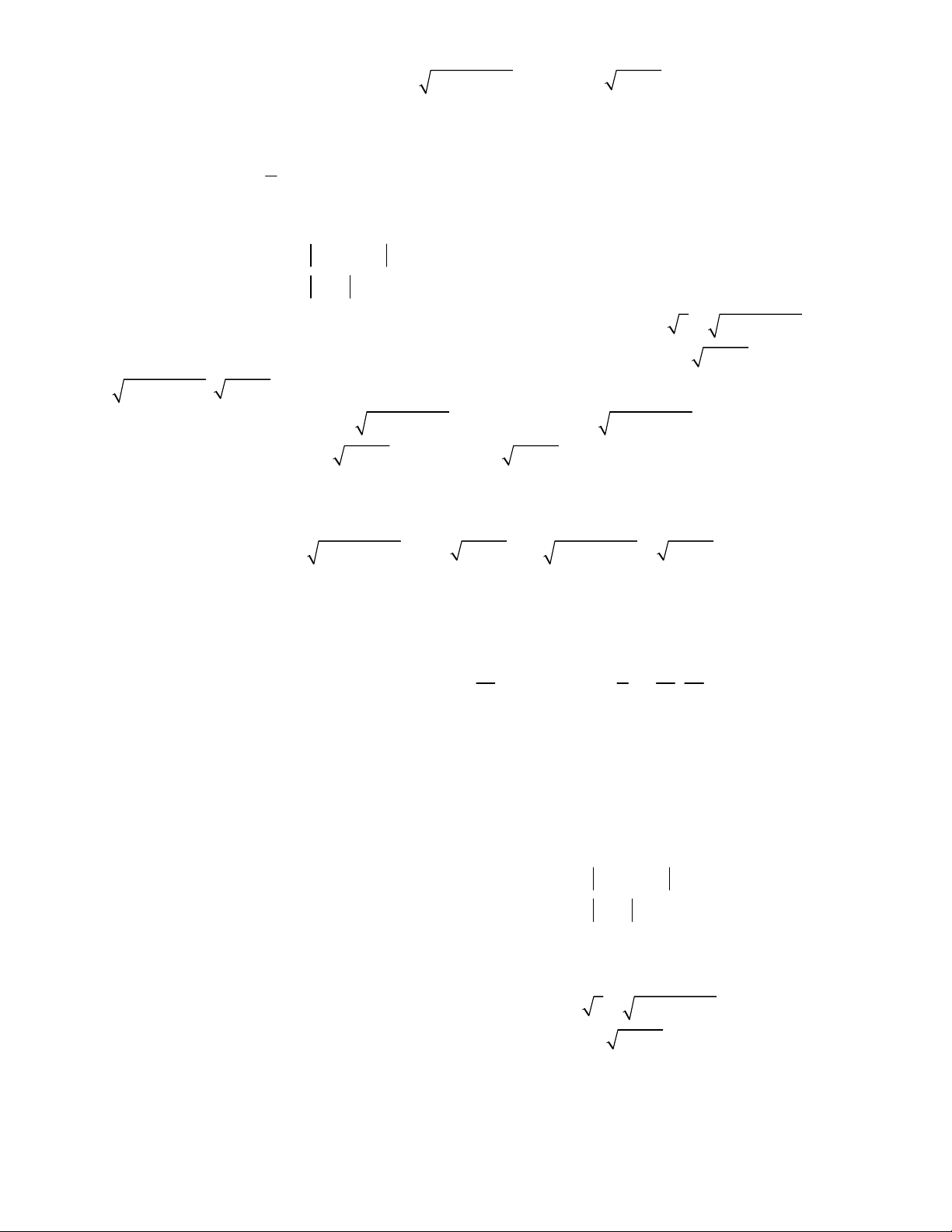
LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

14

B

à

i

t

o

á

n

1

7

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

     

 

2

3 2 13 3 2 4 2 2 3 4 3 6 7 2 ,

;

2 4 4 7 8 .

x y x y x x x y

x y

x xy y y



         







   







.

Lời giải.

Điều kiện

3

3 2 4 0;

4

x y x

   

. Phương trình thứ hai của hệ tương đương với

     

 

2

2 2 2

2

4 4 4 2 4 4 4 1 2 2 2 1

2 2 12 2 1

1 2 2 1 1 2 2 1

1 2 1 1 3

2 1

3 3 2 4

1 2 2 1 1 3 2 2 7 3 3 2 4 9

2 2 6 2 6 1 4 3 9

x xy y x y x x x y x

x yx y

x y x y

x x

x

x y

x y x y x y

x x x

              



     

         

 

 

   

   

     

 

 

  





  

            

  

   

  

      

  

3

1

4 3 3x











 





Dẫn đến

 

3 2 4; 4 3 1;3

x y x    . Mặt khác, phương trình thứ nhất của hệ biến đổi về

   

     

3 2 4 3 2 4 6 3 2 4 9 3 2 4

4 3 4 3 6 4 3 9 4 3 1

x y x y x y x y

x x x x

         

      

Xét hàm số

 

 

    

 

3

2 2

6

9 ; 1;3 3 12 9 3 1 3 0; 1;3

f

t t t t t f t t t t t t



            

.

Suy ra hàm số đang xét liên tục và nghịch biến trên miền

 

1;3

. Ta thu được

 

   

1 3 2 4 4 3 3 2 4 4 3

3 2 4 4 3 2 7

f x y f x x y x

x y x y x

         

       

Lúc đó

       

 

2 2 2 2

2

2 2 1 2 5 2 1

14

5 14 21

5 24 28 0 2; ; 2; , ;

5

2 5 10

x

y x x x

x x x x y

         



    

       

 



  

     

Kết luận hệ phương trình đề bài có hai nghiệm kể trên.

N

h

ậ

n

x

é

t

.

L

ớ

p

b

à

i

t

o

á

n

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

c

h

ứ

a

2

ẩ

n

h

à

m

c

ă

n

t

h

ứ

c

,

t

r

o

n

g

đ

ó

í

t

n

h

ấ

t

m

ộ

t

ẩ

n

h

à

m

c

h

ứ

a

đ

ồ

n

g

t

h

ờ

i

h

a

i

b

i

ế

n

x

v

à

y

,

t

h

a

o

t

á

c

h

ặ

n

m

i

ề

n

g

i

á

t

r

ị

c

h

o

n

ó

k

h

ó

k

h

ă

n

h

ơ

n

v

ớ

i

ẩ

n

h

à

m

ộ

t

b

i

ế

n

.

Á

p

d

ụ

n

g

n

h

ậ

n

x

é

t

ạ

i

b

à

i

t

o

á

n

s

ố

1

4

,

b

à

i

t

o

á

n

1

6

v

à

1

7

c

h

ú

n

g

t

a

v

ẫ

n

t

h

ự

c

h

i

ệ

n

t

ư

ơ

n

g

t

ự

,

t

h

i

ế

t

l

ậ

p

t

ổ

n

g

b

ì

n

h

p

h

ư

ơ

n

g

v

à

đ

á

n

h

g

i

á

c

h

ặ

n

,

n

h

â

n

t

h

ê

m

h

ằ

n

g

s

ố

v

à

c

ô

n

g

t

ừ

n

g

v

ế

c

á

c

b

ấ

t

đ

ẳ

n

g

t

h

ứ

c

   

 

2

2 12 2 1

2 2 2 1

2 1

1 2 2 1 1 2 2 1 1 2 2 1

1 2 1 1 3 2 2 6

3

3 2 4 3

1

3 2 2 7 3 3 2 4 9

2 6 1 4 3 9

1 4 3 3

x yx y

x y x

x

x y x y x y

x x x

x y

x y x y

x x

x



     

 

      

 

 

  





              

  

  

  

       

  





  



      

 



  

  

    

 

  





T

h

i

ế

t

n

g

h

ĩ

t

h

i

ế

t

l

ậ

p

t

ổ

n

g

c

á

c

b

ì

n

h

p

h

ư

ơ

n

g

k

h

ô

n

g

p

h

ả

i

l

à

p

h

ư

ơ

n

g

c

á

c

h

d

u

y

n

h

ấ

t

,

d

ù

n

ó

l

à

t

ố

i

ư

u

.

C

h

ú

n

g

t

a

k

h

ô

n

g

t

h

ể

c

ứ

b

ó

b

u

ộ

c

m

ã

i

t

r

o

n

g

k

h

u

ô

n

k

h

ổ

k

h

ó

k

h

ă

n

đ

ó

đ

ư

ợ

c

,

b

ở

i

đ

ô

i

k

h

i

g

ă

m

b

ì

n

h

p

h

ư

ơ

n

g

c

ũ

n

g

k

h

ô

n

g

d

ễ

d

à

n

g

ì

.

N

ế

u

s

ử

d

ụ

n

g

đ

i

ề

u

k

i

ệ

n

g

h

i

ệ

m

c

ủ

a

p

h

ư

ơ

n

g

t

r

ì

n

h

b

ậ

c

h

a

i

2

2 4 4 7 8x xy y y   

t

h

ì

s

ẽ

n

h

ư

t

h

ế

n

à

o

,

c

h

ú

n

g

t

a

c

ù

n

g

t

h

ử

n

g

h

i

ệ

m

v

ớ

i

b

à

i

t

o

á

n

1

7

t

h

e

o

p

h

ư

ơ

n

g

á

n

t

h

ủ

c

ô

n

g

n

à

y

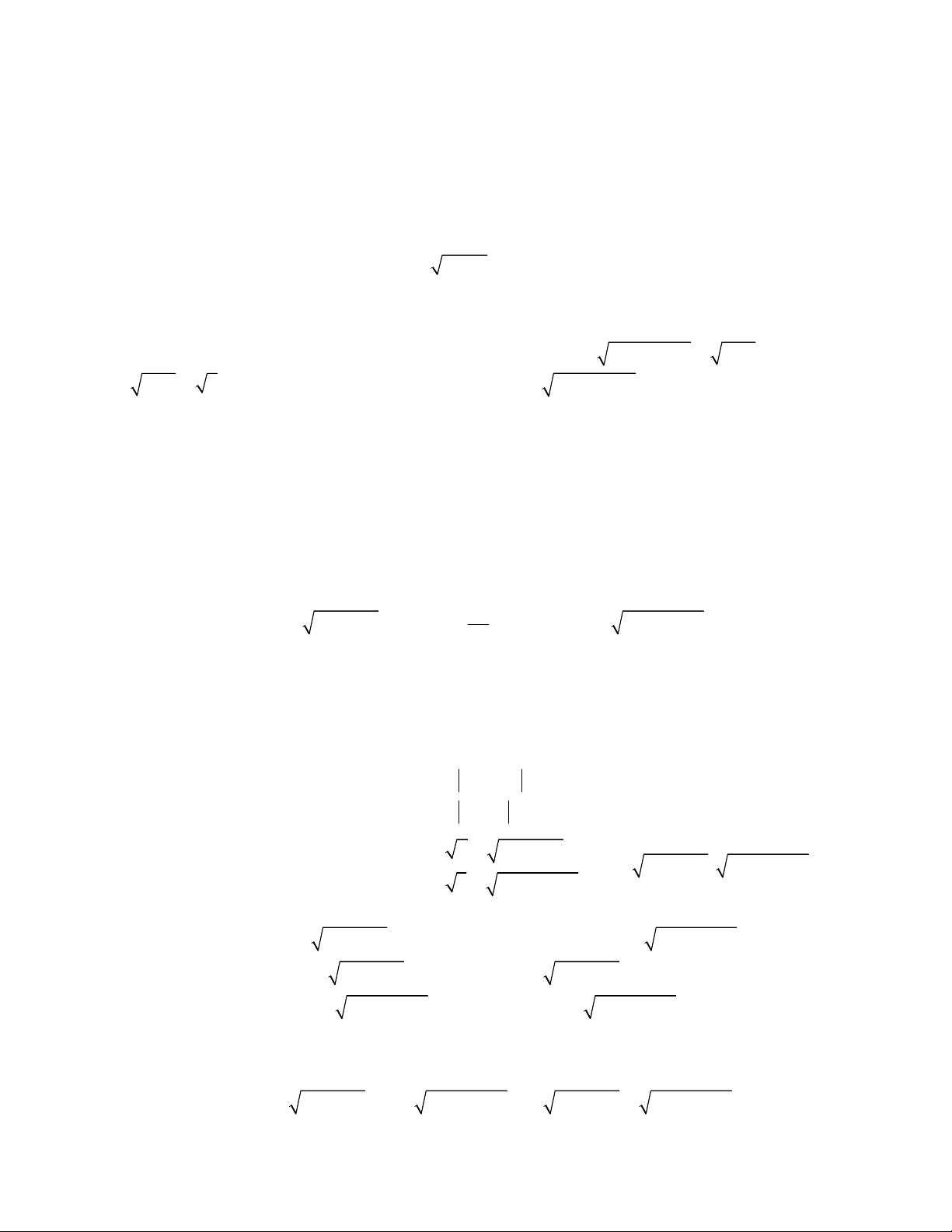
LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

15



P

h

ư

ơ

n

g

t

r

ì

n

h

b

ậ

c

h

a

i

t

h

e

o

ẩ

n

x

:

2

2 4 4 8 7 0

x xy y y

    

B

i

ệ

t

h

ứ

c

 

2

2 2

4

2 4 8 7 4 16 14

y

y y y y





       

.

Đ

i

ề

u

k

i

ệ

n

g

h

i

ệ

m

2

0 4 16 14 0 1, 2 3

y y y



        

.



P

h

ư

ơ

n

g

t

r

ì

n

h

b

ậ

c

h

a

i

t

h

e

o

ẩ

n

y

:

 

2

4

4 2 2 7 0

y

y x x



   

.

B

i

ệ

t

h

ứ

c

   

2

2 2

4

4 4 4 2 7 4 16 12

x

x x x x





        

.

Đ

i

ề

u

k

i

ệ

n

g

h

i

ệ

m

  

2

0 4 16 12 0 4 1 3 0 1 3

x x x x x



            

.



X

u

ấ

t

p

h

á

t

ừ

1 3 1 4 3 9 1 4 3 3

x x x

         

,

x

ử

l

ý

x

o

n

g

ẩ

n

h

à

m

đ

ơ

n

g

i

ả

n

.

T

i

ế

p

t

ụ

c

1,2 3 3 1, 2 6 2 2,4

1 3 3 3 9 3 3 9

3

3 2 7 1 3 2 4 10,6 1 3 2 4 10,6

y y y

x x x

x y x y x y

           

  

 

  

     

  

              

M

à

10

,6 9 3





d

o

đ

ó

s

ẽ

k

h

ô

n

g

c

ó

đ

i

ể

m

t

ự

a

c

h

ắ

c

h

ắ

n

3

2 4 3

x

y



 

.

T

h

ấ

t

b

ạ

i

.

R

õ

r

à

n

g

s

ử

d

ụ

n

g

đ

i

ề

u

k

i

ệ

n

g

h

i

ệ

m

p

h

ư

ơ

n

g

t

r

ì

n

h

b

ậ

c

h

a

i

c

h

o

c

h

í

n

h

x

á

c

m

i

ề

n

g

i

á

t

r

ị

c

ủ

a

t

ừ

n

g

b

i

ế

n

,

t

u

y

n

h

i

ê

n

k

h

i

m

à

h

a

i

b

i

ế

n

c

h

ú

n

g

r

à

n

g

b

u

ộ

c

v

ớ

i

n

h

a

u

t

h

ì

đ

i

ề

u

n

à

y

l

ạ

i

d

ẫ

n

đ

ế

n

c

h

ặ

n

m

i

ề

n

k

h

ô

n

g

c

h

ặ

t

c

h

ẽ

,

p

h

ạ

m

v

i

r

ộ

n

g

,

t

h

ậ

m

c

h

í

p

h

ả

n

t

á

c

d

ụ

n

g

,

l

à

m

c

h

o

h

à

m

s

ố

p

h

í

a

s

a

u

đ

ơ

n

đ

i

ệ

u

m

ộ

t

c

á

c

h

“

l

u

n

g

l

a

y

,

m

ờ

ả

o

”

,

c

h

ư

a

k

ể

c

ó

m

ộ

t

s

ố

b

ạ

n

h

o

a

n

g

t

ư

ở

n

g

t

h

e

o

k

i

ể

u

10

,6 9



,

d

ẫ

n

đ

ế

n

đ

á

n

h

b

à

i

c

ù

n

,

l

à

m

l

i

ề

u

ă

n

h

i

ề

u

n

ữ

a

c

ơ

.

T

h

ô

n

g

q

u

a

đ

â

y

,

c

ó

t

h

ể

t

h

ấ

y

m

ộ

t

b

à

i

t

o

á

n

h

ỏ

r

ú

t

r

a

n

h

i

ề

u

b

à

i

h

ọ

c

l

ớ

n

,

l

i

ê

n

h

ệ

m

ộ

t

c

h

ú

t

r

o

n

g

c

u

ộ

c

s

ố

n

g

,

t

r

o

n

g

t

ì

n

h

y

ê

u

,

c

h

ú

n

g

t

a

k

h

ô

n

g

n

ê

n

q

u

á

đ

ể

ý

,

s

o

i

m

ó

i

,

c

h

ặ

t

c

h

ẽ

,

c

h

i

l

y

,

c

ứ

n

g

n

h

ắ

c

,

g

i

á

o

đ

i

ề

u

,

n

g

ư

ợ

c

l

ạ

i

c

ầ

n

h

ẹ

n

h

à

n

g

,

t

ì

n

h

c

ả

m

,

b

ì

n

h

t

ĩ

n

h

,

k

h

o

a

n

d

u

n

g

m

ớ

i

t

ạ

o

r

a

s

ự

c

â

n

b

ằ

n

g

,

h

ò

a

t

h

u

ậ

n

,

g

ắ

n

b

ó

l

â

u

d

à

i

,

c

ó

t

h

ể

l

ấ

y

d

ẫ

n

c

h

ứ

n

g

c

â

u

t

ụ

c

n

g

ữ

“

L

ạ

t

m

ề

m

b

u

ộ

c

h

ặ

t

”

t

r

o

n

g

k

h

o

t

à

n

g

v

ă

n

h

ọ

c

V

i

ệ

t

N

a

m

.

Bài toán 18.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

   

 

2

27

10 4 9 9 3 3 13 3 3 7,

2

;

2 5 2 0.

x y x y x y x y x y

x y

x y x y xy



           









    





.

Lời giải.

Điều kiện

4

0;3 3 7 0

x

y x y



    

. Phương trình thứ hai của hệ tương đương với

   

 

2

2 2 2 2 2

2

2 2

2

2 5 2 0 2 2 1 4 4 1

1 11 1

1

1 1 2 0

1

2 1

1

2 1 2 2 4 2

2

1

2 1

2

2 4 4 2 4 4

4 3 3 2 3 3 3 7 9

x xy y x y x xy y x y x xy y

x yx y

x y x y

x y

x y x y

              



     

        

 

 

        

   



      





 

  





 

       

 

  

 

       

 





4

2

4

; 3 3 7 1;2

3

3 3 7 3

x y x y

x y



 



     



   





Phương trình thứ nhất của hệ tương đương với

     

   

     

2

10 4 9 2 2 3 2 3 3 13 3 3 7

2

4 4 9 4 12 4

2 3 3 7 3 3 7 9 3 3 7 12 3 3 7 1

x y x y x y x y x y

x y x y x y x y



          



         

          

Xét hàm số

 

 

    

 

3

2 2

2

9 12 ; 1;2 6 18 12 6 1 2 0, 1;2

f

t t t t t f t t t t t t



             

.

Như vậy hàm số liên tục và nghịch biến trên miền

 

1

;2

nên

 

   

1 4 3 3 7 4 3 3 7

4 3 3 7 2 4 3

f x y f x y x y x y

x y x y x y

           

        

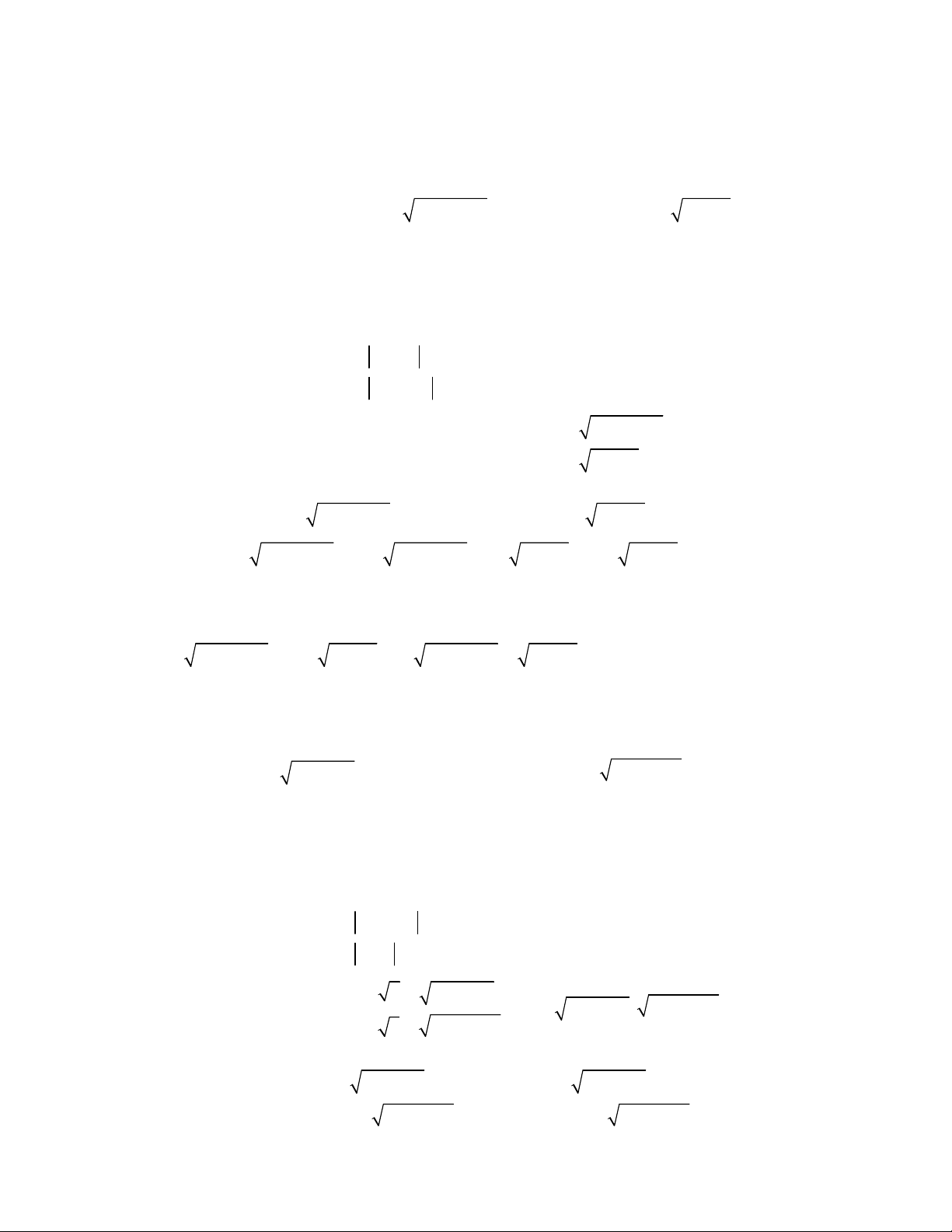
LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

16

Khi đó

     

2

2 2 2

2

2 2

2

2 5 2 2 0 4 4 10 4 4 0

4

3 2 4 3 10 4 2 4 3 0 18 6 3 0, 0

x

xy y x y x xy y x y

y y y y y y y y

          



             

Phương trình ẩn y ở trên vô nghiệm nên hệ đã cho vô nghiệm.

B

à

i

t

o

á

n

1

9

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

     

 

2

2 3 2 3 9 1 4 4 ,

;

2 2 5 2 2 0.

x y x y x y x y x y

x y

x xy y x y



         







    







.

Lời giải.

Điều kiện các căn thức xác định. Phương trình thứ hai của hệ tương đương với

   

 

2

2 2 2 2

2

4 4 2 2 2 1 1 2 1 1

2 12 1

1 2 1 1 2 1

1 1 1 2 0

1 1

0 2 3 2

2 2 3 4 2 2 3 4

6 3 3 0 4 4 4

0 4 2

x xy y x xy y x y x y x y

x yx y

x y x y

x y

x y x y

x y

              



   

       

 

 

   

   

        

  

 

   







   

       

 



  

  

       

  

 





Phương trình thứ nhất của hệ biến đổi về

       

 

3

2 3 2

2 3 2 3 3 2 3 4 4 3 4

2 3 3 2 3 4 3 4 1

x y x y x y x y x y x y

x y x y x y x y

           

         

Xét hàm số

 

 

   

 

3

2 2

3

; 0;2 3 6 3 2 0, 0;2

f

t t t t f t t t t t t



          

.

Hàm số đang xét nghịch biến và liên tục trên miền

 

0

;2

nên

 

   

1 2 3 4 2 3 4 2 3 4 1f x y f x y x y x y x y x y x y                 

.

Lúc này

     

2

2 2

2

1 1 1 3 3

x

y x y y



       

(Vô nghiệm). Vậy hệ phương trình đã cho vô nghiệm.

B

à

i

t

o

á

n

2

0

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

   

 

2

2 2

2 26 8 15 3 2 23 5,

;

2 2 2 2 1 0.

x y x y x y x x x x

x y

x xy y x y



           







     







.

Lời giải.

Điều kiện các căn thức xác định. Phương trình thứ hai của hệ tương đương với

   

 

 

2

2 2 2

2

2 2 2 1 4 4 4 1 2 4

1 21 4

2 1 2 3 1

2 2 2 0 4

2 2

2 4

6 8 3

6 8 9

8; 5 2;3

5 5 25

5 5 5

x xy y x y x x x y x

x yx y

x y x y

x x

x

x y

x y x x

x x

              



     

        

 

 

   

   

     

 

 

  







   





       

 

   



   





Phương trình thứ nhất của hệ tương đương

   

2

2 2 2

2

8 8 15 8 36 8

2

5 5 15 5 36 5

x

y x y x y x y

x x x x x x x x

         



         

Xét hàm số

 

 

    

 

3

2 2

2

15 36 ; 2;3 6 30 36 6 2 3 0; 2;3

f

t t t t t f t t t t t x



             

.

LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

17

Vậy hàm số đang xét liên tục và nghịch biến trên miền

 

2;3

. Suy ra

 





2

2 2 2

8 5 8 5 8 5 3

f x y f x x x y x x x y x x y x                   

.

Khi đó phương trình thứ hai lại trở thành

 

2

2 4 2 2

2

4 3 2 2 3

2 2 3 6 9 2 6 2 1 0

2 2 8 10 0 1 2 8 9 0 1

x x x x x x x

         

           

Ta có

 

 

3

2

8 9; 0;4

f

x x x x   

. Do đó

   

2

4 2 2

6 8; 0 ;

3

3 3

f x x f x x x

 

 

       

 

 

.

Khảo sát hàm số ta thu được

     

 

0

;4

2

32 2 32

0

9; 9 ; 4 105 9 0

3

3 3 3 3 3

x

f

f f Min f x f



   



       



  

   

.

Do vậy

 

 

2

3

1 2 8 9 0, 0;4

x x x x       , phương trình (1) vô nghiệm.

Kết luận hệ phương trình đã cho vô nghiệm.

N

h

ậ

n

x

é

t

.

N

g

o

à

i

p

h

ư

ơ

n

g

p

h

á

p

x

â

y

d

ự

n

g

m

i

ề

n

g

i

á

t

r

ị

c

á

c

ẩ

n

t

h

ô

n

g

q

u

a

p

h

ư

ơ

n

g

t

r

ì

n

h

b

ậ

c

h

a

i

,

c

á

c

b

ạ

n

c

ó

t

h

ể

s

ử

d

ụ

n

g

m

ộ

t

d

ạ

n

g

t

ư

ơ

n

g

t

ự

đ

ơ

n

g

i

ả

n

h

ơ

n

,

m

à

k

h

ô

n

g

t

h

ô

n

g

q

u

a

b

i

ế

n

đ

ổ

i

,

đ

ó

l

à

p

h

ư

ơ

n

g

t

r

ì

n

h

c

h

ứ

a

ẩ

n

t

r

o

n

g

d

ấ

u

g

i

á

t

r

ị

t

u

y

ệ

t

đ

ố

i

,

c

ụ

t

h

ể

l

à

t

ổ

n

g

c

ủ

a

c

á

c

g

i

á

t

r

ị

t

u

y

ệ

t

đ

ố

i

.

C

h

ú

ý

r

ằ

n

g

1

2 3 2

... ; 0

...

n

A k

A A A A k k A k

 



       







K

ế

t

h

ợ

p

b

i

ế

n

đ

ổ

i

d

ạ

n

g

t

ư

ơ

n

g

đ

ồ

n

g

h

à

m

s

ố

c

ủ

a

p

h

ư

ơ

n

g

t

r

ì

n

h

c

ò

n

l

ạ

i

,

k

ế

t

h

ợ

p

c

h

i

a

t

r

ư

ờ

n

g

h

ợ

p

g

i

ả

i

p

h

ư

ơ

n

g

t

r

ì

n

h

c

h

ứ

a

d

ấ

u

g

i

á

t

r

ị

t

u

y

ệ

t

đ

ố

i

t

a

t

h

u

đ

ư

ợ

c

l

ờ

i

g

i

ả

i

b

à

i

t

o

á

n

.

B

à

i

t

o

á

n

2

1

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

   

 

2

2 2

1

1 1,

;

2 1 1 9 1 2 2 2.

x y

x x y y x y y y y

    







          







.

Lời giải.

Điều kiện

1

x





. Phương trình thứ nhất của hệ tương đương với





2

1 1

1 1 1 0 2

1 1 1

1 1 1 0 2

1 1

1 1 3

1

; 2 0;3

2

2 8

2 2 8

x

x x

x y

y y

y

x

x y y

y y

  

     

 



      

  

     

 

 







  





      

 

   







Phương trình thứ hai trở thành

   









2

2 2

3 2

2 2

2 1 1 9 1 2 2 2 9 2

2 1 9 1 2 2 9 2

x x x y y y y y y

x x y y y y

           

         

Xét hàm số

  



    



3

2 2

2 9 ; 0;3 6 18 6 3 0, 0;3

f t t t t f t t t t t t



          

.

Dẫn đến hàm số đang xét liên tục và nghịch biến trên miền





0

;3

. Ta thu được

 





2

2 2

1

2 1 2 1

f

x f y y x y y x y y



           

.

Phương trình thứ nhất khi đó lại trở thành

LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

18

2 2

1 2 1 2

1 1 1 1 0

1

1 1 1 0

0

1 0 1

1 1 0

y y

y y y y

y y y y y y y

y y

y y y y

    

 

 

 

      

 

 



           



   

 

 

 

 

    

 

 

.

Kết luận hệ đã cho có nghiệm duy nhất

1

; 0

x

y



.

B

à

i

t

o

á

n

2

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

3

2

3 3 2,

;

1 1.

x y x y

x y



   







  







.

Lời giải.

Phương trình thứ hai của hệ ta suy ra

 

2

1

1 0 1 2

1

1 1; 0;2

1 1 1 0 2

1 1

x

x x

x y x y

y y

y





     

 



        

  

     

 

 





.

Phương trình thứ nhất biến đổi

   

3

2

3

2 2 3 2 3 2

3

3 1 3 6 3 3 1 3 1 3

x

x x x x y y x x y y



            

.

Xét hàm số

 

 

   

 

3

2 2

3

; 0;2 3 6 3 2 0, 0;2

f

t t t t f t t t t t t



          

.

Hàm số trên liên tục và nghịch biến trên miền

 

0

;2

nên thu được

   

1

f

x f y x y



   

.

Phương trình thứ hai trở thành

2

0

1 0

1 5 1 5

1

;

2 2

0

1 0

x

x x

x x x

x

x x

 







  





  



 





   

























 





.

Từ đây đi đến hệ có hai nghiệm.

B

à

i

t

o

á

n

2

3

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

3

2 3

9

21 51 117,

;

2 1 2.

x y y y x

x y



    







   







.

Lời giải.

Phương trình thứ hai suy ra

 

2 2

2 2 2

2 1 2

1 2

0 4 1 1 5

1

; 2 3;5

1

3 3 2 1

x

x y

y

x x

x y

y y

  

   





     

 

   

 







    

 

      

 

      

 

Phương trình thứ nhất lại tương đương

           

3

3 2

3 2 2 3 2 2

3 2 3 2

51

47 9 21 70

3

3 1 3 6 3 45 45 6 12 8 3 12 12 45 90

1 3 1 45 1 2 3 2 45 2

x x y y y

x x x x x x y y y y y y

x x x y y y

     



                

           

Xét hàm số

 

 

    

 

3

2 2

3

45 ; 3;5 3 6 45 3 3 5 0, 3;5

f

t t t t t f t t t t t t



               

.

Hàm số đang xét liên tục và nghịch biến trên miền

 

3;5



. Ta thu được

   

1

2 1 2 1 2

f

x f y x y y x



         

.

Phương trình thứ hai trở thành

2

2 2 2 2 2

x

x x x



       

.

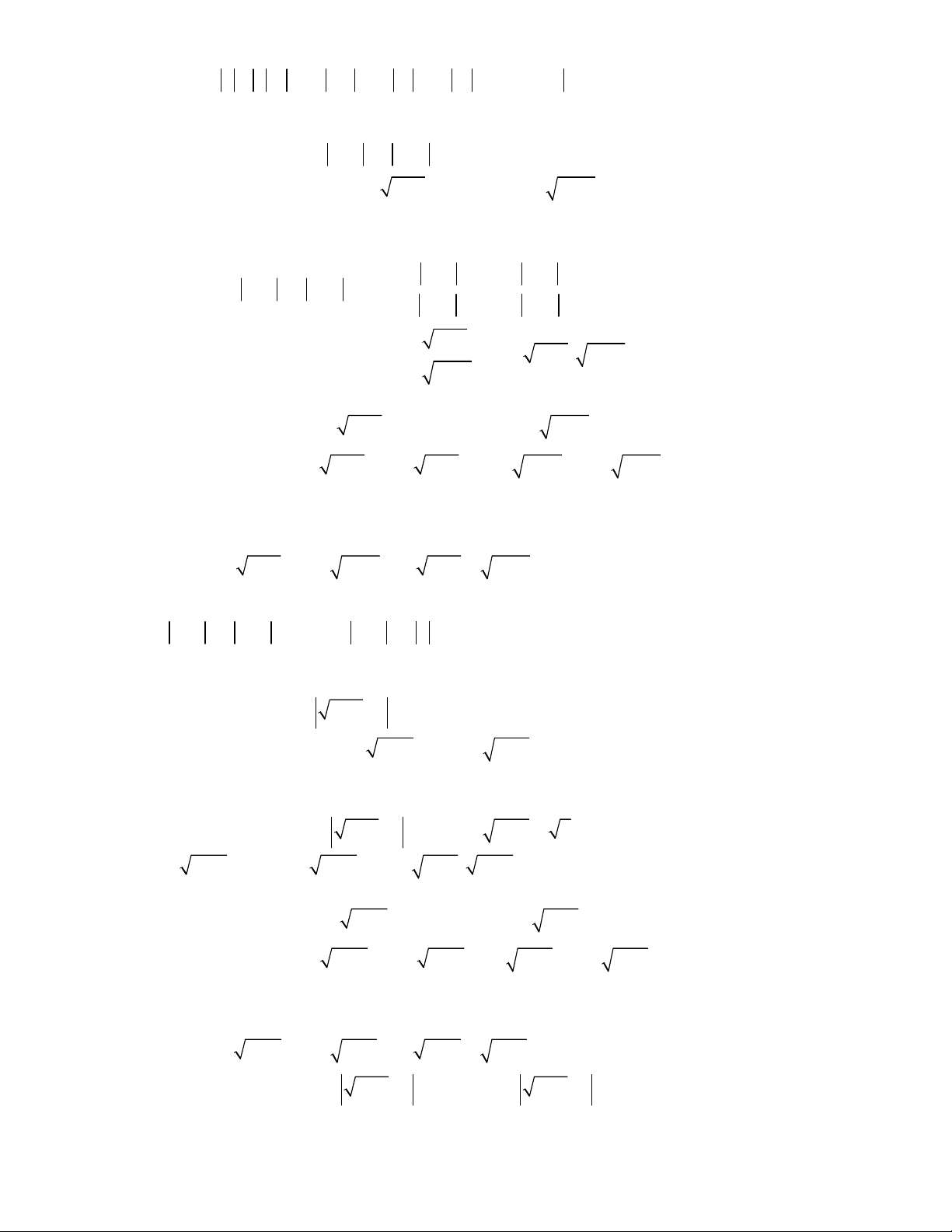
LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

19

Áp dụng bất đẳng thức

2 2 2 2 4 2

a b a b x x x x

            

, phương trình ẩn x vô nghiệm.

Kết luận bài toán đã cho vô nghiệm.

B

à

i

t

o

á

n

2

4

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

2 1 3 1 6,

;

1 2 1 3 2 2 2 3 .

x y

x x y y

    







      







.

Lời giải.

Điều kiện

1

; 1

x

y



. Phương trình thứ nhất của hệ suy ra

 

2 1 6 1 3

3

1 3

2

1 3 1 6

2

1 2

3

1 6 1 2

0 1 1

5 1 1

1; 2 0;1

3 2 1

0 2 1

x x

x

x y

y

y y

x

x y

y

     



  



 

      

  



  



  



 

 



  

   





     

 

   

  







Phương trình thứ hai biến đổi về

       

3 2 3 2

2

1 1 3 1 2 2 2 3 2

2

1 3 1 2 2 3 2

x

x x y y y

x x y y

        

       

Xét hàm số

 

 

   

3

2 2

2

3 ; 0;1 6 6 6 1 0

f

t t t t f t t t t t





       

.

Hàm số đang xét liên tục và nghịch biến trên miền

 

0

;1

nên ta có

   

1 2 1 2 1 2 1

f x f y x y x y y x             

.

Lúc đó lại có

1

1 1

2 1 3 1 6 2 1 3 6

2 2 3 6 5 4

x x

x

x y x x

x x x

 

 

 

 

 



   

   

      

   

 

 

.

Kết luận hệ phương trình đã cho vô nghiệm.

B

à

i

t

o

á

n

2

5

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

   

 

1 1 1,

;

3 3 1 1 3 3 6.

x y

x x y y x y



   









       





.

Lời giải.

Điều kiện

3 1; 1

x y

    

.

Từ phương trình thứ nhất ta có

1 1 1 1 0 1 2

y x y         .

Mặt khác

 

1 3 2 0 3 2 1; 3 0;2

x x x y x            .

Phương trình thứ hai biến đổi về

       

3

2 3 2

3

3 3 3 1 1 3 1

3

3 3 1 3 1

x

x x y y y

x x y y

        

       

Xét hàm số

 

 

   

 

3

2 2

3 ; 0;2 3 6 3 2 0, 0;2

f t t t t f t t t t t t



          

.

Hàm số trên liên tục và nghịch biến trên miền đang xét, suy ra

   

3 1 3 1 3 1 2

f x f y x y x y y x

             

.

Khi đó phương trình thứ nhất trở thành

1 1 2 1 1 1 1 0

x x x x

          

.

Xét hai trường hợp

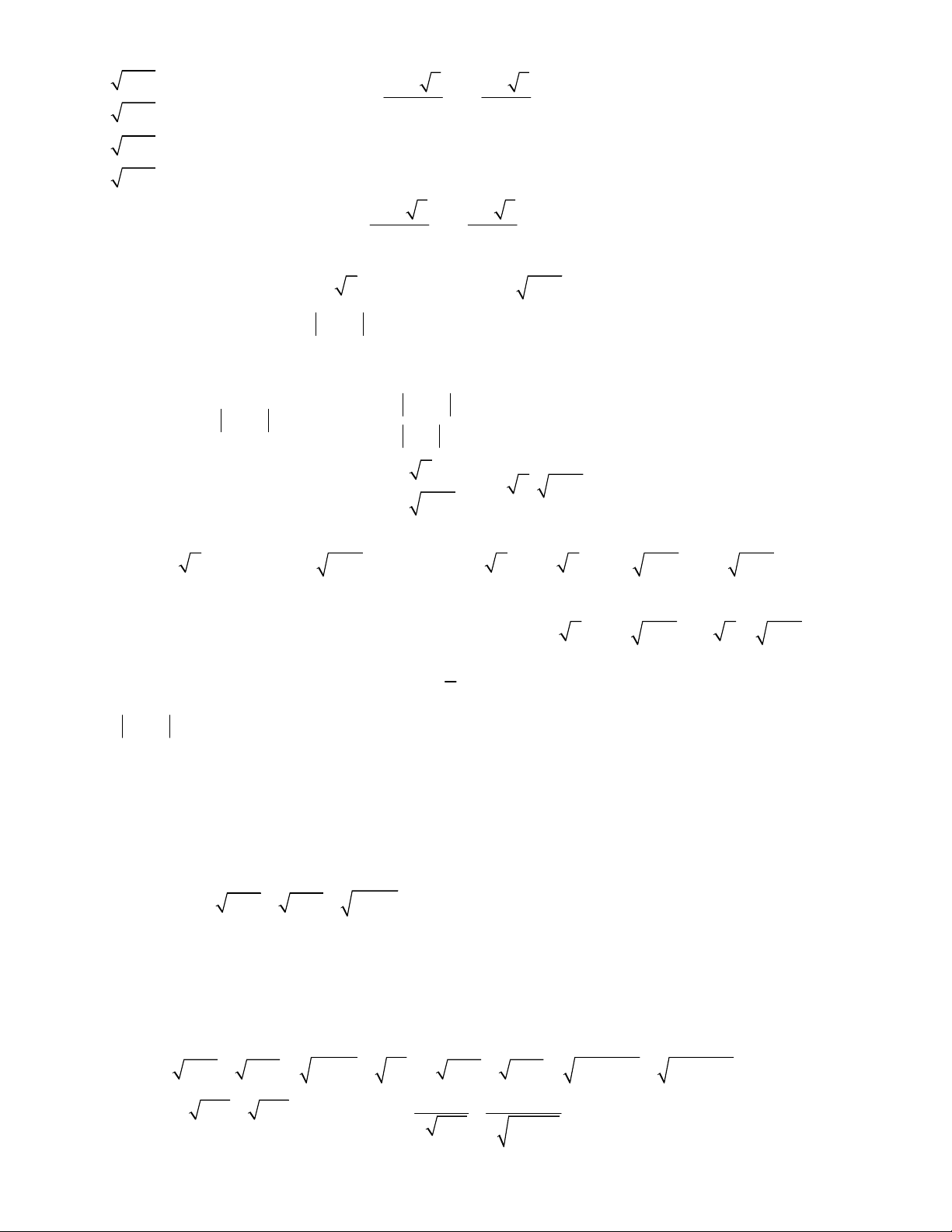
LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

20

o

2

0

1 1

1 5 3 5

;

2 2

1 0

1

x

x y

x x





 



  



   

 

  

  







.

o

1 1 0 0

2 1 1

1 2

x x x

x

x x



   

 



   

  

   

  

 





.

Kết luận hệ đã cho có nghiệm duy nhất

1

5 3 5

;

2

x

y

  

 

.

B

à

i

t

o

á

n

2

6

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

   

 

2

3 2 1 1 3,

;

2 3 1 1

x x y x y y

x y



     







   







.

Lời giải.

Điều kiện

0

; 1

x

y



. Phương trình thứ hai của hệ suy ra

 

 

2

2 3 1

1 2 3 1 1 2

2

3 1 1

1

1 1 0 2

1 1

0 2

1 4

; 1 0;1

1 1 1

0 1 1

x

x x

x y

y y

y

x

x y

y

  

      

 



      

  



    

 

 







 





    

 

   

  







Phương trình thứ nhất biến đổi về

   

       

3

2 3 2

2 3 2 1 1 3 1 2 3 2 1 3 1

x x x y y y x x y y

           

.

Xét hàm số

 

 

   

3

2 2

2

3 ; 0;1 6 6 6 1 0

f

t t t t f t t t t t





       

.

Hàm số đang xét liên tục và nghịch biến trên miền

 

0;1

nên ta có

   

1 1 1f x f y x y x y       

.

Thu được

2

3

2

3

2

2 3 1

2 4 0

2 3 1

2 3 2 3

2 3 1 2 2 0

x

x x

x

x x x x













  





  





  



   





 

 



  

 



     

 



Kết luận hệ phương trình đã cho vô nghiệm.

B

à

i

t

o

á

n

2

7

.

T

r

í

c

h

l

ư

ợ

c

â

u

3

,

Đ

ề

t

h

i

t

u

y

ể

n

s

i

n

h

Đ

ạ

i

h

ọ

c

;

M

ô

n

T

o

á

n

;

K

h

ố

i

A

v

à

k

h

ố

i

A

1

;

Đ

ề

t

h

i

c

h

í

n

h

t

h

ứ

c

,

B

ộ

G

i

á

o

d

ụ

c

v

à

Đ

à

o

t

ạ

o

V

i

ệ

t

N

a

m

;

K

ỳ

t

h

i

t

u

y

ể

n

s

i

n

h

n

ă

m

2

0

1

3

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

4

2 2

1 1 2 ,

;

2 1 6 1 0.

x x y y

x y

x x y y y



     







     







.

Lời giải.

Điều kiện

1x 

. Phương trình thứ hai của hệ tương đương với

   

2

1 2 1 4 1 4 4 0 0

x

x y y y y x y y y y



            

.

Khi đó phương trình thứ nhất trở thành

 

4 4 4 4

4 4

1

1 2 1 1 1 1 1 1x x y y x x y y



               

.

Xét hàm số

 

4

1 1, 1f t t t t    

thì

 

3

4

1

0

, 1

2

1

4 1

f

t t

t





   





. Hàm số đồng biến với

1t 

.

LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

21

Dễ thấy

 

 

4

1 1

f x f y x y

      

. Thay thế vào phương trình thứ hai thu được

   

 

2

4

7 4

0

4

2 4 0

2

4 0

y

y y y y y y

g y y y y





       





   



Để ý rằng

   

6

3

7

8 1 0, 0

g

y y y y g y





     

đồng biến, liên tục với

0

y



. Hơn nữa

 

1

0 1

g

y



 

.

Từ đây ta thu được hai nghiệm

     

;

1;0 , 2;1

x

y 

.

N

h

ậ

n

x

é

t

.

Đ

â

y

l

à

n

ă

m

t

h

ứ

h

a

i

d

ạ

n

g

t

o

á

n

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

s

ử

d

ụ

n

g

t

í

n

h

c

h

ấ

t

đ

ơ

n

đ

i

ệ

u

h

à

m

s

ố

x

u

ấ

t

h

i

ệ

n

t

r

o

n

g

c

â

u

3

,

k

ỳ

t

h

i

t

u

y

ể

n

s

i

n

h

Đ

ạ

i

h

ọ

c

m

ô

n

T

o

á

n

c

h

í

n

h

t

h

ứ

c

(

k

h

ô

n

g

k

ể

c

â

u

5

P

h

â

n

l

o

ạ

i

t

h

í

s

i

n

h

t

r

o

n

g

Đ

ề

t

h

i

t

u

y

ể

n

s

i

n

h

m

ô

n

T

o

á

n

Đ

ạ

i

h

ọ

c

k

h

ố

i

A

n

ă

m

2

0

1

0

)

.

M

ứ

c

đ

ộ

m

i

ề

n

g

i

á

t

r

ị

c

ủ

a

b

i

ế

n

c

ũ

n

g

t

ư

ơ

n

g

t

ự

b

à

i

t

o

á

n

1

,

Đ

ề

t

h

i

t

u

y

ể

n

s

i

n

h

k

h

ố

i

A

n

ă

m

2

0

1

2

,

t

u

y

n

h

i

ê

n

h

ì

n

h

t

h

ứ

c

v

ô

t

ỷ

c

ủ

a

p

h

ư

ơ

n

g

t

r

ì

n

h

t

h

ứ

n

h

ấ

t

k

h

i

ế

n

h

i

ề

u

b

ạ

n

t

h

í

s

i

n

h

t

ỏ

r

a

l

ú

n

g

t

ú

n

g

,

e

n

g

ạ

i

,

k

h

ó

n

h

ì

n

h

ậ

n

,

c

h

ố

n

g

p

h

á

.

K

h

ả

n

ă

n

g

t

ư

d

u

y

l

i

n

h

o

ạ

t

,

k

ế

t

n

ố

i

k

i

ế

n

t

h

ứ

c

l

à

t

r

ọ

n

g

t

â

m

,

s

o

n

g

h

à

n

h

v

ớ

i

n

ó

k

ỹ

n

ă

n

g

t

í

n

h

t

o

á

n

c

ẩ

n

t

h

ậ

n

,

c

h

í

n

h

x

á

c

đ

ư

ợ

c

x

â

y

d

ự

n

g

n

g

a

y

t

ừ

n

h

ữ

n

g

b

à

i

t

o

á

n

h

ỏ

n

h

ư

t

h

ế

n

à

y

.

T

r

o

n

g

c

u

ộ

c

s

ố

n

g

,

t

h

à

n

h

b

ạ

i

l

à

đ

i

ề

u

t

h

ư

ờ

n

g

t

h

ấ

y

,

n

h

ư

n

g

k

h

ô

n

g

v

ì

t

h

ế

m

à

c

h

ú

n

g

t

a

n

ả

n

c

h

í

,

c

h

ù

n

b

ư

ớ

c

,

t

r

á

i

l

ạ

i

c

ầ

n

l

ạ

c

q

u

a

n

,

t

i

n

t

ư

ở

n

g

,

c

ố

g

ắ

n

g

i

ữ

l

ấ

y

l

ề

,

m

ạ

n

h

d

ạ

n

,

t

á

o

b

ạ

o

,

t

h

ẳ

n

g

t

h

ắ

n

b

ả

o

v

ệ

c

h

â

n

l

ý

,

l

à

m

c

h

ủ

m

ộ

t

p

h

ầ

n

b

ầ

u

t

r

ờ

i

k

h

o

a

h

ọ

c

!

N

g

o

à

i

c

á

c

h

p

h

â

n

t

í

c

h

b

ì

n

h

p

h

ư

ơ

n

g

n

h

ư

t

r

ê

n

,

c

á

c

b

ạ

n

c

ó

t

h

ể

c

o

i

p

h

ư

ơ

n

g

t

r

ì

n

h

t

h

ứ

h

a

i

c

ó

d

ạ

n

g

ẩ

n

x

,

t

h

a

m

s

ố

y

 

2

1 6 1 0

x

x y y y



    

.

B

i

ệ

t

h

ứ

c

 

2

1 6 1 4

y

y y y y





      

v

à

đ

i

ề

u

k

i

ệ

n

c

ó

n

g

h

i

ệ

m

0

4 0 0

y





    

.

B

à

i

t

o

á

n

2

8

.

T

r

í

c

h

l

ư

ợ

c

â

u

8

,

T

h

ử

s

ứ

c

t

r

ư

ớ

c

k

ỳ

t

h

i

Đ

ạ

i

h

ọ

c

2

0

1

5

,

Đ

ề

s

ố

2

,

T

ạ

p

c

h

í

T

o

á

n

h

ọ

c

v

à

t

u

ổ

i

t

r

ẻ

,

N

h

à

x

u

ấ

t

b

ả

n

G

i

á

o

d

ụ

c

V

i

ệ

t

N

a

m

;

S

ố

4

9

,

T

h

á

n

g

1

n

ă

m

2

0

1

4

.

T

á

c

g

i

ả

P

h

ạ

m

T

r

ọ

n

g

T

h

ư

–

G

i

á

o

v

i

ê

n

t

r

ư

ờ

n

g

T

H

P

T

C

h

u

y

ê

n

N

g

u

y

ễ

n

Q

u

a

n

g

D

i

ê

u

,

T

ỉ

n

h

Đ

ồ

n

g

T

h

á

p

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

4

2

3

2 5 ,

;

2 2 8 4 0.

x x y y

x y

x x y y y



     







     







.

Lời giải.

Điều kiện

2

x



.

Phương trình thứ hai của hệ tương đương với

   

2

2 2 4 4 4 2 4 0

x x y y y y x y y y

           

.

Khi đó phương trình thứ nhất trở thành

 

4 4

4

2

2 5 5x x y y



      

.

Xét hàm số

   

3

4

2

5; 0 1 0, 0

5

t

f t t t t f t t

t



         



.

Như vậy hàm số trên liên tục và đồng biến trên miền

0t 

. Ta thu được

 

   

 

4

2 2

4 3

2

3

2

2 2

0

4 1 4 0

1

4 1

f

x f y x y y x

y

y y y y y y

g y y y

         





 



       

 

 

  





Hàm số

 

g

y

liên tục và đồng biến với

   

0

1 1

y

g y g y



   

.

Kết luận hệ phương trình có các nghiệm

     

;

2;0 , 3;1

x

y 

.

B

à

i

t

o

á

n

2

9

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

3

2

2 2

4

12 9 1 2 2 1,

;

2 5 3 2 3 1 0.

x x x y y

x y

x x y y



     







      







.

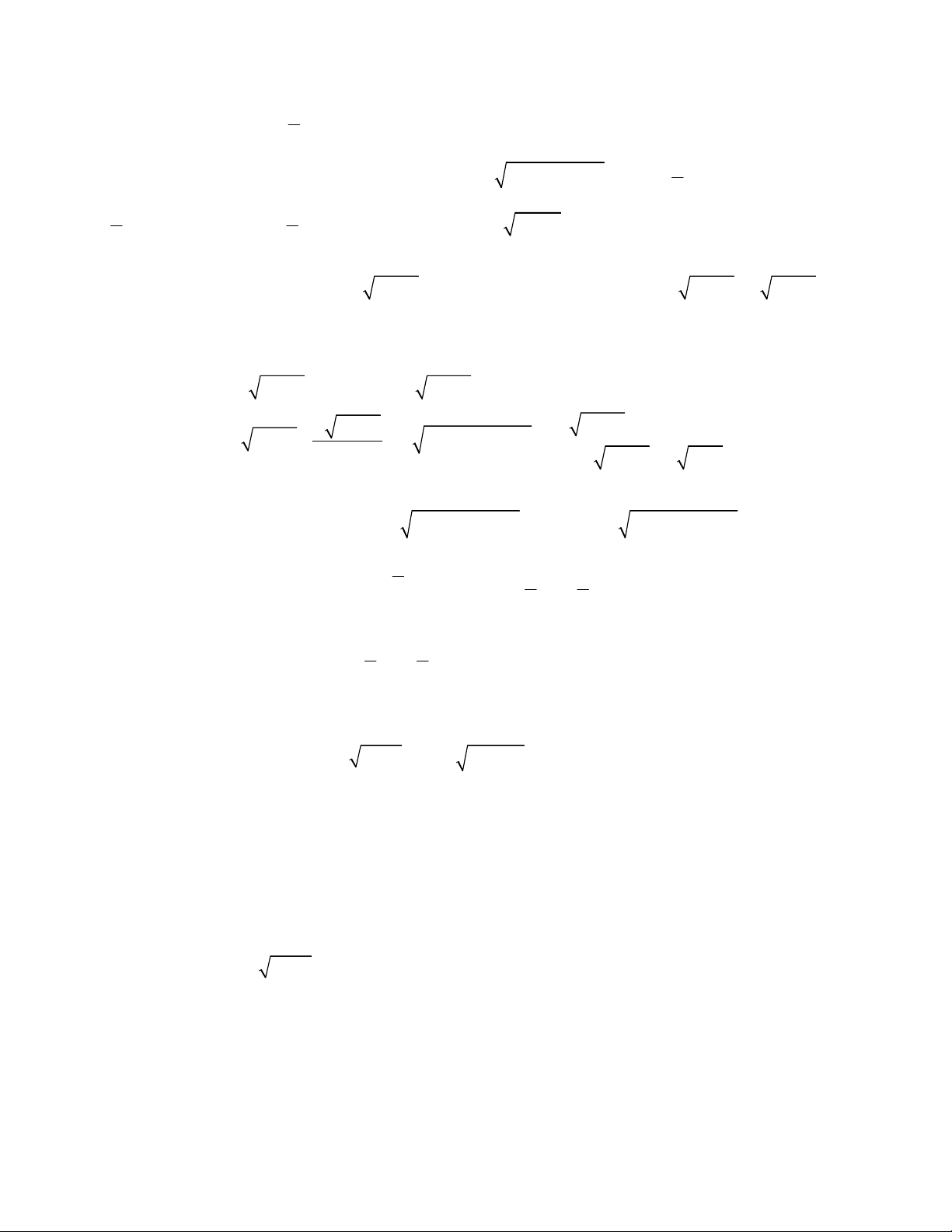
LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

22

Lời giải.

Điều kiện

2

2 1 0

1

2 3 1 0

2

 



  



   



y

y y

.

Phương trình thứ hai của hệ tương đương

  

2

3

2 3 1 2 3 1 0 1

2

x x y y x

            

.

Suy ra

2

1

0 ( 1)

2

4



    

x

và

0 2 1 1 1 2 1 0        

y y

.

Phương trình thứ nhất của hệ tương đương với

       

3

2

8 24 18 2 4 2 2 21 2 2 3 2 2 1 2 2 3

1

1x x x y y x x y y

y

            





Xét hàm số

3

( ) 3 f t t t

trên

 

1

;1



ta có đạo hàm

 

 

2

'

3 3 3 1 ,

0

1;1

f

t t t t       

.

Dẫn đến hàm số liên tục, đồng biến trên miền

 

1;1



.

Thu được

 

2 2 2 1 2 2 2 1f x f y x y        

. Thay vào phương trình thứ hai ta được

 

  

     

 

2

1 0

2 1

1 2 1 . 2 1 1

2

1 2 1 2 1

2 1 0 2 1

1 2 1 4 4 4 2 1 1 1 2 2 1 1

2 1

1

1 3

; 1; , ;1

1

2

2 2

1

1 2 2

y

y y y

y

y y y y y y

y

x

y



 

 

      



   



  

 

 

 



         

 

 







   



     





   



   







 







Vậy hệ đã cho có các nghiệm

 

1 3

,

1; , ;1 .

2 2



  



 



  

   

x

y

B

à

i

t

o

á

n

3

0

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

3

3 2

2 2 2

3

3 2,

;

1 2 3 2 .

x y y x

x y

x x y y



   







    







.

Lời giải.

Điều kiện

1

1;0 2

x

y



   

.

Từ điều kiện ta có

   

1

0;2 , 0;2

x

y  

. Phương trình thứ nhất của hệ biến đổi thành

     

3

2

3 2 2 3 2 3 2

3

3 1 3 6 3 3 1 3 1 3x x x x x y y x x y y



             

.

Xét hàm số

     

 

3 2 2

3

3 0, 0;2

f

t t t f t t t t



       

. Hàm số nghịch biến, liên tục trên

 

0

;2

.

Do đó

     

1

f

x f y x y



     

. Thay thế vào phương trình thứ hai của hệ

 

2

2 4 2 2 2 2

2 2 1 4 4 4 4 8 0 0 1x x x x x x x x y              

.

Cặp giá trị này nghiệm đúng hệ ban đầu, kết luận

 

 

0;1

S 

.

N

h

ậ

n

x

é

t

.

H

a

i

b

à

i

t

o

á

n

2

9

v

à

3

0

m

ở

m

à

n

c

h

o

l

ớ

p

b

à

i

t

o

á

n

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

v

ô

t

ỷ

g

i

ả

i

đ

ư

ợ

c

h

ỉ

t

h

ô

n

g

q

u

a

s

ử

d

ụ

n

g

t

í

n

h

c

h

ấ

t

đ

ơ

n

đ

i

ệ

u

h

à

m

s

ố

đ

ơ

n

t

h

u

ầ

n

   

f

u f v



,

t

r

o

n

g

đ

ó

t

h

a

o

t

á

c

đ

á

n

h

g

i

á

d

ấ

u

đ

ạ

o

h

à

m

c

ó

đ

ộ

k

h

ó

d

i

ễ

n

t

i

ế

n

t

h

e

o

x

u

h

ư

ớ

n

g

“

v

ừ

a

t

ă

n

g

,

v

ừ

a

g

i

ả

m

”

.

C

ụ

t

h

ể

g

i

ả

m

ứ

c

đ

ộ

c

h

ặ

n

m

i

ề

n

g

i

á

t

r

ị

b

i

ế

n

,

g

i

ả

m

t

ừ

p

h

ư

ơ

n

g

t

r

ì

n

h

b

ậ

c

h

a

i

x

u

ố

n

g

đ

i

ề

u

k

i

ệ

n

x

á

c

đ

ị

n

h

đ

ơ

n

g

i

ả

n

,

t

u

y

n

h

i

ê

n

m

ứ

c

đ

ộ

p

h

ứ

c

t

ạ

p

g

i

a

t

ă

n

g

d

o

c

h

ứ

a

c

ă

n

t

h

ứ

c

ở

b

i

ể

u

t

h

ứ

c

h

ố

t

c

h

ặ

n

.

C

á

c

b

ạ

n

l

ư

u

ý

t

à

i

l

i

ệ

u

n

à

y

k

h

ô

n

g

đ

ề

c

ậ

p

đ

ế

n

l

ớ

p

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

c

ó

đ

ị

n

h

ư

ớ

n

g

.

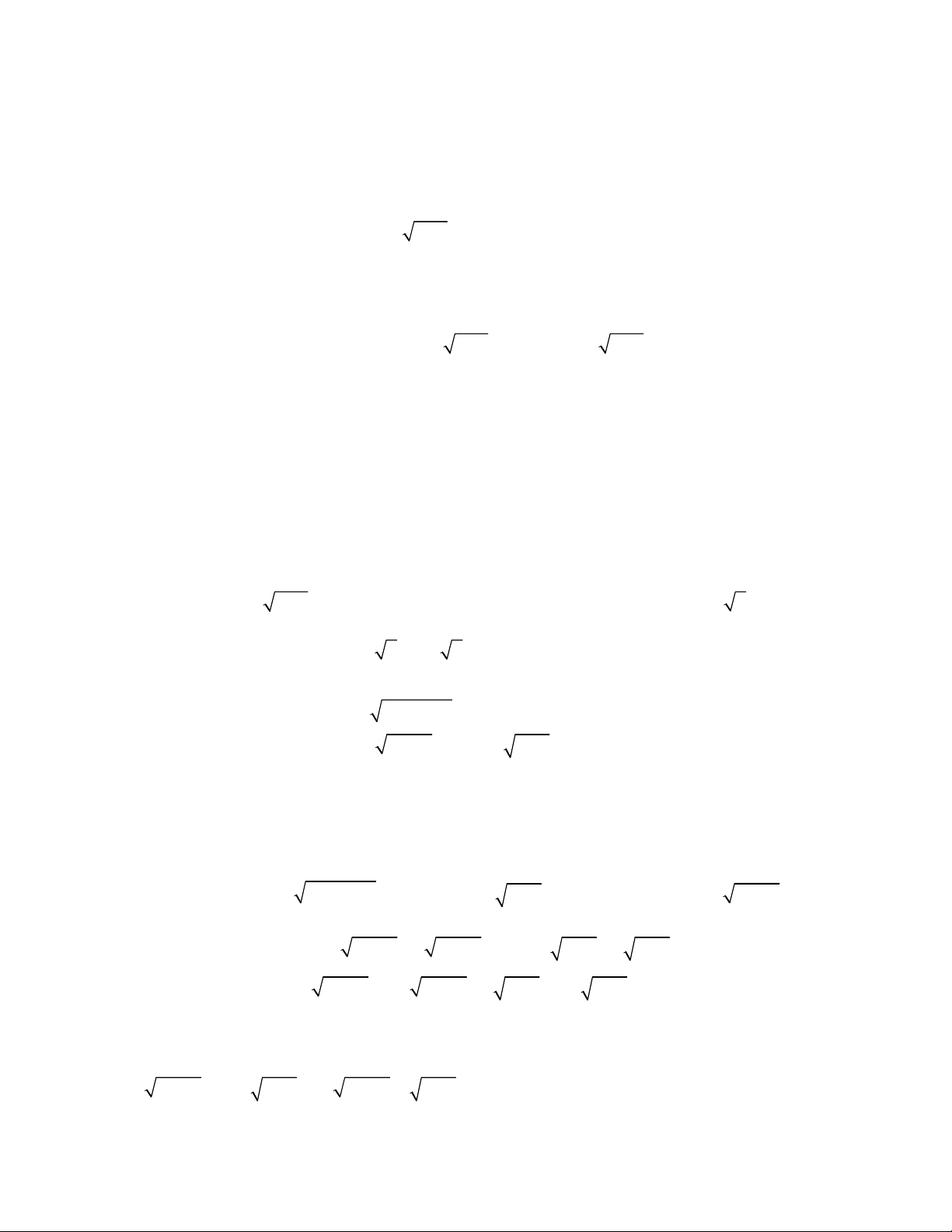
LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

23

1

.

P

h

â

n

t

í

c

h

p

h

ư

ơ

n

g

t

r

ì

n

h

t

h

ứ

n

h

ấ

t

,

t

ì

m

q

u

a

n

h

ệ

h

a

i

ẩ

n

.

2

.

T

h

a

y

t

h

ế

v

à

o

p

h

ư

ơ

n

g

t

r

ì

n

h

c

ò

n

l

ạ

i

v

à

s

ử

d

ụ

n

g

c

ô

n

g

c

ụ

h

à

m

s

ố

(

p

h

ư

ơ

n

g

t

r

ì

n

h

m

ộ

t

ẩ

n

)

.

T

r

ọ

n

g

t

â

m

t

à

i

l

i

ệ

u

l

à

s

ử

d

ụ

n

g

t

í

n

h

c

h

ấ

t

đ

ơ

n

đ

i

ệ

u

đ

ơ

n

t

h

u

ầ

n

h

o

ặ

c

k

h

ả

o

s

á

t

h

à

m

s

ố

,

t

ì

m

g

i

á

t

r

ị

l

ớ

n

h

ấ

t

–

g

i

á

t

r

ị

l

ớ

n

h

ấ

t

c

ó

s

ử

d

ụ

n

g

c

h

ặ

n

m

i

ề

n

g

i

á

t

r

ị

b

i

ế

n

,

t

ổ

n

g

h

ò

a

c

á

c

k

i

ế

n

t

h

ứ

c

đ

ạ

i

s

ố

,

l

ư

ợ

n

g

i

á

c

,

b

ấ

t

đ

ẳ

n

g

t

h

ứ

c

,

…

Đ

i

ề

u

n

à

y

đ

ò

i

h

ỏ

i

c

á

c

b

ạ

n

đ

ộ

c

g

i

ả

c

ầ

n

t

ỉ

n

h

t

á

o

,

n

h

ạ

y

b

é

n

,

t

ì

m

đ

i

ề

u

k

i

ệ

n

c

h

í

n

h

x

á

c

h

o

b

à

i

t

o

á

n

đ

ể

c

ó

n

h

ữ

n

g

đ

á

n

h

g

i

á

n

g

ắ

n

g

ọ

n

h

ấ

t

,

t

ố

i

ư

u

n

h

ấ

t

.

B

à

i

t

o

á

n

3

1

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

3 2 3

1 2 1,

;

12 8 3 2.

x y x

x y

y x x y



   







   







.

Lời giải.

Điều kiện

1x 

.

Biến đổi phương trình thứ nhất của hệ

 

2

1 1 2 1 1 1 1 1 0 1y x x y x y             

.

Từ đây dẫn đến

1

;2 1 1

y

x



 

. Phương trình thứ hai của hệ tương đương

 

   

3 3 2

3

3 8 12 2

3 8 12 6 1 3 2 1

3 2 1 3 2 1

y y x x

y y x x x x

y y x x

   

       

     

Xét hàm số

 

3

3 ; 1f t t t t  

thì

 

2

3

3 3 1 0, 1

f

t t t t





     

.

Hàm số liên tục và đồng biến trên miền đang xét. Thu được

   

2

1 2 1

f

y f x y x



   

.

Phương trình thứ nhất lại trở thành

2

0 2

2

2 1 4 2 2

4 4 4 4 8 8 0

x x

x x x

x x x x x

  

 

       

 

      

 

.

Suy ra hệ có nghiệm duy nhất

 

; 4 2 2;7 4 2

x y    .

B

à

i

t

o

á

n

3

2

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

   

 

3

2

2,

;

3 4 3 2 3 1.

y x x

x y

x x y y



   







    







.

Lời giải.

Điều kiện

3

2

0

1

3

2 0

1

0

x x

x

y





 









 

 













Từ phương trình thứ nhất

3

2

2 0 2 1 1

y

x x y y



        

. Đồng thời

1 3 2 1

x x

   

.

Phương trình thứ hai của hệ tương đương với

   

3

2 3 2 2 3 2 1 1 2 1

3 2 2 3 2 1 2 1

x

x x y y y

x x y y



       

       

Xét hàm số

 

3

2 ; 1f t t t t  

ta có đạo hàm

 

2

3 2 0, 1f t t t



    

.

Như vậy hàm số

 

f t

liên tục và đồng biến trên miền đang xét.

Thu được

   

3 2 1 3 2 1 3 2 1 3 1f x f y x y x y y x             

.

Với điều kiện

1x 

, phương trình thứ nhất khi đó trở thành

LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

24

   

 

 

2

3 2

2 2

3

3 2 9 1 1 2

1 1

1

;4 5;4 5

9

9 2 8 11 0

x x x x x x x

x x

x

x x x x x

         

 

 

     

 

      

 

Dẫn đến hệ có các nghiệm

   

; 1;2 , 4 5;11 3 5 , 4 5;11 3 5

x y      .

N

h

ậ

n

x

é

t

.

Đ

ể

x

â

y

d

ự

n

g

c

á

c

b

à

i

t

o

á

n

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

d

ạ

n

g

t

ư

ơ

n

g

t

ự

c

ũ

n

g

k

h

ô

n

g

q

u

á

k

h

ó

.



B

à

i

t

o

á

n

s

ố

3

2

c

á

c

b

ạ

n

c

ó

t

h

ể

đ

ể

ý

p

h

é

p

đ

á

n

h

g

i

á

m

i

ề

n

g

i

á

t

r

ị

3

2 2 0 2 1 1

y x x y y

         

,

l

à

h

o

à

n

t

o

à

n

t

ự

n

h

i

ê

n

,

t

ư

ơ

n

g

ứ

n

g

b

ư

ớ

c

n

g

o

ặ

t

đ

ầ

u

t

i

ê

n

,

c

ơ

b

ả

n

k

h

i

c

h

ú

n

g

t

a

t

h

ự

c

h

i

ệ

n

b

ì

n

h

p

h

ư

ơ

n

g

h

a

i

v

ế

.

Đ

ồ

n

g

t

h

ờ

i

p

h

ư

ơ

n

g

t

r

ì

n

h

t

h

ứ

h

a

i

c

ủ

a

h

ệ

c

ó

d

ạ

n

g

t

ư

ơ

n

g

đ

ồ

n

g

h

à

m

s

ố

   

f u f v



d

ễ

d

à

n

g

t

h

i

ế

t

l

ậ

p

.

C

h

ú

ý

r

ằ

n

g

c

á

c

ă

n

t

h

ứ

c

ẩ

n

h

à

m

3

2; 1

u

x v y



  

đ

ộ

c

l

ậ

p

v

ớ

i

r

i

ê

n

g

l

ẻ

t

ừ

n

g

b

i

ế

n

ê

n

t

h

a

o

t

á

c

đ

á

n

h

g

i

á

ẩ

n

h

à

m

l

à

h

ế

t

s

ứ

c

t

h

u

ậ

n

l

ợ

i

,

n

ó

s

ẽ

r

ấ

t

p

h

ứ

c

t

ạ

p

n

ế

u

c

h

ứ

a

h

a

i

b

i

ế

n

.



B

à

i

t

o

á

n

s

ố

3

1

k

h

ô

n

g

n

ằ

m

n

g

o

à

i

p

h

ạ

m

v

i

c

h

ặ

n

m

i

ề

n

g

i

á

t

r

ị

n

h

ư

n

g

c

ó

m

ộ

t

s

ố

y

ế

u

t

ố

g

â

y

k

h

ó

k

h

ă

n

.

C

ụ

t

h

ể

l

à

d

ự

a

t

r

ê

n

ề

n

t

ả

n

g

đ

i

ề

u

k

i

ệ

n

x

á

c

đ

ị

n

h

,

t

a

t

ạ

m

y

ê

n

t

â

m

v

ớ

i

1x 

,

k

h

i

m

a

n

h

n

h

a

t

ấ

n

c

ô

n

g

p

h

ư

ơ

n

g

t

r

ì

n

h

t

h

ứ

n

h

ấ

t

,

ý

t

ư

ở

n

g

đ

ơ

n

g

i

ả

n

h

ấ

t

l

à

s

u

y

r

a

1

0

x

y



 

n

h

ư

b

à

i

t

o

á

n

3

2

,

t

u

y

n

h

i

ê

n

d

o

c

ó

h

a

i

b

i

ế

n

t

h

a

m

g

i

a

n

ê

n

k

h

ô

n

g

t

i

ế

p

c

ậ

n

đ

ư

ợ

c

ẩ

n

y

,

k

h

ô

n

g

t

o

à

n

d

i

ệ

n

.



Ý

t

ư

ở

n

g

t

ạ

o

b

ạ

o

h

ơ

n

đ

ố

i

v

ớ

i

b

à

i

t

o

á

n

3

1

l

à

s

ử

d

ụ

n

g

b

i

ế

n

đ

ổ

i

t

ư

ơ

n

g

đ

ư

ơ

n

g

(

b

ì

n

h

p

h

ư

ơ

n

g

h

a

i

v

ế

)

,

m

ứ

c

đ

ộ

x

ấ

u

n

h

ấ

t

l

à

p

h

ư

ơ

n

g

t

r

ì

n

h

b

ậ

c

h

a

i

t

ổ

n

g

q

u

á

t

h

a

i

ẩ

n

v

ớ

i

m

ộ

t

r

o

n

g

h

a

i

ẩ

n

x

h

o

ặ

c

y

t

r

ở

t

h

à

n

h

t

h

a

m

s

ố

.

C

ụ

t

h

ể

 

2

2 2

1

0

1 0

2

1 2 5 0

2

2 2 1 4 4

x y

x x y y y

x xy y x y x

  







 



    



     





P

h

ư

ơ

n

g

t

r

ì

n

h

b

ậ

c

h

a

i

ẩ

n

x

,

t

h

a

m

s

ố

y

c

ó

b

i

ệ

t

h

ứ

c

 

2

1 2 5 4 4

y

y y y y





       

.

Đ

i

ề

u

k

i

ệ

n

c

ó

n

g

h

i

ệ

m

l

à

0 4 4 0 1y y



      

.

T

h

à

n

h

c

ô

n

g

.



M

ộ

t

p

h

ư

ơ

n

g

h

ư

ớ

n

g

k

h

á

c

l

à

 

2

1 1 2 1 1 1 1 1 0 1y x x y x y             

.

Đ

â

y

l

à

n

g

ụ

ý

b

a

n

đ

ầ

u

c

ủ

a

t

á

c

g

i

ả

,

c

ũ

n

g

c

h

í

n

h

l

à

c

ơ

s

ở

c

h

o

l

ờ

i

g

i

ả

i

p

h

í

a

t

r

ê

n

.

T

u

y

n

h

i

ê

n

đ

ể

đ

ả

m

b

ả

o

y

ế

u

t

ố

t

ự

n

h

i

ê

n

,

c

h

ắ

c

h

ắ

n

c

á

c

b

ạ

n

đ

ộ

c

g

i

ả

n

ê

n

t

h

ự

c

h

i

ệ

n

t

ậ

p

k

ế

t

h

a

i

b

i

ế

n

v

ề

h

a

i

b

i

ế

n

c

h

i

ế

n

t

u

y

ế

n

1

2 1 1 2 1

x

y x y x x



       

.

T

h

ự

c

h

i

ệ

n

đ

ặ

t

ẩ

n

p

h

ụ

2

1

; 0 1

x

t t x t



    

,

d

ẫ

n

đ

ế

n

b

i

ể

u

d

i

ễ

n

 

2 2

1

1 2 2 2

y

t t t t f t



      

.

H

à

m

s

ố

ẩ

n

t

n

à

y

c

ó

n

h

i

ề

u

c

á

c

h

đ

á

n

h

g

i

á

,

d

ù

n

g

h

ằ

n

g

đ

ẳ

n

g

t

h

ứ

c

h

o

ặ

c

k

h

ả

o

s

á

t

h

à

m

s

ố

b

ậ

c

h

a

i

–

p

a

r

a

b

o

l

,

đ

ề

u

l

à

n

h

ữ

n

g

k

ỹ

n

ă

n

g

c

ơ

b

ả

n

.

T

r

o

n

g

t

r

ư

ờ

n

g

h

ợ

p

h

à

m

s

ố

c

ó

d

ạ

n

g

t

ổ

n

g

q

u

á

t

b

ậ

c

h

a

i

h

o

ặ

c

b

ậ

c

b

a

,

p

h

ư

ơ

n

g

á

n

t

ố

i

ư

u

l

à

n

ê

n

s

ử

d

ụ

n

g

c

ô

n

g

c

ụ

đ

ạ

o

h

à

m

–

h

à

m

s

ố

 

3 2

f t at bt ct

f

t at bt ct d

  



  

B

à

i

t

o

á

n

3

.

T

r

í

c

h

l

ư

ợ

c

â

u

3

,

T

h

ử

s

ứ

c

t

r

ư

ớ

c

k

ỳ

t

h

i

Đ

ạ

i

h

ọ

c

2

0

1

5

,

Đ

ề

s

ố

2

;

N

ă

m

h

ọ

c

2

0

1

3

–

2

0

1

4

;

T

ạ

p

c

h

í

T

o

á

n

h

ọ

c

v

à

t

u

ổ

i

t

r

ẻ

,

N

h

à

X

u

ấ

t

b

ả

n

G

i

á

o

d

ụ

c

V

i

ệ

t

N

a

m

;

S

ố

4

3

6

,

T

h

á

n

g

1

0

n

ă

m

2

0

1

3

.

T

á

c

g

i

ả

:

H

u

ỳ

n

h

N

g

u

y

ễ

n

L

u

â

n

L

ư

u

–

N

g

u

y

ễ

n

T

h

ị

D

u

y

A

n

.

G

i

á

o

v

i

ê

n

T

r

u

n

g

t

â

m

B

ồ

i

d

ư

ỡ

n

g

v

ă

n

h

ó

a

T

h

ă

n

g

L

o

n

g

,

T

p

.

H

ồ

C

h

í

M

i

n

h

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

3

2

4

3 1 2 1 0,

;

2 2 1 0.

x x y y

x y

x x y y



    







    







.

Lời giải.

LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

25

Điều kiện

1

0

2

y



 

. Từ điều kiện ta có

1

0

0 2 1 1

2

y



     

. Từ phương trình thứ hai của hệ

   

2

1

2

2 1 0 2 1 0 0 0 2 1

2

x

x y y x x x x



               

.

Biến đổi phương trình thứ nhất của hệ

         

3

8

6 2 2 2 1 2 3 2 2 1 2 1 3 2 1 1

x

x y y x x y y y             

.

Xét hàm số

 

 

 

 

3

2 2

3

; 0;1 3 3 3 1 0, 0;1

f

t t t t f t t t t



          

.

Hàm số liên tục và nghịch biến trên miền đang xét dẫn đến

   

 

2

4 1

1 2 2 1 2 2 1

2

x

f x f y x y y



          .

Phương trình thứ hai trở thành

 

2

2 2

2

0

1

;0

2 2 8 0

2

2 1 2 8

4 4 1 2 8

0

1

;0

1

1 1 1

;0

;0 ; 0; , ;0

2

2 2 2

1 1

;

12 4 1 0

2 6

x

x x x x

x x

x x x

x

x x y

x

x x













 



 

     





 



 



  









   





















 



 



 

    





 

 



        

     

  

 



 

    

 



 



 

 

  

 











 











Kết luận hệ đã cho có hai nghiệm kể trên.

B

à

i

t

o

á

n

3

4

.

T

r

í

c

h

l

ư

ợ

c

â

u

I

.

2

;

Đ

ề

t

h

i

c

h

ọ

n

h

ọ

c

s

i

n

h

g

i

ỏ

i

l

ớ

p

1

2

T

H

P

T

;

M

ô

n

T

o

á

n

;

Đ

ề

t

h

i

c

h

í

n

h

t

h

ứ

c

;

S

ở

G

i

á

o

d

ụ

c

v

à

Đ

à

o

t

ạ

o

T

ỉ

n

h

H

ả

i

D

ư

ơ

n

g

;

N

ă

m

h

ọ

c

2

0

1

2

–

2

0

1

3

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

   

 

3

3 1 9 1 ,

;

1 1 1.

x x y y

x y



    









   





.

Lời giải.

Điều kiện

1; 1y x 

. Phương trình thứ hai của hệ dẫn đến

1

1 1 1

y

x



   

.

Biến đổi phương trình thứ nhất

   

3

1 3 1x x y y



    

.

Xét hàm số

   

 

3

2 2

3

; 1 3 3 3 1 0, 1

f

t t t t f t t t t





         

.

Như vậy hàm số trên liên tục và đồng biến trên miền đang xét, thu được

   

 

1 1f x f y x y      

.

Phương trình thứ hai lại trở thành

  

 

1

1 1 1 1;2

1 2 0

x

x x x x x

x x







         



  





.

Kết luận hệ có hai nghiệm

     

; 1;2 , 2;5

x y 

.

B

à

i

t

o

á

n

3

5

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

2

3

2

1

1,

1

;

2 1 2.

x x

y y

y

x y

x x y







  











   







.

Lời giải.

LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

26

Điều kiện

1

y





. Từ phương trình thứ hai của hệ ta có

 

3 2 3

2

2 1 1, 2 3 0

1 11

1

3 0 1 0 1

2

4

x x y y x x

x

x x x x x



         

 

 



          





 

 

 

 



Phương trình thứ nhất của hệ tương đương với

   

 

3

2 2 3 2 2 2

2 1 1 2 1 1 2 1 1

x x y y x x y y y           .

Xét hàm số

   

3

2

; 1 3 2 0, 1

f

t t t t f t t t





       

.

Hàm số trên liên tục và đồng biến trên miền

1t 

. Thu được

   





2

1

1 1

f

x f y x y



    

.

Thay thế vào phương trình thứ hai

 

3

3 2

2

2 2 0 1 2 0

1 7

1

0 1 0 0

2

4

x x x x x x x x

x x x y y



          





 



         





 

 

 

 

Kết luận hệ có nghiệm duy nhất

1; 0

x y

 

.

B

à

i

t

o

á

n

3

6

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

   

 

2

3

1 3,

;

3 1 2 1 .

y x x

x y

x x y y x



    







     







.

Lời giải.

Điều kiện

1

; 2 1 0; 3

x

y x y



    

.

Từ phương trình thứ nhất của hệ ta có

2

3

1 3 0 4 2, 1 3 4 1

y

x x x y y



             

.

Kết hợp

1

2

1 1

1 2 1 4

2

1 2

x

y y x

y x

 



 

 



 

  

   



 





Phương trình thứ hai của hệ tương đương

   

     

   

3

2 2

3 2 3

3 3 1 3 2 1 2 1 3 2 1

1

3 1 2 1 2 2 1

x x x x x y x y x

x x y x y x

           



         

Xét hàm số

     

3

2 2

3 ; 2 3 6 3 2 0, 2

f t t t t f t t t t t t



          

.

Hàm số trên liên tục và đồng biến trên miền

2t 

nên thu được

   

 

2

1 2 1 1 2 1 2 1 2 1

f x f y x x y x x x y x x y                  

.

Phương trình thứ nhất trở thành

2

3 1 3 1 0 1; 1x x x x x y          

. Hệ có nghiệm duy nhất.

N

h

ậ

n

x

é

t

.

B

à

i

t

o

á

n

s

ố

3

6

c

ó

h

a

i

ẩ

n

h

à

m

k

h

ó

n

h

ậ

n

b

i

ế

t

n

u

ô

i

g

i

ấ

u

t

r

o

n

g

p

h

ư

ơ

n

g

t

r

ì

n

h

t

h

ứ

h

a

i

c

ủ

a

h

ệ

.

V

ấ

n

đ

ề

p

h

á

t

h

i

ệ

n

ẩ

n

h

à

m

n

à

y

đ

ã

đ

ư

ợ

c

t

r

ì

n

h

b

à

y

t

r

o

n

g

t

à

i

l

i

ệ

u

H

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

c

h

ứ

a

c

ă

n

t

h

ứ

c

p

h

ầ

n

t

h

ứ

5

.

Ẩ

n

h

à

m

t

h

ứ

n

h

ấ

t

ạ

m

t

h

ờ

i

c

h

ư

a

t

h

ể

k

h

a

i

p

h

á

,

k

h

ô

n

g

q

u

á

k

h

ó

đ

ể

n

h

ậ

n

r

a

ẩ

n

h

à

m

t

h

ứ

h

a

i

2 1v y x  

,

v

ấ

n

đ

ề

t

i

ế

p

t

h

e

o

l

à

x

â

y

d

ự

n

g

d

ạ

n

g

t

ư

ơ

n

g

đ

ồ

n

g

h

à

m

s

ố

   

f

u f v



n

h

ư

t

h

ế

n

à

o

,

v

à

đ

i

ề

u

n

à

y

c

ó

k

h

ả

t

h

i

h

a

y

k

h

ô

n

g

,

đ

ố

i

v

ớ

i

b

à

i

t

o

á

n

t

r

ê

n

.

C

á

c

b

ạ

n

đ

ộ

c

g

i

ả

c

ầ

n

p

h

â

n

b

i

ệ

t

r

õ

r

à

n

g

h

a

i

t

r

ư

ờ

n

g

h

ợ

p

x

ả

y

r

a

,

m

a

n

h

n

h

a

c

h

o

c

á

c

b

ư

ớ

c

b

i

ể

n

đ

ổ

i

c

ó

l

ý

o

   

2 2 1, 1

y x m y x m

    

.

o

   

3

2

1 2 1 2 1

y

y y x y x



     

LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

27

T

r

ư

ờ

n

g

h

ợ

p

t

h

ứ

n

h

ấ

t

   

2 2 1, 1

y x m y x m

    

k

h

i

đ

ó

v

ế

p

h

ả

i

p

h

ư

ơ

n

g

t

r

ì

n

h

c

h

ú

n

g

t

a

k

h

a

i

t

r

i

ể

n

r

a

c

ó

d

ạ

n

g

   

2 1 2 1 1 2 1y x y x m y x       

.

Đ

i

ề

u

n

à

y

k

h

ẳ

n

g

đ

ị

n

h

à

m

s

ố

g

ố

c

t

ố

i

t

h

i

ể

u

c

ó

d

ạ

n

g

 

3

2

f

t at bt ct



 

,

t

r

o

n

g

đ

ó

0

ac



.

H

ệ

s

ố

b

c

ó

t

h

ể

t

ồ

n

t

ạ

i

h

o

ặ

c

k

h

ô

n

g

,

n

ế

u

c

ó

t

h

ì

h

à

m

s

ố

s

ẽ

c

à

n

g

p

h

ứ

c

t

ạ

p

,

v

ì

2

bt

k

h

ô

n

g

c

h

ứ

a

c

ă

n

ê

n

g

ư

ờ

i

t

h

i

ế

t

l

ậ

p

b

à

i

t

o

á

n

s

ẽ

s

ử

d

ụ

n

g

t

h

ê

m

b

ớ

t

l

à

m

c

h

o

n

ó

ẩ

n

g

i

ấ

u

đ

i

r

ấ

t

d

ễ

d

à

n

g

.

T

r

ư

ờ

n

g

h

ợ

p

t

h

ứ

h

a

i

,

c

h

í

n

h

l

à

b

à

i

t

o

á

n

s

ố

4

1

,

đ

ả

m

b

ả

o

c

h

ắ

c

h

ắ

n

h

à

m

s

ố

   

3

2

, 0

f t at bt c

  

,

đ

i

ề

u

n

à

y

s

ẽ

t

ă

n

g

c

ư

ờ

n

g

t

ố

c

đ

ộ

c

h

o

c

á

c

t

h

a

o

t

á

c

l

ậ

p

l

u

ậ

n

c

ủ

a

c

á

c

b

ạ

n

.

T

h

i

ế

t

l

ậ

p

h

à

m

s

ố

v

ớ

i

1

a



         

   

     

3

3 2 3

3

3 2 3 2 2

3

3 2 3 2

3 3 1 2 1 2 1 2 1

3 3 2 2 1 2 1

3 3 2 2 2 1

x x y y x x m b x m y x b y x

x x m xm m bx bxm bm b y x y x

x m b x m bm b x by m bm b y x

               

            

            

Đ

ồ

n

g

n

h

ấ

t

h

ệ

s

ố

         

3

2 3

3 2

3 3

3

1 3 1 2 1 2 2 1

3 2 2 3

1

m b

b

x x y x y x

m bm b

m

m bm b

 





 

 





           



  







  



.

B

à

i

t

o

á

n

3

7

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

   

 

2

3 2 3 3 ,

;

4 1 1 4 2 5 5 2 12 3 3 .

xy x x x y x

x y

y x y x x x x y



     







         







.

Lời giải.

Điều kiện

1

0; 2

y

x x



  

. Phương trình thứ nhất của hệ tương đương với

          

 

3

2 3 3 2 3

3

3 2 0 2

2 0

x

x x x y y x x x x x y

x

y x x y x x

y

x x

           







         





  



Với

2 0

y x x y x

     

. Kết hợp

5 2 1

2

0

1 1

x

y x



 









 

 

  







Phương trình thứ hai của hệ tương đương với

   

 

   

3

4

1 1 3 3 3 15 6 4 5 2 5 2

4

1 3 1 4 5 2 3 5 2

y

x y x y x x x x

y

x y x x x

           



         

Xét hàm số

     

3

2 2

4

3 ; 1 12 6 6 2 1 0, 1

f

t t t t f t t t t t t





         

.

Hàm số trên liên tục và đồng biến trên miền đang xét, dẫn đến

   

1 5 2 1 5 2 1 5 2 4

f y x f x y x x y x x y x                

.

Khi đó

2

5

2 4 2 5 2

4 16 16 5 2

2

7

5 9 5

7 5 7 5

;

4 4

4

14 11 0

4 4

x

y x x x x

x x x

x

x y

x

x x





       



   













 

 

     

 

   



  

 





 

 



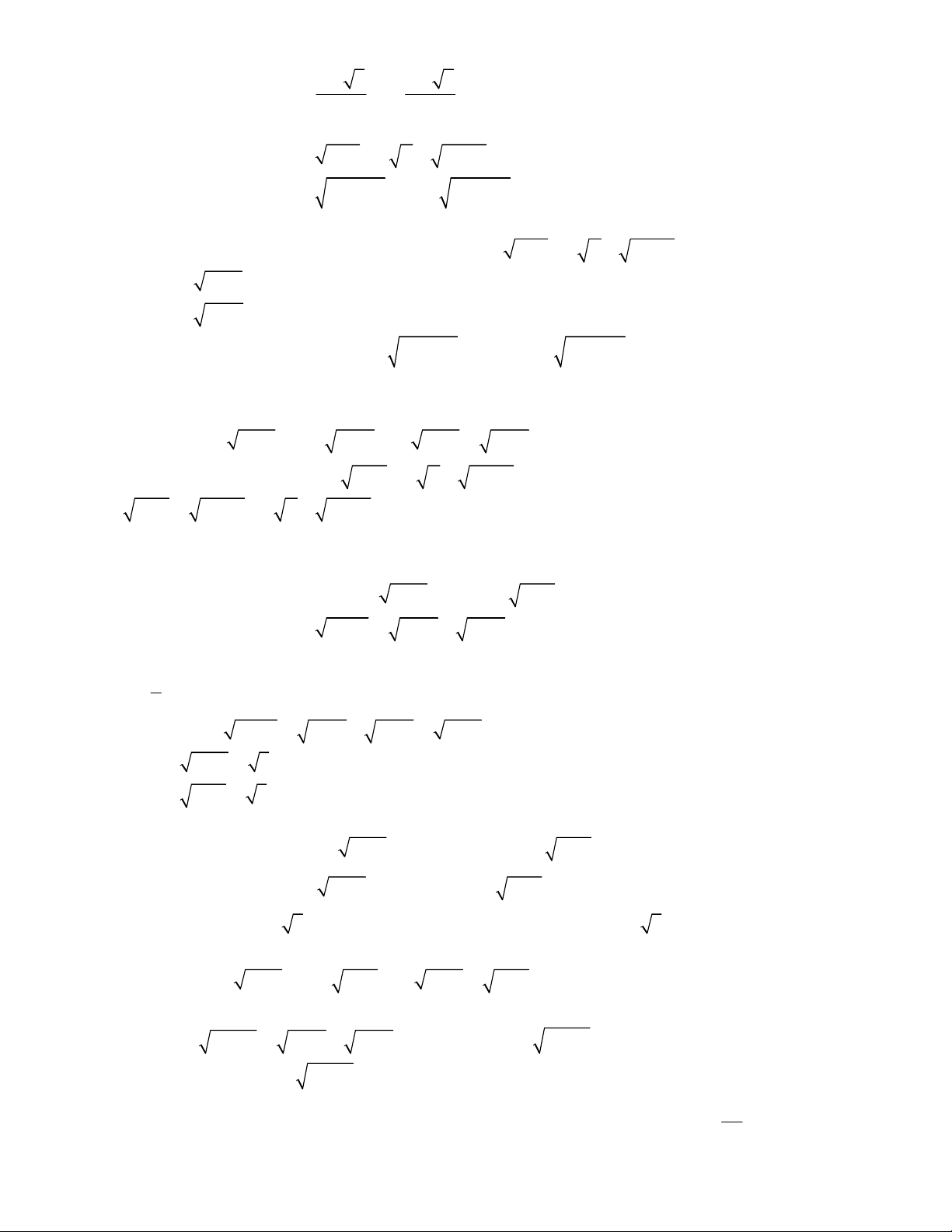
LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

28

Kết luận hệ có nghiệm duy nhất

7

5 9 5

;

4

x y

 

 

.

B

à

i

t

o

á

n

3

8

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

   

 

3

1 2 2 1,

;

2 3 4 3 6.

x y y

x y

x x y y



   







     







.

Lời giải.

Điều kiện

1

; 0

x

y



. Từ phương trình thứ nhất của hệ ta có

1

2 2 1 1 1 1 2

x

y y x x



        

.

Kết hợp

2 2

2

0

4 2

x

y



 









 



 







Phương trình thứ hai của hệ tương đương với

       

3

2

3 2 4 3 4

x

x y y



     

.

Xét hàm số

     

3

2 2

3

; 2 3 6 3 2 0, 2

f

t t t t f t t t t t t





         

.

Hàm số trên liên tục và đồng biến trên miền đang xét nên thu được

   

2 4 2 4 2 4 2

f x f y x y x y x y

             

.

Khi đó phương trình thứ nhất trở thành

 

1 2 2 1y y y

    

.

Để ý rằng

1

2 1 2 2 1, 0

y

y y y y



      

.

Dẫn đến (*) có nghiệm khi

   

0 2 ; 2;0

y x x y    

là nghiệm duy nhất của hệ.

B

à

i

t

o

á

n

3

9

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

   

 

4 2 2 4 1 1 9 9 9,

;

5 1 2 2.

x x y y x y

x y

x y y



       







    







.

Lời giải.

Điều kiện

1

;

2

5

x

y



. Từ phương trình thứ hai của hệ

5

1 2 2 2 2 2, 2 5 1 4 1

x

y y y x x



             

.

Do đó

2 3

1

2

1 3

x

y



 









 



 







Phương trình thứ nhất của hệ tương đương với

       

 

   

3

4

2 2 9 2 4 1 1 9 1

4

2 9 2 4 1 9 1

x x x y y y

x x y y

        



       

Xét hàm số

 

3

2

4 9 ; 3

f t t t t   ta có

   

2

12 18 6 2 3 0, 3

f t t t t t t



       .

Hàm số trên liên tục và đồng biến trên miền đang xét nên thu được hệ thức

   

2 1 2 1 2 1 1

f x f y x y x y x y             

.

Phương trình thứ hai của hệ trở thành

    

        

2

5 6 2 2 5 6 2 2 4

3 6 2 4 9 2 4 2 2

26

2 9 2 4 2 0 2 5 26 0 2;

5

y y y y y y

y y y y y

y y y y y y

         

        

 

            

 

 

 

LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

29

Từ đây dẫn đến hệ có hai nghiệm

   

21

26

;

1;2 , ;

5

x

y







 





.

N

h

ậ

n

x

é

t

.

T

h

ô

n

g

q

u

a

3

9

b

à

i

t

o

á

n

m

ở

đ

ầ

u

t

à

i

l

i

ệ

u

,

c

ó

l

ẽ

n

h

i

ề

u

b

ạ

n

đ

ộ

c

g

i

ả

đ

ã

đ

ị

n

h

ì

n

h

r

õ

r

à

n

g

h

ư

ớ

n

g

đ

i

đ

á

n

h

g

i

á

m

i

ề

n

g

i

á

t

r

ị

c

ủ

a

c

á

c

b

i

ế

n

t

r

o

n

g

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

.

M

ộ

t

c

â

u

h

ỏ

i

đ

ặ

t

r

a

l

à

l

à

m

t

h

ế

n

à

o

đ

ể

x

â

y

d

ự

n

g

c

á

c

b

à

i

t

o

á

n

t

ư

ơ

n

g

t

ự

,

v

ì

m

ộ

t

đ

i

ề

u

b

ă

n

k

h

o

ă

n

l

à

p

h

ư

ơ

n

g

t

r

ì

n

h

c

h

ố

t

c

h

ặ

n

(

T

)

c

ủ

a

c

h

ú

n

g

t

a

(

p

h

ư

ơ

n

g

t

r

ì

n

h

p

h

ụ

c

v

ụ

đ

á

n

h

g

i

á

ẩ

n

)

c

ó

h

a

i

v

a

i

t

r

ò

o

Đ

á

n

h

g

i

á

ẩ

n

.

o

G

i

ả

i

n

g

h

i

ệ

m

.

V

a

i

t

r

ò

t

h

ứ

n

h

ấ

t

h

ì

c

ó

t

h

ể

m

u

ô

n

h

ì

n

h

v

ạ

n

t

r

ạ

n

g

,

đ

a

c

h

i

ề

u

,

ở

đ

â

y

t

á

c

g

i

ả

t

ạ

m

d

ừ

n

g

c

h

â

n

v

ớ

i

p

h

ư

ơ

n

g

t

r

ì

n

h

b

ậ

c

h

a

i

t

ổ

n

g

q

u

á

t

v

à

p

h

ư

ơ

n

g

t

r

ì

n

h

c

h

ứ

a

c

ă

n

b

ậ

c

h

a

i

(

h

a

i

ẩ

n

c

ơ

b

ả

n

)

t

r

o

n

g

p

h

ạ

m

v

i

b

i

ế

n

đ

ổ

i

t

ư

ơ

n

g

đ

ư

ơ

n

g

–

n

â

n

g

c

a

o

l

ũ

y

t

h

ừ

a

,

b

ậ

c

t

r

o

n

g

c

ă

n

c

a

o

n

h

ấ

t

l

à

b

ậ

c

n

h

ấ

t

h

o

ặ

c

q

u

y

(

T

)

v

ề

m

ộ

t

r

o

n

g

c

á

c

d

ạ

n

g

đ

ặ

c

t

h

ù

   

i

f

x g x



 

v

ớ

i

   

i

f x g x



 

   

i i

f x g x





v

ớ

i

   

i i

f x g x

  

.

S

ỡ

d

ĩ

n

h

ư

v

ậ

y

v

ì

k

h

i

t

h

i

ế

t

l

ậ

p

h

à

m

s

ố

,

t

ì

m

đ

ư

ợ

c

m

ố

i

l

i

ê

n

h

ệ

g

i

ữ

a

h

a

i

ẩ

n

,

t

h

a

y

t

h

ế

n

g

ư

ợ

c

l

ạ

i

p

h

ư

ơ

n

g

t

r

ì

n

h

(

T

)

t

h

ì

t

h

a

o

t

á

c

g

i

ả

i

n

g

h

i

ệ

m

t

r

ở

n

ê

n

đ

ơ

n

g

i

ả

n

v

à

k

h

ả

t

h

i

.

T

r

o

n

g

c

á

c

t

r

a

n

g

t

i

ế

p

t

h

e

o

t

á

c

g

i

ả

s

ẽ

g

i

ớ

i

t

h

i

ệ

u

c

á

c

b

à

i

t

o

á

n

v

ớ

i

c

ă

n

b

ậ

c

b

a

,

d

ự

a

t

r

ê

n

c

ơ

s

ở

p

h

ư

ơ

n

g

t

r

ì

n

h

(

T

)

g

i

ả

i

b

ằ

n

g

ẩ

n

p

h

ụ

đ

ư

a

v

ề

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

.

N

h

â

n

d

ị

p

n

à

y

t

ô

i

c

ũ

n

g

x

i

n

c

h

i

a

s

ẻ

m

ộ

t

k

i

n

h

n

g

h

i

ệ

m

t

r

o

n

g

v

i

ệ

c

x

â

y

d

ự

n

g

h

à

m

s

ố

t

ạ

i

p

h

ư

ơ

n

g

t

r

ì

n

h

c

ò

n

l

ạ

i

(

A

)

,

l

ấ

y

đ

i

ể

n

h

ì

n

h

b

à

i

t

o

á

n

s

ố

3

9

n

h

é

.

C

á

c

b

ư

ớ

c

đ

ạ

i

k

h

á

i

n

h

ư

s

a

u



L

ự

a

c

h

ọ

n

h

ị

t

h

ứ

c

h

o

p

h

ư

ơ

n

g

t

r

ì

n

h

(

T

)

,

2

2 2 2 2, 2 4

ax

b y y y ax b



           

.

D

ấ

u

đ

ẳ

n

g

t

h

ứ

c

x

ả

y

r

a

k

h

i

2

y



.



T

h

à

n

h

t

h

ử

l

ấ

y

n

g

h

i

ệ

m

đ

ẹ

p

2

; 1 5 1 6 2 7 3...

y

x ax b x x x



        

N

h

ư

v

ậ

y

t

a

t

h

u

đ

ư

ợ

c

1

2

x

y













T

r

ê

n

đ

â

y

l

ư

u

ý

c

h

ỉ

c

ầ

n

c

ố

ý

“

g

i

ả

v

ờ

”

n

g

h

i

ệ

m

đ

ẹ

p

2

; 1

y

x



m

à

t

h

ô

i

,

v

ì

s

a

u

k

h

i

t

h

i

ế

t

l

ậ

p

đ

ư

ợ

c

q

u

a

n

h

ệ

h

à

m

s

ố

đ

ố

i

v

ớ

i

p

h

ư

ơ

n

g

t

r

ì

n

h

(

A

)

,

đ

ặ

c

b

i

ệ

t

l

ạ

i

c

ó

d

ạ

n

g

n

h

ị

t

h

ứ

c

b

ậ

c

n

h

ấ

t

2

ẩ

n

mx

ny p





,

t

h

a

y

t

h

ế

v

à

o

p

h

ư

ơ

n

g

t

r

ì

n

h

(

T

)

c

h

ú

n

g

t

a

l

u

ô

n

l

u

ô

n

g

i

ả

i

đ

ư

ợ

c

,

m

ộ

t

k

h

i

v

á

n

đ

ã

đ

ó

n

g

t

h

u

y

ề

n

,

l

ú

c

đ

ó

c

ò

n

q

u

a

n

t

â

m

g

ì

đ

ế

n

g

h

i

ệ

m

x

ấ

u

h

a

y

đ

ẹ

p

l

à

m

g

ì

n

ữ

a

,

n

g

h

i

ệ

m

x

ấ

u

t

h

ì

c

à

n

g

i

ấ

u

đ

ư

ợ

c

b

ả

n

c

h

ấ

t

,

c

h

ố

n

g

p

h

á

m

ò

n

g

h

i

ệ

m

,

đ

i

ể

n

h

ì

n

h

p

h

i

v

ụ

3

9

c

ó

c

ặ

p

n

g

h

i

ệ

m

“

n

g

o

à

i

g

i

á

t

h

ú

”

m

à

v

ẫ

n

t

h

ỏ

a

m

ã

n

h

ệ

b

a

n

đ

ầ

u

đ

ó

t

h

ô

i

,

 

21 26

;

5

x

y











 

.



B

ư

ớ

c

t

i

ế

p

t

h

e

o

l

à

l

ự

a

c

h

ọ

n

d

ạ

n

g

t

h

ứ

c

h

à

m

s

ố

,

t

í

n

h

c

h

ấ

t

đ

ơ

n

đ

i

ệ

u

l

à

đ

ồ

n

g

b

i

ế

n

v

ì

m

i

ề

n

g

i

á

t

r

ị

c

ủ

a

c

h

ú

n

g

t

a

k

h

á

c

ơ

b

ả

n

1

2

x

y











,

t

h

a

y

v

ì

đ

ộ

p

h

ứ

c

t

ạ

p

1

2

1

2

x

y



 







 



t

h

ư

ờ

n

g

d

ù

n

g

c

h

o

t

r

ư

ờ

n

g

h

ợ

p

đ

ơ

n

đ

i

ệ

u

n

g

h

ị

c

h

b

i

ế

n

.



N

ó

i

t

ớ

i

v

ấ

n

đ

ề

h

à

m

s

ố

l

ạ

i

c

ó

n

h

i

ề

u

d

ạ

n

g

,

c

ó

t

h

ể

d

ạ

n

g

đ

a

t

h

ứ

c

,

p

h

â

n

t

h

ứ

c

h

o

ặ

c

h

ứ

a

c

ả

h

à

m

s

i

ê

u

v

i

ệ

t

,

n

h

ư

n

g

t

h

ô

i

đ

ể

a

n

t

o

à

n

ê

n

s

ử

d

ụ

n

g

h

à

m

s

ố

đ

a

t

h

ứ

c

,

đ

ả

m

b

ả

o

l

u

ô

n

l

i

ê

n

t

ụ

c

,

d

ự

k

i

ế

n

ẩ

n

h

à

m

l

à

s

ẽ

l

à

h

a

i

c

ă

n

t

h

ứ

c

n

h

ỏ

x

í

u

,

s

a

u

k

h

i

t

r

i

ể

n

k

h

a

i

s

ẽ

x

u

ấ

t

h

i

ệ

n

q

u

a

n

h

ệ

b

ậ

c

n

h

ấ

t

mx

ny p





,

n

ế

u

k

h

ô

n

g

t

h

ì

x

ô

i

h

ỏ

n

g

b

ỏ

n

g

k

h

ô

n

g

.

C

á

c

p

h

ư

ơ

n

g

á

n

đ

ư

ợ

c

x

e

m

x

é

t

b

a

o

g

ồ

m

Ẩ

n

h

à

m

1

1 1 2 2 2

2 2

1

1 1 2 2 2

2

1

1 1 2 2 2

;

u a x b y c v a x b y c



     



     



     



H

à

m

s

ố

 

2

3

2

4 3 2

...

f t at bt ct

f t at bt ct d

f t at bt ct dt e



  



   



    





LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

30



B

à

i

t

o

á

n

3

9

t

á

c

g

i

ả

l

ự

a

c

h

ọ

n

2 3

1

2

1 3

x

y



 









 



 







H

i

ể

n

h

i

ê

n

c

o

n

s

ố

3

l

à

m

ộ

t

s

ố

v

ô

t

ỷ

,

l

ẻ

t

ó

e

l

o

e

,

n

h

ư

n

g

c

h

ú

n

g

t

a

k

h

ô

n

g

n

h

ấ

t

h

i

ế

t

x

â

y

d

ự

n

g

h

à

m

s

ố

c

ó

đ

ạ

o

h

à

m

p

h

ả

i

c

h

ứ

a

n

ó

.

L

ự

a

c

h

ọ

n

b

i

ể

u

t

h

ứ

c

đ

ạ

o

h

à

m

   

f

t t t k







v

ớ

i

 

0

0;

f

t t t k





  

.

D

ễ

t

h

ấ

y

r

ằ

n

g

n

ế

u

c

ó

đ

i

ề

u

k

i

ệ

n

0 3

k 

t

h

ì

   

0, 3 0

f t t t k t k



      

,

t

h

e

o

l

ý

t

h

u

y

ế

t

d

ấ

u

c

ủ

a

n

h

ị

t

h

ứ

c

b

ậ

c

n

h

ấ

t

,

p

h

ạ

m

v

i

c

h

ư

ơ

n

g

t

r

ì

n

h

Đ

ạ

i

s

ố

l

ớ

p

1

0

T

H

P

T

.

H

à

m

s

ố

l

ậ

p

t

ứ

c

đ

ồ

n

g

b

i

ế

n

.



C

h

ọ

n

g

a

y

 

3

1,5 3

2

k f t t t









    









,

p

h

á

h

ữ

u

t

ỷ

đ

ư

a

v

ề

   

2

3 2 3

f

t t t t t





  

.

K

h

i

đ

ó

l

ấ

y

n

g

u

y

ê

n

h

à

m

n

g

ư

ợ

c

t

r

ở

l

ạ

i

,

h

i

ệ

n

g

u

y

ê

n

h

ì

n

h

à

m

s

ố

g

ố

c

 

2

3 2

2

3

2 3

3

2

t t t t C   



.

T

ấ

t

n

h

i

ê

n

k

h

ô

n

g

n

ê

n

đ

è

o

b

ồ

n

g

t

h

ê

m

h

ằ

n

g

s

ố

C

v

ì

t

ấ

t

y

ế

u

h

a

i

v

ế

c

ủ

a

(

A

)

đ

ề

u

c

ó

C

s

ẽ

x

ả

y

r

a

t

r

i

ệ

t

i

ê

u

h

o

à

n

t

o

à

n

.

T

i

ế

p

t

ụ

c

p

h

á

h

ữ

u

t

ỷ

,

l

ấ

y

h

à

m

s

ố

d

ạ

n

g

đ

a

t

h

ứ

c

h

ệ

s

ố

n

g

u

y

ê

n

 

3

2 3 2

2

3

6

4 9

3

2

f

t t t t t

 

   

 

 

.



T

r

i

ể

n

k

h

a

i

p

h

á

t

u

n

g

h

ỏ

a

m

ù

t

h

e

o

h

a

i

ẩ

n

h

à

m

2

; 1

u

x v y



  

,

t

ứ

c

l

à

b

i

ế

n

đ

ổ

i

n

g

ư

ợ

c

l

ờ

i

g

i

ả

i

   

       

 

   

3

4

2 2 4 1 1 9 9 9

4

2 2 9 2 4 1 1 9 1

4

2 9 2 4 1 9 1

x x y y x y

x x x y y y

x x y y

       



        



       

G

h

é

p

c

á

c

p

h

ư

ơ

n

g

t

r

ì

n

h

(

T

)

,

(

A

)

k

i

ế

n

l

ậ

p

đ

ư

ợ

c

đ

ề

b

à

i

t

h

e

o

đ

ú

n

g

ý

đ

ồ

t

ù

y

ý

.

T

r

ê

n

đ

â

y

t

á

c

g

i

ả

m

ạ

o

m

u

ộ

i

s

ử

d

ụ

n

g

m

ộ

t

s

ố

n

g

ô

n

t

ừ

n

h

ạ

y

c

ả

m

“

g

i

ả

v

ờ

”

,

“

n

g

o

à

i

g

i

á

t

h

ú

”

,

“

v

á

n

đ

ã

đ

ó

n

g

t

h

u

y

ề

n

”

,

“

đ

è

o

b

ồ

n

g

”

,

…

t

o

à

n

h

ữ

n

g

n

g

ô

n

t

ừ

t

r

o

n

g

t

ì

n

h

y

ê

u

v

à

h

ô

n

h

â

n

,

g

i

a

đ

ì

n

h

…

T

h

ự

c

r

a

đ

â

y

c

h

ỉ

l

à

l

ồ

n

g

h

é

p

c

h

ủ

ý

t

r

o

n

g

q

u

á

t

r

ì

n

h

t

h

i

ế

t

l

ậ

p

m

ộ

t

b

à

i

t

o

á

n

h

ỏ

,

m

ộ

t

b

à

i

t

o

á

n

v

ô

t

r

i

v

ô

g

i

á

c

,

c

ó

đ

ô

i

c

h

ú

t

n

é

t

đ

ẹ

p

ẩ

n

c

h

ứ

a

t

r

o

n

g

t

ư

d

u

y

p

h

ả

n

b

i

ệ

n

.

N

h

ư

n

g

,

t

r

o

n

g

c

u

ộ

c

s

ố

n

g

,

t

r

o

n

g

t

ì

n

h

y

ê

u

,

g

i

a

đ

ì

n

h

v

à

n

h

ữ

n

g

t

h

ứ

t

h

â

n

t

h

ư

ơ

n

g

,

c

h

ú

n

g

t

a

k

h

ô

n

g

n

ê

n

l

à

m

t

h

ế

,

k

h

ô

n

g

đ

ư

ợ

c

l

à

m

t

h

ế

,

d

ù

t

r

o

n

g

s

u

y

n

g

h

ĩ

,

v

ì

b

ấ

t

c

ứ

l

ý

d

o

g

ì

,

n

h

ư

n

h

ữ

n

g

m

á

n

h

k

h

ó

e

t

r

ê

n

k

i

a

,

h

ã

y

s

ố

n

g

c

h

â

n

t

h

à

n

h

,

c

ó

t

r

á

c

h

n

h

i

ệ

m

,

n

g

h

ĩ

a

v

ụ

,

k

h

ô

n

g

c

h

ố

i

b

ỏ

,

v

ụ

l

ợ

i

,

l

u

ô

n

l

u

ô

n

g

i

ữ

v

ữ

n

g

v

à

c

h

á

y

b

ỏ

n

g

t

ì

n

h

c

ả

m

,

c

h

ủ

k

i

ế

n

v

ẹ

n

t

o

à

n

,

t

r

o

n

g

s

á

n

g

,

t

h

ủ

y

c

h

u

n

g

,

đ

ú

n

g

đ

ạ

o

l

ý

l

à

m

n

g

ư

ờ

i

,

đ

ú

n

g

p

h

o

n

g

t

ụ

c

,

t

ậ

p

q

u

á

n

c

ủ

a

t

ổ

t

i

ê

n

,

c

ủ

a

đ

ấ

t

n

ư

ớ

c

V

i

ệ

t

N

a

m

n

g

h

ì

n

ă

m

v

ă

n

h

i

ế

n

.

Ô

i

,

t

ả

n

m

ạ

n

m

ấ

t

r

ồ

i

,

c

h

ế

t

m

ấ

t

h

ô

i

.

B

à

i

t

o

á

n

4

0

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

   

 

3

1

1 2 4 3 1 3 1,

;

1 1 1.

x y x y x y y y

x y



        







   







.

Lời giải.

Điều kiện

1; 1 0

y x y

   

.

Từ phương trình thứ hai của hệ

3

1

1 1 1 1 1 2

x

y x x



        

.

Dẫn đến

1 2

1

4

3 1 4

3

1 2

x y

y



  



 







 

 







Phương trình thứ nhất của hệ tương đương với

       

 

   

3

1 1 2 1 3 1 3 1 2 3 1

1

2 1 3 1 2 3 1

x y x y x y y y y

x y x y y y

           



         

Xét hàm số

     

3

2 2

2

; 2 3 4 3 4 0, 2

f

t t t t f t t t t t t





         

.

Hàm số liên tục và đồng biến trên miền đang xét nên ta được

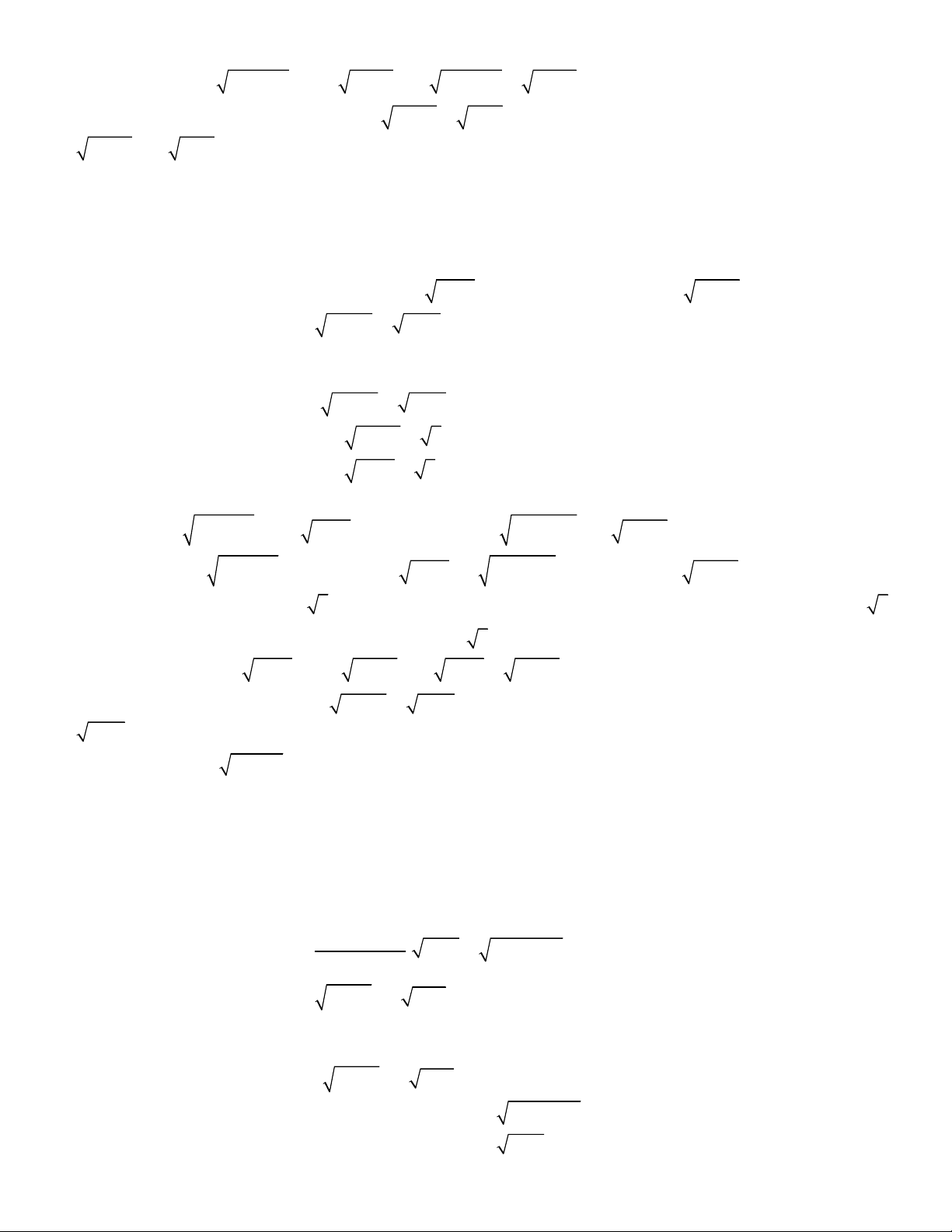
LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

31

 

   

1 3 1 1 3 1 1 3 1 2f x y f y x y y x y y x y

                  .

Phương trình thứ hai của hệ khi đó trở thành

3

2 1 1 1

y y

   

.

Đặt

 

3

2

3

2 1 ; 1 2 2 1 2 1 1

y a y b a b y y

          

. Ta có hệ phương trình

 

   

3

2 2

3 2

1 1

1

0

; 1;2

2 2 1 1 1 3 0

1

2 1

b a b a

a b

b

x y

a a a a a a

a

a b

   

 

 





 

    

   

       



 



 

 

.

Kết luận hệ đã cho có nghiệm duy nhất kể trên.

B

à

i

t

o

á

n

4

1

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

     

 

3

2

2 2 9 15 1 2 4 11 2 1,

;

3 5 2 2.

x y x y y x y y

x y

y x



        







   







.

Lời giải.

Điều kiện

2

; 0

x

x y



 

.

Phương trình thứ hai của hệ dẫn đến

3

3 5 2 2 2 3 5 8 3 3 1y x y y y           

.

Do đó kết hợp

2

1 3

1 2 1 3

2 3

3

y

x x y

x y



 

  

 



 

  

  

 

 





Phương trình thứ nhất của hệ tương đương

   

         

3

3 3

4 18 15 15 15 4 2 1 18 2 1

4 15 18 4 2 1 15 2 1 18 2 1

x y x y y x y y

x y x y x y y y y

          



           

Xét hàm

 

3 2

4 15 18 ; 3

f t t t t t    ta có

 

  

2

12

30 18 6 2 5 3 6 1 2 3 0, 3

f

t t t t t t t t



           

.

Như vậy hàm số trên liên tục và đồng biến trên miền

3

t  . Ta có hệ thức

 

   

2 1 2 1 2 1 1f x y f y x y y x y y x y               

.

Phương trình thứ hai của hệ trở thành

3

3 2 2 2

x x

   

.

Đặt

2

2 , 0 2

x u u x u

     

thì

 

2

3 2 3 2

3 2

2

3 8 6 12 8 3 12 0

3 8 2

0 0

0

3 12 0

0 2 1

0

u u u u u u u

u u

u

u u u

u x y

u



 

       



  

 

  

 





 





  



      









Kết luận hệ phương trình có nghiệm duy nhất

2

; 1

x

y



.

B

à

i

t

o

á

n

4

2

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

3

2

15

. 3 2 3,

4 2 15

;

2 2 1 1

x

x x y

x y

y x





   



 







   





.

Lời giải.

Điều kiện

1

;2 3 0;4 2 15 0

x

x y x y



     

.

Từ phương trình thứ hai của hệ ta có

3

3 3

3

2 2 1 1 1 2 1 1 1

y x y y y x            

.

Kết hợp đồng thời

2 3 2

1 2 2 3 4

1 1 3 4

3 2

x y

y y x y

x x x

x



  

      

  



  

   

   

  

 





LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

32

Phương trình thứ nhất của hệ tương đương

   

 

3

2

15 3 4 2 15 2 3

2

3 3 21 3 2 2 3 2 3 21 2 3

2 3 21 3 2 2 3 21 2 3

x x x y x y

x x x x y x y x y

x x x y x y

      



           

          

Xét hàm số

   

 

3

2 2

2

21 ; 2 6 21 3 2 7 0, 2

f

t t t t f t t t t





         

.

Hàm số liên tục và đồng biến trên miền đang xét, dẫn đến

 

   

3 2 3 3 2 3

3 2 3 1; 1

f x f x y x x y

x x y x y x y

          

         

Kết luận hệ đã cho có nghiệm duy nhất.

B

à

i

t

o

á

n

4

3

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

   

 

3 3

2

4

3

2 3 3 2 2 ,

;

2 1.

x y y x x

x y

y x x



     









   





.

Lời giải.

Điều kiện

1

;3 2 0

x

x y



  

.

Từ phương trình thứ hai của hệ ta có

2

2 2

4

3

2

1 1 2 1 1 1 1

y

x x y y y



            

.

Kết hợp

1 1 3 2 4

3 2 2; 2 2 2

1 2 2 4

y x y

x y x

x x

     

 

      

 

  

 

.

Phương trình thứ nhất của hệ trở thành

         

3

2 3 3 2 2 2 3 2 2x y x y x x



        

.

Xét hàm số

     

3

2 2

3

; 2 3 6 3 2 0, 2

f

t t t t f t t t t t t





         

.

Hàm số trên liên tục và đồng biến trên miền đang xét nên thu được

 

   

3 2 2 2 3 2 2 2 3 2 2 2

f x y f x x y x x y x x y                 

.

Khi đó

1

x

x y





  



 



. Hệ có nghiệm duy nhất

1x

y



.

B

à

i

t

o

á

n

4

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

3

2 2 2

1 2 1,

;

3 5 8 1 2 1 2 1.

y x

x y

x x x y x y x y



   







        







.

Lời giải.

Điều kiện

2

x



. Phương trình thứ nhất của hệ dẫn đến

3

1

2 1 1 1 1 2

y

x y y



        

.

Kết hợp

2

2 1 9

2 1 3

2

1 3

x

x y

y

x







  



  



 

  



 







Phương trình thứ hai tương đương với

     

   

3

2 2 2 2 2

3 2

2 2 2

3 3 1 4 2 1 4 2 1 2 1 2 1

1 4 1 2 1 2 1 4 2 1

x x x x x x y x y x y

x x x y x y x y

             

           

Xét hàm số

     

3

2 2

4

; 3 3 8 3 8 0, 3

f

t t t t f t t t t t t





         

.

Hàm số trên liên tục và đồng biến trên miền đang xét nên ta được

 





2

2 2 2

1

2 1 1 2 1 2 1 2 1

f

x f x y x x y x x x y x y



               

.

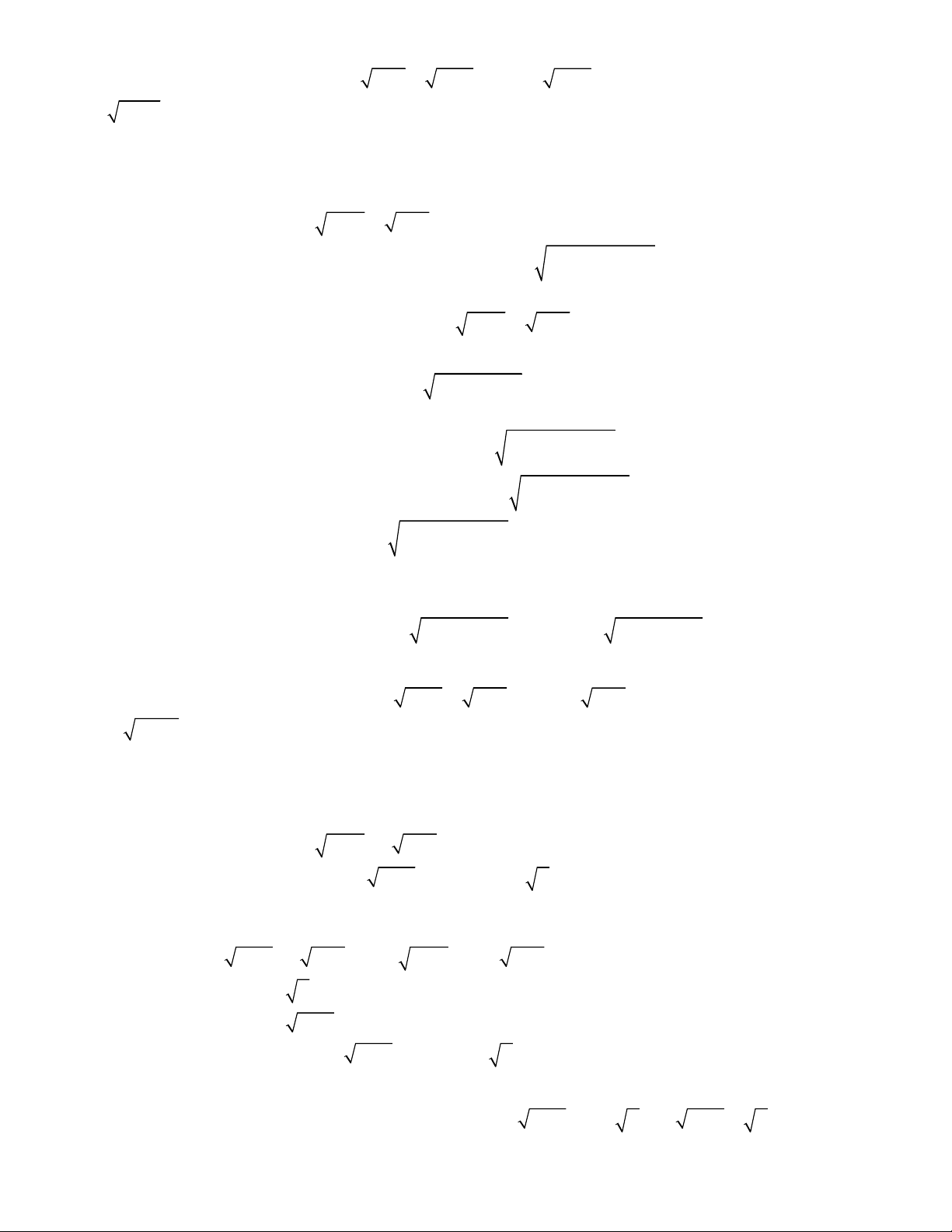
LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

33

Thay thế vào phương trình thứ nhất lại có

3

1 2 1

x x

   

. Đặt

2

, 0 2

x

u u x u



    

.

Suy ra

 

2

3 2 3 2

3 2

2 3 0

1 3 3 1 2 3 0

1 1

0

0 0

0

u u u

u u u u u u u

u u

u

u u

u



  

 

       

 

  

    

   

 





 





.

Từ đây ta có nghiệm duy nhất

2

; 2

x

y



.

B

à

i

t

o

á

n

4

5

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

3

2 2

7 1 2,

;

27 27 21 30 1 9 6 1 .

y x

x y

x x x y x y



   







      







.

Lời giải.

Điều kiện

1x 

. Phương trình thứ nhất của hệ dẫn đến

3

7 1 2 2, 1 7 8 1y x x y y           

.

Kết hợp đồng thời

2

3 1 4

1

9 6 1 16

9 6 1 4

x

y

x y

 



 







 

  



  







Phương trình thứ hai của hệ tương đương với

   

     

   

 

3

2 2 2

3

3 2 2 2 2

3

3 2

2 2

27 18 21 4 5 9 6 1 9 6 1

27

27 9 1 5 9 6 1 9 6 1 5 9 6 1

3 1 5 3 1 9 6 1 5 9 6 1

x x x x y x y

x x x x x x y x y

x x x y x y

        



           

          

Xét hàm số

     

3

2 2

5

; 4 3 10 3 10 0, 4

f

t t t t f t t t t t t





         

.

Hàm số đã cho liên tục và đồng biến trên miền đang xét, suy ra

   





2

2 2

3

1 9 6 1 3 1 9 6 1

9

6 1 9 6 1

f

x f x y x x y

x

x x y x y



         



      

Khi đó phương trình thứ nhất của hệ trở thành

3

7 1 2

x x

   

. Đặt

2

1

, 0 1

x

u u x u



    

.

Ta có hệ

2

3 2 3 2

3

2

1

8

6 12 8 5 12 0

8 2

0

1

0

x

u u u u u u u

u u

u

y

u







       





  

    

   









 



Kết luận hệ phương trình có nghiệm duy nhất

   

; 1;1

x y 

.

B

à

i

t

o

á

n

4

6

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

3

2

2 1 1,

;

2 2 2 .

y x

x y

x x x y y y



   







     







.

Lời giải.

Điều kiện

1; 0

x y

 

. Xuất phát từ phương trình thứ nhất của hệ

3

2 2 1 1 2 1 2 1 1 2 1 1x x y x y y              

.

Kết hợp

1

1 1

1 2 1

2 1

y

y y

x x

x





 

 



 

  

  

 

 





Phương trình thứ hai biến đổi về

     

2 2 2x x x y y y

      

.

Xét hàm số

     

3

2 2

;

1 3 2 3 2 0, 1

f

t t t t f t t t t t t





         

.

Hàm số trên liên tục và đồng biến trên miền

1t 

nên

 

   

2 2 2

f x f y x y x y         

.

LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

34

Phương trình thứ nhất khi đó trở thành

3

2 1 1

x x

  

. Đặt

3

2

3

;

1 , 0 1

x

a x b b a b



     

.

Kết hợp

2

1

a

b





dẫn đến hệ

 

2

3

2

3 2

3

2

1

2 1

2

1

4 2 3 0

1

2

1

4 5 3 0 1 1 1

4 5 3 0; 0

a

b

a

a b

b

a

a b

a a a

a

a a a x y

a a













 





 

 

  



 

 



 

   

 



 



 









          





   



Kết luận hệ có nghiệm duy nhất

   

;

1;1

x

y 

.

B

à

i

t

o

á

n

4

7

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

3

2

1 1,

;

1 1

.

2 1 2 1

y x

x y



   







  



 





.

Lời giải.

Điều kiện

1

;

2

x

y





. Từ phương trình thứ nhất của hệ ta có

3

2

1 1 1 2 1 1

y

x y y



        

.

Kết hợp

2 1 1

1

2 1 1

x

y

x

y



 









 



 







Phương trình thứ hai biến đổi

 

2

2 2 2

2 2 2 1 2 1

2 1 2 1 2 1 2 1

x y x y



        



  

.

Xét hàm số

   

 

3

2

2 1

2 2

; 1 2 0, 1

t

f t t t f t t t

t t t





         

. Hàm số đồng biến trên miền

1t 

nên

 

   

2 1 2 1 2 1 2 1 2 1 2 1

f x f y x y x y x y              

.

Phương trình thứ nhất trở thành

3

2 1 1x x   

.

Đặt

 

3 2

3

2 ; 1 0 1

x a x b b a b

       

. Phương trình đã cho trở thành

1a b 

. Ta thu được hệ

      

3

2 3 2

1 1

1

2 0 0;1; 2 2;1;10

1

2 0

a b b a

a a a a x

a b a a a

   

 

         

 

    

 

.

Kết luận hệ có các cặp nghiệm

       

; 1;1 , 2;2 , 10;10

x y 

.

Nhận xét.

Đ

ố

i

v

ớ

i

b

à

i

t

o

á

n

s

ố

4

7

,

n

h

ì

n

t

h

o

á

n

g

q

u

a

p

h

ư

ơ

n

g

t

r

ì

n

h

t

h

ứ

h

a

i

c

ủ

a

h

ệ

,

m

ộ

t

s

ố

b

ạ

n

đ

ộ

c

g

i

ả

v

ộ

i

v

à

n

g

k

ế

t

l

u

ậ

n

h

a

i

b

i

ế

n

b

ằ

n

g

n

h

a

u

l

à

t

h

i

ế

u

c

ơ

s

ở

,

n

g

u

y

ê

n

d

o

n

ế

u

k

h

ô

n

g

c

ó

đ

á

n

h

g

i

á

1t 

t

h

ì

h

à

m

s

ố

t

h

u

đ

ư

ợ

c

k

h

ô

n

g

h

o

à

n

t

o

à

n

đ

ơ

n

đ

i

ệ

u

t

r

ê

n

m

ộ

t

m

i

ề

n

.

Y

ế

u

t

ố

đ

á

n

h

g

i

á

c

h

ặ

n

m

i

ề

n

g

i

á

t

r

ị

c

á

c

b

i

ế

n

t

r

o

n

g

t

ư

ơ

n

g

đ

ồ

n

g

h

à

m

s

ố

l

à

v

ô

c

ù

n

g

q

u

a

n

t

r

ọ

n

g

,

b

à

i

t

o

á

n

à

y

n

g

o

à

i

p

h

ư

ơ

n

g

á

n

t

r

ê

n

c

á

c

b

ạ

n

c

ó

t

h

ể

s

ử

d

ụ

n

g

đ

ạ

i

l

ư

ợ

n

g

l

i

ê

n

h

ợ

p

–

t

r

ụ

c

ă

n

t

h

ứ

c

–

h

ệ

t

ạ

m

t

h

ờ

i

n

h

ư

s

a

u

 

1

1 1 1

2 1 2 1 2 1 2 1

2

2 1 2 1

2 1. 2 1

2

1. 2 1 2 1 2 1

2

1. 2 1 2 1 2 1 2

x y x y

x y y x

x y

x y x y

x y

x y x y

x y

x y x y

      

   



  

     

 



   









     





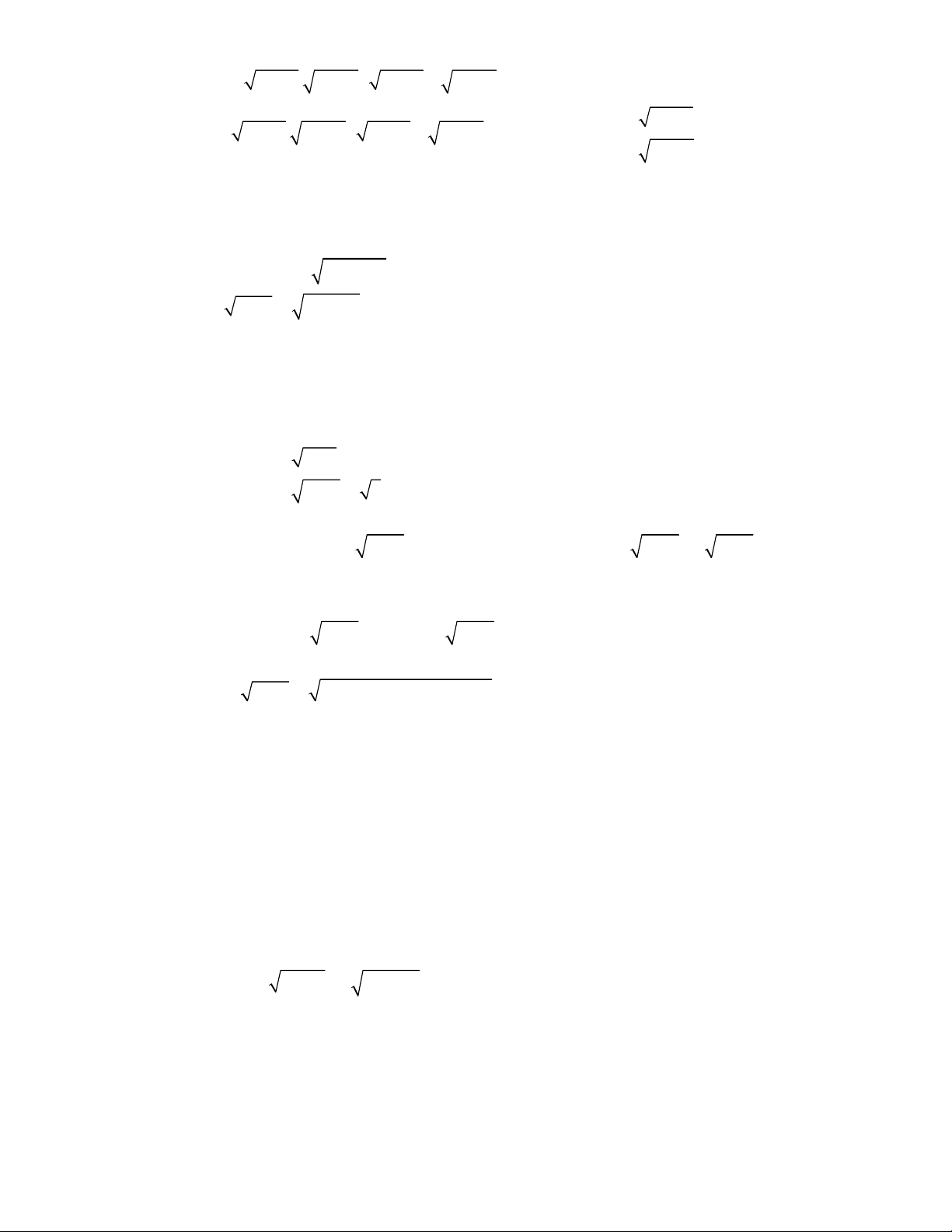
LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

35

X

ử

l

ý

p

h

ư

ơ

n

g

t

r

ì

n

h

a

i

ẩ

n

 

2 1. 2 1 2 1 2 1 2

x y x y

     

k

h

á

đ

ơ

n

g

i

ả

n

s

ở

d

ĩ

 

2 1. 2 1 2 1 2 1 2

x y x y

     

v

ớ

i

2 1 1

1

2 1 1

x

y

x

y



 









 



 







T

u

y

n

h

i

ê

n

ế

u

đ

ằ

n

g

t

h

ằ

n

g

x

ô

n

g

p

h

a

,

k

h

ô

n

g

c

ó

đ

á

n

h

g

i

á

t

h

ì

s

ẽ

k

h

ó

t

ì

m

r

a

l

ố

i

t

h

o

á

t

.

B

à

i

t

o

á

n

4

8

.

T

r

í

c

h

l

ư

ợ

c

â

u

4

;

Đ

ề

t

h

i

đ

ề

n

g

h

ị

O

l

y

m

p

i

c

3

0

t

h

á

n

g

4

(

D

à

n

h

c

h

o

c

á

c

t

ỉ

n

h

M

i

ề

n

T

r

u

n

g

–

T

â

y

N

g

u

y

ê

n

–

N

a

m

B

ộ

)

;

M

ô

n

T

o

á

n

;

K

h

ố

i

1

0

;

L

ầ

n

t

h

ứ

1

7

;

N

ă

m

2

0

1

;

Đ

ơ

n

v

ị

t

r

ư

ờ

n

g

T

H

P

T

C

h

u

y

ê

n

H

ù

n

g

V

ư

ơ

n

g

;

T

ỉ

n

h

G

i

a

L

a

i

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

3

3 2

2

3

2 3 ,

;

3 2 8 .

x x y y

x y

x y y



   







  







.

Lời giải.

Điều kiện

 

2

3

0 0 3

0

8

8 0

x

y y y y

y

y y















       

  







   

 



Kết hợp

1 1

2 1 1

0 3 3

3 3 1

x

x x

y y

y



 

  

 



 

  

  

  

 





Phương trình thứ nhất của hệ tương đương với

       

3

2

3

3 1 3 3 3 1 3 1 3 3 3 3x x x x y y x x y y y



               

.

Xét hàm số

   

3 2

3

; 1 3 3 0, 1

f

t t t t f t t t





       

.

Vậy hàm số liên tục và đồng biến trên miền đang xét. Dẫn đến

   

 

2

1 3 1 3 2 1 3 2 2

f x f y x y x x y y x x

                 

.

Thay thế vào phương trình thứ hai ta có

 

4 3 2 4 3 2

3 2

3

2 4 8 8 12 8 8 17 6 0

3

5 2 0

5 2 0 1

x x x x x x x x x

x

x x x x

x x x



          







     



   



Xét hàm số

 

3

2

5 2 0; 2

g x x x x x

     

ta có

 

2

3 2 5 0,g x x x x



     

.

Hàm số này liên tục và đồng biến trên toàn trục số thực nên

   

2

2 12 0

x

Min g x g



  

.

Phương trình (1) vô nghiệm nên hệ có nghiệm duy nhất

3; 1x y 

.

B

à

i

t

o

á

n

4

9

.

T

r

í

c

h

l

ư

ợ

c

â

u

1

,

Đ

ề

t

h

i

đ

ề

n

g

h

ị

O

l

y

m

p

i

c

3

0

t

h

á

n

g

4

(

c

á

c

t

ỉ

n

h

M

i

ề

n

T

r

u

n

g

–

T

â

y

N

g

u

y

ê

n

–

N

a

m

B

ộ

)

M

ô

n

T

o

á

n

;

K

h

ố

i

1

0

;

L

ầ

n

t

h

ứ

1

8

;

N

ă

m

2

0

1

2

;

Đ

ơ

n

v

ị

t

r

ư

ờ

n

g

T

H

P

T

C

h

u

y

ê

n

T

r

ầ

n

H

ư

n

g

Đ

ạ

o

;

T

ỉ

n

h

B

ì

n

h

T

h

u

ậ

n

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

3

3 2

2 2 2

12 6 16 0,

;

4 2 4 5 4 0.

x x y y

x y

x x y y



    







    







.

Lời giải.

Điều kiện

 

2

4

0

2

0 4

4 0

x

y

y y



 



 









 

 







Từ điều kiện

2 2 0 2 4

0 4 0 4

x x

y y

     

 



 

   

 

Phương trình thứ nhất của hệ tương đương

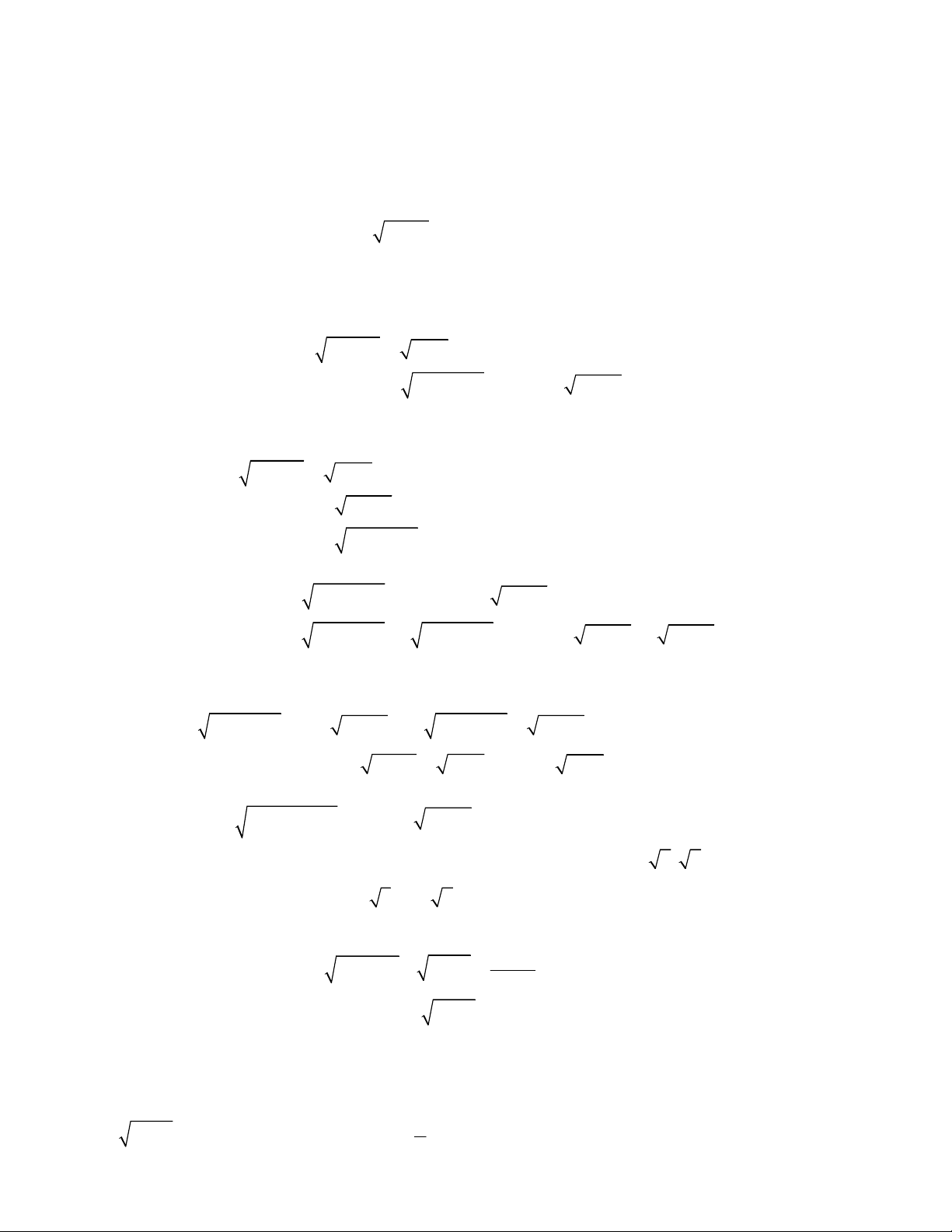
LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

36

 

     

3

2 2 3 2

3

2

3 2

6

12 8 6 4 4 6

2

6 2 6

x

x x x x y y

x

x y y

       

      

Xét hàm số

 

 

   

 

3

2 2

6

; 0;4 3 12 3 4 0, 0;4

f

t t t t f t t t t t t



          

.

Như vậy hàm số đã cho liên tục và nghịch biến trên

 

0

;4

. Ta thu được

     

2

f

x f y x y



     

.

Thế vào phương trình thứ hai ta có

 

2 2 4 2 2

4

2 2 2

4

6 3 4 16 48 36 36 9

16

57 0 16 57 0 0

x

x x x x

x

x x x x

       



      

Từ đây suy ra hệ có nghiệm duy nhất

0

; 2

x

y



.

Bài toán 50. Giải hệ phương trình

 

2

3

2

3 5 2 1,

;

3 5 2 3 2 5.

y x

x y

x y x y x x



   







      







.

Lời giải.

Điều kiện

2

2; 5 0

x x y

   

.

Từ phương trình thứ nhất

2

2 2 2

3

5 2 1 1 3 5 1 3 6 2

y

x y y y



          

.

Kết hợp

2 2

2

5 3

2 2 5 9

2 5 9

5

3

x

y y x

y x



 

  

 



 

  

   



 







Phương trình thứ hai của hệ tương đương

 

   

2

2 2 2

5 8 5 2 5 8 2 5

5 5 8 5 2 5 2 5 8 2 5

x y x y x x

x y x y x y x x x

        

             

Xét hàm số

   

3

2

8

; 3 3 8 0, 3

f

t t t t f t t t





       

.

Hàm số liên tục và đồng biến trên miền đang xét. Thu được

 





 

2

2 2 2

5

2 5 5 2 5 5 2 5

f

x y f x x y x x y x y x



                

.

Thay thế vào phương trình thứ nhất lại có

3

3 5 2 1

x x

   

. Đặt

2

2 , 0 2

x t t x t

     

.

Ta có

 

 

3

2

2 2 3 2

3

3 2

3

2 5 1 3 1 1 3 1 3 3 1

3

0 3 0 0 2 2; 2

t

t t t t t t t

t

t t t t x y



            



           

Dẫn đến hệ có hai cặp nghiệm

 

   

; 2; 3 , 2; 2

x y   .

Bài toán 51. Giải hệ phương trình

 

2

4 2 2 4

9

2 2 1 ,

4

;

32 64 1 16 2 1 .

x

x x y

x y

x y y y x





   









     





.

Lời giải.

Điều kiện

1 1

0 2

y

x

  





 



Ta có

2

0

1 1

y



 

và từ điều kiện dẫn đến

0 1

2

x

 

. Phương trình thứ hai của hệ tương đương với

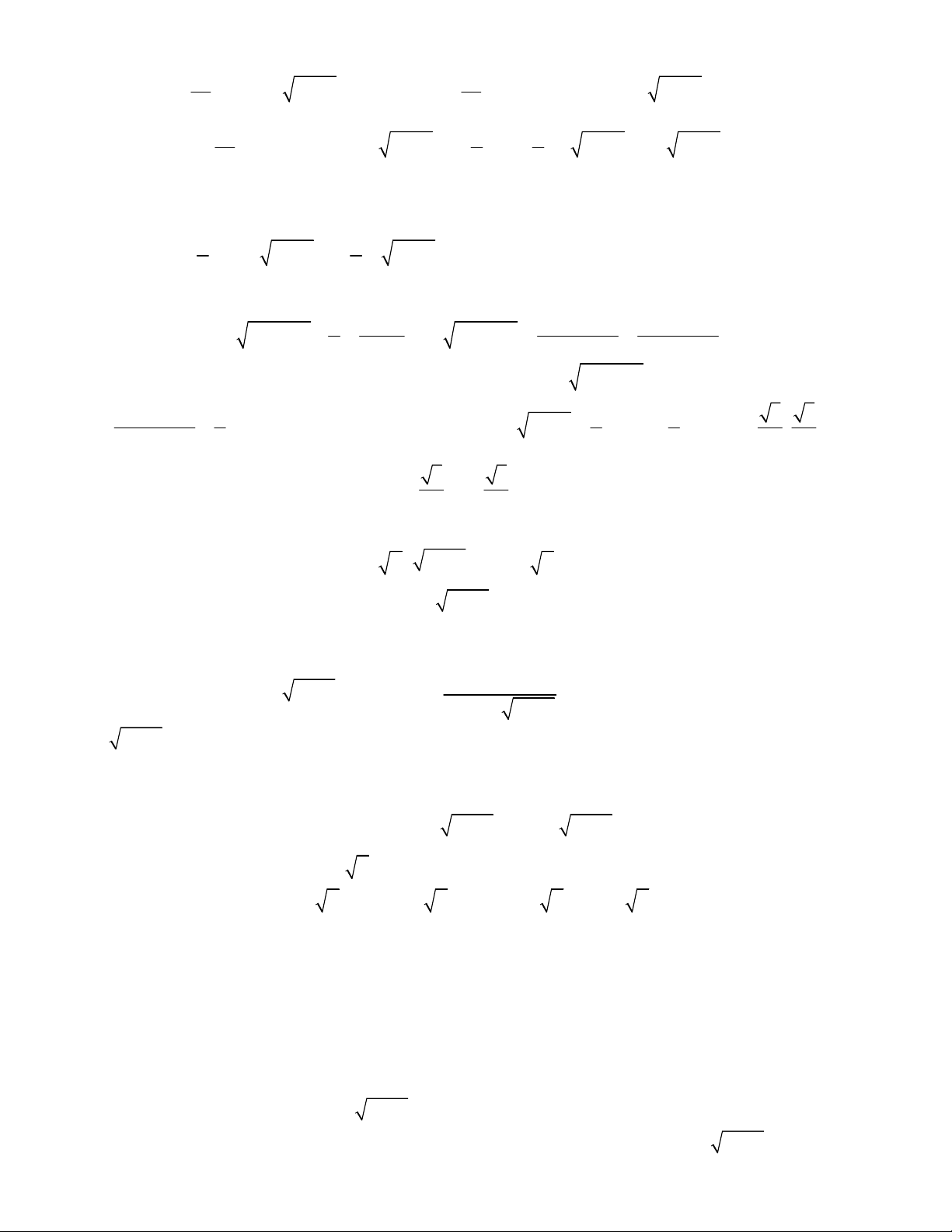
LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

37

 





 

4

2 2 4 4 2 2

4

2

2 2 2 2

2

4 1 2 1 2 2 1 4 1

16 16

2 1 4 1 4. 1 4 1

16 2 2

x x

y y y x x y y y

x x x

x y y y y

            

 



           





 

Xét hàm số

   

 

4

3 3

4 ; 1 4 4 4 1 0, 1f t t t t f t t t t



          

.

Hàm số này liên tục và nghịch biến trên miền đang xét.

Thu được

 





2 2

1

2 2

x x

f

f y y







     





 

.

Khi đó phương trình thứ nhất của hệ trở thành

   

 

2

1 8

9 2 9

2 2 2 2

2 4 4 4

x

x x x x

 

  

       .

Áp dụng bất đẳng thức liên hệ trung bình cộng – trung bình nhân thì

 

2

2 2 2

x

x x x



   

.

Ngoài ra

 

2

1 8

8

2

4 4

x  

 

nên dẫn đến

2

1 3 3 3

1

1 ;

1 0

2

4 2 2

x

x y y y

x

 







 



        

  

 

 



 

.

Đối chiếu điều kiện ta có hai nghiệm

 

3 3

;

1; , 1;

2

x

y

   







  



  

   

.

Bài toán 52. Giải hệ phương trình

   

 

2

2 2 2

1 1 3 ,

;

1 1.

x y x y y

x y

y y x x



    









    





.

Lời giải.

Điều kiện

0

y



. Nhận xét phương trình thứ hai

 

4 2

2 2 2

2 2

1 1

1 1 1 0,

0 0

1 1

y y

x x

y y x x y y x

y y

x x

 

 



            

 

 

  

 



Rõ ràng

2

1 1,x x

   

và

0

y



không thỏa mãn hệ phương trình đã cho.

Với

1y 

, xét hàm số

   

2

;

1 2 1 0, 1

f

t t t t f t t t





       

.

Hàm số đang xét liên tục và đồng biến trên miền đang xét.

Phương trình thứ hai của hệ tương đương

 





2

1 1

f y f x y x

    

.

Thay thế vào phương trình đầu tiên, đặt

; 1y t t 

thì

   

 

2

6 3 2 5 2

2

3 2

3 3 3 0

3 3 0 3 3 0

1 2 3 3 0 1 1; 0

y y y y y y y y y y y

t t t t t t t t

t t t t t t y x

       

         

          

Kết luận hệ đã cho có nghiệm duy nhất

0

; 1

x

y



.

Nhận xét.

B

à

i

t

o

á

n

s

ố

5

2

n

à

y

t

á

c

g

i

ả

n

g

h

ĩ

r

ằ

n

g

đ

a

s

ố

c

á

c

b

ạ

n

đ

ộ

c

g

i

ả

đ

ề

u

q

u

a

n

s

á

t

h

ấ

y

s

ự

t

ư

ơ

n

g

đ

ồ

n

g

h

à

m

s

ố

t

ạ

i

p

h

ư

ơ

n

g

t

r

ì

n

h

t

h

ứ

h

a

i

 

2

f

t t t





.

T

u

y

n

h

i

ê

n

đ

ạ

o

h

à

m

c

ủ

a

n

ó

   

2

1

f

t t t f t t





   

c

h

ư

a

x

á

c

đ

ị

n

h

d

ấ

u

r

õ

r

à

n

g

.

Đ

ể

ý

t

h

ê

m

ộ

t

c

h

ú

t

c

ó

t

h

ể

t

h

ấ

y

h

i

ể

n

h

i

ê

n

2

1 1,x x

   

n

h

ư

n

g

ẩ

n

h

à

m

y

l

ạ

i

k

h

ô

n

g

đ

ồ

n

g

b

ộ

v

ì

m

i

ề

n

c

h

ặ

n

y

ế

u

(

đ

i

ề

u

k

i

ệ

n

x

á

c

đ

ị

n

h

)

0

y



.

N

h

ư

n

g

l

ạ

i

c

ó

 

2

1

0, 1

t

t t t t



    

d

o

v

ậ

n

d

ụ

n

g

đ

ặ

c

t

í

n

h

2

1 1,x x

   

,

k

h

i

đ

ó

LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

38

d

ẫ

n

đ

ế

n

t

ì

n

h

t

r

ạ

n

g

2

0 1 0

y y y y

     

,

k

ế

t

h

ợ

p

0

y



c

h

ẳ

n

g

p

h

ả

i

1

0

y



 

h

a

y

s

a

o

,

v

à

t

i

ế

p

t

ụ

c

l

ậ

p

l

u

ậ

n

m

ở

r

a

c

á

n

h

c

ử

a

l

ờ

i

g

i

ả

i

.

L

ư

u

ý

đ

ố

i

v

ớ

i

t

r

ư

ờ

n

g

h

ợ

p

t

ổ

n

g

q

u

á

t

c

á

c

b

ạ

n

ê

n

đ

ặ

t

2

1 , 1x t t  

c

h

ẳ

n

g

h

ạ

n

,

đ

ộ

c

l

ậ

p

ẩ

n

v

ề

h

a

i

c

h

i

ế

n

t

u

y

ế

n

,

đ

á

n

h

g

i

á

 

2

;

1

g

t at bt c t



  

.

S

ử

d

ụ

n

g

đ

ạ

i

l

ư

ợ

n

g

l

i

ê

n

h

ợ

p

–

t

r

ụ

c

ă

n

t

h

ứ

c

n

h

ư

t

r

ê

n

c

ũ

n

g

l

à

m

ộ

t

p

h

ư

ơ

n

g

c

á

c

h

a

y

,

đ

ộ

c

đ

á

o

,

t

h

ú

v

ị

 

4

2

2 2 2

2 2

1 1

1 1 1 0,

0 0

1 1

y y

x x

y y x x y y x

y y

x x

 

 



            

 

 

  

 



B

à

i

t

o

á

n

5

3

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

   

 

2

1 1 ,

;

2 1 1 2 2 2 3 3 3.

x y x

x y

x x y y x y



   







       







.

Lời giải.

Điều kiện

1

;

1

2

x

y



. Phương trình thứ nhất tương đương

1

2 1 1 2 1 1 1 1 0 1

2 1

x

x y x x x y y x x

x x



                

 

.

Kết hợp

1 2 1

1

2 3 1

x

y



  









 



  







Phương trình thứ hai của hệ tương đương với

       

 

   

3 3

2 1 1 3 1 2 2 2 3 2

2

1 3 1 2 2 3 2

x x x y y y

x x y y

        



       

Xét hàm số

     

3

2 2

2 3 ; 1 6 6 6 1 0, 1f t t t t f t t t t t t



          

.

Hàm số trên liên tục và đồng biến trên miền đang xét nên thu được

 

   

1 2 1 2 1 2 2 1f x f y x y x y x y                

.

Phương trình thứ nhất trở thành

 

2

1 2 2 1 2 2 2 2

1

5

2 2 1 1

2

4

8 1 0

x x x x x x x

x

x x x y

x x

         





        



  



Kết luận hệ đã cho có nghiệm duy nhất

5

1

;

2

x

y  

.

N

h

ậ

n

x

é

t

.

S

ử

d

ụ

n

g

đ

ạ

i

l

ư

ợ

n

g

l

i

ê

n

h

ợ

p

–

t

r

ụ

c

ă

n

t

h

ứ

c

t

ì

m

i

ề

n

g

i

á

t

r

ị

b

i

ế

n

l

à

m

ộ

t

c

á

c

h

đ

á

n

h

g

i

á

đ

ơ

n

g

i

ả

n

,

t

h

u

ầ

n

t

ú

y

,

t

r

ê

n

t

h

ự

c

t

ế

n

ó

v

ẫ

n

l

à

b

i

ế

n

đ

ổ

i

t

ư

ơ

n

g

đ

ư

ơ

n

g

,

c

h

ỉ

s

ử

d

ụ

n

g

k

i

ế

n

t

h

ứ

c

ă

n

t

h

ứ

c

s

ơ

đ

ẳ

n

g

t

r

o

n

g

c

h

ư

ơ

n

g

t

r

ì

n

h

Đ

ạ

i

s

ố

l

ớ

p

9

T

H

C

S

,

t

h

i

ế

t

n

g

h

ĩ

n

ó

k

h

ô

n

g

q

u

á

k

h

ó

đ

ể

đ

ô

n

g

đ

ả

o

c

á

c

b

ạ

n

á

p

d

ụ

n

g

.

X

é

t

r

i

ê

n

g

t

r

ư

ờ

n

g

h

ợ

p

b

à

i

t

o

á

n

s

ố

5

3

,

c

ó

t

h

ể

l

ậ

p

l

u

ậ

n

h

ẹ

n

h

à

n

g

h

ơ

n

h

ư

s

a

u

2 1 1 0 2 1 2 1 1x x y x x x x x            

.

B

à

i

t

o

á

n

5

4

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

2 2

2 2 1 ,

;

4 3 2 1 2 3 1.

x y y

x y

x y y y x x



   







      







.

Lời giải.

Điều kiện

1

2;

2

x y

 

.

LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

39

Từ phương trình thứ nhất của hệ ta có

1

0

2 2 1 1 0 1

2

1

y

x

y y y y

y





         





.

Kết hợp

1 1

2

1

2 1 1

x

y



 









 



 







Phương trình thứ hai của hệ tương đương với

     

2 2

2 1 3 1 4 4 1 3 2 1

1 3 1 2 1 3 2 1

x x x y y y

x x y y

        

        

Xét hàm số

   

4 3

3 ; 1 4 3 0, 1f t t t t f t t t



        

.

Hàm số

 

f t

liên tục và đồng biến trên miền

1t 

. Dẫn đến hệ quả

 

   

1 2 1 1 2 1 1 2 1 2f x f y x y x y x y

               .

Chú ý xét

2 ; 1x y y 

.

Khi đó, phương trình thứ nhất trở thành

   

    

2

2 2 2 1 2 2 3 1 2 2 1 1 2 2 1

1

2

1 4 2 1 7 6 1 0 1 7 1 0 ;1

7

y

y y y y y y y y y

             







              









Đối chiếu, kết luận nghiệm

2

; 1

x

y



.

B

à

i

t

o

á

n

5

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

   

 

2

2 3 6,

;

11 5 2 1.

2

x x y

x y

x y x x



   









    







.

Lời giải.

Điều kiện

1

; 2

x

y



.

Từ phương trình thứ nhất của hệ ta có

2

2 2 3 6 3 6 0 2

2 2

x

x x y y x

x x



         

 

.

Kết hợp các điều kiện

2

2 4

2 2 1 5

2 1 5 2

x y

x x y

y x

x



 

  

 



 

  

  

 

  





Phương trình thứ hai tương đương

   

     

11 2 10 2 1

11 2 1 2 1 11 2 1

x y x y x x

x y x y x y x x x

     

          

Xét hàm số

   

3

2

11 ; 2 3 11 0, 2f t t t t f t t t



        

.

Như vậy hàm số trên liên tục và đồng biến trên miền

2t 

. Thu được

 

   

2 1 2 1 2 1 1f x y f x x y x x y x y x               

.

Thay thế trở lại phương trình thứ nhất ta có

 

2

3

2 2 2 2 3 3

2

2 3 3

2

1

2 2

2 2 2 1

4

2

x

x x x

x

x x

x

x x

x





   





   











 

 

   

 











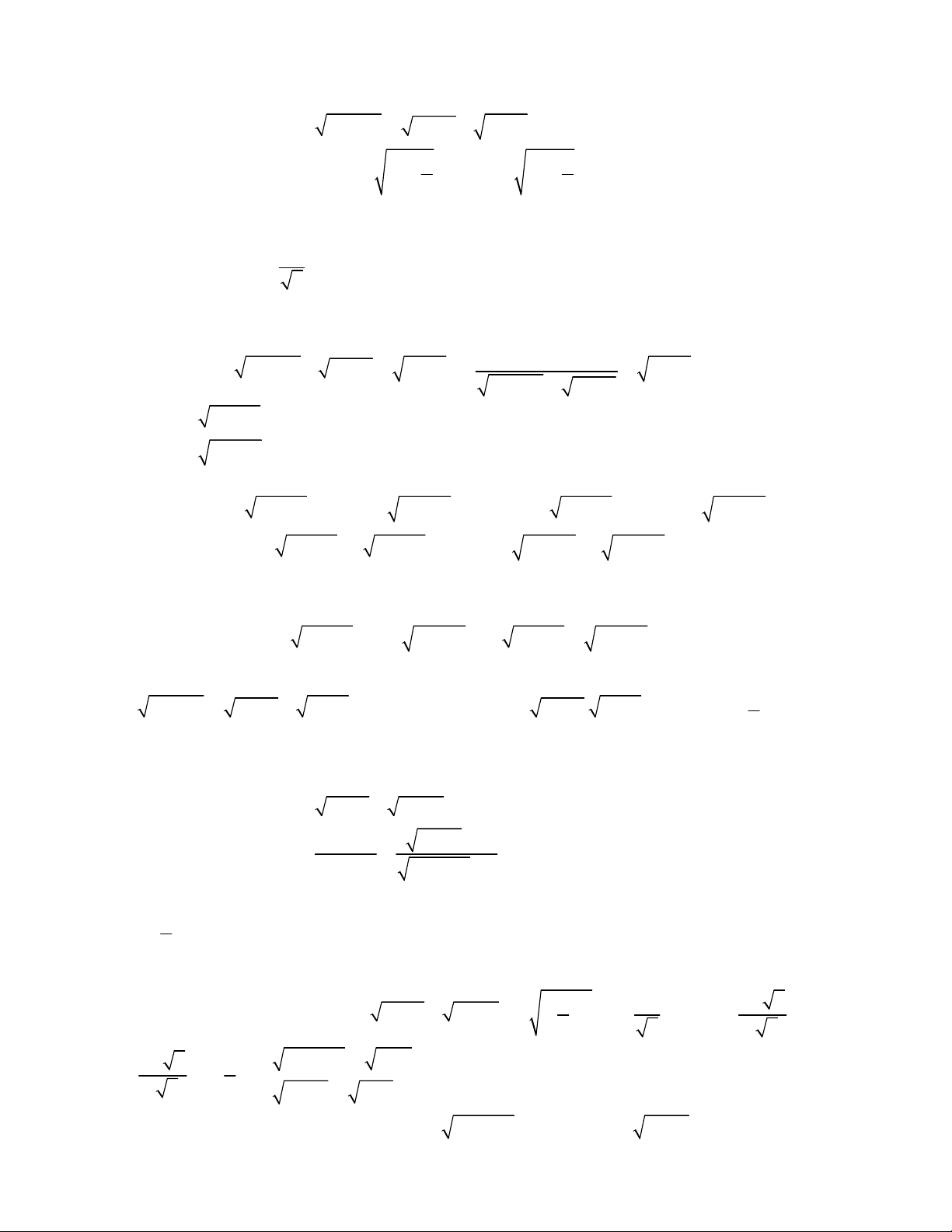
LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

40

Kết luận hệ phương trình ban đầu vô nghiệm.

B

à

i

t

o

á

n

5

6

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

   

 

2

2 2 2 2

2 2 1 1,

;

1 1

2 2 .

2 2

x x x y

x y

x x y y



    







    







.

Lời giải.

Điều kiện

2

1

2 1

2

2 0

1

2 1 0

y

x

x x

y

x











 



 

 

 







 



Từ phương trình thứ nhất

2

2 2 2

2

1

2 2 1 1 1 0 1 1

2 2 1

x

x x x y y x x

x x x



            

  

.

Kết hợp

2

1

2

1 1

1

2

1 1

x

y





























Phương trình thứ hai của hệ tương đương với

       

   

 

2 2 2 2 2 2 2 2

2 2 2 2 2 2

2 2 1 2 2 1 2 4 2 1 2 4 2 1

2 1 2 1 3 2 1 2 1 2 1 3 2 1

x x y y x x y y

x x x y y y

          

          

Xét hàm số

   

3 2

3

; 1 3 3 0, 1

f

t t t t f t t t





       

.

Hàm số đang xét liên tục và đồng biến trên miền tương ứng. Thu được hệ quả

 









2

2 2 2 2 2

2

1 2 1 2 1 2 1

f

x f y x y x y



         

.

Khi đó phương trình thứ nhất trở thành

2

2 2 2 2

1

2

2 1 1 2 2 2 2 1. 1 0 ; 1;1

2

x

x x x x x x x x x x







               





 

.

Kết hợp

1x 

ta có hai nghiệm

     

; 1;1 , 1; 1

x y

 

.

B

à

i

t

o

á

n

5

7

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

2 1 4 3 1 3 ,

;

2 1 2

1

.

2 1

1 2

x x y

x y

y

x y

y

x y



    







 

 







  





.

Lời giải.

Điều kiện

3

;

2 1 0

4

0

1 4

x

y

x y





 









  



Từ phương trình thứ nhất của hệ ta có

3 1 1 2

3 2 1 4 3 2. 1 1 1

4

2 3 2

y x x y



            .

Kết hợp

1 2,32

1

2 3

;

4

3 2

2

1 2,13

x y

y x

y



  





  



 





Phương trình thứ hai của hệ tương đương

 

1 1 2 2 1 2 1 2x y x y y y

         

.

LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

41

Xét hàm số

       

2

3 2 2

2 2 ; 3 4 3 4 0, 2,13

f t t t t t t f t t t t t t



            .

Như vậy hàm số liên tục và đồng biến trên miền

2

,13

t 

nên thu được

 

   

1 2 1 1 2 1 1 2 1

f x y f y x y y x y y x y                 

.

Phương trình thứ nhất trở thành

   

2 2

2

1 4 3 3 1 2 2 1 2 4 3 6 2

2

1 2 2 1 1 4 3 2 4 3 1 0

2 1 1

2

1 1 4 3 1 0 1

4

3 1

x x x x x x

x x x x

x

x x

x



         

          



 





        











Kết luận hệ phương trình đã cho có nghiệm duy nhất

1x

y



.

N

h

ậ

n

x

é

t

.

C

á

c

b

ạ

n

c

ó

t

h

ể

s

ử

d

ụ

n

g

b

ấ

t

đ

ẳ

n

g

t

h

ứ

c

l

i

ê

n

h

ệ

t

r

u

n

g

b

ì

n

h

c

ộ

n

g

–

t

r

u

n

g

b

ì

n

h

n

h

â

n

v

ớ

i

đ

i

ể

m

r

ơ

i

đ

ể

x

ử

l

ý

p

h

ư

ơ

n

g

t

r

ì

n

h

ệ

q

u

ả

ẩ

n

x

t

h

u

đ

ư

ợ

c

n

h

ư

s

a

u

2

1 1 4 3 1 6 2

2

1 4 3 3 1

2

2 2

x

x x

x

x x



   



      

.

D

ấ

u

đ

ẳ

n

g

t

h

ứ

c

x

ả

y

r

a

k

h

i

2 1 4 3 1 1x x x     

.

B

à

i

t

o

á

n

5

8

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

3

2

3

2 3 3 3 4 1 ,

;

1 2 1.

x x xy y x y y y

x y

x y y



      







   







.

Lời giải.

Điều kiện

1

;

2

x

y



.

Từ phương trình thứ hai của hệ ta có

1

2

1 0 1

1

x

y

x y

x

y

 



    





.

Kết hợp đồng thời

1 1

1 2 1 1

x y x y

y y

   

 



 

  

 

Phương trình thứ nhất của hệ tương đương với

 

   

         

3

2

3 2 2 3 2

3 2 2 3 3 2

3 3

3 2 3 3 3 4 1

3 3 3 9 12 3 2

3

3 3 8 12 6 1 3 2 1

3 2 1 3 2 1

x x xy y x y y y

x x y xy y y y x

x x y xy y x y y y y y

x y x y y y

      

       



          

        

Xét hàm số

   

3

2

3

; 1 3 3 0, 1

f

t t t t f t t t





       

.

Hàm số đang xét liên tục và đồng biến trên miền

1t 

. Hệ quả

     

2 1 2 1 3 1f x y f y x y y x y           

.

Khi đó phương trình thứ hai trở thành

 

2

1

2 1 3 2 1 3 3 1 2 2 1

1

1 3 1 3

2 2 1 1 2 0 ;

4 4 4

x y y y y y y y y y

y y y y y



           





 

 

        

 

 

 

Đối chiếu điều kiện

1

1 3 3 3 7

;

2

4 4

y

y x





  

là nghiệm duy nhất của hệ đã cho.

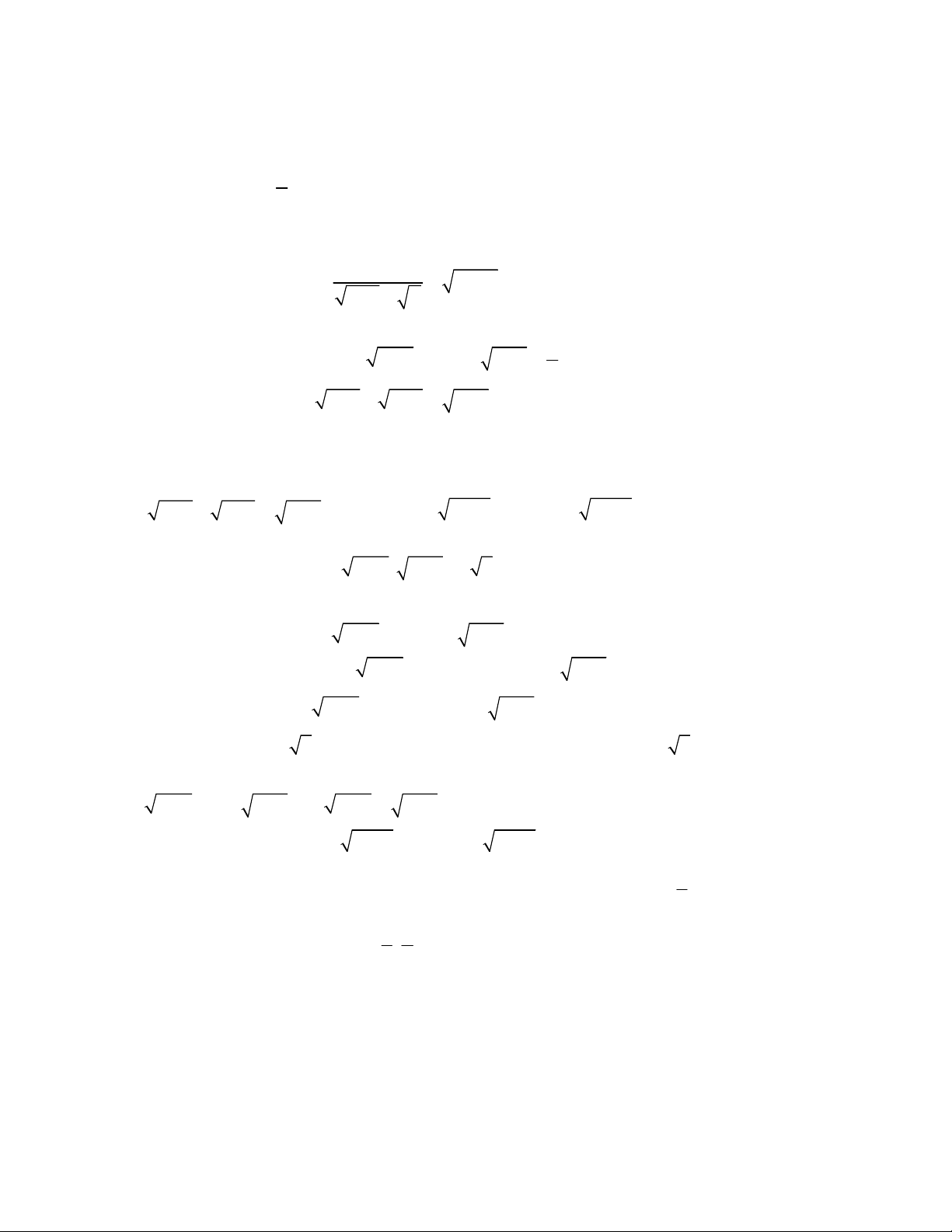
LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

42

N

h

ậ

n

x

é

t

.

T

h

o

á

n

g

q

u

a

b

à

i

t

o

á

n

5

8

,

q

u

a

n

s

á

t

p

h

ư

ơ

n

g

t

r

ì

n

h

t

h

ứ

n

h

ấ

t

d

ễ

t

h

ấ

y

s

ẽ

x

u

ấ

t

h

i

ệ

n

h

a

i

ẩ

n

h

à

m

đ

ề

u

k

h

ô

n

g

c

h

ứ

a

c

ă

n

t

h

ứ

c

,

t

r

o

n

g

đ

ó

c

h

ắ

c

h

ắ

n

c

ó

ẩ

n

h

à

m

c

h

ứ

a

h

a

i

b

i

ế

n

x

v

à

y

.

B

i

ế

n

đ

ổ

i

m

ộ

t

c

h

ú

t

c

á

c

b

ạ

n

d

ễ

d

à

n

g

đ

ư

a

v

ề

d

ạ

n

g

h

à

m

s

ố

         

3 3

3

2 1 3 2 1x y x y y y



      

.

R

õ

r

à

n

g

d

o

đ

i

ề

u

k

i

ệ

n

1

;

2

x

y



,

h

a

i

b

i

ế

n

c

ù

n

g

p

h

e

c

á

n

h

v

ớ

i

n

h

a

u

n

ê

n

s

ử

d

ụ

n

g

n

ề

n

t

ả

n

g

n

à

y

t

h

i

ế

t

l

ậ

p

c

á

c

đ

á

n

h

g

i

á

c

h

o

đ

ạ

i

l

ư

ợ

n

g

x

y



l

à

b

ấ

t

k

h

ả

t

h

i

.

T

r

o

n

g

t

r

ư

ờ

n

g

h

ợ

p

n

à

y

k

h

é

o

l

é

o

s

ử

d

ụ

n

g

đ

ạ

i

l

ư

ợ

n

g

l

i

ê

n

h

ợ

p

,

t

h

ự

c

r

a

l

à

đ

i

ề

u

k

i

ệ

n

t

i

ê

n

q

u

y

ế

t

c

ó

n

g

h

i

ệ

m

c

ủ

a

p

h

ư

ơ

n

g

t

r

ì

n

h

t

h

ứ

h

a

i

c

h

ú

n

g

t

a

l

ạ

i

c

ó

c

o

n

đ

ư

ờ

n

g

t

h

u

ậ

n

l

ợ

i

,

t

ư

ở

n

g

c

h

ừ

n

g

k

h

ô

n

g

t

h

ể

1

2 1 0 1

1

x

y

y x y

x

y



     





.

B

à

i

t

o

á

n

5

9

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

     

 

9

3 3 1 1 9,

2

;

1 1 1.

x x y y x y

x y

x x y



       









    





.

Lời giải.

Điều kiện

1

1; 1

x

y



   

.

Từ phương trình thứ hai của hệ ta có

2 2

1 0 1

1 1 1 1 2 2 1 1 2 1

1 2 3

y y

x x y y x y x

y y

  

 

               

 

  

 

Kết hợp

1 1 2 3 4

3; 1 2;2

1 3 2 1 4

x x

x y

y y

     

 

 

    

 

 

    

 

.

Phương trình thứ nhất của hệ tương đương

   

       

 

   

3

2

3 3 2 1 1 9 9 18

2

3 3 9 3 2 1 1 9 1

2

3 9 3 2 1 9 1

x x y y x y

x x x y y y

x x y y

       



        



       

Xét hàm số

 

3

2

2 9 ; 2;2

f t t t t

 

  

 

ta có

   

2

6 18 6 3 0, 2;2

f t t t t t t

 



      

 

.

Dẫn đến hàm số liên tục, nghịch biến trên miền đang xét.

Thu được

   

3 1 3 1 3 1 2

f x f y x y x y y x

             

. Khi đó

2

2 2 2

1 2 2 1 1 2 1

1 0 1

3

1;

5

2 1 4 4 5 2 3 0

y x x x

x x

x

x x x x x

       

   

 

 

    

   

      

 

 

Kết luận hệ có hai nghiệm

   

3

7

; 1;1 , ;

5

x y





  









.

N

h

ậ

n

x

é

t

.

C

á

c

b

ạ

n

đ

ộ

c

g

i

ả

d

ễ

t

h

ấ

y

t

o

à

n

b

ộ

c

á

c

b

à

i

t

o

á

n

t

ừ

5

2

đ

ế

n

6

0

đ

ề

u

s

ử

d

ụ

n

g

k

ỹ

t

h

u

ậ

t

l

i

ê

n

h

ợ

p

–

t

r

ụ

c

ă

n

t

h

ứ

c

đ

ố

i

v

ớ

i

m

ộ

t

r

o

n

g

h

a

i

p

h

ư

ơ

n

g

t

r

ì

n

h

c

ủ

a

h

ệ

,

p

h

ụ

c

v

ụ

c

h

ặ

n

m

i

ề

n

g

i

á

t

r

ị

c

ủ

a

c

á

c

b

i

ế

n

,

d

ẫ

n

đ

ế

n

s

ự

đ

ơ

n

đ

i

ệ

u

c

ủ

a

h

à

m

s

ố

t

r

ê

n

m

ộ

t

m

i

ề

n

.

N

g

o

à

i

r

a

đ

ể

k

h

a

i

t

h

á

c

v

à

n

â

n

g

c

a

o

,

p

h

á

t

r

i

ể

n

đ

ặ

c

t

í

n

h

c

h

ặ

n

m

i

ề

n

ẩ

n

h

à

m

c

ó

t

h

ể

s

ử

d

ụ

n

g

l

i

ê

n

h

ợ

p

h

ứ

c

t

ạ

p

h

ơ

n

,

đ

á

n

h

g

i

á

–

b

ấ

t

đ

ẳ

n

g

t

h

ứ

c

,

ẩ

n

p

h

ụ

,

…

v

ấ

n

đ

ề

n

à

y

s

ẽ

đ

ư

ợ

c

đ

ề

c

ậ

p

s

a

u

.

Q

u

ý

đ

ộ

c

g

i

ả

l

ư

u

ý

đ

ố

i

v

ớ

i

c

ô

n

g

c

ụ

đ

ạ

o

h

à

m

–

h

à

m

s

ố

,

n

g

o

à

i

t

í

n

h

c

h

ấ

t

đ

ơ

n

đ

i

ệ

u

   

f u f v u v  

,

c

h

ú

n

g

t

a

c

ò

n

c

ó

t

h

ể

t

ì

m

g

i

á

t

r

ị

l

ớ

n

h

ấ

t

–

g

i

á

t

r

ị

n

h

ỏ

n

h

ấ

t

c

ủ

a

h

à

m

s

ố

t

h

ô

n

g

q

u

a

k

h

ả

o

s

á

t

s

ự

b

i

ế

n

t

h

i

ê

n

h

o

ặ

c

đ

ồ

t

h

ị

h

à

m

s

ố

.

D

ư

ớ

i

đ

â

y

l

à

m

ộ

t

l

ớ

p

b

à

i

t

o

á

n

m

ớ

i

đ

ạ

i

d

i

ệ

n

c

h

o

n

h

ậ

n

x

é

t

r

ê

n

,

h

y

v

ọ

n

g

c

á

c

b

ạ

n

t

i

ế

p

c

ậ

n

m

ộ

t

c

á

c

h

t

ố

t

n

h

ấ

t

.

LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

43

B

à

i

t

o

á

n

6

0

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

   

 

2

3

3 2 2

1 3 1,

;

4 3 5 35 34 0.

x y y

x y

x y x y x y



   







      







.

Lời giải.

Điều kiện

0

y



.

Từ phương trình thứ nhất ta có

   

2

1

1 3 1 1 1 2 0

x

y y x x



          

.

Phương trình thứ hai của hệ trở thành

   

3

2 3 2

4

5 3 35 34 0 34

x

x x y y y f x g y



         

.

Xét hàm số

 

3

2

4 5f x x x x  

trên miền

 

2;0



ta có

   

2

5

3

8 5; 0 1;

3

f

x x x f x x







     

 

 

.

Trên miền

 

2;0



thì hàm số

 

f x

đồng biến, liên tục, do đó

 

 

 

2

;0

2

34

x

M

in f x f







  

.

Xét hàm số

 

3 2

3

35 ; 0

g

y y y y y



  

, dễ thấy ngay hàm số đồng biến nên

   

0

y

M

in g y g





.

Như vậy

   

34

Min

f x g x



 





 

. Dấu đẳng thức xảy ra khi

2

; 1

x

y



 

.

Cặp giá trị này không thỏa mãn hệ ban đầu, kết luận bài toán vô nghiệm.

N

h

ậ

n

x

é

t

.

M

ấ

u

c

h

ố

t

l

à

c

ô

n

g

v

i

ệ

c

h

ặ

n

m

i

ề

n

g

i

á

t

r

ị

c

ủ

a

ẩ

n

h

à

m

,

c

ũ

n

g

k

h

ô

n

g

q

u

á

k

h

ó

,

t

ư

ơ

n

g

t

ự

đ

á

n

h

g

i

á

t

ổ

n

g

b

ì

n

h

p

h

ư

ơ

n

g

     

2

3

0 1 1 3 1 1 1 2 0

y

y x y y x x



             

.

T

u

y

n

h

i

ê

n

p

h

ư

ơ

n

g

t

r

ì

n

h

t

h

ứ

h

a

i

k

h

ô

n

g

c

ó

d

ạ

n

g

t

ư

ơ

n

g

đ

ồ

n

g

h

à

m

s

ố

   

f

u f v u v



 

.

T

h

ự

c

t

ế

n

ó

c

ó

d

ạ

n

g

t

ổ

n

g

h

a

i

h

à

m

s

ố

đ

ộ

c

l

ậ

p

v

ớ

i

t

ừ

n

g

b

i

ế

n

   

3 2 3 2

4

5 3 35 5 5

x

x x y y y f x g y



       

.

M

ộ

t

đ

i

ề

u

m

a

y

m

ắ

n

v

ì

đ

â

y

c

h

í

n

h

l

à

đ

i

ề

u

k

i

ệ

n

đ

ẳ

n

g

t

h

ứ

c

k

h

i

c

á

c

h

à

m

s

ố

đ

ạ

t

g

i

á

t

r

ị

l

ớ

n

h

ấ

t

v

ớ

i

m

i

ề

n

t

ư

ơ

n

g

ứ

n

g

 

 

 

 

 

     

3

2

2;0

3 2

0

4

5 ; 2;0 2 34

3

35 ; 0 1 39

x

y

f

x x x x x Max f x f

g y y y y y Max g y g









        



     

B

à

i

t

o

á

n

6

1

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

2

3

3 2

4 1 2 ,

;

2 2 3 .

x y y

x y

y x x x x y



   







    







.

Lời giải.

Điều kiện

0

x



. Phương trình thứ nhất của hệ tương đương với

 

2

3 2

2

4 2 2 3 1 3

4 2

1 3 0 1 0 1

x

x y y y y y

x

y y y y y

         

 

         

Phương trình thứ hai tương đương

   

3

2

3 2 2 0 0

y y x x x x f y g x

        

.

Xét hàm số

 

3

2; 1

f

y y y y



  

thì

   

2

3

3 0, 1

f

y y y f y



     

liên tục, đồng biến.

Dẫn đến

   

1

0

f

y f





.

Xét hàm số

   

2

2 ; 0 2 1 3g x x x x x x g x x x



        .

Ta có

 

1

0

2 3 1 0 ;1 ;1

2

4

g x x x x x



  





       

   

   

.

Khảo sát sự biến thiên hàm này với miền đang xét ta có

     

1

0

0; ; 1 0 0

4

16

g g g g x

 



   





 

.

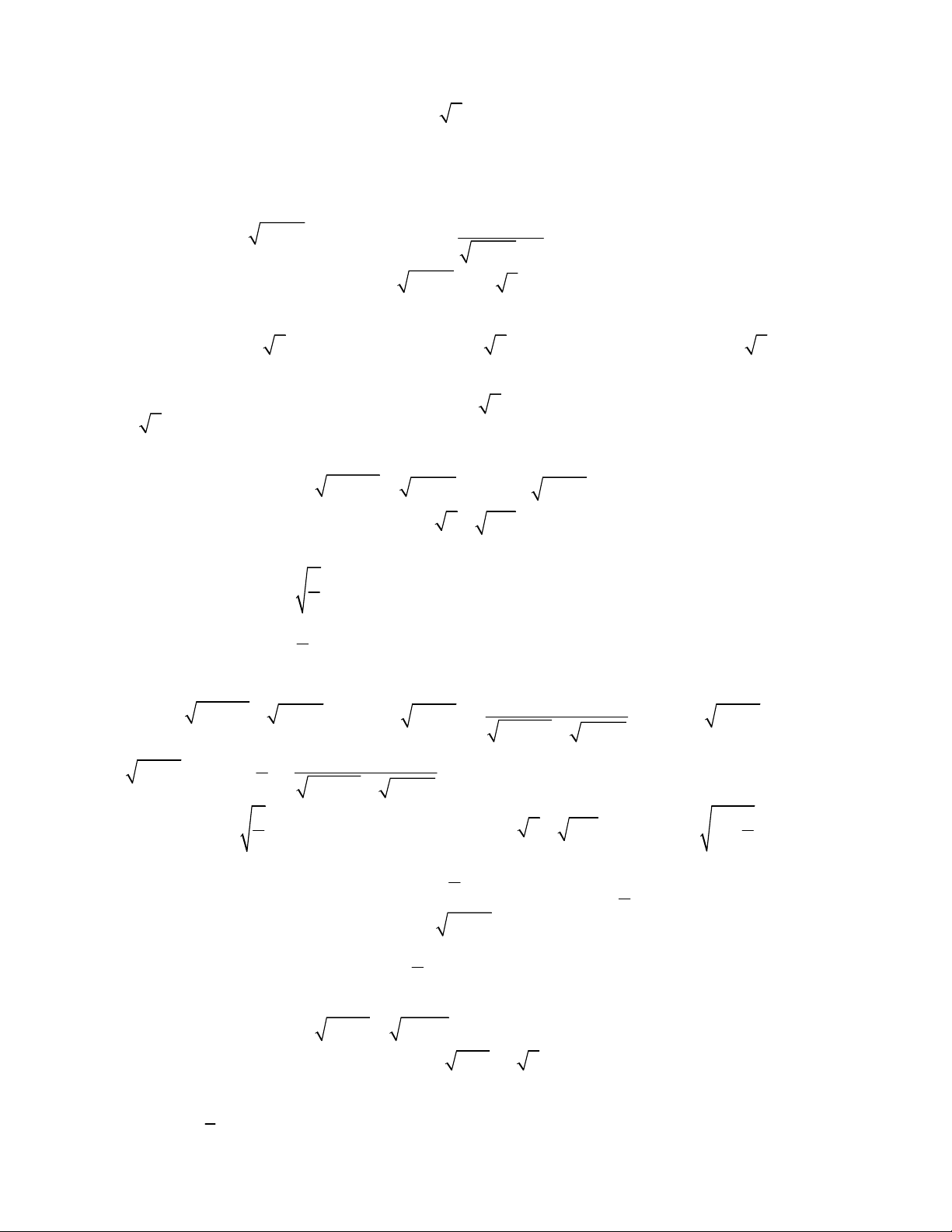
LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

44

Vậy

   

0

f

y g x





. Dấu đẳng thức xảy ra khi

 

     

2

1

;

0;1 , 1;1

1

y

x

y

x x







 









.

Thử lại thu được nghiệm của hệ là

   

;

0;1

x

y 

.

N

h

ậ

n

x

é

t

.

B

à

i

t

o

á

n

à

y

n

g

o

à

i

t

h

a

o

t

á

c

s

ử

d

ụ

n

g

đ

ạ

i

l

ư

ợ

n

g

l

i

ê

n

h

ợ

p

–

t

r

ụ

c

ă

n

t

h

ứ

c

 

2

3 2

2

4 2 2 3 1 3

4 2

x

x y y y y y

x

         

 

.

H

o

à

n

t

o

à

n

c

ó

t

h

ể

đ

á

n

h

g

i

á

t

h

u

ầ

n

t

ú

y

 

3

2 2

2 4 1 4 1 3 1 3 0

y y x y y y

           

.

N

g

o

à

i

r

a

c

á

c

b

ạ

n

h

ọ

c

s

i

n

h

n

h

ỏ

t

u

ổ

i

c

ó

t

h

ể

k

h

ô

n

g

n

h

ấ

t

h

i

ế

t

s

ử

d

ụ

n

g

c

ô

n

g

c

ụ

h

à

m

s

ố

 

   

 

2

3 2 3

3 2 2 0 3 2 1 0 1 2 1 0

y y x x x x y y x x y y x x

                 

.

R

õ

r

à

n

g

   

 

   

 

2

1

2 0, 1

1 2 1 0

1

0, 0

y y y

y y x x

x x x



    



     





  





.

B

à

i

t

o

á

n

6

2

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

2

3

2

3

2 3 2 1 2 1,

;

7 2 11.

x x y y

x y

x x x x xy



     







    







.

Lời giải.

Điều kiện

2

3

2; 0

3

2 0

1

2

1 0

2

x

y



 





  

 

 

 









Phương trình thứ nhất của hệ tương đương với

 

2

3 1

3 2 3 2 1 2 1 1 2 1

3 2 3 2

x x

x x y y y y

x x



         

  

.

Vì

 

2

1

3 1

1

1 2 1 0, 0 3 1 0

0

2

3 2 3 2

x

x x

y y y x x

x

x x







          





  



Kết hợp với điều kiện

2

1

3

x x  

. Khi đó

 

3

2

1

7 2 1 1 8.1 2.1. 11

2

x x x x xy

        

.

Phương trình thứ hai của hệ có nghiệm khi

 

2

1

1;

1

2

1

;

2

1

2 1 0

x y

y y



 





 





  



(Thỏa mãn hệ ban đầu).

Kết luận hệ đã cho có nghiệm duy nhất

1

;

2

x

y



.

B

à

i

t

o

á

n

6

3

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

2

3

2 3

3 1 2 2 ,

;

3 4 5 1 6 6.

y y x

x y

y y x x x



   







     







.

Lời giải.

Điều kiện

1

1;

3

x y

  

.

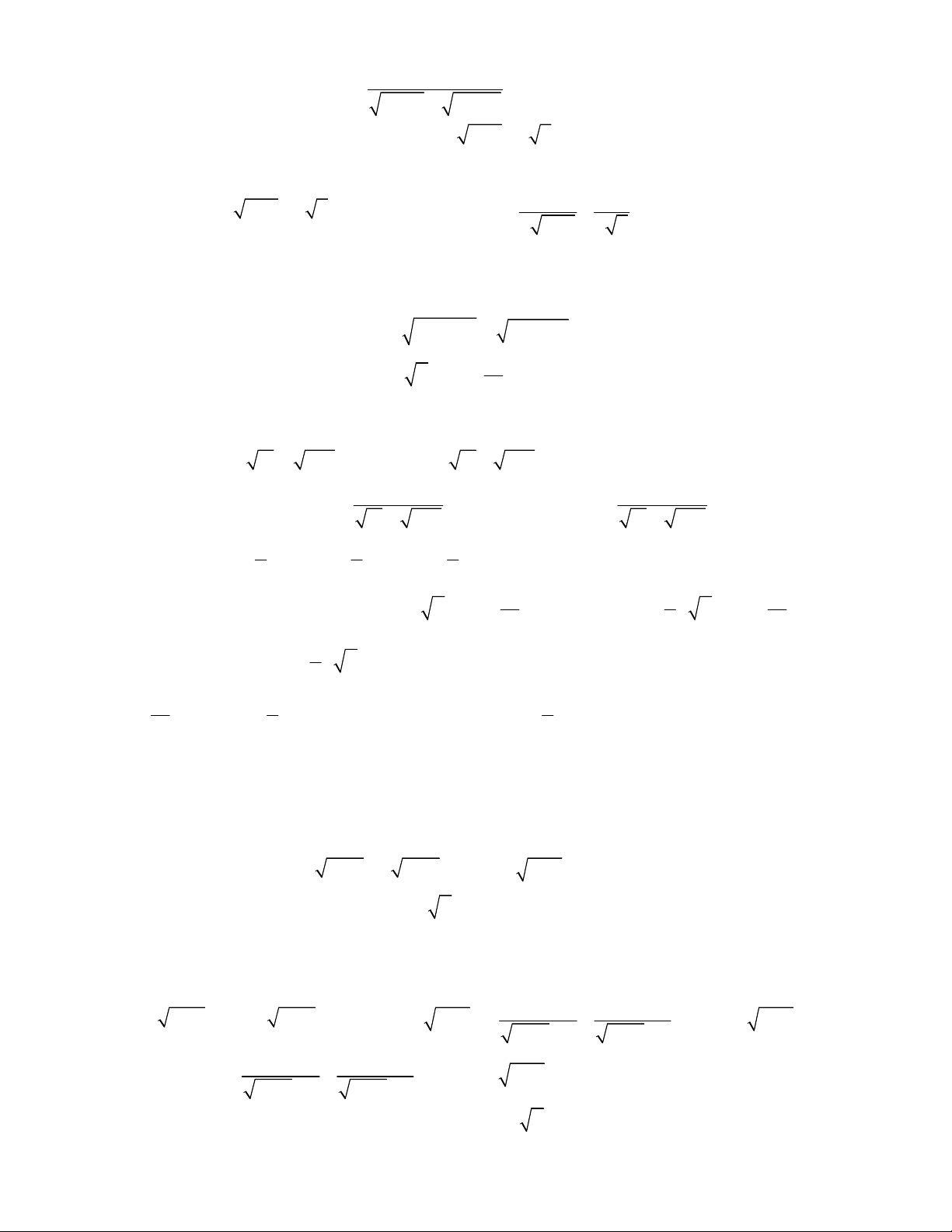
LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

45

Phương trình thứ nhất của hệ tương đương

2

1

0

1 0 1

3

1 2 2

y

x

y y

y





     



 

.

Phương trình thứ hai tương đương

 

   

3

2 3

3 4 5 1 6 6 6

y y x x x f y g x

        

.

Xét hàm số

 

3

2

3 4 ; 1f y y y y  

ta có

 

2

9 8 0, 1f y y y y



    

.

Xét hàm số

 

3

5 1 6 ; 1g x x x x x    

ta có

 

2

5 3

3 0, 1

2 1 2

g x x x

x x



     



.

Hai hàm số liên tục đồng biến trên miền tương ứng dẫn đến

       

1

1 1 7 6

f

y g x f g



     

.

Thử lại nghiệm không thỏa mãn, hệ vô nghiệm.

B

à

i

t

o

á

n

6

4

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

   

 

2

3

2

4

3 1 1,

;

19

2 5 .

2

x y x y x y

x y

y y x y y



      







   







.

Lời giải.

Điều kiện căn thức xác định

0

x

y





. Đặt

x

y t





thì phương trình thứ nhất trở thành

    

2

4

3 1 1 4 1 3 1 0

2 1 1

2 1 2 1 0 2 1 2 1 0

3

1 3 1

1 1 1

2

2 2

t

t t t t t

t

t t t t

t x y x y

         



 

         





   

 

       

Khi đó phương trình thứ hai trở thành

3

2 3 2

19

1 19

2

5 2 5

2

2 2

y

y x y y y y y y y

 



        





 

.

Xét hàm số

 

3 2

1

2

5

2

f

y y y y y y







   





 

, hàm số liên tục và đồng biến.

Lại có

 

19 3

1

1;

2 2

f

y x



  

. Hệ có nghiệm duy nhất

 

3

; ;1

2

x y















.

N

h

ậ

n

x

é

t

.

B

à

i

t

o

á

n

à

y

k

h

ô

n

g

q

u

á

k

h

ó

n

h

ậ

n

t

h

ấ

y

p

h

ư

ơ

n

g

t

r

ì

n

h

t

h

ứ

n

h

ấ

t

c

ó

d

ạ

n

g

p

h

ư

ơ

n

g

t

r

ì

n

h

v

ô

t

ỷ

m

ộ

t

b

i

ế

n

s

ố

x

y t





,

g

i

ả

i

b

ằ

n

g

p

h

ư

ơ

n

g

p

h

á

p

s

ử

d

ụ

n

g

đ

ạ

i

l

ư

ợ

n

g

l

i

ê

n

h

ợ

p

–

t

r

ụ

c

ă

n

t

h

ứ

c

.

T

h

a

y

t

h

ế

v

à

o

p

h

ư

ơ

n

g

t

r

ì

n

h

t

h

ứ

h

a

i

t

h

u

đ

ư

ợ

c

h

à

m

s

ố

m

ộ

t

b

i

ế

n

y

,

l

i

ê

n

t

ụ

c

v

à

đ

ồ

n

g

b

i

ế

n

c

ơ

b

ả

n

.

B

à

i

t

o

á

n

6

5

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

3

2

2 7 1 1 8,

;

1 3 5 8 .

x x y y

x y

x y y x y



      







     







.

Lời giải.

Điều kiện

1

; 2

y

x



 

.

Phương trình thứ nhất của hệ tương đương với

 

3

2 2

2

3 2 2 7 3 1 1 1 1

2 2 7 3

1 1

2 1 1 0 2 0 2

2 2 7 3

x

x x y y y y

x x

x y y x x

x x



            

   

 

           

 

   

 

Phương trình thứ hai của hệ trở thành

   

3

2 3

3 2 3 8 4 0 0

x x x y y y f x g y

         

.

Xét hàm số

 

3

2

3

2 ; 2

f

x x x x x



  

ta có

 

2

3

6 2 0, 2

f

x x x x





    

.

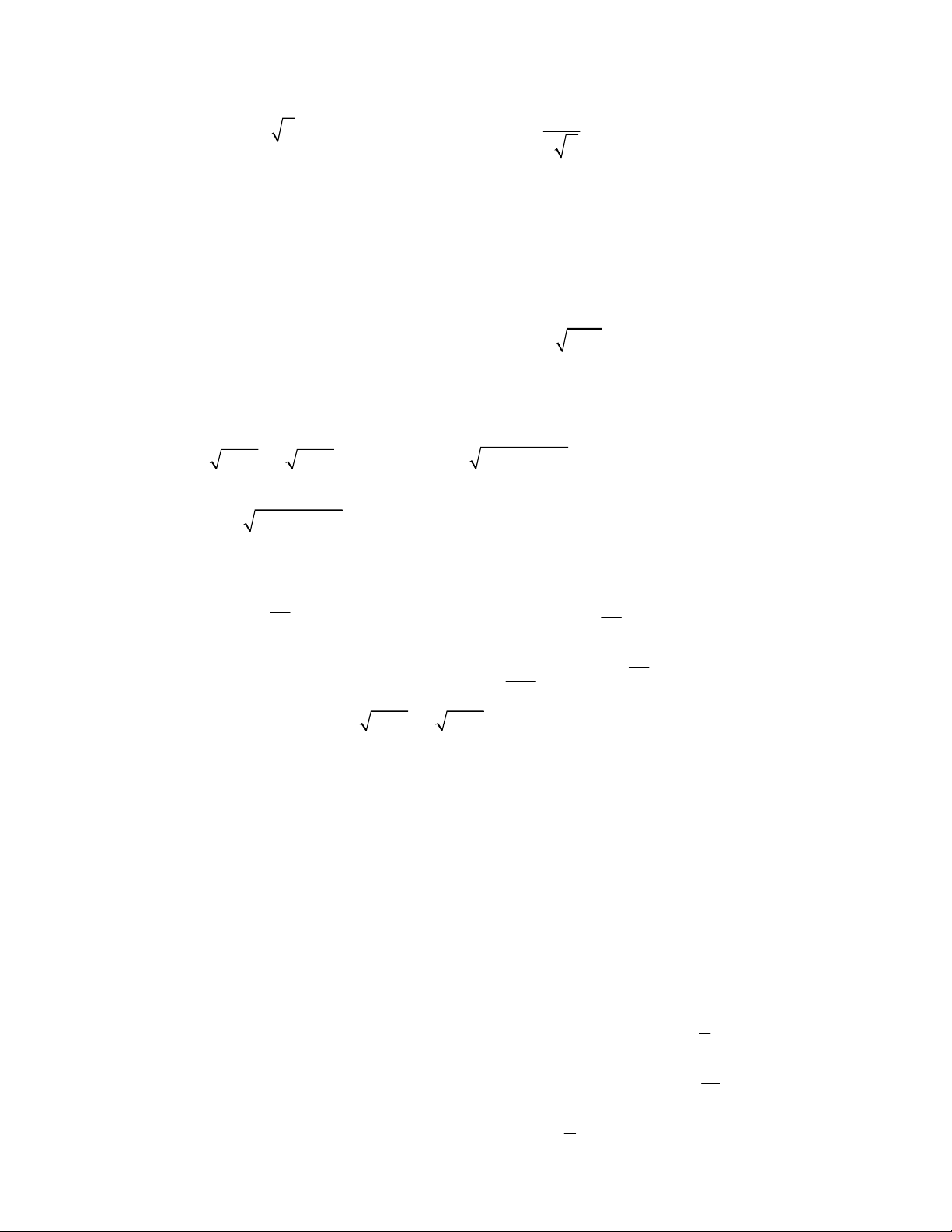
LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

46

Dễ thấy hàm số đồng biến liên tục nên

   

2

2 0

x

Min f x f



 

.

Xét hàm số

 

3

3 8 4; 0

g y y y y y

    

ta có

 

2

1

9

8 0, 1

2

g

y y y

y





    

.

Hàm số này cũng liên tục, đồng biến suy ra

   

1

0

y

Min

g x g





Tóm lại ta thu được

   

0

Min f x g y

 





 

, dấu đẳng thức xảy ra khi và chỉ khi

2

; 1

x

y



.

Cặp giá trị này thỏa mãn hệ đề bài nên là nghiệm duy nhất của hệ.

N

h

ậ

n

x

é

t

.

Đ

ố

i

v

ớ

i

b

à

i

t

o

á

n

s

ố

6

5

n

à

y

,

c

ả

h

a

i

h

ì

n

h

t

h

ứ

c

ủ

a

c

á

c

p

h

ư

ơ

n

g

t

r

ì

n

h

m

ộ

t

v

à

h

a

i

đ

ề

u

p

h

ứ

c

t

ạ

p

,

t

ỏ

r

a

k

h

á

b

ấ

t

l

ợ

i

c

h

o

c

h

ú

n

g

t

a

.

T

u

y

n

h

i

ê

n

m

ộ

t

s

ố

b

ạ

n

h

ọ

c

s

i

n

h

q

u

e

n

t

h

u

ộ

c

v

ớ

i

k

ỹ

t

h

u

ậ

t

l

i

ê

n

h

ợ

p

–

t

r

ụ

c

ă

n

t

h

ứ

c

t

r

o

n

g

p

h

ư

ơ

n

g

t

r

ì

n

h

v

ô

t

ỷ

c

ó

t

h

ể

d

ễ

d

à

n

g

n

h

ậ

n

r

a

c

á

c

h

p

h

á

đ

ề

,

c

h

ỉ

c

ầ

n

c

h

ú

ý

r

ằ

n

g

 

3

1

1 0, 1

y

y y



   

s

ẽ

t

ì

m

i

ề

n

g

i

á

t

r

ị

c

ủ

a

b

i

ế

n

x

c

h

ặ

t

h

ơ

n

s

o

v

ớ

i

2

x





.

N

h

i

ề

u

b

ạ

n

h

ọ

c

s

i

n

h

v

ộ

i

v

à

n

g

x

é

t

n

g

a

y

c

á

c

h

à

m

s

ố

đ

ộ

c

l

ậ

p

   

,

f

x g y

s

ẽ

g

ặ

p

h

ả

i

t

r

ở

n

g

ạ

i

d

ấ

u

đ

ạ

o

h

à

m

k

h

ô

n

g

x

á

c

đ

ị

n

h

 

2

3

6 2; 2?

f

x x x x





   

.

N

g

o

à

i

r

a

c

á

c

b

ạ

n

c

ó

t

h

ể

g

i

ả

i

b

ấ

t

p

h

ư

ơ

n

g

t

r

ì

n

h

s

a

u

đ

ể

t

ì

m

r

a

2

x



 

2

2 2

2

2 2 7 8 5 30 4 9 14 64

34 5 0

4

9 14 34 5 16 9 14 25 2 340 1156

5

34

5

2

5 34

34

2

466

2

9 484 932 0 5

9

x x x x x

x

x x x x x x x

x

x x

         

 







          





























    



















 

 



 

  













H

o

ặ

c

ó

t

h

ể

x

é

t

h

à

m

s

ố

đ

ồ

n

g

b

i

ế

n

       

2 2 7; 2 8; 2 2

g x x x g g x g x

       

.

B

à

i

t

o

á

n

6

,

t

r

í

c

h

l

ư

ợ

c

Đ

ề

t

h

i

c

h

ọ

n

Đ

ộ

i

t

u

y

ể

n

d

ự

t

h

i

H

S

G

Q

u

ố

c

g

i

a

M

ô

n

T

o

á

n

;

T

r

ư

ờ

n

g

T

H

P

T

C

h

u

y

ê

n

Đ

H

S

P

,

T

r

ự

c

t

h

u

ộ

c

Đ

ạ

i

h

ọ

c

S

ư

p

h

ạ

m

H

à

N

ộ

i

;

N

ă

m

h

ọ

c

2

0

1

0

–

2

0

1

.

B

à

i

t

o

á

n

6

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

  

 

2

2 2

2 3 4 2 3 4 18,

;

7 6 14 0.

x x y y

x y

x y xy x y



    







     







.

Lời giải.

Điều kiện

;x y



.

Coi phương trình thứ hai của hệ lần lượt là phương trình bậc hai ẩn x và ẩn y, ta có

   

2

2 2

7 6 14 0 1

6 7 14 0 2

x y x y y

y x y x x



     





     





Điều kiện có nghiệm của hai phương trình trên là

2

1

2

7

1

3 10 7 0

3

10

3 16 20 0

2

3

y

y y

x x

x



 





     

 



 

     





 





Xét hàm số

     

2

3

2 3 4; 4 3; 0

4

f t t t t f t t f t t

 

         



.

LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

47

Do đó các hàm số

 

2

10

2

3 4; 2;

3

f

x x x x







  









và

 

2

7

2

3 4; 1;

3

f

y y y y







  









đều liên tục, đồng biến.

Suy ra

       

.

2 . 1 6.3 18

f

x f y f f



 

.

Dấu đẳng thức xảy ra khi và chỉ khi

2; 1x y 

. Hệ phương trình đề bài có nghiệm duy nhất.

N

h

ậ

n

x

é

t

.

Đ

ố

i

v

ớ

i

b

à

i

t

o

á

n

6

n

à

y

,

v

i

ệ

c

p

h

â

n

t

í

c

h

b

ì

n

h

p

h

ư

ơ

n

g

p

h

ư

ơ

n

g

t

r

ì

n

h

a

i

đ

ã

t

r

ở

n

ê

n

k

h

ó

k

h

ă

n

(

k

h

ô

n

g

p

h

ả

i

t

h

ự

c

h

i

ệ

n

đ

ư

ợ

c

)

,

n

ế

u

c

ó

n

ó

t

ư

ơ

n

g

t

ự

v

i

ệ

c

t

ì

m

g

i

á

t

r

ị

n

h

ỏ

n

h

ấ

t

c

ủ

a

t

a

m

t

h

ứ

c

b

ậ

c

h

a

i

h

a

i

ẩ

n

x

v

à

y

.

R

õ

r

à

n

g

c

h

ú

n

g

t

a

c

h

ọ

n

p

h

ư

ơ

n

g

á

n

í

t

c

h

ô

n

g

a

i

h

ơ

n

,

s

ử

d

ụ

n

g

đ

i

ề

u

k

i

ệ

n

c

ó

n

g

h

i

ệ

m

c

ủ

a

p

h

ư

ơ

n

g

t

r

ì

n

h

b

ậ

c

h

a

i

ẩ

n

x

v

à

ẩ

n

y

l

ầ

n

l

ư

ợ

t

.

S

a

u

k

h

i

x

ử

l

ý

t

r

i

ệ

t

đ

ể

m

i

ề

n

g

i

á

t

r

ị

c

ủ

a

x

v

à

y

,

đ

ể

ý

s

ự

t

ư

ơ

n

g

đ

ồ

n

g

i

ữ

a

h

a

i

b

i

ể

u

t

h

ứ

c

ở

p

h

ư

ơ

n

g

t

r

ì

n

h

t

h

ứ

n

h

ấ

t

.

T

r

ư

ờ

n

g

h

ợ

p

h

a

i

b

i

ể

u

t

h

ứ

c

k

h

á

c

n

h

a

u

,

c

á

c

b

ạ

n

v

ẫ

n

h

o

à

n

t

o

à

n

c

ó

t

h

ể

s

ử

d

ụ

n

g

k

i

ế

n

t

h

ứ

c

h

à

m

s

ố

h

o

ặ

c

á

c

k

ỹ

n

ă

n

g

k

h

á

c

ủ

a

b

ấ

t

đ

ẳ

n

g

t

h

ứ

c

đ

ể

t

ì

m

r

a

2

; 1

x

y



.

G

i

ả

d

ụ

p

h

ư

ơ

n

g

t

r

ì

n

h

t

h

ứ

n

h

ấ

t

c

ó

d

ạ

n

g

  

2 3

4

6 2 54

x

x y



  

h

a

y

t

h

ậ

m

c

h

í

c

ó

d

ạ

n

g

k

h

ủ

n

g

b

ố

đ

ạ

i

k

h

á

i

n

h

ư

     

3

2 7 4 9

1 3 3 105; 1 38

x x x y y x x y y

         

.

C

h

ú

n

g

t

a

v

ẫ

n

s

ử

d

ụ

n

g

t

í

c

h

a

i

h

à

m

đ

ồ

n

g

b

i

ế

n

   

.

f

x g y

đ

ể

t

h

u

đ

ư

ợ

c

2

; 1

x

y



.

B

à

i

t

o

á

n

6

7

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

3

3 2 2

2 2

3

20 2 5 39 100,

;

4 4 3 .

x y x xy y x

x y

x y xy y x



     







    







.

Lời giải.

Điều kiện

;x

y



. Coi phương trình thứ hai của hệ lần lượt là phương trình bậc hai ẩn x và ẩn y, ta có

 

2

2 2

3

4 4 0

4

3 4 0

x

x y y y

y y x x x



    



    

Các điều kiện có nghiệm là

2

1 2

2

7

1

3 10 7 0

3

0; 0

4

3 4 0

0

3

y

y y

x x

x



 





   

 

     

 

  







 





Phương trình thứ nhất của hệ trở thành

 

   

3

3 2 2 2 2

3 2 3 2

3 3 20 2 4 3 4 5 39 100

3 18 45 3 3 8 108 108

x y x y x x y y x

x x x y y y f x g y

         

         

Xét hàm số

 

3

2

4

3

18 45; 0;

3

f

x x x x







  





 

thì

 

2

4

9

36 45 0, 0;

3

f

x x x x









    





 

.

Hàm số liên tục, đồng biến trên miền đó nên

 

4

0

;

3

4

892

3

9

x

M

ax f x f







 

 

 

 

 

 

.

Xét hàm số

 

3 2

7

3

3 8 ; 1;

3

g

y y y y y







   





 

thì

   

2

2 4

9

6 8; 0 ;

3

g

y y y g y y





 

       

 

 

.

Trên miền

 

7

1

;

3

7

4 80

1;

3

3 9

y

y Max g y g







 

 



  

   

 

 

   

, suy ra

   

108

Ma

x f x g y 

 

 

.

Dấu đẳng thức xảy ra khi

4

3

x

y



. Thử lại, kết luận hệ đã cho có nghiệm duy nhất

4

3

x

y



.

N

h

ậ

n

x

é

t

.

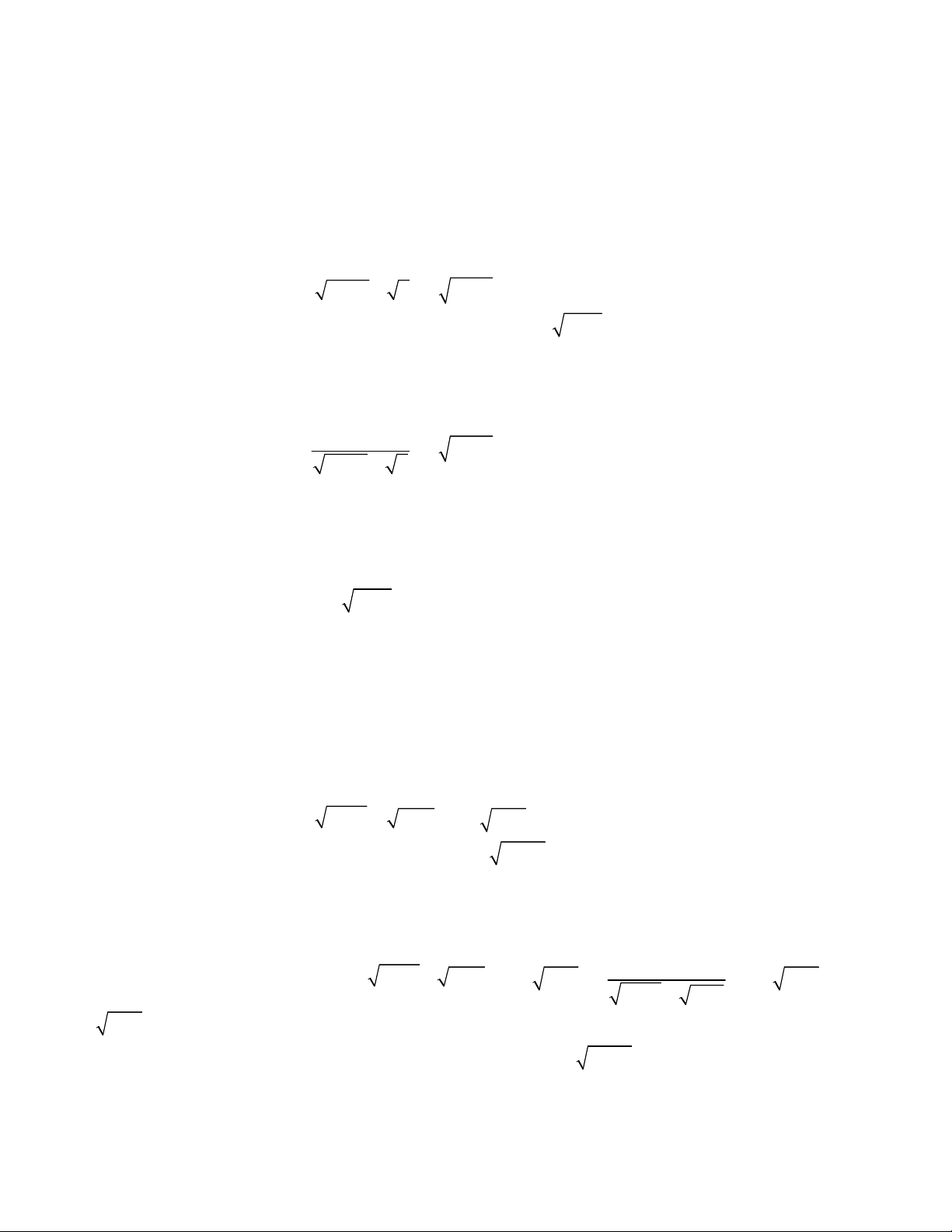
LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

48

B

à

i

t

o

á

n

3

,

đ

i

ề

u

k

i

ệ

n

p

h

ư

ơ

n

g

t

r

ì

n

h

b

ậ

c

h

a

i

c

ủ

a

h

a

i

ẩ

n

x

,

y

c

ó

l

ẽ

đ

ã

t

r

ở

n

ê

n

q

u

e

n

t

h

u

ộ

c

.

T

u

y

n

h

i

ê

n

p

h

ư

ơ

n

g

t

r

ì

n

h

t

h

ứ

n

h

ấ

t

c

ủ

a

h

ệ

c

ó

h

ì

n

h

t

h

ứ

c

k

h

á

m

ù

m

ị

t

,

n

h

ằ

n

g

n

h

ị

t

,

k

h

ó

c

h

ị

u

,

n

g

u

y

ê

n

d

o

t

í

c

h

x

y

d

í

n

h

v

à

o

n

h

a

u

,

m

u

ố

n

s

ử

d

ụ

n

g

h

à

m

s

ố

t

h

ô

n

g

t

h

ư

ờ

n

g

c

h

ú

n

g

t

a

t

h

ư

ờ

n

g

c

ô

l

ậ

p

h

a

i

b

i

ế

n

,

x

é

t

h

e

o

c

ù

n

g

m

ộ

t

ư

ơ

n

g

đ

ồ

n

g

h

à

m

h

o

ặ

c

h

a

i

h

à

m

k

h

á

c

n

h

a

u

,

n

h

ư

n

g

đ

ò

i

h

ỏ

i

p

h

ả

i

đ

ồ

n

g

b

ộ

đ

ể

đ

ạ

t

đ

ư

ợ

c

d

ấ

u

đ

ẳ

n

g

t

h

ứ

c

.

C

h

ú

ý

m

ộ

t

c

h

ú

t

p

h

ư

ơ

n

g

t

r

ì

n

h

t

h

ứ

h

a

i

c

ó

t

h

ể

s

ử

d

ụ

n

g

p

h

é

p

t

h

ế

2

4 3 4

xy y x x y    

,

t

ừ

đ

ó

s

u

y

r

a

 

   

3

3 2 2 2 2

3 2 3 2

3

3 20 2 4 3 4 5 39 100

3

18 45 3 3 8 108 108

x

y x y x x y y x

x x x y y y f x g y

         

         

B

à

i

t

o

á

n

6

8

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

2

4

3 2 3

2 1 7 1 ,

;

2 4 2 1 1 4 .

x x y

x y

x x x x y y



   







      







.

Lời giải.

Điều kiện

2

1 0; 0

0

,5

1 1

1

;4 0

x x

x

y

  







 

  



 



Phương trình thứ nhất của hệ suy ra

2

1

7 1 0 1

2 1

x

y x

x x



    

 

.

Xét hàm số

   

4 3 2 3 2

2 4 2 1; 1 8 12 2 2

f x x x x x x f x x x x



          

.

Ta có

   

 

    

2

2 1 4 2 1 2 1 1 4 2 1 0, 1f x x x x x x x x



           





 

.

Do đó hàm số liên tục và đồng biến trên miền đang xét nên

   

1

1 0

x

Min f x f



 

.

Mặt khác

 

 

3

1

;1 1 1 4 0

y

y y y



      

.

Do đó phương trình thứ hai của hệ có nghiệm khi các dấu đẳng thức xảy ra, tức là

3

1

1 0

x

y







 









.

Kết luận hệ có nghiệm duy nhất kể trên.

N

h

ậ

n

x

é

t

.

N

g

o

à

i

p

h

ư

ơ

n

g

á

n

s

ử

d

ụ

n

g

h

à

m

s

ố

v

ớ

i

đ

a

t

h

ứ

c

b

ậ

c

b

ố

n

b

i

ế

n

x

,

c

á

c

b

ạ

n

c

ó

t

h

ể

s

ử

d

ụ

n

g

p

h

â

n

t

í

c

h

t

h

u

ầ

n

t

ú

y

n

h

ư

s

a

u

   

 

2

4

3 2 2

2

4 2 1 1 2 1 0, 1

f

x x x x x x x x



         

B

à

i

t

o

á

n

6

9

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

3

3 2

1 9 2 1,

;

5 8 2 3 2 1 12.

x x y y

x y

x x x y y



    







     







.

Lời giải.

Điều kiện

3

1

9

1

;9 0

1

1 0;2 1 0

x

x x

y

y y





  





 



   



Phương trình thứ nhất của hệ tương đương

3

3 3

3

10

1 9 2 1 2 1

1 1

x x

x x y y y y

x x

 

       

  

.

Vì

 

3

3 2

2

1 0, 1 10 0 2 2 5 0 2 0 2

y

y y x x x x x x x



                

.

Phương trình thứ hai của hệ tương đương với

 

     

3

2

5 8 2 3 2 1 12 12

x x x y y f x g y

        

.

Xét hàm số

 

 

3

2

5 8 ; 2;9

f x x x x x   

ta có

    

 

2

3 10 8 3 2 3 4 0, 2;9

f x x x x x x



        

.

Hàm số này liên tục và đồng biến trên miền đang xét nên

 

 

 

2

;9

2

4

x

M

in f x f





.

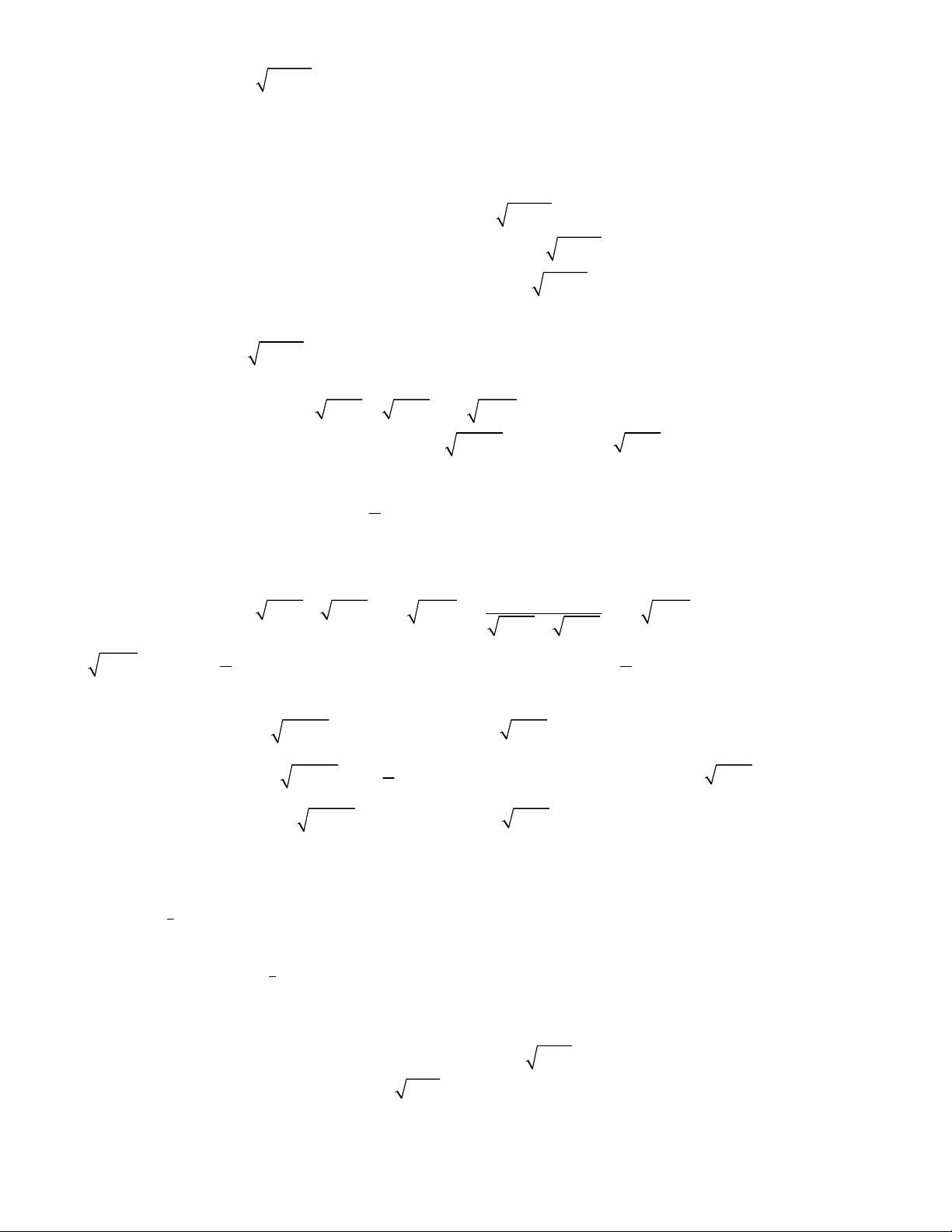
LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

49

Xét hàm số

   

2 3 2 1; 1g y y y y   

là hàm liên tục, đồng biến nên

   

1

2.4 8

y

Min

g y g





 

.

D

o

đ

ó

p

h

ư

ơ

n

g

t

r

ì

n

h

t

h

ứ

h

a

i

c

ó

n

g

h

i

ệ

m

k

h

i

c

á

c

d

ấ

u

đ

ẳ

n

g

t

h

ứ

c

x

ả

y

r

a

,

t

ứ

c

l

à

2

; 1

x

y



.

Cặp giá trị này thỏa mãn hệ nên là nghiệm duy nhất của hệ.

N

h

ậ

n

x

é

t

.

N

g

o

à

i

c

ô

n

g

c

ụ

h

à

m

s

ố

v

ớ

i

đ

a

t

h

ứ

c

b

ậ

c

b

a

ẩ

n

x

c

á

c

b

ạ

n

đ

ọ

c

n

h

ỏ

t

u

ổ

i

c

ó

t

h

ể

s

ử

d

ụ

n

g

p

h

â

n

t

í

c

h

 

     

3

2

3 2

2

5

8 2 3 2 1 12

5

8 4 2 3 2 1 8

2

1 2 3 2 1 8

x

x x y y

x x x y y

x x y y

     



      



     

C

h

ú

ý

t

h

ê

m

r

ằ

n

g

   

 

2

1 0

2 3 2 1 2.4 8

x

y y



  





   





B

à

i

t

o

á

n

7

0

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

3

5

3 5 2 ,

;

17 6 1 3 2 31 8 117.

x x y y

x y

x y y y x x x



    







        







.

Lời giải.

Điều kiện

2

5

0; 3 0; 8 0

2

3

2

0;3 2 0

3 5

x x x

y

y y

x



     









 

   





  



Phương trình thứ nhất của hệ tương đương với

2 2

5 3 5 2 5 2

5 3

x

x x y y y y

x x



       

  

.

Vì

2

5 2 0, ;2 2 2 0 1

3

y y y x x





        

 

 

. Như vậy

 

2

3;1 ; ;2

3

x

y





  

 





.

Phương trình thứ hai của hệ tương đương với

 

   

3

6 1 3 2 17 31 8 117 117

y y y x x x x f y g x

   

           

   

.

Xét hàm số

   

2

6

1 3 2; ;2

3

f

y y y y y

 



   









và hàm số

 

 

3

17

31 8; 3;1

g

x x x x x x      

.

Dễ thấy các hàm đơn lẻ

6 ; 1; 3 2

y y y

 

và

3

17 ; 31; 8

x x x x

  

đều là các hàm số đồng biến, liên tục trên từng

miền tương ứng với hai biến x, y. Các hàm ban đầu là tổ hợp tổng – tích các hàm đồng biến nên đều đồng biến, hơn

nữa đều nhận giá trị dương trên miền xác định.

Dẫn đến

     

 

 

2

3;

1

;3

3

2

18; 1 99

x

y

Ma

x f y f Max g x g





 



 

 



  

.

Khi đó

       

 

2

3;1

;3

3

18

99 117

x

y

f

x g y Max f y Max g x





 



 

 



    

.

Phương trình thứ hai có nghiệm khi các dấu cực trị xảy ra đồng thời, tức là

1; 2

x y

 

(Thỏa mãn hệ).

B

à

i

t

o

á

n

7

1

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

   

 

3

2 3

2 3 2

4

2 4 13 5 3 1,

;

17 2 3 1 6 2 4 1 .

x x x y y y

x y

x x x y y y



     







      







.

Lời giải.

Điều kiện

1

; 1

y

x



. Phương trình thứ nhất của hệ biến đổi thành

LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

50

   

 

3

2 3

2

3 3 2

3 2

2

2 5 4 13 3 1

3 1 2 5 4 1 14 1 2 1 14 14

3 4

8

3 1 6 0 2 2 4 0

1

2

3 2

2 2 4 0 2 0 2

1 2

x x x y y y

y y y x x x x x

y y

y y y y y y

y y

y y y y y

y y

     

            

 



          





 

 

 

          

 

 

 

Phương trình thứ hai của hệ tương đương với

   

     

2

3 2

4

2 3 2

4

17 2 3 1 6 2 4 1

17 2 3 1 6 8 2 2

x x x y y y

x x x y y y f x g y

      

          

Xét hàm số

     

2

4

17 2 3 1 6 1 6

f x x x x f

     

.

Xét hàm số

 

3 2

8

; 2

g

y y y y y



  

ta có

 

2

3

2 8 0, 2

g

y y y y





    

nên hàm số đồng biến, liên tục.

Suy ra

       

2

4 6 4 2

g

y g f x g y



      

. Dấu đẳng thức xảy ra khi

2; 1y x 

.

Thử lại ta thu được nghiệm duy nhất của hệ.

N

h

ậ

n

x

é

t

.

B

à

i

t

o

á

n

7

1

c

ó

m

ứ

c

đ

ộ

k

h

ó

n

h

ỉ

n

h

ơ

n

m

ộ

t

c

h

ú

t

s

o

v

ớ

i

c

á

c

b

à

i

t

o

á

n

t

r

ư

ớ

c

,

k

h

ô

n

g

s

ử

d

ụ

n

g

đ

ạ

i

l

ư

ợ

n

g

l

i

ê

n

h

ợ

p

l

i

ê

n

h

ợ

p

đ

ơ

n

t

h

u

ầ

n

,

t

á

c

g

i

ả

m

ạ

o

m

u

ộ

i

s

ử

d

ụ

n

g

đ

ặ

c

t

í

n

h

k

h

ô

n

g

â

m

c

ủ

a

c

á

c

b

i

ể

u

t

h

ứ

c

 

2

f

x g x

t

r

o

n

g

đ

ó

 

0

g

x



v

ớ

i

đ

i

ề

u

k

i

ệ

n

c

ă

n

t

h

ứ

c

ủ

a

b

à

i

t

o

á

n

.

Đ

ể

t

ì

m

đ

i

ề

u

k

i

ệ

n

c

ủ

a

b

i

ế

n

y

,

n

g

o

à

i

l

ờ

i

g

i

ả

i

n

h

ư

t

r

ê

n

c

ó

t

h

ể

s

ử

d

ụ

n

g

t

í

n

h

đ

ơ

n

đ

i

ệ

u

c

ủ

a

h

à

m

s

ố

n

h

ư

s

a

u

   

3

2 3

3 3 2

2 5 4 13 3 1

3 1 2 5 4 1

x x x y y y

g y y y y x x x f x

     

        

D

ễ

t

h

ấ

y

c

á

c

h

à

m

   

,

f

x g y

đ

ề

u

đ

ồ

n

g

b

i

ế

n

v

ớ

i

đ

i

ề

u

k

i

ệ

n

1

; 1

y

x



n

ê

n

       

3

1 14 3 1 14 2 2

f x f g y y y y g y

         

.

B

à

i

t

o

á

n

7

2

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

  

 

2

1 3 2 1 ,

;

2 11 20 4 5 13.

x x x x y

x y

x x x y y



     







     







.

Lời giải.

Điều kiện

1

3

x



. Phương trình thứ nhất của hệ tương đương với

     

2

2 4

1 3 2 1 2 1

1 3

x

x x x x y x x y

x x



         

  

.

Rõ ràng

  

 

2

2 4

2 1 0, 1;3 , 0 2 4 0 2

1 3

x

x x y x y x x

x x



             

  

 .

Phương trình thứ hai của hệ tương đương với

 

2

3

2 2 3 2

2

11 20 4 4 1 13 2 11 20 2 1 13

x

x x y y x x x y



            

.

Xét hàm số

 

 

3

2

11 20 ; 2;3

f

x x x x x   

ta có

    

 

2

6

22 20 2 5 3 0, 2;3

f

x x x x x x



        

.

Hàm số liên tục và đồng biến trên miền đang xét nên

 

 

 

2;3

2

12

x

M

in f x f





.

Hơn nữa

   

2

3 2

2

1 1 2 11 20 2 1 12 1 13

y

x x x y



          

.

Do đó phương trình thứ hai có nghiệm khi các dấu đẳng thức xảy ra, tức là

2

x y

 

.

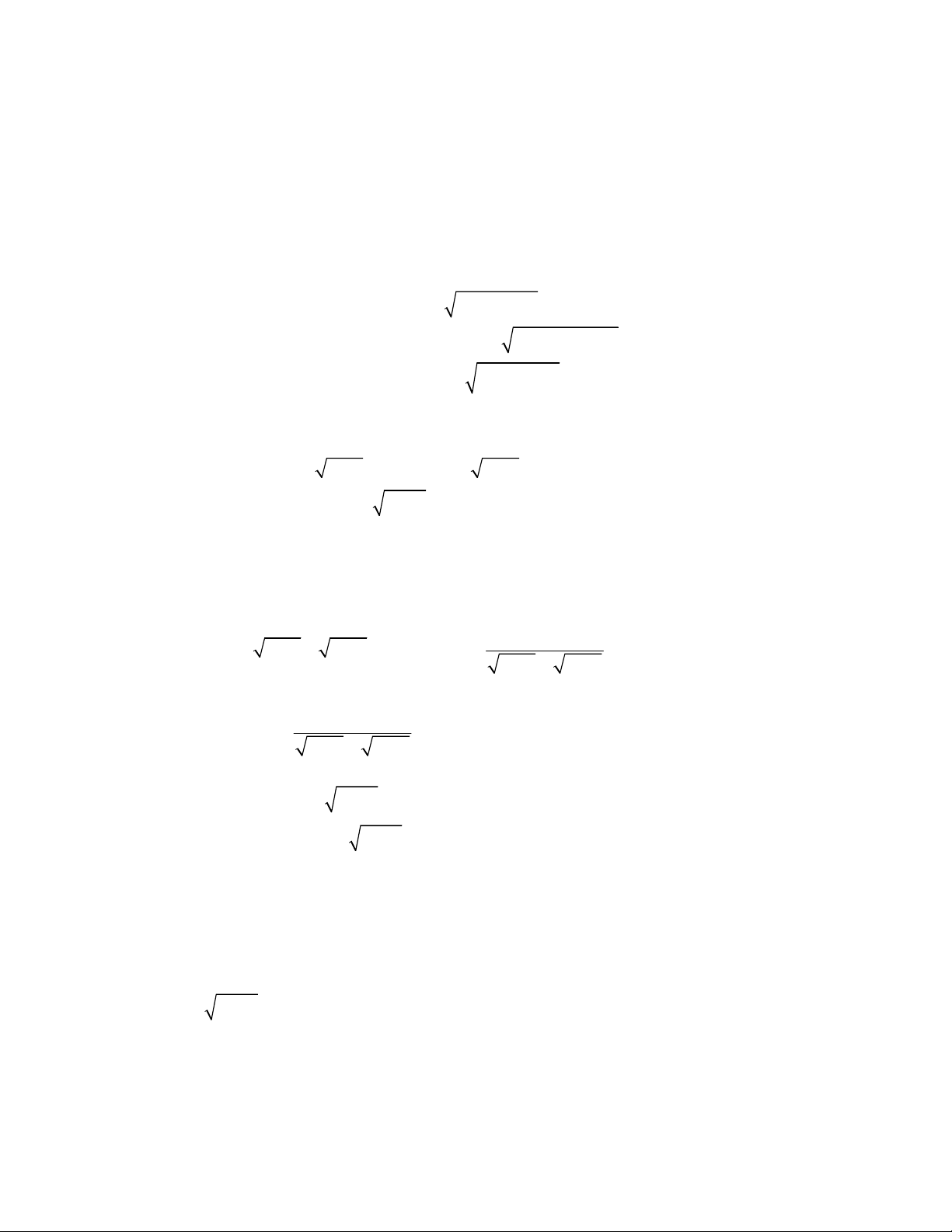
LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

51

Thử lại, kết luận hệ có nghiệm duy nhất kể trên.

N

h

ậ

n

x

é

t

.



B

ư

ớ

c

n

g

o

ặ

t

q

u

y

ế

t

đ

ị

n

h

ư

ớ

n

g

đ

i

c

ủ

a

c

á

c

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

t

r

o

n

g

l

ớ

p

b

à

i

t

o

á

n

à

y

l

à

s

ử

d

ụ

n

g

đ

ạ

i

l

ư

ợ

n

g

l

i

ê

n

h

ợ

p

–

c

h

ặ

n

m

i

ề

n

g

i

á

t

r

ị

,

t

h

ô

n

g

t

h

ư

ờ

n

g

c

h

ú

n

g

t

a

t

h

ư

ờ

n

g

c

ô

l

ậ

p

b

i

ế

n

t

h

e

o

h

ư

ớ

n

g

   

F

x G y



,

t

ừ

đ

ó

đ

á

n

h

g

i

á

c

ự

c

t

r

ị

   

F

x G y



đ

ể

b

ậ

t

n

g

ư

ợ

c

t

r

ở

l

ạ

i

t

ì

m

đ

ư

ợ

c

m

i

ề

n

g

i

á

t

r

ị

b

i

ế

n

c

ò

n

l

ạ

i

.

T

u

y

n

h

i

ê

n

b

à

i

t

o

á

n

7

2

k

h

ô

n

g

c

ò

n

đ

ơ

n

g

i

ả

n

h

ư

t

h

ế

n

ữ

a

,

k

h

i

v

i

ệ

c

ô

l

ậ

p

b

i

ế

n

l

à

k

h

ô

n

g

t

h

ể

,

h

o

à

n

t

o

à

n

c

á

c

b

ạ

n

c

ó

t

h

ể

t

h

a

y

t

h

ế

c

á

c

h

à

m

   

F

x G y



b

ở

i

   

;

F

x y G x y



,

t

h

ậ

m

c

h

í

c

ò

n

p

h

ứ

c

t

ạ

p

h

ơ

n

ữ

a

   

;

; ;... ; ; ;...

F

x y z G x y z



,

đ

ố

i

v

ớ

i

h

ệ

k

h

ô

n

g

m

ẫ

u

m

ự

c

n

h

i

ề

u

ẩ

n

.



L

ư

u

ý

c

ó

t

h

ể

s

ử

d

ụ

n

g

b

i

ế

n

đ

ổ

i

t

h

u

ầ

n

t

ú

y

t

h

a

y

c

h

o

p

h

ư

ơ

n

g

á

n

đ

ạ

o

h

à

m

–

h

à

m

s

ố

    

3

2 2

3 2 2

2 2

2

11 20 4 5 13

2

11 20 12 4 4 1 1

2

3 2 2 1 1

x x x y y

x x y

     



       



     

C

h

ú

ý

t

i

ế

p

t

ụ

c

  

2

3 0, 2 2 3 2 0, 2

x

x x x x



        

.

B

à

i

t

o

á

n

7

3

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

3

2 3 2 3 2

6

2 2,

;

1 1 4 4 8 16 12.

x y y x

x y

y y xy y x x x



     







       







.

Lời giải.

Điều kiện

3

2

0;6 0

2

6

1

0

x x

x

y

   



 





 



 



Phương trình thứ nhất của hệ tương đương với

3

4 2

6 2 2 2

6 2

x

x x y y y y

x x



         

  

.

Xét hàm số

 

3

2; 1f y y y y   

ta có

 

2

3 1 0,f y y y



    

nên hàm liên tục, đồng biến.

Dẫn đến

   

 

1

4

2

1

0 0 4 2 0 2 2;2

6 2

y

x

Min

f y f x x x

x x







          

  

.

Phương trình thứ hai của hệ tương đương

 

   

2

3 2 2 3 2

2

2 3 3 2

1 1 4 4 7 16 12

1 1 2 7 16 12 1

y y x xy y x x x

y y x y x x x

        

        

Xét hàm số

 

 

3

2

7

16 12; 2;2

g

x x x x x     

.

Ta có

    

 

2

3

14 16 2 3 8 0, 2;2

g

x x x x x x



         

vì

 

2 0

2;2

3 8 0

x

 



  



 



.

Hàm số liên tục và đồng biến trên miền

 

 

 

 

2

;2

2

;2 2 0

x

M

ax g x g





  

.

Trong khi đó

 

2

3

1 1 2 0, 1;y y x y y x

         

.

Phương trình (1) có nghiệm khi và chỉ khi các dấu cực trị xảy ra

3

1 0

2

0

1

2

y

x

y

x



 









  

 











Kết luận hệ có nghiệm duy nhất kể trên.

N

h

ậ

n

x

é

t

.

LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

52

C

á

c

b

ạ

n

đ

ộ

c

g

i

ả

n

h

ỏ

t

u

ổ

i

d

ù

c

h

ư

a

c

ó

t

r

o

n

g

t

a

y

c

ô

n

g

c

ụ

đ

ạ

o

h

à

m

–

h

à

m

s

ố

h

o

à

n

t

o

à

n

c

ó

t

h

ể

x

ử

l

ý

c

á

c

b

à

i

t

o

á

n

t

ư

ơ

n

g

t

ự

b

ằ

n

g

c

á

c

h

s

ử

d

ụ

n

g

p

h

â

n

t

í

c

h

n

h

â

n

t

ử

t

h

u

ầ

n

t

ú

y



T

h

a

y

t

h

ế

k

h

ả

o

s

á

t

 

3

2; 1f y y y y   

b

ở

i

   

2

3

2

1 2 0, 1

y

y y y y



      

.



T

h

a

y

t

h

ế

k

h

ả

o

s

á

t

 

 

3

2

7 16 12; 2;2

g x x x x x     

b

ằ

n

g

 

   

2 3 2 2 3 2

2

2 3 2 2

1 1 4 4 7 16 12

1 1 4 4 2 3

y y x xy y x x x

y y x xy y x x

        

        

C

h

ú

ý

 

   

 

2

3

2

1 1 2 0, 1;

2 3 0; 2;2

y y x y y x

x x x



       







     





B

à

i

t

o

á

n

7

4

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

2

3

2 3 2

2

1

1 17 1,

3 2

;

2 6 4 7 2 1 2.

x

x y y

x x

x y

x x x y y y x





   



  







       





.

Lời giải.

Điều kiện

1

2

; 1

2

x

y



 

. Phương trình thứ nhất của hệ tương đương với

 

   

2

3

2 1 17 1

3 2 1 2 17 1

1 1

17 1

3 2 1 2

1 1

1

17 1

3

2 1 2

x x x y y

x x

x y y

x x

x

x y y

x

      

        

 

    

   

 



    





   

 

Ta có

 

2

17

1 0, 1

x

y y y



   

và

1 1 1

0

, ;2

2

3

2 1 2

x

x x







  







  

 

nên

1

0 1

x



  

.

Xét hàm số

 

 

 

 

3

2 2

2 6 ; 1;2 3 4 6 0, 1;2

f x x x x x f x x x x



          

.

Hàm này liên tục và đồng biến trên miền

 

     

1

1;2 1 3

x

f x Min f x f



    

.

Xét hàm số

   

3

2 2

4 ; 1 3 2 4 0, 1g y y y y y g y y y y



          

.

Hàm này liên tục và đồng biến trên miền đang xét nên

     

1

5 0

y

g

y Min g y g





  

.

Lại có

 

3 2 3 2

2

1 1, 1 2 6 4 2 1 3 5 2

x

x x x x y y y x



             

.

Phương trình thứ hai của hệ có nghiệm khi và chỉ khi

1x y 

, hệ có nghiệm duy nhất.

N

h

ậ

n

x

é

t

.

C

ó

t

h

ể

n

h

ậ

n

t

h

ấ

y

b

à

i

t

o

á

n

7

4

t

h

o

ạ

t

i

ê

n

c

ó

v

ẻ

“

d

ễ

t

h

ở

”

h

ơ

n

s

o

v

ớ

i

c

á

c

b

à

i

t

o

á

n

t

r

ư

ớ

c

v

ì

h

ầ

u

n

h

ư

b

ạ

n

đ

ọ

c

n

à

o

c

ũ

n

g

q

u

a

n

s

á

t

h

ấ

y

b

i

ể

u

t

h

ứ

c

l

i

ê

n

h

ợ

p

đ

ư

ợ

c

b

ố

t

r

í

s

ẵ

n

v

ớ

i

p

h

ư

ơ

n

g

t

r

ì

n

h

đ

ầ

u

t

i

ê

n

 

2

2 1

1 17 1

3 2

x

x y y

x x



   

  

.

X

ô

n

g

p

h

a

c

h

ú

n

g

t

a

đ

á

n

h

g

i

á

l

i

ê

n

h

o

à

n

 

2

2 1

1 17 1 1 1

3 2

x

x y y

x x



     

  

.

T

u

y

n

h

i

ê

n

đ

ế

n

đ

â

y

x

u

ấ

t

h

i

ệ

n

t

â

m

l

ý

“

m

ừ

n

g

h

ụ

t

”

v

ì

b

ì

n

h

t

h

ư

ờ

n

g

s

ử

d

ụ

n

g

2 1

0

3 2

x

x x





  

c

ơ

m

à

.

LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

53

T

i

n

h

t

ế

m

ộ

t

c

h

ú

t

c

ó

t

h

ể

n

h

ậ

n

t

h

ấ

y

n

g

a

y

v

i

ệ

c

g

i

ả

i

b

ấ

t

p

h

ư

ơ

n

g

t

r

ì

n

h

2 1

1 3 2 1

3 2

x

x x



     

  

.

T

i

ế

p

t

ụ

c

b

i

ế

n

đ

ổ

i

2

3

1 2 3 3 2 2 2

0

1

1 2

2 0

x

x x x x x x

x

x x



           







  

 

   

  



N

g

o

à

i

r

a

c

ó

t

h

ể

t

r

i

ệ

t

i

ê

u

s

ố

1

b

ằ

n

g

c

á

c

h

s

ử

d

ụ

n

g

l

i

ê

n

h

ợ

p

h

ằ

n

g

s

ố

t

ư

ơ

n

g

t

ự

l

ờ

i

g

i

ả

i

p

h

í

a

t

r

ê

n

.

B

à

i

t

o

á

n

7

5

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

3

3 2 2

2

1 3 2 3 4,

;

1 2 1 2 3 5.

x x y y

x y

x y y x y y x



     







       







.

Lời giải.

Điều kiện

2

1

;

3

y



. Phương trình thứ nhất của hệ tương đương với

   

 

   

3

2

2 1 1 3 2 1 3 2

2 1 3 1

1 2

2 1 1 3 2 1

2 3

1 1 2

2 1 1 3 2 1

x x y y

x x

y y

x x

x y y

x x

       

 

    

   

 

     

 

   

 

Để ý rằng

   

2

1

2 0, 1

y

y y



   

và

2 3 2

0,

3

2 1 1 3 2 1

x

x x

   

   

nên dẫn đến

1

0 1

x



  

.

Phương trình thứ hai của hệ tương đương với

 

2

2 3 3 2

2

3 2

2

3 2 1 5

2

1 3 5

x

y xy y x x x y

y x y y x x x



      



      

Ta có

   

2

0

; 1 0, 1 2 1 0

y

x y y y y x y y



         

.

Hàm số

 

3

2

3 ; 1f x x x x x   

là hàm liên tục, đồng biến vì

 

2

3 2 3 0,f x x x x



     

;

   

1 5

f x f

 

.

Phương trình thứ hai có nghiệm khi các dấu đẳng thức đồng thời xảy ra, tức là

0

1

1 0; 1

x y

y x

 



  



  



.

Kết luận hệ có nghiệm duy nhất.

N

h

ậ

n

x

é

t

.

B

à

i

t

o

á

n

s

ố

7

5

n

à

y

đ

ã

c

ó

c

ô

l

ậ

p

h

a

i

h

à

m

s

ố

t

ạ

i

p

h

ư

ơ

n

g

t

r

ì

n

h

đ

ầ

u

t

i

ê

n

c

ủ

a

h

ệ

,

c

h

ú

n

g

t

a

t

h

ự

c

h

i

ệ

n

đ

á

n

h

g

i

á

n

g

a

y

l

ậ

p

t

ứ

c

.

N

g

o

à

i

p

h

ư

ơ

n

g

á

n

s

ử

d

ụ

n

g

l

i

ê

n

h

ợ

p

h

ằ

n

g

s

ố

n

h

ư

t

r

ê

n

   

 

   

3

2

2 1 3 2 3 4 2 1 1 3 2 1 3 2

2 1 3 1

1 2

2 1 1 3 2 1

2 3

1 1 2

2 1 1 3 2 1

x x y y x x y y

x x

y y

x x

x y y

x x

              

 

    

   

 

     

 

   

 

C

á

c

b

ạ

n

c

ó

t

h

ể

s

ử

d

ụ

n

g

p

h

â

n

t

í

c

h

t

h

u

ầ

n

t

ú

y

đ

ể

t

h

u

đ

ư

ợ

c

h

à

m

ẩ

n

x

l

ớ

n

h

ơ

n

b

ằ

n

g

2

.

   

2

3

2

1 3 2 3 2 2 1 2 2 2

x

x y y y y



          

.

Đ

ế

n

đ

â

y

c

ó

t

h

ể

g

i

ả

i

b

ấ

t

p

h

ư

ơ

n

g

t

r

ì

n

h

2 1 3 2 2

x x

   

h

o

ặ

c

x

é

t

h

à

m

s

ố

đ

ề

u

k

h

ả

t

h

i

,

n

h

a

n

h

c

h

ó

n

g

.

X

é

t

h

à

m

 

2 1 3 2;3 2

t x x x x

    

l

à

h

à

m

đ

ồ

n

g

b

i

ế

n

ê

n

   

1 2 1t x t x   

.

LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

54

B

à

i

t

o

á

n

7

6

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

3

2

3

3 2 2 2 2

2 7

1 0,

;3 10

2 2 3 15 1 3 2 17.

x

y

x yx x

x x y xy x y x xy





  



  





       





.

Lời giải.

Điều kiện

3

2

3

10

3

10

1

1 0

x

y



  

 



 

  

 





Phương trình thứ nhất của hệ tương đương với









 

3

3 2 3 3 2

3

3 2

3 3 2

2

3

3 3 2

3 10 1 0 3 2 3 10 1 1

1 1

3 2 3 10 1 1

1 1

3 2 3 10 1 1

x x y x x y

x x y

y

x

x x y

              

 

  

     

 

   

 

     

 

Ta có

2

2 3 3

1 1

0, ; 0

1 1 3 2 3 10

y

y x x

    

     

 nên từ (1) ta có

3

1 0 1 1x x x     

.

Phương trình thứ hai của hệ tương đương với

 

   

3

2 2 2 2

3 2 2 2 3 2 2

2 2 3 2 2

2

3 2 2

2

2 3 2 3 15 1 17

2

2 2 2 15 1 17

2

2 2 1 2 15 1 17

1

2 15 1 17 2

x x y xy x xy x y

x x y xy x xy x x x x y

x x xy y x y x x x y

x x y x x x y

       



          



          

        

X

é

t

h

à

m

   

3

2 2

2

; 1 3 2 2 0,f x x x x x f x x x x





         



.

Hàm số liên tục, đồng biến trên toàn trục số nên

     

1

1 2

x

f x Min f x f



  

.

Mặt khác

 

2

3

2 2

2

1

0, 1

1

2 15 1 0 2 15.1 17

1 1,

x x y x

x x y x x x y

y y



    





          



   







.

Phương trình (2) có nghiệm khi các dấu cực trị xảy ra, nghĩa là

 

2

1

1 0

0

1; 0

x

x x y

y

x y







  





 



 







Thử lại thỏa mãn hệ ban đầu, kết luận hệ có nghiệm duy nhất kể trên.

N

h

ậ

n

x

é

t

.



V

ớ

i

m

o

t

i

p

t

ư

ơ

n

g

t

ự

,

k

h

i

c

á

c

h

à

m

p

h

ụ

c

v

ụ

c

h

ố

t

c

h

ặ

n

đ

ã

p

h

ơ

i

b

à

y

,

h

o

à

n

t

o

à

n

c

ó

t

h

ể

g

i

ả

i

b

ấ

t

p

h

ư

ơ

n

g

t

r

ì

n

h

c

ơ

b

ả

n

,

m

ặ

c

d

ù

c

ó

v

ấ

t

v

ả

h

ơ

n

3

3 2 3 3 2

3 3 3 3 3 3 3

3 3

3

3 3

3

6 3 3 6 3

3

10 1 0 10 3 1 1

10 3 1 10 4 2 3 3 3

3 0 3

3

1

3

0 3

1 3

6 9 3 7 6 0

x x y x x y

x x x x x x x

x x

x

x x x x x

            

              

 

  





 



     



  



 

 

 

 



 

      

 

 

 



M

ộ

t

c

h

ú

ý

k

h

á

c

l

à

t

r

ả

i

d

ọ

c

á

c

b

à

i

t

o

á

n

7

3

đ

ế

n

7

6

,

c

á

c

p

h

ư

ơ

n

g

t

r

ì

n

h

p

h

ụ

c

ủ

a

h

ệ

b

a

n

đ

ầ

u

k

h

ô

n

g

c

ò

n

đ

ơ

n

g

i

ả

n

h

ư

t

r

ư

ớ

c

,

t

ứ

c

l

à

k

h

ô

n

g

c

ò

n

d

ạ

n

g

h

à

m

s

ố

đ

ộ

c

l

ậ

p

đ

ể

c

h

ú

n

g

t

a

t

h

a

o

t

á

c

   

f

x g y k





,

b

a

o

g

ồ

m

v

i

ệ

c

LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

55

t

ì

m

c

ự

c

t

r

ị

c

ủ

a

c

á

c

h

à

m

   

,

f x g y

,

c

h

o

d

ù

   

,

f x g y

c

ó

l

à

t

ổ

h

ợ

p

t

ổ

n

g

-

t

í

c

h

c

ủ

a

c

á

c

h

à

m

đ

ơ

n

đ

i

ệ

u

v

ớ

i

t

ừ

n

g

b

i

ế

n

.

P

h

ạ

m

v

i

m

ớ

i

c

ủ

a

c

á

c

b

à

i

t

o

á

n

t

r

ê

n

l

à

h

à

m

s

ố

l

i

ê

n

k

ế

t

,

t

ứ

c

l

à

h

à

m

s

ố

đ

ơ

n

đ

i

ệ

u

l

à

t

ổ

h

ợ

p

t

ổ

n

g

–

t

í

c

h

c

ủ

a

c

á

c

h

à

m

đ

ơ

n

đ

i

ệ

u

v

ớ

i

h

a

i

b

i

ế

n

k

h

á

c

n

h

a

u

.



C

ụ

t

h

ể

l

à

b

à

i

t

o

á

n

s

ố

7

4

v

ớ

i

h

à

m

t

ổ

n

g

c

ộ

n

g

 

3

2 3 2

2 6 4 7 2 1 2

x x x y y y x

       

.

C

á

c

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

7

3

,

7

5

,

7

6

m

ứ

c

đ

ộ

c

a

o

h

ơ

n

k

h

i

đ

ã

đ

ư

ợ

c

b

ố

t

r

í

l

ồ

n

g

h

é

p

đ

ạ

i

l

ư

ợ

n

g

k

h

ô

n

g

â

m

h

a

i

b

i

ế

n

 

;M x y

.



B

à

i

t

o

á

n

s

ố

7

3

c

ó

   

2

73

;

2

M

x y x y





.

 

   

2

3 2 3 2

2 3 2 2 3 2

2

2 3 3 2

1

1 4 4 8 16 12

1 1 4 4 7 16 12

1

1 2 7 16 12

y y xy y x x x

y y x xy y x x x

y y x y x x x

       

         



        



B

à

i

t

o

á

n

s

ố

7

5

c

ó

   

2

75

;

M

x y y x y





.

 

3

3 2 2

2 2 3 3 2

2

3 2

1 2 1 2 3 5

2

3 2 1 5

2

1 3 5

x y y x y y x

x y xy y x x x y

y x y y x x x

       



       



       



B

à

i

t

o

á

n

s

ố

7

6

c

ó

   

2

7

6

;

1

M

x y x x y



 

 

   

3 2 2 2 2

3 2 2 2 3 2 2

2 2 3 2 2

2

3 2 2

2

2 3 2 3 15 1 17

2

2 2 2 15 1 17

2

2 2 1 2 15 1 17

1

2 15 1 17

x x y xy x xy x y

x x y xy x xy x x x x y

x x xy y x y x x x y

x x y x x x y

       



          



          

         

B

à

i

t

o

á

n

7

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

   

     

 

3

2

3 2 1 1 3 8,

;

2 2 2 5 7 .

x y y y x

x y

x y y y x y x x



      







      







Lời giải.

Điều kiện

1y 

.

Phương trình thứ hai của hệ đã cho tương đương với

       

      

   

2

3

2

3

2

3

2

2 4 2 3 2

2

2 2 2 3 2

1

2 3 2

x y y y x y x y y x x

x y y x y y y x x

x y y x x



         



         

      

Dễ thấy

       

2

3

1

1 2 0, 1 3 2 0 1 2 0

2

x

x y y y x x x x

x





              



 



Xét

1x 

thì

 

2 1 1 53

y y

   

(Vô nghiệm).

Xét

2

x





thì phương trình thứ nhất của hệ trở thành

 

       

3

2

9

24 19 2 1 1 0

2

5 2 1 1 1 0 1

x

x x y y y

       

        

Để ý rằng

     

2

5 2 1 1 1 0, 2; 1

x

x y y y x y



           

.

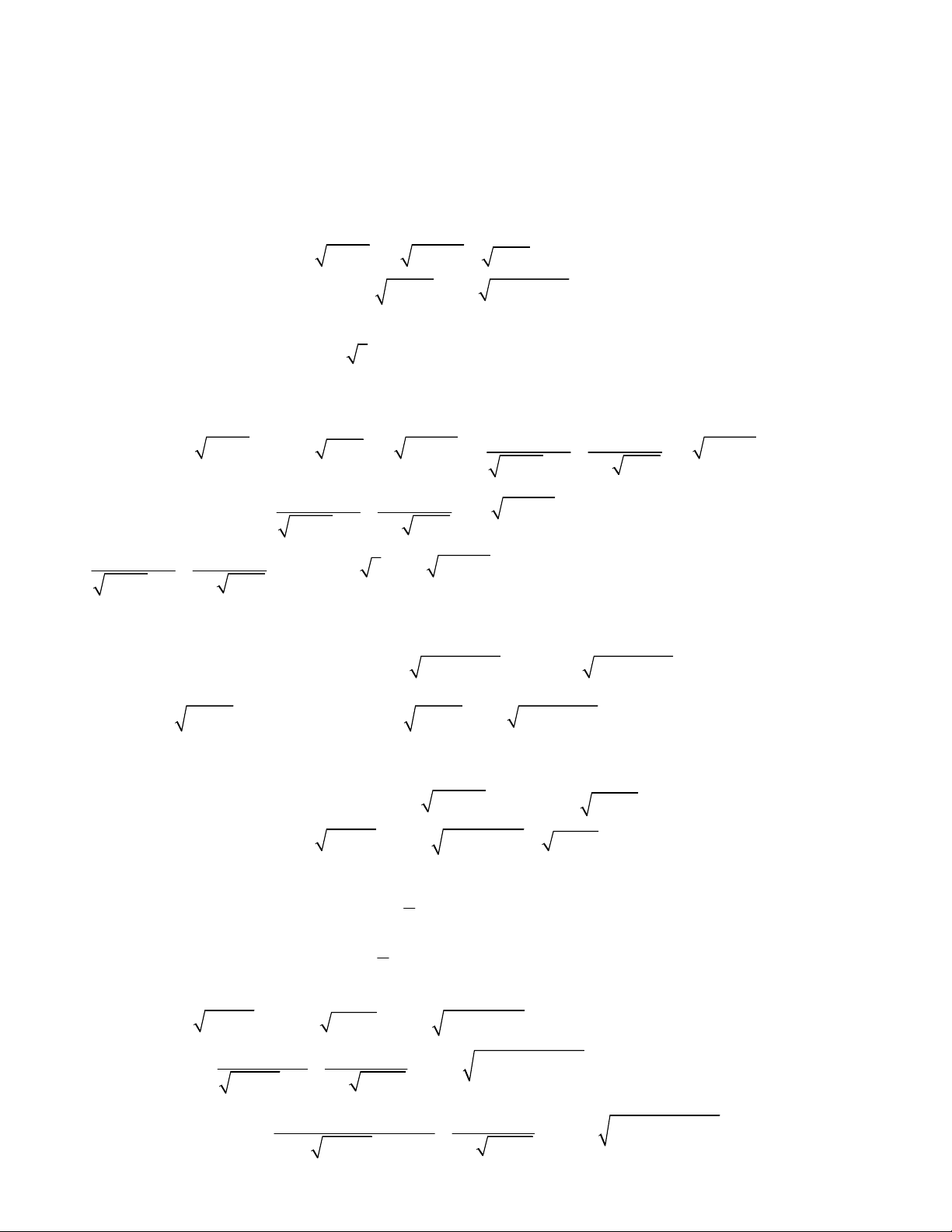
LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

56

Phương trình (1) có nghiệm khi và chỉ khi các dấu đẳng thức xảy ra, nghĩa là

2

; 1

x

y



 

.

Cặp số

2

; 1

x

y



 

thỏa mãn hệ nên là nghiệm duy nhất của bài toán.

N

h

ậ

n

x

é

t

.

M

ấ

u

c

h

ố

t

c

ủ

a

b

à

i

t

o

á

n

7

l

à

b

i

ế

n

đ

ổ

i

p

h

ư

ơ

n

g

t

r

ì

n

h

t

h

ứ

n

h

ấ

t

,

đ

i

ề

u

n

à

y

c

ó

t

h

ể

m

a

n

h

n

h

a

t

ừ

v

i

ệ

c

h

ú

n

g

t

a

p

h

á

n

đ

o

á

n

c

ặ

p

n

g

h

i

ệ

m

2

; 1

x

y



 

c

ủ

a

h

ệ

t

ừ

p

h

ư

ơ

n

g

t

r

ì

n

h

t

h

ứ

h

a

i

.

K

ế

t

h

ợ

p

c

á

c

k

i

ế

n

t

h

ứ

c

v

ề

b

ấ

t

đ

ẳ

n

g

t

h

ứ

c

A

M

–

G

M

,

t

ừ

đ

ó

đ

ư

a

r

a

h

ư

ớ

n

g

đ

i

t

h

i

ế

t

l

ậ

p

h

ạ

n

g

t

ử

   

2

3

2 1 2 0

x

x x x



    

đ

ể

t

h

u

đ

ư

ợ

c

l

ờ

i

g

i

ả

i

n

h

ư

t

r

ê

n

.

B

à

i

t

o

á

n

7

8

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

3

2

33 3 3

3 10 2 1,

;

6 17 2 9 34.

x y x x

x y

y y y x x x



     







     







.

Lời giải.

Điều kiện

 

3

2

3

2

3

0;10 0

3

2

2 0; 1 0

0

x x

x

x y y

y



   





 





 

   











Phương trình thứ nhất của hệ tương đương với

 

3

2 2

3

2

3

1

3 2 1 2 10 10

1 2

3 2

1 1

1 10

1 2

3 2

x x

x

x y x y x

x

x y x

x

 



         





 

 

 

    

 

 

 

 

Ta có

2

3

1 1

0, 3;2 ; 10 0,

1 2

3 2

x x

x y x y

x

 

 

        

 

 

 



nên

 

1

0 1 1;2

x

x x     

.

Xét hàm số

 

 

 

 

3

2

9; 1;2 3 2 0, 1;2

f

x x x x f x x x



         

.

Hàm số liên tục và đồng biến trên miền đang xét nên

   

 

 

3

33 3

1;2

1

8 2 9 2 17 2 9 17.1.2 34

x

f

x Min f x f x x x x x





          

.

Hơn nữa

   

3

3 3 3 3

6 0, 0 6 17 2 9 34

y y y y y y y x x x

           

.

Phương trình thứ hai có nghiệm khi các dấu đẳng thức xảy ra, tức là

1

; 0

x

y



.

B

à

i

t

o

á

n

7

9

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

2

3

5 3

3

6 2 2 3 17 1 3 2 12,

;

3 1 1997 3 2 3 2 1.

x x x x y y

x y

x y y x



      









      





.

Lời giải.

Điều kiện

 

2 5

3

0

3 0;3 1 0

2

3 2 0;3 2 0

3

x

x x x

y x

y



 





   

 



 

   











Phương trình thứ hai của hệ tương đương với

   

 

     

5 3

3

2

3

5

4 3 2

2

3

5

3 1 2 1 3 2 1997 3 2

3 3 2 2

1997 1 2

1 3 2

3 1 2

3 1

2

1 1997 1 2 1

1 3 2

3 1 2

x x y y

x x

y y

x

x x x x

x y y

x

       

 

    

 

 

 

   

 

     

 

 

 

 

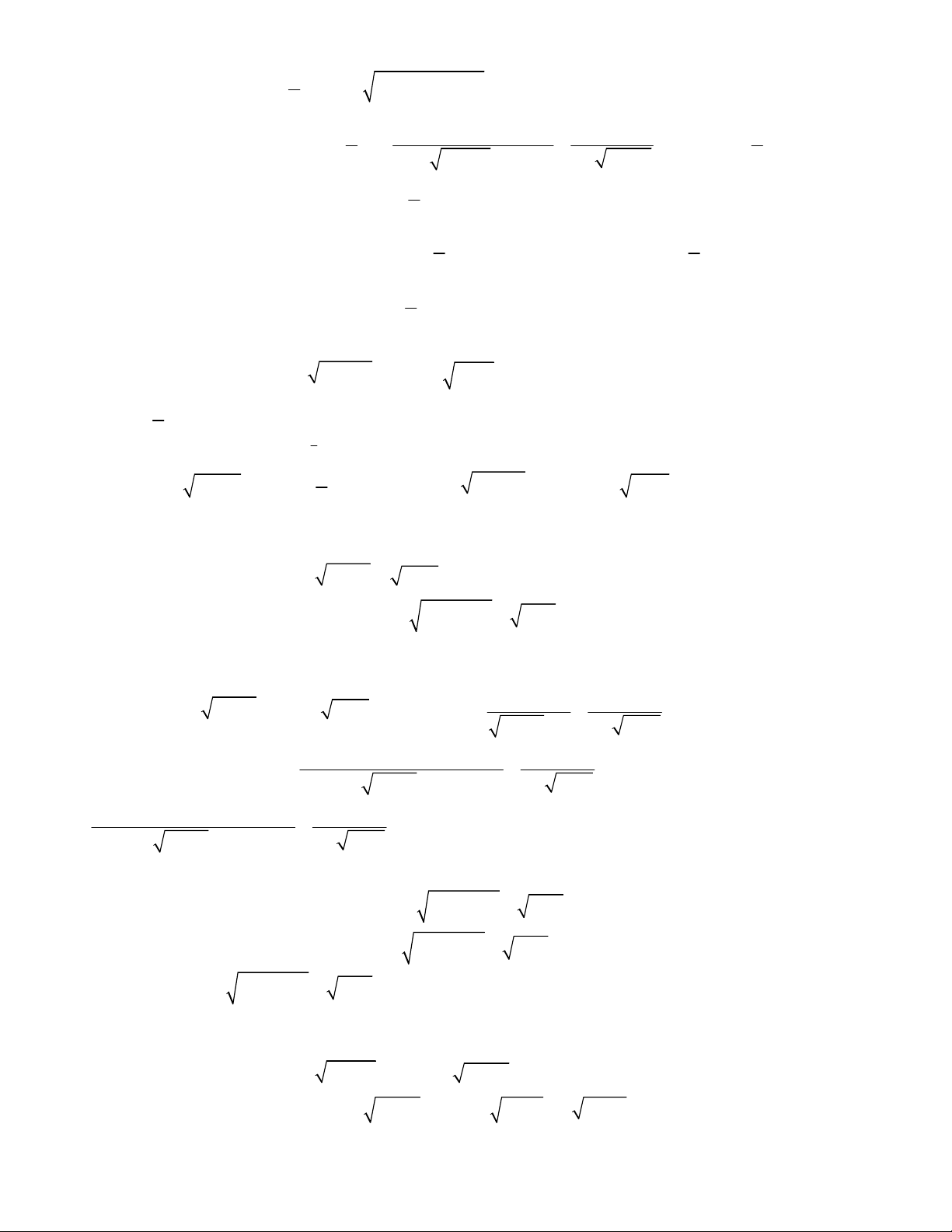
LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

57

T

a

t

h

ấ

y

       

2

3

2

1

2 0, 1997 1 2 0

3

y

y y y y



       

.

Hơn nữa

 

4

3 2

4 3 2

5

3 1

3 2 3

1 0, 0; 0, 0;

2 2

1 3 2

3 1 2

x x x x

x x x x x x

x

   

   

           

   

 

   

 

.

Do đó từ (1) thu được

3

1

0 1 1;

2

x

x x







    









.

X

é

t

đ

ồ

n

g

t

h

ờ

i

c

á

c

h

à

m

s

ố

   

3

2

3 2

3 3

2 2; 1; 3 2 0, 1;

2

3

; 1; 3 3 0,

2

f x x x x f x x x

g x x x x g x x x



  





        



  

   







        

 

 



Hai hàm số trên đều liên tục và đồng biến trên miền tương ứng.

Trong khi đó

 

   

3

6 2 2 3 6

h x x x x x f x g x

     là tổ hợp hai hàm đồng biến nên nó đồng biến, ngoài

ra ta có

       

3

1

;

2

3

1

; 6 1 . 1 6.2 12

2

x

h x Minh x f g







 

 







    





 

.

Thêm nữa

 

2

3 3

2

1

3 2 0, 6 2 2 3 17 1 4 12

3

y

y y x x x x y y



           

.

Phương trình thứ nhất của hệ có nghiệm khi các dấu đẳng thức đồng thời xảy ra, tức là

1

; 1

x

y



.

B

à

i

t

o

á

n

8

0

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

2

7

4

2 2 2

8

2 6 2,

;

5 13 3 1 2 17.

x x x y

x y

x y x y y x y



     







      







.

Lời giải.

Điều kiện

1

;0 2

y

x



 

. Phương trình thứ nhất của hệ tương đương với

   

7

2 2

7

1 1

8 3 1 2 6 6

1 2

8 3

x x

x x x y x y

x

 

          

 

 

     

6 5 4 3 2

2

7

1

6 1

1

2

8 3

x x x x x x

x x y

x

 

     

    

 

 

 

 

Ta có

 

6

5 4 3 2

2

7

1 1

0, 0;6 0, ,

1 2

8 3

x x x x x x

x x y x y

x

     

       

 

 



.

Từ (1) thu được

 

1

0 1 1;2

x

x x     

. Phương trình thứ hai của hệ tương đương

 

   

 

4

2 2 2 2

2

2 2 2

2

13 3 1 4 17

13

3 1 4 17 2

x

x y y x y y y

x y x y y y

       

       

Rõ ràng

   

2

2 2

0

;13 3 1 4 13.1 0 4 17

x

y x y y y



        

.

Phương trình (2) có nghiệm khi các dấu đẳng thức đồng thời xảy ra, tức là

1x

y



.

B

à

i

t

o

á

n

8

1

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

   

 

3

2

4 3 3

3 1 2 1 3 2 2 4,

;

1 3 2 1 8 7.

x y x y x

x y

x y x y y x



      







       







.

Lời giải.

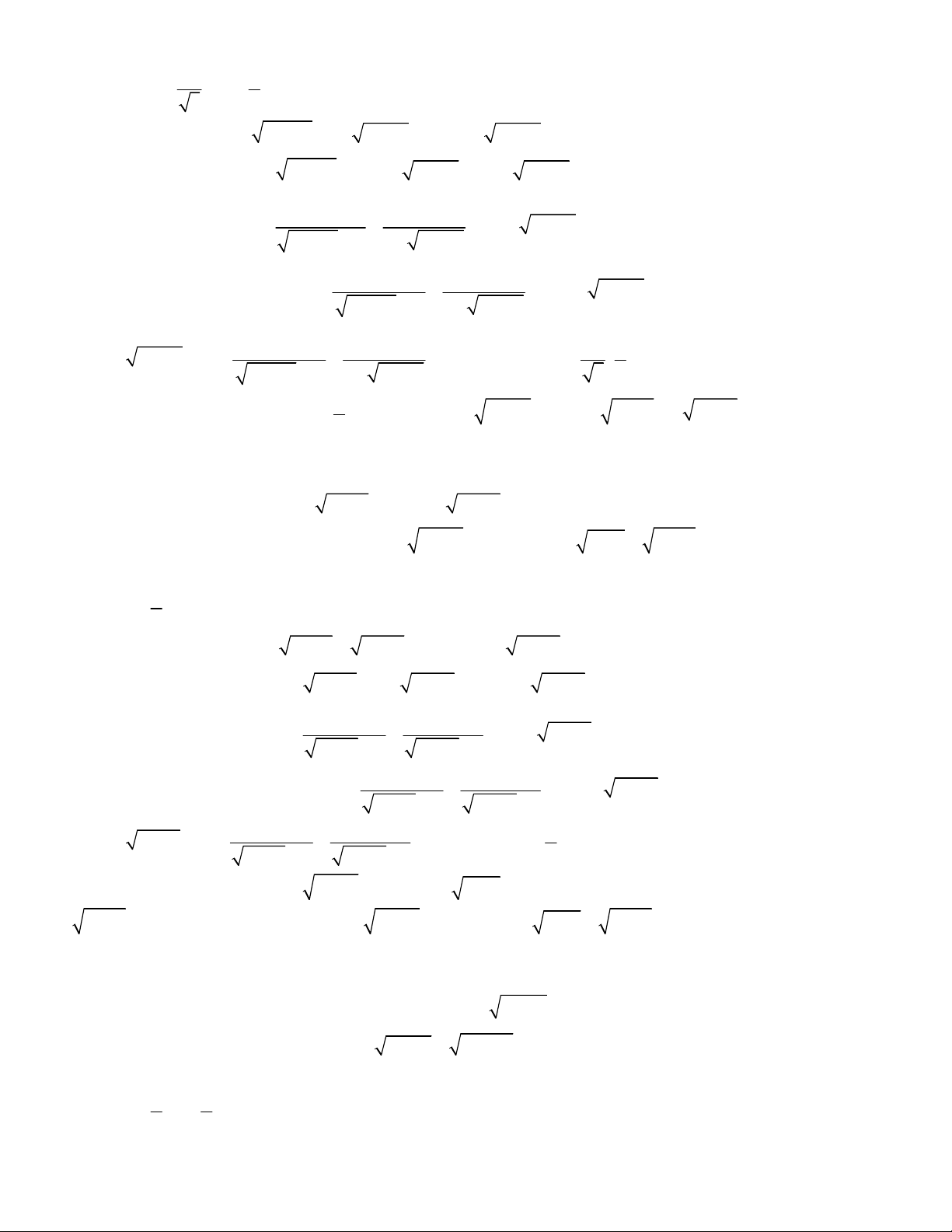
LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

58

Điều kiện

3

1 3

1;

2

3

y x

   

. Phương trình thứ nhất của hệ tương đương với

 

3

2

3

2

3

2

3

1 1 3 2 2 3 2 3 2

3 1 2 1 3 2 3 2

3 1

2 2

3 2

1 3 2

3 1 2

3 1

2

1

3 2 1

1

3 2

3 1 2

x x y y x x

x x y x

x

y x

x

x x

x y x

x

        

        



    

 

 

 

 

 

     

 

 

 

 

Ta có

 

2

3

3 1

2 1 3

3 2 0; 0, ; ;

2

1 3 2 3

3 1 2

x x

y x y x

x

 

 

         

 

 

 

 

 .

Từ (1) ta có

3

1

0 1 1;

2

x

x x







    









. Khi đó

   

4

3 3

1

3 2 1 8 2.2 0 1.3 7

x

y x y y x



         

.

Phương trình thứ hai của hệ có nghiệm khi các dấu đẳng thức xảy ra, tức là

1x

y



.

B

à

i

t

o

á

n

8

2

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

   

 

2

3 3 3

3 1 2 1 2 1 2 1,

;

3 1 3 3 2 3 1 22.

x y x y x

x y

x y y y x y y



      







         







.

Lời giải.

Điều kiện

1

; 1

2

x y 

. Phương trình thứ nhất của hệ tương đương với

 

   

 

2

3 1 2 1 2 2 2 1 2 1

3 1 2 2 1 1 2 1

3 1 2 1

2 1

3 1 2 2 1 1

3 2

1 2 1

3 1 2 2 1 1

x x y y x x

x x y x

x x

y x

x x

x y x

x x

        

        

 

    

   

 

     

 

   

 

Ta có

 

2

3 2 1

2 1 0; 0, ;

2

3 1 2 2 1 1

y x y x

x x

        

   

 nên

1 0 1x x   

.

Khi đó các hàm số con

2

3 3

3

1; 3; 3 2; 3

x

y y y x y



    

đều là các hàm đồng biến.

Do

3

1 0

y

 

nên

 

   

 

2

3 3 3

; 3 1 3 3 2 3 1 1;1 22

f x y x y y y x y y f

           

.

Dấu đẳng thức xảy ra khi

1x y 

. Hệ phương trình có nghiệm duy nhất.

B

à

i

t

o

á

n

8

3

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

4

3 2

3

4 3 2 3 2 1 2.

;

2 1 5 4 3 2 5 2.

x x x y y x

x y

y x x y x



      









      





.

Lời giải.

Điều kiện

4

2

;

5

3

x

y



. Phương trình thứ hai của hệ tương đương với

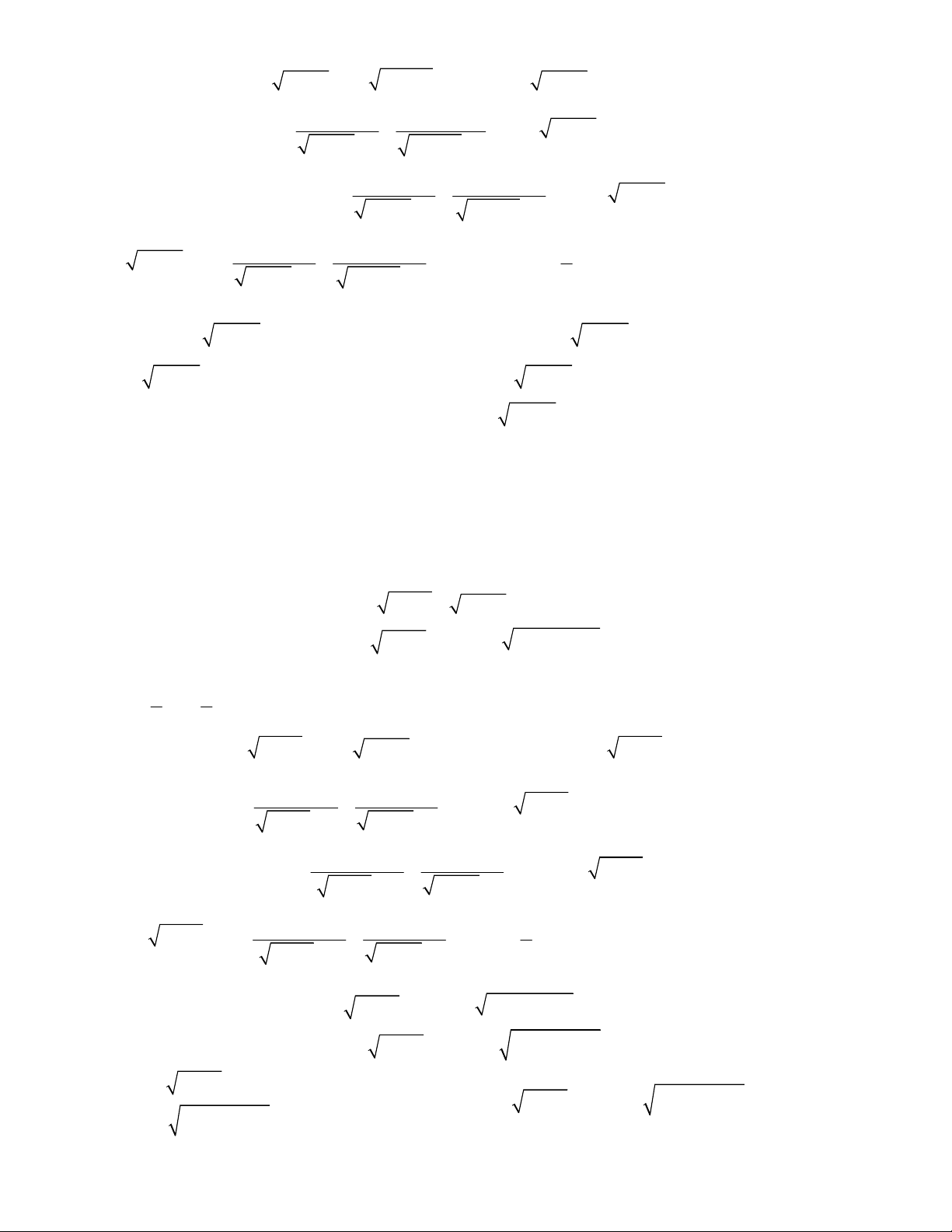
LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

59

 

3

2

3

2

3

2

3

5

4 1 3 2 1 2 5 4 5 4

3 1

5 1

5 4

5 4 1

3 2 1

3 1

5

1

5 4

5 4 1

3 2 1

x x y y x x

x

y x

x

x x

x y x

x

         



    

 

 

 

 

     

 

 

 

 

Ta có

 

2

3

3 1

5 4

5 4 0; 0, ;

5

5 4 1

3 2 1

x x

y x y x

x

 

        

 

 nên

1

0 1

x



  

.

Phương trình thứ nhất của hệ tương đương với

 

   

2

3

2

3 2

2 3 2 3 2 3 3 1 0 3 2 1 0 1

x x y y x x x x x y x x               .

Rõ ràng

 

2

3 3

3 2 0; 1 0; 1; 3 2 1 0

x y x x x y x y x x

              

 .

Do đó (1) có nghiệm khi các dấu đẳng thức xảy ra, hay

3

2

1

x

y

x y

x









  









.

Kết luận hệ đã cho có nghiệm duy nhất kể trên.

Nhận xét.

Các bài toán 78, 80, 81, 82, 83 đều có dạng cô lập hàm số dạng phức tạp

   

;

F

x y G x y



, trong đó việc phát

hiện biểu thức

 

;G

x y

không còn là điều đơn giản, yêu cầu bạn đọc hết sức chú ý và khéo léo tách ghép.

B

à

i

t

o

á

n

8

4

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

   

 

3

3 2

3

2

2 5 3 4 3 2 11,

;

1 4 1 2 1 2 2 1 .

y x x x y y

x y

x y x x x x



       







      







.

Lời giải.

Điều kiện

3

1

;

4

x y

 

. Phương trình thứ nhất của hệ tương đương với

 





3

2 3 3

3

2

3

2

3

3 3 2 4 3 1 2 1 2 1 3 3

3 1

4 1

1 3

4 3 1

3 2

3 1

4

1 1 3

4 3 1

3 2

x x y y y x x

x

y x

x

x x

x y x

x

            



     

 

 

 

 

 

      

 

 

 

 

Ta có





 

2

3

3 1

4 3

1 3 0; 0, ;

4

4 3 1

3 2

x x

y x x y

x

 

         

 

 



nên

1

0 1

x



  

.

Phương trình thứ hai của hệ tương đương với

   

       

3

2

3

2

1 4 1 2 1 2 2 1

1 4 1 2 1 1 1

x y x x x x

      

       

Khi đó

 

     

3

2

1 4 1 0, 1

1 4 1 2 1 1

2 1 1 2 1 . , 1

x y x

x

y x x x x

x

x x x x x



    





      





      





.

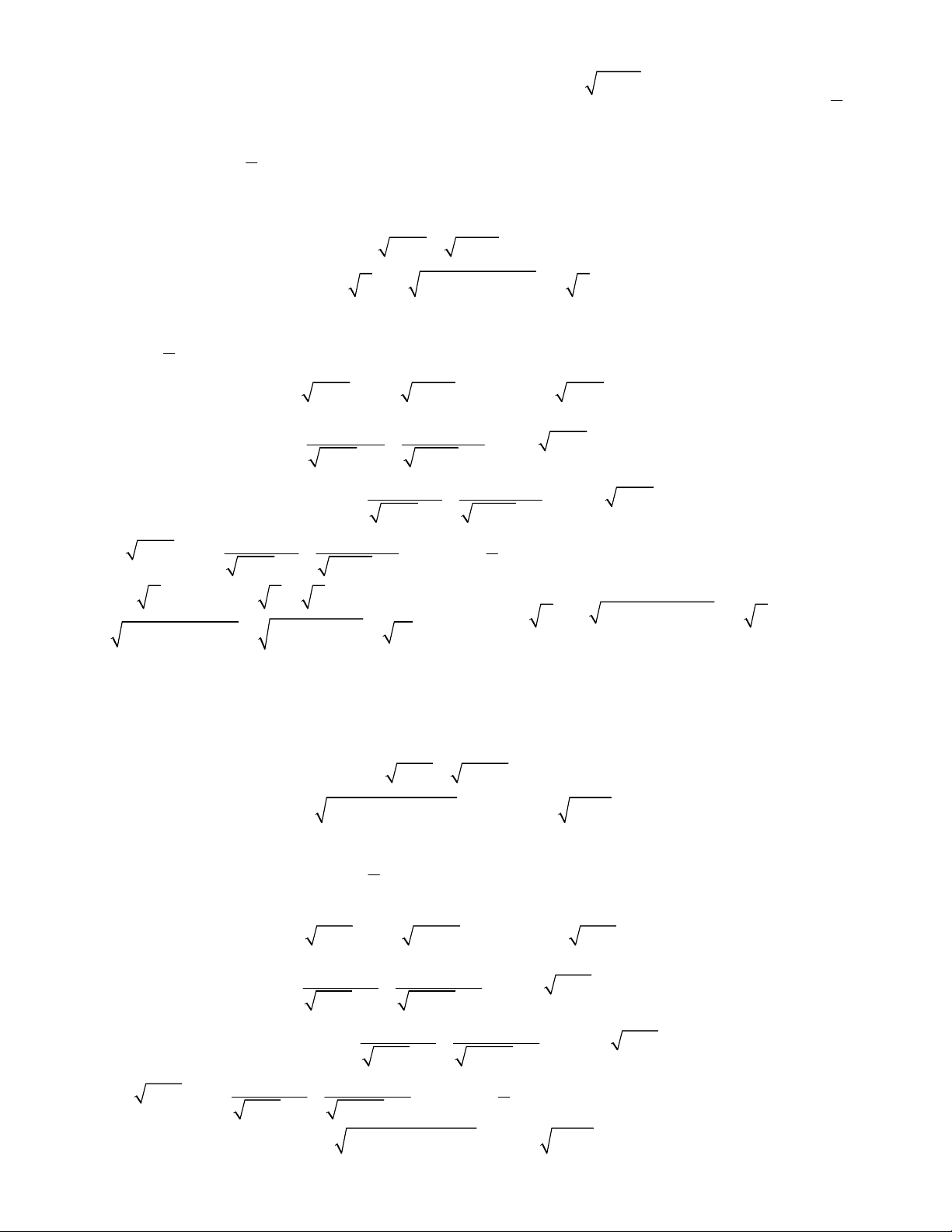
LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

60

Phương trình (1) có nghiệm khi và dấu đẳng thức xảy ra, tức là

 

3

2

1

4 1 0

1

; 1;

4

1

0

x y

x x y

x



  









  



















.

Xét trường hợp

 

1

;

1;

4

x

y















không thỏa mãn hệ. Xét

 

2

1

1 2 0 1

x

y x y



      

.

Kết luận hệ có nghiệm duy nhất kể trên.

B

à

i

t

o

á

n

8

5

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

2

3

2

3

2 7 2 4 1 19,

;

2 4 4 .

y x x y x

x y

x y x y y x y



      







     







.

Lời giải.

Điều kiện

1

;

0

4

x

y



 

. Phương trình thứ nhất của hệ tương đương với

 

2

7 2 2 4 1 3 2 2 2

7

2

4 8

2

2 2 4 1 3

7 4

2

1 4 1 3

x x y y x x

x

y x

x x

x y x

x x

         



    

   

 

     

 

   

 

Ta có

 

2

7 4 1

2 0; 0, ;

4

2 1 4 1 3

y x x y

x x

         

   



nên

2 0 2

x x

   

.

Khi đó

 

3 3

2

33 2 3 3

3

2 2

2 4 4

4 4 2 0

x y x y y

x y x x x x y

x y y x y x x



     



      



        





.

Phương trình thứ hai của hệ có nghiệm khi

2 0 2

x x

y y

  

 



 

  

 

Kết luận hệ có nghiệm duy nhất

2

; 2

x

y



.

B

à

i

t

o

á

n

8

6

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

2

2 3

17 6 8 2 7 9 62,

;

5 2 2 1 2 1997 1.

y x x x y

x y

x x y x x y



      







     







.

Lời giải.

Điều kiện

2

7

1;5 2 2 1 0;

2

y x x y x

      

.

Phương trình thứ nhất của hệ tương đương với

 

   

 

2

17

8 3 2 7 3 9 6 8 8

17

1 2 1

3 8

8 3 2 7 3

17 2

1

3 8

8

3 2 7 3

x x y y x x

x x

y x

x x

x y x

x x



        



    

   

 

     

 

   

 

Ta có

 

2

17 2 7

3 8 0; 0, ; 1

2

8 3 2 7 3

y x x y

x x

         

   

nên thu được

1 0 1x x   

.

Phương trình thứ hai tương đương với

2

2 3

5

2 2 1 1997 1 2

x

x y x y x



    

.

LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

61

Ta có

 

2

2 3 2 2 2

1

; 1 5 2 2 1 1997 1 5 2 1 4 1 4 2

x

y x x y x y x x x x x x



              

.

Do đó phương trình thứ hai có nghiệm khi dấu đẳng thức xảy ra, tức là

1x

y



.

B

à

i

t

o

á

n

8

7

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

2

3

4 2 2 2

5 4 2 3 3 2 9,

;

2 4 4 2 1 .

x y x y y x

x y

x y y y y y x y y



       







        







.

Lời giải.

Điều kiện các căn thức xác định.

Phương trình thứ nhất của hệ tương đương với

 

2

5 4 3 3 2 2 1 2 1 3 3

5

5 1

1 3

5 4 3 3 2

5 1

1 1 3

5 4 3 3 2

x x y y y x x

x

y x

x x

x y x

x x

            



     

   

 

      

 

   

 

Ta có

 

2

5 1 4

1 3 0; 0, ;

5

5 4 3 3 2

y x x y

x x

          

   



nên dẫn đến

1 0 1x x   

.

Khi đó

 

2

3

4 2 4 2 4 4 2

2

2 2

2 2 1 1

4 4 4 4 1 2 1 2 1

x y y y y y y y y y y

y y x x y y y



           







        



Suy ra

3 4 2 2 2

2

4 4 2 1

x

y y y y y x y y



       

.

Phương trình thứ hai của hệ có nghiệm khi và chỉ khi

 

2

1

1 0

x

y













 



 







Đáp số nghiệm duy nhất

   

;

1;1

x

y 

.

B

à

i

t

o

á

n

8

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

   

 

2

3

2 2

3

3 2

4

1 4 8 4 4 ,

;

1 2 4 2 1 .

y x y y x x xy xy

x y

x x y y y y



      







     







.

Lời giải.

Điều kiện

1

2

y



. Phương trình thứ nhất của hệ tương đương với

   

 

     

2

3

2

2 2

4 4 4 8 5 1

4 4 4 4 1 1

2 2 1 1

y x y y x y y x x x

y x y x x

       

        

     

Rõ ràng

     

2

1

2

0, 2 1 1 0

2

1

x

y x y y x x

x







         







o Xét trường hợp

2

1 3 3

0

0;

2

2 2

x

y y y



  



    

 







  

. Loại

0

y



và

 

1

3

;

2

x

y

 



 





không thỏa mãn hệ.

o Xét

   

3

3 2 2 2

1

1 2 4 2 1 2 2 . 2 .

2

x

x x y y y y y y y y



         

.

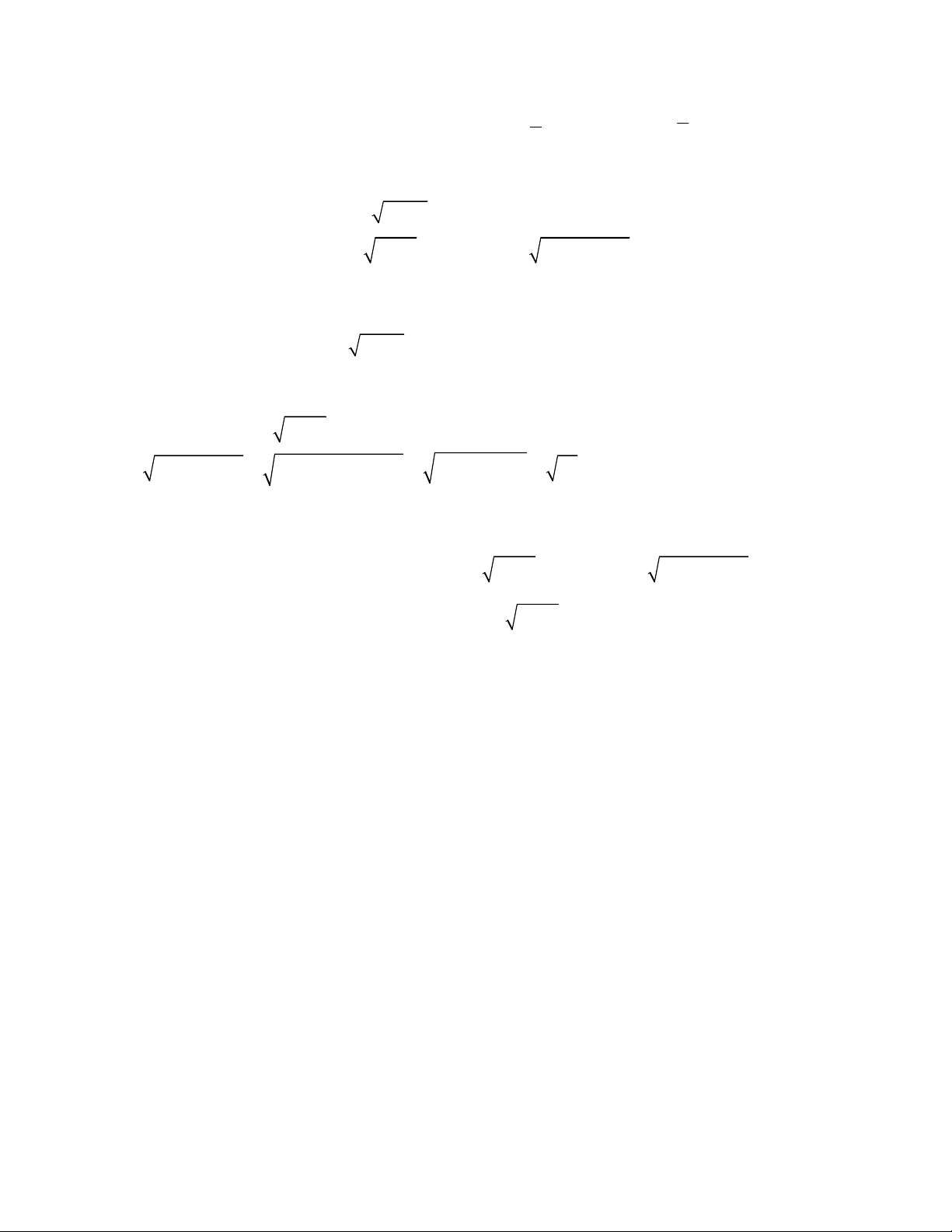
LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

62

Phương trình thứ hai có nghiệm khi và chỉ khi

 

2

0

;

3

1

1;

2

x y

y x y

x y



 



  

 



 



 

 

 



.

Kết luận hệ vô nghiệm.

B

à

i

t

o

á

n

8

9

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

   

 

3

2

3 3 2

1

4 5 1 ,

;

1 1 2 6 2 2 1 5 .

y x x x

x y

x y x x y y y



   







       







.

Lời giải.

Điều kiện

3

1; 4

y x

  

.

Từ phương trình thứ nhất của hệ

   

3

3 2

0

1 4 0, 1 1 0

1

x

y x y x x

x





        







Xét trường hợp

 

3

0

1 .2 0 1

x

y y



    

, cặp số

   

;

0;1

x

y 

không thỏa mãn hệ.

Xét trường hợp

 

3

1

1 1 0, 1; 1

x

x y y x



       

.

Bên cạnh đó

 

2

2 2 2 2 2

2 2 1 2 1 1 0, 1y y y y y y y y y y             

.

Xét hàm số

   

3

2

2 6; 1 3 2 0, 1f x x x x f x x x



         

.

Hàm số liên tục và đồng biến trên





1

;



.

Do đó thu được

     

1

1 5

x

f x Min f x f



  

suy ra

 

3

3 2

1 1 2 6 2 2 1 0 5. 5x y x x y y y y         

.

Phương trình thứ hai của hệ có nghiệm khi và chỉ khi

 

3

1 1 0

1

1 0

1

x y

x

y

x



  









  

 













Kết luận hệ phương trình đề bài có nghiệm duy nhất

1x

y



.

N

h

ậ

n

x

é

t

.

T

h

ô

n

g

t

h

ư

ờ

n

g

t

r

ư

ớ

c

đ

â

y

s

a

u

k

h

i

c

h

ặ

n

m

i

ề

n

g

i

á

t

r

ị

c

á

c

b

i

ế

n

t

h

à

n

h

c

ô

n

g

,

k

h

i

l

à

m

v

i

ệ

c

v

ớ

i

p

h

ư

ơ

n

g

t

r

ì

n

h

c

u

ố

i

c

ù

n

g

c

h

ú

n

g

t

a

đ

ề

u

t

ì

m

g

i

á

t

r

ị

n

h

ỏ

n

h

ấ

t

,

g

i

á

t

r

ị

l

ớ

n

h

ấ

t

c

ủ

a

t

ổ

h

ợ

p

c

á

c

h

à

m

s

ố

(

d

ạ

n

g

đ

ộ

c

l

ậ

p

v

à

d

ạ

n

g

l

i

ê

n

k

ế

t

)

,

n

h

ư

n

g

v

ẫ

n

g

i

ữ

v

ữ

n

g

t

í

n

h

c

h

ấ

t

h

u

ầ

n

t

ú

y

v

ớ

i

m

ộ

t

b

ê

n

l

à

h

ằ

n

g

s

ố

   

; ; ...

f x y g x y const

  

.

V

ớ

i

c

ô

n

g

c

ụ

đ

ạ

o

h

à

m

–

k

h

ả

o

s

á

t

h

à

m

s

ố

t

r

o

n

g

t

a

y

v

à

c

á

c

đ

á

n

h

g

i

á

c

ơ

b

ả

n

,

t

h

ậ

m

c

h

í

c

h

ỉ

c

ầ

n

p

h

â

n

t

í

c

h

n

h

â

n

t

ử

,

t

á

c

h

n

h

ó

m

t

h

í

c

h

ợ

p

,

v

ớ

i

c

h

ú

ý

đ

i

ể

m

b

i

ê

n

c

á

c

g

i

á

t

r

ị

n

g

h

i

ệ

m

c

á

c

b

ạ

n

c

ó

t

h

ể

h

o

à

n

t

o

à

n

x

ử

l

ý

t

ố

t

p

h

ầ

n

l

ớ

n

c

á

c

b

à

i

t

o

á

n

t

ư

ơ

n

g

t

ự

.

S

o

s

á

n

h

v

ớ

i

c

á

c

b

à

i

t

o

á

n

t

r

ư

ớ

c

,

c

á

c

b

ạ

n

đ

ộ

c

g

i

ả

c

ó

t

h

ể

t

h

ấ

y

c

á

c

b

à

i

t

o

á

n

8

4

,

8

5

,

8

6

,

8

7

,

8

,

8

9

đ

ã

n

â

n

g

c

ấ

p

đ

ộ

h

ơ

n

m

ộ

t

b

ậ

c

,

s

ở

d

ĩ

d

ạ

n

g

t

h

ứ

c

p

h

ứ

c

t

ạ

p

h

ơ

n

,

k

h

i

v

ế

p

h

ả

i

k

h

ô

n

g

c

ò

n

l

à

h

ằ

n

g

s

ố

       

;

; ... ; ; ...

;

; ... ; ; ...

f

x y g x y F x y G x y

f x y g x y F x y G x y



   



   

N

g

ư

ờ

i

t

a

t

h

ư

ờ

n

g

n

ó

i

“

…

T

ì

n

h

m

ấ

t

v

u

i

l

ú

c

đ

ã

v

ẹ

n

c

â

u

t

h

ề

,

Đ

ờ

i

c

h

ỉ

đ

ẹ

p

k

h

i

h

ã

y

c

ò

n

d

a

n

g

d

ở

,

T

h

ư

v

i

ế

t

đ

ừ

n

g

x

o

n

g

,

t

h

u

y

ề

n

t

r

ô

i

c

h

ớ

đ

ỗ

,

C

h

o

n

g

à

n

s

a

u

l

ơ

l

ử

n

g

v

ớ

i

n

g

à

n

x

ư

a

…

”

(

N

g

ậ

p

n

g

ừ

n

g

–

H

ồ

D

z

ế

n

h

;

1

9

4

3

)

Đ

â

y

l

à

n

g

u

y

ê

n

g

ố

c

ủ

a

c

â

u

n

ó

i

“

T

ì

n

h

c

h

ỉ

đ

ẹ

p

k

h

i

c

ò

n

d

a

n

g

d

ở

”

…

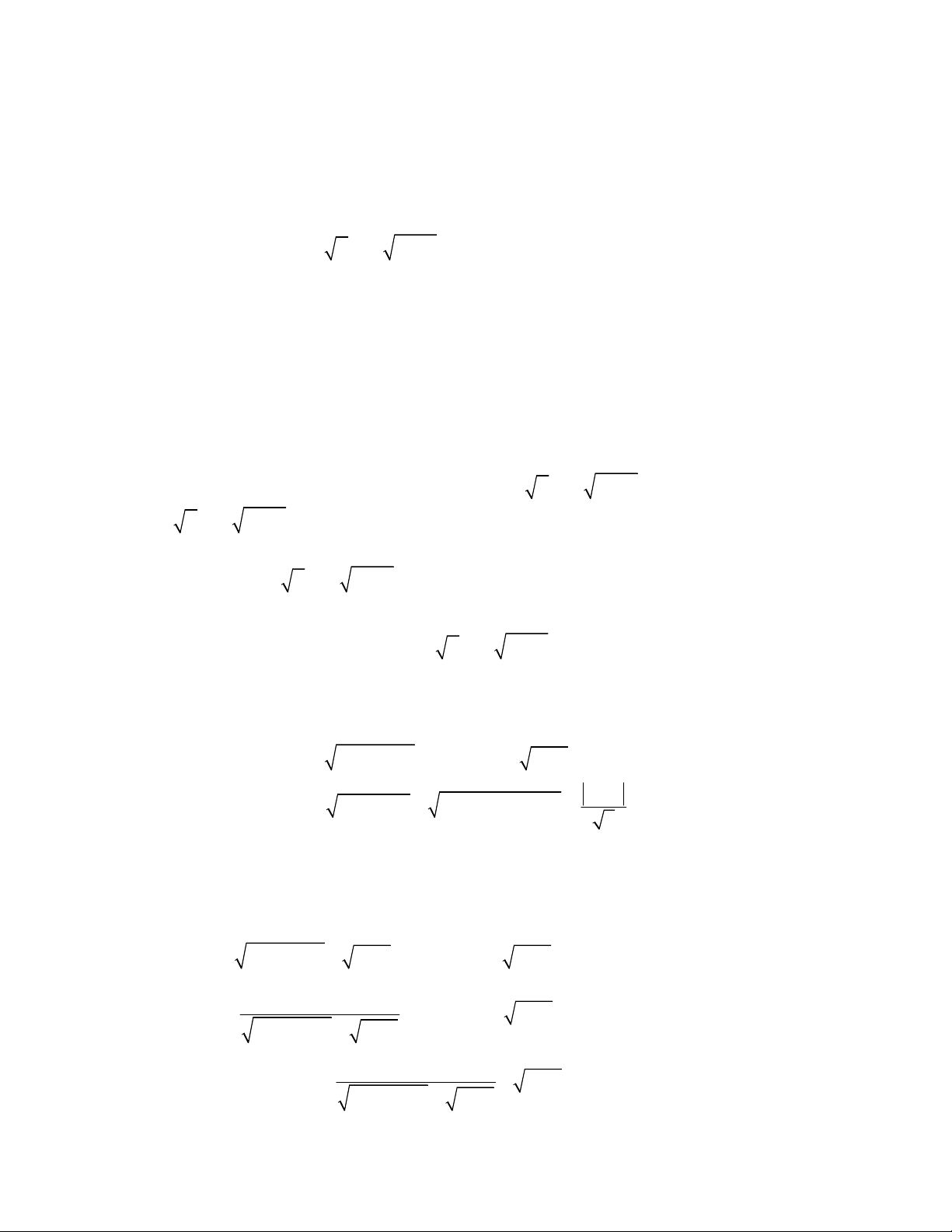
LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

63

L

à

m

ộ

t

n

g

ư

ờ

i

q

u

a

n

i

ệ

m

t

ì

n

h

y

ê

u

đ

ẹ

p

l

à

n

g

ẫ

u

h

ứ

n

g

,

v

ẹ

n

t

o

à

n

,

s

o

n

s

ắ

c

,

t

h

ủ

y

c

h

u

n

g

,

g

ắ

n

b

ó

t

ì

n

h

n

g

h

ĩ

a

v

à

t

r

á

c

h

n

h

i

ệ

m

,

n

h

ư

n

g

t

á

c

g

i

ả

c

h

ợ

t

h

ấ

y

n

h

ữ

n

g

p

h

é

p

s

o

s

á

n

h

đ

á

n

h

g

i

á

l

ơ

l

ử

n

g

t

r

ê

n

c

ũ

n

g

c

ó

p

h

ầ

n

đ

ồ

n

g

đ

i

ệ

u

,

k

h

i

m

à

c

h

ú

n

g

t

a

s

ử

d

ụ

n

g

c

á

c

d

ữ

k

i

ệ

n

v

à

c

á

c

b

ư

ớ

c

h

ố

t

c

h

ặ

n

l

ú

c

n

à

o

c

ũ

n

g

m

ộ

t

n

ử

a

,

l

ú

c

n

à

o

c

ũ

n

g

h

ờ

h

ữ

n

g

,

l

ú

c

t

h

ă

n

g

l

ú

c

g

i

á

n

g

,

k

h

ô

n

g

đ

ư

ờ

n

g

l

ố

i

r

õ

r

à

n

g

,

k

h

ô

n

g

t

h

e

o

m

ộ

t

q

u

ỹ

đ

ạ

o

c

ố

đ

ị

n

h

,

c

à

n

g

l

à

m

c

h

o

b

à

i

t

o

á

n

t

r

ở

n

ê

n

đ

ộ

c

đ

á

o

,

đ

ẹ

p

đ

ẽ

l

ạ

k

ỳ

,

đ

ò

i

h

ỏ

i

í

t

n

h

i

ề

u

s

ự

k

h

é

o

l

é

o

,

t

i

n

h

t

ế

v

à

m

ộ

t

c

h

ú

t

m

a

y

m

ắ

n

c

ủ

a

n

g

ư

ờ

i

g

i

ả

i

b

à

i

t

o

á

n

.

B

à

i

t

o

á

n

9

0

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

3

3 2 2

2 3

3

2 10 15 2 4 3 4 ,

;

6 17 1 19 97 72.

x y y x x y

x y

y y x x



     







    





.

Lời giải.

Điều kiện

1y 

. Phương trình thứ nhất của hệ tương đương với

   

       

3

2 3 2

3 2 3 2

2 2

3

12 15 6 2 10 16 8

3

4 5 2 2 5 8 4

3

1 2 2 2 1

x x x y y y

x x y y

      



      



    

Chú ý rằng

       

2

1

2 2 1 0, 1 3 1 2 0

2

x

y y y x x

x





         







 Xét trường hợp

1x 

thì phương trình thứ hai trở thành

2

6

17 1 6

y



 

.

Dễ thấy

2

6

17 1 6, 1 1

y

y y y



     

là nghiệm duy nhất, khi đó

   

;

1;1

x

y 

.

 Xét trường hợp

2

x



thì phương trình thứ hai viết lại

   

2 3

6

17 1 19 97 72 0 0

y

y x x f x g y



       

.

Xét hàm số

 

3

19 97 72; 2

f x x x x

   

ta có

 

2

57 97 0, 2

f x x x



    

nên hàm số đồng biến.

Suy ra

   

2 30

f x f

 

, hơn nữa

 

2

6

17 1 6

g

y y y



  

nên

   

36 0

f x g y

  

.

Trường hợp này vô nghiệm.

Kết luận hệ ban đầu có duy nhất nghiệm

   

;

1;1

x

y 

.

Bài toán 91. Giải hệ phương trình

 

2 2 3 2

2 2

2

2 1 4 3 1,

;

2 3 2 2 1 .

2

x y x y y y y y

x y

y x y x y x



         









      







.

Lời giải.

Điều kiện

2

2 3 0

2

1 0; 3

x y

x y y

  







   



Phương trình thứ nhất của hệ tương đương với

 

   

 

   

 

     

2

2 1 3 2 3 1 1

2 2

2 3 1 1

2 1 3

2

3 1 1 1

2 1 3

x y y x y y y y

x y

x y y y y

x y y

x y y y y

x y y

          

 

       

   

 

 

       

 

   

 

Để ý rằng

 

2

3 0 2 2 3 2 1 2 3 1 0

x

y x y x y x x x y x



                

.

LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

64

Lại có

2

3 0

2

1 3

y

x y y

  



  

nên từ (1) ta được

   

2

1

1 1 0

1

y

y y

y

 



   







 Xét trường hợp

 

   

2

0 3

1

; 3; 1 , 3; 1

1

x y x

y x y

y y

 

   



       



   

 

.

Các cặp số trên không thỏa mãn

2

3

x

y





nên đều bị loại.

 Xét trường hợp

1y 

. Xuất phát

 

2

0

2

x y

x y x y



     , dẫn đến

 

2

2 2 2 2 2

2 2 1 1

2

x

y

x

y

x y x x y x x y



         

.

Mặt khác

2 2

1

2 3 0 2 3 2 2 1

2

x

y

y x y y x y x y x





           

.

Phương trình thứ hai của hệ có nghiệm khi các dấu đẳng thức xảy ra, tức là

 

2

1 0

1

0

1

2

3 0

x

x y

y

x

y



 











 

 









 





Thử lại, kết luận hệ có nghiệm duy nhất kể trên.

N

h

ậ

n

x

é

t

.

C

á

c

b

à

i

t

o

á

n

t

ừ

8

đ

ế

n

9

0

c

á

c

p

h

é

p

c

h

ặ

n

m

i

ề

n

g

i

á

t

r

ị

d

i

ễ

n

t

i

ế

n

t

h

u

ậ

n

l

ợ

i

,

k

h

i

m

à

đ

á

n

h

g

i

á

đ

ư

ợ

c

d

ự

a

t

r

ê

n

b

ố

t

r

í

h

à

m

s

ố

m

ộ

t

b

i

ế

n

   

f

x g y



.

P

h

é

p

đ

á

n

h

g

i

á

c

ự

c

t

r

ị

h

à

m

s

ố

   

f

x g y



l

à

d

ễ

d

à

n

g

,

c

h

ỉ

c

ầ

n

s

ử

d

ụ

n

g

c

á

c

p

h

é

o

b

i

ế

n

đ

ổ

i

t

ư

ơ

n

g

đ

ư

ơ

n

g

–

p

h

â

n

t

í

c

h

n

h

â

n

t

ử

h

o

ặ

c

a

o

h

ơ

n

l

à

c

ô

n

g

c

ụ

đ

ạ

o

h

à

m

–

h

à

m

s

ố

n

ế

u

c

ầ

n

t

h

i

ế

t

.

L

ư

u

ý

n

h

ỏ

l

à

đ

ơ

n

v

ị

Q

q

u

y

ế

t

đ

ị

n

h

m

i

ề

n

g

i

á

t

r

ị

c

ó

d

ạ

n

g

t

h

ứ

c

2

A B

,

t

ổ

n

g

q

u

á

t

2

k

A B

,

c

ụ

t

h

ể

   

 

   

2

88

2

89 89

2

90 90

1

2 1 1 ; 0

2

1

1 ; 0

0

1

3 1 2 ; 0

2

x

Q x x Q

x

Q x x Q

x

Q x x Q

x







    











   











    







T

á

c

g

i

ả

x

â

y

d

ự

n

g

l

o

ạ

t

b

à

i

t

o

á

n

c

ó

đ

ạ

i

l

ư

ợ

n

g

n

h

ạ

y

c

ả

m

n

à

y

đ

ể

c

ả

n

h

t

ỉ

n

h

b

ạ

n

đ

ọ

c

t

r

ư

ờ

n

g

h

ợ

p

2

0

k

A

A B

B





 







T

ấ

t

n

h

i

ê

n

c

á

c

t

r

ư

ờ

n

g

h

ợ

p

m

a

y

m

ắ

n

l

à

n

g

o

ạ

i

l

ệ

k

h

i

t

ậ

p

n

g

h

i

ệ

m

c

ủ

a

c

h

ú

n

g

b

a

o

h

à

m

n

h

a

u

,

v

í

d

ụ

   

2

1

1 2 0 2

2

x

x x x

x





      



 



h

o

ặ

c

   

2

3

3 2 0 2

2

y

y y y

y





     







.

T

r

o

n

g

t

r

ư

ờ

n

g

h

ợ

p

k

h

ô

n

g

b

a

o

h

à

m

v

ớ

i

t

ậ

p

n

g

h

i

ệ

m

r

ờ

i

n

h

a

u

,

c

á

c

b

ạ

n

c

ầ

n

h

ế

t

s

ứ

c

t

ỉ

n

h

t

á

o

,

c

ẩ

n

t

h

ậ

n

v

à

l

ậ

t

đ

i

l

ậ

t

l

ạ

i

,

b

ă

n

k

h

o

ă

n

s

u

y

n

g

h

ĩ

t

ì

m

t

ò

i

đ

ế

n

c

ù

n

g

.

M

ặ

c

d

ù

c

h

ỉ

l

à

n

h

ữ

n

g

k

i

ế

n

t

h

ứ

c

r

ấ

t

đ

ơ

n

g

i

ả

n

,

c

ơ

b

ả

n

h

ư

n

g

r

ấ

t

d

ễ

n

h

ầ

m

l

ẫ

n

v

à

t

h

i

ế

u

t

r

ư

ờ

n

g

h

ợ

p

,

d

ẫ

n

đ

ế

n

t

i

n

h

t

h

ầ

n

b

à

i

t

o

á

n

b

ị

t

ổ

n

h

ạ

i

n

g

h

i

ê

m

t

r

ọ

n

g

d

o

đ

ô

i

k

h

i

m

ấ

t

n

g

h

i

ệ

m

h

a

y

n

g

h

i

ệ

m

n

g

o

ạ

i

l

a

i

…

m

à

t

r

o

n

g

q

u

á

t

r

ì

n

h

g

i

ả

i

t

o

á

n

,

l

à

m

v

i

ệ

c

,

k

ể

c

ả

t

r

o

n

g

c

u

ộ

c

s

ố

n

g

c

h

ú

n

g

t

a

t

h

ư

ờ

n

g

v

ô

t

ì

n

h

n

g

ộ

n

h

ậ

n

,

k

ể

c

ả

v

ô

t

â

m

q

u

ê

n

đ

i

n

h

ữ

n

g

t

h

ứ

t

h

â

n

t

h

ư

ơ

n

g

n

h

ư

t

h

ế

.

Đ

á

n

g

c

h

ú

ý

h

ơ

n

c

ả

l

à

b

à

i

t

o

á

n

s

ố

9

1

,

v

ớ

i

đ

ạ

i

l

ư

ợ

n

g

q

u

y

ế

t

đ

ị

n

h

c

h

ặ

n

   

2

91

1

Q

y y



 

,

t

u

y

n

h

i

ê

n

p

h

é

p

l

i

ê

n

h

ợ

p

t

h

i

ế

t

l

ậ

p

đ

ạ

i

l

ư

ợ

n

g

n

à

y

l

à

b

ấ

t

n

g

ờ

,

đ

ộ

c

đ

á

o

v

à

c

ầ

n

k

h

a

i

t

h

á

c

n

h

i

ề

u

.

LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

65

 

   

 

   

 

     

2

2 1 3 2 3 1 1

2 2

2 3 1 1

2 1 3

2

2 3 1 1 1

2

1 3

x y y x y y y y

x y

x y y y y

x y y

x y y y y

x y y

          

 

       

   

 

 

       

 

   

 

K

h

ô

n

g

i

ố

n

g

c

á

c

b

à

i

t

o

á

n

t

r

ư

ớ

c

t

h

ư

ờ

n

g

d

ẫ

n

đ

ế

n

2

2 0

x y

  

,

n

h

ư

n

g

x

u

i

x

ẻ

o

l

à

c

h

o

d

ù

n

h

ư

t

h

ế

t

h

ì

v

ẫ

n

c

h

ư

a

c

ó

g

ì

k

h

ở

i

s

ắ

c

t

r

o

n

g

l

ậ

p

l

u

ậ

n

.

N

é

t

i

n

h

t

ế

t

h

ể

h

i

ệ

n

ở

đ

i

ề

u

m

à

í

t

a

i

n

g

ờ

t

ớ

i

 

2

2 2

2

3 0 2 2 3 2 1 2 3 1 0

x

y x y x y x x x y x



                

.

H

ơ

n

ữ

a

p

h

ư

ơ

n

g

t

r

ì

n

h

ệ

q

u

ả

c

ũ

n

g

đ

ư

ợ

c

t

h

i

ế

t

l

ậ

p

t

h

e

o

m

o

t

i

p

đ

á

n

h

g

i

á

l

ơ

l

ử

n

g

,

đ

ò

i

h

ỏ

i

t

ổ

n

g

h

ò

a

l

i

ê

n

h

ệ

,

p

h

ả

n

b

i

ệ

n

v

à

c

h

í

n

h

x

á

c

,

t

ừ

n

g

b

ư

ớ

c

t

i

ệ

m

c

ậ

n

đ

á

p

s

ố

c

u

ố

i

c

ù

n

g

.

B

à

i

t

o

á

n

9

2

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

2

2 2 2

3

2 4 2 4 7 6 1 ,

;

3 1 4 5 3 2 1 .

x y x y x y y x

x y

x x y x y x y



        







       







.

Lời giải 1.

Điều kiện

2

2 2

4

5 0;3 2 1 0

7

0;3 2 4 0

x

y x y

x y x y





    







    





Phương trình thứ nhất của hệ tương đương với

 

2

2 2 2 2

2

2 2 2

2 2

2 2 2

2 2

3 2 4 7 2 3 7 6 1

2 3

2 3 7 6 1

3 2 4 7

1

2 3 7 6 1

3 2 4 7

x y x y x y x y y x

x y

x y x y y x

x y x y

x y x y y x

x y x y

           

 

       

    

 

 

       

 

    

 

Ta có

2

1

7

0

3

2 4 7

x y

x y x y



  



   

.

Bên cạnh đó

 

2

4

5 0 2 3 4 5 2 1 0

x

y x y x y x



          

, dẫn đến

 

2

0

6 1 0

1

y

y x

x





  







Xét trường hợp

 

2

3

2

3 0

3 3

0

; ;0 , ;0

2

2 2

0

x

x y

y x y

y





  







 



     



  



   





   







, loại vì

4

5 0

x

y



 

.

Xét trường hợp

 

2 2

1

3 1 0 3 1 4 5 0

x

x x x y



       

.

Nhận xét

 

2

2 2

0

2

x

y x y x y



    

và áp dụng

,

M

M M





ta có

   

2

2 2 2 2 2 2

3

2 1 2 1 2

x

y x y x x y x y x y



          

.

Kết hợp lại ta được

 

2

2 2

3 1 4 5 3 2 1

x x y x y x y       

.

Phương trình thứ hai của hệ có nghiệm khi và chỉ khi

4

5 0

1

0

x

y

x

x y

y

x

y

  













 













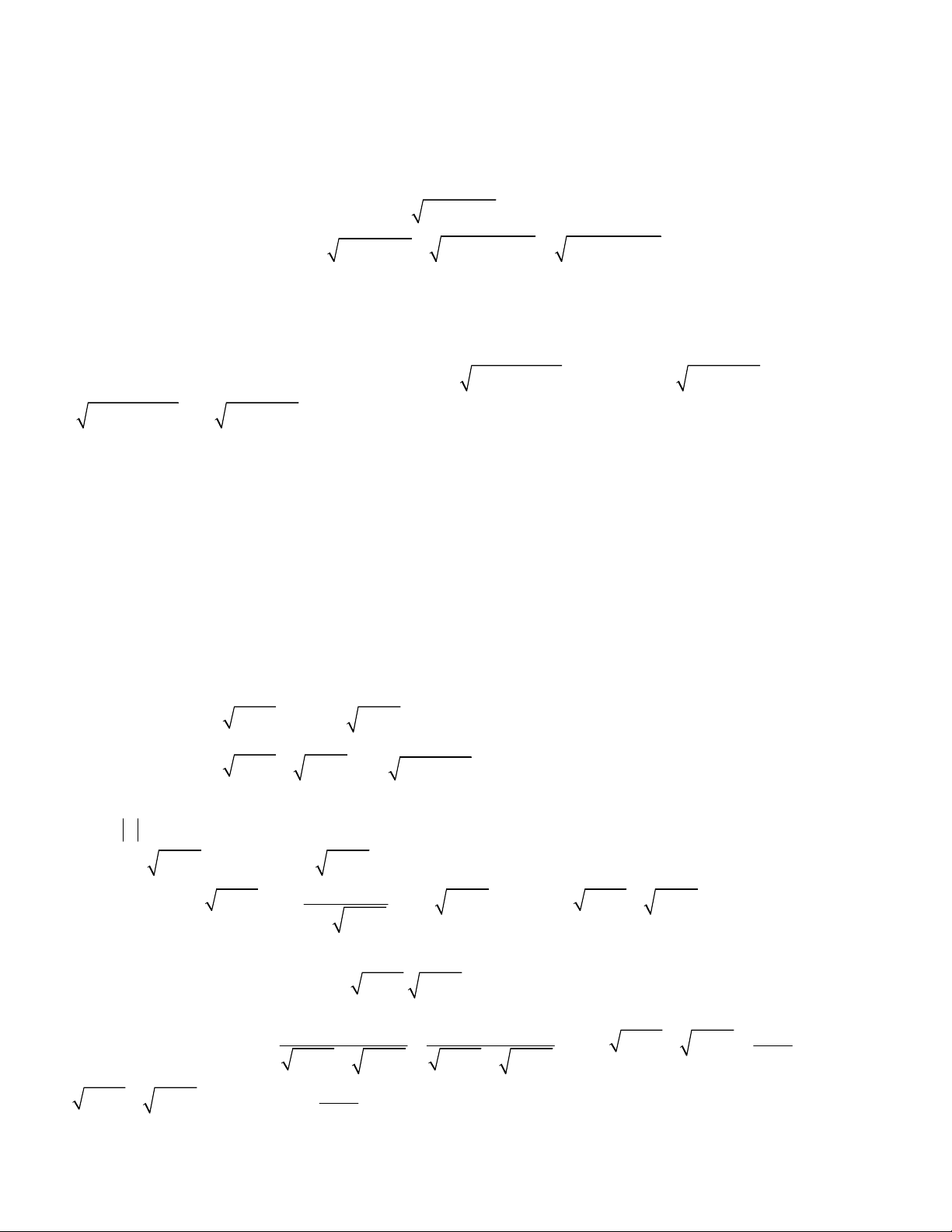
LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

66

Kết luận hệ phương trình đề bài có nghiệm duy nhất

1x

y



.

Lời giải 2.

Điều kiện

2

2 2

4 5 0;3 2 1 0

7

0;3 2 4 0

x y x y



     







    





Xét trường hợp

1x 

ta có

 

2

2 2 2 2 2

2

2 2 2 2

2

1 3 1 0 3 1 4 5 0

3 1 4 5 3 2 1 3 2 1

0

1 1 1

2 3 2 1

1 0

x x x x y

x y x x y x y x y

x y

x x

x xy y x y

x x y

        

           

 



 





       

 

    

   





Khi đó dấu đẳng thức xảy ra nên

0

; 1 1

x

y x x y



    

.

Xét trường hợp ngược lại,

1x 

ta có

 

2

2 2 2

6 1 0 3 2 4 2 4 7 0

y x x y x y x y

          

.

Đặt

 

2 2 2 2 2

3

2 4 ; 7 , 0; 0 2 4 1

x

y a x y b a b x y a b



            

. Thu được

   

        

2 2 2 2

2

1 0 0

0

1 0

0

2 3

a a b b a b a b b

a b a b a b b a b a b b

a b x y

        



         





 

     

Kết hợp đồng thời

 

2

3

2

4 2 0 2 1 0 1 1

5 4 0

x y

x

x x x x y

x y



 



          





 



.

Vậy hệ phương trình ban đầu có nghiệm duy nhất kể trên.

Bài toán 93.

T

r

í

c

h

l

ư

ợ

c

â

u

8

;

T

h

ử

s

ứ

c

t

r

ư

ớ

c

k

ỳ

t

h

i

Đ

ạ

i

h

ọ

c

2

0

1

5

;

Đ

ề

s

ố

2

;

T

ạ

p

c

h

í

T

o

á

n

h

ọ

c

v

à

t

u

ổ

i

t

r

ẻ

,

N

h

à

x

u

ấ

t

b

ả

n

G

i

á

o

d

ụ

c

V

i

ệ

t

N

a

m

;

S

ố

4

5

0

,

T

h

á

n

g

1

2

n

ă

m

2

0

1

4

.

T

á

c

g

i

ả

N

g

u

y

ễ

n

T

ấ

t

T

h

u

–

G

i

á

o

v

i

ê

n

T

r

ư

ờ

n

g

T

H

P

T

C

h

u

y

ê

n

L

ư

ơ

n

g

T

h

ế

V

i

n

h

;

T

ỉ

n

h

Đ

ồ

n

g

N

a

i

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h









 

2

2 2

1 1 1,

;

1 1 8 14 17.

x x y y

x y

x y y x



    









      





.

Lời giải.

Điều kiện

1

y



.

Nhận xét

2

1

, 1 0

y

y y y y



      



. Do đó phương trình thứ nhất tương đương với

 

2

2 2 2

2

1

1 1 1 1

1

x x y y y x x y

y y

           

 

.

Khi hai vế cùng dấu ta có

2

2 2 2 2 2 2 2

2 2 2 2 2 2

1 1

2

2 1. 1

0 0

x y x y x y y x

y xy y x y x y

xy xy

 

     



       

 

 

 

Ngoài ra từ (1) ta lại có

2 2

2 2 2 2

2 1 1

0 1 1

1 1 1 1

x y

y x x y

y x

x y x y

 

        



     

.

Do

2

1

1 1 1 0; 1 0 1x y y x y x

y x

           



.

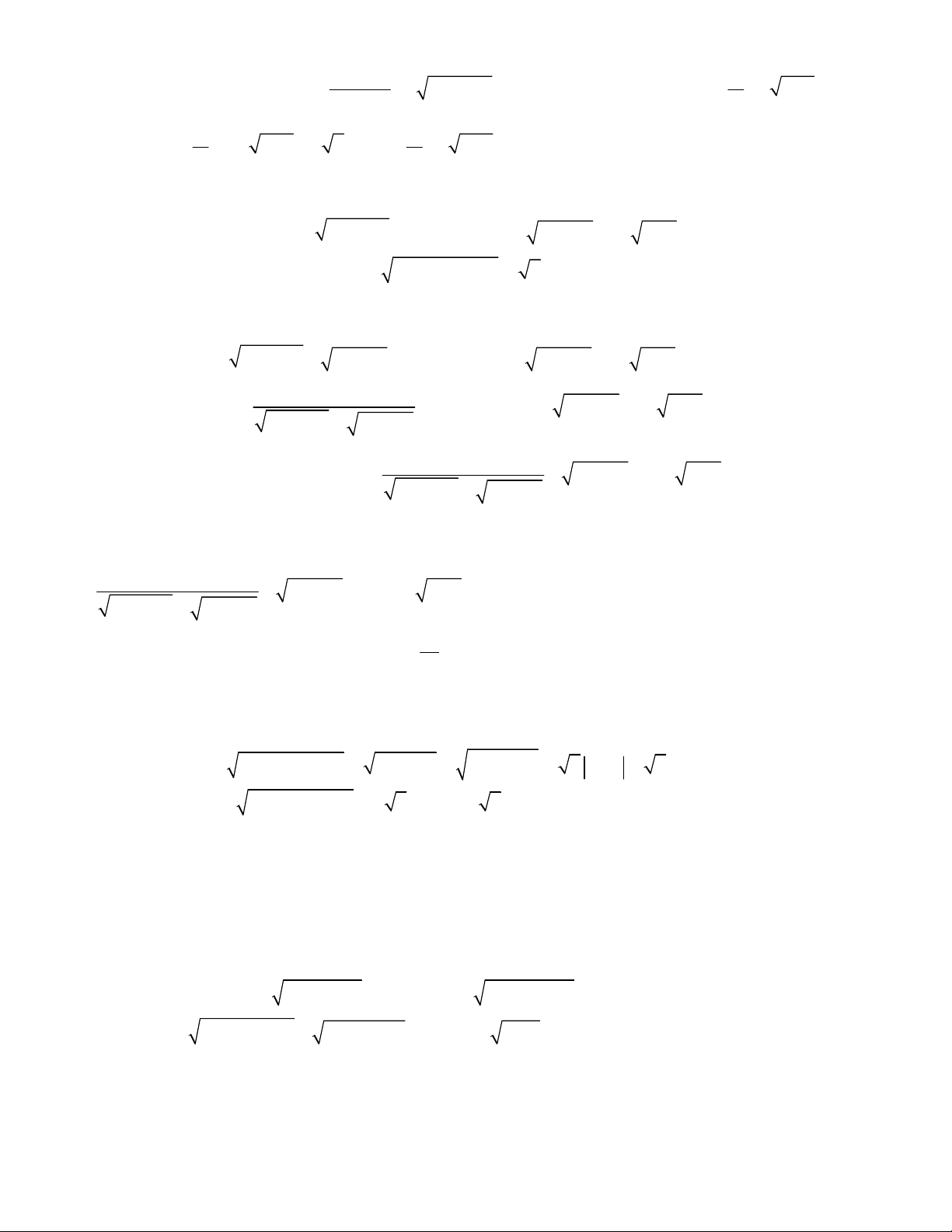
LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

67

Phương trình thứ hai của hệ trở thành

 

2

1

8 4 17

y x

   



. Đặt





 

2

1

;

0;1 8 4 17 2

t

y x t t

t



     

.

Rõ ràng

2

1

0

1 1;8 4 8 4 16 8 4 17

t

t t

t



         

, (2) vô nghiệm.

Kết luận hệ phương trình ban đầu vô nghiệm.

B

à

i

t

o

á

n

9

4

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

2 2 4

3

3 2 2

3

20 3 17 13 17 6 1,

;

2 1 6 17 5 2 2 .

x x y y x y

x y

y x y x



      







    







.

Lời giải.

Điều kiện

2

6 17 5 0;17 6 0

x y y

    

. Phương trình thứ nhất của hệ tương đương với

 

2 2 4

3

2

2 4

3

2

2 4

3

2

3 20 17 6 3 17 14 17 6 1

3 17 14

3 17 14 17 6 1

3 20 17 6

1

3 17 14 17 6 1

3 20 17 6

x y x y y x y

x y

x y y x y

x y

x y y x y

x y

        

 

      

  

 

 

      

 

  

 

Nhận thấy

 

2

6

17 11 0 3 17 14 6 17 11 3 1 0

x

y x y x y x



          

.

Lại có

4

3

2

0

1

17 6 0 1 0

1

3 20 17 6

x

y x y

y

x y





      





  



 Xét

 

0

14

0 ; 0;

17 14 0

17

x

x x y

y





 

   



 

  

 



, không thỏa mãn hệ.

 Xét

3

1 2 1 1 0

y y

    

và

2

2 2

6 17 5 6 12 0

x y x

    

.

Hơn nữa

 

2

2 2 2

4 1 0 4 8 4 0 6 12 2 4 4 2 2

x x x x x x x            

dẫn đến

   

2

2 2

6

17 5 6 12 2 2 2 2 2 2

x

y x x x x



        

.

Kết hợp ta được

 

   

3

2 2

2 1 6 17 5 1. 2 2 2 2

y x y x x

      

.

Phương trình thứ hai của hệ có nghiệm khi dấu đẳng thức xảy ra, tức là

1 0

2

0 1

1

x

x y

y











   









.

Vậy hệ phương trình đã cho có nghiệm duy nhất kể trên.

B

à

i

t

o

á

n

9

5

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

   

 

2

2 2 3 2

3 3 4 1 1 3 2 5,

;

2 3 1 2 3 5 4 3.

x y x y y y x y

x y

y x y x y x x x y x y xy



        









            





.

Lời giải.

Điều kiện

2

2 2 2

;

4 1

3 2 5 0;2 3 1 0

x

y x y

x y x y



  





     





Phương trình thứ nhất của hệ tương đương với

LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

68

   

 

2

2 2 2 3

2 2 2 2 2 3

2

2 2 2 3

2 2

2 2 2 3

2 2

3 3 4 1 3 2 5 1

4 1 3 2 5 3 4 4 1 1

3 4

3 4 4 1 1

4 1 3 2 5

1

3 4 4 1 1

4 1 3 2 5

x y x y x y y y

x y x y x y x y y y

x y

x y x y y y

x y x y

x y x y y y

x y x y

        

            

 

       

    

 

 

       

 

    

 

Ta có

 

2

3 5 0 3 4 2 3 5 1 0

x

y x y x y x



          

.

Lại có

 

2 2 3

2 2

0

1

4 1 0 1 0

1

4 1 3 2 5

y

x y y y

y

x y x y





       





    



 Xét trường hợp

     

2

0

; 2;0 , 2;0

4

0

y

y x y

x





    



 



, không thỏa mãn hệ.

 Xét trường hợp

1y 

, kết hợp

1 1

1

y x

x y y

 

 



 

 

 

Khi đó chú ý

 

2 2

2

0 2

x y x y x y

     

ta được

 

2

2 2 2 2 2

2

2 2

2

3 1 1 2

2 3 1 0

x

y y x y x y

x y x y x y x y

       

         

Ngoài ra

 

2

2 2

2 2 3 2 3 2 2

1

0 2 3 1

2 3 1 2 3 5

y y x y y x y y xy

y

x y x y x x x y x x y xy



       



            

Xét hiệu giữa hai vế phương trình thứ hai

 

3

2 2

3 2 2

2

3

4

3

1 2 4 4

1 2 0, 1,

x x y xy x y xy

x x y xy x y

x x y x y

      

 

 

 

       







        



Như vậy phương trình thứ hai của hệ có nghiệm khi dấu đẳng thức xảy ra, tức là

3

1

; 2 0

1

;

1; 1

x

x y

y

x

y x y







  





 



 



B

à

i

t

o

á

n

9

6

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

   

 

3

2

2 2

2

4 3 4 7 4 5 1 ,

;

8 9 1 4 3 1 2 2 1 .

x y x y x y y

x y

y x y y x y x



       









       





.

Lời giải.

Điều kiện

2

4 3 0;4 5 0;8 9

x y x y x y

      

.

Phương trình thứ nhất của hệ tương đương với





 

3

2

2 2

2

3

2

4 3 2 5 4 5 4 5 1

2

4 5

4

5 4 5 1

4

3 2 5

x y y x y x y y

x y

x y x y y

x y y



        







      



 

LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

69

 

3

2

4

5 4 5 1

4

3 2 5

x y x y y

x y y

 

 



      

 

  

 

Ta có

 

2

8

9 0 4 5 8 9 4 1 0

x

y x y x y x



          

.

Kết hợp

 

3

2

4

5 0 1 0 1

4

3 2 5

x

y y y

x

y y



       



 

.

Rõ ràng

   

2

8 9 1 4 3 1 0, 1 2 2 1 0

y x y y x y y x

           

.

Lại có

 

2

2 2 2

2

1 0 2 4 2 0 4 4 2 2 1 2 1

x

x x x x x x



           

nên

   

 

2

1 4 3 1 4 4 2 1 2 1 2 1

1 2 0 1 4 3 1 2 2 1

y x y x x x x

y y x y x

           

        

Ngoài ra

   

2

8

9 0 8 9 1 4 3 1 2 2 1

y

x y y x y y x y x



          

.

Phương trình thứ hai của hệ có nghiệm khi

8 9 0 1

1 0; 1 1

x y x

x y y

   

 



 

   

 

Kết luận hệ phương trình đề bài có nghiệm duy nhất kể trên.

B

à

i

t

o

á

n

9

7

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

2 2

2 2 2

3 3 2 4 5 6 1 6,

;

2 2 5 5 2 1 2 .

x y x y y y x

x y

y x y x y y x y



        







      







.

Lời giải.

Điều kiện

2

1

;

2; 3 3 0

2

6; 6

y x y x y

y x





    









  



Phương trình thứ nhất của hệ tương đương với

 

2

3 3 6 2 2 3 6 1 6

2 3

2 2 3 6 1 6

3 3 6

1

2 3 2 6 1 6

3 3 6

x y y x y y y x

x y

x y y y x

x y y

x y y y x

x y y

          

 

       

   

 

 

       

 

   

 

Ta có

   

2

0 2 3 2 2 1 0

x

y x y x y x



          

.

Lại có

2

1

2 6 0

3

3 6

y

x y y

  



  

dẫn đến

 

6

1 6 0

1

x

y x

y

 



   







Xét trường hợp

2

6

33

2

3 0

2

x

y

x

y







 





   

 

 



 







(Loại vì không thỏa mãn hệ).

Xét trường hợp

 

2 2 2 2 2

2 2

2

0

1 0 2 5 5 2 0 2 2 5 5 2 1 2

2 1

y x y

y x y x y x y x y y x y

y y y



  



              





  





.

Phương trình thứ hai của hệ có nghiệm khi và chỉ khi

1x

y



.

LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

70

B

à

i

t

o

á

n

9

8

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

2

2 5 6 3 10 8 1 ,

;

2 1 4 5 4 1 2 .

y x y x x y x

x y

y x y x y x



       









      





.

Lời giải.

Điều kiện

2

4

5 0; 0

4

1 0

x y x

x y



  







 



Phương trình thứ nhất của hệ tương đương với

 

2 2

2

2 2 5 8 3 2 3 8 1

2 3

3 2 3 8 1

2 2 5 8

2

2 3 3 8 1

2 2 5 8

y x x y x x y x

y x

y x x y x

y x x

y x x y x

y x x

         

 

      

   

 

 

      

 

   

 

Ta có nhận xét

 

2

4

5 0 2 3 4 5 2 1 0

x

y y x x y y



          

.

Lại có

 

2

0

2

3 8 0 1 0

1

2 2 5 8

x

x y x

y

y x x





      





   



 Xét trường hợp

 

2

0

3 3

0

; 0; , 0;

3

2

3 0

2

x

x x y

y

y x









  







    



  



   



  



   





; không thỏa mãn.

 Xét

 

1 2 1 0 2 1 4 5 0

y y y x y

        

.

Ngoài ra

 

2 2 2

4

1 4 2 2 1 4 5 4 1 2

x

y x x y x y x y x



          

.

Phương trình thứ hai của hệ có nghiệm khi các dấu đẳng thức xảy ra, tức là

1x

y



.

B

à

i

t

o

á

n

9

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

2

2 2 2

4 3 5 4 5 1 ,

;

6 7 6 7 2 1.

x y x y x x y

x y

x y x y y y x x



      







          





.

Lời giải.

Điều kiện

2

4

0; 1

6

7;6 7

x

y x

x y y x



  





  



Phương trình thứ nhất của hệ tương đương với

 

2

2 2 2 2

2

2 2 2

2 2

2 2 2

2 2

4 4 3 4 4 5 1

3 4

3 4 4 5 1

4 4

1

3 4 4 5 1

4 4

x y x x y x x y

x y

x y x x y

x y x

x y x x y

x y x

        

 

      

  

 

 

      

 

  

 

Nhận xét

 

2

6 7 0 3 4 6 7 3 1 0

x y x y x y x

           

.

Lại có

 

2

2 2

0

1

4 0 5 1 0

1

4 4

x

x x y

y

x y x





      





  



LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

71

 Xét

2

0

4

3 4 0

x

y

x y







 

 



  



(Không thỏa mãn điều kiện).

 Xét

1

0 6 7 6 6 1 1

y

y y x y y x x



         

.

Ngoài ra

6 7

7 7 14 2

6 7

x y

x y x y

y x

 



     



 



và

6 7 0

x y

  

.

Kết hợp ta có

6

7 6 7 2 1

x

y x y y y x x



        

.

Phương trình thứ hai của hệ có nghiệm khi và chỉ khi

6

7 0

1

2

1

x

y

x

y



 











 

 











Kết luận hệ phương trình có duy nhất nghiệm.

B

à

i

t

o

á

n

1

0

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

   

 

2

2 2 3

2 2

3 5 3 2 3 1 ,

;

2 3 2 1 2 3 2.

x x y x y x y x y

x y

x y y x y x y



         







        







.

Lời giải.

Điều kiện

2

3

5 0

2

3

2 3

x x y

x y





  











 



Phương trình thứ nhất của hệ tương đương với

   

 

2

2 2 3

2

2 2 3

2

2 2 3

2

3 5 2 3 2 2 3 1

2

2 2 3 1

3 5 2 3

1

2 2 3 1

3 5 2 3

x x y x y x y x y x y

x y

x y x y x y

x x y x y

x y x y x y

x x y x y

            

 

       

     

 

 

       

 

     

 

Ta nhận xét

 

2

3 0 2 2 3 1 0

x

y x y x y x



          

.

Lại có

2

1

2

3 0

3 5 2 3

x y

x x y x y



  

     

dẫn đến

 

2 3

0

1 0

1

x

x y

y





  







 Nếu

2

0

2

0

x

y

x y







 

 





 



(Không thỏa mãn hệ ban đầu).

 Nếu

 

1 2 1 0 2 3 2 1 2 3 0

y y x y y x y

           

.

Ta có

 

2 3

3 6 2

2 3

x y

x y x y

x y

 



     



 



.

Ngoài ra

 

2 2

2 2 2 2 2 2

0

2 2 4 2

x

y x y xy x y x y x y



           

.

Vậy

 

2

2 3 2 1 2 3 22

x y y x y x y

        

.

Phương trình thứ hai của hệ có nghiệm khi

2 2 3

1

; 1

x y x y

x y

x y y

   



  



 



, nghiệm duy nhất.

N

h

ậ

n

x

é

t

.

LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

72

C

á

c

b

à

i

t

o

á

n

t

ừ

8

đ

ế

n

1

0

k

h

ô

n

g

n

ằ

m

n

g

o

à

i

p

h

ạ

m

v

i

l

ớ

p

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

s

ử

d

ụ

n

g

t

ổ

n

g

h

ò

a

đ

á

n

h

g

i

á

–

h

à

m

s

ố

v

ớ

i

đ

i

ề

u

k

i

ệ

n

t

i

ê

n

q

u

y

ế

t

c

h

ặ

n

m

i

ề

n

g

i

á

t

r

ị

m

ộ

t

b

i

ế

n

t

h

ô

n

g

q

u

a

đ

ạ

i

l

ư

ợ

n

g

l

i

ê

n

h

ợ

p

,

d

ù

r

ằ

n

g

m

ứ

c

đ

ộ

c

ò

n

d

ừ

n

g

l

ạ

i

đ

ơ

n

g

i

ả

n

v

ớ

i

m

ộ

t

ẩ

n

m

à

t

h

ô

i

.

B

ì

n

h

t

h

ư

ờ

n

g

c

á

c

b

à

i

t

o

á

n

t

r

ư

ớ

c

đ

ó

c

h

ú

n

g

t

a

b

i

ế

n

đ

ổ

i

v

ề

d

ạ

n

g

     

;

; ;

f

x y A x y g x y







 

.

S

a

u

đ

ó

d

ù

n

g

đ

ặ

c

t

í

n

h

 

;

0

; 0

;

0

A

x y

f x y

g x y



























v

ớ

i

m

ọ

i

g

i

á

t

r

ị

;x

y

t

h

u

ộ

c

t

ậ

p

x

á

c

đ

ị

n

h

D

,

 

;A x y

t

h

ư

ờ

n

g

l

à

d

ạ

n

g

c

ă

n

t

h

ứ

c

.

T

ừ

b

à

i

t

o

á

n

s

ố

9

1

t

r

ở

đ

i

,

m

ọ

i

t

h

ứ

k

h

ô

n

g

c

ò

n

đ

ơ

n

t

h

u

ầ

n

ữ

a

,

m

à

d

ự

a

t

r

ê

n

k

ế

t

h

ợ

p

h

à

i

h

ò

a

c

á

c

đ

ạ

i

l

ư

ợ

n

g

k

h

ô

n

g

â

m

d

ự

a

t

r

ê

n

đ

i

ề

u

k

i

ệ

n

x

á

c

đ

ị

n

h

D

,

v

ớ

i

v

ă

n

p

h

o

n

g

   

; ;

f x y U h x y

g x y V k x y

 



 





T

r

o

n

g

đ

ó

U

,

V

l

à

b

i

ể

u

t

h

ứ

c

k

h

ô

n

g

â

m

b

ấ

t

k

ỳ

,

c

ò

n

   

;

; ;

h

x y k x y

k

h

ô

n

g

â

m

v

ớ

i

m

ọ

i

g

i

á

t

r

ị

;

x

y D



.

C

á

c

b

ạ

n

đ

ộ

c

g

i

ả

d

ễ

t

h

ấ

y

r

ấ

t

k

h

ó

k

h

ă

n

h

ơ

n

k

h

i

đ

ề

b

à

i

s

ử

d

ụ

n

g

h

ệ

s

ố

t

u

y

ế

n

t

í

n

h

c

h

e

g

i

ấ

u

đ

i

b

ả

n

c

h

ấ

t

   

 

1 1

2 2

; ;

; 0; 0

; ;

i

f x y mU n h x y

m n

g x y m V n k x y

 

 



 





.

C

á

c

b

ạ

n

l

ư

u

ý

v

ớ

i

b

i

ế

n

đ

ổ

i

     

;

; ;

f

x y A x y g x y







 

,

v

a

i

t

r

ò

c

ủ

a

   

; , ;g x y g x y

k

h

ô

n

g

b

ì

n

h

đ

ẳ

n

g

,

t

ạ

m

t

h

ờ

i

c

h

ú

n

g

t

a

x

é

t

r

ư

ờ

n

g

h

ợ

p

 

;

g

x y Q



,

đ

ơ

n

v

ị

q

u

y

ế

t

đ

ị

n

h

m

i

ề

n

g

i

á

t

r

ị

m

ộ

t

b

i

ế

n

.

C

ó

t

h

ể

l

ấ

y

c

á

c

đ

i

ể

n

h

ì

n

h

v

ớ

i

U

;

V

v

à

đ

ạ

i

l

ư

ợ

n

g

q

u

y

ế

t

đ

ị

n

h

m

i

ề

n

g

i

á

t

r

ị

Q

n

h

ư

s

a

u



B

à

i

t

o

á

n

9

1

.

 

     

   

2

91

2

92 91 91 91

2

91 91

2 1

; 2 3 ; ; 2 0

; 1 1

U x x

h x y x y f x y U h x y x y

Q g x y y y



  



         





   





.

H

ệ

s

ố

t

u

y

ế

n

t

í

n

h

1

;

1

.



B

à

i

t

o

á

n

9

2

.

 

   

2

92

2

92

92 92 92

2

92 91

2 1

; 4 5 ; ; 2 3 0

; 6 1

U x

h x y x y f x y U h x y x y

Q g x y y x



 



         





  





.

H

ệ

s

ố

t

u

y

ế

n

t

í

n

h

2

;

1

.



B

à

i

t

o

á

n

9

4

.

 

   

2

94

2

94

94 94 94

4

3

94 94

3 1

; 6 17 11 ; ; 3 17 14 0

; 1

U x

h x y x y f x y U h x y x y

Q g x y x y



 



         





  





.

H

ệ

s

ố

t

u

y

ế

n

t

í

n

h

3

;

1

.



B

à

i

t

o

á

n

9

5

.

 

   

2

95

2

95

95 95 95

2 3

95 95

1

;

2 3 5 ; ; 3 4 0

;

1

U x

h x y x y f x y U h x y x y

Q g x y y y



 





        







 





.

H

ệ

s

ố

t

u

y

ế

n

t

í

n

h

1

;

1

.



B

à

i

t

o

á

n

9

6

.

 

   

2

96

2

96

96 96 96

3

96 96

4 1

; 8 9 ; ; 4 5 0

; 1

U x

h x y x y f x y U h x y x y

Q g x y y



 



         





  





.

H

ệ

s

ố

t

u

y

ế

n

t

í

n

h

4

;

1

.

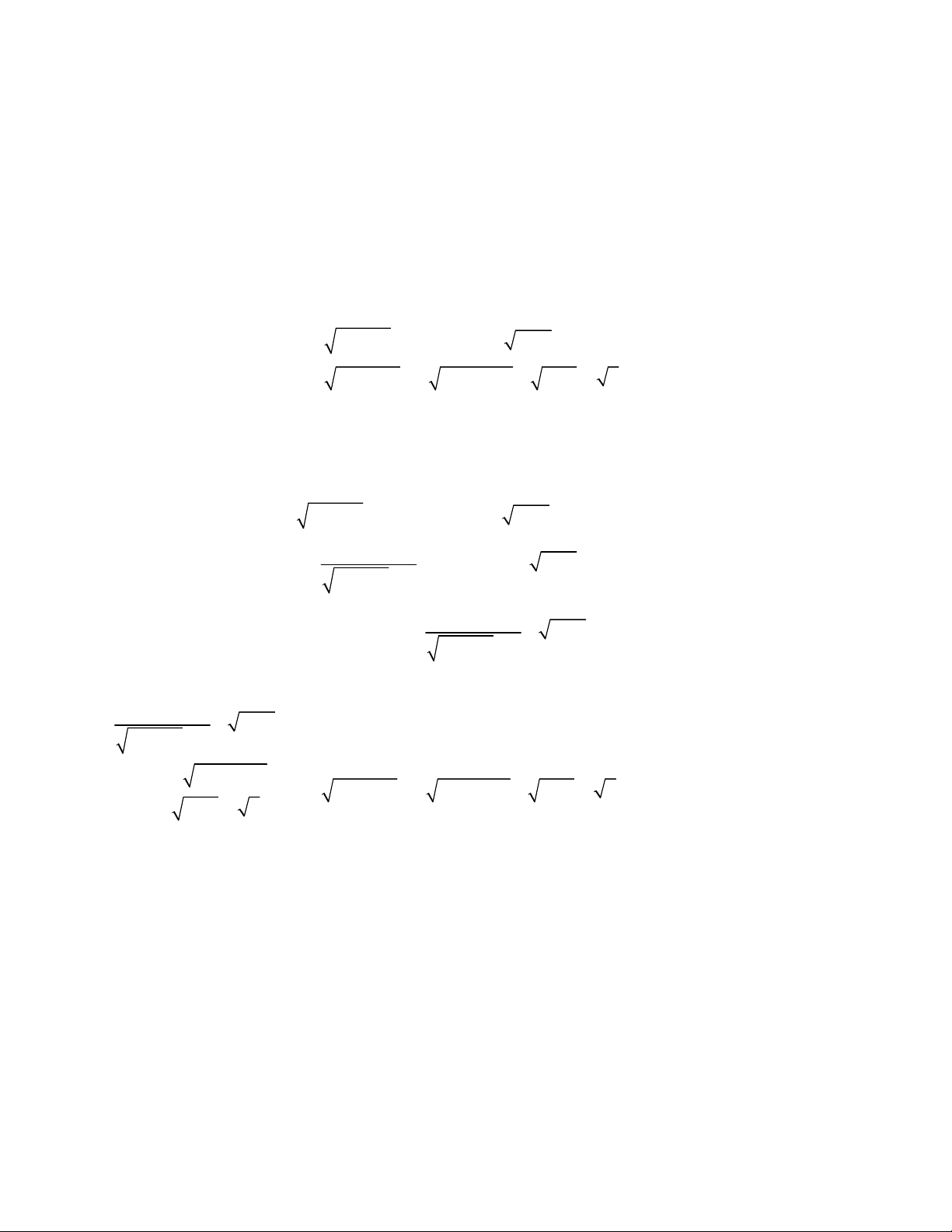
LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

73

C

á

c

b

à

i

t

o

á

n

t

i

ế

p

t

h

e

o

t

ư

ơ

n

g

t

ự

.

T

r

ê

n

đ

â

y

t

á

c

g

i

ả

đ

ã

l

ấ

y

t

r

ư

ờ

n

g

h

ợ

p

đ

ơ

n

g

i

ả

n

h

ấ

t

n

g

h

i

ệ

m

1x

y



,

l

ự

a

c

h

ọ

n

b

ì

n

h

p

h

ư

ơ

n

g

 

2

1

U

x





v

à

g

h

é

p

t

h

ê

m

h

ệ

s

ố

t

u

y

ế

n

t

í

n

h

,

c

h

ư

a

đ

ả

đ

ộ

n

g

t

ớ

i

 

;h

x y

,

t

ạ

m

t

h

ờ

i

 

;h

x y

l

à

c

h

í

n

h

b

ằ

n

g

m

ộ

t

r

o

n

g

c

á

c

b

i

ể

u

t

h

ứ

c

d

ư

ớ

i

c

ă

n

b

ậ

c

h

a

i

c

ủ

a

p

h

ư

ơ

n

g

t

r

ì

n

h

t

h

ứ

h

a

i

.

V

ề

m

ặ

t

h

ẩ

m

ỹ

,

c

á

c

h

ệ

s

ố

t

u

y

ế

n

t

í

n

h

;

i

m n

n

à

y

v

ừ

a

g

i

ấ

u

đ

i

b

ả

n

c

h

ấ

t

l

i

ê

n

h

ợ

p

b

a

n

đ

ầ

u

,

v

ừ

a

g

i

ả

m

t

h

i

ể

u

s

ự

c

ồ

n

g

k

ề

n

h

,

t

ạ

o

r

a

s

ự

g

ọ

n

g

à

n

g

,

đ

ẹ

p

m

ắ

t

c

h

o

 

;f

x y

c

ũ

n

g

n

h

ư

t

o

à

n

b

ộ

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

.

C

h

ú

n

g

t

a

h

o

à

n

t

o

à

n

c

ó

t

h

ể

đ

à

o

s

â

u

,

c

ả

i

t

i

ế

n

,

p

h

ứ

c

t

ạ

p

h

ó

a

b

ằ

n

g

c

á

c

h

t

h

a

y

đ

ổ

i

n

g

h

i

ệ

m

b

à

i

t

o

á

n

v

à

c

á

c

h

ệ

s

ố

t

u

y

ế

n

t

í

n

h

;

i

m n

,

c

ũ

n

g

n

h

ư

 

;h

x y

k

h

ô

n

g

c

ò

n

l

à

m

ộ

t

r

o

n

g

c

á

c

ă

n

t

h

ứ

c

n

ữ

a

,

n

ó

đ

ư

ợ

c

t

h

a

y

t

h

ế

b

ở

i

s

ự

l

ồ

n

g

h

é

p

h

ệ

s

ố

t

u

y

ế

n

t

í

n

h

v

ớ

i

c

á

c

b

i

ể

u

t

h

ứ

c

d

ư

ớ

i

d

ấ

u

c

ă

n

,

k

h

i

đ

ó

h

ệ

b

a

n

đ

ầ

u

s

ẽ

c

h

ứ

a

n

h

i

ề

u

d

ấ

u

c

ă

n

,

đ

ặ

t

ẩ

n

p

h

ụ

b

ị

v

ô

h

i

ệ

u

h

ó

a

m

ặ

c

d

ù

c

h

ú

n

g

c

ó

m

ố

i

l

i

ê

n

h

ệ

v

ớ

i

n

h

a

u

,

t

i

ế

c

r

ằ

n

g

đ

ó

l

à

m

ố

i

l

i

ê

n

h

ệ

t

u

y

ế

n

t

í

n

h

m

à

k

h

ô

n

g

p

h

ả

i

a

i

a

i

c

ũ

n

g

d

ễ

d

à

n

g

n

h

ậ

n

r

a

.

B

à

i

t

o

á

n

1

0

1

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

2 2 3

3 3 4 3 1 ,

;

2 2 3 1 2.

x y x y x y

x y

x y y x y y



      







        





.

Lời giải.

Điều kiện

2

3 0; 3; 2 3 0

3

0; 1

x y x x y

x y y



      





   



Phương trình thứ nhất của hệ tương đương với

 

2

2 3

2

2 3

2

2 3

2

3 2 3 4 3 1

3 4

3 4 3 1

3 2

1

3 4 3 1

3 2

x y x y x y

x y

x y x y

x y

x y x y

x y

       

 

      

 

 

 

      

 

 

 

Ta nhận xét

       

2 2

2

3

4 1 2 3 5 1 2 2 3 0

x

y x x y x x y x y



              

.

Hơn nữa

3

2

1

3

0 1 0 1

3

2

x

y y

x

y



      



.

Khi đó

2

3 0

1

2 2 3 1 2

1 2

y x y

y x y y x y y

y



  



          



 





.

Phương trình thứ hai có nghiệm khi các dấu đẳng thức xảy ra tức là

2

3

4 1 0

1

2 2 3 0

x y y

x

y

x y x y



    











 







     



Thử lại, kết luận hệ có nghiệm duy nhất.

N

h

ậ

n

x

é

t

.

B

à

i

t

o

á

n

s

ố

1

0

1

m

ở

m

à

n

c

h

i

ế

n

d

ị

c

h

ệ

s

ố

t

u

y

ế

n

t

í

n

h

1

;

1

;

1

v

ớ

i

b

ì

n

h

p

h

ư

ơ

n

g

 

2

1

x



c

á

c

b

i

ể

u

t

h

ứ

c

d

ư

ớ

i

d

ấ

u

c

ă

n

,

t

ấ

t

n

h

i

ê

n

t

ạ

m

d

ừ

n

g

c

h

â

n

t

ạ

i

p

h

é

p

l

i

ê

n

h

ợ

p

m

ộ

t

c

ă

n

t

h

ứ

c

v

ớ

i

h

ằ

n

g

s

ố

,

đ

ồ

n

g

n

g

h

ĩ

a

đ

ạ

i

l

ư

ợ

n

g

 

2

; 3 4

f x y x y

  

l

ộ

l

i

ễ

u

n

g

à

y

t

ạ

i

p

h

ư

ơ

n

g

t

r

ì

n

h

t

h

ứ

n

h

ấ

t

c

ủ

a

h

ệ

.

C

ụ

t

h

ể

     

   

 

       

2

101

1 2

1 1 1

2 2

2

1

; ; 2; ; 2 3

1

; 1 2 3 5 1 2 2 3 0 ; 3 4

U

x h x y x y h x y x y

m n p

f x y x x y x x y x y f x y x y





      





  





                  

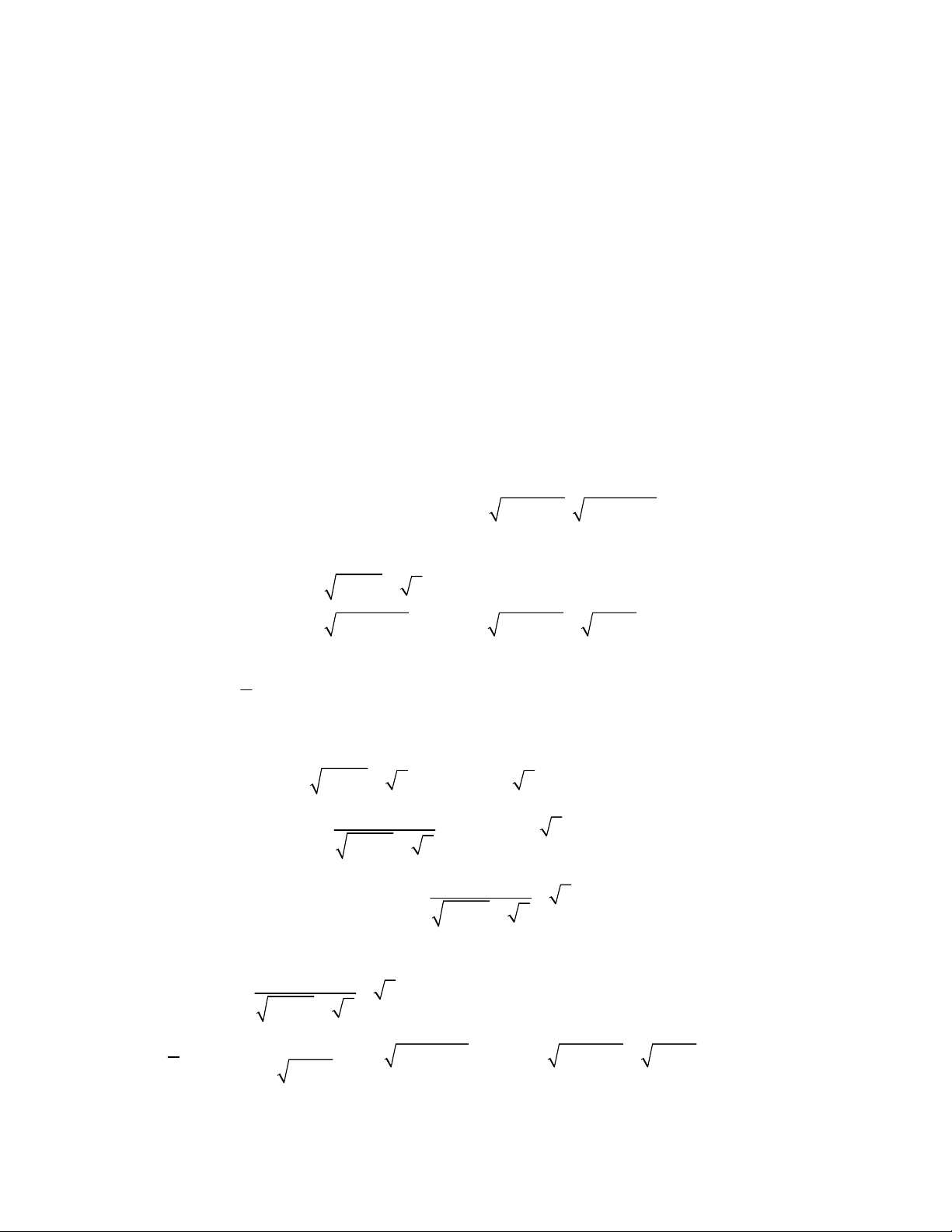
LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

74

N

g

o

à

i

r

a

c

á

c

b

ạ

n

c

ó

t

h

ể

l

ự

a

c

h

ọ

n

h

ệ

s

ố

t

u

y

ế

n

t

í

n

h

k

i

ể

u

k

h

á

c

,

đ

ả

m

b

ả

o

h

ệ

s

ố

c

h

ứ

a

x

(

h

o

ặ

c

h

ệ

s

ố

c

h

ứ

a

y

)

c

ủ

a

đ

ạ

i

l

ư

ợ

n

g

 

;f

x y

s

u

y

b

i

ế

n

b

ằ

n

g

0

,

 

;f

x y

s

ẽ

l

ậ

p

t

ứ

c

t

r

ở

n

ê

n

h

ỏ

n

h

ắ

n

,

x

i

n

h

t

ư

ơ

i

.

     

   

 

     

 

2

101

1 2

1 1 1

2 2

2

1

; ; 2; ; 2 3

2; 1; 3

;

2 1 4 7 11 2 1 2 3 2 3 0

;

2 7 9

U x h x y x y h x y x y

m n p

f x y x x y x x y x y

f x y x y



       





  







             



  

T

h

ậ

m

c

h

í

t

h

a

y

đ

ổ

i

U

n

ế

u

m

u

ố

n

h

ệ

s

ố

k

h

ô

n

g

c

h

ứ

a

y

     

   

 

       

2

101

1 2

1 1 1

2 2

2

1 ; ; 2; ; 2 3

2; 2; 1

;

2 1 3 4 7 2 1 2 2 2 3 0 ; 2 3 5

U y h x y x y h x y x y

m n p

f

x y y x y y x y x y f x y y x





      





  







                 

N

h

ư

n

g

c

á

c

b

ạ

n

b

i

ế

t

k

h

ô

n

g

,

đ

ể

c

ó

t

h

ể

c

ó

đ

ư

ợ

c

l

i

ê

n

k

ế

t

       

2 2

2

3

4 1 2 3 5 1 2 2 3 0

x

y x x y x x y x y



              

.

C

h

ú

n

g

t

a

c

ầ

n

đ

i

ề

u

k

i

ệ

n

t

i

ê

n

q

u

y

ế

t

n

h

ư

t

h

ế

n

à

o

,

b

ở

i

v

ì

c

á

i

g

ì

h

ệ

q

u

ả

c

ũ

n

g

c

ầ

n

s

ự

t

ổ

c

h

ứ

c

v

à

b

ố

t

r

í

t

ừ

t

r

ư

ớ

c

đ

ó

.

K

h

ô

n

g

q

u

á

k

h

ó

c

h

ỉ

c

ầ

n

c

ó

s

ự

h

i

ệ

n

d

i

ệ

n

c

ủ

a

c

á

c

b

i

ể

u

t

h

ứ

c

2; 2 3x y x y   

t

r

o

n

g

c

ă

n

t

h

ứ

c

b

ậ

c

h

a

i

t

ạ

i

p

h

ư

ơ

n

g

t

r

ì

n

h

t

h

ứ

h

a

i

,

h

o

ặ

c

h

ỉ

c

ầ

n

c

ă

n

t

h

ứ

c

b

ậ

c

h

ẵ

n

đ

ạ

i

l

o

ạ

i

n

h

ư

6

4

2

; 2 3

x

y x y



  

s

ẽ

l

à

m

ấ

t

p

h

ư

ơ

n

g

h

ư

ớ

n

g

đ

ặ

t

ẩ

n

p

h

ụ

c

ủ

a

đ

a

s

ố

c

á

c

b

ạ

n

q

u

e

n

v

ớ

i

t

h

ủ

p

h

á

p

n

à

y

.

B

à

i

t

o

á

n

1

0

2

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

2

2 2

2 3 1 ,

;

3 4 3 2 2 2 1 1.

y x y x y

x y

x y y x y y



     







        







.

Lời giải.

Điều kiện

2

1

0;

2

2 0; 3 4

y

x y

x y x y



  







    



Phương trình thứ nhất của hệ tương đương với

 

2

2 2

2

2 2

2

2 2

2

2 2 2 1

2

2 2 1

2

1

2 2 1

2

y x y x y

y x

y x y

y x

y x y

y x

      

 

     

 

 

 

     

 

 

 

Nhận xét

       

2

2 4 2 1 2 4 6 2 1 3 4 2 0

y

x y x y y x y x y



              

.

Do đó

2

2 0

y x

  

, lại có

2

1

2 0 1 0

1

2

y

y x





     



 

 



Kết hợp với

 

3

2 0

1

3 4 3 2 2 2 1 1

2

2 1 1

y

y y x y y x y y

y

 







            











.

Vì vậy phương trình thứ hai của hệ có nghiệ khi

1

3 4 2 0

y

x y

x y x y





  



     



.

Kết luận hệ có nghiệm duy nhất.

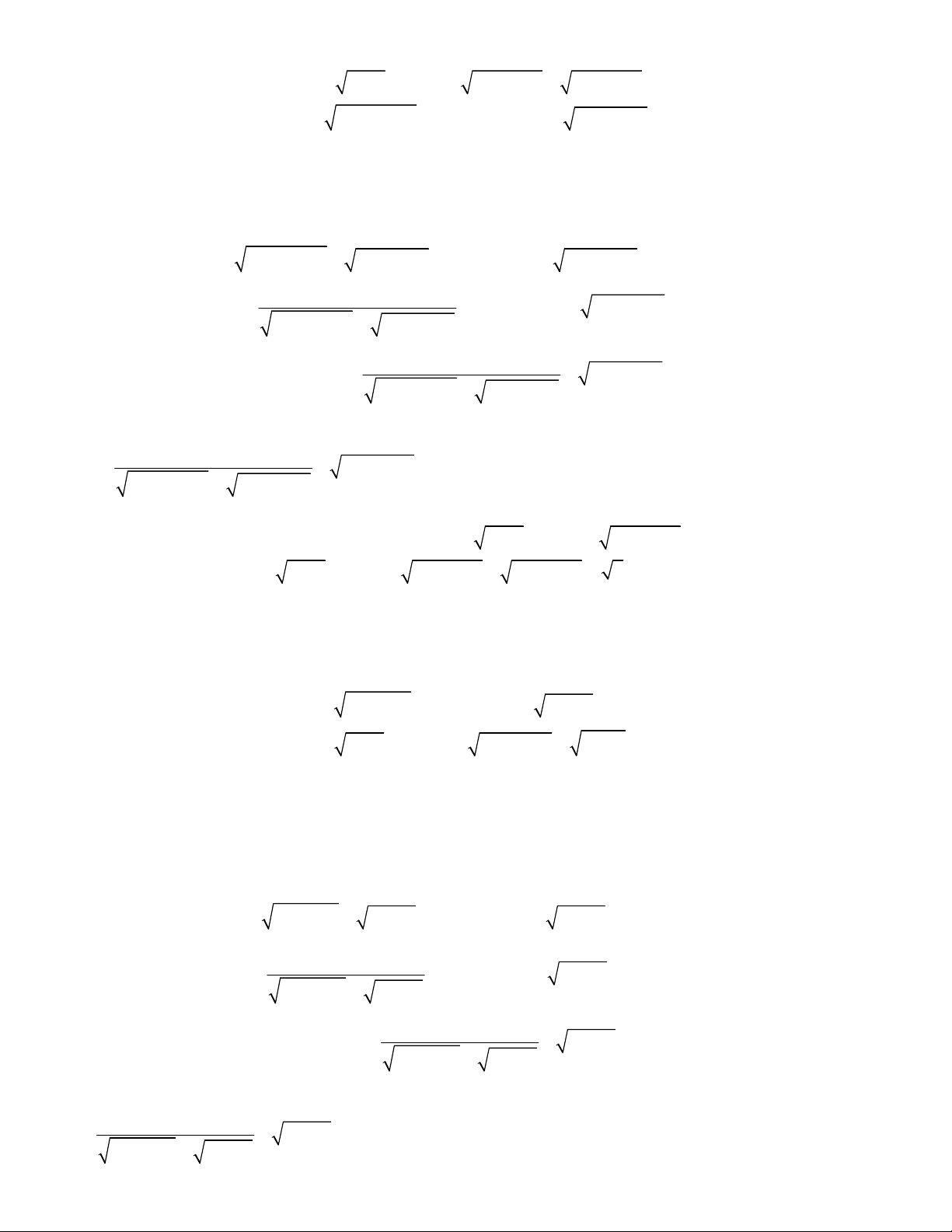
LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

75

B

à

i

t

o

á

n

1

0

3

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

2

2 1 2 1 4 1 2,

;

4 5 4 3 1 4 5 1.

y x y x x y x y

x y

y x y y x x y y



        







         







.

Lời giải.

Điều kiện

2

;2 1 0; 4 5 0

4 1 0; 4 5 0

x y x y y x

x y x y



      





    



Phương trình thứ hai tương đương với

 

2

4

5 4 5 4 3 4 5 1

4 3

4 3 4 5 1

4

5 4 5

y x x y y y x x y y

y y x

y y x x y y

y

x x y

           

 

       



   

 

2

1

4 3 4 5 1

4 5 4 5

y y x x y y

y x x y

 

 

       





    

 

.

Nhận xét

       

2 2

2

4

3 1 3 2 1 1 2 1 0

y

y x y x y y x y x y



             

.

Hơn nữa

2

1

4

5 0 1 0 1

4

5 4 5

x

y y y

y

x x y



       



   

.

Khi đó ta có

 

1 2 1 0 2 1 2 1 0

2 1 2 1 4 1 4 2

x y x x y x y x x y

y x y x x y x y

            

          

Phương trình thứ nhất của hệ có nghiệm khi

; 1

1

2 1 0

x y y

x y

x y x y

 



  



    



.

Kết luận bài toán có nghiệm duy nhất kể trên.

B

à

i

t

o

á

n

1

0

4

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

3

2

3 3

2

2 7 2 5 9 2 7 3 1 ,

;

2 1 2 3 3 2.

x y x y y y

x y

x x y y x y y



      







       







.

Lời giải.

Điều kiện

2

3

2 7 0;2 7 0

2 3 0;

3 0

x y y

x y x y

y



   





  





 



Phương trình thứ nhất của hệ tương đương với

 

3

2

3

2

3

2

2 7 2 7 2 5 7 2 7 3 1

2 2 5 9

2 5 7 2 7 3 1

2 7 2 7

2

5 9 2 7 3 1

2 7 2 7

x y y x y y y

x y

x y y y

x y y

x y y y

x y y

        

 

      

  

 

 



     





  

 

Nhận xét

   

2

5 7 2 1 3 2 3 0

x

y x x y x y



        

.

Lại có

 

3

2

2 7 0 3 1 0 1

2

7 2 7

y y y

x

y y

       



 

.

LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

76

Khi đó

 

3

3 3

3

1

1 2 1 0 2 1 2 3 3 0 0 2 2

3

4

x y

y y x x y y x y y

y

 





               











.

Phương trình thứ hai của hệ có nghiệm khi và chỉ khi

2

1

2

7 2 7

1

2

3 0

y

x

y y

y

x

y x y













  

 









   



Thử lại kết luận hệ có nghiệm duy nhất

1x y 

.

B

à

i

t

o

á

n

1

0

5

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

2

2 2 3

2

2 17 6 3 15 5 3 1,

;

2 2 1 2 1 1.

x y x y x y y

x y

x y xy x y x y



      









       





.

Lời giải.

Điều kiện

2 2

2

2; 2 1 0

2

1;17 6 0

15

5 3 0

x y x y

x y

    







 





  



Phương trình thứ nhất của hệ tương đương với

 

2

2 2 2 3

2

2 2 3

2 2

2 2 3

2 2

3 17 6 15 5 3 2 3 17 6 1

3

2 3

2

3 17 6 1

17

6 15 5 3

3

2

3 17 6 1

17

6 15 5 3

x y x y x y x y y

x y

x y x y y

x y x y

x y x y y

x y x y

         

 

      

   

 

 



     





   

 

Nhận xét

     

2

3 3 2 2 1 2 1 0

x

y x y x y x



         

.

Hơn nữa

2

3

2 2

3

17

6 0 1 0 1

17

6 15 5 3

x

y y y

x

y x y



      



  

.

Kết hợp

2

2 2 1 0

2 1 1 0

2 1 2 1 1

x y xy x y

x y x

x y



     



     



   





Dẫn đến

2

2 1 2 1 1

x

y xy x y x y



      

. Phương trình thứ hai có nghiệm khi

1x

y



.

Thử lại kết luận hệ có nghiệm duy nhất

1x

y



.

B

à

i

t

o

á

n

1

0

6

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

   

 

2

2 2 2

2 4 3 2

3 4 2 4 7 2 1 1 ,

;

2 3 3 1 1 .

x y x y x x y

x y

y x y x x y x



        









       





.

Lời giải.

Điều kiện

2

4

3 2

2 3; 1

1

0;3 4 0

x y x

x y x y



  







    





Phương trình thứ nhất của hệ tương đương với

LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

77

   

 

   

 

   

 

2

2 2 2 2

2

2 2 2

2 2

2 2 2

2 2

3 4 7 2 3 7 2 1 1

2 3

2 3 7 2 1 1

3 4 7

1

2 3 7 2 1 1

3 4 7

x y x x y x x y

x y

x y x x y

x y x

x y x x y

x y x

          

 

       

   

 

 

       

 

   

 

Nhận xét

 

2

3 1 1 2 3 0

x

y x x x y



        

.

Lại có

 

2

2 2

1

7

0 2 1 1 0

3 4 7

x x y

x y x



     

   

.

Vì

2

4

3 4 2

2 3 0

1 0 2 1 0 1 0 1

1

y x y

x x y y

x y x x



  



          



   





Dẫn đến

2

4 3 2

2

3 3 1 1

y

x y x x y x



      

.

Phương trình thứ hai có nghiệm khi dấu đẳng thức xảy ra tức là

2

3

2

3 1 0 1

1

; 1 0

x

y x x

y

x





    











 





Thử lại kết luận hệ có nghiệm duy nhất

1x y 

.

B

à

i

t

o

á

n

1

0

7

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

2

2 2

3 2 3

3 3 3 2 1 1 ,

;

5 2 1 1 .

x y x y x x y

x y

x y y x x y x



       









       





.

Lời giải.

Điều kiện

2

2 3

2 3 2 3

3

3 3

2 1 0; 1 0 2 0; 1

2

0; 1 0 1 0

x y

x x x y x

x

y x y x y



 



 



        



 

        



Phương trình thứ nhất của hệ tương đương với

 

2

2 2 2

2

2 2

3 3 2 1 2 2 1 1

2

2 2 1 1

3 3 2 1

1

2 2 1 1

3 3 2 1

x y x x y x x y

x y

x y x x y

x y x

x y x x y

x y x

         

 

      

   

 

 

      

 

   

 

Nhận xét

   

2

1

2 1 2 1 0

x

x y x x y x



          

.

Hơn nữa

 

2

1

; 2 1 0 1 0 1

3

3 2 1

x

x x y y

x

y x



       



  

.

Dẫn đến

3

2 3

2 3 2

1 0

5 2 1 1

1

y x

x

y y x x y x

x

y x x



 





       





  





.

Do đó phương trình thứ hai của hệ có nghiệm khi

2

2 0

1

0; 1

x y x y

x y

x

y



     

  



  



Kết luận hệ phương trình có nghiệm duy nhất kể trên.

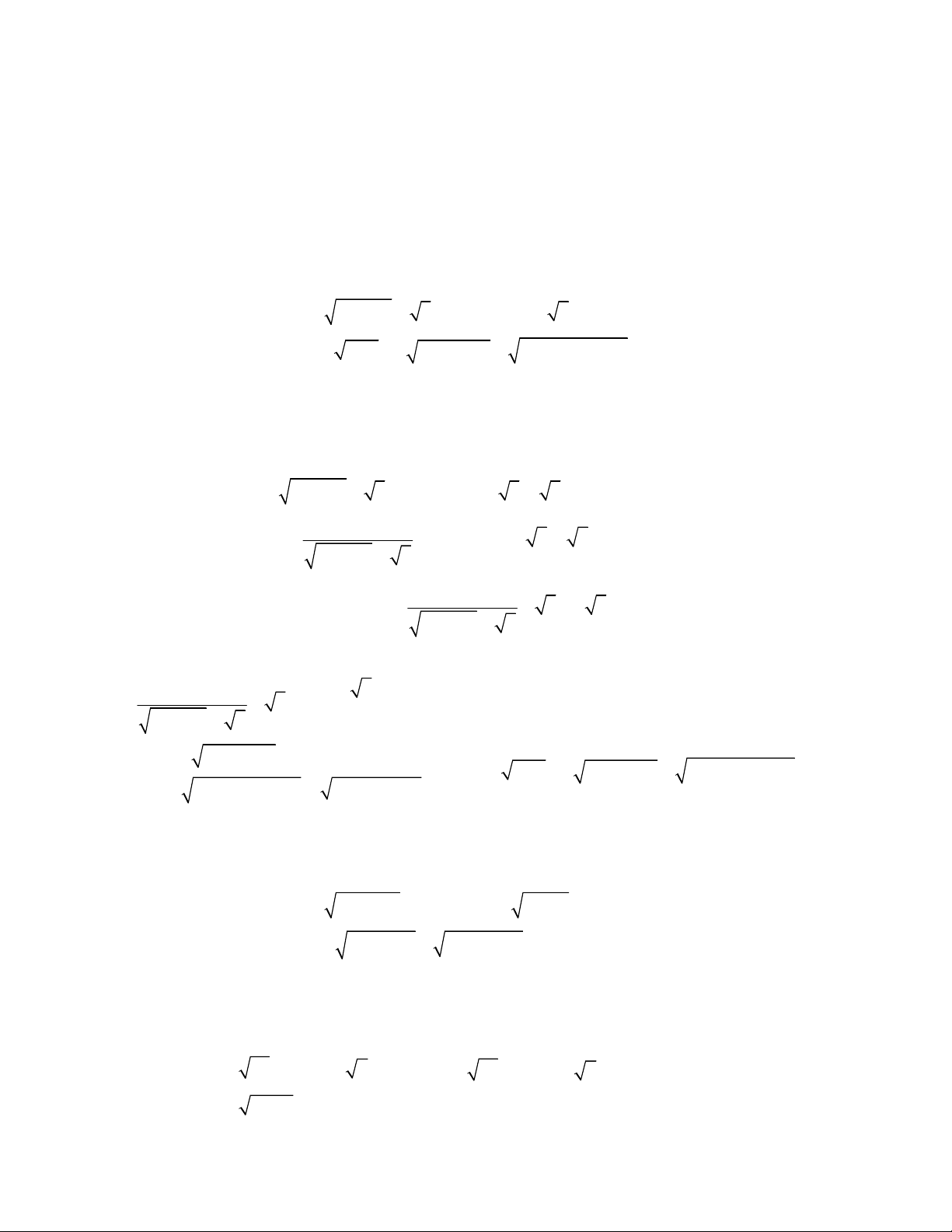
LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

78

N

h

ậ

n

x

é

t

.

B

à

i

t

o

á

n

s

ố

1

0

7

c

h

ú

n

g

t

a

c

ó

     

2

1

; 2 1 2 1 0

x

f x y x y x x y x



           

.

R

õ

r

à

n

g

t

r

ê

n

đ

â

y

c

ó

s

ử

d

ụ

n

g

     

2

1

2

1

; ; 2; ; 1

U

x h x y x y h x y x



     

,

t

r

o

n

g

đ

ó

 

1

;h

x y

l

à

b

i

ể

u

t

h

ứ

c

d

ư

ớ

i

c

ă

n

,

c

ò

n

đ

ạ

i

l

ư

ợ

n

g

 

2

; 1h x y x 

t

ừ

t

r

ê

n

t

r

ờ

i

r

ơ

i

x

u

ố

n

g

,

c

ũ

n

g

k

h

ô

n

g

â

m

đ

ấ

y

c

h

ứ

n

h

ư

n

g

m

à

k

h

a

i

q

u

ậ

t

đ

ư

ợ

c

n

ó

r

a

v

ô

c

ù

n

g

k

h

ó

k

h

ă

n

.

Đ

ể

t

ự

n

h

i

ê

n

h

ơ

n

c

á

c

b

ạ

n

c

ó

t

h

ể

x

ử

l

ý

t

h

e

o

p

h

ư

ơ

n

g

á

n

s

a

u

   

2

2 1 2

x

y x x x y x x x y



          

v

ớ

i

 

1 0; 1

; 2

U x x x

h x y x y

    







  





B

à

i

t

o

á

n

1

0

8

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

   

 

2

2 3

2

2 3 2 4 5 1 ,

;

4 1 2 3 2 .

x y x y x y

x y

x x x y x y x y x



     









        





.

Lời giải.

Điều kiện

2

0;2 3 0

1; 2 0

x

y x y

x x y x y





   







   





Phương trình thứ nhất của hệ tương đương với

   

2

2 3

2

2 3

2

2 3

2

2 3 2 3 3 5 1

2 3

2 3 3 5 1

2 3

1

2 3 3 5 1

2 3

x y x y x y

x y

x y x y

x y

x y x y

x y

      

 

     

 

 

 

     

 

 

 

Nhận xét

 

2

1

2 3 2 1 2 3 0

x

x y x x x y



        

.

Lại có

 

3

2

5 1 0

1

1; 3 0 1 1

2 3

1

x y

x y y

x y

x



 



       



 







.

Khi đó

2 2

2

3 0

1

2 1 1 2 .

x

x y

x

y

x y x y x x





 









 





       





nên

2

4

1 2 3 2

x

x x y x y x y x



       

.

Phương trình thứ hai của hệ có nghiệm khi

1 2 3 0

1

x x y

x y

    



  



 



.

B

à

i

t

o

á

n

1

0

9

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

2

2 2 2 2 3

2 2 3

2

3 2 2 1 ,

;

1 2 1 3 2 1.

x y x y y x y

x y

y y x y x y y



       







       





.

Lời giải.

Điều kiện

 

2

0 1

1 0

2 1

2 1 0

y x



  

 







 

 

  





Xét trường hợp

 

2

2 2

3

2 2 1

3 2 2 1

0

1 2 1

x x x

y x

x



   

 



   





 

 



.

Xét trường hợp

1x 

thì phương trình thứ nhất của hệ tương đương với

LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

79

 

2

2 2 2 2 3

2 2 2 2 2 2 3

2 2

2 2 2 3

2 2 2

2 2 2 3

2 2 2

2 3 2 2 1

2 2 2 2 2 1

2

2 2 2 1

2 2

1

2 2 2 1

2 2

x y x y y y x

x y y x y y y x

x y

x y y y x

x y y

x y y y x

x y y

       

          

 

       

  

 

 

       

 

  

 

Nhận xét

  

1

3 1 0

x

x x



   

, suy ra

 

  

2 2 2 2 2

2

2 3 2 1 3 1 2 1 0

x

y x x y x x x y x



             

.

Khi đó kết hợp

2

3 3

2 2 2

1

2

0 2 1 0 2 1 1 1

2

y

y x y x y

x

y y



           



 

.

Ta có ngay

 

2

1 2 1 0

y y x y x

    

.

Xét hàm số

   

3

2

3

2 ; 1 9 2 0, 1

f

y y y y f y y y





       

, hàm số liên tục và đồng biến trên





1

;



.

Khảo sát sự biến thiên thu được

     

2

2 3

1

1 1 1 2 1 3 2 1

y

Min f y f y y x y x y y



         

.

Phương trình thứ hai của hệ có nghiệm khi và chỉ khi

2

1

; 1 1

2

1 0

x y

x

y x y

y

x



 





   







 



.

Thử lại, kết luận hệ có nghiệm duy nhất

1x y 

.

B

à

i

t

o

á

n

1

0

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

   

 

2

2 2 2 2 2 3

2 2 2

2 3 2 3 6 3 2 5 ,

;

2 1 3 3 2 5 2 2 1 1.

x x y x x y y x y

x y

y x y x x x y x



        









         





.

Lời giải.

Điều kiện

2

2 2

2

3

0; 1

3

2 5 0;3 2 5 0

2 2 1 0

x y x x

y x y x

x x y



   





    





   



.

Phương trình thứ nhất của hệ tương đương với

 

2

2 2

2 2 2 2 2 2 3 2

2 2

2 2 2 3 2

2 2 2

2

2 2 3 2

2

2 2

2 1 3 3 2 5 2 2 1 1

2 2 6 3 2 5 2 3 5 3 2 5

2 3 5

2 3 5 3 2 5

2 2 6 3 2 5

1

2 3 5 3 2 5

2 2 6 3 2 5

y x y x x x y x

x x y y x x y y x y x

x y

x y y x y x

x x y y x

x y y x y x

x x y y x

         

           

 

       

    

 

 

       

 

    

 

Nhận xét

   

2 2 2

1

2 1 0 2 3 5 2 1 3 2 5 0

1

x

x x x y x x y x

x





           



 



.

Từ đó kết hợp

2

3 2 3 2

2 2 2

1

3

2 5 0 0 1 1

2

2 6 3 2 5

y

x y x y x y

x

x y y x



          



   

.

LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

80

Khi đó

2

1 0

1

2

2 1 2 1 1

y

x

y

x x y x x x



 



 





      





Suy ra

2 2 2

2

1 3 3 2 5 2 2 1 1

y

x y x x x y x



        

.

Phương trình thứ hai của hệ có nghiệm khi

2

2 2

1

3 2 5 0 1

1

1;2 3 5 0

x y x x

y

y x y





    











   





Thử lại, kết luận hệ có nghiệm duy nhất kể trên.

N

h

ậ

n

x

é

t

.

T

h

e

o

l

ố

i

m

ò

n

,

c

h

ú

n

g

t

a

v

ẫ

n

c

h

ủ

đ

ạ

o

c

ô

n

g

p

h

á

m

ộ

t

r

o

n

g

h

a

i

p

h

ư

ơ

n

g

t

r

ì

n

h

,

t

ì

m

i

ề

n

g

i

á

t

r

ị

m

ộ

t

b

i

ế

n

t

h

e

o

b

i

ế

n

c

ò

n

l

ạ

i

v

ớ

i

s

ự

l

ư

u

t

â

m

s

á

t

s

a

o

đ

i

ề

u

k

i

ệ

n

x

á

c

đ

ị

n

h

.

K

h

ô

n

g

i

ố

n

g

n

h

ư

n

h

ữ

n

g

b

à

i

t

o

á

n

t

r

ư

ớ

c

,

b

à

i

t

o

á

n

s

ố

1

0

c

ó

đ

i

ề

u

k

i

ệ

n

x

á

c

đ

ị

n

h

p

h

ứ

c

t

ạ

p

h

ơ

n

,

k

h

i

m

à

b

i

ế

n

x

c

ó

t

ậ

p

g

i

á

t

r

ị

n

ằ

m

t

r

ê

n

h

a

i

k

h

o

ả

n

g

r

ờ

i

n

h

a

u

l

à



 



;

1 1;x



   

.

T

a

t

h

ấ

y

    

0

x p

x p x q p q

x q





    







.

N

h

ư

v

ậ

y

  

 

0, ; ;

x m

x p x q p q m n

x n





     







.

N

g

o

à

i

r

a

c

ó

t

h

ể

l

ự

a

c

h

ọ

n

t

h

e

o

c

á

c

h

k

h

á

c

n

h

ư

s

a

u

   

 

2

2 2 2 2 2 2

2

3 5 1 2 1 3 2 5 1 1 3 2 5

x

y x x x y x x x y x



               

.

B

à

i

t

o

á

n

1

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

2

2 2 2 3

2 2 2

3

4 3 6 3 5 1,

;

2 2 4 5 1 .

x y y x y y y x

x y

x y x y x y x y



        









         





.

Lời giải.

Điều kiện các căn thức xác định. Phương trình thứ nhất của hệ tương đương với

 

2

2 2 2 3

2 2

2 2 3

2 2

2 2 3

2 2

3 4 3 5 3 5 3 5 1

3 5

3 5 3 5 1

3 4 3 5

1

3 5 3 5 1

3 4 3 5

x y y y x y y y x

x y y

x y y y x

x y y y

x y y y x

x y y y

          

  

       

   

 

 

       

 

   

 

Ta có

   

2

2 2 2 2 2 2

3

5 2 1 4 7 2 1 2 4 5 0

x

y y x x y x y x x y y x



                 

.

Lại có

3

2

1

3

5 0 1 0 1

3

4 3 5

y

x x

x

y y y



      



  

.

Lúc đó

 

2

2 2 2

2 2

2 4 5 0

2 2 4 5 1

1

x y x

x y x y x y x y

y x y y y



   



          



    





.

Do đó phương trình thứ hai của hệ có nghiệm khi

2

1

4 5 2 0

x

y

y x x y











     



Kết luận hệ phương trình ban đầu có nghiệm duy nhất.

B

à

i

t

o

á

n

1

2

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

3

3 3 2 2 4 1 0,

;

2 2 3 2 1 2 0.

x y x y y

x y

x x y x y y x y



      







        







.

Lời giải.

LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

81

Điều kiện

3

3 0; 0

0

; 3 3 0

0;2 3 0

2

3 0; 2 0

2

0

x y y

x y x y

x y



   



    



     

 



    







 



Phương trình thứ nhất của hệ tương đương với

 

3 3

3 3 2 2 3 2 1 0

3 3 2 2 3 1

x y x y y y

x y y x y y y

       

        

 

3

2 3

2 2 3 1

3 3

1

2 3 2 1

3 3

x y

x y y y

x y y

x y y y

x y y

 

     

  

 

 

     

 

  

 

Nhận xét

   

2

3

2 1 2 0, 0

x

x x x x



      

nên

   

3 3

2 3 3 2 2 3 2 0

x y x x x y x y

           

.

Lại có

3

1

2

0 1 0 1 1

3

y

y y y

x

y y



       



 

.

Với

 

2

0

1

2

2 3 2 1 2 0

1

2 1 2 0

x x y

x y

x x y x y y x y

y

y x y



 

 







         





   







.

Phương trình thứ hai của hệ có nghiệm khi

0 1

2 3 2 0 1

x y x

x y x y y

  

 



 

      

 

Thử lại, kết luận hệ phương trình có nghiệm duy nhất

1x y 

.

N

h

ậ

n

x

é

t

.

S

a

u

m

ộ

t

h

ờ

i

g

i

a

n

d

à

i

g

i

a

o

t

r

a

n

h

,

p

h

ư

ơ

n

g

á

n

s

ử

d

ụ

n

g

c

h

i

ế

n

t

h

u

ậ

t

d

u

k

í

c

h

t

h

u

ầ

n

t

ú

y

d

ọ

c

t

h

e

o

c

h

i

ế

n

t

u

y

ế

n

9

1

đ

ế

n

1

c

h

ỉ

v

ớ

i

v

ũ

k

h

í

h

ạ

n

g

n

h

ẹ

d

ạ

n

g

n

h

ị

t

h

ứ

c

b

ậ

c

n

h

ấ

t

–

t

a

m

t

h

ứ

c

b

ậ

c

h

a

i

,

v

ề

c

ơ

b

ả

n

c

h

ú

n

g

t

a

đ

ã

x

ử

l

ý

đ

ư

ợ

c

p

h

ầ

n

l

ớ

n

c

á

c

đ

ơ

n

v

ị

t

r

i

n

h

s

á

t

,

t

i

ề

n

t

i

ê

u

c

ủ

a

đ

ị

c

h

q

u

â

n

.

T

u

y

n

h

i

ê

n

,

c

à

n

g

đ

i

s

â

u

v

à

o

c

h

í

n

h

d

i

ệ

n

c

u

ộ

c

h

i

ế

n

,

k

h

i

m

à

t

ì

n

h

ì

n

h

p

h

ứ

c

t

ạ

p

h

ơ

n

v

ớ

i

c

h

i

ế

n

t

r

a

n

h

q

u

y

ư

ớ

c

,

v

ớ

i

c

á

c

t

h

à

n

h

l

ũ

y

k

i

ê

n

c

ố

,

c

ạ

m

b

ẫ

y

g

i

ă

n

g

n

h

ư

m

ạ

n

g

n

h

ệ

n

,

c

ầ

n

s

ử

d

ụ

n

g

v

ũ

k

h

í

h

ạ

n

g

n

ặ

n

g

,

k

i

n

h

n

g

h

i

ệ

m

x

ư

ơ

n

g

m

á

u

t

í

c

h

l

ũ

y

,

á

p

đ

ả

o

b

i

ể

n

g

ư

ờ

i

v

à

n

h

ữ

n

g

b

ư

ớ

c

đ

i

k

h

é

o

l

é

o

,

c

ẩ

n

t

h

ậ

n

.

B

à

i

t

o

á

n

s

ố

1

2

m

ở

m

à

n

q

u

y

m

ô

k

h

i

U

c

ó

d

ạ

n

g

đ

a

t

h

ứ

c

m

ộ

t

ẩ

n

b

ậ

c

b

a

,

k

ế

t

h

ợ

p

s

ử

d

ụ

n

g

h

ệ

s

ố

t

u

y

ế

n

t

í

n

h

1

;

1

;

1

v

ớ

i

c

á

c

b

i

ể

u

t

h

ứ

c

k

h

ô

n

g

â

m

   

 

     

2

3

1

1 1 1

2

3 3

3

2 1 2 0, 0

; 2 3 0 1

; 2 0

;

2 3 3 2 2 3 2 0

U

x x x x x

h x y x y m n p

h x y x y

f x y x y x x x y x y



        



      





   







            

Đ

i

ể

m

đ

á

n

g

c

h

ú

ý

h

ơ

n

l

à

đ

a

t

h

ứ

c

b

ậ

c

b

a

k

h

ô

n

g

c

ó

đ

ặ

c

t

í

n

h

k

h

ô

n

g

â

m

v

ố

n

c

ó

n

h

ư

t

a

m

t

h

ứ

c

b

ậ

c

h

a

i

,

đ

ể

t

h

i

ế

t

l

ậ

p

đ

i

ề

u

n

à

y

c

á

c

b

ạ

n

c

h

ú

ý

b

ố

t

r

í

đ

i

ề

u

k

i

ệ

n

c

h

o

c

á

c

b

i

ế

n

t

r

ư

ớ

c

đ

ó

:

   

2

0

,

n

x

a mx n x

m



    

.

V

í

d

ụ

n

h

ư

   

2

3 2

2

3

2

3 2

2 1 0, 1 3 2 2 0, 1

1

2 0, 2 3 2 0, 2

1

4 0, 4 2 7 4 0, 4

x x x x x x x

x x x x x x

x x x x x x x

             



           



            

LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

82

V

ì

 

;f x y

c

ủ

a

c

h

ú

n

g

t

a

y

ê

u

c

ầ

u

t

h

ẩ

m

ĩ

c

a

o

,

h

ơ

n

ữ

a

c

á

c

b

i

ể

u

t

h

ứ

c

U

v

à

 

;

i

h x y

c

h

u

i

v

à

o

t

r

o

n

g

c

ă

n

t

h

ứ

c

n

ê

n

c

ầ

n

g

ọ

n

g

à

n

g

,

đ

ẹ

p

m

ắ

t

,

t

r

á

n

h

c

ồ

n

g

k

ề

n

h

,

v

ì

v

ậ

y

n

ê

n

c

h

ọ

n

l

ự

a

h

ệ

s

ố

s

a

o

c

h

o

k

h

u

y

ế

t

h

ạ

n

g

t

ử

b

ậ

c

h

a

i

h

o

ặ

c

b

ậ

c

n

h

ấ

t

đ

ể

t

ạ

o

r

a

đ

a

t

h

ứ

c

h

ì

n

h

t

h

ứ

c

b

a

h

ạ

n

g

t

ử

   

 

   

 

   

 

2

3

2

2 3

2

2 3

2

4 4 4 4 12 16

3

6 6 9 6 27 54

2

1 1 4 4 1 1 4 3 1

x

x x x x x x

x x x x x x x



       



       



       

T

ừ

đ

ó

t

a

c

ó

t

h

ể

m

ở

r

ộ

n

g

U

l

ê

n

c

á

c

đ

a

t

h

ứ

c

b

ậ

c

b

ố

n

v

à

c

a

o

h

ơ

n

ữ

a

,

k

i

ế

n

l

ậ

p

c

á

c

b

à

i

t

o

á

n

y

ê

u

c

ầ

u

t

ư

d

u

y

t

ổ

n

g

t

h

ể

.

B

à

i

t

o

á

n

1

3

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

3

2 3 2

3 17 3 13 19 4 17 21 0,

;

17 4 5 6 6 7 4 21 5.

x x y x x y y

x y

x y y x y y x



        







         





.

Lời giải.

Điều kiện các căn thức xác định. Phương trình thứ nhất của hệ tương đương với

 

3

2 3 2

3 2

3 17 4 17 3 13 17 4 17 4 17 21

4 1

3 13 17

3 13 17 4 17

4 17 21

3 17 4 17

4 1

1

3 13 17 4 17

4 17 21

3 17 4 17

x x y y x x y y y

y

x x y

x x y y

y

x x y y

y

x x y y

y

x x y y

           



  

      

 

   

 



 

      

 

 

   

 

Nhận xét

   

2

3

2

3

9 5 1 5 0, 0

x

x x x x x



       

, dẫn đến

   

3

2 3 2

3

13 17 3 9 5 3 4 5 6 7 0

x

x y x x x x y x y



            

.

Lại có

 

3

2

4 1

1

4 17 0 0 1

4 17 21

3 17 4 17

y

y y

y

x x y y



      

 

   

.

Khi đó

6

7 0

17

4 5 6 6 7 4 21 5

4

21 25 5

y x y

x y y x y y x

y



  





        





 





.

Vì dấu đẳng thức không xảy ra nên hệ phương trình đã cho vô nghiệm.

N

h

ậ

n

x

é

t

.

Đ

ố

i

v

ớ

i

b

à

i

t

o

á

n

à

y

t

a

t

h

ấ

y

     

   

 

3

2 3 2

3 2

;

3 13 17 3 9 5 3 4 5 6 7 0

; 4 17 21

1

; 4 17 0

3 17 4 17

f x y x x y x x x x y x y

g x y g y y

T x y y

x x y y



             

   

   

   

C

á

c

đ

ạ

i

l

ư

ợ

n

g

t

h

a

m

g

i

a

   

3

2

1 2

3

9 5; ; 4 5; ; 6 7

U

x x x h x y x y h x y x y



        

.

H

ệ

s

ố

t

u

y

ế

n

t

í

n

h

     

1

1 1 1 2 1 1 1

; ; ; ; 1; 3; 1

f x y mU n h x y p h x y m n p

     

.

Đ

ạ

i

l

ư

ợ

n

g

k

h

ô

n

g

â

m

ộ

t

b

i

ế

n

U

c

ó

d

ạ

n

g

đ

a

t

h

ứ

c

b

ậ

c

b

a

3

2

3

9 5

U

x x x



  

,

n

h

ư

đ

ã

n

ó

i

b

ạ

n

đ

ọ

c

ó

t

h

ể

x

ử

l

ý

U

t

h

e

o

p

h

â

n

t

í

c

h

n

h

â

n

t

ử

h

o

ặ

c

p

h

ư

ơ

n

g

p

h

á

p

h

à

m

s

ố

n

ế

u

m

u

ố

n



P

h

â

n

t

í

c

h

   

2

3

2

3 9 5 1 5 0, 0

x x x x x x

        

.



X

é

t

h

à

m

s

ố

 

3 2

3

9 5, 0

t

x x x x x



    

t

a

c

ó

     

2

3

6 9; 0 1; 3

t

x x x t x x

 



     

.

LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

83

R

õ

r

à

n

g

         

0

0 5; 1 0 1 0

x

t t t x Mint x t



     

.

B

à

i

t

o

á

n

1

4

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

3

2 2

3 5 2 11 15 4 1 ,

;

7 15 5 11 4 4 .

x y x y y y

x y

x y y x y x y x x x



       









         





.

Lời giải.

Điều kiện

3

2 2

3

5 0; 15 0;7 15 0

5

11 0; 4 4 0; 0

x

y y x y

x y x y x x x





      







      





Phương trình thứ nhất của hệ tương đương với

 

3 3

3

3 5 15 2 10 15 4 1

2 10

2 10 15 4 1

3 5 15

1

2 10 15 4 1

3 5 15

x y y x y y y

x y

x y y y

x y y

x y y y

x y y

         

 

      

   

 

 

      

 

   

 

Vì

   

2

3

12

16 2 4 0, 0

x

x x x x



      

nên

   

3

2

10 12 16 7 15 5 11 0

x

y x x x y x y



          

.

Lại có

 

3

1

15

0 4 1 0 1

3 5 15

y

y y

x y y



      

   

.

Suy ra

 

2

2 2

5 11 0

4 4 2

y x y

x y x x y x x y x x



  





       





.

Từ đó

2

7 15 5 11 4 4

x y y x y x y x x x

         

.

Phương trình thứ hai của hệ có nghiệm khi và chỉ khi

7

15 5 11 0

2

0

1

x

y x y

x

y

     









  

 











Kết luận hệ có nghiệm duy nhất

2

; 1

x

y



.

N

h

ậ

n

x

é

t

.

B

à

i

t

o

á

n

s

ố

1

4

c

ó

c

á

c

đ

ạ

i

l

ư

ợ

n

g

đ

ơ

n

g

i

ả

n

h

ơ

n

     

 

     

3

; 2 10 12 16 7 15 5 11 0

1

; 15 0

3 5 15

; 4 1

f x y x y x x x y x y

T x y y

x y y

g x y g y y

            

   

   

  

V

ớ

i

s

ự

t

h

a

m

g

i

a

c

ủ

a

   

3

1

2

12 16; ; 7 15; ; 5 11

U x x h x y x y h x y x y

        

.

B

à

i

t

o

á

n

1

5

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

3

2

4

8

3 3 8 2 5 1,

;

2 2 4 3 16 1 2 .

x y x y y

x y

x y x y x y xy y x



      









         





.

Lời giải.

Điều kiện các căn thức xác định.

Phương trình thứ nhất của hệ tương đương với

LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

84

 

3

3 3

3

8 3 3 8 2 3 2 1

8 3 3 8 2 3 1

8 2 3

8 2 3 1

8 3 3

1

8 2 3 1

8 3 3

x y x y y y

x y y x y y y

x y

x y y y

x y y

x y y y

x y y

       

        

 

     

  

 

 

     

 

  

 

Nhận xét

   

2

3

4

3 1 2 1 1 0, 0

x

x x x x



      

, dẫn đến

 

   

3 3

8

2 3 2 4 3 1 2 2 4 3 0

x

y x x x y x y



          

.

Lại vì

3

1

0 1 0 1 1

8

3 3

y y y y

x

y y

        



 

.

Khi đó

 

2

4

3 0

0

1

16

1 16 2

x

y x y

x

y

x

y y x x





  









 





   





Thu được

 

2

4

2

2 4 3 16 1 2

x

y x y x y xy y x



        

.

Phương trình thứ hai của hệ có nghiệm khi

3

8

2 3 0

1

2

2 4 3 0 ; 1

2

1

x

y

x

y x y x y

y





 





       









.

Thử lại, kết luận hệ có nghiệm duy nhất kể trên.

Nhận xét.

C

á

c

đ

ơ

n

v

ị

t

h

a

m

g

i

a

l

i

ê

n

h

ợ

p

b

a

o

g

ồ

m

   

 

   

3

1

; 0; ; 1

8 3 3

; 8 2 3 2 4 3 1 2 2 4 3 0

T x y y g x y y

x y y

f x y x y x x x y x y

    

  

            

Đ

á

n

g

c

h

ú

ý

h

ơ

n

c

ả

l

à

h

ệ

s

ố

t

u

y

ế

n

t

í

n

h

c

ủ

a

U

đ

ã

t

ă

n

g

l

ê

n

   

3

1

2 1 1 1

4 3 1; ; 2 2; ; 4 3; 2; 1

U x x h x y x y h x y x y m n p

           

.

K

h

i

v

i

ế

t

đ

ế

n

b

à

i

t

o

á

n

s

ố

1

5

n

à

y

,

n

g

à

y

1

5

.

0

4

.

2

0

1

5

,

t

á

c

g

i

ả

đ

a

n

g

đ

ọ

c

d

ở

d

a

n

g

m

ộ

t

r

u

y

ệ

n

g

ắ

n

,

m

à

k

h

ô

n

g

l

ú

c

x

e

m

l

ạ

i

t

h

ì

r

a

n

ó

l

à

t

r

u

y

ệ

n

d

à

i

2

c

h

ư

ơ

n

g

,

v

à

c

ũ

n

g

k

ế

t

h

ợ

p

x

e

m

d

a

n

g

d

ở

m

ộ

t

b

ộ

p

h

i

m

,

b

ộ

p

h

i

m

c

h

ỉ

c

ó

m

ộ

t

ậ

p

t

h

ô

i

:

B

o

n

g

b

ó

n

g

l

ê

n

t

r

ờ

i

.

B

ộ

p

h

i

m

s

ả

n

x

u

ấ

t

b

ở

i

H

ã

n

g

p

h

i

m

t

r

u

y

ề

n

h

ì

n

h

,

Đ

à

i

t

r

u

y

ề

n

h

ì

n

h

V

i

ệ

t

N

a

m

n

ă

m

1

9

7

,

c

h

u

y

ể

n

t

h

ể

t

ừ

t

á

c

p

h

ẩ

m

c

ù

n

g

t

ê

n

c

ủ

a

n

h

à

v

ă

n

N

g

u

y

ễ

n

N

h

ậ

t

Á

n

h

v

i

ế

t

n

ă

m

1

9

1

,

k

h

i

t

ô

i

c

ò

n

r

ấ

t

n

h

ỏ

,

m

ã

i

g

i

ờ

đ

â

y

k

h

i

k

h

ô

n

g

c

ò

n

g

ồ

i

t

r

ê

n

g

h

ế

n

h

à

t

r

ư

ờ

n

g

t

ô

i

m

ớ

i

b

i

ế

t

đ

ế

n

t

á

c

p

h

ẩ

m

h

i

ệ

n

t

h

ự

c

v

à

đ

ậ

m

c

h

ấ

t

n

h

â

n

v

ă

n

h

ư

t

h

ế

.

H

ô

m

n

a

y

l

à

m

ộ

t

b

u

ổ

i

c

h

i

ề

u

t

h

ứ

4

m

ù

a

x

u

â

n

ă

m

2

0

1

5

,

t

i

ế

t

r

ờ

i

đ

ầ

u

h

è

đ

ẹ

p

v

à

c

ó

g

i

ó

l

ộ

n

g

v

i

v

u

,

t

ô

i

l

à

m

v

i

ệ

c

t

ạ

i

m

ộ

t

n

g

ô

i

n

h

à

n

h

ỏ

k

h

u

ấ

t

r

o

n

g

k

h

u

đ

ô

t

h

ị

m

ớ

i

Y

ê

n

H

ò

a

,

q

u

ậ

n

C

ầ

u

G

i

ấ

y

,

t

r

u

n

g

t

â

m

t

h

ủ

đ

ô

H

à

N

ộ

i

,

k

ế

b

ê

n

d

ò

n

g

s

ô

n

g

T

ô

L

ị

c

h

đ

e

n

g

ò

m

,

x

ấ

u

x

í

n

h

ư

n

g

q

u

e

n

t

h

u

ộ

c

v

à

n

h

i

ề

u

k

ỷ

n

i

ệ

m

đ

ố

i

v

ớ

i

n

g

ư

ờ

i

t

h

a

h

ư

ơ

n

g

x

ứ

n

g

ư

ờ

i

.

M

ặ

c

d

ù

b

ê

n

k

i

a

l

à

c

o

n

đ

ư

ờ

n

g

L

á

n

g

x

e

c

ộ

n

g

ù

n

g

ụ

t

,

b

o

n

c

h

e

n

v

à

đ

ô

n

g

đ

ú

c

n

h

ư

n

g

c

h

ú

n

g

t

ô

i

c

h

ẳ

n

g

q

u

a

n

t

â

m

,

h

ó

a

r

a

g

i

ữ

a

c

á

i

n

ơ

i

p

h

ồ

n

h

o

a

đ

ô

h

ộ

i

n

à

y

v

ẫ

n

c

ó

n

h

ữ

n

g

k

h

u

v

ắ

n

g

l

ặ

n

g

,

t

h

a

n

h

b

ì

n

h

đ

ế

n

l

ạ

t

h

ư

ờ

n

g

.

G

i

ữ

a

k

h

ô

n

g

i

a

n

t

ĩ

n

h

m

ị

c

h

ấ

y

,

t

ô

i

n

g

ồ

i

m

ộ

t

m

ì

n

h

,

đ

ọ

c

h

ế

t

2

c

h

ư

ơ

n

g

v

à

x

e

m

t

ậ

p

h

i

m

n

h

ẹ

n

h

à

n

g

,

l

ò

n

g

t

r

à

n

g

ậ

p

n

h

i

ề

u

c

ả

m

x

ú

c

.

B

ộ

p

h

i

m

B

o

n

g

b

ó

n

g

m

ù

a

h

è

đ

ư

ợ

c

h

u

y

ể

n

t

h

ể

,

t

u

y

n

ộ

i

d

u

n

g

k

h

ô

n

g

s

á

t

v

ớ

i

c

h

í

n

h

t

r

u

y

ệ

n

v

à

l

ư

ợ

c

b

ỏ

n

h

i

ề

u

c

h

i

t

i

ế

t

đ

á

n

g

q

u

ý

,

đ

ắ

t

g

i

á

c

ầ

n

t

h

i

ế

t

,

l

à

m

t

ô

i

b

ă

n

k

h

o

ă

n

x

e

n

l

ẫ

n

t

i

ế

c

n

u

ố

i

.

T

r

o

n

g

p

h

i

m

t

ì

n

h

c

ờ

c

ó

d

i

ễ

n

x

u

ấ

t

v

ô

c

ù

n

g

h

ồ

n

h

i

ê

n

,

t

i

n

h

t

ế

,

v

ô

t

ư

c

ủ

a

n

h

d

i

ễ

n

v

i

ê

n

H

o

à

n

g

T

ù

n

g

,

t

ô

i

c

h

ợ

t

n

h

ậ

n

r

a

đ

ó

l

à

m

ộ

t

n

h

â

n

v

ậ

t

p

h

ả

n

d

i

ệ

n

t

r

o

n

g

l

o

ạ

t

p

h

i

m

Đ

ộ

i

đ

ặ

c

n

h

i

ệ

m

n

h

à

C

2

1

m

à

t

ô

i

r

ấ

t

h

í

c

h

,

h

a

i

a

n

h

e

m

h

a

y

c

ù

n

g

x

e

m

ỗ

i

k

h

i

m

a

y

m

ắ

n

c

ó

d

ị

p

c

h

i

ế

u

l

ạ

i

t

r

ê

n

s

ó

n

g

V

T

V

1

Đ

à

i

t

r

u

y

ề

n

h

ì

n

h

Q

u

ố

c

g

i

a

.

T

ô

i

t

h

í

c

h

g

ọ

i

l

à

Đ

à

i

t

r

u

y

ề

n

h

ì

n

h

Q

u

ố

c

g

i

a

h

ơ

n

l

à

Đ

à

i

t

r

u

y

ề

n

h

ì

n

h

V

i

ệ

t

N

a

m

v

ì

n

ó

t

h

â

n

t

h

ư

ơ

n

g

v

à

d

u

y

n

h

ấ

t

,

c

h

ứ

a

đ

ự

n

g

m

ộ

t

p

h

ầ

n

t

h

ờ

i

ấ

u

t

h

ơ

,

b

ê

n

g

i

a

đ

ì

n

h

,

b

ê

n

g

ư

ờ

i

t

h

â

n

.

LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

85

Q

u

ả

t

h

ự

c

ó

k

h

á

c

b

i

ệ

t

v

ớ

i

n

h

ữ

n

g

k

ê

n

h

p

h

i

m

t

r

u

y

ệ

n

c

h

u

y

ê

n

g

h

i

ệ

p

v

à

n

h

ữ

n

g

k

ê

n

h

đ

a

c

h

i

ề

u

l

o

ạ

n

x

ạ

t

h

ô

n

g

t

i

n

.

Đ

ó

l

à

k

ê

n

h

t

h

ờ

i

s

ự

c

h

í

n

h

t

h

ố

n

g

,

k

ê

n

h

v

ă

n

h

ó

a

,

g

i

ả

i

t

r

í

,

t

i

n

t

ứ

c

t

ổ

n

g

h

ợ

p

t

r

u

y

ề

n

t

h

ố

n

g

đ

ố

i

v

ớ

i

đ

ồ

n

g

b

à

o

c

ả

n

ư

ớ

c

,

v

ớ

i

n

h

â

n

d

â

n

m

i

ề

n

ú

i

,

h

ả

i

đ

ả

o

,

v

ớ

i

c

á

c

h

i

ế

n

s

ĩ

b

i

ê

n

p

h

ò

n

g

v

à

c

á

c

m

i

ề

n

q

u

ê

t

h

ô

n

d

ã

.

C

h

a

o

ô

i

,

n

à

o

l

à

V

T

V

1

,

V

T

V

2

,

V

T

V

3

n

è

…

v

à

Đ

à

i

p

h

á

t

h

ì

n

h

t

r

u

y

ề

n

h

ì

n

h

T

h

á

i

B

ì

n

h

t

h

â

n

y

ê

u

c

ủ

a

q

u

ê

h

ư

ơ

n

g

t

ô

i

n

ữ

a

.

B

a

o

n

ă

m

t

h

á

n

g

v

ớ

i

c

h

i

ế

c

m

à

n

h

ì

n

h

n

h

ỏ

x

í

u

t

ừ

đ

e

n

t

r

ắ

n

g

c

h

u

y

ể

n

s

a

n

g

m

à

u

v

ớ

i

n

h

ữ

n

g

k

h

u

n

g

i

ờ

p

h

i

m

q

u

e

n

t

h

u

ộ

c

,

t

ô

i

n

h

ớ

l

ắ

m

.

n

h

ữ

n

g

b

ộ

p

h

i

m

k

ị

c

h

t

í

n

h

,

c

h

â

n

t

h

ự

c

v

à

đ

ậ

m

t

í

n

h

n

h

â

n

v

ă

n

h

a

y

c

ù

n

g

x

e

m

v

ớ

i

m

ẹ

n

g

à

y

n

h

ỏ

c

h

i

ề

u

t

h

ứ

b

ả

y

,

c

h

ủ

n

h

ậ

t

…

n

à

o

l

à

C

ả

n

h

s

á

t

h

ì

n

h

s

ự

,

H

o

a

c

ỏ

m

a

y

,

P

h

í

a

t

r

ư

ớ

c

l

à

b

ầ

u

t

r

ờ

i

,

S

ó

n

g

n

g

ầ

m

,

V

ù

n

g

t

r

ờ

i

b

ì

n

h

y

ê

n

,

Đ

ư

ờ

n

g

đ

ờ

i

…

.

K

h

ô

n

g

b

i

ế

t

c

ó

p

h

ả

i

v

ì

n

h

ữ

n

g

i

á

t

r

ị

ấ

y

m

à

g

i

ờ

đ

â

y

t

ô

i

t

r

ở

n

ê

n

s

u

y

n

g

h

ĩ

,

h

à

n

h

đ

ộ

n

g

v

à

m

ơ

ư

ớ

c

m

ộ

t

c

á

c

h

t

h

ậ

n

t

r

ọ

n

g

h

a

y

k

h

ô

n

g

?

T

i

ế

p

c

ậ

n

v

ớ

i

t

á

c

p

h

ẩ

m

n

à

y

,

t

ô

i

ấ

n

t

ư

ợ

n

g

s

â

u

s

ắ

c

v

ề

n

h

â

n

v

ậ

t

N

g

u

y

ễ

n

M

i

n

h

T

h

ư

ờ

n

g

v

à

g

i

a

đ

ì

n

h

a

n

h

,

v

ề

b

ố

P

h

o

n

g

,

m

ẹ

T

u

ệ

c

ủ

a

n

h

,

v

ề

b

é

N

h

i

,

v

ề

c

ô

b

é

T

à

i

K

h

ô

n

v

à

h

ơ

n

t

h

ế

n

ữ

a

…

N

g

h

ĩ

a

c

ử

c

a

o

đ

ẹ

p

c

ủ

a

c

h

ú

P

h

o

n

g

–

b

ố

c

ủ

a

n

h

T

h

ư

ờ

n

g

ở

đ

ầ

u

t

á

c

p

h

ẩ

m

,

v

à

c

ủ

a

T

h

ư

ờ

n

g

ở

c

u

ố

i

t

á

c

p

h

ẩ

m

,

t

ư

ơ

n

g

t

ự

h

à

n

h

đ

ộ

n

g

v

ừ

a

b

ấ

t

đ

ắ

c

d

ĩ

,

v

ừ

a

đ

a

u

t

h

ư

ơ

n

g

c

ủ

a

n

h

g

i

á

o

l

à

n

g

t

ê

n

T

r

i

ệ

u

t

r

o

n

g

N

h

ữ

n

g

b

à

i

h

ọ

c

n

ô

n

g

t

h

ô

n

(

N

g

u

y

ễ

n

H

u

y

T

h

i

ệ

p

)

,

h

a

y

v

i

ệ

c

l

à

m

c

a

o

t

h

ư

ợ

n

g

c

ủ

a

c

ô

b

é

T

h

u

t

r

o

n

g

T

â

m

h

ồ

n

m

ẹ

(

N

g

u

y

ễ

n

H

u

y

T

h

i

ệ

p

)

.

C

h

ắ

c

n

h

i

ề

u

b

ạ

n

đ

ọ

c

b

i

ế

t

đ

ế

n

T

â

m

h

ồ

n

m

ẹ

c

ũ

n

g

l

à

b

ộ

p

h

i

m

đ

ặ

c

b

i

ệ

t

c

ù

n

g

t

ê

n

c

h

u

y

ể

n

t

h

ể

,

d

ẫ

n

đ

ế

n

t

ê

n

t

u

ổ

i

c

ô

b

é

P

h

ù

n

g

H

o

a

H

o

à

i

L

i

n

h

,

e

m

b

é

H

à

N

ộ

i

–

n

ữ

d

i

ễ

n

v

i

ê

n

c

h

í

n

h

x

u

ấ

t

s

ắ

c

n

h

ấ

t

ạ

i

L

i

ê

n

h

o

a

n

p

h

i

m

Á

–

P

h

i

n

ă

m

2

0

1

k

h

i

m

ớ

i

1

2

t

u

ổ

i

.

V

ề

“

B

o

n

g

b

ó

n

g

l

ê

n

t

r

ờ

i

”

,

t

á

c

p

h

ẩ

m

đ

ư

ợ

c

v

i

ế

t

d

ự

a

t

r

ê

n

k

h

u

n

g

c

ả

n

h

m

i

ề

n

N

a

m

,

k

h

i

t

á

c

g

i

ả

đ

ã

c

h

u

y

ể

n

đ

ế

n

s

i

n

h

s

ố

n

g

t

ạ

i

t

h

à

n

h

p

h

ố

H

ồ

C

h

í

M

i

n

h

,

n

g

ô

n

g

ữ

t

r

o

n

g

t

r

u

y

ệ

n

m

a

n

g

đ

ậ

m

n

é

t

N

a

m

b

ộ

m

ộ

c

m

ạ

c

v

à

c

ó

k

h

á

c

b

i

ệ

t

v

ớ

i

m

i

ề

n

B

ắ

c

,

t

u

y

n

h

i

ê

n

v

ớ

i

d

i

ễ

n

x

u

ấ

t

đ

ặ

c

s

ắ

c

ủ

a

n

h

H

o

à

n

g

T

ù

n

g

v

à

t

ậ

p

t

h

ể

a

n

h

c

h

ị

h

ọ

c

s

i

n

h

l

ớ

p

1

2

A

1

t

r

ư

ờ

n

g

T

H

P

T

P

h

a

n

Đ

ì

n

h

P

h

ù

n

g

n

i

ê

n

k

h

ó

a

1

9

4

–

1

9

7

,

Q

u

ậ

n

B

a

Đ

ì

n

h

,

n

h

ữ

n

g

c

o

n

p

h

ố

Q

u

á

n

T

h

á

n

h

,

L

ê

D

u

ẩ

n

,

đ

o

ạ

n

đ

ư

ờ

n

g

s

ắ

t

B

ắ

c

–

N

a

m

b

ê

n

C

ô

n

g

v

i

ê

n

T

h

ố

n

g

n

h

ấ

t

,

C

ô

n

g

v

i

ê

n

T

h

ủ

L

ệ

,

…

t

ấ

t

c

ả

đ

ề

u

l

à

m

t

o

á

t

l

ê

n

v

ẻ

đ

ẹ

p

d

u

n

g

d

ị

v

ố

n

c

ó

c

ủ

a

đ

ấ

t

v

à

n

g

ư

ờ

i

t

h

ủ

đ

ô

,

c

ủ

a

t

u

ổ

i

h

ọ

c

t

r

ò

v

à

n

ề

n

v

ă

n

h

ó

a

đ

ấ

t

n

ư

ớ

c

.

“

B

ó

n

g

b

ó

n

g

l

ê

n

t

r

ờ

i

,

n

h

ữ

n

g

q

u

ả

b

ó

n

g

đ

ã

b

a

y

c

a

o

v

à

d

ư

ờ

n

g

n

h

ư

s

ắ

p

s

ử

a

t

a

n

v

à

o

m

â

y

t

r

ắ

n

g

.

T

h

ế

l

à

c

h

ú

n

g

đ

ã

đ

ế

n

ơ

i

đ

ị

n

h

đ

ế

n

.

V

à

c

h

ẳ

n

g

b

a

o

l

â

u

n

ữ

a

,

p

h

ú

c

l

à

n

h

s

ẽ

đ

ế

n

v

ớ

i

a

i

t

i

n

v

à

o

s

ự

v

ĩ

n

h

ằ

n

g

c

ủ

a

n

h

ữ

n

g

đ

i

ề

u

t

ố

t

đ

ẹ

p

.

B

ấ

t

g

i

á

c

T

h

ư

ờ

n

g

m

ỉ

m

c

ư

ờ

i

v

ớ

i

ý

n

g

h

ĩ

c

ủ

a

m

ì

n

h

v

à

v

ừ

a

d

õ

i

m

ắ

t

h

e

o

n

h

ữ

n

g

c

h

ấ

m

l

i

t

i

n

v

à

o

n

ề

n

m

â

y

t

r

ắ

n

g

,

a

n

h

v

ừ

a

x

ú

c

đ

ộ

n

g

t

ự

h

ỏ

i

k

h

ô

n

g

b

i

ế

t

r

o

n

g

c

ơ

m

a

n

h

ữ

n

g

m

ơ

ư

ớ

c

m

à

c

o

n

g

ư

ờ

i

k

ý

t

h

á

c

,

n

h

ữ

n

g

q

u

ả

b

ó

n

g

l

ê

n

t

r

ờ

i

k

i

a

đ

a

n

g

m

a

n

g

t

h

e

o

đ

i

ề

u

n

g

u

y

ệ

n

ư

ớ

c

n

à

o

c

ô

b

ạ

n

h

ỏ

c

h

â

n

t

h

à

n

h

v

ừ

a

g

ử

i

g

ắ

m

c

h

o

a

n

h

”

.

V

à

t

á

c

g

i

ả

c

h

ợ

t

h

ấ

y

a

n

h

T

h

ư

ờ

n

g

đ

ư

ợ

c

g

ặ

p

c

ô

b

é

T

à

i

K

h

ô

n

(

L

à

)

,

t

r

o

n

g

p

h

i

m

t

ê

n

L

ụ

a

–

c

ô

b

é

m

ồ

c

ô

i

t

h

ô

n

g

m

i

n

h

đ

ư

ợ

c

m

ẹ

T

u

ệ

c

ủ

a

n

h

c

ư

n

g

n

h

ấ

t

l

ớ

p

đ

ã

l

à

m

ộ

t

đ

i

ề

u

m

a

y

m

ắ

n

,

m

ộ

t

đ

i

ề

u

d

i

ệ

u

k

ỳ

m

à

n

h

à

v

ă

n

s

ắ

p

x

ế

p

.

C

ũ

n

g

l

à

m

ộ

t

á

c

p

h

ẩ

m

d

à

n

h

c

h

o

t

h

i

ế

u

n

h

i

c

ủ

a

n

h

à

v

ă

n

N

g

u

y

ễ

n

N

h

ậ

t

Á

n

h

,

c

ũ

n

g

c

ó

t

í

n

h

t

i

ế

t

“

Ă

n

h

i

ề

u

k

ẹ

o

s

ú

n

r

ă

n

g

”

,

n

h

ư

n

g

k

h

ô

n

g

p

h

ả

i

l

à

k

ẹ

o

k

é

o

n

h

ư

t

r

o

n

g

B

o

n

g

b

ó

n

g

l

ê

n

t

r

ờ

i

đ

â

u

,

m

à

c

ô

b

é

t

r

o

n

g

C

ô

g

á

i

đ

ế

n

t

ừ

h

ô

m

q

u

a

(

1

9

8

9

)

b

ị

s

ú

n

r

ă

n

g

t

h

ự

c

s

ự

,

V

i

ệ

t

A

n

…

m

ộ

t

c

á

i

t

ê

n

r

ấ

t

x

i

n

h

x

ắ

n

,

đ

ặ

c

b

i

ệ

t

m

à

t

ô

i

â

u

y

ế

m

đ

ặ

t

c

h

o

m

ộ

t

c

ô

g

á

i

1

8

t

u

ổ

i

n

h

ỏ

n

h

ắ

n

,

b

é

b

ỏ

n

g

,

c

ũ

n

g

h

ơ

i

h

ơ

i

s

ú

n

r

ă

n

g

(

t

r

ẹ

o

t

r

ọ

)

v

à

t

i

n

h

n

g

h

ị

c

h

k

h

ô

n

g

k

é

m

T

à

i

K

h

ô

n

c

ơ

c

h

ứ

,

c

ô

b

é

m

à

t

ô

i

y

ê

u

t

h

ư

ơ

n

g

n

h

ấ

t

r

ê

n

đ

ờ

i

.

M

ọ

i

n

g

ư

ờ

i

s

i

n

h

r

a

đ

ề

u

c

ó

q

u

y

ề

n

b

ì

n

h

đ

ẳ

n

g

,

c

ó

q

u

y

ề

n

s

ố

n

g

v

à

m

ư

u

c

ầ

u

h

ạ

n

h

p

h

ú

c

…

đ

ã

l

à

đ

i

ề

u

ư

ớ

c

,

c

h

ú

n

g

t

a

c

ó

q

u

y

ề

n

,

m

i

ễ

n

s

a

o

n

ó

c

h

â

n

c

h

í

n

h

v

à

k

h

ô

n

g

x

ấ

u

,

n

h

ư

t

h

ế

l

à

đ

ẹ

p

đ

ẽ

.

Đ

ố

i

v

ớ

i

c

á

c

b

à

i

t

o

á

n

t

ừ

1

0

đ

ế

n

1

5

,

t

h

o

ạ

t

n

h

ì

n

k

h

ô

n

g

í

t

b

ạ

n

c

ả

m

t

h

ấ

y

m

ô

n

g

l

u

n

g

,

v

ô

h

ư

ớ

n

g

v

ì

h

ì

n

h

t

h

ứ

c

g

ọ

n

g

à

n

g

v

à

k

h

ó

b

ấ

u

v

í

u

c

ủ

a

n

ó

,

n

h

ư

n

g

v

ì

t

h

ế

l

i

ệ

u

c

ó

c

ầ

n

ư

ớ

c

l

à

m

đ

ư

ợ

c

h

a

y

k

h

ô

n

g

,

k

h

ô

n

g

,

c

h

ỉ

c

ầ

n

c

h

ú

ý

m

ộ

t

c

h

ú

t

v

à

k

h

é

o

l

é

o

b

i

ế

n

đ

ổ

i

,

c

ẩ

n

t

h

ậ

n

t

r

o

n

g

c

á

c

l

i

ê

n

k

ế

t

l

à

c

ó

t

h

ể

h

o

à

n

t

o

à

n

x

ử

l

ý

ổ

n

t

h

ỏ

a

v

ớ

i

m

ộ

t

l

ờ

i

g

i

ả

i

l

o

g

i

c

,

c

h

í

n

h

x

á

c

.

B

à

i

t

o

á

n

1

6

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

4

4 3

3 2 2

3

8 5 4 10 ,

;

3 1 2 2 2 1 .

x y x y y y

x y

y x y y y x x y



     









        





.

Lời giải.

Điều kiện

4

3 2 2

8

5 0; 0

2

; 2 2 1 0

x

y y

x y y y x



   







    





Phương trình thứ nhất của hệ tương đương với

 





 

4

4 3

4 4 3

3

8 5 4 5 5

3 8 5 2 4 5

x y x y y y y

x

y y x y y y y



     

        

LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

86

 

4

3

4

4 3

4

3 4 5

4 5

8 5 2

3

4 5

8 5 2

x y

x

y y y y

x

y y

x

y y y y

x y y

 

     

  

 

 

     

 

  

 

Nhận xét

 

4

5 4 3 4 2 0

x

y x x x y



       

nên

 

   

2

2 2

4 2

4

3 1 2 3 1 1 2 0,x x x x x x x x

 



           







.

Lại có

4

3

0

8

5 2

y

x y y

 



 

nên

 

3

5

6

0

1 0

1

y

y y y y

y y

y

y y















      

 



 











Xét trường hợp

 

4

0

5

; 5

5

0

y

x











  

 

 

 







Tất cả các cặp số thu được không thỏa mãn

2

x

y





, loại.

Xét trường hợp

 

3

2 2 2 2

3

1 2 0

3 1 0

1

1 0

2 2 1 2

y x y

y

y y x x y



   

 





  

 

 

    







Mặt khác

 

2 2

2 2 2 2

0

2 2

x

y x y x y x y x y x y



          

.

Dẫn đến

 

3

2 2

3

1 2 2 2 1

y

x y y y x x y



       

. Dấu đẳng thức

3

1

2 1 0

1

;

0

x

x y y

y

x

y x y







   



 

 



 



Thử lại, kết luận hệ có nghiệm duy nhất

1x

y



.

N

h

ậ

n

x

é

t

.

B

à

i

t

o

á

n

s

ố

1

6

n

à

y

c

h

ú

n

g

t

a

c

ó

c

á

c

đ

ơ

n

v

ị

t

h

a

m

g

i

a

l

i

ê

n

h

ợ

p

n

h

ư

s

a

u

     

   

3

4

3

;

0; ;

8 5 2

; 4 5 4 3 4 2 0

T

x y y g x y g y y y

x y y

f x y x y x x x y

     

  

         

T

r

o

n

g

đ

ó

 

   

2

2 2

4 2

4

3 1 2 3 1 1 2 0,U x x x x x x x x

 



            







.

H

ệ

s

ố

t

u

y

ế

n

t

í

n

h

 

1

1 1

; 2; 1; 4

h x y x y m n

    

.

Đ

i

ể

m

đ

á

n

g

l

ư

u

ý

l

à

đ

ạ

i

l

ư

ợ

n

g

k

h

ô

n

g

â

m

U

đ

ã

t

ă

n

g

c

ấ

p

t

r

ở

t

h

à

n

h

đ

a

t

h

ứ

c

b

ậ

c

b

ố

n

m

ộ

t

ẩ

n

.

Đ

a

p

h

ầ

n

c

á

c

b

ạ

n

đ

ọ

c

q

u

e

n

s

ử

d

ụ

n

g

b

ấ

t

đ

ẳ

n

g

t

h

ứ

c

C

a

u

c

h

y

đ

ề

u

b

i

ế

t

đ

ế

n

đ

á

n

h

g

i

á

c

o

n

v

ớ

i

đ

i

ể

m

r

ơ

i

1x 

đ

i

ể

n

h

ì

n

h

n

h

ư

2 3

4 5

2

1 0, ; 3 2 0, 0

4 3 0, ; 6 5 0, 0,...

x

x x x x x

x x x x x x

         



X

ử

l

ý

c

á

c

đ

ạ

i

l

ư

ợ

n

g

n

à

y

c

ó

t

h

ể

s

ử

d

ụ

n

g

p

h

â

n

t

í

c

h

n

h

â

n

t

ử

h

o

ặ

c

ô

n

g

c

ụ

đ

ạ

o

h

à

m

–

h

à

m

s

ố

r

ấ

t

h

u

ậ

n

t

i

ệ

n



P

h

â

n

t

í

c

h

 

   

2

2 2

4 2

4 3 1 2 3 1 1 2 0,U x x x x x x x x

 

             

 



.



X

é

t

h

à

m

s

ố

 

4

3;U t x x x x



   



.

Đ

ạ

o

h

à

m

   

3

4 4; 0 1 1t x x t x x x



      

d

ẫ

n

đ

ế

n

     

1 1

x

t x Mint x t



  



.

N

g

o

à

i

r

a

đ

ơ

n

v

ị

q

u

y

ế

t

đ

ị

n

h

m

i

ề

n

g

i

á

t

r

ị

b

i

ế

n

y

c

ũ

n

g

c

ó

m

ộ

t

s

ố

đ

i

ể

m

c

h

ư

ớ

n

g

n

g

ạ

i

d

ù

l

à

k

i

ế

n

t

h

ứ

c

h

ế

t

s

ư

c

ơ

b

ả

n

 

3 3

5

6

0

1 0

1

y

Q y y y y

y y

y

y y















       

 



 











LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

87

V

ì

v

ậ

y

c

ầ

n

x

e

m

x

é

t

ổ

n

g

t

h

ể

h

a

i

t

r

ư

ờ

n

g

h

ợ

p

x

ả

y

r

a

,

k

h

u

y

ế

n

c

á

o

n

ê

n

d

ù

n

g

t

r

ự

c

t

i

ế

p

h

ư

ơ

n

g

t

r

ì

n

h

l

i

ê

n

h

ợ

p

s

ẽ

t

h

u

đ

ư

ợ

c

n

g

a

y

k

ế

t

q

u

ả

k

h

ô

n

g

t

h

ỏ

a

m

ã

n

đ

i

ề

u

k

i

ệ

n

x

á

c

đ

ị

n

h

,

c

h

ư

a

k

ể

t

h

ỏ

a

m

ã

n

h

ệ

b

a

n

đ

ầ

u

(

t

í

n

h

t

h

e

o

đ

a

s

ố

)

.

Đ

ể

á

c

đ

ộ

c

h

ơ

n

ữ

a

,

n

g

ư

ờ

i

r

a

đ

ề

c

ó

t

h

ể

b

ố

t

r

í

c

h

o

t

r

ư

ờ

n

g

h

ợ

p

n

g

h

i

ệ

m

đ

ặ

c

b

i

ệ

t

n

à

y

n

g

h

i

ệ

m

đ

ú

n

g

p

h

ư

ơ

n

g

t

r

ì

n

h

d

ẫ

n

đ

ế

n

m

ấ

t

n

g

h

i

ệ

m

v

ố

n

c

ó

c

ủ

a

b

à

i

t

o

á

n

,

đ

i

ề

u

n

à

y

t

ấ

n

c

ô

n

g

m

ạ

n

h

m

ẽ

v

à

o

m

ộ

t

b

ộ

p

h

ậ

n

h

ữ

n

g

t

h

í

s

i

n

h

v

ộ

i

v

à

n

g

,

k

h

ô

n

g

c

ẩ

n

t

h

ậ

n

.

B

à

i

t

o

á

n

1

7

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

4

2 4 2

2 3

2 2 5 7 3 2,

;

4 5 7 3 7 3 2 10.

x x y x x y y

x y

x x y y y y



       









       





.

Lời giải.

Điều kiện

4

2

3

2 0

4

5 0

7

3

x x y

y



  





 









Phương trình thứ nhất của hệ tương đương với

 

4

2 4 2

4 2 4 2

4 2

2

2 5 3 7 3 3 7 3 2

2

2 7 3 5 3 7 3 7 3 2

2 5 3

7 1

5 3 7 3

7

3 2

2

7 3

7

1

2

5

3 7 3

7 3 2

2

7 3

x x y x x y y y

x x y y x x y y y

x x y

y

x x y y

y

x x y y

y

x x y y

y

x x y y

          



           

  



      

 

   

 



 

      

 

 



  

 

Ta nhận xét

 

   

2

2 2

4 2

4

3 1 2 3 1 1 2 0,x x x x x x x x

 



           







.

Suy ra

 

4

2 4 2

5

3 4 3 4 5 0

x

x y x x x x y



        

.

Lại do

4

2

7 3 0 1 0 1

2

7 3

y y y

x

x y y

       



  

.

Khi đó

2

3

7

3 10

1 0 4 5 7 3 7 3 2 10

7 3 2

y y

y x x y y y y

y



 



           



 





.

Phương trình thứ hai của hệ có nghiệm khi các dấu đẳng thức xảy ra tức là

2

4

5 0

1

4 3 0

1

x x y

x

x x

y



  









  

 











Thử lại, kết luận hệ có nghiệm duy nhất

1x

y



.

B

à

i

t

o

á

n

1

8

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

3

2

3

2 2 2 ,

;

3 4 1 2 5 3 2 1 .

y x y y x y y

x y

x y y x y x



       









       





.

Lời giải.

Điều kiện

3

2

0

; 0

3

4 0;2 5 3 0

y

x y y

x y x y



   







    





Phương trình thứ nhất của hệ tương đương với

LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

88

 

3

2 2 2 2 2

2

2 2 2 2

2

1

2 2 2 1

2

y x y y y x y y

y x

y x y y

         

 

      

   

 

 

      

 

   

 

Nhận xét

     

2

3

3 3

3

2 2 2 0, 0 2 3 2 3 4 0

y

y y y y y x y y x y



                

.

Bên cạnh đó

3

1

2

0 1 0 1 1

2

y

y y y

y x y y



        

   

.

Vì thế

 

2

2 2 2 2

1

0 2 5 4 2 2 2 1 1 2 5 3 1

y

x y x x x x x y x



               

.

Hơn nữa

   

2

1 2 0 1 2 5 3 2 1 3 4 1 2 5 3 2 1

y y x y x x y y x y x

                 

.

Phương trình thứ hai của hệ có nghiệm khi

 

2

3

1

0

1

3

4 3 2 0

1

x

y y y

y

















     

 













Thử lại, kết luận hệ phương trình ban đầu có nghiệm duy nhất

1x

y



.

B

à

i

t

o

á

n

1

9

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

4

3 4 2

3 1 2 5 4 5,

;

2 3 2 1 2.

y x y x x

x y

x x y x y x y



       









       





.

Lời giải.

Điều kiện

4

2

3 0

0

3 1 0

x

y

x

y x





 









  



Phương trình thứ nhất của hệ tương đương với

 

4

3 1 4 2 3 4 4 5

2 3 1

2 3 4

4 5

3 1 4

1 1

2 3 4

4 5

3 1 4

y x x y x x x

y x x

x

y x x

x

y x x

x

y x x

          

  

    

 

   

 



 

     

 

 

   

 

Nhận xét

 

   

2

2 2

4 2

4

3 1 2 3 1 1 2 0

y

y y y y y y

 



         





.

Dẫn đến

 

4

2 3 4 3 2 2 3 0

y x y y x y

        

.

Lại thấy

4

1

4

0 1 0 1

3

1 4

x

x x

y

x x



      



  

.

Khi

2 3 0

1 2 3 1

1

x x y

x x x y x

x



  



      









.

Mặt khác

 

2

3

4 4 4 2 2 3 4 2

2 1 2 2 2 1 1 2 1 1

x y y y y y x y y

             

.

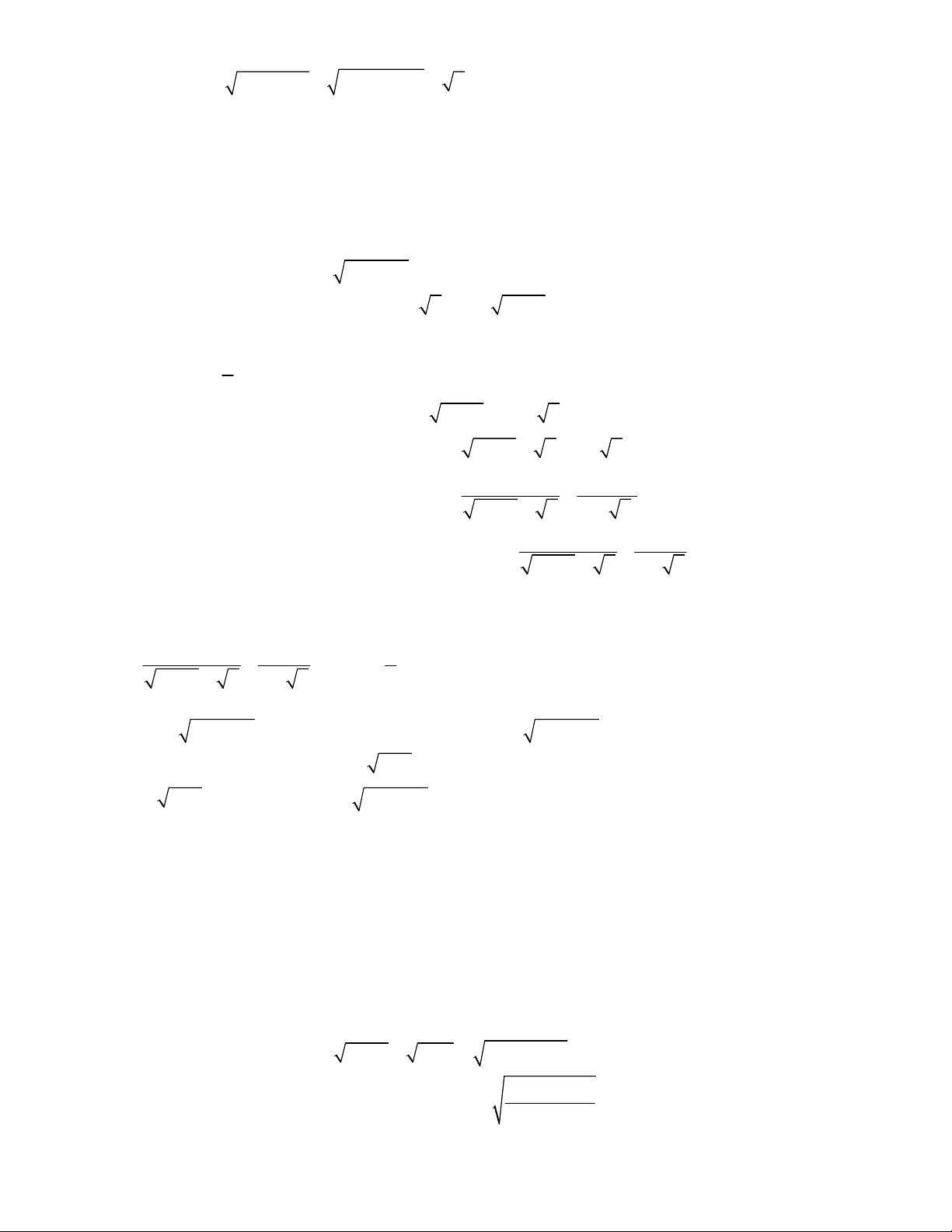
LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

89

Kết hợp tổng thể ta có

3 4 2

2

3 2 1 2

x

x y x y x y



      

.

Phương trình thứ hai của hệ có nghiệm khi

 

4

2

3 2 3 0

1

; 1

1

0

x y y x

x

x y

y



     











 

 







 





Kết luận hệ phương trình ban đầu có nghiệm duy nhất

1x

y



.

B

à

i

t

o

á

n

1

2

0

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

3

2

5 2 3 6 3 7,

;

2 1 2 1 4 3 .

x y x x x y

x y

x y x x x y



      







      







.

Lời giải.

Điều kiện

1

2

;

2

x

y x



 

. Phương trình thứ hai của hệ tương đương với

 

   

 

     

2

3

3 2 2 1 2

3 2 2 1

1

3 2

2 1

1

3 2 1

2 1

x y x y x x x

x y x y x x x x

x x

x

x y x y

x x x x

x

x y x y x

x

x x x



      

         



      

  





       







 





Xét hàm số

   

2

3 2; 2 2 3 0, 2f t t t t f t t t



         

.

Hàm số liên tục và đồng biến trên miền đang xét dẫn đến

   

2 0

f t f

 

.

Bên cạnh đó

1 1

0, 1 0 1

2

2 1

x

x x x

x x x x

        

  

.

Phương trình thứ nhất của hệ tương đương với

   

3

2

5

2 3 3 1 3 3 6 5 2 3 1 6

x

y x x x x y x y x y x



               

.

Dễ thấy

 

3

1 0, 1x x   

và hàm

 

5 2 3 ; 2

g t t t t x y

     

đồng biến, liên tục.

Do đó

       

3

5

2 3 2 6 5 2 3 1 6

g

t t t g x y x y x



           

.

Phương trình có nghiệm khi

2

1

1 0

x y

x

 



  



 



(Thỏa mãn hệ ban đầu).

N

h

ậ

n

x

é

t

.

B

à

i

t

o

á

n

s

ố

1

2

0

c

h

ú

n

g

t

a

đ

ã

s

ử

d

ụ

n

g

k

ỹ

t

h

u

ậ

t

l

i

ê

n

h

ợ

p

v

ớ

i

b

i

ế

n

x

đ

ể

c

ô

l

ậ

p

c

á

c

đ

ạ

i

l

ư

ợ

n

g

;x x y

.

T

u

y

n

h

i

ê

n

c

ầ

n

h

ế

t

s

ứ

c

h

ú

ý

c

h

ứ

n

g

m

i

n

h

 

0

f

x y





v

ớ

i

     

2

3

2

f

x y x y x y



    

.

K

h

ô

n

g

q

u

á

k

h

ó

k

h

i

n

h

ậ

n

r

a

đ

â

y

l

à

t

a

m

t

h

ứ

c

b

ậ

c

h

a

i

m

ộ

t

ẩ

n

;

2

t

x y t



 

d

o

đ

i

ề

u

k

i

ệ

n

x

á

c

đ

ị

n

h

.

D

o

đ

ó

c

ó

t

h

ể

b

i

ế

n

đ

ổ

i

n

h

ư

s

a

u

      

2

3

2 1 2 0, 2

x

y x y x y x y x y



           

.

B

à

i

t

o

á

n

1

2

1

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

2

3

4

2

2 1 3 2 2 3

;

2 2

2 4 5 .

3 2 4

x x y y

x y

x x

x x y y

x x



      







 

     

 





.

Lời giải.

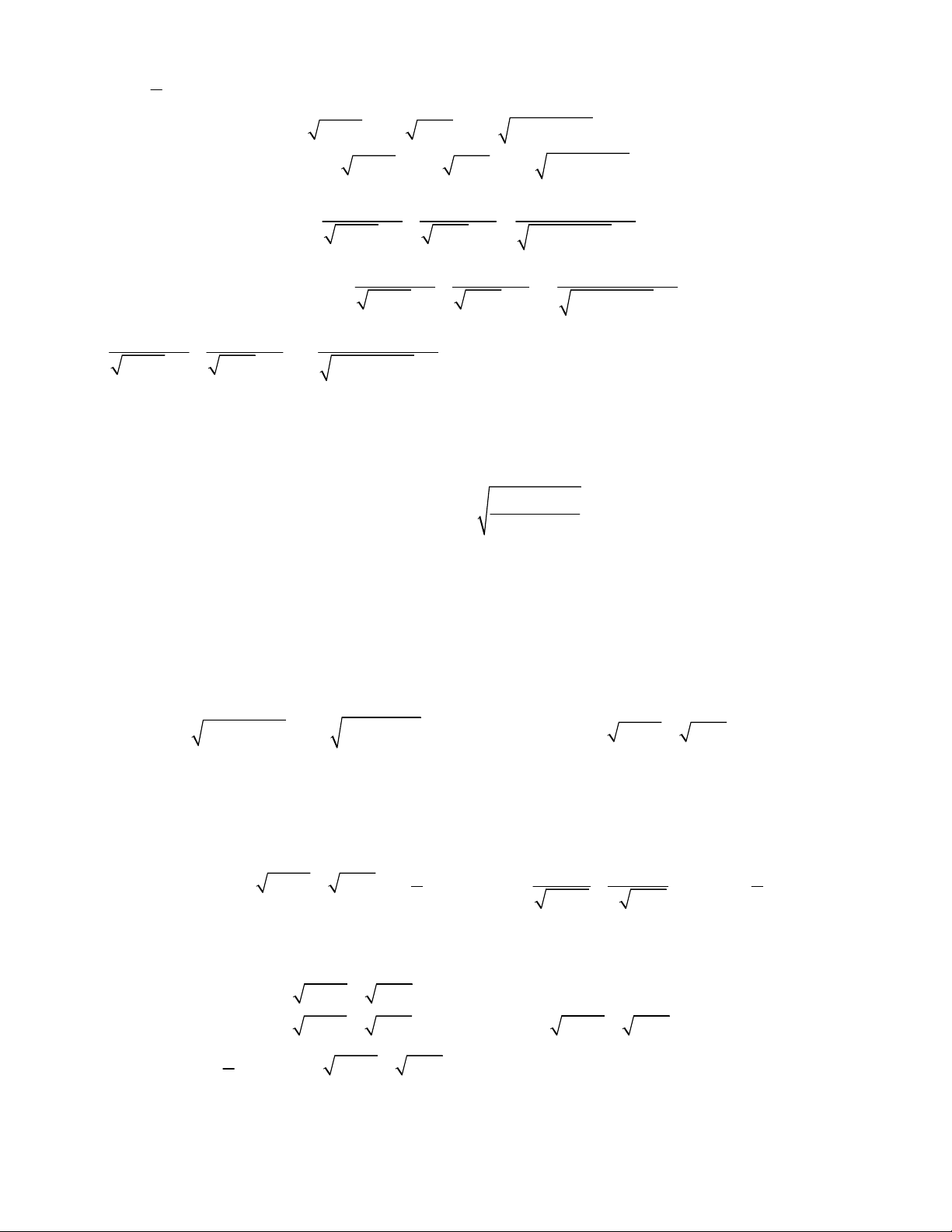
LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

90

Điều kiện

1

2

x



. Phương trình thứ nhất của hệ tương đương với

 

   

2

2 1 2 3 2 2 2 1

2

2 1 1 3 2 2 2 1

2

1 1

1

2 1 1 3 2

2

2 1

x

x y y

x x y y

x y

x

x x

y y

        



        



  

   

  

 

2

1

2 1

1

2 1 1 3 2

2 2 1

y

x

x x

y y



 

   

 

   

 

  

Rõ ràng

 

2

1

2 1

0; 0

2 1 1 3 2

2 2 1

y

x x

y y



  

   

  

nên ta được

1 0 1x x   

.

Xét hàm số

   

3

2

2 ; 1 3 2 0, 1f x x x x f x x x



        

.

Hàm số liên tục và đồng biến trên miền

   

1 1 1

x f x f

    

.

Lại có

 

2

4 2 3 4

4 3 1 2 3 0, 2 4 5 1 0 2 1

y y y y y y x x y y

                  



.

Mặt khác

 

2

2 2

2 1 0 0 2 2 3 2 4 1

3 2 4

x x

x x x x x

x x

 

          

 

.

Do đó phương trình thứ hai của hệ có nghiệm khi các dấu đẳng thức xảy ra, tức là

1

0

1

0

y

x

x y

x











  











.

Thử lại ta thu được nghiệm duy nhất của hệ.

N

h

ậ

n

x

é

t

.

V

ớ

i

b

à

i

t

o

á

n

s

ố

1

2

1

,

đ

ể

c

h

ặ

n

m

i

ề

n

g

i

á

t

r

ị

1x 

,

c

á

c

b

ạ

n

h

o

à

n

t

o

à

n

c

ó

t

h

ể

s

ử

d

ụ

n

g

b

ấ

t

p

h

ư

ơ

n

g

t

r

ì

n

h

ẩ

n

x

v

ớ

i

đ

á

n

h

g

i

á

g

i

ả

m

t

h

e

o

h

ằ

n

g

đ

ẳ

n

g

t

h

ứ

c

n

h

ư

s

a

u

 

2

2 3 1 1 3 1 3 4

y

y y



        

d

ẫ

n

đ

ế

n

2 2 1 3 4

x x

   

.



S

ử

d

ụ

n

g

đ

ạ

i

l

ư

ợ

n

g

l

i

ê

n

h

ợ

p

–

h

ệ

t

ạ

m

t

h

ờ

i

c

h

ú

n

g

t

a

s

ẽ

q

u

y

v

ề

l

ờ

i

g

i

ả

i

m

ớ

i

c

ù

n

g

b

ả

n

c

h

ấ

t

l

ờ

i

g

i

ả

i

t

r

ê

n

.



S

ử

d

ụ

n

g

p

h

é

p

b

i

ế

n

đ

ổ

i

t

ư

ơ

n

g

đ

ư

ơ

n

g

–

n

â

n

g

l

ũ

y

t

h

ừ

a

(

b

ì

n

h

p

h

ư

ơ

n

g

)

t

r

o

n

g

t

r

ư

ờ

n

g

h

ợ

p

n

à

y

l

à

c

h

ắ

c

h

ắ

n

t

u

y

n

h

i

ê

n

c

ũ

n

g

k

h

á

d

à

i

d

ò

n

g

,

v

ì

c

ầ

n

g

i

ả

i

p

h

ư

ơ

n

g

t

r

ì

n

h

c

h

ứ

a

c

ă

n

,

p

h

ư

ơ

n

g

t

r

ì

n

h

b

ậ

c

h

a

i

c

ó

k

è

m

t

h

e

o

đ

i

ề

u

k

i

ệ

n

.



S

ử

d

ụ

n

g

c

ô

n

g

c

ụ

đ

ạ

o

h

à

m

–

h

à

m

s

ố

(

l

i

ê

n

c

h

ư

ơ

n

g

t

r

ì

n

h

Đ

ạ

i

s

ố

-

G

i

ả

i

t

í

c

h

l

ớ

p

1

–

1

2

c

ấ

p

T

H

P

T

)

c

ũ

n

g

l

à

h

ư

ớ

n

g

đ

i

t

á

o

b

ạ

o

,

n

h

a

n

h

g

ọ

n

X

é

t

h

à

m

s

ố

 

1

2

2 1 3;

2

f

x x x x



   

t

a

c

ó

 

2

1 1

0, ;

2

2 1 2 3

f x x

x x









    





 





.

H

à

m

s

ố

l

i

ê

n

t

ụ

c

v

à

đ

ồ

n

g

b

i

ế

n

t

r

ê

n

m

i

ề

n

t

ư

ơ

n

g

ứ

n

g

d

ẫ

n

đ

ế

n

   

1

4 1

f

x f x



  

.



Đ

á

n

h

g

i

á

đ

ơ

n

t

h

u

ầ

n

c

ũ

n

g

r

ấ

t

p

h

ù

h

ợ

p

v

ớ

i

c

á

c

b

ạ

n

h

ọ

c

s

i

n

h

n

h

ỏ

t

u

ổ

i

1

2 2 1 3 4

1 2 2 1 3 4

1

2 2 1 3 4

2

x

x x

x x x



     



     





     





d

ẫ

n

đ

ế

n

2 2 1 3 4 1x x x     

.

LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

91

B

à

i

t

o

á

n

1

2

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

3

2

3

2 3 5 2 4

;

1

2 3 .

2

x x x x y

x y

y

x x y x y



     









    







.

Lời giải.

Điều kiện

2

3

2

3 0

x

y













 



Phương trình thứ nhất của hệ tương đương với

 

3 2 1 3 2 4 2 6

3 1

1

2 2 3

3 2 1 3 2

3 1

1

2 2 3

3

2 1 3 2

x x x x y

x x

x

x y

x x

x

x x y

x x

       



    

   

 



    

 

   

 

Ta có

3 1 2

2 3 0; 0, 1 0 1

3

3 2 1 3 2

x

x y x x x

x x

           

   

.

Do

 

2

3 2 3 2 2 2

1

1 0

x

x x x x x y x y



        

.

Lại có

 

2

2 2 2 2 2 2

0

2

x y

x

y

x

y x y x y x y x y





           

.

Từ đó dẫn đến

3

2 2 2 3 2

1 1

2 3

2 2 2

x y y y

x y x y x x y x y

  

           .

Phương trình thứ hai của hệ có nghiệm khi các dấu đẳng thức xảy ra, hay

2

3 1 0

1

0

x

y x

x

y

x

y

    









 

 













Thử lại, kết luận hệ có nghiệm duy nhất kể trên.

N

h

ậ

n

x

é

t

.

V

ẫ

n

v

ớ

i

m

o

t

i

p

s

ử

d

ụ

n

g

đ

ạ

i

l

ư

ợ

n

g

l

i

ê

n

h

ợ

p

c

h

ố

t

c

h

ặ

n

m

i

ề

n

g

i

á

t

r

ị

m

ộ

t

b

i

ế

n

,

l

ư

u

ý

b

à

i

t

o

á

n

à

y

k

h

ó

c

ó

t

h

ể

đ

ộ

c

l

ậ

p

g

i

ả

i

b

ấ

t

p

h

ư

ơ

n

g

t

r

ì

n

h

ẩ

n

x

n

h

ư

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

1

2

v

ì

đ

ã

đ

ư

ợ

c

g

ă

m

đ

ạ

i

l

ư

ợ

n

g

k

h

ô

n

g

â

m

2

3 0

x

y



 

n

ộ

i

t

ạ

i

p

h

ư

ơ

n

g

t

r

ì

n

h

t

h

ứ

h

a

i

,

đ

ó

l

à

c

h

ư

ớ

n

g

n

g

ạ

i

v

ậ

t

c

ả

n

t

r

ở

v

à

c

h

ắ

c

h

ẳ

n

đ

ã

p

h

á

v

ỡ

k

ế

h

o

ạ

c

h

n

g

â

y

t

h

ơ

c

ủ

a

n

h

i

ề

u

b

ạ

n

đ

ọ

c

.

   

3 1

1 2 2 3

3 2 1 3 2

x

x x y

x x

 

    

 

   

 

v

ớ

i

v

a

i

t

r

ò

     

;

. ; ;

f

x y T x y g x y



.

T

r

o

n

g

đ

ó

o

 

;f x y

v

ẫ

n

c

ò

n

t

r

ẻ

c

o

n

v

ớ

i

d

ạ

n

g

   

;0

f x f x



,

h

ơ

n

ữ

a

v

ẫ

n

c

ò

n

l

à

n

h

ị

t

h

ứ

c

.

o

 

;g

x y

c

ò

n

h

ẹ

n

h

à

n

g

k

h

i

t

r

ù

n

g

l

ặ

p

b

i

ể

u

t

h

ứ

c

d

ư

ớ

i

c

ă

n

 

;

2 3

g

x y x y



 

.

o

 

3 1

;

3 2 1 3 2

x

T x y

x x

 

   

b

ư

ớ

c

đ

ầ

u

x

u

ấ

t

h

i

ệ

n

b

i

ế

n

t

r

ê

n

t

ử

t

h

ứ

c

(

m

ộ

t

b

i

ế

n

)

.

S

a

u

k

h

i

k

h

a

i

p

h

á

đ

i

ề

u

k

i

ệ

n

1x 

,

r

õ

r

à

n

g

đ

â

y

k

h

ô

n

g

p

h

ả

i

m

ố

i

q

u

a

n

h

ệ

h

a

i

b

i

ế

n

,

v

ì

v

ậ

y

k

h

ô

n

g

t

h

ể

t

h

a

y

t

h

ế

v

à

o

m

à

u

n

g

d

u

n

g

i

ả

i

n

g

h

i

ệ

m

,

s

u

y

n

g

h

ĩ

t

h

ư

ờ

n

g

n

h

ậ

t

l

à

c

h

u

ẩ

n

b

ị

t

i

n

h

t

h

ầ

n

đ

á

n

h

g

i

á

p

h

ư

ơ

n

g

t

r

ì

n

h

t

h

ứ

h

a

i

,

b

ở

i

h

ì

n

h

t

h

ứ

c

n

ó

c

h

o

t

h

ấ

y

đ

ã

đ

ư

ợ

c

b

ố

t

r

í

v

i

ệ

n

b

i

n

h

đ

ó

n

l

õ

n

g

c

h

ặ

n

đ

ứ

n

g

đ

à

t

i

ế

n

q

u

â

n

c

ó

v

ẻ

m

ạ

n

h

m

ẽ

c

ủ

a

m

ì

n

h

.

K

h

ô

n

g

q

u

á

k

h

ó

c

á

c

b

ạ

n

đ

ề

u

n

h

ậ

n

x

é

t

2

3 0

x

x y



 

c

h

o

d

ù

α

0

x





đ

i

c

h

ă

n

g

n

ữ

a

,

v

ì

đ

ã

d

ự

đ

o

á

n

t

r

ư

ớ

c

d

ấ

u

đ

ẳ

n

g

t

h

ứ

c

d

à

n

h

c

h

o

n

g

h

i

ệ

m

x

ả

y

r

a

k

h

i

1

;2 3 0 1

x

x y x y



     

.

LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

92

C

h

í

n

h

v

ì

t

h

ế

c

h

ú

n

g

t

a

m

a

n

h

n

h

a

c

h

u

y

ể

n

đ

à

t

ấ

n

c

ô

n

g

t

h

e

o

h

ư

ớ

n

g

3

2

1

, 1

2

y

x y x



   

,

v

à

m

a

y

m

ắ

n

đ

ã

đ

ế

n

t

h

e

o

ư

ớ

c

n

g

u

y

ệ

n

,

b

ở

i

v

ì

 

2

3

2 2 3 2 3

2 2 1 2 2 1 2 1 2

x y y y x y y x y

           

.

T

ấ

t

n

h

i

ê

n

k

h

i

t

h

ự

c

h

à

n

h

c

ầ

n

k

h

é

o

l

é

o

đ

ố

i

v

ớ

i

c

á

c

k

i

ế

n

t

h

ứ

c

ơ

b

ả

n

 

2

3

3 2 2

2 2

3 2 3 2

2

1 2, 1 2 2 1 1

11 1

1

2 2

2

x

y x x y y y y

yy y

y

x y x y



          

 





      

B

à

i

t

o

á

n

1

2

3

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

2

3 2

3

3 2 1 5 ,

;

2 3 2 2 3 1.

x x x y x

x y

x y x x x y y



     









       





.

Lời giải.

Điều kiện

2

3 2

1

;

2 3 0

2

2 2 3 0

x

y x

x x y





  







   



Phương trình thứ nhất của hệ tương đương với

   

 

2

3

2 2 1 2 3

3 2 2 1 1 2 3

1

2 1

2 3

3 2 2 1 1

2

1

2 3

3

2 2 1 1

x x x x x x y x

x x x x y x

x x x x

y x

x x

x

y x

x

       

        

 

    

   

 



    





   

 

Ta có

2

2 1

2 3 0; 0, 1 0 1

2

3 2 2 1 1

x x

y x x x x

x x

           

   

.

Xét hàm số

   

3

2

; 1 3 2 0, 1

f

x x x x f x x x





       

.

Rõ ràng hàm liên tục và đồng biến nên ta thu được

     

1

1 1

x

f x Min f x f



   

.

Suy ra

 

2

3

2 2 2 2

2

2 3 1 2 3 2 2 2 1 1

x

x y y y y y y



            

.

Vì thế

3

2 2 3 2

2

2 3 1 1 2 3 2 2 3 1

x

x y y y x y x x x y y



              

.

Phương trình thứ hai của hệ có nghiệm khi và chỉ khi

1

0

1

1 0

1

y

x

y

x

 











 

 











Thử lại, kết luận hệ phương trình có nghiệm duy nhất

1x

y



.

N

h

ậ

n

x

é

t

.



B

i

ể

u

t

h

ứ

c

l

i

ê

n

h

ợ

p

x

u

ấ

t

h

i

ệ

n

b

i

ế

n

t

r

ê

n

t

ử

t

h

ứ

c

   

2

; ;0

3 2 2 1 1

x x

T x y T x

x x

  

   

.



 

2

;

2 3

g

x y y x



 

l

à

đ

a

t

h

ứ

c

h

a

i

b

i

ế

n

k

h

ô

n

g

â

m

.



Đ

ơ

n

v

ị

q

u

y

ế

t

đ

ị

n

h

m

i

ề

n

g

i

á

t

r

ị

b

i

ế

n

x

l

à

   

;

;0 1

Q

f x y f x x



  

.



Đ

á

n

h

g

i

á

3

2

1

x



 

c

ó

t

h

ể

q

u

a

b

i

ế

n

đ

ổ

i

t

ư

ơ

n

g

đ

ư

ơ

n

g

,

k

h

ô

n

g

n

h

ấ

t

h

i

ế

t

s

ử

d

ụ

n

g

h

à

m

s

ố

LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

93

 

3

2

2 1 0 1 1 0, 1x x x x x x         

v

ì

2

1 1 0, 1x x x     

.



Đ

á

n

h

g

i

á

2

2 2 1 1y y y    

c

ó

t

h

ể

d

ù

n

g

b

ấ

t

đ

ẳ

n

g

t

h

ứ

c

p

h

ụ

 

2

a b a b

  

.

 

2

2 2

2 2 2 1 1 2 2 1 1y y y y y y          

.

B

à

i

t

o

á

n

1

2

4

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

2

3

3 2 2

2

2 0,

;

2 3.

x x y y

x y

x x xy y y



     







     







.

Lời giải.

Điều kiện

 

3 2

2 0 1 2 0 1y y y y y y         

.

Phương trình thứ nhất của hệ suy ra

  

2

3

2

2 0 1 2 0 2 1

x

x y y x x x



             

.

Phương trình thứ hai biến đổi về

 

  

2

3

2 2 2

2 2

1 1

1

3 2 1

3 2 3 2

y y

y

x x xy y y x y x

y y

 



          

   

.

Mà

  

2

1 1

0, 1; 0, 1, 1 0 1 1

3 2

y y

y x y y x x x x y

y

 

                

 

 .

Vậy hệ đề bài có nghiệm duy nhất

1x

y



.

N

h

ậ

n

x

é

t

.

K

h

ô

n

g

q

u

á

k

h

ó

đ

ể

c

h

ú

n

g

t

a

n

h

ậ

n

r

a

đ

i

ề

u

k

i

ệ

n

 

3

2

2 0 1 2 0 1y y y y y y         

.

Đ

i

ề

u

k

i

ệ

n

à

y

m

a

y

m

ắ

n

v

ì

n

ó

đ

ộ

c

l

ậ

p

v

ớ

i

m

ộ

t

b

i

ế

n

,

k

h

ô

n

g

b

ấ

t

l

ợ

i

n

h

ư

c

á

c

r

à

n

g

b

u

ộ

c

h

a

i

b

i

ế

n

.

H

ơ

n

ữ

a

v

ớ

i

c

h

ú

ý

đ

ó

,

d

ễ

d

à

n

g

s

u

y

r

a

đ

ư

ợ

c

2

3

1 3 2

y



  

,

v

ì

t

h

ế

 

3

2 2

2

2 1 0

x

x xy y x y x



       

V

ì

b

i

ể

u

t

h

ứ

c

đ

ã

đ

ư

ợ

c

b

ố

t

r

í

s

ẵ

n

đ

ạ

i

l

ư

ợ

n

g

x

á

c

đ

ị

n

h

d

ư

ơ

n

g

2

x y

n

ê

n

t

ấ

t

y

ế

u

1

0 1 1

x

x x



    

.

S

ự

đ

ố

i

l

ậ

p

n

à

y

d

ẫ

n

đ

ế

n

l

ờ

i

g

i

ả

i

n

g

ắ

n

g

ọ

n

,

n

h

ẹ

n

h

à

n

g

.

B

à

i

t

o

á

n

1

2

5

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h





 

3

2 3

3 2 3

2 3 4 4,

;

2 6 2 8 .

x x x y y

x y

x x xy y y



     







     







.

Lời giải.

Điều kiện

 

3

2

3 4 0 1 4 0 1y y y y y y         

. Phương trình thứ nhất của hệ tương đương

 

3

2 3 2

2 4 3 4 0 1 2 4 0 1x x x y y x x x x              

.

Phương trình thứ hai biến đổi

   





 

3

2

3 2

3

2 1

1 2 1 2 8 3 2 1

8 3

y

x x y x y x y x

y



         

 

.

Mà

 

3

2

3

2 1

0, 1; 2 0, , 1 1 0 1 1

8 3

y

y x y x y x x x y

y



                

 

 .

Thử lại ta thấy hệ có nghiệm duy nhất

1x

y



.

N

h

ậ

n

x

é

t

.

B

à

i

t

o

á

n

à

y

c

ũ

n

g

k

h

ô

n

g

q

u

á

k

h

ó

k

h

a

i

t

h

á

c

đ

i

ề

u

k

i

ệ

n

 

3

2

3 4 0 1 4 0 1y y y y y y         

.

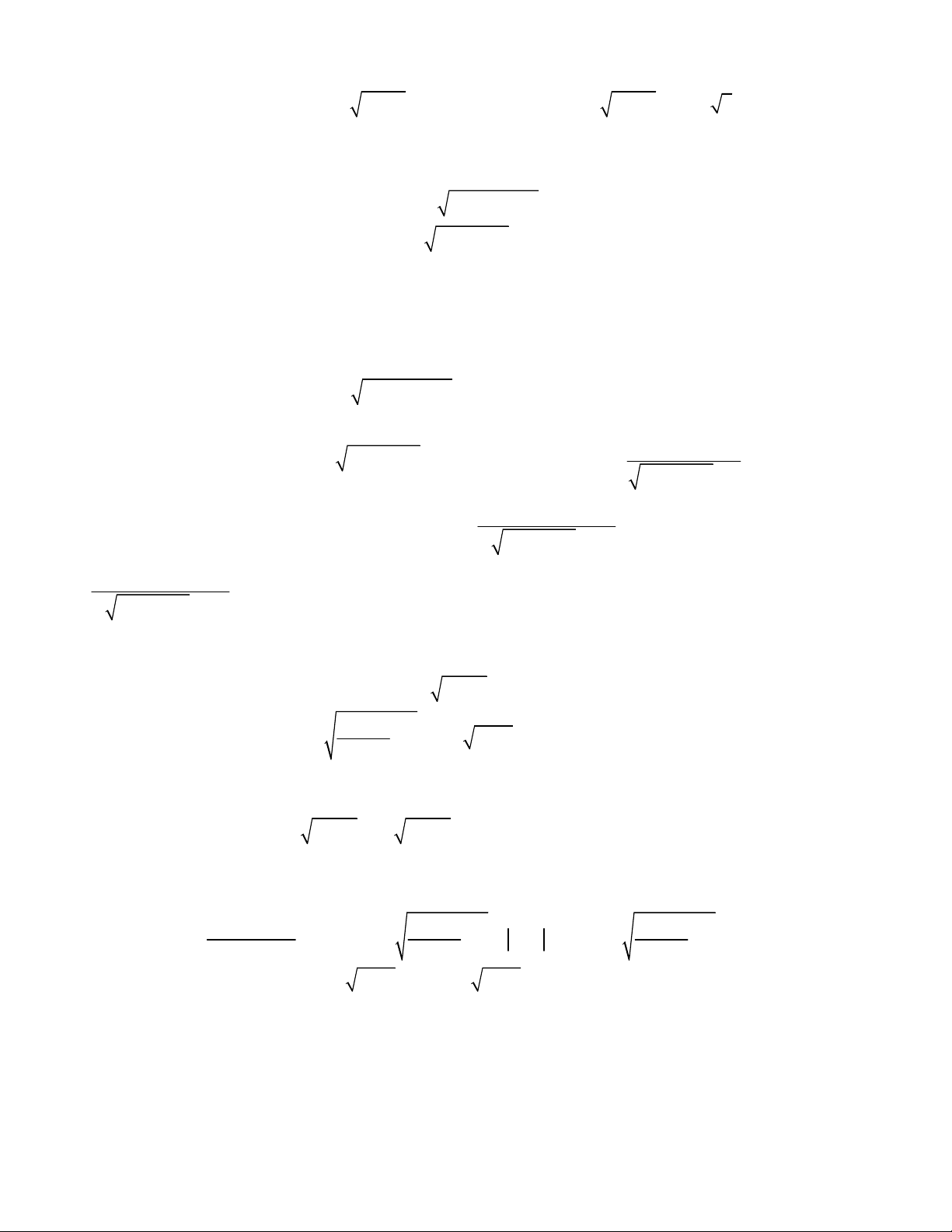
LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

94

C

ă

n

t

h

ứ

c

h

ứ

a

y

t

ạ

i

p

h

ư

ơ

n

g

t

r

ì

n

h

t

h

ứ

h

a

i

đ

ộ

c

l

ậ

p

n

ê

n

c

ũ

n

g

d

ễ

d

à

n

g

đ

á

n

h

g

i

á





   

 

3

2 3 3 2 3

2 2

2 6 2 8 2 2 2 8 6 2 9 6 0

1 2 1 0 2 1 0 1

x x xy y y x x xy y y

x x y x x y x x

               

          

B

à

i

t

o

á

n

1

2

6

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

3

2 3

3

2

2 2 3 5 5,

;

2 2.

x x x y y

x y

xy x y y y



     







    







.

Lời giải.

Điều kiện

 

   

2

3

1 2 2 5 0 1 1 5 0

2 3 5 0

1

2 0

y y y y y y

y y

y

y y



 



        



  

  

 

   

  

  



  



 

  



.

Phương trình thứ nhất của hệ biến đổi

 

3

2 3 2

2 2 5 2 3 5 0 1 2 3 5 0 1x x x y y x x x x              

.

Phương trình thứ hai của hệ tương đương với

   

3

2

2 2 2 2 1 2 1

2 2

y y

xy y x y y y x x

y y

 

           

  

  

 

2

3

1 2

2 2

y y y

x y

y y

  

   

  

Ta có

 

2

3

1 2

0; 2 0, 1 1 0 1 1

2 2

y y y

y y x x x y

y y

  

            

  

.

Kết luận hệ có nghiệm duy nhất

1

; 1

x

y



.

B

à

i

t

o

á

n

1

2

7

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

2

2 3 2 5 ,

;

3 3

2 1.

2

x x y

x y

x

x x y



   











    





.

Lời giải.

Điều kiện

2

2; 5

y y

  

. Phương trình thứ nhất biến đổi

 

2

2 2 2 2

1

2 2 5 2 5 2 5 1 4 2 2

x

y y y y y



              

.

Lại có

 

2

2 2

2 2 2

2

1 0 3 2 3 2 2 1 2 1

3 2 3 3 3 3 3

1 1 1 1

2 2 2

x x x x x x

x x x x

x x x x x x

         

   

            

Từ phương trình thứ hai của hệ dẫn đến

2

1 1 2 2 2 2

y

y y y



        

.

Khi đó các dấu đẳng thức cũng xảy ra nên

2

1

0

2

1

0

y

x

y

x











  

 













Thử lại không thỏa mãn hệ nên kết luận hệ vô nghiệm.

N

h

ậ

n

x

é

t

.

P

h

ư

ơ

n

g

t

r

ì

n

h

t

h

ứ

n

h

ấ

t

c

ủ

a

h

ệ

đ

a

p

h

ầ

n

b

ạ

n

đ

ọ

c

đ

ề

u

n

h

ậ

n

r

a

đ

ặ

c

đ

i

ể

m

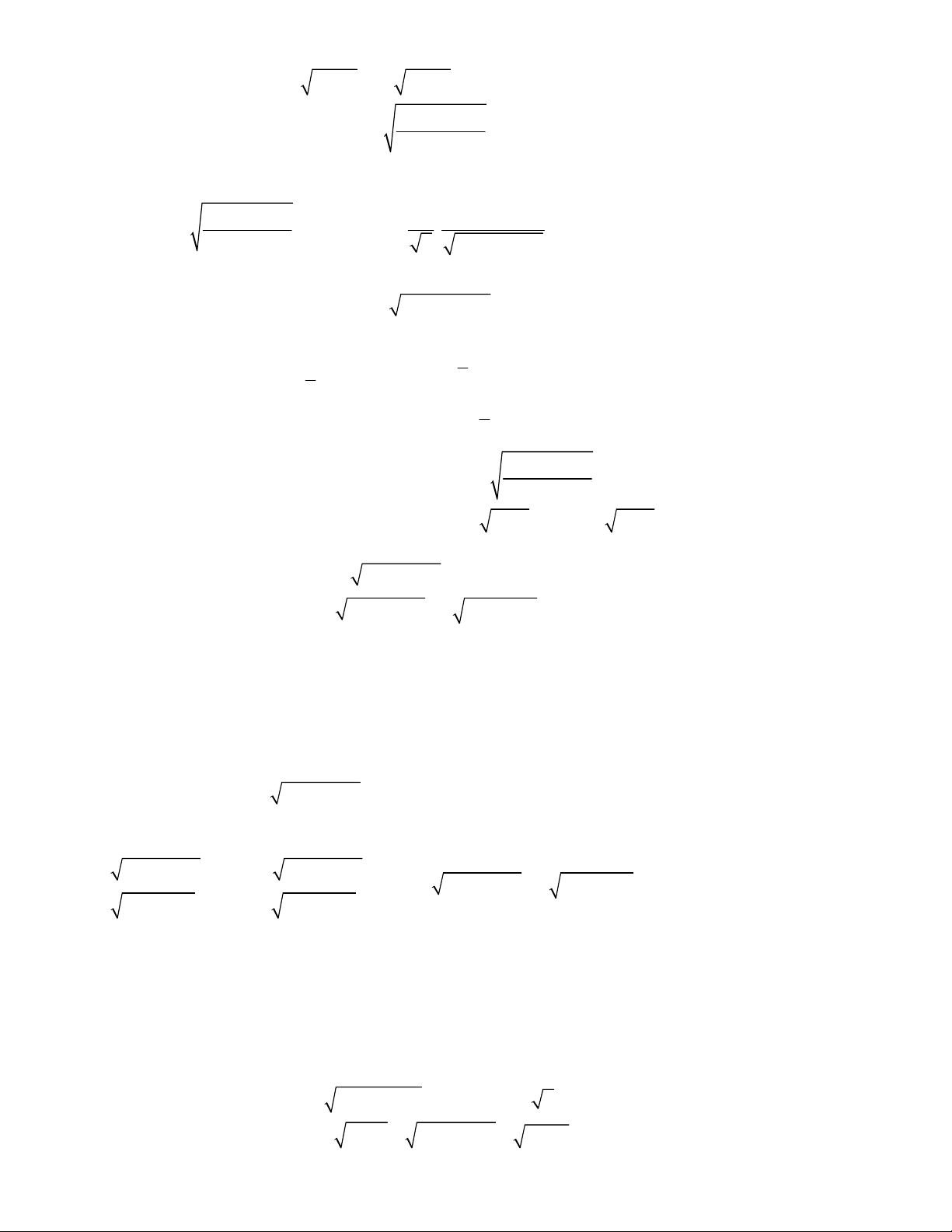
LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

95

 

2

2 2 2 2

1

2 2 5 2 5 2 5 1 4 2 2

x

y y y y y



              

.

T

u

y

n

h

i

ê

n

p

h

ư

ơ

n

g

t

r

ì

n

h

t

h

ứ

h

a

i

c

ó

đ

ạ

i

l

ư

ợ

n

g

2

3 2 3

2

x x

x

 



g

â

y

k

h

ó

k

h

ă

n

t

r

o

n

g

v

i

ệ

c

đ

á

n

h

g

i

á

.

L

ờ

i

g

i

ả

i

t

r

ê

n

s

ử

d

ụ

n

g

l

à

r

ấ

t

h

u

ầ

n

t

ú

y

v

à

c

ơ

b

ả

n

,

n

h

ư

n

g

n

g

h

ĩ

đ

ư

ợ

c

n

h

ư

t

h

ế

c

ầ

n

m

ộ

t

s

ự

l

i

n

h

o

ạ

t

v

à

k

h

é

o

l

é

o

n

h

ấ

t

đ

ị

n

h

.

K

h

ô

n

g

n

h

ấ

t

h

i

ế

t

n

h

ư

t

h

ế

,

c

á

c

b

ạ

n

c

ó

t

h

ể

s

ử

d

ụ

n

g

c

ô

n

g

c

ụ

đ

ạ

o

h

à

m

–

k

h

ả

o

s

á

t

h

à

m

s

ố

n

h

ư

s

a

u

X

é

t

h

à

m

s

ố

   

2

3

2 3 1 3 1

.

1

2

3

2 3

x

x x

f x x f x

x x

  





   



.

D

ễ

t

h

ấ

y

 

2

3 1 0

0 3 1 6 4 6

9 6 1 6 4 6

1

3

1

3

5

1;

3 2 5 0

3

x

f x x x x

x x x x

x

x x

 





      



    





 





 

 

   

 

 

 

 

  

 





 



L

ậ

p

b

ả

n

g

b

i

ế

n

t

h

i

ê

n

h

à

m

s

ố

t

a

t

h

ấ

y

   

2

3 2 3

1

1 1

2

x

x x

Min

f x f x



 



   



.

L

ú

c

n

à

y

đ

ã

c

ó

đ

ò

n

b

ẩ

y

đ

ể

c

h

ặ

n

m

i

ề

n

g

i

á

t

r

ị

b

i

ế

n

y

c

ò

n

l

ạ

i

2 1 1 2 2 2 2

y y y y

         

.

B

à

i

t

o

á

n

1

2

8

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

3

2 3

2 3 1,

;

3 3 2 2 .

x x x y y

x y

y x x x y y x y



     







      







.

Lời giải.

Điều kiện

 

2

3

2 2

3

2

1 3 0

2 3 0

1

3

3 0 3 3

1

2

0

1 2 0

x x x

x x

x

x x x x

y

y y

y y y



   



  













     

  









  

   







Từ phương trình thứ nhất của hệ ta có

 

   

3

3 3

2

2 3 1 1 1 2 0

1 2 0 1 2 1 7 0 1

x x x y y y y

y y y y y y

           

 

           

 

Khi đó

2

2 3

3 3

3

3 1 3 3

3 3 2 2

2 2 2 2

x x y x x y

y

x x x y y x y

y

y x y y x

 

     

 



       



     

 

 

.

Phương trình thứ hai của hệ có nghiệm khi và chỉ khi các dấu đẳng thức đồng thời xảy ra, tức là

1x

y



.

Thử lại thấy thỏa mãn, vậy hệ có nghiệm duy nhất.

N

h

ậ

n

x

é

t

.

P

h

ư

ơ

n

g

t

r

ì

n

h

t

h

ứ

n

h

ấ

t

c

ủ

a

h

ệ

đ

ư

ợ

c

ô

l

ậ

p

b

i

ế

n

ê

n

t

ì

m

đ

i

ề

u

k

i

ệ

n

c

h

ặ

t

c

h

ẽ

c

h

o

t

o

à

n

t

h

ể

h

a

i

b

i

ế

n

k

h

ô

n

g

m

ấ

y

k

h

ó

k

h

ă

n

.

P

h

ư

ơ

n

g

t

r

ì

n

h

t

h

ứ

h

a

i

c

ủ

a

h

ệ

t

u

y

c

á

c

h

ạ

n

g

t

ử

l

à

t

ổ

h

ợ

p

c

ă

n

t

h

ứ

c

–

đ

ơ

n

t

h

ứ

c

h

a

i

b

i

ế

n

h

ư

n

g

d

o

đ

i

ề

u

k

i

ệ

n

t

ì

m

đ

ư

ợ

c

m

ạ

n

h

m

ẽ

1

; 1

x

y



n

ê

n

d

ễ

d

à

n

g

đ

á

n

h

g

i

á

n

h

ẹ

n

h

à

n

g

.

B

à

i

t

o

á

n

1

2

9

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

4

3 3 2

3 3 3

2

1 1 ,

;

1 2 3 4.

x y x x x

x y

x y x y xy



     







      







.

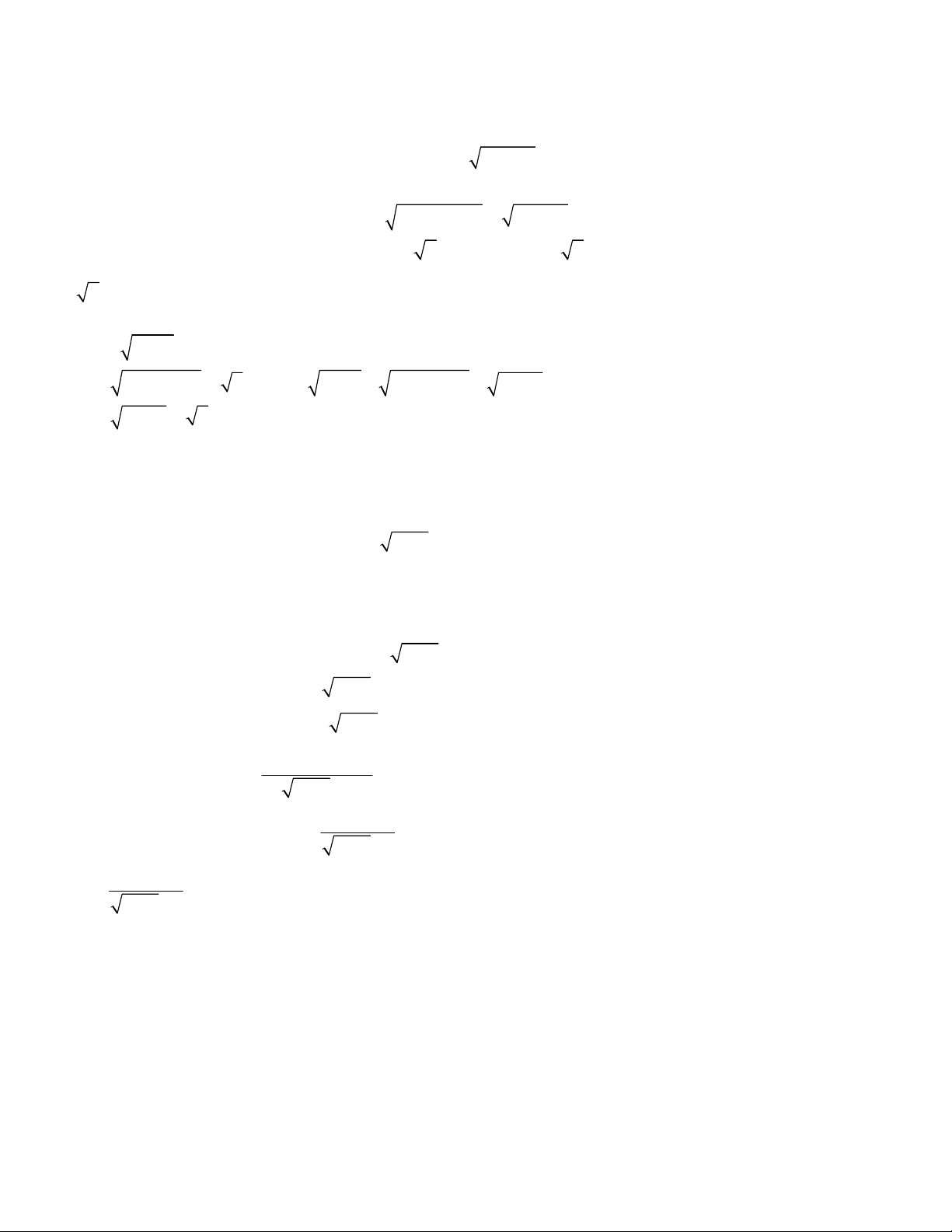
LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

96

Lời giải.

Điều kiện

1

0

y

x











Ta có

   

2

2 4 4 2 2 4 2

1 0 2 2 2 1 1 2 2 1

x x x x x x x

            

.

Xét phương trình thứ nhất của hệ

4 3 4 2

3 2 2 3

1

2 1 2 2 1

2

y

x y x x

x x x x x x



      



      

Đặt

;

0

x

t t





dẫn đến

 

5

4 3 2

6

1 2

2

0 1 0 1 1

0

t t t t t t

t t

t t x

t



     



 



        

 









.

Khi đó

3

3 3 3 3

1

0

2

4 2 1 2 3 4

3

4 2

x y

x y x y x y xy

xy



 





          





  





.

Phương trình thứ hai của hệ có nghiệm khi và chỉ khi các dấu đẳng thức xảy ra tức là

1x

y



.

Thử lại ta thấy thỏa mãn hệ, kết luận bài toán có nghiệm duy nhất

   

;

1;1

x

y 

.

B

à

i

t

o

á

n

1

3

0

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

2

4

6

3 2

1 2 7 4 44,

;

4 30 21 6 4.

x x x y y

x y

y x x x y



       









    





.

Lời giải.

Điều kiện

2

x



. Phương trình thứ nhất của hệ tương đương với

 

  

    

 

     

2

2 4

2

2 2

2 1 2 1 2 2 14 49 4 44

2 1 2 2 11 4 4

2 1 2 1 2 9 9 4 3

2 1 3

3 2 3 1 2 3

2 1

3 2 3 1 1 2 1

2 1

x x x x x x x y y

x x x x y y

x x

x x y y y

x

x x y y

x

            

       

         

 

       

 

 

 

       

 

 

 

 

Rõ ràng

 

2

1

2

3 0, 2

2 1

x

x x

x



   

 

nên từ (1) suy ra

3

0 3

x



  

.

Xét phương trình thứ hai của hệ

 

6

3 2

2

4 3 2 3 2

6 5 4 21 30 9

1 2 3 4 5 4 21 30 9 0 2

y y x x x

y y y y y x x x

     

          

Ta có

 

2

4

3 2 4 3 2 2 2

2 3 4 5 2 2 4 5 2 1 3 0,y y y y y y y y y y y y y

                  

.

Hơn nữa xét hàm số

 

3 2

4 21 30 9; 3

f x x x x x

    

.

Đạo hàm

   

2

12

42 30 0, 3

f

x x x x f x





     

đồng biến, liên tục nên

   

3

0

f

x f





.

Phương trình (3) có nghiệm khi và chỉ khi

 

2

3

1 0

1

3

x

y

x







 





 









LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

97

Thử lại cặp giá trị thấy thỏa mãn hệ đề bài. Kết luận nghiệm duy nhất

3

; 1

x

y



.

N

h

ậ

n

x

é

t

.

P

h

ư

ơ

n

g

t

r

ì

n

h

t

h

ứ

n

h

ấ

t

c

ủ

a

h

ệ

c

ó

v

ế

p

h

ả

i

l

à

m

ộ

t

đ

ạ

i

l

ư

ợ

n

g

m

ộ

t

b

i

ế

n

 

4

44

f

y y y



 

.

T

h

ô

n

g

t

h

ư

ờ

n

g

n

h

i

ề

u

b

ạ

n

đ

ọ

c

q

u

e

n

t

h

u

ộ

c

v

ớ

i

b

ấ

t

đ

ẳ

n

g

t

h

ứ

c

đ

ề

u

d

ễ

d

à

n

g

n

h

ậ

n

r

a

m

ấ

u

c

h

ố

t

v

ấ

n

đ

ề

 

4

44 4 3 41 41

M

y y y y



      

v

ớ

i

4

4 3 0,y y y

     

.

T

h

ự

c

r

a

đ

i

ề

u

n

à

y

đ

ư

ợ

c

t

á

c

g

i

ả

x

â

y

d

ự

n

g

t

ừ

b

ấ

t

đ

ẳ

n

g

t

h

ứ

c

l

i

ê

n

h

ệ

t

r

u

n

g

b

ì

n

h

c

ộ

n

g

–

t

r

u

n

g

b

ì

n

h

n

h

â

n

v

ớ

i

b

ố

n

s

ố

t

h

ự

c

k

h

ô

n

g

â

m

n

h

ư

s

a

u

4 4 4

4

1

1 1 4 4 4 4 3 0

y

y y y y y



        

.

N

g

o

à

i

b

ả

n

c

h

ấ

t

đ

ẳ

n

g

t

h

ứ

c

n

h

ư

t

r

ê

n

c

á

c

b

ạ

n

h

o

à

n

t

o

à

n

s

ử

d

ụ

n

g

p

h

â

n

t

í

c

h

n

h

â

n

t

ử

t

ư

ơ

n

g

t

ự

l

ờ

i

g

i

ả

i

h

o

ặ

c

ô

n

g

c

ụ

đ

ạ

o

h

à

m

–

k

h

ả

o

s

á

t

h

à

m

s

ố



 

   

2

2 2

4 2

4

3 1 2 3 1 1 2 0

y

y y y y y y

 



         





.



X

é

t

h

à

m

s

ố

   

4

3

4

3; 4 4

f

y y y y f y y





     



.

T

a

c

ó

 

0 1f y y



  

.

K

h

ả

o

s

á

t

s

ự

b

i

ế

n

t

h

i

ê

n

t

a

đ

ư

ợ

c

   

1

0

y

M

in f y f







.

S

a

u

c

ô

n

g

đ

o

ạ

n

à

y

n

h

i

ề

u

b

ạ

n

x

ô

n

g

p

h

a

t

ấ

n

c

ô

n

g

b

ấ

t

p

h

ư

ơ

n

g

t

r

ì

n

h

ẩ

n

x

d

ạ

n

g

 

2

2 1 2 2 11 7 0

x x x x

     

.

T

u

y

n

h

i

ê

n

đ

â

y

l

à

b

ấ

t

p

h

ư

ơ

n

g

t

r

ì

n

h

m

ộ

t

ẩ

n

c

h

ứ

a

t

a

m

t

h

ứ

c

b

ê

n

g

o

à

i

c

ă

n

t

h

ứ

c

n

ê

n

k

h

ô

n

g

p

h

ả

i

m

ộ

t

đ

i

ề

u

đ

ơ

n

g

i

ả

n

,

c

ó

t

h

ể

n

ó

i

p

h

ư

ơ

n

g

á

n

l

i

ê

n

h

ợ

p

ở

t

r

ê

n

l

à

t

ố

i

ư

u

.

P

h

ư

ơ

n

g

t

r

ì

n

h

ệ

q

u

ả

t

h

ự

c

h

ấ

t

l

à

h

a

i

h

à

m

đ

ộ

c

l

ậ

p

m

ộ

t

b

i

ế

n

   

6

3 2

6

5 4 21 30 9

N

y y x x x g y f x



       

.



V

ớ

i

h

à

m

s

ố

b

i

ế

n

y

,

t

h

ự

c

h

à

n

h

p

h

ư

ơ

n

g

á

n

   

 

2

4 3 2

1

2 3 4 5

g

y y y y y y



    

c

ầ

n

l

ư

u

ý

p

h

â

n

t

í

c

h

b

ì

n

h

p

h

ư

ơ

n

g

 

2

4

3 2 4 3 2 2 2

2 3 4 5 2 2 4 5 2 1 3 0,y y y y y y y y y y y y y

                  

.



N

g

o

à

i

r

a

c

ó

t

h

ể

s

ử

d

ụ

n

g

c

ô

n

g

c

ụ

h

à

m

s

ố

v

ớ

i

   

5

6

6; 0 1

g

y y g y y





   

.



H

à

m

s

ố

b

i

ế

n

x

c

ó

t

h

ể

s

ử

d

ụ

n

g

p

h

â

n

t

í

c

h

n

h

â

n

t

ử

 

3

2

4

21 30 9; 3

f

x x x x x



   

.

B

à

i

t

o

á

n

1

3

1

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

2

2 2

1

4 3 2 1 ,

;

4 3 6 3 2 1.

y

x y

x

x y

x x y x y





   









     





.

Lời giải.

Điều kiện

3

2

x 

. Phương trình thứ nhất của hệ tương đương với

 

        

2

2 2 2

2

4 3 2 1 4 3 1 1 2

1

1 1 1 1

4 3 1 4 3 1

x x xy x y x x x x xy y

x x

x

x x y x x x y

x x

            



 

           

 

   

 

Ta có

 

2

3

0; 1 0, 1 0 1

4

4 3 1

x

x y x x x x

x

           

 

.

Lại có

 

2

2 2 2

2

2 2 2 2 2 2

0 2 0 2 4 2 0

6 3 4 4 2 6 3 2 2

x y x xy y x xy y

x

y x xy y x y x y x y x y

         



           

Hơn nữa

2

2 2 2

1

4 3 1 4 3 6 3 2 1

x

x x x y x y



         

.

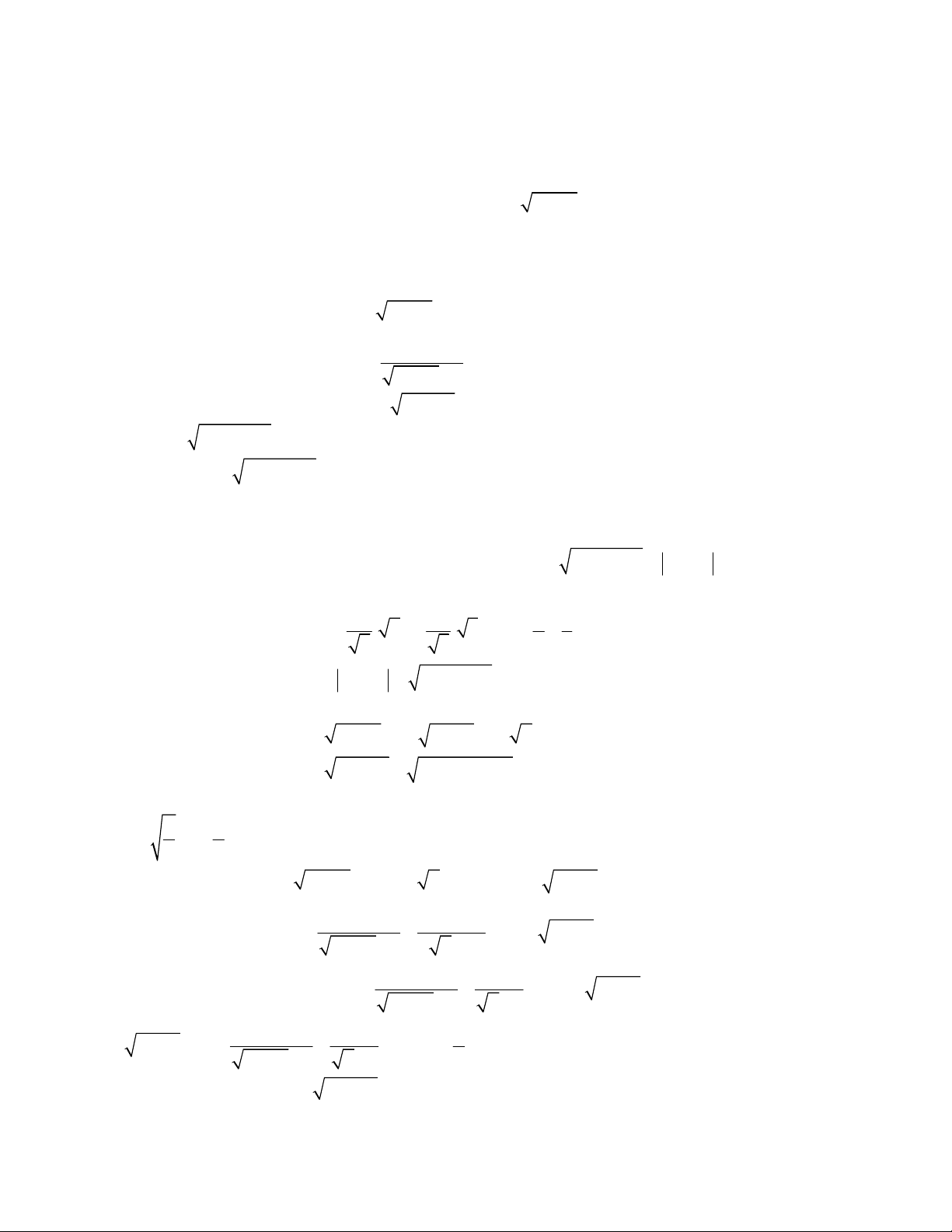
LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

98

Phương trình thứ hai có nghiệm khi và chỉ khi

0

1

x y

x

 



  







.

Kết luận hệ phương trình đề bài có nghiệm duy nhất

1x y 

.

N

h

ậ

n

x

é

t

.



S

a

u

k

h

i

t

h

ự

c

h

i

ệ

n

q

u

y

đ

ồ

n

g

c

h

ú

n

g

t

a

q

u

y

p

h

ư

ơ

n

g

t

r

ì

n

h

t

h

ứ

n

h

ấ

t

v

ề

p

h

ư

ơ

n

g

t

r

ì

n

h

a

i

ẩ

n

h

ỗ

n

t

ậ

p

c

ă

n

t

h

ứ

c

,

h

ơ

n

ữ

a

h

a

i

ẩ

n

d

í

n

h

v

à

o

n

h

a

u

g

â

y

t

â

m

l

ý

h

o

a

n

g

m

a

n

g

2

4

3 2 1

x

x xy x y



   

.

T

r

o

n

g

t

r

ư

ờ

n

g

h

ợ

p

n

à

y

c

ầ

n

h

ế

t

s

ứ

c

b

ì

n

h

t

ĩ

n

h

t

h

i

ế

t

l

ậ

p

đ

ạ

i

l

ư

ợ

n

g

k

h

ô

n

g

â

m

,

k

h

ô

n

g

q

u

á

k

h

ó

n

h

ậ

n

t

h

ấ

y

đ

ó

l

à

h

ằ

n

g

đ

ẳ

n

g

t

h

ứ

c

   

2

;

g x y x y

 

,

c

ũ

n

g

l

à

đ

ơ

n

v

ị

q

u

y

ế

t

đ

ị

n

h

 

;M x y

q

u

e

n

t

h

u

ộ

c

.

B

i

ể

u

t

h

ứ

c

ò

n

l

ạ

i

c

h

ứ

a

đ

ộ

c

b

i

ế

n

x

n

ê

n

s

ử

d

ụ

n

g

l

i

ê

n

h

ợ

p

g

i

ả

i

b

ấ

t

p

h

ư

ơ

n

g

t

r

ì

n

h

l

à

p

h

ù

h

ợ

p

 

    

2

2 2

2

4 3 1 1 2

1

1 1

4 3 1

x x x x xy y

x x

x x x y

x

      



     

 



K

h

i

đ

ã

x

u

ấ

t

h

i

ệ

n

m

i

ề

n

g

i

á

t

r

ị

2

1

4 3 1

x



  

l

à

đ

i

ề

u

t

ấ

t

y

ế

u

.

V

ấ

n

đ

ề

t

i

ế

p

t

h

e

o

l

à

h

a

i

đ

ạ

i

l

ư

ợ

n

g

t

ư

ơ

n

g

ứ

n

g

l

ọ

t

l

ạ

i

2

6

3 2

x

y x y





,

r

õ

r

à

n

g

l

à

b

ấ

t

đ

ẳ

n

g

t

h

ứ

c

l

à

c

h

ứ

n

g

m

i

n

h

t

h

u

ậ

n

c

h

i

ề

u

l

ớ

n

h

ơ

n

ê

n

t

a

c

ả

m

q

u

a

n

t

h

e

o

h

ư

ớ

n

g

2

6

3 2

x

y x y



 

.

S

ử

d

ụ

n

g

b

i

ế

n

đ

ổ

i

t

ư

ơ

n

g

đ

ư

ơ

n

g

t

ư

ơ

n

g

t

ự

l

ờ

i

g

i

ả

i

 

2

2 2 2 2

2

2 2 2 2 2 2

0 2 0 2 4 2 0

6 3 4 4 2 6 3 2 2

x y x xy y x xy y

x

y x xy y x y x y x y x y

         



           

S

ử

d

ụ

n

g

b

ấ

t

đ

ẳ

n

g

t

h

ứ

c

B

u

n

y

a

k

o

v

s

k

y

h

a

i

b

ộ

s

ố

v

ớ

i

đ

i

ể

m

r

ơ

i

 

2

2 2 2 2

2

1 4 1

2 . 6 . 3 6 3 6 3

6

3

6 3

2 2 6 3

x y x y x y x y

x y x y x y

 

       

 

 

     

B

à

i

t

o

á

n

1

3

2

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

2

2 4 2

3

2 2 2 1 2 2 ,

;

3 2 3 2 1 1.

x x y x x x y

x y

x x y x y



     







      







.

Lời giải.

Điều kiện

4

2

1

;

;3 2 1 0

3

2

x y x y



   

. Phương trình thứ nhất tương đương với

 

   

 

2

3 2 1 1 2 2 1 2 1

3 1 1

2 1

3 2 1 1

3

1 2 1

3 2 1 1

x x x x x y y

x x x

x y

x x

x

x x y

x x

        

 

    

  

 

     

 

  

 

Ta có

 

2

3

2

1 0; 0,

3

2 1 1

x

x y x

x x



     



 

dẫn đến

1

0 1

x



  

.

Khi đó

2

4 2

1

x

x x x



   

và

2

3 2 1, 1x x   

. Ta có các nhận xét

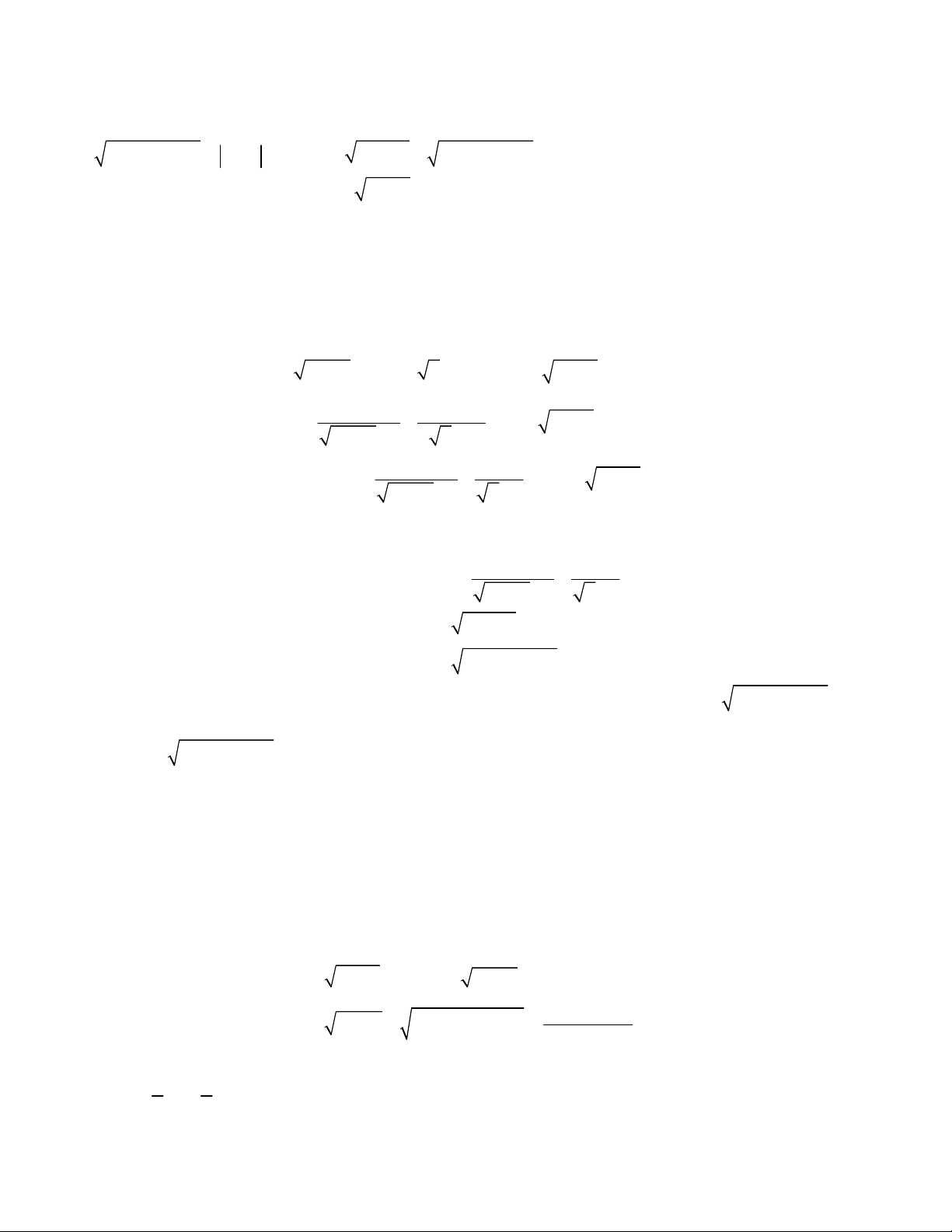
LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

99

   

 

   

4

2 2 2 2 2 2 2 2

2

2 2

2 2 4 2

3

2 1 3 2 1 2 1 2

0 2 3 2 1

x

y x y x y x x y

x

y x y x y x y x y



         

          

Từ đó

4 2 2 4 2

3

2 1 3 2 3 2 1 1

x

y x y x y x x y x y



            

.

Dấu đẳng thức xảy ra khi và chỉ khi

1

2

1

0

x

x y

y

x

x y





 





 





  

 



Kết luận hệ phương trình đã cho có nghiệm duy nhất

1x

y



.

N

h

ậ

n

x

é

t

.

B

à

i

t

o

á

n

s

ố

1

3

2

v

ì

p

h

ư

ơ

n

g

t

r

ì

n

h

t

h

ứ

n

h

ấ

t

c

ó

c

á

c

đ

ạ

i

l

ư

ợ

n

g

b

ậ

c

t

h

ấ

p

h

ơ

n

ê

n

t

a

s

ẽ

c

h

u

y

ể

n

t

r

ọ

n

g

t

â

m

t

ấ

n

c

ô

n

g

đ

ố

i

t

ư

ợ

n

g

n

à

y

.

T

h

o

ạ

t

i

ê

n

q

u

a

n

s

á

t

c

h

ú

n

g

t

a

t

h

ấ

y

l

ạ

i

c

ó

y

ế

u

t

ố

d

í

n

h

k

é

p

g

â

y

b

ấ

t

l

ợ

i

c

h

o

v

i

ệ

c

ô

l

ậ

p

b

i

ế

n

,

n

h

ư

n

g

c

h

ú

ý

m

ộ

t

c

h

ú

t

s

ẽ

t

h

ấ

y

n

ó

p

h

ụ

c

v

ụ

c

h

o

h

ằ

n

g

đ

ẳ

n

g

t

h

ứ

c

–

d

ự

k

i

ế

n

đ

ơ

n

v

ị

q

u

y

ế

t

đ

ị

n

h

d

ấ

u

 

;M

x y

 

   

 

2

3 2 1 1 2 2 1 2 1

3 1 1

2 1

3 2 1 1

3

1 2 1

3 2 1 1

x x x x x y y

x x x

x y

x x

x

x x y

x x

        

 

    

  

 

     

 

  

 

Tổng thể biểu thức biến x ta sử dụng phép liên hợp công phá, một điều chú ý hơn là biểu thức liên hợp xuất hiện

biến số trên tử thức, vẫn chỉ là một biến, sẽ phức tạp hơn rất nhiều nếu có sự tham gia của hai biến

   

2

3

;

;0

3

2 1 1

x

T

x y T x

x x

  



 

.

Tương tự bài toán số 131, tách tương đồng đánh giá

 

2

4

2

3 2 1 1

3 2 1 2

x

x y x y









  







Rõ ràng (1) tất yếu do miền giá trị

1 0 1x x   

. Vì bất đẳng thức cùng chiều nên cần

4 2

3

2 1

x

y x y



  

.

Biến đổi tương đương

 

4

2 4 2 2 2 4 2 2

2

4 4 2

4 2 2 2

2

4 2

3

2 1 3 2 1 2 3 2 1 0

1

2 2 0

3 2 2 1 0

3 2 1 0

x y x y x y x xy y x x y xy

x x x x y

x x x xy y

x x x y



              





    



       



    



Hai hướng đi này đều khả quan vì

 

  

 

2

4 4 2 4 2 2

2 2

4 2 2 2

1 2 2 1 2 1 0, 1

3 2 1 0 1 3 1 0, 1

x x x x y x x x x y x

x x x y x x x y x

             

            

B

à

i

t

o

á

n

1

3

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

2

3

2 3 2 4 ,

;

4 3

3 2 2 2 .

2

x x y x y x

x y

x xy

y x y



     







 

    







.

Lời giải.

Điều kiện

2 2

;

3

y

x



. Phương trình thứ nhất của hệ tương đương với

LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

100

 

2

3 2 3 2 1 2 3 2 3 2

3 1

1

3 2

3 2 1

3 2

1 3

1 3 2

3 2 1

3 2

x x x y y x x

x x

x

y x

x

x x

x y x

x

         



    

 

 

 



     

 

 

 

 

Nhận xét

 

2

1 3 2

3

2 0; 0,

3

2 1

3 2

x x

y x x

x





     





 

nên

1

0 1

x



  

.

Khi đó áp dụng bất đẳng thức liên hệ trung bình cộng – trung bình nhân ta có

 

2

2 2

2

3 2 1 2 2 4 3 4 3

3 2 2 2

2 2 2 2

y x y x y x xy

y x y

        

        .

Do đó phương trình thứ hai có nghiệm khi dấu đẳng thức xảy ra tức là

2

3

2 1

1

2 2

y y

x

y

x y

  







 



  



Kết luận hệ ban đầu có nghiệm duy nhất

1x

y



.

N

h

ậ

n

x

é

t

.



L

ư

u

ý

d

ạ

n

g

p

h

ư

ơ

n

g

t

r

ì

n

h

c

h

ố

t

c

h

ặ

n

s

ử

d

ụ

n

g

l

i

ê

n

h

ợ

p

–

t

r

ụ

c

ă

n

t

h

ứ

c

     

;

. ; ;

f

x y T x y g x y



.

V

ớ

i

t

ậ

p

x

á

c

đ

ị

n

h

D

,

t

a

c

ó

 

;

0, ;

T

x y x y D



 

.

Đ

ơ

n

v

ị

q

u

y

ế

t

đ

ị

n

h

m

i

ề

n

g

i

á

t

r

ị

m

ộ

t

b

i

ế

n

c

ó

t

h

ể

x

o

a

y

c

h

u

y

ể

n

q

u

a

n

h

   

 

;

; , ;

;

f x y Q

f x y g x y

g x y Q















M

ộ

t

r

o

n

g

h

a

i

đ

ơ

n

v

ị

   

;

, ;

f

x y g x y

k

h

ô

n

g

â

m

đ

ể

p

h

ụ

c

v

ụ

đ

ơ

n

v

ị

Q

p

h

á

t

h

u

y

h

i

ệ

u

q

u

ả

.

C

h

ú

n

g

t

a

đ

ã

b

i

ế

t

l

ú

c

đ

ó

     

1

1 1 1 2

1 1 1 1 2

; ; ;

f x y mU n h x y p h x y

g x y mU n h x y p h x y

  



  





T

r

i

ể

n

k

h

a

i

m

ứ

c

đ

ộ

p

h

ứ

c

t

ạ

p

đ

ư

ợ

c

t

ù

y

n

g

h

i

l

ự

a

c

h

ọ

n

.



C

á

c

b

ạ

n

đ

ề

u

c

ó

t

h

ể

n

h

ậ

n

t

h

ấ

y

b

à

i

t

o

á

n

s

ố

1

3

c

ó

p

h

ư

ơ

n

g

t

r

ì

n

h

t

h

ứ

n

h

ấ

t

đ

ư

ợ

c

x

â

y

d

ự

n

g

k

h

é

o

l

é

o

,

t

r

ư

ớ

c

h

ế

t

l

à

h

ì

n

h

t

h

ứ

c

n

g

ắ

n

g

ọ

n

h

ư

n

g

s

ự

g

ắ

n

k

ế

t

c

ă

n

t

h

ứ

c

h

ỗ

n

t

ạ

p

đ

ậ

p

t

a

n

h

y

v

ọ

n

g

c

ô

l

ậ

p

h

a

i

b

i

ế

n

;x y

.

V

ớ

i

t

ư

t

ư

ở

n

g

á

p

đ

ặ

t

n

g

h

i

ệ

m

đ

ẹ

p

đ

ẽ

1x

y



,

đ

ạ

i

l

ư

ợ

n

g

k

h

ô

n

g

â

m

 

;g

x y

d

ự

a

t

r

ê

n

t

ư

t

ư

ở

n

g

t

h

u

ầ

n

t

ú

y

v

ớ

i

b

ì

n

h

p

h

ư

ơ

n

g

h

i

ệ

u

 

2

k

a b



,

đ

ả

m

b

ả

o

d

ấ

u

đ

ẳ

n

g

t

h

ứ

c

x

ả

y

r

a

k

h

i

1a

b x y



  

.

C

h

i

a

s

ẻ

v

ề

p

h

ư

ơ

n

g

c

á

c

h

t

h

i

ế

t

l

ậ

p

đ

ơ

n

v

ị

 

;g

x y

,

b

ạ

n

đ

ọ

c

ó

t

h

ể

c

ó

n

h

i

ề

u

l

ự

a

c

h

ọ

n

 

2

2 2

; 2 1 ; ; 1 3 1 ; ; 1 3 ;...

g x y x y g x y x y g x y y x          



V

à

h

ơ

n

t

h

ế

n

ữ

a

.

T

u

y

n

h

i

ê

n

đ

ể

ý

r

ằ

n

g

p

h

ư

ơ

n

g

t

r

ì

n

h

t

h

ứ

n

h

ấ

t

v

ố

n

đ

ã

c

ầ

n

c

á

c

ă

n

t

h

ứ

c

m

ộ

t

b

i

ế

n

x

đ

ể

p

h

ụ

c

v

ụ

l

i

ê

n

h

ợ

p

đ

á

n

h

g

i

á

m

i

ề

n

g

i

á

t

r

ị

x

,

n

ế

u

c

h

ọ

n

l

ự

a

n

h

ư

t

h

ế

v

ô

t

ì

n

h

l

à

m

c

h

o

x

u

ấ

t

h

i

ệ

n

3

c

ă

n

t

h

ứ

c

t

r

ở

l

ê

n

,

h

ì

n

h

t

h

ứ

c

b

à

i

t

o

á

n

c

ồ

n

g

k

ề

n

h

m

à

k

h

ó

g

i

ấ

u

đ

ư

ợ

c

ý

đ

ồ

b

a

n

đ

ầ

u

c

ủ

a

c

h

ú

n

g

t

a

,

n

h

ư

b

à

i

t

o

á

n

s

ố

1

3

2

.

Ở

đ

â

y

t

á

c

g

i

ả

đ

ã

l

ự

a

c

h

ọ

n

t

r

ù

n

g

l

ặ

p

c

ă

n

t

h

ứ

c

t

h

ứ

h

a

i

t

ứ

c

l

à

 

2

; 3 2

g x y y x  

c

ũ

n

g

v

ì

n

h

ữ

n

g

l

ý

d

o

n

h

o

n

h

ỏ

đ

ó

.



Đ

ố

i

v

ớ

i

p

h

ư

ơ

n

g

t

r

ì

n

h

t

h

ứ

h

a

i

c

ủ

a

h

ệ

,

ý

t

ư

ở

n

g

đ

á

n

h

g

i

á

b

ấ

t

đ

ẳ

n

g

t

h

ứ

c

l

à

h

o

à

n

t

o

à

n

t

ự

n

h

i

ê

n

v

ì

h

a

i

v

ế

c

ó

s

ự

x

u

ấ

t

h

i

ệ

n

c

ủ

a

2

x

t

ư

ơ

n

g

ứ

n

g

t

r

o

n

g

c

ă

n

,

n

g

o

à

i

c

ă

n

.

S

ự

b

ằ

n

g

n

h

a

u

c

ủ

a

h

a

i

n

h

â

n

t

ử

2

2; 2

x y

 

g

ợ

i

ý

đ

ế

n

b

ấ

t

đ

ẳ

n

g

t

h

ứ

c

l

i

ê

n

h

ệ

t

r

u

n

g

b

ì

n

h

c

ộ

n

g

–

t

r

u

n

g

b

ì

n

h

n

h

â

n

(

A

M

–

G

M

h

a

y

C

a

u

c

h

y

)

,

t

u

y

n

h

i

ê

n

l

à

đ

á

n

h

g

i

á

t

r

ộ

i

,

n

g

h

ĩ

a

l

à

v

ế

t

r

á

i

n

h

ỏ

t

h

u

a

v

ế

p

h

ả

i

,

b

ư

ớ

c

đ

ầ

u

đ

ã

t

h

o

á

t

k

h

ỏ

i

k

ì

m

h

ã

m

đ

á

n

h

g

i

á

g

i

ả

m

v

ế

t

r

á

i

p

h

ư

ơ

n

g

t

r

ì

n

h

 

2

2 2

2

3 2 1 2 2 4 3 4 3

3 2 2 2

2 2 2 2

y x y x y x xy

y x y

        

       

.

LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

101



S

a

u

k

h

i

x

ử

l

ý

đ

ế

n

b

ư

ớ

c

2

4 3

2

x y

 

t

h

ấ

y

s

a

i

k

h

á

c

h

ú

t

í

t

v

ớ

i

2

4 3

2

x xy

 

,

l

ú

c

n

à

y

m

i

ề

n

g

i

á

t

r

ị

1x 

p

h

á

t

h

u

y

t

á

c

d

ụ

n

g

,

k

h

i

m

à

2

4

4 , 1; 0

3

y

xy x y



    

.

B

à

i

t

o

á

n

1

3

4

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

    

   

 

3

43 10 7 4 3 4 ,

;

3 7 3 4 3 6 5 7 4.

y x y x

x y

x y x x y y



   







     







.

Lời giải.

Điều kiện

7

4 0;3 4 0

y

x



  

.

Phương trình thứ hai của hệ tương đương với

     

 

2

3 7 3 4 3 7 7 4 5 7 4

3 7 3 4 7 4 5 7 4

3 7

5 7 4

3 4 7 4

x y x x y y y y

x y x y y y

x y

y y

x y

       

       



   

  

Vì

 

2

3

7

0

; 7 4 0 5 0

3

4 7 4

x y

y y

x y





    



 

.

Khi đó áp dụng bất đẳng thức liên hệ trung bình cộng – trung bình nhân ta có

       

   

10 7 4 3 4 5.2 7 4 3 4 5 3 4 7 4

5 3 7 8 5.3 35 40 .3 35 8 3 43

y x y x x y

x y x y y x y y y x

        

          

Phương trình thứ hai của hệ có nghiệm khi

3 7

35

; 5

5

3

x y

y





  







.

N

h

ậ

n

x

é

t

.

B

à

i

t

o

á

n

s

ố

1

3

4

t

á

c

g

i

ả

t

r

í

c

h

l

ư

ợ

c

t

r

o

n

g

m

ộ

t

à

i

l

i

ệ

u

,

k

h

ô

n

g

r

õ

t

á

c

g

i

ả

,

k

h

i

n

h

ậ

n

t

h

ấ

y

s

ự

t

ư

ơ

n

g

đ

ồ

n

g

ý

t

ư

ở

n

g

v

ớ

i

t

à

i

l

i

ệ

u

n

à

y

,

t

h

u

ộ

c

l

ớ

p

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

s

ử

d

ụ

n

g

c

h

ặ

n

m

i

ề

n

g

i

á

t

r

ị

–

b

ấ

t

đ

ẳ

n

g

t

h

ứ

c

–

h

à

m

s

ố

.

C

á

c

b

ạ

n

c

ó

t

h

ể

c

ó

m

ộ

t

s

ố

q

u

a

n

s

á

t

n

h

ư

s

a

u

o

P

h

ư

ơ

n

g

t

r

ì

n

h

t

h

ứ

h

a

i

c

ủ

a

h

ệ

g

ợ

i

ý

t

ư

ở

n

g

l

i

ê

n

h

ợ

p

   

3 7 3 4 3 6 5 7 4

3 7 3 4 3 7 5 7 4

x y x x y y

x y x x y y y

     

       

o

H

i

ệ

u

h

a

i

c

ă

n

t

h

ứ

c

t

h

i

ế

t

l

ậ

p

b

ì

n

h

p

h

ư

ơ

n

g

h

i

ệ

u

 

     

2

3

7 . 3 7 3 7

3 7 3 4 7 4

3

4 7 4 3 4 7 4

x

y x y x y

x y x y

  

     



    

.

o

Đ

i

ể

m

ú

t

 

35

5

0 5 ; ;5

3

y

y x y







    





 

k

h

i

3 7x y

.

o

S

ự

x

u

ấ

t

h

i

ệ

n

c

ủ

a

3x

t

ạ

i

h

a

i

v

ế

p

h

ư

ơ

n

g

t

r

ì

n

h

t

h

ứ

n

h

ấ

t

d

ẫ

n

d

ắ

t

b

ấ

t

đ

ẳ

n

g

t

h

ứ

c

A

M

–

G

M

         

10 7 4 3 4 5.2 7 4 3 4 5 3 4 7 4 5 3 7 8

y x y x x y x y

           

.

L

ư

u

ý

n

ế

u

v

ộ

i

v

à

n

g

s

ử

d

ụ

n

g

á

p

đ

ặ

t

đ

i

ề

u

k

i

ệ

n

t

ì

m

đ

ư

ợ

c

5

y



s

ẽ

b

ị

v

ư

ớ

n

g

v

ì

   

5

3 7 8 3 7 8

x

y y x y



   

v

à

c

ầ

n

c

h

ứ

n

g

m

i

n

h

3

7 8 3 43 5

x

y x y



    

,

n

g

ư

ợ

c

.

C

ầ

n

k

h

é

o

l

é

o

v

à

n

h

ẹ

n

h

à

n

g

c

h

i

a

c

ắ

t

c

á

c

đ

ơ

n

v

ị

đ

ố

i

p

h

ư

ơ

n

g

   

5

3 7 8 5.3 35 40 .3 35 8 3 43

x

y x y y x y y y x         

.

S

ở

d

ĩ

n

h

ư

t

h

ế

v

ì

c

ầ

n

đ

ể

ý

t

r

i

ệ

t

i

ê

u

h

a

i

đ

ạ

i

l

ư

ợ

n

g

t

r

ù

n

g

l

ặ

p

3xy

.

C

ó

t

h

ể

t

h

ô

n

g

q

u

a

b

ắ

c

ầ

u

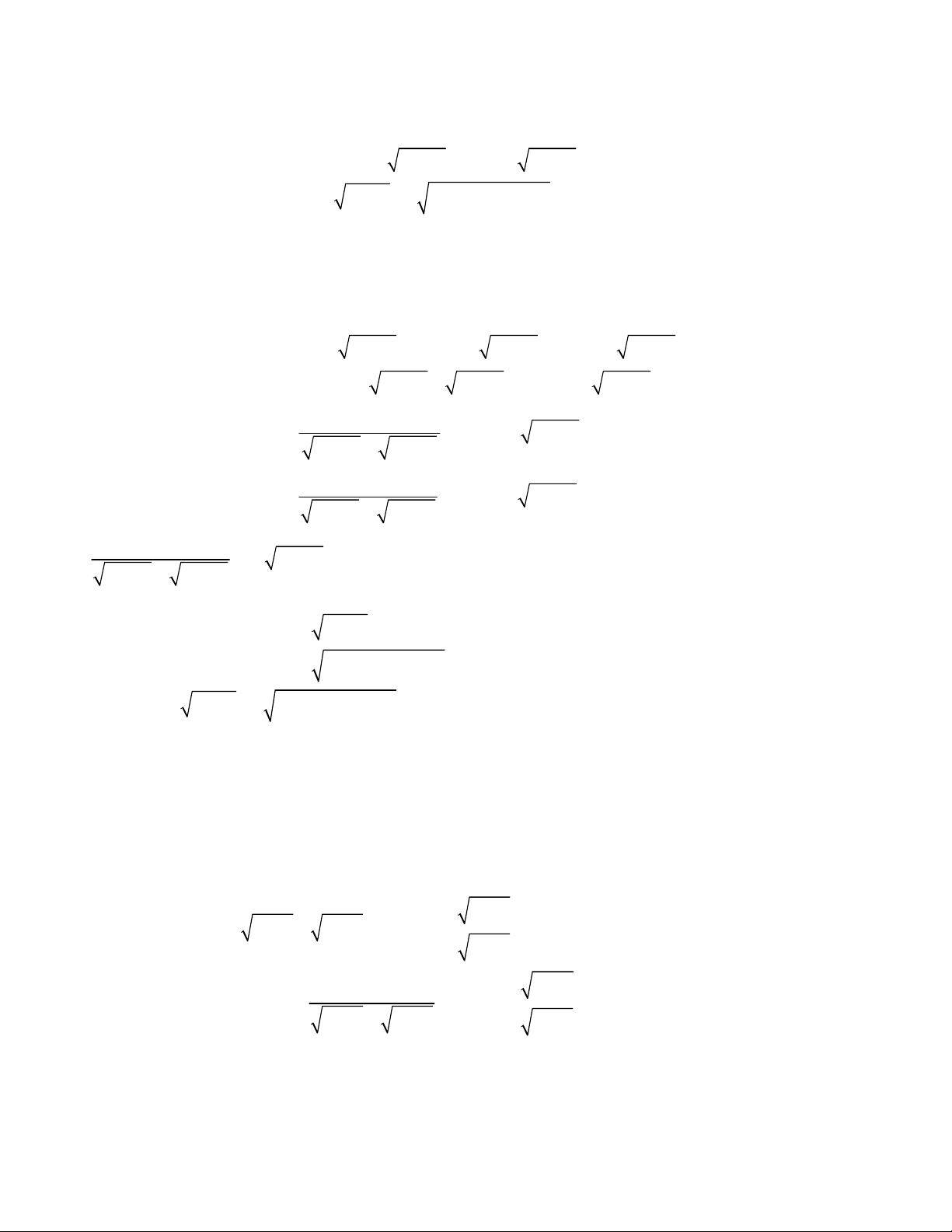
LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

102

 

5 3 7 8 15 35 40 3 35 40

3 35 40 3 43 8 40 5

x y x y xy y

xy y xy y y y

       

       

B

à

i

t

o

á

n

1

3

5

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

   

 

3

3 3 3

2

3 2 5 ,

;

4 3 2 1 10 1 18 .

x y x y x x y

x y

y x y x y y



    







      







.

Lời giải.

Điều kiện

 

3

0; 5 0; 3 0

1

10 1 0

x y x y y

x y





    







 





Phương trình thứ nhất của hệ tương đương với

     

 

   

 

2

2 3 2 5 2 1 5

2 3 5 2 1 5

2 .2 2

2 1 5

3 5

2 2

2 1 5

3 5

x y x y x y x y y x y

x y x y x y y x y

x y x y

y x y

x y x y

x y

y x y

x y x y

       

       

 

   

  



   

  

Ta có

 

2

0

, 5 0 1 0 1

3 5

x y

x

y y y

x y x y





      

  

, do đó

3

10 1 0 1 0

y x

    

.

Áp dụng bất đẳng thức liên hệ trung bình cộng – trung bình nhân AM – GM ta có

 

3

3 3

3 3 3

4 3 4 4 8

2 1 10 1 1 10 1 10

y y y

x y x y x y

     

       

Kết hợp

 

3

3 3 3 3 3 3 3

1

4 3 2 1 10 1 10 8 10 8 18

y

y x y x y y x y y y x y y



               

.

Phương trình thứ hai của hệ có nghiệm khi các dấu đẳng thức xảy ra tức là

3

4

2

10

1 1

1

y

x

y

x

y



 









  

 











Thử lại trên toàn bộ hệ ta thu được nghiệm

2; 1x y 

.

N

h

ậ

n

x

é

t

.



T

ổ

n

g

q

u

á

t

d

à

n

h

c

h

o

p

h

ư

ơ

n

g

t

r

ì

n

h

q

u

y

ế

t

đ

ị

n

h

m

i

ề

n

g

i

á

t

r

ị

,

m

o

t

i

p

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

s

ố

1

3

4

     

   

; .

h x y f x

mx ny f x g y

h x y g y



 



  

 





t

h

ỏ

a

m

ã

n

     

f

x g y k mx ny



 

.

K

h

i

đ

ó

s

ẽ

x

u

ấ

t

h

i

ệ

n

h

ệ

q

u

ả

 

   

2

; .

h x y f x

k mx ny

f x g y

h x y g y

















R

õ

r

à

n

g

l

à

 

;h x y

t

h

i

ê

n

b

i

ế

n

v

ạ

n

h

ó

a

,

t

ạ

m

d

ừ

n

g

c

h

â

n

v

ớ

i

m

ộ

t

ẩ

n

.

Đ

ố

i

v

ớ

i

b

à

i

t

o

á

n

s

ố

1

3

5

n

à

y

,

b

a

n

đ

ầ

u

t

á

c

g

i

ả

l

ự

a

c

h

ọ

n

 

;

1

h

x y y





t

h

ô

i

,

n

h

ư

n

g

m

à

c

h

ợ

t

h

ấ

y

n

h

ư

t

h

ế

h

ơ

i

l

ộ

l

i

ễ

u

v

ì

2

x

y x y





n

g

h

e

c

h

ừ

n

g

n

ó

“

t

h

â

n

t

h

i

ế

t

”

q

u

á

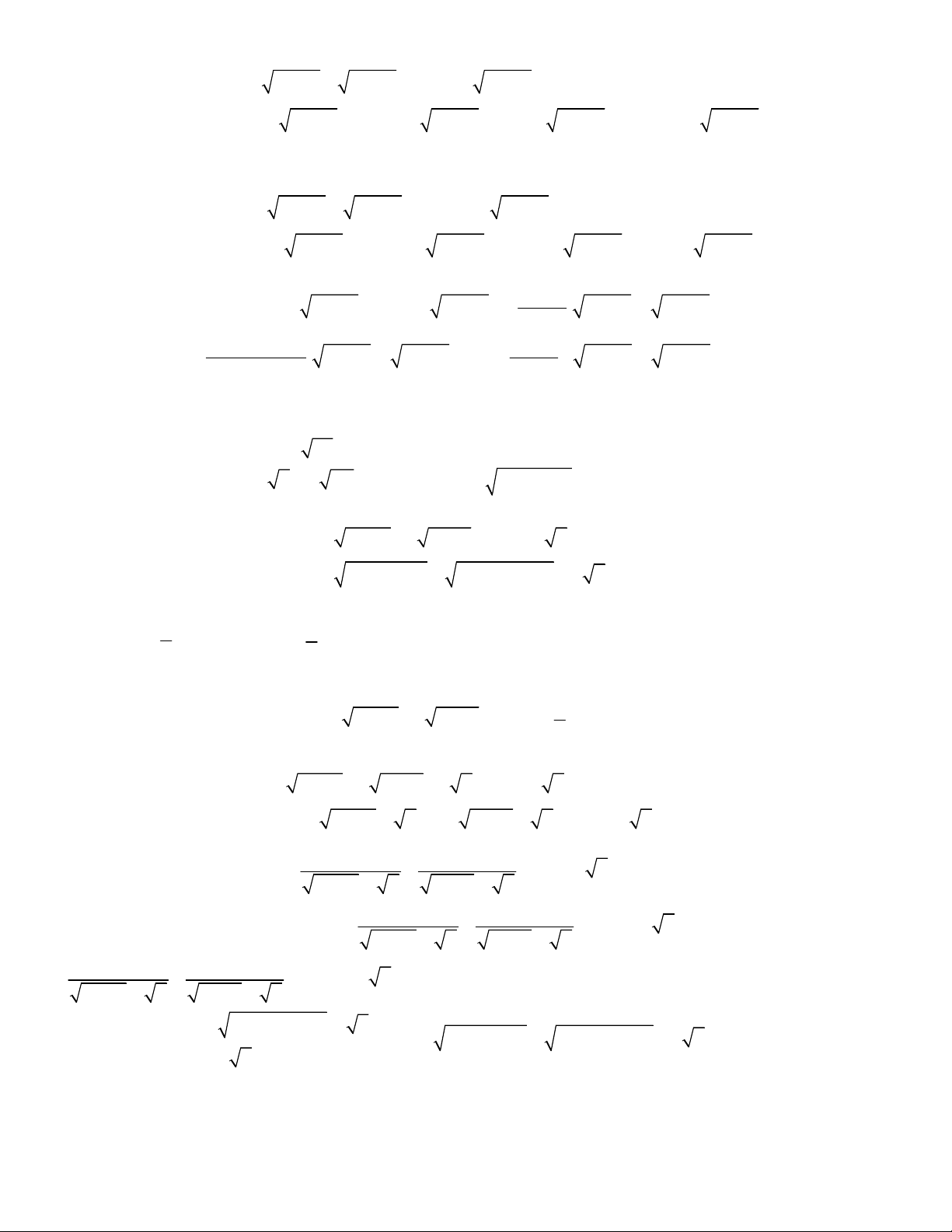
LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

103

 

       

2

3 5 1 5

2

3 2 5 1 5 1 5

x

y x y x y y x y

x

y x y x y x y y x y x y x y



     

            



R

ắ

p

t

â

m

l

à

m

c

h

o

n

ó

k

h

ô

n

g

n

g

ó

c

đ

ầ

u

d

ậ

y

đ

ư

ợ

c

,

k

h

u

y

n

h

ư

ớ

n

g

ọ

n

g

à

n

g

t

r

i

ệ

t

i

ê

u

ẩ

n

y

,

m

ạ

o

m

u

ộ

i

c

h

ọ

n

l

ự

a

đ

a

t

h

ứ

c

   

;

2 1

h

x y y





 

       

2

3 5 2 1 5

2

3 2 5 2 1 5 2 5

x

y x y x y y x y

x

y x y x y x y y x y x x y



     

           

C

á

c

b

ạ

n

c

ó

t

h

ể

d

ọ

a

m

a

c

h

o

á

n

t

â

m

l

ý

b

ằ

n

g

b

i

ế

n

đ

ổ

i

   

2

3 2 5 . 3 5

2

x y

x

y x y x x y x y x y

x



       



.

H

o

ặ

c

t

i

ế

p

t

ụ

c

2

2 2 2 2

.

3 5 1 . 3 5

2

x y y

x

y x y x y x y

x

   

 

       

 

 

 

.



Đ

ố

i

v

ớ

i

p

h

ư

ơ

n

g

t

r

ì

n

h

t

h

ứ

h

a

i

c

ủ

a

h

ệ

,

đ

ể

á

p

d

ụ

n

g

đ

ư

ợ

c

b

ấ

t

đ

ẳ

n

g

t

h

ứ

c

l

i

ê

n

h

ệ

t

r

u

n

g

b

ì

n

h

c

ộ

n

g

–

t

r

u

n

g

b

ì

n

h

n

h

â

n

h

ấ

t

h

i

ế

t

c

á

c

b

ạ

n

c

ầ

n

c

ó

3

10 1 0 1 0

y x

    

,

đ

ơ

n

g

i

ả

n

v

ì

đ

i

ề

u

k

i

ệ

n

t

i

ê

n

q

u

y

ế

t

l

à

c

á

c

h

ạ

n

g

t

ử

t

h

a

m

g

i

a

k

h

ô

n

g

â

m

,

d

ạ

n

g

t

h

ứ

c

2

ab a b 

k

h

i

;

0

a

b



.

Đ

ơ

n

c

ử

c

h

ú

n

g

t

a

c

ó

2 2 2 2.1 2 1  

đ

ú

n

g

v

à

       

2 2 . 1 2 1     

s

a

i

.

B

à

i

t

o

á

n

1

3

6

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

2

3 3

2

3 2 3 2 1 4 ,

;

7 4 5 2 3.

x x y x

x y

y y x y xy y x



    







      







.

Lời giải.

Điều kiện

2

3

1

5

4

5 0

x

y y





 



 

 



  



 



Từ phương trình thứ nhất của hệ ta có

2

3 2 3 2 1 0, 4 0 4

3

x

x x y y



          

.

Kết hợp điều kiện thu được

1y 

, lúc này biến đổi phương trình thứ nhất

 

   

 

   

 

   

2 3 2 3 2 1 5 1

2 3 2 3 2 1 1

4 1 3 1

1

3 2 2 1

4 3

1 1

3 2 2 1

x x x y x

x x x x y x

x x

y x

x x x x

x y x

x x x x

     

       

 

   

   

 

    

 

   

 

Vì

 

4 3

0; 1 0, 1 1 0 1

3 2 2 1

y x y x x

x x x x

          

   

.

Kết hợp

3 3

2 3 3

1

0

2 4 2

7

4 5 2 3

1 0

1

x

x y xy

y y x y xy y x

y

y x



 

   







       



 









.

Toàn bộ các dấu đẳng thức xảy ra khi và chỉ khi

1x

y



, cặp số này thỏa mãn hệ ban đầu.

N

h

ậ

n

x

é

t

.

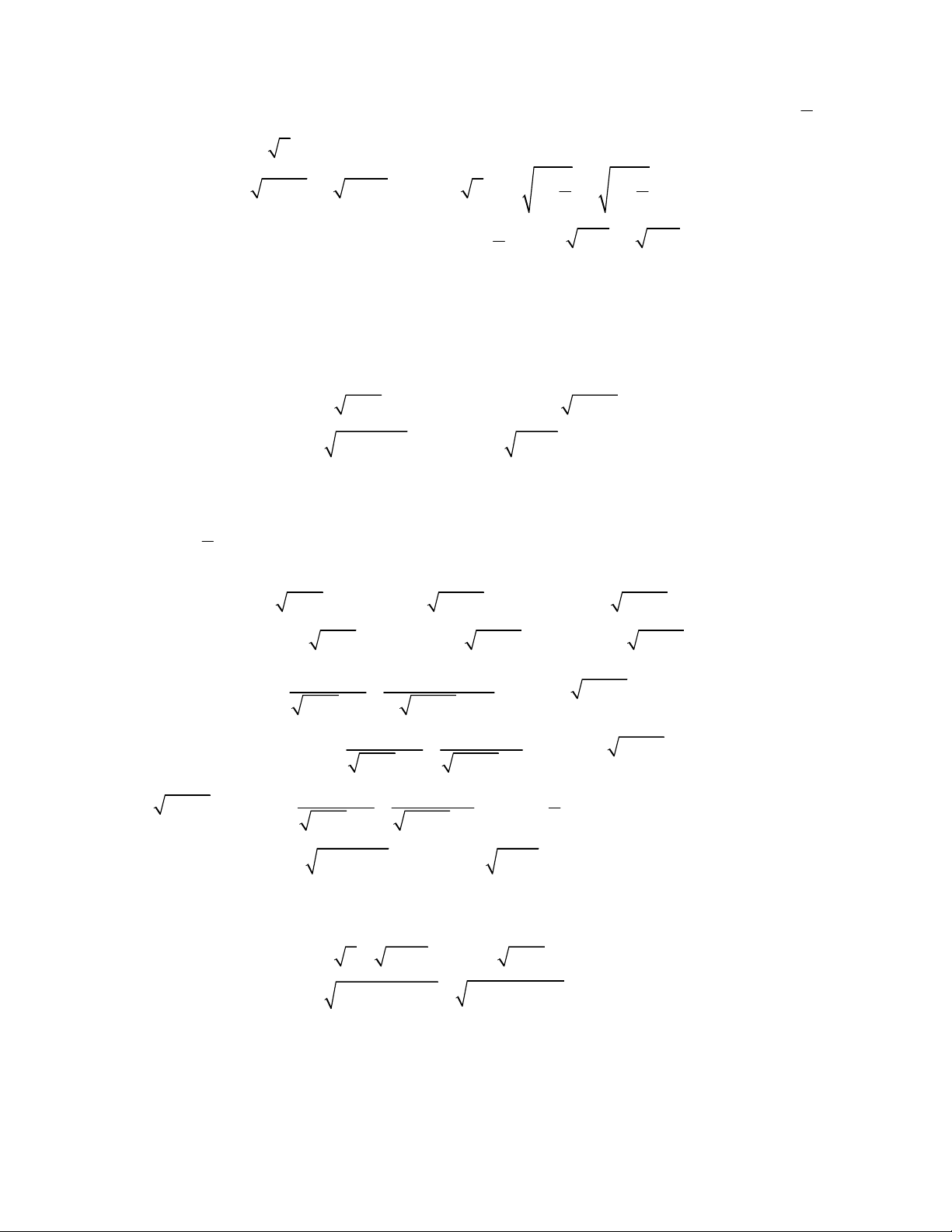
LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

104

Đ

ố

i

v

ớ

i

b

à

i

t

o

á

n

s

ố

1

3

6

n

à

y

,

c

ả

m

g

i

á

c

đ

ầ

u

t

i

ê

n

l

à

h

a

i

b

i

ế

n

đ

ã

m

a

y

m

ắ

n

đ

ư

ợ

c

b

ố

t

r

í

c

h

o

c

h

ú

n

g

t

a

d

ạ

n

g

c

ô

l

ậ

p

.

T

h

à

n

h

t

h

ử

k

h

ô

n

g

p

h

á

n

đ

o

á

n

đ

ư

ợ

c

n

g

h

i

ệ

m

1x 

đ

ể

t

i

ế

n

h

à

n

h

l

i

ê

n

h

ợ

p

,

m

ộ

t

s

ố

b

ạ

n

d

ự

a

t

r

ê

n

c

ơ

s

ở

2

3

x



,

c

h

i

a

c

ả

h

a

i

v

ế

p

h

ư

ơ

n

g

t

r

ì

n

h

t

h

ứ

n

h

ấ

t

c

h

o

x

,

đ

ư

a

v

ề

d

ạ

n

g

 

2 1

2

3 2 3 2 1 4 2 3 3 2 4

x

x y x y

x x



         

.

S

a

u

đ

ó

t

ấ

t

y

ế

u

đ

ặ

t

ẩ

n

p

h

ụ

v

à

h

y

v

ọ

n

g

t

ấ

n

c

ô

n

g

t

h

e

o

l

ố

i

m

ò

n

1

2

3 3 2 4

t

t t y

x



     

.

M

ộ

t

đ

i

ề

u

k

h

ô

n

g

m

a

y

x

ả

y

r

a

,

đ

i

ề

u

k

i

ệ

n

x

á

c

đ

ị

n

h

y

c

ủ

a

m

ì

n

h

l

à

h

a

i

t

ậ

p

h

ợ

p

r

ờ

i

n

h

a

u

1 5

y y

   

,

n

h

ư

v

ậ

y

đ

á

n

h

g

i

á

t

h

e

o

m

ộ

t

c

h

i

ề

u

l

à

k

h

ó

k

h

ă

n

v

à

k

h

ô

n

g

t

o

à

n

v

ẹ

n

.

Đ

ể

ý

m

ộ

t

c

h

ú

t

c

ó

t

h

ể

t

h

ấ

y

g

i

ả

n

l

ư

ợ

c

đ

i

đ

ư

ợ

c

đ

i

ề

u

k

i

ệ

n

à

y

,

b

ằ

n

g

c

á

c

h

s

ử

d

ụ

n

g

đ

i

ề

u

k

i

ệ

n

c

ó

n

g

h

i

ệ

m

n

g

a

y

c

h

í

n

h

p

h

ư

ơ

n

g

t

r

ì

n

h

t

r

ê

n

4 0

1

1 5

y

y y

 



 



   



.

B

à

i

t

o

á

n

1

3

7

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

3

3 3 1 4 4 3,

;

2 2 1 2.

x x x y x x

x y

x y x y y



      







      







.

Lời giải.

Điều kiện

3

2

0

3

1

;

4

x

y

y x





 





 





Phương trình thứ nhất của hệ tương đương với

 

    

 

3

2 3 4 3 3 1 4 3

3

2 3 4 3 1 1 4 3

1 4 3 1

1 4 3

3 2 4 3 1

4 3

1 1 4 3

3

2 4 3 1

x x x x x x y x

x x x x y x

x x x x

y x

x x

x

x y x

x x

         



        

  

    

   



 

     

 

   

 

Lại có

 

3

4 3

3

1

4 3 0, 1; 0,

4

3

2 4 3 1

x

y x y x

x x





       



  

dẫn đến

1

0 1

x



  

.

Khi đó

 

3 3

3

2

0

1

2

2 1 2

1

2

4

x y

x

x y x y y

y

x y

  







       





  



.

Phương trình thứ hai của hệ có nghiệm khi dấu đẳng thức xảy ra tức là

1x y 

.

B

à

i

t

o

á

n

1

3

8

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

  

 

5

3 2

2 3 1 1 3,

;

1 4 2 .

x x y x

x y

y y x x y x y



    







      







.

Lời giải.

Điều kiện

  

5

3 2

5 3 2

0

1 4 0 1 4

2 0

x

y y y y

x x y











       

 

 

  



Từ phương trình thứ nhất của hệ ta có

1

0 1

y



   

, kết hợp điều kiện ta được

1y 

.

LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

105

 

   

 

   

2

3 3 1 3 1 3

3 1 2 1

1 3

2 3 3 1 3

3 2

1

1 3

2

3 3 1 3

x x x x y x

x x

y x

x x x x

x y x

x x x x

        

 

    

    

 



    





    

 

Ta có

 

3 2

0, 1 3 0, 1

2 3 3 1 3

y x y

x x x x

      

    

dẫn đến

1

0 1

x



  

.

Khi đó ta để ý

 

5

3 2 2 3 5 3 2 2 2

2

2 0 2 2 2

x

x x x x x x x y x y



         

.

Hơn nữa

   

2 2

2 2 2 2

0 2 2 2 2

x y x y x y x y x y x y           

, dẫn đến

  

5

3 2 2 2 5 3 2

2 2 2 1 4 2

x x y x y x y y y x x y x y             

.

Phương trình thứ hai của hệ có nghiệm khi và chỉ khi

1

x

x y





  







.

B

à

i

t

o

á

n

1

3

9

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

3

2 2

6 2 8 2 0,

;

1 3 5 4.

y x x x

x y

y x xy y



     







     





.

Lời giải.

Điều kiện

2

0 2; 1; 3 5 0

x y x xy y

     

.

Phương trình thứ nhất tương đương với

 

   

 

3

6

2 8 2 1

2 3 8 2 1

2 1 2 1

1

3 8 2

2 2

1 1

3 8 2

x x x x y x

x x

y x

x x x x

x y x

x x x x

       

       

 

   

   

 

    

 

   

 

Ta có

 

3

2 2

0; 1 0, 1 1 0 1

3 8 2

y x y x x

x x x x

          

   

.

Khi đó

2

2 3 2 2

1; 1 3 5 9 1 3 5 3

x y x xy y y x xy y

           

.

Phương trình thứ hai có nghiệm khi các dấu đẳng thức xảy ra, tức là

1x y 

. Hệ có nghiệm duy nhất.

Nhận xét.

D

ạ

n

g

t

h

ứ

c

     

;

. ; ;

f

x y T x y g x y



.

       

   

 

       

     

 

136

3

137

138

3

139

4 3

; 1; ; ; ; 1

3 2 2 1

4 3

; 1; ; ; ; 1 4 3

3 2 4 3 1

3 2

; 1; ; ; ; 1 3

2 3 3 1 3

2 2

; 1; ; ; ; 1

3 8 2

Q f x y x T x y g x y y x

x x x x

x

Q f x y x T x y g x y y x

x x

Q f x y x T x y g x y y x

x x x x

Q f x y x T x y g x y y x

x x x x

      

   



       

   

       

    

      

   

LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

106

T

r

ả

i

d

ọ

c

t

h

e

o

t

u

y

ế

n

đ

ư

ơ

n

g

1

3

6

–

1

3

9

,

c

á

c

b

ạ

n

c

ó

t

h

ể

t

h

ấ

y

đ

ạ

i

l

ư

ợ

n

g

q

u

y

ế

t

đ

ị

n

h

m

i

ề

n

g

i

á

t

r

ị

m

ộ

t

b

i

ế

n

Q

l

à

đ

ơ

n

g

i

ả

n

d

ư

ớ

i

d

ạ

n

g

n

h

ị

t

h

ứ

c

b

ậ

c

n

h

ấ

t

,

t

u

y

n

h

i

ê

n

đ

ơ

n

v

ị

 

;g

x y

c

ò

n

l

ạ

i

p

h

ù

t

r

ợ

Q

,

v

ẫ

n

x

u

ấ

t

h

i

ệ

n

v

ớ

i

h

a

i

b

i

ế

n

h

ư

n

g

t

r

ô

n

g

r

ấ

t

r

ơ

t

r

ụ

i

v

à

k

h

ó

b

ấ

u

v

í

u

,

k

h

ô

n

g

c

ò

n

l

à

d

ạ

n

g

b

ì

n

h

p

h

ư

ơ

n

g

q

u

e

n

t

h

u

ộ

c

,

c

ầ

n

h

ế

t

s

ứ

c

l

ư

u

t

â

m

đ

ế

n

đ

i

ề

u

k

i

ệ

n

x

á

c

đ

ị

n

h

c

ủ

a

b

à

i

t

o

á

n

,

t

h

ậ

m

c

h

í

l

à

đ

i

ề

u

k

i

ệ

n

c

ó

n

g

h

i

ệ

m

đ

ể

x

ử

l

ý

b

ằ

n

g

đ

ư

ợ

c

.

B

à

i

t

o

á

n

1

4

0

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

   

 

   

 

3

4

2

2 1 2 1 1 ,

;

2 1 5 27 2 1 2 1.

x x x x x y x

x y

y y x x



      







     







.

Lời giải.

Điều kiện

 

3

1

2

5 0

x

y













 



Từ phương trình thứ nhất của hệ ta có

   

3

1

2

2 1 2 1 0, 1 0 1

2

x

x x x x x y x y



            

.

Kết hợp điều kiện

 

3

1 5 0 1y y y    

. Phương trình thứ nhất tương đương

 

3

2

3

2 2 2 1 1

2

1

2 1

2 2

2

1

1 1

2 1

2 2

x x x x x y x

x x x

x

y x

x x

x x x

x y x

x x

x x x

       

 



   

 

  

 

 

 

    

 

 

  

 

Vì

 

2

3

2

1

0; 1 0 1 0 1

2 1

2 2

x x x

y x x x

x x

x x x

 

        

 

  

.

N

h

ậ

n

x

é

t

 

2

2 2 2 2

2

1 0 2 4 2 0 6 3 4 4 1 2 1

x

x x x x x x x



            

.

Áp dụng bất đẳng thức Bunyakovsky ta lại có

 

   

2

2 4 4

2 4 2 4

4

6 3 3 2. 2 3.1 18 9 2 1 27 2 1

6 3 27 2 1 2 1 6 3 27 2 1

x x x x

x x x x x

       

         

D

o

đ

ó

 

     

3

4 4

2

1 5 27 2 1 27 2 1 2 1

y

y x x x



      

.

Phương trình thứ hai của hệ có nghiệm khi các dấu đẳng thức xảy ra tức là

1x y 

.

B

à

i

t

o

á

n

1

4

1

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

  

 

2

3

2 2 1 1,

;

2 1 2 3 .

x y x y

x y

y x y x y



    







    







.

Lời giải.

Điều kiện

0

x

y











Phương trình thứ nhất của hệ tương đương với

LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

107

 

2

3

2 2 1 2 1

2 1

1

3 2 1

1 2

1

3

2 1

x x y x y y

y x

x

y

x x x

y

x y

x x x

      



   

  

 



   





  

 

Rõ ràng

 

2

1 2

1 0; 0, 0 1 0 1

3 2 1

y

y y x x

x x x

          

  

.

Áp dụng bất đẳng thức liên hệ trung bình cộng – trung bình nhân ta có

  

1 2 1 2 2 2 4

2 1 2 2 2 3

2

2 2

y x y x y

y

x y x y x y x x y

     



            

.

Do đó phương trình thứ hai có nghiệm khi dấu đẳng thức xảy ra tức là

1

2

1 2

x

y

x

y















 









 



Kết luận hệ phương trình có nghiệm duy nhất kể trên.

N

h

ậ

n

x

é

t

.

Đ

ố

i

v

ớ

i

c

á

c

b

ạ

n

đ

ộ

c

g

i

ả

c

h

ư

a

l

à

m

q

u

e

n

v

ớ

i

l

ớ

p

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

s

ử

d

ụ

n

g

l

i

ê

n

h

ợ

p

c

h

ặ

n

m

i

ề

n

g

i

á

t

r

ị

b

i

ế

n

k

ế

t

h

ợ

p

b

ấ

t

đ

ẳ

n

g

t

h

ứ

c

–

đ

á

n

h

g

i

á

t

h

ì

b

à

i

t

o

á

n

à

y

t

h

ự

c

s

ự

k

h

ó

.

C

ù

n

g

v

ớ

i

m

o

t

i

p

c

á

c

b

à

i

t

o

á

n

t

r

ư

ớ

c

,

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

s

ố

1

4

1

c

ó

đ

ạ

i

l

ư

ợ

n

g

t

h

a

m

g

i

a

l

i

ê

n

h

ợ

p

 

;T

x y

b

ắ

t

đ

ầ

u

x

u

ấ

t

h

i

ệ

n

h

a

i

ẩ

n

,

t

r

o

n

g

k

h

i

đ

ơ

n

v

ị

q

u

y

ế

t

đ

ị

n

h

m

i

ề

n

g

i

á

t

r

ị

v

à

đ

ơ

n

v

ị

c

ò

n

l

ạ

i

k

h

ô

n

g

q

u

á

k

h

ó

đ

ể

n

h

ậ

n

r

a

 

1 2 2

; 0; , 0

3

3 2 1

y

T x y x y

x x x

      

  

v

à

   

2

; 1

g x y y

 

.

B

à

i

t

o

á

n

1

4

2

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

2

1 4 3 1 ,

;

2 1 2 2 2 .

2

x x y x y y x x

x y

y x

y x x y x



      









      







.

Lời giải.

Điều kiện

3

1

2

; 2

4 2

x

y



  

.

Phương trình thứ nhất của hệ tương đương với

   

 

   

 

2

2 1 4 3 2 1

1 3 1

1

2 1 4 3

x x x y x x y y x

x x y x

y x

x x x x

       

 

   

   

   

2

3

1 1

2 1 4 3

x y

x y x

x x x x

 

    

 

   

 

.

Ta có

 

2

3

3 1

0

, ; 2 , ;2 ; 1 0

4

2

2 1 4 3

x y

x y y x

x x x x

   



      



  

   

   

nên

1

0 1

x



  

.

Á

p

d

ụ

n

g

b

ấ

t

đ

ẳ

n

g

t

h

ứ

c

l

i

ê

n

h

ệ

t

r

u

n

g

b

ì

n

h

c

ộ

n

g

–

t

r

u

n

g

b

ì

n

h

n

h

â

n

k

h

i

đ

ó

 

2

2 2

2 1 1 2 1 2

2 1 2 2

2 2 2

3 4

2

2 2 2

y x x y

x x y x y x y x

x

     

       

       

   

LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

108

Phương trình thứ hai có nghiệm khi dấu đẳng thức xảy ra tức là

2

1 2 1

2 1 1

1

0; 1

y x

x y x y

y

x



   



     







 



.

So sánh với điều kiện ta có nghiệm duy nhất

1x

y



.

B

à

i

t

o

á

n

1

4

3

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

3

2

2 1 2 ,

;

3 2 2 1 2 1.

x y x y y y x x y

x y

y x y x y



     







     







.

Lời giải.

Điều kiện

2

; 0

3

y x

 

. Phương trình thứ nhất tương đương với

   

 

   

    

   

2

2 2 2 1

2

2 2 2 1

1

2

2 2 2 1

1

2 2 2 2 1

x y x y x y x y y x y y

x y x y x y y x y y

x y x y y x

x y x y x y y

x y y x

x y x y x y y



       



       

  

 

     

 

 

     

Ta có

 

2

0

; 0,

3

2

2 2 2 1

x y

y

x y x y x y y





  



    

nên

1 0 1x x   

.

Khi đó

 

2

3

2 1 0, 1 2 2x x x x x

     

, kết hợp bất đẳng thức liên hệ trung bình cộng – trung bình nhân thì

 

3

3 2 1 2 1 4 2 2

3

2 2 1 2 1 2 1

2

2 2

x x y x y

y

x y x y x y

     



          

.

Phương trình thứ hai của hệ có nghiệm khi dấu đẳng thức đồng thời xảy ra , nghĩa là

3

2 1

2

1 1

1

y

x

y x y

x











   









.

So sánh với điều kiện ta có nghiệm duy nhất của hệ

1x

y



.

B

à

i

t

o

á

n

1

4

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

   

 

2

4 4 3

3

5 2 3 ,

;

3 2 1 1 2 .

x y x y x y y

x y

x x y x xy



    







      







.

Lời giải.

Điều kiện

2

0

2

0

3

0

3

2

y

x

xy

y

x









 

 

 

 





Phương trình thứ nhất của hệ tương đương với

     

 

2

3 2 3 1

3 2 3 1 3 1

3 2

x y x y x y y x y

x y

x

y x y y x y x y

x

y y

     



        

 

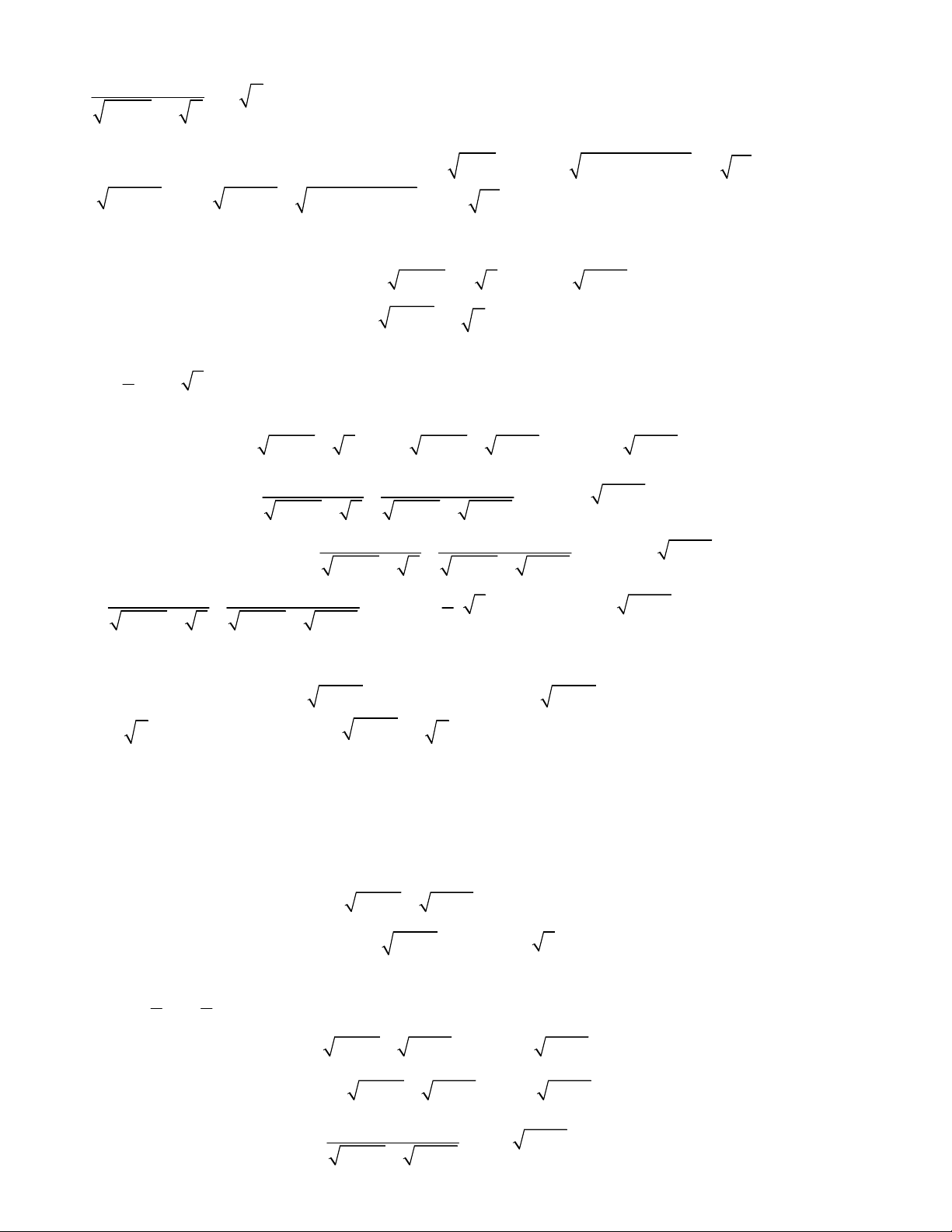
LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

109

Ta có

 

2

0; 0 1 0 1

3

2

x y

y x x

x

y y



      



.

Khi đó áp dụng bất đẳng thức liên hệ trung bình cộng – trung bình nhân ta có

4

4 3 4 4 4 4 4 4 3

4

1 1 1 4 4 1 2

x y x x y x y xy x y x xy

             

.

Lại có

2 2 4 4 3

3

2 1 3 2 1 1 2

x

x x y x xy



        

.

Phương trình thứ hai có nghiệm khi các dấu đẳng thức xảy ra tức là

1x

y



.

B

à

i

t

o

á

n

1

4

5

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

2

3

3 5 2

2 7 6 1 2 1,

;

2 2 2 2 1.

x y x x x y x

x y

x y x y x y y



     







       





.

Lời giải.

Điều kiện

3

6

2

; 0

7

x

y



 

.

Phương trình thứ nhất của hệ tương đương với

   

 

   

 

   

2

7

6 2 7 6 2 1 1 2 1

6 1 5 1

1 2 1

7 6 7 6 2 1

6 5

1

1 2 1

7

6 7 6 2 1

x x x y x x y x

x x y x

y x

x x x x

x y

x

y x

x

x x x

        

 

    

    

 



    





    

 

Dễ thấy

 

2

3

6

5 6

0

, ; 2 , 0; 1 2 1 0

7

6 7 6 2 1

x y

x y y x

x x x x

 



       





    

 

.

Từ đó

5

1 0 1 1

x x x

     

.

Áp dụng bất đẳng thức liên hệ trung bình cộng – trung bình nhân lại có

3

2 3 3 3 2

2 2 2 2 2 2

y x y x x y x y

        

.

Hơn nữa

5 3 3 2 5

2

1;2 2 2 2 2 2 1

y

y x x y x y y x y



         

.

Phương trình thứ hai của hệ có nghiệm khi các dấu đẳng thức xảy ra, tức là

3

1

0

1 1

2

y

x y x y

y

x



 



    











.

Đối chiếu điều kiện ta thu được các nghiệm duy nhất

1x

y



.

B

à

i

t

o

á

n

1

4

6

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

2

3 2

3

2 2 1 1 2 ,

;

1 2 1 7 7.

y x x y x

x y

y y x x x



     









     





.

Lời giải.

Điều kiện

2 1

;

3 2

x

y



. Phương trình thứ nhất của hệ tương đương với

 

   

 

2

3

2 2 1 2 2 1 2 1

3

2 2 1 2 1

1

2 1

3 2 2 1

y

x x y y x x

y

x x y x

y x

x x



      



     



   

  

LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

110

Ta có

 

2

1

0, ; 2 1 0 1 0 1

2

3 2 2 1

y

y y x x x

x x

          

  

.

Khi đó xét hàm số

     

3

2 2

7 7

7 ; 1 3 2 3 2 0, 1

2 2

f x x x x x f x x x x x x

x x



             

.

Hàm số liên tục và đồng biến trên miền





1

;



dẫn đến

       

2

3

2

1

7 1 2 1 7 7

x

f

x Min f x f y y x x x



        

.

Phương trình thứ hai của hệ có nghiệm khi các dấu đẳng thức xảy ra tức là

1x y 

.

Kết luận hệ có nghiệm duy nhất kể trên.

B

à

i

t

o

á

n

1

4

7

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

3

2

2 1 ,

;

2 2 1 3 2 1 5 .

x

x y

y

x y

y y x xy



  









   





.

Lời giải.

Điều kiện

1

;

2 2

x y

 

. Phương trình thứ nhất của hệ tương đương với

 

   

 

2 2

2

2 2 1 2 2 1 2

2 1

2 2 1

2 1

y x x y y x x y y x x

y x

y x x y x y x

x x

        



       

 

Ta thấy

 

2

2 1

0, ; 0 1 0 1

2

2 1

y

y y x x x

x x

         

 

.

Khi đó áp dụng bất đẳng thức liên hệ trung bình cộng – trung bình nhân ta có

 

3

2 2 1 3 2 1 2 1 1 2 1 1 1 2 3 2 3 5y y x y y x xy y xy xy xy

               .

Phương trình thứ hai của hệ có nghiệm khi và chỉ khi dấu đẳng thức xảy ra tức là

1x y 

.

Vậy hệ phương trình đề bài có nghiệm duy nhất

1x y 

.

Nhận xét.

Đ

ố

i

v

ớ

i

c

á

c

b

à

i

t

o

á

n

1

4

1

đ

ế

n

1

4

7

l

à

l

ớ

p

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

s

ử

d

ụ

n

g

p

h

é

p

l

i

ê

n

h

ợ

p

l

i

n

h

o

ạ

t

x

ử

l

ý

m

i

ề

n

g

i

á

t

r

ị

b

i

ế

n

x

,

k

h

ô

n

g

c

ô

l

ậ

p

đ

ư

ợ

c

h

a

i

b

i

ế

n

đ

ộ

c

l

ậ

p

,

t

r

o

n

g

đ

ó

b

i

ể

u

t

h

ứ

c

l

i

ê

n

h

ợ

p

 

;T x y

đ

ề

u

c

h

ứ

a

h

a

i

b

i

ế

n

,

d

ù

r

ằ

n

g

c

ò

n

đ

ơ

n

đ

ộ

c

m

ộ

t

p

h

â

n

t

h

ứ

c

n

h

ư

n

g

t

h

ự

c

s

ự

k

h

ó

p

h

á

t

h

i

ệ

n

,

đ

ể

l

à

m

đ

ư

ợ

c

đ

i

ề

u

n

à

y

c

á

c

b

ạ

n

c

ầ

n

t

ư

d

u

y

c

a

o

đ

ộ

,

b

ằ

n

g

m

ọ

i

g

i

á

l

à

m

x

u

ấ

t

h

i

ệ

n

c

á

c

đ

ạ

i

l

ư

ợ

n

g

k

h

ô

n

g

â

m

 

;g

x y

n

h

ư

b

ì

n

h

p

h

ư

ơ

n

g

,

l

ũ

y

t

h

ừ

a

b

ậ

c

h

ẵ

n

,

c

ă

n

t

h

ứ

c

,

n

h

â

n

t

ử

,

…

t

ù

y

t

h

e

o

đ

i

ề

u

k

i

ệ

n

x

á

c

đ

ị

n

h

,

t

h

ậ

m

c

h

í

đ

i

ề

u

k

i

ệ

n

c

ó

n

g

h

i

ệ

m

c

ủ

a

p

h

ư

ơ

n

g

t

r

ì

n

h

n

h

ư

c

á

c

b

ạ

n

đ

ã

t

h

ấ

y

.

R

i

ê

n

g

đ

ố

i

v

ớ

i

b

à

i

t

o

á

n

s

ố

1

4

7

,

n

g

o

à

i

p

h

ư

ơ

n

g

á

n

l

i

ê

n

h

ợ

p

c

á

c

b

ạ

n

c

ó

t

h

ể

s

ử

d

ụ

n

g

b

ấ

t

đ

ẳ

n

g

t

h

ứ

c

l

i

ê

n

h

ệ

g

i

ữ

a

t

r

u

n

g

b

ì

n

h

c

ộ

n

g

–

t

r

u

n

g

b

ì

n

h

n

h

â

n

A

M

–

G

M

v

ớ

i

đ

i

ể

m

r

ơ

i

m

a

y

m

ắ

n

2

2 1 2 . 2

x

y y x

y

    

.

T

i

ế

p

t

ụ

c

s

ử

d

ụ

n

g

b

ấ

t

p

h

ư

ơ

n

g

t

r

ì

n

h

đ

i

đ

ế

n

2 2 1 2 2 1 2 1 1x x x x x x x         

.

B

à

i

t

o

á

n

1

4

8

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

2

3 2 2 2 1 ,

;

3 3 2 5 4.

x y x y x x

x y

x x y x y x



     







    







.

Lời giải.

Điều kiện

2

;

0

3

x

y



. Phương trình thứ nhất của hệ tương đương với

LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

111

 

2

3

2 2 2 1

3 2 2 2 1 2

x x y x y x

x

x y x x y y x x



    



       

   

 

2

2 1 2 1

3 2 2 1

2 2

1

3 1 2 1

x y x

y x

x x x x

y

x y x

x x x x

 

   

   

 

    

 

   

 

Ta thấy

 

2

2 2

0, 0; 0

3 1 2 1

y

y y x

x x x x

     

   

nên dẫn đến

1

0 1

x



  

.

Phương trình thứ hai tương đương với

   

 

2

2 2

2 2 3 5 4 2 3 5 4x x y y x x x x y x x x

            

.

Khi đó xét hàm số

   

2

5

2 3 5 ; 1 4 3 0, 1

2

f x x x x x f x x x

x



          

.

Hàm số liên tục và đồng biến trên miền đang xét nên

     

 

2

1

1 4 2 3 5 4

x

f x Min f x f x y x x x



        

.

Vì vậy phương trình (*) có nghiệm khi và chỉ khi

;

1

x

y y x

x

y

x









 









.

Kết luận hệ phương trình đã cho có nghiệm duy nhất

1x y 

.

B

à

i

t

o

á

n

1

4

9

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

2

3

4

3 ,

2

;

3 1 2 1 4 .

y x x

x x

y

x y

x x x y



 

 











   







.

Lời giải.

Điều kiện

0; 0

x y

 

. Phương trình thứ nhất của hệ tương đương với

     

 





 

3

2 3 2

3

2

3 2

3

2 3 4 2 3 2 2 2

2

2 3 2 2

3 2

y x x x y x y x x y x y y x x

y x x

y x x x y y x x y x

x x x

            

 

         

 

Ta thấy

 

2

3

2

3

1

2

0, 0; 0 0 1 0

1 0

3 2

x

y

y y x x x x x

x

x x x







           



  

 



Đối chiếu điều kiện đi đến hai khả năng

0 1x x  

.



1

0

4 2

8

x

y y



   

, cặp số

1

0

;

8

 

 





không thỏa mãn hệ.



1 3 1 2

x x x

   

. Khi đó nhận xét

 

2

4 4 2 2 4 2

2 2 2 1 1 2 2 1

x x x x x y

         

.

Dẫn đến

 

4

2 2 2

4

3

1 2 1 3 1 1 1 4 4

x

x x y y y y



         

.

Phương trình thứ hai của hệ có nghiệm khi các dấu đẳng thức xảy ra tức là

 

2

1 1 0

1

0; 1

x x

x y

y x y



   



  





  



.

Đối chiếu điều kiện ta được nghiệm duy nhất

   

; 1;1

x y 

.

LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

112

B

à

i

t

o

á

n

1

5

0

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

   

 

3

2

5

8

3 4 8 4 12,

;

4 3 3

2 2 3 .

2

y x x y x x y y

x y

x x y

x x y y x



       







 

   







.

Lời giải.

Điều kiện

 

2

8

0

2

0 2

0

3

0

x x

x

x y x y

y

x



 







 



  



 













Phương trình thứ nhất của hệ tương đương với





 

3 2

2

3 3

8

8 4 4 2 2 8 8

7 8 1 8

2 8 2 8

8

8 8 8

y x x x y y y x x

y x x y x x x

y x y x

x x x x x x

          

    

         

     

Xét trường hợp

   

0

; 4;0

4

2

8 0

y

x y

x

y x











   

 

 

   





bị loại.

Xét

 

2

3

8

0 0, 0; 2 8 0

8 8

y x x

y y y x

x x x

 

        

  

dẫn đến

1

0 1

x



  

.

Áp dụng bất đẳng thức liên hệ trung bình cộng – trung bình nhân ta lại có

   

5

2 4 3 4 3 3 4 3 3

2 2 3

2 2 2 2

x x y y x x y x x y

x x y y x

       

       do

5

, 1x x x  

.

Phương trình thứ hai của hệ có nghiệm khi các dấu đẳng thức xảy ra hay

2

1

4 3

1

1 2 8 0

x x y

x

y x

y

x y x



 







  

 







     



K

ế

t

l

u

ậ

n

h

ệ

b

a

n

đ

ầ

u

c

ó

n

g

h

i

ệ

m

d

u

y

n

h

ấ

t

.

B

à

i

t

o

á

n

1

5

1

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

2

4

3 2

2

1 3

6 8 3 8 ,

;

2 3 4 3 6 .

x

y x y y

x y

x x

x y x y





     









   





.

Lời giải.

Điều kiện

1

;

0

2

x

y



. Phương trình thứ nhất của hệ tương đương với

 

   

4

2

4 2

2

4 2

2

3

1

2 2 1

3 2 6 8 2 0

2

3 2 1

2 2 2 1

1

6 8 2 0

2

1 1

3 1

6 8 3 0

2

2 1 1

3 1

1 3

2

x

y y y

x x

y y y

x x

x

y y y

x x

x

y y

x







       

 

 

 

 



      



      

 



    

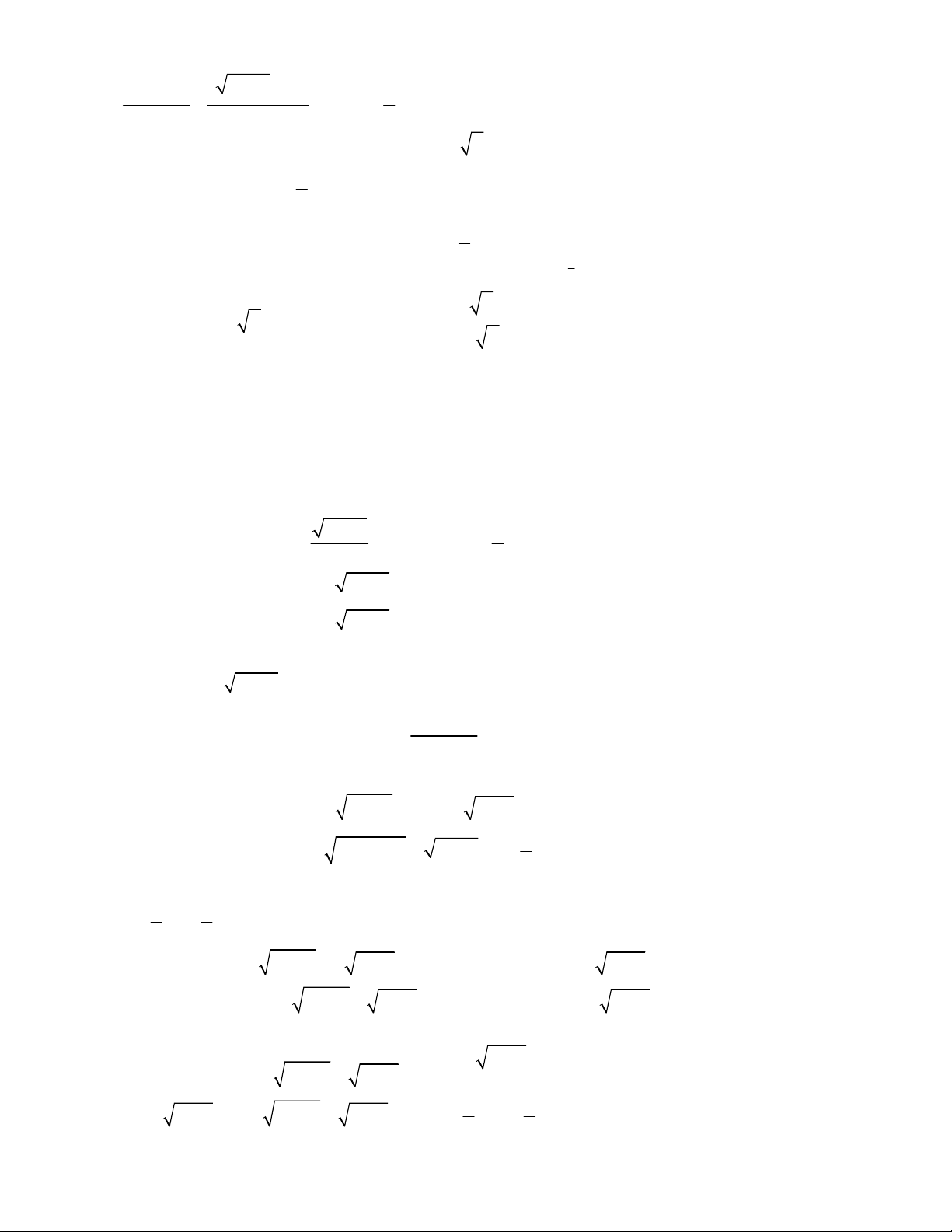
LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

113

Để ý rằng

 

   

2

3

2 1 1

3 1

1

0, 1 3 0 1

2

x

x y y y

x

 



         

.

Phương trình thứ hai của hệ trở thành

   

3

2

2 3 3 6 4 0 0

x x y y f x g y

       

.

Xét hàm số

 

3

2

1

2

3 ;

2

f

x x x x



 

thì

   

2

0

6 6 ; 0

1

x

f x x x f x

x





 

   







Lập bảng biến thiên hàm

 

f

x

, rõ ràng trên miền

   

1

;

2

1

;

1 1

2

x

Min f x f





 

 

 







    





 

.

Xét hàm số

 

 

3 6 4; 0;1

g y y y y    thì

 





3 1

0

, 0;1

y

f y y

y





   

.

Hàm số này nghịch biến nên

 

 

 

0

;1

1

y

M

in g y g





. Như vậy

   

0

f x g y

 

.

Dấu đẳng thức xảy ra khi

1x

y



. Thử lại vào hệ ban đầu ta có cặp nghiệm

   

;

1;1

x

y 

.

Nhận xét.

Thao tác biến đổi phương trình thứ nhất của hệ hết sức thú vị, việc tạo ra các hằng đẳng thức như thế trên thực

tế không phải một điều dễ thấy, nó manh nha từ cái nhìn bất đẳng thức AM – GM (BĐT Cauchy, liên hệ giữa trung

bình cộng và trung bình nhân). Xét phương trình thứ nhất của hệ

 

2 4

2 4 2

2

4 2

2 1 3

6 8 3 8

2 1 3 8 3 6 8

2 1 3 1 6 8 2

x

y x y y

x x

x x x x y y y

x x x y y y



     

       

       

Khi đó rõ ràng

 

   

2

4

2

3

4 2

2

2 1 1

2 1 3 1 6 8 2

2

6 8 2 1 1 1 3 0 1

3

1

x

x x x x y y y x

x

y y y y y y

x

 



        

            



B

à

i

t

o

á

n

1

5

2

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

3

2

4

2

3 1,

;

3

2 1 2 1 1 .

2

y x y y x y y y x

x y

x y x x y



       







     







.

Lời giải.

Điều kiện

1

;

2

x

y



. Phương trình thứ nhất của hệ tương đương với

 





 

3 2

3

2

3

1 2 1

2 1 2 1

1

y x y y x y y y x y x y

y

x y x y y y y x y x y

y

x x

y x y

x y x y

         



          





   

  

Ta thấy

 

2

3

1

0; 0, ,

2

y

x y x y x y x y



          

.

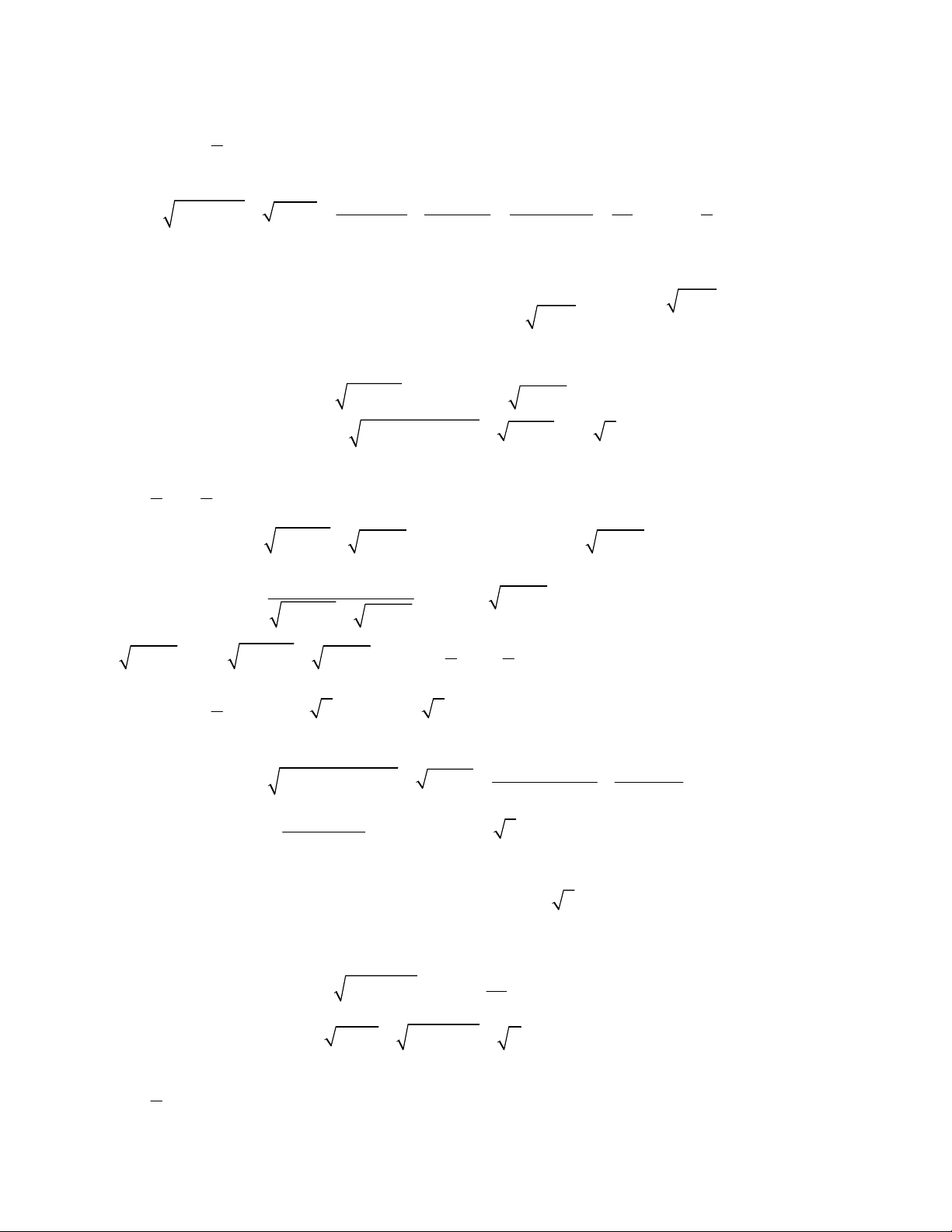
LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

114

Dẫn đến

 

3

2

1

0 1 0

1 0

x

x x x x

x





     



  



Kết hợp điều kiện

4

1

2

x

x x x



   

.

Áp dụng bất đẳng thức liên hệ trung bình cộng – trung bình nhân cho phương trình thứ hai

 

4

2

1 1 2 1 3 2 2 3 3

2

1 2 1 1 1

2

2 2 2 2

x

y x x y x

x

y x y x y



    



          

.

Hệ có nghiệm khi tất cả các dấu đẳng thức xảy ra tức là

2

1

2 1 1 ;

1

x y

x x y

y x y



 

 







   



  





  



.

Kết luận hệ ban đầu vô nghiệm.

B

à

i

t

o

á

n

1

5

3

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

  

 

2 2

3 2 2 3 3 3 1,

;

3 2 1 3 2 5 4 4 .

y x y x y x y x x y

x y

y x x x x y



        







      







.

Lời giải.

Điều kiện

4

1

;

5

2

x

y



. Phương trình thứ nhất của hệ tương đương với





 

2

3

3 2 1 2 1 3 3

1

3

3 3

y

x y x y x x x x y x y

y x x

x x y

x y x y



         



    

  

Vì

 

2

4 1

1

3 0; 3 3 0; .

5

2

x

x y x y x y x y



          

dẫn đến

 

2

1

0 1 0

0

x

x x x x

x





     







Kết hợp điều kiện

4

1 1

5

x

x x x x x



     

.

Áp dụng bất đẳng thức liên hệ trung bình cộng – trung bình nhân với phương trình thứ hai ta có

  

2

1 3 2 5 4 1

2

1 3 2 5 4

2 2

8 2 6

4 3 4 3

2

y x x

x y

x y x x y



   



    

 

      

Hệ có nghiệm khi toàn bộ các dấu đẳng thức xảy ra tức là

2 1 3 2

1

5

4 1

y x

x

y

x

  

















 





Thử lại, kết luận hệ ban đầu có nghiệm duy nhất

1x y 

.

B

à

i

t

o

á

n

1

5

4

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

3

3 3

3

2

1 ,

;

2 1 2 1.

x

x x y y

y

x y

x x x y y x



    









      





.

Lời giải.

Điều kiện

3

1

;

0; 0

2

x

y x x y



   

.

Phương trình thứ nhất tương đương với

LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

115





 

3

2

3 2

3

2

3

2

3

2 2 2 2 2

2

y x x y y x y

y

x x y x y y y x y x y

y

x x

y x y

x x y x y

    



        





  

   

Ta thấy

 

2

3

2 0; 2 0; 0

y x y x x y x y y

         

nên

 

3

2

1

0 1 0

1 0

x

x x x x

x





     



  



Kết hợp điều kiện

3

3 3

1

3 4

2

x

x x x x x x



      

.

Áp dụng bất đẳng thức liên hệ trung bình cộng – trung bình nhân cho phương trình thứ hai

3

3 3

1 2 1 1 1 3 2 4 2

2 1 2 1

2 2 2 2 2

x x x y y x x x

x x x y y x

        

           

.

Hệ có nghiệm khi tất cả các dấu đẳng thức xảy ra tức là

3

2 1 1

1

2

x

x x y

y

x y

y

x y



    





  











.

Thử lại, kết luận hệ ban đầu có nghiệm duy nhất

1x

y



.

B

à

i

t

o

á

n

1

5

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

     

 

3

4

1 3 2 3,

;

2 5 4 3 3.

x y x y x y x y y

x y

x x y y x



       









      





.

Lời giải.

Điều kiện

3

4

3

0; 0

3; 2 5 0

4

3 0

x y x y

y x x

y y x

   





    







  



Phương trình thứ nhất của hệ tương đương với

     

 

   

2

3

2 3 3

3 2 2 3 3

3

1

3 2 2 3 3

x y x y x y x y x y y

x y x y x y x y y

x y x

x y x y x y y



       

        

 

 

     

Ta thấy

 

2

0; 3 3 0 1 0 1

3

2 2

x y

x y y x x

x

y x y



         



 

.

Với phương trình thứ hai của hệ

Xét hàm số

   

3

2

5; 1 3 2 0, 1

f

x x x x f x x x





        

.

Hàm số liên tục và đồng biến trên miền đang xét dẫn đến

     

3

1

1 4 2 5 2

x

f x Min f x f x x



      

.

Lại có

4

4 3 4 4

y y x y y

     

. Xét hàm số

   

3

4 4; 0 1 1g y y g y y y



      

.

Khảo sát hàm số này ta có

     

4

1

1 4 3 1

y

g

y Min g y g y y x





      



.

Như vậy

3

4

2

5 4 3 3

x

x y y x



     

. Dấu đẳng thức xảy ra khi

1x

y



.

LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

116

B

à

i

t

o

á

n

1

5

6

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

2

3 2 2

4 3 6 3 4 ,

;

2 1 3 5 1 1 2 .

y y x y x

x y

x xy y x y x



    









        





.

Lời giải.

Điều kiện

2

3

0

2

1 0

x

y

x xy y

 







  



Phương trình thứ nhất của hệ tương đương với

 

3

2

3 2

2

3 2

4

3 6 3 12

3 4 3 4 4 7 12

3 2 4 7 12

y y x y y x

x y y x y y y y y

x y y y y y

    

        

      

Rõ ràng

 

2

3

2 2

5

23

4

7 12 0 1 5 12 0 1 0 1

2

4

y

y y y y y y y y





 



              





 

 

 

 

.

Từ đây

 

2

3

2 2 3 2 2 2 3

1

2 1 2 1 1 1 2 1 1

y

y y x xy y x xy y x y x xy y



                  

.

Lại có

   

2

2 2

1

0 2 1 0 3 6 4 4

x

x x x x



        

, nên

 

2

2 2 2 2 2 2

1

3 5 1 3 6 4 4 2 3 5 1 2

y

x y x x x x x y x



              

.

Phương trình thứ hai của hệ có nghiệm khi các dấu đẳng thức xảy ra tức là

1 0; 1

1

0; 2 0

x y

x y x

  



  



   



.

Kết luận hệ ban đầu có nghiệm duy nhất

1x

y



.

N

h

ậ

n

x

é

t

.

T

r

ê

n

đ

â

y

c

á

c

b

ạ

n

v

ừ

a

t

i

ế

p

c

ậ

n

v

ớ

i

m

ộ

t

l

o

ạ

t

c

á

c

b

à

i

t

o

á

n

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

v

ô

t

ỷ

k

ế

t

h

ợ

p

đ

á

n

h

g

i

á

–

h

à

m

s

ố

-

b

ấ

t

đ

ẳ

n

g

t

h

ứ

c

(

t

ừ

t

h

í

d

ụ

1

2

0

đ

ế

n

t

h

í

d

ụ

1

5

)

,

v

ớ

i

h

ư

ớ

n

g

đ

i

c

h

ặ

n

m

i

ề

n

g

i

á

t

r

ị

c

ủ

a

m

ộ

t

r

o

n

g

h

a

i

b

i

ế

n

b

ằ

n

g

c

á

c

h

s

ử

d

ụ

n

g

đ

ạ

i

l

ư

ợ

n

g

l

i

ê

n

h

ợ

p

–

t

r

ụ

c

ă

n

t

h

ứ

c

v

ớ

i

đ

ầ

y

đ

ủ

c

á

c

h

ì

n

h

t

h

ứ

c

đ

a

d

ạ

n

g

,

p

h

o

n

g

p

h

ú

.

P

h

ư

ơ

n

g

t

r

ì

n

h

c

h

ố

t

c

h

ặ

n

s

ử

d

ụ

n

g

l

i

ê

n

h

ợ

p

–

t

r

ụ

c

ă

n

t

h

ứ

c

     

;

. ; ;

f

x y T x y g x y



.

V

ớ

i

t

ậ

p

x

á

c

đ

ị

n

h

D

,

t

a

c

ó

 

;

0, ;

T

x y x y D



 

.

Đ

ơ

n

v

ị

q

u

y

ế

t

đ

ị

n

h

m

i

ề

n

g

i

á

t

r

ị

m

ộ

t

b

i

ế

n

c

ó

t

h

ể

x

o

a

y

c

h

u

y

ể

n

q

u

a

n

h

   

 

;

; , ;

;

f x y Q

f x y g x y

g x y Q















M

ộ

t

r

o

n

g

h

a

i

đ

ơ

n

v

ị

   

; , ;f x y g x y

k

h

ô

n

g

â

m

đ

ể

p

h

ụ

c

v

ụ

đ

ơ

n

v

ị

Q

p

h

á

t

h

u

y

h

i

ệ

u

q

u

ả

.

C

h

ú

n

g

t

a

đ

ã

b

i

ế

t

l

ú

c

đ

ó

     

1

1 1 1 2

1 1 1 1 2

; ; ;

f x y mU n h x y p h x y

g x y mU n h x y p h x y

  



  





B

i

ể

u

t

h

ứ

c

t

h

a

m

g

i

a

l

i

ê

n

h

ợ

p

 

;T

x y

t

ừ

d

ễ

đ

ế

n

k

h

ó

,

t

ừ

x

u

ấ

t

h

i

ệ

n

h

ằ

n

g

s

ố

t

r

ê

n

t

ử

t

h

ứ

c

t

i

ế

n

d

ầ

n

đ

ế

n

m

ộ

t

b

i

ế

n

,

h

a

i

b

i

ế

n

ằ

m

t

r

ê

n

t

ử

t

h

ứ

c

.

Đ

ó

l

à

c

h

ư

a

k

ể

đ

ế

n

   

;

, ;

f

x y g x y

x

o

a

y

c

h

u

y

ể

n

k

h

ô

n

g

n

g

ừ

n

g

q

u

a

b

ì

n

h

p

h

ư

ơ

n

g

,

l

ũ

y

t

h

ừ

a

b

ậ

c

h

ẵ

n

,

c

ă

n

t

h

ứ

c

t

ù

y

t

h

e

o

đ

i

ề

u

k

i

ệ

n

x

á

c

đ

ị

n

h

.

T

ừ

b

à

i

t

o

á

n

1

5

6

,

c

h

ú

n

g

t

a

t

ạ

m

r

ờ

i

x

a

t

h

i

ê

n

h

ư

ớ

n

g

l

i

ê

n

h

ợ

p

,

q

u

a

y

t

r

ở

l

ạ

i

k

h

a

i

t

h

á

c

t

í

n

h

c

h

ấ

t

k

h

ô

n

g

â

m

d

ự

a

t

r

ê

n

c

á

c

t

ổ

n

g

b

ì

n

h

p

h

ư

ơ

n

g

,

c

ũ

n

g

l

à

m

ộ

t

m

ả

n

h

đ

ấ

t

q

u

e

n

t

h

u

ộ

c

n

h

ư

n

g

k

h

ô

n

g

k

é

m

p

h

ầ

n

m

à

u

m

ỡ

.

B

à

i

t

o

á

n

1

5

7

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

   

 

3

4

2 2 2 3 2 2

3

2 2 1 3 ,

;

3 3 2 4 10 2 3.

y x x x y

x y

x x y x y y y y x x y



    







        







.

Lời giải.

LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

117

Điều kiện

2

2 4 10 0; 3 0

y y x x y

    

.

Phương trình thứ nhất của hệ tương đương với

 

3

2 3 2

2

3 2

3

6 2 1 3

2

1 2 1 3 3 3 5

1 3 3 5

y x x x y

x

x x x y x y x x x

x x y x x x

    



          

       

Rõ ràng ta phải có

 

   

2

3

2 2

3

5 0 1 2 5 0 1 1 4 0 1

x

x x x x x x x x







              





.

Khi đó

 

4 3

3

4 2 2 2 3 3 2 2 3

3 3

3

2

3

3 3 3

x x

x

x y x y y x x y xy y x y x y

x









          









.

Hơn nữa

 

2

2 2 2 2 2

2 4 10 2 4 10 6 9 3 2 4 10 3 3y y x y y y y y y y x y y                

.

Do đó

4

2 2 2 3 2 2

3

3 2 4 10 3 2 3

x

x y x y y y y x x y y x y



           

.

Phương trình thứ hai có nghiệm khi các dấu đẳng thức xảy ra tức là

1; 1 0

1

3

0

1

3

x y

x

y

x

x y



  









 

 









 



Kết luận bài toán có nghiệm duy nhất

1x y 

.

N

h

ậ

n

x

é

t

.

Đ

ể

t

h

i

ế

t

k

ế

l

ớ

p

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

n

à

y

k

h

ô

n

g

q

u

á

k

h

ó

,

đ

i

ề

u

q

u

a

n

t

r

ọ

n

g

l

à

g

i

ấ

u

đ

ư

ợ

c

á

c

b

ả

n

c

h

ấ

t

ổ

n

g

b

ì

n

h

p

h

ư

ơ

n

g

v

à

l

à

m

g

ọ

n

p

h

ư

ơ

n

g

t

r

ì

n

h

k

h

a

i

t

r

i

ể

n

c

ủ

a

c

h

ú

n

g

t

a

.

L

ấ

y

t

h

í

d

ụ

b

à

i

t

o

á

n

s

ố

1

5

7

,

ấ

n

đ

ị

n

h

n

g

h

i

ệ

m

đ

ẹ

p

1x

y



,

g

i

ả

đ

ị

n

h

s

ử

d

ụ

n

g

b

ì

n

h

p

h

ư

ơ

n

g

đ

ể

l

ậ

p

h

ư

ơ

n

g

t

r

ì

n

h

c

h

ố

t

c

h

ặ

n

m

i

ề

n

g

i

á

t

r

ị

c

ủ

a

t

ừ

n

g

b

i

ế

n

t

h

e

o

d

ạ

n

g

t

h

ứ

c

 

   

 

   

2

1

3 1

1

3 2

k

x x y t x

k x x y t y



   



   





C

á

c

b

ạ

n

t

ạ

m

t

h

ờ

i

l

ấ

y

t

r

ư

ờ

n

g

h

ợ

p

đ

ơ

n

g

i

ả

n

h

ấ

t

1

k



.

N

ế

u

s

ử

d

ụ

n

g

(

1

)

t

h

ì

m

ụ

c

t

i

ê

u

c

h

ặ

n

m

i

ề

n

g

i

á

t

r

ị

b

i

ế

n

x

v

à

s

ử

d

ụ

n

g

(

2

)

l

à

m

ụ

c

t

i

ê

u

c

h

ặ

n

m

i

ề

n

g

i

á

t

r

ị

b

i

ế

n

y

.

T

ấ

t

c

ả

b

ạ

n

đ

ọ

c

đ

ề

u

b

i

ế

t

n

ế

u

k

h

a

i

t

r

i

ể

n

b

ì

n

h

p

h

ư

ơ

n

g

v

ế

t

r

á

i

n

h

ư

t

r

ê

n

s

ẽ

x

u

ấ

t

h

i

ệ

n

p

h

ầ

n

l

ớ

n

đ

a

t

h

ứ

c

h

ứ

a

x

.

 

   

2

1 3 2 1 2 1 3 3 3 3 1 2 1 3x x y x x x x y x y x x y x x y                 

.

V

ì

t

h

ế

s

ử

d

ụ

n

g

(

1

)

s

ẽ

t

ố

i

ư

u

h

ơ

n

(

2

)

k

h

i

b

ố

t

r

í

 

3 2

t

x ax bx cx d



  

đ

ể

t

r

i

ệ

t

i

ê

u

(

t

ấ

t

n

h

i

ê

n

c

h

ỉ

t

r

i

ệ

t

i

ê

u

m

ộ

t

b

i

ế

n

)

đ

ư

ợ

c

đ

ạ

i

l

ư

ợ

n

g

2

3 3 1M x x y   

.

M

ộ

t

c

â

u

h

ỏ

i

đ

ặ

t

r

a

l

à

v

ì

s

a

o

c

h

ú

n

g

t

a

l

ạ

i

l

ự

a

c

h

ọ

n

đ

a

t

h

ứ

c

b

ậ

c

b

a

t

h

a

y

v

ì

t

a

m

t

h

ứ

c

b

ậ

c

h

a

i

,

m

ộ

t

k

h

ả

n

ă

n

g

q

u

e

n

t

h

u

ộ

c

v

à

c

à

n

g

l

à

m

g

ọ

n

g

à

n

g

p

h

ư

ơ

n

g

t

r

ì

n

h

c

h

ố

t

.



T

r

ư

ớ

c

t

i

ê

n

m

ờ

i

c

á

c

b

ạ

n

q

u

a

n

s

á

t

c

á

c

đ

i

ể

n

h

ì

n

h

s

a

u

   

 

2

2 2

2 4 2

1

3 2 1; 1 3 3 4 4

1 3 2 4 4 1 ; 1 3 9 6 1;...

x

x y x x x x y x x

x x y x x x x y x x

           

V

ớ

i

d

ạ

n

g

t

h

ứ

c

t

r

ê

n

c

h

ú

n

g

t

a

k

h

ô

n

g

k

h

a

i

t

h

á

c

đ

ư

ợ

c

đ

i

ề

u

g

ì

t

r

ừ

d

ạ

n

g

n

h

â

n

t

ử

p

h

ứ

c

t

ạ

p

.

H

ơ

n

ữ

a

h

a

i

v

ế

đ

ề

u

c

ó

d

ạ

n

g

b

ì

n

h

p

h

ư

ơ

n

g

,

đ

ặ

c

t

í

n

h

k

h

ô

n

g

â

m

l

à

h

i

ể

n

h

i

ê

n

.



T

i

ế

p

t

h

e

o

l

à

c

á

c

t

h

í

d

ụ

   

 

2

2 2

2 4 2

1 3 3 4; 1 3 3 4 3

1

3 2 2 5 2 ; 1 3 5 6 1;...

x x y x x x x y x x

           

           

V

ớ

i

c

á

c

t

h

í

d

ụ

t

h

u

ộ

c

m

ụ

c

2

,

c

h

ú

n

g

t

a

k

h

a

i

t

h

á

c

đ

ư

ợ

c

m

i

ề

n

g

i

á

t

r

ị

b

i

ế

n

x

.

LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

118

N

g

o

à

i

r

a

c

ò

n

t

r

i

ệ

t

i

ê

u

đ

ư

ợ

c

đ

ạ

i

l

ư

ợ

n

g

M

đ

ư

a

v

ề

p

h

ư

ơ

n

g

t

r

ì

n

h

ế

t

s

ứ

c

đ

ẹ

p

m

ắ

t

 

2

1

3 3 4

3 3 1 2 1 3 3 4

3

5 2 1 3

x x y x x

x x y x x y x x

y

x x y

     

         



   

T

u

y

n

h

i

ê

n

  

2

1

3 4 0 1 4 0

4

x

x x x x

x





       



 



M

i

ề

n

g

i

á

t

r

ị

b

i

ế

n

x

t

h

u

ộ

c

h

a

i

t

ậ

p

h

ợ

p

r

ờ

i

n

h

a

u

n

ê

n

g

â

y

b

ấ

t

l

ợ

i

c

h

o

q

u

á

t

r

ì

n

h

đ

á

n

h

g

i

á

t

i

ế

p

t

h

e

o

.

Đ

ể

c

o

c

ụ

m

đ

ư

ợ

c

m

i

ề

n

g

i

á

t

r

ị

t

r

ê

n

b

ắ

t

b

u

ộ

c

ầ

n

c

ó

t

h

ê

m

y

ế

u

t

ố

t

ạ

i

p

h

ư

ơ

n

g

t

r

ì

n

h

t

h

ứ

h

a

i

.

T

h

í

d

ụ

n

h

ư

s

ự

x

u

ấ

t

h

i

ệ

n

c

ủ

a

c

á

c

ă

n

,

h

o

ặ

c

m

ộ

t

p

h

ư

ơ

n

g

t

r

ì

n

h

đ

á

n

h

g

i

á

t

ạ

o

r

a

m

i

ề

n

đ

ố

i

l

ậ

p

n

h

ư

4

2

2 2

;

2 1; 3; 3 4;...

1

2

2; 2 1 ; 3 2

2

3

k

k k

x

x x x

N x x N x x N x x

  



          



V

ấ

n

đ

ề

n

à

y

t

á

c

g

i

ả

s

ẽ

x

i

n

đ

ề

c

ậ

p

s

a

u

.

T

h

a

y

đ

ổ

i

t

h

e

o

h

ư

ớ

n

g

đ

a

t

h

ứ

c

b

ậ

c

b

a

b

ấ

t

k

ỳ

c

ó

n

g

h

i

ệ

m

h

ữ

u

t

ỷ

   

 

2

3 2 3 2

2 2

3 2 3

1

3 6 11 6; 1 3 3 4 5

1 3 2 2 7 4 ; 1 3 9 ;...

x

x y x x x x x y x x

x x y x x x x x y x x



           

           

K

h

a

i

t

h

á

c

m

i

ề

n

g

i

á

t

r

ị

   

 

3

2

3 2 2

3

6 11 6 0 1 2 3 0

1 2

4

5 0 1 5 5 0

2 7 4 0 1 3 4 0

x

x x x x x x

x

x x x x x

x x x x x x





         



 





      

        

C

á

c

m

i

ề

n

đ

ề

u

r

ờ

i

n

h

a

u

v

à

t

ỏ

r

a

p

h

ứ

c

t

ạ

p

,

k

h

i

k

h

ô

n

g

c

ó

s

ự

h

ỗ

t

r

ợ

đ

i

ề

u

k

i

ệ

n

à

o

s

a

u

đ

ó

.



D

ự

a

t

r

ê

n

h

ữ

n

g

t

h

ử

n

g

h

i

ệ

m

t

r

ê

n

b

ư

ớ

c

đ

ầ

u

c

h

ú

n

g

t

a

s

ử

d

ụ

n

g

đ

a

t

h

ứ

c

b

ậ

c

b

a

v

ớ

i

n

g

h

i

ệ

m

d

u

y

n

h

ấ

t

v

à

c

ó

c

á

c

h

ệ

s

ố

t

h

í

c

h

ợ

p

n

h

ấ

t

m

ụ

c

t

i

ê

u

t

r

i

ệ

t

i

ê

u

đ

ạ

i

l

ư

ợ

n

g

M

 

   

2

3 2

1 3 3 3 1 2 1 3 3

x x y x x y x x y t x ax x x d              

.

D

o

n

g

h

i

ệ

m

ấ

n

đ

ị

n

h

b

ằ

n

g

1

n

ê

n

a

v

à

d

đ

ư

ợ

c

x

á

c

đ

ị

n

h

k

h

á

đ

ơ

n

g

i

ả

n

 

3

2

3

1; 1 0 5

2

; 1 0 6

3

; 1 0 7

t

x ax x x d

a f d

   

    



   



   

L

ư

u

ý

q

u

á

t

r

ì

n

h

c

h

ọ

n

a

v

à

d

c

ũ

n

g

c

ầ

n

c

h

í

n

h

x

á

c

,

k

h

é

o

l

é

o

,

t

r

á

n

h

t

ạ

o

r

a

đ

a

t

h

ứ

c

h

a

i

n

g

h

i

ệ

m

.

B

à

i

t

o

á

n

1

5

8

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

2

3

2

2 4 1 ,

;

2 2 4 .

y y x x x y y

x y

x x x y y



      







   







.

Lời giải.

Điều kiện

2 2

2

2 0; 4 0

2

0; 0

y y x x x y

x y y





    



  



Phương trình thứ hai của hệ tương đương với

 

2

3 2 3 2

2 2 2 2 4 2 2 4x x x y x y x x x x x y x x x              

.

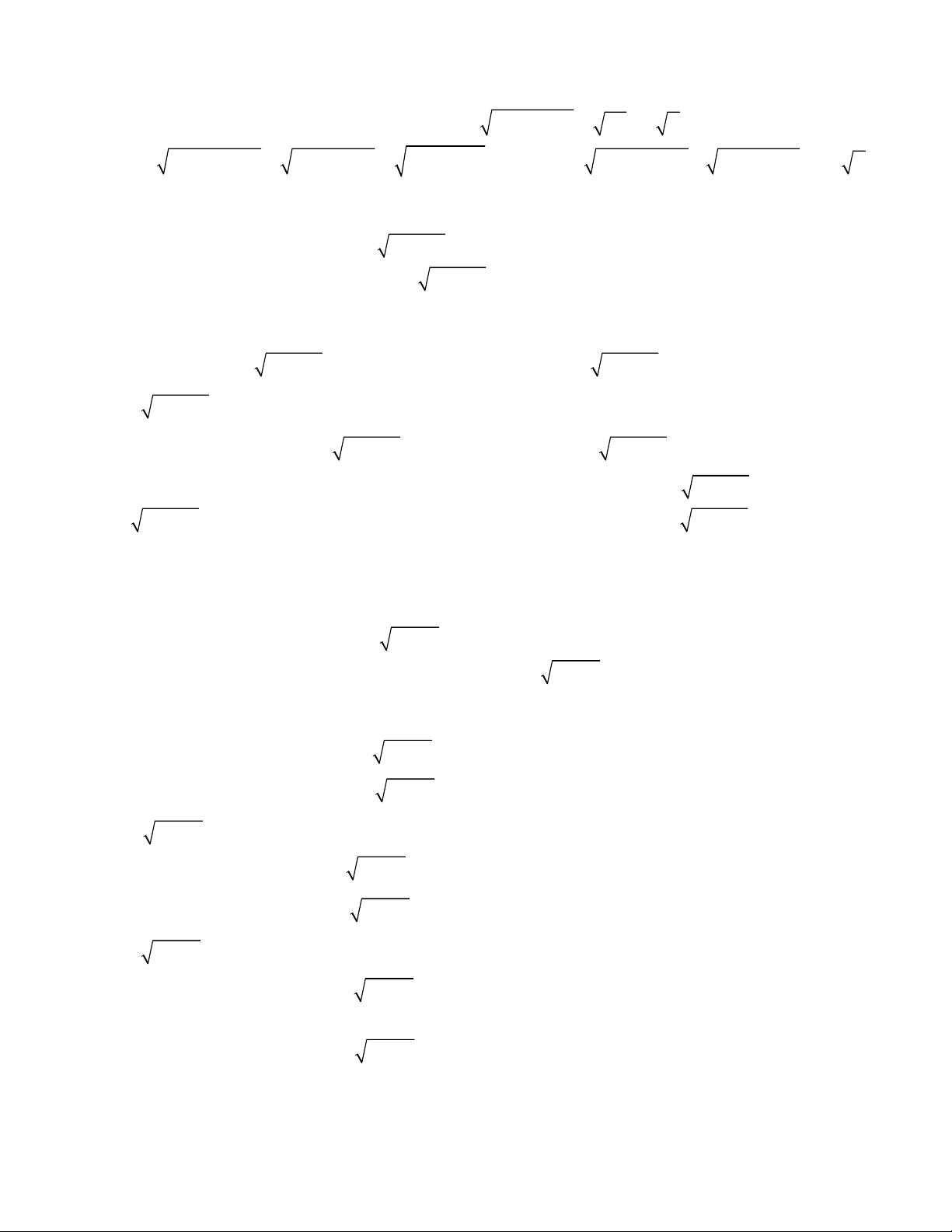
LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

119

Rõ ràng

 

   

2

3

2 2

2

4 0 1 2 4 0 1 1 3 0 1

x

x x x x x x x x







              





.

Khi đó

 

2 2 2

1 1 0 4 4 4 4 2

x x x x x x x y y x x y y y

              

.

Lại có

 

2

1

2 2 2 2 1 1 1

x

y y x y y y



         

dẫn đến

2

2 4 1

y

y x x x y y



     

.

Phương trình thứ nhất có nghiệm khi các dấu đẳng thức xảy ra tức là

1x

y



.

B

à

i

t

o

á

n

1

5

9

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

3

2

3 2 4 2 1,

;

7 2 3 2 2 4.

x x x y x y

x y

y x y x y y



    







    







.

Lời giải.

Điều kiện

3 2 0

x y

 

. Phương trình thứ nhất của hệ tương đương với

 

2

3

2

3 2

2 3 2 3 2 3 3 1 3 2 1

x x x y x y x x x x x y x

            

.

Dễ thấy

 

2

3

3 2 0 1 0 1 0 1x x y x x x          

.

Phương trình thứ hai trở thành

 

2

2 3 2 3 2 4 4 3 2 4 4

y y x y x y x y x y x

          

.

Lại có

 

2

3 2 4 4, 1y x y x x     

nên phương trình thứ hai có nghiệm khi

3 2

3

2 1

1

y

x y

x

x y x y

x











   











.

Kết luận hệ có nghiệm duy nhất

1x

y



.

B

à

i

t

o

á

n

1

6

0

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

3 2

3 2 2

2 2 4 4 2 1,

;

2 6 5 2 2 2 2.

y y x y y y x

x y

y y y x x x x y



     







      







.

Lời giải.

Điều kiện

2

0

x

y





. Phương trình thứ nhất của hệ tương đương với

 

2

3 2

2

3

2 2 2 3 3 1

2 1

y y x y x y y y y

y x y y

       

    

Rõ ràng

 

2

3

2 0 1 0 1y x y y y       

. Biến đổi phương trình thứ hai

 

2

3 2

2

3

2

2 2 2 3 3 1 0

2

2 1 0

x x x y x y y y y

x x y y



       



    

Dễ thấy

 

2

3

2 2 1 0, 1x x y y y      

.

Phương trình thứ hai có nghiệm khi

2

1

0

1

2

x

x y

x

y

x y



 









 

 







 



Thử lại, kết luận hệ ban đầu có nghiệm duy nhất kể trên.

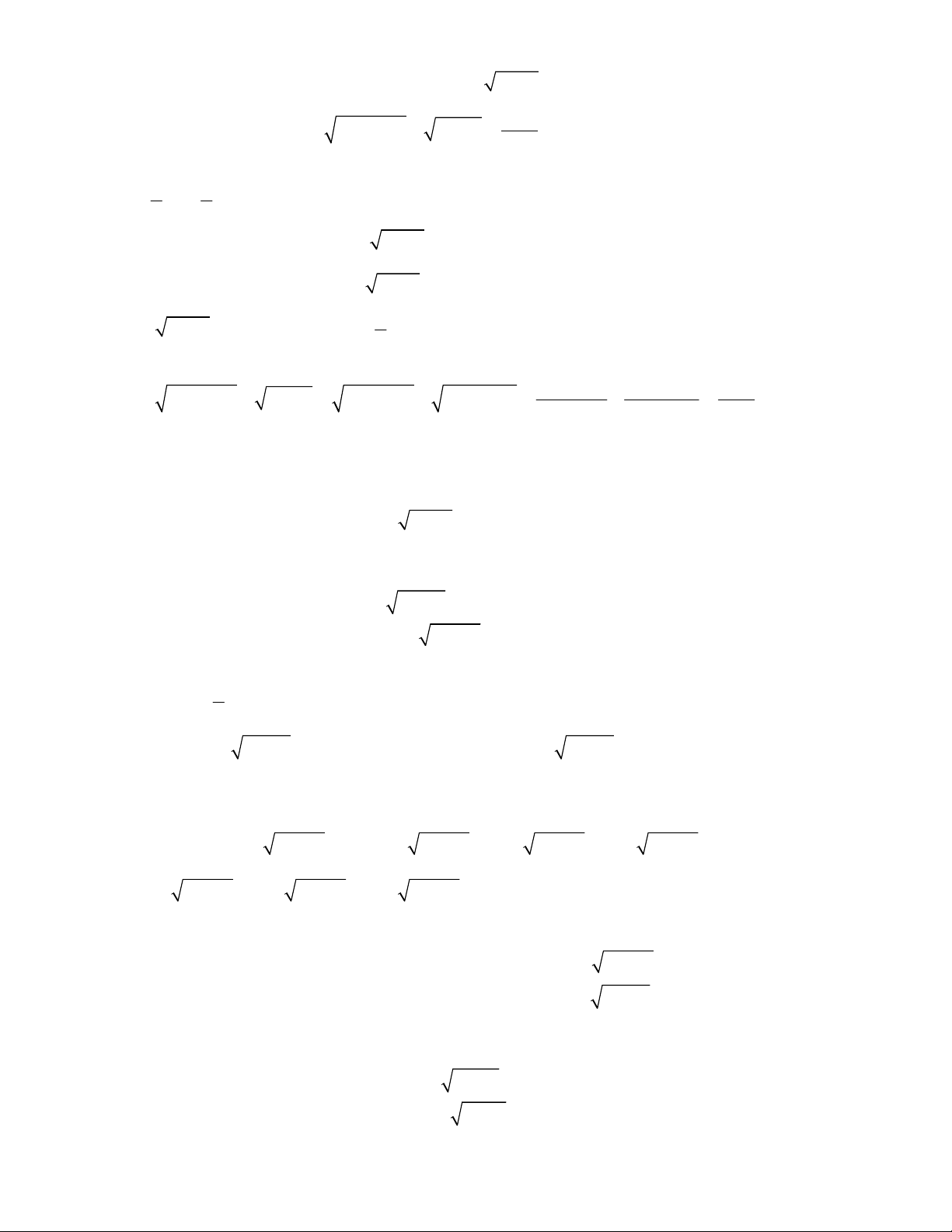
LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

120

B

à

i

t

o

á

n

1

6

1

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

2

2 2

3

2 2 1 1 1,

;

3

2 1 3 2 3 .

2

xy x y xy x x y

x y

x

x y y y



       









     





.

Lời giải.

Điều kiện

1

2

;

2 3

x

y



. Phương trình thứ nhất của hệ tương đương với

 

2

2 2

2

2 1 2 1 2 1

2

1 1

x

y y x x x xy y y

x

y x x y y



       



     

Rõ ràng

 

2

1

2

1 0, 1 0 1

2

x

y x x y x y y



          

.

Khi đó áp dụng bất đẳng thức liên hệ trung bình cộng – trung bình nhân ta có

     

2

1 3 2 3

2

1 3 2 2 1 3 2 3

2

2 2

x

y y y x

x

y y x y y y y



   



         

.

Phương trình thứ hai của hệ có nghiệm khi và chỉ khi các dấu đẳng thức xảy ra, nghĩa là

2 1; 3 2

1

1; 0

1

2 1

x y y x

x

y x y

y

y x



   







   

 







 



Thử lại, kết luận hệ phương trình đề bài có nghiệm duy nhất

1x

y



.

B

à

i

t

o

á

n

1

6

2

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

3

2

3 3

5 2 2 8 ,

;

1 2 2 1 2 2.

x x x y y

x y

y y x x



   







    







.

Lời giải.

Điều kiện

3

1

2

;

2

x

y x



. Phương trình thứ nhất của hệ tương đương với

 

2

3 2 3 2

2 2 2 5 2 8 2 5 2 8x x x y x y x x x x x y x x x              

.

Rõ ràng

 

3

2 2

5

2 8 0 1 5 6 8 0 1

x

x x x x x x



         

.

Khi đó phương trình thứ hai tương đương với





2

3 3 3 3 3

2 2 1 2 1 2 1 1 2 1 2 1 1

y y x x x x y x

            

.

Lại thấy





2

3 3 3

1 2 1 1 2 1 2 1 1

x x x y x

         

.

Phương trình thứ hai có nghiệm khi các dấu đẳng thức xảy ra tức là

3

1

2

1

2

x

y

x

y

x

x y















 

 







 





Thử lại, kết luận hệ phương trình đề bài có nghiệm duy nhất

1x y 

.

B

à

i

t

o

á

n

1

6

3

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

2

4

2

2 4 3,

;

2 5 3 4 2 1.

x y x y

x y

x y x y



   







   







.

Lời giải.

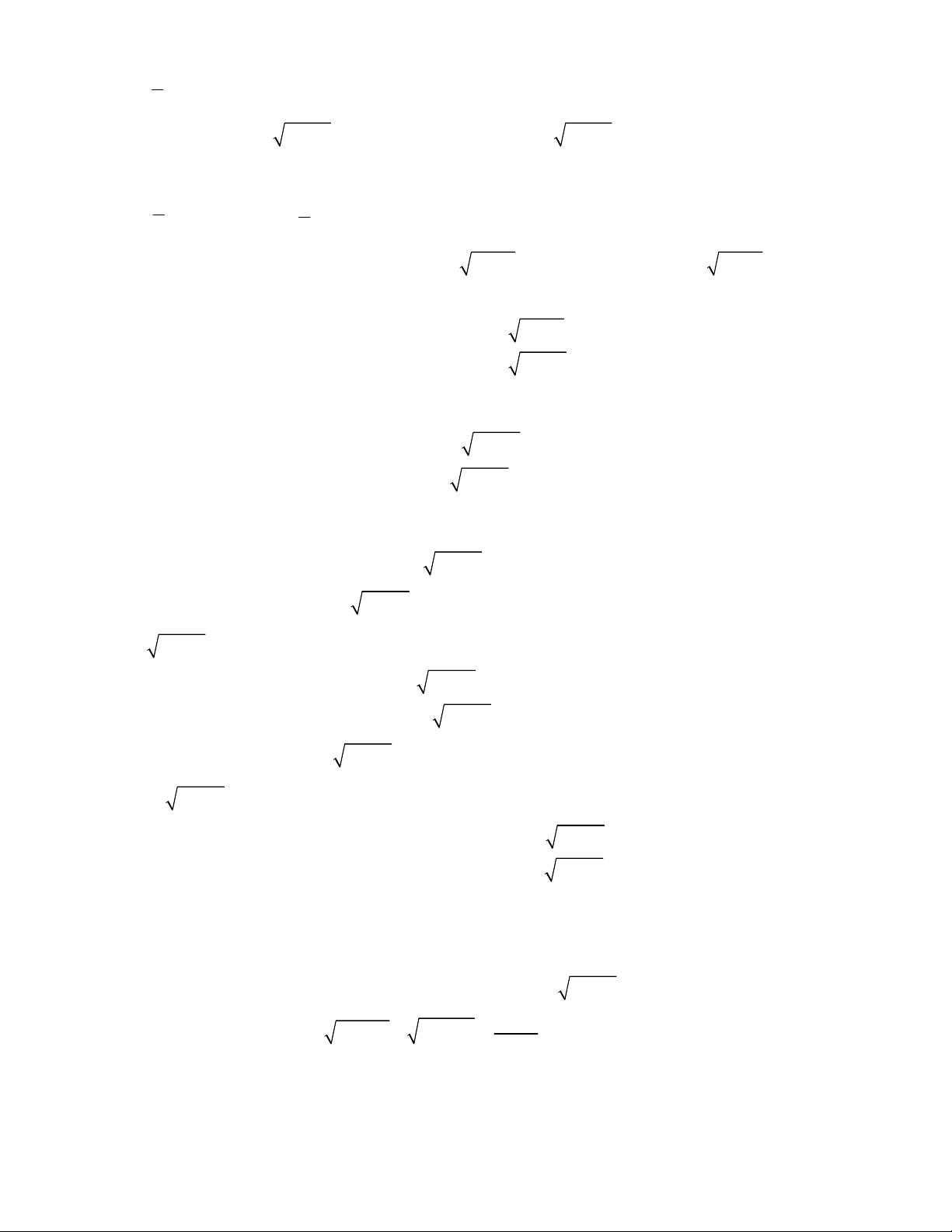
LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

121

Điều kiện

3

4

y



. Phương trình thứ nhất của hệ tương đương với

 

2

2 4 4

2 4 3 4 3 4 5 4 3 4 5x x y y y y x y y y            

.

Như vậy

 

3

2

4

1 5 0

4 5 0

1

0 1

1

2

y

y y y

y y

y



    



  

 



    

 



 



.

Phương trình thứ hai của hệ tương đương với

   

2

2 2 2 1 2 1 1 2 2 1 1

x x y y y x y y          

.

Rõ ràng

1 0 1y y   

. Các dấu đẳng thức xảy ra khi

1

2

1

4

3

y

x

y

x

y













 

 













Kết luận hệ phương trình có nghiệm duy nhất

1x

y



.

B

à

i

t

o

á

n

1

6

4

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

3

2

4 2 1 3 2 2,

;

1 2 1 2 3 2 .

x x x x y x y

x y

y y y x x



      







     







.

Lời giải.

Điều kiện

3 0;3 0

y x x y

   

. Phương trình thứ nhất của hệ tương đương với

 

2

3 2

2

3

2 1 2 1 3 3 3 3 1

1

3 1

x x x x y x y x x x

x

x y x

          



    

Ta có

 

2

3

1 3 0 1 0 1x x y x x        

. Phương trình thứ hai tương đương với

 

2

2 3 1 2 1 3 2

2

1 2 1 3 3 2 1 1

1

3 1 1

y y y y x x

y

y y y x y x y y x

y

y x y x

      



           



      

Rõ ràng

 

2

1 3 1 0 1 0 1y y x y x x          

.

Hệ có nghiệm khi toàn bộ các dấu đẳng thức xảy ra, tức là

1 3

1

3

1

y

y x

x

x x y

y

x





 











  

 













Kết luận hệ phương trình ban đầu có nghiệm duy nhất

1x

y



.

B

à

i

t

o

á

n

1

6

5

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

2 3

3

2

7 2 5 ,

;

5

3 2 2 .

2

y xy x y x y x y

x y

x

xy y x



      









   







.

Lời giải.

Điều kiện

2

5 0;3 2 0

2

0

x y xy

y x

   











Phương trình thứ nhất của hệ tương đương với

LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

122

 

2

2 3 2

2

3 2

2 2 5 5 5 7

5

5 7

x xy y x y x y x y x x x

x y x y x x x

          



      

Rõ ràng chúng ta có

 

   

2

3

2 2

5 7 0 1 2 7 0 1 1 6 0 1x x x x x x x x x

 

               

 

.

Sử dụng điều này và áp dụng bất đẳng thức liên hệ trung bình cộng – trung bình nhân ta có

 

3

2

3 2 1 2 1 5

3 2 2 3 2 2

2 2 2

xy xy x x

xy y x xy x y x

    

          .

Phương trình thứ hai có nghiệm khi các dấu đẳng thức xảy ra tức là

3

3 2 1;2 1

1

5 ; 1

xy xy x

x y

x y x y x



   



  



   





.

Kết luận hệ ban đầu có nghiệm duy nhất

1x y 

.

B

à

i

t

o

á

n

1

6

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

2

3

2 2 2 2

3

2 ,

;

3 3 2.

4

y y x y y x x

x y

x y y x y



    











    







.

Lời giải.

Điều kiện

0

; 0

y

x



. Phương trình thứ nhất của hệ tương đương với

 

   

2

2 3 2

2 2 3 2

2 2

3 2

2 3

2

2 3

3

x y x y x y y x x x x

x

x y y y y x x x x x

x y y x x x x

        



        

       

Ta có

 

3

2 2

3 0 1 2 3 0 1x x x x x x x          

.

Áp dụng bất đẳng thức liên hệ trung bình cộng – trung bình nhân với phương trình thứ hai

   

 

3

2

2 2 2 2

2 3

3 4

4 3 4 3

2

3 4

4 3

2

x xy

x y x x y

x y y

 

   

 

 

Thu được

   

 

3

3 2 2 3

2 2 2 3

3

2 2 2 2

3 4 3 4

4 3 4 3 4

2 2 2

3 3 2

4

x y

x xy x y y

x y x y y

x y

x y y x y



   

      



     

Phương trình thứ hai của hệ có nghiệm khi các dấu đẳng thức xảy ra tức là

2

2 2 3

;

1

3 3 4

y x x y

x y

x y x y y



 



  



   





.

Kết luận hệ phương trình có nghiệm duy nhất kể trên.

B

à

i

t

o

á

n

1

6

7

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

3

2

3 2 2 2 7,

;

17 6 10 2 3 5 3 2 2.

x x x y y y xy

x y

x y x y x x



     







       







.

Lời giải.

LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

123

Điều kiện

2 ;3 5 3 0

17 6 10 0

x y y x

x y

   





  



Phương trình thứ nhất của hệ tương đương với

 

2

2 2 3 2

2

3 2

2 2 2 2 3 2 2 7

2 3 2 2 7

x xy y x x x y x y x x x

x y x x y x x x

          

        

Rõ ràng chúng ta có

 

3

2 2

3

2 2 7 0 1 3 5 7 0 1

x

x x x x x x



         

.

Khi đó áp dụng bất đẳng thức liên hệ trung bình cộng – trung bình nhân cho phương trình thứ hai

 

2

17 6 10

17

6 10 17 6 10 9 3 5

2

2 3 5 3 3 5 3

x x y

x y x x y x y

x y x x y x

  



       



    

Dẫn đến

 

2

17

6 10 2 3 5 3 4 2 2 2

x

y x y x x x x



         

.

Phương trình thứ hai có nghiệm khi và chỉ khi

17

6 10 1; 1

1

3 5 3

1

2

0

x y x

x

x x y

y

x

y x x y



   









  

 







    



Kết luận hệ phương trình ban đầu có nghiệm duy nhất

1x

y



.

B

à

i

t

o

á

n

1

6

8

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

2

3 2

2

2 1 ,

;

2 2 1 2 .

x y y

x

x y

x y x y x



  









   





.

Lời giải.

Điều kiện

0

; 0

x

y





.

Phương trình thứ nhất của hệ tương đương với

 

   

2

2 3 3

2

2 1 2 1 2 2 2

2 2 2

x y y x x y y x y x xy

x

x x x y y x x x x y x x

          

          

Rõ ràng ta có

 

3

2

2 0 1 2 2 0 1x x x x x x         

.

Áp dụng bất đẳng thức liên hệ trung bình cộng – trung bình nhân ta có

 

2

3 2

2 1 2

2 1

2 2

x y x y x

x x x y

   

     .

Phương trình thứ hai của hệ có nghiệm khi các dấu đẳng thức xảy ra nghĩa là

2

1

x

y

x y x y

x









   











.

Đối chiếu và thử lại ta được nghiệm duy nhất của hệ

1x y 

.

B

à

i

t

o

á

n

1

6

9

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

2

4

3 6 4,

;

1

3 2 2 .

2

x y xy

x y

y

x xy x



  









   







.

Lời giải.

LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

124

Điều kiện

2

;

0

3

x

y



. Phương trình thứ nhất của hệ tương đương với

   

2

2 2

3 2 3 4 3 3 4

x y xy x x x y x x

         

.

Rõ ràng

  

2

1

3 4 0 1 4 0

4

x

x x x x

x





       



 



Kết hợp điều kiện ta được

4

1

x

x x



 

. Áp dụng bất đẳng thức Cauchy thu được

4

1

3 2 1 1

3 2 2 2

2 2 2 2

x

x y y y

x xy x x



   

       

.

Hệ có nghiệm khi dấu đẳng thức xảy ra hay

3

2 1

1

x

x y x y

x









   









.

Đối chiếu và thử lại ta được nghiệm duy nhất của hệ

1x y 

.

B

à

i

t

o

á

n

1

7

0

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

3

2

2 2

5 4 2 2 11,

;

1

3 2 2 .

x x xy y

x y

x y y x y x y

x



   







      







.

Lời giải.

Điều kiện

2

0; 0

x

y x



 

.

Phương trình thứ nhất của hệ tương đương với

 

3

2

3

2 3 2 2 5 6 11

2 2 2 2 5 6 11

2 2 5 6 11

x y x x y x x

x x x y x y x x

x x y x x

 

     

 

 

       

 

     

Rõ ràng

 

3

2

5

6 11 0 1 5 5 11 0 1

x

x x x x x



        

.

Phương trình thứ hai của hệ tương đương với

 

3

2 2

2 3 2

2

3

2 2 1

2 2 2 3 3 1 0

2

1 0

x xy xy x x xy x y

x x y y x y y x x x

x x y y x

      

         



    

Vì

 

2

3

1 0 2 1 0

x x x y y x

       

.

Phương trình trên có nghiệm khi dấu đẳng thức xảy ra, nghĩa là

2

1

2

x

y y

x

y

x

x y



 











 







 



Đối chiếu và thử lại ta được nghiệm duy nhất của hệ

1x

y



.

B

à

i

t

o

á

n

1

7

1

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

3

2

3

1 2 2 3 2 ,

;

2 3 2.

y x y

x

x y

x y y x



   









  





.

Lời giải.

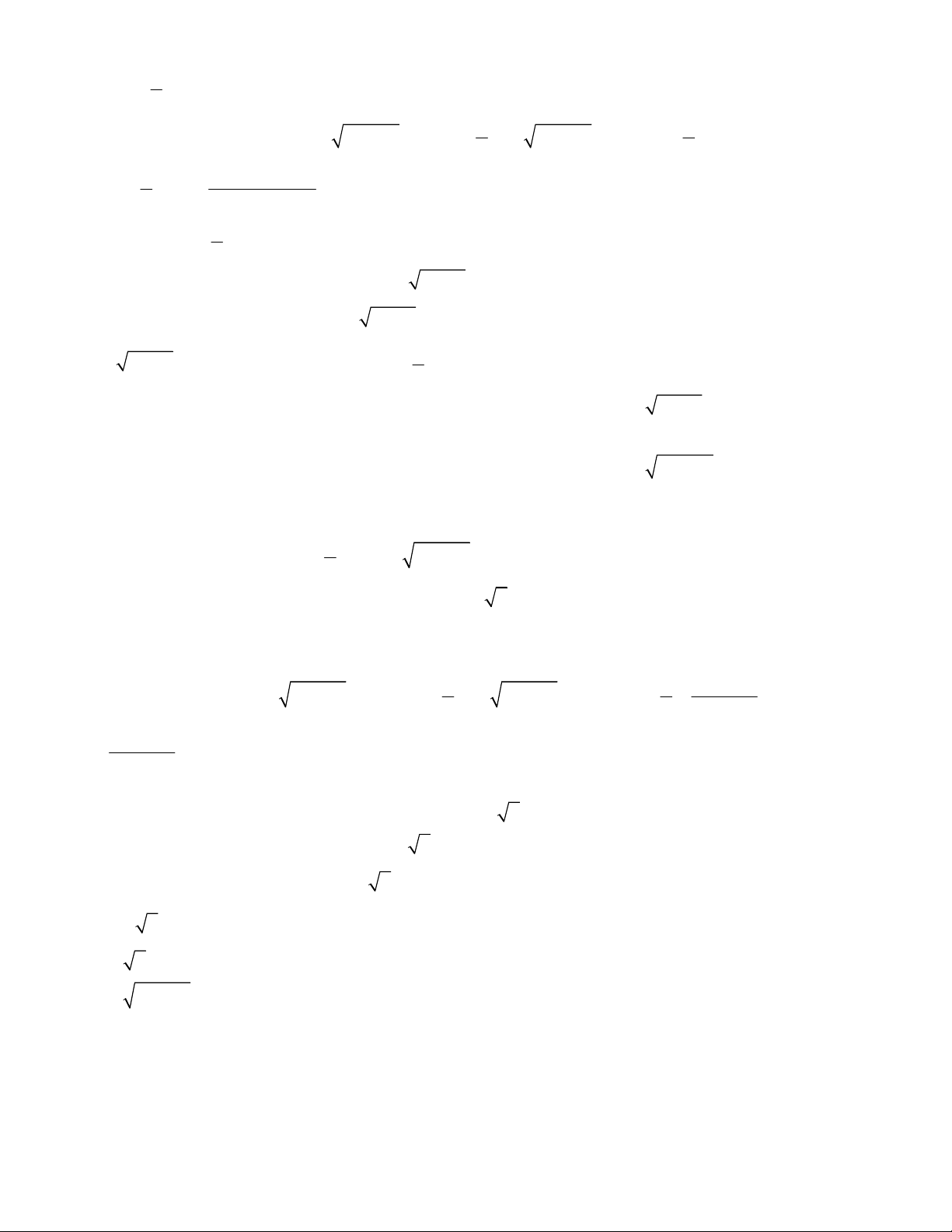
LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

125

Điều kiện

2

;

3 2

3

x

x y



. Phương trình thứ nhất của hệ tương đương với

 

2

3

2 2 3 2 1 3 3 2 1 3x y x y x x y x

x



         

.

Ta thấy

  

1

3 1 1

3

3 0 0

1 0

x

x x

x

x x



 



    



  



Kết hợp điều kiện

2

1

3

x



 

. Phương trình thứ hai trở thành

 

   

2

3

2

3 2 2 3 2 3 2 0

3 2 1 2 0

x y x y x x

x y x x

       

      

Rõ ràng

 

   

2

3 2 1 2 0,

3

x y x x x

       

.

Phương trình thứ hai có nghiệm khi đồng bộ các dấu đẳng thức xảy ra nghĩa là

3

2 0

1

0 1

3 2 1

x y

x

x y



  





   





 



.

Đối chiếu và thử lại ta được nghiệm duy nhất của hệ

1x

y



.

B

à

i

t

o

á

n

1

7

2

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

2

3

2 2 ,

;

2 2 1 2 2 .

y x x y

x

x y

x y x y x xy



  









    





.

Lời giải.

Điều kiện

2

2 ; 0

x y x

 

. Phương trình thứ nhất của hệ tương đương với





 

3

2

2 2 2 2 2

3 1

3 3

2 2 2 3 2 3

x

x y x x y x x x y x x

x x x



            .

Rõ ràng

 

3

3 1

0 1 0

x

x x

x



    

. Kết hợp với

0 1x x  

.

Phương trình thứ hai tương đương với

 

2

2 2 2

2

2 1 2 2

2

2 2 1

1

x

y x y x xy

x y x y x xy y

x y x y x

    



     



    

Vì

 

2

1 1

x x y x y x

      

. Hệ có nghiệm khi tất cả các dấu đẳng thức xảy ra.

Nghĩa là

2

0

1

2

1

x y x y

x

y x

y

x



   









  

 













Đối chiếu điều kiện ta được nghiệm duy nhất

1x

y



.

LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

126

B

à

i

t

o

á

n

1

7

3

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

2

2 2

3

5 4 2 ,

;

2 2 2 1 2 .

x x y y

x

x y

x x y y x y



  









    





.

Lời giải.

Điều kiện

2

2 2 2

2

5

4 ; 0

5 4 ;2 0

2

;2 0

2

0; 0

x y x

x y x y

x y x

 



  







 



 



 





Phương trình thứ nhất của hệ tương đương với

 

2

2 2 2

6 6

2

5 4 5 4 5 5 4 5x x x y x y x x x y x x x

x x



           

Rõ ràng

 

2

3

2

1 6 6

6 5 6

5 0 0 0

x x x

x x

x x x

  

 

      

.

Chú ý điều kiện

2

6 6

0 0

x x

x

 

  

nên thu được

1 0 1x x   

.

Phương trình thứ hai của hệ tương đương với





 

2

2 2 2 2 2

2

2 2 2 2

2

2 2 2

2 2 2 2 2 0

2 2 2 0

2 1

2 0

2 2

x y y x y y x y x y

x y y x y x y

x x

x y y

x y x y

        

       



    

  

Lại có





 

2

2 2

2 1

2 0; 0, 1

2 2

x x

x y y x

x y x y



     

  

.

Phương trình thứ hai có nghiệm khi các dấu đẳng thức xảy ra tức là

2

1

5

4

x y y

x

y

x

y x



 













 







 





Đối chiếu điều kiện và thử lại ta được nghiệm duy nhất

1x

y



.

B

à

i

t

o

á

n

1

7

4

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

3

2 2

4

2

2 ,

;

1 2 2 .

y x y y x

y

x y

y x y x x



   









    





.

Lời giải.

Điều kiện

2

0

2

0

2

y x y

x

y x

y

x



 







 



 







Phương trình thứ nhất tương đương với





2

2 2 3 2

2

2 3 2

4

2

2 2 2

4

2 2

y x y y x y y y y

y

x y y y y

y



      



     

Nhận thấy rằng khi đó

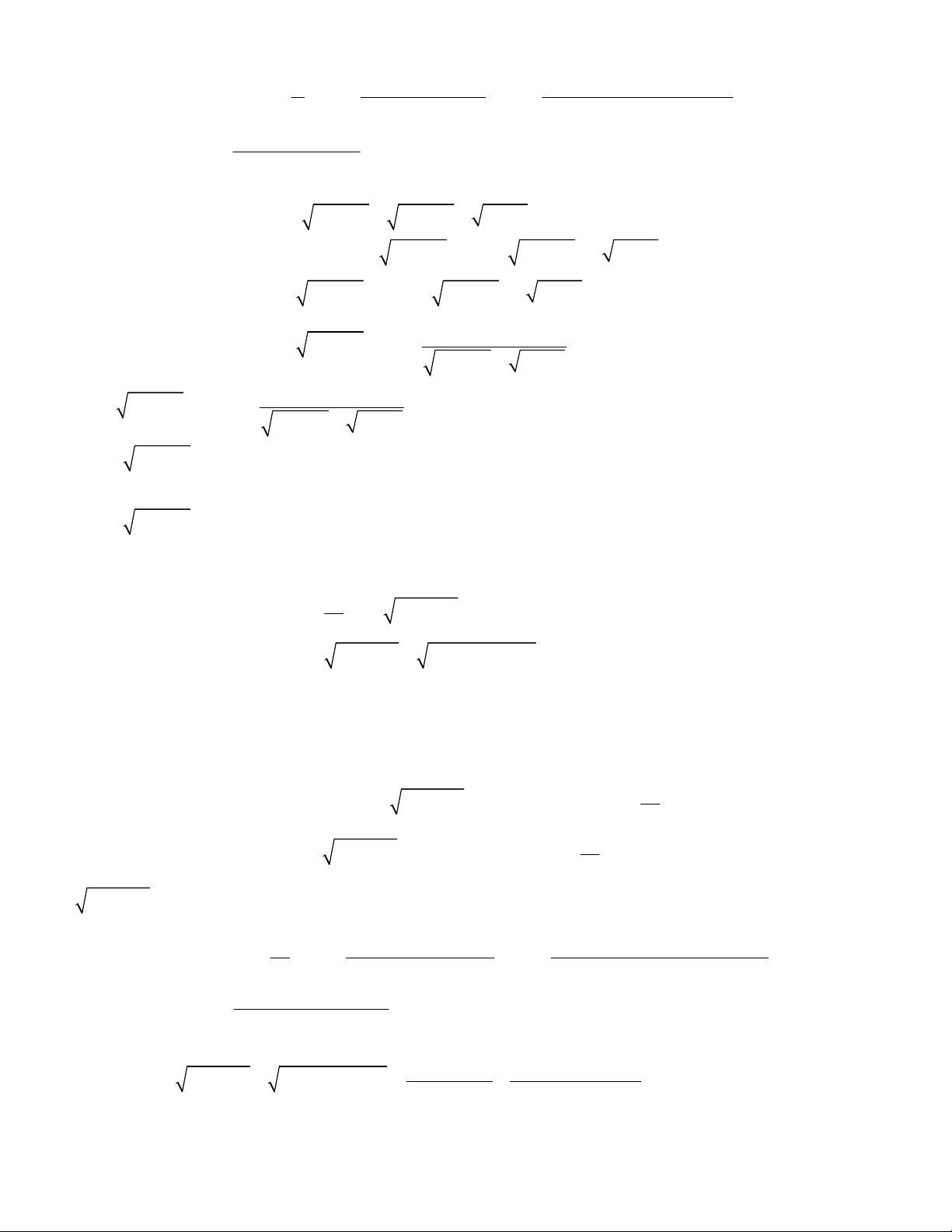
LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

127

 

3

2

4 3 2

3 2

1

2 5 4

4 3 4

2

0 0 0

y

y y y

   

  



      

.

Chú ý điều kiện

3

2

5 4

0

0 1 0 1

y

y y

y

y y

y



 



     

.

Phương trình thứ hai tương đương với









 

2

2 2

2 2 2 2 2

2

2 2 2

2

2 2

2 2 2 0

2

2 2 2 2 2 2 0

2

2 2 2 2 0

4 1

2 0 1

2 2

y x y x y x x

y x x y x x y x x

y x x y x x

y

y x x

      



        



      



    

  

Rõ ràng





 

2

4 1

2 0; 0, 1

2 2

y

y x x y

y x x



     

  

nên (1) có nghiệm khi các dấu đẳng thức xảy ra.

Nghĩa là

2

2 2

2

1

1 0; 1

1

2

y

x x

y x x

x

y x y

y

x y

y x y



 



 











   

  







 







Đối chiếu điều kiện và thử lại ta được nghiệm duy nhất

1x

y



.

B

à

i

t

o

á

n

1

7

5

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

3

2

3 2 4 2 3 4 4

17

2

2 3 3 2 ,

;

2 2 2 .

y x y x x

x

x y

x y y y x y x



   









     





.

Lời giải.

Điều kiện

3

2 3 2

4 2 3 4 2 3

2

; 0 2 ; 0

2

2 0 2 2 0

x

y x x y x

y y x y y x

 

   

 



 



    

 

 

Phương trình thứ nhất của hệ tương đương với





3

2 3 2 2 3 2

2

3 2 3 2

17

2 2 2 2 9 6

17

2 2 9 6

x y y x y y x x x

x

y y x x x

x

       



     

Vì





2

3

2

2 0

x y y

  

nên

 

3

2

4 3 2

3 2

1 2 11 17 17

17 2 9 6 17

2 9 6 0 0 0

x x x x

x x x

   

  

       

.

Lại có điều kiện

3

2

2 11 17 17

0 0

x x x

x

  

  

, dẫn đến

1

0 1

x



  

, và

4

1

x

.

Áp dụng bất đẳng thức liên hệ trung bình cộng – trung bình nhân AM – GM cho phương trình thứ hai

3

2 4 2 3

3

2 4 2 3 4 4 4

2 1 2 2 1

2 2 2 1

2 2

x y y y x

x y y y x y y x

    

         

.

Hệ có nghiệm khi các dấu đẳng thức xảy ra, nghĩa là ta có hệ điều kiện sau

LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

128

3

2

3 2

4 2 3

3 2 2

3 2

2 1

2 2 1

1

2

2 1

1

; 0

2

x y

y y x

x

y y x

x

y

x

y

x y y



 



 



  





 



 

 

  







 

 



Đối chiếu điều kiện và thử lại ta được nghiệm duy nhất

1x

y



.

B

à

i

t

o

á

n

1

7

6

.

G

i

ả

i

h

ệ

p

h

ư

ơ

n

g

t

r

ì

n

h

 

2

3

2

5 2 2 ,

;

2 3 3 1 3 2 .

y xy x x x y y

x y

x y x y x x y



     







      







.

Lời giải.

Điều kiện

2 0

3 3 1 0

x y

 





  



Phương trình thứ nhất của hệ tương đương với

 

2

2 3 2

2 2 2 3 2

2

3 2

2

2 2 2 2 2 2 5

2

2 2 2 2 2 5

2

2 2 5

x y x xy y x x y x x x

x

y x x y x x xy y x x x

x

y x x y x x x

         



          



       

Khi đó rõ ràng

 

3 2 2

2 2 5 0 1 3 5 0 1x x x x x x x          

.

Sử dụng điều này, kết hợp bất đẳng thức liên hệ trung bình cộng – trung bình nhân cho phương trình sau

 

2

3 3 1 1

2 2 3 2 1 3 2

2

x

x y x y

x

y x x y x y x y x



   



         

.

Phương trình thứ hai của hệ có nghiệm khi toàn bộ các dấu đẳng thức xảy ra, tức là

2 3 3 1 1

1

2 0

1

x y x y

x

x y x x y

y

x

    









     

 











Đối chiếu điều kiện và thử lại ta được nghiệm duy nhất

1x

y



.

17.6

LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

129

Lời kết.

Bài toán số 176 cũng là bài toán cuối cùng của tài liệu Lý thuyết giải hệ phương trình chứa căn phần thứ 7, chủ

đạo kết hợp phép thế, ẩn phụ, tính chất đơn điệu hàm số với kỹ thuật liên hợp – phân tích chặn miền giá trị, đánh

giá thuần túy và tổng hòa toàn bộ các kỹ năng giải phương trình vô tỷ, tuy nhiên nó chỉ là chút chia sẻ phần nào

của tác giả. Kiến thức hàm số, đồ thị hàm số và các kỹ thuật giải phương trình bậc cao, vô tỷ khác chắc hẳn các

bạn học sinh đã thuần thục, đáng lưu ý hơn hết là cách tìm miền giá trị của các biến, đây là mấu chốt và là điểm

nhấn của từng bài toán, là đòn quyết định tính đơn điệu của hàm số đang xét trên một miền, và tất nhiên điều này

không đơn giản, như các bạn đã thấy, nó đòi hỏi quan sát tinh tế, một chút tư duy, liên hệ, biến đổi đại số và một

chút bất đẳng thức – cực trị vừa đủ! Mong muốn các bạn độc giả chú ý kỹ lưỡng và rút được nhiều kinh nghiệm quý

báu cho bản thân mình.

Tác giả chúc các bạn học sinh, các thầy cô giáo và toàn thể các bạn độc giả sức khỏe, vui vẻ, bình tĩnh, tự tin,

bứt phá, đánh bật đề thi, đạt kết quả cao trong các kỳ thi tương lai sắp tới, chúc cho cô bé tôi yêu thương nhất đạt

điểm 10 tối đa môn Toán trong kỳ thi THPT Quốc gia năm 2015 và hơn thế nữa.

“Học, học nữa, học mãi”

(Vladimir Ilyich Ulyanov)

Người ta thường nói “Học để biết, học để làm việc, học để cùng chung sống”. Tuy nhiên với con người học là

chưa đủ, quan trọng là sống, điều này là vô cùng khó. Sinh ra và lớn lên trên đất nước nhiều đau thương, sục sôi

dòng máu chảy trong mình không thay đổi được, thừa hưởng chế độ y tế và giáo dục để phát triển, đó là ân huệ

của cha mẹ, của thế hệ trước, của non sông ban tặng cho mỗi công dân. Tư tưởng cá nhân luôn tồn tại trong mỗi

người, đó là sự phân công xã hội và tất yếu nảy sinh do bản năng, vì thế nó thường vượt qua ngưỡng cửa tập thể,

dễ lầm đường lạc lối. Thiết nghĩ sống tốt, hữu ích, đúng đạo lý, khoan dung, không dẫm đạp đồng bào, diệt trừ ác

độc, hơn nữa để an toàn và thoải mái cần chiếm lĩnh khoa học, cùng nhau vững bước làm chủ tri thức, làm chủ

tương lai, cùng nhau mang sức trẻ và ý chí kiên cường xây dựng bức tường thành bảo vệ mẹ già, vợ dại, con thơ

trước sự dòm ngó của ngoại bang. Quyết tâm xây dựng tổ quốc Việt Nam hòa bình, công chính, dân chủ, vững bền,

giàu mạnh, sánh vai cùng các nước trong khu vực, như Liên Bang Nga, Cộng hòa Hồi giáo Iran, CHDCND Triều

Tiên, hay ít nhất là CHND Trung Hoa láng giềng chẳng hạn.

Facebook Mâu Thuẫn – Yêu Thương.

Thủ đô Hà Nội, ngày 09 tháng 05 năm 2015.

------------------------------HẾT------------------------------

LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

130

I

.

M

Ộ

T

S

Ố

T

À

I

L

I

Ệ

U

T

H

A

M

K

H

Ả

O

1. Bài tập nâng cao và một số chuyên đề toán 8.

Bùi Văn Tuyên; NXB Giáo dục Việt Nam; 2004.

2. Bài tập nâng cao và một số chuyên đề toán 9.

Bùi Văn Tuyên; NXB Giáo dục Việt Nam; 2005.

3. Nâng cao và phát triển toán 8, tập 1 – tập 2.

Vũ Hữu Bình; NXB Giáo dục Việt Nam; 2004.

4. Nâng cao và phát triển toán 9, tập 1 – tập 2.

Vũ Hữu Bình; NXB Giáo dục Việt Nam; 2005.

5. Toán nâng cao Đại số 10.

Nguyễn Huy Đoan; NXB Giáo dục Việt Nam; 1999.

6. Bài tập nâng cao và một số chuyên đề Đại số 10.

Nguyễn Huy Đoan; Đặng Hùng Thắng; NXB Giáo dục Việt Nam; 2006.

7. Tài liệu chuyên toán: Đại số 10 – Bài tập Đại số 10.

Đoàn Quỳnh – Doãn Minh Cường – Trần Nam Dũng

– Đặng Hùng Thắng; NXB Giáo dục Việt Nam; 2010.

8. Một số chuyên đề Đại số bồi dưỡng học sinh giỏi THPT.

Nguyễn Văn Mậu – Nguyễn Văn Tiến và

một số tác giả; NXB Giáo dục Việt Nam; 2009.

9. Tuyển tập các bài toán hay và khó Đại số 9.

Nguyễn Đức Tấn – Đặng Đức Trọng – Nguyễn Cao Huynh

– Vũ Minh Nghĩa – Bùi Ruy Tân – Lương Anh Văn; NXB Giáo dục Việt Nam; 2002.

10. Một số phương pháp chọn lọc giải các bài toán sơ cấp, tập 1 – tập 3.

Phan Đức Chính – Phạm Văn Điều – Đỗ Văn Hà – Phạm Văn Hạp

– Phạm Văn Hùng – Phạm Đăng Long – Nguyễn Văn Mậu

– Đỗ Thanh Sơn – Lê Đình Thịnh; NXB Đại học Quốc gia Hà Nội; 1997.

11. Bài giảng chuyên sâu Toán THPT: Giải toán Đại số 10.

Lê Hồng Đức – Nhóm Cự Môn; NXB Hà Nội; 2011.

12. Phương pháp giải phương trình và bất phương trình.

Nguyễn Văn Mậu; NXB Giáo dục Việt Nam; 1994.

13. Toán bồi dưỡng học sinh phổ thông trung học – quyển 1; Đại số.

Hàn Liên Hải – Phan Huy Khải – Đào Ngọc Nam – Nguyễn Đạo Phương

– Lê Tất Tôn – Đặng Quan Viễn; NXB Hà Nội; 1991.

14. Phương trình và hệ phương trình không mẫu mực.

Nguyễn Đức Tấn – Phan Ngọc Thảo; NXB Giáo dục Việt Nam; 1996.

15. Chuyên đề bồi dưỡng Toán cấp ba; Đại số.

Nguyễn Sinh Nguyên; NXB Đà Nẵng; 1997.

16. Giải toán Đại số sơ cấp (Dùng cho học sinh 12 chuyên, luyện thi đại học).

Trần Thành Minh – Vũ Thiện Căn – Võ Anh Dũng; NXB Giáo dục Việt Nam; 1995.

17. Những dạng toán điển hình trong các kỳ thi tuyển sinh Đại học và Cao đẳng; Tập 3.

Bùi Quang Trường; NXB Hà Nội; 2002.

18. Ôn luyện thi môn Toán THPT theo chủ đề; Tập một: Đại số và lượng giác.

Cung Thế Anh; NXB Giáo dục Việt Nam; 2011.

19. Phương pháp giải toán trọng tâm.

Phan Huy Khải; NXB Đại học Sư phạm; 2011.

20. Các bài giảng luyện thi môn Toán; Tập 2.

Đức Chính – Vũ Dương Thụy – Đào Tam – Lê Thống Nhất; NXB Giáo dục Việt Nam; 1993.

21. 500 Bài toán chọn lọc Đại số - Hình học 10.

Lê Hoành Phò; NXB Đại học Quốc gia Hà Nội; 2012.

22. Tam thức bậc hai và ứng dụng.

LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

131

Lê Sĩ Đồng – Lê Minh Tâm; NXB Giáo dục Việt Nam; 2003.

23. Chuyên đề Bất đẳng thức và ứng dụng trong đại số.

Nguyễn Đức Tấn; NXB Giáo dục Việt nam; 2003.

24. 23 Chuyên đề giải 1001 bài toán sơ cấp ; Quyển 1.

Nguyễn Văn Vĩnh – Nguyễn Đức Đồng

và một số đồng nghiệp (NKTH); NXB Giáo dục Việt Nam; 2002.

25. Phương pháp giải toán bất đẳng thức và cực trị.

Nguyễn Văn Dũng – Võ Quốc Bá Cẩn – Trần Quốc Anh; NXB ĐHQG Hà Nội; 2011.

26. Các bài giảng về bất đẳng thức Cauchy.

Nguyễn Vũ Lương – Phạm Văn Hùng – Nguyễn Ngọc Thắng; NXB ĐHQG Hà Nội; 2008.

27. Cẩm nang luyện thi Đại học Ứng dụng hàm số Giải toán Đại số và Giải tích.

Huỳnh Nguyễn Luân Lưu – Nguyễn Thị Duy An; NXB ĐHQG Hà Nội ;2014.

28. Tư duy logic tìm tòi lời giải Hệ phương trình.

Mai Xuân Vinh – Phạm Kim Chung – Phạm Chí Tuân

– Đào Văn Chung – Dương Văn Sơn ; NXB ĐHQG Hà Nội; 2015.

29. Bồi dưỡng học sinh giỏi toán Trung học cơ sở, Đại số.

Nguyễn Thị Thanh Thủy – Phạm Minh Phương

– Trần Văn Tấn; NXB Giáo dục Việt Nam; 2014.

30. 9 Chuyên đề Đại số Trung học cơ sở.

Vũ Hữu Bình; NXB Giáo dục Việt Nam; 2014.

31. Hệ phương trình và phương trình chứa căn thức.

Nguyễn Vũ Lương – Phạm Văn Hùng – Nguyễn Ngọc Thắng; NXB ĐHQG Hà Nội; 2006.

32. Đề thi tuyển sinh vào lớp 10 hệ THPT Chuyên trực thuộc đại học và THPT Chuyên các tỉnh thành.

33. Đề thi tuyển sinh vào lớp 10 hệ THPT hệ đại trà các địa phương trên toàn quốc.

34. Đề thi học sinh giỏi môn toán khối 8 đến khối 12 các cấp.

35. Đề thi tuyển sinh Đại học – Cao đẳng môn Toán (chính thức – dự bị) qua các thời kỳ.

36. Đề thi Olympic 30 tháng 4 Toán học khối 10, khối 11 các tỉnh miền Trung và Nam bộ (1995 – 2013).

37. Các tạp chí toán học: Tạp chí Toán học và tuổi trẻ; Tạp chí Toán tuổi thơ 2 THCS; Tạp chí Kvant...

38. Các diễn đàn toán học: Boxmath.vn; Math.net.vn; Mathscope.org; Onluyentoan.vn; Diendantoanhoc.net;

Math.net.vn; K2pi.net; Mathlink.ro;...

39. Một số trang mạng học tập thông qua facebook; twiter;...

LÝ THUYẾT GIẢI HỆ PHƯƠNG TRÌNH CHỨA CĂN THỨC (PHẦN 8)

_______________________________________________________________________________________________________________________________________________________________

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

CREATED BY GIANG SƠN; GACMA1431988@GMAIL.COM TRUNG ĐOÀN HOÀNG SA; QUÂN ĐOÀN TĂNG THIẾT GIÁP

132

T

H

Â

N

T

H

Ể

T

Ạ

I

N

G

Ụ

C

T

R

U

N

G

T

I

N

H

T

H

Ầ

N

T

Ạ

I

N

G

Ụ

C

N

G

O

Ạ

I

D

Ụ

C

T

H

À

N

H

Đ

Ạ

I

S

Ự

N

G

H

I

Ệ

P

T

I

N

H

T

H

Ầ

N

C

Á

N

H

Y

Ế

U

Đ

Ạ

I

-

Sử dụng hàm số chặn miền giá trị giải hệ chứa căn (hệ chứa căn phần 8) – Lương Tuấn Đức

Thông tin :

Tài liệu liên quan:

Chuyên đề một số phương pháp đếm trong các bài toán tổ hợp

Các dạng toán vectơ Toán 10 thường gặp

Các dạng toán mệnh đề và tập hợp Toán 10 thường gặp

Đề cương giữa học kỳ 1 Toán 10 năm 2024 – 2025 trường THPT Hoàng Văn Thụ – Hà Nội

Đề cương giữa học kỳ 1 Toán 10 năm 2024 – 2025 trường THPT Xuân Đỉnh – Hà Nội