Sử dụng thuật toán Forward and Backward propagation để giải quyết bài toán Heart Disease | Bài thảo luận Lập trình python

lOMoAR cPSD| 45315597
TRƯỜNG ĐẠI HỌC THƯƠNG MẠI
KHOA HTTT KINH TẾ - THƯƠNG MẠI ĐIỆN TỬ -----&----- BÀI THẢO LUẬN
HỌC PHẦN: LẬP TRÌNH VỚI PYTHON
CHỦ ĐỀ: Sử dụng thuật toán Forward and Backward
propagation để giải quyết bài toán Heart Disease Nhóm: 15 Lớp Học Phần: 231_INFO4511_01
Giáo Viên Bộ Môn: Nguyễn Thị Thanh Tâm lOMoAR cPSD| 45315597 MỤC LỤC
A. MỞ ĐẦU .............................................................................................................................. 3
LỜI CẢM ƠN ........................................................................................................................ 3
LỜI NÓI ĐẦU ....................................................................................................................... 3
B. NỘI DUNG ........................................................................................................................... 5
1. CÁC LÝ THUYẾT LIÊN QUAN ................................................................................... 5
1.1. Mạng nơ -ron nhân tạo ................................................................................................ 5
1.2. Suy giảm độ dốc (Gradient Descent) .......................................................................... 6
2. LÍ THUYẾT FORWARD AND BACKWARD PROPAGATION ................................ 7
2.1. Lan truyền xuôi (Forward Propagation) ...................................................................... 7
2.2. Lan truyền ngược (Backward Propagation) ................................................................ 8
3. MÔ TẢ DỮ LIỆU ........................................................................................................... 10
4. MÔ TẢ BÀI TOÁN ........................................................................................................ 11
4.1. Mô tả bài toán ............................................................................................................ 11
4.2. Sử dụng thuật toán Forward and Backward Progation ............................................. 12
5. SỬ DỤNG PYTHON ĐỂ GIẢI QUYẾT BÀI TOÁN ................................................. 12
C. KẾT LUẬN.........................................................................................................................13 2 lOMoAR cPSD| 45315597 A. MỞ ĐẦU LỜI CẢM ƠN
Lời đầu tiên, nhóm chúng em xin gửi lời cảm ơn chân thành đến trường Đại Học
Thương Mại đã đưa học phần “Lập trình với Python” vào chương trình giảng dạy. Đặc
biệt, nhóm chúng em xin gửi lời cảm ơn sâu sắc đến giảng viên đã dạy dỗ, truyền đạt
những kiến thức quý báu cho chúng em trong suốt thời gian học tập vừa qua. Trong thời
gian học tập, chúng em đã có thêm cho mình nhiều kiến thức bổ ích, tinh thần hoc tâp
hiệu quả, nghiêm túc. Đây chắc chắn sẽ là những kiến thức quý báu là hành trang để
chúng em có thể vững bước sau này.
Lập trình với Python là học phần rất thú vị vô cùng bổ ích và có tính thực tế cao.
Đảm bảo cung cấp đủ kiến thức, gắn liền với nhu cầu thực tiễn của sinh viên. Tuy nhiên,
do vốn kiến thức còn nhiều hạn chế và khả năng tiếp thu thực tế còn nhiều bỡ ngỡ. Mặc
dù nhóm đã cố gắng hết sức nhưng bài thảo luận nhóm khó có thể tránh khỏi những
thiếu sót và nhiều chỗ còn chưa chính xác, kính mong cô xem xét và góp ý để bài thảo
luận của nhóm được hoàn thiện hơn ạ. LỜI NÓI ĐẦU
Trái tim là bộ phận quan trọng của cơ thể chúng ta. Nếu tim hoạt động không tốt
sẽ ảnh hưởng đến các bộ phận khác của cơ thể con người như não, thận,... Một số yếu
tố làm tăng nguy cơ mắc bệnh tim như: cholesterol, huyết áp cao, thiếu tập thể dục, hút
thuốc và béo phì,... Tổ chức Y tế Thế giới (WHO) ước tính có 12 triệu ca tử vong xảy ra
trên toàn thế giới, trong đó bệnh tim là nguyên nhân chính gây tử vong. Ví dụ, năm
2008, 17,3 triệu người chết vì bệnh tim và WHO ước tính đến năm 2030, gần 23,6 triệu
người sẽ chết vì bệnh tim. Chính vì thế, để giảm nguy cơ mắc bệnh tim, cần phải dự
đoán. Việc phát hiện và dự đoán bệnh là một nhiệm vụ khó khăn trong môi trường y tế,
phát hiện bệnh tim từ nhiều yếu tố là một vấn đề đa tầng có thể dẫn đến những giả định
tiêu cực và những hậu quả khó lường. Lượng dữ liệu (hồ sơ) khổng lồ là nguồn tài
nguyên chính cần được xử lý và phân tích để khai thác kiến thức cho phép hỗ trợ tiết
kiệm chi phí và ra quyết định.
Với sự phát triển như vũ bão của công nghệ, nhất là trong lĩnh vực trí tuệ nhân tạo
(AI), hiện nay người ta đã và đang liên tục phát triển các giải pháp của các vấn đề trong
mọi lĩnh vực, trong đó có các giải pháp kết hợp AI để tăng khả năng điều trị trong lĩnh
vực y tế, một ví dụ cụ thể hơn đó là mô hình chẩn đoán khả năng mắc bệnh tim dựa trên
các số liệu theo dõi mà máy móc có thể tự động ghi nhận liên tục với tần suất cao trong 3 lOMoAR cPSD| 45315597
thời gian dài. Vậy nhóm 15 học phần Lập trình với Pyhton sẽ tìm hiểu xem thuật toán
Forward and Backward propagation giải quyết bài toán bệnh tim như thế nào. 4 lOMoAR cPSD| 45315597 B. NỘI DUNG
1. CÁC LÝ THUYẾT LIÊN QUAN
1.1. Mạng nơ -ron nhân tạo
Mạng neural nhân tạo hay thường gọi ngắn gọn là mạng neural (tiếng Anh là
artificial neural network - ANN hay neural network) là một mô hình toán học hay mô
hình tính toán được xây dựng dựa trên các mạng neural sinh học. Nó gồm có một nhóm
các neural nhân tạo (nút) nối với nhau, và xử lý thông tin bằng cách truyền theo các kết
nối và tính giá trị mới tại các nút (cách tiếp cận connectionism đối với tính toán). Trong
nhiều trường hợp, mạng neural nhân tạo là một hệ thống thích ứng (adaptive system) tự
thay đổi cấu trúc của mình dựa trên các thông tin bên ngoài hay bên trong chảy qua
mạng trong quá trình học. Trong thực tế sử dụng, nhiều mạng neural là các công cụ mô
hình hóa dữ liệu thống kê phi tuyến. Chúng có thể được dùng để mô hình hóa các mối
quan hệ phức tạp giữa dữ liệu vào và kết quả hoặc để tìm kiếm các dạng/mẫu trong dữ liệu.
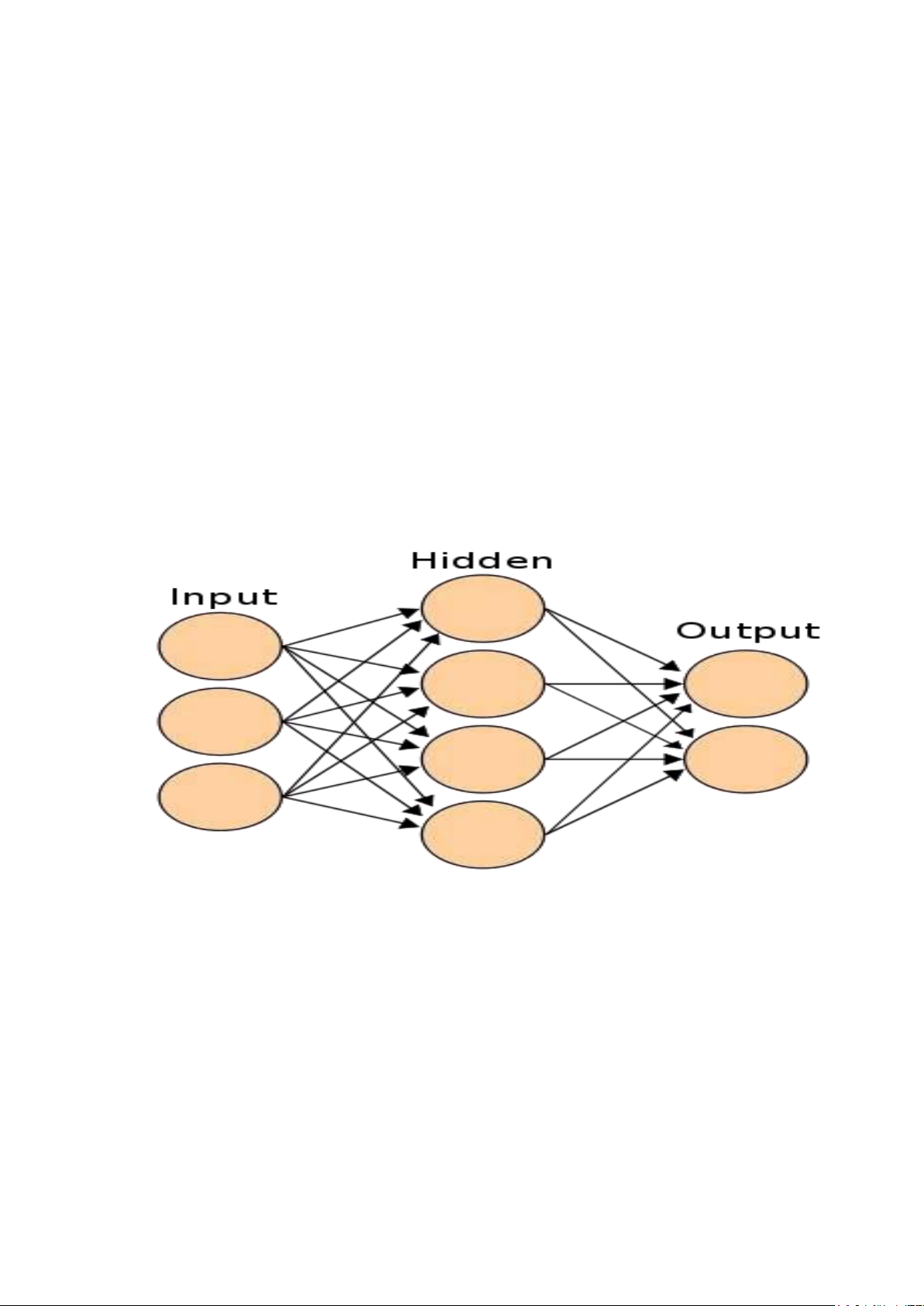
Hình 1:Hình mẫu về mạng nơ tron nhân tạo
Mạng thần kinh học (học ở đây có nghĩa là đã được huấn luyện) thông qua việc xử
lý các ví dụ, mỗi ví dụ đều chứa đầu vào và kết quả đã biết, hình thành các kết hợp có
trọng số xác suất giữa hai thành phần này, chúng được lưu trữ trong cấu trúc dữ liệu của
chính mạng. Việc huấn luyện mạng nơ-ron từ một ví dụ nhất định thường được tiến hành
bằng cách xác định sự khác biệt giữa đầu ra đã xử lý của mạng (thường là dự đoán) và
một đầu ra mục tiêu. Sự khác biệt này chính là lỗi. Mạng sau đó điều chỉnh các kết hợp
có trọng số của nó theo một quy tắc học tập và sử dụng giá trị lỗi này. Các điều chỉnh
liên tiếp sẽ khiến mạng nơ-ron tạo ra đầu ra ngày càng giống với đầu ra mục tiêu. Sau 5 lOMoAR cPSD| 45315597
một số lượng đủ lớn các điều chỉnh này, việc huấn luyện có thể được kết thúc dựa trên
một số tiêu chí nhất định. Đây là một hình thức của học có giám sát.
Các hệ thống như vậy "học" thực hiện các tác vụ bằng cách xem xét các ví dụ,
thông thường không cần được lập trình với các quy tắc cụ thể cho nhiệm vụ. Ví dụ, trong
thị giác máy tính, chúng có thể học cách xác định các hình ảnh chứa mèo bằng cách
phân tích các hình ảnh mẫu đã được gắn nhãn thủ công là "có mèo" hoặc "không có
mèo" và sử dụng kết quả để xác định mèo trong các hình ảnh khác. Chúng làm điều này
mà không cần bất kỳ kiến thức trước nào về mèo, ví dụ như chúng có lông, đuôi, râu và
khuôn mặt giống mèo. Thay vào đó, chúng tự động tạo ra các đặc điểm nhận dạng từ
các ví dụ mà chúng xử lý.
1.2. Suy giảm độ dốc (Gradient Descent)
Suy giảm độ dốc (còn thường được gọi là giảm dần độ dốc nhất) là một phương
pháp tối ưu hóa toán học không bị ràng buộc. Đây là thuật toán lặp bậc nhất để tìm
cực tiểu cục bộ của hàm đa biến khả vi . Ý tưởng là thực hiện các bước lặp lại theo
hướng ngược lại với độ dốc (hoặc độ dốc gần đúng) của hàm tại điểm hiện tại, bởi vì
đây là hướng đi xuống dốc nhanh nhất. Ngược lại, bước theo hướng của gradient sẽ dẫn
đến mức cực đại cục bộ của hàm đó, thủ tục sau đó được gọi là tăng dần độ dốc. Nó đặc
biệt hữu ích trong học máy để giảm thiểu hàm chi phí hoặc tổn thất. Không nên nhầm
lẫn việc giảm độ dốc với các thuật toán tìm kiếm cục bộ, mặc dù cả hai đều là các phương
pháp lặp lại để tối ưu hóa. Sự giảm dần độ dốc thường được quy cho Augustin-Louis
Cauchy, người đầu tiên đề xuất nó vào năm 1847. Jacques Hadamard đã đề xuất một
cách độc lập một phương pháp tương tự vào năm 1907. Các đặc tính hội tụ của nó cho
các bài toán tối ưu hóa phi tuyến tính lần đầu tiên được nghiên cứu bởi Haskell Curry
vào năm 1944 với phương pháp này ngày càng được nghiên cứu và sử dụng rộng rãi
trong những thập kỷ tiếp theo. Một phần mở rộng đơn giản của suy giảm độ dốc là giảm
độ dốc ngẫu nhiên, đóng vai trò là thuật toán cơ bản nhất được sử dụng để tạo hầu hết
các mạng nơ-tron học hiên nay. 6 lOMoAR cPSD| 45315597
Hình 2: Hình mô tả về gradient descent
2. LÍ THUYẾT FORWARD AND BACKWARD PROPAGATION
2.1. Lan truyền xuôi (Forward Propagation) a, Khái niệm
Lan truyền xuôi là quá trình tính toán cũng như lưu trữ các biến trung gian (bao
gồm cả đầu ra) của mạng nơ-ron theo thứ tự từ tầng đầu vào đến tầng đầu ra. Bây giờ ta
sẽ thực hiện qua từng bước trong cơ chế vận hành của mạng nơ-ron sâu có một tầng ẩn.
Điều này nghe có vẻ tẻ nhạt nhưng theo như cách nói dân giã, bạn phải “tập đi trước khi tập chạy”.
Lan truyền xuôi trong mạng nơ-ron là quá trình mà mạng nơ-ron đưa ra dự đoán.
Dữ liệu đầu vào được "truyền xuôi" qua từng tầng của mạng tới tầng cuối cùng, cũng là
tầng đầu ra chứa dự đoán của mạng. b, Nhiệm vụ
Quá trình truyền tải thông tin từ một điểm đầu đến một điểm cuối mà không có sự
can thiệp hay xử lý cụ thể nào đến dữ liệu.
Tính toán đầu ra của mô hình dựa trên đầu vào. Trong quá trình này, thông tin chạy
từ lớp đầu vào qua các lớp ẩn và cuối cùng đến lớp đầu ra thông qua các phép toán trong
mạng neural. Forward propagation có thể được xem như là quá trình lan truyền thông
tin từ trước đến sau trong mạng neural để tính toán kết quả dự đoán 7 lOMoAR cPSD| 45315597
c, Cơ chế hoạt động
Dữ liệu được truyền từ điểm xuất phát trên mạng đến điểm đích thông qua các thiết
bị mạng như router hay switch. Các thiết bị này chỉ kiểm tra và chuyển tiếp gói tin dựa
trên thông tin địa chỉ đích và địa chỉ nguồn có trong gói tin. Tuy nhiên, không có sự xử
lý thông tin hay biến đổi gói tin trong quá trình này.
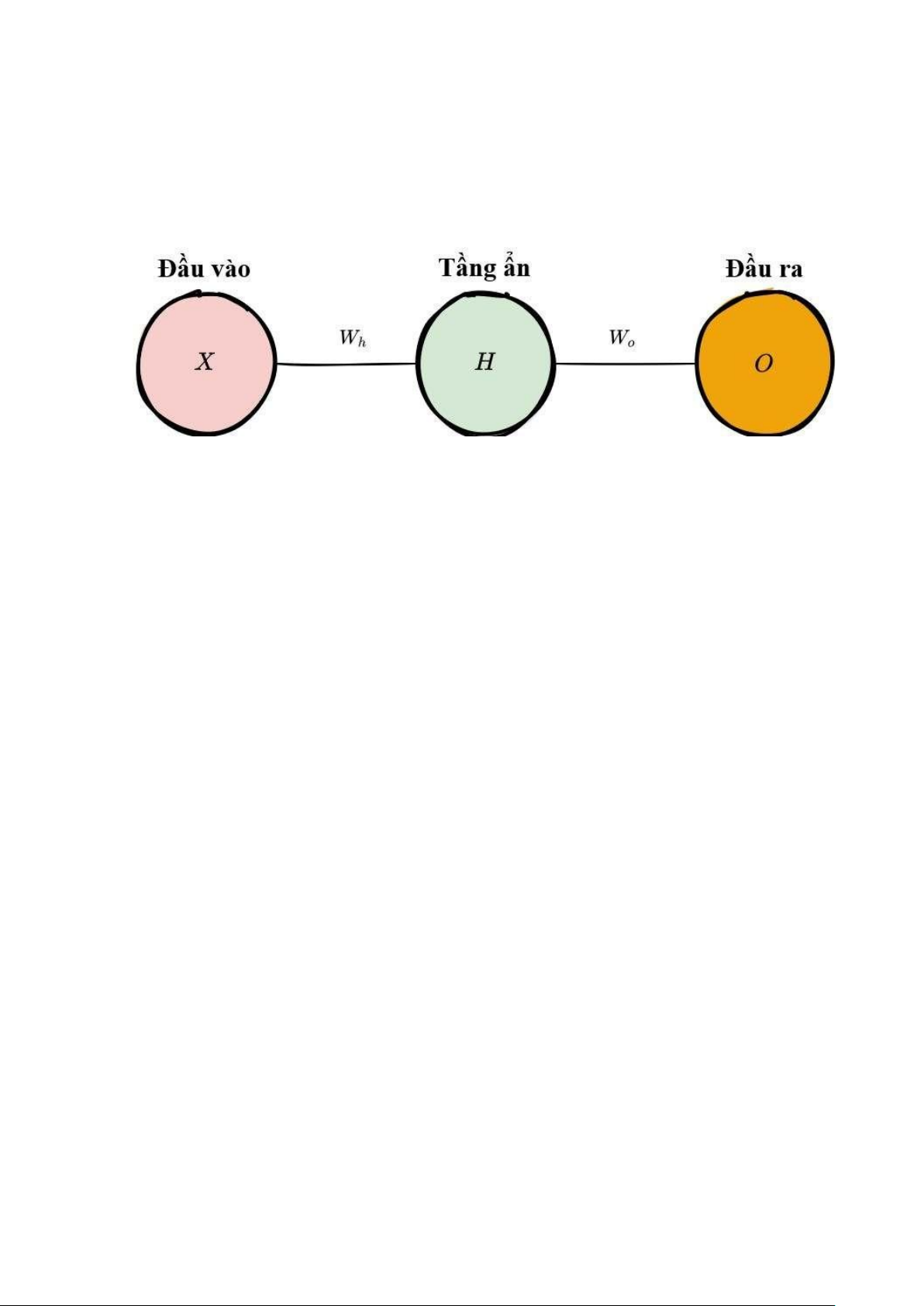
Với một mạng nơ-ron đơn giản chỉ có 1 tầng ẩn như hình minh hoạ trên với mỗi
tầng chỉ có 1 nơ-ron, quá trình lan truyền xuôi có thể được mô tả bằng công thức toán học như sau: Dự đoán = A(A(XWh)Wo)
trong đó A là hàm kích hoạt (ví dụ như ReLU - Đơn vị chỉnh lưu tuyến tính), X là đầu
vào của mạng, Wℎ và Wo lần lượt là trọng số của từng tầng trong mạng.
1.Định trọng số đầu vào khi truyền dữ liệu đầu vào tới tầng ẩn bằng cách nhân X với trọng số ẩn Wℎ.
2.Áp dụng hàm kích hoạt ở tầng ẩn và truyền kết quả tới tầng đầu ra.
3.Lặp lại bước 2, tuy nhiên lần này với X là kết quả H mà tầng ẩn trả về. Ta thu được kết quả dự đoán O.
2.2. Lan truyền ngược (Backward Propagation) a, Khái niệm
Backward propagation (lan truyền ngược) là phương pháp tính gradient của
các tham số mạng nơ-ron. Nói một cách đơn giản, phương thức này duyệt qua
mạng nơ-ron theo chiều ngược lại, từ đầu ra đến đầu vào, tuân theo quy tắc dây chuyền trong giải tích.
Các hệ thống học sâu có thể học các mẫu cực kỳ phức tạp và chúng thực
hiện điều này bằng cách điều chỉnh trọng số của chúng. Trọng số của một mạng
lưới thần kinh sâu được điều chỉnh chính xác như thế nào? Chúng được điều
chỉnh thông qua một tiến trình gọi là lan truyền ngược. Nếu không có lan truyền
ngược, các mạng lưới thần kinh sâu sẽ không thể thực hiện các tác vụ như nhận
dạng hình ảnh và diễn giải ngôn ngữ tự nhiên. Hiểu cách lan truyền ngược hoạt
động là rất quan trọng để hiểu các mạng thần kinh sâu nói chung, vì vậy, hãy tìm lOMoAR cPSD| 45315597
hiểu sâu về lan truyền ngược và xem quy trình được sử dụng như thế nào để điều
chỉnh trọng số của mạng.
Lan truyền ngược có thể khó hiểu và các tính toán được sử dụng để thực
hiện lan truyền ngược có thể khá phức tạp. Bài viết này sẽ cố gắng cung cấp cho
bạn một sự hiểu biết trực quan về lan truyền ngược, sử dụng ít trong cách tính
toán phức tạp. Tuy nhiên, một số cuộc thảo luận về toán học đằng sau lan truyền ngược là cần thiết. b, Nhiệm vụ
Nhiệm vụ chính của Backward propagation (hay còn gọi là
backpropagation) là tính toán đạo hàm cho các trọng số của mạng neural network.
Quá trình này được sử dụng trong quá trình huấn luyện để cập nhật các trọng số
sao cho mô hình mạng neural có thể học được từ dữ liệu.
Cụ thể, quá trình backward propagation bắt đầu bằng việc tính toán đạo hàm
của hàm mất mát (loss function) theo các trọng số của mạng. Điều này cho phép
đo lường mức độ ảnh hưởng của mỗi trọng số đến sự sai khác giữa đầu ra tính
toán và giá trị thực tế.
Sau đó, mạng neural sử dụng đạo hàm này để điều chỉnh các trọng số sao
cho giảm thiểu hàm mất mát. Thông qua quá trình lan truyền ngược, các đạo hàm
này được truyền lại theo lượt theo lớp ngược lại từ lớp đầu ra đến lớp đầu vào, từ
đó tính toán được gradient cho từng trọng số. Gradient này được sử dụng để cập
nhật trọng số thông qua một thuật toán tối ưu hóa như Gradient Descent.
Tóm lại, nhiệm vụ của backward propagation là tính toán đạo hàm của hàm
mất mát theo các trọng số của mạng neural network và sử dụng các đạo hàm này
để cập nhật trọng số, từ đó cải thiện hiệu suất và khả năng học của mô hình.
c, Cơ chế hoạt động
Thông thường được sử dụng trong các hệ thống như mạng nơ-ron nhân tạo (neural
networks) để cập nhật trọng số giữa các lớp nơ-ron. Khi mạng nơ-ron cho ra kết quả đầu
ra, thông tin này được truyền ngược từ lớp cuối cùng lại lớp đầu tiên để tính toán sự thay
đổi trọng số giữa các lớp nơ-ron để cải thiện độ chính xác và hiệu suất của mạng. Ví dụ:
Đạo hàm tiến bắt đầu từ một nút đầu vào và di chuyển dần tới nút cuối cùng
cần tính đạo hàm. Tại mỗi nút, nó sẽ tính tổng tất cả các đường đầu vào của nó.
Đương nhiên là mỗi đường như vậy thể hiện một cách ảnh hưởng tới nút tương
ứng bởi đầu vào. Bằng cách lấy tổng của chúng, ta sẽ thu được tổng tất cả các
cách ảnh hưởng tới nút tương ứng bởi tất cả các đầu vào. Hay nói cách khác, nó
chính là đạo hàm của nút tương ứng đó. lOMoAR cPSD| 45315597 Chain Forward
Mặc dù có thể bạn không nghĩ cách tính này dựa theo phương pháp đồ thị,
nhưng đạo hàm tiến rất gần với cách tính đạo hàm theo mà bạn được học trong
các bài giảng về giải tích.
Ngược lại, đạo hàm ngược lại bắt đầu từ đầu ra (điểm cần tính) cho tới đầu
vào (điểm bắt đầu). Tại mỗi nút, nó sẽ nhóm tất cả các cạnh xuất phát từ nút tương ứng đó. Chain Backward
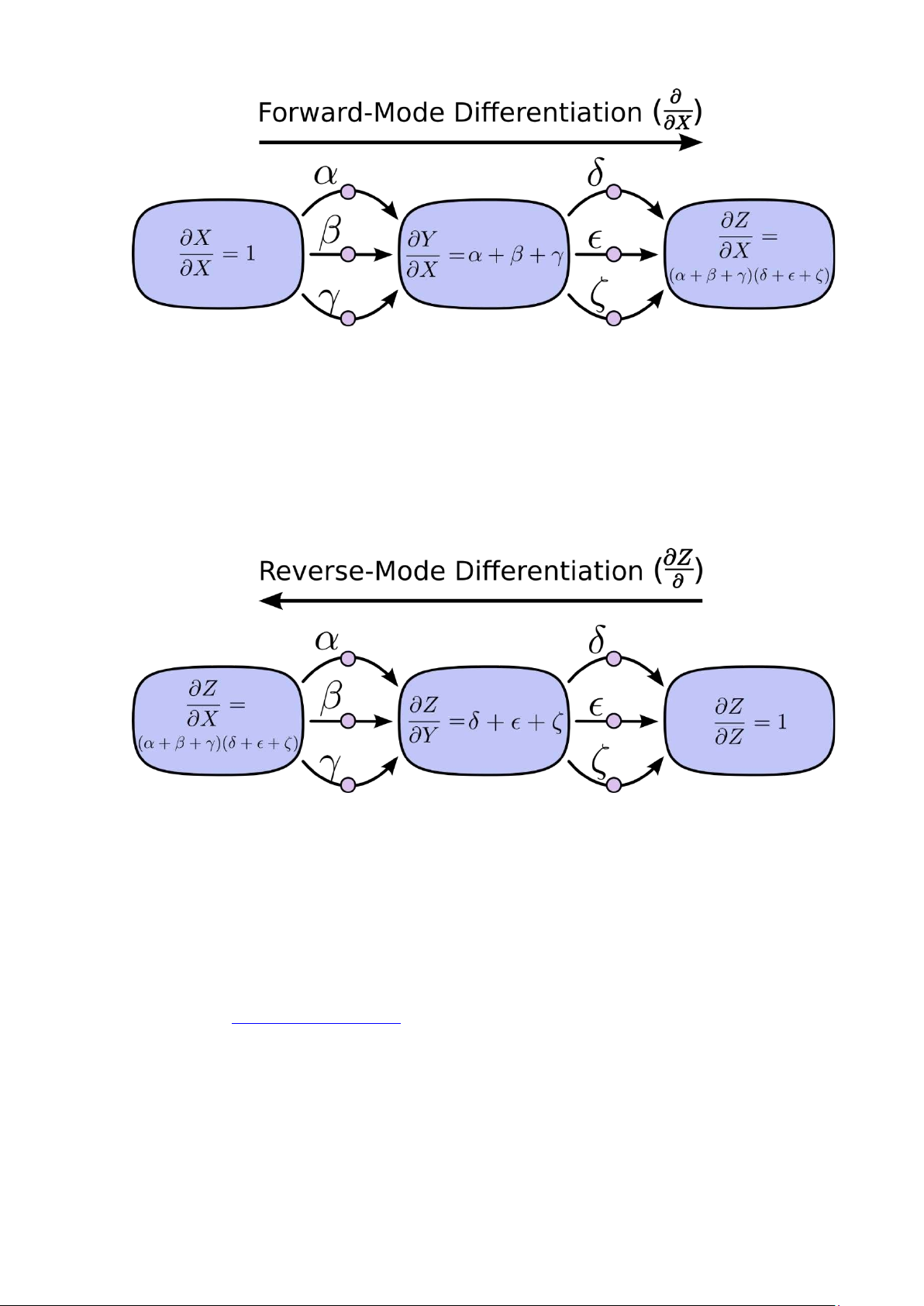
Đạo hàm tiến theo dõi một đầu vào ảnh hưởng tới tất cả các nút ra sao, còn
đạo hàm ngược thể hiện tất cả các nút ảnh hưởng tới 1 nút đầu vào thế nào. Nói
cách khác, đạo hàm tiến áp dụng phép toán ∂/∂X cho tất cả các nút, còn đạo hàm
ngược áp dụng phép toán ∂Z/∂ cho tất cả các nút.
3. MÔ TẢ DỮ LIỆU
Dữ liệu heart disease nhóm sử dụng có các thuật ngữ sau: 1.
Tuổi (Age): Đây là thông tin về độ tuổi của người được khảo sát. 2.
Giới tính (Sex): Thông tin về giới tính của người được khảo sát. Trong trường
hợpnày, có thể có giá trị 0 hoặc 1. Giá trị 0 thường đại diện cho giới tính nữ và giá trị 1
đại diện cho giới tính nam. 10 lOMoAR cPSD| 45315597 3.
Loại đau ngực (CP - Chest Pain): Đây là thông tin về loại đau ngực mà người
đượckhảo sát có thể trải qua. Có thể có các giá trị từ 0 đến 3, mỗi giá trị đại diện cho
một loại đau ngực khác nhau. 4.
Huyết áp nghỉ ngơi (Trestbps - Resting Blood Pressure): Đây là thông tin về
huyếtáp của người được khảo sát trong thời gian nghỉ ngơi. 5.
Mức cholesterol (Chol - Cholesterol): Đây là thông tin về mức độ cholesterol
trongmáu của người được khảo sát. 6.
Đường huyết lúc đói (FBS - Fasting Blood Sugar): Đây là thông tin về mức
đườnghuyết khi người được khảo sát đang trong tình trạng đói. 7.
Điện tâm đồ lúc nghỉ ngơi (Restecg - Resting Electrocardiographic Results): Đây
làthông tin về kết quả của điện tâm đồ khi người được khảo sát đang nghỉ ngơi. 8.
Mức nhịp tim tối đa (Thalach - Maximum Heart Rate Achieved): Đây là thông
tinvề mức độ nhịp tim tối đa của người được khảo sát. 9.
Đau ngực khi gắng sức (Exang - Exercise Induced Angina): Đây là thông tin về
việcngười được khảo sát có trải qua đau ngực khi gắng sức hay không. Giá trị 0 thường
đại diện cho không có đau ngực khi gắng sức và giá trị 1 đại diện cho có đau ngực khi gắng sức. 10.
Mức chênh lệch ST (Oldpeak): Đây là thông tin về mức chênh lệch của đoạn
STtrong điện tâm đồ so với thời gian nghỉ ngơi ban đầu. 11.
Đường cong ST (Slope - Slope of the ST Segment): Đây là thông tin về
dạngđường cong của đoạn ST trên điện tâm đồ. 12.
Số lượng động mạch lớn bị hẹp (Ca): Đây là thông tin về số lượng các động
mạchlớn bị hẹp trong hệ mạch tim của người được khảo sát. 13.
Hình ảnh động mạch (Thal - Thallium Stress Test): Đây là thông tin về hình
ảnhcủa động mạch trong điện tâm đồ. 14.
Mắc bệnh hay không (Target): Đây là thông tin về việc người được khảo sát
cómắc bệnh tim mạch hay không. Giá trị 1 thường đại diện cho mắc bệnh và giá trị 0
đại diện cho không mắc bệnh. 4. MÔ TẢ BÀI TOÁN
4.1. Mô tả bài toán
Trong bài toán Heart Disease - Classifications, các đặc điểm bệnh nhân sẽ
được chuyển thành đầu vào cho mô hình học máy. Mô hình học máy sẽ sử dụng
các thuật toán học máy để học mối quan hệ giữa các đặc điểm bệnh nhân và khả
năng mắc bệnh tim mạch. 11 lOMoAR cPSD| 45315597
Ví dụ, mô hình học máy có thể sử dụng mạng nơ-ron để học mối quan hệ
này. Mạng nơ-ron sẽ có một số lớp nơ-ron, mỗi lớp sẽ có một chức năng cụ thể.
Lớp đầu tiên sẽ nhận đầu vào là các đặc điểm bệnh nhân. Các lớp tiếp theo sẽ xử
lý đầu vào và tạo ra một đầu ra. Đầu ra này sẽ là khả năng mắc bệnh tim mạch của bệnh nhân.
Sau khi mô hình được học, mô hình có thể được sử dụng để dự đoán khả
năng mắc bệnh tim mạch của bệnh nhân mới. Để thực hiện việc này, các đặc điểm
của bệnh nhân mới sẽ được chuyển thành đầu vào cho mô hình. Mô hình sẽ sử
dụng các trọng số đã học để tính toán khả năng mắc bệnh tim mạch của bệnh nhân.
4.2. Sử dụng thuật toán Forward and Backward Progation
4.2.1. Forward propagation
Trong quá trình forward propagation, các đặc điểm bệnh nhân sẽ được
chuyển thành đầu vào cho mô hình học máy. Mô hình học máy sẽ sử dụng các
thuật toán học máy để học mối quan hệ giữa các đặc điểm bệnh nhân và khả năng mắc bệnh tim mạch.
Ví dụ, mô hình học máy có thể sử dụng mạng nơ-ron để học mối quan hệ
này. Mạng nơ-ron sẽ có một số lớp nơ-ron, mỗi lớp sẽ có một chức năng cụ thể.
Lớp đầu tiên sẽ nhận đầu vào là các đặc điểm bệnh nhân. Các lớp tiếp theo sẽ xử
lý đầu vào và tạo ra đầu ra. Đầu ra này sẽ là khả năng mắc bệnh tim mạch của bệnh nhân.
4.2.2. Backward propagation
Trong quá trình backward propagation, mô hình học máy sẽ sử dụng đầu ra
của mô hình để tính toán sai số. Sai số này sẽ được sử dụng để cập nhật các trọng số của mô hình.
Ví dụ, nếu đầu ra của mô hình là 0,5, có nghĩa là bệnh nhân có 50% khả
năng mắc bệnh tim mạch. Nếu bệnh nhân thực tế không mắc bệnh tim mạch, thì
mô hình đã dự đoán sai. Sai số này sẽ được sử dụng để cập nhật các trọng số của
mô hình, giúp mô hình cải thiện khả năng dự đoán của mình.
5. SỬ DỤNG PYTHON ĐỂ GIẢI QUYẾT BÀI TOÁN
5.1. Code python import pandas as pd
import numpy as np from matplotlib import pyplot as plt data =
pd.read_csv('heart_disease.csv') data.info() for i in 12 lOMoAR cPSD| 45315597
range(data.shape[1]): print("Các giá
trị duy nhất trong cột {} là
{}".format(i,data.iloc[:,i].unique())) y = data.target.values x_d =
data.drop(["target"], axis=1) x = (x_d - np.min(x_d))/(np.max(x_d)- np.min(x_d)) from
sklearn.model_selection import
train_test_split x_train, x_test, y_train, y_test =
train_test_split(x,y,test_size=0.2,rando
m_state=40) # Đảo ngược ma trận để
có các đặc trưng trong hàng và các
mẫu trong cột x_train = x_train.T x_test = x_test.T def
initialize_weights_and_bias(dimensio n):
weight_parameters = np.full([dimension, 1], 0.01)
bias_parameter = 0.0 return weight_parameters, bias_parameter
# Định nghĩa hàm sigmoid def sigmoid(z): y_head = 1 /
(1 + np.exp(-z)) return y_head def
forward_backward_propagation(w, b, x_train, y_train):
# Forward propagation (lan truyền xuôi) z = np.dot(w.T, x_train) + b
y_head = sigmoid(z) loss = -y_train * np.log(y_head) - (1 - y_train) *
np.log(1 - y_head) cost = (np.sum(loss)) / x_train.shape[1] #
x_train.shape[1] dùng để tỷ lệ
# Backward propagation (lan truyền ngược) derivative_weight = (np.dot(x_train,
((y_head - y_train).T))) / x_train.shape[1] derivative_bias = np.sum(y_head - y_train) /
x_train.shape[1] gradients = {"derivative_weight": derivative_weight, "derivative_bias":
derivative_bias} return cost, gradients
# Cập nhật học các tham số def update(w, b, x_train, y_train,
learning_rate, number_of_iterarion): 13 lOMoAR cPSD| 45315597
cost_list = [] cost_list2 = [] # Được sử dụng để in ra các giá trị cost
cho mỗi lần lặp index = []
for i in range(number_of_iterarion):
# Lan truyền xuôi và lan truyền ngược để tìm cost và gradients
cost, gradients = forward_backward_propagation(w, b, x_train, y_train) cost_list.append(cost)
# Cập nhật w = w - learning_rate *
gradients["derivative_weight"] b = b - learning_rate * gradients["derivative_bias"]
# In các giá trị cost if i % 10 == 0:
cost_list2.append(cost) index.append(i)
print("Cost after iteration %i: %f" % (i, cost)) #
Cập nhật học các tham số weights and bias
parameters = {"weight": w, "bias": b}
plt.plot(index, cost_list2) plt.xticks(index,
rotation='vertical') plt.xlabel("Number of
Iteration") plt.ylabel("Cost") plt.show()
return parameters, gradients, cost_list # Hàm dự đoán
def predict(w, b, x_test): # x_test là đầu vào lan truyền xuôi
z = sigmoid(np.dot(w.T, x_test) + b) Y_prediction =
np.zeros((1, x_test.shape[1]))
# Nếu nhỏ hơn hoặc bằng 0.5 dự đoán là không mắc bệnh, còn lớn hơn dự đoán 1 là có
for i in range(z.shape[1]): if z[0, i] <= 0.5: Y_prediction[0, i] = 0 else:
Y_prediction[0, i] = 1 return Y_prediction def logistic_regression(x_train,
y_train, x_test, y_test, learning_rate, num_iterations): dimension = x_train.shape[0]
w, b = initialize_weights_and_bias(dimension) parameters, gradients,
cost_list = update(w, b, x_train, y_train, learning_rate, num_iterations)
y_prediction_test = predict(parameters["weight"], parameters["bias"], x_test)
print("Score of Logistic Regression for Heart Disease Data by using Backward Propagation: {} %".format( 14 lOMoAR cPSD| 45315597
100 - np.mean(np.abs(y_prediction_test - y_test)) * 100))
logistic_regression(x_train, y_train, x_test, y_test, learning_rate=5, num_iterations=310) 5.2.Kết quả
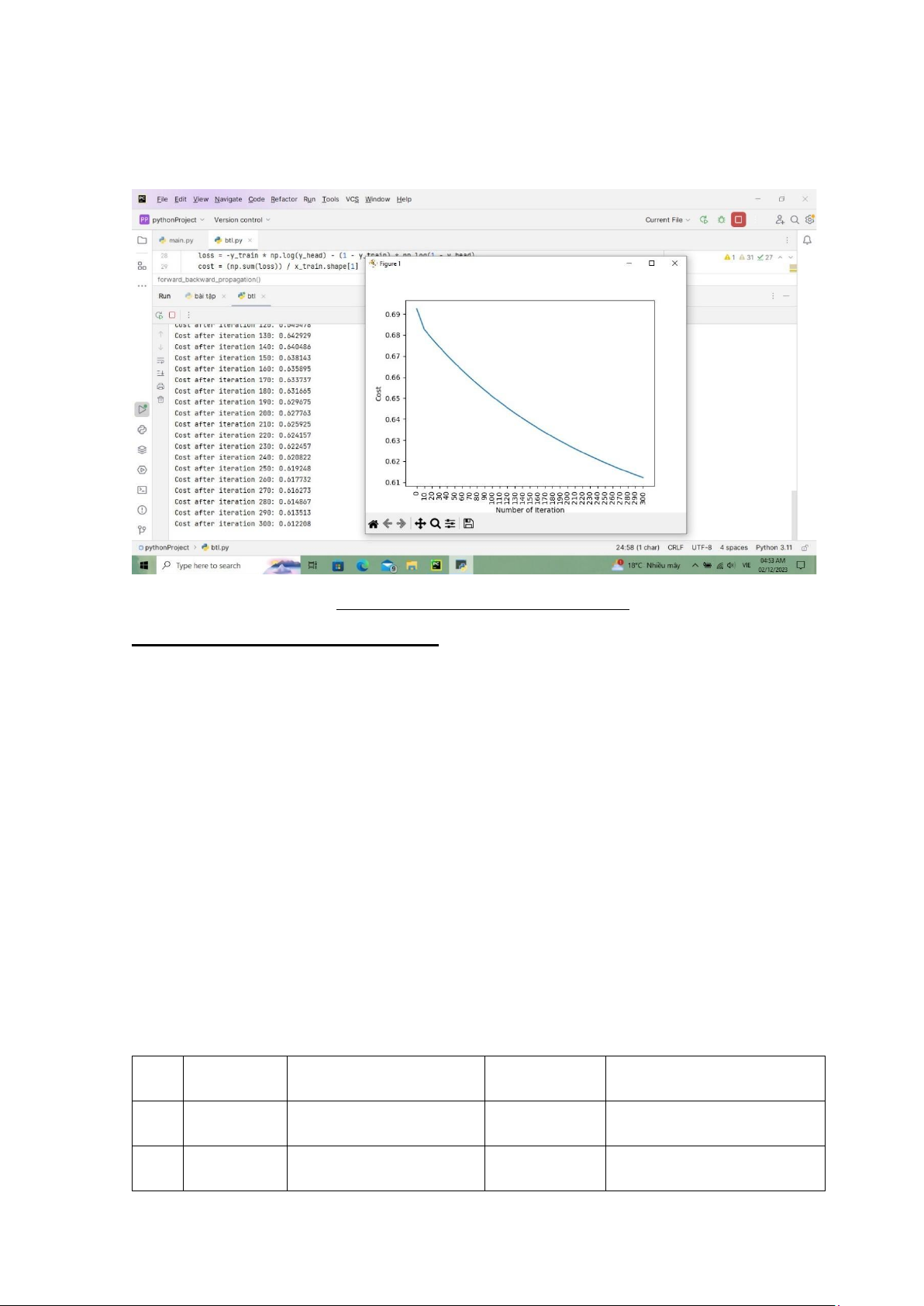
Hinh 3:Biểu đồ sau khi chạy thuật toán
Độ chính xác của thuật toán là :68,33% C. KẾT LUẬN
-Việc áp dụng thuật toán “Forward and Backward Progation” và các lý
thuyết có liên quan đã giúp nâng cao hiệu quả đáng kể khi xử lý bài toán Heart Diese như trên.
-Việc tìm hiểu về các lý thuyết giúp bọn em hiểu rõ hơn về thuật toán cũng
như cách vận hành của nó ,cách áp dụng thuật toán vào các bài toán khác Ngoài
ra thông qua thuật toán cũng giúp ta hiểu hơn về cách vận hành của một mạng
thần kinh học cũng như sự logic trong cách hoạt động của mạng nơ -ron góp phần
cho hoạt động của thuật toán trở nên trơn tru hơn
-Qua đó thấy được tầm quan trọng cũng như tính ứng dụng cao của các
thuật toán vào các bài toán nhiều dữ liệu. Giúp tiết kiệm thời gian, tang độ chính
xác của thuật toán lên mức đáng kẻ giảm thiểu sai số xuống mức thấp nhất
Bảng phân công nhiệm vụ STT MSV Họ và tên Chức vụ Nhiệm vụ 1 23D190069 Vũ Đức Huy Nhóm trưởng
Làm báo cáo,thuyết trình 2 23D190070 Vũ Thị Lan Hương Thành viên Làm slide 15 lOMoAR cPSD| 45315597 3 23D190071 Phan Nam Khánh Thành viên Mô tả bài toán 4
23D190072 Nguyễn Thị Ngọc Lan Thành viên Thực hiện code 5
23D190073 Hoàng Thị Ngọc Linh Thành viên Mô tả dữ liệu
Nhiệm vụ chung của cả nhóm:
-Tìm hiểu về thuật toán -Tìm hiểu về code 16