Sửa đề mẫu 2 - chương 1 2 - Toán cao cấp c2 | Trường Đại Học Duy Tân

Điều kiện của phép cộng hai ma trận: cùng cấp Điều kiện của phép nhân ma trận với 1 số: ko có điều kiện Điều kiện của phép nhân hai ma trận: số cột của ma trận trước bằng số hàng của ma trận sau Điều kiện của phép nhân lũy thừa ma trận: ma trận vuông. Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời bạn đọc đón xem!

7 4 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Môn: Toán cao cấp c2 (mth 102)

Trường: Đại học Duy Tân

Thông tin:

5 trang 1 tháng trước

Tác giả:

Profile Mai Nguyệt
DTU – Khoa Khoa học Tự nhiên B Thân Thị Quỳnh Dao
Họ và tên: ……………………………………………. Lớp: …… 1
Kiểm tra
1. Cho hai ma trận
5 7
A
3 4
và
2 1
B 3 5
1 0
. Khi đó
T
là ma trận
A.
5 3
7 4
B.
2 3 1
1 5 0
C.
2 1
3 5
1 0
D. không xác định được
Điều kiện của phép cộng hai ma trận: cùng cấp
Điều kiện của phép nhân ma trận với 1 số: ko có điều kiện
Điều kiện của phép nhân hai ma trận: số cột của ma trận trước bằng số hàng của ma trận sau
Điều kiện của phép nhân lũy thừa ma trận: ma trận vuông
Điều kiện của phép chuyển vị ma trận: ko có điều kiện
2. Cho ma trận
1 5 1
A
3 2 4
. Khi đó
-3A
là ma trận
A.
3 5 1
9 2 4
B.
1 15 1
3 6 4
C.
3 15 1
9 6 4
D.
3 15 3
9 6 12
3. Trong các ma trận sau, ma trận nào có dạng bậc thang?
A. B C. D. .
4. Cho ma trận A Phép biến đổi nào sau đây là phép biến đổi sơ cấp hàng trên A?
3x5 .
A.
1 2
h h
B.
2 2
h 0h
C.
2 2 1
h 3h h
D.
1 1 2
h 2h 3h
5. Cho ma trận
4 4
A
. Khẳng định nào sau đây đúng?
A.
2 2
A A
B.
2 4
A A
C .
2 8
A A
D.
2 16
A A
6. Ma trận con của ma trận là ma trận:
A. B. C. D.
DTU – Khoa Khoa học Tự nhiên B Thân Thị Quỳnh Dao
2
Họ và tên: ……………………………………………. Lớp: ……
7. Cho phép biến đổi ma trận sau:
1 1
3h h
A B
. Khi đó:
A.
A B
B.
A B
C.
3
A B
D. 3
A B
8. Cho
m 2 2 p 4 3
A B C
. Xác định n, p?
A. m = p = 5 B. m = p = 2 C. m = 4; p = 3 D. m = 3; p = 4
9. Cho hai ma trận
0 1
A
1 0
và
1 1
B
2 3
. Khẳng định nào sau đây là đúng?
A. AB = A B. AB = B C. AB = BA D Cả 3 đáp án A, B, C đều sai. .
10. Cho hai ma trận
1 2 3
1 0 6
4 2 0
A
,
1 1 4
2 0 2
3 6 0
B
. Khi đó,
A.
A B
B.
A B
C.
2
A B
D. đáp án khác
11. Xác định giá trị của định thức
0 1 3
0 2 5
0 3 7
D
?
A B. C. D. .
12. Cho
2 1
m 5
A
,
det 0
A
khi:
A. m < 10 B. m > 10 C. m =10 D. với mọi
m
13. Cho hai ma trận:
1 2 3 1 2 3
2 1 ; 4 2 2 ( 0)
0 0 2 2
A b B b a
a a a a
. Khẳng định nào sau đây đúng?
A.
1
2
A B
B.
2
A B
C.
A B
D.
A B
14. Cho hai định thức:
1 2
3 2 1 5 4 8
D 5 4 8 ; D 3 2 1
1 0 2 1 0 2
. Khẳng định nào sau đây đúng?
DTU – Khoa Khoa học Tự nhiên B Thân Thị Quỳnh Dao
3
Họ và tên: ……………………………………………. Lớp: ……
A.
1 2
D D
B .
1 2
D D
C.
2 1
D 2D
D.
2 1
D 2D
15. Cho hai định thức:
1 2
1 2 3 3 2 5
D 3 2 5 ; D 1 2 3
3 3 3
a b c a b c
. Khẳng định nào sau đây đúng?
A.
2 1
D 3D
B.
2 1
D 3D
C.
1 2
D 3D
D.
1 2
D 3D
16. Ma trận nào sau đây là ma trận khả nghịch?
A. B C. D. .
1. Xác định hạng của ma trận
1 4 6
0 1 5
0 2 10
A
?
A. r(A) = 1 B r(A) = 2 C. r(A) = 3 D. r(A) = 4 .
2. Cho ma trận
1 1 2
0 2 0
0 m 0
A
. Tìm giá trị của m để
3
r A
?
A. m = 0 B. m =1 C. m = 2 D không tồn tại giá trị m .
3. Ma trận hệ số tự do của hệ phương trình
2 3 1
9
x y
x y
là
A.
2 3
1 1
B.
2 1
1 9
C.
2 3 1
1 1 9
D .
1
9
4. Cho ma trận
4 6
A
. Khẳng định nào sau đây đúng?
A.
0 ( ) 4
r A
B.
0 ( ) 4
r A
C.
0 ( ) 4
r A
D .
0 ( ) 4
r A
5. Ma trận nghịch đảo của ma trận
1 1
1 0
A
là:
A.
1
1 1
1 0
A
B.
1
0 1
1 1
A
C.
1
0 1
1 1
A
D.
1
1 0
1 1
A
DTU – Khoa Khoa học Tự nhiên B Thân Thị Quỳnh Dao
4
Họ và tên: ……………………………………………. Lớp: ……
6. Cho ma trận
m 2
2 m
A
. Tập các giá trị m để ma trận
A
không khả nghịch là
A.
m = 2
B.
m = -2
C .
m = 2
D.
m 2
7. Hệ phương trình có ma trận hệ số mở rộng là
1 2 3 2
0 1 1 0
0 0 0 0
A
thì họ nghiệm tổng quát của hệ có:
A. 1 ẩn cơ bản B 2 ẩn cơ bản C. 3 ẩn cơ bản D. vô số ẩn cơ bản .
8. Hệ phương trình tuyến tính thuần nhất có ma trận hệ số là
1 2 3 5
0 9 4 2
0 0 0 0
A
thì họ nghiệm tổng quát
của hệ có:
A. 0 ẩn cơ bản B. 1 ẩn cơ bản C 2 ẩn cơ bản D. 3 ẩn cơ bản .
9. Hệ phương trình tuyến tính thuần nhất có ma trận hệ số là
2
1 0 3
0 5 6
0 5 m 2m 6
A
có vô số nghiệm
khi:
A. m
0
B. m
2
C. m
0
và m
2
D m.
0
hoặc m
2
10. Cho ma trận
1 0 m
0 0 m
0 m m 1 0
A
. Tìm giá trị của m để
1
r A
?
A. m = 0 B. m =1 C. m = 0
m = 1 D. đáp án khác
11. Tìm giá trị m để hệ phương trình có ma trận hệ số mở rộng là
2
2 1 0 0
0 3 1 0
0
0 0 1
A
m
vô nghiệm?
A. m
1
B. m
1
C. m
1
D không có giá trị m .
DTU – Khoa Khoa học Tự nhiên B Thân Thị Quỳnh Dao
5
Họ và tên: ……………………………………………. Lớp: ……
12. Cho hệ phương trình
1
2 2
0 0
x y z
y z
z
, có thể chọn ẩn nào làm ẩn cơ bản?
A.
,
x y
B.
,
x z
C.
,
y z
D A.,B.,C. đều đúng .
13. Cho hệ phương trình tuyến tính
4 1
10 3 6 3
x y m
x y m
. Khẳng định nào sau đây đúng?
A. Hệ vô nghiệm, m
B Hệ có nghiệm,. m
C. Hệ có vô số nghiệm, m
D. tất cả đều sai
14. Trong các hệ phương trình sau đây, hệ nào là hệ Cramer? không phải
A.
4 2
10 3 1
x y
x y
B.
4 2 1
6 3
x y
x y
C .
0
3 3 2
x y
x y
D.
5
3 2
x y
x y
15. Hệ phương trình có ma trận hệ số mở rộng là
2 1
0
m
0 m m 1
A
có nghiệm duy nhất khi:
A. m
0
B. m
1
C. m
0
hoặc m
1
D m.
0
và m
1
16. Tập nghiệm của một hệ phương trình tuyến tính thuần nhất là tập hợp:
A. Rỗng B. có 1 phần tử C. có ít nhất 1 phần tử D. có vô số các phần tử
| 1/5
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

DTU – Khoa Khoa học Tự nhiên B Thân Thị Quỳnh Dao Kiểm tra 2 1 5  7   1. Cho hai ma trận A  và B  3 5 . Khi đó   T A B là ma trận 3  4     1 0    2 1 5 3  2 3 1   A.  B. C. 3 5 7 4  
D. không xác định được    1  5 0   1 0   
Điều kiện của phép cộng hai ma trận: cùng cấp
Điều kiện của phép nhân ma trận với 1 số: ko có điều kiện
Điều kiện của phép nhân hai ma trận: số cột của ma trận trước bằng số hàng của ma trận sau
Điều kiện của phép nhân lũy thừa ma trận: ma trận vuông
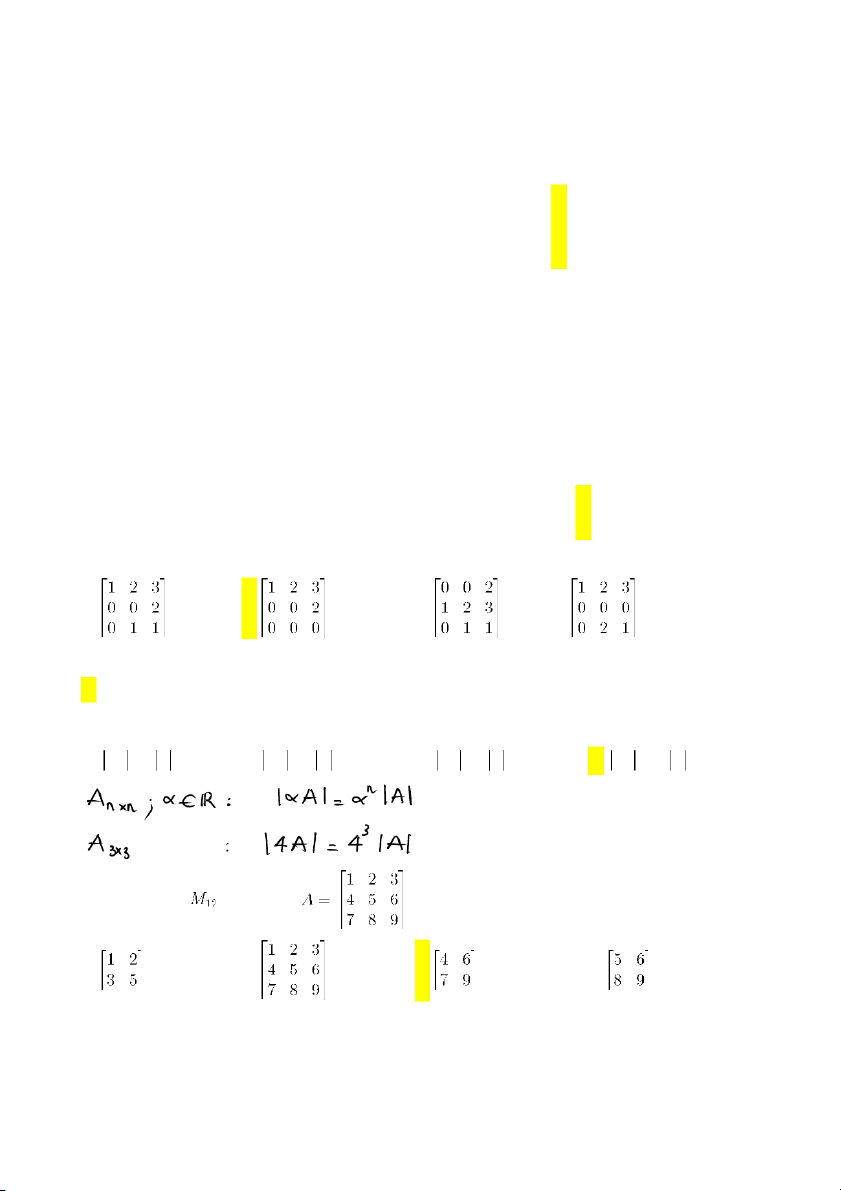
Điều kiện của phép chuyển vị ma trận: ko có điều kiện 1  5 1  2. Cho ma trận A  . Khi đó -3A 3  là ma trận  2 4   3 5 1  1 15 1   3  1  5 1  3 15 3 A.  B.   C.   D.    9 2 4    3 6 4  9  6  4   9 6 12
3. Trong các ma trận sau, ma trận nào có dạng bậc thang? A. B. C. D.
4. Cho ma trận A3x5 . Phép biến đổi nào sau đây là phép biến đổi sơ cấp hàng trên A? A. h  h B. h  0h C. h  3h  h D. h  2h  3h 1 2 2 2 2 2 1 1 1 2 5. Cho ma trận A
. Khẳng định nào sau đây đúng? 44 A. 2A  2 A B. 2 A  4 A C. 2A  8 A D. 2A  16 A 6. Ma trận con của ma trận là ma trận: A. B. C. D.
Họ và tên: ……………………………………………. Lớp: …… 1
DTU – Khoa Khoa học Tự nhiên B Thân Thị Quỳnh Dao 3 
7. Cho phép biến đổi ma trận sau: 1 h 1 h A  B . Khi đó: A. A  B B. A   B C. A  3 B D. 3 A  B 8. Cho   . Xác định n, p? m A 2 B2 p C   4 3 A. m = p = 5 B. m = p = 2 C. m = 4; p = 3 D. m = 3; p = 4      9. Cho hai ma trận 0 1 A    và 1 1 B  
 . Khẳng định nào sau đây là đúng? 1  0     2 3   A. AB = A B. AB = B C. AB = BA
D. Cả 3 đáp án A, B, C đều sai.  1 2 3 1 1  4     10. Cho hai ma trận A  1  0 6   , B  2 0 2   . Khi đó,  4 2 0   3 6 0   A. A  B B. A   B C. A  2 B D. đáp án khác 0 1 3
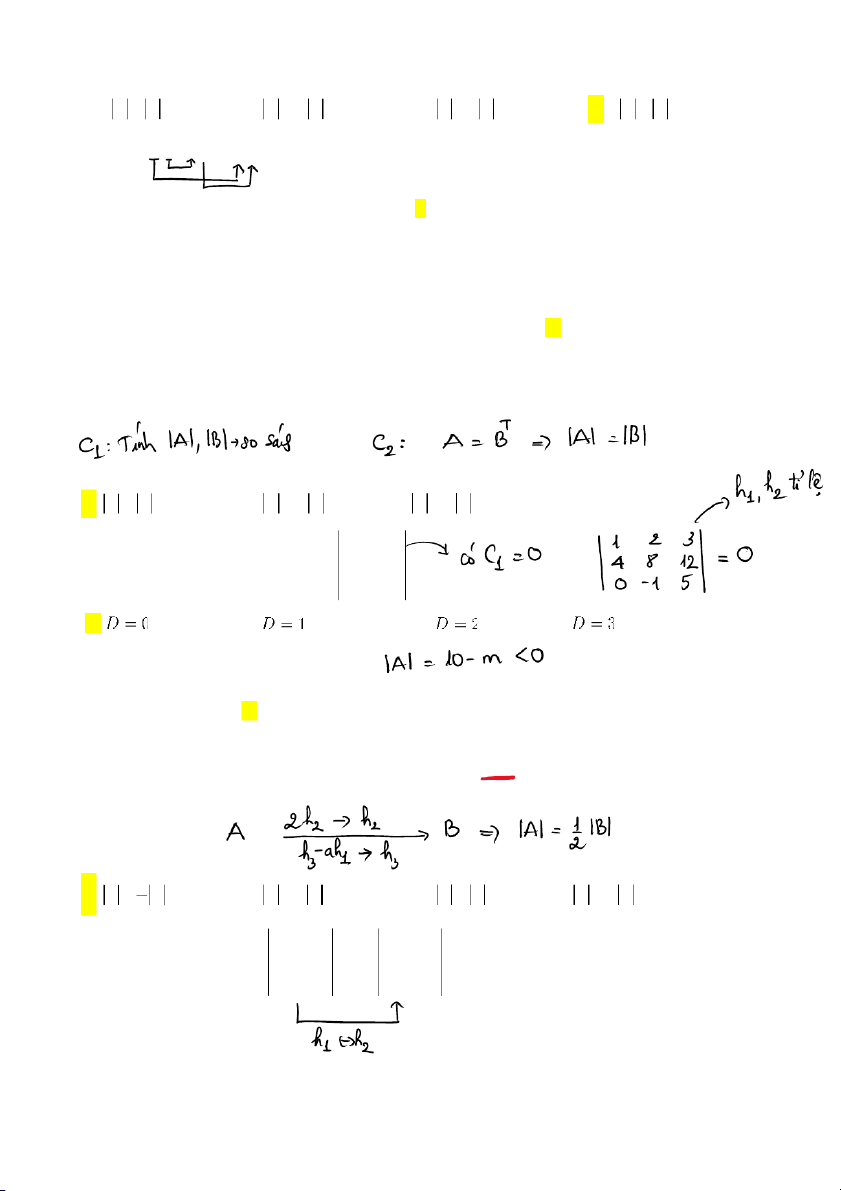
11. Xác định giá trị của định thức D  0 2 5 ? 0 3 7 A. B. C. D.  2 1 12. Cho A    , det A  0 khi: m 5 A. m < 10 B. m > 10 C. m =10 D. với mọi m   1 2 3 1 2 3     
13. Cho hai ma trận: A 2 b 1 ; B  4 2b 2 (a 0)    
. Khẳng định nào sau đây đúng? a 0 a 0 2  a 2  a     1 A. A  B B. A  2 B C. A  B D. A   B 2 3 2 1 5 4 8
14. Cho hai định thức: D  5 4 8 ; D  3
2 1 . Khẳng định nào sau đây đúng? 1 2 1 0 2 1 0 2 2
Họ và tên: ……………………………………………. Lớp: ……
DTU – Khoa Khoa học Tự nhiên B Thân Thị Quỳnh Dao A. D  D B. D  D C. D  2D D. D  2D 1 2 1 2 2 1 2 1 1 2 3 3 2 5
15. Cho hai định thức: D  3  2 5 ; D  1 2
3 . Khẳng định nào sau đây đúng? 1 2 a b c 3a 3b 3c A. D  3D B. D  3D C. D  3D D. D  3D 2 1 2 1 1 2 1 2
16. Ma trận nào sau đây là ma trận khả nghịch? A. B. C. D. 1 4 6 
1. Xác định hạng của ma trận   A  0  1 5  ? 0 2 10   A. r(A) = 1 B. r(A) = 2 C. r(A) = 3 D. r(A) = 4 1 1  2 2.   Cho ma trận A  0 2
0 . Tìm giá trị của m để r  ?   A  3 0 m 0   A. m = 0 B. m =1 C. m = 2
D. không tồn tại giá trị m 2x  3 y  1
3. Ma trận hệ số tự do của hệ phương trình  là  x  y  9   2 3   2 1  2 3 1 1   A.  B.   C.   D.    1 1    1 9  1  1  9  9   4. Cho ma trận
. Khẳng định nào sau đây đúng? 4 A 6  A. 0  r(A)  4 B. 0  r(A)  4 C. 0 r (A)  4 D. 0  r (A)  4 1  1 
5. Ma trận nghịch đảo của ma trận A  là: 1  0    1  1  0 1 0 1   1 0 A. 1 A  B. 1 A  C. 1 A  D. 1 A  1  0         1   1 1 1     1 1 3
Họ và tên: ……………………………………………. Lớp: ……
DTU – Khoa Khoa học Tự nhiên B Thân Thị Quỳnh Dao m 2  6. Cho ma trận A  
. Tập các giá trị m để ma trận A không khả nghịch là 2 m   A. m = 2 B. m = -2 C. m =  2 D. m  2  1 2 3 2  
7. Hệ phương trình có ma trận hệ số mở rộng là   A  0 1 
1 0 thì họ nghiệm tổng quát của hệ có:     0 0 0 0   A. 1 ẩn cơ bản B. 2 ẩn cơ bản C. 3 ẩn cơ bản D. vô số ẩn cơ bản 1 2 3 5  
8. Hệ phương trình tuyến tính thuần nhất có ma trận hệ số là A 0 9 4 2 
thì họ nghiệm tổng quát   0 0 0 0     của hệ có: A. 0 ẩn cơ bản B. 1 ẩn cơ bản C. 2 ẩn cơ bản D. 3 ẩn cơ bản 1  0 3   
9. Hệ phương trình tuyến tính thuần nhất có ma trận hệ số là   A  0 5 6   có vô số nghiệm   2 0  5 m  2m  6   khi: A. m  0 B. m  2
C. m 0 và m 2 D. m  0 hoặc m  2 1 0 m   10. Cho ma trận A  0 0 m 
 . Tìm giá trị của m để r   A  1 ? 0 mm    1 0  A. m = 0 B. m =1 C. m = 0 m = 1 D. đáp án khác 2 1 0 0  
11. Tìm giá trị m để hệ phương trình có ma trận hệ số mở rộng là   A  0 3 vô nghiệm?  1 0  2  0 0 m  1 0   A. m  1 B. m  1  C. m 1 D. không có giá trị m 4
Họ và tên: ……………………………………………. Lớp: ……
DTU – Khoa Khoa học Tự nhiên B Thân Thị Quỳnh Dao x   y  z  1 
12. Cho hệ phương trình  2y 
z  2 , có thể chọn ẩn nào làm ẩn cơ bản?  0z  0  A. , x y B. x,z C. y,z D. A.,B.,C. đều đúng  4x  y m 1
13. Cho hệ phương trình tuyến tính 
. Khẳng định nào sau đây đúng? 10x 3y  6m 3  A. Hệ vô nghiệm, m  
B. Hệ có nghiệm,m 
C. Hệ có vô số nghiệm,m  D. tất cả đều sai
14. Trong các hệ phương trình sau đây, hệ nào không phải là hệ Cramer?  4x  y  2 4 x 2 y  1  x  y  0  x  y  5 A.  B.  C.  D.  1  0x  3y  1 6x  y  3 3  x  3y  2 x  3 y  2 2 1 0 
15. Hệ phương trình có ma trận hệ số mở rộng là A    có nghiệm duy nhất khi:   0 mm    1 m   A. m  0 B. m  1
C. m 0 hoặc m 1 D. m  0 và m  1
16. Tập nghiệm của một hệ phương trình tuyến tính thuần nhất là tập hợp: A. Rỗng B. có 1 phần tử
C. có ít nhất 1 phần tử
D. có vô số các phần tử 5
Họ và tên: ……………………………………………. Lớp: ……