APPLIED STATISTICS COURSE CODE: ENEE1006IU Lecture 10: Chapter 6: t-Test
(3 credits: 2 is for lecture, 1 is for lab-work)
Instructor: TRAN THANH TU Email: tttu@hcmiu.edu.vn tttu@hcmiu.edu.vn 1 T-TEST
• For example, two methods for making a chemical analysis are compared to see if the
new one is equivalent to the older standard method; algae are grown under different
conditions to study a factor that is thought to stimulate growth; etc.
“Do two different methods of doing A give different results?”
“Can we be highly confident that the difference is positive or negative?”
“How large might the difference be?”
• One experimental design is to make a series of tests using treatment A and then to
independently make a series of tests using method B. Independent t-test
• A second way of designing the experiment is to pair the samples according to time,
technician, batch of material, or other factors that might contribute to a difference
between the two measurements Paired t-test tttu@hcmiu.edu.vn 2
6.1. PAIRED T-TEST FOR ASSESSING THE AVERAGE OF DIFFERENCES
•Two samples are said to be paired when each data point in the first sample is
matched and related to a unique data point in the second sample.
•Paired experiments are used when it is difficult to control all factors that might influence the outcome.
•If these factors cannot be controlled, the experiment is arranged so they are
equally likely to influence both of the paired observations. Paired data are
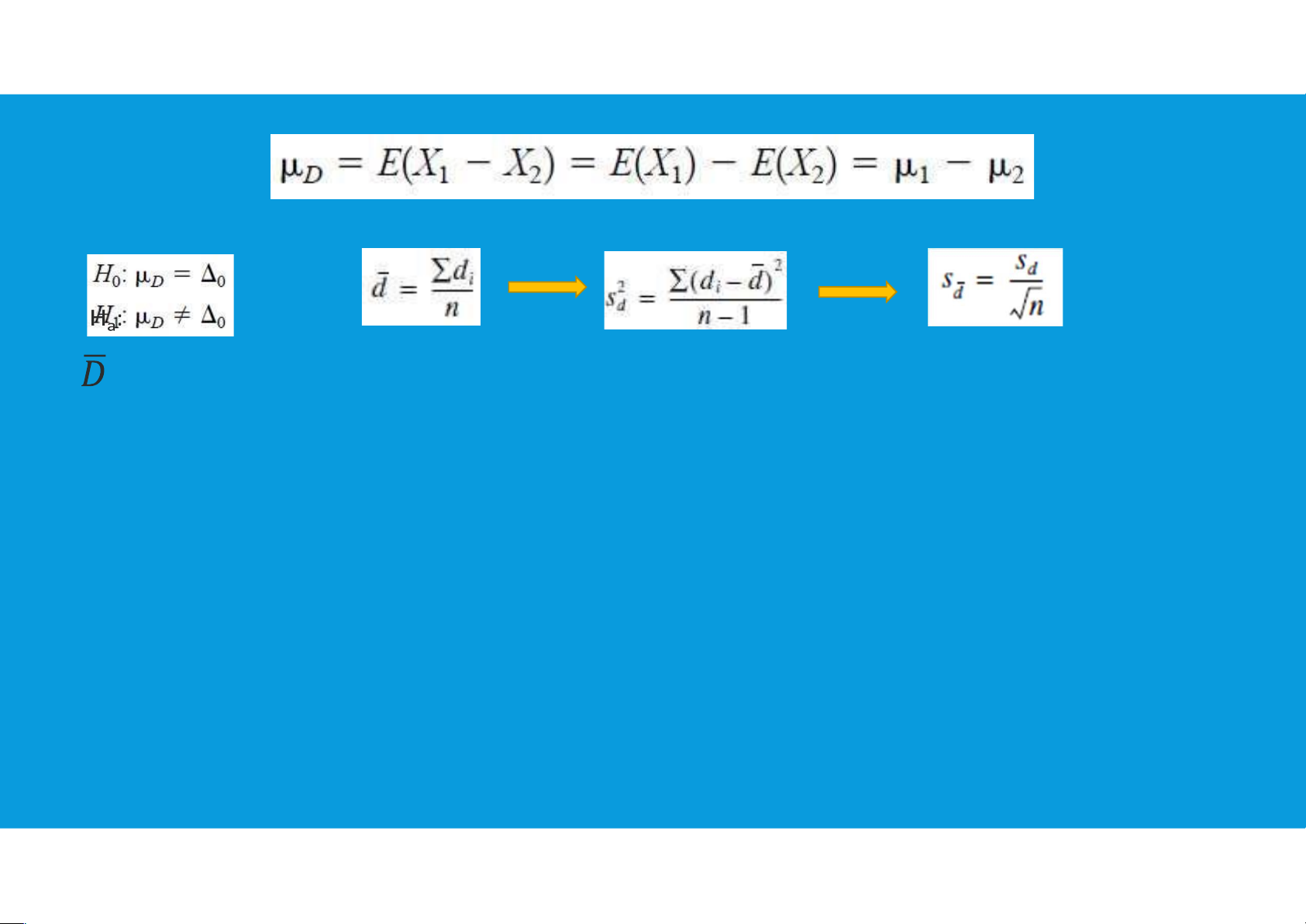
evaluated using the paired t-test •The classical null hypothesis is:
“The difference between the two methods is zero.” tttu@hcmiu.edu.vn 3
6.1. PAIRED T-TEST FOR ASSESSING THE AVERAGE OF DIFFERENCES
•The paired t-test examines the average of the differences between paired observations
•Let (X11, X21), (X12, X22), … , (X1n, X2n) be a set of n paired observations where: -µ1 and
are the mean and variance of the population represented by X1 -µ2 and
are the mean and variance of the population represented by X2
Define the differences between each pair of observations as Dj=X1j - X2j, (j= 1, 2, …, n)
The Dj’s are assumed to be normally distributed with mean µD and variance tttu@hcmiu.edu.vn 4
6.1. PAIRED T-TEST FOR ASSESSING THE AVERAGE OF DIFFERENCES
: the sample average of the n differences D1, D2, … , Dn SD: the
sample standard deviation of these differences tttu@hcmiu.edu.vn 5 : : : tttu@hcmiu.edu.vn 6
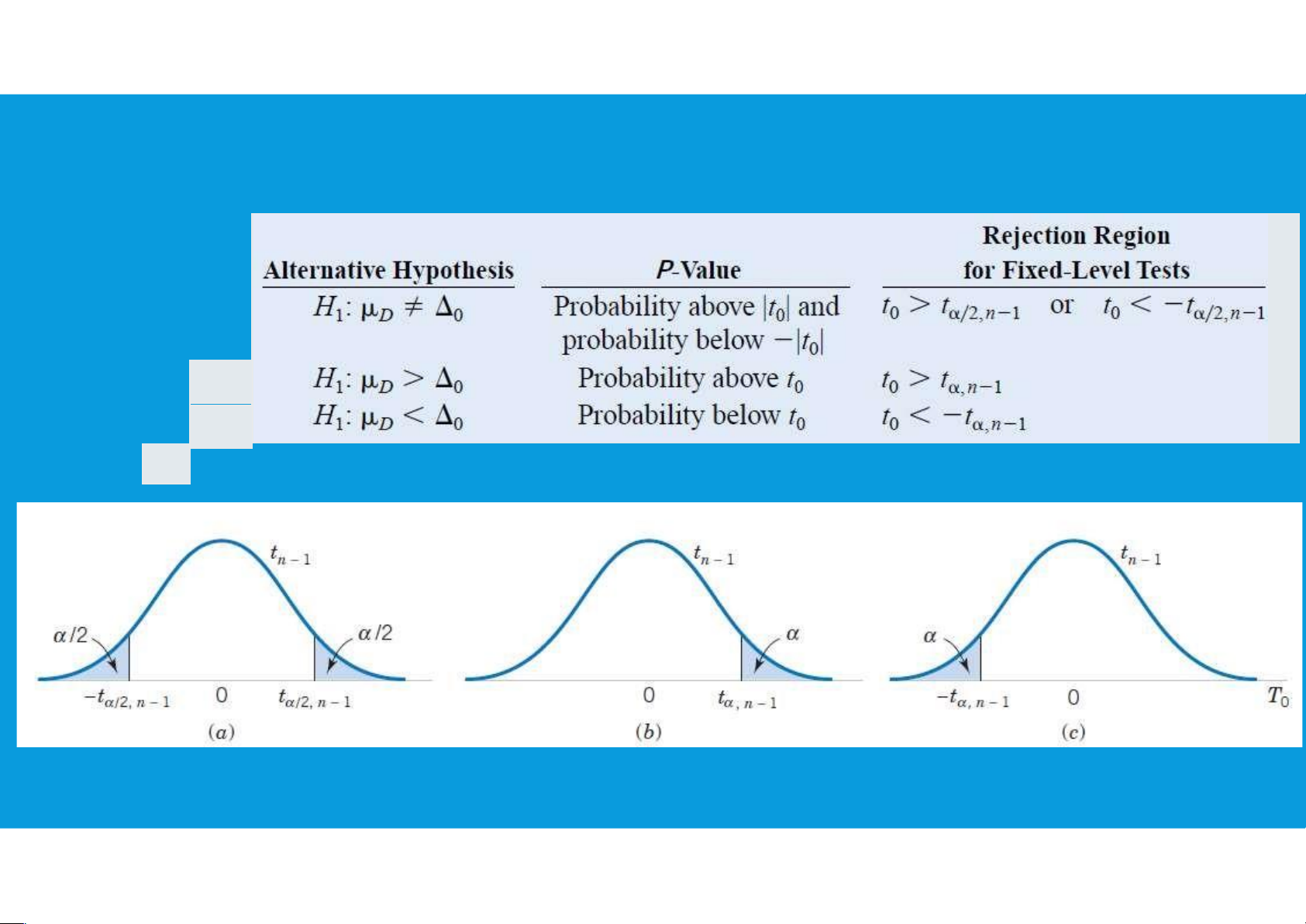
6.1. PAIRED T-TEST FOR ASSESSING THE AVERAGE OF DIFFERENCES Ha: Ha: Ha: tttu@hcmiu.edu.vn 7
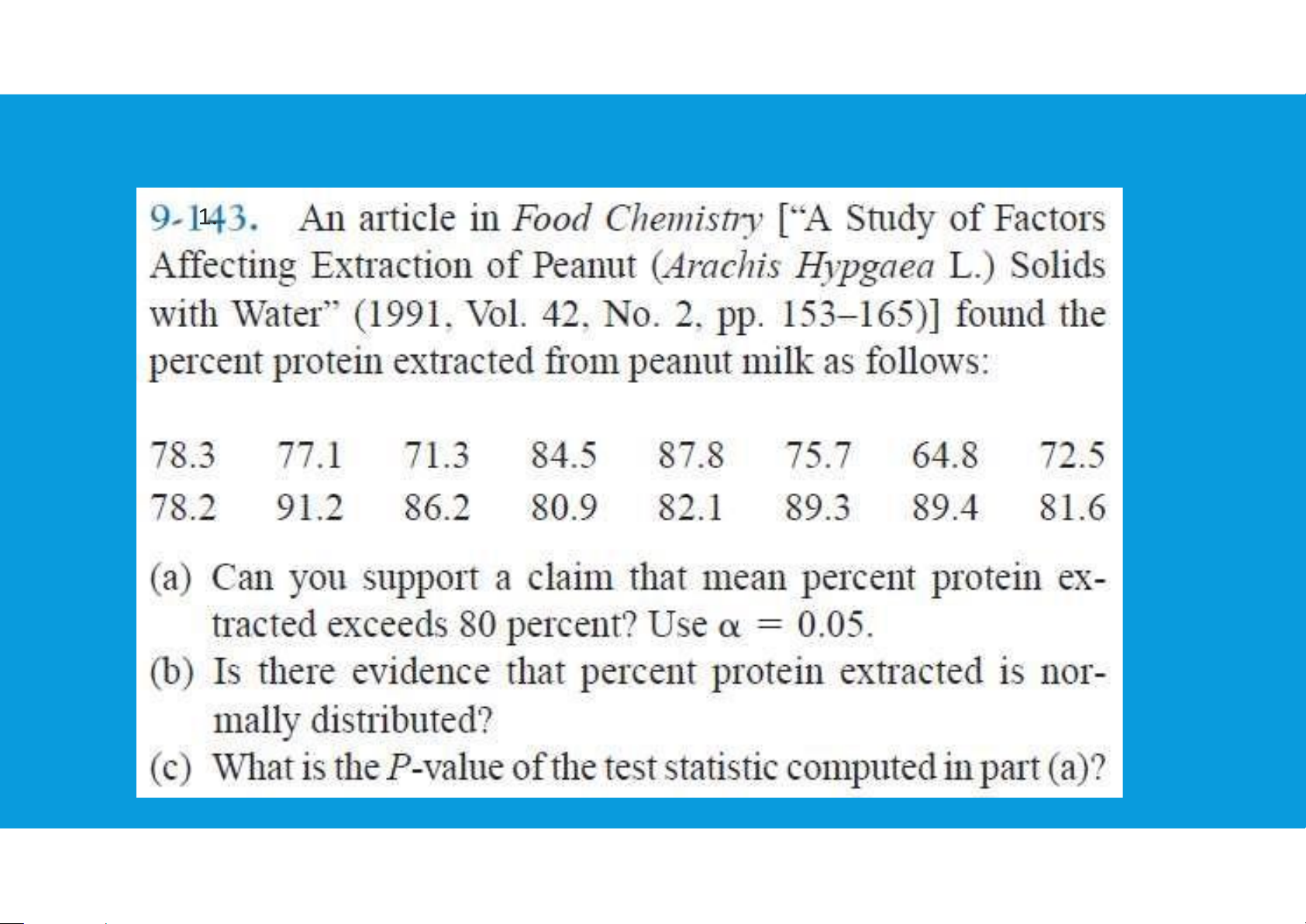
6.1. PAIRED T-TEST FOR ASSESSING THE AVERAGE OF DIFFERENCES tttu@hcmiu.edu.vn 8 End of file 1. Any questions? tttu@hcmiu.edu.vn 8
6.2. INDEPENDENT T-TEST FOR ASSESSING THE DIFFERENCE OF TWO AVERAGES
•A t-test on the difference of the averages would conclude that A and B are not different.
•Sometimes it is not possible to pair the tests, and then the averages of the two
treatments must be compared using the independent t-test. Example:
•Even if water specimens were collected on the same day, there will be differences
in storage time, distribution time, water use patterns, and other factors.
•Two independently distributed random variables y1 and y2 have, respectively, mean
values η1 and η2 and variances and
6.2. INDEPENDENT T-TEST FOR ASSESSING THE DIFFERENCE OF TWO AVERAGES
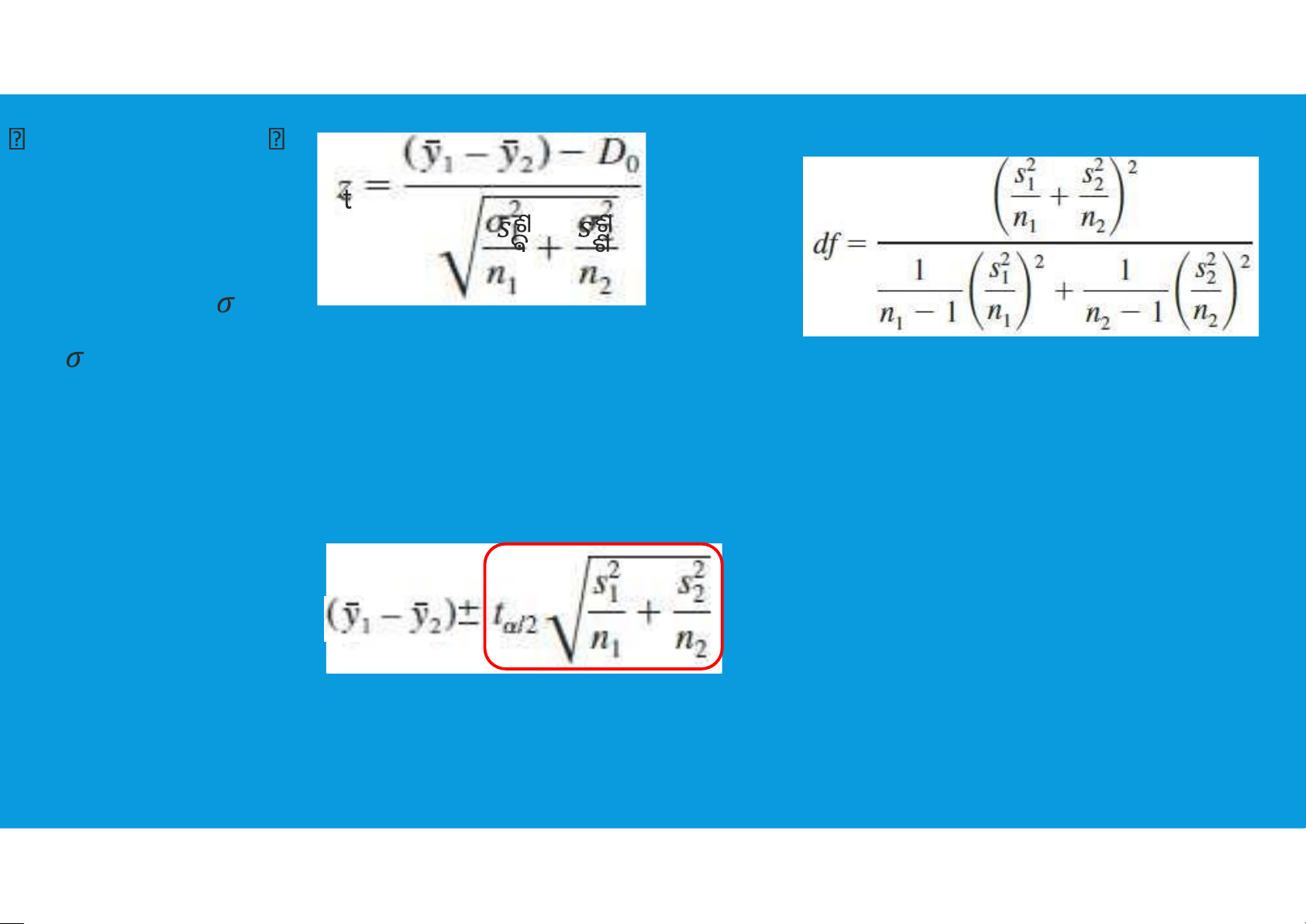
•The usual statement of the problem is in terms of testing the null hypothesis that
the difference in the means is zero:
•but we prefer viewing the problem in terms of the confidence interval of the difference tttu@hcmiu.edu.vn 10
6.2. INDEPENDENT T-TEST FOR ASSESSING THE DIFFERENCE OF TWO AVERAGES Usually the variances estimator of variance: tttu@hcmiu.edu.vn 11 test statistic used Degree of freedom for t distribution: for the case where ଵ and ଶ are unknown:
Interval estimate of the difference between two population means: Margin of error
6.2. INDEPENDENT T-TEST FOR ASSESSING THE DIFFERENCE OF TWO AVERAGES
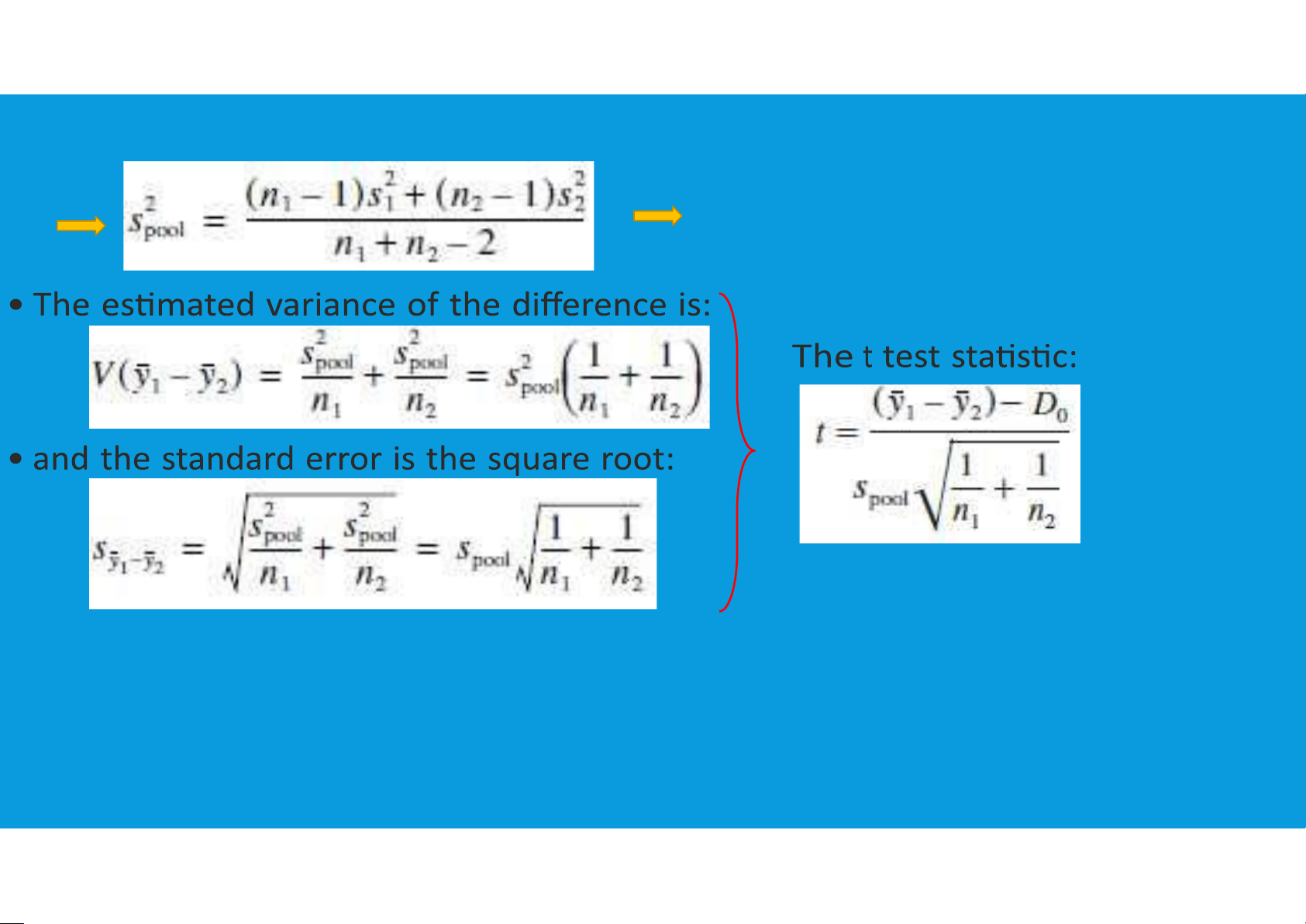
These can be pooled if they are of equal magnitude. tttu@hcmiu.edu.vn 12
Assuming this to be true, the pooled estimate of the variance is:
This is the weighted average of the variances,
where the weights are the degrees of freedom of each variance.
To construct the (1−α)100% percent confidence interval use the t statistic for α/2 and
ν=n1+n2−2 degrees of freedom tttu@hcmiu.edu.vn 13
6.3. HYPOTHESIS TESTS ABOUT THE DIFFERENCE BETWEEN THE PROPORTIONS OF TWO POPULATIONS
•Similar application for the proportion: tttu@hcmiu.edu.vn 14 tttu@hcmiu.edu.vn 15
6.3. HYPOTHESIS TESTS ABOUT THE DIFFERENCE BETWEEN THE PROPORTIONS OF TWO POPULATIONS
•This test statistic applies to large sample situations where n1p1, n1(1 − p1), n2p2,
and n2(1 − p2) are all greater than or equal to 5.
•Interval estimate of the difference between two population proportions: tttu@hcmiu.edu.vn 16 l End of file 2. Any questions? tttu@hcmiu.edu.vn 15 EXERCISES l tttu@hcmiu.edu.vn 16 EXERCISES