Tài liệu bồi dưỡng học sinh giỏi, Olympic chuyên đề dãy số

Tài liệu gồm 63 trang, được biên soạn bởi tác giả Nguyễn Thanh Tâm (trường THPT Tây Ninh, tỉnh Tây Ninh), hướng dẫn phương pháp giải một số dạng toán nâng cao về dãy số và giới hạn của dãy số, đây là các bài toán thường xuất hiện trong các đề thi học sinh giỏi và Olympic môn Toán THPT.

96 48 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 2: Dãy số. Cấp số cộng và cấp số nhân (KNTT)

Môn: Toán 11

Thông tin:

63 trang 8 tháng trước

Tác giả:

Profile Kim Oanh
TỔ TOÁN
TRƯỜNG THPT TÂY NINH
9-9-2020
Biên soạn: NGUYỄN THANH TÂM
Email: thanhtamstn@gmail.com
Tel: 0986318518
TÀI LIỆU
BỒI DƯỠNG HỌC SINH GIỎI, OLYMPIC
CHUYÊN ĐỀ: DÃY SỐ
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 1
NỘI DUNG CHUYÊN ĐỀ
- Phương pháp tìm số hạng của dãy số cho bởi một hệ thức truy hồi tuyến
tính.
- Liên phân số.
- Sai phân.
- Các phương pháp tìm số hạng của dãy số.
- Các khái niệm dãy con, dãy tuần hoàn và chu kì.
- Mối liên hệ giữa tính hội tụ của dãy số và dãy con.
- Tìm giới hạn của dãy số.
- Các bài toán thường gặp về dãy số.
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 2
PHẦN I
XÁC ĐỊNH DÃY SỐ
A. XÁC ĐỊNH DÃY SỐ BẰNG PHƯƠNG PHÁP QUY NẠP, PHƯƠNG PHÁP ĐỔI BIẾN.
1. Xác định dãy số bằng phương pháp quy nạp.
Để chứng minh mệnh đề chứa biến A(n) đúng với mọi số nguyên dương n ( bằng phương
pháp quy nạp), ta thực hiện theo các bước như sau:
Bước 1 (bước cơ sở hay bước khởi đầu): Kiểm tra A(n) đúng với n = 1.
Bước 2 (bước quy nạp): Giả sử A(n) đúng với n=k (k≥1,k∈N)
ta chứng minh A(n) đúng với n = k+1.
Bước 3: Kết luận: A(n) đúng với mọi số nguyên dương n.
Bài 1: Cho dãy số
( )
n
x
như sau:
a) Tính
1 2 3
, , .x x x
b) Tìm số hạng tổng quát ( số hạng thứ n).
Giải
a) Ta có
1
2
2 2cos
2
x
==
;
2
3
2
2 2 2 1 2 1 cos 2cos
2 4 2
x



= + = + = + =




32
34
2 2 1 cos 2cos
22
xx


= + = + =


.
b) Ta suy ra :
1
2cos , 1,2,...
2
n
n
xn
+
= =
Với n =1
1
2cos 2.
4
x
==
n =1 công thức đúng.
Giả sử công thức đúng với n=k (k≥1,k∈N) nghĩa là
1
2cos , 1
2
k
k
xk
+
=
Ta chứng minh công thức đúng với n=k+1 (k≥1,k∈N) nghĩa là
1
2
2cos , 1
2
k
k
xk
+
+
=
.
Thậy vậy:
1
12
2 2 1 cos 2cos
22
kk
kk
xx

+
++

= + = + =


Vậy công thức tổng quát của dãy số trên là:
1
2cos , 1,2,...
2
n
n
xn
+
= =
Bài 2: Cho dãy số
( )
n
x
như sau:
( )
1
1
3
21
, 1,2,...
1 1 2
n
n
n
x
x
xn
x
+
=
+−
= =
+−
. Tính
2003
x
Giải
Từ công thức
( )
tan tan
tan
1 tan .tan
xy
xy
xy
+
+=
−
.
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 3
Ta có:
2
2
tan 2 1
2tan
8
8
1 tan tan2. tan 2tan 1 0
4 8 8 8
1 tan
tan 1 2
8
8
=−
= = = + − =
−
= − −
Vì
tan 0
8
nên
tan 2 1
8
=−
,
1
3 tan ,
3
x
==
2
tan tan
38
tan
38
1 tan .tan
38
x



+

= = +


−
,
3
tan tan
3 8 8
tan 2
38
1 tan .tan
3 8 8
x


++



= = +



−+


Suy ra công thức tổng quát
( )
tan 1 , 1,2,...
38
n
x n n


= + − =


Với n=1
1
tan 0. 3,
38
x


= − =


đúng
Giả sử công thức đúng với n = k (k≥1,k∈N) nghĩa là
( )
tan 1 , 1
38
k
x k k


= + −


Ta chứng minh công thức đúng với n = k+1 (k≥1,k∈N) nghĩa là
1
tan , 1
38
k
x k k

+

= +


.
Thậy vậy:
( )
( )
( )
1
tan 1 tan
3 8 8
tan 1 tan , 1
3 8 8 3 8
1 tan 1 .tan
3 8 8
k
k
x k k k
k
+

+ − +


= = + − + = +

− + −


Vậy công thức tổng quát của dãy số trên là:
( )
tan 1 , 1,2,...
38
n
x n n


= + − =


BÀI TẬP TƯƠNG TỰ
Bài 1: Cho dãy số
( )
n
x
như sau:
( )
1
1
3
3
23
, 1,2,...
1 3 2
n
n
n
x
x
xn
x
+
=
+−
= =
+−
. Tính
2010
x
Hướng dẫn: ta có:
tan 2 3
12
=−
Công thức tổng quát của dãy số trên là:
( )
tan 1 , 1,2,...
6 12
n
x n n


== + − =


.
Bài 2: Tìm số hạng tổng quát của dãy số
( )
n
x
như sau:
1
1
1
3
, 1,2,...
1 3.
n
n
n
x
x
xn
x
+
=
+
= =
−
.
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 4
2. Xác định dãy số bằng phương pháp đổi biến (đặt ẩn phụ)
Chú ý:
1) Hàm số bậc hai
( )
2
f x ax bx c= + +
có đỉnh
;
22
bb
Af
aa


−−




thì đặt
2
b
Xx
a
=+
.
2) Hàm số bậc ba
( )
32
f x ax bx cx d= + + +
có điểm uốn
;
33
bb
Af
aa


−−




thì đặt
3
b
Xx
a
=+
.
3) Hàm số bậc bốn
( )
4 3 2
f x ax bx cx dx e= + + + +
có điểm uốn
;
44
bb
Af
aa


−−




thì đặt
4
b
Xx
a
=+
.
CÁC VÍ DỤ
Bài 1: Tìm dãy số
( )
n
x
biết
2
11
; , 1,2,...
n
x x ax bx c n
+
= = + + =
trong đó
2
2
0,
4
bb
ac
a
−
=
.
Hướng dẫn: đặt
2
nn
b
yx
a
=+
Ta được:
2
1
, 1,2,....
2 2 2
n n n
b b b
y a y b y c n
a a a
+
− = − + − + =
2
2
1
2
.
2 4 2
n
n n n
by
b b b
y a y b y c
a a a a
+


− = − + + − +




2 2 2
2
1
2
2 4 2 4
n n n n
b b b b b
y ay by by
a a a a
+
−
− = − + + − +
2
1
, 1,2,...
nn
y ay n
+
= =
Suy ra:
( )
2
2 2 2 1 1 2 1
1 2 1
... , 1,2,...
nn
n n n
y ay a ay a y n
− − −
−−
= = = = =
Vậy
21
2 1 1 2 1 2 1 1
1
, 1,2,...
2 2 2
n
n n n
n
b b b
x a y a n
a a a
−
− − − − −

= − = + − =


Thử lại bằng quy nạp.
Bài 2 (HSG QG 2000 – 2001): Cho dãy số
( )
n
x
như sau:
( )
11
2
, , 1,2,...
3 2 2 1 1
n
n
n
x
x x n
nx
+
= = =
++
Hãy tính tổng của 2001 số hạng đầu của dãy số
( )
n
x
Giải.
Ta thấy
0, 1,2,...
n
xn =
Do đó
( )
( )
1
1
11
2 2 1 , 1,2,...
2 2 1 1
n
n
n n n
x
x n n
n x x x
+
+
= = + + =
++
Đặt
2
n
n
u
x
=
Khi đó
1
3u =
và
( ) ( )( )
1
4 2 1 2 1 2 1 , 1,2,...
n n n
u n u u n n n
+
= + + = + − =
Vậy
( )( )
2 2 1 1
, 1,2,...
2 1 2 1 2 1 2 1
n
n
xn
u n n n n
= = = − =
+ − − +
Do đó
1 2 2001
1 1 1 1 1 1 1 4002
... ... 1
1 3 3 5 4001 4003 4003 4003
x x x
+ + + = − + − + + − = − =
.
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 5
3. Một số phép biến đổi bởi công thức lượng giác.
Bài 3: Xác định dãy số
( )
n
y
thỏa điều kiện
2
11
; 2 1, 1,2,...
nn
y R y y n
+
= − =
Giải.
* Nếu
1
1y
thì tồn tại
sao cho
1
cos y
=
.
Khi đó
2 2 1
23
2cos 1 cos2 , cos2 ,..., cos2
n
n
y y y
−
= − = = =
.
* Nếu
1
1y
xét số thực β sao cho
2
11
2
11
2
11
1
11
2 1 0
2
1
yy
yy
yy
= + −

= + − + =


= − −
Vậy: nếu đặt
2
11
1yy
= + −
thì
2
1 1 1
1 1 1
;1
2
y y y


= + = − −


Ta có:
2
2
1
2
1 1 1 1
2 1 ,
22
y



= + − = +


2
22
21
2
1 1 1 1
2 1 2 1
22
yy



= − = + − = +


.
Giả sử:
1
1
2
2
11
,
2
n
n
n
y
−
−

=+


khi đó
1
1
2
22
1
22
1 1 1 1
21
22
nn
nn
n
y


−
−
+

= + − = +



Vậy
1
1
2
2
11
, 1,2,...
2
n
n
n
yn
−
−

= + =


.
Bài 4: Xác định dãy số
( )
n
y
thỏa điều kiện
3
11
; 4 3 , 1,2,...
n n n
y R y y y n
+
= − =
Giải.
* Nếu
1
1y
thì tồn tại
sao cho
1
cos y
=
.
Khi đó:
3 2 1
23
4cos 3cos cos3 , cos3 ,..., cos3
n
n
y y y
−
= − = = =
.
* Nếu
1
1y
, xét số thực β sao cho
2
11
2
11
2
11
1
11
2 1 0
2
1
yy
yy
yy
= + −

= + − + =


= − −
Vậy: nếu đặt
2
11
1yy
= + −
thì
2
1 1 1
1 1 1
;1
2
y y y


= + = − −


Ta có:
0
0
3
3
1
3
1 1 1 1 1 1
4 3 ,
2 2 2
y


= + − + = +


3
33
2 1 1
3
1 1 1 1 1 1
4 3 4 3
2 2 2
y y y
= − = + − + = +
.
Giả sử:
1
1
3
3
11
2
n
n
n
y
−
−

=+


.
Khi đó:
11
11
3
3 3 3
1
3 3 3
1 1 1 1 1 1
43
2 2 2
n n n
n n n
n
y
−−
−−
+
= + − + = +
.
Vậy:
1
1
3
3
11
, 1,2,...
2
n
n
n
yn
−
−

= + =


.
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 6
Bài 5: Xác định dãy số
( )
n
u
như sau:
( )
3*
11
; 3 0 ,
n n n
x x ax x a n N
+
= = +
Giải
Đặt
2
nn
xy
a
=
khi đó
3*
11
; 4 3 ,
2
n n n
a
y y y y n N
+
= = +
.
Xét số thực β sao cho
2
11
2
11
2
11
1
11
2 1 0
2
1
yy
yy
yy
= + +

= − − − =


= − +
Vậy: nếu đặt
2
11
1yy
= + +
thì
(
)
2
1 1 1
1 1 1
;1
2
y y y


= − = − − +


Ta có:
0
0
3
3
1
3
1 1 1 1 1 1
43
2 2 2
y


= − + − = −


3
33
2 1 1
3
1 1 1 1 1 1
4 3 4 3
2 2 2
y y y
= + = − + − = −
.
Giả sử:
1
1
3
3
11
2
n
n
n
y
−
−

=−


.
Khi đó:
11
11
3
3 3 3
1
3 3 3
1 1 1 1 1 1
43
2 2 2
n n n
n n n
n
y
−−
−−
+
= − + − = −
.
Vậy:
11
33
22
1
1 1 , 1,2,...
2 4 2 4
nn
n
a a a a
xn
a
−−


= + + + − + =



.
BÀI TẬP ÁP DỤNG
Bài 3: Cho dãy số
( )
n
x
xác định như sau:
2*
11
11
; 4 ,
22
nn
x x x n N
+
− = −
Đặt
1
1
1 2 3
4
...
n
n
n
n
x
u
x x x x
−
+
=
Tìm số hạng tổng quát của dãy số
( )
n
u
Giải.
Đặt
1
2
nn
xy=
ta được dãy số
( )
n
y
thỏa điều kiện
22
1 1 1 1
11
2 ; 2 1, 1,2,...
22
n n n n
y x y y y y n
++
= = − = − =
Theo kết quả bài 3 trên, ta được :
1
1
2
2
11
2
n
n
n
y
−
−

=+


.
Với:
22
1 1 1 1
1 2 4 1y y x x
= + − = + −
. Đặt:
1
1
2
2
1
2
n
n
nn
zy
−
−

= = +


.
Khi đó:
21
21
2
2
1
1 2 3
2 2 2
2
22
1
...
1 1 1 1
...
n
n
n
n
n
n
z
z z z z


−
−
+
+
=
+ + + +
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 7
21
21
2
2
2 2 2
2
22
11
1 1 1 1 1
...
n
n
n
n


−
−


−+




=
− + + + +
1
1
2
2
2
2
2
2
11
11
...
1
1
n
n
n
n
n
n

+
+


−+



+


= = = −


−

−


Vì:
24
n n n
z y x==
nên
1
1 1 1
1 2 3 1 2 3 1 2 3
44
... 4 ... ...
n
n n n
n
n n n
z x x
z z z z x x x x x x x x
−
+ + +
==
.
Vậy: Số hạng tổng quát của dãy số
( )
n
u
là
1
1
2
*
2
11
,
1
n
n
n
u n N
+
+

+
= −

−

.
Bài 4 (Đề nghị OLYMPIC 30/04/1999): Xác định số hạng tổng quát của dãy số
( )
n
u
như sau:
3*
11
2; 9 3 ,
n n n
u u u u n N
+
= = +
Giải.
Đặt
2
3
nn
ux=
khi đó
3*
11
3; 4 3 ,
n n n
x x x x n N
+
= = +
Theo kết quả bài 5 trên, ta có:
11
33
22
1 3.2 3 4 3.2 3 4
11
2 2 4 2 4
nn
n
x
−−


= + + + − +



( ) ( )
11
33
1
3 10 3 10 , 1,2,...
2
nn
n
−−

= + + − =


Bài 5 (Đề nghị OLYMPIC 30/04/2004): Xác định số hạng tổng quát của dãy số
( )
n
u
như sau:
3 2 *
11
3
; 24 12 6 15 6,
6
n n n n
u u u u u n N
+
= = − + −
Giải
Đặt
61
nn
ux=−
khi đó
3*
11
2; 4 3 ,
n n n
x x x x n N
+
= = +
Theo kết quả bài 5 trên ta
( ) ( )
11
33
1
2 5 2 5 2 , 1,2,...
26
nn
n
xn
−−

= + + − + =


Cách 2: Đặt
61
nn
ux=−
Khi đó
3*
11
2; 4 3 ,
n n n
x x x x n N
+
= = +
Xét phương trình
2
4 1 0 2 5; 2 5x x x x− − = = + = −
Phương trình có 2 nghiệm
12
,xx
thỏa
12
12
4
.1
xx
xx
+=
=−
.
Ta chứng minh:
( )
11
33
12
1
2
nn
n
u x x
−−
=+
Suy ra:
( ) ( )
11
33
1
2 5 2 5 2 , 1,2,...
26
nn
n
un
−−

= + + − + =


Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 8
B. Phương pháp lặp.
Để tìm số hạng tổng quát của dãy số
( )
n
u
bằng phương pháp lặp ta thường tìm các hàm số
f(x) và h(x) sao cho
( ) ( )
( )
( )
1
*
nn
f u h f u
−
=
. Sử dụng (*) liên tiếp ta thu được:
( ) ( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
1 2 2 2 0
... **
n n n n n
f u h f u h h f u h f u h f u
− − −
= = = = =
Từ (**) ta tìm được
0
u
. Hàm số f được gọi là hàm số phụ, còn hàm số h được gọi là hàm số
lặp.
CÁC VÍ DỤ
Bài 1: Tìm số hạng tổng quát của dãy số
( )
n
x
cho như sau:
11
3; 7 1, 1,2,...
nn
x x x n
+
= = − =
Giải:
Gọi c là nghiệm của phương trình f(x) = x trong đó f(x) = 7x – 1.
Ta có :
1
71
6
c c c− = =
.
Xét:
11
11
7 1 7 1 , 1,2,...
66
n n n n
x x x x n
++
= − − = − − =
Ta được:
1
1 7 1
7 7 , 1,2,...
6 6 6
n n n
x x x n
+

− = − = − =


Vậy:
2 1 1
1 2 1
1 1 1 1 17
7 7 ... 7 7 .
6 6 6 6 6
nn
n n n
x x x x
−−
−−
− = − = − = = − =
Suy ra:
1
17 1
.7 , 1,2,...
66
n
n
xn
−
= + =
Bài 2.Cho dãy số
( )
n
x
được xác định như sau:
*
11
54
5; ,
2
n
n
n
x
x x n N
x
+
+
= =
+
.
Chứng minh rằng:
*
4,
n
x n N
.Tính
2013
x
Giải
Gọi c là nghiệm của phương trình f(x) = x, trong đó f(x)
54
2
n
n
x
x
+
=
+
Xét:
2
1
54
3 4 0
4
2
c
c
c c c
c
c
=−
+
= − − =
=
+
.
Ta có:
1
54x =
.
Giả sử:
*
4,
n
x n N
.
Ta chứng minh:
*
1
4,
n
x n N
+
Nếu
1
4
n
x
+
=
thì
54
4 5 4 4 8 4
2
n
n n n
n
x
x x x
x
+
= + = + =
+
(mâu thuẫn).
Vậy:
*
4,
n
x n N
.
Ta có:
1 1 1 1
1 1 1 1
5 4 4 5 4 1
4 4 ; 1 1 6
2 2 2 2
n n n n
nn
n n n n
x x x x
xx
x x x x
− − − −
− − − −
+ − + +
− = − = + = + =
+ + + +
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 9
Suy ra:
21
12
1
1 2 1
1 1 1
1
6 6 ... 6 6
4 4 4 4
nn
n n n
n n n
x x x
x
x x x x
−
−−
−−
+ + +
+
= = = = =
− − − −
Do đó:
( )
*
4.6 1
1 6 4 ,
61
n
n
n n n
n
x x x n N
+
+ = − =
−
Vậy:
2013
2013
2013
4.6 1
61
x
+
=
−
.
Bài 3: Tìm số hạng tổng quát của dãy số
( )
n
x
cho như sau:
2
11
; 14 56, 1,2,...
n n n
x R x x x n
+
= = − + =
Giải
Gọi c là nghiệm của phương trình f(x) = x, trong đó f(x) =
( )
2
14 56f x x x= − +
.
22
14. 56 15 56 0 7; 8c c c c c c c= − + − + = = =
Xét:
( )
( ) ( )
11
2
22
2
1 1 1 1
7 14 49 7 ... 7 7 , 1,2,...
nn
n n n n
x x x x x n
−−
− − −
− = − + = − = = − = − =
Vậy: Số hạng tổng quát của dãy số
( )
n
x
là
( )
1
2
7 7 , 1,2,...
n
n
xn
−
= + − =
Bài 4: Tìm số hạng tổng quát của dãy số
( )
n
u
cho như sau:
2
11
2
; 3 4 , 1,2,...
3
n n n
u R u u u n
+
= = + + =
Giải.
Ta biến đổi:
22
11
2
3 4 3 9 12 2.
3
n n n n n n
u u u u u u
++
= + + = + +
Đặt
3
n
n
x
u =
.
Ta được:
2
11
3 ; 4 2, 1,2,...
n n n
x R x x x n
+
= = + + =
( )
2
2
11
2 4 4 2 , 1,2,...
n n n n
x x x x n
++
+ = + + = + =
Suy ra:
( ) ( )
( )
2
1
22
2
1 2 1
2 2 2 ... 2
n
n n n
x x x x
−
−−
+ = + = + = = +
Vậy:
( )
( )
1
1
2
2
3 2 2
3 2 2
3
n
n
nn
xu
−
−
+−
= + − =
.
Lớp hàm
( )
22
ax
gx
b c x
=
+
Ta có:
( )
22
2 2 2 2
dax b ax dc x
d g x d
b c x b c x
−+
− = − =
++
Ta cần chọn a, b, c, d sao cho
( )
2
2 2 2 2
d 2db ax dc x d x d x x− + = − = − +
2
2
2
22
1
1
bd d b d
a d a d
dc
c
d
==
= =


=
=
.
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 10
Bài 5: Tìm số hạng tổng quát của dãy số
( )
n
x
cho như sau:
11
2
8
; , 1,2,...
4
n
n
n
x
x R x n
x
+
= = =
+
Giải.
Nếu
2
=−
thì
2, 1,2,...
n
xn= − =
Xét
2
−
. Ta có:
( )
( )
2
2
1
1 1 1
2 2 2
1 1 1
22
8 2 8 8
2 2 1
4 4 4
n
n n n
n
n n n
x
x x x
x
x x x
−
− − −
− − −
−
−+
− = − = =
+ + +
( )
( )
2
2
1
1 1 1
2 2 2
1 1 1
22
8 2 8 8
2 2 2
4 4 4
n
n n n
n
n n n
x
x x x
x
x x x
−
− − −
− − −
+
++
+ = + = =
+ + +
Xét hàm số:
( )
2
2
x
fx
x
−
=
+
.
Ta thấy:
( ) ( ) ( )
( ) ( ) ( )
2
11
2
22
22
1
1 2 1
1
22
... 3
22
nn
nn
n n n
nn
xx
f x f x f x f x f
xx
−−
−
−−
−

−−
= = = = = = =

++

Đặt:
( )
1
2
n
f

−
=

nên
2
22
21
n
n
n
x
x
x
−
−
= =
++
Vậy: Số hạng tổng quát của dãy số
( )
n
x
là
1
1
2
2
2
21
1
, 1,2,...
2
1
1
n
n
n
xn
−
−

−

−


+



= =
−

+

+

Lớp hàm
( )
3
2
x ax
gx
bx c
+
=
+
Ta có :
( )
3 3 2
22
x ax x bdx ax cd
g x d d
bx c bx c
+ − + −
− = − =
++
Ta cần chọn a, b, c, d sao cho
( )
3
3 2 3 2 2 3
33x bdx ax cd x d x dx d x d− + − = − = − + −
22
32
33
33
bd d b
a d a d
dc d c d
==


= =


==

.
Bài 6. Tìm số hạng tổng quát của dãy số
( )
n
x
xác định như sau:
3
11
2
6
0; , 1,2,...
32
nn
n
n
xx
x x n
x
+
+
= = =
+
Giải.
Chọn
2c =
nên
3, 6, 2b a d= = =
( )
( )
3
3 3 2
1
2 2 2
2
6 3 2 6 2 2
2 2 1
3 2 3 2 3 2
n
n n n n n
n
n n n
x
x x x x x
x
x x x
+
−
+ − + −
− = − = =
+ + +
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 11
( )
( )
3
3 3 2
1
2 2 2
2
6 3 2 6 2 2
2 2 2
3 2 3 2 3 2
n
n n n n n
n
n n n
x
x x x x x
x
x x x
+
+
+ + + +
+ = + = =
+ + +
Xét hàm số
( )
2
2
x
fx
x
−
=
+
ta thấy
( ) ( ) ( )
( ) ( ) ( )
2
11
3
33
33
1
1 2 1
1
22
... 3
22
nn
nn
n n n
nn
xx
f x f x f x f x f
xx
−−
−
−−
−

−−
= = = = = = =


++

Đặt
( )
1
3
n
f

−
=

nên
2
22
1
2
n
n
n
x
x
x
−
+
= =
−
+
Vậy: Số hạng tổng quát của dãy số
( )
n
x
là
1
1
3
3
2
21
2
, 1,2,...
2
1
2
n
n
n
xn
−
−


−

+


+


= =

−
−

+

Lớp hàm
( )
42
3
x ax b
gx
cx dx
++
=
+
Ta có :
( )
4 2 4 3 2
33
x ax b x cex ax dex b
g x e e
cx dx cx dx
+ + − + − +
− = − =
++
Ta cần chọn a, b, c, d, e sao cho
( )
4
4 3 2 4 3 2 2 3 4
4 6 4ex cex ax dex b x e x ex e x e− + − + = − = − + − +
22
32
44
4e 4
66
44
ce c
a e a e
de e d e
b e b e
==


==



==


==

.
Bài 7. Tìm số hạng tổng quát của dãy số
( )
n
x
xác định như sau:
42
11
3
12 4
0; , 1,2,...
48
nn
n
nn
xx
x x n
xx
+
++
= = =
+
Giải.
Chọn:
2e =
khi đó
12, 4, 4, 8a b c d= = = =
.
Ta thấy:
0, 1,2,...
n
xn =
Do đó:
( )
( )
4
4 2 4 3 2
1
3 3 3
2
12 4 4 2 12 8 2 4
2 2 1
4 8 4 8 4 8
n
n n n n n n
n
n n n n n n
x
x x x x x x
x
x x x x x x
+
+
+ + + + + +
+ = + = =
+ + +
( )
( )
4
4 2 4 3 2
1
3 3 3
2
12 4 4 2 12 8 2 4
2 2 2
4 8 4 8 4 8
n
n n n n n n
n
n n n n n n
x
x x x x x x
x
x x x x x x
+
−
+ + − + − +
− = − = =
+ + +
.
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 12
Xét hàm số
( )
2
, 0.
2
x
f x x
x
−
=
+
Ta suy ra:
( ) ( ) ( )
( ) ( ) ( )
2
11
4
44
44
1
1 2 1
1
22
... 3
22
nn
nn
n n n
nn
xx
f x f x f x f x f
xx
−−
−
−−
−

−−
= = = = = = =


++

Đặt:
( )
1
4
n
f

−
=

.
Nên:
2
22
1
2
n
n
n
x
x
x
−
+
= =
−
+
Vậy: Số hạng tổng quát của dãy số
( )
n
x
là
1
1
4
4
2
21
2
, 1,2,...
2
1
2
n
n
n
xn
−
−


−

+


+


= =

−
−

+

BÀI TẬP TƯƠNG TỰ.
Bài 1: Tìm số hạng tổng quát của dãy số
( )
n
u
cho như sau:
2
11
6
; 5 4 , 1,2,...
5
n n n
u R u u u n
+
= = − − − =
Giải.
Đặt
5
n
n
x
u =−
Khi đó.
22
11
1 1 4 6
4 6, 1,2,...
5 5 5 5
n n n n n n
x x x x x x n
++
− = − + − = − + =
( )
2
2
11
2 4 4 2 , 1,2,...
n n n n
x x x x n
++
− = − + = − =
Suy ra:
( ) ( )
( )
2
1
22
2
1 2 1
2 2 2 ... 2
n
n n n
x x x x
−
−−
− = − = − = = −
Vậy:
( ) ( )
(
)
11
22
1
3 2 2 5 2 2
5
nn
nn
xu

−−
= + + = − + +
.
Bài 2: Tìm số hạng tổng quát của dãy số
( )
n
u
cho như sau:
32
11
; 25 15 3 , 1,2,...
n n n n
u R u u u u n
+
= = − + =
Giải.
Đặt
5
n
n
x
u =
ta được
32
11
5 ; 3 3 , 1,2,...
n n n n
x R x x x x n
+
= = − + =
( )
3
32
1
1 3 3 1 1 , 1,2,...
n n n n n
x x x x x n
+
− = − + − = − =
Suy ra:
( ) ( )
( )
2
1
33
3
1 2 1
1 1 1 ... 1
n
n n n
x x x x
−
−−
− = − = − = = −
Vậy:
( )
( )
1
1
3
3
5 1 1
5 1 1
5
n
n
nn
xu
−
−
−+
= − + =
.
Bài 3: Tìm số hạng tổng quát của dãy số
( )
n
u
cho như sau:
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 13
2
11
2
3 6 1
; , 1,2,...
9 6 5
nn
n
nn
uu
u R u n
uu
+
+−
= = =
−+
Hướng dẫn: Đặt
31
nn
xu=−
. Biến đổi đưa về dạng
1
2
8
, 1,2,...
4
n
n
n
x
xn
x
+
= =
+
.
Bài 4: Tìm số hạng tổng quát của dãy số
( )
n
x
cho như sau:
3
11
2
12
0; , 1,2,...
34
nn
n
n
xx
x x n
x
+
+
= = =
+
Giải.
Chọn
4c =
nên
3, 12, 2b a d= = =
( )
( )
3
3 3 2
1
2 2 2
2
12 6 12 8
2 2 1
3 4 3 4 3 4
n
n n n n n
n
n n n
x
x x x x x
x
x x x
+
−
+ − + −
− = − = =
+ + +
( )
( )
3
3 3 2
1
2 2 2
2
12 6 12 8
2 2 2
3 4 3 4 3 4
n
n n n n n
n
n n n
x
x x x x x
x
x x x
+
+
+ + + +
+ = + = =
+ + +
Xét hàm số
( )
2
2
x
fx
x
−
=
+
.
Ta thấy:
( ) ( ) ( )
( ) ( ) ( )
2
11
3
33
33
1
1 2 1
1
22
... 3
22
nn
nn
n n n
nn
xx
f x f x f x f x f
xx
−−
−
−−
−

−−
= = = = = = =

++

Đặt
( )
1
3
n
f

−
=

nên
2
22
21
n
n
n
x
x
x
−
+
= =
+−
Vậy: Số hạng tổng quát của dãy số
( )
n
x
là
1
1
3
3
2
21
2
, 1,2,...
2
1
2
n
n
n
xn
−
−

−

+


+



= =
−

−

+

Bài 5: Tìm số hạng tổng quát của dãy số
( )
n
u
xác định như sau:
3
11
2
96
; , 1,2,...
367
nn
n
nn
uu
u u n
uu
+
+−
= = =
−+
Hướng dẫn: Đặt
1
nn
xu=−
. Biến đổi đưa về dạng:
3
1
2
12
, 1,2,...
34
nn
n
n
xx
xn
x
+
+
= =
+
Bài 6: Tìm số hạng tổng quát của dãy số
( )
n
u
xác định như sau:
( )
2
*
11
42
4 4 1
;,
16 24 1
nn
n
nn
uu
u R u n N
uu
+
+
= =
++
.
Giải.
Ta thấy
*
nN
tồn tại
n
u
. Nếu
1
2
=−
thì
1
2
n
u =−
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 14
Ta xét
1
2
−
ta có :
( )
( )
4
3 4 3 2
1
4 2 4 2 4 2
21
32 8 16 32 24 8 1
2 1 1 1
16 24 1 16 24 1 16 24 1
n
n n n n n n
n
n n n n n n
u
u u u u u u
u
u u u u u u
+
+
+ + + + +
+ = + = =
+ + + + + +
( )
( )
4
3 4 3 2
1
4 2 4 2 4 2
21
32 8 16 32 24 8 1
2 1 1 2
16 24 1 16 24 1 16 24 1
n
n n n n n n
n
n n n n n n
u
u u u u u u
u
u u u u u u
+
−−
+ − + − + −
− = − = =
+ + + + + +
Xét hàm số
( )
21
21
x
fx
x
−
=
+
.
Ta thấy:
( ) ( ) ( )
( ) ( ) ( )
2
11
4
44
44
1
1 2 1
1
2 1 2 1
... 3
2 1 2 1
nn
nn
n n n
nn
uu
f u f u f u f u f
uu
−−
−
−−
−

−−
= = − = − = − = = − = −

++

Đặt
( )
1
4
n
f

−
=

nên
21
1
2 1 2 2
n
n
n
u
u
u
−
−
= − =
++
Vậy: Số hạng tổng quát của dãy số
( )
n
x
là:
Nếu
1
2
=−
thì
1
2
n
u =−
Nếu
1
2
−
thì
1
1
4
4
21
1
2
, 1,2,...
21
21
21
n
n
n
un
−
−
−

−

+

= =

−

+


+



Bài 7. (HSG QG 2010)
Cho dãy số
( )
n
u
xác định như sau:
1
1 1 1
11
5
2 2.3 , 2,3,...
n n n
n
nn
u
u u n
− − −
+−
=
= + + =
a) Tìm số hạng tổng quát của dãy số
( )
n
u
.
b) Chứng minh rằng
( )
n
u
là dãy số giảm .
Giải
a) Theo giả thiết ta có
( ) ( ) ( )
1 1 1 2 2 2 1 1 2 2 1 2 1
1 2 2
2 2.3 2 2.3 2 2.3 2 2 2 3 3 ...
n n n n n n n n n n n n n n
n n n n
u u u u
− − − − − − − − − − − − −
− − −
= + + = + + + + = + + + + =
( ) ( )
2 1 2 1
1
2 ... 2 2 2 3 ... 3 3
n n n n
u
− − − −
= + + + + + + + +
( ) ( )
11
2 1 2 3 1 3
5 2 2 3
1 2 1 3
nn
nn
−−
−−
= + + = +
−−
vậy
2 3 , 2,3,...
nn
n
n
un= + =
b)Ta có
( ) ( ) ( )
1 1 1 1
2 3 2 3 3 2 3 3 2 3 3.2 3 2 3 , 2,3,...
n n n n n n n n n n n n n n
nn
n
un
+ + + +
= + + + = + = + + =
vậy
1
, 2,3,...
nn
u u n
+
=
Hay
( )
n
u
là dãy số giảm.
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 15
C. XÁC ĐỊNH DÃY SỐ BẰNG PHƯƠNG PHÁP SAI PHÂN.
• Cho dãy số
( )
n
x
. Xét phương trình
( ) ( )
0 1 1
... 1
n k n k k n
a x a x a x g n
+ + −
+ + + =
Trong đó g(n) là hàm
số theo n, và
01
, ,...,
k
a a a
là các hẳng số. khi dó phương trình
( )
0 1 1
... 0 2
n k n k k n
a x a x a x
+ + −
+ + + =
được gọi là Phương trình sai phân tuyến tính thuần nhất tương ứng với phương trình (1)
• phương trình
( )
1
01
... 0 3
kk
k
a a a

−
+ + + =
được gọi là Phương trình đặc trưng của (2).
• Nghiệm tổng quát của phương trình (1) sẽ có dạng
*
, 1,2,...
n n n
x x x n= + =
Trong đó
n
x
là
nghiệm tổng quát của phương trình sai phân tuyến tính thuần nhất (2), còn
*
n
x
là nghiệm riêng
của phương trình (1).
I./PHƯƠNG TRÌNH SAI PHÂN TUYẾN TÍNH BẬC NHẤT.
1/ phương trình sai phân tuyến tính thuần nhất bậc nhất .
Định nghĩa:Phương trình sai phân tuyến tính thuần nhất bậc nhất với hệ số hằng là
phương trình có dạng:
1
0
nn
ax bx
+
+=
, n=0,1,2,3…(1.1). Trong đó a≠0,b≠0 là những số cho trước.
Phương trình đặc trưng của (1,1)
aλ + b = 0
,phương trình nầy có nghiệm là
λ = -
b
a
.
Vậy nghiệm tổng quát của phương trình sai phân (1.1) có dạng:
. , 1,2,3...
n
n
x C n
==
Ví dụ:
1
2
nn
xx
+
=
và
1
3x =−
n = 0,1,2,3…có công thức tổng quát
( )
3 .2
n
n
x =−
2/ phương trình sai phân tuyến tính không thuần nhất bậc nhất .
Định nghĩa : Phương trình sai phân tuyến tính không thuần nhất bậc nhất là phương
trình có dạng:
1n n n
ax bx d
+
+=
, n=0,1,2,3…(1.3). Trong đó a≠0, b là những hằng số, dn là các số
nào đó.
Ta thường viết dưới dạng :
1n n n
x qx d
+
=+
n = 0,1,2,3… (1.4) .
Ví dụ : Tìm nghiệm của phương trình
01
1; 5 3 2 , 1,2,3...
n
nn
x x x n
+
= + = =
Giải
Phương trình đặc trưng
5 3 0
+=
có nghiệm
3
5
=−
.
Nghiệm tổng quát của phương trình thuần nhất là
3
5
n
n
xC

=−


.
Tìm nghiệm riêng của phương trình không thuần nhất là
*
.2
n
n
xa=
.
Thay vào phương trình ta được
1
1
5. .2 3. .2 2
13
n n n
a a a
+
+ = =
. Do đó
*
1
.2
13
n
n
x =
Nghiệm tổng quát của phương trình là
31
.2
5 13
n
n
xC

= − +


. Vì
0
1x =
nên
1 12
1
13 13
CC+ = =
Vậy
12 3 1
.2
13 5 13
n
n
n
x

= − +


.
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 16
Dưới đây ta sẽ ta tìm nghiêm riêng của phương trình sai phân.
DẠNG 1. Dãy số
10
1
2
nn
ux
n
u qu b
.
Nếu q = 1 thì (un) là cấp số cộng có công sai d = b nên :
1
1
n
u u n b
.
Nghiệm tổng quát của phương trình thuần nhất
1nn
uu
+
=
là
n
uC=
.
Nghiệm riêng của phương trình không thuần nhất là
*
.
n
u c n=
.
Thay vào phương trình ta được
1nn
u u d
+
=+
ta được
( )
1c n cn d c d+ = + =
Nghiệm tổng quát của phương trình là
n
u C nd=+
.
Vì
00
ux=
cho trước thì
0n
u x nd=+
hay
1
1
n
u u n b
Đây chính là công thức tổng quát của cấp số cộng.
Nếu q≠1 Nghiệm tổng quát của phương trình thuần nhất
1
.
nn
u qu
+
=
là
.
n
n
u C q=
d = b là đa thức bậc 0 với mọi n nên phương trình có nghiêm riêng
*
n
uc=
Thay vào phương trình ta được
1nn
u qu b
+
=+
ta được
1
b
c qc b c
q
.
Vậy nghiệm tổng quát của phương trình là
.
1
n
n
b
u C q
q
=+
−
BÀI TẬP ÁP DỤNG.
Bài 1 Xác định số hạng tổng quát của dãy số (un ) được xác định bởi :
a)
11
1, 2 2
nn
u u u n
. b)
11
3, 2 2
nn
u u u n
.
c)
11
2, 3 + 2 2
nn
u u u n
d)
11
2, 3 1 2
nn
u u u n
.
e)
11
1
, 2
2 2 3
n
n
n
u
u u n
u
.
Giải
a)
11
1, 2 2
nn
u u u n
Nghiệm tổng quát của phương trình thuần nhất
1nn
uu
+
=
là
n
uC=
.
Nghiệm riêng của phương trình không thuần nhất là
*
.
n
u a n=
.
Nghiệm tổng quát của phương trình là
.
n
u C an=+
.
Vì
12
11uu= = −
thì hệ phương trình
13
2 1 2
C a C
C a a
+ = =


+ = − = −

Vậy công thức tổng quát
3 2 , 2
n
u n n
.
b)
11
3, 2 2
nn
u u u n
Nghiệm tổng quát của phương trình thuần nhất
1
2
nn
uu
+
=
là
.2
n
n
uC=
.
1
3
3 3 .2
2
u c c
. Nghiệm tổng quát của phương trình là
1
3.2
n
n
u
−
=
.
c)
11
2, 3 + 2 2
nn
u u u n
.
Nghiệm tổng quát của phương trình thuần nhất
1
3
nn
uu
+
=
là
.3
n
n
uC=
.
Nghiệm riêng của phương trình không thuần nhất là
*
n
ua=
.
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 17
Nghiệm tổng quát của phương trình là
.3
n
n
u C a=+
.
Vì
12
28uu= =
thì hệ phương trình
3 2 1
9 8 1
C a C
C a a
+ = =


+ = = −

Vậy công thức tổng quát
3 1, 1
n
n
un
.
d)
11
2, 3 1 2
nn
u u u n
.
Nghiệm tổng quát của phương trình thuần nhất
1
3
nn
uu
+
=
là
.3
n
n
uC=
.
Nghiệm riêng của phương trình không thuần nhất là
*
n
ua=
.
Nghiệm tổng quát của phương trình là
.3
n
n
u C a=+
.
Vì
12
27uu= − = −
thì hệ phương trình
5
32
6
97
1
2
C
Ca
Ca
a
=−
+ = −

+ = −
=
Vậy công thức tổng quát
1
51
.3
22
n
n
u
.
e)
11
1
, 2
2 2 3
n
n
n
u
u u n
u
.
Ta có:
1
0u
bằng quy nạp ta được
0
n
u
.
Từ giả thiết suy ra
1
13
2
nn
uu
. Đặt
1
n
n
v
u
khi đó
1
3 2 2
nn
v v n
với
1
2v
Áp dụng kết quả câu c ta được
1
1
31
n
n
un
.
BÀI TẬP RÈN LUYỆN.
Bài 1: Xác định số hạng tổng quát của dãy số (un ) được xác định bởi :
a/
11
4, 2 2
nn
u u u n
. ĐS:
22
n
un
.
b/
11
2, 3 2
nn
u u u n
. ĐS:
1
2.3
n
n
u
.
c/
11
1, 3 6 2
nn
u u u n
. ĐS:
1
4.3 3 2
n
n
un
.
d/
11
1, 4 +2 2
nn
u u u n
. ĐS:
1
42
2
33
n
n
un
.
Bài 2: Xác định số hạng tổng quát của dãy số (un ) được xác định bởi :
a/
1
1
3
1
1
n
n
n
u
n
u
u
u
. b/
1
1
2
1
21
n
n
n
u
n
u
u
u
Bài 3 (Lạng Sơn 2009 – 2010): Cho của dãy số (xn ) được xác định bởi:
1
1
2
1
3
2
n
n
n
x
n
x
x
x
.
Tìm công thức tổng quát của dãy số (xn ) theo n
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 18
DẠNG 2. Dãy số
10
1
nn
ux
u qu f n
trong đó f(n) là đa thức bậc k theo n, q là hằng số.
Nếu q = 1 ta tìm nghiệm riêng của phương trình không thuần nhất là
( )
*
.
n
u n g n=
.
với
( )
.n g n
là đa thức bậc k+1 của n có hệ số tự do bằng 0.
Nếu q ≠1 ta tìm nghiệm riêng của phương trình không thuần nhất là
( )
*
n
u g n=
.
với g(n) là đa thức bậc k.
BÀI TẬP ÁP DỤNG.
Bài 2: Xác định số hạng tổng quát của dãy số (un ) được xác định bởi :
a/
11
2, 2 1 2
nn
u u u n n
. b/
11
2, 2 +3n - 1 1
nn
u u u n
.
Giải
a/
11
2, 2 1 2
nn
u u u n n
Phương trình đặc trưng
10
−=
có nghiệm
1
=
.
Nghiệm tổng quát của phương trình thuần nhất là
n
uC=
.
Tìm nghiệm riêng của phương trình không thuần nhất là
( )
*
n
u n an b=+
.
Ta phân tích
2
2
2 1 1 1 1n g n g n an bn a n b n
1
2
n
n
31
3 5 2
a b a
a b b
*2
2
n
u g n n n
.
Nghiêm tông quát của phương trình là
2
2
n
u C n n= + +
Vì
0
2u =
thì
2
2 1 2.1 1CC= + + = −
. Vậy:
2
21
n
u n n
.
b/
11
2, 2 +3n 1 1
nn
u u u n
.
Phương trình đặc trưng
20
−=
có nghiệm
2
=
.
Nghiệm tổng quát của phương trình thuần nhất là
.2
n
n
uC=
.
Tìm nghiệm riêng của phương trình không thuần nhất là
( ) ( )
*
n
u g n an b= = +
.
Ta phân tích
3 1 2 1n an b a n b
1
2
n
n
23
55
a b a
bb
35g x n
Nghiệm tổng quát của phương trình là
.2 5 3
n
n
u C n= − −
Vì
1
2u =
thì
2 .2 5.1 3 5CC= − − =
. Vậy công thức tổng quát
5.2 3n 5 1
n
n
un
BÀI TẬP RÈN LUYỆN.
Bài 3: Xác định số hạng tổng quát của dãy số (un ) được xác định bởi:
a/
1
1
4
52
nn
u
u u n
ĐS:
2
51
2
22
n
u n n
.
b/
1
2
1
1
1
2
nn
u
n
u u n
. ĐS:
32
21
1
33
n
u n n n
.
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 19
c/
1
1
1
3 2 1
nn
u
u u n
ĐS:
2
3. 2
3
n
n
un
.
d/
1
32
1
2
3 2 9 9 3
nn
u
u u n n n
ĐS:
3
2.3
n
n
un
DẠNG 3. Dãy số
00
1
0
.
n
n n k
ux
u qu P n
Nếu q = α ta tìm nghiệm riêng của phương trình không thuần nhất là
( )
*
..
n
nk
u nQ n
=
.
với
( )
.
k
nQ n
là đa thức bậc k+1 của n có hệ số tự do bằng 0 .
Nếu q ≠α ta tìm nghiệm riêng của phương trình không thuần nhất là
( )
*
.
n
nk
u Q n
=
.
với
( )
k
Qn
là đa thức bậc k.
BÀI TẬP ÁP DỤNG.
Bài 3: Xác định số hạng tổng quát của dãy số (un ) được xác định bởi :
a./
11
1, 3 +2 2
n
nn
u u u n
b)
11
3, +3.4 2
n
nn
u u u n
Giải
a./
11
1, 3 +2 2
n
nn
u u u n
Phương trình đặc trưng
30
−=
có nghiệm
3
=
.
Nghiệm tổng quát của phương trình thuần nhất là
.3
n
n
uC=
.
Tìm nghiệm riêng của phương trình không thuần nhất là
( )
*
.2
n
n
u g n a==
.
Thay vào phương trình ta được
11
.2 3. .2 2 2
n n n
a a a
++
= + = −
ta được.
( )
*1
2
n
n
u g n
+
= = −
Vậy nghiệm tổng quát của phương trình là
1
.3 2
nn
n
uC
+
=−
Vì
1
1u =
thì
2
5
1 .3 2
3
CC= − =
Vậy công thức tổng quát
11
5.3 2 1
nn
n
un
b)
11
3, +3.4 2
n
nn
u u u n
Phương trình đặc trưng
10
−=
có nghiệm
1
=
.
Nghiệm tổng quát của phương trình thuần nhất là
n
uC=
.
Tìm nghiệm riêng của phương trình không thuần nhất là
( )
*
.4
n
n
u g n a==
.
Thay vào phương trình ta được
ta được.
( )
*1
4
n
n
u g n
+
==
Vậy nghiêm tông quát của phương trình là
1
4
n
n
uC
+
=+
Vì
1
3u =
thì
3 4 1CC= + = −
Vây :
41
n
n
u
.
b)
11
6, 3 +5.3 1
n
nn
u u u n
Phương trình đặc trưng
30
−=
có nghiệm
3
=
.
Nghiệm tổng quát của phương trình thuần nhất là
.3
n
n
uC=
.
Tìm nghiệm riêng của phương trình không thuần nhất là
( )
*
. .3
n
n
u n g n a==
.
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 20
Thay vào phương trình ta được
( )
1
5
. 1 3 . 3 5.3
3
n n n
a n a n a
+
+ = + =
ta được
*1
5
.3 5. .3
3
nn
n
u n n
−
==
Vậy nghiêm tông quát của phương trình là
1
.3 5. 3
nn
n
u C n
−
=+
Vì
1
6u =
thì
1
6 .3 5.1
3
CC= + =
Vây :
11
3 5. 3
nn
n
un
−−
=+
BÀI TẬP RÈN LUYỆN.
Bài 4 Xác định số hạng tổng quát của dãy số (un ) được xác định bởi :
a./
11
4, 2 +7.5 1
n
nn
u u u n
ĐS:
57
.2 .3
33
nn
n
u
b)
11
4, 2 +3.2 1
n
nn
u u u n
ĐS:
1
4.2 3 .2
nn
n
un
c)
1
1
17
5
1
32
n
nn
u
n
uu
ĐS:
1
3 .2
5
nn
n
u
.
DẠNG 4. Dãy số
10
1
2
.
n
nn
ux
n
u au b f n
Giả sử
( )
.
n
n
d f n b
=+
khi đó nghiệm riêng của phương trình
* 1 2
n n n
x x x=+
BÀI TẬP ÁP DỤNG.
Bài 3: Xác định số hạng tổng quát của dãy số (un ) được xác định bởi:
2
11
5, 2 +3.2 +
n
nn
u u u n
.
Giải
2
1
2
2 +3.2 1
2 +3.2 +n
22
n
nn
n
nn
nn
xx
uu
y y n
Từ
11
1
3 .2 3 .2
nn
n
x x n
;
12
1
6 .2 2 3
n
n
y y n n
.
1 1 2
11
3 2 +3n. 2 2 3
nn
n
u x y n n
Vậy
2 1 2
1
2 +3. 2 2 3
2
nn
n
u n n
BÀI TẬP RÈN LUYỆN.
Bài 1: Xác định số hạng tổng quát của dãy số (un ) được xác định bởi :
a)
1
1
1
23
n
nn
u
n
u u n
ĐS:
11
11.2 3 2
nn
n
un
b)
1
4
1
2 7.5 3.2
nn
nn
u
n
uu
ĐS:
1
10 7
3 .2 .5
33
nn
n
un
Bài 2: Xác định số hạng tổng quát của dãy số (un ) được xác định bởi:
2*
11
1, 2 +2.2 +
n
nn
u u u n n N
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 21
ĐS:
1 2 2
5.2 .2 2 3, 1,2,...
n
n
u n n n n
Bài 3: Xác định số hạng tổng quát của dãy số (un ) được xác định bởi :
11
2, 5 +2.3 6.7 +12 2
nn
nn
u u u n
ĐS:
1 1 1
157.5 3 3.7 3
n n n
n
u
II./ PHƯƠNG TRÌNH SAI PHÂN BẬC HAI.
I. Phương trình sai phân tuyến tính thuần nhất bậc hai .
Định nghĩa: Phương trình sai phân tuyến tính thuần nhất bậc hai với hệ số hằng là
phương trình có dạng:
21
0
n n n
ax bx cx
++
+ + =
,n=0,1,2,3…(1.1).Trong đó a≠0,b,c là những số cho
trước.
Nếu c = 0 Phương trình nầy là phương trình tuyến tính bậc nhất.
Trường hợp 1: Phương trình đặc trưng
2
aλ + b = 0 c
+
có 2 nghiệm là
( )
1 2 1 2
λ , λ

.
Thì nghiệm tổng quát của phương trình sai phân (1.1) có dạng:
1 1 2 2
.
nn
n
x C C

=+
.
Ví dụ : Tìm nghiệm của phương trình sai phân
01
21
7; 6
3 28
n n n
xx
x x x
++
= = −
=+
Giải
Phương trình đặc trưng
2
3 28 0

− − =
có 2 nghiệm
12
4; 7

= − =
.
Nên nghiệm tổng quát của phương trình thuần nhất có dạng
( )
12
4 .7
n
n
n
x C C= − +
.
Với điều kiên ban đầu
n = 0,
0
7x =
, ta có
0 1 2
7x C C= + =
; n = 1,
1
6x =−
ta có
1 1 2
4 7 6x C C= − + = −
. suy ra
12
5; 2CC==
Vậy nghiệm tổng quát phương trình với điều kiện ban đầu là
( )
5 4 2.7
n
n
n
x = − +
LƯU Ý: Với điều kiên ban đầu
01
5; 9xx= = −
thì
( )
1
47
n
n
n
x
−
= − − +
.
BÀI TẬP RÈN LUYỆN.
Tìm nghiệm tổng quát của phương trình sai phân:
a)
01
21
8; 3
12
n n n
xx
x x x
++
==
=−
ĐS:
5.3 3. 4
n
n
n
x
b)
01
21
2; 8
8 9 0
n n n
xx
x x x
++
= = −
+ − =
ĐS:
19
n
n
x
Trường hợp 2: Phương trình đặc trưng
2
aλ + b = 0c
+
có nghiệm kép là
12
λ
=
.
Thì nghiệm tổng quát của phương trình sai phân (1.1) có dạng:
1 1 2 1
.
nn
n
x C C n

=+
.
Ví dụ : Tìm nghiệm của phương trình sai phân
01
21
1; 2
10 25
n n n
xx
x x x
++
= − =
=−
Giải
Phương trình đặc trưng
2
10 25 0

− + =
có nghiệm kép
12
5

==
.
Nên nghiệm tổng quát của phương trình thuần nhất có dạng
( )
12
.5
n
n
x C nC=+
.
Với điều kiên ban đầu n = 0,
0
1x =−
ta có
01
1xC= = −
;
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 22
n = 1,
1
2x =
, ta có
( )
1 1 2
.5 2x C C= + =
suy ra
12
7
1;
5
CC= − =
Vậy nghiệm tổng quát phương trình với điều kiện ban đầu là
7
1 .5
5
n
n
xn

= − +


BÀI TẬP RÈN LUYỆN
Tìm nghiệm tổng quát của phương trình sai phân:
a)
01
21
1; 16
8 16
n n n
xx
x x x
++
==
=−
ĐS:
1 3 4
n
n
xn
b)
01
21
33; 162
69
n n n
xx
x x x
++
==
=−
ĐS:
4 7 .3
n
n
xn
c)
12
21
1; 3
21
n n n
xx
x x x
++
==
=−
ĐS:
12
n
xn
Trường hợp 3: Phương trình đặc trưng
2
aλ + b = 0c
+
vô nghiệm .
Thì nghiệm tổng quát của phương trình sai phân (1.1) có dạng:
12
( cosn sin )
n
n
x r C C n

=+
.
Trong đó
2 2 2
; arctan ; ; ; 4 .
2a 2a
Bb
r A B A B b ac
A
−
= + = = = = −
Ví dụ : Tìm nghiệm của phương trình sai phân
01
21
1
1;
2
n n n
xx
x x x
++
==
=−
Giải
Phương trình đặc trưng
2
10

− + =
có nghiệm
1,2
13
2
i
=
.
Ta có
22
1 3 1
; ; 1; arctan arctan
12 2 2 2 3
3
bB
A B r A B
aA
= − = = = = + = = = =
(Shift - mode 2 –
13
22
i+
- Shift 2(cmplx) – 3 = máy hiện
1
1
3
Thì
1;
3
r
==
)
Nên nghiệm tổng quát của phương trình thuần nhất có dạng
12
cos sin
33
n
nn
x C C

=+
.
Với điều kiên ban đầu
0
1x =
ta có
01
1xC==
;
n = 1,
1
1
2
x =
. ta có
1 1 2
1
cos .sin
3 3 2
x C C

= + =
suy ra
12
1; 0CC==
Vậy nghiệm tổng quát phương trình với điều kiện ban đầu là
cos
3
n
n
x
=
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 23
II. Phương trình sai phân tuyến tính bậc hai .
Định nghĩa : Phương trình sai phân tuyến tính bậc hai không thuần nhất là phương
trình có dạng:
21n n n n
ax bx cx d
++
+ + =
, n=0,1,2,3…(1.2). Trong đó a,b,c là những hằng số, dn là
hàm số của biến số tự nhiên n. n = 0,1,2,3… (1.4) .
DẠNG 5. Dãy số
1 0 2 0
21
;
. . .
n
n n n
u x u y
nN
a u bu cu d
• Nếu phương trình (*) có 2 nghiệm phân biệt khác α. Thì
*
2
.
n
n
d
u
a b c
• Nếu phương trình (*) có 2 nghiệm phân biệt có 1 nghiệm u= α. Thì
1
*
..
2
n
n
nd
u
ab
.
• Nếu phương trình (*) có nghiệm kép u= α. Thì
2
*
. 1 .
2
n
n
n n d
u
a
BÀI TẬP ÁP DỤNG
Bài 1: Xác định số hạng tổng quát của dãy số (un ) được xác định bởi:
a/
01
21
1; 3
4 +3 5.2
n
n n n
uu
nN
u u u
Giải
Phương trình đặc trưng
2
4 3 0

− + =
có 2 nghiệm
12
1; 3

==
.
Nghiệm tổng quát của phương trình thuần nhất có dạng
12
.3
n
n
u C C=+
.
Nghiệm riêng của phương trình không thuần nhất có dạng
*
5.2
5.2
4 8 3
n
n
n
u = = −
−+
.
Nên nghiệm tổng quát của phương trình có dạng
12
.3 5.2
nn
n
u C C= + −
.
Với
0
1u
ta được
12
51CC+ − = −
; Với
1
3u
ta được
12
3 5.2 3CC+ − =
Ta có hệ phương trình
1
12
12
2
9
4
2
3 13 1
2
C
CC
CC
C
Vậy
2
1
3 1 5.2
2
nn
n
u
.
b/
01
21
1; 3
5 +6 5.2
n
n n n
uu
nN
u u u
Phương trình đặc trưng
2
5 6 0

− + =
có 2 nghiệm
12
2; 3

==
.
Nghiệm tổng quát của phương trình thuần nhất
12
.2 .3
nn
n
u C C=+
Nghiệm riêng của phương trình không thuần nhất:
1
*1
5 .2
5 .2
45
n
n
n
n
un
−
−
= = −
−
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 24
Nên nghiệm tổng quát của phương trình có dạng
12
5
.2 .3 .2
2
n n n
n
u C C n= + −
.
Với
0
1u
ta được
12
1CC+ = −
; Với
1
3u
ta được
12
2 3 5 3CC+ − =
Ta có hệ phương trình
1 2 1
1 2 2
1 11
2 3 8 10
C C C
C C C
Vậy
11
11.2 10.3 5 .2 10.3 5 22 .2
n n n n n
n
u n n
..
c/
01
12
1; 3
2
4 +4 3.2
n
n n n
uu
n
u u u
Phương trình đặc trưng
2
4 4 0

− + =
có 2 nghiệm
12
2

==
.
Nghiệm tổng quát của phương trình thuần nhất có dạng
12
( ).2
n
n
u C C n=+
.
Nghiệm riêng của phương trình không thuần nhất
( )
( )
2
*3
3 . 1 2
3 . 1 2
2
n
n
n
nn
u n n
−
−
−
= = −
Nghiệm tổng quát của phương trình có dạng
( )
3
12
( ).2 3 1 2
nn
n
u C C n n n
−
= + + −
.
Ta có
1
12
12
1
1
1;
3
2
2
C
CC
CC
. Vậy
23
3 8 .2
n
n
u n n
d/
01
12
3; 0
2
3 28 60
n n n
uu
n
u u u
Phương trình
2
3 28 0xx
có 2 nghiệm
4; 7xx
Công thức tổng quát
60
. 4 .7 . 4 .7 2
1 3 28
nn
nn
n
u a b a b
Với
01
3; 0uu
23
3; 2
4 7 2 0
ab
ab
ab
. Vậy
3. 4 2.7 2
n
n
n
u
BÀI TẬP RÈN LUYỆN.
Bài 1: Xác định số hạng tổng quát của dãy số (un ) được xác định bởi :
a/
01
12
9; 45
2
2 8 27.5
n
n n n
uu
n
u u u
b/
01
1
12
9; 45
2
8 15 2.5
n
n n n
uu
n
u u u
c/
01
12
1; 496
2
16 64 128.8
n
n n n
uu
n
u u u
d/
01
12
5; 8
2
6 9 2.3 4
nn
n n n
uu
n
u u u
e/
01
12
6; 0
2
3 2 5
n n n
uu
n
u u u
f/
24
12
5; 17
2
21
n n n
uu
n
u u u
.
Bài 2 (HSG Tỉnh LS 2008-2009): Dãy số
n
u
xác định như sau:
01
1
1
1; 2 (1)
2
(2)
3
nn
n
uu
uu
u
−
+
==
+
=
(với n =
1, 2,3,…). Tìm
n
u
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 25
DẠNG 6: Dãy số
1 0 2 0
21
;
1
..
n n n
u x u y
n
a u bu c u f n
trong đó f(n) là đa thức theo n bậc k.
* Nếu
0abc+ +
thì nghiệm riêng của phương trình không thuần nhất là
( )
*
nk
u g n=
là đa thức bậc k của n.
* Nếu
0abc+ + =
và
20ab+
thì nghiệm riêng của phương trình không thuần nhất
là
( )
*
.
nk
u n g n=
* Nếu
0abc+ + =
và
20ab+=
thì nghiệm riêng của phương trình không thuần nhất
là
( )
*2
.
nk
u n g n=
BÀI TẬP ÁP DỤNG.
Bài 1: Xác định số hạng tổng quát của dãy số (un ) được xác định bởi :
a/
01
2
12
1; 3
2
5 +6 2 2 1
n n n
uu
n
u u u n n
Giải
Phương trình đặc trưng
2
5 6 0

− + =
có 2 nghiệm
12
2; 3

==
.
Nghiệm tổng quát của phương trình thuần nhất
12
.2 .3
nn
n
u C C=+
.
Nghiệm riêng của phương trình không thuần nhất có dạng
*2
n
u kn ln t= + +
.
Thay vào phương trình ta được:
2
22
2 2 1 ln 5 1 l 1n n kn t k n n t
2
6 2 l 2k n n t
Cho lần lượt n=0,n=1,n=2 ta có hệ phương trình
19 7 2 1 1
7 5 2 5 8
3 2 13 19
k l t k
k l t l
k l t t
ta được
*2
8 19
n
u n n
Nên Nghiệm tổng quát của phương trình có dạng
2
12
.2 .3 8 19
nn
n
u C C n n= + + + +
.
Với
0
1u
ta được
12
19 1CC+ + = −
; Với
1
3u
ta được
12
2 3 1 8 19 3CC+ + + + =
Ta có hệ phương trình
1 2 1
1 2 2
20 35
2 3 25 15
C C C
C C C
Vậy
2
15.3 35.2 8 19
nn
n
u n n
.
b/
01
12
1; 4
2
3 +2 2 1
n n n
uu
n
u u u n
Giải
Phương trình đặc trưng
2
3 2 0

− + =
có 2 nghiệm
12
1; 2

==
. (a+b+c=0)
Nghiệm tổng quát của phương trình thuần nhất
12
.2
n
n
u C C=+
.
Nghiệm riêng của phương trình không thuần nhất có dạng
*
()
n
u n kn l=+
.
Thay vào phương trình ta được :
2 1 5 1 1 6 2 2 ln n kn l n k n l n k n
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 26
Cho lần lượt n=0,n=1 ta có hệ phương trình
51
1; 6
33
kl
kl
kl
suy ra
*2
6
n
u n n
Nên nghiệm tổng quát của phương trình có dạng
2
12
.2 6
n
n
u C C n n= + − −
.
Với
0
1u
ta được
12
1CC+=
; Với
1
4u
ta được
12
2 1 6 4CC+ − − =
Ta có hệ phương trình
1 2 1
1 2 2
1 10
2 11 9
C C C
C C C
Vậy
12
5.2 6 9
n
n
u n n
.
BÀI TẬP RÈN LUYỆN.
Bài 1: Xác định số hạng tổng quát của dãy số (un ) được xác định bởi :
a./
01
12
8; 3
2
12 3 2
n n n
uu
n
u u u n
b/
01
12
3; 2
2
4 5 12 8
n n n
uu
n
u u u n
III. Phương trình sai phân tuyến tính bậc ba
DẠNG 8. Dãy số
0 0 1 0 2 0
1 2 3
;;
3
0
n n n n
u x u y u z
n
u au bu cu
Để tìm công thức tổng quát của dãy số
n
u
ta làm như sau:
Xét phương trình đặc trưng x
3
+ ax
2
+bx+c=0.(*)
* Nếu phương trình (*) có 3 nghiệm phân biệt
1 2 3
,,x x x
.Thì
1 2 3
...
nnn
n
u p x q x k x
.
* Nếu phương trình (*) có 2 nghiệm phân biệt
1 2 3
x x x
.Thì
13
.
nn
n
u p qn x k x
.
* Nếu phương trình (*) có nghiệm bội 3
1 2 3
x x x
.Thì
2
1
..
n
n
u p nq k n x
Bài 4: Xác định số hạng tổng quát của dãy số (un ) được xác định bởi:
0 1 2
1 2 3
0; 1; 3
3
7 11 5 0
n n n n
u u u
n
u u u u
Phương trình
32
7 11 5 0x x x
có 2 nghiệm
1 2 3
1, 5x x x
Công thức tổng quát
.5
n
n
u p qn k
Cho n=0,n=1,n=2 và giải hệ phương trình ta được
1 3 1
,,
16 4 16
p q k
.
Vậy
1 3 1
5
16 4 16
n
n
un
.
DẠNG 9. Dãy số
0 0 1 0 2 0
1 2 3
;;
3
n n n n n
u x u y u z
n
u au bu cu d
Trường hợp đặc biệt
n
d f n
là đa thức bậc k của n.Tìm
gn
là đa thức cùng bậc
fn
* Nếu phương trình (*) có 3 nghiệm phân biệt
1 2 3
,,x x x
.Thì
*
n
x g n
* Nếu phương trình (*) có 2 nghiệm phân biệt
1 2 3
x x x
.Thì
*
n
x ng n
.
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 27
* Nếu phương trình (*) có nghiệm bội 3
1 2 3
x x x
.Thì
*2
n
x n g n
Bài 5: Xác định số hạng tổng quát của dãy số (un ) được xác định bởi :
0 1 2
2
1 2 3
4; 26; 74
3
6 11 6 6 4 8
n n n n
u u u
n
u u u u n n
Phương trình
32
6 11 6 0x x x
có 3 nghiệm
1 2 3
1; 2; 3x x x
Nghiệm riêng
*2
n
x g n n an bn c
thay vào phương trình ta được
2
2
22
6 1 1 1 11 2
2 2 6 3 3 3
g n n an bn c n a n b n c n
a n b n c n a n b n c
lần lượt cho n=0,n=1,n=2 ta được hệ phương trình
5 2 4
8 3 1; 2; 5
5 2 4
a b c
a c a b c
a b c
nên
* 3 2
25
n
x g n n n n
Nghiệm tổng quát của phương trình đã cho có dạng
32
.2 .3 2 5
nn
n
x p q k n n n
Thay vào điều kiện ban đầu
0 1 2
4; 26; 74x x x
suy ra
5; 1; 1p q k
Vậy số hạng tổng quát của dãy số là
32
2 5 5 2 3
nn
n
u n n n
Trường hợp đặc biệt
.
n
n
d p n
* Nếu phương trình (*) có 3 nghiệm phân biệt
1 2 3
,,x x x
khác α .Thì
*
.
n
n
x p n
* Nếu phương trình (*) có 3 nghiệm phân biệt có
1
x
.Thì
*
.
n
n
x p n n
.
* Nếu phương trình (*) có nghiệm bội 3
1 2 3
x x x
.Thì
*2
.
n
n
x n p n
Bài 6: Xác định số hạng tổng quát của dãy số (un ) được xác định bởi :
1 2 3
22
1 2 3
3; 20; 89
3
6 11 6 2 2.3
nn
n n n n
u u u
n
u u u u
Phương trình
32
6 11 6 0x x x
có 3 nghiệm
1 2 3
1; 2; 3x x x
Phương trình đặc trưng có nghiệm x=2 nên Nghiệm riêng
2
.2
n
n
x cn
thay vào phương
trình
1 2 3
6 11 6 2
n
n n n n
u u u u
ta được
32
3 .2 12 .2 11 .2 1 1c c c c
Do đó
2
.2
n
n
xn
.
Phương trình đặc trưng có nghiệm x=3 nên Nghiệm riêng
3
.3
n
n
x dn
thay vào phương
trình
1 2 3
6 11 6 2.3
n
n n n n
u u u u
ta được
32
3 .3 12 .3 11 .3 6 1c c c c
Do đó
2
.3
n
n
xn
.
Nghiệm tổng quát của phương trình đã cho có dạng
.2 .3 .2 .3
n n n n
n
x p q k n n
Thay vào điều kiện ban đầu
1 2 3
3; 20; 89u u u
suy ra
1
1; 1;
3
p q k
Vậy số hạng tổng quát của dãy số là
1
1 1 2 3 1 3
nn
n
u n n
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 28
IV. HỆ PHƯƠNG TRÌNH SAI PHÂN TUYẾN TÍNH VỚI HỆ SỐ HẰNG.
DẠNG 10: Dãy số
1 1 1
1 1 1
;
, :
;
n n n
nn
n n n
x x ax by
xy
y y cx dy
.
Một trong các cách giải hệ nầy là đưa về phương trình sai phân tuyến tính bậc hai
Từ
1 2 1 1n n n n n n
x ax by x ax by
+ + + +
= + = +
và
1
.
n n n
by x ax
+
=−
Từ
( )
11
0
n n n n n n
y cx dy by bcx bdy b
++
= + = +
.
Vậy
( )
( ) ( )
2 1 1 1 1
.
n n n n n n n n n n
x ax bcx bdy ax bcx d x x a d x bc ad x
+ + + + +
= + + = + + − = + + −
Phương trình :
21
0
n n n
x a d x ad bc x
chính là phương trình sai phân tuyến
tính bậc hai với điều kiện
0 1 0 0
; . .x x a x b y
từ đó ta xác định được
n
x
thay vào hệ đã
cho ta được
n
y
.
Bài 1: Tìm công thức tổng quát của 2 dãy số
01
01
0; 3
, :
6; 5
n n n
nn
n n n
x x x y
xy
y y x y
Giải
Ta có
( )
2 1 1 1 1
3 5 3 5 3 2 8 .
n n n n n n n n n n
x x x y x x x x x x
+ + + + +
= + − = + − − = +
Phương trình đăc trưng:
2
2 8 0 2; 4
Do đó công thức tổng quát
( )
2 .4
n
n
n
x a b= − +
vì
0 0 1
0; 6 6x y x= = =
nên ta có:
01
2 4 6 1
a b a
a b b
+ = = −


− + = =

từ đó suy ra:
( ) ( )
( )
( )
1
3 2 2 4.4 3 4 2 4 5 2
n n n
n n n
n n n
y u u
+
= − = − + − − − = + −
Vậy số hạng tổng quát
( )
( )
24
5 2 4
n
n
n
n
n
n
x
y
= − − +
= − +
Bài 2: Tìm công thức tổng quát của 2 dãy số
1 1 1
1 1 1
2; 2
, :
1; 2
n n n
nn
n n n
x x x y
xy
y y x y
Giải
1 2 2 1 2 1 2
2 2 2 2 2
n n n n n n n n
x x x y x x x x
12
43
n n n
x x x
và
1
5x
từ đó ta xác định được
11
1
11
1 3 2 3 1
22
nn
n n n n
x y x x
BÀI TẬP TƯƠNG TỰ.
Bài 1: Tìm công thức tổng quát của 2 dãy số
01
01
1; 4 2
, :
1;
n n n
nn
n n n
x x x y
xy
y y x y
ĐS: số hạng tổng quát
11
2 ; 2 , 1,2,...
nn
nn
x y n
−−
= = =
Bài 2: Tìm công thức tổng quát của 2 dãy số
1 1 1
1 1 1
3; 4 2
, :
1; 3
n n n
nn
n n n
x x x y
xy
y y x y
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 29
DẠNG 11. Dãy số phân tuyến tính
1
1
1
2
n
n
n
u
n
au b
u
cu d
Để tìm công thức tổng quát của dãy số
n
u
ta làm như sau:
Giải hệ phương trình
1 1 1
1 1 1
;
;
n n n
n n n
x x ax by
y y cx dy
khi đó
n
n
n
x
u
y
là nghiệm của phương
trình đã cho .Thật vậy ta có
1
1 1 1 1
1
1 1 1
1
n
n n n n n
n
n
n n n n
n
x
ab
x ax by y au b
u
x
y cx dy cu d
cd
y
Bài 3: Xác định số hạng tổng quát của dãy số (un ) được xác định bởi :
1
1
1
2
1
21
2
n
n
n
u
n
u
u
u
Giải
Xét hệ phương trình
0 1 1
0 1 1
2; 2
1; 2
n n n
n n n
x x x y
y y x y
theo bài 2 dạng 10 hệ có nghiệm là:
1
1
1
1
1
31
31
2
1
31
31
2
n
n
n
n
n
n
n
n
n
x
x
u
y
y
vậy
1
1
31
31
n
n
n
u
Bài 4: Xác định số hạng tổng quát của dãy số (un ) được xác định bởi :
1
1
1
1
2
23
n
n
n
u
n
u
u
u
Giải
Xét hai dãy số
( )
n
x
và
( )
n
y
như sau:
11
11
1; 2
1
1; 2 3
n n n
n n n
x x x y
n
y y x y
1,2,...n=
Ta có :
( ) ( )
1 1 1 1 1
2 2 2 3 4 3 2
n n n n n n n n n
x x y x x y x x y
+ + + + +
= + = + + = + +
( )
1 1 1
4 3 4
n n n n n n
x x x x x x
+ + +
= + + − = +
.
Vậy dãy số
( )
n
x
thỏa điều kiện
1 2 1 1
1; 3; 4 0, 1.
n n n
x x x x x n
++
= = − − =
Phương trình đăc trưng:
2
4 1 0 2 5; 2 5
Do đó công thức tổng quát
( ) ( )
2 5 2 5
nn
n
x a b= − + +
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 30
vì
12
1; 3xx==
nên ta có:
( ) ( )
53
1
25
2 5 2 5 3
35
25
a
ab
ab
b
+
=−
+=


− + + =
−

=
nên
( ) ( )
3 5 3 5
2 5 2 5 , 1
2 5 2 5
nn
n
xn
− − −
= − + +
.
từ đó suy ra
( ) ( )
5 1 5 1
2 5 2 5 , 1
2 5 2 5
nn
n
yn
+−
= − + +
.
Vậy
( ) ( )
( ) ( )
3 5 3 5
2 5 2 5
2 5 2 5
,1
5 1 5 1
2 5 2 5
2 5 2 5
nn
n
nn
un
− − −
− + +
=
+−
− + +
BÀI TẬP TƯƠNG TỰ
Bài 3: Xác định số hạng tổng quát của dãy số (un ) được xác định bởi
a/
1
1
1
1
1
2
54
n
n
n
u
n
u
u
u
ĐS:
1
2
5.2 3
n
n
u
b/
1
1
1
2
1
51
3
n
n
n
u
n
u
u
u
ĐS:
7
3
n
n
u
n
.
V. PHƯƠNG PHÁP TUYẾN TÍNH HÓA.
1) Phương pháp biểu diễn nghiệm dưới dạng tuyến tính .
Bài 1: Cho dãy số
12
2
1
2
1
3
2
n
n
n
xx
n
x
x
x
. Chứng minh rằng mọi số hạng của dãy số đều là số nguyên.
Giải
Tìm số hạng tổng quát của dãy số dưới dạng
12
(*)
n n n
x ax bx c
Cho n = 3,4,5 ta được
3 4 5
3; 11; 41x x x
thay vào (*) ta được
3
3 11 4; 1; 0
11 3 41
abc
a b c a b c
a b c
suy ra
12
4
n n n
x x x
Bằng quy nạp ta chứng minh được
12
4
n n n
x x x
là dạng tuyến tính của dãy số đã
cho.
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 31
Do
12
1xx
nguyên nên
12
4
n n n
x x x
của dãy số đã cho đều là số nguyên.
Bài 2: Cho dãy số
1
2
1
1
1
2 3 2
n n n
x
n
x x x
. Chứng minh rằng mọi số hạng của dãy số đều
là số nguyên.
Giải
Tìm số hạng tổng quát của dãy số dưới dạng
12
(*)
n n n
x ax bx c
Cho n=3,4,5 ta được
2 3 4 5
3; 11; 41; 153x x x x
thay vào (*) ta được
3 11
11 3 41 4; 1; 0
41 11 153
abc
a b c a b c
a b c
suy ra
12
4
n n n
x x x
Bằng quy nạp ta chứng minh được
12
4
n n n
x x x
là dạng tuyến tính của dãy số đã cho.
Do
12
1; 3xx
nguyên nên
12
4
n n n
x x x
của dãy số đã cho đều là số nguyên.
BÀI TẬP RÈN LUYỆN
Bài 1: Tuyến tính hóa phương trình
2
01
0; 5 24 1
n n n
x x x x
.
ta được
2 3 4 5
1; 10; 99; 980x x x x
nên
12
10
n n n
x x x
ĐS: Số hạng tổng quát của dãy số
6
5 2 6 5 2 6
24
nn
n
x
Bài 2: Tuyến tính hóa phương trình
23
0 1 2 1
1, 2;
n n n
x x x x x
.
Hướng dẫn: lấy lôgarit cơ số e 2 vế
23
2 1 2 1
ln 2ln 3ln
n n n n n n
x x x x x x
Đặt
ln
nn
vu
khi đó phương trình trở thành
21
23
n n n
v v v
Bài 3: Tìm số hạng tổng quát của dãy số
11
2
1;
23
n
n
n
x
xx
x
Hướng dẫn
2
1
2
2
1
23
1 2 3
1
23
n
n
n
n n n n
n
x
x
x
x x x x
x
.
Đặt
1
n
n
v
x
khi đó phương trình trở thành
2
1
2 3 1
n n n
v v v
2) Phương pháp đặt ẩn phụ.
Xác định công thúc tổng quát của dãy số
12
12
21
11
;
23
.
32
nn
n
nn
uu
uu
u
uu
Ta thấy
0
n
un
vì nếu
0
n
u
nào đó thì
12
0; 0
nn
uu
suy ra
12
0; 0uu
.
Đặt
1
n
n
v
u
khi đó
12
32
n n n
v v v
. Công thức tổng quát
1
12
n
n
v
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 32
Vậy
1
1
21
n
n
u
.
3) Phương pháp biến đổi tương đương.
Tìm nghiệm của phương trình
2
0 1 1
2; 6 33; 3 8 1
n n n
u u u u u
.
Giải
Chuyển vế và bình phương 2 vế ta được.
2 2 2
11
6 9 8 1
n n n n n
u u u u u
hay
22
11
61
n n n n
u u u u
Thay n + 1 bởi n ta được
22
11
61
n n n n
u u u u
.
Cộng theo từng vế ta được
1 1 1
60
n n n n n
u u u u u
.
Vì
2
1
3 8 1 0
n n n
u u u
nên
1 1 1
3 9 0
n n n n
u u u u
0
n
u
.
Suy ra
11
60
n n n
u u u
. Phương trình đặc trưng
2
6 1 0xx
có nghiệm
3 2 2x
Số hạng tổng quát của dãy số dưới dạng
3 2 2 3 2 2
nn
n
u k l
.
Từ các giá trị ban đầu
01
2; 6 33uu
suy ra
8 66 8 66
;
88
kl
Vậy Số hạng tổng quát của dãy số là
8 66 8 66
3 2 2 3 2 2
88
nn
n
u
.
Nhận xét: Phương trình đã cho là bậc nhất nhưng phi tuyến (có chứa căn) nên khi biến đổi tương
đương , nó trở thành phương trình tuyến tính bậc hai.
BÀI TẬP RÈN LUYỆN
Bài 1: Tìm số hạng tổng quát
0
2
1
1
;:
5 24 8
n
n n n
u
u
u u x
.
ĐS:
11
6 2 6 2
5 2 6 5 2 6
2 6 2 6
nn
n
u
.
Bài 2: Xác định số hạng tổng quát của dãy số (un ) được xác định bởi :
a/
23
0 1 2 1
1; 2;
n n n
u u u u u
hd: đặt
ln
nn
vu
ta có
21
v 2 3
n n n
vv
.
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 33
PHẦN 2
XÁC ĐỊNH GIỚI HẠN CỦA DÃY SỐ.
I. Sử dụng định nghĩa giới hạn dãy Số.
1. Định nghĩa giới hạn dãy Số.
Định nghĩa 1: Ta nói dãy số
( )
n
x
có giới hạn hữu hạn là a ( ký hiệu
lim
n
n
xa
→+
=
) nếu với
mọi số dương ε cho trước ( nhỏ bao nhiêu tùy ý ) tồn tại một số tự nhiên
0
n
sao cho :
0
,
n
x a n n
−
.
Định nghĩa 2: Dãy số
( )
n
x
được gọi là hội tụ nếu tồn tại
aR
sao cho
lim
n
n
xa
→+
=
. Khi
đó ta còn nói dãy số
( )
n
x
hội tụ về a. Một dãy số không hội tụ gọi là dãy số phân kỳ.
Định nghĩa 3: Ta nói dãy số
( )
n
x
dần tới dương vô cực (ký hiệu
lim
n
n
x
→+
= +
) nếu với
mỗi số dương M (lớn bao nhiêu cũng được ) tồn tại một số tự nhiên
0
n
sao cho:
0
,
n
x M n n
.
Định nghĩa 4: Ta nói dãy số
( )
n
x
dần tới âm vô cực (ký hiệu
lim
n
n
x
→+
= −
) nếu với mỗi
số âm m (nhỏ bao nhiêu cũng được ) tồn tại một số tự nhiên
0
n
sao cho :
0
,
n
x m n n
2. Giới hạn riêng, dãy con.
Định nghĩa 5: Cho tập hợp A≠∅ và A
.R
Số x được gọi là cận trên của tập A nếu với mọi
aA
ta có
ax
. Lúc này ta nói tập A bị
chặn trên.
Số x được gọi là cận dưới của tập A nếu với mọi
aA
ta có
ax
. Lúc này ta nói tập A bị
chặn dưới,
Cận trên bé nhất (nếu có) của tập A được gọi là cận trên đúng của tập hợp A, ký hiệu: supA.
Cận dưới bé nhất (nếu có) của tập A được gọi là cận dưới đúng của tập hợp A, ký hiệu inf A.
Lưu ý: sup A có thể không thuộc A. Nếu sup A thuộc A thì đó chính là giá trị lớn nhất của
A, ký hiệu Max A.
Tương tự: inf A có thể không thuộc A. Nếu inf A thuộc A thì đó chính là giá trị nhỏ nhất
của A, ký hiệu min A.
Định lý 1: Tập con khác rỗng A của R nếu bị chặn trên thì có sup A, nếu bị chặn dưới thì có
infA
Định lý 2: (Đặc trưng của cận trên đúng, cận dưới đúng)
,
sup
0, : .
M x x A
MA
a A a M

=
−
,
inf
0, : .
m x x A
mA
a A a m

=
+
Trong thực hành ta thường áp dụng định lý sau:
Định lý 3: Cho tập hợp A≠∅ và A
.R
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 34
Nếu tập hợp A bị chặn trên thì tồn tại dãy số
( )
n
x
trong A sao cho
lim sup
n
n
xA
→+
=
.
Nếu tập hợp A bị chặn dưới thì tồn tại dãy số
( )
n
x
trong A sao cho
lim inf
n
n
xA
→+
=
.
Định nghĩa 6: Dãy con
( )
k
n
x
của dãy số
( )
n
x
là dãy mà các phần tử của nó được trích từ
dãy số
( )
n
x
ra, trong đó các chỉ số
k
n
thỏa mãn điều kiện
1 2 1
lim , ... ...
k k k
k
n n n n n
+
→+
= +
Ví dụ : Xét dãy số
( )
n
x
Dãy số
( )
2n
x
(tức là dãy số
2 4 6
, , ,...xxx
) là dãy con của dãy số
( )
n
x
.
Dãy số
( )
21n
x
−
(tức là dãy số
1 3 5
, , ,...x x x
) là dãy con của dãy số
( )
n
x
.
Hai dãy
( )
2n
x
và
( )
21n
x
−
được gọi là 2 dãy con kề nhau của dãy số
( )
n
x
.
Định nghĩa 7: Dãy con
( )
k
n
x
của dãy số
( )
n
x
là hội tụ thì giới hạn của nó được gọi là giới
hạn riêng của dãy số
( )
n
x
.
Ví dụ : Xét dãy số
( )
n
x
với
( )
1 , 1,2,3,...
n
n
xn= − =
khi đó dãy số này không có giới hạn, tuy
nhiên 1 và -1 là các giới hạn riêng của dãy số
( )
n
x
vì
2
lim 1
n
n
x
→+
=
và
21
lim 1
n
n
x
−
→+
=−
.
Định nghĩa 8: Giới hạn riêng lớn nhất của dãy số
( )
n
x
được gọi là giới hạn trên của nó và
ký hiệu là
lim
n
n
x
→+
( hay
lim sup
n
n
x
→+
).
Giới hạn riêng bé nhất của dãy số
( )
n
x
được gọi là giới hạn dưới của nó và ký hiệu là
lim
n
n
x
→+
( hay
lim inf
n
n
x
→+
).
Quy ước:
Nếu
1
sup , ,...
nn
xx
+
= +
với mọi n thì
lim
n
n
x
→+
= +
.
Nếu
1
inf , ,...
nn
xx
+
= −
với mọi n thì
lim
n
n
x
→+
= −
.
Định lý 4: (Cantor) Cho
1 1 2 2
; , ; ,..., ; ,...
nn
a b a b a b
là dãy đoạn thắt dần (tức là
11
; ; , 1;2;3,...
n n n n
a b a b n
++
=
và
( )
lim 0
nn
n
ba
→+
−=
. Khi đó tồn tại một điểm a thuộc mọi
đoạn
;
nn
ab
.
Định lý 5 : (Bolzano – Weierstrass) Từ một dãy số bị chặn bất kỳ
( )
n
x
đều có thể trích ra
một dãy con
( )
k
n
x
hội tụ.
Định lý 6 : Mọi dãy số thực
( )
n
x
đều có giới hạn trên và giới hạn dưới.
Hệ quả 1: Mọi dãy bị chặn
( )
n
x
, Nếu x là giới hạn trên của dãy thì.
*
00
0, : ,
n
n N x x n n

+
.
Hệ quả 2: Mọi dãy bị chặn
( )
n
x
,
Nếu x là giới hạn trên của dãy thì ∀ε>0 và ∀k∈N,tồn tại
:.
k
kn
n k x x
−
Nếu x là giới hạn dưới của dãy thì ∀ε>0 và ∀k∈N,tồn tại
:.
k
kn
n k x x
+
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 35
Định lý 7 : dãy số
( )
n
x
hội tụ khi và chỉ khi nó bị chặn và
lim
n
n
x
→+
lim
n
n
x
→+
=
Định lý 8 : dãy số
( )
n
x
có giới hạn (hữu hạn hoặc ±∞) khi và chỉ khi
lim sup lim inf
nn
nn
xx
→+ →+
=
. Khi đó
lim lim sup lim inf
n n n
n n n
x x x
→ →+ →+
==
.
3. Tiêu chuẩn Cauchy.
Định nghĩa 9: Ta nói dãy số
( )
n
x
là dãy Cauchy hoặc dãy cơ bản nếu với mọi số dương ε
cho trước tồn tại số tự nhiên n0 sao cho
0
,,
nm
x x n m n
−
.
Chú ý: 1)
( )
lim lim 0 lim 0
n n n
n n n
x a x a x a
→+ →+ →+
= − = − =
2) Nếu
lim
n
n
xa
→+
=
thì
lim
n
n
xa
→+
=
.
3)
lim
n
n
x
→+
=
nghĩa là
n
x
có thể lớn bao nhiêu cũng được miễn là n đủ lớn.
Định lý 9 (Tiêu chuẩnCauchy): dãy số
( )
n
x
hội tụ khi và chỉ khi dãy số
( )
n
x
là dãy
Cauchy.
4. Một số bài toán áp dụng.
Bài 1. Cho dãy số
( )
n
x
là dãy số bị chặn trên và thỏa mãn điều kiện
( )
21
13
, 1,2,... 1
44
n n n
x x x n
++
+ =
. Chứng minh rằng dãy số
( )
n
x
có giới hạn hữu hạn khi n tăng
lên vô hạn.
Giải
Đặt
1
3
1,2,...
4
n n n
y x x n
+
= + =
Do đó
( )
1 2 1 1
33
= y 1,2,... 2
44
n n n n n n
y x x x x n
+ + + +
= + + =
suy ra dãy số
( )
n
y
là dãy số tăng.
Vì dãy số
( )
n
x
bị chặn trên nên tồn tại số M sao cho
, 1,2,...
n
x M n =
do đó
( )
1
3 3 7
M+ M= 1,2,... 3
4 4 4
n n n
M
y x x n
+
= + =
dãy số
( )
n
y
là bị chặn trên
Từ (2) và (3) dãy số
( )
n
y
là dãy số hội tụ.
Đặt
lim
n
n
yb
→+
=
và
4
7
b
a=
Ta chứng minh
lim
n
n
xa
→+
=
.
0

vì
lim
n
n
yb
→+
=
nên tồn tại
00
:,
8
n
n N y b n n
−
Do đó với mọi
0
nn
ta có
1
37
8 4 4
n n n
a
y b x x
+
− = + −
( ) ( )
11
33
44
n n n n
x a x a x a x a
++
= − + − − − −
Suy ra
10
3
,
48
nn
x a x a n n
+
− − +
.(4)
Trong (4) lần lượt lấy
0 0 0
, 1, 2,...n n n n n n= = + = +
00
1
3
,
48
nn
x a x a
+
− − +
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 36
0 0 0
2
21
3 3 3
.
4 8 4 4 8 8
n n n
x a x a x a
++

− − + − + +


.
0 0 0 0
2 3 3
3 2 1
3 3 3 3 3 3
. . 1
4 8 4 4 8 8 4 8 4 4
n n n n
x a x a x a x a
+ + +

− − + − + + − + + +



.
….
0 0 0
12
3
1
3 3 3 3 3
4
... . ... 1 .
3
4 8 4 4 4 4 8
1
4
k
k k k k
n k n n
x a x a x a

−−
+


−





− − + + + + + = − +




−


0 0 0
3 3 3
1
4 8 4 4 2
k k k
n k n n
x a x a x a

+

− − + − − +



với k đủ lớn.
Điều này có nghĩa là
n
xa
−
, với n đủ lớn, tức là
lim
n
n
xa
→+
=
.
Vậy dãy số
( )
n
x
là dãy số hội tụ.
Bài 2. (Đề thi vô địch Matxcơva). Chứng minh rằng dãy số
( )
n
x
với
( )
2
sin
n
xn=
, không tiến tới 0
khi
n →+
Giải
Ta có
( )
sin sin cos cos sin sin cos sin cosx y x y x y x y y x− = − +
Do đó:
( )
sin sin sinx y x y− +
Giả sử
( )
2
lim sin 0
n
n
→+
=
.
Khi đó với
( )
*2
00
1
sin2, : sin ,
16
n N n n n

=
Với
0
nn
ta có:
( ) ( ) ( )
22
22
sin 2 1 sin 1 sin 1 sin 2n n n n n

+ = + − + +

( ) ( ) ( ) ( )
sin2 sin 2 3 2 1 sin 2 3 sin 2 1 2 2 4n n n n
= + − + + + + + =

Do đó :
11
sin2 4 4. sin2 sin2
16 4
= =
.Điều mâu thuẩn nầy chứng tỏ dãy số đã cho
không tiến tới 0 khi
n →+
.
Bài 3.(Đề thi vô địch toàn Liên Xô). Cho dãy số
( )
n
a
,Biết
1
lim 0
2
n
n
n
a
a
+
→+

−=


. Chứng minh
rằng :
lim 0
n
n
a
→+
=
.
Giải
∀ε>0, vì
1
lim 0
2
n
n
n
a
a
+
→+

−=


nên
*
1
00
:,
2
n
n
a
n N a n n
−
−
.
Với ε>0 tồn tại
*
kN
sao cho
0
2
n
k
a
. Khi đó với mọi số tự nhiên
0
m n k+
ta có:
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 37
1 1 1
11
11
2 2 2 2 2
m m m
m m m m m
a a a
a a a a a
− − −
−−

= − + − + +


2 2 3 3
2 2 3
1 1 1 1 1 1
2 2 2 2 2 2 2 2 2 2
m m m m
a a a a
− − − −
+ + = + + + + + = + + +
0
00
0
0 0 0
11
2
1
1
11
2
... ... 2 2
1
2 2 2 2 2 2 2
1
2
mn
nn
n
m n m n m n
kk
aa
a
−
− − − − −
−

+ + + + + + = − + + =


−
Như vậy ta chứng minh được:
( )
*
1 0 1
0, :n n k N n n
= +
ta có
3
n
a
có nghĩa
là
lim 0
n
n
a
→+
=
.
Mở rộng Bài 3 được thể hiện qua bài 4 sau đây.
Bài 4.Tìm tất cả các số thực t sao cho với mọi dãy số
( )
n
x
thỏa mãn
( )
1
lim 0
nn
n
tx x
+
→+
−=
,ta suy ra
lim 0
n
n
x
→+
=
.
Giải Ta có
( ) ( )
( )
11
lim 0 lim 0 1
n n n n
nn
tx x x tx
++
→+ →+
− = − =
Xét dãy số
( )
n
x
với
,
n
n
x t n N=
. Khi đó dãy số
( )
n
x
thỏa mãn (1).
Nếu
lim lim 0
n
n
nn
xt
→+ →+
==
thì
1t
. Ngược lại,giả sử
1t
.Ta chứng minh rằng với mọi
dãy số
( )
n
x
sao cho
( )
1
lim 0
nn
n
x tx
+
→+
−=
ta luôn có
lim 0
n
n
x
→+
=
. Vì
( )
1
lim 0
nn
n
x tx
+
→+
−=
nên với mọi
ε > 0,tồn tại
*
0
nN
sao cho
10
,
nn
x tx n n
+
−
.
Do đó
0
nn
ta có:
1nn
x tx
+
−
2
1nn
tx t x t
−
−
.
….
0
00
00
1
1
nn
n n n n
nn
t x t x t
−
− − +
+
−
.
Suy ra
( )
( )
( )
0 0 0
0 0 0
11
2
1 1 1 1
...
n n n n n n
n n n n n n n n
x t x x tx tx t x t x t x
− + − − +
+ + − +
− = − + − + + −
00
00
1
2
1 1 1
...
n n n n
n n n n n n
x tx tx t x t x t x
− − +
+ − +
− + − + + −
( )
0
0
1
2
1
1
1 ...
11
nn
nn
t
t t t
tt
−+
−
−
+ + + + =
−−
.
Vì
1t
nên tồn tại
*
0
nN
sao cho
0
0
1
1
,
nn
n
t x n n
−+
.
Từ (2) và (3) suy ra
01
n n n +
ta có:
( )
0 0 0 0
0 0 0 0
1 1 1 1
1 1 1
1
1
n n n n n n n n
n n n n n n n
x x t x t x x t x t x
t

− + − + − + − +
+ + +
= − + − + +
−
Vậy với mọi ε > 0,tồn tại
*
2 2 0 1
:n N n n n = +
sao cho
12
1
1,
1
n
x n n
t
+

+


−

Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 38
nghĩa là
lim 0
n
n
x
→+
=
. Vậy tất cả các số t cần tìm là
1t
.
Bài 5. (Đề nghị Olympic 30/4/2000) Cho dãy số
( )
n
x
thỏa mãn
0 , , 1,2,...
n m n m
x x x n m
+
+ =
,
Chứng minh rằng dãy số
n
x
n



có giới hạn hữu hạn.
Giải
Gọi
1
12
, ,..., , ,...
1 2 1
nn
xx
xx
A
nn
+

=

+

Khi đó tập A bị chặn dưới bởi số 0 nên tồn tại ìnf A Ta
chứng minh
lim inf A
n
n
x
n
→+
=
với mọi ε > 0 cho trước, theo tính chất của cận dưới đúng, tồn tại m
sao cho
( )
inf A inf A+ 1
2
m
x
m

.
Với n là số tự nhiên bất kỳ,khi đó tồn tại hai số nguyên dương q và r sao cho
,0 1n mq r r m= + −
Khi đó
...
n mq r m m m r m r
x x x x x x qx x
+
= + + + + = +
(xem
0
0x =
)
Do đó:
( )
inf A . inf A+ 2
2
n m r m m
rr
x qx x x qx
xx
n qm r m qm r r n
+
= + +
++
Đặt
1 2 1
max , ,...,
m
x x x
−
=
với
01rm −
thì
r
x
do đó với
2
n
ta có
0.
22
r
x
n

=
.
Bởi vậy từ (2) ta suy ra
( )
2
inf A inf A+ inf A+ , n> 3
22
m
x
m
+ =
inf A lim inf A+ , >0
n
n
x
n

→+
Vậy
lim inf A
n
n
x
n
→+
=
.
Bài 6: Cho dãy số
( )
n
x
thỏa mãn
*
0 . , ,
n m n m
x x x n m N
+
,Chứng minh rằng
lim
n
n
n
x
→+
tồn tại và
hữu hạn.
Giải
Với mọi n =1,2,3 …ta có
( )
11
0 0 .
n
n
nn
x x x x
vậy dãy số
( )
n
n
x
bị chặn.
Gọi
lim
m
m
m
Lx
→+
=
. khi đó tồn tại dãy con
( )
k
k
m
m
x
của dãy số
( )
m
m
x
sao cho
lim
k
k
m
m
m
xL
→+
=
Với mỗi n cố định tùy ý ta có thể viết
k k k
m nl r=+
trong đó
0,1,2,..., 1
k
rn−
do đó
theo giả thiết ta có
( )
..
l
k k k k k k
k
m nl r nl r n r
x x x x x x
+
=
Bởi vậy với mọi k=1,2,…, ta có
( )
( )
( )
( )
( )
( )
1 1 1
1
.
.
ll
k k k
k
k
k k k
k k k k
k
kk
m m m
m
r
m n l r
n
m n r n r n r
l
x x x x x x x
+
+
= =
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 39
( )
( )
1
1
, 1,2,...
k
k
kk
m
m
n
m n r
x x x k =
cho
k → +
ta được
( )
1
, 1,2,...
n
n
n
n
L x x n = =
Suy ra
lim lim lim lim
m m m m
m m m m
m m m m
x x x x
→+ →+ →+ →+
=
.
Vậy dãy số
( )
n
n
x
hội tụ.
Tương tự cách giải bài nầy ta chứng minh được dãy số
n
x
n



bài 5 hội tụ.
Bài tập tương tự
Bài 1: Cho dãy số
( )
n
x
là dãy số bị chặn trên và thỏa mãn điều kiện
( )
21
12
, 1,2,... 1
33
n n n
x x x n
++
+ =
. Chứng minh rằng dãy số
( )
n
x
có giới hạn hữu hạn khi n tăng
lên vô hạn.
Bài 2: (Đề thi HSG QG 1988) Cho dãy số
( )
n
u
là dãy số bị chặn , thỏa mãn điều kiện
21
2 ; , 1,2,...
n n n n
u u u u M n
++
+ =
có nhất thiết hội tụ không ?.
Bài 3: Giả sử các số hạng của dãy số
( )
n
x
thỏa mãn:
*
1, 1 1, ,
n n m n m n m
x x x x x x n m N
+
+ − + +
,
a) Chứng minh rằng dãy số
n
x
n



có giới hạn hữu hạn.
b) Chứng minh rằng nếu
lim
n
n
x
aR
n
→+
=
thì
1 1, 1,2,...
n
na x na n− + =
Giải.
a) Gọi
1
nn
yx=+
và
1
nn
Zx=−
, khi đó
1 ; 1
n m n m n m n m
y x z x
+ + + +
= + = −
và
0 1 2 , , 1,2,...
n m n m n m n m
y x x x y y n m
++
= + + + = + =
( )
0 1 1 1 , , 1,2,...
n m n m n m n m
z x x x z z n m
++
= − + − − = + =
Theo bài 5, suy ra dãy số
n
y
n



hội tụ và dãy số
n
z
n



hội tụ .
Mà ta có
( )
11
1
22
nn
n n n
xx
x y z
n n n n
+ − −

= = −


nên dãy số
n
x
n



hội tụ.
b) nếu
lim
n
n
y
aR
n
→+
=
thì
1
1
lim lim lim lim
n n n
n n n n
y x x
a
n n n n
→+ →+ →+ →+
+
= = + =
Do đó theo lời giải bài 5 ta có
( )
1
1, 1,2,... 1
nn
n
yx
a a x na n
nn
+
− =
.
Mặt khác:
1
1
lim lim lim lim
n n n
n n n n
z x x
a
n n n n
→+ →+ →+ →+
−
= = − = −
nên
( )
1
1, 1,2,... 2
nn
n
zx
a a x na n
nn
−
− + =
Từ (1) và (2) suy ra
1 1, 1,2,...
n
na x na n− + =
.
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 40
II. XÁC ĐỊNH SỐ HẠNG TỔNG QUÁT RỒI TÍNH GIỚI HẠN.
1) Phương pháp. Để tìm
lim
n
n
x
→+
ta thực hiện như sau:
Bước 1: tìm số hạng tổng quát của dãy số
n
x
.
Bước 2: Sử dụng các công thức sau tìm
lim
n
n
x
→+
.
2) Các kết quả thường dùng .
•
( )
0 0 0
ln 1
sin 1
lim 1,lim 1,lim ln
x
x x x
x
xa
a
x x x
→ → →
+
−
= = =
.
•
11
lim 1 ; lim 1
xx
xx
ee
xx
→+ →−
+ = + =
•
( ) ( )
11
00
lim 1 ; lim 1
xx
xx
x e x e
+−
→→
+ = + =
.
• Nếu
1q
thì
lim 0
n
x
q
→+
=
.
• Nếu f(x) là hàm số liên tục trên K thì
( )
( )
lim lim
n n n
nn
f x f x x K
→+ →+
=
và dãy số
n
x
hội tụ
đến
aK
3. Các bài toán.
Bài 1: ( Đề HSG Hà nội năm học 2011 – 2012 ) Cho dãy số
( )
n
u
được xác định bởi:
1
1
1
nn
u
u u n
+
=
=+
. Tìm
1
lim
n
n
n
u
u
→+
+
Giải
Công thức tổng quát
( )
2
1
2
2
n
u n n= − +
Nên
2
2
2
1
2
12
1
2
lim lim lim 1
12
2
1
n
n n n
n
u
nn
nn
u n n
nn
→+ →+ →+
+
−+
−+
= = =
++
++
.
Bài 2: (Đề Olympic Toán SV – 2013) Cho dãy số
( )
n
x
được xác định bởi:
( )
1
2
2
1
1 2 1, 1,2,...
nn
x a R
n x n x n n
+
=
+ = + + =
. Tìm
lim
n
n
x
→+
Giải
Ta phân tích
( )
2
2
2 1 1n n n+ = + −
Ta có :
( ) ( ) ( )
2 2 2
2 2 2
11
1 2 1 1 1
n n n n
n x n x n n x n x n n
++
+ = + + + = + + −
( ) ( )
22
22
1
11
nn
n x n n x n
+
+ − + = −
Do đó :
( ) ( )
22
2 2 2 2
11
1 1 ... 1 1 1
nn
n x n n x n x a
−
− = − − − = = − = −
Suy ra công thức tổng quát
2
2
1
n
an
x
n
−+
=
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 41
nên
2
22
11
lim lim lim 1 1
n
n n n
a n a
x
nn
→+ →+ →+
− + −

= = + =


Bài 3: (Đề Olympic 30/40/ 2013 ) Tìm dãy số
( )
n
x
được xác định bởi:
( ) ( ) ( )
1
22
1
0
1
3 2 2 1 4 .
nn
x
n
n x n x n
+
+ = + + +
Giải
Ta có:
( ) ( ) ( ) ( ) ( ) ( ) ( )
2 2 2 2
11
3 2 2 1 4 3 2 2 1 3 2 2 1
n n n n
n x n x n n x n x n n
++
+ = + + + + = + + + − +
( ) ( ) ( ) ( ) ( )
( )
( )
( )
2 2 2 2
11
3 2 3 2 2 1 2 1 3 2 1 2 1 1
n n n n
n x n n x n n x n x
++
+ − + = + − + + − = + −
(*)
Đặt
2
1
nn
yx=−
thay vào (*) ta được
( )
( )
1
21
32
nn
n
yy
n
+
+
=
+
Do đó
( )
( ) ( )
1
1 1 1
21
2 2 2 1
. ...
3 2 3 1 3 3 2
n
n
n
n
y y y
n n n
+
+
+

==

+ + +

suy ra
lim 0
n
n
y
→+
=
Vậy
( )
1
lim 1 0
n
n
xx
→+
=
.
Bài 4: (Đề Olympic 30/40/ 2013) Cho dãy số
( )
n
x
được xác định bởi :
1
1
1
14 51
, 1,2,...
5 18
n
n
n
x
x
xn
x
+
=
−−
= =
+
Tìm
2013
x
và
lim
n
n
x
→+
.
Giải.
Công thức tổng quát
( )
1
1
34 33.3
11.3 10
n
n
n
x
−
−
−
=
−
nên
( )
2012
2013
2012
34 33.3
11.3 10
x
−
=
−
Nên
( )
1
1
34 33.3
lim lim 3
11.3 10
n
n
n
nn
x
−
−
→+ →+
−
= = −
−
Bài 5: (Đề đề nghị Olympic 30/4 năm 2015 Chuyên An Giang) Cho dãy số
( )
n
u
được xác định
bởi :
1
1
2010
7 7 , 2.
n
nn
u
u u n
−
=
= +
Tính
lim
7
n
n
n
u
n
→+
Hướng dẫn: Công thức tổng quát
1
2003.7 .7 , 1
nn
n
u n n
−
= +
nên
1
2003.7 .7 2003
lim lim lim 1 1
.7 .7 7
nn
n
nn
n n n
u
n
n n n
−
→+ →+ →+
+

= = + =


Bài 6: (Đề Olympic Toán SV 2012 ) Cho dãy số
( )
n
a
được xác định bởi :
1
1
12
, 1,2,...
nn
a
n
a a n
nn
+
=
+
= − =
Tìm ∝ để dãy số
( )
n
a
có giới hạn hữu hạn.
Giải
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 42
Dãy số
( )
n
x
như sau :
, 1,2,...
n
n
a
xn
n
= =
Ta có
( )
( )
1
2
, 1,2,... 2
1
nn
x x n
nn
+
= − =
+
21
2
1.2
xx=−
;
32
2
2.3
xx=−
;…;
( )
1
2
1
nn
xx
nn
+
=−
+
cộng theo từng vế ta được
( )
11
1 1 1 1 1 1 1
2 ... 2 1 ...
1.2 2.3 1 2 2 1
n
x x x
n n n n


= − + + + = − − + − + −



−−


( )
11
21
1
21
n
xx
nn
−

= − − = −


Như vây
( ) ( )
1
2 1 2 2, 1,2,...
nn
a nx nx n n n
= = − − = − + =
Do đó dãy số
( )
n
a
có giới hạn hữu hạn
2 0 2

− = =
.
Bài 7 : (Đề HSG Gia lai 2012 - 2013) Cho dãy số
( )
n
a
được xác định bởi:
( )
1
1
1 2013
, 1,2,...
n
n
aR
na
an
n
+
=
++
= =
a) Tìm số hạng tổng quát của dãy số
( )
n
a
b) Tìm ∝ để dãy số
( )
n
a
có giới hạn hữu hạn và tính giới hạn trong trường hợp đó.
Giải
a) Ta có
( )
( )( ) ( ) ( )( )
1
1
1 2013
2013
, 1,2,...
1 2 1 1 2
n
nn
n
na
aa
an
n n n n n n n n
+
+
++
= = = +
+ + + + +
Xét dãy số
( )
n
x
như sau:
( )
, 1,2,...
1
n
n
a
xn
nn
= =
+
khi đó
1
2
x
=
Làm tương tự bài 6
Như vây
( ) ( )
( ) ( )
22
1
2013 2013 2013
1 1 2 , 1,2,...
4 2 4 2
nn
a n n x n n x n n n n n

= + = + + + − = + + − =


Do đó dãy số
( )
n
a
có giới hạn hữu hạn
2013 2013
0
2 4 2
+ = = −
b) Lúc này
2013 2013
lim lim
22
nn
a
→+ →+

= − = −


.
Bài 8: (Đề HSG Bunggari 2000) Cho dãy số
( )
n
x
được xác định như sau:
12
2
3
21
1;
, 1,2,...
n n n
x x a
x x x n
++
==
= =
a là hằng số dương.
Chứng minh rằng dãy số
( )
n
x
hội tụ và tính giới hạn của dãy số nầy.
Giải
Ta thấy
0, 1,2,...
n
xn =
nên từ
( )
1
2
3
2 1 2 1
21
ln ln ln , 1,2,...
33
n n n n n n
x x x x x x n
+ + + +
= = + =
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 43
Đặt
ln
nn
ux=
ta được dãy số
( )
n
u
như sau :
12
21
0; ln
21
, 1,2,...
33
n n n
u u a
u u u n
++
==
= + =
Xét phương trình đặc trưng :
2
1
3 2 1 0 1;
3
− − = = = −
Do đó
1
3
n
n
u A B

= + −


vì
12
0; lnu u a==
nên
3ln
0
3
4
9ln
ln
94
B
a
A
A
Ba
A a B
−=
=



+ = =
Nên
3ln 9ln 1
, 1,2,...
4 4 3
n
n
aa
un

= + − =


suy ra
3ln
lim
4
n
n
a
u
→+
=
vì
1
lim 0
3
n
n→+

−=


Vì hàm số
( )
x
f x e=
liên tục trên R nên ta có:
( )
3ln 3
3
lim
ln
44
4
lim lim
n
nn
a
u
u
a
n
nn
x e e e e a
→+
→+ →+
= = = = =
.
Bài 9: (Đề nghị Olympic 30/4/ 2012) Cho dãy số
( )
n
x
được xác định như sau:
12
2
3
21
1; 2012
, 1,2,...
n n n
xx
x x x n
++
==
= =
.
Chứng minh rằng dãy số
( )
n
x
hội tụ và tính giới hạn của dãy số nầy.
Đây trường hợp riêng của bài 8.
Bài 10: Cho dãy số
( )
n
x
được xác định như sau :
01
11
1; 5
6 , 1,2,...
n n n
xx
x x x n
+−
==
= − =
Hãy tìm
lim 2
nn
n
xx
→+
ký hiệu :
a a a=−
chỉ lấy phần lẻ của a.
Giải
Công thức tổng quát
( )( ) ( )( ) ( ) ( )
2 1 2 1
11
2 1 3 2 2 2 1 3 2 2 2 1 2 1
2 2 2 2
n n n n
nn
xx
++
= + + + − − = + + −
( ) ( )
2 1 2 1
1
2 2 1 2 1 , 0,1,2...
2
nn
n
xn
++

= + + − =


Do đó
( ) ( ) ( )
2 1 2 1 2 1
1
2 2 1 2 1 2 1 , 0,1,2...
2
n n n
n
xn
+ + +

− − = + − − =


Mà
( )
21
0 2 1 1, 0,1,2,...
n
n
+
− =
nên
( )
21
2 2 1 , 0,1,2...
n
n
xn
+
= − =
Do đó
( )
42
1
2 1 2 1 , 0,1,2...
22
n
nn
x x n
+

= + − =


suy ra
( )
( )
42
11
lim 2 lim 1 2 1 , 0,1,2...
2 2 2 2
n
nn
nn
x x n
+
→+ →+

= + − = =


Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 44
Bài 11: Tìm giới hạn của dãy số
( )
n
x
được xác định bởi:
1
2 2 2 2 ... 2 , 1,2,...
n
n
n
xn
+
= − + + + =
Giải
Đặt
1
2 2 ... 2 , 1,2,...
n
n
un
+
= + + + =
Bằng quy nạp ta Chứng minh được
1
2cos , 1,2,...
2
n
n
un
+
= =
Ta có
21
1 1 2 2
2 2 2cos 2 2 1 cos 2 2.2sin 2 sin
2 2 2 2
n n n n
n
n n n n
x
+
+ + + +

= − = − = =


Vậy
2
2
sin
2
lim lim
22
2
n
n
nn
n
x

+
→+ →+
+
==
(do
0
sin
lim 1
x
x
x
→
=
)
Bài 12: Tìm giới hạn của dãy số
( )
n
x
được xác định bởi:
2 2 2
. ... , 1,2,...
2
22
2 2 ... 2
n
n
xn= =
+
+ + +
Giải
Theo bài 10 ta có
2 3 2 1
1 1 1
. ..... , 1,2,...
cos cos cos
2 2 2
n
n
xn
+
= =
Theo công thức nhân đội
1
sin .cos sin2
2
=
nên
2 1 2 1
2 3 2 1 2 1 2 3 2 2
sin sin
22
1
cos .cos ....cos sin cos .cos ....cos sin
2 2 2 2 2 2 2 2 2

++
++
==
nn
n
n n n n
x
2 1 2 1
2 2 3 2 1 2 1 2
sin sin
22
... , 1,2,...
11
cos .cos ....cos sin
2 2 2 2 2 2

++
−−
= = = =
nn
n n n
n
Vậy
21
21
sin
2
lim lim
22
2
n
n
nn
n
x

+
→+ →+
+
==
(do
0
sin
lim 1
x
x
x
→
=
).
BÀI TẬP TƯƠNG TỰ
Bài 1 (Đề HSG Tây Ninh năm học 2014 – 2015 ) Cho dãy số
( )
n
x
được xác định bởi :
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 45
( ) ( )
1
2
2
11
1
5
1 4 2 . , 1,
n n n n
x
n x n x n x x n n N
++
=
+ = + +
. Tìm
lim
n
n
x
→+
Giải
Dùng quy nạp chứng minh
0, 1,
n
x n n N
Chia 2 vế cho
1
.
nn
xx
+
ta được
( )
( )
2
2
1
1
4 2 , 1,
nn
n
n
n n n N
xx
+
+
= + +
Đặt
2
n
n
n
y
x
=
ta có
( )
2
2
1
1 4 2
nn
n y n y n
+
+ = + +
Ta phân tích
( )
2
2
4 2 2 1 2n n n+ = + −
do đó:
( ) ( ) ( )
( ) ( )
2 2 2
2 2 2
11
1 2 1 2 1 2 2
n n n n
n y n y n n n y n y
++
+ = + + − + − = −
( )
( )
( )
2
2
11
1 2 ... 1 2 3
n
n y y
−
= − − = = − =
( )
2
2
3
2 3 2
nn
n y y
n
− = = +
22
22
3 2 1
32
n
n
nn
x
n x n
+
= = =
+
vậy
2
2
1
lim lim
3 2 2
n
nn
n
x
n
→+ →+

==

+

Bài 2: (Đề HSG Tp Hồ Chí Minh năm học 2012 – 2013 )
Cho dãy số
( )
n
u
được xác định bởi :
1
*
1
1
5
34
,
21
n
n
n
u
u
u n N
u
+
=
+
=
+
Chứng minh rằng dãy số
( )
n
u
có giới hạn hữu hạn và tìm giới hạn đó
Hd: Công thức tổng quát
( )
( )
1
1
1
3. 1 4.5
3. 1 2.5
n
n
n
n
n
u
−
+
−
−+
=
−+
nên
( )
( )
1
1
1
3. 1 4.5
lim lim 2
3. 1 5
n
n
n
n
n
nn
u
−
+
−
→+ →+
−+
==
−+
.
Bài 3: Tìm giới hạn của dãy số
( )
1
4
5
0 1 2 1
0; 0; , 1,2,...
n n n
u u u u u n
++
= =
Kết quả
45
99
01
lim
n
n
u u u
→+
=
.
III. SỬ DỤNG ĐỊNH LÍ WEIERSTRASS ĐỂ CHỨNG MINH DÃY SỐ CÓ GIỚI HẠN.
1) Một số kiến thức thường dùng.
Định nghĩa 10 : Cho dãy số
( )
n
x
, ta nói dãy số đó:
Đơn điệu tăng nếu
1
, 1,2,...
nn
x x n
+
=
Đơn điệu giảm nếu
1
, 1,2,...
nn
x x n
+
=
Đơn điệu tăng thực sự nếu
1
, 1,2,...
nn
x x n
+
=
Đơn điệu giảm thực sự nếu
1
, 1,2,...
nn
x x n
+
=
Dãy số đơn điệu tăng và đơn điệu giảm gọi chung là Dãy số đơn điệu.
Định nghĩa 11 : Cho dãy số
( )
n
x
ta nói dãy số
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 46
Bị chặn trên nếu tồn tại số M sao cho
, 1,2,...
n
x M n =
Bị chặn dưới nếu tồn tại số m sao cho
, 1,2,...
n
x m n =
Bị chặn nếu nó bị chặn trên và bị chặn dưới.
Định lý 9: (định lý Weierstrass) Nếu dãy số
( )
n
u
tăng và bị chặn trên (hoặc giảm và bị
chặn dưới) đều hội tụ .
Chú ý:
i) Nếu dãy số
( )
n
x
tăng và không bị chặn trên thì
lim
n
n
x
→+
= +
và khi đó
1
lim 0
n
n
x
→+
=
.
Nếu dãy số
( )
n
x
giảm và không bị chặn dưới thì
lim
n
n
x
→+
= −
và khi đó
1
lim 0
n
n
x
→+
=
.
ii) Dãy số tăng (giảm) hội tụ khi và chỉ khi nó bị chặn trên (bị chặn dưới)
iii) Cho 2 dãy
( ) ( )
,
nn
xy
khi đó
, 1,2,...
nn
x y n =
thì
lim lim
nn
nn
xy
→+ →+
.
Định lý 10: Mọi dãy hội tụ đều bị chặn.
Phương pháp :
Bước 1:Xét xem dãy số đã cho tăng hay giảm.
– Nếu tăng thì chứng minh
, 1,2,...
n
x L n =
để suy ra dãy bị chặn trên.
– Nếu giảm thì chứng minh
, 1,2,...
n
x L n =
để suy ra dãy bị chặn dưới.
Bước 2:Sử dụng kết quả bước 1 để chứng minh dãy số đơn điệu.
Bước 3:Sử dụng định lý Weierstrass để chứng minh dãy số đã cho hội tụ.Sau đó, Giả sử
dãy số đã cho hội tụ về L, từ
( )
1
, 1,2,...
nn
x f x n
+
= =
khi
n →+
và sử dụng tính liên tục của
hàm f ta được
( )
L f L=
.Vậy giới hạn của dãy số đã cho là nghiệm của phương trình
( )
x f x=
.
BÀI TẬP ÁP DỤNG.
Bài 1. Chứng minh rằng dãy số
( )
n
u
cho bởi công thức
1
1
2
2
nn
u
uu
+
=
=+
với n≥1 có giới hạn và tìm
giới hạn đó.
Giải
Ta có
1
2u =
và
1
2
nn
uu
+
=+
nên
0
n
u
n
.
* Ta chứng minh
2
n
u
n
(1).
Với n=1 Ta có
1
2u =
< 2 thì (1) đúng .
Giả sử bất đẳng thức đúng với n = k thì
2
k
u
ta chứng minh bất đẳng thức đúng với n = k+1 thì
1
2
k
u
+
Thật vậy
1
2 2 2 2
nn
uu
+
= + + =
vậy
2
n
u
n
.
Chứng minh dãy số
( )
n
u
tăng .
Xét
2
1
2 2 0 1 2
n n n n n n n
u u u u u u u
+
+ − − −
mà
02
n
u
nên
1nn
uu
+
.
Vậy dãy số
( )
n
u
có giới hạn.
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 47
Đặt
lim
n
ua=
thì 0≤a≤2 và
1
2 lim lim 2
n n n n
u u u u
+
= + = +
2
2 2 0 1 2a a a a a v a = + − − = = − =
vì
0
n
u
nên
lim 0
n
ua=
vậy
lim 2
n
u =
.
Bài 2: Chứng minh rằng dãy số
( )
n
u
cho bởi công thức
1
1
2
1
2
n
n
u
u
u
+
=
=−
n≥2 có giới hạn và tìm giới
hạn đó.
Giải
Công thức tổng quát
1
1
n
n
u
n
+
=
+
ta chứng minh dãy số
( )
n
u
giảm và bị chặn bởi 1
và
1
lim lim lim 1 1
11
n
n
u
nn

= = − =

++

. vậy
lim 1
n
u =
Bài 3: Cho dãy số
( )
n
x
được xác định bởi
11
3
; 3 2, 2,3,...
2
nn
x x x n
−
= = − =
Chứng minh rằng dãy số
( )
n
x
có giới hạn khi
n →+
, tìm giới hạn đó.
Hướng dẫn :
Cách 1: Bằng quy nạp chứng minh
3
2, 1,2,...
2
n
xn =
Xét
2
1
32
3 2 0
32
nn
n n n n
nn
xx
x x x x
xx
+
− + −
− = − − =
−+
vì
3
;2
2
n
x



Vậy dãy số
( )
n
x
tăng và bị chặn trên nên hội tụ
Đặt
lim
n
n
xa
→+
=
khi đó
3
;2
2
a



Từ
1
3 2, 2,3,...
nn
x x n
−
= − =
cho
n →+
ta được
11
lim lim 3 2 3lim 2
n n n
nn
n
x x x
−−
→+ →+
→+
= − = −
hay
3 2 2a a a= − =
.
Vậy
lim 2
n
n
x
→+
=
.
Cách 2: Bằng quy nạp chứng minh
3
2, 1,2,...
2
n
xn =
Xét hàm số
( )
3
3 2, ;2
2
f x x x

= −


.Khi đó
( )
1
, 1,2,...
nn
x f x n
+
= =
Ta có
( )
33
' 0, ;2
2
2 3 2
f x x
x

=

−

do đó f(x) là hàm tăng trên
3
;2
2



Ta có
( )
2 1 1 1
3 5 3
3 2 3. 2
2 2 2
x f x x x= = − = − = =
suy ra dãy số
( )
n
x
tăng.
Bài 4: (HSG QG năm 2012) Cho dãy số
( )
n
x
được xác định bởi
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 48
( )
1
1
3
2
2 , 2,3,...
3
nn
x
n
x x n
n
−
=
+
= + =
Chứng minh rằng dãy số
( )
n
x
có giới hạn hữu hạn, tính giới hạn đó.
Hướng dẫn
Bằng quy nạp chứng minh
1
2
, 3,4,...
1
n
n
xn
n
−
+
=
−
suy ra dãy số
( )
n
x
bị chặn dưới bởi số 0.
Với
3n
ta có
( )
( )
1
1 1 1
2 2 1
2
20
33
n
n n n n
n n x
n
x x x x
nn
−
− − −
+ − −
+

− = + − =
Vậy dãy số
( )
n
x
giảm và bị chặn dưới nên có giới hạn hữu hạn.
Đặt
lim
n
n
xa
→+
=
cho
n →+
ta được
( ) ( )
11
2 1 2
lim lim 2 lim lim 2
3 3 3
n n n
n n n n
n
x x x
nn
−−
→+ →+ →+ →+
+

= + = + +


hay
( )
1
21
3
a a a= + =
.
Vậy
lim 1
n
n
x
→+
=
.
Bài 5: Cho trước
0a
, xét dãy số
( )
n
x
thỏa mãn điều kiên
0
n
xa
và
( )
2
1
,
4
nn
a
x a x n N
+
−
Chứng minh rằng dãy số đã cho có giới hạn và tìm giới hạn đó.
Hướng dẫn: ta có
0
n
xa
dãy số
( )
n
u
bị chặn.
Áp dụng bất đẳng thức cauchy
( ) ( )
2
1 1 1
2 2
4
n n n n n n
a
x a x x a x a x x n
+ + +
+ − − =
suy ra dãy số
( )
n
x
giảm và bị chặn dưới nên có giới hạn hữu hạn
Đặt
( )
lim 0
n
x x x=
ta có
( ) ( )
22
1 1 1
lim
44
n n n n
aa
x a x x a x
+ + +
− −
( )
2
2
10
4 2 2
a a a
x x x x

− − =


. vậy
lim
2
n
a
x =
.
Bài 6: Cho dãy số
( )
n
x
được xác định bởi
12
1
0;
2
xx==
và
( )
3
11
1
1 , 2,3,...
3
n n n
x x x n
+−
= + + =
Chứng minh rằng dãy số
( )
n
x
có giới hạn hữu hạn, tính
lim
n
n
x
→+
Giải
Ta chứng minh
( )
51
0 , 1,2,... 2
2
n
xn
−
=
Ta có
12
51
0,
2
xx
−

Giả sử
1
5 1 5 1
0 ,0
22
nn
xx
−
−−
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 49
Khi đó
( )
3
3
11
1 1 5 1 5 1 5 1
0 1 1
3 3 2 2 2
n n n
x x x
+−

− − −

= + + + + =


Theo nguyên lý quy nạp (2 ) đúng. Ta chứng minh dãy số
( )
n
x
tăng.
Ta có:
1 2 3 1 2 3
1 1 1 1
0; , 1 0
2 3 2 2
x x x x x x

= = = + + =


Giả sử
2 1 1
,
n n n n
x x x x
− − −

Khi đó
( ) ( )
( )
( )
( )
3 3 3 3
1 1 1 2 1 1 2
11
1 1 0
33
n n n n n n n n n n
x x x x x x x x x x
+ − − − − − −

− = + + − + + = − + −

Vậy
1
, 1,2,...
nn
xx
+

nên dãy số
( )
n
x
có giới hạn.
Đặt
lim
n
n
xa
→+
=
cho
n →+
ta được
( )
( )
( )
32
1
1 5 1
1 1 1 0
15
32
2
a
a a a a a a a
a
=
−
= + + − + − = =
−
=
.
Vậy
51
lim
2
n
n
x
→+
−
=
.
Bài 7: Cho dãy số
( )
n
x
thỏa mãn điều kiên
1
0, 0xa
và
*
1
1
,
2
nn
n
a
x x n N
x
+

= +


Chứng minh rằng dãy số đã cho có giới hạn và tìm giới hạn đó.
Hướng dẫn:
Ta có
21
1
1
2
a
x x a
x

= +


do đó bằng quy nạp và bất đẳng thức cauchy ta suy ra
, 2,3,...
n
x a n =
Mặt khác
1
1
2
11
1 , 2,3,...
2 2 2 2
n
nn
nn
x
aa
x x n
x x a
+
+
= + + = =
Vậy dãy số
( )
n
x
giảm và bị chặn dưới bởi
a
nên hội tụ.
Đặt
lim
n
n
xl
→+
=
cho
n →+
ta được
( )
22
1
2
2
a
l l l l a l a l a
l

= + = + =


.
Vậy
lim
n
n
xa
→+
=
.
Bài 8: Cho dãy số
( )
n
x
được xác định bởi
( )
3
3
2 8 1, 1,2,3,...
n
x n a n n a R= + + =
a) Tìm a sao cho dãy số
( )
n
x
có giới hạn hữu hạn.
b) Tìm a sao cho
( )
n
x
là dãy số tăng (kể từ số hạng nào đó)
Giải
a) Nếu
1a =−
thì dãy số
( )
n
x
có giới hạn hữu hạn vì :
(
)
( )
3
3
2
2 3 3
3
3
1
lim lim 2 8 1 lim 0
4 2 8 1 8 1
n
n n n
x n n
n n n n
→+ →+ →+
−
= − + = =
+ + + +
.
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 50
Giả sử dãy số
( )
n
x
có giới hạn hữu hạn vì
( )
33
33
2 8 1 1 8 1
n
x n n a n= − + + + +
mà dãy số
( )
n
x
có giới hạn hữu hạn nên dãy số
( )
n
y
với
( )
3
3
1 8 1, 1,2,...
n
y a n n= + + =
cũng có giới hạn
hữu hạn . Mà
3
3
lim 8 1
n
n
→+
+ = +
nên từ dãy số
( )
n
y
có giới hạn hữu hạn suy ra
1 0 1aa+ = = −
Vậy dãy số
( )
n
x
có giới hạn hữu hạn khi và chỉ khi
1a =−
b) Dãy số
( )
n
x
là dãy số tăng (kể từ số hạng nào đó) khi và chỉ khi tồn tại số nguyên dương
0
n
sao cho
10
,
nn
x x n n
+
.Ta có
( ) ( )
( )
33
33
33
33
1
2 2 8 1 1 2 8 1 8 1 1 8 1 2
nn
x x n a n n n a n n
+
+ + + + + + + + − + −
( )
( )
( )
( )
( )
( )
(
)
(
)
3
3
2
2
33
33
33
33
8 1 1 8 1
2
8 1 1 8 1 1 8 1 8 1
a n n
n n n n

+ + − +

−
+ + + + + + + +
( )
( )
( )
( )
( )
(
)
(
)
2
2
2
33
33
33
33
24 24 8
2
8 1 1 8 1 1 8 1 8 1
a n n
n n n n
++
−
+ + + + + + + +
( )
( )
( )
( )
( )
(
)
(
)
2
2
2
33
33
33
33
24 24 8
24
lim 2 2 1
444
8 1 1 8 1 1 8 1 8 1
n
a n n
a
a
n n n n
→+
++
− − −
++
+ + + + + + + +
Vậy dãy số
( )
n
x
tăng (kể từ số hạng nào đó) khi và chỉ khi
1a −
BÀI TẬP TƯƠNG TỰ
Bài 1: Cho dãy số
( )
n
u
cho bởi công thức
1
12
2
nn
n
uu
u
+

=+


và
1
0u
a) Chứng minh rằng
2, 2
n
un
b) Chứng minh rằng dãy số
( )
n
u
có giới hạn và tìm giới hạn.
Bài 2: (Đề HSG Tp Hồ Chí Minh năm học 2012 – 2013)
Cho dãy số
( )
n
u
được xác định bởi :
1
1
5
u =
và
*
1
34
,
21
n
n
n
u
u n N
u
+
+
=
+
Chứng minh rằng dãy số
( )
n
u
có giới hạn hữu hạn và tìm giới hạn đó
Bài 3: (HSG Gia Lai năm 2004)
Cho dãy số
( )
n
x
được xác định bởi
1
2004x =
và
( )
1
21
1 , 1,2,3,...
31
nn
n
x x n
n
+
+
= + =
+
Chứng minh rằng dãy số
( )
n
x
có giới hạn hữu hạn, tính giới hạn đó.
Hướng dẫn: tương tự bài 4 trên.
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 51
Bài 4: Chứng minh rằng cho bởi công thức
( )
( )
1
01
1
1
1
4
n
nn
u
n
uu
+

−
có giới hạn và tìm giới hạn đó.
Hướng dẫn: tương tự bài 5 trên
Bài 5: Cho dãy số
( )
n
x
được xác định bởi
1
5
2
x =
và
3*
1
20 21
12 ,
1
n n n
n
x x x n N
n
+
+
= − +
+
Chứng minh rằng dãy số
( )
n
x
có giới hạn hữu hạn, tính giới hạn đó.
Hướng dẫn.
- Chứng minh :
*
2,
n
x n N
.
- Chứng minh
1
, 1,2,...
nn
xx
+

nên dãy số
( )
n
x
có giới hạn.
Đặt
lim
n
n
xa
→+
=
cho
n →+
ta được Vậy
lim 2
n
n
x
→+
=
.
Bài 6: Cho dãy số
( )
n
x
được xác định bởi
1
2011
2010
x =
và
2*
1
2 4999
2,
2499
n n n
n
x x x n N
n
+
+
= − +
+
Chứng minh rằng dãy số
( )
n
x
có giới hạn hữu hạn, tính giới hạn đó.
Hướng dẫn.
- Chứng minh :
*
1,
n
x n N
.
- Chứng minh
1
, 1,2,...
nn
xx
+

nên dãy số
( )
n
x
có giới hạn.
Đặt
lim
n
n
xa
→+
=
cho
n →+
ta được Vậy
lim 1
n
n
x
→+
=
.
Bài 7: Cho dãy số
( )
n
x
thỏa mãn điều kiên
1
0, 0xa
và
*
1
2
1
2,
3
nn
n
a
x x n N
x
+

= +


Chứng minh rằng dãy số đã cho có giới hạn và tìm giới hạn đó.
Hướng dẫn: Ta có
3
2 1 1
2
1
1
3
a
x x x a
x

= + +


tương tự bài 7 trên
Bài 8: Cho dãy số
( )
n
x
được xác định bởi
( )
2
1, 1,2,...
n
x n a n n a R= + + =
a) Tìm a sao cho dãy số
( )
n
x
có giới hạn hữu hạn.
b) Tìm a sao cho
( )
n
x
là dãy số tăng (kể từ số hạng nào đó)
tương tự bài 8 trên
Bài 9: (T10/404) Cho dãy số
( )
n
x
xác định bởi
1
5
2
x =
và
3
1
20 21
12
1
n n n
n
x x x
n
+
+
= − +
+
. Chứng minh
dãy số
( )
n
x
có giới hạn và tìm giới hạn đó.
Bài 10: (HSG Tây ninh 2014) Cho dãy số
( )
n
u
xác định bởi
1
2u =
và
*
1
15
2
nn
n
u u n
u
+

= +


Chứng minh rằng
( )
52
n
un
Tìm
lim
n
u
.
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 52
IV. GIỚI HẠN CỦA DÃY TỔNG.
Bài 1. Cho dãy số
( )
n
a
xác định bởi
1
*
2
1
2
1
n n n
a
nN
a a a
+
=
= − +
. Tìm
1
1
lim , 1;2;3...
n
i
i
n
a
=
=
Để tiến hành giải bài toán trên ta tiến hành theo các bước sau.
Bước 1: Chỉ ra
lim
n
a = +
.
Bước 2: tính tổng
1
1
n
i
i
a
=
Bước 3: Tìm
1
1
lim
n
i
i
a
=
.
Giải
Do
1
21a =
và
( )
2
1
1 , 1;2;3...
n n n
a a a n
+
− = − =
nên
1 2 3
1 2 ...a a a =
tức là dãy số nầy tăng (1).
Ta chứng minh dãy số
( )
n
a
không bị chặn trên (2).
Thật vậy, nếu dãy số
( )
n
a
bị chặn trên thì
( )
n
a
hội tụ Giả sử
( )
lim 1
n
a a a=
khi đó
( )
2
11a a a a= + − =
(mâu thuẩn).
Từ (1) và (2)suy ra
lim
n
a = +
.
Ta có
( )
1
1
1 1 1
1 1 , 1;2;...
11
i i i
i i i
a a a i
a a a
+
+
− = − = − =
−−
suy ra
11
11
1 1 1 1
11
1 1 1
nn
ii
i i i n
a a a a
==
++

= − = − →

− − −


khi
n→+
.
Vậy
1
1
lim 1
n
i
i
a
=
=
khi
n→+
.
Bài 2 : Cho dãy số
( )
n
x
xác định bởi
1
2
1
1
2008
n n n
x
x x x
+
=
=+
n =1;2;3; Tìm
12
2 3 1
lim ...
n
n
x
xx
x x x
+

+ + +


Giải
Ta có
2
1
2008 0, 1;2;3...
n n n
x x x n
+
− = =
nên dãy số
( )
n
x
là dãy số tăng và dương .Ta
chứng minh
( )
n
x
không bị chặn trên.
Thật vậy, nếu dãy số
( )
n
x
bị chặn trên thì
( )
n
x
hội tụ Giả sử
( )
lim 0
n
x a a=
khi đó
2
2008 0a a a a= + =
(vô lý).suy ra
lim
n
x = +
.
Biến đổi
2
1
11
1 1 1
2008
2008
k
k k k
k k k
x
x x x
x x x
+
++

= + = −


suy ra
12
2 3 1 1 1
1 1 1
...
2008
n
nk
x
xx
x x x x x
++

+ + + = −


Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 53
Vậy
12
2 3 1
1
lim ...
2008
n
n
x
xx
x x x
+

+ + + =


.
Bài 3: Cho dãy số
( )
, 1,2,...
n
xn=
xác định bởi
1
2
1
1
2
4
2
n n n
n
x
x x x
x
+
=
++
=
Chứng minh rằng dãy
( )
n
y
với
2
1
1
, 1;2;3...
n
n
i
i
yn
x
=
==
có giới hạn hữu hạn. Tìm
lim
n
y
.
Giải
Từ giải thiết ta thấy
0 1
n
xn
nên
22
1
2
44
2
0, 1
22
4
n n n n n n
n
n n n
n n n
x x x x x x
x
x x x n
x x x
+
+ + + −
− = − = =
++
Do đó dãy số
( )
n
x
tăng.
Giả sử
( )
lim 0
n
x a a=
khi đó
2
4
0
2
a a a
aa
++
= =
(vô lý).
Suy ra
lim
n
x = +
.
Từ
( )
2
2
1 1 1
2
1
1
4
1 1 1
11
2
n n n
n n n n
nn
n
x x x
x x x x n
xx
x
+ + +
+
+
++
= = + = −
Suy ra
22
1
1 1 2 2 3 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1
... 6
n
n
i
i n n n n
y
x x x x x x x x x x x
=
+ + +

= = + − + − + + − = − = −


Do đó
6 1
n
yn
và dãy số
( )
n
y
tăng vì
1
1
1
n n n
n
y y y
x
+
+
= +
Vậy dãy số
( )
n
y
có giới hạn hữu hạn và
lim 6
n
y =
Bài 4 : Cho dãy số
( )
n
a
xác định bởi
( )( )( )
1
*
1
1
1 2 3 1
n n n n n
a
nN
a a a a a
+
=
= + + + +
đặt
1
1
, 1;2;3...
2
n
n
i
i
yn
x
=
==
+
Tìm
lim
n
y
.
Giải
Từ công thức xác định dãy suy ra
2
5a =
và
0 1;2;3...
n
an =
ta biến đổi .
( )( )( )
( )( )
22
1 2 3 1 3 3 2 1
n n n n n n n n
a a a a a a a a+ + + + = + + + +
( ) ( )
2
22
3 2 3 1
n n n n
a a a a= + + + +
=
2
31
nn
aa++
với n ≥1.
22
1 1 1
3 1 3 3 ... 3 3
nn
n n n n n
a a a a a a
+−
= + + =
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 54
Bằng quy nap ta chì ra được
1
3 2
n
n
an
−
.Nên
1
lim lim 3
n
n
n
a
−
→+
= +
ta lại có
2
1
31
n n n
a a a
+
= + +
( )( )
2
1
1 3 2 1 2
n n n n n
a a a a a
+
+ = + + = + +
nên
( )( )
1
1 1 1 1
1 1 2 1 2
n n n n n
a a a a a
+
= = −
+ + + + +
1
1 1 1
2 1 1
n n n
a a a
+
=−
+ + +
Do đó
11
1 1 1 1
1 1 1 1 1 1 1 1
2 1 1 1 1 2 1 2
nn
n
ii
i i i n n
y
x x x x x x
==
+ + +

= = − = − = − →

+ + + + + +


Vậy
1
lim
2
n
y =
khi
n→+
.
Bài 5. Xét dãy số thực
( )
( )
1
n
xn
xác định bởi
( )
1
32
1
1
2 5 4
n n n n
x a a R
n
x x x x
+
=

= − +
. Tìm tất cả các giá trị
của a để dãy số
( )
n
x
có giới hạn hữu hạn. Hãy tìm giới hạn của dãy số
( )
n
x
trong các trường
hợp đó.
Giải
Xét hàm số
( )
32
2 5 4f t t t t= − +
.Khi đó dãy số đã cho có dạng
( )
*
1nn
x f x n N
+
=
ta có
( ) ( )( )
2
' 6 10 4 2 3 2 1f t t t x x= − + = − −
và
( ) ( )( )
1 2 3f x x x x x− = − −
. Từ đó suy ra
( )
f x x=
khi
0x =
hoặc
1x =
hoặc
3
2
x =
và khi
0x
thì
( )
f x x
, khi
3
2
x
thì
( )
f x x
.
Bằng cách lập bảng biến thiên của hàm số
( )
fx
ta có khi
3
0
2
x
thì
( )
3
0
2
fx
.
Từ các nhận xét trên ta thu được:
(i) Với
( )
;0x −
luôn luôn có
( ) ( )
;0fx −
.
(ii) Với
3
0;
2
x



luôn luôn có
( )
3
0;
2
fx



.
(iii) Với
3
;
2
x

+


luôn luôn có
( )
3
;
2
fx

+


.
Ta xét các trường hợp cụ thể :
Trường hợp 1: a<0 theo (i) thì mọi
0
n
x
và
( )( )
1
1 2 3 0
n n n n n
x x x x x
+
− = − −
do đó dãy
số
( )
n
x
là dãy giảm nên có giới hạn
lim
n
xb=
khi đó
3
0;1;
2
b



và b<a mâu thuẫn vì a<0. Suy
ra dãy số
( )
n
x
không có giới hạn hữu hạn ứng với a<0.
Trường hợp 2: a=0. Khi đó dãy số
( )
n
x
là dãy hằng và
lim 0
n
x =
.
Trường hợp3:
3
0
2
a
theo (ii) thì mọi
3
0
2
n
x
và
( )
2
1
1 1 1 1
n n n n
x x x x
+
− − − −
do
3
0;
2
n
x



nên
( )( )
1 2 1 1
nn
xx− −
.
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 55
Bằng phương pháp quy nạp từ
1
11
nn
xx
+
− −
suy ra
1
11
n
xa
+
− −
với mọi n nguyên
dương.
do
3
0;
2
a



nên
1
1
2
a −
suy ra
lim 1
n
x =
Trường hợp 4:
3
2
a =
Khi đó dãy số
( )
n
x
là dãy hằng và
3
lim
2
n
x =
.
Trường hợp 5:
3
2
a
theo (iii) thì mọi
3
;
2
n
x

+


và
1
0
nn
xx
+
−
do đó dãy số
( )
n
x
là
dãy tăng. Nếu tồn tại giới hạn hữu hạn
lim
n
xb=
thì
3
0;1;
2
b



và b>0 ( vô lý).
Kết luận: Dãy số
( )
n
x
có giới hạn hữu hạn khi và chỉ khi
3
0;
2
a



.
Khi a = 0 thì
lim 0
n
x =
.
Khi
01a
thì
lim 1
n
x =
.
Khi
3
1
2
a
thì
3
lim
2
n
x =
Bài 6. Xét dãy số
( )
( )
1;2;3...
n
xn=
xác định bởi
0
1
1
1
1
n
n
x
x
x
+
=
=+
+
.Vớin=1;2;3…và
𝛼
là số cho trước
lớn hơn 1. Tìm
lim
n
x
.
Giải
Nhận xét: với
0
1x
=
thì
1
n
x
với n=1;2;3…..
Xét hàm số
( )
1
1
1
ft
t
=+
+
.Khi đó dãy số đã cho có dạng
( )
*
1nn
x f x n N
+
=
ta có
( )
( )
2
1
'0
1
2 1 1
1
ft
t
t
−
=
++
+
và
( )
1
'
8
ft
với x>1
Vì f(1)>1 và f(2)<2 nên phương trình
( )
f x x=
có nghiệm duy nhất trong
( )
1;2
. Gọi
nghiệm đó là L
Theo định lý Lagrange thì với mọi L≠x>1 tồn tại c>1 sao cho
( ) ( )
( ) ( ) ( )
1
'
8
f x f L
f c f x f L x L
xL
−
= − −
−
và
( )
( )
1
8
nn
f x f L x L− −
Hay
1
10
11
... 1
88
n
nn
x L x L x
+
+

− − −


suy ra
lim
n
xL=
Ta cần xác định L. giải phương trình
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 56
( )
3
1 1 1 25
12
1 3 3 27
f x x x x x
x
= + = + − + =
+
ta được
43 177 43 177 1
54 18 54 18 3
L = + + − −
trong khoảng
( )
1;2
.
Vậy
43 177 43 177 1
lim
54 18 54 18 3
n
x = + + − −
.
Bài 7: Xét dãy số
( )
( )
1;2;3...
n
xn=
xác định bởi
1
2
1
2,1
2 8 4
2
n n n
n
x
x x x
x
+
=
− + + −
=
.Với mỗi số nguyên
dương n , đặt
2
0
1
1
4
n
n
i
i
y
x
=
+
=
−
Tìm
lim
n
y
.
Giải
Nhận xét: ta có
( )( )
2
2
2 8 4
4 3 2
2
x x x
x x x
− + + −
− = − −
.
Phương trình không có nghiệm khi x>2. Do đó
1 2 3
2,1 ...x x x
(1).
Mặt khác từ công thức truy hồi của dãy
( )
n
x
ở giả thiết bài toán ta suy ra
( )
2
2 2 2 2
1 1 1 1
2 2 8 4 4 4 4 8 4 8 4
n n n n n n n n n n n n
x x x x x x x x x x x x
+ + + +
− + = + − + + − + − = + −
.
( )( )
22
1 1 1 1 1
4 2 3 6 4 3 2
n n n n n n n n
x x x x x x x x
+ + + + +
− = − + − − = + −
11
2 2 2 2
11
1 1 1 1
3 2 1
1 1 1 1 1 1
2 2 2 2
4 4 4 4
nn
n n n n
n n n n
xx
x x x x
x x x x
++
++
+ + + +
+ + +
= = = + = −
− − − −
− − − −
(2).
Từ (1) và (2) ta thấy tồn tại
lim
n
x
và
2
1
1
1 1 1
lim lim lim 0
22
4
nn
n
xx
x
+
+
= − =
−−
−
suy ra
lim
n
x = +
.
Do đó
2
11
1 1 1 1
1
1 1 1 1 1 1
10
2 2 2 2 2
4
nn
n
ii
n n n n
n
y
x x x x x
x
==
+ + +
+

= = − = − = −

− − − − −
−


Vậy
lim 10
n
y =
.
Bài 8. Cho dãy số
( )
n
x
xác định bởi
1
2
1
2
1
2
1;2;...
1
n
n
nn
a
n
a
a
aa
+
=
=
=
−+
a) Chứng minh rằng dãy số
( )
n
a
có giới hạn hữu hạn và tìm giới hạn đó.
b) Đặt
12
...
nn
b a a a= + + +
với mỗi số nguyên dương n.Tìm phần nguyên
n
b
và giới hạn
lim
n
n
b
→
.
Giải
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 57
Ta có
2
2
13
1 0 0 1
24
n n n n
a a a a n

− + = − +


.
Mặt khác
( )
2
2
1
22
1
0
11
nn
n
n n n
n n n n
aa
a
a a a
a a a a
+
−−
− = − =
− + − +
(1) .
Do đó chứng minh quy nạp ta được:
n n 1 1
1
0 a a ... a
2
.
Vậy dãy số
( )
n
a
là dãy giảm bị chặn dưới bởi 0, suy ra tồn tại
lim
n
n
aa
→
=
và (1) s
b) Ta có
2
1
22
11
1
1 1 1 1
11
1 1 1 1
11
nn
n n n
n n n n
n n n n
aa
a a a
a a a a
a a a a
+
++
−
− = − = = + = −
− − − −
− + − +
do đó
11
1 1 1 1
1 1 1 1 1
2
1 1 1 1 1
nn
ni
ii
n n n n
ba
a a a a a
==
+ + +

= = − = − = −

− − − − −


vì
n 1 n n
n1
11
0 a 2 1 1 b 0 b 0
2 1 a
và
lim 0 lim 2 1 1
nn
nn
ab
→ →
= = − =
.
Bài 9: Cho dãy số
( )
n
a
xác định bởi
12
1aa==
và
( )
1
1
, 2,3,...
1
n
nn
a
a a n
nn
−
+
= + =
+
Chứng minh rằng
dãy số
( )
n
a
có giới hạn hữu hạn.
Giải
Ta thấy
*
0,
n
a n N
do đó suy ra dãy số
( )
n
a
là dãy số tăng. Theo giả thiết ta có:
( ) ( ) ( )
1 1 2
11
...
1 1 1
n n n
n n n
a a a
a a a
n n n n n n
− − −
+−

= + = + + =

+ + −

( ) ( ) ( )( )
1 2 3
21
2
...
1 1 2 1 3.4 2.3
n n n
a a a
aa
a
n n n n n n
− − −
= + + + + + +
+ − − −
( ) ( ) ( )( )
( )
1 2 3
11
... 1 *
1 1 2 1 3.4 2.3
n n n
a a a
n n n n n n
− − −
= + + + + + +
+ − − −
Bằng quy nạp ta chứng minh
5
, 3,4,...
3
n
an =
Ta có
1
32
1 7 5
1
2.3 6 6 3
a
aa= + = + =
Giả sử
5
, :3
3
k
a k N k n
khi đó từ (*) ta có:
( ) ( ) ( )( )
1
5 1 1 1 1 1 1
... 1
3 1 1 2 1 4.5 3.4 2.3
n
a
n n n n n n
+

+ + + + + + +

+ − − −

Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 58
5 1 1 1 1 1 1 1 1
... 1
3 1 1 4 5 12 6
5 1 1 5 5 1 5 20 5
.
3 4 1 4 3 4 4 12 3
n n n n
n

= − + − + + − + + +

+−


= − + + = =

+

dãy số
( )
n
a
tăng và bị chặn trên nên dãy số
( )
n
a
có giới hạn hữu hạn.
Lưu ý: Giả sử
, :3
k
a k N k n
ta chứng minh
1n
a
+
từ (*) ta có:
( ) ( ) ( )( )
1
1 1 1 1 5
...
1 1 2 1 4.5 4
n
a
k k k k k k
+

+ + + + +

+ − − −

1 1 5 5
4 1 4 4k
+

= − +

+

Để
1n
a
+
thì
55
43

+
= =
.
BÀI TẬP RÈN LUYỆN.
Bài 1. Cho dãy số
( )
n
x
xác định bởi
1
3x =
và.Tìm
12
1 1 1
lim ...
1 1 1
n
x x x

+ + +

− − −

Bài 2. Cho dãy số
( )
n
x
xác định bởi
1
1xa=
và
2
1nn
xx
+
=
.Tìm
12
2 3 1
lim ...
1 1 1
n
n
x
xx
x x x
+

+ + +

− − −

Bài 3. Cho dãy số
( )
n
x
xác định bởi
1
2x =
và
( )
2
1
1
1
2
nn
xx
+
=+
n=1,2,…. Đặt
1
1
1
n
n
k
k
S
x
=
=
+
.Tìm
phần nguyên
2008
S
và tìm
lim
n
S
.
Bài 4. Cho dãy số
( )
n
x
xác định bởi
1
1xa=
và
( )
2
1
2003 2002 1
n n n
x x x n
+
= +
Tìm
1
1
lim
1
n
k
k
k
x
x
=
+
−
.
Bài 5. Cho dãy số
( )
n
x
xác định bởi
1
1xa=
và
( )
2
1
1
1
nn
n
n
xx
xn
x
+
+−
=
Tìm
2
1
1
lim
1
n
k
k
x
=
−
.
Bài 6. Cho dãy số
( )
n
x
xác định bởi
1
8x =
và
( )
( )
2
1
1
7 25 1,2,..
3
n n n
x x x n
+
= − + =
Tìm
1
1
lim
2
n
k
k
x
=
−
.
Bài 7. Cho dãy số
( )
n
x
xác định bởi
1
2009x =
và
( )
2
1
1
n n n
x x x
+
=+
Tìm
1
1
lim
1
n
k
k
x
=
+
.
Bài 8. Cho dãy số
( )
n
x
xác định bởi
1
2x =
và
( )
4
1
3
1
1
1
nn
n
nn
xx
xn
xx
+
−+
=
−+
Chứng minh dãy số
( )
n
y
xác đinh bởi
3
1
1
n
n
k
k
y
x
=
=
có giới hạn và tìm giới hạn đó.
Bài 9. (HSG Gia Lai năm 2011 – 2012) Cho dãy số
( )
n
a
xác định bởi
12
24, 60aa==
và
( )( )
1
1
, 2,3,...
12
n
nn
a
a a n
n n n
−
+
= + =
++
Chứng minh rằng dãy số
( )
n
a
có giới hạn hữu hạn..
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 59
V. PHƯƠNG PHÁP SO SÁNH DÃY SỐ .
1) Đinh lý 11 (Nguyên lý kẹp) Nếu ba dãy số
( ) ( ) ( )
,,
n n n
x y z
thỏa điều kiện
0
,
n n n
y x z n n
và
lim lim
nn
nn
y z L
→+ →+
==
thì
lim
n
n
xL
→+
=
.
CÁC BÀI TOÁN.
Bài 1: (Đề Olympic toán SV toàn quốc 2003) Cho dãy số
( )
n
x
xác định bởi
( )
12
... , 1,2,...
2! 3! 1 !
k
k
xk
k
= + + + =
+
Hãy tính
1 2 2003
lim ...
n n n
n
n
x x x
→+
+ + +
Giải
Vì
( )
1
1
0
2!
kk
k
xx
k
+
+
− =
+
nên
1 2 2002 2003
0 ... ...x x x x
Ta có :
( )
( )
( ) ( )
11
11
1 ! 1 ! ! 1 !
k
k
k k k k
+−
= = −
+ + +
.
Do đó
( ) ( ) ( )
1 2 1 1 1 1 1 1
... 1 ... 1
2! 3! 1 ! 2! 2! 3! ! 1 ! 1 !
k
k
x
k k k k

= + + + = − + − + + − = −


+ + +

Ta có:
2003 1 2 2003 2003
... 2003 .
n n n n n
x x x x x + + +
suy ra
1
2003 1 2 2003 2003
... 2003 .
n n n
n
n
x x x x x + + +
nên
1
1 2 2003
11
1 ... 2003 1 .
2004! 2004!
n n n
n
n
x x x

− + + + −


Vì
1
1 1 1
lim 1 2003 lim 1 1
2004! 2004! 2004!
n
nn→+ →+
− = − = −
Suy ra
1 2 2003
1
lim ... 1 .
2004!
n n n
n
n
x x x
→+
+ + + = −
Bài 2: (Đề Olympic 30/4/ 2011) Cho dãy số
( )
n
u
xác định bởi
1
0ua=
và
1
, 1,2,...
nn
n
n
u u k
u
+
= + =
Tìm giới hạn của dãy
n
u
n



.
Giải
Ta có
21
1
2
2 2 2uu
u
= +
.Giả sử
,2
n
u n n
Khi đó,
( )
( )
( )( )
2
1
1
1
10
nn
nn
n
nn
u u n
u n u n
un
uu
+
−−
− + +
− + = =
Theo nguyên lý quy nạp suy ra
,2
n
u n n
, do đó
1, 2,3,...
n
u
n
n
=
.
Từ đây ta được
( )
1 1 2
1 2 ... 1
n n n n
n
n
u u u u u n
u
+−
= + + + + −
suy ra
( )
22
22
1 1 1 *
nn
uu
u n u
n n n n n
−−
+ +
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 60
Từ (*) cho
n →+
và sử dụng giới hạn kẹp ta được
lim 1
n
n
u
n
→+
=
.
Bài 3 (Đề Olympic 30/4/ 2001):
Cho dãy số
( )
n
u
xác định bởi
0
1
2
u =
và
2
1
1
, 1,2,...,
k
kk
u
u u k n
n
−
−
= + =
. Tìm
lim
n
n
u
→+
.
Giải
Từ giải thiết ta có:
( )
22
1 1 1 1 1 1k k k k k k k k k k
n u u u nu nu u u u u u
− − − − − −
− = − + − =
( )( )
( )
1
1 1 1
1 1 1 1
1 1 1 1
1
kk
k k k k k
k k k k k k
uu
u u n u u u
u u n u u u n u
−
− − −
− − − −
−
− + = = − =
++
Do
0 1 2
1
...
2
u u u=
nên từ (1) ta suy ra
( )
1
1 1 1
, 1,2,... 2
kk
kn
u u n
−
− =
Từ (2) thay k = 1,2,… n.
Rồi cộng các bất đẳng thức ta được:
( )
0
1 1 1
1 1 1 1, 1,2,... 2
nk
nn
u u k n
u u u
− =
Nên từ (1) ta suy ra
( )
1
1 1 1
, 1,2,... 3
1
kk
kn
u u n
−
− =
+
Trong (3) thay k= 1,2,… n . rồi cộng các bất đảng thức ta được
0
1 1 1 2 1
2 1,
1 1 1 2
n
nn
n n n n
u n N
u u n u n n n
++
− − =
+ + + +
.Mà
1
lim 1
2
n
n
n
→+
+
=
+
Vậy
lim 1
n
n
u
→+
=
Bài 4 (Đề Olympic 30/4/ 2006):
Cho dãy số
( )
n
u
xác định bởi
1
12x
và
2
1
1 , 1,2,...
2
n
nn
x
x x n
+
= + + =
Tìm
lim
n
n
x
→+
?
Giải
Ta có
( )
( )
2
2
2
1
1 1 3 3
1 2 2 1 , 1,2,...
2 2 2 2 2
n
n n n n n
x
x x x x x n
+
= + − = − − − = − − + =
Bằng quy nạp ta chứng minh
1, 1,2,...
n
xn =
Theo giả thiết ta có
1
1x
Giả sử
1
n
x
,
Khi đó từ
2
1 2 3 2 0
n n n
x x x − +
hay
22
3
1 0 1 .
2 2 2 2
n n n
nn
x x x
xx− + − −
Do đó
2
1
1 1 1 2 2 1 1
2 2 2
n n n
nn
x x x
xx
+

= + − + − = − = − =


vì
( )
2
n
x
Vậy theo nguyên lý quy nạp ta suy ra
1, 1,2,...
n
xn =
Như vậy ta chứng minh được
3
1 , 2,3,...
2
n
xn =
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 61
Đặt
2a =
khi đó
2
1
2
a
aa= + −
.
Do đó, ta có:
( )
( )
2
2 2 2
1
1
11
22
n n n n n
a
x a x x a x a x a
+

− = + − − + − = − − −


( )
11
.1 . 2
22
n n n n
x a x a x a a x= − − + = − − −
mà
21
n
ax− −
nên
1 1 1
2
1 1 1
...
2 2 2
n n n
n
x a x a x a x a
+−
− − − −
Vậy
1
1
1
0 2 , 2,3,...
2
n
n
x a x
−
− − =
vì
1
1
lim 0
2
n
n
−
→+
=
nên theo nguyên lý kẹp ta được
lim 2
n
n
xa
→+
==
.
BÀI TẬP TƯƠNG TỰ
Bài 1 (Đề vô địch Singapore 1997): Cho dãy số
( )
n
u
xác định bởi
0
1
2
u =
và
2
1
1
, 1,2,..., 1
k
kk
u
u u k n
n
−
−
= + = −
. Chứng minh rằng
1
11
n
u
n
−
. Hướng dẫn: xem bài giải bài 3.
Bài 2 (HSG Gia Lai 1996): Cho dãy số
( )
n
x
xác định bởi
1
1
3
x =
và
2
1
1, 1,2,...
2
n
n
x
xn
+
= − =
Chứng minh rằng dãy số
( )
n
a
có giới hạn hữu hạn và tìm giới hạn đó.
Hướng dẫn:
Bằng quy nạp ta chứng minh
1 0, 2,3,...
n
xn− =
Giả sử
lim
n
n
xL
→+
=
khi
n →+
Ta giải phương trình:
2
13
1 1 3
2
13
L
L
LL
L
=+
= − = −
=−
.
Ta chứng minh
1
12
3
0 , 2,3,...
2
n
n
x L x L n
−
+

− − =


Bài 2: Cho trước
0;1a
, xét dãy số
( )
n
x
xác định bởi
1
2
a
x =
và
2
1
, 1,2,...
22
n
n
x
a
xn
+
= − =
.
Chứng minh rằng dãy số
( )
n
x
có giới hạn hữu hạn và tìm giới hạn đó.
Hướng dẫn :
Bằng quy nạp ta chứng minh
11
, 2,3,...
82
n
xn− =
Giả sử:
lim
n
n
xL
→+
=
khi
n →+
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 62
Ta giải phương trình:
2
2
2
2
11
11
22
11
La
aL
L L a
La
=+−
= − = + −
= − + −
.
Ta chứng minh:
1
1
, 2,3,...
22
n
n
a
x L L n
−

− − =


Vây:
2
lim 1 1
n
n
xa
→+
=+−
.
Bài 3: Cho trước
( )
0;a +
, xét dãy số
( )
n
x
xác định bởi
1
2
a
x =
( )
1
2 , 1,2,...
n n n
x x ax n
+
= − =
.
Chứng minh rằng nếu
0, 1,2,...
n
xn =
thì dãy số
( )
n
x
có giới hạn hữu hạn và tìm giới hạn đó.
Hướng dẫn:
Ta có
( )
2 1 1 1 1
2 0,2 0,1 1x x ax ax ax= − − − −
.Nhưng vì
1
0, 0xa
nên
1
11ax−
suy
ra
*
1
1 1,ax n N−
Ta có:
( ) ( )
2
22
11
11
2 1 1 2 2 1 1
n n n n n n n n n
x x ax ax ax ax a x ax ax
aa
++
− = − − − = − − = − + = −
1
24
2
1 2 1
1 1 1 ... 1
n
n n n
ax ax ax ax
−
−−
− = − = − = = −
Vậy:
( )
1
2
lim 1 lim 1 0
n
nn
nn
ax ax
−
→+ →+
− = − =
do
*
1
1 1,ax n N−
Do đó:
( )
1
lim 1 0 lim 1 lim
n n n
n n n
ax ax x a
−
→+ →+ →+
− = = =
.
Bài 4 (HSG QG năm 2012): Cho dãy số
( )
n
x
được xác định bởi
( )
1
1
3
2
2 , 2,3,...
3
nn
x
n
x x n
n
−
=
+
= + =
Chứng minh rằng dãy số
( )
n
x
có giới hạn hữu hạn, tính giới hạn đó.
Giải
Ta có :
( )
1 1 1
2 2 2 2 2 5
1 1 1 1 , 10
3 3 5
n n n n
nn
x x x x n
n n n n n
− − −
++

− = − + − + − +


.
Đặt
5
max 1; , 10, 11
kk
y x k n
k

= −


* Nếu
1
nn
yx=−
thì
1 1 1
2 5 2 4
1 .2
5 5 5
n n n n
y x y y
n
− − −

− + =


.
* Nếu
5
n
y
n
=
thì
1
5
1
nn
yy
n
−
=
−
.
Vậy :
( )
n
y
là dãy giảm, bị chặn dưới bởi số 0 nên có giới hạn hữu hạn.
Ta chứng minh: a = 0.
Suy ra nên
lim 1 0
n
n
x
→+
−=
. Do đó
lim 1
n
n
x
→+
=
| 1/63
| | Tải xuống

Có thể bạn quan tâm:

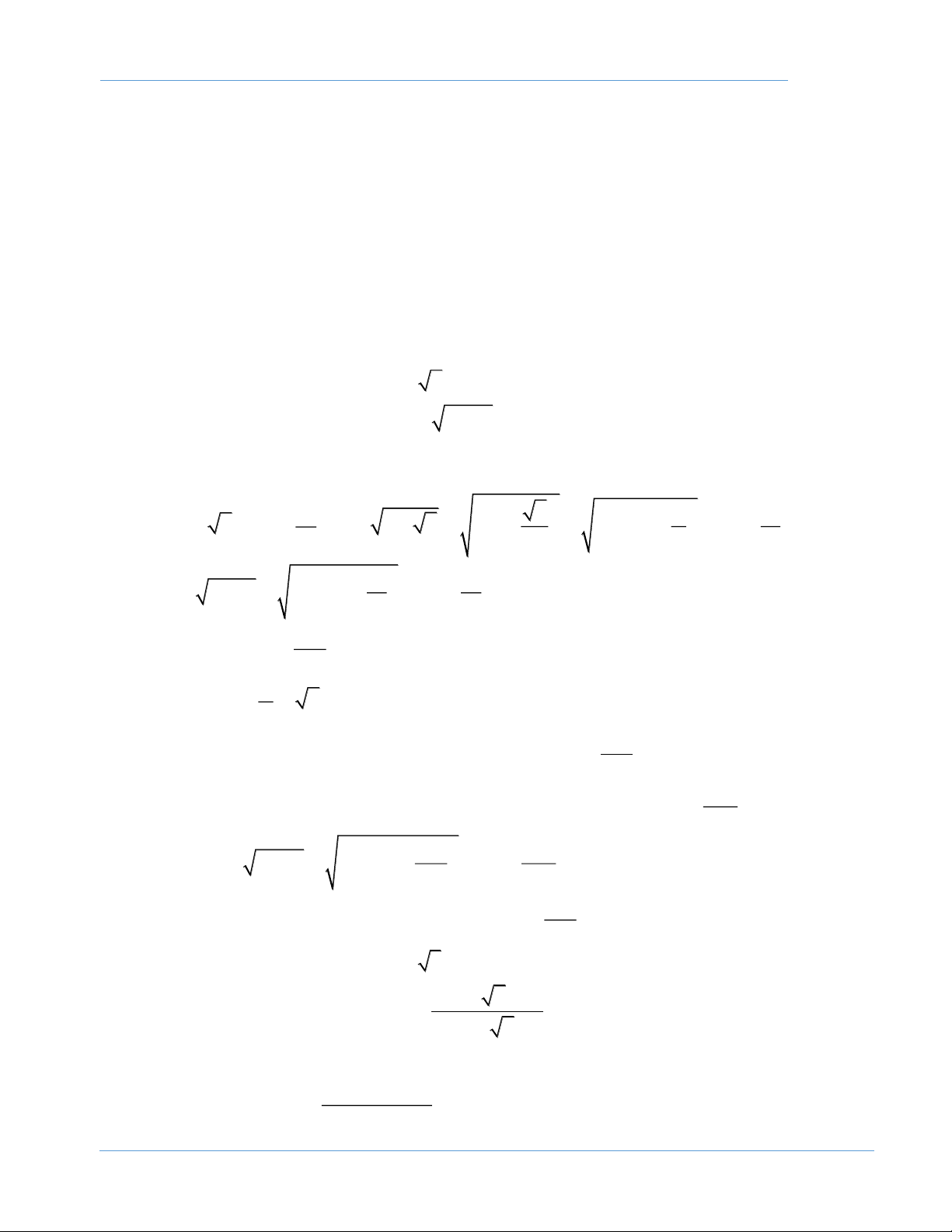
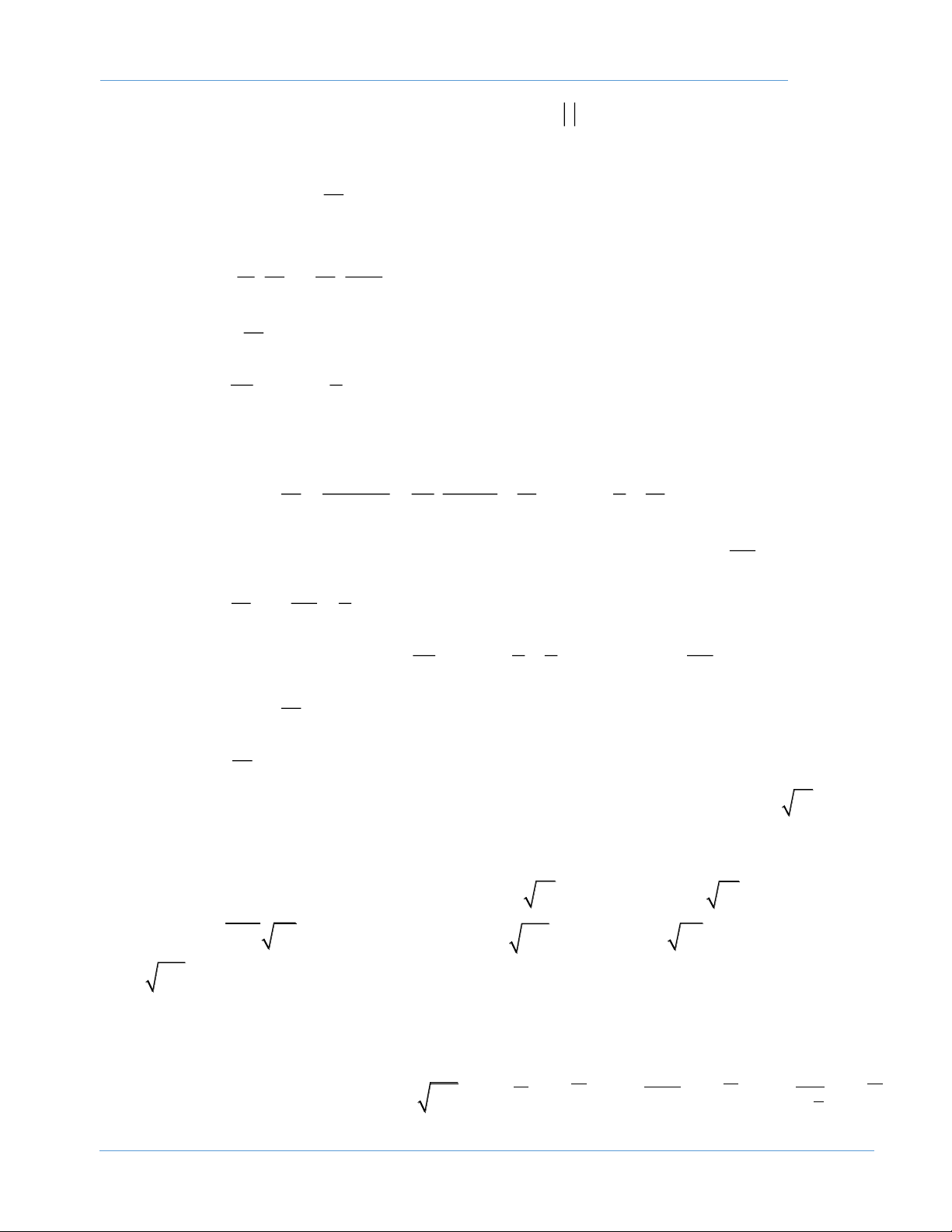
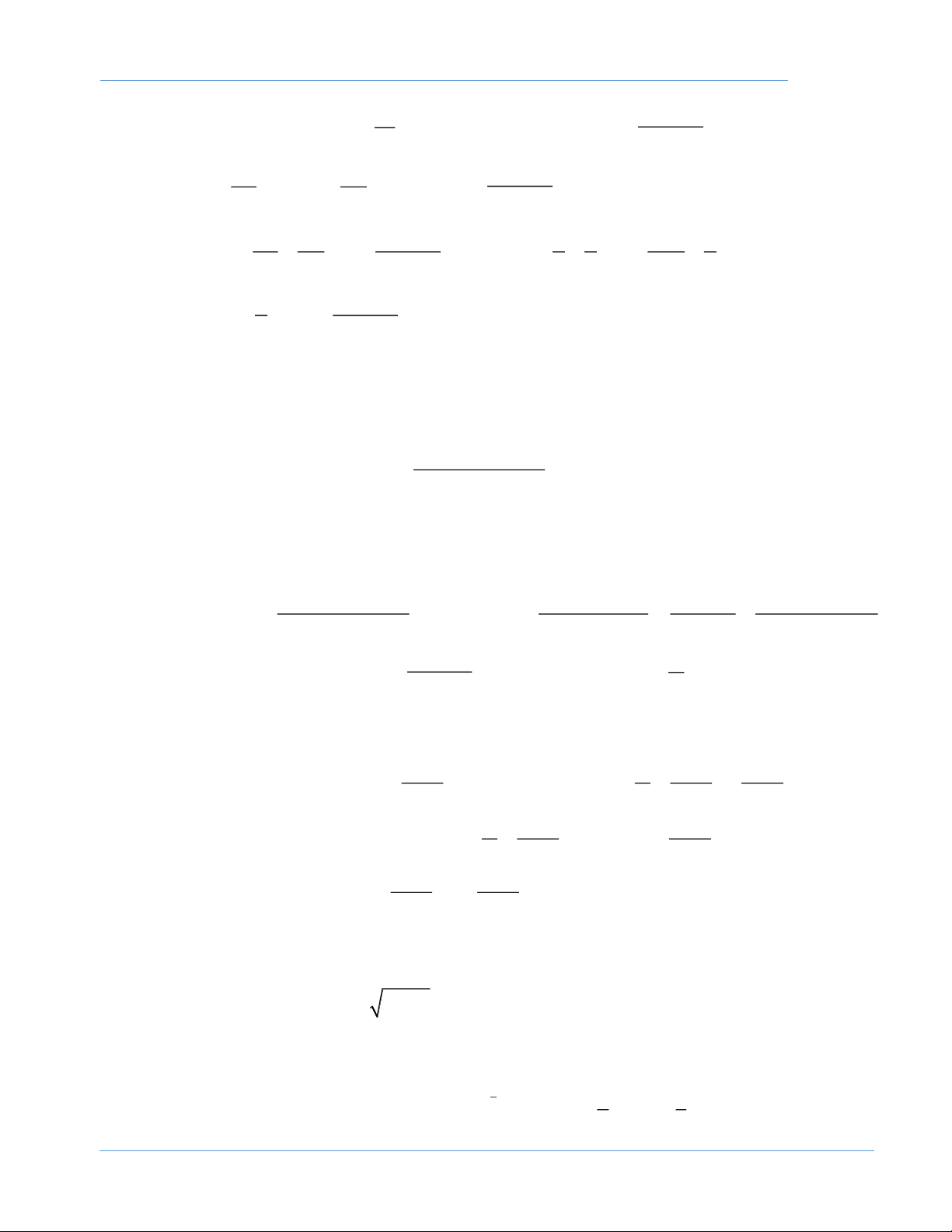
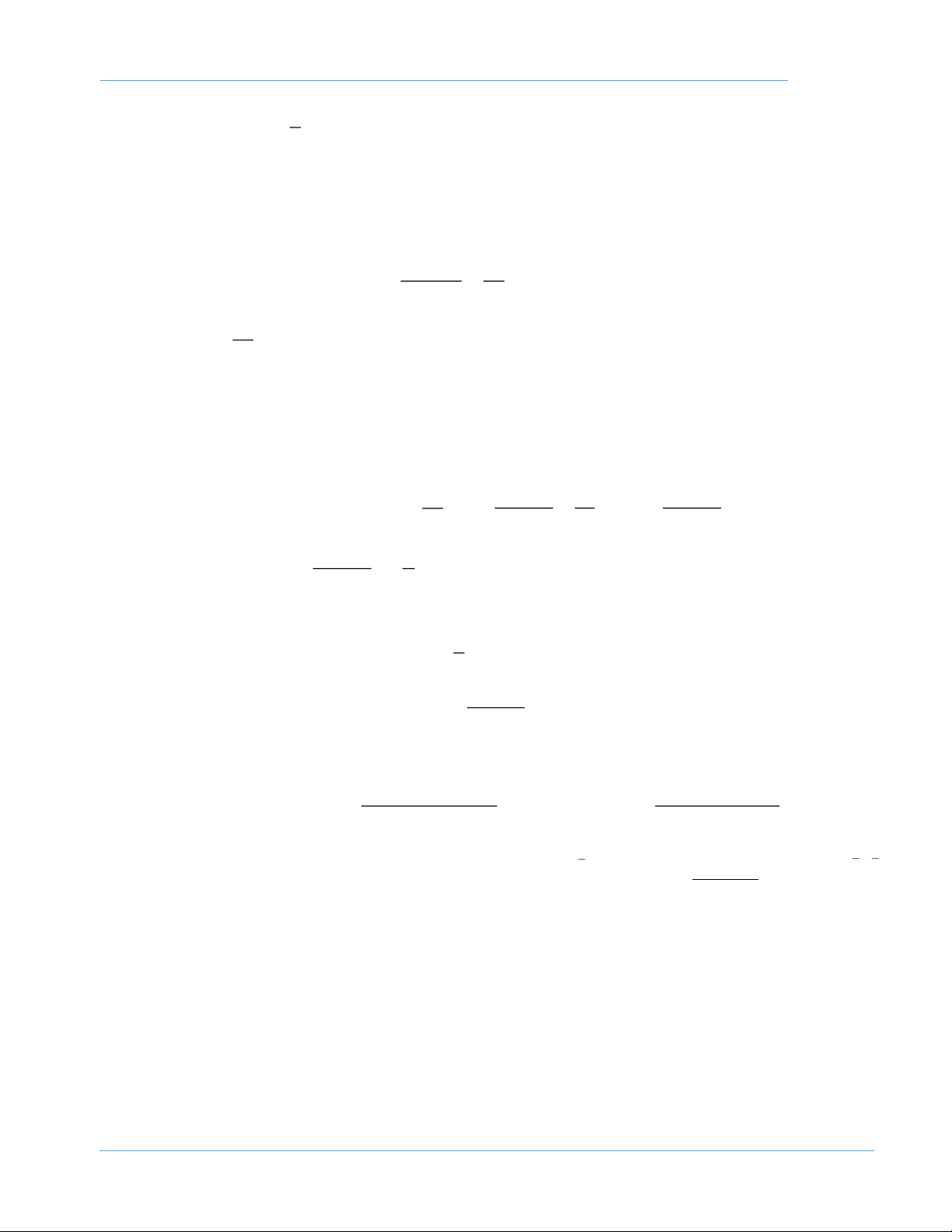
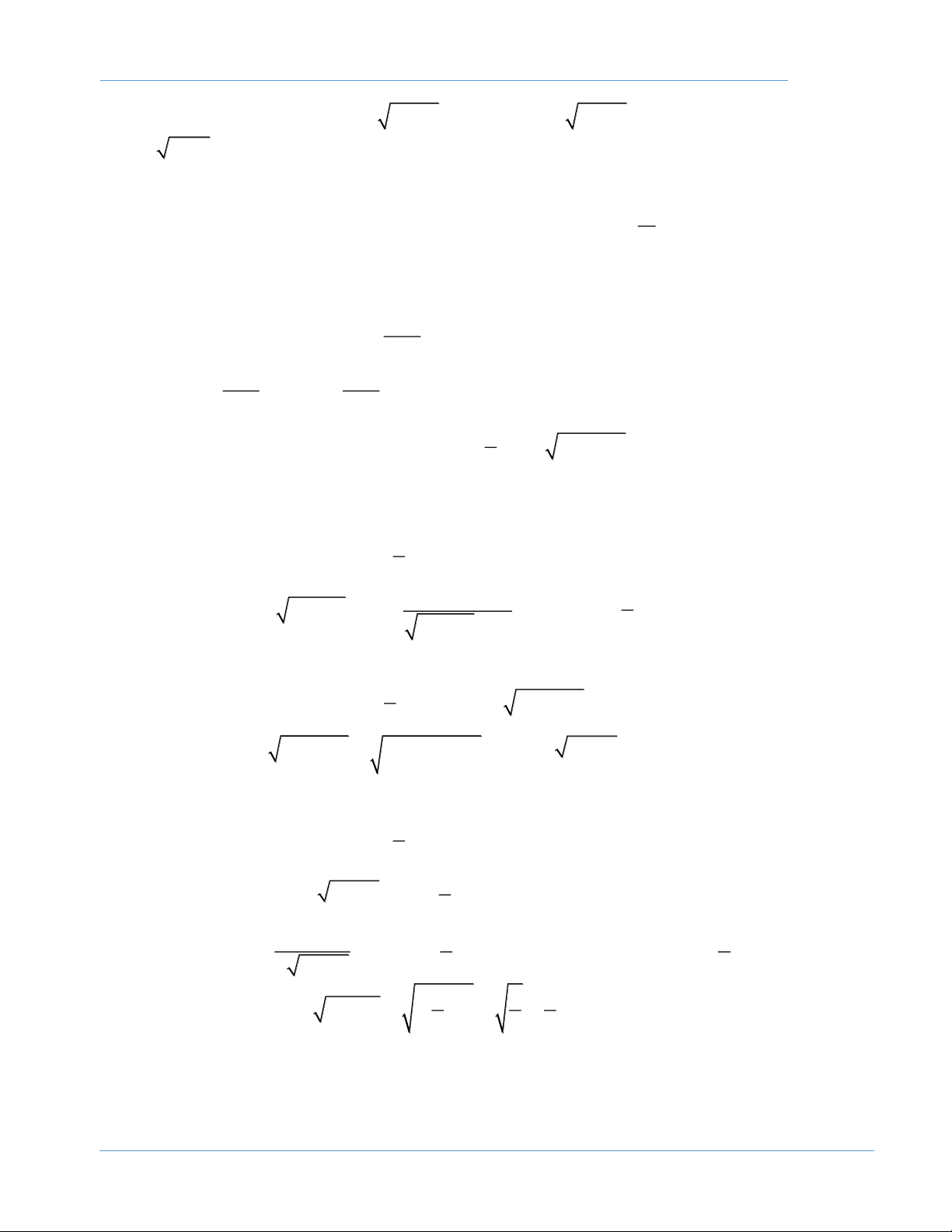
Preview text:

TỔ TOÁN
TRƯỜNG THPT TÂY NINH TÀI LIỆU
BỒI DƯỠNG HỌC SINH GIỎI, OLYMPIC
CHUYÊN ĐỀ: DÃY SỐ
Biên soạn: NGUYỄN THANH TÂM Email: thanhtamstn@gmail.com Tel: 0986318518 9-9-2020
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
NỘI DUNG CHUYÊN ĐỀ
- Phương pháp tìm số hạng của dãy số cho bởi một hệ thức truy hồi tuyến tính. - Liên phân số. - Sai phân.
- Các phương pháp tìm số hạng của dãy số.
- Các khái niệm dãy con, dãy tuần hoàn và chu kì.
- Mối liên hệ giữa tính hội tụ của dãy số và dãy con.
- Tìm giới hạn của dãy số.
- Các bài toán thường gặp về dãy số.
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 1
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020 PHẦN I XÁC ĐỊNH DÃY SỐ
A. XÁC ĐỊNH DÃY SỐ BẰNG PHƯƠNG PHÁP QUY NẠP, PHƯƠNG PHÁP ĐỔI BIẾN.
1. Xác định dãy số bằng phương pháp quy nạp.
Để chứng minh mệnh đề chứa biến A(n) đúng với mọi số nguyên dương n ( bằng phương
pháp quy nạp), ta thực hiện theo các bước như sau:
Bước 1 (bước cơ sở hay bước khởi đầu): Kiểm tra A(n) đúng với n = 1.
Bước 2 (bước quy nạp): Giả sử A(n) đúng với n=k (k≥1,k∈N)
ta chứng minh A(n) đúng với n = k+1.
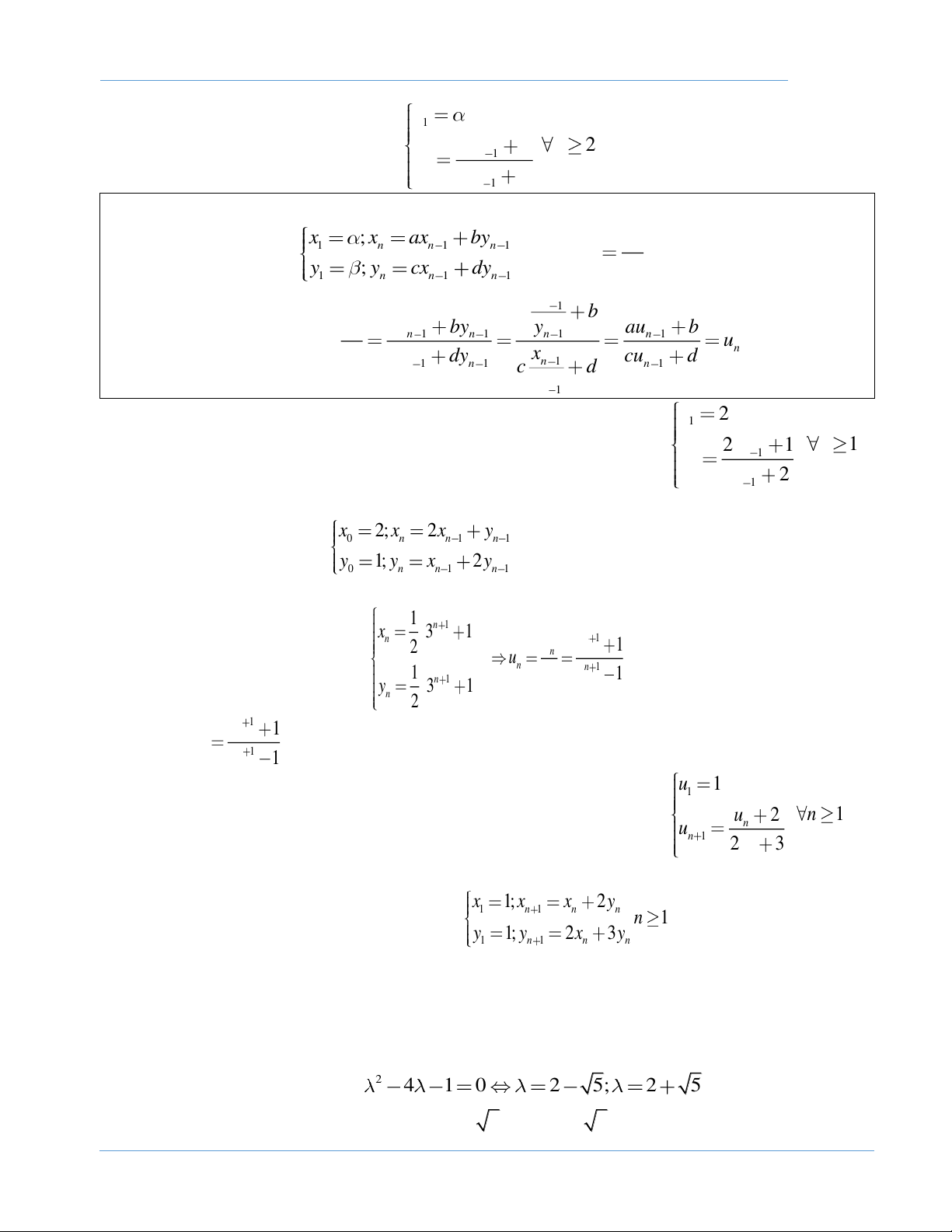
Bước 3: Kết luận: A(n) đúng với mọi số nguyên dương n. x = 2
Bài 1: Cho dãy số ( x như sau: 1  n )
x = 2 + x , n  =1,2,...  n 1+ n
a) Tính x , x , x .
b) Tìm số hạng tổng quát ( số hạng thứ n). 1 2 3 Giải   2      a) Ta có x = 2 = 2cos ; x = 2 + 2 = 21+  = 2 1+ cos = 2cos   1 2 2 2 3 2    4  2    
x = 2 + x = 2 1+ cos = 2cos . 3 2   3 4  2  2  b) Ta suy ra : x = 2cos , n  =1,2,... n n 1 2 +  Với n =1 x = 2cos
= 2. n =1 công thức đúng. 1 4 
Giả sử công thức đúng với n=k (k≥1,k∈N) nghĩa là x = 2cos , k  1 k k 1 2 + 
Ta chứng minh công thức đúng với n=k+1 (k≥1,k∈N) nghĩa là x = 2cos , k  1. k 1 + k +2 2     Thậy vậy: x = 2 + x = 2 1+ cos = 2cos k 1 + k   k 1 + k +2  2  2 
Vậy công thức tổng quát của dãy số trên là: x = 2cos , n  =1,2,... n n 1 2 + x = 3 1 
Bài 2: Cho dãy số ( x như sau:  x + 2 −1 . Tính x n ) n x = , n  =1,2,... 2003 n 1 +  1+  (1− 2)xn Giải x + y Từ công thức (x + y) tan tan tan = 1− . tan . x tan y
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 2
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020    2 tan tan = 2 −1    8   8 Ta có: 2 1 = tan = tan 2. =  tan + 2tan −1 = 0   4 8   2 8 8 1− tan tan = 1 − − 2 8  8   Vì tan  0 nên tan = 2 −1, 8 8        + +  tan + tan tan tan        3 8  8     x = 3 = tan , 3 8 x = = tan + , x = = tan + 2   1   3 2    3 8  3       3 8  1− tan .tan 1− tan + .tan   3 8  3 8  8    
Suy ra công thức tổng quát x = tan + n − n  = n  ( ) 1 , 1, 2,...   3 8      Với n=1 x = tan − 0. = 3, đúng 1    3 8     
Giả sử công thức đúng với n = k (k≥1,k∈N) nghĩa là x = tan + k − k   k  ( ) 1 , 1   3 8     
Ta chứng minh công thức đúng với n = k+1 (k≥1,k∈N) nghĩa là x = tan + k , k   1. k 1 +    3 8       tan +  (k − )1 + tan   3 8  8          Thậy vậy: x = = tan + k −1 + = tan + k , k  1 k 1 +  ( )      (        − + k −  ) 3 8 8 3 8 1 tan 1 .tan   3 8  8    
Vậy công thức tổng quát của dãy số trên là: x = tan + n − n  = n  ( ) 1 , 1, 2,...   3 8 
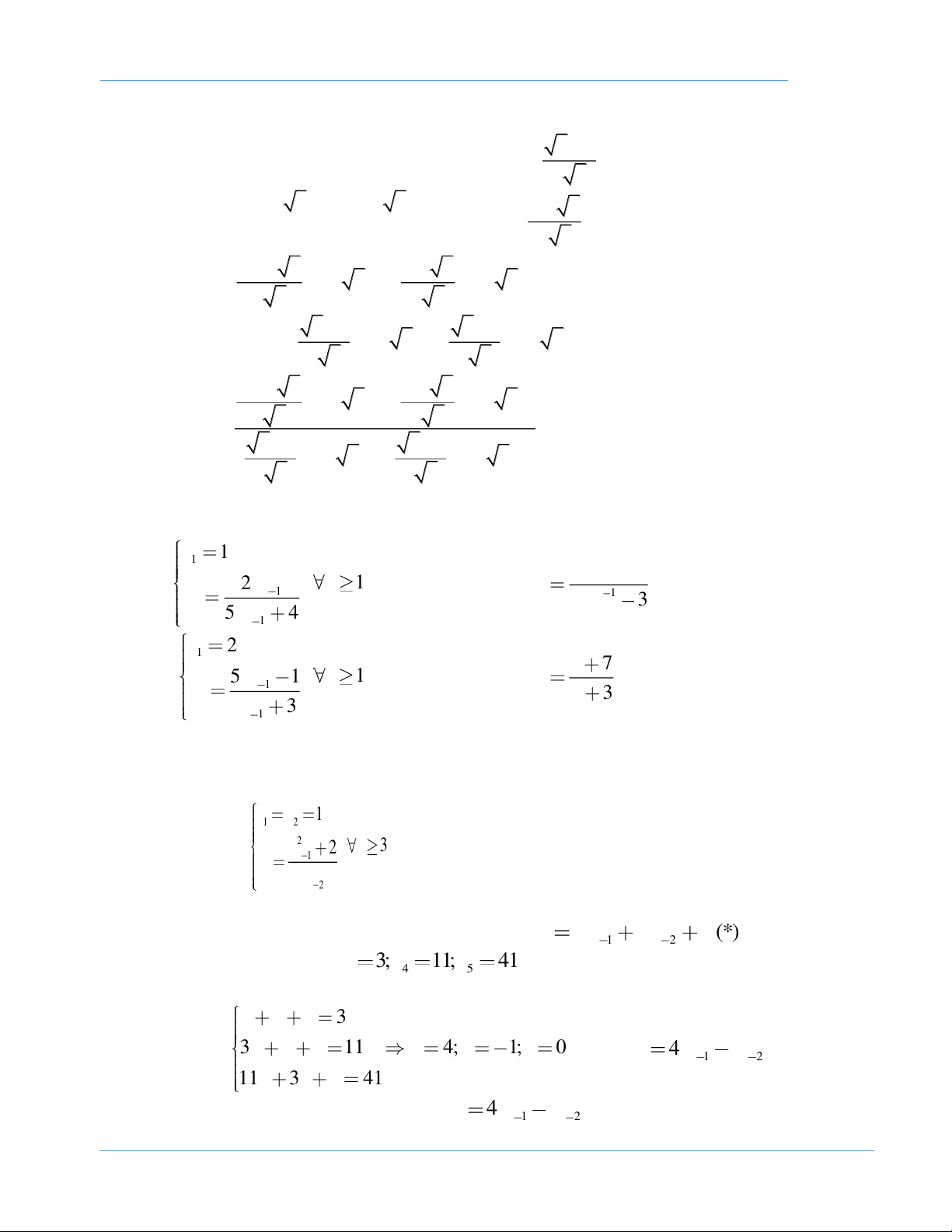
BÀI TẬP TƯƠNG TỰ  3 x = 1 3 
Bài 1: Cho dãy số ( x như sau:  . Tính x n ) x + 2 − 3 2010 nx = , n  = 1,2,... n 1 +  1+  ( 3−2)xn  Hướng dẫn: ta có: tan = 2 − 3 12    
Công thức tổng quát của dãy số trên là: x == tan + n − n  = . n  ( ) 1 , 1, 2,...   6 12  x =1 1 
Bài 2: Tìm số hạng tổng quát của dãy số ( x như sau:  + . n ) x 3 n x = , n  =1,2,...
n 1+ 1− 3.xn
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 3
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
2. Xác định dãy số bằng phương pháp đổi biến (đặt ẩn phụ) Chú ý: bb  b 1) Hàm số bậc hai ( ) 2
f x = ax + bx + c có đỉnh A − ; f −  
 thì đặt X = x + .  2a  2a  2abb  b 2) Hàm số bậc ba ( ) 3 2
f x = ax + bx + cx + d có điểm uốn A − ; f −  
 thì đặt X = x + .
 3a  3a  3abb  b 3) Hàm số bậc bốn ( ) 4 3 2
f x = ax + bx + cx + dx + e có điểm uốn A − ; f −  
 thì đặt X = x + .
 4a  4a  4a CÁC VÍ DỤ 2 b − 2b
Bài 1: Tìm dãy số ( x biết 2 x = ; x = ax +bx + , c n
 =1,2,... trong đó a  0,c = . n ) 1 n 1 + 4a b
Hướng dẫn: đặt y = x + n n 2a 2 bb   b  Ta được: y − = a y − + b y − + c, n  = 1,2,.... n 1 +     2 n a  2 n a   2a  2 bby b   b  2 ny − = ay − +  + b y − + . c n 1 + n   2 2aa 4 n a   2a  2 2 2 b b b b − 2b 2  y − = ay − by + + by − + 2
y = ay , n  =1,2,... n 1 + + 2 n n a 4 n a 2a 4a n 1 n − − − Suy ra: y = ay = a ay = = a y n  = n n− ( n− )2 2 2 2n 1 1 2n 1 ... , 1, 2,... 1 2 1 2n 1 − − − − b − −  b b Vậy 2n 1 1 2n 1 2n 1 1 x = a y − = a  + − , n  =1,2,... n 1   2a  2a  2a Thử lại bằng quy nạp. 2 x
Bài 2 (HSG QG 2000 – 2001): Cho dãy số ( x như sau: x = , n x = , n  =1,2,... n ) 1 n 1 + 3 2(2n + ) 1 x +1 n
Hãy tính tổng của 2001 số hạng đầu của dãy số ( x n ) Giải.
Ta thấy x  0, n  =1,2,... n x 1 1 Do đó n x =  = 2 2n +1 + , n  = 1,2,... n 1 + 2(2n + ) ( ) 1 x + 1 x x n n 1 + n 2 Đặt u =
Khi đó u = 3 và u
= 4 2n +1 + u u = 2n +1 2n −1 , n  =1,2,... n 1 + ( ) n n ( )( ) n x 1 n 2 2 1 1 Vậy x = = = − n  = n u n + n − n − n + n ( )( ) , 1, 2,... 2 1 2 1 2 1 2 1 1 1   1 1   1 1  1 4002
Do đó x + x + ... + x = − + − + ...+ − = 1− = . 1 2 2001       1 3   3 5   4001 4003  4003 4003
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 4
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
3. Một số phép biến đổi bởi công thức lượng giác.
Bài 3: Xác định dãy số ( y thỏa điều kiện 2 y  ; R y = 2y −1, n  =1,2,... n ) 1 n 1 + n Giải.
* Nếu y  1 thì tồn tại  sao cho cos = y . 1 1 Khi đó 2 2 1 y 2cos  1 cos 2, y cos 2 ,..., y cos 2n− = − = = =  . 2 3 n
* Nếu y  1 xét số thực β sao cho 1 2     = y + y −1 1 1 1 1 2 y =  +
  − 2y  +1 = 0   1   1     2 2
 = y − y −1  1 1   Vậy: nếu đặt 1 1 1 2
 = y + y −1 thì 2 y =  + ; = y − y −1 1 1 1   1 1 2     Ta có: 2  2 1  1  1  1  1  1  1  1  2 y = 2   +   −1 =  + , 2 2
y = 2 y −1 = 2   +   −1 =  + . 1     2 2     2     2 1 2 2     2       2      Giả sử: n 1 1 − 1 1 n− 1 1 n 1 2 y =   +  khi đó 1 2 2 y = 2  +  − =  + + −   n 1 n− , 1 n 2 1 1 n n 2    2 2 2     2       Vậy n 1 1 − 1 2 y =   +   = . − n n , 1, 2,... 1 n 2 2   
Bài 4: Xác định dãy số ( y thỏa điều kiện 3 y  ; R y
= 4y −3y , n  =1,2,... n ) 1 n 1 + n n Giải.
* Nếu y  1 thì tồn tại  sao cho cos = y . 1 1 Khi đó: 3 2 1 y 4cos  3cos cos3, y cos3 ,..., y cos3n− = − = = =  . 2 3 n 2     = + −
* Nếu y  1, xét số thực β sao cho y y 1 1 1 1 1 2 = +  − + =   1 y   2 y  1 0 1   1     2 2
 = y − y −1  1 1 1  1  1 Vậy: nếu đặt 2
 = y + y −1 thì 2 y =  + ; = y − y −1 1 1 1   1 1 2     3         Ta có: 0 1 1 1 1 1 1 3 y = 4   +   − 3  +   =   + , 0 1 3 2     2      2     3 1  1  1  1  1  1  3 3
y = 4 y − 3y = 4   +   − 3  +   =  + . 2 1 1   3 2     2      2       Giả sử: n 1 1 − 1 3 y =   +  . n 1 n − 3 2    3         Khi đó: n 1 − n 1 1 1 1 − 1 1 n 1 3 3 3 y = 4  +  −   +  =  + . + −  −   n 3 1 n 1 1 3 3 3n n 2     2     2       Vậy: n 1 1 − 1 3 y =   +   = . − n n , 1, 2,... 1 n 3 2   
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 5
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
Bài 5: Xác định dãy số (u như sau: 3 x = ; x
= ax + 3x a  0 , n   N 1 n 1 + n n ( ) * n ) Giải 2  Đặt x = y khi đó a 3 * = = +   . n n y ; y 4 y 3y , n N + a 1 1 2 n n n 2     = y + y +1 Xét số thực β sao cho 1 1 1 1 2 y =  −
  − 2y  −1 = 0   1   1     2 2  = y − y +1  1 1   Vậy: nếu đặt 2
 = y + y +1 thì 1 1 1 y =  − ; = −   ( 2 y − y + 1 1 1 1 ) 1 1 2     3         Ta có: 0 1 1 1 1 1 1 3 y = 4   −   + 3  −   =   −  0 1 3 2     2      2     3 1  1  1  1  1  1  3 3
y = 4 y + 3y = 4   −   + 3  −   =  − . 2 1 1   3 2     2      2       Giả sử: n 1 1 − 1 3 y =   −  . n 1 n − 3 2    3         Khi đó: n 1 − n 1 1 1 1 − 1 1 n 1 3 3 3 y = 4  −  +   −  =  − . + −  −   n 3 1 n 1 1 3 3 3n n 2     2     2     n 1 − n 1 − 3 3   2 2         Vậy: 1 a a a a   x =  + +1 +  − +1 , n  =1,2,.... n a  2 4   2 4         BÀI TẬP ÁP DỤNG 1 1
Bài 3: Cho dãy số ( x xác định như sau: 2 * x  − ; x = 4x − , n   N n ) 1 n 1 + 2 n 2 1 4 −n x Đặt n 1 u + =
Tìm số hạng tổng quát của dãy số (u n ) n x x x ...x 1 2 3 n Giải. 1 1 1 Đặt x =
y ta được dãy số ( y thỏa điều kiện 2 2 y = 2x ; y
= y −  y = 2y −1, n  =1,2,... n ) n 2 n 1 1 n 1 + n n 1 + 2 2 n  
Theo kết quả bài 3 trên, ta được : n 1 1 − 1 2 y =   +  . n 1 n − 2 2      Với: 2 2
 = y + y −1 = 2x + 4x −1 . Đặt: n 1 − 1 2 = =  + . 1 1 1 1 z 2 y   n 1 n n − 2    2n 1  + n Khi đó: 2 z +  n 1 = z z z ...z       2 n 1 1 2 3 n 1 − 2 1 2 1 2 1  +  +     + ...  +  2 n 1 2 − 2 2          
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 6
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020  1      n 1 2  − 1 n 1    +  2  −    +  2n      n n 1 + 2 2     =   1   +1 = ... = =  −          n 1+ 2       − 2 n 1 1 1 − 2 1 2 1 2 1  −  +  + n 1 1      + ...  +  2   −  2 n 1 2 − 2 2             2n    1 z 4x 4 −n x
Vì: z = 2y = 4x nên n 1 + n 1 + n 1 + = = . n n n z z z ...z 4n x x x ...x x x x ...x 1 2 3 n 1 2 3 n 1 2 3 n n 1 + 2    +
Vậy: Số hạng tổng quát của dãy số (u là 1 1 * =  −   . n ) u   + n N n , 1 n 2     −1
Bài 4 (Đề nghị OLYMPIC 30/04/1999): Xác định số hạng tổng quát của dãy số (u như sau: n ) 3 * u = 2;u
= 9u + 3u , n   N 1 n 1 + n n Giải. 2 Đặt u = x khi đó 3 * x = 3; x
= 4x + 3x , n   N n + 3 n 1 n 1 n n
Theo kết quả bài 5 trên, ta có: n 1 − n 1 − 3 3   2 2 1  3.2 3 4   3.2 3 4    n 1 − n 1 − 3 3 1   x =  + +1 +  − +1
= (3+ 10) +(3− 10) , n  =1,2,... n  2  2 4   2 4          2  
Bài 5 (Đề nghị OLYMPIC 30/04/2004): Xác định số hạng tổng quát của dãy số (u như sau: n ) 3 3 2 * u = ;u
= 24u −12 6u +15u − 6, n   N 1 n 1 + n n n 6 Giải
Đặt u = 6x −1khi đó 3 * x = 2; x
= 4x + 3x , n   N n n 1 n 1 + n n n 1 − n 1 − 3 3 1  
Theo kết quả bài 5 trên ta x = + + − + n  = n (2 5 ) (2 5) 2 , 1, 2,...  2 6  
Cách 2: Đặt u = 6x −1 n n Khi đó 3 * x = 2; x
= 4x + 3x , n   N 1 n 1 + n n Xét phương trình 2
x − 4x −1 = 0  x = 2 + 5; x = 2 − 5 x + x = 4
Phương trình có 2 nghiệm x , x thỏa 1 2  . 1 2 x .x = 1 −  1 2 n 1 − n 1 1 − Ta chứng minh: u = x + x n ( 3 3 1 2 ) 2 n 1 − n 1 − 3 3 1   Suy ra: u = + + − + n  = n (2 5 ) (2 5) 2 , 1, 2,...  2 6  
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 7
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
B. Phương pháp lặp.
Để tìm số hạng tổng quát của dãy số (u bằng phương pháp lặp ta thường tìm các hàm số n )
f(x) và h(x) sao cho f (u ) = h( f (u
* . Sử dụng (*) liên tiếp ta thu được: n n 1 − )) ( )
f (u ) = h( f (u = h h f u = h f u = ... = h f u ** n n 1 − ))
( ( ( n−2))) 2( ( n−2)) n ( ( 0))( )
Từ (**) ta tìm được u . Hàm số f được gọi là hàm số phụ, còn hàm số h được gọi là hàm số 0 lặp. CÁC VÍ DỤ
Bài 1: Tìm số hạng tổng quát của dãy số ( x cho như sau: x = 3; x = 7x −1, n  =1,2,... n ) 1 n 1 + n Giải:
Gọi c là nghiệm của phương trình f(x) = x trong đó f(x) = 7x – 1. 1
Ta có : 7c −1 = c c = . 6 1 1 Xét: x
= 7x −1  x − = 7x −1− , n  =1,2,... n 1 + n n 1 + 6 n 6 1 7  1  Ta được: x
− = 7x − = 7 x − , n  =1,2,... n 1 +   6 n 6 n  6  1  1   1    n− 1 n− 17 Vậy: 2 1 1 x − = 7 x − = 7 x − = ... = 7 x − = 7 . nn 1−   n−2   1  6  6   6   6  6 17 n− 1 Suy ra: 1 x = .7 + , n  =1,2,... n 6 6 5x + 4
Bài 2.Cho dãy số ( x được xác định như sau: n * x = 5; x = , n   N n ) 1 n 1 + x + . 2 n Chứng minh rằng: * x  4, n
  N .Tính x n 2013 Giải 5x + 4
Gọi c là nghiệm của phương trình f(x) = x, trong đó f(x) n = x + 2 n 5c + 4 c = 1 − Xét: 2
= c c − 3c − 4 = 0   . c + 2 c = 4 Ta có: x = 5  4 . 1 Giả sử: * x  4, n   N . n Ta chứng minh: * x  4, n   N n 1 + 5x + 4 Nếu x = 4 thì n
= 4  5x + 4 = 4x + 8  x = 4 n 1 + x + (mâu thuẫn). 2 n n n n Vậy: * x  4, n   N . n 5x + 4 x − 4 5x + 4 x +1 Ta có: n 1 − n 1 − n 1 − n 1 x − 4 = − 4 = ; x +1 = +1 = 6 − n x + 2 x + 2 n x + 2 x + 2 n 1 − n 1 − n 1 − n 1 −
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 8
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020 x +1 x +1 x +1 + − − − x n n n n 1 Suy ra: 1 2 2 1 1 = 6 = 6 = ... = 6 = 6n x − 4 x − 4 x − 4 x − 4 n n 1 − n−2 1 4.6n + n 1 Do đó: x +1 = 6 x −  x = n   N n ( 4 n ) * , n 6n − 1 2013 4.6 +1 Vậy: x = 2013 2013 6 − . 1
Bài 3: Tìm số hạng tổng quát của dãy số ( x cho như sau: n ) 2 x =   ; R x
= x −14x + 56, n  =1,2,... 1 n 1 + n n Giải
Gọi c là nghiệm của phương trình f(x) = x, trong đó f(x) = f ( x) 2
= x −14x + 56. 2 2
c = c −14.c + 56  c −15c + 56 = 0  c = 7;c = 8 n 1 − n 1 − 2 2 2 Xét: 2 x − 7 = x
−14x + 49 = x − 7 = ... = x − 7 =  − 7 , n  = 1,2,... n n 1 − n 1 − ( n 1− ) ( 1 ) ( ) n
Vậy: Số hạng tổng quát của dãy số ( x là x  − = + − n  = n ( ) 1 2 7 7 , 1, 2,... n )
Bài 4: Tìm số hạng tổng quát của dãy số (u cho như sau: n ) 2 2 u =   ; R u
= 3u + 4u + , n  =1,2,... 1 n 1 + n n 3 Giải. 2 Ta biến đổi: 2 2 u
= 3u + 4u +  3u = 9u +12u + 2. n 1 + n n n 1 + 3 n n x Đặt n u = . n 3 Ta được: 2 x = 3  ; R x
= x + 4x + 2, n  =1,2,... 1 n 1 + n n x
+ 2 = x + 4x + 4 = x + n  = + n n ( 2 n+ )2 2 , 1, 2,... n 1 1 2 n 1 − 2 2 2
Suy ra: x + 2 = x + = x + = = x + n ( 2 2 ... 2 n 1 − ) ( n−2 ) ( 1 ) − 2n −  + − 2n 3 2 2 Vậy: x =  + −  u = . n (3 2) ( ) 1 1 2 n 3 ax
Lớp hàm g ( x) = 2 2 b + c x ax d
b − ax + dc x
Ta có: d − g ( x) 2 2 = d − = 2 2 2 2 b + c x b + c x
Ta cần chọn a, b, c, d sao cho b − ax + dc x = (d − x)2 2 2 2 2 d
= d − 2dx + x  2 bd = d b  = d  
 a = 2d  a = 2d .   2 dc = 1 1 2  c =  d
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 9
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020 8x
Bài 5: Tìm số hạng tổng quát của dãy số ( x cho như sau: x =   ; n R x = , n  =1,2,... n ) 1 n 1 + 2 4 + xn Giải. Nếu  = 2 − thì x = 2 − , n  =1,2,... n 8x 2x −8x + 8 2 − − − − (2 x n 1 n 1 n 1 n 1 − )2 2 Xét   2
− . Ta có: 2 − x = 2 − = = 1 n 2 2 2 ( ) 4 + x 4 + x 4 + x n 1 − n 1 − n 1 − 8x 2x + 8x + 8 2 + − − − (2 x n n n n− )2 2 1 1 1 1 2 + x = 2 + = = 2 n 2 2 2 ( ) 4 + x 4 + x 4 + x n 1 − n 1 − n 1 − − x
Xét hàm số: f ( x) 2 = 2+ . x Ta thấy: 2 ( − x  − x − −  f x − = =   =  f x  =  f x  = =  f x  =  f   n ) 2 2  ( n− ) 2   ( n− ) 22 n n n n ...   ( ) 1 2   ( ) 1 2 1 3 1 2 1  ( ) 2 + x 2 + x nn 1 −  − 2 − x 2 − 2 Đặt:  =  ( ) 1 2n f    nên n =   x = 2 n + x 1+  n n 1 − 2    2 −  2 1  −      1+    
Vậy: Số hạng tổng quát của dãy số ( x là x =  = − n n , 1, 2,... n ) 1 n 2  2 −  1+    1+  x + ax
Lớp hàm g ( x) 3 = 2 bx + c x + ax
x − bdx + ax − cd
Ta có : g ( x) 3 3 2 − d = − d = 2 2 bx + c bx + c
Ta cần chọn a, b, c, d sao cho x − bdx + ax − cd = ( x − d )3 3 2 3 2 2 3
= x − 3dx + 3d x − d bd = 3d b  = 3   2 2
 a = 3d  a = 3d .   3 2 dc = d c = d  
Bài 6. Tìm số hạng tổng quát của dãy số ( x xác định như sau: n ) 3 x + 6x x =   0; n n x = , n  = 1,2,... 1 n 1 + 2 3x + 2 n Giải.
Chọn c = 2 nên b = 3,a = 6,d =  2 − x + x x − x + x − (x 2 6 3 2 6 2 2 n )3 3 3 2 x − 2 n n = − 2 n n n = = 1 n 1 + 2 2 2 ( ) 3x + 2 3x + 2 3x + 2 n n n
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 10
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020 + x + x x + x + x + (x 2 6 3 2 6 2 2 n )3 3 3 2 x + 2 n n = + 2 n n n = = 2 n 1 + 2 2 2 ( ) 3x + 2 3x + 2 3x + 2 n n n x −
Xét hàm số f ( x) 2 = ta thấy x + 2 3 ( x −  x − − −  f x − = =   =  f x  =  f x  = =  f x  =  f   n ) 2 2    ( n− ) 3   ( n− ) 23 n n n n ...   ( ) 1 3   ( ) 1 3 1 3 1 2 1  ( ) x + 2 x + 2 nn 1−  − x − 2 2 + 2 Đặt  =  ( ) 1 3n f    nên n =   x = n x + 2 1−  n n 1 − 3     − 2  2 1  +      + 2   
Vậy: Số hạng tổng quát của dãy số ( x là   n ) x =  = − n n , 1, 2,... 1 n 3   − 2  1−    + 2  
x + ax + b
Lớp hàm g ( x) 4 2 = 3 cx + dx
x + ax + b
x − cex + ax − dex + b
Ta có : g ( x) 4 2 4 3 2 − e = − e = 3 3 cx + dx cx + dx
Ta cần chọn a, b, c, d, e sao cho x − cex + ax − dex + b = ( x − e)4 4 3 2 4 3 2 2 3 4
= x − 4ex + 6e x − 4e + e ce = 4e c  = 4   2 2 a = 6ea = 6e     . 3 2 de = 4e d = 4e    4  4 b  = e b  = e
Bài 7. Tìm số hạng tổng quát của dãy số ( x xác định như sau: n ) 4 2 x +12x + 4 x =   0; n n x = , n  =1,2,... 1 n 1 + 3 4x + 8x n n Giải.
Chọn: e = 2 khi đó a = 12,b = 4,c = 4, d = 8 .
Ta thấy: x  0, n  =1,2,... n Do đó: + x + x + x + x + x + x + (x 2 12 4 4 2 12 8 2 4 n )4 4 2 4 3 2 x + 2 n n = + 2 n n n n = = 1 n 1 + 3 3 3 ( ) 4x + 8x 4x + 8x 4x + 8x n n n n n n − x + x + x − x + x − x + (x 2 12 4 4 2 12 8 2 4 n )4 4 2 4 3 2 x − 2 n n = − 2 n n n n = = 2 n 1 + 3 3 3 ( ) 4x + 8x 4x + 8x 4x + . 8x n n n n n n
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 11
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020 x −
Xét hàm số f ( x) 2 = , x   0. x + 2 Ta suy ra: 4 ( x −  x − − −  f x − = =   =  f x  =  f x  = =  f x  =  f   n ) 2 2    ( n− ) 4   ( n− ) 24 n n n n ...   ( ) 1 4   ( ) 1 4 1 3 1 2 1  ( ) x + 2 x + 2 nn 1−  − Đặt:  =  ( ) 1 4n f    . x − 2 2 + 2 Nên: n =   x = n x + 2 1−  n n 1 − 4     − 2  2 1  +      + 
Vậy: Số hạng tổng quát của dãy số ( x là 2     n ) x =  = − n n , 1, 2,... 1 n 4   − 2  1−    + 2  
BÀI TẬP TƯƠNG TỰ.
Bài 1: Tìm số hạng tổng quát của dãy số (u cho như sau: n ) 6 2 u =   ; R u = 5
− u − 4u − , n  =1,2,... 1 n 1 + n n 5 Giải. x 1 1 4 6 Đặt n u = − Khi đó. 2 2
− x = − x + x −  x = x − 4x + 6, n  =1,2,... n + + 5 n 1 n n n 1 5 5 5 5 n n x
− 2 = x − 4x + 4 = x − n  = + n n ( 2 n+ )2 2 , 1, 2,... n 1 1 2 n 1 − 2 2 2
Suy ra: x − 2 = x − = x − = = x − n ( 2 2 ... 2 n 1 − ) ( n−2 ) ( 1 ) n 1 − n 1 − 2 1 2 Vậy: x =  + +  u = −  + + . n (3 2) 2 n ((5 2) 2) 5
Bài 2: Tìm số hạng tổng quát của dãy số (u cho như sau: n ) 3 2 u =   ; R u
= 25u −15u + 3u , n  =1,2,... 1 n 1 + n n n Giải. x Đặt n u = ta được 3 2 x = 5  ; R x
= x −3x + 3x , n  =1,2,... n + 5 1 n 1 n n n x
−1 = x − 3x + 3x −1 = x − n  = + n n n ( n )3 3 2 1 , 1, 2,... n 1 2 n 1 − 3 3 3
Suy ra: x −1 = x − = x − = = x − n ( 1 1 ... 1 n 1 − ) ( n−2 ) ( 1 ) − 3n −  − + 3n 5 1 1 Vậy: x =  − +  u = . n (5 ) ( ) 1 1 1 1 n 5
Bài 3: Tìm số hạng tổng quát của dãy số (u cho như sau: n )
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 12
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020 2 3u + 6u −1 u =   ; n n R u = , n  =1,2,... 1 n 1 + 2 9u − 6u + 5 n n 8x
Hướng dẫn: Đặt x = 3u −1. Biến đổi đưa về dạng n x = , n  =1,2,... n n n 1 + 2 4 + . xn
Bài 4: Tìm số hạng tổng quát của dãy số ( x cho như sau: n ) 3 x +12x x =   0; n n x = , n  = 1,2,... 1 n 1 + 2 3x + 4 n Giải.
Chọn c = 4 nên b = 3, a = 12, d = 2  x +12x
x − 6x +12x − 8 (x −2 n n n n n n )3 3 3 2 x − 2 = − 2 = = 1 n 1 + 2 2 2 ( ) 3x + 4 3x + 4 3x + 4 n n n x +12x
x + 6x +12x + 8 (x + 2 n n n n n n )3 3 3 2 x + 2 = + 2 = = 2 n 1 + 2 2 2 ( ) 3x + 4 3x + 4 3x + 4 n n n x −
Xét hàm số f ( x) 2 = x+ . 2 Ta thấy: 3 ( x −  x − − −  f x − = =   =  f x  =  f x  = =  f x  =  f   n ) 2 2  ( n− ) 3   ( n− ) 23 n n n n ...   ( ) 1 3   ( ) 1 3 1 3 1 2 1  ( ) x + 2 x + 2 nn 1−  − x − 2 2 + 2 Đặt  =  ( ) 1 3n f    nên n =   x = x + 2 n 1−  n n 1 − 3     − 2  2 1  +       + 2    
Vậy: Số hạng tổng quát của dãy số ( x là x =  = − n n , 1, 2,... n ) 1 n 3   − 2  1−   + 2 
Bài 5: Tìm số hạng tổng quát của dãy số (u xác định như sau: n ) 3 u + 9u − 6 u = ; n n u = , n  = 1,2,... 1 n 1 + 2 3u − 6u + 7 n n 3 x +12x
Hướng dẫn: Đặt x = u −1. Biến đổi đưa về dạng: n n x = , n  =1,2,... n n n 1 + 2 3x + 4 n
Bài 6: Tìm số hạng tổng quát của dãy số (u xác định như sau: n ) 4u u + n ( 2 4 n )1 * u =   ; R u = , n   N 1 n 1 + 4 2 16u + 24u + . 1 n n Giải. 1 1 Ta thấy * n
  N tồn tại u . Nếu  = − thì u = − n 2 n 2
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 13
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020 1 Ta xét   − ta có : 2 32u + 8u
16u + 32u + 24u + 8u +1 (2u + n n n n n n n )4 3 4 3 2 1 2u +1 = +1 = = 1 n 1 + 4 2 4 2 4 2 ( ) 16u + 24u +1 16u + 24u +1 16u + 24u + 1 n n n n n n 32u + 8u 1
− 6u + 32u − 24u + 8u −1 −(2u − n n n n n n n )4 3 4 3 2 1 2u −1 = −1 = = 2 n 1 + 4 2 4 2 4 2 ( ) 16u + 24u +1 16u + 24u +1 16u + 24u + 1 n n n n n n x −
Xét hàm số f ( x) 2 1 = 2x+ . 1 Ta thấy: 4 ( u −  u − − −  f u − = = −  = −  f u  = −  f u  = = − f u  = − f   n ) 2 1 2 1  ( n− ) 4   ( n− ) 24 n n n n ...   ( ) 1 4   ( ) 1 4 1 3 1 2 1  ( ) 2u +1 2u +1 nn 1−  − 2u −1 1−  Đặt  =  ( ) 1 4n f    nên n = −  u = 2u +1 n 2 + 2 n
Vậy: Số hạng tổng quát của dãy số ( x là: n ) n 1 − 4  2 −1 1−   1 1 1   + 2 
Nếu  = − thì u = − Nếu  − thì u = , n  = 1,2,... 2 n 2 2 n n 1 − 4    2 −1 2 1  +      2 +1    Bài 7. (HSG QG 2010) u  = 5  1
Cho dãy số (u xác định như sau:  n ) n 1 − n 1 − n 1 n u
= u + 2 + 2.3 − , n  = 2,3,...  n 1+ n 1 −
a) Tìm số hạng tổng quát của dãy số (u . n )
b) Chứng minh rằng (u là dãy số giảm . n ) Giải a) Theo giả thiết ta có n n 1 − n 1 − n 1 u = u + 2 + 2.3 − = u − − − − − + + + + = u − − − − − + + + + = n n− ( n 2 n 2 n 2 2 2.3 n− ) n 1 n 1 n 2 2 2.3 n− ( n 2 n 1 2 2 ) 2( n 2 n 1 3 3 ... 1 2 2 ) ( n 1−) ( n 1 2 1 2 3 1 3 − − − ) u ( n−2 n 1 2 ... 2 2 − ) 2( n−2 n 1 3 ... 3 3 − = + + + + + + + + = 5 + + 2 = 2n + 3n 1 ) 1− 2 1− 3 vậy n
u = 2n + 3n , n  = 2,3,... n + + + + b)Ta có n 1 n n n u = + +  + = + = +  + n  = n
( n n) n n ( n n) ( n n) n n 1 n 1 n 1 2 3 2 3 3 2 3 3 2 3 3.2 3 2 3 , 2,3,...
vậy u u , n
 = 2,3,... Hay (u là dãy số giảm. n ) n n 1 +
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 14
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
C. XÁC ĐỊNH DÃY SỐ BẰNG PHƯƠNG PHÁP SAI PHÂN.
• Cho dãy số (x . Xét phương trình a x + a x
+...+ a x = g n 1 Trong đó g(n) là hàm 0 n+k 1 n+k 1 − k n ( ) ( ) n )
số theo n, và a ,a ,..., a là các hẳng số. khi dó phương trình a x + a x +...+ a x = 0 2 0 n+k 1 n+k 1 − k n ( ) 0 1 k
được gọi là Phương trình sai phân tuyến tính thuần nhất tương ứng với phương trình (1) • phương trình k k 1 a a  − +
+...+ a = 0 3 được gọi là Phương trình đặc trưng của (2). 0 1 k ( )
• Nghiệm tổng quát của phương trình (1) sẽ có dạng *
x = x + x , n
 =1,2,... Trong đó x là n n n n
nghiệm tổng quát của phương trình sai phân tuyến tính thuần nhất (2), còn * x là nghiệm riêng n của phương trình (1).
I./PHƯƠNG TRÌNH SAI PHÂN TUYẾN TÍNH BẬC NHẤT.
1/ phương trình sai phân tuyến tính thuần nhất bậc nhất .
Định nghĩa:Phương trình sai phân tuyến tính thuần nhất bậc nhất với hệ số hằng là
phương trình có dạng: ax
+bx = 0 , n=0,1,2,3…(1.1). Trong đó a≠0,b≠0 là những số cho trước. n 1 + n
Phương trình đặc trưng của (1,1) aλ + b = 0 ,phương trình nầy có nghiệm là λ = - b . a
Vậy nghiệm tổng quát của phương trình sai phân (1.1) có dạng: x = . n
C  , n =1, 2,3... n Ví dụ: x = 2x và x = 3
− n = 0,1,2,3…có công thức tổng quát x = − n ( ) 3 .2n n 1 + n 1
2/ phương trình sai phân tuyến tính không thuần nhất bậc nhất .
Định nghĩa : Phương trình sai phân tuyến tính không thuần nhất bậc nhất là phương trình có dạng: ax
+bx = d , n=0,1,2,3…(1.3). Trong đó a≠0, b là những hằng số, d n 1 + n n n là các số nào đó.
Ta thường viết dưới dạng : x
= qx + d n = 0,1,2,3… (1.4) . n 1 + n n
Ví dụ : Tìm nghiệm của phương trình x =1; 5x
+ 3x = 2n,n =1,2,3... 0 n 1 + n Giải 3
Phương trình đặc trưng 5 + 3 = 0 có nghiệm  = − . 5 n  3 
Nghiệm tổng quát của phương trình thuần nhất là x = C − . n    5 
Tìm nghiệm riêng của phương trình không thuần nhất là * x = .2n a . n 1 n + n n 1
Thay vào phương trình ta được 1 5. .2 a + 3. .2 a = 2  a = . Do đó * x = .2n 13 n 13  3 1 1 12
Nghiệm tổng quát của phương trình là x = C −
+ .2n . Vì x =1nên C + = 1  C = n    5 13 0 13 13 n 12  3  1 Vậy x = − + .2n . n   13  5  13
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 15
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
Dưới đây ta sẽ ta tìm nghiêm riêng của phương trình sai phân. u x DẠNG 1. Dãy số 1 0 n 2 . u qu b n n 1
Nếu q = 1 thì (un) là cấp số cộng có công sai d = b nên : u u n 1 b . n 1
Nghiệm tổng quát của phương trình thuần nhất u
= u là u = C . n 1 + n n
Nghiệm riêng của phương trình không thuần nhất là * u = . c n . n
Thay vào phương trình ta được u
= u + d ta được c(n + )
1 = cn + d c = d n 1 + n
Nghiệm tổng quát của phương trình là u = C + nd . n
Vì u = x cho trước thì u = x + nd hay u u n 1 b 0 0 n 0 n 1
Đây chính là công thức tổng quát của cấp số cộng.
Nếu q≠1 Nghiệm tổng quát của phương trình thuần nhất u = .
q u là u = . n C q n 1 + n n
d = b là đa thức bậc 0 với mọi n nên phương trình có nghiêm riêng * u = c n b
Thay vào phương trình ta được u
= qu + bta đượcc qc b c . n 1 + n 1 q b
Vậy nghiệm tổng quát của phương trình là u = . n C q + n 1− q BÀI TẬP ÁP DỤNG.
Bài 1 Xác định số hạng tổng quát của dãy số (un ) được xác định bởi : a) u 1,u u 2 n 2 . b) u 3,u 2u n 2. 1 n n 1 1 n n 1 c) u 2,u 3u + 2 n 2 d) u 2,u 3u 1 n 2. 1 n n 1 1 n n 1 1 u e) u , n u n 2 . 1 n 1 2 2u 3 n Giải a) u 1,u u 2 n 2 1 n n 1
Nghiệm tổng quát của phương trình thuần nhất u
= u là u = C . n 1 + n n
Nghiệm riêng của phương trình không thuần nhất là * u = . a n . n
Nghiệm tổng quát của phương trình là u = C + . a n. n C  + a =1 C  = 3
Vì u =1 u = 1
− thì hệ phương trình   1 2  C  + 2a = 1 − a = 2 −
Vậy công thức tổng quát u 3 2 , n n 2 . n b) u 3,u 2u n 2 1 n n 1
Nghiệm tổng quát của phương trình thuần nhất u
= 2u là u = .2n C . n 1 + n n 3 − u 3 3 . c 2 c
. Nghiệm tổng quát của phương trình là 1 u = 3.2n . 1 n 2 c) u 2,u 3u + 2 n 2 . 1 n n 1
Nghiệm tổng quát của phương trình thuần nhất u
= 3u là u = .3n C . n 1 + n n
Nghiệm riêng của phương trình không thuần nhất là * u = a . n
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 16
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
Nghiệm tổng quát của phương trình là u = .3n C + a. n  + =  =
Vì u = 2  u = 8 thì hệ phương trình 3C a 2 C 1   1 2  9  C + a = 8 a = 1 −
Vậy công thức tổng quát u 3n 1, n 1. n d) u 2,u 3u 1 n 2. 1 n n 1
Nghiệm tổng quát của phương trình thuần nhất u
= 3u là u = .3n C . n 1 + n n
Nghiệm riêng của phương trình không thuần nhất là * u = a . n
Nghiệm tổng quát của phương trình là u = .3n C + a. n  5 C = −  + = −  Vì u = 2 − u = 7
− thì hệ phương trình 3C a 2  6 1 2    9  C + a = 7 − 1 a =  2 5 n 1
Vậy công thức tổng quát 1 u .3 . n 2 2 1 u e) u , n u n 2 . 1 n 1 2 2u 3 n Ta có: u
0 bằng quy nạp ta được u 0 . 1 n 1 3 1 Từ giả thiết suy ra 2 . Đặt v khi đó v 3v 2 n 2 với v 2 u u n u n n 1 1 n 1 n n 1
Áp dụng kết quả câu c ta được u n 1. n 3n 1 BÀI TẬP RÈN LUYỆN.
Bài 1: Xác định số hạng tổng quát của dãy số (un ) được xác định bởi : a/ u 4,u u 2 n 2 . ĐS: u 2n 2 . 1 n n 1 n b/ u 2,u 3u n 2 . ĐS: 1 u 2.3n . 1 n n 1 n c/ u 1,u 3u 6 n 2 . ĐS: n 1 u 4.3 3 n 2 . 1 n n 1 n n 1 4 2 d/ u 1,u 4u +2 n 2 . ĐS: u n 2. 1 n n 1 n 3 3
Bài 2: Xác định số hạng tổng quát của dãy số (un ) được xác định bởi : u 3 1 u 2 1 a/ u n 1 . b/ u n 1 n u n n 1 u u 1 n 1 n 2u 1 n x 2 1
Bài 3 (Lạng Sơn 2009 – 2010): Cho của dãy số (xn ) được xác định bởi: 3x n 1 . n xn 1 x 2 n
Tìm công thức tổng quát của dãy số (xn ) theo n
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 17
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020 u x 1 0 DẠNG 2. Dãy số
trong đó f(n) là đa thức bậc k theo n, q là hằng số. u qu f n n 1 n
Nếu q = 1 ta tìm nghiệm riêng của phương trình không thuần nhất là * u = . n g n . n ( ) với .
n g (n) là đa thức bậc k+1 của n có hệ số tự do bằng 0.
Nếu q ≠1 ta tìm nghiệm riêng của phương trình không thuần nhất là * u = g n . n ( )
với g(n) là đa thức bậc k. BÀI TẬP ÁP DỤNG.
Bài 2: Xác định số hạng tổng quát của dãy số (un ) được xác định bởi : a/ u 2,u u 2n 1 n 2 . b/ u 2,u
2u +3n - 1 n 1 . 1 n n 1 1 n 1 n Giải a/ u 2,u u 2n 1 n 2 1 n n 1
Phương trình đặc trưng  −1 = 0 có nghiệm  = 1.
Nghiệm tổng quát của phương trình thuần nhất là u = C . n
Tìm nghiệm riêng của phương trình không thuần nhất là *
u = n an + b . n ( ) 2 Ta phân tích 2 2n 1 g n g n 1 an bn a n 1 b n 1 n 1 a b 3 a 1 * 2 u g n n 2n . n n 2 3a b 5 b 2
Nghiêm tông quát của phương trình là 2
u = C + n + 2n n Vì u = 2 thì 2
2 = C +1 + 2.1  C = 1 − . Vậy: 2 u n 2n 1. 0 n b/ u 2,u 2u +3n 1 n 1. 1 n 1 n
Phương trình đặc trưng  − 2 = 0 có nghiệm  = 2 .
Nghiệm tổng quát của phương trình thuần nhất là u = .2n C . n
Tìm nghiệm riêng của phương trình không thuần nhất là *
u = g n = an + b . n ( ) ( ) Ta phân tích 3n 1 an b 2 a n 1 b n 1 a b 2 a 3 g x 3n 5 n 2 b 5 b 5
Nghiệm tổng quát của phương trình là u = .
C 2n − 5n − 3 n Vì u = 2 thì n 2 = .
C 2 − 5.1− 3  C = 5 . Vậy công thức tổng quát u 5.2 3n 5 n 1 1 n
BÀI TẬP RÈN LUYỆN.
Bài 3: Xác định số hạng tổng quát của dãy số (un ) được xác định bởi: u 4 5 1 a/ 1 ĐS: 2 u n n 2 . u u 5n 2 n 2 2 n 1 n u 1 1 2 1 b/ n 1 . ĐS: 3 2 u n n n 1. 2 u u 2n n 3 3 n 1 n
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 18
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020 u 1 n 2 c/ 1 ĐS: u 3. n 2 . 3u 2u n 1 n 3 n 1 n u 2 1 d/ ĐS: 3 u 2.3n n 3 2 u 3u 2n 9n 9n 3 n n 1 n u x 0 0 DẠNG 3. Dãy số 0 u qu P n . n n 1 n k
Nếu q = α ta tìm nghiệm riêng của phương trình không thuần nhất là * u = .
n Q (n). n  . n k với .
n Q n là đa thức bậc k+1 của n có hệ số tự do bằng 0 . k ( )
Nếu q ≠α ta tìm nghiệm riêng của phương trình không thuần nhất là *
u = Q (n). n  . n k
với Q n là đa thức bậc k. k ( ) BÀI TẬP ÁP DỤNG.
Bài 3: Xác định số hạng tổng quát của dãy số (un ) được xác định bởi : a./ u 1,u 3u +2n n 2 b) u 3,u u +3.4n n 2 1 n n 1 1 n n 1 Giải a./ u 1,u 3u +2n n 2 1 n n 1
Phương trình đặc trưng  − 3 = 0 có nghiệm  = 3 .
Nghiệm tổng quát của phương trình thuần nhất là u = .3n C . n
Tìm nghiệm riêng của phương trình không thuần nhất là *
u = g (n) = .2n a . n
Thay vào phương trình ta được n 1 + n n 1 . a 2 3. . a 2 2 + = +  a = 2 − ta được. * u g (n) 1 2n+ = = − n
Vậy nghiệm tổng quát của phương trình là n n 1 u . C 3 2 + = − n 5 Vì u =1 thì 2
1 = C.3 − 2  C = 1 3
Vậy công thức tổng quát n 1 n 1 u 5.3 2 n 1 n b) u 3,u u +3.4n n 2 1 n n 1
Phương trình đặc trưng  −1 = 0 có nghiệm  = 1.
Nghiệm tổng quát của phương trình thuần nhất là u = C . n
Tìm nghiệm riêng của phương trình không thuần nhất là *
u = g (n) = .4n a . n
Thay vào phương trình ta được n 1 + n n 1 . a 4 . a 4 3.2 + = +  a = 4ta được. * u g (n) 1 4n+ = = n
Vậy nghiêm tông quát của phương trình là 1 u C 4n+ = + n
Vì u = 3 thì 3 = C + 4  C = 1 − 1 Vây : u 4n 1. n b) u 6,u
3u +5.3n n 1 1 n 1 n
Phương trình đặc trưng  − 3 = 0 có nghiệm  = 3 .
Nghiệm tổng quát của phương trình thuần nhất là u = .3n C . n
Tìm nghiệm riêng của phương trình không thuần nhất là * u = . n g (n) = . a 3n . n
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 19
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020 n + n n 5
Thay vào phương trình ta được . a (n + ) 1 1 3 = . a 3 n + 5.3  a = 3 5 ta được * n n 1 u .3 n 5. .3 n − = = n 3
Vậy nghiêm tông quát của phương trình là n n 1 u . C 3 5. 3 n − = + n 1
Vì u = 6 thì 6 = C.3 + 5.1 C = 1 3 Vây : n 1 − n 1 u 3 5. 3 n − = + n
BÀI TẬP RÈN LUYỆN.
Bài 4 Xác định số hạng tổng quát của dãy số (un ) được xác định bởi : 5 n 7 a./ u 4,u
2u +7.5n n 1 ĐS: u .2 .3n 1 n 1 n n 3 3 b) u 4,u
2u +3.2n n 1 ĐS: n n 1 u 4.2 3 . n 2 1 n 1 n n 17 u n 1 c) 1 5 n 1 ĐS: u 3 .2n . n 5 u 3u 2n n 1 n u x 1 0 DẠNG 4. Dãy số n 2 u au . n b f n n n 1
Giả sử d = f (n) + . n
b khi đó nghiệm riêng của phương trình * 1 2
x = x + x n n n n BÀI TẬP ÁP DỤNG.
Bài 3: Xác định số hạng tổng quát của dãy số (u n
n ) được xác định bởi: 2 u 5,u 2u +3.2 +n . 1 n 1 n Giải x 2x +3.2n 1 n n n 2 u 2u +3.2 +n n 1 n 2 y 2 y n 2 n n Từ n 1 n 1 x x 3 .2 3 . n 2 ; n 1 2 y y 6 .2 n 2n 3 . n 1 n 1 n 1 n 1 2 u x y 3 2 +3n. 2 n 2n 3 n 1 1 n n 1 Vậy 2 1 2 u 2 +3. 2 n 2n 3 n 2
BÀI TẬP RÈN LUYỆN.
Bài 1: Xác định số hạng tổng quát của dãy số (un ) được xác định bởi : u 1 1 a) n 1 ĐS: n 1 n 1 u 11.2 3 n 2 n u 2u 3n n n n u 4 1 10 n 7 b) n 1 ĐS: 1 u 3n .2 .5n n u 2u 7.5n 3.2n 3 3 n n
Bài 2: Xác định số hạng tổng quát của dãy số (un ) được xác định bởi: n 2 * u 1,u
2u +2.2 +n n N 1 n 1 n
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 20
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020 ĐS: n 1 2 2 u 5.2 . n 2 n 2n 3, n 1, 2,... n
Bài 3: Xác định số hạng tổng quát của dãy số (un ) được xác định bởi : u 2,u 5u +2.3n 6.7n +12 n 2 1 n n 1 ĐS: n 1 n 1 n 1 u 157.5 3 3.7 3 n
II./ PHƯƠNG TRÌNH SAI PHÂN BẬC HAI.
I. Phương trình sai phân tuyến tính thuần nhất bậc hai .
Định nghĩa: Phương trình sai phân tuyến tính thuần nhất bậc hai với hệ số hằng là
phương trình có dạng: ax
+ bx + cx = 0,n=0,1,2,3…(1.1).Trong đó a≠0,b,c là những số cho n+2 n 1 + n trước.
Nếu c = 0 Phương trình nầy là phương trình tuyến tính bậc nhất.
Trường hợp 1: Phương trình đặc trưng 2
aλ + b + c = 0 có 2 nghiệm là λ , λ   . 1 2 ( 1 2)
Thì nghiệm tổng quát của phương trình sai phân (1.1) có dạng: x = C . n n
 + C . n 1 1 2 2 x = 7; x = 6 −
Ví dụ : Tìm nghiệm của phương trình sai phân 0 1  x = 3x + 28xn+2 n 1 + n Giải
Phương trình đặc trưng 2
 − 3 − 28 = 0 có 2 nghiệm  = 4 − ; = 7. 1 2
Nên nghiệm tổng quát của phương trình thuần nhất có dạng n x = C 4 − + C .7n . n 1 ( ) 2
Với điều kiên ban đầu
n = 0, x = 7 , ta có x = C + C = 7 ; n = 1, x = 6 − 0 0 1 2 1 ta có x = 4 − C + 7C = 6
− . suy ra C = 5;C = 2 1 1 2 1 2 n
Vậy nghiệm tổng quát phương trình với điều kiện ban đầu là x = 5( 4 − ) + 2.7n n n
LƯU Ý: Với điều kiên ban đầu x = 5; x = 9 − thì x − = − − + . n ( ) n 1 4 7 0 1
BÀI TẬP RÈN LUYỆN.
Tìm nghiệm tổng quát của phương trình sai phân: x = 8; x = 3 n a) 0 1  ĐS: x 5.3n 3. 4 x = 12x − xn n + 2 n n 1 + x = 2; x = 8 − n b) 0 1  ĐS: x 1 9 x + 8x − 9x = 0  n n + 2 n 1 + n
Trường hợp 2: Phương trình đặc trưng 2
aλ + b + c = 0 có nghiệm kép là λ =  . 1 2
Thì nghiệm tổng quát của phương trình sai phân (1.1) có dạng: x = C . n n
 + C n. n 1 1 2 1 x = 1 − ; x = 2
Ví dụ : Tìm nghiệm của phương trình sai phân 0 1  x = 10x − 25xn+2 n 1 + n Giải
Phương trình đặc trưng 2
 −10 + 25 = 0 có nghiệm kép  =  = 5. 1 2
Nên nghiệm tổng quát của phương trình thuần nhất có dạng x = (C + nC .5n . n 1 2 )
Với điều kiên ban đầu n = 0, x = 1
− ta có x = C = 1 − ; 0 0 1
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 21
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020 7
n = 1, x = 2 , ta có x = C + C .5 = 2 suy ra C = 1 − ;C = 1 ( 1 2) 1 1 2 5  7 
Vậy nghiệm tổng quát phương trình với điều kiện ban đầu là x = 1 − + n .5n n    5 
BÀI TẬP RÈN LUYỆN
Tìm nghiệm tổng quát của phương trình sai phân: x = 1; x = 16 a) 0 1  ĐS: x 1 3n 4n x = 8x −16xn n + 2 n +1 n
x = 33; x = 162 b) 0 1  ĐS: x 4 7n .3n x = 6x − 9xn n + 2 n 1 + nx = 1; x = 3 c) 1 2  ĐS: x 1 2n x = 2x −1xn n + 2 n +1 n
Trường hợp 3: Phương trình đặc trưng 2
aλ + b + c = 0 vô nghiệm .
Thì nghiệm tổng quát của phương trình sai phân (1.1) có dạng: n
x = r (C cosn + C sin n) . n 1 2 B b −  Trong đó 2 2 2 r =
A + B ; = arctan ; A = ; B =
; = b − 4ac. A 2a 2a  1 x = 1; x =
Ví dụ : Tìm nghiệm của phương trình sai phân 0 1  2
x = x − xn+2 n +1 n Giải 1 i 3
Phương trình đặc trưng 2
 −  +1 = 0 có nghiệm   = . 1,2 2 b 1  3 B 1  Ta có 2 2 A = − = ;B = = ;r =
A + B = 1; = arctan = arctan = 12 2 2a 2 A 3 3 1 3 1  (Shift - mode 2 – + i
- Shift 2(cmplx) – 3 = máy hiện 1  Thì r = 1; = ) 2 2 3 3 nn
Nên nghiệm tổng quát của phương trình thuần nhất có dạng x = C cos + C sin . n 1 2 3 3
Với điều kiên ban đầu x =1ta có x = C =1; 0 0 1 1   1 n = 1, x =
. ta có x = C cos + C .sin = 1 2 1 1 2 3 3 2
suy ra C =1;C = 0 1 2 n
Vậy nghiệm tổng quát phương trình với điều kiện ban đầu là x = cos n 3
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 22
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
II. Phương trình sai phân tuyến tính bậc hai .
Định nghĩa : Phương trình sai phân tuyến tính bậc hai không thuần nhất là phương trình có dạng: ax
+ bx + cx = d , n=0,1,2,3…(1.2). Trong đó a,b,c là những hằng số, d n+2 n 1 + n n n là
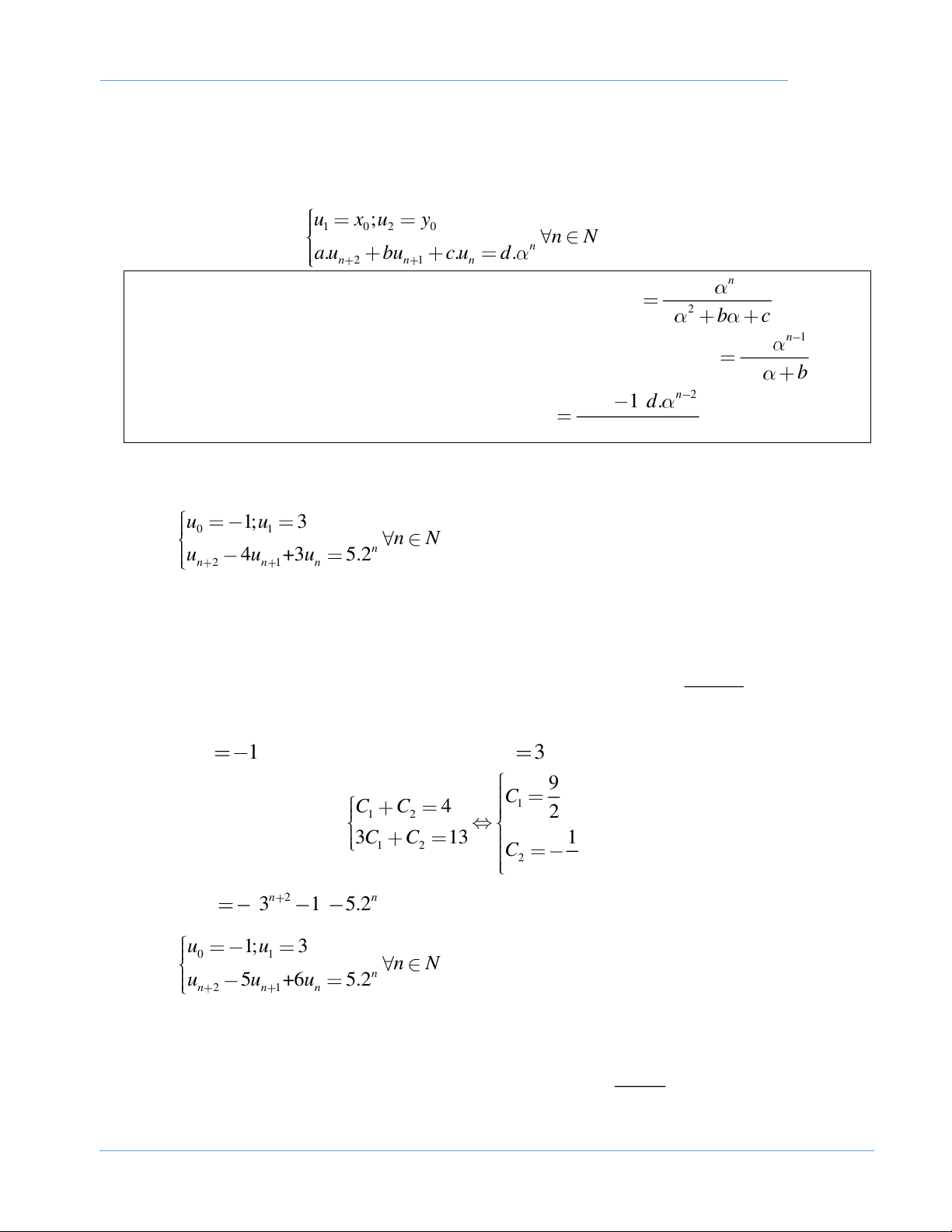
hàm số của biến số tự nhiên n. n = 0,1,2,3… (1.4) . u x ;u y 1 0 2 0 DẠNG 5. Dãy số n N . a u bu . c u d. n n 2 n 1 n • d. n
Nếu phương trình (*) có 2 nghiệm phân biệt khác α. Thì * u n 2 a b c n 1 • . n d.
Nếu phương trình (*) có 2 nghiệm phân biệt có 1 nghiệm u= α. Thì * u . n 2a b n 2 . n n 1 d.
• Nếu phương trình (*) có nghiệm kép u= α. Thì * u n 2a BÀI TẬP ÁP DỤNG
Bài 1: Xác định số hạng tổng quát của dãy số (un ) được xác định bởi: u 1;u 3 0 1 a/ n N u 4u +3u 5.2n n 2 n 1 n Giải
Phương trình đặc trưng 2
 − 4 + 3 = 0 có 2 nghiệm  =1; = 3. 1 2
Nghiệm tổng quát của phương trình thuần nhất có dạng u = C .3n + n C . 1 2 5.2n
Nghiệm riêng của phương trình không thuần nhất có dạng * u = = 5 − .2n . n 4 − 8 + 3
Nên nghiệm tổng quát của phương trình có dạng u = C .3n + C −5.2n . n 1 2 Với u
1ta được C + C − 5 = 1 − ; Với u
3 ta được 3C + C − 5.2 = 3 0 1 2 1 1 2 9 C1 C C 4 2
Ta có hệ phương trình 1 2 3C C 13 1 1 2 C2 2 1 Vậy n 2 u 3 1 5.2n . n 2 u 1;u 3 0 1 b/ n N u 5u +6u 5.2n n 2 n 1 n
Phương trình đặc trưng 2
 − 5 + 6 = 0 có 2 nghiệm  = 2; = 3. 1 2
Nghiệm tổng quát của phương trình thuần nhất u = C .2n + C .3n n 1 2 n 1 5 . n 2 −
Nghiệm riêng của phương trình không thuần nhất: * n 1 u 5 . n 2 − = = − n 4 − 5
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 23
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020 n n 5
Nên nghiệm tổng quát của phương trình có dạng u = C .2 + C .3 − .2n n . n 1 2 2 Với u
1ta được C + C = 1 − ; Với u
3ta được 2C +3C −5 = 3 0 1 2 1 1 2 C C 1 C 11
Ta có hệ phương trình 1 2 1 2C 3C 8 C 10 1 2 2 Vậy n n n 1 n n 1 u 11.2 10.3 5 . n 2 10.3 5n 22 .2 .. n u 1;u 3 0 1 c/ n 2 u 4u +4u 3.2n n n 1 n 2
Phương trình đặc trưng 2
 − 4 + 4 = 0 có 2 nghiệm  =  = 2 . 1 2
Nghiệm tổng quát của phương trình thuần nhất có dạng u = (C + C ) n .2n n . 1 2 3 . n n −1 2n− * ( ) 2
Nghiệm riêng của phương trình không thuần nhất u = = 3 . n n − − n ( ) n 3 1 2 2
Nghiệm tổng quát của phương trình có dạng u (C C ) n .2n 3n n − = + + − . n ( ) n 3 1 2 1 2 C 1 1 1 Ta có C 1; 3 C . Vậy 2 3 u 3n n 8 .2n 1 2 n C C 2 1 2 2 u 3;u 0 d/ 0 1 n 2 u 3u 28u 60 n n 1 n 2 Phương trình 2 x 3x 28 0 có 2 nghiệm x 4; x 7 n n 60 n
Công thức tổng quát u . a 4 . b 7 . a 4 . b 7n 2 n 1 3 28 a b 2 3 n Với u 3;u 0 a 3;b 2 . Vậy u 3. 4 2.7n 2 0 1 n 4a 7b 2 0
BÀI TẬP RÈN LUYỆN.
Bài 1: Xác định số hạng tổng quát của dãy số (un ) được xác định bởi : u 9;u 45 u 9;u 45 0 1 0 1 a/ n 2 b/ n 2 u 2u 8u 27.5n 1 u 8u 15u 2.5n n n 1 n 2 n n 1 n 2 u 1;u 496 u 5;u 8 0 1 0 1 c/ n 2 d/ n 2 u 16u 64u 128.8n u 6u 9u 2.3n 4n n n 1 n 2 n n 1 n 2 u 6;u 0 u 5;u 17 e/ 0 1 n 2 f/ 2 4 n 2 . u 3u 2u 5 u 2u u 1 n n 1 n 2 n n 1 n 2 u  =1;u = 2 (1) 0 1 
Bài 2 (HSG Tỉnh LS 2008-2009): Dãy số u xác định như sau:  + (với n = n u 2u n n 1 u − = (2)  n 1+  3 1, 2,3,…). Tìm u n
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 24
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020 u x ;u y 1 0 2 0 DẠNG 6: Dãy số n
1 trong đó f(n) là đa thức theo n bậc k. . a u bu . c u f n n 2 n 1 n
* Nếu a + b + c  0 thì nghiệm riêng của phương trình không thuần nhất là * u = g
n là đa thức bậc k của n. n k ( )
* Nếu a + b + c = 0 và 2a + b  0 thì nghiệm riêng của phương trình không thuần nhất là * u = . n g n n k ( )
* Nếu a + b + c = 0 và 2a + b = 0 thì nghiệm riêng của phương trình không thuần nhất là * 2 u = n .g n n k ( ) BÀI TẬP ÁP DỤNG.
Bài 1: Xác định số hạng tổng quát của dãy số (un ) được xác định bởi : u 1;u 3 0 1 a/ n 2 2 u 5u +6u 2n 2n 1 n n 1 n 2 Giải
Phương trình đặc trưng 2
 − 5 + 6 = 0 có 2 nghiệm  = 2; = 3. 1 2
Nghiệm tổng quát của phương trình thuần nhất u = C .2n + C .3n n . 1 2
Nghiệm riêng của phương trình không thuần nhất có dạng * 2
u = kn + ln + t . n
Thay vào phương trình ta được: 2 2 2 2 2n 2n 1 kn ln t 5 k n 1 l n 1 t 6 k n 2 l n 2 t
Cho lần lượt n=0,n=1,n=2 ta có hệ phương trình 19k 7l 2t 1 k 1 7k 5l 2t 5 l 8 ta được * 2 u n 8n 19 n k 3l 2t 13 t 19
Nên Nghiệm tổng quát của phương trình có dạng n n 2
u = C .2 + C .3 + n + 8n +19 . n 1 2 Với u
1ta được C + C +19 = 1 − ; Với u
3ta được 2C + 3C +1+ 8 +19 = 3 0 1 2 1 1 2 C C 20 C 35
Ta có hệ phương trình 1 2 1 2C 3C 25 C 15 1 2 2 Vậy n n 2 u 15.3 35.2 n 8n 19 . n u 1;u 4 b/ 0 1 n 2 u 3u +2u 2n 1 n n 1 n 2 Giải
Phương trình đặc trưng 2
 − 3 + 2 = 0 có 2 nghiệm  =1; = 2 . (a+b+c=0) 1 2
Nghiệm tổng quát của phương trình thuần nhất u = C .2n + n C . 1 2
Nghiệm riêng của phương trình không thuần nhất có dạng * u = ( n kn + l) . n
Thay vào phương trình ta được : 2n 1 n kn l 5 n 1 k n 1 l 6 n 2 k n 2 l
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 25
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
Cho lần lượt n=0,n=1 ta có hệ phương trình 5k l 1 k 1;l 6 suy ra * 2 u n 6n 3k l 3 n
Nên nghiệm tổng quát của phương trình có dạng n 2
u = C .2 + C − n − 6n . n 1 2 Với u
1ta được C + C =1; Với u
4ta được 2C + C −1− 6 = 4 0 1 2 1 1 2 C C 1 C 10
Ta có hệ phương trình 1 2 1 2C C 11 C 9 1 2 2 Vậy n 1 2 u 5.2 n 6n 9 . n
BÀI TẬP RÈN LUYỆN.
Bài 1: Xác định số hạng tổng quát của dãy số (un ) được xác định bởi : u 8;u 3 u 3;u 2 a./ 0 1 n 2 b/ 0 1 n 2 u u 12u 3n 2 u 4u 5u 12n 8 n n 1 n 2 n n 1 n 2
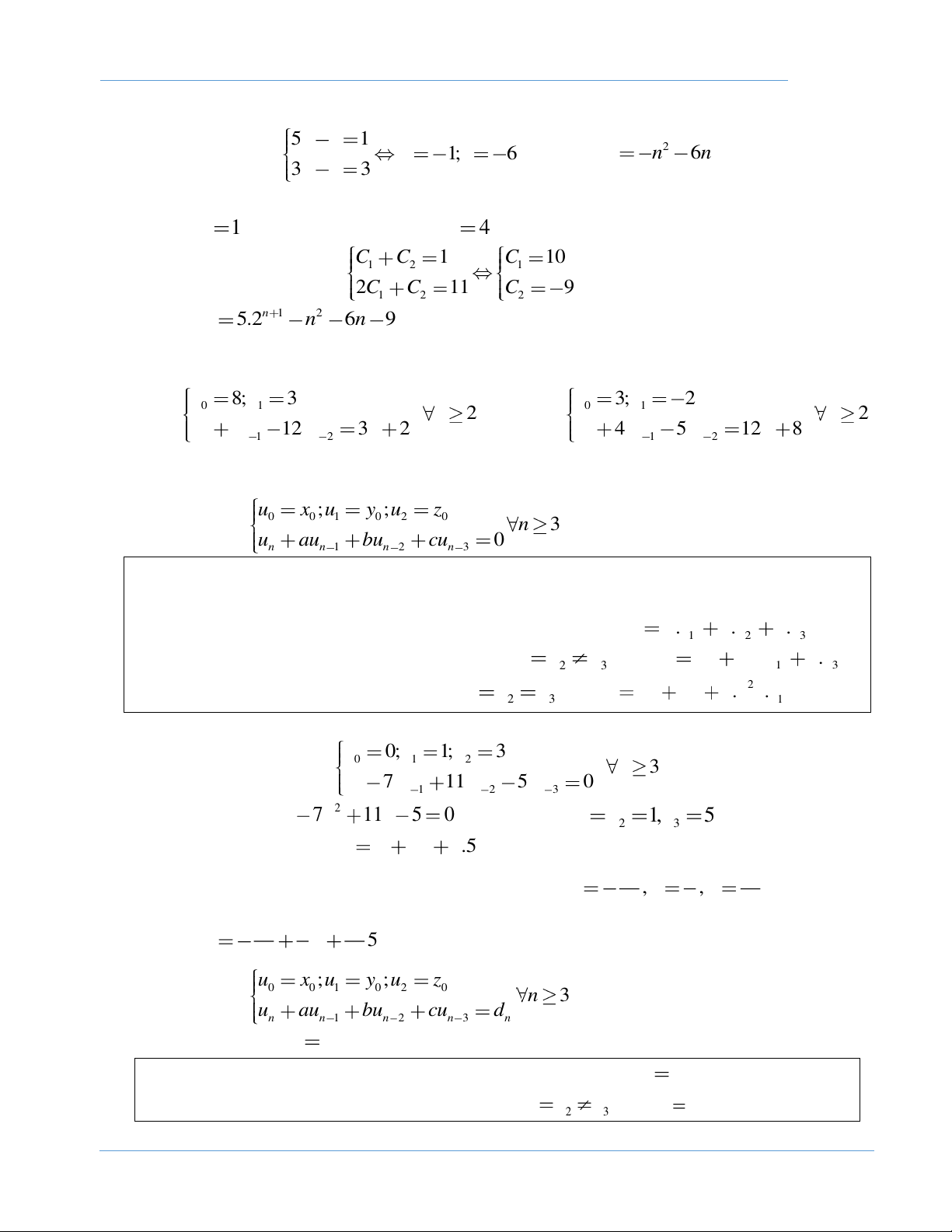
III. Phương trình sai phân tuyến tính bậc ba u x ;u y ;u z DẠNG 8. Dãy số 0 0 1 0 2 0 n 3 u au bu cu 0 n n 1 n 2 n 3
Để tìm công thức tổng quát của dãy số u ta làm như sau: n
Xét phương trình đặc trưng x3+ ax2+bx+c=0.(*)
* Nếu phương trình (*) có 3 nghiệm phân biệt x , x , x .Thì u . n p x . n q x k. n x . 1 2 3 n 1 2 3
* Nếu phương trình (*) có 2 nghiệm phân biệt x x x .Thì n u p qn x k. n x . 1 2 3 n 1 3
* Nếu phương trình (*) có nghiệm bội 3 x x x .Thì 2 u p nq k.n . n x 1 2 3 n 1
Bài 4: Xác định số hạng tổng quát của dãy số (un ) được xác định bởi: u 0;u 1;u 3 0 1 2 n 3 u 7u 11u 5u 0 n n 1 n 2 n 3 Phương trình 3 2 x 7x 11x 5 0 có 2 nghiệm x x 1, x 5 1 2 3
Công thức tổng quát u p qn k.5n n 1 3 1
Cho n=0,n=1,n=2 và giải hệ phương trình ta được p , q , k . 16 4 16 1 3 1 Vậy u n 5n . n 16 4 16 u x ;u y ;u z DẠNG 9. Dãy số 0 0 1 0 2 0 n 3 u au bu cu d n n 1 n 2 n 3 n
Trường hợp đặc biệt d
f n là đa thức bậc k của n.Tìm g n là đa thức cùng bậc f n n
* Nếu phương trình (*) có 3 nghiệm phân biệt x , x , x .Thì * x g n 1 2 3 n
* Nếu phương trình (*) có 2 nghiệm phân biệt x x x .Thì * x ng n . 1 2 3 n
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 26
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
* Nếu phương trình (*) có nghiệm bội 3 x x x .Thì * 2 x n g n 1 2 3 n
Bài 5: Xác định số hạng tổng quát của dãy số (un ) được xác định bởi : u 4;u 26;u 74 0 1 2 n 3 2 u 6u 11u 6u 6n 4n 8 n n 1 n 2 n 3 Phương trình 3 2 x 6x 11x 6 0 có 3 nghiệm x 1; x 2; x 3 1 2 3 Nghiệm riêng * 2 x g n n an bn
c thay vào phương trình ta được n 2 2 g n n an bn c 6 n 1 a n 1 b n 1 c 11 n 2 2 2 a n 2 b n 2 c 6 n 3 a n 3 b n 3 c 5a 2b c 4
lần lượt cho n=0,n=1,n=2 ta được hệ phương trình 8a c 3 a 1;b 2; c 5 5a 2b c 4 nên * 3 2 x g n n 2n 5n n
Nghiệm tổng quát của phương trình đã cho có dạng n n 3 2 x p . q 2 k.3 n 2n 5n n
Thay vào điều kiện ban đầu x 4; x 26; x 74suy ra p 5; q 1; k 1 0 1 2
Vậy số hạng tổng quát của dãy số là 3 2 u n 2n 5n 5 2n 3n n
Trường hợp đặc biệt d p n . n n
* Nếu phương trình (*) có 3 nghiệm phân biệt x , x , x khác α .Thì * x p n . n 1 2 3 n
* Nếu phương trình (*) có 3 nghiệm phân biệt có x .Thì * x p n . n n . 1 n
* Nếu phương trình (*) có nghiệm bội 3 x x x .Thì * 2 x n p n . n 1 2 3 n
Bài 6: Xác định số hạng tổng quát của dãy số (un ) được xác định bởi : u 3;u 20;u 89 1 2 3 n 3 n 2 n 2 u 6u 11u 6u 2 2.3 n n 1 n 2 n 3 Phương trình 3 2 x 6x 11x 6 0 có 3 nghiệm x 1; x 2; x 3 1 2 3
Phương trình đặc trưng có nghiệm x=2 nên Nghiệm riêng 2 x c .2n n thay vào phương n trình u 6u 11u 6u 2n ta được 3 2 3 .2 c 12 .2 c 11 .2 c 1 c 1 n n 1 n 2 n 3 Do đó 2 x .2n n . n
Phương trình đặc trưng có nghiệm x=3 nên Nghiệm riêng 3 x d .3n n thay vào phương n trình u 6u 11u 6u 2.3n ta được 3 2 3 . c 3 12 . c 3 11 . c 3 6 c 1 n n 1 n 2 n 3 Do đó 2 x .3n n . n
Nghiệm tổng quát của phương trình đã cho có dạng x p . q 2n k.3n . n 2n . n 3n n 1
Thay vào điều kiện ban đầu u 3;u 20;u 89 suy ra p 1; q 1; k 1 2 3 3
Vậy số hạng tổng quát của dãy số là n n 1 u 1 n 1 2 3n 1 3 n
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 27
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
IV. HỆ PHƯƠNG TRÌNH SAI PHÂN TUYẾN TÍNH VỚI HỆ SỐ HẰNG. x ; x ax by DẠNG 10: Dãy số 1 n n 1 n 1 x , y : . n n y ; y cx dy 1 n n 1 n 1
Một trong các cách giải hệ nầy là đưa về phương trình sai phân tuyến tính bậc hai Từ x
= ax +by x = ax +by và by = x −ax . n 1 + n n n+2 n 1 + n 1 + n n 1 + n Từ y
= cx + dy by = bcx + bdy b  0 . n 1 + n n n 1 + n n ( ) Vậy x
= ax + bcx + bdy = ax + bcx + d x − x = a + d x + bc − ad x . n+2 n 1 + n n n 1 + n ( n 1+ n) ( ) n 1+ ( ) n
Phương trình : x a d x ad bc x
0 chính là phương trình sai phân tuyến n 2 n 1 n
tính bậc hai với điều kiện x ; x . a x .
b y từ đó ta xác định được x thay vào hệ đã 0 1 0 0 n
cho ta được y . n x 0; x 3x y
Bài 1: Tìm công thức tổng quát của 2 dãy số 0 n 1 x , y : n n n n y 6; y 5x y 0 n 1 n n Giải Ta có x
= 3x + 5x − y = 3x + 5x − x − 3x = 2x + 8x . n+2 n 1 + n n n 1 + n ( n 1+ n ) n 1 + n
Phương trình đăc trưng: 2 2 8 0 2; 4 n
Do đó công thức tổng quát x = a ( 2 − ) + .
b 4n vì x = 0; y = 6  x = 6 n 0 0 1 a + b = 0 a = 1 − nên ta có:     2 − a + 4b = 6 b  =1 n n n
từ đó suy ra:  y = u − 3u = 2 2 −
+ 4.4n − 3 4n − 2 − = 4n + 5 2 − n n 1 + n ( ) ( ( ) ) ( ) x = −  ( n 2 − ) + 4n n
Vậy số hạng tổng quát  ny = 5  ( 2 − ) + 4n n x 2; x 2x y
Bài 2: Tìm công thức tổng quát của 2 dãy số 1 n n 1 n 1 x , y : n n y 1; y x 2y 1 n n 1 n 1 Giải x 2x x 2y 2x x 2 x 2x x 4x 3x và x 5 n n 1 n 2 n 2 n 1 n 2 n 1 n 2 n n 1 n 2 1 1 n 1
từ đó ta xác định được 1 n 1 x 1 3 y x 2x 3 1 n n n 1 2 n 2
BÀI TẬP TƯƠNG TỰ. x 1; x 4x 2y
Bài 1: Tìm công thức tổng quát của 2 dãy số 0 n 1 x , y : n n n n y 1; y x y 0 n 1 n n ĐS: số hạng tổng quát n 1 − n 1 x 2 ; y 2 − = = , n  =1,2,... n n x 3; x 4x 2y
Bài 2: Tìm công thức tổng quát của 2 dãy số 1 n n 1 n 1 x , y : n n y 1; y x 3y 1 n n 1 n 1
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 28
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020 u1
DẠNG 11. Dãy số phân tuyến tính au b n 2 n 1 un cu d n 1
Để tìm công thức tổng quát của dãy số u ta làm như sau: n x ; x ax by x Giải hệ phương trình 1 n n 1 n 1 khi đó n u
là nghiệm của phương n y ; y cx dy y 1 n n 1 n 1 n xn 1 a b x ax by y au b
trình đã cho .Thật vậy ta có n n 1 n 1 n 1 n 1 u n y cx dy xn 1 cu d n n 1 n 1 n 1 c d yn 1 u 2 1
Bài 3: Xác định số hạng tổng quát của dãy số (un ) được xác định bởi : 2u 1 n 1 n 1 un u 2 n 1 Giải x 2; x 2x y Xét hệ phương trình 0 n n 1 n 1 y 1; y x 2y 0 n n 1 n 1
theo bài 2 dạng 10 hệ có nghiệm là: 1 n 1 x 3 1 n n 1 2 x 3 1 n u n n 1 1 y n 1 3 1 y 3 1 n n 2 n 1 3 1 vậy u n n 1 3 1 u 1 1
Bài 4: Xác định số hạng tổng quát của dãy số (un ) được xác định bởi : u 2 n 1 n un 1 2u 3 n Giải x 1; x x 2y Xét hai dãy số ( n n n x và ( y như sau: 1 1 n 1 n ) n ) y 1; y 2x 3y 1 n 1 n n n  = 1,2,... Ta có : x
= x + 2y = x + 2 2x + 3y = x + 4x + 3 2y n 1 + n 1 + n 1 + n 1 + ( n n ) n 1 + n ( n)
= x + 4x + 3 x − x = 4x + x . n 1 + n ( n 1+ n) n 1 + n
Vậy dãy số ( x thỏa điều kiện x =1; x = 3; x
−4x − x = 0,n 1. n ) 1 2 n 1 + n 1 + n
Phương trình đăc trưng: 2 4 1 0 2 5; 2 5 n n
Do đó công thức tổng quát x = a − + b + n (2 5) (2 5)
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 29
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020 vì x =1; x = 3 1 2  5 + 3  + =  = − 1 a a b   2 5 nên ta có: (   2 − 5 
)a+(2+ 5)b =3  3− 5 b =  2 5 3 − − 5 n 3 − 5 n nên x = − + + n   . n (2 5) (2 5) , 1 2 5 2 5 5 +1 n 5 −1 n từ đó suy ra y = − + + n   . n (2 5) (2 5) , 1 2 5 2 5 3
− − 5 ( − )n 3− 5 n 2 5 + (2+ 5) 2 5 2 5 Vậy u = , n  1 n 5 +1( − )n 5 −1 n 2 5 + (2+ 5) 2 5 2 5
BÀI TẬP TƯƠNG TỰ
Bài 3: Xác định số hạng tổng quát của dãy số (un ) được xác định bởi u 1 1 2 a/ 2u n 1 ĐS: u n 1 u n n 1 n 5.2 3 5u 4 n 1 u 2 1 n 7 b/ 5u 1 n 1 ĐS: u . n 1 u n n n 3 u 3 n 1
V. PHƯƠNG PHÁP TUYẾN TÍNH HÓA.
1) Phương pháp biểu diễn nghiệm dưới dạng tuyến tính . x x 1 1 2 Bài 1: Cho dãy số 2 x
2 n 3. Chứng minh rằng mọi số hạng của dãy số đều là số nguyên. n 1 xn xn 2 Giải
Tìm số hạng tổng quát của dãy số dưới dạng x ax bx c (*) n n 1 n 2
Cho n = 3,4,5 ta được x 3; x 11; x 41 3 4 5 thay vào (*) ta được a b c 3 3a b c 11 a 4;b 1; c 0 suy ra x 4x x n n 1 n 2 11a 3b c 41
Bằng quy nạp ta chứng minh được x 4x x
là dạng tuyến tính của dãy số đã n n 1 n 2 cho.
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 30
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020 Do x x 1nguyên nên x 4x x
của dãy số đã cho đều là số nguyên. 1 2 n n 1 n 2 x 1 1 Bài 2: Cho dãy số
n 1. Chứng minh rằng mọi số hạng của dãy số đều 2 x 2x 3x 2 n 1 n n là số nguyên. Giải
Tìm số hạng tổng quát của dãy số dưới dạng x ax bx c (*) n n 1 n 2
Cho n=3,4,5 ta được x 3; x 11; x 41; x 153thay vào (*) ta được 2 3 4 5 3a b c 11 11a 3b c 41 a 4;b 1;c 0 41a 11b c 153 suy ra x 4x x n n 1 n 2
Bằng quy nạp ta chứng minh được x 4x x
là dạng tuyến tính của dãy số đã cho. n n 1 n 2 Do x 1; x 3nguyên nên x 4x x
của dãy số đã cho đều là số nguyên. 1 2 n n 1 n 2
BÀI TẬP RÈN LUYỆN
Bài 1: Tuyến tính hóa phương trình 2 x 0; x 5x 24x 1 . 0 n 1 n n ta được x 1; x 10; x 99; x 980 nên x 10x x 2 3 4 5 n n 1 n 2 6 n n
ĐS: Số hạng tổng quát của dãy số x 5 2 6 5 2 6 n 24
Bài 2: Tuyến tính hóa phương trình 2 3 x 1, x 2; x x x . 0 1 n 2 n 1 n
Hướng dẫn: lấy lôgarit cơ số e 2 vế 2 3 x x x ln x 2ln x 3ln x n 2 n 1 n n 2 n 1 n Đặt v
lnu khi đó phương trình trở thành v 2v 3v n n n 2 n 1 n x
Bài 3: Tìm số hạng tổng quát của dãy số x 1; n x 1 n 1 2 2 3 xn 2 x 1 2 3 x n n 2 3 Hướng dẫn x 1 . n 1 2 2 2 3 x x x x x n 1 n n n n 1 Đặt v
khi đó phương trình trở thành 2 v 2v 3v 1 n x n 1 n n n
2) Phương pháp đặt ẩn phụ. 1 1 u ;u 1 2 2 3
Xác định công thúc tổng quát của dãy số u .u n 1 n 2 un 3u 2u n 2 n 1 Ta thấy u
0 n vì nếu u
0 nào đó thì u 0;u 0 suy ra u 0;u 0 . n n n 1 n 2 1 2 1 Đặt v khi đó v 3v 2v
. Công thức tổng quát 1 v 1 2n n u n n 1 n 2 n n
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 31
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020 1 Vậy u . n n 1 2 1
3) Phương pháp biến đổi tương đương.
Tìm nghiệm của phương trình 2 u 2;u 6 33;u 3u 8u 1 . 0 1 n 1 n n Giải
Chuyển vế và bình phương 2 vế ta được. 2 2 2 u 6u u 9u 8u 1 hay 2 2 u 6u u u 1 n 1 n 1 n n n n 1 n 1 n n
Thay n + 1 bởi n ta được 2 2 u 6u u u 1. n n n 1 n 1
Cộng theo từng vế ta được u u u 6u u 0 . n 1 n n 1 n n 1 Vì 2 u 3u 8u 1 0 nên u 3u 9u u 0 u 0 . n 1 n n n 1 n n 1 n 1 n Suy ra u 6u u
0. Phương trình đặc trưng 2 x 6x 1 0 có nghiệm x 3 2 2 n 1 n n 1 n n
Số hạng tổng quát của dãy số dưới dạng u k 3 2 2 l 3 2 2 . n 8 66 8 66
Từ các giá trị ban đầu u 2;u 6 33 suy ra k ;l 0 1 8 8 8 66 n 8 66 n
Vậy Số hạng tổng quát của dãy số là u 3 2 2 3 2 2 . n 8 8
Nhận xét: Phương trình đã cho là bậc nhất nhưng phi tuyến (có chứa căn) nên khi biến đổi tương
đương , nó trở thành phương trình tuyến tính bậc hai.
BÀI TẬP RÈN LUYỆN u 1 0
Bài 1: Tìm số hạng tổng quát ; u : . n 2 u 5u 24x 8 n 1 n n n 1 n 1 6 2 6 2 ĐS: u 5 2 6 5 2 6 . n 2 6 2 6
Bài 2: Xác định số hạng tổng quát của dãy số (un ) được xác định bởi : a/ 2 3 u 1;u 2;u u u hd: đặt v lnu ta có v 2v 3v . 0 1 n 2 n 1 n n n n 2 n 1 n
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 32
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020 PHẦN 2
XÁC ĐỊNH GIỚI HẠN CỦA DÃY SỐ.
I. Sử dụng định nghĩa giới hạn dãy Số.
1. Định nghĩa giới hạn dãy Số.
Định nghĩa 1: Ta nói dãy số ( x có giới hạn hữu hạn là a ( ký hiệu lim x = a ) nếu với n ) n n→+
mọi số dương ε cho trước ( nhỏ bao nhiêu tùy ý ) tồn tại một số tự nhiên n sao cho : 0
x − a   , n   n . n 0
Định nghĩa 2: Dãy số ( x được gọi là hội tụ nếu tồn tại a R sao cho lim x = a . Khi n ) n n→+
đó ta còn nói dãy số ( x hội tụ về a. Một dãy số không hội tụ gọi là dãy số phân kỳ. n )
Định nghĩa 3: Ta nói dãy số ( x dần tới dương vô cực (ký hiệu lim x = + ) nếu với n ) n n→+
mỗi số dương M (lớn bao nhiêu cũng được ) tồn tại một số tự nhiên n sao cho: x M, n   n . 0 n 0
Định nghĩa 4: Ta nói dãy số ( x dần tới âm vô cực (ký hiệu lim x = − ) nếu với mỗi n ) n n→+
số âm m (nhỏ bao nhiêu cũng được ) tồn tại một số tự nhiên n sao cho : x  , m n   n 0 n 0
2. Giới hạn riêng, dãy con.
Định nghĩa 5: Cho tập hợp A≠∅ và A  . R
Số x được gọi là cận trên của tập A nếu với mọi a A ta có a x . Lúc này ta nói tập A bị chặn trên.
Số x được gọi là cận dưới của tập A nếu với mọi a A ta có a x . Lúc này ta nói tập A bị chặn dưới,
Cận trên bé nhất (nếu có) của tập A được gọi là cận trên đúng của tập hợp A, ký hiệu: supA.
Cận dưới bé nhất (nếu có) của tập A được gọi là cận dưới đúng của tập hợp A, ký hiệu inf A.
Lưu ý: sup A có thể không thuộc A. Nếu sup A thuộc A thì đó chính là giá trị lớn nhất của
A, ký hiệu Max A.
Tương tự: inf A có thể không thuộc A. Nếu inf A thuộc A thì đó chính là giá trị nhỏ nhất
của A, ký hiệu min A.
Định lý 1: Tập con khác rỗng A của R nếu bị chặn trên thì có sup A, nếu bị chặn dưới thì có infA
Định lý 2: (Đặc trưng của cận trên đúng, cận dưới đúng) M  , x x   A
M = sup A       0, a
  A: a M −. m  , x x   A
m = inf A       0, a
  A: a m + .
Trong thực hành ta thường áp dụng định lý sau:
Định lý 3: Cho tập hợp A≠∅ và A  . R
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 33
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
Nếu tập hợp A bị chặn trên thì tồn tại dãy số ( x trong A sao cho lim x = sup A . n ) n n→+
Nếu tập hợp A bị chặn dưới thì tồn tại dãy số ( x trong A sao cho lim x = inf A . n ) n n→+
Định nghĩa 6: Dãy con ( x
của dãy số ( x là dãy mà các phần tử của nó được trích từ n ) nk )
dãy số ( x ra, trong đó các chỉ số n thỏa mãn điều kiện lim n = + ,
n n  ...  n n  ... n ) k k 1 2 k k 1 + k→+
Ví dụ : Xét dãy số ( x n ) Dãy số ( x
(tức là dãy số x , x , x ,...) là dãy con của dãy số ( x . n ) 2n ) 2 4 6 Dãy số ( x
(tức là dãy số x , x , x ,... ) là dãy con của dãy số ( x . n ) 2n 1 − ) 1 3 5 Hai dãy ( x và ( x
được gọi là 2 dãy con kề nhau của dãy số ( x . n ) 2n 1 − ) 2n )
Định nghĩa 7: Dãy con ( x
của dãy số ( x là hội tụ thì giới hạn của nó được gọi là giới n ) nk )
hạn riêng của dãy số ( x . n ) n
Ví dụ : Xét dãy số ( x với x = − n  =
khi đó dãy số này không có giới hạn, tuy n ( )1 , 1, 2,3,... n )
nhiên 1 và -1 là các giới hạn riêng của dãy số ( x vì lim x = 1và lim x = 1 − . n ) 2n 2n 1 − n→+ n→+
Định nghĩa 8: Giới hạn riêng lớn nhất của dãy số ( x được gọi là giới hạn trên của nó và n )
ký hiệu là lim x ( hay lim sup x ). n n n→+ n→+
Giới hạn riêng bé nhất của dãy số ( x được gọi là giới hạn dưới của nó và ký hiệu là n )
lim x ( hay lim inf x ). n n n→+ n→+ Quy ước:
Nếu supx , x ,... = + với mọi n thì lim x = + . n n 1 +  n n→+
Nếu inf x , x ,... = − với mọi n thì lim x = − . n n 1 +  n n→+
Định lý 4: (Cantor) Cho a ;b , a ;b ,..., a ;b ,... là dãy đoạn thắt dần (tức là 1 1   2 2   n n
a ;b a ;b , n
 =1;2;3,... và lim (b − a = . Khi đó tồn tại một điểm a thuộc mọi n n ) 0 n 1 + n 1 +   n nn→+
đoạn a ;b . n n
Định lý 5 : (Bolzano – Weierstrass) Từ một dãy số bị chặn bất kỳ ( x đều có thể trích ra n ) một dãy con ( x hội tụ. nk )
Định lý 6 : Mọi dãy số thực ( x đều có giới hạn trên và giới hạn dưới. n )
Hệ quả 1: Mọi dãy bị chặn ( x , Nếu x là giới hạn trên của dãy thì. n ) *    0, n
  N : x x +, n   n . 0 n 0
Hệ quả 2: Mọi dãy bị chặn ( x , n )
Nếu x là giới hạn trên của dãy thì ∀ε>0 và ∀k∈N,tồn tại n
  k : x x −. k k n
Nếu x là giới hạn dưới của dãy thì ∀ε>0 và ∀k∈N,tồn tại n
  k : x x +. k k n
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 34
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
Định lý 7 : dãy số ( x hội tụ khi và chỉ khi nó bị chặn và lim x = lim x n ) n n n→+ n→+
Định lý 8 : dãy số ( x có giới hạn (hữu hạn hoặc ±∞) khi và chỉ khi n )
lim sup x = lim inf x . Khi đó lim x = lim sup x = lim inf x . n n n n n n→+ n→+ n→ n→+ n→+
3. Tiêu chuẩn Cauchy.
Định nghĩa 9: Ta nói dãy số ( x là dãy Cauchy hoặc dãy cơ bản nếu với mọi số dương ε n )
cho trước tồn tại số tự nhiên n −   0 sao cho x x , , n m n . n m 0
Chú ý: 1) lim x = a  lim ( x − a) = 0  lim x − a = 0 n n n n→+ n→+ n→+
2) Nếu lim x = a thì lim x = a . n n n→+ n→+
3) lim x =  nghĩa là x có thể lớn bao nhiêu cũng được miễn là n đủ lớn. n n n→+
Định lý 9 (Tiêu chuẩnCauchy): dãy số ( x hội tụ khi và chỉ khi dãy số ( x là dãy n ) n ) Cauchy.
4. Một số bài toán áp dụng.
Bài 1. Cho dãy số (x là dãy số bị chặn trên và thỏa mãn điều kiện n ) 1 3 x
x + x , n
 =1,2,... 1 . Chứng minh rằng dãy số (x có giới hạn hữu hạn khi n tăng n ) n+2 n 1 + n ( ) 4 4 lên vô hạn. Giải 3 3 3 Đặt y = x + x n
 =1,2,...Do đó y = x + x x + x = y n  =1,2,... 2 n 1 + n+2 n 1 + n 1 + n n ( ) n n 1 + 4 n 4 4
suy ra dãy số ( y là dãy số tăng. n )
Vì dãy số ( x bị chặn trên nên tồn tại số M sao cho x M, n  =1,2,... n ) n 3 3 7M do đó y = x + x  M+ M= n
 =1,2,... 3 dãy số ( y là bị chặn trên n ) n n 1 + n ( ) 4 4 4
Từ (2) và (3) dãy số ( y là dãy số hội tụ. n ) 4b
Đặt lim y = b và
= a Ta chứng minh lim x = a .    0 n n n→+ 7 n→+ 
vì lim y = b nên tồn tại n N : y − b  , n
  n Do đó với mọi n n ta có n 0 n 0 0 n→+ 8  3 7a  3 3
y − b = x + x − = ( x − a +
x − a x
− a − x − a n 1 + ) ( n ) n n 1 + + 8 4 n 4 n 1 4 4 n 3  Suy ra x
− a x − a + , n   n .(4) n 1 + n 0 4 8
Trong (4) lần lượt lấy n = n ,n = n +1,n = n + 2,... 0 0 0 3  x
− a x − a + , + 0 n 1 0 4 n 8
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 35
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020 2 3   3  3   x − a x − a +  x − a + . + + +   . 0 n 2 0 n 1 0 4 8  4 n  4 8 8 2 3 3 3  3 3   3   3 3        x − a x − a +  x − a + . +  x − a + .      + +1 + + +    . 0 n 3 0 n 2 0 n 1 0 4 8 4 4 8 8 4 n 8  4 4          …. k  3     − k k 1 − k −2 k 1       3    3   3  3  3     4  x a ... x a .    ... 1      x a .  −   − + + + + + = − + +   0 n k 0 n 0  4  8   4   4  4   4 n  8  3    1−   4   k k k 3   3       3   x − a x − a +   1−     x − a +   +   với k đủ lớn. 0 n k 0 n 0 4 8  4       4 n  2  
Điều này có nghĩa là x − a   , với n đủ lớn, tức là lim x = a . n n n→+
Vậy dãy số ( x là dãy số hội tụ. n )
Bài 2. (Đề thi vô địch Matxcơva). Chứng minh rằng dãy số ( x với x = ( 2 sin n , không tiến tới 0 n ) n ) khi n → + Giải
Ta có sin ( x − y) = sin xcos y − cos xsin y  sin x cos y + sin y cos x
Do đó: sin ( x − y)  sin x + sin y Giả sử ( 2 lim sin n ) = 0 . n→+ 1 Khi đó với *  = sin 2, n   N : sin( 2 n  , n   n 0 ) 0 16 2 2
Với n n ta có: ( n + ) = (n + ) 2 − n   (n + ) 2 sin 2 1 sin 1 sin 1 + sin n  2 0  
sin 2 = sin (2n + 3) − (2n + ) 1   sin 
(2n +3) + sin(2n + ) 1  2 + 2 = 4 1 1 Do đó : sin 2  4 = 4. sin 2 =
sin 2 .Điều mâu thuẩn nầy chứng tỏ dãy số đã cho 16 4
không tiến tới 0 khi n → + .  a
Bài 3.(Đề thi vô địch toàn Liên Xô). Cho dãy số (a ,Biết lim n a − = 0   . Chứng minh n ) n 1 + n→+  2 
rằng : lim a = 0 . n n→+ Giảia a ∀ε>0, vì lim n a − = 0  nên * n 1 n N : a −   −  , n   n . n 1 +  0 n 0 n→+  2  2 an Với ε>0 tồn tại *
k N sao cho 0
  . Khi đó với mọi số tự nhiên m n + k ta có: 2k 0
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 36
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020 aa a 1 1 m 1 − m 1 − m 1 a = a − +  a − − + a   + a mmm m 1 − m 1 −  2  2 2 2 2 1  1   1  1  1    1   +  + a =  + + a   + +  + a =  + + + am−2    2 m−2 2 m−3 3 m−3 2  2  2 2 2 2  2  2 2 2 1 1    − 1 m−n a a 0 n  1  n 0 0 2 ...   + + + ...+ + a   + =  2 − +  2 +  =    2 m−n 1 − m−n n k m−n 1 − 0 0 0 0 2 2 2 2 1 2  2  2k 1− 2
Như vậy ta chứng minh được:    0, n  = (n + k) *  N : n
  n ta có a  3 có nghĩa 1 0 1 n là lim a = 0 . n n→+
Mở rộng Bài 3 được thể hiện qua bài 4 sau đây.
Bài 4.Tìm tất cả các số thực t sao cho với mọi dãy số ( x thỏa mãn lim (tx − x = 0 ,ta suy ra n n 1 + ) n ) n→+ lim x = 0 . n n→+
Giải Ta có lim (tx − x
= 0  lim x − tx = 0 1 n n 1 + ) ( n 1+ n ) ( ) n→+ n→+
Xét dãy số ( x với n x = t , n
  N . Khi đó dãy số (x thỏa mãn (1). n ) n ) n
Nếu lim x = lim n
t = 0 thì t  1. Ngược lại,giả sử t  1.Ta chứng minh rằng với mọi n n→+ n→+
dãy số ( x sao cho lim ( x
− tx = 0 ta luôn có lim x = 0 . Vì lim (x − tx = 0 nên với mọi n 1 + n ) n 1 + n ) n ) n n→+ n→+ n→+ ε > 0,tồn tại *
n N sao cho x −tx  , n   n . 0 n 1 + n 0 Do đó n
  n ta có: x −tx   0 n 1 + n 2 tx − t xt  . n n 1 − …. − − + n−n n n n n 1 0 0 0 t x − t xt  . n 1 + n 0 0 − + − − + Suy ra n 0 n 1 x −t x
= x −tx + tx −t x + + t x −t x + n ( n+ n ) ( 2 ... n n n n n 1 1 n n 1 − ) ( 0 0 1 n 1 + n 0 0 0 ) 2 − − 1 + 0 0
x − tx + tx − t x + ... n n n n + t x − t x n 1 + n n n 1 − + 0 n 1 0 n n−n 1 + 2 n− − n 1 t 1
 (1+ t + t +...+ t ) 0 0  =    1− t 1− . t − +
Vì t  1nên tồn tại *
n N sao cho n n 1 0 t x   , n   n . 0 0 n 1
Từ (2) và (3) suy ra n
  n + n ta có: 0 1 − + − + − + − + x = x − t x + t xx − t x + t x   +  n+ ( n n n n n n n n 1 0 1 n+ n ) 0 1 0 1 0 1 1 1 n n 1 + n n 0 0 0 0 1− t  1 
Vậy với mọi ε > 0,tồn tại *
n N : n = n + n sao cho x   +1, n   n 2 2 0 1 n 1 + 2 1 t  −  
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 37
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
nghĩa là lim x = 0 . Vậy tất cả các số t cần tìm là t  1. n n→+
Bài 5. (Đề nghị Olympic 30/4/2000) Cho dãy số ( x thỏa mãn 0  xx + x , , n m =1,2,... , n ) n+m n mx  Chứng minh rằng dãy số n
 có giới hạn hữu hạn. n  Giải  x x x x  Gọi 1 2 n n 1 A =  , ,..., ,
+ ,... Khi đó tập A bị chặn dưới bởi số 0 nên tồn tại ìnf A Ta  1 2 n n +1  x
chứng minh lim n = inf A với mọi ε > 0 cho trước, theo tính chất của cận dưới đúng, tồn tại m n→+ n x  sao cho inf A m   inf A+ ( ) 1 . m 2
Với n là số tự nhiên bất kỳ,khi đó tồn tại hai số nguyên dương q và r sao cho
n = mq + r,0  r m −1 Khi đó x = x
x + x +...+ x + x = qx + x (xem x = 0 ) n mq+r m m m r m r 0 x qx + x x qx xx Do đó: inf A n m r m   = . m r +  inf A+ r + (2) n qm + r m qm + r r 2 n 2
Đặt maxx , x ,..., x
=  với 0  r m −1thì x   do đó với n  1 2 m−  1 rx   ta có 0 r   . = . n 2 2 x   2
Bởi vậy từ (2) ta suy ra inf A m   inf A+ + = inf A+, n  > (3) m 2 2  x
 inf A  lim n  inf A+,   >0 n→+ n x Vậy lim n = inf A . n→+ n
Bài 6: Cho dãy số ( x thỏa mãn * 0  xx .x , ,
n mN ,Chứng minh rằng lim n x tồn tại và n ) n+m n m n n→+ hữu hạn. Giải n
Với mọi n =1,2,3 …ta có 0  x x
  x x vậy dãy số (n x bị chặn. n ) n ( 0 n . 1 ) n 1
Gọi L = lim m x . khi đó tồn tại dãy con ( km x
của dãy số (m x sao cho m ) mk ) m m→+ lim mk x = L mk m→+
Với mỗi n cố định tùy ý ta có thể viết m = nl + r trong đó r n − do đó k 0,1,2,...,  1 k k k k
theo giả thiết ta có x = x
x .x x x m nl +r nl r ( n) l .r k k k k k k 1 1 1 k k 1 l l
Bởi vậy với mọi k=1,2,…, ta có m m m m n l +r r m k xx x = x x = x + x m
( n) ( r ) k ( n) . ( r ) k ( n)n. k k k k k k k ( kr ) k k l
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 38
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020 m m n kx x x k  =
cho k → + ta được L  ( x = x n  = n ) 1 n n , 1, 2,... m ( n)n k ( kr ) 1 1 k , 1, 2,...
Suy ra lim m x  lim m x  lim m x = lim m x . m m m m m→+ m→+ m→+ m→+
Vậy dãy số ( n x hội tụ. n )  x
Tương tự cách giải bài nầy ta chứng minh được dãy số n   bài 5 hội tụ. n
Bài tập tương tự
Bài 1: Cho dãy số ( x là dãy số bị chặn trên và thỏa mãn điều kiện n ) 1 2 x
x + x , n
 =1,2,... 1 . Chứng minh rằng dãy số (x có giới hạn hữu hạn khi n tăng n ) n+2 n 1 + n ( ) 3 3 lên vô hạn.
Bài 2: (Đề thi HSG QG 1988) Cho dãy số (u là dãy số bị chặn , thỏa mãn điều kiện n ) 2u
u + u ; u M, n
 =1,2,... có nhất thiết hội tụ không ?. n+2 n 1 + n n
Bài 3: Giả sử các số hạng của dãy số ( x thỏa mãn: n ) *
x  1, x + x −1  x
x + x +1, , n m N , n n m n+m n mx
a) Chứng minh rằng dãy số n
 có giới hạn hữu hạn.  n x
b) Chứng minh rằng nếu lim n = a R thì na −1 x na +1, n  =1,2,... n n→+ n Giải.
a) Gọi y =1+ x và Z =1− x , khi đó y =1+ x ;z =1− x và n n n n n+m n+m n+m n+m 0  y =1+ x
 2+ x + x = y + y , , n m =1,2,... n+m n+m n m n m 0  z =1− x 1+ − − = +  = + +
(1 x x ) z z , ,nm 1,2,... n m n m n m n my   z  Theo bài 5, suy ra dãy số n
 hội tụ và dãy số n   hội tụ .  n   n x 1+ x − − xy z   x n n (1 n ) 1 Mà ta có n n = = −   nên dãy số n   hội tụ. n 2n 2  n n   n y y x +1 x 1
b) nếu lim n = a R thì lim n = lim n
= lim n + lim = a n→+ n n→+ n→+ n→+ n n n n →+ n y 1+ x
Do đó theo lời giải bài 5 ta có n n a   a
x na −1, n  =1,2,... . n ( ) 1 n n z 1− x 1 x
Mặt khác: lim n = lim n = lim
− lim n = −a nên n→+ n→+ n→+ n n n n →+ n z x −1 n n −a   a
x na +1, n  =1,2,... n (2) n n
Từ (1) và (2) suy ra na −1 x na +1, n  =1,2,.... n
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 39
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
II. XÁC ĐỊNH SỐ HẠNG TỔNG QUÁT RỒI TÍNH GIỚI HẠN.
1) Phương pháp. Để tìm lim x ta thực hiện như sau: n n→+
Bước 1: tìm số hạng tổng quát của dãy số x . n
Bước 2: Sử dụng các công thức sau tìm lim x . n n→+
2) Các kết quả thường dùng . sin x ln (1+ x) x − • a 1 lim =1,lim =1,lim = ln a . x 0 → x 0 → x 0 x x → x x x     • 1 1 lim 1 + = ; e lim 1 + = e     x→+ xx →−   x  1 1
• lim (1+ x)x = ;
e lim (1+ x)x = e . + − x→0 x→0
• Nếu q 1 thì lim n q = 0 . x→+
• Nếu f(x) là hàm số liên tục trên K thì lim f (x ) = f
  và dãy số x hội tụ →+ (lim x x K n n →+ ) n n n n đến a K 3. Các bài toán.
Bài 1: ( Đề HSG Hà nội năm học 2011 – 2012 ) Cho dãy số (u được xác định bởi: n ) u  =1 u 1  . Tìm lim n u = u + nn→+ u n 1 + n n 1 + Giải 1
Công thức tổng quát u = n − n + n ( 2 2) 2 1 2 − + 2 1 2 u n − n + 2 Nên lim n = lim = lim n n =1 . 2 n→+ n u
→+ n + n + 2 n→+ 1 2 n 1 + 1+ + 2 n n
Bài 2: (Đề Olympic Toán SV – 2013) Cho dãy số ( x được xác định bởi: n )
x = a R  1 (  . Tìm lim x n n +  )2 2 1 x
= n x + 2n +1, n  = 1,2,... n→+ n 1 + n Giải
Ta phân tích n + = (n + )2 2 2 1 1 − n 2 2 2 Ta có : (n + ) 2 1 x
= n x + 2n +1  n + x = n x + n + − n + n ( ) 2 1 n+ n ( ) 2 1 n 1 1 2 2  (n + ) 1 x − + = − + (n ) 2 2 1 n x n n 1 n 2 2 Do đó : 2 2
n x − n = (n − ) 1 x − − = = − = − − (n ) 2 2 1 ... 1 x 1 a 1 n n 1 1 2 a −1+ n
Suy ra công thức tổng quát x = n 2 n
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 40
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020 2 a −1+ na −1 nên lim x = lim = lim 1+ =1 n   2 2 n→+ n→+ n n →+  n
Bài 3: (Đề Olympic 30/40/ 2013 ) Tìm dãy số ( x được xác định bởi: n ) x  0  1  n  3  (n + 2) 1 2 x = 2 + + + + (n ) 2 1 x n 4 . n 1 n ( ) Giải Ta có: 3(n + 2) 2 x = 2(n + ) 2 1 x + n +  n + x = n + x + n + − n + + n ( 4) 3( 2) 2 2 n+ ( ) 2 1 3 2 2 1 n 1 1 n ( ) ( )  3(n + 2) 2 x
− 3(n + 2) = 2(n + ) 2 1 x − 2 n +  n + x − = n + x − + (*) n ( )1 3( 2)( 2n+ )1 2( ) 1 ( 2 1 n 1 1 n ) 2(n + ) 1 Đặt 2
y = x −1 thay vào (*) ta được y = y n n n 1 + 3(n + 2) n + 2(n + ) n 1 1 2n 2  2  1 Do đó y = . ... y =
y suy ra lim y = 0 n 1 +   3(n + 2) 3(n + ) 1 1 1 3  3  n + 2 n n→+ Vậy lim x = ( 1 x  0 . n 1 ) n→+
Bài 4: (Đề Olympic 30/40/ 2013) Cho dãy số ( x được xác định bởi : n ) x =1 1   1 − 4x − 51 Tìm x và lim x . n x = , n  = 1,2,... 2013 n n→+ n 1 +  5x +18  n Giải. n 1 34 − 33.3 − 2012 34 − 33.3
Công thức tổng quát x = nên x = n ( n 1 2013 11.3 − −10) ( 2012 11.3 −10) n 1 34 − 33.3 − Nên lim x = lim = − n − n→+ n→+ ( 3 n 1 11.3 −10)
Bài 5: (Đề đề nghị Olympic 30/4 năm 2015 Chuyên An Giang) Cho dãy số (u được xác định n ) u  = 2010  1 u bởi :  Tính lim n u
 = 7u + 7n, n   2.  →+ 7n n n n n 1 −
Hướng dẫn: Công thức tổng quát n 1 u 2003.7 − = + . n 7n, n  1 nên n n 1 u 2003.7 − + . n 7n  2003  lim n = lim = lim +1 =1   →+ . n 7n →+ . n 7n n n n→+  7n
Bài 6: (Đề Olympic Toán SV 2012 ) Cho dãy số (a được xác định bởi : n ) a =  1   n +1 2 a = a − , n  =1,2,...  n 1+ nn n
Tìm ∝ để dãy số (a có giới hạn hữu hạn. n ) Giải
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 41
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020 a 2
Dãy số ( x như sau : n x = , n
 =1,2,... Ta có x = x − , n  = 1,2,... 2 n ) n n 1 + n n n(n + ) ( ) 1 2 2 2 x = x − ; x = x − ;…; x = x −
cộng theo từng vế ta được 2 1 n 1 + n 1.2 3 2 2.3 n(n + ) 1  1 1 1   1 1 1 1  x = x − 2 + + ...+
 = x − 2 1− + −...+ − n 1     1.2 2.3 n  (n − ) 1 1   2 2 n −1 n   1  2(n − ) 1 = x − 2 1− = x −
Như vây a = nx = nx − 2 n −1 =  − 2 n + 2, n  =1,2,... n n 1 ( ) ( ) 1   1  n n
Do đó dãy số (a có giới hạn hữu hạn  − 2 = 0   = 2 . n )
Bài 7 : (Đề HSG Gia lai 2012 - 2013) Cho dãy số (a được xác định bởi: n ) a =   R 1   (n + ) 1 a + 2013 na = , n  =1,2,... n 1 +  n
a) Tìm số hạng tổng quát của dãy số (a n )
b) Tìm ∝ để dãy số (a có giới hạn hữu hạn và tính giới hạn trong trường hợp đó. n ) Giải (n + ) 1 a + 2013 a a n 2013 a) Ta có n 1 a = , n  =1,2,... + n  = + n 1 + n (n + ) 1 (n + 2) n(n + ) 1 n(n + ) 1 (n + 2) a
Xét dãy số ( x như sau: n x = n  = khi đó x = n ) n n(n + ) , 1, 2,... 1 1 2 Làm tương tự bài 6 Như vây    a = n n + x = n n + x + n + n − = n + n + − n  = n ( ) 1 n ( ) 2013 1 ( 2013 2013 2 2) ( 2 , 1, 2,... 1 )  4  2 4  2  2013 2013
Do đó dãy số (a có giới hạn hữu hạn + = 0   = − n ) 2 4 2  2013  2013 b) Lúc này lim a = lim − = −    . n→+ n→+  2  2
Bài 8: (Đề HSG Bunggari 2000) Cho dãy số ( x được xác định như sau: n )
x = 1; x = a  1 2  a là hằng số dương. 2 3 x = x x , n  = 1,2,...  n+2 n 1 + n
Chứng minh rằng dãy số ( x hội tụ và tính giới hạn của dãy số nầy. n ) Giải 2 1
Ta thấy x  0, n
 =1,2,... nên từ x = x x
 ln x = ln x + ln x , n  =1,2,... n+2 ( n 1+ n)1 2 3 n n+2 n 1 + 3 3 n
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 42
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020 u  = 0;u = ln a 1 2 
Đặt u = ln x ta được dãy số (u như sau :  n ) n n 2 1 u
= u + u , n  =1,2,...  n+2 n 1 +  3 3 n 1
Xét phương trình đặc trưng : 2
3 − 2 −1 = 0   = 1; = − 3  B  3ln a n − = =  A 0 A 1     3  4
Do đó u = A + B −
vì u = 0;u = ln a nên    n    3  1 2 B 9ln aA ln a  + = B =  9  4 n n 3ln a 9 ln a  1  3ln a  1  Nên u = + − , n
 = 1,2,...suy ra lim u = vì lim − = 0 n     4 4  3  n n→+ 4 n→+  3  3ln a 3 3 lim u Vì hàm số ( ) x
f x = e liên tục trên R nên ta có: lim x = lim n un n e = e →+ = e = ( ln 4 a e = a . n )4 4 n→+ n→+
Bài 9: (Đề nghị Olympic 30/4/ 2012) Cho dãy số ( x được xác định như sau: n )
x = 1; x = 2012  1 2  . 2 3 x = x x , n  = 1,2,...  n+2 n 1 + n
Chứng minh rằng dãy số ( x hội tụ và tính giới hạn của dãy số nầy. n )
Đây trường hợp riêng của bài 8.x =1; x = 5
Bài 10: Cho dãy số ( x được xác định như sau : 0 1  n ) x
= 6x − x , n  =1,2,...  n 1+ n n 1 − Hãy tìm lim x ký hiệu : 
a = a − a chỉ lấy phần lẻ của a. →+  2x n nn Giải Công thức tổng quát + +     x = + + + − −  x = + + − n ( )( )n ( )( )n n   ( )2n 1 ( )2n 1 1 1 2 1 3 2 2 2 1 3 2 2 2 1 2 1   2 2 2 2  + +    x = + + − n  = n ( )2n 1 ( )2n 1 1 2 2 1 2 1 , 0,1, 2... 2   2n 1 + 2n 1 + 2n 1 1 +   Do đó 2x − − = + − − n  = n ( 2 )1 ( 2  )1 ( 2 )1 , 0,1, 2... 2   n+ n+ Mà  ( − )2 1 0 2 1 1, n  = 0,1,2,... nên x = − n  = n ( )2 1 2 2 1 , 0,1, 2... n+   Do đó x x = + − n  = n n  ( )4 2 1 2 1 2 1 , 0,1, 2...   2 2  suy ra +   x x = + − = n  =   n→+ ( n n) →+ ( )4n 2 1 1 lim 2 lim 1 2 1 , 0,1, 2... 2 2 n  2 2
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 43
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
Bài 11: Tìm giới hạn của dãy số ( x được xác định bởi: x = 2n 2 − 2 + 2 + ... + 2 , n  =1,2,... n ) n n 1 + Giải
Đặt u = 2 + 2 + ... + 2 , n
 =1,2,...Bằng quy nạp ta Chứng minh được n n 1 +  u = 2cos , n  =1,2,... n n 1 2 +      +  Ta có n n n 2 n 1 x = 2 2 − 2cos = 2 2 1− cos = 2 2.2sin = 2 sin n   n 1 + n 1 + n+2 n+2 2  2  2 2  sin n+2   sin x Vậy 2 lim x = lim = (do lim =1 ) n n→+ 2 n→+  2 x 0 → x n+2 2
Bài 12: Tìm giới hạn của dãy số ( x được xác định bởi: n ) 2 2 2 x = . ... , n  =1,2,... n 2 2 + 2 2 + 2 + ... + 2 n Giải 1 1 1 Theo bài 10 ta có x = . ..... , n  =1,2,... n    cos cos cos 2 3 2n 1 2 2 2 + 1
Theo công thức nhân đội sin.cos = sin 2 nên 2   sin sin 2n 1 + 2n 1 2 2 + x = n     = 1     cos .cos ....cos sin cos .cos ....cos sin 2 3 2n 1 + 2n 1 + 2 3 2n 2 2 2 2 2 2 2 2 2 2 n   sin sin 2n 1 + 2n 1 2 2 + = = ... = ,n = 1, 2,... 1     1 cos .cos ....cos sin 2 2 3 2n 1 − 2n 1 − 2 2 2 2 2 2 2 n  sin 2n 1  +  sin x Vậy 2 lim x = lim = (do lim =1). n n→+ 2 n→+  2 x 0 → x 2n 1 2 + BÀI TẬP TƯƠNG TỰ
Bài 1 (Đề HSG Tây Ninh năm học 2014 – 2015 ) Cho dãy số ( x được xác định bởi : n )
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 44
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020  1 x =  1 5  . Tìm lim x n (  n→+ n +  )2 2 1 x = n x
+ 4n + 2 x .x , n
  1,n N n n 1 + ( ) n 1+ n Giải
Dùng quy nạp chứng minh x  0, n  1,nN n (n + )2 2 1 n
Chia 2 vế cho x .x = + (4n + 2), n
 1,nN n 1 + ta được n x x n 1 + n 2 n Đặt y = ta có (n + )2 2 1 y = n y + 4n + 2 n + x n 1 n n
Ta phân tích n + = (n + )2 2 4 2 2 1 − 2n do đó: (n + )2 1 y = n y + 2 n + − n n + y − = n y − + n ( )2 1 2 ( )2 2 2 1 ( 2 n+ ) 2 2 n 1 1 ( n ) = (n − )2 1 ( y − 2 = = − = − ) 2 ... 1 y 2 3 n 1 ( 1 ) 3 2 2 3 + 2n 1 n 2
n ( y − 2) = 3  y = + 2 = =  x = n n 2 n 2 n 2 n x 3 + 2n n 2  n  1 vậy lim x = lim   = n 2 n→+
n→+  3 + 2n  2
Bài 2: (Đề HSG Tp Hồ Chí Minh năm học 2012 – 2013 )  1 u =  1  5
Cho dãy số (u được xác định bởi :  n ) 3u + 4 n * u  = , n   N n 1 +  2u +1  n
Chứng minh rằng dãy số (u có giới hạn hữu hạn và tìm giới hạn đó n ) n n 3.(− ) n 1 1 + 4.5 − 3.(− ) n 1 1 + 4.5 −
Hd: Công thức tổng quát u = nên lim u = lim = 2 . n n+ n n 1 + 3.(− ) 1 n 1 1 + 2.5 − n→+ n→+ 3.(− ) n 1 1 + 5 − 4 5
Bài 3: Tìm giới hạn của dãy số u  0;u  0;u = u u n  = Kết quả 9 9 lim u = u u . n+ ( n n+ )1 4 5 , 1, 2,... 0 1 2 1 n 0 1 n→+
III. SỬ DỤNG ĐỊNH LÍ WEIERSTRASS ĐỂ CHỨNG MINH DÃY SỐ CÓ GIỚI HẠN.
1) Một số kiến thức thường dùng.
Định nghĩa 10 : Cho dãy số ( x , ta nói dãy số đó: n )
Đơn điệu tăng nếu xx , n  =1,2,... n 1 + n
Đơn điệu giảm nếu xx , n  =1,2,... n 1 + n
Đơn điệu tăng thực sự nếu xx , n  =1,2,... n 1 + n
Đơn điệu giảm thực sự nếu xx , n  =1,2,... n 1 + n
Dãy số đơn điệu tăng và đơn điệu giảm gọi chung là Dãy số đơn điệu.
Định nghĩa 11 : Cho dãy số ( x ta nói dãy số n )
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 45
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
Bị chặn trên nếu tồn tại số M sao cho x M, n  =1,2,... n
Bị chặn dưới nếu tồn tại số m sao cho x  , m n  =1,2,... n
Bị chặn nếu nó bị chặn trên và bị chặn dưới.
Định lý 9: (định lý Weierstrass) Nếu dãy số (u tăng và bị chặn trên (hoặc giảm và bị n )
chặn dưới) đều hội tụ . Chú ý: 1
i) Nếu dãy số ( x tăng và không bị chặn trên thì lim x = + và khi đó lim = 0 . n ) n n→+ n→+ xn 1
Nếu dãy số ( x giảm và không bị chặn dưới thì lim x = − và khi đó lim = 0 . n ) n n→+ n→+ xn
ii) Dãy số tăng (giảm) hội tụ khi và chỉ khi nó bị chặn trên (bị chặn dưới)
iii) Cho 2 dãy ( x ), y khi đó x y , n
 =1,2,... thì lim x  lim y . n ( n) n n n n n→+ n→+
Định lý 10: Mọi dãy hội tụ đều bị chặn. Phương pháp :
Bước 1:Xét xem dãy số đã cho tăng hay giảm.
– Nếu tăng thì chứng minh x  , L n
 =1,2,... để suy ra dãy bị chặn trên. n
– Nếu giảm thì chứng minh x  , L n
 =1,2,... để suy ra dãy bị chặn dưới. n
Bước 2:Sử dụng kết quả bước 1 để chứng minh dãy số đơn điệu.
Bước 3:Sử dụng định lý Weierstrass để chứng minh dãy số đã cho hội tụ.Sau đó, Giả sử
dãy số đã cho hội tụ về L, từ x = f x , n
 =1,2,... khi n →+ và sử dụng tính liên tục của n 1 + ( n)
hàm f ta được L = f (L) .Vậy giới hạn của dãy số đã cho là nghiệm của phương trình x = f ( x) . BÀI TẬP ÁP DỤNG. u  = 2
Bài 1. Chứng minh rằng dãy số (u cho bởi công thức 1 
với n≥1 có giới hạn và tìm n ) u  = 2 + un 1+ n giới hạn đó. Giải
Ta có u = 2 và u
= 2 + u nên u  0 n   . 1 n 1 + n n
* Ta chứng minh u  2 n   (1). n
Với n=1 Ta có u = 2 < 2 thì (1) đúng . 1
Giả sử bất đẳng thức đúng với n = k thì u  2 ta chứng minh bất đẳng thức đúng với n = k+1 thì k u
 2 Thật vậy u = 2 + u  2 + 2 = 2 vậyu  2 n   . k 1 + n 1 + n n
Chứng minh dãy số (u tăng . n ) Xét 2 u
u  2 + u u u − u − 2  0  1
−  u  2 mà 0  u  2nên u u . n 1 + n n n n n n n n 1 + n
Vậy dãy số (u có giới hạn. n )
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 46
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
Đặt limu = a thì 0≤a≤2 và u
= 2 + u  limu = lim 2 + u n n 1 + n n n 2
a = 2 + a a − a − 2 = 0  a = 1
− v a = 2 vì u  0nênlimu = a  0 vậylimu = 2 . n n n u  = 2 1 
Bài 2: Chứng minh rằng dãy số (u cho bởi công thức 
1 n≥2 có giới hạn và tìm giới n ) u = 2 − n 1 +  un hạn đó. Giải n
Công thức tổng quát u =
ta chứng minh dãy số (u giảm và bị chặn bởi 1 n ) n 1 + n +1 n  1  và lim u = lim = lim 1− =1 . vậylimu =1 n   n +1  n +1 n 3
Bài 3: Cho dãy số ( x được xác định bởi x = ; x = 3x − 2, n  = 2,3,... n ) 1 1 − 2 n n
Chứng minh rằng dãy số ( x có giới hạn khi n → + , tìm giới hạn đó. n )
Hướng dẫn : 3
Cách 1: Bằng quy nạp chứng minh  x  2, n  =1,2,... 2 n 2 −x + 3x − 2 3  Xét x − x = 3x − 2 n n − x =  0 vì x  ; 2 n 1 + n n n n   3x − 2 + x 2  n n
Vậy dãy số ( x tăng và bị chặn trên nên hội tụ n ) 3 
Đặt lim x = a khi đó a  ; 2 Từ x = 3x − 2, n
 = 2,3,...cho n →+ ta được n   n n 1 − n→+ 2  lim x = lim 3x
− 2 = 3lim x − 2 hay a = 3a − 2  a = 2. n n 1 − n 1 − n→+ n→+ n→+ Vậy lim x = 2 . n n→+ 3
Cách 2: Bằng quy nạp chứng minh  x  2, n  =1,2,... 2 n  
Xét hàm số f ( x) 3 = 3x − 2, x   ; 2 
 .Khi đó x = f x , n  =1,2,... n 1 + ( n) 2     3  Ta có f ( x) 3 3 ' =  0, x   ; 2 
 do đó f(x) là hàm tăng trên ; 2   2 3x − 2 2   2  3 5 3
Ta có x = f x = 3x − 2 = 3. − 2 =
 = x suy ra dãy số (x tăng. n ) 2 ( 1) 1 1 2 2 2
Bài 4: (HSG QG năm 2012) Cho dãy số ( x được xác định bởi n )
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 47
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020 x = 3 1   n + 2 x = x + n  =  n ( 2 , 2,3,... n 1 − )  3n
Chứng minh rằng dãy số ( x có giới hạn hữu hạn, tính giới hạn đó. n ) Hướng dẫn n + 2
Bằng quy nạp chứng minh x  , n  = 3,4,... n 1 − n − 1
suy ra dãy số ( x bị chặn dưới bởi số 0. n ) n + 2
2 n + 2 − n −1 x   n− 
Với n  3 ta có x − x = x + − x =  n n− ( 2 n− ) ( ) 1 0 1 1 n 1 − 3n 3n
Vậy dãy số ( x giảm và bị chặn dưới nên có giới hạn hữu hạn. n )
Đặt lim x = a cho n → + ta được n n→+ n + 2   1 x = x + = + x
+ hay a = (a + 2)  a =1. n ( 1 2 lim lim 2 lim lim 2 n 1 − )   ( n 1− ) n→+ n→+ 3 n n →+  3 3 n n →+  3 Vậy lim x = 1 . n n→+ a
Bài 5: Cho trước a  0 , xét dãy số ( x thỏa mãn điều kiên 0  x a và x a − xn   N n ( , n 1 + ) 2 n ) n 4
Chứng minh rằng dãy số đã cho có giới hạn và tìm giới hạn đó.
Hướng dẫn: ta có 0  x a dãy số (u bị chặn. n ) n
Áp dụng bất đẳng thức cauchy a
x + a − xx a − x
= a x x n   n ( n+ ) 2 n ( n+ ) 2 2 1 1 n 1 + 4 n
suy ra dãy số ( x giảm và bị chặn dưới nên có giới hạn hữu hạn n ) 2 2 a a
Đặt lim x = x( x  0 ta có x a − x   x a − xn ( lim n 1 + ) n 1 + ( n 1 + ) n ) 4 4 2 (    − a x) 2 a a a x 1   x −  0  x =   . vậy lim x = . 4  2  2 n 2 1 1
Bài 6: Cho dãy số ( x được xác định bởi x = 0; x = và x = + x + x n  = n+ ( 3 1 , 2,3,... 1 n n 1 − ) n ) 1 2 2 3
Chứng minh rằng dãy số ( x có giới hạn hữu hạn, tính lim x n ) n n→+ Giải 5 −1
Ta chứng minh 0  x  , n  =1,2,... n (2) 2 5 −1 5 −1 5 −1
Ta có 0  x , x  Giả sử 0  x  ,0  x  1 2 − 2 n 1 2 n 2
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 48
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020 3   1 1  5 −1  5 −1 5 −1 Khi đó 0  x = + x + x   +   +    = n+ ( 3 1 1 1 n n 1 − ) 3 3  2 2  2      
Theo nguyên lý quy nạp (2 ) đúng. Ta chứng minh dãy số ( x tăng. n ) 1 1  1  1
Ta có: x = 0; x = , x = 1+
+ 0 =  x x x Giả sử x x , x x 1 2 3   1 2 3 − − − 2 3  2  2 n 2 n 1 n 1 n 1 1 Khi đó x
− x =  + x + x − + x + x  = x − x + x − xn+ n ( 3 1 n n−  ) ( 3 1 n− n− ) ( n n− ) ( 3 3 0 1 1 1 2 1 n 1 − n−2 ) 3 3
Vậy x x , 1
 ,2,...nên dãy số (x có giới hạn. n ) n n 1 +
Đặt lim x = a cho n → + ta được n n→+ a =1 1  − a = ( 5 1 3
1+ a + a )  (a − ) 1 ( 2 a + a − ) 1 = 0  1 5  a = −  . 3 a = 2  2 5 −1 Vậy lim x = . n n→+ 2 1  a
Bài 7: Cho dãy số ( x thỏa mãn điều kiên x  0,a  0 và * x =  x + , n   N n ) 1 n 1 + 2 n xn
Chứng minh rằng dãy số đã cho có giới hạn và tìm giới hạn đó. Hướng dẫn: 1  a  Ta có x =
x +   a do đó bằng quy nạp và bất đẳng thức cauchy ta suy ra 2 1 2 x  1  x 1 a 1 a x a, n
 = 2,3,... Mặt khác n 1+ = +  +
= 1 x x , n  = 2,3,... n 2 n 1 + x 2 2x 2 2 n a n n
Vậy dãy số ( x giảm và bị chặn dưới bởi a nên hội tụ. n ) 1  a
Đặt lim x = l cho n → + ta được 2 2 l = l +
 2l = l + a l = a   (l a). n n→+ 2  l
Vậy lim x = a . n n→+
Bài 8: Cho dãy số ( x được xác định bởi 3 3
x = 2n + a 8n +1, n
 = 1,2,3,... a R n ( ) n )
a) Tìm a sao cho dãy số ( x có giới hạn hữu hạn. n )
b) Tìm a sao cho ( x là dãy số tăng (kể từ số hạng nào đó) n ) Giải a) Nếu a = 1
− thì dãy số (x có giới hạn hữu hạn vì : n ) − lim x = lim n − n + = = . n n→+ n→+ ( 1 3 3 2 8 1) lim 0 n→+ 3 3
4n + 2n 8n +1 + (8n + )2 2 3 3 1
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 49
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
Giả sử dãy số ( x có giới hạn hữu hạn vì 3 3
x = 2n − 8n +1 + a + n + mà dãy số n ( ) 3 3 1 8 1 n )
(x có giới hạn hữu hạn nên dãy số (y với y = a + n + n  = cũng có giới hạn n ( ) 3 3 1 8 1, 1, 2,... n ) n ) hữu hạn . Mà 3 3
lim 8n +1 = + nên từ dãy số ( y có giới hạn hữu hạn suy ra n ) n→+
a +1 = 0  a = 1 −
Vậy dãy số ( x có giới hạn hữu hạn khi và chỉ khi a = 1 − n )
b) Dãy số ( x là dãy số tăng (kể từ số hạng nào đó) khi và chỉ khi tồn tại số nguyên dương n n ) 0 sao cho xx , n   n .Ta có n 1 + n 0 3 x
x  2n + 2 + a 8 n + +  n + n +  a n + + − n +  − + n ( )3 3 1 1 2 8 1 (38 1 1 8 1 2 n 1 ( )3 3 3 3 ) a 8  (n + )3 1 +1− ( 3 8n + ) 1     (  2 − 8(n + ) 1 +1)2 +( 8(n + ) 1 +1)( 3 8n +1) +( 3 3 3 8n +1)2 3 3 3 3 a ( 2 24n + 24n + 8)  (  2 − 8(n + ) 1 +1)2 + ( 8(n + ) 1 +1)( 3 8n +1) + ( 3 3 3 8n +1)2 3 3 3 3 a ( 2 24n + 24n + 8) 24a  lim  −   −  a  − n→+ ( 2 2 1 + + 8(n + ) 1 +1)2 + ( 8(n + ) 1 +1)( 3 8n +1) + ( 3 4 4 4 3 3 8n +1)2 3 3 3 3
Vậy dãy số ( x tăng (kể từ số hạng nào đó) khi và chỉ khi a  1 − n )
BÀI TẬP TƯƠNG TỰ 1  2 
Bài 1: Cho dãy số (u cho bởi công thức u
= u +  và u  0 n ) n 1 + 2 n u  1 n
a) Chứng minh rằng u  2, n   2 n
b) Chứng minh rằng dãy số (u có giới hạn và tìm giới hạn. n )
Bài 2: (Đề HSG Tp Hồ Chí Minh năm học 2012 – 2013) 1 3u + 4
Cho dãy số (u được xác định bởi : u = và n * u = , n   N n ) 1 + 5 n 1 2u + 1 n
Chứng minh rằng dãy số (u có giới hạn hữu hạn và tìm giới hạn đó n )
Bài 3: (HSG Gia Lai năm 2004) 2n +1
Cho dãy số ( x được xác định bởi x = 2004 và x = x +1 , n  =1,2,3,... n 1 + ( n ) n ) 1 3n + 1
Chứng minh rằng dãy số ( x có giới hạn hữu hạn, tính giới hạn đó. n )
Hướng dẫn: tương tự bài 4 trên.
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 50
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020 0  u 1 n
Bài 4: Chứng minh rằng cho bởi công thức  (n  )1 1
có giới hạn và tìm giới hạn đó. u 1− u   n 1+ ( n )  4
Hướng dẫn: tương tự bài 5 trên 5 20n + 21
Bài 5: Cho dãy số ( x được xác định bởi x = và 3 * x = x −12x + , n   N n ) 1 + 2 n 1 n n n + 1
Chứng minh rằng dãy số ( x có giới hạn hữu hạn, tính giới hạn đó. n ) Hướng dẫn. - Chứng minh : * x  2, n   N . n
- Chứng minh x x , 1
 ,2,...nên dãy số (x có giới hạn. n ) n n 1 +
Đặt lim x = a cho n → + ta được Vậy lim x = 2 . n n n→+ n→+ 2011 2n + 4999
Bài 6: Cho dãy số ( x được xác định bởi x = và 2 * x = x − 2x + , n   N n ) 1 + 2010 n 1 n n n + 2499
Chứng minh rằng dãy số ( x có giới hạn hữu hạn, tính giới hạn đó. n ) Hướng dẫn. - Chứng minh : * x  1, n   N . n
- Chứng minh x x , 1
 ,2,...nên dãy số (x có giới hạn. n ) n n 1 +
Đặt lim x = a cho n → + ta được Vậy lim x = 1 . n n n→+ n→+ 1  a
Bài 7: Cho dãy số ( x thỏa mãn điều kiên x  0,a  0 và * x = 2x + , n   N n ) 1 n 1 + n 2 3 xn
Chứng minh rằng dãy số đã cho có giới hạn và tìm giới hạn đó. 1  a Hướng dẫn: Ta có 3
x =  x + x +
  a tương tự bài 7 trên 2 1 1 2 3 x  1 
Bài 8: Cho dãy số ( x được xác định bởi 2
x = n + a n +1, n
 = 1,2,... a R n ( ) n )
a) Tìm a sao cho dãy số ( x có giới hạn hữu hạn. n )
b) Tìm a sao cho ( x là dãy số tăng (kể từ số hạng nào đó) n )
tương tự bài 8 trên 5 20n + 21
Bài 9: (T10/404) Cho dãy số ( x xác định bởi x = và 3 x = x −12x + n ) 1 n 1 + n n 2 n + . Chứng minh 1
dãy số ( x có giới hạn và tìm giới hạn đó. n ) 1  5 
Bài 10: (HSG Tây ninh 2014) Cho dãy số (u xác định bởi u = 2 và * u = u +  n   n ) 1 n 1 + 2 n un
Chứng minh rằng u  5 (n  2 Tìm limu . n ) n
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 51
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
IV. GIỚI HẠN CỦA DÃY TỔNG. a = 2  n 1 1
Bài 1. Cho dãy số (a xác định bởi * 
nN . Tìm lim  ,n =1;2;3... n ) 2
a = a − a +1  = a n 1 + n n i 1 i
Để tiến hành giải bài toán trên ta tiến hành theo các bước sau.
Bước 1: Chỉ ra lima = + . n n 1
Bước 2: tính tổng  i 1 = ai n 1 Bước 3: Tìm lim  . i 1 = ai Giải
Do a = 2 1và a
− a = a −1 ,n =1;2;3... nên 1 2 = a a a ... n 1 + n ( n )2 1 1 2 3
tức là dãy số nầy tăng (1).
Ta chứng minh dãy số (a không bị chặn trên (2). n )
Thật vậy, nếu dãy số (a bị chặn trên thì (a hội tụ Giả sử lim a = a a n ( ) 1 n ) n )
khi đó a = a + (a − )2 1
a =1 (mâu thuẩn).
Từ (1) và (2)suy ra lima = + . n 1 1 1 Ta có a −1= a a −1  = − , i = 1; 2;... i 1 + i ( i ) a a −1 a − 1 i i i 1 + n 1 n  1 1  1 suy ra  =  −  =1− →1 − − − khi n → +. i 1 = a = a a a i i 1 1 1 1  i i 1 +  n 1 + n 1 Vậy lim  =1khi n →+. i 1 = aix =1    1 x x x
Bài 2 : Cho dãy số ( x xác định bởi  n =1;2;3; Tìm 1 2 lim + +... n +  n ) 2
x = 2008x + xx x x   n 1 + n n 2 3 n 1 + Giải Ta có 2 x
− x = 2008x  0,n =1;2;3... nên dãy số (x là dãy số tăng và dương .Ta n ) n 1 + n n
chứng minh ( x không bị chặn trên. n )
Thật vậy, nếu dãy số ( x bị chặn trên thì ( x hội tụ Giả sử lim x = a(a  0 khi đó n ) n ) n ) 2
a = 2008a + a a = 0 (vô lý).suy ra lim x = + . n x 1  1 1  Biến đổi 2 x = 2008 k x + x  =  −  k 1 + k k x 2008 x x k 1 +  k k 1 +  x x x 1  1 1  suy ra 1 2 + +... n + =  −  x x x 2008 x x 2 3 n 1 +  1 k 1 + 
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 52
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020 x x x  1 Vậy 1 2 lim  + +... n +  = . x x x 2008  2 3 n 1 +   1 x =  1  2
Bài 3: Cho dãy số ( x ), n =1, 2,... xác định bởi n 2
x + 4x + xn n n x = n 1 +  2 n 1
Chứng minh rằng dãy ( y với y = 
, n = 1; 2;3... có giới hạn hữu hạn. Tìm lim y . n ) n 2 n i 1 = xi Giải
Từ giải thiết ta thấy x  0 n  1 nên n 2 2
x + 4x + x
x + 4x − x x n n n n n n 2 n x − x = − x = =  0, n   1 n 1 + n n 2 2 2
x + 4x + x n n n
Do đó dãy số ( x tăng. n ) 2
a + 4a + a
Giả sử lim x = a (a  0 khi đó a =  a = 0 (vô lý). n ) 2 Suy ra lim x = + . n 2
x + 4x + x n n n 1 1 1 Từ 2 x =
x = x x +1  = − n  1 n 1 + n 1 + n ( n 1 + ) 2 2 x x x n 1 + n n 1 + n 1 1  1 1   1 1   1 1  1 1 1 Suy ra y =  =
+  −  +  −  +...+  −  = − = 6 − n 2 2 = x x x x x x x x x x x i 1 i 1  1 2   2 3   n n 1 +  1 n 1 + n 1 + 1
Do đó y  6 n
 1và dãy số ( y tăng vì y = y +  y n ) n n 1 + n n xn 1 +
Vậy dãy số ( y có giới hạn hữu hạn và lim y = 6 n ) na =1 1 
Bài 4 : Cho dãy số (a xác định bởi *  n N n ) a
= a a +1 a + 2 a + 3 +1  n 1+ n ( n )( n )( n )  n 1 đặt y = 
, n = 1; 2;3... Tìm lim y . n + n i 1 = x 2 i Giải
Từ công thức xác định dãy suy ra a = 5và a  0 n
 =1;2;3... ta biến đổi . 2 n
a (a + )(a + )(a + ) + = ( 2 a + a )( 2 1 2 3 1 3 a + 3a + 2) +1 n n n n n n n n = (a + a )2 2 + ( 2 3
2 a + 3a ) +1 = 2
a + 3a +1 với n ≥1. n n n n n n 2 2 a
= a + 3a +1 3a  3 a  ...  3na = 3n n 1 + n n n n 1 − 1
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 53
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020 −
Bằng quy nap ta chì ra được n 1 a 3 −  n   2.Nên 1
lim a  lim 3n = + ta lại có n n n→+ 2 a = a + 3a +1 2
a +1 = a + 3a + 2 = a +1 a + 2 nên n 1 + n n ( n )( n ) n 1 + n n 1 1 1 1 = = −  1 1 1 = − a +1 a +1 a + 2 a +1 a + 2 a + 2 a +1 a + 1 n 1 + ( n )( n ) n n n n n 1 + n 1 n  1 1  1 1 1 1 1 Do đó y =  =  −  = − = − → n + + + + + + i 1 = x 2 = x x x x x i i 1 1 1 1 1 2 1 2  i i 1 +  1 n 1 + n 1 + 1 Vậy lim y = khi n → +. n 2
x = a aR  1 ( )
Bài 5. Xét dãy số thực ( x )(n  ) 1 xác định bởi  n
 1 . Tìm tất cả các giá trị n 3 2
x = 2x − 5x + 4xn 1+ n n n
của a để dãy số ( x có giới hạn hữu hạn. Hãy tìm giới hạn của dãy số ( x trong các trường n ) n ) hợp đó. Giải
Xét hàm số f (t) 3 2
= 2t − 5t + 4t .Khi đó dãy số đã cho có dạng x = f x n   N ta có n+ ( n ) * 1 f (t ) 2 '
= 6t −10t + 4 = 2(3x − 2)(x − )
1 và f ( x) − x = x( x − ) 1 (2x − )
3 . Từ đó suy ra f ( x) = xkhi 3 3
x = 0hoặc x = 1hoặc x =
và khi x  0 thì f ( x)  x , khi x
thì f ( x)  x. 2 2 3
Bằng cách lập bảng biến thiên của hàm số f ( x) ta có khi 0  x  thì  f ( x) 3 0  . 2 2
Từ các nhận xét trên ta thu được: (i) Với x (− ;0
 )luôn luôn có f (x)(− ;0  ).  3    (ii) Với x  0; 
 luôn luôn có f ( x) 3  0;  .  2   2   3    (iii) Với x  ; + 
 luôn luôn có f (x) 3  ; +   .  2   2 
Ta xét các trường hợp cụ thể :
Trường hợp 1: a<0 theo (i) thì mọi x  0 và x
− x = x x −1 2x − 3  0 do đó dãy n 1 + n n ( n )( n ) n  3 
số ( x là dãy giảm nên có giới hạn lim x = b khi đó b 0;1;   và bn ) n  2 
ra dãy số ( x không có giới hạn hữu hạn ứng với a<0. n )
Trường hợp 2: a=0. Khi đó dãy số ( x là dãy hằng và lim x = 0. n ) n 3 3
Trường hợp3: 0  a
theo (ii) thì mọi 0  x  và x
−1  x −1 x −1  x −1 n 1 + ( n )2 2 n 2 n n  3  do x  0; nên ( x − x −  . n ) 1 (2 n ) 1 1 n    2 
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 54
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
Bằng phương pháp quy nạp từ x
−1  x −1 suy ra x −1  a −1 với mọi n nguyên n 1 + n n 1 + dương.  3  1 do a  0; 
 nên a −1  suy ra lim x =1  2  2 n 3 3
Trường hợp 4: a =
Khi đó dãy số ( x là dãy hằng và lim x = . n ) 2 n 2 3  3 
Trường hợp 5: a
theo (iii) thì mọi x  ; + 
 và x − x  0 +
do đó dãy số ( x là n ) 2 n  2  n 1 n  3 
dãy tăng. Nếu tồn tại giới hạn hữu hạn lim x = b thì b  0;1;   và b>0 ( vô lý). n  2   3
Kết luận: Dãy số ( x có giới hạn hữu hạn khi và chỉ khi a  0; . n )    2
Khi a = 0 thì lim x = 0. n
Khi 0  a 1thì lim x =1. n 3 3 Khi 1 a  thì lim x = 2 n 2 x = 0 
Bài 6. Xét dãy số ( x )(n =1;2;3.. )
. xác định bởi  1
.Vớin=1;2;3…và 𝛼 là số cho trước n x = 1+  n 1+ x +1  n
lớn hơn 1. Tìm lim x . n Giải
Nhận xét: với x = 1thì x 1 với n=1;2;3….. 0 n
Xét hàm số f (t ) 1 = 1+ x = f x n   N +
t + .Khi đó dãy số đã cho có dạng n 1 ( n ) * 1 1 − ta có f '(t ) =  0và f (t) 1 '  với x>1 ( 8 t + )2 1 2 1 1+ t +1
Vì f(1)>1 và f(2)<2 nên phương trình f ( x) = xcó nghiệm duy nhất trong (1; 2) . Gọi nghiệm đó là L
Theo định lý Lagrange thì với mọi L≠x>1 tồn tại c>1 sao cho
f ( x) − f (L) = f (c) f (x)− f (L) 1 '  x − L f x
− f L x − L x − và ( n ) ( ) 1 L 8 8 n n 1 + 1  1  Hay x
− L x − L  ... 
x −1 suy ra lim x = L n 1 + n   0 8  8  n
Ta cần xác định L. giải phương trình
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 55
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020 3     f ( x) 1 1 1 25 = x  1+ = x x + − 2 x + =     x +1  3   3  27 43 177 43 177 1 ta được L = + + − − trong khoảng (1;2). 54 18 54 18 3 43 177 43 177 1 Vậy lim x = + + − − . n 54 18 54 18 3 x = 2,1 1 
Bài 7: Xét dãy số ( x )(n =1;2;3.. ) . xác định bởi 2 
.Với mỗi số nguyên n
x − 2 + x + 8x − 4 n n nx = n 1 +  2 n 1
dương n , đặt y =  Tìm lim y . n 2 − n i =0 x 4 i 1 + Giải 2
x − 2 + x + 8x − 4 Nhận xét: ta có 2
x − 4 = (x −3)(x − 2). 2
Phương trình không có nghiệm khi x>2. Do đó 2,1 x x x  ... (1). 1 2 3
Mặt khác từ công thức truy hồi của dãy ( x ở giả thiết bài toán ta suy ra n )
(2x − x + 2 = x + x −  x + x + − x x + x − x = x + x − + . n )2 2 2 2 2 8 4 4 4 4 8 4 8 4 n 1 n n n 1 + n n 1 + n n 1 + n n n 2 2
x − 4 = x x − 2x + 3x − 6  x − 4 = x + 3 x − 2 n 1 + n 1 + n n 1 + n n 1 + ( n 1+ )( n ) 1 x + 3 x + 2 +1 + + 1 1 1 1 1 n 1 n 1  = = = +  = − 2 2 2 2 x − 2 x − 4 x − 4 x − 2 x − 4 x − (2). 4 x − 2 x − 2 n n 1 + n 1 + n 1 + n 1 + n 1 + n n 1 + 1 1 1
Từ (1) và (2) ta thấy tồn tại lim x và lim = lim − lim = 0 n 2 x − suy ra 4 x − 2 x − 2 n 1 + n n 1 + lim x = + . n n 1 n  1 1  1 1 1 Do đó y =  =  −  = − =10 − n 2 − − − − − − i 1 = x 4 + i 1 = x 2 x 2 x 2 x 2 x 2 n 1  n n 1 +  1 n 1 + n 1 +
Vậy lim y =10 . n  1 a =  1  2
Bài 8. Cho dãy số ( x xác định bởi n =1; 2;... n ) 2 ana = n 1 + 2  a − a +1  n n
a) Chứng minh rằng dãy số (a có giới hạn hữu hạn và tìm giới hạn đó. n )
b) Đặt b = a + a +... + a với mỗi số nguyên dương n.Tìm phần nguyên b và giới hạn n n 1 2 n lim b . n n→ Giải
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 56
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020 2  1  3 Ta có 2
a − a +1 = a −
+  0  a  0 n  1. n nn   2  4 n a −a a − n n ( n )2 2 1 Mặt khác a − a = − a =  0 n 1 + n 2 n 2 a − a +1 a − a + (1) . 1 n n n n 1
Do đó chứng minh quy nạp ta được: 0 a a ... a . n n 1 1 2
Vậy dãy số (a là dãy giảm bị chặn dưới bởi 0, suy ra tồn tại lim a = a và (1) s n ) n n→ 2 a a −1 1 1 1 1 b) Ta có a −1 n = −1 n =  = a +  a = − n 1 + 2 2 a − a +1 a − a + 1 a −1 n a −1 n a −1 a −1 n n n n n 1 + n n 1 + n n n  1 1  1 1 1
do đó b = a =  −  = − = 2 − n i − − − − − i 1 = i 1 = a 1 a 1 a 1 a 1 1 an 1+ nn 1 + 1 n 1 + 1 1 vì 0 a 2 1 1 b 0 b 0 n 1 n n và 2 1 an 1
lim a = 0  lim b = 2 −1 =1 . n n n→ n→ a
Bài 9: Cho dãy số (a xác định bởi a = a =1và n 1 a = a − +
, n = 2,3,... Chứng minh rằng n ) 1 2 n 1 + n n(n + ) 1
dãy số (a có giới hạn hữu hạn. n ) Giải Ta thấy * a  0, n
  N do đó suy ra dãy số (a là dãy số tăng. Theo giả thiết ta có: n ) n a aan 1 − n 1 − n−2 a = + a = +  + a  = ... n 1 + − n(n + ) 1 n n(n + ) 1 (n −  ) n 1 1 na a a a a n 1 − n−2 n−3 2 1 = ( + ) + + + + + + a n n 1 (n − ) 1 n
(n − 2)(n − ) ... 2 1 3.4 2.3 a a a 1 1 n 1 − n−2 n−3 = + + + + + +
n(n + ) (n − ) n
(n − )(n − ) ... ( 1 ) * 1 1 2 1 3.4 2.3 5
Bằng quy nạp ta chứng minh a  , n  = 3,4,... n 3 a 1 7 5 Ta có 1 a = a + =1+ =  3 2 2.3 6 6 3 5
Giả sử a  , k
  N :3  k n khi đó từ (*) ta có: k 3 5  1 1 1 1  1 1 a   + + + ...+  + + +1 n 1 + 3 n(n + ) 1 (n − ) 1 n (n − 2)(n −  ) 1 4.5 3.4 2.3 
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 57
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020 5  1 1   1 1   1 1  1 1 = − + − + ...+ − + + +1      
3  n n +1  n −1 n   4 5  12 6 5  1 1  5 5 1 5 20 5 = − +  . + = =   3  4 n +1  4 3 4 4 12 3
dãy số (a tăng và bị chặn trên nên dãy số (a có giới hạn hữu hạn. n ) n )
Lưu ý: Giả sử a  , k
 N :3 k nta chứng minh a  k n 1 +  1 1 1 1  5 từ (*) ta có: a    + + + ...+  + n 1 + k (k + ) 1 (k − ) 1 k (k − 2)(k −  ) 1 4.5 4   1 1  5  5  + =  + − +  5 5   Để a  thì =    = .  + 4 k +1  4 4 n 1 4 3
BÀI TẬP RÈN LUYỆN.  1 1 1 
Bài 1. Cho dãy số ( x xác định bởi x = 3 và.Tìm lim + +...+  n ) 1 x −1 x −1 x −1  1 2 n   x x x
Bài 2. Cho dãy số ( x xác định bởi x = a 1 và 2 x = x .Tìm 1 2 lim + +... n +  n ) 1 n 1 + n x −1 x −1 x −1  2 3 n 1 +  1 n 1
Bài 3. Cho dãy số ( x xác định bởi x = 2 và x
= x + n=1,2,…. Đặt S =  .Tìm n+ ( 2 1 1 n ) n ) 1 2 n + k 1 = x 1 kS2008 phần nguyên và tìm limS . n n x
Bài 4. Cho dãy số ( x xác định bởi x = a 1 và 2 2003x
= x + 2002x n 1 Tìm lim k  . n 1 + n n ( ) n ) 1 − k 1 = x 1 k 1 + 2 x + x −1 n 1
Bài 5. Cho dãy số ( x xác định bởi x = a 1 và n n x = n  1 Tìm lim  . n 1 + ( ) n ) 1 x 2 − k = x 1 n 1 k 1 n 1
Bài 6. Cho dãy số ( x xác định bởi x = 8 và x = x − x + n = Tìm lim  . n+ ( 2 7 25 1,2,.. 1 n n )( ) n ) 1 3 − k 1 = x 2 k n 1
Bài 7. Cho dãy số ( x xác định bởi x = 2009 và x = x x +1 Tìm lim  . n 1 + n ( n )2 n ) 1 + k 1 = x 1 k 4 x − x +1
Bài 8. Cho dãy số ( x xác định bởi x = 2 và n n x = n 1 y n 1 + ( ) n ) 1 3 x − x +
Chứng minh dãy số ( n ) 1 n n n 1
xác đinh bởi y = 
có giới hạn và tìm giới hạn đó. n 3 k 1 = xk
Bài 9. (HSG Gia Lai năm 2011 – 2012) Cho dãy số (a xác định bởi a = 24,a = 60và n ) 1 2 an 1 a = a − + , n = 2,3,... a
có giới hạn hữu hạn.. n 1 + n n(n + ) 1 (n +
Chứng minh rằng dãy số ( n ) 2)
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 58
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020
V. PHƯƠNG PHÁP SO SÁNH DÃY SỐ .
1) Đinh lý 11 (Nguyên lý kẹp) Nếu ba dãy số ( x ),( y ), z thỏa điều kiện n n ( n)
y x z , n
  n và lim y = lim z = L thì lim x = L . n n n 0 n n n n→+ n→+ n→+ CÁC BÀI TOÁN.
Bài 1: (Đề Olympic toán SV toàn quốc 2003) Cho dãy số ( x xác định bởi n ) 1 2 k x = + + ...+ k  = Hãy tính lim n n x + x + ... n n + x k (k + ) , 1, 2,... 2! 3! 1 ! 1 2 2003 n→+ Giải k +1 Vì x − x =  0
0  x x  ...  xx ... k 1 + k (k + nên 2)! 1 2 2002 2003 k (k + ) − Ta có : 1 1 1 1 ( = = − . k + ) 1 ! (k + ) 1 ! k! (k + ) 1 ! 1 2 k  1   1 1   1 1  1 Do đó x = + + ...+ = − + − + +      −  = − k (k ) 1 ...      k  (k ) 1 2! 3! 1 ! 2! 2! 3! ! 1 ! + +  (k + ) 1 ! Ta có: n n n  + +... n +  2003 n x x x x x . 2003 1 2 2003 2003 1 suy ra n n n xx + x + ... n + x  2003n x . 2003 1 2 2003 2003 1 1   n n n 1 nên 1 n −
x + x + ...+ x  2003n 1− . 1 2 2003   2004!  2004! 1  1   1  1 Vì lim 1− = 2003n lim 1− =1−     n→+  2004! n→+   2004! 2004! n n n 1
Suy ra lim n x + x + ... + x =1− . 1 2 2003 n→+ 2004!
Bài 2: (Đề Olympic 30/4/ 2011) Cho dãy số (u xác định bởi u = a  0 và n ) 1 nu u = u + , k
 = 1,2,... Tìm giới hạn của dãy n   . n 1 + n un n Giải 2 Ta có u = u +
 2 2  2.Giả sử u  , n n   2 2 1 u n 1 2
u − n +1 u + n
u −1 u − n Khi đó, u − n +1 n n n n = =  0 n 1 + ( ) ( ) ( )( ) u u n n u
Theo nguyên lý quy nạp suy ra u  , n n
  2, do đó n 1, n  = 2,3,... . n n n
Từ đây ta được u = u +
u +1 u + 2  ...  u + n −1 n 1 + n n n 1 − 2 ( ) un u u n − 2 u u − 2 suy ra n 2 n 2 1   + 1 1+ ( ) * n n n n n
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 59
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020 u
Từ (*) cho n → + và sử dụng giới hạn kẹp ta được lim n = 1 . n→+ n
Bài 3 (Đề Olympic 30/4/ 2001): 1 2 u
Cho dãy số (u xác định bởi u = và k 1 u = u − + , k
 =1,2,...,n . Tìm lim u . n ) 0 − 2 k k 1 n n n→+ Giải
Từ giải thiết ta có: n(u − u
= u nu − nu + u u −u = u u k k − ) 2 2 1 k 1 − k k 1 − k k 1 − k 1 − k k 1 −  ( u − u u − u n + u = u u −  =  − = k k − ) ( k − ) 1 1 1 1 k k 1 1 1 1 k k 1 − ( ) u u n + u u u n + u k k 1 − k 1 − k 1 − k k 1 − 1 1 1 1 Do
= u u u  ... nên từ (1) ta suy ra −  , k  =1,2,...n(2) 0 1 2 2 u u n k 1 − k Từ (2) thay k = 1,2,… n.
Rồi cộng các bất đẳng thức ta được: 1 1 1 − 1  1
u 1 u  1, k  = 1,2,...n(2 n k ) u u u 0 n n 1 1 1 Nên từ (1) ta suy ra −  , k  = 1,2,...n(3) u u n + 1 k 1 − k
Trong (3) thay k= 1,2,… n . rồi cộng các bất đảng thức ta được 1 1 n 1 n n + 2 n +1 + −    n 1 2 − =   u  1, n   N lim =1 u u n +1 u n +1 n +1 n + .Mà 2 n n→+ n + 2 0 n n Vậy lim u = 1 n n→+
Bài 4 (Đề Olympic 30/4/ 2006): 2 x
Cho dãy số (u xác định bởi 1 x  2 và x =1 n + x + , n
 =1,2,... Tìm lim x ? n ) 1 n 1 + n 2 n n→+ Giải 2 x 1 1 2 3 3 Ta có x =1 n + x − = − x − x − = − x − +  n  = n+ n ( 2 2 2 1 , 1, 2,... 1 n n ) ( n ) 2 2 2 2 2
Bằng quy nạp ta chứng minh x 1, n  =1,2,... n
Theo giả thiết ta có x 1 1 Giả sử x 1, n 2 2 x 3 x x Khi đó từ 2
1  x  2  x − 3x + 2  0 hay n − x +1  0 nx − 1 n − . n n n 2 2 n n 2 2 2  x x x Do đó x =1 n
+  x −  1+1 n − = 2 n −
= 2 −1=1 vì (x  2 n ) n 1 + n 2 2 2  
Vậy theo nguyên lý quy nạp ta suy ra x 1, n  =1,2,... n 3
Như vậy ta chứng minh được 1  x  , n  = 2,3,... n 2
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 60
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020 2 a
Đặt a = 2 khi đó a = 1+ a − . 2 2  a  1 Do đó, ta có: 2 x
− a = 1+ x − x − 1+ a −  = x − a − x − a n+ n n ( n ) ( 2 2 1 n )  2  2 1 = x − a −
x + a = x − a − a − x n ( n ) 1 . 1 . 2 2 n 2 n
mà 2 − a − x  1 n 1 1 1 nên x
− a x − a x − a  ...  x − a n 1 + n 2 n 1 − n 1 2 2 2 1
Vậy 0  x − a x − 2 , = 2,3,... n n 1 − 1 2 1 vì lim
= 0 nên theo nguyên lý kẹp ta được lim x = a = 2 . 1 →+ n 2n− n n→+
BÀI TẬP TƯƠNG TỰ 1
Bài 1 (Đề vô địch Singapore 1997): Cho dãy số (u xác định bởi u = và n ) 0 2 2 u 1 k 1 u = u − + , k
 =1,2,...,n −1. Chứng minh rằng 1−  u 1. Hướng dẫn: xem bài giải bài 3. k k 1 − n n n 1 2 x
Bài 2 (HSG Gia Lai 1996): Cho dãy số ( x xác định bởi x = và n x = −1, n  =1,2,... n ) 1 + 3 n 1 2
Chứng minh rằng dãy số (a có giới hạn hữu hạn và tìm giới hạn đó. n ) Hướng dẫn:
Bằng quy nạp ta chứng minh 1
−  x  0, n  = 2,3,... n
Giả sử lim x = L khi n → + n n→+ 2 LL =1+ 3
Ta giải phương trình: L = −1  
L = 1− 3 . 2 L =1− 3 n 1 −  3  Ta chứng minh 0  x − L   
x − L , n  = 2,3,... n 1 + 2 2   a 2 a x
Bài 2: Cho trước a 0; 
1 , xét dãy số ( x xác định bởi x = và n x = − , n  =1,2,... . n ) 1 + 2 n 1 2 2
Chứng minh rằng dãy số ( x có giới hạn hữu hạn và tìm giới hạn đó. n ) Hướng dẫn : 1 1
Bằng quy nạp ta chứng minh −  x  , n  = 2,3,... 8 n 2
Giả sử: lim x = L khi n → + n n→+
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 61
Chuyên đề : Dãy số và giới hạn của dãy số - Bồi dưỡng học sinh giỏi, Olympic 2020 2 2  a L L = 1+ a −1
Ta giải phương trình: 2 L = −  
L = 1+ a −1 . 2 2 2
L = − 1+ a −1 n 1 −  1  a
Ta chứng minh: x − L  − L , n  = 2,3,... n    2  2 Vây: 2
lim x = 1+ a −1. n n→+ a
Bài 3: Cho trước a (0;+) , xét dãy số ( x xác định bởi x = x
= x 2 − ax , n  =1,2,.... n 1 + n ( n ) n ) 1 2
Chứng minh rằng nếu x  0, n
 =1,2,... thì dãy số (x có giới hạn hữu hạn và tìm giới hạn đó. n ) n Hướng dẫn:
Ta có x = x 2 − ax  0,2 − ax  0,1− ax  1
− .Nhưng vì x  0,a  0 nên 1− ax 1 suy 2 1 ( 1 ) 1 1 1 1 ra * 1− ax  1, n   N 1 Ta có: 1 x − = x
− ax −  ax − = − ax
− ax = a x − ax + = − ax + n ( n ) 1 2 1 1 n+ n ( 2 n ) 2 2 2 2 1 1 n 1 1 n n n a a n 1 − 2 4 2
 1− ax = 1− ax = 1− ax = ... = 1− ax n n 1 − n−2 1 n− Vậy: ( −ax = − ax = do * 1− ax  1, n   N n ) 1 2 lim 1 lim 1 0 n 1 n→+ n→+ Do đó: ( − ax ) 1 lim 1
= 0  lim ax =1 lim x = a− . n n n n→+ n→+ n→+ x = 3 1 
Bài 4 (HSG QG năm 2012): Cho dãy số ( x được xác định bởi n )  n + 2 x = x + n  =  n ( 2 , 2,3,... n 1 − )  3n
Chứng minh rằng dãy số ( x có giới hạn hữu hạn, tính giới hạn đó. n ) Giải Ta có : n + 2 n +   x − = x − +  x − +  x − + n   . n ( 2 2 2 2 5 1 1 1 1 , 10 n 1 − ) n 1 −  n 1−  3n n 3n n 5  n   5 
Đặt y = max  x −1 ; , k   10, n   11 k kk  2  5  2 4
* Nếu y = x −1 thì y x −1 +  .2y = y   . n n n n 1 − n 1 − n 1 − 5  n  5 5 5 5 * Nếu y = thì y  = y n − n n n 1 n − . 1
Vậy : ( y là dãy giảm, bị chặn dưới bởi số 0 nên có giới hạn hữu hạn. n ) Ta chứng minh: a = 0.
Suy ra nên lim x −1 = 0 . Do đó lim x = 1 n n n→+ n→+
GV: Nguyễn Thanh Tâm – Trường THPT Tây Ninh Trang 62