



Preview text:
CHỦ ĐỀ HAI ĐƯỜNG THẲNG VUÔNG GÓC I. KIẾN THỨC TRỌNG TÂM
1) Tích vô hướng của hai vectơ trong không gian
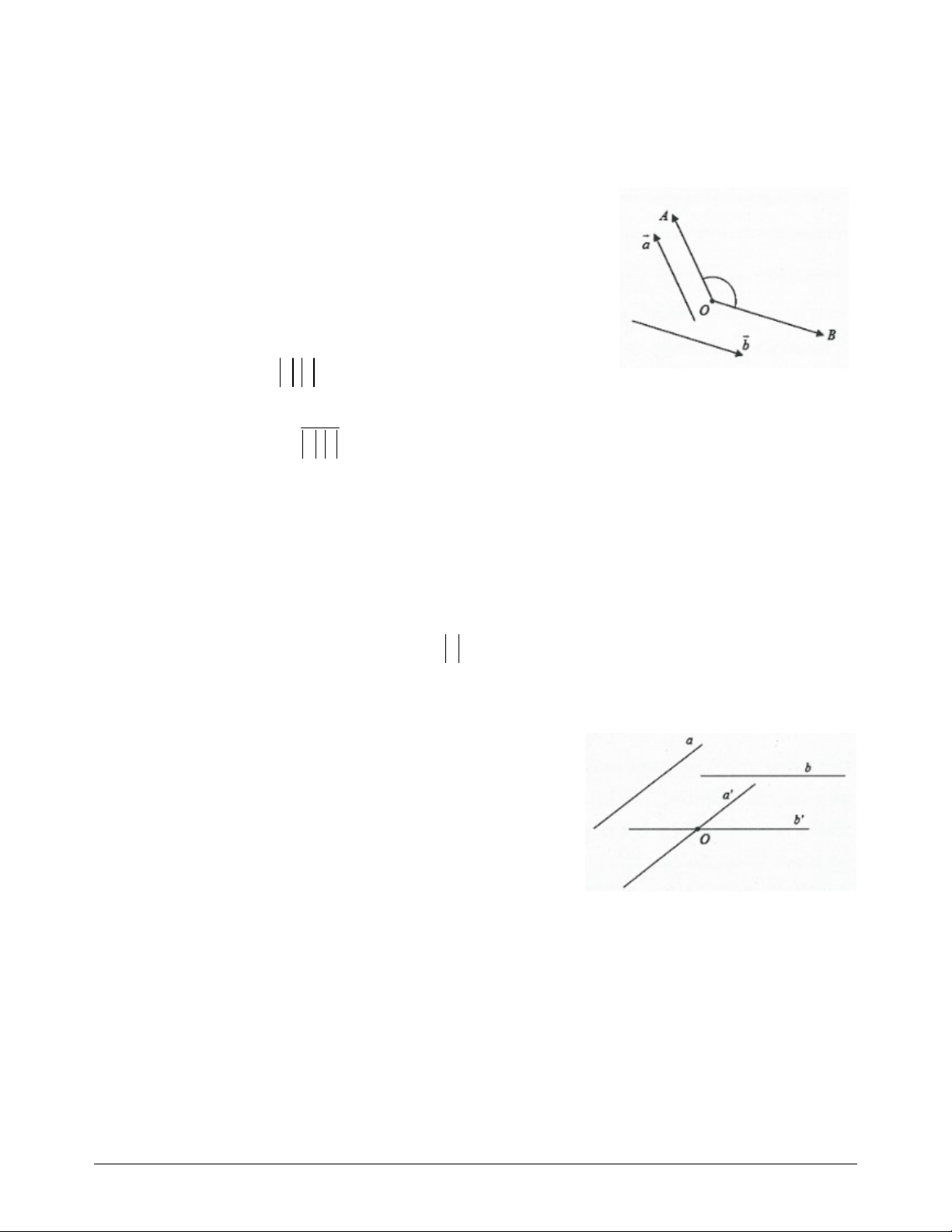
Góc giữa hai vectơ a và b khác 0 được định nghĩa bằng góc
AOB với OA a ; OB b .
Nếu a hoặc b bằng 0 ta quy ước góc giữa chúng có thể nhận một giá trị tùy ý.
Tích vô hướng của hai vectơ a và b là một số, được ký hiệu . a b và được xác định bởi . a b a . b cos ;
a btừ đó suy ra cosin góc giữa hai a b vectơ a và b là a b . cos ; a . b
Đặc biệt khi a b cos ; a b 0 . a b 0 .
Tính chất của tích vô hướng:
Cho 3 vectơ a ; b ; c và số thực k . Khi đó ta có: i) . a b . b a . ii) a b c . a b . a c . 2 2 iii) ka.b k . a b . a kb. iv) a a .
2) Góc giữa hai đường thẳng trong không gian Định nghĩa:
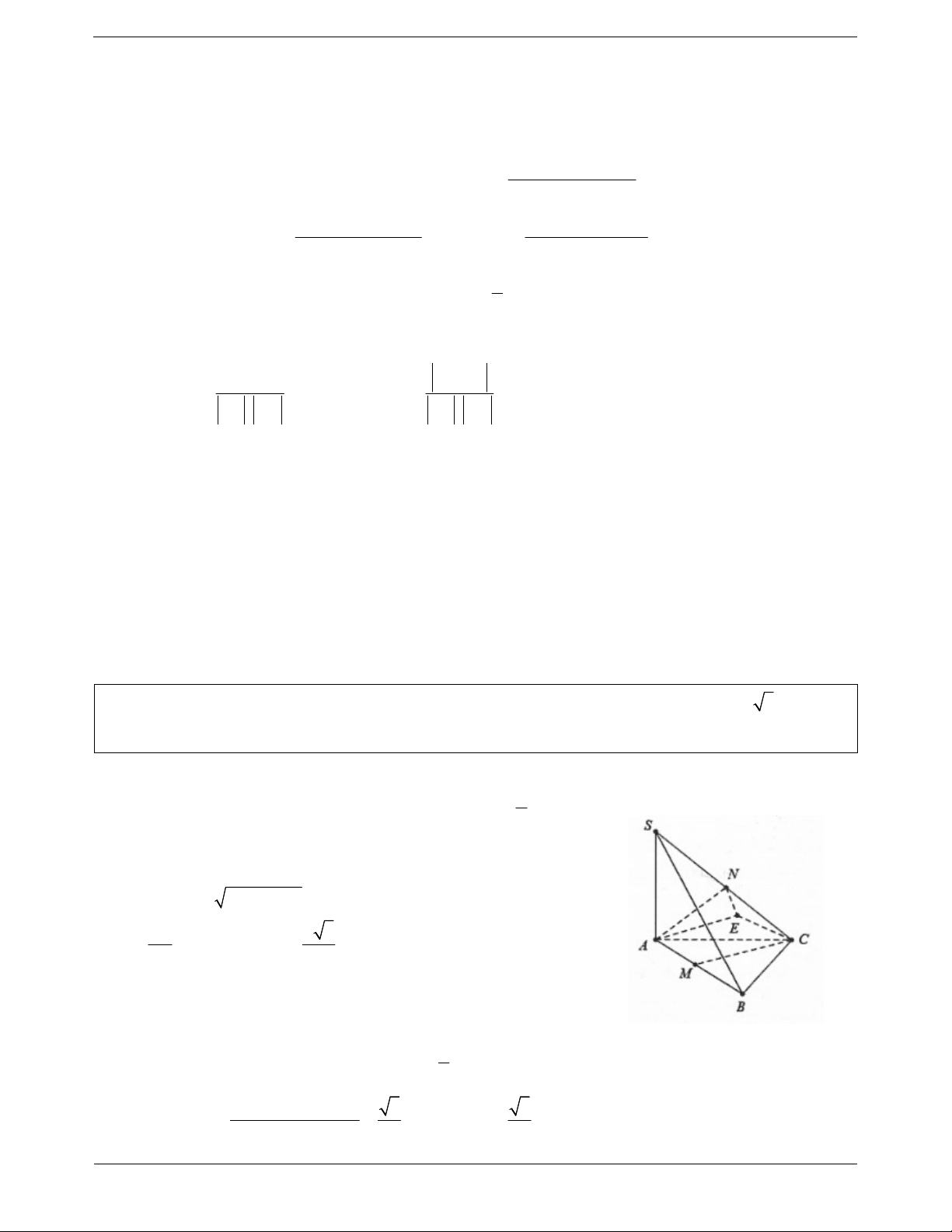
Trong không gian cho 2 đường thẳng a , b bất kỳ. Từ một điểm O
nào đó ta vẽ 2 đường thẳng a , b lần lượt song song với a và
b . Ta nhận thấy rằng khi điểm O thay đổi thì góc giữa 2 đường
thẳng a và b không thay đổi.
Do đó ta có định nghĩa:
Định nghĩa: Góc giữa 2 đường thẳng a và b trong không gian là
góc giữa 2 đường thẳng a và b cùng đi qua một điểm và lần lượt song song với a và b .
Cách xác định góc giữa hai đường thẳng:
Để xác định góc giữa 2 đường thẳng a và b ta có thể lấy điểm O thuộc một trong hai đường thẳng đó rồi
vẽ một đường thẳng qua O và song song với đường thẳng còn lại.
Nếu u là vectơ chỉ phương của đường thẳng a và v là vectơ chỉ phương của đường thẳng b và u;v
thì góc giữa 2 đường thẳng a và b bằng nếu 0 90 và bằng 180 nếu 90 180 .
Nếu 2 đường thẳng a và b song song hoặc trùng nhau thì góc giữa chúng bằng 0 . Trang 1
Góc giữa hai đường thẳng là góc có số đo 0 180 .
Phương pháp tính góc giữa hai đường thẳng:
Để tính góc giữa hai đường thẳng trong không gian ta cần nhớ các công thức sau: AB AC BC
– Định lý hàm số cosin trong tam giác ABC : 2 2 2 cosBAC 2.A . B AC BA BC AC CA CB AB Tương tự ta có: 2 2 2 cos ABC và 2 2 2 cos ACB . 2.B . A BC 2.C . A CB 1
Chú ý công thức đặc biệt: A . B AC A . B AC cos BAC 2 2 2 AB AC BC . 2
– Tính góc giữa hai đường thẳng AB và CD ta tính góc giữa hai vectơ AB và CD dựa vào công thức A . B CD AB CD A . B CD cos ;
cos A ;
B CD AB . CD AB . CD
Từ đó suy ra góc giữa hai đường thẳng AB và CD .
3) Hai đường thẳng vuông góc
Hai đường thẳng được gọi là vuông góc nếu góc giữa chúng bằng 90 .
Ký hiệu: a b hoặc b a a//b
Mối quan hệ giữa quan hệ song song và vuông góc: c b c a
II. HỆ THỐNG VÍ DỤ MINH HỌA
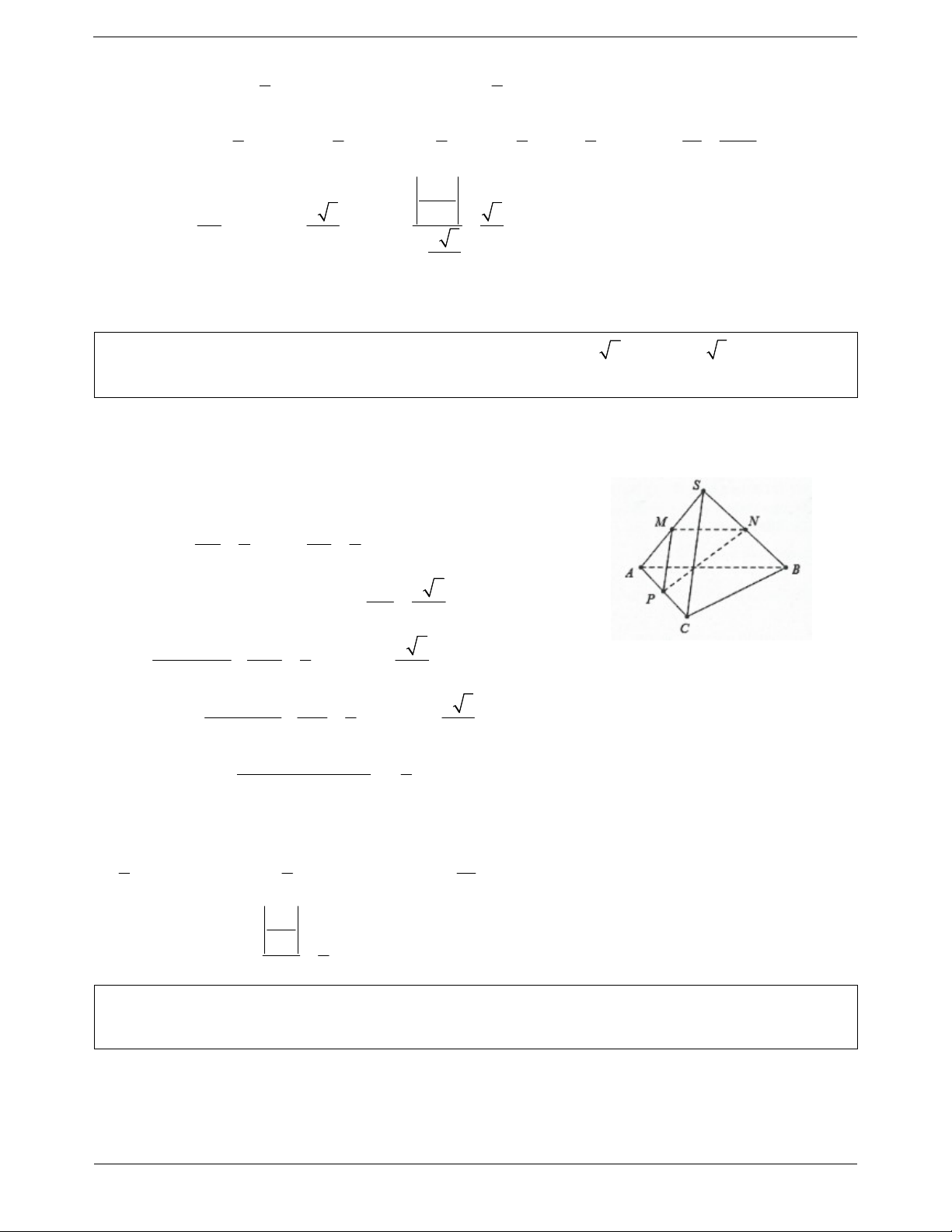
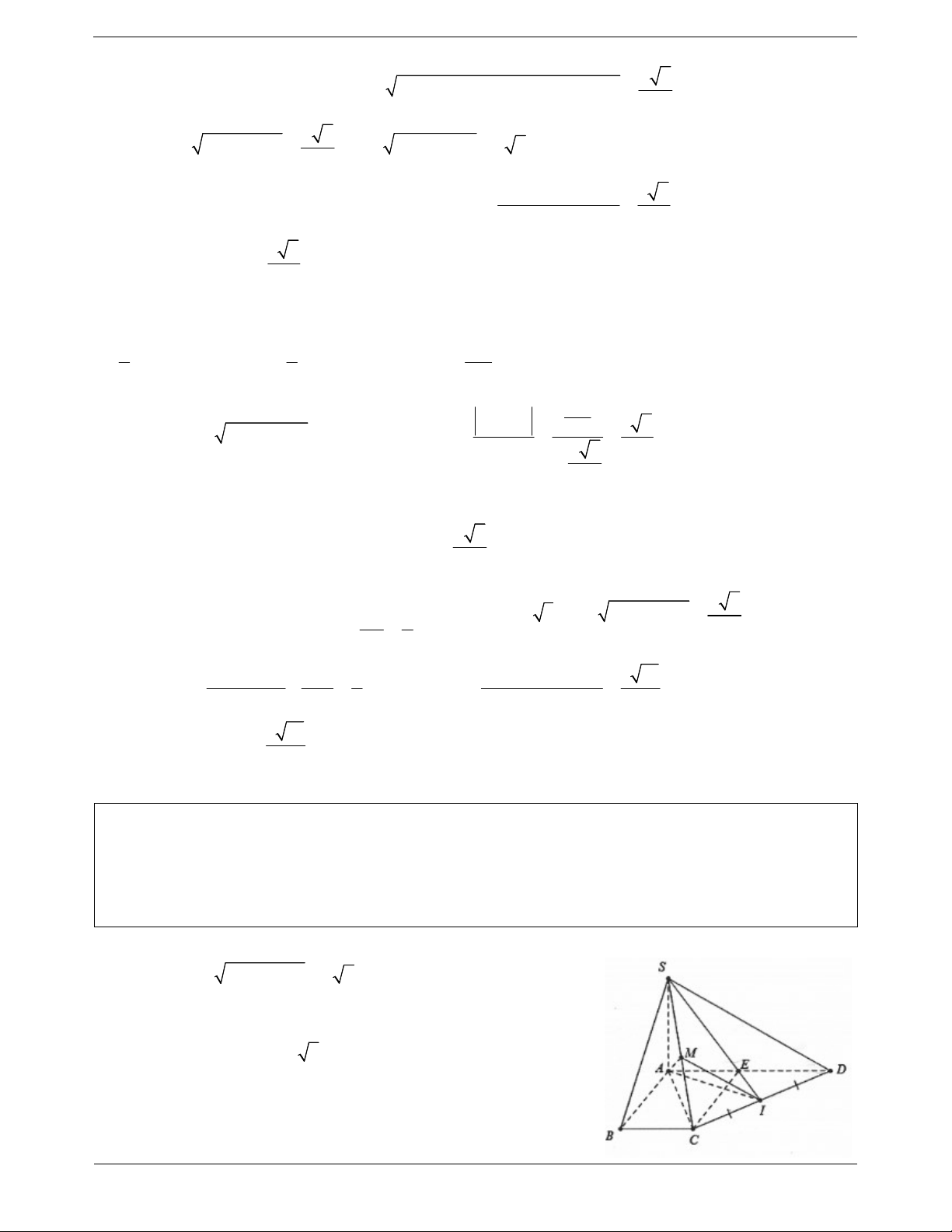
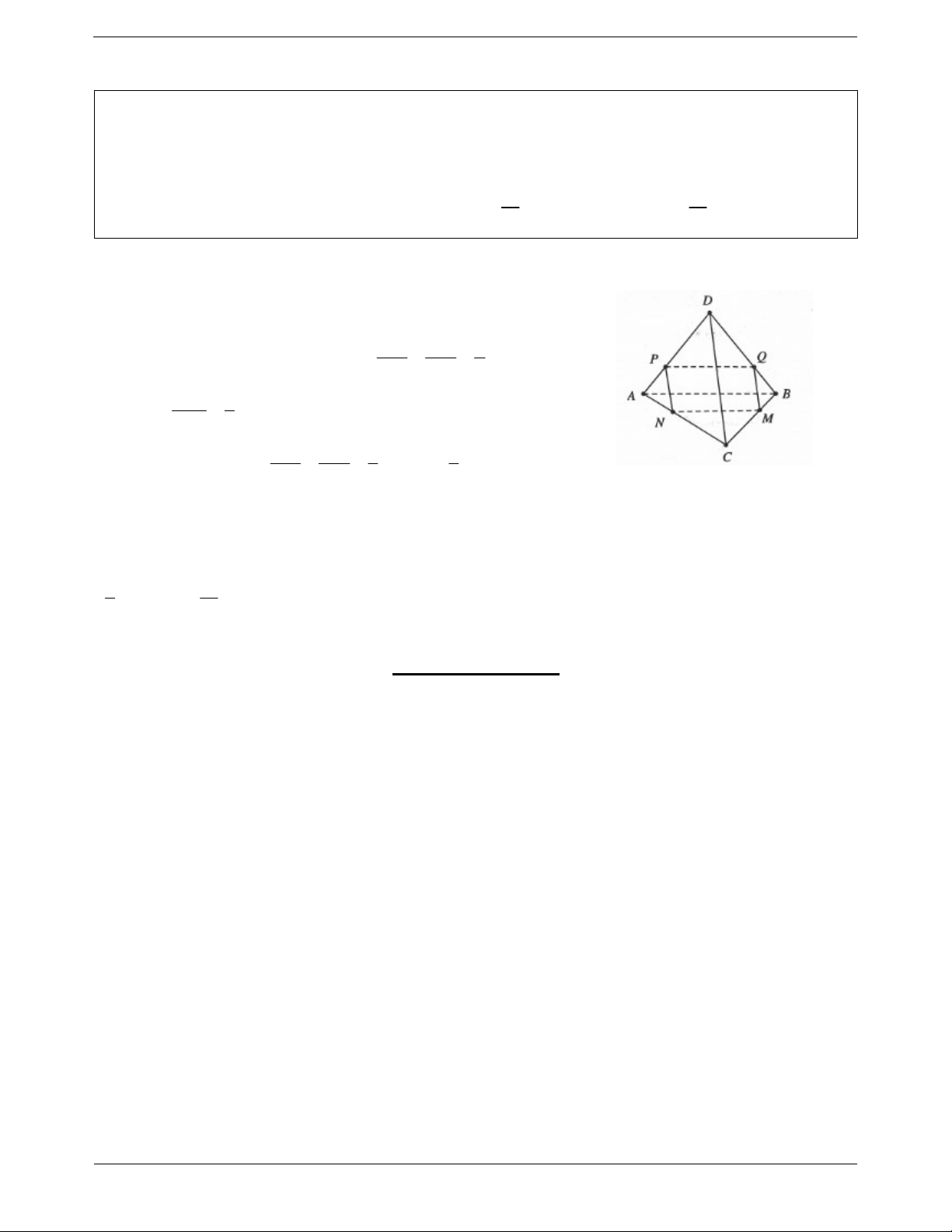
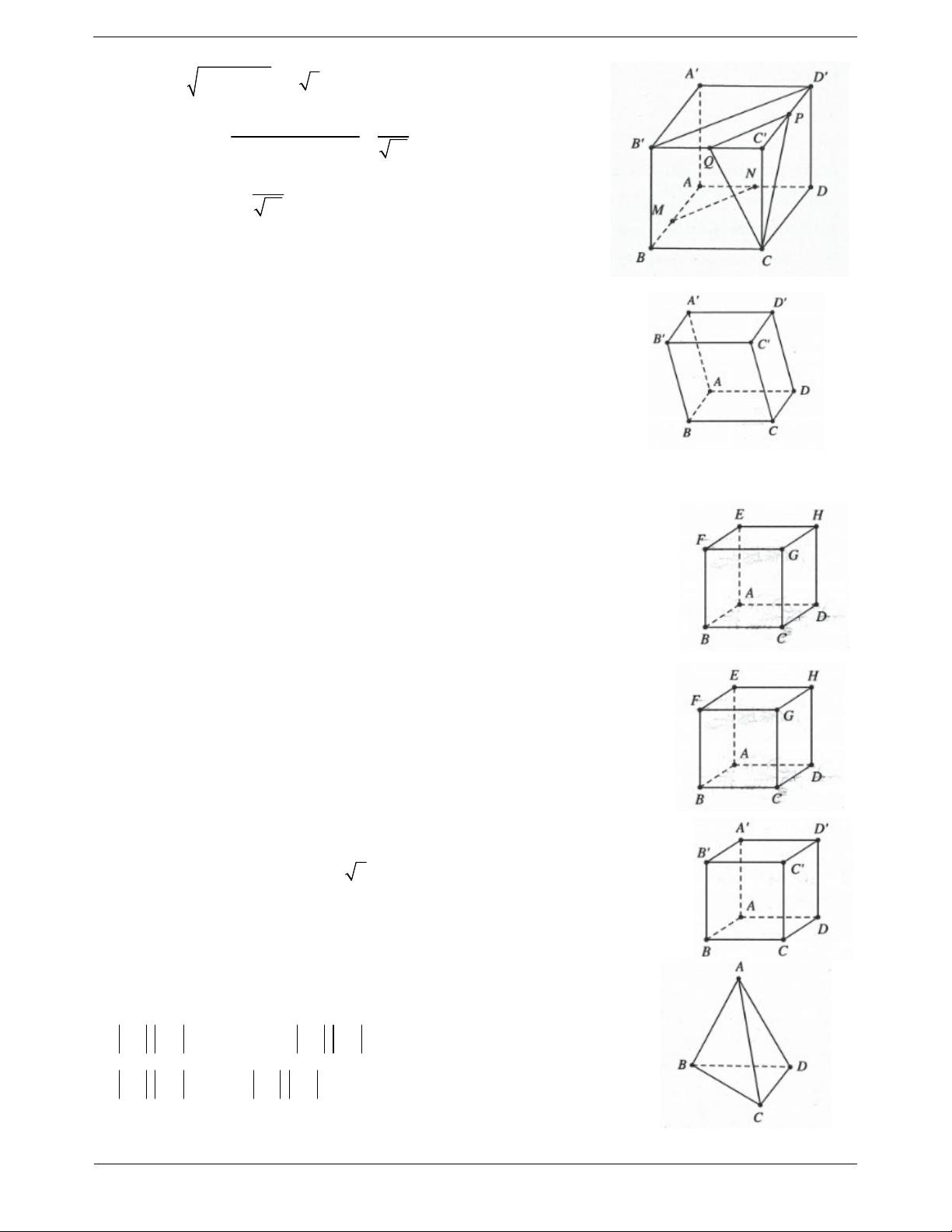
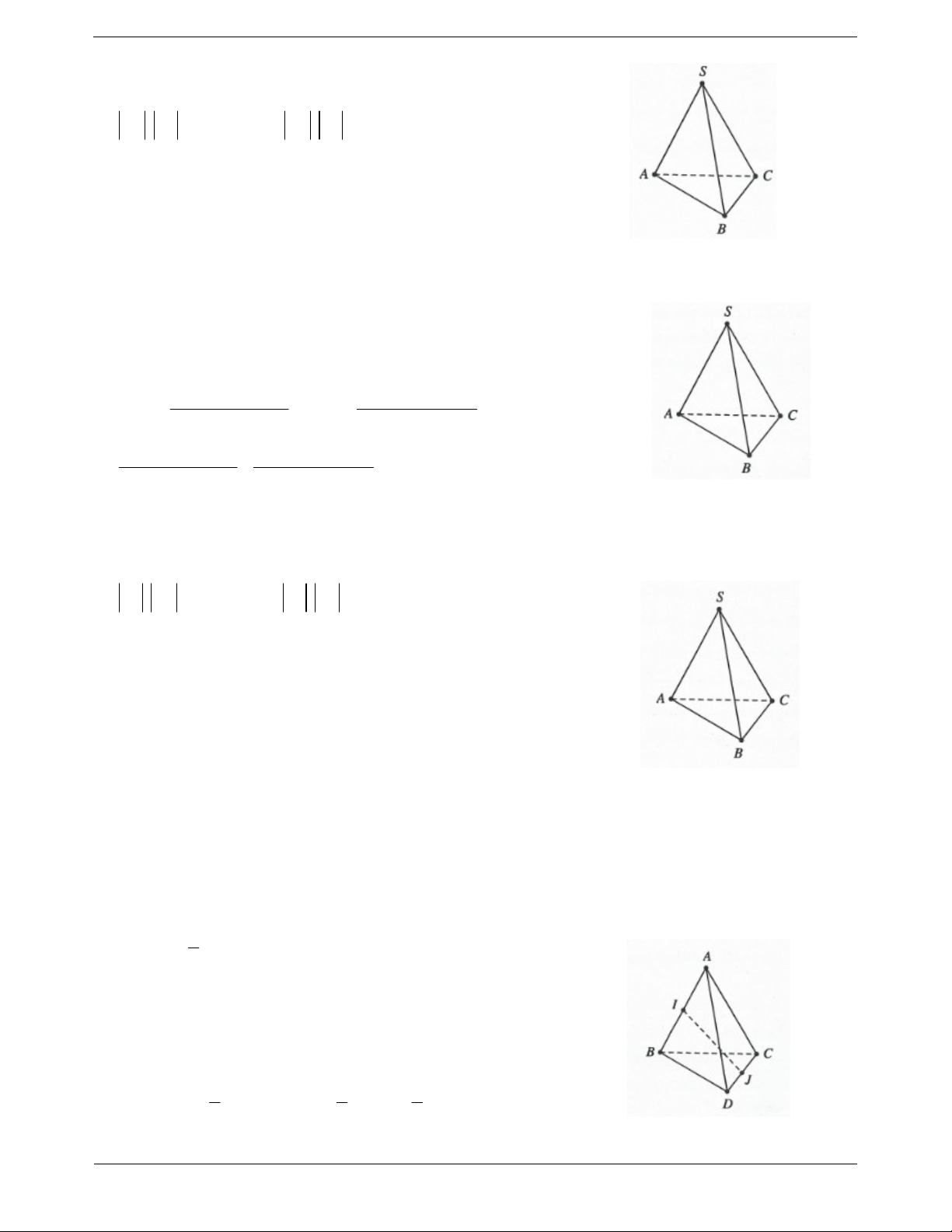
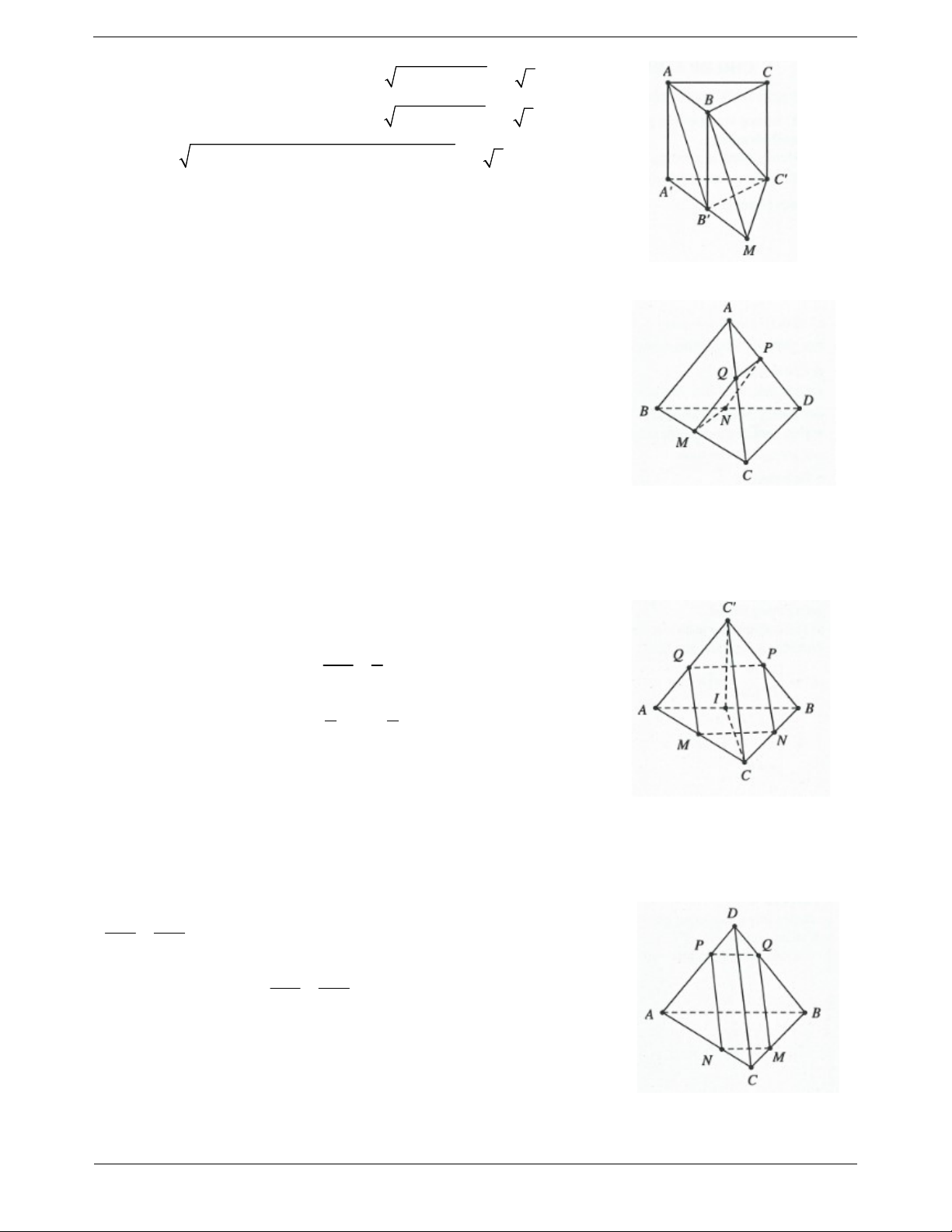
Ví dụ 1. Cho hình chóp S.ABC có đáy là tam giác đều cạnh a , SA ABC và SA a 3 . Gọi M ,
N lần lượt là trung điểm AB và SC . Tính cosin của góc giữa hai đường thẳng AN và CM . Lời giải: a
Cách 1: Dựng hình bình hành AMCE suy ra AM CE . 2 Khi đó AE//CM AN;CM AN;AE . Mặt khác 2 2
SC SA AC 2a độ dài đường trung tuyến AN là SC a 3 AN a . AE CM . 2 2 Do A
BC đều nên CM AM AMCE là hình chữ nhật.
Khi đó CE AE mà CE SA CE SAE CE SE . 1 S
EC vuông tại E có đường trung tuyến EN SC a . 2 AN AE NE Ta có: 2 2 2 3 cosNAE 3 0 cos . 2.AN.AE 4 4 Trang 2
1 1
Cách 2: Ta có: AN AS AC;CM AM AC AB AC . 2 2
1 1 1 1 2 2 1 a 3a
Khi đó AN.CM AS AC 2 AB AC A . B AC AC 2 a cos 60 . 2 2 4 2 4 2 8 2 3a SC a 3 8 3 Lại có AN a; CM cos= . 2 2 a 3 4 . a 2
Bình luận: Dựa vào hai cách làm trên ta thấy rằng, trong một số trường hợp, việc sử dụng công cụ vectơ
để tính góc giữa hai đường thẳng giúp bài toán trở nên dễ dàng hơn rất nhiều!
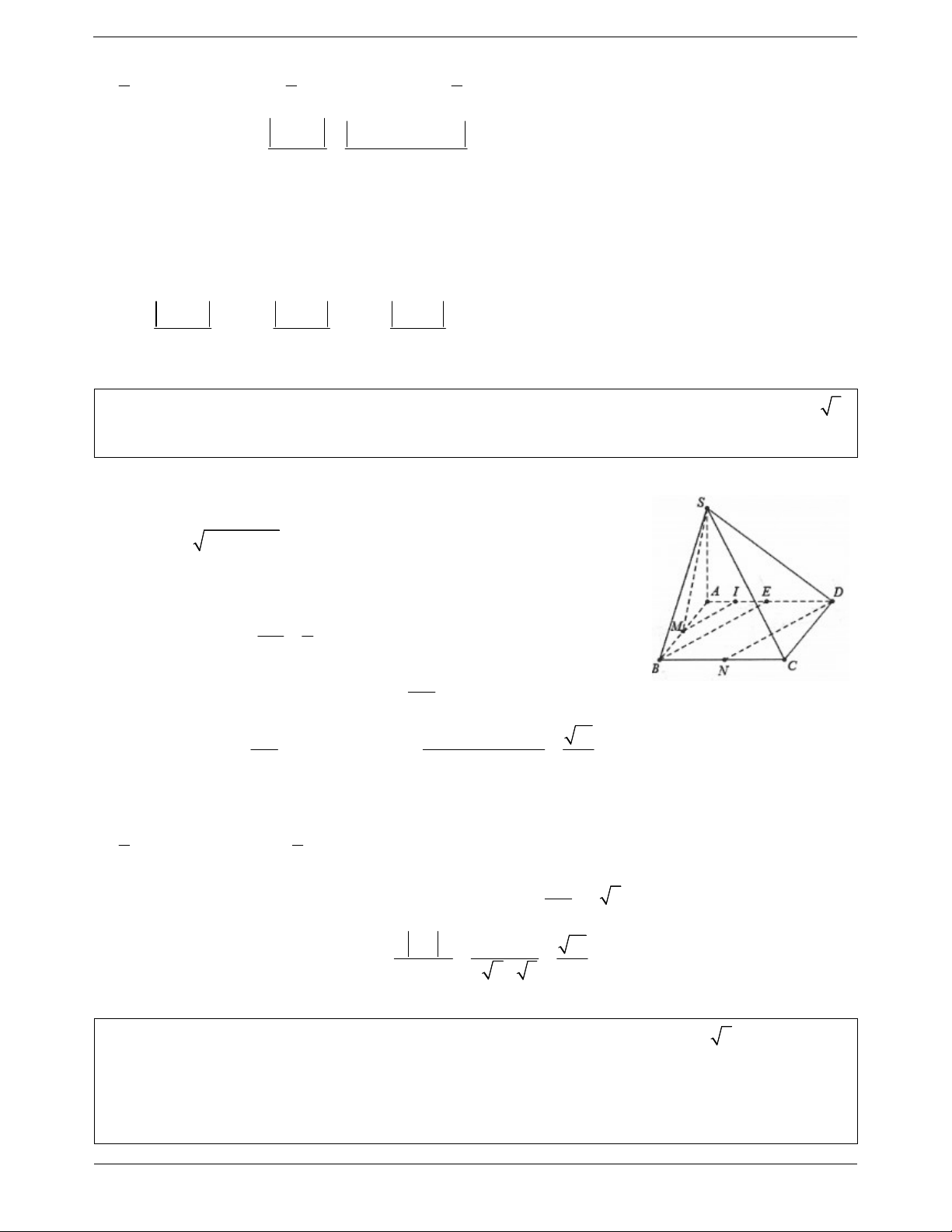
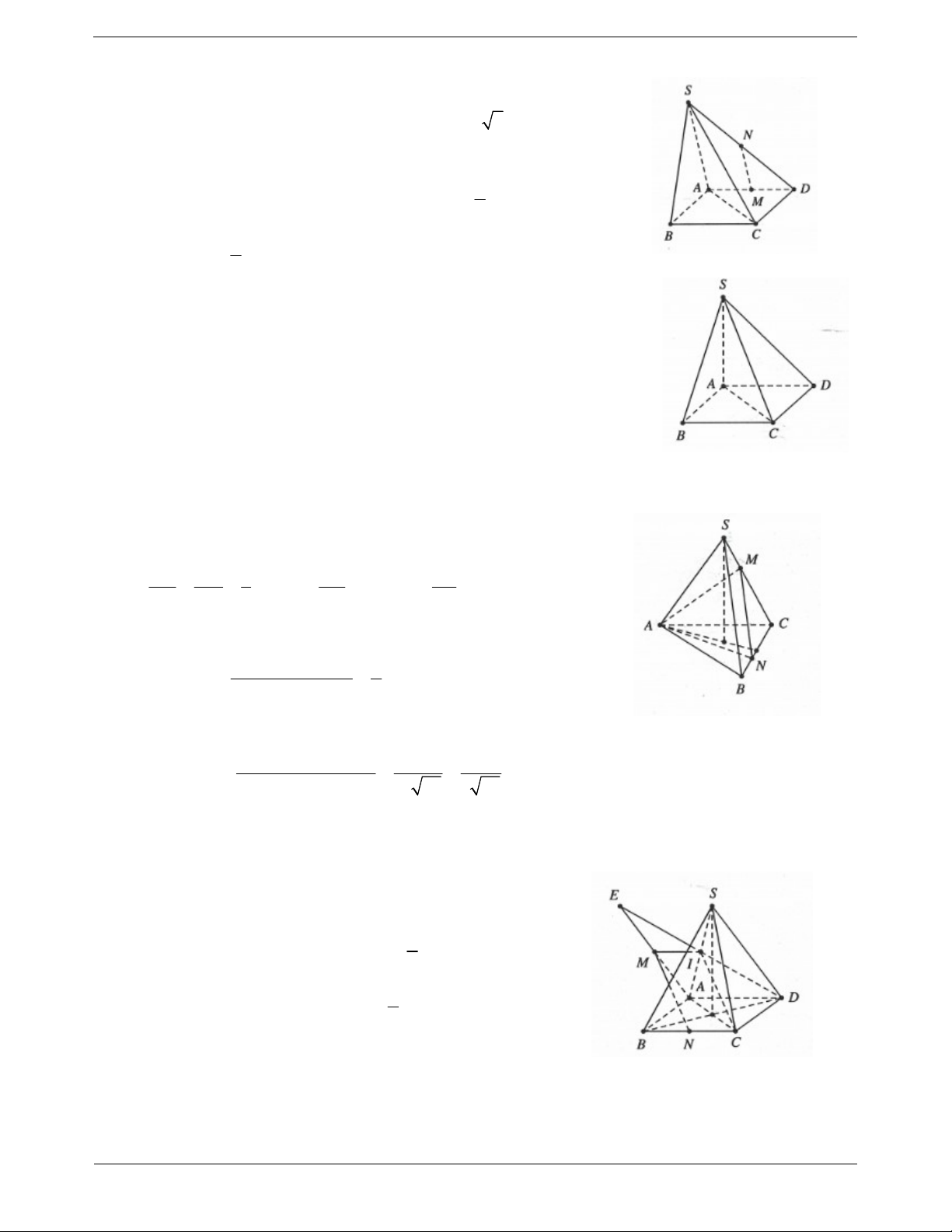
Ví dụ 2. Cho hình chóp S.ABC có SA SB SC AB ;
a AC a 2 và BC a 3 . Tính cosin góc
giữa hai đường thẳng SC và AB . Lời giải:
Cách 1: Gọi M , N, P lần lượt là trung điểm S , A SB và AC . MP//SC Khi đó SC AB MP MN ; ; . MN //AB AB a SC a Ta có MN ; MP . 2 2 2 2 AC a 2 Mặt khác S
AC vuông tại S SP . 2 2 2 2 2 BA BC AC 3 a 6 2 2 BP a BP . 2 4 2 2 2 2 2 PS PB SB 3 a 3 Suy ra 2 2 PN a NP . 2 4 4 2 MN MP NP Khi đó 2 2 2 1 cosNMP NMP SC AB 120 ; 60 . 2.MN.MP 2
Cách 2: Ta có: AB SB SA A .
B SC SB SA.SC S . B SC S . A SC 1 SB SC AC 1 SA SC AB 2 a 2 2 2 2 2 2 . 2 2 2 2 a 2 1 Suy ra cos SC; AB
SC; AB 60. . a a 2
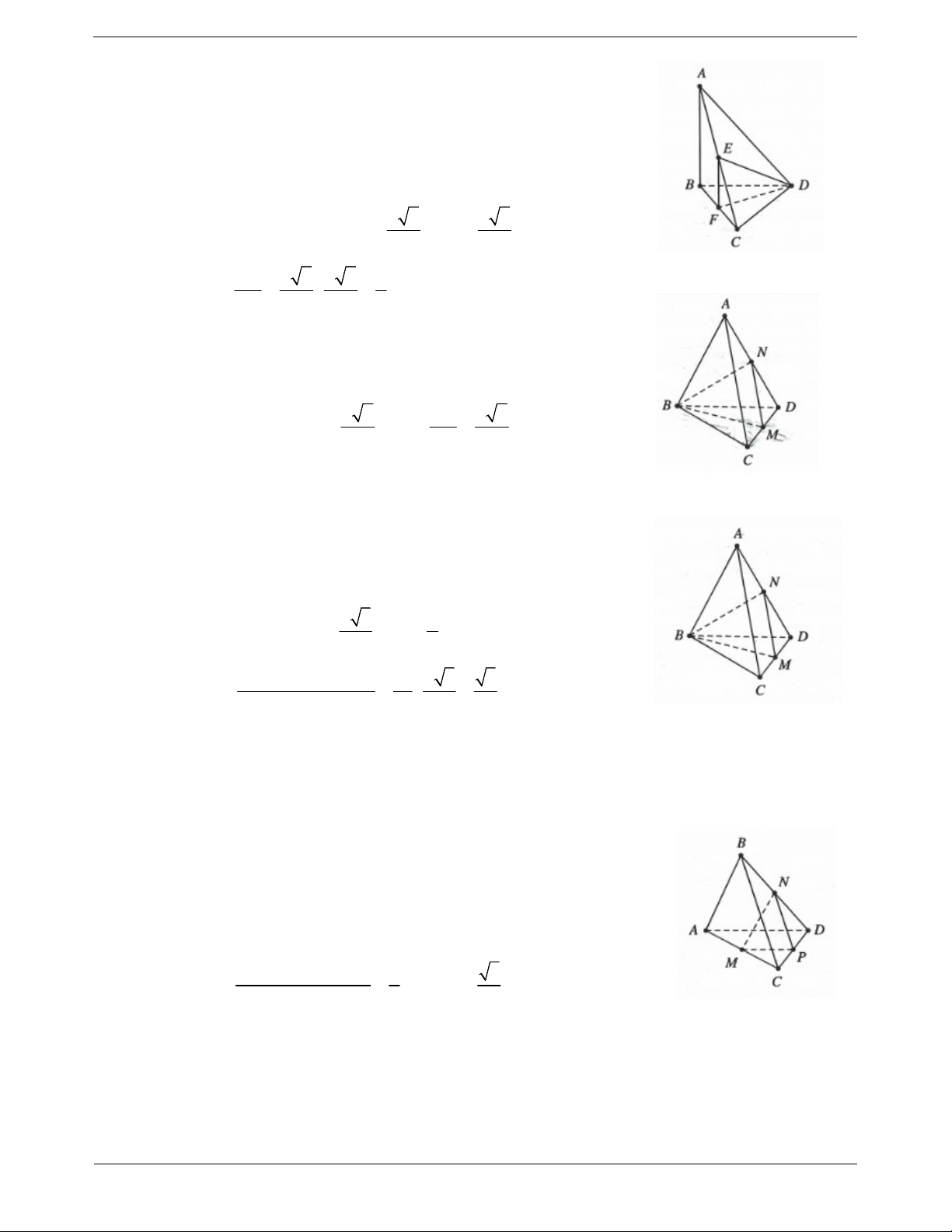
Ví dụ 3. Cho tứ diện ABCD có AB x ,CD x ; AC y , BD y , BC z , AD z . Tính góc giữa hai 1 2 1 2 1 2 đường thẳng BC và AD . Lời giải:
Ta có BC.DA BC DC CA C . B CD C . B CA Trang 3 1 1 1 2 2 2 CB CD BD 2 2 2 CB CA AB 2 2 2 2 AB CD BD CA 2 2 2 2 2 2 2 BC.DA x x y y Khi đó cos BC; DA 1 2 1 2 . BC.DA 2z z 1 2 BC; AD
Đặc biệt: Nếu AB CD x; AC BD y và BC AD z ta đặt AB;CD thì ta có: AC;BD 2 2 2 2 2 2 x y y z z x cos = ; cos = ; cos = . 2 2 2 z x y
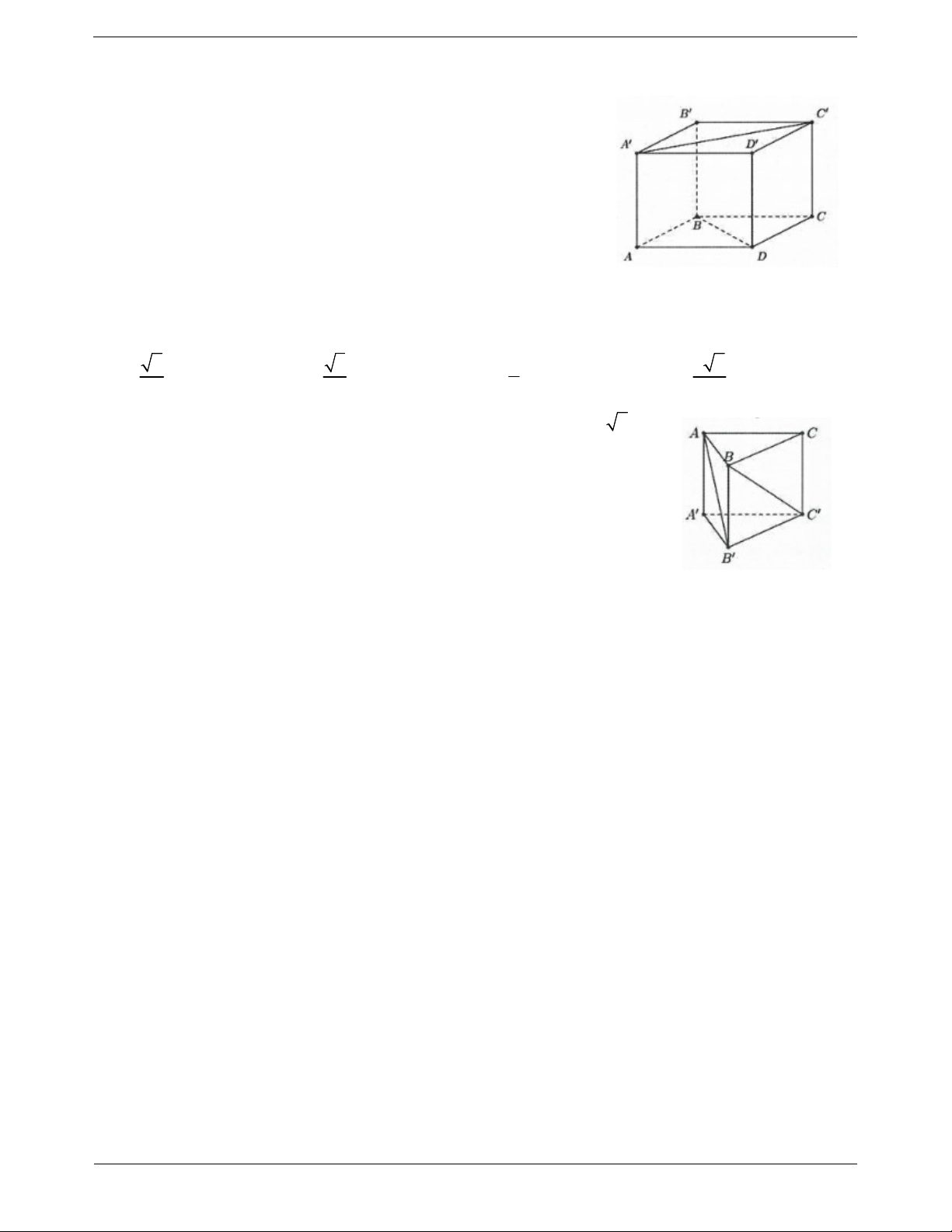
Ví dụ 4. Cho hình chóp S.ABCD có đáy là hình vuông ABCD cạnh 2a , SA ABCD và SB a 5 .
Gọi M là trung điểm AB và N là trung điểm BC . Tính cosin góc giữa hai đường thẳng SM và DN . Lời giải:
Cách 1: Do SA ABCD . Ta có: 2 2
SA SB AB a . Gọi E là trung điểm của AD và I là trung
điểm AE . Dễ thấy BNDE là hình bình hành và MI là đường trung bình
trong tam giác ABE . Khi đó DN //BE//MI . AE a Ta có: AM a; AI . 2 2 2 5a Mặt khác: 2 2 2 2 2
SM SA AM 2a ; SI . 4 2 5a 2 2 2 SM MI SI 10 2 2 2 MI AI AM . Do vậy cos SMI cosSM; DN 4 2.SM.MI 5
Cách 2: Ta có: SM.DN SM SN SD SM.SN SM.SD 1 1 2 2 2 SM SN MN 2 2 2 SM SD MD 2 2 AC Mặt khác: 2 2 2 2 2 2 2
SN SA AN SA AB BN 6a , MN a 2 , 2 2 2 2 SD 5a , MD 5a . 2 2 2 2a 2a 10 Do đó 2
SM .DN 2a cos SM ; DN . SM .DN a 2.a 5 5
Ví dụ 5. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật có AB ;
a AD a 2 , SA ABCD và SA 2a .
a) Tính cosin góc giữa hai đường thẳng BC và SD .
b) Gọi I là trung điểm của CD . Tính cosin góc giữa hai đường thẳng SB và AI . Trang 4 Lời giải:
a) Do BC //AD SD; BC SD; AD SDA AD AD 1 S
AD vuông tại A cos SDA . 2 2 SD AD SA 3
b) Gọi M , K lần lượt là trung điểm của AB và SA thì MK là đường trung
bình của tam giác SAB . Khi đó MK //SB , mặt khác MC//AI . Suy ra SB AI MK CM ; ; . 2 2 SB SA AB a 5 3a Ta có: 2 2 MK ; MC MB BC ; 2 2 2 2 2 2 KC KA AC 2a . 2 2 2 KM MC KC 1 1 Khi đó cos KMC cosS ; B AI . 2.KM.MC 3 5 3 5
Cách 2: Ta có: S .
B AI SB SI SA S . B SI S . B SA 1 1 2 2 2 SB SI BI 2 2 2 SB SA AB 2 2 2 25a 3a Do 2 2 2 2 2 2 2 2
SB 5a ; SI SA AD DI ; AI AD DI IB . 4 2 2 a 2 S . B AI a 1 Suy ra SB AI c SB AI 2 . os ; . 2 S . B AI 3a 3 5 a 5. 2
Ví dụ 6. Cho hình chóp S.ABCD có đáy là hình thoi cạnh a ,
ABC 60 . Tam giác SAB cân tại S và
thuộc mặt phẳng vuông góc với đáy. Biết rằng SC tạo với đáy một góc 30 . Tính cosin của góc giữa a) SD và BC .
b) DH và SC , với H là chân đường cao hạ từ S xuống mặt đáy ABCD . Lời giải: a) Do AB BC a, ABC 60 A BC đều cạnh a .
Gọi H là trung điểm của AB , do tam giác SAB tại S nên SH AB . SAB ABCD Mặt khác SH ABC . AB SAB ABCD a 3 A BC đều nên CH ,SC; ABC SCH 30 2 a
Ta có: SH HC tan 30 . 2 Trang 5 a 7 Do ABC 60 2 2
BAD 120 HD AH AD 2AH.AD cos120 . 2 a 2 Suy ra 2 2 2 2 SA SH HA , SD SH HD a 2 . 2 DS DA SA
Mặt khác AD//BC BC SD AD SD 2 2 2 5 2 ; ; ,cos SDA . 2.DS.DA 8 Do vậy BC SD 5 2 cos ; . 8
b) Ta có SC.DH SC SH SD S . C SH SC.SD 1 SH SC HC 1 SC SD CD 2 3a 2 2 2 2 2 2 2 2 4 2 3a SC.DH 3 7 Mặt khác 2 2 SC SH HC a SC DH 4 cos ; SC.DH a 7 14 . a 2 DH / /BI
Cách 2: Gọi I là trung điểm CD a 7 DH BI 2 MI / /SC a 2
Gọi M là trung điểm SD SC a . Lại có 2 2
BD a 3; SB SH HB . MI 2 2 2 2 2 2 BD BS SD 5 MI IB MB Do đó 2 2 BM a 2 2 2 3 17 cos MIB . 2 4 4 2.IM.IB 14 Suy ra DH SC 3 17 cos ; . 14
Ví dụ 7. Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B có AD 2AB 2CD 2a và
SA ABCD . Biết rằng SC tạo với đáy một góc 60. Tính cosin góc giữa: a) BC và SD .
b) AI và SD với I là trung điểm CD . Lời giải: a) Ta có: 2 2 AC AB BC a 2 .
Do SA ABCD SC; ABC SCA 60 .
Khi đó SA AC tan 60 a 6 . Do AD BC BC SD AD SD / / ; ; . Trang 6 AD AD Mặt khác cos ADS 2 2 SD SA AD 2a 10 cosBC; SD . 2 2 6a 4a 5
b) Gọi E là trung điểm AD AE DE BC a ABCE là hình vuông cạnh a . 1
Do CE AD ACD vuông tại C . 2 a 2 Ta có: 2 2
CD CE ED a 2 ID . 2
1 1
Lại có: AI.SD SI SA.SD SI.SD S . A SD 2 2 2 SI SD DI 2 2 2 SA SD AD 2 2 2 2 5a 17a Trong đó 2 2 2 2 2 2 AI AC CI SI SA AI . 2 2 2 2 3a 3a 3 Do đó 2
AI.SD 3a cos AI;SD . AI.SD a 10 5 .a 10 2 MI / /SD a 10 SC
Cách 2: Gọi M là trung điểm SC SD a 10 , AI , AM a 2 . MI 2 2 2 2 IA IM AM Khi đó 2 2 2 3 cos MIA . 2.I . A IM 5
Ví dụ 8. Cho hình lăng trụ ABC.A B C
có đáy là tam giác đều cạnh a , hình chiếu của điểm A xuống
mặt đáy ABC trùng với trung điểm của BC . Biết cạnh bên tạo với mặt đáy một góc 60 .
a) Tính tan góc tạo bởi B C và A C .
b) Cosin góc tạo bởi CC và AB . Lời giải
a) Gọi H là trung điểm BC . Ta có: BC / /B C B C ; AC BC; AC ACH . Mặt khác A H
ABC AA ; ABC AAH 60 . a 3 3a AH A H AH tan 60 . 2 2 A H Xét tam giác vuông A H C ta có tan A C H 3. HC Vậy tan B C AC ; 3 .
b) Do CC AA CC AB AA AB / / ; ; Trang 7 Ta có: 2 2
AA AH HA a 3 a 10 AA AB AB AB A H HB cos 2 2 2 3 2 2 AAB . 2 2.AA .AB 4 Vậy CC AB 3 cos ; . 4
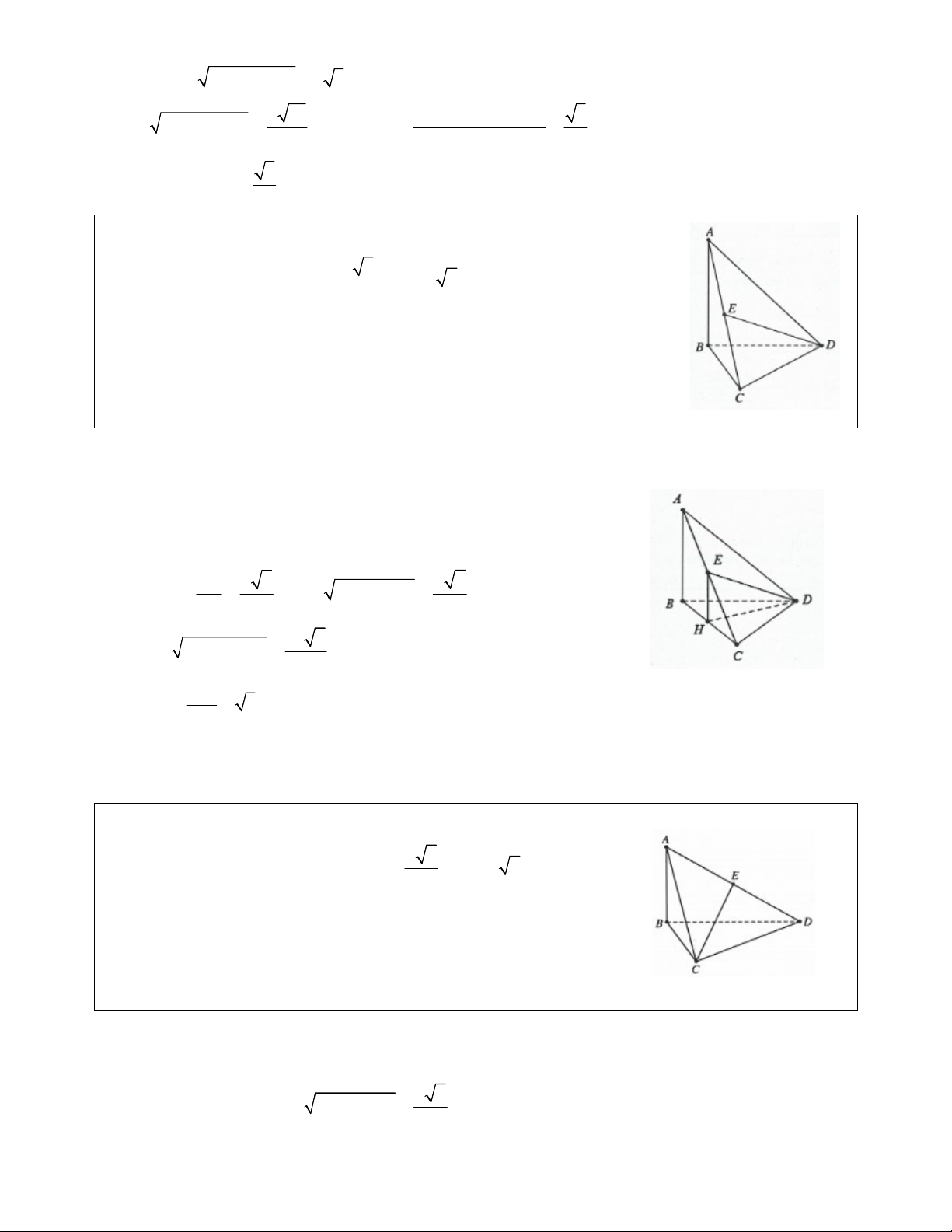
Ví dụ 9. Cho tứ diện ABCD có AB vuông góc với mặt phẳng BCD . Biết tam a 6
giác BCD vuông tại C và AB
, AC a 2,CD a . Gọi E là trung điểm 2
của AC (tham khảo hình vẽ bên). Góc giữa hai đường thẳng AB và DE bằng A. 45 B. 60 C. 30 D. 90 Lời giải
Gọi H là trung điểm của BC khi đó
EH / / AB EH BCD EH HD . Suy ra AB DE EH DE ; ; AB a 6 a 2 Ta có: 2 2 HE , BC AC AB 2 4 2 3a 2 2 2 DH DC CH 4 DH tan DEH 3 DEH 60 . EH Vậy AB; DE EH;DE DEH 60 . Chọn B.
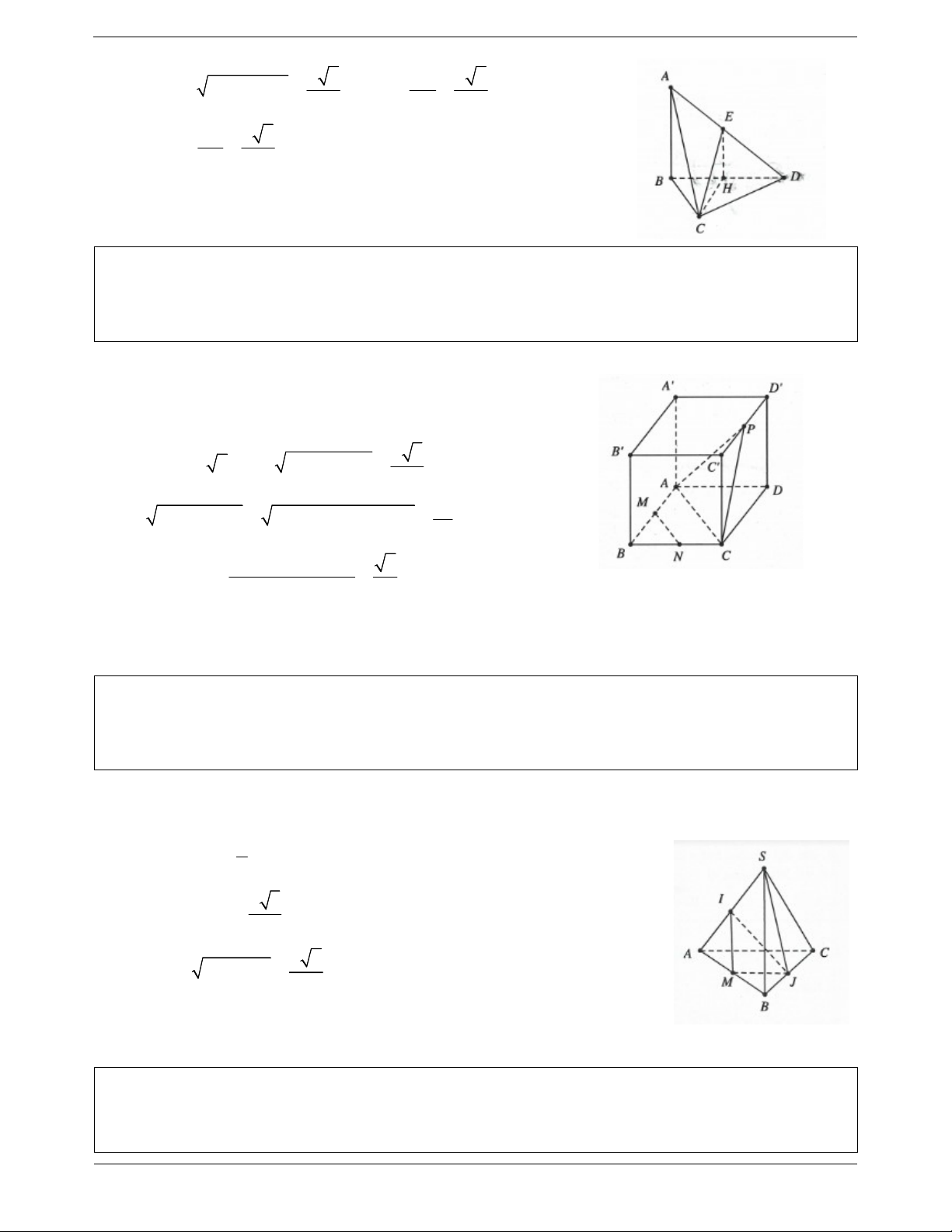
Ví dụ 10. Cho tứ diện ABCD có AB vuông góc với mặt phẳng BCD . a 6
Biết tam giác BCD vuông tại C và AB
, AC a 2,CD a . Gọi E 2
là trung điểm của AC (tham khảo hình vẽ bên). Góc giữa hai đường thẳng AB và CE bằng A. 60 B. 45 C. 30 D. 90 Lời giải
Gọi H là trung điểm BD EH / / AB EH BCD a 2 Vậy EH CH , ta có 2 2 BC AC AB 2 Trang 8 a 6 BD a 6 Suy ra 2 2 BD BC CD CH 2 2 4 AB a 6 Lại có EH
CH EHC vuông cân tại H 2 4 Do đó AB;CE EH;CE CEH 45 . Chọn B.
Ví dụ 11. Cho hình lập phương ABC . D A B C D
cạnh a . Gọi M , N, P lần lượt là trung điểm các cạnh AB, BC, C D
. Xác định góc giữa hai đường thẳng MN và AP . A. 60 B. 90 C. 30 D. 45 Lời giải
Dễ thấy MN là đường trung bình trong tam giác ABC nên MN AC MN AP AC AP / / ; ; . a 5 Lại có 2 2
AC a 2,CP CC C P 2 3a 2 2 2 2 2
AP AP AA AD D P AA 2 AP AC CP Do đó 2 2 2 2 cosCAP 2.A . P AC 2 CAP MN CP 45 ; . Chọn D.
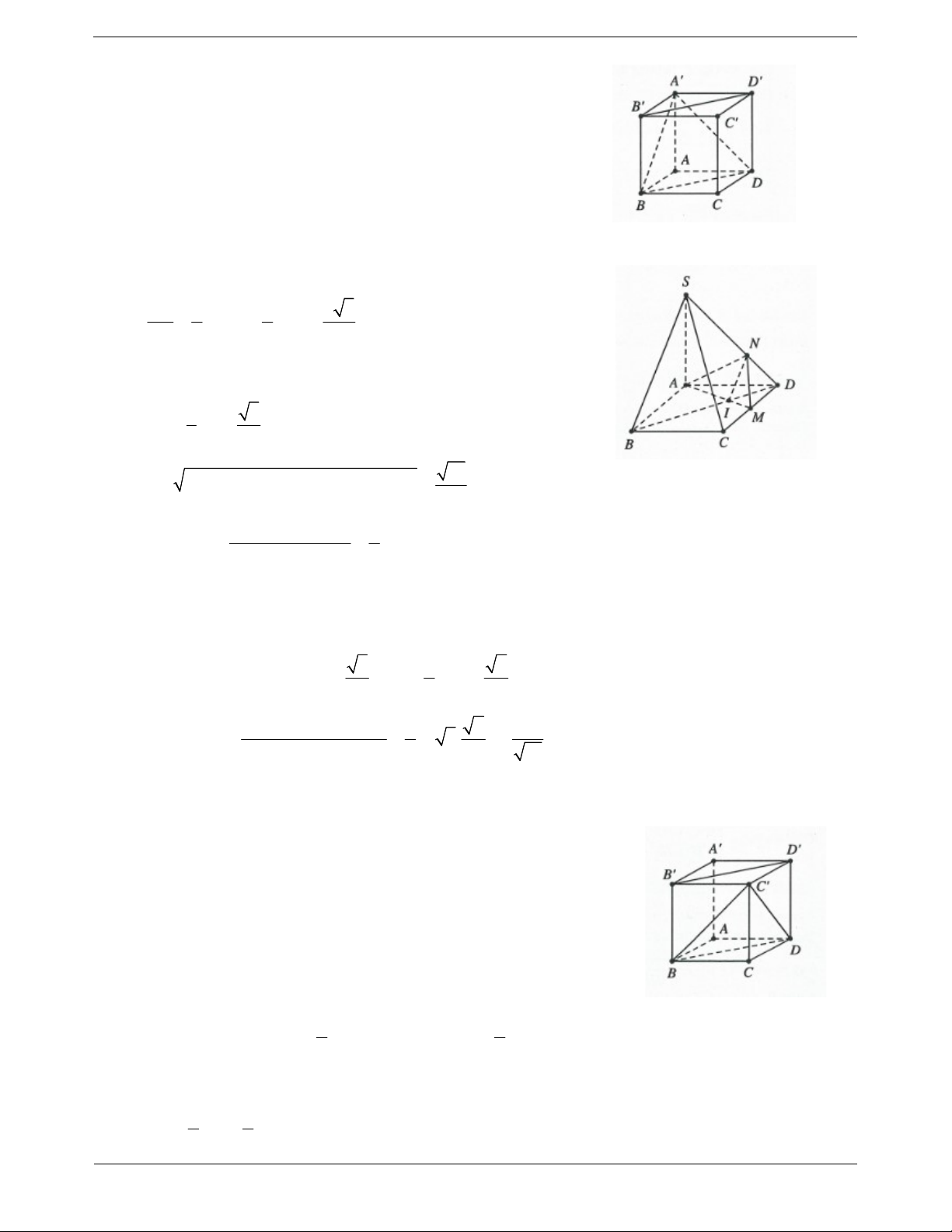
Ví dụ 12. Cho hình chóp S.ABC có tất cả các cạnh đều bằng a . Gọi I , J lần lượt là trung điểm của S ,
A BC . Tính số đo của góc hợp bởi IJ và SB . A. 45 B. 30 C. 60 D. 90 Lời giải
Gọi M là trung điểm AB thì MI, MJ lần lượt là đường trung bình của tam giác ASB và ABC . a Ta có: MI MJ 2 a 3 Mặt khác JA JS
tam giác JSA cân tại J JI SA 2 a 2 Khi đó 2 2 2 2 2 IJ SJ SI
MI MJ IJ nên tam giác MIJ vuông 2 cân tại M IJ SB IJ IM ; ; 45 . Chọn A.
Ví dụ 13. Cho hình chóp tứ giác đều S.ABCD đáy ABCD là hình vuông, E là điểm đối xứng với D
qua trung điểm SA . Gọi M , N lần lượt là trung điểm của AE và BC . Góc giữa hai đường thẳng MN và BD bằng Trang 9 A. 90 B. 60 C. 45 D. 75 Lời giải
Gọi I là trung điểm SA thì MICN là hình bình hành nên MN / /CI BD AC Mặt khác
(với O là tâm của hình vuông ABCD ) BD SO
Suy ra BD SAC BD CI BD MN Vậy MN BD ; 90 . Chọn A.
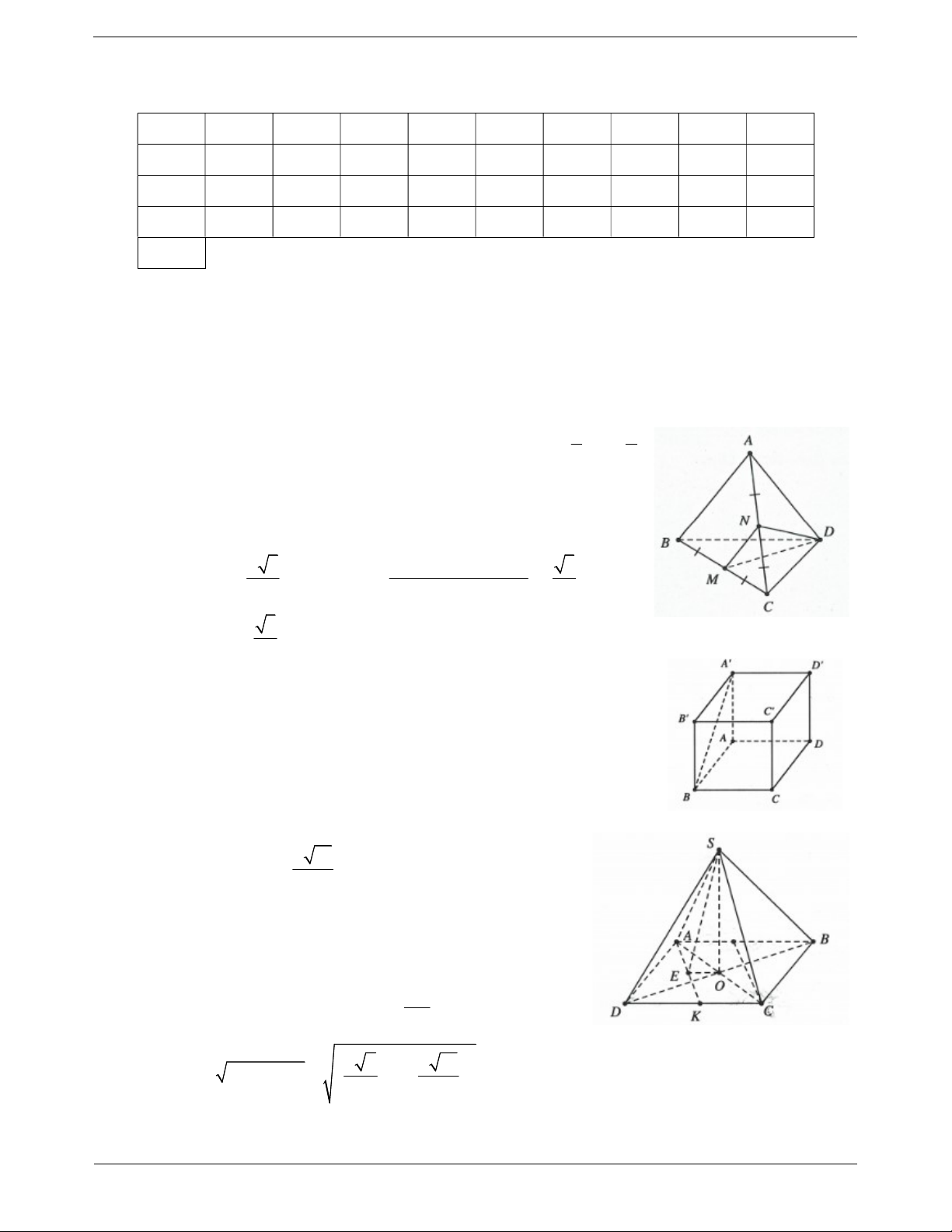
Ví dụ 14. Cho hình lăng trụ tam giác đều ABC.A B C
có AB a và AA a 2 . Góc giữa hai đường
thẳng AB và BC bằng A. 30 B. 90 C. 45 D. 60 Lời giải
Gọi E là điểm thuộc AB sao cho B A B E
Ta có ABEB là hình bình hành nên AB / /BE 1 Lại có AE 2a, B C AE E
AC vuông tại C 2 Khi đó 2 2 C E A E
AC a 3, BE AB a 3 2 2 BC BB C B a 3 B
EC là tam giác đều. Do đó AB ; BC BE;BC EBC 60 . Chọn D.
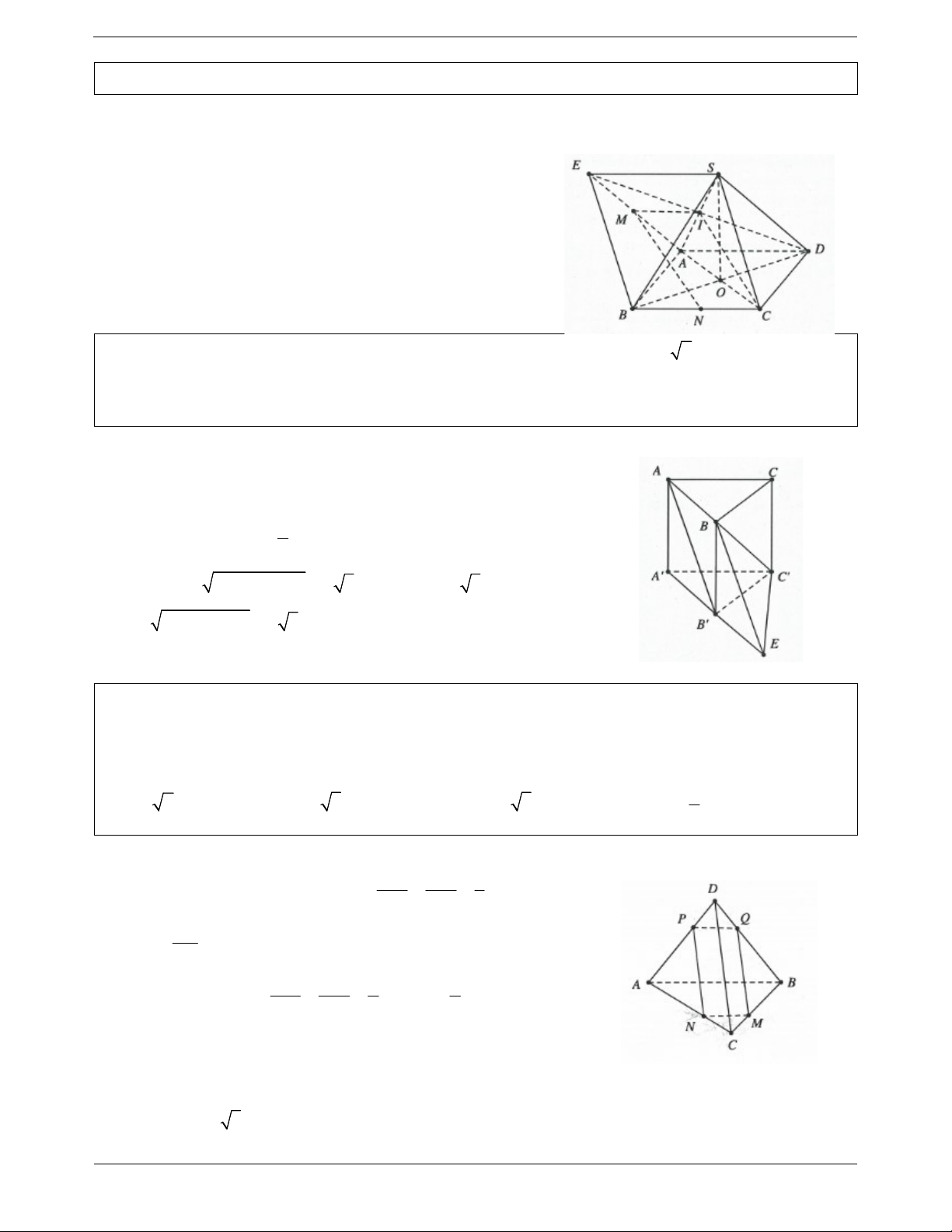
Ví dụ 15. Cho tứ diện ABCD có AB 6, CD 3, góc giữa AB và CD là 60 và điểm M trên BC sao
cho BM 2MC . Mặt phẳng P qua M song song với AB và CD cắt AC, AD, BD lần lượt tại
N, P,Q . Diện tích MNPQ bằng 3 A. 2 2 B. 3 C. 2 3 D. 2 Lời giải MN CM 1
Do MN / / AB , theo định lý Talet ta có AB CB 3 AB MN 2 3 MQ BM 2 2 Tương tự MQ / /CD MQ CD 2 CD BC 3 3
Lại có MN / / AB , MQ CD MN MQ AB CD / / ; ; 60 Khi đó S S MN MQ MN MQ 2 . sin ; MNPQ MNQ
2.2.sin 60 2 3 . Chọn C. Trang 10
Ví dụ 16. Cho tứ diện ABCD có AB vuông góc với CD , AB 4, CD 6 . M là điểm thuộc cạnh BC
sao cho MC 2BM . Mặt phẳng P qua M song song với AB và CD . Diện tích thiết diện của P với tứ diện là 17 16 A. 5 B. 6 C. D. 3 3 Lời giải
Mặt phẳng P qua M song song với AB và CD cắt AC, AD, BD lần lượt tại N , P,Q . MN CM 2
Do MN / / AB , theo định lý Talet ta có AB CB 3 2AB 8 MN 3 3 MQ BM 1 1 Tương tự MQ / /CD MQ CD 2 CD BC 3 3
Lại có MN / / AB , MQ CD MN MQ AB CD / / ; ; 90 Khi đó S S MN MQ MN MQ 2 . sin ; MNPQ MNQ 8 16 .2.sin 90 . Chọn D. 3 3 BÀI TẬP TỰ LUYỆN
Câu 1. Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hai đường thẳng cùng vuông góc với một đường thẳng thì song song với nhau.
B. Một đường thẳng vuông góc với một trong hai đường thẳng vuông góc với nhau thì song song với đường thẳng còn lại.
C. Hai đường thẳng cùng vuông góc với một đường thẳng thì vuông góc với nhau.
D. Một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia.
Câu 2. Trong không gian cho 3 đường thẳng phân biệt a,b, c . Khẳng định nào sau đây đúng?
A. Nếu a / /b và c a thì c b
B. Nếu góc giữa a và c bằng góc giữa b và c thì a / /b
C. Nếu a và b cùng vuông góc với c thì a / /b
D. Nếu a và b cùng nằm trong mặt phẳng / /c thì góc giữa a và c bằng góc giữa b và c
Câu 3. Cho hai đường thẳng phân biệt a,b và mặt phẳng P , trong đó a P . Mệnh đề nào sau đây là sai? Trang 11
A. Nếu b P thì b / /a
B. Nếu b P thì b a
C. Nếu b / /a thì b P
D. Nếu b a thì b / / P
Câu 4. Cho tứ diện đều ABCD cạnh a . Gọi M là trung điểm BC . Tính cosin góc giữa hai đường thẳng AB, DM . 3 3 3 1 A. B. C. D. 2 6 3 2
Câu 5. Cho hình lập phương ABC . D A B C D
. Góc giữa hai đường thẳng BA ,CD bằng A. 90 B. 60 C. 30 D. 45
Câu 6. Cho hình chóp tứ giác đều S.ABCD có AB a,O là trung điểm AC và SO b . Gọi là a 14
đường thẳng đi qua C, chứa trong mặt phẳng ABCD và khoảng cách từ O đến là . Giá 6
trị lượng giác cos SA, bằng 2a a 2a a A. B. C. D. 2 2 3 4b 2a 2 2 2b 4a 2 2 3 2b 4a 2 2 3 4b 2a
Câu 7. Cho hình chóp S.ABCD có đáy là hình vuông ABCD , cạnh bên SA vuông góc với mặt phẳng
đáy. Đường thẳng SD tạo với mặt phẳng SAB một góc 45. Gọi I là trung điểm của cạnh CD . Góc
giữa hai đường thẳng BI và SD bằng (số đo góc được làm tròn đến hàng đơn vị) A. 39 B. 42 C. 51 D. 48
Câu 8. Cho hình chóp S.ABCD đều có SA AB a . Góc giữa SA và CD là A. 60 B. 30 C. 90 D. 45
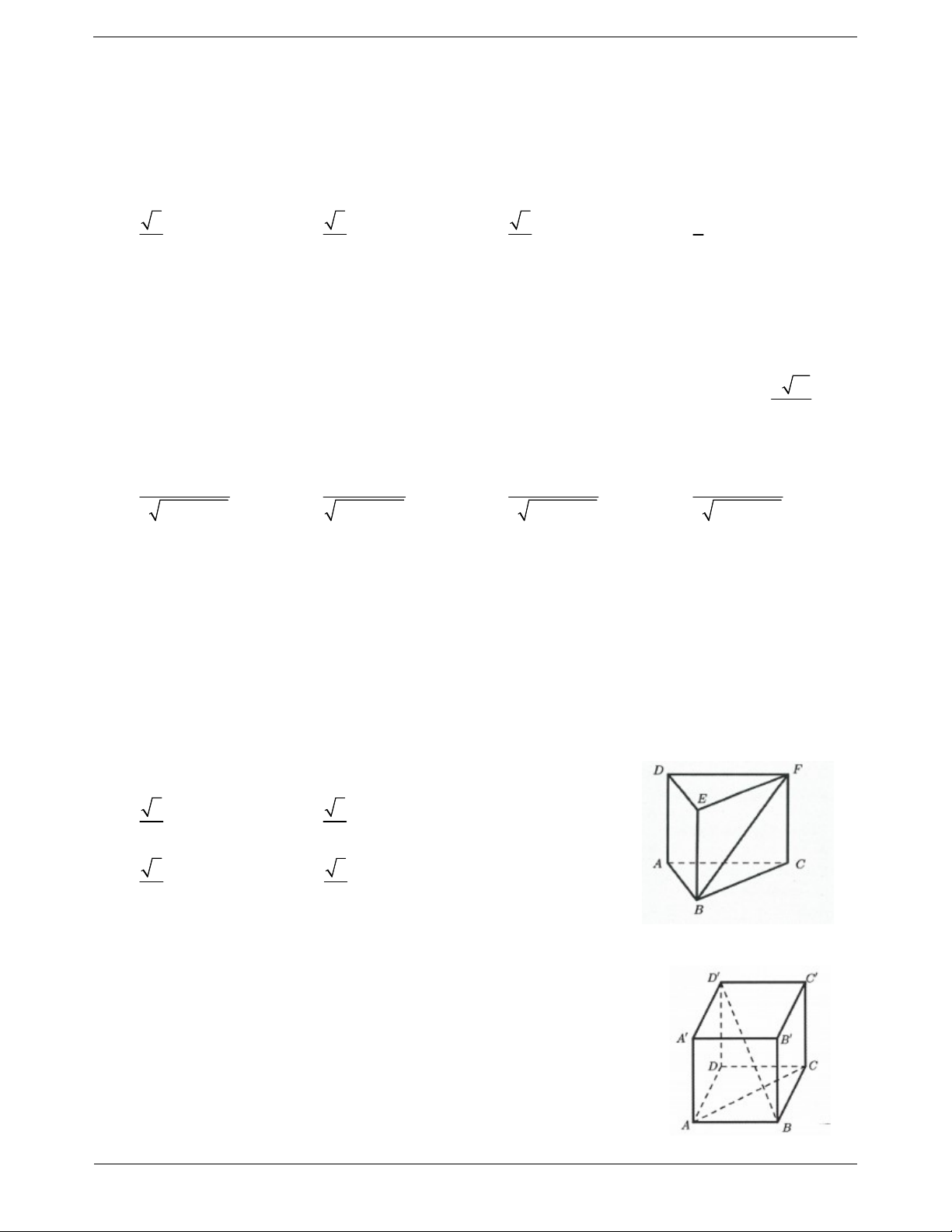
Câu 9. Cho lăng trụ tam giác đều ABC.DEF có cạnh bằng a , chiều cao bằng 2a . Tính cosin góc tạo bởi hai đường thẳng AC, BF 5 3 A. B. 10 5 5 3 C. D. 5 10
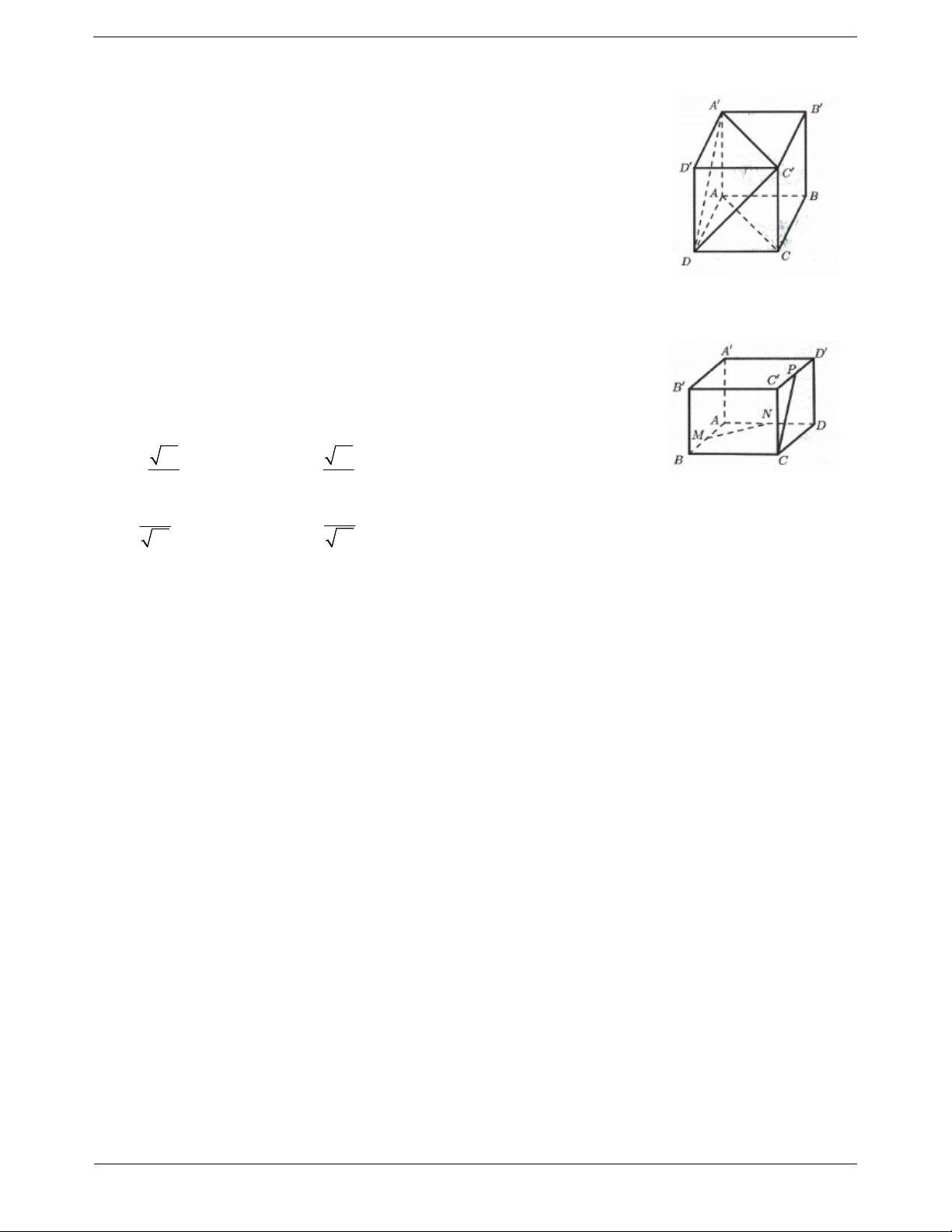
Câu 10. Cho hình lập phương ABC . D A B C D
(tham khảo hình vẽ). Góc
giữa hai đường thẳng AC và BD là A. 30 B. 90 C. 60 Trang 12 D. 45
Câu 11. Cho hình lập phương ABC . D A B C D
(tham khảo hình vẽ). Góc giữa
hai đường thẳng AC và A D là A. 45 B. 30 C. 60 D. 90
Câu 12. Cho hình lập phương ABC . D A B C D
. Gọi M , N, P lần lượt là
trung điểm của các cạnh AB, AD,C D
. Cosin của góc giữa hai đường thẳng MN,CP bằng 10 15 A. . B. 5 5 1 3 C. D. 10 10 Câu 13. Cho hình hộp ABC . D A B C D
. Giả sử tam giác AB C và A D
C đều có 3 góc nhọn. Góc giữa
hai đường thẳng AC và AD là góc nào sau đây? A. AB C B. DA C C. BB D D. BDB
Câu 14. Cho hình lập phương ABC . D A B C D
. Chọn khẳng định sai? A. Góc giữa AC và B D bằng 90 B. Góc giữa AA và B D bằng 60 C. Góc giữa AD và B C bằng 90
D. Góc giữa BD và AC bằng 90
Câu 15. Cho hình lập phương ABC .
D EFGH . Hãy xác định góc giữa cặp vectơ AB và DH ? A. 45 B. 90 C. 60 D. 120
Câu 16. Cho hình lập phương ABC .
D EFGH . Hãy xác định góc giữa cặp vectơ AB và EG ? A. 90 B. 60 C. 45 D. 120
Câu 17. Cho hình lập phương ABC . D A B C D
.Góc giữa AC và DA là A. 45 B. 90 C. 60 D. 120
Câu 18. Cho tứ diện ABCD có AB AC AD và BAC
BAD 60 . Hãy xác định góc giữa cặp vectơ AB và CD ? A. 60 B. 45 C. 120 D. 90
Câu 19. Cho hình chóp S.ABC có SA SB SC và ASB BSC CSA , BAC BAD 60 . Hãy xác
định góc giữa cặp vectơ AB và SC ? A. 120 B. 45 C. 60 D. 90 Trang 13
Câu 20. Cho hình chóp S.ABC có SA SB và CA CB . Tính số đo của góc giữa hai đường thẳng chéo nhau SC và AB . A. 30 B. 45 C. 60 D. 90
Câu 21. Cho hình chóp S.ABC có AB AC và SAC
SAB . Tính số đo của góc giữa hai đường thẳng chéo nhau SA và BC . A. 30 B. 45 C. 60 D. 90
Câu 22. Cho tứ diện ABCD có AB AC AD và BAC BAD 60 ,
CAD 90 . Gọi I và J lần lượt
là trung điểm của AB và CD . Hãy xác định góc giữa cặp vectơ AB và IJ ? A. 120 B. 90 C. 45 D. 45
Câu 23. Cho hình chóp S.ABCD có đáy là hình vuông ABCD cạnh a và các cạnh bên đều bằng a . Gọi
M và N lần lượt là trung điểm AD và SD . Số đo của góc MN, SC bằng A. 45 B. 30 C. 90 D. 60
Câu 24. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB a . Cạnh bên SA ABCD ,
SA a . Góc giữa hai đường thẳng SB,CD bằng A. 90 B. 60 C. 30 D. 45
Câu 25. Cho hình chóp đều S.ABC có SA 9a, AB 6a . Gọi M là điểm thuộc cạnh SC sao cho 1
SM MC . Cosin của góc giữa hai đường thẳng SB, AM ? 2 7 1 19 14 A. B. C. D. 2 48 2 7 3 48
Câu 26. Cho hình chóp S.ABCD đều có đáy là hình vuông ABCD , E là điểm đối xứng của D qua
trung điểm SA . Gọi M , N lần lượt là trung điểm AE , BC . Tính góc giữa đường thẳng MN và BD . A. 60 B. 90 C. 45 D. 75
Câu 27. Cho hình lập phương ABC . D A B C D
.Góc giữa hai đường thẳng BA và B D bằng A. 45 B. 90 C. 30 D. 60
Câu 28. Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng 2, cạnh
SA 1và vuông góc với đáy. Gọi M là trung điểm CD . Tính cos với là góc
tạo bởi hai đường thẳng SB và AM . 2 2 A. B. 5 5 1 4 C. D. 2 5 Trang 14
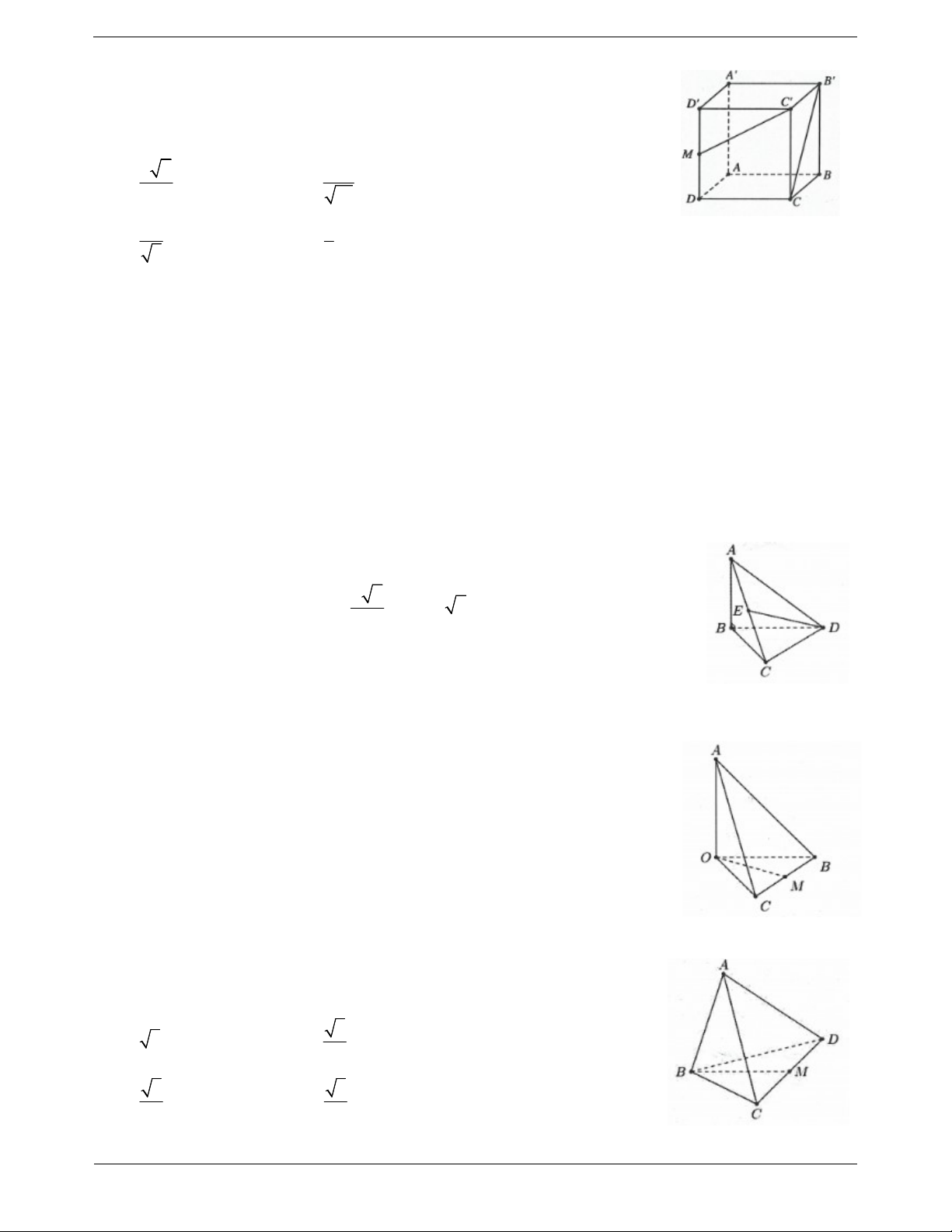
Câu 29. Cho hình lập phương ABC . D A B C D
. Gọi M là trung điểm
DD (tham khảo hình vẽ bên). Tính cosin của góc giữa hai đường thẳng B C và C M . 2 2 1 A. B. 9 10 1 1 C. D. 3 3
Câu 30. Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O , SA nằm trên đường vuông góc với
mặt phẳng ABCD . Trong các khẳng định sau, khẳng định nào sai? A. AD SC B. SA BD C. SO BD D. SC BD
Câu 31. Cho hình lập phương ABC . D A B C D
. Tính số đo góc giữa hai đường thẳng BC và B D . A. 60 B. 90 C. 30 D. 45
Câu 32. Cho tứ diện ABCD có AB CD . Gọi I, J , E, F lần lượt là trung điểm AC, BC, BD, AD . Góc giữa IE và JF bằng A. 30 B. 45 C. 90 D. 60
Câu 33. Cho tứ diện ABCD có AB vuông góc với mặt phẳng BCD . Biết tam a 6
giác BCD vuông tại C và AB
, AC a 2,CD a . Gọi E là trung điểm 2
AC (tham khảo hình vẽ bên). Góc giữa AB và DE bằng A. 45 B. 60 C. 30 D. 90
Câu 34. Cho tứ diện OABC có O ,
A OB,OC đôi một vuông góc với nhau và
OA OB OC . Gọi M là trung điểm BC (tham khảo hình vẽ bên). Góc giữa
hai đường thẳng AB và OM bằng A. 90 B. 30 C. 45 D. 60
Câu 35. . Cho tứ diện đều ABCD . Gọi M là trung điểm CD . Cosin của góc
giữa hai đường thẳng AC và BM bằng 3 A. 3 B. 3 3 3 C. D. 6 2 Trang 15
Câu 36. Cho hình hộp chữ nhật ABC . D A B C D
(tham khảo hình vẽ
bên) có AD a, BD 2a . Góc giữa hai đường thẳng AC và BD là A. 60 B. 120 C. 90 D. 30
Câu 37. Cho tứ diện ABCD có AD 14, BC 6 . Gọi M , N lần lượt là trung điểm của các cạnh
AC, BD . Gọi là góc giữa hai đường thẳng BC và MN . Biết MN 8, tính sin . 2 3 1 2 2 A. B. C. D. 4 2 2 3
Câu 38. Cho lăng trụ tam giác đều ABC.A B C
có AB a và AA a 2 . Góc
giữa hai đường thẳng AB và BC bằng A. 30 B. 90 C. 45 D. 60
Câu 39. Cho tứ diện ABCD có AB vuông góc với CD . Mặt phẳng P song song với AB và CD lần
lượt cắt BC, DB, AD, AC tại M , N, P,Q . Tứ giác MNPQ là hình gì? A. Hình thang. B. Hình bình hành. C. Hình chữ nhật.
D. Tứ giác không phải hình thang.
Câu 40. Trong không gian cho hai tam giác đều ABC và ABC có chung cạnh AB và nằm trong hai mặt
phẳng khác nhau. Gọi M , N, P,Q lần lượt là trung điểm các cạnh AC,CB, BC và C A . Tứ giác MNPQ là hình gì? A. Hình bình hành. B. Hình chữ nhật. C. Hình vuông. D. Hình thang.
Câu 41. Cho tứ diện ABCD có AB vuông góc với CD , AB CD 6 . M là điểm thuộc cạnh BC sao
cho MC xBM 0 x
1 . Mặt phẳng P song song với AB và CD lần lượt cắt BC, DB, AD, AC tại
M , N, P,Q . Diện tích lớn nhất của tứ giác bằng bao nhiêu? A. 9. B. 11. C. 10. D. 8. Trang 16
ĐÁP ÁN VÀ LỜI GIẢI BẢI TẬP TỰ LUYỆN 1-D 2-A 3-B 4-B 5-D 6-C 7-C 8-A 9-A 10-B 11-B 12-C 13-B 14-B 15-B 16-C 17-C 18-D 19-D 20-D 21-D 22-B 23-C 24-D 25-D 26-B 27-D 28-A 29-B 30-A 31-A 32-C 33-B 34-D 35-C 36-C 37-B 38-D 39-C 40-C 41-A
Câu 1: Trong không gian một đường thẳng vuông góc với một trong hai đường thẳng song song thì
vuông góc với đường thẳng kia. Chọn D.
Câu 2: Nếu a / /b và c a thì c b . Chọn A.
Câu 3: Khẳng định sai là B. Chọn B. 1 a
Câu 4: Gọi N là trung điểm của AC thì MN / / AB và MN AB 2 2
(tính chất đường trung bình) Khi đó AB DM NM DM ; ; a MD MN DN 3 Lại có DM DN 2 2 2 3 cos DMN 0 . 2 2.M . D MN 6 Vậy AB DM 3 cos ; . Chọn B. 6
Câu 5: Do CD / / AB nên BA ;CD BA;AB ABA 45 . Chọn D.
Câu 6: Gọi K là điểm thuộc CD sao cho AK / / a 14 Dựng OE AK thì OE 6
Mặt khác SO AK AE SOE Ta có S ; A S ;A AK SAE AE
Xét tam giác vuông SAK ta có cos SAK SA 2 2 a 2 a 14 Trong đó 2 2 AE OA OE 2 6 Trang 17 2 a a 2a 2 2 2 a AE , SA OA SO b o c s SAK = . Chọn C. 3 2 2 a 2 2 a 2 3 2 4b 3 b 2 DA AB
Câu 7: Đặt AB 2a , do DA SAB DA SA Do đó S ; D SAB
DSA 45 SA AD 2a
Gọi K là trung điểm AB DK / /BI Do đó BI SD DK SD ; ;
Mặt khác SD 2a 2, SK DK a 5 DS DK SK Suy ra 2 2 2 10 cos SDK 2.DS.DK 5 SDK 50,77 . Chọn C.
Câu 8: Ta có AB / /CD nên SA CD SA AB ; ;
Mặt khác S.ABCD là chóp đều nên SA SB do đó tam giác SAB đều nên SAB 60 . Vậy SA CD SA AB ; ; SAB 60 . Chọn A.
Câu 9: Ta có AC / /DF AC BF DF BF ; ; Mặt khác 2 2
BD BF 4a a a 5, DF a FD FB BD Do đó 2 2 2 5 cos DFB 0 2.F . D FB 10 Vậy AC BF 5 cos ; . Chọn A. 10 AC BD Câu 10: Ta có
AC BDD AC BD AC BB
Vậy góc giữa hai đường thẳng AC và B D là 90 . Chọn B.
Câu 11: Đặt AB a , ta có AC AC AC AD AC AD / / ; ;
Mặt khác AD DC A C
a 2 ADC là tam giác đều nên DAC 60 Vậy AC AD AC A D ; ;
DAC 60 . Chọn B.
Câu 12: Đặt AD 2a , gọi Q là trung điểm B C thì PQ / /B D
/ /MN do đó MN CP PQ CP ; ; B D 2a 2 Ta có PQ a 2 2 2 Trang 18 CQ CP a2 2 2 a a 5 PQ PC CQ Do đó 2 2 2 1 cos CPQ 2.P . Q PC 10 Vậy MN CP 1 cos ; . Chọn C. 10
Câu 13: Ta có AC / / AC ( AB C D là hình bình hành) Mà DA C
nhọn nên AC; A D AC ; AD DAC Chọn B.
Câu 14: Ta có AA ; B D BB ;B D BB C
90 . Khẳng định B sai. Chọn B.
Câu 15: Vì DH AE ( ADHE là hình vuông) Nên A ; B DH A ;BAE
BAE 90 ( ABFE là hình vuông). Chọn B.
Câu 16: Vì EG AC ( AEGC là hình vuông) Nên A ; B EG A ;BAC
BAC 45 ( ABCD là hình vuông). Chọn C.
Câu 17: Gọi a là độ dài cạnh của hình lập phương. Khi đó, tam giác AB C là
tam giác đều AB B C
CA a 2 B C A 60
Lại có DA / /CB nên AC; DA AC;CB ACB 60 . Chọn C.
Câu 18: Ta có A .
B CD AB AD AC A . B AD A . B AC AB . AD cos A ; B AD AB . AC cos A ; B AC
AB . AD cos 60 AB . AC cos 60 . Mà AC AD A .
B CD 0 AB;CD 90 . Chọn D. Trang 19
Câu 19: Ta có SC.AB SC SB SA SC.SB SC.SA
SC . SB cosSC;SB SC . SA cosSC;SA SC.S . B cos BSC SC.S . A cos ASC . Mà SA SB SC và BSC ASC SC.AB 0
Do đó SC; AB 90 . Chọn D.
Câu 20: Xét SC.AB CS CB CA CS.CA CS.CB CS.C . A cos SCA CS.C . B cos SCB 2 2 2 2 2 2 SC CA SA SC CB SB CS.C . A CS.C . B 2.SC.CA 2.SC.CB 2 2 2 2 2 2 SC CA SA SC CB SB SA SB 0 (do ) 2 2 C A CB Vậy SC AB . Chọn D.
Câu 21: Xét S .
A BC SASC SB S . A SC S . A SB SA . SC cosS ; A SC SA . SB cos SAB S . A SC.cos ASC S . A S . B cos SAB (1) SA chung Ta có AB AC S AB S AC (c – g – c) SAB SAC SC SB Suy ra (2) ASC ASB Từ (1) và (2) suy ra S .
A BC 0 . Vậy SA BC . Chọn D.
Câu 22: Xét tam giác ICD có J là trung điểm
1 CD IJ IC ID 2 AB AC Tam giác ABC có
ABC đều CI AB BAC 60
Tương tự ta có ABD đều nên DI AB
1 1 1
Ta có IJ.AB IC ID.AB IC.AB I . D AB 0 2 2 2 Trang 20 IJ AB A ; B IJ 90. Chọn B.
Câu 23: Do ABCD là hình vuông cạnh a AC a 2 2 2 2 2
AC 2a SA SC SAC vuông tại S 1
Ta có MN là đường trung bình của DSA NM SA 2
1 Khi đó NM .SC S .
A SC 0 MN SC MN; SC 90 . 2 Chọn C.
Câu 24: Vì AB / /CD nên S ; B CD S ;B AB SBA
Ta có SA ABCD SA AB mà SA AB a
SAB vuông cân tại A SBA 45 . Vậy SB CD ; SBA 45 .Chọn D.
Câu 25: Kẻ MN / /SB N BC SB; AM MN; AM AMN BN SM 1 BC SC Ta có BN 2a; SM 3a BC SC 3 3 3 Suy ra 2 2 2 2 AN AB BN 2A . B BN.cos 60 28a SA SC AC Lại có 2 2 2 7 cos ASC 2.S . A SC 9 Suy ra 2 2 2 AM SA SM SA SM 2 2 . .cos ASC 48a AM MN AN Do đó 2 2 2 56 14 cos AMN . 2.AM .MN 12 48 3 48 Chọn D.
Câu 26: Gọi I là trung điểm SA I là trung điểm ED Suy ra MI / / AD
MI là đường trung bình EAD 1 MI AD 2 1
Ta có NC / / AD NC / /MI mà NC AD NC MI 2
Do đó MNCI là hình bình hành MN / /IC MN BD IC BD ; ;
Lại có BD SAC BD IC nên IC BD ; 90 . Trang 21 Chọn B. Câu 27: Vì B D
/ /BD nên BA ; B D BA;BD A B D Xét A B
D có AB BD DA (3 đường chéo của ba mặt) Suy ra A B D đều ABD 60 . Chọn D
Câu 28: Gọi I AM BD nên IDM IBA IM 1 2 2 5 IA AM IA 2 3 3
Kẻ IN / /SB N SD nên S ; B AM IN; AI AIN 1 5 Ta có IN SB ; 3 3 17 Và 2 2 AN AD DN 2A . D DN.cos ADN ; 3 AI IN AN Suy ra 2 2 2 2 cos AIN . Chọn A. 2.AI.IN 5
Câu 29: Gọi N là trung điểm AD MN / / AD mà AD / / B C MN / /B C Do đó B C ;C M MN;C M C M N 5 1 2 Tam giác C M N có C M C N ; MN AD 2 2 2 C M MN C N Suy ra 2 2 2 1 2 1 cos C M N : 5. . Chọn B. 2.C M .MN 2 2 10 SA BD Câu 30: Ta có
BD SAC BD SO . Chọn A. AC BD Câu 31: Ta có B D
/ /BD BC ; B D BC ;BD C B D Tam giác C B
D có BC DC BD (3 đường chéo 3 mặt bên) Suy ra C B
D là tam giác đều C B D 60 . Chọn A. 1 1
Câu 32: Ta có IF / /CD, IF CD và EJ / /CD, EJ CD 2 2
Suy ra IF / /EJ, IF EJ
IJEF là hình bình hành 1 1
Lại có IJ AB CD IJ IF IJEF là hình thoi IE JF . Chọn C. 2 2 Trang 22
Câu 33: Gọi F là trung điểm BC EF / / AB Do đó A ; B DE EF;DE DEF BC CD Ta có
CD ABC CD AC AB CD a 6 a 6
Tam giác DEF vuông tại F , có EF ; DE 4 2 EF a 6 a 6 1 Suy ra cos DEF : DEF 60 . Chọn B. DE 4 2 2
Câu 34: Gọi N là trung điểm AB MN / / AC Do đó AC;OM MN;OM OMN a 2 AC a 2
Tam giác OMN có OM ON ; MN 2 2 2 Suy ra OM ON MN OMN đều OMN 60 Chọn D.
Câu 35: Gọi N là trung điểm AD MN / / AC Do đó AC; BM MN;BM BMN a 3 a
Tam giác BMN có BM BN ; MN 2 2 BM MN BN a a Suy ra 2 2 2 2 3 3 cos BMN : . 2.BM .MN 4 2 6 Chọn C. AC B D Câu 36: Ta có AC BDD B A C BD . Chọn C. AC B B
Câu 37: Gọi P là trung điểm CD NP / /BC Do đó MN; BC MN;NP MNP
Tam giác MNP có MN 8, MP 7, NP 3 MN PN MP Suy ra 2 2 2 1 3 cos MNP sin . 2.MN.PN 2 2 Chọn B.
Câu 38: Gọi M là điểm đối xứng với A qua B AB / /BM Do đó AB ; BC BM;BC MBC Trang 23 Tam giác BB M vuông tại 2 2 B BM BB B M a 3 Tam giác BB C vuông tại 2 2
B BC BB B C a 3 Và 2 2 MC B M B C 2B M .B C .cos MB C a 3 Suy ra BMC đều MBC 60 . Chọn D. P ABC MQ Câu 39: MQ / / AB P / / AB
Tương tự ta có NP / / AB NP / /MQ và PQ / /MN / /CD
Do đó tứ giác MNPQ là hình bình hành AB CD
Mặt khác AB / /MQ PQ MQ do đó tứ giác MNPQ là hình chữ C D / /PQ nhật. Chọn C.
Câu 40: Đặt cạnh các tam giác đều bằng a .
Gọi I là trung điểm AB thì CI AB
Mặt khác C I AB nên AB AIC AB CC CC a
Lại có MQ / /CC và MQ
(tính chất đường trung bình), 2 2 a a
tương tự ta có NP / /CC , NP , PQ 2 2 MQ / /CC
Suy ra MNPQ là hình thoi, mặt khác PQ / / AB C C AB
MQ PQ suy ra MNPQ là hình vuông. Chọn C.
Câu 41: Do MN / / AB , theo định lý Talet ta có MN CM x MN . x AB 6x AB CB MQ BM Tương tự MQ / /CD 1 x CD BC
MQ 1 xCD 61 x
Lại có MN / / AB , MQ CD MN MQ AB CD / / ; ; 90 Khi đó S S MN MQ MN MQ 2 . sin ; MNPQ MNQ Trang 24 x x x x x 2 2 36 1 sin 90 36 36 9 6 3 9 Do đó S 9 MNPQ . Chọn A. max Trang 25




