Tài liệu chủ đề hàm số liên tục

Tài liệu gồm 36 trang, bao gồm kiến thức trọng tâm, hệ thống ví dụ minh họa và bài tập trắc nghiệm tự luyện chủ đề hàm số liên tục, có đáp án và lời giải chi tiết; giúp học sinh lớp 11 tham khảo khi học chương trình Đại số và Giải tích 11 chương 4.

25 13 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 2: Dãy số. Cấp số cộng và cấp số nhân (KNTT)

Môn: Toán 11

Thông tin:

36 trang 5 tháng trước

Tác giả:

Profile Kim Oanh
Trang 1
CHỦ ĐỀ HÀM SỐ LIÊN TỤC
I. KIẾN THỨC TRỌNG TÂM
1) Hàm số liên tục tại một điểm
Giả sử hàm số
f
xác định trên khoảng
;
a b
và
0
x a b
. Hàm số
f
được gọi là liên tục tại
điểm
0
x
nếu:
0
0
lim
x x
f x f x
Hàm số không liên tục tại điểm
0
x
được gọi là gián đoạn tại điểm
0
x
và điểm
0
x
được gọi là
điểm gián đoạn của hàm số
f x
Theo định nghĩa trên, hàm số
f x
xác định trên khoảng
;
a b
là liên tục tại điểm
0
;
x a b
nếu và chỉ nếu
0
lim
x x
f x
và
0
lim
x x
f x
tồn tại và
0
lim
x x
f x
=
0
lim
x x
f x
=
0
f x
2) Hàm số liên tục trên một khoảng, trên một đoạn
Hàm số
f x
xác định trên khoảng
;
a b
được gọi là liên tục trên khoảng đó, nếu nó liên tục tại
mọi điểm của khoảng đó.
Hàm số
f x
xác định trên đoạn
;
a b
được gọi là liên tục trên đoạn đó, nếu nó liên tục trên
khoảng
;
a b
và
lim
x a
f x f a
,
lim
x b
f x f b
(liên tục bên phải tại
a
và bên trái tại
b
)
Chú ý:
- Đồ thị của một hàm số liên tục trên một khoảng là một “đường liền” trên khoảng đó.
- Tính liên tục của một hàm số:
Tổng, hiệu, tích, thương của hai hàm số liên tục tại một điểm là những hàm số liên tục tại
điểm đó (giá trị của mẫu tại điểm đó phải khác 0)
Hàm đa thức và hàm phân thức hữu tỉ liên tục trên tập xác định của chúng.
Các hàm
sin
y x
,
cos
y x
,
tan
y x
,
cot
y x
liên tục trên tập xác định của chúng.
3) Tính chất của hàm số liên tục
Định lí: (Định lí về giá trị trung gian của hàm số liên tục)
Giả sử hàm số
f
liên tục trên đoạn
;
a b
. Nếu
f a f b
thì với mỗi số thực
M
nằm giữa
f a
và
f b
, tồn tại ít nhất một điểm
;
c a b
sao cho
f c M
.
Hệ quả 1: Nếu hàm
f
liên tục trên
;
a b
và
. 0
f a f b
thì tồn tại ít nhất một điểm
;
c a b
sao cho
0
f c
.
Hệ quả 2: Nếu hàm
f
liên tục trên
;
a b
và
0
f x
vô nghiệm trên
;
a b
thì hàm số
f
có dấu
không đổi trên
;
a b
.
Trang 2
II. PHÂN DẠNG TOÁN VÀ HỆ THỐNG VÍ DỤ MINH HỌA
Dạng 1. Xét tính liên tục của hàm số tại một điểm
Để xét sự liên tục của hàm số
y f x
tại điểm tại
0
x
ta thực hiện các bước :
Bước 1 : Tính
0
f x
Bước 2 : Tính
0
lim
x x
f x
(trong nhiều trường hợp để tính
0
lim
x x
f x
ta cần tính
0
lim
x x
f x
và
0
lim
x x
f x
Bước 3 : So sánh
0
lim
x x
f x
và
0
f x
rồi rút ra kết luận.
Chú ý : hàm số không liên tục tại
0
x
thì được gọi là gián đoạn tại
0
x
Ví dụ 1. Xét tính liên tục của hàm số tại điểm được chỉ ra :
a)
3
1
1
1 1
x
khi x
f x
x
khi x
(tại
1
x
) b)
3 2
1
1
1
1
4
x
khi x
x
f x
khi x
(tại
1
x
)
Lời giải:
a
Ta có:
1 3
1 1
1 1
f
1 1
3
lim lim 1 1
1
x x
x
f x f
x
hàm số liên tục tại
1
x
b
Ta có :
1
1
4
f
.
1 1 1 1
3 2 3 2 3 2
1
lim lim lim lim 1
1
3 2
1 3 2
x x x x
x x x
f x f
x
x
x x
Vậy hàm số liên tục tại
1
x
.
Ví dụ 2. Xét tính liên tục của hàm số tại điểm được chỉ ra:
a)
2 3
2
2 7 5
2
3 2
1 2
x x x
khi x
f x
x x
khi x
(tại
2
x
) b)
2
5
5
2 1 3
5 3 5
x
khi x
x
f x
x khi x
(tại
5
x
)
Lời giải:
a
Ta có:
2 1
f
Mà
2
2 3 2
2
2 2 2 2
2 3 1
2 7 5 3 1
lim lim lim lim 1 2
3 2 2 1 1
x x x x
x x x
x x x x x
f x f
x x x x x
Vậy hàm số liên tục tại
2
x
Trang 3
b
Ta có:
2
5 5 5 3 3
f
.
Lại có
2
5 5
lim lim 5 3 3
x x
f x x
Và
5 5 5 5
5 2 1 3
5 2 1 3
lim lim lim lim 3
2
2 1 3
2 1 3 2 1 3
x x x x
x x
x x
f x
x
x x
Từ đó
5
5 lim
x
f f x
hàm số liên tục tại
5
x
.
Ví dụ 3. Xét tính liên tục của hàm số tại điểm được chỉ ra:
a)
1 cos 0
1 0
x khi x
f x
x khi x
(tại
0
x
) b)
1
1
2 1
2 1
x
khi x
f x
x
x khi x
(tại
1
x
)
Lời giải:
a
Ta có:
0 1 cos0 0
f
.
Lại có
0 0
0 0
lim lim 1 1
lim lim 1 cos
x x
x x
f x x
f x x
nên không tồn tại giới hạn hàm số tại
0
x
Vậy hàm số không liên tục tại
0
x
.
b
Ta có:
1 2.1 2
f
.
Lại có
1 1
1 1 1 1
lim lim 2 2
1 2 1
1 2 1
lim lim lim lim 2
1
2 1
2 1 2 1
x x
x x x x
f x x
x x
x x
f x
x
x x
Rõ ràng
1 1
lim lim 1
x x
f x f x f
nên hàm số liên tục tại
1
x
.
Ví dụ 4. Tìm
,
m n
để hàm số liên tục tại điểm được chỉ ra:
a)
2
1
2 3 1
x khi x
f x
mx khi x
(tại
1
x
)
b)
3 2
2 2
1
1
3 1
x x x
khi x
f x
x
x m khi x
(tại
1
x
)
Lời giải
a
Ta có:
2
1 1
lim lim 1
x x
f x x
Lại có
1 1
lim lim 2 3 2 3
x x
f x mx x
Hàm số liên tục
2 3 1 2
x x
Trang 4
b
2
3 2
2
1 1 1 1
1 2
2 2
lim lim lim lim 2 3
1 1
x x x x
x x
x x x
f x x
x x
Hàm số liên tục
3 3 0
m m
Ví dụ 5. Tìm
,
m n
để hàm số liên tục tại điểm được chỉ ra:
a)
2
1
6
0, 3
3
3
m khi x
x x
f x khi x x
x x
n khi x
(tại
0
x
và
3
x
)
b)
2
2
2
2
2
x x
khi x
f x
x
m khi x
(tại
2
x
)
Lời giải
a
Khi
0; 3
x x
thì
2
3 2
6 2
3 3
x x
x x x
f x
x x x x x
0 0
lim lim
x x
f x m m
Hàm
f x
liên tục tại
0 0
2 2
0 lim lim 1
x x
x
x m
x x
3 3
lim lim
x x
f x n n
Hàm
f x
liên tục tại
3 3
2 2 5
3 lim lim 1
3
x x
x
x n
x x
2
2 2 2 2
2 1
2
lim lim lim lim 1 3
2 2
x x x x
x x
x x
b f x x
x x
Hàm
f x
liên tục tại
0 3
x m
Dạng 2. Xét tính liên tục của hàm số trên khoảng, đoạn
Để chứng minh hàm số
y f x
liên tục trên một khoảng, đoạn ta dùng các định nghĩa về hàm
số liên tục trên khoảng, đoạn và các nhận xét để suy ra kết luận.
Khi nói xét tính liên tục của hàm số (mà không nói rõ gì hơn) thì ta hiểu phải xét tính liên tục trên
tập xác định của nó.
Tìm các điểm gián đoạn của hàm số tức là xét xem trên tập xác định của nó hàm số không liên tục
tại các điểm nào
Trang 5
Ví dụ 1. Xét tính liên tục của các hàm số sau trên tập xác định của chúng :
a)
3
3
2
1
1
4
1
3
x x
khi x
x
f x
khi x
b)
2
3 4 2
5 2
2 1 2
x x khi x
f x khi x
x khi x
Lời giải
a
3
3
3 3 2
1 1 1 1
1 1
2 1 4
lim lim lim lim 1
1 1 1 3
x x x x
x x
x x
f x
x x x x
 
Do đó, hàm số này liên tục tại
1
x
2
2 2
lim 3 4 =2; lim 2 1 5
x x
b x x x
Mà
5
f x
khi
2
x
nên
2
2 2
lim lim lim
x
x x
f x f x f x
Do đó, hàm số đã cho liên tục khi
2
x
Ví dụ 2. Xét tính liên tục của các hàm số sau trên tập xác định của chúng :
a)
2
4
2
2
4 2
x
khi x
f x
x
khi x
b)
2
2
2
2
2 2 2
x
khi x
f x
x
khi x
Lời giải
a
Hàm số
f x
liên tục với
2
x
1
2
2 2 2 2
2 2
4
lim lim lim lim 2 2 2 4.
2 2
x x x x
x x
x
f x x
x x
2
2 4 lim 2
x
f f x f f x
liên tục tại
2
x
2
Từ
1
và
2
ta có
f x
liên tục trên
.
b
Hàm số
f x
liên tục với
2
x
1
2
2 2 2 2
2 2
2
lim lim lim lim 2 2 2 2 2.
2 2
x x x x
x x
x
f x x
x x
2
2 2 2 lim 2
x
f f x f f x
liên tục tại
2
x
2
Từ
1
và
2
ta có
f x
liên tục trên
.
Ví dụ 3. Tìm các giá trị của
m
để các hàm số sau liên tục trên tập xác định của chúng:
a)
2
2
2
2
2
x x
khi x
f x
x
m khi x
b)
2
1
2 1
1 1
x x khi x
f x khi x
mx khi x
Lời giải
Trang 6
a
Hàm số
f x
liên tục với
2
x
.
Do đó
f x
liên tục trên
f x
liên tục tại
2
2 lim 2
x
x f x f
1
Ta có
2
2 2 2 2
2 1
2
lim lim lim lim 1 2 1 3; 2 .
2 2
x x x x
x x
x x
f x x f m
x x
Khi đó
1
3 3
m m
.
b
Ta có:
2
1 1 1 1
lim lim 1 1; lim lim 1 1 2; 1 2.
x x x x
f x mx m f x x x f
1 1
YCBT lim lim 1 1 2 1.
x x
f x f x f m m
Ví dụ 4. Xét tính liên tục của các hàm số sau trên tập xác định của chúng :
a)
3 2
2 2
1
1
3 1
x x x
khi x
f x
x
x m khi x
b)
2
1
2 3 1
x khi x
f x
mx khi x
Lời giải
a
Hàm số
f x
liên tục với
1
x
.
Do đó
f x
liên tục trên
f x
liên tục tại
1
1 lim 1
x
x f x f
1
Ta có
1 3.1 3.
f m m
2
3 2
2
1 1 1 1
1 2
2 2
lim lim lim lim 2 1 2 3.
1 1
x x x x
x x
x x x
f x x
x x
Khi đó
1 3 3 0.
m m
b
Ta có
1 2 .1 3 2 3.
f m m
2 2
1 1 1 1
lim lim 2 3 ; lim lim 1 1.
x x x x
f x mx f x x
1 1
YCBT lim lim 1 2 3 1 2 3 2.
x x
f x f x f m m m
Dạng 3. Ứng dụng tính liên tục trong giải phương trình
Biến đổi phương trình về dạng:
0
f x
Tìm hai số
a
,
b
sao cho
. 0
f a f b
(Dùng chức nắng TABLE của máy tính (Mode 7)
tìm cho nhanh)
Chứng minh
f x
liên tục trên
;
a b
từ đó suy ra
0
f x
có nghiệm
Chú ý :
- Nếu
. 0
f a f b
thì phương trình có nghiệm thuộc
;
a b
Trang 7
- Để chứng minh
0
f x
có ít nhất
n
nghiệm trên
;
a b
, ta chia đoạn
;
a b
thành
n
khoảng
nhỏ rời nhau, rồi chứng minh trên mỗi khoảng đó phương trình có ít nhất một nghiệm.
Ví dụ 1. Chứng minh rằng các phương trình sau có 3 nghiệm phân biệt:
a)
3
3 1 0
x x
b)
3
2 6 1 3
x x
Lời giải:
a
Dễ thấy hàm
3
3 1
f x x x
liên tục trên
R
.
Ta có:
2 1
2 . 1 0
1 3
f
f f
f
tồn tại một số
1 1
2; 1 : 0 1 .
a f a
0 1
0 . 1 0
1 1
f
f f
f
tồn tại một số
2 2
0;1 : 0 2 .
a f a
1 1
1 . 2 0
2 3
f
f f
f
tồn tại một số
3 3
1;2 : 0 3 .
a f a
Do ba khoảng
2; 1 , 0;1
và
1;2
đôi một không giao nhau nên phương trình
3
3 1 0
x x
có ít
nhất 3 nghiệm phân biệt.
Mà phương trình bậc 3 thì chỉ có tối đa là 3 nghiệm nên
3
3 1 0
x x
có đúng 3 nghiệm phân biệt.
b
Đặt
3 3
3
1 1 2 6 1 0
x t x t t t
.
Xét hàm số
3
2 6 1
f t t t
liên tục trên
R
.
Ta có:
2 . 1 3.5 0
0 . 1 1. 3 0
1 . 2 3.5 0
f f
f f
f f
tồn tại 3 số
1 2
t t
và
3
t
lần lượt thuộc 3 khoảng đôi một không giao
nhau là
2; 1 , 0;1
và
1;2
sao cho
1 2 3
0
f t f t f t
và do đây là phương trình bậc 3 nên
0
f t
có đúng 3 nghiệm phân biệt.
Ứng với mỗi giá trị
1 2
,
t t
và
3
t
ta tìm được duy nhất một giá trị
x
thỏa mãn
3
1
x t
và hiển nhiên 3 giá
trị này khác nhau nên PT ban đầu có đúng 3 nghiệm phân biệt.
Ví dụ 2. Chứng minh rằng các phương trình sau luôn có nghiệm:
a)
5
3 3 0
x x
b)
4 3 2
3 1 0
x x x x
Lời giải:
a
Xét
5
3 3.
f x x x
lim
x
f x


tồn tại một số
1
0
x
sao cho
1
0.
f x
lim
x
f x


tồn tại một số
2
0
x
sao cho
2
0.
f x
Trang 8
Từ đó
1 2
. 0
f x f x
luôn tồn tại một số
0 2 1 0
; : 0
x x x f x
nên phương trình
5
3 3 0
x x
luôn có nghiệm.
b
Xét
4 3 2
3 1
f x x x x x
liên tục trên
R
Ta có:
1 3 0
f
lim
x
f x


tồn tại một số
0
a
sao cho
0
f a
.
2
3 0
x x
nên luôn tồn tại một số
0
0;
x a
thỏa mãn
0
0
f x
nên phương trình
4 3 2
3 1 0
x x x x
luôn có nghiệm.
Ví dụ 3. Chứng minh rằng các phương trình sau luôn có nghiệm với mọi giá trị của tham số:
a)
3
2 2
1 1 3 0
m x x x
b)
cos cos 2 0
x m x
c)
2cos 2 2sin 5 1
m x x
Lời giải:
a
Xét
1
1
m
m
. Phương trình có dạng
2
3 0
x x
nên PT có nghiệm
Với
1
1
m
m
giả sử
3
2 2
1 1 3
f x m x x x
f x
liên tục trên R nên
f x
liên tục trên
1;0
Ta có
2
1 1 0; f 0 1 0 1 .f 0 0
f m f
Do đó PT luôn có nghiệm với mọi giá trị của tham số
m
b
Đặt
cos cos2
f x x m x f x
liên tục trên R
Ta có
1 3 1 3
0; f 0 .f 0
4 4 4 4
2 2
f f
Do đó PT luôn có nghiệm với mọi giá trị của tham số
m
c
Đặt
2cos 2 2sin5 1
f x m x x f x
liên tục trên R
Ta có
3
2 1 0; 2 1 0 .f 0
4 4 4 4
f f f
Do đó PT luôn có nghiệm với mọi giá trị của tham số
m
Ví dụ 4. Chứng minh rằng phương trình
2
0
ax bx c
luôn có nghiệm
1
0;
3
x
với
0
a
và
2 6 19 0
a b c
.
Lời giải:
Đặt
2
f x ax bx c f x
liên tục trên R
Trang 9
Nếu
0
c
thì
0
f x
có 2 nghiệm là
0
1
3
x
x
Nếu
0
c
, ta có
1 1
0 ; f 2 6 18
3 9 3 18 18
a b c
f c c a b c
2
1
0 .f 0
3 18
c
f
. Do đó
0
f x
có nghiệm trong
1
0;
3
a
Ta có:
0 1 cos 0 0
f
.
Lại có
0 0
0 0
lim lim 1 1
lim lim 1 cos
x x
x x
f x x
f x x
nên không tồn tại giới hạn hàm số tại
0
x
Vậy hàm số không liên tục tại
0
x
.
b
Ta có:
1 2.1 2
f
.
Lại có
1 1
1 1 1 1
lim lim 2 2
1 2 1
1 2 1
lim lim lim lim 2
1
2 1
2 1 2 1
x x
x x x x
f x x
x x
x x
f x
x
x x
Rõ ràng
1 1
lim lim 1
x x
f x f x f
nên hàm số liên tục tại
1
x
.
Ví dụ 5. Cho các phương trình sau
4 3
3 0
x x
,
5 3
16 20 0
x x
,
7 4
4 0
x x
. Số phương trình có
nghiệm là ?
A. 0 B. 1 C. 2 D. 3
Lời giải:
Hàm số
4 3
3
f x x x
liên tục trên
nên liên tục trên
0;2
.
Mà
0 . 2 0 0
f f f x
có ít nhất một nghiệm thuộc khoảng
0;2
.
Hàm số
5 3
16 20
g x x x
liên tục trên
nên liên tục trên
3;5
.
Mà
3 . 5 0 0
f f f x
có ít nhất một nghiệm thuộc khoảng
3;5
.
Hàm số
7 4
4
h x x x
liên tục trên
nên liên tục trên
0;2
.
Mà
0 . 2 0 0
f f f x
có ít nhất một nghiệm thuộc khoảng
0;2
.
Như vậy cả ba phương trình đã cho đều có nghiệm. Chọn D
Ví dụ 6. Phương trình
5 3
5 4 1 0
x x x
có số nghiệm là ?
A. 3 B. 5 C. 1 D. 4
Lời giải:
Hàm số
5 3
5 4 1
f x x x x
liên tục trên
.
Trang 10
Ta kiểm tra được
2 3 1 1
2 . 0; . 0 0; 0 . 0; . 1 ; 1 . 3 <0.
3 2 2 2
f f f f f f f f f f
Từ đó trên mỗi khoảng
3 3 1 1
2; , ;0 , 0; , ;1 , 1;3
2 2 2 2
thì
0
f x
đều có ít nhất một
nghiệm.
Mà
0
f x
là phương trình bậc 5 nên nó có tối đa 5 nghiệm.
Do đó số nghiệm của phương trình là 5. Chọn B.
BÀI TẬP TỰ LUYỆN
Câu 1. Hàm số
1
3
4
f x x
x
liên tục trên
A.
4;3
B.
4;3
C.
4;3
D.
; 4 3;
 
Câu 2. Hàm số
3
cos sin
2sin 3
x x x x
f x
x
liên tục trên
A.
1;1
B.
1;5
C.
3
;
2

D.
Câu 3. Cho hàm số xác định và liên tục trên R với
2
3 2
, 1
1
x x
f x x
x
. Tính
1
f
A.
2
B.
1
C.
0
D.
1
Câu 4. Cho hàm số
f x
xác định và liên tục trên
3;3
với
3 3
, 0.
x x
f x x
x
Tính
0
f
A.
2 3
3
B.
3
C.
1
D.
0
Câu 5. Cho hàm số
f x
xác định và liên tục trên
4;

với
, 0
4 2
x
f x x
x
.
Tính
0
f
A. 0 B. 2 C. 4 D. 1
Câu 6. Tìm giá trị của tham số
m
để hàm số
2
2
2
2
2
x x
khi x
f x
x
m khi x
liên tục tại
2
x
A. 0 B. 1 C. 2 D. 3
Câu 7. Tìm giá trị của tham số
m
để hàm số
3 2
2 2
1
1
3 1
x x x
khi x
f x
x
x m khi x
liên tục tại
1
x
A. 0 B. 2 C. 4 D. 6
Trang 11
Câu 8. Tìm giá trị của tham số
k
để hàm số
1
1
1
1 1
x
khi x
y f x
x
k khi x
liên tục tại
1
x
A.
1
2
B. 2 C.
1
2
D. 0
Câu 9. Biết rằng hàm số
3
3
1 2
3
x
khi x
f x
x
m khi x
liên tục tại
3,
x m
là tham số.
Khẳng định nào sau đây đúng?
A.
3;0
m B.
3
m
C.
0;5
m D.
5;m

Câu 10. Tìm giá trị của tham số
m
để hàm số
2
1
sin 0
0
x khi x
f x
x
m khi x
liên tục tại
0
x
A.
2; 1
m
B.
2
m
C.
0;5
m D.
5;m
Câu 11. Tìm giá trị của tham số
m
để hàm số
tan
0
0 0
x
khi x
f x
x
khi x
liên tục trên khoảng nào dưới
đây?
A.
0;
2
B.
;0
2
C.
;
4 4
D.
;
 
Câu 12. Biết rằng
0
sin
lim 1
x
x
x
. Tìm giá trị thực của tham số
m
để hàm số
sin
1
1
1
x
khi x
f x
x
m khi x
liên tục tại
1
x
A.
B.
C.
1
D.
1
Câu 13. Biết rằng
sin
lim 1
x
x
x
. Tìm giá trị thực của tham số
m
để hàm số
2
1 cos
x
khi x
x
f x
m khi x
liên tục tại
x
A.
2
B.
2
C.
1
2
D.
1
2
Trang 12
Câu 14. Hàm số
4
2
3 1
4
1; 0
1 0
khi x
x
f x khi x x
x x
khi x
liên tục tại
A. Mọi điểm
0, 1
x x
B. Mọi điểm x
C. Mọi điểm trừ
1
x
D. Mọi điểm trừ
0
x
Câu 15. Số điểm gián đoạn của hàm số
2
0,5 1
1
1; 1
1
1 1
khi x
x x
f x khi x x
x
khi x
là
A. 0 B. 1 C. 2 D. 3
Câu 16. Có bao nhiêu giá trị thực của tham số
m
để hàm số
2 2
khi 2
1 x khi 2
m x x
f x
m x
liên tục trên
A. 2 B. 1 C. 0 D. 3
Câu 17. Biết rằng hàm số
khi 0;4
1 khi 4;6
x x
f x
m x
liên tục trên
0;6
. Khẳng định nào sau đây là
đúng?
A.
2
m
B.
2 3
m
C.
3 5
m
D.
5
m
Câu 18. Có bao nhiêu giá trị của tham số
a
để hàm số
2
3 2
khi 1
1
khi 1
x x
x
x
f x
a x
liên tục trên
A. 1 B. 2 C. 0 D. 3
Câu 19. Có bao nhiêu giá trị của tham số
a
để hàm số
2
1
khi 1
1
khi 1
x
x
f x
x
a x
liên tục trên đoạn
0;1 ,
a
là tham số. Khẳng định nào dưới đây là đúng?
A.
a
là một số nguyên B.
a
là một số vô tỉ
C.
5
a
D.
0
a
Câu 20. Xét tính liên tục của hàm số
1
khi 1
2 1
2 khi 1
x
x
f x
x
x x
. Khẳng định nào dưới dây đúng?
A.
f x
không liên tục trên
B.
f x
không liên tục trên
0;2
C.
f x
gián đoạn tại
1
x
D.
f x
không liên tục trên
Trang 13
Câu 21. Tìm giá trị nhỏ nhất của
a
để hàm số
2
2
5 6
khi 3
4 3
1 khi 3
x x
x
f x
x x
a x x
liên tục tại
3
x
A.
2
3
B.
2
3
C.
4
3
D.
4
3
Câu 22. Tìm giá trị lớn nhất của
a
để hàm số
3
2
3 2 2
khi 2
2
1
khi 2
4
x
x
x
f x
a x x
liên tục tại
2
x
A. 3 B. 0 C. 1 D. 2
Câu 23. Xét tính liên tục của hàm số
1 cos khi 0
1 khi 0
x x
f x
x x
. Khẳng định nào sau đây đúng ?
A.
f x
liên tục tại
0
x
B.
f x
liên tục trên
;1

C.
f x
không liên tục trên
D.
f x
gián đoạn tại
1
x
Câu 24. Tìm các khoảng liên tục của hàm số
cos khi 1
2
1 khi 1
x
x
f x
x x
. Mệnh đề nào sau đây là sai?
A. Hàm số liên lục tại
1
x
B. Hàm số liên tục trên các khoảng
;1 ; 1;
 
C. Hàm số liên tục tại
1
x
D. Hàm số liên tục trên khoảng
1;1
Câu 25. Cho hàm số
2
khi 1, 0
0 khi 0
khi 1
x
x x
x
f x x
x x
. Hàm số
f x
liên tục tại
A. Mọi điểm x
B. Mọi điểm trừ
0
x
C. Mọi điểm trừ
1
x
D. Mọi điểm trừ
0
x
và
1
x
Câu 26. Cho hàm số
2
1
khi 3, 1
1
4 khi 1
1 khi 3
x
x x
x
f x x
x x
. Hàm số
f x
liên tục tại
A. Mọi điểm
x
B. Mọi điểm trừ
1
x
C. Mọi điểm trừ
3
x
D. Mọi điểm trừ
1
x
và
3
x
Câu 27. Số điểm gián đoạn của hàm số
2
2 khi 0
+1 khi 0 2
3 1 khi 2
x x
f x x x
x x
.
Trang 14
A. 1 B. 2 C. 3 D. 0
Câu 28. Tính tổng
S
gồm tất cả các giá trị
m
để hàm số
2
2
+ khi 1
2 khi 1
-1 khi 1
x x x
f x x
m x x
liên tục tại
1
x
A.
1
B. 0 C.
1
D. 2
Câu 29. Cho hàm số
2
3
cos khi 0
khi 0 1
1
khi 1
x x x
x
f x x
x
x x
. Hàm số liên tục tại
A. Mọi điểm
x
B. Mọi điểm trừ
0
x
C. Mọi điểm trừ
1
x
D. Mọi điểm trừ
0
x
và
1
x
Câu 30. Tìm
a
để hàm số
2 2
khi 2
2
2 khi 2
x
x
f x
x
x a x
liên tục tại
2
x
A.
15
4
B.
15
4
C.
1
4
D.
1
Câu 31. Tìm tất cả các giá trị của
m
để hàm số
1 1
khi 0
1
khi 0
1
x x
x
x
f x
x
m x
x
liên tục tại
0
x
A.
1
m
B.
2
m
C.
1
m
D.
0
m
Câu 32. Cho hàm số
2
2
3 2
khi 2
2 2
- 4 6 khi 2
x x
x
f x
x
m x m x
,
m
là tham số. Có bao nhiêu giá trị của
m
để
hàm số đã cho liên tục tại
2
x
?
A. 1 B. 2 C. 0 D. 3
Câu 33. Tìm tất cả các giá trị của tham số
m
để hàm số
2
2
khi 2
2
4 khi 2
x x
x
f x
x
mx x
liên tục tại
2
x
A.
3
m
B.
2
m
C.
2
m
D. Không tồn tại
m
Câu 34. Tìm
m
để hàm số
2
2
2 2 khi 2
5 5 khi 2
x x x
y f x
x m m x
liên tục trên
?
A.
2; 3
m m
B.
2; 3
m m
C.
1; 6
m m
D.
1; 6
m m
Trang 15
Câu 35. Cho hàm số
2016
2
khi 1
2018 1 2018
khi 1
x x
x
f x
x x
k x
. Tìm
k
để hàm số
f x
liên tục tại
1
x
.
A.
2 2019
k B.
2017 2018
2
k C.
1
k
D.
2016
2019
2017
Câu 36. Cho hàm số
2
2
2 2 khi 1
2
khi 1
1
x x
f x
x a
x
x
. Gía trị của
a
để hàm số liên tục tại
0
1
x
A. 1 B.
2
C. 3 D. 4
Câu 37. Cho hàm số
3
1
khi 1
1
1 khi 1
x
x
f x
x
x
. Hãy chọn kết luận đúng.
A.
y
liên tục phải tại
1
x
B.
y
liên tục tại
1
x
C.
y
liên tục trái tại
1
x
D.
y
liên tục trên
Câu 38. Tìm giá trị của tham số
a
để hàm số
2
5 6
khi 3
3
khi 3
x x
x
f x
x
a x
liên tục tại
3
x
A.
0
a
B.
1
a
C.
1
a
D.
2
a
Câu 39. Tìm
m
để hàm số
3
2 - -1
khi 1
1
1 khi 1
x x
x
f x
x
mx x
liên tục trên
.
A.
4
3
B.
1
3
C.
4
3
D.
2
3
Câu 40. Tìm giá trị thực của tham số
m
để hàm số
3 2
2 2
khi 1
1
3 khi 1
x x x
x
f x
x
x m x
liên tục
tại
1
x
A.
0
m
B.
6
m
C.
4
m
D.
2
m
Câu 41. Cho hàm số
2
2
4 2
khi 0
5
2 khi 0
4
x
x
x
f x
a x
. Tìm giá trị thực của tham số
a
để hàm số
f x
liên tục tại
0
x
A.
3
4
a
B.
4
3
a
C.
4
3
a
D.
3
4
a
Trang 16
Câu 42. Tìm
a
để hàm số
2
1
khi 1
1
khi 1
x
x
f x
x
a x
liên tục tại điểm
0
1
x
.
A.
0
a
B.
1
a
C.
2
a
D.
1
a
Câu 43. Cho hàm số
5 1 2
khi 1
1
1
khi 1
4
x
x
x
f x
mx m x
, (
m
là tham số). Giá trị
m
để hàm số liên tục
trên
là
A.
0
m
B.
1
2
m
C.
2
m
D.
1
m
Câu 44. Tìm giá trị của tham số
m
để hàm số
2
3 2
khi 1
1
khi 1
x x
x
f x
x
m x
liên tục tại
1
x
.
A.
1
m
B.
2
m
C.
1
m
D.
2
m
Câu 45. Hàm số nào dưới đây gián đoạn tại điểm
1
x
?
A.
2
1
1
x
y
x x
B.
2
2
1
x
y
x
C.
2
1 1
y x x x
D.
2
1
1
x x
y
x
Câu 46. Cho hàm số
2
6
khi 2
2
2 1 khi 2
x x
x
f x
x
ax x
. Xác định
a
để hàm số liên tục tại điểm
2
x
A.
2
a
B.
1
a
C.
1
a
D.
1
2
a
Câu 47. Tìm giá trị thực của tham số
m
để hàm số
2
1 khi 2
+m khi 2
x x
f x
x x
liên tục tại
2
x
A.
1
m
B.
0
m
C.
3
m
D.
6
m
Câu 48. Cho hàm số
sin
khi 0
khi 0
x
x
f x
x
a x
. Tìm
a
để
f x
liên tục tại
0
x
A.
1
B.
1
C. 2 D. 0
Câu 49. Cho hàm số
2
khi 2
3 1 khi 2
x m x
f x
x x
(
m
là tham số). Tìm giá trị thực của tham số
m
để hàm
số đã cho liên tục tại
0
2
x
A.
2
m
B.
1
m
C.
0
m
D.
3
m
Trang 17
Câu 50. Tìm giá trị của tham số
m
sao cho hàm số
2
2
3 7 6
khi 3
3
5 2 khi 3
x x
x
f x
x
x mx x
liên tục với mọi
x
thuộc
.
A.
7
m
B.
3
m
C.
2
m
D.
0
m
Câu 51. Giá trị của tham số
m
sao cho hàm số
4 2
khi 0
5
2 khi 0
4
x
x
x
f x
m x x
liên tục tại
0
x
là
A. 3 B.
4
3
C.
1
8
D.
1
2
Câu 52. Giá trị của tham số
a
sao cho hàm số
1
khi 1
1
1
khi 1
2
x
x
x
f x
ax x
liên tục tại điểm
1
x
là
A.
1
2
B.
1
C. 1 D.
1
2
Câu 53. Tìm tất cả các giá trị thực của tham số
m
để hàm số
2
16
khi 4
4
1 khi 4
x
x
f x
x
mx x
liên tục trên
.
A.
8
m
hoặc
7
4
m
B.
8
m
hoặc
7
4
m
C.
7
4
m
D.
7
4
m
Câu 54. Cho hàm số
2
1
khi 1
1
khi 1
x
x
f x
x
m x
, với
m
tham số thực. Tìm
m
để hàm số
f x
liên tục tại
1
x
A.
2
m
B.
2
m
C.
1
m
D.
1
m
Câu 55. Cho hàm số
2
3
khi 3
3
2 3 khi 3
x
x
f x
x
x
. Tìm khẳng định đúng trong các khẳng định sau :
I
f x
liên tục tại
3
x .
II
f x
gián đoạn tại
3
x .
III
f x
liên tục trên
.
A. Chỉ I và II. B. Chỉ I và III.
C. Cả I, II, III đều đúng. D. Chỉ II và III.
Trang 18
Câu 56. Cho hàm số
2
3 2
khi 2
2
2 1 khi 2
x x
x
f x
x
m x
. Với giá trị nào của
m
sau đây để hàm số
f x
liên
tục tại
2
x
.
A. 0 B. 1 C. 2 D.
1
Câu 57. Có bao nhiêu giá trị thực của tham số
m
để hàm số
2
3 2
khi 2
2
1 khi 2
x x
x
f x
x
m x x
liên tục trên
?
A. 0 B. 1 C. 2 D. 3
Câu 58. Tìm
P
để hàm số
2
4 3
, x>1
1
6 3, 1
x x
y
x
Px x
liên tục trên
?
A.
5
6
B.
1
2
C.
1
6
D.
1
3
Câu 59. Cho
,
a b
là hai số thực sao cho hàm số
2
, 1
1
2 1 1
x ax b
x
f x
x
ax x
liên tục trên
?
Tính
a b
A. 0 B.
1
C.
5
D. 7
Câu 60. Cho hàm số
2
2
2 2
khi 1
3 2
8 khi 1
ax a x
x
f x
x
a x
. Có bao nhiêu giá trị của tham số
a
để
hàm số liên tục tại
1
x
A. 1 B. 0 C. 3 D. 2
Câu 61. Cho hàm số
3 1, khi 0
1 2 1
khi 0
x a x
f x
x
x
x
. Tìm tất cả các giá trị của tham số
a
để hàm
số liên tục tại
0
x
A.
1
a
B.
3
a
C.
2
a
D.
4
a
Câu 62. Tìm
m
để hàm số
2
16
khi 4
4
1 khi 4
x
x
f x
x
mx x
liên tục tại điểm
4
x
A.
8
B. 8 C.
7
4
D.
7
4
Trang 19
Câu 63. Cho hàm số
3
8
khi 2
2
2 1 khi 2
x
x
f x
x
m x
. Tìm
m
để hàm số liên tục tại
0
2
x
A.
3
2
B.
13
2
C.
11
2
D.
1
2
Câu 64. Cho hàm số
2
khi 1
3 2
khi 1
1
x mx x
f x
x
x
x
. Tìm
m
để hàm số đã cho liên tục tại
1
x
A.
3
4
B.
1
3
C. 0 D. 2
Câu 65. Cho hàm số
2
1 cos
khi 0
1 khi 0
x
x
f x
x
x
. Khẳng định nào trong các khẳng định sau là đúng?
A.
f x
có đạo hàm tại
0
x
B.
f x
liên tục tại
0
x
C.
2 0
f
D.
f x
gián đoạn tại
0
x
Câu 66. Tìm
a
để các hàm số
2
4 1 1
khi 0
2 1
3 khi 0
x
x
f x
ax a x
x
liên tục tại
0
x
A.
1
4
B.
1
2
C.
1
6
D. 1
Câu 67. Cho hàm số
khi 0
1 khi 0
x m x
f x
mx x
. Tìm tất cả các giá trị thực của
m
để
f x
liên tục trên
A. 1 B. 0 C.
1
D.
2
Câu 68. Cho hàm số
sin khi 1
1 khi 1
x x
f x
x x
. Mệnh đề nào sau đây đúng?
A. Hàm số liên tục trên
B. Hàm số liên tục trên các khoảng
; 1

và
1;

C. Hàm số liên tục trên các khoảng
;1

và
1;

D. Hàm số gián đoạn tại
1
x
Câu 69. Hàm số
2
16
khi 4
2
3 khi 4
x
x
f x
x
x m x
liên tục tại
0
4
x
khi
m
nhận giá trị là
A. 44 B.
20
C.
20
D.
44
Trang 20
Câu 70. Cho hàm số
2 1 5
khi 4
4
2 khi 4
x x
x
f x
x
a x
. Tìm tất cả các giá trị của tham số
a
để hàm số
liên tục tại
4
x
A.
5
2
a
B.
11
6
a
C.
3
a
D.
2
a
Câu 71. Cho hàm số
2
2 7 6
khi 2
2
1
khi 2
2
x x
x
x
f x
x
a x
x
. Biết
a
là giá trị để hàm số
f x
liên tục tại
2
x
. Tìm số nghiệm nguyên của bất phương
2
7
0
4
x ax
A. 1 B. 4 C. 3 D. 2
Câu 72. Tìm giá trị thực của tham số
m
để hàm số
2
2
khi 2
2
khi 2
x x
x
f x
x
m x
liên tục tại
2
x
A.
3
m
B.
1
m
C.
2
m
D.
0
m
Câu 73. Cho các mệnh đề:
1 .
Nếu hàm số
y f x
liên tục trên
;
a b
và
. 0
f a f b
thì tồn tại
0
;
x a b
sao cho
0
0
f x
.
2 .
Nếu hàm số
y f x
liên tục trên
;
a b
và
. 0
f a f b
thì phương trình
0
f x
có nghiệm.
3 .
Nếu hàm số
y f x
liên tục, đơn điệu trên
;
a b
và
. 0
f a f b
thì phương trình
0
f x
có
nghiệm duy nhất trên
;
a b
.
Trong ba mệnh đề trên
A. Có đúng hai mệnh đề sai. B. Cả ba mệnh đề đều đúng.
C. Cả ba mệnh đề đều sai. D. Có đúng một mệnh đề sai.
Câu 74. Cho hàm số
3
4 4 1
f x x x
. Mệnh đề nào sau đây sai?
A. Hàm số đã cho liên tục trên
B. Phương trình
0
f x
không có nghiệm trên khoảng
;1

C. Phương trình
0
f x
có nghiệm trên khoảng
2;0
D. Phương trình
0
f x
có ít nhất hai nghiệm trên khoảng
1
3;
2
Trang 21
Câu 75. Cho phương trình
4 2
2 5 1 0
x x x
. Mệnh đề nào sau đây đúng?
A. Phương trình không có nghiệm trong khoảng
1;1
.
B. Phương trình không có nghiệm trong khoảng
2;0
.
C. Phương trình chỉ có một nghiệm trong khoảng
2;1
.
D. Phương trình có ít nhất hai nghiệm trong khoảng
0;2
.
Câu 76. Cho hàm số
3
3 1
f x x x
. Số nghiệm của phương trình
0
f x
trên
là
A. 0 B. 1 C. 2 D. 3
Câu 77. Cho hàm số
f x
liên tục trên đoạn
1;4
sao cho
1 2
f
,
4 7
f
. Có thể nói gì về số
nghiệm của phương trình
5
f x
trên đoạn
1;4
:
A. Vô nghiệm. B. Có ít nhất một nghiệm.
C. Có đúng một nghiệm. D. Có đúng hai nghiệm.
Câu 78. Có tất cả bao nhiêu giá trị nguyên của tham số
m
thuộc khoảng
10;10
để phương trình
3 2
3 2 2 3 0
x x m x m
có bai nghiệm phân biệt
1 2 3
, ,
x x x
thỏa mãn
1 2 3
1
x x x
?
A. 19 B. 18 C. 4 D. 3
ĐÁP ÁN VÀ LỜI GIẢI BẢI TẬP TỰ LUYỆN
1-C 2-D 3-D 4-B 5-C 6-D 7-A 8-C 9-B 10-C
11-A 12-A 13-C 14-B 15-B 16-A 17-A 18-C 19-A 20-D
21-A 22-C 23-C 24-A 25-A 26-D 27-A 28-B 29-C 30-B
31-B 32-A 33-A 34-A 35-A 36-B 37-A 38-B 39-A 40-A
41-D 42-C 43-B 44-A 45-B 46-C 47-A 48-A 49-B 50-D
51-C 52-C 53-D 54-C 55-B 56-A 57-B 58-C 59-D 60-D
61-C 62-D 63-C 64-A 65-D 66-C 67-C 68-C 69-B 70-B
71-D 72-A 73-D 74-B 75-D 76-D 77-B 78-C
Câu 1: Điều kiện
3 0 4
4;3
4 0 3
x x
D
x x
hàm số liên tục trên
4;3
.
Xét tại
3
x
, ta có
3 3
1 1
lim lim 3 3
4 7
x x
f x x f
x
Hàm số liên tục trái tại
3
x
. Vậy hàm số liên tục trên
4;3
. Chọn C
Câu 2: Vì
2sin 3 0
x
với mọi
x D
nên hàm số liên tục trên
. Chọn D
Trang 22
Câu 3: Vì
f x
liên tục trên
nên
2
1 1 1
3 2
1 lim lim lim 2 1
1
x x x
x x
f f x x
x
. Chọn D.
Câu 4: Vì
f x
liên tục trên
3;3
nên suy ra
0 0 0
3 3 2 1
0 lim lim lim
3 3 3
x x x
x x
f f x
x
x x
. Chọn B.
Câu 5: Vì
f x
liên tục trên
4;

nên suy ra
0 0 0
0 lim lim lim 4 2 4
4 2
x x x
x
f f x x
x
. Chọn C.
Câu 6: Tập xác định
D
, chứa
2
x
. Theo giả thiết thì ta phải có
2
2 2 2
2
2 lim lim lim 1 3.
2
x x x
x x
m f f x x
x
Chọn D.
Câu 7: Hàm số xác định với mọi x
. Theo giả thiết thì ta có
1
3 1 lim
x
m f f x
Suy ra
2
3 2
2
1 1 1
1 2
2 2
3 lim lim lim 2 3 0
1 1
x x x
x x
x x x
m x m
x x
. Chọn A.
Câu 8: Hàm số
f x
có TXĐ:
0;D

. Điều kiện bài toán tương đương vợi
1 1 1
1 1 1 1
1 1 lim lim lim .
1 2 2
1
x x x
x
k y y k
x
x
Chọn C.
Câu 9: Hàm số
f x
có TXĐ là
1;

. Theo giả thiết thì ta phải có
3 3 3 3
3 1 2
3
3 lim lim lim lim 1 2 4.
3
1 2
x x x x
x x
x
m f f x x
x
x
Chọn B.
Câu 10: Với mọi
0
x
, ta có :
2 2
1
0 sin 0
f x x x
x
khi
0
0 lim 0.
x
x f x
Theo giả thiết thì ta phải có:
0
0 lim 0.
x
m f f x
Chọn C.
Câu 11: Tập xác định:
\ |
2
D k k Z
.
Ta có
0 0 0
tan sin 1 1
lim lim lim . 1. 1 0 0
cos cos
x x x
x x
f x f f x
x x x x
không liên tục tại
0
x
.
Chọn A.
Câu 12: Tập xác định
D
. Điều kiện bài toán tương đương với
1 1
sin
1 lim lim
1
x x
x
m f f x
x
1 1 1
sin sin 1 sin 1
= lim lim lim .
1 1 1
x x x
x x x
x x x
*
.
Trang 23
Đặt
1
t x
thì
0
t
khi
1
x
. Do đó
*
trở thành :
0
sin
lim . .
t
t
m
t
Chọn A.
Câu 13: Hàm số xác định với mọi
x
. Điều kiện của bài toán trở thành:
2
2 2
2cos
1 cos
2
lim lim lim
x x x
x
x
m f f x
x x
2
2
2
2sin sin
1
2 2 2 2
lim lim
2
2 2
x x
x x
x
x
*
Đặt
0
2 2
x
t
khi
1
x
. Khi đó
*
trở thành:
2
2
0
1 sin 1 1
lim .1 .
2 2 2
t
t
m
t
Chọn C.
Câu 14: Hàm số
y f x
có TXĐ:
D
Dễ thấy hàm số
y f x
liên tục trên mỗi khoảng
; 1 , 1;0
 và
0;

.
1
Xét tại
1,
x
ta có
2
4
2
2
1 1 1 1
1 1
lim lim lim lim 1 3 1 .
1
x x x x
x x x x
x x
f x x x f
x x x x

hàm số
y f x
liên tục tại
1.
x
2
Xét tại
0
x
, ta có
2
4
2
2
0 0 0 0
1 1
lim lim lim lim 1 1 0 .
1
x x x x
x x x x
x x
f x x x f
x x x x
hàm số
y f x
liên tục tại
0
x
. Chọn B.
Câu 15: Hàm số
y f x
có TXĐ:
D
.
Hàm số
2
1
1
x x
f x
x
liên tục trên mỗi khoảng
; 1 , 1;1
 và
1;

.
1
Xét tại
1,
x
ta có
2
1 1 1
1
1
lim lim lim 1
1 1 2
x x x
x x
x
f x f
x x
Hàm số liên tục tại
1.
x
2
Xét tại
1
x
, ta có
2
1 1 1
2
1 1 1
1
lim lim lim
1 1
1
lim lim lim
1 1
x x x
x x x
x x
x
f x
x x
x x
x
f x
x x


Hàm số
y f x
gián đoạn tại
1
x
. Chọn B.
Trang 24
Câu 16: TXĐ:
D
. Hàm số liên tục trên mỗi khoảng
;2 , 2; .
 
Khi đó
f x
liên tục trên
f x
liên tục tại
2
x
2
2 2
lim 2 lim lim 2 .
x
x x
f x f f x f x f
*
Ta có
2
2
2 2
2 2 2
2 2
2 4
1
lim lim 1 2 1 * 4 2 1
1
2
lim lim 4
x x
x x
f m
m
f x m x m m m
m
f x m x m
Chọn A.
Câu 17: Dễ thấy hàm số
f x
liên tục trên mỗi khoảng
0;4
và
4;6
. Khi đó hàm số liên tục trên
đoạn
0;6
khi và chỉ khi hàm số liên tục tại
4, 0, 6
x x x
.
Tức là ta cần có
0
6
4 4
lim 0
lim 6
lim lim 4
x
x
x x
f x f
f x f
f x f x f
*
0 0
lim lim 0
0 0 0
x x
f x x
f
6 6
lim lim 1 1
6 1
x x
f x m m
f m
4 4
4 4
lim lim 2
lim lim 1 1 ;
4 1
x x
x x
f x x
f x m m
f m
Khi đó
*
trở thành
1 2 1 2.
m m
Chọn A.
Câu 18: Hàm số
f x
liên tục trên
;1

và
1,

.
Khi đó hàm số đã cho liên tục trên
khi nó liên tục tại
1
x
, tức là ta cần có
1
1 1
lim 1 lim lim 1
x
x x
f x f f x f x f
*
Ta có
1 1
1 1
2 khi 1
lim lim 2 1
khi 1
lim lim 2 1
2 khi 1
x x
x x
x x
f x x
f x a x
f x x
x x
*
không thỏa mãn.
Vậy không tồn tại giá trị
a
thỏa yêu cầu. Chọn C.
Trang 25
Câu 19: Hàm số xác định và liên tục trên
0;1
.
Khi đó
f x
liên tục trên
0;1
khi và chỉ khi
1
lim 1
x
f x f
*
Ta có
2
1 1 1
1
* 4.
1
lim lim lim 1 1 4
1
x x x
f a
a
x
f x x x
x
Chọn A.
Câu 20: Dễ thấy hàm số liên tục trên
;1

và
1;

.
Ta có
1 1
1 1 1
1 2
lim lim 2 2
1
lim lim lim 2 1 2
2 1
x x
x x x
f
f x x f x
x
f x x
x
liên tục tại
1
x
Vậy hàm số
f x
liên tục trên
. Chọn D.
Câu 21: Điều kiện bài toán trở thành:
3 3
lim lim 3
x x
f x f x f
*
Ta có
2
2
3 3 3
2 3
3 3
3 1 3
2 4 3
5 6
lim lim lim 3
1
4 3
lim lim 1 1 3 .
x x x
x x
f a
x x x
x x
f x
x
x x
f x a x a
min
2 2
* .
3 3
a a
Chọn A.
Câu 22: Ta cần có
2 2
lim lim 2
x x
f x f x f
*
Ta có
2
3
max
2 2
2 2
2 2
7
2 2
4
3 2 2 1
lim lim * 1 1.
2 4
1 7
lim lim 2 .
4 4
x x
x x
f a
x
f x a a
x
f x a x a
Chọn C.
Câu 23: Hàm số xác định với mọi
x
Ta có
f x
liên tục trên
;0
 và
0;

.
Trang 26
Mà
0 0
0 0
0 1
lim lim 1 cos 1 cos 0 0
lim lim 1 0 1 1
x x
x x
f
f x x f x
f x x
gián đoạn tại
0
x
. Chọn C.
Câu 24: Ta có
f x
liên tục trên
; 1 , 1;1
 và
1;

.
Lại có
1 1
1 cos 0
2
lim lim 1 2
x x
f
f x
f x x
gián đoạn tại
1
x
. Chọn A.
Câu 25: Hàm số
y f x
có TXĐ:
D
.
Dễ thấy hàm số
y f x
liên tục trên mỗi khoảng
;0 , 0;1
 và
1;

.
Ta có
2
0 0 0
2
0 0 0
0 0
lim lim lim 0
lim lim lim 0
x x x
x x x
f
x
f x x f x
x
x
f x x
x
liên tục tại
0
x
Lại có
2
1 1 1
2
1 1 1
1 1
lim lim lim 1
lim lim lim 1
x x x
x x x
f
x
f x x f x
x
x
f x x
x
liên tục tại
1
x
Vậy hàm số
y f x
liên tục trên
. Chọn A.
Câu 26: Hàm số
y f x
có TXĐ:
D
.
Dễ thấy hàm số
y f x
liên tục trên mỗi khoảng
;1 , 1;3
 và
3;

.
Ta có
2
1 1 1
1 4
1
lim lim lim 1 2
1
x x x
f
f x
x
f x x
x
gián đoạn tại
1
x
Lại có
2
3 3 3
3 2
1
lim lim lim 1 4
1
x x x
f
f x
x
f x x
x
gián đoạn tại
3
x
Chọn D.
Câu 27: Hàm số
y h x
có TXĐ:
D
.
Trang 27
Dễ thấy hàm số
y h x
liên tục trên mỗi khoảng
;0 , 0;2
 và
2;

.
Ta có
0 0
0 1
lim lim 2 0
x x
h
f x
h x x
không liên tục tại
0
x
Lại có
2
2 2
2 2
2 5
lim lim 1 5
lim lim 3 1 5
x x
x x
h
h x x f x
h x x
liên tục tại
2
x
. Chọn A.
Câu 28: Hàm số xác định với mọi
x
Điều kiện bài toán trở thành
1 1
lim lim 1
x x
f x f x f
*
Ta có
2 2 2
1 1
2
1 1
1 2
lim lim 1 1 * 1 2
lim lim 2
x x
x x
f
f x m x m m
f x x x
1 0.
m S
Chọn B.
Câu 29: Hàm số
y f x
có TXĐ:
D
.
Dễ thấy hàm số
y f x
liên tục trên mỗi khoảng
;0 , 0;1
 và
1;

.
Ta có
0 0
2
0 0
0 0
lim lim cos 0
lim lim 0
1
x x
x x
f
f x x x f x
x
f x
x
liên tục tại
0
x
Lại có
2
1 1
3
1 1
1 1
1
lim lim
1 2
lim lim 1
x x
x x
f
x
f x f x
x
f x x
không liên tục tại
1
x
Chọn C.
Câu 30: Ta có
2 2 2
2 2 2 4
2 4 ,lim lim lim
2
2 2 2
x x x
x x
f a f x
x
x x
2
1 1
lim
4
2 2
x
x
Để hàm số đã cho liên tục tại điểm
2
x
thì
2
1 15
2 lim 4
4 4
x
f f x a a
. Chọn B.
Câu 31: Ta có
0
lim 0 1
x
f x f m
Trang 28
Lại có:
0 0 0 0
1 1 1 1 2
lim lim lim lim
1 1 1 1
x x x x
x x x x x
f x
x
x x x x x
0
2 2
lim 1.
2
1 1
x
x x
Để hàm số đã cho liên tục tại điểm
0
x
thì
1 1 2
m m
. Chọn B.
Câu 32: Ta có
2
2
lim 2 2 4 6
x
f x f m m
Mặt khác
2
2 2 2 2
2 2 1 2
1 2
3 2
lim lim lim lim
2 4
2
2 2
2 2
x x x x
x x x
x x
x x
f x
x
x
x
x
2
lim 2 2 1 4
x
x x
Do đó hàm số đã cho liên tục tại điểm
2
x
khi
2 2
2 4 6 4 2 4 2 0 1
m m m m m
. Vậy có 1
giá trị của
m
. Chọn A
Câu 33: Ta có
2
lim 2 2 4
x
f x f m
Lại có :
2
2 2 2 2
2
2
lim lim lim lim 2
2 2
x x x x
x x
x x
f x x
x x
Để hàm số liên tục tại điểm
2
x
thì
2 4 2 3
m m
. Chọn A.
Câu 34: Ta có
2
lim 2 4 2 2 2 4
x
f x f
Mặt khác
2 2
2 2
lim lim 5 5 10 5
x x
f x x m m m m
Hàm số liên tục với mọi
2
x
, như vậy để hàm số đã cho liên tục trên
thì hàm số liên tục tại điểm
2
x
khi và chỉ khi
2 2
2
4 10 5 5 6 0
3
m
m m m m
m
. Chọn A.
Câu 35: Ta có
1
f k
2016
2016
1 1 1
1 1
2
lim lim lim
2018 1 2018
2018 1 2018
2018 1 2018
x x x
x x
x x
f x
x x
x x
x x
2015 2014
1
1 1 1
lim 2018 1 2018
2017 1
x
x x x x x
x x
x
2015 2014
1
1 1
2016 1
lim 2018 1 2018 .2 2019 2 2019
2017 2017
x
x x x
x x
Do đó hàm số liên tục tại điểm
1 2 2019
x k . Chọn A.
Câu 36: Ta có
2
1 1 1
2 2
lim 1 0, lim lim
1 2
x x x
x a a
f x f f x
x
Trang 29
Để hàm số liên tục tại điểm
0
1
x
thì
2
0 2
2
a
a
. Chọn B.
Câu 37: Ta có
1
lim 1 1
x
f x f
Mặt khác
2
3
2
1 1 1 1
1 1
1
lim lim lim lim 1 3
1 1
x x x x
x x x
x
f x x x
x x
Do
1 1
lim lim
x x
f x f x
nên hàm số đã cho không liên tục tại điểm
1
x
Mặt khác
1
lim 1 1
x
f x f
nên hàm số liên tục phải tại điểm
1
x
. Chọn A.
Câu 38: Ta có
2
3 3 3 3
2 3
5 6
3 3,lim lim lim lim 2 1
3 3
x x x x
x x
x x
f f x x
x x
Để hàm số liên tục tại điểm
3
x
thì
3
lim 3 1
x
f x f a
. Chọn B.
Câu 39: Hàm số đã cho liên tục với mọi
1
x
Ta có:
3 3
1 1 1
2 1 2 2 1
1 1,lim lim lim
1 1
x x x
x x x x
f m f x
x x
3
1 1
3 32 2
3 3 3
2 1
2 2 1
lim 1 lim 1 1
3 3
1 1 1
x x
x
x x x x x
Để hàm số đã cho liên tục tại
1
x
thì
1 4
1
3 3
m m
. Chọn A.
Câu 40: Ta có:
1 3
f m
và
2
3 2
1 1 1
1 2 1
2 2
lim lim lim
1 1
x x x
x x x
x x x
f x
x x
2
2
1 1
2 1
lim lim 2 3
1
x x
x x
x
x
Để hàm số đã cho liên tục tại
1
x
thì
3 3 0
m m
. Chọn A.
Câu 41: Ta có
5
0 2
4
f a
và
2 2
2
0 0 0
2 2
4 2 4 4
lim lim lim
4 2
x x x
x x
f x
x
x x
2
0
1 1
lim
4
4 2
x
x
Để hàm số đã cho liên tục tại điểm
0
x
thì
5 1 3 3
2 2
4 4 2 4
a a a
. Chọn D.
Câu 42: Ta có
2
1 1 1 1
1 1
1
lim lim lim lim 1 2
1 1
x x x x
x x
x
f x x
x x
Lại có
1
f a
, để hàm số liên tục tại điểm
1
x
thì
2
a
. Chọn C.
Trang 30
Câu 43: Ta có
1
1 1
lim 1 2
4 4
x
f x f m m m
Lại có:
1 1 1 1
5 1
5 1 2 5 1 4
lim lim lim lim
1
1 5 1 2 1 5 1 2
x x x x
x
x x
f x
x
x x x x
1
5 5
lim
4
5 1 2
x
x
Để hàm số liên tục trên
thì hàm số phải liên tục tại điểm
1
x
Khi đó
1 5 1
2
4 4 2
m m
. Chọn B.
Câu 44: Ta có
2
1 1 1
3 2
lim lim lim 2 1
1
x x x
x x
f x x
x
Hàm số đã cho liên tục tại
1
x
khi
1
lim 1 1
x
f x f m
. Chọn A.
Câu 45: Hàm số
2
2
1
x
y
x
bị gián đoạn tại
1
x
. Chọn B.
Câu 46:
2
2 2 2
6
lim lim lim 3 5
2
x x x
x x
f x x
x
Và
2 2
lim lim 2 1 1 4 ; 2 2 .2 1 1 4
x x
f x ax a f a a
Hàm số đã cho liên tục tại
2
x
khi
2 2
lim lim 2 1 4 5 1
x x
f x f x f a a
. Chọn C.
Câu 47: Ta có
2 2
lim lim 1 3
x x
f x x
;
Và
2
2 2
lim lim 4; 2 4
x x
f x x m m f m
Hàm số đã cho liên tục tại
2
x
khi
2 2
lim lim 2 4 3 1
x x
f x f x f m m
. Chọn A.
Câu 48: Ta có
0 0
sin
lim lim 1; 0
x x
x
f x f a
x
Hàm số liên tục tại
0
x
khi
0
lim 0 1
x
f x f a
. Chọn A.
Câu 49: Ta có
2
2 2
lim lim 4 ;
x x
f x x m m
Và
2 2
lim lim 3 1 5; 2 4 ;
x x
f x x f m
Hàm số liên tục tại
2
x
khi
2 2
lim lim 2 4 5 1
x x
f x f x f m m
. Chọn B.
Câu 50: Hàm số đã cho liên tục trên khoảng
;3 , 3;
 
Ta có
2
3 3 3
3 7 6
lim lim lim 3 2 3.3 2 11
3
x x x
x x
f x x
x
;
Trang 31
Và
2
3 3
lim lim 5 2 15 11; 2 15 11
x x
f x x mx m f m
Hàm số liên tục tại
3
x
khi
3 3
lim lim 3 15 11 11 0
x x
f x f x f m m
Vậy
0
m
là giá trị để hàm số liên tục trên
. Chọn D
Câu 51: Ta có
0 0 0
4 2 1 1
lim lim lim ;
4
4 2
x x x
x
f x
x
x
Và
0 0
5
lim lim 2 2 ; 0 2
4
x x
f x m x m f m
Hàm số liên tục tại
0
x
khi
0 0
1 1
lim lim 0 2
4 8
x x
f x f x f m m
. Chọn C.
Câu 52: Ta có
1 1 1
1 1 1
lim lim lim ;
1 2
1
x x x
x
f x
x
x
Và
1 1
1 1 1
lim lim ; 1
2 2 2
x x
f x ax a f a
Hàm số liên tục tại
1
x
khi
1 1
1 1
lim lim 1 1
2 2
x x
f x f x f a a
. Chọn C
Câu 53: Hàm số đã cho liên tục trên khoảng
;4 , 4;

Ta có
2
4 4 4
16
lim lim lim 4 8;
4
x x x
x
f x x
x
Và
4 4
lim lim 1 4 1; 4 4 1
x x
f x mx m f m
Hàm số liên tục tại
4
x
khi
4 4
7
lim lim 4 4 1 8
4
x x
f x f x f m m
Vậy
7
4
m
là giá trị để hàm số liên tục trên
. Chọn D.
Câu 54: Ta có
2
1 1 1
1
lim lim lim 1 2; 1
1
x x x
x
f x x f m
x
Hàm số liên tục tại
1
x
khi
1
lim 1 1
x
f x f m
. Chọn C.
Câu 55: Ta có
2
3 3 3
3
lim lim lim 3 2 3 3
3
x x x
x
f x x f
x
Suy ra hàm số đã cho liên tục tại
3
x
Hàm số liên tục trên
. Chọn B.
Câu 56: Ta có
2
2 2 2
3 2
lim lim lim 1 1;
2
x x x
x x
f x x
x
Và
2 2
lim lim 2 1 2 1;
x x
f x m m
Hàm số liên tục tại
2
x
khi
2 2
lim lim 2 1 1 0
x x
f x f x m m
. Chọn A.
Trang 32
Câu 57: Hàm số đã cho liên tục trên khoảng
;2 , 2;

Ta có
2
2 2 2
3 2
lim lim lim 1 1;
2
x x x
x x
f x x
x
Và
2 2
lim lim 2 2 ;
x x
f x x mx m
Hàm số liên tục tại
2
x
khi
2 2
1
lim lim 2 2 1
2
x x
f x f x m m
Vậy
1
2
m
là giá trị để hàm số liên tục trên
. Chọn B.
Câu 58: Ta có
2
1 1 1 1
1 3
4 3
lim lim lim lim 3 2
1 1
x x x x
x x
x x
f x x
x x
Lại có
1 1
lim lim 6 3 1 6 3
x x
f x Px f P
Hàm số liên tục trên
khi hàm số liên tục tại
1
x
Khi đó
1
2 6 3
6
P P
. Chọn C.
Câu 59: Ta có
1 2 1
f a
Để hàm số đã cho liên tục trên
thì hàm số liên tục tại điểm
1
x
Khi đó
2
1 1
lim lim 2 1 *
1
x x
x ax b
f x a
x
Suy ra
2
1 1 1
x ax b x x b a b
Ta có:
1
* lim 2 1 1 2 1
x
x b a b a
(2)
Giải hệ
1
và
2
ta được
3
7
4
a
a b
b
. Chọn D.
Câu 60: Ta có
2
1 8
f a
, mặt khác
2
1 1
2 2
lim lim
3 2
x x
ax a x
f x
x
1 1
2 1
lim . 3 2 lim 2 . 3 2 4 2
3 4
x x
ax x
x ax x a
x
Hàm số liên tục tại điểm
1
x
khi
2 2
0
8 4 2 4 0
4
a
a a a a
a
Vậy có 2 giá trị của tham số
a
. Chọn D.
Câu 61: Ta có
0 0
lim lim 3 1 1
x x
f x x a a
Mặt khác
0 0 0 0
1 2 1 1 2 1 2
lim lim lim lim 1
1 2 1
1 2 1
x x x x
x x
f x
x
x
x x
Trang 33
Hàm số đã cho liên tục tại điểm
0 1 1 2
x a a
. Chọn C.
Câu 62: Ta có
4 4
lim lim 1 4 1
x x
f x mx m
Lại có:
2
4 4 4 4
4 4
16
lim lim lim lim 4 8
4 4
x x x x
x x
x
f x x
x x
Để hàm số liên tục tại điểm
4
x
thì
7
4 1 8
4
m m
. Chọn D.
Câu 63: Ta có
2
3
2 2 2
2 2 4
8
2 2 1,lim lim lim
2 2
x x x
x x x
x
f m f x
x x
2
2
lim 2 4 12
x
x x
Để hàm số liên tục tại điểm
0
2
x
thì
11
2 1 12
2
m m
. Chọn C.
Câu 64: Ta có
2
1 1
lim lim 1
x x
f x x mx m
Lại có:
1 1 1 1
3 2 3 4 1
lim lim lim lim
1
1 3 2 1 3 2
x x x x
x x x
f x
x
x x x x
1
1 1
lim
4
3 2
x
x
Để hàm số đã cho liên tục tại điểm
1
x
thì
1 3
1
4 4
m m
. Chọn A.
Câu 65: Ta có
2
2
2
2
0 0 0 0
2sin sin
1 cos 1 1
2 2
0 0,lim lim lim lim
2 2
4.
2
2
x x x x
x x
x
f f x
x
x
x
Suy ra hàm số gián đoạn và không có đạo hàm tại điểm
0
x
. Chọn D.
Câu 66: Ta có
2
0 0 0
4 1 1 4 1 1
0 3,lim lim lim
2 1
2 1 4 1 1
x x x
x x
f f x
ax a x
x ax a x
0
4 4 2
lim
2 2 1 2 1
2 1 4 1 1
x
a a
ax a x
Hàm số liên tục tại điểm
0
x
khi
2 1
3
2 1 6
a
a
. Chọn C.
Trang 34
Câu 67: Ta có
0 0
lim lim
x x
f x x m m
Mặt khác
0 0
lim lim 1 1
x x
f x mx
Hàm số liên tục trên
khi hàm số liên tục tại điểm
0
x
suy ra
1 1
m m
. Chọn C.
Câu 68: Ta có
1 1 1 1
lim lim 1 2, lim lim sin sin 0
x x x x
f x x f x x
Suy ra hàm số không liên tục tại điểm
1
x
Lại có
1 1 1 1
lim lim sin sin 0, lim lim 1 0
x x x x
f x x f x x
Do đó hàm số liên tục tại điểm
1
x
. Chọn C.
Câu 69: Ta có
4
lim 4 12
x
f x f m
Lại có:
2
4 4 4 4
4 4
16
lim lim lim lim 4 2 32
4
2
2
x x x x
x x
x
f x x x
x
x
x
Hàm số liên tục tại điểm
4
x
khi
12 32 20
m m
. Chọn B.
Câu 70: Ta có
4 4
2 1 5
2 1 5
4 2, lim lim
4
4 2 1 5
x x
x x
x x
f a f x
x
x x x
4 4
4 1 1
lim lim
6
2 1 5
4 2 1 5
x x
x
x x
x x x
Hàm số liên tục tại điểm
4
x
khi
1 11
2
6 6
a a
. Chọn B.
Câu 71: Ta có
2 2
1 1
lim lim 2
2 4
x x
x
f x a a f
x
Mặt khác
2
2 2 2 2
2 7 6
2 2 3
2 2 3
lim lim lim lim
2 2 2
x x x x
x x
x x
x x
f x
x x x
2
lim 2 3 1
x
x
Hàm số liên tục tại điểm
2
x
khi
1 3
1
4 4
a a
.
Bất phương trình
2 2
7 3 7 7
0 0 1
4 4 4 4
x ax x x x
Kết hợp
1;0
x Z x . Chọn D
Trang 35
Câu 72: Ta có
2
2 2 2
2 1
2
2 ,lim lim lim 1 3
2 2
x x x
x x
x x
f m x
x x
Để hàm số liên tục tại điểm
2
x
thì
3
m
. Chọn A.
Câu 73: Nếu hàm số
y f x
liên tục trên
;
a b
và
. 0
f a f b
thì tồn tại
0
;
x a b
sao cho
0
0
f x
phương trình
0
f x
có ít nhất một nghiệm trên khoảng
;
a b
.
Mệnh đề
1
và
2
đúng và mệnh đề
3
sai. Chọn D.
Câu 74: Hàm
f x
là hàm đa thức nên liên tục trên
A đúng.
Ta có
1 1 0
0
2 23 0
f
f x
f
có nghiệm
1
x
trên
2;1
, mà
2; 1 2;0 ;1

B sai và C đúng. Chọn B.
Câu 75: Xét hàm số
4 2
2 5 1
f x x x x
là hàm số liên tục trên
Ta có:
1 3, 1 1, 0 1
f f f
Do đó
0 . 1 0
0 . 1 0
f f
f f
Phương trình
0
f x
có nghiệm trên mỗi khoảng
1;0
và
0;1
Do đó các khẳng định A, B,C sai. Chọn D.
Câu 76: Hàm số
3
3 1
f x x x
liên tục trên
Ta có:
2 3, 1 1, 0 1, 2 2
f f f f
Suy ra phương trình
0
f x
có nghiệm trên mỗi khoảng
2;1
,
1;0
,
0;2
Mà phương trình
0
f x
có tối đa 3 nghiệm nên nó có 3 nghiệm. Chọn D.
Câu 77: Ta có
5 5 0
f x g x f x
Mặt khác
1 1 5 3 0
g f
và
4 4 5 2 0
g f
Suy ra phương trình
5
f x
có ít nhất một nghiệm trên đoạn
1;4
. Chọn B.
Câu 78: Đặt
3 2
3 2 2 3
f x x x m x m
Ta có:
lim
x
f x


, để phương trình có nghiệm
1
1
x
thì
1 0
f
1 3 2 2 3 0 5 0 5
m m m m
Trang 36
Lại có
1 1 3 23
1 3 0
2 8 4 8
f m m
và
lim
x
f x


Do đó với
5
m
thì phương trình đã cho có ba nghiệm phân biệt
1 2 3
, ,
x x x
thỏa mãn
1 2 3
1
x x x
.
Kết hợp
, 10;10 9; 8; 7; 6
m Z m m
. Chọn C.
| 1/36
| | Tải xuống

Có thể bạn quan tâm:

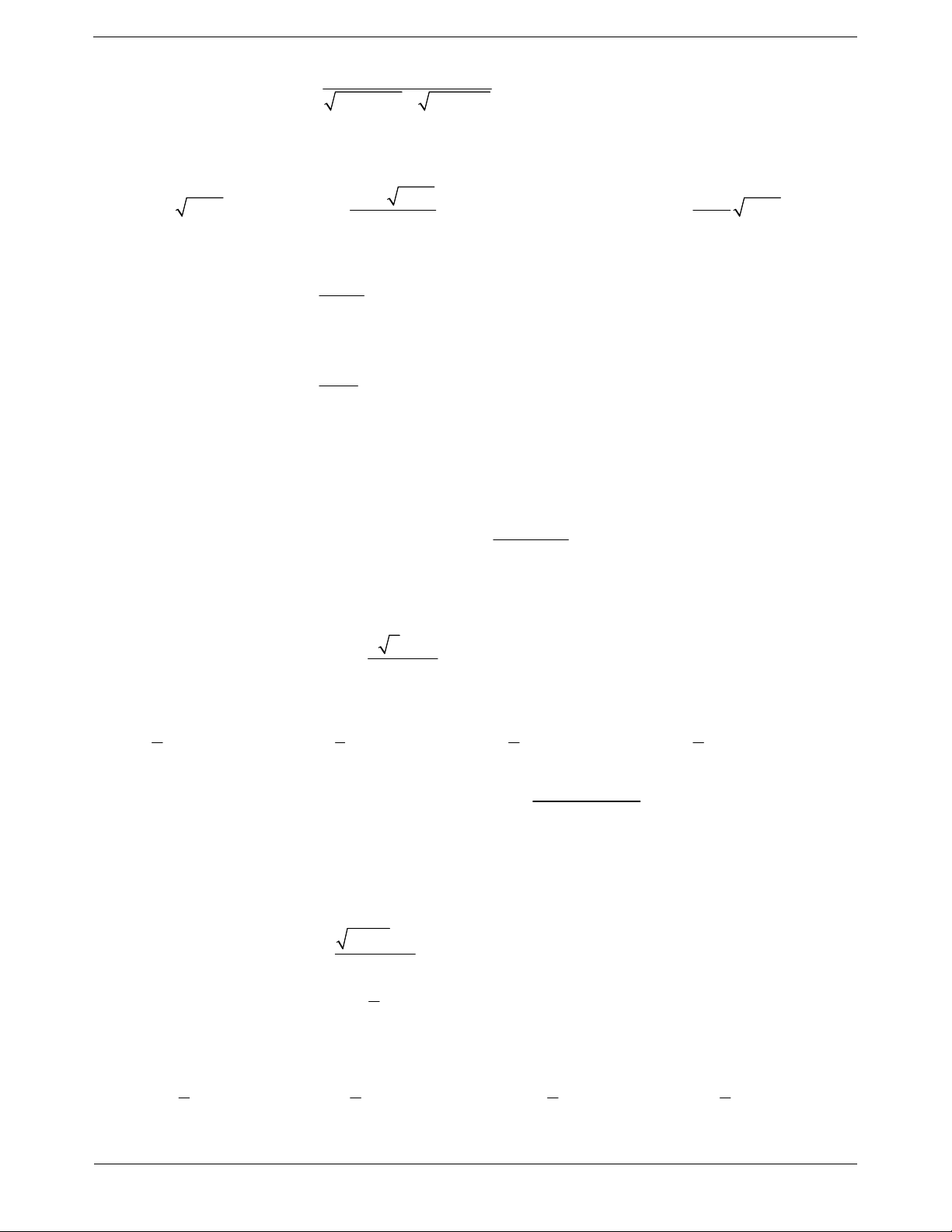
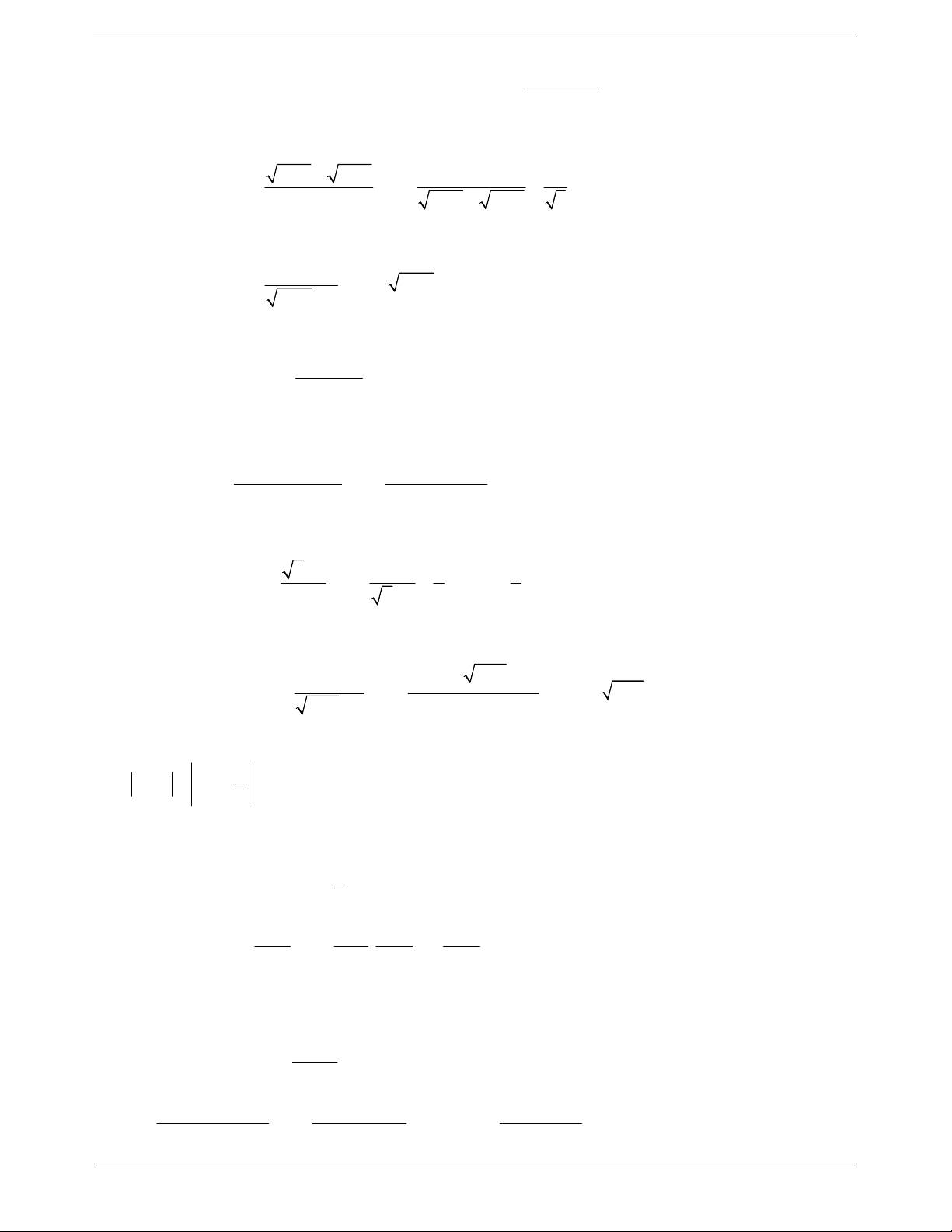
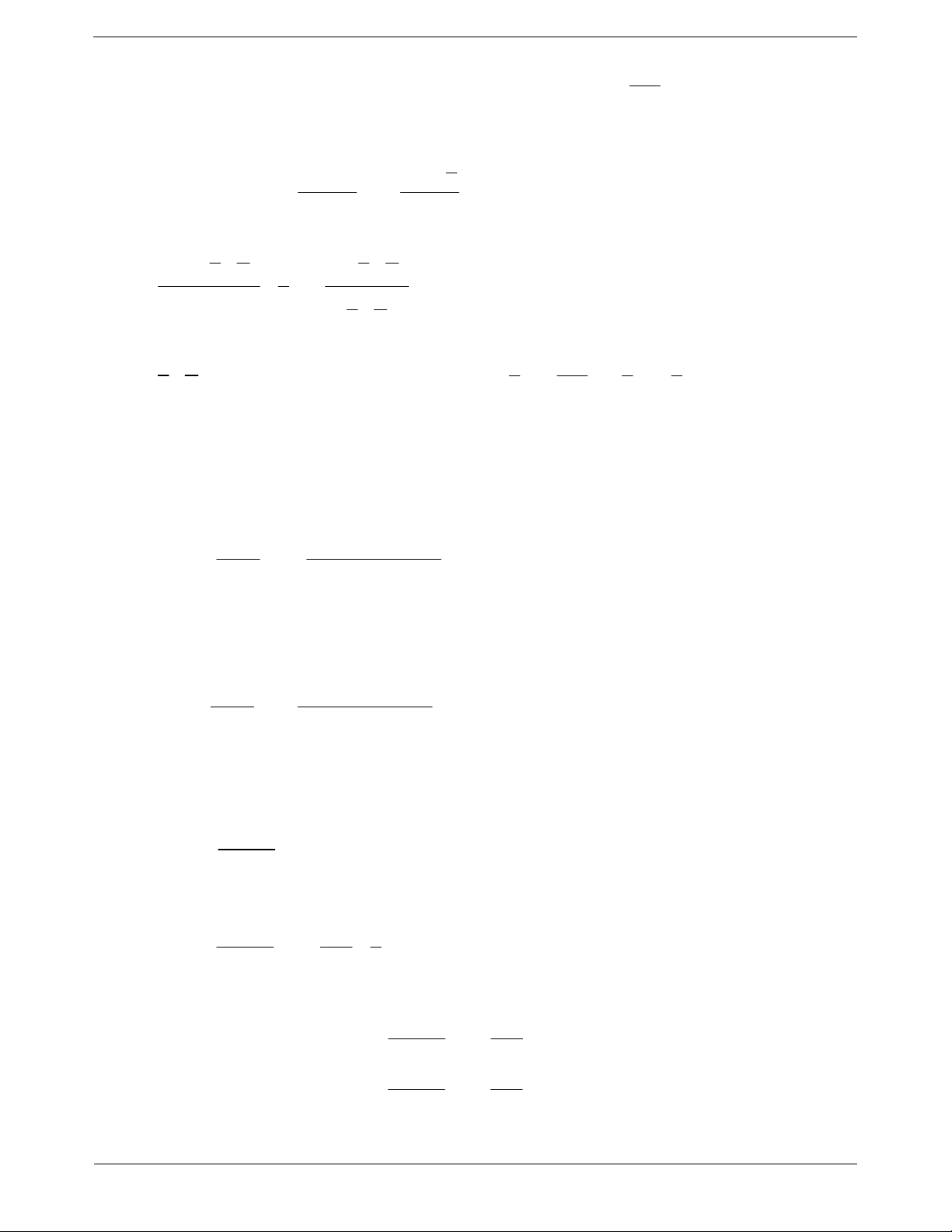
Preview text:

CHỦ ĐỀ HÀM SỐ LIÊN TỤC I. KIẾN THỨC TRỌNG TÂM
1) Hàm số liên tục tại một điểm
 Giả sử hàm số f xác định trên khoảng a;b và x  ;
a b . Hàm số f được gọi là liên tục tại 0  
điểm x nếu: lim f  x  f  x 0  0 x 0 x
 Hàm số không liên tục tại điểm x được gọi là gián đoạn tại điểm x và điểm x được gọi là 0 0 0
điểm gián đoạn của hàm số f  x
 Theo định nghĩa trên, hàm số f  x xác định trên khoảng a;b là liên tục tại điểm x  ; a b 0  
nếu và chỉ nếu lim f  x và lim f x tồn tại và lim f  x = lim f  x = f  x 0  x         0 x x 0 x x 0 x x 0 x
2) Hàm số liên tục trên một khoảng, trên một đoạn
 Hàm số f  x xác định trên khoảng a;bđược gọi là liên tục trên khoảng đó, nếu nó liên tục tại
mọi điểm của khoảng đó.
 Hàm số f  x xác định trên đoạn  ;
a b được gọi là liên tục trên đoạn đó, nếu nó liên tục trên
khoảng a;b và lim f  x  f a , lim f  x  f b (liên tục bên phải tại a và bên trái tại b ) x a  x b  Chú ý:
- Đồ thị của một hàm số liên tục trên một khoảng là một “đường liền” trên khoảng đó.
- Tính liên tục của một hàm số:
 Tổng, hiệu, tích, thương của hai hàm số liên tục tại một điểm là những hàm số liên tục tại
điểm đó (giá trị của mẫu tại điểm đó phải khác 0)
 Hàm đa thức và hàm phân thức hữu tỉ liên tục trên tập xác định của chúng.
 Các hàm y  sin x , y  cos x , y  tan x , y  cot x liên tục trên tập xác định của chúng.
3) Tính chất của hàm số liên tục
 Định lí: (Định lí về giá trị trung gian của hàm số liên tục)
Giả sử hàm số f liên tục trên đoạn  ;
a b . Nếu f a  f b thì với mỗi số thực M nằm giữa f a
và f b , tồn tại ít nhất một điểm c  ;
a b sao cho f c  M .
 Hệ quả 1: Nếu hàm f liên tục trên  ;
a b và f a. f b  0 thì tồn tại ít nhất một điểm c  ;
a b sao cho f c  0 .
 Hệ quả 2: Nếu hàm f liên tục trên a;b và f  x  0 vô nghiệm trên  ;
a b thì hàm số f có dấu không đổi trên  ; a b . Trang 1
II. PHÂN DẠNG TOÁN VÀ HỆ THỐNG VÍ DỤ MINH HỌA
 Dạng 1. Xét tính liên tục của hàm số tại một điểm
Để xét sự liên tục của hàm số y  f  x tại điểm tại x ta thực hiện các bước : 0  Bước 1 : Tính f x 0 
 Bước 2 : Tính lim f x (trong nhiều trường hợp để tính lim f x ta cần tính lim f  x và x   0 x x 0 x x 0 x lim f x x   0 x
 Bước 3 : So sánh lim f x và f x rồi rút ra kết luận. 0  x 0 x
Chú ý : hàm số không liên tục tại x thì được gọi là gián đoạn tại x 0 0
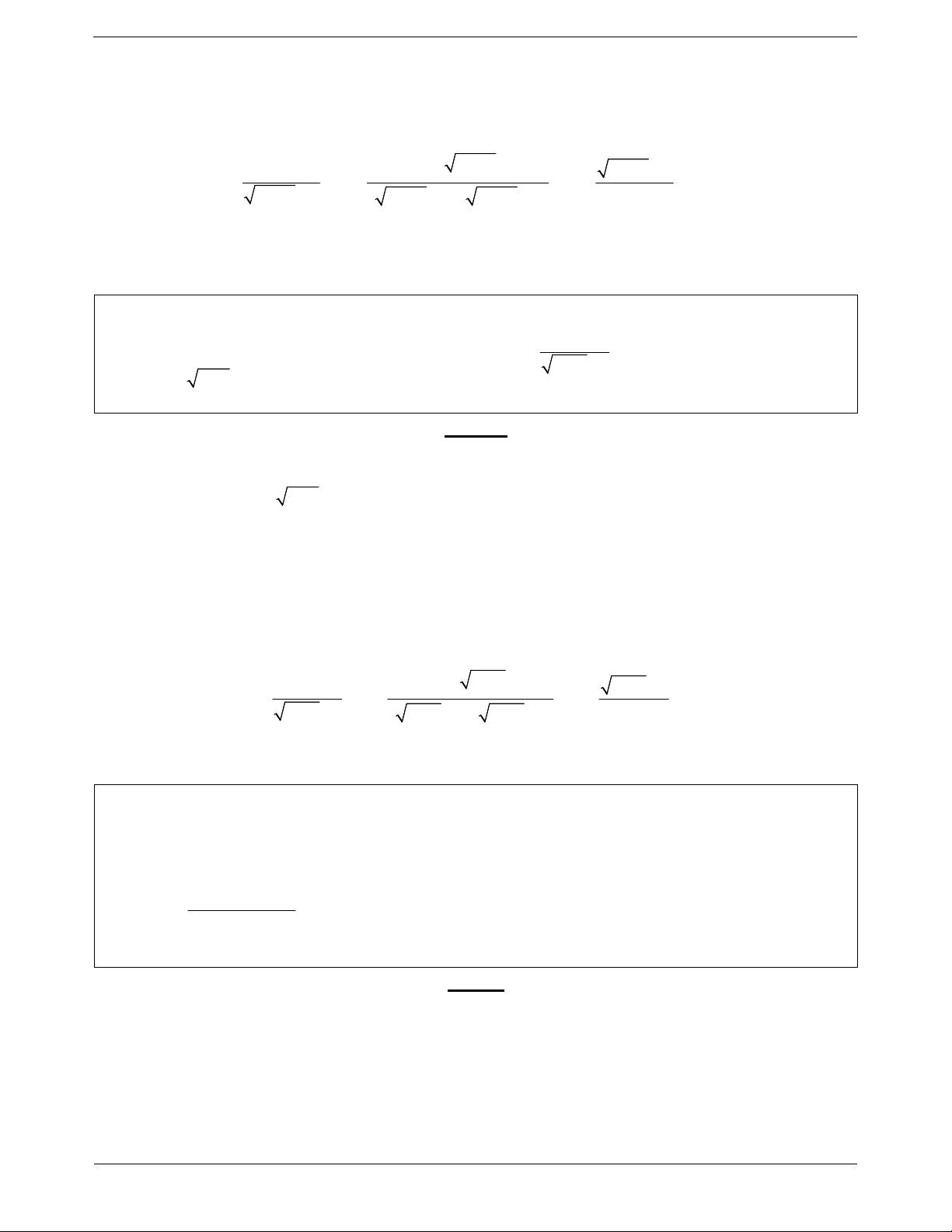
Ví dụ 1. Xét tính liên tục của hàm số tại điểm được chỉ ra :   x  3 x  3  2  khi x  1  khi x  1  a) f  x   x 1 (tại x  1) b) f  x x 1   (tại x  1)  1 1 khi x  1  khi x 1 4 Lời giải:   a Ta có: f   1 3 1   1 1  1  f  x x 3 lim  lim  1   f  
1  hàm số liên tục tại x  1 x 1  x1 x 1 b Ta có : f   1 1  . 4  x32
 x32 x32 f  x 1 lim  lim    f x x x   lim lim 1 1 x x   1  x  3  2   1 1 1 x 1  x  3  2
Vậy hàm số liên tục tại x  1.
Ví dụ 2. Xét tính liên tục của hàm số tại điểm được chỉ ra: 2 3 2  7x  5x  x  x  5  khi x  2 khi x  5  a) f  x 2   x  3x  2
(tại x  2 ) b) f  x  2x 1  3  (tại x  5) 1  khi x  2   x 5  2 3 khi x  5 Lời giải: a Ta có: f 2 1 2  7x  5x  x x  2 2 2 3 x  3x   2 1 x  3x 1 Mà lim f  x  lim  lim  lim 1  f 2 2 x2 x2 x2 x  3x  2 x  2x   x2 1 x     1
Vậy hàm số liên tục tại x  2 Trang 2
b Ta có: f      2 5 5 5  3  3 .
Lại có lim f x  lim  x  52  3  3 x 5 x 5     x  x 5 2x 13 5  2x 1  3 Và lim f  x  lim  lim  lim  3 x 5 x 5 x 5 2x 1  3
  2x 13 2x 1 3 x 5     2
Từ đó f 5  lim f  x  hàm số liên tục tại x  5. x5
Ví dụ 3. Xét tính liên tục của hàm số tại điểm được chỉ ra:     x 1 x khi x    khi x  1 a) f  x 1 cos 0   (tại x  0 )
b) f  x   2  x 1 (tại x  1)  x 1 khi x  0 2x khi x 1 Lời giải:
a Ta có: f 0  1 cos0  0 .
 lim f x  lim x 1 1  Lại có x0 x0 
nên không tồn tại giới hạn hàm số tại x  0
lim f  x  lim 1 cos x x0 x0
Vậy hàm số không liên tục tại x  0 . b Ta có: f   1  2.1  2  .
lim f x  lim 2x  2  x 1  x 1    Lại có  1 x  1 2 x x   1    f  x 2 x 1 lim  lim  lim  lim  2  x 1  x 1  x 1  2  x 1   
 2x  1 2x   x 1 1   1 
Rõ ràng lim f  x  lim f  x  f  
1 nên hàm số liên tục tại x  1. x 1 x 1  
Ví dụ 4. Tìm m, n để hàm số liên tục tại điểm được chỉ ra: 2 x khi x 1 a) f  x   (tại x  1) 2mx  3 khi x  1  3 2  x  x  2x  2  khi x  1 b) f  x   x 1 (tại x  1) 3  x  m khi x 1 Lời giải a Ta có: lim f  x 2  lim x  1 x 1 x 1  
Lại có lim f  x  lim 2mx  3  2x  3 x 1 x 1  
Hàm số liên tục  2x  3  1  x  2 Trang 3 x  x  2x  2 x   1  2 3 2 x  2 b lim f  x  lim  lim  lim 2 x  2  3 x 1  x 1  x 1  x 1 x 1 x 1 
Hàm số liên tục  3  3  m  m  0
Ví dụ 5. Tìm m, n để hàm số liên tục tại điểm được chỉ ra: m khi x 1  2  x  x  6 a) f  x   
 (tại x  0 và x  3) x  x    khi x 0, x 3 3 n khi x  3 2  x  x  2  khi x  2 b) f  x   x  2 (tại x  2 ) m khi x  2 Lời giải 2 x  x  6
x 3x  2 x  2
a Khi x  0; x  3 thì f  x    x  x  3 x  x  3 x
 lim f x  lim m  m x0 x0 x  2  2 
Hàm f  x liên tục tại x  0  m  lim  lim 1     x0 x0 x  x 
 lim f x  limn  n x3 x3 x  2  2  5
Hàm f  x liên tục tại x  3  n  lim  lim 1    x3 x3 x  x  3 2     b x x x x lim f  x 2  2  1  lim  lim  limx   1  3 x2 x2 x2 x2 x  2 x  2
Hàm f  x liên tục tại x  0  m  3
 Dạng 2. Xét tính liên tục của hàm số trên khoảng, đoạn
 Để chứng minh hàm số y  f x liên tục trên một khoảng, đoạn ta dùng các định nghĩa về hàm
số liên tục trên khoảng, đoạn và các nhận xét để suy ra kết luận.
 Khi nói xét tính liên tục của hàm số (mà không nói rõ gì hơn) thì ta hiểu phải xét tính liên tục trên tập xác định của nó.
 Tìm các điểm gián đoạn của hàm số tức là xét xem trên tập xác định của nó hàm số không liên tục tại các điểm nào Trang 4
Ví dụ 1. Xét tính liên tục của các hàm số sau trên tập xác định của chúng : 3  x  x  2 2 khi x  1   x  3x  4 khi x  2 3   a) f  x x 1   b) f  x  5  khi x  2 4  khi x  1    2x 1 khi x  2 3  Lời giải 3 3 x  x  2 x 1 x 1  1  4 a lim f x    lim  lim  lim 1  3 3  2  x 1  x1 x 1  x1 x 1 x 1  x  x 1 3
Do đó, hàm số này liên tục tại x  1 b lim       2 x 3x 4 =2; lim 2x  1 5 x 2 x 2  
Mà f  x  5 khi x  2 nên  lim f  x  lim f  x  lim f  x x2 x 2 x2 
Do đó, hàm số đã cho liên tục khi x  2
Ví dụ 2. Xét tính liên tục của các hàm số sau trên tập xác định của chúng : 2  x  4 2  x  2  khi x  2  khi x  2  a) f  x   x  2 b) f  x   x  2 4 khi x  2   2 2 khi x  2 Lời giải
a Hàm số f  x liên tục với x  2   1 2 x  x  x  lim f x 4  2 2  lim  lim  lim  x  2  2   2  4  . x 2  x2 x 2  x2 x  2 x  2
f 2  4  lim f  x  f 2  f  x liên tục tại x  2 2 x2 Từ  
1 và 2 ta có f  x liên tục trên  .
b Hàm số f  x liên tục với x   2  1 2 x  x 2x 2 2  lim f  x  lim  lim
 lim x  2  2  2  2 2. x 2 x 2 x 2 x 2 x  2 x  2
f  2  2 2  lim f x  f  2  f x liên tục tại x  2 2 x 2 Từ  
1 và 2 ta có f  x liên tục trên  .
Ví dụ 3. Tìm các giá trị của m để các hàm số sau liên tục trên tập xác định của chúng: 2  x  x  2 2 x  x khi x  1  khi x  2  a) f  x   x  2
b) f  x  2 khi x 1 m khi x  2  mx 1 khi x 1  Lời giải Trang 5
a Hàm số f  x liên tục với x  2 .
Do đó f  x liên tục trên   f  x liên tục tại x  2  lim f  x  f 2  1 x2 2 x  x  2 x  2 x 1 Ta có lim f  x     lim  lim
 lim x 1  2 1  3; f 2  . m x2 x2 x2 x  2 x  2     x2 Khi đó   1  3  m  m  3 .
b Ta có: lim f  x  lim mx  
1  m 1; lim f  x  lim           2 x x 1 1 2; f   1 2. x 1  x 1  x 1  x 1 
YCBT  lim f  x  lim f  x  f  
1  m 1  2  m  1. x 1 x 1  
Ví dụ 4. Xét tính liên tục của các hàm số sau trên tập xác định của chúng : 3 2  x  x  2x  2  khi x  1 2 x khi x 1 a) f  x   x 1 b) f  x   2mx  3 khi x  1 3  x  m khi x 1 Lời giải
a Hàm số f  x liên tục với x   1.
Do đó f  x liên tục trên   f  x liên tục tại x  1  lim f x  f   1  1 x 1  Ta có f   1  3.1 m  m  3. x  x  2x  2 x  1 2 3 2 x  2 lim f  x  lim  lim  lim 2 x  2 1 2  3. x 1  x 1  x 1  x 1 x 1 x 1  Khi đó  
1  3  m  3  m  0. b Ta có f   1  2 . m 1 3  2m  3.
lim f  x  lim 2mx  3; lim f x 2 2  lim x 1  1. x 1 x 1 x 1 x 1    
YCBT  lim f  x  lim f  x  f  
1  2m  3  1  2m  3  m  2. x 1 x 1  
 Dạng 3. Ứng dụng tính liên tục trong giải phương trình
 Biến đổi phương trình về dạng: f x  0
 Tìm hai số a , b sao cho f a. f b  0 (Dùng chức nắng TABLE của máy tính (Mode 7) tìm cho nhanh)
 Chứng minh f  x liên tục trên  ;
a b từ đó suy ra f  x  0 có nghiệm Chú ý :
- Nếu f a. f b  0 thì phương trình có nghiệm thuộc  ; a b Trang 6
- Để chứng minh f  x  0 có ít nhất n nghiệm trên a;b , ta chia đoạn  ; a b thành n khoảng
nhỏ rời nhau, rồi chứng minh trên mỗi khoảng đó phương trình có ít nhất một nghiệm.
Ví dụ 1. Chứng minh rằng các phương trình sau có 3 nghiệm phân biệt: a) 3 x  3x 1  0 b) 3 2x  6 1 x  3 Lời giải:
a Dễ thấy hàm f  x 3
 x  3x 1 liên tục trên R . Ta có:  f  2  1  
 f 2. f     tồn tại một số a  2  ;1 : f a  0 1 . 1    1    f    1 0 1  3  f  0  1  
 f 0. f     tồn tại một số a  0;1 : f a  0 2 . 2    2     f    1 0 1  1   f    1  1     f  
1 . f 2   tồn tại một số a  1;2 : f a  0 3 . 3    3    f    0 2  3 Do ba khoảng 2;  1 , 0; 
1 và 1;2 đôi một không giao nhau nên phương trình 3 x  3x 1  0 có ít
nhất 3 nghiệm phân biệt.
Mà phương trình bậc 3 thì chỉ có tối đa là 3 nghiệm nên 3
x  3x 1  0 có đúng 3 nghiệm phân biệt. b Đặt 3 3 3
1 x  t  x  1 t  2t  6t 1  0 . Xét hàm số f t 3
 2t  6t 1 liên tục trên R .  f 2. f   1  3  .5  0 
Ta có:  f 0. f   1  1. 3
   0  tồn tại 3 số t , t và t lần lượt thuộc 3 khoảng đôi một không giao 1 2 3  f    1 . f 2  3.5  0 nhau là 2;  1 , 0; 
1 và 1;2 sao cho f t  f t  f t  0 và do đây là phương trình bậc 3 nên 1   2   3
f t  0 có đúng 3 nghiệm phân biệt.
Ứng với mỗi giá trị t , t và t ta tìm được duy nhất một giá trị x thỏa mãn 3
x  1 t và hiển nhiên 3 giá 1 2 3
trị này khác nhau nên PT ban đầu có đúng 3 nghiệm phân biệt.
Ví dụ 2. Chứng minh rằng các phương trình sau luôn có nghiệm: a) 5 x  3x  3  0 b) 4 3 2
x  x  3x  x 1  0 Lời giải: a Xét f  x 5  x  3x  3.
lim f  x    tồn tại một số x  0 sao cho f  x  0. 1  1 x
lim f  x    tồn tại một số x  0 sao cho f  x  0. 2  x 2 Trang 7
Từ đó f  x . f x  0  luôn tồn tại một số x  x ; x : f x  0 nên phương trình 5 x  3x  3  0 0  2 1  0  1   2  luôn có nghiệm. b Xét f  x 4 3 2
 x  x  3x  x 1 liên tục trên R Ta có: f   1  3   0
lim f  x    tồn tại một số a  0 sao cho f a  0 . x 2
 x  x  3  0 nên luôn tồn tại một số x  0;a thỏa mãn f  x  0 nên phương trình 0  0   4 3 2
x  x  3x  x 1  0 luôn có nghiệm.
Ví dụ 3. Chứng minh rằng các phương trình sau luôn có nghiệm với mọi giá trị của tham số: a)   m x  3 2 2 1 1  x  x  3  0 b) cos x  m cos 2x  0
c) m2cos x  2  2sin5x 1 Lời giải: m 1 a Xét  . Phương trình có dạng 2
x  x  3  0 nên PT có nghiệm m  1  m  1 Với 
giả sử f  x    m x  3 2 2 1 1  x  x  3 m  1
f  x liên tục trên R nên f  x liên tục trên 1;0 Ta có f   2
1  m 1  0; f 0  1  0  f   1 .f 0  0
Do đó PT luôn có nghiệm với mọi giá trị của tham số m
b Đặt f  x  cos x  mcos 2x  f  x liên tục trên R    1  3  1     3  Ta có f   0; f    0  f .f  0          4  2  4  2  4   4 
Do đó PT luôn có nghiệm với mọi giá trị của tham số m
c Đặt f  x  m2cos x  2  2sin5x 1 f x liên tục trên R           3  Ta có f   2 1  0; f   2 1  0  f .f  0          4   4   4   4 
Do đó PT luôn có nghiệm với mọi giá trị của tham số m  1
Ví dụ 4. Chứng minh rằng phương trình 2
ax  bx  c  0 luôn có nghiệm x  0;  với a  0 và 3   2a  6b 19c  0 . Lời giải: Đặt   2
f x  ax  bx  c  f  x liên tục trên R Trang 8 x  0
 Nếu c  0 thì f x  0 có 2 nghiệm là  1 x   3   1  a b 1 c
Nếu c  0 , ta có f 0  c; f    c  2a  6b 18c      3  9 3 18 18 2     1  c  1  f 0 .f    0  
. Do đó f  x  0 có nghiệm trong 0;    3  18  3 
a Ta có: f 0 1 cos0  0 .
 lim f x  lim x 1 1  Lại có x0 x0 
nên không tồn tại giới hạn hàm số tại x  0
lim f  x  lim 1 cos x x0 x0
Vậy hàm số không liên tục tại x  0 . b Ta có: f   1  2.1  2  .
lim f x  lim 2x  2  x 1  x 1    Lại có  1 x  1 2 x x   1    f  x 2 x 1 lim  lim  lim  lim  2  x 1  x 1  x 1  2  x 1   
 2x  1 2x   x 1 1   1 
Rõ ràng lim f  x  lim f  x  f  
1 nên hàm số liên tục tại x  1. x 1 x 1  
Ví dụ 5. Cho các phương trình sau 4 3 x  x  3  0 , 5 3 x 16x  20  0 , 7 4
x  x  4  0 . Số phương trình có nghiệm là ? A. 0 B. 1 C. 2 D. 3 Lời giải: Hàm số f  x 4 3
 x  x  3 liên tục trên  nên liên tục trên 0;2 .
Mà f 0. f 2  0  f  x  0 có ít nhất một nghiệm thuộc khoảng 0;2 . Hàm số g  x 5 3
 x 16x  20 liên tục trên  nên liên tục trên 3;5 .
Mà f 3. f 5  0  f  x  0 có ít nhất một nghiệm thuộc khoảng 3;5 . Hàm số h x 7 4
 x  x  4 liên tục trên  nên liên tục trên 0;2 .
Mà f 0. f 2  0  f  x  0 có ít nhất một nghiệm thuộc khoảng 0;2 .
Như vậy cả ba phương trình đã cho đều có nghiệm. Chọn D Ví dụ 6. Phương trình 5 3
x  5x  4x 1  0 có số nghiệm là ? A. 3 B. 5 C. 1 D. 4 Lời giải: Hàm số f  x 5 3
 x  5x  4x 1 liên tục trên  . Trang 9  2   3   1   1 
Ta kiểm tra được f 2. f   0; f  . f   
 0  0; f 0. f  0; f . f       1 ; f   1 . f 3 <0.  3   2   2   2  
3   3   1   1 
Từ đó trên mỗi khoảng 2;  ,  ;0 , 0; , ;1 ,       
 1;3 thì f  x  0 đều có ít nhất một 
2   2   2   2  nghiệm.
Mà f  x  0 là phương trình bậc 5 nên nó có tối đa 5 nghiệm.
Do đó số nghiệm của phương trình là 5. Chọn B. BÀI TẬP TỰ LUYỆN Câu 1. Hàm số f  x 1  3  x  liên tục trên x  4 A. 4;  3 B. 4;3 C.  4  ;  3 D.  ;  43; 3 x  x cos x  sin x
Câu 2. Hàm số f  x  liên tục trên 2sin x  3  3   A. 1;  1 B. 1;  5 C. ;    D.   2  2 x  3x  2
Câu 3. Cho hàm số xác định và liên tục trên R với f  x  , x   1. Tính f   1 x 1 A. 2 B.1 C. 0 D. 1  x    x
Câu 4. Cho hàm số f  x xác định và liên tục trên 3;  3 với f  x 3 3  , x   0. x Tính f 0 2 3 A. B. 3 C. 1 D. 0 3 x
Câu 5. Cho hàm số f  x xác định và liên tục trên 4; với f  x  , x  0 . x  4  2 Tính f 0 A. 0 B. 2 C. 4 D. 1 2  x  x  2  khi x  2
Câu 6. Tìm giá trị của tham số m để hàm số f  x   x  2 liên tục tại x  2 m khi x  2 A. 0 B. 1 C. 2 D. 3 3 2  x  x  2x  2  khi x  1
Câu 7. Tìm giá trị của tham số m để hàm số f  x   x 1 liên tục tại x  1 3  x  m khi x 1 A. 0 B. 2 C. 4 D. 6 Trang 10  x 1  khi x  1
Câu 8. Tìm giá trị của tham số k để hàm số y  f x   x 1 liên tục tại x  1 k 1 khi x 1 1 1 A. B. 2 C.  D. 0 2 2  3  x  khi x  3
Câu 9. Biết rằng hàm số f  x   x 1  2
liên tục tại x  3, m là tham số. m khi x  3
Khẳng định nào sau đây đúng? A. m 3;0 B. m  3 C. m 0;5 D. m 5;  1 2 x sin khi x  0
Câu 10. Tìm giá trị của tham số m để hàm số f  x   x liên tục tại x  0 m khi x  0 A. m  2  ;  1 B. m  2  C. m 0;5 D. m 5;  tan x  khi x  0
Câu 11. Tìm giá trị của tham số m để hàm số f  x   x
liên tục trên khoảng nào dưới 0 khi x  0 đây?           A. 0;   B.  ;0   C.  ;   D.  ;    2   2   4 4  sin x sin x  khi x  1 Câu 12. Biết rằng lim
 1. Tìm giá trị thực của tham số m để hàm số f  x   x 1 x0 x m khi x 1 liên tục tại x  1 A.   B.  C. 1 D. 1 1 cos x sin x khi x    Câu 13. Biết rằng lim
 1. Tìm giá trị thực của tham số m để hàm số f  x  x  2 x x  m khi x   liên tục tại x     1 1 A. B.  C. D.  2 2 2 2 Trang 11 3  khi x  1  4  x  4
Câu 14. Hàm số f  x   khi x  1
 ; x  0 liên tục tại 2 x  x 1 khi x 0 
A. Mọi điểm x  0, x  1 B. Mọi điểm x  
C. Mọi điểm trừ x  1
D. Mọi điểm trừ x  0 0,5 khi x  1    x x 1
Câu 15. Số điểm gián đoạn của hàm số f  x     khi x  1; x  1 là 2 x 1 1 khi x 1  A. 0 B. 1 C. 2 D. 3 2 2 m x khi x  2
Câu 16. Có bao nhiêu giá trị thực của tham số m để hàm số f  x   liên tục trên  1 m  x khi x  2  A. 2 B. 1 C. 0 D. 3  x khi x 0;4
Câu 17. Biết rằng hàm số f  x    
liên tục trên 0;6. Khẳng định nào sau đây là 1   m khi x   4;6 đúng? A. m  2 B. 2  m  3 C. 3  m  5 D. m  5 2  x  3x  2  khi x  1
Câu 18. Có bao nhiêu giá trị của tham số a để hàm số f  x   x 1 liên tục trên  a khi x 1  A. 1 B. 2 C. 0 D. 3 2  x 1  khi x  1
Câu 19. Có bao nhiêu giá trị của tham số a để hàm số f  x   x 1 liên tục trên đoạn a khi x 1
0; 1,a là tham số. Khẳng định nào dưới đây là đúng? A. a là một số nguyên B. a là một số vô tỉ C. a  5 D. a  0  x 1  khi x  1
Câu 20. Xét tính liên tục của hàm số f  x   2  x 1
. Khẳng định nào dưới dây đúng? 2x khi x 1
A. f  x không liên tục trên 
B. f  x không liên tục trên 0;2
C. f  x gián đoạn tại x  1
D. f  x không liên tục trên  Trang 12 2  x  5x  6  khi x  3
Câu 21. Tìm giá trị nhỏ nhất của a để hàm số f  x   4x  3  x liên tục tại x  3  2 1   a x khi x  3 2 2 4 4 A.  B. C.  D. 3 3 3 3 3  3x  2  2  khi x  2 
Câu 22. Tìm giá trị lớn nhất của a để hàm số f  x x  2   liên tục tại x  2 1  2 a x  khi x  2  4 A. 3 B. 0 C. 1 D. 2   x x  
Câu 23. Xét tính liên tục của hàm số f  x 1 cos khi 0  
. Khẳng định nào sau đây đúng ?  x 1 khi x  0
A. f  x liên tục tại x  0
B. f  x liên tục trên  ;   1
C. f  x không liên tục trên 
D. f  x gián đoạn tại x  1   x  x 
Câu 24. Tìm các khoảng liên tục của hàm số f  x cos khi 1   2
. Mệnh đề nào sau đây là sai? x 1 khi x 1 
A. Hàm số liên lục tại x  1
B. Hàm số liên tục trên các khoảng  ;   1 ;1;
C. Hàm số liên tục tại x  1
D. Hàm số liên tục trên khoảng 1;  1 2  x khi x 1,x  0  x 
Câu 25. Cho hàm số f  x  0 khi x  0
. Hàm số f  x liên tục tại  x khi x 1   A. Mọi điểm x  
B. Mọi điểm trừ x  0
C. Mọi điểm trừ x  1
D. Mọi điểm trừ x  0 và x  1 2  x 1 khi x  3,x 1  x 1 
Câu 26. Cho hàm số f  x  4 khi x 1
. Hàm số f  x liên tục tại  x 1 khi x  3   A. Mọi điểm x  
B. Mọi điểm trừ x  1
C. Mọi điểm trừ x  3
D. Mọi điểm trừ x  1 và x  3 2x khi x  0 
Câu 27. Số điểm gián đoạn của hàm số f  x 2
 x +1 khi 0  x 2 . 3  x 1 khi x  2  Trang 13 A. 1 B. 2 C. 3 D. 0 2 x +x khi x 1 
Câu 28. Tính tổng S gồm tất cả các giá trị m để hàm số f  x  2 khi x  1 liên tục tại x 1  2 m x -1 khi x  1  A. 1 B. 0 C. 1 D. 2 x cos x khi x  0  2  x
Câu 29. Cho hàm số f  x  
khi 0  x  1. Hàm số liên tục tại 1 x  3 x khi x 1  A. Mọi điểm x  
B. Mọi điểm trừ x  0
C. Mọi điểm trừ x  1
D. Mọi điểm trừ x  0 và x  1  x  2  2  khi x  2
Câu 30. Tìm a để hàm số f  x   x  2 liên tục tại x  2 2x  a khi x  2 15 15 1 A. B.  C. D. 1 4 4 4  1 x  1 x  khi x  0 
Câu 31. Tìm tất cả các giá trị của m để hàm số   x f x   liên tục tại x  0 1 x m  khi x  0  1 x A. m  1 B. m  2 C. m  1 D. m  0 2  x  3x  2  khi x  2
Câu 32. Cho hàm số f  x   x  2  2
, m là tham số. Có bao nhiêu giá trị của m để  2 m x - 4m  6 khi x  2
hàm số đã cho liên tục tại x  2 ? A. 1 B. 2 C. 0 D. 3 2  x  2x  khi x  2
Câu 33. Tìm tất cả các giá trị của tham số m để hàm số f  x   x  2 liên tục tại x  2 mx 4 khi x  2 A. m  3 B. m  2 C. m  2 D. Không tồn tại m 2
x  2 x  2 khi x  2
Câu 34. Tìm m để hàm số y  f x   liên tục trên  ? 2 5
 x  5m  m khi x  2 A. m  2; m  3 B. m  2  ;m  3  C. m  1;m  6 D. m  1  ;m  6  Trang 14 2016  x  x  2  khi x  1
Câu 35. Cho hàm số f  x   2018x 1  x  2018
. Tìm k để hàm số f  x liên tục tại k khi x 1 x  1 . 2017 2018 2016 A. k  2 2019 B. k  C. k  1 D. 2019 2 2017 2 2x  2 khi x 1 
Câu 36. Cho hàm số f  x  2x  a
. Gía trị của a để hàm số liên tục tại x  1 khi x  1 0  2  x 1 A. 1 B. 2 C. 3 D. 4 3 1   x  khi x  1
Câu 37. Cho hàm số f  x   1 x
. Hãy chọn kết luận đúng. 1  khi x 1
A. y liên tục phải tại x  1
B. y liên tục tại x  1
C. y liên tục trái tại x  1 D. y liên tục trên  2  x  5x  6  khi x  3
Câu 38. Tìm giá trị của tham số a để hàm số f  x   x  3 liên tục tại x  3 a khi x  3 A. a  0 B. a  1 C. a  1  D. a  2 3 2 x - x -1  khi x  1
Câu 39. Tìm m để hàm số f  x   x 1 liên tục trên  . mx1 khi x 1 4 1 4 2 A.  B.  C. D. 3 3 3 3 3 2  x  x  2x  2  khi x  1
Câu 40. Tìm giá trị thực của tham số m để hàm số f  x   x 1 liên tục 3  x  m khi x 1 tại x  1 A. m  0 B. m  6 C. m  4 D. m  2 2  x  4  2  khi x  0 2  Câu 41. Cho hàm số   x f x  
. Tìm giá trị thực của tham số a để hàm số  5 2a  khi x  0  4
f  x liên tục tại x  0 3 4 4 3 A. a   B. a  C. a   D. a  4 3 3 4 Trang 15 2  x 1  khi x  1
Câu 42. Tìm a để hàm số f  x   x 1
liên tục tại điểm x  1. 0 a khi x 1 A. a  0 B. a  1 C. a  2 D. a  1  5x 1  2  khi x  1 
Câu 43. Cho hàm số f  x x 1  
, ( m là tham số). Giá trị m để hàm số liên tục 1 mx  m  khi x 1  4 trên  là 1 A. m  0 B. m  C. m  2 D. m  1 2 2  x  3x  2  khi x  1
Câu 44. Tìm giá trị của tham số m để hàm số f  x   x 1 liên tục tại x  1. m khi x 1 A. m  1 B. m  2 C. m  1 D. m  2
Câu 45. Hàm số nào dưới đây gián đoạn tại điểm x  1? x 1 2 x  2 A. y  B. y  2 x  x 1 x 1 2 x  x 1 C. y   x   2 1 x  x   1 D. y  x 1 2  x  x  6  khi x  2
Câu 46. Cho hàm số f  x   x  2
. Xác định a để hàm số liên tục tại điểm x  2 2ax 1 khi x  2 1 A. a  2 B. a  1 C. a  1  D. a  2 x 1 khi x  2
Câu 47. Tìm giá trị thực của tham số m để hàm số f  x   liên tục tại x  2 2 x +m khi x  2  A. m  1 B. m  0 C. m  3 D. m  6 sin x  khi x  0
Câu 48. Cho hàm số f  x   x
. Tìm a để f  x liên tục tại x  0 a khi x  0 A. 1 B. 1 C. 2 D. 0 2 x  m khi x  2
Câu 49. Cho hàm số f  x  
( m là tham số). Tìm giá trị thực của tham số m để hàm 3  x 1 khi x  2
số đã cho liên tục tại x  2 0 A. m  2 B. m  1 C. m  0 D. m  3 Trang 16 2 3x  7x  6  khi x  3
Câu 50. Tìm giá trị của tham số m sao cho hàm số f  x   x  3 liên tục với mọi  2 x   5mx  2 khi x  3 x thuộc  . A. m  7 B. m  3 C. m  2 D. m  0  x  4  2  khi x  0 
Câu 51. Giá trị của tham số m sao cho hàm số   x f x  
liên tục tại x  0 là 5 2m  x khi x  0  4 4 1 1 A. 3 B. C. D.  3 8 2  x 1  khi x  1 
Câu 52. Giá trị của tham số a sao cho hàm số f  x x 1  
liên tục tại điểm x  1 là 1 ax  khi x 1  2 1 1 A. B. 1 C. 1 D.  2 2 2  x 16  khi x  4
Câu 53. Tìm tất cả các giá trị thực của tham số m để hàm số f  x   x  4 liên tục trên  . mx 1 khi x  4 7 7 A. m  8 hoặc m  B. m  8 hoặc m   4 4 7 7 C. m   D. m  4 4 2  x 1  khi x  1
Câu 54. Cho hàm số f  x   x 1
, với m tham số thực. Tìm m để hàm số f  x m khi x 1 liên tục tại x  1 A. m  2 B. m  2 C. m  1 D. m  1 2  x  3 khi x  3 
Câu 55. Cho hàm số f  x   x  3
. Tìm khẳng định đúng trong các khẳng định sau :  2 3 khi x  3
I f x liên tục tại x  3 .
II f x gián đoạn tại x  3 .
III f x liên tục trên  . A. Chỉ I và II. B. Chỉ I và III.
C. Cả I, II, III đều đúng. D. Chỉ II và III. Trang 17 2  x  3x  2  khi x  2
Câu 56. Cho hàm số f  x   x  2
. Với giá trị nào của m sau đây để hàm số f  x liên 2m1 khi x  2 tục tại x  2 . A. 0 B. 1 C. 2 D. 1 2  x  3x  2  khi x  2
Câu 57. Có bao nhiêu giá trị thực của tham số m để hàm số f  x   x  2   1 m   x khi x  2 liên tục trên  ? A. 0 B. 1 C. 2 D. 3 2  x  4x  3  , x  >1
Câu 58. Tìm P để hàm số y   x 1 liên tục trên  ? 6Px 3, x   1 5 1 1 1 A. B. C. D. 6 2 6 3 2  x  ax  b  , x  1
Câu 59. Cho a, b là hai số thực sao cho hàm số f  x   x 1 liên tục trên  ? 2ax 1 x 1 Tính a  b A. 0 B. 1 C. 5  D. 7 2
ax  a  2 x  2  khi x  1
Câu 60. Cho hàm số f  x   x  3  2
. Có bao nhiêu giá trị của tham số a để  2 8   a khi x 1
hàm số liên tục tại x  1 A. 1 B. 0 C. 3 D. 2 3  x  a 1, khi x  0 
Câu 61. Cho hàm số f  x   1 2x 1
. Tìm tất cả các giá trị của tham số a để hàm  khi x  0  x
số liên tục tại x  0 A. a  1 B. a  3 C. a  2 D. a  4 2  x 16  khi x  4
Câu 62. Tìm m để hàm số f  x   x  4
liên tục tại điểm x  4 mx 1 khi x  4 7 7 A. 8 B. 8 C.  D. 4 4 Trang 18 3  x 8  khi x  2
Câu 63. Cho hàm số f  x   x  2
. Tìm m để hàm số liên tục tại x  2 0 2m1 khi x  2 3 13 11 1 A. B. C. D.  2 2 2 2 2 x  mx khi x 1 
Câu 64. Cho hàm số f  x   x  3  2
. Tìm m để hàm số đã cho liên tục tại x  1  khi x  1  x 1 3 1 A.  B. C. 0 D. 2 4 3 1   cos x  khi x  0
Câu 65. Cho hàm số f  x 2   x
. Khẳng định nào trong các khẳng định sau là đúng? 1  khi x  0
A. f  x có đạo hàm tại x  0
B. f  x liên tục tại x  0 C. f  2  0
D. f  x gián đoạn tại x  0  4x 1 1  khi x  0
Câu 66. Tìm a để các hàm số f  x 2  ax  2a   1 x liên tục tại x  0 3  khi x  0 1 1 1 A. B. C.  D. 1 4 2 6  x  m x 
Câu 67. Cho hàm số f  x khi 0  
. Tìm tất cả các giá trị thực của m để f  x mx 1 khi x  0 liên tục trên  A. 1 B. 0 C. 1  D. 2    x x  
Câu 68. Cho hàm số f  x sin khi 1  
. Mệnh đề nào sau đây đúng? x 1 khi x  1 
A. Hàm số liên tục trên 
B. Hàm số liên tục trên các khoảng  ;    1 và 1;
C. Hàm số liên tục trên các khoảng  ;   1 và 1;
D. Hàm số gián đoạn tại x  1 2  x 16  khi x  4
Câu 69. Hàm số f  x   x  2
liên tục tại x  4 khi m nhận giá trị là 0 3  x m khi x  4 A. 44 B. 20 C. 20 D. 44 Trang 19  2x 1  x  5  khi x  4
Câu 70. Cho hàm số f  x   x  4
. Tìm tất cả các giá trị của tham số a để hàm số a  2 khi x  4 liên tục tại x  4 5 11 A. a  B. a   C. a  3 D. a  2 2 6 2  2x  7x  6  khi x  2 
Câu 71. Cho hàm số f  x x  2  
. Biết a là giá trị để hàm số f  x liên tục tại  1 x a  khi x  2  2  x 7
x  2 . Tìm số nghiệm nguyên của bất phương 2 x  ax   0 4 A. 1 B. 4 C. 3 D. 2 2  x  x  2  khi x  2
Câu 72. Tìm giá trị thực của tham số m để hàm số f  x   x  2 liên tục tại x  2 m khi x  2 A. m  3 B. m  1 C. m  2 D. m  0
Câu 73. Cho các mệnh đề:  
1 . Nếu hàm số y  f  x liên tục trên a;b và f a. f b  0 thì tồn tại x  ; a b sao cho 0   f  x  0 . 0 
2. Nếu hàm số y  f x liên tục trên a;b và f a. f b  0 thì phương trình f x  0 có nghiệm.
3. Nếu hàm số y  f x liên tục, đơn điệu trên  ;ab và f a. f b  0 thì phương trình f x  0 có
nghiệm duy nhất trên  ; a b . Trong ba mệnh đề trên
A. Có đúng hai mệnh đề sai.
B. Cả ba mệnh đề đều đúng.
C. Cả ba mệnh đề đều sai.
D. Có đúng một mệnh đề sai.
Câu 74. Cho hàm số f  x 3  4
 x  4x 1. Mệnh đề nào sau đây sai?
A. Hàm số đã cho liên tục trên 
B. Phương trình f x  0 không có nghiệm trên khoảng  ;   1
C. Phương trình f  x  0 có nghiệm trên khoảng 2;0  1 
D. Phương trình f  x  0 có ít nhất hai nghiệm trên khoảng 3;    2  Trang 20 Câu 75. Cho phương trình 4 2
2x  5x  x 1  0 . Mệnh đề nào sau đây đúng?
A. Phương trình không có nghiệm trong khoảng 1;  1 .
B. Phương trình không có nghiệm trong khoảng 2;0 .
C. Phương trình chỉ có một nghiệm trong khoảng  2  ;  1 .
D. Phương trình có ít nhất hai nghiệm trong khoảng 0;2 .
Câu 76. Cho hàm số f  x 3
 x  3x 1. Số nghiệm của phương trình f x  0 trên  là A. 0 B. 1 C. 2 D. 3
Câu 77. Cho hàm số f  x liên tục trên đoạn 1;4 sao cho f  
1  2 , f 4  7 . Có thể nói gì về số
nghiệm của phương trình f  x  5 trên đoạn 1;4: A. Vô nghiệm.
B. Có ít nhất một nghiệm.
C. Có đúng một nghiệm. D. Có đúng hai nghiệm.
Câu 78. Có tất cả bao nhiêu giá trị nguyên của tham số m thuộc khoảng 10;10 để phương trình 3 2
x  3x  2m  2 x  m  3  0 có bai nghiệm phân biệt x , x , x thỏa mãn x  1 x  x ? 1 2 3 1 2 3 A. 19 B. 18 C. 4 D. 3
ĐÁP ÁN VÀ LỜI GIẢI BẢI TẬP TỰ LUYỆN 1-C 2-D 3-D 4-B 5-C 6-D 7-A 8-C 9-B 10-C 11-A 12-A 13-C 14-B 15-B 16-A 17-A 18-C 19-A 20-D 21-A 22-C 23-C 24-A 25-A 26-D 27-A 28-B 29-C 30-B 31-B 32-A 33-A 34-A 35-A 36-B 37-A 38-B 39-A 40-A 41-D 42-C 43-B 44-A 45-B 46-C 47-A 48-A 49-B 50-D 51-C 52-C 53-D 54-C 55-B 56-A 57-B 58-C 59-D 60-D 61-C 62-D 63-C 64-A 65-D 66-C 67-C 68-C 69-B 70-B 71-D 72-A 73-D 74-B 75-D 76-D 77-B 78-C 3   x  0 x  4 Câu 1: Điều kiện     D   4  ; 
3  hàm số liên tục trên 4;3 . x  4  0 x  3   1  1
Xét tại x  3, ta có lim f  x  lim 3  x    f   3 x 3 x 3    x  4  7
 Hàm số liên tục trái tại x  3. Vậy hàm số liên tục trên  4  ;  3 . Chọn C
Câu 2: Vì 2sin x  3  0 với mọi x    D   nên hàm số liên tục trên  . Chọn D Trang 21 2 x  3x  2
Câu 3: Vì f  x liên tục trên  nên f   1  lim f  x  lim
 lim x  2  1. Chọn D. x 1  x 1  x 1 x 1 
Câu 4: Vì f  x liên tục trên 3;  3 nên suy ra    f    f  x x 3 3 x 2 1 0 lim  lim  lim  . Chọn B. x0 x0 x0 x x  3  3  x 3
Câu 5: Vì f  x liên tục trên 4; nên suy ra  x
f 0  lim f  x  lim  lim    . Chọn C.     x 4 2 4 x 0 x 0 x 0 x  4  2
Câu 6: Tập xác định D   , chứa x  2 . Theo giả thiết thì ta phải có 2   m  f    f  x x x 2 2 lim  lim  limx   1  3. Chọn D. x2 x2 x2 x  2
Câu 7: Hàm số xác định với mọi x   . Theo giả thiết thì ta có 3 m  f   1  lim f  x x 1  x  x  2x  2 x  1 2 3 2 x  2 Suy ra 3  m  lim  lim  lim  2
x  2  3  m  0 . Chọn A. x 1  x 1  x 1 x 1 x 1 
Câu 8: Hàm số f  x có TXĐ: D  0; . Điều kiện bài toán tương đương vợi  k   y   x 1 1 1 1 1 1  lim y  lim  lim   k   . Chọn C. x 1  x 1  x 1 x 1  x 1 2 2
Câu 9: Hàm số f  x có TXĐ là 1; . Theo giả thiết thì ta phải có  x 3 x x1 2 3 
m  f 3  lim f x  lim  lim   lim     Chọn B.      x 1 2 4. x 3 x 3 x 3 x 3 x 1  2 x  3
Câu 10: Với mọi x  0 , ta có : 0  f x 1 2 2
 x sin  x  0 khi x  0  lim f  x  0. x x0
Theo giả thiết thì ta phải có: m  f 0  lim f  x  0. Chọn C. x0  
Câu 11: Tập xác định: D   \   k | k  Z  .  2  tan x sin x 1 1 Ta có lim f  x  lim  lim .  1.
 1  0  f 0  f x không liên tục tại x  0 . x0 x0 x0 x x cos x cos x Chọn A.
Câu 12: Tập xác định D   . Điều kiện bài toán tương đương với      f  x sin x m f 1 lim  lim x 1  x 1  x 1 sin  x    sin x   1          sin x  1 = lim lim lim .    * . x 1  x 1  x 1 x 1 x 1   x   1  Trang 22 sin t Đặt t    x  
1 thì t  0 khi x  1. Do đó * trở thành : m  lim   .    . Chọn A. t0 t
Câu 13: Hàm số xác định với mọi x   . Điều kiện của bài toán trở thành: 2 x 2cos  m  f    f  x 1 cos x 2 lim  lim  lim x   x    x  2 x   x  2 2        2 x x 2sin  sin        2 2  1  2 2   lim  lim    * x   x  2 2 x     x        2 2     x  2 1  sin t  1 1 Đặt t  
 0 khi x 1. Khi đó * trở thành: 2 m  lim  .1  .   Chọn C. 2 2 t0 2  t  2 2
Câu 14: Hàm số y  f  x có TXĐ: D  
Dễ thấy hàm số y  f  x liên tục trên mỗi khoảng  ;    1 , 1  ;0 và 0;.   1 Xét tại x  1  , ta có x  x x  x   1  2 4 x  x   f x 1 lim  lim  lim  lim  2
x  x 1  3  f 1 . 2  x 1  x1 x1 x  x x  x     x1 1
 hàm số y  f x liên tục tại x  1.
2 Xét tại x  0 , ta có x  x x  x   1  2 4 x  x   f x 1 lim  lim  lim  lim 2 x  x 1  1  f 0 . 2  x0 x0 x0 x  x x  x     x0 1
 hàm số y  f x liên tục tại x  0 . Chọn B.
Câu 15: Hàm số y  f  x có TXĐ: D   . x x 1 Hàm số f  x   
liên tục trên mỗi khoảng  ;    1 ,  1  ;  1 và 1;. 2 x 1   1 Xét tại x  1  , ta có  f x x  x  1 x 1 lim  lim  lim   f 1 2   x 1  x1 x 1 x 1  x 1 2
 Hàm số liên tục tại x  1.   f  x x  x  1 x lim  lim  lim       2     2 Xét tại    x  1 , ta có x 1 x 1 x 1 x 1 x 1    f  x x  x  1 x lim  lim  lim     2 x 1  x 1    x 1 x 1   x 1
 Hàm số y  f  x gián đoạn tại x 1. Chọn B. Trang 23
Câu 16: TXĐ: D   . Hàm số liên tục trên mỗi khoảng  ;  2, 2;.
Khi đó f  x liên tục trên   f  x liên tục tại x  2
 lim f  x  f 2  lim f  x  lim f x  f 2.   * x 2 x 2 x 2     f  2 2  4m m  1 
Ta có lim f x lim 1 m x 2  1 m * 2 4m 21 m             1 x2 x2 m    f  x 2 2 2  2 lim  lim m x  4m x2 x2 Chọn A.
Câu 17: Dễ thấy hàm số f  x liên tục trên mỗi khoảng 0;4 và 4;6 . Khi đó hàm số liên tục trên
đoạn 0;6 khi và chỉ khi hàm số liên tục tại x  4, x  0, x  6 .
 lim f x  f 0 x0 
Tức là ta cần có lim f  x  f 6 * x6 
 lim f  x  lim f  x  f 4 x4 x4
 lim f x  lim x  0   x 0 x 0     f  0  0  0
lim f x  lim 1 m 1 m   x 6 x 6     f  6 1 m
 lim f x  lim x  2 x4 x4   
lim f x  lim 1 m  1 ; m x4 x4   f 4 1 m 
Khi đó * trở thành 1 m  2  m 1  2. Chọn A.
Câu 18: Hàm số f  x liên tục trên  ;   1 và 1,  .
Khi đó hàm số đã cho liên tục trên  khi nó liên tục tại x  1, tức là ta cần có lim f  x  f  
1  lim f  x  lim f x  f   1 * x 1 x 1 x 1    x  2 khi x  1
lim f  x  lim 2  x 1     Ta có f  x x 1  x 1  a khi x 1   
 * không thỏa mãn. lim f  
x  lim x  2  1 2  x khi x  1 x 1  x 1  
Vậy không tồn tại giá trị a thỏa yêu cầu. Chọn C. Trang 24
Câu 19: Hàm số xác định và liên tục trên 0;  1 .
Khi đó f  x liên tục trên 0; 
1 khi và chỉ khi lim f  x  f   1   * x 1   f   1  a  Ta có 2        x Chọn A. f x   x            x  * a 4. 1 lim lim lim 1 1 4 x 1  x 1  x 1  x 1   
Câu 20: Dễ thấy hàm số liên tục trên  ;   1 và 1; .   f  1  2   
Ta có lim f  x  lim  2  x  2
 f x liên tục tại x  1 x 1  x 1     f  x x 1 lim  lim  lim             2 x 1 2 x 1  x 1  x 1  2 x 1    
Vậy hàm số f  x liên tục trên  . Chọn D.
Câu 21: Điều kiện bài toán trở thành: lim f  x  lim f  x  f 3 * x 3 x 3    f 3 2  1 3a   2    x  2 4x 3 5 6  x x x 
Ta có lim f  x  lim  lim  3  x3 x3 x3 4x  3  x  1 x  lim f x  lim       2 1 a x 3 1 3a . x3 x3     2 2 *  a    a   . Chọn A. min 3 3
Câu 22: Ta cần có lim f  x  lim f  x  f 2   * x 2 x 2    f 2 7 2  2a   4  3  3x  2  2 1
Ta có lim f  x  lim   *  a  1   a  1. Chọn C.   max x2 x2 x  2 4     lim f  x 1 7 2 2  lim a x   2a  .   x2 x2   4  4
Câu 23: Hàm số xác định với mọi x  
Ta có f  x liên tục trên  ;  0 và 0;. Trang 25   f 0  1 
Mà lim f  x  lim 1 cos x 1 cos 0  0  f x gián đoạn tại x  0 . Chọn C. x0 x0 
 lim f x  lim x 1  0 1 1 x0 x0
Câu 24: Ta có f  x liên tục trên  ;    1 ,  1  ;  1 và 1; .     f    1  cos   0    Lại có  2  
 f  x gián đoạn tại x  1. Chọn A.
 lim f x  lim x   1  2 x   1 x   1     
Câu 25: Hàm số y  f  x có TXĐ: D   .
Dễ thấy hàm số y  f  x liên tục trên mỗi khoảng  ;  0, 0;  1 và 1;.   f 0  0  2  x
Ta có lim f  x  lim
 lim x  0  f x liên tục tại x  0 x0 x0 x0 x   2  x  lim f  x  lim  lim x  0 x0 x0 x0 x    f   1  1  2  x
Lại có lim f  x  lim
 lim x  1  f  x liên tục tại x 1 x 1  x 1  x 1 x    2  x lim f  x  lim  lim x  1 x 1  x 1  x 1 x  
Vậy hàm số y  f  x liên tục trên  . Chọn A.
Câu 26: Hàm số y  f  x có TXĐ: D   .
Dễ thấy hàm số y  f  x liên tục trên mỗi khoảng ;  
1 , 1;3 và 3; .  f   1  4  Ta có 2  1  f  x x
 gián đoạn tại x 1 lim f  x  lim  lim x   1  2 x 1  x 1  x 1  x 1   f 3  2  Lại có 2  1  f x x
 gián đoạn tại x  3 lim f  x  lim  lim  x   1  4 x 3 x 3  x 3 x 1     Chọn D.
Câu 27: Hàm số y  h x có TXĐ: D   . Trang 26
Dễ thấy hàm số y  h x liên tục trên mỗi khoảng  ;
 0, 0;2 và 2; . h0 1  Ta có 
 f x không liên tục tại x  0 lim hx    lim 2x  0 x 0 x 0   h2  5  
Lại có lim h x  lim   
liên tục tại x  2 . Chọn A.    2 x 1 5 f x x2 x2 
 lim hx  lim 3x   1  5 x2 x2
Câu 28: Hàm số xác định với mọi x  
Điều kiện bài toán trở thành lim f  x  lim f  x  f   1 * x 1 x 1    f    1  2 
Ta có lim f x  lim           2 m x  2 1 m 1 * 2 m 1 2 x 1  x 1   lim f x  lim      2 x x 2 x 1  x 1   m  1   S  0. Chọn B.
Câu 29: Hàm số y  f  x có TXĐ: D   .
Dễ thấy hàm số y  f  x liên tục trên mỗi khoảng  ;  0, 0;  1 và 1;.   f 0  0  
Ta có lim f  x  lim x cos x  0  f  x liên tục tại x  0 x0 x0  2  x lim f  x  lim  0 x0 x0  1 x  f   1  1  2  x 1
Lại có lim f  x  lim
  f x không liên tục tại x  1 x 1  x 1  1 x 2  lim f x 3  lim x 1 x 1  x 1  Chọn C. x  2  2 x  2  4
Câu 30: Ta có f 2  4  a,lim f  x  lim  lim x2 x2 x2 x  2
x  2 x  2  2 1 1  lim  x2 x  2  2 4 1 15
Để hàm số đã cho liên tục tại điểm x  2 thì f 2  lim f x  4  a   a   . Chọn B. x2 4 4
Câu 31: Ta có lim f  x  f 0  m 1 x 0  Trang 27 1 x  1 x 1 x 1 x 2  x
Lại có: lim f  x  lim  lim  lim x 0 x 0 x 0 x
  1 x  1 x  x 0     x  1 x  1 x  2  2   lim   1  . x 0  1 x  1 x 2
Để hàm số đã cho liên tục tại điểm x  0 thì m 1  1   m  2  . Chọn B.
Câu 32: Ta có lim f  x  f 2 2  2m  4m  6 x 2  2     x  2  2 x 1 x  2 x 3x 2 x 1 x 2 Mặt khác lim f  x         lim  lim  lim x 2 x 2 x 2 x  2  2  x  2  4 x 2     x  2 x  2  2  lim       x 2 2x  1 4 x2
Do đó hàm số đã cho liên tục tại điểm x  2 khi 2 2
2m  4m  6  4  2m  4m  2  0  m  1. Vậy có 1 giá trị của m . Chọn A
Câu 33: Ta có lim f  x  f 2  2m  4 x 2  2 x  2x x x  2 Lại có : lim f x    lim  lim  lim x  2 x 2 x 2  x 2  x 2 x 2 x 2     
Để hàm số liên tục tại điểm x  2 thì 2m  4  2  m  3. Chọn A.
Câu 34: Ta có lim f  x  f 2  4  2 2  2  4 x 2 
Mặt khác lim f  x  lim         2 5x 5m m  2 10 5m m x2 x2
Hàm số liên tục với mọi x  2 , như vậy để hàm số đã cho liên tục trên  thì hàm số liên tục tại điểm m  2 x  2 khi và chỉ khi 2 2
4  10  5m  m  m  5m  6  0   . Chọn A. m  3 Câu 35: Ta có f   1  k x  x  2  2016 2016 x   1   x   lim f  x 1  lim  lim x 1  x 1  x 1     2018x 1 x  2018 2018x 1 x 2018 2018x 1  x  2018 x  1 2015 2014 x  x  x   1   x   1  lim 2018x 1  x  2018 x 1    2017 x   1  2015 2014 x  x  x   1 1 2016 1  lim 2018x 1  x  2018  .2 2019  2 2019 x 1    2017 2017
Do đó hàm số liên tục tại điểm x  1  k  2 2019 . Chọn A. 2x  a 2  a
Câu 36: Ta có lim f  x  f  
1  0, lim f  x  lim     2 x 1  x 1  x 1  x 1 2 Trang 28 2  a
Để hàm số liên tục tại điểm x  1 thì 0   a  2 . Chọn B. 0 2
Câu 37: Ta có lim f  x  f   1  1 x 1  1 x 1 x 2 3 1 x  x 
Mặt khác lim f  x  lim  lim  lim         2 1 x x  3 x 1  x 1   x 1   x 1 1 x 1 x 
Do lim f  x  lim f  x nên hàm số đã cho không liên tục tại điểm x  1 x 1 x 1  
Mặt khác lim f  x  f  
1  1 nên hàm số liên tục phải tại điểm x  1. Chọn A. x 1  2 x  5x  6 x  2 x  3
Câu 38: Ta có f 3  3,lim f x     lim  lim  limx  2 1 x3 x3 x3 x3 x  3 x  3
Để hàm số liên tục tại điểm x  3 thì lim f  x  f 3  a  1. Chọn B. x3
Câu 39: Hàm số đã cho liên tục với mọi x  1 2 x  x 1 2 x  2 1 x Ta có: f   1  m 1,lim f  x 3 3  lim  lim x 1  x 1  x 1 x 1  x 1  2  3 x 1       2  2 1   lim 1  lim 1  1  x 1        3 x   3 2 3 x  x  x 1     3 2 3 x  x   3 3 1 1 1      1 4
Để hàm số đã cho liên tục tại x  1 thì m 1    m   . Chọn A. 3 3 3 2 2 x  x  2x  2 x x 1  2 x 1 Câu 40: Ta có: f  
1  3  m và lim f  x      lim  lim x 1  x 1  x 1 x 1  x 1  2x 2x 1  lim  lim 2 x  2  3 x 1  x 1 x 1 
Để hàm số đã cho liên tục tại x  1 thì 3  m  3  m  0 . Chọn A. 2 2 x  4  2 x  4  4 Câu 41: Ta có f   5
0  2a  và lim f  x  lim  lim 4 2 x0 x0 x0 2 x x  2x  4  2 1 1  lim  x0 2 x  4  2 4 5 1 3 3
Để hàm số đã cho liên tục tại điểm x  0 thì 2a  
 2a   a  . Chọn D. 4 4 2 4 2 x 1 x 1 x 1 Câu 42: Ta có lim f x     lim  lim  limx   1  2 x 1  x 1  x 1  x 1 x 1 x 1  Lại có f  
1  a , để hàm số liên tục tại điểm x  1 thì a  2 . Chọn C. Trang 29 1 1
Câu 43: Ta có lim f  x  f   1  m  m   2m  x 1  4 4 5x 1  2 5x 1 4 5 x   1
Lại có: lim f  x  lim  lim  lim x 1 x 1  x 1 x 1   x   1  5x 1  2 x 1     x   1  5x 1  2 5 5  lim  x 1  5x 1  2 4
Để hàm số liên tục trên  thì hàm số phải liên tục tại điểm x  1 1 5 1 Khi đó 2m    m  . Chọn B. 4 4 2 2 x  3x  2
Câu 44: Ta có lim f  x  lim  limx  2  1 x 1  x 1  x 1 x 1 
Hàm số đã cho liên tục tại x  1 khi lim f  x  f   1  m  1. Chọn A. x 1  2 x  2 Câu 45: Hàm số y 
bị gián đoạn tại x  1. Chọn B. x 1 2 x  x  6 Câu 46: lim f x  lim  lim x  3  5 x 2 x 2  x 2 x 2    
Và lim f  x  lim  2  ax   1  1 4 ; a f 2  2  . a 2 1  1 4a x 2 x 2  
Hàm số đã cho liên tục tại x  2 khi lim f  x  lim f  x  f 2  1 4a  5  a  1. Chọn C. x 2 x 2  
Câu 47: Ta có lim f  x  lim  x   1  3; x 2 x 2   Và lim f  x  lim         2 x m m 4; f 2 m 4 x2 x2
Hàm số đã cho liên tục tại x  2 khi lim f  x  lim f  x  f 2  m  4  3  m  1  . Chọn A. x 2 x 2   sin x
Câu 48: Ta có lim f  x  lim  1; f 0  a x0 x0 x
Hàm số liên tục tại x  0 khi lim f  x  f 0  a 1. Chọn A. x0
Câu 49: Ta có lim f  x  lim       2 x m 4 ; m x2 x2
Và lim f  x  lim 3x   1  5; f 2  4  ; m x 2 x 2  
Hàm số liên tục tại x  2 khi lim f  x  lim f  x  f 2  m  4  5  m  1. Chọn B. x 2 x 2  
Câu 50: Hàm số đã cho liên tục trên khoảng  ;  3,3; 2 3x  7x  6 Ta có lim f  x  lim
 lim 3x  2  3.3 2 11; x 3 x 3  x 3 x 3     Trang 30 Và lim f  x  lim          2 x
5mx 2 15m 11; f 2 15m 11 x3 x3
Hàm số liên tục tại x  3 khi lim f  x  lim f  x  f 3  15m 11 11  m  0 x 3 x 3  
Vậy m  0 là giá trị để hàm số liên tục trên  . Chọn D x  4  2 1 1
Câu 51: Ta có lim f  x  lim  lim  ; x 0 x 0 x 0 x     x  4  2 4  5 
Và lim f x  lim 2m  x  2 ; m f   0  2m x 0 x 0    4  1 1
Hàm số liên tục tại x  0 khi lim f  x  lim f  x  f 0  2m   m  . Chọn C. x 0 x 0   4 8 x 1 1 1
Câu 52: Ta có lim f  x  lim  lim  ; x 1 x 1  x 1 x 1     x 1 2  1  1 1
Và lim f  x  lim ax   a  ; f   1  a    x 1 x 1    2  2 2 1 1
Hàm số liên tục tại x  1 khi lim f  x  lim f  x  f   1  a    a  1. Chọn C x 1 x 1   2 2
Câu 53: Hàm số đã cho liên tục trên khoảng  ;  4, 4; 2 x 16 Ta có lim f x  lim  lim x  4  8; x 4 x 4  x 4 x 4    
Và lim f  x  lim mx  
1  4m 1; f 4  4m 1 x 4 x 4   7
Hàm số liên tục tại x  4 khi lim f  x  lim f  x  f 4  4m 1  8  m  x 4 x 4   4 7
Vậy m  là giá trị để hàm số liên tục trên  . Chọn D. 4 2 x 1
Câu 54: Ta có lim f x  lim  lim x   1  2; f   1  m x 1  x 1  x 1 x 1 
Hàm số liên tục tại x  1 khi lim f  x  f   1  m  1. Chọn C. x 1  2 x  3
Câu 55: Ta có lim f x  lim
 lim x  3  2 3  f  3 x 3 x 3 x 3 x  3
Suy ra hàm số đã cho liên tục tại x  3  Hàm số liên tục trên  . Chọn B. 2 x  3x  2
Câu 56: Ta có lim f x  lim  lim x   1  1; x 2 x 2  x 2 x 2    
Và lim f  x  lim 2m   1  2m 1; x 2 x 2  
Hàm số liên tục tại x  2 khi lim f  x  lim f  x  2m 1  1  m  0 . Chọn A. x 2 x 2   Trang 31
Câu 57: Hàm số đã cho liên tục trên khoảng  ;  2, 2; 2 x  3x  2 Ta có lim f x  lim  lim x   1  1; x 2 x 2  x 2 x 2    
Và lim f  x  lim  x  mx  2  2 ; m x 2 x 2   1
Hàm số liên tục tại x  2 khi lim f  x  lim f  x  2  2m 1  m  x 2 x 2   2 1
Vậy m  là giá trị để hàm số liên tục trên  . Chọn B. 2 2 x  4x  3 x 1 x  3 Câu 58: Ta có lim f x     lim  lim  lim x  3  2  x 1 x 1  x 1  x 1 x 1 x 1     
Lại có lim f  x  lim 6Px  3  f   1  6P  3 x 1 x 1  
Hàm số liên tục trên  khi hàm số liên tục tại x  1 1
Khi đó 2  6P  3  P  . Chọn C. 6 Câu 59: Ta có f   1  2a 1
Để hàm số đã cho liên tục trên  thì hàm số liên tục tại điểm x  1 2 x  ax  b
Khi đó lim f  x  lim  2a 1  * x 1  x 1  x 1 Suy ra 2
x  ax  b   x  
1  x  b  a  1 b  1
Ta có: *  lim x  b  2a 1  1 b  2a 1(2) x 1  a  3 Giải hệ   1 và 2 ta được   a  b  7 . Chọn D. b   4 2 ax  a  2 x  2 Câu 60: Ta có f   2
1  8  a , mặt khác lim f  x    lim x 1  x 1  x  3  2 ax  2x  1  lim . x    ax  x    a  x  3 2 lim 2. x  3 2 4 2 1 1 x  3  4 a  0
Hàm số liên tục tại điểm x  1 khi 2 8  a  4a  2 2  a  4a  0   a  4
Vậy có 2 giá trị của tham số a . Chọn D.
Câu 61: Ta có lim f  x  lim 3x  a   1  a 1 x 0 x 0   1 2x 1 1 2x 1 2
Mặt khác lim f  x  lim  lim  lim 1 x 0 x 0 x 0 x  x 1 2x   x 0 1      1 2x 1 Trang 32
Hàm số đã cho liên tục tại điểm x  0  a 1  1  a  2 . Chọn C.
Câu 62: Ta có lim f  x  lim mx   1  4m 1 x 4 x 4   2 x 16 x  4 x  4 Lại có: lim f x     lim  lim  lim x  4  8 x 4 x 4  x 4  x 4 x 4 x 4      7
Để hàm số liên tục tại điểm x  4 thì 4m 1  8  m  . Chọn D. 4 x  8 x  2 2 3 x  2x  4
Câu 63: Ta có f 2  2m 1,lim f  x  lim  lim x2 x2 x2 x  2 x  2  lim 2 x  2x  4 12 x2 11
Để hàm số liên tục tại điểm x  2 thì 2m 1  12  m  . Chọn C. 0 2
Câu 64: Ta có lim f  x  lim       2 x mx 1 m x 1  x 1  x  3  2 x  3  4 x 1
Lại có: lim f  x  lim  lim  lim x 1 x 1  x 1 x 1  x   1  x  3  2 x 1    
x  1 x 3  2 1 1  lim  x 1  x  3  2 4 1 3
Để hàm số đã cho liên tục tại điểm x  1 thì m 1   m  . Chọn A. 4 4 2 2 x  x  2sin sin 1 cos x 1   1 Câu 65: Ta có f    f  x 2 2 0 0,lim  lim  lim  lim    2 2 x0 x0 x0 x0 x  x  2 x 2 4.      2 2   
Suy ra hàm số gián đoạn và không có đạo hàm tại điểm x  0 . Chọn D. 4x 1 1 4x 11
Câu 66: Ta có f 0  3,lim f  x  lim  lim 2 x0 x0 ax  2a   x0 1 x xax  2a   1  4x 1  1 4 4 2  lim   x0 ax  2a   1  4x 1  1 22a   1 2a 1 2 1 
Hàm số liên tục tại điểm x  0 khi  3  a  . Chọn C. 2a 1 6 Trang 33
Câu 67: Ta có lim f x  lim       x m m x0 x0
Mặt khác lim f  x  lim mx   1  1 x 0 x 0  
Hàm số liên tục trên  khi hàm số liên tục tại điểm x  0 suy ra m  1  m  1. Chọn C.
Câu 68: Ta có lim f  x  lim  x  
1  2, lim f  x  lim sin  x  sin  0 x 1 x 1 x 1 x 1    
Suy ra hàm số không liên tục tại điểm x  1
Lại có lim f x  lim sin x  sin  
   0, lim f x  lim x   1  0 x   1  x   1  x   1  x   1         
Do đó hàm số liên tục tại điểm x  1  . Chọn C.
Câu 69: Ta có lim f  x  f 4 12  m x 4  2 x 16 x  4 x  4 Lại có: lim f  x     lim  lim  lim x  4        x 2 32 x4 x4 x4  x  4 x4 x 2 x  2
Hàm số liên tục tại điểm x  4 khi 12  m  32  m  20 . Chọn B. 2x 1  x  5 2x 1 x  5
Câu 70: Ta có f 4  a  2, lim f  x     lim x4 x4 x  4
x  4 2x 1 x 5 x  4 1 1  lim  lim 
x4  x  4 2x 1  x  5 x4 2x 1  x  5 6 1 11
Hàm số liên tục tại điểm x  4 khi a  2   a   . Chọn B. 6 6  1 x  1
Câu 71: Ta có lim f x  lim a   a   f   2 x 2 x 2    2  x  4 2 2x  7x  6 x  2 2x  3 2 x 2x 3 Mặt khác lim f  x     lim  lim  lim x 2 x 2  x 2 x 2  x  2 x 2     x  2  lim       2x 3 1 x2 1 3
Hàm số liên tục tại điểm x  2 khi a   1  a  . 4 4 7 3 7 7 Bất phương trình 2 2
x  ax   0  x  x   0    x  1 4 4 4 4
Kết hợp x  Z  x   1  ;  0 . Chọn D Trang 34 2 x  x  2 x  2 x 1 Câu 72: Ta có f 2     , m lim  lim  limx   1  3 x2 x2 x2 x  2 x  2
Để hàm số liên tục tại điểm x  2 thì m  3 . Chọn A.
Câu 73: Nếu hàm số y  f  x liên tục trên a;b và f a. f b  0 thì tồn tại x  ; a b sao cho 0  
f  x  0  phương trình f  x  0 có ít nhất một nghiệm trên khoảng a;b. 0  Mệnh đề  
1 và 2 đúng và mệnh đề 3 sai. Chọn D.
Câu 74: Hàm f  x là hàm đa thức nên liên tục trên   A đúng.  f    1  1  0 Ta có 
 f  x  có nghiệm x trên 2;  1 , mà  f 1    0 2  23  0 2;  1   2  ;0   ;  
1  B sai và C đúng. Chọn B.
Câu 75: Xét hàm số f  x 4 2
 2x  5x  x 1 là hàm số liên tục trên  Ta có: f   1  3  , f   1  1  , f 0 1  f  0. f   1  0 Do đó 
 Phương trình f  x  0 có nghiệm trên mỗi khoảng 1;0 và 0;  1  f  0. f   1  0
Do đó các khẳng định A, B,C sai. Chọn D. Câu 76: Hàm số f  x 3
 x  3x 1 liên tục trên  Ta có: f 2  3  , f   1  1, f 0  1  , f 2  2
Suy ra phương trình f x  0 có nghiệm trên mỗi khoảng 2;  1 , 1;0 , 0;2
Mà phương trình f  x  0 có tối đa 3 nghiệm nên nó có 3 nghiệm. Chọn D.
Câu 77: Ta có f  x  5  g x  f  x  5  0 Mặt khác g   1  f  
1  5  3  0 và g 4  f 4  5  2  0
Suy ra phương trình f  x  5 có ít nhất một nghiệm trên đoạn 1;4. Chọn B. Câu 78: Đặt f  x 3 2
 x  3x  2m  2 x  m  3
Ta có: lim f  x   , để phương trình có nghiệm x  1 thì f   1  0 x 1
 1 3  2m  2  m  3  0  m  5  0  m  5 Trang 35  1   1 3 23 Lại có f
    m 1 m  3   0  
và lim f  x    2  8 4 8 x Do đó với m  5
 thì phương trình đã cho có ba nghiệm phân biệt x , x , x thỏa mãn x  1 x  x . 1 2 3 1 2 3
Kết hợp m  Z, m 10;10  m   9  ;8; 7  ;  6 . Chọn C. Trang 36