Tài liệu đọc môn Sức bền vật liệu | Trường Đại học Bách Khoa Hà Nội

SỨC BỀN VẬT LIỆU 1 TÀI LIỆU ĐỌC TẬP THỂ TÁC GIẢ:
PGS TS NGUYỄN MẠNH CƯỜNG TS NGUYỄN THÁI TẤT HOÀN TS TRẦN ĐÌNH LONG TS LÊ THỊ BÍCH NAM TS NGUYỄN DANH TRƯỜNG
NHÓM CHUYÊN MÔN CƠ HỌC VẬT LIỆU VÀ KẾT CẤU KHOA CƠ ĐIỆN TỬ TRƯỜNG CƠ KHÍ
ĐẠI HỌC BÁCH KHOA HÀ NỘI HÀ NỘI, 10/2023 MỤC LỤC
CHƯƠNG 1 MỞ ĐẦU ....................................................................................................... 4
1.1 Đối tượng và nhiệm vụ của môn học ................................................................... 4
1.2 Mô hình nghiên cứu ............................................................................................. 5
1.3 Ôn lại một số khái niệm cơ bản trong tĩnh học .................................................... 7
1.4 Nội lực ................................................................................................................ 10
1.5 Phân loại biến dạng cơ bản của thanh ................................................................ 13
1.6 Biểu đồ nội lực ................................................................................................... 15
CHƯƠNG 2 KÉO NÉN ĐÚNG TÂM, CẮT HAY TRƯỢT ........................................... 18
2.1 Kéo, nén đúng tâm .................................................................................................. 18
2.2 Cắt hay trượt ........................................................................................................... 21
2.3 Định luật Hooke ...................................................................................................... 23
2.4 Tính chất cơ học của vật liệu .................................................................................. 23
2.5 Ứng suất cho phép và hệ số an toàn ....................................................................... 29
2.6 Thanh siêu tĩnh chịu kéo nén đúng tâm .................................................................. 32
CHƯƠNG 3 XOẮN THUẦN TÚY THANH MẶT CẮT NGANG TRÒN .................... 33
3.1 Khái niệm ................................................................................................................ 33
3.2 Biểu đồ moment xoắn ............................................................................................. 35
3.3 Quan hệ giữa ứng suất tiếp, biến dạng và moment xoắn trên mặt cắt ngang ......... 37
3.4 Điều kiện bền và điều kiện cứng ............................................................................ 42
3.5 Bài toán siêu tĩnh khi xoắn ..................................................................................... 43
CHƯƠNG 4 UỐN NGANG PHẲNG THANH THẲNG ................................................ 45
4.1 Giới thiệu ................................................................................................................ 45
4.2 Quan hệ giữa lực cắt, moment uốn và tải trọng ...................................................... 47
4.3 Biểu đồ lực cắt và moment uốn .............................................................................. 50
4.4 Uốn thuần túy .......................................................................................................... 55
4.5 Uốn ngang phẳng .................................................................................................... 69 4.6
Đặc trưng hình học mặt cắt ngang .......................................................................... 82
CHƯƠNG 5 TRẠNG THÁI ỨNG SUẤT, TRẠNG THÁI BIẾN DẠNG VÀ THUYẾT BỀN ........ 91 2
5.1 Trạng thái ứng suất ................................................................................................. 91
5.2 Trạng thái ứng suất phẳng ...................................................................................... 99
5.3 Trạng thái biến dạng ............................................................................................. 102
5.3 Quan hệ giữa ứng suất và biến dạng, định luật Hooke tổng quát ......................... 108
5.4 Thuyết bền ............................................................................................................ 111
TÀI LIỆU THAM KHẢO .............................................................................................. 115 3 CHƯƠNG 1 MỞ ĐẦU Nội dung:
• Đối tượng và nhiệm vụ của môn học, mô hình nghiên cứu.
• Ngoại lực, các loại liên kết và phản lực liên kết
• Nội lực và các thành phần nội lực
• Phân loại biến dạng cơ bản của thanh • Biểu đồ nội lực
1.1 Đối tượng và nhiệm vụ của môn học
1.1.1 Nhiệm vụ của môn học
Sức bền vật liệu là một môn học nghiên cứu về ứng xử cơ học của vật rắn khi chịu tác
dụng của ngoại lực. Sức bền vật liệu còn được gọi là Cơ học vật rắn biến dạng hay là Cơ học của vật liệu.
Nhiệm vụ của môn học nghiên cứu về độ bền, độ cứng và độ ổn định của vật rắn bao
gồm chi tiết máy, kết cấu hay công trình. Trong đó độ bền là khả năng chịu lực mà
không bị phá hủy của vật rắn, độ bền của vật rắn liên quan đến đại lượng ứng suất. Độ
cứng là khả năng của kết cấu và các phần tử của nó chống lại ngoại lực về mặt biến
dạng, đủ độ cứng tức là biến dạng của kết cấu không vượt quá giá trị cho phép. Độ ổn
định là khả năng bảo toàn dạng xác định ban đầu của kết cấu trong quá trình chịu lực.
Sư hiểu biết về ứng xử cơ học của vật rắn khi chịu tác dụng của ngoại lực sẽ giúp cho
người kỹ sư đưa ra các thiết kế đảm bảo an toàn cho mọi kết cấu như bánh răng, trục
truyền, cầu, máy bay hay nhà cửa,…Vì vậy Sức bền vật liệu là môn khoa học kỹ thuật
cơ sở của nhiều ngành kỹ thuật.
1.1.2 Đối tượng của môn học
Trong sức bền vật liệu, vật rắn được nghiên cứu là vật rắn biến dạng. Đó là vật rắn
thực dưới tác dụng của lực thì vật rắn bị thay đổi hình dáng và kích thước. Những
thông số đặc trưng cho ứng xử cơ học của vật rắn đó là ứng suất, biến dạng và chuyển
vị. Những thông số này phụ thuộc vào tính chất vật lý của vật liệu được khảo sát. Vì
vậy các vật rắn được khảo sát là các chi tiết máy, kết cấu hay công trình được làm từ
vật liệu thực như thép, gỗ, bê tông, nhựa, composite, …
Đây là môn học được xây dựng kết hợp giữa lý thuyết và thực nghiệm. Thực nghiệm
giúp xác định được các tính chất vật lý của vật liệu. Từ đó những nghiên cứu lý thuyết
sẽ đưa ra các công thức và phương trình để dự đoán những ứng xử cơ học của vật rắn.
1.2 Mô hình nghiên cứu
1.2.1 Về mặt hình học.
Các vật rắn trong thực tế được chia thành 3 dạng kết cấu chính là kết cấu dạng thanh,
kết cấu dạng tấm vỏ và kết cấu dạng khối.
- Kết cấu dạng thanh là loại kết cấu mà kích thước một phương lớn hơn rất nhiều so
với hai phương còn lại. Các kết cấu dạng thanh hay gặp trong thực tế đó là trục
truyền, dầm, cột, thanh treo, … Ví dụ cột có chiều dài lớn hơn rất nhiều so với đường kính của cột.
- Kết cấu dạng tấm, vỏ là loại kết cấu mà có kích thước hai phương lớn hơn rất nhiều
so với phương còn lại. Kích thước chiều dài, chiều rộng của tấm lớn hơn rất nhiều
so với bề dày của tấm. Các kết cấu dạng tấm, vỏ hay gặp trong thực tế đó là mái
nhà, sàn nhà, bồn chứa, thân máy bay, cánh máy bay, vỏ ô tô, …
- Kết cấu dạng khối là loại kết cấu mà có kích thước theo ba phương xấp xỉ nhau.
Kết cấu dạng khối hay gặp trong thực tế đó là bánh răng, bi trong ổ bi, viên gạch, …
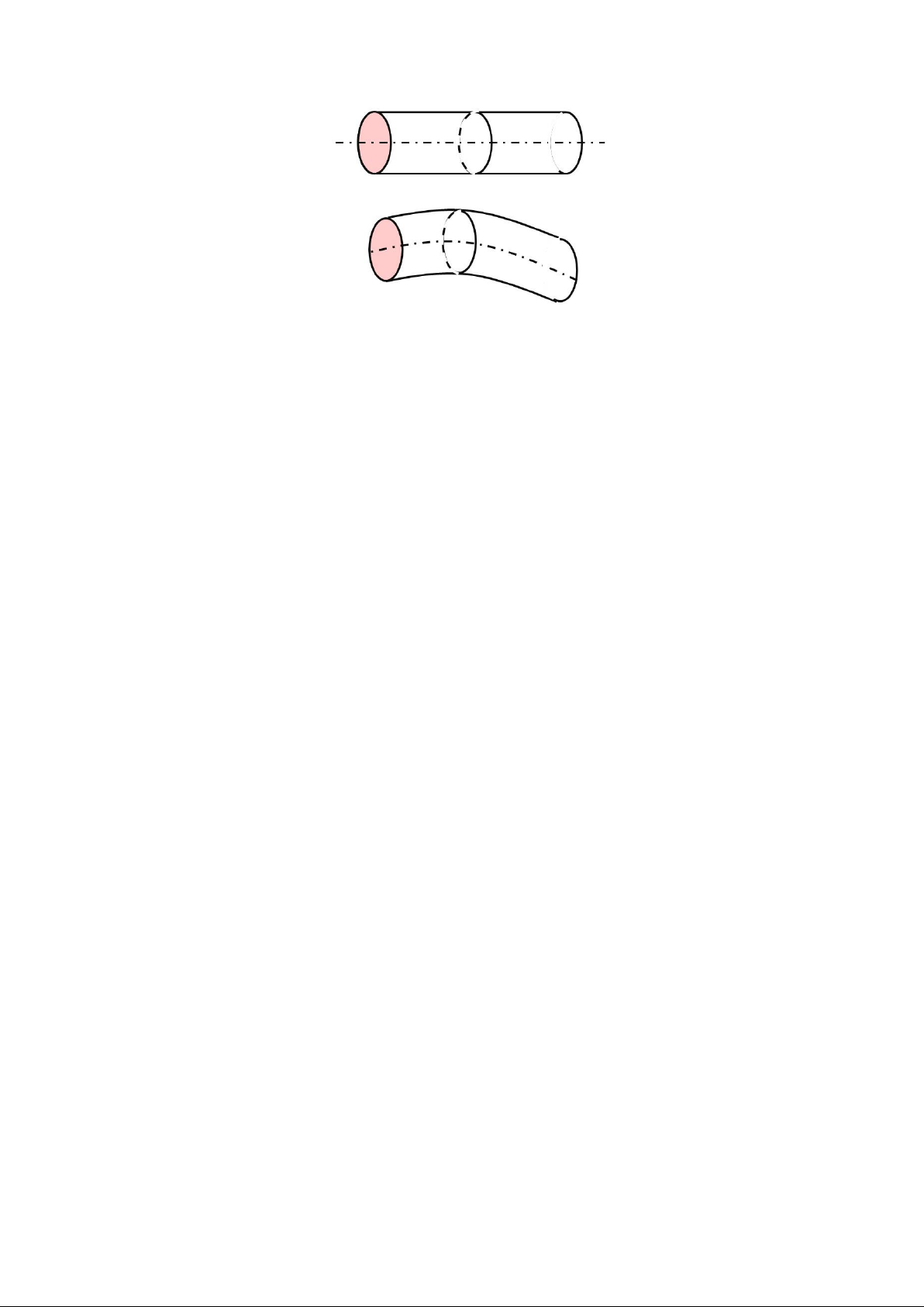
Hình 1.1 Kết cấu dạng thanh
Đối tượng được khảo sát nhiều nhất của sức bền vật liệu đó là các kết cấu dạng thanh.
Thanh là một kết cấu khi trọng tâm của hình phẳng chuyển động trên một quỹ đạo và
hình phẳng luôn vuông góc với quỹ đạo đó. Quỹ đạo đó gọi là trục thanh. Thanh thẳng
nếu quỹ đạo này là đường thẳng và thanh cong nếu quỹ đạo này là đường cong.
1.2.2 Về mặt vật lý
Về mặt vật lý, vật liệu được khảo sát tuân theo các giả thuyết sau: Giả thiết 1:
Vật liệu được coi là liên tục, đồng chất và đẳng hướng. -
Liên tục nghĩa là vật liệu điền đầy mọi thể tích của vật rắn. -
Đồng chất nghĩa là tính chất vật lý như nhau tại mọi điểm -
Đẳng hướng nghĩa là tính chất vật lý và cơ học như nhau theo mọi phương. Giả thiết 2:
Vật liệu được coi là đàn hồi tuyệt đối. Khi chịu tác dụng của ngoại lực thì vật rắn biến
dạng biến dạng, khi ngừng tác dụng thì vật rắn trở về trạng thái như ban đầu và biến
dạng này tỷ lệ với lực tác dụng. Giả thiết 3:
Những biến dạng và chuyển vị của vật rắn được khảo sát là bé. Vì vậy có thể áp dụng
nguyên lý cộng tác dụng.
1.3 Ôn lại một số khái niệm cơ bản trong tĩnh học 1.3.1 Ngoại lực
Ngoai lực là tác dụng của môi trường bên ngoài hay của vật thể khác lên vật đang xét.
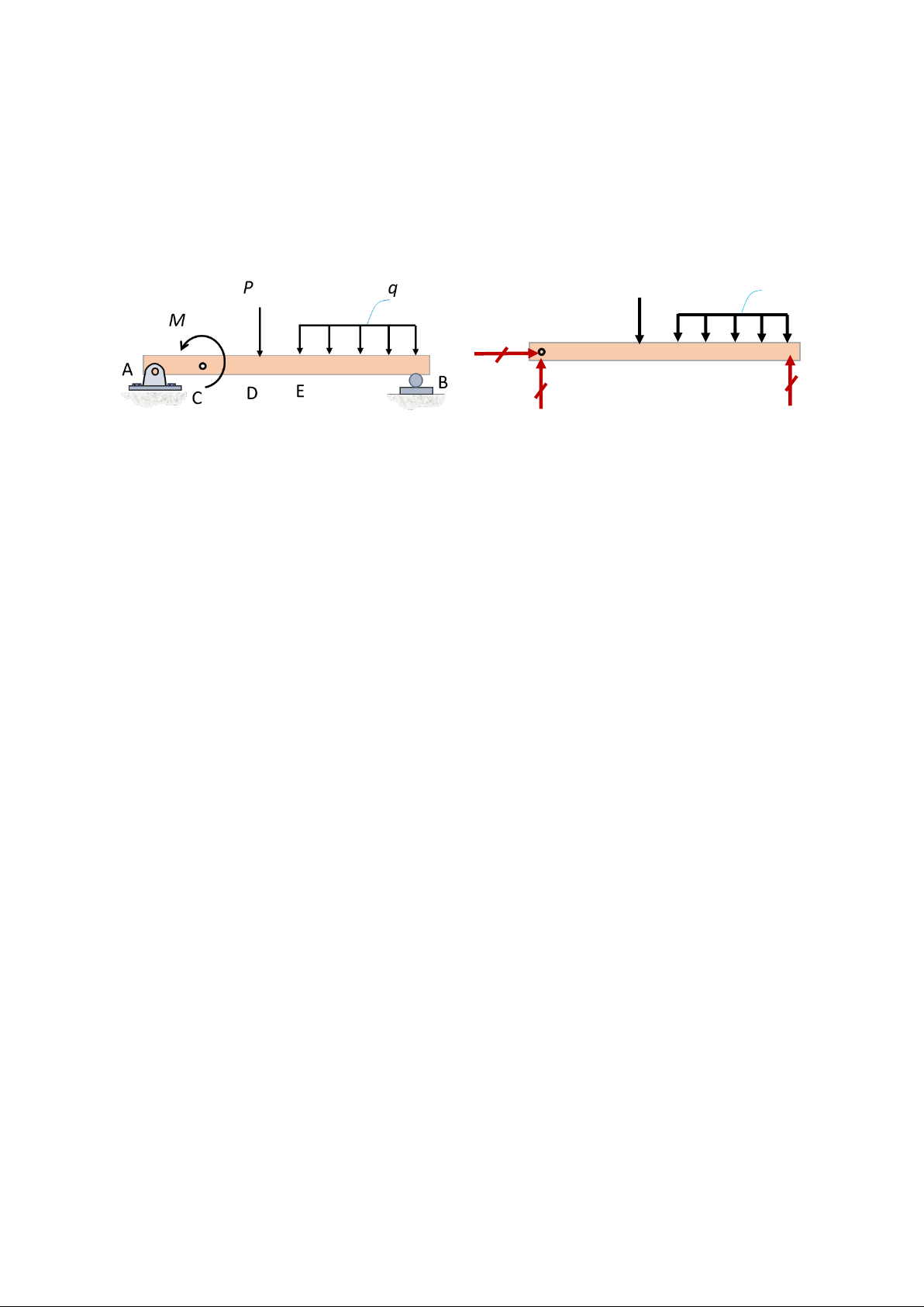
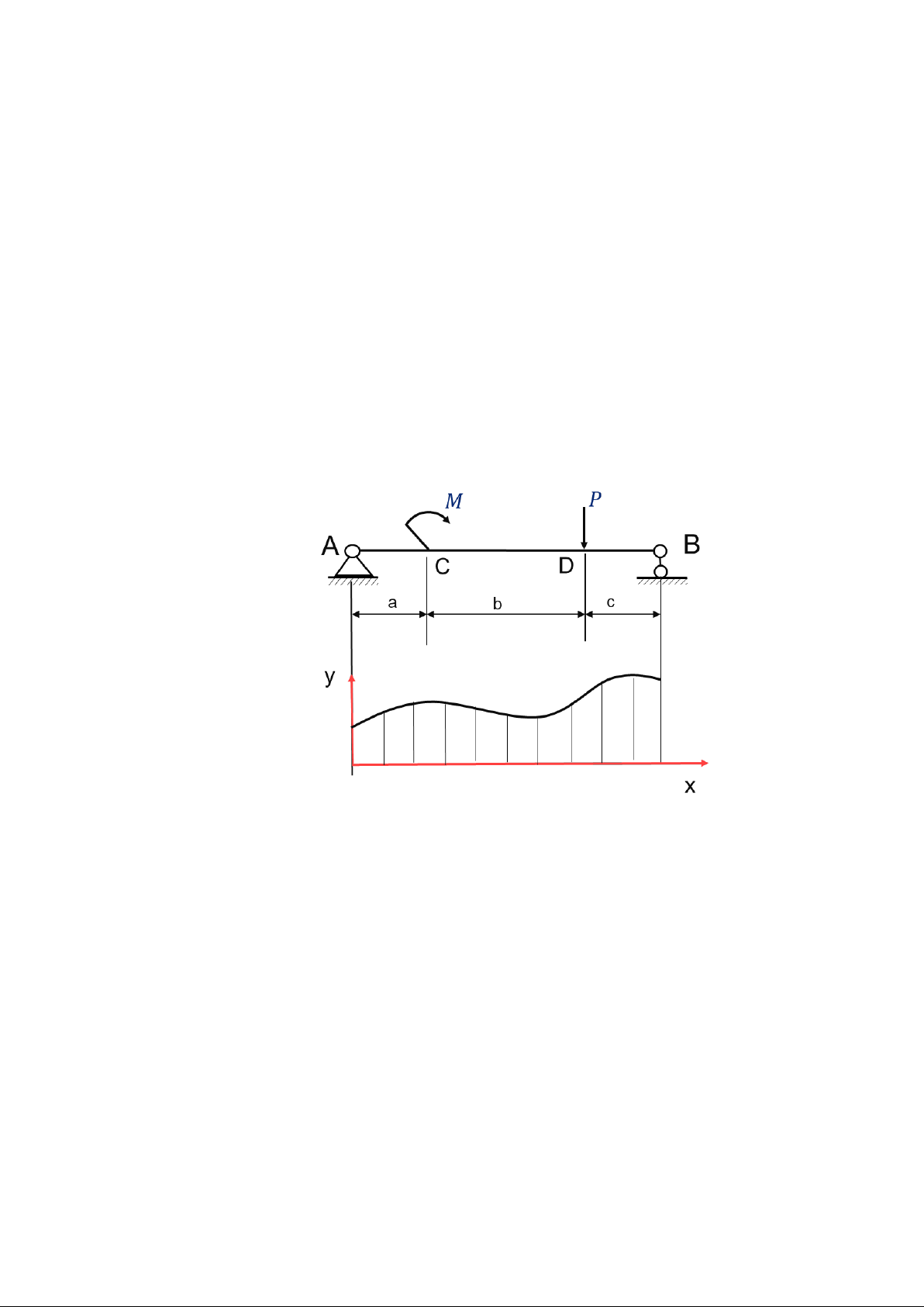
Ngoại lực bao gồm tải trọng và phản lực liên kết. M P q A x A A y B y
Hình 1.2 Các dạng tải trọng và phản lực liên kết
Tải trọng là tác dụng của môi trường bên ngoài lên vật thể đang xét. Tải trọng thường
có phương, chiều, độ lớn và điểm đặt đã biết trước.
Các dạng tải trọng là:
• Tải trọng tập trung P: là lực tập trung tại một điểm. Đơn vị là N, kN
• Tải trọng phân bố q: là tải trọng phân bố trên bề mặt [N/m2] hoặc tải trọng phân bố trên chiều dài [N/m]
• Moment tập trung M: là moment tác dụng tại một điểm. Đơn vị là [Nm], [kNm]
• Moment phân bố m: moment phân bố trên chiều dài. Đơn vị là [Nm/m], [kNm/m]
Phản lực liên kết là lực phát sinh tại chỗ tiếp xúc của vật thể với vật thể khác. Phụ thuộc
vào loại liên kết sẽ có phản lực liên kết tương ứng. Chiều và độ lớn của phản lực liên kết là chưa xác định.
Hình 1.2 mô hình hóa một thanh chịu các tác dụng của các loại tải trọng khác nhau, tựa
trên hai gối tưa tại A và B. Trong hình 1.2, các tải trọng tác dụng lên thanh bao gồm
lực tập trung P đặt tại D, moment tập trung M tại C và hệ lực phân bố q bằng hằng số
trên đoạn EB. Các phản lực liên kết bao gồm Ax, Ay và By phát sinh tại vị trí liên kết.
Vì vật rắn đang xét là vật rắn cân bằng ở trạng thái tĩnh, nên tải trọng và phản lực liên
kết tác dụng lên vật rắn phải tuân theo phương trình cân bằng.
1.3.2 Các loại liên kết và phản lực liên kết
Để xác định được phương của phản lực liên kết ta cần phải xác định được loại liên kết
tại đó. Theo nguyên tắc nếu chuyển vị thẳng bị giới hạn theo phương nào thì sẽ xuất
hiện phản lực liên kết theo phương đó. Tương tự nếu góc xoay bị giới hạn theo phương
nào thì cũng sẽ xuất hiện moment theo phương đó. Sau đây là một số dạng liên kết cơ
bản trong kỹ thuật được cho trong bảng 1.1.
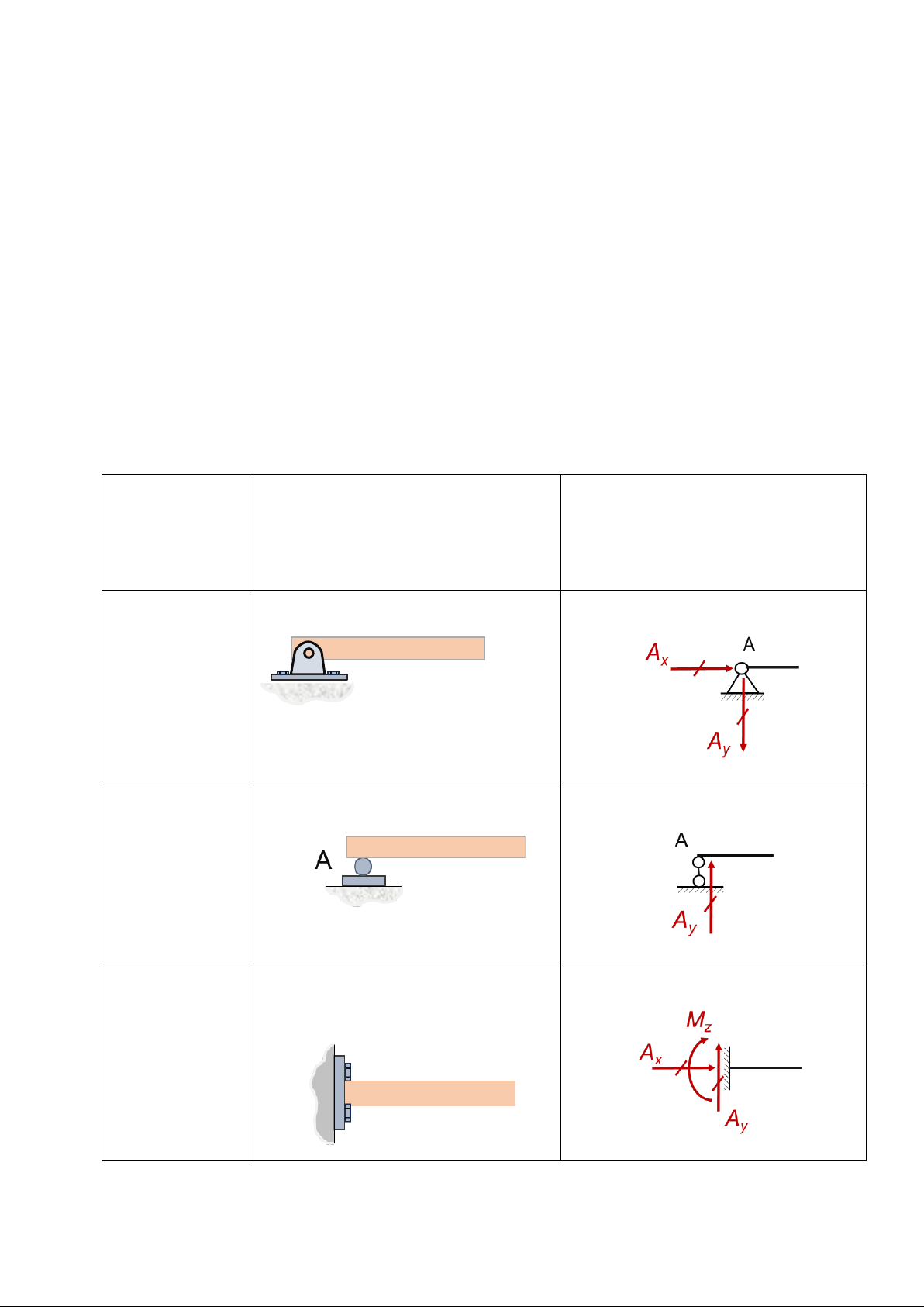
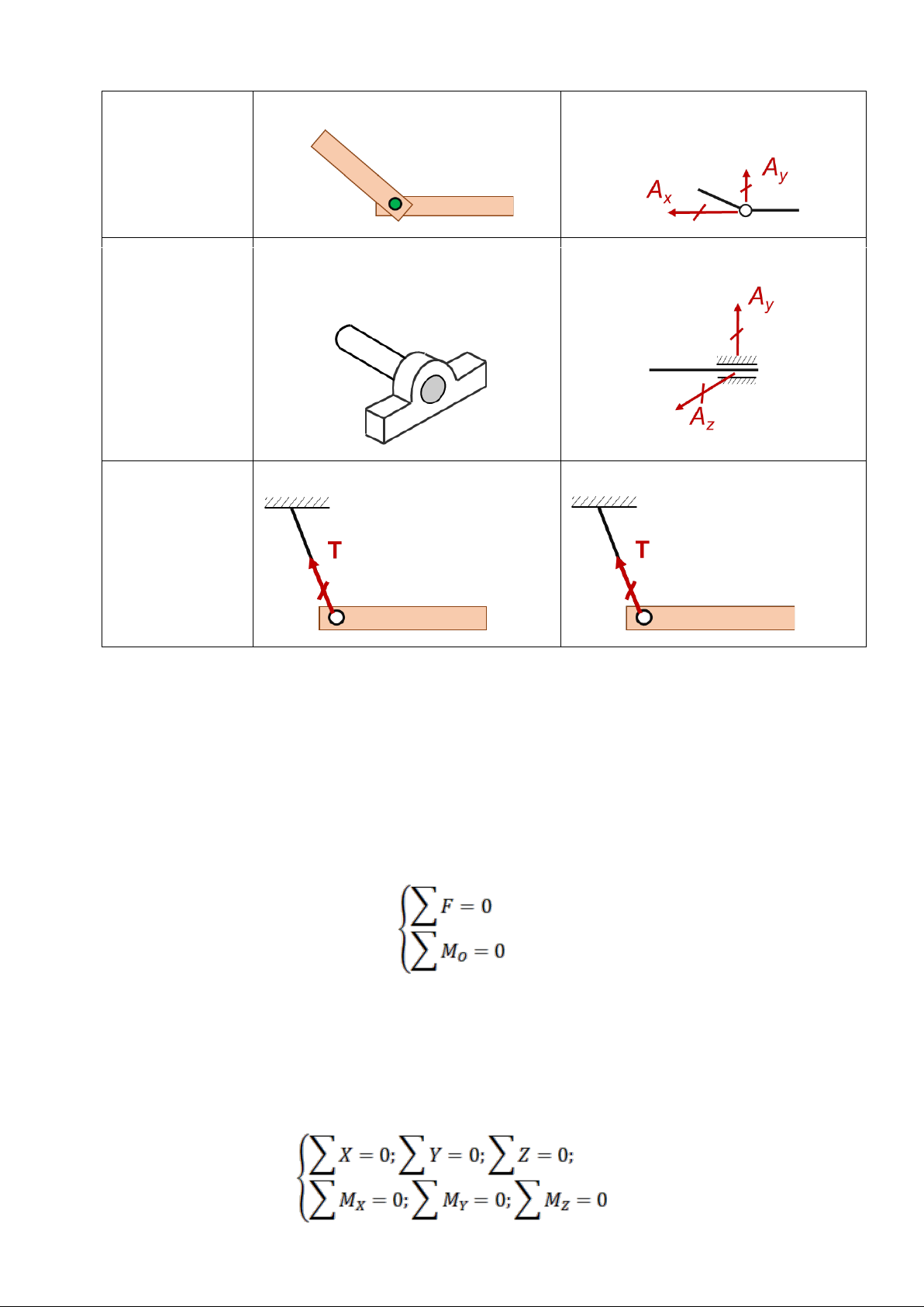
Bảng 1.1. Các loại liên kết và phản lực liên kêt tương ứng Loại liên kết
Hình ảnh liên kết
Mô hình hóa và phản lực liên kết tương ứng Gối tựa cố A định Gối tựa di động Ngàm hoặc mối hàn A Liên kết khớp A Liên kết ổ đỡ hoặc ổ lăn Liên kết cáp treo hoặc thanh treo
1.3.3 Phương trình cân bằng và cách xác định phản lực liên kết
Như đã nói ở trên vật rắn đang xét là vật rắn cân bằng. Để vật rắn cân bằng tổng các
lực và tổng moment tác dụng lên vật rắn bằng không. Ta có các phương trình cân bằng: (1.1)
Trên vật rắn, ta thiết lập hệ tọa độ Descaster Oxyz, khi chiếu vector lực chính và
vector moment chính lên các trục tọa độ ta sẽ được 6 phương trình cân bằng như sau: (1.2)
Trong bài toán phẳng để vận rắn cân bằng ta chỉ cần hạn chế 3 bậc tự do, tương ứng
với 3 phương trình cân bằng như sau: (1.3) Hoặc (1.4)
Giải các phương trình cân bằng ta sẽ xác định được giá trị của các phản lực liên kết. 1.4 Nội lực
1.4.1 Nội lực và phương pháp mặt cắt
Giữa các phần tử vật chất trong vật rắn có lực tương tác để vật rắn giữ nguyên hình
dạng và kích thước. Khi chịu tác dụng của ngoại lực thì lực tương tác này sẽ tăng
lên để chống lại tác dụng bên ngoài. Độ tăng của lực tương tác bên trong vật thể
dưới tác dụng của ngoại lực chính là nội lực.
Để xác định được nội lực tại một vị trí nào đó trong vật thể ta sẽ sử dụng phương pháp mặt cắt.
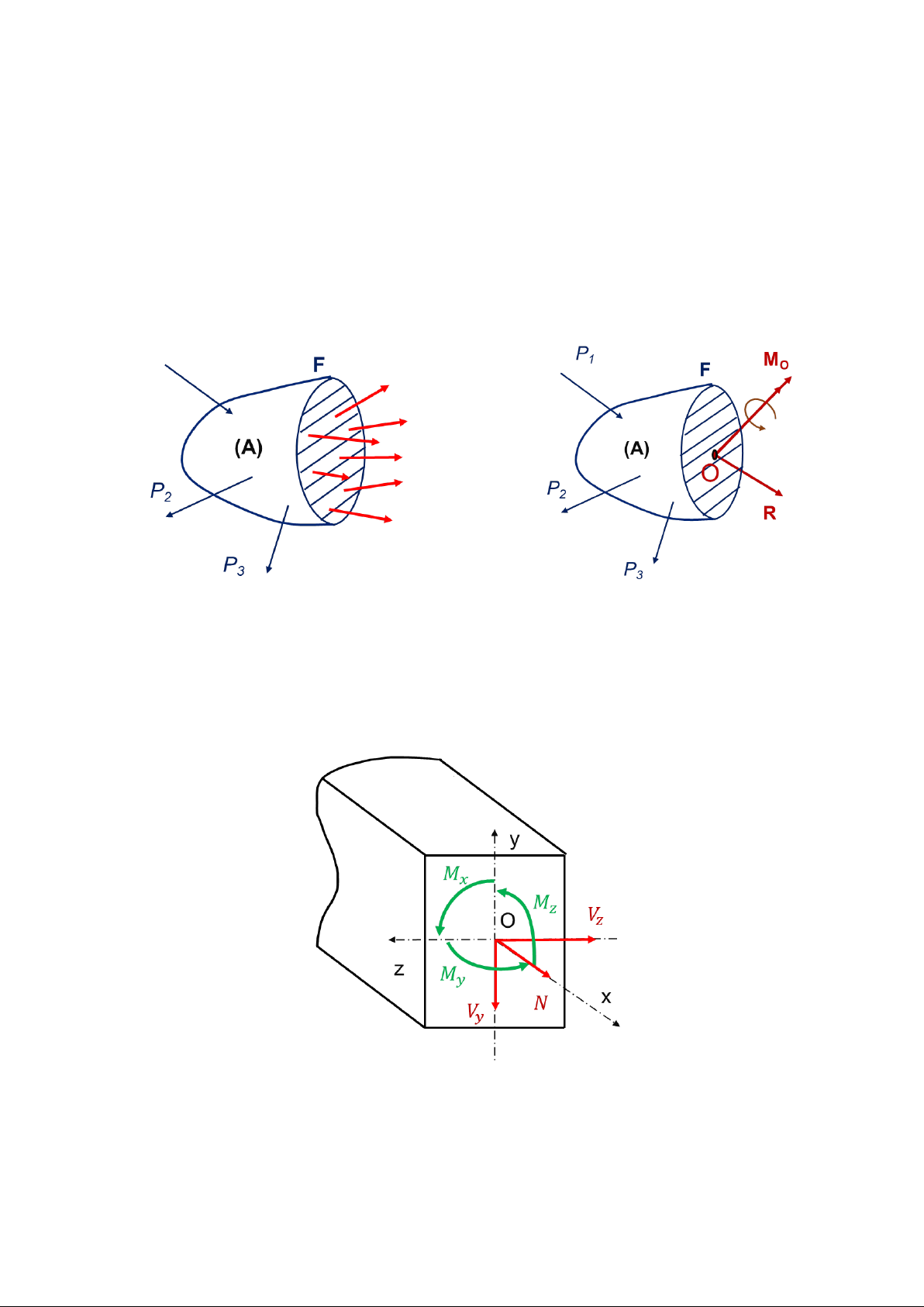
Hình 1.3 Phương pháp mặt cắt
Xét một vật rắn cân bằng dưới tác dụng của ngoại lực P1, P2, ... Pn như hình 1.3. Để
xác định giá trị nội lực tại mặt cắt K nào đó trong vật thể, ta sử dụng mặt phẳng (π)
đi qua K chia vật thể thành 2 phần (A) và (B). Ta xét cân bằng của phần (A), ta thấy
lực tương tác của phần (B) tác dụng lên phần (A) chính là hệ nội lực tại mặt cắt
đang xét (hình 1.4 a). Dời hệ lực này về tâm O của mặt cắt ngang, hệ lực này sẽ
tương đương với một vector lực chính R và một vector moment chính M0 (hình 1.4
b). Để phần (A) cân bằng thì hệ nội lực này phải cân bằng với các ngoại lực tác
dụng vào phần (A) và được xác định nhờ giải các phương trình cân bằng. a) b)
Hình 1.4. Nội lực tại mặt cắt
1.4.2 Các thành phần nội lực
Hình 1.5. Các thành phần nội lực trên mặt cắt ngang trong bài toán không gian a)
Bài toán không gian
Xét một đoạn thanh có mặt cắt ngang hình chữ nhật như hình 1.5. Trên mặt cắt
ngang này ta đặt vào một hệ trục tọa độ Oxyz, với trục x trùng với trục của thanh,
trục y và z nằm trên mặt phẳng của mặt cắt ngang, chiều trục theo quy tắc bàn tay
phải. Khi chiếu vector lực chính R và vector moment chính MO lên các trục tọa độ
ta sẽ được 6 thành phần tương ứng như sau:
- Hình chiếu của vector R lên trục x ta gọi là lực dọc, ký hiệu là N. Đơn vị [N], [kN]
- Hình chiếu của vector R lên trục y ta gọi là lực cắt, ký hiệu là Vy. Đơn vị [N], [kN]
- Hình chiếu của vector R lên trục z ta gọi là lực cắt, ký hiệu là Vz. Đơn vị [N], [kN]
Lực dọc có phương dọc theo trục của thanh và vuông góc với mặt cắt ngang. Lực
cắt nằm trên mặt cắt ngang và vuông góc với trục của thanh.
- Thành phần moment quay quanh trục x, gây xoắn trục của thanh ta gọi là
moment xoắn, ký hiệu là Mx. Đơn vị [Nm], [kNm], [Ncm], [kNcm],…
- Thành phần moment quay quanh trục y, gây uốn trục của thanh ta gọi là
moment uốn, ký hiệu là My. Đơn vị [Nm], [kNm], [Ncm], [kNcm],… - Thành phần
moment quay quanh trục z, gây uốn trục của thanh ta gọi là moment uốn, ký hiệu
là Mz. Đơn vị [Nm], [kNm], [Ncm], [kNcm],…
Như vậy trong trường hợp tổng quát trên mặt cắt ngang sẽ có 6 thành phần nội lực,
bao gồm 3 lực và 3 moment. b) Bài toán phẳng
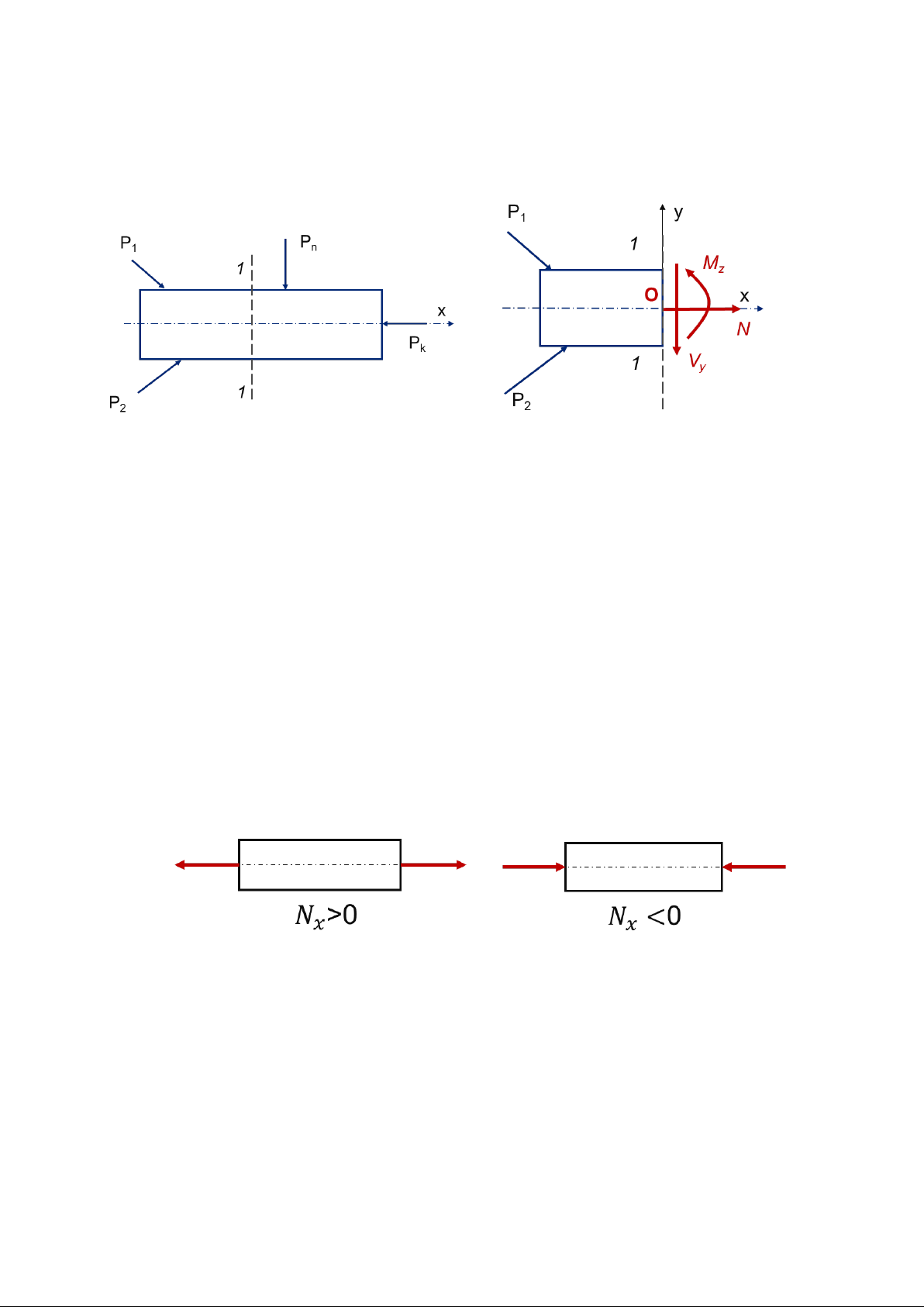
Xét một thanh cân bằng dưới tác dụng của các ngoại lực cùng nằm trên một mặt
phẳng chứa trục x của thanh như hình 1.6. Để xác định nội lực tại mặt cắt 1-1, ta
chia thanh thành 2 phần và xét cân bằng của phần bên trái. Các thành phần nội lực
tại mặt cắt 1-1 cũng nằm trên mặt phẳng nói trên, bao gồm: -
Lực dọc N - dọc theo trục của thanh -
Lực cắt Vy – theo phương y, vuông góc với trục của thanh -
Moment uốn Mz – quay quanh trục z và gây uốn trục thanh.
Để xác định được các thành phần nộ lực tại mặt cắt 1-1 ta cũng sử dụng các phương trình cân bằng.
Hình 1.6. Các thành phần nội lực trên mặt cắt ngang trong bài toán phẳng
1.5 Phân loại biến dạng cơ bản của thanh
Như đã xét ở trên, trong trường hợp tổng quát trên mặt cắt ngang của thanh có 6
thành phần nội lực, trong bài toán phẳng trên mặt cắt ngang có 3 thành phần nội
lực, ở đây ta chỉ xét các trường hợp biến dạng cơ bản của thanh. Đối với một thanh
chịu lực sẽ có các dạng biến dạng cơ bản sau:
1. Biến dạng kéo nén
Biến dạng kéo nén xảy ra khi trên mặt cắt ngang của thanh chỉ có duy nhất một
thành phần nội lực là lực dọc Nx.
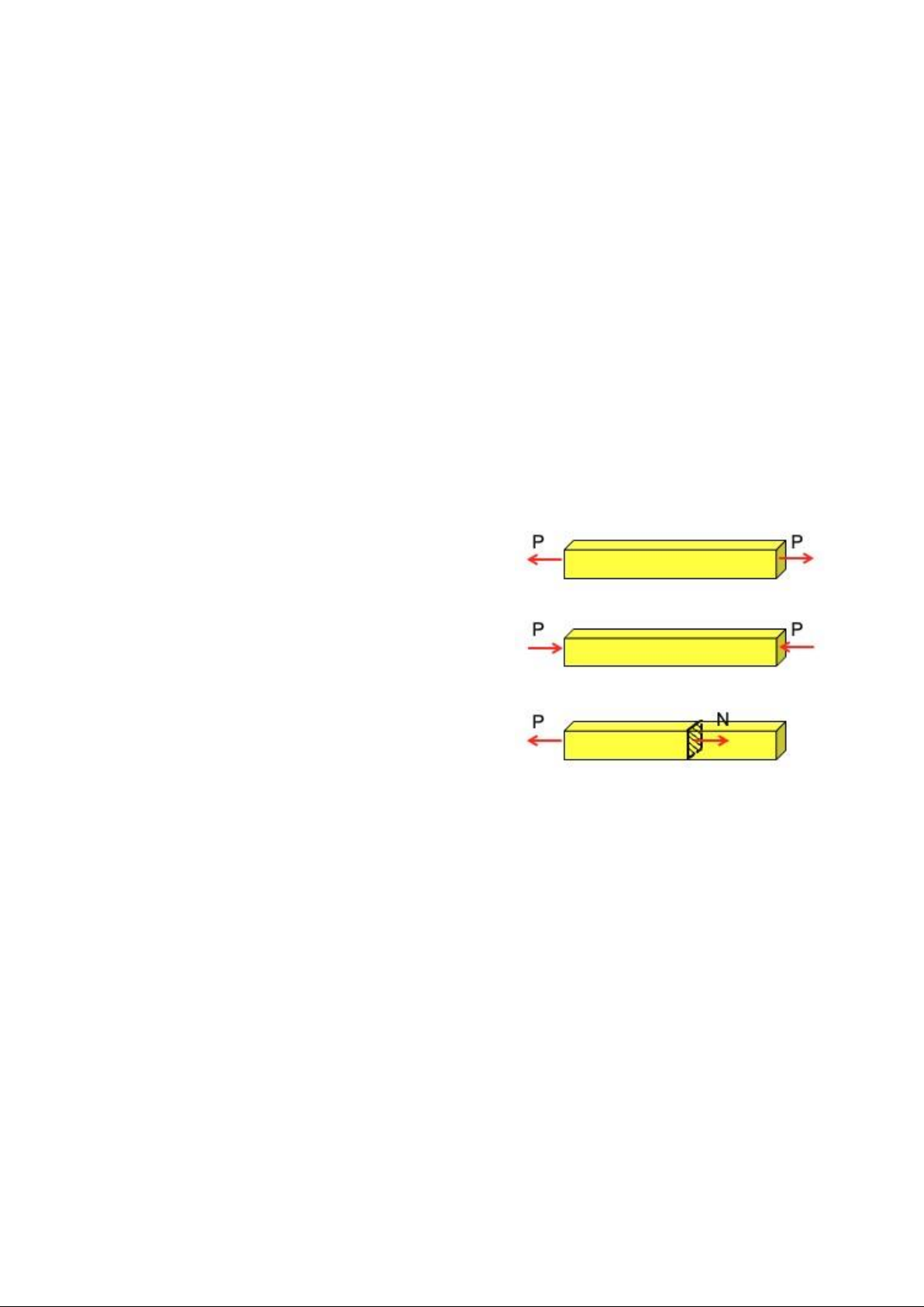
Hình 1.7. Quy ước dấu của lực dọc
Quy ước dấu của lực dọc như hình 1.7:
- Lực dọc Nx được coi là dương nếu như có chiều hướng ra ngoài mặt cắt, gây kéo thanh.
- Lực dọc Nx được coi là âm nếu như có chiều hướng vào trong mặt cắt, gây nén thanh.
2. Biến dạng uốn thuần túy
Biến dạng uốn thuần túy xảy ra khi trên mặt cắt ngang của thanh chỉ có duy nhất
một thành phần nội lực là moment uốn Mz (hoặc My)
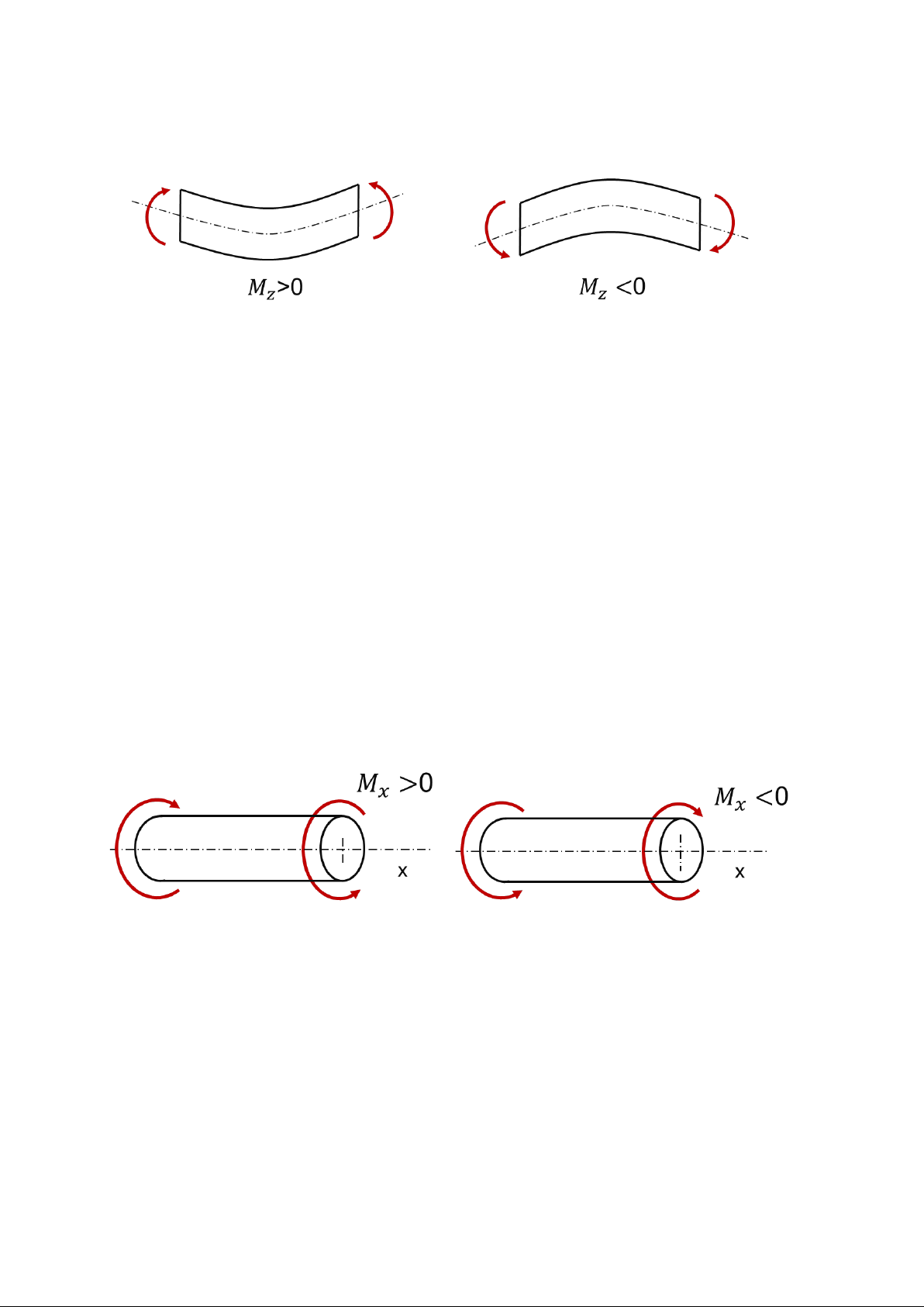
Hình 1.8. Quy ước dấu của moment uốn
Quy ước dấu của moment uốn như hình 1.8:
- Moment uốn được coi là dương nếu như chiều moment làm căng thớ dưới của thanh.
- Moment uốn được coi là âm nếu như chiều moment làm căng thớ trên của thanh.
3. Biến dạng xoắn
Biến dạng xoắn xảy ra khi trên mặt cắt ngang của thanh chỉ có duy nhất một thành
phần nội lực là moment xoắn Mx.
Hình 1.9. Quy ước dấu của moment xoắn
Quy ước dấu của moment xoắn như hình 1.9:
- Moment xoắn được coi là dương nếu như nhìn vào mặt cắt moment có chiều
quay ngược chiều kim đồng hồ.
- Moment xoắn được coi là âm nếu như nhìn vào mặt cắt moment có chiều
quay cùng chiều kim đồng hồ.
4. Biến dạng cắt hoặc biến dạng trượt
Biến dạng cắt hay còn gọi là biến dạng trượt xảy ra khi trên mặt cắt ngang của thanh
có thành phần nội lực là lực cắt Vy (hoặc Vz)
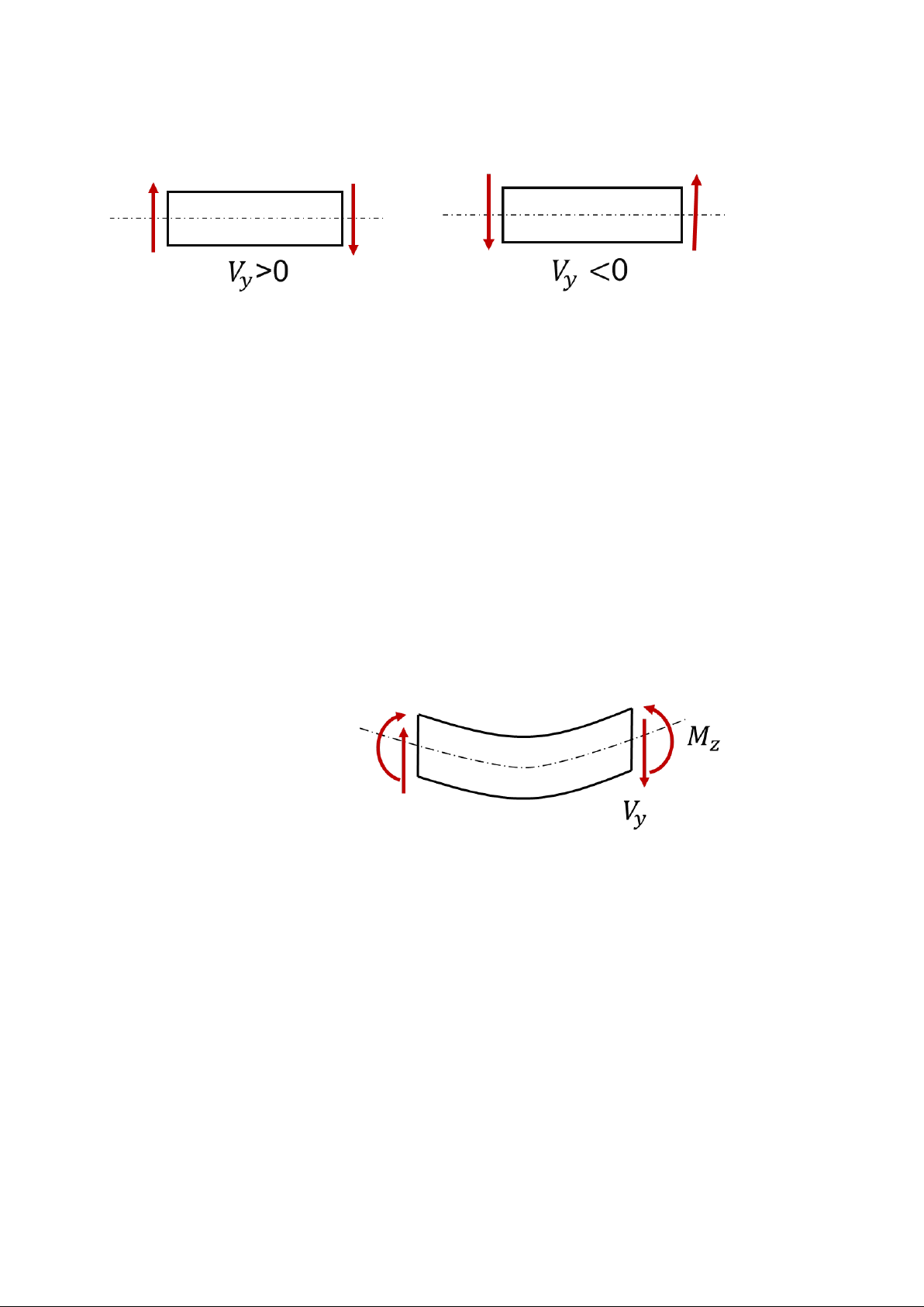
Hình 1.10. Quy ước dấu của lực cắt
Quy ước dấu của lực cắt như hình 1.10:
- Lực cắt được coi là dương nếu như quay pháp tuyến của mặt cắt ngang một
góc 900 theo chiều kim đồng hồ chiều trùng với chiều lực cắt.
- Lực cắt được coi là âm nếu như quay pháp tuyến của mặt cắt ngang một góc
900 ngược chiều kim đồng hồ trùng với chiều lực cắt.
5. Biến dạng uốn ngang phẳng
Trong trường hợp trên mặt cắt ngang của thanh có cả moment uốn và lực cắt cùng
nằm trên mặt phẳng ta gọi là thanh chịu uốn ngang phẳng (Hình 1.11)
Hình 1.11. Thanh chịu uốn ngang phẳng
1.6 Biểu đồ nội lực
Định nghĩa: Biểu đồ nội lực là đường biểu diễn sự biến thiên của nội lực theo vị trí
mặt cắt ngang trên thanh.
Biểu đồ nội lực được biểu diễn như sau: -
Trục hoành là trục song song với trục của thanh (trục x) -
Tung độ là độ lớn của nội lực tại mặt cắt tương ứng -
Như vậy tương ứng với các thành phần nội lực trên mặt cắt ngang thì ta cũng
có các biểu đồ nội lực tương ứng: biểu đồ lực dọc N, biểu đồ lực cắt V, biểu
đồ moment uốn Mz hoặc My, biểu đồ moment xoắn Mz. -
Theo quy ước: lực dọc, biểu đồ lực cắt và biểu đồ moment xoắn nếu có giá
trị dương sẽ vẽ phía bên trên trục hoành. Ngược lại, giá trị âm sẽ vẽ phía dưới trục hoành. -
Biểu đồ moment uốn được quy ước: moment căng thớ nào thì sẽ vẽ về phía
thớ đó, do vậy moment uốn có giá trị dương sẽ vẽ phía dưới trục hoành và
ngược lại moment uốn âm sẽ vẽ phía trên trục hoành.
Hình 1.12. Cách biểu diễn biểu đồ nội lực
Trình tự các bước vẽ biểu đồ nội lực như sau:
Bước 1: Mô hình hóa kết cấu
Trong bước này cần xác định loại kết cấu, dạng liên kết và các dạng tải trọng của
kết cấu thực để mô hình hóa kết cấu một cách chính xác. Việc mô hình hóa chính
xác sẽ cho kết quả khảo sát gần với thực tế chịu lực của kết cấu.
Bước 2: Xác định giá trị của các phản lực liên kết
Sau khi mô hình hóa kết cấu, ta tách các liên kết và thay vào các phản lực liên kết
tương ứng. Sử dụng các phương trình cân bằng để xác định giá trị của các phản lực liên kết nói trên.
Bước 3: Chia đoạn và xác định nội lực trên từng đoạn thanh
Dựa trên tải trọng tác dụng vào thanh ta sẽ chia thanh thành các đoạn tương ứng.
Trên mỗi đoạn thanh ta sẽ sử dụng phương pháp mặt cắt để xác định được các thành
phần nội lực và giá trị của nội lực trên từng đoạn. Việc xác định giá trị nội lực cũng
dựa vào phương trình cân bằng
Bước 4: Vẽ biểu đồ nội lực
Sau khi xác định được nội lực trên từng đoạn thanh, ta sẽ đi vẽ các biểu đồ nội lực cho thanh.
Quan sát biểu đồ nội lực giúp ta biết được sự phân bố nội lực trên từng vị trí của
thanh và những vị trí có giá trị nội lực lớn là những vị trí nguy hiểm khi khảo sát độ bền của kết cấu.
CHƯƠNG 2 KÉO NÉN ĐÚNG TÂM, CẮT HAY TRƯỢT Nội dung: • Kéo nén đúng tâm • Cắt hay trượt • Định luật Hooke
• Tính chất cơ học của vật liệu
• Ứng suất cho phép và hệ số an toàn
• Thanh siêu tĩnh chịu kéo nén đúng tâm
2.1 Kéo, nén đúng tâm
2.1.1 Vẽ biểu đồ lực dọc
a) Nhắc lại khái niệm bài toán kéo nén đúng tâm (KNĐT)
Định nghĩa: Một thanh được gọi là chịu kéo
(nén) đúng tâm (dọc trục) là thanh chịu lực
sao cho mọi mặt cắt ngang của nó chỉ có một
thành phần nội lực là N. Hình 2.1
b) Vẽ biểu đồ lực dọc bằng phương pháp mặt cắt
Các bước vẽ biểu đồ lực dọc bằng phương pháp mặt cắt như sau:
Bước 1: Tính phản lực liên kết. Từ phương trình cân bằng trên cảc thanh bao gồm
tổng các tải trọng và các phản lực liên kết bằng 0, từ đó chiếu xuống trục dọc của
thanh ta tìm được các phản lực liên kết.
Bước 2: Sử dụng phương pháp mặt cắt để tính thành phần lực dọc trên từng đoạn
thanh. Từ phương trình cân bằng trên từng đoạn thanh bao gồm tổng các ngoại lực
và nội lực bằng 0, từ đó ta tính được thành phần nội lực dọc.
Bước 3: Trên cơ sở kết quả tại Bước 2, ta vẽ biểu đồ lực dọc.
c) Vẽ biểu đồ lực dọc bằng quy tắc vẽ nhanh
Các bước vẽ biểu đồ lực dọc bằng phương pháp vẽ nhanh như sau:
Bước 1: Tính phản lực liên kết. Từ phương trình cân bằng trên cảc thanh bao gồm
tổng các tải trọng và các phản lực liên kết bằng 0, từ đó chiếu xuống trục dọc của
thanh ta tìm được các phản lực liên kết.
Bước 2: Vẽ biểu đồ lực dọc đi từ trái sang phải như sau:
- Nơi nào có lực tập trung thì biểu đồ lực dọc có bước nhảy, chiều nhảy ngược
với chiều của lực tập trung, trị số bước nhảy bằng trị số lực tập trung.
- Nơi nào có lực phân bố có cường độ cố định thì biểu đồ lực dọc ở đó là đường thẳng.
2.1.2 Ứng suất pháp
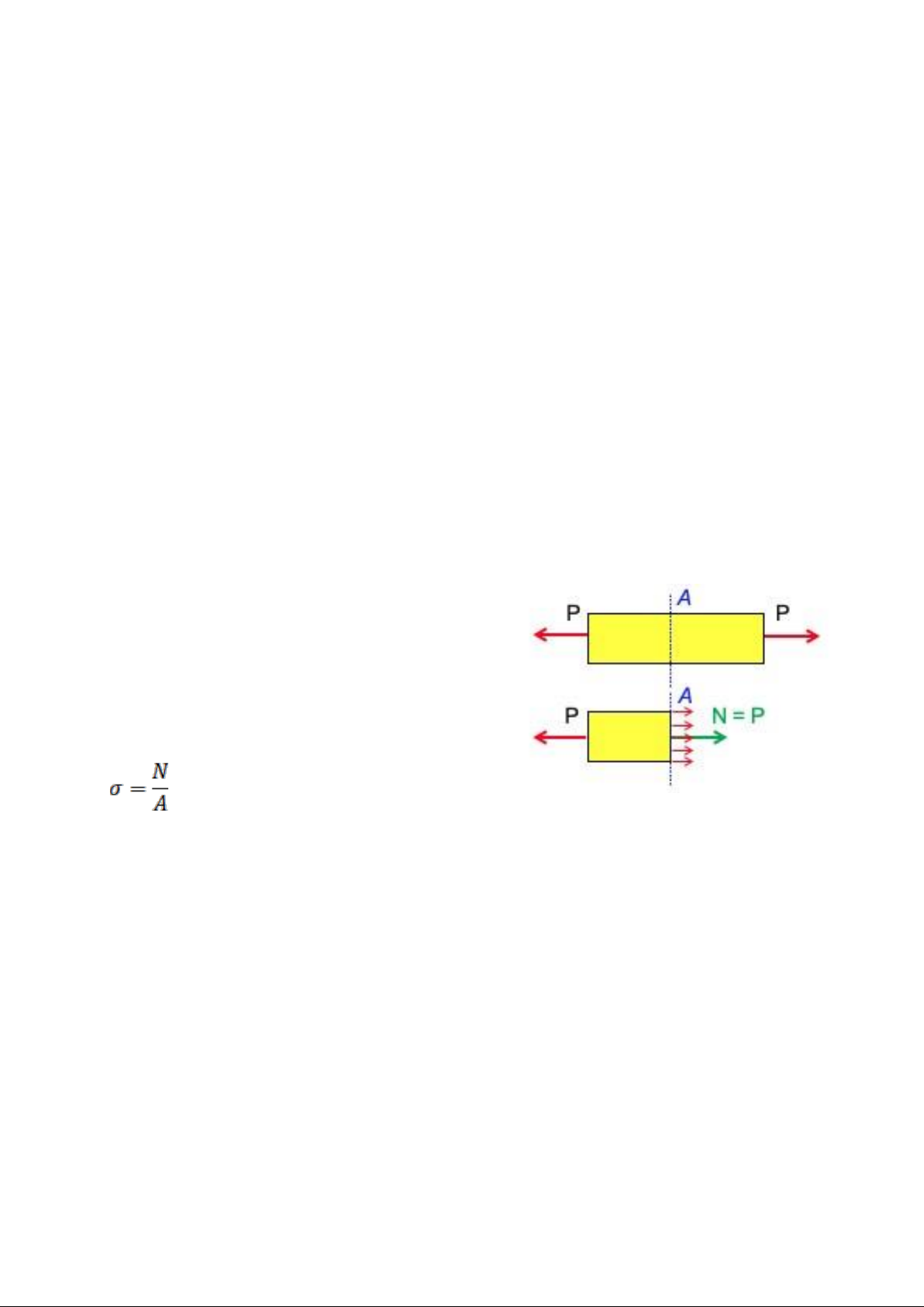
Định nghĩa: Khi thanh chịu kéo đúng
tâm, trên mỗi mặt cắt ngang A vuông góc
với trục thanh, thì thành phần nội lực là
lực dọc N. Ta gọi ứng suất pháp tại các
điểm trên mặt cắt A là tỉ số Hình 2.2
Ứng suất pháp nằm vuông góc với mặt cắt, vì thế còn được gọi là ứng suất pháp
tuyến. Đơn vị của ứng suất pháp là N/m2, Pascal. Dấu của ứng suất pháp được quy
định như sau: chiều dương hướng từ mặt cắt ra ngoài vật thể, làm cho vật thể bị kéo;
ngược lại chiều âm hướng từ mặt cắt vào bên trong vật thể, làm cho vật thể bị nén.