


































































































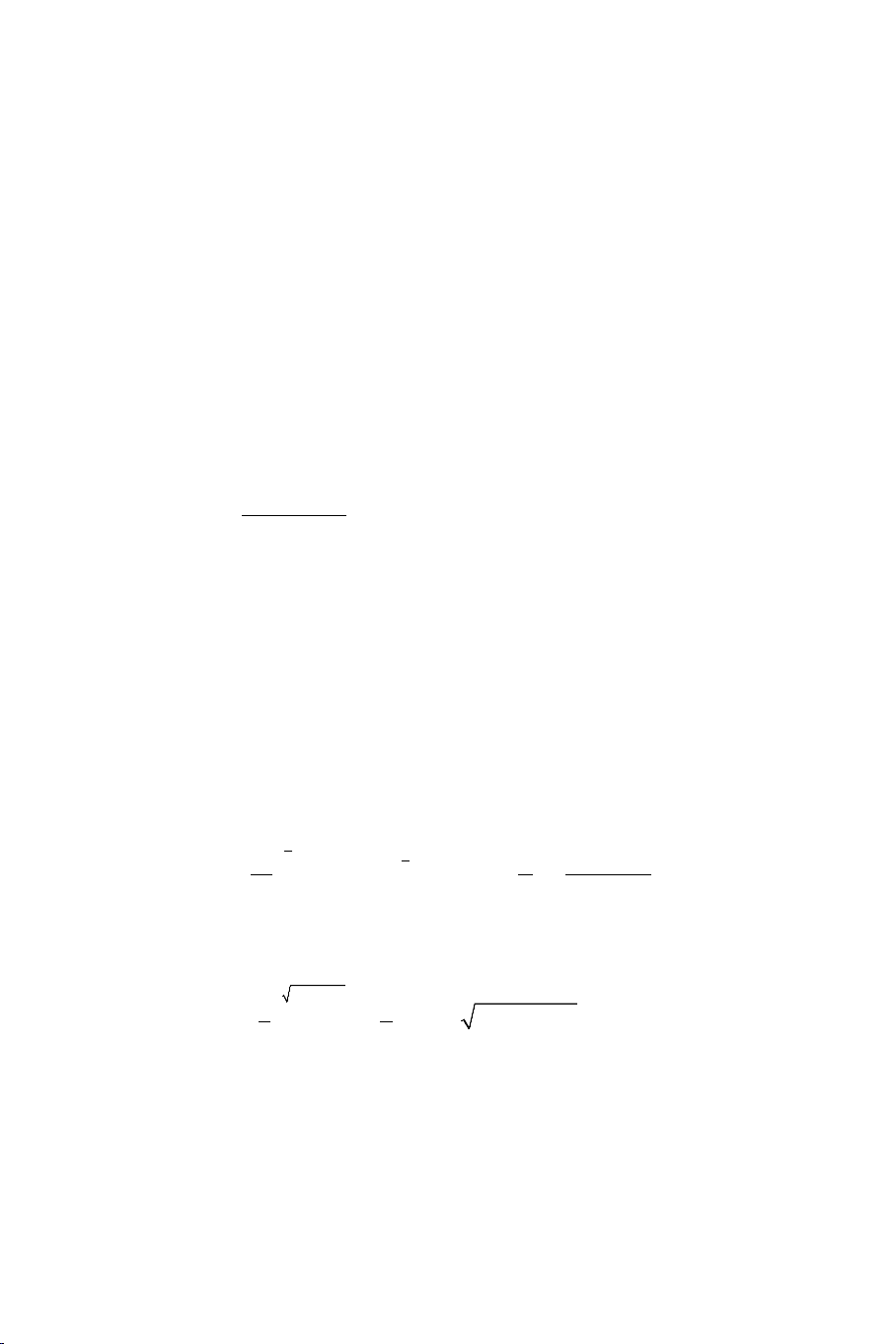



Preview text:
Chương VI
HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT Bài 1
PHÉP TÍNH LŨY THỪA
A. TÓM TẮT LÝ THUYẾT
I. KHÁI NIỆM LŨY THỪA
1. Lũy thừa với số mũ nguyên
Lũy thừa với số mũ nguyên dương. Cho a ∈ và *
n ∈ . Khi đó n a = . a . a ....
a a (n thừa số a).
Lũy thừa với số mũ nguyên âm, lũy thừa với số mũ 0 −n 1 Cho a ∈ \{ } 0 và * n∈ . Ta có: 0 1 a =
;a =1;a = a . n a
Lũy thừa với số mũ nguyên có các tính chất tương tự tính chất của lũy thừa
với số mũ nguyên dương. Chú ý: 0 0 và − ( *
0 n n∈ ) không có nghĩa. 2. Căn bậc n
Cho số thực b và số nguyên dương n ≥ 2 .
Số a được gọi là căn bậc n của số b nếu n a = b .
Khi n lẻ, b∈ : Tồn tại duy nhất một căn bậc n của số b là n b .
Khi n chẵn và b < 0 thì không tồn tại căn bậc n của số b.
Khi n chẵn và b = 0 thì có duy nhất một căn bậc n của số b là n 0 = 0.
Khi n chẵn và b > 0 có 2 căn bậc n của số thực b là n b và n − b .
3. Lũy thừa với số mũ hữu tỷ m
Cho số thực a > 0 và số hữu tỷ r = , trong đó m∈ ; n∈ , 2 n ≥ . Khi n m đó r n n m
a = a = a . 5
4. Lũy thừa với số mũ vô tỷ
Giả sử a là một số dương và α là một số vô tỷ và (rn ) là một dãy số hữu tỷ
sao cho lim r = α . Khi đó = . n lim nr a aα n→+∞ n→+∞
II. TÍNH CHẤT CỦA LŨY THỪA VỚI SỐ MŨ THỰC
Cho hai số dương a; b và ;
m n∈ . Khi đó ta có các công thức sau. Nhóm công thức 1 Nhóm công thức 2 1. m. n m n a a a + = m m 1. n n m
a = a = ( n a ) m a m−n 1 2. a m 0 −n a = = ⇔ = n n a a n n n
2. . = ( ) , n .n n a b ab
a b = ab 3. ( )n m m.n a = a n n n 3. a a = , a a = n n n b b b b B. CÁC DẠNG TOÁN. DẠNG 1:
RÚT GỌN VÀ TÍNH GIÁ TRỊ BIỂU THỨC CHỨA LŨY THỪA Phương pháp:
Sử dụng phối hợp linh hoạt các tính chất của lũy thừa.
Chọn a,b là các số thực dương, x, y là các số thực tùy ý, ta có: x − a x+y x = . y a a a và x y a = . y a x x
x . x ( )x ; a a a b ab = = ;( x a )y xy = a x b b . Ví dụ 1. Tính 1 ( )0 ( )2 4 2 ; 4,72 ; 3 ; 2 ( ; 4) 3− − − . Lời giải Ta có: 6 = ( )0 = (− )2 1 2 2; 4,72 1; 3 = ( 3 − )( 3 − ) = 9; 4 = = (− ) 3− 1 1 2 2.2.2.2 16; 4 = = − . ( 4 − )3 64
Ví dụ 2. Đưa các biểu thức sau về dạng lũy thừa 3 2 4 b a
1) a a (a > 0) . 2) . 3) 5 3 (a,b > 0). 0,75 16 a b .Lời giải 1 1 1 3 3 2 2 1) 2 2 4 a a = .
a a = a = a . 1 2.(2 )1 2 2 3 5 3 13 6 2 4 2 − 2) 6 = = = 2 . 0,75 16 (2 )3 3 4 2 4 1 1 2 2 − 2 5 15 15 b a b a b 3) 5 3 15 15 = . = a .b = . 1 1 a b a 5 15 a b
Ví dụ 3. Rút gọn các biểu thức sau đây: 1) (a − )4 5 . 2) 4 2
81a b (b ≤ 0). 3) 4 8 x (x + )4 1 (x ≤ − ) 1 . Lời giải
1) (a − )4 = (a − )2 5 5 . 2) 4 2 2 2 81a b = 9a b = 9
− a b (do b ≤ 0 ) 3) 4 8 x (x + )4 2 2
1 = x . x +1 = −x (x + ) 1 (do x ≤ 1 − ⇔ x +1≤ 0 ). 2024 2025
Ví dụ 4. Tính giá trị của biểu thức P = (5+ 2 6) .(5− 2 6) Lời giải
Ta có: (5+ 2 6)(5− 2 6) = 25− 24 =1. 7 Do đó P = ( + )2024 ( − )2025 5 2 6 . 5 2 6 = (5+ 2 6)(5−2 6) 2024 . (5−2 6)=5−2 6.
Ví dụ 5. Không dùng máy tính, hãy tính giá trị các biểu thức sau 1 3 5 7 − 1 1 1 2 1) 2 3 4 3 2 4
A = 3 .5 : 2 : 16 : 5 .3 .2 6 2) 3 3 5 3 B 4. 2. 8 3. 3. 3 = + . 3) C = ( 1+ 2 2 2 −
) 1−−2 2 +( 1+ 2 1− 2) 4+ 2 25 5 .5 8 .4 : 2 . Lời giải 1 1 3 5 7 − 1 1 1 2 3 1 5 1 7 1 + + 2 + 1) 2 3 4 3 2 4 2 2 3 3 4 4 4
A = 3 .5 : 2 : 16
: 5 .3 .2 = 3 .5 .2 : 2 = (3 .5 .2 .2− )1 2 2 2 4 1 − 15 2 = 3.5.2 = 2 2) 1 6 1 6 6 5 1 17 3 17 18 3 5 3 5 3 3 5 3 2 6 2 6 2 18 10
B = 4. 2. 8 + 3. 3. 3 =
2 .2 + 3.3 = 2 + 3 = 2 + 3 . 3) + + − −
C = (25 + −5 ).5− − +(8 + .4 − ) + ( 2 2 2 2 2 5 5 ) ( 3 3 2 2 2 2 2 .2 1 2 2 2 1 2 2 1 2 1 2 4 2 ) : 2 = + 1+2 2 4+ 2 5 2 5+ 2 1 − 2 1 36 = 5 − 5 + = 5 − + 2 = . 4+ 2 2 5 5 1 − 1 −
Ví dụ 6. Cho a = (2 + 3) ,b = (2 − 3) . Tính A (a ) 1− (b ) 1 1 1 − = + + + . Lời giải − Ta có: a = ( + ) 1 1 2 3 = = 2 − 3 . 2 + 3 8 − b = ( − ) 1 1 2 3 = = 2 + 3 . 2 − 3 Suy ra − − − −
A (a )− (b )− = + + +
= ( − + ) 1 +( + + ) 1 = ( − ) 1 +( + ) 1 1 1 1 1 2 3 1 2 3 1 3 3 3 3 1 1 6 = + = = 1. 3− 3 3+ 3 9 − 3
Ví dụ 7. Rút gọn các biểu thức sau: 4 a + ab a − b 1) P = −
(a > 0,b > 0). 4 4 4 4 a + b a − b 3 1 + 2− 3 2) a .a Q = (a > 0). ( + a − ) 2 2 2 2 2 1 1 1 − y y 3) 2 2
K = x − y 1− 2
+ (x > 0, y > 0) . x x Lời giải 1)Ta có
( a)2 + ab ( a)2 − + − ( b a ab a b )2 4 4 4 4 4 P = − = − 4 4 4 4 4 4 4 4 a + b a − b a + b a − b 4 a ( 4 4 a + b ) ( 4 4 a − b )( 4 4 a + b ) = − 4 4 4 4 a + b a − b 4 = − ( 4 4 + ) 4 a a b = − b 3 1 3 1 2 3 + + − 2 + − 3 3 a .a = a = a 3 a 2) Ta có: 5 ( . ) ⇒ = = 2+2 ( Q a 2+2)( 2− − 2 2 2 ) 2 2 − = = a a a a − 2 1 1 2 3) Rút gọn 2 2
x − y = ( x − y ) 1 − 2 1 − 2 2 − − 1− 2 y y y + = −1 y x x = = x x x x y x − 9 2 x
Vậy K = ( x − y )2 = x . y − x
Ví dụ 8. Biết 9x + 9−x = 23. Tính 3x + 3−x . Lời giải Ta có: x − x x x −x − x + = ⇔ + + = ⇔ ( x −x + )2 2 2 9 9 23 3 2.3 .3 3 25 3 3
= 25 ⇒ 3x + 3−x = 5. DẠNG 2:
CHỨNG MINH ĐẲNG THỨC LŨY THỪA Phương pháp:
Để chứng minh đẳng thức ta thường sử dụng các phương pháp sau :
1.Biến đổi tương đương.
2.Biến đổi vế trái thành vé phải hoặc vế phải thành vế trái.
3.Biến đổi hai vế về đại lượng thứ 3.
Ví dụ 1. Chứng minh đẳng thức 4 2 3 42 3 2 . Lời giải
Biến đổi vế trái ta có: VT
2 2 3 2 3 1 3 2 3 1 3 1 3 1 3 1 3 1 2 VP(dpcm)
Ví dụ 2. Chứng minh đẳng thức 3 3 7 5 2 75 2 2 . Lời giải 3 3
VT 2 2 63 2 1 2 2 63 2 1 . 3 2 3 2 3 3 2 3 2 3 2 1 2 3 2 3 2 1
3 3 3 3 2 1 2 1 2 1 2 1 2 VP(dpcm). 10
Ví dụ 3. Chứng minh rằng nếu 1 x 2 thì
x 2 x1 x2 x1 2 . Lời giải
VT x
1 2 x11 x 1 2 x11 .
x 2 x 2 1 1
1 1 x11 x11 . x1 1 1 x 1 . Do 1 x 2 4 1 1 2 3 3 a 8a b b
Ví dụ 4. Chứng mnh rằng 3 3 1 2 a . 2 2 a 3 3 3 a 2 ab 4b Lời giải
a a8b 1 3 3 3 a 2 b VT . 2 2 2 2 3 3 3 3 a a ab b
3 a a8b 3 a 2 2 3 3 3 3 3 3 a 2 2 2 b a a b b 3 2
a a8b 2 3 2 3
a a VP . a8b
Ví dụ 5. Chứng minh đẳng thức 1 1 1 1 3 3 3 3
8ba a b a 2b ab . 1 1 2 1 1 2 6 3 3 3 3 3 3 2a b
4a 2a b b Lời giải 1 1 2 1 1 2 1 1 1 1 3 3 3 3 3 3 3 3 3 3
a b 4a 2a b b
2a b
a 2b 8b a VT . 1 1 2 1 1 2 6 3 3 3 3 3 3 2a b
4a 2a b b 1 1 1 1 1 1 1 1 3 3 3 3 3 3 3 3
8ba 4a b 2 a b 24a b a b 2 . 1 1 6 8a b 11 8ba 6
8ba 6ab ab VP . 6 8 1 6 8ba a b
Ví dụ 6. Chứng minh đẳng thức sau: 1
1 1 2a 2a2 4 12a , a 0. 1 a
1 1 2a 2a2 1 2 4 Lời giải Biến đổi vế trái 1 2a 2a 1 1 1 2 2 2 1 2a 2 2 2 2 a 4 4 VT . 1 2a 2a 1 1 1 2 2 2 1 2a 2 2 2 2 a 4 4 1 a a 2 1 1 2 2
1 2a 2a 4 2 . 1 1 2 2 2 1
1 2a 2a a a 4 2
1 22a 22a 1 2a a 2 1 22 2a 1 12a 1 VP . a a 2 1 1 2 a 2 2 2 1 2a a a 2 2 1 22 ( 2 3 a − )1( 2 3 3 3 3 a + a + a )
Ví dụ 7. Chứng minh rằng 3 = a +1. 4 3 3 a − a Lời giải ( 3 a − ) 1 ( 3 a + ) 3 1 a ( 2 3 3 a + a + ) 1 VT = 3
= a +1 = VP (đpcm). 3 a ( 3 3 a − ) 1 DẠNG 3: BÀI TOÁN THỰC TẾ Phương pháp:
Giả sử số tiền gốc là A ; lãi suất là r% / kì hạn gửi ( có thể là tháng, quý hay năm ). 12
+ Số tiền nhận được cả gốc và lãi sau n kì hạn gửi là 1 n A r .
+ Số tiền lãi nhận được sau n kì hạn gửi là
1 n A A 1 n A r r 1 .
Ví dụ 1. Bà Hạnh gửi 100 triệu vào tài khoản định kỳ tính lãi kép với lãi
suất là 8% / năm. Tính số tiền lãi thu được sau 10 năm. Lời giải
Áp dụng công thức tính lãi kép, sau 10 năm số tiền cả gốc và lãi bà Hạnh
thu về là n A r 10 1
100 1 0,08 215,892 triệu đồng.
Suy ra số tiền lãi bà Hạnh thu về sau 10năm là 215,892100 115,892 triệu đồng.
Ví dụ 2. Tỉ lệ tăng dân số hàng năm ở Việt Nam được duy trì ở mức 1,05%
. Biết rằng, dân số của Việt Nam ngày 1 tháng 4 năm 2014 là 90.728.900
người. Với tốc độ tăng dân số như thế thì vào ngày 1 tháng 4 năm 2030
thì dân số của Việt Nam là Lời giải
Dân số vào ngày 1 tháng 4 năm 2030 là: ×( + )16 90.728.900 1 1,05% =107.232.574 người.
Ví dụ 3. Một người muốn gửi tiết kiệm ở ngân hàng và hi vọng sau 4 năm
có được 850 triệu đồng để mua nhà. Biết lãi suất ngân hàng mỗi tháng
trong thời điểm hiện tại là 0,45% . Hỏi người đó mỗi tháng phải gửi vào
ngân hàng tối thiểu bao nhiêu tiền để đủ số tiền mua nhà ? ( giả sử số tiền
mỗi tháng là như nhau và lãi suất trong 4 năm là không thay đổi). Lời giải
Giả sử người này gửi tiền ở thời điểm t nào đó , kể từ thời điểm này sau 4
năm (48 tháng) ông muốn có số tiền 850 triệu. Như vậy rõ ràng ta có thể coi
đây là bài toán gửi tiền định kì đầu tháng. Áp dụng bài toán 5 ta có số tiền Ar
phải gửi mỗi tháng là : m .
1 r 1 rn 1 13
Theo bài ra n 48,r 0,45%,A 850 thay vào ta được 850.0,45% m 15,833 triệu đồng.
1 0,45% 1 0,45%48 1
Ví dụ 4. Một bà mẹ Việt Nam anh hùng được hưởng số tiền là 4 triệu đồng
trên một tháng (chuyển vào tài khoản của mẹ ở ngân hàng vào đầu tháng).
Từ tháng 1 năm 2016 mẹ không đi rút tiền mà để lại ngân hàng và được
tính lãi suất 1% trên một tháng. Đến tháng 12 năm 2016 mẹ rút toàn bộ số
tiền (gồm số tiền của 12 tháng và số tiền đã gửi tháng 1). Hỏi khi đó mẹ
lĩnh về bao nhiêu tiền ? (kết quả làm tròn theo đơn vị nghìn đồng). Lời giải
Nếu ban đầu gửi vào a đồng, từ đầu tháng sau gửi thêm a đồng (không
đổi) vào đầu mỗi tháng với lãi suất r% trong n tháng thì tổng số tiền thu được là : a A a
r rn 4 1 1 1 4
1 1% 1 1%11 1 4 50,73 r 1% triệu đồng.
Ví dụ 5. [Đề thử nghiệm Bộ GD&ĐT 2017] Số lượng của loại vi khuẩn A
trong một phòng thí nghiệm được tính theo công thức ( ) = (0).2t s t s , trong
đó s(0) là số lượng vi khuẩn A lúc ban đầu, s(t) là số lượng vi khuẩn A
có sau t phút. Biết sau 3 phút thì số lượng vi khuẩn A là 625 con. Hỏi sau
bao lâu, kể từ lúc ban đầu, số lượng vi khuẩn A là 10 triệu con? Lời giải s 3
Ta có: s(3) = s(0) 3 .2 ⇒ s(0) ( ) = = 78,125 nghìn con 8
Do đó s(t) =10 triệu con =10000 nghìn con khi = s( ) t t 10000 10000 0 .2 ⇒ 2 = = 128 78,125
Ví dụ 6. Cường độ của ánh sáng I khi đi qua môi trường khác với không
khí, chẳng hạn như sương mù hay nước,...sẽ giảm dần tùy theo độ dày
của môi trường và một hằng số µ gọi là khả năng hấp thu ánh sáng tùy
theo bản chất môi trường mà ánh sáng truyền đi và được tính theo công thức = . −µx
I I e với x là độ dày của môi trường đó và tính bằng mét, I 0 0 14
là cường độ ánh sáng tại thời điểm trên mặt nước. Biết rằng nước hồ
trong suốt có µ =1,4 . Cường độ ánh sáng giảm đi bao nhiêu lần khi
truyền trong hồ đó từ độ sâu 3m xuống đến độ sâu. 1 x Số e : lim 1 + =
e , e = 2,718281828.... x→+∞ x Lời giải
Cường độ ánh sáng ở độ sâu 3m là 1 − ,4.3 4 − ,2 I = I .e = I .e 1 0 0
Cường độ ánh sáng ở độ sâu 30m là 1 − ,4.30 42 I I .e I . − = = e 2 0 0 4 − ,2 I e Ta có 1 16 =
= 2,6081.10 nên cường độ ánh sáng giảm đi 16 2,6081.10 42 − I e 2 lần.
Ví dụ 7. E.coli là vi khuẩn đường ruột gây tiêu chảy, đau bụng dữ dội. Cứ
sau 20 phút thì số lượng vi khuẩn E. coli tăng gấp đôi. Ban đầu, chỉ có 40
vi khuẩn E. coli trong đường ruột. Hỏi sau bao nhiêu giờ, số lượng vi
khuẩn E.coli lớn hơn 671088640 con? Lời giải 1
Vì cứ sau 20 phút (bằng giờ) số lượng vi khuẩn tăng gấp đôi nên số 3
lượng vi khuẩn tăng theo quy luật
N = N .2n = 40.2n > ⇒ n > 1
. Vậy sau ít nhất 24. = 8 giờ n 671088640 24 0 3
thì số vi khuẩn đạt mức lớn hơn 671088640 con.
C. BÀI TẬP TỰ LUYỆN.
Bài 1: Cho hàm số f (x) = ( x + x + )3 2 2 2
3 1 . Tính giá trị của f ( ) 1
Bài 2: Rút gọn biểu thức 1 a) 3 6
P = x x với x > 0 . 5 3 3
b)Q = b : b với b > 0 . 15 4 3 6 4
c) P = x . x với x 0 1 d) 1− 2 2+ 2 2 P = 3 .3 .9 Bài 3: Tính 1 0,25 3 a) A 0,2 1 8 32 . 64 27 3 4 2 3 4 1 5 2 1 32 2 2 25 2 b) B . 5 4 3 4 a b a ab c) C . 4 4 4 4 a b a b a b d) D ab: với 2 2 a b .
a b2 3 3 3 3 3 a b
Bài 4: Rút gọn các biểu thức sau 1 π a) π π 2 4π E x y xy . 4 1 2 3 3 3
a a a b) F . 1 3 1 4 4 4
a a a 1 5 3 6 6 a − 3a + 2
a − a + a c) A = + 3 6 a −1 a 7 1 + 2− 7 . = a a P d) ( − a ) 2+2 2 2
Bài 5: Chứng minh rằng nếu 2 3 4 2 2 3 4 2
x + x y + y + y x = a thì 2 2 2 3 3 3
x + y = a .
Bài 6: Chu kì bán rã của nguyên tố phóng xạ poloni 210 là 138 ngày (
nghĩa là sau 138 ngày khối lượng của nguyên tố đó chỉ còn 1 nửa). Tính 16
khối lượng còn lại của 40 gam poloni 210 sau 7314 ngày ( khoảng 20 năm). 2n
Bài 7:Cho biết f (n) = , vói n∈ . Tính 2n +1 S = f ( 1000) − + f ( 999) − ++ f ( 1
− ) + f (0) + f (1) ++ f (1000)
D. BÀI TẬP TRẮC NGHIỆM − ( − ) 3 − 3 2 2 1 2 : 4 3 . +
Câu 1:Tính giá trị của biểu thức 9 K = 3 − 3 − 2 ( )0 1 5 .25 0,7 . + 2 2 8 5 33 A. . B. . C. . D. . 3 3 3 13
Câu 2: Biết rằng 3 2 . . n x x
x = x với x > 0 . Tìm n. 2 4 A. n = 2 . B. n = . C. n = . D. n = 3. 3 3 + a + .(a − )1 3 2 3 1 3
Câu 3: Cho biểu thức P =
, với a > 0 . Mệnh đề nào sau 1+ 3 a đây là đúng? 1 1 A. 3 P = a . B. P = .
C. P = a . D. P = . a 3 a
Câu 4: Cho 2x = 5. Giá trị của biểu thức x 1 2 4 2 x T + − = + bằng: 504 104 104 504 A. . B. . C. . D. . 5 5 25 25 2x + 2−x − 3
Câu 5: Cho 4x + 4−x = 34 . Tính giá trị của biểu thức T = . x 1 + 1 1− 2 − 2 −x 3 3 3 3 A. T = . B. T = . C. T − = . D. T = . 4 11 11 13 17 1 2 2025 1 1 1
Câu 6: Tích (2025 )! 1 1 ...1 + + +
được viết dưới dạng 1 2 2025 b a , khi đó ( ;
a b) là cặp nào trong các cặp sau? A. (2026;2025) . B. (2027;2026). C. (2023;2022) . D. (2024;2023) .
Câu 7:Một khu rừng có trữ lượng gỗ 5
4.10 mét khối. Biết tốc độ sinh
trưởng của các cây trong rừng đó là 4% mỗi năm. Hỏi sau 10 năm khu
rừng đó có số mét khối gỗ gần nhất với số nào? A. 5 5,9.10 . B. 5 5,92.10 . C. 5 5,93.10 . D. 5 5,94.10 .
Câu 8: Chị Phương Anh vay trả góp ngân hàng MSB số tiền 500 triệu
đồng với lãi suất 10,8 %/năm, mỗi tháng trả 15 triệu đồng. Sau ít nhất
bao nhiêu tháng thì chị Phương Anh trả hết nợ? A. 39 tháng. B. 41 tháng. C. 40 tháng. D. 42 tháng.
Câu 9:Chu kì bán rã của nguyên tố phóng xạ ponoli 210 là 138 ngày (nghĩa
là sau 138 ngày khối lượng của nguyên tố đó chỉ còn một nửa). Thời
gian phân rã phóng xạ ponoli 210 để từ 20 gam còn lại 15 2,22.10− gam
gần đúng với đáp án nào nhất?
A. Khoảng 18 năm.
B. Khoảng 21 năm. C. Khoảng 19 năm. D. Khoảng 20 năm. 1 1 1+ + 2 2
Câu 10:Bài …: Cho f ( x) x (x+ ) 1 = e . Biết rằng m
( )1. (2). (3)... (2025) = n f f f f e với ,
m n là các số tự nhiên và mn là
phân số tối giản. Tính 2 m − n A. 2 m − n = 1 − . B. 2 m − n =1. C. 2 m − n = 2026. D. 2 m − n = 2026 − . 18
E. HƯỚNG DẪN GIẢI
BÀI TẬP TỰ LUYỆN 3
Bài 1: Ta có f ( ) 2 1 = 6 = 6 6 . Bài 2: 1 1 1 a)Ta có 3 6 2
P = x ⋅ x = x = x . 5 1 5 1 4 − b)Ta có 3 3 3 3 3
Q = b :b = b = b 4 4 4 c)Ta có 3 6 4 3 6 2
P x . x x .x x . x 1 d)Ta có 1 2 2 2 2 1 22 2 1 4 P 3 .3 .9 3 3 81. Bài 3: 1 1 1 3 3 3 2 1 2 7 1 a) A 5 2 5 6 2 4 2 2 . 3 2 3 6 2 2 1 5 5 ( 3 2) 3 2 2 1 2 2 2 2 5 2 2 2 2 4 1 b) B . 5 2 3 5 5 3 9 2 4 4 a b4 4
a b 4 a4 4 a b c) 4 4 4 4 C
a b a b . 4 4 4 4 a b a b d) D 2 3 2 3
a ab b ab 3 3 : a b2 3 3 . D 2 3 2
a ab b 3 3
a b2 3 3 a b2 3 3 2 : : a b2 3 3 1. Bài 4: a) π π π π π π π π π π π π 2 2 2 2 2 2 4 2 π π E x y x y x y x y x y x y x y . 4 1 4 2 3 3 3 3 2
a a a a a a b) F a . 1 3 1 1 a 1 4 4 4 4
a a a a 19 1 5 3 6 6 a − 3a + 2
a − a + a c)Ta có A = + 3 6 a −1 a ( a − ) 2 2 3 3 3 6 3 3
1 a + a − 2
a a − a +1 = + 3 6 a −1 a 2 2 3 3 3 3 3
= a + a − 2 + a − a +1 = 2 a −1. 7 1 + 2− 7 3 a .a a d)Ta có : 5 P = = = ( a + − 2−2 ) 2 2 2 a a
Bài 5: Biến đổi tương đương ta có 2 3 4 2 2 3 4 2 3 4
x + x y + y + y x = a ⇔ x (3 2 3 2 x + y ) 3 4 + y (3 2 3 2
y + x ) = a ( 2 3 2 x y ) 4 3 4 x y ⇔ + + = a ⇔ ( 2 3 2 x + y )3 3 3 3 = a 2 3 2 3 2 3
⇔ x + y = a (đpcm).
Bài 6: Ta có 7314 ngày tương ứng 53 chu kì.
Nên khối lượng còn lại của 40 gam poloni 210 sau 7314 ngày bằng 53 1 15 40 = 4,44.10− (gam) . 2 1 2n n Bài 7:Ta có 2
f (n) + f (−n) = + = 1. 2n +1 1 +1 2n 1 2001
Vậy S = [ f (1000) + f ( 1000) −
]++[ f (1) + f ( 1 − )]+ = . 2 2
BÀI TẬP TRẮC NGHIỆM
1.D 2.C 3.B 4.A 5.C 6.A 7.B 8.C 9.D 10.A Câu 1: Chọn D 20 − ( − ) 3 − 3 2 2 1 2 : 4 3 . + 4 6 − 6 5 9 2.2 + 3 .3 2 +1 33 Ta có K = = = = . 3 − 3 − 4 3 3 + + − 1 5 .5 1.2 5 2 13 3 2 5 .25 + (0,7)0 . 2 Câu 2: Chọn C 1 1 1 5 1 5 1 5 4 + Ta có: 3 3 3 2 2 2 2 2 2 2 6 2 6 3
x. x . x = x . x .x = x . x = x .x = x = x . Câu 3: Chọn B + a + .(a − )1 3 2 3 1 3 (1− 3)(1+ + 3 2 3 ) 2+ 3 2 − 3 a .a a .a a 1 Ta có: P = = = = = . 1+ 3 1+ 3 1+ 3 1+ 3 a a a a a
Câu 4: Chọn A 2 x+ −x x 2 x 4 4 504 Ta có: T = 4 + 2 = 4 .4 + = + = + = . x (2 )2 1 2 2 .4 4.5 2 2x 5 5 Câu 5: Chọn C Ta có: x − x x − x + = ⇔ + + = ⇔ ( x − x + )2 2 2 4 4 34 2 2 2 36 2 2
= 36 ⇔ 2x + 2−x = 6
(Do 2x + 2−x > 0 ). 6 − 3 3 3 − Khi đó: T = = = .
1− 2(2x + 2−x ) 1− 2.6 11 Câu 6: Chọn A 1 2 2025 1 1 1 Ta có (2025 )! 1 1 ...1 + + + 1 2 2025 2 2025 = (2025 ) 2 3 2026 2025 ! . ... = 2026
. Suy ra a = 2026,b = 2025 . 2 2025 1 2 2025 Câu 7: Chọn B
Số lượng gỗ sau 10 năm là : 5 10
4.10 .(1+ 0,04) = 592097,714 . Câu 8:Chọn C
Sau tháng thứ nhất số tiền còn lại là T = 500 1+ 0,9% −15 1 ( ) . 21
Sau tháng thứ hai số tiền còn lại là
T = T (1+ 0,9%) −15 = 500(1+ 0,9%)2 −15 1+ 0,9% −15. 2 1 ( )
Sau tháng thứ n số tiền còn lại là T = T + − n n . − 1 0,9% 15 1 ( ) = ( + )n − ( + )n 1− − ( + )n−2 500 1 0,9% 15 1 0,9% 15 1 0,9% −...15(1+ 0,9%) −15 n − + = 500(1+ 0,9%)n 1 (1 0,9%) −15 1−(1+0,9%) Để T = ⇒ + = ⇔ n ≈ . n ( )n 10 0 1 0,9% 39,81 7
Vậy sau ít nhất 40 tháng thì trả hết nợ. Câu 9: Chọn D
Gọi t (ngày) là số chu kì bán rã. Khi đó ta có phương trình: 1 t 15 20. = 2, 22.10− ⇒ t ≈ 53 . 2 Câu 10: Chọn A Đặt g (x) 1 1 = 1+ + 2 x ( 1+ x)2 Với x > 0 ta có 2 2 1 1
x + x +1 + x . x +1 (x + x+ )2 2 2 2 1 g (x) ( ) ( ) = 1+ + = = 2 x (1+ x)2 x(x + ) 1 x(x + ) 1 2 x + x +1 1 1 1 = = 1+ = 1+ − x(x + ) 1 x(x + ) 1 x x +1 Suy ra g ( )
1 + g (2) + g (3) +⋅⋅⋅+ g (2025) 1 1 1 1 1 1 1 1 1 = 1+ − + 1+ − + 1+ − + ⋅⋅⋅+ 1+ − = 2018 − 2 2 2 3 3 4 2017 2018 2018 22 Khi đó 2 1 2026 1 − m ( ) ( ) ( ) (
) g( ) g( ) g( ) g( ) 2026 1 2 3 2025 − + + +⋅⋅⋅+ 2026 2026 1 . 2 . 3 ... 2025 = = = = n f f f f e e e e . Do đó 2
m = 2026 −1, n = 2026. Vậy 2 2 2
m − n = 2026 −1− 2026 = 1 − . 23 Bài 2 LÔGARIT
A. TÓM TẮT LÝ THUYẾT
I. Định nghĩa lôgarit.
Cho hai số dương a, b với a ≠ 1. Số α thỏa mãn đẳng thức aα = b được
gọi là logarit cơ số a của b và kí hiệu là log b a .
Nghĩa là: = log b ⇔ aα α = .b a Chú ý:
Logarit thập phân là logarit cơ số 10. Viết : log b = log b = lg b 10
Logarit tự nhiên là logarit cơ số e . Viết : log b = ln b e
Không có logarit của số 0 và số âm vì aα > 0, α ∀ .
Cơ số của logarit phải dương và khác 1 (a ≠ 1)
Theo định nghĩa của logarit, ta có: log 1 = 0; log a = 1 a a ;
log ba = b, ∀b∈ loga b a
b, b ,b 0 a ; = ∀ ∈ > . II. Tính chất:
1. Logarit của một tích:
Cho 3 số dương a, b , b 1
2 với a ≠ 1, ta có log (b .b ) = log b + log b a 1 2 a 1 a 2
2. Logarit của một thương: b
Cho 3 số dương a, b , b a ≠ 1 2 với 1, ta có 1 log
= log b − log b a a 1 a 2 b2
Đặc biệt: với a, b > 0, a ≠ 1 1 log = − log b a a b
3. Logarit của lũy thừa:
Cho a, b > 0, a ≠ 1, với mọi α , ta có log bα = α log b a a Đặc biệt: n 1 log b = log b a a n 1
4. Công thức đổi cơ số: log b
Cho 3 số dương a, b, c với a ≠ 1,c ≠ 1, ta có log c b = a log a c 1
Đặc biệt: log c = và 1 với α ≠ 0 . a log a log α b = log b a a α c
B. CÁC DẠNG TOÁN. DẠNG 1:
TÍNH GIÁ TRỊ CỦA BIỂU THỨC Phương pháp:
+ Sử dụng công thức, tính chất và các quy tắc về logarit
Ví dụ 1. Tính giá trị của biểu thức 3
P = log2 8+ log3 27 − log5 5 . Lời giải Ta có: 3
P = log2 8+ log3 27 − log5 5 3 3 3
= log2 2 + log3 3 − log5 5 = 3+ 3−3 = 3.
Ví dụ 2. Tính giá trị của biểu thức P = ln (2e) − log100 . Lời giải
Ta có: P = ln (2e) − log100 2
= ln 2 + ln e − log10 = ln 2 +1− 2 = ln 2 −1.
Ví dụ 3. Tính giá trị của biểu thức log2 3 P = 2 − log 3 . 3 Lời giải Ta có: log2 3 P = 2
− log 3 = 3− log 3 = 3− 2 =1. 3 1 2 3
Ví dụ 4. Tính giá trị biểu thức ln 9 P = log5 3.log2 5− . ln 4 Lời giải Ta có: ln 9 P = log5 3.log2 5− = log 5.log 3− log 9 ln 4 2 5 4 2 = log 3− log 2 2 = − = 2 3 log2 3 log2 3 0.
Ví dụ 5. Cho a là số thực dương, a khác 1 . Tính giá trị biểu thức P = log a a a . a 2 Lời giải 1 1 Ta có P = log a a a = log a a a = a a a a ( 4 8 . . ) 1 2 4 8 loga . . a 1 1 1 7 + + 7 8 4 2 8 = log a = a = . a loga 8 DẠNG 2:
Biến đổi, rút gọn, biểu diễn biểu thức chứa logarit Phương pháp:
+ áp dụng các tính chất, quy tắc tính logarit, đổi cơ số
Ví dụ 6. Với số dương a tùy ý, rút gọn biểu thức log(8a) − log(2a) Lời giải b Áp dụng công thức log = b − c a loga loga , ta có: c ( ) ( ) 8 log 8 log 2 log a a a − = = log 4. 2a
Ví dụ 7. Rút gọn biểu thức log2
P = 2 a + log ( b
a (a > 0,a ≠ ) 1 . a ) Lời giải
Áp dụng các tính chất của logarit ta được P = a + b .
Ví dụ 8. Cho a,b,c,d là các số thực dương tùy ý. Rút gọn biểu thức:
= log a + log b + log c − log a P . b c d d Lời giải
Với a,b,c,d là các số thực dương, ta có:
log a .b . c = − a a log a P = log : = log1 = 0. b c d d d d
Ví dụ 9. Cho a,b là các số thực dương và a khác 1 . Rút gọn biểu thức: 3 6 P = log b + b a log . 2 a Lời giải
Với a,b là các số thực dương và a khác 1, ta có: 1 P = 3log b + b = 6log b . a 6. log 2 a a 3
Ví dụ 10. Cho a,b là các số thực dương và khác 1 . Rút gọn biểu thức: log b a b − a ( ) 3 3 2 logb 2 a P = 2 log b + a 1 Lời giải
Với a,b là các số thực dương và khác 1, ta có: 3 2 log a + b − b − a a loga ( 3 2 logb logb ) P = 2 log b + a 1 1 2log b + 3 + 2log b − + a a log b a 3 2log b = a = 2 log b + 2 log b + a 1 a 1 2 log b + a 1 2 log b a 2 = = = 2log a . 2 log b +1 log b b a a DẠNG 3:
TÍNH LOGARIT THEO LOGARIT KHÁC
DẠNG 3.1:TÍNH LOGARIT THEO 1 LOGARIT KHÁC
Ví dụ 11. Cho log 2 = a . Tính log 18 theo a . 3 3 Lời giải Ta có: log 18 = log ( 2 2.3 ) 2
= log 2 + log 3 = log 2 + 2 = a + 2 . 3 3 3 3 3
Ví dụ 12. Cho b = log 3. Tính log 25 theo b . 5 81 Lời giải Ta có: 2 1 1 1 log = = = = . 81 25 log 4 5 2. log 3 3 5 4 2log5 3 b 2
Ví dụ 13. Cho a = log m với 0 < m ≠ 1. Tính A = log m m 16 2 theo a . Lời giải Từ giả thiết ta có: 4 4 = log + a A m = + = + = + = . m 16
logm16 1 4logm 2 1 1 log m a 2
Ví dụ 14. Cho log 3 = a . Tính log 18 theo a . 12 24 4 Lời giải 1 1 2a Ta có a = log 3 = = ⇔ log 3 = . 12 2 log 12 1+ 2log 2 1− a 3 3 ( 2a 2 1+ 2. log 3 .2 2 ) 1+2log 3 1− a 1+ 3a Khi đó: log 18 = = = = . log 2 .3 3+ log 3 2a 3− a 2 ( ) 2 24 3 2 3+ 1- a
Ví dụ 15. Cho log 15 = a . Tính A = log 15 theo a . 3 25 Lời giải
Ta có: log 15 = a ⇔ log 3+ log 5 = a ⇔ log 5 = a −1. 3 3 3 3 Khi đó: log 15 1+ log 5 a 3 3 A = log 15 = = = . 25 log 25 2log 5 2 a −1 3 3 ( )
DẠNG 3.2:TÍNH LOGARIT THEO 2 LOGARIT KHÁC
Ví dụ 16. Cho log 5 = a;log 5 = .
b Tính log 6 tính theo a và b . 2 3 5 Lời giải + Ta có: 1 1 1 1 log 6 = log 2 + log 3 a b = + = + = . 5 5 5 log 5 log 5 a b ab 2 3
Ví dụ 17. Cho a = log 2, b = ln 2 . Hãy biểu diễn ln800 theo a và b . Lời giải
Ta có: ln800 = 3ln 2 + 2ln10 = 3ln 2 + 2ln 2.log 10 2 . 2ln 2 = 3ln 2 + 2 = 3 b b + . log 2 a 121
Ví dụ 18. Cho a = log 11 , b = log 5 . Hãy biểu diễn log theo a và 25 2 625 16 b . Lời giải Ta có: 121 1 log = log 121− log 16 1 = log 11− log 2 . 625 ( 5 5 ) 16 4 5 5 2 5 1 1 Mà a = log 11 1 = = = 121 1 = − 25 log 11; log 2 nên log a . 5 2 5 log 5 b 625 16 b 2
DẠNG 3.3:TÍNH LOGARIT THEO 3 LOGARIT KHÁC
Ví dụ 19. Cho a = log 5;b = log 7;log 3 . Tính log 1260 theo a,b, . c 3 2 2 6 Lời giải log 35 log 5 + log 7 Ta có: log 1260 = 2 + log 35 2 = + 2 2 = + 6 6 2 2 . log 6 1+ log 3 2 2 +
Mà log 5 = log 3.log 5 = ac ac b = + 2 2 3 nên log 1260 2 . 6 1+ c
Ví dụ 20. Cho log 5 = a; log 7 = ;
b log 12 = c . Tính log 4200. 9 2 4 18 Lời giải log 12 2 + log 3 Ta có: 2 2 c = log 12 = = ⇔ log 3 = 2c − 2 4 log 4 2 2 . 2 log 5 log 5 2 2 a = log 5 = = ⇔ log 5 = 2a log 3 9 log 9 2log 3 2 2 2 2
= 2a (2c − 2) = 4ac − 4a . log 4200 log ( 3 2 2 .3.5 .7 2 ) Khi đó: 2 log 4200 = = 18 log 18 log ( 2 2 2.3 2 ) 3+ log 3+ 2log 5 + log 7 2 2 2 = 1+ 2log 3 2
3+ 2c − 2 + 2(4ac − 4a) + b 8ac −8a + b + 2c +1 = = 1+ 2(2c − 2) 4c − 3 .
C. BÀI TẬP TỰ LUYỆN.
Bài 1: Không sử dụng máy tính, hãy tính: a) 1 log 2 8 6 b) log 2 1 4 c) 4 log 3 3 d) log 0,125 0,5 Bài 2: Tính a) log23 4 b) log9 2 27 log 2 c) 3 9 d) log827 4
Bài 3: Rút gọn biểu thức a) log 6.log 9.log 2 3 8 6 b) 2 4 log b + b a log 2 a
Bài 4: Tính giá trị biểu thức ln 9 P = log5 3.log2 5− . ln 4
Bài 5: Tìm các số thực dương a biết log . a log a = 32 2 . 2
Bài 6: Cho a , b là các số thực dương khác 1 và thỏa mãn ab ≠ 1. Rút gọn
biểu thức P = (log b + a + b − b a − a logb 2)(loga logab )logb 1
Bài 7: Đặt a = log 3 và b = log 3. Hãy tính log 45 theo a và b 2 5 6
D. BÀI TẬP TRẮC NGHIỆM
Câu 1: Với mọi số thực dương a,b, x, y và a,b ≠ 1, mệnh đề nào sau đây sai? A) 1 1 log = . B) log xy = x + y . a ( ) loga log a x log x a a C) x log a x = x . D) log = x − y . a loga log b .loga logb a y
Câu 2: Cho a > 0;a ≠1. Tìm mệnh đề đúng trong các mệnh đề sau? A. log n x = n x .
B. log x có nghĩa x ∀ ∈ . a loga a C. log a = log x y = x y x ∀ > a . loga .loga ; 0 a 0 . D. ( ) . 7
Câu 3: Cho a là số thực dương bất kì. Tìm khẳng định đúng trong các khẳng định sau: A. 3 1 log a = log a .
B. log(3a) = 3log a . 3 C. ( a) 1 log 3 = log a . D. 3
log a = 3log a . 3
Câu 4: Cho a là số thực dương khác 1. Tính I = log a . a 1
A. I = . B. I = 2
− . C. I = 0. D. I = 2 . 2
Câu 5: Cho a,b > 0 , a ≠ 1 thỏa log b = . Tính 3 P = log b . a 3 2 a 9 1
A. P =18. B. P = 2 . C. P = . D. P = . 2 2
Câu 6: Trong các mệnh đề sau, mệnh đề nào đúng? A) log bα = α
b với mọi số a,b dương và . a loga a ≠ 1 B) 1 log b =
với mọi số a,b dương và a ≠1. a log a b C) log b + c =
bc với mọi số a,b dương và a ≠ 1. a loga loga D) log log a c b =
với mọi số a,b dương và a ≠1. a log b c
Câu 7: Cho a,b là hai số thực dương tùy ý và b ≠1.Tìm kết luận đúng.
A) ln a + lnb = ln(a + b) . B) ln(a + b) = ln . a lnb .
C) ln a − lnb = ln(a − b) . D) ln log a a = . b lnb
Câu 8: Cho hai số dương a, b (a ≠ )
1 . Mệnh đề nào dưới đây SAI? A) log a =
. B) log aα = α . a 2a a
C) log = . D) logab a = b . a 1 0
Câu 9: Với các số thực dương a,b bất kì. Mệnh đề nào dưới đây đúng?
A) log(ab) = log .
a logb . B) a log log a = . b logb
C) log(ab) = log a + logb .
D) log a = logb − log a . b 8
Câu 10: Với các số thực dương a,b bất kì. Mệnh đề nào dưới đây đúng?
A) ln(ab) = ln a + lnb . B) a ln ln a = . b lnb C) ln(ab) = ln . a lnb .
D) ln(a) = lnb − ln a . b
Câu 11: Cho a,b,c > 0 , a ≠ 1 và số α ∈ , mệnh đề nào dưới đây sai? A) log c
a = c . B) a log a = . a 1 C) log bα = α b .
D) log b − c = b − c . a loga log a loga a
Câu 12: Cho a > 0,a ≠1, biểu thức D = log a có giá trị bằng bao nhiêu? 3 a A) 3
− . B) 3. C) 1 . D) 1 − . 3 3
Câu 13: Với a và b là hai số thực dương, a ≠ 1. Giá trị của 3 loga b a bằng 1 1 A) 3
b . B) b . C) 3b . D) 3 b . 3
Câu 14: Cho hai số thực dương a, b và a ≠ 1. Khẳng định nào đúng ? A) 1
log ab = + log b . B) 2021 2021log ab = + b . a 1 log a 2 a a C) 2020 log a b = + b . D) 2018 log a b = + b a 2018(1 loga ) . a 2020 loga
Câu 15: Nếu log 4 = a thì log 4000 bằng
A) 3+ a . B) 4 + b . C) 3+ 2a .
Câu 16: Đặt a = log 15;b = log 10. Hãy biểu diễn 3 3
log 50 theo a và b. 3
A) log 50 = (a + b − )
1 . B) log 50 = 3(a + b − ) 1 . 3 3
C) log 50 = 2(a + b − )
1 . D) log 50 = 4(a + b − ) 1 3 3
Câu 17: Cho a,b,c là các số dương (a,b ≠1) . Trong các mệnh đề sau,
mệnh đề nào là mệnh đề đúng? A) b 1 log =
b . B) logb a a = b . a ( ) log 3 a 3 a C) log = α . D) log c = c b . a logb .log α b log b a a a
Câu 18: Với các số thực dương a, b bất kì. Mệnh đề nào dưới đây đúng? 9 3 A) 2
log ( a ) =1+ 3log a + log b . 2 2 2 b 3 B) 2a 1 log (
) =1+ log a + log b . 2 2 2 b 3 3 C) 2
log ( a ) =1+ 3log a − log b . 2 2 2 b 3 D) 2a 1 log (
) =1+ log a − log b . 2 2 2 b 3
E. HƯỚNG DẪN GIẢI
BÀI TẬP TỰ LUYỆN Bài 1: a) 1 3 log log (2− = ) = 3. − log 2 = 3 − 2 2 2 8 b) 1 1 log 2 = log = − = − − 2 .log 2 2 1 2 2 2 2 4 c) 4 1 1 log 3 = log 3 = 3 3 4 4 d) 3
log 0,125 = log (0,5) = 3log 0,5 = 3 0,5 0,5 0,5 Bài 2: a) log23 log23 log2 3 2 2 2 4 = (2 ) = (2 ) = 3 = 9 1 3 3 b) log9 2 3log9 2 log9 2 log9 2 3 2 2 2 27 = (3 ) = (9 ) = (9 ) = 2 = 2 2 log 2 log 2 c) 3 3 log 2 3 4 4 4 9 = (( 3) ) = (( 3) ) = 2 =16 d) 3 3
log 27 = log 3 = log 3 = log 3 3 8 2 2 2 3 nên log23 log23 log8 27 2 2 2 4 = (2 ) = (2 ) = 3 = 9 Bài 3: a) 2 2 2
log 6.log 9.log 2 = (log 6.log 2).log 3 = log 2. log 3 = 3 3 8 6 3 6 2 3 2 3 3 b) 2 4 2 2 2 log b + b = b + b = b = b a log log a a loga 2loga 4log 2 a 10 Bài 4: Ta có: ln 9 P = log5 3.log2 5− = log 5.log 3− log 9 ln 4 2 5 4 2 = log 3− log 2 2 = − = 2 3 log2 3 log2 3 0. Bài 5 : Ta có: log .
a log a = 32 ⇔ 2log .
a log a = 32 ⇔ (log a)2 =16 2 2 2 2 2 4 a = 2 =16 log a = 4 2 ⇔ ⇔ . = − 4 − 1 log a 4 2 a = 2 = 16
Bài 6: Ta có P = (log b + a + b − b a − a logb 2)(loga logab )logb 1 1 log = log b + + 2log b a b − a − a a b ab a a ( ) logb 1 log log 2 log b + b + b a 2loga 1 log = .log a b − a − a logb 1 log b + b a 1 loga ( b + a )2 2 log 1 log = . b a
.log a − = (log b + b a − = b a
)1.loga .logb 1 log b 1 . log b + b a a 1 loga a 2 2a log (3 .5) 2log 3 log 3.log 5 + + b 2ab + a Bài 7: 2 2 2 3 log 45 = = = = 6 log (3.2) 1+ log 3 1+ a ab + b 2 2 TRẮC NGHIỆM
1.A 2.A 3.D 4.D 5.C 6.A 7.A 8.A 9.C 10.A
11D 12C 13D 14C 15A 16C 17D 18A Câu 1: Chọn A.
Với mọi số thực dương a,b, x, y và a,b ≠1. Ta có: 1 1 − 1 log = x ≠ . a loga x log x a
Vậy A sai. Theo các tính chất logarit thì các phương án B,C và D đều đúng. Câu 2: ChọnA. 11 log x x ∀ > a có nghĩa 0 ⇒ câu B sai log a = a 1 ⇒ câu C sai. log x y = x + y x ∀ > a ( . ) loga loga ; 0 ⇒ câu D sai. Câu 3: ChọnD. 3
log a = 3log a ⇒ A sai, D đúng.
log(3a) = log3+ log a ⇒ B,C sai. Câu 4: ChọnD.
I = log a = 2log a = a a 2 . Câu 5: ChọnC. 3 3 9
Vì a,b > 0 nên ta có: P = log b = = . a .3 2 2 2 Câu 6: Chọn A. Câu 7: Chọn A.
Theo tính chất làm Mũ-Log. Câu 8: Chọn A. Câu 9: Chọn C.
log(ab) = log a + logb . Câu 10: Chọn A. Câu 11: Chọn D.
Theo tính chất của logarit, mệnh đề sai là log b − c = b − c . a loga loga
Câu 12: Chọn C.Ta có: 1 1
D = log a = log a = . 3 a 3 a 3
Câu 13: Chọn D.Áp dụng công thức: logab a = b Câu 14: Chọn C. 12
log ab = 2(log a + b a a loga ) = 2 + 2log b a . ab = ( 2018 2018log 2018 + b a loga ) 2020 log a b = a + b a 2020.loga loga = 2020 + log b a Câu 15: Chọn A. = ( 3) 3
log 4000 log 4.10 = log 4 + log10 = log 4 + 3 = a + 3. Câu 16: Chọn C.
Ta có log 50 = log 50 = 2log 50 = 2log 10.5 1 3 3 3 ( ) 2 3 = 2(log 10 + log 5 3 3 ) = 2(log 10 + log 15 − log 3 3 3 3 ) = 2(a + b − ) 1 Câu 17: Chọn D. Câu 18: Chọn A. Ta có: 3 2a 3 log (
) = log (2a ) − log b 2 2 2 b 3
= log 2 + log a − log b 2 2 2
=1+ 3log a − log b 2 2 13 Bài 3.1 HÀM SỐ MŨ
A. TÓM TẮT LÝ THUYẾT I. Hàm số mũ
Cho số thực a > 0 và a ≠ 1. Hàm số có dạng x
y = a được gọi là hàm số mũ cơ số a .
— Tập xác định: D = .
— Tập giá trị: T = (0,+∞)
— Hàm số liên tục trên .
— Nếu a >1 thì hàm số x
y = a đồng biến trên . lim x a = +∞ ; lim x a = 0 x→+∞ x→−∞
— Nếu 0 < a <1 thì hàm số x
y = a nghịch biến trên . lim x a = 0 ; lim x a = +∞ x→+∞ x→−∞
II. Đồ thị của hàm số mũ Đồ thị hàm số x
y = a đi qua điểm (1;a), cắt trục tung tại điểm (0;1) và
nằm phía trên trục hoành 1 B. CÁC DẠNG TOÁN.
DẠNG 1: So sánh các cặp số Phương pháp:
Với a >1, nếu x < y thì x y a < a .
Với 0 < a < 1, nếu x < y thì x y a > a . Ví dụ 1. So sánh 2 3 a) 0,7 và 0,7− b) 2 3 5 và 3 2 5 8 3 3 c) 3 và d) 0,4 3 và 3 4 4 0,3 e) 20 4 và 7 64 f) (0,2) và 1 Lời giải 2 3 a) 0,7 0,7− <
vì cơ số a = 0,7 <1 b) 2 3 3 2 5 < 5 8 3 3 3 c) > 4 4 0,4 0,5 d) 3 < 3 = 3 20 3 7 7 e) 4 < (4 ) = 64 0,3 0 f) (0, 2) < (0, 2) =1 Ví dụ 2. So sánh a) 300 2 và 200 3 b) 99 3 và 21 11 c) 444 333 và 333 444 1 −
Ví dụ 3. Viết các số sau theo thứ tự tăng dần : 0 3 ; 3 ; 0,2 32 4 13 15
Ví dụ 4. Tìm các số thực dương a thỏa 7 8
a < a 2
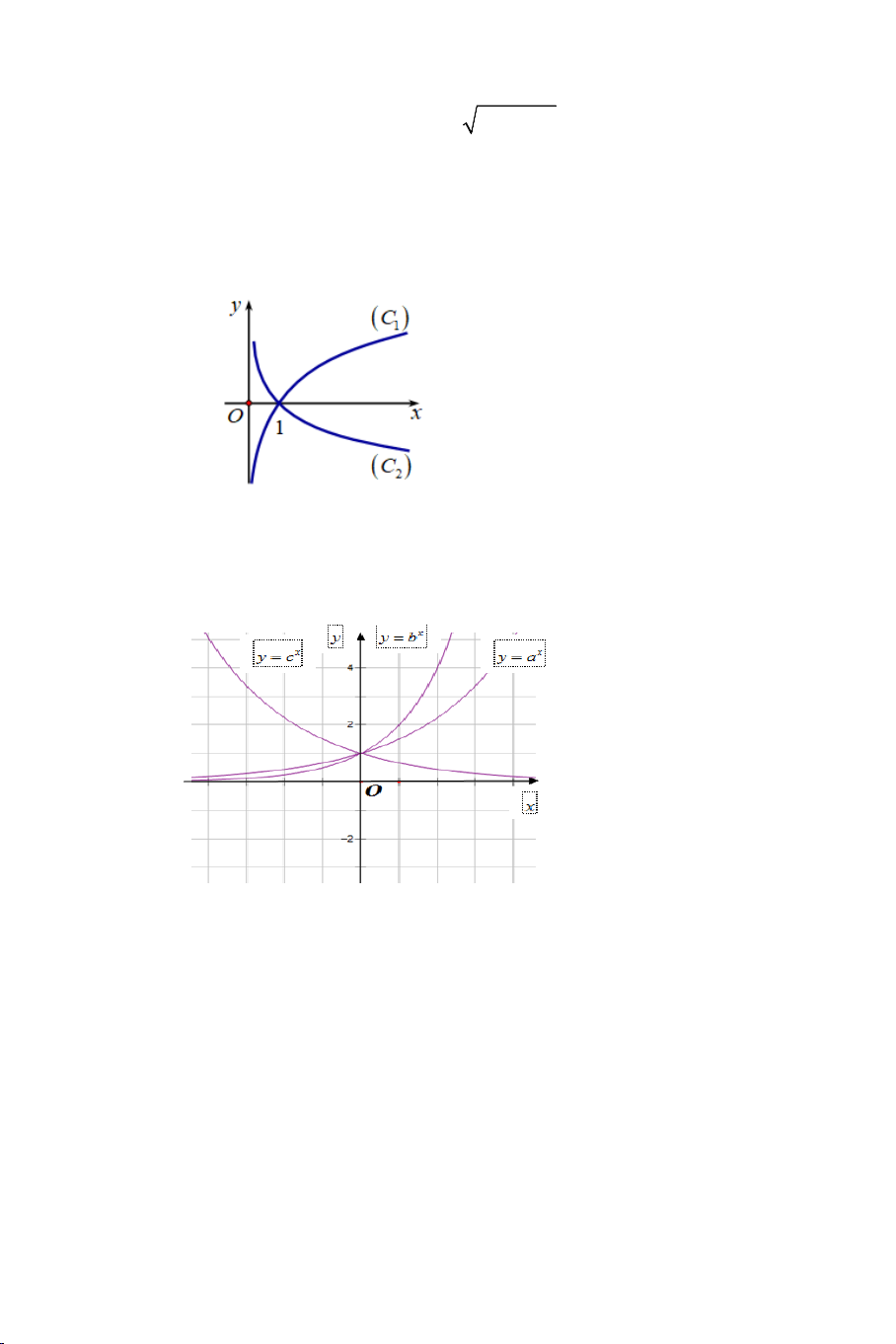
DẠNG 2: Đồ thị của hàm số mũ
Ví dụ 5. Xét tính đồng biến, nghịch biến của các hàm số sau trên ? x a) (0,6)x y = y = ( 10 −3) e) 1 x y = f) 2 x y − = b) 3 1 x π y = y = g) 4x c) 3 2 x y = d) π x
Ví dụ 6. Vẽ đồ thị hàm số 2x
y = và đồ thị hàm số 1 y = 2
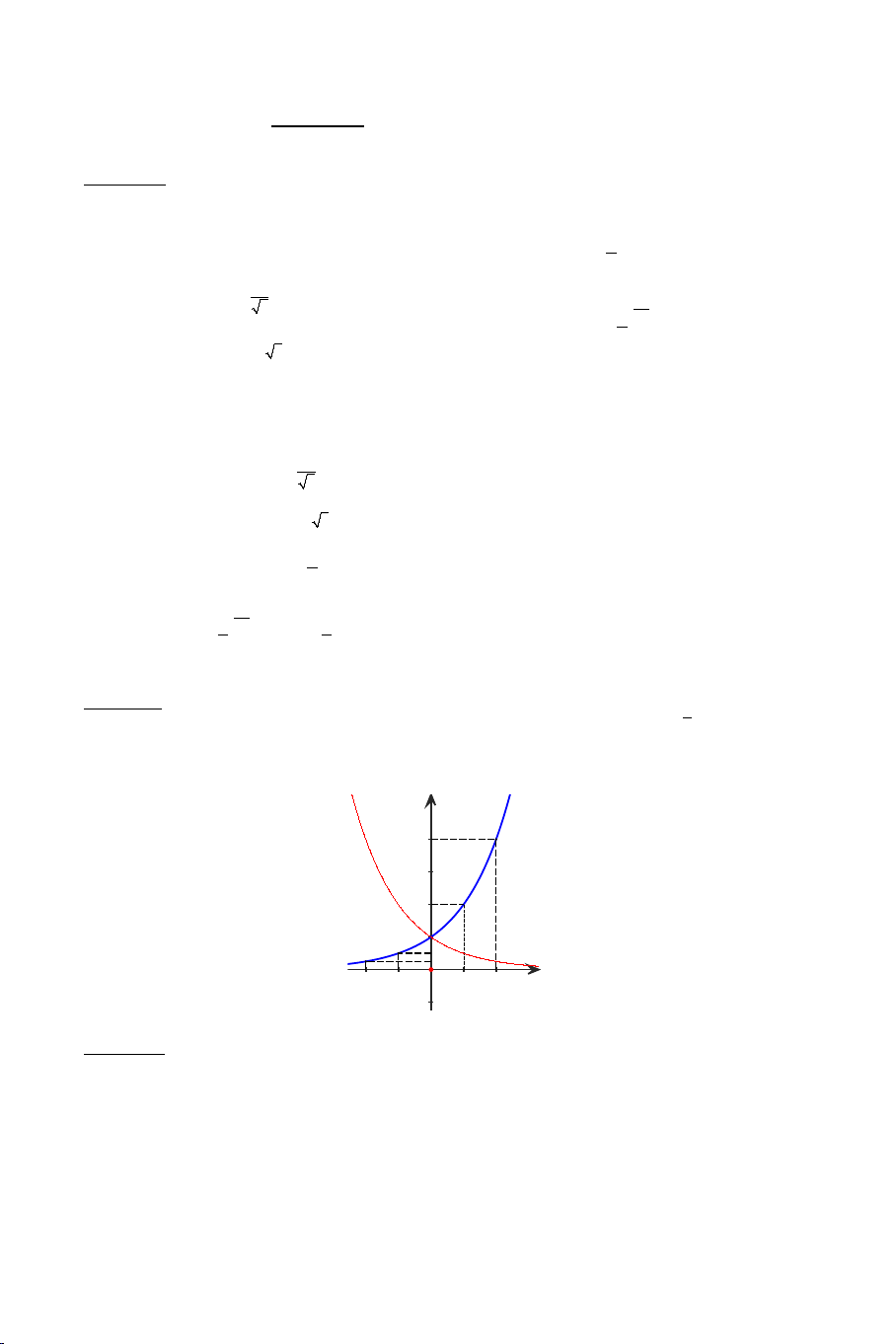
Ví dụ 7. Cho các hàm số x y = a , x y = b , x
y = c (0 < a, b, c ≠ ) 1 có đồ thị
như hình vẽ bên dưới. Hãy so sánh các số a,b,c ? x y = c y x y = b x y = a 1 O x 3
DẠNG 3: Bài toán thực tế
Ví dụ 7. Trong vật lí, sự phân rã của các chất phóng xạ được biểu diễn bởi t 1 T
công thức m(t) m =
, trong đó m là khối lượng ban đầu của chất 0 2 0
phóng xạ (tại thời điểm t = 0 ); T là chu kì bán rã (từ là khoảng thời gian
để một nửa khối Iượng chất phóng xạ bị biến thành chất khác). Chu kì bán
rã của Cacbon 14 C là khoảng 5730 năm. Người ta tìm được trong một mẫu
đồ cổ một lượng Cacbon và xác định được nó đã mất khoảng 25 lượng
Cacbon ban đầu của nó. Hỏi mẫu đồ cổ có tuổi là bao nhiêu? Lời giải
Ta có: m(t) = (100% − 25%)m = 75%m 0 0 t 5330 1 Khi đó, ta có: 75%m m = ⋅
⇔ t = 5730⋅log 0,75 ≈ 2378 (năm). 0 0 0,5 2 4
C. BÀI TẬP TỰ LUYỆN.
Bài 1: So sánh các cặp số sau: a) 2 2 và ( )3 2 3 2 2 b) 0, 2− và 0, 2−
Bài 3: Hàm số sau đây đồng biến hay nghịch biến trên ? ( 2)x y = . a) 1 x y = . b) 2 2 x y = . c) 3 x e y = . d) π Bài 3: Cho hàm số x
y = a có đồ thị như hình bên. Tìm giá trị của a ?
Bài 4: Cho số thực a dương khác 1. Biết rằng bất kì đường thẳng nào
song song với trục Ox mà cắt các đồ thị 4x y = và x
y = a , trục tung
lần lượt tại M , N , A thì AN = 2AM . Tìm giá trị của a ? 5
Bài 5: Số lượng của loại vi khuẩn A trong một phòng thí nghiệm được tính
theo công thức ( ) = (0).2t s t s
, trong đó s(0) là số lượng vi khuẩn A lúc ban
đầu, s(t) là số lượng vi khuẩn A có sau t phút. Biết sau 3 phút thì số
lượng vi khuẩn A là 625 nghìn con. Hỏi sau bao lâu, kể từ lúc ban đầu, số
lượng vi khuẩn A là 10 triệu con? 6
D. BÀI TẬP TRẮC NGHIỆM Câu 1:
Trong các khẳng định sau, khẳng định nào sai?
A. Nếu a >1 thì x y
a > a khi và chỉ khi x > y .
B. Nếu a >1 thì x y
a ≤ a khi và chỉ khi x ≤ y
C. Nếu 0 < a <1 thì x y
a > a khi và chỉ khi x > y .
D. Nếu 0 < a ≠ 1 thì x y
a = a khi và chỉ khi x = y . Câu 2:
Trong các khẳng định sau, khẳng định nào sai? 2017 2018 2018 2017 A. ( 2 − ) 1 > ( 2 − ) 1 . B. ( 3 − ) 1 > ( 3 − ) 1 . 2018 2017 2 2 C. 2 1+ 3 2 > 2 . D. 1− < 1− . 2 2 Câu 3:
Hàm số nào dưới đây đồng biến trên tập xác định của nó? 2 x e x x A. y = x . B. y = .
C. y = ( 2) .
D. y = (0,5) . 3 π Câu 4:
Hàm số nào dưới đây đồng biến trên . 1 x π A. y = . B. y = . 5x 4 1 e x C. y = ( . D. y = . 7 − 5)x 3 Câu 5:
Đường cong trong hình sau là đồ thị của hàm số nào trong bốn hàm số sau: x
A. y = ( 2) . B. 2 y = x . C. 2x y = .
D. y = x +1. 7 Câu 6:
Đồ thị hình bên là của hàm số nào? y 3 1 1 − O x x x x 1 x 1
A. y = ( 3) . B. y = .
C. y = ( 2) . D. y = . 2 3 Câu 7: Cho hai hàm số x = , x
y a y = b với a,b là hai số thực dương khác
1, lần lượt có đồ thị là (C ) và (C ) như hình bên. 1 2
Mệnh đề nào dưới đây là đúng?
A. 0 < a < b < 1.
B. 0 < b < 1 < a .
C. 0 < a < 1 < b .
D. 0 < b < a < 1. Câu 8:
Cho ba số thực dương a,b,c khác 1. Đồ thị các hàm số x = , x = , x
y a y b y = c được cho trong hình vẽ bên 8
Mệnh đề nào dưới đây đúng?
A. a < b < c . B. a < c < b .
C. b < c < a .
D. c < a < b . Câu 9:
Hình vẽ dưới đây là đồ thị của các hàm số mũ x = , x = , x y a y b y = c y x y = a x y = c 1 x y = b O x
Khẳng định nào dưới đây đúng?
A. a > b > c .
B. a > c >1 > b .
C. b > c >1 > a .
D. b > a > c . x x 1 x
Câu 10: Cho bốn hàm số y = ( 3) , y = , 4x y = , 1 y = và bốn 3 4 đường cong (C C C C
1 ) , ( 2 ) , ( 3 ) , ( 4 ) như hình vẽ bên. Hỏi các đồ
thị trên lần lượt tương ứng với hình vẽ nào? A. (C C C C C C C C
2 ) , ( 3 ) , ( 4 ) , ( 1 ) .
B. ( 4 ), ( 3 ) ,( 2 ),( 1) . C. (C C C C C C C C
4 ) , ( 1 ) , ( 3 ) , ( 2 ) .
D. ( 1) , ( 2 ), ( 3 ) , ( 4 ). 9
E. HƯỚNG DẪN GIẢI
BÀI TẬP TỰ LUYỆN
Bài 1: So sánh các cặp số sau: 3 a) Vì 3 3 2 < nên 2 2 2 < 2 = ( 2) 2 b) Vì 3 − < 2 − 2 nên 3 − 2 − 2 0,2 > 0,2
Bài 2: Hàm số sau đây đồng biến hay nghịch biến trên ? a) Hàm số ( 2)x y = đồng biến x b) Hàm số 1 y = nghịch biến 2 x c) Hàm số 2 y = nghịch biến 3 x d) Hàm số e y = nghịch biến π
Bài 3: Đồ thị hàm số đi qua (2;3) nên 2
3 = a ⇒ a = 3. Bài 4:
Vì AN = 2AM nên ( 1 ; 4x M x , ( 2 1 2 ; x N x a− − . 1 ) 1 ) Ta có x − x 1 1 1 2 1 4 = a ⇔ 4 = ⇔ a = . 2 a 2 Bài 5: s 3
Sau 3 phút ta có: s( ) = s( ) 3 3 0 .2 ⇒ s(0) ( ) = = 78125. 3 2
Tại thời điểm t số lượng vi khuẩn A là 10 triệu con nên ta có: ( ) s t t ( ) = (0).2t s t s t 10.000.000 ⇔ 2 = ⇔ =
⇔ 2t =128 ⇔ t = 7 . s( ) 2 0 78125 10
BÀI TẬP TRẮC NGHIỆM 1.C 2.B 3.C 4.C 5.C 6.D 7.B 8.B 9.B 10.C 11 Bài 3.2 HÀM SỐ LÔGARIT
A. TÓM TẮT LÝ THUYẾT I. Hàm số lôgarit
Cho số thực a > 0 và a ≠ 1.
Hàm số dạng y = log x được gọi là hàm số lôgarit cơ số a . a
— Tập xác định: D = (0;+∞)
— Tập giá trị: T =
— Hàm số liên tục trên (0;+∞) .
— Nếu a >1 thì hàm số y = log x đồng biến trên (0;+∞) . a
lim y = lim log x = +∞ ; lim y = lim log x = −∞ a x→+∞ x→+∞ →0+ →0+ a x x
— Nếu 0 < a <1 thì hàm số y = log x nghịch biến trên (0;+∞) . a
lim y = lim log x = −∞ ; lim y = lim log x = +∞ a x→+∞ x→+∞ →0+ →0+ a x x
II. Đồ thị của hàm số lôgarit
Đồ thị hàm số y = log x đi qua điểm (a;1) , cắt trục hoành tại điểm (1;0) a
và nằm bên phải trục tung. 1 B. CÁC DẠNG TOÁN.
DẠNG 1: So sánh các cặp số Phương pháp:
Với a >1, nếu x < y thì log x < y . a loga
Với 0 < a <1, nếu x < y thì log x > y . a loga Ví dụ 1. So sánh g) log 3 log 5 0,2 và 0,2 log 9 1 1 h) 5 và log 5 8 i) log 5 log 4 3 và 7 6 5 3
Ví dụ 2. Tìm số lớn nhất trong các số sau log ; log ; log ; log 2 3 5 3 6 1 2 3 3
Ví dụ 3. Có bao nhiêu giá trị nguyên m thỏa log ( 2
m − m + 2 ≥ log 22 1 ) ? 1 2 2 Lời giải. Ta có log ( 2 m − m + 2) 2 2
≥ log 22 ⇔ m − m + 2 ≤ 22 ⇔ m − m − 20 ≤ 0 − 4 ≤ m ≤ 5 1 1 . 2 2
Từ đó suy ra có 10 giá trị nguyên m thỏa đề bài. 2
DẠNG 2: Đồ thị của hàm số lôgarit
Ví dụ 4. Xét tính đồng biến, nghịch biến của các hàm số sau trên tập xác định? = h) y = log x y logπ x 0,6 y = log x k) 3 1 1 i) 3 y = logπ y = log x l) x 4 j) 2− 3 Hướng dẫn giải
a) Hàm số y = log x nghịch biến trên khoảng (0;+∞) 0,6
b) Hàm số y = log x nghịch biến trên khoảng (0;+∞) 1 3 c) Hàm số y = log
x nghịch biến trên khoảng (0;+∞) 2− 3 d) Hàm số y = log +∞
π x đồng biến trên khoảng (0; ) 3 1 e) y = log = −
đồng biến trên khoảng (0;+∞) π logπ x x 4 4
Ví dụ 5. Vẽ đồ thị hàm số y = log x và đồ thị hàm số y = log x 2 1 2 Hướng dẫn giải y 4 3 2 1 -2 -1 1 2 O x -1
Ví dụ 6. Cho a và b là các số thực dương khác 1. Biết rằng bất kì đường
thẳng nào song song với trục tung mà cắt các đồ thị y = log x , a
y = log x và trục hoành lần lượt tại A , B và H ta đều có b
2HA = 3HB (hình vẽ bên dưới). Tìm hệ thức liên hệ giữa a và b . 3 Hướng dẫn giải
Ta có : HA = log x và HB = −log x . a b
2HA = 3HB ⇔ 2log x = − x a 3logb 1 ⇔ log x = log ⇒ = 3 3 2
⇒ a. b =1⇒ a .b =1. − x a 1 a 3 3 b b 4
DẠNG 3: Bài toán thực tế
Ví dụ 7. Cường độ trận động đất M (Richter) được cho bởi công thức
M = logA − logA , với A là biên độ rung chấn tối đa và A là một biên độ 0 0
chuẩn (hằng số). Đầu thế kỷ 20, một trận động đất ở San Francisco có
cường độ 8,3 độ Richter. Cũng trong cùng năm đó, một trận động đất khác
ở Nam Mỹ có cường độ 9,3 độ Richter. Hỏi trận động đất ở Nam Mỹ có
biên độ gấp mấy lần biên độ trận động đất ở San Francisco? Lời giải Gọi ,
A B lần lượt là biên độ rung chấn tối đa trận động đất ở San Francisco và ở Nam Mỹ.
Trận động đất ở San Francisco có cường độ 8,3 độ Richter nên A A 8,3
8,3 = log − log ⇔ 8,3 = log ⇔ = 10 A A A ⇔ A = 0 0 8,3 A A 10 0 0
Trận động đất ở Nam Mỹ có cường độ 9,3 độ Richter nên B B 9,3
9,3 = log − log ⇔ 9,3 = log ⇔ = 10 B B A ⇔ A = 0 0 9,3 A A 10 0 0 A B A − A 1 Khi đó 8,3 9,3 A = = ⇒ = 10 ⇔ = ⇔ B =10 A 0 8,3 9,3 10 10 B B 10
Vậy trận động đất ở Nam Mỹ có biên độ gấp 10 lần biên độ trận động đất ở San Francisco. 5
C. BÀI TẬP TỰ LUYỆN.
Bài 1: So sánh các cặp số : logπ 3 và logπ 5
Bài 2: Tìm tập xác định của các hàm số sau : y = log ( 2 x −1 2 ) c) = log 3x y − 2 2 ( ) d) 1 y = e) 2 − log x 3
Bài 3: Vẽ đồ thị hàm số y = log x 1 a) 4 b) y = log x 1 y = log c) 2 x
Bài 4: Một nguồn âm đặt ở O đẳng hướng trong không gian có công suất
truyền âm P không đổi. Biết rằng cường độ âm tại một điểm cách nguồn một đoạn R là P I =
và mức cường độ âm tại điểm đó là = log I L Ben 2 4π R I0
với I là hằng số. Như vậy có thể thấy rằng R luôn tỉ lệ với − /2 10 L . Áp 0
dụng tính chất này để tính mức cường độ âm tại trung điểm M của đoạn
thẳng AB biết mức cường độ âm tại A, B lần lượt là L = L = . A 20 dB, B 60 dB
và O nằm trên đoạn thẳng AB.
Bài 5: Các nhà khoa học thực hiện nghiên cứu trên một nhóm học sinh
bằng cách cho họ xem một danh sách các loài động vật và sau đó kiểm tra
xem họ nhớ được bao nhiêu % mỗi tháng. Sau t tháng, khả năng nhớ trung
bình của nhóm học sinh tính theo công thức M (t) = 75 − 20ln(t + ) 1 ,t ≥ 0
(đợn vị %). Hỏi khoảng thời gian ngắn nhất bao lâu thì số học sinh trên nhớ
được danh sách đó dưới 10%?
Bài 6: Trong một bản hợp ca, coi mọi ca sĩ đều hát với cùng cường độ âm
và coi cùng tần số. Khi một ca sĩ hát thì mức cường độ ân là 68 dB. Khi cả
ban hợp ca cùng hát thì đo được mức cường độ âm là 80 dB. Tính số ca sĩ 6
có trong ban hợp ca đó biết mức cường độ ân L được tín theo công thức =10log I L
. Trong đó I là cường độ âm và I là cường độ âm chuẩn. I 0 0
D. BÀI TẬP TRẮC NGHIỆM Câu 1.
Cho a là số thực lớn hơn 1. Mệnh đề nào sau đây đúng?
A. Hàm số y = log x đồng biến trên . a
B. Hàm số y = log x nghịch biến trên . a
C. Hàm số y = log x đồng biến trên (0;+∞). a
D. Hàm số y = log x nghịch biến trên (0;+∞). a Câu 2.
Tìm tập xác định D của hàm số y = log ( 2
x − 2x − 3 . 2 ) A. D = (− ; ∞ − ] 1 ∪[3;+∞). B. D = [ 1; − ] 3 . C. D = (− ; ∞ − ) 1 ∪ (3;+∞) . D. D = ( 1; − 3) . Câu 3.
Tìm tất cả các giá trị thực của tham số m để hàm số y = ( 2
log x − 2mx + m) có tập xác định là .
A. m < 0 ; m >1.
B. 0 < m <1.
C. m ≤ 0 ; m ≥1.
D. 0 ≤ m ≤1. Câu 4.
Hàm số nào sau đây đồng biến trên khoảng (0;+∞)? A. y = log .x
B. y = log x e . 2 2 2
C. y = log x D. y = log π . x e . 3 4 Câu 5.
Cho hai số thực a và b , với 1< a < b . Khẳng định nào dưới đây
là khẳng định đúng ? A. log b < < a .
B. 1< log b < a . a log a 1 logb b C. log a < b < .
D. log a < < b . b 1 log b loga 1 a 7 Câu 6.
Cho các số thực dương a,b với a ≠1 và log b < . Khẳng định a 0
nào sau đây là đúng?
0 < b <1< a
0 < b <1< a A. B.
0 < a <1< b 1 < a,b
0 < a,b <1
0 < b,a <1 C. D. 1 < a,b
0 < a <1< b Câu 7.
Đường cong trong hình bên là đồ thị của một hàm số trong bốn
hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây.
Hỏi hàm số đó là hàm số nào?
A. y = log x .
B. y = log x +1 . 2 ( ) 2
C. y = log x +1.
D. y = log x +1 . 3 ( ) 3 Câu 8. Cho a, ,
b c là các số thực dương khác 1. Hình vẽ bên là đồ thị
của ba hàm số y = log x y = log x y = log x Mệnh đề nào sau c . b , a , đây đúng?
A. a < c < . b
B. a < b < .c
C. b < a < .c
D. b > a > .c Câu 9.
Cho điểm H (4;0) đường thẳng x = 4 cắt hai đồ thị hàm số
y = logx và y = logx lần lượt tại hai điểm a b , A B và sao cho
AB = 2BH . Khẳng định nào sau đây đúng ? 8 A. 3 b = a . B. 3 a = b .
C. a = 3b .
D. b = 3a .
Câu 10. Hàm số y = log x y = x a và
logb có đồ thị như hình vẽ dưới đây.
Đường thẳng y = 3 cắt hai đồ thị tại các điểm có hoành độ x , 1 x . x = 2x , 2 Biết rằng 2
1 giá trị của a bằng b 1 A. . B. 3. C. 3 2. D. 2. 3
E. HƯỚNG DẪN GIẢI
BÀI TẬP TỰ LUYỆN Bài 1: log > π 3 logπ 5 Bài 2: 9
a) y = log ( 2x −1 2 ) Điều kiện xác định: 2
x −1 > 0 ⇔ x < 1 − ∨ x > 1 .
Tập xác định là D = ( ; −∞ − ) 1 ∪(1;+∞) b) log 3x y = − 2 2 ( )
Điều kiện xác định: 3x − 2 > 0 ⇔ 3x > 2 ⇔ x > log 2. 3 .
Tập xác định là D = (log 2;+∞ . 3 ) c) 1 y = 2 − log x 3
Điều kiện xác định: 2 − log x > 0 ⇔ log x < 2 ⇔ 0 < x < 9 3 3
Tập xác định là D = (0;9) . Bài 4:
M là trung điểm AB ⇒ 2R = R + R M A B
Do R tỉ lệ với −L/2 − M L /2 10 − 30 10 2.10 10 10− ⇒ = + 10 − 30 10 +10− ⇒ L = − = dB M 2.log 20,6 2 Bài 5:
Theo đề ta có: 75 − 20ln(t + ) 1 ≤10% ⇔ ln(t + ) 1 ≥ 3,25 ⇔ t ≥ 24,79
Vậy cần ít nhất 25 tháng để số học sinh trên nhớ được danh sách đó dưới 10% Bài 6: Ta có: I I =10log I L = 68 và L = =
I = nI ⇒ n = n 10lg n 80 . n I n 1 I I 0 0 1 Gọi n là số ca sĩ. I I I 1 L − L =10log
−10log n =10log n n 1 I I I 0 0 1 n L − 1 L 80−68 In 10 10 5 6 ⇒ n = =10 =10 = 10 ≈16 I1 10
BÀI TẬP TRẮC NGHIỆM 1.C 2.C 3.B 4.B 5.D 6.A 7.D 8.B 9.A 10.C Câu 1: Chọn C. Câu 2: ChọnC. x > 3 Hàm số xác định 2
⇔ x − 2x − 3 > 0 ⇔ . x < 1 −
Vậy tập xác định của hàm số là D = (− ; ∞ − ) 1 ∪ (3;+∞) . Câu 3: ChọnB. a > 0 Ycbt 2
⇔ x − 2mx + m > 0, 0 x ∀ ∈ ⇔ ⇔ < m <1. 2
∆' = m − m < 0
Câu 4: ChọnB. Vì cơ số e a = >1. 2 Câu 5: ChọnD. log b > a ⇔ b > a loga loga 1
Ta có : b > a >1⇔ ⇔ log a < < b b 1 loga . log b > a ⇔ > a b logb 1 logb Câu 6: Chọn A. . Câu 7: Chọn D.
Dựa vào đồ thị thấy có tiệm cận đứng x = 1 − . Loại đáp án A, C
Đồ thị hàm số đi qua điểm có tọa độ (2; ) 1 Câu 8: Chọn B.
Kẻ đường thẳng y =1 cắt đồ thị các hàm số y = log x y = x y = x a , logb , logc
lần lượt tại các điểm có hoành độ x = a, x = b, x = . c
Dựa vào đồ thị ta thấy a < b < .c Câu 9: Chọn A. Ta có : 4 4
AB = 2BH ⇔ log = 3 log ⇔ logb = 3 loga a b 4 4 .
Từ đồ thị hàm số ta có b a b a 3
log = 3 log ⇒ log = 3log ⇒ b = a 4 4 4 4 . 11 Câu 10: Chọn C. Từ đồ thị, suy ra: • x x =
1 là nghiệm của phương trình log = ⇔ = b 3 nên 3 log x x b b 3 . 1 1 • x x =
2 là nghiệm của phương trình log = ⇔ = a 3 nên 3 log x x a a 3 . 2 2 3 a a Do 3 3 3 x = 2x →a = 2.b ⇔ = 2 ⇔ = 2. 2 1 b b 12 Bài 4
PHƯƠNG TRÌNH BẤT PHƯƠNG TRÌNH MŨ VÀ LOGARIT
A. TÓM TẮT LÝ THUYẾT 0 < a ≠1 • f (x) g(x) a = a ⇔ a =1 hoặc . f
( x) = g ( x)
f (x) < g (x), khi a >1 • f (x) g(x) a < a ⇔
. (các trường hợp dấu ≤ ; > ; ≥ f
( x) > g ( x), khi 0 < a <1
giải tương tự theo quy tắc so sánh hai lũy thừa cùng cơ số). 0 < a ≠1, 0 b >
• Phương trình f (x) a = b ⇔ . f ( x) = log b a • Phương trình f (x) g(x) f (x) g(x) a = b ⇔ log a = b ⇔ f x = g x b a loga ( ) ( ).loga hoặc f (x) g(x) log a = b ⇔ f x a = g x . b logb ( ).logb ( )
• Bất phương trình f (x) g(x) f (x) g(x) a < b ⇔ log a < b ⇔ f x < g x b a loga ( ) ( ).loga nếu a >1 hoặc f (x) g(x) log a > b ⇔ f x > g x
b nếu 0 < a <1. a loga ( ) ( ).loga 0 < a ≠1 • log f x = g x ⇔ . a
( ) loga ( ) f (x)= g(x)>0 g ( x) > 0
• log g x = f x < a ≠ ⇔ g x = a ⇔ . a ( ) ( ) ( 0 ) 1 loga ( ) f (x) loga g ( x) f (x) = a
f (x) > g (x) > 0, khi 0 < a <1 • log f x < g x ⇔ (các trường hợp bất a
( ) loga ( ) 0< f
(x) < g(x), khi a >1
phương trình mang dấu khác làm tương tự theo quy tắc so sánh 2 logarit cùng cơ số). g (x) > 0 g ( x) > 0
• log g x < f x < a ≠ ⇔ nếu a >1 hoặc a ( ) ( ) ( 0 )1 g f x ( x) f (x) < a g ( x) ( ) > a
nếu 0 < a <1. Các trường hợp khác làm tương tự. Chú ý: B. CÁC DẠNG TOÁN. DẠNG 1:
ĐƯA VỀ CÙNG CƠ SỐ Phương pháp:
+ Nắm vững khái niệm cơ bản
Ví dụ 1. Giải các phương trình sau: 1 2 x +2 a) 2x−3 1 27 = . 3 1 3 b) x+ x x + 2 2 2x 1 9 2 2 3 − − = − . c) log ( 2 x − x + 2 =1 2 )
d) log x +1 +1= log 3x −1 2 ( ) 2 ( ) Lời giải 2 x +2 a) Ta có: 2x−3 1 27 = 2 6x−9 − x −2 ⇔ 3 = 3 2
⇔ 6x − 9 = −x − 2 2
⇔ x + 6x − 7 = 0 3 x =1 ⇔ . x = 7 −
Vậy tập nghiệm của phương trình là {1; } 7 − . 1 3 3 1 b) Ta có x+ x+ x+ x x + 2 2 2x 1 − x 2x 1 − 2 2 9 − 2 = 2 − 3 ⇔ 9 + 3 = 2 + 2 x 1 x x x 4 9 .9 2 2.2 2.2 .9x 3 2.2x ⇔ + = + ⇔ = 3 3 9 x 9 9 ⇔ = ⇔ x = log . 9 2 2 2 2 2 2 x = 0 c) log ( 2 x − x + 2) 2
=1 ⇔ x − x + 2 = 2 ⇔ . 2 x =1
d) Điều kiện xác định 1 x > . 3
log x +1 +1= log 3x −1 ⇔ log x +1 .2 = log 3x −1 2 ( ) 2 ( ) 2 ( ) 2 ( ) . ⇔ 2(x + )
1 = 3x −1⇔ x = 3
Vậy tập nghiệm phương trình là S = { } 3 .
Ví dụ 2. Giải các bất phương trình sau: 1 3 a) 2 x 2 ≤ . 5 5 b) 2 − > ( )2 1 8 .2 2 x x x . x− c) ( )x− ( ) 1 1 x 1 5 2 5 2 + + ≥ − . d) log ( 2 13 − x ≥ 2 . 3 ) Lời giải 2 1 3 a) 2 x 2 ≤ . 5 5 Vì 2 −
<1 nên bất phương trình 1 1 3x 1 ⇔ ≥ 3 ⇔ ≥ 0 ⇔ 0 < x ≤ 5 x x 3 b) 2 − > ( )2 1 8 .2 2 x x x . Bất phương trình 2
x 1−x > ( )2x 2 2 3x 1−x x 3x 1 8 .2 2 ⇔ 2 .2
> 2 ⇔ 2 + −x > 2x 2 2
⇔ 3x +1− x > x ⇔ x − 2x −1< 0 ⇔ 1− 2 < x <1+ 2 .
Vậy tập nghiệm của bất phương trình là S = (1− 2;1+ 2). x− c) ( )x− ( ) 1 1 x 1 5 2 5 2 + + ≥ − . ( x− −x − −
5 + 2)x ≥ ( 5 − 2) 1 − + ⇔ ( 5 + 2)x + x x ≥ ( 5 + 2)1 1 1 x 1 1 1 ⇔ x −1≥ x +1 (1− x)(x + 2) x ≥1 ⇔ ≤ 0 ⇔ . x +1 2 − ≤ x < 1 − d) log ( 2 13 − x ≥ 2 . 3 ) − > < Bất phương trình ( − x ) 2 2 2 13 x 0 x 13 log 13 ≥ 2 ⇔ ⇔ 3 2 2 13 − x ≥ 9 x ≤ 4
− 13 < x < 13 ⇔ ⇔ 2 − ≤ x ≤ 2 . 2 − ≤ x ≤ 2
Vậy tập nghiệm của bất phương trình log ( 2 13 − x ≥ 2 là [ 2; − 2] . 3 ) DẠNG 2:
PHƯƠNG PHÁP ĐẶT ẨN PHỤ Phương pháp: g(x) = > g(x) f a = ( < a ≠ ) t a 0 0 0 1 ⇔ . f (t) = 0
Ta thường gặp các dạng: ● 2 f (x) f (x) . m a + . n a + p = 0 . ● f (x) f (x) . m a + . n b + p = 0 , trong đó . a b =1. Đặt f (x) t = a ( t> 0), suy ra f (x) 1 b = . t ● 2 f (x) . m a + . n ( . a b)f (x) 2 f (x) + . p b = 0 . Chia hai vế cho 2 f (x) b và đặt 3 f (x) a t = > 0 . b t = log g x a ( )
f log g x = < a ≠ ⇔ a ( ) 0 ( 0 )1 f (t) . = 0
Ví dụ 3. Giải các phương trình sau: a) 3.9x 10.3x − + 3 = 0 . b) 2 2 x +x x +x 1 4 2 + + − 3 = 0 .
c) (2 3)x (2 3)x − + + = 4. d) x x 2x 1 9 6 2 + − = . Lời giải a) 3.9x 10.3x − + 3 = 0 . Phương trình 2 3.3 x 10.3x ⇔ − + 3 = 0 . Đặt 3x
t = > 0. Phương trình trở thành 2 1
3t −10t + 3 = 0 ⇔ t = hoặc t = 3 . 3 Với 1 x 1
t = ⇒ 3 = ⇔ x = 1 − 3 3 Với = 3 ⇔ 3x t = 3 ⇔ x =1. Vậy S = { 1; − } 1 . b) 2 2 x +x x +x 1 4 2 + + − 3 = 0 .
Phương trình tương đương với 2 2
4x +x + 2.2x +x − 3 = 0 . t =1 Đặt 2 2x x t + =
, t > 0 . Phương trình trở thành 2t + 2t − 3 = 0 ⇔ . t = 3 − (l) = + x 0
Với t =1, ta được 2x x 2 2
=1 ⇔ x + x = 0 ⇔ . x = 1 −
c) (2 3)x (2 3)x − + + = 4.
Ta có: (2 3)x .(2 3)x x x − +
=1. Đặt t = ( − ) t > ⇒ ( + ) 1 2 3 , 0 2 3 = . t Phương trình trở thành: 1 2
t + = 4 ⇒ t − 4t +1 = 0 ⇔ t = 2 ± 3 . t
Với = 2 − 3 ⇒ (2 − 3)x t = 2 − 3 ⇔ x =1. Với = + ⇒ ( − )x = + ⇔ ( − )x − t = ( − ) 1 2 3 2 3 2 3 2 3 2 3 ⇔ x = 1 − . d) x x 2x 1 9 6 2 + − = . 4 2x x Phương trình x x 2x 1 + x x x 3 3 9 − 6 = 2 ⇔ 9 − 6 = 2.4 ⇔ − = 2 (∗ ) . 2 2 x Đặt 3 =
t với t > 0 , phương trình (∗) trở thành 2 t = 1 − l 2 ( )
t − t − 2 = 0 ⇔ . t = 2 x Với 3 t 2 = ⇔ = 2 ⇔ x = log 2 > 0 . 3 2 2
Ví dụ 4. Giải các phương trình sau: a) 5 log + x = . x 2 log2 2 b) 2 log 4x − log 2x = 5 . 2 ( ) ( ) 2 c) log x x = . x (125 ) 2 .log 1 25 d) 2
log x + log x +1 =1. 2 2 Lời giải a) 5 log + x = . x 2 log2 2
Điều kiện phương trình: x > 0, x ≠1. 5 1 5 + x = ⇔ + x = ⇔ x − x + = x ( )2 5 log 2 log log log log 1 0 2 2 2 2 2 log x 2 2 2 log x = 2 2 x = 4 ⇔ 1 ⇔ log x = 2 x = 2 2 Suy ra S = { 2; } 4 . b) 2 log 4x − log 2x = 5 . 2 ( ) ( ) 2
Điều kiện: x > 0.
log (4x) − log (2x) = 5 ⇔ 1+ log 2x − 2log 2x − 5 = 0 2 ( ( ))2 2 2 2 2 ( ) x = 2 log 2x = 2 . 2 2 ( ) log 2x 4 ⇔ = ⇔ ⇔ 2 ( ) 1 log 2x = 2 − x = 2 ( ) 8 c) log x x = . x (125 ) 2 .log 1 25
Điều kiện x > 0; x ≠1. 2 Ta có x x x x = ⇔ + = x ( ) 2 1 log 125 .log 1 logx125 logx log 1 25 ( ) 5 2 5 ⇔ (3.log + x = x 5 ) 2 1 log 4 5
Đặt log x = t phương trình tương đương: 5 x = 5 3 t =1 log x =1 2 2 5 1 t 4 t 3t 4 0 + = ⇔ + − = ⇔ ⇔ ⇔ 1 . t t = 4 − log x = 4 − 5 x = 625 d) 2
log x + log x +1 =1. 2 2 x > 0 x > 0 Điều kiện 1 ⇔ ⇔ x ≥ . log x +1≥ 1 0 ≥ 2 x 2 2
Đặt log x +1 = t , (t ≥ 0) 2
⇒ log x = t −1 ta có phương trình 2 2 (t − )2 2 1 + t =1 4 2
⇔ t − 2t + t = 0 ⇔ t ( 3t − 2t + )
1 = 0 ⇔ t (t − )( 2 1 t − 2t + ) 1 = 0 t = ( 0 / t m) t =1 ( / t m) ⇔ 1 − + 5 t = ( / t m) . 2 1 − − 5 t = (loai) 2 Với t = 0 thì 1 log x 1 x 2− = − ⇔ = . Với t =1 thì 0
log x = 0 ⇔ x = 2 . 2 2 1− 5 Với 1 − + 5 − t 1 5 = thì 2 log x = ⇔ x = 2 . 2 2 2
Ví dụ 5. Giải các bất phương trình sau: a) − + ( )2 1 3 2. 3 x x ≤ 7 . 2 1 1 + b) 1 x 1 3 x + > 12. 3 3
c) 6.4x 13.6x 6.9x − + > 0 . d) ( 2
3 x − 9) x 1 x 1 3 − 3 + −1 ≤ 0. 27 Lời giải a) − + ( )2 1 3 2. 3 x x ≤ 7 . Bất phương trình 3 x 2 ⇔
+ 2.3 ≤ 7 ⇔ 2.3 x − 7.3x + 3 ≤ 0 . 3x 6 Đặt 3x
t = , t > 0 . Bất phương trình trở thành 2 1
2t − 7t + 3 ≤ 0 ⇔ ≤ t ≤ 3. 2 1
⇒ ≤ 3x ≤ 3 ⇔ −log 2 ≤ x ≤1. 3 2
Vậy S = [−log 2;1 . 3 ] 2 1 1 + b) 1 x 1 3 x + > 12. 3 3 1 Đặt 1 x t =
(t > 0) . Khi đó bất phương trình đã cho trở thành 3 2
t + t >12 ⇔ (t − 3)(t + 4) > 0 ⇔ t > 3 . 1
Từ đó suy ra: 1 x 1 > 3 ⇔ < 1 − ⇔ 1 − < x < 0 . 3 x
Tập nghiệm của bất phương trình là S = ( 1; − 0).
c) 6.4x 13.6x 6.9x − + > 0 . Ta có 2 x x x 2 x 2 x 6.4 13.6 6.9 0 6. 13. − + > ⇔ − + 6 > 0 3 3 2 x 3 > 3 2 x < 1 − ⇔ ⇔ x x >1 2 2 < 3 3 d) ( 2
3 x − 9) x 1 x 1 3 − 3 + −1 ≤ 0. 27 Điều kiện x 1+ x 1 3 1 0 3 + − ≥ ⇔ ≥1 ⇔ x ≥ 1 − . Ta có x = 1
− là một nghiệm của bất phương trình. Với x x x 1 > 1
− , bất phương trình tương đương với ( 2 3 9) 3 − − ≤ 0 . 27 Đặt 3x
t = > 0 , ta có ( 2t ) 1 9 t − − ≤
0 ⇔ (t − )(t + ) 1 3 3 t − ≤ 0 27 27 t ≤ 3 − ⇔ 1 . ≤ t ≤ 3 27 Kết hợp điều kiện 3x
t = > 0 ta được nghiệm 1 ≤ t ≤ 3 27 7 1 ⇔ ≤ 3x ≤ 3 ⇔ 3 − ≤ x ≤1. 27
Ví dụ 6. Giải các bất phương trình sau: a) 2
log x − 5log x − 6 ≤ 0 . 2 2 b) 2 5 2
log x − 25log x − 75 ≤ 0 . 5 5 2 c) 16log x 3log x 2 2 − < 0 . 2
log x + 3 log x +1 2 2 d) log 5x + 2 + 2.log > . x 2 3 2 ( ) (5 +2) Lời giải a) 2
log x − 5log x − 6 ≤ 0 1 . 2 2 ( )
Điều kiện: x > 0 (*)
Đặt t = log x 2 . 2 ( ) (2) ( )1 thành 2 1
t − 5t − 6 ≤ 0 ⇔ 1
− ≤ t ≤ 6⇔−1≤ log x ≤ 6 ⇔ ≤ x ≤ 64 . 2 2 So với (*) : ( ) 1 1 ⇔ ≤ x ≤ 4 6 . Vậy 1 S ;64 = . 2 2 b) 2 5 2
log x − 25log x − 75 ≤ 0 . 5 5
Điều kiện x > 0 . 2 5 2
log x − 25log x − 75 ≤ 0 ⇔ 2
4log x − 4log x − 3 ≤ 0 5 5 5 5 ⇔ 1 3
− ≤ log x ≤ ⇔ 1 ≤ x ≤ 125 . 5 2 2 5 2 c) 16log x 3log x 2 2 − < 0 . 2
log x + 3 log x +1 2 2
Đặt t = log x . 2
Bất phương trình có dạng 3 − < < − 16t 6t t ( t − ) t 1, 2 2 1 2 − < 0 ⇔ < ⇔ 2t + 3 t +1 (2t + 3)(t + ) 0 1 1 0 < t < . 2 3 − < log x < 1 − 1 1 2 < x < Khi đó 2 ⇔ 2 2 2 . 1 0 < log x < 2 1 < x < 2 2 d) log 5x + 2 + 2.log > . x 2 3 2 ( ) (5 +2) 8
Đặt log 5x + 2 = t . Do 5x + 2 > 2 với mọi x nên log 5x + 2 > log 2 =1hay 2 ( ) 2 ( ) 2 t >1.
Bất phương trình đã cho trở thành: 2 2
t + > 3 ⇔ t − 3t + 2 > 0(do t >1) t t <1 ⇔ . t > 2
Đối chiếu với t >1ta lấy t > 2 . Khi đó log 5x + 2 > 2 ⇔ 5x > 2 ⇔ x > log 2 . 2 ( ) 5
Vậy bất phương trình có nghiệm là S = (log 2;+∞ . 5 ) DẠNG 3:
PHƯƠNG PHÁP MŨ HÓA, LOGARIT 2 VẾ Phương pháp:
Dựa vào định nghĩa logarit.
Ví dụ 7. Giải các phương trình sau: a) 2x 1+ x 1− 3 3 .25 = . 25 b) 2x x 1+ 1 3 .4 − = 0. 3x
c) log ( 2x 1− x 1 3 3 − − +1 = x . 3 ) Lời giải a) 2x 1+ x 1− 3 3 .25 = . 25 2 x 1 + Phương trình 2x+ x− 3 3 1 2 1 1 x 1 3 .25 = ⇔ = ⇔ 3 = . (*) x 1 25 3 25 − .25 25x
Lấy logarit cơ số 3 hai vế của (*) , ta được 2 x 1 ⇔ log 3 = log 3 3 25x x = 0 2 1 2 1 x xlog x xlog 0 ⇔ = ⇔ − = ⇔ . 3 3 1 25 25 x = log3 25 b) 2x x 1+ 1 3 .4 − = 0. 3x Ta có 2 x x 1 + 1 3 .4 − = 0 x(x+ ) 1 x 1 + x(x+ ) ( 1 x 1+) x(x+ ) 1 x 1 3 .4 1 log 3 .4 0 log3 log 4 + ⇔ = ⇔ = ⇔ + = 0. 3x 9 ⇔ x(x + ) 1 log3 + (x + ) 1 log 4 = 0 ⇔ ( = − x + )(x + ) x 1 1
log3 log 4 = 0 ⇔ x = − log 4 3
c) log ( 2x 1− x 1 3 3 − − +1 = x . 3 )
log ( 2x 1− x 1 3 3 − − +1 = x 2x 1 − x 1 3 3 − ⇔ − +1 = 3x 2 3 x 4.3x ⇔ − + 3 = 0 3 ) 3x = 3 x =1 ⇔ ⇔ . 3x =1 x = 0 d) .
Ví dụ 8. Giải các bất phương trình sau: a) 2 10x ex < . b) 2x−2x 1 2 − ≤ 3. Lời giải a) 2 10x ex < . Ta có 2 x x < ⇔ ( 2x )< ( x e e ) 2 10 log 10 log ⇔ x − .
x loge < 0 ⇔ x∈(0;loge) . b) 2x−2x 1 2 − ≤ 3. 2 x −2x 1 2 − ≤ 3 2
⇔ (x −1) − 2 ≤ log 3 2 ⇔ (x −1) ≤ log 12 2 2
⇔ 1− log 12 ≤ x ≤1+ log 12 . 2 2
Vậy tập nghiệm S = 1 − log 12;1+ log 12 2 2 . DẠNG 4:
PHƯƠNG PHÁP PHÂN TÍCH THÀNH NHÂN TỬ Phương pháp: A = 0 + . A B = 0 ⇔ B = 0 A > 0 A < 0 + . A B > 0 ⇔ hoặc . B > 0 B < 0 A > 0 A < 0 + . A B < 0 ⇔ hoặc . B < 0 B > 0
Ví dụ 9. Giải các phương trình sau: 2 2 2 x −4x+3 x +7x+6 2x +3x+9 5 + 5 = 5 +1. Lời giải 2 2 2 x −4x+3 x +7x+6 2x +3x+9 5 + 5 = 5 +1. 10 2 2 2 2 2 x −4x+3 x +7x+6 2x +3x+9 5 + 5 = 5 +1 2 2 x x x x
(x −4x+3)+(x +7x+ − + + + 6 4 3 7 6 ) ⇔ 5 + 5 = 5 +1. 2
a = x − 4x + 3 Đặt
, ta được phương trình: 2 b
= x + 7x + 6 5a =1 a = 0
5a + 5b = 5a+b +1
5a 5b 5a.5b ⇔ + = +1 (5a )1(1 5b ⇔ − − ) = 0 ⇔ ⇔ 5b =1 b = 0 x =1 2
x − 4x + 3 = 0 x = 3 Khi đó ⇔
. Tập nghiệm của phương trình là 2
x + 7x + 6 = 0 x = 1 − x = 6 − { 6 − ; 1; − 1; } 3 . Ví dụ 10.
Giải các bất phương trình sau:
log x + log x ≥1+ log .xlog x . 2 3 2 3 Lời giải
a) log x + log x ≥1+ log .xlog x . 2 3 2 3
Điều kiện xác định: x > 0 . Ta có:
log x + log x ≥1+ log .xlog x ⇔ log x −1 log x −1 ≤ 0 2 3 2 3 ( 2 )( 3 ) log x −1≤ 0 2 0 < x ≤ 2 log x −1≥ 0 ≥ 3 x 3 ⇔ ⇔ ⇔ 2 ≤ x ≤ 3 . log x 1 0 − ≥ x ≥ 2 2
log x −1≤ 0 0 < x ≤ 3 3
C. BÀI TẬP TỰ LUYỆN.
Bài 1: Giải các phương trình sau: a) 2 2x −5x+3 2 =1 b) log x −1 = 2 3 ( ) c) log x = log ( 2 x − x . 2 2 )
d) log x + log (x −1) =1 2 2 e) 2x x 1+ 1 3 .4 − = 0. 3x f) 2 2 ( )1 8 8 5 2 .5 0,01. 10 x x x − − − = .
g) (7 4 3)x (2 3)x + + + = 6 . h) 3+3x 3−3x 4+x 4−x 3 3 + 3 + 3 + 3 =10 .
Bài 2: Giải các bất phương trình sau 11 a) 2x 1+ 3 3 > 3 −x . b) log 2x −1 ≥ 0 . 0,5 ( ) 2 x −4x c) 1 < 8 . 2
d) 3log x −1 + log 2x −1 ≤ 3. 3 ( ) 3 ( ) 3
e) log (log ( 2x −1 ≤ 1 − . 1 2 ) 2 f) 1 log > log x − 7 . 1 2 2 ( ) x + 4x − 5 2 2 2 g) 2 2x 2 log − − log x x x − < 2 . 3 1 3 3 3 h) log (log 9x − ≤ . x 72 1 3 ( )
Bài 3: Tìm tất cả các giá trị thực của tham số m để các bất phương trình sau
nghiệm đúng với mọi x∈ . 2 x +2mx 1 + 2x−3m a) 2 e ≤ e 2 b) ( 2 x + ) > ( 2 ln 2 3 ln x + ax + ) 1 .
Bài 4: Tìm m để phương trình log 2018x + m = log 1009x có nghiệm. 6 ( ) 4 ( )
Bài 5: Tìm tham số m để phương trình x x+3 2
4 + 7 = 2 + m + 6m có nghiệm x∈(1;3) .
Bài 6: Tìm giá trị nguyên dương của tham số m để bất phương trình 2 2 x −3x+m
x −3x+m −2+x 2x−3 9 + 2.3 < 3 có nghiệm
Bài 7: Cho bất phương trình: 9x + ( − ) 1 .3x m + m > 0 ( )
1 . Tìm tất cả các giá trị
của tham số m để bất phương trình ( ) 1 nghiệm đúng x ∀ ≥1.
D. BÀI TẬP TRẮC NGHIỆM
Câu 1: Tổng các nghiệm thực của phương trình 2x−3x+8 2x 1 3 9 − = bằng A) 7 − . B) 5 . C) 6 . D) 7 .
Câu 2: Nghiệm của phương trình log x +1 =1− log x − 5 là 7 ( ) 7 ( ) A) x = 6 . B) x = 2 − . C) x = 2, −
x = 6 . D) x =12 .
Câu 3: Phương trình log ( 2
x − 2 + log 5x − 8 = 0 có hai nghiệm x , x . 2 ) 1 ( ) 1 2 2
Tổng P = x + x là 1 2 A) 3 . B) 0 . C) 6 . D) 5 . 12 x 1 +
Câu 4: Nghiệm của phương trình 1 2 = 125 x là 25 A) 1 − . B) 1. C) 1 − . D) 4 . 8 4 3x 1 −
Câu 5: Phương trình 2x−4 1 3 =
có hai nghiệm x , x . Tính x x . 9 1 2 1 2 A) 2 − . B) 5 − . C) 6 . D) 6 − .
Câu 6: Tổng tất cả các nghiệm thực của phương trình
log .xlog 32x + 4 = 0 bằng 2 2 ( ) A) 7 . B) 9 . C) 1 . D) 1 . 16 16 32 2
Câu 7: Số nghiệm thực của phương trình 1−x 3 4 − −1− 0 là 2x A) 0 . B) 1. C) 3 . D) 2 .
Câu 8: Số nghiệm thực của phương trình 3log (2x − )
1 − log (x − 5)3 = 3 3 1 3 A) 3 . B) 1. C) 2 . D) 0 .
Câu 9: Tổng các nghiệm của phương trình 2
log 3x + log 9x − 7 = 0 bằng 3 ( ) 3 ( ) A) 84 . B) 28 . C) 244 . D) 244 . 81 81 3
Câu 10: Tổng các nghiệm của phương trình log 7 − 3x = 2 − x là 3 ( ) A) 3 . B) 7 . C) 1. D) 2 .
Câu 11: Gọi a b (
, a < b) là các nghiệm của phương trình x x 1 + x 1 6 6 2 3 + + = + . Tính giá trị của 3a 2b P = + . A) 17 . B) 7 . C) 31. D) 5 .
Câu 12: Tìm m để phương trình 2
log x − m + 3 log x + 3m −1 = 0 có 2 3 ( ) 3
nghiệm x , x sao cho x .x = 27. 1 2 1 2 A) m =1.. B) 4 m = . . C) m = 25.. D) 28 m = .. 3 3
Câu 13: Có bao nhiêu giá trị nguyên của tham số m để phương trình
9x − (2 − 2)3x m
− m + 4 = 0 có hai nghiệm phân biệt A) 3 . B) 1. C) 2 . D) Vô số.
Câu 14: Biết rằng tập hợp tất cả các giá trị thực của tham số m để
phương trình (2 + 3)x + (2 − 3)x m
=1 có hai nghiệm phân biệt là khoảng ( ;
a b) . Tính T = 3a + 8b . A) T = 5 . B) T = 7 . C) T = 2 . D) T =1. 13 2 x −3x−2
Câu 15: Tập nghiệm của bất phương trình 1 ≥ 4 là 2 A) (− ; ∞ 0]∪[3;+∞) . B) (− ;0 ∞ ] . C) [3;+∞) . D) [0; ] 3 .
Câu 16: Tập nghiệm của bất phương trình log ( 2
x − 3x + 2 + log x −1 ≤1 3 ) 1 ( ) 3 là
A) S = (2;+ ∞) . B) S = (2;5]. C) S = [1;5] .
D) S = (1;+ ∞) . Câu 17: Số nghiệm nguyên của bất phương trình log (x − ) 1 + log (11− 2x) ≥ 0 là 2− 3 2+ 3 A) 2 . B) 3 . C) 4 . D) 1.
Câu 18: Cho bất phương trình log ( 2
x − x − 2 ≥ log x −1 +1, tìm số 2 ) 0,5 ( )
nghiệm nguyên thuộc đoạn [0; ] 2021 . A) 2020 . B) 2019 . C) 2018 . D) 2021.
Câu 19: Gọi S là tập tất hợp tất cả các nghiệm nguyên dương thỏa mãn
bất phương trình 2x−5x 12 2 +
− 4096 < 0 . Tính tổng tất cả các giá trị nghiệm đó A) 14 . B) 12 . C) 10 . D) 8 .
Câu 20: Biết tập nghiệm của bất phương trình 2.9x 5.6x 3.4x − + < 0 là
( ;ab), với a,b∈. Tìm a + 3 .b A) 1. B) 2 . C) 3 . D) 4 .
Câu 21: Số nghiệm nguyên của bất phương trình 2
4log x − log x +1≤ 0 là 4 2 2 A) 3 . B) Vô số. C) 2 . D) 1. Câu 22: Biết rằng tập nghiệm của bất phương trình
(3 5)x (3 5)x 3.2x + + − < là khoảng ( ;
a b) , hãy tính S = b − a A) S = 2 . B) S = 3. C) S =1. D) S = 4 .
Câu 23: Tập nghiệm của bất phương trình log 2x +1 > 1 − là 1 ( ) 2 A) 1 1 ; − . B) 1 − ; ∞ . C) 1 ;+∞ . D) 1 1 − ; . 2 2 2 2 2 2
Câu 24: Tập nghiệm của bất phương trình 1− 2 log
x > 0 có dạng ( ;ab). 1 x 3
Tính T = 3a − 2b . A) T = 0 . B) T = 1 − . C) T =1. D) 2 T = − . 3 14
Câu 25: Có bao nhiêu số nguyên dương y sao cho ứng với mỗi y có tối
thiểu một số nguyên x và không quá 3 số nguyên x thỏa mãn
2x − 4.(5x − y) < 0 A) 15501. B) 78000 . C) 15600 . D) 15500 . Câu 26: Số nghiệm nguyên của bất phương trình 2 2 2x 15 − x 100 + x 10 + x−50 2 2 − 2
+ x − 25x +150 < 0 là A) 6 . B) 3 . C) 5 . D) 4 .
Câu 27: Có bao nhiêu số nguyên dương y sao cho ứng với mỗi y có
nhiều nhất 10 số nguyên x thỏa mãn ( x+4 3 − )
1 (3x − y − ) 1 < 0 ? A) 2187 . B) 59048 . C) 59049 . D) 2186 .
Câu 28: Có bao nhiêu giá trị nguyên của m để bất phương trình 2
log x + mlog x ≥ m nghiệm đúng với mọi giá trị của x∈(0;+∞) . 3 3 A) 5 . B) 6 . C) 4 . D) 7 .
Câu 29: Gọi E là tập hợp tất cả các số nguyên dương y sao cho ứng với
mỗi số y có không quá 4031 số nguyên x thỏa mãn 2 2
log x − 3ylog x + 2y < 0 . Tập E có bao nhiêu phần tử? 2 2 A) 6 . B) 5 . C) 8 . D) 4 .
E. HƯỚNG DẪN GIẢI
BÀI TẬP TỰ LUYỆN
Bài 1: Giải các phương trình sau: a) 2 2x −5x+3 2 =1 x =1 Ta có 2 2x −5x+3 2 =1 2 2x −5x+3 0 ⇔ 2 = 2 2
⇔ 2x − 5x + 3 = 0 ⇔ 3 . x = 2 b) log x −1 = 2 3 ( )
Điều kiện x −1> 0 ⇔ x >1
Ta có log x −1 = 2 ⇔ x −1= 9 ⇔ x =10 (thỏa mãn điều kiện) 3 ( )
Vậy tập nghiệm của phương trình đã cho là S = { } 10 . c) log x = log ( 2 x − x . 2 2 ) 15 x > 0 x > 0 x > 0 Điều kiện ⇔ ⇔ ⇔ x >1. 2
x − x > 0 x ( x − ) 1 > 0 x −1 > 0 x = 0 Ta có log x = log ( 2 x − x 2
⇔ x = x − x 2
⇔ x − 2x = 0 ⇔ . 2 2 ) x = 2
Đối chiếu điều kiện, phương trình có tập nghiệm là S = { } 2 .
d) log x + log (x −1) =1 2 2 x > 0 Điều kiện ⇔ x >1 x −1 > 0
Ta có log x + log (x −1) =1 ⇔ log x x −1 =1 ⇔ x − x = 2
⇔ x − x − 2 = 0 2 ( ) 2 2 2 2 x = 1 − ⇔ x = 2
Đối chiếu điều kiện, phương trình có tập nghiệm là S = { } 2 . e) 2x x 1+ 1 3 .4 − = 0. 3x Ta có: 2x x+ 1 2 3 .4 −
= 0 ⇔ 3x .4x+ = 3−x ⇔ log ( 2 1 1 x x 1 3 .4 + = log 3−x . x 3 ) 3 3 2 ⇔ x + (x + ) 2
1 log 4 = −x ⇔ x + 1+ log 4 x + log 4 = 0 * . 3 ( 3 ) 3 ( )
Do đó T = x x + x + x = − 1+ log 4 + log 4 = 1. − 1 2 1 2 ( 3 ) 3 f) 2 2 ( )1 8 8 5 2 .5 0,01. 10 x x x − − − = . ( ) 2 9− 5−5x − = 2 8 x 10 .10 8−x 2−5x 2 2.5 ⇔ 10 =10
⇔ 8 − x = 2 − 5x ⇔ x = 1 − ; x = 6
g) (7 4 3)x (2 3)x + + + = 6 . (7 4 3)x (2 3)x + + + = 6 ( ) 1 x 2 ( ) ( )2 1 2 3 (2 3)x 6 0 (2 3)x (2 3)x ⇔ + + + − = + + + − 6 = 0 (2) Đặt (2 3)x t = + > 0 Khi đó: ( t = n 2) 2 2 ( )
⇔ t + t − 6 = 0 ⇔ t = 3 − (l) Với = 2 ⇔ (2 + 3)x t = 2 ⇔ x = log( 2 . 2+ 3) h) 3+3x 3−3x 4+x 4−x 3 3 + 3 + 3 + 3 =10 . 3+3x 3−3x 4+x 4−x 3 3 + 3 + 3 + 3 =10 ( ) 1 16 ( ) 3x 27 x 81 3 3x 1 x 1 3 1 ⇔ 27.3 + + 81.3 + =10 ⇔ 27. 3 + + 81. 3 + = 10 2 3x x 3x x ( ) 3 3 3 3 Cosi Đặt x 1 x 1 t = 3 + ≥ 2 3 . = 2 3x 3x 3 3 x 1 3x 2x 1 x 1 1 3x 1 3 ⇒ t = 3 + = 3 + 3.3 . + 3.3 . + ⇔ 3 + = t − 3t x x 2x 3x 3 3 3 3 3 3 x 3 Khi đó:( ) 3 3 3 10 10
2 ⇔ 27(t − 3t) + 81t =10 ⇔ t = ⇔ t = > 2 (n) 27 3 Với 10 x 1 10 t = => 3 + = x (3) 3 3 3 y = 3 (n) Đặt 3x
y = > 0 . Khi đó: (3) 1 10 2 y 3y 10y 3 0 ⇔ + = ⇔ − + = ⇔ 1 y 3 y = (n) 3 Với = 3 ⇒ 3x y = 3 ⇔ x =1 Với 1 x 1
y = ⇒ 3 = ⇔ x = 1 − . 3 3
Bài 2: Giải các bất phương trình sau a) 2x 1+ 3 3 > 3 −x . 2x 1 + 3−x 2 3
> 3 ⇔ 2x +1 > 3 − x ⇔ 3x > 2 ⇔ x > . 3 b) log 2x −1 ≥ 0 . 0,5 ( ) Điều kiện: 1
2x −1> 0 ⇔ x > (*) . 2 log (2x − )
1 ≥ 0 ⇔ 2x −1≤ (0,5)0 ⇔ 2x ≤ 2 ⇔ x ≤1. 0,5
Giao với điều kiện (*) suy ra bất phương trình đã cho có tập nghiệm là 1 S ;1 = . 2 2 x −4x c) 1 < 8 . 2 Ta có 2 2 x −4x x −4x 3 1 1 1 − 8 < ⇔ < 2 2 2 . x <1 2 2
⇔ x − 4x > 3
− ⇔ x − 4x + 3 > 0 ⇔ x >3
Vậy tập nghiệm của bất phương trình là S = (− ; ∞ ) 1 ∪ (3;+∞) . 17
d) 3log x −1 + log 2x −1 ≤ 3. 3 ( ) 3 ( ) 3 x >1 x −1 > 0 Điều kiện: ⇔ 1 ⇔ x >1 (*). 2x −1 > 0 x > 2 3log x −1 + log
2x −1 ≤ 3 ⇔ 3log x −1 + 3log 2x −1 ≤ 3 3 ( ) 3 ( ) 3 3 ( ) 3 ( )
⇔ log x −1 + log 2x −1 ≤1 ⇔ log x −1 2x −1 ≤1 3 ( ) 3 ( ) 3 ( )( ) ( −
⇔ x − )( x − ) 2 1
1 2 1 ≤ 3 ⇔ 2x − 3x − 2 ≤ 0 ⇔ ≤ x ≤ 2 . 2
So điều kiện (*) suy ra bất phương trình có tập nghiệm là S = (1;2] .
e) log (log ( 2x −1 ≤ 1 − . 1 2 ) 2
log ( 2x −1 > 0 2 ) Điều kiện: 2
⇔ x −1 >1 ⇔ x∈(− ; ∞ − 2) ∪( 2;+ ∞) . 2 x −1> 0 ( ( − x ) (x ) 1 2 2 1 log log 1 1 log 1 − ≤ − ⇔ − ≥ = 2 ⇔ ( 2 x −1 ≥ 4 1 2 2 ) 2 2 2
⇔ x ≥ 5 ⇔ x∈(− ; ∞ − 5 ∪ 5;+ ∞ ).
Giao với điều kiện, bất phương trình có tập nghiệm là S = (− ; ∞ − 5 ∪ 5;+ ∞ ). f) 1 log > log x − 7 . 1 2 2 ( ) x + 4x − 5 2 Ta có: 1 log
> log x −7 ⇔ log x + 4x −5 > log x − 7 2 ( ) ( 2 1 2 2 ) 2 ( ) x + 4x − 5 2 x > 7 . x − 7 > 0 x > 7 ⇔ ⇔ ⇔ x < 2 − ⇔ x > 7 2 2
x + 4x − 5 > x − 7
x + 3x + 2 > 0 x > 1 − 2 2 g) 2 2x 2 log − − log x x x − < 2 . 3 1 3 3 3 18 2 2 2 2x 2 log − − log x x x − < 2 3 1 3 3 3 2 2x x − > 0 3 ⇔ 2 2 1 − < log x x − < 2 3 3 3 0 < x < 2 1 ⇔ ⇔ < x <1 1 2 < x <1 2 h) log (log 9x − ≤ . x 72 1 3 ( )
Ta có: log (log (9x − ≤ x 72) 1 3 ) 9x − 72 > 0 0 < x ≠ 1 9x > 73 ⇔ ⇔
log (9x − 72) > 0 x 3
log (9 − 72) ≤ x 3 log (9x − 72) ≤ x 3 x > log 73 9 ⇔ ⇔ log 73 < x ≤ 2 9 x ≤ 2
Bài 3: Tìm tất cả các giá trị thực của tham số m để các bất phương trình sau
nghiệm đúng với mọi x∈ . 2 x +2mx 1 + 2x−3m a) 2 e ≤ e 2 2 2 x +2mx 1 + 2x−3m x +2mx 1 + 2 − x+3 2 e 2 2 m 2 ≤ ⇔ ≤
⇔ x + 2mx +1≥ 2 − x + 3m e 2 e e 2 ⇔ x + 2(m + )
1 x +1− 3m ≥ 0 (∗) .
Bất phương trình có nghiệm đúng với mọi x∈ khi và chỉ khi bất phương
trình (∗) có nghiệm đúng với mọi x∈ . 2 ∆′ ≤ 0
m + 5m ≤ 0 ⇔ ⇔ ⇔ m∈[ 5 − ; 0]. a > 0 1 > 0 (ld) Vậy m∈[ 5
− ; 0] thỏa yêu cầu bài toán. b) ( 2 x + ) > ( 2 ln 2 3 ln x + ax + ) 1 . 19
x + ax + >
ln(2x + 3) > ln(x + ax + ) 2 1 0 2 2 1 , x ∀ ∈ ⇔ , x ∀ ∈ 2 2
2x + 3 > x + ax +1 x + ax +1> 0 ( ) 2 2 1 ∆
( ) = a − 4 < 0 1 ⇔ , x ∀ ∈ ⇔ ⇔ 2 − < a < 2 . 2
x − ax + 2 > 0 (2) 2 ∆ ( = a − 8 < 0 2)
Bài 4: Tìm m để phương trình log 2018x + m = log 1009x có nghiệm. 6 ( ) 4 ( )
2018x + m = 6t
Đặt log 2018x + m = log 1009x = t ⇒ ⇒ 2.4t + = 6t m 6 ( ) 4 ( ) 1009 x = 4t ⇔ = 2. − 4t + 6t m . Đặt ( ) 2.4t 6t f t = −
+ . Ta có: ′( ) = 6t ln 6 − 2.4t f t .ln 4 . t Xét f ′(t) 3 2ln 4 = 0 ⇒ = =
log 16 ⇔ t = log log 16 . 3 ( 6 ) 6 2 ln 6 2 Bảng biến thiên: Phương trình
f (t) = m có nghiệm khi và chỉ khi
m ≥ f log log 16 ≈ 2 − ,01. 3 ( 6 ) 2
Bài 5: Tìm tham số m để phương trình x x+3 2
4 + 7 = 2 + m + 6m có nghiệm x∈(1;3) . Ta có: x x+3 2 x x 2
4 + 7 = 2 + m + 6m ⇔ 4 − 8.2 = m + 6m − 7 ( )1.
Đặt 2x = t , với x∈(1;3) thì t ∈(2;8) .
Phương trình đã cho trở thành 2 2
t − 8t = m + 6m − 7 (2) .
Xét hàm số f (t) 2
= t − 8t,t ∈(2;8) .
Ta có f ′(t) = 2t −8 ; f ′(t) = 0 ⇔ t = 4∈(2;8) . Lại có f (2) = 12 − ; f (4) f (8) = 16 − ; = 0 .
Mà hàm f (t) xác định và liên tục trên t∈(2;8) nên 16
− ≤ f (t) < 0 .
Do đó phương trình (2) có nghiệm trên t ∈(2;8) 2 ⇔ 16
− ≤ m + 6m − 7 < 0 ⇔ 7 − < m <1.
Bài 6: Tìm giá trị nguyên dương của tham số m để bất phương trình 2 2 x −3x+m
x −3x+m −2+x 2x−3 9 + 2.3 < 3 có nghiệm Điều kiện 2
x − 3x + m ≥ 0 . 20 2 2 2 x − x+m
x − x+m − +x x− x − x+m 2 2 3 3 2 2 3 2 3
x −3x+m +x 1 2 9 + 2.3 < 3 ⇔ 3 + .3 < .3 x 9 27 Vì 2 3 x > 0, x
∀ ∈ nên chia 2 vế bất phương trình cho 2 3 x , ta được: 2 2
2 x −3x+m x −3 3 2 3 x+m +x 1 2
x − x+m − x 2 2 2 3 2
x −3x+m −x 1 ⇔ + . < ⇔ 3 + .3 − < 0 2x 2 3 9 3 x 27 9 27
( 2x− x+m−x) 2 2 3 2 2
x −3x+m −x 1 ⇔ + −
< ⇔ ( 2x−3x+m−x ) 2 2x−3x+m−x 1 3 .3 0 3 + .3 − < 0 9 27 9 27 Đặt 2 3 3 x x m x t − + − =
(điều kiện: t > 0 ), bất phương trình trở thành: 2 2 1 1 1 t + t −
< 0 ⇔ − < t < 9 27 3 9 So điều kiện, ta có: 1 2
x −3x+m −x 1 2 − 2 0 < t < ⇔ 3
< = 3 ⇔ x − 3x + m − x < 2 − 9 9 2 2
x − 3x + m ≥ 0
x − 3x + m ≥ 0 2 x 3x m x 2 x 2 0 ⇔ − + < − ⇔ − > ⇔ x > 2
⇒ 4 − m > 2 ⇔ m < 2 2
x − 3x + m < x − 4x + 4
x < 4 − m .
Do m nguyên dương nên m =1 thỏa mãn.
Thử lại ta có m =1 thỏa yêu cầu bài toán.
Bài 7: Cho bất phương trình: 9x + ( − ) 1 .3x m + m > 0 ( )
1 . Tìm tất cả các giá trị
của tham số m để bất phương trình ( ) 1 nghiệm đúng x ∀ ≥1. Đặt 3x
t = . Vì x ≥1⇒ t ≥ 3 Bất phương trình đã cho thành: 2 t + (m − )
1 .t + m > 0 nghiệm đúng t ∀ ≥ 3 2 t − t ⇔
> −m nghiệm đúng t ∀ ≥ 3. t +1
Xét hàm số g (t) 2 = t − + t ∀ ≥ g (t) 2 2 , 3, ' =1− > 0, t ∀ ≥ 3. Hàm số t +1 (t + )2 1
đồng biến trên [3;+∞) và g ( ) 3
3 = . Yêu cầu bài toán tương đương 2 3 3
−m ≤ ⇔ m ≥ − 2 2
BÀI TẬP TRẮC NGHIỆM 1.D 2.A 3.D 4.C 5.D 6.B 7.B 8.B 9.C 10.D
11.D 12.A 13.B 14.C 15.A 16.D 17.B 18.B 19.B 20.C
21.C 22.A 23.A 24.D 25.A 26.D 27.D 28.D 29.A 30.A 21 Câu 1: Chọn D 2 x −3x+8 2x 1 3 9 − = 2 x −3x+8 2(2 − ) 1 ⇔ 3 = 3 x 2
⇔ x − 3x + 8 = 4x − 2 2
⇔ x − 7x +10 = 0 x = 2 ⇔
. Vậy tổng hai nghiệm của phương trình là 7. x = 5 Câu 2: Chọn A x +1 > 0 x > 1 − Điều kiện ⇔ ⇔ x > 5 . x − 5 > 0 x > 5
log x +1 =1− log x − 5 7 ( ) 7 ( )
⇔ log x +1 + log x − 5 =1 7 ( ) 7 ( )
⇔ log x +1 x − 5 =1 7 ( )( ) ⇔ (x + ) 1 (x − 5) = 7 2
⇔ x − 4x −12 = 0 x = 6 ⇔ x = 2−
So với điều kiện, phương trình đã cho có 1 nghiệm x = 6 . Câu 3: Chọn D x > 2 2
Điều kiện x − 2 > 0 ⇔ x < − 2 8 ⇔ x > . 5 x − 8 > 0 5 8 x > 5
Với điều kiện trên ta có phương trình log ( 2
x − 2 + log 5x − 8 = 0 2 ) 1 ( ) 2 ⇔ log ( 2
x − 2 − log 5x − 8 = 0 2 ) 2 ( ) ⇔ log ( 2
x − 2 = log 5x − 8 2 ) 2 ( ) x = 2 2 2
⇔ x − 2 = 5x − 8 ⇔ x − 5x + 6 = 0 ⇔
(Thoả mãn điều kiện trên). x = 3
Vậy tổng P = x + x = 2 + 3 = 5 . 1 2 Câu 4: Chọn C x 1 +
Ta có: 1 =125 ⇔ (5− )(x+ )1 = (5 )2 2 2 3 x x . 25 22 2 − x−2 6x 1 ⇔ 5 = 5 ⇔ 2
− x − 2 = 6x ⇔ x = − . 4
Câu 5: Chọn D 3x 1− Ta có 2x− 1 2 4 x −4 6 − x+2 2 2 3 = ⇔ 3 = 3 ⇔ x − 4 = 6
− x + 2 ⇔ x + 6x − 6 = 0 9
Do ∆ = 36 + 4.6 = 60 > 0 nên phương trình đã cho có 2 nghiệm x , x . 1 2
Theo hệ thức Vi-ét x x = 6 − . 1 2 Câu 6: Chọn B
Điều kiện xác định: x > 0 . Khi đó
log .xlog 32x + 4 = 0 ⇔ log .
x log x + 5 + 4 = 0 2 ( 2 ) 2 2 ( ) 1 log = 1 x x = − 2
⇔ log x + 5.log x + 4 = 0 2 2 ⇔ ⇔ . 2 2 log x = 4 − 1 2 x = 16
Do đó tổng tất cả các nghiệm của phương trình đã cho bằng 9 . 16 Câu 7: Chọn B Ta có: 1− 3 4 3 4 x − −1 = 0 ⇔ − − 1 = 0 x 2 2 2 x 2x x = 2x x 2 1 ⇔ 2 + 3.2 − 4 = 0 ⇔
⇒ 2x =1⇒ x = 0 . 2x = 4 − Câu 8: Chọn B 2x −1 > 0
Điều kiện xác định: ⇔ x > 5 x − 5 > 0
Với điều kiện trên phương trình tương đương:
log 2x −1 + log x − 5 =1 ⇔ log 2x −1 . x − 5 =1 3 ( ) ( ) 3 ( ) 3 ( ) ⇔ (2x − ) 1 .(x − 5) = 3 2
⇔ 2x −11x + 5 = 3 11− 105 x = (tm) 4 ⇔
. Vậy phương trình có 1 nghiệm thực. 11+ 105 x = (ktm) 4 Câu 9: Chọn C Xét phương trình 2
log 3x + log 9x − 7 = 0 1 3 ( ) 3 ( ) ( )
ĐK: x > 0 . Phương trình 23 ( ) 2
1 ⇔ log 3x + log 3x + log 3 − 7 = 0 3 ( ) 3 ( ) 3 . 2
⇔ log 3x + log 3x − 6 = 0 3 ( ) 3 ( )
Đặt t = log 3x 3 ( ) t = 3 − log 3x = 3 − 3 ( ) Phương trình ( )
1 trở thành 2t + t − 6 = 0 ⇔ hoặc t = 2 log 3x = 2 3 ( ) 3 − 1 3x = 3 x = ⇔ ⇔ 81 2 (thỏa mãn) . 3x 3 = x = 3 1 244
Tổng các nghiệm của phương trình (1) là + 3 = 81 81 . Câu 10: Chọn D Ta có: ( x − ) 2 x 2−x x 3
log 7 3 = 2 − x ⇔ 7 − 3 = 3 ⇔ 7 − 3 = . 3 3x + x 7 13 7 + 13 3 = > 0 x = log3 2x x 2 2 ⇔ 3 − + 7.3 − 9 = 0 ⇔ ⇔ . − x 7 13 7 − 13 3 = > 0 x = log3 2 2 + − + − Khi đó 7 13 7 13 7 13 7 13 2 log + log = log . = log 3 = 2 . 3 3 3 3 2 2 2 2
Vậy tổng các nghiệm của phương trình đã cho là 2. Câu 11: Chọn D x x 1 + x 1 6 6 2 3 + + = + x x x 1 + x 1 2 .3 2 3 + ⇔ − − + 6 = 0
2x (3x 2) 3(3x ⇔ − − − 2) = 0 ( 3x − 2 = 0 3x = 2 x = log 2 3x 2)(2x ⇔ − − 3) = 0 ⇔ ⇔ 3 ⇔ . 2x − 3 = 0 2x = 3 x = log 3 2
Vì a < b nên a = log 2, lo b = g 3 . 3 2 Vậy a b log3 2 log2 3 P = 3 + 2 = 3 + 2 = 2 + 3 = 5 . Câu 12: Chọn A
Đặt t = log x 3
Phương trình trở thành : 2t − (m + 2)t + 3m −1= 0
Phương trình có hai nghiệm ⇔ ∆ ≥ 0
⇔ (m + 2)2 − 4(3m − ) 1 ≥ 0 2
⇔ m − 8m + 8 ≥ 0 m ≥ 4 + 2 2
⇔ m≤4−2 2 24 x .x = 27 1 2 1 t t2 ⇔ 3 .3 = 27 1 t +t2 ⇔ 3 = 27 m+2 ⇔ 3 = 27 (Vi − et) ⇔ m + 2 = log 27 3 ⇔ m =1(nhận). Câu 13: Chọn B Đặt = 3x t
(t > 0) . Phương trình 9x −(2 − 2)3x m
− m + 4 = 0 có hai nghiệm
phân biệt khi và chỉ khi phương trình 2t − (2m − 2)t − m + 4 = 0 có hai
nghiệm dương phân biệt. ∆ = (m − )2 2 ' 1 + m − 4 > 0
m − m − 3 > 0
⇔ S = 2m − 2 > 0 ⇔ m >1 P m 4 0 = − + > m < 4 1− 13 m < 2 1+ 13 m > 2 1+ 13 ⇔ ⇔ < m < 4 2 m >1 m < 4
Vậy có một giá trị nguyên của m là 3 thỏa mãn yêu cầu đề bài. Câu 14: Chọn C
Đặt (2 + 3)x = t , (t > 0) ⇒ ( − ) 1 2 3 x = . t Phương trình trở thành m 2
t + =1 ⇔ t − t + m = 0 (*) . t
Phương trình đã cho có hai nghiệm phân biệt khi và chỉ khi (*) có 2 ∆ =1− 4m > 0 nghiệm dương phân biệt 1 ⇔ t
+ t =1 > 0 ⇔ 0 < m < . 1 2 4 t .t = m > 0 1 2 Do đó 1
a = 0;b = ⇒ T = 3a + 8b = 2 . 4 Câu 15: Chọn D 25 2 x −3x−2 2 x −3x−2 2 − Ta có: 1 ≥ 1 1 4 ⇔ ≥ 2 2 2 2
⇔ x − 3x − 2 ≤ 2 − 2
⇔ x − 3x ≤ 0 ⇔ 0 ≤ x ≤ 3 . Câu 16: Chọn B Ta có log ( 2
x − 3x + 2 + log x −1 ≤1 3 ) 1 ( ) 3 ⇔ log ( 2
x − 3x + 2 − log x −1 ≤ log 3 3 ) 3 ( ) 3 ⇔ log ( 2
x − 3x + 2 ≤ log 3 x −1 3 ) 3 ( ) 2
x − 3x + 2 > 0 2
⇔ 0 < x − 3x + 2 ≤ 3(x − ) 1 ⇔ 2
x − 6x + 5 ≤ 0 x <1
⇔ x > 2 ⇔ 2 < x ≤ 5. 1 ≤ x ≤ 5
Vậy bất phương trình đã cho có tập nghiệm S = (2;5].
Câu 17: Chọn B Điều kiện 11 1< x < . Ta có log (x − ) 1 + log (11− 2x) ≥ 0 2 2− 3 2+ 3 ⇔ (x − ) 1 log 1 + log ≥ 0 2− 3 2− 3 11− 2x x −1 log ⇔ ≥ 0 2− 3 11− 2x x −1 ⇔ ≤1 11− 2x x ≤ 4 3x −12 0 ⇔ ≤ ⇔ 11 11− 2x x > 2
Kết hợp điều kiện suy ra 1< x ≤ 4
Vậy bất phương trình có 3 nghiệm nguyên . Câu 18: Chọn B 26 log ( 2
x − x − 2 ≥ log x −1 +1 2 ) 0,5 ( ) ⇔ log ( 2
x − x − 2 ≥ log x −1 +1 2 ) 1 ( ) 2 ⇔ log ( 2
x − x − 2 + log x −1 ≥1 2 ) 2 ( )
⇔ log ( 2x − x − 2 . x −1 ≥1 2 ) ( ) 2
x − x − 2 > 0 ⇔ x −1> 0
( 2x − x −2 )(x − )1 ≥ 2 2
x − x − 2 > 0 ⇔ x −1> 0 3 2
x − 2x − x ≥ 0 x < 1 − x > 2 ⇔ x >1 1− 2 ≤ x ≤ 0 x ≥1+ 2 ⇔ x ≥1+ 2
Vì x là số nguyên và thuộc đoạn [0; ]
2021 nên x∈{3;4;....; } 2021 .
Vậy có 2019 giá trị . Câu 19: Chọn C Ta có 2 2 x −5x 12 2 + − 4096 < 0 x −5x 12 2 + ⇔ < 4096 2 x −5x 12 + 12 ⇔ 2 < 2 2
⇔ x − 5x +12 <12 2
⇔ x − 5x < 0 ⇔ 0 < x < 5 .
Do x nguyên dương nên x∈{1;2;3 }
;4 , suy ra S = {1;2;3 } ;4 . Vậy tổng tất cả
các giá trị của S là 1+ 2 + 3 + 4 =10. Câu 20: Chọn C Ta có:
2.9x − 5.6x + 3.4x < 0 9 x 3 x 2. 5. ⇔ − + 3 < 0 . 4 2 3 x 3 ⇔ 1< < ⇔ 0 < x < 1 2 2
Vậy tập nghiệm bất phương trình là S = (0; )
1 suy ra a = 0; b =1⇒ a + 3b = 3 27 Câu 21: Chọn A TXĐ: D = (0;+∞) . Ta có 2
4log x − log x +1≤ 0 4 2 2 1 2
⇔ 4. log x − log x +1≤ 0 . 2 2 4 2 ⇔ (log x − )2 1 − log x +1≤ 0 2 2
Đặt t = log x , ta được: (t − )2 2
1 − t +1≤ 0 ⇔ t − 3t + 2 ≤ 0 ⇔ 1≤ t ≤ 2 . 2
Suy ra 1≤ log x ≤ 2 ⇔ 2 ≤ x ≤ 4 (Thỏa mãn ĐKXĐ). 2
Vậy bất phương trình có 3 nghiệm nguyên x = 2, x = 3, x = 4 . Câu 22: Chọn A x x +
Ta có (3 5)x (3 5)x 3.2x + + − < . 3 5 2 ⇔ + < 3. 2 3 + 5 x + Đặt 3 5 t = với t > 0 . 2 1 − + ⇔ t + < 3 2
⇔ t − 3t +1< 0 3 5 3 5 ⇔ < t < t 2 2 3 − 5 3 + 5 x 3 + 5 − + ⇔ < 3 5 3 5 < ⇔ log < x < log 2 2 2 3+ 5 3+ 5 2 2 2 2 ⇔ 1
− < x <1 ⇒ (a;b) = ( 1; − ) 1 ⇒ S = 2 . Câu 23: Chọn D 1 2x +1 > 0 x > − Ta có ( x + ) 1 − 2 log 2 1 > 1 − ⇔ ⇔ . 1 1 2x +1< 1 2 2 x < 2
Vậy tập nghiệm của bất phương trình đã cho là 1 1 S ; = − . 2 2 Câu 24: Chọn A 28 1 1 − 2x − 0 < x < > 0 1 2x > 0 2 Bất phương trình 1− 2 log x > 0 x ⇔ x ⇔ ⇔ 1 1 x 1 − 2x 1 −3x x > 3 <1 < 0 3 x x x <0 1 1 ⇔ < x < . 3 2 1 a =
Nên tập nghiệm của bất phương trình là 1 1 3 S = ; ⇒ . 3 2 1 b = 2 Do đó 1 1
T = 3a − 2b = 3. − 2. = 0. 3 2 Câu 25: Chọn D
Điều kiện xác định: 2x ≥ 4 ⇔ x ≥ 2 . Xét y + ∈ 2x − 4 > 0 x > 2
2x − 4.(5x − y) < 0 ⇔ ⇔ . 5x − y < 0 x < log y 5
Từ yêu cầu bài toán suy ra: 3 < log y ≤ 6 ⇔ 125 < y ≤15625 . 5
Vậy có 15500 số nguyên dương y thỏa yêu cầu bài toán. Câu 26: Chọn D Ta có 2 2 2x 15 − x 100 + x 10 + x−50 2 2 − 2
+ x − 25x +150 < 0 . 2 2 2x 15 − x 100 + x 10 + x−50 2 ⇔ − + x − x + − ( 2 2 2 2
15 100 x +10x − 50) < 0 . Đặt 2
a = 2x −15x +100 , 2
b = x +10x − 50 .
Khi đó bất phương trình trở thành: 2a − 2b + a − b < 0 ⇔ 2a − − > 2b a − − b ( )1 Xét hàm số ( ) = 2t f t
− − t có ′( ) = 2t f t
− ln 2 −1< 0 với t ∀ ∈ .
Suy ra f (t) nghịch biến trên . Bất phương trình
( )1 ⇔ a < b 2 2
⇔ 2x −15x +100 < x +10x − 50 2
⇔ x − 25x +150 < 0 ⇔ 10 < x <15.
Mà x∈ nên x∈{11;12;13; }
14 . Vậy bất phương trình có 4 nghiệm nguyên. Câu 27: Chọn D Ta có ( x+4 3 − )
1 (3x − y − ) 1 < 0 ⇔ ( 4 3 .3x − )
1 (3x − y − ) 1 < 0 ( ) 1
Vì y nguyên dương nên 1 y +1 > , khi đó ta có: 4 3 29 ( ) 1 1 ⇔
< 3x < y +1 1 ⇔ log
< log 3x < log y +1 3 3 3 ( ) 4 3 81 ⇔ 4
− < x < log y +1 ⇔ x∈( 4 − ;log y +1 . 3 ( )) 3 ( )
Ứng với mỗi số nguyên dương y có nhiều nhất 10 số nguyên x∈( 4 − ;log y +1 3 ( ))
⇔ 0 < log y +1 ≤ 7 7
⇔ 1< y +1≤ 3 ⇔ 0 < y ≤ 2186 . 3 ( )
Vậy có 2186 giá trị nguyên y thỏa mãn yêu cầu bài toán. Câu 28: Chọn A
Đặt t = log x . Với mọi x∈(0;+∞) ta có t ∈ 3 . Bất phương trình 2
log x + mlog x ≥ m trở thành 2t + mt − m ≥ 0 . 3 3 2
log x + mlog x ≥ m nghiệm đúng với mọi giá trị của x∈(0;+∞) 3 3 2
⇔ t + mt − m ≥ 0, t ∀ ∈ ⇔ ∆ ≤ 0 2
⇔ m + 4m ≤ 0 ⇔ 4 − ≤ m ≤ 0. Vậy m∈{0; 1 − ; 2 − ; 3 − ;− } 4 . Câu 29: Chọn A
Điều kiện x > 0 .
Đặt t = log x , bất phương trình trở thành 2 2
t − 3yt + 2y < 0 (*). 2 ( y)2 2 2 3 4.2y y 0, y + ∆ = − =
> ∀ ∈ , tam thức có hai nghiệm t = y ∨ t = 2y .
Do đó (*) ⇔ y < t < 2y hay y 2
< log < 2 ⇔ 2 < < 2 y y x y x . 2 Vì x, y + ∈ nên ∈ = { y y 2 2 +1;2 + 2; ... ;2 y x A − } 1 .
Số phần tử của tập A là ( 2y ) ( y ) 2 2 1 2 1 1 2 y 2y − − + + = − −1.
Giả thiết bài toán có không quá 4031 số nguyên x nên ta có: 2 2 y 2y − −1≤ 4031. 2
⇔ 2 y − 2y − 4032 ≤ 0 ⇔ 63
− ≤ 2y ≤ 64 ⇔ y ≤ 6 . Vì y +
∈ nên y ∈ E = {1;2;3;4;5; }
6 . Số phần tử của tập hợp E là 6. 30
BÀI TẬP ÔN TẬP CUỐI CHƯƠNG VI
A. BÀI TẬP TỰ LUẬN B.
Bài 1. Tìm tập xác định của các hàm số sau? a) y = log ( 2 2x − x x 3 ) d) 2
y = 3 −1 − log (x − 2) 2 b) 1 2 2 − = x y x − 3 e) y = log 10 1 − x x +1 c) y = log 2 2 2 x − 3x + 2
Bài 2.Tính giá trị các biểu thức sau a) A = ( 3 log 100a ) biết 1 log a = ; 3 3 b b) B = + log
ab với a,b là các số thực dương và a >1, 9 a a b
a ≠ b thỏa mãn log b = a 3; 2020 2020
c) C = ln (2 2 + 3) + ln(3− 2 2) ; d) 2 2 2
D =1+ 2 log 2 + 3 log 2 +....+ 2018 log 2; 3 2018 2 2 2
Bài 3.Tính giá trị các biểu thức sau theo biểu thức đã cho
a) Tính log16 theo a = log 2;
b) Tính log9000 theo a = log3;
c) Tính log 2 theo a = log 9 ; 3 6
d) Tính log 24 theo a = log 27 ; 36 12
Bài 4.Tính giá trị các biểu thức sau theo các biểu thức đã cho
a) Tính log 5 theo a = log 5;b = log 5 ; 6 2 3
b) Tính log 30 theo a = log3;b = log 2 ; 125
c) Tính log301350 theo Choa = log30 3; b = log30 5. d) Tính lo 140 g
63 theo a = log2 3;b = log3 5;c = log7 2;
Bài 5.Giải các phương trình sau: a) x 1 3 = ; b) 2x 1 2 − = 3 ; 9 c) 2x 2x 3 e − − =1; d) x x 1 + x+3 2 .15 = 3 .
Bài 6.Giải các phương trình sau: 5 a) 1 log x = ; b) log 2x −1 = 2 3 ( ) ; 1 2 4 c) (x − )2 log 1 = 2;
d) log2 x(x −1) =1 ; e) 2
(x − 2)[log (x − 5x + 6) +1] = 0; 0.5
f) log x + log x + log x = log .x 2 3 4 20 g) log x
2(9 − 2 ) = 3 − x ; h) log x 3(3 − 8) = 2 − x .
Bài 7.Giải các phương trình sau: a) x 1 3 − = 27 b) x 1− 3−2 4 = 8 x ; c) 2x−x−4 1 2 = ; d) 2 2 x−2x 1 + 2 − x +x 1 3.5 5.3 + = . 16 2 3 x −x+2 x −2 e) (3+ 2 2) = (3− 2 2) .
Bài 8.Giải các phương trình sau: a) 2
log(x − 6x + 7) = log(x − 3) ;
b) log x + log (x −1) =1 2 2 ;
c) log (x + 3) − log (x −1) = 2 − log 8 4 4 4 ;
d) log x + log x + log x = 6 3 ; 3 1/3
e) log (x −1) + log (x +1) =1+ log (7 − x) 1/2 1/2 ; 1/ 2 f) log (x + )2 1 + 2 = log
4 − x + log (4 + x)3 4 . 2 8
Bài 9.Giải các phương trình sau a) x x x 1 12.3 3.15 5 20 ;
b) log 3x4 .log x log x 2 3 3 ;
c) 2x 2.3x 6x 2 ; d) 2 2 2 x −4x+3 x +7x+6 2x +3x+9 5 + 5 = 5 +1; e) 2 2 x x 1 x 1 2 2 2 2 x 2x 6
Bài 10.Giải các phương trình sau 2 a) x −4 x−2 2 = 5 ; b) x x 3 2 5 = 7 ; x x2 −2x x 3 c) 2 .3 = ; d) x x 1 5 .8 100. 2
Bài 11.Giải các bất phương trình sau: x a) 2x ≤ 5; b) 1 > 27 ; c) x−2 5 3 > 3 −x ; 3 2 x −2 1 x 1 d) 2x 1 2 − < 8; e) ≥ ; f) x 1 3 − .5x ≤ 75 . 2 8
Bài 12.Giải các bất phương trình sau a) log x ≥1; b) log x > 2 ; 1 2 c) log 2x +1 ≤1 2 2 ( ) ; d) log − < . π ( x 2x) 0
Bài 13.Giải các bất phương trình sau x+2 1 a) x 1 3 − > 27 ; b) x 1 2 − x −x−9 5 ≥ 5 ; c) ≥ 3−x 3 ; x 2x d) 1 x 1 > 3 + ; e) 2 2− x +5x−6 1 3 ≥ . 9 3x
Bài 14.Giải các bất phương trình sau
a) log x − 3 ≥ log 4 ; 1 ( ) 1 2 2
b) log(3− 2x) ≥ log(x + ) 1 . c) 2
ln x ≥ 2ln (x + ) 1 ; d) 3 log x > 3 − log x − 2 3 1 ( ); 3 e) 1 log 4x − 9 > log ; 1 ( ) 2 x +10 2 f) log x +1 ≤ log 2 − x + 4 0.8 ( ) 1.25 ( );
g) log x +1 − 2log 5 − x <1− log x − 2 2 ( ) 4 ( ) 2 ( ) . 7
Bài 15. a. Tìm tất cả các giá trị thực của tham số m để bất phương trình 2 x +2mx 1 + 2x−3 2 e m ≤
nghiệm đúng với mọi x ∈ . e 2
b.Tìm tất cả giá trị của tham số thực m sao cho bất phương trình 9x − 2( + ) 1 .3x m
− 3− 2m > 0 nghiệm đúng với mọi số thực x . C. BÀI TẬP TỰ LUẬN Câu 1.
Với α là số thực bất kì, đẳng thức nào sau đây sai? α α
A) 10α = ( 10) . B) α 2 10 =10 . C) ( α )2 10 100α = . D) (10α )2 2 10α = . Câu 2.
Cho a > 0 , b > 0 và x , y là các số thực bất kỳ. Đẳng thức nào sau đây đúng?
A) ( + )x = x + x a b a b .
B) x+y = x + y a a a . x C) a = x y xy x a . −x b
D) a b = (ab) . b Câu 3.
Cho a là số thực dương và ,
m n là số nguyên dương ( , m n ≥ 2) .
Đẳng thức nào sau đây đúng? n n
A) n m = m n a a .
B) a = m a . m a n
C) n .m = nm a a a .
D) n m = m a a . Câu 4.
Cho x > 0 . Biểu thức 9 P = . x x bằng 11 10 A) 9 x . B) 9 x . 1 8 C) 9 x . D) 9 x . Câu 5.
Cho x > 0 . Biểu thức 3 2 4
P = x x bằng 2 7 A) 3 P = x . B) 12 P = x . 31 3 C) 12 P = x . D) 4 P = x . Câu 6. Cho ( 2 m n − )
1 < ( 2 − )1 . Khi đó, khẳng định nào sau đây là đúng?
A) m = n .B) m < n .
C) m > n .
D) m ≤ n . Câu 7.
Tìm tập tất cả các giá trị của a để 21 5 7 2
a > a ? 8 A) (0;+∞). B) (0; )
1 . C) (1;+ ∞) . D) 5 2 ; . 21 7 Câu 8.
Tập xác định D của hàm số y = (x − )13 1 là:
A) D = (1;+∞) .B) D = C) D = \{ } 1 . D) D = (−∞ ) ;1 . Câu 9.
Tìm tập xác định D của hàm số y (x x ) 3 2 2 − = − − . A) D = (− ; ∞ − ) 1 ∪ (2;+ ∞) .
B) D = \{ 1; − } 2 .
C) D = .
D) D = (0;+ ∞) .
Câu 10. Với a là số thực dương tùy ý, log 9a bằng 3 ( )
A) 1 + log a .
B) 2log a C) (log a . D) 2 + log a . 3 )2 3 2 3 3
Câu 11. Với a là số thực dương tùy ý, 25 log bằng 5 a
A) 2 − log a .
B) 5 .C) 2 .
D) 5 − log a . 5 log a log a 5 5 5 Câu 12. Với ;
a b là các số thực dương và a ≠1, khi đó 3 log b bằng 2 a
A) 6log b .B) 3
− log b .C) 2 log b . D) 3 log b . a 2 a 3 a 2 a
Câu 13. Với x là số thực dương tùy ý, 3 log x bằng 2
A) 3 + log x .
B) 1 log x .C) (log x . D) 3log x . 2 )3 2 2 3 2
Câu 14. Cho a = log 15, l
b = og 10 . Hãy biểu diễn log 50 theo a và b . 3 3 3
A) 2(a −1+ b) B) 2(a +1+ b) C) 2(a −1− b)
D) 2(a +1+ b)
Câu 15. Đặt a = log 3 và b = log 3 . Hãy biểu diễn log 45 theo a và b 2 5 6 bằng: 2 A) 2 log 45 + = a ab . B) 2 2 log 45 − = a ab . 6 ab 6 ab 2 C) a 2 log 45 + = ab . D) 2a 2 log 45 − = ab . 6 ab + b 6 ab + b Câu 16. Nếu 2
log a + log b = 5 và 2
log a + log b = 7 thì giá trị ab bằng: 8 4 4 8 A) 18 2 . B) 9 2 . C) 8 . D)
Câu 17. Cho log 4 = a, log 4 = b . Hãy biểu diễn log 80 theo a và b . 3 5 12
A) a + 2ab .B) a − 2ab . C) a + 2ab .
D) a − 2ab . ab + b ab + b ab − b ab − b 9
Câu 18. Tập xác định của hàm số y = 1− log x là 2 A) (− ;2
∞ ] .B) [0;2]. C) (0; ) 1 . D) (0;2].
Câu 19. Cho hai hàm số y = log x , y = log x với a , b là hai số thực a b
dương, khác 1và có đồ thị lần lượt là (C , (C như hình vẽ. 2 ) 1 )
Khẳng định nào sau đây SAI?
A) 0 < b < a <1.
B) a >1.C) 0 < b <1< a . D)
Câu 20. Hình bên là đồ thị hàm số = x y a , = x y b , = x
y c (0 < a,b,c ≠1) được
vẽ trên cùng một hệ trục tọa độ. Khẳng định nào sau đây là khẳng định đúng?
A) a > b > c .B) c > b > a .C) a > c > b .
D) b > a > c .
Câu 21. Cho a,b,c dương và khác 1. Các hàm số y = log x , y = log x , a b
y = log x có đồ thị như hình vẽ c 10
Khẳng định nào dưới đây đúng?
A) a > c > b .B) a > b > c .C) c > b > a .
D) b > c > a .
Câu 22. Cho các hàm số = x
y a ; y = log x ; y = log x có đồ thị như hình b c
vẽ. Chọn mệnh đề đúng?
A) b < c < a .B) a < c < b . C) c < b < a .
D) c < a < b .
Câu 23. Biết hàm số ( ) = a f x
có đồ thị đối xứng với đồ thị hàm số 2 b .3x = 3x y
qua đường thẳng x = 1
− như hình vẽ bên dưới. Biết a,b là
các số nguyên. Chọn khẳng định đúng trong các khẳng định sau: 11
A) a + b = 5 .B) a + 2b = 7 .C) 2a − b = 0 . D) 3 a + b =12 .
Câu 24. Nghiệm của phương trình x 1 3 − = 27 là
A) x = 4 .B) x = 3.
C) x = 2 . D) x =1.
Câu 25. Nghiệm của phương trình 2x−4 2 = 2x là
A) x =16 .B) x = 16 − . C) x = 4 − . D) x = 4 .
Câu 26. Tìm tập nghiệm S của phương trình log x −1 + log x +1 = 3 . 2 ( ) 2 ( ) A) S = { } 3
B) S = {− 10; 10} C) S = { 3 − ; } 3 D)
Câu 27. Tập nghiệm của phương trình log x 5 − x =1 6 ( ) A) {1; } 6 − . B) {2; } 3 . C) { 1; − } 6 . D)
Câu 28. Phương trình 3−4
5 x = 25 có nghiệm là
A) x = 4 . B) 1 x = − . C) 1 x = . D) 4 4
Câu 29. Tổng các nghiệm của phương trình log x + log (x − 3)3 = 2 bằng 2 8 bao nhiêu? A) 3 . B) 0 . C) 4 . D)
Câu 30. Tính tổng S = x + x biết x và x là các giá trị thực thỏa mãn 1 2 1 2 x−3
đẳng thức 2x−6x 1+ 1 2 = . 4
A) S = 8 . B) S = 5 − .
C) S = 4 . D)
Câu 31. Tích các nghiệm của phương trình xlog x + 6 = 2x + 3log x bằng 2 2 bao nhiêu? A) 7 . B) 0 . C) 12 . D)
Câu 32. Tích các nghiệm của phương trình x x 1 + x 1 10 10 2 5 + + = + bằng bao nhiêu? A) 7 . B) 0 . C) 1. D) 12
Câu 33. Cho hai số thực a,b với 1< a < b . Khẳng định nào sau đây là đúng? x x
A) a <1⇔ x > b 0. B) <1 ⇔ x > 0.
C) log b < D) a 1. b a
Câu 34. Tính tích các nghiệm thực của phương trình 2x 1− 2x+3 2 = 3 A) 3 − log 3 . B) 1− log 3. C) 1 − . D) 2 2
Câu 35. Tập nghiệm bất phương trình: 2x > 8 là:
A) (−∞;3) .B) [3;+ ∞) . C) (3;+ ∞) . D) (−∞ ] ;3 .
Câu 36. Tập nghiệm của bất phương trình 2 4
3 −x ≥ 27 là: A) [ 1; − ] 1 .B) (−∞ ] ;1 . C) − 7; 7 . D) [1;+∞) . 1
Câu 37. Tìm tập nghiệm S của bất phương trình 1− 1 2 > x x . 16
A) S = (2;+ ∞) .B) S = (− ;0
∞ ) .C) S = (0;+ ∞) . D) S = (− ; ∞ + ∞) . 2 x −3x 10 − x−2
Câu 38. Tìm số nghiệm nguyên của bất phương trình 1 1 > . 3 3
A) 1.B) 0 . C) 9 . D) 11.
Câu 39. Tập nghiệm của bất phương trình log x ≥1 là:
A) (10;+∞) .B) (0;+∞). C) [10;+∞) . D) (− ;1 ∞ 0) .
Câu 40. Tìm tập nghiệm S của bất phương trình log x +1 < log 2x −1 . 1 ( ) 1 ( ) 2 2
A) S = (2;+∞) .B) S = ( 1;
− 2) .C) S = (− ;2 ∞ ) . D) 1 S ;2 = . 2 Câu 41. Số nghiệm nguyên của bất phương trình
log 15x + 2 > log 13x + 8 là: 0,8 ( ) 0,8 ( )
A) Vô số.B) 4 . C) 2 . D) 3 .
Câu 42. Tập nghiệm của bất phương trình x x 8 4 2 + > là :
A) [8;+∞) .B) (− ;8
∞ ) . C) (0;8) . D) (8;+∞) . − x
Câu 43. Tập nghiệm S của bất phương trình x+2 1 5 < là: 25 A) S = (− ;2
∞ ) .B) S = (−∞ )
;1 .C) S = (1;+∞) . D) S = (2;+∞) .
Câu 44. Tập nghiệm của bất phương trình 2
5x −x < 25 là: 13
A) (2;+∞) .B) (− ; ∞ ) 1 ∪ (2;+∞).C) ( 1; − 2) . D) .
Câu 45. Tập nghiệm của bất phương trình 2x 1 3 − > 27 là: A) 1 ; +∞
.B) (3;+∞) .C) 1
;+∞ .D) (2;+∞) . 2 3 x−
Câu 46. Nghiệm của bất phương trình ( )x− ( ) 1 1 x 1 5 2 5 2 + + ≥ − là: A) 3 − ≤ x < 1 − .
B) x ≥1 . C) 2 − ≤ x < 1
− hoặc x ≥1 . D) 2
− < x <1. 1−3 2 x 25
Câu 47. Tìm tập nghiệm S của bất phương trình: ≥ . 5 4 1 1 A) S = ; −∞
.B) S = [1;+∞) .C) S = (−∞ ] ;1 . D) S = ;+∞ . 3 3 Câu 48. Số nghiệm nguyên của bất phương trình ( x x − )3−x− > ( + ) 1+ 1 x+3 10 3 10 3 là:
A) 2 .B) 1. C) 0 . D) 3 .
Câu 49. Tập nghiệm của bất phương trình log 2x +1 < log 1− x +1 là: 5 ( ) 5 ( ) A) 1 S ;1 = − .B) 4 S = −∞ ; .C) 1 4 S = − ; . D) 1 4 S = − ; . 2 7 2 7 2 7
Câu 50. Bất phương trình log x + log x ≤ 3 có tập nghiệm là ( ; a b]. Tính 1 3 3
T = a + 3b .
A) T = 0 .B) T = 27 .
C) T = 81. D) T = 9 . 14
BÀI TẬP ÔN TẬP CUỐI CHƯƠNG VI
D. HƯỚNG DẪN GIẢI BÀI TẬP TỰ LUẬN
Bài 1: a.Hàm số y = log ( 2
2x − x xác định khi và chỉ khi 3 ) 2
2x − x > 0 ⇔ 0 < x < 2 .
Vậy tập xác định của hàm số D = (0;2) . b) Hàm số 1 2 2 − = x y
xác định khi và chỉ khi 1
1− 2x ≥ 0 ⇔ x ≤ . 2
Vậy tập xác định của hàm số 1 D ; = −∞ . 2 c) Hàm số 10 log − = x y xác định 2 2 x − 3x + 2 10 − x x <1 ⇔ > 0 ⇔ 2 x − 3x + 2 2 < x <10
Vậy tập xác định của hàm số D = (−∞ ) ;1 ∪ (2;10). d) Hàm số x 2
y = 3 −1 − log (x − 2) xác định 2 3 x −1≥ 0 x ≥ 0 ⇔ ⇔ x − 2 ≠ 0 x ≠ 2
Vậy tập xác định của hàm số D = [0;+ ∞) \{ } 2 . x − 3 x < 1 − e) Hàm số x − 3 y = log xác định ⇔ > 0 ⇔ 1 x +1 x +1 x > 3 2
Vậy tập xác định của hàm số D = (−∞;−1) ∪ (3;+ ∞) Bài 2. a) ( 3 a ) 3 log 100
= log100 + log a = 2 + 3log a = 5 . b) 3
log b = 3 ⇒ b = a do đó a (a )3 3 3 2 B = + log aa = a a 1+ log = − = − 1 1 0 2 9 a a 3 a 15 c) C = ( + )2020 + ( − )2020 = ( + )2020( − )2020 ln 2 2 3 ln 3 2 2 ln 2 2 3 3 2 2 )=ln1=0 . n n +1 3 3 3 3 ( ( ))2
d) Ta có 1 + 2 + 3 + ...+ n = . 4 Mặt khác 2 2 2
D =1+ 2 log 2 + 3 log 2 + ....+ 2018 log 2 3 2018 2 2 2 2 2 2
=1+ 2 log 2 + 3 log 2 + ....+ 2018 log 2 1 1 1 2 3 2018 2 2 2 3 3 3
=1+ 2 log 2 + 3 log 2 + ....+ 2018 log 2 3 3 3 =1+ 2 + 3 + ...+ 2018 2 2 2 ( + ) 2 2018 2018 1 = 2 2 =1009 .2019 . 2
Bài 3.a) log16 = 4log 2 = 4a . b) = ( 2 3
log9000 log 3 .10 ) = 2log3+ 3 = 2a + 3 . c) log 9 2 2 2 − = 2log 3 ⇔ a = ⇔ log 2 +1 = ⇔ log 2 = a .. 6 2.3 log 2.3 3 a 3 a 3 d) Ta có 3 log 27 = = a . 12 log ( 2 2 .3 3 ) Suy ra 3 − = a hay 3 log 2 = a (a ≠ 0 vì 1+ 2log 2 3 2a 3
a = log 27 > log 1). 12 12 9 − 3 1+ a Khi đó: log 24 3log 2 +1 2a 9 − 3 3 log 24 = = = = a . 36 log 36 2log 2 + 2 6 − 2a 6 + 2a 3 3 2 + 2a Bài 4.a) Ta có: log 5 1 1 = ;
a log 5 = b nên log 2 = ;log 3 = . 2 3 5 5 a b 1 1 1 log 5 = = = = ab . 6
log 6 log 2 + log 3 1 1 a + b 5 5 5 + a b b) Ta có: lg30 lg(3.10) log3 + log10 log3 +1 a +1 log 30 = = = = = . 125 lg125
1000 log1000 − log8 3 − 3log 2 3(1− b) lg 8 c) Ta có 2 1350 = 30.3 .5 suy ra
log 1350 =1+ 2log 3 + log 5 =1+ 2a + . b 30 30 30 16 d) Ta có + . log 63 2 log 7 ac + a c 2 1 = log 3, 3 3 log 63 = = = . 7 140
log 140 2log 2 + log 5 + log 7 abc + 2c +1 3 3 3 3 Bài 5.a) x 1 x 2 3 3 3− = ⇔ = ⇔ x = 2 − . 9 b) 2x 1− 1 2
= 3 ⇔ 2x −1 = log 3 ⇔ x = 1+ log 3 ⇔ x = log 6 . 2 ( 2 ) 2 2 x = − x − x− 1 c) 2 2 3 2 e
=1 ⇔ x − 2x − 3 = 0 ⇔ . x = 3 d) x x 1+ x+3 2 .15 = 3 ⇔ x x 1+ 2 2 .5 = 3 ⇔ x 9 10 = ⇔ 9
x = log = log9 − log5 5 5
⇔ x = 2log3 − log5. 1 Bài 6.a) 2 1 1 1 log x = ⇔ x = ⇔ x = . 1 2 4 2 4 b) log (2x − ) 2
1 = 2 ⇔ 2x −1= 3 ⇔ x = 5 3 c) (x − )2 log
1 = 2 ⇔ 2log x −1 = 2 ⇔ x =11
log x −1 =1⇔ x −1 =10 ⇔ (tm) . x = 9 −
Vậy tập nghiệm của phương trình là S = {11;− } 9 . x = 1 −
d) log [x(x −1)] =1⇔ x(x − ) 2
1 = 2 ⇔ x − x − 2 = 0 ⇔ 2 x = 2
Vậy phương trình có hai nghiệm là x = 1, − x = 2 1 2 x > 3 e) Điều kiện: 2
x − 5x + 6 > 0 ⇔ ; x < 2 x − 2 = 0 (x − 2)log
( 2x −5x +6 +1 = 0 ⇔ . 0,5 ) log
( 2x −5x +6 +1= 0 0.5 )
+) x − 2 = 0 ⇔ x = 2 (không thỏa mãn điều kiện). 17 +) log ( 2
x − 5x + 6 +1 = 0 ⇔ 2
x − 5x + 6 = 2 ⇔ 2
x − 5x + 4 = 0 ⇔ 0.5 ) x =1 ( Thỏa mãn đk). x = 4
Vậy tập nghiệm của phương trình là S = {1; } 4 .
f) Điều kiện: x > 0 .
Ta có: log x + log 2.log x + log 2.log x = log 2.log x 2 3 2 4 2 20 2 ⇔ log .
x 1+ log 2 + log 2 − log 2 = 0 ⇔ log x = 0 ⇔ x =1(nhận) 2 ( 3 4 20 ) 2
Vậy phương trình có nghiệm duy nhất x =1. g) x x 3−x x 8
log (9 − 2 ) = 3 − x ⇔ 9 − 2 = 2 ⇔ 9 − 2 = 2 2x Đặt = 2x t ,t > 0 8 t =1 Ta được phương trình: 2
9 − t = ⇔ t − 9t + 8 = 0 ⇔ t t = 8
+)t =1 ⇔ x = 2
+)t = 8 ⇔ x = 256
Vậy phương trình có hai nghiệm là x = 2, x = 256 1 2 h) x x 2−x x 9
log (3 − 8) = 2 − x ⇔ 3 − 8 = 3 ⇔ 3 − 8 = 3 3x Đặt = 3x t , t > 0 9 t = 1 − Ta được phương trình: 2
t − 8 = ⇔ t − 8t − 9 = 0 ⇔ t t = 9 +) 1 t = 1 − ⇔ x = 3
+) t = 9 ⇔ x =19683
Vậy phương trình có hai nghiệm là 1 x = , x =19683 1 2 3 Bài 7.a) x 1 3 − = 27 x 1 − 3
⇔ 3 = 3 ⇔ x −1 = 3 ⇔ x = 4 . 18 2x b) x 1− 3−2x 2 512 4 = 8 ⇔ = 8 ⇔ 2 x = 2048 8x 11 ⇔ 2 = 2 ⇔ 8x =11 6 4 2 x 11 ⇔ x = . 8 x = x −x− − 0 c) 2 4 4 2 2 2
= 2 ⇔ x − x − 4 = 4
− ⇔ x − x = 0 ⇔ . x =1
Vậy tập nghiệm của phương trình là S = {0; } 1 . 2 2 x 2x 1 2 − x +x 1 + − + d) Ta có: 2 2 x−2x 1 + 2 − x +x 1 + 5 5 5 5 3.5 = 5.3 ⇔ = ⇔ = 2 2x x − + 1 3 + 3 3 3 x = 0 2 2x x 1 1 ⇔ − + + = ⇔ 1 . x = 2
Vậy tập nghiệm của phương trình là 1 S 0; = . 2 f) Nhận xét: ( + )( − ) 1 − 3 2 2 3 2 2 =1⇒ 3 − 2 2 = = (3+ 2 2) 1, 3 + 2 2 Nên ta có: ( x x x x x x +
) 2− + =( − ) 3− ⇔( + ) 2− + =( + ) 3 2 2 2 2− 3 2 2 3 2 2 3 2 2 3 2 2 x = 0 2 3 3 2 x x 2 2 x x x x 0 ⇔ − + = − ⇔ + − = ⇔ − ± . 1 5 x = 2 − ±
Vậy tập nghiệm của phương trình là 1 5 S 0; = . 2 x = 5 2
x − x + = x − Bài 8.a) 2 log( 6 7 3
x − 6x + 7) = log(x − 3) ⇔
⇔ x = 2 ⇔ x = 5. x − 3 > 0 x > 3
b) log x + log (x −1) =1 * 2 2 ( ) 19 x > 0 Đk: ⇔ x >1 x −1 > 0 ( x = −
*) ⇔ log (x(x − )
1 ) =1⇔ x(x − ) 1 2
1 = 2 ⇔ x − x − 2 = 0 ⇔ 2 x = 2
Đối chiếu với Đk ta được nghiệm phương trình là x = 2
c) log (x + 3) − log (x −1) = 2 − log 8 ; 4 4 4 ĐKXĐ: x >1. Ta có: x + 3 x + 3
log (x + 3) − log (x −1) = 2 − log 8 ⇔ log = log 2 ⇔ = 2 ⇔ x = 5 4 4 4 4 4 ( ) x −1 x −1 (nhận)
d) log x + log x + log x = 6 ; 3 3 1/3 ĐKXĐ: x > 0 . Ta có:
log x + log x + log x = 6 ⇔ log x + 2log x − log x = 6 ⇔ log x = 3 ⇔ x = 27 3 3 1/3 3 3 3 3 (nhận)
e) log (x −1) + log (x +1) =1+ log (7 − x) ; 1/2 1/2 1/ 2
ĐKXĐ: 1< x < 7 . Ta có:
log (x −1) + log (x +1) =1+ log (7 − x) ⇔ log ((x −1)(x +1)) = 2log (7 − x 1/2 1/2 1/ 2 1/2 1/2 1 x = 3(N) 2 2
⇔ (x −1)(x +1) = (x − 7) ⇔ x +14x − 51 = 0 ⇔ 2 x = 17 − (L) ( x + )2 1 > 0 x ≠ 1 − 4 − < x < 4
f) Điều kiện: 4 − x > 0 ⇔ x < 4 ⇔ x ≠ 1 − ( + x)3 x > > 4 4 0 − Ta có log (x + )2 1 + 2 = log
4 − x + log (4 + x)3 4 2 8
⇔ log x +1 + log 4 = log (4 − x) + log (4 + x) 2
⇔ 4 x −1 =16 − x 2 2 2 2 20 x ≥1 x ≥ 1 2 4x 4 16 − = − x x = 2 − + 2 6 hay x = 2 − − 2 6 ⇔ ⇔ x 1 < x <1 2 4 − x + 4 =16 − x x = 2 − hay x = 6 x = 2 − + 2 6 ⇔ (thỏa mãn điều kiện). x = 2 −
Vậy tập nghiệm của phương trình là S = { 2; − 2 − + 2 6}.
Bài 9. a) Phương trình đã cho tương đương với 12.3x + 3.3x.5x − 5.5x − 20 = 0
⇔ 3.3x (5x + 4) − 5(5x + 4) = 0 ⇔ (3.3x − 5).(5x + 4) = 0
5x + 4 = 0 (VN ) ⇔ 3.3x − 5 = 0 ( ) 1
Giải phương trình (1) ta có : x 5
3 = ⇔ x = log 5 −1. 3 3
Vậy phương trình có nghiệm là x = log 5 −1. 3 4 3 x − 4 > 0 x > b) Điều kiện : 4 ⇔ 3 ⇔ x > . x > 0 3 x > 0
Phương trình đã cho tương đương với log 3x − 4 −1.log x = 0 2 ( ) 3
log 3x − 4 −1 = 0 log 3x − 4 =1 2 ( ) 2 ( ) ⇔ ⇔ log x = 0 x =1 KTM 3 ( )
⇔ 3x − 4 = 2 ⇔ x = 2 (TM ) .
Vậy phương trình có nghiệm là x = 2 .
c) Phương trình đã cho tương đương với
2.3x − 2x.3x = 2− 2x ⇔ 3x (2− 2x ) = 2− 2x ⇔ (2− 2x )(3x − ) 1 = 0 21 2− 2x = 0 2x = 2 x =1 ⇔ ⇔ ⇔ . 3x −1= 0 3x =1 x = 0
Vậy phương trình có nghiệm là x∈{0; } 1 . d) Ta có: 2 2 2 2 2 2 x −4x+3 x +7x+6 2x +3x+9 x −4x+3 x +7x+6 2x +3x+9 5 + 5 = 5 +1 ⇔ 5 + 5 = 5 +1. 2
a = x − 4x + 3 Đặt
, ta được phương trình: 2
b = x + 7x + 6 5a 5b 5a+ + =
b +1⇔ 5a + 5b = 5a.5b +1 a a
⇔ ( − a )( − b ) 5 =1 = 0 1 5 1 5 = 0 ⇔ ⇔ b . 5 =1 b = 0 x =1 2 x 4x 3 0 − + = x = 3 Khi đó ⇔ . 2
x + 7x + 6 = 0 x = 1 − x = 6 − e) Phương trình 2 x − ( x )
x ( x ) ( x )( 2 1 x 1 2 2 1 2 2 1 2 1 2 − ⇔ − = − ⇔ − − 2x ) = 0 x x x = 0 2 −1= 0 2 =1 x = 0 x = 0 ⇔ ⇔ ⇔ ⇔ ⇔ 2 2 ± x 1 − x x 1 − x 2 2 1 5 2 − 2 = 0 2 = 2 x −1 = x
x − x −1 = 0 x = 2 . Bài 10.a) Ta có: 2 x = x − x− 2 4 2 2 2 = 5
⇔ x − 4 = (x − 2)log 5 ⇔ x − 2 (x + 2) = (x − 2)log 5 ⇔ 2 ( ) 2 x = log 5− 2
b) Lấy logarit cơ số 5 hai vế ta có: x 3x 2x x x 3 log 5 log 7 3 2 .log 7 = ⇔ =
⇔ = log 7 ⇔ x = log log 7 5 5 5 5 3 ( 5 ) 2 2 .
Vậy phương trình có nghiệm là: x = log log 7 . 3 ( 5 ) 2
c)Phương trình tương đương: 2x− x 3 2 2 x −2x 1 + 1−x ( x− )2 1 −( x− ) 1 2 .2 = ⇔ 2 = 3 ⇔ 2 = 3 (*) 3x 22
Lấy logarit cơ số 2 hai vế của (*), ta được (x − )2 1 = −(x − ) 1 .log 3 2 x =1
(x )1(x 1 log 3 0 ⇔ − − + = ⇔ . 2 ) 2 x 1 log 3 log = − = 2 2 3 x =1
Vậy phương trình có nghiệm là: 2 . x log = 2 3
d) Điều kiện: x ≠ 1 − . 3x 2−x
Phương trình tương đương x x 1+ 2 2 x−2 x 1 5 .2 2 .5 5 2 + = ⇔ = (*)
Lấy logarit cơ số 5 hai vế của (*), ta được ( ) 2 2 − − = x x .log 2 5 x +1 x = 2 (TM )
⇔ (x − 2)(x +1+ log 2 = 0 ⇔ . 5 ) x = −log 2 −1 TM 5 ( ) x = 2
Vậy phương trình có nghiệm là: . x = −log 2 − 1 5
Bài 11.a) 2x ≤ 5 ⇔ x ≤ log 5 . 2 x x 3 − b) Ta có: 1 1 1 27 > ⇔ > ⇔ x < 3 − . 3 3 3
Vậy tập nghiệm của bất phương trình là S = (−∞; 3 − ) . c) Ta có: x−2 5−x 7
3 > 3 ⇔ x − 2 > 5 − x ⇔ x > . 2
Vậy tập nghiệm của bất phương trình là 7 S ; = + ∞ . 2 d) Ta có 2 2 x 1− x 1 − 3 2 < 8 ⇔ 2 < 2 ⇔ 2 x −1< 3 ⇔ 2 − < x < 2 .
Vậy tập nghiệm của bất phương trình đã cho là S = ( 2; − 2).
e) Bất phương trình đã cho tương đương với 23 2 x −2x 3 1 1 2 2 ≥
⇔ x − 2x ≤ 3 ⇔ x − 2x − 3 ≤ 0 ⇔ 1 − ≤ x ≤ 3 2 2
Vậy tập nghiệm của bất phương trình đã cho là S = [ 1; − ] 3 .
f) Ta có: x 1− x 1 x x x 2
3 .5 ≤ 75 ⇔ .3 .5 ≤ 75 ⇔ 15 ≤ 225 =15 ⇔ x ≤ 2 . 3
Vậy tập nghiệm của bất phương trình là S = (−∞;2].
Bài 12.a) log x ≥1⇔ x ≥10 b) 1
log x > 2 ⇔ 0 < x < 1 4 2 c) 1 1
log 2x +1 ≤1⇔ 0 ≤ 2x +1≤ 2 ⇔ − ≤ x ≤ 2 ( ) 2 2
x − 2x ≥ 0 1 − 2 < x ≤ 0
d) log x − x < ⇔ ⇔ π ( 2 ) 2 2 0 2
x − 2x <1 2 < x ≤1+ 2
Bài 13. a) x 1− x 1 − 3
3 > 27 ⇔ 3 > 3 ⇔ x −1> 3 ⇔ x > 4.
b) Ta có bất phương trình tương đương với 2 2
x −1≥ x − x − 9 ⇔ x − 2x − 8 ≤ 0 ⇔ 2 − ≤ x ≤ 4
Vậy tập nghiệm của bất phương trình đã cho là S =[ 2; − 4]. c) Ta có x ≥ x ≥ x+ x+ x 0 0 2 2 1 − x 1 1 3 > ⇔ ≥ ⇔ x + 2
≤ x ⇔ x + 2 ≥ 0 ⇔ x ≥ 2 − ⇔ x ≥ 2 3 3 3 2 x + 2 ≤ x x ≥ 2 x ≤ 1 −
Vậy tập nghiệm của bất phương trình đã cho là S = [2;+∞).
d) Điều kiện: x ≠ 1 − . x 2x 2 1 x x x x x + − x+ 2 2 1 1 2 1 > 3 ⇔ 3 > 3 ⇔ 2 − x > ⇔
+ 2x < 0 ⇔ 2x +1 < 0 9 x +1 x +1 x +1 2x(x + 2) x < 2 − ⇔ < 0 ⇔ (thỏa điều kiện). x +1 1 − < x < 0 24
Vậy tập nghiệm của bất phương trình là S = (− ; ∞ 2 − ) ∪ ( 1; − 0) . e) Ta có: 2 − x + x− 1 2 2 5 6 2− x +5x−6 − x 2 3 ≥ ⇔ 3
≥ 3 ⇔ 2 − x + 5x − 6 ≥ −x 3x 2
x + 5x − 6 ≥ 0 x ≤ 6 − ∨ x ≥1 2 x 5x 6 x 2 ⇔ + − ≤ + ⇔ x + 2 ≥ 0 ⇔ x ≥ 2 − 2
x + 5x − 6 ≤ (x + 2)2 x ≤ 10 ⇔1≤ x≤10
Vậy tập nghiệm của bất phương trình là S = [1;10]. x − 3 ≤ 4
Bài 14.a) Bất phương trình log x − 3 ≥ log 4 ⇔ 1 ( ) 1 x − 3 > 0 2 2 x ≤ 7 ⇔ ⇔ 3 < x ≤ 7 . x > 3
Vậy tập nghiệm của bất phương trình đã cho là S = (3;7]. b) Ta có x > 1 − ( x − x) ≥ (x + ) +1> 0 2 log 3 2 log 1 ⇔ ⇔ 2 ⇔ 1 − < x ≤ . 3
− 2x ≥ x +1 x ≤ 3 3
Vậy tập nghiệm của bất phương trình đã cho là 2 S 1; = − . 3 2 x > 0 x ≠ 0 c) Điều kiện: ⇔ ⇔ 1 − < x ≠ 0 . x +1 > 0 x > 1 − Ta có: 2
ln x ≥ 2ln(x + ) 1 ⇔ 2 x ≥ (x + )2 2 ln ln
1 ⇔ x ≥ (x + )2 1 ⇔ 1
2x +1≤ 0 ⇔ x ≤ − . 2
Kết hợp với điều kiện ta được tập nghiệm 1 S 1; = − − . 2 3 x > 0 x > 0 d) Đk: ⇔ ⇔ x > 2 . x − 2 > 0 x > 2 25 Ta có: 3 log x > 3 − log x − 2 ⇔ 3 1 ( ) 3
3log x > 3log x − 2 ⇔ x > x − 2 ⇔ 0 > 2
− (thỏa mãn ∀x∈ ) 3 3 ( )
Kết hợp với điều kiện ta được tập nghiệm S = (2;+ ∞) .
e) Điều kiện của bất phương trình là 9 x > . 4
Khi đó bất phương trình đã cho thành
log 4x − 9 > log x +10 19
⇔ 4x − 9 < x +10 ⇔ x < . (Do 1 ( ) 1 ( ) 3 2 2 1 a = <1). 2
So điều kiện ta được 9 19 < x < . 4 3 x > 1 − f) Điều kiện: ⇔ 1 − < x < 2 x < 2 Ta có log x +1 ≤ log 2
− x + 4 ⇔ log x +1 ≤ log 2 − x + 4 0.8 ( ) 1.25 ( ) 4 ( ) 5 ( ) 5 4 log x +1 ≤ −log 2
− x + 4 ⇔ log x +1 2 − x + 4 ≤ 0 4 ( ) 4 ( ) 4 ( )( ) 5 5 5 2 2 1− 7 1+ 7 ⇔ 2
− x + 2x + 4 ≥1 ⇔ 2
− x + 2x + 3 ≥ 0 ⇔ ≤ x ≤ 2 2
Kết hợp với điều kiện ta có tập nghiệm của bất phương trình là 1− 7 1+ 7 T = ; . 2 2
g) Ta có log x +1 − 2log 5 − x <1− log x − 2 2 ( ) 4 ( ) 2 ( ) 2 < x < 5 ⇔
log x +1 − log 5 − x <1− log x − 2 2 ( ) 2 ( ) 2 ( ) 2 < x < 5
⇔ log x+1 +log x−2 x 2 ( ) 2 ( ) 2 2 ( ) 2 < x < 5 ⇔
log x +1 . x − 2 < log 10 − 2 x 2 ( ) ( ) 2 ( ) 26 2 < x < 5 2 < x < 5 ⇔ ( ⇔ x + )
1 .(x − 2) <10 − 2x 2
x + x −12 < 0 2 < x < 5 ⇔
⇔ 2 < x < 3. 4 − < x < 3
Vậy tập nghiệm của bất phương trình là (2; 3) . 2 x +2mx 1 + 2x−3m 2 x +2mx 1 + 2 − x+3m Bài 15. a. 2 e ≤ 2 2 , ∀x∈ ⇔ ≤ , ∀x∈ e 2 e e ⇔ 2 x + 2mx +1≥ 2 − x + 3m , ∀x∈ 2 ⇔ x + 2(m + )
1 x +1− 3m ≥ 0 ,
∀x∈ (*) . ⇔ 2
∆′ = m + 5m ≤ 0 ⇔ 5 − ≤ m ≤ 0 .
Bài 15.b.Ta có: 9x − 2( + ) 1 .3x m
− 3 − 2m > 0 ⇔ ( x )2 3
− 2.3x − 3 > (3x + ) 1 .2m ⇔ (3x + )
1 (3x − 3) > (3x + )
1 .2m ⇔ 3x − 3 > 2 ⇔ 3x m > 3 + 2m Vậy 9x − 2( + ) 1 .3x m
− 3 − 2m > 0,∀x∈ 3
⇔ 3 + 2m ≤ 0 ⇔ m ≤ − . 2
E. HƯỚNG DẪN GIẢI BÀI TẬP TRẮC NGHIỆM 1 2C 3A 4B 5D 6C 7B 8 9B 10 11 12 13 14 15 D A D A D D A C
16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
B A D A D A D B A D A B C C C
31 32 33 34 35 36 37 38 39 40 41 42 43 44 45
C C A D C A C C C D D D D C D 46 47 48 49 50 C B D D C Câu 30. Chọn C Câu 31. Chọn C
Điều kiện x > 0 .
Ta có xlog x + 6 = 2x + 3log x ⇔ xlog x + 6 − 2x − 3log x = 0 2 2 2 2 x − 3 = 0 x = 3
⇔ (x − 3)(log x − 2 = 0 ⇔ ⇔ 2 ) log x − 2 = 0 x = 4 2
Vậy: tích các nghiệm của phương trình xlog x + 6 = 2x + 3log x 2 2 bằng 12 27 Câu 32. Chọn C Ta có x x 1 + x 1 10 10 2 5 + + = + x x x x
⇔ 2 .5 + 2.5 − 2.2 − 5.5 = 0 5x − 2 = 0 x = log 2
⇔ (5x − 2).(2x − 5) = 0 ⇔ 5 ⇔ 2x − 5 = 0 x = log 5 2
Vậy: tích các nghiệm của phương trình log bằng log 5.log 2 =1 2 2 5 Câu 33. Chọn A Câu 34. Chọn D Ta có: 2 x 1 − 2x+3 2 2 2 = 3
⇔ x −1 = (2x + 3)log 3 ⇔ x − (2log 3)x −1− 3log 3 = 0 2 2 2 . (1) Do 1.( 1 − − 3log 3) = 1
− − 3log 3 < 0 nên phương trình (1) có 2 2 2
nghiệm thực trái dấu x , x . Khi đó theo định lý Vi-et, ta có: 1 2 1 − − 3log 3 2 x x = = 1 − − 3log 3 = −log 54 . 1 2 2 2 1 Câu 35. Chọn C Ta có: x x 3
2 > 8 ⇔ 2 > 2 ⇔ x > 3.
Vậy tập nghiệm bất phương trình là S = (3;+∞). Câu 36. Chọn A Ta có: 2 4 3 −x ≥ 27 ⇔ 2 4−x 3 3 ≥ 3 ⇔ 2 4 − x ≥ 3 2 ⇔ x ≤1 ⇔ 1 − ≤ x ≤1.
Vậy, tập nghiệm của bất phương trình đã cho là: S = [ 1; − ] 1 . Câu 37. Chọn C 1 4 2 1 1 x x x 1 − − − 4 x − x + 4 2 >
⇔ 2 > 2 x ⇔ x −1 > − ⇔ > 0 ⇔ x > 0 . 16 x x
Vậy, tập nghiệm của bất phương trình đã cho là S = (0;+ ∞) . Câu 38. Chọn C 2 x −3x 10 − x−2 Ta có: 1 1 > 2
⇔ x − 3x −10 < x − 2 3 3 x ≥ 5 2 x − 3x −10 ≥ 0 x ≤ 2 − x ≥ 5 ⇔ x − 2 > 0
⇔ x > 2 ⇔ x ≤ 2 −
⇔ 5 ≤ x <14 . 2
x − 3x −10 < (x − 2)2 x <14 2 < x <14 28
Vì x nguyên nên nhận x∈{5;6;7;8;9;10;11;12;1 } 3 . Câu 39. Chọn C x > 0 log x ≥1⇔ ⇔ x ≥10. x ≥10
Vậy bất phương trình đã cho có tập nghiệm là [10;+∞). Câu 40. Chọn D
x +1 > 2x −1
Ta có log x +1 < log 2x −1 ⇔ 1 ⇔ < x < 2 . 1 ( ) 1 ( ) 2x−1>0 2 2 2
Vậy bất phương trình đã cho có tập nghiệm là 1 S ;2 = . 2 Câu 41. Chọn D Điều kiện 2 x > − . 15 Khi đó,
log 15x + 2 > log 13x + 8 ⇔ 15x + 2 <13x + 8 ⇔ 2x < 6 ⇔ x < 3 . 0,8 ( ) 0,8 ( )
Tập nghiệm bất phương trình là: 2 T ;3 = − 15
Vì x nguyên nên x∈{0;1; } 2 . Câu 42. Chọn D x x 8 4 2 + > 2x x 8 2 2 + ⇔ >
⇔ 2x > x + 8 ⇔ x > 8 . Câu 43. Chọn D − x x+2 1 x+2 5 < ⇔ x 5 < (5)2 ⇔ 2 < x . 25 Câu 44. Chọn C Ta có 2 5x −x < 25 2
⇔ x − x < 2 ⇔ 1
− < x < 2 ⇔ x∈( 1; − 2) .
Vậy tập nghiệm của bất phương trình đã cho là S = ( 1; − 2) . Câu 45. Chọn D Ta có: 2x 1
3 − > 27 ⇔ 2x −1> 3 ⇔ x > 2 .
Vậy tập nghiệm của bất phương trình là: (2;+∞) . 29 Câu 46. Chọn C Ta có 1 5 − 2 = . 5 + 2 ( − x− x 5 + 2) ≥ ( 5 + 2)1 2 1 − x x + x − x+ 1 2 1 ⇔ x −1≥ ⇔ ≥ 0 ⇔ x∈[ 2 − ;− ) 1 ∪[1;+∞) x +1 x +1 . Câu 47. Chọn B 1−3 2 x 25 1−3x 2 − ≥ 2 2 ⇔ ≥
⇔ 1− 3x ≤ 2 − ⇔ x ≥1 . 5 4 5 5
Vậy tập nghiệm của bất phương trình là: S = [1;+∞) . Câu 48. Chọn D ( x x x x − )3−x− > ( + ) 1+ x+ ⇔ ( + ) −3 x− > ( + ) 1+ 1 3 1 x+3 10 3 10 3 10 3 10 3 ĐK: x ≠ 1 x ≠ 3 − x − 3 x +1 8 − BPT ⇔ > ⇔
> 0 ⇔ (x −1)(x + 3) < 0 ⇔ 3
− < x <1→ x∈ x −1 x + 3 (x −1)(x + 3) . Câu 49. Chọn D 1 2x +1 > 0 x > − Đk: 1 ⇔
2 ⇔ − < x <1 . 1 − x > 0 2 x <1 Ta có:
log 2x +1 < log 1− x +1 ⇔ . 5 ( ) 5 ( )
log 2x +1 < log 1− x + log 5 . ⇔ log 2x +1 < log 5 − 5x 5 ( ) 5 ( ) 5 ( ) 5 ( ) 5 4
⇔ 2x +1< 5 − 5x ⇔ x < . 7
Kết hợp điều kiện (*) suy ra bất phương trình đã cho có tập nghiệm: 1 4 S ; = − . 2 7 Câu 50. Chọn C
Điều kiện x > 0 . Ta có 30
log x + log x ≤ 3 ⇔ −log x + 2log x ≤ 3 1 3 3 3 3
⇔ log x ≤ 3 ⇔ x ≤ 27 3
Kết hợp với điều kiện ta có tập nghiệm của bất phương trình là T = (0;27]
Do đó a = 0;b = 27 . Vậy T = 0 + 3.27 = 81 31
Document Outline
- Bài 1. PHÉP TÍNH LŨY THỪA - 23T
- Bài 2. LOGARIT - 13T
- Bài 3. HÀM SỐ MŨ - 11T
- Bài 4. HÀM SỐ LOGARIT - 12T
- Bài 5. PT - BPT MŨ LOGA - 30T
- Bài 6. BÀI TẬP ÔN TẬP CHƯƠNG 6 -30T




