


























Preview text:
Giáo Viên Toán _Trường THPT Tuy Phong HÌNH HOÏC 10 CHƯƠNG I VECTƠ LỜI NÓI ĐẦU
Quý đọc giả, quý thầy cô và các em học sinh thân mến!
Nhằm giúp các em học sinh có tài liệu tự học môn Toán,
tôi biên soạn cuốn giải toán trọng tâm của lớp 10.
Nội dung của cuốn tài liệu bám sát chương trình chuẩn và
chương trình nâng cao về môn Toán đã được Bộ Giáo dục và Đào tạo quy định. Nội dung gồm 3 phần
Phần 1. Kiến thức cần nắm
Phần 2. Dạng bài tập có hướng dẫn giải và bài tập đề nghị
Phần 3. Phần bài tập trắc nghiệm.
Cuốn tài liệu được xây dựng sẽ còn có những khiếm
khuyết. Rất mong nhận được sự góp ý, đóng góp của quý
đồng nghiệp và các em học sinh.
Mọi góp ý xin gọi về số 0355334679 – 0916.620.899 Email: lsp02071980@gmail.com Chân thành cảm ơn. Lư Sĩ Pháp
Gv_Trường THPT Tuy Phong – Bình Thuận MỤC LỤC CHƯƠNG I VECTƠ
§1. Các định nghĩa ................................................................ 1 – 4
§2. Tổng và hiệu của hai vectơ ............................................. 5 – 11
§3. Tích của vectơ với một số ............................................... 12 – 19
§4. Hệ tọa độ .......................................................................... 20 – 26
ÔN TẬP CHƯƠNG I ............................................................ 27 – 32
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp CHƯƠNG I. VECTƠ
§1. CÁC ĐỊNH NGHĨA
A. KIẾN THỨC CẦN NẮM 1. Khái niệm vectơ
- Vectơ là một đoạn thẳng có hướng, nghĩa là trong hai điểm mút của
đoạn thẳng, đã chỉ rõ điểm nào là điểm đầu, điểm nào là điểm cuối. A
- Vectơ có điểm đầu A, điểm cuối B được kí hiệu là AB và đọc là B “vectơ AB” a x
- Vectơ cón được kí hiệu là a,b, x, y,...khi không cần chỉ rõ điểm đầu và điểm cuối của nó.
2. Vectơ cùng phương, vectơ cùng hướng
- Đường thẳng đi qua điểm đầu và điểm cuối của một vectơ được gọi là giá của vectơ đó.
- Hai vectơ được gọi là cùng phương nếu giá của chúng song song hoặc trung nhau.
- Như vậy, hai vectơ cùng phương thì chúng chỉ có thể cùng hướng hoặc ngược hướng
- Ba điểm A, B và C thẳng hàng khi và chỉ khi hai vectơ AB và AC cùng phương 3. Hai vectơ bằng nhau
- Độ dài của vectơ là khoảng cách giữa điểm đầu và điểm cuối của vectơ đó. Độ dài của AB được
kí hiệu là AB , như vậy AB = AB
- Vectơ có độ dài bằng 1 gọi là vectơ đơn vị
- Hai vectơ được gọi là bằng nhau nếu chúng cùng hướng và cùng độ dài. Nếu hai vectơ a và b
bằng nhau thì ta viết a = b
- Khi cho trước một vectơ a và điểm O, thì ta luôn tìm được một điểm A duy nhất sao cho OA = a 4. Vectơ - không
- Vectơ có điểm dầu và điểm cuối trùng nhau gọi là vectơ_không, kí hiệu 0 , nghĩa là
0 = AA = BB = MM = ...với mọi điểm A, B, M,… và AA = 0 = 0
- Vectơ_không cùng phương, cùng hướng với mọi vectơ B. BÀI TẬP
Bài 1.1. Cho hai vectơ không cùng phương a và b . Có hay không một vectơ cùng phương với hai vectơ đó? HD Giải Có. Đó là vectơ_không
Bài 1.2.Cho ba vectơ a,b,c đều khác vectơ không. Các khẳng định sau đây đúng hay sai?
a) Nếu hai vectơ a và b cùng phương với c thì a và b cùng phương
b) Nếu a và b cùng ngược hướng với c thì a và b cùng hướng. HD Giải a) Đúng b) Đúng
Bài 1.3. Gọi C là trung điểm của đoạn thẳng AB. Các khẳng định sau đây đúng hay sai?
a) AC và BC cùng hướng
b) AC và AB cùng hướng
c) AB và BC ngược hướng d) AB = BC e) AC = BC f) AB = 2 BC HD Giải a) Sai b) Đúng c) Đúng d) Sai e) Đúng f) Đúng
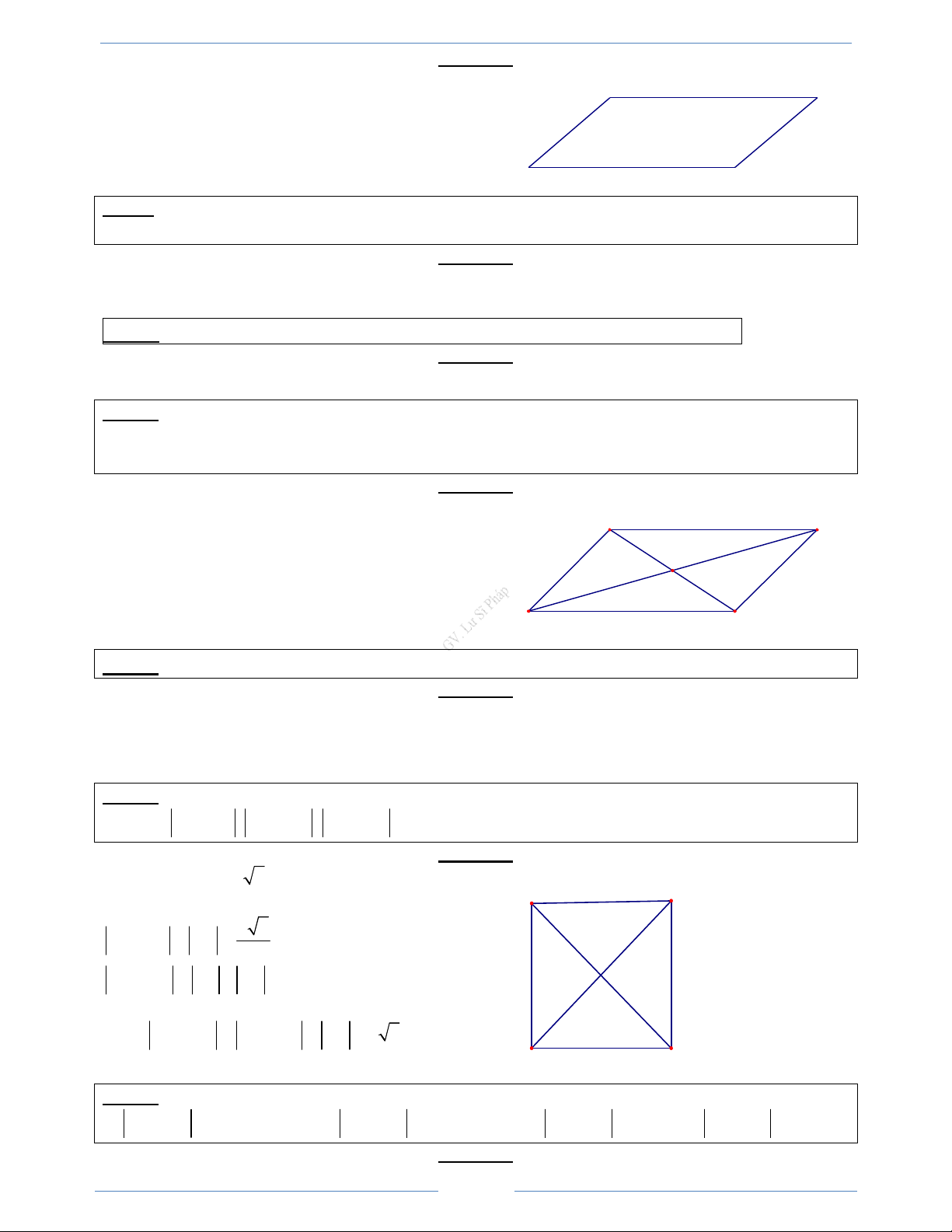
Bài 1.4.Cho tứ giác ABCD. Chứng minh rằng tứ giác đó là hình bình hành khi và chỉ khi AB = DC HD Giải
Nếu tứ giác ABCD là hình bình hành thì AB =
DC và hai vectơ AB và DC cùng hướng. Vậy 1 Chương I. Vectơ
0916 620 899 – 0355 334 679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp AB = DC B
Ngược lại, nếu AB = DC thì AB = DC, AB//DC. C
Vậy tứ giác ABCD là hình bình hành A D
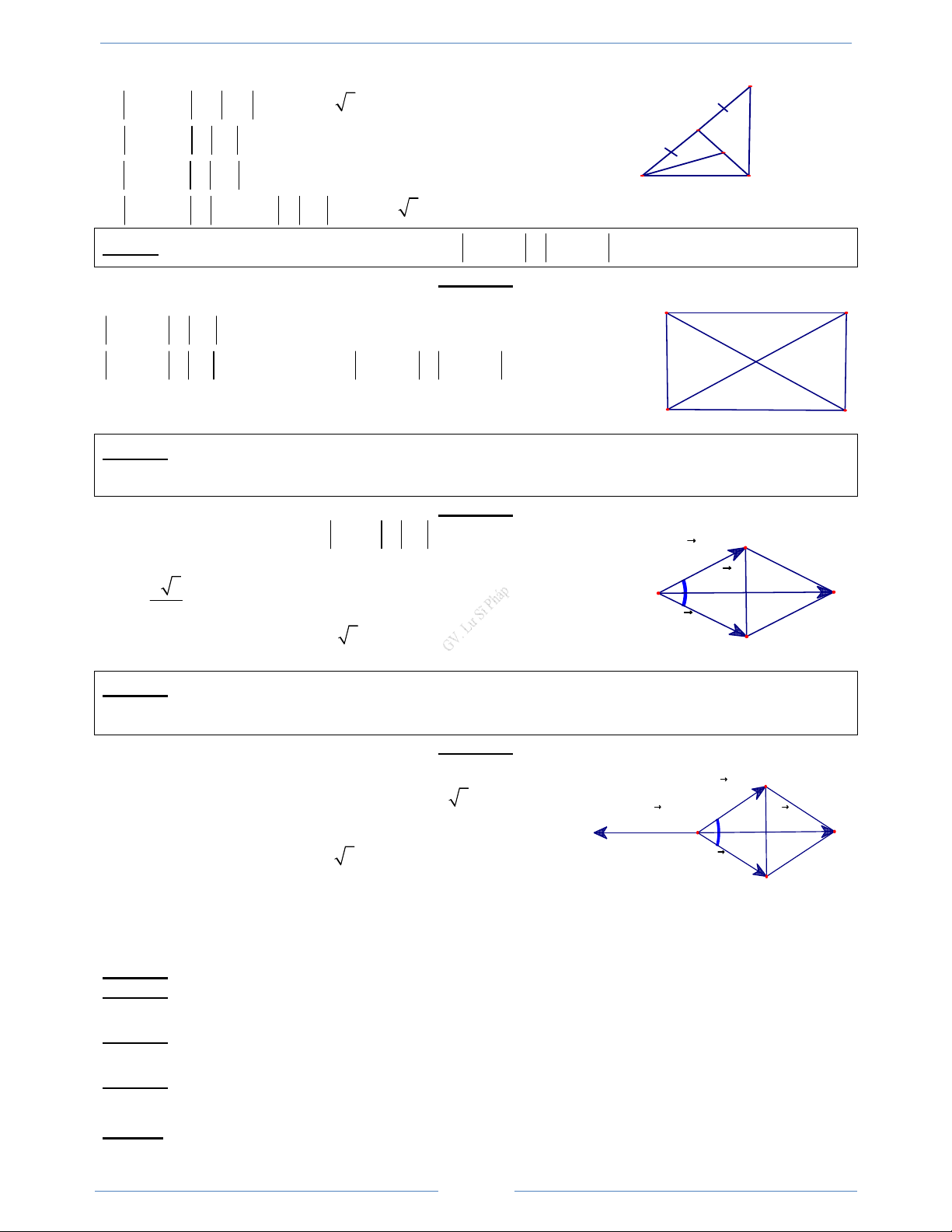
Bài 1.5.Cho lục giác đều ABCDEF có tâm O.
a) Hãy tìm các vectơ khác 0 và cùng phương với OA
b) Hãy tìm các vectơ bằng vectơ AB HD Giải
a) Các vectơ vectơ khác 0 và cùng phương với B C OA là D ,
A AD, BC, CB, AO, OD, DO, EF , FE
b) Các vectơ bằng vectơ AB : OC, ED, FO A D O F E
C. BÀI TẬP TỰ LUYỆN
Bài 1.6. Cho lục giác đều ABCDEF. Hãy vẽ các vectơ bằng vectơ AB và có
a) Các điểm đầu là B, F, C
b) Các điểm cuối là F, D, C
Bài 1.7. Cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm các cạnh AB, AC và BC. Hãy xác định
các vectơ cùng hướng với các vectơ BP, PN
Bài 1.8. Cho tam giác ABC. Có bao nhiêu vectơ khác vectơ 0 có điểm đầu điểm cuối là các đỉnh của tam giác ABC
Bài 1.9. Cho tam giác ABC cân ở A, đường cao AH. Các câu sau đây đúng hay sai? a) AB = AC b) AB = AC c) AB = CA d) HC = BH
Bài 1.10. Cho từ giác ABCD. Gọi M, N, P và Q lần lượt là trung điểm các cạnh AB, BC, CD và DA.
Chứng minh rằng NP = MQ và PQ = NM
Bài 1.11. Cho tứ giác ABCD. Chứng minh rằng nếu AB = DC thì AD = BC
D. BÀI TẬP TRẮC NGHIỆM
Câu 1. Cho ba điểm ,
A B, C phân biệt. Mệnh đề nào dưới đây đúng?
A. Điều kiện cần để ,
A B, C thẳng hàng là AB = AC.
B. Điều kiện cần và đủ để , A ,
B C thẳng hàng là AB cùng phương với AC.
C. Điều kiện đủ để ,
A B, C thẳng hàng là với mọi M , MA cùng phương với A . B
D. Điều kiện cần để ,
A B, C thẳng hàng là với mọi M , MA cùng phương với A . B
Câu 2. Cho hình thoi ABCD cạnh a và BAD = 60° . Đẳng thức nào dưới đây đúng?
A. BD = AC.
B. BC = D . A
C. AB = A . D D. BD = . a
Câu 3. Cho lục giác đều ABCDEF tâm .
O Số các vectơ bằng OC có điểm đầu và điểm cuối là các đỉnh của lục giác là A. 6. B. 3. C. 4. D. 2.
Câu 4. Cho AB ≠ 0 và một điểm C. Có bao nhiêu điểm D thỏa mãn AB = CD ? A. Vô số. B. 1. C. 2. D. 0.
Câu 5. Gọi M , N lần lượt là trung điểm của các cạnh A ,
B AC của tam giác đều ABC . Hỏi cặp vectơ
nào dưới đây cùng hướng? 2 Chương I. Vectơ
0916 620 899 – 0355 334 679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp
A. MA và M . B
B. AN và C . A
C. MN và C . B
D. AB và M . B
Câu 6. Hai vectơ được gọi là bằng nhau khi và chỉ khi
A. Chúng trùng với một trong các cặp cạnh đối của một tam giác đều.
B. Chúng cùng hướng và độ dài của chúng bằng nhau.
C. Giá của chúng trùng nhau và độ dài của chúng bằng nhau.
D. Chúng trùng với một trong các cặp cạnh đối của một hình bình hành.
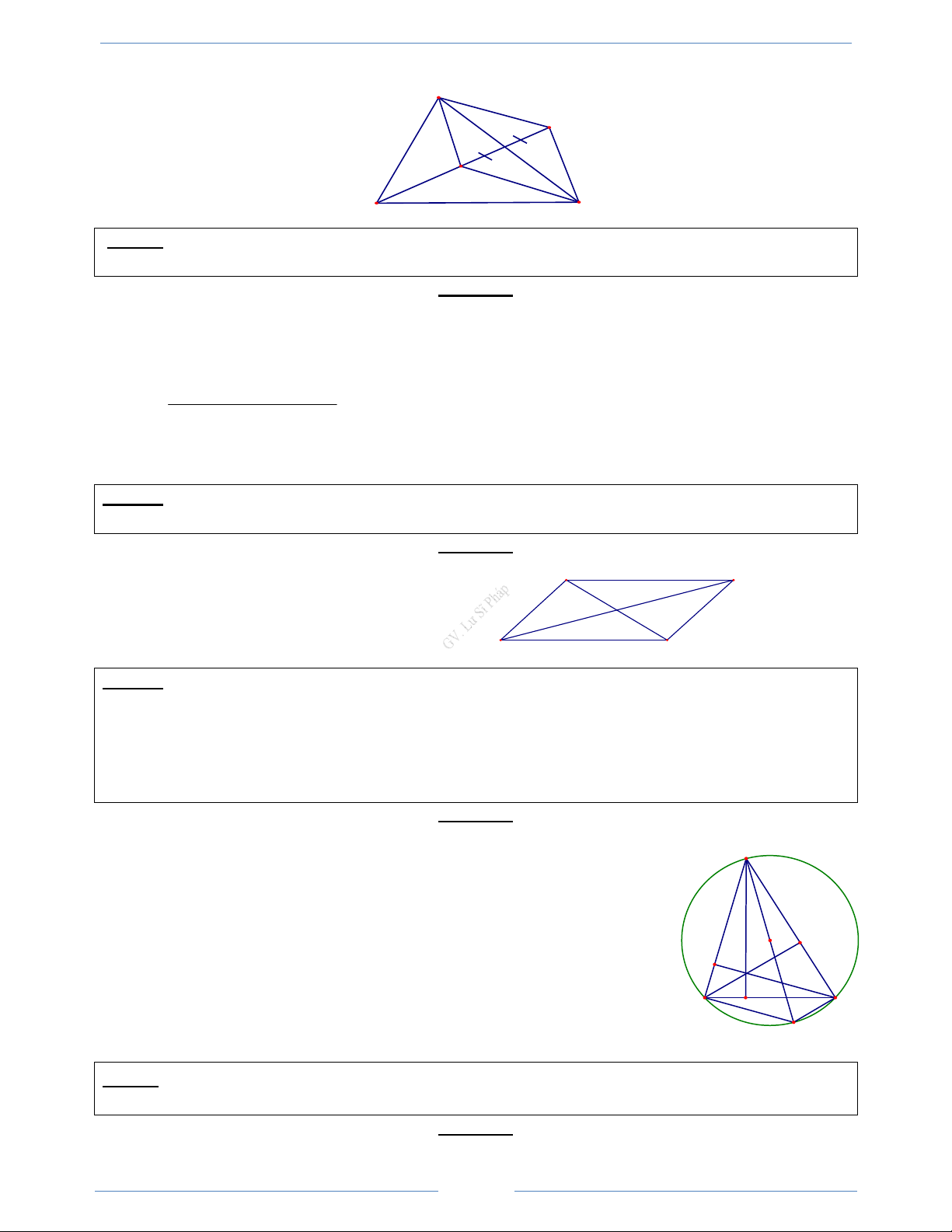
Câu 7. Cho tam giác ABC có trực tâm H . Gọi D là điểm đối xứng với B qua tâm O của đường tròn
ngoại tiếp tam giác ABC . Khẳng định nào dưới đây đúng?
A. HA = CD và AD = HC và OB = OD .
B. HA = CD và AD = CH .
C. HA = CD và AD = HC .
D. HA = CD và AC = CH .
Câu 8. Cho lục giác đều ABCDEF tâm .
O Số các vectơ khác vectơ - không, cùng phương với OC có
điểm đầu và điểm cuối là các đỉnh của lục giác là A. 9. B. 4. C. 6. D. 7.
Câu 9. Cho tam giác ABC đều cạnh a . Gọi M là trung điểm BC . Khẳng định nào dưới đây đúng? a 3 a 3 A. AM = . B. AM = . C. AM = . a
D. MB = MC. 2 2
Câu 10. Mệnh đề nào dưới đây sai?
A. AA = 0.
B. 0 cùng hướng với mọi vectơ.
C. AB > 0.
D. 0 cùng phương với mọi vectơ.
Câu 11. Cho tứ giác ABC .
D Gọi M , N, ,
P Q lần lượt là trung điểm của A ,
B BC, C , D D . A Khẳng
định nào dưới đây sai?
A. MN = AC .
B. MN = Q . P
C. QP = MN .
D. MQ = N . P
Câu 12. Với DE (khác vectơ - không) thì độ dài đoạn ED được gọi là A. Giá của E . D
B. Độ dài của E . D
C. Phương của E . D
D. Hướng của E . D
Câu 13. Vectơ có điểm đầu là D , điểm cuối là E được kí hiệu là A. E . D B. DE. C. DE. D. DE .
Câu 14. Cho tứ giác ABCD . Có bao nhiêu vectơ khác vectơ - không có điểm đầu và cuối là các đỉnh của tứ giác? A. 4. B. 6. C. 8. D. 12.
Câu 15. Cho lục giác đều ABCDEF có tâm .
O Đẳng thức nào dưới đây sai?
A. AB = E . D
B. AB = AF .
C. OD = BC.
D. OB = OE.
Câu 16. Cho bốn điểm phân biệt , A , B C, .
D Điều kiện nào trong các đáp án A, B, C, D sau đây là điều
kiện cần và đủ để AB = CD ?
A. ABCD là hình bình hành.
B. ABDC là hình bình hành.
C. AC = BD.
D. AB = CD.
Câu 17. Cho bốn điểm phân biệt , A ,
B C, D thỏa mãn AB = CD . Khẳng định nào dưới đây sai?
A. ABCD là hình bình hành.
B. AB cùng hướng C . D
C. AB cùng phương C . D
D. AB = CD .
Câu 18. Gọi O là giao điểm của hai đường chéo hình chữ nhật ABCD . Mệnh đề nào dưới đây đúng?
A. OA = OC.
B. OB và OD cùng hướng.
C. AC và BD cùng hướng.
D. AC = BD . 3 Chương I. Vectơ
0916 620 899 – 0355 334 679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp
Câu 19. Cho tam giác ABC. Có bao nhiêu vectơ khác vectơ - không có điểm đầu và điểm cuối là các đỉnh , A , B C ? A. 4. B. 9. C. 3. D. 6.
Câu 20. Gọi M , N lần lượt là trung điểm của các cạnh A ,
B AC của tam giác đều ABC . Đẳng thức nào dưới đây đúng?
A. BC = 2 MN .
B. MA = M . B
C. AB = AC.
D. MN = BC.
Câu 21. Cho hình vuông ABCD . Khẳng định nào dưới đây đúng? A. AC = B . D
B. AB = C . D
C. AB = BC .
D. Hai vectơ AB, AC cùng hướng.
Câu 22. Mệnh đề nào dưới đây đúng?
A. Không có vectơ nào cùng phương với mọi vectơ.
B. Có ít nhất hai vectơ có cùng phương với mọi vectơ.
C. Có vô số vectơ cùng phương với mọi vectơ.
D. Có duy nhất một vectơ cùng phương với mọi vectơ.
Câu 23. Cho AB ≠ 0 và một điểm C. Có bao nhiêu điểm D thỏa mãn AB = CD ? A. Vô số. B. 2. C. 0. D. 1.
Câu 24. Gọi O là giao điểm của hai đường chéo của hình bình hành ABCD . Đẳng thức nào dưới đây sai? A. CB = D . A
B. OB = D . O
C. OA = OC.
D. AB = DC. ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 4 Chương I. Vectơ
0916 620 899 – 0355 334 679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp
§2. TỔNG VÀ HIỆU CỦA HAI VECTƠ
A. KIẾN THỨC CẦN NẮM 1. Tổng của hai vectơ
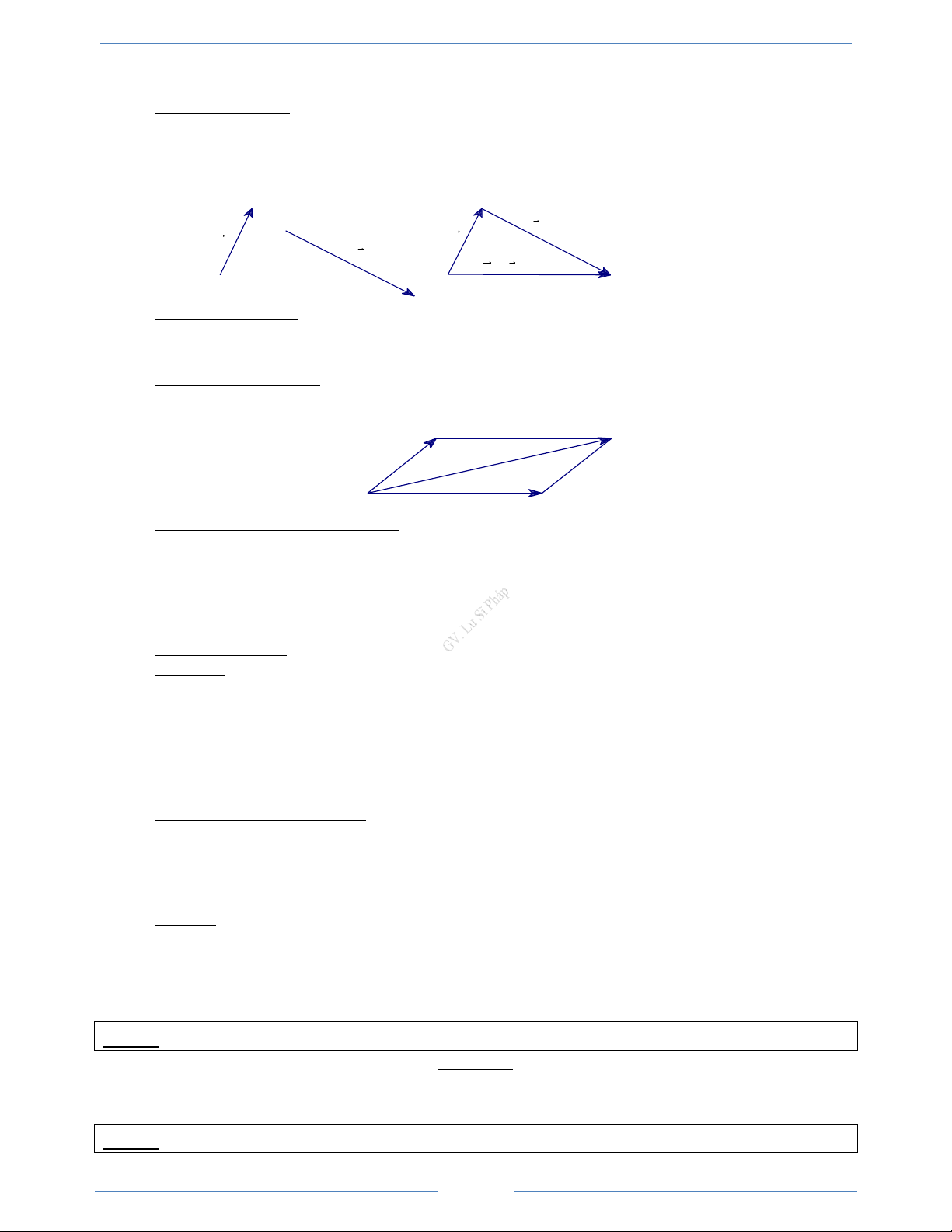
- Cho hai vectơ a và b . Lấy một điểm A tuỳ ý, vẽ AB = a và BC = b . Vectơ AC được gọi là tổng
của hai vectơ a và b . Ta kí hiệu tổng của hai vectơ a và b là a + b . Vậy AC = a + b
- Phép toán tìm tổng của hai vectơ còn được gọi là phép công vectơ. B b a a b A a + b C 2. Các quy tắc cần nhớ a. Quy tắc ba điểm
Với ba điểm A, B, C tuỳ ý, ta luôn có AB + BC = AC
b. Quy tắc hình bình hành
Nếu ABCD là hình bình hành thì ta có: AB + AD = AC B C A D
3. Tính chất của phép cộng các vectơ
Với ba vectơ a,b, c tuỳ ý, ta có
a) a + b = b + a ( Tính chất giao hoán)
b) (a + b) + c = a + (b + c) (Tính chất kết hợp)
c) a + 0 = 0 + a = a (Tính chất của vectơ_không) 4. Hiệu của hai vectơ a) Vectơ đối
- Nếu tổng của hai vectơ a và b là vectơ_không, thì ta nói a là vectơ đối của vectơ b , hoặc vectơ
b là vectơ đối của vectơ a .
- Vectơ đối của vectơ a kí hiệu là - a . Như vậy: a + (- a ) = (- a ) + a = 0
- Nhận xét: Vectơ đối của vectơ a là vectơ ngược hướng với vectơ a và có cùng độ dài với a .
- Đặc biệt, vectơ đối của vectơ 0 l2 vectơ 0
b) Định nghĩa hiệu của hai vectơ
- Cho hai vectơ a và b . Ta gọi hiệu của hai vectơ a và b là vectơ a + (- b ). Kí hiệu a - b . Như
vậy a − b = a + ( b − )
- Qui tắc về hiệu của vectơ: Với ba điểm O, A, B tuỳ ý, ta có: AB = OB − OA 5. Áp dụng
- Điểm I là trung điểm của đoạn thẳng AB khi và chỉ khi IA + IB = 0
- Điểm G là trọng tâm của tam giác ABC khi và chỉ khi GA + GB + GC = 0 B. BÀI TẬP
Bài 2.1.Chứng minh rằng với bốn điểm bất kì A, B, C, D, ta có AC + BD = AD + BC HD Giải
Ta dùng qui tắc ba điểm, ta có AC = AD + DC
Khi đó vt = AC + BD = AD + DC + BD = AD + BD + DC = AD + BC = vp (đpcm)
Bài 2.2. Cho hình bình hành ABCD và một điểm M tuỳ ý. Chứng minh rằng MA + MC = MB + MD 5 Chương I. Vectơ
0916 620 899 – 0355 334 679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp HD Giải
Ta sử dụng quy tắc ba điểm B C
vt = MA + MC = MB + BA + MD + DC
= MB + MD + (BA+ DC) = MB + MD +(BA+ AB)
, vì ABCD là hình bình hành = A D
MB + MD + BB = MB + MD + 0 = vp
Bài 2.3 Chứng minh rằng đối với từ giác ABCD bất kì, ta luôn có
a) AB + BC + CD + DA = 0
b) AB + CD = CB + AD HD Giải
a) vt = AB + BC + CD + DA = AC + CA = AA = 0 = vp (đpcm)
b) AB − AD = CB − CD ⇔ DB = DB (luôn đúng; áp dụng qui tắc ba điểm trừ)
Bài 2.4.Cho bốn điểm A, B, C, D và E. Chứng minh rằng AC + DE − DC − CE + CB = AB HD Giải
Ta có vt = AC + DE − DC − CE + CB = AC + CB + DE − (DC +CE) = AB + DE − DE = AB = vp (đpcm)
Bài 2.5.Cho hình bình hành ABCD có tâm O. Chứng minh rằng
a) CO − OB = BA
b) AB − BC = DB
c) DA − DB = OD − OC
d) DA − DB + DC = O
e) OA + OB + OC + OD = O HD Giải
a) Ta có CO = OA (Vì O là trung điểm của AC) B C
nên vt = CO − OB = OA − OB = BA = vp
b) Vì ABCD là hình bình hành, nên ta có
BC = AD . Do đó vt = AB − AD = DB = vp O
c), d), e) học sinh tự chứng minh. A D
Bài 2.6. Chứng minh rằng AB = CD khi và chỉ khi trung điểm của hai đoạn thẳng AD và BC trùng nhau. HD Giải
Gọi I, J lần lượt là trung điểm của AD và BC. Ta có
AB = CD ⇔ AI + IJ + JB = CJ + JI + ID
⇔ ( AI − ID)+ IJ = (CJ − JB)+ JI ⇔ IJ = JI ⇔ IJ = 0 ⇔ I ≡ J
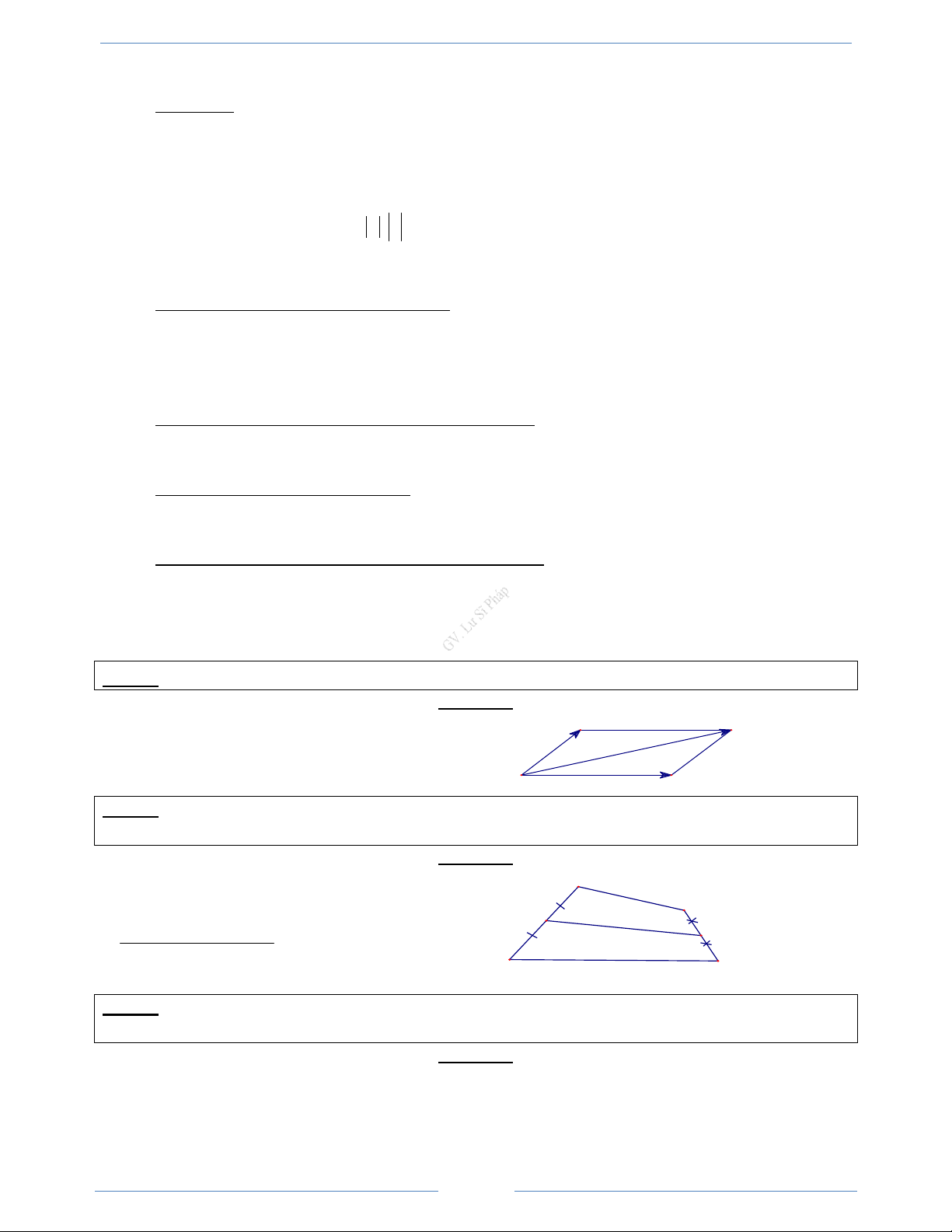
Bài 2.7. Cho hình vuông ABCD cạnh a, có tâm O.
Hãy tính OA − CB ; AB + CD ; CD − DA HD Giải
Ta có AC = BD = a 2 , A B
OA − CB = CO − CB = BO . Do đó a 2
OA − CB = BO = 2 O
AB + CD = AB + CD = 2a ( Vì AB và DC là hai vectơ cùng hướng)
Ta có CD − DA = CD − CB = BD = a 2 ( Vì D C DA = CB )
Bài 2.8.Cho tam giác đều ABC có cạnh bằng a. Tìm: a) AB + AC = ?
b) AB − AC = ? c) AB + BC = ?
d) AB − BC = ? HD Giải 6 Chương I. Vectơ
0916 620 899 – 0355 334 679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp
Gọi AH là đường cao của tam giác đều ABC. D là đối xứng của A qua B. Ta có D
a) AB + AC = 2 AH = 2AH = a 3 B
b) AB − AC = CB = CB = a H
c) AB + BC = AC = AC = a A C
d) AB − BC = BD − BC = CD = CD = a 3
Bài 2.9.Cho tam giác ABC. Chứng minh rằng nếu CA + CB = CA − CB thì tam giác ABC vuông tại C. HD Giải
Vẽ hình bình hành CADB. Ta có CA + CB = CD (qui tắc hbh). Do đó A D
CA + CB = CD = CD .
CA − CB = BA = BA . Từ giả thiết CA + CB = CA − CB suy ra CD = AB
Vậy tứ giác CADB là hình chữ nhật. Từ đó ta có tam giác CAB vuông tại C. C B
Bài 2.10.Cho hai lực 1 F và 2
F có điểm đặt O và tạo với nhau một góc 600. Tìm cường độ tổng hợp lực
của hai lực ấy, biết rằng cường độ của hai lực 1 F và 2 F đều là 100N. HD Giải Ta có + = = . Do đó + = = 1 F 2 F F OA 1 F 2 F OA OA B
Mặt khác, Vẽ hình thoi OCBA, ta có tam giác OCB đều nên F1 a 3 600 F OH = và O A OA = 2OH 2 H F
Vậy cường độ của hợp lực là 100 3 N. 2 C
Bài 2.11.Cho ba lực F = M , = và =
cùng tác động vào một vật tại điểm M và vật đứng 1 A 2 F MB 3 F MC
yên. Cho biết cường độ của
. Tìm cường độ và hướng của lực 1 F và 2 F đều là 100N và 0 AMB = 60 3 F HD Giải
Vật đứng yên do đó F + F + F = 0 . Vẽ hình thoi MAEB, ta có 1 2 3 A + = = và lực F1 1 F 2 F 4 F ME 4
F có cường độ là 100 3 N. Ta có F M F
F + F = 0 , do đó 3 4 600 4 3 3
F là vectơ đối của 4 F . E H Như vậy 3
F có cường độ là 100 3 N và ngược hướng với 4 F F2 B
C. BÀI TẬP TỰ LUYỆN
Bài 2.12. Cho ngũ giác ABCDE. Chứng minh AB + BC + CD = AE − DE
Bài 2.13. Cho lục giác đều ABCDEF và M là một điểm tuỳ ý.
Chứng minh rằng MA + MC + ME = MB + MD + MF
Bài 2.14. Cho tam giác ABC. Các điểm M, N và P lần lượt là trung điểm các cạnh AB, AC và BC. Chứng
minh rằng với điểm O bất kì, ta có OA + OB + OC = OM + ON + OP
Bài 2.15. Cho lục giác đều ABCDEF tâm O. Chứng minh rằng
a) AB + CD + EF + BC + DE + FA = O
b) OA + OB + OC + OD + OE + OF = O
Bài 2.16. Cho hai lực F ; 1 2
F có điểm đặt tại O và tạo với nhau một góc 1200. Tìm cường đô tổng hợp hai 7 Chương I. Vectơ
0916 620 899 – 0355 334 679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp
lực ấy, biết rằng hai lực F ; 1 2
F có đều cường đô là 100N.
Bài 2.17. Cho tam giác ABC. Bên ngoài tam giác vẽ các hình bình hành ABIJ, BCPQ và CARS. Chứng
minh rằng: RJ + IQ + PS = 0
Bài 2.18. Cho sáu điểm A, B, C, D, E, F.
Chứng minh rằng: AD + BE + CF = AE + BF + CD = AF + BD + CE
Bài 2.19. Cho lục giác đều ABCDEF tâm O. Chứng minh rằng:
a) AB + CD + EF + BC + DE + FA = O
b) OA + OB + OC + OD + OE + OF = O
D. BÀI TẬP TRẮC NGHIỆM
Câu 1. Cho hình bình hành ABCD . Đẳng thức nào sau đây đúng?
A. AB − BC = AC.
B. AB − BC = D . B
C. AB − BC = B . D
D. AB − BC = C . A
Câu 2. Cho hình bình hành ABCD có O là giao điểm của hai đường chéo. Đẳng thức nào sau đây sai?
A. OA + OB + OC + OD = 0.
B. AC = AB + A . D
C. BA + BC = DA + DC .
D. AB + CD = AB + C . B
Câu 3. Cho hình bình hành ABCD có O là giao điểm của hai đường chéo. Hỏi vectơ ( AO − DO) bằng
vectơ nào trong các vectơ sau? A. DC. B. AC. C. B . A D. B . C
Câu 4. Cho hình bình hành ABCD có O là giao điểm của hai đường chéo. Gọi E, F lần lượt là trung
điểm của AB, BC . Đẳng thức nào sau đây sai?
A. BE + BF − DO = 0.
B. OC = EB + E . O
C. OA + OC + OD + OE + OF = 0.
D. DO = EB − E . O
Câu 5. Cho a và b là các vectơ khác 0 với a là vectơ đối của b . Khẳng định nào sau đây sai?
A. Hai vectơ a, b cùng độ dài.
B. Hai vectơ a, b chung điểm đầu.
C. Hai vectơ a, b cùng phương.
D. Hai vectơ a, b ngược hướng.
Câu 6. Cho tam giác ABC đều cạnh a . Tính AB + AC . a 3
A. AB + AC = 2a 3.
B. AB + AC = . 2
C. AB + AC = 2 . a
D. AB + AC = a 3.
Câu 7. Cho hình thoi ABCD có AC = 2a và BD = .
a Tính AC + BD .
A. AC + BD = 5 . a
B. AC + BD = a 3.
C. AC + BD = a 5.
D. AC + BD = 3 . a
Câu 8. Cho tam giác ABC cân ở A , đường cao AH . Khẳng định nào sau đây sai?
A. BC = 2HC.
B. HC = −H . B
C. AB = AC .
D. AB = A . C
Câu 9. Cho AB = C
− D. Khẳng định nào sau đây đúng?
A. ABCD là hình bình hành.
B. AB + DC = 0.
C. AB và CD cùng hướng.
D. AB và CD cùng độ dài.
Câu 10. Cho hai điểm A và B phân biệt. Điều kiện để I là trung điểm AB là:
A. AI = BI.
B. IA = I . B
C. IA = I . B
D. IA = −I . B
Câu 11. Cho tam giác ABC và điểm M thỏa mãn điều kiện MA − MB + MC = 0 . Mệnh đề nào sau đây sai? 8 Chương I. Vectơ
0916 620 899 – 0355 334 679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp
A. BA + BC = BM.
B. MA = B . C
C. MABC là hình bình hành.
D. AM + AB = AC.
Câu 12. Cho tam giác ABC vuông cân đỉnh A, đường cao AH . Khẳng định nào sau đây sai?
A. AH + HB = AH + HC .
B. AH − AB = AH − AC.
C. BC − BA = HC − H . A
D. AH = AB − AH .
Câu 13. Cho tam giác ABC đều cạnh a, H là trung điểm của BC . Tính CA − HC . a 7 A. a CA − HC = .
B. CA − HC = . 2 2 3 2 3 C. a a CA − HC = .
D. CA − HC = . 2 3
Câu 14. Cho hình bình hành ABCD. Gọi G là trọng tâm của tam giác ABC. Mệnh đề nào sau đây đúng?
A. GA + GC + GD = B . D
B. GA + GC + GD = C . D
C. GA + GC + GD = . O
D. GA + GD + GC = C . D
Câu 15. Cho tam giác ABC. Tập hợp tất cả các điểm M thỏa mãn đẳng thức MB − MC = BM − BA là
A. đường thẳng qua A và song song với BC.
B. đường thẳng A . B
C. trung trực đoạn BC.
D. đường tròn tâm ,
A bán kính BC.
Câu 16. Cho tam giác ABC với M là trung điểm BC. Mệnh đề nào sau đây đúng?
A. AM + MB + BA = 0.
B. MA + MB = A . B
C. MA+ MB = MC.
D. AB + AC = AM.
Câu 17. Cho ba điểm phân biệt ,
A B, C . Đẳng thức nào sau đây đúng?
A. AB − BC = C . A
B. CA − BA = BC.
C. AB + AC = BC.
D. AB + CA = C . B
Câu 18. Điều kiện nào là điều kiện cần và đủ để I là trung điểm của đoạn thẳng AB ? A. IA = I . B
B. IA = I . B
C. IA + IB = 0.
D. IA − IB = 0.
Câu 19. Cho ba điểm ,
A B, C phân biệt. Khẳng định nào sau đây đúng?
A. AB + AC = BC.
B. MP + NM = N . P
C. CA+ BA = C . B
D. AA + BB = A . B
Câu 20. Cho tam giác ABC đều cạnh .
a Mệnh đề nào sau đây đúng?
A. AB = BC = C . A
B. CA = −A . B
C. AB = BC = CA = . a
D. CA = −B . C
Câu 21. Cho hình chữ nhật ABCD. Khẳng định nào sau đây đúng?
A. AB − AD = AB + AD .
B. BC + BD = AC − AB .
C. AC = B . D
D. AB + AC + AD = 0.
Câu 22. Tam giác ABC có AB = AC = a và BAC =120° . Tính AB + AC . A. a
AB + AC = .
B. AB + AC = 2 . a
C. AB + AC = a 3.
D. AB + AC = . a 2
Câu 23. Gọi O là tâm của hình vuông ABCD . Vectơ nào trong các vectơ dưới đây bằng CA?
A. DC −C . B B. O − A+O . C
C. BA + D . A
D. BC + A . B
Câu 24. Cho lục giác đều ABCDEF có tâm .
O Đẳng thức nào sau đây sai?
A. OA + OC + OE = 0.
B. OA + OC + OB = E . B
C. AB + CD + EF = 0.
D. BC + EF = A . D 9 Chương I. Vectơ
0916 620 899 – 0355 334 679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp
Câu 25. Cho đường tròn O và hai tiếp tuyến MT, MT′ (T và T′ là hai tiếp điểm). Khẳng định nào sau đây đúng? A. OT = O − T .′
B. MT = MT .′
C. MT + MT ′ = TT .′
D. MT = MT .′
Câu 26. Cho ba điểm phân biệt , A ,
B C. Mệnh đề nào sau đây đúng?
A. AB − CA = BC.
B. AB + BC = AC.
C. AB + BC + CA = 0.
D. AB = BC ⇔ CA = BC .
Câu 27. Cho đường tròn O và hai tiếp tuyến song song với nhau tiếp xúc với (O) tại hai điểm A và . B
Mệnh đề nào sau đây đúng? A. OA = O − . B B. AB = O − . B
C. OA = −O . B
D. AB = −B . A
Câu 28. Gọi O là tâm hình vuông ABCD . Tính OB −OC .
A. OB − OC = A . B
B. OB −OC = BC.
C. OB − OC = D . A
D. OB − OC = OD − O . A
Câu 29. Tính tổng MN + PQ + RN + NP + QR . A. M . P B. MN. C. P . R D. M . R
Câu 30. Mệnh đề nào sau đây sai?
A. Nếu ba điểm phân biệt ,
A B, C nằm tùy ý trên một đường thẳng thì AB + BC = AC .
B. Nếu G là trọng tâm tam giác ABC thì GA + GB + GC = 0.
C. Nếu ABCD là hình bình hành thì CB + CD = C . A
D. Nếu M là trung điểm đoạn thẳng AB thì MA+ MB = 0.
Câu 31. Cho tam giác ABC với M , N, P lần lượt là trung điểm của BC, C ,
A AB . Khẳng định nào sau đây sai?
A. MN + NP + PM = 0.
B. PB + MC = M . P
C. AB + BC + CA = 0.
D. AP + BM + CN = 0.
Câu 32. Cho hình vuông ABCD cạnh .
a Tính AB − DA .
A. AB − DA = a 2.
B. AB − DA = 2 . a
C. AB − DA = 0.
D. AB − DA = . a
Câu 33. Cho tam giác ABC vuông cân tại C và AB = 2. Tính độ dài của AB + A . C
A. AB + AC = 5.
B. AB + AC = 2 5.
C. AB + AC = 3.
D. AB + AC = 2 3.
Câu 34. Cho tam giác ABC có M thỏa mãn điều kiện MA + MB + MC = 0 . Xác định vị trí điểm M .
A. M trùng với C.
B. M là trọng tâm tam giác ABC.
C. M là điểm thứ tư của hình bình hành ACBM .
D. M là trung điểm của đoạn thẳng A . B
Câu 35. Cho tam giác ABC vuông tại A và có AB = 3, AC = 4. Tính CA + AB .
A. CA + AB = 13.
B. CA + AB = 2 13.
C. CA + AB = 5.
D. CA + AB = 2.
Câu 36. Cho bốn điểm phân biệt , A B, C, .
D Mệnh đề nào sau đây đúng?
A. AB + AD = CD + C . B
B. AB + BC + CD = D . A
C. AB + BC = CD + D . A
D. AB + CD = AD + C . B
Câu 37. Cho hình vuông ABCD . Khẳng định nào sau đây đúng?
A. AD = CB .
B. AB = C . D
C. AC = B . D
D. AB = BC. 10 Chương I. Vectơ
0916 620 899 – 0355 334 679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp
Câu 38. Cho hình vuông ABCD cạnh a , tâm .
O Tính OB + OC . a 2
A. OB + OC = .
B. OB + OC = a 2. 2 C. a
OB + OC = .
D. OB + OC = . a 2
Câu 39. Cho tam giác ABC có AB = AC và đường cao AH. Đẳng thức nào sau đây đúng?
A. HB + HC = 0.
B. AB = A . C
C. AB + AC = AH.
D. HA + HB + HC = 0.
Câu 40. Cho hình bình hành ABCD . Tập hợp tất cả các điểm M thỏa mãn đẳng thức
MA + MB − MC = MD là
A. tập rỗng.
B. một đoạn thẳng.
C. một đường tròn.
D. một đường thẳng.
Câu 41. Cho tam giác ABC vuông cân tại A có AB = a . Tính AB + AC . a 2
A. AB + AC = a 2.
B. AB + AC = . 2
C. AB + AC = 2 . a
D. AB + AC = . a
Câu 42. Gọi O là tâm hình bình hành ABCD . Đẳng thức nào sau đây sai?
A. BC − BA = DC − D . A
B. OA − OB = C . D
C. OB − OC = OD − O . A
D. AB − AD = D . B
Câu 43. Cho tam giác ABC và điểm M thỏa mãn MB + MC = AB . Tìm vị trí điểm M .
A. M là trung điểm của AC.
B. M là trung điểm của A . B
C. M là trung điểm của BC.
D. M là điểm thứ tư của hình bình hành ABCM .
Câu 44. Gọi M , N, P lần lượt là trung điểm các cạnh AB, BC, CA của tam giác ABC. Hỏi vectơ
MP + NP bằng vectơ nào trong các vectơ sau? A. A . P B. B . P C. MN.
D. MB + N . B
Câu 45. Gọi G là trọng tâm tam giác vuông ABC với cạnh huyền BC = 12. Tính độ dài của vectơ
v = GB + GC .
A. v = 4.
B. v = 2.
C. v = 2 3. D. v = 8. ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 11 Chương I. Vectơ
0916 620 899 – 0355 334 679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp
§3. TÍCH CỦA VECTƠ VỚI MỘT SỐ
A. KIẾN THỨC CẦN NẮM 1. Định nghĩa
- Cho số k ≠ 0 và vectơ a . Tích của vectơ a với số k là một vectơ, kí hiệu k. a , được xác định như sau:
+ Nếu k ≥ 0 thì vectơ k. a cùng hướng với vectơ a
+ Nếu k < 0 thì vectơ k. a ngược hướng với vectơ a
+ Độ dài của vectơ k. a bằng k . a
- Phép lấy tích của vectơ với một số gọi là phép nhân vectơ với số(hoặc phép nhân số với vectơ)
- Ta qui ước 0.a = 0, k.0 = 0
2. Tính chất của phép nhân vectơ với một số
Với hai vectơ a và b bất kì, với mọi số thực h và k, ta có
i) k (a +b) = ka + kb
ii) (h + k )a = ha + ka
iii) h (ka) = (hk)a iv) 1.a = a,( 1 − )a = −a
3. Trung điểm của đoạn thẳng và trọng tâm của tam giác
- Nếu I là trung điểm của AB thì với mọi điểm M, ta có MA + MB = 2MI
- Nếu G là trọng tâm của tam giác ABC thì với mọi điểm M, ta có MA + MB + MC = 3MG
4. Điều kiện để hai vectơ cùng phương
- Điều kiện cần và đủ để hai vecrtơ a và b ( b ≠ 0 ) cùng phương là có một số k để a = k.b
- Ba điểm phân biệt A, B, C thẳng hàng khi và chỉ khi có số k ≠ 0 để AB = k AC
5. Phân tích một vectơ theo hai vectơ không cùng phương
Cho hai vectơ a và b không cùng phương. Khi đó mọi vectơ x đều phân tích được một cách duy
nhất theo hai vectơ a và b , nghĩa là có duy nhất cặp số h, k sao cho x = ha + kb B. BÀI TẬP
Bài 3.1.Cho hình bình hành ABCD.Chứng minh rằng AB + AC + AD = 2AC HD Giải
Theo quy tắc hình bình hành ta có B C
AB + AD = AC . Do đó
vt = ( AB + AD) + AC = AC + AC = 2AC = vp A D
Bài 3.2.Gọi M và N lần lượt là trung điểm các cạnh AB và CD của tứ giác ABCD. Chứng minh rằng:
2MN = AC + BD = BC + AD HD Giải Ta có B
MN = MA + AC + CN + C M
MN = MB + BD + DN N
2MN = AC + BD A D
Phần còn lại chứng minh tương tự
Bài 3.3.Cho tam giác ABC có G là trọng tâm. Chứng minh rằng
a) GA + GB + GC = 0
b) MA + MB + MC = 3MG , với mọi M HD Giải
a) Trọng tâm G nằm trên đường trung tuyến CM và GC = 2GM. Để tính tổng GA + GB , ta dựng hình
bình hành AGBC’. Muốn vậy, ta lấy điểm C’ sao cho M là trung điểm của GC’.
Khi đó GA + GB = GC ' = CG . Do đó GA + GB + GC = CG + GC = CC = 0
b)vt = MG + GA + MG + GB + MG + GC = (GA+GB +GC) +3MG = 3MG = vp 12 Chương I. Vectơ
0916 620 899 – 0355 334 679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp
(vì GA + GB + GC = 0 chứng minh trên) A C' G C B
Bài 3.4.Cho hai tam giác ABC và A’B’C’ lần lượt có trọng tâm là G và G’. Chứng minh rằng :
3GG ' = AA' + BB ' + CC ' HD Giải Ta có
AA ' = AG + GG ' + G ' A'
+BB ' = BG + GG '+ G 'B '
CC ' = CG + GG ' + G 'C '
AA ' + BB ' + CC ' = 3GG '
Vì G là trọng tậm của tamgiác ABC nên GA + GB + GC = 0 và G’ là trọng tậm của tam giác A’B’C’ nên
G ' A ' + G ' B ' + G 'C ' = 0 .
Bài 3.5. Gọi O là tâm của hình bình hành ABCD. Chứng minh rằng với mọi điểm M bất kì, ta luôn có
MA + MB + MC + MD = 4MO HD Giải
Ta có MA + MC = 2MO (Vì O là trung điểm AC) B C
Và MB + MD = 2MO (Vì O là trung điểm của BD)
Vậy MA + MB + MC + MD = 4MO O A D
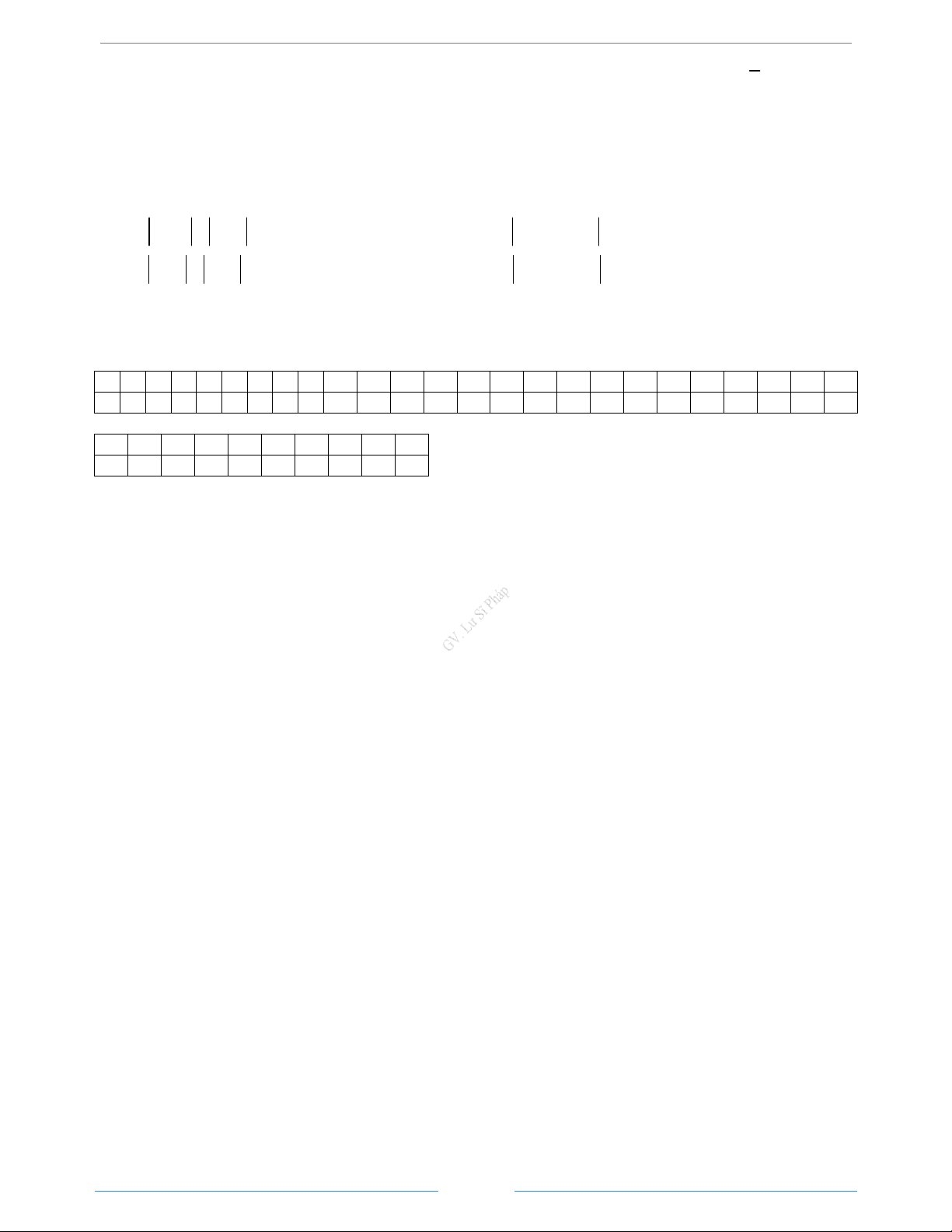
Bài 3.6. Cho tam giác ABC nội tiếp đường tròn tâm O, H là trực tậm của tam giác, D là điểm đối xứng của A qua O.
a) Chứng minh rằng tứ giác HCDB là hình bình hành b) Chứng minh:
i) HA + HD = 2HO ; ii) HA + HB + HC = 2HO ; iii) OA + OB + OC = OH
c) Glà trọng tâm của tam giác ABC. Chứng minh: OH = 3OG . Từ đó có kết luân gì về ba điểm O, H, G ? HD Giải
a) Vì AD là đường kính của đường tròn tâm O nên BD ⊥ AB, DC ⊥ AC . Ta A
có BH ⊥ AC,CH ⊥ AB nên suy ra CH // BD và BH //DC. Vậy tứ giác HBDC là hình bình hành.
b) Vì O là trung điểm của AD nên có HA + HD = 2HO (1)
Vì HBDC là hình bình hành nên ta có HB + HC = HD . Vậy (1) suy ra
HA + HB + HC = 2HO (2) O H
Theo qui tắc ba điểm, ta có OA + OB + OC = OH (3)
c) G là trọng tâm của tam giác ABC,ta có OA + OB + OC = 3OG B C
Từ (3), suy ra OH = 3OG . Vậy ba điểm O, H, G thẳng hàng. D
Bài 3.7.Cho tam giác ABC có trung tuyến AM (M là trung điểm của BC). Phân tích vectơ AM theo hai
vectơ AB và AC . HD Giải 13 Chương I. Vectơ
0916 620 899 – 0355 334 679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp
Gọi N, P lần lượt là trung điềm của AB và AC. A 1 1
Ta có tứ giác ANMP là hình bình hành nên AM = AN + AP = AB + AC 2 2 P
Ta có thể chứng minh cách khác N 1 1
Ta có M là trung điểm của BC nên 2AM = AB + AC ⇒ AM = AB + AC 2 2 B C M
Bài 3.8.Cho tam giác ABC. Gọi M là trung điểm của AB và N là một điểm trên cạnh AC sao cho NA = 2
NC. Gọi K là trung điểm của MN. Phân tích vectơ AK theo hai vectơ AB và AC . HD Giải
Ta có K là trung điểm của MN, nên A 1 1 1 AK = (AM + 1 1 2
AN ) = AB + AC = AB + AC 2 2 2 3 4 3 M N K B C
Bài 3.9. Cho tam giác ABC.
a) Tìm điểm K sao cho KA + 2KB = CB
b) Tìm điểm M sao cho MA + MB + 2MC = O HD Giải
a)KA + 2KB = CB ⇔ KA + 2KB = KB − KC A
⇔ KA + KB + KC = 0
⇔ K là trọng tâm của tam giác ABC I
b)MA + MB + 2MC = O ⇔ 2MI + 2MC = O (I là trung điểm của AB) K M
Hay MI + MC = O ⇔ M là trung điểm của IC B C
Bài 3.10.Cho tam giác đều ABC có O là trọng tâm và điểm M một điểm tuỳ ý trong tam giác. Gọi D, E, F 3
lần lượt là chân đường vuông góc hạ từ M đến BC, AC, AB.Chứng minh rằng: MD + ME + MF = MO 2 HD Giải
Qua M kẻ các đường thẳng A K K / / A ;
B K K / / AC, K K / / 1 4 2 5 3 6 BC K ( 5
K , K ∈ BC, K , K ∈ AC, K , K ∈ AB) 1 2 3 4 5 6 K F 4 Ta có E 1 K6 K3
MD + ME + MF = (M + + + + + M 1 K
MK2 MK3 MK4 MK5 MK6 ) 2 O 1
= (MA+ MB + MC)(1) 2 K D K C B (Vì 1 2
MK AK , MK CK , MK BK , là các hình bình hành) 5 4 3 2 1 6
Mặt khác, O là trọng tâm của tam giác ABC, nên MA + MB + MC = 3MO 1 3
Từ (1) suy ra MD + ME + MF = .3OM = OM 2 2 14 Chương I. Vectơ
0916 620 899 – 0355 334 679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp
C. BÀI TẬP TỰ LUYỆN
Bài 3.11. Cho bốn điểm O, A, B, C sao cho OA + 2OB − 3OC = 0 . Chứng minh rằng ba điểm A, B, C thẳng hàng
Bài 3.12. Cho tam giác ABC và hai điểm I, J thoả IA + 3IC = 0 và JA + 2JB + 3JC = 0 . Chứng minh rằng
ba điểm I, J, B thẳng hàng..
Bài 3.13. Cho tam giác ABC có trọng tâm G và hai điểm M, N thoả 3MA + 4MB = 0 và NB − 3NC = 0 .
Chứng minh rằng ba điểm M, N, G thẳng hàng.
Bài 3.14. Cho tam giác ABC có trọng tâm G và hai điểm M, N thoả MA − 2MB = 0 và 3NA + 2NC = 0
a) Xác định hai điểm M, N
b) Tính vectơ MN theo hai vectơ AB và AC
c) Tính vectơ MG theo hai vectơ AB và AC . Suy ra ba điểm M, N, G thẳng hàng
Bài 3.15. Cho tam giác ABC. Gọi K điểm đối xứng của trọng tâm G qua B
a) Chứng minh rằng KA − 5KB + KC = O
b) Tính vectơ AB và AC theo hai vectơ AG và AK
Bài 3.16. Cho tam giác ABC. Gọi P là trung điểm của AB và Q là một điểm trên cạnh AC sao cho QC =
2QA. Gọi K là trung điểm của PQ, D là trung điểm BC. Chứng minh rằng 1 1 1 1
a) AK = AB + AC
b) KD = AB + AC 4 6 4 3
Bài 3.17. Cho hình chữ nhật ABCD có AB = 4, BC = 3. Gọi M, K lần lượt là trung điểm của BC, CD.
a) Tính AM và AK theo hai vectơ AB và AD
b) Tính : AM + AK
Bài 3.18. Cho hai hình bình hành ABCD và AB’C’D’ có chung đỉnh A.Chứng minh rằng
a) CC ' = BB ' + DD '
b) Hai tam giác BC’D và B’CD’ có cùng trọng tâm
Bài 3.19. Cho tam giác ABC. Gọi I là điểm thoả mãn điều kiện: IA + 2IB + 3IC = 0
a) Chứng minh rằng I là trọng tâm của tam giác BCD, với D là trung điểm của cạnh AC
b) Biểu thị vectơ AI theo hai vectơ AB và AC
Bài 3.20. Cho tam giác ABC. Gọi M là một điểm trên cạnh BC sao cho MB = 2MC. Chứng minh rằng 1 2 AM = AB + AC 3 3
Bài 3.21. Cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm các cạnh BC, AC và AB.chứng minh
rằng AM + BN + CP = 0
Bài 3.22. Cho tam giác ABC có G là trọng tâm. Các điểm M, N và P lần lượt là trung điểm các cạnh
AB, BC và CA. Chứng minh rằng GN + GN + GP = 0
Bài 3.23. Cho tam giác ABC. Hãy xác định điểm M thoả mãn điểu kiện: MA − MB − MC = O
D. BÀI TẬP TRẮC NGHIỆM
Câu 1. Cho tam giác ABC và điểm M thỏa mãn MA = MB + MC. Khẳng định nào sau đây đúng ? A. ,
A M và trọng tâm tam giác ABC thẳng hàng.
B. AM + BC = 0.
C. Ba điểm C, M , B thẳng hàng.
D. AM là phân giác trong của góc BAC.
Câu 2. Cho tam giác ABC, điểm M thuộc cạnh AB sao cho 3 AM = AB và N là trung điểm của AC.
Tính MN theo AB và AC. 15 Chương I. Vectơ
0916 620 899 – 0355 334 679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp 1 1 1 1
A. MN = AC − A . B
B. MN = AC + A . B 2 3 2 3 1 1 1 1
C. MN = AC − A . B
D. MN = AB + AC. 2 3 2 3
Câu 3. Cho tam giác ABC có G là trọng tâm và I là trung điểm của BC. Đẳng thức nào sau đây đúng ? 1
A. GB + GC = 2GI.
B. GB + GC = G . A
C. GA = 2GI.
D. IG = − I . A 3
Câu 4. Cho tam giác ABC. Hai điểm M , N chia cạnh BC theo ba phần bằng nhau BM = MN = NC.
Tính AM theo AB và AC. 1 2 1 2
A. AM = AB − AC.
B. AM = AB + AC. 3 3 3 3 2 1 2 1
C. AM = AB − AC.
D. AM = AB + AC. 3 3 3 3
Câu 5. Cho tam giác ABC có M là trung điểm của BC. Tính AB theo AM và BC. 1 1
A. AB = AM + BC.
B. AB = BC + AM. 2 2 1 1
C. AB = AM − BC.
D. AB = BC − AM. 2 2
Câu 6. Cho hình chữ nhật ABCD và I là giao điểm của hai đường chéo. Tập hợp các điểm M thỏa mãn
MA + MB = MC + MD là
A. trung trực của đoạn thẳng A . B
B. trung trực của đoạn thẳng A . D +
C. đường tròn tâm AC AB BC I , bán kính .
D. đường tròn tâm I, bán kính . 2 2
Câu 7. Gọi G là trọng tâm tam giác ABC . Đặt GA = a, GB = b . Hãy tìm ,
m n để có BC = ma + n . b
A. m =1,n = 2. B. m = 1 − ,n = 2 − .
C. m = 2,n = 1. D. m = 2 − ,n = 1 − .
Câu 8. Cho hình vuông ABCD có tâm là .
O Mệnh đề nào sau đây sai ?
A. AC + DB = 2 A . B
B. AB + AD = 2A . O 1 1
C. AD + DO = − C . A
D. OA + OB = C . B 2 2
Câu 9. Cho hai điểm ,
A B phân biệt và cố định, với I là trung điểm của A .
B Tập hợp các điểm M thỏa
mãn đẳng thức MA + MB = MA − MB là
A. đường trung trực đoạn thẳng AB I . A
B. đường tròn tâm I, đường kính . 2
C. đường tròn đường kính A . B
D. đường trung trực của đoạn thẳng A . B
Câu 10. Cho tam giác đều ABC và điểm I thỏa mãn IA = 2I .
B Mệnh đề nào sau đây đúng ? CA + 2 CA + 2 CA − 2 A. CB CB CB CI = . B. CI = .
C. CI = −CA + 2C . B D. CI = . −3 3 3
Câu 11. Cho hình chữ nhật ABCD và số thực k > 0. Tập hợp các điểm M thỏa mãn đẳng thức
MA + MB + MC + MD = k là
A. một điểm.
B. một đoạn thẳng.
C. một đường thẳng.
D. một đường tròn.
Câu 12. Cho tứ giác ABC .
D Trên cạnh AB, CD lấy lần lượt các điểm M , N sao cho 3 AM = 2 AB và
3 DN = 2 DC. Tính vectơ MN theo hai vectơ AD, BC. 16 Chương I. Vectơ
0916 620 899 – 0355 334 679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp 1 1 1 2
A. MN = AD + BC.
B. MN = AD − BC. 3 3 3 3 1 2 2 1
C. MN = AD + BC.
D. MN = AD + BC. 3 3 3 3
Câu 13. Cho hình bình hành ABC .
D Đẳng thức nào sau đây đúng ?
A. AC − AD = C . D
B. AC + BD = 2BC.
C. AC + BC = A . B
D. AC − BD = 2C . D
Câu 14. Cho tam giác ABC có M là trung điểm của BC, G là trọng tâm của tam giác ABC. Khẳng
định nào sau đây đúng ? 1 2 2
A. AG = AB + AC.
B. AI = AB + 3AC. 3 2 3 2 1
C. AG = (AB + AC).
D. AG = (AB + AC). 3 3
Câu 15. Cho tam giác ABC có M là trung điểm của BC, I là trung điểm của AM . Khẳng định nào sau đây đúng ?
A. IB + 2IC + IA = 0.
B. IB + IC + 2IA = 0.
C. 2IB + IC + IA = 0.
D. IB + IC + IA = 0.
Câu 16. Cho tam giác ABC có M là trung điểm của BC, I là trung điểm của AM . Khẳng định nào sau đây đúng ? 1 1 1 1
A. AI = AB + AC.
B. AI = AB − AC. 4 2 4 2 1 1
C. AI = (AB + AC).
D. AI = (AB − AC). 4 4
Câu 17. Cho tam giác ABC có G là trọng tâm. Mệnh đề nào sau đây đúng ? 2
A. AB + AC + BC = 0.
B. AB + AC = A . G 3
C. BA+ BC = 3B . G
D. CA+ CB = C . G
Câu 18. Cho tam giác ABC và một điểm M tùy ý. Mệnh đề nào sau đây đúng ?
A. 2MA + MB − 3MC = AC + 2BC.
B. 2MA + MB − 3MC = 2AC + BC.
C. 2MA + MB −3MC = 2CA+ C . B
D. 2MA + MB − 3MC = 2CB −C . A
Câu 19. Cho hai điểm ,
A B phân biệt và cố định, với I là trung điểm của A .
B Tập hợp các điểm M
thỏa mãn đẳng thức 2MA + MB = MA + 2MB là
A. đường trung trực đoạn thẳng I . A
B. đường tròn tâm , A bán kính A . B
C. đường trung trực của đoạn thẳng A . B
D. đường tròn đường kính A . B
Câu 20. Cho hình bình hành ABC .
D Tính AB theo AC và B . D 1 1 1
A. AB = AC − B . D
B. AB = AC − B . D 2 2 2 1 1 1
C. AB = AM − BC.
D. AB = AC + B . D 2 2 2
Câu 21. Cho tam giác ABC vuông tại ,
A M là trung điểm của BC. Khẳng định nào sau đây đúng ? A. BC
AM = MB = MC.
B. MB = MC.
C. MB = − MC. D. AM = . 2
Câu 22. Cho hình bình hành ABCD có M là trung điểm của A .
B Khẳng định nào sau đây đúng ? 1 1
A. DM = DC − BC.
B. DM = DC + BC. 2 2 17 Chương I. Vectơ
0916 620 899 – 0355 334 679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp 1 1
C. DM = CD + BC.
D. DM = CD − BC. 2 2
Câu 23. Cho tam giác ABC và điểm M thỏa mãn 2MA + MB = C .
A Khẳng định nào sau đây là đúng ?
A. M trùng C.
B. M là trọng tâm của tam giác ABC. C. M trùng . A D. M trùng . B
Câu 24. Cho tam giác đều ABC cạnh a, trọng tâm .
G Ttập hợp các điểm M thỏa mãn
MA + MB = MA + MC là
A. đường trung trực của đoạn BC.
B. đường tròn đường kính BC.
C. đường tròn tâm a G, bán kính .
D. đường trung trực đoạn thẳng AG. 3
Câu 25. Cho tam giác OAB vuông cân tại O, cạnh OA = .
a Tính 2OA − OB . A. . a
B. (1+ 2) .a
C. a 5.
D. 2a 2.
Câu 26. Cho tam giác ABC , gọi M là trung điểm AB và N là một điểm trên cạnh AC sao cho
NC = 2NA . Gọi K là trung điểm của MN . Khi đó 1 1 1 1
A. AK = AB − AC.
B. AK = AB − AC. 6 4 4 6 1 1 1 1
C. AK = AB + AC.
D. AK = AB + AC. 4 6 6 4
Câu 27. Cho hình thang ABCD có đáy là AB và C .
D Gọi M và N lần lượt là trung điểm của AD và
BC. Khẳng định nào sau đây sai ? 1
A. MN = ( AD + BC).
B. MN = MD + CN + DC. 2 1
C. MN = AB − MD + BN.
D. MN = (AB + DC). 2
Câu 28. Cho ba điểm , A ,
B C không thẳng hàng và điểm M thỏa mãn đẳng thức vectơ
MA = x MB + y MC. Tính giá trị biểu thức P = x + . y
A. P = 3.
B. P = 2.
C. P = − 2.
D. P = 0.
Câu 29. Cho tam giác đều ABC cạnh .
a Biết rằng tập hợp các điểm M thỏa mãn đẳng thức
2MA + 3MB + 4MC = MB − MA là đường tròn cố định có bán kính .
R Tính bán kính R theo . a A. a a a a R = . B. R = . C. R = . D. R = . 2 6 3 9
Câu 30. Cho tam giác ABC. Gọi M và N lần lượt là trung điểm của AB và AC. Khẳng định nào sau đây sai ? 1
A. CN = − AC.
B. AC = 2NC.
C. BC = − 2MN.
D. AB = 2AM. 2
Câu 31. Cho hình bình hành ABCD có M là giao điểm của hai đường chéo. Mệnh đề nào sau đây sai ?
A. MA + MB = MC + M . D
B. AB + BC = AC.
C. AB + AD = A . C
D. BA + BC = 2 BM .
Câu 32. Cho tam giác ABC . Có bao nhiêu điểm M thỏa mãn MA + MB + MC = 3? A. Vô số. B. 2. C. 3. D. 1.
Câu 33. Cho tam giác ABC có G là trọng tâm và M là trung điểm BC. Khẳng định nào sau đây sai ? 18 Chương I. Vectơ
0916 620 899 – 0355 334 679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp 2
A. GB + GC = GM.
B. AB + AC = 3A . G
C. GA = BG + C . G
D. GA = − AM. 3
Câu 34. Cho tam giác ABC và đặt a = BC, b = AC. Cặp vectơ nào sau đây cùng phương?
A. 5a + b, −10 a − 2b.
B. a + b, a − b.
C. 2a + b, a + 2b.
D. 2a − b, a − 2b.
Câu 35. Cho tam giác OAB vuông cân tại O, cạnh OA = .
a Khẳng định nào sau đây sai ?
A. 11OA − 6OB = 5 . a
B. 3OA + 4OB = 5 . a
C. 2OA + 3OB = 5 . a
D. 7 OA − 2OB = 5 . a ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
26 27 28 29 30 31 32 33 34 35 19 Chương I. Vectơ
0916 620 899 – 0355 334 679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp
§4. HỆ TRỤC TOẠ ĐỘ
A. KIẾN THỨC CẦN NẮM
1. Trục và độ dài đại số trên trục
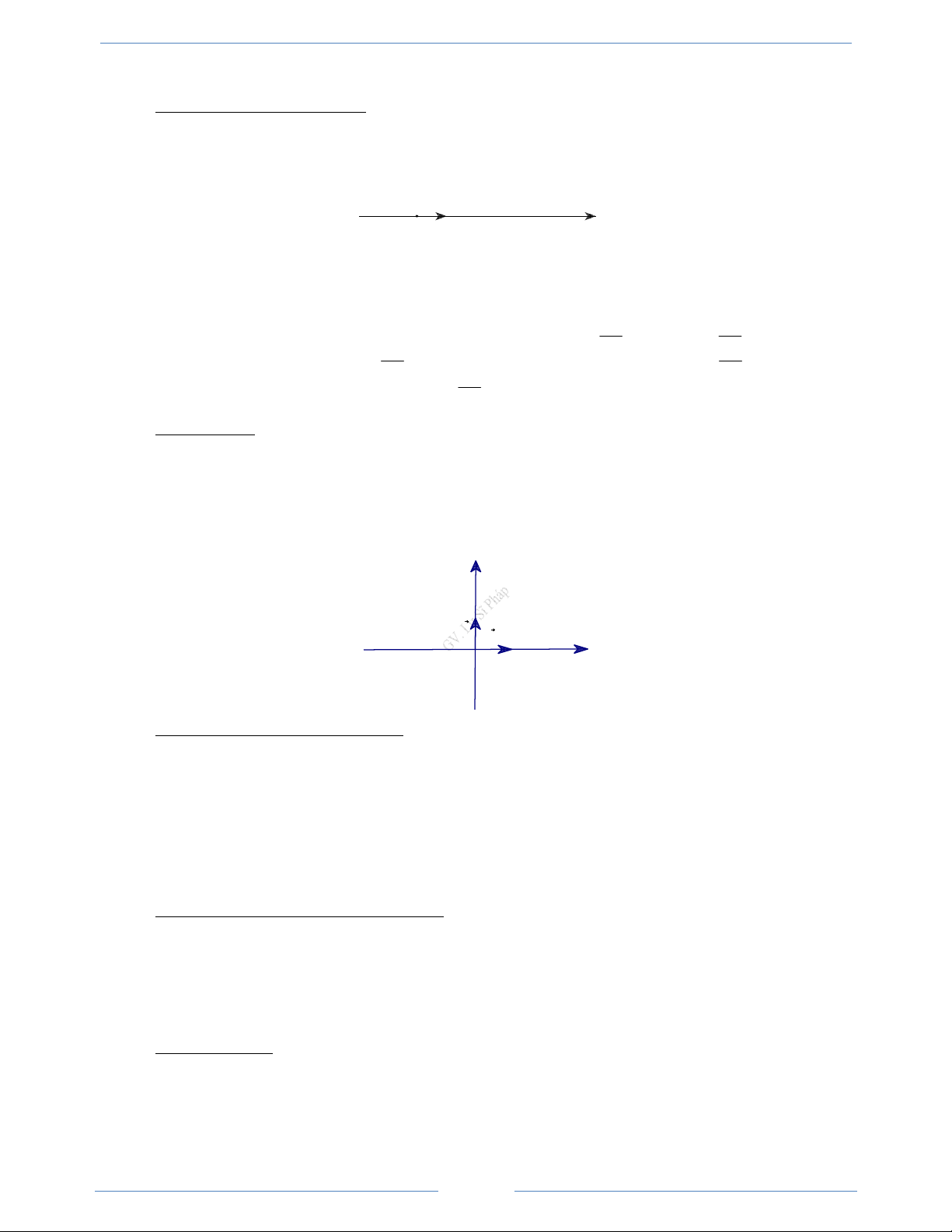
- Trục toạ độ (trục) là một đường thẳng trên đó đã xác định một điểm O và một vectơ đơn vi i có
độ dài bằng 1. Điểm O gọi là gốc toạ độ, vectơ i gọi là vectơ đơn vị của trục toạ độ. → i O x
- Kí hiệu (O,i)
- Ta gọi số k là toạ độ của điểm M trên trục (O,i) khi OM = ki
- Cho hai điểm A và B trên trục (O,i). Khi đó có duy nhất số a sao cho AB = ai . Ta gọi số a đó là
độ dài đại số của vectơ AB đối với trục đã cho. Như vậy AB = A .
B i và kí hiệu AB = a
- Nếu AB cùng hướng với i thì AB = AB , còn nếu AB ngược hướng với i thì AB = −AB
- Nếu điểm A(a) và B(b) trên trục (O,i) thì AB = b − a 2. Hệ trục toạ độ
- Hệ trục toạ đô như hình vẽ. Nó bao gồm hai trục toạ đô Ox và Oy vuông góc với nhau
- Vectơ đơn vị trên trục Ox là i , vectơ đơn vị trên trục Oy là j
- Điểm O gọi là gốc toạ độ. Trục Ox gọi là trục hoành, trục Oy gọi là trục tung
- Hệ trục toạ độ vuông góc cón gọi đơn giản là hệ trục toạ độ và kí hiệu Oxy hay (O,i, j) y j i x O
3. Toạ độ của vectơ đối hệ trục toạ độ
- Đối cới hệ trục toạ độ (O,i, j) , nếu u = xi + y j thì cặp số ( ;x y) được gọi là toạ độ của vectơ u , kí hiệu u = ( ;
x y) hay u( ;
x y) . Số thứ nhật x gọi là hoành độ, số thứ hai y gọi là tung độ của vectơ u
- Nhận xét: Hai vectơ bằng nhau khi và chi khi chúng có hoành độ bằng nhau và tung độ bằng nhau. x = x ' Nếu u( ;
x y), v(x '; y ') thì u = v ⇔ y = y '
4. Biểu thức toạ độ của các phép toán vectơ Cho u( ;
x y), v(x '; y ') . Khi đó, ta có
i) u + v = (x + x'; y + y ');u − v = (x − x '; y − y ')
ii) k.u = (k ; x ky ), k ∀ ∈ ℝ
iii) Vectơ u cùng phương với vectơ v ≠ 0 khi và chỉ khi có số k sao cho x = kx ', y = ky ' 5. Tọa độ của điểm
- Trong mặt phẳng toạ độ Oxy, toạ độ của vectơ OM được gọi là toạ độ của điểm M. Như vậy cặp
số (x; y) được gọi là toạ độ của điểm M khi và chỉ khi OM = (x; y) và kí hiệu M = ( ;
x y) hay M (x; y) . Số x gọi lài hoành độ, y gọi là tung đô của điểm M
- Liên hệ giữa toạ độ điểm và toạ độ của vectơ trong mặt phẳng: Cho hai điểm 20 Chương I. Vectơ
0916 620 899 – 0355 334 679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp
A( x ; y ), B ( x ; y , ta có AB = ( x − x ; y − y B A B A ) A A B B )
6. Toạ độ trung điểm của đoạn thẳng. Toạ độ trọng tâm cụa tam giác
- Cho đoạn thẳng AB có A( x ; y ), B(x ; y . Toạ độ trung điểm I (x ; y của AB được xác định I I ) A A B B ) + + như sau: x x y y A B x = , A B y = I 2 I 2
- Cho tam giác ABC, có A( x ; y ), B(x ; y và C ( x ; y . Khi đó toạ độ trọng tậm G( x ; y G G ) C C ) A A B B ) + + + +
được xác định như sau: x x x y y y A B C x = , A B C y = G 3 G 3 B. BÀI TẬP
Bài 4.1.Tìm toạ độ của các vectơ sau a) a = 2i b) b = −3 j
c) c = 3i − 4 j
d) d = 0, 2i + 3 j 1 1
e) e = ( j −i)
f) f = i − 5 j g) g = 0,15i +1,3 j
h) h = π i − ( 0 cos 24 ) j 2 3 HD Giải a) a = (2;0) b) b = (0; 3 − ) c) c = (3; 4 − ) d) d = (0,2; 3)
Phần còn lại đọc giả làm tương tự
Bài 4.2.Cho các vectơ a = (1;2),b = ( 3 − ;1),c = (−4; 2
− ). Tìm toạ độ các vectơ sau 1 1
a) u = 2a − 3b + c
b) v = −a + b − c
c) w = 3a + 2b + 4c 3 2 HD Giải
a) u = 2a − 3b + c = 2(1;2) − 3( 3 − ;1) + (−4; 2 − ) = (7;1) 2
Tương tự ta có b)v = 0;− ,c)w = ( 1 − 9;0) 3
Bài 4.3. Trong mặt phẳng hệ trục toạ độ Oxy, cho các điểm A(2; 0), B(0;4), C(1;3).
a) Chứng minh A, B, C là ba đỉnh của một tam giác
b) Tìm toạ độ trọng tâm của tam giác ABC HD Giải 2 − 4
a) Ta có AB = (−2;4) và AC = (−1;3) . Do
≠ nên hai vectơ AB, AC không cùng phương, suy ra A, −1 3
B, C không thẳng hàng và chúng là ba đỉnh của một tam giác. + + + + b) Gọi x x x y y y
G ( x ; y là trọng tâm của tam giác ABC, ta có A B C x = , A B C y = . G G ) G 3 G 3 7 Vậy G 1; 3
Bài 4.4.Cho hình bình hành ABCD có A(-1;-2), B(3;2), C(4;-1). Tìm toạ độ điểm D HD Giải
Gọi D ( x ; y . Tứ giác ABCD là hình bình D D ) B C
hành, nên ta có AB = DC
Ta lại có AB = (4;4) và DC = (4 − ; x −1− y) A 4 − x = 4 x = 0 D
Do đó AB = DC ⇔ ⇔ −1− y = 4 y = 5 − Vậy D(0;-5)
Bài 4.5. Cho tam giác ABC. Các điểm M(1;0), N(2;2) và P(-1;3) lần lượt là trung điểm các cạnh BC, CA
và AB. Tìm toạ độ các đỉnh của tam giác ABC. HD Giải 21 Chương I. Vectơ
0916 620 899 – 0355 334 679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp
Ta gọi toạ độ các đỉnh là A( x ; y ), B(x ; y và A A B B ) A
C ( x ; y C C )
Ta có tứ giác NAPM là hình bình hành, suy ra P N NA = MP
NA = ( x − 2; y − 2), MP = (−2;3) .Suy ra: A A x − 2 = −2 x = 0 B C A A M ⇔ . y − 2 = 3 y = 5 A A
Vậy toạ độ điểm A (0;5)
Phần còn lại, làm tương tư B(-2;1) và C(4;-1)
Bài 4.6.Cho ba điểm A(-1;1), B(1;3), C(-2;0). Chứng minh ba điểm A, B, C thẳng hàng. HD Giải
Ta có AB = (2;2), AC = ( 1 − ; 1 − ) . Vậy AB = 2
− AC . Do đó ba điểm A, B, C thẳng hàng.
Bài 4.7.Cho bốn điểm A(0;1), B(1;3),C(2,7) và D(0;3). Chứng minh hai đường thẳng AB và CD song song. HD Giải
Ta có AB = (1;2),CD = ( 2
− ;−4) . Vậy AB = 2
− AC , do đó hai đường thẳng AB và CD song song hoặc trùng nhau.
Ta lại có AC = (2;6) , mà AB = (1;2) . Vậy hai vectơ AB, AC không cùng phương. Do đó điểm C không thuộc đường thẳng AB Vậy AB // CD.
Bài 4.8.Cho các điểm A’(-4;1), B’(2; 4), C’(2;-2) lần lượt là trung điểm các cạnh BC, CA và AB của tam
giác ABC. Tính toạ độ các đỉnh của tam giác ABC. Chứng minh rằng trọng tâm của các tam giác ABC và A’B’C’ trùng nhau. HD Giải
Giải tương tư nhu bài 4.5, tìm được A(8;1),B(-4;-5) và C(-4;7)
Toạ độ trọng tâm của tam giác ABC là G(0;1) và toạ độ trong tâm của tam giác A’B’C’là G’(0;1) Vậy G trùng với G’.
Bài 4.9. Cho vectơ a = (2;−2),b = (1;4) . Hãy phân tích vectơ c = (5;0) theo hai vectơ a và b . HD Giải 2h + k = 5 h = 2
Giả sử c = ha + k ;
b h, k ∈ ℝ . Khi đó, ta có ⇔
. Vậy c = 2a + b
−2h + 4k = 0 k = 1
Bài 4.10.Cho ba điểm A(2;5), B(1;1), C(3;3)
a) Tìm toạ độ điểm D sao cho AD = 3AB − 2AC
b) Tìm toạ độ của điểm E sao cho ABCE là hình bình hành. Tìm toạ độ tâm của hình bình hành đó. HD Giải
a) Gọi D(x;y), Ta có AB = ( 1 − ; 4 − ), AC = (1;−2) .
x − 2 = 3(−1) − 2.1 x = −3
AD = 3AB − 2 AC ⇔ ⇔ . Vậy D(-3;-3) y − 5 = 3( 4 − ) − 2( 2 − ) y = −3
b) Cọi E(x;y). Tứ giác ABCE là hình bìh hành, suy ra AE = BC , x − 2 = 2 x = 4 do đó ⇔ . Vậy E(4;7) y − 5 = 2 y = 7 5
Gọi I(x;y) là tâm của hình bình hành, cũng là trung điểm của AC. Vậy I ;4 2
Bài 4.11. Cho tam giác ABC có A(-1;1), B(5;-3), đỉnh C nằm trên trục Oy và trọng tâm G nằm trên trục
Ox. Tìm toạ độ đỉnh C, G. HD Giải 22 Chương I. Vectơ
0916 620 899 – 0355 334 679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp 1 − +5+ 0 x = 4 G 3 x =
Ta có C ∈Oy ⇒ C(0; y ),G ∈Ox ⇒ G(x ;0) . Do đó G ⇔ 3 . C G 1−3+ 0 yC = y = 2 3 C 4
Vậy G ;0;C(0;2) 3
Bài 4.12.Trong mặt phẳng toạ độ Oxy, cho hai điểm A(4;0), B(2;-2). Đường thẳng AB cắt trục Oy tại
điểm M. Trong ba điểm A, B, M, điểm nào nằm giữa hai điểm còn lại. HD Giải
Gọi M (0; y) , ta có AB = ( 2 − ;−2), AM = ( 4
− ; y) . Vì ba điểm A, B, M thẳng hàng nên vectơ AB và
AM cùng phương, suy ra y = -4. Vậy M(0;-4). Khi đó AB = ( 2 − ;−2), AM = ( 4 − ; 4
− ) , suy ra AM = 2AB .
Vậy điểm B nằm giữa hai điểm A và M.
C. BÀI TẬP TỰ LUYỆN
Bài 4.13. Cho a = (1; 2
− ),b = (0;3) . Tìm tọa độ của các vectơ sau x = a + b, y = a − b, z = 3a − 4b
Bài 4.14. Cho A(-1;8), B(1;6), C(3;4). Chứng minh rằng ba điểm A, B, C thẳng hàng.
Bài 4.15. Cho bốn điểm A(-2;-3), B(3;7), C(0;3), D(-4;-5). Chứng minh rằng hai đường thẳng AB và Cd song song với nhau.
Bài 4.16. Cho tam giác ABC. Các điểm M(1;1), N(2;3), P(0;-4) lần lượt là trung điểm các cạnh BC, CA,
AB. Tìm toạ độ các đỉnh của tam giác, toạ độ trọng tâm của tam giác ABC và MNP
Bài 4.17. Cho tam giác ABC, có A(-5;6), B(-4;-1), C(4;3). Tìm toạ độ trung điểm I của AC, toạ độ điểm
D sao cho từ giác ABCD là hình bình hành.
D. BÀI TẬP TRẮC NGHIỆM
Câu 1. Trong hệ tọa độ Oxy, cho hai điểm A(2; 3
− ), B(4;7). Tìm tọa độ trung điểm I của đoạn thẳng A . B A. I (8; 2 − ) 1 .
B. I (6;4).
C. I (2;10).
D. I (3;2).
Câu 2. Trong hệ tọa độ Oxy, cho tam giác ABC có M (2;3), N (0; 4 − ), P( 1
− ;6) lần lượt là trung điểm
của các cạnh BC, C ,
A AB . Tìm tọa độ đỉnh A ? A. A(1; 1 − 0).
B. A(1;5). C. A(−3;− ) 1 . D. A( 2 − ; 7 − ).
Câu 3. Cho a = (2; 4
− ), b = (−5;3). Tìm tọa độ của u = 2a − .b A. u = ( 1 − ;5). B. u = (9; 1 − ) 1 . C. u = (9; 5 − ). D. u = (7; 7 − ).
Câu 4. Cho u = (3; 2
− ), v = (1;6). Khẳng định nào sau đây là đúng?
A. 2u + v, v cùng phương.
B. u, v cùng phương.
C. u − v và b = (6; 2 − 4) cùng hướng.
D. u + v và a = ( 4
− ;4) ngược hướng.
Câu 5. Trong hệ tọa độ Oxy, cho tam giác ABC có A(3;5), B(1;2), C (5;2). Tìm tọa độ trọng tâm G
của tam giác ABC ? 9 9
A. G (9;9).
B. G (3;3). C. G ( 3 − ; 3 − ).
D. G ; . 2 2
Câu 6. Trong hệ trục tọa độ ( ; O ;
i j ) , tọa độ của vectơ i + j là 23 Chương I. Vectơ
0916 620 899 – 0355 334 679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp A. (1; ) 1 . B. (1;− ) 1 . C. ( 1 − ; ) 1 . D. (0; ) 1 .
Câu 7. Trong hệ tọa độ Oxy, cho tam giác ABC có A(6; )
1 , B (−3;5) và trọng tâm G (−1; ) 1 . Tìm tọa độ đỉnh C ? A. C ( 6 − ; 3 − ). B. C ( 3 − ;6).
C. C (6;−3).
D. C (−6;3).
Câu 8. Trong hệ tọa độ Oxy, cho ba điểm A( 1 − ; )
1 , B (1;3), C (−2;0). Khẳng định nào sau đây sai?
A. BA+ 2CA = 0. B. ,
A B, C thẳng hàng. 2
C. BA = BC.
D. AB = 2A . C 3
Câu 9. Khẳng định nào sau đây là đúng?
A. u = (4;2), v = (8;3) cùng phương.
B. a = (6;3), b = (2; ) 1 ngược hướng. C. a = ( 5 − ;0), b = ( 4
− ;0) cùng hướng.
D. c = (7;3) là vectơ đối của d = ( 7 − ;3).
Câu 10. Trong hệ tọa độ Oxy, cho tam giác ABC có B (9;7), C (11;− )
1 . Gọi M , N lần lượt là trung
điểm của AB, AC. Tìm tọa độ vectơ MN ? A. MN = (2; 8 − ).
B. MN = (1;−4).
C. MN = (10;6).
D. MN = (5;3).
Câu 11. Trong hệ tọa độ Oxy, cho hai điểm A(1;2), B( 2
− ;3) . Tìm tọa độ đỉểm I sao cho IA+ 2IB = 0. 8 2 A. I 1 − ; . B. I (2; 2 − ).
C. I (1;2).
D. I 1; . 3 5
Câu 12. Trong hệ tọa độ Oxy, cho tam giác ABC có C (−2; 4
− ), trọng tâm G(0;4) và trung điểm cạnh
BC là M (2;0). Tổng hoành độ của điểm A và B là A. 4. B. 8. C. −2. D. 2.
Câu 13. Cho a = ( 1 − ;2), b = (5; 7
− ). Tìm tọa độ của vectơ a − .b A. (6; 9 − ). B. (4;−5). C. ( 6 − ;9). D. ( 5 − ; 1 − 4).
Câu 14. Trong hệ tọa độ Oxy, cho bốn điểm A(3; 2 − ), B(7; ) 1 , C (0; ) 1 , D ( 8
− ;−5). Khẳng định nào sau đây đúng?
A. AB, CD cùng hướng. B. ,
A B, C, D thẳng hàng.
C. AB, CD là hai vectơ đối nhau.
D. AB, CD ngược hướng.
Câu 15. Trong hệ tọa độ Oxy, cho ba điểm A(1; )
1 , B (3;2), C (6;5). Tìm tọa độ điểm D để tứ giác
ABCD là hình bình hành.
A. D (4;3).
B. D (3;4).
C. D (4;4).
D. D (8;6).
Câu 16. Trong hệ tọa độ Oxy, cho bốn điểm A(1; ) 1 , B (2;− )
1 , C (4;3), D(3;5). Khẳng định nào sau đây đúng?
A. AC, AD cùng phương.
B. G (9;7) là trọng tâm tam giác BC . D
C. AB = C . D
D. Tứ giác ABCD là hình bình hành.
Câu 17. Trong hệ tọa độ Oxy, cho hình chữ nhật ABCD có A(0;3) , D(2; ) 1 và I ( 1 − ;0) là tâm của
hình chữ nhật. Tìm tọa độ tung điểm của cạnh BC. A. (−3;−2). B. (−4;− ) 1 . C. (1;2). D. (−2;−3).
Câu 18. Cho a = ( 5
− ;0), b = (4; x). Tìm x để hai vectơ a, b cùng phương.
A. x = 0.
B. x = −1.
C. x = −5.
D. x = 4. 24 Chương I. Vectơ
0916 620 899 – 0355 334 679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp
Câu 19. Cho a = (3;−4), b = (−1;2). Tìm tọa độ của vectơ a + . b A. ( 4 − ;6). B. (2;−2). C. (4;−6). D. (−3;−8).
Câu 20. Trong hệ tọa độ Oxy, cho hình bình hành OABC , điểm C thuộc trục hoành. Khẳng định nào sau đây đúng?
A. AB có tung độ khác 0. B. Hai điểm ,
A B có tung độ khác nhau.
C. C có hoành độ bằng 0.
D. x + x − x = 0. A C B
Câu 21. Trong hệ tọa độ Oxy, cho A(5;2), B(10;8). Tìm tọa độ của vectơ AB?
A. AB = (15;10).
B. AB = (2;4).
C. AB = (5;6).
D. AB = (50;16).
Câu 22. Cho u = 2i − j và v = i + xj . Xác định x sao cho u và v cùng phương. 1 1
A. x = 2 .
B. x = −1 .
C. x = − .
D. x = . 2 4
Câu 23. Trong hệ tọa độ Oxy , cho hai điểm A(2; 3
− ), B(3;4). Tìm tọa độ điểm M thuộc trục hoành sao cho ,
A B, M thẳng hàng. 5 1 17
A. M − ;− .
B. M ;0.
C. M (1;0).
D. M (4;0). 3 3 7
Câu 24. Trong hệ tọa độ Oxy, cho tam giác ABC có A( 2
− ;2), B(3;5) và trọng tâm là gốc tọa độ
O (0;0). Tìm tọa độ đỉnh C ?
A. C (1;7). B. C ( 1 − ; 7 − ).
C. C (2;−2). D. C ( 3 − ; 5 − ).
Câu 25. Trong hệ tọa độ Oxy, cho ba điểm A(0;−3), B(2; )
1 , D (5;5) Tìm tọa độ điểm C để tứ giác
ABCD là hình bình hành. A. C ( 7 − ; 9 − ). B. C (3; ) 1 . C. C ( 3 − ;− ) 1 .
D. C (7;9).
Câu 26. Cho a = ( ; x 2), b = ( 5 − ; ) 1 , c = ( ;
x 7). Tìm x biết c = 2a + 3b .
A. x = −15.
B. x = 3.
C. x = 15.
D. x = 5.
Câu 27. Trong hệ tọa độ Oxy, cho bốn điểm A(−5; 2 − ), B( 5
− ;3), C (3;3), D(3; 2
− ). Khẳng định nào sau đây đúng?
A. OA + OB = OC.
B. AB, CD cùng hướng.
C. ABCD là hình chữ nhật. D. I ( 1 − ; )
1 là trung điểm AC.
Câu 28. Trong hệ tọa độ Oxy, cho tam giác ABC có A(1;− )
1 , N (5;−3) và C thuộc trục Oy , trọng tâm
G của tam giác thuộc trục Ox . Tìm tọa độ điểm C.
A. C (0;−4.)
B. C (2;4.)
C. C (0;2 ).
D. C (0;4 ).
Câu 29. Trong hệ tọa độ Oxy, cho ba điểm A(1;0), B(0;3) và C ( 3 − ; 5
− ). Tìm điểm M thuộc trục
hoành sao cho biểu thức P = 2MA − 3MB + 2MC đạt giá trị nhỏ nhất.
A. M (4;0). B. M ( 4 − ;0).
C. M (16;0).
D. M (−16;0).
Câu 30. Trong hệ tọa độ Oxy, cho ba điểm A(1;3), B(−1;2), C (−2; )
1 . Tìm tọa độ của vectơ AB − AC. A. (−1; ) 1 . B. (−5; 3 − ). C. (1; ) 1 . D. (−1;2).
Câu 31. Trong hệ tọa độ Oxy, cho tam giác ABC có A(1; )
1 , B (−2;−2), C (7;7). Khẳng định nào sau đây đúng?
A. AB, AC cùng hướng.
B. B ở giữa hai điểm A và C. 25 Chương I. Vectơ
0916 620 899 – 0355 334 679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp
C. A ở giữa hai điểm B và C.
D. G (2;2) là trọng tâm tam giác ABC.
Câu 32. Trong hệ tọa độ Oxy, cho bốn điểm A(2; ) 1 , B (2;− ) 1 , C ( 2 − ; 3 − ), D( 2 − ;− )
1 . Xét hai mệnh đề:
(I). ABCD là hình bình hành.(II). AC cắt BD tại M (0;− )1.
Khẳng định nào sau đây đúng?
A. Chỉ (I) đúng.
B. Chỉ (II) đúng.
C. Cả (I) và (II) đều đúng.
D. Cả (I) và (II) đều sai.
Câu 33. Trong hệ tọa độ Oxy, cho điểm M (3; 4
− ). Gọi M ,1M lần lượt là hình chiếu vuông góc của 2 M trên Ox,O .
y Khẳng định nào đúng?
A. OM + OM = 3; 4 − .
B. OM = 4. 1 2 ( ) 2
C. OM − OM = −3;−4 . D. OM = 3 − . 1 2 ( ) 1
Câu 34. Cho ba vectơ a = (2; )
1 , b = (3;4), c = (7;2). Giá trị của k, h để c = k.a + . h b là
A. k = 3, 4; h = 0 − ,2.
B. k = 2,5; h = 1 − ,3.
C. k = 4,6; h = 5 − ,1.
D. k = 4, 4; h = 0 − ,6.
Câu 35. Trong hệ tọa độ Oxy, cho A(−1;5), B(5;5), C ( 1 − ;1 )
1 . Khẳng định nào sau đây đúng?
A. AB, AC cùng hướng. B. ,
A B, C thẳng hàng.
C. AB, AC cùng phương. D. AB, AC không cùng phương. ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
26 27 28 29 30 31 32 33 34 35 26 Chương I. Vectơ
0916 620 899 – 0355 334 679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp ÔN TẬP CHƯƠNG I
Bài 1. Cho hình chữ nhật ABCD. Gọi O là giao điểm của hai đường chéo AC và BD.
a) Với m tùy ý, hãy chứng minh MA + MC = MB + MD
b) Chứng minh rằng AB + AD = AB − AD HD Giải
a) MA + MC = 2OM và MB + MD = 2OM . Vậy MA + MC = MB + MD
b) AB + AD = AC ⇒ AB + AD = AC, AB − AD = DB . Vì hai đường chéo hình chữ nhật bằng nhau nên
AB + AD = AB − AD .
Bài 2. Cho tam giác ABC. Gọi I, K lần lượt là trung điểm của BC và BI. Chứng minh: 1 1 3 1
a) AK = AB + AI
b) AK = AB + AC 2 2 4 4 HD Giải 1 1
a) Vì K là trung điểm của BI nên AK = AB + AI (1) 2 2 1 1 3 1
b) Vì I là trung điểm của BC nên AI = AB + AC (2). Thay (2) vào (1), ta có AK = AB + AC . 2 2 4 4
Bài 3. Cho tam giác ABC có trọng tâm G. Gọi M, N, P lần lượt là trung điểm các cạnh AB, BC và CA.
a) Chứng minh rằng GM + GN + GP = 0
b) Chứng minh rằng AN + BP + CM = 0 HD Giải 1
a) Ta có GM + GN + GP = (GA+GB +GB +GC +GC + GA) = GA+GB + GC = 0 2 1 1
b) Ta có AN + BP + CM = ( AB + AC + BC + BA+ CB +CA) = .0 = 0 2 2
Bài 4. Cho hai hình bình hành ABCD và AB’C’D’ có chung đỉnh A. Chứng minh rằng
a) CC ' = BB ' + DD '
b) Hai tam giác BC’D và B’CD’ có cùng trọng tâm. HD Giải a) Ta có B C
CC ' = AC ' − AC = AB ' + AD ' − AB − AD = ( AB '− AB) + ( AD'− AD) B' = BB '+ DD ' A D
b) Từ CC ' = BB ' + DD ' , với mọi điểm G ta có C'
GC ' − GC = GB ' − GB + GD ' − GD ⇔ GB + GD + GC ' = GB ' + GD ' + GC D'
Suy ra GB + GD + GC ' = 0 ⇔ GB ' + GD ' + GC = 0 . Vậy nếu G là trọng tâm
của tam giác BC’D thì G cũng là trọng tâm tam giác B’CD’.
Bài 5. Chứng minh rằng với hai vectơ không cùng phương a và b , ta có a − b < a + b < a + b HD Giải
Từ điểm O bất kì, ta vẽ OA = a , AB = b . Vì a và b không cùng A
phương nên ba điểm O, A, B không thằng hàng. Khi đó, trong tam giác OAB ta có: b a
OA − AB < OB < OA + AB hay là a − b < a + b < a + b a + b B O
Bài 6. Cho tam giác ABC và đường thẳng d. Tìm điểm M trên đường thẳng d sao cho vectơ
u = MA + MB + 2MC có độ dài nhỏ nhất. HD Giải 27 Chương I. Vectơ
0916 620 899 – 0355 334 679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp
Với mọi điểm O, ta có
u = MA + MB + 2MC = OA − OM + OB − OM + 2OC − 2OM = OA + OB + OC − 4OM
Ta chọn điểm O sao cho v = OA + OB + 2OC = 0
Gọi G là trọng tâm của tam giác ABC. Ta có v = OA + OB + 2OC = 4OG + GC 1
Bởi vậy, để v = 0 , ta chọn điểm Osao cho GO = GC 4
Vậy, ta có u = −4OM ⇒ u = 4OM . Độ dài của vectơ u nhỏ nhất khi và chỉ khi 4OM nhỏ nhất hay M là
hình chiếu vuông góc của O trên d.
Bài 7. Cho tam giác ABC. Hãy xác định các điểm M, N, P, Q sao cho
a) MA + MB − 2MC = 0
b) NA + NB + 2NC = 0
c) PA − PB + 2PC = 0
d) QA − QB + QC = 0 HD Giải
a) Gọi I là trung điểm của AB, thì ta có MA + MB − 2MC = 0 khi và chỉ khi
2(MI − MC) = 0 ⇔ CI = 0. Không có điểm M nào như thế.
b) Ta có NA + NB + 2NC = 0 ⇔ 2(NI + NC) = 0. N là trung điểm của CI 1
c) PA − PB + 2PC = 0 ⇔ BA + 2PC = 0 ⇔ PC = AB . Như vậy, nếu lấy điểm D sao cho ABCD là 2
hình bình hành thì P là trung điểm của CD.
d) QA − QB + QC = 0 ⇔ BA + QC = 0 ⇔ QC = AB . Q là điểm sao cho ABCQ là hình bình hành.
Bài 8. Trong mặt phẳng toạ độ Oxy, cho ba điểm A(-1;3), B(4;2), C(3;5)
a) Chứng minh rằng ba điểm A, B, C không thẳng hàng
b) Tìm toạ độ điểm D sao cho AD = −3BC
c) Tìm toạ độ điểm E sao cho O là trọng tâm của tam giác ABE HD Giải
a) Ta có AB = (5;−1), BC = (−1;3) . 5 1 − Vì ≠
nên hai vectơ AB, BC không cùng phương, nghĩa là ba điểm A, B, C không thẳng hàng. 1 − 3 b) Gọi D( ;
x y) , ta có AD = (x +1; y − 3) và −3BC = (3; 9 − ) . x +1 = 3 x = 2 Ta có AD = 3 − BC ⇔ ⇔ . Vậy D(2; −6) y − 3 = −9 y = −6 1 − + 4 + x = 0 x = 3 − c) Gọi 3 E( ;
x y) và O là trọng tâm của tam giác ABE. Ta có ⇔ . Vậy E(−3;−5) 3 + 2 + y y = 5 − = 0 3
Bài 9. Trong mặt phẳng toạ độ Oxy, cho điểm G(1;2). Tìm toạ độ điểm A thuộc Ox và điểm B thuộc Oy
sao cho G là trọng tâm của tam giác OAB. HD Giải x + 0 + 0 0 + y + 0 Gọi ( A ;
x 0), B(0; y) . G là trọng tâm của tam giác OAB khi và chỉ khi = 1 và = 2 3 3 Vậy (
A 3; 0), B(0; 6)
Bài 10. Trong mặt phẳng toạ độ Oxy, cho hai điểm A(1;4) và B(2;2). Đường thẳng đi qua A và B cắt trục
Ox tại M và cắt trục Oy tại N. Tính diện tích tam giác OMN. HD Giải
Gọi M (0; x), N (0; y) . Khi đó AB = (1;−2), AM = (x −1; 4
− ), AN = (−1; y − 4) x −1 4 −
Vì AB, AM cùng phương nên =
⇒ x = 3 . Vậy M (3;0) 1 2 − 28 Chương I. Vectơ
0916 620 899 – 0355 334 679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp 1 − y − 4
Và AB, AN cùng phương nên =
⇒ y = 6 . Vậy M (0;6) 1 −2 1 1 3.6
Diện tích tam giác OMN là S = OM .ON = OM ON = = 9 (đvdt). 2 2 2
BÀI TẬP TỰ LUYỆN
Bài 11. Cho bố điểm A, B, C, D. Tìm các vectơ:
a) u = AB + DC + BD + CA
b) v = AB + CD + BC + DA
Bài 12. Cho lục giác đều ABCDEF và điểm M tuỳ ý.
Chứng minh rằng: MA + MC + ME = MB + MD + MF
Bài 13. Cho tam giác ABC có trung tưyến AM. Trên cạnh AC lấy hai điểm E và F sao cho AE = EF =
FC, BE cắt trung tuyến AM tại N. Tính u = AE + AF + AN + MN
Bài 14. Cho hai điểm A và B. Điểm M thoả mãn điều kiện MA + MB = MA − MB . Chứng minh rằng 1 OM =
AB , với O là trung điểm của AB. 2
Bài 15. Cho tam giác ABC và một điểm M tuỳ ý. Chứng minh rằng vectơ u = MA + MB − 2MC không
phụ thuộc vào vị trí điểm M. Hãy dựng điểm D sao cho CD = u .
Bài 16. Cho đoạn thẳng AB và điểm I sao cho 2IA + 3IB = 0
a) Tìm số k sao cho AI = k AB 2 3
b) Chứng minh rằng với mọi điểm M, ta có MI = MA + MB 5 5
Bài 17. Cho các vectơ a = (2;1),b = (3;−4),c = (−7;2) .
a) Tìm toạ độ các vectơ sau u = 3a + 2b − 4c
b) Tìm x sao cho x + a = b − c
c) Tìm các số h và k sao cho c = ha + kb
Bài 18. Cho hai vectơ u = (3;−4),v = (2;5)
a) Tìm toạ độ các vectơ u + v,u − v và 2u + 3v
b) Tìm a sao cho w = (a;16) và u cùng phương. Khi đó u và w cùng hướng hay ngược hướng?
Bài 19. Trong mặt phẳng toạ độ Oxy, cho các điểm A(-3;6), B(9;-10), C(-5;4).
a) Chứng minh ba điểm A, B, C không thẳng hành
b) Tìm toạ độ trung điểm I của BC và toạ độ trong tâm G của tam giác ABC
c) Tìm toạ độ điểm D sao cho tứ giác BGCD là hình bình hành.
Bài 20. Trong mặt phẳng toạ độ Oxy, choa các điểm A(4;0), B(8;0), C(0;4), D(0;6) và M(2;3)
a) Chứng minh rằng ba điểm B, C, M thẳng hàng và A, D, M thẳng hàng
b) Gọi P, Q, R lần lượt là trung điểm của các đoạn thẳng OM, AC và BD. Chứng minh rằng ba điểm P, Q, R thẳng hàng
Bài 21. Trong mặt phẳng toạ độ Oxy, cho hai điểm A(2;8) và B(4;4). Đường thẳng đi qua A và B cắt trục
Oy tại M và cắt trục Ox tại N. Tính diện tích tam giác OMN.
Bài 22. Trong mặt phẳng toạ độ Oxy, cho điểm G(2;4). Tìm toạ độ điểm A thuộc Oy và điểm B thuộc Ox
sao cho G là trọng tâm của tam giác OAB.
Bài 23. Trong mặt phẳng toạ độ Oxy, cho ba điểm A(-2; 4), B(1; 3), C(3; 2)
a) Chứng minh rằng ba điểm A, B, C không thẳng hàng
b) Tìm toạ độ điểm D sao cho AD = −3BC
c) Tìm toạ độ điểm E sao cho O là trọng tâm của tam giác ACE
BÀI TẬP TRẮC NGHIỆM
Câu 1. Cho tam giác ABC đều cạnh .
a Mệnh đề nào sau đây đúng?
A. AB = BC = CA = .
a B. CA = −BC.
C. AB = BC = C . A
D. CA = −A . B
Câu 2. Cho lục giác đều ABCDEF tâm .
O Số các vectơ bằng OC có điểm đầu và điểm cuối là các đỉnh 29 Chương I. Vectơ
0916 620 899 – 0355 334 679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp của lục giác là A. 6. B. 2. C. 3. D. 4.
Câu 3. Cho tam giác ABC với M , N, P lần lượt là trung điểm của BC, C ,
A AB . Khẳng định nào sau đây sai?
A. MN + NP + PM = 0.
B. PB + MC = M . P
C. AB + BC + CA = 0.
D. AP + BM + CN = 0.
Câu 4. Cho AB ≠ 0 và một điểm C. Có bao nhiêu điểm D thỏa mãn AB = CD ? A. Vô số. B. 1. C. 2. D. 0.
Câu 5. Gọi M , N, P lần lượt là trung điểm các cạnh AB, BC, CA của tam giác ABC. Hỏi vectơ
MP + NP bằng vectơ nào trong các vectơ sau? A. MN.
B. MB + N . B C. A . P D. B . P
Câu 6. Cho lục giác đều ABCDEF có tâm .
O Đẳng thức nào dưới đây sai?
A. AB = E . D
B. AB = AF .
C. OD = BC.
D. OB = OE.
Câu 7. Vectơ có điểm đầu là D , điểm cuối là E được kí hiệu là A. DE. B. DE. C. DE . D. E . D
Câu 8. Cho tam giác ABC có AB = AC và đường cao AH. Đẳng thức nào sau đây đúng?
A. HB + HC = 0.
B. AB = AC.
C. AB + AC = AH.
D. HA + HB + HC = 0.
Câu 9. Cho AB = C
− D . Khẳng định nào sau đây đúng?
A. ABCD là hình bình hành.
B. AB + DC = 0.
C. AB và CD cùng hướng.
D. AB và CD cùng độ dài.
Câu 10. Hai vectơ được gọi là bằng nhau khi và chỉ khi
A. Chúng trùng với một trong các cặp cạnh đối của một tam giác đều.
B. Chúng cùng hướng và độ dài của chúng bằng nhau.
C. Giá của chúng trùng nhau và độ dài của chúng bằng nhau.
D. Chúng trùng với một trong các cặp cạnh đối của một hình bình hành.
Câu 11. Gọi O là tâm hình vuông ABCD . Tính OB − OC .
A. OB − OC = BC.
B. OB − OC = D . A
C. OB − OC = OD − O . A
D. OB − OC = A . B
Câu 12. Với DE (khác vectơ - không) thì độ dài đoạn ED được gọi là
A. Độ dài của E . D
B. Hướng của E . D
C. Giá của E . D
D. Phương của E . D
Câu 13. Cho ba điểm phân biệt , A ,
B C . Đẳng thức nào sau đây đúng?
A. AB + CA = C . B
B. AB − BC = C . A
C. CA − BA = BC.
D. AB + AC = BC.
Câu 14. Cho hình vuông ABCD . Khẳng định nào dưới đây đúng?
A. Hai vectơ AB, AC cùng hướng.
B. AC = B . D
C. AB = C . D
D. AB = BC .
Câu 15. Cho hình thoi ABCD cạnh a và BAD = 60° . Đẳng thức nào dưới đây đúng? A. BC = D . A B. BD = . a
C. BD = AC.
D. AB = A . D
Câu 16. Cho bốn điểm phân biệt ,
A B, C, .
D Điều kiện nào trong các đáp án A, B, C, D sau đây là điều
kiện cần và đủ để AB = CD ?
A. AB = CD.
B. ABDC là hình bình hành.
C. AC = BD.
D. ABCD là hình bình hành.
Câu 17. Cho đường tròn O và hai tiếp tuyến song song với nhau tiếp xúc với (O) tại hai điểm A và . B
Mệnh đề nào sau đây đúng?
A. OA = O − . B B. AB = O − . B
C. OA = −O . B
D. AB = −B . A
Câu 18. Cho lục giác đều ABCDEF tâm .
O Số các vectơ khác vectơ - không, cùng phương với OC có 30 Chương I. Vectơ
0916 620 899 – 0355 334 679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp
điểm đầu và điểm cuối là các đỉnh của lục giác là A. 9. B. 6. C. 7. D. 4.
Câu 19. Cho tứ giác ABC .
D Gọi M , N, ,
P Q lần lượt là trung điểm của A ,
B BC, C , D D . A Khẳng
định nào dưới đây sai? A. MN = Q . P
B. QP = MN .
C. MQ = N . P
D. MN = AC .
Câu 20. Cho tam giác ABC đều cạnh a . Gọi M là trung điểm BC . Khẳng định nào dưới đây đúng? A. a a MB = MC. B. 3 AM = . C. AM = . a D. 3 AM = . 2 2
Câu 21. Cho tam giác ABC vuông cân đỉnh A , đường cao AH . Khẳng định nào sau đây sai?
A. BC − BA = HC − H . A
B. AH = AB − AH .
C. AH + HB = AH + HC .
D. AH − AB = AH − AC.
Câu 22. Cho hai điểm A và B phân biệt. Điều kiện để I là trung điểm AB là:
A. AI = BI.
B. IA = IB.
C. IA = I . B
D. IA = −I . B
Câu 23. Điều kiện nào là điều kiện cần và đủ để I là trung điểm của đoạn thẳng AB ?
A. IA = I . B
B. IA + IB = 0.
C. IA − IB = 0.
D. IA = IB.
Câu 24. Mệnh đề nào dưới đây sai?
A. 0 cùng phương với mọi vectơ.
B. 0 cùng hướng với mọi vectơ.
C. AB > 0.
D. AA = 0.
Câu 25. Cho hình bình hành ABCD . Đẳng thức nào sau đây đúng?
A. AB − BC = D . B
B. AB − BC = B . D
C. AB − BC = C . A
D. AB − BC = AC.
Câu 26. Gọi M , N lần lượt là trung điểm của các cạnh A ,
B AC của tam giác đều ABC . Hỏi cặp vectơ
nào dưới đây cùng hướng?
A. MN và C . B
B. AB và M . B
C. MA và M . B
D. AN và C . A
Câu 27. Tính tổng MN + PQ + RN + NP + QR . A. M . P B. MN. C. P . R D. M . R
Câu 28. Cho ba điểm ,
A B, C phân biệt. Khẳng định nào sau đây đúng?
A. AA + BB = A . B
B. AB + AC = BC.
C. MP + NM = N . P
D. CA + BA = C . B
Câu 29. Cho ba điểm ,
A B, C phân biệt. Mệnh đề nào dưới đây đúng?
A. Điều kiện cần để ,
A B, C thẳng hàng là AB = AC.
B. Điều kiện cần và đủ để , A ,
B C thẳng hàng là AB cùng phương với AC.
C. Điều kiện đủ để ,
A B, C thẳng hàng là với mọi M , MA cùng phương với A . B
D. Điều kiện cần để ,
A B, C thẳng hàng là với mọi M , MA cùng phương với A . B
Câu 30. Cho tam giác ABC. Có bao nhiêu vectơ khác vectơ - không có điểm đầu và điểm cuối là các đỉnh , A , B C ? A. 4. B. 9. C. 3. D. 6.
Câu 31. Cho AB ≠ 0 và một điểm C. Có bao nhiêu điểm D thỏa mãn AB = CD ? A. Vô số. B. 0. C. 1. D. 2.
Câu 32. Cho hình vuông ABCD . Khẳng định nào sau đây đúng?
A. AB = BC.
B. AB = C . D
C. AC = B . D
D. AD = CB .
Câu 33. Mệnh đề nào dưới đây đúng?
A. Không có vectơ nào cùng phương với mọi vectơ.
B. Có duy nhất một vectơ cùng phương với mọi vectơ.
C. Có ít nhất hai vectơ có cùng phương với mọi vectơ.
D. Có vô số vectơ cùng phương với mọi vectơ.
Câu 34. Cho tam giác ABC có trực tâm H . Gọi D là điểm đối xứng với B qua tâm O của đường tròn 31 Chương I. Vectơ
0916 620 899 – 0355 334 679
Tài liệu học tập Toán 10 GV. Lư Sĩ Pháp
ngoại tiếp tam giác ABC . Khẳng định nào dưới đây đúng?
A. HA = CD và AD = CH .
B. HA = CD và AD = HC .
C. HA = CD và AC = CH .
D. HA = CD và AD = HC và OB = OD .
Câu 35. Gọi M , N lần lượt là trung điểm của các cạnh A ,
B AC của tam giác đều ABC . Đẳng thức nào dưới đây đúng?
A. BC = 2 MN .
B. AB = AC.
C. MN = BC.
D. MA = M . B
Câu 36. Cho tam giác ABC với M là trung điểm BC. Mệnh đề nào sau đây đúng?
A. AB + AC = AM.
B. AM + MB + BA = 0.
C. MA + MB = A . B
D. MA + MB = MC.
Câu 37. Cho tam giác ABC cân ở A , đường cao AH . Khẳng định nào sau đây sai?
A. AB = AC.
B. HC = −H . B
C. AB = AC .
D. BC = 2HC.
Câu 38. Cho tứ giác ABCD . Có bao nhiêu vectơ khác vectơ - không có điểm đầu và cuối là các đỉnh của tứ giác? A. 4. B. 6. C. 8. D. 12.
Câu 39. Cho ba điểm phân biệt , A , B .
C Mệnh đề nào sau đây đúng?
A. AB − CA = BC.
B. AB + BC + CA = 0.
C. AB = BC ⇔ CA = BC .
D. AB + BC = AC.
Câu 40. Mệnh đề nào sau đây sai?
A. Nếu ba điểm phân biệt , A ,
B C nằm tùy ý trên một đường thẳng thì AB + BC = AC .
B. Nếu G là trọng tâm tam giác ABC thì GA + GB + GC = 0.
C. Nếu ABCD là hình bình hành thì CB + CD = C . A
D. Nếu M là trung điểm đoạn thẳng AB thì MA + MB = 0.
Câu 41. Gọi O là giao điểm của hai đường chéo hình chữ nhật ABCD . Mệnh đề nào dưới đây đúng?
A. AC = BD .
B. OB và OD cùng hướng.
C. AC và BD cùng hướng.
D. OA = OC.
Câu 42. Gọi O là tâm hình bình hành ABCD . Đẳng thức nào sau đây sai?
A. BC − BA = DC − D .
A B. OA − OB = C . D
C. OB − OC = OD − O . A
D. AB − AD = D . B
Câu 43. Gọi O là giao điểm của hai đường chéo của hình bình hành ABCD . Đẳng thức nào dưới đây sai?
A. OA = OC.
B. CB = D . A
C. AB = DC.
D. OB = D . O
Câu 44. Cho a và b là các vectơ khác 0 với a là vectơ đối của b . Khẳng định nào sau đây sai?
A. Hai vectơ a, b cùng độ dài.
B. Hai vectơ a, b chung điểm đầu.
C. Hai vectơ a, b cùng phương.
D. Hai vectơ a, b ngược hướng.
Câu 45. Cho bốn điểm phân biệt , A ,
B C, D thỏa mãn AB = CD . Khẳng định nào dưới đây sai?
A. AB cùng hướng C . D
B. AB cùng phương C . D
C. AB = CD .
D. ABCD là hình bình hành. ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 32 Chương I. Vectơ
0916 620 899 – 0355 334 679