Tài liệu học tập chuyên đề tính giá trị biểu thức, dãy số quy luật

CÂU LẠC BỘ TOÁN HỌC VQMC BAN CHUYÊN MÔN KHỐI 7 TÀI LIỆU HỌC TẬP CHUYÊN ĐỀ 1 NGƯỜI SOẠN : LÊ THANH PHONG MÃ TÀI LIỆU : 7MTL – 001 MÔN HỌC : TOÁN LỚP : 7M NĂM HỌC : 2024 – 2025 NIÊN KHÓA : 2023 – 2027
BỒI DƯỠNG HỌC SINH GIỎI LỚP 7M
CHUYÊN ĐỀ 1: TÍNH GIÁ TRỊ BIỂU THỨC, DÃY SỐ QUY LUẬT MỤC LỤC TÀI LIỆU HỌC TẬP
CHUYÊN ĐỀ 1 – TÍNH GIÁ TRỊ BIỂU THỨC, DÃY SỐ QUY LUẬT
A. LÝ THUYẾT VÀ PHƯƠNG PHÁP ............................................................................. 3
I. TÍNH GIÁ TRỊ BIỂU THỨC ..................................................................................... 3
1. Thực hiện phép tính cơ bản .................................................................................... 3
a) Phương pháp .......................................................................................................... 3
b) Lý thuyết ............................................................................................................... 3
2. Thực hiện phép tính với phân số ............................................................................ 6
a) Dạng 1. Lũy thừa và phân số ................................................................................. 6
b) Dạng 2. Phân số trên phân số ................................................................................ 6
3. Biến đổi cơ bản......................................................................................................... 7
a) Dạng 1. Cho trước giả thiết ................................................................................... 7
b) Dạng 2. Biến đổi từ biểu thức không có giả thiết ................................................. 7
II. DÃY SỐ QUY LUẬT ................................................................................................. 8
1. Liên quan đến tổng dãy số ...................................................................................... 8
a) Dạng 1. Tổng dãy số cách đều .............................................................................. 8
b) Dạng 2. Tìm số hạng ở vị trí bất kỳ trong dãy cách đều ....................................... 8
2. Liên quan đến tích ................................................................................................... 9
a) Dạng 1. Tính tổng tích các số tự nhiên liên tiếp ................................................... 9
b) Dạng 2. Tổng của dãy bình phương liên tiếp. ....................................................... 9
c) Dạng 3. Dạng dãy khác ....................................................................................... 10
3. Liên quan đến lũy thừa ......................................................................................... 10
a) Dạng 1. Dãy tính tổng dãy lũy thừa cùng cơ số .................................................. 10
b) Dạng 2. Dãy tính tổng dãy lũy thừa cùng cơ số dấu đan xen ............................. 11
4. Liên quan đến phân số .......................................................................................... 11
a) Dạng 1. Tính tổng dãy phân số theo quy luật (tử - mẫu) .................................... 11
b) Dạng 2. Rút gọn phân số ..................................................................................... 12
5. Khác ........................................................................................................................ 13
a) Dạng 1. So sánh dãy tổng quát ............................................................................ 13
b) Dạng 2. Dãy tổng các lập phương ....................................................................... 13
TÀI LIỆU HỌC TẬP CHUYÊN ĐỀ 1 LỚP 7M
c) Dạng 3. Tính tổng dãy có các chữ số giống nhau ............................................... 14
B. LUYỆN TẬP.................................................................................................................. 14
I. TÍNH GIÁ TRỊ BIỂU THỨC ................................................................................... 14
II. DÃY SỐ QUY LUẬT ............................................................................................... 14
III. MỘT SỐ BÀI TẬP TRONG ĐỀ THI ................................................................... 15
C. BẢN QUYỀN TÀI LIỆU VÀ PHẠM VI SỬ DỤNG ................................................. 16
1. Bản quyền ................................................................................................................... 16
2. Phạm vi sử dụng ........................................................................................................ 16 Trang 2 7MTL – 001
TÀI LIỆU HỌC TẬP CHUYÊN ĐỀ 1 LỚP 7M
CHUYÊN ĐỀ 1: TÍNH GIÁ TRỊ BIỂU THỨC, DÃY SỐ QUY LUẬT Lớp 7M
A. LÝ THUYẾT VÀ PHƯƠNG PHÁP
I. TÍNH GIÁ TRỊ BIỂU THỨC
1. Thực hiện phép tính cơ bản a) Phương pháp
- Sử dụng các phép toán cơ bản như: cộng, trừ, nhân, chia, nâng lên lũy thừa, khai phương, số thập phân
vô hạn tuần hoàn, ... và thực hiện đúng theo thứ tự thực hiện phép tính.
- Một số biểu thức thì còn phải sử dụng các tính chất như: giao hoán, kết hợp, phân phối, ... khi thực hiện. b) Lý thuyết * Lũy thừa
- Định nghĩa: Lũy thừa bậc n của một số thực x , ký hiệu n
x là tích của n thừa số x n * . - Tổng quát: n x   . x .
x ..x  x  , n   * n thõa sè x - Quy ước: 0 x  1  x  0 .
- Các công thức lũy thừa: SỐ NỘI DUNG VÍ DỤ 1 m . n m n a a a   5 4 9 2 .2  2 2 m : n mn a a  a a  0 5 6 1 5 : 5 5  3 .   m m m a b ab   4 4 4 4 2 .1,5 2.1,5  3 m m a  a  4 a : b  a :bm m m   b    2 2 2 2 8 : 4 8 : 4  2 m    0 b  b  n 5  m . m n a  a  3 2 2.3 6 6  6  6  1 1 n 1 6 a  n  a  5 10   n  , 0 a 5 10 10000 7  n n m 3 m  3 2 2  a  a 8 5  5  5
+ Lưu ý: Điều kiện: m, n   (trường hợp không nêu điều kiện của m, n). * Phân phối
- Phân phối phép nhân với phép cộng (áp dụng tương tự đối với phép trừ).
ab  ac  ad  ae  af  ... az  a b  c  d  e  f ... z a a a a  1 1 1 1  A     ...  a   ...  a  0, Õ n u a  0 th× A = 0 b c d z  b c d z  - Lưu ý: 1 1
+ Khi có dạng tính chất phân phối trên nhưng lại là phép chia (ví dụ: a :  b : ta nên biến đổi phép 2 2
chia về phép nhân trước, sau đó mới áp dụng tính chất phân phối phép nhân với phép cộng) Trang 3 7MTL – 001
TÀI LIỆU HỌC TẬP CHUYÊN ĐỀ 1 LỚP 7M
* Một số tính chất khác SỐ TÊN PHÉP CỘNG PHÉP NHÂN 1 Giao hoán a  b  b  a ab  ba 2 Kết hợp
a b c  a b c a b c  a b c 3 Số đối a  a  0 Không có
* Tính số thập phân vô hạn tuần hoàn
- Số thập phân vô hạn tuần hoàn đơn:
+ Định nghĩa sử dụng: Là số thập phân vô hạn tuần hoàn có chu kỳ bắt đầu ngay sau dấu “,”.
+ Cách tính (chuyển về dạng phân số):
• B1: Lấy phần chu kỳ làm tử số.
• B2: Mẫu số là các chữ số 9, số chữ số 9 bằng số chữ số của chu kỳ.
• B3: Rút gọn phân số (nếu có).
+ Ví dụ tính: Tính: 0,3
• B1: Tìm được tử số là “3”.
• B2: Vì phần chu kỳ có 1 chữ số nên số chữ số 9 có 1 chữ số. Suy ra mẫu số là “9”. • 3 1
B3 Tìm được phân số là . Rút gọn được . Vậy   1 0, 3  . 9 3 3
- Số thập phân vô hạn tuần hoàn tạp:
+ Định nghĩa sử dụng: Là số thập phân vô hạn tuần hoàn có chu kỳ không bắt đầu ngay sau dấu “,”.
+ Cách tính (chuyển về dạng phân số):
• B1: Lấy phần thập phân (bao gồm cả chu kỳ) rồi trừ đi phần không thuộc chu kỳ làm tử.
• B2: Mẫu số là các chữ số 9 và 0. Số chữ số 9 là số chữ số phần chu kỳ, còn số chữ số 0 là số chữ
số phần không thuộc chu kỳ.
• B3: Rút gọn phân số (nếu có). + Ví dụ: Tính: 0,15  1
• B1: Lấy tử bằng 151 – 15 = 136.
• B2: Theo phương pháp trên, mẫu số sẽ là: “900”. • 136 34 B3: Được phân số là:  . Vậy   34 0,15 1  . 900 225 225
- Số thập phân vô hạn tuần hoàn dạng đặc biệt:
+ Định nghĩa sử dụng: Là số thập phân vô hạn tuần hoàn có phần chu kỳ được bắt đầu bằng các chữ số 0
và kết thúc bằng các chữ số khác 0, có phần nguyên bằng 0.
+ Cách tính (chuyển về dạng phân số):
• B1: Lấy phần chữ số khác 0 của phần chu kỳ làm tử.
• B2: Mẫu số là các chữ số 9, số chữ số 9 bằng số chữ số 0 của phần chu kỳ cộng 1.
• B3: Rút gọn (nếu có).
+ Ví dụ tính: Tính. 0,0017 .
• B1: Tìm được tử số là “17”.
• B2: Vì phần chu kỳ có 2 chữ số nên số số chữ số 9 có 2 + 1 = 3 (chữ số). Suy ra mẫu số là “999”. • 17
B3: Tìm được phân số là
. Do không thể rút gọn được nữa nên   17 0, 0017  . 999 999
Lưu ý: Đối với những số mà có dạng tương tự, tuy nhiên có phần nguyên khác 0 ta tách phần nguyên ra. * Giá trị tuyệt đối a  a a  0 Để tính a ta lưu ý:
. (Chuyên đề giá trị tuyệt đối sẽ nói cụ thể). a  a a  0 Trang 4 7MTL – 001
TÀI LIỆU HỌC TẬP CHUYÊN ĐỀ 1 LỚP 7M
* Phép khai phương cơ bản
- Định nghĩa về căn bậc hai số học:
+ Ký hiệu: x  x  0
+ Giải thích kết quả căn bậc hai số học: Là số a không âm sao cho 2 a  x .
- Giải thích phép khai phương: Phép khai phương chính là cách tính giá trị căn bậc hai số học của một số
không âm. Tuy nhiên đối với lớp 7, khi sử dụng phép khai phương chủ yếu biến đổi được về dạng 2 x . Ví dụ: 2
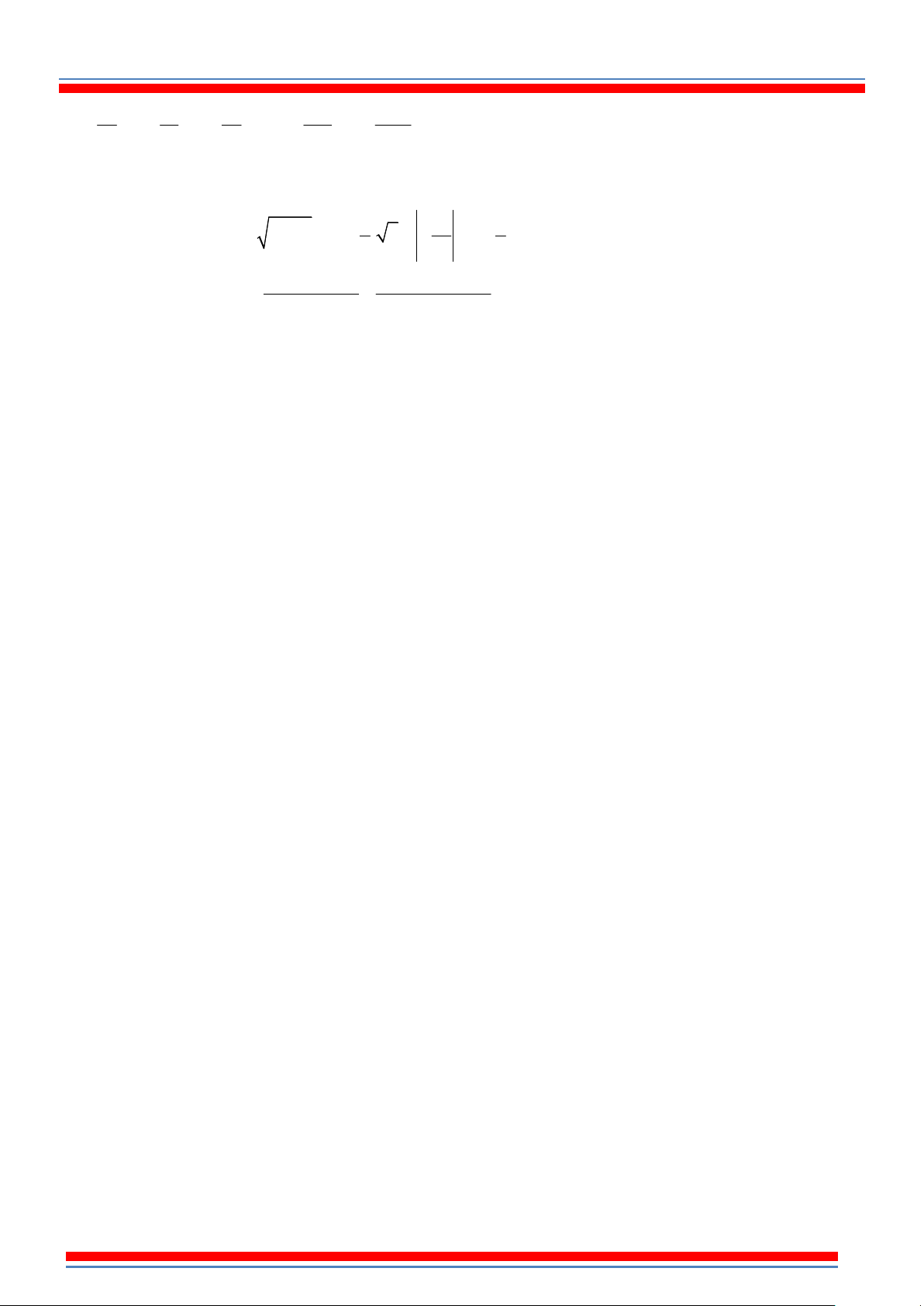
25  5 . Trong trường hợp này, phép khai phương sẽ có công thức đơn giản như ở dưới. - Công thức đơn giản: 2 x  x  x  0 2 x  x  x  0
* Thứ tự thực hiện phép tính
- Đối với biểu thức không chứa ngoặc:
Lũy thừa, căn bậc hai số học Nhân, chia Cộng, trừ
- Đối với biểu thức có chứa dấu ngoặc:
+ Trong ngoặc trước, ngoài ngoặc sau.
+ Thứ tự ngoặc làm trước:      
* Quy tắc dấu ngoặc và chuyển vế - Quy tắc dấu ngoặc: + Bảng quy tắc: TRƯỚC NGOẶC KHI PHÁ NGOẶC VÍ DỤ Dấu cộng “+” Giữ nguyên dấu
2  3 5  2  3 5 Dấu trừ “–” Đổi dấu
2  3 5  2  3 5
+ Lưu ý: Trước những số không viết hẳn dấu thì dấu của những số đó là dấu cộng “+”. - Quy tắc chuyển vế: + Đẳng thức và vế:
• Đẳng thức: Là mối quan hệ giữa hai vế, hai vế được nối với nhau bởi dấu “=”. Biểu thị giá trị của hai vế bằng nhau.
• Vế: Trong đẳng thức bao gồm vế trái và vế phải. Ví dụ: A = B thì A là vế trái, B là vế phải.
• Lưu ý: Khi một vế trong đẳng thức biến đổi như cộng thêm, trừ đi, nhân thêm, chia đi thì vế còn
lại cũng phải làm tương tự để đảm bảo được đẳng thức (đảm bảo được “=” của chúng). + Quy tắc:
• Khi chuyển một số từ vế này qua vế khác (chuyển vế) thì ta phải đổi dấu của chúng. Từ “+” thành
“–”, từ “–” thành “+”. • Ví dụ: A  B  C A  C  B
Ta thấy chuyển “+B” từ vế trái sang vế phải đổi thành “–B” Trang 5 7MTL – 001
TÀI LIỆU HỌC TẬP CHUYÊN ĐỀ 1 LỚP 7M
2. Thực hiện phép tính với phân số
a) Dạng 1. Lũy thừa và phân số * Phương pháp:
• B1: Phân tích tất cả các số ra thừa số nguyên tố rồi thu gọn.
• B2: Đặt thừa số chung trên cả tử và mẫu rồi rút gọn.
• B3: Tính phần còn lại. 6 5 9 4 .9  6 .120 * Ví dụ: Tính: A  4 4 11 8 .27  6
• B1: Phân tích ra thừa số nguyên tố.
2 6.3 5 2.39 2 2 3 .2 .3.5 A 
2 4.3 4 2.311 3 3 12 10 9 9 3 2 .3  2 .3 .2 .3.5 A  12 12 11 11 2 .3  2 .3 12 10 12 10 2 .3  2 .3 .5 A  12 12 11 11 2 .3  2 .3
• B2: Đặt thừa số chung trên cả từ và mẫu và rút gọn. 12 10 2 .3 (1 5) A  11 11 2 .3 (2.3 1) 2.(1 5) A  3.(61)
• B3: Tính phần còn lại. 2.6 4 A   3.5 5
b) Dạng 2. Phân số trên phân số * Phương pháp:
• B1: Biến đổi tất cả các số thập phân, … về dạng phân số.
• B2: Biến đổi các phân số trên tử và dưới mẫu về cùng tử.
• B3: Đặt thừa số chung sao cho tử và mẫu xuất hiện thừa số chung khác. • B4: Rút gọn. 13 13 13   * Ví dụ: Tính: 2011 2012 2024 A  12 12 12   2011 2012 2024
• B1: Biến đổi tất cả các số thập phân, … về dạng phân số.
Đã được biến đổi sẵn.
• B2: Biến đổi các phân số trên tử và dưới mẫu về cùng tử.
Đã được biến đổi sẵn.
• B3: Đặt thừa số chung sao cho tử và mẫu xuất hiện thừa số chung khác.  1 1 1  13      2011 2012 2024 A    1 1 1  12      2011 2012 2024  • B4: Rút gọn. 13 A  12 Trang 6 7MTL – 001
TÀI LIỆU HỌC TẬP CHUYÊN ĐỀ 1 LỚP 7M 3. Biến đổi cơ bản
a) Dạng 1. Cho trước giả thiết * Phương pháp:
- Dựa vào giả thiết bài toán cho, đi tìm ra hướng biến đổi để:
• Xuất hiện giả thiết từ đó thay giả thiết vào biểu thức.
• Các biểu thức liên quan đến giả thiết. 3a  2b 3a  2024
* Ví dụ: Tính giá trị biểu thức: A  
, biết a  b  1012;a  404,8;5a  2 . b 5a  2024 5a  2b
- Nhìn vào biểu thức ta nhận thấy các biểu thức đều chứa các “chữ”, chỉ có 2024 là số “riêng”. Từ đó ta
suy nghĩ có thể biến đổi 2024 thành các “chữ” không.
- Quay về giả thiết ta thấy: a  b  1012 mà 2024  2.1012 vậy ta có thể thay a  b  1012 vào để 2024
biến đổi thành các “chữ”. • Ta có: 3a  2b 3a  2024 A   5a  2024 5a  2b 3a  2b 3a  2.1012 A   5a  2.1012 5a  2b
• Thay a b 1012 vào 2012 ta được: 3a  2b 3a  2.a  b A   5a  2.a  b 5a  2b 3a  2b 3a  2a  2b A   5a  2a  2b 5a  2b 3a  2b 5a  2b A   3a  2b 5a  2b A  11 A  2 Vậy A = 2.
- Lưu ý: Các giả thiết a  404,8;5a  2b chỉ để cho các phân số tồn tại (hay điều kiện của phân số).
b) Dạng 2. Biến đổi từ biểu thức không có giả thiết * Phương pháp:
- Nhìn vào biểu thức và tìm các mối liên quan, quan hệ, hướng đi để biến đổi.
• Phân số: Thường biến đổi để rút gọn tử và mẫu.
• Biểu thức bình thường: Thường biến đổi về tổng số đối, nhân cho 0, … 2023.2024 1 * Ví dụ: Tính: 2 2024  2023
Nhận xét: Biểu thức trên là một phân số nên ta thử tìm mối quan hệ để rút gọn tử và mẫu. • Ta thử biến đổi: 2 2
2024  2023  2023  2023 1  20232023   1 1  2023.2024 1
• Ta thấy khi biến đổi xong, tử và mẫu giống nhau. Do đó, rút gọn được.  • 2023.2024 1 Vậy tính:
 1 (cần trình bày các bước biến đổi rõ hơn). 2 2024  2023 Trang 7 7MTL – 001
TÀI LIỆU HỌC TẬP CHUYÊN ĐỀ 1 LỚP 7M II. DÃY SỐ QUY LUẬT
1. Liên quan đến tổng dãy số
a) Dạng 1. Tổng dãy số cách đều * Phương pháp:
Sử dụng công thức tổng quát để tính tổng dãy số cách đều. * Công thức tổng quát:
- Để tính tổng một dãy số mà các số là các số liên tiếp cách đều nhau ta cần thực hiện:  • SC S§
B1: Tính số số hạng: SSH  1. KC SC S§.SSH
• B2: Tính tổng dựa vào công thức: T  2
Ghi chú: SSH: Số số hạng, SC: Số cuối, SĐ: Số đầu, KC: Khoảng cách cách đều, T: Tổng.
* Ví dụ: Tính giá trị biểu thức: S  2  4  6  8 10 ...100
• B1: Tính số số hạng của dãy. 100  2 98 Số số hạng của S là: 1  1  49 1  50 2 2
• B2: Tính tổng của dãy. 100 2.50 S  2 S  102.25  2550 * Lưu ý:
• Trong khi làm các bài tập có thể lược bỏ qua bước tính số số hạng của dãy (không khuyến khích).
• Theo cách tính số số hạng, thì số số hạng của dãy số tự nhiên liên tiếp từ 1 đến n là n.
b) Dạng 2. Tìm số hạng ở vị trí bất kỳ trong dãy cách đều * Phương pháp:
Vận dụng công thức tính số số hạng và tính tổng của dãy cách đều từ đó biến đổi và lấy được công thức
tính một số hạng ở vị trí bất kỳ. * Công thức tổng quát:
- Để tìm số đầu, số cuối của dãy ta biến đổi như sau:
• B1: Biến đổi công thức tính SSH. SC  S§ SSH  1 KC SC  S§ SSH 1  KC
SSH  1.KC  SC S§ SC  S§  SSH   1 .KC
• B2: Từ đây, ta tìm được số đầu, số cuối bằng cách biến đổi còn lại:
Tìm số đầu: S§  SC  SSH   1 .KC
Tìm số cuối: SC  SSH   1 .KC  S§
Ghi chú: SSH: Số số hạng, SC: Số cuối, SĐ: Số đầu, KC: Khoảng cách cách đều.
* Ví dụ: Tìm số hạng thứ 25 của dãy sau: 1, 4, 7, 10, ...
B1: Sử dụng công thức sẵn, không biến đổi.
B2: Số hạng thứ 25 của dãy là: 25   1 .3 1  73 . * Lưu ý:
- Số cuối ở đây chính là số hạng bất kỳ trong dãy chúng ta cần tìm.
- Trong khi làm có thể lược bỏ bước 1 (không khuyến khích). Trang 8 7MTL – 001
TÀI LIỆU HỌC TẬP CHUYÊN ĐỀ 1 LỚP 7M 2. Liên quan đến tích
a) Dạng 1. Tính tổng tích các số tự nhiên liên tiếp * Phương pháp:
- Thường với dạng bài này số lớn nên ta không thể tính tất cả các tích rồi tính tổng được mà ta cần tìm
cách triệt tiêu dựa vào quy luật.
- Sử dụng dãy A để thực hiện mô phỏng các bước làm: A 1.2  2.3  3.4 ... 99.100 .
• B1: Tìm cách triệt tiêu A
Nhận xét: Khoảng cách trong mỗi tích trong biểu thức A đều giống nhau và cùng bằng 1.
Mở rộng tích các số liên tiếp xung quanh 1.2 ta được 0.1.2.3, thấy 3 – 0 = 3. Mở rộng tích các số
liên tiếp xung quanh 2.3 ta được 1.2.3.4, thấy 4 – 1 = 3; .... Dựa vào đó, ta tìm được cách triệt tiêu
bớt tích trong A bằng cách nhân thêm 3 và tách số 3 đó tháng các hiệu hai số được mở rộng (3 – 0; 4 – 1; ....).
3A  1.2.3  2.3.3  3.4.3  ... 99.100.3
3A  1.2.3 0  2.3.4  
1  ... 99.100.101 98
• B2: Thực hiện biến đổi tiếp
3A  1.2.3  0.1.2  2.3.4 1.2.3  ...  99.100.101 98.99.100
3A  1.2.31.2.3  2.3.4  2.3.4 ... 98.99.100  98.99.100  99.100.101 0 3A  99.100.101 A  33.100.101  333300 * Cách làm chung:
- Từ phương pháp và cách làm mô phỏng trên ta có thể nắm được cách làm chung
• B1: Tìm hai số được mở rộng của mỗi tích như trên.
• B2: Nhân vào dãy một số là hiệu của hai số tìm được.
• B3. Thực hiện tách số đó thành hiệu hai số mở rộng.
• B4: Thực hiện biến đổi tiếp. - Chú ý:
+ Cách làm trên chỉ áp dụng đối với dãy có các tích mà ít nhất có 1 tích còn lại trong dãy có chung thừa số với nó.
+ VD: S  2.4  4.6  ... 8.10 , A  3.5  5.7 ...  9.11.
+ Không áp dụng phương pháp này đối với dãy: 1.2  3.4  5.6  ... . n n   1 và các dãy tương tự.
b) Dạng 2. Tổng của dãy bình phương liên tiếp. * Phương pháp:
- Sử dụng cách “đưa lạ về quen”. Tìm cách đưa về các dãy trên. - Lấy 2 2 2
S 1  2 ...100 làm ví dụ mô tả cách làm.
• B1: Tách các số để xuất hiện dạng 1. 2 2 2 S  1  2  ... 100
S  1.1 2.2  ...100.100 A  1.0   1  2.1  1  ... 100.99   1
A  1.0 11.2  2  ...  99.100 100
A  1.2 ... 99.100  1 2 ...100
• B2: Thực hiện các phép tính còn lại
Ta thấy 2 dạng quen thuộc nên ta chỉ cần thực hiện tính các dãy đó rồi tính tổng là ra A. * Lưu ý:
- Đối với những dãy có dạng a   a2   na2 2 2 ...
ta biến đổi về thành 2 a  2 2 2
1  2  ...  n  (a là hằng). Trang 9 7MTL – 001
TÀI LIỆU HỌC TẬP CHUYÊN ĐỀ 1 LỚP 7M
c) Dạng 3. Dạng dãy khác * Phương pháp:
- Dựa vào kinh nghiệm, kiến thức được rèn luyện qua các bài tập để phán đoán, tìm tòi quy luật và cách biển đổi.
- Cố gắng “đưa lạ về quen”. * Dãy mô phỏng
Dãy tổng tích của các cặp số tự nhiên liên tiếp.
• Mô phỏng: A  1.2  3.4  5.6  ... . n n   1 .
Đối với dãy trên ta thử biến đổi bằng cách tách các thừa số sau trong mỗi tích thành tổng với 1.
Mục đích là để xuất hiện các tổng có nhóm lại được thành một dãy đã “quen”. 1.2  1.1  1  1.11 3.4  3.3  1  3.3  3 ... . n n   1  . n n  n • Khi đó A trở thành:
A  1.11 3.3  3  ... . n n  n A  1.1 3.3... .
n n  1 3 ... n
• Từ đó, ta chỉ cần tính hai dãy đã “quen” để ra kết quả.
3. Liên quan đến lũy thừa
a) Dạng 1. Dãy tính tổng dãy lũy thừa cùng cơ số * Phương pháp:
- Dựa vào cách làm chung khi gặp dãy có dạng tính tổng lũy thừa có cùng cơ số.
- Biến đổi dựa vào kinh nghiệm. * Dãy mô phỏng: 2 3     ... n A a a a  a - Quan sát:
• Các cơ số đều là a.
• Số mũ của mỗi cơ số trong dãy tăng dần và khoảng cách mỗi số mũ là 1. - Biến đổi:
• B1: Tìm cách triệt tiêu. Từ việc quan sát trên ta có thể nhân vào cả hai vế số a với mục đích khi
nhân như vậy số hạng “trước” trong dãy A sẽ biến thành số hạng “sau kề nó” trong dãy A. 2 3 A  a  a  a  ... n  a aA  a  2 3 a  a  a  ... n  a  2 3 n n 1
aA  a  a  ...  a  a 
• B2: Khi đó lấy dãy mới (dãy vừa nhân được) trừ cho dãy cũ (dãy A) để triệt tiêu các số. 2 3 A  a  a  a  ... n  a 2 3 n n 1
aA  a  a  ... a  a  aA  A   2 3 n n 1
a  a  ... a  a    2 3 a  a  a  ... n  a  a   n 1 1 A  a   a n 1 a   a A  a  1 a 1 * Lưu ý:
- Đối với dãy mà cơ số bằng 1 ta không làm theo cách này.
- Có thể áp dụng tương tự với dãy có cơ số là phân số.
* CÁCH LÀM SẼ NÊU SAU KHI TÌM HIỂU XONG DẠNG 2. Trang 10 7MTL – 001
TÀI LIỆU HỌC TẬP CHUYÊN ĐỀ 1 LỚP 7M
b) Dạng 2. Dãy tính tổng dãy lũy thừa cùng cơ số dấu đan xen * Phương pháp:
- Dựa vào cách làm chung khi gặp dãy có dạng tính tổng lũy thừa có cùng cơ số.
- Biến đổi dựa vào kinh nghiệm. * Dãy mô phỏng: 2 3 1      ... n n V v v v  v  v - Quan sát:
• Các cơ số đều là v.
• Số mũ của mỗi cơ số trong dãy tăng dần và khoảng cách mỗi số mũ là 1.
• Các dấu “+”, “–” được đan xen với mỗi lũy thừa. - Biến đổi:
• B1: Giống với dạng 1. 2 3 n 1 V  v  v  v  ...  n  v  v vV  v  2 3 n 1 v  v  v  ...  n  v  v  2 3 n 1  n n 1 vV  v  v ...  v  v  v 
• B2: Khi đó lấy dãy mới (dãy vừa nhân được) cộng cho dãy cũ (dãy A) để triệt tiêu các số. 2 3 n 1 V  v  v  v  ...  n  v  v vV  v  2 3 n 1 v  v  v  ...  n  v  v  vV V   2 3 n 1  n n 1
v  v ... v  v  v     2 3 n 1 v  v  v ...  n  v  v  v   n 1 1 V  v   v n 1 v   v V  v    1 v 1 * Lưu ý:
- Dãy trên không áp dụng nếu cơ số là -1.
- Phương pháp trên cũng đúng với cơ số là phân số. CÁCH LÀM
- Từ các dạng trên ta có thể rút ra cách làm đối với những dạng tương tự như sau:
• B1: Nhân 2 vế cơ số mũ “khoảng cách giữa các số mũ”.
• B2.1: Đối với dãy toàn cộng : “Dãy mới” TRỪ đi “dãy cũ”.
• B2.2: Đối với dãy cộng trừ xen kẽ: “Dãy mới” CỘNG với “dãy cũ”.
- Lưu ý: Đối với dãy có cơ số là phân số, ngoài nhân 2 vế với cơ số thì ta có thể nhân vào 2 vế với mẫu
chung của các phân số đó với cách làm như trên.
4. Liên quan đến phân số
a) Dạng 1. Tính tổng dãy phân số theo quy luật (tử - mẫu) * Phương pháp:
- Tách tử số thành hiệu hai thừa số dưới mẫu để tách phân số thành hiệu hai phân số.
- Nhân thêm để thực hiện được phương pháp tách tử số. a n  a n n  a n 1 1 - Biến đổi 1 phân số:      n n  a n n  a
n n  a nn  a n n  a
* Cách làm đối với dãy CÓ hiệu hai thừa số dưới mẫu đã bằng với tử.
• B1: Biến đổi từng phân số thành hiệu hai phân số.
• B2: Nhóm các phân số cùng mẫu để triệt tiêu.
• B3: Thực hiện phép tính còn lại. Trang 11 7MTL – 001
TÀI LIỆU HỌC TẬP CHUYÊN ĐỀ 1 LỚP 7M
* Cách làm đối với dãy KHÔNG có hiệu hai thừa số dưới mẫu bằng với tử. - Cách 1: Thay tử số
Có thể sử dụng khi tất cả tử số của các phân số trong dãy đều giống nhau, hiệu hai thừa số dưới mẫu cũng
giống nhau hoặc các trường hợp đặc biệt khác.
Chú ý: Để có thể thực hiện các dãy mà không tạm thời làm thay đổi giá trị của dãy ta làm theo cách sau.
• B1: Nhân vào dãy một phân số với tử số của nó là tử chung của dãy và mẫu số là hiệu hai thừa số
dưới mẫu của dãy đồng thời thay tử chung bằng hiệu hai thừa số dưới mẫu.
• B2: Biến đổi dãy mới theo cách làm đối với dãy có hiệu hai thừa số dưới mẫu bằng với tử.
• B3: Thực hiện các phép tính còn lại. m m m - Ví dụ: Tính:   ...
biết a  a  a  a  ...  a  a  k k  m . 2 1 3 2 n n 1    a a a a a a 1 2 2 3 n 1  n
• B1: Nhân thêm phân số vào dãy và thay tử. m m m m  k k   ...    ...  a a a a a a k a a a a 1 2 2 3 n 1  n  1 2 n 1  n  • B2: Biến đổi. m  k k  m  1 1 1 1  m  1 1   ...     ...       k a a a a k a a a a k a a  1 2 n 1  n   1 2 n 1  n   1 n 
• B3: Thực hiện phép tính còn lại. m  1 1  m a  a m a  a n 1  n 1     .  k a a k a .a k a .a  1 n  1 n  1 n 
- Chú ý: Việc nhân thêm phân số vào dãy với tử và mẫu được nêu như trên thực chất là việc đặt tử chung
ra bên ngoài thay bằng hiệu hai thừa số dưới mẫu. Khi biến đổi xong thì cuối cùng cần chia dãy đó với
hiệu hai thừa số dưới mẫu và nhân tử chung đã đặt ra ngoài. Nếu tử chung là m, hiệu hai thừa số dưới  1 1 
mẫu là k, dãy sau biến đổi là  
 thì có được dãy ban đầu sẽ có giá trị là: a a  1 n   1 1   1 1  m  1 1  . m    : k  m : k.       a a a a k a a  1 n   1 n   1 n  - Cách 2: Thay mẫu số.
• Phương pháp: Dựa vào sự quan sát tử số và mẫu số. Đối với dạng này có nhiều bài không thể áp
dụng được cách làm chung cần phải dựa vào sự quan sát và đặc điểm của từng bài khác nhau. Tuy
nhiên đối với những dạng bài cơ bản có thể tham khảo cách làm chung sau đây.
o Nhân thêm vào dãy một phân số sao cho hiệu hai thừa số dưới mẫu bằng với tử.
o Lưu ý: Thường áp dụng đối với các dãy không có tử số chung.
b) Dạng 2. Rút gọn phân số
* Phương pháp: Biến đổi tử số, mẫu số của các phân số thành dạng tích các thừa số. Từ đó rút gọn các thừa số chung. * Cách làm chung
• B1: Tính các biểu thức trong ngoặc (nếu có) thành phân số.
• B2: Tách tử số và mẫu số thành tích (nếu cần).
• B3: Rút gọn các thừa số chung.  1  1   1 
* Ví dụ: Lấy dãy A  1 1 .... 1      làm ví dụ.  2  3   99 
• B1: Tính các biểu thức thành phân số. 3 4 100 A  . .... 2 3 99
• B2: Tách tử số và mẫu số (đã được tách sẵn). Trang 12 7MTL – 001
TÀI LIỆU HỌC TẬP CHUYÊN ĐỀ 1 LỚP 7M
• B3: Rút gọn các thừa số chung. 100 A   50 2 5. Khác
a) Dạng 1. So sánh dãy tổng quát * Phương pháp:
- Tính các dãy tổng quát.
- Sử dụng phép biển đổi so sánh đơn giản: xét hiệu, ... 1 1 1 1 * Ví dụ: Chứng minh M    ...  2 3 100 2 2 2 2 • B1: Tính M 1 1 1 M   ... 2 3 100 2 2 2 1 1 1 2M   ... 2 99 2 2 2  1 1 1   1 1 1  2M  M    ...    ...  2 99   2 3 100   2 2 2   2 2 2  1 1 M   100 2 2
• B2: Biến đổi so sánh cơ bản 1 1 1 1 1 1 Do   0 nên   hay M  . 100 2 2 100 2 2 2 2 1 Vậy M  . 2
b) Dạng 2. Dãy tổng các lập phương n n 1
* Dãy tổng các lập phương từ 1 đến n: 1  2  ... n  1 2 ... n  2 2 2 3 3 3  4
* Phương pháp: Sử dụng thẳng hoặc chứng minh bằng phương pháp Quy nạp (khuyến khích). n n 1 3 3 3  2 2
Chứng minh: 1  2  ... n  n   * (1) 4 1 . 11 3  2 2 2 1.2 Với n = 1 ta thấy: 1   1 (luôn đúng). 4 4 k k 1 3 3 3  2 2
Giả sử (1) đúng với n = k k  
* tức là: 1  2  ... k  . 4 2 2 k 1 k  2
Với n = k + 1, ta chứng minh: 1  2  ... k  3 3 3     1  . 4 Thật vậy: 2 2 2     
  k  3     k  k  3 k k  1 k 1 2 ... 1 1 2 ... 1   k  3 1  k  2 3 3 3 3 3 1 .  k   1 4 4   k  4k  4 k  2 1 . 2 2 k  2k  2k  4
k 1 .k k  2  2 k  2  2
  2      2 2     k    k 1 .k 2 1 .    4 4 4 4
Suy ra, (1) đúng với n = k + 1, do đó theo nguyên lý quy nạp (1) sẽ đúng với mọi n là số nguyên dương (hay đpcm). Trang 13 7MTL – 001
TÀI LIỆU HỌC TẬP CHUYÊN ĐỀ 1 LỚP 7M
c) Dạng 3. Tính tổng dãy có các chữ số giống nhau * Phương pháp:
Chứng minh, biến đổi sử dụng công thức tổng quát. *Công thức tổng quát n 1 a 10   10 
Với a là chữ số, n là số số hạng ta có: a  aa  aaa  ... a . a ..aa     n. 9 9 n ch÷ sè a   B. LUYỆN TẬP
I. TÍNH GIÁ TRỊ BIỂU THỨC
Bài 1. [7MTL00101]. Tính giá trị các biểu thức sau: 2,9 a) Q  900  7 7 3  . 3  3 .2 162.108 16  15    4    3  0, 6 . .   2025 1  4  71 b) K   2 3  2   5  5 .      5   12  9 4 7 5 4 5 2 .27 .12  6 .81 .8 c) V  4 4 7 10 20 16 .18 .9  4 .24.3 d) N    2 3
2024. 5. 5  2  :11 1  62025
Bài 2. [7MTL00102]. Tính giá trị các biểu thức sau:  1   1 a) 2
H  0, 75  2  0,75  3 .      3   9  x  3y x 3 b) T  biết:  . x  y y 5  z  x  y  c) C  1 1 1     ; x ;
y z  0 và x  y  z  0.  x  y  z 
Bài 3. [7MTL00103]. Tính giá trị các biểu thức sau: 3  1  3 1 a) V  16 .  13 .   5  3  5 9 5 14 12 2 11 b) Q      15 25 9 7 25
30.4  90.12 179.24  24 c) M  18  6.27 12.54   1  d) C  99  1  ,3  5.2   7  2 99 3 9   99 .   4 3 90 27 81  99    3  II. DÃY SỐ QUY LUẬT
Bài 1. [7MTL00104]. Tính giá trị các biểu thức sau: 32 6 9 1 19 a) D      3.7 7.41 41.10 10.51 51.14  1 1 1 1 1 1   1 1 1 
b) L  1    ...     ...      2 3 4
2023 2024 2025  1013 1014 2025  Trang 14 7MTL – 001
TÀI LIỆU HỌC TẬP CHUYÊN ĐỀ 1 LỚP 7M
Bài 2. [7MTL00105]. Thực hiện yêu cầu:
a) Kiểm tra số tạo bởi 3 chữ số tận cùng của biểu thức T có chia hết cho 9 hay không, biết:
T  8  88  888  ... 88...88  20  . 88 ch÷ sè 8
b) Tính giá trị biểu thức của D, biết: D  A  B và 2 2 2
A  1  2  ...  99 , B  1.2  2.3  ... 98.99 .
Bài 3. [7MTL00106]. Tính giá trị các biểu thức sau: a) H   4 8 2020 2024       2 4 2022 2024 5. 1 2 2 ... 2 2 1 2  2  ...  2  2  1 1 1 1 1 1 b) P  3.  5.  7. ...15. 17. 19. 1.2 2.3 3.4 7.8 8.9 9.10
Bài 4. [7MTL00107]. Thực hiện yêu cầu: 1 1 1 1 1 1 a) Cho A     ...  . So sánh A  với 0. 2 2 2 2 2 4 5 6 2023 2024 2 b) Cho 2 3 4
1.2  2.2  3.2  4.2 ... .2n P n
. Tìm số tự nhiên n thỏa mãn sao cho: P   n 10 2 2   1 . 1 2 n c) D    ... n  * . 4 4 4 4.1 1 4.2 1 4.n 1 c.1. Chứng tỏ: 4 n    2 n  n   2 4 1 2 2 1 2n  2n  
1 n   *. (Đọc về phần nhân đa thức cho đa thức).
c.2. Tính giá trị biểu thức của D.
c.3. Tính giá trị của D khi n  100 . 2 4 6 2023 1 d) Cho T  . . ... . Chứng minh rằng: 2 T  . 3 5 7 2024 1013
III. MỘT SỐ BÀI TẬP TRONG ĐỀ THI
Bài 1. [7MTL00108]. Tính giá trị các biểu thức sau: (Câu 1. Đề thi Olympic mở rộng, 2023 – 2024, trường THCS Lập Thạch) 196  2 3  7   7 11  1931 7  a) A  .   :  .        .  13 196 98 13  1931 3862 25 2        1 2 3 2023   ...  2024 b) 2023 2022 2021 1 B  . 1 1 1 1  ...  2 3 2024
Bài 2. [7MTL00109]. Tính giá trị các biểu thức sau: (Bài 1. Đề thi chọn HSG cấp huyện, 2023 – 2024,
Phòng GD&ĐT Lương Tài) 2 3  1 3 1 1) A  16 . 13 .   . 5  3  5 81 6 5 9 4 .9  6 .120 2) B  . 4 12 11 8 .3  6 2  1  1  1   1  3) M  1 1 1 .... 1       . 3  2.4  3.5  4.6   2022.2024 
Bài 3. [7MTL00110]. (Câu 1. Đề thi Olympic cấp huyện, 2023 – 2024, Hội đồng thi Olympic trường THCS Lập Thạch) 1) Thực hiện phép tính  2 3  191 33  7 11  1011 9  a)  .  :  .        191 382 17 34   1011 2022 25 2       0   b) 2 1 25 2023 11  72 1 :    2 4  2024  Trang 15 7MTL – 001
TÀI LIỆU HỌC TẬP CHUYÊN ĐỀ 1 LỚP 7M  1  1  1   1  1  c) 1 1 1 .... 1 1  2  2  2   2  2   2  3  4   99 100 
2) Tính giá trị biểu thức: A   x  y  z  2023 2 25
biết 3x  4y  5z  3x  4y và 2x  y  z 19 .
Bài 4. [7MTL00111]. (Bài 1. Đề KS Học sinh giỏi cấp huyện, 2023 – 2024, Phòng GD&ĐT Tiền Hải) 2   1) Thực hiện phép tính:  2 1 2 1 3 5  0,5. . 9   : 1    3 3  3  12 5 6 2 10 3 5 2 2 .3  4 .9 5 .7  25 .49
2) Rút gọn biểu thức: A   12 6 4 5 3 3 9 3 2 .3  8 .3 125 .7  5 .14
C. BẢN QUYỀN TÀI LIỆU VÀ PHẠM VI SỬ DỤNG I. Bản quyền
Bản quyền thuộc về Câu lạc bộ Toán học VQMC – Ban Chuyên môn Khối 7
Với mã tài liệu là: 7MTL – 001 II. Phạm vi sử dụng
Tài liệu này được sử dụng với bất kỳ ai có mong muốn, được chia sẻ miễn phí TUY NHIÊN
KHÔNG ĐƯỢC SỬ DỤNG TÀI LIỆU NÀY VỚI MỤC ĐÍCH THƯƠNG MẠI ------------------- Trang 16 7MTL – 001