Tài liệu học tập môn Toán 11 – La Tuấn Duy (Tập 1)

Với mục đích giúp học sinh tự học chương trình Toán 11 (Đại số và Giải tích 11 và Hình học 11) trong kỳ nghỉ hè năm 2019, thầy La Hồ Tuấn Duy biên soạn tài liệu học tập môn Toán 11 (Tập 1)

68 34 lượt tải Tải xuống

Chia sẻ Báo cáo tài liệu

TÀI LIỆU HỌC TẬP

Năm học: 2019 – 2020

TOÁN 11

TẬP 1

Cuốn sách này của: ______________________________

Biên soạn & giảng dạy: Thầy Duy – THPT Gia Định

LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 1

PHẦN 1:

HÀM SỐ LƯỢNG GIÁC – PHƯƠNG TRÌNH LƯỢNG GIÁC

BÀI 1: ÔN TẬP CÔNG THỨC LƯỢNG GIÁC

A. TÓM TẮT LÝ THUYẾT

1. Giá trị lượng giác của một cung

Trên đường tròn lượng giác (hình 1.1) cho cung



có sđ

AM 



Hình 1.1

Gọi

 

;

M M

M x y

thì ta có:

sin

y OK  

cos

x OH  

 

sin

tan ; cos 0

cos



 



 

 

cos

cot ; sin 0

sin



 



 

Lưu ý:

1. Các giá trị

sin 

;

cos 

xác định với mọi

  

. Và ta có:

 

sin 2 sin , ;k k      

 

cos 2 cos , .k k      

1 sin 1  

;

1 cos 1  

tan 

xác định với mọi

 

k k



    

và

 

tan tank   

cot 

xác định với mọi

 

,k k   

và

 

cot cotk   

2. Công thức lượng giác

Hệ thức cơ bản Cung liên kết

2 2

sin cos 1a a

 

tan .cot 1a a 

sin

tan

cos



cos

cot

sin



1 tan

cos

 

1 cot

sin

 

cos ñoiá

sin buø

phuï cheùo

hôn keùm cheoù sin



 

sin sin

tan tan

cot cot

cos cos

cos

a a



  

 

LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 2

Công thức cộng Công thức nhân đôi – nhân ba – hạ bậc

 

sin sin . cos cos . sina b a b a b  

 

cos cos . cos sin . sina b a b a b 



 

tan tan

tan

1 tan . tan

a b



 



 

tan tan

tan

1 tan . tan

a b



 



sin 2 2 sin .cosa a a

2 2

cos 2 cos sin

2 cos 1

1 2 sin

a a a

 

sin . cos sin 2

1 cos 2

sin

1 cos 2

cos

a a a













 















sin 3 3 sin 4 sina a a 

(3sin – 4sin)

cos 3 4 cos 3 cosa a a 

(4cô – 3 cô)

Công thức biến đổi tổng thành tích Công thức biến đổi tích thành tổng

sin sin 2 sin . cos

2 2

a b a b

a b

 

 

sin sin 2 cos . sin

2 2

a b a b

a b

 

 

cos cos 2 cos . cos

2 2

a b a b

a b

 

 

cos cos 2 sin . sin

2 2

a b a b

a b

 

  

   

sin . cos sin sin

a b a b a b

 

   

 

 

   

cos . sin sin sin

a b a b a b

 

   

 

 

   

cos . cos cos cos

a b a b a b

 

   

 

 

   

sin . sin cos cos

a b a b a b

 

    

 

 

Một số công thức khác

Công thức tính

sin , cos 

theo

tan





sin cos 2 sin

a a a



 







  











 

cos sin 2 cos

a a a



 







 











 



2 2 2

sin . cos sin 2

a a a



4 4 2

1 cos 4

cos sin 1 sin 2

a a a



   

6 6 2

3 cos 4

cos sin 1 sin 2

a a a



   

Đăt

tan





sin

cos

tan



















 



















3. Biểu diễn cung lượng giác trên đường tròn lượng giác

Cung lượng giác



 

 

 

được biểu diễn bởi

điểm trên đường tròn lượng giác.

Bước 1: Xác định điểm

biểu diễn cung



Bước 2: Xác định

1m 

điểm còn lại trên đường tròn lượng giác cách đều điểm

Ví dụ:

1. Cung lượng giác

3 3

x k

  

   

được biểu diễn bởi một điểm

tại vị trí



LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 3

2. Cung lượng giác

6 6

x k

  

   

được biểu diễn bởi hai điểm

tại các vị trí



và



3. Cung lượng giác

4 2 4

k k

   

   

thì có bốn điểm

tại các vị trí



;



B. CÁC DẠNG TOÁN

Dạng 1: Biến đổi biểu thức lượng giác

Phương pháp:

Sử dụng công thức lượng giác. Thông thường ta thực hiện như sau:



Có hệ số tự do



biến đổi cho mất số



Có mũ cao



hạ bậc



Có tích



biến đổi thành tổng



Có tổng



nhóm hạng tử và biến đổi thành tích

Các ví dụ

Câu 1. Biến đổi biểu thức sau thành tổng

cos . cos 2 . cos 3P x x x

___________________________

Câu 2. Biến đổi biểu thức sau thành tổng

sin . sin . sin

3 3

P x x x

 

   

 

 

 

  

 

 

 

 

 

   

___________________________

LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 4

Câu 3. Biến đổi biểu thức sau thành tích

sin 2 cos 2 1P x x  

___________________________

Câu 4. Biến đổi biểu thức sau thành tích

sin sin 2 sin 3P x x x  

___________________________

Câu 5. Biến đổi biểu thức sau thành tích

1 cos cos 2 cos 3P x x x   

___________________________

Câu 6. Biến đổi biểu thức sau thành tích

2 2 2 2

cos cos 2 sin 3 sin 4P x x x x   

___________________________

Câu 7. Biến đổi biểu thức sau thành tích

 

8 8 10 10

sin cos 2 sin cos

P x x x x

   

___________________________

Câu 8. Biến đổi biểu thức sau thành tích

sin 6 2 sin 3 cos cos 2P x x x x  

___________________________

LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 5

Dạng 2: Rút gọn, chứng minh biểu thức lượng giác

Các ví dụ

Câu 9. Chứng minh rằng:

4 4 2

1 1

sin cos cos 2

2 2

x x x

  

___________________________

Câu 10. Chứng minh rằng

6 6

5 3 cos 2

sin cos

2 2 8

x x x

 

___________________________

Câu 11. Rút gọn biểu thức

   

4 4 6 6

3 sin cos 2 sin cos

P x x x x

   

___________________________

Câu 12. Rút gọn biểu thức

2 2 2

2 2

sin sin sin

3 3

P x x x

 

   

 

 

 

    

 

 

 

 

 

   

___________________________

LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 6

Câu 13. Rút gọn biểu thức

3 3

cos 3 sin sin 3 cosP x x x x 

___________________________

Dạng 3: Biểu diễn cung lượng giác trên đường tròn lượng giác

Phương pháp:

Bước 1: Đưa cung về dạng



 



có

điểm trên đường tròn lượng giác biểu diễn cung

Bước 2: Xác định điểm

biểu diễn cung



trên đường tròn lượng giác

Bước 3: Xác định

1m 

điểm còn lại trên đường tròn lượng giác

cách đều

điểm

Các ví dụ

Câu 14. Xác định các điểm trên đường tròn lượng giác biểu diễn cung

x k



 

 

k  

___________________________

Câu 15. Xác định các điểm trên đường tròn lượng giác biểu diễn cung

x k



  

 

k  

___________________________

Câu 16. Xác định các điểm trên đường tròn lượng giác biểu diễn cung

x k



 





___________________________

LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 7

Câu 17. Xác định các điểm trên đường tròn lượng giác biểu diễn cung

x k



  

 

k  

___________________________

Câu 18. Xác định các điểm trên đường tròn lượng giác biểu diễn cung

x k



 

 

k  

___________________________

Câu 19. Xác định các điểm trên đường tròn lượng giác biểu diễn cung





 

k  

___________________________

Câu 20. Xác định các điểm trên đường tròn lượng giác biểu diễn cung





 

k  

___________________________

Câu 21. Xác định các điểm trên đường tròn lượng giác biểu diễn cung

3 2

 

 

 

k  

___________________________

LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 8

BÀI 2: PHƯƠNG TRÌNH LƯỢNG GIÁC CƠ BẢN

Dạng 1: Phương trình

sin u m

Phương pháp:

1. Dạng cơ bản:

sin u m

 



1 1m m   

: Phương trình vô nghiệm



1 1m  

: Với

sinm 

, ta có:

 

1 sin sin

u k

 



  



 



  



  





 

k  

Đặc biệt:

sin 0

sin 1 2

x x k







  



   





     





 

k  

2. Dạng mở rộng:

 

sin sin

u v k



 



 



  



  







(Với

,u v

là các biểu thức theo biến

)

Các ví dụ

Câu 1. Giải phương trình

sin 2 1x 

___________________________

Câu 2. Giải phương trình

sin 3 0x 

___________________________

Câu 3. Giải phương trình

sin 1

2 6



 







  











 

___________________________

LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 9

Câu 4. Giải phương trình

sin 5



___________________________

Câu 5. Giải phương trình

sin 2

 

___________________________

Câu 6. Giải phương trình

2 sin 3 0

2 6



 







  











 

___________________________

Câu 7. Giải phương trình

sin 3 sin 2

x x



 







 











 

___________________________

Câu 8. Tìm các nghiệm của phương trình

sin 2

3 2



 







  











 

trong khoảng

 

; 

___________________________

LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 10

Câu 9. Tìm các nghiệm của phương trình

sin 2 sin

6 3

x x

 

   

 

 

 

  

 

 

 

 

 

   

thỏa

2x 

___________________________

Câu 10. Giải phương trình

2 sin 2 0



 







  











 

và biểu diễn các nghiệm trên đường tròn lượng

giác

___________________________

Dạng 2: Phương trình

cos u m

Phương pháp:

1. Dạng cơ bản:

cosu m

 



1 1m m   

: Phương trình vô nghiệm



1 1m  

: Với

cosm 

, ta có:

 

1 cos cos

u k

 



 



 



  



  





 

k  

Đặt biệt:

cos 0

cos 1 2

x x k



 





   



  





    





 

k  

LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 11

2. Dạng mở rộng:

 

cos cos

u v k





 



  



  







(Với

,u v

là các biểu thức theo biến

)

Các ví dụ

Câu 11. Giải phương trình

cos 3 1x 

___________________________

Câu 12. Giải phương trình

cos 0



 







 











 

___________________________

Câu 13. Giải phương trình

cos 2 1



 







  











 

___________________________

Câu 14. Giải phương trình

cos 2

x 

___________________________

Câu 15. Giải phương trình

2 cos 1 0

3 6



 







  











 

___________________________

LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 12

Câu 16. Giải phương trình

cos 2 cos

4 4

x x

 

   

 

 

 

  

 

 

 

 

 

   

___________________________

Câu 17. Tìm các nghiệm của phương trình

2 cos 3 0



 







  











 

trong đoạn

3;6

 



 

 

___________________________

Câu 18. Giải phương trình

cos

3 2



 







  











 

và biểu diễn các nghiệm trên đường tròn lượng giác

___________________________

Dạng 3: Phương trình

tan u m

và

cot u m

Phương pháp:

1. Dạng cơ bản:



tan u m

tan tanu u k      

 

k  



cotu m

cot cotu u k      

 

k  

LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 13

2. Dạng mở rộng:

 

tan tan

cot cot

u v u v k k



    



(Với

,u v

là các biểu thức theo biến

)

Các ví dụ

Câu 19. Giải phương trình

tan 2 3x  

___________________________

Câu 20. Giải phương trình

3 cot 3 3 0x  

___________________________

Câu 21. Giải phương trình

tan 2 tan

x x



 







 











 

___________________________

Câu 22. Giải phương trình

cot 3 cot2

x x



 







 











 

___________________________

LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 14

Dạng 4: Đưa về phương trình cơ bản

Phương pháp:



Đưa dấu

" "

vào trong

 

sin sin

tan tan

cot cot

cos cos

a a



  



Chuyển giữa

sin

và

cos

sin cos

cos sin

a a



 







 











 

 







 











 



Chuyển giữa

tan

và

cot

tan cot

cot tan

1 1

cot ; tan

tan cot

a a



 







 











 

 







 











 

 



Chú ý các dạng sau

Có

2 2

sin , cosu u



hạ bậc

 

sin sin sin sin

u v u v    

sin cos sin sin

u v u v



 







   











 

 

cos cos cos cos

u v u v    

cos sin cos cos

u v u v



 







   











 

tan cot tan tan

u v u v



 







   











 

tan . cot 1 tan tan tan

cot

u v u u v

    

Các ví dụ

Câu 23. Giải phương trình

sin 2

6 2



 







 











 

___________________________

LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 15

Câu 24. Giải phương trình

cos 2

4 4



 







 











 

___________________________

Câu 25. Giải phương trình

sin 2 sin

3 6

x x

 

   

 

 

 

   

 

 

 

 

 

   

___________________________

Câu 26. Giải phương trình

cos 3 cos 0

x x



 







  











 

___________________________

Câu 27. Giải phương trình

2 9

sin 3 cos

3 4

x x

 

   

 

 

 

  

 

 

 

 

 

   

___________________________

Câu 28. Giải phương trình

sin 2 cos 0

x x



 







  











 

___________________________

LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 16

Câu 29. Giải phương trình

2 2

sin 5 cos 3 0

3 4

x x

 

   

 

 

 

   

 

 

 

 

 

   

___________________________

Câu 30. Giải phương trình

sin 3 sin 3 3

5 5

x x

 

   

 

 

 

   

 

 

 

 

 

   

___________________________

Câu 31. Giải phương trình

tan 3 tan 2 0

x x



 







  











 

___________________________

Câu 32. Giải phương trình

tan 4 cot 2

3 6

x x

 

   

 

 

 

  

 

 

 

 

 

   

___________________________

LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 17

Dạng 5: Phương trình tích

Phương pháp:



Biến đổi phương trình về dạng

. 0

A B







 











Chú ý các công thức sau

1. Công thức nhân đôi

________________________________________________________

2. Công thức hạ bậc

________________________________________________________

3. Công thức tổng thành tích:

________________________________________________________

4. Công thức tích thành tổng

________________________________________________________

Các ví dụ

Câu 33. Giải phương trình

1 cos cos 2 0x x  

___________________________

Câu 34. Giải phương trình

sin 4 cos 4 1 0x x  

___________________________

LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 18

Câu 35. Giải phương trình

sin 3 sin 4 sin 5 0x x x  

___________________________

Câu 36. Giải phương trình

cos 3 sin 2 cos 0x x x  

___________________________

Câu 37. Giải phương trình

cos 6 cos 3 cos 7 cos 4x x x x

___________________________

Câu 38. Giải phương trình

sin 3 sin sin 8 sin 4 0x x x x 

___________________________

BÀI TẬP RÈN LUYỆN

Bài 1: Giải các phương trình sau

2 sin 4 3 0



 







  











 

1 2 cos 3 0



 







  











 

sin 4 sin 2 0

x x



 







  











 

2 9

sin 3 cos

3 4

x x

 

   

 

 

 

  

 

 

 

 

 

   

LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 19

sin 3 sin 2 0

x x



 







  











 

sin 2 cos 0

x x



 







  











 

3 cot 20 1 0

 







  











 

tan 3 tan 2 0

x x



 







  











 

tan 4 cot 2

x x



 







 











 

tan . cot2 1x x 

Bài 2: Giải các phương trình sau

sin

2 6 2



 







 











 

3 3

cos

2 4 4



 







 











 

2 2

2 7

sin 3 sin

3 5

x x

 

   

 

 

 

  

 

 

 

 

 

   

2 2

sin 5 cos 0

x x



 







  











 

sin 3 sin 3 3

5 5

x x

 

   

 

 

 

   

 

 

 

 

 

   

cos cos 3

9 18

x x

 

   

 

 

 

   

 

 

 

 

 

   

cos 3 sin 3 2

3 6

x x

 

   

 

 

 

   

 

 

 

 

 

   

Bài 3: Tìm nghiệm của các phương trình sau trong khoảng đã cho

sin 2

 

với

 



 

tan 2 15 1

 

với

0 0

180 90x  

2 2

cos 2 sin

x x



 







 











 

với



Bài 4: Giải các phương trình sau

sin 2 cos 2 1 0x x  

1 cos 2 cos 4 0x x  

1 cos cos 2 cos 3 0x x x   

sin sin 2 sin 3 sin 4 0x x x x   

cos 5 cos 6 cos 7 0x x x  

sin 6 sin 2 cos 3 cosx x x x

2 2 2 2

sin sin 2 cos 3 cos 4x x x x  

2 2 2 2

sin 2 sin 3 sin 4 sin 5 2x x x x   

LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 20

BÀI 3: GIẢI PHƯƠNG TRÌNH LƯỢNG GIÁC

BẰNG PHƯƠNG PHÁP ĐẶT ẨN PHỤ

Dạng 1: Phương trình bậc hai đối với một hàm số lượng giác

Phương pháp:

Dang Đặt ẩn phụ Điều kiện

sin sin 0a x b x c  

cos cos 0a x b x c  

tan tan 0a x b x c  

cot cot 0a x b x c  

4 2

sin sin 0a x b x c  

sin sin 0

a x b x c

  

4 2

cos cos 0a x b x c  

cos cos 0

a x b c

  

MỘT SỐ ĐẲNG THỨC ĐÁNG NHỚ

●

sin cos sin 2

a a a



●

2 2 2 2

cos 2 cos sin 2 cos 1 1 2 sina a a a a     

●

  

4 4 2 2 2 2

cos sin cos sin cos sin cos 2a a a a a a a

    

●

4 4 2

1 3 1cos 4

sin cos 1 sin 2

2 4

a a a



   

●

6 6 2

3 5 3 cos 4

sin cos 1 sin 2

4 8

a a a



   

Các ví dụ

Câu 1. Giải phương trình

sin 2 3 sin 2 2 0x x  

___________________________

LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 21

Câu 2. Giải phương trình

sin 3 cos 3 1 0x x  

___________________________

Câu 3. Giải phương trình

cos 4 3 sin2 2 0x x  

___________________________

Câu 4. Giải phương trình





tan 3 1 tan 3 0

x x

   

___________________________

Câu 5. Giải phương trình

cot 2 3

sin 2

 

___________________________

Câu 6. Giải phương trình

4 2

4 sin 12 cos 7x x 

___________________________

LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 22

Câu 7. Giải phương trình

cos2 3 cos 4 0x x  

___________________________

Câu 8. Giải phương trình

cos 4 12 sin cos 5 0x x x  

___________________________

Câu 9. Giải phương trình

2 cos 3 cos 4 sin 2 1 0x x x  

___________________________

Câu 10. Giải phương trình

cos 5 .cos cos 4 .cos2 3 cos 1x x x x x  

___________________________

Câu 11. Giải phương trình

4 4

cos sin cos 4 0x x x  

___________________________

LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 23

Câu 12. Giải phương trình

4 4

sin cos sin cos 0x x x x  

___________________________

Câu 13. Giải phương trình

6 6

15 1

cos sin cos 2

8 2

x x x

  

___________________________

Dạng 2: Phương trình đưa về bậc hai

Phương pháp:

Dang Đăt ân phu Chú ý

1 1

sin sin 0

sin

a x b x c

   

 

 

 

    

 

 

 

 

 

   

1 1

cos cos 0

cos

a x b x c

   

 

 

 

    

 

 

 

 

 

   

 

2 2

tan cot tan cot 0

a x x b x x c

    

Các ví dụ

Câu 14. Giải phương trình

1 1

4 sin 4 sin 7 0

sin

x x

   

 

 

 

    

 

 

 

 

 

   

___________________________

LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 24

Câu 15. Giải phương trình

4 2

2 cos 9 cos 1 0

cos

x x

   

 

 

 

    

 

 

 

 

 

   

___________________________

Câu 16. Giải phương trình

 

3 tan cot 4 tan cot 2 0

x x x x



    

___________________________

Dạng 3: Phương trình đối xứng – phản đối xứng

Phương pháp:

●

sin cos 2 sin

a a a



 







  











 

●

sin cos 2 sin

a a a



 







  











 

●

cos sin 2 cos

a a a



 







  











 

●

cos sin 2 cos

a a a



 







  











 

Dang Đặt ẩn phụ Điều kiện

 

sin cos sin .cos 0

a x x b x x c

   

sin cos sin .cos 0

a x x b x x c

   

 

sin cos sin . cos 0

a x x b x x c

   

sin cos sin .cos 0

a x x b x x c

   

LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 25

Các ví dụ

Câu 17. Giải phương trình

 

2 sin 2 3 3 sin cos 5 0x x x   

___________________________

Câu 18. Giải phương trình

2 sin cos 3 sin 2 2 0.

x x x

   

___________________________

Câu 19. Giải phương trình

cos sin 2 sin 2 1

x x x

  

___________________________

BÀI TẬP RÈN LUYỆN

Bài 1: Giải các phương trình sau





4 cos 2 2 1 3 cos 2 3 0

x x

   

cos 2 3 cos 4 cos

x x 

cos 2 3 cos 4 cos

x x 

cos 4 12sin 1 0x x  

5 7

sin 2 3 cos 1 2 sin

2 2

x x x

 

   

 

 

 

    

 

 

 

 

 

   

4 6

sin cos2 4 sin 0x x x  

LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 26

 

5 sin 2 3 1 sin tanx x x  

3 3

cos 8 sin cos cos sin 1 0x x x x x   

 

4 4

5 1 cos 2 sin cosx x x   

10.

6 2

3 cos 4 8 cos 2 cos 3 0x x x   

Bài 2:

1. Tìm

5;2

 

 

 

 

nghiệm đúng phương trình

2 sin 5 sin 2 0x x  

2. Tìm tất cả các nghiệm của phương trình

2 cos 2 4 cos 1 0x x  

thỏa



Bài 3: Giải các phương trình sau

1 1

4 sin 4 sin 7 0

sin

x x

   

 

 

 

    

 

 

 

 

 

   

1 1

cos 2 cos 1

cos

x x

 







   











 

 

2 2

1 1 5

tan cot 1 0

sin cos

x x

    

1 1 10

cos sin

cos sin 3

x x

   

1 1 2

cos sin

sin cos 3

x x

    

Bài 4: Giải các phương trình sau

sin cos 7 sin 2 1x x x  

sin 2 2 2(sin cos ) 5x x x  

cos sin 2 sin 2 1

x x x

  

sin cos sin cos 1

x x x x

  

3 3

sin cos 1 sin 2

x x x

  

3 3

cos sin cos 2x x x 

3 3

cos sin 2 sin2 sin cosx x x x x   

Bài 5: Giải các phương trình sau

4 4

sin cos sin 2

x x x

  

4 4 2

sin cos 2 sin 2 sin 2 0

x x x

   

6 6

sin cos sin2x x x 

6 6 2

cos sin 4 cos 2x x x 

8 8

sin cos

x x

 

8 8 2

sin cos cos 2

x x x

 

 

8 8 10 10

sin cos 2 sin cos cos 2

x x x x x

   

 

1 sin cos 2 sin

cos

1 tan

x x x



 







  











 





6 6

2 2

sin cos 1

tan 2

cos sin

x x







10.

 

6 6

2 cos sin sin cos

2 2 sin

x x x x

 





LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 27

BÀI 4: PHƯƠNG TRÌNH CỔ ĐIỂN

Cơ sở

1. Công thức cộng:

_________________________________________________________

2. Nếu

2 2

1X Y 

thì luôn tồn tại góc



sao cho

sin

cos





















3. Các công thức nhân đôi, hạ bậc, nhân ba, tổng thành tích và tích thành tổng.

Dạng 1:

sin cosa u b u c 

Điều kiện có nghiệm:

2 2 2

a b c 

Phương pháp:

_______________________________________________________

 Chú ý: Dạng

sin cosa u b u c 

giải tương tự

Các ví dụ

Câu 1. Giải phương trình

3 sin cos 1x x 

___________________________

Câu 2. Giải phương trình

3 cos2 sin2 2x x  

___________________________

LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 28

Câu 3. Giải phương trình

cos 3 3 sin 3 1

4 4

x x

 

   

 

 

 

   

 

 

 

 

 

   

___________________________

Câu 4. Giải phương trình

3 sin 4 cos 5x x 

___________________________

Câu 5. Giải phương trình

3sin 3 cos 3 1 4 sinx x x  

___________________________

Câu 6. Tìm tất cả các nghiệm của phương trình

 

sin cos 3 cos 2 2

x x x

  

thỏa



___________________________

LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 29

Dạng 2:

sin cos sina u b u c v 

Điều kiện:

2 2 2

a b c 

Phương pháp:

_______________________________________________________

 Chú ý: Dạng

sin cos cos .sin

a u b u c v c v



 







   











 

giải tương tự

Các ví dụ

Câu 7. Giải phương trình

sin 3 3 cos 3 2 sin2x x x 

___________________________

Câu 8. Giải phương trình

sin 3 3 cos 3 2 cos 5x x x 

___________________________

LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 30

Câu 9. Giải phương trình

3 sin 7 cos 7 2 sin 5

x x x



 







  











 

___________________________

Câu 10. Giải phương trình

3 cos5 2 sin 3 .cos2 sin 0x x x x  

___________________________

Dạng 3:

sin cos sin cosa u b u c v d v  

Điều kiện:

2 2 2 2

a b c d  

Phương pháp:

_______________________________________________________

LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 31

Các ví dụ

Câu 11. Giải phương trình

sin cos 2 sin 2 cosx x x x  

___________________________

Câu 12. Giải phương trình

sin 7 cos 2 3(sin 2 cos 7 )x x x x  

___________________________

Câu 13. Giải phương trình

3(sin 2 cos 3 ) cos 2 sin 3x x x x  

___________________________

BÀI TẬP RÈN LUYỆN

Bài 1: Giải các phương trình sau

cos 7 3 sin7 2x x  

sin cos 3 cos 2

2 2

x x

 







  











 

5 sin2 12cos2 13x x 

3 sin 4 cos 3x x 

2sin 3 sin2 3x x 

 

2 cos2 6 cos sinx x x

 

3 sin 3 3 cos 9 1 4 sin 3x x x  

4 sin 1 3 sin 3 cos3x x x  

 

4 4

4 sin cos 3 sin 4 2

x x x

  

10.

2 cos 2 4 sin cos 1 0

x x x



 







   











 

LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 32

11.

cos 7 cos5 3 sin2 1 sin7 sin5x x x x x  

Bài 2: Giải các phương trình sau

sin 3 3 cos 3 2sin2x x x 

3 sin 7 cos 7 2 sin 5

x x x



 







  











 

cos 3 sin 2 cos 2 0

x x x



 







   











 

3 cos 2 sin 2 2 sin 2 2 2

x x x



 







   











 

3 cos 5 2 sin 3 cos 2 sin 0x x x x  

 

sin 8 cos 6 3 sin 6 cos 8x x x x

  

 

cos 3 sin 3 cos sin 3x x x x

  

4 sin 2 3 cos 2 5 cos 3 0

x x x



 







   











 

Bài 3: Giải các phương trình sau

3 3 cos 2

cos

2 sin





tan 3

cos

 

3 1

8 sin

cos sin

x x

 

 

  

1 2 sin cos

1 2 sin 1 sin

x x





 

cos sin 2

2 cos sin 1

x x





 

cos 3 sin

cos 3 sin 1

x x

 

 

cos2 3 sin2 3 sin cos 4 0x x x x    

 

sin cos sin 2 3 cos 3 2 cos 4 sin

x x x x x x

   

3 3

4 sin cos 3 4 cos sin 3 3 3 cos 4 3x x x x x  

10.

 

6 6

8 sin cos 3 3 cos 2 11 3 3 sin 4 9 sin 2x x x x x

    

Bài 4:

1. Có bao nhiêu giá trị nguyên của tham số

thuộc đoạn

10;10

 



 

 

để phương trình

sin 3 cos 2

3 3

x x m

 

   

 

 

 

   

 

 

 

 

 

   

vô nghiệm.

2. Cho hàm số

sin 2 cos 1

cos sin 2

x x

 



 

 

a. Chứng minh tập xác định của hàm số

 

là



b. Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số

 

trên



3. Cho hàm số

2 sin 2 cos 2

sin 2 cos 2 3

x x





 

. Goi

và

lần lượt là GTLN và GTNN của hàm số đã cho.

Tính

S M m 

LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 33

BÀI 5: PHƯƠNG TRÌNH ĐẲNG CẤP

Cơ sở

Công thức cơ bản:

sin

tan

cos



1 tan

cos

 

Dạng 1: Phương trình đẳng cấp bậc hai

2 2

sin sin cos cosa u b u u c u d  

 



Phương pháp: Xét 2 trường hợp:

Trường hợp 1:

_______________________________________________________

Trường hợp 2:

_______________________________________________________

Các ví dụ

Câu 1. Giải phương trình

2 2

sin 5 sin cos 6 cos 0x x x x  

___________________________

Câu 2. Giải phương trình

2 2

3 sin 2 sin 2 cos 2 4 cos 2 2x x x x  

___________________________

LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 34

Câu 3. Giải phương trình

2 2

2 sin 3 3 sin 6 4 cos 3 2x x x  

___________________________

Câu 4. Giải phương trình

2 2

6 sin 2 sin 4 8 cos 2 4x x x  

___________________________

Câu 5. Giải phương trình

2 2

3 sin 5 cos 2 cos 2 4 sin 2x x x x  

___________________________

Câu 6. Giải phương trình :

1 3 sin 2 2 tanx x 

___________________________

Câu 7. Giải phương trình :

1 3 tan 2 sin 2x x 

___________________________

LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 35

Dạng 2: Phương trình đẳng cấp bậc ba

3 2 2 3

sin sin cos sin cos cos sin cosa u b u u c u u d u e u f u    

 



Phương pháp: Xét 2 trường hợp:

Trường hợp 1:

_______________________________________________________

Trường hợp 2:

_______________________________________________________

Các ví dụ

Câu 8. Giải phương trình

2 cos sin 3x x

___________________________

Câu 9. Giải phương trình

3 3 2

4 sin 3 cos 3 sin sin cos 0x x x x x   

___________________________

LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 36

Câu 10. Giải phương trình

 

sin 3 tan cos 4 sin cosx x x x x  

___________________________

Câu 11. Giải phương trình

   

sin tan 1 3 sin cos sin 3

x x x x x

   

___________________________

Câu 12. Giải phương trình

 

3 3

4 sin cos cos 3 sinx x x x

  

___________________________

Câu 13. Giải phương trình

2 2 cos 3 cos sin 0

x x x



 







   











 

___________________________

LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 37

BÀI TẬP RÈN LUYỆN

Bài 1: Giải các phương trình sau

2 2

2 cos 6 sin cos 6 sin 1x x x x  

2 2

cos 3 sin 2 1 sinx x x  

2 2

cos sin cos 2 sin 1 0x x x x   

2 2

9 sin 30 sin cos 25 cos 25x x x x  

 

2 2 sin cos cos 3 2 cosx x x x

  

sin 2 2 sin 2 cos 2x x x 

Bài 2: Giải các phương trình sau

3 2 2

3 sin 2 sin cos sin cosx x x x x 

6 sin 2 cos 5 sin 2 cosx x x x 

sin 4 sin cos 0x x x  

3 3

sin cos sin cosx x x x  

3 2 2 3

sin 4 sin cos 5 sin cos 2 cos 0x x x x x x   

Bài 3: Giải các phương trình sau

5 sin 4 cos

6 sin 2 cos

2 cos 2

x x

 

 

tan cot 2 sin 2 cos 2x x x x  

   

sin tan 1 3 sin cos sin 3

x x x x x

   

8 cos cos 3

x x



 







 











 

 

2 2

tan . sin 2 sin 3 cos 2 sin . cosx x x x x x  

 

3 3 5 5

cos sin 2 cos sin

x x x x

  

LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 38

BÀI 6: PHƯƠNG TRÌNH ĐƯA VỀ DẠNG TÍCH

1. Phương trình tổng quát

sin 2 cos 2 sin cos 0a x b x c x d x e    

Cơ sở

1. Công thức nhân đôi:

_________________________________________________________

2. Phân tích bậc hai thành nhân tử:

_________________________________________________________

3. Phương trình tích:

_________________________________________________________

Phương pháp

_________________________________________________________

Các ví dụ

Câu 1. Giải phương trình

sin 2 cos 2 sin 5 cos 3 0x x x x    

___________________________

Câu 2. Giải phương trình

cos 2 3 sin 2 9 sin 6 cos 8x x x x   

___________________________

LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 39

Câu 3. Giải phương trình

cos 4 3 sin 4 9 cos 2 3 sin 2 5 0x x x x    

___________________________

Câu 4. Giải phương trình

 

6 6

8 sin cos 3 3 cos 2 11 3 3 sin 4 9 sin 2x x x x x

    

___________________________

Câu 5. Giải phương trình

2 sin 4 2 sin cos 3 cos 2 2

x x x x



 







   











 

___________________________

2. Phương trình đưa về dạng tích

Cơ sở

1. Công thức hạ bậc:

__________________________________________________________

LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 40

2. Công thức biến đổi

Tổng thành tích

________________________

Tích thành tổng

________________________

3. Phương trình tích:

_________________________________________________________

Phương pháp

Bước 1: Sử dụng các công thức hạ bậc, biến đổi tổng thành tích, tích thành tổng để xuất hiện nhân tử

chung

Bước 2: Nhóm hạng tử và đưa về phương trình tích hoặc các dạng phương trình đã biết.

Các ví dụ

Câu 6. Giải phương trình

sin 7 sin sin 5 sin 3x x x x

___________________________

Câu 7. Giải phương trình

sin 5 cos 3 sin 9 cos 7x x x x

___________________________

Câu 8. Giải phương trình

cos cos 3 sin 2 sin 6 sin 4 sin 6x x x x x x 

___________________________

LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 41

Câu 9. Giải phương trình

sin sin 2 sin 3 0x x x  

___________________________

Câu 10. Tìm tổng các nghiệm trong khoảng



 

















 

của phương trình

2 sin 3 sin 7 1 sin 5x x x  

___________________________

Câu 11. Giải phương trình

1 cos cos 2 cos 3 0x x x   

___________________________

Câu 12. Giải phương trình

1 sin sin 2 cos cos 2 cos 3x x x x x    

___________________________

LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 42

Câu 13. Giải phương trình

2 2 2

sin sin 2 sin 3

x x x

  

___________________________

Câu 14. Giải phương trình

2 2 2 2

sin sin 3 cos 2 cos 4x x x x  

___________________________

Câu 15. Giải phương trình

8 cos 1 cos 4x x 

___________________________

BÀI TẬP RÈN LUYỆN

Bài 1: Giải các phương trình sau

sin 2 cos 2 sin 3 cos 2x x x x   

sin 2 2 cos 2 sin 4 cos 1x x x x   

9 sin 6 cos 3 sin 2 cos 2 8x x x x   

2 2 sin 2 cos 2 7 sin 2 2 cos 4 0x x x x    

  

2 cos 1 2 sin cos sin 2 sinx x x x x   

  

2 sin 1 3 cos 4 2 sin 4 4 cos 3

x x x x

    

1 sin cos sin 2 cos 2 0x x x x    

sin 2 2 cos sin 1

tan 3

x x x

  





LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 43





3 sin 2 cos 2 5 sin 2 3 cos 3 3

2 cos 3

x x x x

     





Bài 2: Giải các phương trình sau

sin 4 sin 5 sin 3 sin 4 sin 2 sinx x x x x x 

sin cot 5 cos 9x x x

4 sin 3 cos 2 1 6 sin 8 sinx x x x  

2 cos cos 2 cos 3 7 7 cos 2x x x x 

cos 22 3 cos18 3 cos14 cos10 0x x x x   

cos cos 2 cos 3 cos 4 0x x x x   

2 sin 2 sin 7 1 sinx x x  

sin sin 2 sin 3 1 cos cos 2x x x x x    

sin sin 2 sin 3 cos cos 2 cos 3x x x x x x    

10.

sin sin 2 sin 3

cos cos 2 cos 3

x x x

 



 

Bài 3: Giải các phương trình sau

2 2 2

cos cos 2 cos 3 1x x x  

2 2 2 2

cos cos 2 cos 3 cos 4 2x x x x   

2 2 2

sin sin 2 sin 3

x x x

  

. 4.

2 2 2 2

sin 3 sin 4 sin 5 sin 6x x x x  

2 2 2 2

sin sin 3 cos 2 cos 4x x x x  

2 2 2 2

sin 3 cos 4 sin 5 cos 6x x x x  

2 2 2

sin sin 2 sin 3 2x x x  

2 2 2

sin cos 2 cos 3x x x 

sin

2 2

5 9

cos 3 sin 7 2 2 cos

4 2 2

x x



 







   











 

10.

3 3 3

sin cos 3 cos sin 3 sin 4x x x x x 

11.

 

3 3 5 5

sin cos 2 sin cos

x x x x

  

12.

 

6 6 8 8

sin cos 2 sin cos

x x x x

  

13.

 

8 8 10 10

sin cos 2 sin cos cos 2

x x x x x

   

14.

1 1

2 2 sin

4 sin cos

x x



 







  











 

LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 44

BÀI 7: MỘT SỐ PHƯƠNG PHÁP KHÁC

1. Phương pháp đặt ẩn số mới

Cơ sở

1. Công thức cộng: _______________________________________________

_________________________________________________________

2. Công thức nhân đôi, nhân ba: ________________________________________

_________________________________________________________

Phương pháp

Đặt ẩn mới

để đưa về phương trình lượng giác chứa các cung

,2 , 3 ...t t t

Các ví dụ

Câu 1. Giải phương trình

sin 2 5 sin cos 3

3 6

x x x

 

   

 

 

 

   

 

 

 

 

 

   

___________________________

Câu 2. Giải phương trình

32 cos sin 6 1

x x



 







  











 

___________________________

LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 45

Câu 3. Giải phương trình

8 cos cos 3

x x



 







 











 

___________________________

Câu 4. Giải phương trình

3 1 3

sin sin

10 2 2 10 2

x x 

   

 

 

 

  

 

 

 

 

 

   

___________________________

Câu 5. Giải phương trình

sin 3 sin

2 4 4 2

x x 

   

 

 

 

  

 

 

 

 

 

   

___________________________

LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 46

2. Phương pháp đánh giá

Cơ sở

2 2

A B









  











A B









  











A B



















 

 

 



 











Phương pháp

Biến đổi phương trình về các dạng

1,2, 3

nêu trên.

Các ví dụ

Câu 6. Giải phương trình

sin cos 8 2

x x



 







  











 

___________________________

Câu 7. Giải phương trình

2 2 2 2

cos 4 cos 8 2 sin 12 sin 16x x x x   

___________________________

Câu 8. Giải phương trình

2 2

4 cos 3 tan 4 3 cos 2 3 tan 4 0x x x x    

___________________________

LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 47

Câu 9. Giải phương trình

 

cos 4 cos 2 5 sin 3x x x

  

___________________________

BÀI 8: HÀM SỐ LƯỢNG GIÁC

A. TÓM TẮT LÝ THUYẾT

I. Hàm số lượng giác

1. Hàm số sin: là quy tắc đặt tương ứng mỗi số thực

x  

với số thực

sin 1;1

 

 

 

 

: 1;1

sin

x x

 

 

 

 





Kí hiệu:

siny x



Tập xác định:

D  



Tập giá trị:

1;1

 

 

 

 



 

sin sin ,x x x

     

nên

siny x

là hàm số lẻ.

2. Hàm số cos: là quy tắc đặt tương ứng mỗi số thực

x  

với số thực

cos 1;1

 

 

 

 

: 1;1

cos

x x

 

 

 

 





Kí hiệu:

cosy x



Tập xác định:

D  



Tập giá trị:

1;1

 

 

 

 



 

cos cos ,x x x

    

nên

cosy x

là hàm số chẵn.

3. Hàm số tan: được xác định bởi công thức

sin

tan

cos

y x

 



Tập xác định:

D k



 

 

 

 

 

 





Tập giá trị:

T  



 

tan tan ,x x x

     

nên

tany x

là hàm số lẻ.

4. Hàm số cot: được xác định bởi công thức

cos

cot

sin

y x

 



Tập xác định:

 

D k





Tập giá trị:

T  



 

cot cot ,x x x

     

nên

tany x

là hàm số lẻ.

LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 48

II. Sự biến thiên và đồ thị của hàm số lượng giác

1. Hàm tuần hoàn

Cho hàm số

 

y f x

xác định trên

Nếu tồn tại số dương

sao cho

,x D 

ta có:

   

x T D x T D

f x T f x





   







 





thì ta nói

tuần hoàn

Số nhỏ nhất trong các số

nói trên gọi là

chu kỳ tuần hoàn

của hàm

2. Hàm số sin:

Xét hàm số

siny x

trên đoạn

0;2

 

 

 

Bảng biến thiên:

Hàm số

siny x

tuần hoàn với chu kỳ

2

Đồ thị:

3. Hàm số cos:

Xét hàm số

cosy x

trên đoạn

0;2

 

 

 

Bảng biến thiên:

Hàm số

cosy x

tuần hoàn với chu kỳ

2

Đồ thị:

3. Hàm số tan:

Xét hàm số

tany x

trên đoạn

;

2 2

 

 

 



 

 

Bảng biến thiên:

Hàm số tăng trên đoạn

;

2 2

 

 

 



 

 

và tuần hoàn với chu kỳ



Đồ thị:

LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 49













4. Hàm số cot:

Xét hàm số

coty x

trên đoạn

;

2 2

 

 

 



 

 

Bảng biến thiên:

Hàm số giảm trên đoạn

;

2 2

 

 

 



 

 

và tuần hoàn với chu kỳ



Đồ thị:













2

2

Lưu ý: Các hàm số

   

sin ; cos

y ax b y ax b   

tuần hoàn với chu kỳ



Các hàm số

   

tan ; cot

y ax b y ax b   

tuần hoàn với chu kỳ



Dạng 1. Tìm tập xác định của hàm số lượng giác

Phương pháp



có nghĩa

0A 



có nghĩa

0B 



có nghĩa

0B 

LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 50

Các ví dụ

Câu 10. Tìm tập xác định của hàm số

1 cos

sin 2





___________________________

Câu 11. Tìm tập xác định của hàm số

tan 3

y x



 







 











 

___________________________

Câu 12. Tìm tập xác định của hàm số

cot 2

y x



 







 











 

___________________________

Câu 13. Tìm tập xác định của hàm số

1 cos







___________________________

Câu 14. Tìm tập xác định của hàm số

1 1

sin cos

x x

 

___________________________

LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 51

Câu 15. Tìm tập xác định của hàm số

tan 2 cot2y x x 

___________________________

Câu 16. Tìm tập xác định của hàm số

sin 3 cos

cos 3 sin

x x







___________________________

Dạng 2: Xét tính chẵn lẻ của hàm số lượng giác

Cơ sở

1. Tập

đối xứng

x D x D     

   

x D x D

f x f x





    









 





 

y f x

là hàm số chẵn

   

x D x D

f x f x





    









  





 

y f x

là hàm số lẻ

Các ví dụ

Câu 17. Xét tính chẵn lẻ của hàm số

sin 2y x

___________________________

Câu 18. Xét tính chẵn lẻ của hàm số

cos



___________________________

LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 52

Câu 19. Xét tính chẵn lẻ của hàm số

tany x

___________________________

Câu 20. Xét tính chẵn lẻ của hàm số

tan 2 sin 3y x x 

___________________________

Câu 21. Xét tính chẵn lẻ của hàm số

2 sin 3y x 

___________________________

Dạng 3: Tìm chu kỳ tuần hoàn của hàm số lượng giác

Cơ sở

1. Các hàm số

   

sin ; cos

y ax b y ax b   

tuần hoàn với chu kỳ



2. Các hàm số

   

tan ; cot

y ax b y ax b   

tuần hoàn với chu kỳ



3. Hàm số

 

y f x

có chu kỳ

, hàm số

 

g x

có chu kỳ

thì hàm số

   

y f x g x 

có chu kỳ

với

là số dương nhỏ nhất chia hết cho

và

Các ví dụ

Câu 22. Tìm chu kỳ tuần hoàn của hàm số

sin 2y x

___________________________

LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 53

Câu 23. Tìm chu kỳ tuần hoàn của hàm số

cos 3

y x



 







 











 

___________________________

Câu 24. Tìm chu kỳ tuần hoàn của hàm số

cos 2 tan 2y x x 

___________________________

Câu 25. Tìm chu kỳ tuần hoàn của hàm số

cos 3 cot2y x x 

___________________________

Dạng 4: Tìm GTLN – GTNN của hàm số

Cơ sở

1 sin 1a  

1 cos 1a  

0 sin 1a 

0 cos 1a 

Các ví dụ

Câu 26. Tìm GTLN – GTNN của hàm số

2 sin 3y x 

___________________________

Câu 27. Tìm GTLN – GTNN của hàm số

1 3 cos 2y x 

___________________________

LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 54

Câu 28. Tìm GTLN – GTNN của hàm số

sin cosy x x 

___________________________

Câu 29. Tìm GTLN – GTNN của hàm số

sin 2 3 cos 2 1y x x  

___________________________

Câu 30. Tìm GTLN – GTNN của hàm số

cos 2 4 cos 3y x x  

___________________________

Câu 31. Tìm GTLN – GTNN của hàm số

cos 4 4 sin 2 1y x x  

___________________________

LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 55

LƯỢNG GIÁC TRONG ĐỀ THI 2002 – 2014

Bài 1 (ĐH A2002) Tìm nghiệm thuộc khoảng

 

0;2

của phương trình:

cos 3 sin 3

5 sin cos 2 3

1 2 sin 2

x x

 









  













 

ĐS:

;

3 3

x x

 

 

Bài 2 (ĐH B2002) Giải phương trình:

2 2 2 2

sin 3 cos 4 sin 5 cos 6x x x x  

ĐS:

 

;

9 2

k k

x x k

 

  



Bài 3 (ĐH D2002) Tìm

thuộc đoạn

0;14

 

 

 

nghiệm đúng của phương trình:

cos 3 4 cos 2 3 cos 4 0x x x   

ĐS:

3 5 7

; ; ;

2 2 2 2

x x x x

   

   

Bài 4 (ĐH A2003) Giải phương trình:

cos 2 1

cot 1 sin sin 2

1 tan 2

x x x

   



ĐS:

 

x k k



  



Bài 5 (ĐH B2003) Giải phương trình:

cot tan 4 sin 2

sin 2

x x x

  

ĐS:

 

x k k



   



Bài 6 (ĐH D2003) Giải phương trình:

2 2 2

sin tan cot 0

2 4 2

x x



 







  











 

ĐS:

2 ;

x k x k



  

    

Bài 7 (ĐH A2004) Cho tam giác

ABC

không tù, thỏa mãn điều kiện

cos2 2 2 cos 2 2 cos 3A B C  

Tính ba góc của tam giác

ABC

. ĐS:

90 ; 45A B C    

Bài 8 (ĐH B2004) Giải phương trình:

 

5 sin 2 3 1 sin tanx x x  

ĐS:

; 2

6 6

x k x k

 

    

Bài 9 (ĐH D2004) Giải phương trình:

  

2 cos 1 2 sin cos sin 2 sinx x x x x   

ĐS:

2 ;

3 4

x k x k

 

     

Bài 10 (ĐH A2005) Giải phương trình:

2 2

cos 3 cos 2 cos 0x x x 

ĐS:

 

x k



 



Bài 11 (ĐH B2005) Giải phương trình:

1 sin cos sin 2 cos 2 0x x x x    

ĐS:

2 ;

3 4

x k x k

 

     

Bài 12 (ĐH D2005) Giải phương trình:

4 4

cos sin cos sin 3 0

4 4 2

x x x x

 

   

 

 

 

     

 

 

 

 

 

   

ĐS:

 

x k k



  



Bài 13 (ĐH A2006) Giải phương trình:

 

6 6

2 cos sin sin cos

2 2 sin

x x x x

 





ĐS:

 

x k k



  



Bài 14 (ĐH B2006) Giải phương trình:

cot sin 1 tan tan 4

x x x

 







  











 

ĐS:

;

12 12

x k x k

 

   

Bài 15 (ĐH D2006) Giải phương trình:

LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 56

cos 3 cos 2 cos 1 0x x x   

ĐS:

; 2

x k x k



 

   

Bài 16 (ĐH A2007) Giải phương trình:

   

2 2

1 sin cos 1 cos sin 1 sin 2x x x x x

    

ĐS:

2 ; 2 ;

2 4

x k x k x k

 

  

     

Bài 17 (ĐH B2007) Giải phương trình

2 sin 2 sin 7 1 sinx x x  

ĐS:

2 5 2

; ;

8 4 18 3 18 3

k k k

x x x

     

     

Bài 18 (ĐH D2007) Giải phương trình:

sin cos 3 cos 2

2 2

x x

 







  











 

ĐS:

2 ; 2

2 6

x k x k

 

    

Bài 19 (ĐH A2008) Giải phương trình:

1 1 7

4 sin

sin 4

sin



 







  







 





 



















 

ĐS:

; ;

4 8 8

x k x k x k

  

       

Bài 20 (ĐH D2008) Giải phương trình:

3 3 2 2

sin 3 cos sin cos 3 sin cosx x x x x x  

ĐS:

;

4 2 3

x x k

  



    

Bài 21 (ĐH D2008) Giải phương trình:

 

2 sin 1 cos 2 sin 2 1 2 cosx x x x   

ĐS:

;

3 4

x k x k

 

     

Bài 22 (ĐH A2009) Giải phương trình:

 

  

1 2 sin cos

1 2 sin 1 sin

x x





 

ĐS:

 

18 3

x k

 

   



Bài 23 (ĐH B2009) Giải phương trình:

 

sin cos sin 2 3 cos 3 2 cos 4 sin

x x x x x x

   

ĐS:

2 ;

6 42 7

x k x

  

    

Bài 24 (ĐH D2009) Giải phương trình:

3 cos 5 2 sin 3 cos 2 sin 0x x x x  

ĐS:

;

18 3 6 2

k k

x x

   

    

Bài 25 (ĐH A2010) Giải phương trình:

 

1 sin cos 2 sin

cos

1 tan

x x x



 







  











 





ĐS:

2 ; 2

6 6

x k x k

 

    

Bài 26 (ĐH B2010) Giải phương trình:

 

sin 2 cos 2 cos cos 2 sin 0

x x x x x

   

ĐS:

 

4 2

x k

 

  



Bài 27 (ĐH D2010) Giải phương trình

sin 2 cos2 3 sin cos 1 0x x x x    

ĐS:

2 ; 2

6 6

x k x k

 

   

Bài 28 (ĐH A2011) Giải phương trình:

1 sin 2 cos 2

2 sin sin 2

1 cot

x x

 





ĐS:

; 2

2 4

x k x k

 

   

Bài 29 (ĐH B2011) Giải phương trình:

LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 57

sin 2 cos sin cos cos2 sin cosx x x x x x x   

ĐS:

2 ;

2 3 3

x k x

  

   

Bài 30 (ĐH D2011) Giải phương trình:

sin 2 2 cos sin 1

3 tan

x x x

  





ĐS:

 

x k k



  



Bài 31 (ĐH A2012) Giải phương trình:

3 sin 2 cos 2 2 cos 1x x x  

ĐS:

; 2 ; 2

2 3

x k x k x k

 

  

    

Bài 32 (ĐH B2012) Giải phương trình:





2 cos 3 sin cos cos 3 sin 1

x x x x x

   

ĐS:

 

2 2

2 ;

3 3

x k x k

 

   



Bài 33 (ĐH D2012) Giải phương trình:

sin 3 cos 3 sin cos 2 cos2x x x x x   

ĐS:

; 2 ; 2

4 2 12 12

x x k x k

   

 

      

Bài 34 (ĐH A2013) Giải phương trình:

1 tan 2 2 sin

x x



 







  











 

ĐS:

; 2

4 3

x k x k

 

     

Bài 35 (ĐH B2013) Giải phương trình:

sin 5 2 cos 1x x 

ĐS:

2 2

;

6 3 14 7

k k

x x

   

     

Bài 36 (ĐH D2013) Giải phương trình:

sin 3 cos 2 sin 0x x x  

ĐS:

; 2 ; 2

4 2 6 6

x x k x k

   

 

      

Bài 37 (ĐH A2014) Giải phương trình

sin 4 cos 2 sin 2x x x  

ĐS:

 

x k k



   



Bài 38 (ĐH B2014) Giải phương trình:

 

2 sin 2 cos 2 sin 2x x x

  

ĐS:

 

x k k



   



QUAN HỆ SONG SONG ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 58

PHẦN 2: HÌNH HỌC KHÔNG GIAN

BÀI 1: ĐẠI CƯƠNG VỀ ĐƯỜNG THẲNG VÀ MẶT PHẲNG

A. TÓM TẮT LÝ THUYẾT

1. Khái niệm



Mặt phẳng: là đối tượng cơ bản của hình học không gian. Mặt phẳng được biểu diễn bằng một hình bình

hành hoặc một miền góc và ghi tên của mặt phẳng vào một góc của hình biểu diễn

Để kí hiệu mặt phẳng, ta dùng chữ cái in hoa hoặc chữ Hi Lạp đặt trong dấu ngoặc

 

. Ví dụ: mặt

phẳng

 

mặt phẳng

 





Điểm thuộc mặt phẳng: Cho điểm

và mặt phẳng

 

Khi điểm

thuộc mặt phẳng

 

ta nói

nằm trong

 

hay

 

chứa

. Kí hiệu:

 

A P

Khi điểm

không thuộc mặt phẳng

 

, ta nói

nằm ngoài

 

hay

 

không chứa

. Kí hiệu :

 

A P



Đường thẳng nằm trong mặt phẳng: Cho đường thẳng

và mặt phẳng

 

. Khi mọi điểm thuộc

đều

nằm trong

 

, ta nói

nằm trong

 

hay

 

chứa

. Kí hiệu:

 

d P

2. Hình biểu diễn của một hình không gian

Để nghiên cứu hình học không gian, người ta thường vẽ các hình không gian lên giấy, lên bảng. Hình vẽ đó

gọi là hình biểu diễn của một hình không gian.



Một vài hình biểu diễn của hình lập phương



Một vài hình biểu diễn của hình tứ diện

QUAN HỆ SONG SONG ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 59

3. Quy tắc biểu diễn hình không gian



Hình biểu diễn của đường thẳng là đường thẳng, của đoạn thẳng là đoạn thẳng.



Hình biểu diễn của hai đường thẳng song song là hai đường thẳng song song, của hai đường thẳng cắt

nhau là hai đường thẳng cắt nhau.



Hình biểu diễn phải giữ nguyên quan hệ thuộc giữa điểm và đường thẳng.



Dùng nét liền để biểu diễn cho đường nhìn thấy, nét đứt biểu diễn cho đường bị che khuất

4. Các tính chất thừa nhận

Tính chất 1: Có một và chỉ một đường thẳng đi qua hai điểm phân biệt.

Tính chất 2: Có một và chỉ một mặt phẳng đi qua ba điểm không thẳng hàng.

Tính chất 3: Nếu một đường thẳng có hai điểm phân biệt cùng thuộc một mặt phẳng thì đường thẳng đó

nằm hoàn toàn trên mặt phẳng.

   

M AB P M P   

Tính chất 4: Có bốn điểm không cùng thuộc một mặt phẳng.

Tính chất 5: Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng có một đường thẳng chung duy

nhất chứa tất cả các điểm chung của hai mặt phẳng đó.

Đường thẳng chung đó được gọi là

giao tuyến

của hai mặt phẳng

Kí hiệu:

   

P Q  

Tính chất 6: Trên mỗi mặt phẳng các, kết quả đã biết trong hình học phẳng đều đúng.

5. Cách xác định mặt phẳng

Một mặt phẳng hoàn toàn xác định khi biết:



Nó đi qua ba điểm không thẳng hàng.



Nó đi qua một điểm và một đường thẳng không đi qua điểm đó.



Nó chứa hai đường thẳng cắt nhau.

Các kí hiệu:



 

ABC

là kí hiệu mặt phẳng đi qua ba điểm không thẳng hàng

, ,A B C

( h1)



 

,M d

là kí hiệu mặt phẳng đi qua

và điểm

M d

(h2)



 

1 2

,d d

là kí hiệu mặt phẳng xác định bởi hai đường thẳng cắt nhau

1 2

,d d

(h3)

(h1)

(h2)

(h3)

QUAN HỆ SONG SONG ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 60

6. Hình chóp và hình tứ diện



Hình chóp: Trong mặt phẳng

 

cho đa giác lồi

1 2

...

A A A

. Lấy điểm

nằm ngoài

 

Lần lượt nối

với các đỉnh

1 2

, ,...,

A A A

ta được

tam giác

1 2 2 3 1

, ,...,

SAA SA A SA A

. Hình gồm đa giác

1 2

...

A A A

và

tam giác

1 2 2 3 1

, ,...,

SAA SA A SA A

được gọi là hình chóp , kí hiệu là

1 2

. ...

S A A A

Ta gọi

là đỉnh, đa giác

1 2

...

A A A

là đáy , các đoạn

1 2

, ,...,

SA SA SA

là các cạnh bên,

1 2 2 3 1

, ,...,

A A A A A A

là các cạnh đáy, các tam giác

1 2 2 3 1

, ,...,

SAA SA A SA A

là các mặt bên.



Hình tứ diện: Cho bốn điểm

, , ,A B C D

không đồng phẳng. Hình gồm bốn tam giác

, ,ABC ABD

ACD

và

BCD

được gọi là tứ diện

ABCD

Tứ diện có bốn mặt là các tam giác đều gọi là tứ diện đều

7. Thiết diện (hay mặt cắt):

Thiết diện của hình không gian H khi cắt bởi mặt phẳng

 

là phần chung của H và

 

Ví dụ:



Thiết diện (mặt cắt) là:



Thiết diện (mặt cắt) là:

QUAN HỆ SONG SONG ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 61

MỘT SỐ HÌNH THƯỜNG GẶP

Tứ diện

ABCD

Hình chóp

.S ABC

Hình chóp

.S ABCD

, đáy là tứ giác lồi, các cạnh

đối không song song

Hình chóp

.S ABCD

, đáy là hình bình hành

Hình chóp

.S ABCD

, đáy là hình thang

Hình chóp

.S ABCD

, đáy là hình thang vuông

tại

và

MÔT SÔ KI HIÊU

A d



M a b

 

 



 

M d

 

 



   

   

 

A d

 

   

  

QUAN HỆ SONG SONG ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 62

B. CÁC DẠNG TOÁN

Vấn đề 1: Tìm giao tuyến của hai mặt phẳng

Phương pháp:

Muốn tìm giao tuyến của hai mặt phẳng. Ta tìm hai điểm chung thuộc cả hai mặt phẳng.

Nối hai điểm chung đó được giao tuyến cần tìm.

   

A P Q

AB P Q

B P Q





 



  





 





Các ví dụ

Câu 1: Cho tứ diện

ABCD

. Gọi

là trung điểm

. Trên cạnh

lấy điểm

sao cho

2AN NC

. Hãy xác định giao tuyến:

   

DMN ABD

____________________________

   

DMN BCD



___________________________

   

DMC DNB

___________________________

Câu 2: Cho bốn điểm

, , ,A B C D

không đồng phẳng. Trên cạnh

,AB AC

lấy các điểm

,M N

sao cho

,M N

không là trung điểm của

,AB AC

. Gọi

là trung điểm

. Tìm

   

MNK BCD

___________________________

QUAN HỆ SONG SONG ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 63

Câu 3: Cho hình chóp

.S ABCD

có đáy là tứ giác lồi, các cạnh đối không song song. Tìm giao tuyến của

 

SAC

và

 

SBD

___________________________

 

SAB

và

 

SCD

___________________________

 

SAD

và

 

SBC

___________________________

Câu 4: Cho hình chóp

.S ABCD

có đáy

ABCD

là tứ giác lồi, các cạnh đối không song song. Gọi

là

điểm thuộc cạnh

sao cho

2SM MA

. Tìm giao tuyến:

   

MBD SAC

___________________________

   

MBC SAD



___________________________

   

MBC SCD

___________________________

QUAN HỆ SONG SONG ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 64

Câu 5: Cho tứ diện

ABCD

. Lấy

trên đoạn

,AB

trên đoạn

sao cho

không song song với

và

nằm trong

BCD

. Xác định giao tuyến:

   

MNI BCD

____________________________

   

MNI ACD



____________________________

   

MNI ABD

____________________________

Câu 6: Cho hình chóp

.S ABCD

có đáy là hình bình hành. Gọi

, ,M N P

lần lượt là trung điểm

, ,BC CD SA

. Xác định giao tuyến:

   

MNP SAB

____________________________

   

MNP SAD

____________________________

   

MNP SBC

____________________________

   

MNP SCD

____________________________

QUAN HỆ SONG SONG ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 65

BÀI TẬP RÈN LUYỆN

Câu 1: Cho tứ diện

ABCD

. Gọi

,M N

lần lượt là trung điểm của

và

.AD

a. Xác định giao tuyến của

 

MAD

và

 

NBC

b. Trên cạnh

lấy điểm

, trên cạnh

lấy điểm

. Xác định giao tuyến của

 

NBC

và

 

DIJ

Câu 2: Cho hình chóp

.S ABC

. Gọi

là trung điểm của

là trọng tâm tam giác

SAC

. Trên

cạnh

lấy điểm

sao cho

2AN NB

a. Xác định giao tuyến của

 

MNG

và

 

SAC

. b. Xác định giao tuyến của

 

MNG

và

 

SAB

Câu 3: Cho hình chóp

.S ABCD

có đáy

ABCD

là tứ giác lồi, các cạnh đối không song song,

cắt

tại

. Trên cạnh

lấy điểm

sao cho

3SA SM

. Trên cạnh

lấy điểm

sao cho

3SD ND

a. Xác định giao tuyến của

 

SAC

và

 

SBD

. b. Xác định giao tuyến của

 

SAB

và

 

SCD

c. Xác định giao tuyến của

 

MNO

và

 

ABCD

. d. Xác định giao tuyến của

 

MNO

và

 

SAB

Câu 4: Cho hình chóp

.S ABCD

có đáy là hình chữ nhật, tâm

. Gọi

,M N

lần lượt là trung điểm của

và

a. Xác định giao tuyến của

 

SAC

và

 

SBD

b. Xác định giao tuyến

của

 

AMN

và

 

SAC

c. Gọi

là giao điểm của

với

là giao điểm của

với

. Ba điểm

, ,P A Q

có thẳng hàng

không? Vì sao?

Câu 5: Cho hình chóp

.S ABCD

có đáy là hình bình hành. Trên

,SA SD

lấy điểm

,M N

sao cho

MS ND

MA NS

 

. Gọi

là trung điểm

a. Xác định giao tuyến của

 

MNP

và

 

ABCD

. b. Xác định giao tuyến của

 

MNP

và

 

SAB

c. Xác định giao tuyến của

 

MNP

và

 

SCD

. d. Xác định giao tuyến của

 

MNP

và

 

SAC

Câu 6: Cho tứ diện

ABCD

. Gọi

,M N

lần lượt là các điểm nằm trong

ABC

và

ACD

. Không xét các

trường hợp song song.

a. Xác định giao tuyến của

 

AMN

và

 

BCD

. b. Xác định giao tuyến của

 

BMN

và

 

BCD

Câu 7*: Cho hình chóp

.S ABCD

có đáy

ABCD

là tứ giác lồi, các cạnh đối không song song,

cắt

tại

. Trên cạnh

lấy điểm

sao cho

3MA MS

. Gọi

là trọng tâm

SCD

. Xác định giao

tuyến của

 

MOG

với các mặt của hình chóp

.S ABCD

Câu 8**: Cho tứ diện

ABCD

. Gọi

, ,M N P

lần lượt là các điểm nằm trong các

,ABC ACD 

và

BCD

. Không xét các trường hợp song song, hãy xác định giao tuyến của

 

MNP

với các mặt của tứ

diện.

QUAN HỆ SONG SONG ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 66

Vấn đề 2: Tìm giao điểm của đường thẳng và mặt phẳng

Phương pháp:

Để tìm giao điểm của đường thẳng

và mặt phẳng

 

, ta tìm giao điểm của

với một đường



nằm

trong

 

   

 

d I I d

I d P

P I P

 

 

   

 

   

 

 

    

 

 

Cách xác định



(khi chưa có sẵn)

Bước 1: Chọn mặt phẳng

 

chứa

Bước 2: Tìm

   

P Q  

Bước 3: Trong

 

d I  

 

I d

I d P

I P









   





  





Các ví dụ

Câu 1: Cho tứ diện

ABCD

. Gọi

lần lượt là trung điểm

. Trên cạnh

lấy điểm

sao cho

2AN NC

. Hãy xác định giao điểm:

 

MN BCD



____________________________

 

CD IMN



___________________________

Câu 2: Cho hình chóp

.S ABC

. Trên cạnh

,SA SC

lấy điểm

,M N

sao cho

SA SC

SM NC

 

. Gọi

là

trọng tâm

ABC

. Xác định giao điểm

QUAN HỆ SONG SONG ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 67

 

MN ABC



___________________________

 

AB GMN

___________________________

 

MN SBG

___________________________

 

NG SAB

___________________________

Câu 3: Cho tứ diện hình chóp

.S ABCD

có đáy là tứ giác lồi, các cạnh đối không song song. Gọi

là

trung điểm của

. Xác định giao điểm

 

BD SAC



___________________________

 

AM SBD

___________________________

 

SB ADM



___________________________

QUAN HỆ SONG SONG ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 68

Câu 4: Cho tứ diện hình chóp

.S ABCD

có đáy là hình bình hành tâm

. Trên cạnh

,SA SD

lấy điểm

,M N

sao cho

3SA SM

3SD ND

. Gọi

là trung điểm của

. Tìm giao điểm của:

 

CD MNP

____________________________

 

SB MNP



___________________________

 

SC MNP

___________________________

Câu 5: Cho tứ diện

ABCD

. Gọi

là trung điểm

,BC

là điểm nằm trong

ACD

. Trên cạnh

lấy điểm

sao cho

cắt mặt phẳng

 

BCD

. Tìm giao điểm của:

 

E MG BCD 

____________________________

 

F AD MGI 

___________________________

QUAN HỆ SONG SONG ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 69

BÀI TẬP RÈN LUYỆN

Câu 1: Cho tứ diện

ABCD

. Gọi

,M N

lần lượt là trung điểm của

,BC AB

, điểm

thuộc cạnh

sao

cho

3CD PD

a. Tìm giao điểm của

và

 

MNP

. b. Tìm giao điểm của

và

 

MNP

Câu 2: Cho hình chóp

.S ABC

. Trên cạnh

,AB BC

lấy điểm

,M N

sao cho

MA NB

MB NC

 

. Gọi

là

trọng tâm

SAC

. Tìm giao điểm của

với

 

MNG

Câu 3: Cho tứ diện

ABCD

. Gọi

là trung điểm của

,AB

là trọng tâm

ACD

a. Tìm giao điểm của

và

 

BCD

b. Gọi

là điểm đối xứng của

qua

. Tìm giao điểm của

với

 

BCD

Câu 4: Cho hình chóp

.S ABCD

có đáy là tứ giác lồi, các cạnh đối không song song. Gọi

là giao điểm

của

và

.BD

Trên cạnh

,SA SD

lần lượt lấy các điểm

,M N

sao cho

không song song với

.AD

a. Tìm giao điểm của

và

 

MNO

. b. Tìm giao điểm của

với

 

MNO

c. Gọi

là trung điểm

. Tìm giao điểm của

với

 

MNO

Câu 5: Cho hình chóp

.S ABCD

có đáy là hình bình hành. Gọi

là trung điểm của

a. Tìm giao điểm của

và

 

SBD

b. Tìm giao điểm của

và

 

ABM

Câu 6*: Cho hình chóp

.S ABCD

có đáy là hình thang, đáy lớn

. Trên cạnh

, ,SA SB CD

lần lượt lấy

, ,M N P

sao cho

SA SB CD

SM NB CP

  

a. Tìm giao điểm của

và

 

SAD

b. Tìm giao điểm của

với

 

MNP

Câu 7*: Cho tứ diện

ABCD

. Gọi

, ,M N P

lần lượt là các điểm nằm trong tam giác

,ABC ACD

và

BCD

sao cho

cắt mặt phẳng

 

ACD

a. Tìm giao điểm của

và

 

BCD

. b. Tìm giao điểm của

và

 

MNP

Câu 8*: Cho hình chóp

.S ABCD

có đáy là một tứ giác lồi. Gọi

là điểm nằm trong tam giác

SCD

a. Tìm giao điểm của

và

 

SAC

. b. Tìm giao điểm của

và

 

ABM

QUAN HỆ SONG SONG ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 70

Vấn đề 3: Chứng minh ba điểm thẳng hàng – ba đường thẳng đồng quy

Phương pháp:

1. Chứng minh ba điểm thẳng hàng:

Để chứng minh ba điểm

, ,A B C

thẳng hàng. Ta chứng minh

, ,A B C

cùng thuộc giao tuyến của hai mặt

phẳng.

   

, ,

A P Q

B P Q A B C

C P Q





 



  





 





thẳng hàng.

2. Chứng minh ba đường thẳng đồng quy:

Chứng minh ba đường

, ,a b c

đồng quy.

Bước 1: Gọi

I a b 

Bước 2:

 

   

I a P

I P Q

I b Q





 



  





 





Bước 3: Chứng minh

   

c P Q 

I c 

Vậy

, ,a b c

đồng quy.

Các ví dụ

Câu 1: Trong không gian, cho mặt phẳng

 



và mặt phẳng

 

ABC

. Biết

 

AB M

 

 

AC N 

 

BC P 

. Hình vẽ sau đúng hay sai ? Vì sao?

___________________________

Câu 2: Cho tứ diện

ABCD

. Gọi

là trung điểm

, điểm

trên cạnh

sao cho

4AB AN

điểm

trên cạnh

sao cho

4AD PD

. Gọi

, ,I J K

lần lượt là giao điểm của

và

. Chứng minh rằng

, ,I J K

thẳng hàng.

___________________________

QUAN HỆ SONG SONG ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 71

Câu 3: Cho hình chóp

.S ABCD

có đáy là hình bình hành. Gọi

,H K

lần lượt là trung điểm của

,SB SD

a. Tìm giao điểm

của

và

 

SAC

, giao điểm

của

và

 

AHK

___________________________

b. Gọi

,M HI BC 

N KI CD 

. Chứng minh

rằng

, ,A M N

thẳng hàng

___________________________

Câu 4: Cho hình chóp

.S ABCD

có đáy là hình thang, đáy lớn

. Gọi

là trung điểm

a. Tìm giao điểm

của

và

 

ADM

___________________________

b. Chứng minh rằng

, ,AD BC MN

đồng quy.

___________________________

QUAN HỆ SONG SONG ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 72

Câu 5: Cho hình chóp

.S ABCD

có đáy là tứ giác lồi, các cạnh đối không song song. Gọi

, ,M N P

lần

lượt là các điểm thuộc cạnh

, ,SA SB SD

a. Tìm giao tuyến

của

 

SAB

và

 

SCD

____________________________

b. Tìm giao điểm

của

và

 

MNP

___________________________

c. Chứng minh rằng

,MN PQ

và

đồng quy.

___________________________

Câu 6: Cho hình chóp

.S ABCD

có đáy là hình thang, đáy lớn

2AB CD

. Gọi

là giao điểm của

và

là trung điểm

. Trên cạnh

lấy điểm

sao cho

4 3SN SA

a. Tìm giao điểm

của

và

 

ABCD

___________________________

b. Tìm giao điểm

của

với

 

OMN

, giao điểm

của

với

 

OMN

___________________________

QUAN HỆ SONG SONG ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 73

c. Chứng minh

, ,OI CD JK

đồng quy.

___________________________

d. Gọi

là trung điểm của

. Chứng minh

, ,S H O

thẳng hàng.

___________________________

Câu 7: Cho hình chóp

.S ABCD

có đáy là hình bình hành tâm

. Gọi

,H K

lần lượt là trung điểm

và

a. Tìm giao điểm

của

và

 

SAC

___________________________

b. Tìm giao điểm

của

và

 

CHK

___________________________

b. Tìm giao điểm

của

và

 

CHK

___________________________

c. Chứng minh

, ,IK AD JC

đồng quy.

___________________________

d. Gọi

là trung điểm của

là trọng tâm

ACD

. Chứng minh

, ,S E G

thẳng hàng.

___________________________

QUAN HỆ SONG SONG ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 74

BÀI TẬP RÈN LUYỆN

Câu 1: Cho hình chóp

.S ABCD

có đáy là hình thang, đáy lớn

. Gọi

là trung điểm của

.SD

a. Tìm giao tuyến

của

 

SAB

và

 

SCD

b. Tìm giao điểm

của

và

 

ABM

c. Gọi

là giao điểm của

và

. Chứng minh rằng

,AN BM

và

đồng quy.

Câu 2: Cho hình chóp

.S ABC

. Gọi

là trung điểm của

.SA

Gọi

,N P

là các điểm trên

và

sao

cho

AN SP

AB SC

 

a. Tìm giao điểm

của

và

 

MNP

b. Chứng minh rằng

,MN PQ

và

đồng quy.

Câu 3: Cho tứ diện

ABCD

. Gọi

,M N

lần lượt là trung điểm của

,AB BC

là trọng tâm

ACD

a. Tìm giao điểm

của

và

 

BCD

b. Tìm giao điểm

của

với

 

MNG

và giao điểm

của

với

 

MNG

c. Chứng minh rằng

,MQ NP

và

đồng quy.

Câu 4: Cho hình chóp

.S ABCD

có đáy là hình thang, đáy lớn

2AB CD

. Gọi

là giao điểm của

và

là trung điểm của

là trung điểm

. Chứng minh rằng

, ,S I O

thẳng hàng.

Câu 5: Cho hình chóp

.S ABCD

có đáy là hình bình hành. Gọi

, ,M N P

lần lượt là trung điểm của

, ,BC CD

. Điểm

di động trên đoạn

a. Tìm giao điểm

của

và

 

MNK

, giao điểm

của

và

 

MNK

b. Gọi

là giao điểm của

và

. Chứng minh rằng điểm

luôn thuộc một đường thẳng cố định

di động trên đoạn

Câu 6*: Cho hình chóp

.S ABCD

có đáy là tứ giác lồi, các cạnh đối không song song. Gọi

là trung

điểm

. Trên cạnh

lấy điểm

a. Tìm giao điểm

của

và

 

SBD

b. Gọi

là giao điểm của

và

,BD

là giao điểm của

và

. Chứng minh rằng

luôn đi

qua một điểm cố định khi

di động trên cạnh

QUAN HỆ SONG SONG ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 75

Vấn đề 4: Tìm thiết diện của hình chóp khi cắt bởi một mặt phẳng

Phương pháp:

Nếu mặt phẳng

 



cắt các mặt của hình chóp (Mặt bên và mặt đáy – nếu có) theo các

đoạn giao tuyến

nối tiếp nhau, tạo thành một đa giác phẳng thì ta gọi đa giác này là

thiết diện

hay

mặt cắt

của mặt

phẳng

 



và hình chóp.

Ở hình dươi, thiết diện tạo bởi mặt phẳng

 



và hình chóp S.ABCD là tứ giác

MNPQ

Thông thường, để xác định các thiết diện, ta làm theo hai cách sau:

Cách 1: Tìm giao tuyến đầu tiên của mặt phẳng

 



với một mặt phẳng nào đó của hình chóp, giao

tuyến này dễ tìm được. Sau đó kéo dài giao tuyến này cắt các cạnh khác của hình chóp, từ đó ta tìm được

các đoạn giao tuyến tiếp theo. Đa giác giới hạn bởi các đoạn giao tuyến này là thiết diện cần tìm.

Cách 2: Tìm giao điểm của

 



với các cạnh của hình chóp (cạnh bên và cạnh đáy) (

 



có thể chỉ cắt

một số cạnh, chứ không nhất thiết phải cắt tất cả các cạnh). Nối các giao điểm lại thành một đa giác, là

thiết diện cần tìm

Các ví dụ

Câu 1: Cho tứ diện

ABCD

. Gọi

,M N

là các điểm nằm trên cạnh

,AB AC

sao cho

không song

song với

. Gọi

là trung điểm của

. Xác định thiết diện của tứ diện

ABCD

cắt bởi mặt

phẳng

 

MNI

___________________________

QUAN HỆ SONG SONG ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 76

Câu 2: Cho tứ diện

ABCD

. Gọi

,M N

là các điểm nằm trên cạnh

,AB AC

sao cho

không song

song với

. Gọi

là điểm nằm trong

BCD

. Xác định thiết diện của tứ diện

ABCD

cắt bởi

mặt phẳng

 

MNI

___________________________

Câu 3: Cho hình chóp

.S ABCD

có đáy là tứ giác lồi, các cạnh đối không song song. Trên cạnh

lấy

điểm

. Xác định thiết diện của hình chóp

.S ABCD

cắt bởi mặt phẳng

 

ABM

___________________________

Câu 4: Cho hình chóp

.S ABCD

có đáy là tứ giác lồi, các cạnh đối không song song. Gọi

là giao điểm

của

và

,BD

,M N

là các điểm nằm trên cạnh

,SA SD

sao cho

không song song với

. Xác định thiết diện của hình chóp

.S ABCD

cắt bởi mặt phẳng

 

OMN

___________________________

QUAN HỆ SONG SONG ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 77

Câu 5: Cho hình chóp

.S ABCD

có đáy là hình bình hành tâm

. Gọi

,M N

lần lượt là trung điểm

,SB SD

. Xác định giao điểm của

với mặt phẳng

 

AMN

, từ đó suy ra thiết diện của hình

chóp

.S ABCD

cắt bởi mặt phẳng

 

AMN

___________________________

Câu 6: Cho hình chóp

.S ABC

. Trên cạnh

lấy điểm

. Gọi

và

lần lượt là các điểm nằm trong

tam giác

SBC

và

ABC

sao cho

cắt mặt phẳng

 

ABC

. Xác định giao điểm của

với

 

ABC

và thiết diện của hình chóp

.S ABC

cắt bởi mặt phẳng

 

MNP

___________________________

BÀI TẬP RÈN LUYỆN

Câu 1: Cho tứ diện

.S ABC

. Gọi

,M N

lần lượt là điểm nằm trên cạnh

,SA SC

và

là điểm trong tam

giác

ABC

. Tìm thiết diện của hình chóp và mặt phẳng

 

MNP

Câu 2: Cho hình chóp

.S ABCD

có đáy là tứ giác lồi, các cạnh đối không song song. Gọi

là điểm nằm

trên cạnh

sao cho

3SA SM

là trọng tâm

SCD

là giao điểm của

và

. Xác định

thiết diện của hình chóp

.S ABCD

cắt bởi

 

MGO

QUAN HỆ SONG SONG ĐỀ CƯƠNG TOÁN 11

GV: TUẤN DUY – THPT Gia Định 78

Câu 3: Cho hình chóp

.S ABCD

có đáy là hình bình hành tâm

. Gọi

,M N

lần lượt là trung điểm của

,SB SD

. Trên cạnh

lấy điểm

sao cho

3SP PC

. Xác định thiết diện của hình chóp

.S ABCD

cắt

bởi mặt phẳng

 

MNP

Câu 4: Cho hình chóp

.S ABCD

, có đáy là tứ giác lồi, các cạnh đối không song song. Gọi

, ,M N P

lần lượt

là trung điểm

, ,SA BC CD

. Xác định thiết diện của hình chóp cắt bởi mặt phẳng

 

MNP

Cho hình chóp

.S ABCD

có đáy là hình thang, đáy lớn

.AB

Gọi

,E F

lần lượt là trọng tâm

SBC

và

SCD

a. Xác định giao điểm của

với

 

AEF

b. Xác định thiết diện của hình chóp

.S ABCD

cắt bởi mặt phẳng

 

AEF

Câu 5: Cho hình chóp

.S ABCD

có đáy là hỉnh bình hành. Gọi

,H K

lần lượt là trung điểm của

và

, điểm

thuộc cạnh

. Tìm thiết diện của hình chóp cắt bởi mặt phẳng

 

HKL

Câu 6: Cho hình chóp

.S ABCD

có đáy là hình bình hành tâm

, Gọi

, ,M N I

lần lượt thuộc

, ,AB BC SO

. Tìm thiết diện của hình chóp với mặt phẳng

 

MNI

Bấm Tải xuống để xem toàn bộ.

| 1/79

| | Tải xuống

Preview text:

TÀI LIỆU HỌC TẬP
Năm học: 2019 – 2020 TOÁN 11 TẬP 1
Cuốn sách này của: ______________________________
Biên soạn & giảng dạy: Thầy Duy – THPT Gia Định LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11 PHẦN 1:
HÀM SỐ LƯỢNG GIÁC – PHƯƠNG TRÌNH LƯỢNG GIÁC
BÀI 1: ÔN TẬP CÔNG THỨC LƯỢNG GIÁC A. TÓM TẮT LÝ THUYẾT
1. Giá trị lượng giác của một cung  
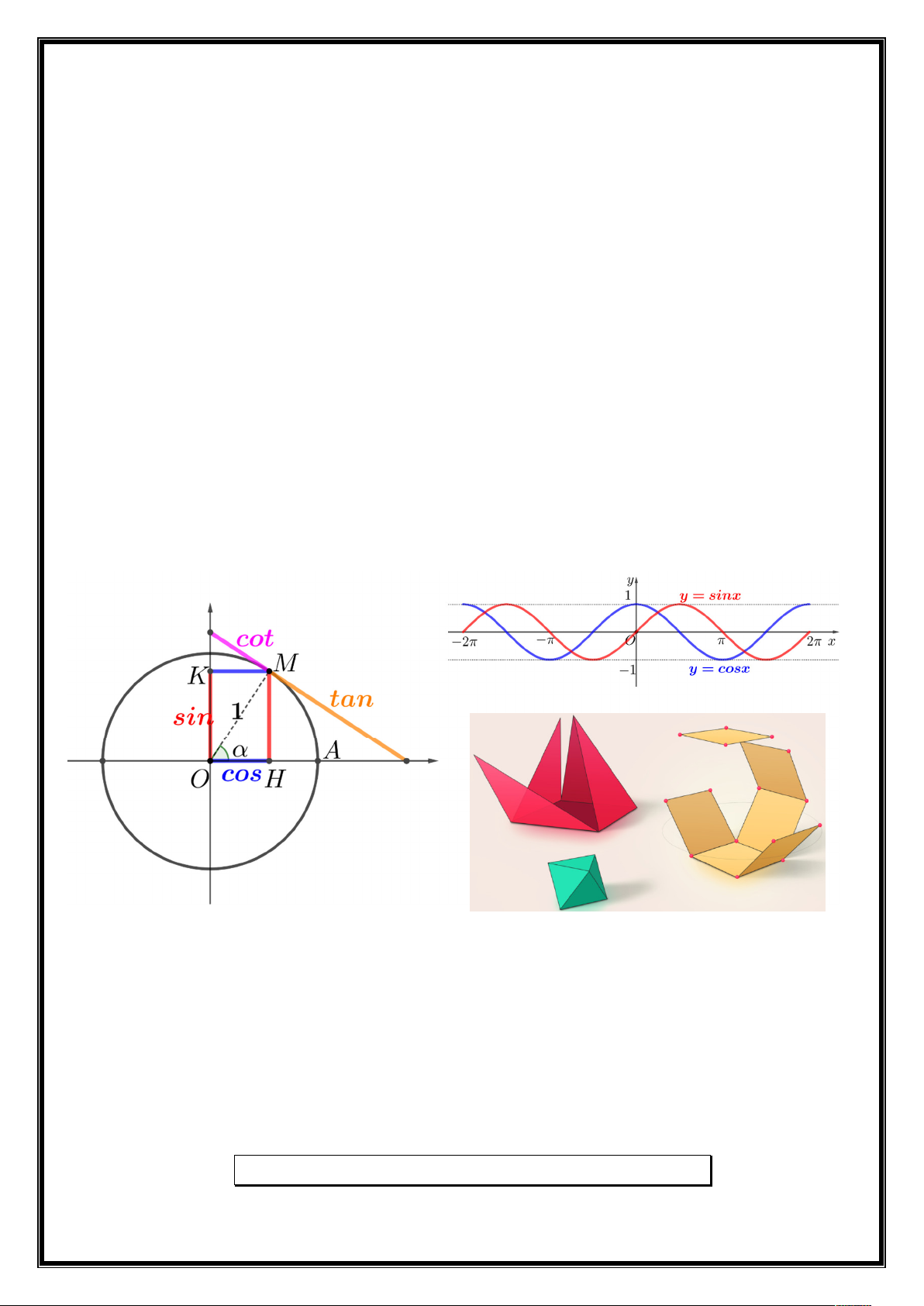
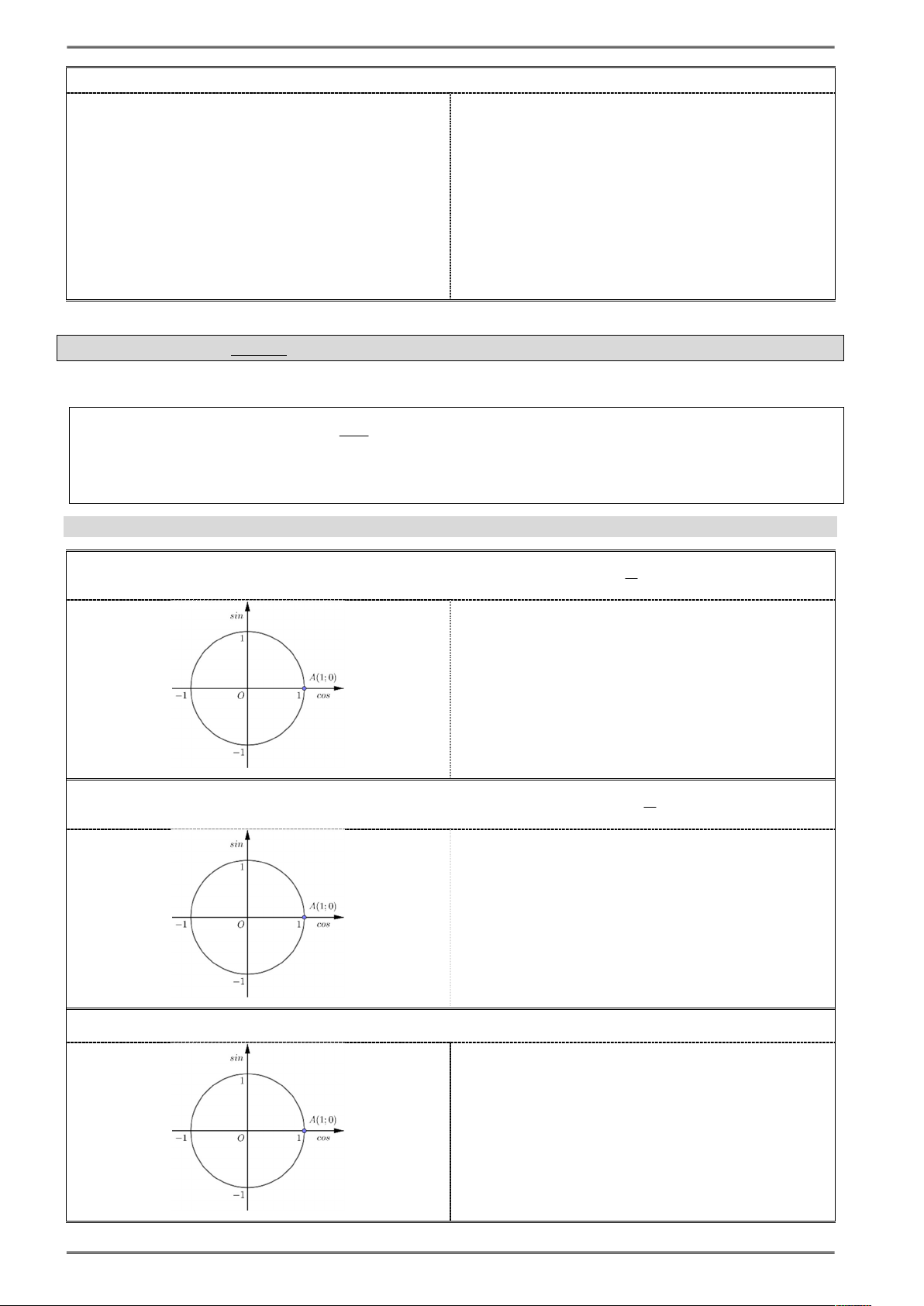
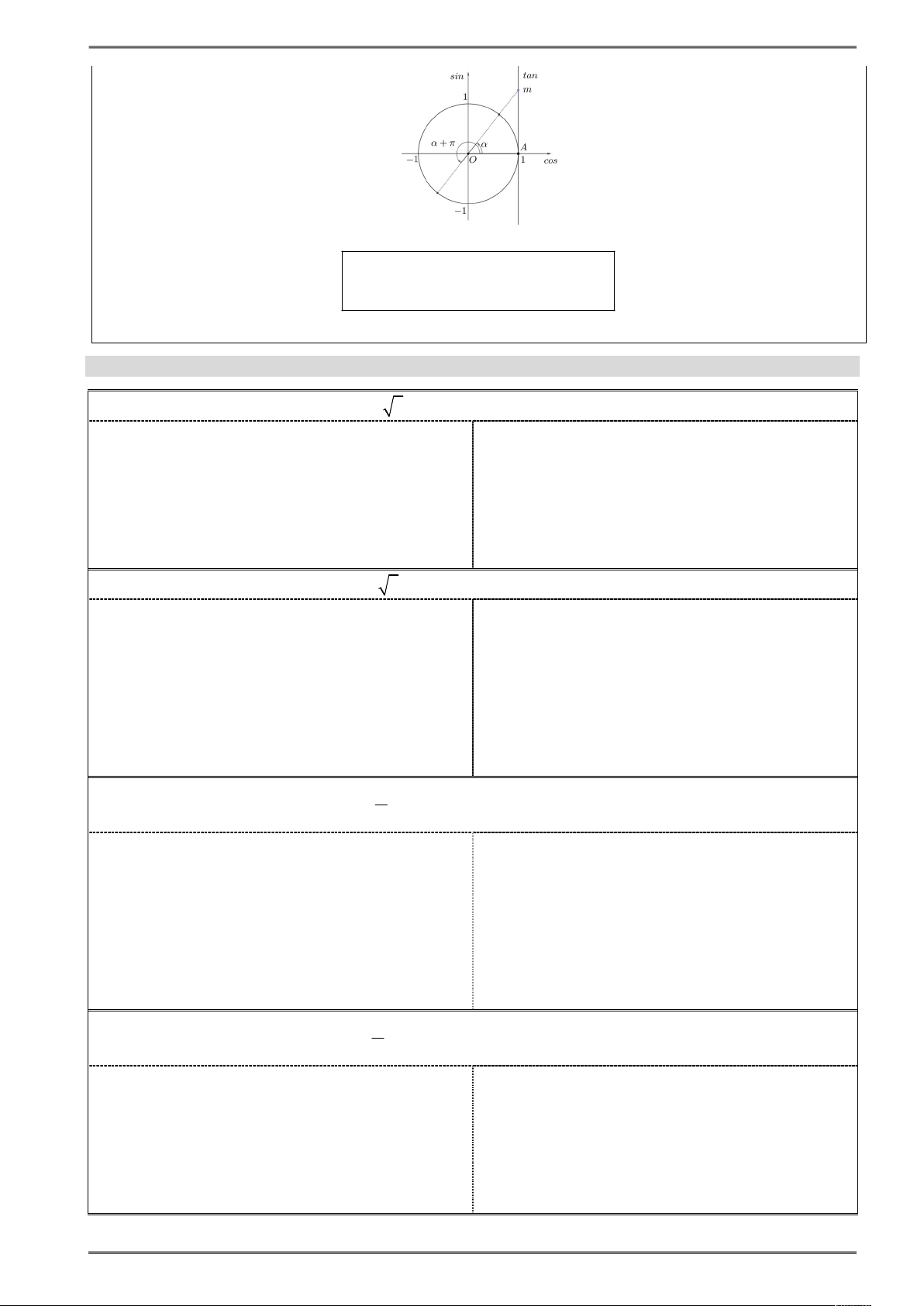
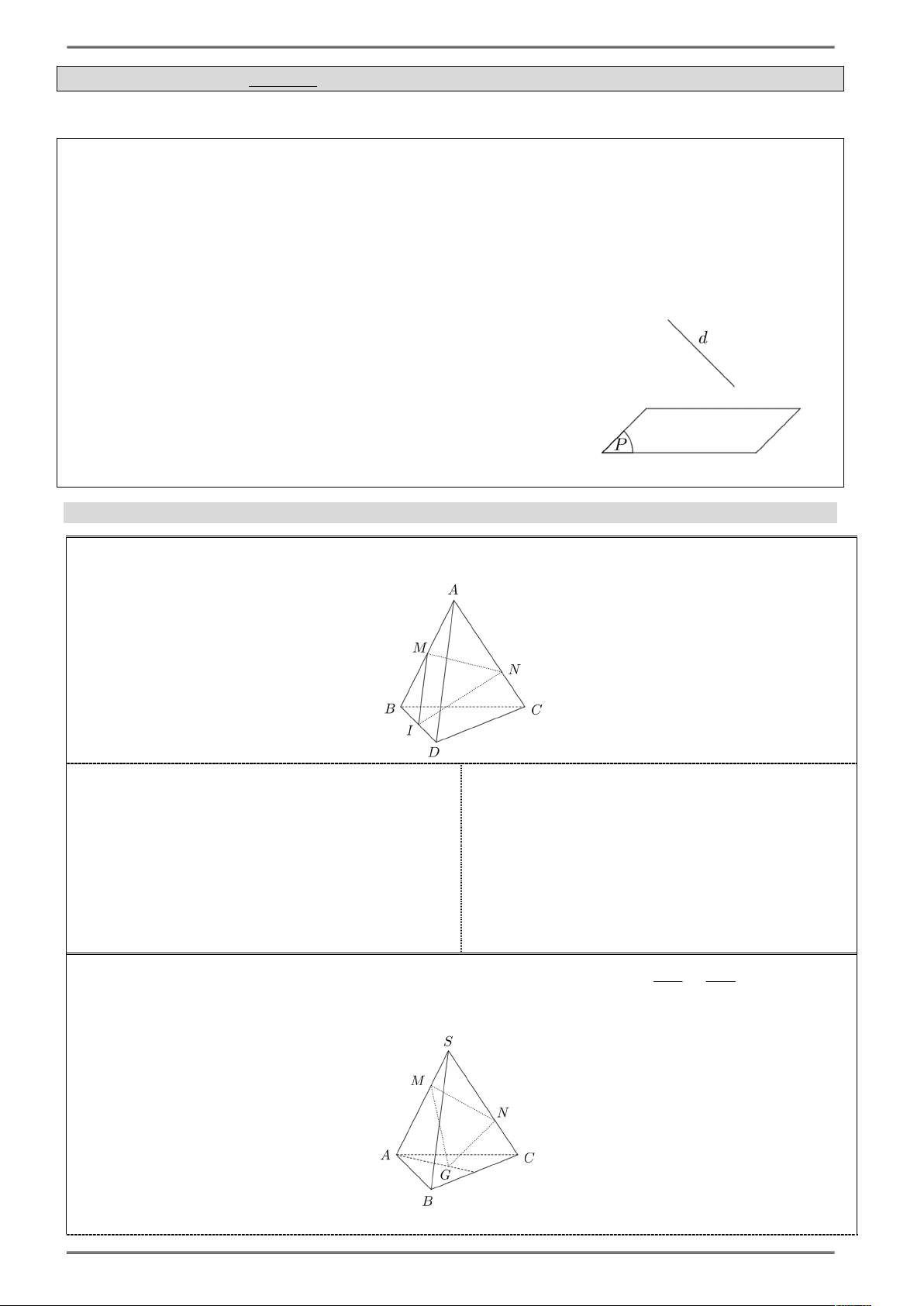
Trên đường tròn lượng giác (hình 1.1) cho cung AM có sđ AM   : Hình 1.1
Gọi M x ;y thì ta có: M M 
sin   y  OK
cos   x  OH M M sin  cos  tan   ;cos   0 cot   ;sin   0 cos  sin  Lưu ý:
1. Các giá trị sin  ; cos  xác định với mọi    . Và ta có:
sin   k2  sin ,  k  ; 
cos   k2  cos ,  k  .  2. 1
  sin   1 ; 1   cos   1 
3. tan  xác định với mọi    k ,
 k   và tan  k  tan  . 2
4. cot  xác định với mọi   k ,
 k   và cot  k  cot  .
2. Công thức lượng giác Hệ thức cơ bản Cung liên kết 2 2
sin a  cos a  1 tana.cota  1 sin a
sina  sin  a   tan a  cos ñoiá cosa sin buø
 tana  tan  a   cosa cota  phuï cheùo
cota  cot a   sina 
cosa  cos a 1 hôn keùm cheo ù sin 2 1  tan a  2
 cos  a 2 cos a 1 2 1  cot a  2 sin a
GV: TUẤN DUY – THPT Gia Định 1 LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11 Công thức cộng
Công thức nhân đôi – nhân ba – hạ bậc
sin a  b  sina.cosb  cosa.sinb
sin 2a  2 sina. cosa 2 2
cos 2a  cos a  sin a
cos a  b  cosa.cosb  sina.sinb 2  2 cos a  1   a  b tana tanb tan  2  1  2 sin a
1  tana. tanb  1    s
 ina.cosa  sin 2a a b tan a tanb tan   2
1  tan a. tanb  1  cos 2a  2  s  in a   2   1  cos 2a 2 c  os a   2  3
sin 3a  3 sin a  4 sin a (3sin – 4sỉn) 3
cos 3a  4 cos a  3 cosa (4cổ – 3 cô)
Công thức biến đổi tổng thành tích
Công thức biến đổi tích thành tổng a  b a b 1
sina  sinb  2 sin . cos sina. cosb sin 
a b sina b     2 2   2 a  b a b 1
sina  sinb  2 cos . sin cosa. sinb sin 
a b sina b     2 2 2   a  b a b 1
cosa  cosb  2 cos . cos cosa. cosb cos 
a b cosa b     2 2   2 a  b a b 1
cosa  cosb  2 sin . sin  
sina. sinb   cos 
a b cosa b 2 2 2    Một số công thức khác Công thức tính sin ,
 cos  theo t  tan 2   
sina  cosa  2 sin a       t   Đặt tan  4  2     2t 
cosa  sina  2 cos a      s  in    2   4   1  t  2  1  t  1  c  os   2 2 2 sin a. cos a  sin 2a 2  1  t 4  2t tan   1 3  1 cos 4a 2  4 4 2  1  t
cos a  sin a  1  sin 2a   2 4 3 5  3 cos 4a 6 6 2
cos a  sin a  1  sin 2a  4 8
3. Biểu diễn cung lượng giác trên đường tròn lượng giác k2
Cung lượng giác x   
k   được biểu diễn bởi m điểm trên đường tròn lượng giác. m
Bước 1: Xác định điểm M biểu diễn cung  .
Bước 2: Xác định m  1 điểm còn lại trên đường tròn lượng giác cách đều điểm M . Ví dụ:   k2 
1. Cung lượng giác x   k2  
được biểu diễn bởi một điểm M tại vị trí . 3 3 1 3
GV: TUẤN DUY – THPT Gia Định 2 LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11   k2  7
2. Cung lượng giác x   k  
được biểu diễn bởi hai điểm M tại các vị trí và . 6 6 2 6 6  k  k2
 3 5 7
3. Cung lượng giác x    
thì có bốn điểm M tại các vị trí , , ; . 4 2 4 4 4 4 4 4 B. CÁC DẠNG TOÁN
Dạng 1: Biến đổi biểu thức lượng giác Phương pháp:
Sử dụng công thức lượng giác. Thông thường ta thực hiện như sau:
 Có hệ số tự do  biến đổi cho mất số
 Có mũ cao  hạ bậc
 Có tích  biến đổi thành tổng
 Có tổng  nhóm hạng tử và biến đổi thành tích Các ví dụ Câu 1.
Biến đổi biểu thức sau thành tổng P  cos x. cos 2x. cos 3x
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________         Câu 2.
Biến đổi biểu thức sau thành tổng P  sin   x . sin x. sin   x   3     3 
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
GV: TUẤN DUY – THPT Gia Định 3 LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11 Câu 3.
Biến đổi biểu thức sau thành tích P  sin 2x  cos 2x  1
___________________________ ___________________________
___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ Câu 4.
Biến đổi biểu thức sau thành tích P  sin x  sin 2x  sin 3x
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ Câu 5.
Biến đổi biểu thức sau thành tích P  1  cos x  cos 2x  cos 3x
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ Câu 6.
Biến đổi biểu thức sau thành tích 2 2 2 2
P  cos x  cos 2x  sin 3x  sin 4x
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________ Câu 7.
Biến đổi biểu thức sau thành tích 8 8 P  x  x   10 10 sin cos
2 sin x  cos x 
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________ Câu 8.
Biến đổi biểu thức sau thành tích P  sin 6x  2 sin 3x cos x  cos 2x
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________
GV: TUẤN DUY – THPT Gia Định 4 LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11
Dạng 2: Rút gọn, chứng minh biểu thức lượng giác Các ví dụ 1 1 Câu 9. Chứng minh rằng: 4 4 2
sin x  cos x   cos 2x 2 2
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ x x 5  3 cos 2x
Câu 10. Chứng minh rằng 6 6 sin  cos  2 2 8
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
Câu 11. Rút gọn biểu thức P   4 4 x  x  6 6 3 sin cos
2 sin x  cos x
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________  2   2     
Câu 12. Rút gọn biểu thức 2 2 2 P  sin x  
  sin x  sin x      3     3 
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
GV: TUẤN DUY – THPT Gia Định 5 LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11
Câu 13. Rút gọn biểu thức 3 3
P  cos 3x sin x  sin 3x cos x
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________
Dạng 3: Biểu diễn cung lượng giác trên đường tròn lượng giác Phương pháp: k2
Bước 1: Đưa cung về dạng x   
 có m điểm trên đường tròn lượng giác biểu diễn cung x m
Bước 2: Xác định điểm M biểu diễn cung  trên đường tròn lượng giác
Bước 3: Xác định m  1 điểm còn lại trên đường tròn lượng giác cách đều điểm M Các ví dụ 
Câu 14. Xác định các điểm trên đường tròn lượng giác biểu diễn cung x 
 k2 k   2 ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ 
Câu 15. Xác định các điểm trên đường tròn lượng giác biểu diễn cung x  
 k2 k   4 ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
Câu 16. Xác định các điểm trên đường tròn lượng giác biểu diễn cung x  k k   ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
GV: TUẤN DUY – THPT Gia Định 6 LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11 
Câu 17. Xác định các điểm trên đường tròn lượng giác biểu diễn cung x  
 k k   2 ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ 
Câu 18. Xác định các điểm trên đường tròn lượng giác biểu diễn cung x 
 k k   4 ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ k2
Câu 19. Xác định các điểm trên đường tròn lượng giác biểu diễn cung x  k   3 ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ k
Câu 20. Xác định các điểm trên đường tròn lượng giác biểu diễn cung x  k   2 ___________________________ ___________________________ ___________________________ ___________________________ ___________________________  k
Câu 21. Xác định các điểm trên đường tròn lượng giác biểu diễn cung x   k   3 2 ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
GV: TUẤN DUY – THPT Gia Định 7 LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11
BÀI 2: PHƯƠNG TRÌNH LƯỢNG GIÁC CƠ BẢN
Dạng 1: Phương trình sin u  m Phương pháp:
1. Dạng cơ bản: sin u  m   1
 m  1  m  1
 : Phương trình vô nghiệm  1
  m  1 : Với m  sin  , ta có:   
u    k2 1 sin u sin      k   u
      k2 
sinx  0  x  k    Đặc biệt: s
 in x  1  x   k2 k    2   s
 in x  1  x    k2  2 2. Dạng mở rộng: u
  v  k2 sin u sin v    k   
u    v  k2 
(Với u, v là các biểu thức theo biến x ) Các ví dụ Câu 1.
Giải phương trình sin 2x  1
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________ Câu 2.
Giải phương trình sin 3x  0
___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ x     Câu 3.
Giải phương trình sin     1  2 6 
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
GV: TUẤN DUY – THPT Gia Định 8 LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11 1 Câu 4.
Giải phương trình sin 5x  2
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ 1 Câu 5.
Giải phương trình sin 2x   3
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ x     Câu 6.
Giải phương trình 2 sin     3  0  2 6 
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________  5    Câu 7.
Giải phương trình sin 3x    sin 2x   4 
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________      1 Câu 8.
Tìm các nghiệm của phương trình sin 2  x       ;    trong khoảng    3  2
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
GV: TUẤN DUY – THPT Gia Định 9 LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11           Câu 9.
Tìm các nghiệm của phương trình sin 2
 x    sin x     x   thỏa 2  6     3 
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________     
Câu 10. Giải phương trình 2 sin x     2  0 
và biểu diễn các nghiệm trên đường tròn lượng  4  giác
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________
Dạng 2: Phương trình cos u  m Phương pháp:
1. Dạng cơ bản: cos u  m   1
 m  1  m  1
 : Phương trình vô nghiệm  1
  m  1 : Với m  cos  , ta có:   
u    k2 1 cos u cos      k   u      k2    c
 osx  0  x   k  2  Đặt biệt: c
 os x  1  x  k2 k    c  osx  1
  x    k2 
GV: TUẤN DUY – THPT Gia Định 10 LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11 2. Dạng mở rộng: u
  v  k2 cos u cos v    k    u  v   k2 
(Với u, v là các biểu thức theo biến x ) Các ví dụ
Câu 11. Giải phương trình cos 3x  1
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________     
Câu 12. Giải phương trình cos x     0   4 
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________     
Câu 13. Giải phương trình cos 2  x    1   3 
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ 3
Câu 14. Giải phương trình cos 2x  2
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ x    
Câu 15. Giải phương trình 2 cos     1  0   3 6 
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
GV: TUẤN DUY – THPT Gia Định 11 LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11  3        
Câu 16. Giải phương trình cos 2  x    cos x      4     4 
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________     
Câu 17. Tìm các nghiệm của phương trình 2 cos x     3  0      trong đoạn 3; 6  4   
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________      1
Câu 18. Giải phương trình cos x      
và biểu diễn các nghiệm trên đường tròn lượng giác  3  2
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________
Dạng 3: Phương trình tan u  m và cot u  m Phương pháp: 1. Dạng cơ bản:
 tan u  m  tan u  tan   u    k k  
 cotu  m  cotu  cot   u    k k  
GV: TUẤN DUY – THPT Gia Định 12 LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11 2. Dạng mở rộng:
tan u  tan v  u  v  k k  
cotu  cotv  u  v  k k  
(Với u, v là các biểu thức theo biến x ) Các ví dụ
Câu 19. Giải phương trình tan 2x   3
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
Câu 20. Giải phương trình 3 cot 3x  3  0
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________     
Câu 21. Giải phương trình tan 2
 x    tan x   6 
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________     
Câu 22. Giải phương trình cot3x    cot 2x   4 
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
GV: TUẤN DUY – THPT Gia Định 13 LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11
Dạng 4: Đưa về phương trình cơ bản Phương pháp:
 Đưa dấu " " vào trong
 sina  sin  a  
 tana  tan  a  
 cota  cot a  
 cosa  cos a
 Chuyển giữa sin và cos  
sin  a  cosa 2    
cos  a  sina 2 
 Chuyển giữa tan và cot  
tan  a  cota 2   
cot a  tana   2  1 1  cota;  tana tana cota  Chú ý các dạng sau Có 2 2 sin ,
u cos u  hạ bậc
sin u   sin v  sin u  sin  v      
sin u  cos v  sin u  sin   v   2 
cos u   cos v  cos u  cos   v    
cos u  sin v  cos u  cos   v   2     
tan u  cotv  tan u  tan   v   2  1
tan u. cotv  1  tan u 
 tan u  tan v cotv Các ví dụ      1
Câu 23. Giải phương trình 2 sin 2  x      6  2
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________
GV: TUẤN DUY – THPT Gia Định 14 LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11      3
Câu 24. Giải phương trình 2 cos 2  x      4  4
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________          
Câu 25. Giải phương trình sin 2
 x     sin x      3     6 
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________     
Câu 26. Giải phương trình cos 3x    cos x  0   3 
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________  2   9     
Câu 27. Giải phương trình sin 3x    cos x      3     4 
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________     
Câu 28. Giải phương trình sin 2
 x    cos x  0   4 
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
GV: TUẤN DUY – THPT Gia Định 15 LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11          
Câu 29. Giải phương trình 2 2 sin 5
 x    cos 3x    0   3     4 
___________________________ ___________________________
___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________    4     
Câu 30. Giải phương trình sin 3x    sin   3x  3   5     5 
___________________________ ___________________________
___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________     
Câu 31. Giải phương trình tan 3x    tan 2x  0   4 
___________________________ ___________________________
___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________         
Câu 32. Giải phương trình tan 4x 
  cot  2x   3     6 
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________
GV: TUẤN DUY – THPT Gia Định 16 LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11
Dạng 5: Phương trình tích Phương pháp: A  0
 Biến đổi phương trình về dạng . A B 0     B  0 
 Chú ý các công thức sau 1. Công thức nhân đôi
________________________________________________________
________________________________________________________
________________________________________________________ 2. Công thức hạ bậc
________________________________________________________
________________________________________________________
3. Công thức tổng thành tích:
________________________________________________________
________________________________________________________
________________________________________________________
________________________________________________________
4. Công thức tích thành tổng
________________________________________________________
________________________________________________________
________________________________________________________
________________________________________________________ Các ví dụ
Câu 33. Giải phương trình 1  cos x  cos 2x  0
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
Câu 34. Giải phương trình sin 4x  cos 4x  1  0
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
GV: TUẤN DUY – THPT Gia Định 17 LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11
Câu 35. Giải phương trình sin 3x  sin 4x  sin 5x  0
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________
Câu 36. Giải phương trình cos 3x  sin 2x  cos x  0
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________
Câu 37. Giải phương trình cos 6x cos 3x  cos 7x cos 4x
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________
Câu 38. Giải phương trình sin 3x sin x  sin 8x sin 4x  0
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________ BÀI TẬP RÈN LUYỆN
Bài 1: Giải các phương trình sau           a. 2 sin 4x    3  0    x     b. 1 2 cos 3 0    3   3        2   9      c. sin 4x    sin 2x  0  sin 3x    cos x     d.        5   3   4 
GV: TUẤN DUY – THPT Gia Định 18 LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11  2     3    e. sin 3x    sin 2x  0  sin 2  x    cos x  0  f.    3   4  x         g. 0
3 cot  20   1  0   x    x   h. tan 3 tan 2 0   2   4       i. tan 4x    cot 2x  x x   j. tan . cot 2 1  3 
Bài 2: Giải các phương trình sau x     1 3x     3 a. 2 sin      cos      b. 2   2 6  2  2 4  4  2  7           c. 2 2 sin 3x    sin   x   x    x   d. 2 2 sin 5 cos 0    3     5   3     4      4         e. sin 3x    sin   3x  3  cos   x  cos  x  3  f.        5     5   9  18     5      g. cos 3x    sin   3x  2   3     6 
Bài 3: Tìm nghiệm của các phương trình sau trong khoảng đã cho 1
a. sin 2x   với x  0;  2 b.  0
tan 2x  15   1 với 0 0 18  0  x  90      c. 2 2 cos 2x  sin x     x   với 2  3 
Bài 4: Giải các phương trình sau
a. sin 2x  cos 2x  1  0
b. 1  cos 2x  cos 4x  0
c. 1  cos x  cos 2x  cos 3x  0
d. sin x  sin 2x  sin 3x  sin 4x  0
e. cos 5x  cos 6x  cos 7x  0
f. sin 6x sin 2x  cos 3x cos x g. 2 2 2 2
sin x  sin 2x  cos 3x  cos 4x h. 2 2 2 2
sin 2x  sin 3x  sin 4x  sin 5x  2
GV: TUẤN DUY – THPT Gia Định 19 LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11
BÀI 3: GIẢI PHƯƠNG TRÌNH LƯỢNG GIÁC
BẰNG PHƯƠNG PHÁP ĐẶT ẨN PHỤ
Dạng 1: Phương trình bậc hai đối với một hàm số lượng giác Phương pháp: Dạng Đặt ẩn phụ Điều kiện 2
a sin x b sin x c  0 2
a cos x b cos x c  0 2
a tan x b tan x c  0 2
a cot x b cotx c  0 4 2
a sin x b sin x c  0 2
a sin x b sin x  c  0 4 2
a cos x b cos x c  0 2
a cos x b cos  c  0
MỘT SỐ ĐẲNG THỨC ĐÁNG NHỚ 1
● sin a cos a  sin 2a 2 ● 2 2 2 2
cos 2a  cos a  sin a  2 cos a  1  1  2 sin a ● 4 4 a  a   2 2 a  a 2 2 cos sin cos sin
cos a  sin a  cos 2a 1 3  1 cos 4a ● 4 4 2
sin a  cos a  1  sin 2a  2 4 3 5  3 cos 4a ● 6 6 2
sin a  cos a  1  sin 2a  4 8 Các ví dụ Câu 1. Giải phương trình 2
sin 2x  3 sin 2x  2  0
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________
GV: TUẤN DUY – THPT Gia Định 20 LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11 Câu 2. Giải phương trình 2
sin 3x  cos 3x  1  0
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ Câu 3.
Giải phương trình cos 4x  3 sin 2x  2  0
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ Câu 4. Giải phương trình 2 tan x   3   1 tan x  3  0
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ 1 Câu 5. Giải phương trình  cot 2x  3 2 sin 2x
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ Câu 6. Giải phương trình 4 2
4 sin x  12 cos x  7
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
GV: TUẤN DUY – THPT Gia Định 21 LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11 Câu 7. Giải phương trình 4
cos 2x  3 cos x  4  0
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________ Câu 8.
Giải phương trình cos 4x  12 sin x cos x  5  0
___________________________ ___________________________
___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ Câu 9. Giải phương trình 2
2 cos 3x cos x  4 sin 2x  1  0
___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________
Câu 10. Giải phương trình 2
cos 5x.cos x  cos 4x.cos 2x  3 cos x  1
___________________________ ___________________________
___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
Câu 11. Giải phương trình 4 4
cos x  sin x  cos 4x  0
___________________________ ___________________________
___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
GV: TUẤN DUY – THPT Gia Định 22 LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11
Câu 12. Giải phương trình 4 4
sin x  cos x  sin x cos x  0
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ 15 1
Câu 13. Giải phương trình 6 6
cos x  sin x  cos 2x  8 2
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
Dạng 2: Phương trình đưa về bậc hai Phương pháp: Dạng
Đặt ẩn phụ Chú ý  1     1  2 a sin x   b   sin x     c  0  2       sin x   sin x   1     1  2 a cos x   b   cos x     c  0  2       cos x   cos x  a  2 2
tan x  cot x  b tan x  cotx  c  0 Các ví dụ  1   1     
Câu 14. Giải phương trình 2 4 sin x    4 sin x    7  0  2       sin x   sin x 
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
GV: TUẤN DUY – THPT Gia Định 23 LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11  4   2     
Câu 15. Giải phương trình 2 2cos x    9
 cos x  1  0  2       cos x  cos x 
___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________
Câu 16. Giải phương trình  2 3 tan x cot 
x   4tan x  cotx  2  0
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________
Dạng 3: Phương trình đối xứng – phản đối xứng Phương pháp:          
● sin a  cos a  2 sin a     a  a  a     ● sin cos 2 sin    4   4           
● cos a  sin a  2 cos a     a  a  a     ● cos sin 2 cos    4   4  Dạng Đặt ẩn phụ Điều kiện
a sin x  cosx b sin x.cosx c  0
a sin x  cos x b sin x.cos x  c  0
a sin x  cosx b sin x.cosx c  0
a sin x  cos x  b sin x. cos x  c  0
GV: TUẤN DUY – THPT Gia Định 24 LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11 Các ví dụ
Câu 17. Giải phương trình 2 sin 2x  3 3 sin x  cos x   5  0
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
Câu 18. Giải phương trình 2 sin x  cos x  3 sin 2x  2  0.
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
Câu 19. Giải phương trình cos x  sin x  2 sin 2x  1
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ BÀI TẬP RÈN LUYỆN
Bài 1: Giải các phương trình sau x 1. 2
4 cos 2x  21  3cos2x  3  0 2. 2
cos 2x  3 cos x  4 cos 2 x 3. 2
cos 2x  3 cos x  4 cos 4. 2
cos 4x  12 sin x 1  0 2  5  7     5. sin 2  x    3 cos x     1  2 sin x  x  x  x   6. 4 6 sin cos 2 4 sin 0  2     2 
GV: TUẤN DUY – THPT Gia Định 25 LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11 7. x     x  2 5 sin 2 3 1 sin tan x 8. 3 3
cos 8x  sin x cos x  cos x sin x 1  0 9.   x  4 4 5 1 cos
 2  sin x  cos x 10. 6 2
3 cos 4x  8 cos x  2 cos x  3  0 Bài 2: 1. Tìm x  5;2   
 nghiệm đúng phương trình 2
2 sin x  5 sin x  2  0
2. Tìm tất cả các nghiệm của phương trình 2 cos 2x  4 cos x  1  0 thỏa x  5
Bài 3: Giải các phương trình sau  1     1  1  1  2   2   1. 4 s  in x    4 s  in x    7  0  2. cos x   2cos x    1 2         sin x   sin x  2 cos x  cos x  1 1 5 1 1 10 3.  
tan x  cot x  1  0 4. cos x   sin x   2 2   sin x cos x 2 cos x sin x 3 1 1 2
5. cos x  sin x     sin x cos x 3
Bài 4: Giải các phương trình sau
1. sin x  cos x  7 sin 2x  1
2. sin 2x  2 2(sin x  cos x)  5
3. cos x  sin x  2 sin 2x  1
4. sin x cos x  sin x  cos x  1 3 5. 3 3
sin x  cos x  1  sin 2x 6. 3 3
cos x  sin x  cos 2x 2 7. 3 3
cos x  sin x  2 sin 2x  sin x  cos x
Bài 5: Giải các phương trình sau 11 3 1. 4 4
sin x  cos x   sin 2x 2. 4 4 2
sin  cos x  2 sin 2x  sin 2x  0 8 4 3. 6 6
sin x  cos x  sin 2x 4. 6 6 2
cos x  sin x  4 cos 2x 1 17 5. 8 8
sin x  cos x  6. 8 8 2
sin x  cos x  cos 2x 8 16   
1  sin x  cos 2x sin x        5  4  1 7. 8 8
sin x  cos x  2 10 10
sin x  cos x  cos 2x 8.  cos x 4 1  tan x 2 6 6 6 6 sin x  cos x 1
2cos x  sin x  sin x cos x 9.  tan 2x 10.  0 2 2 cos x  sin x 4 2  2 sin x
GV: TUẤN DUY – THPT Gia Định 26 LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11
BÀI 4: PHƯƠNG TRÌNH CỔ ĐIỂN Cơ sở 1. Công thức cộng:
_________________________________________________________
_________________________________________________________
_________________________________________________________
_________________________________________________________ X   sin   2. Nếu 2 2
X Y  1 thì luôn tồn tại góc  sao cho  Y   cos  
3. Các công thức nhân đôi, hạ bậc, nhân ba, tổng thành tích và tích thành tổng.
Dạng 1: a sin u  b cos u  c Điều kiện có nghiệm: 2 2 2
a  b  c Phương pháp:
_______________________________________________________
_______________________________________________________
_______________________________________________________
_______________________________________________________
_______________________________________________________
_______________________________________________________
_______________________________________________________
_______________________________________________________
 Chú ý: Dạng a sin u b cos u  c giải tương tự Các ví dụ Câu 1.
Giải phương trình 3 sin x  cos x  1
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ Câu 2.
Giải phương trình 3 cos 2x  sin 2x   2
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
GV: TUẤN DUY – THPT Gia Định 27 LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11           Câu 3.
Giải phương trình cos 3x 
  3 sin 3x    1   4     4 
___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ Câu 4.
Giải phương trình 3 sin x  4 cos x  5
___________________________ ___________________________
___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ 3 Câu 5.
Giải phương trình 3 sin x  3 cos 3x  1  4 sin x
___________________________ ___________________________
___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________ Câu 6.
Tìm tất cả các nghiệm của phương trình  x  x 2 sin cos
 3 cos 2x  2 thỏa x  3
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________
GV: TUẤN DUY – THPT Gia Định 28 LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11
Dạng 2: a sin u  b cos u  c sin v Điều kiện: 2 2 2
a  b  c Phương pháp:
_______________________________________________________
_______________________________________________________
_______________________________________________________
_______________________________________________________
_______________________________________________________
_______________________________________________________
_______________________________________________________
_______________________________________________________     
Chú ý: Dạng a sin u  b cos u  c cos v  .
c sin   v  giải tương tự  2  Các ví dụ Câu 7.
Giải phương trình sin 3x  3 cos 3x  2 sin 2x
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ Câu 8.
Giải phương trình sin 3x  3 cos 3x  2 cos 5x
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
GV: TUẤN DUY – THPT Gia Định 29 LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11      Câu 9.
Giải phương trình 3 sin 7x  cos 7x  2 sin 5  x     6 
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________
Câu 10. Giải phương trình 3 cos 5x  2 sin 3x. cos 2x  sin x  0
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________
Dạng 3: a sin u  b cos u  c sin v  d cos v Điều kiện: 2 2 2 2
a  b  c  d Phương pháp:
_______________________________________________________
_______________________________________________________
_______________________________________________________
_______________________________________________________
_______________________________________________________
_______________________________________________________
_______________________________________________________
_______________________________________________________
_______________________________________________________
_______________________________________________________
_______________________________________________________
GV: TUẤN DUY – THPT Gia Định 30 LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11 Các ví dụ
Câu 11. Giải phương trình sin x  cos 2x  sin 2x  cos x
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
Câu 12. Giải phương trình sin 7x  cos 2x 
3(sin 2x  cos 7x)
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
Câu 13. Giải phương trình 3(sin 2x  cos 3x )  cos 2x  sin 3x
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ BÀI TẬP RÈN LUYỆN
Bài 1: Giải các phương trình sau 2  x x   
1. cos 7x  3 sin 7x   2 2. sin
 cos   3 cos x  2   2 2 
3. 5 sin 2x  12 cos 2x  13
4. 3 sin x  4 cos x  3 2
5. 2 sin x  3 sin 2x  3 6. 2 cos 2x 
6 cosx  sinx 3 3
7. 3 sin 3x  3 cos 9x  1  4 sin 3x
8. 4 sin x 1  3 sin x  3 cos 3x      9.  4 4
4 sin x  cos x   3 sin 4x  2 10. 2 cos 2
 x    4 sin x cos x  1  0   6 
GV: TUẤN DUY – THPT Gia Định 31 LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11
11. cos 7x cos 5x  3 sin 2x  1  sin 7x sin 5x
Bài 2: Giải các phương trình sau     
1. sin 3x  3 cos 3x  2 sin 2x
2. 3 sin 7x  cos 7x  2 sin 5  x     6           
3. cos x  3 sin x  2 cos 2  x    0  x  x   x     4. 3 cos 2 sin 2 2 sin 2 2 2    3   6 
5. 3 cos 5x  2 sin 3x cos 2x  sin x  0
6. sin 8x  cos 6x 
3 sin 6x  cos 8x  3   
7. cos 3x  sin x 
3 cosx  sin 3x
8. 4 sin 2x  3 cos 2x  5 cos 3x    0   2 
Bài 3: Giải các phương trình sau 3  3 cos 2x 1 1.  cos x 2. tan x  3  2 sin x cos x 3 1
12sinxcosx 3. 8 sin x   4.  3 cos x sin x
1 2sinx1 sinx cos x  sin 2x 2 5.  3
6. cos x  3 sin x  2
2 cos x  sin x  1
cos x  3 sin x  1
7. cos 2x  3 sin 2x  3 sin x  cos x  4  0 8. x  x x  x   3 sin cos sin 2 3 cos 3
2 cos 4x  sin x  3 3
9. 4 sin x cos 3x  4 cos x sin 3x  3 3 cos 4x  3 10.  6 6
8 sin x  cos x  3 3 cos 2x  11  3 3 sin 4x  9 sin 2x Bài 4:
1. Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn  10;10    để phương trình         sin x     3 cos x       2m  vô nghiệm.  3     3 
sin x  2 cos x  1 2. Cho hàm số y    1
cos x  sin x  2
a. Chứng minh tập xác định của hàm số   1 là  .
b. Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số   1 trên  .
2 sin 2x  cos 2x 3. Cho hàm số y 
. Gọi M và m lần lượt là GTLN và GTNN của hàm số đã cho.
sin 2x  cos 2x  3
Tính S  M  m .
GV: TUẤN DUY – THPT Gia Định 32 LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11
BÀI 5: PHƯƠNG TRÌNH ĐẲNG CẤP Cơ sở Công thức cơ bản: sina 1 1. tan a  2. 2  1  tan a cosa 2 cos a
Dạng 1: Phương trình đẳng cấp bậc hai 2 2
a sin u  b sin u cos u  c cos u  d   
Phương pháp: Xét 2 trường hợp: Trường hợp 1:
_______________________________________________________
_______________________________________________________
_______________________________________________________
_______________________________________________________
_______________________________________________________ Trường hợp 2:
_______________________________________________________
_______________________________________________________
_______________________________________________________
_______________________________________________________
_______________________________________________________ Các ví dụ Câu 1. Giải phương trình 2 2
sin x  5 sin x cos x  6 cos x  0
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ Câu 2. Giải phương trình 2 2
3 sin 2x  sin 2x cos 2x  4 cos 2x  2
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
GV: TUẤN DUY – THPT Gia Định 33 LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11 Câu 3. Giải phương trình 2 2
2 sin 3x  3 sin 6x  4 cos 3x  2
___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ Câu 4. Giải phương trình 2 2
6 sin 2x  sin 4x  8 cos 2x  4
___________________________ ___________________________
___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ Câu 5. Giải phương trình 2 2
3 sin x  5 cos x  2 cos 2x  4 sin 2x
___________________________ ___________________________
___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________ Câu 6.
Giải phương trình : 1  3 sin 2x  2 tan x
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ Câu 7.
Giải phương trình : 1  3 tan x  2 sin 2x
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________
GV: TUẤN DUY – THPT Gia Định 34 LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11
Dạng 2: Phương trình đẳng cấp bậc ba 3 2 2 3
a sin u  b sin u cos u  c sin u cos u  d cos u  e sin u  f cos u   
Phương pháp: Xét 2 trường hợp: Trường hợp 1:
_______________________________________________________
_______________________________________________________
_______________________________________________________
_______________________________________________________
_______________________________________________________
_______________________________________________________
_______________________________________________________ Trường hợp 2:
_______________________________________________________
_______________________________________________________
_______________________________________________________
_______________________________________________________
_______________________________________________________
_______________________________________________________
_______________________________________________________ Các ví dụ Câu 8. Giải phương trình 3
2 cos x  sin 3x
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ Câu 9. Giải phương trình 3 3 2
4 sin x  3 cos x  3 sin x  sin x cos x  0
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
GV: TUẤN DUY – THPT Gia Định 35 LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11
Câu 10. Giải phương trình 2
sin x  3 tan x  cos x 4 sin x  cos x
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________
Câu 11. Giải phương trình 2
sin x tan x  
1  3 sin x cos x  sin x  3
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________
Câu 12. Giải phương trình  3 3
4 sin x  cos x  cos x  3 sin x
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________    
Câu 13. Giải phương trình 3 2 2 cos x
    3 cos x  sin x  0   4 
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________
GV: TUẤN DUY – THPT Gia Định 36 LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11 BÀI TẬP RÈN LUYỆN
Bài 1: Giải các phương trình sau 1. 2 2
2 cos x  6 sin x cos x  6 sin x  1 2. 2 2
cos x  3 sin 2x  1  sin x 3. 2 2
cos x  sin x cos x  2 sin x  1  0 4. 2 2
9 sin x  30 sin x cos x  25 cos x  25 5.  x  x 2 2 2 sin cos
cos x  3  2 cos x 6. 2
sin 2x  2 sin x  2 cos 2x
Bài 2: Giải các phương trình sau 1. 3 2 2
3 sin x  2 sin x cos x  sin x cos x 2. 3
6 sin x  2 cos x  5 sin 2x cos x 3. 3
sin x  4 sin x  cos x  0 4. 3 3
sin x  cos x  sin x  cos x 5. 3 2 2 3
sin x  4 sin x cos x  5 sin x cos x  2 cos x  0
Bài 3: Giải các phương trình sau 5 sin 4x cos x 1. 3
6 sin x  2 cos x 
2. tan x  cot x  2 sin 2x  cos 2x  2 cos 2x     3. 2
sin x tan x  
1  3 sin x cos x  sin x  3 4. 3 8 cos x     cos 3x   3  5. 2 2
tan x. sin x  2 sin x  3cos 2x  sin x.cos x 6. 3 3 x  x   5 5 cos sin
2 cos x  sin x
GV: TUẤN DUY – THPT Gia Định 37 LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11
BÀI 6: PHƯƠNG TRÌNH ĐƯA VỀ DẠNG TÍCH
1. Phương trình tổng quát a sin 2x  b cos 2x  c sin x  d cos x  e  0 Cơ sở 1. Công thức nhân đôi:
_________________________________________________________
_________________________________________________________
_________________________________________________________
_________________________________________________________
2. Phân tích bậc hai thành nhân tử:
_________________________________________________________
_________________________________________________________ 3. Phương trình tích:
_________________________________________________________ Phương pháp
_________________________________________________________
_________________________________________________________
_________________________________________________________
_________________________________________________________
_________________________________________________________ Các ví dụ Câu 1.
Giải phương trình sin 2x  cos 2x  sin x  5 cos x  3  0
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________ Câu 2.
Giải phương trình cos 2x  3 sin 2x  9 sin x  6 cos x  8
___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________
GV: TUẤN DUY – THPT Gia Định 38 LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11 Câu 3.
Giải phương trình cos 4x  3 sin 4x  9 cos 2x  3 sin 2x  5  0
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ Câu 4. Giải phương trình  6 6
8 sin x  cos x 3 3 cos2x  11 3 3 sin 4x  9 sin 2x
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________     Câu 5.
Giải phương trình 2 sin 4x 
  2 sin x cos x  3 cos 2x  2   4 
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
2. Phương trình đưa về dạng tích Cơ sở 1. Công thức hạ bậc:
__________________________________________________________
__________________________________________________________
GV: TUẤN DUY – THPT Gia Định 39 LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11 2. Công thức biến đổi Tổng thành tích Tích thành tổng
________________________ ________________________
________________________ ________________________
________________________ ________________________
________________________ ________________________ 3. Phương trình tích:
_________________________________________________________ Phương pháp
Bước 1: Sử dụng các công thức hạ bậc, biến đổi tổng thành tích, tích thành tổng để xuất hiện nhân tử chung
Bước 2: Nhóm hạng tử và đưa về phương trình tích hoặc các dạng phương trình đã biết. Các ví dụ Câu 6.
Giải phương trình sin 7x sin x  sin 5x sin 3x
___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ Câu 7.
Giải phương trình sin 5x cos 3x  sin 9x cos 7x
___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ Câu 8.
Giải phương trình cos x cos 3x  sin 2x sin 6x  sin 4x sin 6x
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________
GV: TUẤN DUY – THPT Gia Định 40 LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11 Câu 9.
Giải phương trình sin x  sin 2x  sin 3x  0
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________    
Câu 10. Tìm tổng các nghiệm trong khoảng 0;   x  x   x  của phương trình 2 2 sin 3 sin 7 1 sin 5  2 
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
Câu 11. Giải phương trình 1  cos x  cos 2x  cos 3x  0
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
Câu 12. Giải phương trình 1  sin x  sin 2x  cos x  cos 2x  cos 3x
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
GV: TUẤN DUY – THPT Gia Định 41 LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11 3
Câu 13. Giải phương trình 2 2 2
sin x  sin 2x  sin 3x  2
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________
Câu 14. Giải phương trình 2 2 2 2
sin x  sin 3x  cos 2x  cos 4x
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________
Câu 15. Giải phương trình 4
8 cos x  1  cos 4x
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________ BÀI TẬP RÈN LUYỆN
Bài 1: Giải các phương trình sau
1. sin 2x  cos 2x  sin x  3 cos x  2
2. sin 2x  2 cos 2x  sin x  4 cos x  1
3. 9 sin x  6 cos x  3 sin 2x  cos 2x  8
4. 2 2 sin 2x  cos 2x  7 sin x  2 2 cos x  4  0 5. 2 cos x  
1 2 sin x  cosx  sin 2x  sin x 6.  x   x  x   2 2 sin 1 3 cos 4 2 sin 4  4 cos x  3
sin 2x  2 cos x  sin x  1
7. 1  sin x  cos x  sin 2x  cos 2x  0 8.  0 tan x  3
GV: TUẤN DUY – THPT Gia Định 42 LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11
3 sin 2x  cos 2x  5 sin x  2  3cosx  3  3 9.  1 2 cos x  3
Bài 2: Giải các phương trình sau
1. sin 4x sin 5x  sin 3x sin 4x  sin 2x sin x
2. sin x cot 5x  cos 9x 3. 3
4 sin 3x cos 2x  1  6 sin x  8 sin x
4. 2 cos x cos 2x cos 3x  7  7 cos 2x
5. cos 22x  3 cos 18x  3 cos 14x  cos 10x  0
6. cos x  cos 2x  cos 3x  cos 4x  0 7. 2
2 sin 2x  sin 7x  1  sin x
8. sin x  sin 2x  sin 3x  1  cos x  cos 2x
sin x  sin 2x  sin 3x
9. sin x  sin 2x  sin 3x  cos x  cos 2x  cos 3x 10.  3
cos x  cos 2x  cos 3x
Bài 3: Giải các phương trình sau 1. 2 2 2
cos x  cos 2x  cos 3x  1 2. 2 2 2 2
cos x  cos 2x  cos 3x  cos 4x  2 3 3. 2 2 2
sin x  sin 2x  sin 3x  . 4. 2 2 2 2
sin 3x  sin 4x  sin 5x  sin 6x 2 5. 2 2 2 2
sin x  sin 3x  cos 2x  cos 4x 6. 2 2 2 2
sin 3x  cos 4x  sin 5x  cos 6x 7. 2 2 2
sin x  sin 2x  sin 3x  2 8. 2 2 2
sin x  cos 2x  cos 3x  5x    9x
9. cos 3x  sin 7x  2sin2 2     2 cos  x x  x x  x  10. 3 3 3 sin cos 3 cos sin 3 sin 4  4 2  2 11. 3 3 x  x   5 5 sin cos
2 sin x  cos x  12. 6 6 x  x   8 8 sin cos
2 sin x  cos x  5     1 1 13. 8 8
sin x  cos x  2 10 10
sin x  cos x  cos 2x 14. 2 2 sin x      4  4  sin x cos x
GV: TUẤN DUY – THPT Gia Định 43 LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11
BÀI 7: MỘT SỐ PHƯƠNG PHÁP KHÁC
1. Phương pháp đặt ẩn số mới Cơ sở
1. Công thức cộng: _______________________________________________
_________________________________________________________
_________________________________________________________
2. Công thức nhân đôi, nhân ba: ________________________________________
_________________________________________________________
_________________________________________________________ Phương pháp
Đặt ẩn mới t để đưa về phương trình lượng giác chứa các cung t, 2t, 3t... Các ví dụ         Câu 1. Giải phương trình sin 2
 x    5 sin x     cos 3x   3     6 
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________   6   Câu 2.
Giải phương trình 32 cos x
    sin 6x  1   4 
___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________
GV: TUẤN DUY – THPT Gia Định 44 LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11     Câu 3. Giải phương trình 3 8 cos x     cos 3x   3 
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ 3 x  1   3x      Câu 4. Giải phương trình sin     sin     10 2 2 10 2 
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ 3x   x      Câu 5. Giải phương trình sin     3 sin      2 4     4 2
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
GV: TUẤN DUY – THPT Gia Định 45 LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11 2. Phương pháp đánh giá Cơ sở A   B A   0     A   0  A      1. 2 2
A  B  0  
2. A  B  0   3. A      B   0         B  B 0  B      Phương pháp
Biến đổi phương trình về các dạng 1, 2, 3 nêu trên. Các ví dụ     Câu 6.
Giải phương trình sin x
    cos 8x  2   4 
___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________ Câu 7. Giải phương trình 2 2 2 2
cos 4x  cos 8x  2  sin 12x  sin 16x
___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________ Câu 8. Giải phương trình 2 2
4 cos x  3 tan x  4 3 cos x  2 3 tan x  4  0
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________
GV: TUẤN DUY – THPT Gia Định 46 LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11 Câu 9. Giải phương trình  x  x 2 cos 4 cos 2  5  sin 3x
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
BÀI 8: HÀM SỐ LƯỢNG GIÁC A. TÓM TẮT LÝ THUYẾT I. Hàm số lượng giác
1. Hàm số sin: là quy tắc đặt tương ứng mỗi số thực x   với số thực sin x  1;1     y :   1;1      x  sin x
Kí hiệu: y  sin x
 Tập xác định: D    Tập giá trị: T  1;1      sin  x
   sin x, x   nên y  sin x là hàm số lẻ.
2. Hàm số cos: là quy tắc đặt tương ứng mỗi số thực x   với số thực cos x  1;1     y :   1;1      x  cos x
Kí hiệu: y  cos x
 Tập xác định: D    Tập giá trị: T  1;1      cos x
   cos x, x   nên y  cos x là hàm số chẵn. sin x
3. Hàm số tan: được xác định bởi công thức y  tan x  cos x     
Tập xác định: D   \   k  2   
 Tập giá trị: T    tan x
   tan x, x   nên y  tan x là hàm số lẻ. cos x
4. Hàm số cot: được xác định bởi công thức y  cot x  sin x
 Tập xác định: D   \ k
 Tập giá trị: T    cot x
   cotx, x   nên y  tan x là hàm số lẻ.
GV: TUẤN DUY – THPT Gia Định 47 LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11
II. Sự biến thiên và đồ thị của hàm số lượng giác 1. Hàm tuần hoàn
Cho hàm số y  f x  xác định trên D . x  T  ,
D x T  D 
Nếu tồn tại số dương T sao cho x  D, ta có:  
thì ta nói f tuần hoàn f
 x T   f x  
Số nhỏ nhất trong các số T nói trên gọi là chu kỳ tuần hoàn của hàm f 2. Hàm số sin:
Xét hàm số y  sin x trên đoạn 0; 2   . Bảng biến thiên:
Hàm số y  sin x tuần hoàn với chu kỳ 2 Đồ thị: 3. Hàm số cos:
Xét hàm số y  cos x trên đoạn 0; 2   . Bảng biến thiên:
Hàm số y  cos x tuần hoàn với chu kỳ 2 Đồ thị: 3. Hàm số tan:   
Xét hàm số y  tan x trên đoạn  ;   2 2    Bảng biến thiên:   
Hàm số tăng trên đoạn  ;  
và tuần hoàn với chu kỳ  2 2    Đồ thị:
GV: TUẤN DUY – THPT Gia Định 48 LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11 y x     3  O     3 2 2 2 2 4. Hàm số cot:   
Xét hàm số y  cot x trên đoạn  ;   2 2    Bảng biến thiên:   
Hàm số giảm trên đoạn  ;  
và tuần hoàn với chu kỳ  2 2    Đồ thị: y    2   3  O   3 2 x  2 2 2 2 2
Lưu ý: Các hàm số y  sin ax  b; y  cosax  b tuần hoàn với chu kỳ a 
Các hàm số y  tan ax  b; y  cotax  b tuần hoàn với chu kỳ a
Dạng 1. Tìm tập xác định của hàm số lượng giác Phương pháp
 A có nghĩa  A  0 A 
có nghĩa  B  0 B A 
có nghĩa  B  0 B
GV: TUẤN DUY – THPT Gia Định 49 LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11 Các ví dụ 1  cos x
Câu 10. Tìm tập xác định của hàm số y  sin 2x
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________    
Câu 11. Tìm tập xác định của hàm số y  tan 3x     6 
___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________    
Câu 12. Tìm tập xác định của hàm số y  cot 2  x     4 
___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________ 1  cos x
Câu 13. Tìm tập xác định của hàm số y  1  cos x
___________________________ ___________________________
___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ 1 1
Câu 14. Tìm tập xác định của hàm số y   sin x cos x
___________________________ ___________________________
___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________
GV: TUẤN DUY – THPT Gia Định 50 LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11
Câu 15. Tìm tập xác định của hàm số y  tan 2x  cot 2x
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
sin x  3 cos x
Câu 16. Tìm tập xác định của hàm số y 
cos x  3 sin x
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
Dạng 2: Xét tính chẵn lẻ của hàm số lượng giác Cơ sở
1. Tập D đối xứng  x  D  x   D
x  D  x   D  2.   y  f x    là hàm số chẵn f   x
   f x 
x  D  x   D  3.   y  f x    là hàm số lẻ f  x    f   x  Các ví dụ
Câu 17. Xét tính chẵn lẻ của hàm số y  sin 2x
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ 1
Câu 18. Xét tính chẵn lẻ của hàm số y  cos x
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
GV: TUẤN DUY – THPT Gia Định 51 LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11
Câu 19. Xét tính chẵn lẻ của hàm số 2 y  tan x
___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________
Câu 20. Xét tính chẵn lẻ của hàm số y  tan 2x  sin 3x
___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________
Câu 21. Xét tính chẵn lẻ của hàm số y  2 sin x  3
___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
Dạng 3: Tìm chu kỳ tuần hoàn của hàm số lượng giác Cơ sở 2
1. Các hàm số y  sin ax  b; y  cosax  b tuần hoàn với chu kỳ a 
2. Các hàm số y  tan ax  b; y  cotax  b tuần hoàn với chu kỳ a
3. Hàm số y  f x  có chu kỳ T , hàm số g x  có chu kỳ T thì hàm số y  f x   g x  có chu kỳ T 1 2
với T là số dương nhỏ nhất chia hết cho T và T 1 2 Các ví dụ
Câu 22. Tìm chu kỳ tuần hoàn của hàm số y  sin 2x
___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________
GV: TUẤN DUY – THPT Gia Định 52 LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11    
Câu 23. Tìm chu kỳ tuần hoàn của hàm số y  cos 3x     6 
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
Câu 24. Tìm chu kỳ tuần hoàn của hàm số y  cos 2x  tan 2x
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
Câu 25. Tìm chu kỳ tuần hoàn của hàm số y  cos 3x  cot 2x
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
Dạng 4: Tìm GTLN – GTNN của hàm số Cơ sở
1. 1  sin a  1 2. 1   cosa  1 3. 2 0  sin a  1 4. 2 0  cos a  1 Các ví dụ
Câu 26. Tìm GTLN – GTNN của hàm số y  2 sin x  3
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
Câu 27. Tìm GTLN – GTNN của hàm số y  1  3 cos 2x
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
GV: TUẤN DUY – THPT Gia Định 53 LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11
Câu 28. Tìm GTLN – GTNN của hàm số y  sin x  cos x
___________________________ ___________________________
___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________
Câu 29. Tìm GTLN – GTNN của hàm số y  sin 2x  3 cos 2x  1
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________
Câu 30. Tìm GTLN – GTNN của hàm số y  cos 2x  4 cos x  3
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________
Câu 31. Tìm GTLN – GTNN của hàm số y  cos 4x  4 sin 2x  1
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________
GV: TUẤN DUY – THPT Gia Định 54 LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11
LƯỢNG GIÁC TRONG ĐỀ THI 2002 – 2014
Bài 1 (ĐH A2002) Tìm nghiệm thuộc khoảng 0;2 của phương trình:  cos 3x sin 3x    5 5sin x     cos 2x  3  x  ;x   ĐS: 
1  2 sin 2x  3 3
Bài 2 (ĐH B2002) Giải phương trình: k k 2 2 2 2
sin 3x  cos 4x  sin 5x  cos 6x ĐS: x  ;x  k   9 2
Bài 3 (ĐH D2002) Tìm x thuộc đoạn 0;14 
 nghiệm đúng của phương trình:  3 5 7
cos 3x  4 cos 2x  3 cos x  4  0 ĐS: x  ;x  ;x  ;x  2 2 2 2
Bài 4 (ĐH A2003) Giải phương trình: cos 2x 1  2 cot x  1 
 sin x  sin 2x ĐS: x 
 k k   1  tan x 2 4
Bài 5 (ĐH B2003) Giải phương trình: 2 
cotx  tan x  4 sin 2x  ĐS: x  
 k k   sin 2x 3
Bài 6 (ĐH D2003) Giải phương trình: x    x  2 2 2
sin    tan x  cot  0 
x    k  x    k  ĐS: 2 ; 2 4  2 4
Bài 7 (ĐH A2004) Cho tam giác ABC không tù, thỏa mãn điều kiện
cos 2A  2 2 cos B  2 2 cosC  3
Tính ba góc của tam giác ABC. ĐS: A  90 ;
 B  C  45
Bài 8 (ĐH B2004) Giải phương trình:  5 x     x  2 5 sin 2 3 1 sin tan x ĐS: x   k ;  x   k2 6 6
Bài 9 (ĐH D2004) Giải phương trình:    2 cos x  
1 2 sin x  cos x  sin 2x  sin x ĐS: x    k2 ;
 x    k 3 4
Bài 10 (ĐH A2005) Giải phương trình: k 2 2
cos 3x cos 2x  cos x  0 ĐS: x  k   2
Bài 11 (ĐH B2005) Giải phương trình: 2 
1  sin x  cos x  sin 2x  cos 2x  0 ĐS: x    k2 ;
 x    k 3 4
Bài 12 (ĐH D2005) Giải phương trình:         3  4 4
cos x  sin x  cos x
  sin 3x     0  x   k k    ĐS:    4     4  2 4
Bài 13 (ĐH A2006) Giải phương trình:  6 6
2 cos x  sin x  sin x cos x 5  0 ĐS: x 
 k2 k   2  2 sin x 4
Bài 14 (ĐH B2006) Giải phương trình:  x   5
cot x  sin x 1
  tanx tan   4  x   k ;  x   k  ĐS:  2 12 12
Bài 15 (ĐH D2006) Giải phương trình:
GV: TUẤN DUY – THPT Gia Định 55 LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11 2
cos 3x  cos 2x  cos x  1  0 ĐS: x  k ;  x    k2 3
Bài 16 (ĐH A2007) Giải phương trình:    2  x x   2 1 sin cos
1  cos xsin x  1  sin 2x ĐS: x  k2 ;  x   k2 ;
 x    k 2 4
Bài 17 (ĐH B2007) Giải phương trình  k  k2 5 k2 2
2 sin 2x  sin 7x 1  sin x ĐS: x   ;x   ;x   8 4 18 3 18 3
Bài 18 (ĐH D2007) Giải phương trình: 2  x x    
sin  cos   3 cos x  2  x 
 k  x    k   ĐS: 2 ; 2  2 2  2 6
Bài 19 (ĐH A2008) Giải phương trình: 1 1 7    5   4 sin   x ĐS: x    k ;
 x    k ;  x   k sin x     3     4  4 8 8 sin x     2 
Bài 20 (ĐH D2008) Giải phương trình:  k  3 3 2 2
sin x  3 cos x  sin x cos x  3 sin x cos x ĐS: x  
;x    k 4 2 3
Bài 21 (ĐH D2008) Giải phương trình: 2 
2 sin x 1  cos 2x  sin 2x  1  2 cos x ĐS: x    k ;  x   k 3 4
Bài 22 (ĐH A2009) Giải phương trình:
12sinxcosx  k2   ĐS: x    k    x   x  3 1 2 sin 1 sin 18 3
Bài 23 (ĐH B2009) Giải phương trình:   k2 x  x x  x   3 sin cos sin 2 3 cos 3
2 cos 4x  sin x ĐS: x    k2 ;  x   6 42 7
Bài 24 (ĐH D2009) Giải phương trình:  k  k
3 cos 5x  2 sin 3x cos 2x  sin x  0 ĐS: x   ;x    18 3 6 2
Bài 25 (ĐH A2010) Giải phương trình:   
1  sin x  cos 2x sin x       4  1  7  cos x ĐS: x    k2 ;  x   k2 1  tan x 2 6 6
Bài 26 (ĐH B2010) Giải phương trình:   k
sin 2x  cos 2x cos x  cos 2x  sin x  0 ĐS: x   k   4 2
Bài 27 (ĐH D2010) Giải phương trình  5
sin 2x  cos 2x  3 sin x  cos x  1  0 ĐS: x   k2 ;  x   k2 6 6
Bài 28 (ĐH A2011) Giải phương trình:
1  sin 2x  cos 2x  
 2 sin x sin 2x ĐS: x   k ;  x   k2 2 1  cot x 2 4
Bài 29 (ĐH B2011) Giải phương trình:
GV: TUẤN DUY – THPT Gia Định 56 LƯỢNG GIÁC ĐỀ CƯƠNG TOÁN 11   k2
sin 2x cos x  sin x cos x  cos 2x  sin x  cos x ĐS: x   k2 ;  x   2 3 3
Bài 30 (ĐH D2011) Giải phương trình:
sin 2x  2 cos x  sin x  1   0 ĐS: x 
 k2 k   3  tan x 3
Bài 31 (ĐH A2012) Giải phương trình:  2
3 sin 2x  cos 2x  2 cos x  1 ĐS: x   k ;  x  k2 ;  x   k2 2 3
Bài 32 (ĐH B2012) Giải phương trình: 2 k2
2cosx  3 sin xcosx  cosx  3 sin x  1 ĐS: x   k2 ;  x  k   3 3
Bài 33 (ĐH D2012) Giải phương trình:  k 7 
sin 3x  cos 3x  sin x  cos x  2 cos 2x ĐS: x   ;x   k2 ;  x    k2 4 2 12 12
Bài 34 (ĐH A2013) Giải phương trình:    
1  tan x  2 2 sin x      
x    k x    k   ĐS: ; 2  4  4 3
Bài 35 (ĐH B2013) Giải phương trình:  k2  k2 2
sin 5x  2 cos x  1 ĐS: x    ;x    6 3 14 7
Bài 36 (ĐH D2013) Giải phương trình:  k  7
sin 3x  cos 2x  sin x  0 ĐS: x  
;x    k2 ;  x   k2 4 2 6 6
Bài 37 (ĐH A2014) Giải phương trình 
sin x  4 cos x  2  sin 2x ĐS: x  
 k2 k   3
Bài 38 (ĐH B2014) Giải phương trình: 3
2 sin x  2 cos x  2  sin 2x ĐS: x  
 k2 k   4
GV: TUẤN DUY – THPT Gia Định 57 QUAN HỆ SONG SONG ĐỀ CƯƠNG TOÁN 11
PHẦN 2: HÌNH HỌC KHÔNG GIAN
BÀI 1: ĐẠI CƯƠNG VỀ ĐƯỜNG THẲNG VÀ MẶT PHẲNG A. TÓM TẮT LÝ THUYẾT 1. Khái niệm
 Mặt phẳng: là đối tượng cơ bản của hình học không gian. Mặt phẳng được biểu diễn bằng một hình bình
hành hoặc một miền góc và ghi tên của mặt phẳng vào một góc của hình biểu diễn
Để kí hiệu mặt phẳng, ta dùng chữ cái in hoa hoặc chữ Hi Lạp đặt trong dấu ngoặc   . Ví dụ: mặt
phẳng P , mặt phẳng .
 Điểm thuộc mặt phẳng: Cho điểm A và mặt phẳng P .
Khi điểm A thuộc mặt phẳng P , ta nói A nằm trong P  hay P  chứa A . Kí hiệu: A  P 
Khi điểm A không thuộc mặt phẳng P , ta nói A nằm ngoài P  hay P  không chứa A . Kí hiệu : A  P 
 Đường thẳng nằm trong mặt phẳng: Cho đường thẳng d và mặt phẳng P . Khi mọi điểm thuộc d đều
nằm trong P , ta nói d nằm trong P  hay P  chứa d . Kí hiệu: d  P 
2. Hình biểu diễn của một hình không gian
Để nghiên cứu hình học không gian, người ta thường vẽ các hình không gian lên giấy, lên bảng. Hình vẽ đó
gọi là hình biểu diễn của một hình không gian.
 Một vài hình biểu diễn của hình lập phương
 Một vài hình biểu diễn của hình tứ diện
GV: TUẤN DUY – THPT Gia Định 58 QUAN HỆ SONG SONG ĐỀ CƯƠNG TOÁN 11
3. Quy tắc biểu diễn hình không gian
 Hình biểu diễn của đường thẳng là đường thẳng, của đoạn thẳng là đoạn thẳng.
 Hình biểu diễn của hai đường thẳng song song là hai đường thẳng song song, của hai đường thẳng cắt
nhau là hai đường thẳng cắt nhau.
 Hình biểu diễn phải giữ nguyên quan hệ thuộc giữa điểm và đường thẳng.
 Dùng nét liền để biểu diễn cho đường nhìn thấy, nét đứt biểu diễn cho đường bị che khuất
4. Các tính chất thừa nhận
Tính chất 1: Có một và chỉ một đường thẳng đi qua hai điểm phân biệt.
Tính chất 2: Có một và chỉ một mặt phẳng đi qua ba điểm không thẳng hàng.
Tính chất 3: Nếu một đường thẳng có hai điểm phân biệt cùng thuộc một mặt phẳng thì đường thẳng đó
nằm hoàn toàn trên mặt phẳng.
M  AB  P  M  P
Tính chất 4: Có bốn điểm không cùng thuộc một mặt phẳng.
Tính chất 5: Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng có một đường thẳng chung duy
nhất chứa tất cả các điểm chung của hai mặt phẳng đó.
Đường thẳng chung đó được gọi là giao tuyến của hai mặt phẳng
Kí hiệu:   P   Q
Tính chất 6: Trên mỗi mặt phẳng các, kết quả đã biết trong hình học phẳng đều đúng.
5. Cách xác định mặt phẳng
Một mặt phẳng hoàn toàn xác định khi biết:
 Nó đi qua ba điểm không thẳng hàng.
 Nó đi qua một điểm và một đường thẳng không đi qua điểm đó.
 Nó chứa hai đường thẳng cắt nhau. Các kí hiệu:
 ABC  là kí hiệu mặt phẳng đi qua ba điểm không thẳng hàng , A , B C ( h1)
 M,d là kí hiệu mặt phẳng đi qua d và điểm M  d (h2)
 d ,d là kí hiệu mặt phẳng xác định bởi hai đường thẳng cắt nhau d ,d (h3) 1 2  1 2 M d2 C A d α B α d1 α (h1) (h2) (h3)
GV: TUẤN DUY – THPT Gia Định 59 QUAN HỆ SONG SONG ĐỀ CƯƠNG TOÁN 11
6. Hình chóp và hình tứ diện
 Hình chóp: Trong mặt phẳng P  cho đa giác lồi AA ...A . Lấy điểm S nằm ngoài P . 1 2 n
Lần lượt nối S với các đỉnh A , A ,..., A ta được n tam giác SA A , SA A ,..., SA A . Hình gồm đa giác 1 2 n 1 2 2 3 n 1
A A ...A và n tam giác SA A ,SA A ,...,SA A được gọi là hình chóp , kí hiệu là S.A A ...A . 1 2 n 1 2 2 3 n 1 1 2 n
Ta gọi S là đỉnh, đa giác A A ...A là đáy , các đoạn SA , SA ,..., SA là các cạnh bên, A A , A A ,..., A A 1 2 n 1 2 n 1 2 2 3 n 1
là các cạnh đáy, các tam giác SA A , SA A ,..., SA A là các mặt bên. 1 2 2 3 n 1
 Hình tứ diện: Cho bốn điểm , A ,
B C, D không đồng phẳng. Hình gồm bốn tam giác ABC, ABD,
ACD và BCD được gọi là tứ diện ABCD .
Tứ diện có bốn mặt là các tam giác đều gọi là tứ diện đều
7. Thiết diện (hay mặt cắt):
Thiết diện của hình không gian H khi cắt bởi mặt phẳng P  là phần chung của H và P  Ví dụ:
 Thiết diện (mặt cắt) là:
 Thiết diện (mặt cắt) là:
GV: TUẤN DUY – THPT Gia Định 60 QUAN HỆ SONG SONG ĐỀ CƯƠNG TOÁN 11
MỘT SỐ HÌNH THƯỜNG GẶP Tứ diện ABCD
Hình chóp S .ABC
Hình chóp S .ABCD , đáy là tứ giác lồi, các cạnh
Hình chóp S .ABCD , đáy là hình bình hành đối không song song
Hình chóp S .ABCD , đáy là hình thang vuông
Hình chóp S .ABCD , đáy là hình thang tại A và D
MỘT SỐ KÍ HIỆU A  d
M  a  b A  
M  d   d  
    
A  d  
S    
GV: TUẤN DUY – THPT Gia Định 61 QUAN HỆ SONG SONG ĐỀ CƯƠNG TOÁN 11 B. CÁC DẠNG TOÁN
Vấn đề 1: Tìm giao tuyến của hai mặt phẳng Phương pháp:
Muốn tìm giao tuyến của hai mặt phẳng. Ta tìm hai điểm chung thuộc cả hai mặt phẳng.
Nối hai điểm chung đó được giao tuyến cần tìm. A   P  Q     B   P  
Q AB P Q  Các ví dụ Câu 1:
Cho tứ diện ABCD . Gọi M là trung điểm AB . Trên cạnh AC lấy điểm N sao cho AN  2NC
. Hãy xác định giao tuyến:
b. DMN   BCD ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
c. DMC   DNB
a. DMN   ABD ___________________________ ___________________________ ____________________________ ___________________________ ____________________________ ___________________________ ____________________________ ___________________________ ____________________________ ___________________________ ____________________________ ___________________________ Câu 2: Cho bốn điểm , A ,
B C, D không đồng phẳng. Trên cạnh AB, AC lấy các điểm M, N sao cho M, N
không là trung điểm của AB, AC . Gọi K là trung điểm AD . Tìm MNK   BCD ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
GV: TUẤN DUY – THPT Gia Định 62 QUAN HỆ SONG SONG ĐỀ CƯƠNG TOÁN 11 Câu 3:
Cho hình chóp S .ABCD có đáy là tứ giác lồi, các cạnh đối không song song. Tìm giao tuyến của
b. SAB và SCD ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
c. SAD và SBC 
a. SAC  và SBD ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________ Câu 4:
Cho hình chóp S .ABCD có đáy ABCD là tứ giác lồi, các cạnh đối không song song. Gọi M là
điểm thuộc cạnh SA sao cho SM  2MA . Tìm giao tuyến:
b. MBC   SAD ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
c. MBC   SCD
a. MBD  SAC  ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
GV: TUẤN DUY – THPT Gia Định 63 QUAN HỆ SONG SONG ĐỀ CƯƠNG TOÁN 11 Câu 5:
Cho tứ diện ABCD . Lấy M trên đoạn A ,
B N trên đoạn AC sao cho MN không song song với
BC và I nằm trong BCD . Xác định giao tuyến:
b. MNI   ACD ____________________________ ____________________________ ____________________________ ____________________________ ____________________________ ____________________________
c. MNI   ABD
a. MNI   BCD ____________________________ ____________________________ ____________________________ ____________________________ ____________________________ ____________________________ ____________________________ ____________________________ ____________________________ ____________________________ ____________________________ ____________________________ Câu 6:
Cho hình chóp S .ABCD có đáy là hình bình hành. Gọi M, N, P lần lượt là trung điểm BC, C ,
D SA . Xác định giao tuyến: ____________________________ ____________________________ ____________________________ ____________________________ ____________________________
c. MNP   SBC  ____________________________ ____________________________ ____________________________
a. MNP   SAB ____________________________
____________________________ ____________________________
____________________________ ____________________________
____________________________ d. MNP   SCD 
____________________________ ____________________________
____________________________ ____________________________
____________________________ ____________________________
b. MNP   SAD ____________________________
____________________________ ____________________________
____________________________ ____________________________
GV: TUẤN DUY – THPT Gia Định 64 QUAN HỆ SONG SONG ĐỀ CƯƠNG TOÁN 11 BÀI TẬP RÈN LUYỆN
Câu 1: Cho tứ diện ABCD . Gọi M, N lần lượt là trung điểm của BC và AD.
a. Xác định giao tuyến của MAD và NBC .
b. Trên cạnh AB lấy điểm I , trên cạnh CD lấy điểm J . Xác định giao tuyến của NBC  và DIJ  .
Câu 2: Cho hình chóp S.ABC . Gọi M là trung điểm của BC , G là trọng tâm tam giác SAC . Trên
cạnh AB lấy điểm N sao cho AN  2NB .
a. Xác định giao tuyến của MNG  và SAC  .
b. Xác định giao tuyến của MNG  và SAB.
Câu 3: Cho hình chóp S .ABCD có đáy ABCD là tứ giác lồi, các cạnh đối không song song, AC cắt BD
tại O . Trên cạnh SA lấy điểm M sao cho SA  3SM . Trên cạnh SD lấy điểm N sao cho SD  3ND
a. Xác định giao tuyến của SAC  và SBD.
b. Xác định giao tuyến của SAB và SCD .
c. Xác định giao tuyến của MNO và ABCD .
d. Xác định giao tuyến của MNO và SAB.
Câu 4: Cho hình chóp S.ABCD có đáy là hình chữ nhật, tâm O . Gọi M, N lần lượt là trung điểm của SB và SD .
a. Xác định giao tuyến của SAC  và SBD.
b. Xác định giao tuyến AE của AMN  và SAC  .
c. Gọi P là giao điểm của ME với BC , Q là giao điểm của NE với CD . Ba điểm P, , A Q có thẳng hàng không? Vì sao?
Câu 5: Cho hình chóp S.ABCD có đáy là hình bình hành. Trên ,
SA SD lấy điểm M, N sao cho MS ND 1  
. Gọi P là trung điểm BC . MA NS 3
a. Xác định giao tuyến của MNP  và ABCD .
b. Xác định giao tuyến của MNP  và SAB.
c. Xác định giao tuyến của MNP  và SCD .
d. Xác định giao tuyến của MNP  và SAC  .
Câu 6: Cho tứ diện ABCD . Gọi M, N lần lượt là các điểm nằm trong ABC và ACD . Không xét các trường hợp song song.
a. Xác định giao tuyến của AMN  và BCD.
b. Xác định giao tuyến của BMN  và BCD.
Câu 7*: Cho hình chóp S .ABCD có đáy ABCD là tứ giác lồi, các cạnh đối không song song, AC cắt
BD tại O . Trên cạnh SA lấy điểm M sao cho MA  3MS . Gọi G là trọng tâm SCD . Xác định giao
tuyến của MOG  với các mặt của hình chóp S.ABCD .
Câu 8**: Cho tứ diện ABCD . Gọi M, N, P lần lượt là các điểm nằm trong các A  BC, A  CD và
BCD . Không xét các trường hợp song song, hãy xác định giao tuyến của MNP với các mặt của tứ diện.
GV: TUẤN DUY – THPT Gia Định 65 QUAN HỆ SONG SONG ĐỀ CƯƠNG TOÁN 11
Vấn đề 2: Tìm giao điểm của đường thẳng và mặt phẳng Phương pháp:
Để tìm giao điểm của đường thẳng d và mặt phẳng P , ta tìm giao điểm của d với một đường  nằm trong P : d     I I   d            P I      
P I d P  
Cách xác định  (khi chưa có sẵn)
Bước 1: Chọn mặt phẳng Q chứa d
Bước 2: Tìm   P  Q I   d 
Bước 3: Trong Q : d    I      I     
P I d P  Các ví dụ Câu 1:
Cho tứ diện ABCD . Gọi M , I lần lượt là trung điểm AB , BD . Trên cạnh AC lấy điểm N
sao cho AN  2NC . Hãy xác định giao điểm:
a. MN  BCD
b. CD  IMN  ____________________________ ___________________________ ____________________________ ___________________________ ____________________________ ___________________________
____________________________ ___________________________
____________________________ ___________________________ SA SC Câu 2:
Cho hình chóp S.ABC . Trên cạnh ,
SA SC lấy điểm M, N sao cho   3 . Gọi G là SM NC
trọng tâm ABC . Xác định giao điểm
GV: TUẤN DUY – THPT Gia Định 66 QUAN HỆ SONG SONG ĐỀ CƯƠNG TOÁN 11
a. MN  ABC  ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
b. AB  GMN 
d. NG  SAB ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
c. MN  SBG ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________ Câu 3:
Cho tứ diện hình chóp S.ABCD có đáy là tứ giác lồi, các cạnh đối không song song. Gọi M là
trung điểm của SC . Xác định giao điểm
a. BD  SAC 
c. SB  ADM  ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________
___________________________ ___________________________
b. AM  SBD ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
GV: TUẤN DUY – THPT Gia Định 67 QUAN HỆ SONG SONG ĐỀ CƯƠNG TOÁN 11 Câu 4:
Cho tứ diện hình chóp S.ABCD có đáy là hình bình hành tâm O . Trên cạnh S , A SD lấy điểm
M, N sao cho SA  3SM , SD  3ND . Gọi P là trung điểm của BC . Tìm giao điểm của:
b. SB  MNP  ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
c. SC  MNP
a. CD  MNP  ___________________________ ____________________________ ___________________________ ____________________________ ___________________________ ____________________________ ___________________________
____________________________ ___________________________ ____________________________ ___________________________ ____________________________ ___________________________
____________________________ ___________________________
____________________________ ___________________________ Câu 5:
Cho tứ diện ABCD . Gọi I là trung điểm BC, G là điểm nằm trong ACD . Trên cạnh AB
lấy điểm M sao cho MG cắt mặt phẳng BCD. Tìm giao điểm của: ____________________________ ____________________________ ____________________________ ____________________________
b. F  AD  MGI  ___________________________ ___________________________
a. E  MG  BCD ___________________________ ____________________________ ___________________________ ____________________________ ___________________________ ____________________________ ___________________________ ____________________________ ___________________________ ____________________________ ___________________________
____________________________ ___________________________
GV: TUẤN DUY – THPT Gia Định 68 QUAN HỆ SONG SONG ĐỀ CƯƠNG TOÁN 11 BÀI TẬP RÈN LUYỆN
Câu 1: Cho tứ diện ABCD . Gọi M , N lần lượt là trung điểm của BC, AB , điểm P thuộc cạnh CD sao
cho CD  3PD .
a. Tìm giao điểm của BD và MNP .
b. Tìm giao điểm của AD và MNP  MA NB
Câu 2: Cho hình chóp S.ABC . Trên cạnh AB, BC lấy điểm M , N sao cho   2 . Gọi G là MB NC
trọng tâm SAC . Tìm giao điểm của SA với MNG.
Câu 3: Cho tứ diện ABCD . Gọi M là trung điểm của AB, G là trọng tâm ACD .
a. Tìm giao điểm của MG và BCD.
b. Gọi N là điểm đối xứng của B qua A . Tìm giao điểm của NG với BCD
Câu 4: Cho hình chóp S.ABCD có đáy là tứ giác lồi, các cạnh đối không song song. Gọi O là giao điểm
của AC và BD. Trên cạnh S ,
A SD lần lượt lấy các điểm M, N sao cho MN không song song với AD.
a. Tìm giao điểm của CD và MNO .
b. Tìm giao điểm của SB với MNO
c. Gọi P là trung điểm SC . Tìm giao điểm của AP với MNO
Câu 5: Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M là trung điểm của SC .
a. Tìm giao điểm của AM và SBD
b. Tìm giao điểm của SD và ABM 
Câu 6*: Cho hình chóp S.ABCD có đáy là hình thang, đáy lớn AB . Trên cạnh S ,
A SB,CD lần lượt lấy SA SB CD
M, N, P sao cho    3 . SM NB CP
a. Tìm giao điểm của NP và SAD
b. Tìm giao điểm của SD với MNP 
Câu 7*: Cho tứ diện ABCD . Gọi M, N , P lần lượt là các điểm nằm trong tam giác ABC, ACD và BCD
sao cho MN cắt mặt phẳng ACD .
a. Tìm giao điểm của MN và BCD.
b. Tìm giao điểm của AD và MNP .
Câu 8*: Cho hình chóp S.ABCD có đáy là một tứ giác lồi. Gọi M là điểm nằm trong tam giác SCD .
a. Tìm giao điểm của BM và SAC  .
b. Tìm giao điểm của SD và ABM  .
GV: TUẤN DUY – THPT Gia Định 69 QUAN HỆ SONG SONG ĐỀ CƯƠNG TOÁN 11
Vấn đề 3: Chứng minh ba điểm thẳng hàng – ba đường thẳng đồng quy Phương pháp:
1. Chứng minh ba điểm thẳng hàng:
Để chứng minh ba điểm , A ,
B C thẳng hàng. Ta chứng minh , A ,
B C cùng thuộc giao tuyến của hai mặt phẳng. A   P  Q B 
  P  Q  , A , B C  thẳng hàng. C   P  Q 
2. Chứng minh ba đường thẳng đồng quy:
Chứng minh ba đường a, , b c đồng quy.
Bước 1: Gọi I  a  b I   a   P Bước 2:     I   b  
Q I P Q 
Bước 3: Chứng minh c  P  Q  I  c Vậy a, , b c đồng quy. Các ví dụ Câu 1:
Trong không gian, cho mặt phẳng  và mặt phẳng ABC . Biết AB    M ,
AC    N , BC    P . Hình vẽ sau đúng hay sai ? Vì sao? ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ Câu 2:
Cho tứ diện ABCD . Gọi M là trung điểm AC , điểm N trên cạnh AB sao cho AB  4AN ,
điểm P trên cạnh AD sao cho AD  4PD . Gọi I,J, K lần lượt là giao điểm của MN và BC ,
MP và CD , NP và BD . Chứng minh rằng I,J, K thẳng hàng. ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
GV: TUẤN DUY – THPT Gia Định 70 QUAN HỆ SONG SONG ĐỀ CƯƠNG TOÁN 11 Câu 3:
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi H , K lần lượt là trung điểm của SB, SD ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
b. Gọi M  HI  BC, N  KI CD . Chứng minh rằng ,
A M, N thẳng hàng
a. Tìm giao điểm E của HK và SAC  , giao điểm ___________________________
I của SC và AHK  ___________________________ ___________________________ ___________________________
___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________ Câu 4:
Cho hình chóp S.ABCD có đáy là hình thang, đáy lớn AB . Gọi M là trung điểm SB .
a. Tìm giao điểm N của SC và ADM  .
b. Chứng minh rằng A ,
D BC, MN đồng quy. ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
GV: TUẤN DUY – THPT Gia Định 71 QUAN HỆ SONG SONG ĐỀ CƯƠNG TOÁN 11 Câu 5:
Cho hình chóp S.ABCD có đáy là tứ giác lồi, các cạnh đối không song song. Gọi M, N , P lần
lượt là các điểm thuộc cạnh , SA SB,SD .
b. Tìm giao điểm Q của SC và MNP  ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
c. Chứng minh rằng MN , PQ và SI đồng quy.
a. Tìm giao tuyến SI của SAB và SCD ___________________________ ____________________________ ___________________________
____________________________ ___________________________ ____________________________ ___________________________ ____________________________ ___________________________ ____________________________ ___________________________ ____________________________ ___________________________
____________________________ ___________________________ Câu 6:
Cho hình chóp S.ABCD có đáy là hình thang, đáy lớn AB  2CD . Gọi O là giao điểm của AC
và BD , M là trung điểm SB . Trên cạnh SA lấy điểm N sao cho 4SN  3SA .
a. Tìm giao điểm I của MN và ABCD ___________________________ ___________________________ ___________________________ ___________________________
b. Tìm giao điểm J của SD với OMN  , giao điểm
K của SC với OMN  ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
GV: TUẤN DUY – THPT Gia Định 72 QUAN HỆ SONG SONG ĐỀ CƯƠNG TOÁN 11
c. Chứng minh OI ,CD,JK đồng quy.
d. Gọi H là trung điểm của DM . Chứng minh ___________________________
S, H,O thẳng hàng. ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________ Câu 7:
Cho hình chóp S.ABCD có đáy là hình bình hành tâm O . Gọi H , K lần lượt là trung điểm SB và SD .
b. Tìm giao điểm J của AB và CHK  . ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
c. Chứng minh IK, AD,JC đồng quy. ___________________________
a. Tìm giao điểm E của HK và SAC  . ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
___________________________ d. Gọi E là trung điểm của OK , G là trọng tâm
ACD . Chứng minh S, E,G thẳng hàng.
b. Tìm giao điểm I của SA và CHK  . ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________
GV: TUẤN DUY – THPT Gia Định 73 QUAN HỆ SONG SONG ĐỀ CƯƠNG TOÁN 11 BÀI TẬP RÈN LUYỆN
Câu 1: Cho hình chóp S.ABCD có đáy là hình thang, đáy lớn AD . Gọi M là trung điểm của SD.
a. Tìm giao tuyến SI của SAB và SCD .
b. Tìm giao điểm N của SC và ABM .
c. Gọi O là giao điểm của AC và BD . Chứng minh rằng AN , BM và SO đồng quy.
Câu 2: Cho hình chóp S.ABC . Gọi M là trung điểm của S .
A Gọi N, P là các điểm trên AB và SC sao AN SP 3 cho   . AB SC 4
a. Tìm giao điểm Q của BC và MNP.
b. Chứng minh rằng MN , PQ và SB đồng quy.
Câu 3: Cho tứ diện ABCD . Gọi M, N lần lượt là trung điểm của AB, BC . G là trọng tâm ACD .
a. Tìm giao điểm I của MG và BCD.
b. Tìm giao điểm P của CD với MNG và giao điểm Q của AD với MNG.
c. Chứng minh rằng MQ, NP và BD đồng quy.
Câu 4: Cho hình chóp S.ABCD có đáy là hình thang, đáy lớn AB  2CD . Gọi O là giao điểm của AC
và BD , M là trung điểm của SA , I là trung điểm CM . Chứng minh rằng S, I,O thẳng hàng.
Câu 5: Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M, N , P lần lượt là trung điểm của BC ,CD,
SA . Điểm K di động trên đoạn AP .
a. Tìm giao điểm E của SB và MNK  , giao điểm F của SD và MNK  .
b. Gọi I là giao điểm của ME và NF . Chứng minh rằng điểm I luôn thuộc một đường thẳng cố định
K di động trên đoạn AP .
Câu 6*: Cho hình chóp S.ABCD có đáy là tứ giác lồi, các cạnh đối không song song. Gọi M là trung
điểm SD . Trên cạnh SC lấy điểm N .
a. Tìm giao điểm I của AN và SBD.
b. Gọi E là giao điểm của MI và BD, F là giao điểm của MN và CD . Chứng minh rằng EF luôn đi
qua một điểm cố định khi N di động trên cạnh SC .
GV: TUẤN DUY – THPT Gia Định 74 QUAN HỆ SONG SONG ĐỀ CƯƠNG TOÁN 11
Vấn đề 4: Tìm thiết diện của hình chóp khi cắt bởi một mặt phẳng Phương pháp:
Nếu mặt phẳng   cắt các mặt của hình chóp (Mặt bên và mặt đáy – nếu có) theo các đoạn giao tuyến
nối tiếp nhau, tạo thành một đa giác phẳng thì ta gọi đa giác này là thiết diện hay mặt cắt của mặt
phẳng   và hình chóp.
Ở hình dươi, thiết diện tạo bởi mặt phẳng   và hình chóp S.ABCD là tứ giác MNPQ
Thông thường, để xác định các thiết diện, ta làm theo hai cách sau:
Cách 1: Tìm giao tuyến đầu tiên của mặt phẳng   với một mặt phẳng nào đó của hình chóp, giao
tuyến này dễ tìm được. Sau đó kéo dài giao tuyến này cắt các cạnh khác của hình chóp, từ đó ta tìm được
các đoạn giao tuyến tiếp theo. Đa giác giới hạn bởi các đoạn giao tuyến này là thiết diện cần tìm.
Cách 2: Tìm giao điểm của   với các cạnh của hình chóp (cạnh bên và cạnh đáy) (   có thể chỉ cắt
một số cạnh, chứ không nhất thiết phải cắt tất cả các cạnh). Nối các giao điểm lại thành một đa giác, là thiết diện cần tìm Các ví dụ Câu 1:
Cho tứ diện ABCD . Gọi M, N là các điểm nằm trên cạnh AB, AC sao cho MN không song
song với BC . Gọi I là trung điểm của BD . Xác định thiết diện của tứ diện ABCD cắt bởi mặt phẳng MNI  ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
GV: TUẤN DUY – THPT Gia Định 75 QUAN HỆ SONG SONG ĐỀ CƯƠNG TOÁN 11 Câu 2:
Cho tứ diện ABCD . Gọi M, N là các điểm nằm trên cạnh AB, AC sao cho MN không song
song với BC . Gọi I là điểm nằm trong BC 
D . Xác định thiết diện của tứ diện ABCD cắt bởi
mặt phẳng MNI  ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ Câu 3:
Cho hình chóp S.ABCD có đáy là tứ giác lồi, các cạnh đối không song song. Trên cạnh SD lấy
điểm M . Xác định thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng ABM  ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ Câu 4:
Cho hình chóp S.ABCD có đáy là tứ giác lồi, các cạnh đối không song song. Gọi O là giao điểm
của AC và BD, M, N là các điểm nằm trên cạnh S ,
A SD sao cho MN không song song với
AD . Xác định thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng OMN  ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
GV: TUẤN DUY – THPT Gia Định 76 QUAN HỆ SONG SONG ĐỀ CƯƠNG TOÁN 11 Câu 5:
Cho hình chóp S.ABCD có đáy là hình bình hành tâm O . Gọi M, N lần lượt là trung điểm
SB,SD . Xác định giao điểm của SC với mặt phẳng AMN  , từ đó suy ra thiết diện của hình
chóp S.ABCD cắt bởi mặt phẳng AMN  ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________ Câu 6:
Cho hình chóp S.ABC . Trên cạnh SA lấy điểm M . Gọi N và P lần lượt là các điểm nằm trong
tam giác SBC và ABC sao cho MN cắt mặt phẳng ABC . Xác định giao điểm của MN với
ABC và thiết diện của hình chóp S.ABC cắt bởi mặt phẳng MNP ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________ ___________________________
___________________________ ___________________________ BÀI TẬP RÈN LUYỆN
Câu 1: Cho tứ diện S.ABC . Gọi M, N lần lượt là điểm nằm trên cạnh ,
SA SC và P là điểm trong tam
giác ABC . Tìm thiết diện của hình chóp và mặt phẳng MNP.
Câu 2: Cho hình chóp S.ABCD có đáy là tứ giác lồi, các cạnh đối không song song. Gọi M là điểm nằm
trên cạnh SA sao cho SA  3SM , G là trọng tâm S
 CD , O là giao điểm của AC và BD . Xác định
thiết diện của hình chóp S.ABCD cắt bởi MGO
GV: TUẤN DUY – THPT Gia Định 77 QUAN HỆ SONG SONG ĐỀ CƯƠNG TOÁN 11
Câu 3: Cho hình chóp S.ABCD có đáy là hình bình hành tâm O . Gọi M, N lần lượt là trung điểm của
SB,SD . Trên cạnh SC lấy điểm P sao cho SP  3PC . Xác định thiết diện của hình chóp S.ABCD cắt
bởi mặt phẳng MNP.
Câu 4: Cho hình chóp S.ABCD , có đáy là tứ giác lồi, các cạnh đối không song song. Gọi M, N, P lần lượt là trung điểm S ,
A BC, CD . Xác định thiết diện của hình chóp cắt bởi mặt phẳng MNP.
Cho hình chóp S.ABCD có đáy là hình thang, đáy lớn AB. Gọi E, F lần lượt là trọng tâm S  BC và S  CD .
a. Xác định giao điểm của SC với AEF  .
b. Xác định thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng AEF 
Câu 5: Cho hình chóp S.ABCD có đáy là hỉnh bình hành. Gọi H , K lần lượt là trung điểm của BC và
CD , điểm L thuộc cạnh SA . Tìm thiết diện của hình chóp cắt bởi mặt phẳng HKL .
Câu 6: Cho hình chóp S.ABCD có đáy là hình bình hành tâm O , Gọi M, N , I lần lượt thuộc AB, BC, SO
. Tìm thiết diện của hình chóp với mặt phẳng MNI  .
GV: TUẤN DUY – THPT Gia Định 78

Tài liệu học tập môn Toán 11 – La Tuấn Duy (Tập 1)

Thông tin :

Tài liệu liên quan:

Đề cương giữa kỳ 1 Toán 11 năm 2024 – 2025 trường THPT Sơn Động 3 – Bắc Giang

Đề cương giữa kỳ 1 Toán 11 năm 2024 – 2025 trường THPT Châu Văn Liêm – Cần Thơ

Tài liệu chuyên Toán chủ đề hàm số lũy thừa, hàm số mũ và hàm số logarit

Hệ thống kiến thức và phương pháp giải Toán 11 GDPT 2018 – Võ Công Trường

Chuyên đề toán thực tế giới hạn và hàm số liên tục Toán 11