










Preview text:
LÝ THUYẾT XÁC SUẤT
Phần I. BIẾN CỐ - XÁC SUẤT
1. Phép thử - biến cố
- Thực hiện các điều kiện để nghiên cứu: Phép thử
- Thực hiện phép thử các Kết cục
- Các kết cục quan tâm Biến cố
+ Biến cố chắc chắn: kí hiệu là , U
+ Biến cố không thể có: kí hiệu là , V
+ Biến cố ngẫu nhiên: thường kí hiệu là A, B, C hoặc A , 1 A ,…, 2 An, B ,…, B 1 m 2. Xác suất
Xác suất của một biến cố là con số đặc trưng cho khả năng khách quan xuất hiện biến cố đó
khi thực hiện phép thử. Xác suất của biến cố A được kí hiệu là P(A)
+ Xác suất phải là số thuộc đoạn [0; 1] : 0 P(A) 1
+ P(U) = 1 ; P(V) = 0
3. Định nghĩa cổ điển về xác suất 3.1. Định nghĩa m m A
A : số kết cục thuận lợi cho biến cố A n P(A) = nA
A : số kết cục duy nhất, đồng khả năng khi thực hiện phép thử
3.2. Các phương pháp tính Liệt kê - suy luận
Dùng sơ đồ (sơ đồ Venn, dạng bảng, dạng tập hợp)
Dùng các công thức của giải tích Tổ hợp * Hoán vị Với một bộ n phần tử, có !
n cách sắp xếp có thứ tự, mỗi cách là một hoán vị, n! gọi là n
giai thừa: n! = n(n-1)(n-2)….2.1 * Chỉnh hợp Từ một bộ
n phần tử, lấy ra một bộ có thứ tự gồm k phần tử, số cách có thể lấy là chỉnh n! k k
hợp chập k của , kí hiệu n A A n
n = (n k )! * Tổ hợp Từ một bộ
n phần tử, lấy ra một bộ không có thứ tự gồm k phần tử, số cách có thể lấy là ! n k k
tổ hợp chập k của , kí hiệu là n
Cn Cn= !k(n k)!
3.3. Ưu nhược điểm
- Không phải tiến hành phép thử, không tốn kém
- Nếu số kết cục vô hạn không tính được
- Không biểu diễn được các kết cục duy nhất đồng khả năng, khái niệm đồng khả năng....
Tài liệu Xác suất Thống kê Hoangld@neu.edu.vn
4. Định nghĩa thống kê về xác suất
Thực hiện phép thử thực sự n quan sát n
Biến cố A xuất hiện kA lần kA là của biến cố tần số A kA Tần suất f(A) = n lim
Xác suất P(A) = n f(A)
Với n đủ lớn, P(A) f (A)
5. Nguyên lý xác suất lớn và nhỏ
P(A) là rất nhỏ thì có thể coi là biến cố A sẽ không xảy ra khi thực hiện một phép thử.
P(A) là rất lớn thì có thể coi là biến cố A sẽ xảy ra khi thực hiện một phép thử.
Phần II. CÁC ĐỊNH LÝ XÁC SUẤT
Hai biến cố A và B bằng nhau : A xảy ra B xảy ra, kí hiệu A = B. Nếu A = B P(A) = P(B)
1. Định lý nhân xác suất 1.1. Biến cố tích
C là tích của hai biến cố A và B nếu C xảy ra khi A và B đồng thời xảy ra. Kí hiệu C = A.B
1.2. Xác suất có điều kiện
Xác suất để biến cố B xảy ra khi A đã xảy ra gọi là xác suất của B trong điều kiện A
Kí hiệu P(B/A) hoặc P(BA)
1.3. Tính độc lập và phụ thuộc
A và B được gọi là độc lập với nhau nếu việc biến cố này xảy ra hay không xảy ra không tác
động đến khả năng xảy ra biến cố kia và ngược lại. Nếu chúng không độc lập phụ thuộc
A, B độc lập P(A/B) = P(A) và P(B/A) = P(B) 1.4. Định lý
P(AB) = P(A).P(B/A) = P(B).P(A/B) :
Hệ quả 1 A, B độc lập P(AB) = P(A).P(B) P( ) A.B :
Hệ quả 2 P(A/B) = P( ) B P(B) 0 1.5. Mở rộng n A = A i 1 1A2…A = n
Ai A xảy ra khi các Ai đồng thời xảy ra (i = 1,.., ) n A1, A2,…, A n là
độc lập từng đôi Ai , Aj độc lập ( i j) n n
là độc lập toàn phần nếu các tổ hợp bất kỳ là độc lập, khi đó P( i 1 A i 1 i) = P(Ai)
2. Định lý cộng xác suất
2.1. Biến cố tổng
C là tổng của hai biến cố A và B nếu C xảy ra khi ít nhất một trong hai biến cố A B xảy ra. hoặc Kí hiệu C = A + B
Tài liệu Xác suất Thống kê Hoangld@neu.edu.vn
2.2. Tính xung khắc và không xung khắc
Hai biến cố A và B được gọi là xung khắc với nhau nếu chúng không thể đồng thời cùng xảy ra trong một phép thử.
A, B xung khắc A.B = P(AB) = 0 2.3. Định lý
P(A + B) = P(A) + P(B) – P(A.B) : Nếu Hệ quả
A, B xung khắc P(A + B) = P(A) + P(B) 2.4. Mở rộng n A = A + i 1 1 A2 + …+ An =
Ai A xảy ra khi ít nhất Ai xảy ra (i = 1,.., ) n n n A i 1 i 1 1, A2,…, A n
là xung khắc từng đôi nếu hai biến cố bất kì là xung khắc P( Ai) = P(Ai)
3. Nhóm đầy đủ các biến cố 3.1. Nhóm đầy đủ Các biến cố A ,1 A ,…, 2
An được gọi là một nhóm đầy đủ các biến cố nếu khi thực hiện một
phép thử thì kết cục sẽ là một và chỉ một trong các biến cố đó. Mỗi biến cố là một phân hoạch Khi đó
Ai.Aj = V ( i ≠ j) và A + 1 A2 + … + A = U n n P(A ) P(A ) i i i1 = 1 ij = 1 – P(Aj)
3.2. Biến cố đối lập
Biến cố đối lập của A kí hiệu là A , khi A và A tạo thành nhóm đầy đủ biến cố P(A) + P( A ) = 1 4. Công thức Bernoulli 4.1. Lược đồ
Thực hiện phép thử độc lập n
Với 1 phép thử, biến cố A hoặc A xuất hiện
Lược đồ Bernouli (B) với hai tham số n và p
P(A) = p không đổi, P( A ) = 1 – p = q 4.2. Công thức
Với lược đồ (B), xác suất để trong phép thử độc lập, n
A xuất hiện đúng k lần, kí hiệu P (k) n k P Cn n(k) = pk qn-k
Tài liệu Xác suất Thống kê Hoangld@neu.edu.vn
Phần III. BIẾN NGẪU NHIÊN – QUI LUẬT PHÂN PHỐI XÁC SUẤT
1. Biến ngẫu nhiên Khái niệm
Biến ngẫu nhiên là một đại lượng mà trong kết quả của phép thử sẽ chỉ nhận một và chỉ một
giá trị có thể có tùy thuộc kết cục của phép thử ngẫu nhiên.
Thường kí hiệu là X, Y, Z, các giá trị có thể có : x , x 1
2,…, xn ; y1, y2,…, ym
(X = xi) là một biến cố ngẫu nhiên có xác suất tương ứng P(X = xi) Phân loại
- BNN rời rạc - BNN liên tục
2. Quy luật phân phối xác suất
Là mô tả mối liên hệ giữa giá trị có thể có và xác suất tương ứng của biến ngẫu nhiên
2.1. Bảng phân phối xác suất
Chỉ dùng cho biến ngẫu nhiên rời rạc.
X nhận các giá trị có thể có x1, x , …, x 2
n rời rạc với xác suất tương ứng P(X = xi) = pi (i = 1n) X x1 x2 … xi … xn P p1 p2 … pi … pn
Tính chất : do (X = xi) tạo thành nhóm đầy đủ các biến cố n pi 0 pi 1 và i1 = 1
2.2. Hàm phân phối xác suất
- Dùng cho cả BNN rời rạc và liên tục.
Với số thực x , (
) là biến cố xác định, X < x
P(X < x) là duy nhất
Định nghĩa.
F(x) = P(X < x) x
- Hàm phân phối xác suất phản ánh khả năng, độ tập trung để X ở về phía trái giá trị xác định
- Đồ thị hàm phân phối xác suất BNN rời rạc có dạng bậc thang
- Đồ thị hàm phân phối xác suất BNN liên tục là đường liên tục Tính chất. Tính chất 1. 0 F(x) 1 Tính chất 2.
F(x) không giảm : x1 < x 2 F(x ) 1 F(x ) 2 :
Hệ quả 1 P(a X < b) = F(b) – F(a) : Nếu Hệ quả 2
X liên tục thì P(X =x ) = 0 0 :
Hệ quả 3 X liên tục: P(
a X < ) = b P( < a X b)
= P(a < X < ) = b
P(a X ) = b
F(b) – F(a) Tính chất 3.
F(– ) = 0 ; F( + ) = 1 : Nếu Hệ quả 4
X chỉ [a ; ] thì b
F(x) = 0 x và a
F(x) = 1 x >b
2.3. Hàm mật độ xác suất
Định nghĩa.
f(x) = F’( x) x Tính chất. Tính chất 1.
f(x) 0 x
Tài liệu Xác suất Thống kê Hoangld@neu.edu.vn b
f (x)dx Tính chất 2. P( < a X < ) = b a x
f (x)dx Tính chất 3. F(x) =
f (x)dx Tính chất 4. = 1 f(x) f(x) x dx F(x) a b 1 F(b ) F(a x ) 3. Các tham số 0 đặc trưng
Tìm những tham số đặc trưng để so sánh và đánh giá về biến ngẫu nhiên một cách đơn giản.
3.1. Kì vọng (Expected value) – E(X)
Định nghĩa. n x p i i
E(X) = i 1 với X rời rạc
x.f (x)dx E(X) = với X liên tục
Kì vọng có thể hiểu như trung bình số học của dãy số khi số lượng tăng lên vô hạn.
Kì vọng đặc trưng cho độ lớn về mặt trung bình của biến ngẫu nhiên, có cùng đơn vị với X Tính chất. với là hằng số C E( ) = C C
E(C.X) = C.E(X) n n
E( X ) E (X ) i i
E(X + Y) = E(X) + E(Y) i 1 i 1
3.2. Phương sai (Variance – Var) – V(X) Định nghĩa.
Là trung bình của bình phương sai lệch giữa giá trị có thể có và kì vọng của biến ngẫu nhiên
V(X) = E[X – E(X)]2 = E(X2) – [E(X)]2 với X rời rạc với X liên tục
Tài liệu Xác suất Thống kê Hoangld@neu.edu.vn n n 2 2 2
[ x E( X )] x p [ E( X )] i i i i 1 i 1 2 2 2
[ x E( X )] f ( x )dx x f ( x )dx [ E( X )] i i
Phương sai dùng để đánh giá sự phân tán/ tập trung / đồng đều/ dao động của biến ngẫu
nhiên quanh giá trị trung bình của nó.
Phương sai có đơn vị đo là bình phương đơn vị của X . Tính chất. V( ) = 0 C
V(C + X) = V(X)
V(C.X) = C V 2 (X) n n
V ( X ) V (X ) i i
V(X Y) = V(X) + V(Y) nếu X và Y độc lập i 1 i 1 : Xi độc lập
Độ lệch chuẩn. (Standard deviation – Sd, ; Standard error – Se.) V (X X = )
- Cho biết về trung bình, giá trị cá biệt sai lệch với kì vọng bao nhiêu
- Độ lệch chuẩn có cùng đơn vị đo với X.
3.3. Giá trị tới hạn
Với biến ngẫu nhiên X có quy luật phân phối xác suất
, giá trị tới hạn mức (0 1) của quy luật
là số thực ký hiệu sao cho:
P(X > ) =
Tài liệu Xác suất Thống kê Hoangld@neu.edu.vn
Phần IV. MỘT SỐ QUY LUẬT PHÂN PHỐI XÁC SUẤT THÔNG DỤNG
1. Quy luật Không- Một - A(p) X có bảng phân phối X 0 1 Với , q = 1 – p > 0 p P q p Hay Px = P( ) = X = x
px q1-x với x = {0, 1}
được gọi là phân phối theo quy luật “Không-Một” với tham số p, kí hiệu X ~ A(p) X ~ A(p)
E(X) = p p 1 ( p) V(X) = =
p.q p(1 – p) (X) =
2. Quy luật Nhị thức (Binomial) - B(n ; p) 2.1. Định nghĩa
BNN rời rạc X nhận giá trị có thể có {0, 1,…, n}với xác suất được tính bằng công thức Bernoulli x P C
x = P(X = x) =
n px qn-x ( x = 0 n ;
p > 0 ; p + q = 1), được gọi là tuân theo quy luật Nhị
thức với hai tham số n và p. Kí hiệu X ~ B(n ; p)
Bảng phân phối xác suất X 0 1 … x … n P 0 C 1 C … x C … n C n p0 qn n p1qn-1 n px qn-x n pn q0
X tuân theo quy luật nhị thức chính là tổng của n biến ngẫu nhiên tuân theo quy luật Không-Một X ~ B(n; )
p X = nY với Y ~ A(p)
2.2.Tham số đặc trưng
X ~ B(n ; p) E(X) = np
V(X) = npq = (1 – np p) (X) = np 1 ( p)
3. Quy luật phân phối Chuẩn (Normal) - N( ; 2) 3.1. Định nghĩa
BNN liên tục X nhận các giá trị trong khoảng (– , + ) được gọi là phân phối theo quy luật
Chuẩn với hai tham số và 2 nếu hàm mật độ xác suất có dạng 2 ( x ) 1 f(x) 2 2 f (x) e 2
Kí hiệu X ~ N( , 2 )
Khi đó hàm phân phối xác suất có dạng x
F(x) f (x dx ).
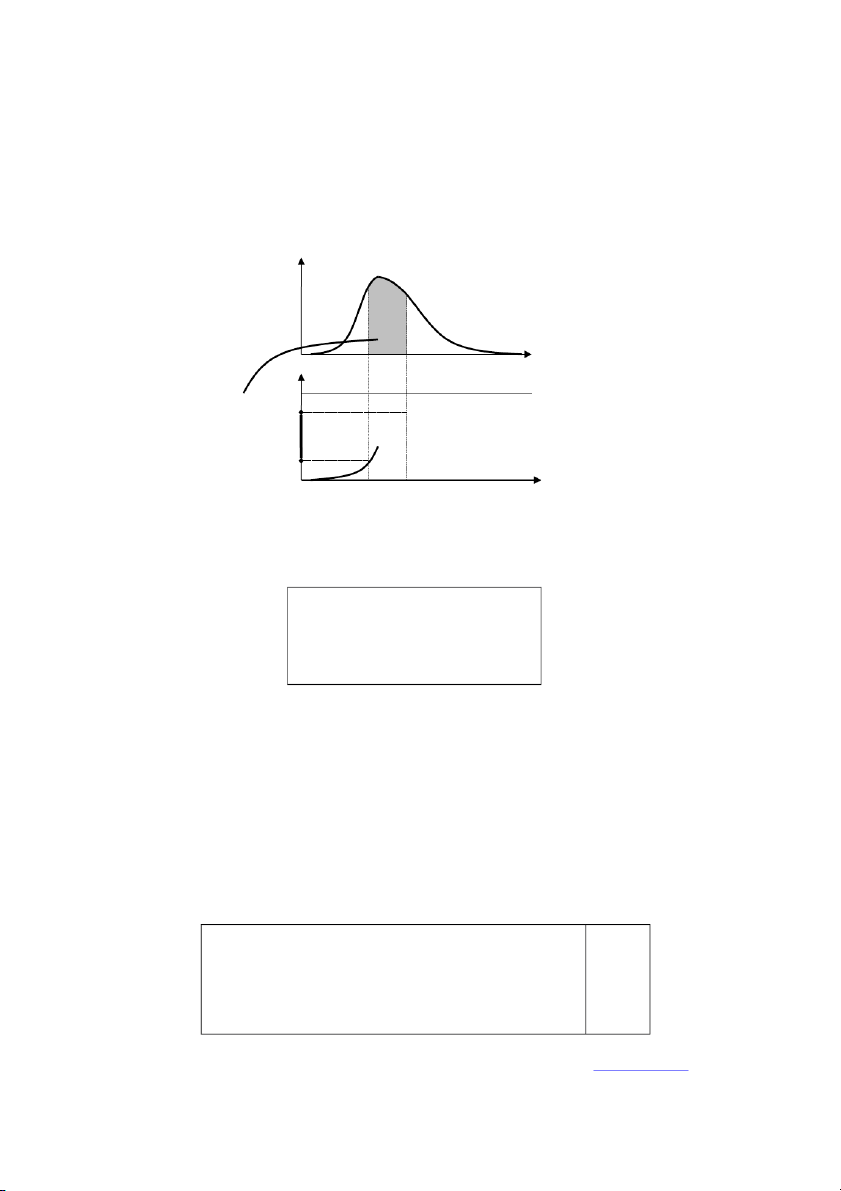
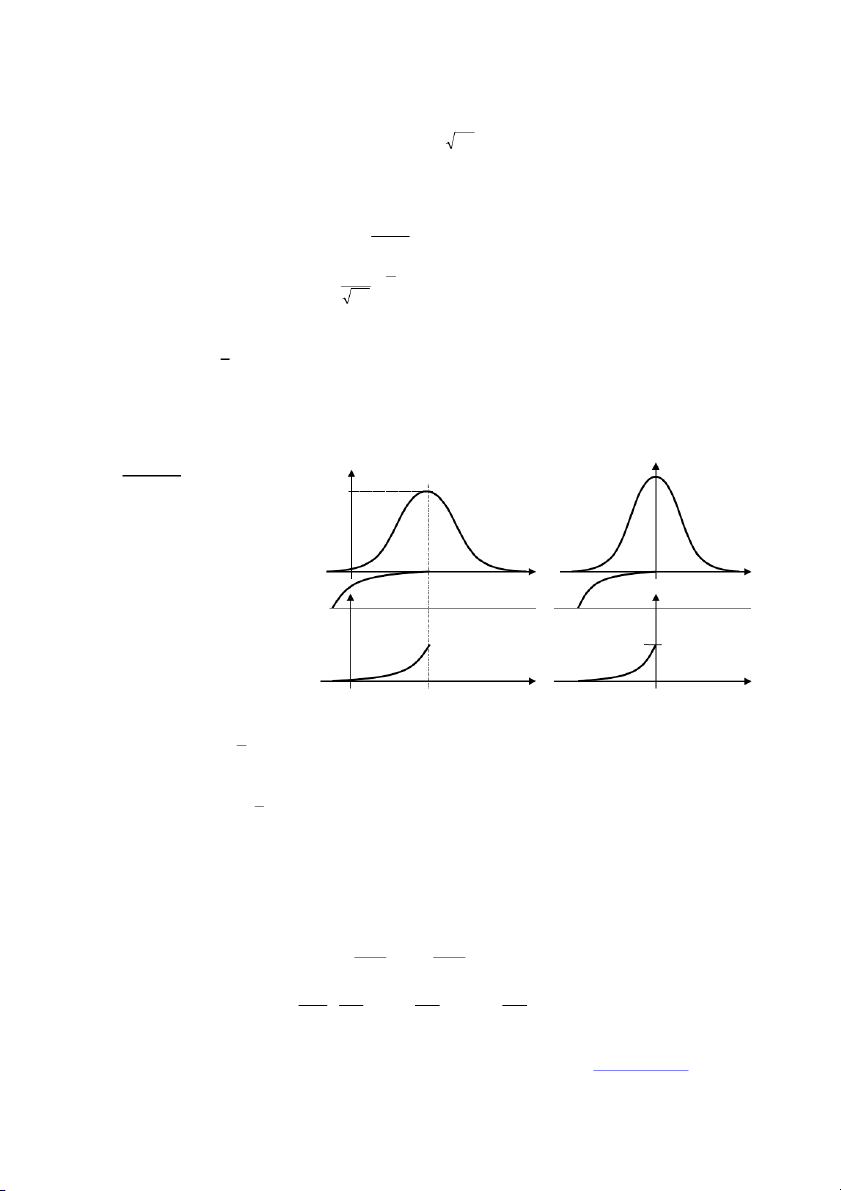
Đồ thị f(x) Dương với x
Đối xứng trục: đường x = 0
Ox là tiệm cận ngang x F(x) 1
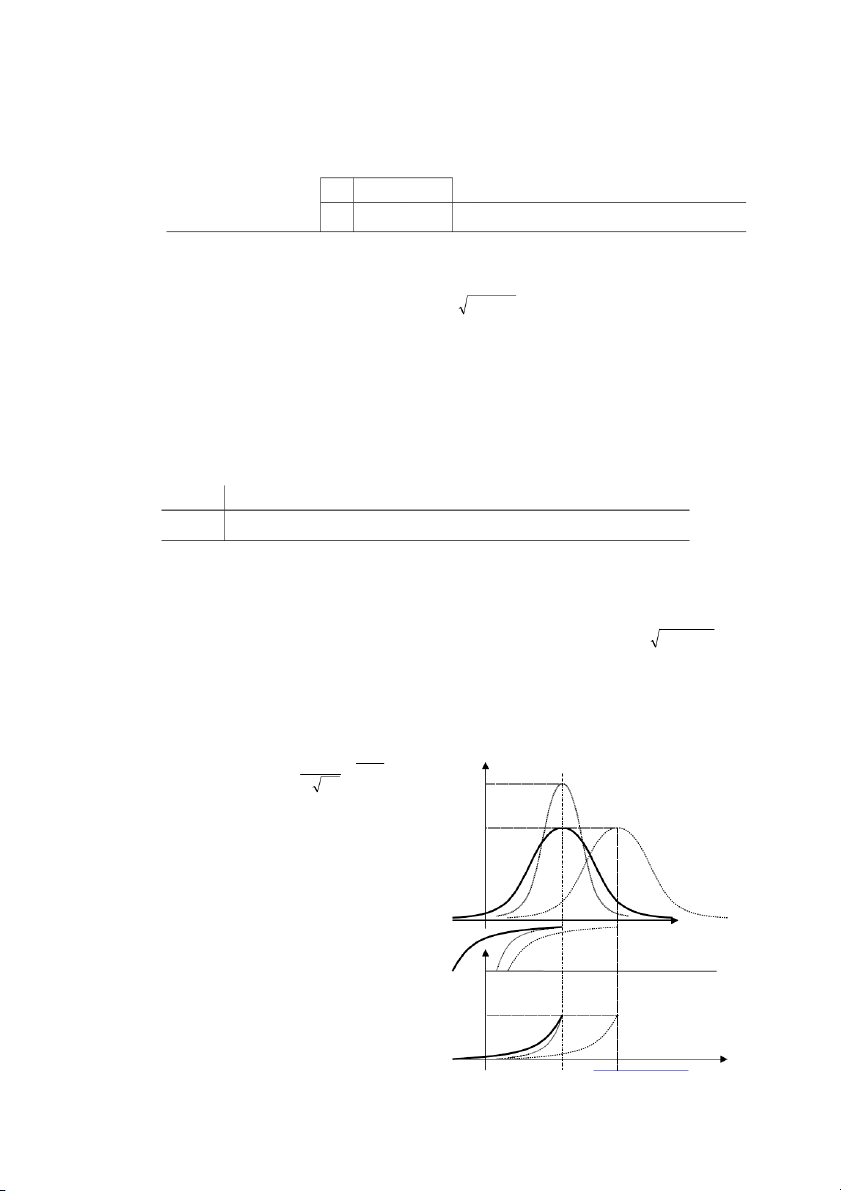
thay đổi dịch chuyển 0.5 1 tăng thấp, bẹt (u) 0 giảm cao, nhọn 0.5 u x (u)
Tài liệu Xác suất Thống kê 0 Hoangld@neu.edu.vn x
3.2. Tham số đặc trưng f(x) x
X ~ N( , 2 ) E(X) = 0 2 2
V(X) = 2 (X) = =
3.3. Biến ngẫu nhiên Chuẩn hóa (Standard Normal) – N( 0 ; 1 )
Biến ngẫu nhiên Chuẩn hóa là BNN phân phối chuẩn có kì vọng bằng 0 và phương sai bằng 1. X
Nếu X ~ N( , 2 ), xét BNN U =
, thì U là BNN có phân phối Chuẩn hóa N(0, 1). 2 1 u u 2 f ( ) u ( ) u e F u ( ) u
( ) (u)du Khi đó 2 và
Đồ thị (u) đối xứng qua trục tung, đồ thị (u) đối xứng qua điểm (0, ½ ). 1
(x) = + (x). 0 2
o(u) = (u) – 0.5, u
( u ) P( 0U u ) ( u )du 0
( u ) P(U u ) 0.5 0 0 Tính chất:
( u ) ( u ) 0 0 , ( u ) 0.5 U>5 0 1 ( P U ) a ( ) a ( ); a 0 2 1 ( P U ) a 1 ( ) a ( ) a ; 0 2 ( P a U ) b ( ) b ( ) a 0 (b) 0 (a). 3.4. Công thức.
Cho BNN phân phối chuẩn X ~ N( , 2 ) b a P a X b . 0 0
X b b b
P(X b) P P U 0 ,5 0
Tài liệu Xác suất Thống kê Hoangld@neu.edu.vn
X a a a
P(X a)P P U 0,5 0
3.5. Giá trị tới hạn chuẩn. Kí hiệu là U : với U ~ N(0, 1) thì P(U > U) = .
Tính chất: U1- = – U .
Các giá trị này được cho trong bảng số hoặc suy ra từ xác suất cho trước:
U0.025 = 1.96; U0.975 = - U0.025 = -1.96
Cho P(U < 1.96) = 0.975 P(U > 1.96) = 1 - 0.975 = 0.025 U = 1.96 0.025
Cho P(U < 1.25) = 0.8944 (1,25) 0.8944
3.6. Sự hội tụ về quy luật Chuẩn
Định lý giới hạn trung tâm (Khái quát). Tổng một số vô hạn (hoặc đủ lớn) BNN có cùng
quy luật phân phối, kì vọng, phương sai hữu hạn sẽ phân phối chuẩn.
Tổ hợp tuyến tính của các biến ngẫu nhiên phân phối chuẩn sẽ phân phối chuẩn, với kì vọng
và phương sai là tổ hợp tuyến tính tương ứng của các kì vọng, phương sai thành phần. 2 (n)
4. Quy luật Khi bình phương (Chi-squared) - n 2 Xi Nếu X i ~ N(0, 1) (i = 1 )
n thì BNN 2 = i 1
sẽ phân phối theo quy luật “Khi-bình 2 phương” với n (
bậc tự do df: degree of freedom), kí hiệu 2 ~ (n) 2
Giá trị tới hạn mức (
với n bậc tự do của phân phối Khi-bình phương : kí hiệu n) sao 2 cho P( 2 ( n >
) ) = , được cho trong bảng số. 2( 29 ) 2( 24 ) 42 .56 12 4 . 0.05 0 9.75
Giá trị này có thể suy ra từ các xác suất cho trước: 2 29 P(2(29) 42 56 ( ) . 0 0.5 < 42.56) = 0.95
P(2(29) > 42.56) = 0.05
5. Quy luật Student - T(n) U 2
Nếu U ~ N(0, 1); 2 ~ 2(n) thì BNN T =
/ n sẽ tuân theo quy luật Student với bậc tự do. n Kí hiệu T ~ T( ) n
Giá trị tới hạn mức với n bậc tự do của phân phối Student kí hiệu t (n) sao cho
P(T > t (n)) = .
Giá trị được cho trong bảng số. t (n) = – t1- (n) t1(n) = – t0(n) = +
Khi n thì quy luật Student hội tụ về quy luật Chuẩn hóa (n>30)
Giá trị này có thể tra bảng phụ lục hoặc suy ra từ xác suất cho sẵn (24 ) (24 ) (29 ) (29 ) t . t . t . t . . 2 462 . 2 462 . 2 064 . 2 064 0 025 0 975 0 01 0 99 (24 ) Cho P(T 2.064 ) 0 975 . P(T . ) . t . . 2 064 ( ) 2 064 0 025 ( 24 ) 24 0 025
6. Quy luật Fisher-Snedecor - F(n1; n2) V / n 1 1 Nếu V V / n 1 ~ 2(n ), 1 V 2 ~ 2(n ) 2 thì BNN F = 2
2 sẽ tuân theo quy luật Fisher-Snedecor với 2
bậc tự do n1 và n2 Kí hiệu F ~ F(n1, n ) 2
Tài liệu Xác suất Thống kê Hoangld@neu.edu.vn
Giá trị tới hạn mức với bậc tự do n và n 1
2 của phân phối Fisher kí hiệu F (n1 2 , n ) sao cho
P(F > F (n1 2 , n )) = 1 Tính chất F F (n , n (n1, n2) = ) 1 a 2 1
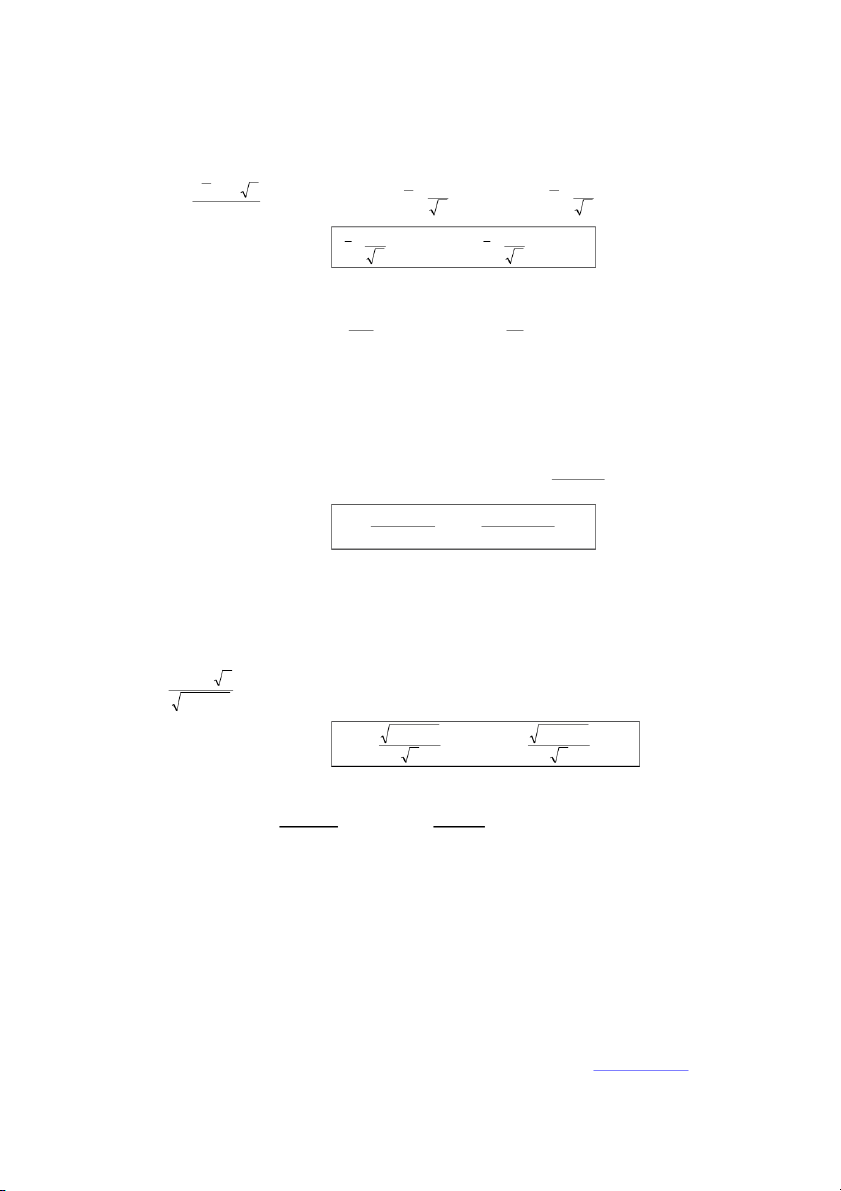
Giá trị này có thể tra bảng phụ lục hoặc suy ra từ xác suất cho sẵn ( 6 5 , ) 1 1 ( 0 1,5 ) 1 ( 5,6 ) 1 ( 5 1,0 ) f f 0 9 . 5 0 9 . 75 f 4 39 . f 3 52 . 0 0 . 5 0.025 4 39 . 3.52 (5 6 , ) P( F . ) . P( F . ) . Cho f . ( , ) 4 39 0 05 ( , ) 4 39 0 95 5 6 5 6 . 4 39 0 05 P( F
3.52 ) 0.975 P( F
3. 52) 0.025 (15 1 , 0 ) Cho f 3.52 ( 15 1 , 0) ( 15 1 , 0) 0. 025 THỐNG KÊ TOÁN
Chương 5. CƠ SỞ LÝ THUYẾT MẪU 0B 1. Khái niệm 3B
Nghiên cứu một hiện tượng, vấn đề - Tập hợp chứa nó
- Dấu hiệu nghiên cứu
- Biến ngẫu nhiên gốc X
+ Quy luật phân phối xác suất + Tham số đặc trưng - Số liệu Hai phương thức:
- Nghiên cứu toàn bộ tập hợp chứa dấu hiệu nghiên cứu: nghiên cứu Tổng thể
- Nghiên cứu một phần của tổng thể, đủ thông tin đặc trưng: nghiên cứu Mẫu 2. Tổng thể 4B
18B2.1. Mô tả tổng thể
Tổng thể là tập hợp tất cả các phần tử chứa đựng dấu hiệu nghiên cứu.
Phần tử trong tổng thể là rời rạc hoặc có thể rời rạc hóa.
Số lượng phần tử: N , N là kích thước tổng thể, có thể N = +
X là BNN của dấu hiệu , X = {x1, x2, … , xN}
Nếu chỉ có k giá trị có thể có (k nhóm) x , 1 x , … , 2
xk với tần số tương ứng N , 1 N , …, 2 Nk Ni Đặt p N i =
là tần suất tổng thể, pi = P(X = xi), thì mô tả tổng thể X x1 x2 … xk k N 57B Tần số N1 N2 … Nk
0 Ni N (i = 1k), Ni = N Tần suất p1 p2 … pk
0 pi 1 (i = 1k), pi = 1
2.2. Tham số đặc trưng của tổng thể 19B N k 1 1 x N x i i i
Trung bình tổng thể N i1 N i 1 k
m p x E( X ) i i i 1
: Trung bình tổng thể = Kì vọng BNN X
Tài liệu Xác suất Thống kê Hoangld@neu.edu.vn 1 N 1 k 2 2 2 2
(x ) N x i i i
Phương sai tổng thể N i 1 N i 1
2 = V(X) : Phương sai tổng thể = Phương sai BNN X 2
Độ lệch chuẩn =
Tần suất tổng thể
Nếu biến cố A xuất hiện trong tổng thể M lần tần suất tổng thể của biến cố A M
p = N = P(A) 3. Mẫu ngẫu nhiên 5B
3.1. Định nghĩa mẫu 20B
Mẫu ngẫu nhiên kích thước
n là tập hợp của n biến ngẫu nhiên độc lập X ,1 X ,…, 2 X n được
thành lập từ biến ngẫu nhiên X trong tổng thể nghiên cứu và có cùng quy luật phân phối xác suất với X
Kí hiệu : W = (X , 1 X ,…, 2 Xn) , Xi là BNN
E(X1) = … = E(X ) = n
m V(X ) = … = 1 V(X ) = n 2 3.2. Mô tả mẫu 21B
Quan sát đúng lần (lấy mẫu kích thước n ), khi đó n X = 1 x , 1 X = 2 x ,…, 2
Xn = x n là số cụ thể
mẫu cụ thể = ( w x , 1 x ,…, 2 x ) n
Nếu giá trị có thể có là x , 1 x ,…, 2
xk với tần số tương ứng n , 1 n ,…, 2
nk hoặc tần suất tương ứng f ,1
f2, …, fk với fi = ni/n w
thì có thể mô tả mẫu xi x1 x2 … xk ni n1 n2 … nk fi f1 f2 … fk
- Có thể ghép lớp giá trị của mẫu và lấy giá trị ở giữa để đại diện cho lớp giá trị đó.
4. Các tham số đặc trưng của mẫu 6B
4.1. Khái niệm thống kê 22B
Với W = (X1, X ,…, 2 X ), n
thống kê trên mẫu là một hàm số của các thành phần mẫu Xi
Kí hiệu G = f (X1, X ,…, X 2 n ).
Khi đó G cũng là một biến ngẫu nhiên, có phân phối xác suất xác định, có thể không giống biến
ngẫu nhiên gốc, nhưng mang thông tin về X.
Với mẫu cụ thể w = (x ,
1 x2,…, x ), thống kê n
G nhận giá trị cụ thể : g = f (x , x 1 ,…, x 2 n) n 1 X Xi 4.2. Trung bình mẫu n i1 23B 2
X là biến ngẫu nhiên có E( X ) = m và
V( X ) = n ( X ) = Se( X )= n
Mẫu cụ thể w: n k 1 1 x x n x i i i n i1 n i1
Tài liệu Xác suất Thống kê Hoangld@neu.edu.vn 1 n 2 * 2 S ( X m ) i
4.3. Phương sai mẫu khi biết trung bình tổng thể n i 1 24B
4.4. Phương sai mẫu khi không biết trung bình tổng thể 25B n 1 (X X 2) n 1 2 i
Độ lệch bình phương trung bình MS = n i1
E(MS) = n n
1 ( X X 2) n i MS Phương sai mẫu
S2 = n 1 i1 = n 1 E(S ) = 2 2
Mẫu cụ thể w: k 1 n s2
n (x x 2 2 2 ) ( ) i i x x n 1 i 1 n 1
Căn bậc hai của phương sai cho độ lệch chuẩn mẫu 2 * 2 2 * 2 S* = S S = S s* = s s = s 4.5. Tần suất mẫu 26B XA
Nếu biến cố A xuất hiện X n
A lần thì tần suất mẫu: f = p 1 ( p) p(1 p ) Tham số đặc trưng
E(f) = p V(f) = n Se(f) = n mA Với mẫu cụ thể f = n
Chương 6. ƯỚC LƯỢNG THAM SỐ 1. Khái niệm 9B
Ước lượng (Estimate) là tính toán một cách gần đúng nhất giá trị của một tham số chưa biết,
dựa trên thông tin cho trước.Tham số là của tổng thể, thông tin là từ mẫu (ngẫu nhiên hoặc cụ thể).
Có 2 phương thức: Ước lượng điểm và ước lượng khoảng
1.1. Ước lượng điểm 35B
Ước lượng bởi 1 giá trị ˆ
(là thống kê trên mẫu ngẫu nhiên, và là con số theo mẫu cụ thể) ˆ
f ( X , X ,...X )
36BPhương pháp hàm ước lượng : xây dựng thống kê 1 2 n là 1 hàm của
các biến ngẫu nhiên, nó được gọi là hàm ước lượng của
Tiêu chuẩn 37B ˆ
Không chệch (unbias) : E( ) = Hiệu quả (
): không chệch và phương sai nhỏ nhất efficient Hiệu quả nhất Tốt nhất ( ) best estimate ˆ Vững : n : ˆ
hội tụ theo xác suất về khi n Đủ : ˆ
chứa toàn bộ thông tin trong mẫu về
Tài liệu Xác suất Thống kê Hoangld@neu.edu.vn
1.2. Ước lượng khoảng 11B Khái niệm 41B
Tìm một khoảng ngẫu nhiên (G , G 1 ) sao cho xác suất 2
rơi vào khoảng đó là đủ lớn
P(G1 < < G ) = 1 – 2
với (1 – ) đủ lớn, đủ nhỏ. (1 – ) là , ( độ tin cậy G , 1 G ) là 2 khoảng tin cậy I = G – 2
G là độ dài khoảng tin cậy 1 Nếu G ,
1 G hữu hạn : khoảng tin cậy 2 2 phía
( - , G ) : khoảng tin cậy 2
tối đa (phía trái) ; (G1,+ ) : khoảng tin cậy tối thiểu (phía phải) Phương pháp 42B
Với W = (X1, X ,…, 2
X ) xây dựng thống kê n
G tương ứng với có quy luật PPXS xác định
G f ( X , X ,..., X , ) 1 2 n
Với 2 giá trị 1 và 2 đủ nhỏ sao cho 1 + 2 = , tương ứng là cặp giá trị tới hạn g , g 1 1 2 P( G g P(G g g G g ) ) 1 1 1 , 2 2 P( 1 1
2 ) = 1 – 1 – 2 = 1 – g G g
Biến đổi tương đương từ ( 1 1
2 ) về (G 1< < G2) sẽ cho ước lượng khoảng cần tìm.
Với mẫu cụ thể, ta tính được 2 giá trị cụ thể của G , G 1 2, ký hiệu là g và g 1 : 2 qua mẫu cụ thể, với
độ tin cậy là (1 – ) , tham số của biến ngẫu nhiên gốc X sẽ nằm trong khoảng (g1,g ) 2
2. Ước lượng khoảng Trung bình tổng thể phân phối chuẩn 12B
(Ước lượng kì vọng toán biến ngẫu nhiên phân phối chuẩn)
X ~ N( , 2), với mẫu W kích thước , ước lượng cho tham số n chưa biết.
51B2.1. Khi biết phương sai tổng thể 2 (X ) n Vì U = ~ N(0,1) nên ( X ) n Pu u 1 1 P X
u X u 1 2 2 1 1 n n = 1 – Với mẫu cụ thể (còn gọi là KTC Khoảng tin cậy 2 phía x u x u / 2 / 2 n n đối xứng) x u Khoảng tin cậy tối đa n x u
Khoảng tin cậy tối thiểu n 2 I u / 2 2
Với khoảng tin cậy đối xứng n
, là độ chính xác của ước lượng, phản ánh
mức độ sai lệch của trung bình mẫu so với trung bình tổng thể với mức xác suất (1 – ) cho trước
Để độ dài khoảng tin cậy đối xứng không vượt quá một đoạn I : 0
I ≤ I (hoặc 0 ≤ 0) 2 4 2 2 ' n u 2 n' u 2 / 2 I 2 / 2 kích thước mẫu ’
n nguyên dương thỏa mãn 0 hoặc 0
Tài liệu Xác suất Thống kê Hoangld@neu.edu.vn
Nếu muốn độ dài khoảng tin cậy giảm đi k lần (độ chính xác của ước lượng tăng k lần)
thì kích thước mẫu tăng k2 lần.
52B2.2. Khi chưa biết phương sai tổng thể 2 , chỉ biết phương sai mẫu S2 ( X ) n S S T ~ T (n ) 1 P X t (n ) 1 X t n / 2 ( ) 1 / 2 1 S nên n n s s Tối đa
Khoảng tin cậy đối xứng x t (n ) 1 x t (n ) 1 / 2 / 2 n n
Tối thiểu
Với khoảng tin cậy đối xứng I ≤ I0 4 2 S 2 S ' 2 n t (n ) 1 ' 2 n t (n ) 1 2 / 2 I 2 / 2 kích thước mẫu 0 hoặc 0
3. Ước lượng khoảng Phương sai tổng thể phân phối chuẩn 13B
(Ước lượng phương sai biến ngẫu nhiên phân phối chuẩn)
53B3.1. Khi chưa biết trung bình tổng thể 2 (n ) 1 S
Với mẫu, tính được phương sai S2, (s2 với mẫu cụ thể) 2 = 2 ~ 2( – 1) n (n ) 1 2 s Tối đa 2 (n ) 1 2 s Khoảng tin cậy 2 phía 2 (n ) 1 2 ( n
Tối thiểu ) 1 / 2 1 / 2
54B3.2. Khi đã biết trung bình tổng thể
4. Ước lượng khoảng Tần suất tổng thể 14B
(Ước lượng tham số p của biến ngẫu nhiên phân phối Không-Một)
( f p) n p 1 ( p) N(0, 1) f 1 ( f ) f 1 ( f ) Tối đa
Khoảng tin cậy đối xứng f u / 2 p f u/2 n n
Tối thiểu
Kích thước mẫu tối thiểu để độ dài khoảng tin cậy đối xứng không vượt quá I cho trước 0 4 f 1 ( f ) f 1 ( f ) 2 ' n u 2 ' n u 2 / 2 I 2 / 2 0 hoặc 0
Chương 7. KIỂM ĐỊNH GIẢ THIÊT 1. Khái niệm 15B
1.1. Giả thiết thống kê 43B
Nghiên cứu vấn đề thông qua dấu hiệu , kiểm tra xem có hay không có một hoặc một số tính
chất nào đó (Đúng hoặc Sai) Kiểm định giả thiết.
Tài liệu Xác suất Thống kê Hoangld@neu.edu.vn
Dấu hiệu đặc trưng bởi (các) biến ngẫu nhiên, kiểm tra dựa trên BNN về một tính chất Thống
kê Giả thiết thống kê (gồm 3 loại)
Cặp giả thiết. H : giả thiết gốc ( o
null-hypothesis) và H : giả thiết đối ( 1 alternative-hypothesis)
Cặp giả thiết về tham số của tổng thể H : H : H : 0 0 0 0 0 0 H : H : H : 1 0 1 0 1 0
Kết quả kiểm định.
Bác bỏ giả thiết này (cho rằng nó Sai) Chấp nhận giả thiết kia
(cho rằng nó Đúng). Có thể có sai lầm.
2 loại Sai lầm.
Loại 1: Bác bỏ một điều đúng
Loại 2 : Chấp nhận 1 điều sai
1.2. Phương pháp Kiểm định 44B
Với mẫu ngẫu nhiên W, giả thiết gốc H . Xây dựng o
thống kê G trên mẫu tương ứng với H , o nếu
Ho đúng, với 1 miền trên trục số kí hiệu là W thì: P(G W /Ho ) = cho trước đủ nhỏ.
G là tiêu chuẩn kiểm định
là mức ý nghĩa của kiểm định, thường cho trước, là xác suất mắc sai lầm loại 1
W là miền bác bỏ
Quy tắc kiểm định.
Với mẫu cụ thể w( ), tính giá trị thống kê n
G gọi là giá trị quan sát: gqs
Nếu gqs W Bác bỏ Ho Nếu gqs W
Chưa có cơ sở bác bỏ Ho
2. Kiểm định tham số của một tổng thể 16B
2.1. Kiểm định trung bình tổng thể phân phối chuẩn 45B
2.1.1. Khi đã biết phương sai tổng thể 2 55B
2.1.2. Khi chưa biết phương sai tổng thể Tiêu chuẩn Cặp giả thuyết Miền bác bỏ Ho (X ) n H : 0 0 0
Tqs > t H : /2(n – 1) T = S 1 0 H : (x ) n 0 0 0 T H :
qs > t (n – 1) T s 1 0 qs = H : 0 0
Tqs < – t(n – 1) H : 1 0
2.2. Kiểm định phương sai tổng thể phân phối chuẩn 46B
X ~ N( , 2) với 2 chưa biết, cần kiểm định Tiêu chuẩn Cặp giả thuyết Miền bác bỏ H0 2 2 2 ( n ) 1 S H : 2 2 0 0 (n ) 1 qs / 2 2 2 H : 2 2 2 2 = 0 1 0 (n ) 1 qs 1 / 2 2 (n ) 1 s 2 H : 2 0 0 2 2 2 2 ( n ) 1 2 2 qs qs = 0 H : 1 0
Tài liệu Xác suất Thống kê Hoangld@neu.edu.vn 2 H : 2 0 0 2 2 n qs ( ) 1 2 H : 2 1 1 0
47B2.3. Kiểm định tần suất tổng thể Tiêu chuẩn Cặp giả thuyết Miền bác bỏ H0 H : p p 0 0
Uqs > u H : p p /2
( f p ) n 1 0 0 p 1 ( p ) H : p p U 0 0 0 0 qs = Uqs > u H : p p 1 0 H : p p 0 0
Uqs < – u H : p p 1 0
Tài liệu Xác suất Thống kê Hoangld@neu.edu.vn




