Tài liệu ôn tập lý thuyết thi tốt nghiệp Trung học Phổ thông môn Toán

Tài liệu gồm 21 trang, được biên soạn bởi thầy giáo Huỳnh Phú Sĩ, hướng dẫn học sinh lớp 12 ôn tập lý thuyết để chuẩn bị cho kỳ thi tốt nghiệp Trung học Phổ thông môn Toán. Mời bạn đọc đón xem!

121 61 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu ôn thi THPTQG môn Toán

Môn: Toán

Thông tin:

21 trang 6 tháng trước

Tác giả:

Profile M. Hậu
TRƯỜNG THCS-THPT MỸ THUẬN
TRƯỜNG THCS-THPT MỸ THUẬN
TỔ TOÁN
TỔ TOÁN
TÀI LIỆU ÔN THI T ỐT NGHIỆP
TÀI LIỆU ÔN THI T ỐT NGHIỆP
TRUNG HỌC PHỔ THÔNG
TRUNG HỌC PHỔ THÔNG
MÔN TOÁN
MÔN TOÁN
You can win
if you want
MỤCLỤC TÀILIỆUÔNTHITỐTNGHIỆPTHPTMÔNTOÁN
MỤC LỤC
Chủ đề 1. Khảo sát sự biến thiên và đồ thị của hàm số. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
1. Sựbiếnthiêncủahàmsố.................................................................. 2
2. Cựctrịcủahàmsố........................................................................ 2
3. Giátrịlớnnhấtvàgiátrịnhỏnhấtcủahàmsố............................................. 3
4. Đườngtiệmcận............................................................................ 3
5. Khảosátđồthịhàmsố.................................................................... 3
Chủ đề 2. Lũy thừa - Mũ - Logarit. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
1. Lũythừa................................................................................... 6
2. Hàmsốlũythừa........................................................................... 7
3. Logarit.................................................................................... 7
4. Hàmsốmũvàhàmsốlogarit.............................................................. 8
5. Phươngtrìnhmũvàphươngtrìnhlogarit................................................... 9
6. Bấtphươngtrìnhmũvàbấtphươngtrìnhlogarit............................................ 9
Chủ đề 3. Nguyên hàm - Tích phân và ứng dụng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
1. Nguyênhàm............................................................................... 10
2. Tíchphân................................................................................. 10
3. Ứngdụngcủatíchphântronghìnhhọc.................................................... 11
Chủ đề 4. Số phức. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
1. Sốphức................................................................................... 12
2. Phépcộng,trừ,nhân,chiasốphức......................................................... 12
Chủ đề 5. Khối đa diện . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
1. Kháiniệmvềhìnhđadiệnvàkhốiđadiện................................................. 13
2. Khốiđadiệnđều.......................................................................... 13
3. Thểtíchkhốiđadiện...................................................................... 13
Chủ đề 6. Khối tròn xoay. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14
1. Hìnhnónvàhìnhtrụ...................................................................... 14
2. Hìnhcầu.................................................................................. 14
Chủ đề 7. Phương pháp tọa độ trong không gian . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16
1. HệtọađộOxyz............................................................................ 16
2. Phươngtrìnhmặtcầu...................................................................... 17
3. Phươngtrìnhmặtphẳng................................................................... 17
4. Phươngtrìnhđườngthẳng................................................................. 18
Chủ đề 8. Dãy số - Quy tắc đếm - Xác suất - Góc - Khoảng cách . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
1. Dãysố..................................................................................... 19
2. Quytắcđếm............................................................................... 19
3. Xácsuất................................................................................... 20
4. GócvàKhoảngcáchtrongkhônggian..................................................... 20
TổToán 1 TrườngTHCS-THPTMỹThuận
Chủđề1.Khảosátsựbiếnthiênvàđồthịcủahàmsố TÀILIỆUÔNTHITỐTNGHIỆPTHPTMÔNTOÁN
Chủđề1.
KHẢO SÁT SỰ BIẾN THIÊN VÀ ĐỒ THỊ
CỦA HÀM SỐ
1 SỰ BIẾN THIÊN CỦA HÀM SỐ
1 Tính đơn điệu và dấu của đạo hàm
!
○ Nếuf
′
(x)> 0,∀x ∈ K thìf(x) ............... trênK.
○ Nếuf
′
(x)< 0,∀x ∈ K thìf(x) ............... trênK.
○ Nếuf
′
(x)=0,∀x ∈ K thìf(x) ............... trênK.
2 Quy tắc xét tính đơn điệu của hàm số
Quy tắc − é
Bước1. Tìm..................
Bước2. Tìm............ f
′
(x).Tìmx đểf
′
(x)...... hoặc..................
Bước3. Lậpbảng...............
Bước4. Kếtluậnvềcáckhoảngđồngbiến,nghịchbiếncủahàmsố.
2 CỰC TRỊ CỦA HÀM SỐ
1 Các khái niệm
!
• Nếuf(x)đạtCĐtạix
0
thìtagọix
0
làđiểmCĐcủa.........,f
(
x
0
)
làgiátrịCĐcủa.........,cònđiểm
M
(
x
0
;f
(
x
0
))
làđiểmCĐcủa..........Tagọitươngtựđốivớicựctiểu.
• CácđiểmCĐvàCTđượcgọichunglà...............,giátrịCĐvàgiátrịCTđượcgọichunglà
......... củahàmsố.
• Nếuf(x) xácđịnhtrênK vàđạtcựctrịtạix
0
thìf
′
(
x
0
)
=....
O
x
y
x
1
y
1
x
2
y
2
Điểmcựcđạicủa...............
Giátrịcựctiểucủa...............
Điểmcựctiểucủa...............
Giátrịcựcđạicủa...............
ĐiểmcựcđạiA
(
x
1
;y
1
)
của...............
ĐiểmcựctiểuB
(
x
2
;y
2
)
của...............
2 Điều kiện đủ để hàm số có cực trị
!
○ Nếuf
′
(
x
0
)
> 0 khix < x
0
vàf
′
(
x
0
)
< 0 khix > x
0
thìx
0
làmộtđiểm......... củahàmsốf(x).
○ Nếuf
′
(
x
0
)
< 0 khix < x
0
vàf
′
(
x
0
)
> 0 khix > x
0
thìx
0
làmộtđiểm......... củahàmsốf(x).
TổToán 2 TrườngTHCS-THPTMỹThuận
Chủđề1.Khảosátsựbiếnthiênvàđồthịcủahàmsố TÀILIỆUÔNTHITỐTNGHIỆPTHPTMÔNTOÁN
3 Quy tắc tìm cực trị
Quy tắc 1 − é
Bước1. Tìm..................
Bước2. Tìm............ f
′
(x).Tìmx đểf
′
(x)...... hoặc..................
Bước3. Lậpbảng...............
Bước4. Kếtluậnvềcácđiểmcựctrị.
Quy tắc 2 − é
Bước1. Tìm..................
Bước2. Tìm............ f
′
(x).Tìmx đểf
′
(x)...0.
Bước3. Tìmđạohàmcấp... rồitínhcácgiátrịf
′′
(x).
Bước4. Kếtluậnvềcácđiểmcựctrị.
3 GIÁ TRỊ LỚN NHẤT VÀ GIÁ TRỊ NHỎ NHẤT CỦA HÀM SỐ
1 Định nghĩa
!
○ SốM đượcgọilàgiátrịlớnnhấtcủaf(x)trênD nếuf(x) ... M, ∀x ∈ D và∃x
0
∈ D saochof
(
x
0
)
... M.
KíhiệuM =max
D
f(x).
○ Sốm đượcgọilàgiátrịnhỏnhấtcủaf(x)trênD nếuf(x) ... m, ∀x ∈ D và∃x
0
∈ D saochof
(
x
0
)
... m.
Kíhiệum =min
D
f(x).
2 Cách tìm GTLN & GTNN của hàm số trên một đoạn
Quy tắc − é
Bước1. Tìm..................
Bước2. Tìm............ f
′
(x).Tìmx đểf
′
(x)...0.
Bước3. Tìmđạohàmcấp... rồitínhcácgiátrịf
′′
(x).
Bước4. Kếtluậnvềcácđiểmcựctrị.
!
Lưu ý:
Nếuf
′
(x) không......... trên[a;b] thìf
(
x
)
đạtGTLNvàGTNNtạicácđầumútcủa[a;b].
4 ĐƯỜNG TIỆM CẬN
1 Tiệm cận ngang
!
Đường thẳng y = y
0
được gọi là tiệm cận
ngangcủađồthịhàmsốy = f
(
x
)
nếu......
trongcácđiềukiệnsauđượcthỏamãn:
○ lim
x→+∞
f(x)=... ○ lim
x→−∞
f(x)=...
2 Tiệm cận đứng
!
Đườngthẳngx =x
0
đượcgọilàtiệmcậnđứng
củađồthịhàmsốy =f
(
x
)
nếu...... trong
cácđiềukiệnsauđượcthỏamãn:
○ lim
x→x
+
0
f(x)=......
○ lim
x→x
+
0
f(x)=......
○ lim
x→x
−
0
f(x)=......
○ lim
x→x
−
0
f(x)=......
5 KHẢO SÁT ĐỒ THỊ HÀM SỐ
1 Hàm số y =ax
3
+bx
2
+cx +d (a =0)
TổToán 3 TrườngTHCS-THPTMỹThuận
Chủđề1.Khảosátsựbiếnthiênvàđồthịcủahàmsố TÀILIỆUÔNTHITỐTNGHIỆPTHPTMÔNTOÁN
b
2
−3ac...0và a...0
O
x
y
−1
3
1
−1
y =x
3
−3x +1
b
2
−3ac...0và a...0
O
x
y
−1
2
y =−
x
3
3
+
x
2
2
+2x
b
2
−3ac...0và a...0
O
x
y
1
1
y =
x
3
3
−x
2
+x +
2
3
b
2
−3ac...0và a...0
O
x
y
y =x
3
+x
2
+2x − 1
b
2
−3ac...0và a...0
O
x
y
2
y =2−x
3
b
2
−3ac...0và a...0
O
x
y
y =1− x −x
3
2 Hàm số y =ax
4
+bx
2
+c (a =0)
a, b...... dấu và a...0
O
x
y
−3
y =x
4
+2x
2
−3
a, b...... dấu và a...0
O
x
y
√
2
−3
−
√
2
−1
y =
x
4
2
−2x
2
−1
TổToán 4 TrườngTHCS-THPTMỹThuận
Chủđề1.Khảosátsựbiếnthiênvàđồthịcủahàmsố TÀILIỆUÔNTHITỐTNGHIỆPTHPTMÔNTOÁN
a, b...... dấu và a...0
O
x
y
1
y =−2x
4
−x
2
+1
a, b...... dấu và a...0
O
x
y
1
2
−1
1
y =−x
4
+2x
2
+1
3 Hàm số y =
ax +b
cx +d
(c =0, ad −bc =0)
y
′
...0
O
x
y
−1
−1
2
y =
2x − 1
x +1
y
′
...0
O
x
y
1
−1
1
y =
x +1
x − 1
4 Sự tương giao của các đồ thị
!
Giảsửhàmsốy =f(x) cóđồthị
(
C
1
)
vàhàmsốy =g(x) cóđồthị
(
C
2
)
.
Đểtìmhoànhđộgiaođiểmcủa
(
C
1
)
và
(
C
2
)
,tagiảiphươngtrình............
TổToán 5 TrườngTHCS-THPTMỹThuận
Chủđề2.Lũythừa-Mũ-Logarit TÀILIỆUÔNTHITỐTNGHIỆPTHPTMÔNTOÁN
Chủđề2.
LŨY THỪA - MŨ - LOGARIT
1 LŨY THỪA
1 Lũy thừa với số mũ nguyên
Chon ∈ N
∗
,a ∈ R.
Lũythừabậcn củaa là......... của... thừasốa.
a
n
=a ·a · a···a · a
| {z }
n sốa
Sốa gọilà.........,sốn gọilà.........
Chú ý: Vớia =0 tacó
• a
0
=... • a
−n
=......
2 Căn bậc n
Chosốb ∈ R vàsốn ∈ N
∗
(n ≥ 2).
Nếua
n
=b thìa đượcgọilà............... củab.
○ Vớin lẻ:có............... cănbậcn củab
○ Vớin chẵn:
– Nếub < 0 thì........................
– Nếub =0 thì........................
– Nếub > 0 thì........................
!
•
n
√
a ·
n
√
b =......
•
n
√
a
n
√
b
=......
•
n
√
a
m
=......
•
n
√
a
n
=
(
a nếun......
|a| nếun......
3 Tính chất của lũy thừa với số mũ thực
!
Choa, b > 0 lànhữngsốthực;m, n lànhữngsốthựctùyý.
• a
m
·a
n
=......
•
a
m
a
n
=......
•
(
a
m
)
n
=......
•
(
ab
)
m
=......
•
a
b
m
=......
○ Vớia > 1:a
m
> a
n
⇔ m...n
○ Vớia < 1:a
m
> a
n
⇔ m...n
TổToán 6 TrườngTHCS-THPTMỹThuận
Chủđề2.Lũythừa-Mũ-Logarit TÀILIỆUÔNTHITỐTNGHIỆPTHPTMÔNTOÁN
2 HÀM SỐ LŨY THỪA
1 Định nghĩa
!
Chosốthựcα.
Hàmsốy =...... đượcgọilàhàmsốlũythừa.
Tập xác định của hàm số lũy thừa − é
Tậpxácđịnhcủahàmsốlũythừax
α
tùythuộcvàogiátrịcủa...
○ Nếuα ∈ Z
+
:tậpxácđịnhlà.........
○ Nếuα ∈ Z
−
:tậpxácđịnhlà.........
○ Nếuα /∈ Z:tậpxácđịnhlà.........
2 Khảo sát hàm số lũy thừa
Trongtrườnghợptổngquát,takhảosáthàmsốy =x
α
trênkhoảng.........
y =x
α
,α > 0 y =x
α
,α < 0
Sựbiếnthiên
Giớihạnđặcbiệt
Tiệmcận
Đồthị
O
x
y
α > 1
α =1
α < 1
1
1
O
x
y
α < 0
1
1
3 LOGARIT
1 Định nghĩa
Chohaisố...... a, b vớia.......
Sốα thỏamãnđẳngthứca
α
=b đượcgọilà........................ vàkíhiệulà.......
α =...... ⇔ a
α
=b
Sốa gọilà.........,sốn gọilà.........
Chú ý: Khôngcólôgaritcủasố...... vàsố0.
Tính chất − é
• log
a
1=...
• log
a
a =...
• a
log
a
b
=...
• log
a
a
b
=...
TổToán 7 TrườngTHCS-THPTMỹThuận
Chủđề2.Lũythừa-Mũ-Logarit TÀILIỆUÔNTHITỐTNGHIỆPTHPTMÔNTOÁN
2 Quy tắc tính lôgarit
!
Chobasố...... a, b, c vớia.......Tacó
• log
a
(
b · c
)
=...............
• log
a
b
c
=...............
• log
a
b
α
=.........,∀α
• log
a
b =
log
c
...
log
c
...
(c =1)
• log
a
b =
1
......
(b =1)
• log
a
α
b =......log
a
b (α =0)
3 Lôgarit thập phân và lôgarit tự nhiên
Lôgarit thập phân − é
Lôgaritthậpphânlàlôgaritcơsố....
logb =......
Lôgarit tự nhiên − é
Lôgarittựnhiênlàlôgaritcơsố...
lnb =......
4 HÀM SỐ MŨ VÀ HÀM SỐ LOGARIT
1 Hàm số mũ
Chosốthực...... a =....
Hàmsốy =...... đượcgọilàhàm số mũ cơsố....
!
Chosố...... a =... vàhàmhợpu =u(x).Tacó:
•
(
a
x
)
′
=.........
•
(
e
x
)
′
=.........
•
(
a
u
)
′
=.........
•
(
e
u
)
′
=.........
y =a
x
,a > 1 y =a
x
,0< a < 1
Sựbiếnthiên
Tiệmcận
Đồthị
O
x
y
a > 1
1
1
a
O
x
y
a < 1
1
1
a
2 Hàm số lôgarit
Chosốthực...... a =....
Hàmsốy =...... đượcgọilàhàm số lôgarit cơsố....
!
Chosố...... a =... vàhàmhợpu =u(x).Tacó:
•
(
log
a
x
)
′
=.........
1
xlna
•
(
lnx
)
′
=.........
1
x
•
(
log
a
u
)
′
=.........
1
xlna
•
(
lnu
)
′
=.........
1
xlna
TổToán 8 TrườngTHCS-THPTMỹThuận
Chủđề2.Lũythừa-Mũ-Logarit TÀILIỆUÔNTHITỐTNGHIỆPTHPTMÔNTOÁN
y =log
a
x,a > 1 y =log
a
x,0< a < 1
Tậpxácđịnh
Sựbiếnthiên
Tiệmcận
Đồthị
O
x
y
a > 1
1
a
1
O
x
y
5 PHƯƠNG TRÌNH MŨ VÀ PHƯƠNG TRÌNH LOGARIT
1 Phương trình mũ
Phươngtrìnhmũcơbảncódạng......... (a > ...,
a =...).
b > 0
b ≤ 0
2 Phương trình lôgarit
Phươngtrìnhlôgarit cơ bản có dạng ............
(a > ...,a =...).
log
a
x =b ⇔ x =......
6 BẤT PHƯƠNG TRÌNH MŨ VÀ BẤT PHƯƠNG TRÌNH LOGARIT
1 Bất phương trình mũ
Bấtphươngtrìnhmũcơbảncódạng......... hoặc
......... hoặc ......... hoặc ......... (a > ...,
a =...).
a
x
> b a > 1 0< a < 1
b > 0
b ≤ 0
2 Bất phương trình lôgarit
Bất phương trình lôgarit cơ bản có dạng
............ hoặc ............ hoặc ............
hoặc............ (a > ...,a =...).
log
a
x > b a > 1 0< a < 1
Nghiệm
TổToán 9 TrườngTHCS-THPTMỹThuận
Chủđề3.Nguyênhàm-Tíchphânvàứngdụng TÀILIỆUÔNTHITỐTNGHIỆPTHPTMÔNTOÁN
Chủđề3.
NGUYÊN HÀM - TÍCH PHÂN VÀ ỨNG
DỤNG
1 NGUYÊN HÀM
1 Tính chất của nguyên hàm
!
Tínhchất1.
Z
f
′
(x)dx =..................
Tínhchất2.
Z
k · f(x)dx =............ (k làhằngsố)
Tínhchất3.
Z
[f(x)±g(x)] dx =.....................
Bảng nguyên hàm của một số hàm số thường gặp
•
Z
0dx =...............
•
Z
dx =...............
•
Z
x
n
dx =............... (n =−1)
•
Z
1
x
dx =...............
•
Z
e
x
dx =...............
•
Z
a
x
dx =............... (a > 0,a =1)
•
Z
cosx dx =...............
•
Z
sinxdx =...............
•
Z
1
cos
2
x
dx =...............
•
Z
1
sin
2
x
dx =...............
2 Tìm nguyên hàm bằng phương pháp đổi biến số
Định lí − é
Nếu
Z
f(u)dx = F(u)+C vàu = u(x)làhàmsố
cóđạohàmliêntụcthì
Z
f
(
u(x)
)
·u
′
(x)dx =........................
Hệ quả − é
Vớiu =ax +b (a =0)thì
Z
f
(
ax +b
)
dx =...............
3 Phương pháp nguyên hàm từng phần
Định lí − é
Nếuhaihàmsốu =u(x) vàv =v(x) cóđạohàmliêntụctrênK thì
Z
u(x)· v
′
(x)dx =........................
2 TÍCH PHÂN
TổToán 10 TrườngTHCS-THPTMỹThuận
Chủđề3.Nguyênhàm-Tíchphânvàứngdụng TÀILIỆUÔNTHITỐTNGHIỆPTHPTMÔNTOÁN
1 Tính chất của tích phân
!
Tínhchất1.
b
Z
a
k · f(x)dx =............... (k làhằngsố)
Tínhchất2.
b
Z
a
[f(x)±g(x)] dx =...........................
Tínhchất3.
c
Z
a
f(x)dx +
b
Z
c
f(x)dx =............ (a < c < b)
2 Phương pháp tính tích phân từng phần
Định lí − é
Nếuhaihàmsốu =u(x) vàv =v(x) cóđạohàmliêntụctrênK thì
b
Z
a
u(x)· v
′
(x)dx =........................
3 ỨNG DỤNG CỦA TÍCH PHÂN TRONG HÌNH HỌC
1 Hình phẳng giới hạn bởi một
đường cong và trục hoành
Diện tích S của hình phẳng giởi hạn bởi đồ thị của
hàm số y =f(x), trục ......... và hai đường thẳng
x =a, x =b được tính theo công thức
S =
b
Z
a
...... dx
2 Hình phẳng giới hạn bởi hai
đường cong
Diện tích S của hình phẳng giởi hạn bởi đồ thị của
hai hàm số y =f(x), y = g(x) và hai đường thẳng
x =a, x =b được tính theo công thức
S =
b
Z
a
............... dx
3 Thể tích của vật thể
CắtmộtvậtthểV bởihaimặtphẳng(P)và(Q)vuônggócvớitrụcOx lầnlượttạix =a,x =b (a < b).
Cắt V bởi một mặt phẳng tùy ý vuông góc với Ox tại diểm x ∈ [a;b] theo thiết diện có diện tích S(x).
GiảsửS(x)liêntụctrênđoạn[a;b],khiđóvậtthểV cóthể
tíchlà
V =
b
Z
a
............ dx
4 Thể tích khối tròn xoay
Quayhìnhthangconggiớihạnbởiđồthịhàmsốy = f(x),trụchoànhvàhaiđườngthẳngx =a,x =b quanh
trục...... tạothànhmộtkhối............ cóthểtíchlà
V =...
b
Z
a
......... dx
TổToán 11 TrườngTHCS-THPTMỹThuận
Chủđề4.Sốphức TÀILIỆUÔNTHITỐTNGHIỆPTHPTMÔNTOÁN
Chủđề4.
SỐ PHỨC
1 SỐ PHỨC
1 Định nghĩa
Mỗibiểuthứcdạng......... trongđóa, b ∈ ... vài
2
=... đượcgọilàmộtsố phức.
• Đốivớisốphứcz =a+bi,tanóia là............,b là............ củaz.
• Sối đượcgọilà............
• Tậphợpcácsốphứckíhiệulà...... (ThesetofComplexnumbers).
!
• Mỗisốthựca đềulàmộtsốphứcvớiphần ảo
bằng...
• Sốphứcbi cóphần thực bằng... đượcgọilàsố
.........
2 Số phức bằng nhau
Haisốphứcđượcgọilàbằngnhaunếu............ và............ củachúngtươngứngbằngnhau.
a
1
+b
1
i =a
2
+b
2
i ⇔
(
a
1
=...
b
1
=...
3 Biểu diễn hình học của số phức
ĐiểmM(...;...) tronghệtrụctọađộOxy đượcgọilàđiểm............ củasốphứcz =a +bi.
4 Môđun của số phức
Chosốphứcz =a +bi cóđiểmbiểudiễnlàM(a;b).
......... củavectơ
−−Ï
OM đượcgọilàmôđuncủasốphứcz,kíhiệulà......
|z| =.........
5 Số phức liên hợp
Chosốphứcz =a +bi.Tagọi......... làsố phức liên hợp củaz,kíhiệulà....
2 PHÉP CỘNG, TRỪ, NHÂN, CHIA SỐ PHỨC
Chohaisốphứcz
1
=a
1
+b
1
i vàz
2
=a
2
+b
2
i,khiđó:
• z
1
+z
2
=...............
• z
1
−z
2
=...............
• (a +bi)(c +di)=.....................
•
z
1
z
2
=
z
1
·z
2
z
2
·z
2
=.....................
TổToán 12 TrườngTHCS-THPTMỹThuận
Chủđề5.Khốiđadiện TÀILIỆUÔNTHITỐTNGHIỆPTHPTMÔNTOÁN
Chủđề5.
KHỐI ĐA DIỆN
1 KHÁI NIỆM VỀ HÌNH ĐA DIỆN VÀ KHỐI ĐA DIỆN
!
Hình đa diện là hình được tạo bởi một số hữu hạn các ......... thỏa mãn hai tính chất sau:
• Hai đa giác phân biệt chỉ có thể hoặc không có ...... chung, hoặc chỉ có một ...... chung, hoặc chỉ
có một ...... chung.
• Mỗi cạnh của đa giác nào cũng là cạnh chung của đúng ...... đa giác.
Khối đa diện là phần ............ được giới hạn bởi một ...... đa diện, kể cả ...... đa diện đó.
2 KHỐI ĐA DIỆN ĐỀU
!
Khối đa diện đều là khối đa diện ...... có các tính chất sau đây:
• Mỗi mặt của nó là một ..................... p cạnh
• Mỗi đỉnh của nó là đỉnh chung của đúng q mặt.
Khốiđadiệnđềunhưvậyđượcgọilàkhốiđadiệnđềuloại.......
Tứdiệnđều
• ...... đỉnh
• ...... cạnh
• ...... mặt
Lậpphương
• ...... đỉnh
• ...... cạnh
• ...... mặt
Bátdiệnđều
• ...... đỉnh
• ...... cạnh
• ...... mặt
Thậpnhịdiệnđều
• ...... đỉnh
• ...... cạnh
• ...... mặt
Nhịthậpdiệnđều
• ...... đỉnh
• ...... cạnh
• ...... mặt
3 THỂ TÍCH KHỐI ĐA DIỆN
Thể tích khối chóp − é
Thể tích khối chóp có diện tích đáy B và chiều cao
h là
V =.........
Thể tích khối lăng trụ − é
Thể tích khối lăng trụ có diện tích đáy B và chiều
cao h là
V =.........
• Thểtíchkhốihộpchữnhật:..................
• Thểtíchkhốilậpphương:..................
TổToán 13 TrườngTHCS-THPTMỹThuận
Chủđề6.Khốitrònxoay TÀILIỆUÔNTHITỐTNGHIỆPTHPTMÔNTOÁN
Chủđề6.
KHỐI TRÒN XOAY
1 HÌNH NÓN VÀ HÌNH TRỤ
1 Hình nón tròn xoay
!
ChotamgiácOIM vuôngtại I. Khi quay △OIM
quanhcạnhOI thìđường......... OIM tạothành
một...... đượcgọilàhìnhnóntrònxoay,gọitắtlà
............
• HìnhtròntâmI,bánkínhIM gọilà.........
• ĐiểmO gọilà...... củahìnhnón
• ĐoạnOI gọilà.........,đoạnOM làđộdài
............
2 Hình trụ tròn xoay
!
Trongmặtphẳng(P)chohaiđườngthẳngℓ và∆
............ vớinhau,cáchnhaumộtkhoảngr.Khi
quaymặtphẳng(P) xungquanh∆ thìđườngthẳngℓ
sinhramộtmặt......... đượcgọilàmặt...... tròn
xoay,gọitắtlà............
• Đườngthẳng...... gọilàtrục
• Đườngthẳng...... gọilàđườngsinh
• r là......... củamặttrụđó.
Chohìnhnóncóchiềucaoh,độdàiđườngsinhℓ và
bánkínhđáyr.Khiđó:
Diệntíchxung
quanh
Diệntíchtoànphần Thểtích
Chohìnhtrụcóchiềucaoh vàbánkínhđáyr.Khiđó:
Diệntíchxung
quanh
Diệntíchtoànphần Thểtích
2 HÌNH CẦU
!
Tập hợp những điểm M trong ............ cách điểm O cố định một khoảng ............ bằng r > 0
được gọi là mặt cầu tâm O bán kính r. Kíhiệu:.........
• NếuhaiđiểmC, D ∈ S
(
S;r
)
thìđoạnthẳngCD gọilà.............
• Dâycungđiquatâmđượcgọilà............ củamặtcầu.
Điểm nằm trong và nằm ngoài mặt cầu − é
ChomặtcầuS
(
O;r
)
vàđiểmM bấtkì.
• NếuOM =r thìM nằm...... mặtcầuS
(
O;r
)
• NếuOM < r thìM nằm...... mặtcầuS
(
O;r
)
• NếuOM > r thìM nằm...... mặtcầuS
(
O;r
)
Giao của mặt cầu và mặt phẳng − é
Cho mặt cầu S
(
O;r
)
và mặt phẳng (P). Gọi H
là hình chiếu vuông góc của O lên (P), khi đó
OH =d
(
O,(P)
)
.
○ NếuOH > r thì(P)và(S)......... điểmchung.
○ NếuOH =r thì(P) ......... với(S) tại....
Khi đó, (P) gọi là ............, H gọi là
............
○ NếuOH < r thì(P)cắt(S)theogiaotuyếnlà
............ tâm...,bánkínhr
′
=..........
Giao của mặt cầu và đường thẳng − é
Cho mặt cầu S
(
O;r
)
và đường thẳng ∆. Gọi H
là hình chiếu vuông góc của O lên ∆, khi đó
OH =d
(
O,∆
)
.
○ NếuOH > r thì∆ và(S) ......... điểmchung.
○ NếuOH =r thì∆ ......... với(S) tại....
Khi đó, ∆ gọi là ............, H gọi là
............
○ NếuOH < r thì∆ cắt(S) tại... điểm.
TổToán 14 TrườngTHCS-THPTMỹThuận
Chủđề6.Khốitrònxoay TÀILIỆUÔNTHITỐTNGHIỆPTHPTMÔNTOÁN
Tiếp tuyến − é
• QuamộtđiểmM nằmtrênmặtcầu,có...... tiếptuyếnvớimặtcầu.Cáctiếptuyếnnàytạothànhmột
............ củamặtcầu.
• QuamộtđiểmM nằmngoàim ặtcầu,có...... tiếptuyếnvớimặtcầu.Cáctiếptuyếnnàytạothànhmột
......... đỉnhA.
• NếuOM > r thìM nằm...... mặtcầuS
(
O;r
)
Diệntích Thểtích
TổToán 15 TrườngTHCS-THPTMỹThuận
Chủđề7.Phươngpháptọađộtrongkhônggian TÀILIỆUÔNTHITỐTNGHIỆPTHPTMÔNTOÁN
Chủđề7.
PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG
GIAN
1 HỆ TỌA ĐỘ OXYZ
1 Tọa độ điểm và vectơ
Trongkhônggian,hệtrụctọađộOxyz baogồm... trụcOx,Oy,Oz đôimột............
• Cácvectơ
−Ï
i ,
−Ï
j ,
−Ï
k lầnlượtlàcácvectơ.........
trêncáctrụcOx,Oy,Oz.
• ĐiểmO(...;...;...) đượcgọilà...............
• Cácmặtphẳng......,......,...... đượcgọilàcác
mặtphẳngtọađộ.
• ĐiểmM
(
x
0
;y
0
;z
0
)
nếu
−−Ï
OM =...............
2 Biểu thức tọa độ của các phép toán vectơ
Các công thức cần nhớ − é
TrongkhônggianOxyz,chohaivectơ
−Ï
a =
(
a
1
;a
2
;a
3
)
và
−Ï
b =
(
b
1
;b
2
;b
3
)
.Tacó:
•
−Ï
a ±
−Ï
b =.....................
• k ·
−Ï
a =..................
•
−Ï
a =
−Ï
b ⇔
a
1
=...
a
2
=...
a
3
=...
•
−Ï
i =.........,
−Ï
j =.........,
−Ï
k =.........
• Vớivectơ
−Ï
b =
−Ï
0 thì
−Ï
a và
−Ï
b cùngphươngkhivà
chỉkhi∃k ∈ R saochoa
1
= ......,a
2
= ......,
a
3
=......
•
−Ï
AB =........................
• TrungđiểmcủađoạnthẳngAB làM
x
A
+x
B
...
;
.........
2
;
.........
...
• TrọngtâmcủatamgiácABC làG
x
A
+x
B
+x
C
...
;
............
3
;
............
...
3 Tích vô hướng
TrongkhônggianOxyz,tíchvôhướngcủahaivectơ
−Ï
a =
(
a
1
;a
2
;a
3
)
và
−Ï
b =
(
b
1
;b
2
;b
3
)
bằng
−Ï
a ·
−Ï
b =.....................
Độ dài của một vectơ − é
Chovectơ
−Ï
a =
(
a
1
;a
2
;a
3
)
.Khiđó
−Ï
a
=
q
a
2
1
+.........
Góc giữa hai vectơ − é
Góc giữa hai vectơ
−Ï
a =
(
a
1
;a
2
;a
3
)
và
−Ï
b =
(
b
1
;b
2
;b
3
)
đượctínhbởicôngthức
cos
−Ï
a,
−Ï
b
=
−Ï
a ...
−Ï
b
−Ï
a
...
−Ï
b
=.....................
4 Tích có hướng
Trongkhônggian,chohaivectơ
−Ï
a =
(
a
1
;a
2
;a
3
)
và
−Ï
b =
(
b
1
;b
2
;b
3
)
.Tích có hướng củahaivectơ
−Ï
a và
−Ï
b làmột
...... ............ vớicả
−Ï
a và
−Ï
b .
h
−Ï
a,
−Ï
b
i
=
(
............;............;............
)
TổToán 16 TrườngTHCS-THPTMỹThuận
Chủđề7.Phươngpháptọađộtrongkhônggian TÀILIỆUÔNTHITỐTNGHIỆPTHPTMÔNTOÁN
2 PHƯƠNG TRÌNH MẶT CẦU
Định lí − é
TrongkhônggianOxyz,mặtcầu(S) tâmI(a;b;c) bánkínhR cóphươngtrìnhlà
(x − ...)
2
+(y ......)
2
+(z......)
2
=......
Nhận xét: Phươngtrìnhmặtcầunóitrêncóthểviếtdướidạng
x
2
+y
2
+z
2
−......x − ......y − ......z +d =0
trongđóR =
√
a
2
+b
2
+c
2
−... (a
2
+b
2
+c
2
−... > ...)
3 PHƯƠNG TRÌNH MẶT PHẲNG
1 Vectơ pháp tuyến của mặt phẳng
Định nghĩa − é
Chomặtphẳng
(
α
)
.Nếuvectơ
−Ï
n =
−Ï
0 vàcó...... vuônggócvớimặtphẳng
(
α
)
thì
−Ï
n đượcgọilàvectơ
.................. của
(
α
)
.
• Mỗimặtphẳngcó......... vectơpháptuyến.
• Nếu
−Ï
n làvectơpháptuyếncủa
(
α
)
thìk ·
−Ï
n cũnglà..................... của
(
α
)
.
2 Phương trình tổng quát của mặt phẳng
TrongkhônggianOxyz,chomặtphẳng
(
α
)
điquađiểmM
(
x
0
;y
0
;z
0
)
vàcóvectơpháptuyến
−Ï
n = (a;b;c).Khi
đó
a
(
x − ...
)
+...
(
y...y
0
)
+c
(
...−z
0
)
=...
Phương trình mặt phẳng theo đoạn chắn − é
Nếumặtphẳng
(
α
)
cắtcáctrụcOx,Oy,Oz lầnlượttạiA(a;0;0),B(0;b;0) vàC(0;0;c) thì
(
α
)
:
x
a
+
y
b
+
z
c
=...
3 Vị trí tương đối của hai mặt phẳng
TrongkhônggianOxyz chohaimặtphẳng
(
α
)
: A
1
x +B
1
y +C
1
z +D
1
=0 và
(
β
)
: A
2
x +B
2
y +C
2
z +D
2
=0.
!
•
(
α
)
∥
(
β
)
⇔
(
(
A
1
;B
1
;C
1
)
...k
(
A
2
;B
2
;C
2
)
D
1
...kD
2
•
(
α
)
≡
(
β
)
⇔
(
(
A
1
;B
1
;C
1
)
...k
(
A
2
;B
2
;C
2
)
D
1
...kD
2
•
(
α
)
⊥
(
β
)
⇔ ............
4 Khoảng cách từ một điểm đến một mặt phẳng
TrongkhônggianOxyz,khoảngcáchtừđiểmM
(
x
0
;y
0
;z
0
)
đếnmặtphẳng
(
α
)
: Ax+By+Cz+D =0 được
tínhbằng
d
(
M,
(
α
))
=
A... +B...+C...+D
√
...
2
+...
2
+...
2
5 Góc giữa hai mặt phẳng
Giảsử
−Ï
m,
−Ï
n lầnlượtlàvectơpháptuyếncủahaimặtphẳng
(
α
)
,
(
β
)
.Khiđó
cos
((
α
)
,
(
β
))
=
−Ï
m ·
−Ï
n
−Ï
m
·
−Ï
n
TổToán 17 TrườngTHCS-THPTMỹThuận
Chủđề7.Phươngpháptọađộtrongkhônggian TÀILIỆUÔNTHITỐTNGHIỆPTHPTMÔNTOÁN
4 PHƯƠNG TRÌNH ĐƯỜNG THẲNG
1 Phương trình tham số và phương trình chính tắc của đường thẳng
Định nghĩa − é
TrongkhônggianOxyz chođườngthẳng∆điquađiểmM
(
x
0
;y
0
;z
0
)
vànhận
−Ï
u =
(
u
1
;u
2
;u
3
)
làmvectơchỉ
phương.Khiđóphươngtrìnhthamsốcủa∆ códạng
∆:
x =......+......t
y =...... +......t
z =...... +......t
(1)
trongđót là............
!
Nếuu
1
, u
2
, u
3
=0 thìphươngtrình(1)cóthểviếtdướidạngchính tắc nhưsau:
x − ...
...
=
y − ...
...
=
z − ...
...
2 Vị trí tương đối của hai đường thẳng
Hai đường thẳng song song, trùng nhau
Gọi
−Ï
u,
−Ï
v lầnlượtlàvectơchỉphươngcủahaiđườngthẳng∆
1
, ∆
2
vàđiểmM ∈ ∆
1
.
• ∆
1
∥ ∆
2
⇔
(
−Ï
u =k......
M ......∆
2
• ∆
1
≡ ∆
2
⇔
(
−Ï
u =k......
M ......∆
2
Hai đường thẳng cắt nhau, chéo nhau
Chohaiđườngthẳngd:
x =x
0
+u
1
t
y =y
0
+u
2
t
z =z
0
+u
3
t
vàd
′
:
x =x
′
0
+v
1
t
′
y =y
′
0
+v
2
t
′
z =z
′
0
+v
3
t
′
.
• d vàd
′
cắtnhaukhivàchỉkhihệphươngtrình
x
0
+u
1
t =x
′
0
+v
1
t
′
y
0
+u
2
t =y
′
0
+v
2
t
′
z
0
+u
3
t =z
′
0
+v
3
t
′
cóđúng...... nghiệm.
• d vàd
′
chéonhaukhivàchỉkhihaivectơ
−Ï
u,
−Ï
v
............ phươngvàhệphươngtrình
x
0
+u
1
t =x
′
0
+v
1
t
′
y
0
+u
2
t =y
′
0
+v
2
t
′
z
0
+u
3
t =z
′
0
+v
3
t
′
...... nghiệm.
3 Vị trí tương đối của đường thẳng và mặt phẳng
!
Đểtìmgiaođiểmcủađườngthẳng∆:
x =x
0
+u
1
t
y =y
0
+u
2
t
z =z
0
+u
3
t
vàmặtphẳng
(
α
)
: Ax +By +Cz +D =0,taxét
phươngtrình
A
(
x
0
+u
1
t
)
+B
(
y
0
+u
2
t
)
+C
(
z
0
+u
3
t
)
+D =0(1)
• Nếu(1)vônghiệmthì∆.........
(
α
)
• Nếu(1)vôsốnghiệmthì∆.........
(
α
)
• Nếu(1)cóđúngmộtnghiệmthì∆.........
(
α
)
TổToán 18 TrườngTHCS-THPTMỹThuận
Chủđề8.Dãysố-Quytắcđếm-Xácsuất-Góc-Khoảngcách TÀILIỆUÔNTHITỐTNGHIỆPTHPTMÔNTOÁN
Chủđề8.
DÃY SỐ - QUY TẮC ĐẾM - XÁC SUẤT -
GÓC - KHOẢNG CÁCH
1 DÃY SỐ
1 Dãy số
!
Mỗi...... sốu xácđịnhtrêntậpcácsốnguyêndươngN
∗
đượcgọilàmộtdãysốvôhạn(gọitắtlàdãysố).
•
u
n
:dãysốu
1
, u
2
, ...
• u
1
:sốhạng.........
• u
n
:sốhạng...............
2 Cấp số cộng - Cấp số nhân
Cấpsốcộng Cấpsốnhân
Địnhnghĩa
Sốhạngtổngquát
Tínhchất
Tổngn sốhạngđầu
2 QUY TẮC ĐẾM
1 Quy tắc cộng và Quy tắc nhân
Quy tắc cộng − é
Nếumộtcôngviệccóthểđượchoànthànhbởimột
trong hai phươngán,phươngánthứnhấtcóm cách
thựchiện,phươngánthứhaicón cáchthựchiện,thì
có............cáchhoànthànhcôngviệc.
Quy tắc nhân − é
Nếumộtcôngviệccóthểđượchoànthànhbởihai giai
đoạn,giaiđoạnthứnhấtcóm cáchthựchiện,giaiđoạn
thứhaicón cáchthựchiện,thìcó............cáchhoàn
thànhcôngviệc.
2 Chỉnh hợp và Tổ hợp
Chỉnhhợp Tổhợp
Địnhnghĩa
Côngthức
Chúý Chỉnhhợpchậpn củan đượcgọilàmột
............ củan.
C
n−k
n
=......
C
k
n
+C
k+1
n
=......
TổToán 19 TrườngTHCS-THPTMỹThuận
Chủđề8.Dãysố-Quytắcđếm-Xácsuất-Góc-Khoảngcách TÀILIỆUÔNTHITỐTNGHIỆPTHPTMÔNTOÁN
3 XÁC SUẤT
1 Các định nghĩa
!
Phép thử ngẫu nhiên:
Phépthửngẫunhiênlà...........................màtakhôngđoántrướcđược........................củanó,mặcdùđãbiết
............................tấtcảcác.......................cóthểcócủaphépthửđó.
Không gian mẫu:
Khônggianmẫucủamộtphépthửlà.........................các........................cóthểxảyracủaphépthửđó.Kí
hiệu...........
Biến cố − é
Biếncốlàmột.............................của.................................
• Tập∅ làbiếncố...........................
• TậpΩ làbiếncố...........................
• NếuA∩ B =∅ thìtanóihaibiếncốA vàB ...........................
• NếuA =Ω\ B thìtanóihaibiếncốA vàB ...........................,kíhiệuA =...... hoặcB =.......
2 Xác suất của biến cố
!
GiảsửA làbiếncốliênquanđếnmộtphépthửvớikhônggianmẫuΩ,chỉcómộtsốhữuhạnkếtquảđồng
khảnăngxuấthiện.XácsuấtcủabiếncốA làtỉsố..........Kíhiệu:...........Trongđón(A) làsố...................
củabiếncốA,n(Ω) làsố................cóthểxảyracủaphépthử.
Tính chất − é
○ P(∅)=......,P(Ω)=.......
○ ...... ≤ P(A)≤ ......,vớimọibiếncốA.
○ P
A
=............,vớimọibiếncốA.
4 GÓC VÀ KHOẢNG CÁCH TRONG KHÔNG GIAN
1 Góc
Góc giữa đường thẳng và mặt phẳng − é
Chođườngthẳng∆vàmặtphẳng
(
α
)
.
• Nếu∆⊥
(
α
)
thì
∆,
(
α
)
=90
◦
.
• Nếu∆khôngvuônggócvới
(
α
)
thì
∆,
(
α
)
=
(
∆,d
)
vớid làhìnhchiếuvuônggóccủa∆ trên
(
α
)
.
Góc giữa mặt phẳng và mặt phẳng − é
Chohaimặtphẳng
(
α
)
và
(
β
)
.
• Nếu
(
α
)
∥
(
β
)
thì
(
α
)
,
(
β
)
=0
◦
.
• Nếu
(
α
)
∩
(
β
)
=∆ thì
(
α
)
,
(
β
)
=
(
a,b
)
vớia ⊂
(
α
)
,b ⊂
(
β
)
vàa ∩∆∩ b =M.
2 Khoảng cách
Điểm và mặt phẳng − é
ChođiểmS vàmặtphẳng
(
α
)
.GọiH làhìnhchiếu
vuônggóccủaS trên
(
α
)
.Khiđó
SH⊥
(
α
)
vàd
S,
(
α
)
=SH
Hai đường thẳng chéo nhau − é
• Đườngthẳng∆cắthaiđườngthẳngchéonhaua, b
vàcùngvuônggócvớihaiđườngthẳngấyđượcgọi
làđườngvuônggóc......... củaa vàb.
• Nếuđườngthẳngvuônggócchung∆cắthaiđường
thẳngchéonhaua, b lầnlượttạiM, N thìd
a,b
=
.......
TổToán 20 TrườngTHCS-THPTMỹThuận
| 1/21
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

TRƯỜNG THCS-THPT MỸ THUẬN TỔ TOÁN
TÀI LIỆU ÔN THI TỐT NGHIỆP
TRUNG HỌC PHỔ THÔNG MÔN TOÁN O win t can wan You you if MỤC LỤC
TÀI LIỆU ÔN THI TỐT NGHIỆP THPT MÔN TOÁN MỤC LỤC
Chủ đề 1. Khảo sát sự biến thiên và đồ thị của hàm số . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 1.
Sự biến thiên của hàm số . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 2.
Cực trị của hàm số . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 3.
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3 4.
Đường tiệm cận . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3 5.
Khảo sát đồ thị hàm số . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
Chủ đề 2. Lũy thừa - Mũ - Logarit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6 1.
Lũy thừa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6 2.
Hàm số lũy thừa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7 3.
Logarit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7 4.
Hàm số mũ và hàm số logarit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8 5.
Phương trình mũ và phương trình logarit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9 6.
Bất phương trình mũ và bất phương trình logarit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
Chủ đề 3. Nguyên hàm - Tích phân và ứng dụng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10 1.
Nguyên hàm . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10 2.
Tích phân . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10 3.
Ứng dụng của tích phân trong hình học . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11
Chủ đề 4. Số phức. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12 1.
Số phức . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12 2.
Phép cộng, trừ, nhân, chia số phức . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
Chủ đề 5. Khối đa diện . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13 1.
Khái niệm về hình đa diện và khối đa diện . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13 2.
Khối đa diện đều . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13 3.
Thể tích khối đa diện . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
Chủ đề 6. Khối tròn xoay. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14 1.
Hình nón và hình trụ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14 2.
Hình cầu . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14
Chủ đề 7. Phương pháp tọa độ trong không gian . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16 1.
Hệ tọa độ Oxyz . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16 2.
Phương trình mặt cầu . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17 3.
Phương trình mặt phẳng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17 4.
Phương trình đường thẳng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
Chủ đề 8. Dãy số - Quy tắc đếm - Xác suất - Góc - Khoảng cách . . . . . . . . . . . . . . . . . . . . . . . . . . . 19 1.
Dãy số . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19 2.
Quy tắc đếm . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19 3.
Xác suất . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20 4.
Góc và Khoảng cách trong không gian . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20 Tổ Toán 1
Trường THCS-THPT Mỹ Thuận
Chủ đề 1. Khảo sát sự biến thiên và đồ thị của hàm số
TÀI LIỆU ÔN THI TỐT NGHIỆP THPT MÔN TOÁN Chủ đề 1.
KHẢO SÁT SỰ BIẾN THIÊN VÀ ĐỒ THỊ CỦA HÀM SỐ 1
SỰ BIẾN THIÊN CỦA HÀM SỐ
1 Tính đơn điệu và dấu của đạo hàm ○ f ′ x > ∀x ∈ K
f x . . . . . . . . . . . . . . . K Nếu ( ) 0, thì ( ) trên . ! ○ f ′ x < ∀x ∈ K
f x . . . . . . . . . . . . . . . K Nếu ( ) 0, thì ( ) trên . ○ f ′ x ∀x ∈ K
f x . . . . . . . . . . . . . . . K Nếu ( ) = 0, thì ( ) trên .
2 Quy tắc xét tính đơn điệu của hàm số Quy tắc − é
. . . . . . . . . . . . . . . . . . Bước 1. Tìm
. . . . . . . . . . . . f ′ x x f ′ x . . . . . .
. . . . . . . . . . . . . . . . . . Bước 2. Tìm ( ). Tìm để ( ) hoặc
. . . . . . . . . . . . . . . Bước 3. Lập bảng Bước 4.
Kết luận về các khoảng đồng biến, nghịch biến của hàm số. 2
CỰC TRỊ CỦA HÀM SỐ
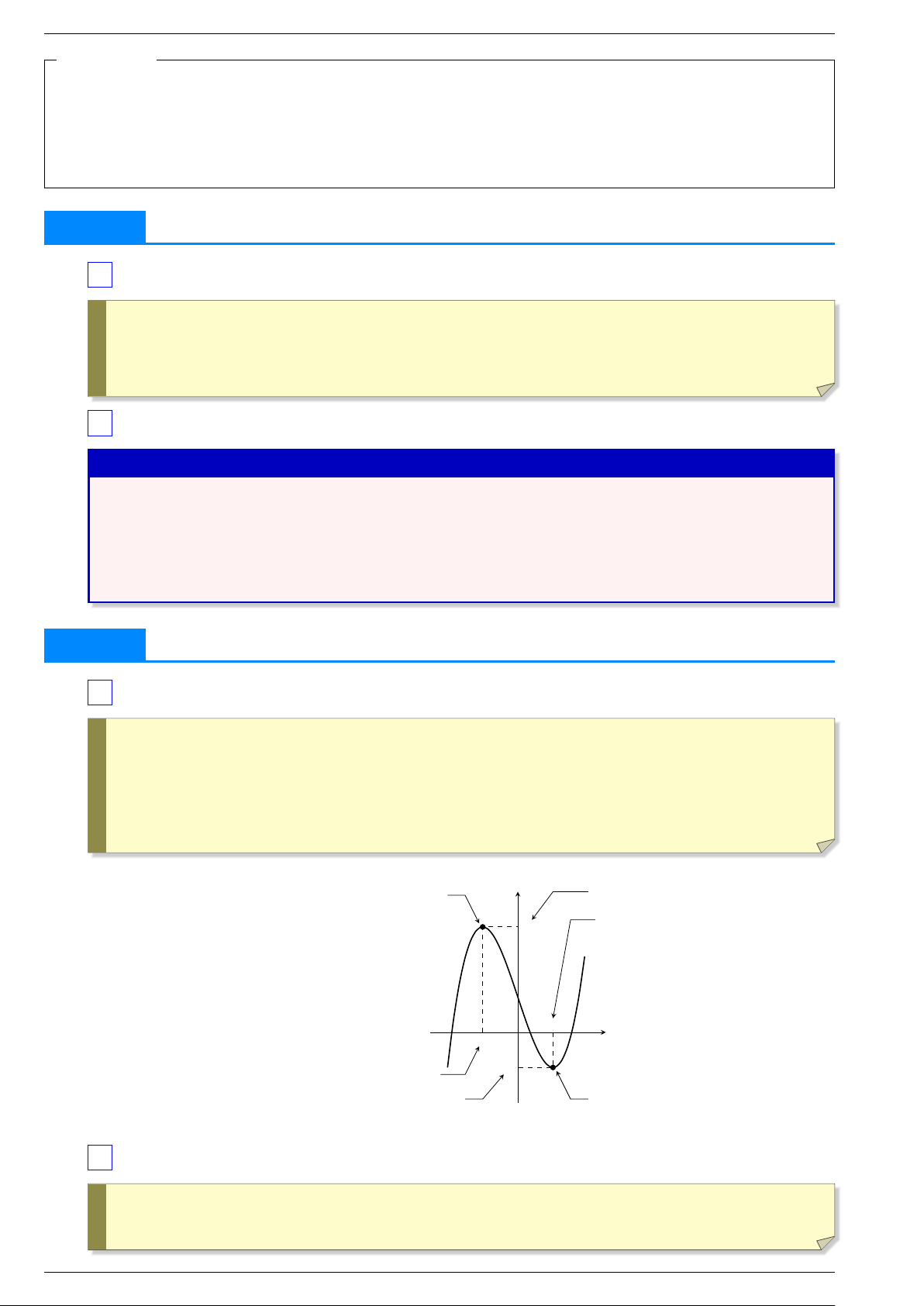
1 Các khái niệm f x x x . . . . . . . . . f x . . . . . . . . . • Nếu ( ) đạt CĐ tại 0 thì ta gọi 0 là điểm CĐ của , ( 0 ) là giá trị CĐ của , còn điểm M x f x . . . . . . . . . ( 0 ; ( 0 )) là điểm CĐ của
. Ta gọi tương tự đối với cực tiểu. !
. . . . . . . . . . . . . . . • Các điểm CĐ và CT được gọi chung là , giá trị CĐ và giá trị CT được gọi chung là
. . . . . . . . . của hàm số. f x K x f ′ x . . . • Nếu ( ) xác định trên và đạt cực trị tại 0 thì ( 0 ) = . y A x y
Giá trị cực đại của ............... Điểm cực đại ( 1 ; 1 ) của ............... y
Điểm cực tiểu của ............... 1 x2 x1 O x y2
Điểm cực đại của ............... B x y
Giá trị cực tiểu của ............... Điểm cực tiểu ( 2 ; 2 ) của ...............
2 Điều kiện đủ để hàm số có cực trị ○ f ′ x > x < x f ′ x < x > x x . . . . . . . . . f x ! Nếu ( 0) 0 khi 0 và ( 0 ) 0 khi 0 thì 0 là một điểm của hàm số ( ). ○ f ′ x < x < x f ′ x > x > x x . . . . . . . . . f x Nếu ( 0 ) 0 khi 0 và ( 0 ) 0 khi 0 thì 0 là một điểm của hàm số ( ). Tổ Toán 2
Trường THCS-THPT Mỹ Thuận
Chủ đề 1. Khảo sát sự biến thiên và đồ thị của hàm số
TÀI LIỆU ÔN THI TỐT NGHIỆP THPT MÔN TOÁN
3 Quy tắc tìm cực trị Quy tắc 1 − é
. . . . . . . . . . . . . . . . . . Bước 1. Tìm
. . . . . . . . . . . . f ′ x x f ′ x . . . . . .
. . . . . . . . . . . . . . . . . . Bước 2. Tìm ( ). Tìm để ( ) hoặc
. . . . . . . . . . . . . . . Bước 3. Lập bảng Bước 4.
Kết luận về các điểm cực trị. Quy tắc 2 − é
. . . . . . . . . . . . . . . . . . Bước 1. Tìm
. . . . . . . . . . . . f ′ x x f ′ x . . . Bước 2. Tìm ( ). Tìm để ( ) 0. . . . f ′′ x Bước 3. Tìm đạo hàm cấp rồi tính các giá trị ( ). Bước 4.
Kết luận về các điểm cực trị. 3
GIÁ TRỊ LỚN NHẤT VÀ GIÁ TRỊ NHỎ NHẤT CỦA HÀM SỐ
1 Định nghĩa ○ M f x D f x . . . M, ∀x ∈ D ∃x ∈ D f x . . . M Số
được gọi là giá trị lớn nhất của ( ) trên nếu ( ) và 0 sao cho ( 0 ) . M f x Kí hiệu = max ( ). ! D ○ m f x D f x . . . m, ∀x ∈ D ∃x ∈ D f x . . . m Số
được gọi là giá trị nhỏ nhất của ( ) trên nếu ( ) và 0 sao cho ( 0 ) . m f x Kí hiệu = min D ( ).
2 Cách tìm GTLN & GTNN của hàm số trên một đoạn Quy tắc − é
. . . . . . . . . . . . . . . . . . Bước 1. Tìm
. . . . . . . . . . . . f ′ x x f ′ x . . . Bước 2. Tìm ( ). Tìm để ( ) 0. . . . f ′′ x Bước 3. Tìm đạo hàm cấp rồi tính các giá trị ( ). Bước 4.
Kết luận về các điểm cực trị. ! Lưu ý: f ′ x . . . . . . . . . a b f x a b Nếu ( ) không trên [ ; ] thì (
) đạt GTLN và GTNN tại các đầu mút của [ ; ]. 4 ĐƯỜNG TIỆM CẬN
1 Tiệm cận ngang
2 Tiệm cận đứng y y x x Đường thẳng = 0 được gọi là tiệm cận Đường thẳng =
0 được gọi là tiệm cận đứng y f x . . . . . . y f x . . . . . .
! ngang của đồ thị hàm số = ( ) nếu của đồ thị hàm số = ( ) nếu trong
trong các điều kiện sau được thỏa mãn:
các điều kiện sau được thỏa mãn: ! ○ f x . . . ○ f x . . . ○ f x . . . . . . ○ f x . . . . . . lim x→ ∞ ( ) = lim x→−∞ ( ) = lim ( ) = lim ( ) = + x→x+ x→x− 0 0 ○ f x . . . . . . ○ f x . . . . . . lim ( ) = lim ( ) = x→x+ x→x− 0 0 5
KHẢO SÁT ĐỒ THỊ HÀM SỐ
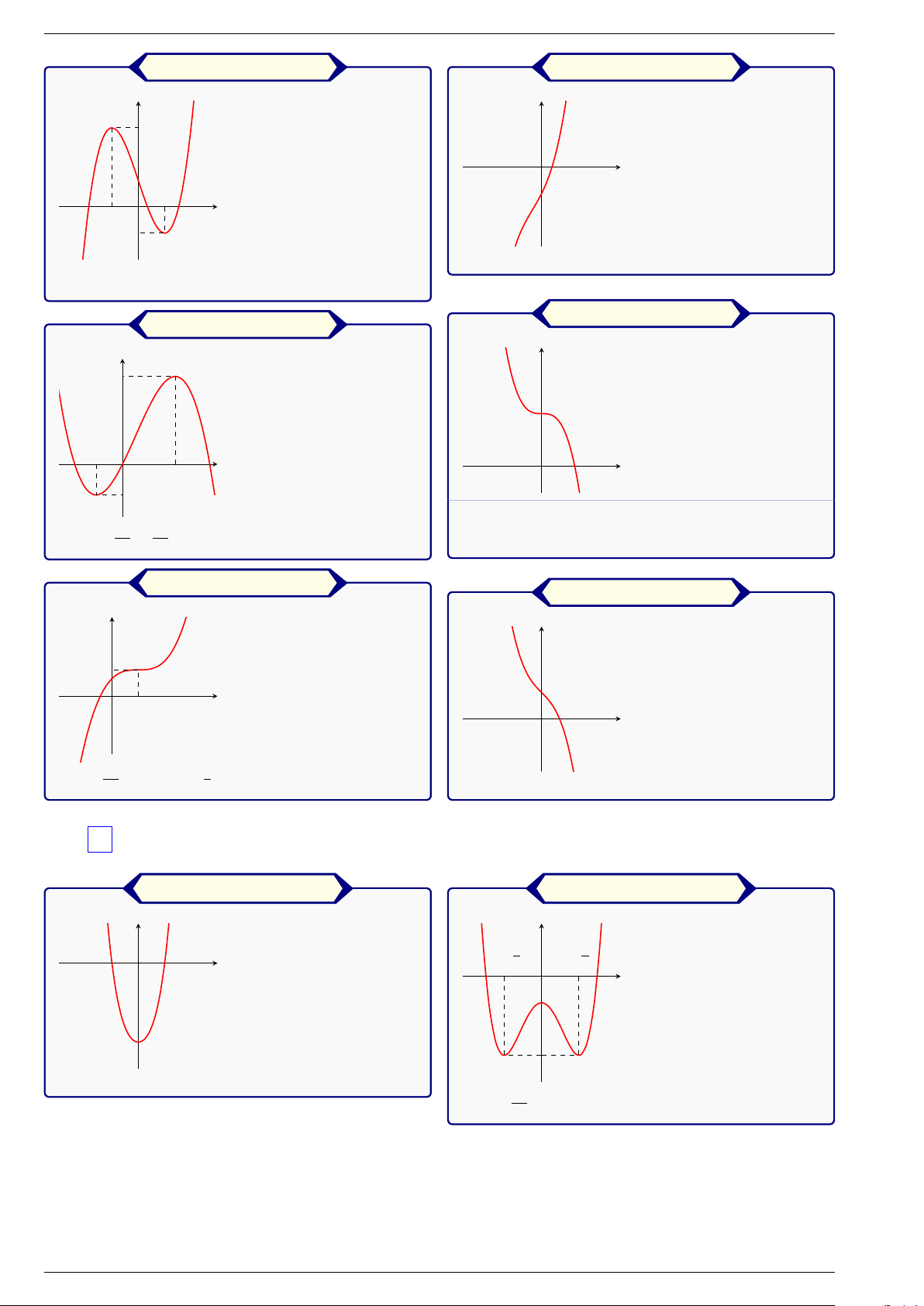
1 Hàm số y ax3 bx2 cx d a ̸ 0 = + + + ( = ) Tổ Toán 3
Trường THCS-THPT Mỹ Thuận
Chủ đề 1. Khảo sát sự biến thiên và đồ thị của hàm số
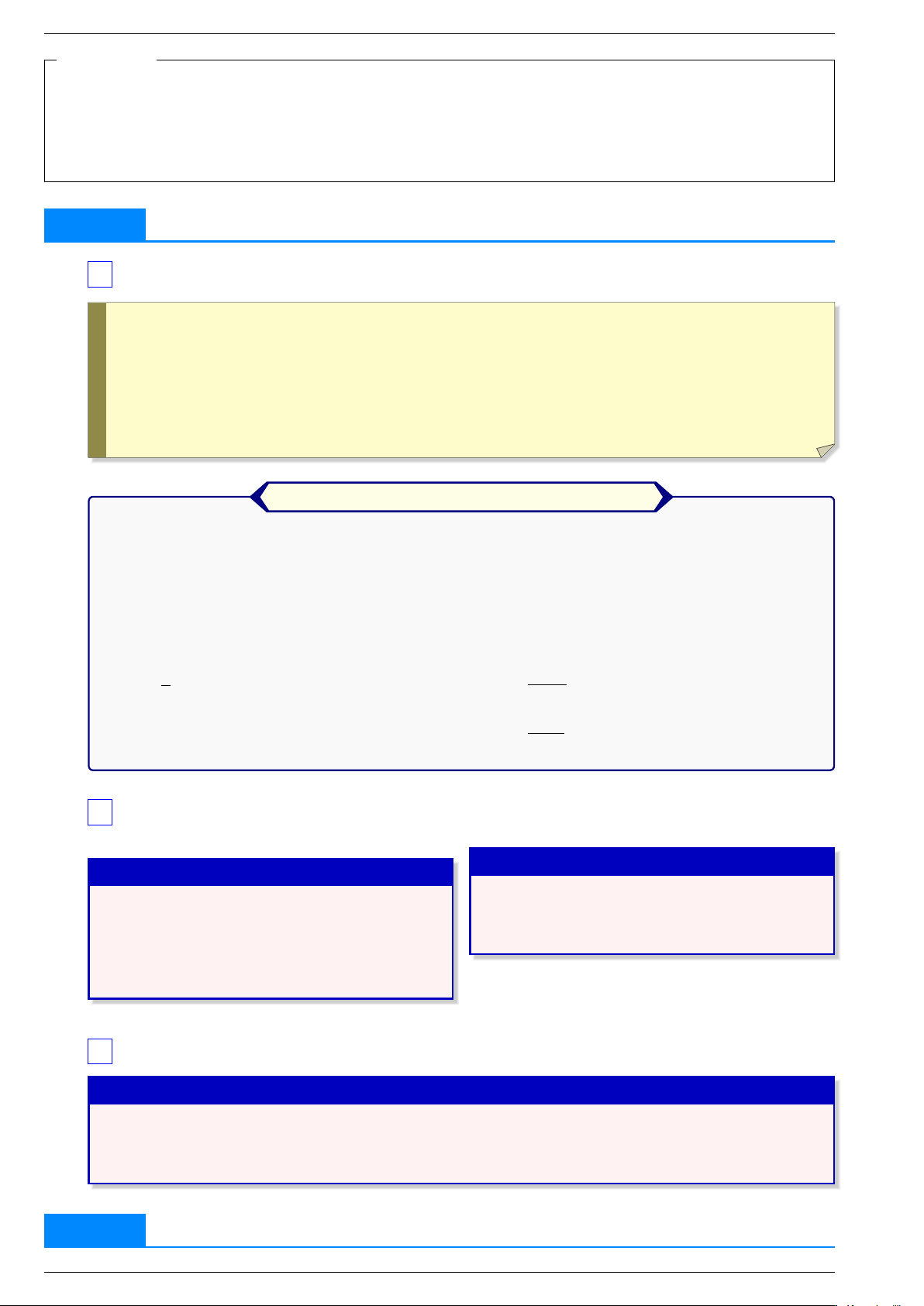
TÀI LIỆU ÔN THI TỐT NGHIỆP THPT MÔN TOÁN b2 − ac . . . và a . . . b2 − ac . . . và a . . . 3 0 0 3 0 0 y y 3 O x O 1 x −1−1 y x3 x2 x − y x = + + 2 1 3 − x = 3 + 1 b2 − ac . . . và a . . . b 3 0 0 2 − ac . . . và a . . . 3 0 0 y y 2 −1 O x O x 2 x3 x2 y − x y − x3 = 2 = + + 2 3 2 b2 − ac . . . và a . . . 3 0 0 b2 − ac . . . và a . . . 3 0 0 y y 1 O x 1 O x x3 y − x 2 2 x = + + y − x − x3 3 3 = 1
2 Hàm số y ax4 bx2 c a ̸ 0 = + + ( = )
a, b . . . . . . dấu và a . . .
a, b . . . . . . dấu và a . . . 0 0 y y O √ √ x − O 2 2 x −1 −3 −3 y x4 x2 − = + 2 3 x4 y − x2 − = 2 1 2 Tổ Toán 4
Trường THCS-THPT Mỹ Thuận
Chủ đề 1. Khảo sát sự biến thiên và đồ thị của hàm số
TÀI LIỆU ÔN THI TỐT NGHIỆP THPT MÔN TOÁN
a, b . . . . . . dấu và a . . .
a, b . . . . . . dấu và a . . . 0 0 y y 1 2 O x O 1 x −1 1 y − x4 − x2 = 2 + 1 y −x4 x2 = + 2 + 1 ax b
3 Hàm số y + c ̸
0, ad − bc ̸ 0 = cx d ( = = ) + y′ . . . y′ . . . 0 0 y y 2 1 O x 1 − − O x 1 1 −1 x − x y 2 1 y + 1 = x = x − + 1 1
4 Sự tương giao của các đồ thị ! y f x C y g x C Giả sử hàm số = ( ) có đồ thị ( 1 ) và hàm số = ( ) có đồ thị ( 2 ). C C . . . . . . . . . . . .
Để tìm hoành độ giao điểm của ( 1 ) và ( 2 ), ta giải phương trình Tổ Toán 5
Trường THCS-THPT Mỹ Thuận
Chủ đề 2. Lũy thừa - Mũ - Logarit
TÀI LIỆU ÔN THI TỐT NGHIỆP THPT MÔN TOÁN Chủ đề 2.
LŨY THỪA - MŨ - LOGARIT 1 LŨY THỪA
1 Lũy thừa với số mũ nguyên n ∈ ∗ N a ∈ R Cho , . n a . . . . . . . . . . . . a Lũy thừa bậc của là của thừa số . an
a · a · a · · · a · a = | {z } n số a a . . . . . . . . . n . . . . . . . . . Số gọi là , số gọi là Chú ý: a ̸ Với = 0 ta có a0 . . . a−n . . . . . . • = • =
2 Căn bậc n b ∈ ∗ R n ∈ N n ≥ Cho số và số ( 2). an b a
. . . . . . . . . . . . . . . b Nếu = thì được gọi là của . ○ n
. . . . . . . . . . . . . . . n b Với lẻ: có căn bậc của ○ n Với chẵn: – b <
. . . . . . . . . . . . . . . . . . . . . . . . Nếu 0 thì – b
. . . . . . . . . . . . . . . . . . . . . . . . Nếu = 0 thì – b >
. . . . . . . . . . . . . . . . . . . . . . . . Nếu 0 thì √ √ √ n a · n b . . . . . . n am . . . . . . • = • = ! √ ( n √ a a n . . . . . . n nếu √ . . . . . . an • = • n b = |a| n . . . . . . nếu
3 Tính chất của lũy thừa với số mũ thực a, b > m, n Cho 0 là những số thực;
là những số thực tùy ý. am · an . . . . . . ab m . . . . . . ! • = • ( ) = am . . . . . . • an = a m am n . . . . . . . . . . . . • • = ( ) = b ○ a >
am > an ⇔ m . . . n Với 1: ○ a <
am > an ⇔ m . . . n Với 1: Tổ Toán 6
Trường THCS-THPT Mỹ Thuận
Chủ đề 2. Lũy thừa - Mũ - Logarit
TÀI LIỆU ÔN THI TỐT NGHIỆP THPT MÔN TOÁN 2 HÀM SỐ LŨY THỪA
1 Định nghĩa ! α Cho số thực . y . . . . . . Hàm số =
được gọi là hàm số lũy thừa.
Tập xác định của hàm số lũy thừa − é xα . . .
Tập xác định của hàm số lũy thừa
tùy thuộc vào giá trị của ○ α ∈ Z+ . . . . . . . . . Nếu : tập xác định là ○ α ∈ − Z . . . . . . . . . Nếu : tập xác định là ○ α / ∈ Z . . . . . . . . . Nếu : tập xác định là
2 Khảo sát hàm số lũy thừa y xα . . . . . . . . .
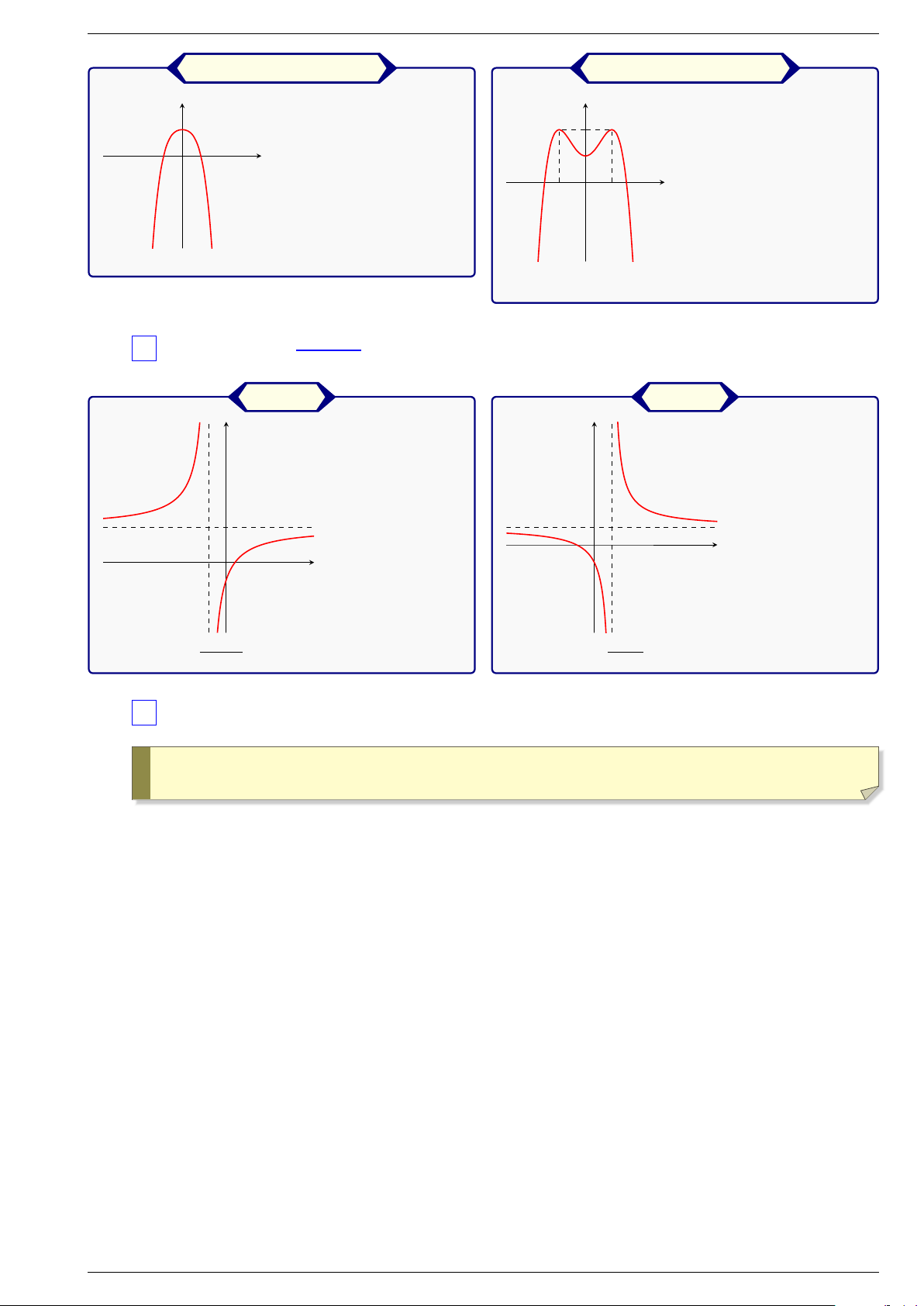
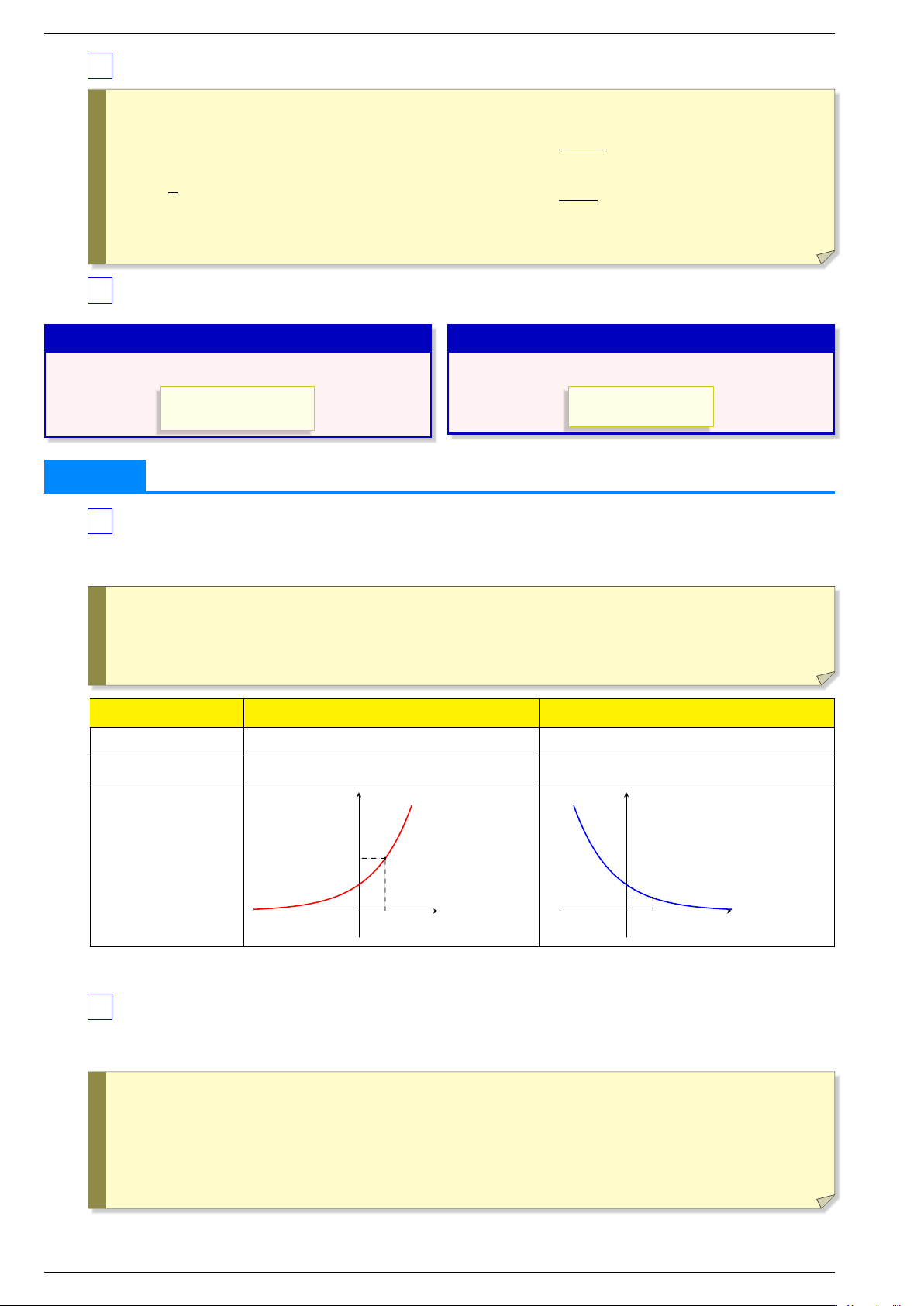
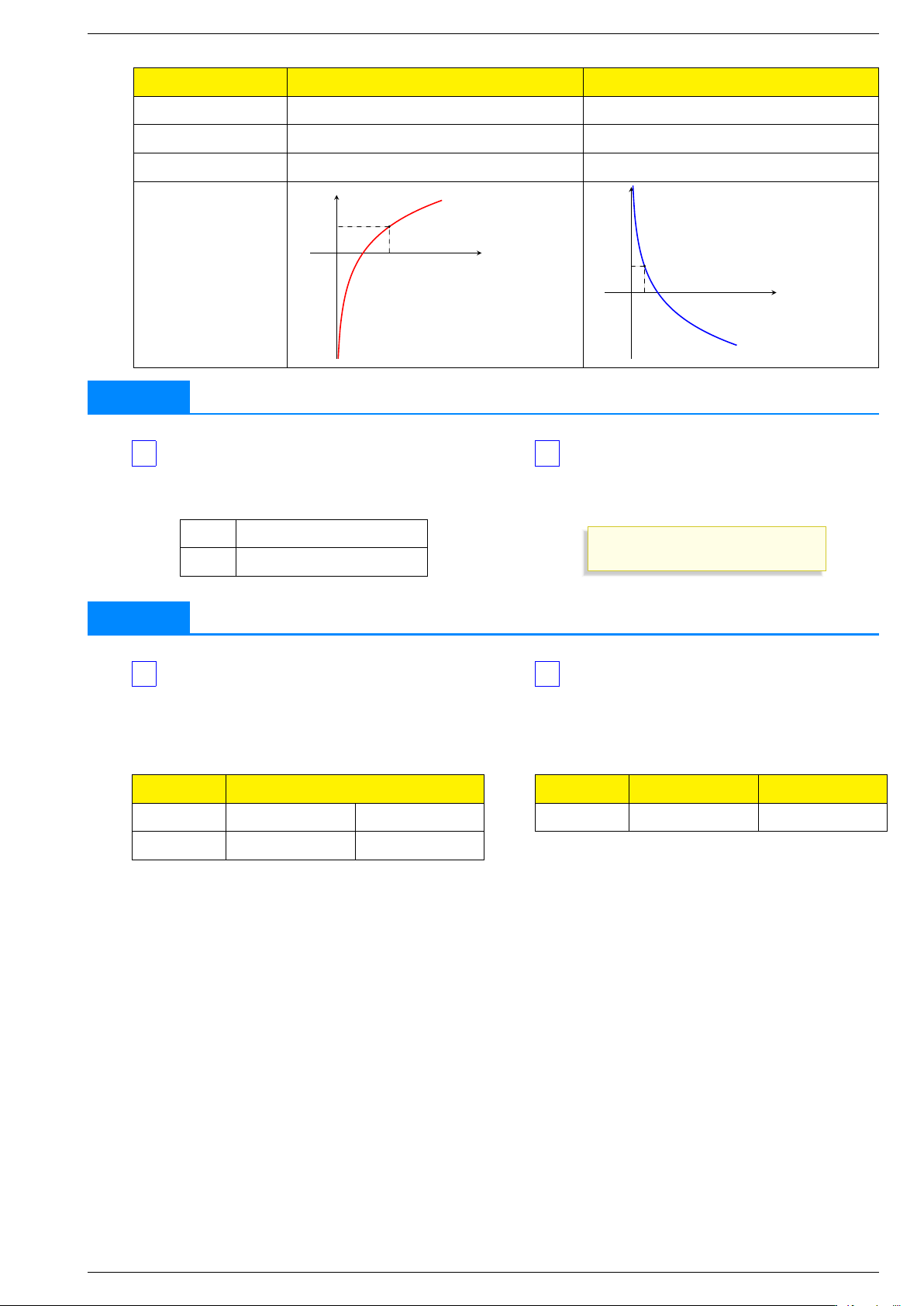
Trong trường hợp tổng quát, ta khảo sát hàm số = trên khoảng y xα α > y xα α < = , 0 = , 0 Sự biến thiên Giới hạn đặc biệt Tiệm cận y y α > 1 α = 1 α < 1 1 1 α < 0 O x O x 1 1 Đồ thị 3 LOGARIT
1 Định nghĩa . . . . . . a, b a . . . . . . Cho hai số với . α aα b
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Số thỏa mãn đẳng thức = được gọi là và kí hiệu là . α . . . . . . ⇔ aα b = = a . . . . . . . . . n . . . . . . . . . Số gọi là , số gọi là Chú ý: . . . . . . Không có lôgarit của số và số 0. Tính chất − é . . . aloga b . . . • loga 1 = • = . . . . . . • loga a = • loga ab = Tổ Toán 7
Trường THCS-THPT Mỹ Thuận
Chủ đề 2. Lũy thừa - Mũ - Logarit
TÀI LIỆU ÔN THI TỐT NGHIỆP THPT MÔN TOÁN
2 Quy tắc tính lôgarit . . . . . . a, b, c a . . . . . . Cho ba số với . Ta có b · c
. . . . . . . . . . . . . . . logc . . . • loga ( ) = c ̸ • loga b = = 1) ! logc . . . ( b
. . . . . . . . . . . . . . . • loga c = 1 b ̸ •
loga b = . . . . . . ( = 1) . . . . . . . . . ∀α . . . . . . α ̸ • loga bα = , • logaα b = loga b ( = 0)
3 Lôgarit thập phân và lôgarit tự nhiên Lôgarit thập phân − é Lôgarit tự nhiên − é . . . . . .
Lôgarit thập phân là lôgarit cơ số .
Lôgarit tự nhiên là lôgarit cơ số b . . . . . . b . . . . . . log = ln = 4
HÀM SỐ MŨ VÀ HÀM SỐ LOGARIT
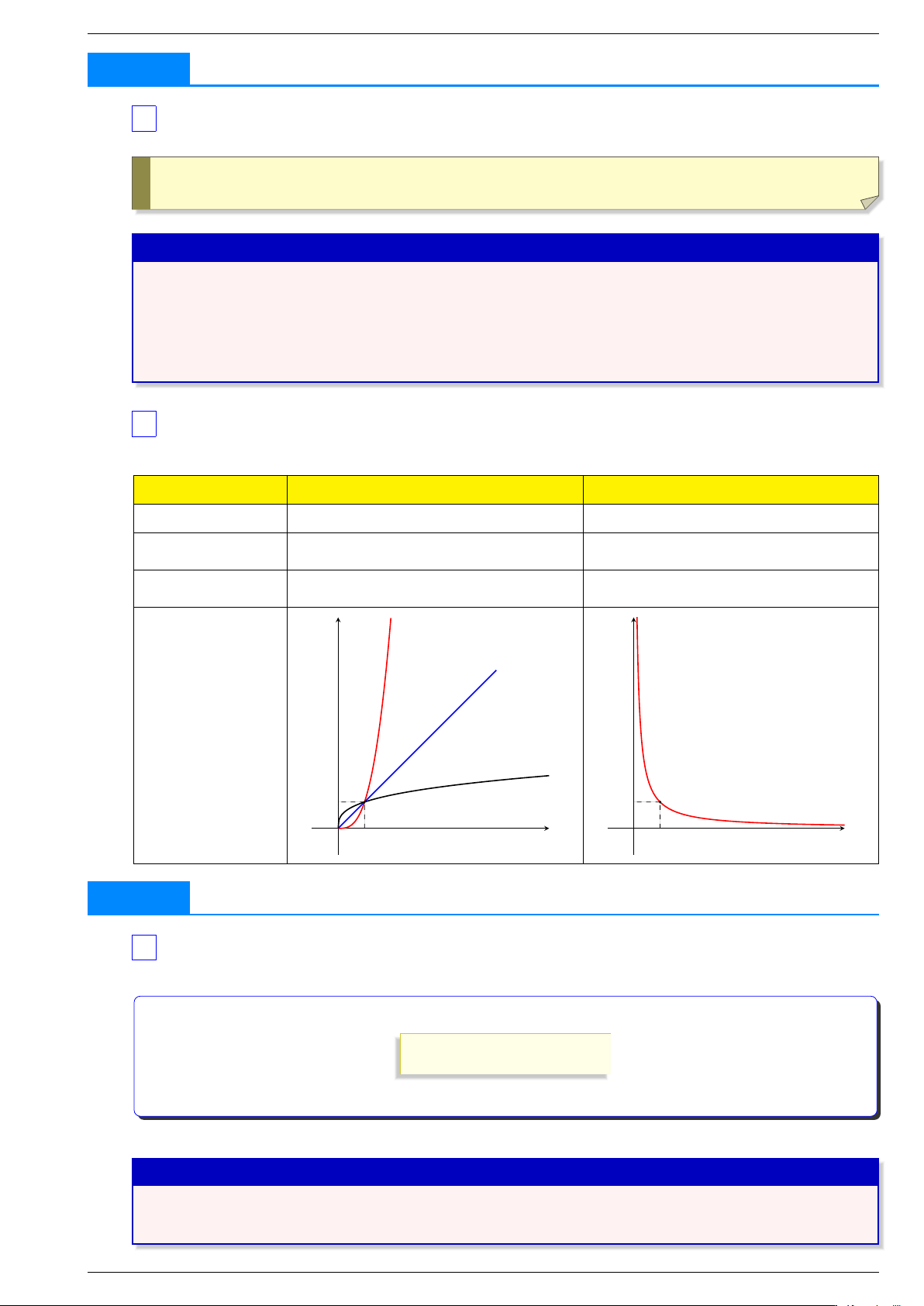
1 Hàm số mũ . . . . . . a ̸ . . . Cho số thực = . y . . . . . . hàm số mũ . . . Hàm số = được gọi là cơ số . . . . . . . a ̸ . . . u u x Cho số = và hàm hợp = ( ). Ta có: ! ax ′ . . . . . . . . . au ′ . . . . . . . . . • ( ) = • ( ) = x ′ . . . . . . . . . u ′ . . . . . . . . . • (e ) = • (e ) = y ax a > y ax < a < = , 1 = , 0 1 Sự biến thiên Tiệm cận y a > 1 y a 1 1 a a < 1 O x O x 1 1 Đồ thị
2 Hàm số lôgarit . . . . . . a ̸ . . . Cho số thực = . y . . . . . . hàm số lôgarit . . . Hàm số = được gọi là cơ số . . . . . . . a ̸ . . . u u x Cho số = và hàm hợp = ( ). Ta có: ′ ′ ! . . . . . . . . . 1 . . . . . . . . . 1 • (loga x ) = x a • (loga u) = x a ln ln x ′ . . . . . . . . . 1 u ′ . . . . . . . . . 1 • (ln ) = x • (ln ) = x a ln Tổ Toán 8
Trường THCS-THPT Mỹ Thuận
Chủ đề 2. Lũy thừa - Mũ - Logarit
TÀI LIỆU ÔN THI TỐT NGHIỆP THPT MÔN TOÁN y a > y < a < = loga x , 1 = loga x , 0 1 Tập xác định Sự biến thiên Tiệm cận y y a > 1 1 O a x 1 1 O a x 1 a < 1 Đồ thị 5
PHƯƠNG TRÌNH MŨ VÀ PHƯƠNG TRÌNH LOGARIT
1 Phương trình mũ
2 Phương trình lôgarit
. . . . . . . . . a > . . . . . . . . . . . . . . .
Phương trình mũ cơ bản có dạng ( , Phương trình lôgarit cơ bản có dạng a ̸ . . . a > . . . a ̸ . . . = ). ( , = ). b > 0 x b ⇔ x . . . . . . loga = = b ≤ 0 6
BẤT PHƯƠNG TRÌNH MŨ VÀ BẤT PHƯƠNG TRÌNH LOGARIT
1 Bất phương trình mũ
2 Bất phương trình lôgarit . . . . . . . . .
Bất phương trình mũ cơ bản có dạng hoặc Bất phương trình lôgarit cơ bản có dạng . . . . . . . . . . . . . . . . . .
. . . . . . . . . a > . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . hoặc hoặc ( , hoặc hoặc a ̸ . . .
. . . . . . . . . . . . a > . . . a ̸ . . . = ). hoặc ( , = ). ax > b a > < a < < a < 1 0 1 loga x > b a > 1 0 1 b > 0 Nghiệm b ≤ 0 Tổ Toán 9
Trường THCS-THPT Mỹ Thuận
Chủ đề 3. Nguyên hàm - Tích phân và ứng dụng
TÀI LIỆU ÔN THI TỐT NGHIỆP THPT MÔN TOÁN Chủ đề 3.
NGUYÊN HÀM - TÍCH PHÂN VÀ ỨNG DỤNG 1 NGUYÊN HÀM
1 Tính chất của nguyên hàm Z f ′ x x
. . . . . . . . . . . . . . . . . . Tính chất 1. ( ) d = ! Z k · f x x
. . . . . . . . . . . . k Tính chất 2. ( ) d = ( là hằng số) Z f x ± g x x
. . . . . . . . . . . . . . . . . . . . . Tính chất 3. [ ( ) ( )] d =
Bảng nguyên hàm của một số hàm số thường gặp Z Z x
. . . . . . . . . . . . . . . ax x
. . . . . . . . . . . . . . . a > a ̸ • 0 d = • d = ( 0, = 1) Z Z x
. . . . . . . . . . . . . . . x x
. . . . . . . . . . . . . . . • d = • cos d = Z Z xn x
. . . . . . . . . . . . . . . n ̸ − x x
. . . . . . . . . . . . . . . • d = ( = 1) • sin d = Z Z 1 x
. . . . . . . . . . . . . . . 1 x
. . . . . . . . . . . . . . . • x d = • = 2 x d cos Z Z x x
. . . . . . . . . . . . . . . 1 x
. . . . . . . . . . . . . . . • e d = • = 2 x d sin
2 Tìm nguyên hàm bằng phương pháp đổi biến số Hệ quả − é Định lí − é u ax b a ̸ Z Với = + ( = 0) thì f u x F u C u u x Nếu ( ) d = ( ) + và = ( ) là hàm số Z f ax b x
. . . . . . . . . . . . . . . ( + ) d =
có đạo hàm liên tục thì Z f u x · u′ x x
. . . . . . . . . . . . . . . . . . . . . . . . ( ( )) ( ) d =
3 Phương pháp nguyên hàm từng phần Định lí − é u u x v v x K Nếu hai hàm số = ( ) và = (
) có đạo hàm liên tục trên thì Z u x · v′ x x
. . . . . . . . . . . . . . . . . . . . . . . . ( ) ( ) d = 2 TÍCH PHÂN Tổ Toán 10
Trường THCS-THPT Mỹ Thuận
Chủ đề 3. Nguyên hàm - Tích phân và ứng dụng
TÀI LIỆU ÔN THI TỐT NGHIỆP THPT MÔN TOÁN
1 Tính chất của tích phân b Z k · f x x
. . . . . . . . . . . . . . . k Tính chất 1. ( ) d = ( là hằng số) a b ! Z f x ± g x x
. . . . . . . . . . . . . . . . . . . . . . . . . . . Tính chất 2. [ ( ) ( )] d = a c b Z Z f x x f x x
. . . . . . . . . . . . a < c < b Tính chất 3. ( ) d + ( ) d = ( ) a c
2 Phương pháp tính tích phân từng phần Định lí − é u u x v v x K Nếu hai hàm số = ( ) và = (
) có đạo hàm liên tục trên thì b Z u x · v′ x x
. . . . . . . . . . . . . . . . . . . . . . . . ( ) ( ) d = a 3
ỨNG DỤNG CỦA TÍCH PHÂN TRONG HÌNH HỌC
1 Hình phẳng giới hạn bởi một
2 Hình phẳng giới hạn bởi hai
đường cong và trục hoành đường cong
Diện tích S của hình phẳng giởi hạn bởi đồ thị của
Diện tích S của hình phẳng giởi hạn bởi đồ thị của hàm số y
f x , trục . . . . . . . . . và hai đường thẳng hai hàm số y f x , y
g x và hai đường thẳng = ( ) = ( ) = ( ) x a, x
b được tính theo công thức x a, x
b được tính theo công thức = = = = b b Z Z S . . . . . . x S
. . . . . . . . . . . . . . . x = d = d a a
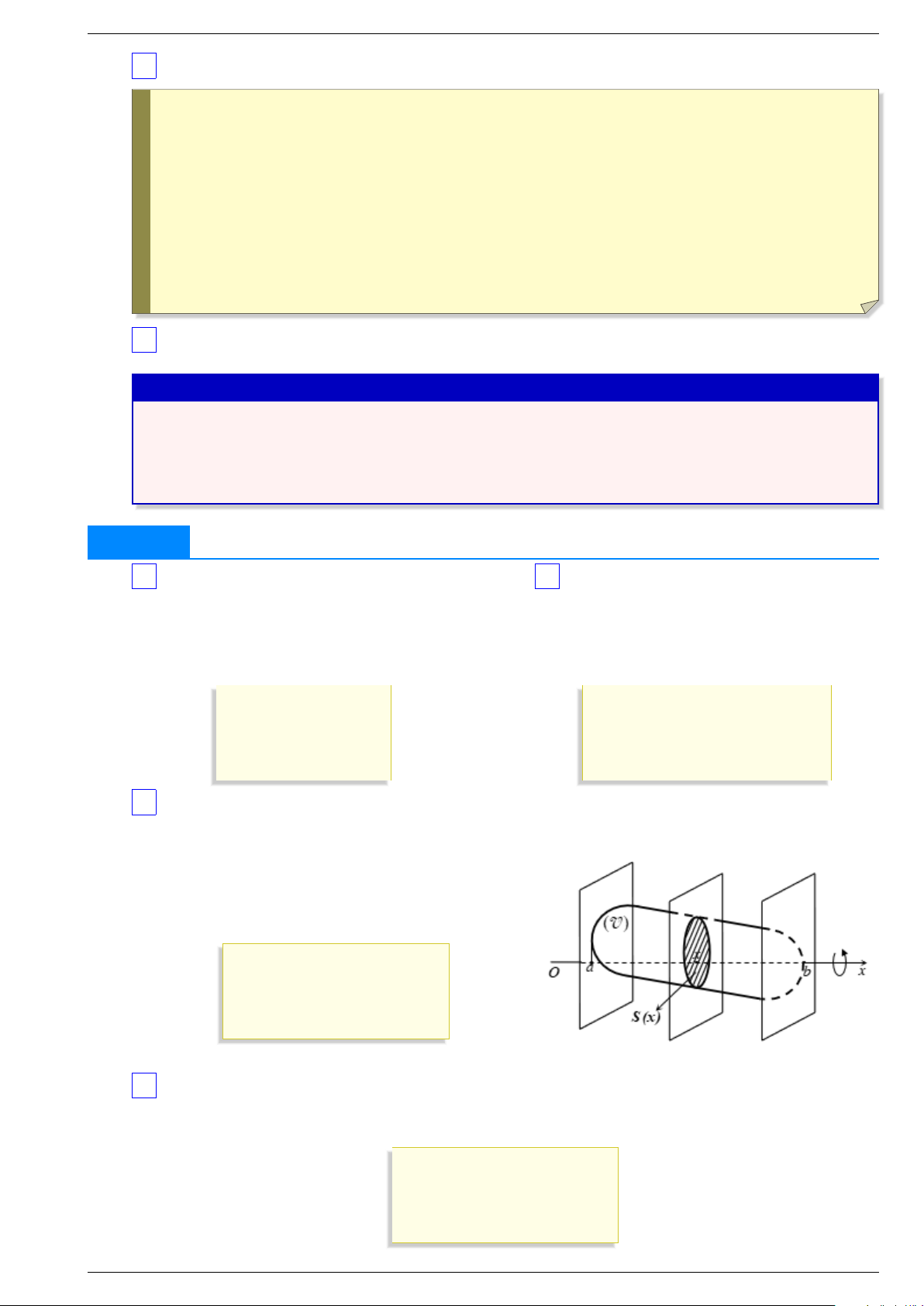
3 Thể tích của vật thể V P Q Ox x a x b a < b Cắt một vật thể bởi hai mặt phẳng ( ) và ( ) vuông góc với trục lần lượt tại = , = ( ). V Ox x ∈ a b S x Cắt bởi một mặt phẳng tùy ý vuông góc với tại diểm [ ; ] theo thiết diện có diện tích ( ). S x a b V Giả sử ( ) liên tục trên đoạn [ ; ], khi đó vật thể có thể tích là b Z V
. . . . . . . . . . . . x = d a
4 Thể tích khối tròn xoay y f x x a x b
Quay hình thang cong giới hạn bởi đồ thị hàm số = (
), trục hoành và hai đường thẳng = , = quanh . . . . . . . . . . . . . . . . . . trục tạo thành một khối có thể tích là b Z V . . . . . . . . . . . . x = d a Tổ Toán 11
Trường THCS-THPT Mỹ Thuận Chủ đề 4. Số phức
TÀI LIỆU ÔN THI TỐT NGHIỆP THPT MÔN TOÁN Chủ đề 4. SỐ PHỨC 1 SỐ PHỨC
1 Định nghĩa . . . . . . . . . a, b ∈ . . . i2 . . . số phức Mỗi biểu thức dạng trong đó và = được gọi là một . z a bi a
. . . . . . . . . . . . b . . . . . . . . . . . . z • Đối với số phức = + , ta nói là , là của . i . . . . . . . . . . . . • Số được gọi là . . . . . . •
Tập hợp các số phức kí hiệu là (The set of Complex numbers). ! a phần ảo bi phần thực . . . • Mỗi số thực
đều là một số phức với • Số phức có bằng được gọi là số . . . . . . . . . . . . bằng
2 Số phức bằng nhau . . . . . . . . . . . . . . . . . . . . . . . .
Hai số phức được gọi là bằng nhau nếu và
của chúng tương ứng bằng nhau. (a . . . a b i a b i ⇔ 1 = 1 + 1 = 2 + 2 b . . . 1 =
3 Biểu diễn hình học của số phức M . . . . . . Oxy . . . . . . . . . . . . z a bi Điểm ( ;
) trong hệ trục tọa độ được gọi là điểm của số phức = + .
4 Môđun của số phức z a bi M a b Cho số phức = + có điểm biểu diễn là ( ; ). −−Ï . . . . . . . . . OM z . . . . . . của vectơ
được gọi là môđun của số phức , kí hiệu là |z| . . . . . . . . . =
5 Số phức liên hợp z a bi . . . . . . . . . số phức liên hợp z . . . Cho số phức = + . Ta gọi là của , kí hiệu là . 2
PHÉP CỘNG, TRỪ, NHÂN, CHIA SỐ PHỨC z a b i z a b i Cho hai số phức 1 = 1 + 1 và 2 = 2 + 2 , khi đó: z z
. . . . . . . . . . . . . . . a bi c di
. . . . . . . . . . . . . . . . . . . . . • 1 + 2 = • ( + )( + ) = z z · z 1 1 2 z − z
. . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . • = = • z z · z 1 2 = 2 2 2 Tổ Toán 12
Trường THCS-THPT Mỹ Thuận
Chủ đề 5. Khối đa diện
TÀI LIỆU ÔN THI TỐT NGHIỆP THPT MÔN TOÁN Chủ đề 5. KHỐI ĐA DIỆN 1
KHÁI NIỆM VỀ HÌNH ĐA DIỆN VÀ KHỐI ĐA DIỆN
Hình đa diện là hình được tạo bởi một số hữu hạn các . . . . . . . . . thỏa mãn hai tính chất sau:
Hai đa giác phân biệt chỉ có thể hoặc không có . . . . . . chung, hoặc chỉ có một . . . . . . chung, hoặc chỉ •
! có một ...... chung.
Mỗi cạnh của đa giác nào cũng là cạnh chung của đúng . . . . . . đa giác. •
Khối đa diện là phần . . . . . . . . . . . . được giới hạn bởi một . . . . . . đa diện, kể cả . . . . . . đa diện đó. 2
KHỐI ĐA DIỆN ĐỀU
Khối đa diện đều là khối đa diện . . . . . . có các tính chất sau đây:
! Mỗi mặt của nó là một ..................... p cạnh •
Mỗi đỉnh của nó là đỉnh chung của đúng q mặt. • . . . . . .
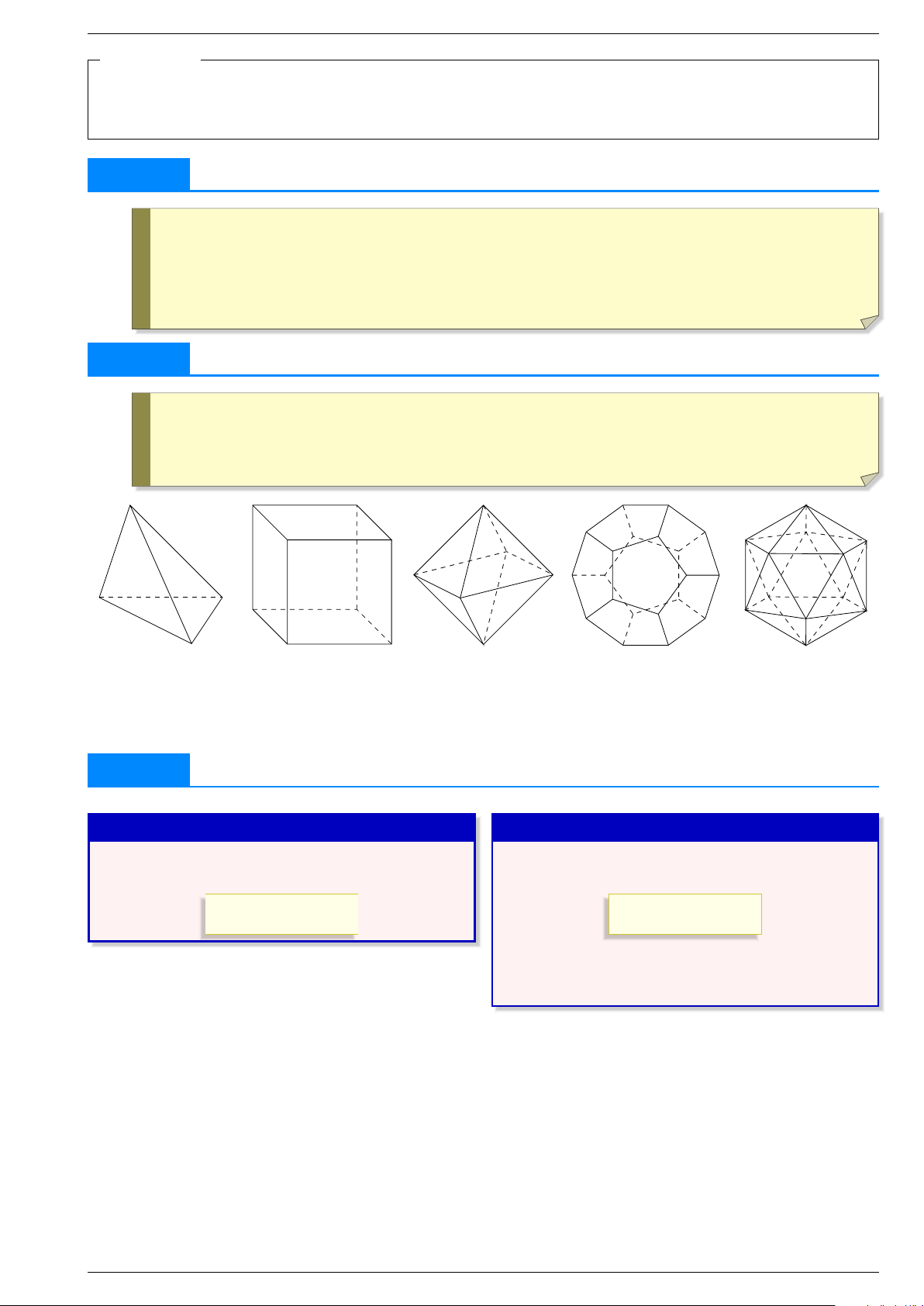
Khối đa diện đều như vậy được gọi là khối đa diện đều loại . Tứ diện đều Lập phương Bát diện đều Thập nhị diện đều Nhị thập diện đều . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . • đỉnh • đỉnh • đỉnh • đỉnh • đỉnh . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . • cạnh • cạnh • cạnh • cạnh • cạnh . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . • mặt • mặt • mặt • mặt • mặt 3
THỂ TÍCH KHỐI ĐA DIỆN
Thể tích khối chóp − é
Thể tích khối lăng trụ − é
Thể tích khối chóp có diện tích đáy B và chiều cao
Thể tích khối lăng trụ có diện tích đáy B và chiều h là cao h là V . . . . . . . . . V . . . . . . . . . = = •
Thể tích khối hộp chữ nhật: .................. •
Thể tích khối lập phương: .................. Tổ Toán 13
Trường THCS-THPT Mỹ Thuận
Chủ đề 6. Khối tròn xoay
TÀI LIỆU ÔN THI TỐT NGHIỆP THPT MÔN TOÁN Chủ đề 6. KHỐI TRÒN XOAY 1
HÌNH NÓN VÀ HÌNH TRỤ
1 Hình nón tròn xoay
2 Hình trụ tròn xoay OIM I △OIM Cho tam giác vuông tại . Khi quay P ℓ OI . . . . . . . . . OIM Trong mặt phẳng ( ) cho hai đường thẳng và ∆ quanh cạnh thì đường tạo thành . . . . . . . . . . . . r . . . . . .
với nhau, cách nhau một khoảng . Khi một
được gọi là hình nón tròn xoay, gọi tắt là P ℓ . . . . . . . . . . . . quay mặt phẳng (
) xung quanh ∆ thì đường thẳng . . . . . . . . . . . . . . . ! sinh ra một mặt được gọi là mặt tròn I IM . . . . . . . . . . . . . . . . . . . . . • Hình tròn tâm , bán kính gọi là ! xoay, gọi tắt là O . . . . . . . . . . . . • Điểm gọi là của hình nón • Đường thẳng gọi là trục OI . . . . . . . . . OM . . . . . . • Đoạn gọi là , đoạn là độ dài • Đường thẳng gọi là đường sinh . . . . . . . . . . . . r . . . . . . . . . • là của mặt trụ đó. h ℓ h r Cho hình nón có chiều cao , độ dài đường sinh và
Cho hình trụ có chiều cao và bán kính đáy . Khi đó: r bán kính đáy . Khi đó: Diện tích xung Diện tích toàn phần Thể tích Diện tích xung Diện tích toàn phần Thể tích quanh quanh 2 HÌNH CẦU
Tập hợp những điểm M trong . . . . . . . . . . . . cách điểm O cố định một khoảng . . . . . . . . . . . . bằng r > 0
được gọi là mặt cầu tâm O bán kính r. . . . . . . . . . ! Kí hiệu: C, D ∈ S S r CD . . . . . . . . . . . . • Nếu hai điểm ( ; ) thì đoạn thẳng gọi là . . . . . . . . . . . . . •
Dây cung đi qua tâm được gọi là của mặt cầu.
Điểm nằm trong và nằm ngoài mặt cầu − é S O r M Cho mặt cầu ( ; ) và điểm bất kì. OM r M . . . . . . S O r • Nếu = thì nằm mặt cầu ( ; ) OM < r M . . . . . . S O r • Nếu thì nằm mặt cầu ( ; ) OM > r M . . . . . . S O r • Nếu thì nằm mặt cầu ( ; )
Giao của mặt cầu và mặt phẳng − é
Giao của mặt cầu và đường thẳng − é S O r P H S O r H Cho mặt cầu ( ; ) và mặt phẳng ( ). Gọi Cho mặt cầu ( ; ) và đường thẳng ∆. Gọi O P O là hình chiếu vuông góc của lên ( ), khi đó là hình chiếu vuông góc của lên ∆, khi đó OH O, P OH O, = d ( ( )). = d ( ∆). ○ OH > r P S . . . . . . . . . ○ OH > r S . . . . . . . . . Nếu thì ( ) và ( ) điểm chung. Nếu thì ∆ và ( ) điểm chung. ○ OH r P . . . . . . . . . S . . . ○ OH r . . . . . . . . . S . . . Nếu = thì ( ) với ( ) tại . Nếu = thì ∆ với ( ) tại . P . . . . . . . . . . . . H . . . . . . . . . . . . H Khi đó, ( ) gọi là , gọi là Khi đó, ∆ gọi là , gọi là . . . . . . . . . . . . . . . . . . . . . . . . ○ OH < r P S ○ OH < r S . . . Nếu thì ( ) cắt ( ) theo giao tuyến là Nếu thì ∆ cắt ( ) tại điểm. . . . . . . . . . . . . . . . r′ . . . . . . . . . tâm , bán kính = . Tổ Toán 14
Trường THCS-THPT Mỹ Thuận
Chủ đề 6. Khối tròn xoay
TÀI LIỆU ÔN THI TỐT NGHIỆP THPT MÔN TOÁN Tiếp tuyến − é M . . . . . . • Qua một điểm nằm trên mặt cầu, có
tiếp tuyến với mặt cầu. Các tiếp tuyến này tạo thành một
. . . . . . . . . . . . của mặt cầu. M . . . . . . • Qua một điểm nằm ngoài mặt cầu, có
tiếp tuyến với mặt cầu. Các tiếp tuyến này tạo thành một . . . . . . . . . A đỉnh . OM > r M . . . . . . S O r • Nếu thì nằm mặt cầu ( ; ) Diện tích Thể tích Tổ Toán 15
Trường THCS-THPT Mỹ Thuận
Chủ đề 7. Phương pháp tọa độ trong không gian
TÀI LIỆU ÔN THI TỐT NGHIỆP THPT MÔN TOÁN Chủ đề 7.
PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN 1 HỆ TỌA ĐỘ OXYZ
1 Tọa độ điểm và vectơ Oxyz . . . Ox Oy Oz . . . . . . . . . . . .
Trong không gian, hệ trục tọa độ bao gồm trục , , đôi một − Ï − Ï − Ï i j k . . . . . . . . .
. . . . . . . . . . . . . . . . . . • Các vectơ , , lần lượt là các vectơ • Các mặt phẳng , , được gọi là các Ox Oy Oz trên các trục , , . mặt phẳng tọa độ. −−Ï O . . . . . . . . .
. . . . . . . . . . . . . . . M x y z OM
. . . . . . . . . . . . . . . • Điểm ( ; ; ) được gọi là • Điểm ( 0 ; 0 ; 0 ) nếu =
2 Biểu thức tọa độ của các phép toán vectơ
Các công thức cần nhớ − é − Ï − Ï Oxyz a a a a b b b b Trong không gian , cho hai vectơ = ( 1 ; 2 ; 3 ) và = ( 1 ; 2 ; 3 ). Ta có: − Ï − Ï − Ï − Ï − Ï a ± b
. . . . . . . . . . . . . . . . . . . . . i . . . . . . . . . j . . . . . . . . . k . . . . . . . . . • = • = , = , = − Ï − Ï − Ï − Ï k · a
. . . . . . . . . . . . . . . . . . − Ï b ̸ a b • = • Với vectơ = 0 thì và cùng phương khi và  ∃k ∈ a . . . . . . a . . . . . . a . . . R chỉ khi sao cho 1 = , 2 = ,  − Ï − Ï  1 = a . . . . . . a b ⇔ a . . . 3 = • = 2 = − Ï  a . . . AB
. . . . . . . . . . . . . . . . . . . . . . . . • = 3 = x x
. . . . . . . . . . . . . . . . . . AB M A + B •
Trung điểm của đoạn thẳng là . . . ; ; . . . 2 x x x
. . . . . . . . . . . . . . . . . . . . . . . . ABC G A + B + C • Trọng tâm của tam giác là . . . ; ; . . . 3
3 Tích vô hướng − Ï − Ï Oxyz a a a a b b b b Trong không gian
, tích vô hướng của hai vectơ = ( 1 ; 2 ; 3 ) và = ( 1 ; 2 ; 3 ) bằng − Ï − Ï a · b
. . . . . . . . . . . . . . . . . . . . . =
Độ dài của một vectơ − é Góc giữa hai vectơ − é − Ï a a a a − Ï − Ï Cho vectơ = ( a a a a b 1 ; 2 ; 3 ). Khi đó Góc giữa hai vectơ = ( 1 ; 2 ; 3 ) và = b b b q ( 1 ; 2 ; 3 )
được tính bởi công thức − Ï a a2 . . . . . . . . . = + 1 − Ï − Ï − Ï − Ï a . . . b a , b
. . . . . . . . . . . . . . . . . . . . . cos = − Ï − Ï = a . . . b
4 Tích có hướng − Ï − Ï − Ï − Ï a a a a b b b b Tích có hướng a b
Trong không gian, cho hai vectơ = ( 1 ; 2 ; 3 ) và = ( 1 ; 2 ; 3 ). của hai vectơ và là một − Ï − Ï
. . . . . . . . . . . . . . . . . . a b với cả và . h− Ï − Ïi a , b
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . = ( ; ; ) Tổ Toán 16
Trường THCS-THPT Mỹ Thuận
Chủ đề 7. Phương pháp tọa độ trong không gian
TÀI LIỆU ÔN THI TỐT NGHIỆP THPT MÔN TOÁN 2
PHƯƠNG TRÌNH MẶT CẦU Định lí − é Oxyz S I a b c R Trong không gian , mặt cầu ( ) tâm ( ; ; ) bán kính có phương trình là x − . . . 2 y . . . . . . 2 z . . . . . . 2 . . . . . . ( ) + ( ) + ( ) =
Nhận xét: Phương trình mặt cầu nói trên có thể viết dưới dạng x2 y2
z2 − . . . . . . x − . . . . . . y − . . . . . . z d + + + = 0 √ R a2 b2 c2 − . . . a2 b2
c2 − . . . > . . . trong đó = + + ( + + ) 3
PHƯƠNG TRÌNH MẶT PHẲNG
1 Vectơ pháp tuyến của mặt phẳng Định nghĩa − é − Ï − Ï − Ï α n ̸ . . . . . . α n Cho mặt phẳng ( ). Nếu vectơ = 0 và có
vuông góc với mặt phẳng ( ) thì được gọi là vectơ
. . . . . . . . . . . . . . . . . . α của ( ). . . . . . . . . . • Mỗi mặt phẳng có vectơ pháp tuyến. − Ï − Ï n α k · n
. . . . . . . . . . . . . . . . . . . . . α • Nếu
là vectơ pháp tuyến của ( ) thì cũng là của ( ).
2 Phương trình tổng quát của mặt phẳng − Ï Oxyz α M x y z n a b c Trong không gian , cho mặt phẳng ( ) đi qua điểm ( 0 ; 0 ; 0 ) và có vectơ pháp tuyến = ( ; ; ). Khi đó a x − . . . . . . y . . . y c . . . − z . . . ( ) + ( 0 ) + ( 0 ) =
Phương trình mặt phẳng theo đoạn chắn − é α Ox Oy Oz A a B b C c Nếu mặt phẳng ( ) cắt các trục , , lần lượt tại ( ; 0; 0), (0; ; 0) và (0; 0; ) thì x y z α . . . ( ) :
a + b + c =
3 Vị trí tương đối của hai mặt phẳng Oxyz α A x B y C z D β A x B y C z D Trong không gian cho hai mặt phẳng ( ) : 1 + 1 + 1 + 1 = 0 và ( ) : 2 + 2 + 2 + 2 = 0. ( ( A B C . . . k A B C A B C . . . k A B C α ( ( ( ( ∥ β ⇔ 1 ; 1 ; 1 ) 2 ; 2 ; 2 ) α ≡ β ⇔ 1 ; 1 ; 1 ) 2 ; 2 ; 2 ) ! • ( ) ( ) D . . . kD • ( ) ( ) D . . . kD 1 2 1 2
α ⊥ β ⇔ . . . . . . . . . . . . • ( ) ( )
4 Khoảng cách từ một điểm đến một mặt phẳng Oxyz M x y z α Ax By Cz D Trong không gian , khoảng cách từ điểm ( 0 ; 0 ; 0 ) đến mặt phẳng ( ) : + + + = 0 được tính bằng A . . . B . . . C . . . D M, α + + + √ d ( ( )) = . . .2 . . .2 . . .2 + +
5 Góc giữa hai mặt phẳng − Ï − Ï m, n α , β Giả sử
lần lượt là vectơ pháp tuyến của hai mặt phẳng ( ) ( ). Khi đó − Ï − Ï m · n α , β cos (( ) ( )) = − Ï − Ï m · n Tổ Toán 17
Trường THCS-THPT Mỹ Thuận
Chủ đề 7. Phương pháp tọa độ trong không gian
TÀI LIỆU ÔN THI TỐT NGHIỆP THPT MÔN TOÁN 4
PHƯƠNG TRÌNH ĐƯỜNG THẲNG
1 Phương trình tham số và phương trình chính tắc của đường thẳng Định nghĩa − é − Ï Oxyz M x y z u u u u Trong không gian
cho đường thẳng ∆ đi qua điểm ( 0 ; 0 ; 0 ) và nhận = ( 1 ; 2 ; 3 ) làm vectơ chỉ
phương. Khi đó phương trình tham số của ∆ có dạng x . . . . . . . . . . . . t  = +  y . . . . . . . . . . . . t ∆ : = + (1)  z . . . . . . . . . . . . t = + t . . . . . . . . . . . . trong đó là u , u , u ̸ chính tắc Nếu 1 2 3
= 0 thì phương trình (1) có thể viết dưới dạng như sau: ! x − . . . y − . . . z − . . . . . . = . . . = . . .
2 Vị trí tương đối của hai đường thẳng
Hai đường thẳng song song, trùng nhau − Ï − Ï u , v , M ∈ Gọi
lần lượt là vectơ chỉ phương của hai đường thẳng ∆1 ∆2 và điểm ∆1 . (− Ï (− Ï u k . . . . . . u k . . . . . . = = ∥ ⇔ ≡ ⇔ • ∆1 ∆2 M . . . . . . • ∆1 ∆2 M . . . . . . ∆2 ∆2
Hai đường thẳng cắt nhau, chéo nhau   x x u t x x′ v t′  =  = +  0 + 1  0 1 d y y u t d′ y y′ v t′ Cho hai đường thẳng : = 0 + 2 và : = + . 0 2   z z u tz z′ v t′ = 0 + 3 = + 0 3 − Ï − Ï d d′ d d′ u , v • và
cắt nhau khi và chỉ khi hệ phương trình • và
chéo nhau khi và chỉ khi hai vectơ . . . . . . . . . . . .
phương và hệ phương trình x u t x′ v t′  = +  0 + 1 0 1  y u t y′ v t′ x u t x′ v t′  0 + 1 = + 1 0 + 2 = +  0 0 2  z u t z′ v t′ y u t y′ v t′ 0 + 2 = + 2 0 + 3 = + 0 0 3  z u t z′ v t′ 0 + 3 = + 3 . . . . . . 0 có đúng nghiệm. . . . . . . nghiệm.
3 Vị trí tương đối của đường thẳng và mặt phẳngx x u t  =  0 + 1 y y u t α Ax By Cz D
Để tìm giao điểm của đường thẳng ∆ : = 0 + 2 và mặt phẳng ( ) : + + + = 0, ta xét  z z u t = 0 + 3 phương trình ! A x u t B y u t C z u t D ( 0 + 1 ) + ( 0 + 2 ) + ( 0 + 3 ) + = 0 (1) . . . . . . . . . α •
Nếu (1) vô nghiệm thì ∆ ( ) . . . . . . . . . α •
Nếu (1) vô số nghiệm thì ∆ ( ) . . . . . . . . . α •
Nếu (1) có đúng một nghiệm thì ∆ ( ) Tổ Toán 18
Trường THCS-THPT Mỹ Thuận
Chủ đề 8. Dãy số - Quy tắc đếm - Xác suất - Góc - Khoảng cách
TÀI LIỆU ÔN THI TỐT NGHIỆP THPT MÔN TOÁN Chủ đề 8.
DÃY SỐ - QUY TẮC ĐẾM - XÁC SUẤT - GÓC - KHOẢNG CÁCH 1 DÃY SỐ
1 Dãy số . . . . . . u N∗ Mỗi số
xác định trên tập các số nguyên dương
được gọi là một dãy số vô hạn (gọi tắt là dãy số). u u , u , . . . • n : dãy số ! 1 2 u • 1 : số hạng ......... u •
n: số hạng ...............
2 Cấp số cộng - Cấp số nhân Cấp số cộng Cấp số nhân Định nghĩa Số hạng tổng quát Tính chất n Tổng số hạng đầu 2 QUY TẮC ĐẾM
1 Quy tắc cộng và Quy tắc nhân Quy tắc cộng − é Quy tắc nhân − é một hai
Nếu một công việc có thể được hoàn thành bởi
Nếu một công việc có thể được hoàn thành bởi giai trong hai m m
phương án, phương án thứ nhất có cách
đoạn, giai đoạn thứ nhất có
cách thực hiện, giai đoạn n n
thực hiện, phương án thứ hai có cách thực hiện, thì thứ hai có
cách thực hiện, thì có ............ cách hoàn
có ............ cách hoàn thành công việc. thành công việc.
2 Chỉnh hợp và Tổ hợp Chỉnh hợp Tổ hợp Định nghĩa Công thức n n n−k . . . . . . Chú ý Chỉnh hợp chập của được gọi là một Cn = . . . . . . . . . . . . n k k+1 . . . . . . của . Cn + Cn = Tổ Toán 19
Trường THCS-THPT Mỹ Thuận
Chủ đề 8. Dãy số - Quy tắc đếm - Xác suất - Góc - Khoảng cách
TÀI LIỆU ÔN THI TỐT NGHIỆP THPT MÔN TOÁN 3 XÁC SUẤT
1 Các định nghĩa
Phép thử ngẫu nhiên:
Phép thử ngẫu nhiên là ........................... mà ta không đoán trước được ........................ của nó, mặc dù đã biết
! ............................ tất cả các ....................... có thể có của phép thử đó. Không gian mẫu:
Không gian mẫu của một phép thử là ......................... các ........................ có thể xảy ra của phép thử đó. Kí hiệu ........... Biến cố − é
Biến cố là một ............................. của ................................. ∅ • Tập
là biến cố ........................... •
Tập Ω là biến cố ........................... A ∩ B ∅ A B • Nếu = thì ta nói hai biến cố và ........................... A \ B A B A . . . . . . B . . . . . . • Nếu = Ω thì ta nói hai biến cố và
..........................., kí hiệu = hoặc = .
2 Xác suất của biến cố A
! Giả sử là biến cố liên quan đến một phép thử với không gian mẫu Ω, chỉ có một số hữu hạn kết quả đồng A . . . . . . . . . n A
khả năng xuất hiện. Xác suất của biến cố là tỉ số
. Kí hiệu: ........... Trong đó ( ) là số ................... A n của biến cố ,
(Ω) là số ................ có thể xảy ra của phép thử. Tính chất − é ○ P ∅ . . . . . . P . . . . . . ( ) = , (Ω) = .
○ . . . . . . ≤ P A ≤ . . . . . . A ( ) , với mọi biến cố . ○ P A . . . . . . . . . . . . A = , với mọi biến cố . 4
GÓC VÀ KHOẢNG CÁCH TRONG KHÔNG GIAN 1 Góc
Góc giữa đường thẳng và mặt phẳng − é
Góc giữa mặt phẳng và mặt phẳng − é α α β
Cho đường thẳng ∆ và mặt phẳng ( ). Cho hai mặt phẳng ( ) và ( ). ⊥ α , α ◦ α ◦ ∥ β α , β • Nếu ∆ ( ) thì ∆ ( ) = 90 . • Nếu ( ) ( ) thì ( ) ( ) = 0 . α , α , d α ∩ β α , β a, b •
Nếu ∆ không vuông góc với ( ) thì ∆ ( ) = (∆ ) • Nếu ( ) ( ) = ∆ thì ( ) ( ) = ( ) d α a ⊂ α b ⊂ β a ∩ ∩ b M với
là hình chiếu vuông góc của ∆ trên ( ). với ( ), ( ) và ∆ = .
2 Khoảng cách
Điểm và mặt phẳng − é
Hai đường thẳng chéo nhau − é S α H a, b Cho điểm và mặt phẳng ( ). Gọi là hình chiếu •
Đường thẳng ∆ cắt hai đường thẳng chéo nhau S α vuông góc của trên ( ). Khi đó
và cùng vuông góc với hai đường thẳng ấy được gọi . . . . . . . . . a b là đường vuông góc của và . SH⊥ α S, α SH ( ) và d ( ) = •
Nếu đường thẳng vuông góc chung ∆ cắt hai đường a, b M, N a, b thẳng chéo nhau lần lượt tại thì d = . . . . . .. Tổ Toán 20
Trường THCS-THPT Mỹ Thuận
Document Outline

  • Khảo sát sự biến thiên và đồ thị của hàm số
    • Sự biến thiên của hàm số
    • Cực trị của hàm số
    • Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
    • Đường tiệm cận
    • Khảo sát đồ thị hàm số
  • Lũy thừa - Mũ - Logarit
    • Lũy thừa
    • Hàm số lũy thừa
    • Logarit
    • Hàm số mũ và hàm số logarit
    • Phương trình mũ và phương trình logarit
    • Bất phương trình mũ và bất phương trình logarit
  • Nguyên hàm - Tích phân và ứng dụng
    • Nguyên hàm
    • Tích phân
    • Ứng dụng của tích phân trong hình học
  • Số phức
    • Số phức
    • Phép cộng, trừ, nhân, chia số phức
  • Khối đa diện
    • Khái niệm về hình đa diện và khối đa diện
    • Khối đa diện đều
    • Thể tích khối đa diện
  • Khối tròn xoay
    • Hình nón và hình trụ
    • Hình cầu
  • Phương pháp tọa độ trong không gian
    • Hệ tọa độ Oxyz
    • Phương trình mặt cầu
    • Phương trình mặt phẳng
    • Phương trình đường thẳng
  • Dãy số - Quy tắc đếm - Xác suất - Góc - Khoảng cách
    • Dãy số
    • Quy tắc đếm
    • Xác suất
    • Góc và Khoảng cách trong không gian