lOMoAR cPSD| 46663874
1. Một công ty có hai phòng chức năng. Phòng A gồm 5 nhân viên nam, 3
nhân viên nữ. Phòng B gồm 6 nhân viên nam, 6 nhân viên nữ. Để kiểm
tra năng lực làm việc của mỗi phòng, giám đốc công ty quyết định chọn
mỗi phòng 3 nhân viên để kiểm tra chuyên môn. Biết rằng mỗi nhân
viên ở phòng A có thể vượt qua kỳ kiểm tra với xác suất 0.8 đối với
nam và 0.9 đối với nữ. Mỗi nhân viên phòng B có thể vượt qua kỳ kiểm
tra với xác suất 0.9 đối với nam và 0.8 đối với nữ. Khả năng vượt qua
kì kiểm tra của phòng nào cao hơn?
A. Không có đủ dữ liệu để đưa ra thông tin cho bài toán.
B. Khả năng cả hai phòng là bằng nhau.
C. Khả năng phòng A cao hơn khả năng phòng B.
D. Khả năng phòng B cao hơn khả năng phòng A. Giải: Phòng A: - Chọn 3 nhân viên nam:
xác xuất cả 3 vượt qua: 0,8.0,8.0,8= 0,512 xác suất
có 2 người vượt qua: 3.0,8.0,8.(1-0,8)=0,384 xác
suất có 1 người vượt qua: 3.0,8.(1−0,8)2=0,096 xác
suất không có người vượt qua: (1−0,8)3=0,008❑❑ - Chọn 2 nam 1 nữ:
xác xuất cả 3 vượt qua: 0,8.0,8.0,9= 0,576 xác
suất có 2 người vượt qua: 3.2.0,8.(1-0,9)= 0,48
xác suất có 1 người vượt qua: 3.[0,8.(1-0,8).(1-0,9)+ 0.9.(1-0,8).(1-0,8)] =0,156
xác suất không có người vượt qua: 0,8.(1-0,8).(1-0,9)+ 0.9.(1- 0,8).(10,8)=0,052 - Chọn 2 nữ 1 nam:
xác xuất cả 3 vượt qua: 0,9.0,9.0,8= 0,648 xác suất
có 2 người vượt qua: 3.[2.0,9.(1-0,8)]= 1,08
xác suất có 1 người vượt qua: 3.[0,9.(1-0,9).(1-0,8)+ 0.8.(1-0,9).(1-0,9)] =0,078
xác suất không có người vượt qua: 0,9.(1-0,9).(1-0,8)+ 0.8.(1- 0,9).(10,9)=0,026 Phòng B - Chọn 3 nhân viên nam: lOMoAR cPSD| 46663874
xác xuất cả 3 vượt qua: 0,9.0,9.0,9= 0,729 xác suất
có 2 người vượt qua: 3.0,9.0,9.(1-0,9)=0,54 xác
suất có 1 người vượt qua: 3.0,9.(1−0,9)2=0,027 xác
suất không có người vượt qua: (1−0,9)3=0,001 - Chọn 2 nam 1 nữ:
xác xuất cả 3 vượt qua: 0,9.0,9.0,8= 0,648 xác
suất có 2 người vượt qua: 3.2.0,9.(1-0,8)= 1,08
xác suất có 1 người vượt qua: 3.[0,9.(1-0,9).(1-0,8)+ 0.8.(1-0,9).(1-0,9)] =0,078
xác suất không có người vượt qua: 0,9.(1-0,9).(1-0,8)+ 0.8.(1- 0,9).(10,9)=0,026 - Chọn 2 nữ 1 nam:
xác xuất cả 3 vượt qua: 0,8.0,8.0,9= 0,576 xác
suất có 2 người vượt qua: 3.2.0,8.(1-0,9)= 0,48
xác suất có 1 người vượt qua: 3.[0,8.(1-0,8).(1-0,9)+ 0.9.(1-0,8).(1-0,8)] =0,156
xác suất không có người vượt qua: 0,8.(1-0,8).(1-0,9)+ 0.9.(1- 0,8).(10,8)=0,052
Tổng xác suất vượt qua kỳ kiểm tra cho cả ba trường hợp: chọn 3 nhân
viên, 2 nam 1 nữ và 2 nữ 1 nam: ⇒ Phòng A:
0,512+0,384+0,096+0,576+0,48+0,156+0,648+1,08+0,078= 4,01
Phòng B: 0,729+0,54+0,027+0,648+1,08+0,078+0,576+0,48+0,156= 4,314
⇒Phòng B có khả năng vượt qua kỳ kiểm tra cao hơn Phòng A
2. Một nhóm bệnh nhân gồm 7 người trong đó có 5 người mắc bệnh A và
6 người mắc bệnh B. Chọn ngẫu nhiên 3 trong số 7 bệnh nhân nói trên.
Tính xác suất để 3 người đó mắc một trong hai loại bệnh. A. 4/7 B. 2/7 C. 1/7 D. 5/7 Giải: n(Ω¿= 7C3 lOMoAR cPSD| 46663874
TH1: 2 người mắc bệnh A và 1 người không mắc bệnh B: 5C2.6C0
TH2: 2 người mắc bệnh B và 1 người không mắc bệnh A: 6C2.5C0
⇒ 5C 2.6C0+6C2.5C0= 5
3. Nếu x là biến ngẫu nhiên nhị thức có n=10 và p=0.8 thì độ lệch chuẩn của x là _________. A. 5,8 B. 1.26 C. 2,09 D. 3,5 Giải:
Var(X)= n.p.q= 10.0,8.(1-0,8)= 1,6 σ (x)= 1,26
4. Cho biến ngẫu nhiên X có hàm mật độ xác suất A. 1/2 B. 3/4 C. 5/7 D. 9/7. Giải: f(x)= f(x)=
xác suất được tính như sau: lOMoAR cPSD| 46663874 P(6=0,5
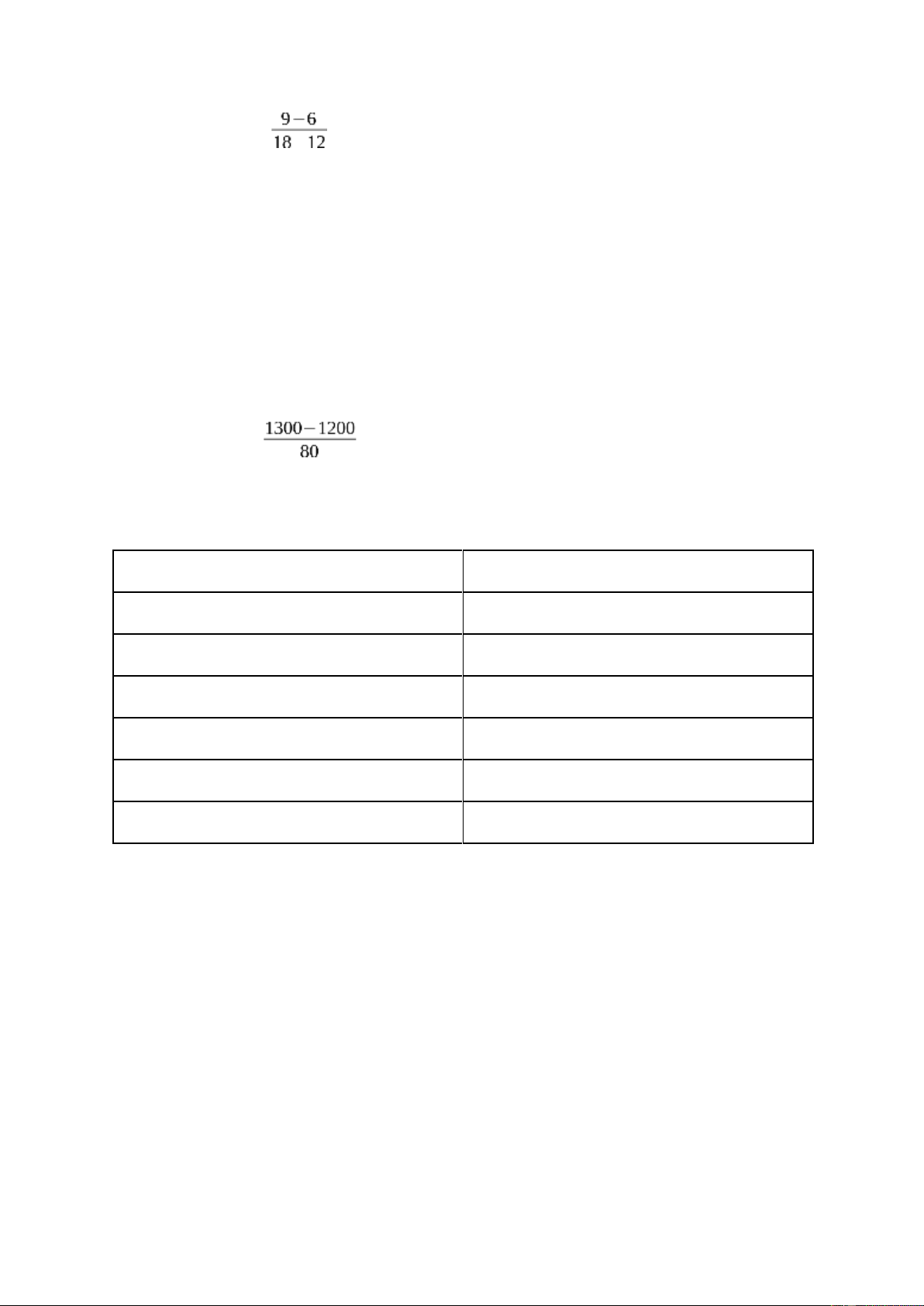
5. Tuổi thọ dự kiến (trung bình) của một loại bóng đèn cụ thể là 1200 giờ với
độ lệch chuẩn là 80 giờ. Tuổi thọ của bóng đèn này có phân bố chuẩn. Xác
suất để một bóng đèn được chọn ngẫu nhiên có tuổi thọ ít hơn 1300 giờ là
bao nhiêu? A. 0.5679 B. 0.0765 C. 0.1345 D. 0.8944 Giải:
Xác suất để một bóng đèn được chọn ngẫu nhiên có tuổi thọ ít hơn 1300 giờ: P(X<1300)=P(Z< ) =P(Z<1,25)= 0,8944
6. Cho bảng phân phối của đại lượng ngẫu nhiên X. Tìm xác suất khi X lớn hơn 20? X F(X) 10 0,1 15 0,1 20 c 25 0,3 30 0,1 35 0,2 A. 0.50 B. 0.60C. 0.41 D. 0,20 Giải: 0,1+0,1+c+0,3+0,1+0,2=1 ⇒c= 0,2
Để xác suất khi x lớn hơn 20:
P(X>20)= P(X=25)+P(X=30)+P(X=35)= 0,3+0,1+0,2=0,6
7. Trong các mệnh đề sau, có bao nhiêu mệnh đề đúng?
i. (−3< ≤4)= (−4≤ ≤3) 𝑃 𝑍 𝑃 𝑍 ii. (
<1.20)= + ( >−1.20) 𝑃 𝑍 𝑃 𝑍 iii. ( ≤0.23)= lOMoAR cPSD| 46663874
+ (−0.23≤ ≤0.23) 𝑃 𝑍 𝑃 𝑍 iv. (1.98≤
≤2.49)= − (−2.49≤ ≤1.98)𝑃 𝑍 𝑃 𝑍 A. 4 B. 2 C. 3 D. 1 Giải:
1. Sai, ta sử dụng tính chất của phân phối chuẩn đối xứng qua gốc tọa độ (Z = 0).
P(−3P(−4≤Z≤3) bao gồm phần từ −4 đến 0 và từ 0 đến 3
Do tính chất đối xứng, P(Z≤3)=P(Z≥−3) và P(Z≤4)=P(Z≥−4)
Tuy nhiên, P(−3khoảng từ -4 đến -3.
2. SAI. P(Z>−1.20) bằng 1−P(Z≤−1.20).
Vì phân phối chuẩn đối xứng qua 0,
P(Z>−1.20)=1−(1−P(Z<1.20)))=P(Z<1.20).
Mệnh đề này là đúng khi: P(Z<1.20)=1/2+P(Z<1.20).
Tuy nhiên, không có cách nào mà P(Z<1.20) lại bằng một nửa của chính nó cộng thêm P(Z<1.20).
3. ĐÚNG. Do tính chất đối xứng, P(Z≤0.23)=1/2+P(−0.23≤Z≤0.23)
Chúng ta biết rằng P(Z≤0.23) có thể được viết là:
P(Z≤0.23)=1/2+P(0≤Z≤0.23).
Tuy nhiên, P(−0.23≤Z≤0.23) không thể viết theo dạng này.
Thực tế, nó có thể viết thành: P(Z≤0.23)≈0.5+P(0≤Z≤0.23)
4. SAI. Ta biết rằng P(Z≤a)+P(Z≥b)= 1 khi a và b đối xứng qua 0.
● P(1.98≤Z≤2.49)= P(Z≤2.49)−P(Z≤1.98)
● P(−2.49≤Z≤1.98) cũng bao gồm hai phần đối xứng.
Mệnh đề này sẽ đúng nếu: P(1.98≤Z≤2.49)≠1/2−P(−2.49≤Z≤1.98) lOMoAR cPSD| 46663874
8. Tỉ lệ người đến khám tại một bệnh viện mắc bệnh A là 40%, trong số những
người mắc bệnh A có 70% mắc cả bệnh B, còn trong số những người không
mắc bệnh A có 30% mắc bệnh B. Xác suất chọn một bệnh nhân mắc bệnh B là bao nhiêu? A. 0.4600 B. 0.3664 C. 0.6300 D. 0.4646 Giải:
Ta gọi: tỉ lệ người đến khám tại một bệnh viện mắc bệnh A là P(A)= 0,4
những người mắc bệnh A có 70% mắc cả bệnh B là P(B|A)= 0,7 những
người không mắc bệnh A có 30% mắc bệnh B là P(B|¬ A)=0,3 Xác suất chọn
một bệnh nhân mắc bệnh B:
P(B)= P(A).P(B|A)+P(B|¬ A¿.P(¬ A¿= 0,4.0,7+0,3.0,6= 0,46
9. Có bao nhiêu biến ngẫu nhiên rời rạc?
i. Số lượng người đến cửa hàng trong 1 giờ.
ii. Số lỗi sai trong 100m vải. iii. Khối lượng của một hộp bánh.
iv. Phần trăm khối lượng công việc đã hoàn thành trong một đơn vị thời gian.
v. Thể tích của một chai nước.
vi. Số sản phẩm được bán ra trong một ngày. vii. Số nốt nhạc trong một bài hát. A. 4 B. 3 C. 5 D. 2 Giải:
1. rời rạc, vì đây là số lượng có thể đếm được.
2. rời rạc vì có thể đếm số lỗi
3. liên tục, vì khối lượng luôn thay đổi
4. liên tục, vì phần trăm số lượng công việc hoàn thành luôn thay đổi
5. liên tục, vì thể tích của nước luôn thay đổi
6. rời rạc, vì có thể đếm được nốt nhạc
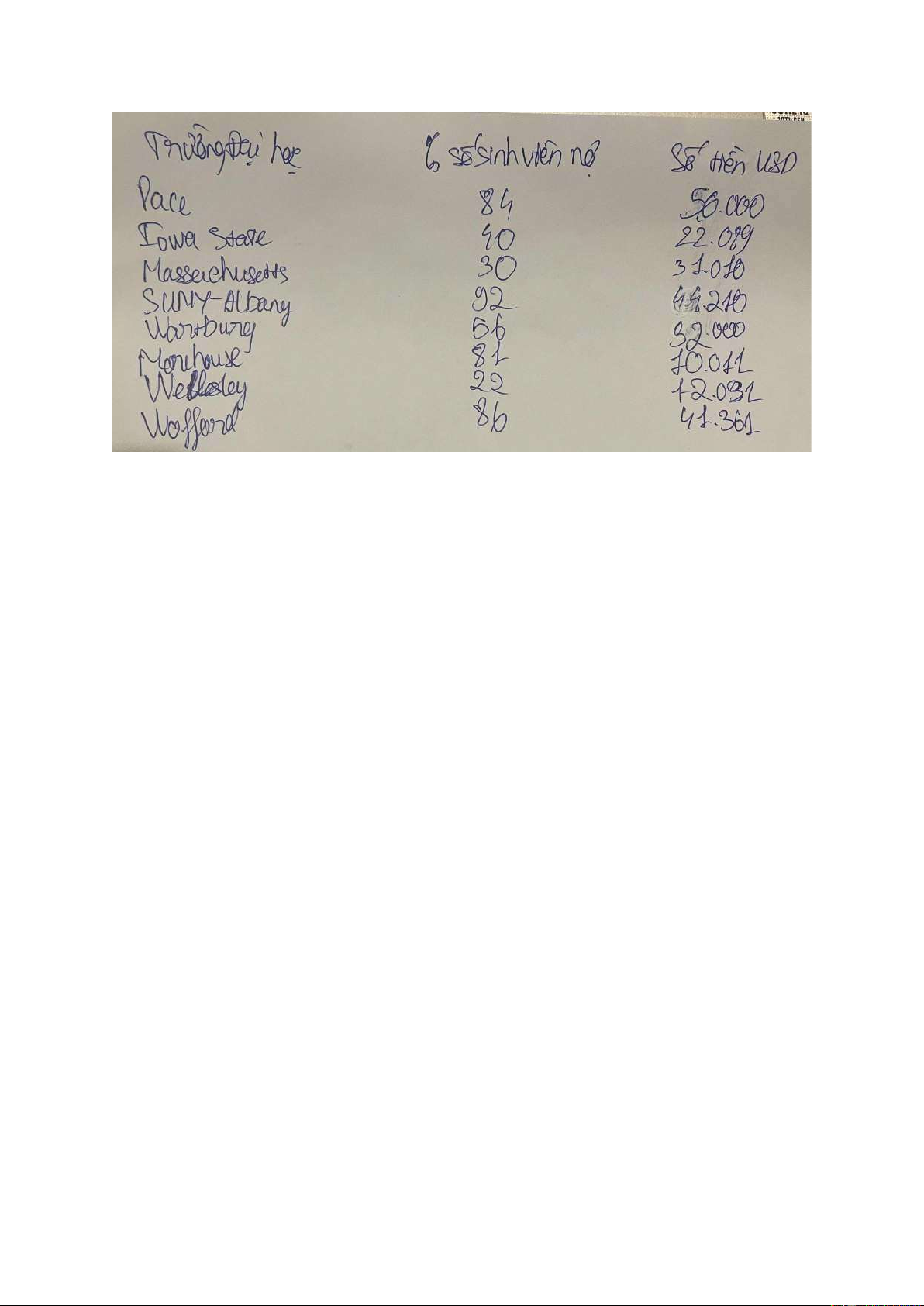
10. Nhiều sinh viên vẫn còn nợ khi tốt nghiệp đại học. Trong bảng sau đây là
tỷ lệ phần trăm sinh viên tốt nghiệp nợ và số nợ trung bình của những sinh
viên tốt nghiệp này tại các trường. lOMoAR cPSD| 46663874
Nếu chọn ngẫu nhiên một trong tám trường này cho một nghiên cứu tiếp theo
về các khoản vay của sinh viên, xác suất chọn một trường có sinh viên tốt
nghiệp với khoản nợ trung bình trên 50000 USD biết rằng sinh viên đó có trên
80% số sinh viên nợ là bao nhiêu? A. 7/8 B. 1/4 C. 1/7 D. 2/5 Giải:
Nhìn vào bảng, ta thấy có 4 trường đáp ứng với yêu cầu % sinh viện nợ
⇒ n(Ω¿= 4 tiếp theo, ta dựa vào số tiền nợ của 4 trường, chỉ duy nhất có 1
trường là đáp ứng yêu cầu đề bài ⇒n(A)= 1 ⇒1/4
11. Ba phòng thí nghiệm được giao nhiệm vụ tạo giống lúa mới. Ba phòng
làm việc độc lập, xác suất thành công tương ứng là 0.5, 0.6 và 0.8. Tính xác
suất không có phòng thành công. A. 0.96 B. 0.78 C. 0.04D. 0.265 Giải:
Vì ba phòng làm việc độc lập, nên P(AB)=P(A).P(B)
xác suất không có phòng thành công: P(¬ A¿=0,5 P(¬B¿=0,4 P(¬C ¿=0,2
⇒P(¬ ABC)=0,5.0,4.0,2=0,04 lOMoAR cPSD| 46663874
12. Một cuộc khảo sát về sinh viên mới trúng tuyển MBA đã cung cấp dữ liệu sau cho 2018 sinh viên. Nộp nhiều hơn một trường Đúng Sai Từ 23 trở xuống 456 332 Nhóm tuổi 24-26 321 225 27-30 298 132 31-35 143 155 Từ 36 trở 50 278
Xác suất để một người nộp đơn được chọn ngẫu nhiên nhỏ hơn 31 tuổi biết
rằng người đó nộp vào nhiều hơn một trường là bao nhiêu? A. 0.8478 B. 0.2352 C. 0.4876 D. 0.5678 Giải:
Để người đó nộp vào nhiều hơn một trường: n(Ω¿=1268
Xác suất để một người nộp đơn được chọn ngẫu nhiên nhỏ hơn 31 tuổi: n(A)=1075 ⇒ =¿0,8478
13. Một mẫu gồm 15 phiếu được chọn ngẫu nhiên, không hoàn lại, từ tổng số
100 phiếu. Mỗi chứng từ trong mẫu được kiểm tra sai sót và số chứng từ
trong mẫu có sai sót được ký hiệu là x. Nếu 40% số phiếu có sai sót thì giá trị
trung bình của x là __________. A. 150 B. 4 C. 10 lOMoAR cPSD| 46663874 D. 6 Giải: Giá trị trung bình: E(x)=n..p= 15.0,4=6
14. Có bao nhiêu phát biểu đúng?
i. Phân phối nhị thức được đặc trưng bởi hai tham số trung bình 𝜇 và phương
sai .𝜎 ii. Phân phối chuẩn là phân phối đối xứng. iii. Vùng diện tích phía dưới
đồ thị của phân phối chuẩn từ -∞ đến +∞ bằng 1. iv. Hệ số tương quan của hai
biến , ( , )= ( ) ( )− (𝑋 𝑌 𝜌 𝑋 𝑌 𝐸 𝑋 𝐸 𝑌 𝐸 𝑋𝑌).
v. Hiệp phương sai của hai biến ,𝑋 𝑌 luôn nhận giá trị từ -1 đến 1. vi.
Trung bình của biến ngẫu nhiên X luôn nhận giá trị không âm. vii.
Phương sai của biến ngẫu nhiên X luôn nhận giá trị không âm. A. 7 B. 1 C. 5 D. 3Gi ải:
1. Đúng, vì n và p đều có trong công thức tính trung bình và phương sai
2. Đúng, vì phân phối chuẩn là một phân phối xác suất đối xứng, nghĩa là
mật độ xác suất của nó bằng nhau ở hai bên của giá trị trung bình ( ). 𝜇
Đồ thị mật độ xác suất của phân phối chuẩn có dạng hình chuông đối xứng.
3. Đúng, vì tổng diện tích dưới đường cong mật độ xác suất của bất kỳ
phân phối xác suất nào cũng bằng 1
4. Sai, vì ( ,𝜌 𝑋 𝑌)= √❑
5. Đúng, vì hiệp phương sai (Cov( , )) của hai biến , thể hiện mức độ 𝑋 𝑌
𝑋 𝑌 liên hệ tuyến tính giữa chúng. Giá trị của Cov( , ) có thể nằm
trong 𝑋 𝑌 khoảng từ -∞ đến +∞.
6. Sai, vì trung bình ( ) của biến ngẫu nhiên X có thể nhận bất kỳ giá trị 𝜇
nào, bao gồm cả giá trị âm.
7. Đúng, vì ^2 luôn không âm vì nó là bình phương của độ lệch chuẩn 𝜎 (
)𝜎 , vốn không thể có giá trị âm.
15. Cho biến ngẫu nhiên X có hàm mật độ xác suất lOMoAR cPSD| 46663874
Tính trung bình của biến ngẫu nhiên =12+2𝑌 X. A. π2 2 π2 B. +3 6 C. π2+2 3 D. 0 Giải:
16. A và B là hai biến cố độc lập và ( )=0.60 và ( )=0.80. Xác suất ( | ) 𝑃 𝐴 𝑃
𝐵 𝑃 𝐵𝐴 là bao nhiêu? A. 0.22 B. 0.31 C. 0,50 D. 0.80 Giải:
Vì hai biến độc lập nên sẽ không ảnh hưởng tới nhau, điều đó đồng nghĩa P(B|A)=P(B)=0,8 lOMoAR cPSD| 46663874
17. Thời gian hoàn thành (từ đầu đến cuối) của một dự án tu sửa tòa nhà có
phân phối chuẩn với trung bình là 150 ngày công và độ lệch chuẩn là 20 ngày
công. Để chắc chắn 95% rằng chúng ta sẽ không chậm trễ trong việc hoàn
thành dự án, chúng ta nên yêu cầu thời gian hoàn thành là _______ ngày làm việc. A. 111 B. 182,9 C. 421 D. 321 Giải: μ=150 σ=20 Vì 95% không chậm trễ: ϕ=(1,645)
⇒d=¿ μ+z .σ= 150+1,645.20= 182,9 (ngày)
18. Xác suất để một cuộc gọi đến đường dây trợ giúp khẩn cấp được trả lời
trong vòng 12 giây là 0.4. Giả sử các cuộc gọi độc lập với nhau. Sử dụng
phép tính xấp xỉ nhị thức, xác suất có ít nhất 60 trong số 120 cuộc gọi được
trả lời trong vòng 12 giây là khoảng ______. A. 0.9898 B. 0.2568 C. 0.0125 D. 0.2312 Giải:
μ=n. p=120.0,4=48
σ2=n. p.q=120.0,4.(1−0,4)=28,8 P(X≥60¿ =P(Z≥2,24¿
⇒P(X≥60)=1−P(X ≤60)=¿ 1-0,9875=0,0125
19. Cho bảng phân phối xác suất X như sau: X F(x) 0 0,25 1 0,25 2 0,5
Đặt =9X+6,5. Tính ( ) và 𝑌 𝐸 𝑌 𝑉𝑎𝑟 𝑌( ). lOMoAR cPSD| 46663874 A. 23 và 44,45 B. 11,25 và 55,69 C. 24,21 và 4,76 D. 55,69 và 11,25 Giải:
E(X)=0.0,25+1.0,25+2.0,5= 1,25 E(X2¿
=0^2.0,25+1^2.0,25+2^2.0,5=2,25
⇒E(Y)=E(9X+6,5)=9.Var(x)=11,25 Var(x)=E(X^2)- [E(X)]^2=0,6875
⇒Var(y)=Var(9x+6,5)=9^2.Var(x)=55,69
20. Một học sinh đoán ngẫu nhiên các câu trả lời cho bài kiểm tra đúng/sai
gồm 8 câu hỏi. Nếu có 60% cơ hội đoán đúng mỗi câu hỏi thì xác suất học
sinh đó đoán sai đúng 2 câu là bao nhiêu? A. 0.234 B. 0.333 C. 0.214 D. 0,113 Giải: n(Ω¿=28=¿256
Xác suất học sinh đó đoán sai đúng 2 câu:
TH1:Học sinh sai 2 câu trong tổng 8 câu: 8C2
TH2: Học sinh đúng 6 câu trong 6 câu: 6C6 ⇒ =0,113