Tài liệu Toán 9 chủ đề góc có đỉnh bên trong đường tròn, bên ngoài đường tròn

GÓC CÓ ĐỈNH BÊN TRONG ĐƯỜNG TRÒN, BÊN NGOÀI ĐƯỜNG TRÒN A. Lý thuyết m
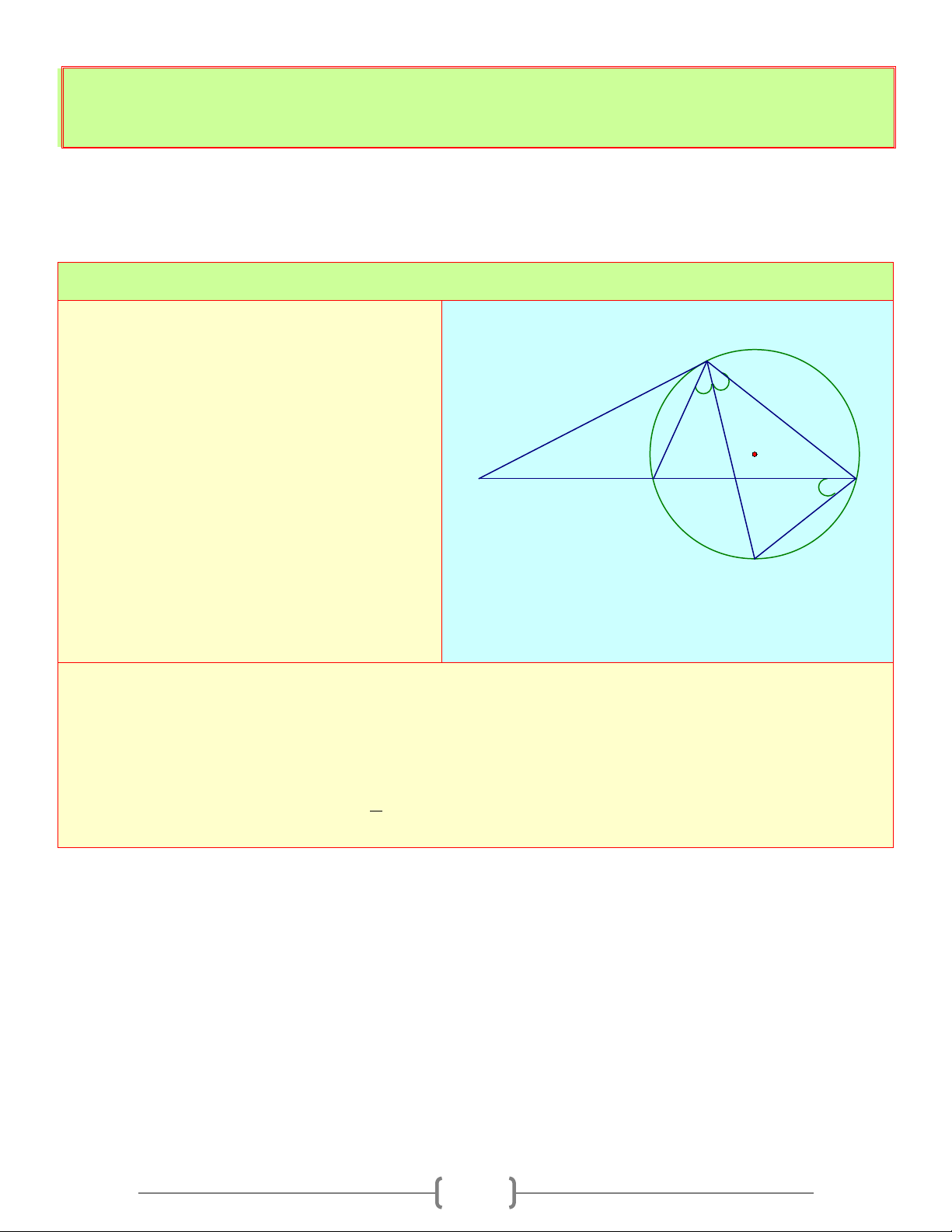
1. Góc có đỉnh bên trong đường tròn D A Góc 
BIC nằm bên trong đường tròn (O) được gọi là góc có đỉnh ở bên I O trong đường tròn. B
*) Định lí 1: Số đo của góc có đỉnh ở bên trong đường tròn bằng nửa tổng n C
số đo hai cung bị chắn, cụ thể ta có:  1 BIC =  sđ AmD +  ( sđ BnC) 2
2. Góc có đỉnh bên ngoài đường tròn
Các góc có đỉnh nằm bên ngoài đường tròn, các cạnh đều có điểm chung với đường được gọi
là góc có đỉnh ở bên ngoài đường tròn.
*) Định lí 2: Số đo của góc có đỉnh ở bên ngoài đường tròn bằng nửa hiệu số đo hai cung bị
chắn, cụ thể ta có:  1 BID =  sđ BmD −  ( sđ AnC) 2 B. Lý thuyết
Dạng 1: Chứng minh hai góc bằng nhau, hai đoạn thẳng bằng nhau
Cách giải: Sử dụng hai định lí về số đo của góc có đỉnh bên trong đường tròn, góc có đỉnh bên ngoài đường tròn. Bài 1:
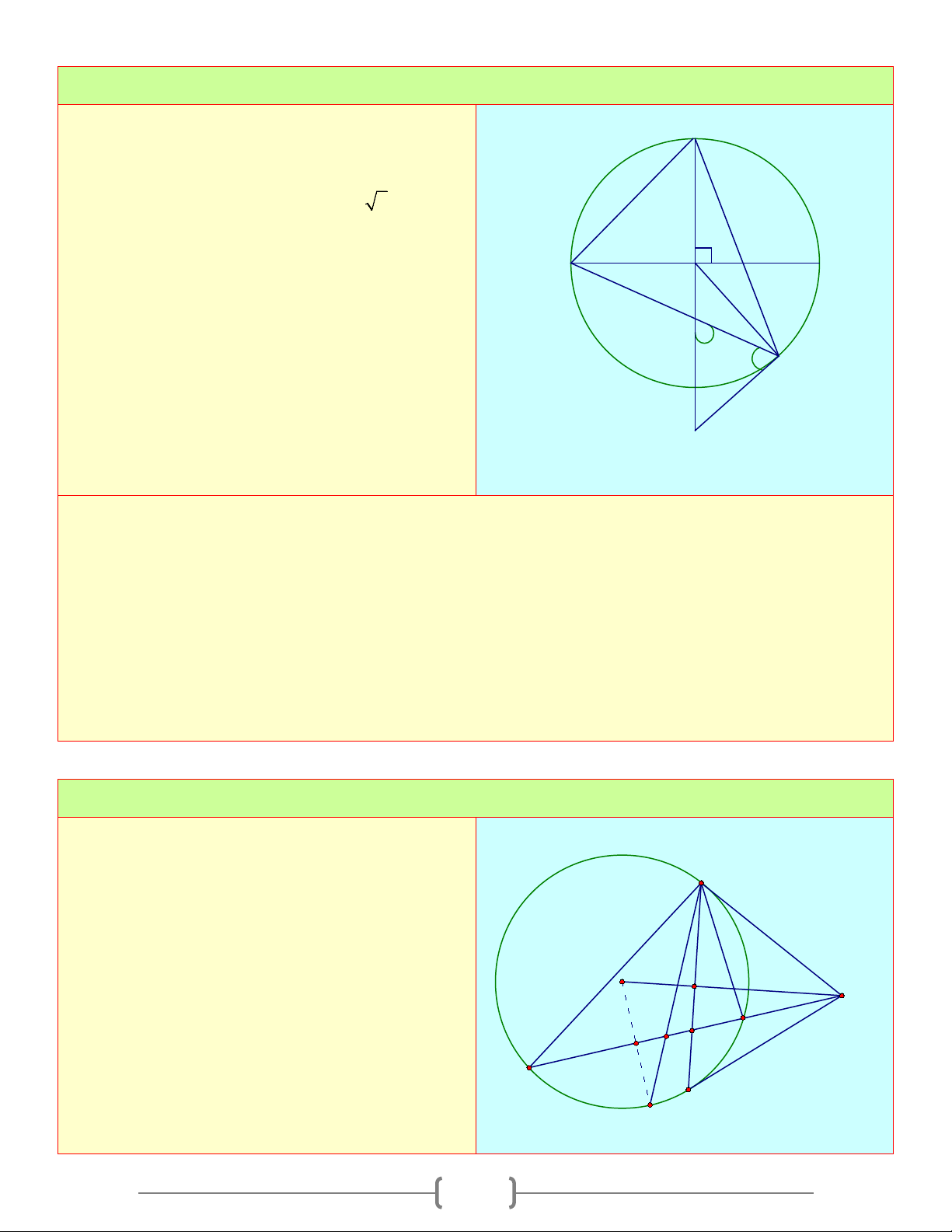
Cho tam giác ABC nội tiếp đường tròn (O) . A
Các tia phân giác của góc B và C cắt nhau D N
tại I và cắt đường tròn lần lượt tại D và E . 1 1 M E 2
Dây CE cắt các cạnh AB và AC lần lượt tại 2 M và N . CMR: I a. A ∆ MN cân b. E ∆ AI, D ∆ AI cân B C
c. ◊AMNI là hình thoi. F Lời giải 1
a) Chứng minh được AI là phân giác của A Xét A ∆ MN , có:  1 M =  sđ AD +  sđ EN 1 ( ) 2  1 N =  sđ EA + 
( sđ CD)⇒ M = N 1 1 1 2
⇒ ∆AMN cân tại A +)  DAI =  1 DI =  sđ CD + 
( sđ CF)⇒∆A ID cân tại D 2 ⇒ DI = DA . Tương tự ta có E
∆ AI cân tại E ⇒ EA = EI
b) Ta có: AE = EI, DA = DI ⇒ DE là đường trung
trực của đoạn AI ⇒ NA = NI ⇒ ∆ANI cân mà  N =  N ⇒  M = 
N ⇒ NI / / AM . 1 2 1 2 tương tự:  N = 
M ⇒ MI / / AN ⇒ là hình bình hành có hai cạnh kề bằng nhau (đpcm) 1 2 Bài 2:
Cho đường tròn (O) và một dây AB . Vẽ C
đường kính CD vuông góc với AB ( D thuộc 2
cung nhỏ AB ). Trên cng nhỏ BC lấy một N 1
điểm N . Các đường thẳng CN và DN lần
lượt cắt đường thẳng AB tại E và F . Tiếp
tuyến của đường tròn tại N cắt đường thẳng A F B I E
AB tại I . CMR: D a. IN ∆ E, IN
∆ F là các tam giác cân b. AE FA AI + = 2 Lời giải
a. Ta có: CD ⊥ AB ⇒  AD =   DB CA =  ; CB 2 Xét IN ∆ E có:  N =  1 N =  sđCN(1) 1 2 2   sđCA −  E = sđ BN =  sđCB −  ( sđ BN ) =  : 2 sđCN : 2(2) 2 Từ  
(1)(2) ⇒ N = E ⇒ ∆INE cân tại I . Tương tự ta có IN
∆ F cân tại I . 1
b. Ta có: IE = IN = IF
AI = AE − IE  AE + AF
 ⇒ 2AI = AE + AF ⇒ AI =
AI = AF + FI  2 Bài 3:
Tam giác ABC nội tiếp đường tròn (O), có: A  0 B =  0 46 ,C = 72
a. Tính A của ∆ABC N
b. Tia phân giác của A cắt đường tròn ở M , O
tia phân giác của B cắt đường tròn ở N . Gọi I
I là giao điểm của AM và BN . Tính các góc B C   BIM; BMI
c. Chứng minh: MB = MC = MI M Lời giải
a. Xét ∆ABC , có A+ B +  0 C = ⇒  0 180 A = 62 b.  0 B = ⇒  0 sđ AC =  0 A = ⇒  0 46 92 ; 62 sđ BC =124 +)  1 MIB =  sđ MB +  0 0 1 124 + 92 0 ( AN) = ( ) = 54 2 2 2  0 =  B I = ⇒ MB = c. 54  MI MB ∆ I cân tại M do   ⇒ dpcm  MB = 
MC ⇒ MB = MC  3 Bài 4:
Cho AB là dây cung của đường tròn (O) . Lấy
I nằm giữa A và B sao cho IA > IB . Gọi D M
là điểm chính giữa cung AB nhỏ. Vẽ dây CD
qua I , tiếp tuyến tại C của đường tròn (O) C
cắt AD ở K O
a. Chứng minh rằng: IK = CK
b. Gọi E là điểm đối xứng của I qua K , EC A I B K E
giao với (O) tại M , Chứng minh rằng ba D
điểm M,O, D thẳng hàng c. .
CACB = CI.CD Lời giải a)  1 CIB =  sdCB +  1 sd AD =  sd BC +  ( ) ( BD) 2 2 1 =  sdCD 2 Mà  1 KIC = 
sdCD ⇒ ∆CIK cân tại K . 2 KE = b)
KI ⇒ KE = KI = KC ⇒ ∆ICE vuông tại K ⇒ ∆ICE nội tiếp đường tròn (K) đường kính KC = KI  IK ⇒  0 ICM = ⇔  0 90
DCM = 90 ⇒ MD là đường kính cả (O) nên M, O, D thẳng hàng.  CAI =    c) Xét CDB(cha . n BC) CA ∆ I, CD ∆ B , có:    
ACI = DCB(c . han .
hai cung.bang.nhau) ⇒ ∆ CA CI
CAI  ∆CDB(gg) ⇒ = ⇔ .
CACB = CI.CD (đpcm). CD CB 4
Dạng 2: Chứng minh hai đường thẳng song song hoặc vuông góc. Chứng minh đẳng thức cho trước
Cách giải: Áp dụng hai định lí về số đo góc có đỉnh bên trong đường tròn, góc có đỉnh bên
ngoài đường tròn để có được các góc bằng nhau, cạnh bằng nhau. Từ đó suy ra điều cần chứng minh Bài 1:
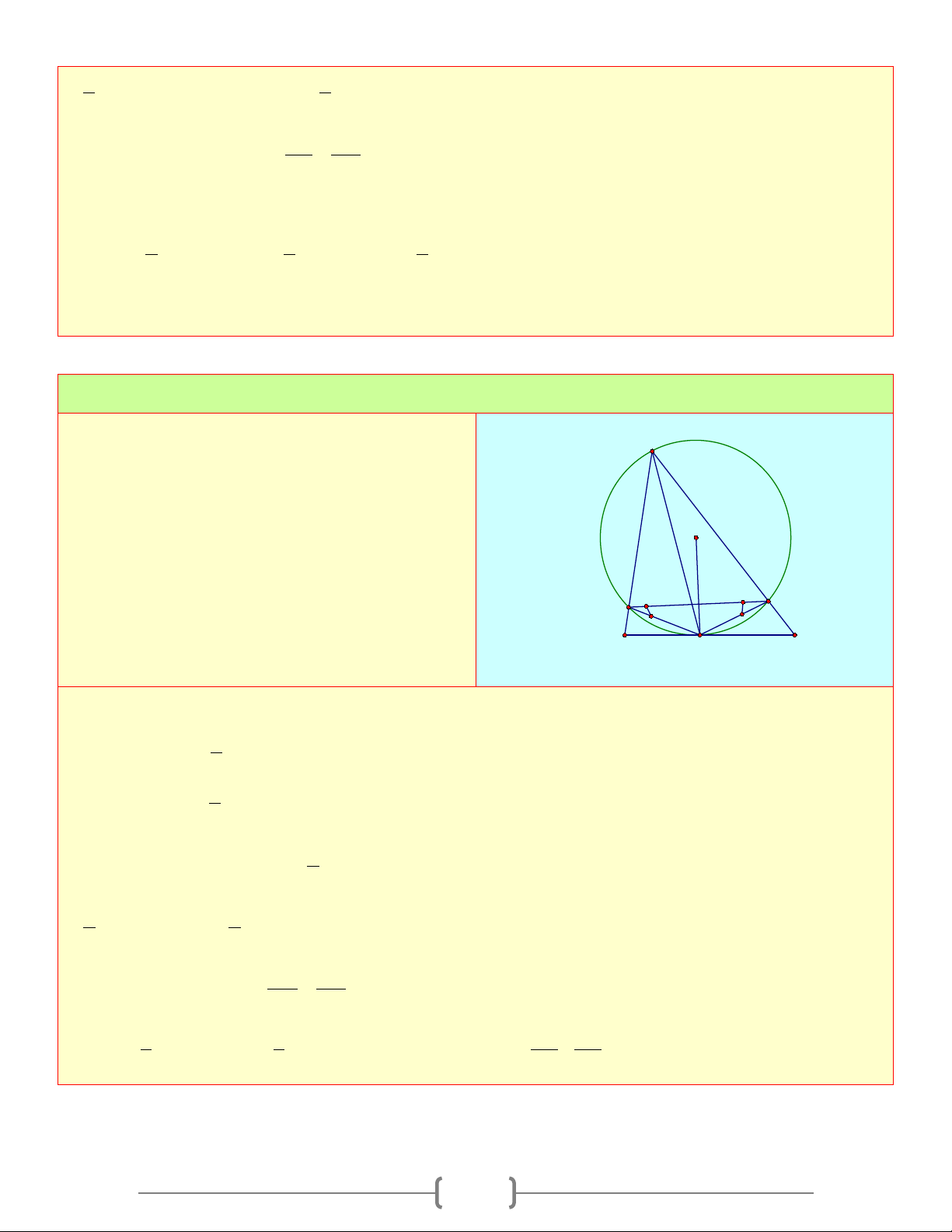
Từ điểm P nằm ngoài đường tròn (O) ,
vẽ tiếp tuyến PA với đường tròn và cát A
tuyến PBC với P, B,C ∈(O).
a) Biết PC = 25c , m PB = 49c . m Đường kính O
của đường tròn là 50c . m Tính PO B P C I
b) Đường phân giác trong của góc A cắt
PB ở I và cắt (O) ở D . Chứng minh DB D
là tiếp tuyến của đường tròn ngoại tiếp ∆AIB . Lời giải
a) Ta có ∆PAC  ∆PBA(gg) 2 ⇒ PA = P . B PC
Xét tam giác vuông PAO (  0 PAO = 90 ) 2 2 2 2 2 2
⇒ PA = PO − OA ⇒ PO = PA + OA ⇒ PO b) Chứng minh được  DBC =  1 DAB = 
CAB ⇒ DB là tiếp tuyến của đường tròn ngoại tiếp ∆AIB 2 5 Bài 2:
Cho đường tròn (O) có hai đường kính AB C
và CD vuông góc với nhau. Trên đường kính
AB lấy điểm E sao cho AE = R 2 Vẽ dây
CF đi qua E . Tiếp tuyến của đường tròn tại E A B
F cắt CD tại M , Vẽ dây AF cắt CD tại N . O Chứng minh N
a) Tia CF là tia phân giác của  BCD F b) MF / /AC D
c) MN,OD,OM là độ dài ba cạnh của của một M tam giác vuông. Lời giải b) Chứng minh được  AFM =  CAF = 
( ACF)⇒ MF //AC c) Chứng minh  MFN = 
MNF ⇒ ∆MNF cân tại M ⇒ MN = MF.
Mặt khác: OD = OF = R
Ta có MF là tiếp tuyến nê ∆OFM vuông ⇒ đpcm. Bài 3:
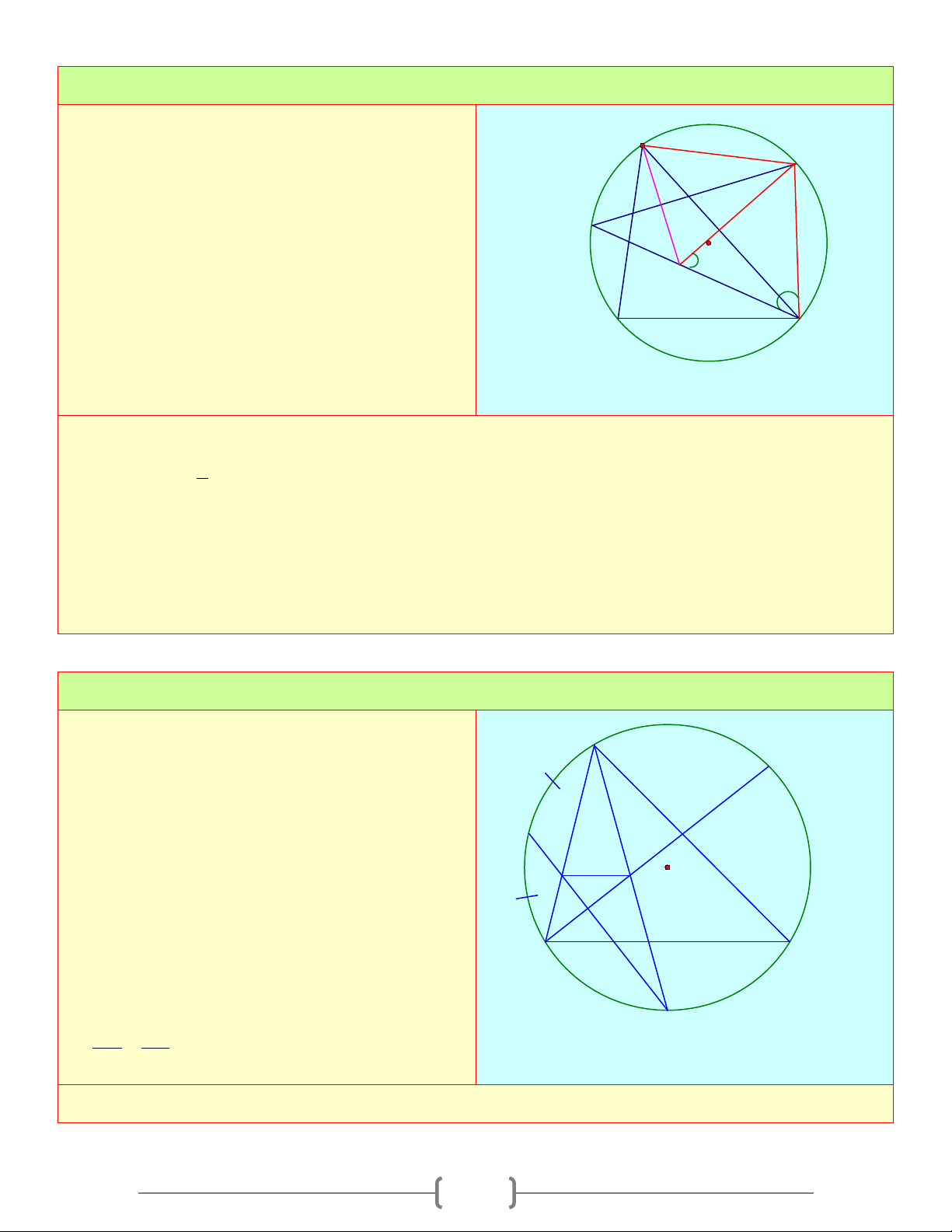
Cho đường tròn (O) và S nằm bên trong
đường tròn. Từ S kẻ hai tiếp tuyến SA và SA' A
( A và A' là tiếp điểm ) và cát tuyến ABC tới
đường tròn. Phân giác của góc BAC cắt BC ở H
D , cắt đường tròn ở E . Gọi H là giao điểm S
của OS và AA', G là giao điểm của OE và D F B
BS còn F là giao điểm của AA' với BC . G C CMR: A' E a. S ∆ AD cân 6 b. SF.SG = . SO SH c. 2
SA = SF.SG Lời giải a.  CE = 
EB ⇒ ∆SAD cân tại S
b. OB = OC = R ⇒ O nằm trên đường trung trực BC  EB = 
EC ⇒ EB = EC ⇒ E nằm trên đường trung trực BC ⇒ OE là đường trung trực của BC ⇒ OE ⊥ BC
+) SO là tia phân giác của tam giác cân ASA' ⇒ SH ⊥ AA' +) ∆ SG OS
OGS  ∆FHS(gg) ⇒ = ⇒ .
SO SH = SF.SG SH SF c. OA ∆
S vuông tại A , 2 2
AH ⊥ OS ⇒ SA = SH.SO ⇒ SA = SF.SG Bài 4:
Cho tam giác ABC nội tiếp đường
tròn (O). Gọi D là một điểm thuộc A
cung AB, qua D kẻ dây DD’ // BC cắt 3 1
AC ở F. Đường thẳng AD’ cắt BC ở E F 1 D' D a. So sánh A ∆ BD, A ∆ EC và A ∆ BE , O A ∆ DC 1 b. B A . D AE = A . B AC C E c. A ∆ FD# A ∆ DB Lời giải a. ⇒  =  ⇒  =  DD'/ /BC BD CD' A A 1 3 Lại có:  D =  '  E 1   ⇒ 
B = E ⇒ ∆ABD  ∆AEC  B =  1 D ' 1 1   +)  1 E =  sd AB −  1 CD =  sd AB −  ( ') ( BD) 2 2 7 1 =  sd AD =   ACD ABE =  1 ADC =  ; sd AC ⇒ A ∆ BE# A ∆ DC(gg) 2 2 b. Ta có ∆ AB AD
AEC  ∆ABD ⇒ = ⇐ A . D AE = A . B AC AE AC
Hoặc ∆ABE  ∆ADC ⇒ ..... c.  1 AFD =  sd AD +  1 CD =  sd AD +  1 BD =  sd ADB =  ( ') ( ) AD'B 2 2 2 +)  = 
BAD' DAF ⇒ A ∆ DF# A ∆ BD '(gg) . Bài 5: Cho A
∆ BC , phân giác AD . Vẽ đường tròn A ( O) đi qua ,
A D và tiếp xúc với BC ở D , 2 1
đường tròn này cắt AB, AC lần lượt ở E và F O . CMR: a. EF / /BC F E b. 1 2
AD = AE.AC 1 c. B D C
AE.AC = A . B AF Lời giải   1  CDF DAF sd FD = =  a) 2   ⇒  =   = 
DAF DAE; D F ⇒ FE / /BC 1 1   1  DFE DAE sd ED  = = 2  b) A =  A ⇒  ED =   1 FD ACD =  sd AED −  ; ( DF) 1 2 2 1 =  sd AED −  1 DE =  sd AE =  ( ) ADE 2 2 AD AE 2
⇒ ∆AED  ∆ADC(gg) ⇒ =
⇒ AD = AE.AC DC AD c.  1 ABD =  sd AFD −  1 ED =  sd FA =  AD AF 2 ( )
ADF ⇒ ∆ADF  ∆ABD ⇒ =
⇒ AD = AF.AB ⇒ AE.AC = AF.AB 2 2 AB AD 8 Bài 6:
Cho ∆ABC nội tiếp đường tròn tâm (O) . Các C
tia phân giác của các góc A và B cắt nhau ở D
I và cắt đường tròn theo thứ tự ở D và E . Chứng minh: E F O
a) ∆BDI là tam giác cân I
b) DE là đường trung trực của IC A B
c) IF / /BC, trong đó F là giao điểm của DE và AC . Lời giải a) Ta có  1 BID =  sd DE = 
DBE ⇒ ∆BID cân tại D 2
b) Chứng minh tương tự ta có ∆IEC cân tại E , ∆DIC cân tại D ⇒ EI = EC;DI = DC ⇒ DE là trung trực của CI
c) F ∈ DE ⇒ FI = FC ⇒  FIC =  FCI = 
ICB ⇒ IF / /BC Bài 7:
Trên đường tròn (O) lấy ba điểm , A B và C . A
Gọi M, N, P theo thứ tự là điểm chính giữa P
của các cung AB, BC,CA . BP cắt AN tại I , M
NM cắt AB tại E . Gọi D là giao điểm của
AN và BC . Chứng minh: E I O
a) ∆BNI là tam giác cân
b) AE.BN = E . B AN B D C c) EI / /BC N d) AN = AB BN BD Lời giải 9
b) Ta có M là điểm chính giữa cung  AB
⇒ NE là phân giác  ⇒ BN = EB BNA
(tính chất đường phân giác) ⇒ BN.AE = N . A BE AN EA d) Ta có ∆ AN AB
ABN  ∆BDN ⇒ = ⇒ đpcm. BN BD 10