Tài liệu Toán 9 chủ đề góc nội tiếp

GÓC NỘI TIẾP A. Lý thuyết M C
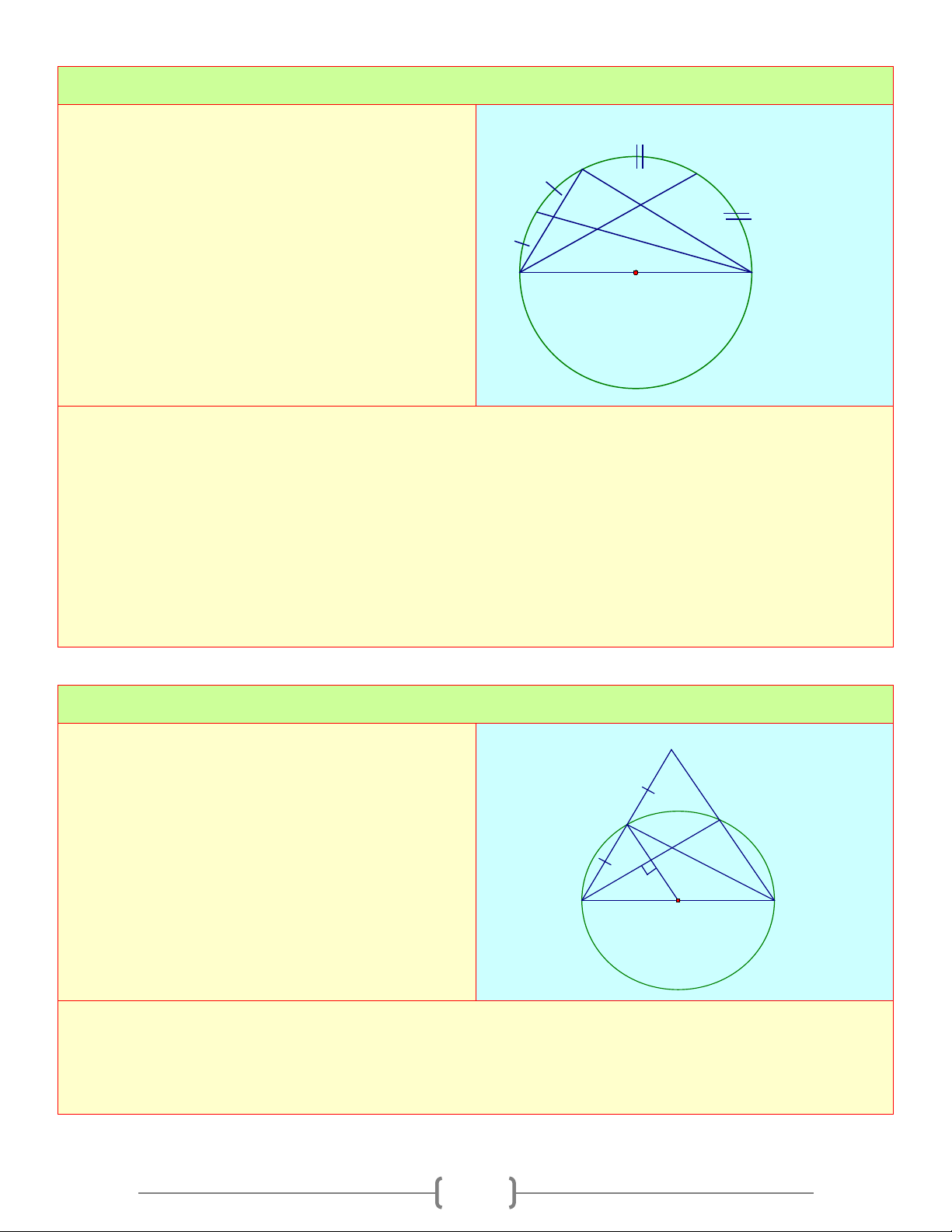
1. Định nghĩa: Góc có đỉnh nằm trên đường tròn và hai cạnh
chứa hai dây cung của đường tròn gọi là góc nội tiếp (  ACB ). N P
Lưu ý: Cung nằm bên trong góc nội tiếp được gọi là cung bị O chắn D B
2. Định lý: Trong một đường tròn, số đo của góc nội tiếp bằng
nửa số đo của cung bị chắn. A  1 ACB = sđ  1 AB = sđ  AOB 2 2
3. Hệ quả: Trong một đường tròn
a) Các góc nội tiếp bằng nhau chắn các cung bằng nhau và ngược lại.  ADB =  MNP ⇔  AB =  MP
b) Các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau  ADB =  ACB
c) Góc nội tiếp (nhỏ hơn hoặc bằng 0
90 ) có số đo bằng nửa số đo của góc ở tâm cùng chắn một cung
d) Góc nội tiếp chắn nửa đường tròn là góc vuông. B. Bài tập
Dạng 1: Chứng minh các góc bằng nhau, các đoạn thẳng bằng nhau
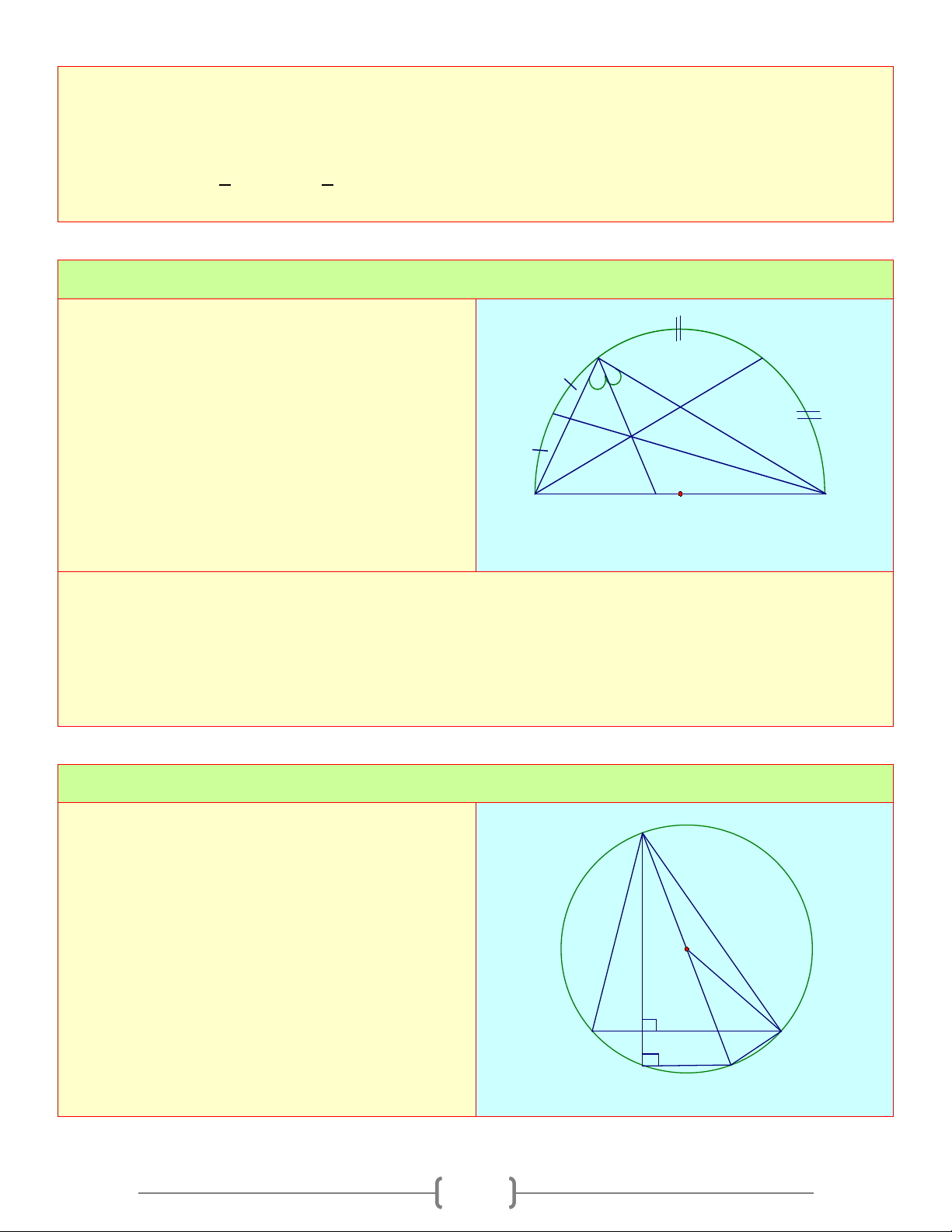
Cách giải: Dùng hệ quả trong phần lý thuyết Bài 1: Cho A
∆ BC cân tại A (  0
A < 90 ). Vẽ đường A
tròn đường kính AB cắt BC tại D , cắt AC tại
E . Chứng minh rằng: a. DB ∆ E cân E b.  1 CBE =  BAC 1 2 B D C Lời giải 1 a)  0
ADB = 90 ⇒ AD ⊥ BC ⇒ AD là phân giác của  A ⇒  =  ⇒  =  A A
BD DE ⇒ BD = DE ⇒ B ∆ ED cân tại 1 2 D b) Ta có  B =  1 A =  DE ⇒  1 B =  BAC . 1 2 1 2 2 Bài 2:
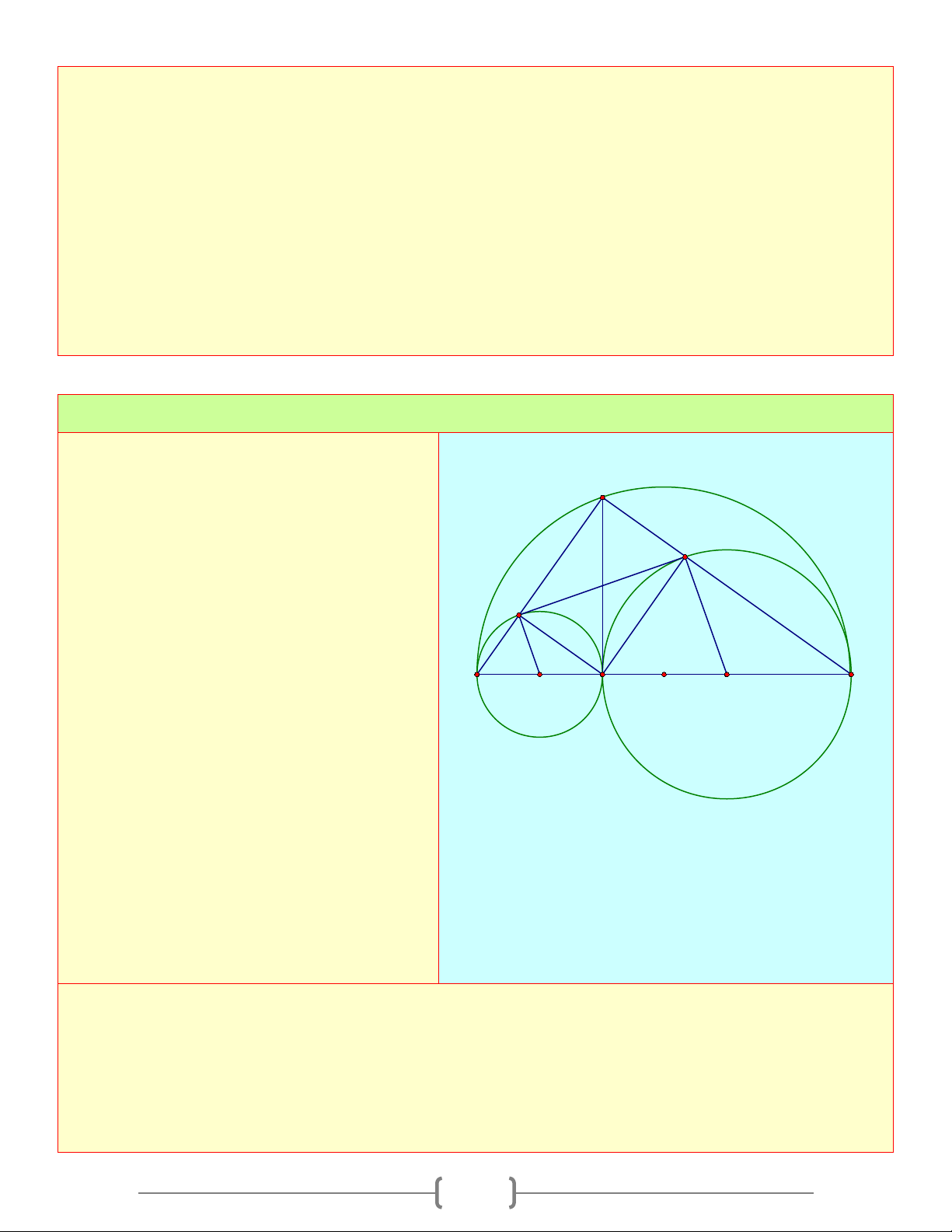
Cho nửa đường tròn (O) đường kính AB và C
dây AC căng cung AC có số đo bằng 600 N
a. So sánh các góc của A ∆ BC M
b. Gọi M và N lần lượt là điểm chính giữa
của các cung AC và BC , hai dây AN và BM I
cắt nhau tại I . Chứng minh rằng CI là tia A B O phân giác của  ACB Lời giải a) Ta có:  0 AC = ⇒  0 BC =
⇒ B < A <  60 120 C
b) AN là phân giác của góc A , BM là phân giác của góc B nên CI là phân giác của góc C (đpcm) Bài 1:
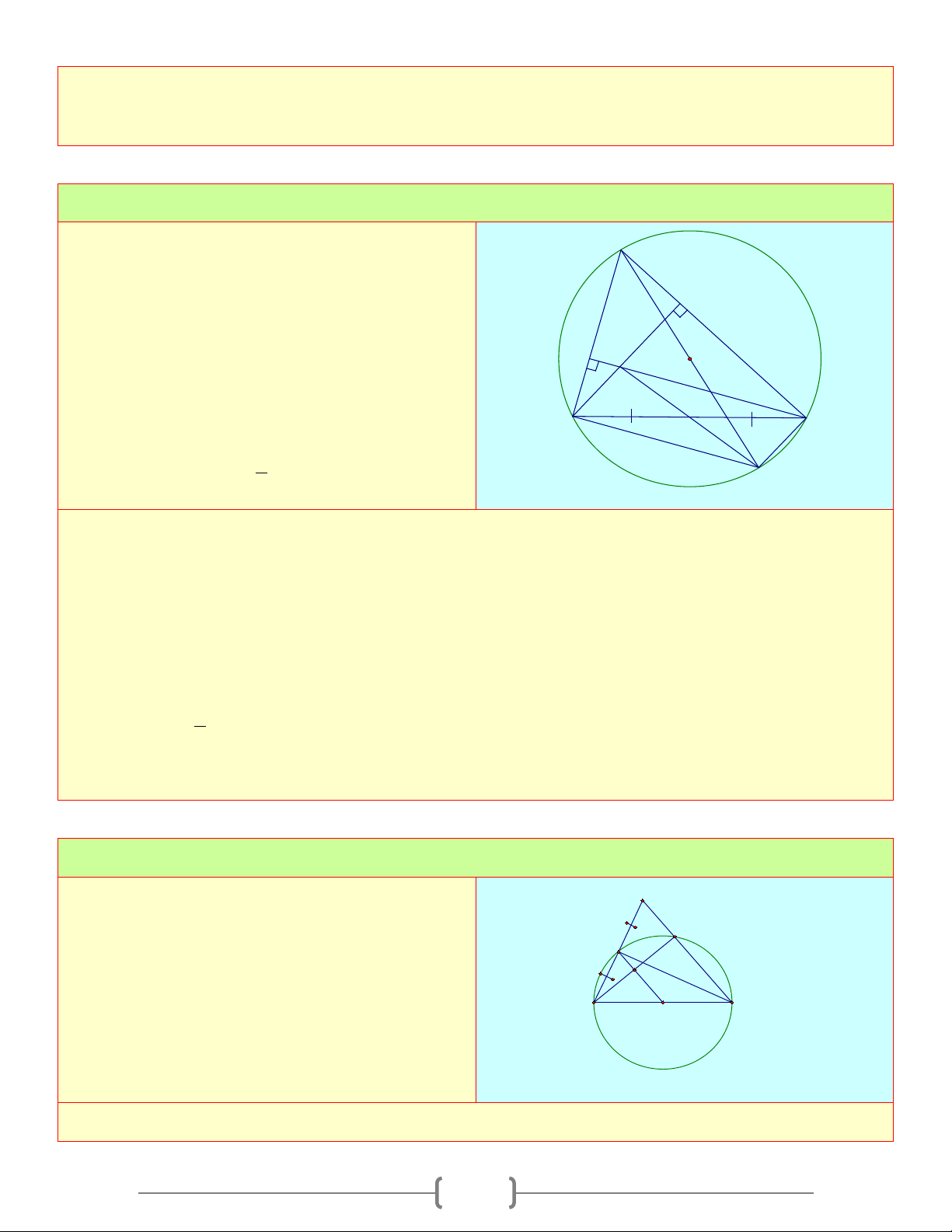
Cho tam giác ABC có ba góc nhọn, đường A cao
AH và nội tiếp đường tròn tâm O , đường kính AM a) Tính  ACM O b) Chứng minh  BAH =  OCA
c) Gọi N là giao điểm của AH với (O) . Tứ B giác H C
BCMN là hình gì? Vì sao? N M 2 Lời giải a) Ta có  0
ACM = 90 (góc nội tiếp) b) Ta có A ∆ BH ∽ A ∆ MC (gg) ⇒  BAH =   OAC OCA =  OAC ⇒  BAH =  ; OCA c)  0
ANM = 90 ⇒ MNBC là hình thang
⇒ BC / /MN ⇒ sđ  BN = sđ  CM ⇒  CBN = 
BCM ⇒ BCMN hình thang cân. Bài 4:
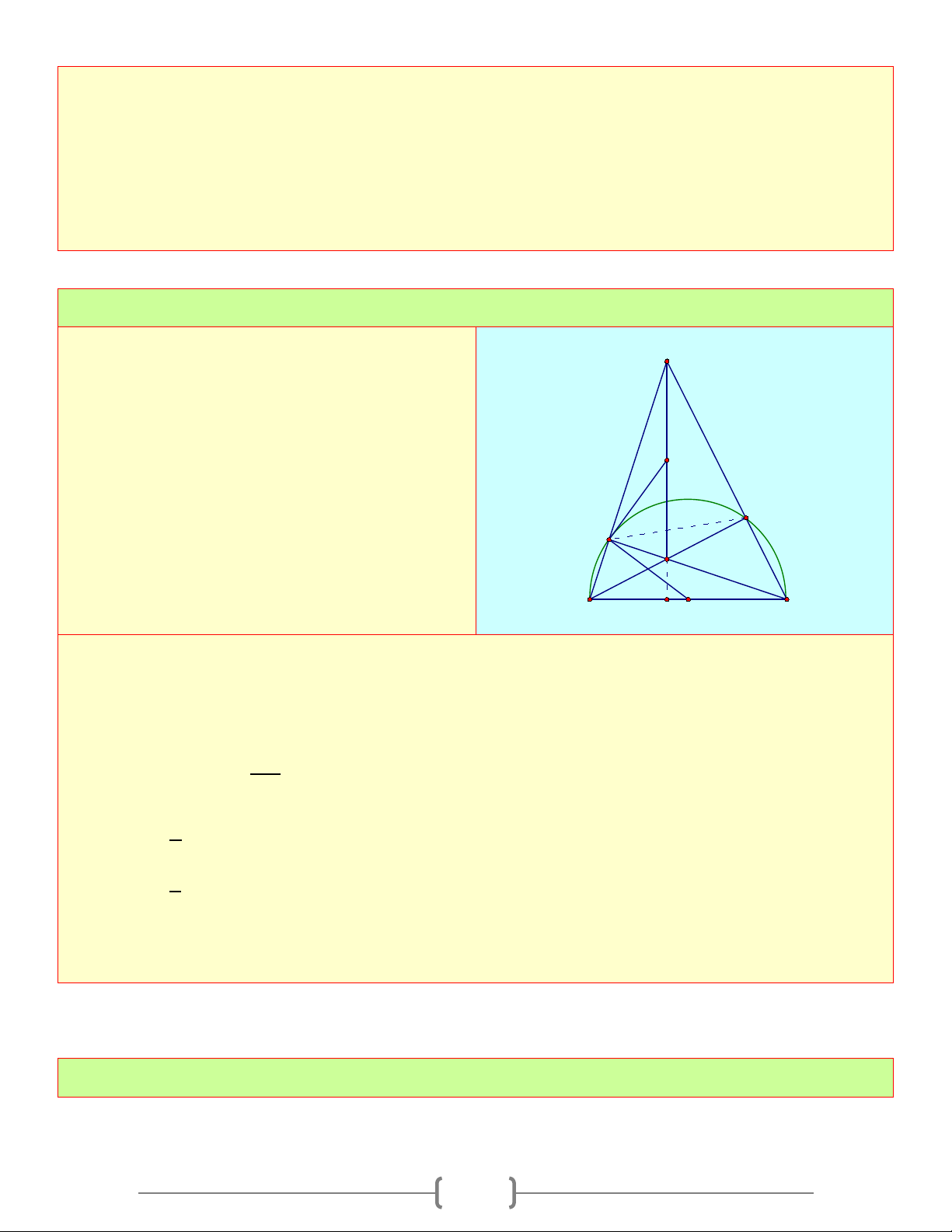
Cho nửa đường tròn (O) đường kính AB.
Lấy M là điểm tùy ý trên nửa đường tròn M
(M khác A và B). Kẻ MH vuông góc với Q
AB ( H ∈ AB ). Trên cùng một nửa mặt
phẳng bờ AB chứa nửa đường tròn (O) P
vẽ hai nửa đường tròn tâm O , đường 1
kính AH và tâm O , đường kính BH. 2 A O O B 1 H 2
Đoạn MA và MB cắt hai nửa đường tròn
(O ) và (O ) lần lượt tại P và Q. Chứng 1 2 minh rằng: a) MH = PQ
b) ∆MPQ  ∆MBA
c) PQ là tiếp tuyến chung của hai đường
tròn (O ) và (O ). 1 2 Lời giải
a) Ta có: ◊MPHQ là hình chữ nhật ⇒ MH = PQ
b) Xét các tam giác vuông AHM và BHM ta có: . MP MA = .
MQ MB ⇒ ∆MPQ  ∆MBA(cgc) c)  PMH =  MBH ⇒  PQH = 
O QB ⇒ PQ là tiếp tuyến của O 2 2 3
Chứng minh tương tự ta có PQ là tiếp tuyến của O . 1
Dạng 2: Chứng minh hai đường thẳng vuông góc, ba điểm thẳng hàng 4 Bài 1:
Cho đường tròn (O) và hai dây MA, MB
vuông góc với nhau. Gọi I, K lần lượt là điểm M K
chính giữa của các cung nhỏ MA và MB. I
a) Chứng minh ba điểm A, O, B thẳng hàng P
b) Gọi P là giao điểm của AK và BI. Chứng A B O
minh P là tâm đường tròn nội tiếp tam giác MAB. Lời giải a) Ta có: M, ,
A B ∈(O) và  0
AMB = 90 ⇒AB là đường kính của đường tròn (O) ⇒ , A O, B thẳng hàng.
b) Ta có: AK, BI là phân giác của góc   MA ; B MBA ⇒
P là tâm đường tròn nội tiếp ∆AMB Bài 2:
Cho đường tròn (O), đường kính AB, điểm D E
thuộc đường tròn. Gọi E là điểm đối xứng với A qua D D K
a) Tam giác ABE là tam giác gì?
b) Gọi K là giao điểm của EB với (O). Chứng A B minh OD ⊥ AK. O Lời giải
a) Xét ∆ABE có BD đồng thời là đường cao, đường trung tuyến nên ∆ABE cân tại B.
b) Xét ∆ABE có OD là đường trung tuyến ⇒ OD / /BE 5
mà: AK ⊥ BE (  0
AKB = 90 ) ⇒ AK ⊥ OD Bài 3:
Cho tam giác ABC nội tiếp đường tròn (O), A
hai đường cao BD và CE cắt nhau tại H. Vẽ đường kính AF D
a) Tứ giác BFCH là hình gì? H O E
b) Gọi M là trung điểm của BC. Chứng minh
rằng ba điểm H, M, F thẳng hàng B M C c) Chứng minh 1 OM = AH. 2 F Lời giải
a) Tứ giác BFCH có các cạnh đối song song nên là hình bình hành.
b) Tứ giác BHCF là hình bình hành mà M là trung điểm của BC nên M là trung điểm của HF
⇒ H, M , F thẳng hàng.
c) Xét ∆AHF có OM là đường trung bình của 1
∆AHF ⇒ OM = AH. 2 Bài 4:
Cho đường tròn (O) đường kính AB, điểm D E
thuộc (O). Gọi E là điểm đối xứng với A qua K D D a. A
∆ BE là tam giác gì A B O
b. Gọi K là giao điểm của EB với (O), Chứng
minh rằng: OD ⊥ AK Lời giải 6 a.  0
ADB = 90 (góc nội tiếp chắn nửa đường tròn) BD ⊥ AE ⇒ 
⇒ ∆ABE cân tại B AD = DE b) OD / /EB  ⇒ OD ⊥ AK AK ⊥ EB Bài 5:
Cho nửa đường tròn (O) đường kính AB = C
2R và điểm C nằm ngoài nửa đường tròn. CA 1
cắt nửa đường tròn tại M, CB cắt nửa đường
tròn tại N. Gọi H là giao điểm của AN và BM I a. CH ⊥ AB 1 N
b. Gọi I là trung điểm của CH. Chứng minh M 1 H
rằng MI là tiếp tuyến của nửa đường tròn (O) 3 A B O Lời giải
a. Ta có H là trực tâm của tam giác ⇒ CH ⊥ AB
b. Cần chứng minh MI ⊥ MO
+) có: C,M,H,  N I; CH  ∈ 2      1  C N ( sd MH) = = 1 1 2     M =   M +)   1  1 3 
N = B = sd AM  →  →  M +  0 IMB = →  0 ( ) 90 OMI = 90 1 1 2   M +  3 0 IMB = 90   B =  1 B ( . ∆ can)  1 3  Bài 6: 7
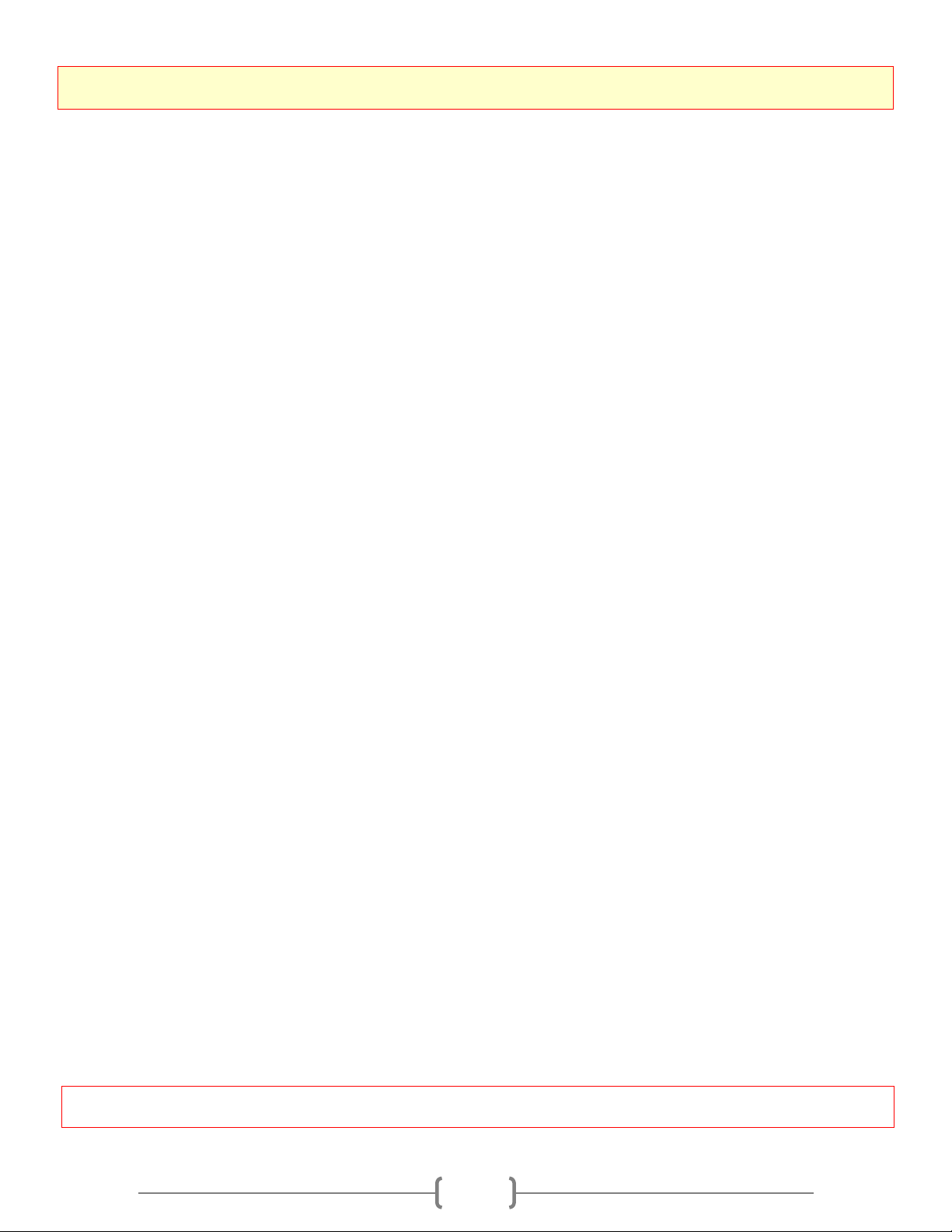
Cho nửa đường tròn (O) đường kính AB và C
điểm C di động trên nửa đường tròn đó. Vẽ
đường tròn (I) tiếp xúc với đường tròn (O) tại I M N
C và tiếp xúc với đưuòng kính AB tại D,
đường tròn này cắt CA, CB lần lượt tại các A D O B
điểm thứ hai là M và N. Chứng minh rằng: a. M, N, I thẳng hàng b. ID ⊥ MN Lời giải a.  0 ACB = ⇒  0 90 MCN = 90 Xét (I), có:  0
ACB = 90 ⇒ N,M , I thẳng hàng
b. Đường tròn (O) và (I) tiếp xúc với nhau tại C nên O, I, C thẳng hàng ∆ICN →  INC =   ICN   INC =  OBC MN / / AB   ⇒  ⇒
 ⇒ ID ⊥ MN ∆OCB →  OBC =  OCB dong.vi 
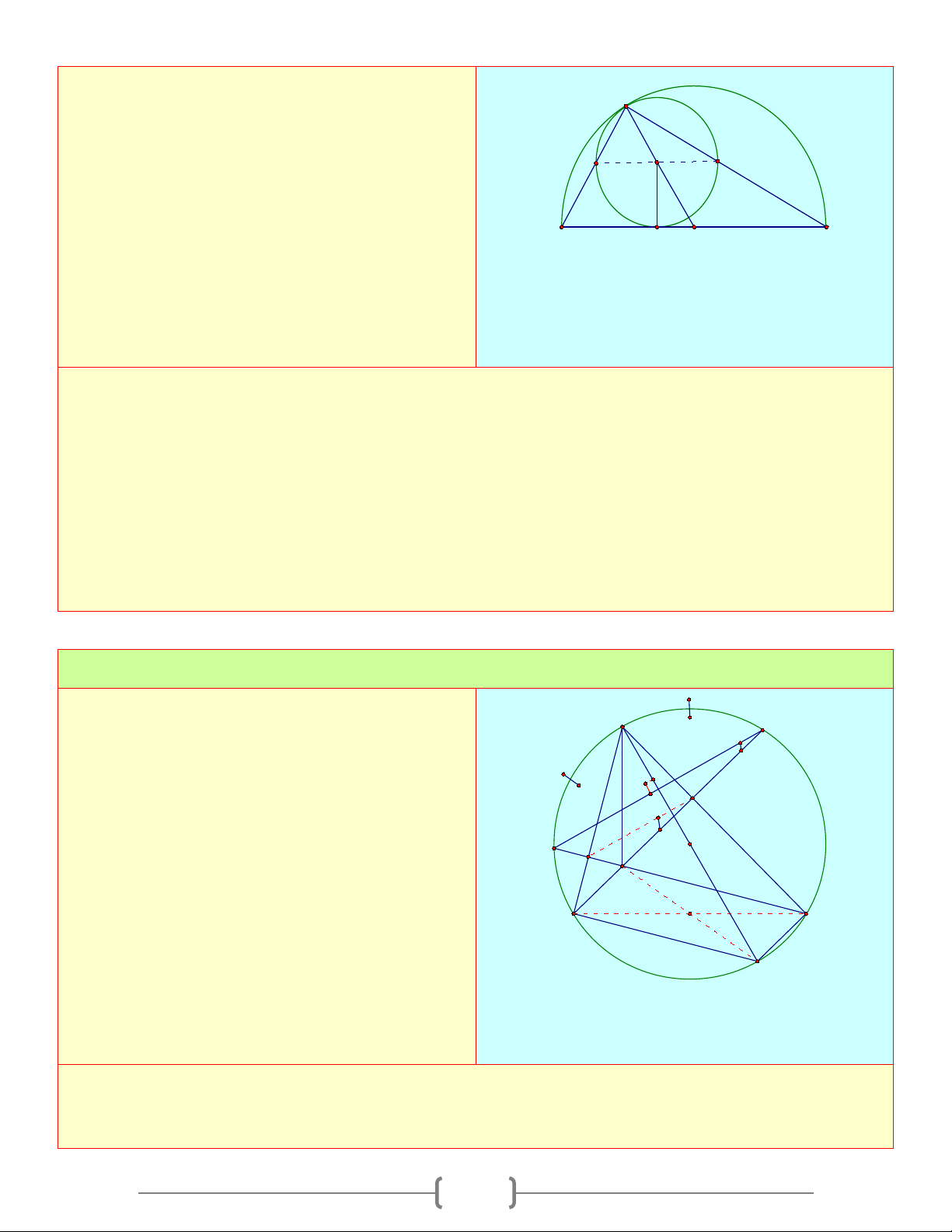
ID ⊥ AB(t. .ctie . p tuyen)    Bài 7: Cho A
∆ BC nhọn nội tiếp đường tròn (O). A E
Đường cao BM, CN cắt nhau tại H và cắt
đường tròn lần lượt tại E và F, chứng minh M rằng
a. A là điểm chính giữa cung FE O F N b. EF // MN 2 1 1 2 c. OA C ⊥ MN B I
d. AH không đổi khi A di động trên cung lớn BC
e. F đối xứng với H qua AB Lời giải a. B =  C (phụ góc  BAC ) ⇒  EA = 
FA (chắn bởi hai góc nội tiếp bằng nhau) ⇒ A là điểm chính 1 1 8 giữa 
FE ⇒ OA ⊥ FE(1) E =   C  E =  b) 2 NMB  ⇒
 ⇒ MN / /FE(2)  NMB =  C  d.vi  2   ⇒ OA ⊥ MN
d) Kẻ đường kính AD và gọi I là trung điểm của BC ⇒ IO ⊥ BC ≡ I Ta có:  CD ⊥ AC  BH / /CD  ACD = 90 ⇒  ⇒ BH AC
t.tu :CH / /  ⊥  BD
⇒ ◊BHCD là hình bình hành.
Mà I là trung điểm của BC nên I là trung điểm của HD +) Xét 1 A
∆ HD,OI = AH ⇔ AH = 2OI ( không đổi ) 2 e. Ta có:  AE =  FA ⇒  ABF = 
ABE ( chắn hai cung bằng nhau ) Xét B
∆ HF có BN là đường cao, đường phân giác nên cân tại B ⇒ BN là đường trung tuyến
⇒ N là trung điểm của FH hay F đối xứng với H qua AB. 9