Tài liệu tự học hàm số lũy thừa, hàm số mũ và hàm số logarit

Tài liệu gồm 47 trang bao gồm lý thuyết, ví dụ mẫu và bài tập tự luyện chủ đề hàm số lũy thừa, hàm số mũ và hàm số logarit, giúp học sinh học tốt chương trình Giải tích 12 chương 2.

75 38 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 6: Hàm số mũ và hàm số lôgarit (KNTT)

Môn: Toán 11

Thông tin:

28 trang 8 tháng trước

Tác giả:

Profile Kim Oanh
CHUYÊN ĐỀ:
CÁC BÀI TOÁN VỀ GIÁ TRỊ LỚN NHẤT, GIÁ TRỊ NHỎ NHẤT
LIÊN QUAN ĐẾN MŨ-LOGARIT
Tác giả: Hoàng Xuân Bính
Nhóm giáo viên Toán tiếp sức Chinh phục kì thi THPT năm 2020
Trong các đề thi thử và đề thi minh họa của BGD&ĐT, các em học sinh gặp nhiều bài toán giá trị
lớn nhất và giá trị nhỏ nhất của các biểu thức mà liên quan đến khái niệm hàm số mũ và logarit.
Bài viết này sẽ giúp các em hiểu rõ cách làm về dạng bài tập này và có hướng giải quyết khi gặp
trong các đề thi.
1. Dạng 1 : Đặt ẩn phụ để biến đổi loga
- Hướng 1 : Với các bài toán mà biểu thức có dạng
log , log
b a
f a b
thì ta có thể đặt ẩn phụ
log
t
a
t b b a
để biến đổi biểu thức đã cho về biểu thức hàm một biến theo
t
.
- Hướng 2 : Với bài toán dạng :
p
u v
a b ab
thì có thể đặt
log
a
t b
1
1 , 1u p t v p
t
từ đó biến đổi biểu thức đã cho về biểu thức hàm một biến theo
t
.
- Hướng 3 :
Với bài toán có dạng:
q
u v p
a b c abc
thì ta đặt
q
u v p
a b c abc t
log
a
u t
,
log
b
v t
,
log
c
p t
,
log
abc
q t
và rút ra được :
1 1 1 1
log
t
abc
a b c q
Các ví dụ minh họa:
Ví dụ 1: Cho
a
,
b
là các số thực dương thỏa mãn
1b
và
a b a
. Tìm giá trị nhỏ nhất của biểu
thức
log 2 log .
a
b
b
a
P a
b
A.
6
. B.
7
. C.
5
. D.
4
.
Đề khảo sát chất lượng – L2 – Chuyên Vĩnh Phúc – 2018-2019
Lời giải
Chọn C
Đặt
log
t
a
t b b a
. Khi đó:
1
1
log 4.log
t t
t
a a
P a a
4 1
1
1
t
t t
Vì
1b
và
a b a
nên
1
1
2
t
.
Khi đó:
4 1 4 1
1
1
1 1
t t
t
P
t t t t
4 1
1 2 .
1
t
t
t t
5
Vậy
min
5P
khi
2
3
t
Ví dụ 2: Xét các số thực
, , ,a b x y
thỏa mãn
1, 1a b
và
3
2 2x y x y
a b ab
. Giá trị nhỏ nhất của biểu
thức
3 4 1P x y
bằng
A.
5
3
. B.
5
3
. C.
3
4
. D.
6
5
.
Đề khảo sát chất lượng-L2-Sở giáo dục Phú Thọ-2019-2020
Lời giải
Chọn A
Giả thiế:
3
2 2x y x y
a b ab
3
3
1
2 log 1 log
3
1
2 log 1 log
3
a a
b b
x y ab b
x y ab a
Đặt
log
a
b t
thì
1 1 1
3 6
x t
t
và
1 1
12
y t
t
Suy ra:
1 1 1 1
1 1
2 3
P t t
t t
1 5 1 5 5
.2 .
6 6 3
t t
t t
.
Vậy giá trị nhỏ nhất của biểu thức
P
là
5
3
.
Ví dụ 3: Cho
, , 0;x y z
, , 1a b c
và
3
x y z
a b c abc
. Giá trị lớn nhất của biểu thức
2
1 1
P z z
x y
thuộc khoảng nào dưới đây?
A.
0;2
. B.
3;
. C.
1;3
. D.
2;4
.
Đề thi thử TN THPT Chuyên Lê Khiết-Quảng Ngãi-2019-2020
Lời giải
Chọn C
Đặt
3
x y z
a b c abc t
( Đk:
1t
). Suy ra
log , log , log
a b c
x t y t z t
và
1
log
3
abc
t
1 1 1
log log log log 3
t t t t
a b c abc
x y z
nên
1 1 1
3
x y z
.
Khi đó:
2
1
3
z
.
Xét hàm số
2
1
( ) 3f z z z
z
, với
0z
.
Ta có:
3 2
2
2 1
( )
z z
f z
z
( ) 0 1f z z
.
Bảng biến thiên
Từ bảng BBT, ta có
0;
max ( ) (1) 2f z f

.
2. Dạng 2 : Sử dụng bất đẳng thức cổ điển
- Bất đẳng thức Cauchy:
0, 0 :
2
a b
a b ab
trong đó tích
.a b
không đổi.
-Bất đẳng thức đẳng thức Cauchy Schwarz:
2
2 2 2 2 2 2
a b c x y z ax by cz
trong đó
ax by cz
có giá trị không đổi.
- Trong dạng này, từ giả thiết của bài toán ta thường thấy xuất hiện dạng biểu thức dạng hàm
đặc trưng :
+
log log log
a a a
u
v u u u v v u v
v
(hoặc
log log
a a
u u v v u v u v
)
+
u v
a u a v u v
Các ví dụ minh họa:
Ví dụ 4: Cho
2
số thực dương
,x y
thỏa mãn
1
3
log 1 1 9 1 1
y
x y x y
.
Giá trị nhỏ nhất của biểu thức
4P x y
là
A.
min
2P
. B.
min
1P
. C.
min
19P
. D.
min
7P
.
Lời giải
Chọn D
Theo giả thiết:
1
3
log 1 1 9 1 1
y
x y x y
3 3
1 log 1 log 1 1 1 9y x y x y
.
3 3
1 log 1 log 1 1 9y x y x
3 3
9
log 1 1 log 1
1
x x y
y
3 3
9 9
log 1 1 log *
1 1
x x
y y
Xét hàm số đặc trưng
3
logf t t t
với
0t
Khi đó:
1
1 0
ln 3
f t
t
với mọi
0t
Suy ra: hàm số
f t
luôn đồng biến và liên tục trên
0;
.
Từ (*) suy ra
9
1 1
1
f x f
y
9
1
1
x
y
9 8
1
1 1
y
x
y y
Vì
0x
nên
0;8y
.
Cách 1: Sử dụng bất đẳng thức Cauchy
Khi đó:
8 9 9 9
4 4 4 1 4 1 5 2 4 1 . 5 7.
1 1 1 1
y
P x y y y y y
y y y y
Vậy
min
7P
khi
9 1
4 1
1 2
y y
y
.
Cách 2: Sử dụng khảo sát hàm số
Xét hàm số
9
4 1
1
g y y
y
với
0; 8y
. Có
2
9
4 0
1
g y
y
1
2
5
2
y
y l
.
Bảng biến thiên của hàm số:
Vậy
min
7P
khi
1
2
y
.
Nhận xét:
+ Với các bài toán mà hàm số được thiết lập như trên, ta có thể sử dụng bất đẳng thức Cauchy để
xác định min của biểu thức P bằng cách biến đổi để xuất hiện tích không đổi của hai biểu thức
chứa biến đều dương là:
4 1y
và
9
1y
.
+ Đối với các em học sinh mà việc áp dụng bất đẳng thức Cauchy chưa thành thạo thì các em có
thể sử dụng phương pháp quen thuộc là khảo sát hàm số thì cũng nhanh chóng thiết lập được đáp
số của bài toán.
+ Ngoài ra, các em có thể sử dụng chức năng bảng giá trị: TABLE. Nhập hàm
9
4 1
1
g x x
x
start
0x
end
1x
step
0,1x
. Khi đó từ bảng giá trị của hàm số
thu được ta cũng có được
min
7P
.
Ví dụ 5: Cho các số thực
,a b
thỏa mãn
2 2 2
2 2 2 1
1 0
a b ab ab b
e e a ab b e
. Gọi
,m M
lần lượt
là giá trị nhỏ nhất, giá trị lớn nhất của biểu thức
1
1 2
P
ab
. Khi đó
m M
bằng
A.
19
5
. B.
2
5
. C.
7
3
. D.
10
3
.
Lời giải
Chọn D
Ta có:
2 2 2
2 2 2 1
1 0
a b ab ab b
e e a ab b e
2 2 2
2 2 2 1
1 0
a b ab b
e a ab b e
2 2 2
2 2 2 1 2
2 1 1
a b ab b
e a ab b e b
.
Xét hàm số đặc trưng:
t
f t e t
với
t
.Có
1 0,
t
f t e t
.
Do đó hàm số
f t
đồng biến trên
. Pt :
2 2 2
1 2 1f a b ab f b
.
2 2 2
2 1a b ab b
2 2
1a ab b
Khi đó:
2
1 a b ab ab
và
2
1 3 3a b ab ab
1
1
3
ab
Suy ra:
1 1 1 1
3
1 2 1 2.1 3
1
1 2.
3
P
ab
nên
1
3,
3
M m
.
Vậy
10
.
3
m M
Ví dụ 6: Cho các số thực dương
,x y
thỏa mãn
2 2
2
2 2
log 2 1
2 2
2
log 2 log 8
3
x y
xy
x y
xy x
. Tìm giá trị nhỏ
nhất của biểu thức:
2 2
2
2 2
2
x xy y
P
xy y
A.
1
2
. B.
5
2
. C.
3
2
. D.
1 5
2
.
Đề kiểm tra chuyên đề lần 4, trường THPT Liễn Sơn-VP-2019-2020
Lời giải
Chọn B
Theo bài ra, ta có:
2 2 2 2 2
2 2
log log 3 2 1 3x y xy x x y xy
2 2 2 2 2 2
2 2 2
log 2 log 3 log 2 3x y x y xy x x xy
2
2 2 2 2 2
2 2
3
log 2 log 3
2
xy x
x y x y x xy
2
2 2 2 2 2
2 2
3
log 2 log 3 1
2
xy x
x y x y x xy
Xét hàm số đặc trưng:
2
log 2f t t t
, có
1
2 0, 0
.ln 2
f t t
t
.
2
2 2
3
1
2
xy x
f x y f
2
2 2
3
2
xy x
x y
2 2
3 1
1
2 2
x x x
y y y
Đặt
x
t
y
2
3 2 0t t
1 2t
.
Ta có:
2 2
2
2 2
2
x xy y
P
xy y
2
2 2
2 1
t t
t
2
2 1
t
t
1 2 1
2 1
2 2 1 2
t
t
1 2 1 5
2 2 1 .
2 2 1 2 2
t
t
. Suy ra:
min
5
2
P
khi
3
2
t
Ví dụ 7: Cho các số thực
3, 1, 1a b c
thỏa mãn:
2 3
3
log log 2 1
2
a b c bc a
bc a
ab ac
ab ca
.
Giá trị nhỏ nhất của
T a b c
thuộc khoảng nào dưới đây?
A.
16;17
. B.
17;18
. C.
18;19
. D.
19;20
.
Thi thử liên trường Thanh Hóa 2019-2020
Lời giải
Chọn B
Theo bài ra, ta có:
( 2 ) ( 3)
( 3)
log log ( 2 ) 1
2
a b c bc a
bc a
ab ac
ab ca
( 2 ) ( 3)
log ( 3) 1 log ( 2 ) 1 1
a b c bc a
bc a ab ac
Đặt
( 2 )
log ( 3)
a b c
t bc a
thì
1
trở thành:
1
2 2t
t
Nhận xét:
0 2 0t VT l
+
0t
thì
1
2 2 . 2VT t
t
. Do đó
2 1t
.
Do đó:
2 3 1 2 3
( 2 ) ( 3) 1.
b c a
a b c bc a
bc a c b a
Áp dụng bất đẳng thức Cauchy Schwarz, ta có:
2
3 2 1 3 2 1
.1 . . .T a b c a b c
a b c a b c
2
3 2 1
.
Dấu “=” xảy ra khi
2
3 3 6
3 2
2 2 6
3 2 1
1 2 3
a b
a
c
b
a b c
c
.
Vậy
2
min 1 2 3 17,19T
.
- Nhận xét: Ta có thể giải
2
2
2 1 2 1 0t t t
1t
* Lỗi thường gặp:
3 3
3
3 2 1 6
3 .3 9 6
a b c abc
a b c abc
tuy nhiên khi áp dụng bất
đẳng thức Cauchy ở đây thì dấu bằng không thể xảy ra được.
3. Dạng 3 : Cực trị hình học
- Hướng 1 :
: 0d ax by c
và
2 2
2
0 0
:C x x y y R
. Khi đó
;d C
có điểm
chung
;d I d R
.
+ Mở rộng trong không gian :
: 0P ax by cz d
và
2 2 2
2
0 0 0
:S x x y y z z R
. Khi đó
;P S
có
điểm chung (
S
có tâm
I
bán kính
R
)
;d I P R
.
- Hướng 2 :
: 0d ax by c
và
2 2
2
0 0
:C x x y y R
sao cho
;d I d R
với
I
là tâm đường tròn
C
khi đó với
,M C N d
thì
;MN d I d R
. Dấu bằng xảy ra
khi
,
M E N A
.
- Hướng 3 :
;A a b
và
2 2
2
0 0
:C x x y y R
sao cho
IA R
với
I
là tâm đường
tròn
C
khi đó với
M C
thì
IA R AM IA R
. Dấu bẳng xảy khi
M D
hoặc
M E
.
Các ví dụ minh họa:
Ví dụ 8: Với các số thực dương
,x y
thay đổi sao cho
2
2 2
2 2
log 2 4 5
x y
x x y y
x y
. Xác
định giá trị lớn nhất của biểu thức
2 1
4
x y
P
x y
.
A.
15 473
31
. B.
15 349
31
. C.
15 39
31
. D.
15 6 14
31
.
Lời giải
Chọn D
Theo bài ra, ta có:
2
2 2
2 2
log 2 4 5
x y
x x y y
x y
2 2 2 2
2 2
log 2 2 1 2 4 4 logx y x y x y x y
2 2 2 2
2 2
log 2 2 2 2 2 2 log 1x y x y x y x y
Xét hàm số đặc trưng:
2
logf t t t
với
0t
. Có
1
1 0, 0
.ln2
f t t
t
.
Do đó hàm số
f t
là hàm số đồng biến. Nên
2 2
1 2 4 4f x y f x y
2 2
2 4 4x y x y
2 2
1 2 9 2x y
.
Ta có:
2 1
4
x y
P
x y
1 2 4 1 0 3P x P y P
Coi
2
là phương trình của đường tròn
C
với tâm
1;2 , 3I R
và
3
là phương trình đường
thẳng
d
Để tồn tại
,x y
thỏa mãn bài toán
,d C
có điểm chung
;d I d R
2 2
1 2 2 4 1
3
1 2
P P P
P P
2
2
7 6 9 2 6 5P P P
2
31 30 9 0P P
15 6 14 15 6 14
31 31
P
.
Ví dụ 9: Với các số thực dương
, ,x y z
thay đổi sao cho
2
2 2 2
2 2
log 4 8 8 2
x y z
x x y y z z
x y z
, gọi giá trị lớn nhất và giá trị nhỏ
nhất của biểu thức
2 2 2
4 7 11 8
6 5 86
x y z x y z
T
x y
thứ tự là
M
và
m
. Khi đó
M m
bằng:
A.
3
2
. B.
1
. C.
5
2
. D.
1
2
.
Đề thi thử TN trường THPT Hải Hậu A- Nạm Định – 2019-2020
Lời giải
Chọn D
+) Ta có
2
2 2 2
2 2
log 4 8 8 2
x y z
x x y y z z
x y z
2 2 2 2 2 2
2 2
log 4 2 2 log 4( 2 2 )x y z x y z x y z x y z
2 2 2 2 2 2
2 2
log 4 2 2 4( 2 2 ) logx y z x y z x y z x y z
(1).
+) Xét hàm đặc trưng
2
log , 0f t t t t
có
1
0, 0
ln 2
f t t t
t
.
+) Ta có
2 2 2 2 2 2
(1) 4 2 2 4 8 8f x y z f x y z x y z x y z
2 2 2
2 4 4 36x y z
.
Khi đó, ta được
4 8 8 4 7 11 8
3 8
6 5 86 6 5 86
x y z x y z
y z
T
x y x y
Ta có:
6 5 86 3 8 6 5 1 3 8 86T x y y z Tx T y z T
6 5 1 3 8 86 0 1Tx T y z T
.
Khi đó ta coi
1
là phương trình mặt phẳng
: 6 5 1 3 8 86 0P Tx T y z T
.
Do đó, tồn tại
, ,x y z
để phương trình mặt phẳng
P
tiếp xúc hoặc cắt mặt cầu
S
với tâm
2;4;4 , 6I R
;d I P R
2 2
2
6 .2 5 1 4 3.4 8 86
6
6 5 1 3
T T T
T T
2
1
720 360 360 0 1
2
T T T
.
Ví dụ 10: Cho các số thực
, , ,a b c d
thỏa mãn
2 2
2
log 4 6 7 1
a b
a b
và
27 81 6 8 1
c d
c d
. Tìm giá
trị nhỏ nhất của biểu thức
2 2
( ) ( )
P a c b d
.
A.
8
5
. B.
49
25
. C.
64
25
. D.
7
5
.
Đề thi KSCL Chuyên Phan Bội Châu-Nghệ An-L2-2019-2020
Lời giải
Chọn B
Ta có:
2 2
2 2
2 2
2
log 4 6 7 1 2 4 6 7 2 3 4
a b
a b a b a b a b
(C).
Khi đó:
3 4 3 4
27 81 6 8 1 3 6 8 1 3 2(3 4 ) 1 0
c d c d c d
c d c d c d
.
Đặt
3 4t c d
, ta có phương trình:
3 2 1 0
t
t
.
Xét hàm số
( ) 3 2 1
t
f t t
có
( ) 3 ln 3 2
t
f t
. Khi đó:
3 0
2
( ) 0 log
ln 3
f t t t
Bảng biến thiên:
Quan sát bbt, ta có
0f t
có nhiều nhất hai nghiệm mà
0 1 0f f
Do đó:
0
1
1
t
t
3 4 0
3 4 1
c d
c d
.
Khi đó: ta coi cặp
;a b
là tập hợp các điểm
;A a b C
có tâm
2;3 , 2I R
; và các cặp
;c d
là tập hợp các điểm
1
; : 3 4 0B c d d x y
hoặc
2
: 3 4 1 0d x y
.
+ Nếu
1
B d
thì
1
18 8
; 2
5 5
AB d I d R
.
+ Nếu
2
B d
thì
2
17 7
; 2
5 5
AB d I d R
.
So sánh hai trường hợp thì
min
7
5
AB
do đó
min
49
25
P
.
Ví dụ 11: Cho
,x y
là hai số thực không âm thoả mãn đẳng thức
2 2
2 2
7
log 6 8 5 0
6 8 2
x y
x y x y
x y
. Giá trị lớn nhất của biểu thức
2 2
T x y
là
A.
4 5
. B.
5 2 5
. C.
10
. D.
10 2 5
.
Đề KSNL Chuyên Nguyễn Thị Minh Khai-Sóc Trăng-2019-2020
Lời giải
Chọn B
Ta có
2 2
2 2
7
log 6 8 5 0
6 8 2
x y
x y x y
x y
2 2 2 2
log 7 7 log 6 8 2 6 8 2x y x y x y x y
(1).
Xét hàm số đặc trưng:
logy f t t t
với
0t
Khi đó:
1
1 0, 0
.ln10
f t t
t
y f t
đồng biến trên khoảng
0;
.
2 2 2 2
1 7 6 8 2 7 6 8 2f x y f x y x y x y
2 2
3 4 20x y
(2).
Ta coi các cặp
;x y
thỏa mãn
2
là các điểm
;A x y
thuộc hình tròn
: 3;4 , 2 5C I R
( kể cả phần nằm bên trong đường tròn đó) mà
0, 0x y
nên tập hợp các điểm
;A x y
là phần
tô màu như hình vẽ dưới.
Gt:
2 2
T x y T OA
với
0;0O
.
Nhận xét:
5 2 5OI R
.
Do đó:
5 2 5T OA OI R
.
max
5 2 5T
khi
A E
.
BÀI TẬP TỰ LUYỆN
Câu 1: Cho các số thực
,x y
thỏa mãn
0 , 1x y
và
3
log 1 1 2 0
1
x y
x y
xy
. Tìm giá
trị nhỏ nhất của
P
với
8
1 2020
9
P x y
.
A.
2021
. B.
2020
. C.
6055
3
. D.
6052
3
.
Câu 2: Cho các số thực
,x y
thỏa mãn đồng thời
0, 1x y
và
2
2 3
2 1 log log
y x
xy x y y
x
.
Tìm giá trị nhỏ nhất của biểu thức:
2
4 3
4
y x
x
P
y y
.
A.
4
. B.
5
. C.
3
D.
6
.
Câu 3: Cho các số thực
,x y
thỏa mãn đồng thời
, 1x y
và
2
5 4 log
4 2
10
5
x y x
y
.
Tìm giá trị nhỏ nhất
của biểu thức:
2 3
40
5
8
x y
P
y
.
A.
21
2
. B.
11
. C.
19
2
D.
8
.
Câu 4: Cho
a
,
b
là các số thực dương thỏa mãn
1b
và
a b a
. Tìm giá trị nhỏ nhất của biểu
thức
log 2 log .
a
b
b
a
P a
b
A.
6
. B.
7
. C.
5
. D.
4
.
Câu 5: Cho các số thực
,a b
thỏa mãn
1.a b
Biết rằng biểu thức
1
log
log
a
ab
a
P
a b
đạt giá trị
lớn nhất khi
.
k
b a
Khẳng định nào sau đây là đúng?
A.
1
0;
2
k
. B.
1
;1
2
k
. C.
3
1;
2
k
. D.
3
;2
2
k
.
Câu 6: Cho các số thực
, , ,a b x y
thỏa mãn
1, 1a b
và
4
x y
a b ab
. Giá trị nhỏ nhất của biểu thức
4 6P x y
thuộc tập nào dưới đây?
A.
9;10
. B.
6;7
. C.
7;8
. D.
8;9
.
Câu 7: Cho các số thực
, , 1a b c
và các số thực dương
, ,x y z
thỏa mãn
6
x y z
a b c abc
. Giá trị
lớn nhất của biểu thức
2
32
4 1P z
x y
thuộc tập nào dưới đây?
A.
34;36
. B.
36; 38
. C.
38; 40
. D.
40;42
.
Câu 8: Cho
, ,a b c
là các số thực dương khác
1
thỏa mãn:
2 2 2
1 1 1
3 5 15
a b c
a b c
. Giá giá trị nhỏ nhất của
biểu thức:
2
1 1 1
8 25P a b c
a b c
thuộc khoảng nào sau đây?
A.
0;20
. B.
20;0
. C.
30; 20
. D.
50; 30
.
Câu 9: Cho
x
,
y
là các số thực dương thỏa mãn
2
4
log 2 4 1
x y
x y
x y
. Giá trị nhỏ nhất của biểu
thức
4 2 2 2
3
3 4 11
4
2
x x y x x
P
y
x y
bằng bao nhiêu?
A.
23
4
. B.
3
. C.
6
. D.
13
2
.
Câu 10: Cho hai số thực dương
a
và
b
thỏa mãn
8 1
4 .2
ab a b
ab
a b
. Giá trị lớn nhất của biểu thức
2
2P ab ab
bằng
A.
3
. B.
1
. C.
5 1
2
. D.
3
17
.
Câu 11: Cho
a
,
b
là hai số thực dương thỏa mãn
5
4 2 5
log 3 4
a b
a b
a b
. Tìm giá trị nhỏ nhất
của biểu thức
2 2
3 5P a b a b
A.
15
. B.
5
. C.
5
. D.
35
.
Câu 12: Cho các số dương
,a b
thỏa mãn
2 3
3 log 2
a b
ab a b
ab
. Tìm giá trị nhỏ nhất của
biểu thức:
2 2
4 26 2020P a b ab
.
A.
1120
. B.
1885
. C.
2021
. D.
1705
.
Câu 13: Cho hai số thực dương
,x y
thỏa mãn
2 2
log log 6 6x x x y y x
. Giá trị nhỏ nhất của
biểu thức
6 8
3 2P x y
x y
.
A.
8 6 2
. B.
59
3
. C.
19
. D.
53
3
.
Câu 14: Cho số thực x, y thỏa mãn
2 2
3
log ( 3) ( 3)
2
x y
x x y y xy
x y xy
. Tìm giá trị lớn
nhất của biểu thức
2 3
6
x y
P
x y
.
A.
69 249
94
. B.
69 249
94
. C.
37 249
94
. D.
43 2 249
94
.
Câu 15: Với các số thực dương
,x y
thay đổi thỏa mãn:
2
2 2
6 2 5
log 12 4 10
1
x y
x x y y
x y
.
Giá trị nhỏ nhất của biểu thức:
3 2 6
2 1
x y
P
x y
thuộc khoảng nào sau đây?
A.
0, 5;0,7
. B.
0,7;0,9
. C.
0, 9;1,1
. D.
0, 3;0,5
.
Câu 16: Cho
,x y
là các số thực dương thỏa mãn:
2
log 2 3 1 2 1 0x y x x y y y
. Khi
biểu thức
2020 2020
log 2.logP x y
đạt giá trị lớn nhất, hãy tính giá trị
2 2
4 5x y
.
A.
2
3
. B.
3
. C.
1
. D.
8
9
.
Câu 17: Cho
,x y
là các số thực dương và
1y
thỏa mãn:
2
5
1 3 5 .ln 1 ln ln
3
x
x y y x y
xy
. Tìm giá trị nhỏ nhất của biểu thức:
32
1 2
25
P x y y
.
A.
103
25
. B.
217
25
. C.
23
25
. D.
48
25
.
Câu 18: Cho
,x y
là hai số thực không âm thoả mãn đẳng thức
2 2
2 2
2
15
log 4 6 8
2 3 3
x y
x x y y
x y
. Giá trị nhỏ nhất của biểu thức
2 2
2 4 5P x y x y
là
A.
26 8 34
. B.
28 4 34
. C.
26 4 34
. D.
28 8 34
.
Hướng dẫn giải bài tập tự luyện
Câu 1: Cho các số thực
,x y
thỏa mãn
0 , 1x y
và
3
log 1 1 2 0
1
x y
x y
xy
. Tìm giá
trị nhỏ nhất của
P
với
8
1 2020
9
P x y
.
A.
2021
. B.
2020
. C.
6055
3
. D.
6052
3
.
Lời giải
Chọn C
Điều kiện:
0 , 1x y
Khi đó
3
log 1 1 2 0
1
x y
x y
xy
3 3
log log 1 1 0x y xy x y xy
3 3
log log 1 1 1x y x y xy xy
Xét hàm số đặc trưng
3
( ) logf t t t
với
0t
Khi đó:
1
'( ) 1 0, 0
ln 3
f t t
t
nên hàm số
( )f t
đồng biến trên khoảng
0;
. Suy ra
1 1 1f x y f xy x y xy
1
1
x
y
x
Suy ra
8
1 2020
9
P x y
8 1
1 2020
9 1
x
x
x
8 2
1 1 2020
9 1
x
x
8 2
2 1 . 2021
9 1
x
x
4
2. 2021
3
6055
3
.
Đẳng thức xảy ra khi
1
2
x
,
1
3
y
(thỏa các điều kiện của đề bài).
Vậy
6055
3
Min
P
.
Câu 2: Cho các số thực
,x y
thỏa mãn đồng thời
0, 1x y
và
2
2 3
2 1 log log
y x
xy x y y
x
.
Tìm giá trị nhỏ nhất của biểu thức:
2
4 3
4
y x
x
P
y y
.
A.
4
. B.
5
. C.
3
D.
6
.
Lời giải
Chọn B
Điều kiện:
0, 1
0, 1
2 3
2 3 0
0
x y
x y
y x
y x
x
.
Ta có :
2
2 3
2 1 log log
y x
xy x y y
x
2
2 3 log 2 log log 2 3 logxy x y y y y x x
2 2
2 3 log log 2 3 logxy x y y y x xy
1
+ Nếu
2
2 3xy y x
thì
1 0
1 0
VT
VP
(do
log 0y
).
+ Nếu
2
2 3xy y x
thì
1 0
1 0
VT
VP
(do
log 0y
).
Do đó, từ
1
suy ra:
2
2 3xy y x
2
1 2 3x y y
.
Ta có:
3
4
x
P xy y
y
2
1
3 3 3
2
4 4
x y
y y
y y
3 3 3 3
2 2 . 2 5
4 4
y y
y y
Vậy
min
5P
khi
7
2
5
y x
.
Câu 3: Cho các số thực
,x y
thỏa mãn đồng thời
, 1x y
và
2
5 4 log
4 2
10
5
x y x
y
.
Tìm giá trị nhỏ nhất
của biểu thức:
2 3
40
5
8
x y
P
y
.
A.
21
2
. B.
11
. C.
19
2
D.
8
.
Lời giải
Chọn A
Gt :
2
5 4 log
4 2
10
5
x y x
y
2
4 2
5 4 log log
5
y
x y x
2
5 4 2 log 2 log log 4 2 log 5 0x y x x y
2 2
5 4 2 log log 5 log 4 2 0 1x y x x y
Vì
1 log 0x x
.
+ Nếu
2
5 4 2 0x y
2
5 4 2x y
1 0VT
(loại).
+ Nếu
2
5 4 2 0x y
2
5 4 2x y
1 0VT
(loại).
+ Nếu
2
5 4 2 0 1 0 /x y VT t m
Vậy
2
1 5 4 2x y
.
Khi đó:
2 3
40
5
8
x y
P
y
3
8 4 2
5
8
y y
y
2
2
9
8
y
y
2
1 1
9
8
y
y y
2
3
1 1 21
3 . . 9
8 2
y
y y
. Dấu bằng xảy ra khi
2, 2x y
.
Câu 4: Cho
a
,
b
là các số thực dương thỏa mãn
1b
và
a b a
. Tìm giá trị nhỏ nhất của biểu
thức
log 2 log .
a
b
b
a
P a
b
A.
6
. B.
7
. C.
5
. D.
4
.
Đề khảo sát chất lượng – L2 – Chuyên Vĩnh Phúc – 2018-2019
Lời giải
Chọn C
Đặt
log
t
a
t b b a
. Khi đó:
1
1
log 4.log
t t
t
a a
P a a
4 1
1
1
t
t t
Vì
1b
và
a b a
nên
1
1
2
t
.
Khi đó:
4 1 4 1
1
1
1 1
t t
t
P
t t t t
4 1
1 2 .
1
t
t
t t
5
Vậy
min
5P
khi
2
3
t
Câu 5: Cho các số thực
,a b
thỏa mãn
1.a b
Biết rằng biểu thức
1
log
log
a
ab
a
P
a b
đạt giá trị
lớn nhất khi
.
k
b a
Khẳng định nào sau đây là đúng?
A.
1
0;
2
k
. B.
1
;1
2
k
. C.
3
1;
2
k
. D.
3
;2
2
k
.
Lời giải
Chọn B
Đặt
log
a
t b
t
b a
(đk:
0 1t
).
Khi đó:
1
log
log
a
ab
a
P
a b
log 1 log
a a
ab b
1 1t t
Xét hàm số:
1 1f t t t
với
0 1t
,
Có
1 3
1 0
4
2 1
f t t
t
Bảng biến thiên:
Vậy
max
9
4
P
khi
3
4
3
4
t b a
do đó:
3
4
k
Câu 6: Cho các số thực
, , ,a b x y
thỏa mãn
1, 1a b
và
4
x y
a b ab
. Giá trị nhỏ nhất của biểu thức
4 6P x y
thuộc tập nào dưới đây?
A.
9;10
. B.
6;7
. C.
7;8
. D.
8;9
.
Lời giải
Chọn D
Giả thiết:
4
x y
a b ab
4
4
log
log
a
b
x ab
y ab
1
1 log
4
1
1 log
4
a
b
x b
y a
Đặt
log
a
t b
(đk:
0t
) thì
1
1
4
x t
và
1 1
1
4
y
t
.
Ta có:
1 1
1 1 6
4
P t
t
29 1 1 29 1 1 33
2 .
4 4 4 4 4
t t
t t
.
Dấu bằng xảy ra khi
3 3
2 ,
4 8
t x y
.
Câu 7: Cho các số thực
, , 1a b c
và các số thực dương
, ,x y z
thỏa mãn
6
x y z
a b c abc
. Giá trị
lớn nhất của biểu thức
2
32
4 1P z
x y
thuộc tập nào dưới đây?
A.
34;36
. B.
36; 38
. C.
38; 40
. D.
40;42
.
Lời giải
Chọn B
Đặt:
6
x y z
a b c abc t
(đk:
1t
).
Ta có:
1
log , log , log ,log
6
a b c abc
x t y t z t t
Suy ra:
1 1 1
log log log log 6
t t t t
a b c abc
x y z
Nhận xét: với
, 0x y
, ta có:
2
4x y xy
1 1 4
x y x y
. Dấu bằng xảy ra khi:
x y
Do đo:
2
32
4 1P z
x y
2
1 1
8. 4 1z
x y
2
1
8 6 4 1z
z
2
1 1
49 4 z
z z
Mà
2 2
3
1 1 1 1
3. . . 3z z
z z z z
nên
49 4.3 37P
.
Dấu bằng xảy ra khi
1z
,
2
5
x y
.
Câu 8: Cho
, ,a b c
là các số thực dương khác
1
thỏa mãn:
2 2 2
1 1 1
3 5 15
a b c
a b c
. Giá giá trị nhỏ nhất của
biểu thức:
2
1 1 1
8 25P a b c
a b c
thuộc khoảng nào sau đây?
A.
0;20
. B.
20;0
. C.
30; 20
. D.
50; 30
.
Lời giải
Chọn D
Đặt
2 2 2
1 1 1
3 5 15
a b c
a b c
t
. Khi đó:
0t
.
+ Nếu
1 0t a b c l
.
+ Nếu
1t
, ta có:
Khi đó:
3
2
log
1
a
t
a
,
5
2
log
1
b
t
b
,
15
2
log
1
c
t
c
.
Suy ra:
2 2 2
1 1 1
log 3 log 5 log 15 0
t t t
a b c
a b c
1 1 1
a b c
a b c
.
Khi đó:
2
1 1 1
8 25P a b c
a b c
2
8 25a b c a b c
2
4 41 41a b c
.
Suy ra:
41P
. Dấu bằng xảy ra khi:
1 1 1
4a b c
a b c
. Ta có thể chọn
3
2
a
thì
5
2
3
.
4
b c
b c
5 13 5 13
,
4 4
b c
Vậy
P
đạt giá trị nhỏ nhất là
41
.
Câu 9: Cho
x
,
y
là các số thực dương thỏa mãn
2
4
log 2 4 1
x y
x y
x y
. Giá trị nhỏ nhất của biểu
thức
4 2 2 2
3
3 4 11
4
2
x x y x x
P
y
x y
bằng bao nhiêu?
A.
23
4
. B.
3
. C.
6
. D.
13
2
.
Lời giải
Chọn A
Điều kiện:
, 0x y
.
Theo giả thiết:
2
4
log 2 4 1
x y
x y
x y
2
4
log 1 2 4
x y
x y
x y
2
4
log 2 4
2 2
x y
x y
x y
2
4
log 2 2 2 2 4
2 2
x y
x y x y
x y
2 2
log 4 2 4 log 2 2 2 2 2 1x y x y x y x y
Xét hàm số đặc trưng
2
log 2f t t t
với
0;t
Ta có:
1
2 0
ln 2
f t
t
với
0;t
nên hàm số
f t
đồng biến trên
0;t
Nên
1 4 2 2 4 2 2 2f x y f x y x y x y x y
.
4 2 2 2
3
3 4 11
4
2
x x y x x
P
y
x y
4 4 2
3
16 12 16 11.2
4
64
y y y y
y
y
1 11
16 4 2
y
y
1 11 23
2 .
16 4 2 4
y
y
.
Vậy
min
23
4
P
khi
2y
.
Nhận xét:
- Đối với bài toán số này, sau khi chúng ta thực hiện việc biểu diễn được
2x y
chỉ cần rút gọn
biểu thức
P
thì việc xác định giá trị
min
P
tương đối đã rõ ràng đối với các em học sinh.
Câu 10: Cho hai số thực dương
a
và
b
thỏa mãn
8 1
4 .2
ab a b
ab
a b
. Giá trị lớn nhất của biểu thức
2
2P ab ab
bằng
A.
3
. B.
1
. C.
5 1
2
. D.
3
17
.
Đề thi thử chuyên Hùng Vương – Gia Lai – lần 1 năm học 2018-2019
Lời giải
Chọn B
Đk:
0, 0,1a b ab
.
Theo giả thiết:
8 1
4 .2
ab a b
ab
a b
2
8 1
.2
2
a b
ab
ab
a b
2 2
.2 2 2 .2 1
a b ab
a b ab
Xét hàm số đặc trưng:
.2
t
f t t
với
0;t
.
Khi đó:
2 .2 .ln 2 0,
t t
f t t t D
nên hàm số
f t
là hàm số đồng biến trên
0;
.
1 2 2 2 2f a b f ab a b ab
1 2 2a b b
.
Vì
, 0 2 0 2a b b b
.
Khi đó:
2
2 1 2 2P ab ab ba b b b
2
1 1 1b
.
Vậy
max
1P
khi
1
, 1
3
a b
.
Câu 11: Cho
a
,
b
là hai số thực dương thỏa mãn
5
4 2 5
log 3 4
a b
a b
a b
. Tìm giá trị nhỏ nhất
của biểu thức
2 2
3 5P a b a b
A.
15
. B.
5
. C.
5
. D.
35
.
Lời giải
Chọn B
Theo bài ra, ta có:
5
4 2 5
log 3 4
a b
a b
a b
5 5
log 4 2 5 log 5 5 4 2 5a b a b a b a b
5 5
log 4 2 5 4 2 5 log 5 5 1a b a b a b a b
Xét hàm số đặc trưng:
5
log 0f t t t t
. Khi đó:
'
1
1 0
ln 5
f t
t
Do đó hàm số
f t
đồng biến nên
1 4 2 5 5f a b f a b
4 2 5 5a b a b
5 3a b
.
2
2 2 2
3 5 5 3 3 5 3 5P a b a b b b b b
2
10 20 5b b
2
10 1 5 5b
.
Vậy GTNN
5P
. Dấu bằng xảy ra khi
2, 1a b
.
Câu 12: Cho các số dương
,a b
thỏa mãn
2 3
3 log 2
a b
ab a b
ab
. Tìm giá trị nhỏ nhất của
biểu thức:
2 2
4 26 2020P a b ab
.
A.
1120
. B.
1885
. C.
2021
. D.
1705
.
Lời giải
Chọn D
Ta có
2 3
3 log 2
a b
ab a b
ab
1 2 3
3 log 2
2
a b
ab a b
ab
2 3
6 log 2 2 4
a b
ab a b
ab
2 3
log 2 2 4 6
a b
ab a b
ab
2 3
log 2 2 2 3
a b
ab a b
ab
log 2 3 2 2 3 log 2 *a b a b ab ab
Xét hàm số đặc trưng
log 2y f t t t
với
0t
. Ta có
1
2 0, 0
ln10
f t t
t
.
Suy ra hàm số
y f t
đồng biến trên khoảng
0;
Do đó
* 2 3 2 3 1f a b f ab a b ab
.
Khi đó, ta có:
2 2
4 26 2020P a b ab
2
2 30 2020a b ab
2
2 30 2 3 2020a b a b
2
2 15 1705a b
.
Vậy
min
1705P
khi
2 15
. 18
a b
a b
nên
3, 6a b
.
Câu 13: Cho hai số thực dương
,x y
thỏa mãn
2 2
log log 6 6x x x y y x
. Giá trị nhỏ nhất của
biểu thức
6 8
3 2P x y
x y
.
A.
8 6 2
. B.
59
3
. C.
19
. D.
53
3
.
Đề kiểm tra học kì I, THPT Minh Khai – Hà Nội, năm học 2019-2020
Lời giải
Chọn C
Điều kiện:
0
0 6
x
y
.
Giả thiết, ta có:
2
2 2 2 2
log log 6 6 log log 6 6x x x y y x x x y x y
2
2 2
2 log log 6 6x x x y x y
2 2
2 2
log log 6 6 1x x x y x y
Xét hàm số
2
logf t t t
với
0t
, ta có:
1
1 0, 0
.ln 2
f t t
t
.
Suy ra hàm số
y f t
đồng biến trên khoảng
0;
.
Do đó:
2 2
1 6 6f x f x y x x y
6x y
.
Với
6x y
thay vào
P
ta được:
6 8 6 8 8 6 3
3 6 2 18 6 9
6 6 2 6 2
y
P y y y y
y y y y y y
.
8 6 3
2 . 2 . 6 9
2 6 2
y
y
y y
19P
.
Dấu bằng xảy ra
8
2
6 3
6
6 2
y
y
y
y
2
2
16
6 4
y
y
4
6 2
y
y
4y
2x
.
Vậy giá trị nhỏ nhất của biểu thức
P
là
19
khi
2
4
x
y
.
Câu 14: Cho số thực x, y thỏa mãn
2 2
3
log ( 3) ( 3)
2
x y
x x y y xy
x y xy
. Tìm giá trị lớn
nhất của biểu thức
2 3
6
x y
P
x y
.
A.
69 249
94
. B.
69 249
94
. C.
37 249
94
. D.
43 2 249
94
.
Đề thi thử TN THPT Lê Hoàn-Thanh Hóa-2019-2020
Lời giải
Chọn B
Đk:
0x y
.
Giả thiết:
2 2
3
log ( 3) ( 3)
2
x y
x x y y xy
x y xy
2 2 2 2
3 3
2 log ( ) 2 log ( 2) 3 3x y x y xy x x y y xy
2 2 2 2
3 3
2 log ( ) 2 (3 3 ) 2 log ( 2) 2x y x y x y xy x y xy
2 2 2 2
3 3
2 log (3 3 ) (3 3 ) 2 log ( 2) ( 2) 1x y x y x y xy x y xy
Xét hàm số đặc trưng:
3
( ) 2 log ( 0)f t t t t
ta có:
2
'( ) 1 0 0
.ln 3
f t t
t
Suy ra: hàm số
f t
đồng biến trên
0;
.
2 2
1 (3 3 ) ( 2)f x y f x y xy
2 2
3 3 2x y x y xy
2 2
2
2
2 2
2
9 3 3 1
3 0
4 2 4 4 2 4
3 3 3 1 3 3 3
1
2 2 4 2 4 2 2 2 2
x x x x
y xy y
x x x x x
y y
Đặt:
3
,
2 2
x x
a y b
thì
2
2
3 3
1 2
2 2
a b
Khi đó:
2 3
6
x y
P
x y
2 3
2
6
2 2
x
y
x x
y
2 3
6
3
a
b
a
2 6 3 0 3
3
Pb
a P P
Ta coi
2
là phương trình đường tròn
C
với
3 3
; , 1
2 2
I R
và
3
là đường thẳng
: 2 6 3 0
3
P
d P x y P
.
Để tồn tại
,a b
khi
,d C
có điểm chung
;d I d R
2
2
3
2 6 3
2 2
1
1
2
3
P
P P
P P
2
188
92 32 0
3
P P
69 249 69 249
94 94
P
. Vậy
max
69 249
94
P
.
Câu 15: Với các số thực dương
,x y
thay đổi thỏa mãn:
2
2 2
6 2 5
log 12 4 10
1
x y
x x y y
x y
.
Giá trị nhỏ nhất của biểu thức:
3 2 6
2 1
x y
P
x y
thuộc khoảng nào sau đây?
A.
0, 5;0,7
. B.
0,7;0,9
. C.
0, 9;1,1
. D.
0, 3;0,5
.
Lời giải
Chọn D
Theo bài ra, ta có:
2
2 2
6 2 5
log 12 4 10
1
x y
x x y y
x y
2 2 2 2
2 2
log 6 2 5 12 4 10 log 1x y x y x y x y
2 2 2 2
2 2
log 2 6 2 5 2 6 2 5 log 1 1 1x y x y x y x y
Xét hàm số đặc trưng cho phương trình:
2
logf t t t
với
0t
.
Ta có:
1
1 0, 0
.ln2
f t t
t
nên hàm số
f t
đồng biến trên khoảng
0;
.
Do đó:
2 2
1 2 6 2 5 1f x y f x y
2 2
2 6 2 5 1x y x y
2 2
6 2 49 2x y
.
Khi đó:
6
2 8
x y
P
x y
2 1 1 8 6 0 3P x P y P
.
Khi đó, ta coi
2
là phương trình của đường tròn
: 6;2 , 7C I R
và
3
là phương trình của
đường thẳng
d
Để tồn tại
,x y
thỏa mãn bài toán
,d C
có điểm chung
;d I d R
2 2
22 14
7
2 1 1
P
P P
2 2 2
22 14 49 2 1 1P P P
2
239 322 98 0P P
161 7 51 161 7 51
239 239
P
Vậy
min
161 7 51
0, 46
239
P
Câu 16: Cho
,x y
là các số thực dương thỏa mãn:
2
log 2 3 1 2 1 0x y x x y y y
. Khi
biểu thức
2020 2020
log 2.logP x y
đạt giá trị lớn nhất, hãy tính giá trị
2 2
4 5x y
.
A.
2
3
. B.
3
. C.
1
. D.
8
9
.
Đề thi thử TN THPT Chuyên Hà Tĩnh-2019-2020
Lời giải
Chọn C
Với
, 0x y
. Ta có:
2
log 2 3 1 2 1 0x y x x y y y
2
log 2 2 1 0 1x y x y x y
+ Nếu
2 1x y
thì
1 0VT
( loại)
+ Nếu
2 1x y
thì
1 0VT
( loại).
+ Nếu
2 1x y
thì
1 0VT
(t/m). Suy ra
1 2 1 1 2x y x y
(đk:
1
0
2
y
).
Khi đó:
2020 2020
log 2.logP x y
2
2020
log .x y
. Mà:
2 2
. 1 2 1 2 . .x y y y y y y
.
Áp dụng bđt Cauchy cho ba số dương, ta có:
3
1 2
. . 1 2
3
y y y
y y y
1
. . 1 2
27
y y y
2020
1
log
27
P
.
Vậy
max 2020
1
log
27
P
khi
2 2
1 1
, 4 5 1
3 3
y x x y
.
Câu 17: Cho
,x y
là các số thực dương và
1y
thỏa mãn:
2
5
1 3 5 .ln 1 ln ln
3
x
x y y x y
xy
. Tìm giá trị nhỏ nhất của biểu thức:
32
1 2
25
P x y y
.
A.
103
25
. B.
217
25
. C.
23
25
. D.
48
25
.
Lời giải
Chọn A
Theo bài ta, ta có:
2
5
1 3 5 .ln 1 ln ln
3
x
x y y x y
xy
2 2
3 5 .ln 1 ln 5 ln 3 1xy y x x x xy y
Nhận xét:
0 ln 1 0x x
.
+ Nếu:
2
3 5xy y x
thì
1 0, 1 0VT VP
( loại).
+ Nếu:
2
3 5xy y x
thì
1 0, 1 0VT VP
( loại).
+ Nếu
2
3 5xy y x
thì
1 1 0VT VP
( thỏa mãn).
Do đó:
2
1 3 5xy y x
2
1 1 5 3x y y
2
5 3
1
y
x
y
(đk:
5
1
3
y
).
Khi đó:
32
1 2
25
P x y y
5 3 32
2
1 25
y
y
y
8 32 57
1
1 25 25
y
y
8 32 57
2 . 1
1 25 25
y
y
103
25
.
Vậy
min
103
25
P
khi
8 32 3
1
1 25 2
y y
y
.
Câu 18: Cho
,x y
là hai số thực không âm thoả mãn đẳng thức
2 2
2 2
2
15
log 4 6 8
2 3 3
x y
x x y y
x y
. Giá trị nhỏ nhất của biểu thức
2 2
2 4 5P x y x y
là?
A.
26 8 34
. B.
28 4 34
. C.
26 4 34
. D.
28 8 34
.
Lời giải
Chọn B
Ta có
2 2
2 2
2
15
log 4 6 8
2 3 3
x y
x x y y
x y
2 2 2 2
2 2
log 15 15 log 2 3 3 4 6 7x y x y x y x y
2 2 2 2
log 15 15 log 4 6 6 4 6 6x y x y x y x y
(1).
Xét hàm số đặc trưng:
2
logy f t t t
với
0t
Khi đó:
1
1 0, 0
.ln 2
f t t
t
y f t
đồng biến trên
khoảng
0;
.
2 2
1 15 4 6 6f x y f x y
2 2
15 4 6 6x y x y
2 2
2 3 4x y
(2).
Ta coi các cặp
;x y
thỏa mãn
2
là các điểm
;M x y
thuộc hình
tròn
: 2;3 , 2C I R
( kể cả phần nằm bên trong đường tròn đó)
Gt:
2 2
2 4 5P x y x y
2 2
1 2 10x y
2
10AM
với
1; 2A
và
34 2
IA R
Khi đó: nên điểm
A
nằm ngoài đường tròn
C
34 2AM IA R
2
34 2 10 28 4 34P
min
28 4 34P
khi
M D
.
| 1/28
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

CHUYÊN ĐỀ:
CÁC BÀI TOÁN VỀ GIÁ TRỊ LỚN NHẤT, GIÁ TRỊ NHỎ NHẤT
LIÊN QUAN ĐẾN MŨ-LOGARIT
Tác giả: Hoàng Xuân Bính
Nhóm giáo viên Toán tiếp sức Chinh phục kì thi THPT năm 2020
Trong các đề thi thử và đề thi minh họa của BGD&ĐT, các em học sinh gặp nhiều bài toán giá trị
lớn nhất và giá trị nhỏ nhất của các biểu thức mà liên quan đến khái niệm hàm số mũ và logarit.
Bài viết này sẽ giúp các em hiểu rõ cách làm về dạng bài tập này và có hướng giải quyết khi gặp trong các đề thi.
1. Dạng 1 : Đặt ẩn phụ để biến đổi loga
- Hướng 1 : Với các bài toán mà biểu thức có dạng f log ,alog b thì ta có thể đặt ẩn phụ b a  t  log t
b  b  a để biến đổi biểu thức đã cho về biểu thức hàm một biến theo t . a
- Hướng 2 : Với bài toán dạng :    p u v a b
ab thì có thể đặt t  log b a    u  p t 1 1 ,v  p 1      
từ đó biến đổi biểu thức đã cho về biểu thức hàm một biến theo t .  t  - Hướng 3 : Với bài toán có dạng:     q u v p a b c
abc thì ta đặt     q u v p a b c abc  t  u  log t a 1 1 1 1
, v  log t , p  log t ,q  log t và rút ra được :    log abc  b c abc t a b c q Các ví dụ minh họa:
Ví dụ 1: Cho a , b là các số thực dương thỏa mãn b  1 và a  b  a . Tìm giá trị nhỏ nhất của biểu a
thức P  log a  2 log    . a b b  b A. 6. B. 7 . C. 5. D. 4 .
Đề khảo sát chất lượng – L2 – Chuyên Vĩnh Phúc – 2018-2019 Lời giải Chọn C 1 41t Đặt t  log t b  b  a . Khi đó: 1 P log t       a a t 4.log a 1 t a a 1t t 1
Vì b  1 và a  b  a nên  t  1. 2 1 41t t 41t t 41t Khi đó: P    1    1  2 .  5 1 t t 1 t t 1t t 2 Vậy P  5 khi t  min 3
Ví dụ 2: Xét các số thực a, ,
b x,y thỏa mãn a  1,b  1 và x 2y x2y 3 a  b
 ab . Giá trị nhỏ nhất của biểu
thức P  3x  4y 1 bằng 5 5 3 6 A. . B. . C. . D. . 3 3 4 5
Đề khảo sát chất lượng-L2-Sở giáo dục Phú Thọ-2019-2020 Lời giải Chọn A  3 1 x  2y  log ab   b a  1 loga  Giả thiế: x 2  y x2y 3 a  b  ab   3  3 1 x   2y  log ab   a b 1 logb   3 1 1  1 1 1 
Đặt log b  t thì x   t      và y    t a 3 6  t  12 t  1  1   1 1  1  5   1 5 5 Suy ra: P  1  t       
 t1  t    .2 t.  . 2  t  3 t  6  t  6 t 3 5
Vậy giá trị nhỏ nhất của biểu thức P là . 3
Ví dụ 3: Cho x,y,z  0; a, , b c  1 và x y z 3
a  b  c  abc . Giá trị lớn nhất của biểu thức 1 1 2
P    z  z thuộc khoảng nào dưới đây? x y A. 0;2. B. 3;. C. 1;3. D. 2;4.
Đề thi thử TN THPT Chuyên Lê Khiết-Quảng Ngãi-2019-2020 Lời giải Chọn C Đặt x y z 3
a  b  c  abc  t ( Đk:t  1). Suy ra x  log t,y  log t,z  log t và a b c 1 log t  abc 3 1 1 1
    log a  log b  log c  log abc  3 1 1 1 nên   3  . t t t t x y z x y z 1 Khi đó: 2 P  3   z  z . z 1 Xét hàm số 2
f(z)  3   z  z , với z  0 . z 3 2 2    1 Ta có: ( ) z z f z  2 z
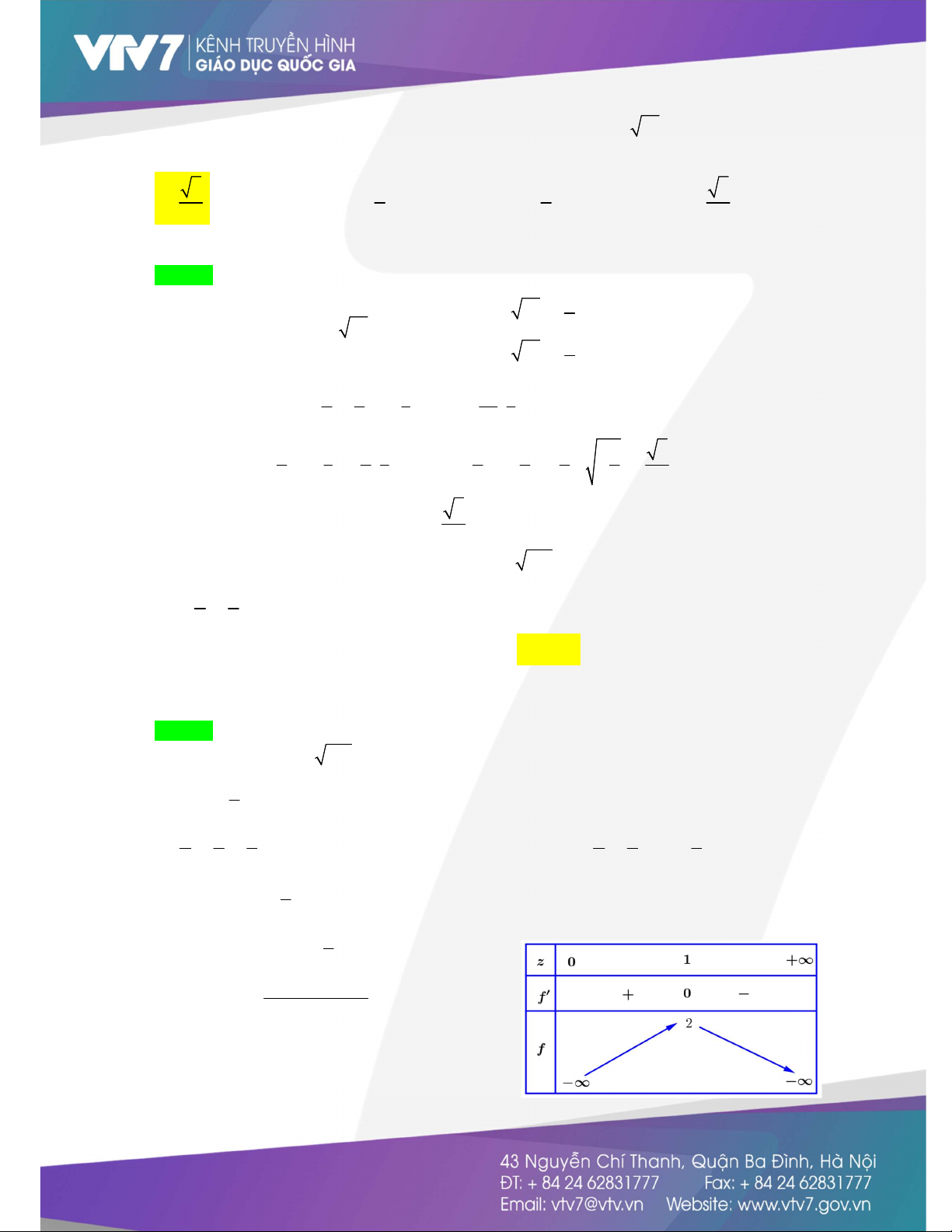
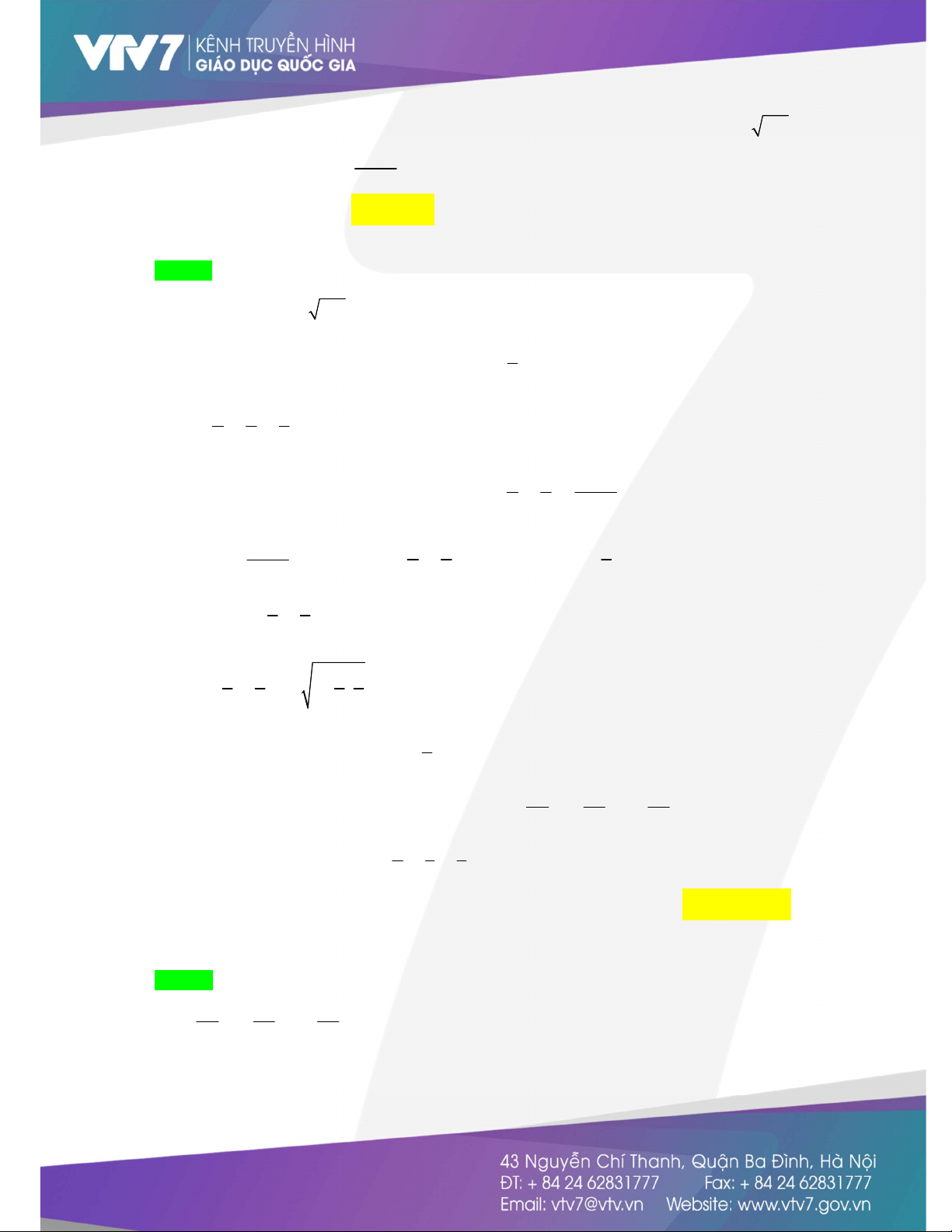
 f (z)  0  z  1. Bảng biến thiên
Từ bảng BBT, ta có max f (z)  f(1)  2 . 0;  
2. Dạng 2 : Sử dụng bất đẳng thức cổ điển a b
- Bất đẳng thức Cauchy: a  0,b  0 :  ab a b 2
trong đó tích . không đổi.
-Bất đẳng thức đẳng thức Cauchy Schwarz:            2 2 2 2 2 2 2 a b c x y z ax by cz
trong đó ax by cz có giá trị không đổi.
- Trong dạng này, từ giả thiết của bài toán ta thường thấy xuất hiện dạng biểu thức dạng hàm đặc trưng : u + log  
   v u  u  log u  v  log v  u  v a   a a v 
(hoặc log u  u  v  log v  u  v u  v ) a a   + u v
a  u  a  v  u  v Các ví dụ minh họa: y 1 
Ví dụ 4: Cho 2 số thực dương x,y thỏa mãn log  x 1 y 1     9  x 1 y  1 . 3       
Giá trị nhỏ nhất của biểu thức P  x  4y là A. P  2 . B. P  1. C. P  19. D. P  7 . min min min min Lời giải Chọn D y 1 
Theo giả thiết: log  x 1 y 1     9  x 1 y  1 3       
y 1log x 1 log y 1        x 1 y  1  9  . 3    3     
y 1log x 1 log y 1 x 1         9  3    3    9  log x  1  x 1   log y  1 3   3   y  1 9 9
 log x  1  x  1   log * 3   3   y  1 y  1
Xét hàm số đặc trưng f t  log t  t với t  0 3 Khi đó: f t 1 
 1  0 với mọi t  0 t ln 3
Suy ra: hàm số f t luôn đồng biến và liên tục trên 0;.   9 9 8 y
Từ (*) suy ra    f x   9 1 1  f       x  1   x  1  y  1 y  1 y  1 y  1
Vì x  0 nên y  0;8.
Cách 1: Sử dụng bất đẳng thức Cauchy Khi đó: 8 y 9 P  x  y   y  y    y   9    y   9 4 4 4 1 4 1 5 2 4 1 .  5  7. y 1 y 1 y  1 y 1 Vậy P  7 khi y   9 1 4 1   y  . min y  1 2
Cách 2: Sử dụng khảo sát hàm số  1 9 y  Xét hàm số g y 9  4y 1 
với y  0;8. Có gy  4   0   2 . y  1   y  2 1  5 y   l  2
Bảng biến thiên của hàm số: 1 Vậy P  7 khi y  . min 2 Nhận xét:
+ Với các bài toán mà hàm số được thiết lập như trên, ta có thể sử dụng bất đẳng thức Cauchy để
xác định min của biểu thức P bằng cách biến đổi để xuất hiện tích không đổi của hai biểu thức 9
chứa biến đều dương là: 4y   1 và . y  1
+ Đối với các em học sinh mà việc áp dụng bất đẳng thức Cauchy chưa thành thạo thì các em có
thể sử dụng phương pháp quen thuộc là khảo sát hàm số thì cũng nhanh chóng thiết lập được đáp số của bài toán.
+ Ngoài ra, các em có thể sử dụng chức năng bảng giá trị: TABLE. Nhập hàm g x 9  4x 1 
start x  0 end x  1 step x  0,1. Khi đó từ bảng giá trị của hàm số x  1
thu được ta cũng có được P  7 . min
Ví dụ 5: Cho các số thực , a b thỏa mãn 2 2 a  b ab   2 2 2 2 1 1 a  b b e e a ab b e        0. Gọi , m M lần lượt 1
là giá trị nhỏ nhất, giá trị lớn nhất của biểu thức P  . Khi đó m  M bằng 1  2ab 19 2 7 10 A. . B. . C. . D. . 5 5 3 3 Lời giải Chọn D Ta có: 2 2 a  b ab   2 2 2 2 1 1 a  b b e e a ab b e        0 2 2 2 a 2b a  b 2 2 1 1 b e a ab b e         0 2 2 2 a 2b a  b 2 2 1 b  2  e  a ab  2b  e  1 b  1.
Xét hàm số đặc trưng:   t
f t  e  t với t   .Có   t
f t  e  1  0, t   .
Do đó hàm số f tđồng biến trên  . Pt :    f  2 2 a  b ab  f  2 1 2 1  b . 2 2 2  a  2b ab  1 b 2 2  a ab b  1 1 Khi đó:    2 1
a b ab  ab và  a b2 1  3ab  3  ab  1  ab   3 1 1 1 1 1 Suy ra:  3  P     nên M  3,m  . 1 1  2ab 1  2.1 3 1  2.   3    3 10 Vậy m  M  . 3 2 2 x  y log  2 2 2 x 2  y  
Ví dụ 6: Cho các số thực dương x,y thỏa mãn 1 log  2
 log 8xy . Tìm giá trị nhỏ 2 2 2 3xy  x 2 2 2x  xy  2y
nhất của biểu thức: P  2 2xy y 1 5 3 1  5 A. . B. . C. . D. . 2 2 2 2
Đề kiểm tra chuyên đề lần 4, trường THPT Liễn Sơn-VP-2019-2020 Lời giải Chọn B
Theo bài ra, ta có: log  2 2 x  y  log  2 3xy  x  2 2  x  2y  1  3xy 2 2  log  2 2 x  y  2 2 2 x  y  log  2 3xy  x  2  x  log 2  3xy 2 2 2
 log x y  2x y  2 2 2 2 2 3xy  x 2  log  x  3xy 2 2 2
 log x y  2x y  2 2 2 2 2 3xy  x 2  log  x  3xy 1 2 2   2
Xét hàm số đặc trưng: f t  log t  2t , có f t 1   2  0, t  0. 2 t.ln2 2 2   2           2   2 2 3 1 xy  x f x y  f    2 2 3xy x x   3 x   1 x                      x y     1  2  2 y 
2 y  2 y  x Đặt t  2
 t  3t  2  0  1  t  2 . y 2 2 2x  xy  2y 2 2t t  2 2 1 2 1 Ta có: P    t   2t  1  2 2xy  y 2t 1 2t 1 2 2t 1 2 1   t   2 1 5 2 2 1 .   5 3 . Suy ra: P  khi t  2 2t 1 2 2 min 2 2 bca   3
Ví dụ 7: Cho các số thực a  3,b  1,c  1 thỏa mãn: log  ab  ac  . a log 2 1 b 2  c bca 3     ab  2ca
Giá trị nhỏ nhất của T  a  b  c thuộc khoảng nào dưới đây? A. 16;17. B. 17;18. C. 18;19. D. 19;20.
Thi thử liên trường Thanh Hóa 2019-2020 Lời giải Chọn B bc(a  3) Theo bài ra, ta có: log  log (ab  2ac)  1 a(b2c) bc(a3) ab  2ca  log b ( c a  3)  1  log (ab  2ac)  1 1 a(b 2  c)   bc(a3)   1 Đặt t  log b (
c a  3) thì  1 trở thành: t   22 a(b 2  c)   t
Nhận xét: t  0 VT 2  0l + t  0 thì VT   1
2  2 t.  2 . Do đó 2  t  1. t b  2c a  3 1 2 3 Do đó: a(b  2c)  b ( c a  3)       1. bc a c b a
Áp dụng bất đẳng thức Cauchy Schwarz, ta có: 2     T  a b c 3 2 1    3 2 1 .1          a.  b.
 c.    3  2  2  1 . a b c  a b c     a b  a   3  3  6    c   
Dấu “=” xảy ra khi  3 2 b     2  2  6   . a  b c   3 2 21 c        1 2  3  Vậy T     2 min 1 2 3  17,19.
- Nhận xét: Ta có thể giải    t   t  t  2 2 2 1 2 1  0  t  1 3 2 1   6
* Lỗi thường gặp: a b c 3 3 3      3 abc.3  9 6 
tuy nhiên khi áp dụng bất a b c abc
đẳng thức Cauchy ở đây thì dấu bằng không thể xảy ra được.
3. Dạng 3 : Cực trị hình học 2 2
- Hướng 1 : d : ax by c  0 2 và C  : x  x
 y y  R . Khi đó d;C có điểm 0   0 chung  d I;d  R .
+ Mở rộng trong không gian :
P:ax by cz d  0 2 2 2 2 và S  : x  x
 y y  z  z  R . Khi đó P;Scó 0   0  0
điểm chung ( S có tâm I bán kínhR )  d I;P  R . 2 2
- Hướng 2 : d : ax by  c  0 2 và C  : x  x  y y  R d I;d  R vớiI 0   0 sao cho  
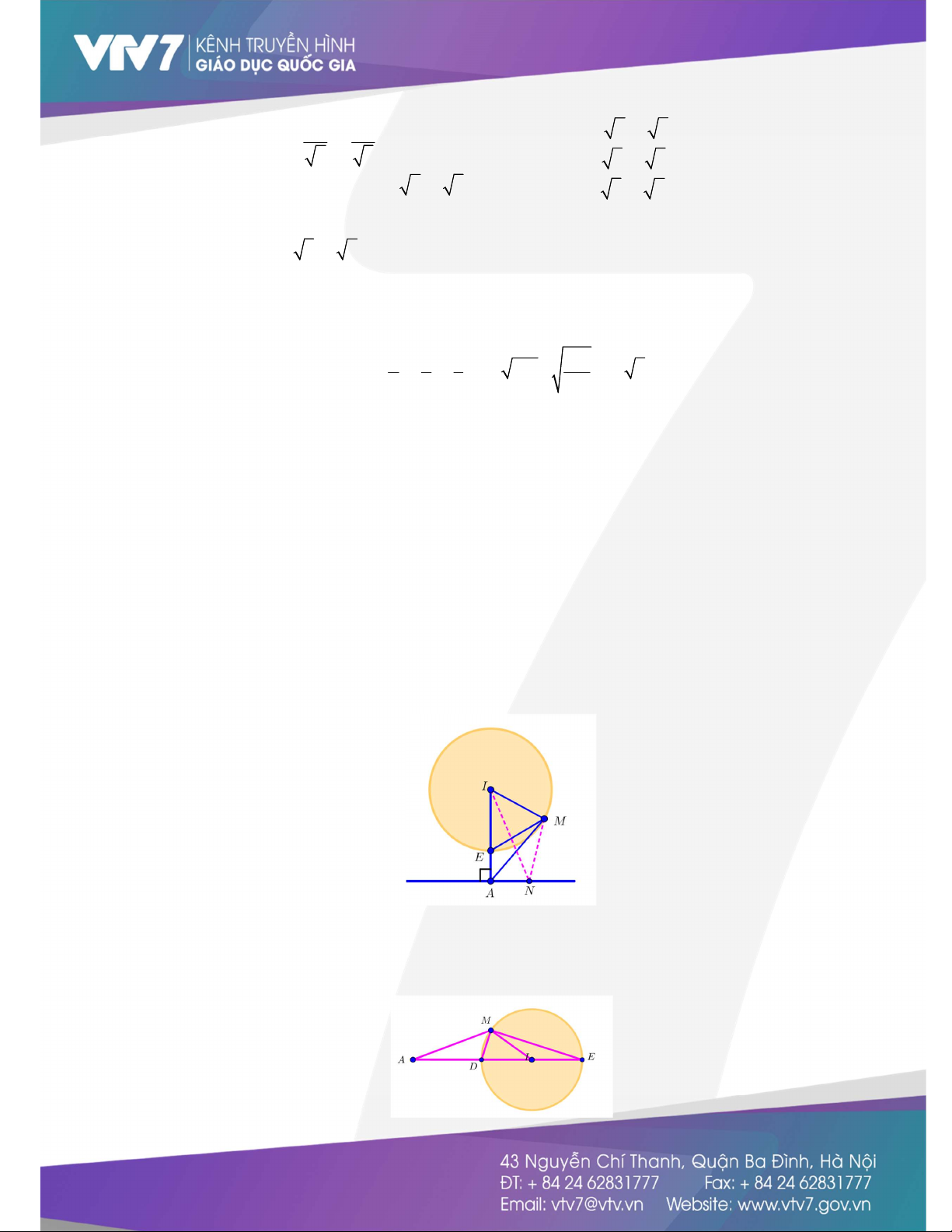
là tâm đường tròn C  khi đó với M  C ,N  d thì MN  d I;d R . Dấu bằng xảy ra khi M  E,N  A. 2 2 - Hướng 3 : Aa;b 2 và C  : x  x  y y  R  vớiI là tâm đường 0   0 sao cho IA R
tròn C  khi đó với M  C  thì IA  R  AM  IA  R . Dấu bẳng xảy khi M  D hoặc M  E . Các ví dụ minh họa: x  2y  2
Ví dụ 8: Với các số thực dương x,y thay đổi sao cho log   
  x x  2  y y  4  5. Xác 2  2 2       x  y  x  2y  1
định giá trị lớn nhất của biểu thức P  . x  y  4 15  473 15  349 15  39 15  6 14 A. . B. . C. . D. . 31 31 31 31 Lời giải Chọn D x  2y  2 Theo bài ra, ta có: log   
  x x  2  y y  4  5 2  2 2       x y 
 log x  2y  21  2x  4y  4  log  2 2 x  y  2 2  x  y 2 2 log 2x 2y 2     2 
x 2y 2 log  2 2 x  y  2 2  x  y 1 2 2  
Xét hàm số đặc trưng: f t  log t  t với t  0. Có f t 1   1  0, t  0. 2 t.ln2
Do đó hàm số f tlà hàm số đồng biến. Nên    f  x  y    f  2 2 1 2 4 4 x  y  2 2
 2x  4y  4  x  y  x  2 y  2 1 2  9 2. x  2y  1 Ta có: P 
 P  1x P 2y  4P 1  0 3 x  y  4
Coi 2 là phương trình của đường tròn C  với tâm I 1;2,R  3 và 3 là phương trình đường thẳng d
Để tồn tại x,y thỏa mãn bài toán d,C  có điểm chung d I;d  R
P  1P 22  4P 1 
 3   P  2   2 7 6 9 2P  6P  5
P  21 P 22 2  31P  30P  9  0 15  6 14 15  6 14   P  . 31 31 Ví dụ 9: Với các số thực dương x, , y z thay đổi sao cho  x  2y  2  log z   
  x x  4  y y  8  z z  8  2 , gọi giá trị lớn nhất và giá trị nhỏ 2  2 2 2        x  y  z  2 2 2
x  y  z  4x  7y 11z  8
nhất của biểu thức T 
thứ tự là M và m . Khi đó M  m 6x  5y  86 bằng: 3 5 1 A.  . B. 1. C.  . D.  . 2 2 2
Đề thi thử TN trường THPT Hải Hậu A- Nạm Định – 2019-2020 Lời giải Chọn D  x  2y  2z  +) Ta có log   
  x x  4  y y  8  z z  8  2 2  2 2 2        x  y  z 
 log 4x  2y  2z log  2 2 2 x  y  z  2 2 2
 x  y  z  4(x  2y  2z) 2 2
 log 4x  2y  2z 4(x  2y  2z)  log  2 2 2 x  y  z  2 2 2  x  y  z (1). 2 2
+) Xét hàm đặc trưng f t  log t t, t  0 có f t 1   t  0, t  0 . 2 t ln2 +) Ta có
 f  x  y  z  f  2 2 2 x  y  z  2 2 2 (1) 4 2 2
 x  y  z  4x  8y  8z
 x  2 y  2 z  2 2 4 4  36 .
4x  8y  8z4x 7y 11z  8 y 3z  8 Khi đó, ta được T   6x  5y  86 6x  5y  86
Ta có: T 6x  5y  86  y  3z  8  6Tx  5T   1 y  3z  8  86T
 6Tx  5T  1y  3z  8  86T  0 1. Khi đó ta coi 
1 là phương trình mặt phẳng P: 6Tx 5T  1y  3z  8  86T  0 . Do đó, tồn tại x, ,
y z để phương trình mặt phẳng P tiếp xúc hoặc cắt mặt cầu S với tâm
6T.2  5T  14  3.4  8  86T
I 2;4;4,R  6  d I;P  R   6 6T2 5T  2 2 1  3 2 1
 720T  360T  360  0  1  T  . 2
Ví dụ 10: Cho các số thực , a ,b ,cd thỏa mãn log
4a  6b  7  1 và 27c81d  6c  8d  1. Tìm giá 2 2 a b  2   
trị nhỏ nhất của biểu thức 2 2 P  (a c)  (b d) . 8 49 64 7 A. . B. . C. . D. . 5 25 25 5
Đề thi KSCL Chuyên Phan Bội Châu-Nghệ An-L2-2019-2020 Lời giải Chọn B 2 2 Ta có: 2 2 log
4a  6b  7  1  a  b  2  4a  6b  7  a  2  b  3  4 (C). 2 2 a b  2        Khi đó: c d 3c4d 3c4 27 81  6  8  1  3  6  8  1  3 d c d c d  2(3c  4d) 1  0 .
Đặt t  3c  4d , ta có phương trình: 3t  2t  1  0 . 2 Xét hàm số ( )  3t f t  2t 1 có ( )  3t f t
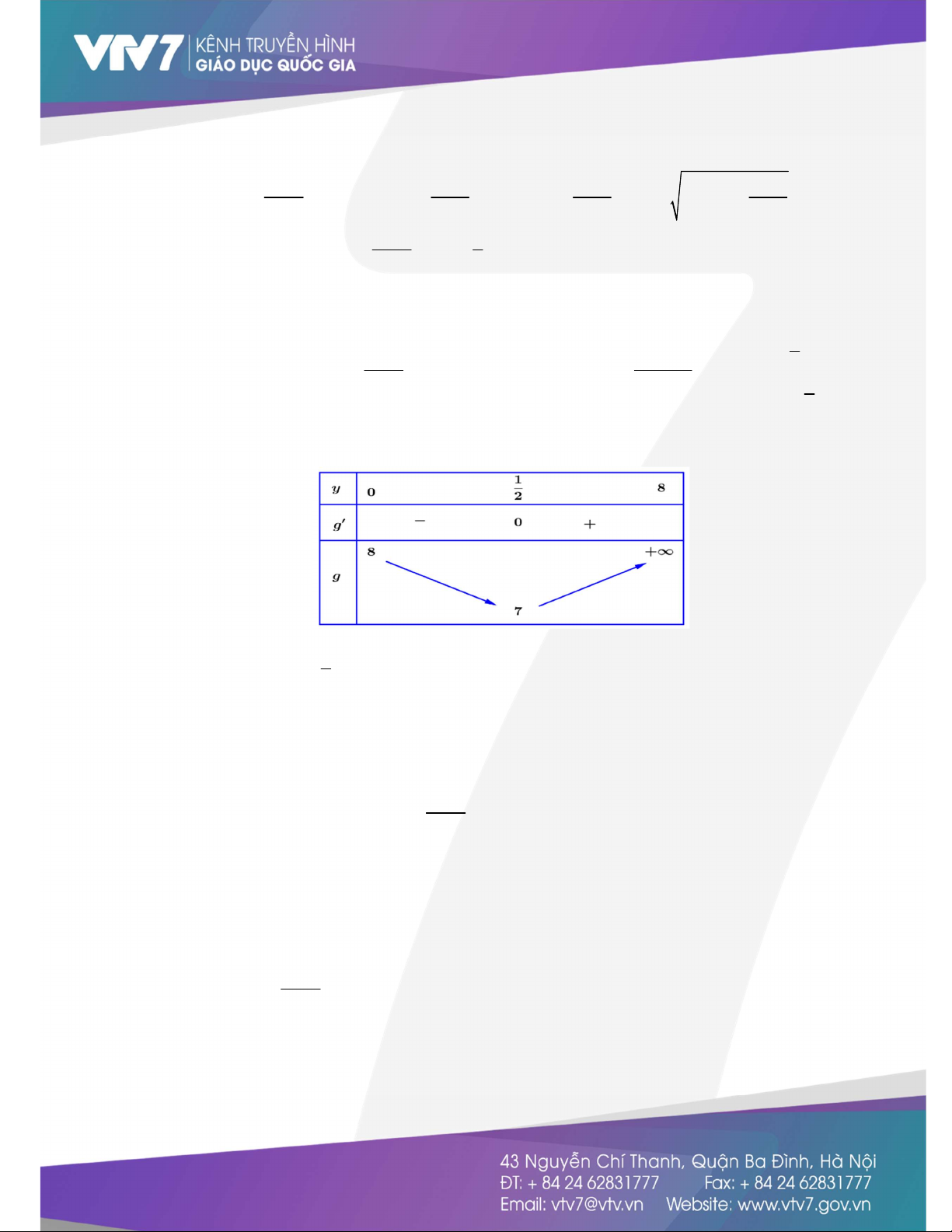
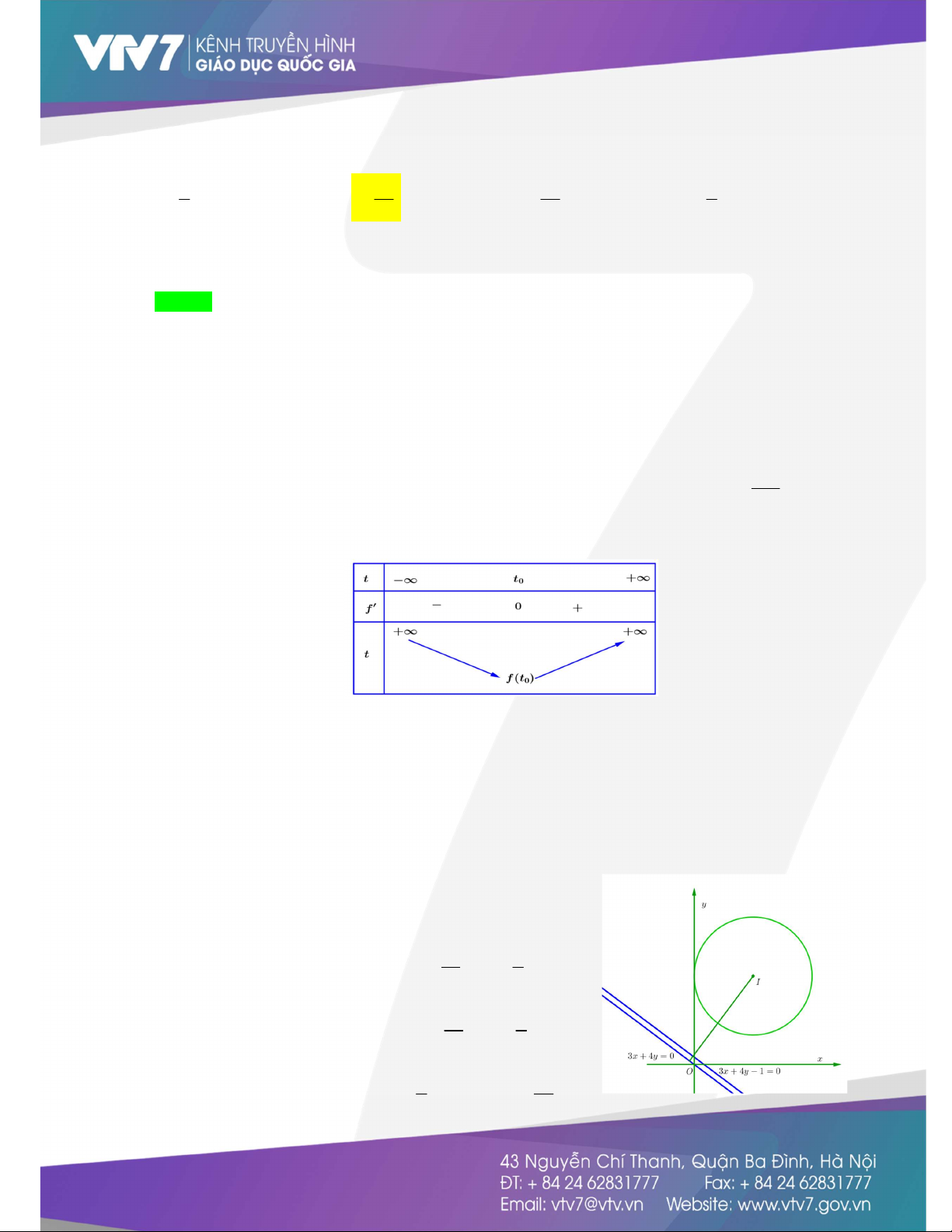
ln 3  2. Khi đó: f (t)  0  t  log  t 3 0 ln 3 Bảng biến thiên:
Quan sát bbt, ta có f t  0 có nhiều nhất hai nghiệm mà f 0  f   1  0 t  3c  4d  0 Do đó:   0 1    t  1  .    3c  4d  1 
Khi đó: ta coi cặp a;b là tập hợp các điểm Aa;b  C  có tâm I 2;3,R  2 ; và các cặp
 ;cd là tập hợp các điểm B ;cdd : 3x  4y  0 hoặc 1 d : 3x  4y 1  0 . 2 18 8
+ Nếu B  d thì AB  d I;d R  2  . 1 1 5 5 17 7
+ Nếu B  d thì AB  d I;d R  2  . 2  2 5 5 7 49
So sánh hai trường hợp thì AB  do đó P  . min 5 min 25 Ví dụ 11: Cho x,y là hai số thực không âm thoả mãn đẳng thức 2 2 x  y  7 2 2 log
 x  y  6x  8y  5  0. Giá trị lớn nhất của biểu thức 2 2 T  x  y là 6x  8y  2 A. 4 5 . B. 5  2 5 . C. 10 . D. 10  2 5 .
Đề KSNL Chuyên Nguyễn Thị Minh Khai-Sóc Trăng-2019-2020 Lời giải Chọn B 2 2 x  y  7 Ta có 2 2 log
 x  y  6x  8y  5  0 6x  8y  2   2 2 x  y   2 2 log
7  x  y  7  log6x  8y  2 6x  8y  2 (1).
Xét hàm số đặc trưng: y  f t  t  logt với t  0 Khi đó: f t 1  1 
 0, t  0  y  f t đồng biến trên khoảng 0;. t.ln10    f  2 2
x  y    f  x  y   2 2 1 7 6 8
2  x  y  7  6x  8y  2
 x  2 y  2 3 4  20 (2).
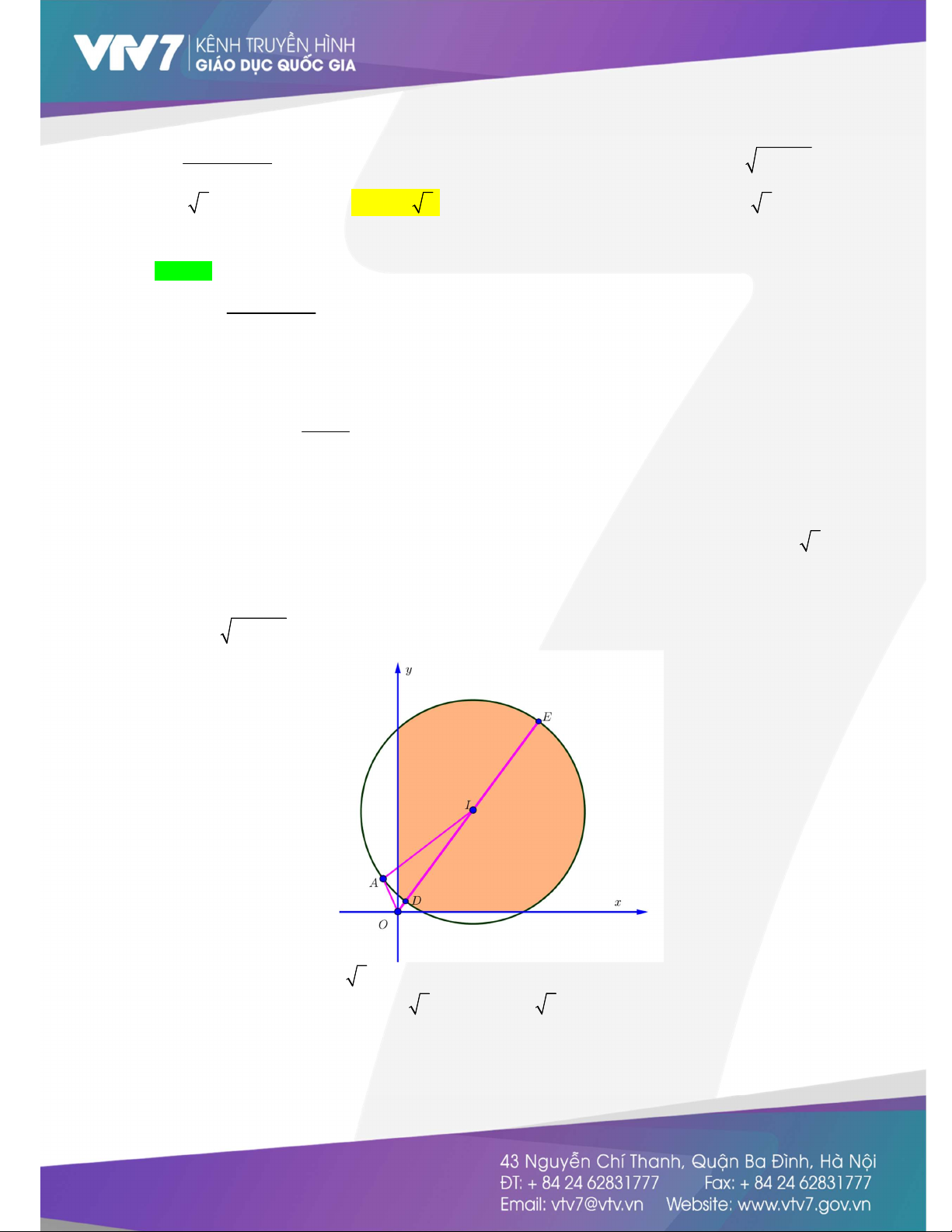
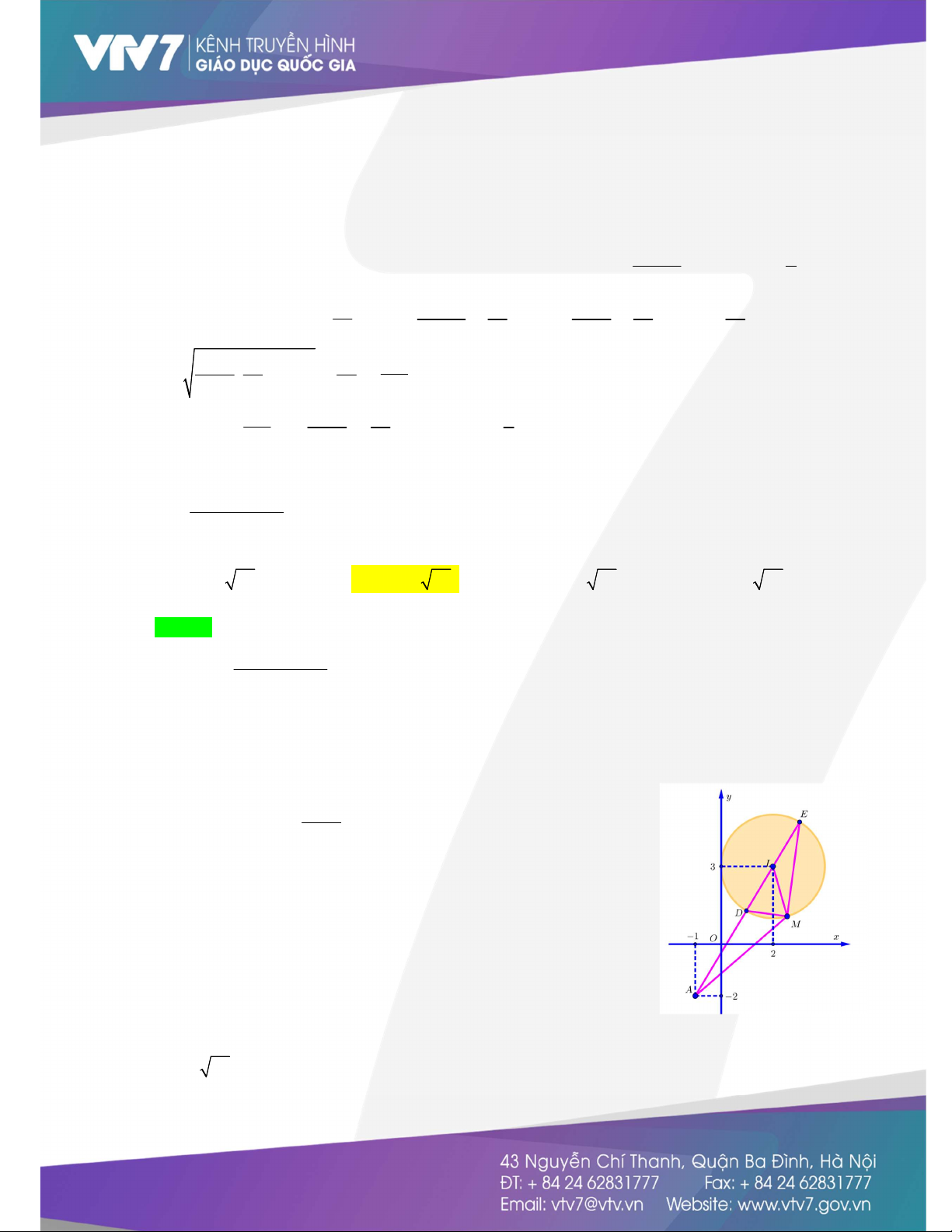
Ta coi các cặp x;y thỏa mãn 2 là các điểm Ax;y thuộc hình tròn C  : I 3;4,R  2 5
( kể cả phần nằm bên trong đường tròn đó) mà x  0,y  0 nên tập hợp các điểm Ax;y là phần
tô màu như hình vẽ dưới. Gt: 2 2
T  x  y T  OA với O 0;0.
Nhận xét:OI  5  R  2 5 .
Do đó: T  OA OI  R  5  2 5 . T  5  2 5 khi A  E . max BÀI TẬP TỰ LUYỆN  x y 
Câu 1: Cho các số thực x,y thỏa mãn 0  x,y  1 và log   
  x  1 y  1  2  0. Tìm giá 3      1xy 8
trị nhỏ nhất của P với P  x   1  y  2020. 9 6055 6  052 A. 2  021. B. 2  020. C. . D. . 3 3 Câu 2: Cho các số thực x,y thỏa mãn đồng thời x  0,y  1và  2     2   3 2 1 log  log y x xy x y y
Tìm giá trị nhỏ nhất của biểu thức: x . 2 y 4x   3 x P   . 4y y A. 4 . B. 5. C. 3 D. 6.  25x 4ylogx 4y  2
Câu 3: Cho các số thực x,y thỏa mãn đồng thời x,y  1 và 10  Tìm giá trị nhỏ nhất 5 . 2 3 40x  y của biểu thức: P   5 . 8y 21 19 A. . B. 11. C. D. 8 . 2 2
Câu 4: Cho a , b là các số thực dương thỏa mãn b  1 và a  b  a . Tìm giá trị nhỏ nhất của biểu a thức P  log a  2 log   . a b b  b A. 6. B. 7 . C. 5. D. 4 . 1 a
Câu 5: Cho các số thực a,b thỏa mãn a  b  1. Biết rằng biểu thức P   log đạt giá trị log a a b ab lớn nhất khi k
b  a . Khẳng định nào sau đây là đúng?  1 1   3 3  A. k   0;         . B. k   ;1 . C. k  1  ; . D. k   ;2.  2 2   2 2 
Câu 6: Cho các số thực a, ,
b x,y thỏa mãn a  1,b  1 và x y 4
a  b  ab . Giá trị nhỏ nhất của biểu thức
P  x  4y  6 thuộc tập nào dưới đây? A. 9;10. B. 6;7. C. 7;8. D. 8;9.
Câu 7: Cho các số thực a, ,
b c  1 và các số thực dương x, , y z thỏa mãn x y z 6
a  b  c  abc . Giá trị 32
lớn nhất của biểu thức 2 P 
 4z  1 thuộc tập nào dưới đây? x  y A. 34;36. B. 36;38. C. 38;40. D. 40;42. a b c Câu 8: Cho a, ,
b c là các số thực dương khác 1 thỏa mãn: 2 2 2 a 1  b 1  1 3 5 15 c  
. Giá giá trị nhỏ nhất của  
biểu thức: P  a b c2 1 1 1  8      25 
thuộc khoảng nào sau đây? a b c A. 0;20. B. 20;0. C. 30;20. D. 50;30. x  4y
Câu 9: Cho x , y là các số thực dương thỏa mãn log   
  2x  4y  1. Giá trị nhỏ nhất của biểu 2  x  y  4 2 2 2 x  3x y  4x 11x thức P   bằng bao nhiêu?   3 4 2 y x y 23 13 A. . B. 3 . C. 6. D. . 4 2 8 ab ab a b  1 
Câu 10: Cho hai số thực dương a và b thỏa mãn 4 .2 
. Giá trị lớn nhất của biểu thức a b 2 P  ab  2ab bằng 5 1 3 A. 3 . B. 1. C. . D. . 2 17 4a  2b  5
Câu 11: Cho a , b là hai số thực dương thỏa mãn log   
  a  3b  4 . Tìm giá trị nhỏ nhất 5  a b  của biểu thức 2 2
P  a b  3a b  5 A. 1  5. B. 5 . C. 5. D. 35 . a  2b  3
Câu 12: Cho các số dương , a b thỏa mãn 3  log
 ab a  2b . Tìm giá trị nhỏ nhất của ab biểu thức: 2 2
P  a  4b  26ab  2020 . A. 1120 . B. 1885 . C. 2021 . D. 1705 .
Câu 13: Cho hai số thực dương x,y thỏa mãn log x  x x  y  log 6  y  6x . Giá trị nhỏ nhất của 2   2   6 8
biểu thức P  3x  2y   . x y 59 53 A. 8  6 2 . B. . C. 19 . D. . 3 3 x  y
Câu 14: Cho số thực x, y thỏa mãn log
 x(x  3)  y(y  3)  xy . Tìm giá trị lớn 3 2 2 x  y  xy  2 x  2y  3
nhất của biểu thức P  . x  y  6 69  249 69  249 37  249 43  2 249 A. . B. . C. . D. . 94 94 94 94 6x  2y  5
Câu 15: Với các số thực dương x,y thay đổi thỏa mãn: log   
  x x 12  y y  4 10 2  2 2       x y 1 . 3x  2y  6
Giá trị nhỏ nhất của biểu thức: P 
thuộc khoảng nào sau đây? 2x  y  1 A. 0,5;0,7. B. 0,7;0,9. C. 0,9;1,  1 . D. 0,3;0,5.
Câu 16: Cho x,y là các số thực dương thỏa mãn: log x  2y  x x  3y  1  y 2y  1  0 . Khi 2       biểu thức P  log
x  2.log y đạt giá trị lớn nhất, hãy tính giá trị 2 2 4x  5y . 2020 2020 2 8 A. . B. 3 . C. 1. D. . 3 9 Câu 17: Cho x,y là các số thực dương và y  1 thỏa mãn:     
x 2y   y   x   x 5 1 3 5 .ln 1  ln    lny  
. Tìm giá trị nhỏ nhất của biểu thức: xy  3 P  x y   32 1  y  2 . 25 103 217 23 48 A. . B. . C. . D. . 25 25 25 25 Câu 18: Cho x,y là hai số thực không âm thoả mãn đẳng thức 2 2 x  y  15 log   2 4x  x  2
6y y  8 . Giá trị nhỏ nhất của biểu thức 2  2x  3y  3 2 2
P  x  y  2x  4y  5 là A. 26  8 34 . B. 28  4 34 . C. 26  4 34 . D. 28  8 34 .
Hướng dẫn giải bài tập tự luyện  x y 
Câu 1: Cho các số thực x,y thỏa mãn 0  x,y  1 và log   
  x  1 y  1  2  0. Tìm giá 3      1xy 8
trị nhỏ nhất của P với P  x   1  y  2020. 9 6055 6  052 A. 2  021. B. 2  020. C. . D. . 3 3 Lời giải Chọn C
Điều kiện: 0  x,y  1 Khi đó    log x y   
  x  1 y  1  2  0 3      1xy
 log x  y  log 1 xy  x  y  xy 1  0 3   3  
 log x  y  x  y  log 1  xy  1  xy 1 3     3      
Xét hàm số đặc trưng f (t)  log t  t với t  0 3 1 Khi đó: f '(t) 
 1  0, t  0 nên hàm số f(t) đồng biến trên khoảng 0;. Suy ra t ln 3
 1  f x y f 1xy  x y  1xy 1 x  y  1  x 8 8 1  x 8 2 Suy ra P  x  
1  y  2020  x  1  2020  x  1 1 2020 9 9 1  x 9 1  x 8  x   2 2 1 .  2021 4  2.  2021 6  055  . 9 1  x 3 3 1 1
Đẳng thức xảy ra khi x  , y  (thỏa các điều kiện của đề bài). 2 3 6055 Vậy P   . Min 3 Câu 2: Cho các số thực x,y thỏa mãn đồng thời x  0,y  1và  2     2   3 2 1 log  log y x xy x y y
Tìm giá trị nhỏ nhất của biểu thức: x . 2 y 4x   3 x P   . 4y y A. 4 . B. 5. C. 3 D. 6. Lời giải Chọn B x   0,y  1  x   0,y  1
Điều kiện: 2y  x  3     .   0 2  y  x  3  0  x  Ta có :  2     2   3 2 1 log  log y x xy x y y x   2
xy  x  2y  3logy  2logy  log2y x  3 logx   2
xy  x  y   y   y x    2 2 3 log log 2 3 log xy   1 V  T   1 0 + Nếu 2 xy  2y  x  3 thì (do logy  0). V  P   1  0 V  T   1 0 + Nếu 2 xy  2y  x  3 thì (do logy  0). V  P   1  0 Do đó, từ   1 suy ra: 2
xy  2y  x  3  x  2y  1  2y  3. 3 x x  2y  1 3 3 3
Ta có: P  xy  y   y   y  2  3 3 3 3  y   2  2 y.  2  5 4 y 4 y 4 y 4 y 4 y 7
Vậy P  5 khi y  2  x  . min 5  25x 4ylogx 4y  2
Câu 3: Cho các số thực x,y thỏa mãn đồng thời x,y  1 và 10  Tìm giá trị nhỏ nhất 5 . 2 3 40x  y của biểu thức: P   5 . 8y 21 19 A. . B. 11. C. D. 8 . 2 2 Lời giải Chọn A  25x 4ylogx 4y  2 4y  2 Gt : 10    2 5x  4ylogx  log    5  5    2
5x  4y  2logx  2logx  log4y  2 log5  0 2  x   y     x      2 5 4 2 log
log 5x log4y 2  0   1  Vì x  1  logx  0 . + Nếu 2 5x 4y  2 0 2
 5x  4y  2 VT  1 0 (loại). + Nếu 2 5x 4y  2  0 2
 5x  4y  2 VT  1  0 (loại). + Nếu 2 5x 4y  
2  0 VT  1  0t / m Vậy   2 1  5x  4y  2. 2 3 40x  y  y   3 8 4 2  y 2 2 y 2 1 1 y Khi đó: P   5   5    9     9 8y 8y y 8 y y 8 2 1 1 y 21 3  3 . .  9 
. Dấu bằng xảy ra khi x  2,y  2 . y y 8 2
Câu 4: Cho a , b là các số thực dương thỏa mãn b  1 và a  b  a . Tìm giá trị nhỏ nhất của biểu a
thức P  log a  2 log    . a b b  b A. 6. B. 7 . C. 5. D. 4 .
Đề khảo sát chất lượng – L2 – Chuyên Vĩnh Phúc – 2018-2019 Lời giải Chọn C 1 41t Đặt t  log t b  b  a . Khi đó: 1 P log t       a a t 4.log a 1 t a a 1t t 1
Vì b  1 và a  b  a nên  t  1. 2 1 41t t 41t t 41t Khi đó: P    1    1  2 .  5 1 t t 1 t t 1t t 2 Vậy P  5 khi t  min 3 1 a
Câu 5: Cho các số thực a,b thỏa mãn a  b  1. Biết rằng biểu thức P   log đạt giá trị log a a b ab lớn nhất khi k
b  a . Khẳng định nào sau đây là đúng?  1 1   3 3  A. k   0;         . B. k   ;1 . C. k  1  ; . D. k   ;2.  2 2   2 2  Lời giải Chọn B Đặt t  log b t
 b  a (đk: 0  t  1). a 1 a Khi đó: P   log
 log ab  1 log b  1  t  1 t log a a b a a ab
Xét hàm số: f t  1  t  1t với 0  t  1, Có f t 1 3  1  0  t  2 1t 4 Bảng biến thiên: 9 3 3 3 Vậy P  khi 4
t   b  a do đó: k  max 4 4 4
Câu 6: Cho các số thực a, ,
b x,y thỏa mãn a  1,b  1 và x y 4
a  b  ab . Giá trị nhỏ nhất của biểu thức
P  x  4y  6 thuộc tập nào dưới đây? A. 9;10. B. 6;7. C. 7;8. D. 8;9. Lời giải Chọn D   1 4 x   log ab x    1 log ba Giả thiết: x y 4 a  b  ab  a     4  4 y   log ab  1 b  y   1 log ab  4 1 1  1
Đặt t  log b (đk: t  0 ) thì x  1 t và y  1     . a 4 4  t  1 1 29 1 1 29 1 1 33
Ta có: P  1 t1   6   t    2 t.  . 4 t 4 4 t 4 4 t 4 3 3
Dấu bằng xảy ra khi t  2  x  ,y  . 4 8
Câu 7: Cho các số thực a, ,
b c  1 và các số thực dương x, , y z thỏa mãn x y z 6
a  b  c  abc . Giá trị 32
lớn nhất của biểu thức 2 P 
 4z  1 thuộc tập nào dưới đây? x  y A. 34;36. B. 36;38. C. 38;40. D. 40;42. Lời giải Chọn B Đặt: x y z 6
a  b  c  abc  t (đk: t  1). 1
Ta có: x  log t,y  log t,z  log t,log t  a b c abc 6 1 1 1
Suy ra:    log a  log b  log c  log abc  6 t t t t x y z 1 1 4
Nhận xét: với x,y  0 , ta có: x  y2  4xy   
. Dấu bằng xảy ra khi: x  y x y x  y 32 1 1  1 Do đo: 2 P   4z  1   2  8.   4z 1   2  8 6    4z  1 x  y x y  z    2 1 1  49  4 z        z z  1 1 1 1 Mà 2 2 3
z    3. z . .  3 nên P  49  4.3  37. z z z z 2
Dấu bằng xảy ra khi z  1, x  y  . 5 a b c Câu 8: Cho a, ,
b c là các số thực dương khác 1 thỏa mãn: 2 2 2 a 1  b 1  1 3 5 15 c  
. Giá giá trị nhỏ nhất của  
biểu thức: P  a b c2 1 1 1  8      25 
thuộc khoảng nào sau đây? a b c A. 0;20. B. 20;0. C. 30;20. D. 50;30. Lời giải Chọn D a b c Đặt 2 2 2 a 1  b 1  1 3 5 15 c    t . Khi đó: t  0.
+ Nếu t  1  a  b  c  0l. + Nếu t  1, ta có: a b c  Khi đó:  log t ,  log t ,  log t . 2 3 a 1 2 5 b 1 2 15 c 1 2 2 2 a 1 b 1 c 1 Suy ra:  
 log 3  log 5  log 15  0 t t t a b c 1 1 1  a b c    . a b c   2
Khi đó: P  a b c2 1 1 1  8      25 
 a b c  8a b c25 a b c  a b c  2 4  41  4  1. 1 1 1 3
Suy ra: P  41. Dấu bằng xảy ra khi: a b c     4 . Ta có thể chọn a  thì a b c 2  5 b  c   2 5  13 5  13  3  b  ,c   4 4  . b c   4
Vậy P đạt giá trị nhỏ nhất là 4  1. x  4y
Câu 9: Cho x , y là các số thực dương thỏa mãn log   
  2x  4y  1. Giá trị nhỏ nhất của biểu 2  x  y  4 2 2 2 x  3x y  4x 11x thức P   bằng bao nhiêu?   3 4 2 y x y 23 13 A. . B. 3 . C. 6. D. . 4 2 Lời giải Chọn A Điều kiện: x,y  0 . x  4y x  4y Theo giả thiết: log   
  2x  4y  1  log    1  2x  4y 2  x  y  2  x  y   x  4      log y      2x  4y x 4  log y   
  2 2x  2y  2 x  4y 2       2 2x  2y 2x  2y
 log x  4y  2 x  4y  log 2x  2y  2 2x  2y 1 2     2      
Xét hàm số đặc trưng f t  log t  2t với t  0; 2 Ta có: f t 1 
 2  0 với t  0; nên hàm số f t đồng biến trên t  0; t ln2 Nên  
1  f x  4y  f 2x  2y  x  4y  2x  2y  x  2y . 4 2 2 2 x  3x y  4x 11x 4 4 2 P   16y 12y  16y 11.2y   y 1 11      3 4 2 y x y 3 64y 4y 16 4y 2 y 1 11 23  2 .   . 16 4y 2 4 23 Vậy P  khi y  2. min 4 Nhận xét:
- Đối với bài toán số này, sau khi chúng ta thực hiện việc biểu diễn được x  2y chỉ cần rút gọn
biểu thức P thì việc xác định giá trị P tương đối đã rõ ràng đối với các em học sinh. min 8 ab ab a b  1 
Câu 10: Cho hai số thực dương a và b thỏa mãn 4 .2 
. Giá trị lớn nhất của biểu thức a b 2 P  ab  2ab bằng 5 1 3 A. 3 . B. 1. C. . D. . 2 17
Đề thi thử chuyên Hùng Vương – Gia Lai – lần 1 năm học 2018-2019 Lời giải Chọn B
Đk: a  0,b  0,1  ab . 8 ab 8 1ab ab a b  1  Theo giả thiết: 4 .2   a b a b   .2  a b 2 2 ab
    a b     2 2 .2 2 2 .2  ab a b ab  1
Xét hàm số đặc trưng:    .2t f t t với t  0;.
Khi đó:    2t  .2t f t
t .ln2  0, t  D nên hàm số f t là hàm số đồng biến trên 0;.
 1  f a b f 22ab  a b  22ab  a12b 2b .
Vì a,b  0  2 b  0  b  2 . Khi đó: 2
P  ab  2ab  ba 1 2b  b2 b  b  2 1 1  1. 1 Vậy P  1 khi a  ,b  1. max 3 4a  2b  5
Câu 11: Cho a , b là hai số thực dương thỏa mãn log   
  a  3b  4 . Tìm giá trị nhỏ nhất 5  a b  của biểu thức 2 2
P  a b  3a b  5 A. 1  5. B. 5 . C. 5. D. 35 . Lời giải Chọn B 4a  2b  5 Theo bài ra, ta có: log      a  3b  4 5  a b 
 log 4a  2b  5  log 5 a b  5 a b  4a  2b  5 5   5      
 log 4a  2b  5  4a  2b  5  log 5 a b  5 a b 1 5     5       1
Xét hàm số đặc trưng: f t  log t  t t  0 . Khi đó: 'f t   1  0 5   t ln5
Do đó hàm số f t đồng biến nên  
1  f 4a  2b  5  f 5a b
 4a  2b  5  5a b  a  5  3b .
P  a b  a b     b2 2 2 2 3 5
5 3 b  35 3bb 5 2  10b  20b  5  b  2 10 1  5  5. Vậy GTNN P  5
 . Dấu bằng xảy ra khi a  2,b  1. a  2b  3
Câu 12: Cho các số dương , a b thỏa mãn 3  log
 ab a  2b . Tìm giá trị nhỏ nhất của ab biểu thức: 2 2
P  a  4b  26ab  2020 . A. 1120 . B. 1885 . C. 2021 . D. 1705 . Lời giải Chọn D a  2b  3 1 a  2b  3 Ta có 3  log
 ab a  2b  3  log     ab a  2b ab 2  ab  a  2b  3      6  log     2ab  2a  4b a 2b 3     log
  2ab 2a  4b  6  ab   ab  a  2b  3  log     2ab  2   a 2b  3  ab 
 loga  2b  3 2a  2b  3  logab 2ab  *
Xét hàm số đặc trưng y  f t  logt  2t với t  0. Ta có f t 1   2  0, t  0 . t ln10
Suy ra hàm số y  f t đồng biến trên khoảng 0; Do đó   *  f a  2b  
3  f ab  a  2b  3  ab  1. Khi đó, ta có: 2 2
P  a  4b  26ab  2020  a  b2 2  30ab  2020  a  b2
2  30a  2b  3 2020  a  b  2 2 15  1705. a   2b  15 Vậy P  1705 khi  nên a  3,b  6. min a  .b  18 
Câu 13: Cho hai số thực dương x,y thỏa mãn log x  x x  y  log 6  y  6x . Giá trị nhỏ nhất của 2   2   6 8
biểu thức P  3x  2y   . x y 59 53 A. 8  6 2 . B. . C. 19 . D. . 3 3
Đề kiểm tra học kì I, THPT Minh Khai – Hà Nội, năm học 2019-2020 Lời giải Chọn C x   0
Điều kiện: 0  y  6. 
Giả thiết, ta có: log x  x x  y  log 6 y 2
 6x  log x  x  log 6  y  x 6  y 2 2 2 2     2
 2 log x  x  log x 6  y  x 6  y 2 2
 log x  x  log x 6  y  x 6  y 1 2 2      2 2    
Xét hàm số f t  log t  t với t  0, ta có: f t 1   1  0, t  0. 2 t.ln2
Suy ra hàm số y  f t đồng biến trên khoảng 0;. Do đó:    f  2 x   f x  y 2 1 6
 x  x 6 y  x  6 y .
Với x  6  y thay vào P ta được:     P   y 6 8 6 8 8 y   6 3 3 6  2y    18  y             .      6y9 6 y y 6 y y y 2 6 y 2  8 y 6 3  2 .  2
. 6 y  9  P  19. y 2 6  y 2 8 y    2 y   16  y   4 Dấu bằng xảy ra y 2      6 3   2    y  4  x  2 .   6   y  2   6 y 6y    4    6 y 2 x   2
Vậy giá trị nhỏ nhất của biểu thức P là 19 khi y  4.  x  y
Câu 14: Cho số thực x, y thỏa mãn log
 x(x  3)  y(y  3)  xy . Tìm giá trị lớn 3 2 2 x  y  xy  2 x  2y  3
nhất của biểu thức P  . x  y  6 69  249 69  249 37  249 43  2 249 A. . B. . C. . D. . 94 94 94 94
Đề thi thử TN THPT Lê Hoàn-Thanh Hóa-2019-2020 Lời giải Chọn B Đk:x  y  0 . x  y Giả thiết: log
 x(x  3)  y(y  3)  xy 3 2 2 x  y  xy  2 2 2 2 2
 2log (x  y) 2log (x  y  xy  2)  x  3x  y  3y  xy 3 3 2 2 2 2
 2log (x  y)  2  (3x  3y)  2log (x  y  xy  2)  x  y  xy  2 3 3 2 2 2 2
 2log (3x  3y)  (3x  3y)  2 log (x  y  xy  2)  (x  y  xy  2) 1 3 3   2
Xét hàm số đặc trưng: f (t)  2 log t  t(t  0) ta có: f '(t)   1  0t  0 3 t.ln 3
Suy ra: hàm số f t đồng biến trên 0;.   2 2
1  f(3x  3y)  f(x  y  xy  2) 2 2
 3x  3y  x  y  xy  2 2 2      2 x  x        9 3x 3x 1 y xy   3 y         0  4     2 4 4 2 4 2 2 2 2  x 3   3x 3x 1  x 3          3x 3 y     y                  1 2 2 4 2 4  2 2  2 2    2 x 3x 2  3     3 Đặt: a  y  ,b  thì a     b        1       2 2 2 2  2     2 x y       3 x  2y  3  2 2a  3 Pb Khi đó: P     a P 2  6P  3  03 x  y  6 x x y    6 b a   6 3 2 2 3 3 3
Ta coi 2là phương trình đường tròn C  với I  ; ,R  1 
và 3 là đường thẳng 2 2    :  2 P d P x  y  6P  3  0 . 3 3  2 P P   6P  3 2 2 Để tồn tại ,
a b khi d,C  có điểm chung dI;d  R   1 P 22 1 2  P 3 188 2  P  92P  32  0 69  249 69  249   P  69 249 . Vậy P   . 3 94 94 max 94 6x  2y  5
Câu 15: Với các số thực dương x,y thay đổi thỏa mãn: log   
  x x 12  y y  4 10 2  2 2       x y 1 . 3x  2y  6
Giá trị nhỏ nhất của biểu thức: P 
thuộc khoảng nào sau đây? 2x  y  1 A. 0,5;0,7. B. 0,7;0,9. C. 0,9;1,  1 . D. 0,3;0,5. Lời giải Chọn D 6x  2y  5 Theo bài ra, ta có: log   
  x x 12  y y  4 10 2  2 2       x  y 1
 log 6x  2y  512x  4y 10  log  2 2 x  y   2 2 1  x  y 2 2 log 26x 2y 5     2 
6x 2y  5 log  2 2 x  y  1  2 2 x  y  1 1 2 2  
Xét hàm số đặc trưng cho phương trình: f t  log t  t với t  0. 2 Ta có: f t 1 
 1  0, t  0 nên hàm số f t đồng biến trên khoảng 0;. t.ln2
Do đó:    f   x  y    f  2 2 1 2 6 2 5
x  y  1   x  y   2 2 2 6 2 5  x  y  1
 x  2 y  2 6 2  492. x  y  6 Khi đó: P 
 2P  1x P  1y  8P  6  03. 2x  y  8
Khi đó, ta coi 2là phương trình của đường tròn C  : I 6;2,R  7 và 3là phương trình của đường thẳng d
Để tồn tại x,y thỏa mãn bài toán  d,C  có điểm chung d I;d  R 22P 14   7  P 2  P 2 P 2 22 14 49 2 1 1        
2P  21 P  21   2  239P  322P  98  0 161 7 51 161  7 51   P  239 239 161 7 51 Vậy P    0,46 min 239
Câu 16: Cho x,y là các số thực dương thỏa mãn: log x  2y  x x  3y  1  y 2y  1  0 . Khi 2       biểu thức P  log
x  2.log y đạt giá trị lớn nhất, hãy tính giá trị 2 2 4x  5y . 2020 2020 2 8 A. . B. 3 . C. 1. D. . 3 9
Đề thi thử TN THPT Chuyên Hà Tĩnh-2019-2020 Lời giải Chọn C
Với x,y  0 . Ta có: log x  2y  x x  3y  1  y 2y  1  0 2      
 log x  2y  x  y x  2y 1  0 1 2       
+ Nếu x  2y  1 thì VT   1  0 ( loại)
+ Nếu x  2y  1 thì VT   1  0 ( loại). 1
+ Nếu x  2y  1 thì VT  
1  0 (t/m). Suy ra  1  x 2y 1  x 12y (đk:0  y  ). 2 Khi đó: P  log x  2.log y  log  2 x.y . Mà: 2 x y    y 2 . 1 2 y  12y.y.y . 2020  2020 2020 y  y  12y
Áp dụng bđt Cauchy cho ba số dương, ta có: 3  y.y.12y 3 1   y.y.12y 1  P  log . 27 2020 27 1 1 1 Vậy P  log khi 2 2
y  ,x   4x  5y  1. max 2020 27 3 3 Câu 17: Cho x,y là các số thực dương và y  1 thỏa mãn:     
x 2y   y   x   x 5 1 3 5 .ln 1  ln    lny  
. Tìm giá trị nhỏ nhất của biểu thức: xy  3 P  x y   32 1  y  2 . 25 103 217 23 48 A. . B. . C. . D. . 25 25 25 25 Lời giải Chọn A    x  5  Theo bài ta, ta có: x
  2y  1  3y 5 .ln  x   1  ln    lny   xy  3  2 xy y   x   
   x    x     2 3 5 .ln 1 ln 5 ln xy  3y 1
Nhận xét: x  0  lnx   1  0 . + Nếu: 2
xy  3y  x  5 thì VT  1  0,VP  1  0( loại). + Nếu: 2
xy  3y  x  5 thì VT  1  0,VP  1 0( loại). + Nếu 2
xy  3y  x  5 thì VT  1 VP  1  0 ( thỏa mãn). 5  3y 5 Do đó:   2
1  xy  3y  x  5    x  2 1
y  1  5  3y  x  (đk: 1  y  ). 2 y 1 3 5  3y 32 8 32 57
Khi đó: P  x y   32 1  y  2   y  2   y  1 25 y  1 25 y  1 25 25 8 32 57 103  2 . y  1   . y  1 25 25 25 103 8 32 3 Vậy P  khi  y  1  y  . min 25 y  1 25 2 Câu 18: Cho x,y là hai số thực không âm thoả mãn đẳng thức 2 2 x  y  15 log   2 4x  x  2
6y y  8 . Giá trị nhỏ nhất của biểu thức 2  2x  3y  3 2 2
P  x  y  2x  4y  5 là? A. 26  8 34 . B. 28  4 34 . C. 26  4 34 . D. 28  8 34 . Lời giải Chọn B 2 2 x  y  15 Ta có log   2 4x  x  2 6y y  8 2  2x  3y  3  log  2 2 x  y  1  2 2
5  x  y  15  log 2x  3y  3  4x  6y  7 2 2     2 2 x  y   2 2 log
15  x  y  15  log4x  6y  6 4x  6y  6 (1).
Xét hàm số đặc trưng: y  f t  t  log t với t  0 2 Khi đó: f t 1  1 
 0, t  0  y  f t đồng biến trên t.ln2 khoảng 0;.    f  2 2 1
x  y  1 5  f 4x  6y  6 2 2
 x  y  15  4x  6y  6  x  2 y  2 2 3  4 (2).
Ta coi các cặp x;y thỏa mãn 2 là các điểm M x;y thuộc hình
tròn C  : I 2;3,R  2 ( kể cả phần nằm bên trong đường tròn đó) 2 2 Gt: 2 2
P  x  y  2x  4y  5  x  1 y   2 10 2
 AM 10 với A1;2 và IA  34  R  2
Khi đó: nên điểm A nằm ngoài đường tròn C   AM  IA R  34 2  P    2
34 2 10  28  4 34  P  28  4 34 khi M  D . min