













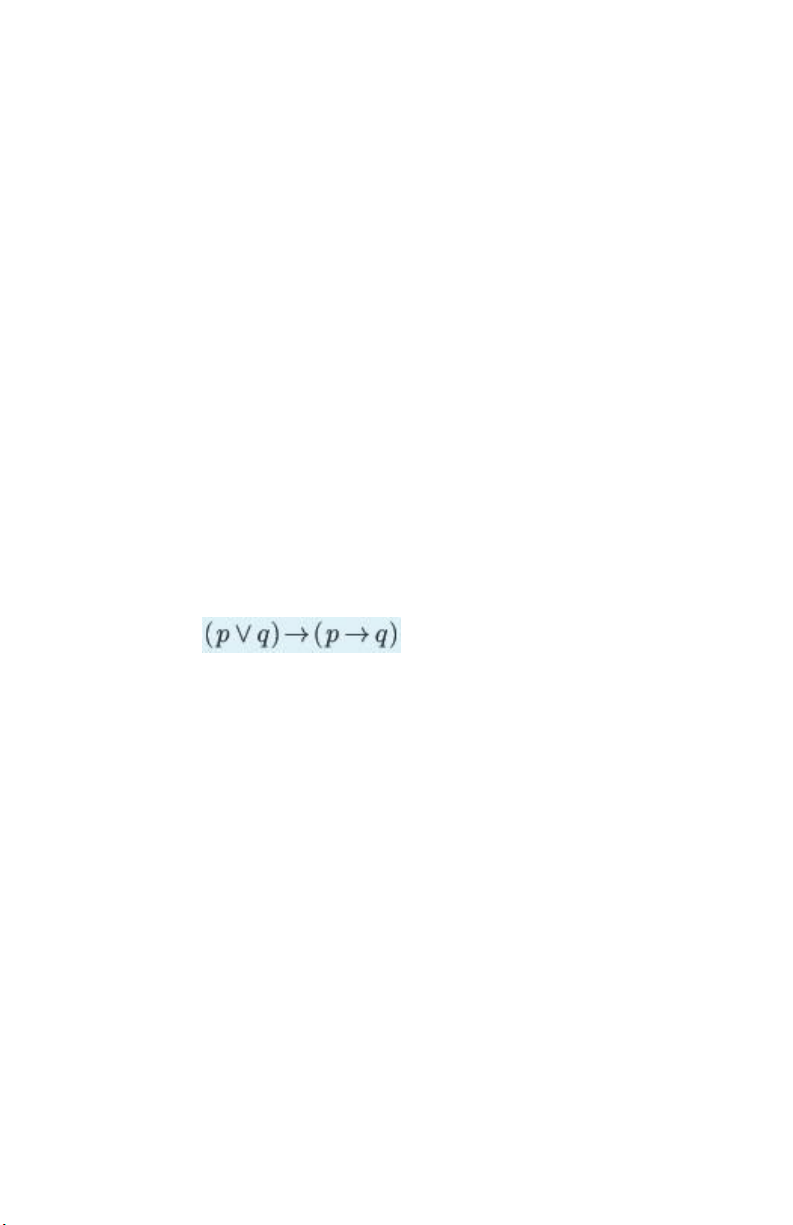







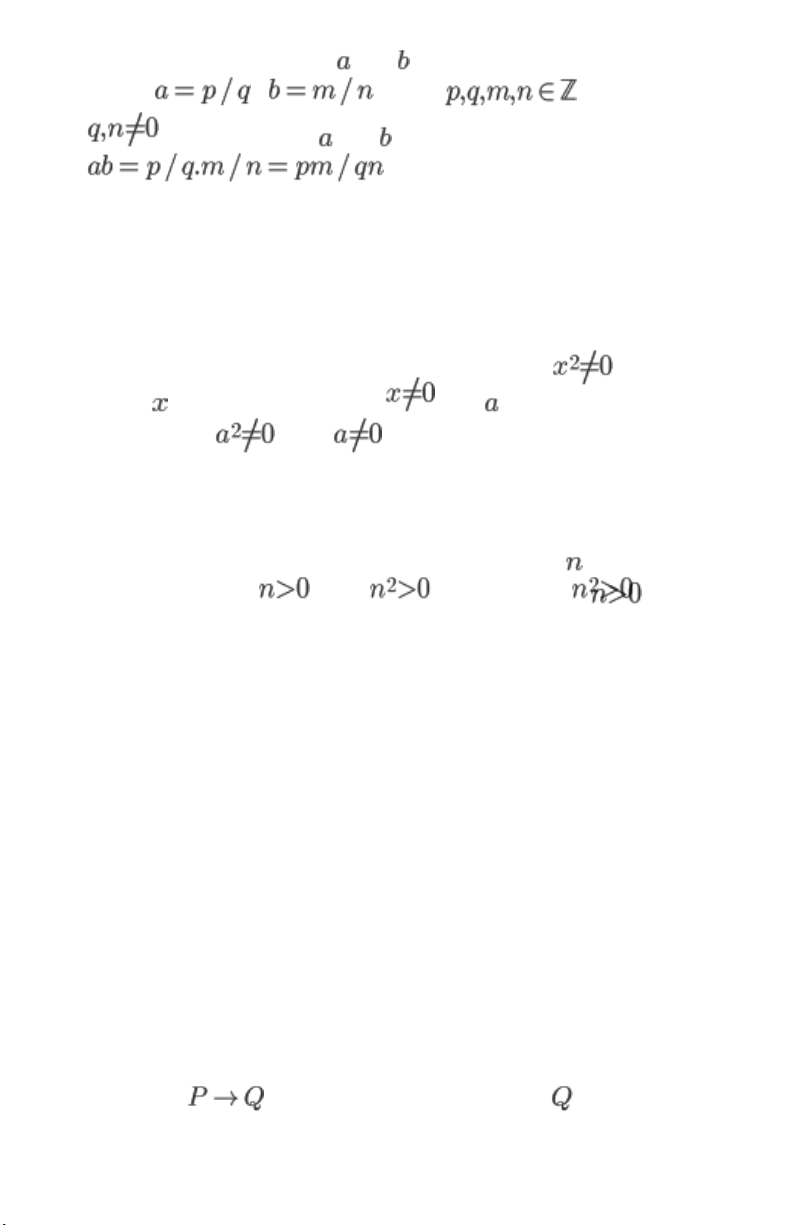









Preview text:
lOMoARcPSD| 40615597
1. What is the inverse of the conditional statement p → q? a. ¬q → ¬p b. ¬q → p c. ¬p → ¬q d. q → p
2. Which of the following propositions is true?
a. 2 is greater than 3 or 3 is a negative integer.
b. 2 Is an odd number and 3 is a positive integer
c. Today is Sunday if only if yesterday was Friday
d. It’s 5 - 2 = 0 then 5 + 7 = 10
3. If p,q,r are proposition then p∨(q∧r) is equivalent to a. (p∨q)∧r b. None of the mentioned. c. (p⋀q)⋁(p∧r) d. (p∨q)∧(p⋁r)
4. What is the negative of the statement p → q? a. p⋀¬q b. ¬q → ¬p c. q → p d. ¬p ⋁ q
5. Find the contrapositive of the following implication “If I get that job, then I am happy”
a. I do not get that job, if I am not happy
b.If I do not get that job, I am not happy
c. I get that job, if I am happy
d. If I do not get that job, then I am happy
6. Let P (x, y) denote the statement "x+y is even". If the domain
of x, y consists of all integers, which of these have truth value TRUE? a.P(3,4) b.∃xP(x,0) c.∀x P(x,0) d.∀x∀y P(x,y) lOMoAR cPSD| 40615597
7.Let P(x) be a predicate. What is the negation of ∃xP(x)? a.∀xP(x) b.None of the mentioned. c.∃x¬P(x) d.∀x¬P(x)
8.Let domain of x includes all students, P(x) be the statement x
can speak English and French fluently. Express the
quantification ∃x¬P(x) in English.
A. All students can speak English and French fluently.
B. There exists a student who can not speak English and French fluently.
C. Every student can not speak English and French fluently.D.
There is a student who can speak English and French fluently.
9. Consider the following argument: "It is a real number such
that n>3 then n2>9. Suppose that n2>9. Then n>3 1.
Determine whether the argument is correct or incorrect. ⇔ Incorrect. 2.
If it is correct, which rule of inference is used? (If it is incorrect, choose None) ⇔ None 3.
If it is incorrect, which fallacy is used? (if it is correct, chooseNone) ⇔
Affirming the conclusion 10. Match the answers.
Prove p→q is true by showing that p is false is ⇔ Vacuous Prove
p→q is true by showing that it q is false, then q must also be false is ⇔ Contradiction
Prove p→q is true by showing that it p is true, then q must also be true is ⇔ Direct.
Prove p→q is true by showing that q is true is ⇔ Trivial
11. If set A is {1,2,3,4} and A - B = 0 then set B can be A. {1,2,3} B. {1,2,3,4,5} C. None of the mentioned lOMoARcPSD| 40615597 D. {1,2,4,5}
12.What is the cardinality of the power set of this set? A = {a, {b}, {ab), {a}} ⇔ 16
13. Let A = {1,2,5,7}, B = {7,4,1,2} and C = {7,4,1,2} What is set (A-B)⋃C? A. None of the mentioned. B. {1,2,4,5,6,7,8} C. {1,2,4,7} D. {7}
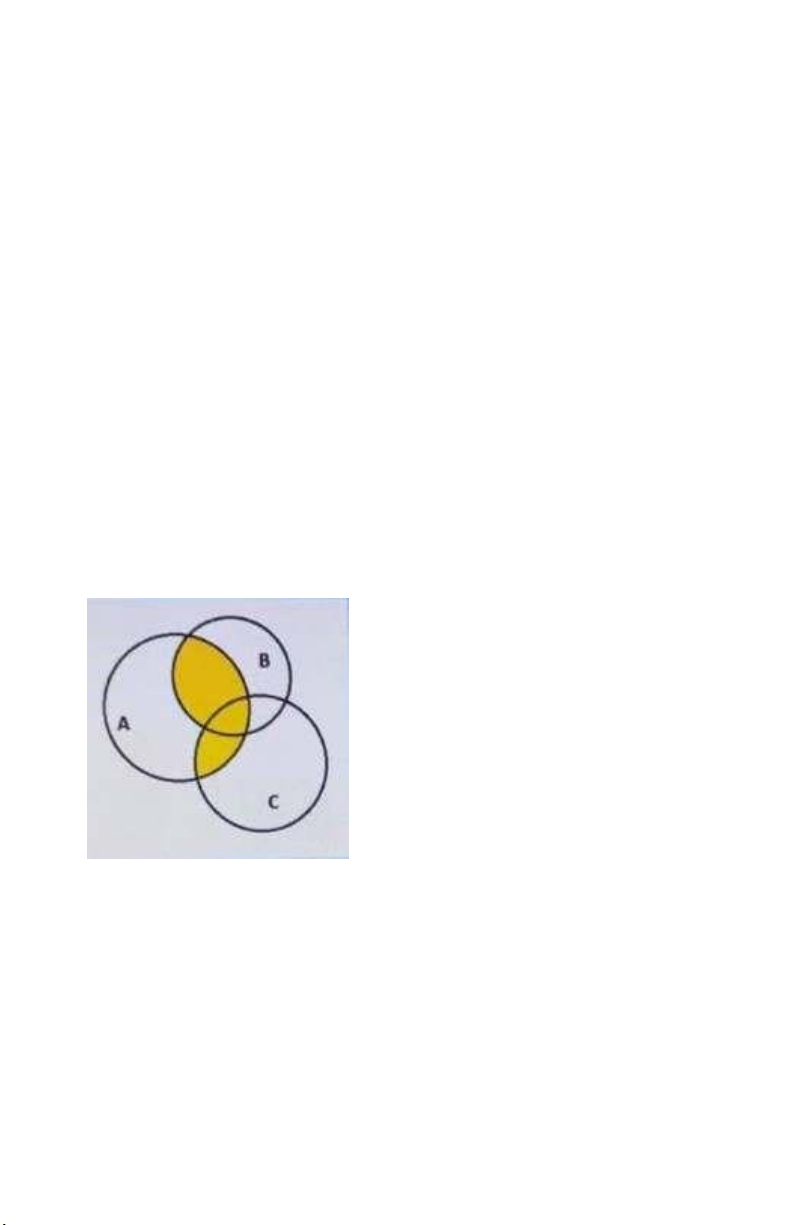
14. For two sets A and B. the set (A - B)⋂B will be A. B B. A⋂B C. A D. None of the mentioned. 15. Let A, B, C be sets
The YELLOW AREA in the above diagram represents A. A⋂B⋂C B. (B⋃C)⋂A C. (A⋂B) - C
16. What is range of the function that assigns to each natural
number its last digit? A. {0,1,2,3,4,5,6,7,8,9}
B. The set of all natural numbers N C. The set of all integers Z D. {1,2,3,4,5,6,7,8,9,10} lOMoAR cPSD| 40615597
17.Let f, g be functions from R+ to R. (R: the set of all real
numbers, R+ the set of all positive real numbers). f(x) = x g(x=
Find all one-to-one (injective) function(s) a. f and g
b. Both f and g are not injective. c. f d. g
18. Let f, g be functions from R to R (R. the set of all real
numbers). f(x) = 2x + 1 g(x) = x2 + 2
Which the following statements are FALSE? A. f is not bijective. B. g is not onto. C. g is one-to-one D. f is one-to-one,
19. Let be a function from R to R: f(x) = 2x+1, g be a function
from R to R: g(x) = x2. Then the composition of g and f is specified by a. gof(x)=2x²+1 b. gof(x)=(2x+1)² c. gof(x)=(2x+1)x²
20.At Thang Long university, each student is given a
student code. A student code is a string beginning with letter
A, followed by 5 decimal digits. How many student codes are there? a. 105 b. 50 c. 510 d. 15
21.How many bit strings are there of length six or less
(including the empty string)? a. 62 b. 64 c. Others lOMoAR cPSD| 40615597 d. 127
22.How many bit strings of length six contain at least four 1s? a.4 b. 22 c. 64 d. 15
23.List all the 2-permutations of (a, b, c). a. ab, ac, ba, bc, ca, cb b. abc c. a,b,c
d. aa, ab, ac, ba, bb, bc, ca, cb, cc
24.Which statement below is FALSE? a. C(n,r) = P(n,r).C(r,r) b. P(n,n) = n! c. C(n,r) = C(n,n - r) d. P(n,r) = C(n,r).P(r,r)
25.How many subsets with at most two elements does a set with
100 elements have? a. 101 + C(100,2) b. C(100,2) c. others d. 2100 - 101
26. Let (an) be the sequence a = 2n, n ∈ N. Which of the
following is a recursive definition of (an)? a. an = 2an - 1 (n ≥ 1) b. an = 4an - 1 (n ≥ 1). c. an= 2an - 1 + 2, (n ≥1) d. an = 4an - 2 (n ≥ 2)
27.Find the solution of the recurrence relation an = 4an-1 - 4an-2,
n∈N, n≥2 with a0 = 2, a = 8?₁ a. an = 2.2n, n ≥0 b. an = n.2n, n ≥0 c. an = 2n.2n, n ≥0
d. an = (n + 1).2n + 1, n ≥0 lOMoAR cPSD| 40615597
28.The Vietnam's GDP (GDP: Gross Domestic Product) is
predicted to grow by 7% annually. Know that the Vietnam's
GDP of 2020 is G0 = 400 (billions dollars). Let Gn, be the GDP n year(s) after 2020.
a. Gn = 1.07Gn - 1 (n≥1) and Gn = 400 x 1.07n
b. Gn = 1.07Gn - 1 (n≥1) and Gn = 400 x (1.07+n).
c. Gn = 400 + 1.07Gn - 1 (n≥1) and Gn = 400 × 1.07n
29. Find f(4) if f is defined recursively by f(0)=0, f(1)=2,
f(n)=2f(n-1) - f(n-2), n≥2 a. 6 b. 8 c. 9 d. 10
30.Let P(n) be the statement that 2+2.3+2.3²+...+2.3n = 3n + 1 - 1
for the positive integer n. We want to prove P(n) is true for all
nonnegative integer in by induction. Basis step. We prove that
P(1) is true. What is P(1)? a. P(1) = 2 b. P(1):2+2.3 = 3² - 1 c. P(1):2 = 3¹-1 d. P(1) = 2+2.3
31.We are going to use the induction method to prove that n! <
nn for all n being integers greater than 1. What do we do in the first step? a. Show that P(1) is true. b. Show that P(3) is true c. Show that P(2) is true. d. Show that P(0) is true.
32.If p, q, r are propositions, then (p→g)⋀(p→r) is logically equivalent to: A. p V (q⋀r) B. p ⋀ (qVr) C. p → (q⋀r) D. p → (qVr)
33. Which of these sentences are propositions?
A. Are online lessons convenient? lOMoAR cPSD| 40615597
B. x2 + 1 > 0, where is a real number.
C. x + y = 7, where x, y are integers. D. 6 + 4 ≠ 10
34. Which of the following proposition is NOT true?
A. Yesterday is Sunday if only if today is Monday.
B. 4 - 3 = 1 if and only if 2 + 2 = 5.
C. 4 is an odd number or 2 is a prime.
D. If 3 - 1 = 1, then 2 < 1.
35.Let p, q, r be propositions. Which of the following statements are true?
A. ¬(p⋀g) ≣ (¬pΛ¬g) B. All of the mentioned. C. (p⋁q) V r ≣ pV(q V r) D. pVq ≣ qVp
36.Which of the following statements is the negation of the
statement "4 is even and 10 is negative"?
A. 4 is odd and 10 is not negative
B. 4 is even or 10 is not negative
C. 4 is odd or 10 is not negative
D. 4 is even and 10 is negative
37.Let p be the statement "You keep your textbook" and q the
statement "It will be a useful reference in your future courses."
What the following statements is the expression of p→q: A. None of the mentioned. B.
If it will be a useful reference in your future courses, then you keep your textbook. C.
You keep your textbook when it will be a useful
reference in your future courses. D.
Your textbook will be a useful reference in your future courses if you keep it.
38.Let Q(x) denote the statement “x2 + 1 > 2x". If the domain
consists of all integers, which of these is NOT true? lOMoAR cPSD| 40615597 A. ∃xP(x) B. P(2) C. ∀xP(x) D. P(0)
39.Let P(x,y) be a predicate. What is negation of ∀x∀yP(x,y)? A. ∃x∃yP(x,y) B. ∀x∀yP(x,y) C. None of the mentioned D. ∃x∃y¬P(x,y)
40.Let P(n) be the proposition "If a and are positive real
numbers, then (a+b)n ≥ an + bn. Prove that P(1) is true. What kind of proof did you use? A. Direct Proof B. Vacuous Proof C. Proof by contraposition D. Trivial Proof
41.Suppose that M, N are sets. How many rows are there in the
membership table which contains M, N, ∅ (the empty set) and
does not contain any other sets? a. 8 b. 3 c. 2 d. 4
42.How many elements does the set have? P({∅, 0, {0}}) Answer: 8
43.Let A, B be sets. If the quantification ∀x(x∈A → x∈B) ⋀
∀x(x∈B → x∈A) is true where the domain of x is the universal set: a. A ⊆ B and B ⊆ A b. A ∈ B and B ∈ A C.A = B d. P(A) = P(B)
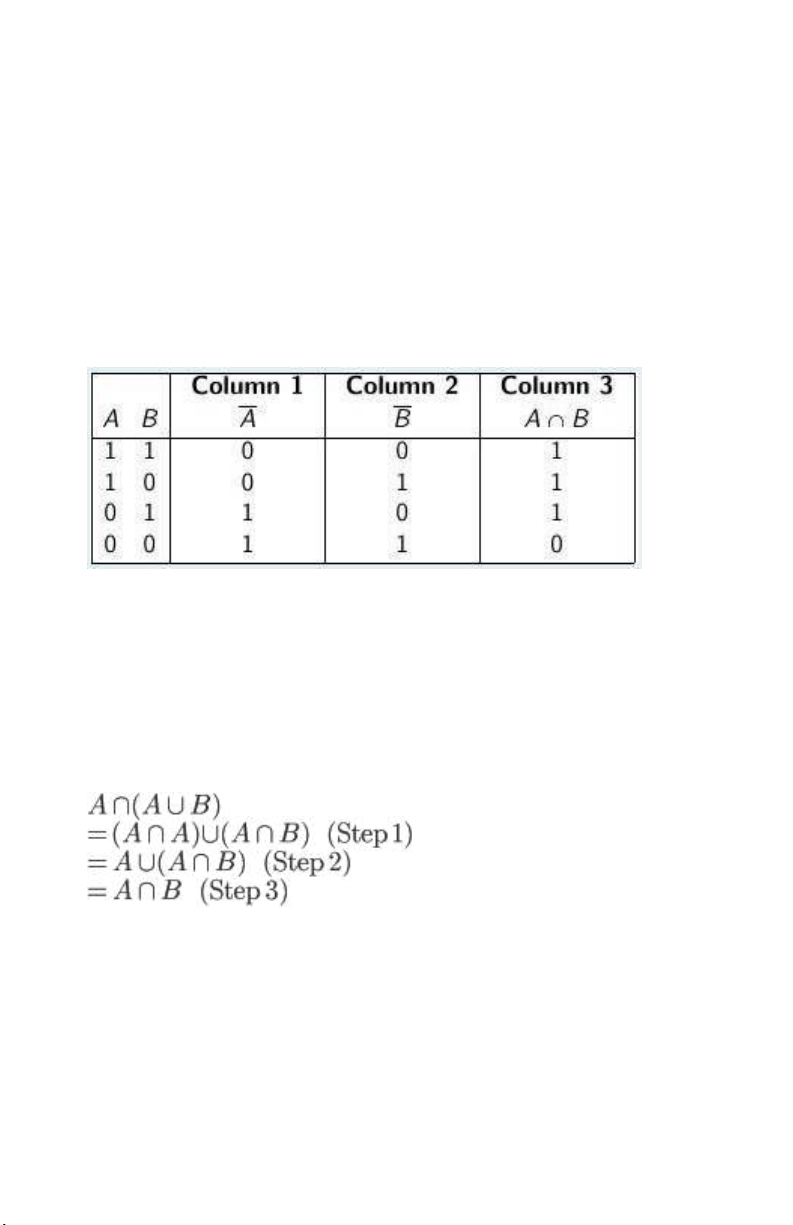
44.Given that A, B are two sets. Among the steps below, which one is FALSE? lOMoARcPSD| 40615597 A∩(A⋃B)
= {x|x∈A ⋀ (x∈A ⋁ x∈B)} (Step1)
= {x|(x∈A ⋀ x∈A) ⋁ x∈B} (Step 2)
= {x|x∈A ⋁ x∈B} (Step 3) = A ⋃ B (Step 4) a. Step 1 b. Step 3 c. Step 2
45.The shaded area of the figure is best described by? A. B - (A⋂B) B. A ⋂ B ⋂ C C. (B - A) - C D. B - (C ⋂ B)
46.Let f be a function from {a, b, c, d, e} to {1, 2, 3, 4, 5}, f(a) =
2, f(b) = 4, f(c) = 2, f(d) = 4, f(e) = 5. What is f({a, c, e})? a. {2,5} b. {1, 3, 4} C. {2,4} d. {2, 4, 5}
47.Let f be functions from R+ to R+ (R+: the set of all positive real numbers). f(x) =
Which the following statement is true? A. f is one-to-one. B. f is bijective. C. f is onto. lOMoAR cPSD| 40615597 D. f is not a function.
48.Let f, g be functions from Z to Z: f(x) = [x2] g(x) = x + 1. Then a. fog(x) = [x+1] b. fog(x) = [x²]+1 c. fog(x) = [(x+1)²]
49.How many strings of length 10 can be made from the
lowercase letters of English alphabet? a. 2610 b. 260 c. 1026 d. others
50.How many bit strings of length six begin or end with two 1s? a. 28 b. 4 c. 64 d. 32
51.How many bit strings of length 20 contain exactly seven 0s? a. 27 b. C(20,7) c. P (20,7) d. 220
52.List all the bit strings of length three. a. 100,010, 001 b. 11, 10, 01, 00 c. 111,000
d. 111, 110, 101, 100, 011, 010, 001, 00053. C(n, k) = a. b. C(n, n - k) c. d. n! k!
54.Which statement below is FALSE? a. C(n,r) = P(n,r).C(r,r) lOMoAR cPSD| 40615597 b. P(n,n) = n! c. C(n,r) = C(n, n - r) d. P(n,r) = C(n,r).P(r,r)
55.How many lowercase letter strings of length 10 which start
with a or end with yz? (Note that the English alphabet has 26 letters) a. 269 +268
b. None of theseC. 269 +268 - 267 d. 267
56.Let {a} be the sequence an = 3*n!, n∈N. Which of the
following is a recursive definition of (an}? a. an = n!.an - 1, n ≥ 1 a0 = 1 b. a , n ≥ 1 a n = n + an - 1 0 = 3 c. a , n ≥ 1 a n = n.an - 1 0 = 3 d. a , n ≥ 1 a n = n! + an - 1 0 = 1
57.What is the solution of the recurrence relation an = n.an - 1, n∈N with a = n!, n ≥0 0 = 1? a. an b. a = 2.n!, n≥0 n c. a = n, n≥0 n d. an = n(n-1), n≥0
58.Assume that the population of the world in 2000 was 6
billion and is growing at the rate of 1.3% a year. Set Pn is the
population of the world n years after 2000. What is recurrence relation for Pn? A. P + 6, n≥1 n = 1.013Pn-1 B. P , n≥1 n = 0.013Pn-1 C. P , n≥1 n = 1.013Pn-1 D. P + 6, n≥1 n = 0.013Pn-1
59.Let (a ), n≥0 be a sequence defined as follows n a + 2, (n ≥2) and a n = an-2 0 = 0, a = 1.₁
What are a2, a3, a4 respectively? a. others b. 1, 2, 3 lOMoAR cPSD| 40615597 c. 3, 5, 7 d. 2,3,4
60.Suppose that we are using the induction method to prove that
P(n) is true for every n≥1. Recall that in the inductive step: for
each k ≥ 1, we prove that if P(k) is true, then P(k+1) is true as well.
What is called the inductive hypothesis?
a. The assumption that P(1) is true.
b. The conclusion that P(k+1) is true. c. None of these.
d. The assumption that P(k) is true.
61.How many onto (surjective) functions from a set with 5
elements to a set with 10 elements are there? Answer: 510 = 9765625 ĐỀ THI THỬ
How many license plates consisting of three letters followed by
three different digits? a. P(26,3). P(10,3) b. P(26,3). 103 c. 263. P(10,3) d. 263. 103
What is the coefficient of X6 in the expansion of (1 - 2x)10? a. 26.C(10, 6) b. -26.C(10, 6) c. C(10, 6) d. 26
The union of two sets {1, 2, 5} and {1, 2, 6} is the set: a. {1, 2, 5, 6} b. {1, 2, 1, 2} c. {1, 5, 6, 3} d. {1, 2, 6, 1}
Let p, q and r be propositions. Construct a proposition which is
true if and only if p and q are true and r is false a. (p ⋀ q) ⋁ r b. p ⋀ q ⋀ r lOMoAR cPSD| 40615597 c. (p ⋀ q) → ¬r d. p ⋀ q ⋀ ¬r
List all the permutations of {x,y,z} a. xyz, xzy, yxz, yzx b. xy, xz, yx, yz, zx, zy
c. xyz, xzy, yxz, yzx, zxy, zyx d. x, y, z
Which of the following is the definition of the sequence of Fibonacci numbers?
a. fn = fn - 1 + fn - 2, f0 = 0, f1 = 1
b. fn = fn - 1 + fn - 2, f0 = 0, f1 = 2
c. fn = fn - 1 + 2fn - 2, f0 = 0, f1 = 1
d. fn = fn - 1 - fn - 2, f0 = 0, f1 = 1
Let f be the function that assigns to a bit string the number of bits in the string. What is f(110110000)? a. 5 b. 4 c. 8 d. 9
What is the solution of the recurrence relation an = an - 1 + 3,
n∈N, n≥1 with a0 = 2, in which N denotes the set of natural numbers. a. an = 2.3n, n≥0 b. an = 2 + 3n, n≥0 c. an = 3n, n≥0 d. an = 2, n≥0
Let P(y) be the statement "y = y3". If the domain is the set of all
the integers. Which of the following is true? A. P(2) B. ∃y P(y) C. P(5) D. ∀y P(y) lOMoARcPSD| 40615597
A model for the number of lobsters caught per year is based on
the assumption that the number of lobsters caught in a year is
the average of the number caught in the three previous years.
Find a recurrence relation for {Ln}, where Ln is the number of
lobsters caught in year $n$, under the assumption for this model.
Let T(x) be the statement “x has visited Tokyo”, where the
domain consists of the students in your class. Express the
statement ∃xT(x) in English.
A. "Every students in your class have visited Tokyo."
B. "Lan (your classmate) has visited Tokyo."
C. "No student in your class has visited Tokyo."
D. "Some student in your class has visited Tokyo."
Let $f$ be the function defined by f: Z → Z, f(n) = 2n + 5, in
which Z denotes the set of all integers. f is one-to-one
Calculate the value of C(10,0) + C(10,1) + ... + C(10,10) a. 1025 b. 1000 c. Other d. 1024 Let P(n) be the statement
for positive integer n. To prove P(n) is true for all positive
integer n by induction, what do we do in the basis step? a. Show that P(2) is true lOMoARcPSD| 40615597
b. Assume that P(k) is true for an arbitrary positive integer $k$
and then show that P(k+1) is true c. Write down P(1) d. Show that P(1) is true
How many bit strings of length 10 contain exactly six 1s? a. 210 b. 26 c. C(10, 6) d. 24
How many bit strings of length 6 start with bit 1 or end with bit 0? a. 26 b. 25 c. 24 d. 26 - 24
Consider the recurrence relation an = an - 1 + 3, n∈N, n≥1, with a0
= 1, in which N denotes the set of natural numbers. Find the value of a3. a. 15 b. 4 c. 19 d. 10
Determine if the following argument is valid or not. ”Phong will
work in an enterprise this summer. Therefore, this summer
Phong will work in an enterprise or he will go travelling.” A.It is not a valid argument. B. It is a valid argument.
A ....... is an unordered collection of objects. A. sequence B. proposition C. set D. function Let P(n) be the statement lOMoARcPSD| 40615597
for positive integer n. To prove P(n) is true for all positive
integer n by induction, what do we do in the inductive step? a. Show that P(2) is true
b. Assume that P(k) is true for an arbitrary positive integer $k$
and then show that P(k+1) is true c. Show that P(1) is true d. Write down P(1)
Which of the following statements is the negation of the
statement: "Jane is young and charming" ? A. "Jane is
not young but she is charming."
B. "Jane is not young and she is not charming."
C. "Jane is young but she is not charming."
D. "Jane is not young or she is not charming."
A compound proposition that is always ..............is called a tautology. A. false B. true
How many rows appear in the truth table for the compound proposition ? A. 8 B. 6 C. 7 D. 4
Let p, q and r be the the propositions
p : We should be honest. q : We
should be dedicated . r : We should be overconfident.
Write the following proposition using p, q and r and logical
connectives: "We should be honest or dedicated but not overconfident." lOMoARcPSD| 40615597
How many elements in the power set of the set A = {-1, 0, 1}? a. 9 b. 4 c. 3 d. 8 Let p, q be propositions,
is called a/an ................. . A. contingency B. tautology C. contradiction D. equivalence
What is the solution of the recurrence relation an = 4an - 1 - 4an - 2,
n∈N, n≥2, with $a_0=1,a_1=4$?
What is the name of the set identity: A ∩ B = B ∩ A? a. Associative law b. Domination law c. Commutative law d. Complement law
Which of the following proposition is true?
p : 5 + 3 = 18 or 5 is a negative integer. q : lOMoARcPSD| 40615597
3 + 3 = 10 if 5 - 3 = 2. r : 1 > 3 and 3 < 6 s : Pigeons can fly. A. p B. s C. q D. r
Let f be the function defined by f: R → Z, , in
which R, Z denote the set of real, integer numbers respectively.
What is the image of the set A = {-2, 1, 2} under the function f?
The compound propositions and are called logically equivalent
if ............... is a tautology.
Which of the following is a proposition? A. Take the dog for a walk. B. . C. How are you feeling today?
D. There is an integer such that . Which of the following is a tautology? A. lOMoARcPSD| 40615597 B. C. None of the mentioned D. is a ............ A. contradiction B. tautology C. none of the mentioned D. contingency What is the negation of ? A. B. C. D.
The negation of the statement "It's cold but it's not snowing today. " is
A. It's not cold or it's not snowing today.
B. It's not cold or it's snowing today.
C. It's snowing but it's not cold today.
D. It's not cold and it's snowing today. is a ............ A. contingency B. none of the mentioned C. contradiction D. tautology
Which of the following is logically equivalent to ? A. B. C. lOMoAR cPSD| 40615597 D. If
is any statement, then which of the following is a tautology? A. B. C. D.
Which of the following is NOT tautology? Select one: A. B. C. D.
“The sum of two negative real numbers is negative.” Is given by? A. B. C. D.
Determine the truth value of statement if the domain consists of all integers. A. False B. True lOMoARcPSD| 40615597
Let , be the following propositional functions: = "Student passes this test."
= "Student studies hard for this test." where
the domain consists of the students in your class. Express the following using , and logical
connectives with quantifier: "Not all students who passed the test did study hard for it." A. B. C. D. In the statement , is the ..........., is is the the ............ and ................
A.Variable, quantifier, predicate
B.Quantifier, predicate, variable
C.Predicate, variable, quantifier
D.Quantifier, variable, predicate Let ,
be the following propositional functions:
= "Student passes this test."
= "Student studies hard for this test." where the
domain consists of the students in your class. Express the following using , and logical
connectives with quantifier: "Not all students will pass the test." A. B. C. D. lOMoARcPSD| 40615597 Let denote “ ”. What is the truth value of the quantifications if the
domain consists of all integers. A.True B.False "Everyone wants to learn
mathematic.” This argument may be true for which
domains? A.All students in your mathematic class B.None of the mentioned
C.All the mathematical learning students in the world D.Both of the mentioned
Use quantifiers and predicates with more than one variable
to express, “There is a student in this class who
has taken at least one course in Discrete Maths.” A.
, where is “ has taken ,” the domain for
consists of all student in this class, and
the domain for consists of all Discrete Maths lectures. B.
, where is “ has taken ,” the domain for
consists of all Discrete Maths lectures,
and the domain for consists of all student in this class. C. , where
is “ has taken ,” the domain
for consists of all student in this class,
and the domain for consists of all Discrete Maths lectures. D. , where is “ has taken ,” the
domain for consists of all student in this class, and the domain
for consists of all Discrete Maths lectures. Determine the truth value of if the domain consists of all real numbers. A.True B.False lOMoARcPSD| 40615597 Let denote the statement “ ”. Which of these have truth value true? A. B. C. D.
A proof covering all the possible cases, such type of
proofs are known as A. Direct proofs B.Vacuous proofs C.Exhaustive proof D.Contrapositive proofs
To prove the statement: ‘There exists a real number such that is irrational and is rational’, we show that there is
satisfying that is irrational and is
rational. Which proof has been used? A.Existence Proof B.Proof by contradiction C.Direct Proof D.Indirect Proof
Given the following statements and the conclusion:
i) If the ice cream on the table is vanilla-flavored, then I
will eat it. ii) I ate the ice cream on the table. iii)
Conclusion: The ice cream is vanilla-flavored.
The conclusion is ..............., using the .................
A.a fallacy; fallacy of denying the hypothesis
B.logical; rule of inference modus ponens
C.a fallacy; fallacy of affirming the conclusion
D.logical; rule of inference modus tollens
To show that “The product of two rational numbers is
rational”, we assume that and are rational, which lOMoARcPSD| 40615597 means , where and . The product of and is then and hence it is rational. Which proof has been used? A.Proof by contradiction B.Direct proof C.Indirect proof D.Trivial proof
Determine wether these are valid arguments. "If
where is a real number, then . Let be a real number with , then . " A.It's valid. B.It's not valid.
Determine whether these are valid arguments. "If is real number such that , then . Suppose that . Then ." A. It's valid. B.It's not valid.
“Peter goes out with friends or it is not sunny” and “It is sunny
or Paul is playing soccer” imply that
A.Peter go out with friends and Paul is playing soccer. B.Peter go out with friends. C.Paul is playing soccer.
D.Peter go out with friends or Paul is playing soccer.
Which rule of inference is used in each of these
arguments, “If it's holiday, then the university will be
closed. The university is not closed today. Thus, it's
not holiday today.” A.Disjunctive syllogism B.Modus tollens C.Modus ponens D.Simplification Proof that
is true based on the fact that is true,
such proofs are known as A.Trivial proofs lOMoARcPSD| 40615597 B.Contrapositive proofs C.Vacuous proofs D.Direct proofs
Let A, B be sets. Find the set A if A-B={1, 3, 5}, B-A={4, 6, 8}, ={0, 2}. a. A={0, 1, 2, 3, 5} b. A={1, 3, 4, 5, 6, 8} c. A={0, 2, 4, 6, 8} d. A={2, 4, 6, 8}
Find a pair of EQUAL sets among the sets given below. A= {a, b, {a}, {b}, {b}}
B={a, b, a, {b}, b} C={{a}, b, a, b, b} D={{a}, b, a, {b}, b} a. B, 1 b. A, 3 c. A, 3
Let A, B be two arbitrary sets. Which of the following
transformation steps is FALSE? a. Step 1 b. Step 3 c. Step 2
In the following membership table, which column is FALSE? lOMoARcPSD| 40615597 a. Column 3 b. Column 1 c. Column 2
Let A be a set with 5 elements, B be a set with 8 elements.
Assume that A and B have 3 elements in common. How
many elements does the set A-B contain? Answer: 2
In the following membership table, which column is FALSE? a. Column 1 b. Column 3 c. Column 2
How many members of the power set of {a, b, c} are there? Answer: 8
Which one of the following transformation steps is FALSE? (A, B are 2 arbitrary sets) a. Step 2 b. Step 1 c. Step 3
How many elements does the Cartesian product of a set A
with 10 elements and a set B with 20 elements have? Answer: 200 lOMoARcPSD| 40615597
Let A, B be sets. Find the set A if A-B={a, b, c}, B-A={d, e, f}, ={a, b, c, d, e, f}.
(Hint: drawing the Venn diagram may help you) a. A={d, e, f} b. A={a, b, c} c. A={a, b, c, d, e} d. A={a, b, c, d, e, f} Let f be a function from X to Y. Suppose that f(x)=y. Then 1) x is the preimage of y. 2) y is the image of x. 3) X is the domain of f. 4) Y is the codomain of f.
Which one of the above statement is FALSE? a. Statement 3
b. None of the statements is false. c. Statement 4 d. Statement 2
Let f, g be functions from Z to Z (Z: the set of all integers). f(n)= g(n)=
List all function(s) which is/are one-
to-one (injective). a. f and g are not injective. b. f, g c. g d. f
Let f be a function from R to R: f(x)=2x+1, g be a function from R to R: .
Then the composition of g and f is specified by a. lOMoARcPSD| 40615597 b. c.
Let f be a function from {a, b, c, d, e} to {1, 2, 3, 4, 5},
f(a)=2, f(b)= 4, f(c)=2, f(d)=4, f(e)=5. What is f({a, c, e})? a. {2, 4} b. {2, 5} c. {2, 4, 5} d. {1, 3, 4}
Given that f is a function from R to R: f(x)= x-2. Then
The INVERSE function of f is specified by a real number. What is this real number? Answer: 2
Let f, g be functions from R to R (R: the set of all real numbers). f(x)= x g(x)=
Find all onto (surjective) function(s). a. g b. f and g c. f
d. None of the given function is surjective.Let f be a function
from R to R (R: the set of all real numbers) and . Find f({-3, -2, -1, 0, 1}). a. {0, 1, 4, 9} b. {9} c. {-3, -2, -1, 0, 1} d. {0, 4, 9}
Let f, g be functions from {1, 2, 3, 4, 5} to {1, 2, 3, 4, 5}.
f(1)=2, f(2)=3, f(3)=4, f(4)=4, f(5)=5, g(1)=2, g(2)=1, g(3)=4, g(4)=3, g{5)=5. lOMoARcPSD| 40615597
Find all one - to - one (injective) function(s)! a. g
b. None of the given functions is one-to-one. c. f d. f and g
Assume that f, g are two functions: f : {Tung, Tuan, Tan, Tren} {7, 8, 9}
f(Tung)=7, f(Tuan)=8, f(Tan)=9, f(Tren)=8 g: {7, 8, 9} {Medium, Good, Excellent}
g(7) = Medium, g(8)=Good, g(9)= Excellent Find (Tuan). Select one: a. Excellent b. Medium c. None of these d. Good Let f, g be functions from to R.
(R: the set of all real numbers, : the set of all
positive real numbers). f(x)= x g(x)=
Find all one-to-one (injective) function(s). a. g b. f and g
c. Both f and g are not injective. d. f
Let f, g be functions from {a, b, c, d} to {1, 2, 3, 4, 5}.
f(a)=2, f(b)=3, f(c)=4, f(d)=5,
g(a)=2, g(b)=5, g(c)=4, g(d)=3.
Find all onto (surjective) function(s)! a. f and g
b. None of the given functions is onto. c. g d. f lOMoAR cPSD| 40615597 1.
what is the solution of the recurrence relation a n
=1+ an-1,n∊N,n≥1 with a0 =3 B. a =n+3, n≥1 n
2. let (an) be the sequence an=n2, n∈N, which of the
following is a recursive definition of (an)? C. an=an- 1+2n-1, n≥1 a0=0
3. the number of r combinations of a set consisting of n (rb.
4. suppose that we are using the induction method to
prove that P(n) is true for every n≥1. in the inductive
step: for each k≥1, suppose that if p(k) is true, what do we do next? b. we prove P(k+1) is true
5. let (an) be the sequence an=4n, n∈N. which of the following is
a recursive definition of (an)? a. a , n≥1 a n=4.an-1 0=1
6. let P(n) be the statement that 2+2.3+2.32+....
+2.3n=3n+1-1 for the positive integer n. we want to
prove P(n) is true for all nonnegative integer n by
induction basis step. we prove that P(n)is true. what is P(1)? b. P(1):2+2.3=32-1
7. which of these statements is true if the domain consists of all integers. a. none of the mentioned
8. find all the true statements among the statements below 1, {∅}⊆{x,∅} 2, {(х)}⊆{x,Ø} 3, Ø∈{х,Ø} b. statement 1 and 3
9. from a group of 8 men and 6 women, 3 people are
selected to form a committee so that at most 1 woman lOMoAR cPSD| 40615597
is on the committee. In how many ways can it be done? b. others 10.
what is the coefficient of x3in(x-1)10? c. 0
11. let (a ), n≥0 be a sequence which is defined n recursively by: a +1(n≥1) What are the 0=2, an=a2n-1
values of a1,a2,a3 respectively? c. a1=5,a2=26,a3=677
12. Nhìn k rõ nhưng đáp án là Incorrect none fallacy….
13. let P(n) be the statement that 2+2.3+2.32+...
+2.3n=3n+1-1 for the nonnegative integer n we want to
prove P(n)is true for as nonnegative integer n by
induction inductive step. for any nonnegative integer
k. assume that P(k) is true, that is 2+2.3+2.32+...
+2.3k=3k+2-1 then we show that P(k+1) is true. What is P(k+1)?
a. 2+2.3+2.32+...+2.3k+1=3k+2-1
14. given that f is a function from R to R: f(x)=x-2. then the
INVERSE function of f is specified by f-1(y)=y+a real
number. what is this real number đáp án: 2
15. let A,B be sets if the quantification
∀x(x∈A→х∈B)Λ∀x(x∈B→x∈A) is true where the
domain of x is the universal set, choose all true statements a. P(A)=P(B) c. A⊆B and В⊆A d. A=B
16. Which one below is the cartesian product of two sets? b. {(1,a),(2,a),(3,a),(1,b)}
17. let P(x)be “x is perfect”. translate the following statement
into logical expression using predicates
logical connectives “no one is perfect” lOMoARcPSD| 40615597 B. 가∃xP(x) 18. let A,B,C be sets
the YELLOW AREA in the above diagram represents a. A∩(ВUC)
19. which of these statements is true if the domain consists of all real numbers b. ∃x(x4=x2)
20. let P(x) be a predicate. what is the negation of ∃xP(x)? d. ∀x ㄱ P(X) 21.
Let p,b propositions. Which of the following ways
DOES NOT express the conditional statement p→q? b. if q,p d. p or q
22. Assume p is true, q is false and ris false. Which of the following is true? a q↔(PΛr)
23. Let p, q be propositions. Which of the following ways
express the biconditional statement p↔q? b. p iff q
d. p is necessary and sufficient for q 24.
let P(x) be a predicate. when is ∃xP(x) false ? lOMoAR cPSD| 40615597 d. P(x) is false for every x
25. If p, q are propositions, then pΛq is logically equivalent to: a. ㄱ(p→가 q)
26. The negation of the statement "It is humid or rainy today" is Select one:
A. it is not humid and it is not rainy today
27. The negation of the statement "3 is a prime or 8 is not
divisible by 3" is Select one:
A. 3 is not a prime and 8 is divisible by 3
28. Which of these statements is false if the domain consists of all integers. c. ∃n(n2=2) d. ∀n(2n>n)
29. Let domain of x include all students, P(x) be the statement
``x can speak English and French fluently". Express the
quantification ∃r 가 P(x) in English.
D. There exists a student who can not speak English and French fluently. 30.
Let f, g be functions from Z to Z(Z the set of
all integers). f(n)=「2] g(n)=]
List all functions) which is/are one-to-one (injective). a. f
32. Let p: This open software is great, q: You
should not use it. Then This open software is
great and you should use it' is best represented by: d. P∧가 q
33. Let pg and r be the propositions: p: Bears
have been seen in the area. q Hiking is safe
on the trail. r:Berries are ripe along the trail. lOMoAR cPSD| 40615597
Write the following proposition using p.q.r and logical
connectives "Bears have not been seen in the area and
hiking on the trail is safe, but berries are ripe along the trail." C. 가 p⋀q∧r
34. If p, q are propositions,then 가(рVq)Λ(pq) is a⋯ d. contradiction
35. Let f, g be functions from (a, b, c, d) to (1, 2, 3, 4, 5).
f(a)=2, f(b)=3, f(c)=4, f(d)=5,
g(a) =2, g(b)=5, g(c)=4, g(d)=3. Find all onto (surjective) functiont(s)!
d. none of the given function is onto
36. Suppose that f is a function from Z to Z (Z: the set of all
integers), f(x)= ] Find f((1, 2, 3, 4). a. (0,1,2)
37. Assume that f, g are two functions: 1:
(Tung, Tuan Tan, Tren)->(7, 8, 9)
f(Tung)=7, f(Tuan) =8, f(Tan)= 9, f(Tren)= 8
g: (7, 8, 9) → (Medium, Good, Excellent)
g(7)=Medium, g(8)= Good, g(9)=Excellent Find go ∫(Tuan). b. good
38. How many bit strings of length six contain at least four 1s? c. 4
39. List all the permutations of (a, b, c).
a. abc, acb, bac, bca, cab, cba
40. We are going to use the induction method to prove
that n!What do we do in the first step? b. show that P(2) is true

