Tập san Toán học số 02

Tài liệu gồm 131 trang, là cuốn Tập san Toán học số 02 do quý thầy, cô giáo Nhóm Giáo Viên Toán Việt Nam biên soạn. Hy vọng Tập san sẽ là sân chơi để quý thầy cô trao đổi kinh nghiệm dạy học cùng các đồng nghiệp thông qua các bài viết của mình; các em học sinh nắm chắc các kiến thức trong chương trình THPT; tiếp cận được với các bài toán mới, hay và lạ.

36 18 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu ôn thi THPTQG môn Toán

Môn: Toán

Thông tin:

131 trang 8 tháng trước

Tác giả:

Profile H. Phượng
https://www.facebook.com/groups/toanvd.vdc
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Tập san
Đổi mới kiểm tra đánh giá theo định hướng
phát triển năng lực người học
Đề xuất cho kỳ thi tốt nghiệp THPT
Trao đổi kinh nghiệm dạy học theo định hướng
tiếp cận năng lực người học
Bàn về một cách tiếp cận khác cho bài toán tính góc giữa đường
thẳng và mặt phẳng
Toàn cảnh đề thi tốt nghiệp THPT môn Toán
Lời giải chi tiết các câu VD – VDC các mã đề gốc 101, 102, 103, 104
Ôn thi tốt nghiệp THPT đợt 2 môn Toán
Phân tích, định hướng tìm lời giải, xây dựng các bài tương tự
các câu VD – VDC
ĐỀ THI TỐT NGHIỆP THPT ĐỢT 1 NĂM 2021
Số 02
8 - 2021
https://www.facebook.com/groups/toanvd.vdc Trang 1
Lời nói đầu
Kỳ thi tốt nghiệp THPT đợt 1 năm 2021 đã diễn ra trong hai ngày 7,8/7/2021.
Buổi thi môn Toán diễn ra vào chiều 7/7/2021, bài thi môn Toán gồm 24 mã đề được lấy
từ 4 mã đề gốc là mã đề 101, 102, 103, 104. Để có góc nhìn đầy đủ vể bài thi môn Toán đợt
1, đồng thời giúp các em học sinh tham gia kỳ thi tốt nghiệp THPT đợt 2 năm 2021 cùng
quý thầy cô có thêm tài liệu ôn tập trong thời gian gấp rút này Nhóm Giáo viên toán Việt
Nam xin trân trọng giới thiệu, ra mắt cùng quý thầy cô và các em ấn phẩm Tập san số 02.
Hy vọng Tập san sẽ là sân chơi để quý thầy cô trao đổi kinh nghiệm dạy học cùng các
đồng nghiệp thông qua các bài viết của mình; các em học sinh nắm chắc các kiến thức trong
chương trình THPT; tiếp cận được với các bài toán mới, hay và lạ. Đặc biệt, rèn luyện tốt
kỹ năng làm bài thi trắc nghiệm môn Toán.
Để hoàn thành Tập san, BQT chân thành cám ơn tất cả các thành viên của nhóm,
hai tổ phản biện đã rất tâm huyết tham gia, xây dựng Tập san.
Trân trọng cám ơn TS Trần Nam Dũng, Ths Hoàng Quân đã tham gia viết bài
cho Tập san và có nhiều đóng góp ý kiến xây dựng cho ban biên tập
Tài liệu tuy đã được nhóm tổ chức làm cẩn thận, phản biện nhiều lần, nhưng không thể
tránh khỏi thiếu sót. Chúng tôi rất mong nhận được ý kiến đóng góp tích cực từ quý thầy cô
cùng các em học sinh. Các ý kiến đóng góp chân thành của quý thầy cô là nguồn động lực để
chúng tôi tiếp tục vững bước trên con đường mới và xây dựng tập san ngày càng chất lượng
hơn. Mọi ý kiến đóng góp, bài viết gửi đăng xin gửi về theo địa chỉ:
mail: nhomGVTVN@gmail.com.
BQT Nhóm Giáo viên toán Việt Nam!
https://www.facebook.com/groups/toanvd.vdc Trang 2
Các thành viên tham gia Tập san
Ban quản trị Nhóm Giáo viên toán Việt Nam
Cô giáo: Ngô Tú Hoa , Lại Nhật Hoan
Thầy giáo: Trần Nam Dũng; Trương Quốc Toản; Nguyễn Khải; Lê Thảo;
Tạ Minh Đức; Nguyễn Ngọc Chi; Lê Tài Thắng, Ngô Nguyễn Quốc Mẫn
Nam Phương; Hoàng Minh Quân; SongMinh Nguyễn.
Cùng các thầy, cô giáo tham gia viết và phản biện: Nguyễn Sỹ, Phong Do, Binh
Hoang, Võ Trọng Trí, Nguyễn Phụ Hoàng Lân, Huỳnh Văn Ánh,
Nguyễn Khắc Thành, Hoàng An Đình, Trần Dức Nội, Lê Thanh Bình,
Ngô Dung, Trương Đức Thịnh, Nguyễn Thanh Hải, Nguyễn Phương,
Chánh Lê Văn, Nguyễn Chiến, Vũ Minh Tư, Nguyễn Thị Hồng Gấm,
Nguyễn Văn Hải; Phạm Tuấn; Song Tử Mắt Nâu; Nguyễn Văn Viễn;
Thân Đức Minh; Phạm Quý; ĐưcThanh Phạm; Dấu Vết Hát.
Trân trọng!
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc Trang 3
Tập san
Số 02
8 - 2021
Đợt 1 của kỳ thi tốt nghiệp THPT đã diễn ra đầu tháng 7 vừa qua, và đợt 2 dự
kiến sẽ diễn ra vào đầu tháng 8. Bỏ qua những áp lực do dịch COVID-19 đem đến,
chúng ta thử cùng đánh giá xem kỳ thi này có giải quyết tốt nhiệm vụ kép mà đó đang
mang trên mình "vừa để xét tốt nghiệp, vừa để tuyển sinh đại học" không?
Tôi nghĩ chúng ta không có vấn đề gì về nhiệm vụ thứ nhất. Đề thi có 25 câu đầu
rất căn bản, đủ để học sinh kiếm 5 điểm hay chí ít cũng không bị liệt. 13-15 câu tiếp
theo có khó hơn, nhưng cũng nhẹ nhàng, dành cho học sinh khá, 10-12 câu cuối thách
thức hơn dành cho học sinh giỏi.
Dưới đây tôi có chọn ngẫu nhiên một mã đề và phân tích 12 câu cuối cùng, tạm
gọi là các câu vận dụng và vận dụng cao. Trong số các câu này, tôi nhận thấy là chỉ có
vài câu (trong đó có 3 câu đầu, 39-41) phù hợp với đề thi trắc nghiệm, còn lại toàn là
những câu tự luận được trắc nghiệm hóa. Học sinh bắt buộc phải giải bài toán, ra đáp
số rồi kiểm tra, so khớp.
Dù sao thì trong số những câu này chỉ có một vài câu tôi đánh giá là không đạt
yêu cầu, còn lại dù không phù hợp lắm nhưng cũng ổn. Rõ ràng là đề của Bộ ra, có quy
trình, có phản biện nên tốt hơn các đề thi thử khá nhiều, ít có những câu trời ơi. Đó là
một điểm cộng của đề thi của Bộ.
Tuy nhiên có một điểm trừ là đề thi của bộ không có bất cứ một câu nào về ứng
dụng của toán học trong thực tiễn, điều làm cho toán khô khan hơn quá nhiều so với
lý, hóa, sinh, nơi mà có rất nhiều những bài toán, bối cảnh thực tiễn. Thực ra thì toán
đâu có xa rời thực tiễn, những bài toán về xác suất, những bài toán cực trị, những bài
toán tính toán hình học. luôn rất thú vị, hấp dẫn, tự nhiên, nó đòi hỏi ở học sinh kỹ
năng đọc hiểu, mô hình hóa, giải quyết vấn đề, đơn giản thôi nhưng cần thiết, thay vì
kiểu học theo tư duy công thức như hiện nay (công thức tính nhanh hiện giờ đang mà
mốt).
Bản thân tôi cho rằng đề thi này chỉ đạt được yêu cầu về phân loại ở tốp dưới và
tốp giữa, còn ở tốp trên thì độ tin cậy không cao, do những bài toán quá khó sẽ tạo
điều kiện cho sự may rủi (trong đề này có khoảng 3-5 bài, tùy đánh giá của mỗi cá
nhân).
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc Trang 4
Tập san
Số 2
8-2021
Do vậy, tôi có đề xuất sau để nâng cao chất lượng và khả năng phân loại của đề
thi.
1. Nếu hướng tới chỉ dùng để xét tốt nghiệp thì vẫn giữ hình thức thi trắc nghiệm,
nhưng bỏ hết những câu khó và không phù hợp trắc nghiệm (ví dụ trong đề đính kèm
chỉ giữ lại các câu 39, 40, 41, 44, 45, 47, 48)
2. Nếu vẫn dùng kỳ thi này với mục tiêu kép thì nên pha trộn hình thức câu hỏi
theo cấu trúc sau:
25 câu trắc nghiệm với độ khó như 25 câu đầu của đề hiện hành.
10 câu điền đáp số lấy các câu từ 26-40, có thể lấy một số câu chân phương như
nói ở phần 1.
35 câu này mỗi câu 0.2 điểm.
3 câu tự luận, trong đó có một câu ở mức trung bình, một câu ở mức độ trung bình
khó (ví dụ như một trong các câu 39, 40, 41, 44, 45, 47, 48) và một câu khó (ví dụ các câu
46, 49, 50). Tránh ra những câu sát thủ hay lắt léo, mẹo mực.
Trong các bài này, có thể là bài ở mức trung bình hay trung bình khó phần tự luận,
hay phần bài toán điền đáp số có thể cho 1 vài bài toán có liên hệ thực tiễn, có sử dụng
mô hình hóa (cấp số nhân, phương trình, hàm số).
Như vậy phần căn bản ta dùng trắc nghiệm còn phần nâng cao hơn ta dùng điền
đáp số và tự luận, một mặt sẽ kiểm tra được rộng và căn bản, mặt khác sẽ tránh được
sự may rủi trong đánh giá tốp trên. Bạn nào được 10 điểm sẽ thực sự là giỏi: cẩn thận
không sai nhảm ở câu dễ và xử lý được các thách thức một cách thật sự ở câu khó.
Vài lời chia sẻ cùng anh chị em trên diễn đàn này. Rất mong nhận được các ý kiến
trao đổi.
12 câu hỏi vận dụng, vận dụng cao trong đề thi tốt nghiệp THPT (mã đề 114)
Câu 39: Có bao nhiêu số nguyên x thỏa mãn
2
3
2 4 [log ( 25) 3] 0
x x
x
A. 24 B. 25 C. Vô số D. 26
Câu này tốt, kiểm tra được các vấn đề về tính đơn điệu của hàm log, mũ, miền xác định của hàm
log. Bài này các phương án nhiễu cùng hay vì các đáp án sai đều liên quan đến một lỗi nào đó
(quên miền xác định, quên x = 2).
Câu 40: Cho hàm số
2
2 2 1
( )
3 1 1
x khi x
f x
x khi x
. Giả sử F là nguyên hàm của f trên R thỏa mãn F(0) = 2.
Giá trị của F(-1) + 2F(2) bằng.
A. 18 B. 20 C. 9 D. 24
Câu này tốt, kiểm tra được về nguyên hàm của hàm số cho trên từng đoạn. Điểm mấu chốt cần
nắm là nguyên hàm phải là hàm liên tục. Có thể nhầm nếu thay nhầm công thức.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc Trang 5
Tập san
Số 2
8-2021
Câu 41: Cho hàm số bậc bốn y = f(x) có đồ thị là đường cong như hình bên. Số nghiệm của phương trình
f(f(x)) = 0 là
A. 10 B. 8 C. 4 D. 12
Câu này tốt, kiểm tra khái niệm hàm hợp. Đây cũng là câu phù hợp với trắc nghiệm vì học sinh
có thể nhẩm được mà không cần đặt bút tính.
Câu 42: Có bao nhiêu số nguyên y sao cho tồn tại
1
;6
3
x
thỏa mãn
2
3 18
27 (1 )27
x xy x
xy
A. 20 B. 21 C. 19 D. 18
Đây là câu dở, rất khó nhưng mà là cái khó không cần thiết, đặc biệt câu này không phù hợp với
trắc nghiệm vì chắc chắn sẽ tạo ra sự may rủi.
Câu 43: Cho hàm số
3 2
( )
f x x ax bx c
với a, b, c là các số thực. Biết hàm số
( ) ( ) '( ) "( )g x f x f x f x
có hai giá trị cực trị là – 5 và 2. Diện tích hình phẳng giới hạn bởi
đường
( )
( ) 6
f x
y
g x
và y = 1 bằng
A. ln10 B. 3ln2 C. ln3 D. ln7
Câu này hơi mẹo quá. Và các đặt vấn đề rất thiếu tự nhiên, không ăn nhập với nhau.
Câu 44: Cho hình hộp chữ nhật ABCD.A’B’C’D’ có đáy là hình vuông, BD = 4a, góc giữa hai mặt phẳng
(A’BD) và (ABCD) bằng 60
0
. Thể tích của khối hộp đã cho bằng
A.
3
16 3a
B.
3
16 3
9
a
C.
3
48 3a
D.
3
16 3
3
a
Câu này ổn, căn bản, chân phương.
Câu 45: Cắt hình nón (N) bởi một mặt phẳng qua đỉnh và mặt phẳng chứa đáy một góc bằng 30
0
ta được
thiết diện là tam giác đều cạnh 2a. Diện tích xung quanh của (N) bằng
A.
2
7
a
B.
2
13
a
C.
2
2 7
a
D.
2
2 13
a
Câu này ổn, căn bản, chân phương, kiểm tra tốt hiểu biết của học sinh về hình nón các các thiết
diện.
Câu 46: Xét các số phức z, w thỏa mãn |z| = 1 và |w| = 2. Khi
| 6 8 |z iw i
đạt giá trị nhỏ nhất, |z –
w| bằng.
A. 3 B.
221
5
C.
5
D.
29
5
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc Trang 6
Tập san
Số 2
8-2021
Câu này tương đối khó, phải nắm vững bất đẳng thức tam giác với các điều kiện xảy ra dấu bằng
mới giải được. Nếu giải bằng hình học thì cũng cần phải hiểu ý nghĩa hình học của phép toán
phức liên hợp và nhân với i. Sẽ chân phương hơn nếu bài này bỏ bớt chữ i trước
w
đi.
Câu 47: Trong không gian Oxyz, cho đường thẳng
1
:
1 1 2
x y z
d
và mặt phẳng (P): x + 2y – 2z + 2 =
0. Hình chiếu vuông góc của d lên (P) là đường thẳng có phương trình
A.
1
2 4 3
x y z
B.
1
2 4 3
x y z
;
C.
1
14 1 8
x y z
D.
1
14 1 8
x y z
.
Câu này bình thường, căn bản, chân phương.
Câu 48: Trên tập hợp các số phức, xét phương trình
2 2
2( 1) 0
z m z m
(m là tham số thực). Có bao
nhiêu giá trị của m để phương trình đó có nghiệm
0
z
thỏa mãn
0
| | 6?
z
A. 1 B. 3 C. 4 D. 2
Câu này ổn, kiểm tra về phương trình bậc hai, định lý Viet và hiểu biết về số phức. Vấn đề mấu
chốt ở đây là biết phân hai trường hợp: trường hợp có hai nghiệm thực và trường hợp có hai
nghiệm phức liên hợp.
Câu 49: Cho hàm số y = f(x) có đạo hàm f’(x) = (x – 9)(x
2
– 16),
x
R. Có bao nhiêu giá trị nguyên dương
của tham số m để hàm số y = f(|x
3
+7x|+m) có ít nhất 3 điểm cực trị?
A. 9 B. 8 C. 16 D. 4
Bài này ổn, liên quan đến đạo hàm của hàm hợp và có thêm chút khó khăn ghi có dấu trị tuyệt
đối.
Câu 50: Trong không gian Oxyz cho hai điểm A(–2;1; –3) và B(1; –3;2). Xét hai điểm M, N thay đổi thuộc
mặt phẳng Oxy sao cho MN = 3. Giá trị lớn nhất của
AM BN
bằng
A.
65
B.
29
C.
26
D.
91
Bài này hay và khó, khai thác các phép biến hình cơ bản như đối xứng, tịnh tiến và bất đẳng thức
tam giác. Nhưng là ý tưởng chỉ dùng được một lần. Sẽ tốt hơn nếu bài này làm tự luận.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc Trang 7
Tập san
Số 02
8 - 2021
Trong chương trình toán THPT, các bài toán về góc giữa đường thẳng và mặt phẳng tuy
không mới. Song, nó vẫn mang tính thời sự trong các bài kiểm tra định kì, các kì thi học sinh
giỏi, kì thi tốt nghiệp trung học phổ thông hằng năm. Bài viết sau đây khai thác một hướng tiếp
cận khác cho bài toán tính góc giữa đường thẳng với mặt phẳng
1. Kiến thức cơ bản
1.1. Định nghĩa
Cho đường thẳng
a
và mặt phẳng
. Góc giữa đường thẳng
a
và hình chiếu
a
của nó
trên mặt phẳng
được gọi là góc giữa đường thẳng
a
và mặt phẳng
.
1.2. Các xác định góc giữa đường thẳng
a
và mặt phẳng
Cách 1:
Bước 1. Tìm
O a
.
Bước 2. Lấy
A a
và dựng
AH
tại
H
.
Khi đó
, ,
a a a AOH
.
Bước 3. Tính số đo của góc
AOH
Chú ý:
0 , 90
a
Cách 2: Tính gián tiếp theo một trong hai hướng sau:
Hướng 1: Chọn một đường thẳng
//d a
mà góc giữa
d
và
có thể tính được.
Từ đó ta có:
, ,a d
Hướng 2: Chọn một mặt phẳng
//
mà góc giữa
a
và
có thể tính được.
Từ đó ta có:
, ,a a
Trao đổi kinh nghiệm dạy học theo định
hướng tiếp cận năng lực người học
Bàn về một cách tiếp cận khác cho bài toán tính góc giữa
đường thẳng và mặt phẳng
Ths. HOÀNG MINH QUÂN
GV Trường THPT chuyên Nguyễn Huệ, Hà Nội
a
a'
H
O
A
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc
Trang 8
Tập san
Số 02
8-2021
Tuy nhiên việc xác định hình chiếu của một điểm lên mặt phẳng không phải lúc nào cũng
thuận lợi. Chính vì vậy, việc đưa ra một cách tiếp cận khác là sử dụng khoảng cách để tính góc giữa
đường thẳng với mặt phẳng nhằm khắc phục khó khăn đó.
1.3. Định hướng tiếp cận
Cho đường thẳng
a
và mặt phẳng
. Để tính góc
giữa đường thẳng
a
và mặt phẳng
, ta tiếp cận thông qua ý tưởng đơn giản khác như sau :
Bước 1: Tìm
O a
.
Bước 2: Tính
,
sin
d A
OA
Cách tiếp cận này thích hợp cho học sinh nắm chắc việc tính khoảng cách từ một điểm đến
một mặt phẳng.
Sau đây chúng tôi đưa ra một số ví dụ minh hoạ với lời giải theo hướng tiếp cận sử dụng
khoảng cách để tính góc giữa đường thẳng với mặt phẳng
2. Ví dụ minh họa
2.1. Áp dụng cho các bài toán khối chóp.
Câu 1: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình chữ nhật,
SA ABCD
. Gọi
G
là trọng
tâm tam giác
ACD
,
I
là trung điểm của
SB
. Biết độ dài các đoạn
SA a
,
3AB a
,
3
2
a
AD
. Góc giữa đường thẳng
IG
và mặt phẳng
SCD
bằng
A.
3
arcsin .
4 13
B.
3
arcsin .
13
C.
3
arcsin .
16
D.
3
arcsin .
16
Lời giải
Chọn A
Có
2SB a
nên tam giác
SAI
đều cạnh
a
.
Gọi
H
là trung điểm của
SI
thì
BI BG
BH BD
nên
//
IG HD
, hay
, ,
IG SCD HD SCD
Có
3
2
a
AH
,
3
2
a
AD
và tam giác
AHD
vuông tại
A
, suy ra
3HD a
Vì
1
4
HS BS
nên
1 1 1
, , ,
4 4 4
d H SCD d B SCD d A SCD d
H
G
I
C
A
D
B
S
a
a'
H
O
A
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc
Trang 9
Tập san
Số 02
8-2021
Mà
2 2 2 2 2 2
1 1 1 1 4 13
9 9d SA AD a a a
3
13
a
d
3
,
4 13
a
d H SCD
Suy ra
,
3 3
sin ,
4 13. 3 4 13
d H SCD
a
HD SCD
HD
a
.
Câu 2: Cho hình chóp đều
.
S ABCD
có đáy
ABCD
là hình vuông tâm
O
cạnh
a
và
2SA a
.
Gọi
,M N
lần lượt là trung điểm của
SD
và
BO
. Gọi
là góc giữa đường thẳng
MN
và mặt phẳng
SCD
thì giá trị
sin
bằng
A.
3 3
7
. B.
2 3
7
. C.
4 3
7
. D.
3
7
.
Lời giải
Chọn A
Ta có:
SBD
là tam giác đều nên
60
SDB
và
6
2
a
SO
Suy ra
2 2 2
2 2 2
9 2 3 2 1 7
2 . cos 60 2. . .
2 8 2 4 2 8
a a a a a
MN MD ND MD ND
14
4
a
MN
Mặt khác
3
, ,
2
d N SCD d O SCD
Mà
2 2 2 2 2 2 2
2
1 1 1 1 2 2 2 14
3 3
,
OC OD OS a a a a
d O SCD
2
2
3 42 3 42
, , ,
14 14 28
a a a
d O SCD d O SCD d N SCD
,
3 42 4 3 3
sin .
28 7
14
d N SCD
a
MN
a
.
Câu 3: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình thoi,
60
BAC
,
SA a
. Tam giác
SAB
là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng
ABCD
. Gọi
là
góc tạo bởi đường thẳng
SB
và mặt phẳng
SCD
. Khi đó
sin
bằng
A.
2
2
. B.
3
2
. C.
6
4
. D.
6
3
.
Lời giải
Chọn C
Gọi
M
là trung điểm của
AB
. Vì tam giác
SAB
là tam giác đều nên
SM AB
.
N
M
O
D
B
C
A
S
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc
Trang 10
Tập san
Số 02
8-2021
Ta có:
,
SAB ABCD
SAB ABCD AB
SM AB SM SAB
SM ABCD
.
Gọi
H
là hình chiếu vuông góc của
B
lên mặt phẳng
SCD
. Suy ra
BH SCD
.
Suy ra
HS
là hình chiếu vuông góc của
BS
lên mặt phẳng
SCD
, do đó:
, ,
SB SCD SB SH BSH
.
Ta có:
,
sin sin
B SCD
d
BH
BSH
SB SB
.
Do
//
BM SCD
, ,
, ,
2 2 2 2 2 2
, ,
3 3
.
. .
6
2 2
4
3 3
2 2
M CD B CD
B SCD M SCD
M CD B CD
a a
SM d SM d
a
d d
SM d SM d
a a
Vậy
;
sin sin
B SCD
d
BH
BSH
SB SB
6
6
4
4
a
a
.
2.2. Áp dụng cho các bài toán khối lăng trụ.
Câu 4: Cho hình lập phương
.
ABCD A B C D
có cạnh bằng
a
. Góc giữa đường thẳng
AD
và
mặt phẳng
A BD
bằng
A.
5
arcsin
3
. B.
6
arcsin
3
. C.
2
arcsin
3
. D.
3
arcsin
3
.
Lời giải
Chọn B
d
(B,(SCD))
H
B
S
SCD
B
A
C
D
M
S
I
O
D
D'
A'
B'
C'
A
B
C
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc
Trang 11
Tập san
Số 02
8-2021
+ Do
/ /
AD BC
nên góc giữa đường thẳng
AD
và mặt phẳng
'
A BD
bằng góc giữa
đường thẳng
'BC
và mặt phẳng
'
A BD
.
+ Do
'AA BD
là tứ diện vuông nên
2 2 2 2
2
1 1 1 1 3
'
, '
AA AB AD a
d A A BD
,
3
a
d A A BD
.
+ Gọi
là góc giữa đường thẳng
'BC
và mặt phẳng
A BD
.
Ta có
2
, 2 ,
6
3
sin
3
2
a
d C A BD d A A BD
BC BC
a
.
Câu 5: Cho hình lăng trụ đều
.
ABC A B C
có cạnh đáy bằng
a
,
3AA a
. Giá trị sin của góc
giữa đường thẳng
BC
và mặt phẳng
A BC
bằng
A.
15
10
. B.
5
10
. C.
15
5
. D.
65
10
.
Lời giải
Chọn A
Gọi
là góc giữa đường thẳng
BC
và mặt phẳng
A BC
.
Ta có:
d ,
sin
C A BC
C B
d ,
A A BC
C B
(vì
AC A BC O
với
O
là trung điểm
AC
).
Gọi
M
là trung điểm của
BC
,
H
là hình chiếu của
A
lên
A M
.
AM BC
BC AA M
AA BC
hay
BC AH
.
Mặt khác
AH A M
nên
AH A BC
hay
d ;
A A BC AH
.
3
2
a
AM
;
2 2
. 15
5
AA AM a
AH
AA AM
;
2 2
2C B BB B C a
.
15
sin
10
.
Câu 6: Cho hình hộp chữ nhật
.
ABCD A B C D
có
1, 2, 3
AB AD AA
.
là mặt phẳng di
động đi qua
B
và song song với
A C
. Gọi
là góc giữa
với đường thẳng
CD
.
Giá trị lớn nhất của
sin
bằng
M
C
B
A'
B'
C'
A
H
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc
Trang 12
Tập san
Số 02
8-2021
A.
7 2
10
. B.
1
. C.
3 10
10
. D.
3 5
7
.
Lời giải
Chọn A
Ta có:
CD
//
BA
, ,CD BA
.
Do
//
A C
nên
chứa đường thẳng
d
qua
B
và song song với
A C
.
;
;
sin
A
A d
d
d
A B A B
.
2 2
10
A B AA AB
.
Dựng
A H d
tại
;A d
H A H d
.
Ta có
d AA
d AHA
d A H
AH d
.
Kẻ
BK AC
tại
K
2 5
5
AH BK
2 2
7 5
5
A H AH AA
7 2
sin
10
A H
A B
.
Dấu “ =” xảy ra khi
A H
.
Vậy
7 2
max sin
10
.
2.3. Bài tập tự luyện
Câu 1: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình chữ nhật với
2 , . AB a BC a
Cạnh
bên
SD a
và
SD
vuông góc với mặt phẳng đáy. Sin của góc tạo bởi đường
thẳng
SB
và mặt phẳng
SAC
bằng
A.
5 3
.
9
B.
6
.
3
C.
6
.
9
D.
30
.
15
Câu 2: Cho hình chóp tứ giác đều
.
S ABCD
có
SA AB a
. Gọi
M
là trung điểm của cạnh
BC
. Tang góc tạo bởi đường thẳng
DM
với mặt phẳng
SAB
bằng?
A.
13
tan
13
. B.
15
tan
5
. C.
26
tan
13
. D.
tan 3
.
Câu 3: Cho hình chóp tứ giác đều
.
S ABCD
có cạnh đáy bằng
a
, tâm
O
. Gọi
M
và
N
lần lượt
là trung điểm của
SA
và
BC
. Biết rằng góc giữa
MN
và
ABCD
bằng
60
, cosin góc
giữa
MN
và mặt phẳng
SBD
bằng
d
A'
D'
C'
B'
B
C
D
A
H
K
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc
Trang 13
Tập san
Số 02
8-2021
A.
41
41
. B.
5
5
. C.
2 5
5
. D.
2 41
41
.
Câu 4: Cho hình chóp tứ giác đều
.
S ABCD
có cạnh đáy bằng
a
. Gọi
O
là tâm của đáy,
E
là
trung điểm cạnh
AD
. Gọi
là góc giữa đường thẳng
CD
và mặt phẳng
SBE
. Biết
2
a
SO
thì
sin
bằng
A.
1
2 6
. B.
3
2
. C.
2
3
. D.
1
6
.
Câu 5: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình bình hành,
2AB a
,
BC a
,
120
ABC
. Cạnh bên
3SD a
và
SD
vuông góc với mặt phẳng đáy. Giá trị
sin
của
góc tạo bởi
SB
và mặt phẳng
SAC
bằng
A.
3
7
. B.
3
4
. C.
3
4
. D.
1
4
.
Câu 6: Cho hình hộp chữ nhật
ABCDA B C D
có đáy
ABCD
là hình vuông. Giá trị lớn nhất của
góc tạo bởi
BD
với mặt phẳng
BDC
bằng
A.
1
arcsin
3
. B.
1
arcsin
3
. C.
1
arcsin
2 3
. D.
1
arcsin
3 2
.
Câu 7: Cho hình hộp
.
ABCD A B C D
có đáy
ABCD
là hình chữ nhật cạnh
; 2AB a AD a
;
I
là trọng tâm tam giác
A C D
. Gọi
là góc giữa đường thẳng
ID
và mặt phẳng
ICB
, biết
3A B a
. Giá trị của
sin
bằng
A.
9
253
. B.
6
11 2
. C.
6
253
. D.
23
11
.
Câu 8: Cho hình lăng trụ đứng
. ' ' 'ABC A B C
có đáy
ABC
là tam giác cân tại
C
,
2AB a
và
0
120
ACB
. Biết
'AA a
. Gọi
I
là trung điểm
AB
thì
sin
của góc giữa đường thẳng
'IA
và mặt phẳng
'
C AB
bằng
A.
2
4
B.
2
2
C.
2 5
3
D.
2 15
3
Câu 9: Cho lăng trụ tam giác đều
.
ABC A B C
, gọi
I
là trung điểm
' 'A B
. Gọi
là góc tạo bởi
'AC
và
'BIC
. Biết
' ; 2AA a AB a
thì giá trị
cos
bằng
A.
15
5
. B.
10
5
. C.
3
5
. D.
2
5
Câu 10: Cho lăng trụ tam giác
ABC
có
, 2 , 60
AB a BC a ABC
. Hình chiếu vuông góc của
'A
lên mặt phẳng
ABC
trùng với trọng tâm
G
của tam giác
ABC
và góc giữa
'AA
tạo
với mặt phẳng
ABC
bằng
60
. Sin của góc tạo bởi
'AA
và mặt phẳng
'
A BC
bằng
A.
9
5 41
. B.
9
4 51
. C.
7
4 51
. D.
9
7 41
.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc Trang 14
Tập san
Số 02
8 - 2021
Toàn cảnh đề thi tốt nghiệp THPT đợt 1 năm 2021
ĐỀ THI, ĐÁP ÁN VÀ LỜI GIẢI CHI TIẾT CÁC CÂU VD – VDC
TRONG ĐỀ THI TỐT NGHIỆP THPT ĐỢT 1 NĂM 2021
Kỳ thi tốt nghiệp THPT đợt 2 năm 2021 sẽ diễn ra vào hai ngày 6,7/8/2021,
để tạo điều kiện cho quý thầy cô cùng các em có tài liệu ôn tập trong thời gian gấp rút này
Nhóm Giáo viên Toán Việt Nam xin gửi tới quý thầy cô và các em Đề thi, đáp án và
lời giải chi tiết các câu VD – VDC của 4 mã đề thi gốc 101, 102, 103, 104 Đề thi tốt
nghiệp THPT đợt 1 Năm 2021
Hy vọng bài viết sẽ giúp quý thầy cô có thêm tài liệu tham khảo; các em học sinh
rèn luyện tốt kỹ năng thi trắc nghiệm môn Toán trong kỳ thi tốt nghiệp THPT đợt 2
năm 2021.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https:/www.facebook.com/groups/toanvd.
Trang 15
Tập san
Số 02
8-2021
Đề thi gồm 06 trang
ĐỀ THI TỐT NGHIỆP THPT ĐỢT 1 NĂM 2021
Bài thi môn: Toán
Thời gian: 90 phút (Không kể thời gian phát đề)
Mã đề thi: 101
Câu 1: Tập nghiệm của bất phương trình
3 2
x
là
A.
3
;log 2
. B.
3
log 2;
. C.
2
;log 3
. D.
2
log 3;
.
Câu 2: Nếu
4
1
d 3
f x x
và
4
1
d 2
g x x
thì
4
1
df x g x x
bằng
A.
1
. B.
5
. C.
5
. D.
1
.
Câu 3: Trong không gian
,Oxyz
cho mặt cầu
S
có tâm
1; 4;0
I
và bán kính bằng
3.
Phương
trình của
S
là:
A.
2 2
2
1 4 9
x y z
. B.
2 2
2
1 4 9
x y z
.
C.
2 2
2
1 4 3
x y z
. D.
2 2
2
1 4 3
x y z
.
Câu 4: Trong không gian
,Oxyz
cho đường thẳng
d
đi qua điểm
3; 1;4
M
và có một vectơ
chỉ phương
2; 4;5
u
. Phương trình của
d
là:
A.
2 3
4
5 4
x t
y t
z t
. B.
3 2
1 4
4 5
x t
y t
z t
. C.
3 2
1 4
4 5
x t
y t
z t
. D.
3 2
1 4
4 5
x t
y t
z t
.
Câu 5: Cho hàm số
y f x
có bảng xét dấu đạo hàm như sau:
Số điểm cực trị của hàm số đã cho là
A.
5.
B.
3
. C.
2
. D.
4
.
Câu 6: Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình bên?
A.
4 2
2 4 1.
y x x
B.
3
3 1y x x
.
C.
4 2
2 4 1
y x x
. D.
3
3 1y x x
.
Câu 7: Đồ thị của hàm số
4 2
4 3
y x x
cắt trục tung tại điểm có tung độ bằng
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https:/www.facebook.com/groups/toanvd.
Trang 16
Tập san
Số 02
8-2021
A.
0
. B.
3
. C.
1
. D.
3
.
Câu 8: Với
n
là số nguyên dương bất kì,
4,n
công thức nào dưới đây đúng?
A.
4
4 !
!
n
n
A
n
. B.
4
4!
4 !
n
A
n
. C.
4
!
4! 4 !
n
n
A
n
. D.
4
!
4 !
n
n
A
n
.
Câu 9: Phần thực của số phức
5 2z i
bằng
A.
5
. B.
2
. C.
5
. D.
2
.
Câu 10: Trên khoảng
0; ,
đạo hàm của hàm số
5
2
y x
là
A.
7
2
2
7
y x
. B.
3
2
2
5
y x
. C.
3
2
5
2
y x
. D.
3
2
5
2
y x
.
Câu 11: Cho hàm số
2
4f x x
. Khẳng định nào dưới đây đúng?
A.
d 2f x x x C
. B.
2
d 4f x x x x C
.
C.
3
d 4
3
x
f x x x C
. D.
3
d 4f x x x x C
.
Câu 12: Trong không gian
,Oxyz
cho điểm
2;3;5A
. Tọa độ vectơ
OA
là
A.
2;3;5
. B.
2; 3;5
. C.
2; 3;5
. D.
2; 3; 5
.
Câu 13: Cho hàm số
y f x
có bảng biến thiên như sau:
Giá trị cực tiểu của hàm số đã cho bằng
A.
1
. B.
5
. C.
3
. D.
1
.
Câu 14: Cho hàm số
y f x
có đồ thị là đường cong trong hình bên. Hàm số đã cho nghịch
biến trên khoảng nào dưới đây?
A.
0;1
. B.
;0
. C.
0; 
. D.
1;1
.
Câu 15: Nghiệm của phương trình
3
log 5 2x
là:
A.
8
5
x
. B.
9x
. C.
9
5
x
. D.
8x
.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https:/www.facebook.com/groups/toanvd.
Trang 17
Tập san
Số 02
8-2021
Câu 16: Nếu
3
0
d 4
f x x
thì
3
0
3 df x x
bằng
A.
36
. B.
12
. C.
3
. D.
4
.
Câu 17: Thể tích của khối lập phương cạnh
5a
bằng
A.
3
5a
. B.
3
a
. C.
3
125a
. D.
3
25a
.
Câu 18: Tập xác định của hàm số
9
x
y
là
A.
. B.
0;
. C.
\ 0
. D.
0;

.
Câu 19: Diện tích
S
của mặt cầu bán kính
R
được tính theo công thức nào dưới đây?
A.
2
16
S R
. B.
2
4
y R
. C.
2
S R
. D.
3
4
3
S R
.
Câu 20: Tiệm cận đứng của đồ thị hàm số
2 1
1
x
y
x
là đường thẳng có phương trình:
A.
1
x
. B.
1
x
. C.
2
x
. D.
1
2
x
.
Câu 21: Cho
0
a
và
1
a
, khi đó
4
log
a
a
bằng
A.
4
. B.
1
4
. C.
1
4
. D.
4
.
Câu 22: Cho khối chóp có diện tích đáy
2
5B a
và chiều cao
h a
. Thể tích của khối chóp đã
cho bằng
A.
3
5
6
a
. B.
3
5
2
a
. C.
3
5a
. D.
3
5
3
a
.
Câu 23: Trong không gian
Oxyz
, cho mặt phẳng
:3 2 1 0
P x y z
. Vectơ nào dưới đây là
một vectơ pháp tuyến của
P
?
A.
1
3;1;2
n
. B.
2
3; 1;2
n
. C.
3
3;1;2
n
. D.
4
3;1; 2
n
.
Câu 24: Cho khối trụ có bán kính đáy
6
r
và chiều cao
3
h
. Thể tích của khối trụ đã cho bằng
A.
108
. B.
36
. C.
18
. D.
54
.
Câu 25: Cho hai số phức
4 2z i
và
3 4w i
. Số phức
z w
bằng
A.
1 6i
. B.
7 2i
. C.
7 2i
. D.
1 6i
.
Câu 26: Cho cấp số nhân
( )
n
u
với
1
3
u
và
2
9
u
. Công bội của cấp số nhân đã cho bằng
A.
6
. B.
1
3
. C.
3
. D.
6
.
Câu 27: Cho hàm số
( ) 2
x
f x e
. Khẳng định nào dưới đây đúng?
A.
2
( )d
x
f x x e C
. B.
( )d 2
x
f x x e x C
.
C.
( )d
x
f x x e C
. D.
( )d 2
x
f x x e x C
.
Câu 28: Trên mặt phẳng tọa độ, điểm
( 3; 4)
M
là điểm biểu diễn của số phức nào dưới đây?
A.
2
3 4z i
. B.
3
3 4z i
. C.
4
3 4z i
. D.
1
3 4z i
.
Câu 29: Biết hàm số
1
x a
y
x
(
a
là số thực cho trước,
1
a
) có đồ thị như trong hình bên.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https:/www.facebook.com/groups/toanvd.
Trang 18
Tập san
Số 02
8-2021
Mệnh đề nào dưới đây đúng?
A.
' 0, 1y x
. B.
' 0, 1y x
. C.
' 0,y x
. D.
' 0,y x
.
Câu 30: Từ một hộp chứa
12
quả bóng gồm
5
quả màu đỏ và
7
quả màu xanh, lấy ngẫu nhiên
đồng thời
3
quả. Xác suất để lấy được
3
quả màu xanh bằng
A.
7
44
. B.
2
7
. C.
1
22
. D.
5
12
.
Câu 31: Trên đoạn
0;3
, hàm số
3
3y x x
đạt giá trị lớn nhất tại điểm
A.
0x
. B.
3x
. C.
1x
. D.
2x
.
Câu 32: Trong không gian
Oxyz
, cho điểm
1;3;2M
và mặt phẳng
: 2 4 1 0P x y z
.
Đường thẳng đi qua
M
và vuông góc với
P
có phương trình là:
A.
1 3 2
1 2 1
x y z
. B.
1 3 2
1 2 1
x y z
.
C.
1 3 2
1 2 4
x y z
. D.
1 3 2
1 2 4
x y z
.
Câu 33: Cho hình chóp
.S ABC
có đáy là tam giác vuông cân tại
B
,
2AB a
và
SA
vuông góc
với mặt phẳng đáy. Khoảng cách từ
C
đến mặt phẳng
SAB
bằng
A.
2a
. B.
2a
. C.
a
. D.
2 2a
.
Câu 34: Trong không gian
Oxyz
, cho hai điểm
1;0;0A
và
4;1; 2B
. Mặt phẳng đi qua
A
và
vuông góc với
AB
có phương trình là
A.
3 2 17 0x y z
. B.
3 2 3 0x y z
.
C.
5 2 5 0x y z
. D.
5 2 25 0x y z
.
Câu 35: Cho số phức
z
thỏa mãn
5 4iz i
. Số phức liên hợp của
z
là
A.
4 5z i
. B.
4 5z i
. C.
4 5z i
. D.
4 5z i
.
Câu 36: Cho hình lắng trụ đứng
.ABC A B C
có tất cả các cạnh bằng nhau ( tham khảo hình bên.
Góc giữa hai đường thẳng
AA
và
BC
là
C'
B'
A
B
C
A'
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https:/www.facebook.com/groups/toanvd.
Trang 19
Tập san
Số 02
8-2021
A.
o
30
. B.
o
90
. C.
o
45
. D.
o
60
.
Câu 37: Với mọi
,a b
thỏa mãn
3
2 2
log log 6a b
, khẳng định nào dưới đây đúng?
A.
3
64a b
. B.
3
36a b
. C.
3
64a b
. D.
3
64a b
.
Câu 38: Nếu
2
0
d 5f x x
thì
2
0
2 1 df x x
bằng
A. 8. B. 9. C. 10. D. 12.
Câu 39: Cho hàm số
2
2 5 1
3 4 1
x khi x
f x
x khi x
. Giả sử
F
là nguyên hàm của
f
trên
thỏa mãn
0 2F
. Giá trị của
1 2 2F F
bằng
A. 27. B. 29. C. 12. D. 33.
Câu 40: Có bao nhiêu số nguyên
x
thỏa mãn
2
3
3 9 log 25 3 0
x x
x
?
A. 27. B. Vô số. C.
26
. D.
25
.
Câu 41: Cho hàm số bậc ba
y f x
có đồ thị là đường cong trong hình bên. Số nghiệm thực
phân biệt của phương trình
1f f x
là
A.
9
. B.
3
. C.
6
. D.
7
.
Câu 42: Cắt hình nón
N
bởi mặt phẳng đi qua đỉnh và tạo với mặt phẳng chứa đáy một góc
bằng
0
60
ta thu được thiết diện là một tam giác đều cạnh
4a
. Diện tích xung quanh của
N
bằng :
A.
2
8 7 a
. B.
2
4 13 a
. C.
2
8 13 a
. D.
2
4 7 a
.
Câu 43: Trên tập hợp các số phức, xét phương trình
2 2
2 1 0z m z m
(m là tham số thực).
Có bao nhiêu giá trị của m để phương trình đó có nghiệm
0
z
thỏa mãn
0
7?z
A.
2
. B.
3
. C.
1
. D.
4
.
Câu 44: Xét các số phức
,z w
thỏa mãn
1z
và
2w
. Khi
6 8 z iw i
đạt giá trị nhỏ nhất,
z w
bằng
A.
221
5
. B.
5
. C.
3
. D.
29
5
.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https:/www.facebook.com/groups/toanvd.
Trang 20
Tập san
Số 02
8-2021
Câu 45: Trong không gian
Oxyz
, cho đường thẳng
d
:
1 2
1 1 1
x y z
và mặt phẳng
: 2 4 0
P x y z
. Hình chiếu vuông góc của
d
trên
P
là đường thẳng có phương
trình:
A.
1 2
2 1 4
x y z
. B.
1 2
3 2 1
x y z
.
C.
1 2
2 1 4
x y z
. D.
1 2
3 2 1
x y z
.
Câu 46: Cho hàm số
3 2
f x x ax bx c
với
, ,a b c
là các số thực. Biết hàm số
g x f x f x f x
có hai giá trị cực trị là
3
và
6
. Diện tích hình phẳng giới
hạn bởi các đường
6
f x
y
g x
và
1y
bằng
A.
2ln3.
B.
ln3.
C.
ln18.
D.
2ln 2.
Câu 47: Có bao nhiêu số nguyên
y
sao cho tồn tại
1
;3
3
x
thỏa mãn
2
3 9
27 1 27
x xy x
xy
.
A.
27
. B.
9
. C.
11
. D.
12
.
Câu 48: Cho khối hộp chữ nhật
. ' ' ' 'ABCD A B C D
có đáy là hình vuông,
2BD a
, góc giữa hai
mặt phẳng
'
A BD
và
ABCD
bằng
0
30
. Thể tích của khối hộp chữ nhật đã cho bằng
A.
3
6 3a
. B.
3
2 3
9
a
. C.
3
2 3a
. D.
3
2 3
3
a
.
Câu 49: Trong không gian
,Oxyz
cho hai điểm
(1; 3; 4), ( 2;1; 2).
A B
Xét hai điểm
M
và
N
thay
đổi thuộc mặt phẳng
( )Oxy
sao cho
2.
MN
Giá trị lớn nhất của
AM BN
bằng
A.
3 5
. B.
61
. C.
13
. D.
53
.
Câu 50: Cho hàm số
y f x
có đạo hàm
2
7 9 , .
f x x x x
Có bao nhiêu giá trị
nguyên dương của tham số
m
để hàm số
3
5
g x f x x m
có ít nhất 3 điểm cực
trị?
A.
6.
B.
7.
C.
5.
D.
4.
……… HẾT ………
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https:/www.facebook.com/groups/toanvd.
Trang 21
Tập san
Số 02
8-2021
ĐỀ THI TỐT NGHIỆP THPT QUỐC GIA NĂM 2021
MÃ ĐỀ 101
Môn: Toán
Thời gian: 90 phút (Không kể thời gian phát đề)
BẢNG ĐÁP ÁN VÀ GIẢI CHI TIẾT
1 2 3 4 5 6 7 8 9 10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
A
C
B
D
D
A
D
D
A
C
C
A
C
A
C
B C
A
B A
B D
B A
B
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
C
B
B
B
A
C
D
B B A
C
A
A
A
C
D
D
B D
C
D
C
D
D
A
Câu 39: Cho hàm số
2
2 5 1
3 4 1
x khi x
f x
x khi x
. Giả sử
F
là nguyên hàm của
f
trên
thỏa mãn
0 2F
. Giá trị của
1 2 2F F
bằng
A. 27. B. 29. C. 12. D. 33.
Lời giải
Chọn A
Dễ thấy hàm số
f
liên tục trên
1 1
2
0 0
1 0 ( )d (3 4) ( )d 5 (1) 7F F f x x x f x x F
.
1 2
1 1
1 2 2 ( )d 2 ( )d 3 (1) 10 16 21 27F F f x x f x x f
.
Câu 40: Có bao nhiêu số nguyên
x
thỏa mãn
2
3
3 9 log 25 3 0
x x
x
A. 27. B. Vô số. C.
26
. D.
25
.
Lời giải
Chọn C
Điều kiện xác định của bất phương trình là
25x
.
Đặt
2
3
( ) 3 9 log 25 3 , 25
x x
A x x x
.
2
3 9 0 0 2
x x
x x
.
3
log 25 3 0 2x x
.
Ta có bảng xét dấu
( )A x
như sau
Từ đó,
2
( ) 0 24; 23;...;0;2
25 0
x
A x x
x
(do
x
).
Kết luận: có
26
nghiệm nguyên thỏa mãn.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https:/www.facebook.com/groups/toanvd.
Trang 22
Tập san
Số 02
8-2021
Câu 41: Cho hàm số bậc ba
( )y f x
có đồ thị là đường cong trong hình bên. Số nghiệm thực
phân biệt của phương trình
1f f x
là
A.
9
. B.
3
. C.
6
. D.
7
.
Lời giải
Chọn D
Từ đồ thị hàm số ta có
1f f x
1 1
2 2
( ) 1 (1)
( ) 0 (2)
( ) 1 2 (3)
f x x và x
f x
f x x và x
Dựa vào đồ thị,
(1)
có đúng 1 nghiệm,
(2)
và
(3)
mỗi phương trình có 3 nghiệm phân
biệt và 7 nghiệm trên phân biệt nhau.
Câu 42: Cắt hình nón
N
bởi mặt phẳng đi qua đỉnh và tạo với mặt phẳng chứa đáy một góc
bằng
0
60
ta thu được thiết diện là một tam giác đều cạnh
4a
. Diện tích xung quanh của
N
bằng :
A.
2
8 7 a
.
B.
2
4 13 a
.
C.
2
8 13 a
.
D.
2
4 7 a
.
Lời giải
Chọn D
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https:/www.facebook.com/groups/toanvd.
Trang 23
Tập san
Số 02
8-2021
Gọi
I
là tâm đáy nón. Ta có thiết diện qua đỉnh là tam giác
SBA
.
Gọi
M
là trung điểm của
AB
. Suy ra
0
60
SMI
.
Do tam giác
SAB
đều cạnh
4a
4 3
2 3
2
a
SM a
.
Xét tam giác
SIM
vuông tại
I
ta có
3 ; 3SI a IM a
.
Xét
IMA
vuông tại
M
ta có
2
2 2 2
3 2 7IA IM MA a a a
.
Khi đó
2
7.4 4 7
xq
S rl a a a
.
Câu 43: Trên tập hợp các số phức, xét phương trình
2 2
2 1 0
z m z m
(
m
là tham số thực).
Có bao nhiêu giá trị của
m
để phương trình đó có nghiệm
0
z
thỏa mãn
0
7?
z
A.
2
. B.
3
. C.
1
. D.
4
.
Lời giải
Chọn B
2 2
( 1) 2 1
m m m
.
+) Nếu
1
0 2 1 0
2
m m
, phương trình có 2 nghiệm thực. Khi đó
0 0
7 7
z z
.
Thế
0
7
z
vào phương trình ta được:
2
14 35 0 7 14
m m m
(nhận).
Thế
0
7
z
vào phương trình ta được:
2
14 63 0
m m
, phương trình này vô nghiệm.
+) Nếu
1
0 2 1 0
2
m m
, phương trình có 2 nghiệm phức
1 2
,z z
thỏa
2 1
z z
. Khi đó
2
2 2
1 2 1
. 7
z z z m
hay
7
m
(loại) hoặc
7
m
(nhận).
Vậy tổng cộng có 3 giá trị của
m
là
7 14
m
và
7
m
.
Câu 44: Xét các số phức
,z w
thỏa mãn
1
z
và
2
w
. Khi
6 8 z iw i
đạt giá trị nhỏ nhất,
z w
bằng
A.
221
5
. B.
5
. C.
3
. D.
29
5
.
Lời giải
Chọn D
Ta có:
2 2
w iw
;
3
z iw z iw
6 8 6 8 10 3 7
P z iw i i z iw
.
Suy ra:
min
7
P
khi
1 10
;
3 4
2 3
. , 0
3 4
5 5
8 6
5 5
6 8 . , 0
8 6
5 5
5 5
k h
z i
z k iw k
z i
i h z iw h
w i
w i
.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https:/www.facebook.com/groups/toanvd.
Trang 24
Tập san
Số 02
8-2021
Vậy
3 4 8 6 29
5 5 5 5 5
z w i i
.
Câu 45: Trong không gian
Oxyz
, cho đường thẳng
d
:
1 2
1 1 1
x y z
và mặt phẳng
: 2 4 0
P x y z
. Hình chiếu vuông góc của
d
trên
P
là đường thẳng có phương
trình:
A.
1 2
2 1 4
x y z
. B.
1 2
3 2 1
x y z
.
C.
1 2
2 1 4
x y z
. D.
1 2
3 2 1
x y z
.
Lời giải
Chọn C
Tọa độ giao điểm
A
của
d
và
P
thỏa mãn hệ phương trình:
1 2
1 1 1
2 4 0
x y z
x y z
0
1
2
x
y
z
0;1;2
A
.
Lấy điểm
1;2;1
B d
. Gọi
H
là hình chiếu của
B
trên
P
.
Phương trình
BH
:
1
2 2
1
x t
y t
z t
Do
H BH P
nên tọa độ điểm
H
thỏa mãn hệ phương trình:
1
2 2
1
2 4 0
x t
y t
z t
x y z
1
3
2
3
4
3
2
3
t
x
y
z
2 4 2
; ;
3 3 3
H
2 1 4
; ;
3 3 3
AH
.
Gọi
d
là hình chiếu vuông góc của
d
trên
P
d
đi qua
A
và
H
d
có một vector chỉ phương là
2;1; 4
u
.
Vậy phương trình đường thẳng
d
là:
1 2
2 1 4
x y z
.
Câu 46: Cho hàm số
3 2
f x x ax bx c
với
, ,a b c
là các số thực. Biết hàm số
g x f x f x f x
có hai giá trị cực trị là
3
và
6
. Diện tích hình phẳng giới
hạn bởi các đường
6
f x
y
g x
và
1y
bằng
A.
2ln3.
B.
ln3.
C.
ln18.
D.
2ln 2.
Lời giải
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https:/www.facebook.com/groups/toanvd.
Trang 25
Tập san
Số 02
8-2021
Chọn D
Ta có
2
3 2
f x x ax b
;
6 2f x x a
;
6
f x
;
g x f x f x f x
6
g x f x f x
.
Vì
g x
có hai giá trị cực trị là
3
và
6
nên
g x
có hai điểm cực trị là
1 2
,x x
và
1
3
g x
,
1
6
g x
.
Phương trình hoành độ giao điểm của hai đường
6
f x
y
g x
và
1y
là
1
6
f x
g x
6
f x g x
6
f x f x f x f x
6 0
f x f x
1
2
0
x x
g x
x x
.
Diện tích hình phẳng giới hạn bởi các đường
6
f x
y
g x
và
1y
là:
2 2 2
2
1
1 1 1
d 6
12
1d d ln 6 ln 2ln 2.
6 6 6 3
x x x
x
x
x x x
g x
f x g x
S x x g x
g x g x g x
Câu 47: Có bao nhiêu số nguyên
y
sao cho tồn tại
1
;3
3
x
thỏa mãn
2
3 9
27 1 27
x xy x
xy
.
A.
27
. B.
9
. C.
11
. D.
12
.
Lời giải
Chọn C
- Khi
0,
y
vì
1
xy
và
1
3
x
nên ta có
3.
y
Với
0
y
, phương trình thành:
2
3 9
27 1 0
x x
vô nghiệm vì
2
3 9 0
1
27 1 27 1 0, ;3
3
x x
x
.
Với
1
y
, phương trình thành:
2
3 10
27 (1 ) 0
x x
x
, có nghiệm vì
2
3 10
1
( ) 27 (1 )
x x
g x x
liên tục trên
1
;3
3
và
1 1
1
. 3 0
3
g g
.
Với
2
y
, phương trình thành:
2
3 11
27 (1 2 ) 0
x x
x
, có nghiệm vì
2
3 11
2
( ) 27 (1 2 )
x x
g x x
liên tục trên
1
;3
3
và
2 2
1
. 3 0
3
g g
.
- Khi
1,
y
xét trên
1
;3
3
, ta có
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https:/www.facebook.com/groups/toanvd.
Trang 26
Tập san
Số 02
8-2021
2
3 9 2
27
27
27 (1 )27 3 log (1 ) 9
log (1 )
3 9 0.
x xy x
xy x xy x
xy
x
x
x y
y
Xét hàm
27
log (1 )
( ) 3 9
xy
g x x y
x
trên
1
;3 .
3
Ta có
2 2
ln(1 ) 1
'( ) 3 3 3 0, ;3 .
ln 27 (1 ) ln 27 n
1 3
3 l 3 ln3 3
xy y
g x x
x x xy x
Do đó, hàm
( )g x
đồng biến trên
1
;3
3
. Vì thế phương trình
( ) 0g x
có nghiệm trên
1
;3
3
khi và chỉ khi
1
(3) 0.
3
g g
Áp dụng bất đẳng thức
ln(1 )u u
với mọi
0u
,
ta có
27
.
3
log (1 3 ) 3
(3) 0
3ln 27
y y
g y y
Do đó
3
1
0 log 1 8 0 1 9
3 3
y
g y y
(do
y
là số nguyên dương).
Vậy
2; 1;1;2;...;9y
hay có 11 giá trị
y
thỏa đề.
Câu 48: Cho khối hộp chữ nhật
. ' ' ' 'ABCD A B C D
có đáy là hình vuông,
2BD a
, góc giữa hai
mặt phẳng
'A BD
và
ABCD
bằng
0
30
. Thể tích của khối hộp chữ nhật đã cho bằng
A.
3
6 3a
. B.
3
2 3
9
a
. C.
3
2 3a
. D.
3
2 3
3
a
.
Lời giải
Chọn D
Gọi
O
là tâm hình vuông
ABCD
. Vì
BD OA
và
'BD AA
nên
' 'BD A OA BD OA
Lại có
'A BD ABCD BD
. Do đó
0
' , ' 30A BD ABCD A OA
(Hình vẽ trên).
Vì tứ giác
ABCD
là hình vuông có
2BD a
nên
OA a
và
2AB AD a
.
Xét tam giác
'A AO
vuông tại
A
có
OA a
và
0
' 30A OA
nên
0
3
' .tan 30
3
a
AA OA
.
Vậy thể tích khối hộp chữ nhật
3
3 2 3
. . ' 2. 2.
3 3
a
V AB AD AA a a a
.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https:/www.facebook.com/groups/toanvd.
Trang 27
Tập san
Số 02
8-2021
Câu 49: Trong không gian
,Oxyz
cho hai điểm
(1; 3; 4), ( 2;1; 2).A B
Xét hai điểm
M
và
N
thay
đổi thuộc mặt phẳng
( )Oxy
sao cho
2.MN
Giá trị lớn nhất của
AM BN
bằng
A.
3 5
. B.
61
. C.
13
. D.
53
.
Lời giải
Chọn D
Vì
. 0
A B
z z
nên
,A B
nằm khác phía so với mặt phẳng
( )Oxy
.
Gọi
,H K
lần lượt là hình chiếu vuông góc của
,A B
lên mặt phẳng
( )Oxy
(1; 3;0), ( 2;1;0)H K
.
Gọi
1
A
là điểm đối xứng của
A
qua
1
( ) (1; 3;4)Oxy A
.
Gọi
2
A
thỏa
1 2
A A MN
1 2
2A A
2
A
đường tròn
( )C
nằm trong mặt phẳng song song với
( )Oxy
và có tâm
1
,A
bán
kính
2R
.
Khi đó:
1 2 2
AM BN A M BN A N BN A B
.
Dấu
" "
xảy ra và
2
A B
đạt giá trị lớn nhất
1 2
A A
ngược hướng với
HK
.
1 2
1 2
6 8
; ;0
5 5
A A
A A HK
HK
2 2
11 23
; ; 4 53
5 5
A A B
.
Vậy giá trị lớn nhất của
AM BN
bằng
53
.
Câu 50: Cho hàm số
y f x
có đạo hàm
2
7 9 , .f x x x x
Có bao nhiêu giá trị
nguyên dương của tham số
m
để hàm số
3
5g x f x x m
có ít nhất 3 điểm cực
trị?
A.
6.
B.
7.
C.
5.
D.
4.
Lời giải
Chọn A
Ta có BBT của hàm
3
5y h x x x
như sau
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https:/www.facebook.com/groups/toanvd.
Trang 28
Tập san
Số 02
8-2021
Ta có
3 3
5 . 5g x x x f x x m
. Rõ ràng
0x
là điểm cực trị của hàm số
y h x
.
Ta có:
3 3
3 3 3
3 3
5 7 5 7
5 0 5 3 5 3
5 3 5 3
x x m x x m
f x x m x x m x x m
x x m x x m
.
Để hàm số
g x
có ít nhất
3
điểm cực trị thì phương trình
0g x
có ít nhất
2
nghiệm
phân biệt khác
0
và
g x
đổi dấu khi đi qua ít nhất
2
trong số các nghiệm đó.
Từ BBT ta có
7 0 7m m
1;2;3; 4;5;6 .m
Vậy có 6 giá trị của
m
thỏa mãn yêu cầu đề bài.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc
Trang 29
Tập san
Số 02
8-2021
Đề thi gồm 05 trang
ĐỀ THI TỐT NGHIỆP THPT ĐỢT 1 NĂM 2021
Bài thi môn: Toán
Thời gian: 90 phút (Không kể thời gian phát đề)
Mã đề thi: 102
Câu 1. Trên khoảng
0;
, đạo hàm của hàm số
5
4
y x
là:
A.
9
4
4
'
9
y x
. B.
1
4
4
'
5
y x
. C.
1
4
5
'
4
y x
. D.
1
4
5
'
4
y x
.
Câu 2. Cho khối chóp có diện tích đáy
2
3B a
và chiều cao
h a
. Thể tích của khối chóp đã
cho bằng:
A.
3
3
2
a
. B.
3
3a
. C.
3
1
3
a
. D.
3
a
.
Câu 3. Nếu
4
1
d 6f x x
và
4
1
d 5g x x
thì
4
1
df x g x x
bằng:
A.
1
. B.
11
. C.
1
. D.
11
.
Câu 4. Tập xác định của hàm số
7
x
y
là:
A.
\ 0
. B.
0;
. C.
0;
. D.
.
Câu 5. Cho hàm số
y f x
có bảng biến thiên như sau:
Giá trị cực đại của hàm số đã cho bằng
A.
3
. B.
1
. C.
5
. D.
1
.
Câu 6. Diện tích
S
của mặt cầu bán kính
R
được tính theo công thức nào dưới đây?
A.
2
4S R
. B.
2
16S R
. C.
2
4
3
S R
. D.
2
S R
.
Câu 7. Trong không gian
Oxyz
, cho đường thẳng
d
đi qua điểm
2;2;1M
và có một vecto chỉ
phương
5; 2; 3u
. Phương trình của
d
là:
A.
2 5
2 2
1 3
x t
y t
z t
. B.
2 5
2 2
1 3
x t
y t
z t
. C.
2 5
2 2
1 3
x t
y t
z t
. D.
5 2
2 2
3
x t
y t
z t
.
Câu 8. Cho hàm số
y f x
có đồ thị là đường cong như hình vẽ. Hàm số
đã cho đồng biến trên khoảng nào dưới đây?
A.
1;1
. B.
; 0
.
C.
0;1
. D.
0;
.
Câu 9. Với
n
là số nguyên dương bất kì,
5n
, công thức nào dưới đây
đúng?
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc
Trang 30
Tập san
Số 02
8-2021
A.
5
!
5! 5 !
n
n
A
n
. B.
5
5!
5 !
n
A
n
. C.
5
!
5 !
n
n
A
n
. D.
5
!
5 !
n
n
A
n
.
Câu 10. Thể tích của khối lập phương cạnh
4a
bằng:
A.
3
64a
. B.
3
32a
. C.
3
16a
. D.
3
8a
.
Câu 11. Cho hàm số
2
3f x x
. Khẳng định nào dưới đây đúng?
A.
2
d 3f x x x x C
. B.
3
d 3
3
x
f x x x C
.
C.
3
d 3f x x x x C
. D.
d 2f x x x C
.
Câu 12. Trên mặt phẳng tọa độ, điểm
3; 2M
là điểm biểu diễn của số phức nào dưới đây?
A.
3
3 2z i
. B.
4
3 2z i
. C.
1
3 2z i
. D.
2
3 2z i
.
Câu 13. Trong không gian
Oxyz
, cho mặt phẳng
: 2 5 3 0P x y z
. Vecto nào dưới đây
là một vecto pháp tuyến của
P
?
A.
2
2;5;1n
. B.
1
2;5;1n
. C.
4
2;5; 1n
. D.
3
2; 5;1n
.
Câu 14. Trong không gian
Oxyz
, cho điểm
4; 1;3A
. Tọa độ của vecto
OA
là
A.
4;1; 3
. B.
4; 1;3
. C.
4;1; 3
. D.
4;1; 3
.
Câu 15. Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?
A.
3
3 1y x x
.
B.
4 2
2 4 1y x x
.
C.
3
3 1y x x
.
D.
4 2
2 4 1y x x
.
Câu 16. Cho cấp số nhân
n
u
với
1
3u
và
2
12u
. Công bội của cấp số nhân đã cho bằng
A.
9
. B.
9
. C.
1
4
. D.
4
.
Câu 17. Cho
0a
và
1a
, khi đó
3
log
a
a
bằng
A.
3
. B.
1
3
. C.
1
3
. D.
3
.
Câu 18. Đồ thị của hàm số
4 2
2 3y x x
cắt trục tung tại điểm có tung độ bằng
A.
1
. B.
0
. C.
2
. D.
3
.
Câu 19. Cho hai số phức
5 2z i
và
1 4w i
. Số phức
z w
bằng:
A.
6 2i
. B.
4 6i
. C.
6 2i
. D.
4 6i
.
Câu 20. Cho hàm số
( ) 1.
x
f x e
Khẳng định nào dưới đây đúng?
A.
1
( )d
x
f x x e C
. B.
( )d
x
f x x e x C
.
C.
( )d
x
f x x e x C
. D.
( )d
x
f x x e C
.
Câu 21. Cho hàm số
( )f x
có bảng xét dấu đạo hàm như sau:
Số điểm cực trị của hàm số đã cho là
A.
5
. B.
3
. C.
2
. D.
4
.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc
Trang 31
Tập san
Số 02
8-2021
Câu 22. Nếu
3
0
( )d 3f x x
thì
3
0
2 ( )df x x
bằng
A.
3
. B.
18
. C.
2
. D.
6
.
Câu 23. Tiệm cận đứng của đồ thị hàm số
1
2
x
y
x
là đường thẳng có phương trình:
A.
1x
. B.
2x
. C.
2x
. D.
1x
.
Câu 24. Trong không gian
Oxyz
cho mặt cầu
( )S
có tâm
0; 2;1I
và bán kính bằng
2
. Phương
trình của
( )S
là:
A.
2 2
2
2 1 2x y z
. B.
2 2
2
2 1 2x y z
.
C.
2 2
2
2 1 4x y z
. D.
2 2
2
2 1 4x y z
.
Câu 25. Phần thực của số phức
6 2z i
bằng
A.
2.
B.
2.
C.
6.
D.
6.
Câu 26. Tập nghiệm của bất phương trình
2 5
x
là
A.
2
;log 5 .
B.
2
log 5; ; .
C.
5
;log 2 .
D.
5
log 2; ; .
Câu 27. Nghiệm của phương trình
5
log 3 2x
là:
A.
25.
B.
32
.
3
C.
32.
D.
25
.
3
Câu 28. Cho khối trụ có bán kính đáy
4r
và chiều cao
3.h
Thể tích của khối trụ đã cho bằng
A.
16 .
B.
48 .
C.
36 .
D.
12 .
Câu 29. Cho hình lăng trụ đứng
. ' ' 'ABC A B C
có tất cả các cạnh bằng nhau (tham khảo hình bên).
Góc giữa hai đường thẳng
'AA
và
'B C
bằng
A.
90 .
B.
45 .
C.
30 .
D.
60 .
Câu 30. Trong không gian, cho hai điểm
0;0;1A
và
2;1;3B
. Mặt phẳng đi qua
A
và vuông
góc với
AB
có phương trình là
A.
2 2 11 0x y z
. B.
2 2 2 0x y z
. C.
2 4 4 0x y z
. D.
2 4 17 0x y z
.
Câu 31. Từ một hộp chứa
10
quả bóng gồm 4 quả màu đỏ và 6 quả màu xanh, lấy ngẫu nhiên
đồng thời
3
quả. Xác suất để lấy được
3
quả màu xanh bằng
A.
1
6
. B.
1
30
. C.
3
5
. D.
2
5
.
Câu 32. Số phức
z
thỏa mãn
6 5iz i
. Số phức liên hợp của
z
là
A.
5 6z i
. B.
5 6z i
. C.
5 6z i
. D.
5 6z i
.
Câu 33. Biết hàm số
1
x a
y
x
(
a
là số thực cho trước,
1a
) có đồ thị như trong hình bên. Mệnh
đề nào dưới đây đúng?
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc
Trang 32
Tập san
Số 02
8-2021
A.
0,y x
. B.
0, 1y x
. C.
0, 1y x
. D.
0,y x
.
Câu 34. Trong không gian
,Oxyz
cho điểm
2;1; 1M
và mặt phẳng
: 3 2 1 0.P x y z
Đường thẳng đi qua
M
và vuông góc với
P
có phương trình là:
A.
2 1 1
1 3 1
x y z
. B.
2 1 1
1 3 2
x y z
.
C.
2 1 1
1 3 1
x y z
. D.
2 1 1
1 3 2
x y z
.
Câu 35. Trên đoạn
2;1
, hàm số
3 2
3 1y x x
đạt giá trị lớn nhất tại điểm
A.
2x
. B.
0x
. C.
1x
. D.
1x
.
Câu 36. Cho hình chóp
.S ABC
có đáy là tam giác vuông cân tại
, 3C AC a
và
SA
vuông góc với
mặt phẳng đáy. Khoảng cách từ
B
đến mặt phẳng
SAC
bằng
A.
3
2
a
. B.
3 2
2
a
. C.
3a
. D.
3 2a
.
Câu 37. Nếu
2
0
( ) 3f x dx
thì
2
0
2 1 df x x
bằng
A.
6
. B.
4
. C.
8
. D.
5
.
Câu 38. Với mọi
,a b
thỏa mãn
3
2 2
log log 8a b
, khẳng định nào dưới đây đúng?
A.
3
64a b
. B.
3
256a b
. C.
3
64a b
. D.
3
256a b
.
Câu 39. Có bao nhiêu số nguyên
x
thỏa mãn
2
2
3 9 log ( 30) 5 0?
x
x
A.
30
. B. Vô số. C.
31
. D.
29
.
Câu 40. Cho hàm số
2
2 1 khi 1
3 2 khi 1
x x
f x
x x
, giả sử
F
là nguyên hàm của
f
trên
thỏa mãn
0 2F
.Giá trị của
1 2 2F F
bằng.
A.
9
. B.
15
. C.
11
. D.
6
.
Câu 41. Cho hàm số bậc ba
y f x
có đồ thị là đường cong trong hình trên. Số nghiệm thực
phân biệt của phương trình
1f f x
là
A.
9
. B.
7
. C.
3
. D.
6
.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc
Trang 33
Tập san
Số 02
8-2021
Câu 42. Xét các số phức
, z w
thỏa mãn
1
z
và
2
w
. Khi
6 8z iw i
đạt giá trị nhỏ nhất
z w
bằng
A.
29
5
. B.
221
5
. C.
3
. D.
5
.
Câu 43. Cho hàm số
3 2
f x x ax bx c
với
, , a b c
là các số thực. Biết hàm số
g x f x f x f x

có hai giá trị cực trị là
4
và
2
. Diện tích hình phẳng giới
hạn bởi các hàm số
6
f x
y
g x
và
1y
bằng
A.
2ln 2
. B.
ln 6
. C.
3ln 2
. D.
ln 2
.
Câu 44. Cho khối hộp chữ nhật
. ' ' ' 'ABCD A B C D
có đáy là hình vuông,
4BD a
, góc giữa hai
mặt phẳng
'
A BD
và
ABCD
=
30
o
. Thể tích của khối hộp chữ nhật đa cho bằng?
A.
3
16 3
9
a
B.
3
48 3a
C.
3
16 3
3
a
D.
3
16 3a
Câu 45. Có bao nhiêu số nguyên
y
sao cho tồn tại
1
; 4
3
x
thỏa mãn
2
3 12
27 1 27
x xy x
xy
?
A.
14
. B.
27
. C.
12
. D.
15
.
Câu 46. Trong không gian
Oxyz
, cho đường thẳng
1 1
:
1 1 2
x y z
d
và mặt phẳng
: 2 3 0
P x y z
. Hình chiếu vuông góc của
d
trên
P
là đường thẳng có phương
trình:
A.
1 1
4 5 13
x y z
. B.
1 1
4 5 1
x y z
. C.
1 1
3 5 1
x y z
. D.
1 1
4 5 13
x y z
.
Câu 47. Cắt hình nón
bởi mặt phẳng đi qua đỉnh và tạo với mặt phẳng chứa đáy một góc
bằng
60
ta được thiết diện là tam giác đều cạnh
2 .a
Diện tích xung quanh của
bằng
A.
2
7
a
. B.
2
13
a
. C.
2
2 7
a
. D.
2
2 13
a
.
Câu 48. Trên tập hợp các số phức, xét phương trình
2 2
2 1 0
z m z m
(
m
là tham số thực).
Có bao nhiêu giá trị của
m
để phương trình đó có nghiệm
0
z
thỏa mãn
0
5
z
?
A.
2
. B.
3
. C.
1
. D.
4
.
Câu 49. Cho hàm số
y f x
có đạo hàm
2
8 9
f x x x
với
x
. Hỏi có bao nhiêu
giá trị nguyên dương của
m
để hàm số
3
6
f x x m
có ít nhất 3 cực trị?
A. 5. B. 7. C. 8. D. 6.
Câu 50. Trong không gian
Oxyz
, cho hai điểm
1; 3; 2
A
,
2;1; 3
B
. Xét hai điểm
M
,
N
thay
đổi trong mặt phẳng
Oxy
sao cho
1
MN
. Giá trị lớn nhất của
AM BN
bằng
A.
17
. B.
41
. C.
37
. D.
61
.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc
Trang 34
Tập san
Số 02
8-2021
BẢNG ĐÁP ÁN ĐỀ 102
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
C
D
D
D
A
A
C
C
C
A
B
D
A
B
D
D
B
D
C
C
D
D
C
D
C
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
A
D
B
B
B
A
C
C
B
B
C
B
B
C
A
B
A
A
C
A
A
A
B
B
C
LỜI GIẢI CHI TIẾT
Câu 39. Có bao nhiêu số nguyên
x
thỏa mãn
2
2
3 9 log ( 30) 5 0?
x x
x
A.
30
. B. Vô số. C.
31
. D.
29
.
Lời giải
Chọn C
Điều kiện xác định:
30x
. Đặt
2
2
( ) 3 9 log 30 5
x x
f x x
Xét phương trình
( ) 0f x
2
2
3 9
log ( 30) 5
x x
x
2
5
2
30 2
x x
x
0
2 (kép)
x
x
.
Ta có bảng xét dấu:
Suy ra bất phương trình
( ) 0f x
có tâp nghiệm là:
30;0 2S
.
Với
29; 28;...; 2; 1;0;2x x
.
Vậy có
31
số nguyên
x
thỏa mãn.
Câu 40. Cho hàm số
2
2 1 khi 1
3 2 khi 1
x x
f x
x x
, giả sử
F
là nguyên hàm của
f
trên
thỏa
mãn
0 2F
. Giá trị của
1 2 2F F
bằng.
A.
9
. B.
15
. C.
11
. D.
6
.
Lời giải
Chọn A
Cách 1:
Ta có:
2
1
2 1 dx x x x c
;
2 3
2
3 2 d 2x x x x c
Suy ra
2
1
3
2
khi 1
d
2 khi 1
x x C x
F x f x x
x x C x
Mà ta có
2
0 2 2F C
.
Mặt khác hàm số
F
là nguyên hàm của
f
trên
nên
y F x
liên tục tại
1x
Suy ra
1
1 1
lim lim 1
x x
F x F x C
.
Khi đó ta có:
2
3
1 khi 1
2 2 khi 1
x x x
F x
x x x
suy ra
1 3
.
2 3
F
F
Vậy
1 2 2 9F F
.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc
Trang 35
Tập san
Số 02
8-2021
Cách 2:
Dễ thấy hàm số
f x
liên tục trên
. Khi đó ta có:
1
2
0
1 0 (3 2)d 1 1 1F F x x F
.
1 2
2
1 1
1 2 2 (3 2)d 2 (2 1)d 3 1 2 4 3 9F F x x x x F
.
Câu 41. Cho hàm số bậc ba
y f x
có đồ thị là đường cong trong hình trên. Số nghiệm thực
phân biệt của phương trình
1f f x
là
A.
9
. B.
7
. C.
3
. D.
6
.
Lời giải
Chọn B
Từ
, 1
1 0
, 1 2
f x a a
f f x f x
f x b b
.
f x a
với
1a
phương trình có một nghiệm
0f x
phương trình có ba nghiệm phân biệt
f x b
với
1 2b
phương trình có 3 nghiệm phân biệt.
Vậy số nghiệm thực phân biệt của phương trình
1f f x
là
7
.
Câu 42. Xét các số phức
, z w
thỏa mãn
1z
và
2w
. Khi
6 8z iw i
đạt giá trị nhỏ nhất,
z w
bằng
A.
29
5
. B.
221
5
. C.
3
. D.
5
.
Lời giải
Chọn A
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc
Trang 36
Tập san
Số 02
8-2021
Ta có
6 8 6 8 10 1 2 7
z i w i i z iw
.
Dấu bằng xảy ra khi và chỉ khi
3 4 3 4
5 5 5 5
6 8 8 6
5 5 5 5
z i z i
iw i w i
.
Khi đó
29
5
z w
.
Câu 43. Cho hàm số
3 2
f x x ax bx c
với
, , a b c
là các số thực. Biết hàm số
g x f x f x f x
có hai giá trị cực trị là
4
và
2
. Diện tích hình phẳng giới
hạn bởi các hàm số
6
f x
y
g x
và
1y
bằng
A.
2ln 2
. B.
ln 6
. C.
3ln 2
. D.
ln2
.
Lời giải
Chọn A
Ta có:
3 2
3 2 6 2
g x f x f x f x x a x a b x a b c
g x f x f x f x
2
3 2 6 2 6
x ax b x a
2
3 2 6 2 6
x a x a b
.
Do
g x
có hai cực trị là
5
và
3
nên
1
2
0
x x
g x
x x
với
1
4
g x
,
2
2
g x
.
Phương trình hoành độ giao điểm
6
1 0
6 6
f x f x g x
g x g x
2
3 2 6 2 6
0 0
6 6
x a x a b g x
g x g x
Phương trình này cũng có hai nghệm phân biệt
1 2
,x x
Như vậy diện tích hình phẳng giới hạn bởi các hàm số
6
f x
y
g x
và
1y
là
2
2
1
1
ln 6 ln 2 6 ln 4 6 2ln 2
6
x
x
x
x
g x
S g x
g x
.
Câu 44. Cho khối hộp chữ nhật
. ' ' ' 'ABCD A B C D
có đáy là hình vuông,
4BD a
, góc giữa hai
mặt phẳng
'
A BD
và
ABCD
=
3 0
o
. Thể tích của khối hộp chữ nhật đã cho bằng ?
A.
3
16 3
9
a
B.
3
48 3a
C.
3
16 3
3
a
D.
3
16 3a
Lời giải
Chọn C
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc
Trang 37
Tập san
Số 02
8-2021
Gọi
O
là trung điểm của
BD
. Ta có:
' 'A AB A AD
suy ra
' 'A B A D
suy ra
'A BD
cân.
Mà
'
'
A BD ABCD BD
A O BD
AO BD
, 30 .A BD ABCD A OA
Xét
A OA
vuông tại
A
có:
tan 30
2
2 2
o
A A A A A A A A
AC BD
AO a
2 3
' 2 .tan30
3
a
A A a
.
Xét hình vuông
ABCD
có:
2 2 2.BD AB AB a
Vậy thể tích của khối hộp chữ nhật bằng:
2
' .V A A AB
=
2
2 3
. 2 2
3
a
a
=
3
16 3
3
a
.
Câu 45. Có bao nhiêu số nguyên
y
sao cho tồn tại
1
;4
3
x
thỏa mãn
2
3 12
27 1 27
x xy x
xy
?
A.
14
. B.
27
. C.
12
. D.
15
.
Lời giải
Chọn A
TH1:
0,y
vì
1xy
và
1
3
x
nên ta có
3.y
Ta có thể kiểm tra trực tiếp để xem xét có nhận
2, 1, 0y y y
hay không.
+) Nếu
2
3 12 2
1
0 ; 4
3
0 27 1 3 12 0
1
4 ; 4
3
x x
x
y x x
x
(trường hợp này loại).
+) Nếu
1y
thỏa mãn.
+) Nếu
2y
thỏa mãn.
TH2: Khi
1,y
ta có:
2
3 12
27 (1 )27
x xy x
xy
2
2
7
3 12 log 1x x xy xy
27
log 1
3 12 0.
xy
x y
x
Xét hàm
27
log 1
3 12
xy
g x x y
x
trên
1
; 4
3
.
Ta có
2 2
ln 1
1
3 3 3 0, ; 4 .
3
ln 27 1 ln 27 3 ln 3 ln 3 3
1
xy
y
g x x
x x xy x
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc
Trang 38
Tập san
Số 02
8-2021
Do đó, hàm
g x
đồng biến trên
1
; 4
3
. Vì thế phương trình
0
g x
có nghiệm trên
1
; 4
3
khi và chỉ khi
1
4 0
3
g g
.
Áp dụng bất đẳng thức
ln 1
u u
với mọi
0
u
, ta có
ln 1 4
4 0
18ln3 3ln3
y
y
g y y
.
Do đó
3
1
0 log 1 11 0 1 12
3 3
y
g y y
(do
y
là số nguyên dương).
Vậy có 14 giá trị nguyên
y
sao cho tồn tại
1
;4
3
x
thỏa mãn
2
3 12
27 1 .27
x xy x
xy
.
Câu 46. Trong không gian
Oxyz
, cho đường thẳng
1 1
:
1 1 2
x y z
d
và mặt phẳng
: 2 3 0
P x y z
. Hình chiếu vuông góc của
d
trên
P
là đường thẳng có phương
trình:
A.
1 1
4 5 13
x y z
. B.
1 1
4 5 1
x y z
.
C.
1 1
3 5 1
x y z
. D.
1 1
4 5 13
x y z
.
Lời giải
Chọn A
Gọi
là đường thẳng cần tìm.
Đường thẳng
d
đi qua
1;0;1
A
có 1 VTCP là:
1;1;2
u
.
Mặt phẳng
P
có 1 VTPT là:
2;1; 1
n
.
Ta có
, 3;5; 1
v u n
;
, 4; 5;13
a n v
.
là hình chiếu của
d
trên
P
đi qua
1;0;1
A
và có 1 VTCP
, 4; 5;13
a n v
.
Suy ra phương trình
:
1 1
4 5 13
x y z
.
Câu 47. Cắt hình nón
bởi mặt phẳng đi qua đỉnh và tạo với mặt phẳng chứa đáy một góc
bằng
60
ta được thiết diện là tam giác đều cạnh
2 .a
Diện tích xung quanh của
bằng
A.
2
7
a
. B.
2
13
a
. C.
2
2 7
a
. D.
2
2 13
a
.
Lời giải
Chọn A
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc
Trang 39
Tập san
Số 02
8-2021
Mặt phẳng
P
cắt hình nón theo thiết diện là tam giác đều
SAB
cạnh
2 2 .a AB a
Kẻ
OH AB
tại
, 3.H AH a SH a
Góc giữa mặt phẳng
SAB
với mặt đáy bằng
3
60 60 .sin 60 .
2
a
SHO SO SH
Mà
2 2 2 2
3 7
4 .
tan 60 2 2
SO a a
OH r AH OH SA h r a
Vậy
2
7
. .2 7 .
2
xq
a
S rl a a
Câu 48. Trên tập hợp các số phức, xét phương trình
2 2
2 1 0z m z m
(
m
là tham số thực).
Có bao nhiêu giá trị của
m
để phương trình đó có nghiệm
0
z
thỏa mãn
0
5z
?
A.
2
. B.
3
. C.
1
. D.
4
.
Lời giải
Chọn B
Ta có
2 1m
.
TH1:
1
0
2
m
thì
0
1
2
z
, suy ra
1
2
m
(loại).
TH2:
1
0
2
m
thì
0
1 2 1 .z m m i
hoặc
0
1 2 1 .z m m i
.
Theo đề bài
2
0
5
5 1 2 1 25
5
m L
z m m
m N
.
TH 3:
1
0
2
m
thì phương trình có hai nghiệm thực phân biệt
Theo đề bài
0 0
5 5z z
.
+ Khi
0
5:z
thế vào phương trình ta được
2
10 15 0 5 10m m m
(nhận).
+ Khi
0
5z
: thế vào phương trình ta được
2
10 35 0m m
vô nghiệm.
Vậy có ba giá trị của
m
.
Câu 49. Cho hàm số
y f x
có đạo hàm
2
8 9
f x x x
với
x
. Hỏi có bao nhiêu
giá trị nguyên dương của
m
để hàm số
3
6 f x x m
có ít nhất 3 cực trị?
A.
5
. B.
7
. C.
8
. D.
6
.
Lời giải
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc
Trang 40
Tập san
Số 02
8-2021
Chọn B
Hàm số
y f x
có
0
f x
tại
8, 3 x x
.
Đặt
3
6 g x f x x m
.
Ta có:
2 3
3 3
3
3 6 6
6 . 6 0
6
x x x
g x f x x m f x x m x
x x
.
Với
0x
là 1 cực trị của
g x
Để
g x
có ít nhất 3 cực trị thì
g x
phải có ít nhất 3 nghiệm bội lẻ hay
3
' 6 0 f x x m
có ít nhất 2 nghiệm.
3
3 3
3
6 3
' 6 0 6 3
6 8
x x m
f x x m x x m
x x m
. Ta có đồ thị
3
6 u x x x
( với
0m
):
Để
3
' 6 0 f x x m
có ít nhất 2 nghiệm thì:
8 0 8 1;7 m m m
.
Vậy có
7
giá trị
m
.
Câu 50. Trong không gian
Oxyz
, cho hai điểm
1; 3; 2A
,
2;1; 3B
. Xét hai điểm
M
,
N
thay
đổi trong mặt phẳng
Oxy
sao cho
1MN
. Giá trị lớn nhất của
AM BN
bằng
A.
17
. B.
41
. C.
37
. D.
61
.
Lời giải
Chọn C
Đề thấy hai điểm
,A B
nằm khác phía so với mặt phẳng
Oxy
.
Gọi
H
lần lượt là hình chiếu vuông góc của
A
lên mặt phẳng
Oxy
, khi đó ta có:
1; 3;0H
.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc
Trang 41
Tập san
Số 02
8-2021
Lấy điểm
1
A
đối xứng với
A
qua mặt phẳng
Oxy
1
1; 3; 2A
. Khi đó
1
AM AM
.
Lấy điểm
2
A
sao cho
1 2
A A MN
. Tứ giác
1 2
AANM
là hình bình hành nên
1 2
AM A N
.
Khi đó ta dễ thấy hai điểm
2
A
và
B
nằm cùng phía so với mặt phẳng
Oxy
.
Do
1MN
nên điểm
N
thuộc đường tròn
C
tâm
M
bán kính
1R MN
nằm trên
mặt phẳng
Oxy
nên điểm
2
A
thuộc vào đường tròn
'C
tâm
1
A
và bán kính
' 1R R
và nằm trong mặt phẳng
2z
.
Ta có:
1 2 2
AM BN A M BN A N BN A B
. Dấu bằng xảy ra khi
2
N A B Oxy
.
Để
AM BN
đạt giá trị lớn nhất thì
2
AB
phải đạt giá trị lớn nhất.
Gọi
K
lần lượt là hình chiếu vuông góc của
B
lên mặt phẳng
2z
, khi đó ta có:
2;1; 2K
và
1BK
,
1
5AK
.
Tam giác
2
BKA
vuông tại
K
nên ta có:
2 2 2
2 2 2
1A B BK KA KA
.
Để
2
AB
phải đạt giá trị lớn nhất thì
2
KA
phải lớn nhất.
Mà
2
2 1 2
' 5 1 6 1 6 37KA A K R A B
Suy ra giá trị lớn nhất của
AM BN
bằng
37
, dấu bằng xảy ra khi
2
N A B Oxy
.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https:/www.facebook.com/groups/toanvd. Trang 42
Tập san
Số 02
8-2021
Đề thi gồm 05 trang
ĐỀ THI TỐT NGHIỆP THPT ĐỢT 1 NĂM 2021
Bài thi môn: Toán
Thời gian: 90 phút (Không kể thời gian phát đề)
Mã đề thi: 103
Câu 1. Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?
A.
3
1
2
2
y x x
. B.
3
1
2
2
y x x
. C.
4 2
1
2
2
y x x
. D.
4 2
1
2
2
y x x
.
Câu 2. Cho cấp số nhân
n
u
với
1
3u
và
2
15u
. Công bội của cấp số nhân đã cho bằng
A.
12
. B.
1
5
. C.
5
. D.
12
.
Câu 3. Cho khối chóp có diện tích đáy
2
7B a
và chiều cao
h a
. Thể tích của khối chóp đã
cho bằng
A.
3
7
6
a
. B.
3
7
2
a
. C.
3
7
3
a
. D.
3
7a
.
Câu 4. Nếu
4
1
( )d 5f x x
và
4
1
( )d 4g x x
thì
4
1
( ) ( ) df x g x x
bằng
A.
1
. B.
9
. C.
1
. D.
9
.
Câu 5. Trong không gian
Oxyz
, cho đường thẳng
d
đi qua điểm
3;1;2M
và có một vectơ
chỉ phương
2;4; 1
u
. Phương trình của
d
là
A.
3 2
1 4
2
x t
y t
z t
. B.
3 2
1 4
2
x t
y t
z t
. C.
3 2
1 4
2
x t
y t
z t
. D.
2 3
4
1 2
x t
y t
z t
.
Câu 6. Diện tích
S
của mặt cầu bán kinh
R
được tính theo công thức nào dưới đây?
A.
2
S R
. B.
2
4
3
S R
. C.
2
4S R
. D.
2
16S R
.
Câu 7. Trong không gian
Oxyz
, cho mặt phẳng
: 2 2 3 0P x y z
. Vectơ nào dưới đây là
một vectơ pháp tuyến của
P
?
A.
3
1;2;2n
. B.
1
1; 2;2n
. C.
4
1; 2; 3n
. D.
2
1;2; 2n
.
Câu 8. Trong không gian
Oxyz
, cho mặt cầu
S
có tâm
0;1; 2I
và bán kinh bằng
3
. Phương
trình của
S
là:
A.
2
2
1 2 9x y z
. B.
2
2
1 2 9x y z
.
C.
2
2
1 2 3x y z
. D.
2
2
1 2 3x y z
.
Câu 9. Cho hàm số
2
1f x x
. Khẳng định nào dưới đây đúng?
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https:/www.facebook.com/groups/toanvd. Trang 43
Tập san
Số 02
8-2021
A.
df x x x x C
. B.
3
d
3
x
f x x x C
.
C.
2
df x x x x C
. D.
d 2f x x x C
.
Câu 10. Cho hàm số
y f x
có bảng xét dấu của đạo hàm như sau:
Số điểm cực trị của hàm số đã cho là:
A.
2
. B.
3
. C.
4
. D.
5
.
Câu 11. Tập xác định của hàm số
6
x
y
là:
A.
0;
. B.
\ 0
. C.
0;
. D.
.
Câu 12. Nếu
3
0
d 2f x x
thì
3
0
3 df x x
bằng
A.
6
. B.
1
. C.
1
. D.
0
.
Câu 13. Trên mặt phẳng tọa độ, điểm
( 2;3)M
là điểm biểu diễn số phức nào dưới đây?
A.
3
2 3z i
. B.
4
2 3z i
. C.
1
2 3z i
. D.
2
2 3z i
.
Câu 14. Cho hàm số
( ) 3
x
f x e
. Khẳng định nào dưới đây đúng?
A.
( )d 3
x
f x x e x C
. B.
( )d
x
f x x e C
.
C.
3
( )d
x
f x x e C
. D.
( )d 3
x
f x x e x C
.
Câu 15. Cho hàm số
( )y f x
có đồ thị là đường cong trong hình bên. Hàm số đã cho đồng biến
trong khoảng nào dưới đây?
A.
( ;2)
. B.
(0;2)
. C.
( 2;2)
. D.
(2; )
.
Câu 16. Đồ thị hàm số
3 2
2 1y x x
cắt trục tung tại điểm có tung độ bằng
A.
3
. B.
1
. C.
1
. D.
0
.
Câu 17. Trên khoảng
(0; )
, đạo hàm của hàm số
4
3
y x
là:
A.
1
3
4
3
y x
. B.
1
3
4
3
y x
. C.
7
3
3
7
y x
. D.
1
3
3
4
y x
.
Câu 18. Cho
0a
và
1a
, khi đó
log
a
a
bằng
A.
2
. B.
2
. C.
1
2
. D.
1
2
.
Câu 19. Trong không gian
Oxyz
cho điểm
(3;2; 4)A
. Tọa độ vectơ
OA
là
A.
(3; 2; 4)
. B.
( 3; 2;4)
. C.
(3;2; 4)
. D.
(3;2;4)
.
Câu 20. Tập nghiệm của phương trình
2 3
x
là
A.
3
(log 2; )
. B.
2
;log 3
. C.
3
;log 2
. D.
2
(log 3; )
.
Câu 21. Cho hai số phức
1 2z i
và
3 4w i
. Số phức
z w
bằng
A.
2 6i
. B.
4 2i
. C.
4 2i
. D.
2 6i
.
Câu 22. Cho hàm số
( )y f x
có bảng biến thiên như hình vẽ sau
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https:/www.facebook.com/groups/toanvd. Trang 44
Tập san
Số 02
8-2021
Giá trị cực đại của hàm số đã cho bằng
A.
3
. B.
0
. C.
2
. D.
1
.
Câu 23. Thể tích khối lập phương cạnh
3a
bằng
A.
3
27a
. B.
3
3a
. C.
3
9a
. D.
3
a
.
Câu 24. Tiệm cận đứng của đồ thị hàm số
2 1
1
x
y
x
là đường thẳng có phương trình
A.
2x
. B.
1x
. C.
1
2
x
. D.
1
.
Câu 25. Phần thực của số phức
3 2z i
bằng:
A.
2
. B.
3
. C.
3
. D.
2.
Câu 26. Nghiệm của phương trình
3
log (2 ) 2x
là:
A.
9
2
x
.
B.
9x
. C.
4x
. D.
8x
Câu 27. Với
n
là số nguyên dương bất kì,
2n
, công thức nào sau đây đúng?
A.
2
2 !
!
n
n
A
n
. B.
2
2!
2 !
n
A
n
. C.
2
!
2! 2 !
n
n
A
n
. D.
2
!
2 !
n
n
A
n
Câu 28. Cho khối trụ có bán kính đáy
2r
và chiều cao
3h
. Thể tích của khối trụ đã cho bằng
A.
12
. B.
18
. C.
6
. D.
4
Câu 29. Trong không gian
Oxyz
, Cho điểm
1;2; 1M
và mặt phẳng
: 2 3 1 0P x y z
Đường thẳng đi qua
M
và vuông góc với mặt phẳng
P
có phương trình là:
A.
1 2 1
2 1 1
x y z
. B.
1 2 1
2 1 3
x y z
.
C.
1 2 1
2 1 1
x y z
. D.
1 2 1
2 1 3
x y z
.
Câu 30. Cho hình lăng trụ đứng
.ABC A B C
có tất cả các cạnh bằng nhau (tham khảo hình bên).
Góc giữa hai đường thẳng
A B
và
CC
bằng:
A.
45
o
. B.
30
o
. C.
90
o
. D.
60
o
.
Câu 31. Cho số phức
z
thỏa mãn
3 2iz i
. Số phức liên hợp của
z
là:
A.
2 3z i
. B.
2 3z i
. C.
2 3z i
. D.
2 3z i
.
Câu 32. Cho hình chóp
.S ABC
có đáy là tam giác vuông cân tại
C
,
AC a
và
SA
vuông góc với
mặt phẳng đáy. Khoảng cách từ
B
đến mặt phẳng
SAC
bằng
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https:/www.facebook.com/groups/toanvd. Trang 45
Tập san
Số 02
8-2021
A.
1
2
a
. B.
2a
. C.
2
2
a
. D.
a
.
Câu 33. Từ một hộp chứa
10
quả bóng gồm
4
quả màu đỏ và
6
quả màu xanh. Lấy ngẫu nhiên
đồng thời
3
quả. Xác suất để lấy được 3 quả màu đỏ bằng
A.
1
5
. B.
1
6
. C.
2
5
. D.
1
30
.
Câu 34. Với mọi
,a b
thỏa mãn
3
2 2
log log 7a b
, khẳng định nào dưới đây đúng?
A.
3
49a b
. B.
3
128a b
. C.
3
128a b
. D.
3
49a b
.
Câu 35. Trong không gian
Oxyz
, cho hai điểm
0;0;1A
và
1;2;3B
. Mặt phẳng đi qua
A
và
vuông góc với
AB
có phương trình là:
A.
2 2 11 0x y z
. B.
2 2 2 0x y z
.
C.
2 4 4 0x y z
. D.
2 4 17 0x y z
.
Câu 36. Trên đoạn
0;3
, hàm số
3
3 4y x x
đạt giá trị nhỏ nhất tại điểm
A.
1x
. B.
0x
. C.
3x
. D.
2x
.
Câu 37. Nếu
2
0
d 6
f x x
thì
2
0
2 1 df x x
bằng
A.
12
. B.
10
. C.
11
. D.
14
Câu 38. Biết hàm số
1
x a
y
x
, (
a
là số thực cho trước và
1a
) có đồ thị như trong hình bên.
Mệnh đề nào dưới đây đúng?
A.
0, 1y x
. B.
0,y x
. C.
0,y x
. D.
0, 1y x
.
Câu 39. Có bao nhiêu số nguyên
x
thỏa mãn
2
2
2 4 log 14 4 0
x x
x
?
A.
14
. B.
13
. C. Vô số. D.
15
.
Câu 40. Cho hàm số
2
2 3 khi 1
3 2 khi 1
x x
f x
x x
. Giả sử
F
là nguyên hàm của
f
trên
thỏa mãn
0 2F
. Giá trị của
1 2 2F F
bằng
A.
23
. B.
11
. C.
10
. D.
21
.
Câu 41. Cho hàm số bậc bốn
y f x
có đồ thị là đường cong trong hình bên dưới.
Số nghiệm thực phân biệt của phương trình
0f f x
là
A.
4
. B.
10
. C.
12
. D.
8
.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https:/www.facebook.com/groups/toanvd. Trang 46
Tập san
Số 02
8-2021
Câu 42. Xét các số phức
,z w
thỏa mãn
1
z
và
2
w
. Khi
6 8z iw i
đạt giá trị nhỏ nhất,
z w
bằng?
A.
3
. B.
29
5
. C.
5
. D.
221
5
.
Câu 43. Trong không gian
Oxyz
, cho đường thẳng
1 2 1
:
1 1 2
x y z
d
và mặt phẳng
( ) : 2 6 0
P x y z
. Hình chiếu vuông góc của
d
trên
( )P
là đường thẳng có phương
trình:
A.
1 2 1
3 1 1
x y z
. B.
1 2 1
3 1 1
x y z
.
C.
1 2 1
1 4 7
x y z
. D.
1 2 1
.
1 4 7
x y z
Câu 44. Có bao nhiêu số nguyên
y
sao cho tồn tại
1
;5
3
x
thỏa mãn
2
3 15
27 1 27
x xy x
xy
.
A.
17
. B.
16
. C.
18
. D.
15
.
Câu 45. Cho khối hộp chữ nhật
.
ABCD A B C D
có đáy là hình vuông,
2BD a
, góc giữa hai mặt
phẳng
A BD
và
ABCD
bằng
60
. Thể tích của khối hộp chữ nhật đã cho bằng
A.
3
2 3
9
a
. B.
3
6 3a
. C.
3
2 3
3
a
. D.
3
2 3a
.
Câu 46. Cho hàm số
3 2
f x x ax bx c
với
a
,
b
,
c
là các số thực. Biết hàm số
g x f x f x f x
có hai giá trị cực trị là
5
và
3
. Diện tích hình phẳng giới
hạn bởi các đường
6
f x
y
g x
và
1y
bằng
A.
2ln3
. B.
ln 2
. C.
ln15
. D.
3ln 2
.
Câu 47. Cắt hình nón
N
bởi mặt phẳng đi qua đỉnh và tạo với mặt phẳng chứa đáy một góc
bằng
0
30 ,
ta được thiết diện là tam giác đều cạnh
4 .a
Diện tích xung quanh của nón
bằng
A.
2
4 7
a
. B.
2
8 7
a
. C.
2
8 13
a
. D.
2
4 13 .a
Câu 48. Trên tập hợp các số phức, xét phương trình
2 2
2 1 0
z m z m
(
m
là tham số thực).
Có bao nhiêu giá trị của
m
để phương trình đó có nghiệm
o
z
thỏa mãn
8
o
z
?
A.
4
. B.
3
. C.
2
. D.
1
.
Câu 49. Trong không gian
Oxyz
, cho hai điểm
1; 3;2
A
và
2;1; 4
B
. Xét hai điểm
M
và
N
thay đổi thuộc mặt phẳng
Oxy
sao cho
4
MN
. Giá trị lớn nhất của
AM BN
bằng
A.
5 2
. B.
3 13
. C.
61
. D.
85
.
Câu 50. Cho hàm số
y f x
có đạo hàm
2
10 25 ,f x x x x
. Có bao nhiêu giá trị
nguyên dương của tham số
m
để hàm số
3
8
g x f x x m
có ít nhất 3 điểm cực trị
A.
9
. B.
25
. C.
5
. D.
10
.
BẢNG ĐÁP ÁN ĐỀ 103
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https:/www.facebook.com/groups/toanvd. Trang 47
Tập san
Số 02
8-2021
1 2 3 4 5 6 7 8 9 10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
B
C
C
D
C
C
B
A
B
C
D
A
C
A
B
C
B
D
C
D
C
A
A
B
C
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
A
D
A
B
A
A
D
D
B
B
A
B
A
D
D
B
D
D
A
D
A
D
B
D
A
LỜI GIẢI CHI TIẾT CÁC CÂU VD – VDC
Câu 39. Có bao nhiêu số nguyên
x
thỏa mãn
2
2
2 4 log 14 4 0
x x
x
?
A.
14
. B.
13
. C. Vô số. D.
15
.
Lời giải
Chọn D
Cách 1
Trường hợp 1:
2
2
2 4 0
log 14 4 0
x x
x
2
2
2 2
14 16
x x
x
2
2 0
2
x x
x
0 2
2
x
x
2x
Trường hợp 2:
2
2
2 4 0
log 14 4 0
x x
x
2
2 0
14 2
x x
x
0
14 0
2
2
14 2
x
x
x
x
x
.
Vậy có 15 giá trị nguyên của
x
thỏa mãn yêu cầu bài toán.
Cách 2:
Điều kiện xác định:
14x
. Đặt
2
2
2 4 log 1( 4) 4
x x
f x x
.
Xét phương trình
( ) 0f x
2
2
log ( )
4
14
2
4
x x
x
2
4
2
14 2
x x
x
0
2 (kép)
x
x
.
Ta có bảng xét dấu:
Suy ra bất phương trình
( ) 0f x
có tập nghiệm là:
14;0 2S
.
Do
13; 12;...; 2; 1;0;2x x
.
Vậy có 15 giá trị nguyên của
x
thỏa mãn yêu cầu bài toán.
Câu 40. Cho hàm số
2
2 3 khi 1
3 2 khi 1
x x
f x
x x
. Giả sử
F
là nguyên hàm của
f
trên
thỏa mãn
0 2F
. Giá trị của
1 2 2F F
bằng
A.
23
. B.
11
. C.
10
. D.
21
.
Lời giải
Chọn D
Ta có
2
1
3
2
3 khi 1
2 khi 1
x x C x
F x
x x C x
.
Ta có
2
1 1
1 1
lim lim 3 4
x x
F x x x C C
.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https:/www.facebook.com/groups/toanvd. Trang 48
Tập san
Số 02
8-2021
3
2 2
1 1
lim lim 2 3
x x
F x x x C C
.
F x
liên tục tại
1 2
1 4 3x C C
(1)
2
0 2 2F C
(2).
Từ (1) và (2) suy ra
1
2
1
2
C
C
2
3
3 1 khi 1
2 2 khi 1
x x x
F x
x x x
.
3
2
1 2 2 1 2 1 2 2 2 3.2 1 21F F
.
Câu 41. Cho hàm số bậc bốn
y f x
có đồ thị là đường cong trong hình bên dưới.
Số nghiệm thực phân biệt của phương trình
0f f x
là
A.
4
. B.
10
. C.
12
. D.
8
.
Lời giải
Chọn B
Ta có:
1
1 0
0
0 1
1
f x a a
f x b b
f f x
f x c c
f x d d
.
Phương trình
f x a
với
1a
vô nghiệm.
Phương trình
f x b
với
1 0b
có 4 nghiệm phân biệt.
Phương trình
f x c
với
0 1c
có 4 nghiệm phân biệt.
Phương trình
f x d
với
1d
có 2 nghiệm phân biệt.
Vậy phương trình
0f f x
có 10 nghiệm.
Câu 42. Xét các số phức
,z w
thỏa mãn
1z
và
2w
. Khi
6 8z iw i
đạt giá trị nhỏ nhất,
z w
bằng?
A.
3
. B.
29
5
. C.
5
. D.
221
5
.
Lời giải
Chọn D
Theo BĐT modun số phức, ta có:
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https:/www.facebook.com/groups/toanvd. Trang 49
Tập san
Số 02
8-2021
3
z iw z iw z w
.
Ta lại có:
6 8 6 8 6 8 6 8 10 3 7
z iw i i z iw i z iw i z iw
.
Dấu bằng xảy ra, khi và chỉ khi:
.
0, 0.
6 8 .
z k iw
k m
i m z iw
Lấy modun 2 vế, ta được:
1
.
1 .2
2
10
10 .3
6 8 .
3
k
z k iw
k
m
i m z iw
m
.
3 4
221
5 5
.
8 6
5
5 5
z i
z w
w i
Câu 43. Trong không gian
Oxyz
, cho đường thẳng
1 2 1
:
1 1 2
x y z
d
và mặt phẳng
( ) : 2 6 0
P x y z
hình chiếu vuông góc của
d
trên
( )P
là đường thẳng có phương
trình:
A.
1 2 1
3 1 1
x y z
. B.
1 2 1
3 1 1
x y z
.
C.
1 2 1
1 4 7
x y z
. D.
1 2 1
.
1 4 7
x y z
Lời giải
Chọn D
Ta có
d
đi qua điểm
1; 2; 1
A
và
1; 2; 1
A
thuộc
( )P
.
Vậy
1; 2; 1
A
là giao điểm của
d
và
( )P
.
Gọi
Q
là mặt phẳng chứa đường thẳng
d
và vuông góc với
P
. Khi đó
Q
có vectơ
pháp tuyến
, 3; 1;1
d
Q P
n u n
.
Đường thẳng
d
là giao tuyến của hai mặt phẳng
P
và
Q
nên có một vecto chỉ
phương là:
( 1; 4;7)
,
Q
d
P
u n n
.
Vậy đường thẳng
d
có
( 1;4;7)
d
u
và đi qua điểm
(1; 2; 1)
A
có phương trình chính
tắc là
1 2 1
.
1 4 7
x y z
Câu 44. Có bao nhiêu số nguyên
y
sao cho tồn tại
1
;5
3
x
thỏa mãn
2
3 15
27 1 27
x xy x
xy
.
A.
17
. B.
16
. C.
18
. D.
15
.
Lời giải
Chọn A
Khi
0,
y
vì
1
xy
và
1
3
x
nên ta có
3.
y
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https:/www.facebook.com/groups/toanvd. Trang 50
Tập san
Số 02
8-2021
Với
0y
, phương trình thành:
2
3 15
27 1 0
x x
, vô nghiệm vì
2
3 15 0
1
27 1 27 1 0, ;5
3
x x
x
.
Với
1y
, phương trình thành:
2
3 16
27 (1 ) 0
x x
x
có nghiệm vì
2
3 16
1
( ) 27 (1 )
x x
g x x
liên tục trên
1
;5
3
và
1 1
1
. 5 0
3
g g
.
Với
2y
, phương trình thành:
2
3 17
27 (1 2 ) 0
x x
x
có nghiệm vì
2
3 16
2
( ) 27 (1 2 )
x x
g x x
liên tục trên
1
;5
3
và
2 2
1
. 5 0
3
g g
.
Khi
1,y
xét trên
1
;5
3
, ta có
2
27
3 2
27
15
27 (1 )27 3 15 log (1 )
log (1 )
3 15 0.
x xy x
xy x x xy xy
xy
x y
x
Xét hàm
27
log (1 )
( ) 3 15
xy
g x x y
x
trên
1
;5 .
3
Ta có
2 2
ln(1 ) 1
'( ) 3 3 3 0, ;5 .
ln 27 (1 )ln 27 n
1 3
3 l 3 ln 3 3
xy y
g x x
x x xy x
Do đó, hàm
( )g x
đồng biến trên
1
;5
3
. Vì thế phương trình
( ) 0g x
có nghiệm trên
1
;5
3
khi và chỉ khi
1
(5) 0.
3
g g
Áp dụng bất đẳng thức
ln(1 )u u
với mọi
0u
, ta
có
27
5
log (1 5 ) 5
(5) 0.
l5 n 27
y y
g y y
Do đó
3
1
0 log 1 14 0 1 15
3 3
y
g y y
(do
y
là số nguyên dương).
Vậy
2; 1;1;2;...;15y
hay có 17 giá trị
y
thỏa đề.
Câu 45. Cho khối hộp chữ nhật
.ABCD A B C D
có đáy là hình vuông,
2BD a
, góc giữa hai mặt
phẳng
A BD
và
ABCD
bằng
60
. Thể tích của khối hộp chữ nhật đã cho bằng
A.
3
2 3
9
a
. B.
3
6 3a
. C.
3
2 3
3
a
. D.
3
2 3a
.
Lời giải
Chọn D
+) Ta có
2 2 ; 2BD a AC a AB a
.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https:/www.facebook.com/groups/toanvd. Trang 51
Tập san
Số 02
8-2021
+)
2
2
2 2
ABCD
S a a
.
+) Góc giữa hai mặt phẳng
A BD
và
ABCD
là góc
A OA
tan .tan 60 3AA AO A OA a a
.
Vậy
2 3
.
. 3.2 2 3
ABCD A B C D ABCD
V AA S a a a
.
Câu 46. Cho hàm số
3 2
f x x ax bx c
với
a
,
b
,
c
là các số thực. Biết hàm số
g x f x f x f x
có hai giá trị cực trị là
5
và
3
. Diện tích hình phẳng giới
hạn bởi các đường
6
f x
y
g x
và
1y
bằng
A.
2ln3
. B.
ln 2
. C.
ln15
. D.
3ln 2
.
Lời giải
Chọn A
3 2
f x x ax bx c
2
3 2f x x ax b
,
6 2f x x a
,
6f x
.
g x f x f x f x
6g x f x f x f x f x f x
.
Do
g x
có hai cực trị là
5
và
3
nên
1
2
0
x x
g x
x x
với
1
3g x
,
2
5g x
.
Ta có:
6
1 0
6 6
f x f x f x
g x g x
1
2
x x
x x
.
Diện tích hình phẳng giới hạn bởi các đường
6
f x
y
g x
và
1y
là
2 2
1 1
6
1 d d
6 6
x x
x x
f x f x f x
S x x
g x g x
2
2
1
1
d 6
ln 6 2ln 3
6
x
x
x
x
g x
g x
g x
.
Câu 47. Cắt hình nón
N
bởi mặt phẳng đi qua đỉnh và tạo với mặt phẳng chứa đáy một góc
bằng
0
30 ,
ta được thiết diện là tam giác đều cạnh
4 .a
Diện tích xung quanh của nón
bằng
A.
2
4 7 a
. B.
2
8 7 a
. C.
2
8 13 a
. D.
2
4 13 .a
Lời giải
Chọn D
Gọi
O
là tâm đáy nón, đỉnh nón là
,S
thiết diện là tam giác đều
.SAB
Kẻ
,OH AB
H
là trung điểm
AB
0
30 .SHO
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https:/www.facebook.com/groups/toanvd. Trang 52
Tập san
Số 02
8-2021
2 3, 2 .SH a HA a
Ta có:
0
.cos30 3 .OH SH a
2 2 2 2
9 4 13.
R HO HA a a a
2
13.4 4 13 .
xq
S Rl a a a
Câu 48. Trên tập hợp các số phức, xét phương trình
2 2
2 1 0
z m z m
(
m
là tham số thực).
Có bao nhiêu giá trị của
m
để phương trình đó có nghiệm
o
z
thỏa mãn
8
o
z
?
A.
4
. B.
3
. C.
2
. D.
1
.
Lời giải
Chọn B
Ta có
8 4
m
.
Trường hợp 1:
1
0
2
m
suy ra phương trình có 2 nghiệm thực
o
z
là nghiệm
thực
8
8
8
o
o
o
z
z
z
thay vào phương trình
2
2
4
16 48 0 /
12
16 80 0( )
m
m m T M
m
m m VN

.
Trường hợp 2:
1
0
2
m
suy ra phương trình sẽ có 2 nghiệm phức, vì
o
z
là
nghiệm nên suy ra
o
z
cũng là nghiệm
2
2
8
8 64 . 64 64
8
o o o o
m
z z z z m
m
.
Kết hợp điều kiện nên ta nhận
8
m
.
Vậy có 3 giá trị
m
thỏa mãn.
Câu 49. Trong không gian
Oxyz
, cho hai điểm
1; 3;2
A
và
2;1; 4
B
. Xét hai điểm
M
và
N
thay đổi thuộc mặt phẳng
Oxy
sao cho
4
MN
. Giá trị lớn nhất của
AM BN
bằng
A.
5 2
. B.
3 13
. C.
61
. D.
85
.
Lời giải
Chọn D
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https:/www.facebook.com/groups/toanvd. Trang 53
Tập san
Số 02
8-2021
Dễ thấy hai điểm
,A B
nằm khác phía so với mặt phẳng
Oxy
.
Gọi
1
A
là điểm đối xứng của
A
qua mặt phẳng
Oxy
suy ra
1
1; 3; 2A
.
Gọi mặt phẳng
P
chứa
1
A
và song song mặt phẳng
Oxy
suy ra
: 2P z
.
Ta gọi
2 1 2
:A A A MN
 
và gọi
K
là hình chiếu của
B
lên
1
2;1; 2 2, 5P K BK KA
Khi đó:
2 2
2 2 1
( 4) 85AM BN A N BN A B BK KA
.
Suy ra giá trị lớn nhất của
AM BN
bằng
85
, dấu bằng xảy ra khi
2
N A B Oxy
.
Câu 50. Cho hàm số
y f x
có đạo hàm
2
10 25 ,f x x x x
. Có bao nhiêu giá trị
nguyên dương của tham số
m
để hàm số
3
8g x f x x m
có ít nhất 3 điểm cực trị
A.
9
. B.
25
. C.
5
. D.
10
.
Lời giải
Chọn A
Cách 1:
Ta có BBT của hàm
3
8y h x x x
như sau
Ta có
3 3
8 . 8g x x x f x x m
. Rõ ràng
0x
là điểm cực trị của hàm
y h x
Ta có:
3 3
3 3 3
3 3
8 10 8 10
8 0 8 5 8 5
8 5 8 5
x x m x x m
f x x m x x m x x m
x x m x x m
.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https:/www.facebook.com/groups/toanvd. Trang 54
Tập san
Số 02
8-2021
Để hàm số
g x
có ít nhất
3
điểm cực trị thì phương trình
0
g x
có ít nhất
2
nghiệm
phân biệt khác
0
và
g x
đổi dấu khi đi qua ít nhất
2
trong số các nghiệm đó.
Từ BBT ta có
10 0 10
m m
1;2;3; 4;5;6;7;8;9 .
m
Vậy có 9 giá trị của
m
thỏa mãn yêu cầu đề bài.
Cách 2:
Với
,f h
là các hàm liên tục trên tập số thực, thì nếu
c
là điểm cực trị của
f h x
thì
c
phải là điểm cực trị của
g
hoặc là
h c
là điểm đạt cực trị của
f
. Bây giờ
10
m
và
với hàm
3
8
h x x m
x
, ta có
f
chỉ có các điểm đạt cực trị là
10, 5
. Trong khi chỉ
có duy nhất điểm đạt cực trị của
h
là
0
cùng với
10
h x m
với mọi
x
, và thêm nữa
thì phương trình
10
h x
có không quá một nghiệm là
0
x
. Bởi vậy,
10
m
không
thỏa mãn yêu cầu.
Khi
9
m
và
5
m
, thì trên từng khoảng mở bên trái và phải số
0
ta có
2
2
23 9
.
8 5
x h x h x x
g x
x
Cho thấy
g x
đổi dấu khi
x
chạy qua
0
và vì thế nó đạt cực trị tại
0.
x
Kết hợp thêm
việc đa thức
9
h x
có đúng hai nghiệm phân biệt khác
0
, và
g x
đổi dấu khi
x
chạy qua các nghiệm đó. Cho thấy
9
m
và
5
m
thỏa yêu cầu.
Nếu
5
m
lúc đó
2
2
2
3 9 .8 25
g x x x h x h x
Ta cũng thấy
g x
đổi dấu
khi
x
chạy qua
0
và hai nghiệm phân biệt khác
0
của
9
h x
, cho thấy là cũng thỏa
mãn.
Vậy
m
là các số nguyên dương nhỏ hơn
10.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https:/www.facebook.com/groups/toanvd. Trang 55
Tập san
Số 02
8-2021
Đề thi gồm 06 trang
ĐỀ THI TỐT NGHIỆP THPT ĐỢT 1 NĂM 2021
Bài thi môn: Toán
Thời gian: 90 phút (Không kể thời gian phát đề)
Mã đề thi: 104
Câu 1: Cho hai số phức
3 2z i
và
1 4w i
. Số phức
z w
bằng
A.
4 2i
. B.
4 2i
. C.
2 6i
. D.
2 6i
.
Câu 2: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?
A.
3
3 1y x x
. B.
4 2
4 1y x x
. C.
3
3 1y x x
. D.
4 2
2 1y x x
.
Câu 3: Nếu
4
1
d 4f x x
và
4
1
d 3g x x
thì
4
1
df x g x x
bằng
A.
1
. B.
7
. C.
1
. D.
7
.
Câu 4: Tiệm cận đứng của đồ thị hàm số
1
2
x
y
x
là đường thẳng có phương trình:
A.
2x
. B.
1x
. C.
2x
. D.
1x
.
Câu 5: Trong không gian
Oxyz
, cho mặt cầu
S
có tâm
1;3;0I
và bán kính bằng
2
. Phương trình
của mặt cầu
S
là:
A.
2 2
2
1 3 2x y z
. B.
2 2
2
1 3 4x y z
.
C.
2 2
2
1 3 4x y z
. D.
2 2
2
1 3 2x y z
.
Câu 6: Tập nghiệm của bất phương trình
2 5
x
là
A.
2
;log 5
. B.
5
log 2;
. C.
5
;log 2
. D.
2
log 5;
.
Câu 7: Thể tích của khối lập phương cạnh
2a
bằng
A.
3
a
. B.
3
2a
. C.
3
8a
. D.
3
4a
.
Câu 8: Trên khoảng
0;
, đạo hàm của hàm số
5
3
y x
là:
A.
5
3
3
8
y x
. B.
2
3
5
3
y x
. C.
2
3
5
3
y x
. D.
2
3
3
5
y x
.
Câu 9: Trong không gian
Oxyz
,
cho điểm
2; 1;4 .A
Tọa độ của véc tơ
OA
là
A.
2;1;4
. B.
2; 1;4
. C.
2;1;4
. D.
2;1; 4
.
Câu 10: Nếu
3
0
d 3f x x
thì
3
0
4 df x x
bằng
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https:/www.facebook.com/groups/toanvd. Trang 56
Tập san
Số 02
8-2021
A.
3
. B.
12
. C.
36
. D.
4
.
Câu 11: Cho cấp số nhân
n
u
với
1
2
u
và
2
10.
u
Công bội của cấp số nhân đã cho bằng
A.
8
. B.
8
. C.
5
. D.
1
5
.
Câu 12: Với
n
là số nguyên dương bất kì ,
3,
n
công thức nào dưới đây đúng ?
A.
3
3 !
!
n
n
A
n
. B.
3
3!
3 !
n
A
n
. C.
3
!
3 !
n
n
A
n
. D.
3
!
3! 3 !
n
n
A
n
.
Câu 13: Cho hàm số
2
2
f x x
. Khẳng định nào dưới đây đúng?
A.
d 2
f x x x C
. B.
3
d 2
3
x
f x x x C
.
C.
2
d 2
f x x x x C
. D.
3
d 2
f x x x x C
.
Câu 14: Cho hàm số
y f x
có bảng biến thiên như sau:
Giá trị cực tiểu của hàm số đã cho bằng
A.
0
. B.
3
. C.
1
. D.
1
.
Câu 15: Trong không gian
Oxyz
, cho mặt phẳng
: 2 4 1 0
P x y z
. Vectơ nào dưới đây là một
vectơ pháp tuyến của
P
?
A.
2
2; 4;1
n
. B.
1
2;4;1
n
. C.
3
2;4; 1
n
. D.
4
2;4;1
n
.
Câu 16: Phần thực của số phức
4 2z i
bằng
A.
2
. B.
4
. C.
4
. D.
2
.
Câu 17: Nghiệm của phương trình
2
log 5 3
x
là
A.
8
5
x
. B.
9
5
x
. C.
8
x
. D.
9
x
.
Câu 18: Tập xác định của hàm số
8
x
y
là
A.
\ 0
. B.
. C.
0;
. D.
0;
.
Câu 19: Cho
0
a
và
1
a
, khi đó
5
log
a
a
bằng
A.
1
5
. B.
1
5
. C.
5
. D.
5
.
Câu 20: Trong không gian
Oxyz
,
cho đường thẳng
d
đi qua điểm
(1;5; 2)
M
và có một vectơ chỉ phương
(3; 6;1)
u
. Phương trình của
d
là:
A.
3
6 5
1 2
x t
y t
z t
. B.
1 3
5 6
2
x t
y t
z t
. C.
1 3
5 6
2
x t
y t
z t
. D.
1 3
5 6
2
x t
y t
z t
.
Câu 21: Trên mặt phẳng tọa độ, điểm
( 4;3)
M
là điểm biểu diễn của số phức nào sau đây?
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https:/www.facebook.com/groups/toanvd. Trang 57
Tập san
Số 02
8-2021
A.
3
4 3z i
. B.
4
4 3z i
. C.
2
4 3z i
. D.
1
4 3z i
.
Câu 22: Cho hàm số
y f x
có bảng xét dấu của đạo hàm như sau:
Số điểm cực trị của hàm số đã cho là
A.
3
. B.
4
. C.
2
. D.
5
.
Câu 23: Cho hàm số
( ) 4
x
f x e
. Khẳng định nào sau đây đúng?
A.
( )d 4
x
f x x e x C
. B.
( )d
x
f x x e C
.
C.
4
( )d
x
f x x e C
. D.
( )d 4
x
f x x e x C
.
Câu 24: Cho hàm số
y f x
có đồ thị là đường cong trong hình bên.
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A.
1;1
. B.
1;
. C.
;1
. D.
0;3
.
Câu 25: Diện tích S của mặt cầu bán kính R được tính theo công thức nào dưới đây?
A.
2
S R
. B.
2
16S R
. C.
2
4S R
. D.
2
4
3
S R
.
Câu 26: Đồ thị hàm số
3 2
2 3 5y x x
cắt trục tung tại điểm có tung độ bằng
A.
5
. B.
0
. C.
1
. D.
2
.
Câu 27: Cho khối chóp có diện tích đáy
2
8B a
và chiều cao
h a
. Thể tích khối chóp đã cho bằng
A.
3
8a
B.
3
4
3
a
. C.
3
4a
. D.
3
8
3
a
.
Câu 28: Cho khối trụ có bán kính đáy
5r
và chiều cao
3h
. Thể tích của khối trụ đã cho bằng
A.
15
B.
75
. C.
25
. D.
45
.
Câu 29: Trong không gian Oxyz, cho điểm
2;1; 2M
và mặt phẳng
: 3 2 1 0.P x y z
Đường
thẳng đi qua M và vuông góc với
P
có phương trình là:
A.
2 1 2
.
3 2 1
x y z
B.
2 1 2
3 2 1
x y z
.
C.
2 1 2
3 2 1
x y z
. D.
2 1 2
3 2 1
x y z
.
Câu 30: Cho hình lăng trụ đứng
.ABC A B C
có tất cả các cạnh bằng nhau (tham khảo hình bên). Góc
giữa hai đường thẳng
AB
và
CC
bằng
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https:/www.facebook.com/groups/toanvd. Trang 58
Tập san
Số 02
8-2021
A.
30
. B.
90
. C.
60
. D.
45
.
Câu 31: Cho hình chóp
.S ABC
có đáy là tam giác vuông cân tại
B
,
4AB a
và
SA
vuông góc với mặt
phẳng đáy. Khoảng cách từ điểm
C
đến mặt phẳng
( )SAB
bằng
A.
4a
. B.
4 2a
. C.
2 2a
. D.
2a
.
Câu 32: Nếu
2
0
d 4f x x
thì
2
0
2 1) df x x
bằng
A.
8
. B.
10
. C.
7
. D.
6
.
Câu 33: Biết hàm số
1
x a
y
x
(
a
là số thực cho trước và
1a
) có đồ thị như trong hình bên.
Mệnh đề nào dưới đây đúng?
A.
0,y x
. B.
0, 1y x
. C.
0,y x
. D.
0, 1y x
.
Câu 34: Cho số phức
z
thỏa mãn
4 3iz i
. Số phức liên hợp của
z
là:
A.
3 4z i
. B.
3 4z i
. C.
3 4z i
. D.
3 4z i
.
Câu 35: Từ một hộp chứa
12
quả bóng gồm
5
quả màu đỏ và
7
quả màu xanh, lấy ngẫu nhiên đồng thời
3
quả. Xác suất để lấy được
3
quả màu đỏ bằng
A.
1
22
. B.
7
44
. C.
5
12
. D.
2
7
.
Câu 36: Với mọi
,a b
thỏa mãn
3
2 2
log log 5a b
, khẳng định nào dưới đây đúng?
A.
3
32a b
. B.
3
25a b
. C.
3
25a b
. D.
3
32a b
.
Câu 37: Trên đoạn
1;2
,
hàm số
3 2
3 1y x x
đạt giá trị nhỏ nhất tại điểm
A.
2x
. B.
0x
. C.
1x
. D.
1x
.
Câu 38: Trong mặt phẳng
Oxyz
, cho hai điểm
1;0;0 3;2;1A B
. Mặt phẳng đi qua
A
và vuông góc với
AB
có phương trình là:
A.
2 2 2 0x y z
. B.
4 2 17 0x y z
.
C.
4 2 4 0x y z
. D.
2 2 11 0x y z
.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https:/www.facebook.com/groups/toanvd. Trang 59
Tập san
Số 02
8-2021
Câu 39: Cho hàm số bậc bốn
y f x
có đồ thị là đường cong trong hình bên . Số nghiệm thực phân
biệt của phương trình
0f f x
là:
A.
12
. B.
10
. C.
8
. D.
4
.
Câu 40: Có bao nhiêu số nguyên
x
thỏa mãn
2
3
2 4 log 25 3 0?
x x
x
A.
24.
B. Vô số. C.
25.
D.
26.
Câu 41: Cho hàm số
2
2 2 1
3 1 1
x khi x
f x
x khi x
. Giả sử
F
là nguyên hàm của
f
trên
thỏa mãn
0 2F
. Giá trị của
1 2 2F F
bằng
A.
18
. B.
20
. C.
9
. D.
24
.
Câu 42: Cắt hình nón
N
bởi mặt phẳng đi qua đỉnh và tạo với mặt phẳng chứa đáy một góc bằng
30
,
ta được thiết diện là tam giác đều cạnh
2a
. Diện tích xung quanh của
N
bằng
A.
2
7 .a
B.
2
13 .a
C.
2
2 13 .a
D.
2
2 7 .a
Câu 43: Trong không gian
Oxyz
, cho đường thẳng
1
:
1 1 2
x y z
d
và mặt phẳng
( ) : 2 2 2 0P x y z
. Hình chiếu vuông góc của
d
lên mặt phẳng
( )P
là đường thẳng có
phương trình:
A.
1
2 4 3
x y z
. B.
1
14 1 8
x y z
. C.
1
2 4 3
x y z
. D.
1
14 1 8
x y z
.
Câu 44: Có bao nhiêu số nguyên
y
sao cho tồn tại
1
;6
3
x
thỏa mãn
2
3 18
27 1 27
x xy x
xy
?
A.
19
. B.
20
. C.
18
. D.
21
.
Câu 45: Trên tập hợp các số phức, xét phương trình
2 2
2 1 0z m z m
(
m
là tham số thực). Có bao
nhiêu giá trị của
m
để phương trình đó có nghiệm
0
z
thoả mãn
0
6z
?
A.
4
. B.
1
. C.
2
. D.
3
.
Câu 46: Cho khối hộp chữ nhật
.ABCD A B C D
có đáy là hình vuông
4BD a
, góc giữa hai mặt phẳng
A BD
và
ABCD
bằng
0
60
. Thể tích của khối hộp chữ nhật đã cho bằng
A.
3
48 3a
. B.
3
16 3
9
a
. C.
3
16 3
3
a
. D.
3
16 3a
.
Câu 47: Cho hàm số
3 2
f x x ax bx c
với
, , a b c
là các số thực. Biết hàm số
g x f x f x f x
có hai giá trị cực trị là
5
và
2
. Diện tích hình phẳng giới hạn
bởi các hàm số
6
f x
y
g x
và
1y
bằng
A.
ln3
. B.
3ln 2
. C.
ln10
. D.
ln 7
.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https:/www.facebook.com/groups/toanvd. Trang 60
Tập san
Số 02
8-2021
Câu 48: Xét các số phức
, z w
thỏa mãn
1
z
và
2
w
. Khi
6 8z iw i
đạt giá trị nhỏ nhất
z w
bằng
A.
29
5
. B.
221
5
. C.
3
. D.
5
.
Câu 49: Trong không gian
,Oxyz
cho hai điểm
( 2;1; 3)
A
và
(1; 3;2).
B
Xét hai điểm
M
và
N
thay
đổi thuộc mặt phẳng
( )Oxy
sao cho
3.
MN
Giá trị lớn nhất của
AM AN
bằng
A.
65
. B.
29
. C.
26
. D.
91
.
Câu 50: Cho hàm số
y f x
có đạo hàm
2
9 16
f x x x
,
x
. Có bao nhiêu giá trị
nguyên dương của tham số
m
để hàm số
3
7
g x f x x m
có ít nhất
3
điểm cực trị?
A.
16
. B.
9
. C.
4
. D.
8
.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https:/www.facebook.com/groups/toanvd. Trang 61
Tập san
Số 02
8-2021
ĐỀ THI THPT QUỐC GIA – NĂM HỌC: 2020 – 2021
ĐỀ CHÍNH THỨC (MÃ ĐỀ 104)
Môn: Toán
Thời gian: 90 phút (Không kể thời gian phát đề)
BẢNG ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
B
C
D
C
C
D
C
B
B
B
C
C
B
C
C
C
A
B
A
D
D
B
A
A
C
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
A
D
B
A
D
A
D
B
A
A
A
B
A
B
D
A
B
D
B
D
D
B
A
A
D
HƯỚNG DẪN GIẢI CHI TIẾT
Câu 39: Cho hàm số bậc bốn
y f x
có đồ thị là đường cong trong hình bên . Số nghiệm thực phân
biệt của phương trình
0f f x
là:
A.
12
. B.
10
. C.
8
. D.
4
.
Lời giải
Chọn B
Ta có:
1 1
1 0 2
0
0 1 3
1 4
f x a a
f x b b
f f x
f x c c
f x d d
.
Từ đồ thị hàm số ta thấy:
Phương trình
1
có: 2 nghiệm
Phương trình
2
có:
4
nghiệm
Phương trình
3
có:
4
nghiệm
Phương trình
4
vô nghiệm
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https:/www.facebook.com/groups/toanvd. Trang 62
Tập san
Số 02
8-2021
Vậy phương trình
0f f x
có tất cả 10 nghiệm thực phân biệt.
Câu 40: Có bao nhiêu số nguyên
x
thỏa mãn
2
3
2 4 log 25 3 0?
x x
x
A.
24.
B. Vô số. C.
25.
D.
26.
Lời giải
Chọn D
Cách 1:
Điều kiện xác định của bất phương trình là
25x
.
Đặt
2
3
( ) 2 4 log 25 3 , 25
x x
A x x x
.
2
2 4 0 0 2
x x
x x
.
3
log 25 3 0 2x x
.
Ta có bảng xét dấu
( )A x
như sau
Từ đó,
2
( ) 0 24; 23;...;0;2
25 0
x
A x x
x
(do
x
).
Kết luận: có
26
nghiệm nguyên thỏa mãn.
Cách 2:
Trường hợp 1:
2
3
2 4 0
log 25 3 0
x x
x
2
2
2 2
25 27
x x
x
2
2 0
2
x x
x
0 2
2
x
x
2x
.
Trường hợp 2:
2
3
2 4 0
log 25 3 0
x x
x
2
2 0
25 2
x x
x
0
25 0 2
2
25 2
x
x x
x
x
.
Vậy có 26 giá trị nguyên của
x
thỏa mãn
2
3
2 4 log 25 3 0
x x
x
.
Câu 41: Cho hàm số
2
2 2 1
3 1 1
x khi x
f x
x khi x
. Giả sử
F
là nguyên hàm của
f
trên
thỏa mãn
0 2F
. Giá trị của
1 2 2F F
bằng
A.
18
. B.
20
. C.
9
. D.
24
.
Lời giải
Chọn A
F
là nguyên hàm của
f
trên
nên
2
1
3
2
2 1
1
x x C khi x
F x
x x C khi x
.
Ta có:
2
0 2 2F C
.
1
Do
F
liên tục tại
1x
nên
1 1
lim lim 1
x x
F x F x F
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https:/www.facebook.com/groups/toanvd. Trang 63
Tập san
Số 02
8-2021
1
1 2 1 1
3 2 3 4 1
C C C C
.
Do đó
2
3
2 1 1
2 1
x x khi x
F x
x x khi x
.
Suy ra
1 2 2 18
F F
.
Câu 42: Cắt hình nón
N
bởi mặt phẳng đi qua đỉnh và tạo với mặt phẳng chứa đáy một góc bằng
30
, ta được thiết diện là tam giác đều cạnh
2a
. Diện tích xung quanh của
N
bằng
A.
2
7 .a
B.
2
13 .a
C.
2
2 13 .a
D.
2
2 7 .a
Lời giải
Chọn B
Ta có:
SAB
đều cạnh
2 3
2 3.
2
a
a SH a
Góc giữa thiết diện và mặt phẳng đáy là
30 .
SHI
Xét
SHI
vuông tại
I
;
3 3
.cos30 3. .
2 2
a
HI SH a
Xét
AHI
vuông tại
H
:
2
2 2 2
9 13
.
4 2
a a
AI AH HI a
Vậy:
2
xq
13
. . . . .2 13 .
2
a
S r l AI SA a a
Câu 43: Trong không gian
Oxyz
, cho đường thẳng
1
:
1 1 2
x y z
d
và mặt phẳng
( ) : 2 2 2 0
P x y z
. Hình chiếu vuông góc của
d
lên mặt phẳng
( )P
là đường thẳng có
phương trình:
A.
1
2 4 3
x y z
. B.
1
14 1 8
x y z
. C.
1
2 4 3
x y z
. D.
1
14 1 8
x y z
.
Lời giải
Chọn D
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https:/www.facebook.com/groups/toanvd. Trang 64
Tập san
Số 02
8-2021
Cách 1
Tọa độ
A d P
thỏa
0
2 2 2 0
0 0;0;1
1 2 2 2
0
1
1 1 2 1 2 4
x
x y z
y A
x y z x y z
z
.
Lấy điểm
1
(1; 1;3) :
1 1 2
x y z
B d
.
Gọi
B
là hình chiếu của điểm
B
lên mặt phẳng
( )P
1 1 3
:
1 2 2
x y z
BB
Tọa độ
B BB P
thỏa
2 2 2 0
1 1 3 2 2 2 5 5
1 2 2 1 4 4 9
x y z
x y z x y z
5 14
1
9 9
5 1 14 1 17
1 2. ; ;
9 9 9 9 9
5 17
3 2.
9 9
x
y B
z
.
14 1 8 1
; ; (14;1;8)
9 9 9 9
AB u u
là vectơ chỉ phương của
AB
.
Vậy
1
:
14 1 8
x y z
AB
là hình chiếu vuông góc của đường thẳng
d
lên
( )P
.
Cách 2
Tọa độ
A d P
thỏa
0
2 2 2 0
0 0;0;1
1 2 2 2
0
1
1 1 2 1 2 4
x
x y z
y A
x y z x y z
z
.
Gọi
'd
là hình chiếu của
d
lên
P
;
+ Đường thẳng
d
có vectơ chỉ phương
1; 1;2 .
u
+ Mặt phẳng
( )P
có vectơ pháp tuyến
(1;2; 2)
n
.
+
, ( 2; 4;3)
a u n
.
+
, (14;1;8)
n a
là vectơ chỉ phương của
( ')d
.
Vậy
1
: .
14 1 8
x y z
d
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https:/www.facebook.com/groups/toanvd. Trang 65
Tập san
Số 02
8-2021
Câu 44: Có bao nhiêu số nguyên
y
sao cho tồn tại
1
;6
3
x
thỏa mãn
2
3 18
27 1 27
x xy x
xy
?
A.
19
. B.
20
. C.
18
. D.
21
.
Lời giải
Chọn B
Cách 1:
Khi
0,
y
vì
1
xy
và
1
3
x
nên ta có
3.
y
Với
0
y
, phương trình thành:
2
3 18
27 1 0
x x
vô nghiệm vì
2
3 18 0
1
27 1 27 1 0, ;6
3
x x
x
.
Với
1
y
, phương trình thành:
2
3 19
27 (1 ) 0
x x
x
, có nghiệm vì
2
3 19
1
( ) 27 (1 )
x x
g x x
liên tục trên
1
;6
3
và
1 1
1
. 6 0
3
g g
.
Với
2
y
, phương trình thành:
2
3 20
27 (1 2 ) 0
x x
x
, có nghiệm vì
2
3 20
2
( ) 27 (1 2 )
x x
g x x
liên tục trên
1
;6
3
và
2 2
1
. 6 0
3
g g
.
Khi
1,
y
xét trên
1
;6
3
, ta có
2
1
27
2
3
7
8 2
27 (1 )27 3 18 log (1 )
log (1 )
3 18 0.
x xy x
xy x x xy xy
xy
x y
x
Xét hàm
27
log (1 )
( ) 3 18
xy
g x x y
x
trên
1
;6 .
3
Ta có
2 2
ln(1 ) 1
'( ) 3 3 3 0, ;6 .
ln27 (1 )ln27 n
1 3
3 l 3 ln3 3
xy y
g x x
x x xy x
Do đó, hàm
( )g x
đồng biến trên
1
;6
3
. Vì thế phương trình
( ) 0
g x
có nghiệm trên
1
;6
3
khi và chỉ khi
1
. (6) 0.
3
g g
Áp dụng bất đẳng thức
ln(1 )
u u
với mọi
0
u
, ta
có
27
.
6
log (1 6 ) 6
(6) 0
6ln 27
y y
g y y
Do đó
3
1
0 log 1 17 0 1 18
3 3
y
g y y
(do
y
là số nguyên dương).
Vậy
2; 1;1;2;...;18
y
hay có 20 giá trị
y
thỏa đề.
Cách 2.
Giả sử
y
là một trong những số nguyên thỏa mãn yêu cầu, lúc đó ta xét phương trình
2
3 18
27 1 27
x xy x
xy
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https:/www.facebook.com/groups/toanvd. Trang 66
Tập san
Số 02
8-2021
trên
1
;6 : 1
3
D x xy
, và trên
D
nó tương đương với
0
f x
, trong đó
2
3
1
3 18 log 1 .
3
f x x y x xy
Ta có vài tính toán sau
2
2
' 6 18 , '' 6 .
3 1 ln3
1 ln3
y y
f x x y f x
xy
xy
Nếu
0
y
, khi ấy vì cần có nghiệm
1
;3
3
x
nên có ngay
2
y
, lúc ấy
1 1
;
3
D
y
trên
D
ta có
3 3
1
3
1 1 1 1 1 2
lim 6 log 1 6 log 1 0.
3 3 3 3 3 3
x
f x y y
Kết hợp
1
lim
x
y
f x


và việc
f
liên tục trên
D
cho thấy
f
có điểm triệt tiêu trên
D
,
nghĩa là trường hợp này cho ta
2, 1
y
thỏa yêu cầu.
Nếu
0
y
, ta có
2
3 18 0
f x x x
với mọi
x D
, vì thế loại.
Nếu
19
y
, lúc đó có
1
3
lim ' 16 17 0
3 ln 3
x
y
f x y y
y
.
Kết hợp việc
'f x
tăng ngặt trên
D
, cho ta
f
tăng ngặt trên
D
và trên
D
có
3
1
3
1 1 1 1
lim 6 log 1
3 3 3 3
x
f x y y
Xét
3
1 1 1 1
6 log 1
3 3 3 3
g y y y
trên
10;
, ta có
3
1 1 2 1 19
' 0, 19 log 1 0
3 3 3 3 3 3
g y g
y
Vậy,
0
g y
với mỗi
19
y
, cho thấy là
0
f x
với mọi
x D
.
Nếu
1 18
y
, thế thì vì
3
1 log 7
18 0
3
g
kết hợp tính tăng ngặt của
g
trên
1;18
ta có
3
1
3
1 1 1
lim 9 log 1 0
3 3 3
x
f x g y y y
.
Còn, theo bất đẳng thức số
e
, ta có
3
6
1
lim 6 log 1 6 6 ln 1 6 0
3
x
f x y y y y
.
Đến đây, theo tính liên tục của
f
, ta thấy nó triệt tiêu trên
D
.
Tóm lại
\ 0
y
và
2 18.
y
Câu 45: Trên tập hợp các số phức, xét phương trình
2 2
2 1 0
z m z m
(
m
là tham số thực). Có bao
nhiêu giá trị của
m
để phương trình đó có nghiệm
0
z
thoả mãn
0
6
z
?
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https:/www.facebook.com/groups/toanvd. Trang 67
Tập san
Số 02
8-2021
A.
4
. B.
1
. C.
2
. D.
3
.
Lời giải
Chọn D
Ta có
2 2
( 1) 2 1
m m m
.
+) Nếu
1
0 2 1 0
2
m m
, phương trình có 2 nghiệm thực. Khi đó
0 0
6 6
z z
.
* Thay
0
6
z
vào phương trình ta được
2 2
36 12 1 0 12 24 0 6 2 3
m m m m m
(thoả mãn).
* Thay
0
6
z
vào phương trình ta được
2 2
36 12 1 0 12 48 0
m m m m
(vô nghiệm).
+) Nếu
1
0 2 1 0
2
m m
, phương trình có 2 nghiệm phức
1 2
,z z
thỏa
2 1
z z
. Khi đó
2
2 2
1 2 1
. 6
z z z m
hay
6
m
(loại) hoặc
6
m
(nhận).
Vậy tổng cộng có 3 giá trị của
m
là
6 2 3
m
và
6
m
.
Câu 46: Cho khối hộp chữ nhật
.
ABCD A B C D
có đáy là hình vuông,
4BD a
, góc giữa hai mặt phẳng
A BD
và
ABCD
bằng
0
60
. Thể tích của khối hộp chữ nhật đã cho bằng
A.
3
48 3a
. B.
3
16 3
9
a
. C.
3
16 3
3
a
. D.
3
16 3a
.
Lời giải
Chọn D
Ta có đáy
ABCD
là hình vuông có
4 2 2BD a AB a
.
Gọi
I
trung điểm
.BD
Vì
4 2BD a BI AI a
.
Tam giác
A AI
vuông tại
A
có:
0
tan 60 2 3
A A
A A a
AI
.
Thể tích của khối hộp chữ nhật đã cho bằng:
2
3
. 2 2 .2 3 16 3
ABCD
V S A A a a a
.
Câu 47: Cho hàm số
3 2
f x x ax bx c
với
, , a b c
là các số thực. Biết hàm số
g x f x f x f x
có hai giá trị cực trị là
5
và
2
. Diện tích hình phẳng giới hạn bởi
các hàm số
6
f x
y
g x
và
1y
bằng
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https:/www.facebook.com/groups/toanvd. Trang 68
Tập san
Số 02
8-2021
A.
ln 3
. B.
3ln 2
. C.
ln10
. D.
ln7
.
Lời giải
Chọn B
Ta có
3 2
3 2 6 2
g x f x f x f x x a x a b x a b c
g x f x f x f x
2
3 2 6 2 6
x ax b x a
2
3 2 6 2 6
x a x a b
.
Vì
y g x
có hai giá trị cực trị là
5
và
2
nên
0
g x
có hai nghiệm phân biệt
1 2
,x x
với
1 2
2, 5
g x g x
.
Phương trình hoành độ giao điểm
6
1 0
6 6
f x f x g x
g x g x
2
3 2 6 2 6
0 0
6 6
x a x a b g x
g x g x
.
Phương trình này cũng có hai nghệm phân biệt
1 2
,x x
Như vậy diện tích hình phẳng giới hạn bởi các hàm số
6
f x
y
g x
và
1y
là
2
2
1
1
ln 6 ln 2 6 ln 5 6 3ln2
6
x
x
x
x
g x
S g x
g x
.
Câu 48: Xét các số phức
, z w
thỏa mãn
1
z
và
2
w
. Khi
6 8z iw i
đạt giá trị nhỏ nhất,
z w
bằng
A.
29
5
. B.
221
5
. C.
3
. D.
5
.
Lời giải
Chọn A
Ta có
6 8 6 8 10 1 2 7
z iw i i z iw
.
Dấu “bằng” xảy ra
6 8
, , 0
6 8
k z i
k l
l iw i
10
, , 0
2 10
k
k l
l
10
5
k
k
.
Từ đó suy ra
3 4 3 4 3 4
5 5 5 5 5 5
.
6 8 8 6 8 6
5 5 5 5 5 5
z i z i z i
iw i w i w i
Vậy
29
5
z w
.
Câu 49: Trong không gian
Ox ,yz
cho hai điểm
( 2;1; 3)
A
và
(1; 3; 2).
B
Xét hai điểm
M
và
N
thay
đổi thuộc mặt phẳng
( )Oxy
sao cho
3.
MN
Giá trị lớn nhất của
AM AN
bằng
A.
65
. B.
29
. C.
26
. D.
91
.
Lời giải
Chọn A
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https:/www.facebook.com/groups/toanvd. Trang 69
Tập san
Số 02
8-2021
Dễ thấy điểm
A
nằm phía dưới, điểm
B
nằm phía trên mặt phẳng
( ).O xy
Gọi
'A
là điểm đối xứng của điểm
A
qua mặt phẳng
( ),O xy
suy ra tọa độ điểm
( 2;1;3).A
Gọi
( )
là mặt phẳng qua
A
và song song với mặt phẳng
( ),O xy
suy ra phương trình mặt
phẳng
( ) : 3 0.z
Trên mặt phẳng
( )
lấy điểm
1
A
sao cho
1
3AA MN
, suy ra
1
A
thuộc
đường tròn
,3A
và tứ giác
1
AAMN
là hình bình hành nên ta có
1
AM AN
.
Nên
1 1
AM BN A M BN AM BN A B
. Gọi
B
là hình chiếu của
B
lên mặt phẳng
( ),
suy ra tọa độ điểm
(1; 3;3)B
.
Ta có
2
2 2
1 1
1 3 65.AB B B B A B A
Câu 50: Cho hàm số
y f x
có đạo hàm
2
9 16f x x x
,
x
. Có bao nhiêu giá trị nguyên
dương của tham số
m
để hàm số
3
7g x f x x m
có ít nhất
3
điểm cực trị?
A.
16
. B.
9
. C.
4
. D.
8
.
Lời giải
Chọn D
Ta có BBT của hàm
3
7y h x x x
như sau:
Ta có
3 3
7 . 7g x x x f x x m
. Rõ ràng
0x
là điểm cực trị của hàm
y h x
.
Ta có:
3 3
3 3 3
3 3
7 9 7 9
5 0 7 4 7 4
7 4 7 4
x x m x x m
f x x m x x m x x m
x x m x x m
.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https:/www.facebook.com/groups/toanvd. Trang 70
Tập san
Số 02
8-2021
Để hàm số
g x
có ít nhất
3
điểm cực trị thì phương trình
0
g x
có ít nhất
2
nghiệm phân
biệt khác
0
và
g x
đổi dấu khi đi qua ít nhất
2
trong số các nghiệm đó.
Từ BBT ta có
9 0 9
m m
1;2;3;4;5;6,7,8 .
m
Vậy có 8 giá trị của
m
thỏa mãn yêu cầu đề bài.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc Trang 86
Tập san
Số 02
8 - 2021
Ôn thi tốt nghiệp THPT đợt 2
Phân tích, định hướng tìm lời giải, xây dựng các bài tương tự các
câu VD – VDC mã đề 102
ĐỀ THI TỐT NGHIỆP THPT ĐỢT 1 NĂM 2021
Buổi thi môn Toán kỳ thi tốt nghiệp THPT đợt 1 năm 2021 diễn ra vào chiều
ngày 7/8/2021. Bài thi môn Toán gồm 24 mã đề, được lấy từ 4 mã đề gốc là: Mã đề
101, 102, 103, 104. Nội dung đề thi nằm trong chương trình THPT, chủ yếu chương
trình lớp 12, trong đó 38 câu đầu ở mức độ nhận biết, thông hiểu được ra trong các mã đề
nhằm kiểm tra kiến thức cơ bản của lớp 11, lớp 12; trong các mã đề từ câu 39 đến câu 45
kiểm tra kiến thức học sinh ở mức độ vận dụng, từ câu 46 đến câu 50 ở mức độ vận dụng
cao đã thể hiện rõ tính phân hoá bằng cách sử dụng tổng hợp các kiến thức trong chương
trình THPT.
Kỳ thi tốt nghiệp THPT đợt 2 năm 2021 sẽ diễn ra trong 2 ngày 6/7/8/2021,
để tạo điều kiện cho quý thầy cô cùng các em có tài liệu ôn tập trong thời gian gấp rút này
Nhóm Giáo viên Toán Việt Nam xin gửi tới quý thầy cô và các em bài viết “Phân
tích, định hướng tìm lời giải, xây dựng các bài tương tự các câu VD – VDC đề thi tốt nghiệp
THPT đợt 1 Năm 2021”
Hy vọng bài viết sẽ giúp quý thầy cô có thêm tài liệu tham khảo; các em học sinh
nắm chắc các kiến thức trong chương trình THPT; tiếp cận được với các bài toán mới,
hay và lạ. Đặc biệt, rèn luyện tốt kỹ năng thi trắc nghiệm môn Toán.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc Trang 87
Tập san
Số 02
8 - 2021
Câu 39. Cắt hình nón
N
bởi mặt phẳng đi qua đỉnh và tạo với mặt phẳng chứa đáy một góc bằng
0
60
ta thu được thiết diện là một tam giác đều cạnh
4a
. Diện tích xung quanh của
N
bằng :
A.
2
8 7 a
.
B.
2
4 13 a
.
C.
2
8 13 a
.
D.
2
4 7 a
.
FB: Trương Quốc Toản – Tạ Minh Đức
Phân tích định hướng tìm Lời giải:
- Đây là bài toán tính diện tích xung quanh của hình nón;
- Để tính diện tích xung quanh của hình nón ta áp dụng công thức
xq
S rl
;
- Trong bài toán này đường sinh
4l a
, nên chúng ta chỉ cần xác định bán kính đáy
r
của
hình nón
N
thông qua giả thiết bài toán;
Lời giải
Chọn D
Gọi
I
là tâm của đường tròn đáy của hình nón.
Ta có thiết diện qua đỉnh là tam giác
SBA
.
Gọi
M
là trung điểm của đoạn thẳng
AB
.
Ta chứng minh được
AB SIM
, suy ra góc giữa mặt phẳng đi qua đỉnh và mặt
phẳng chứa đáy của hình nón là
0
60SMI
.
Do tam giác
SAB
đều cạnh
4a
, suy ra
4 3
2 3
2
a
SM a
.
Xét tam giác
SIM
vuông tại
I
ta có
3 ; 3SI a IM a
.
Xét
IMA
vuông tại
M
ta có
2
2 2 2
3 2 7IA IM MA a a a
.
Vậy diện tích xung quanh của hình nón là
2
7.4 4 7
xq
S rl a a a
.
Bình luận:
- Đây là bài toán tính diện tích xung quanh của hình nón, để làm được bài này yêu cầu các
em học sinh phải nhớ công thức tính diện tích xung quanh của hình nón; cách xác định thiết
diện của mặt phẳng với hình nón và xác định được góc giữa hai mặt phẳng. Tuy dạng toán
này không mới, nhưng để giải quyết được bài toán này thì các em học sinh phải có học lực
khá trở lên.
Hướng phát triển:
Hướng phát triển 1: Thay đổi giả thiết cho chiều cao và diện tích thiết diện. Yêu cầu tính thể
tích của khối nón
Hướng phát triển 2: Thay giả thiết góc bằng bán kính đáy của hình nón. Tính khoảng cách
từ tâm của đáy đến mặt phẳng
Hướng phát triển 3: Giữ nguyên giả thiết, mặt cắt chia khối nón thành hai phần tính thể tích
một phần của khối nón
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc Trang 88
Tập san
Số 02
8 - 2021
Hướng phát triển 4: Thay đổi giả thiết cho bán kính đáy hình nón; mặt phẳng đi qua đỉnh
và tạo với mặt phẳng chứa đáy một góc. Tính diện tích thiết diện.
Hướng phát triển 5: Thay đổi giả thiết bài toán cho bán kính, chiều cao của hình nón. Mặt
phẳng đi qua đỉnh hình nón cắt mặt phẳng chứa đáy là tam giác cân có cạnh đáy cho trước.
Tính góc tạo bởi hai mặt phẳng.
Hướng phát triển 6: Xây dựng các bài toán tương tự trên hình trụ
Các ví dụ minh họa
Câu 1. Cho hình nón có chiều cao bằng
2 5
. Một mặt phẳng đi qua đỉnh hình nón và cắt hình nón
theo một thiết diện là tam giác đều có diện tích bằng
9 3
. Thể tích của khối nón được giới
hạn bởi hình nón đã cho bằng
A.
32 5
3
. B. . C.
32 5
. D.
96
.
Lời giải
Chọn A
Ta có
2 2
2 2
3 3
9 3 36 36
4 4
SAB
AB AB
S AB SA
.
2 2
36 20 4
R OA SA SO
Thể tích của khối nón là
2
1 32 5
3 3
V R h
.
Câu 2. Cho hình nón có đỉnh
S
, đáy là đường tròn tâm
O
sao cho
6 5
SO
, một mặt phẳng
( )
cắt mặt nón theo hai đường sinh
, SA SB
. Biết khoảng cách từ
O
đến mặt phẳng
( )
bằng
2 5
và diện tích tam giác
SAB
bằng
360
. Thể tích khối nón bằng
A.
1325 5
. B.
265 5
. C.
1325 5
. D.
265 5
.
Lời giải
Chọn A
32
S
O
A
B
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc Trang 89
Tập san
Số 02
8 - 2021
Kẻ
, ,( ) 2 5OI AB OH SI OH d O
2 2
2 2 2 2 2 2
1 1 1 1 1 1 1 1 2
45
2 5 6 5
OH SO OI OI OH SO
3 10
2
OI
2
2
2 2
3 10 9 10
6 5
2 2
SI SO OI
1 360
. . . 8 10
2
9 10
2
SAB
SAB
S
S SI AB SI IA IA
SI
2
2
2 2
3 10 5 106
8 10
2 2
r OI IA
2
1 5 106
. . .6 5 1325 5
3 2
V
Câu 3. Cho hình nón đỉnh
,S
đáy là đường tròn
;3O
. Một mặt phẳng đi qua đỉnh của hình nón cắt
đường tròn đáy tại hai điểm
A
và
B
sao cho
5.SA AB
Khoảng cách từ
O
đến mặt phẳng
SAB
bằng
A.
33
.
5
B.
4 33
.
15
C.
33
.
15
D.
2 33
.
15
Lời giải
Chọn B.
Gọi
I
là trung điểm
AB
.
Ta có
AB SO
AB SOI SAB SOI
AB OI
.
Trong
SOI
, kẻ
, OH SI H SI
thì
OH SAB
.
;
d O SAB OH
.
Ta có:
2 2 2 2
5 3 4SO SA OA
.
Ta có:
2
2 2 2
5 11
3
2 2
OI OA AI
.
Tam giác vuông
SOI
có:
2 2 2
1 1 1 1 4 4 33
16 11 15
OH
OH OI SO
.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc Trang 90
Tập san
Số 02
8 - 2021
Vậy
4 33
; .
15
d O SAB OH
Câu 4. Một khối nón có bán kính đáy bằng
2 ,a
đường sinh bằng
7a
(tham khảo hình dưới đây).
Một mặt phẳng qua đỉnh và tạo với đáy của hình nón một góc
0
60
chia khối nón thành hai
phần, gọi
V
là thể tích phần nhỏ hơn. Giá trị của
V
bằng
A.
3
4 3
1 .
9
a
B.
3
4 3
1 .
3
a
C.
3
4 3
3 .
3
a
D.
3
4 3
3 .
9
a
Lời giải
Chọn A.
Giả sử mặt phẳng qua đỉnh và tạo với đáy một góc
0
60
cắt khối nón theo thiết diện là
tam giác
SMN
như hình vẽ.
Gọi
I
là trung điểm của
.MN
Khi đó
,OI MN SI MN
từ giả thiết ta có góc
0
60 .SIO
Xét tam giác
SOM
ta có
2 2
3 .SO SM OM a
Xét tam giác
SIO
ta có
0
3
,
tan60
3
SO a
OI a
từ đó xét trong tam giác
OIM
ta được
0
60 ,IOM
suy ra
0
120 ,NOM
2 0 2
1
. .sin120 3 .
2
OMN
S OM a
Gọi
o
S
là diện tích hình viên phân tạo bởi dây
MN
và cung nhỏ
.MN
Ta có
2 2
0
1 4
. 3 .
3 3
OMN
S OM S a
Thể tích cần tính bằng
2 3
0
1 1 4 4 3
. . 3 . 3 1 .
3 3 3 9
V SO S a a a
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc Trang 91
Tập san
Số 02
8 - 2021
Câu 5. Cắt hình nón đỉnh
I
bởi một mặt phẳng đi qua trục của hình nón ta được một tam giác vuông
cân có cạnh huyền bằng
2a
,
BC
là dây cung của đường tròn đáy hình nón sao cho mặt
phẳng
IBC
tạo với mặt phẳng chứa đáy hình nón một góc
0
60
. Tính theo
a
diện tích
S
của
tam giác
IBC
.
A.
2
3
3
a
S
. B.
2
3
a
S
. C.
2
2
3
a
S
. D.
2
2
3
a
S
.
Lời giải
Chọn C
Tam giác
IDC
vuông cân có
2
2
2
a
DC a IH HC
và
IC a
.
Gọi
E
là trung điểm cạnh
BC
, góc giữa mặt phẳng
( )IBC
và
( )BCD
là
0
60
IEH
.
Trong tam giác
IHE
có
0
6
sin60 3
IH a
IE
.
Tam giác
IEC
có
2 2 2 2
2 3
3 3
CE IC IE a a a
.
Vậy
2
2
.
3
a
S EI EC
.
Câu 6. Cho hình nón đỉnh
S
có bán kính đáy
3,
R
chiều cao
2 2.
h
Mặt phẳng
( )
qua đỉnh
S
cắt đáy của hình nón theo dây cung có độ dài
2
.
3
Tính góc tạo bởi mặt phẳng
( )
và mặt
phẳng chứa đáy của hình nón.
A.
0
30
B.
0
45
C.
0
60
D.
0
75
Lời giải
Chọn C
Gọi
,A B
là hai giao điểm của
( )
với đường tròn đáy, ta có
2
.
3
AB
Gọi
M
là trung điểm
,AB
ta có
,
OM AB SM AB
góc tạo bởi
( )
và mặt đáy
là
SMO
,
2 2
2 6
,
3
OM OB BM
tan 3.
SO
SMO
OM
0
60 .
SMO
M
O
S
A
B
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc Trang 92
Tập san
Số 02
8 - 2021
Câu 7. Cho hình trụ có hai đáy là hai đường tròn tâm
O
và tâm
O
, bán kính đáy
3,
r a
chiều cao
hình trụ
h a
. Mặt phẳng
( )
đi qua trung điểm của
OO
và tạo với
OO
một góc
60
và
( )
cắt đường tròn đáy tâm
O
theo dây cung
AB
. Độ dài đoạn
AB
là:
A.
2a
. B.
3
2
a
. C.
3
2
a
. D.
3a
.
Lời giải
Chọn D
Gọi
M
,
N
lần lượt là trung điểm của
OO
và
AB
. Ta có
,
AB ON AB OO AB OMN
. Gọi
H
là hình chiếu của
O
trên
MN
thì
( )
OH
Ta có
; ; ; 60
OO ABM OO MH OO MN OMN
.
Tam giác
OMN
vuông tại
O
có
.tan
ON OM OMN
3
.tan60
2 2
a a
ON
.
2
2 2 2
3
2 2 2 3 3
4
a
AB NB OB ON a a
.
Câu 8. Cho một hình trụ tròn xoay và hình vuông
ABCD
cạnh
a
có hai đỉnh liên tiếp
,A B
nằm trên
đường tròn đáy thứ nhất của hình trụ, hai đỉnh còn lại nằm trên đường tròn đáy thứ hai của
hình trụ. Mặt phẳng
ABCD
tạo với mặt phẳng chứa đáy hình trụ một góc
45
. Tính diện tích
xung quanh hình trụ?
A.
2
xq
2 3
5
a
S
. B.
2
xq
3
3
a
S
. C.
2
xq
3
4
a
S
. D.
2
xq
3
2
a
S
.
Lời giải
Chọn D
Gọi
, ,P Q E
lần lượt là trung điểm của
, ,
AB CD OO
. Góc giữa
( )ABCD
và mặt đáy là
45
O QE
. Ta có
2
a
EQ
, do đó
2
4
a
O Q EO
.
α( )
B
A
H
M
O'
O
N
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc Trang 93
Tập san
Số 02
8 - 2021
Suy ra
2
2
a
h OO
và
6
4
a
r O C
.
Diện tích xung quanh của hình trụ là
2
xq
6 2 3
2 .
4 2 2
a a a
S
Câu 9. Cho khối trụ có thiết diện qua trục
OO
là một hình vuông cạnh bằng
2
. Mặt phẳng
P
đi
qua trung điểm
I
của
OO
và tạo với mặt phẳng chứa đáy của khối trụ một góc bằng
30
.
Diện tích của thiết diện do
P
cắt khối trụ gần số nào sau đây nhất?
A.
3,6
. B.
3,8
. C.
3,5
. D.
3,7
.
Lời giải
Chọn A
Do thiết diện qua trục là một hình vuông cạnh bằng
2
nên chiều cao của hình
trụ là
2
h
và bán kính đáy là
1R
.
Giả sử giao tuyến của mặt phẳng
P
và đáy chứa tâm
O
là đường thẳng
d
. Gọi
E
là hình chiếu của
O
trên
d
. Khi đó góc giữa
P
và mặt phẳng chứa đáy là góc
30
OEI
.
Trong tam giác vuông
IOE
có
2
tan 3 1
3
3
OI
OEI OE
OE
. Do đó điểm
E
nằm ngoài đường tròn đáy nên thiết diện là Elip.
Trong tam giác vuông có
2 4 3
cos
3
3
2
HM
AMH AM
AM
.
Hay
4 3 2 3
2
3 3
a a
. Mà
2 2 1CD b b
.
Thiết diện là hình elip nên diện tích bằng
2 3
3,62
3
ab
.
Câu 40: Cho hàm số
2
2 5 1
3 4 1
x khi x
f x
x khi x
. Giả sử
F
là nguyên hàm của
f
trên
thỏa mãn
0 2
F
. Giá trị của
1 2 2
F F
bằng
A. 27. B. 29. C. 12. D. 33.
OO
AHM
O
I
M
H
A
C
D
O
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc Trang 94
Tập san
Số 02
8 - 2021
Phân tích định hướng tìm lời giải
Dạng toán: Cho hàm số
F
là nguyên hàm của
f
với
f
là hàm cho bởi nhiều biểu thức. Bài toán yêu
cầu tính giá trị của biểu thức
F
tại một số điểm. Dạng toán này ta có 2 cách làm chính sau
* Cách 1: Tìm hàm số
F
(là tìm các hằng số
1 2
, ,...
C C
) dựa vào các giả thuyết đã cho (như liên tục, có
đạo hàm,
o
F x
,…). Tùy theo yêu cầu bài toán mà sử dụng hàm số
F
đã tìm được một cách phù hợp.
Cụ thể hơn ta có:
Bước 1:
2
1
2
3
2
2 5 1
5 1
3 4 1
4 1
x khi x
x x C khi x
f x F x
x khi x
x x C khi x
.
Bước 2: Tìm các hằng số
1 2
,C C
dựa vào
(0) 2F
và tính liên tục của hàm số.
Bước 3: Tính giá trị của biểu thức
1 2 2
F F
.
* Cách 2: Sử dụng công thức
d
b
a
F b F a f x x
phù hợp. Cụ thể ở bài trên ta làm như sau
Bước 1:
1
0
1 d 0
F f x x F
.
Bước 2: Để ý
1 2 2 1 1 2 2 1 3 1
F F F F F F F
, các biểu thức trong dấu
ngoặc vuông có dạng
d
b
a
f x x
Fb-Nam Phương
Lời giải
* Cách 1
2
1
2
3
2
2 5 1
5 1
3 4 1
4 1
x khi x
x x C khi x
f x F x
x khi x
x x C khi x
.
Vì
2
1
2
3
5 1
0 2 2
4 2 1
x x C khi x
F C F x
x x khi x
.
Hàm số liên tục trên
1 1
lim lim (1)
x x
F x F x F
1 1
1 5 1 4 2 1
C C
2
3
5 1 1
4 2 1
x x khi x
F x
x x khi x
. Vậy
1 2 2 3 2.15 27
F F
.
* Cách 2
Nhận xét: Hàm số
f x
liên tục trên
.
0 0
2
1 1
0 1 d 3 4 d 5 1 0 5 3.
F F f x x x x F
F
1 1
2
0 0
1 0 d 3 4 d 5 1 0 5 7.
F F f x x x x F
F
2 2
1 1
2 1 d 2 5 d 8 2 1 8 15.
F F f x x x x F
F
Do đó
1 2 2 3 2.15 27.
F F
Bình luận:
- Đây là dạng toán thuộc mức độ vận dụng, việc nhận ra hướng giải đòi hỏi học sinh phải nắm chắc
các khái niệm và tính chất của nguyên hàm cũng như các phương pháp tìm nguyên hàm.
Hướng phát triển:
- Không cho điều kiện
( )
F a m
. Yêu cầu tính
( ) ( )F b F c
.
- Thêm điều kiện như: có đạo hàm, liên tục,….
- Thay đổi điều kiện kiện của đề bài bằng cách cho
( ) ( )
F a F b k
. Yêu cầu tính
( ) ( )F n F m
.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc Trang 95
Tập san
Số 02
8 - 2021
Bài tập tương tự
Câu 1: Cho hàm số
2
2 1 khi 1
3 2 khi 1
x x
f x
x x
. Giả sử
F
là nguyên hàm của
f
trên
thỏa mãn
0 2
F
. Giá trị của
1 2 2
F F
bằng
A.
9
. B.
15
. C.
11
. D.
6
.
Lời giải
Chọn A
Ta có:
2
2 1 khi 1
3 2 khi 1
x x
f x
x x
2
1
3
2
khi 1
d
2 khi 1
x x C x
F x f x x
x x C x
.
Mà ta có
2
0 2 2
F C
.
Mặt khác hàm số
F
là nguyên hàm của
f
trên
nên
y F x
liên tục tại
1x
.
Suy ra
1
1 1
lim lim (1) 1
x x
F x F x F C
.
Khi đó ta có:
2
3
1 khi 1
2 2 khi 1
x x x
F x
x x x
suy ra
1 3
.
2 3
F
F
Vậy
1 2 2 9
F F
.
Câu 2: Cho hàm số
2
2 3 khi 1
3 2 khi 1
x x
f x
x x
. Giả sử
F
là nguyên hàm của
f
trên
thỏa mãn
0 2
F
. Giá trị của
1 2 2
F F
bằng
A.
23
. B.
11
. C.
10
. D.
21
.
Lời giải
Chọn D
Dễ thấy hàm số
f
liên tục trên
.
1 1
2
0 0
1 0 ( )d (3 2) ( )d 3 (1) 5
F F f x x x f x x F
.
1 2
1 1
1 2 2 ( )d 2 ( )d 3 (1) 6 12 15 21
F F f x x f x x f
.
Câu 3: Biết rằng
( )F x
liên tục trên
là một nguyên hàm của hàm số
2
3
3 2 khi 2
( ) .
4 18 khi 2
x x
f x
x x
Giá trị
của biểu thức
( 1) (3)
F F
bằng
A.
7.
B.
18.
C.
8.
D.
32.
Lời giải
Chọn B
Ta có:
1 3
2 2
( 1) (3) d d 18
F F f x x f x x
.
Câu 4: Biết rằng
( )F x
liên tục trên
là một nguyên hàm của hàm số
3
1
khi 0
( )
2 1
(2 1) khi 0
x
f x
x
x x
và
(4) ( 1) 8
F F
. Giá trị của biểu thức
( 2) 2 (12)
P F F
bằng
A.
20
. B.
27
. C.
281
16
. D.
121
8
.
Lời giải
Chọn B
Ta có :
4 1
0 0
8 2 (0) (4) (0) ( 1) (0) d d 2 (0) 3
F F F F F f x x f x x F
.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc Trang 96
Tập san
Số 02
8 - 2021
2 12
0 0
( 2) 2 (12) d 2 d 3 (0) 27
P F F f x x f x x F
.
Câu 5: Biết rằng
( )F x
liên tục trên
, là một nguyên hàm của hàm số
3
1 khi 0
( )
(2 1) khi 0
x x
f x
x x
và
19
(3) ( 1)
3
F F
. Giá trị của biểu thức
( 2) (8)
P F F
bằng
A.
20
. B.
27
. C.
58
. D.
29
.
Lời giải
Chọn D
Ta có
3
1 1
4
2 2
2
( ) 1 , 0
3
( )
(2 1)
( ) , 0
8
F x x C x
F x
x
F x C x
.
Do
( )F x
liên tục trên
nên
1 2 1 2
0 0
2 1 13
lim ( ) lim ( ) (0)
3 8 24
x x
F x F x F C C C C
.
Và
1 2 1 2
16 1 19 7
(3) ( 1) 8
3 8 3 8
F F C C C C
. Suy ra
1 2
1 17
,
6 24
C C
.
Tính
1 81 17
(8) ( 2) 18 29
6 8 24
F F
.
Câu 6: Cho hàm số
2
1 khi 1
( )
khi 1
ax x
f x
x b x
với
, a b
là các tham số thực. Biết rằng
( )f x
liên tục và có
đạo hàm trên
.
Tích phân
2
1
( )dI f x x
bằng
A.
1
3
B.
19
3
C.
26
3
D.
25
3
Lời giải
Chọn C
Hàm số liên tục trên
nên sẽ liên tục tại
o
1
x
1 1
lim ( ) lim ( ) (1)
x x
f x f x f
2
1 1
lim( 1) lim( ) (1) 1 1 .
x x
ax x b f a b a b
Hàm số có đạo hàm trên
nên có đạo hàm tại
o
1 1
1 lim ( ) lim ( )
x x
x f x f x
1 1
lim( ) lim(2 ) 2.
x x
a x a
Suy ra
2
2 1 khi 1
2 ( ) .
2 khi 1
x x
a b f x
x x
Do đó:
2 1 2 1 2
2
1 1 1 1 1
26
( )d ( )d ( )d ( 2)d (2 1)d
3
I f x x f x x f x x x x x x
Câu 7: Cho hàm số
2
1 khi 0
( ) .
1 khi 0
ax bx x
f x
ax b x
Biết rằng hàm số
( )f x
có đạo hàm trên
.
Tích phân
1
3
( )dI f x x
bằng
A.
82
3
B.
22
3
C.
14.
D.
10.
Lời giải
Chọn D
+)
( )f x
có đạo hàm trên
( )f x
liên tục trên
( )f x
liên tục tại
0
x
.
( )f x
liên tục tại tại
0
x
0 0
lim ( ) lim ( ) (0)
x x
f x f x f
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc Trang 97
Tập san
Số 02
8 - 2021
2
0 0
lim 1 lim 1 (0)
x x
ax bx ax b f
1 1
b
2.
b
+)
( )f x
có đạo hàm trên
( )f x
có đạo hàm tại
0
x
.
2
0 0 0
2 1 1
( ) (0)
lim lim lim 2 2
0 0
x x x
ax x
f x f
ax
x x
.
0 0 0
2 1 1
( ) (0)
lim lim lim
0 0
x x x
ax
f x f
a a
x x
.
( )f x
có đạo hàm tại
0
x
0 0
( ) (0) ( ) (0)
lim lim
0 0
x x
f x f f x f
x x
2
a
.
Do đó,
2
2 2 1 khi 0
( )
2 1 khi 0
x x x
f x
x x
.
Vậy
1 1
3 3
( )d 2 1 d 10
I f x x x x
.
Câu 8: Cho hàm số
2
3, 1
5 , 1
x x
f x
x x
. Giả sử
F
là nguyên hàm của
f
trên
thỏa mãn
0 1
F
.
Tính
2
2
0 1
cos sin d dI f x x x F x x
A.
142
.
12
B.
112
13
C.
1
12
. D.
13
.
12
Lời giải
Chọn A
Ta có
3
1
2
2
3 , 1
3
5 , 1
2
x
x C x
F x
x
x C x
.
Mà
2
0 1 1
F C
.
Vì
f x
liên tục tại
1x
nên
F x
liên tục tại
1x
1 1
lim lim (1)
x x
F x F x F
1
1 1
5 1 3
2 3
C
1
13
6
C
.
Vậy
3
2
13
3 , 1
3 6
5 1, 1
2
x
x x
F x
x
x x
.
2 2
2 2
0 1 0 1
cos sin d d cos d cos dI f x x x F x x f x x F x x
1 2
0 1
d df x x F x x
1 2
3
0 1
13 142
5 d 3 d
3 6 12
x
x x x x
.
Câu 41: Có bao nhiêu số nguyên
x
thỏa mãn
2
3
3 9 log 25 3 0
x x
x
A. 27. B. Vô số. C.
26
. D.
25
.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc Trang 98
Tập san
Số 02
8 - 2021
Phân tích định hướng tìm lời giải:
- Đây là bài toán giải bất phương trình mũ, lôgarit dạng
. 0f x g x
.
- Để giải bất phương trình chúng ta cần đặt điều kiện sau đó tìm nghiệm của từng phương
trình
0f x
và
0g x
. Tiếp theo lập bảng xét dấu
.f x g x
và tìm tập nghiệm từ đó
kết luận số nghiệm nguyên thỏa mãn bất phương trình.
Fb-Lê Thanh Bình
Lời giải
Chọn C
Ta có điều kiện xác định của bất phương trình là
25x
.
Đặt
2
3
( ) 3 9 log 25 3 , 25
x x
A x x x
.
2
3 9 0 0 2
x x
x x
.
3
log 25 3 0 2x x
.
Ta có bảng xét dấu
( )A x
như sau
Từ đó,
2
( ) 0 24; 23;...;0;2
25 0
x
A x x
x
(do
x
).
Kết luận: có
26
nghiệm nguyên thỏa mãn.
Bình luận:
- Đây là bài toán giải bất phương trình mũ và lôgarit trong đó việc tìm nghiệm của từng
phương trình mũ và lôgarit khá đơn giản. Tuy nhiên qua thực tế thì học sinh thường mắc
các sai sót sau:
Quên không đặt hay để ý điều kiện của lôgarit. Từ đó dẫn đến tập nghiệm là
;0 2
nên kết luận là vô số.
Thiếu nghiệm
2x
nên kết luận là có 25 số nguyên
x
.
Đây là câu hỏi kiểm tra kiến thức ở mức độ vận dụng.
Hướng phát triển:
Hướng phát triển 1: Thay đổi hàm số , hoặc có thể cho thêm 1 hàm số nữa dạng
. . 0f x g x h x
.
Hướng phát triển 2: Thay đổi thành dạng
. 0f x g x
,
. 0f x g x
hay
. 0
f x g x
…
Bài tập tương tự
Câu 1. Tập nghiệm của bất phương trình
2 1
1
3 9 3 3 1 0
27
x x x
chứa bao nhiêu số nguyên ?
A. 2. B. 3. C. 4. D. 5.
Lời giải
Chọn B
Điều kiện
1 1
3 1 0 3 1 1
x x
x
.
+ Ta có
1x
là một nghiệm của bất phương trình.
+ Với
1x
, bất phương trình tương đương với
2
1
3 9 3 0
27
x x
.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc Trang 99
Tập san
Số 02
8 - 2021
Đặt
3 0
x
t
, ta có
2
1
9 0
27
t t
1
3 3 0
27
t t t
3
1
3
27
t
t
.
Kết hợp điều kiện
3 0
x
t
ta được nghiệm
1
3
27
t
1
3 3 3 1
27
x
x
.
Kết hợp điều kiện
1
x
ta được
1 1x
suy ra trường hợp này bất phương trình
có 2 nghiệm nguyên.
Vậy bất phương trình đã cho có tất cả 3 nghiệm nguyên.
Câu 2. Tập nghiệm của bất phương trình
2 2
3 . 54 5.3 9 6 .3 45
x x x
x x x x
là
A.
;1 2;

B.
;1 2;5

C.
;1 5;
 
D.
1; 2 5;

.
Lời giải
Chọn D
Bất phương trình
2 2
3 . 54 5.3 9 6 .3 45
x x x
x x x x
tương đương với:
2 2 2
3 . 9 6 .3 54 5.3 45 0 3 9 6 3 9 5 3 9 0
x x x x x x
x x x x x x
2
2
2
2
3 9 0
1
6 5 0
5
5
3 9 6 5 0
1 2
3 9 0
2
6 5 0
1 5
x
x
x
x
x
x x
x
x
x x
x
x
x x
x
.
Vậy tập nghiệm của bất phương trình đã cho là
1; 2 5;

.
Câu 3. Có bao nhiêu số nguyên
x
thỏa mãn
2
2
3 9 log 32 5 0
x x
x
?
A.
31.
B. Vô số. C.
32
. D.
33
.
Lời giải
Chọn C
Xét hàm số
2
2
3 9 log 30 5
x x
f x x
, với
32
x
.
Cho
2
2
2
5
2
2
3 9 0
3 3
0
0
log 32 5 0
32 2
x x
x x
x
f x
x
x
x
Ta có bảng xét dấu như sau:
Suy ra tập nghiệm của bất phương trình
0
f x
là
32;0 0;2
S
Mặt khác
x
nên
31; 30; 27;......; 2; 1;1
x
.
Vậy có
32
số nguyên
x
thỏa mãn.
Câu 4. Có bao nhiêu số nguyên
x
thỏa mãn
5
log 1. 2 1024 0
x
x
?
A.
6
. B. Vô số. C.
4
. D.
5
.
Lời giải
Chọn C
Điều kiện
5
log 1 0 5
x x
.
Xét hàm số
5
log 1. 2 1024
x
f x x
, với
5
x
.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc Trang 100
Tập san
Số 02
8 - 2021
Cho
5
5
log 1 0
0
10
2 1024 0
x
x
x
f x
x
Ta có bảng xét dấu như sau:
Suy ra tập nghiệm của bất phương trình
0
f x
là
5;10
S
Mặt khác
x
nên
6;7;8;9
x
.
Vậy có
4
số nguyên
x
thỏa mãn.
Câu 5. Có bao nhiêu số nguyên
x
thuộc khoảng
2020;2021
thỏa mãn
2
7 6
7 7
2 .log log
x x
x x
?
A.
2017
. B. Vô số. C.
2016
. D.
2015
.
Lời giải
Chọn C
Điều kiện
0
x
.
Với
0
x
bất phương trình đã cho tương đương với
2
7 6
7 7
2 .log log 0
x x
x x
2
7 6
7
2 1 .log 0
x x
x
Xét hàm số
2
7 6
7
2 1 .log
x x
f x x
, với
0
x
.
Cho
2
2
7 6
7
1
7 6 0
2 1 0
0
6
1
log 0
x x
x
x x
f x
x
x
x
(thỏa mãn điều kiện
0
x
)
Ta có bảng xét dấu như sau:
Suy ra tập nghiệm của bất phương trình
0
f x
là
6; 1
S
.
Mặt khác x là số nguyên thuộc khoảng
2020;2021
nên
1;6;7;8;9;....;2020
x
.
Vậy có
2016
số nguyên
x
thỏa mãn.
Câu 42: Trong không gian
Oxyz
, cho đường thẳng
d
:
1 2
1 1 1
x y z
và mặt phẳng
: 2 4 0
P x y z
. Hình chiếu vuông góc của
d
trên
P
là đường thẳng có phương trình:
A.
1 2
2 1 4
x y z
. B.
1 2
3 2 1
x y z
.
C.
1 2
2 1 4
x y z
. D.
1 2
3 2 1
x y z
.
Phân tích định hướng tìm lời giải:
- Đây là bài toán lập phương trình đường thẳng là hình chiếu vuông góc của một đường
thẳng lên một mặt phẳng.
- Để lập phương trình đường thẳng ta cần biết hai điểm hoặc biết một điểm và một véc tơ
chỉ phương của nó
- Trong lời giải sau đây ta sẽ đi theo hướng lập phương trình đường thẳng
d
là hình chiếu
của
d
trên
P
khi biết hai điểm bằng cách.
+ Tìm
A d P
+ Tìm hình chiếu của
H
của
,
B d B A
lên
P
. Khí đó
d
là đường thẳng
AH
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc Trang 101
Tập san
Số 02
8 - 2021
Fb-Lê Tài Thắng
Lời giải
Chọn C
Tọa độ giao điểm
A
của
d
và
P
thỏa mãn hệ phương trình:
1 2
1 1 1
2 4 0
x y z
x y z
0
1
2
x
y
z
0;1; 2A
.
Lấy điểm
1;2;1B d
. Gọi
H
là hình chiếu của
B
trên
P
.
Phương trình
BH
:
1
2 2
1
x t
y t
z t
Do
H BH P
nên tọa độ điểm
H
thỏa mãn hệ phương trình:
0;1; 2A
1
2 2
1
2 4 0
x t
y t
z t
x y z
1
3
2
3
4
3
2
3
t
x
y
z
2 4 2
; ;
3 3 3
H
2 1 4
; ;
3 3 3
AH
.
Gọi
d
là hình chiếu vuông góc của
d
trên
P
d
đi qua
A
và
H
d
có một vector chỉ phương là
2;1; 4u
.
Vậy phương trình đường thẳng
d
là:
1 2
2 1 4
x y z
.
Nhận xét: Đây là cách làm theo chuẩn tự luận dựa trên tư duy hình học đơn giản.
Cách này hơi dài nhưng học sinh trung bình thì dễ làm.
Bình luận:
- Đây là bài toán lập phương trình đường thẳng, để xác định các yếu tố lập được phương
trình của đường thẳng nói trên học sinh phải có kiến thức tổng hợp liên quan đến tìm tọa
độ giao điểm, tìm hình chiếu của điểm lên mặt. Đặc biệt, học sinh phải nhận ra mẫu chốt
của bài toán là khi tìm hình chiếu của đường thẳng ta cần tìm hình chiếu của hai điểm phân
biệt của đường thẳng đó lên mặt phẳng. Trong trường hợp đường và mặt cắt nhau thì điểm
cắt chính là một điểm trên đường thẳng là hình chiếu đó.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc Trang 102
Tập san
Số 02
8 - 2021
- Ở bài toán này ta có thể dễ thấy
d P ABH
với
ABH
là mặt phẳng chứa
d
và
vuông góc
P
. Vì vậy ta có thêm các hướng giải như sau:
+ Hướng 1: Ta lập mặt phẳng
Q
chứa
d
vuông góc với
P
, khi đó ta tìm
d P Q
.
+ Hướng 2: Tìm véc tơ chỉ phương của
d
là
, ,
P d P
u n u n
và lập phương trình
d
có
VTCP
u
đi qua
A
.
Trong các hướng thì ta chọn hướng 2 là nhanh nhất với bài toán trắc nghiệm.
Lời giải (theo hướng 2)
Chọn C
Tọa độ giao điểm
A
của
d
và
P
thỏa mãn hệ phương trình:
1 2
1 1 1
2 4 0
x y z
x y z
0
1
2
x
y
z
0;1; 2
A
.
Ta có
1,2,1 ; 1,1, 1
P d
n u
nên
, , 4,2, 8
P d P
u n u n

hay chọn
2,1, 4
u
.
Vậy phương trình đường thẳng
d
là:
1 2
2 1 4
x y z
.
Cách này nhanh nhưng đòi hỏi sự tưởng tượng cao, tính toán nhanh, với học sinh khá
trở lên sẽ thích cách này hơn. Nó rất phù hợp cho bài toán trắc nghiệm.
Bài tập tương tự
Câu 1. Cho đường thẳng
1 2 2
( ) :
2 1 1
x y z
d
và mặt phẳng
( ) : 2 3 0
P x y
. Đường thẳng
là hình chiếu vuông góc của đường thẳng
d
trên mặt phẳng
( )P
có phương trình là
A.
1 1 3
1 2 4
x y z
. B.
1 2 2
1 2 4
x y z
.
C.
1 2 2
4 8 5
x y z
. D.
1 1 3
4 8 5
x y z
.
Lời giải
Chọn D
Tọa độ giao điểm
A
của
d
và
( )P
là nghiệm của hệ:
1
2 3 0
1 1;1;3
1 2 2
3
2 1 1
x
x y
y A
x y z
z
.
Lấy
1;2;2
B d
, gọi
H
là hình chiếu của
B
xuống mặt phẳng
( )P
.
Phương trình đường thẳng
1 2
: 2
2
x t
BH y t
z
. Tọa độ điểm
H
là nghiệm của hệ:
2 3 0
1 2
1 13
; ;2
2
5 5
2
x y
x t
H
y t
z
.
Hình chiếu
là đường thẳng đi qua hai điểm
,A H
.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc Trang 103
Tập san
Số 02
8 - 2021
Ta có
4 8
; ; 1
5 5
AH
. Đường thẳng
đi qua
A
có vecto chỉ phương
5 4; 8,5
u AH
.
Phương trình đường thẳng
là:
1 1 3
4 8 5
x y z
.
Câu 2. Trong không gian Oxyz, cho mặt phẳng
: 3 0
P x y z
và đường thẳng
1 2
:
1 2 1
x y z
d
. Hình chiếu vuông góc của
d
trên
P
có phương trình là
A.
1 1 1
1 4 5
x y z
B.
1 1 1
3 2 1
x y z
C.
1 1 1
1 4 5
x y z
D.
1 4 5
1 1 1
x y z
Lời giải
Chọn C
Gọi
M
là giao điểm của
d
với
P
.
Tọa độ của
M
là nghiệm của hệ:
3 1
3 0
2 1 1
1 2
2 1
1 2 1
x y z x
x y z
x y y
x y z
x z z
1;1;1
M
Lấy điểm
0; 1;2
N d
.
Một vec tơ pháp tuyến của mặt phẳng
P
là:
1;1;1
n
.
Gọi
là đường thẳng đi qua
N
và nhận
1;1;1
n
làm vec tơ chỉ phương.
Phương trình đường thẳng
1 2
:
1 1 1
x y z
Gọi
N
là giao điểm của
với
P
.
Tọa độ của
N
là nghiệm của hệ:
2
3
3
3 0
1
1
1 2
3
2
1 1 1
8
3
x
x y z
x y z
x y y
x y z
x z
z
2 1 8
; ;
3 3 3
N
1 4 5 1
; ; 1;4; 5
3 3 3 3
MN u
Đường thẳng cần tìm đi qua điểm
1;1;1
M
và nhận
1;4; 5
u
làm vec tơ chỉ
phương nên có phương trinh
1 1 1
1 4 5
x y z
.
Câu 3. Cho đường thẳng
d
:
2 1
2 3 2
x y z
và mặt phẳng
( )P
:
2 0
x y z
. Phương trình hình
chiếu vuông góc của
d
trên
( )P
là
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc Trang 104
Tập san
Số 02
8 - 2021
A.
1
1 2
2 3
x t
y t
z t
. B.
1
1 2
2 3
x t
y t
z t
.
C.
1
1 2
2 3
x t
y t
z t
. D.
1
1 2
2 3
x t
y t
z t
.
Lời giải
Đường thẳng
d
có véc tơ chỉ phương
2; 3;2
d
u
.
Mặt phẳng
( )P
có véc tơ pháp tuyến
1; 1; 1
P
n
.
Mặt phẳng
( )Q
chứa
d
và vuông góc với
( )P
;
Đường thẳng
'
d
là hình chiếu vuông góc của
d
trên
( )P
,
'
d P Q
Véc tơ pháp tuyến của mặt phẳng
( )Q
là
'
, 5;4;1
Q d P
n u n
Véc tơ chỉ phương của
'
d
là
'
, 3; 6;9 3 1;2; 3
d P Q
u n n
Ta thấy đường thẳng
'
d
thuộc
( )P
nên điểm
0 0
' ( )M d M P
. Thay tọa độ điểm
0
1;1; 2
M
ở đáp án A thấy thỏa mãn phương trình
( )P
.
Câu 4. Trong không gian với hệ tọa độ
,Oxyz
cho mặt phẳng
: 3 0
P x y z
và đường thẳng
1 2
:
1 2 1
x y z
d
. Hình chiếu của
d
trên
P
có
phương trình là đường thẳng
d
. Trong
các điểm sau điểm nào thuộc đường thẳng
d
?
A.
2;5; 4
M
. B.
1;3; 1
P
. C.
1; 1;3
N
. D.
2;7; 6
Q
.
Lời giải
Gọi
A d P
. Vì
: 1 2 ; 1 2 ;2
2
x t
A d y t A t t t
z t
.
Mặt khác
1 2 2 3 0 1A P t t t t
. Vậy
1;1;1
A
.
Lấy
0; 1;2
B d
. Gọi
là đường thẳng qua
B
và vuông góc
P
.
Thì
: 1
2
x t
y t
z t
. Gọi
C
là hình chiếu của
B
lên
P
.
Suy ra
; 1 ;2
C C t t t
.
Mặt khác
2
1 2 3 0
3
C P t t t t
. Vậy
2 1 8
; ;
3 3 3
C
.
Lúc này
d
qua
1;1;1
A
và có một vectơ chỉ phương là
1 4 5
; ;
3 3 3
AC
. Hay
d
nhận
1;4; 5
u
làm một vectơ chỉ phương.
Suy ra
1
: 1 4
1 5
x s
d y s
z s
. Vậy điểm thuộc đường thẳng
d
là
2;5; 4
M
.
Câu 43: (MĐ 101 BGD&ĐT NĂM 2020-2021) Cho hàm số bậc ba
( )y f x
có đồ thị là đường cong
trong hình bên. Số nghiệm thực phân biệt của phương trình
1
f f x
là
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc Trang 105
Tập san
Số 02
8 - 2021
A.
9
. B.
3
. C.
6
. D.
7
.
Phân tích định hướng
o – Bài toán có mức độ VD thuộc dạng “Tương giao đồ thị”, đã xuất hiện nhiều trong đề
thi các năm trước.
O– Ý tưởng: Cho đồ thị, bảng biến thiên,… của hàm số
y f x
. Hỏi số nghiệm của
phương trình
( )f g x
với
là hằng số.
B1: Vẽ đường thẳng
y
, dựa vào đồ thị, bảng biến thiên đã cho đưa phương trình về
dạng
i
g x
.
B2: Tìm nghiệm của phương trình
i
g x
.
FB-Ngonguyen Quocman
Lời giải
Chọn D
Từ đồ thị hàm số ta có
1f f x
1 1
2 2
( ) 1 (1)
( ) 0 (2)
( ) 1 2 (3)
f x x và x
f x
f x x và x
.
Dựa vào đồ thị,
(1)
có đúng 1 nghiệm,
(2)
và
(3)
mỗi phương trình có 3 nghiệm
phân biệt và 7 nghiệm trên phân biệt nhau.
Bình luận:
- Việc “hợp” các
f
vào nhau sẽ gây khó hiểu hoặc nhầm lẫn cho các học sinh chưa gặp
dạng này hoặc học chưa kỹ. Chưa kể, đường thẳng
y
có thể cắt đồ thị hàm số
y f x
ban đầu tại những điểm “không đẹp” là cách làm bài toán “khó gần” thêm. Đôi
khi, để học sinh có thể dễ tiếp cận hơn, quen thuộc hơn, ta có thể “án chừng” các con số
1 2
,x x
như bài trên bởi các giá trị gần đúng, ví dụ như
1 2
1,7; 1,7x x
.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc Trang 106
Tập san
Số 02
8 - 2021
- Có rất nhiều hướng để có thể mở rộng bài toán, như thêm vào trị tuyệt đối, tham số,
thay
bởi hàm số,….hoặc thay vì cho đồ thị, bảng biến thiên của
f x
thì có thể cho đồ
thị hoặc bảng biến thiên của
f x
.
Các ví dụ tương tự:
Câu 1. Cho hàm số bậc ba
y f x
có đồ thị trong hình bên. Số nghiệm của phương trình
0f f x
là
A.
3
. B.
9
. C.
4
. D.
7
.
Lời giải
Chọn D
Từ đồ thị hàm số ta có:
2 (1)
0 0 (2)
1 (3)
f x
f f x f x
f x
Phương trình
(1)
có nghiệm duy nhất, phương trình
(2)
và
(3)
mỗi phương trình có
3 nghiệm phân biệt. Tất cả các nghiệm trên đều phân biệt nhau nên phương trình ban
đầu có tổng cộng 7 nghiệm.
Câu 2. Cho hàm số bậc bốn
y f x
có đồ thị như hình vẽ. Số nghiệm của phương trình
4
1
3
f x
f x
là
A.
3
. B.
2
. C.
4
. D.
6
.
Lời giải
Chọn C
Điều kiện:
3f x
Khi đó ta có:
4
1
1
3 2
f x
f x
f x
. Dựa vào đồ thị, phương trình
1
2
f x
có 4
nghiệm phân biệt.
Câu 3. Cho hàm số bậc bốn
y f x
có đồ thị như hình vẽ. Số nghiệm của phương trình
5
1
3
f f x
f f x
là
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc Trang 107
Tập san
Số 02
8 - 2021
A.
7
. B.
8
. C.
5
. D.
6
.
Lời giải
Chọn D
Để ý rằng
3 1 3 2 0,f f x x
Ta có:
5
1 1 (*)
3
f f x
f f x
f f x
.
Vẽ đường thẳng
1y
, ta có:
0 (1)
(*) 1 (2)
1 (3)
f x
f x a
f x b
Dựa vào đồ thị, phương trình
(1)
có 4 nghiệm phân biệt, phương trình
(2)
vô
nghiệm, phương trình
(3)
có 2 nghiệm phân biệt khác với 4 nghiệm trên. Vậy phương
trình đã cho có tổng cộng 6 nghiệm.
Câu 4. Cho hàm số bậc ba
( )y f x
có đồ thị như hình vẽ.
Số nghiệm của phương trình
( ) 0f f x
là
A.
10
. B.
12
. C.
14
. D.
8
.
Lời giải
Chọn B
Từ đồ thị hàm số ta có:
1
2
0;1 (1)
0 2 (2)
3; (3)
f x x
f f x f x
f x x
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc Trang 108
Tập san
Số 02
8 - 2021
Từ đồ thị
( )y f x
ta suy ra đồ thị
y f x
như hình vẽ
Từ đó dễ thấy phương trình
(1)
có 6 nghiệm, phương trình
(2)
có 4 nghiệm và
phương trình
(3)
có 2 nghiệm phân biệt. Tất cả các nghiệm trên đều phân biệt nhau
nên phương trình ban đầu có tổng cộng 12 nghiệm.
Câu 5. Cho hàm số bậc ba
( )y f x
có đồ thị như hình vẽ.
Số nghiệm của phương trình
1f f x x
là
A.
5
. B.
7
. C.
9
. D.
3
.
Lời giải
Chọn A
( 3; 2)
1 0
(3; )
f x x a f x x a
f f x x f x x f x x
f x x b f x x b

.
Ta có các đường thẳng
; ; y x a y x y x b
như hình vẽ (2 đường không qua
gốc tọa độ đều tạo với 2 trục các tam giác vuông cân).
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc Trang 109
Tập san
Số 02
8 - 2021
Dựa vào đồ thị, phương trình đã cho có đúng 5 nghiệm.
Câu 6. (Chuyên Lam Sơn Thanh Hóa – Lần 3) Cho hàm số
3 2
3 3 4y f x x x x
. Gọi
m
là số
nghiệm thực của phương trình
2 2 3f f x f x
. Khẳng định nào sau đây đúng?
A.
7m
. B.
4m
. C.
6m
. D.
9m
.
Lời giải
Chọn C
Đặt
2t f x
. Khi đó phương trình thành
2
1
2 1
2 1
t
f t t
f t t
2
3 2
3 2
1
1
1
3 13
4 2 1 0
3 4 2 1
2
t
t
t
t t t
t t t t
t
.
3 2
3 2
3 3 4 2 1
3 13
3 3 4 2
2
x x x
x x x
. Mỗi phương trình đều có 3 nghiệm phân biệt lẫn
nhau nên phương trình ban đầu có tổng cộng 6 nghiệm.
Câu 7. Cho hàm số bậc bốn
( )y f x
có đồ thị như hình vẽ.
Số nghiệm của phương trình
2 3
2
f x
f x
f f x
là
A.
5
. B.
6
. C.
2
. D.
3
.
Lời giải
Chọn C
Điều kiện:
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc Trang 110
Tập san
Số 02
8 - 2021
3; 1
1;0
2 0
1
3
f x a
f x b
f f x
f x
f x
.
Đặt
, ;0;1;3t f x t a
.
Khi đó ta có:
2 3 2 3 3
2 (*)
2
t t
t f t f t
f t t t
.
Vẽ đồ thị
3
y
t
ta được
Dựa vào đồ thị,
(*) 3; 1; , 3;4t c c
. So điều kiện nhận
t c f x c
,
phương trình này có 2 nghiệm phân biệt.
Câu 8. Cho hàm số bậc ba
( )y f x
có đồ thị như hình vẽ.
Số nghiệm của phương trình
2f xf x
là
A.
5
. B.
4
. C.
3
. D.
6
.
Lời giải
Chọn D
Ta có:
2
2
2
4
4
f x
xf x
x
f xf x
xf x
f x
x
(do
0x
không là nghiệm)
Ta vẽ thêm các đồ thị
2
y
x
và
4
y
x
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc Trang 111
Tập san
Số 02
8 - 2021
Dựa vào đồ thị, phương trình đã cho tổng cộng có 6 nghiệm.
Câu 9. (MĐ 102 BGD&ĐT NĂM 2019-2020) Cho hàm số bậc ba
( )y f x
có đồ thị là đường cong
như hình vẽ bên dưới.
Số nghiệm thực phân biệt của phương trình
3
( ) 1 0f x f x
là
A.
6
B.
4
C.
5
D.
8
Lời giải
Chọn A
Ta có:
3
3 3 3
3
( ) 6; 5 (1)
( ) 1 0 ( ) 1 ( ) 3; 2 (2)
( ) 0 (3)
x f x a
f x f x f x f x x f x b
x f x
+ Phương trình
(3)
tương đương
1 1
0
,( 6 5)
x
x x x a
.
+ Các hàm số
3
a
g x
x
và
3
b
h x
x
đồng biến trên các khoảng
;0
và
0;
,
và nhận xét rằng
0x
không phải là nghiệm của phương trình
(1)
và
(2)
nên ta có:
f x g x
f x h x
.
+ Trên khoảng
;0
, ta có
0
0 0
lim ; lim 1
lim lim 0
lim lim
x
x
x x
x x
f x f x
g x h x
g x h x

 


nên các phương trình
f x g x
và
f x h x
có nghiệm duy nhất.
+ Trên khoảng
0;
, ta có
0
0 0
lim ; lim 1
lim lim 0
lim lim
x
x
x x
x x
f x f x
g x h x
g x h x

 


nên các phương trình
f x g x
và
f x h x
có nghiệm duy nhất.
Do đó, phương trình
3
( ) 1 0f x f x
có nghiệm phân biệt.
6
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc Trang 112
Tập san
Số 02
8 - 2021
Câu 10. (MĐ 103 BGD&ĐT NĂM 2019-2020) Cho hàm số bậc bốn
y f x
có đồ thị là đường cong
trong hình vẽ bên.
Số nghiệm thực phân biệt của phương trình
2
( ) 2 0f x f x
là
A.
8
. B.
12
. C.
6
. D.
9
.
Lời giải
Chọn D
2
2
2
2
2
( ) 0
( ) 1
( ) 2 0
( ) 2
( ) 3
x f x
x f x a
f x f x
x f x b
x f x c
với
0 a b c
.
Xét phương trình
2
( ) 1 0f
m
x m
x
.
Gọi
,
là hoành độ giao điểm của
: ( )C y f x
và
Ox
;
0
.
2
(1) ( ) 0
f x
m
x
. Đặt
2
( ) ( )g x f x
x
m
Đạo hàm
3
2
( ) ( )
m
g x f x
x
.
Trường hợp 1:
3
2
; ( ) 0; 0 ( ) 0
m
x f x g x
x
Ta có
2
0li , ( )m
x
m
g x g


. Phương trình
0g x
có một nghiệm thuộc
;

.
Trường hợp 2:
x
( ) 0f x
,
2
0
m
x
suy ra
( ) 0 ( , )g x x
.
Trường hợp 3:
3
2
; ( ) 0; 0 ( ) 0
m
x f x g x
x
Ta có
2
0li , ( )m
x
m
g x g

. Phương trình
0g x
có một nghiệm thuộc
( ; )

.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc Trang 113
Tập san
Số 02
8 - 2021
Vậy phương trình
2
m
f x
x
có hai nghiệm
0
m
.
Ta có:
2
( ) 0 0 ( ) 0
x f x x f x
: có ba nghiệm.
Vậy phương trình
1
có 9 nghiệm.
Câu 44: Cho hàm số
3 2
f x x ax bx c
với
, ,a b c
là các số thực. Biết hàm số
g x f x f x f x
có hai giá trị cực trị là
3
và
6
. Diện tích hình phẳng giới hạn
bởi các đường
6
f x
y
g x
và
1y
bằng
A.
2ln3.
B.
ln3.
C.
ln18.
D.
2ln 2.
Phân tích định hướng tìm lời giải:
- Đây là bài toán tính diện tích hình phẳng giới hạn bởi hai đồ thị hàm số trong trường
hơp một đồ thị hàm số là đồ thị của hàm ẩn với giả thiết về cực trị;
- Để giải bài toán đầu tiên cần xác định hai yếu tố: tính chất của hàm ẩn từ giả thiết và
nghiệm của phương trình hoành độ giao điểm của hai đồ thị hai hàm số;
- Trong bài toán này, hai yếu tố trên chỉ xác định được vì hàm ẩn là hàm bậc ba có hai
điểm cực trị với hai giá trị cực trị cho trước và nghiệm của phương trình hoành độ giao
điểm chính là hai điểm cực trị của hàm ẩn.
- Từ đó, áp dụng công thức tính diện tích hình phẳng với lưu ý nếu hàm
f x
không đổi
dấu trên
;a b
thì
b b
a a
f x dx f x dx
.
FB-Phạm Tuấn
Lời giải
Chọn D
Ta có
2
3 2
f x x ax b
;
6 2f x x a
;
6
f x
;
Khi đó
g x f x f x f x
6
g x f x f x
.
Vì
g x
có hai giá trị cực trị là
3
và
6
mà
g x
là hàm bậc ba có hệ số của
3
x
dương nên
g x
có hai điểm cực trị là
1 2
x x
và
1
6
g x
,
2
3
g x
.
Phương trình hoành độ giao điểm của hai đường
6
f x
y
g x
và
1y
là
1
6
f x
g x
6
f x g x
6
f x f x f x f x

6 0
f x f x
1
2
0
x x
g x
x x
.
Diện tích hình phẳng giới hạn bởi các đường
6
f x
y
g x
và
1y
là:
2 2 2
1 1 1
6 6
1d d d
6 6 6
x x x
x x x
f x f x g x f x f x
S x x x
g x g x g x
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc Trang 114
Tập san
Số 02
8 - 2021
2 2
2
1
1 1
d d ln 6 ln12 ln 3 2ln 2.
6 6
x x
x
x
x x
g x g x
x x g x
g x g x
Bình luận:
- Đây là bài toán tính diện tích hình phẳng giới hạn bởi hai đồ thị hàm số trong trường
hơp một đồ thị hàm số là đồ thị của hàm ẩn với giả thiết về cực trị, để xác định các yếu
tố lập được công thức tính diện tích hình phẳng học sinh phải có kiến thức tổng hợp liên
quan đến cực trị, giá trị cực trị của hàm số, tích phân hàm trị tuyệt đối và tích phân hàm
ẩn. Đây là câu hỏi kiểm tra kiến thức ở mức độ VDC.
- Đây là bài toán sử dụng tính chất điểm cực trị của hàm bậc 3 đã gặp trong đề minh họa.
Có thể xây dựng các hướng phát triển đối với tính chấc điểm cực trị của hàm số bậc 3.
- Lưu ý: Với hướng giải dựng hàm của bài toán sẽ gặp khó khăn khi xây dựng lại hàm
6
f x
y
g x
.
Hướng phát triển:
Hướng phát triển 1: Giữ nguyên giả thiết và cho diện tích hình phẳng hỏi giá trị cực trị
còn lại.
Hướng phát triển 2: Thay cho giá trị cực trị của hàm số
g x
cho đồ thị của hàm số
g x
không thay đổi kết luận.
Hướng phát triển 3: Hai hàm số
f x
và
g x
có mối liên hệ bảng biến thiên giữ nguyên
giả thiết về giá trị cực trị của một hàm số có mối liên hệ giữa hai hàm
f x
và
g x
với
cách dựng lại hàm số.
Hướng phát triển 4: Thay đổi giả thiết về giá trị cực trị của hàm
f x
và cho hai hàm số
có mối liên hệ giữa nghiệm và cực trị với các dựng lại hàm số.
Hướng phát triển 5: Sử dụng tính chất hai điểm cực trị và điểm uốn của hàm bậc 3 để xây
dựng lại hàm số và trả lời yêu cầu bài toán về diện tích hình phẳng.
Hướng phát triển 6: Thay đổi giả thiết về cực trị của hàm số
f x
và giữ nguyên hàm
g x
cho thêm điều kiện giá trị tại điểm cực trị của hàm
f x
.
Bài tập tương tự
Câu 1. Cho hàm số
3 2
f x x ax bx c
với
, ,a b c
là các số thực. Biết hàm số
g x f x f x f x
có hai điểm cực trị với giá trị cực tiểu là
3
và diện tích hình
phẳng giới hạn bởi các đường
6
f x
y
g x
và
1y
bằng
2 ln 2
. Giá trị cực đại của hàm
g x
bằng
A.
6.
B.
3.
C.
18.
D.
8.
Lời giải
Chọn A
Ta có:
2
3 2
f x x ax b
;
6 2f x x a
;
6
f x
;
Khi đó
g x f x f x f x
6
g x f x f x
.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc Trang 115
Tập san
Số 02
8 - 2021
Vì
g x
có hai điểm cực trị với giá trị cực tiểu là
3
mà
g x
là hàm bậc ba có hệ số
của
3
x
dương nên
g x
có hai điểm cực trị là
1 2
x x
và
2
3g x
nên
1 2
6 0, ;g x x x x
.
Phương trình hoành độ giao điểm của hai đường
6
f x
y
g x
và
1y
là
1
6
f x
g x
6f x g x
6f x f x f x f x

6 0f x f x
1
2
0
x x
g x
x x
.
Diện tích hình phẳng giới hạn bởi các đường
6
f x
y
g x
và
1y
là:
2 2 2
1 1 1
6 6
1d d d
6 6 6
x x x
x x x
f x f x g x f x f x
S x x x
g x g x g x
2 2
2
1
1 1
1
d d ln 6 ln 6 ln 3 2ln 2.
6 6
x x
x
x
x x
g x g x
x x g x g x
g x g x
Do
1 2 1 1
ln 6 ln3 2ln 2 ln12 6g x g x g x g x
.
Câu 2. Cho hàm số
3 2
2
3
f x x ax bx c
với
, ,a b c
là các số thực. Biết hàm số
g x f x f x f x

có đồ thị như hình vẽ
Diện tích hình phẳng giới hạn bởi các đường
4
f x
y
g x
và
1y
bằng
A.
2ln 3 ln 2.
B.
ln3.
C.
ln12.
D.
2ln 2.
Lời giải
Chọn A
Ta có:
2
2 2f x x ax b
;
4 2f x x a
;
4f x
;
Khi đó
g x f x f x f x

4g x f x f x
.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc Trang 116
Tập san
Số 02
8 - 2021
Từ đồ thị của hàm số
g x
thì
g x
có hai điểm cực trị
1 2
x x
và
1 2
8; 2
g x g x
;
1 2
4 0, ;g x x x x
.
Phương trình hoành độ giao điểm của hai đường
4
f x
y
g x
và
1y
là
1
4
f x
g x
4
f x g x
4
f x f x f x f x

4 0
f x f x
1
2
0
x x
g x
x x
.
Diện tích hình phẳng giới hạn bởi các đường
4
f x
y
g x
và
1y
là:
2 2
1 1
1 1
4 4
x x
x x
f x f x
S dx dx
g x g x
2 2
1 1
4 4
4 4
x x
x x
f x g x f x f x
dx dx
g x g x

2
2
1
1
d ln 4 ln12 ln 2 2ln 3 ln 2.
4
x
x
x
x
g x
x g x
g x
Câu 3. Cho hai hàm số
3 2 2
2 1; 4
f x ax x bx g x cx x d
có bảng biến thiên như sau:
Biết rằng hàm số
' 'y f x g x
có giá trị cực trị là
2
. Khi đó diện tích hình phẳng
giới hạn bởi các đường
; ; 1; 2
y f x y g x x x
bằng
A.
3
4
. B.
3
2
. C.
1
4
. D.
1
2
.
Lời giải
Chọn A
Hàm số
2
4
g x cx x d
đạt giá trị lớn nhất tại
2
x
c
và giá trị lớn nhất bằng
2
1
g
c
nên
2
2 2 4
4 1 1, 1
c d d
c c c
.
Hàm số
g x
có hai nghiệm là
và
nên
g x c x x
.
Hơn nữa
f x
có hai điểm cực trị
x
và
x
nên
2
' 3 4 3f x ax x b a x x
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc Trang 117
Tập san
Số 02
8 - 2021
Do đó
2
12
4 3
3 12 3
' 3 '
3
a
c a
a a ad
c
f x g x ax x f x g x
ad
c c c
b
c
.
Khi đó
2
' ' ' 4 2 4
y f x g x g x g x cx c x d
đạt cực trị tại điểm
4 2 2
1
2
c
x
c c
và giá trị cực trị
2
1 2
y
c
.
Suy ra
2
2 2 2 4
1 1 4 2 1 4 2 2
y c c d c d
c c c c
.
Từ
1
và
2
suy ra
1
c
.
Do đó
3
1
3
3
d
a
b
. Vậy
2
3 2
1
1 3
3 7 4
3 4
S x x x dx
.
Câu 4. Cho hai hàm số
3 2 2
2 1; 4
f x ax x bx g x cx x d
với
, ,a b c
và
d
là các số thực
thỏa mãn
0
ac
. Biết phương trình
0
g x
có hai nghiệm phân biệt là hai điểm cực trị của
hàm số
f x
với hai giá trị cực trị là
1
và
3
. Diện tích hình phẳng giới hạn bởi các đường
; 1
f x g x
y y
f x
bằng
A.
ln 2
. B.
2 ln 2
. C.
ln 6
. D.
2ln 3
.
Lời giải
Chọn A
Hàm số
g x
có hai nghiệm là
và
nên
g x c x x
.
Hơn nữa
f x
có hai điểm cực trị
x
và
x
nên,
1; 3
f f
2
' 3 4 3f x ax x b a x x
Do đó
2
12
4 3
3 12 3
' 3 '
3
a
c a
a a ad
c
f x g x ax x f x g x
ad
c c c
b
c
.
Xét phương trình hoành độ giao điểm của hai đường là
1
f x g x
f x
0 ' 0
x
f x g x f x
x
.
'
1
d f x
f x g x g x g x f x
S dx dx dx dx
f x f x f x f x f x
ln ln 4 ln 2 ln 2
f x
.
Câu 5. Cho hàm số
3 2
1f x x ax bx
với
,a b
là các số thực khác
0
. Biết hàm số
f x
có hai
điểm cực trị
1 2
,x x
thỏa mãn
2 1
2
x x
và
1 2
2
f x f x
. Diện tích hình phẳng giới hạn
bởi các đường
1
; 4
f x
y y
x
bằng
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc Trang 118
Tập san
Số 02
8 - 2021
A.
32
3
. B.
21
2
. C.
11
. D.
10
.
Lời giải
Chọn A
Ta có
2
' 3 2
f x x ax b
và
'' 6 2f x x a
.
Do hàm số
f x
có hai cực trị là
1
x
và
2
x
, nên
1 2
,x x
là hai nghiệm phân biệt của
phương trình
1 2
2
1 2
2
3
3 2 0
.
3
a
x x
x ax b
b
x x
.
Hơn nữa
1 2
2 1
3
a
f x f x f
.
Mà
2 1
2
x x
suy ra
6; 9
a b
.
Hàm số
3 2
6 9 1f x x x x
nên
2
1
6 9
f x
x x
x
.
Xét phương trình hoành độ giao điểm giữa hai đường là
2
1
6 9 4
5
x
x x
x
.
Vậy
1 1
2
5 5
1
4d 6 5 d
f x
S x x x x
x
32
3
.
Câu 6. Cho hàm số
3 2
f x x ax bx c
với
, ,a b c
là các số thực. Biết hàm số
f x
có hai điểm
cực trị
1 2
,x x
thỏa mãn
2 1
2
x x
và hàm số
' ''g x f x f x f x
có
1
6
g x
. Diện
tích hình phẳng giới hạn bởi các đường
1
;
y g x x x
và
2
x x
bằng
A.
8
. B.
4
. C.
2
. D.
16
.
Lời giải
Chọn A
Do hàm số
f x
có hai cực trị là
1
x
và
2
x
thỏa mãn
2 1
2
x x
, nên
2 2
1 2 1 2 1 1 1 1
' 3 3 3 3 6
f x x x x x x x x x x x x x x x
.
Khi đó
3 2
1 1
3
f x x x x x C
và
1
'' 6 6
f x x x
.
Mà
3
1
' '' 6
g x f x f x f x x x C
suy ra
1
6 6 0
g x C C
.
Vậy
2
2 2 2
1 1 1
1
3 3 4
1 1 1
1
d 6 d 6 d 6 8
4
x
x x x
x x x
x
S g x x x x x x x x x x x
.
Câu 45. Cho khối hộp chữ nhật
. ' ' ' 'ABCD A B C D
có đáy là hình vuông,
2BD a
, góc giữa hai mặt
phẳng
'
A BD
và
ABCD
bằng
0
30
. Thể tích của khối hộp chữ nhật đã cho bằng
A.
3
6 3a
. B.
3
2 3
9
a
. C.
3
2 3a
. D.
3
2 3
3
a
.
Phân tích định hướng tìm lời giải:
- Đây là bài toán tính thể tích của khối hộp chữ nhật;
- Để tính khối hộp chữ nhật ta áp dụng công thức
.V B h
;
+ Trong bài toán này
ABCD
B S
dễ dàng tính thông qua giả thiết
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc Trang 119
Tập san
Số 02
8 - 2021
+ Xác định đường cao
h AA
, việc tính
AA
được quy về việc xác lập mỗi liên hệ giữa
góc giữa hai mặt phẳng
'A BD
và
ABCD
với đường chéo của đáy.
Fb-Ngô Dung
Lời giải
Chọn D
Gọi
O
là tâm hình vuông
ABCD
.
Vì
BD OA
và
'BD AA
nên
' 'BD A OA BD OA
Lại có
'A BD ABCD BD
. Do đó
0
' , ' 30A BD ABCD A OA
(Hình vẽ
trên).
Vì tứ giác
ABCD
là hình vuông có
2BD a
nên
OA a
và
2AB AD a
.
Xét tam giác
'A AO
vuông tại
A
có
OA a
và
0
' 30A OA
nên
0
3
' .tan 30
3
a
AA OA
.
Vậy thể tích khối hộp chữ nhật
3
3 2 3
. . ' a 2. 2.
3 3
a
V AB AD AA a a
.
Bình luận:
- Đây là bài toán tính thể tích của khối hộp chữ nhật, để giải quyết được bài toán này
yêu cầu học sinh phải nắm vững công thức tính thể tích khối hộp; cách xác định góc
giữa hai mặt phẳng; thiết lập mỗi liên hệ giữa đường cao với giả thiết đã cho của bài
toán để tính chiều cao của khối hộp. Đây là câu hỏi kiểm tra kiến thức ở mức độ VD.
Hướng phát triển 1: Một bài toán tương tự, tuy nhiên ta thay đổi một chút về giả thiết
đáy. (câu 1)
Hướng phát triển 2: Về cách xác định đường cao, từ đó xác định được góc. (câu 2,3)
Hướng phát triển 3: Thay đổi góc giữa mặt bên và mặt đáy thành góc giữa mặt bên và
mặt bên (câu 4)
Hướng phát triển 4: Ta cho 2 giả thiết về góc, khi đó, giả thiết đường cao được ẩn trong
giả thiết về góc, sử dụng mối quan hệ đó đi xác định đường cao. (câu 5)
Bài tập tương tự
Câu 1. Cho khối hộp chữ nhật
. ' ' ' 'ABCD A B C D
, đáy
ABCD
có
2 2AB AD a
. Góc giữa hai
mặt phẳng
B AD
và
ABCD
bằng
0
45
. Thể tích của khối hộp chữ nhật đã cho bằng
A.
3
4 5
5
a
. B.
3
2 5
5
a
. C.
3
2 5
15
a
. D.
3
8 5
15
a
.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc Trang 120
Tập san
Số 02
8 - 2021
Lời giải
Chọn A
Bài toán hoàn toàn tương tự với đề bài gốc. Vậy nên ta sẽ giải rút gọn như sau:
Gọi
H
là hình chiếu vuông góc của
B
lên cạnh
AC
.
Khi đó ta sẽ có
, 45
B AC ABCD B HB
Dẫn đến
B HB
vuông cân tại
B BB BH
.
Xét tam giác
BAC
vuông tại
, 2 ,
B BA a BC a
khi đó đường cao
2 2 2
2
. 2 . 2
5
2
BA BC a a a
BH
BA BC
a a
.
Vậy
3
.
4 5
. .
5
ABCD A B C D
V BA BC BB a
.
Câu 2. Cho khối lăng trụ tam giác đều
. ' ' 'ABC A B C
có
3AB a
. Gọi
M
là trung điểm
AA
. Góc
giữa hai mặt phẳng
MBC
và
A B C
bằng
30
. Thể tích của khối lăng trụ
.
ABC A B C
đã cho bằng
A.
3
9 3
8
a
. B.
3
9 3
4
a
. C.
3
27 3
8
a
. D.
3
27 3
4
a
.
Lời giải
Chọn D
Gọi
N
là trung điểm
BC
. Khi đó
; ; 30
MBC A B C MN AN MNA
Xét
MAN
có
3 3 3
, 30 3
2 2
a
AN a MNA MA AA a
Vậy
3
.
27 3
4
ABC A B C
V a
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc Trang 121
Tập san
Số 02
8 - 2021
Câu 3. Cho chóp
.
S ABC
có đáy
ABC
là tam giác đều cạnh
a
. Gọi
M
là trung điểm
BC
, chân
đường cao hạ từ
S
xuống mặt phẳng đáy chính là trung điểm
H
của đoạn
AM
. Biết góc
giữa hai mặt phẳng
,
SAB ABC
bằng
60
. Thể tích của hình chóp đã cho bằng
A.
3
3
8
a
. B.
3
3 3
16
a
. C.
3
3
32
a
. D.
3
2
8
a
.
Lời giải
Chọn C
Dựng
HE AB
tại
E
.
Khi đó
, , 60
SAB ABC SE EH SEH
.
Ta có
1 1 3
, ,
2 4 8
a
EH d M AB d C AB
, suy ra
3
.tan 60
8
a
SH EH
Câu 4. Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác vuông cân tại
A
cạnh
AB a
. Hình chiếu
vuông góc của
S
trên mặt phẳng
ABC
trùng với trung điểm
H
của
BC
. Biết góc tạo bởi
hai mặt phẳng
SAC
và
SBC
bằng
60
. Thể tích của khối chóp đã cho bằng
A.
3
24
a
. B.
3
12
a
. C.
3
6
a
. D.
3
2
a
.
Lời giải
Chọn B
Ta có
ABC
vuông cân tại
, 2A AB a BC a
và
2
2
a
AH
.
Ta dựng
HI SA
, khi đó ta có
SA IBC
.
Mà
SA SAB SAC
góc
; ; 60
SAB SAC IB IC
Khi đó có 2TH:
60
BIC
hoặc
120
BIC
.
TH:
60
BIC
. Khi đó
2
BI BC a a BA
vô lý.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc Trang 122
Tập san
Số 02
8 - 2021
TH:
120
BIC
. Khi đó
6 6
3 6
a a
BI CI HI
Ta xét
HSA
vuông tại
2
,
2
a
H HA
và đường cao
6
6 2
a a
HI SH
.
Vậy
3
.
1
. .
6 12
S ABC
a
V SH AB AC
Câu 5. Cho chóp
.
S ABC
, đáy
ABC
là tam giác vuông tại
, 2 , 30
A BC a ABC
. Hai mặt bên
,
SAB SAC
cùng tạo với đáy một góc bằng
60
. Biết hình chiếu vuông góc
H
của
S
xuống mặt đáy nằm trên cạnh
BC
. Thể tích của hình chóp đã cho bằng
A.
3
3 1
12
a
. B.
3
3 1
6
a
. C.
3
3 1
2
a
. D.
3
3 3
4
a
.
Lời giải
Chọn D
Từ
H
dựng
HE AB
tại
E
và
HF AC
tại
F
.
, 60
, 60
SAB ABC SEH
SAC ABC SFH
đặt
HE HF x
Ta có
3
tan tan60 3
3 1
HF x a
C x
FC a x
Suy ra
3
.tan 60
3 1
a
SH HF
Vậy
3
.
1 3 3
. .
6 4
S ABC
V SH AB AC a
.
Câu 46: [TNTHPTQG -MĐ122-Năm 2021] Trên tập hợp các số phức, xét phương trình
2 2
2 1 0
z m z m
(
m
là tham số thực). Có bao nhiêu giá trị của
m
để phương trình đó
có nghiệm
o
z
thỏa mãn
6
o
z
?
A.
2
. B.
3
. C.
1
. D.
4
.
Phân tích định hướng tìm lời giải:
+ Khai thác
6
o
z
. Nếu
0
z
là số thực thì
6
o
z
0
6
z
; Nếu
0
, ; 0
z a bi a b b
thì
2 2
0
z a b
.
+ Trong từng trường hợp
o
z
là nghiệm thực,
o
z
là nghiệm phức không suy biến của
phương trình
2 2
2 1 0
z m z m
ta phải chú ý tới điều kiện tương ứng của
m
để
kiểm tra kết quả.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc Trang 123
Tập san
Số 02
8 - 2021
Ý tư
ởng: Kiểm tra việc một số em học sinh quên không xét trường hợp
o
z
là số thực.
Fb-Khải Nguyễn
Lời giải
Phương trình đã cho có
2 2
( 1) 2 1.
m m m
Nếu
2 1 0
m
thì phương trình có nghiệm thực
0
z
mà
6
o
z
0
6
z
Khi đó ta có:
2 2
2
2
2
2
6 2 1 .6 0
12 48 0
12 24 0
6 2 1 . 6 0
m m
m m
m m
m m
6 2 3
m
(thỏa mãn điều kiện
' 0
).
Nếu
2 1 0
m
thì phương trình có phức không thực
1 2 1
z m i m
Khi đó
6 1 2 1 6
o
z m i m
2
2
1 2 1 6
m m
6
6
m
m
.
Thấy
6
m
thỏa mãn
' 0
và
6
m
không thỏa mãn
' 0
.
Vậy có
3
giá trị của
m
thỏa mãn bài toán.
Bài tập tương tự
Câu 1: [Nhóm Giáo Viên Toán Việt Nam] Trên tập số phức cho phương trình
2
0
z az b
với
,a b
. Biết rằng hai nghiệm của phương trình có dạng
2
w
và
2 5 3w i
với
w
là một
số phức. Giá trị của tổng
T
a b
bằng
A.
81
. B.
82
. C.
100
. D.
64
.
Định hướng
+ Khai thác giả thiết thấy phương trình có hai nghiệm phức không thực. Đây là cơ sở
để áp dụng tính chất về nghiệm phức không thực của phương trình bậc hai.
+ Trên tập hợp các số phức, xét phương trình
2
0
az bz c
với
, ,a b c
và
0
a
.
Khi đó nếu
1 2
,z z
là các nghiệm phức không thực của phương trình thì:
2
4 0
b ac
và
1;2
2
b i
z
a
. Nhận thấy
1 2
z z
;
1 2
b
z z
a
,
2 2
1 2 1 2
c
z z z z
a
;
1 2
z z
a
.
Lời giải
+ Vì
2
w
và
2 5 3w i
với
w
là một số phức là các nghiệm của phương trình đã cho
nên chúng là các nghiệm phức không thực.
+ Gọi
1 2
,z z
là các nghiệm phức không thực của phương trình đã cho
1 2
z z
. Đặt
1
2
z w x yi
(
,x y
)
2
w x yi
2
2 5 3 2 9 2 3
w i x y i z
.
+ Vì
1 2
z z
nên
2 9
2 3
x x
y y
9
1
x
y
. Như vậy
1 2
9 ; 9z i z i
.
+
1 2
1 2
18
82
a z z
b z z
64
a b
Chọn D
Câu 2: [Sưu Tầm Trên Nhóm Giáo Viên Toán Việt Nam] Cho các số thực
a
và
b
sao cho phương
trình
2
0
z az b
có hai nghiệm phức
1 2
,z z
không thực. Trên mặt phẳng tọa độ
Oxy
, gọi
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc Trang 124
Tập san
Số 02
8 - 2021
A
và
B
lần lượt là điểm biểu diễn các số phức
1 2
,z z
. Biết rằng
OAB
có một góc bằng
120
. Mệnh đề nào dưới đây đúng?
A.
2
(2 3)
b a
. B.
2
3
b a
. C.
2
2
b a
. D.
2
b a
.
Định hướng
Dùng tính chất về nghiệm phức không thực của phương trình bậc hai hệ số thực.
Lời giải
+ Vì Phương trình
2
0
z az b
(
,a b
) có hai nghiệm phức
1 2
,z z
không phải là
số thực nên
2
4 0
a b
và
1,2
2
a i
z
.
+ Ta có
1
OA z b
;
2
OB z b
;
2
1 2
4
AB z z b a
. Thấy
OA OB
OAB
cân tại đỉnh
O
. Vì
OAB
cân tại
O
và có một góc bằng
120
nên
120
AOB
2
2 2
2
4 2 cos120
b a b b b b
2
b a
Chọn D
Câu 3: [Chuyên Đại Học Vinh-L2/N2021] Cho các số thực
,b c
sao cho phương trình
2
0
z bz c
có hai nghiệm phức
1 2
,z z
thỏa mãn
1
4 3 1z i
và
2
8 6 4
z i
. Mệnh đề nào sau đây
đúng?
A.
5 4
b c
. B.
5 12
b c
. C.
5 12
b c
. D.
5 4
b c
.
Lời giải
+ Nếu
1 2
,z z
là các nghiệm thực của phương trình đã cho thì từ
1
4 3 1z i
2
1
4 9 1
z
2
1
4 8
z
. Điều này vô lý.
+ Nếu
1 2
,z z
là các nghiệm phức không thực thì
2 1
z z
. Đặt
1
,z x yi x y
2
z x yi
.
1
2
4 3 1
8 6 4
z i
z i
hay
2 2
2 2
4 3 1
8 6 4
x y
x y
2 2
2 2
2 4 3 24
4 4 3 84
x y x y
x y x y
2 2
36
4 3 30
x y
x y
24
5
18
5
x
y
. Suy ra
1
2
24 18
5 5
24 18
5 5
z i
z i
.
+
1 2
1 2
48
5
36
b z z
c z z
5 12
b c
Chọn B
Câu 47: [TNTHPT QG-MĐ122-Năm 2021] Xét các số phức
,z w
thỏa mãn
1
z
và
2
w
. Khi
6 8z i w i
đạt giá trị nhỏ nhất,
z w
bằng
A.
3
. B.
5
. C.
29
5
. D.
221
5
.
Phân tích định hướng tìm lời giải:
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc Trang 125
Tập san
Số 02
8 - 2021
+ Khai thác k
ết luận, thấy cần áp dụng BĐT mô đun
6 8 6 8 10 1
z i w i i z i w z i w
. Kết hợp giả thiết, nghĩ đến
3 2
z i w z i w
. Từ đây suy ra
6 8 7
z i w i
.
+ Tìm
,z w
để đẳng thức ở
1
và
2
xảy ra.
Fb-Khải Nguyễn
Lời giải
+ Ta có
6 8 6 8 10 1
3 2
z i w i i z i w z i w
z i w z i w
6 8 7 3
z i w i
.
+ Đẳng thức ở
1
xảy ra khi và chỉ khi
6 8z i w k i
với
k
và
0
k
. Đẳng
thức ở
2
xảy ra khi và chỉ khi
.
z t i w
với
t
và
0t
. Như thế, đẳng thức ở
1
,
2
đồng thời xảy ra khi và chỉ khi
3 4
5 5
8 6
5 5
z i
w i
hay đẳng thức ở
3
xảy ra khi
và chỉ khi
3 4
5 5
8 6
5 5
z i
w i
.
+ Vậy
min 6 8 7
z i w i
, khi đó
29
5
z w
Chọn C
Bình lu
ận
Đây là bài thi tr
ắc nghiệm về GTNN, GTLN của biểu thức chứa mô đun số phức. Để
giải bài toán nay chỉ cần áp dụng trực tiếp các BĐT mô đun, nhưng yêu cầu phải chỉ
được khi nào đẳng thức xảy ra. Điều này gây khó khăn cho học sinh vì các em khó
nhớ nếu không tự chứng minh được BĐT mô đun.
Các câu tương tự
Câu 1: [Nhóm Giáo Viên Toán Việt Nam] Xét số phức
z
thay đổi thỏa mãn
2.
z i
Biết biểu thức
T 3 2 4
z i z i
đạt giá trị nhỏ nhất khi
z x yi
,x y
. Hiệu
x y
bằng
A.
3 6 13
17
. B.
6 13 3
17
. C.
3 6 13
17
. D.
3 6 13
17
.
Định hướng
Khai thác kết luận: Biểu thức
T 3 2 4
z i z i
đạt giá trị nhỏ nhất. Ta phải “cân
bằng hệ số” (làm xuất hiện thừa số
2
ở biểu thức
3z i
) trước khi áp dụng bất đẳng
thức mô đun bằng đẳng thức sau:
2 1
1 2 1 2
1 2
z z
z z z z
z z
1 2 1 2
, ; 0, 0
z z z z
.
Lời giải
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc Trang 126
Tập san
Số 02
8 - 2021
+ Ta có
4
3 4 4
4
i z i
z i z i i z i i
z i i
2 z
;
2 4
T z i z
2 4 2 17
z i z
1
.
+ Đẳng thức ở
1
xảy ra khi
4 , ,0 1
2
z k i k k
z i
4 8 13 1 2 13
17 17
z i
.
+ Vậy
3 6 13
17
x y
Chọn C
Câu 2: [Sở Nam Định-Năm 2021] Xét các số phức
;z w
thỏa mãn
2 2
2 2 6
z z i
và
3 2 3 6w i w i
. Khi
z w
đạt giá trị nhỏ nhất, hãy tính
z
.
A.
1 2
. B.
2 1
. C.
1
5
. D.
1
5
.
Định hướng
+ Khai thác giả thiết, thấy
2 2
2 2 6
z z i
1 1z i
;
3 2 3 6w i w i
3
2
4
y x
(
, ,w x yi x y
).
+ Khai thác kết luận, viết
1 1
z w i z i
w
1 1i z i
w
2
2
3
1 3 1 *
4
x x
.
Lời giải
+
2 2
2 2 6
z z i
2 2
1 1 1 1 6
z i i z i i
2 2
2 1 1 6
z i i
1 1z i
.
+ Đặt
, ,w x yi x y
. Khi đó
3 2 3 6w i w i
3
2
4
y x
.
+
1 1
z w i z i
w
1 1i z i
w
2
2
3
1 3 1 *
4
x x
.
+ Khi
4
5
x
thì
7
5
y
và
4 7
5 5
w i
. Đẳng thức ở
*
xảy ra khi và chỉ khi
1 1
z i k i w
với
k
và
0
k
. Từ
1 1
z i k i w
1 1
z i k i w
1
3
k
2
5 5
i
z
5
5
z
Chọn D
Câu 3: [Đềtham khảo-2018] Xét các số phức
z x yi
(
,x y
) thỏa mãn
4 3 5
z i
. Khi biểu
thức
1 3 1P z i z i
đạt giá trị lớn nhất, giá trị của
x y
bằng
A.
4
. B.
6
. C.
8
. D.
10
.
Định hướng
+Nhận thấy
1 3 4 3 5
z i z i
,
1 4 3 3 2z i z i i
do đó không tính
được
2 2
1 3 1
z i z i
theo
4 3z i
(
,
là các số thực).
+Tuy nhiên ta lại có
2 2 2 2
1 3 1 2 1 2z i z i z i i
.
Lời giải
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc Trang 127
Tập san
Số 02
8 - 2021
+
2 2 2 2
2 1 3 1 4 1 2
P z i z i z i i
2
2 5
z i
1
.
+
4 3 4 2 4 3 4 2 3 5
z i z i i z i i
2
. Đẳng thức ở
2
xảy ra
khi
, 0
4 3 4 2
4 3 5
k k
z i k i
z i
6 4z i
.
+Từ
1
và
2
suy ra
10 2
P
3
. Đẳng thức ở
3
xảy ra khi và chỉ khi đẳng
thức ở
1
và
2
đồng thời xảy ra
6 4
1 3 1
z i
z i z i
6 4z i
Chọn D
Câu 4: [Chuyên Hùng Vương Bình Dương-L5N2018] Xét các số phức
,z x yi x y
thỏa mãn
1 3 3z i z i
. Khi
1 2 1
z i z i
đạt giá trị lớn nhất,
3 3
x y
bằng
A.
0
. B.
16
. C.
54
. D.
27
.
Lời giải
+ Ta có
1 3 3z i z i
2 2 2 2
1 3 3 1
x y x y
0
x y
.
+ Trong mặt phẳng phức, gọi
M z
,
1 2A i
và
1
B i
. Khi đó,
M
thuộc đường
thẳng
d
có phương trình
0
x y
. Nhận thấy
,A B
nằm cùng một phía đối với
d
.
+
AB
có phương trình:
2 3 0
x y
; Xét hệ
0
3
2 3 0
x y
x y
x y
.
+
1 2 1
z i z i
5
MA MB AB
. Đẳng thức xảy ra khi và chỉ khi ba điểm
M
,
A
,
B
thẳng hàng hay
M
là giao điểm của đường thẳng
AB
và đường thẳng
d
hay
3;3
M
Chọn C
Câu 5: [Sưu Tầm Và Biên Tập] Xét các số phức
,z w
thay đổi thỏa mãn
2
z
,
3 2 1w i
. Khi
2
2 4
z zw
đạt giá trị lớn nhất,
z w
bằng
A.
6
. B.
2 85
5
. C.
2
. D.
2 5
.
Lời giải
+ Đặt
z x yi
với
,x y
thì
2
z z
yi
; Vì
2
z
nên
2 2
4
x y
2 2
y
0 2 4
y
2
2 16
y
.
+
2
2 4
z zw
2
2
z z
z w
4
iy w
4 3 2 3 2
iy i i w
4 3 2 3 2
iy i i w
4 3 2 4
y i
2
4 4 9 2 24
y
. Từ đây suy ra
2
2 4 24 1
z zw
.
+ Đẳng thức ở
1
xảy ra khi và chỉ khi
2
18 14
5 5
z i
w i
. Vậy
2
max 2 4 24
z zw
, khi
đó
6
z w
Chọn A
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc Trang 128
Tập san
Số 02
8 - 2021
Câu 6: [Chuyên Đại Học Vinh-L2/N2021] Cho các số thực
,b c
sao cho phương trình
2
0
z bz c
có hai nghiệm phức
1 2
,z z
thỏa mãn
1
4 3 1z i
và
2
8 6 4
z i
. Mệnh đề nào sau đây
đúng?
A.
5 4
b c
. B.
5 12
b c
. C.
5 12
b c
. D.
5 4
b c
.
Lời giải
+ Nếu
1 2
,z z
là các nghiệm thực của phương trình đã cho thì từ
1
4 3 1z i
2
1
4 9 1
z
2
1
4 8
z
. Điều này vô lý.
+ Nếu
1 2
,z z
là các nghiệm phức không thực thì
2 1
z z
1
8 6 4
z i
.
Ta có
1 1
1 1
1 4 3 4 3 1
4 8 6 8 6 2
z i z i
z i i z
1
1
6
6
z
z
1
6
z
. Đẳng thức ở
1
xảy ra
khi và
chỉ khi
1
4 3z k i
với
k
và
0
k
. Từ đây tính được
1
24 18
5 5
z i
(thỏa mãn
2
) và
2
24 18
5 5
z i
.
+
1 2
1 2
48
5
36
b z z
c z z
5 12
b c
Chọn B
Câu 7: [Chuyên Vinh -L2/N2018] Trong các số phức
z
thỏa mãn
2
1 2z z
, gọi
1
z
và
2
z
lần lượt
là các số phức có mô đun nhỏ nhất và lớn nhất. Khi đó mô đun của số phức
1 2
w z z
bằng
A.
2 2
. B.
2
. C.
2
. D.
1 2
.
Định hướng
+ Khai thác giả thiết:
2
1 2z z
2
2
2 2 2
1 4z z z z
2
2 4
2
4 1
z z z z
.
+
2 2
2
2z z z z zz
2
2
2z z z
2
2 z
.
Lời giải
+ Ta có :
2
1 2z z
2
2
2 2 2
1 4z z z z
2
2 4
2
4 1
z z z z
.
+ Mặt khác:
2 2
2 2
2
2 2 1
z z z z z z
. Suy ra
2 4 2
4 1 2z z z
4 2
6 1 0
z z
1 2 1 2
z
. Đẳng thức ở
1
xảy ra khi và chỉ khi
0
z z
z
là số thuần ảo.
+ Dễ dàng có
1
2 1z i
và
2
2 1z i
. Từ đó
1 2
2 2w z z i
và
2 2
w
Chọn A
Câu 8: [SởGD&ĐTHàNam–L1N2018] Xét các số phức
,z a bi a b
thỏa mãn
2
4 15 1
z z i i z z
. Khi
1
3
2
z i
đạt giá trị nhỏ nhất,
4a b
bằng
A.
7
. B.
6
. C. 5. D.
4
.
Lời giải
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc Trang 129
Tập san
Số 02
8 - 2021
+ Ta có
z a bi z a bi
;
2
4 15 1
z z i i z z
2
2
2 2
a a
b
2
2
2 2
a a
z a i
.
+
2
1 1
3 5
2 2 2 2
a a
z i a i
2
2
2
1
5
2 2 2
a a
a
2
2 2
1 1 1 39
2 2 2 8
a a
39
8
. Khi
1
2
a
thì
1 39
3
2 8
z i
+ Vậy
1 39
min 3
2 8
z i
; Khi đó
4 7
a b
Chọn A
Câu 48: Cho hàm số
y f x
có đạo hàm
2
7 9 , .
f x x x x
Có bao nhiêu giá trị
nguyên dương của tham số
m
để hàm số
3
5
g x f x x m
có ít nhất 3 điểm cực trị?
A.
6.
B.
7.
C.
5.
D.
4.
Phân tích định hướng tìm lời giải:
- Đây là bài toán cực trị hàm hợp có tham số: Tìm tham số
m
để hàm số
,
y f u x m
có
đúng (ít nhất, nhiều nhất)
k
điểm cực trị (1).
- Cách giải bài toán (1):
+ Một số bài mà
,
y f u x m
là hàm số chẵn thì đồ thị hàm số
,
y f u x m
nhận
O y
là trục đối xứng. Khi đó, việc xét số điểm cực trị của hàm số
,
y f u x m
trên
quy về
xét số điểm cực trị của hàm số này trên
0;
. Hàm số
,
y f u x m
có
2 1k
điểm cực trị
khi và chỉ khi
,
y f u x m
có
k
điểm cực trị trên
0;
.
+ Tổng quát: Trong nhiều bài toán, ta sử dụng tính chất (*) sau
Cho hàm số
f x
và
u x
liên tục trên
, khác hàm hằng trên mọi khoảng. Gọi
1 2
, ,...,
n
x x x
là các điểm cực trị của
f x
.
Khi đó:
1) Nếu
0
x
là nghiệm của phương trình
, 1,
i
u x x i n
thì
0
x
cũng là điểm cực trị của hàm
số
f u x
. Hơn nữa, nếu
i
x
là điểm cực đại (cực tiểu) của
f x
thì
0
x
cũng là điểm cực đại
(cực tiểu) của hàm số
f u x
.
Thật vậy, theo định nghĩa cực trị,
i
x
là điểm cực trị của
f x
tồn tại khoảng
;
i i
a b
chứa
i
x
sao cho
i
f x f x
hay
i
f x f x
với mọi
; \
i i i
x a b x
.
Mà
u x
liên tục trên
nên tồn tại khoảng
;
i i
c d
chứa
0
x
sao cho
0
; \ , ; \
i i i i i
u x a b x x c d x
.
Do vậy:
0
f u x f u x
hay
0
f u x f u x
với
0
; \
i i
x c d x
.
Suy ra,
0
x
cũng là điểm cực trị của hàm số
f u x
. Hơn nữa, nếu
i
x
là điểm cực đại (cực
tiểu) của
f x
thì
0
x
cũng là điểm cực đại (cực tiểu) của hàm số
f u x
.
2) Ta có
.
f u x u x f u x
, với mọi
x
. Do đó:
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc Trang 130
Tập san
Số 02
8 - 2021
+ Qua điểm
0
x
mà
u x
đổi dấu thì
f u x
đổi dấu.
+ Nếu
0
x
là điểm cực trị của
u x
thì
0
x
cũng là điểm cực trị của
f u x
.
Từ đó, ta có kết quả sau:
Số điểm cực trị của hàm số
f u x
bao gồm số điểm cực trị của
u x
và số nghiệm của các
phương trình
i
u x x
, với
1,i n
. Đồng thời các nghiệm này phải khác điểm cực trị của
u x
.
FB-Chu Thom
Lời giải
Chọn A
Để ý rằng:
3
5u x x x m
có cùng số điểm cực trị với hàm số
3
5y h x x x
.
Ta có BBT của hàm
3
5y h x x x
như sau:
Suy ra
3
5u x x x m
có đúng 1 điểm cực trị.
Ta có
3 3
5 . 5g x x x f x x m
.
Từ giả thiết
2
7
7 9 0 3
3
x
f x x x x
x
.
Ta có:
3 3
3 3 3
3 3
5 7 5 7
5 0 5 3 5 3
5 3 5 3
u x x x m x x m
f x x m u x x x m x x m
u x x x m x x m
(2).
Hàm số
g x
có ít nhất
3
điểm cực trị
(2) có ít nhất
2
nghiệm phân biệt khác
0
.
Từ bảng biến thiên của hàm số
h x
, ta có
7 0 7m m
.
Mà
m
nên
1;2;3;4;5;6m
Vậy có 6 giá trị của
m
thỏa mãn yêu cầu đề bài.
Bình luận:
- Trong cách giải trên, mấu chốt là tìm được số điểm cực trị của
3
5u x x x m
và tìm
được
m
để hệ (2) có ít nhất
2
nghiệm phân biệt khác
0
. Cả 2 yêu cầu cùng được giải quyết
dựa vào bảng biến thiên của hàm số
3
5y h x x x
.
- Ngoài cách giải trên, ta có thể thấy
3
5g x f x x m
là hàm số chẵn. Vì vậy,
g x
có ít nhất 3 điểm cực trị
g x
có ít nhất 1 điểm cực trị trên khoảng
0;
.
Hướng phát triển:
Hướng phát triển 1: Thay giả thiết cho công thức
f x
thành cho đồ thị hay bảng xét dấu
của
f x
, đồ thị hay bảng biến thiên của
f x
.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc Trang 131
Tập san
Số 02
8 - 2021
Hướng phát triển 2: Thay đổi hàm số
,u x m
.
Hướng phát triển 3: Thay đổi vị trí của trị tuyệt đối, hoặc bỏ trị tuyệt đối, vị trí tham số
m
(
m
không phải hệ số tự do).
Hướng phát triển 4: Thay đổi câu hỏi: Có ít nhất
k
cực trị, có nhiều nhất
k
cực trị, có đúng
k
cực trị.
Bài tập tương tự
Câu 1: Cho hàm số
f x
có bảng xét dấu đạo hàm như sau
Có tất cả bao nhiêu giá trị nguyên dương của tham số
m
để hàm số
4 2
2 3g x f x x m
có ít nhất 7 điểm cực trị?
A.
2
. B.
4
. C.
3
. D.
5
.
Lời giải
Chọn B
Đặt
4 2
2 3u x x x m
. Ta có
u x
có cùng số điểm cực trị với hàm số
4 2
2 3h x x x
. Đồ thị
4 2
2 3h x x x
như sau:
Từ đó suy ra hàm số
4 2
2 3u x x x m
có 5 điểm cực trị.
Từ giả thiết suy ra hàm số
f x
có 2 điểm cực trị là
4; 5x x
.
4 2 4 2
2 3 2 3g x x x m f x x m
.
Ta có
4 2
4 2
4 2
2 3 4
2 3 0
2 3 5
x x m
f x x m
x x m
4 2
4 2
2 3 4
(3).
2 3 5
x x m
x x m
Hàm số
4 2
2 3g x f x x m
có ít nhất 7 điểm cực trị
(3) có ít nhất 2 nghiệm phân
biệt khác điểm cực trị của
u x
5 0 5m m
mà
*
m
nên
1;2;3;4m
.
Câu 2: Cho hàm số
f x
liên tục trên
có đúng 2 điểm cực trị và có đồ thị như hình vẽ
Có tất cả bao nhiêu giá trị nguyên của tham số
m
thuộc
20;20
để hàm số
2
3g x f x x m
có nhiều nhất 7 điểm cực trị?
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc Trang 132
Tập san
Số 02
8 - 2021
A.
21
. B.
20
. C.
22
. D.
19
.
Lời giải
Chọn A
Đặt
2
3u x x x m
g x f u x
.g x u x f u x
.
Xét hàm số
2
3u x x x m
có cùng điểm cực trị với hàm số
2 2 3 2
3 3 3h x x x x x x x
.
Bảng biến thiên của hàm số
3 2
3y x x
như sau:
Suy ra, đồ thị hàm số
y h x
như sau
Từ đồ thị suy ra hàm số
y h x
có 3 điểm cực trị
u x
có 3 điểm cực trị.
Hàm số
g x
có quá 7 điểm cực trị
hệ
2
2
3 1
3 2
u x x x m
u x x x m
có quá 4 nghiệm
phân biệt khác điểm cực trị của
h x
. Ta có
2
2
3 1
3 2
x x m
x x m
.
Do vậy, hệ
2
2
3 1
3 2
u x x x m
u x x x m
có quá 4 nghiệm phân biệt khác điểm cực trị của
h x
1 0
1 4
m
m
1
3
m
m
mà
m
nguyên thuộc
20;20
20;0
3
m
m
có 20 giá trị
của
m
để
g x
có quá 7 điểm cực trị.Vậy số giá trị nguyên của tham số
m
thuộc
20;20
để hàm số
2
3g x f x x m
có nhiều nhất 7 điểm cực trị là
41 20 21
.
Câu 3: Cho hàm số
y f x
có đạo hàm là hàm đa thức bậc 4. Biết hàm số
f x
có đồ thị như
hình
vẽ. Có tất cả bao nhiêu giá trị nguyên của tham số
m
thuộc
10;10
để hàm số
3 2
3 2g x f x mx
có đúng 6 điểm cực trị?
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc Trang 133
Tập san
Số 02
8 - 2021
A.
8.
B.
10.
C.
21.
D.
20.
Lời giải
Chọn D
2 3 2
3 6 3 2 0g x x mx f x mx
3 2
3 2
0
2
(4)
3 2 0
3 2 4
x
x m
u x x mx
u x x mx
.
Nếu
0m
thì (4) có 3 nghiệm phân biệt là
3
0; 2x x
g x
không thể có 6 điểm cực trị.
Nếu
0m
thì ta có bảng biến thiên
g x
có đúng 6 điểm cực trị
(4) có đúng 6 nghiệm
3
3
1
4 2 4
2
m m
.
Nếu
0m
thì ta có bảng biến thiên
g x
có đúng 6 điểm cực trị
(4) có đúng 6 nghiệm
3
3
1
2 4 0
2
m m
.
Vậy,
g x
có đúng 6 điểm cực trị thì
3
1
2
m
hoặc
3
1
2
m
.
Mà
m
nguyên thuộc
10;10
nên có 20 giá trị của
m
.
Câu 4: Cho hàm số
f x
. Biết rằng
f x
là hàm số đa thức bậc bốn có đồ thị như sau
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc Trang 134
Tập san
Số 02
8 - 2021
Tìm tất cả các giá trị thực của tham số
m
để hàm số
2
2
x x
g x f e me
có nhiều điểm cực
trị nhất?
A.
2m
. B.
1m
. C.
1m
. D.
2m
.
Lời giải
Chọn D
Đặt
2
2
x x
u x e me
g x f u x
.g x u x f u x
.
Ta có
2 0
2
0 1
0
3
2
x x
u x e e m
u x
g x u x
u x
u x
(5).
Hàm số
g x
có nhiều điểm cực trị nhất
(5) có nhiều nghiệm nhất
0m
và
2
1
0
3
2
u x
u x
u x
u x
(6) có nhiều nghiệm nhất.
Khi
0m
, ta có
0 lnu x x m
.
Bảng biến thiên
(6) có nhiều nghiệm nhất
2
0
2
2
m
m
m
.
Câu 5: Cho hàm số
y f x
xác định và liên tục trên
và có bảng biến thiên như hình vẽ
Có bao nhiêu giá trị nguyên của tham số
10;10m
để hàm số
5
x
g x f e x m
có
đúng 9 cực trị?
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc Trang 135
Tập san
Số 02
8 - 2021
A.
2
. B.
4
. C.
3
. D.
5
.
Lời giải
Chọn C
Đặt
5
x
u x e x m
g x f u x
.g x u x f u x
.
Hàm số
5
x
u x e x m
có cùng điểm cực trị với hàm số
5
x
h x e x
, với
5
x
h x e x
.
Xét hàm số
5 1 0 0
x x
h x e x h x e x
. Bảng biến thiên
Suy ra đồ thị hàm số
h x
có dạng
Từ bảng biến thiên suy ra hàm số
h x
có 3 điểm cực trị
5
x
u x e x m
có 3
điểm cực trị.
Ta có
5 1
0
5 2
x
x
e x m
f u x
e x m
5 1
(7)
5 2
x
x
e x m
e x m
.
Hàm số
g x
có đúng 9 điểm cực trị
(7) có đúng 6 nghiệm phân biệt khác điểm
cực trị của
u x
0 1 4
2 4
m
m
4 1 0 5 1
2 2
m m
m m
5 2m
,
mà
m
có 3 giá trị của
m
.
Câu 49: [Câu 49 THPT QG 2021– Mã 103] Trong không gian
Oxyz
, cho hai điểm
1; 3;2A
và
2;1; 4B
. Xét hai điểm
M
và
N
thay đổi thuộc mặt phẳng
Oxy
sao cho
4MN
. Giá trị
lớn nhất của
AM BN
bằng
A.
5 2
. B.
3 13
. C.
61
. D.
85
.
Fb-Võ Trọng Trí & Khải Nguyễn
Phân tích định hướng tìm lời giải:
1. Các bài toán quen thu
ộc:
+ Cho hai đi
ểm
,A B
cố định nằm khác phía đối với mặt phẳng
. Xét điểm
M
thay đổi
thu
ộc
, khi đó:
MA MB AB
. Đẳng thức xảy ra khi và chỉ khi
'M M
, trong đó
'M
là giao điểm của
đo
ạn thẳng
AB
với
.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc Trang 136
Tập san
Số 02
8 - 2021
' 'MA MB MA MB AB
. Đẳng thức xảy ra khi và chỉ khi
'M M
, trong đó
'B
là điểm
đ
ối xứng với
B
qua
và
'M
là giao điểm của đoạn thẳng
'AB
với
.
+ Cho hai đi
ểm
,A B
cố định nằm cùng phía đối với mặt phẳng
. Xét điểm
M
thay đổi
thu
ộc
, khi đó:
' 'MA MB MA MB AB
. Đẳng thức xảy ra khi và chỉ khi
'M M
, trong đó
'B
là điểm
đ
ối xứng với
B
qua
và
'M
là giao điểm của đoạn thẳng
'AB
với
.
MA MB AB
. Đẳng thức xảy ra khi và chỉ khi
'M M
, trong đó
'M
là giao điểm của
đo
ạn thẳng
AB
với
.
2. Tr
ở lại bài toán.
Bài toán g
ần gũi với một bài toán quen thuộc là tìm giá trị lớn nhất của
AM BM
v
ới
M
thuộc mặt phẳng
Oxy
. Việc đề cho xuất hiện điểm
N
với ràng buộc
4MN
nên ta có th
ể dùng phép tịnh tiến để biến
'AM BN AM B M
quen thuộc bằng
cách l
ấy điểm
'B
sao cho
'BB N M

.
Lời giải 1
Chọn D
Thấy hai điểm
,A B
nằm khác phía so với mặt phẳng
Oxy
. Gọi
1
B
là điểm đối xứng của
B
qua
Oxy
thì
1
2;1;4B
và
1
BN BN
. Gọi
P
là mặt phẳng đi qua
1
B
và song song với
Oxy
thì
P
có phương trình
4z
. Gọi
H
là hình chiếu vuông góc của điểm
A
lên
P
thì
1; 3;4H
. Gọi
2
B
là điểm sao cho
1 2
B B NM
thì
2
B P
.
Ta có:
2AH
,
1
5BH
,
1 2
4BB MN
(vì
1 2
B B NM
),
1 2
BN B M
(vì
1 2
B B NM
1 2
B N B M
). Trong
P
, điểm
2
B
thay đổi thuộc đường tròn
C
có tâm
1
B
và bán kính
1 2
4R BB
.
AM BN
1 2
AM B N AM B M
2
AB
2
2
2
AH HB
2
2
1 1 2
AH HB B B
85
85AM BN
1
. Đẳng thức ở
1
xảy ra khi và chỉ khi điểm
1
B
nằm giữa hai
điểm
2
B
,
H
và
2
M AB Oxy
.
Vậy
max 85AM BN
.
Lời giải 2
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc Trang 137
Tập san
Số 02
8 - 2021
Dễ thấy hai điểm
,A B
nằm khác phía so với mặt phẳng
Oxy
. Gọi
1
A
là điểm đối xứng
của
A
qua mặt phẳng
Oxy
thì
1
1; 3; 2
A
và
1
AM AM
. Gọi
; ;0M a b
và
; ;0M a b
, ta
có:
2 2
4
a c b d
hay
2 2
16
a c c d
;
1
1; 3;2
AM a b
;
2; 1;4
BN c d
;
1
3; 4; 2
A M BN a c b d
.
1
AM BN AM BN
1 1
AM BN AM BN
2 2
3 4 4
a c b d
2 2
29 2 4 3
a c b d b d a c
2 2
2 3
45 2 4 3
b d a c
85
85
AM BN
. Khi
32 51
; ;0
5 5
M
và
44 67
; ;0
5 5
N
thì
85
AM BN
. Vậy
max 85
AM BN
.
Bình luận:
Đây là bài toán đư
ợc phát triển từ ‘bài toán 2’ trang số 7 trong SGK Hình Học Nâng
Cao l
ớp 11.
Hai thôn n
ằm ở hai vị trí
A
và
B
cách nhau một con sông (xem rằng hai bờ sông là
hai đư
ờng thẳng song song. Người ta dự định xây một chiếc cầu bắc qua sông (cố
nhiên c
ầu phải vuông góc với hai bờ sông và làm hai đoạn đường thẳng từ
A
đến
M
và t
ừ
B
đến
N
. Hãy xác định vị trí chiếc cầu
MN
sao cho
AM BN
ngắn nhất.
L
ấy điểm
'A
sao cho
'
A A M N
 
khi đó
'AM A N
và
AM BN A N BN A B
.
Hư
ớng phát triển
Hư
ớng 1: Tìm giá trị nhỏ nhất của
AM BN
.
Hư
ớng 2: Bỏ bớt ràng buộc điểm
N Oxy
, khi đó
2
A
thuộc mặt cầu tâm
1
A
bán kính bằng
1 2
A A
.
Các bài tập tương tự
Câu 1: [Trần Quốc Luật-THTT tháng 12 năm 2017] Trong không gian với hệ tọa độ
Oxyz
, cho các
điểm
0;0;2
A
và
3;4;1
B
. Tìm giá trị nhỏ nhất của
AX BY
với
,X Y
là các điểm thuộc
mặt phẳng
Oxy
sao cho
1XY
.
A.
3
. B.
5
. C.
2 17
. D.
1 2 5
.
Lời giải 1
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc Trang 138
Tập san
Số 02
8 - 2021
Thấy
0;0;2A
,
3;4;1B
nằm cùng phía đối với mặt phẳng
Oxy
. Gọi
'A
là điểm đối
xứng với điểm
A
qua
Oxy
, khi đó
' 0;0; 2A
và
'AX A X
.
Vì
,X Y Oxy
nên gọi
; ;0X a b
,
; ;0Y c d
. Vì
1XY
nên
2 2
1
a c b d
hay
2 2
1a c b d
.
' ; ;2A X a b
,
3 ;4 ;1YB c d
,
' 3; 4;3A X YB a c b d
.
AX BY 'A X YB
'A X YB
 
'A X YB
 
2 2
3 4 9a c b d
2 2
34 2 3 4a c b d a c b d
35 2 3 4a c b d
35 2 3 4a c b d
2 2
2 2
35 2 3 4 a c b d
5 5AX BY
. Khi
8 32
; ;0
5 15
X
và
11 44
; ;0
5 15
Y
thì
5AX BY
. Vậy
min 5AX BY
.
Lời giải 2
Thấy
0;0;2A
,
3;4;1B
nằm cùng phía đối với mặt phẳng
Oxy
. Gọi
'A
là điểm đối
xứng với điểm
A
qua
Oxy
, khi đó
1
0;0; 2A
và
1
AX A X
.
Gọi
P
là mặt phẳng chứa
1
A
và song song mặt phẳng
Oxy
suy ra
P
có phương trình là
2z
. Gọi
K
là hình chiếu của
B
lên
P
thì
3;4; 2K
, khi đó
3BK
,
1
5KA
.
Lấy điểm
2
A
sao cho
1 2
AA XY
, khi đó
1 2
AX AY
(vì
1 2 1 2
A A XY A X AY
),
2
A P
và trong
P
,
2
A
thuộc đường tròn
C
tâm
1
A
bán kính
1 2
1R AA
(vì
1 2
A A XY
).
1
AX BY AX BY
2 2
AY BY A B
2
2
2
BK KA
2
2
1
BK KA R
5
5 1AX BY
. Đẳng thức ở
1
xảy ra khi và chỉ khi
2
A
là giao điểm thứ nhất của
đường thẳng
1
AK
với
C
(
2
A
thuộc đoạn thẳng
1
AK
) đồng thời
2
Y A B Oxy
.
Vậy
min 5AX BY
.
Câu 2: [Câu 49 THPT QG 2021– Mã 103] Trong không gian
Oxyz
, cho hai điểm
1; 3;2A
và
2;1; 4
B
. Xét hai điểm
M
và
N
thay đổi, trong đó
M
thuộc mặt phẳng
Oxy
và
N
tùy ý
sao cho
4MN
. Giá trị lớn nhất của
AM BN
bằng
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc Trang 139
Tập san
Số 02
8 - 2021
A.
5 2
. B.
3 13
. C.
61
. D.
85
.
Câu 50. Có bao nhiêu số nguyên
y
sao cho tồn tại
1
;6
3
x
thỏa mãn
2
3 18
27 1 27
x xy x
xy
?
A.
19
. B.
21
. C.
20
. D.
18
.
Fb: Nguyễn Sỹ - Nguyễn Thanh Hải
Lời giải
Giả sử tồn tại
y
để phương trình trên có nghiệm
1
;6
3
x
. Suy ra
1 0
xy
Lấy logarit cơ số
27
hai vế, PT đã cho tương đương
2
27
3 18 log 1 0
x y x xy
.
Xét hàm số
2
27
3 18 log 1
f x x y x xy
, với
1
;6
3
x
.
- Với
0
y
, do
1 0
1
3
xy
x
1
y
x
, Suy ra
3 0
y
hay
1; 2
y
.
+) Với
1
y
, ta có
2
27
3 19 log 1
f x x x x
là hàm số liên tục trên
2
;1
3
.
Do
2
11
3
f
và
1
lim
x
f x

suy ra phương trình có nghiệm trên
2
;1
3
.
+) Với
2
y
, ta có
2
27
3 20 log 1 2f x x x x
là hàm số liên tục trên
1 1
;
3 2
.
Phân tích định hướng lời giải
- Đây là bài toán có mức độ VDC (có thể là câu khó nhất của đề thi THPT QG năm 2021).
- Sử dụng phương pháp “Logarit hóa hai vế” để xét phương trình mũ dạng:
; ;
; . , 0 ; 1
f x m g x m
a u x m b a b
(với m là tham số)
Định hướng tìm lời giải:
B1: Dựa vào phương trình đã cho tìm điều kiện cho phương trình.
B2: Coi
y
như tham số, lấy logarit cơ số 27 hai vế, sau đó đưa phương trình về dạng
0
f x
.
B3: Sử dụng kĩ thuật chia miền giá trị của tham số và xét hàm số
f x
. Mục đích để đánh giá
được tính đơn điệu của hàm số
f x
và sử dụng được định lý giá trị trung bình.
Sử dụng các đơn vị kiến thức:
Nếu
f
liên tục trên đoạn
;a b
và
. 0
f a f b
thì phương trình
0
f x
có ít nhất
một nghiệm trên khoảng
;a b
.
Sử dụng kiến thức này đã làm cho việc giải toán trở thành việc thử sai trong việc chọn cặp a, b.
Thay vào đó dùng kết quả sau (không thể giải quyết trọn vẹn việc thử sai nhưng đã giảm thiểu một
phần):
Cho
f
liên tục và đơn điệu trên đoạn trên
;a b
. Khi đó phương trình
0
f x
có nghiệm trên
khoảng
;a b
khi và chỉ khi và
. 0.
f a f b
Nếu
a e
thì hàm số
log 1
a
f x x x
nghịch biến trên
0;
.
Lưu ý:
log 1
a
x x
với mọi
0
x
và
a e
.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc Trang 140
Tập san
Số 02
8 - 2021
Do
1
6
3
f
và
1
2
lim
x
f x
suy ra phương trình có nghiệm trên
1 1
;
3 2
.
- Với
0
y
, phương trình trở thành
2
0
3 18 0
6
x
x x
x
, không thỏa mãn.
- Với
19
y
, ta có
6 18
3 1 ln3
y
f x x y
xy
,
2
2
1
6 0, ;6 .
3
3 1 ln3
y
f x x
xy
Suy ra
f x
đồng biến trên
1
;6
3
. Do đó
1
' 2 18 0
3 3 ln3
y
f x f y
y
vì
3 ln3 1
3 ln3
y
y y
y
Suy ra
f x
là đồng biến trên
1
;6
3
. Suy ra
27
1 17
log 1
3 3 3 3
y y
f x f
.
Xét hàm số
27
log 1 , 0g t t t t
. Dễ thấy
1
1 0, 0
3 3 ln 3
g t t
t
, suy ra
g t
là hàm đồng biến, do đó
1 17 19 17
0
3 3 3 3 3
y
f g g
. Suy ra
1
0 ;6
3
f x x
.
Do đó PT trên không có nghiệm thuộc
1
;6
3
.
- Với
1 18
y
. Do hàm số
2
27
3 18 log 1
f x x y x xy
liên tục trên
1
;6
3
.
Ta lại có hàm số
27
log 1 ,g t t t
đồng biến trên
0;

.
Mà
27
1 17
log 1
3 3 3 3
y y
f
1 17 17
6 0, 1;18
3 3 3 3
y
f g g y
,
Mặt khác
27
6 6 log 1 6 6 6 0, 1;18
f y y g y g y
.
Suy ra
1
. 6 0
3
f f
. Do đó phương trình trên có nghiệm trên
1
;6 .
3
Vậy có tất cả
20
giá trị nguyên của
y
thỏa mãn yêu cầu.
Bình luận:
- Việc sử dụng BĐT Bernoulli để đánh giá như lời giải sau đây là sai:
Có bao nhiêu số nguyên
y
sao cho tồn tại
1
;6
3
x
thỏa mãn
2
3 18
27 1 27
x xy x
xy
?
A.
19
. B.
21
. C.
20
. D.
18
.
Lời giải
Ta có:
2
3 18
27 1 .27
x xy x
xy
2
3 18
27 1
x xy x
xy
2
3 18
27 1 0
x xy x
xy
.
Mặt khác:
2
2
3 18
3 18 2
27 1 1 26 1 1 26 3 18 1
x xy x
x xy x
xy xy x xy x xy
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc Trang 141
Tập san
Số 02
8 - 2021
2
78 25 468x xy x
.
+ Với
19
y
2
3 18 2 2
1
27 1 78 25 468 84 7 0 ;6
3
x xy x
xy x xy x x x x
(loại).
+ Với
3
y
2
3 18
1
27 1 1 3 0 ;6
3
x xy x
xy x x
(loại).
+ Với
2
y
1
2
x
(thỏa mãn).
+ Với
1
y
1x
(thỏa mãn).
+ Với
0
y
2
3 18
27 1
x x
2
3 18 0
x x
0
6
x
x
(loại).
+ Với
1 18
y
. Xét hàm số
2
3 18
27 1
x xy x
f x xy
.
Do
17
1
3 1 0 1;2;....;18
3 3
y
y
f y
và
6
6 27 6 1 0 1;2;....;18
y
f y y
nên phương trình
0
f x
luôn có nghiệm
thuộc
1
;6
3
.
Tóm lại
2; 1;1;2;....;18
y
. Vậy có
20
số nguyên
y
thỏa mãn yêu cầu bài toán.
Lưu ý:
Nếu
1
a
thì
1 1
x
a ax
với
0
x
hoặc
1x
.
Nếu
1
a
thì
1 1
x
a ax
với
0 1x
.
- Khi giảng dạy cho HS chúng ta nên phát biểu bài toán dưới dạng. “Có bao nhiêu giá trị
nguyên của tham số
m
để phương trình
2
3 18
27 1 27
x xm x
xm
có nghiệm thuộc
1
;6
3
? ”
Hướng phát triển:
Hướng phát triển 1: Thay biến
y
bởi tham số
m
quy về bài toán tìm tham số
m
nguyên để
phương trình có nghiệm.
Hướng phát triển 2: Sử dụng phương pháp đánh giá hai vế của phương trình hoặc sử dụng các
bất đẳng thức cơ bản.
Hướng phát triển 3: Sử dụng phương pháp hàm số.
Các ví dụ tương tự:
Hướng phát triển 1: Thay biến
y
bởi tham số
m
quy về bài toán tìm tham số
m
nguyên để phương
trình có nghiệm
Câu 1. Có bao nhiêu số nguyên
m
để phương trình
2
3 15
(1 )27
27
x xm x
xm
có nghiệm
1
;5
3
x
?
A.
16
. B.
18
. C.
15
. D.
17
.
Lời giải
Giả sử tồn tại
m
để phương trình trên có nghiệm
1
;5
3
x
.
Từ phương trình, suy ra
1
xm
. Do
1
;5
3
x
, nên ta có
1
3
m
x
hay
2
m
.
Phương trình đã cho tương đương với
2
3 15
(1 ) 0
27
.
x x xm
xm
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc Trang 142
Tập san
Số 02
8 - 2021
Xét hàm số
2
3 15
127 ( )
x x xm
xx mf
trên khoảng
1
;5
3
Ta có
5 *
(5) 27 1 5 0
m
f m m
và
14
1 1
3 1
3 3
m
f m
,
Xét hàm số:
14
3 1
3
m
m
g m
, ta có
3 0
' 0 14 log 3ln3 12,9g m m m
.
BBT:
Do
3 0
2 0
g
g
và
16 0
15 0
g
g
, kết hợp với BBT suy ra với
m
nguyên lớn hơn
3
và
0 2; 1;...;15g m m
.
+ Với
{ 2; 1;1; ;15}m
ta có
1
(5) 0
3
f f
, nên phương trình
( ) 0f x
luôn có nghiệm
trên khoảng
1
;5
3
.
+ Với
0m
, ta có
( ) 0 0, 5f x x x
không thỏa mãn.
+ Với
16m
; Ta có phương trình
2
3 15 2
(1 ) 3 15 log227 10 7 0
x x xm
f x xm x x xm mx
Xét hàm số
2
27
3 15 log 1x x xx mh mx
trên khoảng
1
;5
3
. Ta có
2
2
1
' 6 15 '' 6 0, ;5 .
1 ln27 3
3 1 ln3
m m
h x x m h x x
mx
mx
Vì
'h x
liên tục trên đoạn
1
;5
3
nên hàm số
'h x
đồng biến trên khoảng
1
;5
3
. Do đó
1
' ' 2 15 0
3 3 ln3
m
h x h m
m
vì
3 ln3m m
nên
1
3 ln3
m
m
.
Suy ra
h x
là đồng biến trên
1
;5
3
. Do đó,
27
1 14
log 1
3 3 3 3
m m
h x h
.
Xét hàm số
27
log 1 , 0g t t t t
. Dễ thấy
1
1 0, 0
3 3 ln3
g t t
t
, suy ra
g t
là hàm đồng biến, do đó
1 14 14
8 0
3 3 3 3
m
h g g
. Suy ra
1
0 ;5
3
h x x
.
Do đó phương trình trên không có nghiệm thuộc khoảng
1
;5
3
.
Vậy
{ 2; 1;1; 2; ;15}m
, hay có 17 giá trị nguyên của tham số
m
.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc Trang 143
Tập san
Số 02
8 - 2021
Câu 2. (Mã đề 101, 2021) Có bao nhiêu số nguyên
y
sao cho tồn tại
1
;3
3
x
thỏa mãn
2
3 9
27 1 27
x xy x
xy
?
A.
27
. B.
9
. C.
11
. D.
12
.
Lời giải
Giả sử tồn tại
y
để phương trình trên có nghiệm
1
;3
3
x
. Suy ra
1 0
xy
Lấy logarit cơ số
27
hai vế, phương trình đã cho tương đương
2
27
3 9 log 1 0
x y x xy
.
Đặt
2
27
3 9 log 1
f x x y x xy
,
1
;3
3
x
. Ta xét các trường hợp sau
Nếu
0
y
thì
1
3
y
x
, suy ra
3
y
hay
1; 2
y
.
+) Với
1
y
thì ta có
1
0
3
f
và
1
lim
x
f x
suy ra phương trình có nghiệm trên
1 1
;1 ;3
3 3
.
+) Tương tự, với
2
y
, phương trình cũng có nghiệm trên
1 1 1
; ;3
3 2 3
.
Nếu
0
y
thì phương trình trở thành
2
0
3 9 0
3
x
x x
x
không thỏa mãn.
Nếu
10
y
, ta có
6 9
3 1 ln3
y
f x x y
xy
,
2
2
1
6 0, ;3 .
3
3 1 ln3
y
f x x
xy
Suy ra
f x
đồng biến trên
1
;3
3
. Do đó
1
' 2 9 0
3 3 ln 3
y
f x f y
y
.
Suy ra
f x
là hàm số đồng biến trên
1
;3
3
. Do đó
27
1 8
log 1
3 3 3 3
y y
f x f
.
Xét hàm số
27
log 1 , 0
g t t t t
. Dễ thấy
1
1 0
3 3 ln3
g t
t
g t
là hàm đồng
biến, suy ra
1 8 10 8
0
3 3 3 3 3
y
f g g
.
Nên phương trình không có nghiệm trên
1
;3
3
trong trường hợp này.
Nếu
1 9
y
thì từ tính đồng biến của
g t
, ta suy ra
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc Trang 144
Tập san
Số 02
8 - 2021
1 8
0, 1 9
3 3 3
y
f g y
,
3 3 0, 1 9
f g y y
.
Điều này dẫn đến phương trình có nghiệm trên
1
;3 .
3
Vậy có
11
giá trị nguyên của
y
thỏa mãn yêu cầu.
Hướng phát triển 2. Sử dụng phương pháp đánh giá hai vế của phương trình hoặc sử
dụng các bất đẳng thức cơ bản.
Câu 3. Có bao nhiêu cặp số nguyên
;x y
thỏa mãn
2020
x
và
2
2 3 2
2 2021 2 2 4
x y x y
x y
?
A.
1
. B.
2020
. C.
2021
. D.
0
.
Lời giải
Chọn B
Nếu
2 2
2 2 3 2 2 3 2
2 2 0 2 2 ,2021 2 2 0 2 2021 2 2 4
x y x y x y x y
x y x y x y
.
Nếu
2 2
2 2 3 2 2 3 2
2 2 0 2 2 ,2021 2 2 0 2 2021 2 2 4
x y x y x y x y
x y x y x y
.
Nếu
2 2
2 2 3 2 2 3 2
2 2 0 2 2 ,2021 2 2 0 2 2021 2 2 4
x y x y x y x y
x y x y x y
.
Vậy
2 2 0 2 2x y x y
, do
2020 2020 1009 1011
x y
.
Do
y
nên có
2021
giá trị, nên có
2021
cặp số
;x y
thỏa mãn.
Câu 4. Có bao nhiêu cặp số nguyên
;x y
với
1 2020
y
thỏa mãn biểu thức sau:
2
3 3
2
2 2 2
log 4 2 log 2
x x
x x x
y
y y y
y
.
A.
11
. B.
15
. C.
10
. D.
6
.
Lời giải
Chọn A
Đặt
2 0
x
a
, suy ra
2
2 2
3 3
2
2
log log
ay a
a ay y ay
y
2
2 2 2
3 3
2
log 2. log 1 1 1 *
a ay y a a a y a
ay y y y a y
Nhận thấy
3 3
* 1, * log 1 log 3 1
Cauchy
a y
VP VT
y a
dẫn đến
1 2
x
a
y
y
.
Do
2
1 2020 1 2 2020 0 log 2020 10,98
x
y x
.
Vì
x
nên
x
có 11 giá trị, mỗi giá trị của
x
tương ứng một giá trị
y
.
Vậy nên có
11
cặp số
;x y
thỏa mãn.
Hướng phát triển 3. Sử dụng phương pháp hàm số.
Câu 5. Có bao nhiêu cặp số nguyên
;x y
với
2 99
x y
thỏa mãn
y x
x y
?
A.
4751
. B.
4750
. C.
4656
. D.
4657
.
Lời giải
Chọn A
Từ
ln ln
ln ln
y x
x y
x y y x x y
x y
, xét hàm số
ln
, 2;99
t
f t t
t
.
Có
2
1 ln
0 2,71
t
f t f t t e
t
.
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
https://www.facebook.com/groups/toanvd.vdc Trang 145
Tập san
Số 02
8 - 2021
Suy ra hàm số
f t
đồng biến trên đoạn
2;e
và nghịch biến trên đoạn
;99
e
.
- TH1.
3 [ ;99]
x x e
thì
ln ln
3
x y
y x
x y
, suy ra có
2
97
4656
C
cặp
;x y
thỏa
mãn.
- TH2.
2
x
thì
ln 2 ln ln 4 ln
4 5, 2
2 4
y y
y y x
y y
có 95 cặp
;x y
thỏa
mãn.
Vậy nên có
4656 95 4751
cặp số
;x y
thỏa mãn.
| 1/131
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Tập san Số 02 8 - 2021
Đổi mới kiểm tra đánh giá theo định hướng
phát triển năng lực người học
Đề xuất cho kỳ thi tốt nghiệp THPT
Trao đổi kinh nghiệm dạy học theo định hướng
tiếp cận năng lực người học
Bàn về một cách tiếp cận khác cho bài toán tính góc giữa đường thẳng và mặt phẳng
Toàn cảnh đề thi tốt nghiệp THPT môn Toán
Lời giải chi tiết các câu VD – VDC các mã đề gốc 101, 102, 103, 104
Ôn thi tốt nghiệp THPT đợt 2 môn Toán
Phân tích, định hướng tìm lời giải, xây dựng các bài tương tự các câu VD – VDC
ĐỀ THI TỐT NGHIỆP THPT ĐỢT 1 NĂM 2021
https://www.facebook.com/groups/toanvd.vdc Lời nói đầu
Kỳ thi tốt nghiệp THPT đợt 1 năm 2021 đã diễn ra trong hai ngày 7,8/7/2021.
Buổi thi môn Toán diễn ra vào chiều 7/7/2021, bài thi môn Toán gồm 24 mã đề được lấy
từ 4 mã đề gốc là mã đề 101, 102, 103, 104. Để có góc nhìn đầy đủ vể bài thi môn Toán đợt
1, đồng thời giúp các em học sinh tham gia kỳ thi tốt nghiệp THPT đợt 2 năm 2021 cùng
quý thầy cô có thêm tài liệu ôn tập trong thời gian gấp rút này Nhóm Giáo viên toán Việt
Nam xin trân trọng giới thiệu, ra mắt cùng quý thầy cô và các em ấn phẩm Tập san số 02.
Hy vọng Tập san sẽ là sân chơi để quý thầy cô trao đổi kinh nghiệm dạy học cùng các
đồng nghiệp thông qua các bài viết của mình; các em học sinh nắm chắc các kiến thức trong
chương trình THPT; tiếp cận được với các bài toán mới, hay và lạ. Đặc biệt, rèn luyện tốt
kỹ năng làm bài thi trắc nghiệm môn Toán.
Để hoàn thành Tập san, BQT chân thành cám ơn tất cả các thành viên của nhóm,
hai tổ phản biện đã rất tâm huyết tham gia, xây dựng Tập san.
Trân trọng cám ơn TS Trần Nam Dũng, Ths Hoàng Quân đã tham gia viết bài
cho Tập san và có nhiều đóng góp ý kiến xây dựng cho ban biên tập
Tài liệu tuy đã được nhóm tổ chức làm cẩn thận, phản biện nhiều lần, nhưng không thể
tránh khỏi thiếu sót. Chúng tôi rất mong nhận được ý kiến đóng góp tích cực từ quý thầy cô
cùng các em học sinh. Các ý kiến đóng góp chân thành của quý thầy cô là nguồn động lực để
chúng tôi tiếp tục vững bước trên con đường mới và xây dựng tập san ngày càng chất lượng
hơn. Mọi ý kiến đóng góp, bài viết gửi đăng xin gửi về theo địa chỉ:
mail: nhomGVTVN@gmail.com.
BQT Nhóm Giáo viên toán Việt Nam!
https://www.facebook.com/groups/toanvd.vdc Trang 1
Các thành viên tham gia Tập san
Ban quản trị Nhóm Giáo viên toán Việt Nam
Cô giáo: Ngô Tú Hoa , Lại Nhật Hoan
Thầy giáo: Trần Nam Dũng; Trương Quốc Toản; Nguyễn Khải; Lê Thảo;
Tạ Minh Đức; Nguyễn Ngọc Chi; Lê Tài Thắng, Ngô Nguyễn Quốc Mẫn
Nam Phương; Hoàng Minh Quân; SongMinh Nguyễn.
Cùng các thầy, cô giáo tham gia viết và phản biện: Nguyễn Sỹ, Phong Do, Binh
Hoang, Võ Trọng Trí, Nguyễn Phụ Hoàng Lân, Huỳnh Văn Ánh,
Nguyễn Khắc Thành, Hoàng An Đình, Trần Dức Nội, Lê Thanh Bình,
Ngô Dung, Trương Đức Thịnh, Nguyễn Thanh Hải, Nguyễn Phương,
Chánh Lê Văn, Nguyễn Chiến, Vũ Minh Tư, Nguyễn Thị Hồng Gấm,
Nguyễn Văn Hải; Phạm Tuấn; Song Tử Mắt Nâu; Nguyễn Văn Viễn;
Thân Đức Minh; Phạm Quý; ĐưcThanh Phạm; Dấu Vết Hát. Trân trọng!
https://www.facebook.com/groups/toanvd.vdc Trang 2
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Tập san Số 02 8 - 2021
Đổi mới kiểm tra đánh giá theo định hướng
phát triển năng lực người học
Đề xuất cho kỳ thi tốt nghiệp THPT TS. TRẦN NAM DŨNG
Giảng viên khoa Toán – Tin học Trường Đại học KHTN, ĐHQG Tp HCM
Đợt 1 của kỳ thi tốt nghiệp THPT đã diễn ra đầu tháng 7 vừa qua, và đợt 2 dự
kiến sẽ diễn ra vào đầu tháng 8. Bỏ qua những áp lực do dịch COVID-19 đem đến,
chúng ta thử cùng đánh giá xem kỳ thi này có giải quyết tốt nhiệm vụ kép mà đó đang
mang trên mình "vừa để xét tốt nghiệp, vừa để tuyển sinh đại học" không?
Tôi nghĩ chúng ta không có vấn đề gì về nhiệm vụ thứ nhất. Đề thi có 25 câu đầu
rất căn bản, đủ để học sinh kiếm 5 điểm hay chí ít cũng không bị liệt. 13-15 câu tiếp
theo có khó hơn, nhưng cũng nhẹ nhàng, dành cho học sinh khá, 10-12 câu cuối thách
thức hơn dành cho học sinh giỏi.
Dưới đây tôi có chọn ngẫu nhiên một mã đề và phân tích 12 câu cuối cùng, tạm
gọi là các câu vận dụng và vận dụng cao. Trong số các câu này, tôi nhận thấy là chỉ có
vài câu (trong đó có 3 câu đầu, 39-41) phù hợp với đề thi trắc nghiệm, còn lại toàn là
những câu tự luận được trắc nghiệm hóa. Học sinh bắt buộc phải giải bài toán, ra đáp
số rồi kiểm tra, so khớp.
Dù sao thì trong số những câu này chỉ có một vài câu tôi đánh giá là không đạt
yêu cầu, còn lại dù không phù hợp lắm nhưng cũng ổn. Rõ ràng là đề của Bộ ra, có quy
trình, có phản biện nên tốt hơn các đề thi thử khá nhiều, ít có những câu trời ơi. Đó là
một điểm cộng của đề thi của Bộ.
Tuy nhiên có một điểm trừ là đề thi của bộ không có bất cứ một câu nào về ứng
dụng của toán học trong thực tiễn, điều làm cho toán khô khan hơn quá nhiều so với
lý, hóa, sinh, nơi mà có rất nhiều những bài toán, bối cảnh thực tiễn. Thực ra thì toán
đâu có xa rời thực tiễn, những bài toán về xác suất, những bài toán cực trị, những bài
toán tính toán hình học. luôn rất thú vị, hấp dẫn, tự nhiên, nó đòi hỏi ở học sinh kỹ
năng đọc hiểu, mô hình hóa, giải quyết vấn đề, đơn giản thôi nhưng cần thiết, thay vì
kiểu học theo tư duy công thức như hiện nay (công thức tính nhanh hiện giờ đang mà mốt).
Bản thân tôi cho rằng đề thi này chỉ đạt được yêu cầu về phân loại ở tốp dưới và
tốp giữa, còn ở tốp trên thì độ tin cậy không cao, do những bài toán quá khó sẽ tạo
điều kiện cho sự may rủi (trong đề này có khoảng 3-5 bài, tùy đánh giá của mỗi cá nhân).
https://www.facebook.com/groups/toanvd.vdc Trang 3
Tập san Số 2
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8-2021
Do vậy, tôi có đề xuất sau để nâng cao chất lượng và khả năng phân loại của đề thi.
1. Nếu hướng tới chỉ dùng để xét tốt nghiệp thì vẫn giữ hình thức thi trắc nghiệm,
nhưng bỏ hết những câu khó và không phù hợp trắc nghiệm (ví dụ trong đề đính kèm
chỉ giữ lại các câu 39, 40, 41, 44, 45, 47, 48)
2. Nếu vẫn dùng kỳ thi này với mục tiêu kép thì nên pha trộn hình thức câu hỏi theo cấu trúc sau:
25 câu trắc nghiệm với độ khó như 25 câu đầu của đề hiện hành.
10 câu điền đáp số lấy các câu từ 26-40, có thể lấy một số câu chân phương như nói ở phần 1.
35 câu này mỗi câu 0.2 điểm.
3 câu tự luận, trong đó có một câu ở mức trung bình, một câu ở mức độ trung bình
khó (ví dụ như một trong các câu 39, 40, 41, 44, 45, 47, 48) và một câu khó (ví dụ các câu
46, 49, 50). Tránh ra những câu sát thủ hay lắt léo, mẹo mực.
Trong các bài này, có thể là bài ở mức trung bình hay trung bình khó phần tự luận,
hay phần bài toán điền đáp số có thể cho 1 vài bài toán có liên hệ thực tiễn, có sử dụng
mô hình hóa (cấp số nhân, phương trình, hàm số).
Như vậy phần căn bản ta dùng trắc nghiệm còn phần nâng cao hơn ta dùng điền
đáp số và tự luận, một mặt sẽ kiểm tra được rộng và căn bản, mặt khác sẽ tránh được
sự may rủi trong đánh giá tốp trên. Bạn nào được 10 điểm sẽ thực sự là giỏi: cẩn thận
không sai nhảm ở câu dễ và xử lý được các thách thức một cách thật sự ở câu khó.
Vài lời chia sẻ cùng anh chị em trên diễn đàn này. Rất mong nhận được các ý kiến trao đổi.
12 câu hỏi vận dụng, vận dụng cao trong đề thi tốt nghiệp THPT (mã đề 114) 2
Câu 39: Có bao nhiêu số nguyên x thỏa mãn 2x  4x [log (x  25) 3]  0 3 A. 24 B. 25 C. Vô số D. 26
Câu này tốt, kiểm tra được các vấn đề về tính đơn điệu của hàm log, mũ, miền xác định của hàm
log. Bài này các phương án nhiễu cùng hay vì các đáp án sai đều liên quan đến một lỗi nào đó
(quên miền xác định, quên x = 2). 2x  2 khi x  1
Câu 40: Cho hàm số f (x)  
. Giả sử F là nguyên hàm của f trên R thỏa mãn F(0) = 2. 2
3x 1 khi x  1 
Giá trị của F(-1) + 2F(2) bằng. A. 18 B. 20 C. 9 D. 24
Câu này tốt, kiểm tra được về nguyên hàm của hàm số cho trên từng đoạn. Điểm mấu chốt cần
nắm là nguyên hàm phải là hàm liên tục. Có thể nhầm nếu thay nhầm công thức.
https://www.facebook.com/groups/toanvd.vdc Trang 4
Tập san Số 2
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8-2021
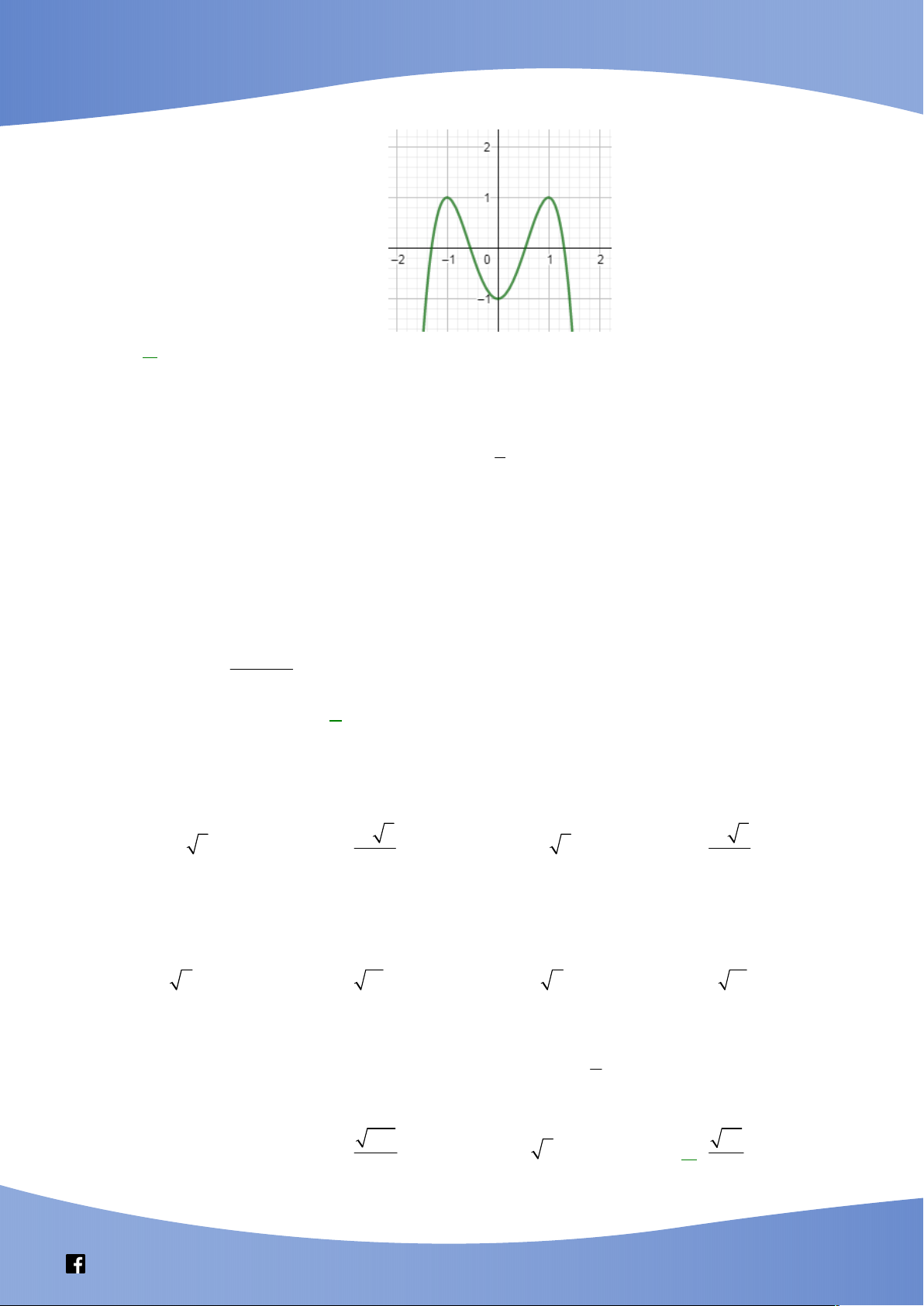
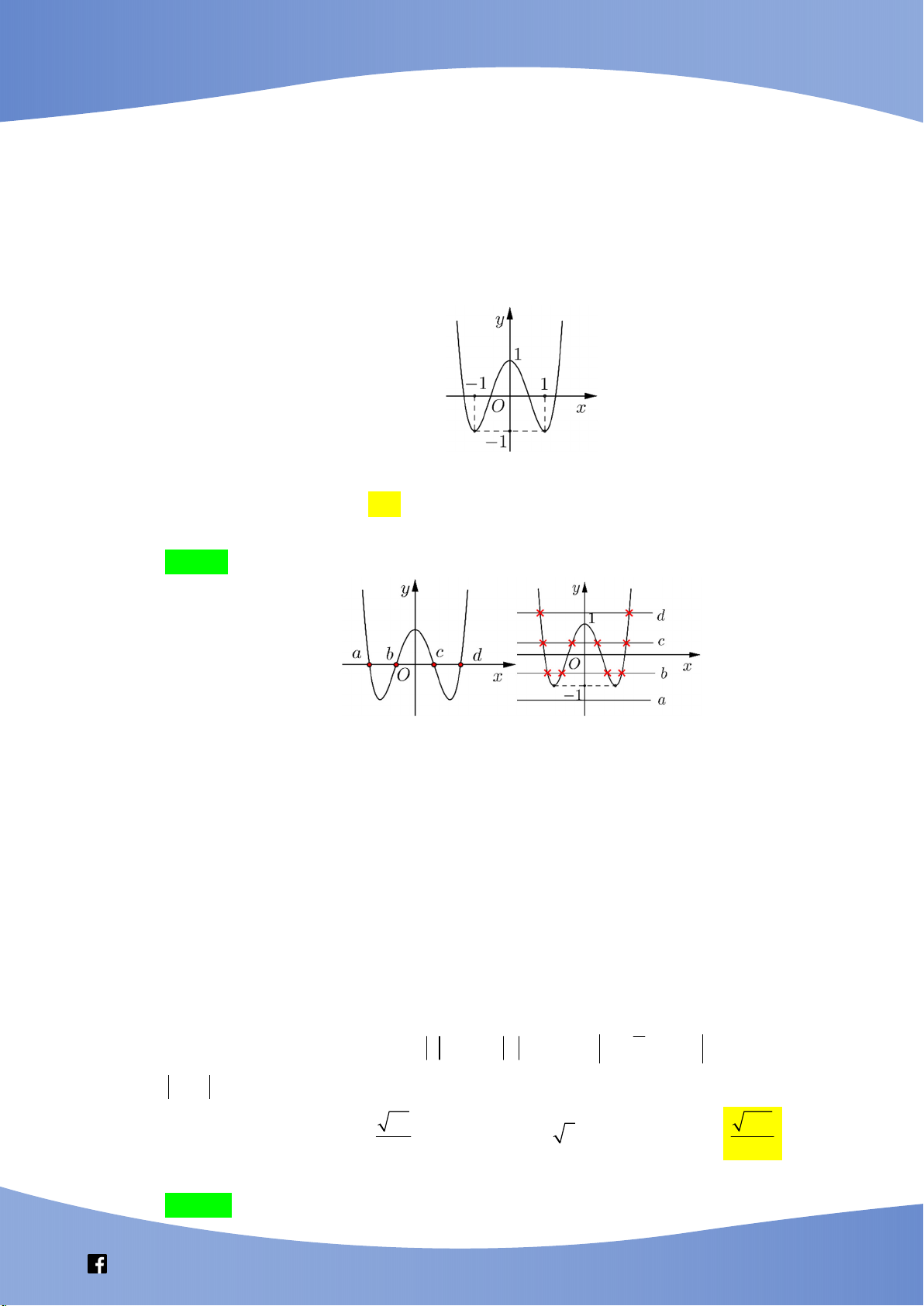
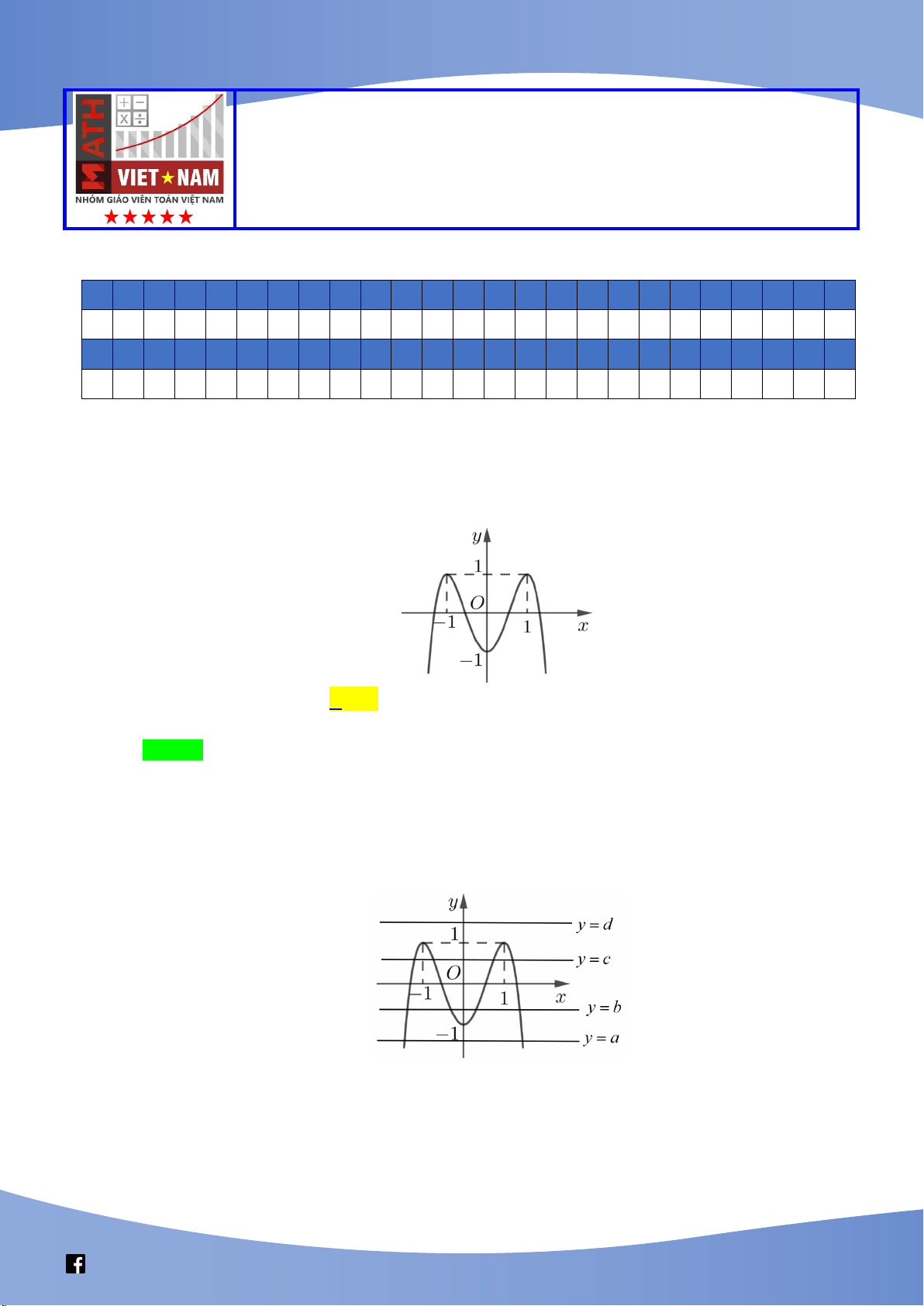
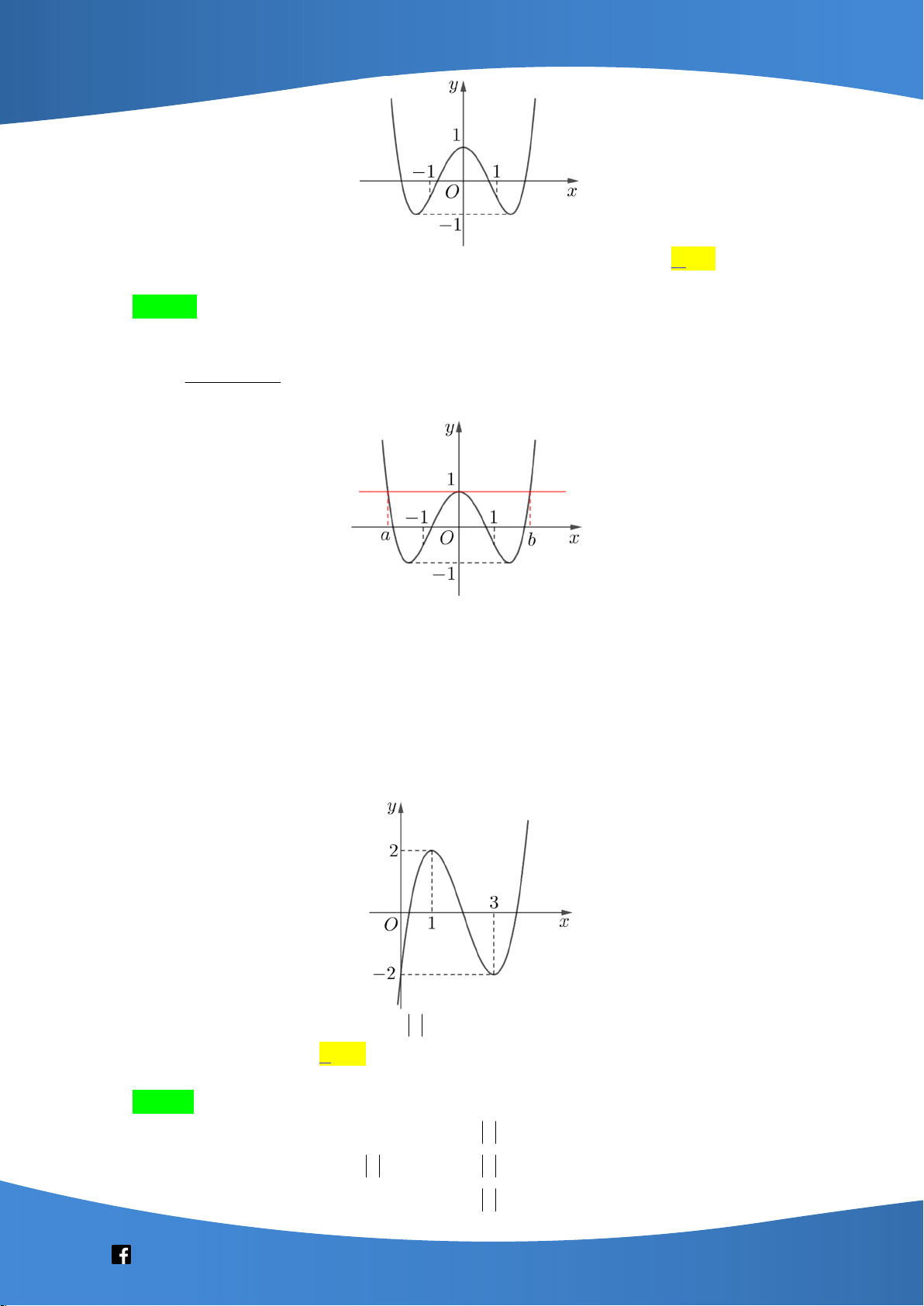
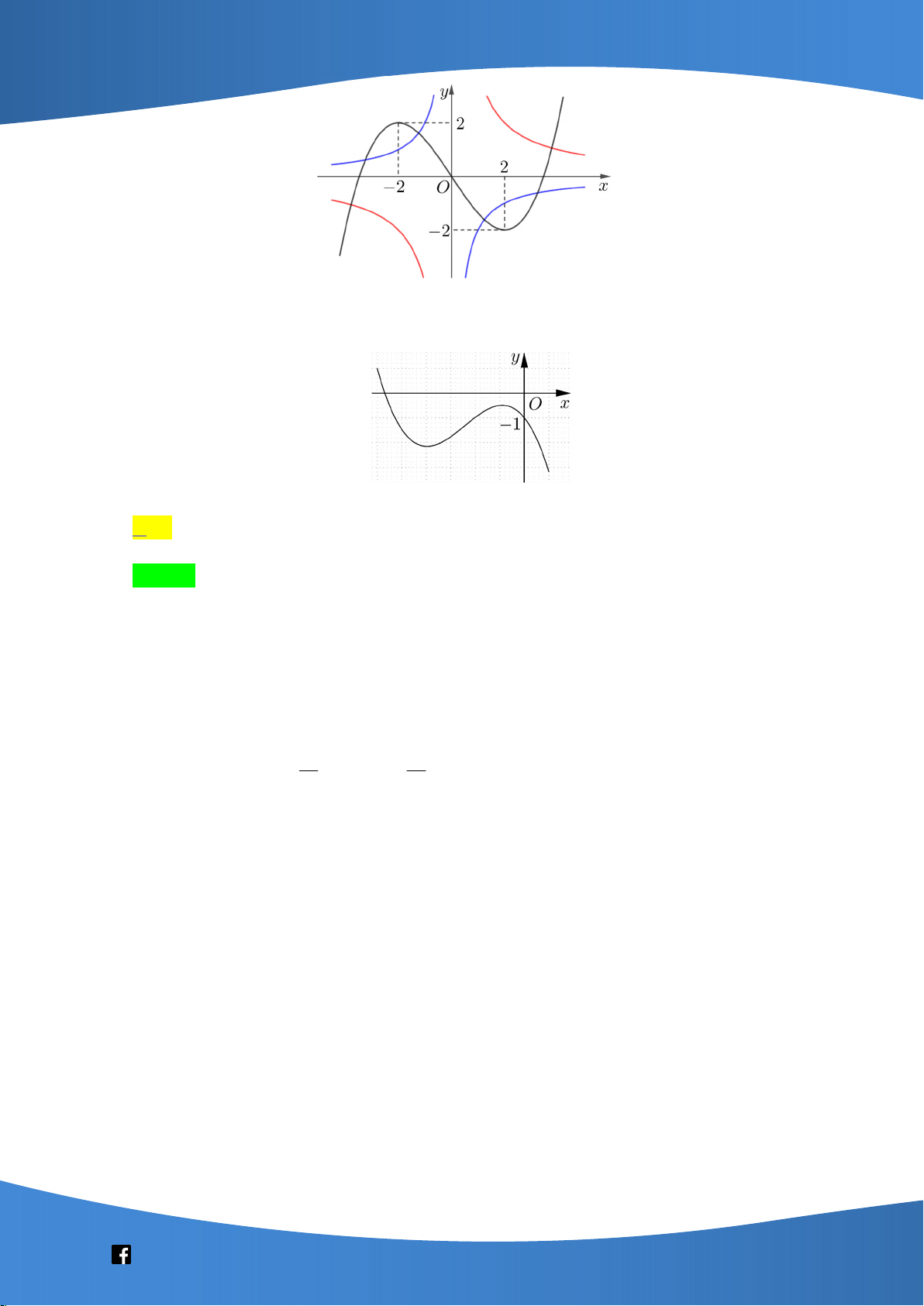
Câu 41: Cho hàm số bậc bốn y = f(x) có đồ thị là đường cong như hình bên. Số nghiệm của phương trình f(f(x)) = 0 là A. 10 B. 8 C. 4 D. 12
Câu này tốt, kiểm tra khái niệm hàm hợp. Đây cũng là câu phù hợp với trắc nghiệm vì học sinh
có thể nhẩm được mà không cần đặt bút tính.  1  2
Câu 42: Có bao nhiêu số nguyên y sao cho tồn tại x  ; 6 3x xy 18 x   thỏa mãn 27  (1 xy)27  3  A. 20 B. 21 C. 19 D. 18
Đây là câu dở, rất khó nhưng mà là cái khó không cần thiết, đặc biệt câu này không phù hợp với
trắc nghiệm vì chắc chắn sẽ tạo ra sự may rủi. Câu 43: Cho hàm số 3 2
f (x)  x ax bx c với a, b, c là các số thực. Biết hàm số
g(x)  f (x)  f '(x)  f "(x) có hai giá trị cực trị là – 5 và 2. Diện tích hình phẳng giới hạn bởi f (x) đường y  và y = 1 bằng g(x)  6 A. ln10 B. 3ln2 C. ln3 D. ln7
Câu này hơi mẹo quá. Và các đặt vấn đề rất thiếu tự nhiên, không ăn nhập với nhau.
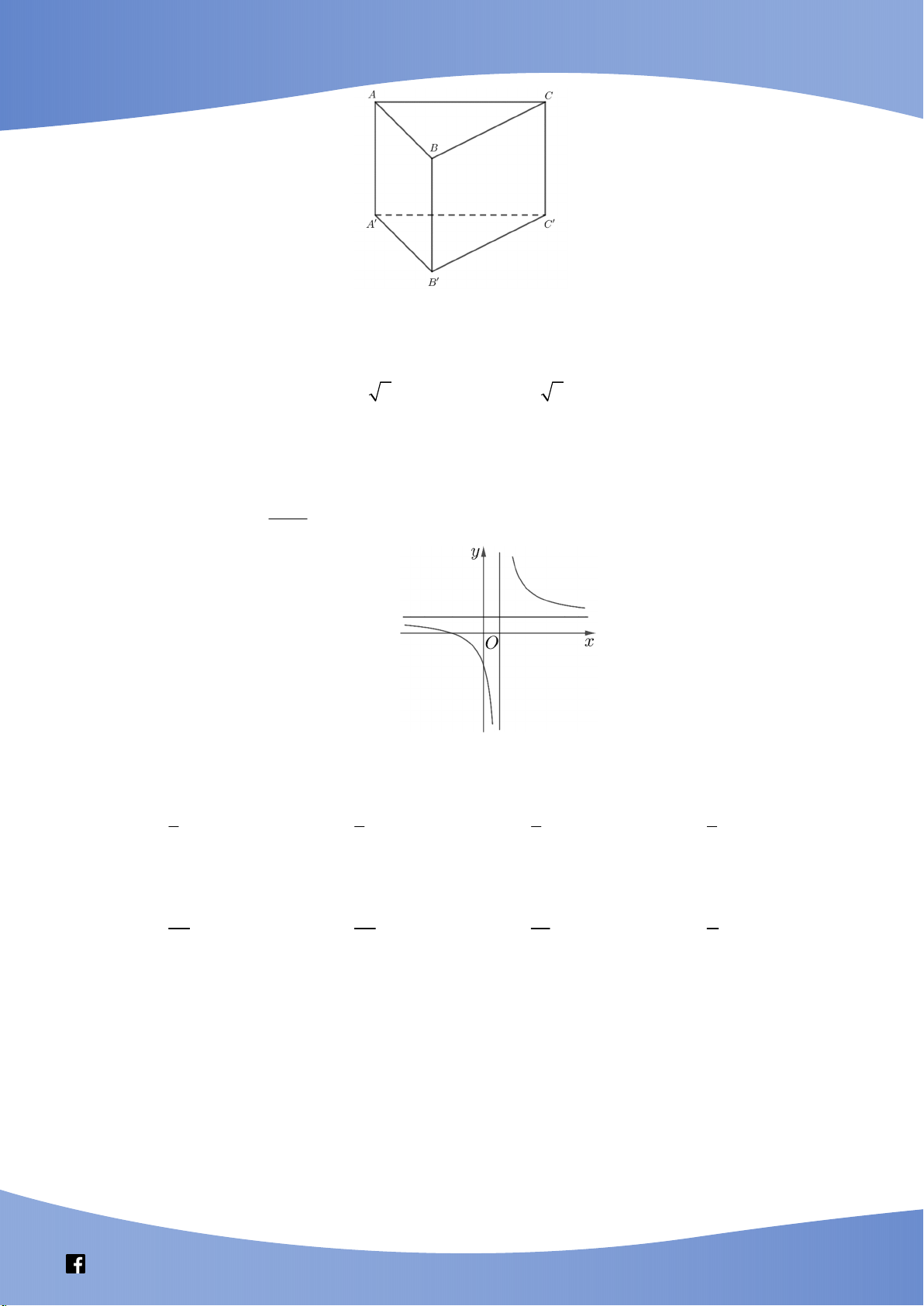
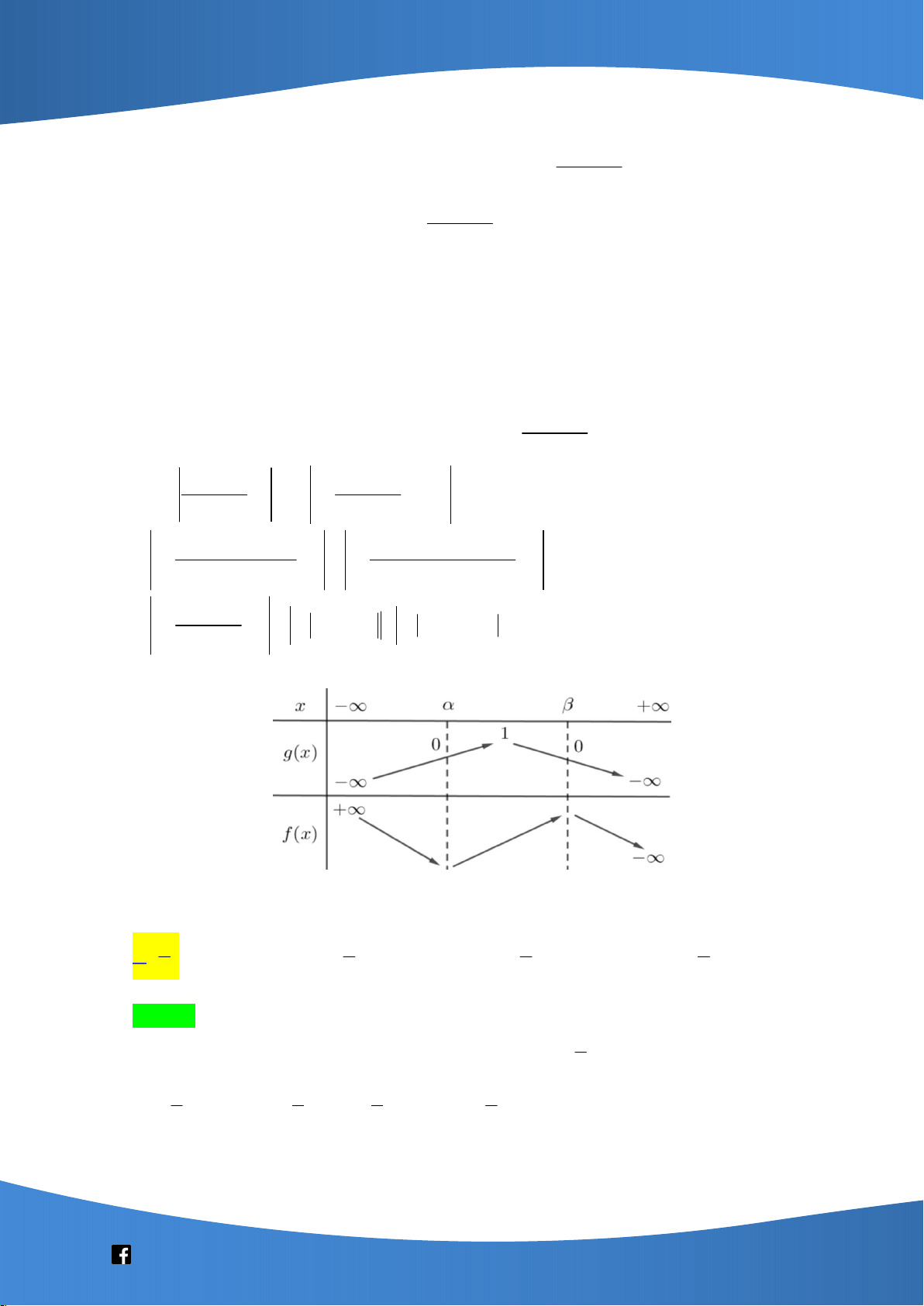
Câu 44: Cho hình hộp chữ nhật ABCD.A’B’C’D’ có đáy là hình vuông, BD = 4a, góc giữa hai mặt phẳng
(A’BD) và (ABCD) bằng 600. Thể tích của khối hộp đã cho bằng 16 3 16 3 A. 3 16 3a B. 3 a C. 3 48 3a D. 3 a 9 3
Câu này ổn, căn bản, chân phương.
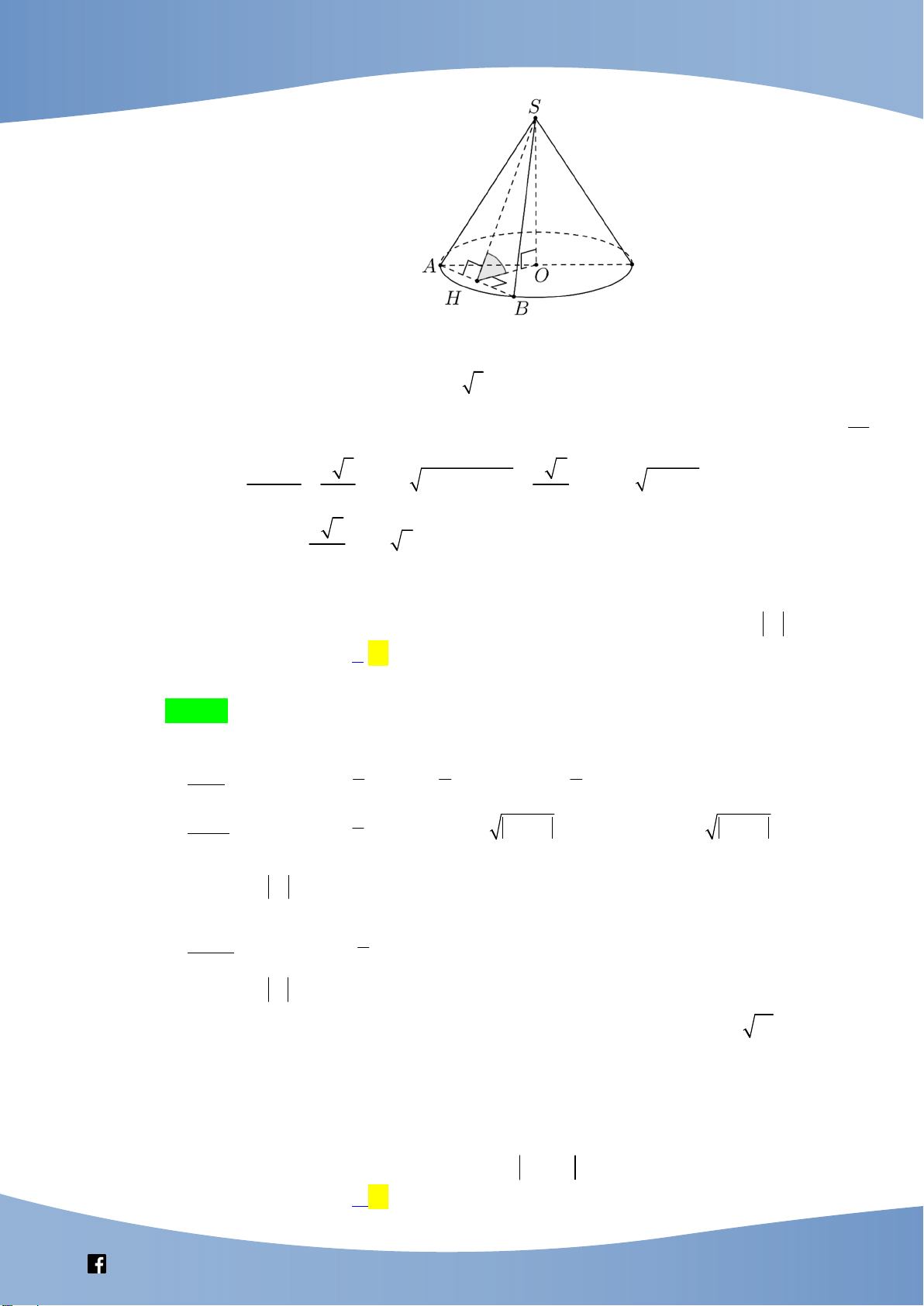
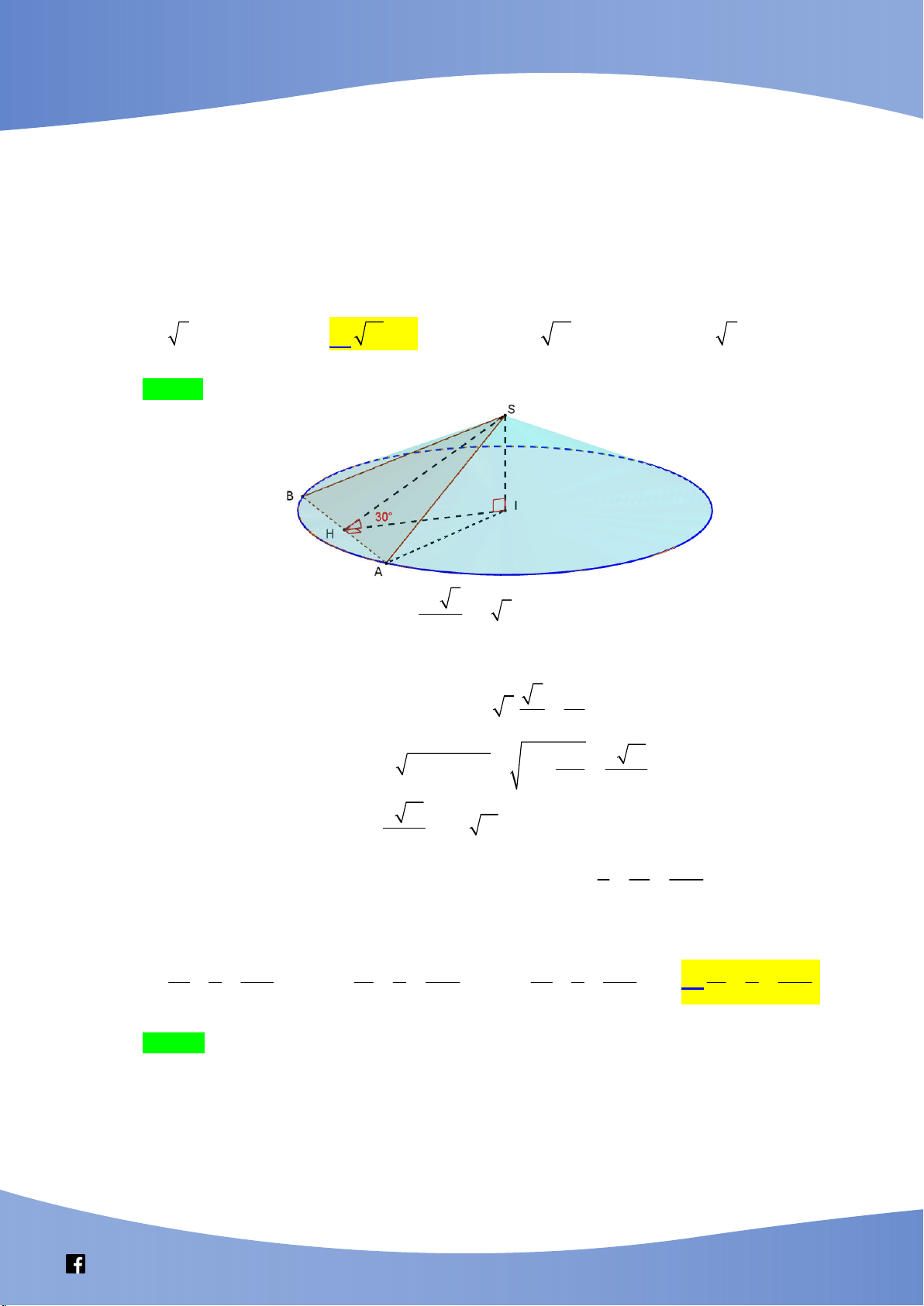
Câu 45: Cắt hình nón (N) bởi một mặt phẳng qua đỉnh và mặt phẳng chứa đáy một góc bằng 300 ta được
thiết diện là tam giác đều cạnh 2a. Diện tích xung quanh của (N) bằng A. 2 7 a B. 2 13 a C. 2 2 7 a D. 2 2 13 a
Câu này ổn, căn bản, chân phương, kiểm tra tốt hiểu biết của học sinh về hình nón các các thiết diện.
Câu 46: Xét các số phức z, w thỏa mãn |z| = 1 và |w| = 2. Khi | z iw  6  8i | đạt giá trị nhỏ nhất, |z – w| bằng. 221 29 A. 3 B. C. 5 D. 5 5
https://www.facebook.com/groups/toanvd.vdc Trang 5
Tập san Số 2
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8-2021
Câu này tương đối khó, phải nắm vững bất đẳng thức tam giác với các điều kiện xảy ra dấu bằng
mới giải được. Nếu giải bằng hình học thì cũng cần phải hiểu ý nghĩa hình học của phép toán
phức liên hợp và nhân với i. Sẽ chân phương hơn nếu bài này bỏ bớt chữ i trước w đi. x y z 1
Câu 47: Trong không gian Oxyz, cho đường thẳng d :  
và mặt phẳng (P): x + 2y – 2z + 2 = 1 1 2
0. Hình chiếu vuông góc của d lên (P) là đường thẳng có phương trình x y z 1 x y z 1 A.   B.   ; 2  4 3 2  4 3 x y z 1 x y z 1 C.   D.   . 14 1 8 14 1 8
Câu này bình thường, căn bản, chân phương.
Câu 48: Trên tập hợp các số phức, xét phương trình 2 2
z  2(m 1)z m  0 (m là tham số thực). Có bao
nhiêu giá trị của m để phương trình đó có nghiệm z thỏa mãn | z | 6? 0 0 A. 1 B. 3 C. 4 D. 2
Câu này ổn, kiểm tra về phương trình bậc hai, định lý Viet và hiểu biết về số phức. Vấn đề mấu
chốt ở đây là biết phân hai trường hợp: trường hợp có hai nghiệm thực và trường hợp có hai
nghiệm phức liên hợp.
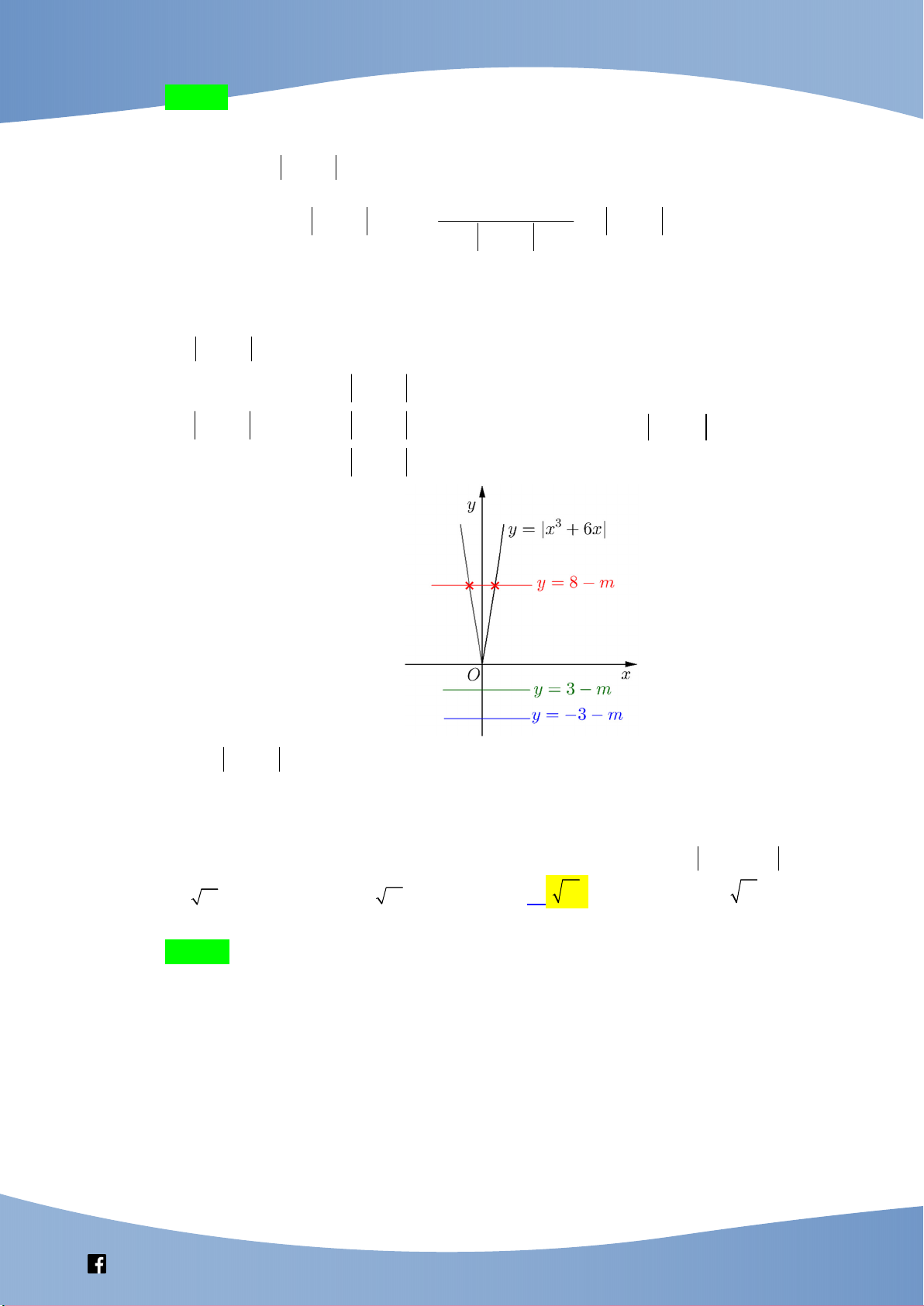
Câu 49: Cho hàm số y = f(x) có đạo hàm f’(x) = (x – 9)(x2 – 16), x R. Có bao nhiêu giá trị nguyên dương
của tham số m để hàm số y = f(|x3+7x|+m) có ít nhất 3 điểm cực trị? A. 9 B. 8 C. 16 D. 4
Bài này ổn, liên quan đến đạo hàm của hàm hợp và có thêm chút khó khăn ghi có dấu trị tuyệt đối.
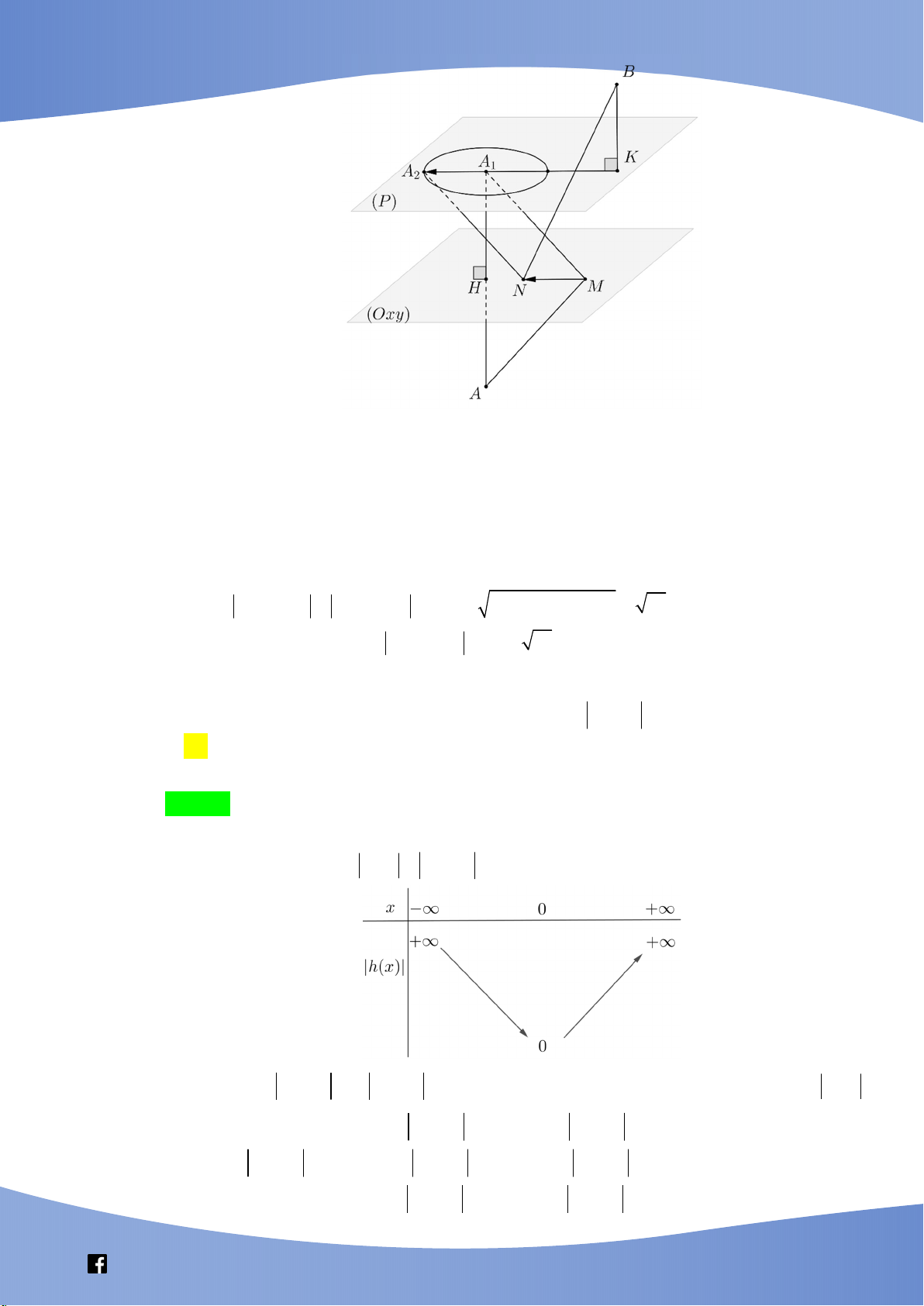
Câu 50: Trong không gian Oxyz cho hai điểm A(–2;1; –3) và B(1; –3;2). Xét hai điểm M, N thay đổi thuộc
mặt phẳng Oxy sao cho MN = 3. Giá trị lớn nhất của AM BN bằng A. 65 B. 29 C. 26 D. 91
Bài này hay và khó, khai thác các phép biến hình cơ bản như đối xứng, tịnh tiến và bất đẳng thức
tam giác. Nhưng là ý tưởng chỉ dùng được một lần. Sẽ tốt hơn nếu bài này làm tự luận.
https://www.facebook.com/groups/toanvd.vdc Trang 6 Tập san
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Số 02 8 - 2021
Trao đổi kinh nghiệm dạy học theo định
hướng tiếp cận năng lực người học
Bàn về một cách tiếp cận khác cho bài toán tính góc giữa
đường thẳng và mặt phẳng Ths. HOÀNG MINH QUÂN
GV Trường THPT chuyên Nguyễn Huệ, Hà Nội
Trong chương trình toán THPT, các bài toán về góc giữa đường thẳng và mặt phẳng tuy
không mới. Song, nó vẫn mang tính thời sự trong các bài kiểm tra định kì, các kì thi học sinh
giỏi, kì thi tốt nghiệp trung học phổ thông hằng năm. Bài viết sau đây khai thác một hướng tiếp
cận khác cho bài toán tính góc giữa đường thẳng với mặt phẳng
1. Kiến thức cơ bản
1.1. Định nghĩa
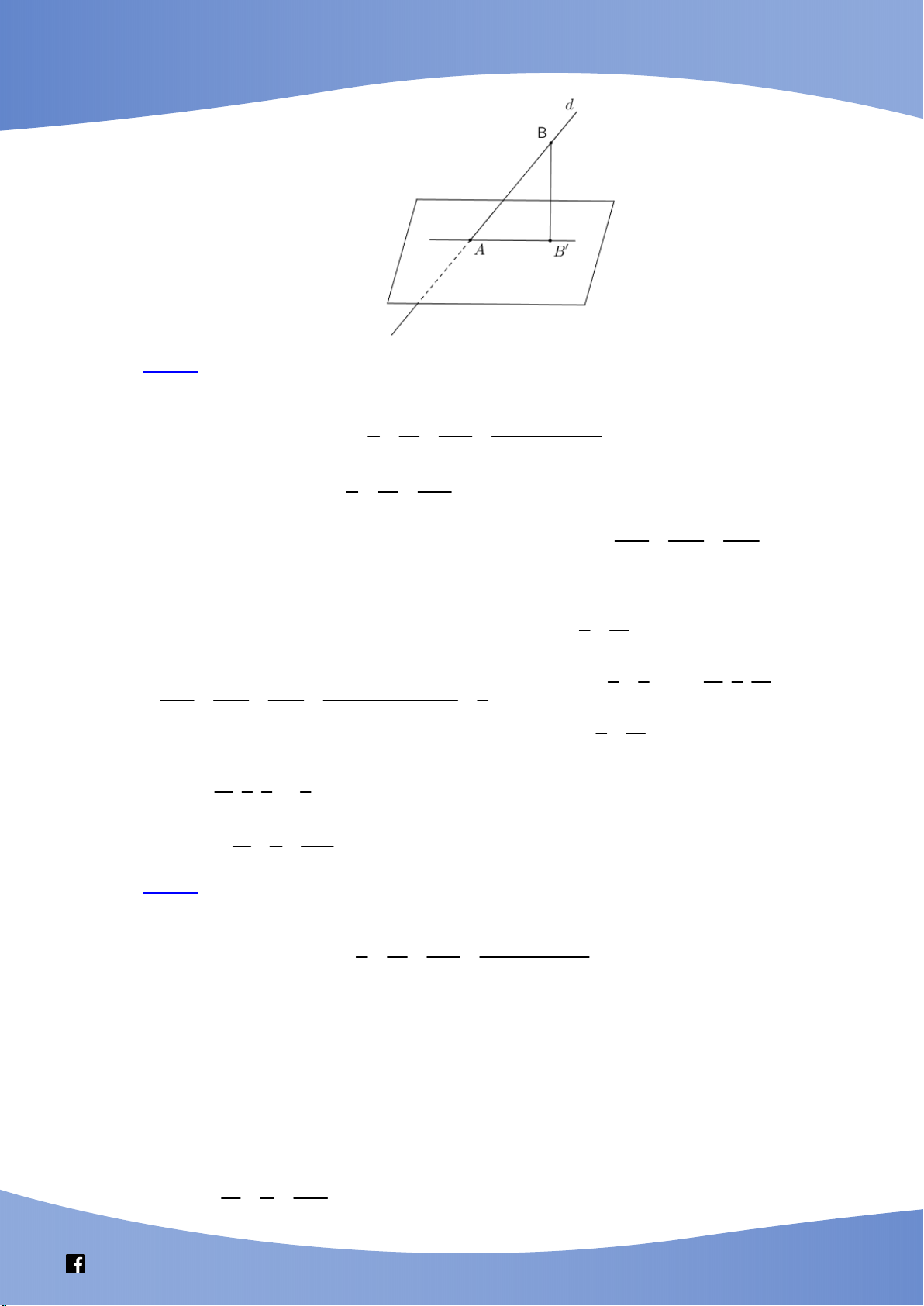
Cho đường thẳng a và mặt phẳng   . Góc giữa đường thẳng a và hình chiếu a của nó
trên mặt phẳng   được gọi là góc giữa đường thẳng a và mặt phẳng   .
1.2. Các xác định góc giữa đường thẳng a và mặt phẳng   Cách 1:
Bước 1. Tìm O a    . a A
Bước 2. Lấy Aa và dựng AH    tại H .
Khi đó a    a a  , ,  AOH . a'   O H
Bước 3. Tính số đo của góc AOH
Chú ý: 0   ,
a    90
Cách 2: Tính gián tiếp theo một trong hai hướng sau:
Hướng 1: Chọn một đường thẳng d // a mà góc giữa d và   có thể tính được.
Từ đó ta có: a,      d,   
Hướng 2: Chọn một mặt phẳng   //   mà góc giữa a và   có thể tính được.
Từ đó ta có: a,      a,   
https://www.facebook.com/groups/toanvd.vdc Trang 7
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8-2021
Tuy nhiên việc xác định hình chiếu của một điểm lên mặt phẳng không phải lúc nào cũng
thuận lợi. Chính vì vậy, việc đưa ra một cách tiếp cận khác là sử dụng khoảng cách để tính góc giữa
đường thẳng với mặt phẳng nhằm khắc phục khó khăn đó.
1.3. Định hướng tiếp cận
Cho đường thẳng a và mặt phẳng   . Để tính góc  giữa đường thẳng a và mặt phẳng
  , ta tiếp cận thông qua ý tưởng đơn giản khác như sau : a A
Bước 1: Tìm O a    . d  , A   a'
Bước 2: Tính sin   O H OA
Cách tiếp cận này thích hợp cho học sinh nắm chắc việc tính khoảng cách từ một điểm đến một mặt phẳng.
Sau đây chúng tôi đưa ra một số ví dụ minh hoạ với lời giải theo hướng tiếp cận sử dụng
khoảng cách để tính góc giữa đường thẳng với mặt phẳng 2. Ví dụ minh họa
2.1. Áp dụng cho các bài toán khối chóp. Câu 1:
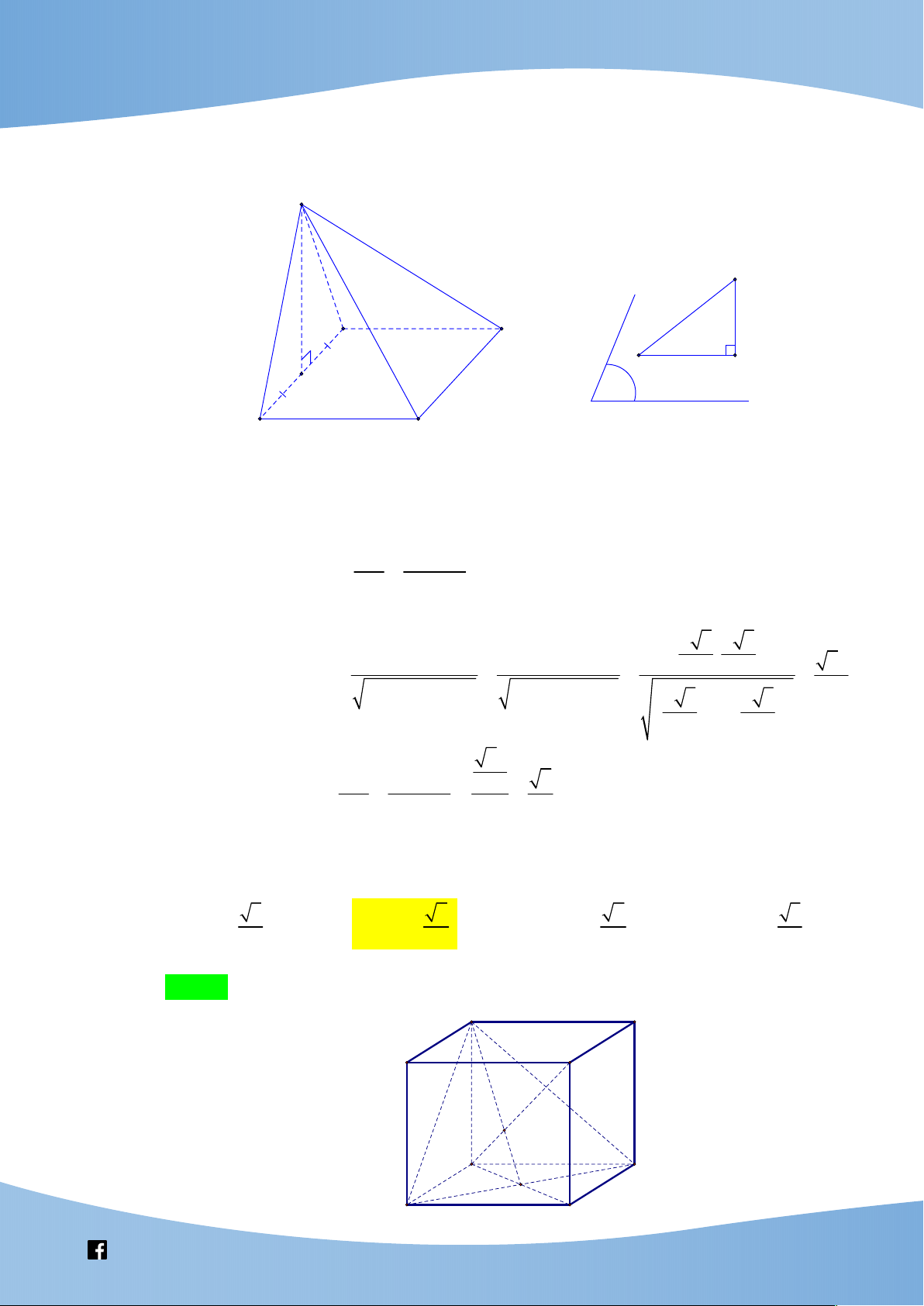
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA   ABCD . Gọi G là trọng
tâm tam giác ACD , I là trung điểm của SB . Biết độ dài các đoạn SA a , AB a 3 , 3a AD
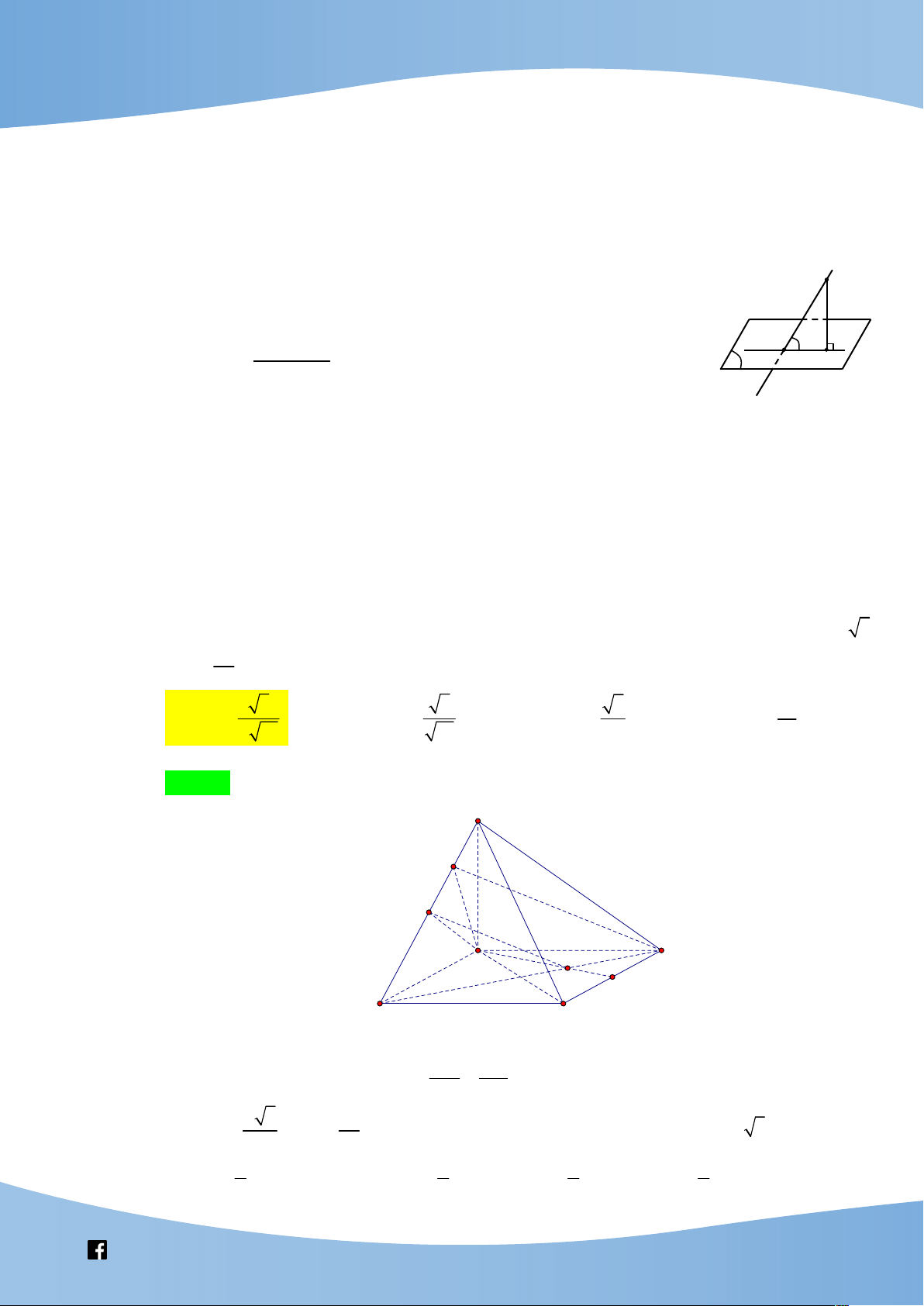
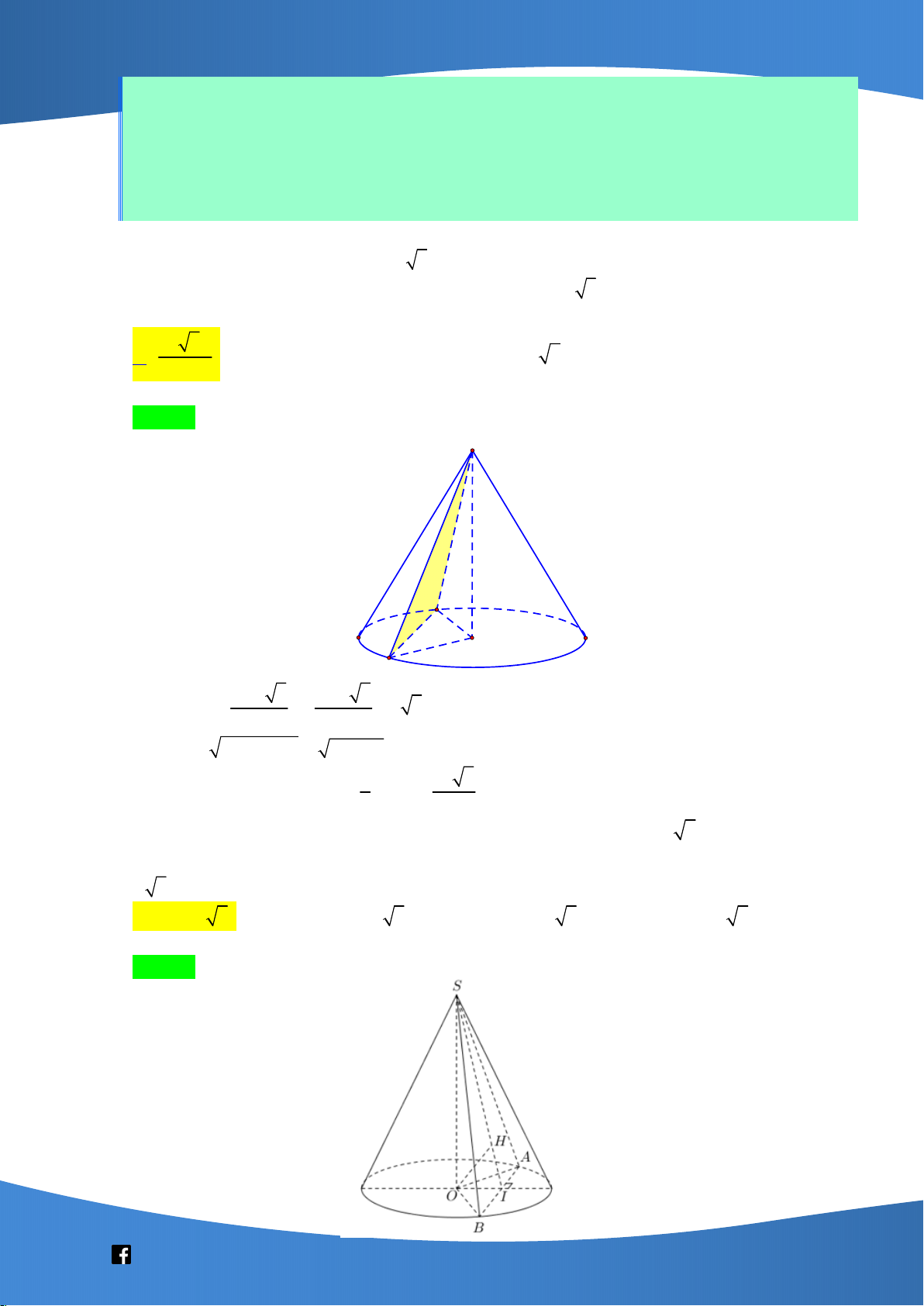
. Góc giữa đường thẳng IG và mặt phẳng SCD bằng 2 3 3 3 3 A. arcsin . B. arcsin . C. arcsin . D. arcsin . 4 13 13 16 16 Lời giải Chọn A S H I A D G B C
Có SB  2a nên tam giác SAI đều cạnh a . BI BG
Gọi H là trung điểm của SI thì 
nên IG // HD , hay IG,SCD  HD,SCD BH BD a 3 3a Có AH  , AD
và tam giác AHD vuông tại A , suy ra HD a 3 2 2 1 1 1 1 Vì HS
BS nên d H ,SCD  d B,SCD  d  ,
A SCD  d 4 4 4 4
https://www.facebook.com/groups/toanvd.vdc Trang 8
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8-2021 1 1 1 1 4 13 3a a Mà       d
d H SCD 3 ,  2 2 2 2 2 2 d SA AD a 9a 9a 13 4 13
d H,SCD 3a 3
Suy ra sin  HD,SCD    . HD 4 13.a 3 4 13 Câu 2:
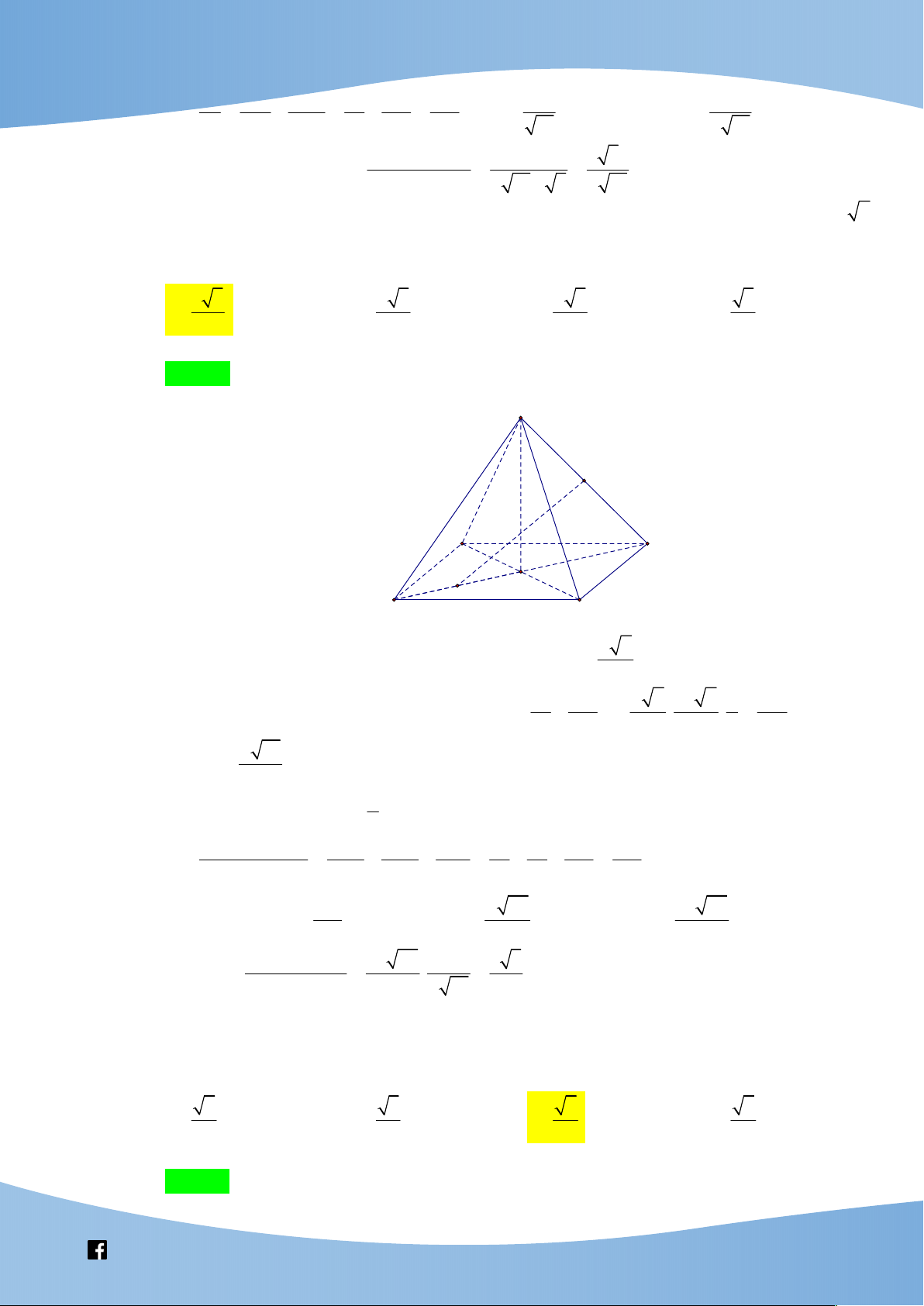
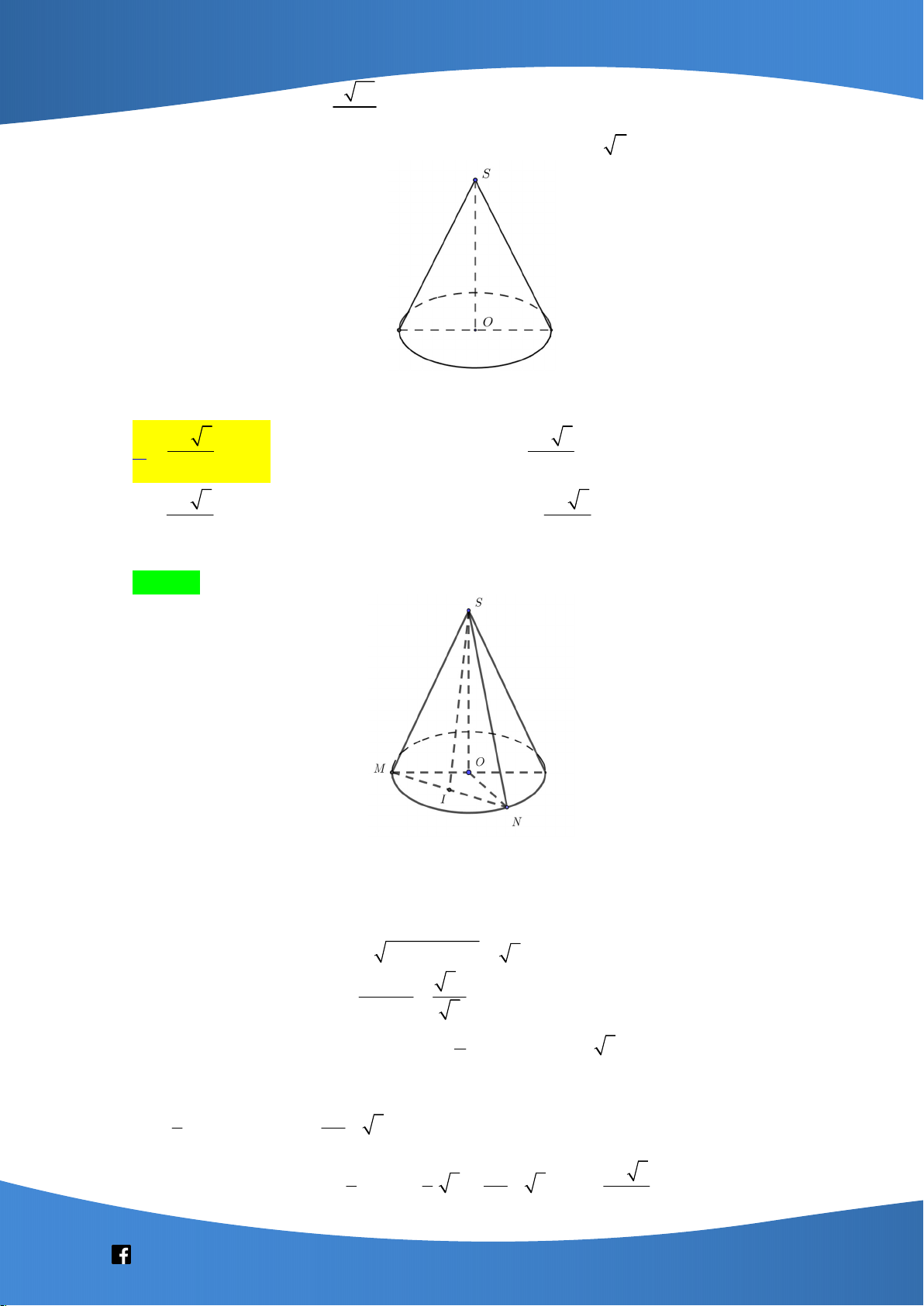
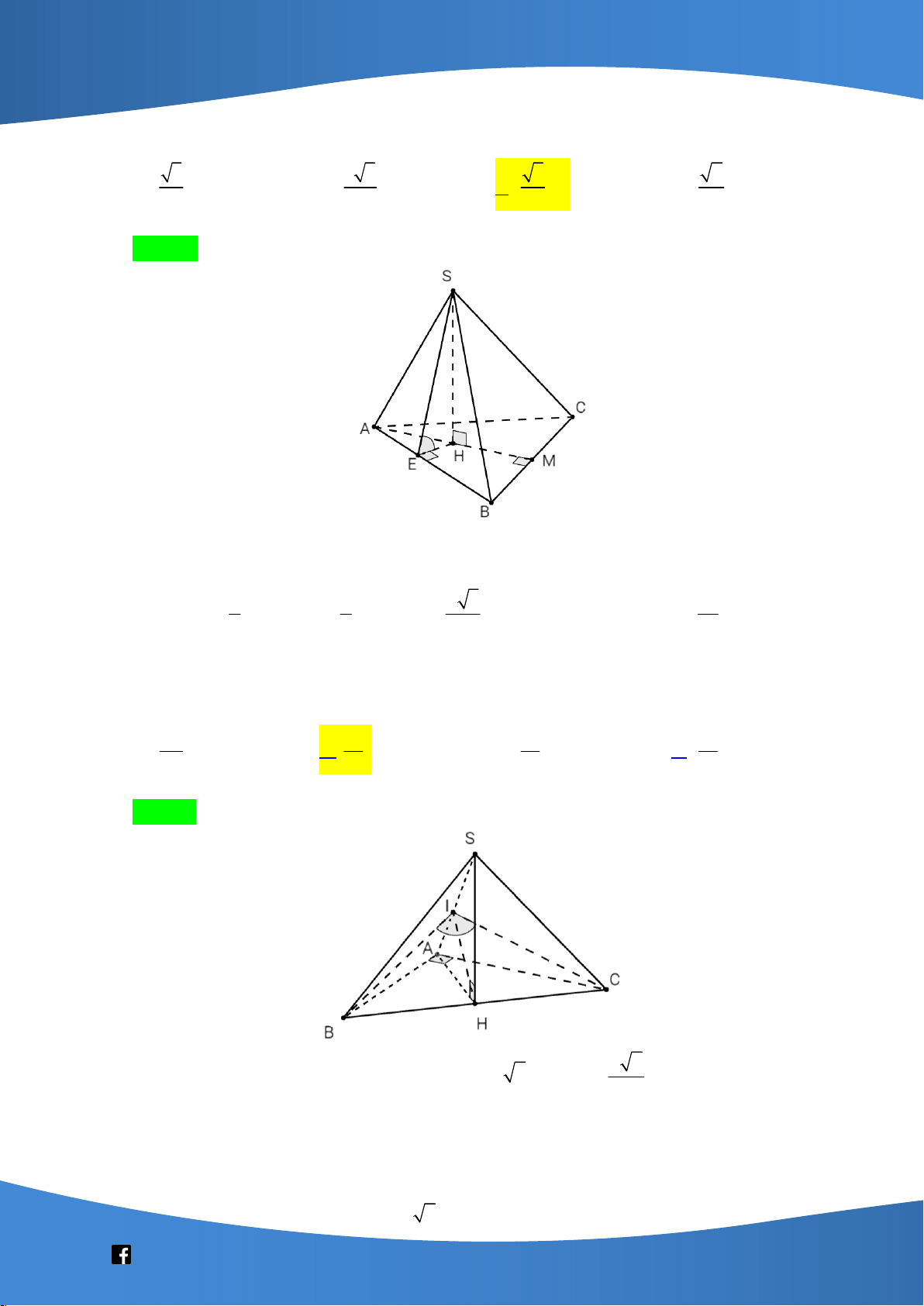
Cho hình chóp đều S.ABCD có đáy ABCD là hình vuông tâm O cạnh a và SA a 2 .
Gọi M , N lần lượt là trung điểm của SD và BO . Gọi là góc giữa đường thẳng MN
và mặt phẳng SCD thì giá trị sin bằng 3 3 2 3 4 3 3 A. . B. . C. . D. . 7 7 7 7 Lời giải Chọn A S M A D N O B C a 6 Ta có: S
BD là tam giác đều nên 
SDB  60 và SO  2 2 2 2 a 9a a 2 3a 2 1 7a Suy ra 2 2 2
MN MD ND  2M . D ND cos 60    2. . .  2 8 2 4 2 8 a 14  MN  4 3
Mặt khác d N,SCD  d O,SCD 2 1 1 1 1 2 2 2 14 Mà        2
d O,SCD 2 2 2 2 2 2 2 OC OD OS a a 3a 3a 2 3a a 42 3a 42 2
d O,SCD 
d O,SCD 
d N,SCD  14 14 28
d N,SCD 3a 42 4 3 3  sin   .  . MN 28 a 14 7 Câu 3:
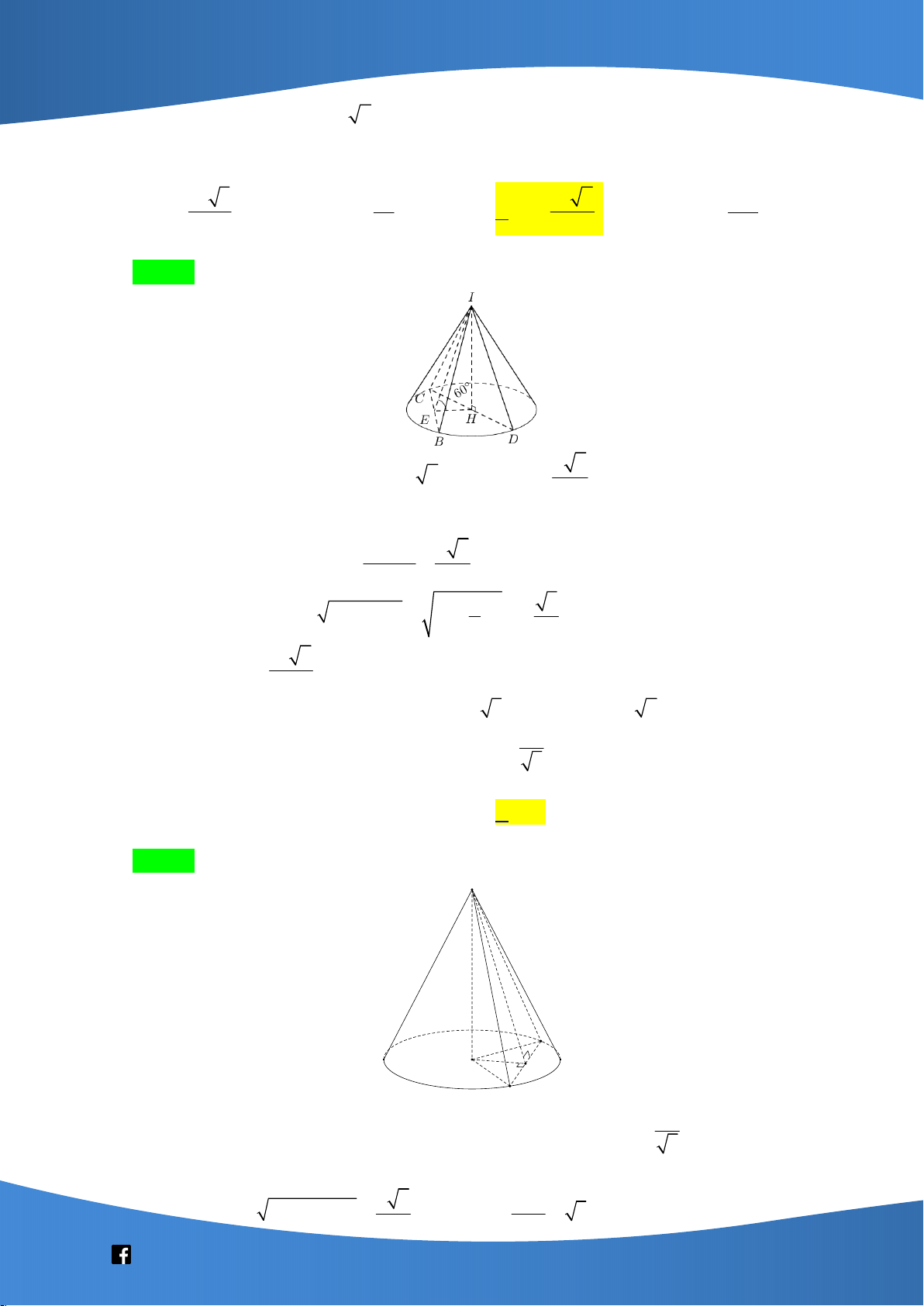
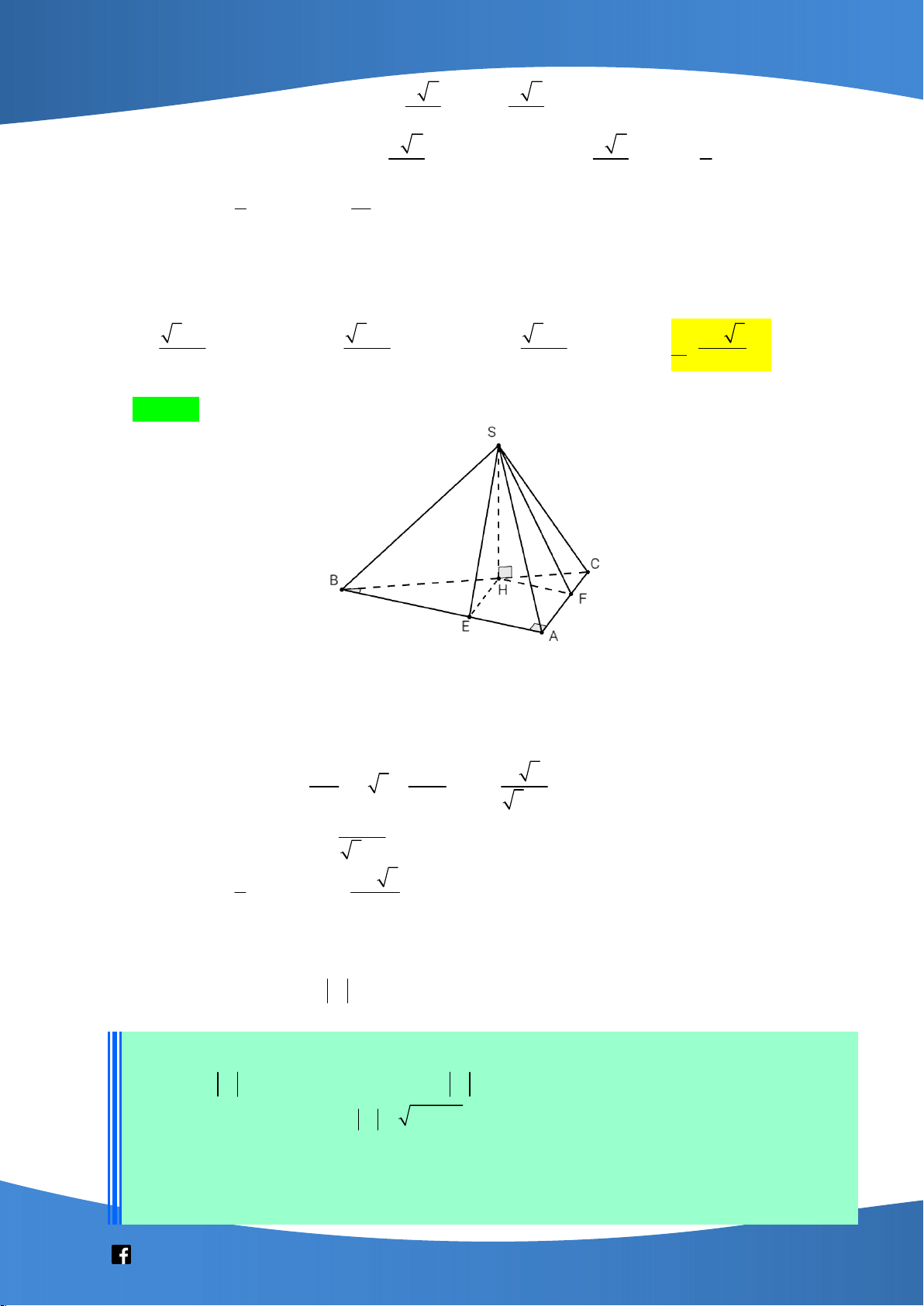
Cho hình chóp S.ABCD có đáy ABCD là hình thoi, 
BAC  60 , SA a . Tam giác SAB
là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng  ABCD . Gọi  là
góc tạo bởi đường thẳng SB và mặt phẳng SCD . Khi đó sin bằng 2 3 6 6 A. . B. . C. . D. . 2 2 4 3 Lời giải Chọn C
Gọi M là trung điểm của AB . Vì tam giác SAB là tam giác đều nên SM AB .
https://www.facebook.com/groups/toanvd.vdc Trang 9
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8-2021
SAB   ABCD  Ta có: 
SAB   ABCD  AB SM   ABCD .
SM AB, SM  SAB  S B B C d(B,(SCD)) S H M SCD A D
Gọi H là hình chiếu vuông góc của B lên mặt phẳng SCD . Suy ra BH  SCD .
Suy ra HS là hình chiếu vuông góc của BS lên mặt phẳng SCD , do đó:
SB SCD   SB SH    , ,  BSH . d BHB, SCD  Ta có:    sin  sin BSH   . SB SB
Do BM // SCDa 3 a 3 . SM .d SM .dM ,CD B,CD 6 2 2 add    
B,SCD
M ,SCD 2 2 2 2 2 2 4 SM d SM dM ,CD B,CD  a 3   a 3       2 2     6a d BHB; SCD  6 Vậy    sin  sin BSH   4   . SB SB a 4
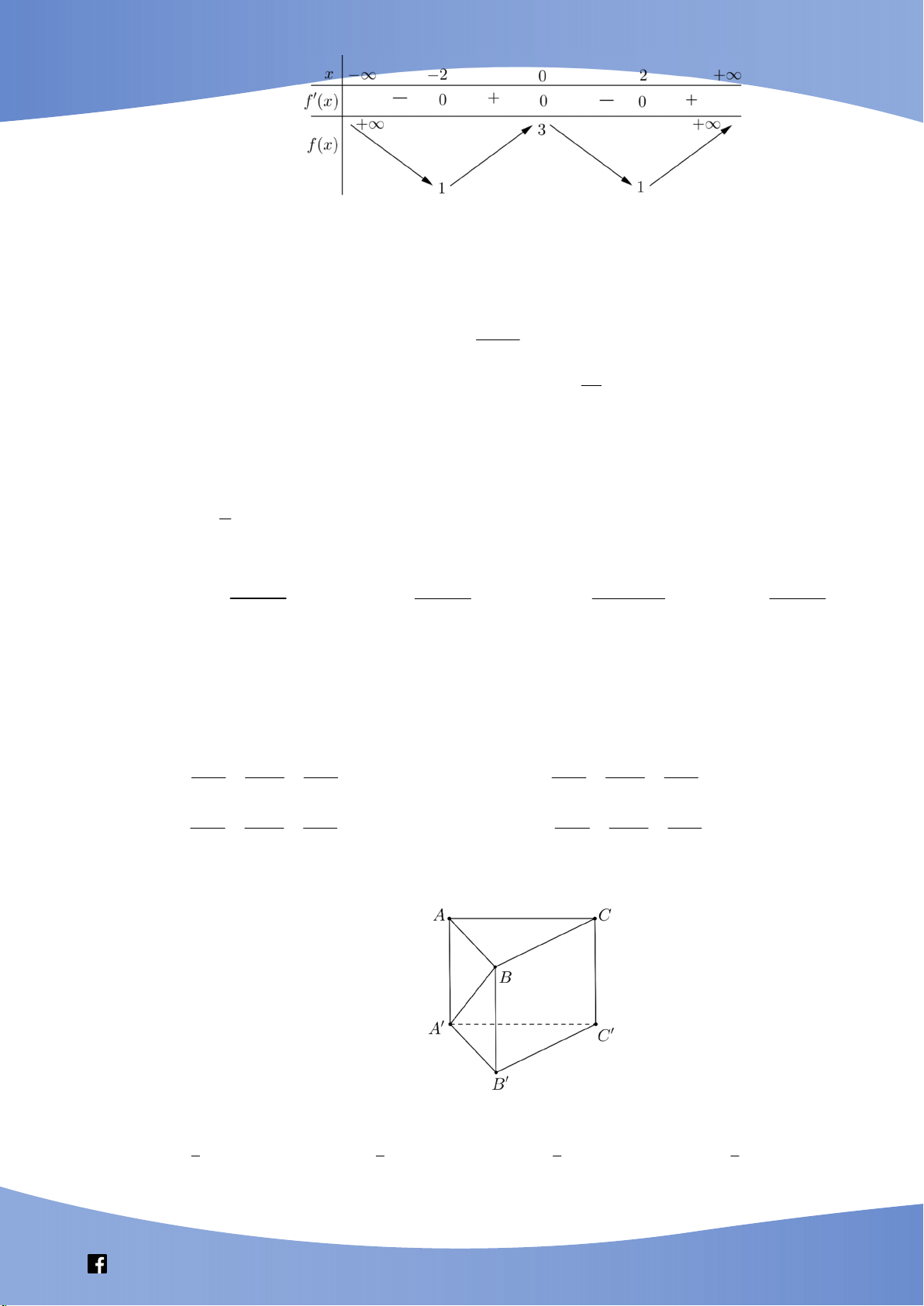
2.2. Áp dụng cho các bài toán khối lăng trụ. Câu 4:
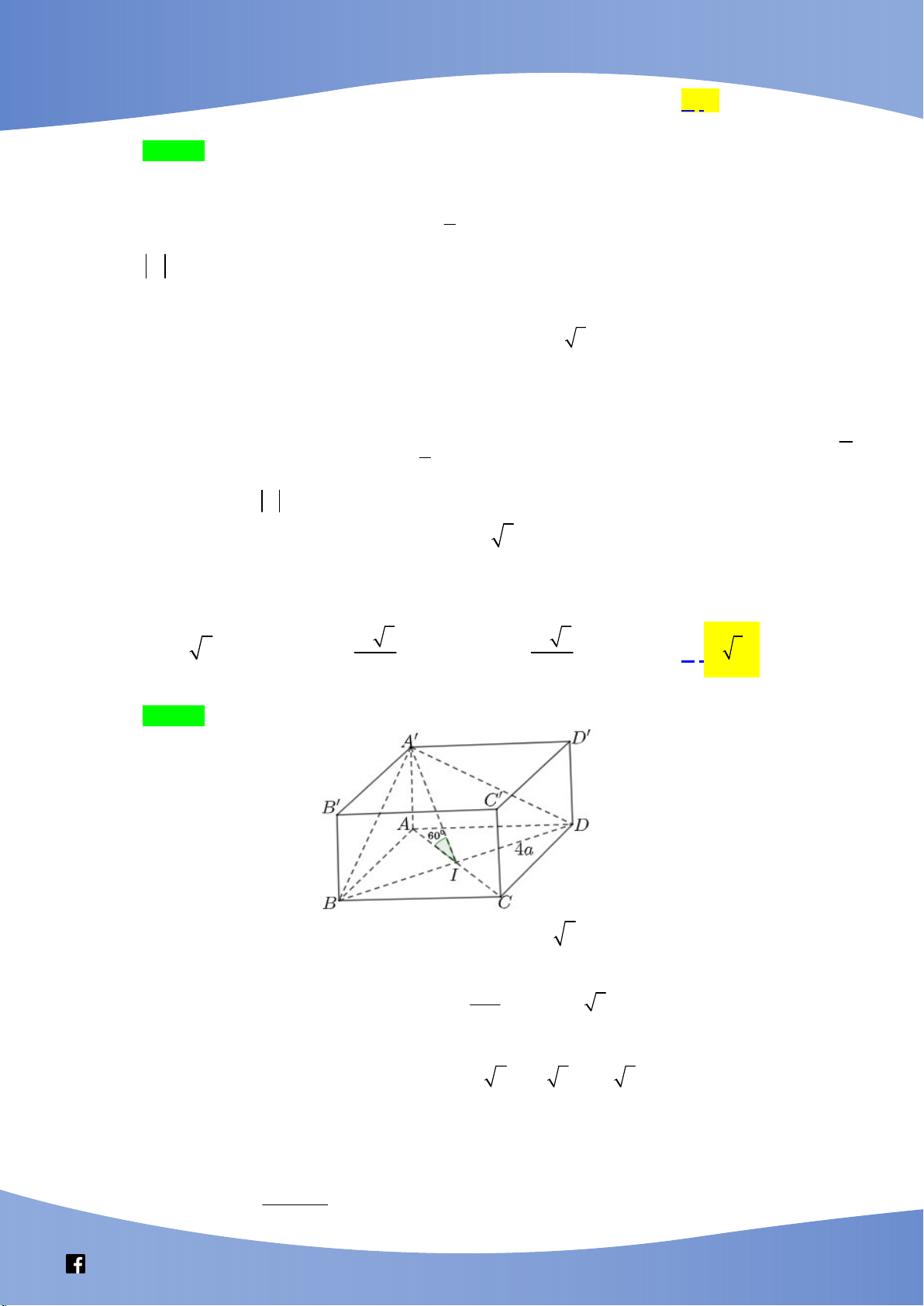
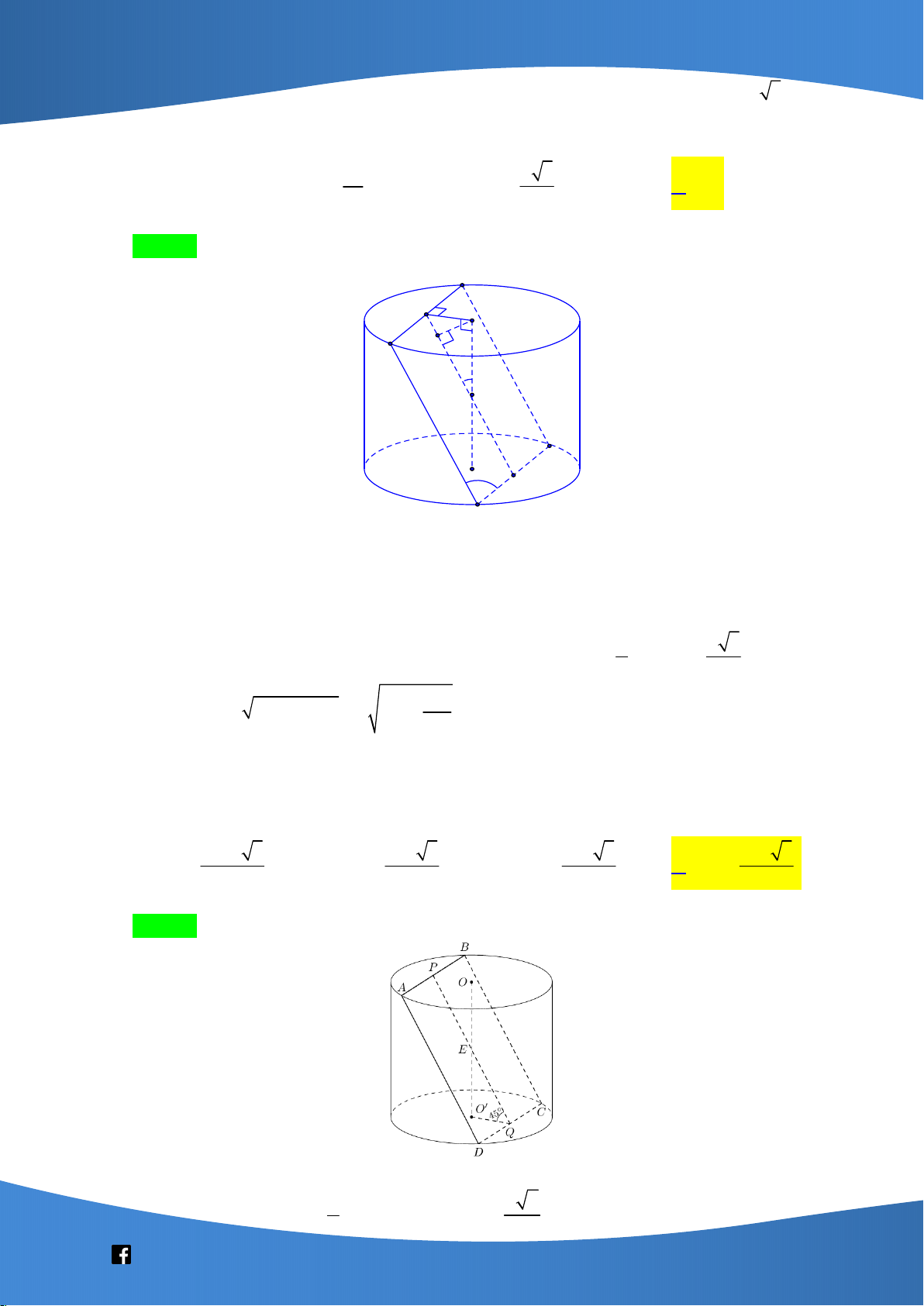
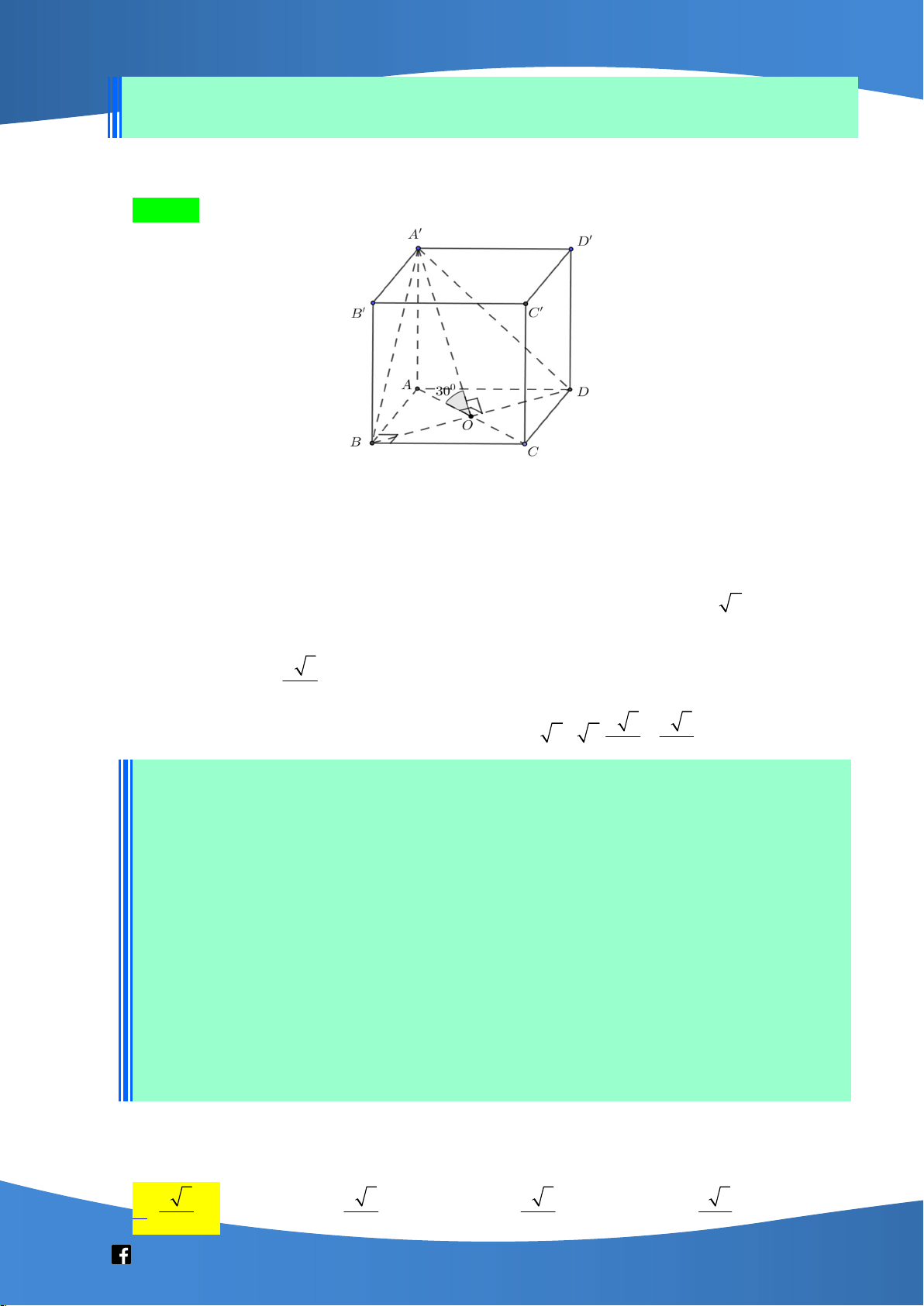
Cho hình lập phương ABC . D A BCD
  có cạnh bằng a . Góc giữa đường thẳng AD và
mặt phẳng  ABD bằng 5 6 2 3 A. arcsin . B. arcsin . C. arcsin . D. arcsin . 3 3 3 3 Lời giải Chọn B A' D' B' C' I D A O B C
https://www.facebook.com/groups/toanvd.vdc Trang 10
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8-2021
+ Do AD / /BC nên góc giữa đường thẳng AD và mặt phẳng  A' BD bằng góc giữa
đường thẳng BC ' và mặt phẳng  A' BD . 1 1 1 1 3
+ Do AA' BD là tứ diện vuông nên     2 d  ,
A A' BD 2 2 2 2 AA' AB AD a   a d ,
A ABD  . 3
+ Gọi  là góc giữa đường thẳng BC ' và mặt phẳng  ABD . 2a
d C , ABD 2d  ,
A ABD 3 6 Ta có sin     . BCBCa 2 3 Câu 5:
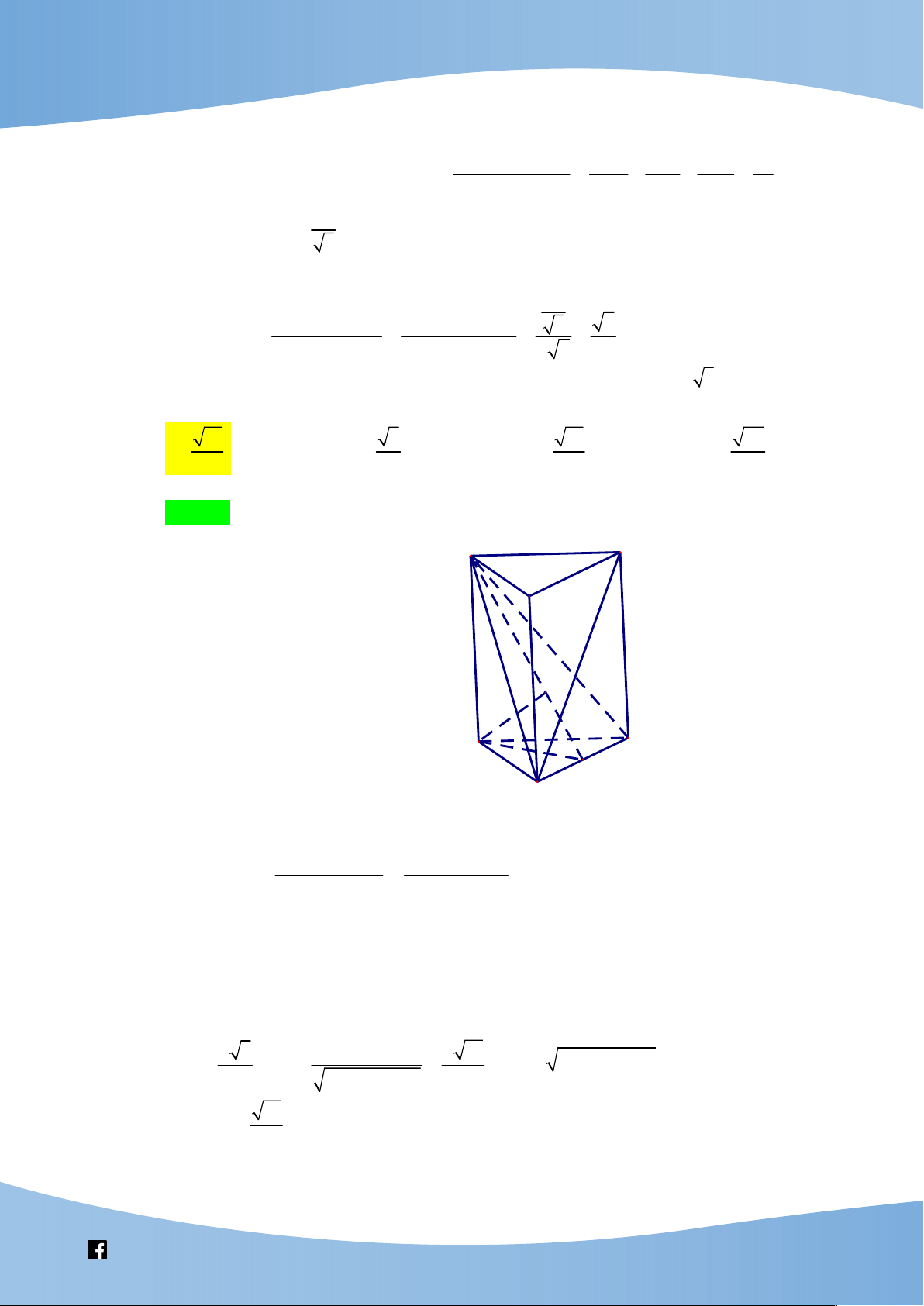
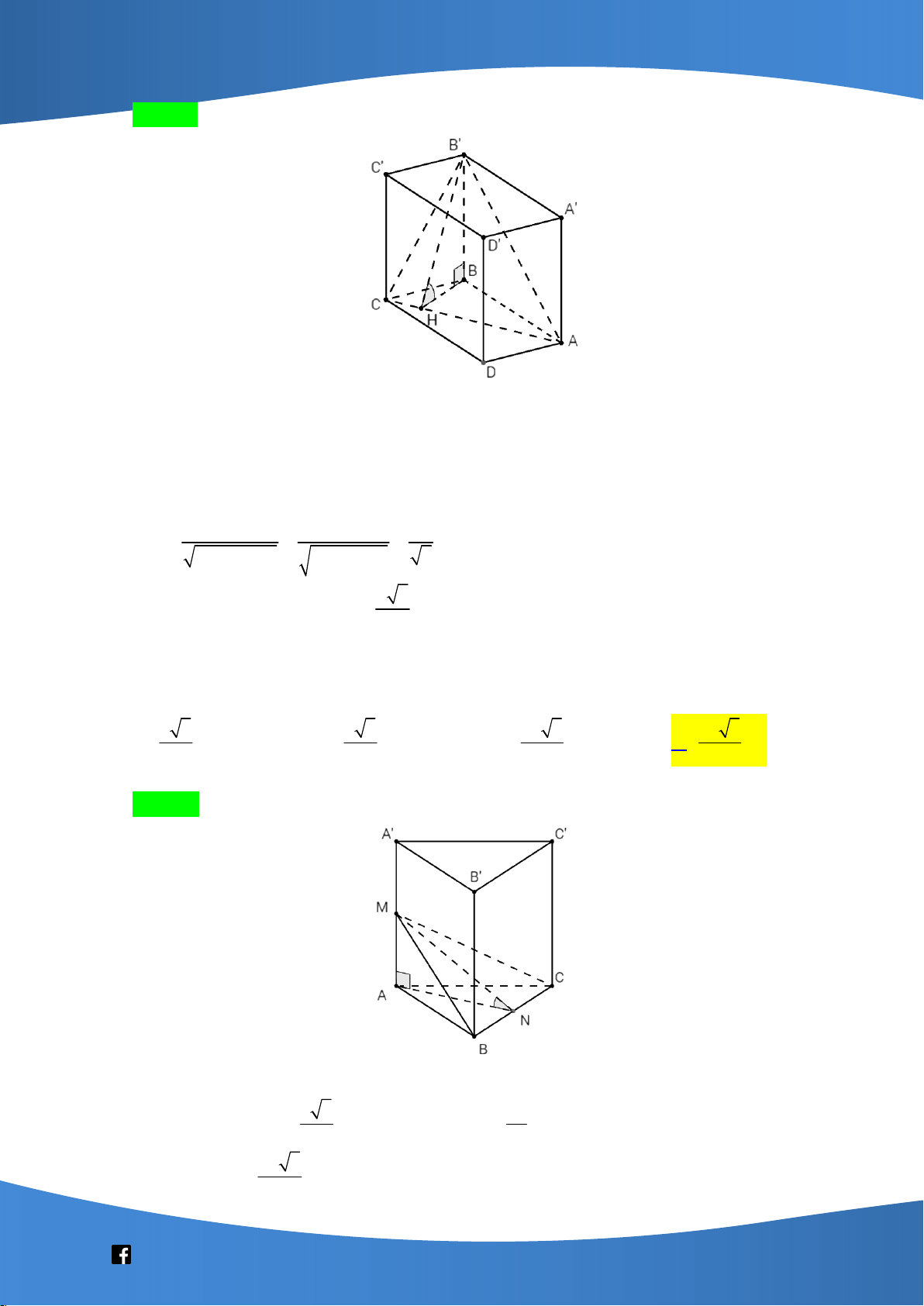
Cho hình lăng trụ đều AB . C A BC
  có cạnh đáy bằng a , AA  a 3 . Giá trị sin của góc
giữa đường thẳng BC và mặt phẳng  ABC  bằng 15 5 15 65 A. . B. . C. . D. . 10 10 5 10 Lời giải Chọn A A' C' B' H A C M B
Gọi  là góc giữa đường thẳng BC và mặt phẳng  ABC  .
d C , ABC  d  ,
A ABC  Ta có: sin  
(vì AC   ABC   O với O là trung điểm C BC BAC ).
Gọi M là trung điểm của BC , H là hình chiếu của A lên AM .
AM BC  BC  AAM  hay BC AH . AA  BC
Mặt khác AH AM nên AH   ABC  hay d  ;
A ABC   AH . a 3 AA .AM a 15 AM  ; AH   ; 2 2 C B
  BB  B C    2a . 2 2 2 5 AA  AM 15  sin  . 10 Câu 6:
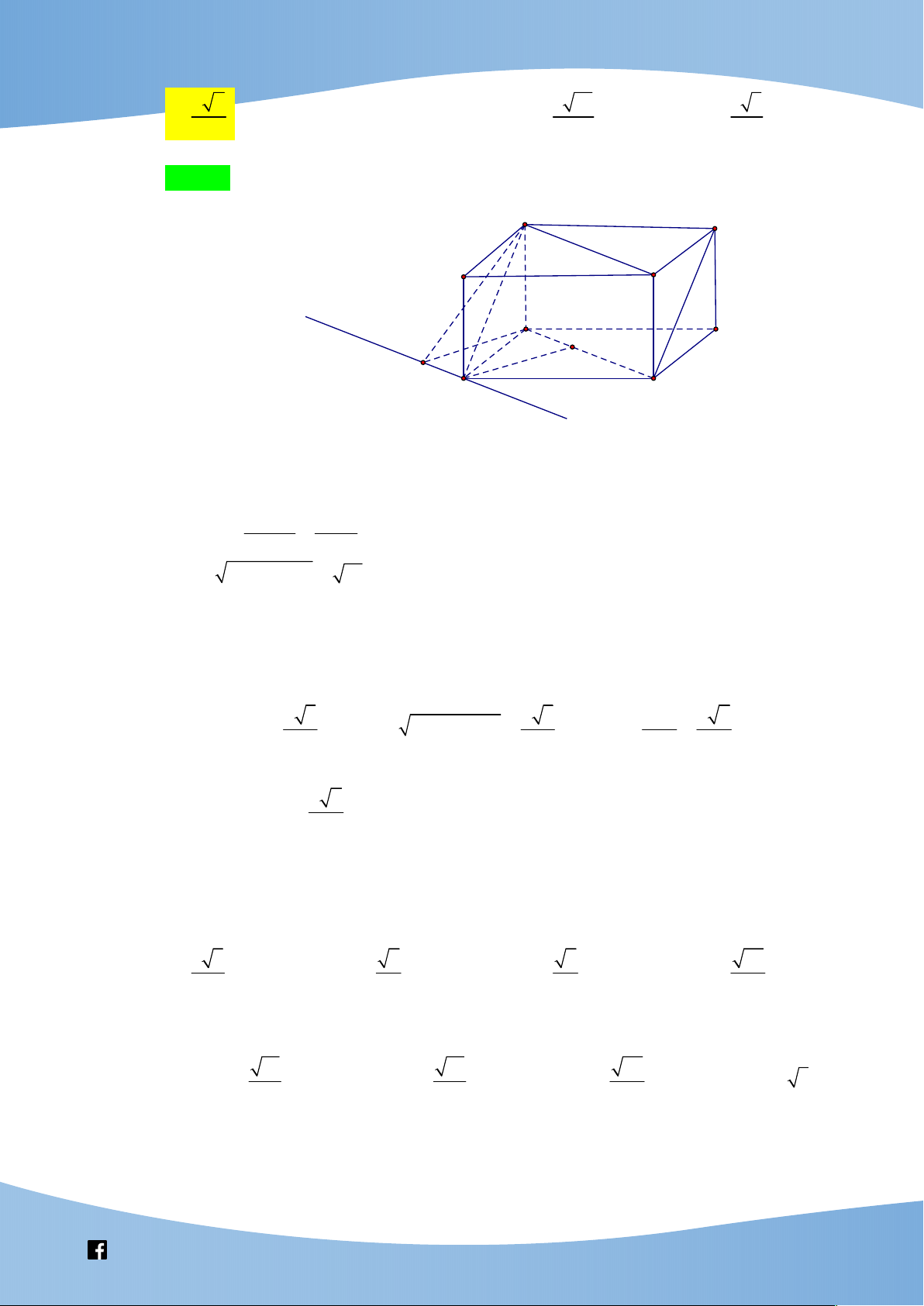
Cho hình hộp chữ nhật ABC . D A BCD
  có AB  1, AD  2, AA  3 .   là mặt phẳng di
động đi qua B và song song với A C
  . Gọi  là góc giữa   với đường thẳng CD .
Giá trị lớn nhất của sin bằng
https://www.facebook.com/groups/toanvd.vdc Trang 11
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8-2021 7 2 3 10 3 5 A. . B. 1 . C. . D. . 10 10 7 Lời giải Chọn A A' D' B' C' d A D K H B C
Ta có: CD // BA  CD ,      BA,   . Do   // A C
  nên   chứa đường thẳng d qua B và song song với A C   . dd A;   A;d   sin   . A BA B  2 2 AB
AA  AB  10 . Dựng A H
d tại H AH d .  A;d   d AA Ta có 
d   AHA  AH d .
d AH
Kẻ BK AC tại K 2 5 7 5 AH 7 2
AH BK  2 2  AH AH AA   sin   . 5 5 AB 10
Dấu “ =” xảy ra khi    AH . 7 2 Vậy max sin   . 10
2.3. Bài tập tự luyện Câu 1:
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB  2a, BC  . a Cạnh
bên SD a và SD vuông góc với mặt phẳng đáy. Sin của góc tạo bởi đường
thẳng SB và mặt phẳng SAC  bằng 5 3 6 6 30 A. . B. . C. . D. . 9 3 9 15 Câu 2:
Cho hình chóp tứ giác đều S.ABCD có SA AB a . Gọi M là trung điểm của cạnh BC
. Tang góc tạo bởi đường thẳng DM với mặt phẳng SAB bằng? 13 15 26 A. tan  . B. tan  . C. tan  . D. tan  3 . 13 5 13 Câu 3:
Cho hình chóp tứ giác đều .
S ABCD có cạnh đáy bằng a , tâm O . Gọi M và N lần lượt
là trung điểm của SA và BC . Biết rằng góc giữa MN và  ABCD bằng 60 , cosin góc
giữa MN và mặt phẳng SBD bằng
https://www.facebook.com/groups/toanvd.vdc Trang 12
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8-2021 41 5 2 5 2 41 A. . B. . C. . D. . 41 5 5 41 Câu 4:
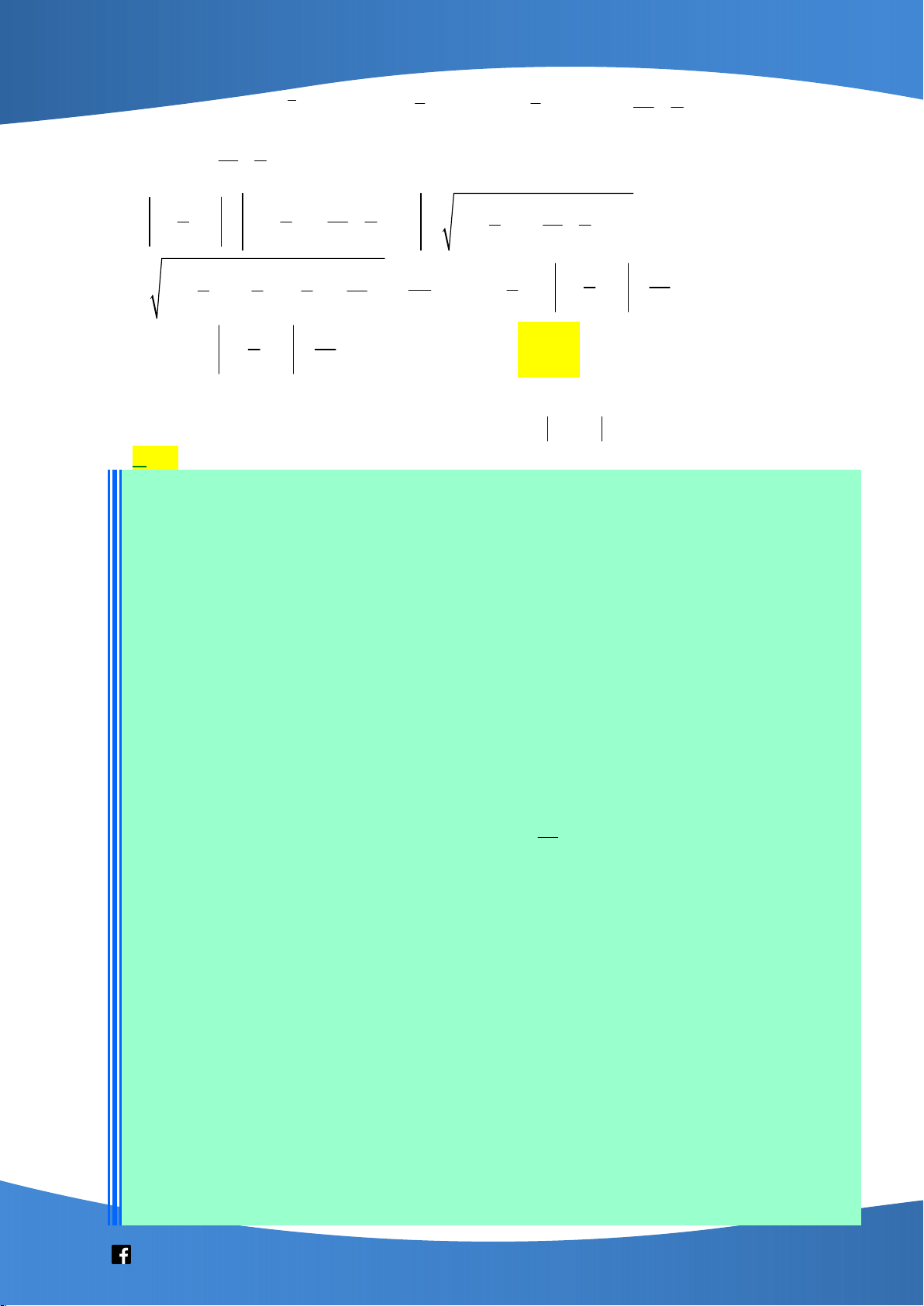
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a . Gọi O là tâm của đáy, E là
trung điểm cạnh AD . Gọi  là góc giữa đường thẳng CD và mặt phẳng SBE . Biết a SO  thì sin bằng 2 1 3 2 1 A. . B. . C. . D. . 2 6 2 3 6 Câu 5:
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, AB  2a , BC a , 
ABC  120 . Cạnh bên SD a 3 và SD vuông góc với mặt phẳng đáy. Giá trị sin của
góc tạo bởi SB và mặt phẳng SAC  bằng 3 3 3 1 A. . B. . C. . D. . 7 4 4 4 Câu 6:
Cho hình hộp chữ nhật ABCDA BCD
  có đáy ABCD là hình vuông. Giá trị lớn nhất của
góc tạo bởi BD với mặt phẳng  BDC bằng 1 1 1 1 A. arcsin . B. arcsin . C. arcsin . D. arcsin . 3 3 2 3 3 2 Câu 7:
Cho hình hộp ABCD.AB CD
  có đáy ABCD là hình chữ nhật cạnh AB  ;
a AD  2a ; I
là trọng tâm tam giác  AC D
  . Gọi  là góc giữa đường thẳng ID và mặt phẳng  ICB , biết A B
  a 3 . Giá trị của sin bằng 9 6 6 23 A. . B. . C. . D. . 253 11 2 253 11 Câu 8:
Cho hình lăng trụ đứng AB .
C A' B 'C ' có đáy ABC là tam giác cân tại C , AB  2a và  0
ACB  120 . Biết AA'  a . Gọi I là trung điểm AB thì sin của góc giữa đường thẳng
IA ' và mặt phẳng C ' AB bằng 2 2 2 5 2 15 A. B. C. D. 4 2 3 3 Câu 9:
Cho lăng trụ tam giác đều AB . C A BC
  , gọi I là trung điểm A' B' . Gọi  là góc tạo bởi
AC ' và  BIC ' . Biết AA'  a; AB  2a thì giá trị cos bằng 15 10 3 2 A. . B. . C. . D. 5 5 5 5
Câu 10: Cho lăng trụ tam giác ABC có 
AB a, BC  2a, ABC  60 . Hình chiếu vuông góc của
A ' lên mặt phẳng  ABC  trùng với trọng tâm G của tam giác ABC và góc giữa AA' tạo
với mặt phẳng  ABC  bằng 60. Sin của góc tạo bởi AA' và mặt phẳng  A ' BC  bằng 9 9 7 9 A. . B. . C. . D. . 5 41 4 51 4 51 7 41
https://www.facebook.com/groups/toanvd.vdc Trang 13
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Tập san Số 02
8 - 2021
Toàn cảnh đề thi tốt nghiệp THPT đợt 1 năm 2021
ĐỀ THI, ĐÁP ÁN VÀ LỜI GIẢI CHI TIẾT CÁC CÂU VD – VDC
TRONG ĐỀ THI TỐT NGHIỆP THPT ĐỢT 1 NĂM 2021
Kỳ thi tốt nghiệp THPT đợt 2 năm 2021 sẽ diễn ra vào hai ngày 6,7/8/2021,
để tạo điều kiện cho quý thầy cô cùng các em có tài liệu ôn tập trong thời gian gấp rút này
Nhóm Giáo viên Toán Việt Nam xin gửi tới quý thầy cô và các em Đề thi, đáp án và
lời giải chi tiết các câu VD – VDC của 4 mã đề thi gốc 101, 102, 103, 104 Đề thi tốt
nghiệp THPT đợt 1 Năm 2021
Hy vọng bài viết sẽ giúp quý thầy cô có thêm tài liệu tham khảo; các em học sinh
rèn luyện tốt kỹ năng thi trắc nghiệm môn Toán trong kỳ thi tốt nghiệp THPT đợt 2 năm 2021.
https://www.facebook.com/groups/toanvd.vdc Trang 14
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8-2021
ĐỀ THI TỐT NGHIỆP THPT ĐỢT 1 NĂM 2021
Bài thi môn: Toán
Thời gian: 90 phút (Không kể thời gian phát đề) Mã đề thi: 101
Đề thi gồm 06 trang Câu 1:
Tập nghiệm của bất phương trình 3x  2 là A.  ;  lo  ;  log 3 log 3;  3 g  2 .
B. log3 2;  . C.  2  . D.  2  . 4 4 4 Câu 2:
Nếu f x dx  3 
và g xdx  2  
thì  f x  g x d  x    bằng 1 1 1 A. 1  . B. 5 . C. 5. D. 1. Câu 3:
Trong không gian Oxyz, cho mặt cầu S  có tâm I 1; 4
 ;0 và bán kính bằng 3. Phương
trình của S  là: 2 2 2 2
A. x     y   2 1 4  z  9 .
B. x     y   2 1 4  z  9 . 2 2 2 2
C. x     y   2 1 4  z  3 .
D. x     y   2 1 4  z  3 . Câu 4:
Trong không gian Oxyz, cho đường thẳng d đi qua điểm M 3; 1
 ; 4 và có một vectơ 
chỉ phương u   2
 ; 4;5 . Phương trình của d là:
x  2  3t
x  3  2t
x  3  2t
x  3  2t    
A. y  4  t .
B. y  1 4t .
C. y  1 4t .
D. y  1 4t .
z  5  4t     z  4  5tz  4  5tz  4  5tCâu 5:
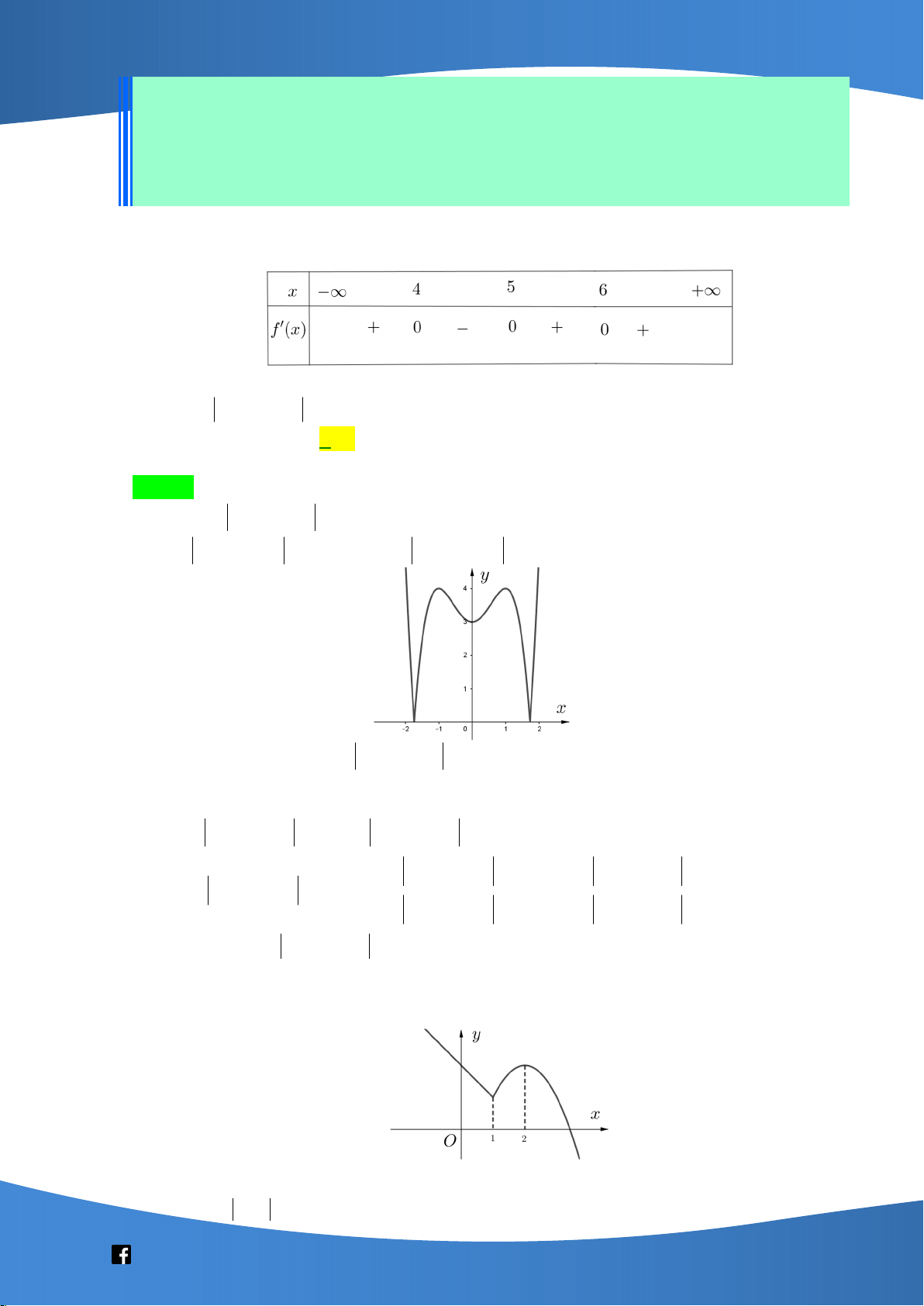
Cho hàm số y f x có bảng xét dấu đạo hàm như sau:
Số điểm cực trị của hàm số đã cho là A. 5. B. 3 . C. 2 . D. 4 . Câu 6:
Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình bên? A. 4 2 y  2
x  4x 1. B. 3
y  x  3x 1. C. 4 2
y  2x  4x 1. D. 3
y x 3x 1. Câu 7: Đồ thị của hàm số 4 2
y  x  4x  3 cắt trục tung tại điểm có tung độ bằng
https:/www.facebook.com/groups/toanvd. Trang 15
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8-2021 A. 0 . B. 3 . C. 1. D. 3  . Câu 8:
Với n là số nguyên dương bất kì, n  4, công thức nào dưới đây đúng? n  4 ! 4! n! n! 4   A. A  . B. 4 A  . C. 4 A  . D. 4 A  . n n! nn  4! n 4  ! n  4! nn  4! Câu 9:
Phần thực của số phức z  5  2i bằng A. 5 . B. 2 . C. 5  . D. 2 . 5
Câu 10: Trên khoảng 0;, đạo hàm của hàm số 2
y x là 7 2 3 2 3 5 3 5  A. 2 y  x . B. 2 y  x . C. 2 y  x . D. 2 y  x . 7 5 2 2
Câu 11: Cho hàm số f x 2
x  4 . Khẳng định nào dưới đây đúng?
A. f xdx  2x C  .
B. f x 2
dx x  4x C  . 3 x
C. f xdx   4x C  .
D. f x 3
dx x  4x C  . 3 
Câu 12: Trong không gian Oxyz, cho điểm A 2
 ;3;5 . Tọa độ vectơ OA là A.  2  ;3;5 . B. 2; 3  ;5 . C.  2  ; 3  ;5 . D. 2; 3  ; 5   .
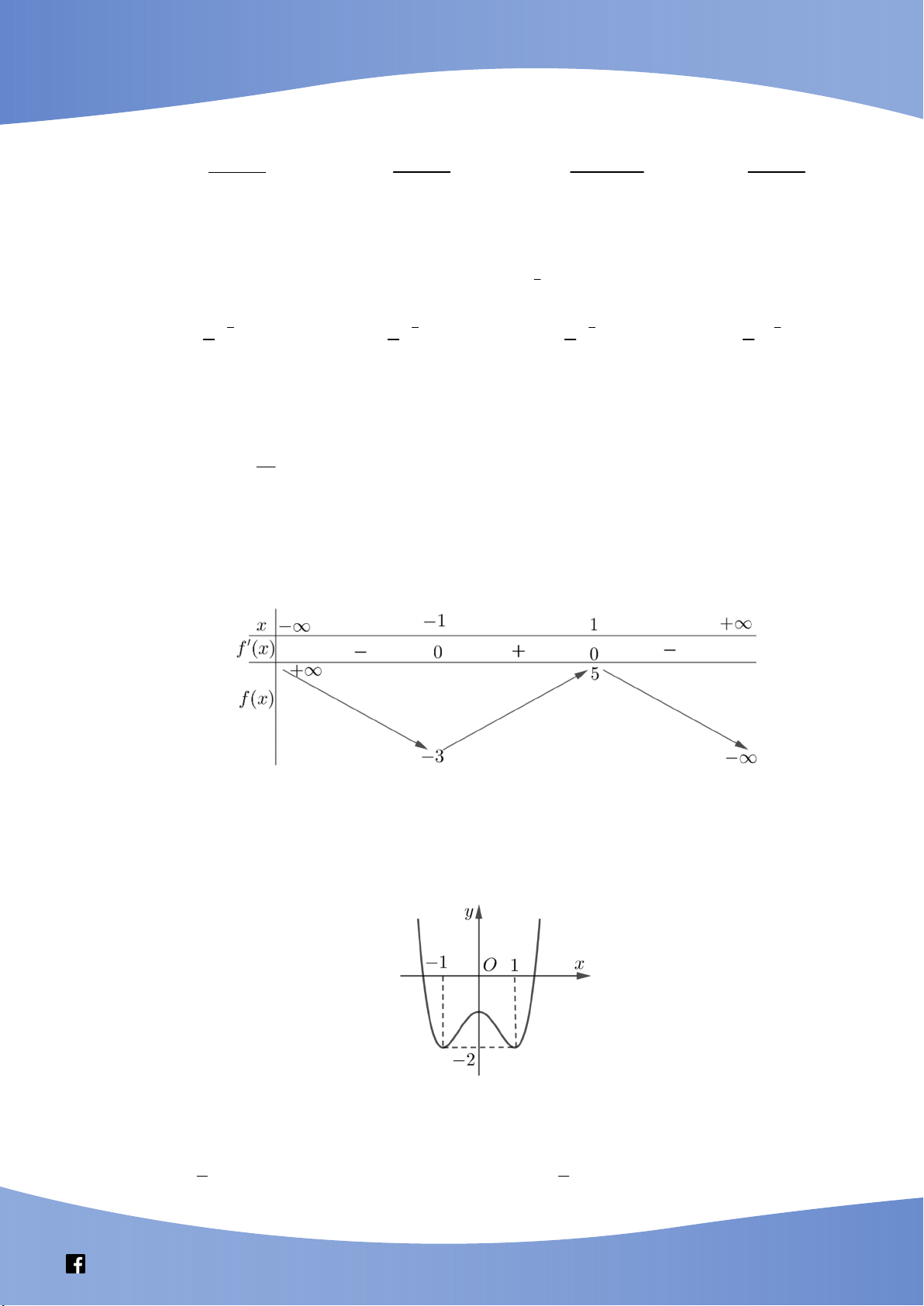
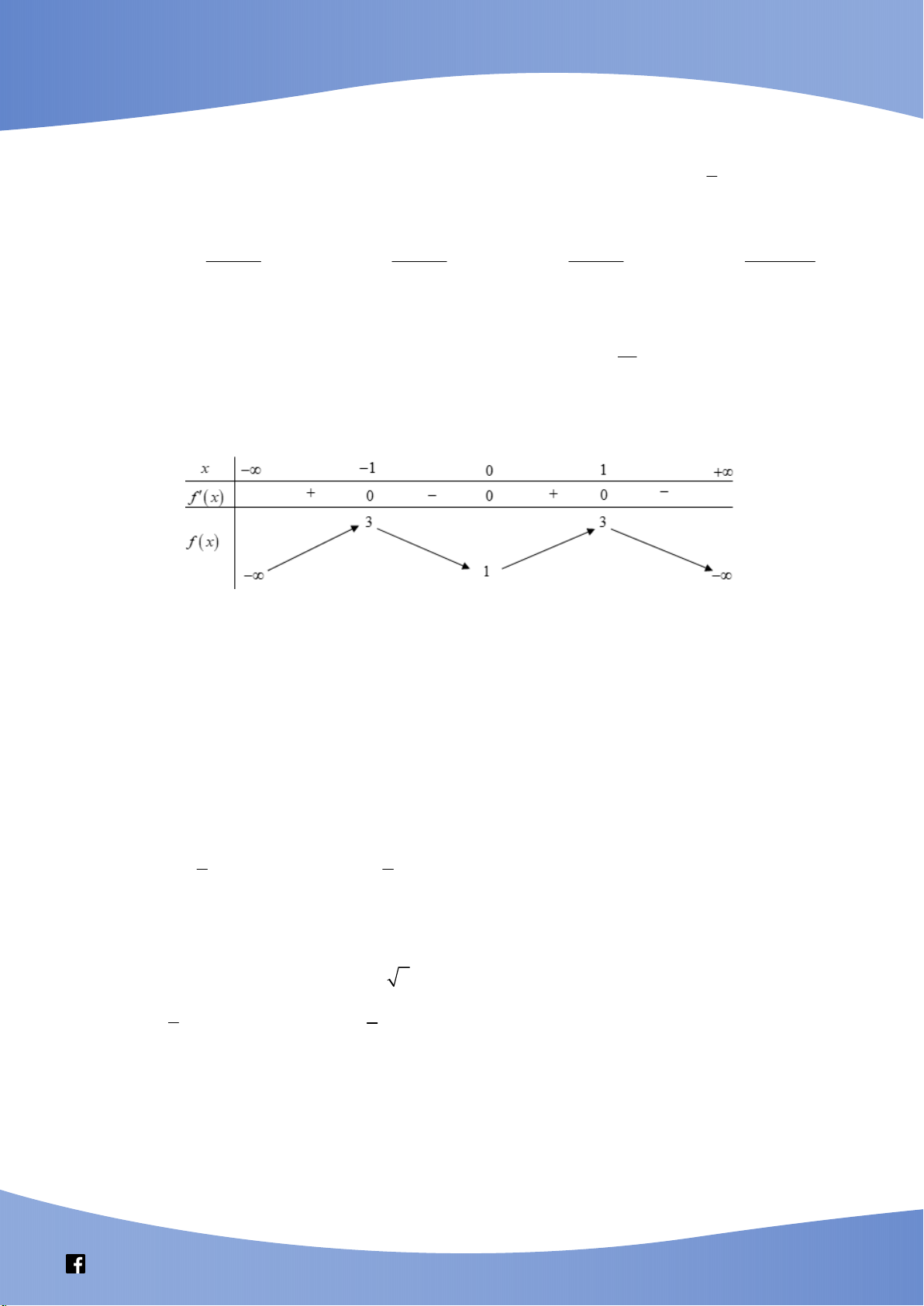
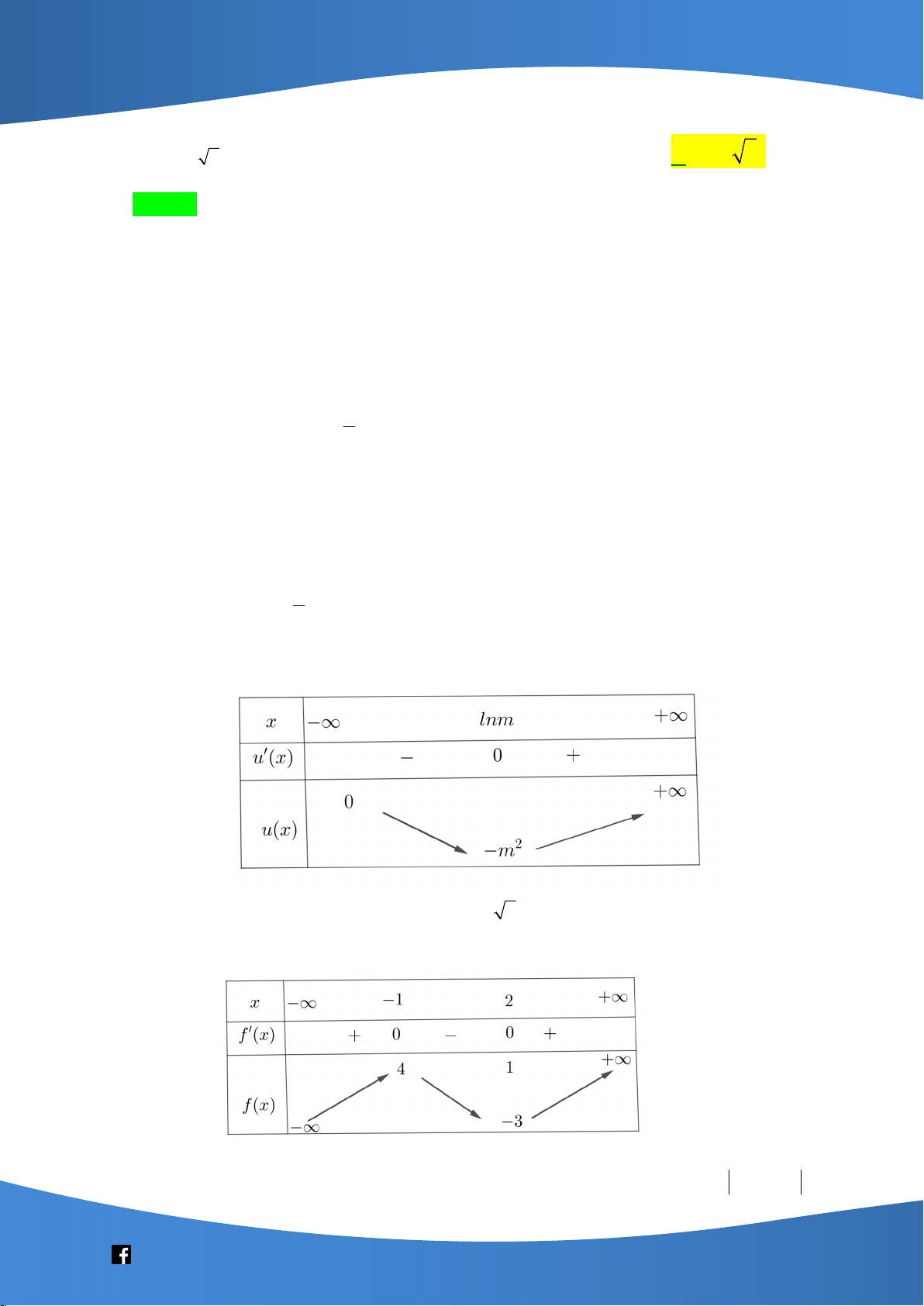
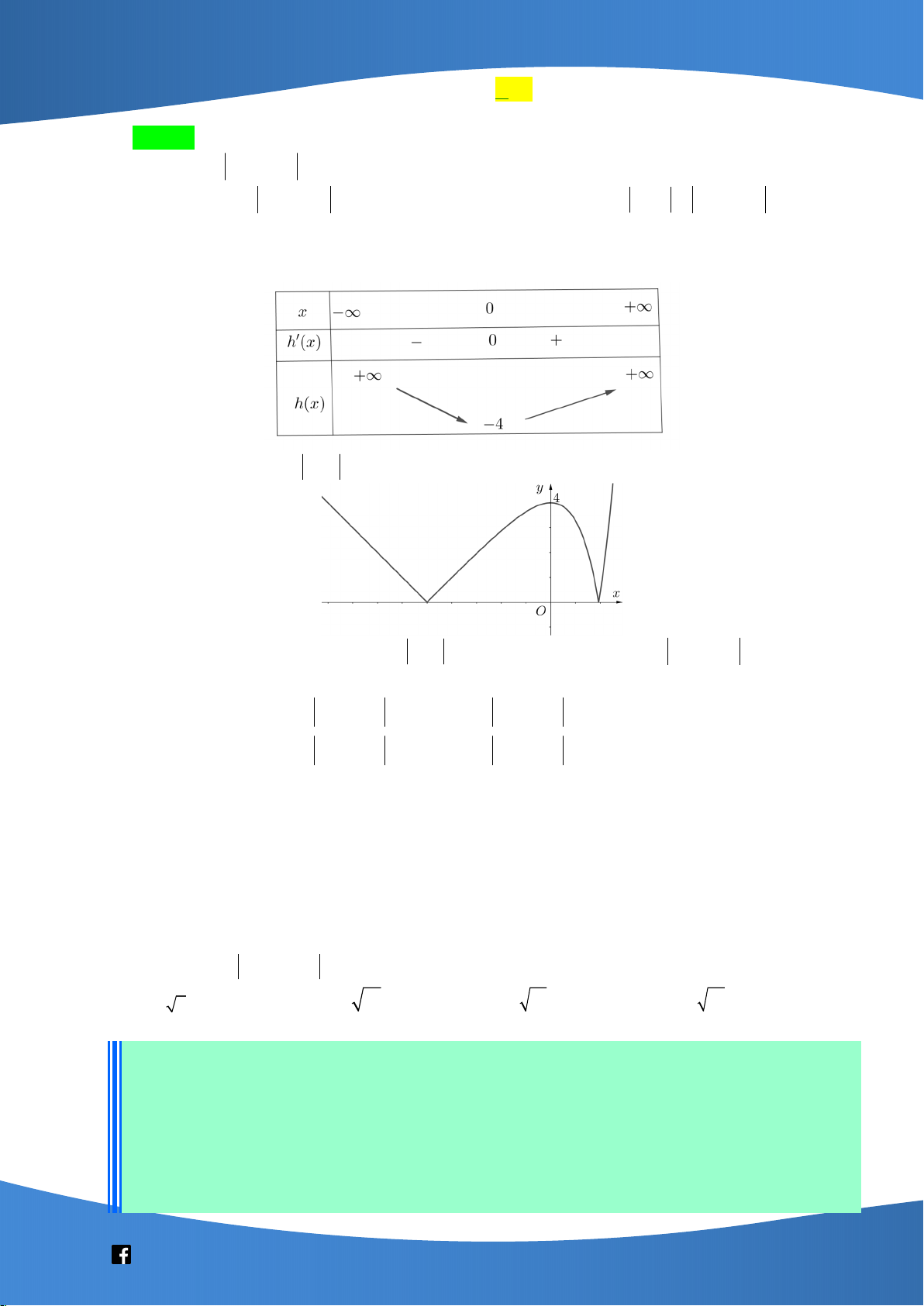
Câu 13: Cho hàm số y f x có bảng biến thiên như sau:
Giá trị cực tiểu của hàm số đã cho bằng A. 1. B. 5 . C. 3  . D. 1.
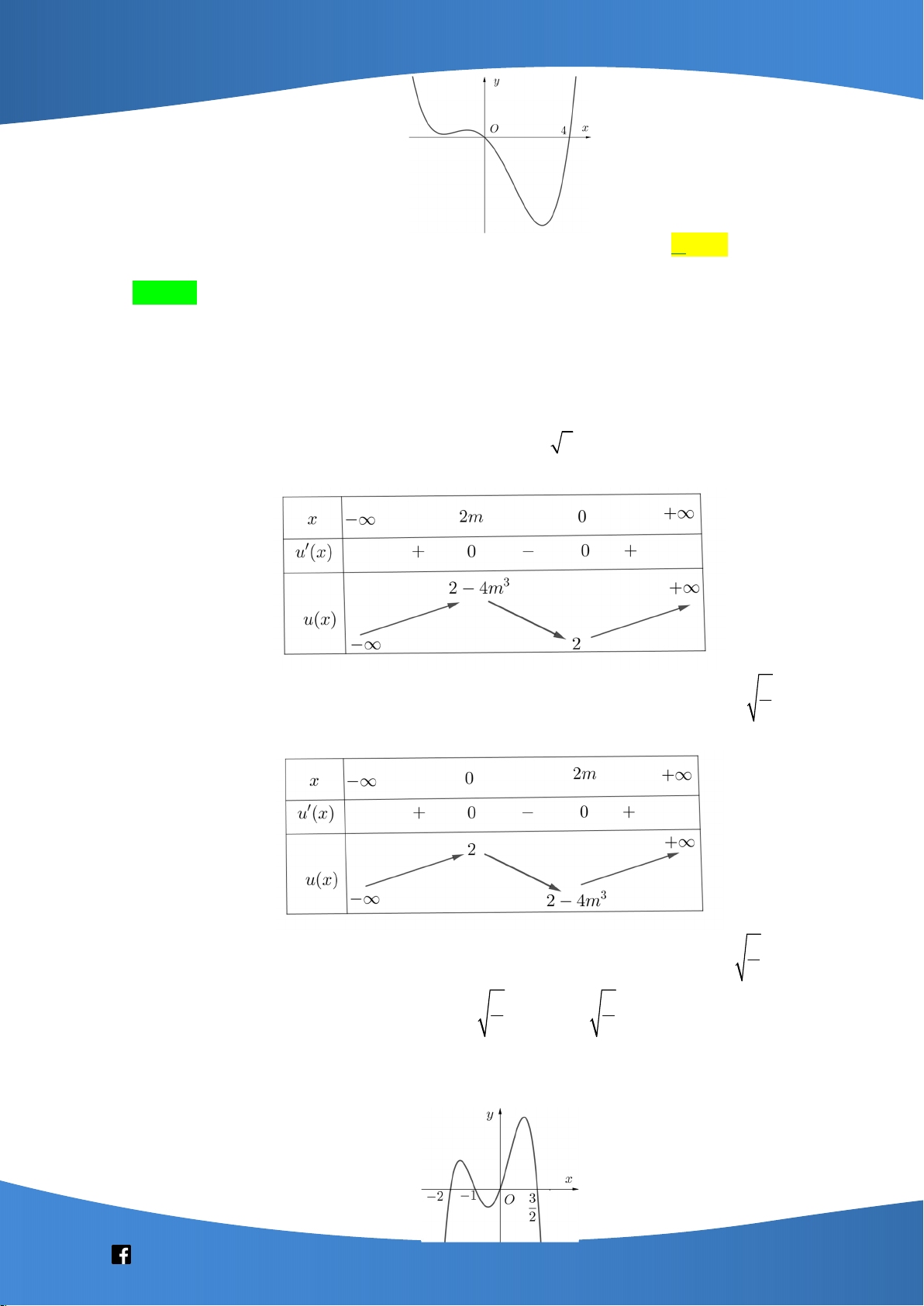
Câu 14: Cho hàm số y f x có đồ thị là đường cong trong hình bên. Hàm số đã cho nghịch
biến trên khoảng nào dưới đây? A. 0;  1 . B.  ;  0 .
C. 0; . D.  1  ;  1 .
Câu 15: Nghiệm của phương trình log 5x  2 là: 3   8 9
A. x  .
B. x  9 .
C. x  . D. x  8 . 5 5
https:/www.facebook.com/groups/toanvd. Trang 16
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8-2021 3 3
Câu 16: Nếu f xdx  4 
thì 3 f xdx  bằng 0 0 A. 36 . B. 12 . C. 3 . D. 4 .
Câu 17: Thể tích của khối lập phương cạnh 5a bằng A. 3 5a . B. 3 a . C. 3 125a . D. 3 25a .
Câu 18: Tập xác định của hàm số 9x y  là A.  .
B. 0; . C.  \   0 . D. 0; .
Câu 19: Diện tích S của mặt cầu bán kính R được tính theo công thức nào dưới đây? 4 A. 2 S  16 R . B. 2 y  4 R . C. 2 S   R . D. 3 S   R . 3 2x  1
Câu 20: Tiệm cận đứng của đồ thị hàm số y
là đường thẳng có phương trình: x  1 1 A. x  1 . B. x  1 . C. x  2 . D. x  . 2
Câu 21: Cho a  0 và a  1, khi đó 4 log a bằng a 1 1 A. 4 . B. . C.  . D. 4 . 4 4
Câu 22: Cho khối chóp có diện tích đáy 2
B  5a và chiều cao h a . Thể tích của khối chóp đã cho bằng 5 5 5 A. 3 a . B. 3 a . C. 3 5a . D. 3 a . 6 2 3
Câu 23: Trong không gian Oxyz , cho mặt phẳng  P :3x y  2z  1  0 . Vectơ nào dưới đây là
một vectơ pháp tuyến của  P  ?     A. 1 n   3  ;1;2 . B. 2 n  3; 1  ;2 . C. 3
n  3;1;2 . D. 4 n  3;1; 2   .
Câu 24: Cho khối trụ có bán kính đáy r  6 và chiều cao h  3. Thể tích của khối trụ đã cho bằng A. 108 . B. 36 . C. 18 . D. 54 .
Câu 25: Cho hai số phức z  4  2i và w  3  4i . Số phức z w bằng
A. 1 6i .
B. 7  2i .
C. 7  2i . D. 1   6i .
Câu 26: Cho cấp số nhân ( ) n u với 1 u  3 và 2
u  9 . Công bội của cấp số nhân đã cho bằng 1 A. 6 . B. . C. 3 . D. 6 . 3
Câu 27: Cho hàm số ( ) x
f x e  2 . Khẳng định nào dưới đây đúng? A. 2 ( )d x f x x eC  . B. ( )d x
f x x e  2x C  . C. ( )d x
f x x e C  . D. ( )d x
f x x e  2x C  .
Câu 28: Trên mặt phẳng tọa độ, điểm M ( 3
 ; 4) là điểm biểu diễn của số phức nào dưới đây? A. z    i z   i 2
z  3 4i . B. 3 z  3   4i . C. 4 3 4 . D. 1 3 4 . x a
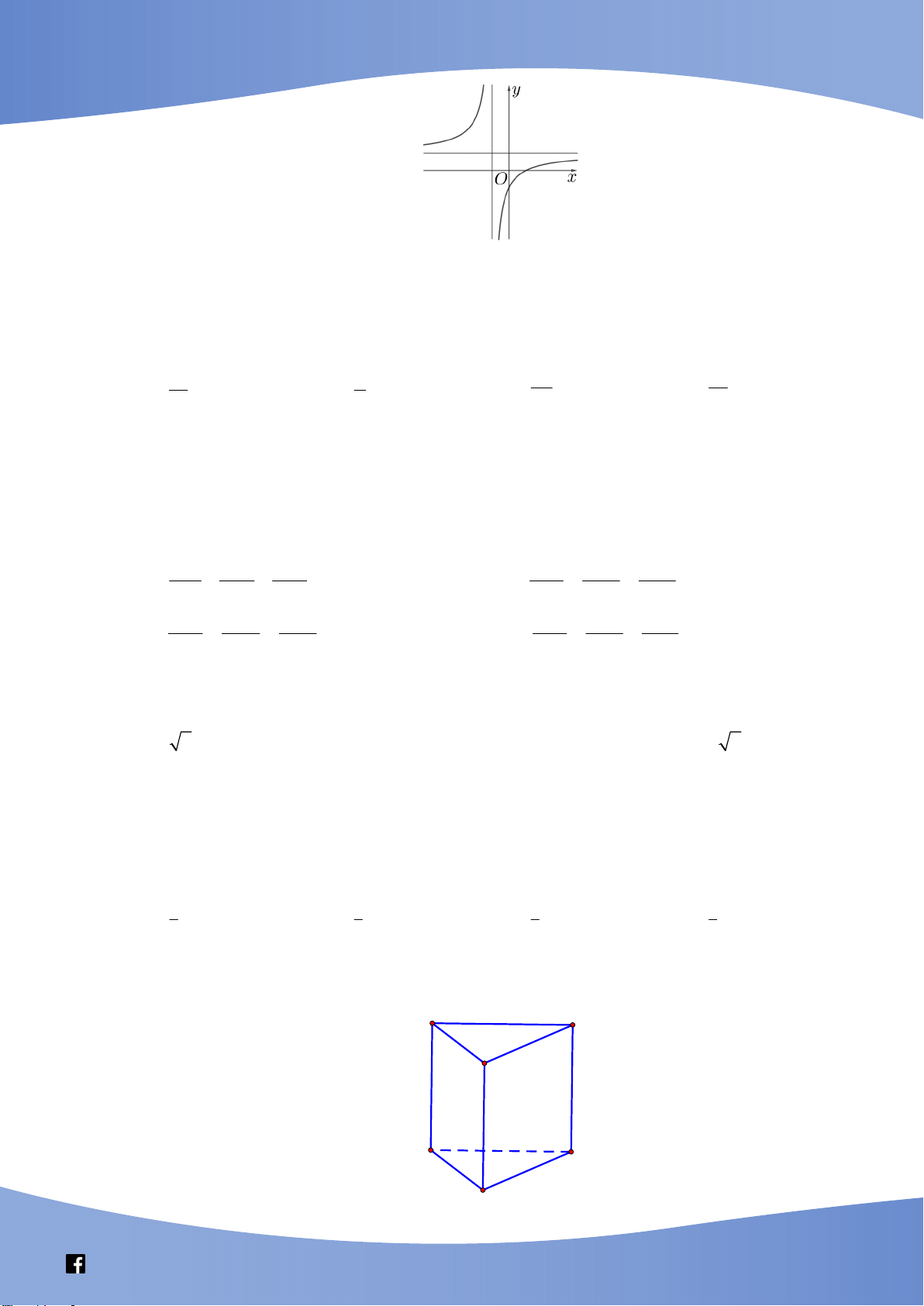
Câu 29: Biết hàm số y
( a là số thực cho trước, a  1) có đồ thị như trong hình bên. x  1
https:/www.facebook.com/groups/toanvd. Trang 17
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8-2021
Mệnh đề nào dưới đây đúng?
A. y'  0, x   1  .
B. y '  0, x   1  .
C. y '  0, x    .
D. y '  0, x    .
Câu 30: Từ một hộp chứa 12 quả bóng gồm 5 quả màu đỏ và 7 quả màu xanh, lấy ngẫu nhiên
đồng thời 3 quả. Xác suất để lấy được 3 quả màu xanh bằng 7 2 1 5 A. . B. . C. . D. . 44 7 22 12
Câu 31: Trên đoạn 0;  3 , hàm số 3
y  x  3x đạt giá trị lớn nhất tại điểm
A. x  0 .
B. x  3 .
C. x  1 . D. x  2 .
Câu 32: Trong không gian Oxyz , cho điểm M  1
 ;3; 2 và mặt phẳng  P :x  2y  4z 1  0 .
Đường thẳng đi qua M và vuông góc với  P có phương trình là: x 1 y  3 z  2 x 1 y  3 z  2 A.   . B.   . 1 2  1 1 2 1 x 1 y  3 z  2 x 1 y  3 z  2 C.   . D.   . 1 2  4 1 2  4
Câu 33: Cho hình chóp S.ABC có đáy là tam giác vuông cân tại B , AB  2a và SA vuông góc
với mặt phẳng đáy. Khoảng cách từ C đến mặt phẳng SAB bằng A. 2a . B. 2a . C. a . D. 2 2a .
Câu 34: Trong không gian Oxyz , cho hai điểm A1;0;0 và B 4;1;2 . Mặt phẳng đi qua A và
vuông góc với AB có phương trình là
A. 3x y  2z 17  0 .
B. 3x y  2z  3  0 .
C. 5x y  2z  5  0 .
D. 5x y  2z  25  0 .
Câu 35: Cho số phức z thỏa mãn iz  5  4i . Số phức liên hợp của z là
A. z  4  5i .
B. z  4  5i . C. z  4   5i . D. z  4   5i .
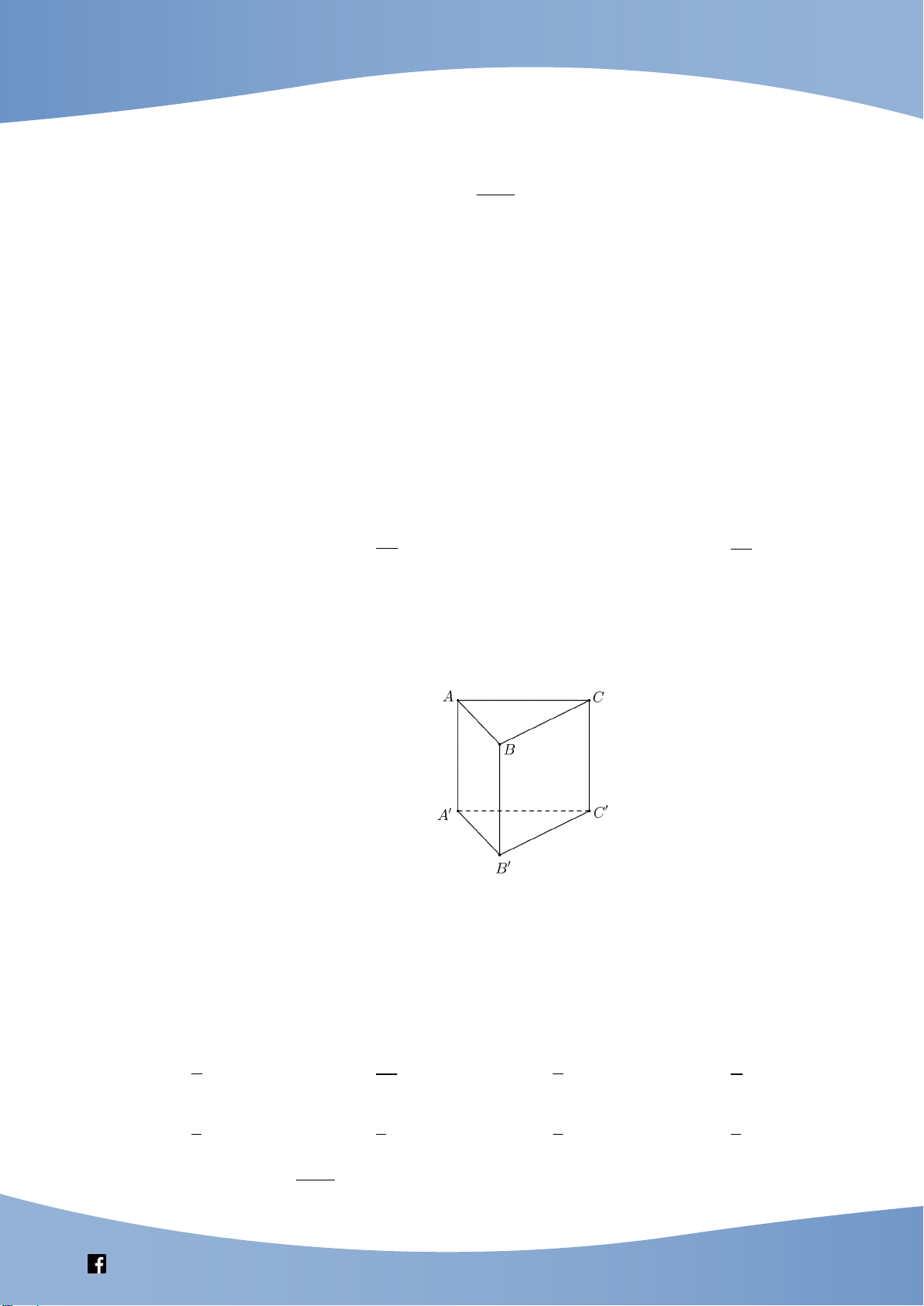
Câu 36: Cho hình lắng trụ đứng AB . C A BC
  có tất cả các cạnh bằng nhau ( tham khảo hình bên.
Góc giữa hai đường thẳng AA và BC là A C B A' C' B'
https:/www.facebook.com/groups/toanvd. Trang 18
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8-2021 A. o 30 . B. o 90 . C. o 45 . D. o 60 .
Câu 37: Với mọi a, b thỏa mãn 3
log a  log b  6 , khẳng định nào dưới đây đúng? 2 2 A. 3 a b  64 . B. 3 a b  36 . C. 3
a b  64 . D. 3
a b  64 . 2 2
Câu 38: Nếu f x dx  5 
thì 2 f x 1 dx    bằng 0 0 A. 8. B. 9. C. 10. D. 12.
2x  5 khi x  1
Câu 39: Cho hàm số f x  
. Giả sử F là nguyên hàm của f trên  thỏa mãn 2
3x  4 khi x  1 
F 0  2 . Giá trị của F  
1  2F 2 bằng A. 27. B. 29. C. 12. D. 33. 2
Câu 40: Có bao nhiêu số nguyên x thỏa mãn 3x 9x  log x  25 3  0  3    ? A. 27. B. Vô số. C. 26 . D. 25 .
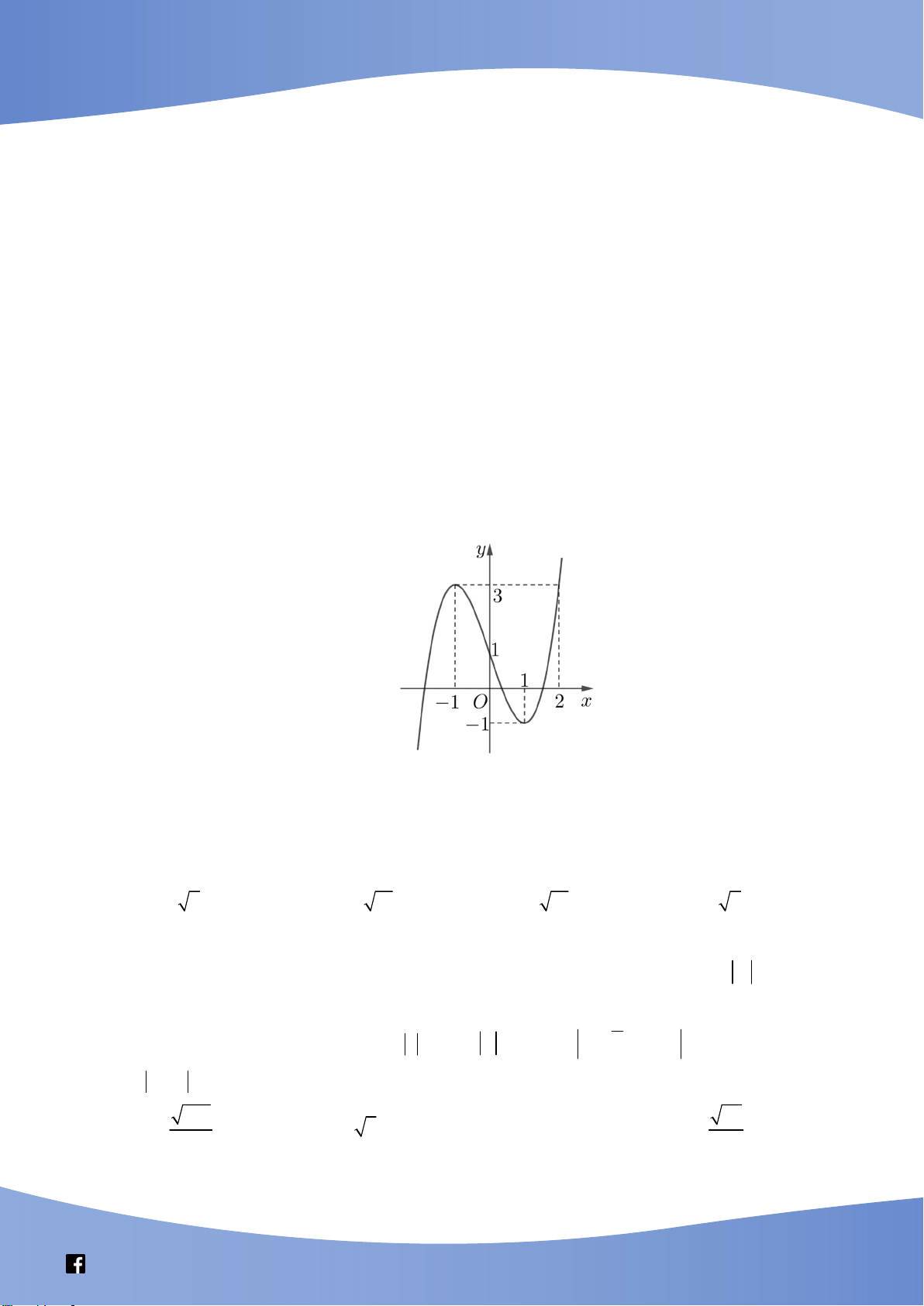
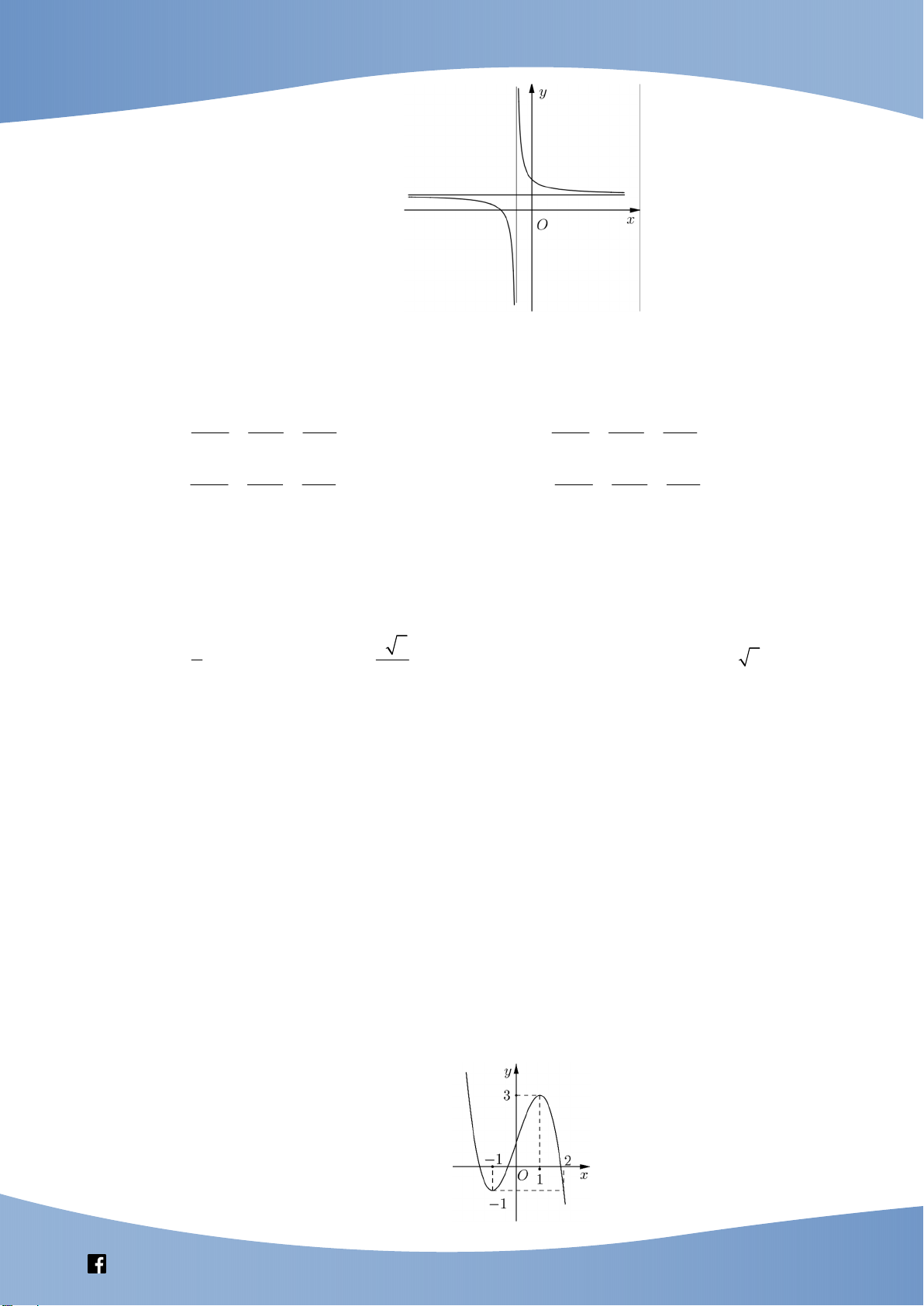
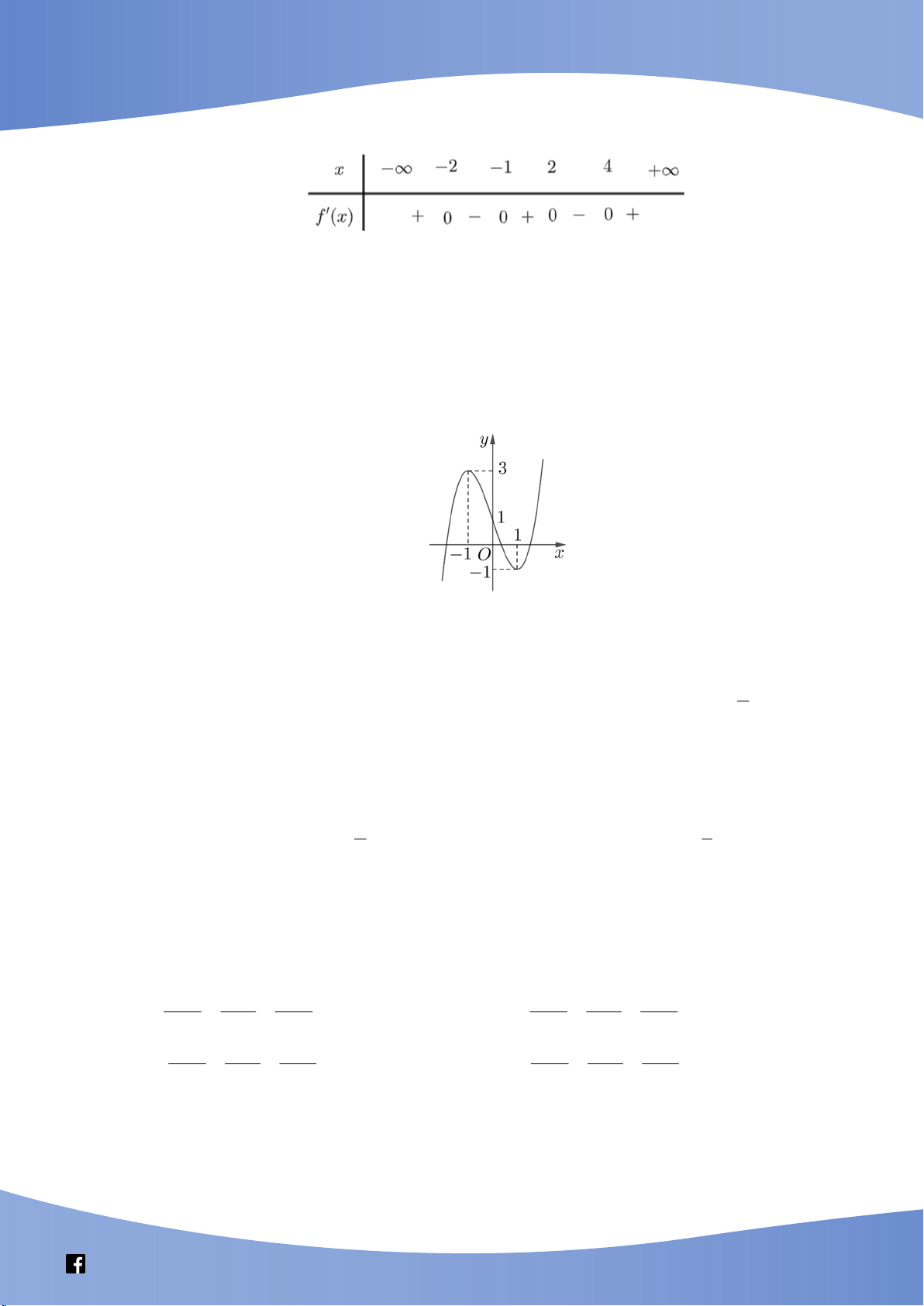
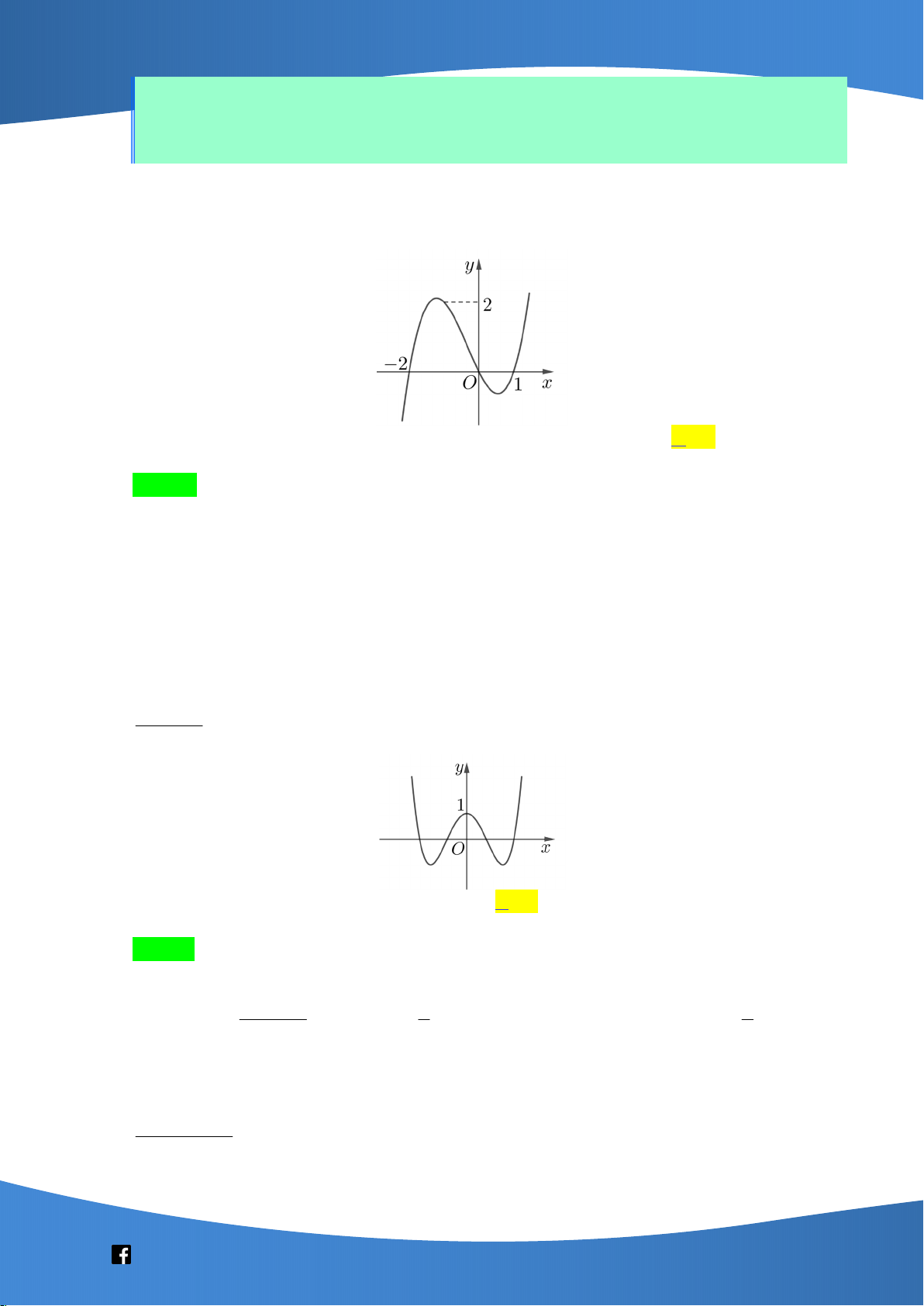
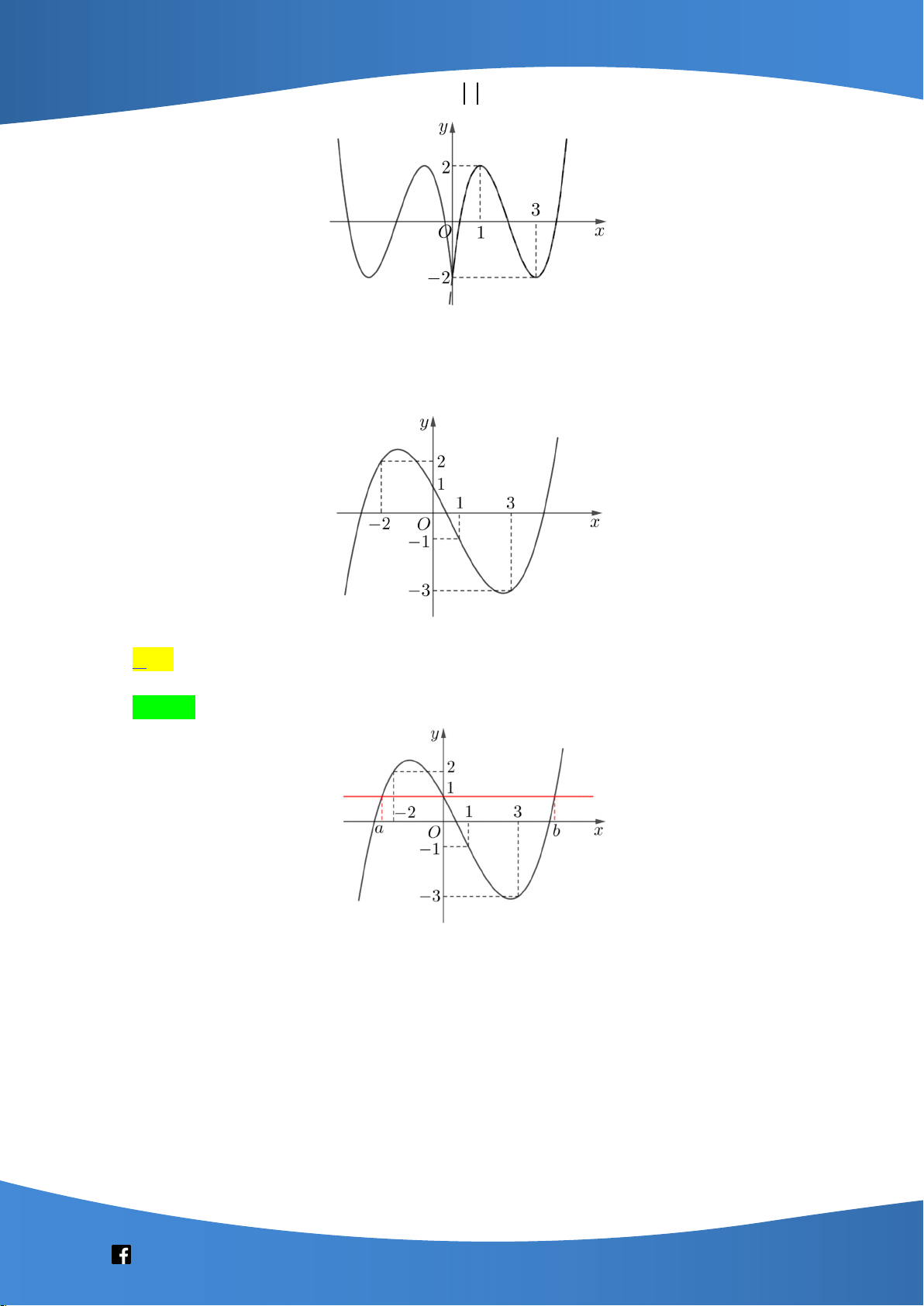
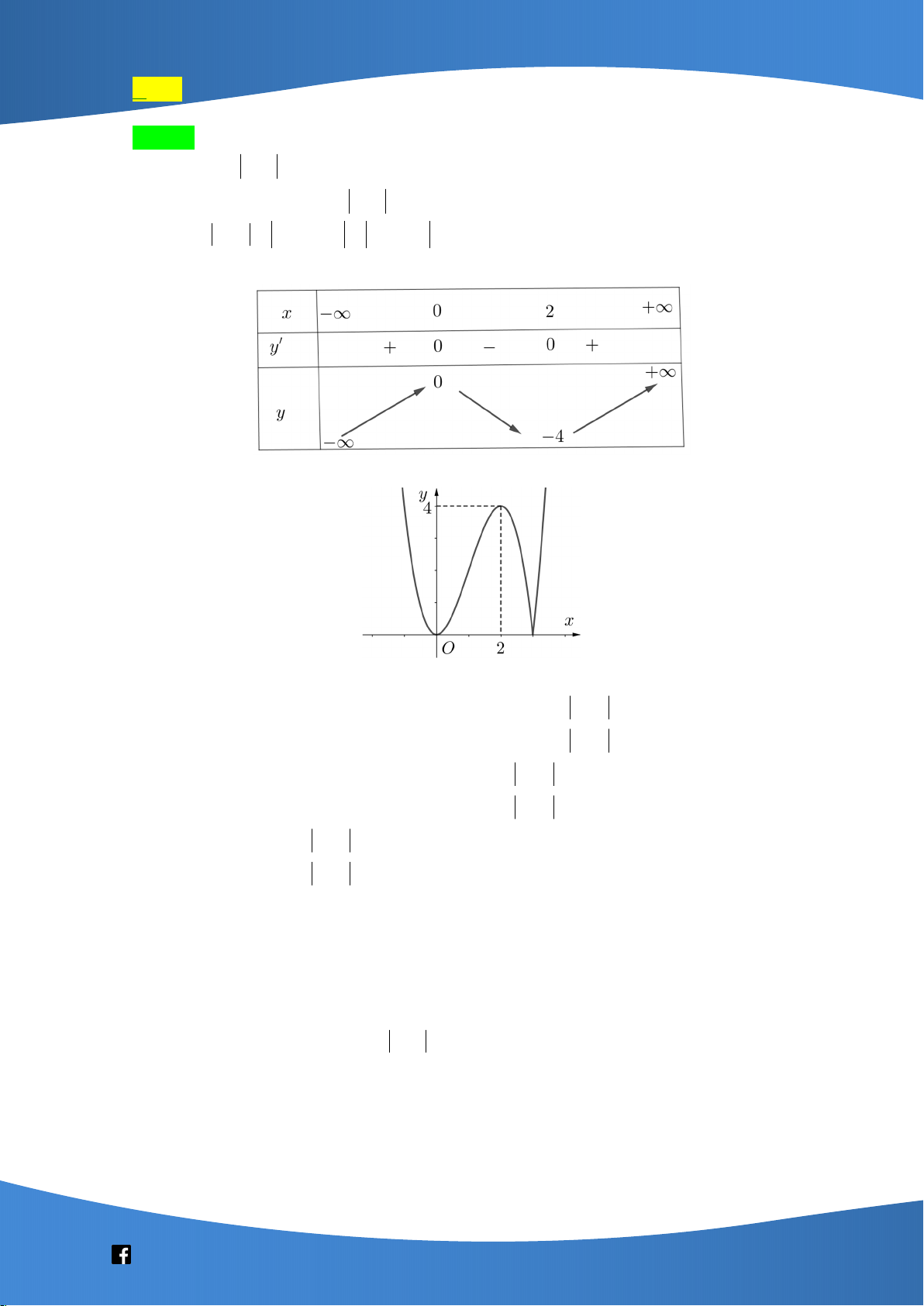
Câu 41: Cho hàm số bậc ba y f x có đồ thị là đường cong trong hình bên. Số nghiệm thực
phân biệt của phương trình f f x 1 là A. 9 . B. 3 . C. 6 . D. 7 .
Câu 42: Cắt hình nón  N  bởi mặt phẳng đi qua đỉnh và tạo với mặt phẳng chứa đáy một góc bằng 0
60 ta thu được thiết diện là một tam giác đều cạnh 4a . Diện tích xung quanh của  N  bằng : A. 2 8 7 a . B. 2 4 13 a . C. 2 8 13 a . D. 2 4 7 a .
Câu 43: Trên tập hợp các số phức, xét phương trình 2
z  m   2 2
1 z m  0 (m là tham số thực).
Có bao nhiêu giá trị của m để phương trình đó có nghiệm z thỏa mãn z  7? 0 0 A. 2 . B. 3 . C. 1. D. 4 .
Câu 44: Xét các số phức z, w thỏa mãn z  1 và w  2 . Khi z iw  6  8i đạt giá trị nhỏ nhất, z w bằng 221 29 A. . B. 5 . C. 3 . D. . 5 5
https:/www.facebook.com/groups/toanvd. Trang 19
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8-2021 x y 1 z  2
Câu 45: Trong không gian Oxyz , cho đường thẳng d :   và mặt phẳng 1 1 1
P :x  2y z  4  0 . Hình chiếu vuông góc của d trên P là đường thẳng có phương trình: x y  1 z  2 x y  1 z  2 A.   . B.   . 2 1 4 3 2 1 x y 1 z  2 x y 1 z  2 C.   . D.   . 2 1 4 3 2 1 Câu 46: Cho hàm số   3 2
f x x ax bx c với a, ,
b c là các số thực. Biết hàm số
g x  f x  f  x  f  x có hai giá trị cực trị là 3
 và 6 . Diện tích hình phẳng giới f x
hạn bởi các đường y  và y  1 bằng g x  6 A. 2ln 3. B. ln 3. C. ln18. D. 2ln 2.  1  2
Câu 47: Có bao nhiêu số nguyên y sao cho tồn tại x  ;3 3x xy 9 x   thỏa mãn 27  1 xy 27 .  3  A. 27 . B. 9 . C. 11. D. 12.
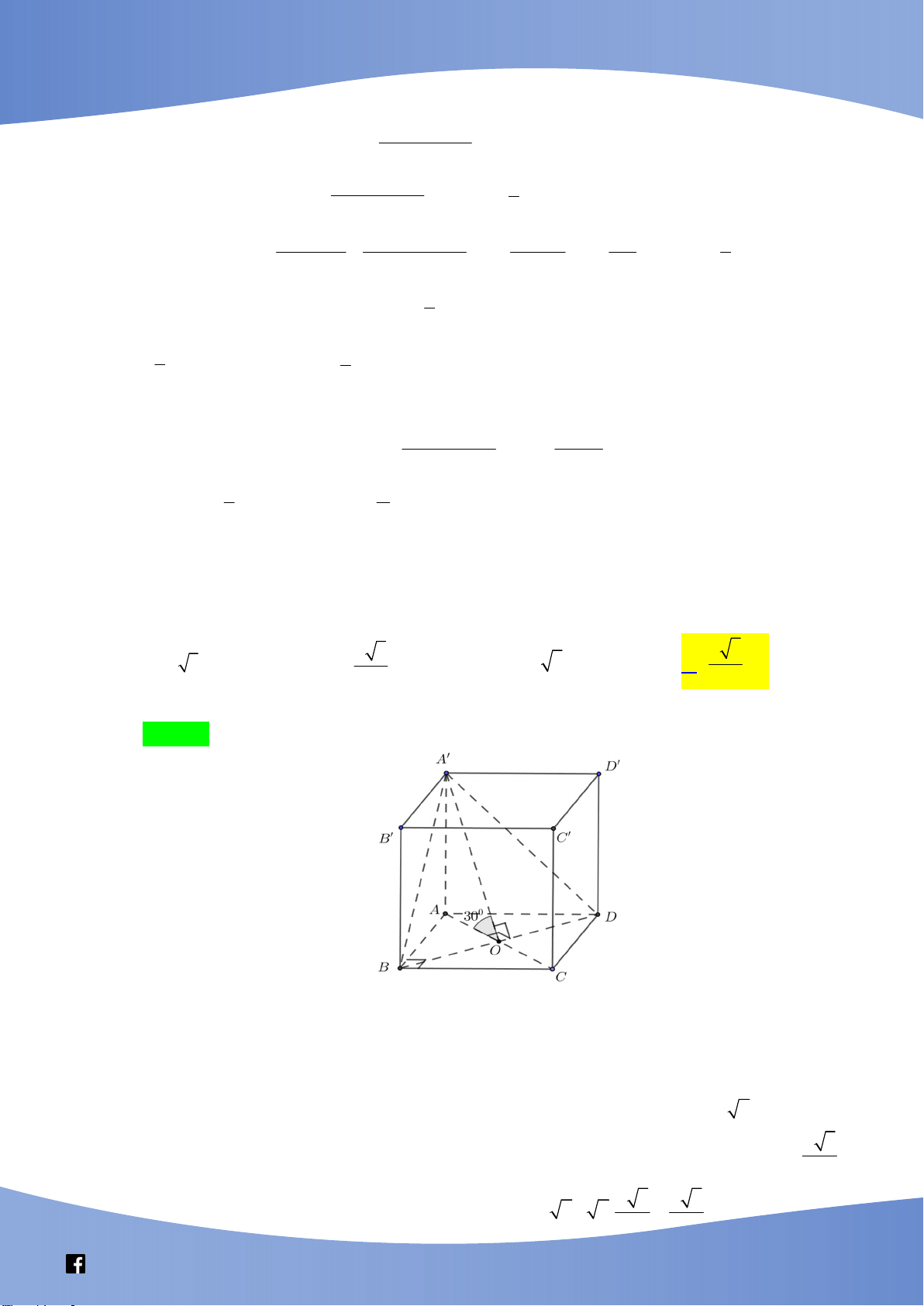
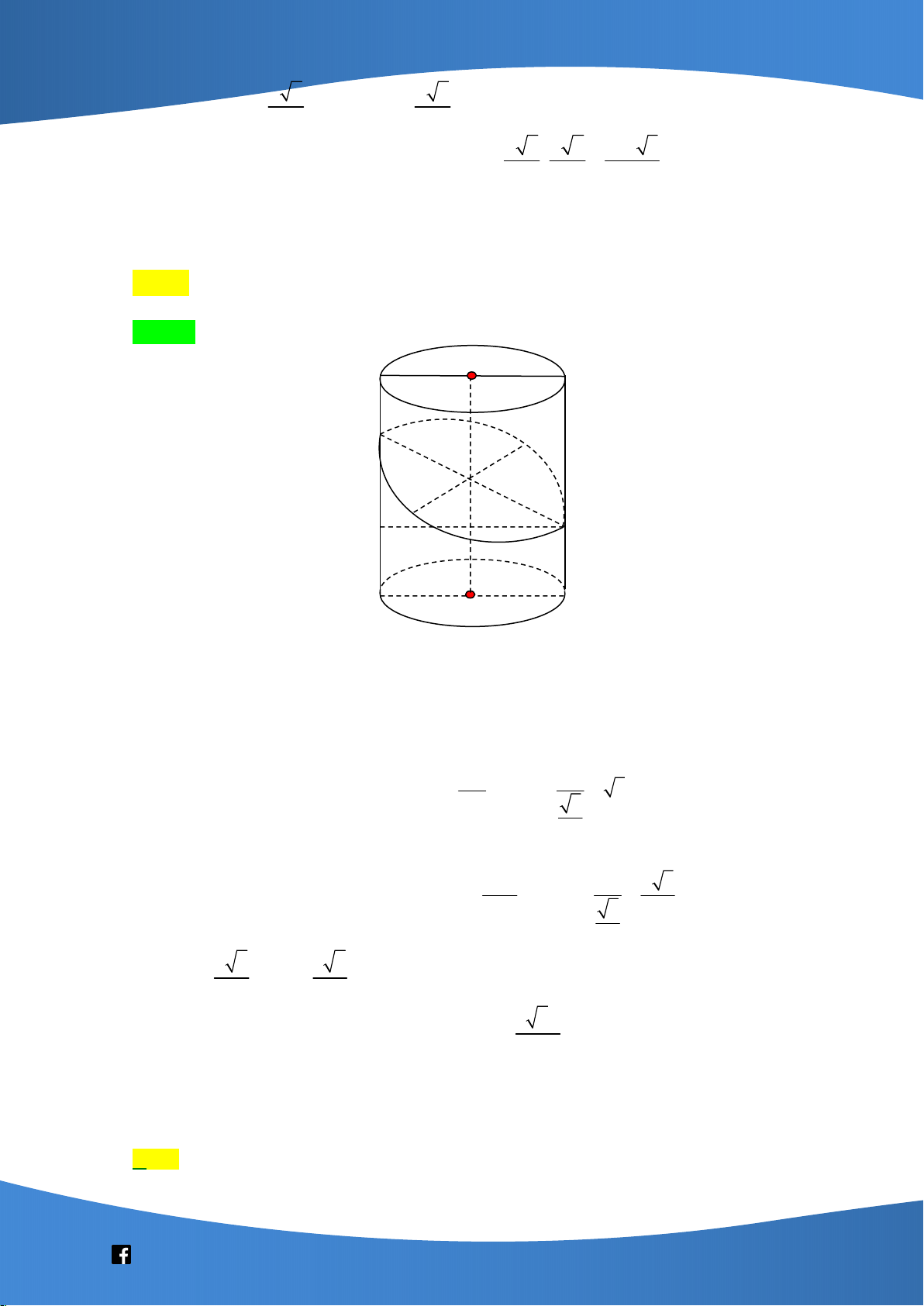
Câu 48: Cho khối hộp chữ nhật ABCD.A ' B 'C ' D ' có đáy là hình vuông, BD  2a , góc giữa hai
mặt phẳng  A' BD và  ABCD bằng 0
30 . Thể tích của khối hộp chữ nhật đã cho bằng 2 3 2 3 A. 3 6 3a . B. 3 a . C. 3 2 3a . D. 3 a . 9 3
Câu 49: Trong không gian Oxyz, cho hai điểm ( A 1; 3  ; 4  ), B( 2
 ;1; 2). Xét hai điểm M và N thay
đổi thuộc mặt phẳng (Oxy) sao cho MN  2. Giá trị lớn nhất của AM BN bằng A. 3 5 . B. 61 . C. 13 . D. 53 .
Câu 50: Cho hàm số y f x có đạo hàm f  x   x   2 7 x  9, x   .  Có bao nhiêu giá trị
nguyên dương của tham số m để hàm số g x  f  3
x  5x m có ít nhất 3 điểm cực trị? A. 6. B. 7. C. 5. D. 4.
……… HẾT ………
https:/www.facebook.com/groups/toanvd. Trang 20
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8-2021
ĐỀ THI TỐT NGHIỆP THPT QUỐC GIA NĂM 2021 MÃ ĐỀ 101 Môn: Toán
Thời gian: 90 phút (Không kể thời gian phát đề)
BẢNG ĐÁP ÁN VÀ GIẢI CHI TIẾT
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
A C B D D A D D A C C A C A C B C A B A B D B A B
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
C B B B A C D B B A C A A A C D D B D C D C D D A
2x  5 khi x  1
Câu 39: Cho hàm số f x  
. Giả sử F là nguyên hàm của f trên  thỏa mãn 2
3x  4 khi x  1 
F 0  2 . Giá trị của F  
1  2F 2 bằng A. 27. B. 29. C. 12. D. 33. Lời giải Chọn A
Dễ thấy hàm số f liên tục trên  1 1 F   1  F 0 2 
f (x)dx
(3x  4) f (x)dx  5  F (1)  7   . 0 0 1  2 F   1  2F 2 
f (x)dx  2
f (x)dx  3 f (1)  1  0 16  21  27   . 1 1 2
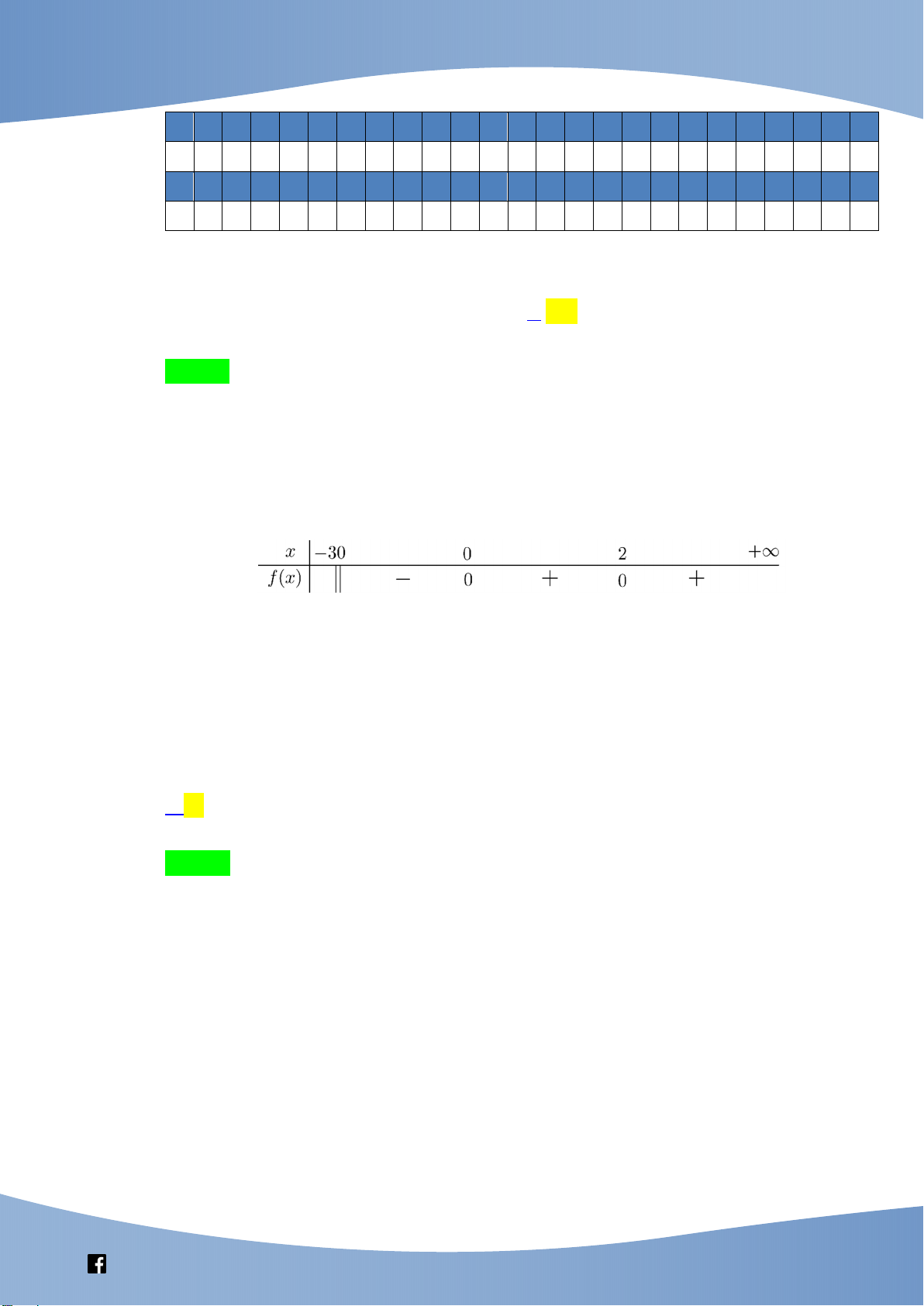
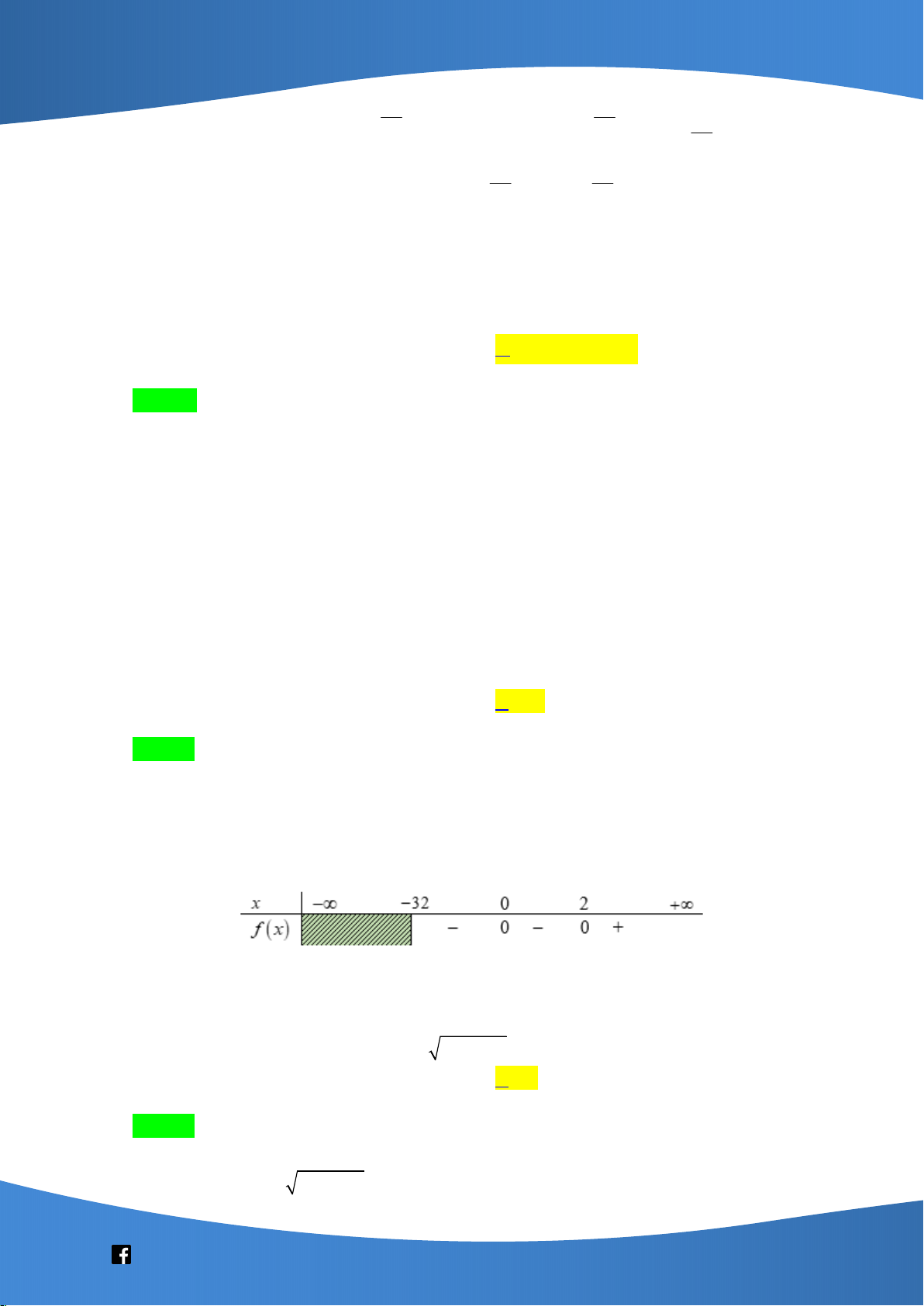
Câu 40: Có bao nhiêu số nguyên x thỏa mãn 3x 9x  log x  25 3  0  3    A. 27. B. Vô số. C. 26 . D. 25 . Lời giải Chọn C
Điều kiện xác định của bất phương trình là x  2  5 . 2
Đặt ( )  3x 9x A x
log x25 3,x  2  5  3    . 2
3x  9x  0  x  0  x  2 .
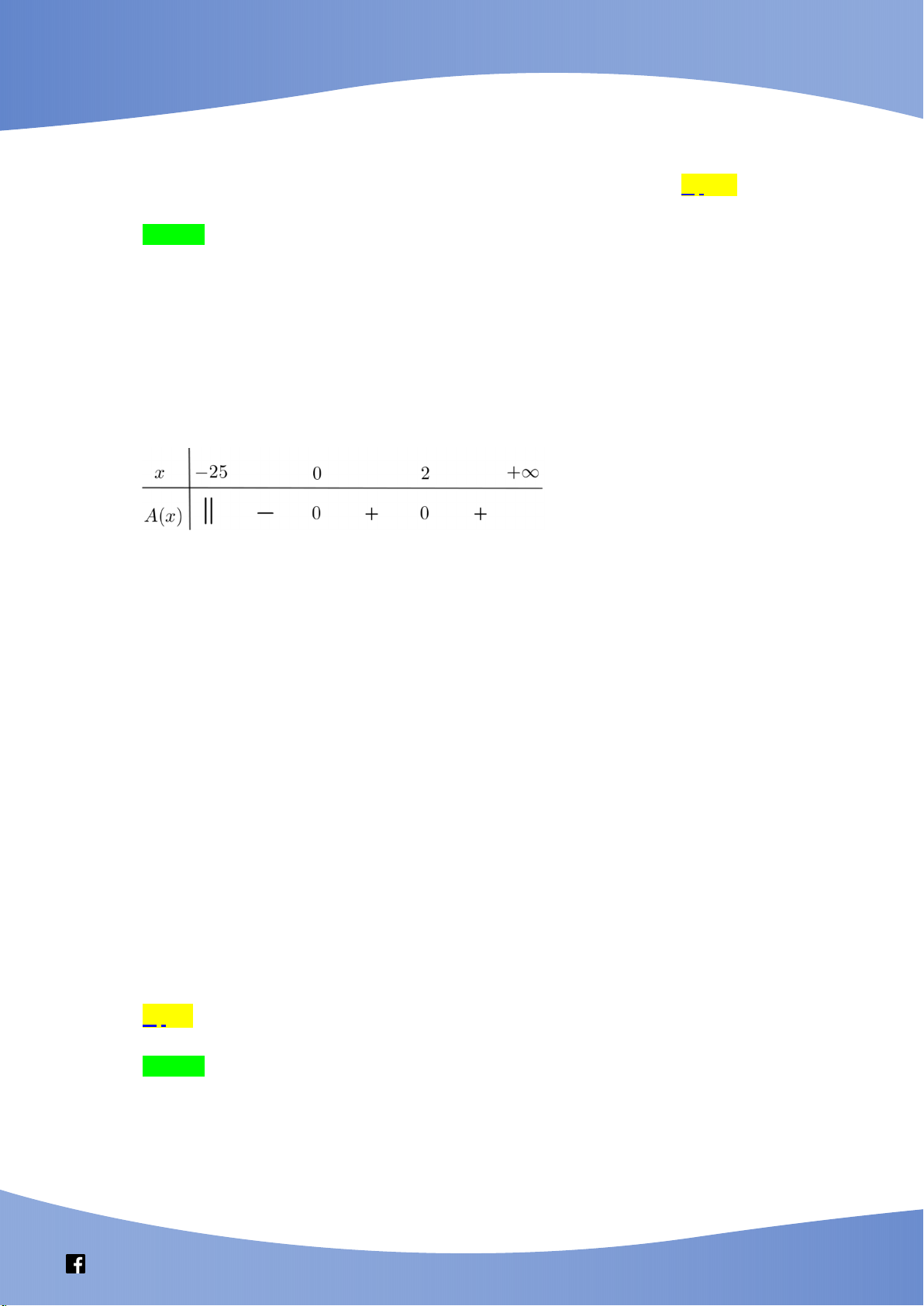
log x  25  3  0  x  2 . 3   Ta có bảng xét dấu ( A x) như sau  x  2 Từ đó, ( A x)  0   x    24  ; 23  ;...;0;  2 (do x   ). 25   x  0 
Kết luận: có 26 nghiệm nguyên thỏa mãn.
https:/www.facebook.com/groups/toanvd. Trang 21
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8-2021
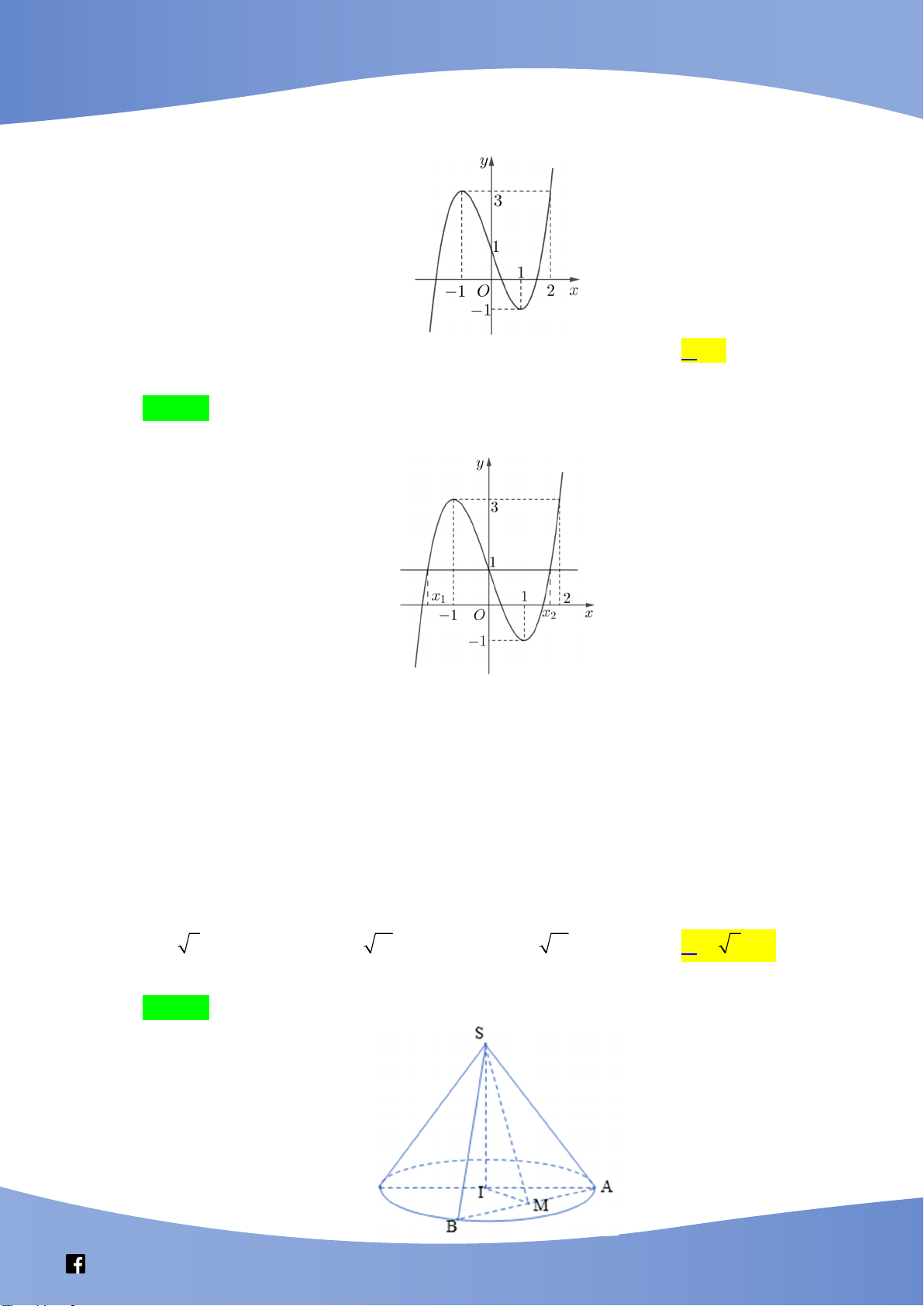
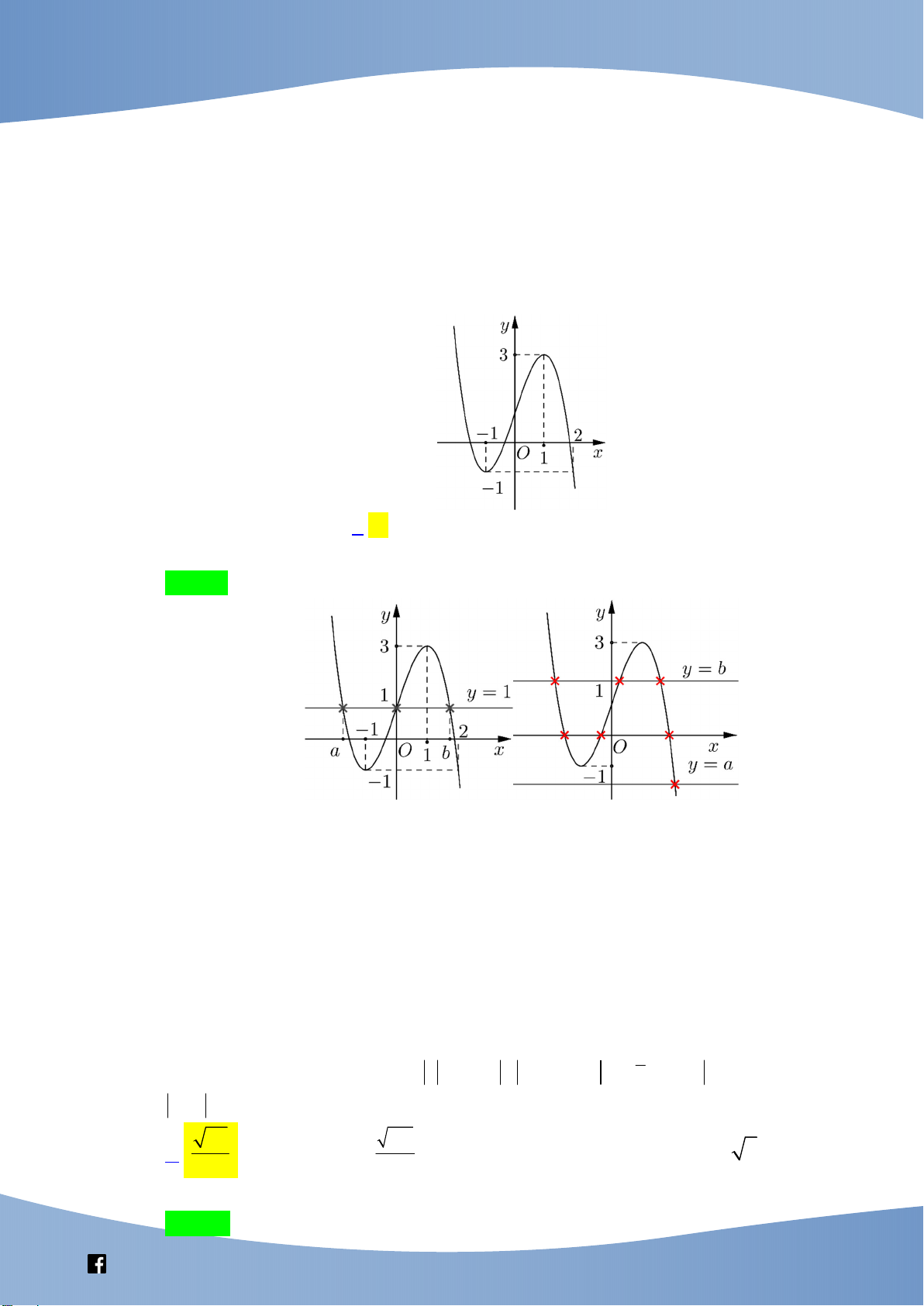
Câu 41: Cho hàm số bậc ba y f (x) có đồ thị là đường cong trong hình bên. Số nghiệm thực
phân biệt của phương trình f f x 1 là A. 9 . B. 3 . C. 6 . D. 7 . Lời giải Chọn D
Từ đồ thị hàm số ta có
f (x)  x và x  1  (1) 1 1
f f x 1   f (x)  0 (2) 
f (x)  x và 1  x  2 (3)  2 2
Dựa vào đồ thị, (1) có đúng 1 nghiệm, (2) và (3) mỗi phương trình có 3 nghiệm phân
biệt và 7 nghiệm trên phân biệt nhau.
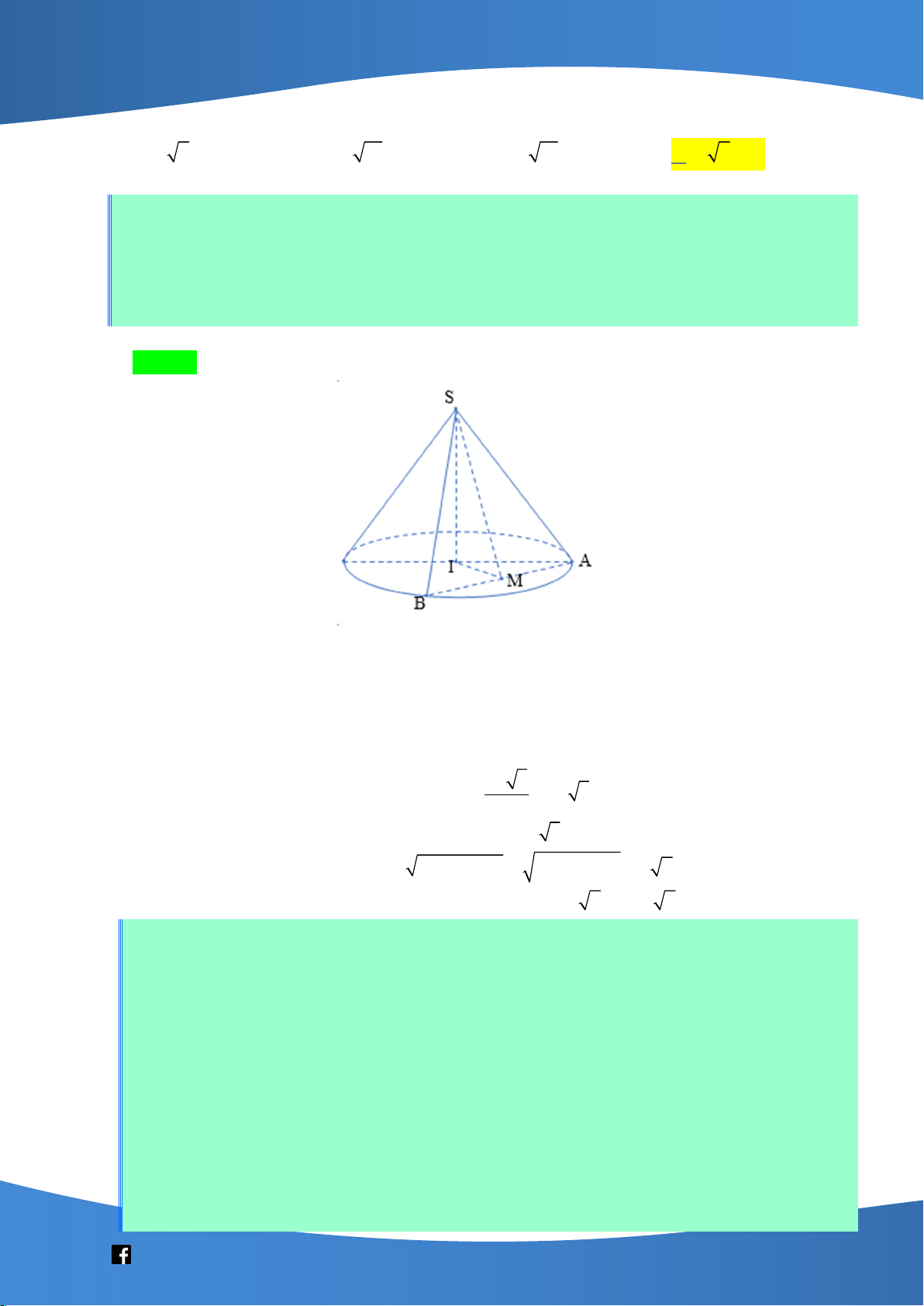
Câu 42: Cắt hình nón  N  bởi mặt phẳng đi qua đỉnh và tạo với mặt phẳng chứa đáy một góc bằng 0
60 ta thu được thiết diện là một tam giác đều cạnh 4a . Diện tích xung quanh của  N  bằng : A. 2 8 7 a . B. 2 4 13 a . C. 2 8 13 a . D. 2 4 7 a . Lời giải Chọn D
https:/www.facebook.com/groups/toanvd. Trang 22
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8-2021
Gọi I là tâm đáy nón. Ta có thiết diện qua đỉnh là tam giác SBA.
Gọi M là trung điểm của AB . Suy ra  0 SMI  60 . 4a 3
Do tam giác SAB đều cạnh 4a SM   2a 3 . 2
Xét tam giác SIM vuông tại I ta có SI  3a; IM a 3 .
Xét IMA vuông tại M ta có IA IM MA a   a2 2 2 2 3 2  a 7 . Khi đó 2
S   rl   a 7.4a  4 7 a . xq
Câu 43: Trên tập hợp các số phức, xét phương trình 2
z  m   2 2
1 z m  0 ( m là tham số thực).
Có bao nhiêu giá trị của m để phương trình đó có nghiệm z thỏa mãn z  7? 0 0 A. 2 . B. 3 . C. 1. D. 4 . Lời giải Chọn B 2 2 
  (m 1)  m  2m 1. 1 +) Nếu 
  0  2m 1  0  m   , phương trình có 2 nghiệm thực. Khi đó 2
z  7  z  7  . 0 0
Thế z  7 vào phương trình ta được: 2
m 14m  35  0  m  7  14 (nhận). 0 Thế z  7
 vào phương trình ta được: 2
m 14m  63  0 , phương trình này vô nghiệm. 0 1 +) Nếu 
  0  2m 1  0  m   , phương trình có 2 nghiệm phức z , z   thỏa 2 1 2
z z . Khi đó 2 2 2
z .z z
m  7 hay m  7 (loại) hoặc m  7  (nhận). 2 1 1 2 1
Vậy tổng cộng có 3 giá trị của m là m  7  14 và m  7  .
Câu 44: Xét các số phức z, w thỏa mãn z  1 và w  2 . Khi z iw  6  8i đạt giá trị nhỏ nhất, z w bằng 221 29 A. . B. 5 . C. 3 . D. . 5 5 Lời giải Chọn D
Ta có: w  2  iw  2 ; z iw z iw  3
P z iw  6  8i  6  8i z iw  10  3  7 .  1 10 k  ; h    2 3  3 4   . ,  0  z   i z k iw k 3 4     5 5 Suy ra: m P in  7 khi 
 z   i   . 6   8i  . h
z iw,h  0 5 5 8 6    w   i  8 6   5 5 w   i   5 5
https:/www.facebook.com/groups/toanvd. Trang 23
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8-2021 3 4  8 6  29
Vậy z w   i   i    . 5 5  5 5  5 x y 1 z  2
Câu 45: Trong không gian Oxyz , cho đường thẳng d :   và mặt phẳng 1 1 1
P :x  2y z  4  0 . Hình chiếu vuông góc của d trên P là đường thẳng có phương trình: x y  1 z  2 x y  1 z  2 A.   . B.   . 2 1 4 3 2 1 x y 1 z  2 x y 1 z  2 C.   . D.   . 2 1 4 3 2 1 Lời giải Chọn C
Tọa độ giao điểm A của d và  P thỏa mãn hệ phương trình:  x y 1 z  2 x  0     1 1 1 
  y  1  A0;1;2 .
x  2y z  4  0  z  2 
Lấy điểm B1;2; 
1  d . Gọi H là hình chiếu của B trên  P . x  1 t
 Phương trình BH :  y  2  2t z 1 t
Do H BH   P nên tọa độ điểm H thỏa mãn hệ phương trình:  1 t    3 x  1 t  2   x
y  2  2t   3  2 4 2   2 1 4      H ; ;    AH  ; ;    . z  1 t  4   3 3 3   3 3 3  y
x  2y z  4  0   3  2  z   3
Gọi d là hình chiếu vuông góc của d trên  P  d đi qua A và H
d  có một vector chỉ phương là u  2;1; 4 . x y 1 z  2
Vậy phương trình đường thẳng d là:   . 2 1 4 Câu 46: Cho hàm số   3 2
f x x ax bx c với a, ,
b c là các số thực. Biết hàm số
g x  f x  f  x  f  x có hai giá trị cực trị là 3
 và 6 . Diện tích hình phẳng giới f x
hạn bởi các đường y  và y  1 bằng g x  6 A. 2ln 3. B. ln 3. C. ln18. D. 2ln 2. Lời giải
https:/www.facebook.com/groups/toanvd. Trang 24
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8-2021 Chọn D Ta có f  x 2
 3x  2ax b ; f  x  6x  2a ; f  x  6 ;
g x  f x  f  x  f  x  g x  f  x  f  x  6 .
Vì g x có hai giá trị cực trị là 3
 và 6 nên g x có hai điểm cực trị là x , x và 1 2 g x  3
 , g x  6 . 1  1  f xf x
Phương trình hoành độ giao điểm của hai đường y  và y  1 là  1 g x  6 g x  6
f x  g x  6
f x  f x  f  x  f  x  6
f  x  f  x  6  0  x xg x 1  0   . x x  2 f x
Diện tích hình phẳng giới hạn bởi các đường y  và y  1 là: g x  6 x x x 2 f x
2  g x 2 
d  g x  6 x 12 S  1dx   d  x
 ln g x 2  6  ln  2 ln 2.    g xg x    g x x   6 x   6   x   x1 6 3 1 1 1  1  2
Câu 47: Có bao nhiêu số nguyên y sao cho tồn tại x  ;3 3x xy 9 x   thỏa mãn 27  1 xy 27 .  3  A. 27 . B. 9 . C. 11. D. 12. Lời giải Chọn C 1
- Khi y  0, vì xy  1
 và x  nên ta có y  3  . 3 2
Với y  0 , phương trình thành: 3x 9
27  x 1  0 vô nghiệm vì 2 x x  1 3 9 0  27
1  27 1  0, x   ;3   .  3  2 2 Với y  1  , phương trình thành: 3x 1  0 27
x  (1 x)  0 , có nghiệm vì 3x 1  0 ( )  27 x g x  (1 x) 1 1   1  liên tục trên ;3  và g .g 3  0 . 1   1   3     3  2 Với y  2  , phương trình thành: 3x 1  1 27
x  (1 2x)  0 , có nghiệm vì 2 3x 1  1 1   1  ( )  27 x g x
 (1 2x) liên tục trên ;3 và g .g 3  0 . 2   2   2  3     3  1 
- Khi y  1, xét trên ;3  , ta có 3   
https:/www.facebook.com/groups/toanvd. Trang 25
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8-2021 2 3x xy 9 x 2 27  (1 xy)27
 3x xy  log (1 xy)  9x 27 log (1 xy) 27  3x  9   y  0. x log (1 xy) 1  Xét hàm 27
g(x)  3x  9   y trên ;3 . x  3    ln(1 xy) y 1 3 1 
Ta có g '(x)  3    3   3   0, x   ;3 . 2 2 x ln 27 x(1 xy) ln 27 3x n l 3 ln 3  3     1 
Do đó, hàm g(x) đồng biến trên ;3 
. Vì thế phương trình g(x)  0 có nghiệm trên 3     1   1  ;3   khi và chỉ khi g g(3)  0.  
Áp dụng bất đẳng thức ln(1 u)  u với mọi u  0 ,  3   3  ta có log (1 3y) 3y 27 g(3)    y    y  . 0 3 3ln 27  1   y  Do đó g  0   log 1
y  8  0  1  y  9  
(do y là số nguyên dương). 3    3   3  Vậy y  2  ; 1  ;1;2;...; 
9 hay có 11 giá trị y thỏa đề.
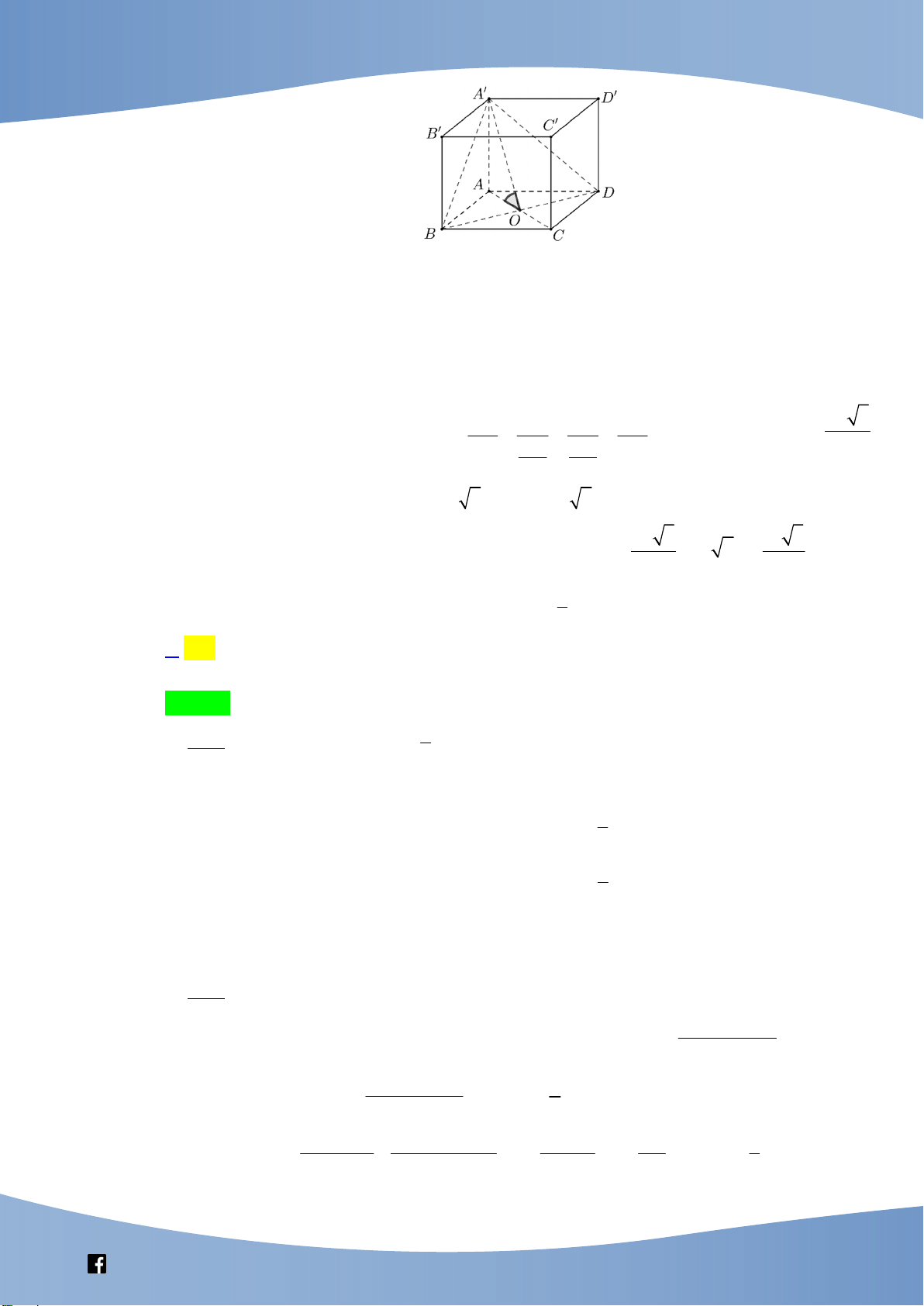
Câu 48: Cho khối hộp chữ nhật ABCD.A ' B 'C ' D ' có đáy là hình vuông, BD  2a , góc giữa hai
mặt phẳng  A' BD và  ABCD bằng 0
30 . Thể tích của khối hộp chữ nhật đã cho bằng 2 3 2 3 A. 3 6 3a . B. 3 a . C. 3 2 3a . D. 3 a . 9 3 Lời giải Chọn D
Gọi O là tâm hình vuông ABCD . Vì BD OA và BD AA' nên
BD   A'OA  BD OA'
Lại có  A' BD  ABCD  BD . Do đó  A BD  ABCD  0 ' ,
A 'OA  30 (Hình vẽ trên).
Vì tứ giác ABCD là hình vuông có BD  2a nên OA a và AB AD a 2 . a 3
Xét tam giác A ' AO vuông tại A có OA a và  0
A'OA  30 nên 0 AA '  . OA tan 30  . 3 a 3 2 3
Vậy thể tích khối hộp chữ nhật 3 V A . B A .
D AA'  a 2.a 2.  a . 3 3
https:/www.facebook.com/groups/toanvd. Trang 26
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8-2021
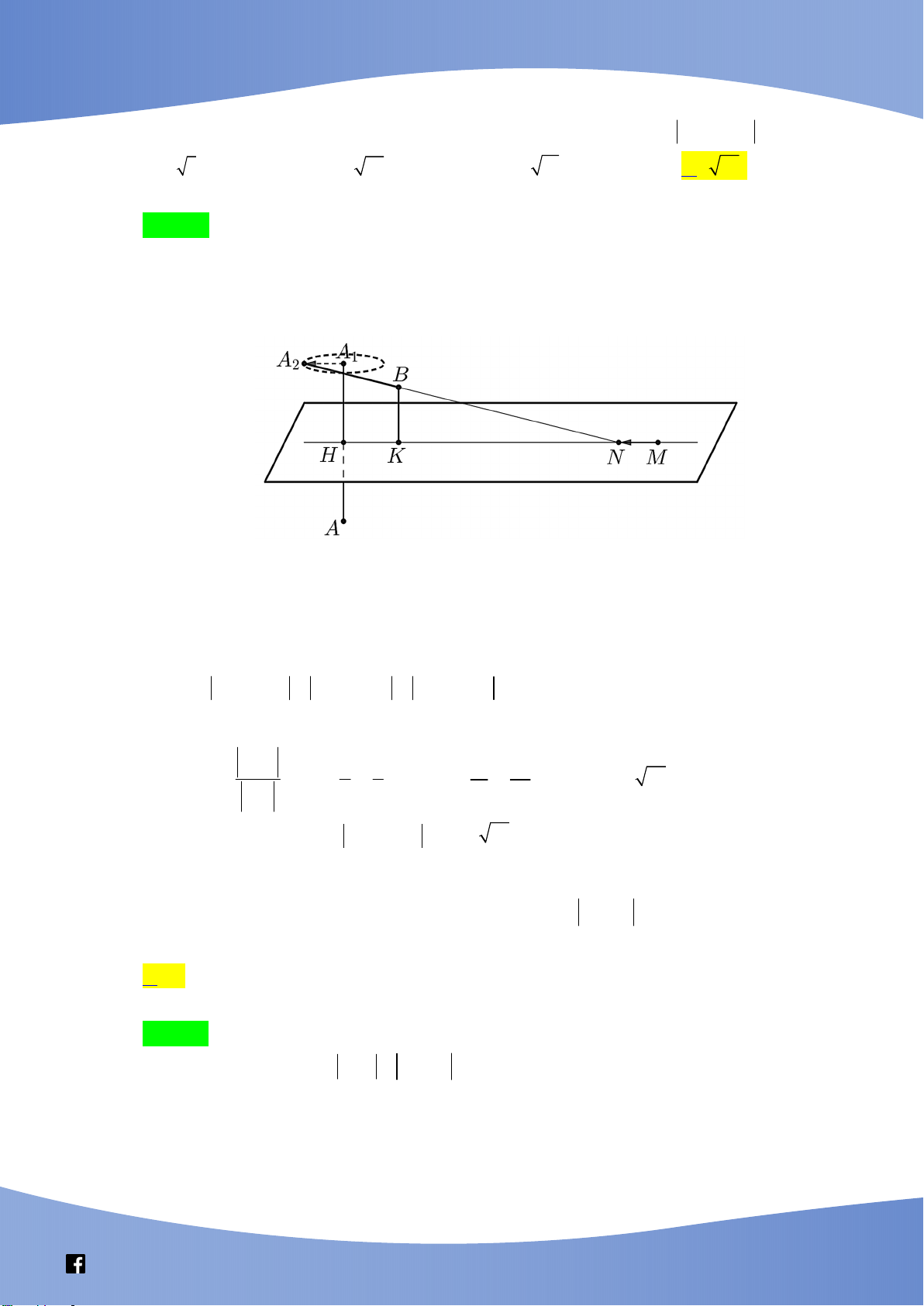
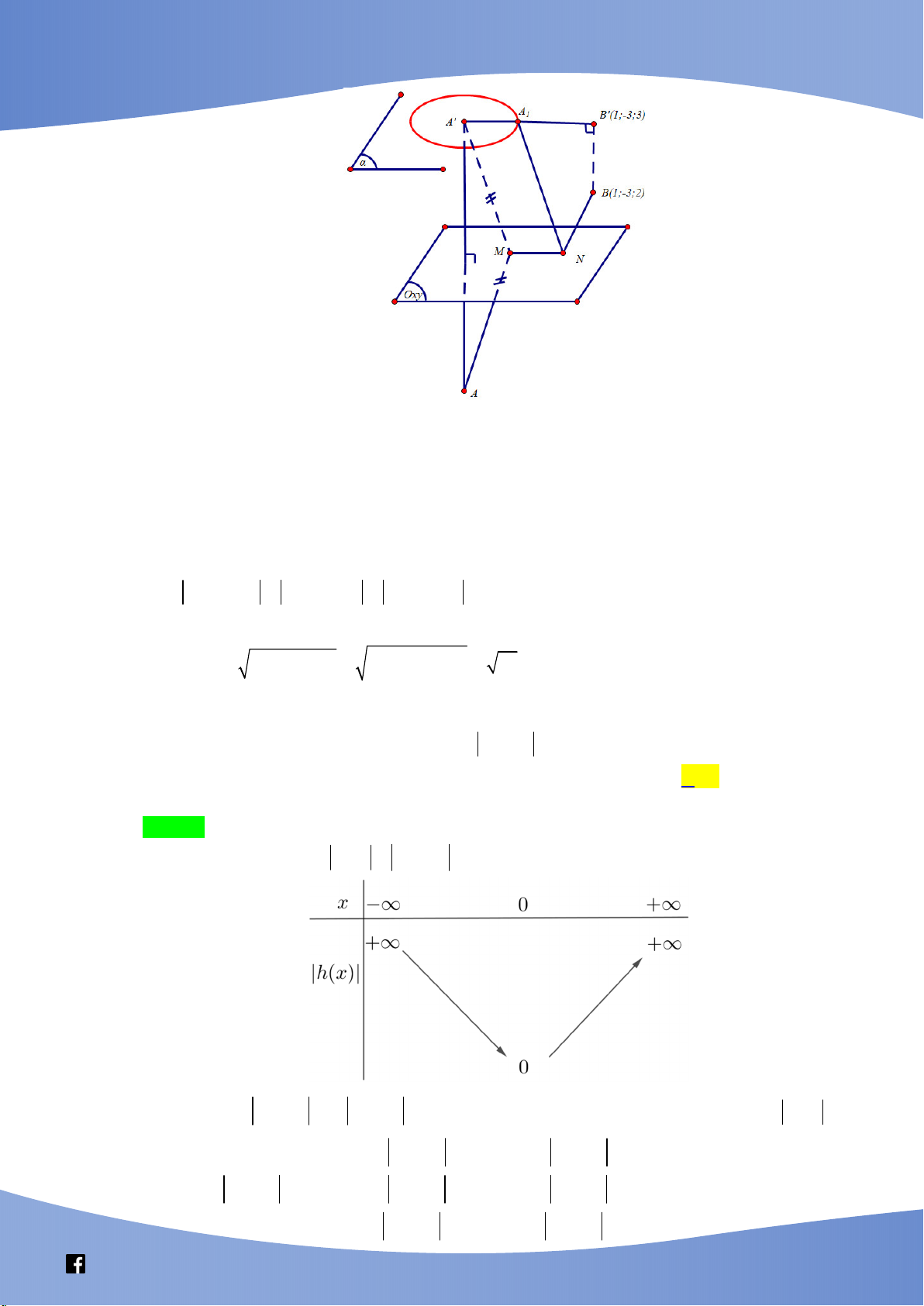
Câu 49: Trong không gian Oxyz, cho hai điểm ( A 1; 3  ; 4  ), B( 2
 ;1; 2). Xét hai điểm M và N thay
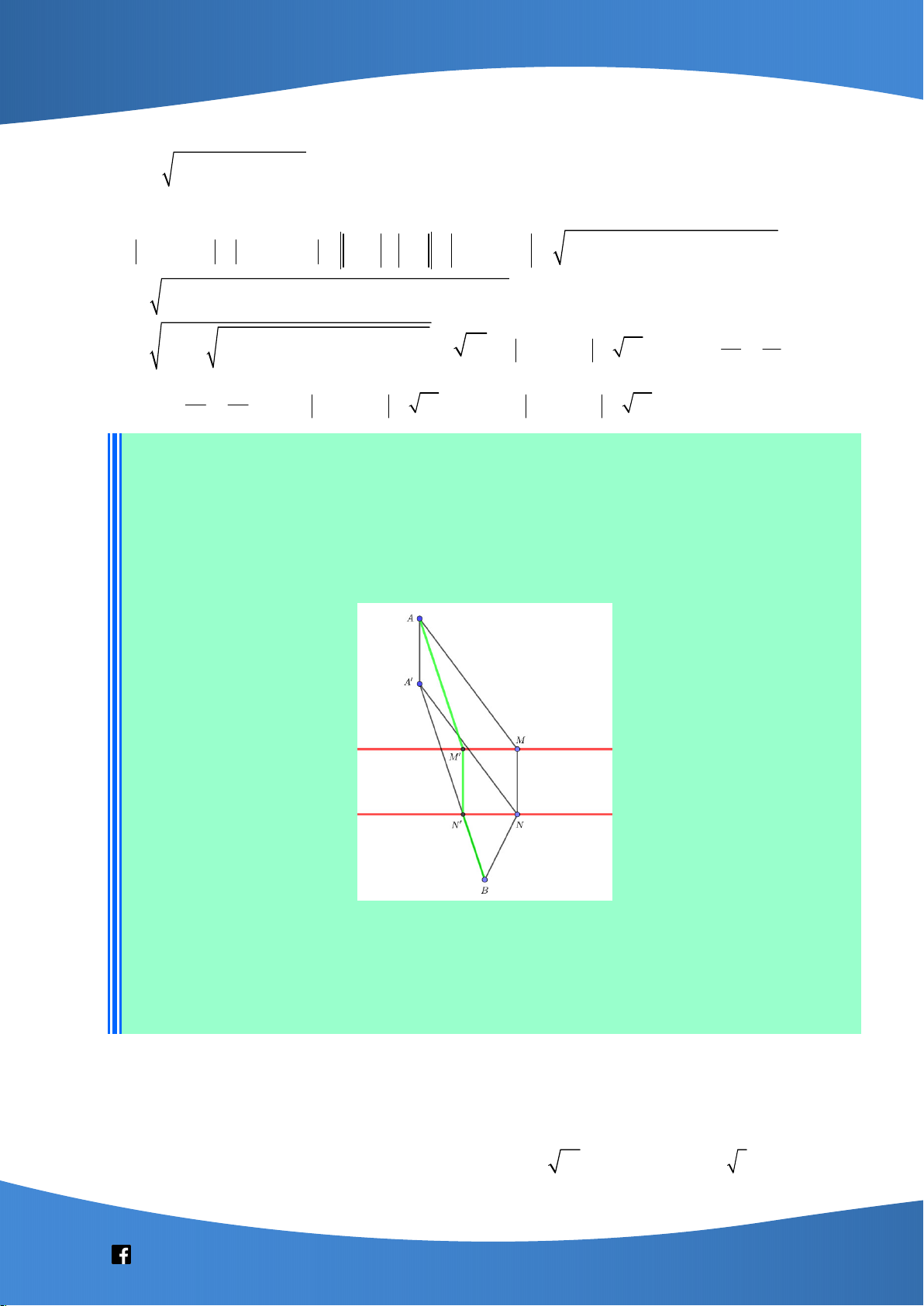
đổi thuộc mặt phẳng (Oxy) sao cho MN  2. Giá trị lớn nhất của AM BN bằng A. 3 5 . B. 61 . C. 13 . D. 53 . Lời giải Chọn D Vì z .z  0 A B nên ,
A B nằm khác phía so với mặt phẳng (Oxy) .
Gọi H , K lần lượt là hình chiếu vuông góc của ,
A B lên mặt phẳng (Oxy)  H (1; 3  ; 0), K ( 2  ;1; 0) . Gọi 1
A là điểm đối xứng của A qua (Oxy)  1 A (1; 3  ; 4) .
  Gọi 2 A thỏa 1 A 2 A MN  1 A 2 A  2  2
A  đường tròn (C) nằm trong mặt phẳng song song với (Oxy) và có tâm 1 A , bán kính R  2 .
Khi đó: AM BN  1 A M BN  2 A N BN  2 A B .   Dấu "  " xảy ra và 2
A B đạt giá trị lớn nhất  1 A 2
A ngược hướng với HK .    1 A 2 A  6 8   11 23    1 A 2 A   HK  ;  ; 0    2 A ;  ; 4    2 A B  53 . HK  5 5   5 5 
Vậy giá trị lớn nhất của AM BN bằng 53 .
Câu 50: Cho hàm số y f x có đạo hàm f  x   x   2 7 x  9, x   .  Có bao nhiêu giá trị
nguyên dương của tham số m để hàm số g x  f  3
x  5x m có ít nhất 3 điểm cực trị? A. 6. B. 7. C. 5. D. 4. Lời giải Chọn A
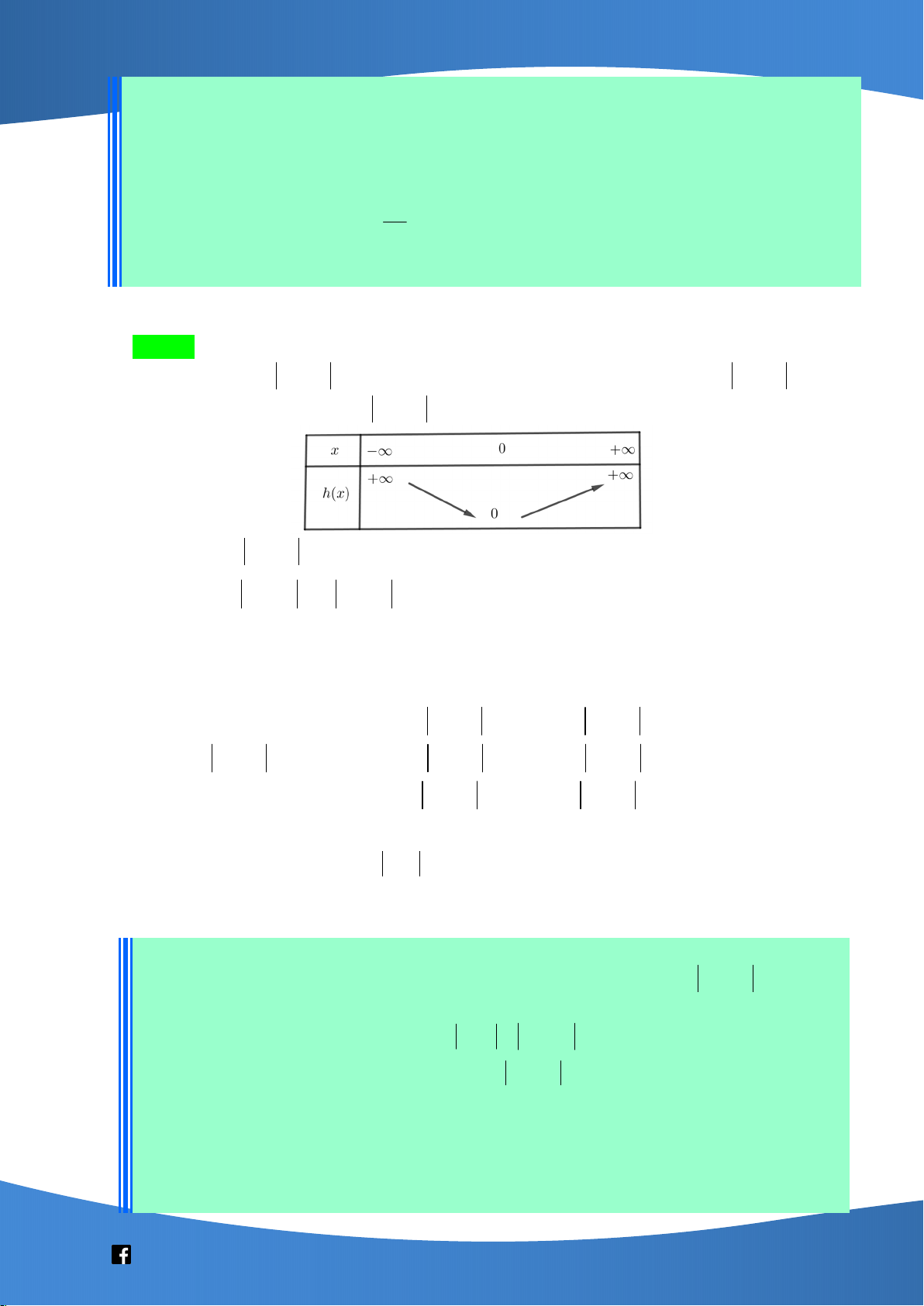
Ta có BBT của hàm y h x 3
x  5x như sau
https:/www.facebook.com/groups/toanvd. Trang 27
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8-2021
Ta có g x 3
x x f  3 5 .
x  5x m . Rõ ràng x  0 là điểm cực trị của hàm số y hx . 3 3
x  5x m  7
x  5x  7  m   Ta có: f  3
x  5x m 3 3
 0   x  5x m  3   x  5x  3  m .   3 3
x  5x m  3 
x  5x  3   m  
Để hàm số g x có ít nhất 3 điểm cực trị thì phương trình g x  0 có ít nhất 2 nghiệm
phân biệt khác 0 và g x đổi dấu khi đi qua ít nhất 2 trong số các nghiệm đó.
Từ BBT ta có 7  m  0  m  7  m 1;2;3;4;5;  6 .
Vậy có 6 giá trị của m thỏa mãn yêu cầu đề bài.
https:/www.facebook.com/groups/toanvd. Trang 28
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8-2021
ĐỀ THI TỐT NGHIỆP THPT ĐỢT 1 NĂM 2021
Bài thi môn: Toán
Thời gian: 90 phút (Không kể thời gian phát đề) Mã đề thi: 102
Đề thi gồm 05 trang 5 Câu 1.
Trên khoảng 0;  , đạo hàm của hàm số 4
y x là: 9 4 1 4 1 5 1 5  A. 4 y '  x . B. 4 y '  x . C. 4 y '  x . D. 4 y '  x . 9 5 4 4 Câu 2.
Cho khối chóp có diện tích đáy 2
B  3a và chiều cao h a . Thể tích của khối chóp đã cho bằng: 3 1 A. 3 a . B. 3 3a . C. 3 a . D. 3 a . 2 3 4 4 4 Câu 3.
Nếu f x dx  6 
và g x dx  5  
thì  f x  g x dx    bằng: 1 1 1 A. 1. B. 11. C. 1. D. 11. Câu 4.
Tập xác định của hàm số 7x y  là: A.  \   0 .
B. 0;  .
C. 0;  . D.  . Câu 5.
Cho hàm số y f x có bảng biến thiên như sau:
Giá trị cực đại của hàm số đã cho bằng A. 3 . B. 1. C. 5 . D. 1. Câu 6.
Diện tích S của mặt cầu bán kính R được tính theo công thức nào dưới đây? 4 A. 2
S  4 R . B. 2
S  16 R . C. 2 S   R . D. 2 S   R . 3 Câu 7.
Trong không gian Oxyz , cho đường thẳng d đi qua điểm M 2; 2;  1 và có một vecto chỉ 
phương u  5;2; 3
  . Phương trình của d là:
x  2  5t
x  2  5t
x  2  5t
x  5  2t    
A. y  2  2t .
B. y  2  2t .
C. y  2  2t .
D. y  2  2t . z  1   3t     z  1 3tz  1 3tz  3   tCâu 8.
Cho hàm số y f x có đồ thị là đường cong như hình vẽ. Hàm số
đã cho đồng biến trên khoảng nào dưới đây? A. 1;  1 .
B. ; 0 . C. 0;  1 . D. 0;  . Câu 9.
Với n là số nguyên dương bất kì, n  5 , công thức nào dưới đây đúng?
https://www.facebook.com/groups/toanvd.vdc Trang 29
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8-2021 n! 5! n! n! A. 5 A  . B. 5 A  . C. 5 A  . D. 5 A  . n 5  ! n  5! nn  5! nn  5! nn  5!
Câu 10. Thể tích của khối lập phương cạnh 4a bằng: A. 3 64a . B. 3 32a . C. 3 16a . D. 3 8a .
Câu 11. Cho hàm số f x 2
x  3 . Khẳng định nào dưới đây đúng? 3 x
A. f x 2
dx x  3x C  .
B. f xdx   3x C  . 3
C. f x 3
dx x  3x C  .
D. f xdx  2x C  .
Câu 12. Trên mặt phẳng tọa độ, điểm M 3; 2 là điểm biểu diễn của số phức nào dưới đây?
A. z  3  2i .
B. z  3  2i . C. z  3   2i . D. z  3   2i . 3 4 1 2
Câu 13. Trong không gian Oxyz , cho mặt phẳng  P  : 2x  5 y z  3  0 . Vecto nào dưới đây
là một vecto pháp tuyến của  P  ?     A. n  2  ;5;1 .
B. n  2;5;1 . C. n  2;5; 1  . D. n  2; 5  ;1 . 3   4   1   2   
Câu 14. Trong không gian Oxyz , cho điểm A4; 1;3 . Tọa độ của vecto OA là
A. 4;1;3 .
B. 4; 1;3 .
C. 4;1; 3 . D. 4;1;3 .
Câu 15. Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên? A. 3
y x  3x  1 . B. 4 2
y  2x  4x  1 . C. 3
y   x  3x  1 . D. 4 2
y  2x  4x  1.
Câu 16. Cho cấp số nhân u với u  3 và u 12 . Công bội của cấp số nhân đã cho bằng n  1 2 1 A. 9 . B. 9  . C. . D. 4 . 4
Câu 17. Cho a  0 và a  1, khi đó 3 loga a bằng 1 1 A. 3 . B. . C.  . D. 3 . 3 3
Câu 18. Đồ thị của hàm số 4 2
y  x  2x  3 cắt trục tung tại điểm có tung độ bằng A. 1. B. 0 . C. 2 . D. 3 .
Câu 19. Cho hai số phức z  5  2i và w  1 4i . Số phức z wbằng:
A. 6  2i .
B. 4  6i .
C. 6  2i . D. 4   6i .
Câu 20. Cho hàm số ( ) x
f x e 1. Khẳng định nào dưới đây đúng? A. 1 ( )d x f x x e    C  . B. ( )d x
f x x e x C  . C. ( )d x
f x x e x C  . D. ( )d x
f x x e C  .
Câu 21. Cho hàm số f (x) có bảng xét dấu đạo hàm như sau:
Số điểm cực trị của hàm số đã cho là A. 5 . B. 3 . C. 2 . D. 4 .
https://www.facebook.com/groups/toanvd.vdc Trang 30
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8-2021 3 3
Câu 22. Nếu f (x)dx  3 
thì 2 f (x)dx  bằng 0 0 A. 3 . B. 18 . C. 2 . D. 6 . x 1
Câu 23. Tiệm cận đứng của đồ thị hàm số y
là đường thẳng có phương trình: x  2 A. x  1  . B. x  2  .
C. x  2 . D. x  1.
Câu 24. Trong không gian Oxyz cho mặt cầu (S) có tâm I 0; 2  
;1 và bán kính bằng 2 . Phương
trình của (S) là: A. 2 2
x   y  2   z  2 2 2 1  2 . B. 2
x   y  2   z   1  2 . C. 2 2
x   y  2   z  2 2 2 1  4 . D. 2
x   y  2   z   1  4 .
Câu 25. Phần thực của số phức z  6  2i bằng A. 2  . B. 2. C. 6. D. 6  .
Câu 26. Tập nghiệm của bất phương trình 2x  5 là A.  ;  log 5 .
B. log 5; ; .
C. ;log 2 . D. log 2; ; . 5  5  2  2 
Câu 27. Nghiệm của phương trình log 3x  2 là: 5   32 25 A. 25. B. . C. 32. D. . 3 3
Câu 28. Cho khối trụ có bán kính đáy r  4 và chiều cao h  3. Thể tích của khối trụ đã cho bằng A. 16 . B. 48. C. 36 . D. 12 .
Câu 29. Cho hình lăng trụ đứng ABC.A ' B 'C ' có tất cả các cạnh bằng nhau (tham khảo hình bên).
Góc giữa hai đường thẳng AA ' và B'C bằng A. 90 .  B. 45 .  C. 30 .  D. 60 . 
Câu 30. Trong không gian, cho hai điểm A0;0; 
1 và B 2;1;3 . Mặt phẳng đi qua A và vuông
góc với AB có phương trình là
A. 2x y  2z 11 0. B. 2x y  2z  2  0 . C. 2x y  4z  4  0 . D. 2x y  4z 17  0 .
Câu 31. Từ một hộp chứa 10 quả bóng gồm 4 quả màu đỏ và 6 quả màu xanh, lấy ngẫu nhiên
đồng thời 3 quả. Xác suất để lấy được 3 quả màu xanh bằng 1 1 3 2 A. . B. . C. . D. . 6 30 5 5
Câu 32. Số phức z thỏa mãn iz  6  5i . Số phức liên hợp của z là
A. z  5  6i . B. z  5   6i .
C. z  5  6i . D. z  5   6i . x a
Câu 33. Biết hàm số y
( a là số thực cho trước, a 1) có đồ thị như trong hình bên. Mệnh x 1
đề nào dưới đây đúng?
https://www.facebook.com/groups/toanvd.vdc Trang 31
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8-2021
A. y  0, x   .
B. y  0, x   1  .
C. y  0, x   1  .
D. y  0, x   .
Câu 34. Trong không gian Oxyz, cho điểm M 2;1;  
1 và mặt phẳng  P : x  3y  2z 1  0.
Đường thẳng đi qua M và vuông góc với  P có phương trình là: x  2 y 1 z 1 x  2 y 1 z 1 A.   . B.   . 1 3  1 1 3  2 x  2 y 1 z 1 x  2 y 1 z 1 C.   . D.   . 1 3  1 1 3  2
Câu 35. Trên đoạn 2;  1 , hàm số 3 2
y x  3x 1 đạt giá trị lớn nhất tại điểm A. x  2  .
B. x  0 . C. x  1  . D. x 1.
Câu 36. Cho hình chóp S.ABC có đáy là tam giác vuông cân tại C, AC  3a và SA vuông góc với
mặt phẳng đáy. Khoảng cách từ B đến mặt phẳng SAC  bằng 3 3 2 A. a . B. a . C. 3a . D. 3 2a . 2 2 2 2 Câu 37. Nếu
f (x)dx  3  thì
2 f x 1 d  x    bằng 0 0 A. 6 . B. 4 . C. 8 . D. 5 .
Câu 38. Với mọi a,b thỏa mãn 3
log a  log b  8 , khẳng định nào dưới đây đúng? 2 2 A. 3
a b  64 . B. 3 a b  256 . C. 3 a b  64 . D. 3
a b  256 . 2
Câu 39. Có bao nhiêu số nguyên x thỏa mãn 3x  9log (x  30)  5  0? 2  A. 30 . B. Vô số. C. 31. D. 29 .
2x 1 khi x  1
Câu 40. Cho hàm số f x  
, giả sử F là nguyên hàm của f trên  thỏa mãn 2
3x  2 khi x  1 
F 0  2 .Giá trị của F  
1  2F 2 bằng. A. 9. B. 15 . C. 11. D. 6 .
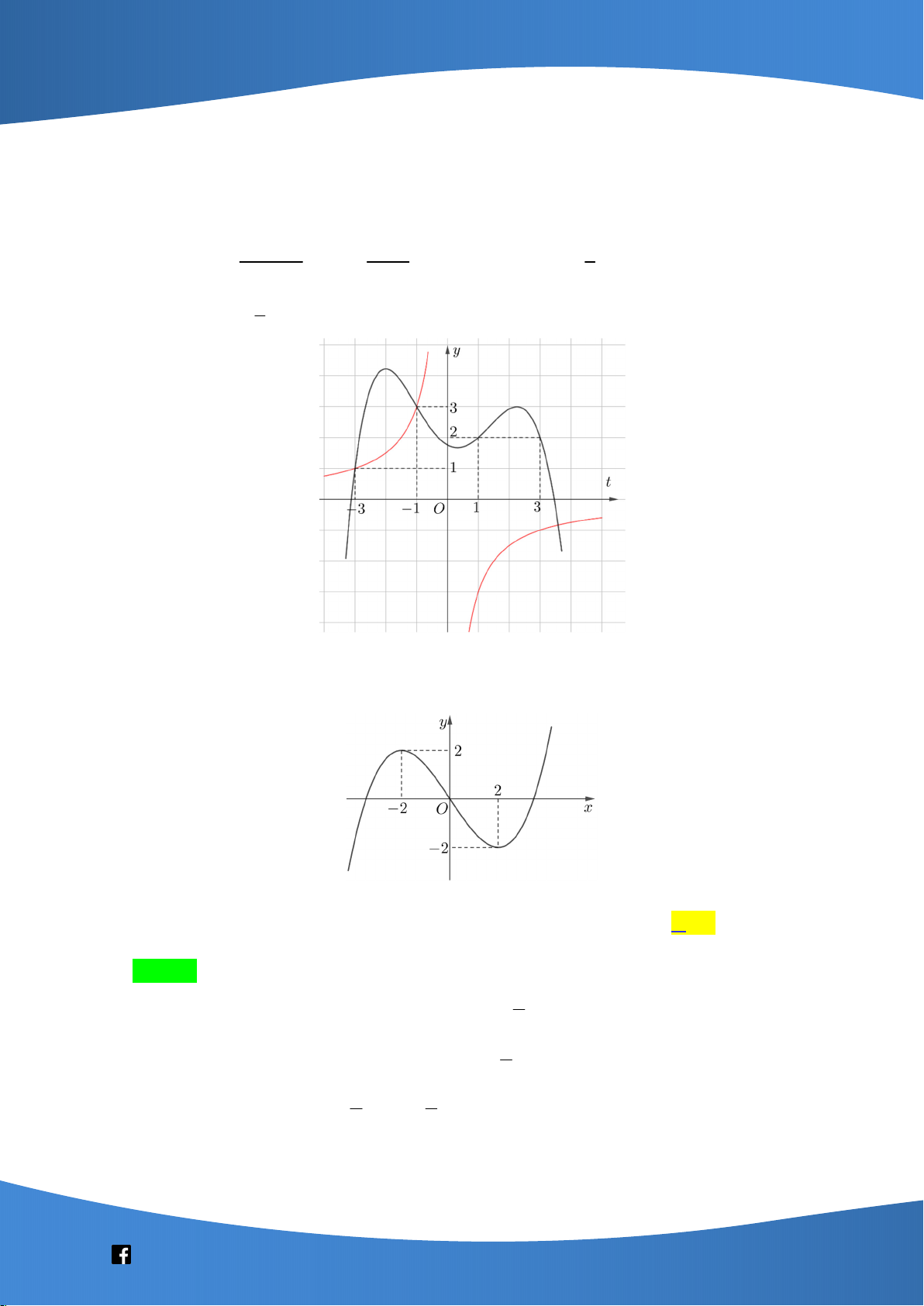
Câu 41. Cho hàm số bậc ba y f x có đồ thị là đường cong trong hình trên. Số nghiệm thực
phân biệt của phương trình f f x  1 là A. 9 . B. 7 . C. 3 . D. 6 .
https://www.facebook.com/groups/toanvd.vdc Trang 32
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8-2021
Câu 42. Xét các số phức z, w thỏa mãn z  1 và w  2 . Khi z iw  6  8i đạt giá trị nhỏ nhất
z w bằng 29 221 A. . B. . C. 3 . D. 5 . 5 5 Câu 43. Cho hàm số   3 2
f x x ax bx c với a, b, c là các số thực. Biết hàm số
g x  f x  f  x  f  x có hai giá trị cực trị là 4 và 2 . Diện tích hình phẳng giới f x
hạn bởi các hàm số y
và y 1 bằng g x  6 A. 2ln 2 . B. ln 6 . C. 3ln 2 . D. ln 2 .
Câu 44. Cho khối hộp chữ nhật ABC .
D A' B 'C ' D ' có đáy là hình vuông, BD  4a , góc giữa hai
mặt phẳng  A' BD và  ABCD = 30o . Thể tích của khối hộp chữ nhật đa cho bằng? 16 3 16 3 A. 3 a B. 3 48 3a C. 3 a D. 3 16 3a 9 3  1  2
Câu 45. Có bao nhiêu số nguyên y sao cho tồn tại x  ; 4 3x xy 12 x   thỏa mãn 27
 1 xy 27 ?  3  A. 14 . B. 27 . C. 12 . D. 15 . x 1 y z 1
Câu 46. Trong không gian Oxyz , cho đường thẳng d :   và mặt phẳng 1 1 2
P : 2x y z  3  0 . Hình chiếu vuông góc của d trên  P là đường thẳng có phương trình: x 1 y z 1 x  1 y z 1 x 1 y z 1 x 1 y z 1 A.   . B.   . C.   . D.   . 4 5 13 4 5 1 3 5  1 4 5 13
Câu 47. Cắt hình nón  bởi mặt phẳng đi qua đỉnh và tạo với mặt phẳng chứa đáy một góc
bằng 60 ta được thiết diện là tam giác đều cạnh 2 .
a Diện tích xung quanh của  bằng A. 2 7a . B. 2 13 a . C. 2 2 7 a . D. 2 2 13 a .
Câu 48. Trên tập hợp các số phức, xét phương trình 2
z  m   2 2
1 z m  0 ( m là tham số thực).
Có bao nhiêu giá trị của m để phương trình đó có nghiệm z thỏa mãn z  5 ? 0 0 A. 2 . B. 3 . C. 1. D. 4 .
Câu 49. Cho hàm số y f x có đạo hàm f  x   x   2 8
x  9 với x   . Hỏi có bao nhiêu
giá trị nguyên dương của m để hàm số f  3
x  6x m có ít nhất 3 cực trị? A. 5. B. 7. C. 8. D. 6.
Câu 50. Trong không gian Oxyz , cho hai điểm A1;  3; 2 , B 2;1;  3 . Xét hai điểm M , N thay
đổi trong mặt phẳng Oxy sao cho MN 1. Giá trị lớn nhất của AM BN bằng A. 17 . B. 41 . C. 37 . D. 61 .
https://www.facebook.com/groups/toanvd.vdc Trang 33
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8-2021
BẢNG ĐÁP ÁN ĐỀ 102
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
C D D D A A C C C A B D A B D D B D C C D D C D C
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
A D B B B A C C B B C B B C A B A A C A A A B B C
LỜI GIẢI CHI TIẾT 2
Câu 39. Có bao nhiêu số nguyên x thỏa mãn 3x  9x log (x  30)  5  0? 2  A. 30 . B. Vô số. C. 31. D. 29. Lời giải Chọn C 2 x x
Điều kiện xác định: x  30 . Đặt f ( )
x  3 9  log x30 5 2     2 3x   9x 2  x  2 xx  0
Xét phương trình f (x)  0       . log (x  30)  5 5  x  30  2 x  2 (kép) 2   Ta có bảng xét dấu:
Suy ra bất phương trình f (x)  0 có tâp nghiệm là: S   3  0;  0   2 .
Với x  x   2  9; 2  8;...; 2  ; 1  ;0;  2 .
Vậy có 31 số nguyên x thỏa mãn. 2 x  1 khi x  1
Câu 40. Cho hàm số f x  
, giả sử F là nguyên hàm của f trên  thỏa 2 3x  2 khi x  1  mãn F 
0  2. Giá trị của F  
1  2F 2 bằng. A. 9. B. 15 . C. 11. D. 6. Lời giải Chọn A Cách 1: Ta có: 2x 1 2
dx x x c 2 3
3x  2 dx x  2x c 1  ;   2 2 
x x C khi x 1 1
Suy ra F x  f x dx   3
x  2x C khi x 1  2
Mà ta có F 0  2  C  2 . 2
Mặt khác hàm số F là nguyên hàm của f trên  nên y F x liên tục tại x  1
Suy ra lim F x   lim F x   C  1 . 1 x 1 x 1   2  x x 1 khi x 1 F    1  3
Khi đó ta có: F x   suy ra  . 3
x  2x  2 khi x 1  F  2  3  Vậy F  
1  2F 2  9.
https://www.facebook.com/groups/toanvd.vdc Trang 34
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8-2021 Cách 2:
Dễ thấy hàm số f x liên tục trên  . Khi đó ta có: 1 F   1  F   2
0  (3x 2)dx  1   F   1 1  . 0 1  2 F   1  2F   2 2 
(3x  2)dx  2 (2x 1
 )dx 3F   1  2 43  9   . 1 1
Câu 41. Cho hàm số bậc ba y f x có đồ thị là đường cong trong hình trên. Số nghiệm thực
phân biệt của phương trình f f x 1 là A. 9. B. 7. C. 3. D. 6. Lời giải Chọn B
f x  ,
a a    1 
Từ f f x 1  f   x  0 .
f x  ,b 1 b  2 
f x  a với a  1 phương trình có một nghiệm
f x  0 phương trình có ba nghiệm phân biệt
f x  b với 1 b  2 phương trình có 3 nghiệm phân biệt.
Vậy số nghiệm thực phân biệt của phương trình f f x 1 là 7.
Câu 42. Xét các số phức ,
z w thỏa mãn z 1 và w  2 . Khi z iw  6 8i đạt giá trị nhỏ nhất,
z w bằng 29 221 A. . B. . C. 3. D. 5 . 5 5 Lời giải Chọn A
https://www.facebook.com/groups/toanvd.vdc Trang 35
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8-2021
Ta có z iw  6  8i  6  8i z iw  10  1  2  7 .  3 4  3 4 z    i z    i    
Dấu bằng xảy ra khi và chỉ khi 5 5 5 5    . 6 8 8 6 iw i     w    i   5 5   5 5 29
Khi đó z w  . 5 Câu 43. Cho hàm số   3 2
f x x ax bx c với a, b, c là các số thực. Biết hàm số
g x  f x  f  x  f  x có hai giá trị cực trị là 4
 và 2. Diện tích hình phẳng giới f x
hạn bởi các hàm số y
và y  1 bằng g x  6 A. 2ln 2 . B. ln 6 . C. 3ln 2 . D. ln 2 . Lời giải Chọn A
Ta có: g x  f x  f  x  f  x 3
x  a   2
3 x  2a b  6 x 2a b c
g x  f  x  f  x  f  x 2
 3x  2ax b  6 x  2a  6 2
 3x  2a  6 x 2a b  6 .  x x
Do g x có hai cực trị là 5
 và 3 nên g x 1  0  
với g x  4
 , g x  2 . 2  1  x x  2
Phương trình hoành độ giao điểm f x
f x  g x  6 2
3x  2a  6 x  2a b  6 g   x   1   0   0   0 g x  6 g x  6
g x   6
g x   6
Phương trình này cũng có hai nghệm phân biệt x , x 1 2 f x
Như vậy diện tích hình phẳng giới hạn bởi các hàm số y  và y  1 là g x  6 2 x g xx S
 ln g x 2  6  ln 2  6  ln 4   6  2 ln 2  . g x x   1 6 x 1
Câu 44. Cho khối hộp chữ nhật ABC .
D A ' B 'C ' D ' có đáy là hình vuông, BD  4a , góc giữa hai
mặt phẳng  A' BD và  ABC
D = 3 0 o . Thể tích của khối hộp chữ nhật đã cho bằng ? 16 3 3 16 3 3 A. 3 a
B. 48 3a C. 3 a D.16 3a 9 3 Lời giải Chọn C
https://www.facebook.com/groups/toanvd.vdc Trang 36
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8-2021
Gọi O là trung điểm của BD . Ta có: A  ' AB A
 ' AD suy ra A'B A'D suy ra A  ' BD cân.
 A ' BD   ABCD  BD
Mà A'O BD   A B
D  ABCD     ,  A OA  30 .   AO BD  2a 3 Xét AO
A vuông tại A có: AA AA AA AA tan 30o      A' A  2 . a tan 30  . AO AC BD 2a 3 2 2
Xét hình vuông ABCD có: BD AB 2  AB  2a 2. 2 a 16 3
Vậy thể tích của khối hộp chữ nhật bằng: V A' . A AB =  a 2 2 3 . 2 2 = 3 a . 3 3  1  2
Câu 45. Có bao nhiêu số nguyên y sao cho tồn tại x ;4   thỏa mãn
3 x xy     12 27 1 27 x xy ?  3  A. 14. B. 27 . C. 12. D. 15 . Lời giải Chọn A  1
TH1: y  0, vì xy  1 và x
nên ta có y  3. 3
Ta có thể kiểm tra trực tiếp để xem xét có nhận y  2, y  1, y  0 hay không.   1  x  0  ; 4    2  3  +) Nếu 3x 1  2 x 2 y 0 27 1 3x 12x 0        
(trường hợp này loại).   1  x  4  ; 4      3 
+) Nếu y  1 thỏa mãn.
+) Nếu y  2 thỏa mãn.
TH2: Khi y  1, ta có: log 1 xy 27   2 3x xy 12 27  (1 )27 x xy 2
 3x 12x  log
1 xy xy  3x 12   y  0. 27   x log 1 xy 27    1 
Xét hàm g x  3x 12   y trên ; 4 . x  3    ln 1 xyy 1 3  1 
Ta có g x  3    3   3   0, x  ; 4 . 2 x ln 27 x 1 xy  2 ln 27 3x ln 3 ln 3  3    
https://www.facebook.com/groups/toanvd.vdc Trang 37
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8-2021  1 
Do đó, hàm g x đồng biến trên ; 4 
. Vì thế phương trình gx  0 có nghiệm trên 3     1   1  ; 4   khi và chỉ khi g g   4  0 .  3   3
Áp dụng bất đẳng thức ln 1 u  u với mọi u  0 , ta có ln1 4yy g 4    y    y  0. 18ln3 3ln3  1   y  Do đó g  0  log 1
y 11  0 1  y 12   3  
(do y là số nguyên dương).  3   3   1  2
Vậy có 14 giá trị nguyên y sao cho tồn tại x ;4 3 x xy 12 x   thỏa mãn 27  1 xy .27 .  3  x  1 y z 1
Câu 46. Trong không gian Oxyz , cho đường thẳng d :   và mặt phẳng 1 1 2
P : 2x y z 3  0. Hình chiếu vuông góc của d trên P là đường thẳng có phương trình: x  1 y z 1 x  1 y z  1 A.   . B.   . 4 5 13 4 5 1 x 1  y z 1  x 1  y z 1  C.   . D.   . 3 5  1 4 5 13 Lời giải Chọn A
Gọi  là đường thẳng cần tìm. 
Đường thẳng d đi qua A 1  ;0; 
1 có 1 VTCP là: u  1;1;2 . 
Mặt phẳng  P có 1 VTPT là: n  2;1;  1 .      
Ta có v  u, n   3;5; 1 ; a  n, v   4; 5;13 .    
 là hình chiếu của d trên  P  đi qua A 1  ;0;  1 và có 1 VTCP   
a   n, v   4; 5;13 .   x  1 y z 1 Suy ra phương trình  :   . 4 5 13
Câu 47. Cắt hình nón  
 bởi mặt phẳng đi qua đỉnh và tạo với mặt phẳng chứa đáy một góc
bằng 60 ta được thiết diện là tam giác đều cạnh 2a. Diện tích xung quanh của    bằng 2 2 2 2
A. 7a .
B. 13a .
C. 2 7a . D. 2 13 a . Lời giải Chọn A
https://www.facebook.com/groups/toanvd.vdc Trang 38
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8-2021
Mặt phẳng  P cắt hình nón theo thiết diện là tam giác đều SABcạnh 2a AB  2 . a
Kẻ OH AB tại H AH  , a SH a 3. a
Góc giữa mặt phẳng  SAB với mặt đáy bằng  3
60  SHO  60  SO SH .sin 60  . 2 SO a 3 a 7 Mà 2 2 2 2 OH    r AH OH
SA h r  4 . a tan 60 2 2 a 7 Vậy 2
S   rl  .
.2a  7 a . xq 2
Câu 48. Trên tập hợp các số phức, xét phương trình 2
z  m   2 2
1 z m  0 ( mlà tham số thực).
Có bao nhiêu giá trị của m để phương trình đó có nghiệm z z  5 0 thỏa mãn ? 0 A. 2. B. 3. C. 1. D. 4. Lời giải Chọn B
Ta có   2m 1.  1 1 1
TH1:   0  m   thì z  , suy ra m   (loại). 2 0 2 2  1
TH2:   0  m   thì z m  1 
2m  1 .i hoặc z m  1  2m  1 .i . 2 0 0 m  5 L 2  
Theo đề bài z  5  m 1  2  m 1  25  . 0      m  5   N    1
TH 3:   0  m   thì phương trình có hai nghiệm thực phân biệt 2
Theo đề bài z  5  z  5  . 0 0 2 + Khi z 5: m 1  0m 1
 5  0 m  5 10 0
thế vào phương trình ta được (nhận). + Khi z  5  0
: thế vào phương trình ta được 2
m  10m  35  0 vô nghiệm.
Vậy có ba giá trị của m.
Câu 49. Cho hàm số y f x có đạo hàm f  x   x   2 8
x  9 với x . Hỏi có bao nhiêu
giá trị nguyên dương của m để hàm số f  3
x  6 x m  có ít nhất 3 cực trị? A. 5. B. 7. C. 8. D. 6. Lời giải
https://www.facebook.com/groups/toanvd.vdc Trang 39
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8-2021 Chọn B
Hàm số y f x có f  x  0 tại x  8, x  3 .
Đặt g x   f  3
x  6 x m  .   2 3x  6 3 x  6x 3 
Ta có: g x 
f x  6x m  . f  3
x  6x m x  0 . 3      x  6x
Với x  0 là 1 cực trị của g x
Để g x có ít nhất 3 cực trị thì 
g x phải có ít nhất 3 nghiệm bội lẻ hay f  3
' x  6 x m   0 có ít nhất 2 nghiệm. 3
x  6x m  3    f ' 3
x  6x m 3
 0   x  6x m  3 . Ta có đồ thị u x 3
x  6 x ( với m  0):  3
x  6x m  8  Để f  3
' x  6 x m   0 có ít nhất 2 nghiệm thì: 8  m  0  m  8  m1;7 .
Vậy có 7 giá trị m.
Câu 50. Trong không gian Oxyz , cho hai điểm A1;  3; 2 , B 2  ;1; 
3 . Xét hai điểm M, N thay
đổi trong mặt phẳng Oxy  sao cho MN 1. Giá trị lớn nhất của AM BN bằng A. 17 . B. 41 . C. 37. D. 61. Lời giải Chọn C
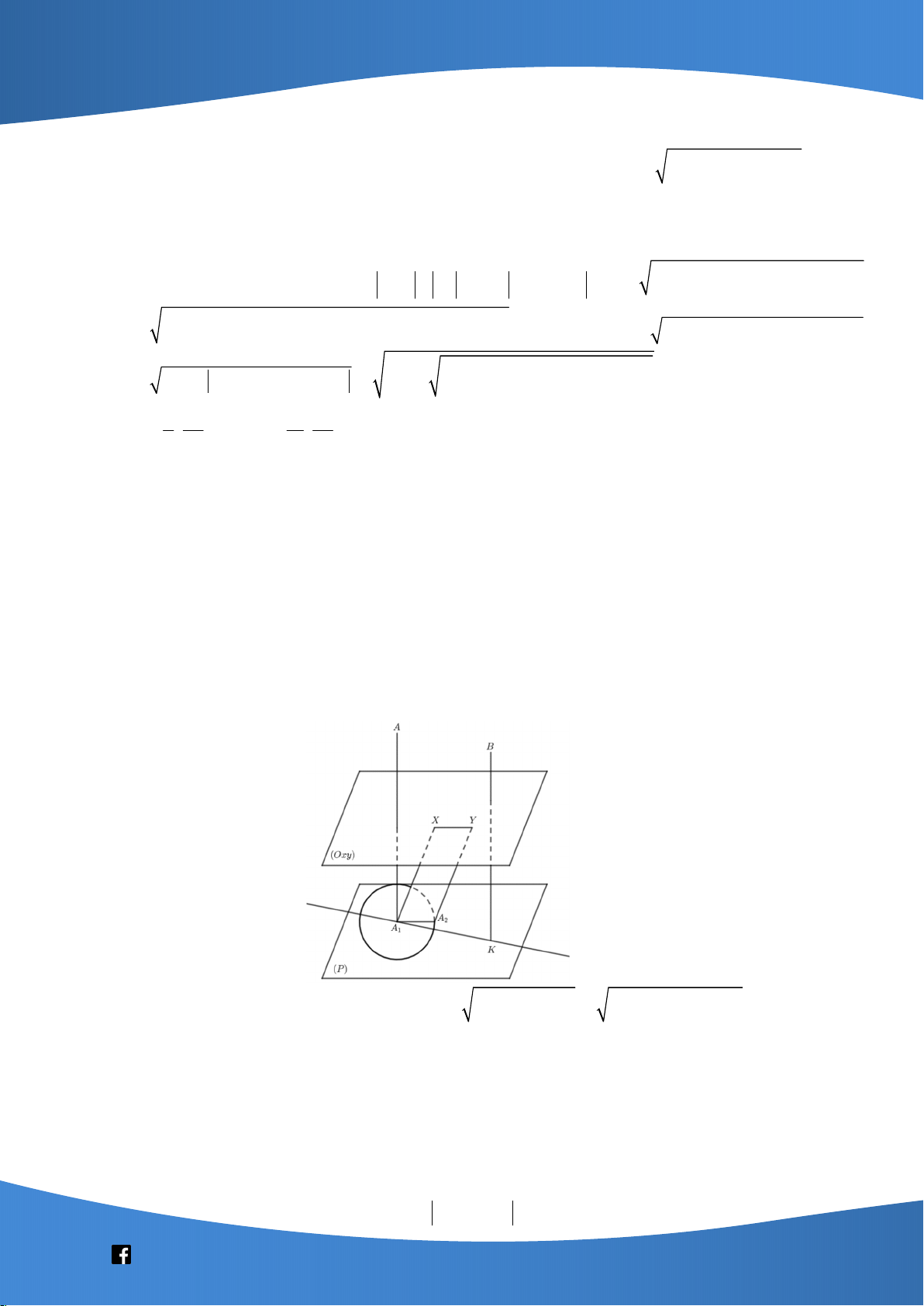
Đề thấy hai điểm A, B nằm khác phía so với mặt phẳng Oxy  .
Gọi H lần lượt là hình chiếu vuông góc của A lên mặt phẳng Oxy  , khi đó ta có: H 1; 3  ;  0 .
https://www.facebook.com/groups/toanvd.vdc Trang 40
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8-2021 Lấy điểm A
Oxy A  1; 3  ; 2 
. Khi đó AM AM 1  
1 đối xứng với A qua mặt phẳng   1 .
  Lấy điểm A A A MN AA NM AM A N 2 sao cho . Tứ giác là hình bình hành nên . 1 2 1 2 1 2
Khi đó ta dễ thấy hai điểm A Oxy
2 và B nằm cùng phía so với mặt phẳng   .
Do MN 1 nên điểm N thuộc đường tròn C tâm M bán kính R MN 1 nằm trên mặt phẳng Ox
y nên điểm A C A R R
2 thuộc vào đường tròn  ' tâm 1 và bán kính ' 1
và nằm trong mặt phẳng z  2  .
Ta có: AM BN A M BN A N BN A B . Dấu bằng xảy ra khi N A B Oxy . 2   1 2 2
Để AM BN đạt giá trị lớn nhất thì A B 2
phải đạt giá trị lớn nhất.
Gọi K lần lượt là hình chiếu vuông góc của B lên mặt phẳng z  2  , khi đó ta có: K 2  ;1; 
2 và BK 1, AK  5 1 .
Tam giác BKA2 vuông tại K nên ta có: 2 2 2 A B BK KA  1  KA . 2 2 2 Để A B KA 2
phải đạt giá trị lớn nhất thì 2 phải lớn nhất. Mà 2
KA A K R '  5 1  6  A B  1 6  37 2 1 2
Suy ra giá trị lớn nhất của AM BN bằng 37, dấu bằng xảy ra khi N A B Oxy . 2  
https://www.facebook.com/groups/toanvd.vdc Trang 41
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8-2021
ĐỀ THI TỐT NGHIỆP THPT ĐỢT 1 NĂM 2021
Bài thi môn: Toán
Thời gian: 90 phút (Không kể thời gian phát đề) Mã đề thi: 103
Đề thi gồm 05 trang Câu 1.
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên? 1 1 1 1 A. 3
y   x  2x  . B. 3
y x  2x  . C. 4 2
y   x  2x  . D. 4 2
y x  2x  . 2 2 2 2 Câu 2.
Cho cấp số nhân u với u  3 và u 15 . Công bội của cấp số nhân đã cho bằng n  1 2 1 A. 1  2 . B. . C. 5 . D. 12 . 5 Câu 3.
Cho khối chóp có diện tích đáy 2
B  7a và chiều cao h a . Thể tích của khối chóp đã cho bằng 7 7 7 A. 3 a . B. 3 a . C. 3 a . D. 3 7a . 6 2 3 4 4 4 Câu 4.
Nếu f (x)dx  5 
và g(x)dx  4  
thì  f (x)  g(x)dx  bằng 1 1 1 A. 1. B. 9  . C. 1. D. 9 . Câu 5.
Trong không gian Oxyz , cho đường thẳng d đi qua điểm M  3
 ;1;2 và có một vectơ 
chỉ phương u  2;4; 
1 . Phương trình của d là
x  3  2t
x  3  2t
x  3  2t
x  2  3t    
A. y  1 4t .
B. y  1 4t .
C. y  1 4t .
D. y  4  t . z  2  t     z  2  tz  2  tz  1   2tCâu 6.
Diện tích S của mặt cầu bán kinh R được tính theo công thức nào dưới đây? 4 A. 2
S   R . B. 2 S   R . C. 2
S  4 R . D. 2 S  16 R . 3 Câu 7.
Trong không gian Oxyz , cho mặt phẳng  P : x  2y  2z  3  0 . Vectơ nào dưới đây là
một vectơ pháp tuyến của  P ?    
A. n  1;2;2 .
B. n  1; 2;2 .
C. n  1; 2; 3 .
D. n  1;2; 2 . 2   4   1   3   Câu 8.
Trong không gian Oxyz , cho mặt cầu S  có tâm I 0;1; 2 và bán kinh bằng 3 . Phương
trình của S  là: A.  
x   y     z  2 2 1 2  9 .
B. x   y     z  2 2 1 2  9 . C.  
x   y     z  2 2 1 2  3 .
D. x   y     z  2 2 1 2  3 . Câu 9.
Cho hàm số f x 2
x 1. Khẳng định nào dưới đây đúng?
https:/www.facebook.com/groups/toanvd. Trang 42
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 3 8-2021 x
A. f xdx x   x C  .
B. f xdx   x C  . 3
C. f x 2
dx x x C  .
D. f xdx  2x C  .
Câu 10. Cho hàm số y f x có bảng xét dấu của đạo hàm như sau:
Số điểm cực trị của hàm số đã cho là: A. 2 . B. 3 . C. 4 . D. 5 .
Câu 11. Tập xác định của hàm số 6x y  là:
A. 0;   . B.  \   0 .
C. 0;  . D.  . 3 3
Câu 12. Nếu f x dx  2 
thì 3 f x dx  bằng 0 0 A. 6 . B. 1. C. 1. D. 0 .
Câu 13. Trên mặt phẳng tọa độ, điểm M ( 2
 ;3) là điểm biểu diễn số phức nào dưới đây?
A. z  2  3i . B. z  2   3i . C. z  2   3i .
D. z  2  3i . 3 4 1 2
Câu 14. Cho hàm số ( ) x
f x e  3 . Khẳng định nào dưới đây đúng? A. ( )d x
f x x e  3x C  . B. ( )d x
f x x e C  . C. 3 ( )d x f x x eC  . D. ( )d x
f x x e  3x C  .
Câu 15. Cho hàm số y f (x) có đồ thị là đường cong trong hình bên. Hàm số đã cho đồng biến
trong khoảng nào dưới đây? A. ( ;  2) . B. (0;2) . C. (2;2) . D. (2;) .
Câu 16. Đồ thị hàm số 3 2
y  x  2x 1cắt trục tung tại điểm có tung độ bằng A. 3 . B. 1. C. 1. D. 0 . 4
Câu 17. Trên khoảng (0;) , đạo hàm của hàm số 3
y x là: 1 4 1 4 7 3 1 3 A. 3 y  x . B. 3 y  x . C. 3 y  x . D. 3 y  x . 3 3 7 4
Câu 18. Cho a  0 và a  1, khi đó log a bằng a 1 1 A. 2 . B. 2 . C.  . D. . 2 2 
Câu 19. Trong không gian Oxyz cho điểm ( A 3;2; 4
 ) . Tọa độ vectơ OA là A. (3; 2  ; 4  ) . B. ( 3  ; 2  ; 4) . C. (3;2; 4  ) . D. (3;2;4) .
Câu 20. Tập nghiệm của phương trình 2x  3 là A. (log 2; )  . B.  ;  log 3 . C.  ;  log 2 . D. (log 3; )  . 3  2  3 2
Câu 21. Cho hai số phức z  1 2i và w  3  4i . Số phức z w bằng
A. 2  6i .
B. 4  2i .
C. 4  2i . D. 2   6i .
Câu 22. Cho hàm số y f (x) có bảng biến thiên như hình vẽ sau
https:/www.facebook.com/groups/toanvd. Trang 43
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8-2021
Giá trị cực đại của hàm số đã cho bằng A. 3 . B. 0 . C. 2 . D. 1.
Câu 23. Thể tích khối lập phương cạnh 3a bằng A. 3 27a . B. 3 3a . C. 3 9a . D. 3 a . 2x  1
Câu 24. Tiệm cận đứng của đồ thị hàm số y
là đường thẳng có phương trình x 1 1
A. x  2 .
B. x  1 . C. x  . D. 1. 2
Câu 25. Phần thực của số phức z  3 2i bằng: A. 2 . B. 3  . C. 3 . D. 2  .
Câu 26. Nghiệm của phương trình log (2x)  2 là: 3 9 A. x x  .
C. x  4 . D. x  8 2 . B. 9
Câu 27. Với n là số nguyên dương bất kì, n  2 , công thức nào sau đây đúng? n  2 ! 2   2! n! n! A. A  . B. 2 A  . C. 2 A  . D. 2 A n n! nn  2! n 2  ! n  2! nn  2!
Câu 28. Cho khối trụ có bán kính đáy r  2 và chiều cao h  3 . Thể tích của khối trụ đã cho bằng A. 12 . B. 18 . C. 6 . D. 4
Câu 29. Trong không gian Oxyz , Cho điểm M 1;2; 
1 và mặt phẳng  P : 2x y  3z 1  0
Đường thẳng đi qua M và vuông góc với mặt phẳng  P có phương trình là: x 1 y  2 z  1 x 1 y  2 z  1 A.   . B.   . 2 1 1 2 1 3 x  1 y  2 z 1 x  1 y  2 z 1 C.   . D.   . 2 1 1 2 1 3
Câu 30. Cho hình lăng trụ đứng AB . C A BC
  có tất cả các cạnh bằng nhau (tham khảo hình bên).
Góc giữa hai đường thẳng A B  và CC bằng: A. 45o . B. 30o . C. 90o . D. 60o .
Câu 31. Cho số phức z thỏa mãn iz  3  2i . Số phức liên hợp của z là:
A. z  2  3i .
B. z  2  3i .
C. z  2  3i .
D. z  2  3i .
Câu 32. Cho hình chóp S.ABC có đáy là tam giác vuông cân tại C , AC a và SA vuông góc với
mặt phẳng đáy. Khoảng cách từ B đến mặt phẳng SAC bằng
https:/www.facebook.com/groups/toanvd. Trang 44
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8-2021 1 2 A. a . B. 2a . C. a . D. a . 2 2
Câu 33. Từ một hộp chứa 10 quả bóng gồm 4 quả màu đỏ và 6 quả màu xanh. Lấy ngẫu nhiên
đồng thời 3 quả. Xác suất để lấy được 3 quả màu đỏ bằng 1 1 2 1 A. . B. . C. . D. . 5 6 5 30
Câu 34. Với mọi a,b thỏa mãn 3
log a  log b  7 , khẳng định nào dưới đây đúng? 2 2 A. 3
a b  49 . B. 3 a b  128 . C. 3
a b  128 . D. 3 a b  49 .
Câu 35. Trong không gian Oxyz , cho hai điểm A0;0; 
1 và B1;2;3 . Mặt phẳng đi qua A và
vuông góc với AB có phương trình là:
A. x  2 y  2z 11  0 .
B. x  2 y  2z  2  0 .
C. x  2 y  4z  4  0 .
D. x  2 y  4z 17  0 .
Câu 36. Trên đoạn 0;  3 , hàm số 3
y x  3x  4 đạt giá trị nhỏ nhất tại điểm
A. x  1 .
B. x  0 .
C. x  3 . D. x  2 . 2 2
Câu 37. Nếu f x dx  6 
thì 2 f x 1 dx    bằng 0 0 A. 12 . B. 10 . C. 11. D. 14 x a
Câu 38. Biết hàm số y
, ( a là số thực cho trước và a  1
 ) có đồ thị như trong hình bên. x 1
Mệnh đề nào dưới đây đúng?
A. y  0, x   1 .
B. y  0, x    .
C. y  0, x    .
D. y  0, x   1. 2
Câu 39. Có bao nhiêu số nguyên x thỏa mãn 2x  4x log x 14  4  0 2     ? A. 14 . B. 13 . C. Vô số. D. 15 .
2x  3 khi x  1
Câu 40. Cho hàm số f x  
. Giả sử F là nguyên hàm của f trên  thỏa mãn 2
3x  2 khi x  1 
F 0  2 . Giá trị của F  
1  2F 2 bằng A. 23. B. 11. C. 10 . D. 21 .
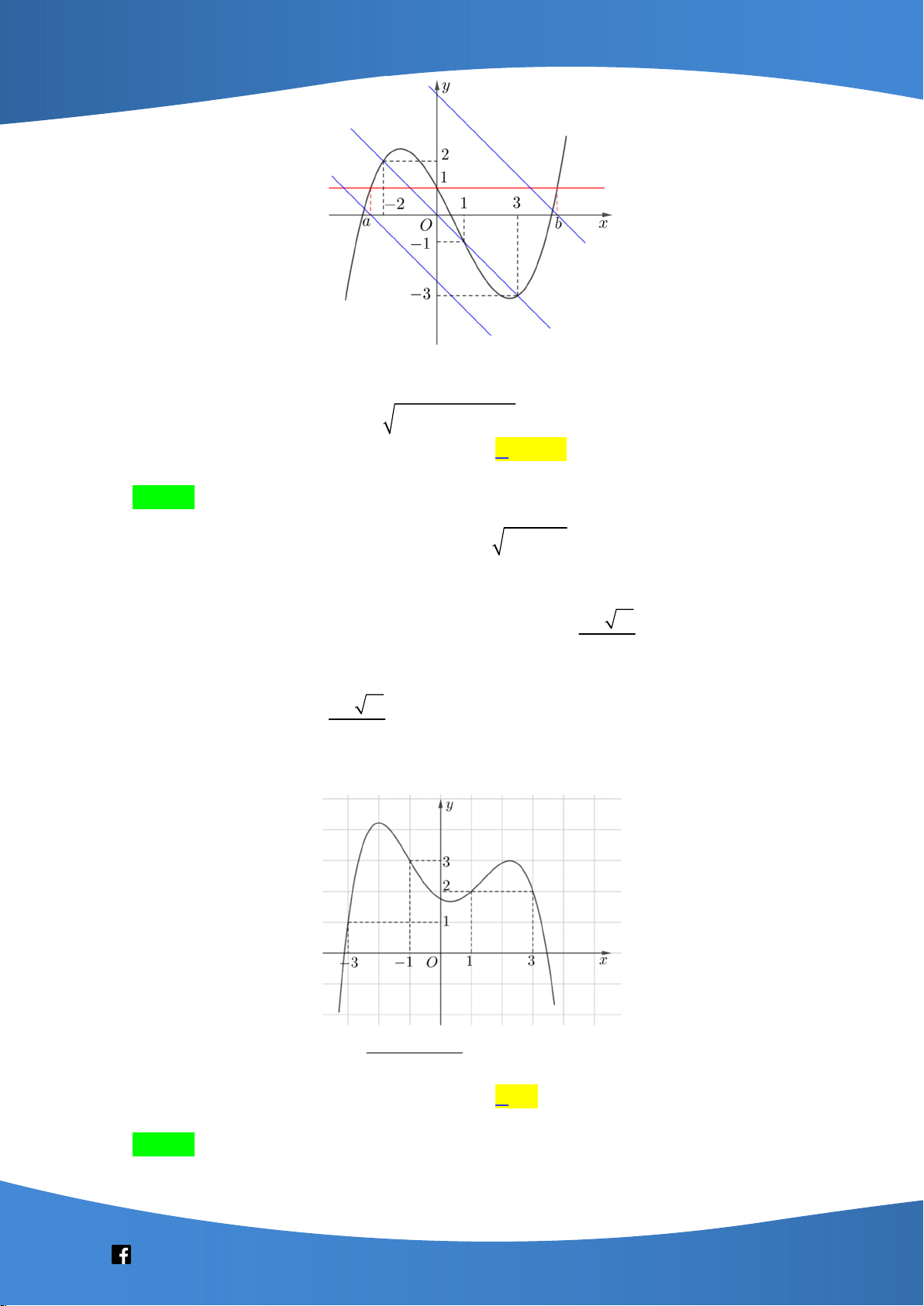
Câu 41. Cho hàm số bậc bốn y f x có đồ thị là đường cong trong hình bên dưới.
Số nghiệm thực phân biệt của phương trình f f x  0 là A. 4 . B. 10 . C. 12 . D. 8 .
https:/www.facebook.com/groups/toanvd. Trang 45
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8-2021
Câu 42. Xét các số phức z, w thỏa mãn z  1 và w  2 . Khi z iw  6  8i đạt giá trị nhỏ nhất,
z w bằng? 29 221 A. 3 . B. . C. 5 . D. . 5 5 x 1 y  2 z  1
Câu 43. Trong không gian Oxyz , cho đường thẳng d :   và mặt phẳng 1 1 2
(P) : x  2 y z  6  0 . Hình chiếu vuông góc của d trên (P) là đường thẳng có phương trình: x  1 y  2 z 1 x 1 y  2 z  1 A.   . B.   . 3 1 1 3 1 1 x  1 y  2 z 1 x 1 y  2 z  1 C.   . D.   . 1 4 7 1 4 7  1  2
Câu 44. Có bao nhiêu số nguyên y sao cho tồn tại x  ;5 3 x xy 15 x   thỏa mãn 27  1 xy  27 .  3  A. 17 . B. 16 . C. 18 . D. 15 .
Câu 45. Cho khối hộp chữ nhật ABC . D A BCD
  có đáy là hình vuông, BD  2a , góc giữa hai mặt phẳng  A B
D và  ABCD bằng 60 . Thể tích của khối hộp chữ nhật đã cho bằng 2 3 2 3 A. 3 a . B. 3 6 3a . C. 3 a . D. 3 2 3a . 9 3 Câu 46. Cho hàm số   3 2
f x x ax bx c với a , b , c là các số thực. Biết hàm số
g x  f x  f  x  f  x có hai giá trị cực trị là 5
 và 3 . Diện tích hình phẳng giới f x
hạn bởi các đường y
và y  1 bằng g x  6 A. 2ln 3 . B. ln 2 . C. ln15 . D. 3ln 2 .
Câu 47. Cắt hình nón  N  bởi mặt phẳng đi qua đỉnh và tạo với mặt phẳng chứa đáy một góc bằng 0
30 , ta được thiết diện là tam giác đều cạnh 4 .
a Diện tích xung quanh của nón bằng A. 2 4 7 a . B. 2 8 7 a . C. 2 8 13 a . D. 2 4 13 a .
Câu 48. Trên tập hợp các số phức, xét phương trình 2
z  m   2 2
1 z m  0 ( m là tham số thực).
Có bao nhiêu giá trị của m để phương trình đó có nghiệm z thỏa mãn z  8 ? o o A. 4 . B. 3 . C. 2 . D. 1.
Câu 49. Trong không gian Oxyz , cho hai điểm A1; 3  ;2 và B 2  ;1; 4
  . Xét hai điểm M và N
thay đổi thuộc mặt phẳng Oxy sao cho MN  4 . Giá trị lớn nhất của AM BN bằng A. 5 2 . B. 3 13 . C. 61 . D. 85 .
Câu 50. Cho hàm số y f x có đạo hàm f  x   x   2 10
x  25,x   . Có bao nhiêu giá trị
nguyên dương của tham số m để hàm số g x  f  3
x  8x m có ít nhất 3 điểm cực trị A. 9 . B. 25 . C. 5 . D. 10 .
BẢNG ĐÁP ÁN ĐỀ 103
https:/www.facebook.com/groups/toanvd. Trang 46
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8-2021
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
B C C D C C B A B C D A C A B C B D C D C A A B C
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
A D A B A A D D B B A B A D D B D D A D A D B D A
LỜI GIẢI CHI TIẾT CÁC CÂU VD – VDC 2
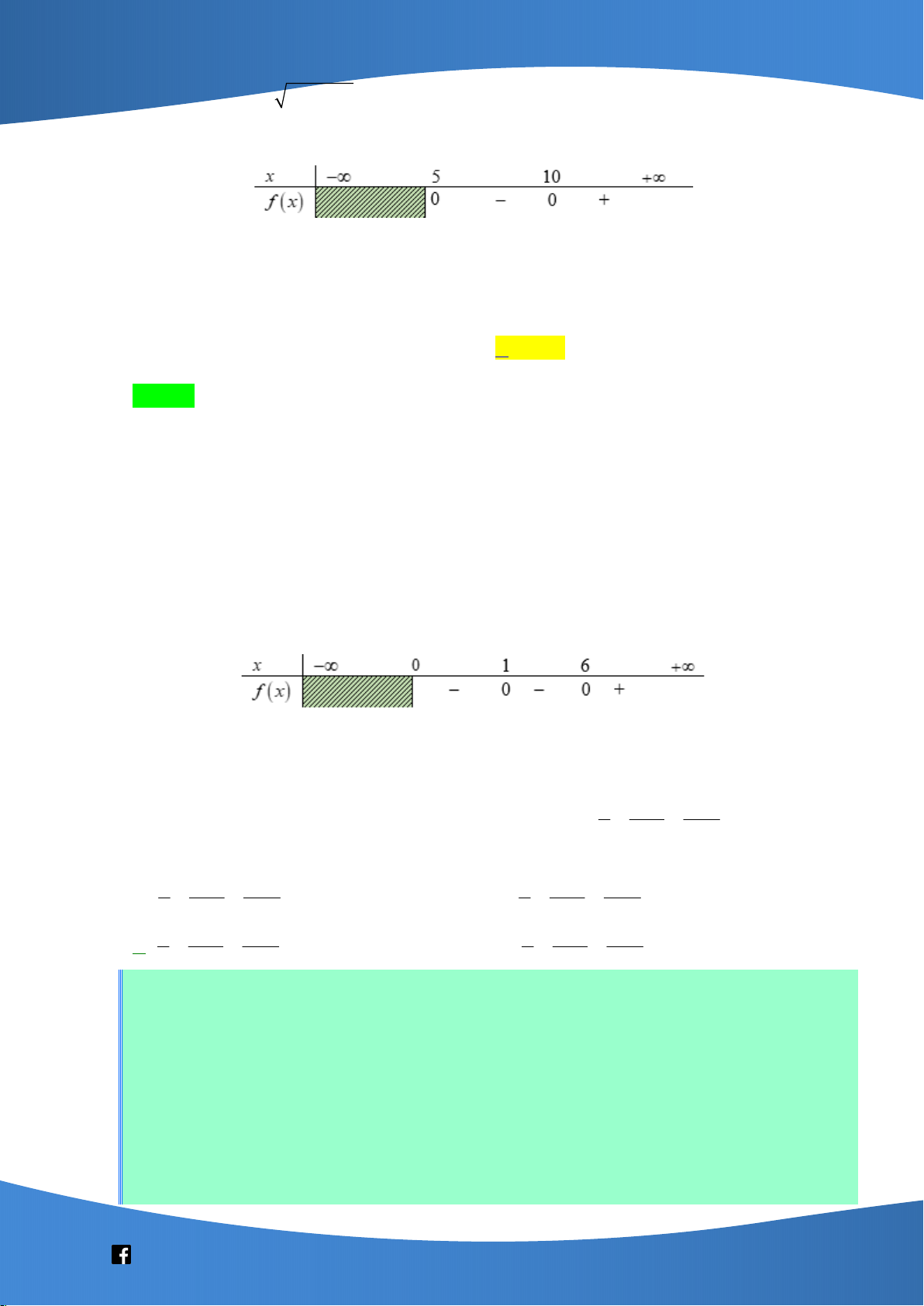
Câu 39. Có bao nhiêu số nguyên x thỏa mãn 2x  4x log x 14  4  0 2     ? A. 14 . B. 13 . C. Vô số. D. 15 . Lời giải Chọn D Cách 1  Trường hợp 1: 2  2
2x  4x  0 x 2  2  2 x 2
x  2x  0 0  x  2         x  2 log x 14  4  0  x 14  16 x  2 x  2 2        Trường hợp 2: x  0 2 
2x  4x  0 2
x  2x  0   1  4  x  0       x  2    . log x 14  4  0  1  4  x  2 x  2 2       1  4  x  2 
Vậy có 15 giá trị nguyên của x thỏa mãn yêu cầu bài toán. Cách 2: 2
Điều kiện xác định: x  1
 4 . Đặt ( )  2x  4x f x
log x14 4 2     . 2 2x  4x 2 x  2xx  0
Xét phương trình f (x)  0      . 4  log (x 14)  4  x 14  2 x  2 (kép) 2   Ta có bảng xét dấu:
Suy ra bất phương trình f (x)  0 có tập nghiệm là: S   1  4;  0   2 .
Do x   x  1  3; 1  2;...; 2  ; 1  ;0;  2 .
Vậy có 15 giá trị nguyên của x thỏa mãn yêu cầu bài toán.
2x  3 khi x  1
Câu 40. Cho hàm số f x  
. Giả sử F là nguyên hàm của f trên  thỏa mãn 2
3x  2 khi x  1 
F 0  2 . Giá trị của F  
1  2F 2 bằng A. 23. B. 11. C. 10 . D. 21 . Lời giải Chọn D 2 
x  3x C khi x  1
Ta có F x 1   . 3
x  2x C khi x  1  2
Ta có lim F x  lim     .    2 x 3x C C 4 1  1 x 1  x 1 
https:/www.facebook.com/groups/toanvd. Trang 47
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 3 8-2021
lim F x  lim     .    x 2x C C 3 2  2 x 1  x 1 
F x liên tục tại x  1  C  4  C  3 (1) 1 2
F 0  2  C  2 (2). 2 2 C  1 
x  3x 1 khi x  1 Từ (1) và (2) suy ra 1 
F x   . C  2 3  2
x  2x  2 khi x  1 
F    F     3       2 1 2 2 1 2 1 2 2 2  3.2   1  21 .
Câu 41. Cho hàm số bậc bốn y f x có đồ thị là đường cong trong hình bên dưới.
Số nghiệm thực phân biệt của phương trình f f x  0 là A. 4 . B. 10 . C. 12 . D. 8 . Lời giải Chọn B
f x  a a    1  f
  x  b 1  b  0
Ta có: f f x  0   .
f x  c 0  c   1 
f x  d d   1 
Phương trình f x  a với a  1  vô nghiệm.
Phương trình f x  b với 1
  b  0 có 4 nghiệm phân biệt.
Phương trình f x  c với 0  c 1 có 4 nghiệm phân biệt.
Phương trình f x  d với d 1 có 2 nghiệm phân biệt.
Vậy phương trình f f x  0 có 10 nghiệm.
Câu 42. Xét các số phức z, w thỏa mãn z  1 và w  2 . Khi z iw  6  8i đạt giá trị nhỏ nhất,
z w bằng? 29 221 A. 3 . B. . C. 5 . D. . 5 5 Lời giải Chọn D
Theo BĐT modun số phức, ta có:
https:/www.facebook.com/groups/toanvd. Trang 48
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8-2021
z iw z iw z w  3 . Ta lại có: z iw 6 8i
 6 8i  z iw         
 6  8i    z iw  6  8i z iw  10  3  7 .  
z k.iw
Dấu bằng xảy ra, khi và chỉ khi: 
k  0, m  0. 6   8i  . m  z iw   1   . k z k iw   1   k.2   2
Lấy modun 2 vế, ta được:      . 10   .3 m 1  0
 6  8i   . m z iw    m    3  3 4 z   i   5 5 221    z w  . 8 6 5 w   i   5 5 x 1 y  2 z 1
Câu 43. Trong không gian Oxyz , cho đường thẳng d :   và mặt phẳng 1 1 2
(P) : x  2 y z  6  0 hình chiếu vuông góc của d trên (P) là đường thẳng có phương trình: x 1 y  2 z 1 x 1 y  2 z 1 A.   . B.   . 3 1 1 3 1 1 x 1 y  2 z 1 x 1 y  2 z 1 C.   . D.   . 1 4 7 1 4 7 Lời giải Chọn D
Ta có d đi qua điểm A1; 2;   1 và A1; 2;   1 thuộc (P) . Vậy A1; 2;  
1 là giao điểm của d và (P) .
Gọi Q là mặt phẳng chứa đường thẳng d và vuông góc với  P . Khi đó Q có vectơ    pháp tuyến n
 u , n    . Q d P 3; 1;  1      
Đường thẳng d là giao tuyến của hai mặt phẳng  P và Q nên có một vecto chỉ phương là:   
ud  n , n   (1; 4; 7) . Q P   
Vậy đường thẳng dcó ud  ( 1
 ; 4;7) và đi qua điểm A(1; 2; 1
 ) có phương trình chính x 1 y  2 z 1 tắc là   . 1 4 7  1  2
Câu 44. Có bao nhiêu số nguyên y sao cho tồn tại x  ;5 3 x xy 15 x   thỏa mãn 27  1 xy  27 .  3  A. 17 . B. 16 . C. 18 . D. 15 . Lời giải Chọn A 1
 Khi y  0, vì xy  1  và x  nên ta có y  3  . 3
https:/www.facebook.com/groups/toanvd. Trang 49
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 2 8-2021 Với y  0 , phương trình thành: 3x 1  5 27 x 1  0 , vô nghiệm vì 2 x x  1 3 15 0  27
1  27 1  0, x   ;5   .  3  2 2 Với y  1  , phương trình thành: 3x 1  6 27
x  (1 x)  0 có nghiệm vì 3x 1  6 ( )  27 x g x  (1 x) 1 1   1  liên tục trên ;5  và g .g 5  0 . 1   1   3     3  2 Với y  2  , phương trình thành: 3x 1  7 27
x  (1 2x)  0 có nghiệm vì 2 1  1 3x 1  6   ( )  27 x g x
 (1 2x) liên tục trên ;5 và g .g 5  0 . 2   2   2  3     3  1 
Khi y  1, xét trên ;5  , ta có 3    2 3x xy 15 x 2 27  (1 xy)27
 3x 15x  log (1 xy)  xy 27 log (1 xy) 27  3x 15   y  0. x log (1 xy) 1  Xét hàm 27
g(x)  3x 15   y trên ;5 . x  3    ln(1 xy) y 1 3 1 
Ta có g '(x)  3    3   3   0, x   ;5 . 2 2 x ln 27 x(1 xy) ln 27 3x n l 3 ln 3 3     1 
Do đó, hàm g(x) đồng biến trên ;5 
. Vì thế phương trình g(x)  0 có nghiệm trên 3     1   1  ;5   khi và chỉ khi g g(5)  0.  
Áp dụng bất đẳng thức ln(1 u)  u với mọi u  0 , ta  3   3  log (1 5 y) 5 y có 27 g(5)    y    y  0. 5 5ln 27  1   y  Do đó g  0   log 1
y 14  0  1  y  15  
(do y là số nguyên dương). 3    3   3  Vậy y  2  ; 1  ;1;2;...;1 
5 hay có 17 giá trị y thỏa đề.
Câu 45. Cho khối hộp chữ nhật ABC . D A BCD
  có đáy là hình vuông, BD  2a , góc giữa hai mặt phẳng  A B
D và  ABCD bằng 60 . Thể tích của khối hộp chữ nhật đã cho bằng 2 3 2 3 A. 3 a . B. 3 6 3a . C. 3 a . D. 3 2 3a . 9 3 Lời giải Chọn D
+) Ta có BD  2a AC  2 ; a AB a 2 .
https:/www.facebook.com/groups/toanvd. Trang 50
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8-2021 +) S  a 2 2 2  2a . ABCD
+) Góc giữa hai mặt phẳng  A B
D và  ABCD là góc  A OA  
AA  AO tan AOA  .
a tan 60  a 3 . Vậy 2 3 VAA .S
a 3.2a  2 3a . ABCD.A BCD   ABCD Câu 46. Cho hàm số   3 2
f x x ax bx c với a , b , c là các số thực. Biết hàm số
g x  f x  f  x  f  x có hai giá trị cực trị là 5
 và 3 . Diện tích hình phẳng giới f x
hạn bởi các đường y
và y  1 bằng g x  6 A. 2ln 3. B. ln 2 . C. ln15 . D. 3ln 2 . Lời giải Chọn A   3 2
f x x ax bx c f  x 2
 3x  2ax b , f  x  6x  2a , f  x  6 .
g x  f x  f  x  f  x  g x  f  x  f  x  f  x  f  x  f  x  6 .  x x
Do g x có hai cực trị là 5
 và 3 nên g x 1  0  
với g x  3 , g x  5  . 2  1  x x  2 f x
f  x  f  x  6  x x Ta có:  1   0 1   . g x  6 g x  6 x x  2 f x
Diện tích hình phẳng giới hạn bởi các đường y  và y  1 là g x  6 2 x f x 2 x
f  x  f  x  6 2
x d  g x  6 x2 S   1dx  dx    
ln gx  6   2ln3 .   g x   g x g x x   6 x x   6   x   6 1 1 1 1
Câu 47. Cắt hình nón  N  bởi mặt phẳng đi qua đỉnh và tạo với mặt phẳng chứa đáy một góc bằng 0
30 , ta được thiết diện là tam giác đều cạnh 4 .
a Diện tích xung quanh của nón bằng A. 2 4 7 a . B. 2 8 7 a . C. 2 8 13 a . D. 2 4 13 a . Lời giải Chọn D
Gọi O là tâm đáy nón, đỉnh nón là S, thiết diện là tam giác đều SA . B Kẻ 
OH AB, H là trung điểm AB 0  SHO  30 .
https:/www.facebook.com/groups/toanvd. Trang 51
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8-2021
SH  2a 3, HA  2 . a Ta có: 0
OH SH.cos 30  3 . a 2 2 2 2
R HO HA  9a  4a a 13. 2
S   Rl   a 13.4a  4 13 a . xq
Câu 48. Trên tập hợp các số phức, xét phương trình 2
z  m   2 2
1 z m  0 ( m là tham số thực).
Có bao nhiêu giá trị của m để phương trình đó có nghiệm z thỏa mãn z  8 ? o o A. 4 . B. 3 . C. 2 . D. 1. Lời giải Chọn B
Ta có   8m  4. 1
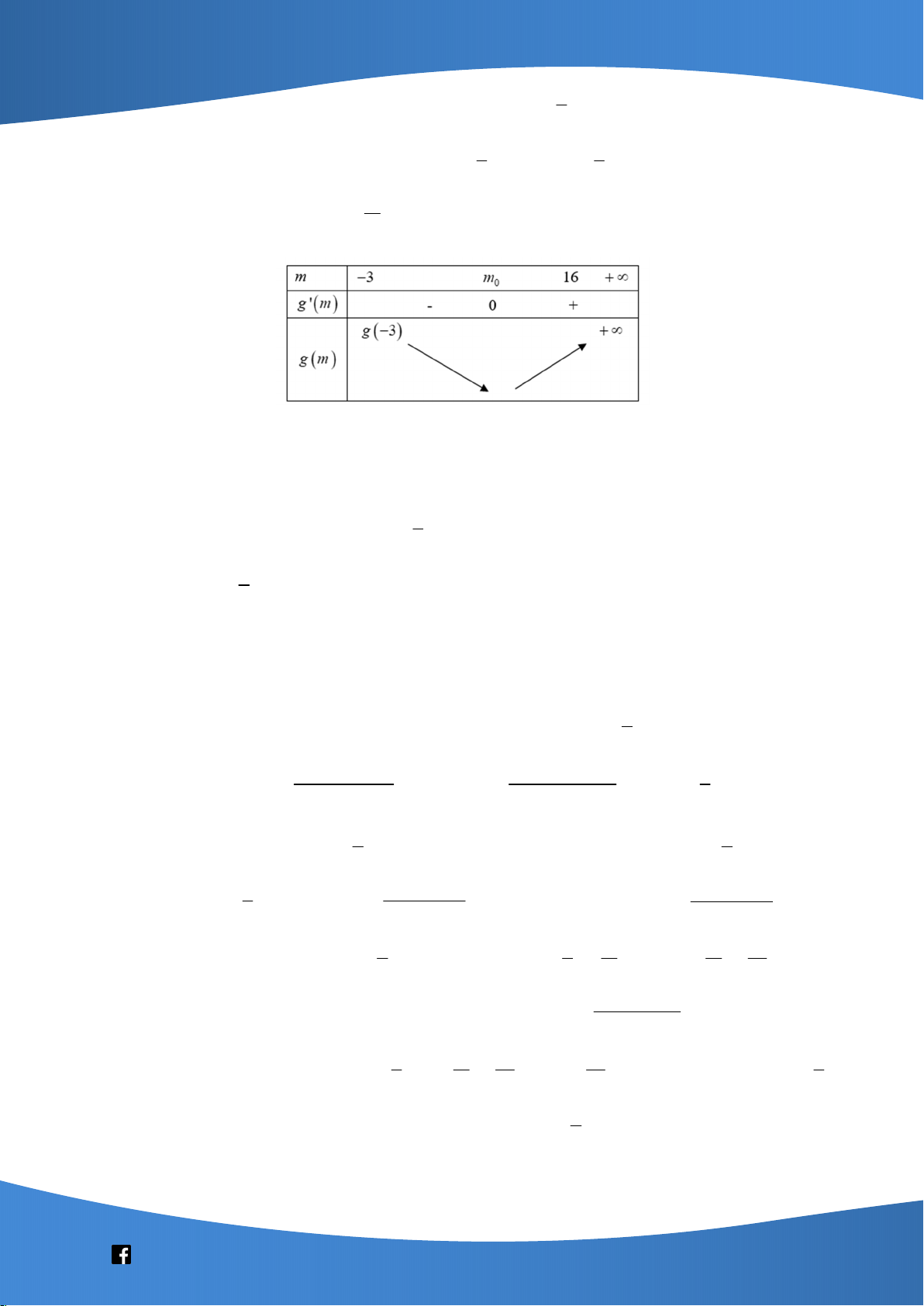
Trường hợp 1:   0  m   suy ra phương trình có 2 nghiệm thực  z là nghiệm 2 o thực  m  4 2  z  8
m 16m  48  0    T / M z  8 o  thay vào phương trình  m  12 . o    z  8  o 2
m 16m  80  0(VN)  1
Trường hợp 2:   0  m   suy ra phương trình sẽ có 2 nghiệm phức, vì z là 2 o
nghiệm nên suy ra z cũng là nghiệm o 2 m  8 2 z  8  z
 64  z .z  64  m  64  . o o o om  8  
Kết hợp điều kiện nên ta nhận m  8  .
Vậy có 3 giá trị m thỏa mãn.
Câu 49. Trong không gian Oxyz , cho hai điểm A1; 3  ;2 và B 2  ;1; 4
  . Xét hai điểm M và N
thay đổi thuộc mặt phẳng Oxy sao cho MN  4 . Giá trị lớn nhất của AM BN bằng A. 5 2 . B. 3 13 . C. 61 . D. 85 . Lời giải Chọn D
https:/www.facebook.com/groups/toanvd. Trang 52
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8-2021 Dễ thấy hai điểm ,
A B nằm khác phía so với mặt phẳng Oxy .
Gọi A là điểm đối xứng của A qua mặt phẳng Oxy suy ra A 1; 3  ; 2  . 1   1
Gọi mặt phẳng  P chứa A và song song mặt phẳng Oxy suy ra  P : z  2  . 1   Ta gọi
A : A A MN và gọi K là hình chiếu của B lên 2 1 2
P  K  2  ;1; 2
   BK  2, KA  5 1 Khi đó: 2 2
AM BN A N BN A B BK  (KA  4)  85 . 2 2 1
Suy ra giá trị lớn nhất của AM BN bằng 85 , dấu bằng xảy ra khi N A B Oxy . 2  
Câu 50. Cho hàm số y f x có đạo hàm f  x   x   2 10
x  25,x   . Có bao nhiêu giá trị
nguyên dương của tham số m để hàm số g x  f  3
x  8x m có ít nhất 3 điểm cực trị A. 9 . B. 25 . C. 5 . D. 10 . Lời giải Chọn A Cách 1:
Ta có BBT của hàm y h x 3
x  8x như sau Ta có  g x 3  x x f  3 8 .
x  8x m. Rõ ràng x  0 là điểm cực trị của hàm y hx 3 3
x  8x m  10
x  8x  10  m   Ta có: f  3
x  8x m 3 3
 0   x  8x m  5   x  8x  5  m .   3 3
x  8x m  5 
x  8x  5   m  
https:/www.facebook.com/groups/toanvd. Trang 53
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8-2021
Để hàm số g x có ít nhất 3 điểm cực trị thì phương trình g x  0 có ít nhất 2 nghiệm
phân biệt khác 0 và g x đổi dấu khi đi qua ít nhất 2 trong số các nghiệm đó.
Từ BBT ta có 10  m  0  m  10  m 1;2;3;4;5;6;7;8;  9 .
Vậy có 9 giá trị của m thỏa mãn yêu cầu đề bài. Cách 2:
Với f ,h là các hàm liên tục trên tập số thực, thì nếu c là điểm cực trị của f hx thì
c phải là điểm cực trị của g hoặc là h c là điểm đạt cực trị của f . Bây giờ m  10 và
với hàm hx 3
x  8x m , ta có f chỉ có các điểm đạt cực trị là 10, 5 . Trong khi chỉ
có duy nhất điểm đạt cực trị của h là 0 cùng với hx  m  10 với mọi x , và thêm nữa
thì phương trình hx  10 có không quá một nghiệm là x  0 . Bởi vậy, m  10 không thỏa mãn yêu cầu.
Khi m  9 và m  5 , thì trên từng khoảng mở bên trái và phải số 0 ta có
3x 8hx 9hx2 2  25 x g x  . x
Cho thấy g x đổi dấu khi x chạy qua 0 và vì thế nó đạt cực trị tại x  0. Kết hợp thêm
việc đa thức hx  9 có đúng hai nghiệm phân biệt khác 0 , và g  x đổi dấu khi x
chạy qua các nghiệm đó. Cho thấy m  9 và m  5 thỏa yêu cầu. 2 2
Nếu m  5 lúc đó g x  x 2
3x  8 hx  9hx  25. Ta cũng thấy gx đổi dấu
khi x chạy qua 0 và hai nghiệm phân biệt khác 0 của hx  9 , cho thấy là cũng thỏa mãn.
Vậy m là các số nguyên dương nhỏ hơn 10.
https:/www.facebook.com/groups/toanvd. Trang 54 Tập san
NHÓM GIÁO VIÊN TOÁN VIỆT NAM Số 02 8-2021
ĐỀ THI TỐT NGHIỆP THPT ĐỢT 1 NĂM 2021
Bài thi môn: Toán
Thời gian: 90 phút (Không kể thời gian phát đề) Mã đề thi: 104
Đề thi gồm 06 trang Câu 1:
Cho hai số phức z  3  2i và w  1 4i . Số phức z w bằng
A. 4  2i .
B. 4  2i .
C. 2  6i . D. 2  6i . Câu 2:
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên? A. 3
y x  3x 1. B. 4 2
y x  4x 1 . C. 3
y  x  3x 1. D. 4 2
y  x  2x 1. 4 4 4 Câu 3:
Nếu f xdx  4 
và g xdx  3  
thì  f x  g x dx    bằng 1 1 1 A. 1. B. 7 . C. 1. D. 7 . x  1 Câu 4:
Tiệm cận đứng của đồ thị hàm số y
là đường thẳng có phương trình: x  2
A. x  2 .
B. x  1 .
C. x  2 . D. x  1 . Câu 5:
Trong không gian Oxyz , cho mặt cầu S  có tâm I  1
 ;3;0 và bán kính bằng 2 . Phương trình
của mặt cầu S  là: 2 2 2 2
A. x     y   2 1 3  z  2 .
B. x     y   2 1 3  z  4 . 2 2 2 2
C. x     y   2 1 3  z  4 .
D. x     y   2 1 3  z  2 . Câu 6:
Tập nghiệm của bất phương trình 2x  5 là A.  ;  log 5 .
B. log 2; . C.  ;  log 2 . D. log 5; . 2  5  5  2  Câu 7:
Thể tích của khối lập phương cạnh 2a bằng A. 3 a . B. 3 2a . C. 3 8a . D. 3 4a . 5 Câu 8:
Trên khoảng 0; , đạo hàm của hàm số 3 y x là: 5 3 2 5 2 5 2  3 A. 3 y x . B. 3 y x . C. 3 y x . D. 3 y x . 8 3 3 5  Câu 9:
Trong không gian Oxyz , cho điểm A2; 1
 ; 4. Tọa độ của véc tơ OA là A.  2  ;1; 4 .
B. 2;1;4 .
C. 2;1;4 . D.  2  ;1; 4 . 3 3 Câu 10: Nếu
f xdx  3 
thì 4 f xdx  bằng 0 0
https:/www.facebook.com/groups/toanvd. Trang 55 Tập san
NHÓM GIÁO VIÊN TOÁN VIỆT NAM Số 02 8-2021 A. 3 . B. 12 . C. 36 . D. 4 .
Câu 11: Cho cấp số nhân u với u  2 và u  10. Công bội của cấp số nhân đã cho bằng n  1 2 1 A. 8 . B. 8 . C. 5 . D. . 5
Câu 12: Với n là số nguyên dương bất kì , n  3, công thức nào dưới đây đúng ? n  3 ! 3! n! n! 3   A. A  . B. 3 A  . C. 3 A  . D. 3 A  . n n! nn  3! nn  3! n 3  ! n  3!
Câu 13: Cho hàm số f x 2
x  2 . Khẳng định nào dưới đây đúng? 3 x A.
f xdx  2x C  . B.
f xdx   2x C  . 3 C. f x 2
dx x  2x C  .
D. f x 3
dx x  2x C  .
Câu 14: Cho hàm số y f x có bảng biến thiên như sau:
Giá trị cực tiểu của hàm số đã cho bằng A. 0 . B. 3 . C. 1. D. 1.
Câu 15: Trong không gian Oxyz , cho mặt phẳng  P : 2x  4 y z 1  0 . Vectơ nào dưới đây là một
vectơ pháp tuyến của  P ?     A. n  2; 4  ;1 .
B. n  2; 4;1 .
C. n  2; 4; 1  . D. n  2  ; 4;1 . 4   3   1   2  
Câu 16: Phần thực của số phức z  4  2i bằng A. 2 . B. 4 . C. 4 . D. 2 .
Câu 17: Nghiệm của phương trình log 5x  3 là 2   8 9 A. x  . B. x  . C. x  8 . D. x  9 . 5 5
Câu 18: Tập xác định của hàm số 8x y  là A.  \   0 . B.  . C. 0;  . D. 0;  .
Câu 19: Cho a  0 và a  1, khi đó 5 log a bằng a 1 1 A. . B.  . C. 5 . D. 5 . 5 5
Câu 20: Trong không gian Oxyz , cho đường thẳng d đi qua điểm M (1;5; 2
 ) và có một vectơ chỉ phương u  (3; 6
 ;1) . Phương trình của d là:
x  3  t
x  1 3t
x  1 3t
x  1 3t     A. y  6   5t .
B. y  5  6t .
C. y  5  6t .
D. y  5  6t .  z 1 2t     z  2  tz  2   tz  2   t
Câu 21: Trên mặt phẳng tọa độ, điểm M ( 4
 ;3) là điểm biểu diễn của số phức nào sau đây?
https:/www.facebook.com/groups/toanvd. Trang 56 Tập san
NHÓM GIÁO VIÊN TOÁN VIỆT NAM Số 02 8-2021 A. z  4   3i .
B. z  4  3i .
C. z  4  3i . D. z  4   3i . 3 4 2 1
Câu 22: Cho hàm số y f x có bảng xét dấu của đạo hàm như sau:
Số điểm cực trị của hàm số đã cho là A. 3 . B. 4 . C. 2 . D. 5 .
Câu 23: Cho hàm số ( ) x
f x e  4 . Khẳng định nào sau đây đúng? A. ( )d x
f x x e  4x C  . B. ( )d x
f x x e C  . C. 4 ( )d x f x x eC  . D. ( )d x
f x x e  4x C  .
Câu 24: Cho hàm số y f x có đồ thị là đường cong trong hình bên.
Hàm số đã cho nghịch biến trên khoảng nào dưới đây? A. 1;  1 .
B. 1;   .
C. ;1 . D. 0;3 .
Câu 25: Diện tích S của mặt cầu bán kính R được tính theo công thức nào dưới đây? 4 A. 2
S   R . B. 2
S  16 R . C. 2
S  4 R . D. 2 S   R . 3
Câu 26: Đồ thị hàm số 3 2 y  2
x  3x  5 cắt trục tung tại điểm có tung độ bằng A. 5 . B. 0 . C. 1 . D. 2 .
Câu 27: Cho khối chóp có diện tích đáy 2
B  8a và chiều cao h a . Thể tích khối chóp đã cho bằng 4 8 A. 3 8a B. 3 a . C. 3 4a . D. 3 a . 3 3
Câu 28: Cho khối trụ có bán kính đáy r  5 và chiều cao h  3 . Thể tích của khối trụ đã cho bằng A. 15 B. 75 . C. 25 . D. 45 .
Câu 29: Trong không gian Oxyz, cho điểm M 2;1; 2 và mặt phẳng  P  : 3x  2 y z 1  0. Đường
thẳng đi qua M và vuông góc với  P có phương trình là: x  2 y 1 z  2 x  2 y 1 z  2 A.   . B.   . 3 2 1  3 2 1 x  2 y 1 z  2 x  2 y 1 z  2 C.   . D.   . 3 2 1 3 2 1 
Câu 30: Cho hình lăng trụ đứng ABC.AB C
  có tất cả các cạnh bằng nhau (tham khảo hình bên). Góc
giữa hai đường thẳng AB và CC bằng
https:/www.facebook.com/groups/toanvd. Trang 57 Tập san
NHÓM GIÁO VIÊN TOÁN VIỆT NAM Số 02 8-2021 A. 30 . B. 90 . C. 60 . D. 45 .
Câu 31: Cho hình chóp S.ABC có đáy là tam giác vuông cân tại B , AB  4a và SA vuông góc với mặt
phẳng đáy. Khoảng cách từ điểm C đến mặt phẳng (SAB) bằng A. 4a .
B. 4 2a .
C. 2 2a . D. 2a . 2 2 Câu 32: Nếu
f xdx  4 
thì 2 f x 1) dx    bằng 0 0 A. 8 . B. 10 . C. 7 . D. 6 . x a
Câu 33: Biết hàm số y
( a là số thực cho trước và a  1) có đồ thị như trong hình bên. x 1
Mệnh đề nào dưới đây đúng?
A. y  0, x    .
B. y  0, x   1 .
C. y  0, x    .
D. y  0, x   1 .
Câu 34: Cho số phức z thỏa mãn iz  4  3i . Số phức liên hợp của z là:
A. z  3  4i .
B. z  3  4i .
C. z  3  4i .
D. z  3  4i .
Câu 35: Từ một hộp chứa 12 quả bóng gồm 5 quả màu đỏ và 7 quả màu xanh, lấy ngẫu nhiên đồng thời
3 quả. Xác suất để lấy được 3 quả màu đỏ bằng 1 7 5 2 A. . B. . C. . D. . 22 44 12 7
Câu 36: Với mọi a, b thỏa mãn 3
log a  log b  5 , khẳng định nào dưới đây đúng? 2 2 A. 3 a b  32 . B. 3 a b  25 . C. 3
a b  25 . D. 3
a b  32 .
Câu 37: Trên đoạn 1;2 , hàm số 3 2
y x  3x 1 đạt giá trị nhỏ nhất tại điểm
A. x  2 .
B. x  0 .
C. x  1 . D. x  1 .
Câu 38: Trong mặt phẳng Oxyz , cho hai điểm A1;0;0 B 3;2; 
1 . Mặt phẳng đi qua A và vuông góc với
AB có phương trình là:
A. 2x  2 y z  2  0 .
B. 4x  2 y z 17  0 .
C. 4x  2 y z  4  0 .
D. 2x  2 y z 11  0 .
https:/www.facebook.com/groups/toanvd. Trang 58 Tập san
NHÓM GIÁO VIÊN TOÁN VIỆT NAM Số 02 8-2021
Câu 39: Cho hàm số bậc bốn y f x có đồ thị là đường cong trong hình bên . Số nghiệm thực phân
biệt của phương trình f f x  0 là: A. 12 . B. 10 . C. 8 . D. 4 . 2
Câu 40: Có bao nhiêu số nguyên x thỏa mãn 2x  4x log x  25 3  0? 3     A. 24. B. Vô số. C. 25. D. 26. 2x  2 khi x  1
Câu 41: Cho hàm số f x  
. Giả sử F là nguyên hàm của f trên  thỏa mãn 2
3x 1 khi x  1 
F 0  2 . Giá trị của F  
1  2F 2 bằng A. 18 . B. 20 . C. 9 . D. 24 .
Câu 42: Cắt hình nón  N  bởi mặt phẳng đi qua đỉnh và tạo với mặt phẳng chứa đáy một góc bằng 30 ,
ta được thiết diện là tam giác đều cạnh 2a . Diện tích xung quanh của  N  bằng A. 2 7 a . B. 2 13 a . C. 2 2 13 a . D. 2 2 7 a . x y z 1
Câu 43: Trong không gian
Oxyz , cho đường thẳng d :   và mặt phẳng 1 1  2
(P) : x  2 y  2z  2  0 . Hình chiếu vuông góc của d lên mặt phẳng (P) là đường thẳng có phương trình: x y z 1 x y z 1 x y z 1 x y z 1 A.   . B.   . C.   . D.   . 2  4 3 14 1 8 2  4 3 14 1 8  1  2
Câu 44: Có bao nhiêu số nguyên y sao cho tồn tại x  ;6 3x xy 18 x   thỏa mãn 27  1 xy 27 ?  3  A. 19 . B. 20 . C. 18 . D. 21 .
Câu 45: Trên tập hợp các số phức, xét phương trình 2
z  m   2 2
1 z m  0 ( m là tham số thực). Có bao
nhiêu giá trị của m để phương trình đó có nghiệm z thoả mãn z  6 ? 0 0 A. 4 . B. 1. C. 2 . D. 3 .
Câu 46: Cho khối hộp chữ nhật ABC . D AB CD
  có đáy là hình vuông BD  4a , góc giữa hai mặt phẳng
ABD và  ABCD bằng 0
60 . Thể tích của khối hộp chữ nhật đã cho bằng 16 3 16 3 A. 3 48 3a . B. 3 a . C. 3 a . D. 3 16 3a . 9 3 Câu 47: Cho hàm số   3 2
f x x ax bx c với a, ,
b c là các số thực. Biết hàm số
g x  f x  f  x  f  x có hai giá trị cực trị là 5 và 2 . Diện tích hình phẳng giới hạn f x
bởi các hàm số y  và y  1 bằng g x  6 A. ln 3 . B. 3ln 2 . C. ln10 . D. ln 7 .
https:/www.facebook.com/groups/toanvd. Trang 59 Tập san
NHÓM GIÁO VIÊN TOÁN VIỆT NAM Số 02 8-2021
Câu 48: Xét các số phức z, w thỏa mãn z  1 và w  2 . Khi z iw  6  8i đạt giá trị nhỏ nhất z w bằng 29 221 A. . B. . C. 3 . D. 5 . 5 5
Câu 49: Trong không gian Oxyz, cho hai điểm ( A 2  ;1; 3  ) và B(1; 3
 ; 2). Xét hai điểm M và N thay
đổi thuộc mặt phẳng (Oxy) sao cho MN  3. Giá trị lớn nhất của AM AN bằng A. 65 . B. 29 . C. 26 . D. 91 .
Câu 50: Cho hàm số y f x có đạo hàm f  x   x   2 9
x 16 , x   . Có bao nhiêu giá trị
nguyên dương của tham số 3 m
để hàm số g x   f x  7x m  có ít nhất 3 điểm cực trị? A. 16 . B. 9. C. 4. D. 8.
https:/www.facebook.com/groups/toanvd. Trang 60 Tập san
NHÓM GIÁO VIÊN TOÁN VIỆT NAM Số 02 8-2021
ĐỀ THI THPT QUỐC GIA – NĂM HỌC: 2020 – 2021
ĐỀ CHÍNH THỨC (MÃ ĐỀ 104) Môn: Toán
Thời gian: 90 phút (Không kể thời gian phát đề) BẢNG ĐÁP ÁN
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
B C D C C D C B B B C C B C C C A B A D D B A A C
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
A D B A D A D B A A A B A B D A B D B D D B A A D
HƯỚNG DẪN GIẢI CHI TIẾT
Câu 39: Cho hàm số bậc bốn y f x có đồ thị là đường cong trong hình bên . Số nghiệm thực phân
biệt của phương trình f f x  0 là: A. 12. B. 10 . C. 8. D. 4. Lời giải Chọn B
f x  a a    1   1  f
  x   b 1  b  0 2
Ta có: f f x  0  .
f x  c0  c   1 3 
f x  d d   1 4 
Từ đồ thị hàm số ta thấy:
Phương trình 1 có: 2 nghiệm
Phương trình 2 có: 4 nghiệm
Phương trình 3 có: 4 nghiệm
Phương trình 4 vô nghiệm
https:/www.facebook.com/groups/toanvd. Trang 61 Tập san
NHÓM GIÁO VIÊN TOÁN VIỆT NAM Số 02 8-2021
Vậy phương trình f f x  0 có tất cả 10 nghiệm thực phân biệt. 2 x x
Câu 40: Có bao nhiêu số nguyên 2 4 l
 og x  25 3  0? x thỏa mãn   3   A. 24. B. Vô số. C. 25. D. 26. Lời giải Chọn D Cách 1:
Điều kiện xác định của bất phương trình là x  25 . 2 x x Đặt ( A )
x  2 4  log x25 3,x  2  5  3    . 2
2x 4x  0  x  0 x  2.
log x  25 3  0  x  2 . 3  
Ta có bảng xét dấu A ( x ) như sau x  2 Từ đó, ( A x)  0   x    2  4; 2  3;...;0;  2 (do x  ). 2  5  x  0 
Kết luận: có 26 nghiệm nguyên thỏa mãn. Cách 2:  Trường hợp 1: 2  2 x 2x
2x  4x  0 2    2 2
x  2 x  0 0   x  2         x  2 .
log x  25  3  0  x  25  27 x  2 x  2 3        Trường hợp 2: x  0 2 
2x  4x  0 2
x  2x  0       x  2  2
 5  x  0  x  2  .
log x  25  3  0  25  x  2 3      2  5  x  2  2 x x
 Vậy có 26 giá trị nguyên của 2 4 l
 og x  25 3  0 x thỏa mãn   3    . 2x  2 khi x  1
Câu 41: Cho hàm số f x  
. Giả sử F là nguyên hàm của f trên  thỏa mãn 2
3x  1 khi x  1  F 
0  2. Giá trị của F  
1  2F 2 bằng A. 18 . B. 20 . C. 9. D. 24. Lời giải Chọn A 2 
x  2x C khi x 1 1
F là nguyên hàm của f trên  nên F x   . 3
x x C khi x 1  2
 Ta có: F 0  2  C  2 . 1 2
 Do F liên tục tại x  1 nên lim F x  lim F x  F 1 x 1 x 1  
https:/www.facebook.com/groups/toanvd. Trang 62 Tập san
NHÓM GIÁO VIÊN TOÁN VIỆT NAM Số 02 8-2021   1
C  3  C  2C  3  4  C 1. 1 2 1 1 2 
x  2x 1 khi x 1
 Do đó F x   . 3 x x  2 khi x 1   Suy ra F  
1  2F 2 18 .
Câu 42: Cắt hình nón  N bởi mặt phẳng đi qua đỉnh và tạo với mặt phẳng chứa đáy một góc bằng 30
, ta được thiết diện là tam giác đều cạnh 2a. Diện tích xung quanh của  N bằng 2 2 2 2 A. 7 a  .
B. 13a .
C. 2 13a . D. 2 7 a  . Lời giải Chọn B 2a 3  Ta có: S
AB đều cạnh 2a SH   a 3. 2 
 Góc giữa thiết diện và mặt phẳng đáy là SHI 30 .  3 3a  Xét S
HI vuông tại I ; HI SH.cos30  a 3.  . 2 2 2 9a a 13  Xét A
HI vuông tại H : 2 2 2 AI
AH HI a   . 4 2 a 13  Vậy: 2 S   .
r l  .AI.SA  .
.2a  13a . xq 2 x y z  1
Câu 43: Trong không gian
O xyz , cho đường thẳng d :   và mặt phẳng 1 1 2
( P ) : x  2 y  2 z  2  0 . Hình chiếu vuông góc của d lên mặt phẳng ( P ) là đường thẳng có phương trình: x y z  1 x y z  1 x y z  1 x y z  1 A.   . B.   . C.   . D.   . 2 4 3 14 1 8 2 4 3 14 1 8 Lời giải Chọn D
https:/www.facebook.com/groups/toanvd. Trang 63 Tập san
NHÓM GIÁO VIÊN TOÁN VIỆT NAM Số 02 8-2021 Cách 1
x  2 y  2z  2  0 x  0  
 Tọa độ A d   P thỏa  x y z 1
x  2 y  2z  2
 y  0  A0;0;  1 .     0   1 1  2 1 2  4 z  1  x y z  1
 Lấy điểm B(1; 1;3)  d :   . 1 1 2 x  1 y  1 z  3
Gọi B là hình chiếu của điểm B lên mặt phẳng ( P )  BB :   1 2 2
 Tọa độ B  BB  P thỏa  5 14 x  1   9 9
x  2 y  2z  2  0    5 1  14 1 17   x 1 y  1 z  3
x  2 y  2z  2  5 5   y  1   2.   B ; ;   .     9 9  9 9 9     1 2 2 1  4  4 9  5 17 z  3  2.    9 9
 14 1 8 1    AB  ; ;
u u  (14;1;8)  
là vectơ chỉ phương của AB .  9 9 9  9 x y z 1  Vậy AB :  
là hình chiếu vuông góc của đường thẳng d lên ( P ) . 14 1 8 Cách 2
x  2 y  2z  2  0 x  0  
 Tọa độ A d   P thỏa  x y z 1
x  2 y  2z  2
 y  0  A0;0;  1 .     0   1 1  2 1 2  4 z  1 
 Gọi d ' là hình chiếu của d lên  P ; 
+ Đường thẳng d có vectơ chỉ phương u  1; 1  ; 2. 
+ Mặt phẳng ( P ) có vectơ pháp tuyến n  (1;2; 2  ) .   
+ a  u, n   (2; 4;3) .    
+ n, a   (14;1;8) là vectơ chỉ phương của (d ') .   x y z  1  Vậy d  :   . 14 1 8
https:/www.facebook.com/groups/toanvd. Trang 64 Tập san
NHÓM GIÁO VIÊN TOÁN VIỆT NAM Số 02 8-2021  1  2
Câu 44: Có bao nhiêu số nguyên y sao cho tồn tại x  ;6   thỏa mãn
3 x xy     18 27 1 27 x xy ?  3  A. 19 . B. 20 . C. 18 . D. 21. Lời giải Chọn B Cách 1: 1
Khi y  0, vì xy  1 và x
nên ta có y  3. 3 2 3x 1  8x
Với y  0 , phương trình thành: 27 1  0 vô nghiệm vì 2 x x  1 3 18 0  27
1 27 1  0, x   ;6   .  3  2 2 Với 3x 1  9x 3x 1  9x
y  1 , phương trình thành: 27
 (1 x)  0 , có nghiệm vì g (x)  27  (1 x) 1 1   1  liên tục trên ; 6  và g .g 6  0 . 1   1  3     3 2 Với 3x 20x
y  2 , phương trình thành: 27
 (1 2x)  0 , có nghiệm vì 2 1   1  3x 20 ( )  27 x g x
 (1 2x) liên tục trên ; 6 và g .g 6  0 . 2   2   2  3     3   1 
 Khi y  1, xét trên ; 6  , ta có 3    2 3 x xy 18 x 2 27  (1  xy)27
 3x 18x  log (1  xy)  xy 27 log (1  xy) 27  3x 18   y  0. x log (1  xy) 1  Xét hàm 27
g ( x)  3x  18   y trên ;6 .   x 3  ln(1 xy) y 1 3 1  Ta có g '( ) x  3   3  3  0, x   ;6 . 2 2 x ln 27 ( x 1 xy)ln 27 3x n l 3 ln3 3      1 
Do đó, hàm g ( x ) đồng biến trên ; 6 
. Vì thế phương trình g ( x)  0 có nghiệm trên 3     1   1  ;6   khi và chỉ khi g .g(6)  0.  
Áp dụng bất đẳng thức ln(1  u)  u với mọi u  0 , ta  3   3  có log (1  6 y) 6 y 27 g (6)    y    y  0. 6 6 ln 27  1   y  Do đó g  0  log 1
y 17  0 1  y 18  
(do y là số nguyên dương). 3    3   3  Vậy y  2  ; 1  ;1;2;...;1 
8 hay có 20 giá trị y thỏa đề. Cách 2.
Giả sử ylà một trong những số nguyên thỏa mãn yêu cầu, lúc đó ta xét phương trình 2
3x xy     18 27 1 27 x xy
https:/www.facebook.com/groups/toanvd. Trang 65 Tập san
NHÓM GIÁO VIÊN TOÁN VIỆT NAM Số 02 8-2021  1  trên D
;6 x  : xy     
1 , và trên D nó tương đương với f   x 0, trong đó  3  1 f x  2
 3x   y  18 x  log 3 1  xy  . 3 2 y y
Ta có vài tính toán sau f ' x  6x y 18 
, f '  x  6  . 31 xyln3 1 xy2 ln3  1   1 1 
Nếu y  0 , khi ấy vì cần có nghiệm x  ;3 
 nên có ngay y  2 , lúc ấy D  ;    trên  3  3 y   D ta có 1 1 1  1  1  2 
lim f x    y  6  log 3 1  y  6  log   3 1   0.   1  3 3 3  3  3  3  x 3 Kết hợp lim
f x   và việc f liên tục trên D cho thấy f có điểm triệt tiêu trên D , 1  x y
nghĩa là trường hợp này cho ta y   2  ,  1 thỏa yêu cầu.
Nếu y  0 , ta có f x 2
 3x  18x  0 với mọi xD, vì thế loại.
Nếu y  19 , lúc đó có y
lim f '  x   y  16   y  17  0 . 1  3  yln 3 x 3
Kết hợp việc f ' x tăng ngặt trên D , cho ta f tăng ngặt trên D và trên D có 1 1 1  1 
lim f x    y  6  log 3 1  y   1  3 3 3  3  x 3 1 1 1  1 
Xét g y   y  6  lo 3 g 1 y   trên 10;   , ta có 3 3 3  3  1 1 2 1  19 
g ' y    0, g 19   log 1   0   3 33  y 3 3 3  3  Vậy, g 
y 0 với mỗi y  19 , cho thấy là f  
x 0 với mọi xD. 1  log 7
Nếu 1  y  18 , thế thì vì g 18 3 
 0 kết hợp tính tăng ngặt của g trên 1;1  8 ta có 3 1 1  1 
lim f x   g y    y  9  log . 3 1  y  0   1  3 3  3  x 3
Còn, theo bất đẳng thức số e , ta có 1
lim f x   6 y  log .
3 1  6 y   6 y  ln 1  6 y   0 x 6  3
Đến đây, theo tính liên tục của f , ta thấy nó triệt tiêu trên D .
Tóm lại y\ 
0 và 2  y  18.
Câu 45: Trên tập hợp các số phức, xét phương trình 2
z  m   2 2
1 z m  0 ( m là tham số thực). Có bao nhiêu giá trị của z m
để phương trình đó có nghiệm z  6 0 thoả mãn ? 0
https:/www.facebook.com/groups/toanvd. Trang 66 Tập san
NHÓM GIÁO VIÊN TOÁN VIỆT NAM Số 02 8-2021 A. 4. B. 1. C. 2. D. 3. Lời giải Chọn D 2 2 Ta có    (m 1
 ) m  2m 1  . 1
+) Nếu   0  2m  1  0  m   , phương trình có 2 nghiệm thực. Khi đó 2
z  6  z  6  . 0 0 * Thay z 6 0
vào phương trình ta được  m   2 2 36 12
1  m  0  m 12m  24  0  m  6  2 3 (thoả mãn). * Thay z  6  0
vào phương trình ta được  m  2 2 36 12
1  m  0  m 12m  48  0 (vô nghiệm). 1
+) Nếu   0  2m  1  0  m   , phương trình có 2 nghiệm phức z , z  z z 1 2 thỏa 2 1 2 2 . Khi đó 2 2
z .z z
m  6 hay m  6 (loại) hoặc m  6  (nhận). 1 2 1
Vậy tổng cộng có 3 giá trị của m là m  6  2 3 và m  6  .
Câu 46: Cho khối hộp chữ nhật ABC . D A BCD
  có đáy là hình vuông, BD  4a , góc giữa hai mặt phẳng
ABD và  ABC D bằng 0
6 0 . Thể tích của khối hộp chữ nhật đã cho bằng 3 16 3 16 3 3 3 3
A. 48 3a . B. a . C. a . D. 16 3a . 9 3 Lời giải Chọn D
Ta có đáy ABCD là hình vuông có BD4aAB2 2a.
Gọi I trung điểm B .
D Vì BD  4a BI AI  2a . AA Tam giác A A
I vuông tại A có: 0 tan 60 
AA  2 3a . AI
Thể tích của khối hộp chữ nhật đã cho bằng: V S A A    a2 3 . 2 2
.2 3a 16 3a . ABCD Câu 47: Cho hàm số   3 2
f x x ax bx c với a, b, c là các số thực. Biết hàm số
g x  f x  f  x  f  x có hai giá trị cực trị là 5
 và 2. Diện tích hình phẳng giới hạn bởi f x các hàm số y  và y  1 bằng g x  6
https:/www.facebook.com/groups/toanvd. Trang 67 Tập san
NHÓM GIÁO VIÊN TOÁN VIỆT NAM Số 02 8-2021 A. ln 3 . B. 3ln 2 . C. ln 10 . D. ln 7 . Lời giải Chọn B Ta có
g x  f x  f  x  f  x 3
x  a   2
3 x  2a b  6 x  2a b c
g x  f  x  f  x  f  x 2
 3x  2ax b  6 x  2a  6 2
 3x  2a  6 x 2a b  6 .
Vì y g x có hai giá trị cực trị là 5
 và 2 nên g x  0 có hai nghiệm phân biệt x , x 1 2 với
g x  2, g x  5  . 1   2 
Phương trình hoành độ giao điểm f x
f x  g x  6 2
3x  2a  6 x  2a b  6 g   x   1   0   0   0 . g x  6 g x  6
g x   6
g x   6
Phương trình này cũng có hai nghệm phân biệt x , x 1 2 f x
Như vậy diện tích hình phẳng giới hạn bởi các hàm số y  và y  1 là g x  6 2 x g xx S
 ln g x 2  6  ln 2  6  ln 5   6  3ln 2  . g x x   1 6 x 1
Câu 48: Xét các số phức z, w thỏa mãn z 1 và w  2 . Khi z iw  6  8i đạt giá trị nhỏ nhất, z w bằng 29 221 A. . B. . C. 3. D. 5 . 5 5 Lời giải Chọn A
Ta có z iw  6  8i  6  8i z iw 10 1 2  7 . k
  z  6  8ik  10  k  10
Dấu “bằng” xảy ra  
, k,l  0  
, k,l  0   . l  iw  6   8i  2 l  10   k  5   3 4  3 4  3 4 z    i z    i z    i  5 5  5 5     5 5 Từ đó suy ra      . 6 8 8 6 8 6 iw iw i        w    i   5 5   5 5   5 5 29
Vậy z w  . 5
Câu 49: Trong không gian Oxyz, cho hai điểm A(2;1; 3) và B(1; 3; 2). Xét hai điểm M và N thay
đổi thuộc mặt phẳng (Oxy) sao cho MN  3. Giá trị lớn nhất của AM AN bằng A. 65. B. 29 . C. 26 . D. 91. Lời giải Chọn A
https:/www.facebook.com/groups/toanvd. Trang 68 Tập san
NHÓM GIÁO VIÊN TOÁN VIỆT NAM Số 02 8-2021
Dễ thấy điểm A nằm phía dưới, điểm B nằm phía trên mặt phẳng (O xy ). Gọi '
A là điểm đối xứng của điểm A qua mặt phẳng (O xy ), suy ra tọa độ điểm A (  2;1;3).
Gọi ( ) là mặt phẳng qua A và song song với mặt phẳng (O xy ), suy ra phương trình mặt
phẳng ( ) : z  3  0. Trên mặt phẳng ( ) lấy điểm A AA   MN 3 A 1 sao cho 1 , suy ra 1 thuộc
đường tròn  A ,3 và tứ giác AAMN AM   AN 1
là hình bình hành nên ta có 1 .
Nên AM BN A M
BN A M BN A B . Gọi B là hình chiếu của B lên mặt phẳng 1 1
( ), suy ra tọa độ điểm B(1; 3;3) .
Ta có AB B B   B A   1 B A    2 2 2 3  65. 1 1
Câu 50: Cho hàm số y f x có đạo hàm f  x   x   2 9 x 16 , x
  . Có bao nhiêu giá trị nguyên dương của tham số 3 m
để hàm số g x   f x  7 x m  có ít nhất 3 điểm cực trị? A. 16 . B. 9. C. 4. D. 8. Lời giải Chọn D
Ta có BBT của hàm y h x 3
x  7 x như sau: 
Ta có g x 3
x x f  3 7 .
x  7x m . Rõ ràng x  0 là điểm cực trị của hàm y hx . 3 3
x  7x m  9
x  7x  9  m   Ta có: f  3
x  5x m 3 3
 0   x  7x m  4   x  7x  4  m .   3 3
x  7x m  4 
x  7x  4   m  
https:/www.facebook.com/groups/toanvd. Trang 69 Tập san
NHÓM GIÁO VIÊN TOÁN VIỆT NAM Số 02 8-2021
Để hàm số g x có ít nhất 3 điểm cực trị thì phương trình g x  0 có ít nhất 2 nghiệm phân
biệt khác 0 và g x đổi dấu khi đi qua ít nhất 2 trong số các nghiệm đó.
Từ BBT ta có 9  m  0  m  9  m   1;2;3;4;5;6,7,  8 .
Vậy có 8 giá trị của m thỏa mãn yêu cầu đề bài.
https:/www.facebook.com/groups/toanvd. Trang 70
NHÓM GIÁO VIÊN TOÁN VIỆT NAM
Tập san Số 02 8 - 2021
Ôn thi tốt nghiệp THPT đợt 2
Phân tích, định hướng tìm lời giải, xây dựng các bài tương tự các câu VD – VDC mã đề 102
ĐỀ THI TỐT NGHIỆP THPT ĐỢT 1 NĂM 2021
Buổi thi môn Toán kỳ thi tốt nghiệp THPT đợt 1 năm 2021 diễn ra vào chiều
ngày 7/8/2021. Bài thi môn Toán gồm 24 mã đề, được lấy từ 4 mã đề gốc là: Mã đề
101, 102, 103, 104. Nội dung đề thi nằm trong chương trình THPT, chủ yếu chương
trình lớp 12, trong đó 38 câu đầu ở mức độ nhận biết, thông hiểu được ra trong các mã đề
nhằm kiểm tra kiến thức cơ bản của lớp 11, lớp 12; trong các mã đề từ câu 39 đến câu 45
kiểm tra kiến thức học sinh ở mức độ vận dụng, từ câu 46 đến câu 50 ở mức độ vận dụng
cao đã thể hiện rõ tính phân hoá bằng cách sử dụng tổng hợp các kiến thức trong chương trình THPT.
Kỳ thi tốt nghiệp THPT đợt 2 năm 2021 sẽ diễn ra trong 2 ngày 6/7/8/2021,
để tạo điều kiện cho quý thầy cô cùng các em có tài liệu ôn tập trong thời gian gấp rút này
Nhóm Giáo viên Toán Việt Nam xin gửi tới quý thầy cô và các em bài viết “Phân
tích, định hướng tìm lời giải, xây dựng các bài tương tự các câu VD – VDC đề thi tốt nghiệp THPT đợt 1 Năm 2021”
Hy vọng bài viết sẽ giúp quý thầy cô có thêm tài liệu tham khảo; các em học sinh
nắm chắc các kiến thức trong chương trình THPT; tiếp cận được với các bài toán mới,
hay và lạ. Đặc biệt, rèn luyện tốt kỹ năng thi trắc nghiệm môn Toán.
https://www.facebook.com/groups/toanvd.vdc Trang 86
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8 - 2021
Câu 39. Cắt hình nón  N  bởi mặt phẳng đi qua đỉnh và tạo với mặt phẳng chứa đáy một góc bằng 0
60 ta thu được thiết diện là một tam giác đều cạnh 4a . Diện tích xung quanh của  N  bằng : A. 2 8 7 a . B. 2 4 13 a . C. 2 8 13 a . D. 2 4 7 a .
FB: Trương Quốc Toản – Tạ Minh Đức
Phân tích định hướng tìm Lời giải:
- Đây là bài toán tính diện tích xung quanh của hình nón;
- Để tính diện tích xung quanh của hình nón ta áp dụng công thức S   rl ; xq
- Trong bài toán này đường sinh l  4a , nên chúng ta chỉ cần xác định bán kính đáy r của
hình nón  N  thông qua giả thiết bài toán; Lời giải Chọn D
Gọi I là tâm của đường tròn đáy của hình nón.
Ta có thiết diện qua đỉnh là tam giác SBA .
Gọi M là trung điểm của đoạn thẳng AB .
Ta chứng minh được AB  SIM  , suy ra góc giữa mặt phẳng đi qua đỉnh và mặt 
phẳng chứa đáy của hình nón là 0 SMI  60 . 4a 3
Do tam giác SAB đều cạnh 4a , suy ra SM   2a 3 . 2
Xét tam giác SIM vuông tại I ta có SI  3a; IM a 3 . Xét I
MA vuông tại M ta có IA IM MA a   a2 2 2 2 3 2  a 7 .
Vậy diện tích xung quanh của hình nón là 2 S
  rl   a 7.4a  4 7 a . xq Bình luận:
- Đây là bài toán tính diện tích xung quanh của hình nón, để làm được bài này yêu cầu các
em học sinh phải nhớ công thức tính diện tích xung quanh của hình nón; cách xác định thiết
diện của mặt phẳng với hình nón và xác định được góc giữa hai mặt phẳng. Tuy dạng toán
này không mới, nhưng để giải quyết được bài toán này thì các em học sinh phải có học lực khá trở lên. Hướng phát triển:
Hướng phát triển 1: Thay đổi giả thiết cho chiều cao và diện tích thiết diện. Yêu cầu tính thể tích của khối nón
Hướng phát triển 2: Thay giả thiết góc bằng bán kính đáy của hình nón. Tính khoảng cách
từ tâm của đáy đến mặt phẳng
Hướng phát triển 3: Giữ nguyên giả thiết, mặt cắt chia khối nón thành hai phần tính thể tích
một phần của khối nón
https://www.facebook.com/groups/toanvd.vdc Trang 87
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8 - 2021
Hướng phát triển 4: Thay đổi giả thiết cho bán kính đáy hình nón; mặt phẳng đi qua đỉnh
và tạo với mặt phẳng chứa đáy một góc. Tính diện tích thiết diện.
Hướng phát triển 5: Thay đổi giả thiết bài toán cho bán kính, chiều cao của hình nón. Mặt
phẳng đi qua đỉnh hình nón cắt mặt phẳng chứa đáy là tam giác cân có cạnh đáy cho trước.
Tính góc tạo bởi hai mặt phẳng.
Hướng phát triển 6: Xây dựng các bài toán tương tự trên hình trụ
Các ví dụ minh họa Câu 1.
Cho hình nón có chiều cao bằng 2 5 . Một mặt phẳng đi qua đỉnh hình nón và cắt hình nón
theo một thiết diện là tam giác đều có diện tích bằng 9 3 . Thể tích của khối nón được giới
hạn bởi hình nón đã cho bằng 32 5 A. . B. 32 . C. 32 5 . D. 96 . 3 Lời giải Chọn A S B O A 2 2 AB 3 AB 3 Ta có 2 2 S  
 9 3  AB  36  SA  36 . SAB 4 4 2 2 R OA SA SO  36  20  4 1 32 5
Thể tích của khối nón là 2
V   R h  . 3 3 Câu 2.
Cho hình nón có đỉnh S , đáy là đường tròn tâm O sao cho SO  6 5 , một mặt phẳng ( )
cắt mặt nón theo hai đường sinh S ,
A SB . Biết khoảng cách từ O đến mặt phẳng ( ) bằng
2 5 và diện tích tam giác SAB bằng 360 . Thể tích khối nón bằng A. 1325 5 . B. 265 5 . C. 1325 5 . D. 265 5 . Lời giải Chọn A
https://www.facebook.com/groups/toanvd.vdc Trang 88
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8 - 2021
Kẻ OI AB, OH SI OH d O, ( )  2 5 1 1 1 1 1 1 1 1 2 3 10          OI  2 2 2 2 2 2 OH SO OI OI OH SO  2  2 45 2 5 6 5 2 2  
SI SO OI  6 52 3 10 9 10 2 2      2  2   1 S 360 S
.SI.AB SI. SAB IA IA    8 10 SAB 2 SI  9 10    2   2  
r OI IA  8 102 3 10 5 106 2 2      2  2   2 1  5 106  V  . .  .6 5  1325 5 3  2    Câu 3.
Cho hình nón đỉnh S, đáy là đường tròn O;3 . Một mặt phẳng đi qua đỉnh của hình nón cắt
đường tròn đáy tại hai điểm A và B sao cho SA AB  5. Khoảng cách từ O đến mặt phẳng
SAB bằng 33 4 33 33 2 33 A. . B. . C. . D. . 5 15 15 15 Lời giải Chọn B.
Gọi I là trung điểm AB .  AB SO Ta có 
AB  SOI   SAB  SOI  . AB OI
Trong SOI  , kẻ OH SI , H SI thì OH  SAB .
d O;SAB  OH . Ta có: 2 2 2 2 SO SA OA  5  3  4 . 2  5  11 Ta có: 2 2 2
OI OA AI  3     .  2  2 1 1 1 1 4 4 33
Tam giác vuông SOI có:      OH  . 2 2 2 OH OI SO 16 11 15
https://www.facebook.com/groups/toanvd.vdc Trang 89
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8 - 2021
Vậy d O SAB 4 33 ;  OH  . 15 Câu 4.
Một khối nón có bán kính đáy bằng 2a, đường sinh bằng a 7 (tham khảo hình dưới đây).
Một mặt phẳng qua đỉnh và tạo với đáy của hình nón một góc 0
60 chia khối nón thành hai
phần, gọi V là thể tích phần nhỏ hơn. Giá trị của V bằng  4 3   4 3  A. 3  1 a .  1 a .  B. 3 9      3    4 3   4 3  C. 3   3 a .    3 a .  D. 3 3      9   Lời giải Chọn A.
Giả sử mặt phẳng qua đỉnh và tạo với đáy một góc 0
60 cắt khối nón theo thiết diện là
tam giác SMN như hình vẽ.
Gọi I là trung điểm của MN. Khi đó OI MN , SI MN từ giả thiết ta có góc 0 SIO  60 .
Xét tam giác SOM ta có 2 2 SO SM OM  3a. SO 3a
Xét tam giác SIO ta có OI  
a, từ đó xét trong tam giác OIM ta được 0 tan 60 3  1 0 IOM  60 , suy ra  0 NOM  120 , 2 0 2 S
.OM .sin120  3a . OMN 2
Gọi S là diện tích hình viên phân tạo bởi dây MN và cung nhỏ MN. Ta có o 1  4 2  2
S   .OM S   3 a . 0   3 OMN  3  1 1 4  4 3   
Thể tích cần tính bằng 2 3 V S . O S  . 3 . a  3 a     1 a . 0 3 3 3  9     
https://www.facebook.com/groups/toanvd.vdc Trang 90
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8 - 2021 Câu 5.
Cắt hình nón đỉnh I bởi một mặt phẳng đi qua trục của hình nón ta được một tam giác vuông
cân có cạnh huyền bằng a 2 , BC là dây cung của đường tròn đáy hình nón sao cho mặt
phẳng  IBC  tạo với mặt phẳng chứa đáy hình nón một góc 0
60 . Tính theo a diện tích S của tam giác IBC . 2 a 3 2 a 2 a 2 2 2a A. S  . B. S  . C. S  . D. S  . 3 3 3 3 Lời giải Chọn C a 2
Tam giác IDC vuông cân có DC a 2  IH HC
và IC a . 2 
Gọi E là trung điểm cạnh BC , góc giữa mặt phẳng (IBC) và (BCD) là 0 IEH  60 . IH a 6
Trong tam giác IHE có IE   . 0 sin 60 3 2 3 Tam giác IEC có 2 2 2 2 CE IC IE a a a . 3 3 2 a 2
Vậy S EI.EC  . 3 Câu 6.
Cho hình nón đỉnh S có bán kính đáy R  3, chiều cao h  2 2. Mặt phẳng ( ) qua đỉnh 2
S cắt đáy của hình nón theo dây cung có độ dài
. Tính góc tạo bởi mặt phẳng ( ) và mặt 3
phẳng chứa đáy của hình nón. A. 0 30 B. 0 45 C. 0 60 D. 0 75 Lời giải Chọn C S A O M B 2 Gọi ,
A B là hai giao điểm của ( ) với đường tròn đáy, ta có AB  . 3
Gọi M là trung điểm AB, ta có OM AB, SM AB  góc tạo bởi ( ) và mặt đáy  2 6 SO  là SMO , 2 2
OM OB BM  ,  tan SMO   3. 0  SMO  60 . 3 OM
https://www.facebook.com/groups/toanvd.vdc Trang 91
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8 - 2021 Câu 7.
Cho hình trụ có hai đáy là hai đường tròn tâm O và tâm O , bán kính đáy r a 3, chiều cao
hình trụ h a . Mặt phẳng ( ) đi qua trung điểm của OO và tạo với OO một góc 60 và ( )
cắt đường tròn đáy tâm O theo dây cung AB . Độ dài đoạn AB là: 3a a 3 A. 2a . B. . C. . D. 3a . 2 2 Lời giải Chọn D B N A O H M O' (α)
Gọi M , N lần lượt là trung điểm của OO và AB . Ta có
AB ON , AB OO  AB  OMN  . Gọi H là hình chiếu của O trên MN thì OH  ( )
Ta có OO  ABM   OOMH
  OOMN    ; ; ;  OMN  60 .  a a 3
Tam giác OMN vuông tại O có ON OM.tan OMN ON  .tan 60  . 2 2 2 3a 2 2 2
AB  2NB  2 OB ON  2 3a   3a . 4 Câu 8.
Cho một hình trụ tròn xoay và hình vuông ABCD cạnh a có hai đỉnh liên tiếp , A B nằm trên
đường tròn đáy thứ nhất của hình trụ, hai đỉnh còn lại nằm trên đường tròn đáy thứ hai của
hình trụ. Mặt phẳng ABCD tạo với mặt phẳng chứa đáy hình trụ một góc 45 . Tính diện tích
xung quanh hình trụ? 2 2 a 3 2  a 3 2  a 3 2  a 3 A. S  . B. S  . C. S  . D. S  . xq 5 xq 3 xq 4 xq 2 Lời giải Chọn D
Gọi P, Q, E lần lượt là trung điểm của AB,CD,OO . Góc giữa ( ABCD) và mặt đáy là  a a 2 O Q
E  45 . Ta có EQ  , do đó O Q   EO  . 2 4
https://www.facebook.com/groups/toanvd.vdc Trang 92
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8 - 2021 a 2 a 6
Suy ra h OO  và r O C   . 2 4 2 a 6 a 2  a 3
Diện tích xung quanh của hình trụ là S  2    . xq 4 2 2 Câu 9.
Cho khối trụ có thiết diện qua trục OO là một hình vuông cạnh bằng 2 . Mặt phẳng  P đi
qua trung điểm I của OO và tạo với mặt phẳng chứa đáy của khối trụ một góc bằng 30 .
Diện tích của thiết diện do  P cắt khối trụ gần số nào sau đây nhất? A. 3, 6 . B. 3,8 . C. 3,5 . D. 3, 7 . Lời giải Chọn A O A C I D H M O
Do thiết diện qua trục OO là một hình vuông cạnh bằng 2 nên chiều cao của hình
trụ là h  2 và bán kính đáy là R  1 .
Giả sử giao tuyến của mặt phẳng  P và đáy chứa tâm O là đường thẳng d . Gọi E
là hình chiếu của O trên d . Khi đó góc giữa  P và mặt phẳng chứa đáy là góc  OEI 30  .  OI 2
Trong tam giác vuông IOE có tan OEI   OE
 3  1. Do đó điểm E OE 3 3
nằm ngoài đường tròn đáy nên thiết diện là Elip.  HM 2 4 3
Trong tam giác vuông AHM có cos AMH   AM   . AM 3 3 2 4 3 2 3 Hay 2a   a
. Mà CD  2b  2  b  1 . 3 3 2 3
Thiết diện là hình elip nên diện tích bằng ab     3, 62 . 3
2x  5 khi x  1
Câu 40: Cho hàm số f x  
. Giả sử F là nguyên hàm của f trên  thỏa mãn 2
3x  4 khi x  1 
F 0  2. Giá trị của F  
1  2F 2 bằng A. 27. B. 29. C. 12. D. 33.
https://www.facebook.com/groups/toanvd.vdc Trang 93
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8 - 2021
Phân tích định hướng tìm lời giải
Dạng toán: Cho hàm số F là nguyên hàm của f với f là hàm cho bởi nhiều biểu thức. Bài toán yêu
cầu tính giá trị của biểu thức F tại một số điểm. Dạng toán này ta có 2 cách làm chính sau
* Cách 1: Tìm hàm số F (là tìm các hằng số C ,C ,... ) dựa vào các giả thuyết đã cho (như liên tục, có 1 2
đạo hàm, F x ,…). Tùy theo yêu cầu bài toán mà sử dụng hàm số F đã tìm được một cách phù hợp. o
Cụ thể hơn ta có: 2
2x  5 khi x  1 
x  5x C khi x  1
Bước 1: f x    F x 1   . 2 3
3x  4 khi x  1 
x  4x C khi x  1  2
Bước 2: Tìm các hằng số C ,C dựa vào F (0)  2 và tính liên tục của hàm số. 1 2
Bước 3: Tính giá trị của biểu thức F   1  2F 2 . b
* Cách 2: Sử dụng công thức F b  F a 
f xdx
phù hợp. Cụ thể ở bài trên ta làm như sau a 1
Bước 1: F   1 
f xdx F 0  . 0
Bước 2: Để ý F  
1  2F 2  F   1  F  
1   2 F 2  F   1   3F   1    
, các biểu thức trong dấu b ngoặc vuông có dạng
f xdxa Fb-Nam Phương Lời giải * Cách 1 2
2x  5 khi x  1 
x  5x C khi x  1
f x    F x 1   . 2 3
3x  4 khi x  1 
x  4x C khi x  1  2 2 
x  5x C khi x  1
Vì F 0  2  C  2  F x 1  . 2  3
x  4x  2 khi x  1 
Hàm số liên tục trên   lim F x  lim F x  F (1)  1 5  C  1 4  2  C  1 1 1 x 1 x 1   2 
x  5x 1 khi x  1
F x   . Vậy F   1  2F 2  3   2.15  27 . 3
x  4x  2 khi x  1  * Cách 2
Nhận xét: Hàm số f x liên tục trên .  0 0
F 0  F   1 
f x dx     2
3x  4dx  5  F  
1  F 0  5  3.  1  1  1 1 F  
1  F 0  f x dx    2
3x  4dx  5  F  
1  F 0  5  7. 0 0 2 2
F 2  F   1 
f x dx  2x  5 dx  8  F 2  F   1  8  15.   1 1 Do đó F   1  2F 2  3   2.15  27. Bình luận:
- Đây là dạng toán thuộc mức độ vận dụng, việc nhận ra hướng giải đòi hỏi học sinh phải nắm chắc
các khái niệm và tính chất của nguyên hàm cũng như các phương pháp tìm nguyên hàm.
Hướng phát triển:
- Không cho điều kiện F (a)  m . Yêu cầu tính F (b)  F (c) .
- Thêm điều kiện như: có đạo hàm, liên tục,….
- Thay đổi điều kiện kiện của đề bài bằng cách cho F (a)  F (b)  k . Yêu cầu tính F (n)  F (m) .
https://www.facebook.com/groups/toanvd.vdc Trang 94
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8 - 2021
Bài tập tương tự 2x 1 khi x  1 Câu 1:
Cho hàm số f x  
. Giả sử F là nguyên hàm của f trên  thỏa mãn 2 3x  2 khi x  1 
F 0  2 . Giá trị của F  
1  2F 2 bằng A. 9 . B. 15 . C. 11. D. 6 . Lời giải Chọn A 2x 1 khi x  1 2 
x x C khi x  1
Ta có: f x  1 
F x  f x dx    . 2 3x  2 khi x  1 3 
x  2x C khi x  1  2
Mà ta có F 0  2  C  2 . 2
Mặt khác hàm số F là nguyên hàm của f trên  nên y F x liên tục tại x  1 .
Suy ra lim F x  lim F x  F (1)  C  1. 1 x 1 x 1   2  x x 1 khi x  1 F    1  3
Khi đó ta có: F x   suy ra  . 3
x  2x  2 khi x  1  F  2  3  Vậy F  
1  2F 2  9 .
2x  3 khi x  1 Câu 2:
Cho hàm số f x  
. Giả sử F là nguyên hàm của f trên  thỏa mãn 2
3x  2 khi x  1 
F 0  2 . Giá trị của F  
1  2F 2 bằng A. 23. B. 11. C. 10 . D. 21 . Lời giải Chọn D
Dễ thấy hàm số f liên tục trên  . 1 1 F   1  F 0 2 
f (x)dx
(3x  2) f (x)dx  3  F (1)  5   . 0 0 1  2 F   1  2F 2 
f (x)dx  2
f (x)dx  3 f (1)  6  12 15  21   . 1 1 2 3   x  2 khi x  2 Câu 3:
Biết rằng F (x) liên tục trên  là một nguyên hàm của hàm số f (x)   . Giá trị 3
4x 18 khi x  2 
của biểu thức F (1)  F (3) bằng A. 7. B. 18. C. 8. D. 32. Lời giải Chọn B 1  3 Ta có: F ( 1  )  F (3) 
f xdx
f xdx  18   . 2 2  1 khi x  0  Câu 4:
Biết rằng F (x) liên tục trên  là một nguyên hàm của hàm số f (x)   2x 1 và  3
(2x 1) khi x  0 
F (4)  F (1)  8 . Giá trị của biểu thức P F (2)  2F (12) bằng 281 121 A. 20 . B. 27 . C. . D. . 16 8 Lời giải Chọn B 4 1 
Ta có : 8  2F (0)  F (4)  F (0)  F ( 1  )  F (0) 
f xdx
f xdx  2  F(0)  3   . 0 0
https://www.facebook.com/groups/toanvd.vdc Trang 95
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8 - 2021 2  12 P F ( 2  )  2F (12) 
f xdx  2
f xdx  3F(0)  27   . 0 0 
x 1 khi x  0 Câu 5:
Biết rằng F (x) liên tục trên  , là một nguyên hàm của hàm số f (x)   và 3
(2x 1) khi x  0  19
F (3)  F (1) 
. Giá trị của biểu thức P F (2)  F (8) bằng 3 A. 20 . B. 27 . C. 58 . D. 29 . Lời giải Chọn D  2 F (x)   x  3 1  C , x  0 1 1   3
Ta có F (x)   . 4 (2x 1) F (x)   C , x  0 2 2   8 2 1 13
Do F (x) liên tục trên  nên lim F (x)  lim F (x)  F (0)  C  
C C C   . 1 2 1 2 x 0 x 0   3 8 24 16 1 19 7 1 17
Và F (3)  F ( 1  )  8   C   C   C C  . Suy ra C  ,C  . 1 2 1 2 3 8 3 8 1 2 6 24 1 81 17
Tính F (8)  F ( 2  )  18     29 . 6 8 24
ax 1 khi x  1 Câu 6:
Cho hàm số f (x)  
với a, b là các tham số thực. Biết rằng f (x) liên tục và có 2
x b khi x  1  2 đạo hàm trên .  Tích phân I f (x)dx  bằng 1  1 19 26 25 A. B. C. D. 3 3 3 3 Lời giải Chọn C
Hàm số liên tục trên  nên sẽ liên tục tại x  1  lim f (x)  lim f (x)  f (1) o x 1 x 1   2
 lim(ax 1)  lim(x b)  f (1)  a 1  1 b a  . b x 1 x 1  
Hàm số có đạo hàm trên  nên có đạo hàm tại x  1  lim f (
x)  lim f (  x) o x 1 x 1  
2x 1 khi x  1
 lim(a)  lim(2x)  a  2. Suy ra a b  2  f (x)   . x 1 x 1   2
x  2 khi x  1  2 1 2 1 2 26 Do đó: 2 I
f (x)dx
f (x)dx
f (x)dx
(x  2)dx  (2x 1)dx        3 1  1  1 1  1 2
ax bx 1 khi x  0 Câu 7:
Cho hàm số f (x)  
. Biết rằng hàm số f (x) có đạo hàm trên .  Tích phân ax b 1 khi x  0  1  I f (x)dx  bằng 3 82 22 A. B.   C. 1  4. D. 10. 3 3 Lời giải Chọn D
+) f (x) có đạo hàm trên   f (x) liên tục trên   f (x) liên tục tại x  0 .
f ( x) liên tục tại tại x  0   lim f (x)  lim f (x)  f (0) x 0 x 0  
https://www.facebook.com/groups/toanvd.vdc Trang 96
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8 - 2021  lim        b
 1  1  b  2.   2 ax bx
1 lim ax b 1 f (0) x 0 x 0  
+) f (x) có đạo hàm trên   f (x) có đạo hàm tại x  0 .   2 ax  2x f x f   1 1 ( ) (0)  lim  lim
 lim ax  2  2 . x 0 x  0 x 0 x  0 x 0   
f (x)  f (0) ax   2   1 1  lim lim   
 lim a a . x 0 x  0 x 0 x  0 x 0   
f (x)  f (0)
f (x)  f (0)
f ( x) có đạo hàm tại x  0  lim  lim  a  2  . x 0 x  0 x 0   x  0 2   2
x  2x 1 khi x  0
Do đó, f (x)   .  2
x 1 khi x  0  1  1  Vậy I
f (x)dx   2  x   1 dx 1  0   . 3  3  2
x  3, x  1 Câu 8:
Cho hàm số f x  
. Giả sử F là nguyên hàm của f trên  thỏa mãn F 0  1. 5  x, x  1   2 2 Tính I
f cos xsin d
x x F x dx   0 1 142 112 1 13 A. . B. C. . D. . 12 13 12 12 Lời giải Chọn A 3
x 3x C , x 1  1  3
Ta có F x   . 2 x 5  x   C , x  1 2   2
Mà F 0  1  C  1. 2
Vì f x liên tục tại x  1 nên F x liên tục tại x  1  lim F x  lim F x  F (1) x 1 x 1   1 1 13  5   1 
 3  C C  . 1 2 3 1 6 3  x 13  3x  , x  1   3 6
Vậy F x   . 2 x 5  x  1, x  1   2   2 2 2 2 I
f cos xsin d
x x F x dx   f cos x d cos x  F x dx     0 1 0 1 1 2 
f xd x F xdx   0 1 1 2 3  x 13  142
 5  xdx   3x  dx     . 3 6 12 0 1   2
Câu 41: Có bao nhiêu số nguyên x thỏa mãn 3x  9x  log x  25  3  0  3    A. 27. B. Vô số. C. 26 . D. 25 .
https://www.facebook.com/groups/toanvd.vdc Trang 97
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8 - 2021
Phân tích định hướng tìm lời giải:
- Đây là bài toán giải bất phương trình mũ, lôgarit dạng f x.g x  0 .
- Để giải bất phương trình chúng ta cần đặt điều kiện sau đó tìm nghiệm của từng phương
trình f x  0 và g x  0 . Tiếp theo lập bảng xét dấu f x.g x và tìm tập nghiệm từ đó
kết luận số nghiệm nguyên thỏa mãn bất phương trình. Fb-Lê Thanh Bình Lời giải Chọn C
Ta có điều kiện xác định của bất phương trình là x  25 . 2
Đặt ( )  3x  9x A x
log x  25 3, x  25  3    . 2
3x  9x  0  x  0  x  2 . log
x  25  3  0  x  2 . 3   Ta có bảng xét dấu ( A x) như sau  x  2 Từ đó, ( A x)  0   x    24  ; 2  3;...; 0;  2 (do x   ). 25   x  0 
Kết luận: có 26 nghiệm nguyên thỏa mãn. Bình luận:
- Đây là bài toán giải bất phương trình mũ và lôgarit trong đó việc tìm nghiệm của từng
phương trình mũ và lôgarit khá đơn giản. Tuy nhiên qua thực tế thì học sinh thường mắc các sai sót sau:
 Quên không đặt hay để ý điều kiện của lôgarit. Từ đó dẫn đến tập nghiệm là  ;0 
2 nên kết luận là vô số.
 Thiếu nghiệm x  2 nên kết luận là có 25 số nguyên x .
Đây là câu hỏi kiểm tra kiến thức ở mức độ vận dụng. Hướng phát triển:
Hướng phát triển 1: Thay đổi hàm số , hoặc có thể cho thêm 1 hàm số nữa dạng
f x.g x.h x  0 .
Hướng phát triển 2: Thay đổi thành dạng f x.g x  0 , f x.g x  0 hay f x.g x  0 …
Bài tập tương tự xx 1  Câu 1.
Tập nghiệm của bất phương trình  2 3  9 x 1 3  3  1  0  
chứa bao nhiêu số nguyên ?  27  A. 2. B. 3. C. 4. D. 5. Lời giải Chọn B Điều kiện x 1  x 1 3 1 0 3      1  x  1  .
+ Ta có x  1 là một nghiệm của bất phương trình. xx 1 
+ Với x  1 , bất phương trình tương đương với  2 3  9 3   0   .  27 
https://www.facebook.com/groups/toanvd.vdc Trang 98
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8 - 2021 t  3   1   1  Đặt 3x t   0 , ta có  2 t  9 t   0   
 t  3t  3 t   0    1 .  27   27    t  3  27 1 1 Kết hợp điều kiện 3x t   0 ta được nghiệm  t  3   3x  3  3   x  1 . 27 27
Kết hợp điều kiện x  1 ta được 1  x  1 suy ra trường hợp này bất phương trình có 2 nghiệm nguyên.
Vậy bất phương trình đã cho có tất cả 3 nghiệm nguyên. Câu 2.
Tập nghiệm của bất phương trình x 2 x 2 3 .  54  5.3  9  6 .3x x x x x  45 là A. ;  1  2;  B. ;  1  2;5 C. ;  1  5; 
D. 1; 2  5;  . Lời giải Chọn D
Bất phương trình x 2 x 2 3 .  54  5.3  9  6 .3x x x x x
 45 tương đương với:  x 2 2     x      x   2 3 . 9 6 .3 54 5.3 45  0 
3x  9  6 3x  9  53x x x x x x x  9  0 x  2  3x    9  0    x  1 2 x 6x 5 0        x  5  3x  9 2
x  6x  5  0   x  5     . x   1  x  2 3   9  0    x  2 2
x  6x  5  0   1  x  5 
Vậy tập nghiệm của bất phương trình đã cho là 1; 2  5;  . 2 Câu 3.
Có bao nhiêu số nguyên x thỏa mãn 3x  9x  log x  32  5  0  2    ? A. 31. B. Vô số. C. 32 . D. 33 . Lời giải Chọn C 2
Xét hàm số    3x  9x f x
log x 30 5  x   . 2    , với 32 2 2 x x x 2  3  9  0  3  3 xx  2
Cho f x  0       log  x  32 5  5  0 x  32  2 x  0  2  
Ta có bảng xét dấu như sau:
Suy ra tập nghiệm của bất phương trình f x  0 là S  32; 0  0; 2
Mặt khác x   nên x 31; 30; 27;......; 2; 1;  1 .
Vậy có 32 số nguyên x thỏa mãn. Câu 4.
Có bao nhiêu số nguyên x thỏa mãn log 1. 2x x  1024  0 ? 5   A. 6 . B. Vô số. C. 4 . D. 5 . Lời giải Chọn C
Điều kiện log x 1  0  x  5 . 5 Xét hàm số    log 1. 2x f x x
1024 , với x  5 . 5  
https://www.facebook.com/groups/toanvd.vdc Trang 99
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8 - 2021  log x 1  0 x  5 Cho f x 5  0     2x 1024  0 x  10  
Ta có bảng xét dấu như sau:
Suy ra tập nghiệm của bất phương trình f x  0 là S  5;10
Mặt khác x   nên x 6;7;8;  9 .
Vậy có 4 số nguyên x thỏa mãn. 2 Câu 5.
Có bao nhiêu số nguyên x thuộc khoảng 2020; 202 
1 thỏa mãn x 7x6 2
.log x  log x ? 7 7 A. 2017 . B. Vô số. C. 2016 . D. 2015 . Lời giải Chọn C
Điều kiện x  0 . 2
Với x  0 bất phương trình đã cho tương đương với x 7x6 2
.log x  log x  0 7 7
  2x7x6 2   1 .log x  0 7 2
Xét hàm số f x   x 7x6 2  
1 .log x , với x  0 . 7 2 x 7 x6 2 2 1  0
x  7x  6  0 x  1
Cho f x  0       (thỏa mãn điều kiện log x  0 x  1 x  6  7   x  0 )
Ta có bảng xét dấu như sau:
Suy ra tập nghiệm của bất phương trình f x  0 là S  6;     1 .
Mặt khác x là số nguyên thuộc khoảng 2020; 202 
1 nên x 1; 6; 7;8;9;....; 202  0 .
Vậy có 2016 số nguyên x thỏa mãn. x y 1 z  2
Câu 42: Trong không gian Oxyz , cho đường thẳng d :   và mặt phẳng 1 1 1 
P : x  2 y z  4  0 . Hình chiếu vuông góc của d trên P là đường thẳng có phương trình: x y 1 z  2 x y 1 z  2 A.   . B.   . 2 1 4  3 2  1 x y 1 z  2 x y 1 z  2 C.   . D.   . 2 1 4  3 2  1
Phân tích định hướng tìm lời giải:
- Đây là bài toán lập phương trình đường thẳng là hình chiếu vuông góc của một đường
thẳng lên một mặt phẳng.
- Để lập phương trình đường thẳng ta cần biết hai điểm hoặc biết một điểm và một véc tơ chỉ phương của nó
- Trong lời giải sau đây ta sẽ đi theo hướng lập phương trình đường thẳng d là hình chiếu
của d trên  P khi biết hai điểm bằng cách.
+ Tìm A d   P
+ Tìm hình chiếu của H của B d , B A lên  P . Khí đó d là đường thẳng AH
https://www.facebook.com/groups/toanvd.vdc Trang 100
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8 - 2021 Fb-Lê Tài Thắng Lời giải Chọn C
Tọa độ giao điểm A của d và  P thỏa mãn hệ phương trình:  x y 1 z  2 x  0     1 1 1 
  y  1  A0;1; 2 .
x  2y z  4  0  z  2 
Lấy điểm B 1; 2; 
1  d . Gọi H là hình chiếu của B trên  P . x  1 t
 Phương trình BH :  y  2  2t z 1 t
Do H BH   P nên tọa độ điểm H thỏa mãn hệ phương trình: A0;1; 2  1 t    3  x  1 t 2   x  
y  2  2t  3  2 4 2   2 1 4      H ; ;    AH  ; ;    . z  1 t  4   3 3 3   3 3 3  y
x  2y z  4  0   3  2 z   3
Gọi d là hình chiếu vuông góc của d trên  P  d đi qua A và H
d có một vector chỉ phương là u  2;1;  4 . x y 1 z  2
Vậy phương trình đường thẳng d là:   . 2 1 4 
Nhận xét: Đây là cách làm theo chuẩn tự luận dựa trên tư duy hình học đơn giản.
Cách này hơi dài nhưng học sinh trung bình thì dễ làm. Bình luận:
- Đây là bài toán lập phương trình đường thẳng, để xác định các yếu tố lập được phương
trình của đường thẳng nói trên học sinh phải có kiến thức tổng hợp liên quan đến tìm tọa
độ giao điểm, tìm hình chiếu của điểm lên mặt. Đặc biệt, học sinh phải nhận ra mẫu chốt
của bài toán là khi tìm hình chiếu của đường thẳng ta cần tìm hình chiếu của hai điểm phân
biệt của đường thẳng đó lên mặt phẳng. Trong trường hợp đường và mặt cắt nhau thì điểm
cắt chính là một điểm trên đường thẳng là hình chiếu đó.
https://www.facebook.com/groups/toanvd.vdc Trang 101
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8 - 2021
- Ở bài toán này ta có thể dễ thấy d    P   ABH  với  ABH  là mặt phẳng chứa d và
vuông góc  P . Vì vậy ta có thêm các hướng giải như sau:
+ Hướng 1: Ta lập mặt phẳng Q chứa d vuông góc với  P , khi đó ta tìm d    P  Q .    
+ Hướng 2: Tìm véc tơ chỉ phương của d là u
 n , u  , n  và lập phương trình d có P d P    
VTCP u đi qua A .
Trong các hướng thì ta chọn hướng 2 là nhanh nhất với bài toán trắc nghiệm.
Lời giải (theo hướng 2) Chọn C
Tọa độ giao điểm A của d và  P thỏa mãn hệ phương trình:  x y 1 z  2 x  0     1 1 1 
  y  1  A0;1; 2 .
x  2y z  4  0  z  2       
Ta có n  1, 2, 
1 ; u  1,1,   1 nên u
 n , u  , n   4, 2, 8 hay chọn P d PP d   
u  2,1, 4. x y 1 z  2
Vậy phương trình đường thẳng d là:   . 2 1 4 
Cách này nhanh nhưng đòi hỏi sự tưởng tượng cao, tính toán nhanh, với học sinh khá
trở lên sẽ thích cách này hơn. Nó rất phù hợp cho bài toán trắc nghiệm.
Bài tập tương tự x 1 y  2 z  2 Câu 1.
Cho đường thẳng (d ) :  
và mặt phẳng (P) : 2x y  3  0 . Đường thẳng  2 1  1
là hình chiếu vuông góc của đường thẳng d trên mặt phẳng (P) có phương trình là x 1 y 1 z  3 x 1 y  2 z  2 A.   . B.   . 1  2 4 1  2 4 x 1 y  2 z  2 x 1 y 1 z  3 C.   . D.   . 4 8  5 4 8  5 Lời giải Chọn D
Tọa độ giao điểm A của d và (P) là nghiệm của hệ:
2x y  3  0 x  1    x 1 y  2
z  2   y  1  A1;1;3 .      2 1  1 z  3 
Lấy B 1; 2; 2  d , gọi H là hình chiếu của B xuống mặt phẳng (P) . x  1   2t
Phương trình đường thẳng  BH  :  y  2  t
. Tọa độ điểm H là nghiệm của hệ: z  2 
2x y  3  0  x  1   2t  1 13    H ; ; 2   . y  2  t  5 5   z  2 
Hình chiếu  là đường thẳng đi qua hai điểm , A H .
https://www.facebook.com/groups/toanvd.vdc Trang 102
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8 - 2021   4  8  Ta có AH ; ; 1  
 . Đường thẳng  đi qua A có vecto chỉ phương  5 5  
u  5AH   .  4; 8,5 x 1 y 1 z  3
Phương trình đường thẳng  là:   . 4 8  5 Câu 2.
Trong không gian Oxyz, cho mặt phẳng  P : x y z  3  0 và đường thẳng x y 1 z  2 d :  
. Hình chiếu vuông góc của d trên  P có phương trình là 1 2 1  x 1 y 1 z 1 x 1 y 1 z 1 A.   B.   1  4  5 3 2  1  x 1 y 1 z 1 x 1 y  4 z  5 C.   D.   1 4 5  1 1 1 Lời giải Chọn C
Gọi M là giao điểm của d với  P .
x y z  3  0
x y z  3 x  1   
Tọa độ của M là nghiệm của hệ:  x y 1
z  2  2x y  1   y  1       1 2 1  x z  2 z  1    M 1;1;  1
Lấy điểm N 0; 1; 2  d . 
Một vec tơ pháp tuyến của mặt phẳng  P là: n  1;1;  1 . 
Gọi  là đường thẳng đi qua N và nhận n  1;1; 
1 làm vec tơ chỉ phương. x y 1 z  2
Phương trình đường thẳng  :   1 1 1
Gọi N  là giao điểm của  với  P .  2 x   3
x y z  3  0
x y z  3     1
Tọa độ của N  là nghiệm của hệ:  x y 1
z  2  x y  1   y     3     1 1 1 x z  2   8 z    3  2 1 8  N ;  ;    3 3 3    1 4 5  1  MN   ;  ;   u 1;4; 5      3 3 3  3 
Đường thẳng cần tìm đi qua điểm M 1;1; 
1 và nhận u  1; 4; 5 làm vec tơ chỉ x 1 y 1 z 1
phương nên có phương trinh   . 1 4 5  x y  2 z 1 Câu 3.
Cho đường thẳng d :  
và mặt phẳng (P) : x y z  2  0 . Phương trình hình 2 3  2
chiếu vuông góc của d trên (P) là
https://www.facebook.com/groups/toanvd.vdc Trang 103
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8 - 2021 x  1 tx  1 tx  1 tx  1 t    
A. y  1 2t .
B. y  1 2t .
C. y  1 2t .
D. y  1 2t . z  2   3t     z  2   3tz  2   3tz  2  3tLời giải 
Đường thẳng d có véc tơ chỉ phương u  2;  3; 2 . d  
Mặt phẳng (P) có véc tơ pháp tuyến n  1; 1;   1 . P
Mặt phẳng (Q) chứa d và vuông góc với (P) ; Đường thẳng '
d là hình chiếu vuông góc của d trên (P) , d '   P  Q   
Véc tơ pháp tuyến của mặt phẳng (Q) là n  u , n   5; 4;1 Q d ' P       
Véc tơ chỉ phương của '
d là u  n , n   3;  6;9  3 1; 2; 3 d ' P Q       Ta thấy đường thẳng '
d thuộc (P) nên điểm M d '  M (P) . Thay tọa độ điểm 0 0 M
1;1;  2 ở đáp án A thấy thỏa mãn phương trình (P) . 0   Câu 4.
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng  P: x y z  3  0 và đường thẳng x y 1 z  2 d :  
. Hình chiếu của d trên  P có phương trình là đường thẳng d . Trong 1 2 1 
các điểm sau điểm nào thuộc đường thẳng d ?
A. M 2;5;  4 .
B. P 1;3;   1 .
C. N 1; 1;3 .
D. Q 2; 7 ;  6 . Lời giảix t
Gọi A d   P  . Vì Ad :  y  1
  2t At ; 1 2t ; 2  t  . z  2  t
Mặt khác A   P  t 1 2t  2  t  3  0  t  1. Vậy A1;1;  1 .
Lấy B 0; 1; 2  d . Gọi  là đường thẳng qua B và vuông góc  P . x t  Thì  :  y  1
  t . Gọi C là hình chiếu của B lên  P .
z  2  t 
Suy ra C    C t; 1 t; 2  t . 2  2 1  8 
Mặt khác C  P  t 1 t  2  t  3  0  t  . Vậy C ; ;   . 3  3 3 3    1  4  5 
Lúc này d qua A1;1; 
1 và có một vectơ chỉ phương là AC  ; ;   . Hay d  3 3 3  
nhận u  1; 4;  5 làm một vectơ chỉ phương. x  1 s
Suy ra d :  y  1 4s . Vậy điểm thuộc đường thẳng d là M 2;5;  4 . z 1 5s
Câu 43: (MĐ 101 BGD&ĐT NĂM 2020-2021) Cho hàm số bậc ba y f (x) có đồ thị là đường cong
trong hình bên. Số nghiệm thực phân biệt của phương trình f f x  1 là
https://www.facebook.com/groups/toanvd.vdc Trang 104
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8 - 2021 A. 9 . B. 3 . C. 6 . D. 7 .
Phân tích định hướng
o – Bài toán có mức độ VD thuộc dạng “Tương giao đồ thị”, đã xuất hiện nhiều trong đề thi các năm trước.
O– Ý tưởng: Cho đồ thị, bảng biến thiên,… của hàm số y f x . Hỏi số nghiệm của
phương trình f g(x)   với  là hằng số.
B1: Vẽ đường thẳng y   , dựa vào đồ thị, bảng biến thiên đã cho đưa phương trình về
dạng g x   . i
B2: Tìm nghiệm của phương trình g x   . i FB-Ngonguyen Quocman Lời giải Chọn D
Từ đồ thị hàm số ta có
f (x)  x và x  1 (1) 1 1
f f x  1   f (x)  0 (2) . 
f (x)  x và 1  x  2 (3)  2 2
Dựa vào đồ thị, (1) có đúng 1 nghiệm, (2) và (3) mỗi phương trình có 3 nghiệm
phân biệt và 7 nghiệm trên phân biệt nhau. Bình luận:
- Việc “hợp” các f vào nhau sẽ gây khó hiểu hoặc nhầm lẫn cho các học sinh chưa gặp
dạng này hoặc học chưa kỹ. Chưa kể, đường thẳng y   có thể cắt đồ thị hàm số
y f x ban đầu tại những điểm “không đẹp” là cách làm bài toán “khó gần” thêm. Đôi
khi, để học sinh có thể dễ tiếp cận hơn, quen thuộc hơn, ta có thể “án chừng” các con số
x , x như bài trên bởi các giá trị gần đúng, ví dụ như x  1  , 7; x  1, 7 . 1 2 1 2
https://www.facebook.com/groups/toanvd.vdc Trang 105
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8 - 2021
- Có rất nhiều hướng để có thể mở rộng bài toán, như thêm vào trị tuyệt đối, tham số,
thay  bởi hàm số,….hoặc thay vì cho đồ thị, bảng biến thiên của f x thì có thể cho đồ
thị hoặc bảng biến thiên của f  x .
Các ví dụ tương tự: Câu 1.
Cho hàm số bậc ba y f x có đồ thị trong hình bên. Số nghiệm của phương trình
f f x  0 là A. 3 . B. 9 . C. 4 . D. 7 . Lời giải Chọn D
f x  2 (1) 
Từ đồ thị hàm số ta có: f f x  0  f   x  0 (2)
f x 1 (3) 
Phương trình (1) có nghiệm duy nhất, phương trình (2) và (3) mỗi phương trình có
3 nghiệm phân biệt. Tất cả các nghiệm trên đều phân biệt nhau nên phương trình ban
đầu có tổng cộng 7 nghiệm. Câu 2.
Cho hàm số bậc bốn y f x có đồ thị như hình vẽ. Số nghiệm của phương trình
4  f x 1 là f x  3 A. 3 . B. 2 . C. 4 . D. 6 . Lời giải Chọn C
Điều kiện: f x  3  4  f x 1 1 Khi đó ta có:
 1  f x 
. Dựa vào đồ thị, phương trình f x  có 4 f x  3 2 2 nghiệm phân biệt. Câu 3.
Cho hàm số bậc bốn y f x có đồ thị như hình vẽ. Số nghiệm của phương trình
5  f f x 1 là
f f x  3
https://www.facebook.com/groups/toanvd.vdc Trang 106
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8 - 2021 A. 7 . B. 8 . C. 5 . D. 6 . Lời giải Chọn D
Để ý rằng f f x  3  1
  3  2  0, x
5  f f x Ta có:
 1  f f x 1 (*) .
f f x  3
f x  0 (1) 
Vẽ đường thẳng y  1, ta có: (*)  f
  x  a  1 (2)
f x  b 1 (3) 
Dựa vào đồ thị, phương trình (1) có 4 nghiệm phân biệt, phương trình (2) vô
nghiệm, phương trình (3) có 2 nghiệm phân biệt khác với 4 nghiệm trên. Vậy phương
trình đã cho có tổng cộng 6 nghiệm. Câu 4.
Cho hàm số bậc ba y f (x) có đồ thị như hình vẽ.
Số nghiệm của phương trình f f ( x )  0 là A. 10 . B. 12 . C. 14 . D. 8 . Lời giải Chọn B
f x   x  0;1 (1) 1   
Từ đồ thị hàm số ta có: f f x   0   f x   2 (2) 
f x   x  3;  (3) 2   
https://www.facebook.com/groups/toanvd.vdc Trang 107
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8 - 2021
Từ đồ thị y f (x) ta suy ra đồ thị y f x  như hình vẽ
Từ đó dễ thấy phương trình (1) có 6 nghiệm, phương trình (2) có 4 nghiệm và
phương trình (3) có 2 nghiệm phân biệt. Tất cả các nghiệm trên đều phân biệt nhau
nên phương trình ban đầu có tổng cộng 12 nghiệm. Câu 5.
Cho hàm số bậc ba y f (x) có đồ thị như hình vẽ.
Số nghiệm của phương trình f f x  x  1 là A. 5 . B. 7 . C. 9 . D. 3 . Lời giải Chọn A
f x  x a  (3; 2  )
f x  x a  
f f x  x  1  f
  x  x  0  f
  x  x .  
f x  x b  (3;)
f x  x b  
Ta có các đường thẳng y  x  ; a y  ;
x y  x b như hình vẽ (2 đường không qua
gốc tọa độ đều tạo với 2 trục các tam giác vuông cân).
https://www.facebook.com/groups/toanvd.vdc Trang 108
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8 - 2021
Dựa vào đồ thị, phương trình đã cho có đúng 5 nghiệm. Câu 6.
(Chuyên Lam Sơn Thanh Hóa – Lần 3) Cho hàm số y f x 3 2
x  3x  3x  4 . Gọi m là số
nghiệm thực của phương trình
f f x  2  2  3  f x . Khẳng định nào sau đây đúng? A. m  7 . B. m  4 . C. m  6 . D. m  9 . Lời giải Chọn C t   1 
Đặt t f x  2 . Khi đó phương trình thành f t   2  1 t   f
 t   2  1 t 2  t  1 t   1 t    1       . 3 2 
t  3t  4t  2   1 t 2 3 2 3 13 t 4t 2t 1 0        t   2 3 2
x  3x  3x  4  2  1  
. Mỗi phương trình đều có 3 nghiệm phân biệt lẫn  3  13 3 2
x  3x  3x  4  2   2
nhau nên phương trình ban đầu có tổng cộng 6 nghiệm. Câu 7.
Cho hàm số bậc bốn y f (x) có đồ thị như hình vẽ.
2 f x  3
Số nghiệm của phương trình
  f x là
f f x  2 A. 5 . B. 6 . C. 2 . D. 3 . Lời giải Chọn C Điều kiện:
https://www.facebook.com/groups/toanvd.vdc Trang 109
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8 - 2021
f x  a  3  ;   1  f
  x  b   1  ;0
f f x  2  0   . f   x  1
f x  3 
Đặt t f x,t  ; a 0;1;  3 . 2t  3 2t  3 3 Khi đó ta có:  t  
f t   2  f t    (*) . f t   2 tt 3
Vẽ đồ thị y   ta được t
Dựa vào đồ thị, (*)  t  3  ; 1  ; 
c ,c 3;4 . So điều kiện nhận t c f x  c ,
phương trình này có 2 nghiệm phân biệt. Câu 8.
Cho hàm số bậc ba y f (x) có đồ thị như hình vẽ.
Số nghiệm của phương trình f xf x  2 là A. 5 . B. 4 . C. 3 . D. 6 . Lời giải Chọn D  2   xf xf x  2   x
Ta có: f xf x  2    
(do x  0 không là nghiệm)
xf x  4 4 
f x   x 2 4
Ta vẽ thêm các đồ thị y   và y x x
https://www.facebook.com/groups/toanvd.vdc Trang 110
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8 - 2021
Dựa vào đồ thị, phương trình đã cho tổng cộng có 6 nghiệm. Câu 9.
(MĐ 102 BGD&ĐT NĂM 2019-2020) Cho hàm số bậc ba y f (x) có đồ thị là đường cong như hình vẽ bên dưới.
Số nghiệm thực phân biệt của phương trình f  3
x f (x) 1  0 là A. 6 B. 4 C. 5 D. 8 Lời giải Chọn A 3
x f (x)  a   6  ; 5   (1)  Ta có: f  3
x f (x) 1  0  f  3 x f (x) 3  1
  x f (x)  b  3  ; 2   (2)  3
x f (x)  0 (3)  x  0
+ Phương trình (3) tương đương  . x x , ( 6
  x a  5  )  1 1 a b
+ Các hàm số g x 
và h x 
đồng biến trên các khoảng  ;
 0 và 0;  , 3 x 3 x
và nhận xét rằng x  0 không phải là nghiệm của phương trình (1) và (2) nên ta có:
f x  g x  .
f x  h x 
 lim f x  ;
 lim f x  1 x  x0  + Trên khoảng  ;
 0 , ta có  lim g x  lim h x  0 nên các phương trình x x 
 lim g x  lim h x   x0 x0
f x  g x và f x  h x có nghiệm duy nhất.
 lim f x  ;
 lim f x  1 x  x0 
+ Trên khoảng 0;  , ta có  lim g x  lim h x  0 nên các phương trình x x 
 lim g x  lim h x   x0 x0
f x  g x và f x  h x có nghiệm duy nhất.
Do đó, phương trình f  3
x f (x) 1  0 có 6 nghiệm phân biệt.
https://www.facebook.com/groups/toanvd.vdc Trang 111
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8 - 2021
Câu 10. (MĐ 103 BGD&ĐT NĂM 2019-2020) Cho hàm số bậc bốn y f x có đồ thị là đường cong trong hình vẽ bên.
Số nghiệm thực phân biệt của phương trình f  2
x f (x)  2  0 là A. 8 . B. 12 . C. 6 . D. 9 . Lời giải Chọn D 2 x f (x)  0  2  f x f (x) a 1 2 x f (x)   2 0    
với 0  a b c . 2
x f (x)  b2  2
x f (x)  c 3  m
Xét phương trình f (x)  1 m  0 . 2     x
Gọi  ,  là hoành độ giao điểm của C  : y f (x) và Ox ;   0   . m m
(1)  f (x) 
 0 . Đặt g(x)  f (x)  2 x 2 x 2m Đạo hàm g (  x)  f (  x)  . 3 x 2m
Trường hợp 1: x   ; f (  x)  0;  0  g (  x)  0 3 x m
Ta có lim g x  , g( )  
 0 . Phương trình g x  0 có một nghiệm thuộc 2 x   ;    .
Trường hợp 2:   x   m f ( ) x  0,
 0 suy ra g(x)  0 x  (,  ) . 2 x 2m
Trường hợp 3: x   ; f (  x)  0;  0  g (  x)  0 3 x m
Ta có lim g x  , g( )  
 0 . Phương trình g x  0 có một nghiệm thuộc ( ; ) . 2 x 
https://www.facebook.com/groups/toanvd.vdc Trang 112
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8 - 2021 m
Vậy phương trình f x  có hai nghiệm m   0 . 2 x Ta có: 2
x f (x)  0  x  0  f (x)  0 : có ba nghiệm. Vậy phương trình   1 có 9 nghiệm.
Câu 44: Cho hàm số   3 2
f x x ax bx c với , a ,
b c là các số thực. Biết hàm số
g x  f x  f  x  f  x có hai giá trị cực trị là 3 và 6 . Diện tích hình phẳng giới hạn f x
bởi các đường y  và y  1 bằng g x  6 A. 2ln 3. B. ln 3. C. ln18. D. 2 ln 2.
Phân tích định hướng tìm lời giải:
- Đây là bài toán tính diện tích hình phẳng giới hạn bởi hai đồ thị hàm số trong trường
hơp một đồ thị hàm số là đồ thị của hàm ẩn với giả thiết về cực trị;
- Để giải bài toán đầu tiên cần xác định hai yếu tố: tính chất của hàm ẩn từ giả thiết và
nghiệm của phương trình hoành độ giao điểm của hai đồ thị hai hàm số;
- Trong bài toán này, hai yếu tố trên chỉ xác định được vì hàm ẩn là hàm bậc ba có hai
điểm cực trị với hai giá trị cực trị cho trước và nghiệm của phương trình hoành độ giao
điểm chính là hai điểm cực trị của hàm ẩn.
- Từ đó, áp dụng công thức tính diện tích hình phẳng với lưu ý nếu hàm f x không đổi b b dấu trên  ; a b thì
f xdx
f xdx   . a a FB-Phạm Tuấn Lời giải Chọn D Ta có f  x 2
 3x  2ax b ; f  x  6x  2a ; f  x  6 ;
Khi đó g x  f x  f  x  f  x  g x  f  x  f  x  6 .
Vì g x có hai giá trị cực trị là 3 và 6 mà g x là hàm bậc ba có hệ số của 3 x
dương nên g x có hai điểm cực trị là x x và g x  6 , g x  3  . 2  1  1 2 f x
Phương trình hoành độ giao điểm của hai đường y  và y  1 là g x  6 f x 1 g x  6
f x  g x  6
f x  f x  f  x  f  x  6
f  x  f  x  6  0 x xg x 1  0   . x x  2 f x
Diện tích hình phẳng giới hạn bởi các đường y  và y  1 là: g x  6 2 x f x 2
x f x  g x 2  6 x
  f  x  f  x  6  S  1dx   d  x   d  x    g xg x   g x     x   6 x   6   x   6   1 1 1
https://www.facebook.com/groups/toanvd.vdc Trang 113
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8 - 2021 x x
2  g x 2 
g x  x   d  x   d
x  ln g x 2  6  ln12  ln 3  2 ln 2.    g x   g x    x   6   x   x1 6   1 1 Bình luận:
- Đây là bài toán tính diện tích hình phẳng giới hạn bởi hai đồ thị hàm số trong trường
hơp một đồ thị hàm số là đồ thị của hàm ẩn với giả thiết về cực trị, để xác định các yếu
tố lập được công thức tính diện tích hình phẳng học sinh phải có kiến thức tổng hợp liên
quan đến cực trị, giá trị cực trị của hàm số, tích phân hàm trị tuyệt đối và tích phân hàm
ẩn. Đây là câu hỏi kiểm tra kiến thức ở mức độ VDC.
- Đây là bài toán sử dụng tính chất điểm cực trị của hàm bậc 3 đã gặp trong đề minh họa.
Có thể xây dựng các hướng phát triển đối với tính chấc điểm cực trị của hàm số bậc 3.
- Lưu ý: Với hướng giải dựng hàm của bài toán sẽ gặp khó khăn khi xây dựng lại hàm f xy  . g x  6 Hướng phát triển:
Hướng phát triển 1: Giữ nguyên giả thiết và cho diện tích hình phẳng hỏi giá trị cực trị còn lại.
Hướng phát triển 2: Thay cho giá trị cực trị của hàm số g x cho đồ thị của hàm số g x
không thay đổi kết luận.
Hướng phát triển 3: Hai hàm số f x và g x có mối liên hệ bảng biến thiên giữ nguyên
giả thiết về giá trị cực trị của một hàm số có mối liên hệ giữa hai hàm f x và g x với cách dựng lại hàm số.
Hướng phát triển 4: Thay đổi giả thiết về giá trị cực trị của hàm f x và cho hai hàm số
có mối liên hệ giữa nghiệm và cực trị với các dựng lại hàm số.
Hướng phát triển 5: Sử dụng tính chất hai điểm cực trị và điểm uốn của hàm bậc 3 để xây
dựng lại hàm số và trả lời yêu cầu bài toán về diện tích hình phẳng.
Hướng phát triển 6: Thay đổi giả thiết về cực trị của hàm số f x và giữ nguyên hàm
g x cho thêm điều kiện giá trị tại điểm cực trị của hàm f x .
Bài tập tương tự Câu 1. Cho hàm số   3 2
f x x ax bx c với , a ,
b c là các số thực. Biết hàm số
g x  f x  f  x  f  x có hai điểm cực trị với giá trị cực tiểu là 3 và diện tích hình f x
phẳng giới hạn bởi các đường y
và y  1 bằng 2 ln 2 . Giá trị cực đại của hàm g xg x  6 bằng A. 6. B. 3. C. 18. D. 8. Lời giải Chọn A Ta có: f  x 2
 3x  2ax b ;
f  x  6x  2a ;
f  x  6 ;
Khi đó g x  f x  f  x  f  x  g x  f  x  f  x  6 .
https://www.facebook.com/groups/toanvd.vdc Trang 114
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8 - 2021
Vì g x có hai điểm cực trị với giá trị cực tiểu là 3 mà g x là hàm bậc ba có hệ số của 3
x dương nên g x có hai điểm cực trị là x x và g x  3  nên 2  1 2
g x  6  0, x
 x ; x . 1 2  f x
Phương trình hoành độ giao điểm của hai đường y  và y  1 là g x  6 f x 1 g x  6
f x  g x  6
f x  f x  f  x  f  x  6
f  x  f  x  6  0  x xg x 1  0   . x x  2 f x
Diện tích hình phẳng giới hạn bởi các đường y  và y  1 là: g x  6 x x x 2 f x
2  f x  g x 2  6 
  f  x  f  x  6  S  1dx   d  x   d  x    g xg x   g x     x   6 x   6   x   6   1 1 1 x x
2  g  x 2 
g x  x   d  x   d
x  ln g x 2  6  ln  
g x  6  ln 3  2ln 2. 1    g x   g x    x   6   x   x1 6   1 1
Do g x g x  ln g x  6  ln 3  2 ln 2  ln12  g x  6 . 1   2    1   1 2 Câu 2.
Cho hàm số f x 3 2 
x ax bx c với , a ,
b c là các số thực. Biết hàm số 3
g x  f x  f  x  f  x có đồ thị như hình vẽ f x
Diện tích hình phẳng giới hạn bởi các đường y  và y  1 bằng g x  4
A. 2 ln 3  ln 2. B. ln 3. C. ln12. D. 2 ln 2. Lời giải Chọn A Ta có: f  x 2
 2x  2ax b ;
f  x  4x  2a ;
f  x  4 ;
Khi đó g x  f x  f  x  f  x  g x  f  x  f  x  4 .
https://www.facebook.com/groups/toanvd.vdc Trang 115
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8 - 2021
Từ đồ thị của hàm số g x thì g x có hai điểm cực trị x x và 1 2
g x  8; g x  2
 ; g x  4  0, x
 x ; x . 1 2  1   2  f x
Phương trình hoành độ giao điểm của hai đường y  và y  1 là g x  4 f x 1 g x  4
f x  g x  4
f x  f x  f  x  f  x  4
f  x  f  x  4  0 x xg x 1  0   . x x  2 f x
Diện tích hình phẳng giới hạn bởi các đường y  và y  1 là: g x  4 x x 2 f x 2  f x  S  1 dx   1 dx   g xg x    x   4 x   4   1 1 2
x f x  g x 2  4 x
  f  x  f  x  4    dx   dx    g x   g x    x   4   x   4   1 1
x2  g x  x   d
x  ln g x 2  4
 ln12  ln 2  2 ln 3  ln 2.   g x   x   x1 4   1 Câu 3.
Cho hai hàm số f x 3 2
ax x bx g x 2 2 1;
cx  4x d có bảng biến thiên như sau:
Biết rằng hàm số y f ' x  g ' x có giá trị cực trị là 2 . Khi đó diện tích hình phẳng
giới hạn bởi các đường y f x; y g x; x  1; x  2 bằng 3 3 1 1 A. . B. . C. . D. . 4 2 4 2 Lời giải Chọn A 2
Hàm số g x 2
cx  4x d đạt giá trị lớn nhất tại x   và giá trị lớn nhất bằng c 2  2   2   2  4 g   1   nên c   4   d  1    d  1,       1 .  c   c   c c
Hàm số g x có hai nghiệm là  và  nên g x  c x   x    .
Hơn nữa f x có hai điểm cực trị x   và x   nên f x 2 '
 3ax  4x b  3a x   x   
https://www.facebook.com/groups/toanvd.vdc Trang 116
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8 - 2021 1
 2a  4  c  3a 3a 12a 3ad   c
Do đó f ' x  g x 2  3ax x   
f ' x  g x . c c c 3ad   b   c
Khi đó y f x  g x  g x  g x 2 ' ' '
cx  4  2cx d  4 đạt cực trị tại điểm 4  2c 2  2  x    1
và giá trị cực trị y 1  2   . 2c cc  2  2   2   2  4 Suy ra y 1  c 1      4  2c 1  d  4  
c d  2   2 .  c   c   c c Từ  
1 và 2 suy ra c  1  . d  3   2  1 1 3 Do đó 3 2
a   . Vậy S
x  3x  7x  4 dx   . 3  3 4 1 b   3   Câu 4.
Cho hai hàm số f x 3 2
ax x bx g x 2 2 1;
cx  4x d với , a ,
b c và d là các số thực
thỏa mãn ac  0 . Biết phương trình g x  0 có hai nghiệm phân biệt là hai điểm cực trị của
hàm số f x với hai giá trị cực trị là 1 và 3 . Diện tích hình phẳng giới hạn bởi các đường
f x  g xy
; y  1 bằng f xA. ln 2 . B. 2 ln 2 . C. ln 6 . D. 2 ln 3 . Lời giải Chọn A
Hàm số g x có hai nghiệm là  và  nên g x  c x   x    .
Hơn nữa f x có hai điểm cực trị x   và x   nên, f    1
 ; f    3 f x 2 '
 3ax  4x b  3a x   x    1
 2a  4  c  3a 3a 12a 3ad   c
Do đó f ' x  g x 2  3ax x   
f ' x  g x . c c c 3ad   b   c
Xét phương trình hoành độ giao điểm của hai đường là
f x  g x x  
 1  f x  g x  0  f ' x  0   . f xx    
f x  g x  g x  g x  f ' x
d f x S  1 dx dx dx dx       f   xf   xf   xf   xf   x 
 ln f x  ln 4  ln 2  ln 2 .  Câu 5.
Cho hàm số f x 3 2
x ax bx 1 với a,b là các số thực khác 0 . Biết hàm số f x có hai
điểm cực trị x , x thỏa mãn x x  2 và f x f x  2 . Diện tích hình phẳng giới hạn 1   2  1 2 2 1 f x 1
bởi các đường y
; y  4 bằng x
https://www.facebook.com/groups/toanvd.vdc Trang 117
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8 - 2021 32 21 A. . B. . C. 11. D. 10 . 3 2 Lời giải Chọn A
Ta có f x 2 '
 3x  2ax b và f '  x  6x  2a .
Do hàm số f x có hai cực trị là x và x , nên x , x là hai nghiệm phân biệt của 1 2 1 2  2a x x   1 2   3 phương trình 2
3x  2ax b  0   . bx .x  1 2   3  a
Hơn nữa f x f x  2   f   1  . 1   2     3 
Mà x x  2 suy ra a  6;b  9 . 2 1 f x 1
Hàm số f x 3 2
x  6x  9x 1 nên 2
x  6x  9 . x
Xét phương trình hoành độ giao điểm giữa hai đường là x  1  2
x  6x  9  4   . x  5   1  f x 1 1  32 Vậy 2 S   4dx
x  6x  5 dx    . x 3 5  5  Câu 6. Cho hàm số   3 2
f x x ax bx c với , a ,
b c là các số thực. Biết hàm số f x có hai điểm
cực trị x , x thỏa mãn x x  2 và hàm số g x  f x  f ' x  f '  x có g x  6  . Diện 1  1 2 2 1
tích hình phẳng giới hạn bởi các đường y g x; x x và x x bằng 1 2 A.8. B. 4. C. 2. D. 16 . Lời giải Chọn A
Do hàm số f x có hai cực trị là x x x x  2 1 và 2 thỏa mãn , nên 2 1
f ' x  3 x x  x x   3 x x 2  3 x x  x x   3 x x 2  6 x x . 1 2 1 2 1 1 1  1  3 2
Khi đó f x   x x  3 x x
C và f '  x  6 x x  6 . 1  1   1 
Mà g x  f x  f ' x  f '  x   x x 3  C  6 suy ra g x C  6  6   C  0 . 1  1 Vậy x x x x 2 2 2 2  1  S
g xdx
x x 3 6 dx  x x 3 6        dx
x x 4  6x  8 1 1 1    .     4   x x x 1 1 1 x1
Câu 45. Cho khối hộp chữ nhật ABCD.A ' B 'C ' D ' có đáy là hình vuông, BD  2a , góc giữa hai mặt
phẳng  A' BD và  ABCD bằng 0
30 . Thể tích của khối hộp chữ nhật đã cho bằng 2 3 2 3 3 A. 3 6 3a . B. 3 a . C. 3 2 3a . D. a . 9 3
Phân tích định hướng tìm lời giải:
- Đây là bài toán tính thể tích của khối hộp chữ nhật;
- Để tính khối hộp chữ nhật ta áp dụng công thức V  . B h ;
+ Trong bài toán này B S
dễ dàng tính thông qua giả thiết ABCD
https://www.facebook.com/groups/toanvd.vdc Trang 118
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8 - 2021
+ Xác định đường cao h AA , việc tính AA được quy về việc xác lập mỗi liên hệ giữa
góc giữa hai mặt phẳng  A' BD và  ABCD với đường chéo của đáy. Fb-Ngô Dung Lời giải Chọn D
Gọi O là tâm hình vuông ABCD .
Vì BD OA và BD AA ' nên BD   A'OA  BD OA'
Lại có  A' BD   ABCD  BD . Do đó  A BD  ABCD  0 ' ,
A 'OA  30 (Hình vẽ trên).
Vì tứ giác ABCD là hình vuông có BD  2a nên OA a và AB AD a 2 .  Xét tam giác 0
A ' AO vuông tại A có OA a và A'OA  30 nên a 3 0 AA '  O . A tan 30  . 3 a 3 2 3
Vậy thể tích khối hộp chữ nhật 3 V A . B A .
D AA '  a 2.a 2.  a . 3 3 Bình luận:
- Đây là bài toán tính thể tích của khối hộp chữ nhật, để giải quyết được bài toán này
yêu cầu học sinh phải nắm vững công thức tính thể tích khối hộp; cách xác định góc
giữa hai mặt phẳng; thiết lập mỗi liên hệ giữa đường cao với giả thiết đã cho của bài
toán để tính chiều cao của khối hộp. Đây là câu hỏi kiểm tra kiến thức ở mức độ VD.
Hướng phát triển 1: Một bài toán tương tự, tuy nhiên ta thay đổi một chút về giả thiết đáy. (câu 1)
Hướng phát triển 2: Về cách xác định đường cao, từ đó xác định được góc. (câu 2,3)
Hướng phát triển 3: Thay đổi góc giữa mặt bên và mặt đáy thành góc giữa mặt bên và mặt bên (câu 4)
Hướng phát triển 4: Ta cho 2 giả thiết về góc, khi đó, giả thiết đường cao được ẩn trong
giả thiết về góc, sử dụng mối quan hệ đó đi xác định đường cao. (câu 5)
Bài tập tương tự
Câu 1. Cho khối hộp chữ nhật ABCD.A ' B 'C ' D ' , đáy ABCD có AB  2 AD  2a . Góc giữa hai mặt phẳng  B A
D và  ABCD bằng 0
45 . Thể tích của khối hộp chữ nhật đã cho bằng 4 5 2 5 2 5 8 5 A. 3 a . B. 3 a . C. 3 a . D. 3 a . 5 5 15 15
https://www.facebook.com/groups/toanvd.vdc Trang 119
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8 - 2021 Lời giải Chọn A
Bài toán hoàn toàn tương tự với đề bài gốc. Vậy nên ta sẽ giải rút gọn như sau:
Gọi H là hình chiếu vuông góc của B lên cạnh AC .
Khi đó ta sẽ có  B A
C   ABCD  ,  B HB  45 Dẫn đến B H
B vuông cân tại B BB  BH .
Xét tam giác BAC vuông tại B, BA  2a, BC a khi đó đường cao B . A BC 2 . a a 2a BH    . 2 2 BA BCa2 2 5 2  a 4 5 Vậy 3 VB . A BC.BB  a .
ABCD. AB CD   5
Câu 2. Cho khối lăng trụ tam giác đều ABC.A' B 'C ' có AB  3a . Gọi M là trung điểm AA . Góc
giữa hai mặt phẳng MBC và  A BC
  bằng 30 . Thể tích của khối lăng trụ ABC.AB C   đã cho bằng 9 3 9 3 27 3 27 3 A. 3 a . B. 3 a . C. 3 a . D. 3 a . 8 4 8 4 Lời giải Chọn D
Gọi N là trung điểm BC . Khi đó MBC   AB C
   MN AN   ; ;  MNA  30 3 3  3a Xét MAN có  AN
a, MNA  30  MA
AA  3a 2 2 27 3 Vậy 3 Va
ABC. AB C   4
https://www.facebook.com/groups/toanvd.vdc Trang 120
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8 - 2021 Câu 3.
Cho chóp S.ABC có đáy ABC là tam giác đều cạnh a. Gọi M là trung điểm BC , chân
đường cao hạ từ S xuống mặt phẳng đáy chính là trung điểm H của đoạn AM . Biết góc
giữa hai mặt phẳng SAB, ABC  bằng 60 . Thể tích của hình chóp đã cho bằng 3 3 3 3 2 A. 3 a . B. 3 a . C. 3 a . D. 3 a . 8 16 32 8 Lời giải Chọn C
Dựng HE AB tại E .
Khi đó SAB  ABC   SE EH   , ,  SEH  60 . 1 1 a 3  3a Ta có EH
d M , AB  d C, AB 
, suy ra SH EH .tan 60  2 4 8 8 Câu 4.
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A cạnh AB a . Hình chiếu
vuông góc của S trên mặt phẳng  ABC trùng với trung điểm H của BC . Biết góc tạo bởi
hai mặt phẳng SAC  và SBC  bằng 60 . Thể tích của khối chóp đã cho bằng 3 a 3 a 3 a 3 a A. . B. . C. . D. . 24 12 6 2 Lời giải Chọn B a 2
Ta có ABC vuông cân tại ,
A AB a BC a 2 và AH  . 2
Ta dựng HI SA , khi đó ta có SA   IBC  .
Mà SA  SAB SAC  góc SAB;SAC   I ; B IC   60    
Khi đó có 2TH: BIC  60 hoặc BIC 120 .  
TH: BIC  60 . Khi đó BI BC a 2  a BA  vô lý.
https://www.facebook.com/groups/toanvd.vdc Trang 121
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8 - 2021   a 6 a 6
TH: BIC 120 . Khi đó BI CI   HI  3 6 a 2 a 6 a Ta xét H
SA vuông tại H , HA
và đường cao HI   SH  . 2 6 2 3 1 a Vậy V
SH .AB.AC S . ABC 6 12 Câu 5.
Cho chóp S.ABC , đáy ABC là tam giác vuông tại  ,
A BC  2a, ABC  30 . Hai mặt bên
SAB,SAC  cùng tạo với đáy một góc bằng 60 . Biết hình chiếu vuông góc H của S
xuống mặt đáy nằm trên cạnh BC . Thể tích của hình chóp đã cho bằng 3 1 3 1 3 1 3  3 A. 3 a . B. 3 a . C. 3 a . D. 3 a . 12 6 2 4 Lời giải Chọn D
Từ H dựng HE AB tại E và HF AC tại F . 
 SAB, ABC       SEH  60  
 đặt HE HF x  
  SAC  ,  ABC    SFH  60   HF x a 3
Ta có tan C  tan 60   3   x FC a x 3 1  3a
Suy ra SH HF. tan 60  3  1 1 3  3 Vậy 3 VSH .A . B AC a . S . ABC 6 4
Câu 46: [TNTHPTQG -MĐ122-Năm 2021] Trên tập hợp các số phức, xét phương trình 2
z  m   2 2
1 z m  0 ( m là tham số thực). Có bao nhiêu giá trị của m để phương trình đó có nghiệm z z o thỏa mãn 6 ? o A. 2. B. 3. C. 1. D. 4.
Phân tích định hướng tìm lời giải:
+ Khai thác z  6 . Nếu z là số thực thì z  6  z  6  ; Nếu o 0 o 0
z a bi , a b ;  b  0 thì 2 2 . 0   z a b 0
+ Trong từng trường hợp z z o là nghiệm thực,
o là nghiệm phức không suy biến của phương trình 2
z  m   2 2
1 z m  0 ta phải chú ý tới điều kiện tương ứng của m để kiểm tra kết quả.
https://www.facebook.com/groups/toanvd.vdc Trang 122
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8 - 2021
Ý tưởng: Kiểm tra việc một số em học sinh quên không xét trường hợp zo là số thực. Fb-Khải Nguyễn Lời giải Phương trình đã cho có 2 2 
  (m 1)  m  2m 1.
 Nếu   2m 1  0 thì phương trình có nghiệm thực  z  z  0 mà 6 oz  6  0 2 6  2 m   2 2 1 .6  m  0
m  12m  48  0 Khi đó ta có:     m  6  2 3
62  2 m   1 .6 2 2  m  0
m 12m  24  0  
(thỏa mãn điều kiện '  0).
 Nếu   2m 1  0 thì phương trình có phức không thực z m 1 i 2  m 1 m  6
Khi đó z  6  m  1  i 2m  1  6  m      m  2 2 1 2 1  6  . om  6  Thấy m  6
 thỏa mãn '  0 và m  6 không thỏa mãn '  0.
Vậy có 3 giá trị của m thỏa mãn bài toán.
Bài tập tương tự Câu 1:
[Nhóm Giáo Viên Toán Việt Nam] Trên tập số phức cho phương trình 2
z az b  0 với
a , b   . Biết rằng hai nghiệm của phương trình có dạng w  2 và 2w  5  3i với w là một
số phức. Giá trị của tổng T  a b bằng A. 81. B. 82 . C. 100 . D. 64 . Định hướng
+ Khai thác giả thiết thấy phương trình có hai nghiệm phức không thực. Đây là cơ sở
để áp dụng tính chất về nghiệm phức không thực của phương trình bậc hai.
+ Trên tập hợp các số phức, xét phương trình 2
a z b z c  0 với a , b, c   và a  0 .
Khi đó nếu z , z 1
2 là các nghiệm phức không thực của phương trình thì: b   i b 2
  b  4ac  0 và z
. Nhận thấy z z ; z z   , 1;2 1 2 2a 1 2 a 2 2 cz z zz  ; z z  . 1 2 1 2 a 1 2 a Lời giải
+ Vì w  2 và 2w  5  3i với w là một số phức là các nghiệm của phương trình đã cho
nên chúng là các nghiệm phức không thực. + Gọi z , zz z 1
2 là các nghiệm phức không thực của phương trình đã cho . Đặt 1 2
z w2  xyi
w x  2  yi  2w  5  3i  2x  9  2y  3 i z 1
( x, y   )       . 2 x  2x 9  x  9
+ Vì z z nên 
. Như vậy z  9 ; i z  9i . 1 2  
y  2y  1 2   3  y  1  a   
z z  1  8 1 2  + 
a b  64 Chọn D b   z z  82  1 2 Câu 2:
[Sưu Tầm Trên Nhóm Giáo Viên Toán Việt Nam] Cho các số thực a và bsao cho phương trình 2
z az b  0 có hai nghiệm phức z , z 1
2 không thực. Trên mặt phẳng tọa độ Oxy , gọi
https://www.facebook.com/groups/toanvd.vdc Trang 123
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8 - 2021
A và B lần lượt là điểm biểu diễn các số phức z , z 1 2 . Biết rằng O
AB có một góc bằng
120 . Mệnh đề nào dưới đây đúng? A. 2
(2  3)b a . B. 2
3b a . C. 2
2b a . D. 2
b a . Định hướng
Dùng tính chất về nghiệm phức không thực của phương trình bậc hai hệ số thực. Lời giải + Vì Phương trình 2
z az b  0 ( a, b   ) có hai nghiệm phức z , z 1 2 không phải là a i  số thực nên 2
  a  4b  0 và z  . 1,2 2
+ Ta có OA z b ; OB z b ; 2
AB z z
4b a . Thấy OA OB 1 2 1 2  O
AB cân tại đỉnh O . Vì O
AB cân tại O và có một góc bằng 120 nên  AOB 120
  b a 2   b 2   b 2 2 4  2 b b cos120 2
b a Chọn D Câu 3:
[Chuyên Đại Học Vinh-L2/N2021] Cho các số thực b , c sao cho phương trình 2
z bz c  0
có hai nghiệm phức z , z
z  43i 1
z 8  6i  4 1 2 thỏa mãn và . Mệnh đề nào sau đây 1 2 đúng?
A. 5b c  4 .
B. 5b c  12 .
C. 5b c  12 .
D. 5b c  4  . Lời giải + Nếu z , z
z  43i 1 1
2 là các nghiệm thực của phương trình đã cho thì từ 1
  z  42 9 1 1
  z  42  8  . Điều này vô lý. 1 + Nếu z , z z z
z x yi , x y  1
2 là các nghiệm phức không thực thì . Đặt 1   2 1
z xyi 2 . 2 2  2 2
z  4  3i  1
x  4   y   3 1   x y
  24x 3y  2  4  1   hay   
z  8  6i  4 2 2  2 2  
x y   44x  3y  8  4 2
  x 8  y  6  4    24  24 18 x z   i 2 2
x y  36   5 1   5 5     . Suy ra  .
4 x  3 y  30  18  24 18 y   z   i   5 2   5 5  48
b    z z   1 2  + 
5  5b c  12  Chọn B
c z z  36  1 2
Câu 47: [TNTHPT QG-MĐ122-Năm 2021] Xét các số phức ,
z w thỏa mãn z 1 và w  2 . Khi z i 
w 68i đạt giá trị nhỏ nhất, z w bằng 29 221 A. 3. B. 5 . C. . D. . 5 5
Phân tích định hướng tìm lời giải:
https://www.facebook.com/groups/toanvd.vdc Trang 124
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8 - 2021
+ Khai thác kết luận, thấy cần áp dụng BĐT mô đun z i 
w  68i  68i z i 
w 10 z i  w  
1 . Kết hợp giả thiết, nghĩ đến z i 
w z i  w  3  
2 . Từ đây suy ra z i 
w  6 8i  7 . + Tìm ,
z w để đẳng thức ở   1 và 2 xảy ra. Fb-Khải Nguyễn Lời giải
z i 
w  6  8i  6  8i z i  
w 10  z i   w   1  + Ta có 
z i  
w z i   w  3 2 
z i 
w 68i  7   3 . + Đẳng thức ở  
1 xảy ra khi và chỉ khi z i w   k 6  8i với k  và k  0 . Đẳng
thức ở 2 xảy ra khi và chỉ khi z t.i w  với t   và t  0 . Như thế, đẳng thức ở  3 4 z    i    1  5 5
, 2 đồng thời xảy ra khi và chỉ khi 
hay đẳng thức ở 3 xảy ra khi 8 6
w    i   5 5  3 4 z    i   5 5 và chỉ khi  . 8 6
w    i   5 5 29
+ Vậy min z i  
w  6 8i  7 , khi đó z w  Chọn C 5 Bình luận
Đây là bài thi trắc nghiệm về GTNN, GTLN của biểu thức chứa mô đun số phức. Để
giải bài toán nay chỉ cần áp dụng trực tiếp các BĐT mô đun, nhưng yêu cầu phải chỉ
được khi nào đẳng thức xảy ra. Điều này gây khó khăn cho học sinh vì các em khó
nhớ nếu không tự chứng minh được BĐT mô đun. Các câu tương tự Câu 1:
[Nhóm Giáo Viên Toán Việt Nam] Xét số phức z thay đổi thỏa mãn z i  2. Biết biểu thức
T  z 3i  2 z  4 i đạt giá trị nhỏ nhất khi z x yi  ,
x y  . Hiệu x y bằng 3  6 13 6 13  3 3  6 13 3  6 13 A. . B. . C. . D.  . 17 17 17 17 Định hướng
Khai thác kết luận: Biểu thức T  z 3i  2 z  4 i đạt giá trị nhỏ nhất. Ta phải “cân
bằng hệ số” (làm xuất hiện thừa số 2 ở biểu thức z  3i ) trước khi áp dụng bất đẳng z z 2 1
thức mô đun bằng đẳng thức sau: z z z
z z , z  ;
z  0, z  0 . 1 2 1 2  1 2 1 2 z z 1 2 Lời giải
https://www.facebook.com/groups/toanvd.vdc Trang 125
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8 - 2021 4i z i
+ Ta có z  3i   z i  4i
z i 
4i  2 z ; T  2 z  4  i z z i 4i
 2 z  4  i z  2 17   1 . z k
4  i,k  ,0  k   1 4  8 13 1 2 13 + Đẳng thức ở   1 xảy ra khi   z   i . z i  2   17 17 3 6 13
+ Vậy x y   Chọn C 17 2 2 Câu 2:
[Sở Nam Định-Năm 2021] Xét các số phức ;
z w thỏa mãn z  2  z  2i  6 và
w3 2i w3 6i . Khi z w đạt giá trị nhỏ nhất, hãy tính z . 1 1 A. 1  2 . B. 2  1 . C. . D. . 5 5 Định hướng 2 2
+ Khai thác giả thiết, thấy z  2  z  2i  6  z 1i 1; w3 2i w3 6i 3  y  
x  2 ( w x y , i  , x y  ). 4
+ Khai thác kết luận, viết z w  1 i w   z 1 i  1 i w z 1i 2      x2 3 1  x  3 1     * .  4  Lời giải 2 2
+ z  2  z  2i  6   z   i   i   2   z   i   i   2 1 1 1 1  6 2 2 2 z 1 i i 1      
 6  z 1i 1   . 3
+ Đặt w x y , i  ,
x y  . Khi đó w32i w36i y   x  2 . 4 2 2  3 
+ z w  1 i w   z 1 i  1 i w z 1i  1 x  x  3 1     * .  4  4 7 4 7
+ Khi x   thì y   và w   
i . Đẳng thức ở * xảy ra khi và chỉ khi 5 5 5 5
z 1i k 1i  
w với k  và k  0 . Từ z 1i k 1i   w 1 2 i 5
z 1 i k 1 i w  k    z    z  Chọn D 3 5 5 5 Câu 3:
[Đềtham khảo-2018] Xét các số phức z x yi ( x, y   ) thỏa mãn z  4  3i  5 . Khi biểu
thức P z 13i z 1 i đạt giá trị lớn nhất, giá trị của x y bằng A. 4. B. 6. C. 8. D. 10 . Định hướng
+Nhận thấy z 1 3i   z  4  3i  5 , z 1 i   z  4  3i  3  2i do đó không tính 2 2
được  z 1 3i   z 1 i theo z  4  3i (,  là các số thực). 2 2 2 2
+Tuy nhiên ta lại có z 1 3i z 1 i 2 z i 1 2i             . Lời giải
https://www.facebook.com/groups/toanvd.vdc Trang 126
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8 - 2021 2 + 2 2 2 2 P 2  z 1 3i z 1 i  4  z i 1 2i           
 2 5 z i   1 .    
+ z i   z  4  3i  4  2i  z  4  3i  4  2i  3 5 2 . Đẳng thức ở 2 xảy ra  k   , k  0  
khi z  4  3i k 4  2i  z  6  4i .
z  43i  5   +Từ  
1 và 2 suy ra P  10 2 3 . Đẳng thức ở 3 xảy ra khi và chỉ khi đẳng
z  6  4i  thức ở  
1 và 2 đồng thời xảy ra  
z  6  4i Chọn D
z 13i z 1  i   Câu 4:
[Chuyên Hùng Vương Bình Dương-L5N2018] Xét các số phức z x yi  ,
x y  thỏa mãn
z 1 3i z  3  i 3 3
. Khi z 1  2i z  1  i đạt giá trị lớn nhất, x y bằng A. 0. B. 16 . C. 54. D. 27 . Lời giải 2 2 2 2
+ Ta có z 1 3i z  3  i   x   1  y   3   x   3  y   1
x y  0 .
+ Trong mặt phẳng phức, gọi M z , 
A 1 2i và B  1
  i . Khi đó, M thuộc đường
thẳng d  có phương trình x y  0 . Nhận thấy ,
A B nằm cùng một phía đối với  d  . x y  0
+ AB có phương trình: x  2 y  3  0 ; Xét hệ 
x y  3 .
x  2 y  3  0 
+ z 1  2i z  1  i MA MB AB  5 . Đẳng thức xảy ra khi và chỉ khi ba điểm
M , A , B thẳng hàng hay M là giao điểm của đường thẳng AB và đường thẳng
d  hay M 3;3 Chọn C Câu 5:
[Sưu Tầm Và Biên Tập] Xét các số phức ,
z w thay đổi thỏa mãn z  2, w3 2i 1. Khi 2
z  2zw  4 đạt giá trị lớn nhất, z w bằng 2 85 A. 6. B. . C. 2. D. 2 5. 5 Lời giải z z 2 2
+ Đặt z x yi với x, y   thì
yi ; Vì z  2 nên x y  4  2  y  2 2
 0  y  2  4   y  2 2  16 . z z + 2
z  2zw  4  2 z
w  4 iy w  4 iy  3  2i  3  2i w 2
 4  iy  3  2i  3  2i w     y  2 4 4 9 2  24 
  4 3   y  2 i  4 . Từ đây suy ra 2
z  2 zw  4  24 1 .  z  2i  + Đẳng thức ở  
1 xảy ra khi và chỉ khi  18 14 . Vậy 2
max z  2zw  4  24 , khi w   i   5 5
đó z w  6 Chọn A
https://www.facebook.com/groups/toanvd.vdc Trang 127
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8 - 2021 Câu 6:
[Chuyên Đại Học Vinh-L2/N2021] Cho các số thực b , c sao cho phương trình 2
z bz c  0
có hai nghiệm phức z , z
z  43i 1
z 8  6i  4 1 2 thỏa mãn và . Mệnh đề nào sau đây 1 2 đúng?
A. 5b c  4 .
B. 5b c  12 .
C. 5b c  12 .
D. 5b c  4  . Lời giải + Nếu z , z
z  43i 1 1
2 là các nghiệm thực của phương trình đã cho thì từ 1
  z  42 9 1 1
  z  42  8  . Điều này vô lý. 1 + Nếu z , z z z 1
2 là các nghiệm phức không thực thì . 2 1 
z  8  6i  4 1 1
  z  4  3i z  4  3i 1  z  6 1 1   1 Ta có     
z  6 . Đẳng thức ở   1 xảy ra 1
4  z  8  6i  8  6i z 2  z  6 1 1     1  khi và 24 18
chỉ khi z k 4
 3i với k  và k  0 . Từ đây tính được (thỏa mãn 1   z   i 1 5 5 2 24 18 ) và z   i . 2 5 5  48
b    z z   1 2  + 
5  5b c  12  Chọn B
c z z  36  1 2 Câu 7:
[Chuyên Vinh -L2/N2018] Trong các số phức z thỏa mãn 2
z  1  2 z , gọi z z 1 và 2 lần lượt
là các số phức có mô đun nhỏ nhất và lớn nhất. Khi đó mô đun của số phức wz z 1 2 bằng A. 2 2 . B. 2. C. 2 . D. 1  2 . Định hướng
+ Khai thác giả thiết: 2 2 z  1  2 z 2 2 2 2  z
 1  z z  4 z
z z2 2 4 2
 4 z z 1. 2 2 2 2
+ z  z   z z 2zz  z z2 2
2 z  2 z . Lời giải + Ta có : 2 2 z  1  2 z 2 2 2 2  z
 1  z z  4 z
z z2 2 4 2
 4 z z 1. 2 2 2 2 2 2 4 2
+ Mặt khác: z   z   z z 2 z  2  z  
1 . Suy ra 4 z z 1  2 z 4 2
z  6 z  1  0  1
  2  z 1 2 . Đẳng thức ở   1 xảy ra khi và chỉ khi
z z  0  z là số thuần ảo. + Dễ dàng có z
2  1 i và z
2  1 i . Từ đó w z z  2 2i và w  2 2 2   1   1 2 Chọn A Câu 8:
[SởGD&ĐTHàNam–L1N2018] Xét các số phức
z a bi  ,
a b thỏa mãn 1
z z   i i z z  2 4 15 1 . Khi z
 3i đạt giá trị nhỏ nhất, a  4b bằng 2 A. 7. B. 6. C. 5. D. 4. Lời giải
https://www.facebook.com/groups/toanvd.vdc Trang 128
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8 - 2021 2 a a
+ Ta có z a bi z a bi ;  z z   i i z z  2 4 15 1  b    2 2 2 2  a a   z a    2 i   . 2 2   2 1  1   a a  2 2 2  1   a a
+ z   3i a     5 i      a     5 2      2  2 2    2  2 2   2 2 2 1  1 1 39      3 9 1 1 39  a   z   3i     a       . Khi a  thì  2  2   2  8 2 8   8 2 1 39 + Vậy min z   3i
; Khi đó a  4b  7 Chọn A 2 8
Câu 48: Cho hàm số y f x có đạo hàm f  x   x   2 7 x  9, x   .  Có bao nhiêu giá trị
nguyên dương của tham số 3 m
để hàm số g x   f x  5x m  có ít nhất 3 điểm cực trị? A. 6. B. 7. C. 5. D. 4.
Phân tích định hướng tìm lời giải:
- Đây là bài toán cực trị hàm hợp có tham số: Tìm tham số m để hàm số y f u x, m có
đúng (ít nhất, nhiều nhất) k điểm cực trị (1).
- Cách giải bài toán (1):
+ Một số bài mà y f u x, m là hàm số chẵn thì đồ thị hàm số y f u x, m nhận O y
là trục đối xứng. Khi đó, việc xét số điểm cực trị của hàm số y f u x, m trên  quy về
xét số điểm cực trị của hàm số này trên 0; 
 . Hàm số y f u x, m có 2k 1 điểm cực trị
khi và chỉ khi y f u x, m cók điểm cực trị trên 0;   .
+ Tổng quát: Trong nhiều bài toán, ta sử dụng tính chất (*) sau
Cho hàm số f x và u x liên tục trên  , khác hàm hằng trên mọi khoảng. Gọi x , x ,..., x 1 2 n
là các điểm cực trị của f x . Khi đó: 1) Nếu x x
0 là nghiệm của phương trình u x   x , i  1, n thì
cũng là điểm cực trị của hàm i  0
số f ux . Hơn nữa, nếu x f x x
i là điểm cực đại (cực tiểu) của
  thì 0 cũng là điểm cực đại
(cực tiểu) của hàm số f ux .
Thật vậy, theo định nghĩa cực trị, x f x a ;b
i là điểm cực trị của   tồn tại khoảng  chứa i i x f x f x f x f x
xa ; b \ x i sao cho    hay    với mọi  . i i   i i i
Mà u x liên tục trên  nên tồn tại khoảng c ; d chứa x sao cho i i  0
u xa ; b  \x , x
 c ; d  \ x . i i i i i  0
Do vậy: f u x  f u x
hay f u x  f u x với x
 c ;d  \ x . i i  0 0  0  Suy ra, x x
0 cũng là điểm cực trị của hàm số f u x . Hơn nữa, nếu
i là điểm cực đại (cực
tiểu) của f x thì x0 cũng là điểm cực đại (cực tiểu) của hàm số f ux . 
2) Ta có  f u x  u x. f u x  
, với mọi x . Do đó:
https://www.facebook.com/groups/toanvd.vdc Trang 129
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8 - 2021  + Qua điểm x ux   0 mà
  đổi dấu thì f ux   đổi dấu. + Nếu x u x x
0 là điểm cực trị của
  thì 0 cũng là điểm cực trị của f ux .
Từ đó, ta có kết quả sau:
Số điểm cực trị của hàm số f ux bao gồm số điểm cực trị của u x và số nghiệm của các
phương trình u x  x , với i  1, n . Đồng thời các nghiệm này phải khác điểm cực trị của i
u x . FB-Chu Thom Lời giải Chọn A
Để ý rằng: u x 3
x  5x m có cùng số điểm cực trị với hàm số y h x 3  x  5x .
Ta có BBT của hàm y h x 3
x  5x như sau:
Suy ra u x 3
x  5x m có đúng 1 điểm cực trị. 
Ta có g x 3
x x f  3 5 .
x  5x m . x  7 
Từ giả thiết f  x   x  7 2
x  9  0  x  3   . x  3   u x 3 3
x  5x m  7
x  5x  7  m   Ta có: f  3
x  5x m  0   ux 3 3
x  5x m  3   x  5x  3  m (2).   u   x 3 3
x  5x m  3 
x  5x  3   m  
Hàm số g x có ít nhất 3 điểm cực trị  (2) có ít nhất 2 nghiệm phân biệt khác 0.
Từ bảng biến thiên của hàm số hx , ta có 7  m  0  m  7 . Mà m
nên m   1;2;3;4;5;  6
Vậy có 6 giá trị của m thỏa mãn yêu cầu đề bài. Bình luận:
- Trong cách giải trên, mấu chốt là tìm được số điểm cực trị của u x 3
x  5x m và tìm
được m để hệ (2) có ít nhất 2 nghiệm phân biệt khác 0. Cả 2 yêu cầu cùng được giải quyết
dựa vào bảng biến thiên của hàm số y h x 3  x  5x .
- Ngoài cách giải trên, ta có thể thấy g x   f  3
x  5 x m  là hàm số chẵn. Vì vậy, g x
có ít nhất 3 điểm cực trị  g x có ít nhất 1 điểm cực trị trên khoảng 0;   .
Hướng phát triển:
Hướng phát triển 1: Thay giả thiết cho công thức f  x thành cho đồ thị hay bảng xét dấu của f  
x , đồ thị hay bảng biến thiên của f x .
https://www.facebook.com/groups/toanvd.vdc Trang 130
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8 - 2021
Hướng phát triển 2: Thay đổi hàm số u x, m .
Hướng phát triển 3: Thay đổi vị trí của trị tuyệt đối, hoặc bỏ trị tuyệt đối, vị trí tham số m
( m không phải hệ số tự do).
Hướng phát triển 4: Thay đổi câu hỏi: Có ít nhất k cực trị, có nhiều nhất k cực trị, có đúng k cực trị.
Bài tập tương tự Câu 1:
Cho hàm số f x có bảng xét dấu đạo hàm như sau
Có tất cả bao nhiêu giá trị nguyên dương của tham số m để hàm số
g x   f  4 2
x  2 x  3  m  có ít nhất 7 điểm cực trị? A. 2. B. 4. C. 3. D. 5. Lời giải Chọn B
Đặt u x 4 2
x  2x  3  m . Ta có u x có cùng số điểm cực trị với hàm số h x  4 2
x  2 x  3 . Đồ thị h x  4 2
x  2 x  3 như sau:
Từ đó suy ra hàm số u x 4 2
x  2x  3  m có 5 điểm cực trị.
Từ giả thiết suy ra hàm số f x có 2 điểm cực trị là x  4; x  5 .  g x 4 2
  x x   mf  .    4 2 2 3
x  2x  3  m 4 2
x  2x  3  m  4 4 2
x  2x 3  4  m 4 2
Ta có f  x  2x 3  m  0     (3). 4 2
x  2x  3  m  5 4 2
x  2x 3  5 m  
Hàm số g x   f  4 2
x  2 x  3  m  có ít nhất 7 điểm cực trị  (3) có ít nhất 2 nghiệm phân
biệt khác điểm cực trị của u x  5  m  0  m  5 mà *
m   nên m   1;2;3;  4 . Câu 2:
Cho hàm số f x liên tục trên  có đúng 2 điểm cực trị và có đồ thị như hình vẽ
Có tất cả bao nhiêu giá trị nguyên của tham số m thuộc  2  0;2  0 để hàm số
g x  f  2
x x  3  m có nhiều nhất 7 điểm cực trị?
https://www.facebook.com/groups/toanvd.vdc Trang 131
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8 - 2021 A. 21. B. 20 . C. 22. D. 19 . Lời giải Chọn A Đặt ux 2
x x 3  m g x  f u x  g x  u x. f u x .
Xét hàm số ux 2
x x 3  m có cùng điểm cực trị với hàm số h x 2 2  x x
x x   3 2 3
3  x  3x . 3 2
Bảng biến thiên của hàm số y x 3x như sau:
Suy ra, đồ thị hàm số y hx như sau
Từ đồ thị suy ra hàm số y hx có 3 điểm cực trị  u x có 3 điểm cực trị. u x 2
x x  3  m  1
Hàm số g x có quá 7 điểm cực trị  hệ  có quá 4 nghiệm u x 2
x x  3  m  2  2
x x  3  1 m
phân biệt khác điểm cực trị của h x . Ta có  . 2
x x  3  2  m  u x 2
x x  3  m  1 Do vậy, hệ 
có quá 4 nghiệm phân biệt khác điểm cực trị của u x 2
x x  3  m  2  h x 1   m  0 m  1 m     2  0;  0     mà   m nguyên thuộc  2  0;2  0  có 20 giá trị 1 m  4  m  3   m   3  
của m để g x có quá 7 điểm cực trị.Vậy số giá trị nguyên của tham số m thuộc  2  0;2 
0 để hàm số g x  f  2
x x  3  m có nhiều nhất 7 điểm cực trị là 41 20  21. Câu 3:
Cho hàm số y f x có đạo hàm là hàm đa thức bậc 4. Biết hàm số f  x có đồ thị như hình
vẽ. Có tất cả bao nhiêu giá trị nguyên của tham số m thuộc  1  0;1  0 để hàm số
g x  f  3 2
x  3mx  2 có đúng 6 điểm cực trị?
https://www.facebook.com/groups/toanvd.vdc Trang 132
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8 - 2021 A. 8. B. 1 0 . C. 21. D. 20. Lời giải Chọn D x  0  x  2m
g x   2
x mxf  3 2 3 6
x  3mx  2  0  (4)  . u x 3 2
x  3mx  2  0  u x 3 2
x  3mx  2  4 
Nếu m  0 thì (4) có 3 nghiệm phân biệt là 3
x  0; x   2 g x không thể có 6 điểm cực trị.
Nếu m  0 thì ta có bảng biến thiên 1
g x có đúng 6 điểm cực trị  (4) có đúng 6 nghiệm 3 3
 4  2  4m m   . 2
Nếu m  0 thì ta có bảng biến thiên 1
g x có đúng 6 điểm cực trị  (4) có đúng 6 nghiệm 3 3
 2  4m  0  m  . 2 1 1
Vậy, g x có đúng 6 điểm cực trị thì 3 m   hoặc 3 m  . 2 2
Mà m nguyên thuộc  1  0;1 
0 nên có 20 giá trị của m . Câu 4:
Cho hàm số f x . Biết rằng f  x là hàm số đa thức bậc bốn có đồ thị như sau
https://www.facebook.com/groups/toanvd.vdc Trang 133
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8 - 2021
Tìm tất cả các giá trị thực của tham số 2 x x m
để hàm số g x  f e  2me  có nhiều điểm cực trị nhất?
A. m   2 .
B. m  1. C. m  1  .
D. m  2 . Lời giải Chọn D Đặt   2x   2 x u x e
me g x  f u x  g x  u x. f u x . 
    2 x x u x e e m  0 
u x  2  
Ta có g x  0  u x  1   (5).
u x  0   3 u x    2
Hàm số g x có nhiều điểm cực trị nhất  (5) có nhiều nghiệm nhất
u x  2 u   x  1
m  0 và u x  0 (6) có nhiều nghiệm nhất.   3
u x   2
Khi m  0, ta có u x  0  x  ln m. Bảng biến thiên m  0
(6) có nhiều nghiệm nhất    m  2 . 2 m  2  Câu 5:
Cho hàm số y f x xác định và liên tục trên  và có bảng biến thiên như hình vẽ
Có bao nhiêu giá trị nguyên của tham số m 1  0;1 
0 để hàm số     x g x f
e x  5  m  có đúng 9 cực trị?
https://www.facebook.com/groups/toanvd.vdc Trang 134
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8 - 2021 A. 2. B. 4. C. 3. D. 5. Lời giải Chọn C Đặt   x
u x e x  5  m g x  f u x  g x  u x. f u x . Hàm số   x
u x e x  5  m có cùng điểm cực trị với hàm số   x
h x e x  5 , với   x
h x e x 5. Xét hàm số   x    5    x h x e x
h x e 1  0  x  0 . Bảng biến thiên
Suy ra đồ thị hàm số hx có dạng
Từ bảng biến thiên suy ra hàm số hx có 3 điểm cực trị    x
u x e x  5  m có 3 điểm cực trị. x
e x 5  m  1  x
e x 5  1   m
Ta có f u x  0     (7) . x
e x 5  m  2 x
e x 5  2  m  
Hàm số g x có đúng 9 điểm cực trị  (7) có đúng 6 nghiệm phân biệt khác điểm
0  1 m  4
4  m 1  0 5  m  1
cực trị của u x        5   m  2  , 2  m  4  m  2 m  2  
mà m có 3 giá trị của m .
Câu 49: [Câu 49 THPT QG 2021– Mã 103] Trong không gian Oxyz , cho hai điểm  A 1; 3  ;2 và B 2  ;1; 4
  . Xét hai điểm M và N thay đổi thuộc mặt phẳng Oxy sao cho MN  4 . Giá trị
lớn nhất của AM BN bằng A. 5 2 . B. 3 13 . C. 61. D. 85.
Fb-Võ Trọng Trí & Khải Nguyễn
Phân tích định hướng tìm lời giải:
1. Các bài toán quen thuộc: + Cho hai điểm ,
A B cố định nằm khác phía đối với mặt phẳng   . Xét điểm M thay đổi
thuộc   , khi đó:
MAMB AB . Đẳng thức xảy ra khi và chỉ khi M M ', trong đó M ' là giao điểm của
đoạn thẳng AB với   .
https://www.facebook.com/groups/toanvd.vdc Trang 135
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8 - 2021
MA MB MA MB '  AB ' . Đẳng thức xảy ra khi và chỉ khi M M ', trong đó B' là điểm
đối xứng với B qua   và M ' là giao điểm của đoạn thẳng AB' với   . + Cho hai điểm ,
A B cố định nằm cùng phía đối với mặt phẳng   . Xét điểm M thay đổi
thuộc   , khi đó:
MAMB MAMB'  AB'. Đẳng thức xảy ra khi và chỉ khi M M ', trong đó B' là điểm
đối xứng với B qua   và M ' là giao điểm của đoạn thẳng AB' với   .
MAMB AB . Đẳng thức xảy ra khi và chỉ khi M M ', trong đó M ' là giao điểm của
đoạn thẳng AB với   .
2. Trở lại bài toán.
Bài toán gần gũi với một bài toán quen thuộc là tìm giá trị lớn nhất của AM BM
với M thuộc mặt phẳng Oxy . Việc đề cho xuất hiện điểm N với ràng buộc MN  4
nên ta có thể dùng phép tịnh tiến để biến AM BN AM B ' M quen thuộc bằng  
cách lấy điểm B' sao cho B B '  N M . Lời giải 1 Chọn D
Thấy hai điểm A, B nằm khác phía so với mặt phẳng Oxy  . Gọi B1 là điểm đối xứng của
B qua Oxy thì B 2
 ;1; 4 và BN BN . Gọi  P là mặt phẳng đi qua B và song song với 1   1 1
Oxy thì P có phương trình z  4 . Gọi H là hình chiếu vuông góc của điểm A lên P
  thì H 1; 3  ; 4 . Gọi B B B NM B P 2 là điểm sao cho thì . 2   1 2
 
 
Ta có: AH  2 , B H  5 BB MN 4 B B NM BN B M B B NM 1 , 1 2 (vì ), (vì 1 2 1 2 1 2
 
B N B M ). Trong  P , điểm B thay đổi thuộc đường tròn C có tâm B và bán kính 1 2 2 1 R B B  4 1 2 . AM BN
AM B N AM B MABAH  HB
AH HB B B 1 1 2 2 2 2 2 2 1 2 2
 85  AM BN  85   1 . Đẳng thức ở  
1 xảy ra khi và chỉ khi điểm B1 nằm giữa hai điểm B
M AB Oxy 2 , H và . 2  
Vậy max AM BN  85 . Lời giải 2
https://www.facebook.com/groups/toanvd.vdc Trang 136
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8 - 2021
Dễ thấy hai điểm A, B nằm khác phía so với mặt phẳng Oxy  . Gọi A1 là điểm đối xứng
của A qua mặt phẳng Oxy thì A 1; 3  ; 2 
và AM AM . Gọi M  ; a ; b  0 và M  ; a ; b  0 , ta 1   1  2 2 2 2
có: a c b d  4 hay a c  c d   16 ; A M a 1;b  3;2 ; 1     
BN  c  2; d 1; 4 ; A M BN a c  3;b d  4; 2  . 1       2 2
AM BN A M BN AM BN AM BN  a c  
3 b d  4  4 1 1 1
 a c2 bd2 292 4
 bd   3 a c    32 51   
    2   2 2 3 45 2 4 3 b d
a c   85  AM BN  85 . Khi M ; ;0    5 5   44 67  và N ; ;0 
 thì AM BN  85 . Vậy max AM BN  85 .  5 5  Bình luận:
Đây là bài toán được phát triển từ ‘bài toán 2’ trang số 7 trong SGK Hình Học Nâng Cao lớp 11.
Hai thôn nằm ở hai vị trí A và B cách nhau một con sông (xem rằng hai bờ sông là
hai đường thẳng song song. Người ta dự định xây một chiếc cầu bắc qua sông (cố
nhiên cầu phải vuông góc với hai bờ sông và làm hai đoạn đường thẳng từ A đến M
và từ B đến N . Hãy xác định vị trí chiếc cầu MN sao cho AM BN ngắn nhất.   Lấy điểm '
A sao cho A A '  M N khi đó AM A' N và AM BN A N   BN A B  . Hướng phát triển
Hướng 1: Tìm giá trị nhỏ nhất của AM BN .
Hướng 2: Bỏ bớt ràng buộc điểm N  Oxy , khi đó A thuộc mặt cầu tâm A bán kính bằng 2 1 A A . 1 2
Các bài tập tương tự Câu 1:
[Trần Quốc Luật-THTT tháng 12 năm 2017] Trong không gian với hệ tọa độ Oxyz , cho các
điểm A0;0; 2 và B3;4; 
1 . Tìm giá trị nhỏ nhất của AX BY với X , Y là các điểm thuộc
mặt phẳng Oxy sao cho XY 1. A. 3. B. 5. C. 2  17 . D. 12 5. Lời giải 1
https://www.facebook.com/groups/toanvd.vdc Trang 137
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8 - 2021
Thấy A0;0; 2 , B3;4; 
1 nằm cùng phía đối với mặt phẳng Oxy . Gọi ' A là điểm đối
xứng với điểm A qua Oxy , khi đó A'0;0; 2
  và AX A' X . 2 2
Vì X ,Y Oxy nên gọi X  ; a ; b 0 , Y  ;
c d;0 . Vì XY 1 nên a c b d 1 hay
a c2  b d 2  1 .     A' X   ; a ;
b 2 , YB  3 ; c 4  d; 
1 , A' X YB  a c  3;b d  4;3 .     2 2 AX BY  ' A X YB
A ' X YB
A ' X YB
 a c  
3 b d  4 9
 a c2 bd2 342 
3 a c 4bd   
35  2 3 a c   4 b d    2 2 2 2 
35  2 3 a c   4 b d   35 2 3  4  a c b d   5  AX BY  5 . Khi  8 32  11 44  X ; ;0   và Y ; ;0 
 thì AX BY  5. Vậy min AX BY   5.  5 15   5 15  Lời giải 2
Thấy A0;0; 2 , B3;4; 
1 nằm cùng phía đối với mặt phẳng Oxy . Gọi ' A là điểm đối
xứng với điểm A qua Oxy , khi đó A 0;0; 2 
và AX A X . 1   1
Gọi  P là mặt phẳng chứa A Oxy P
1 và song song mặt phẳng 
 suy ra   có phương trình là z  2
 . Gọi K là hình chiếu của B lên  P thì K 3;4; 2
  , khi đó BK  3, KA  5 1 .    
  Lấy điểm A A A XY A X A Y
A A XY A X A Y 2 sao cho , khi đó (vì ), 1 2 1 2 1 2 1 2
A P và trong  P , A thuộc đường tròn C tâm A bán kính R A A 1(vì 2   2 1 1 2 A A XY 1 2 ).
AX BY A X BY A Y BY A B BK KA
BK  KA R  5 1 2 2 2 2 2 1 2 2
AX BY  5   1 . Đẳng thức ở  
1 xảy ra khi và chỉ khi A2 là giao điểm thứ nhất của đường thẳng AK C A AK
Y A B Oxy 1
với   ( 2 thuộc đoạn thẳng 1 ) đồng thời . 2  
Vậy min AX BY   5. Câu 2:
[Câu 49 THPT QG 2021– Mã 103] Trong không gian Oxyz , cho hai điểm  A 1; 3  ;  2 và B 2  ;1; 4
  . Xét hai điểm M và N thay đổi, trong đó M thuộc mặt phẳng Oxy và N tùy ý
sao cho MN  4 . Giá trị lớn nhất của AM BN bằng
https://www.facebook.com/groups/toanvd.vdc Trang 138
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8 - 2021 A. 5 2 . B. 3 13 . C. 61. D. 85.  1  2
Câu 50. Có bao nhiêu số nguyên y sao cho tồn tại x  ; 6 3 x xy 18 x   thỏa mãn 27  1 xy27 ?  3  A. 19 . B. 21 . C. 20 . D. 18 .
Phân tích định hướng lời giải
- Đây là bài toán có mức độ VDC (có thể là câu khó nhất của đề thi THPT QG năm 2021).
- Sử dụng phương pháp “Logarit hóa hai vế” để xét phương trình mũ dạng:
f x;mau  ;
x mgx;m .b
, 0  a;b  
1 (với m là tham số)
Định hướng tìm lời giải:
B1: Dựa vào phương trình đã cho tìm điều kiện cho phương trình.
B2: Coi y như tham số, lấy logarit cơ số 27 hai vế, sau đó đưa phương trình về dạng f x  0 .
B3: Sử dụng kĩ thuật chia miền giá trị của tham số và xét hàm số f x . Mục đích để đánh giá
được tính đơn điệu của hàm số f x và sử dụng được định lý giá trị trung bình.
Sử dụng các đơn vị kiến thức: 
Nếu f liên tục trên đoạn a; b và f a. f b  0 thì phương trình f x  0 có ít nhất
một nghiệm trên khoảng a;b .
Sử dụng kiến thức này đã làm cho việc giải toán trở thành việc thử sai trong việc chọn cặp a, b.
Thay vào đó dùng kết quả sau (không thể giải quyết trọn vẹn việc thử sai nhưng đã giảm thiểu một phần):
Cho f liên tục và đơn điệu trên đoạn trên a; b . Khi đó phương trình f x  0 có nghiệm trên
khoảng a;b khi và chỉ khi và f a. f b  0. 
Nếu a e thì hàm số f x  log 1 x x nghịch biến trên 0; . a
Lưu ý: log 1 x x với mọi x  0 và a e. a
Fb: Nguyễn Sỹ - Nguyễn Thanh Hải Lời giải  1 
Giả sử tồn tại y  để phương trình trên có nghiệm x  ; 6 
 . Suy ra 1 xy  0  3 
Lấy logarit cơ số 27 hai vế, PT đã cho tương đương 2
3x  y   18 x  log 1 xy  0 . 27   1  Xét hàm số 2 f  
x  3x y 1  8 x  log
1 xy , với x   ; 6 . 27      3  1   xy  0  1
- Với y  0 , do  1  y   , Suy ra 3
  y  0 hay y 1;   2 . x   x  3 2  +) Với y 2  1  , ta có f  
x  3x 19x  log
1 x là hàm số liên tục trên  ;1 . 27     3   2   2  Do f    11 lim f x   và
  suy ra phương trình có nghiệm trên  ;1   .     3  x 1   3  1  1  +) Với y 2  2  , ta có f  
x  3x  20x  log
1 2x là hàm số liên tục trên  ;  . 27    3   2 
https://www.facebook.com/groups/toanvd.vdc Trang 139
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8 - 2021  1   1 1 
Do f    6 và .  
lim f x   suy ra phương trình có nghiệm trên  ;       3   1   3 2 x       2  x   0
- Với y  0 , phương trình trở thành 2
3x 18x  0  , không thỏa mãn. x   6 
- Với y 19, ta có y
f x  6x y   18  , 31 xyln 3 2 y 1  f   x  6   0, x    ; 6 . 2   31 x y ln 3 3   1  Suy ra f   
x đồng biến trên  ; 6 . Do đó    3  1  y y f  
x f '   2    y 1  8 
 0 vì 3  y  ln 3  y    1 3  3  yln 3 3  yln 3  1  Suy ra f  
x là đồng biến trên  ; 6   . Suy ra  3  1  yy  17
f x  f     log 1     .   27    3  3  3  3 1
Xét hàm số g t  t  log 1 t , t  0 . Dễ thấy gt  1
 0,t  0 , suy ra g t 27       33  tln 3
là hàm đồng biến, do đó 1   y  17 19  17  1 
f    g     g     0 f x  0 x   ;6       . Suy ra     .  3   3  3  3  3  3   1 
Do đó PT trên không có nghiệm thuộc  ; 6   .  3  1   - Với 1 2
y 18 . Do hàm số f  
x  3x y 1  8 x  log
1 xy liên tục trên  ;6 . 27    3    
Ta lại có hàm số g t  t  log
1 t , đồng biến trên 0; . 27   1  yy  17 1   y  17 17 Mà f     log 1      
f    g     g 6   0, y  1;18 , 27            3  3  3  3  3   3  3 3 Mặt khác f   6  6 y  log
1 6 y g 6 y g 6  0, y   1;18 . 27          1   1  Suy ra f . f  
6  0. Do đó phương trình trên có nghiệm trên  ;6 .    3   3 
Vậy có tất cả 20 giá trị nguyên của y thỏa mãn yêu cầu. Bình luận:
- Việc sử dụng BĐT Bernoulli để đánh giá như lời giải sau đây là sai:  1  2
Có bao nhiêu số nguyên y sao cho tồn tại x  ; 6 3 x xy 18 x   thỏa mãn 27  1 xy27 ?  3  A. 19 . B. 21 . C. 20 . D. 18 . Lời giải 2 2 2 Ta có:
3x xy     18 27 1 .27 x xy  3x xy 1  8 27 x 1 xy  3x xy 1  8 27
x 1 xy  0 . 2 2 Mặt khác:       
3x xy 18 3 18 x x xy x xy   xy    2 27 1 1 26 1
1 26 3x xy 18x  1 xy
https://www.facebook.com/groups/toanvd.vdc Trang 140
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8 - 2021 2
 78x  25xy  468x . 2 x xyx  1  + Với y  19  3 18 2 2 27
1 xy  78x  25xy  468x  84x  7x  0 x   ; 6   (loại).  3  2 x xyx  1  + Với y  3  3 18 27
 1 xy  1 3x  0 x   ; 6   (loại).  3  1
+ Với y  2  x  (thỏa mãn). 2
+ Với y  1  x  1 (thỏa mãn). 2 x  0 + Với y  0  3x 1  8 27 x 1  2
3x 18x  0   (loại). x  6 
+ Với 1  y  18 . Xét hàm số   2 3x xy 1  8  27 x f x 1 xy .  1   y Do y 17 f  3 1  0 y     1;2;....;  18 và  3  3   6 6  27 y f
 6y 1  0 y  1;2;....;1 
8 nên phương trình f x  0 luôn có nghiệm  1  thuộc ; 6   .  3  Tóm lại y  2  ; 1;1; 2;....;1 
8 . Vậy có 20 số nguyên y thỏa mãn yêu cầu bài toán. Lưu ý: x
 Nếu a  1 thì 1  a   ax 1 với x  0 hoặc x  1. x
 Nếu a  1 thì 1  a   ax 1 với 0  x 1 .
- Khi giảng dạy cho HS chúng ta nên phát biểu bài toán dưới dạng. “Có bao nhiêu giá trị  1 2 
nguyên của tham số m để phương trình
3 x xm     18 27 1 27 x xm có nghiệm thuộc ;6   ? ”  3 
Hướng phát triển:
Hướng phát triển 1: Thay biến y bởi tham số m quy về bài toán tìm tham số m nguyên để phương trình có nghiệm.
Hướng phát triển 2: Sử dụng phương pháp đánh giá hai vế của phương trình hoặc sử dụng các
bất đẳng thức cơ bản.
Hướng phát triển 3: Sử dụng phương pháp hàm số.
Các ví dụ tương tự:
Hướng phát triển 1: Thay biến y bởi tham số m quy về bài toán tìm tham số m nguyên để phương trình có nghiệm 2
Câu 1. Có bao nhiêu số nguyên 3  15 x
m để phương trình 27 x xm  (1 xm)27 có nghiệm  1  x  ;5   ?  3  A. 16 . B. 18 . C. 15 . D. 17 . Lời giải  1 
Giả sử tồn tại m   để phương trình trên có nghiệm x  ;5   .  3   1  1
Từ phương trình, suy ra xm  1  . Do x  ;5 
 , nên ta có m    3 hay m  2  .  3  x 2
Phương trình đã cho tương đương với 3x 1  5 27
xxm  (1 x ) m  0.
https://www.facebook.com/groups/toanvd.vdc Trang 141
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8 - 2021  1 
Xét hàm số f x 2 3x 1  5  27 xxm  1
(  xm) trên khoảng ;5    3  5m *  1   m 1 Ta có f (5)  27 1
 5m  0 m   và 14 f  3 1 m   ,  3  3  m
Xét hàm số: g mm 14  3 1
, ta có g 'm  0  m  14  log 3ln 3  m  12,9 . 3   3 0 BBT: g   3    0 g  16  0 Do  và 
, kết hợp với BBT suy ra với m nguyên lớn hơn 3  và g   2    0  g  15  0 
g m  0  m 2  ; 1  ;...;1  5 .  1 
+ Với m  {2; 1;1;;15} ta có ff (5)  0  
, nên phương trình f ( x)  0 luôn có nghiệm  3   1  trên khoảng ;5   .  3 
+ Với m  0 , ta có f (x)  0  x  0, x  5 không thỏa mãn.
+ Với m  16 ; Ta có phương trình 2 f x 3x 1  5xxm 2  0  27
 (1 xm)  3x 15x xm  log 27 1 mx  0  1 
Xét hàm số h x 2
 3x 15x xm  log
1 mx trên khoảng ;5 . Ta có 27      3  2 m m  1 
h' x  6x 15  m
h'  x  6   0, x   ;5 .    1 mx ln 27 31 mx2 ln 3  3  1  1 
Vì h' x liên tục trên đoạn ;5 
nên hàm số h' x đồng biến trên khoảng ;5 . Do đó 3      3   1  m m
h ' x  h '  2    m 15 
 0 vì 3  m ln 3  m nên   1.  3  3  mln 3 3  mln 3 1   1  mm  14
Suy ra h x là đồng biến trên ;5 
. Do đó, hx  h   log 1      . 3  27    3  3  3  3 1
Xét hàm số g t   t  log
1 t , t  0 . Dễ thấy gt   1  0, t   0 , suy ra 27   33  t  ln 3  1   m  14 14  1 
g t  là hàm đồng biến, do đó hg   g     8 
 0 . Suy ra hx  0 x   ;5   .  3   3  3 3  3   1 
Do đó phương trình trên không có nghiệm thuộc khoảng ;5   .  3 
Vậy m {2; 1;1; 2;;15} , hay có 17 giá trị nguyên của tham số m .
https://www.facebook.com/groups/toanvd.vdc Trang 142
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8 - 2021  1  Câu 2.
(Mã đề 101, 2021) Có bao nhiêu số nguyên y sao cho tồn tại x  ;3   thỏa mãn  3  2
3 x xy     9 27 1 27 x xy ? A. 27 . B. 9 . C. 11. D. 12 . Lời giải  1 
Giả sử tồn tại y   để phương trình trên có nghiệm x  ;3 
 . Suy ra 1 xy  0  3 
Lấy logarit cơ số 27 hai vế, phương trình đã cho tương đương 2
3x   y  9 x  log 1 xy  0 . 27    1 
Đặt f x 2
 3x   y  9 x  log 1 xy , x
;3 . Ta xét các trường hợp sau 27      3  1 
Nếu y  0 thì  y
 3 , suy ra y  3 hay y 1;   2 . x  1 
+) Với y  1 thì ta có f  0  
và lim f x    suy ra phương trình có nghiệm trên  3  x 1   1   1  ;1  ;3     .  3   3   1 1   1 
+) Tương tự, với y  2 , phương trình cũng có nghiệm trên ;  ;3     .  3 2   3   x  0 
Nếu y  0 thì phương trình trở thành 2
3x  9x  0   không thỏa mãn. x  3  
Nếu y  10 , ta có y
f  x  6x   y  9  , 31 xy ln 3 2 y  1 
f  x  6   0, x   ;3 .   31 xy2 ln3  3  1 
Suy ra f  x đồng biến trên ;3  . Do đó 3     1  y
f  x  f '  2     y  9   0 .  3  3  yln 3 1 
Suy ra f x là hàm số đồng biến trên ;3  . Do đó 3     1  yy  8
f x  f   log 1    . 27    3  3  3  3 1
Xét hàm số g t   t  log
1 t , t  0 . Dễ thấy gt   1
 0 g t  là hàm đồng 27   33  t  ln 3 biến, suy ra  1   y  8 10  8 fg   g   0       .  3   3  3  3  3  1 
Nên phương trình không có nghiệm trên ;3 
 trong trường hợp này.  3  
Nếu 1  y  9 thì từ tính đồng biến của g t  , ta suy ra
https://www.facebook.com/groups/toanvd.vdc Trang 143
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8 - 2021  1   y  8 fg   0, 1   y  9     ,  3   3  3 f  
3  g 3y  0, 1   y  9 .  1 
Điều này dẫn đến phương trình có nghiệm trên ;3 .    3 
Vậy có 11 giá trị nguyên của y thỏa mãn yêu cầu.
Hướng phát triển 2. Sử dụng phương pháp đánh giá hai vế của phương trình hoặc sử
dụng các bất đẳng thức cơ bản. Câu 3. Có bao nhiêu cặp số nguyên  ; x y thỏa mãn x  2020 và 2 x2 y x 3 y2 2  2021
x  2y  2  4 ? A. 1. B. 2020 . C. 2021 . D. 0 . Lời giải Chọn B 2 2 Nếu x2 y 2 x 3 y2
x y    
x y   x2 y x 3 y2 2 2 0 2 2 , 2021 2 2  0  2  2021
x  2y  2  4 . 2 2 Nếu x2 y 2 x 3 y2
x y    
x y   x2 y x 3 y2 2 2 0 2 2 , 2021 2 2  0  2  2021
x  2y  2  4 . 2 2 Nếu x2 y 2 x 3 y2
x y    
x y   x2 y x 3 y2 2 2 0 2 2 , 2021 2 2  0  2  2021
x  2y  2  4 .
Vậy x  2 y  2  0  x  2  2 y , do 2020  x  2020  1009  y  1011 .
Do y   nên có 2021 giá trị, nên có 2021 cặp số  ; x y thỏa mãn.
Câu 4. Có bao nhiêu cặp số nguyên  ;
x y với 1  y  2020 thỏa mãn biểu thức sau:
2x 2 y  2x x x 2 x   log 4  2 y y  log 2 y  . 3   3   2 y A. 11. B. 15 . C. 10 . D. 6 . Lời giải Chọn A 2 2ay a Đặt 2x a   0 , suy ra log  2 2
a ay y  log ay  3  3   2 y 2 2 2 2
a ay y a aa y   a   log  2.   log 1  1 1 * 3 2 3       ay y y y a y     Cauchya ya
Nhận thấy VP   *  1, VT   *  log  1  log 3  1 dẫn đến
 1  y  2x . 3   3 y a   y Do 1   2020  1  2x y
 2020  0  x  log 2020  10,98 . 2
Vì x   nên x có 11 giá trị, mỗi giá trị của x tương ứng một giá trị y .
Vậy nên có 11 cặp số  ; x y thỏa mãn.
Hướng phát triển 3. Sử dụng phương pháp hàm số.
Câu 5. Có bao nhiêu cặp số nguyên  ;
x y với 2  x y  99 thỏa mãn y x
x y ? A. 4751 . B. 4750 . C. 4656 . D. 4657 . Lời giải Chọn A x y y x ln ln ln t
Từ x y y ln x x ln y  
, xét hàm số f t   , t 2;99 . x y t 1 ln t
Có f t  
f t  0  t e  2, 71 . 2   t
https://www.facebook.com/groups/toanvd.vdc Trang 144
Tập san Số 02
NHÓM GIÁO VIÊN TOÁN VIỆT NAM 8 - 2021
Suy ra hàm số f t  đồng biến trên đoạn 2;e và nghịch biến trên đoạn  ; e 99 . ln x ln y
- TH1. x  3  x [ ; e 99] thì 
y x  3 , suy ra có 2 C  4656 cặp  ; x y thỏa x y 97 mãn. ln 2 ln y ln 4 ln y
- TH2. x  2 thì   
y  4  y  5, x  2 có 95 cặp  ; x y thỏa 2 y 4 y mãn.
Vậy nên có 4656  95  4751 cặp số  ; x y thỏa mãn.
https://www.facebook.com/groups/toanvd.vdc Trang 145