Thu Gọn Hệ Lực 2025: Tóm Tắt Lý Thuyết và Bài Tập | Môn Cơ học kết cấu - Đại học Xây Dựng Hà Nội

lOMoAR cPSD| 58933639
1. BÀI TOÁN THU GỌN HỆ LỰC A. TÓM TẮT LÝ THUYẾT
1.1. Thu gọn hệ lực không gian tổng quát
Cho hệ lực không gian (F F F )
1, 2,..., n , ta có các đại lượng: + Véc tơ chính: n R = F + + = 1 F2 ...+ Fn Fk (1.1) k=1 n F Ri Rj Rk = + + R = k x y z k=n1 n n (1.2)
Rx = Fkx,Ry = Fky,Rz = Fkz k=1 k=1 k=1
+ Véctơ mômen chính của hệ lực lấy đối với điểm O: n M = O m FO( )k (1.3) k=1 Trong đó:
mO( )F =OA F (1.4)
N ế u đ ặ t vào O h ệ tr ụ c t ọ a đ ộ Oxyz , ta có: i j k y z x z x y mO () A A A A A A F x y z i j k = A A A = − + F F F F F F y z x z x y F F F ( 1 . 5 ) x y z =(yF zFi xF zF j xF yFk
A z − A y ) −( A z − A x ) +( A y − A x ) v ớ i ( Axyz , , là t a AAA
) ọ a đ ộ đi ể m đ ặ t c ủ a l ự c F ; ,, ijk
là các véc tơ đơn v ị ch ỉ phương c ủ
các trục tọa độ Ox, Oy, Oz.
+ Mômen chính lấy đối với các trục tọa độ: n n n M = = = x
mx(Fk ),My
my(Fk ),Mz mz(Fk ) (1.6) k=1 k=1 k=1 lOMoAR cPSD| 58933639
+ Liên hệ mômen chính lấy đối với các trục tọa độ và véc tơ mô men chính lấy đối với gốc tọa độ O có: n M = + + O
m FO( k ) = M ix M jy M kz (1.7) k=1
+ Thu gọn hệ lực không gian (F F F )
1, 2,..., n về tâm O ta được: ( ) ( ) (1.8) F F F1, 2,..., n R MO ,O trong đó
RO = R = R ix + R i y + R iz (1.9) n M O O k x y z k=1 = m F(
với O là gốc của hệ trục tọa độ Oxyz đã chọn. ) = M i + M j +M k
+ Dạng tối giản của hệ lực: (1.10) • Hệ lực cân bằng: ( (1.11) F F ) 1, 2,...,Fn ~ 0 MRO O==00
• Hệ lực có hợp lực R: )
(F F1, 2,...,Fn ~ R R 0 (1.12) R M .O = 0
Gọi N(x,y,z) là điểm đặt của hợp lực R, khi đó đường tác dụng lực xác định theo công thức Varignon: lOMoAR cPSD| 58933639 i j k yR zR M
z − y = x m () R M x y z
( M , M , M ) zR xR M ( 1 . 13 ) O = O = x y z x − z = y R R R x y z
• H ệ l ự c tương đương v ớ i ng ẫ u l ự c R 0 ( , FF ,..., F ~( , FF ) = ( 1 . 14 ) 1 2 n ) M 0 O
• H ệ l ự c tương đương v ớ i 2 l ự c chéo nhau:
xR y − yRx = Mz (F F ) 1, 2,...,Fn
~ (R R1, 2chéo nhau) R M .O 0 (1.15)
1.2. Thu gọn một số hệ lực đặc biệt
1.2.1. Thu gọn hệ lực phẳng
Cho hệ lực phẳng(F F F )
1, 2,..., n , ta có các đại lượng: + Véc tơ chính: n R = F + + = 1 F2 ...+ Fn Fk (1.16) k=1 n n n R = F = + = = k R ix R j R y ; x Fkx,R y Fky (1.17) k=1 k=1 k=1
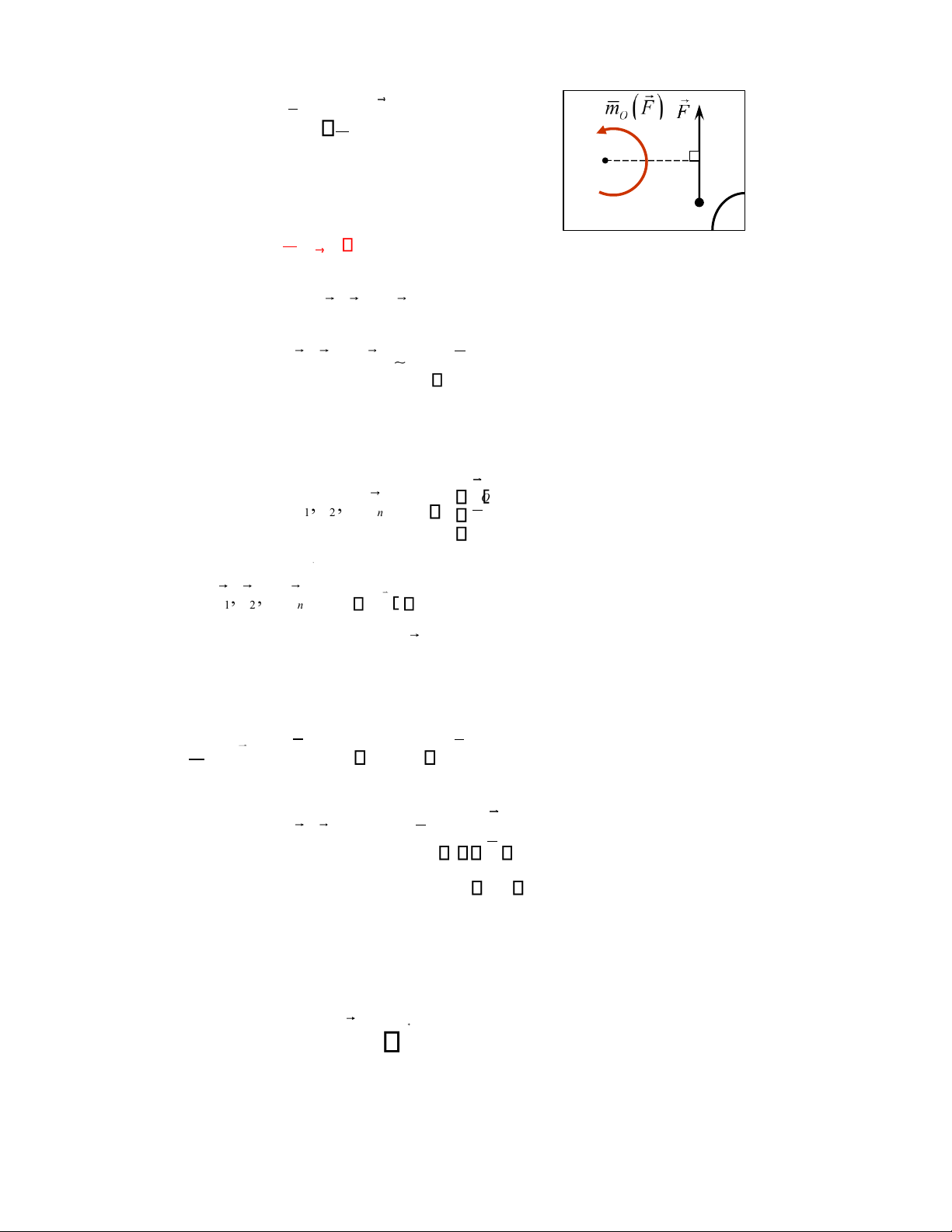
+ Mômen chính của hệ lực lấy đối với điểm O trong mặt phẳng: lOMoAR cPSD| 58933639 n M = O mO( )Fk + k=1 d O Trong đó: _ A P
mO(F)= Fd
+ Thu gọn hệ lực phẳng (F F )
1, 2,...,Fn về tâm O trong mặt phẳng ta được: ( ) ( ) F F1, 2,...,Fn RO ,MO (1.18)
+ Dạng tối giản của hệ lực:
• H ệ l ự c cân b ằ ng: R 0 O = (1.19) ( , FF ,..., F ~0 1 2 n ) M 0 O =
• H ệ l ự c có h ợ p l ự c R : ,
FF ,..., F ~ R 0 1 2 n ) R ( (1.20)
Gọi N(x, y) là điểm đặt của hợp lực RN , khi đó đường tác dụng lực xác định theo công thức Varignon: m (1.21)
O(RN) = MO => xR y − yRx = MO
• Hệ lực tương đương với ngẫu lực (F F ) 1, 2,...,Fn ~ MO R = 0 (1.22) MO 0
1.2.2 Thu gọn hệ ngẫu lực
Hệ ngẫu lực bất kỳ sẽ tương đương với một ngẫu lực có véctơ mômen bằng tổng véctơ
mômen của các ngẫu lực thành phần n M = mk (1.23) k=1 lOMoAR cPSD| 58933639
Hệ ngẫu lực trong mặt phẳng sẽ tương đương với một ngẫu lực có mômen bằng tổng mômen
của các ngẫu lực thành phần n M = mk (1.24) k=1
1.2.3. Thu gọn hệ lực đồng quy
Hệ lực đồng quy sẽ tương đương với một lực, lực đó đạt tại điểm đồng quy và biểu diễn
bằng véctơ chính của hệ lực đó, hoặc tương đương với hệ lực cân bằng nếu véctơ chính của hệ lực đó bằng 0. n R F 0 A = kA
(F , F ,..., F = A A nA ) k 1 1 2 n (1.25) 0 khi F = kA 0 k=1
1.2.4. Thu gọn hệ lực song song cùng chiều
+ Thu gọn hệ lực song song (F F F )
1, 2,..., n về tâm O ta được: ( ) ( )
F F F1, 2,..., n R MO , O (1.26)
trong đó RO ⊥ MO = R MO . O = 0
+ Dạng tối giản của hệ lực:
• Tương đương v ớ i h ệ l ự c cân b ằ ng: R 0 O = (1.27) ( , FF ,..., F ~0 1 2 n ) M 0 O =
• H ệ l ự c có h ợ p l ự c R : ,
FF ,..., F )~ R R 0 ( 1 2 n (1.28) •
Hệ lực tương đương với ngẫu lực (F F ) 1, 2,...,Fn ~ MO MR O= 00 (1.29) lOMoAR cPSD| 58933639
+ Thu gọn hệ lực phân bố: là hệ lực song song cùng chiều được phân bố theo quy luật nào
đó trên một miền xác định của vật. •
Hệ lực phân bố bất kỳ q(x) tác dụng trên đoạn chiều dài AB = L, đơn vị N/m. Hệ lực
tương đương với hợp lực Q của hệ lực có: lOMoAR cPSD| 58933639 F2 = + −F12
F22 2FF1 2 cos , = − y F •
Tọa độ véctơ đề-các: F y F = F i + x F jy x α trong đó F F x = Fsin
,Fy = F cos , nếu thành phần lực Fx x hoặc
Fy ngược chiều trục tọa độ sẽ mang dấu âm “–”. •
Véctơ tổng theo tọa độ đề-các: A z
F = F1 + F2 + F3 + =...
FFxy == FF11xy A
++FF22xy++FF33xy++......
2. Véctơ tọa độ Đề-các: A x
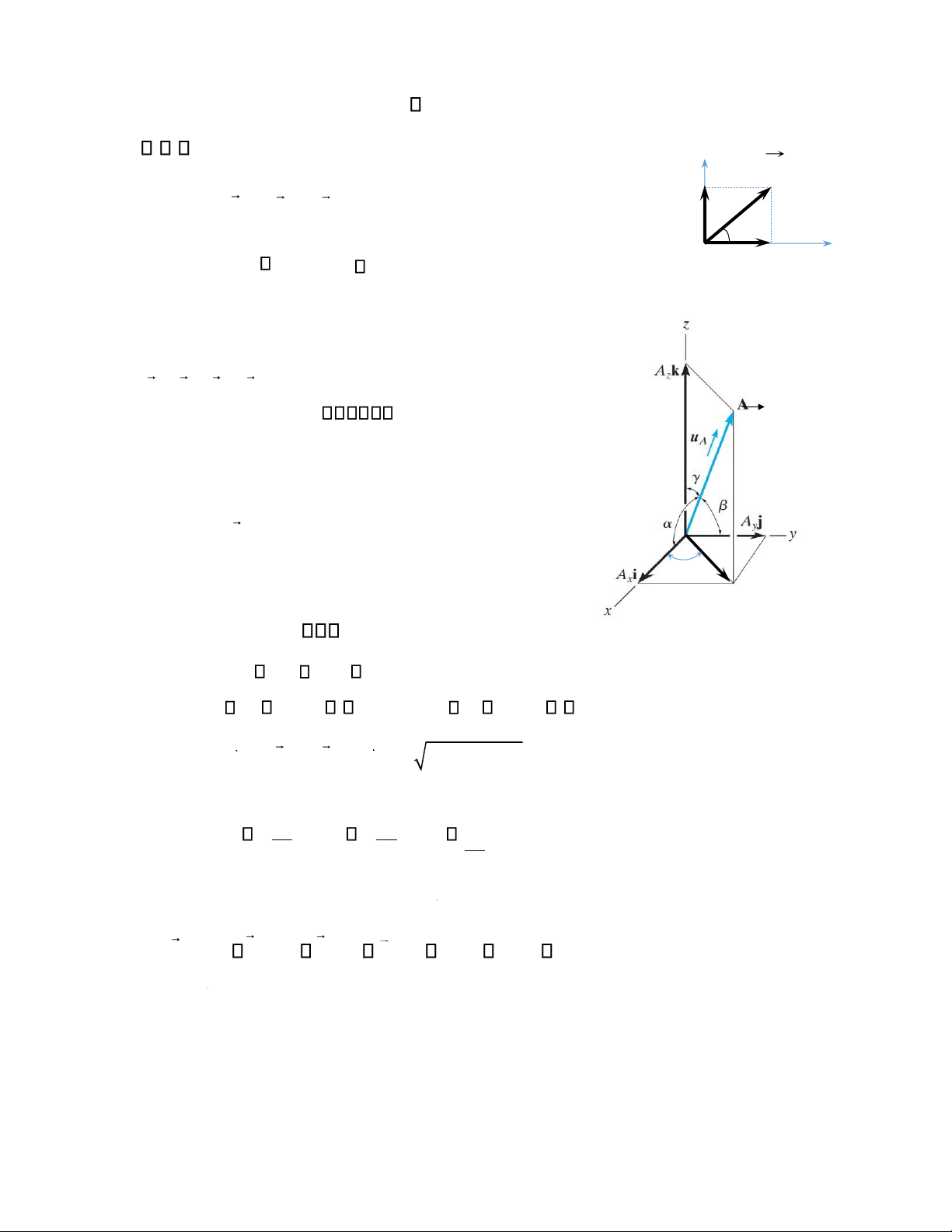
Véctơ Acó độ lớn A, tọa độ theo các trục là ( A x A A A ) θ x,
y, z , tạo với các trục tọa độ Ox, Oy, Oz A' lần lượt các góc là , , . Khi đó ta có:
A Az =cos , A A =sin
A Ax = cos = Asin cos A Ay = sin = Asin sin
A = A ix + A jy + A k Az ; = Ax2 + Ay2 + Az2 cos = Ax , cos = Ay ,cos = Az A A A
Véctơ đơn vị chỉ phương của véctơ A là: u = A
cos i + cos j +cos k; cos2 +cos2 +cos2 =1. lOMoAR cPSD| 58933639
*) Véc tơ F dọc theo phương AB
có tọa độ A x y z( ) A, A, A và ( Bx z : B , B B y , )
AB =( x x i y y j z k B z − A ) ( + B − A ) ( + B − A ) AB = ( 2 2 2 x x y y z z B − A )
+( B − A ) +( B − A ) AB u ( x x y y z z B − A )
i ( B − A) j ( B − A) k = AB = AB + AB + AB x x F y y F z z F
=> F Fu ( B − A ) i ( B − A ) j ( B − A ) k = = AB + AB + AB *)
Tích vô hướng, tích có hướng, hình chiếu của một véc tơ lên 1 phương:
Cho véctơ a = a ix +a jy +a kz và b = +b ix b jy +b kz , α là góc tạo bởi 2 véctơ, khi đó:
+ Tích vô hướng của hai véctơ là đại lượng vô hướng: ab ab= cos
+ Tích có hướng của hai véc tơ là một véctơ vuông góc với mặt phẳng chứa 2 véc tơ thành phần: lOMoAR cPSD| 58933639 Lời giải:
+ Góc tạo bởi trục x và phương hợp lực: lOMoAR cPSD| 58933639 cos = =Rx 66,32 =11,34o R 67,64
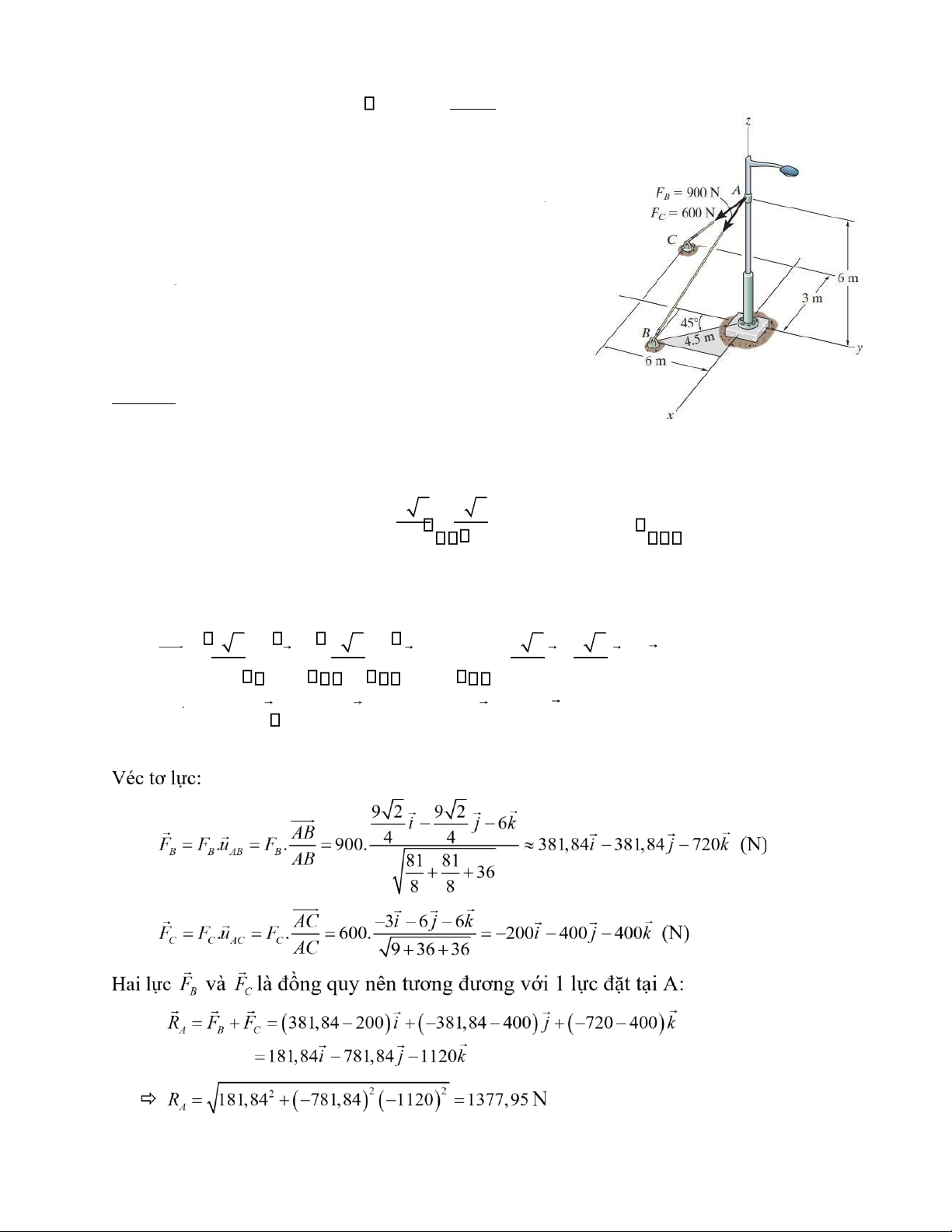
Bài 2. Cột đèn được gia cố bằng dây cáp AC và AB
như hình vẽ. Nếu biết lực căng tác dụng vào cột đèn FC =
600N, FB= 900N, các kích thước như hình vẽ.
Xác định véctơ hợp lực của các lực căng cáp và độ lớn của nó. Lời giải: Tọa độ các điểm:
A là (0, 0, 6); C là (-3, -6, 0).
B là (4,5sin45 ; -4,5cos45 ; o o 0)= 9 24 ; - 9 24 ; 0 Ta có các véc tơ: 9 2 9 2 9 2 9 2 AB = 4 −0 i + − 4 −0
j +(0−6)k = 4 i − 4 j −6k
AC =(−3−0)i +(− −60) j +(0−6)k = −3i −6j −6k lOMoAR cPSD| 58933639
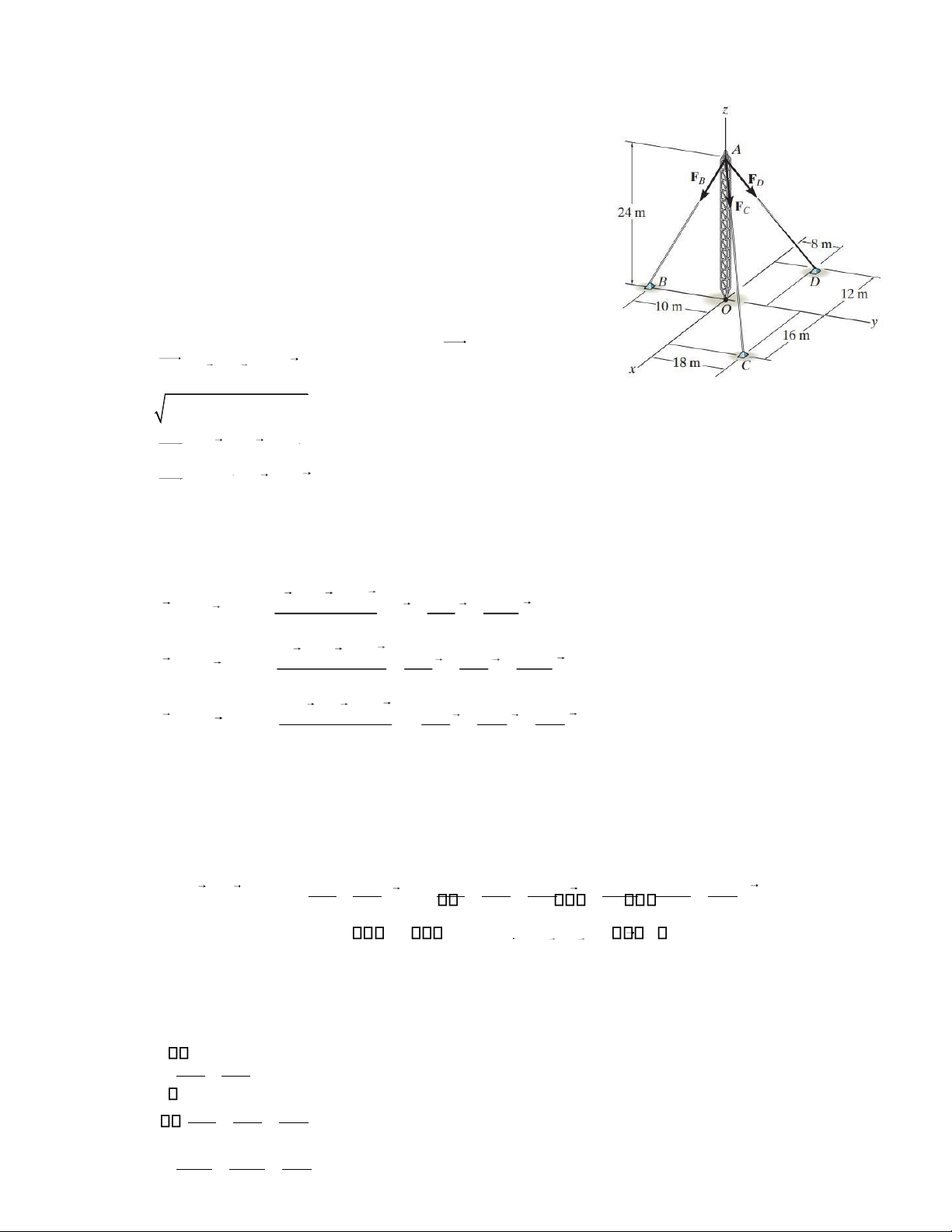
Bài 3. Cột viễn thông được giữ cố định bằng 3 dây cáp với
các lực căng cáp tác dụng lên cột dọc chiều dài mỗi dây
như hình vẽ. Biết hợp lực của chúng dọc từ A đến O và có độ lớn 20kN.
Xác định các lực căng cáp Lời giải: Tọa độ các điểm :
A(0, 0, 24), B(0, -10, 0), C(16, 18, 0), D(-12, 8, 0) Các véc tơ:
AB = 0i −10 j − 24k hoặc
AB= − −(0, 10, 24),
AB= 02 + −( 10)2 + −( 24)2 =26m
AC =16i +18j −24k , AC = 34m
AD = −12i +8j − 24k , AD = 28m Véc tơ lực:
FB = F uB AB = FB.0i −10 j − 24k = −0i
5FB j −12FB k 26 13 13
FC = F uC AC = FC.16i +18 j − 24k =
8FC i + 9FC j −12FC k 34 17 17 17
FD = F uD AD = FD.− + −12i 8 j
24k =−3FD i + 2FD j − 6FD k 28 7 7 7 Véc tơ hợp lực:
RA = FB + FC + FD =
817FC −3F7D i + − 513FB +917FC + 2F7D j −
1213FB +1217FC +6F7D k
Do véc tơ hợp lực dọc AO có độ lớn 20kN nên: RA = 0i + 0 j − 20k Đồng
nhất 2 véc tơ hợp lực ta có:
817FC − 3F7D = 0
−5FB + 9FC + 2FD = 0 lOMoAR cPSD| 58933639 13 17 7
1213FB + 1217FC + 6F7D = 20
Giải ra ta được: FB = 11,94kN; FC = 5,45kN; FD = 5,98kN
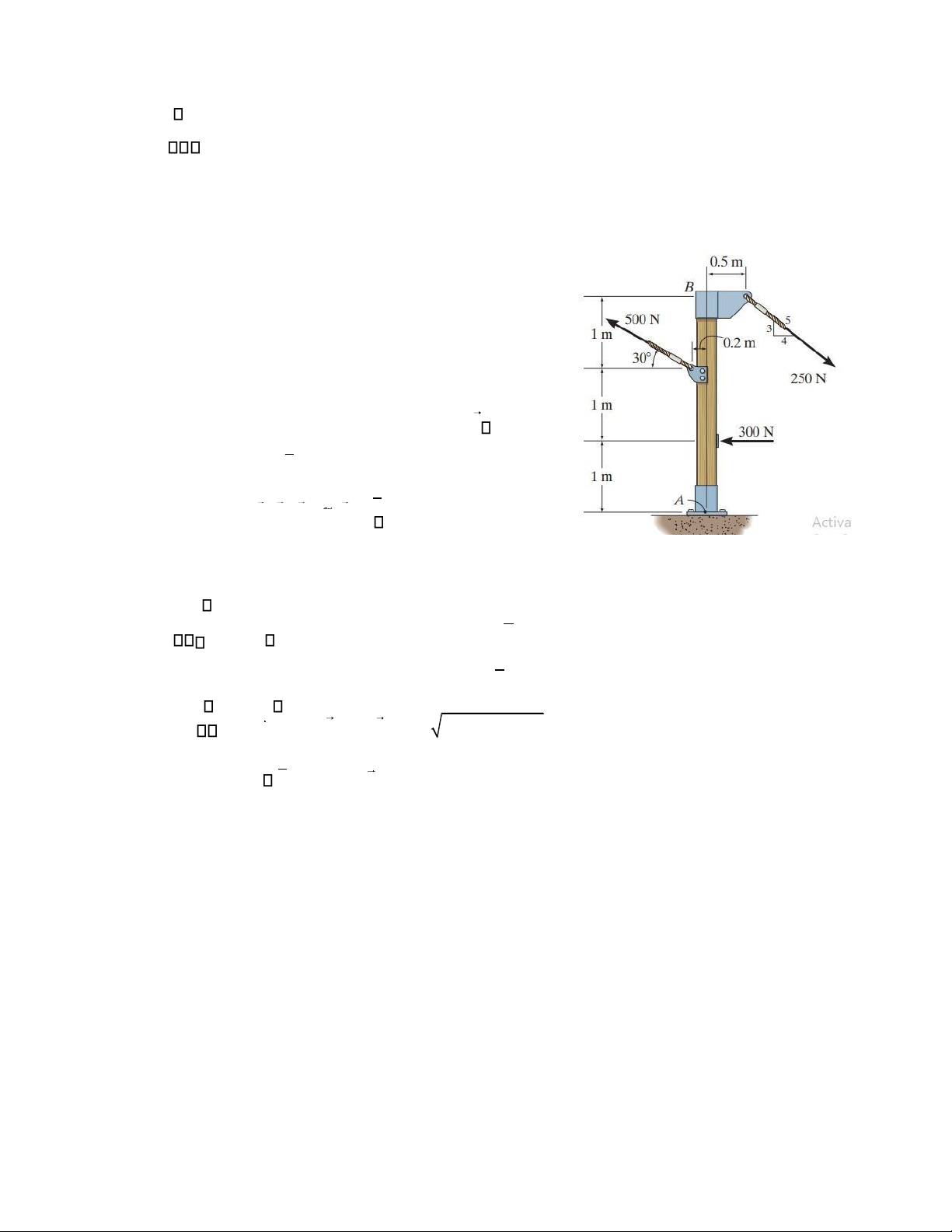
Bài 4. Cho cột AB chịu tác dụng của hệ lực như hình
vẽ. Thu gọn hệ lực tác dụng lên cột AB về chân cột A
(Thay thế hệ lực tác dụng bằng một lực và một ngẫu
lực tại chân cột A) Bài giải:
Đặt lực các lực có độ lớn trên hình là F1 = 300N, F2 =
500N, F3 = 250N. Hệ tọa độ Axy.
Thu gọn hệ lực về chân cột A ta được 1 lực RA và 1
ngẫu lực có mômen MA: (F F F ) ( ) 1, 2, 3 R MA , A
trong đó véc tơ chính được xác định: o 4
R F F Fx = 1x + 2x + 3x = −F F1 − 2 cos30 + F3.5 = −533N R F F F = + + = − + y 1x 2x 3x
0 F2 sin30o − F3.3 =100N 5
 Lực tại A: R = − = A
533i +100j R, A ( 533)−2 +1002 =542,3N lOMoAR cPSD| 58933639 3 3
Ngẫu lực tại A: M = ( )= A mA F F Fk
1.1+ 2 cos30 .2o −F2 sin30 .0,2 4 3 o
−F .5 .3−F . .0,55 = 441Nm F 3 F 1
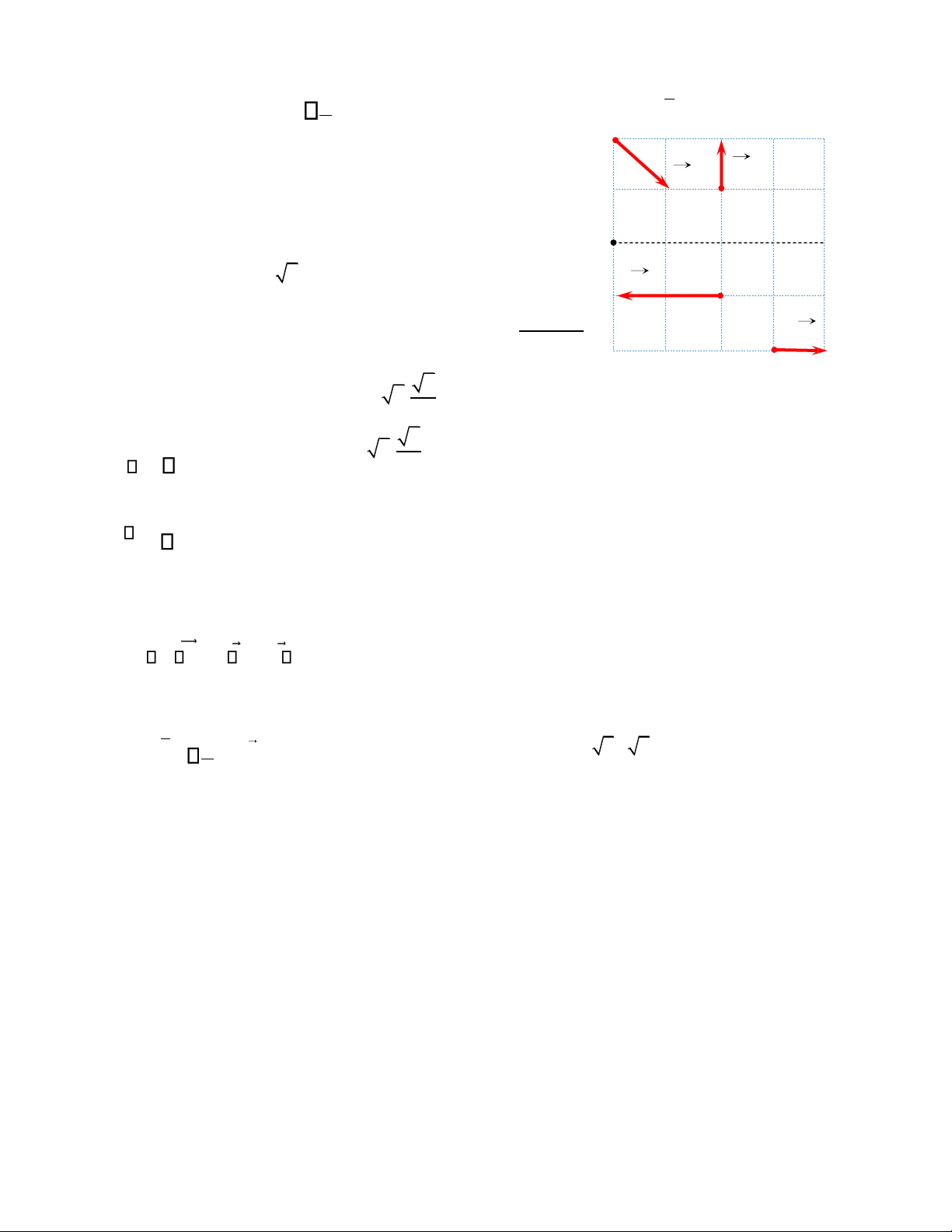
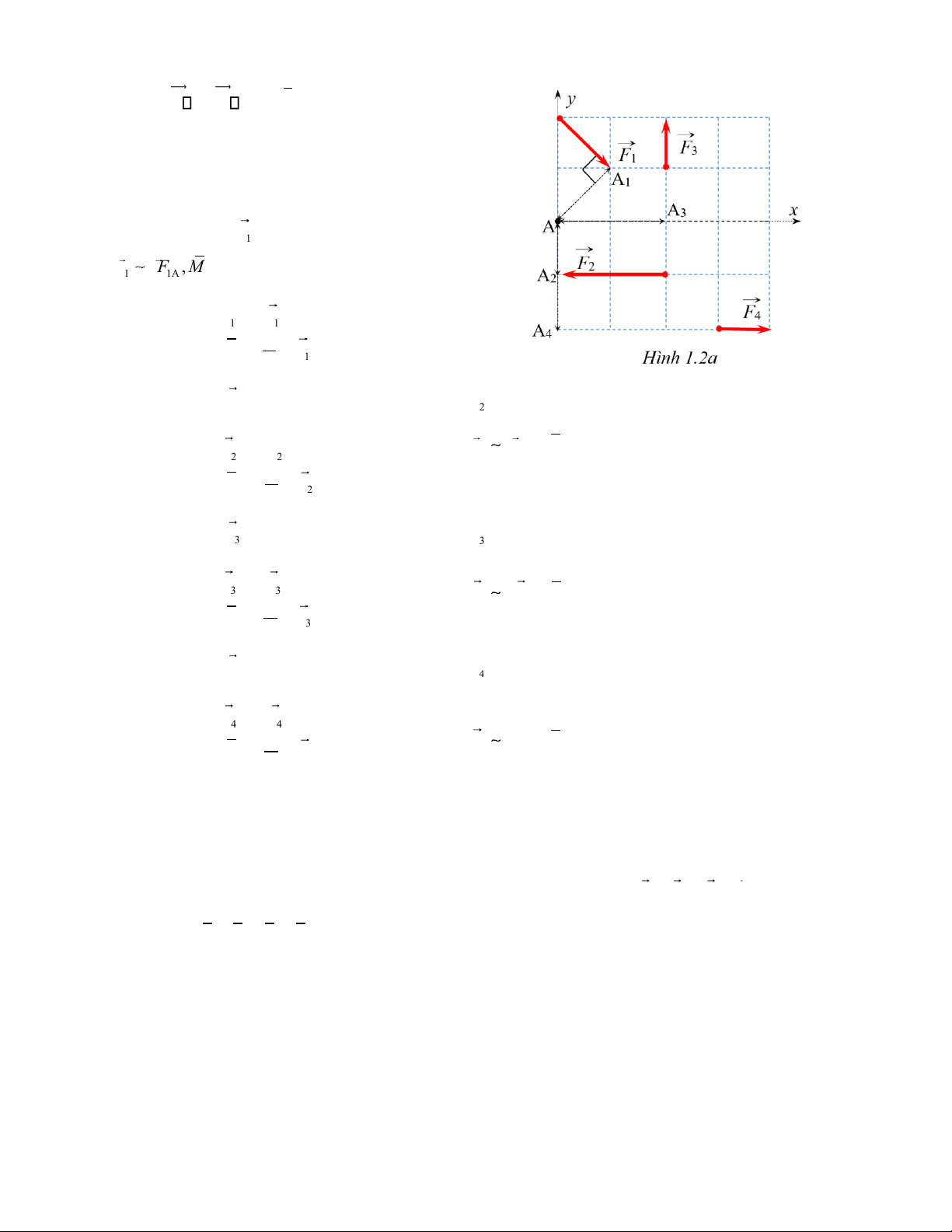
Bài 5. Cho hệ lực phẳng gồm các lực đặt tại các đỉnh của
lưới hình vuông cạnh a, có phương chiều dọc theo các A
cạnh hoặc đường chéo của ô vuông như Hình 1.2. Biết độ
lớn các lực là F = = = = 1
P 2 , F P2 2 , F F P3 4 F 2
Thu gọn hệ lực về A. Dạng tối giản của hệ lực đó. Lời giải: F 4
Đặt vào A hệ trục tọa độ Axy như Hình 1.2a + Ta có véc tơ 2 Hình 1.2 chính của hệ lực: 2. 2 n 2 R = = + =− x
F Fkx 1 cos45o − F F P2 4 2P P+ = 0 k=1 n R = = − = − y Fky
F1sin45o + F3 P 2. + P = 0 k=1 2 Vậy:
R =R ix + R j y= 0
+ Mômen chính của hệ lực lấy đối với điểm A: n
MA = mA(Fk) =−F1.AA1 −F2.AA2 +F3.AA3 +F4.AA4 =−P a2.
2 −P a P a P a.2 + .2 + .2 = 0 k=1
+ Thu gọn hệ lực về A ta được: lOMoAR cPSD| 58933639 R = A = R
=0 , MA 0. Hệ lực đã cho cân bằng.
Chú ý: Ta có thể áp dụng trực tiếp định lý dời lực
song song để thu gọn hệ lực về A như sau: + L ự c F d 1
ị ch chuy ể n v ề A ta đư ợ c: F F M 1 ( 1 A , 1) , trong đó F F = 1 A 1 M m F 1 = A ( 1) 1 =
−F.AA1 = −2Pa + L ự c F d F
2 ị ch chuy ể n v ề A ta đư ợ c: 2 F F = 2 A 2 (F ) 2A,M2 , trong đó M m F 2 = A ( 2) 2 + L ự c F d F
3 ị ch chuy ể n v ề A ta đư ợ c: 3
= −F .AA2 = −2Pa F F = 3 A 3 M m F (F ) 3A,M3 , trong đó 3 = A ( 3) 3 + L ự c F d F
4 ị ch chuy ể n v ề A ta đư ợ c: 4 = F .AA3 = 2Pa F = 4 A F 4 M m F = (F )
4A,M4 , trong đó ( ) 4 A 4 = F4.AA4 = 2Pa ng qui
Như vậy tại A hệ lực ban đầu tương đương với hệ lực đồ (F )
1A,F2A,F3A,F4A và hệ ngẫu lực (M M M M ) 1, 2, 3, 4 lOMoAR cPSD| 58933639
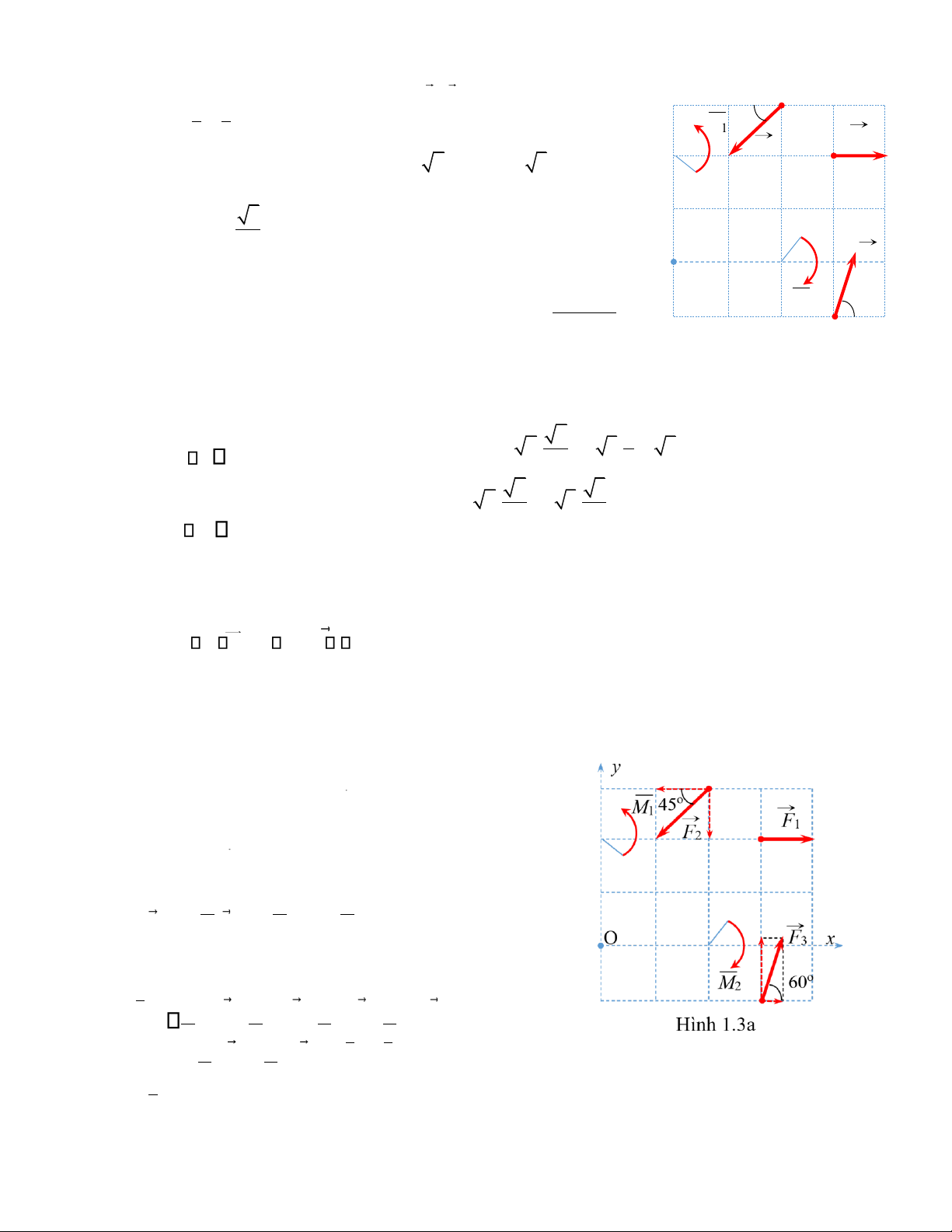
Bài 6. Cho hệ lực phẳng gồm các lực F F F1, 2, 3 và ngẫu lực có M 45 o mô men M M 1 1,
2 đặt tại các đỉnh của lưới hình vuông cạnh a F 1 F 2
như Hình 1.3. Biết độ lớn F = = = 1
2kN, F2 2 2kN ,F3 2 3kN , M1 =
1,5kNm, M2 = 3 kNm, a= 0,5m. 2 O F 3
Thu gọn hệ lực về O. Dạng tối giản của hệ lực. Lời giải: M 2 60 o
Đặt vào O hệ trục tọa độ Oxy như Hình 1.3a + Ta có véc tơ Hình 1.3 chính của hệ lực: n o o 2 1 R = = − x Fkx F1
F2 cos45 + F3 cos60 2 2 2.= − +2 3. = 3kN k=1 2 2 n o o 2 3 R = =− y Fky
F2 sin45 + F3 sin60 =−2 2. +2 3. =1kN k=1 2 2 Vậy:
R =R ix + R j y 0
Chú ý: Ngẫu lực sẽ không có mặt trong phương trình hình chiếu vì nó là hai lực song song
ngược chiều, khi chiếu lên 1 phương nào đó chúng sẽ triệt tiêu cho nhau.
+ Mômen chính của hệ lực lấy đối với điểm O:
Khi tính mômen của lực F3 lấy đối với điểm O, việc xác
định tay đòn của lực là tương đối khó. Khi đó ta có thể phân
tích F3 thành 2 lực đồng qui theo hai phương của trục tọa
độ, khi đó: mO(F3) = mO(F3x)+mO(F3y) = F3 cos60 .o a+ F3 sin60
.3o a Bằng cách trên ta có: n
MO = mO( )Fk =mO( )F1 +mO(F2x)+mO(F2y) k=1
+mO(F3x)+mO(F M M3y)+ +1 2 => M =− O
F a1.2 +F2 cos45 .3o a F− 2 sin45 .2o a+F3 cos60 .o a+F3sin60 .3o a M+ −1 M2 lOMoAR cPSD| 58933639 3 9 3 =− + − +2 3 2+ + −1,5= 5kNm 2 2 2
Như vậy hệ lực phẳng thu gọn về O ta được một lực và một ngẫu lực: R = = O
3.i +1.j , MO 5kNm
+ Dạng tối giản của hệ lực: Do R 0 nên hệ lực tương đương với hợp lực (chú ý rằng hợp
lực này không đặt tại O do M O 0). Hợp lực đó là: RN R 3. i 1. j = = +
, đặt tại N theo phương trình (1.21): x 3 y 5 − = (1.30)
Như vậy, theo phương trình (1.30) ta chỉ xác định được đường tác dụng lực, theo hệ quả
trượt lực thì tác dụng của lực không đổi khi ta trượt nó dọc đường tác dụng lực.
Bài 7. Cột đèn được gia cố bằng dây cáp AC và AB như hình vẽ. Nếu biết lực căng của các
dây FC = 600N, FB= 900N, các kích thước như hình lOMoAR cPSD| 58933639 lOMoAR cPSD| 58933639 , FF R , B R M C A O O Cách ( ) ( ) R R khác: Hệ O = A i j k i j k lực cáp M m R x y z i j k O = o ( 0 0 6 4691,04 1091,04 0
A) = A A A = = + + tương R R R 181,84 781,84 1120 x y z − −
đương với RA , do đó thu gọn hệ lực về O tương đương với thu gọn RA về O. Ta sử dụng định
lý dời lực song song để rời RA từ A về O:
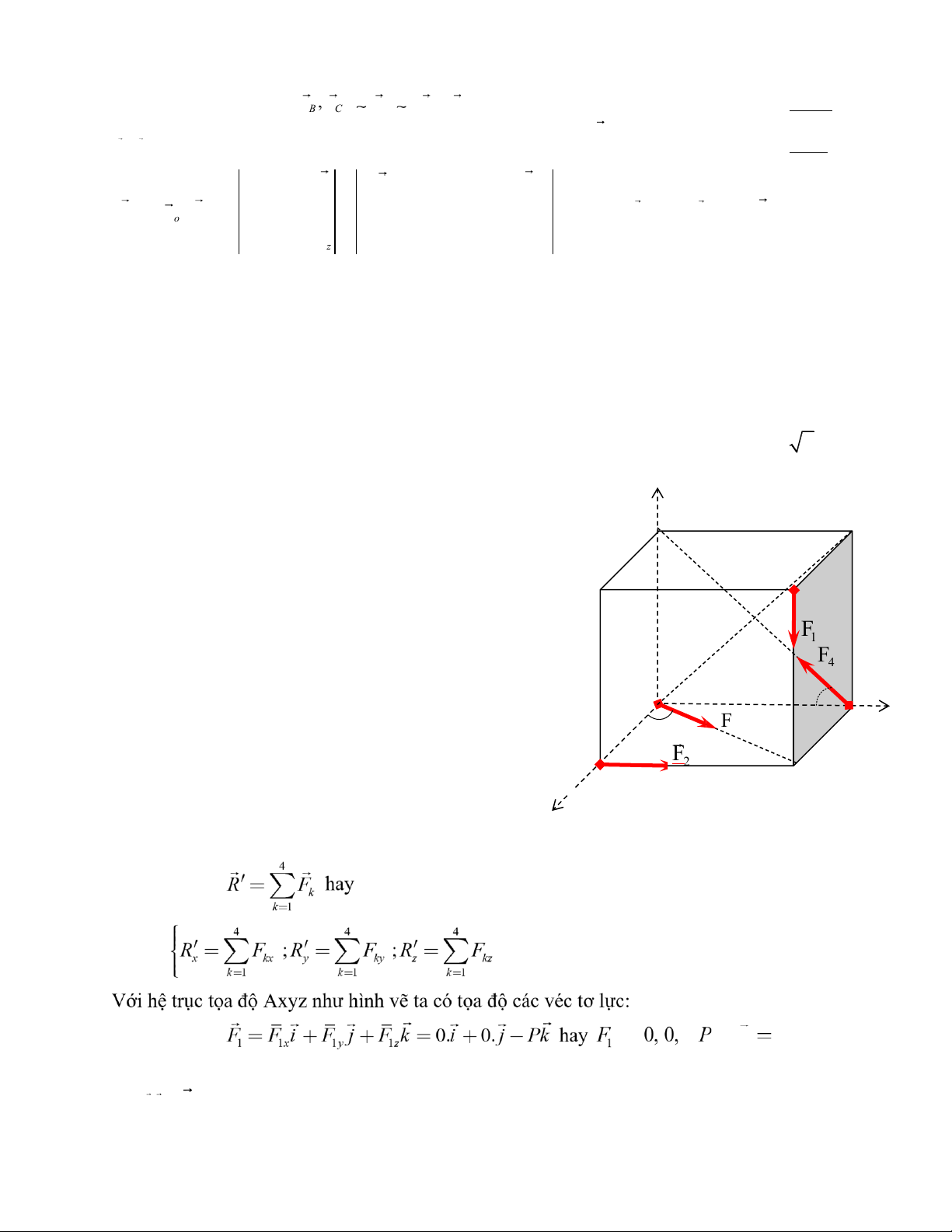
Bài 8. Cho hệ lực đặt tại các đỉnh của hình lập phương ABCD.A’B’C’D’ có cạnh dài a. Các
lực có phương dọc các cạnh như hình vẽ. Độ lớn 1 2 3 4
các lực là: F = F = P, F = F = P 2 . z A’
Chọn hệ trục tọa độ Axyz như hình vẽ. B’
a) Xác định véc tơ chính của hệ lực. C’
b) Xác định mô men chính của hệ lực lấy đối D’ 
với các trục tọa độ. F 1  F
c) Xác định véctơ mômen chính của hệ lực lấy 4 45 o y đối với điểm A. A  F
d) Thu gọn hệ lực về điểm A và nhận xét dạng 3 B 45 o  F
tối giản của hệ lực. C 2 D x Lời giải:
a) Véc tơ chính của hệ lực bằng tổng hình học các véctơ lực thành phần: (31) (32)
với i j k, , lần lượt là các véc tơ đơn vị chỉ phương của trục Ax, Ay và Az. lOMoAR cPSD| 58933639
F2 0.i P j. 0k hay F2 0, P,0 (33)
F3 F3cos45 .oi F3sin45 .o j 0k Pi. P j. 0.k hay F3 P P, ,0 (34) F4 0.i F4 cos45 .o j
F4sin45ok 0.i P j. Pk. hay F4 0, P P, (35)
Thay các biểu thức từ (32) đến (35) vào (31) ta được: R
Pi Pj 0.k hay R P P, ,0 (36)
b) Mômen chính của hệ lực lấy đối với các trục tọa độ.
*) Mômen chính Mx lấy đối với trục x: mômen chính của hệ lực lấy đối với trục x bằng tổng
mômen của các lực thành phần lấy đối với trục x: 4 M m F m F m F m F m F ( 37 ) x x 1 x 2 x 3 x 4 x k k 1 m F FCD Pa ( 38 ) 1 1 . x m F (vì F 2 0 x 2 cắt trục x ) ( 39 ) m F ( vì F 3 0 x 3 cắt trục x ) ( 40 ) AB m F F Pa ( 41 ) x 4 4 . 2
Thay các biểu thức từ (38) đến (41) vào (37): M Pa 0 0 Pa 0 x (42)
*) Mômen chính My lấy đối với trục y: 4 M m F . FBD 0 0 0 Pa y y k 1 k 1 (43) F (my 2 0 vì F 2
song song với trục y; F F3, 4 cắt trục y nên mômen cũng bằng 0) *)
Mômen chính Mz lấy đối với trục z: 4 M m F 0 F . AC 0 0 Pa z z k 2 k 1 (44)
c) Véctơ mômen chính của hệ lực lấy đối với điểm A bằng tổng véctơ mômen của các lực
thành phần lấy đối với điểm A: 4 lOMoAR cPSD| 58933639 MA mA Fk (45) k 1
Với A là gốc của hệ trục tọa độ Axyz, ta cũng có công thức liên hệ mômen: MA M ix M jy M kz hay MA M M Mx, y, z (46)
(Chú ý rằng công thức (46) chỉ đúng khi A là gốc của hệ trục tọa độ!) Như
vậy, từ (42) đến (44) thay vào (46) ta có: MA 0i Paj Pak hay MA 0,Pa Pa, (47)
Cách 2 làm câu b và c: Ta có thể dùng công thức (45) bằng phương pháp giải tích để xác định
M A và suy ra M M Mx, y, z như sau: