Chương 16: Học hiểu về cơ cấu (Phần 2) | Môn Cơ học kết cấu - Đại học Xây Dựng Hà Nội

lOMoAR cPSD| 58933639
16.6. Tâm vận tốc tức thời
Vận tốc của điểm B bất kỳ nằm trên một vật rắn
có thể xác định được trực tiếp bằng cách chọn một
điểm cơ sở A – là điểm có vận tốc bằng không tại
thời điểm khảo sát. Trong trường hợp này, vA = 0, và
do đó, phương trình vận tốc vB = vA + ω rB/A trở
thành vB = ω rB/A. Đối với một vật có chuyển động
phẳng tổng quát, điểm A được chọn như trên được
gọi là tâm vận tốc tức thời (IC), và nó nằm trên trục
quay tức thời. Trục này thẳng góc với mặt phẳng
chuyển động và giao điểm của trục này và mặt phẳng
chuyển động là vị trí của IC. Vì điểm A trùng với IC,
nên vB = ω rB/IC và vì vậy điểm B chuyển động tức
thời quanh IC theo quỹ đạo tròn; nói cách khác, vật
đó quay xung quanh trục quay tức thời. Độ lớn của
vB đơn giản bằng vB = rB/IC, trong đó, là vận
tốc góc của vật. Do vật chuyển động tròn nên hướng
của vB phải vuông góc với rB/IC.
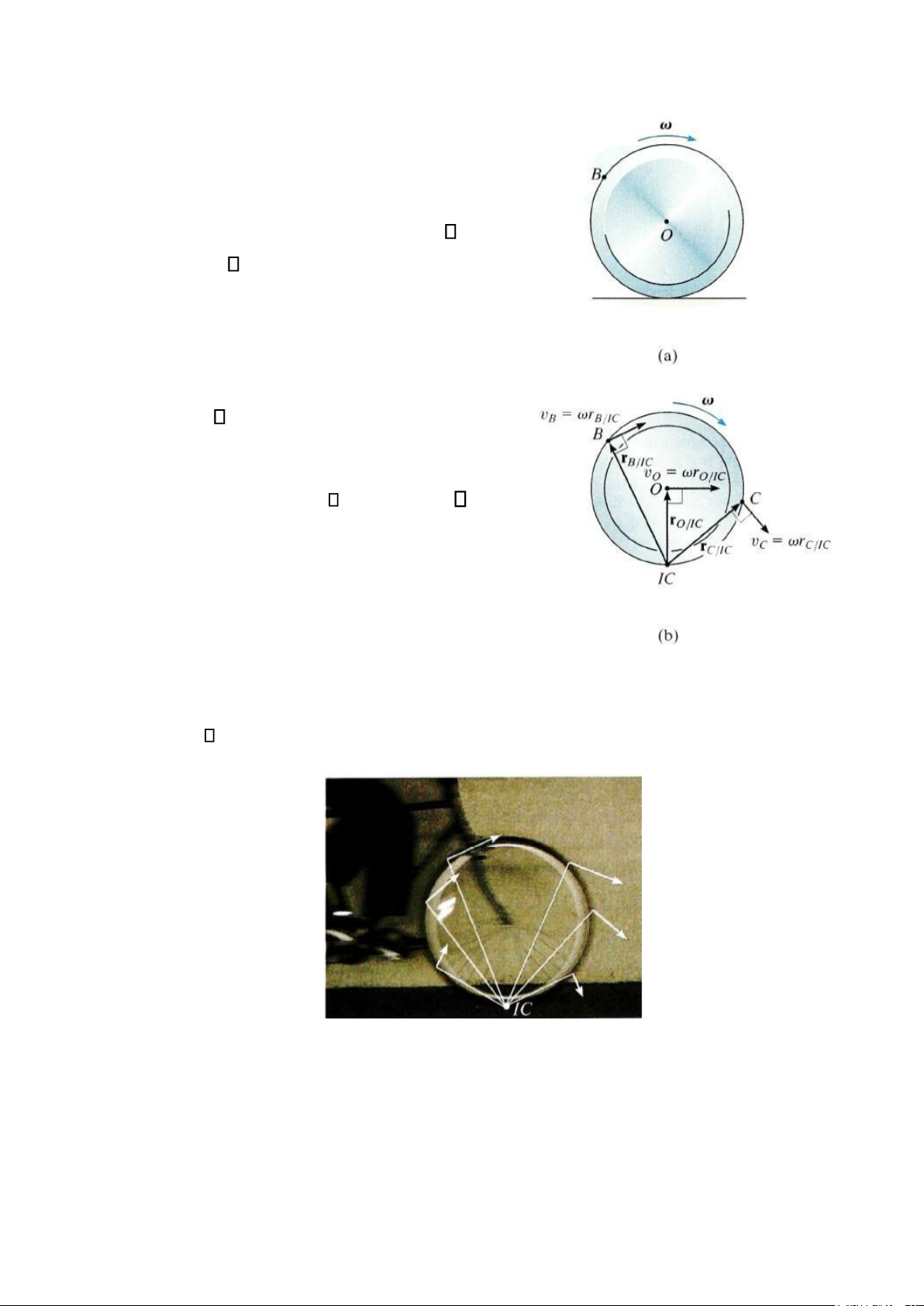
Ví dụ, xét bánh xe trong hình 16-17a. Nếu nó
lăn không trượt thì điểm tiếp xúc với đất có vận tốc
bằng không. Do đó, điểm này chính là IC của bánh
Hình 16-17 xe (Hình 16-17b). Nếu ta coi bánh xe quay xung
quanh điểm này thì vận tốc của điểm B, C, O và vân vân có thể xác định được bằng phương
trình v = r. Ở đây, các khoảng cách theo các tia rB/IC, rC/IC, và rO/IC trên hình 16-17b, được
tính nhờ đặc điểm hình học của bánh xe.
IC của bánh xe đạp này nằm trên mặt đất. Tại đây, ta có thể phần nào thấy nan
hoa trong khi tại đỉnh của bánh xe, chúng trở nên rất mờ. Hãy chú ý xem các
điểm ở vị trí cạnh của bánh xe chuyển động như mô tả trong hình theo vận tốc của chúng. lOMoAR cPSD| 58933639
Vị trí của IC. Để xác định vị trí IC, ta có thể sử dụng điều đã biết là vận tốc của một điểm
trên vật luôn vuông góc với vectơ vị trí tương đối kéo dài từ IC đến điểm đó. Có thể xảy ra một số khả năng sau:
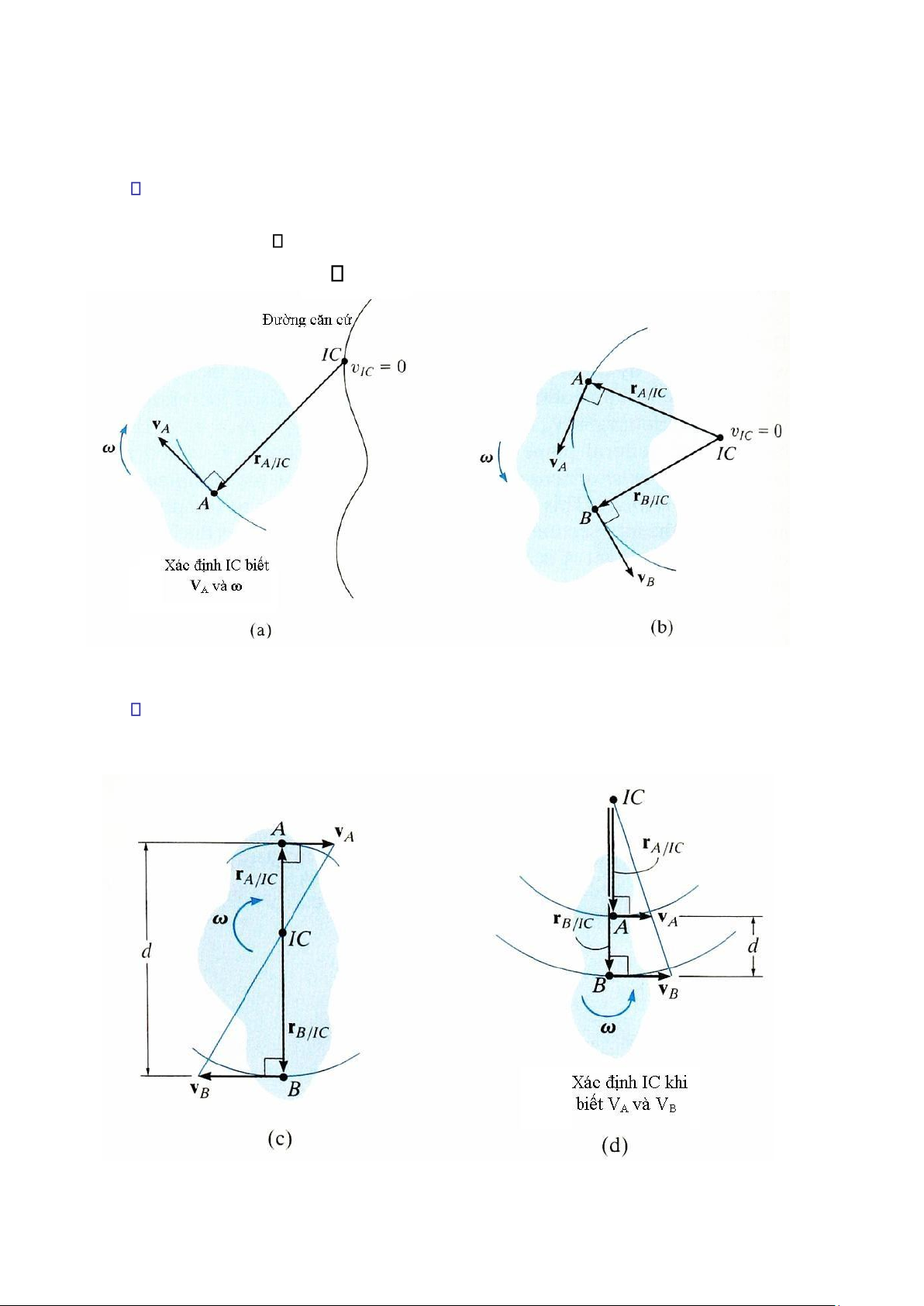
Cho trước vận tốc vA của điểm A trên vật, và vận tốc góc ω của nó (Hình 16-18a).
Trong trường hợp này, IC nằm dọc theo đường thẳng vẽ vuông góc với vA tại A, khoảng cách
từ A đến IC là rA/IC = vA/ . Lưu ý rằng IC nằm dịch lên trên và sang phải vì vA phải tạo ra vận
tốc góc cùng chiều kim đồng hồ quay quanh IC. Hình 16-18
Cho trước phương chiều của hai vận tốc không song song vA và vB, hình 16-18b. Dựng
các đoạn thẳng vuông góc với vA và vB tại A và B. Kéo dài các đoạn thẳng này như trên hình
16-18b, giao điểm của chúng chính là IC tại thời điểm đang xét. Hình 16-18 (tiếp) lOMoAR cPSD| 58933639
Cho trước độ lớn và hướng của hai vận tốc song song vA và vB . Trong trường hợp này,
vị trí của IC được xác định bằng các tam giác tỷ lệ. Các ví dụ về trường hợp này được biểu
diễn trong hình 16-18c và d. Trong cả hai trương hợp này, rA/IC = vA/ và rB/IC = vB/ . Nếu
gọi d là khoảng cách đã biết giữa hai điểm A
và B, thì trong hình 16-18c, rA/IC + rB/IC =
d và trong hình 16-18d, rB/IC – rA/IC = d.
Trong trường hợp đặc biệt, lưu ý rằng nếu vật
chuyển động tịnh tiến, vA = vB thì IC sẽ được
coi là ở xa vô cùng, trong trường hợp này, rA/IC = rB/IC
. Đây chính là trường hợp =
(vA/rA/IC) = (vB/rB/IC) 0.
Thực tế điểm chọn coi là tâm vận tốc tức
thời đối với vật thể, chỉ được sử dụng tại một
thời điểm, vì vật thay đổi vị trí của nó từ thời
điểm này sang thời điểm lân cận (tiếp theo).
Quỹ tích các điểm được xác định bởi vị trí IC
trong khi vật rắn chuyển động được gọi là đường tâm quay(đường
lăn). Mặc dù IC giúp ta xác định vận tốc của
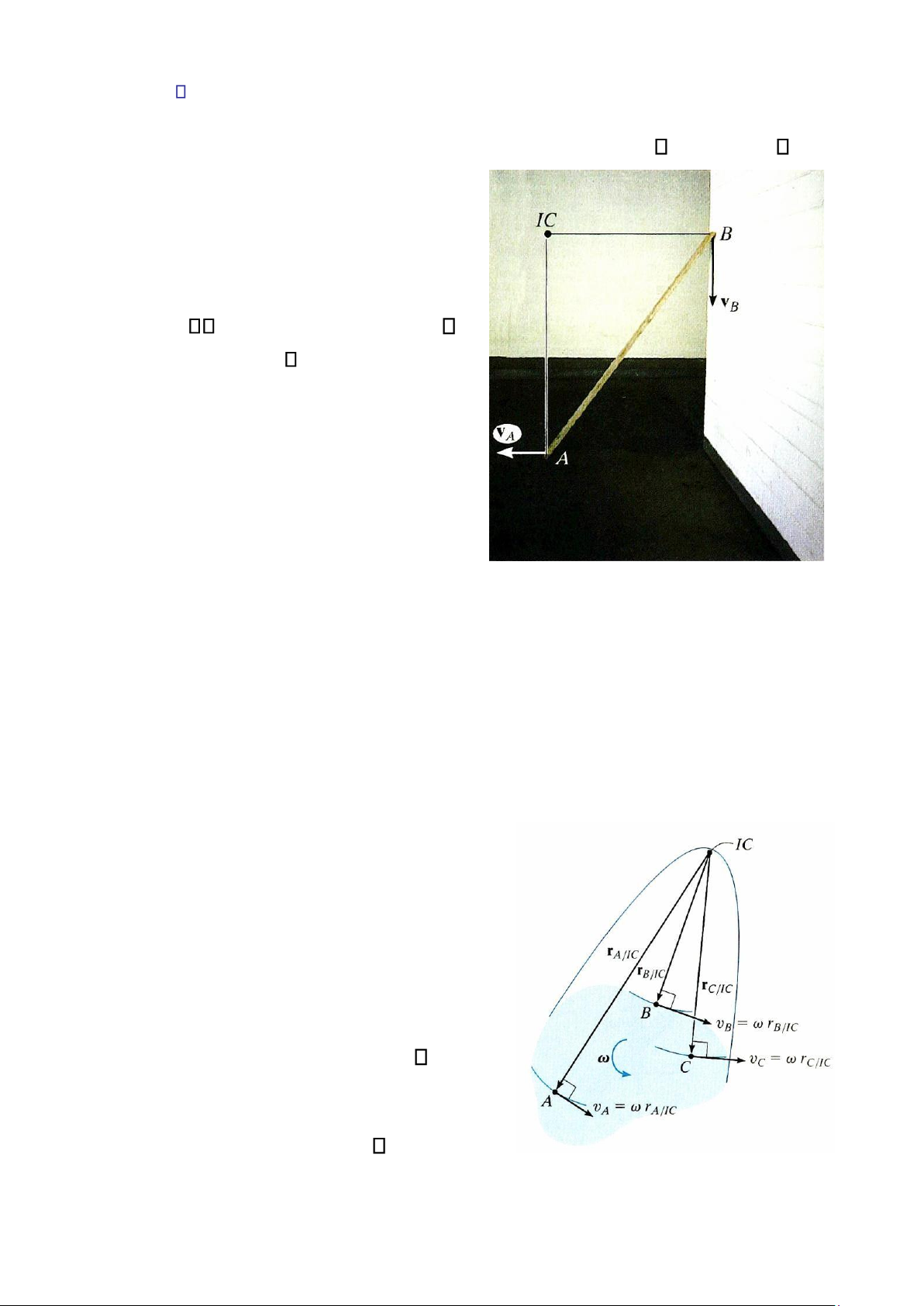
Khi tấm bảng chuyển động xuống dưới sang trái thì nó một điểm bất kì trên vật một cách dễ dàng phụ
thuộc vào mặt phẳng chuyển động. Do đã biết hướng nhưng nói chung gia tốc của nó không bằng các
vận tốc của các đầu của IC như trên Hình. Tại thời điểm này, tấm bảng sẽ A và B, ta xác định được vị trí không
và do đó, nó không được sử dụng để quay tức thời quanh điểm này. Vẽ tấm bảng tại các vị trí xác định
gia tốc tức thời của các điểm trên khác nhau, ta thiết lập được IC tại mỗi trường hợp và vẽ được đường lăn vật.
Trình tự phân tích.
Vận tốc của một điểm trên vật chịu ràng buộc
chuyển động phẳng tổng quát, có thể được xác
định bằng cách xác định vị trí của tâm quay tức
thời có vận tốc bằng không, miễn là vị trí của IC
được xác định đầu tiên bằng cách sử dụng một
trong ba phương pháp đã nêu trên. •
Khi vẽ trên sơ đồ động học trong hình 16-
19, vật được hình dung là “kéo dài và chốt”
tại IC sao cho tại thời điểm khảo sat, nó quay
quanh chốt này với vận tốc góc . •
Độ lớn vận tốc của các điểm A, B và C bất
kì trên vật có thể được xác định bằng cách
sử dụng phương trình v = r, trong đó, r là Hình 16-19
khoảng cách theo các tia từ IC tới mỗi điểm đó. lOMoAR cPSD| 58933639 •
Phương chiều của mỗi véc tơ vận tốc v vuông góc với đường thẳng theo các tia
liên quan r, và vận tốc có hướng - dẫn tới làm di chuyển điểm đó theo hướng nhất
quán với vận tốc góc của đường thẳng theo các tia, hình 16-19. Ví dụ 16.10
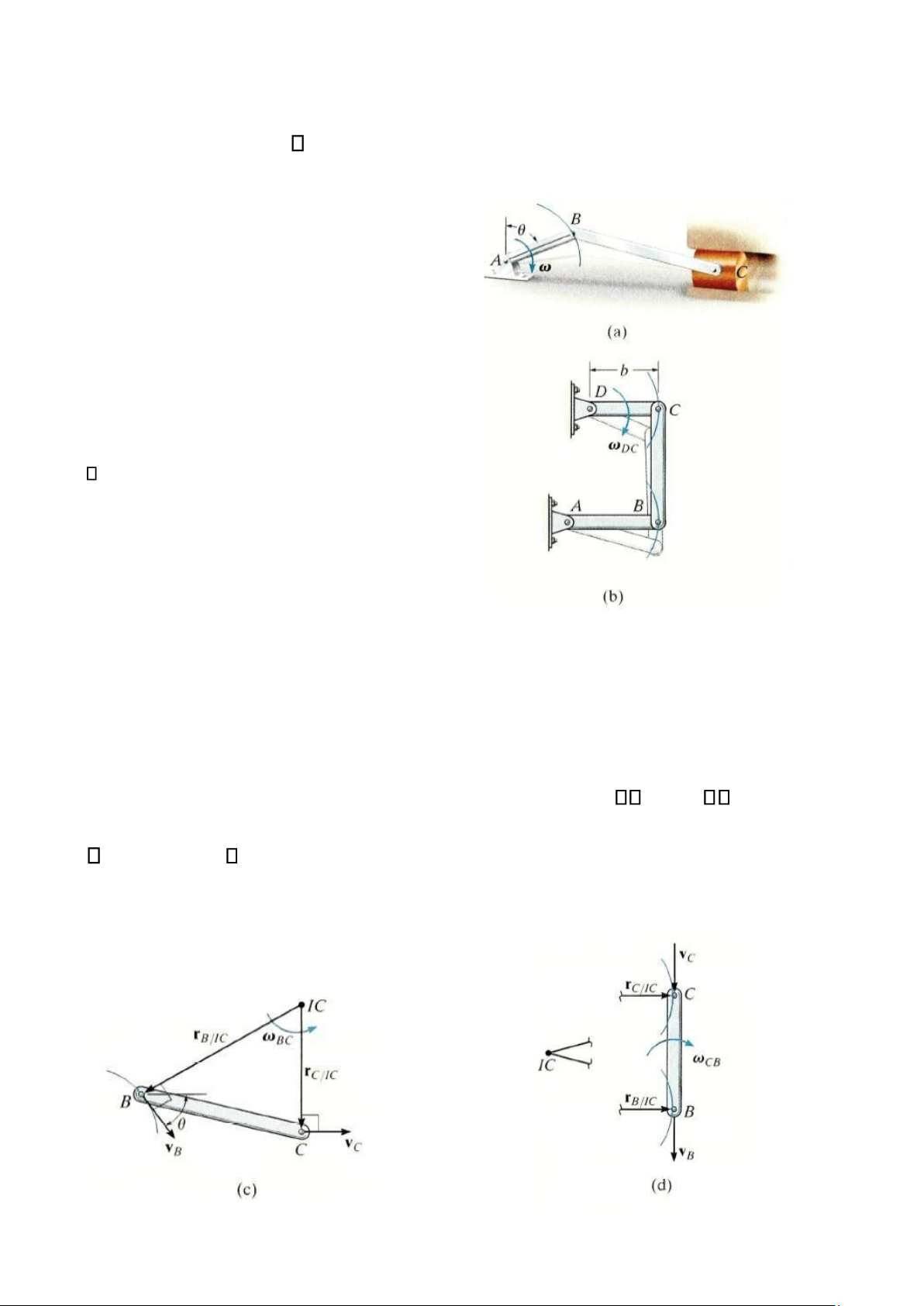
Hãy chứng tỏ việc xác định vị trí của tâm quay
tức thời có vận tốc bằng không của (a) thanh BC
trên hình 16-20a và (b) thanh nối CB trên hình 16- 20b. Bài giải
Phần (a). Như trên hình 16-20a, điểm B có
vận tốc vB, làm thanh AB quay cùng chiều kim
đồng hồ. Điểm B chuyển động theo quỹ đạo tròn,
nên vB vuông góc với AB, và do đó, nó tạo ra góc
so với phương nằm ngang như trên hình
16-20c. Điểm B chuyển động làm piston di
chuyển theo phương ngang lên phía trước với vận
tốc vC . Khi các đường thẳng vẽ vuông góc với vB
và vC; Hình 16-20c, thì chúng giao nhau tại IC.
Phần (b). Các điểm B và C chuyển động theo
quỹ đạo tròn do các thanh AB và DC quanh quay Hình 16-20
một trục cố định. Hình 16-20b. Do vectơ vận tốc
hướng theo phương tiếp tuyến với quỹ đạo nên tại thời điểm khảo sát, vC trên thanh DC
và vB trên thanh AB đều hướng thẳng đứng xuống dưới, dọc theo trục của thanh CB,
hình 16-2d. Các đường thẳng theo các tia được vẽ vuông góc với hai vận tốc này tạo
thành các đường thẳng song song giao nhau tại “vô cùng”; tức là, rC/IC và rB/IC . Vì vậy,
CB = (vC/rC/IC) = 0. Kết quả là thanh CB chuyển động tịnh tiến tức thời. Tuy nhiên,
thời điểm sau đó, CB sẽ dịch chuyển tới vị trí lệch, làm tâm quay tức thời di chuyển tới
vị trí hữu hạn nào đó. lOMoAR cPSD| 58933639 Hình 16-20 (tiếp) Ví dụ 16.11
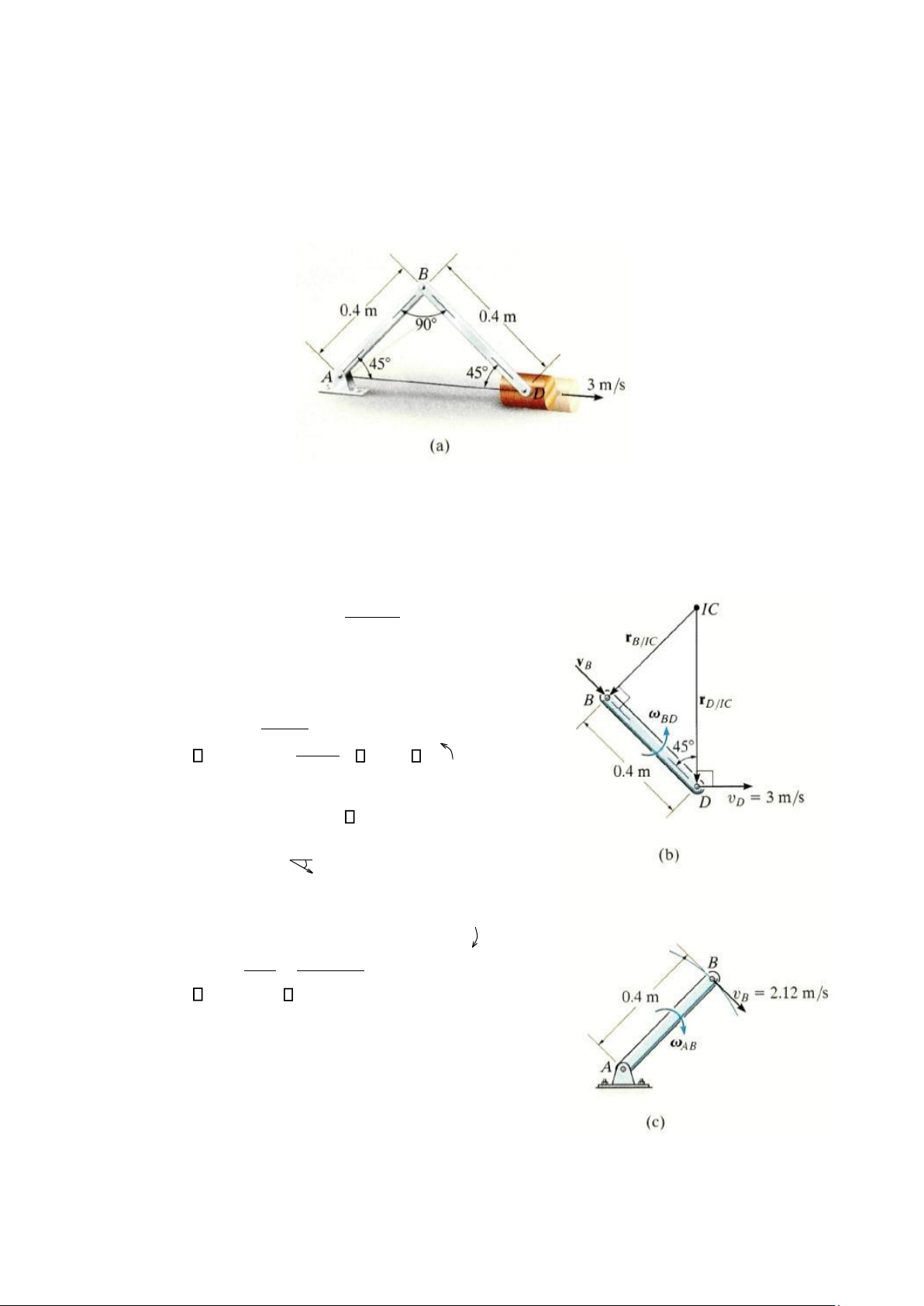
Khối D trong hình 16-21a chuyển động với vận tốc 3 m/s. Xác định vận tốc góc của thanh
BD và AB tại thời điểm như trong hình vẽ. Bài giải
Khi D chuyển động sang phải, nó làm cánh tay đòn AB quay cùng chiều kim đồng hồ quanh
điểm A. Do đó, vB vuông góc với AB. Tâm quay tức thời có vận tốc bằng không của thanh BD
là giao điểm của các đoạn thẳng vuông góc với vB và vD. Hình 16-21b. Từ hình học, ta có, rB/IC = 0.4 tan 450 m = 0.4 m 0.4m rD/IC = cos450 = 0.566 m
Vì đã biết độ lớn của vD, vận tốc góc của thanh BD là vD
3m/ s 5.30 rad/s BD = rD/IC 0.566
Do đó, vận tốc của B là vB = BD (rB/IC ) = 5.30 rad/s (0.4 m) = 2.12 m/s 450
Từ hình 16-21c, ta thu được vận tốc góc của AB như sau: vB
2.12m/ s = 0.53 rad/s AB = rB/ A 0.4m
Chú ý: Thử giải bài toán này bằng cách áp dụng phương
trình vD = vB + vB/D cho thanh BD. lOMoAR cPSD| 58933639 Hình 16-21a, b, c Ví dụ 16.12
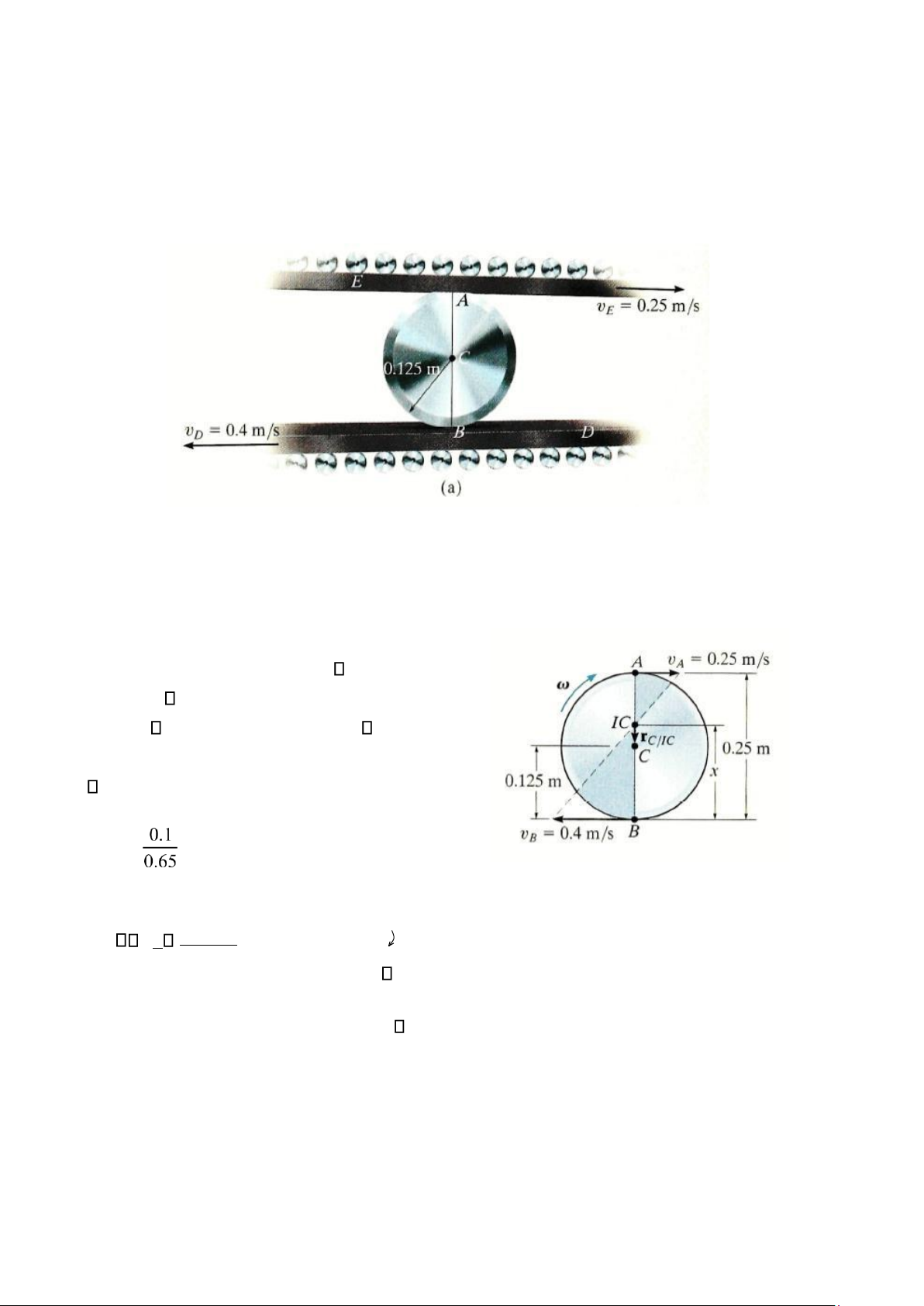
Khối trụ trên hình 16-22a lăn không trượt giữa hai tấm chuyển động E và D. Xác định vận
tốc góc của khối trụ và vận tốc tâm C của nó tại thời điểm như trong hình vẽ.
Hình 16-22a Bài giải
Do khối trụ lăn không trượt, nên các điểm tiếp xúc A và B trên khối trụ lần lượt có cùng
vận tốc với các tấm E và D. Hơn nữa, vận tốc vA và vB song song với nhau, bằng tỷ lệ của các
tam giác vuông, IC được xác định ở điểm trên đường thẳng AB; Hình 16-22b. Giả sử khoảng cách
từ điểm này đến B là x, ta có vB = x 0.4 m/s = x
vA = (0.25 m – x); 0.25 m/s = (0.25 m - x)
Chia hai phương trình trên cho nhau để triệt tiêu , ta thu được
0.4 (0.25 – x) = 0.25x x = = 0.154 m.
Từ đó, vận tốc góc của khối trụ là Hình 16-22 b vB
0.4m/s = 2.60 rad/s x 0.154m
Do đó, vận tốc của tâm C là vB = rC/IC = 2.60 rad/s (0.154 m – 0.1225 m) = 0.0750 m/s lOMoAR cPSD| 58933639 BÀI TẬP
16-78. Giải bài tập 16-51 sử dụng phương pháp tâm quay tức thời có vận tốc bằng không.
16-79. Giải bài tập 16-54 sử dụng phương pháp tâm quay tức thời có vận tốc bằng không.
*16-80. Giải bài tập 16-59 sử dụng phương pháp tâm quay tức thời có vận tốc bằng không.
16-81. Giải bài tập 16-61 sử dụng phương pháp tâm quay tức thời có vận tốc bằng không.
16-82. Giải bài tập 16-62 sử dụng phương pháp tâm quay tức thời có vận tốc bằng không.
16-83. Giải bài tập 16-63 sử dụng phương pháp tâm quay tức thời có vận tốc bằng không.
*16-84. Giải bài tập 16-65 sử dụng phương pháp tâm quay tức thời có vận tốc bằng không. Bài tập 16-85
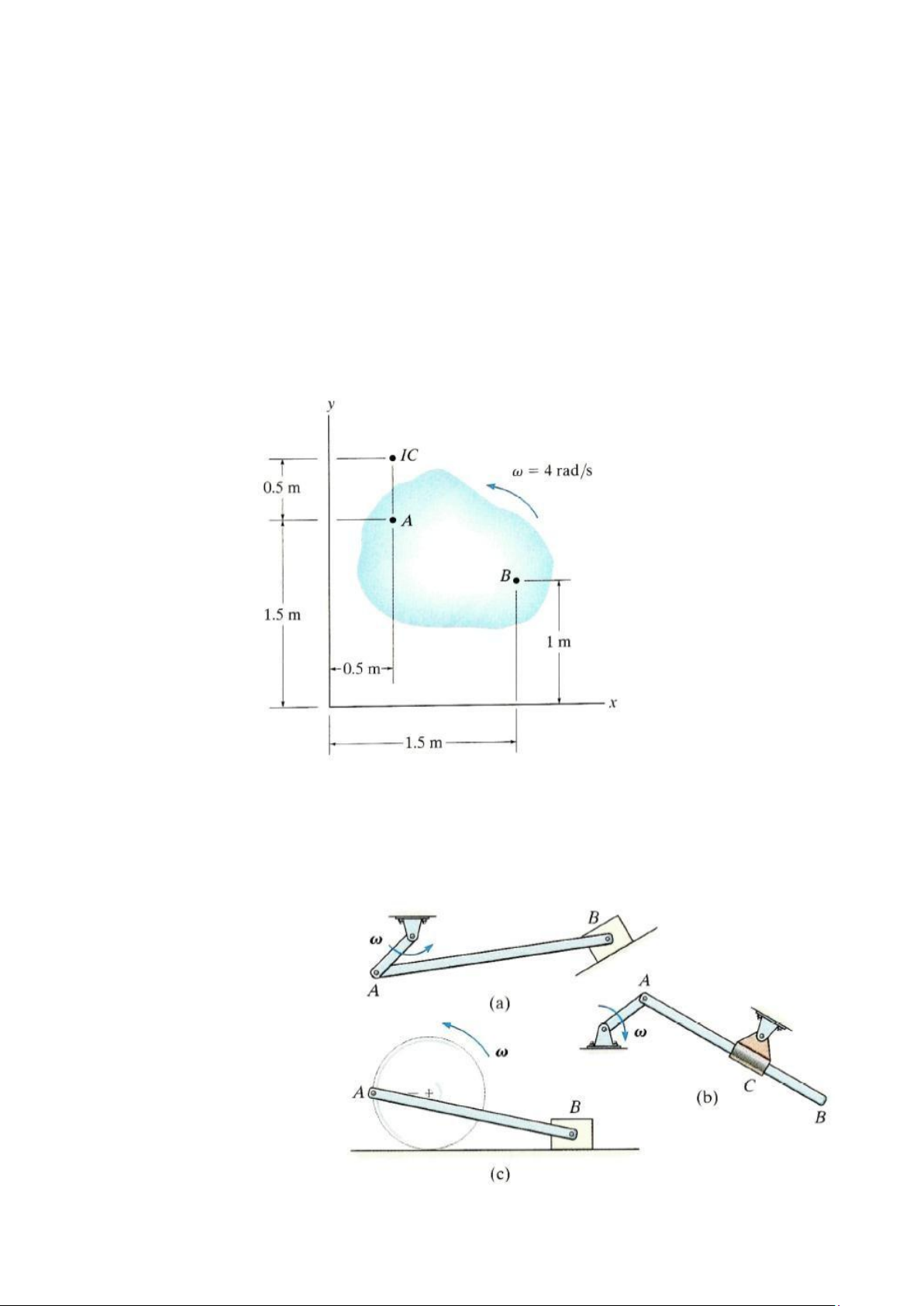
16-85. Tâm quay tức thời có vận tốc bằng không của một vật đặt tại điểm IC (0.5m, 2 m).
Nếu vật đó có vận tốc góc là 4 rad/s như trên
hình 16-85, hãy xác định
vận tốc của điểm B so với điểm A. 16-86. Trong các
trường hợp dưới đây hãy nêu phương pháp hình
học để xác định tâm quay
tức thời có vận tốc bằng
không của thanh AB. Giả sử về hình học lOMoAR cPSD| 58933639 đã biết. Bài tập 16-86
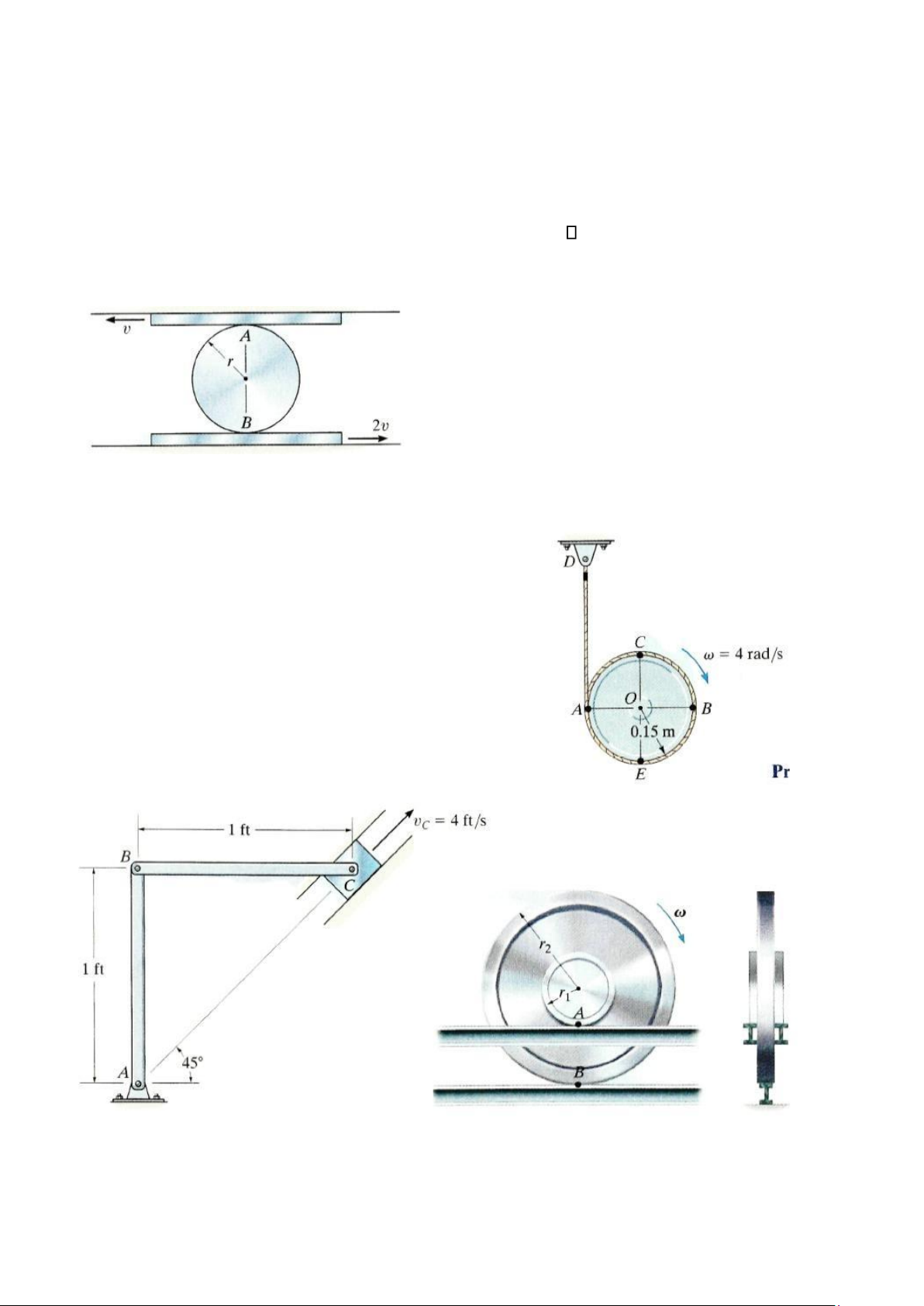
16-87. Đĩa có bán kính r được giới hạn lăn không trượt tại hai điểm A và B. Nếu các tấm
có vận tốc như hình vẽ, hãy xác định vận tốc góc của đĩa.
*16-88. Tại thời điểm như hình vẽ, đĩa quay với vận tốc góc = 4 rad/s. Hãy xác định vận
tốc của các điểm A, B và C.
16-89. Con trượt C di chuyển lên phía trên của thanh nghiêng với vận tốc 4 ft/s. Hãy xác
định vận tốc góc của thanh AB, BC và vận tốc của
điểm B ở thời điểm như trên hình vẽ. Bài tập 16-87 Bài tập 16-88
Hình 16 - 3 Bài tập 16-89 Bài tập 16-90 lOMoAR cPSD| 58933639
16-90. Chứng minh rằng nếu vành bánh xe và trục bánh xe luôn tiếp xúc với ba thanh khi
bánh xe quay thì sẽ xảy ra hiện tượng trượt tại A nếu không xảy ra hiện tượng trượt tại B. Với
những điều kiện này, nếu vận tốc góc của bánh xe là thì vận tốc của điểm A bằng bao nhiêu.
Bài tập 16-91
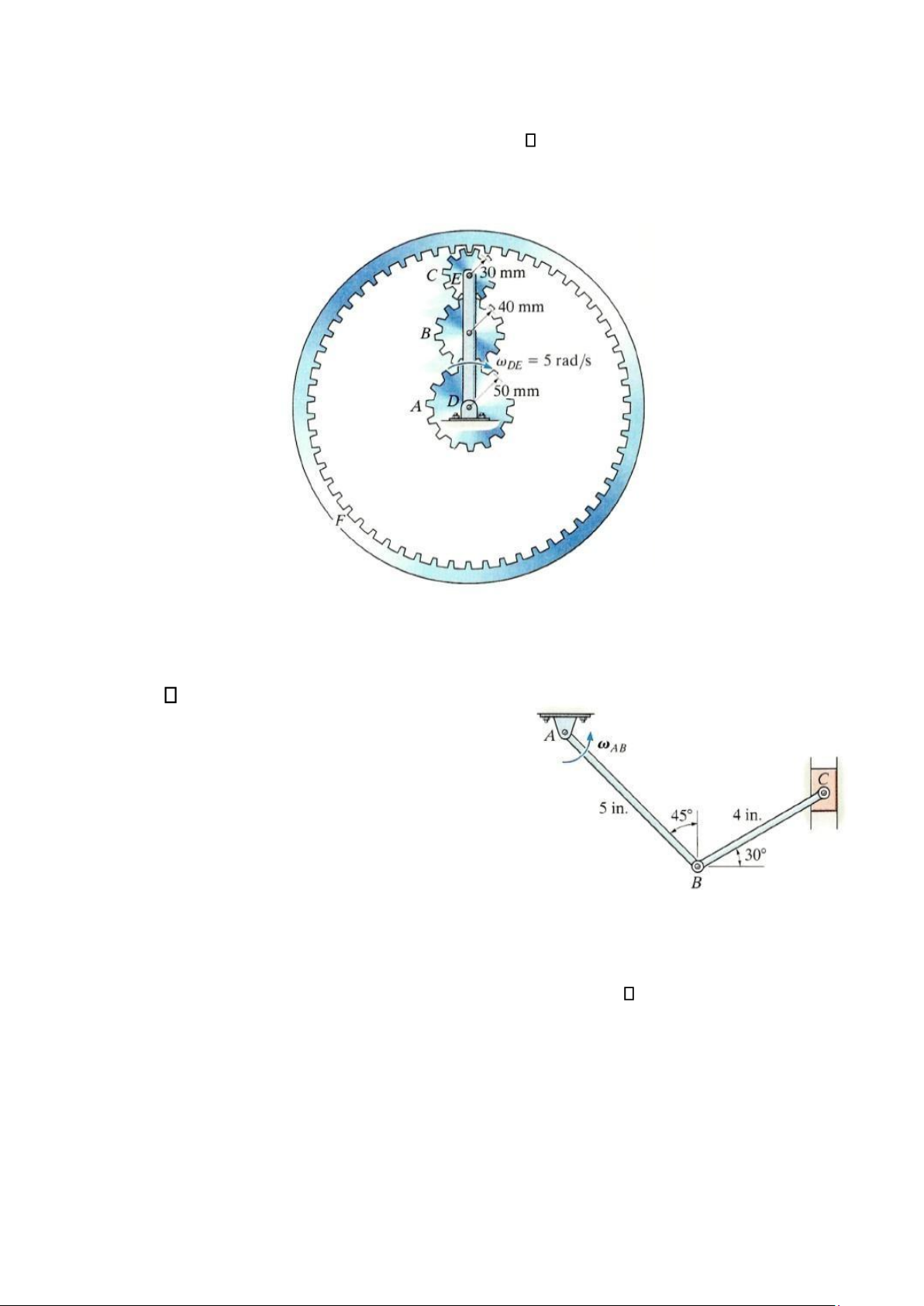
16-91. Bộ truyền động bánh răng Epixic hoạt động bằng cách quay thanh DE với vận tốc
góc DE = 5 rad/s. Nếu vành răng F là cố định, hãy
xác định các vận tốc góc của các bánh răng A, B và C.
* 16-92. Hãy xác định vận tốc góc của thanh AB
tại vị trí như trong hình 16-92; nếu con trượt C
chuyển động lên trên với vận tốc 12 in/s.
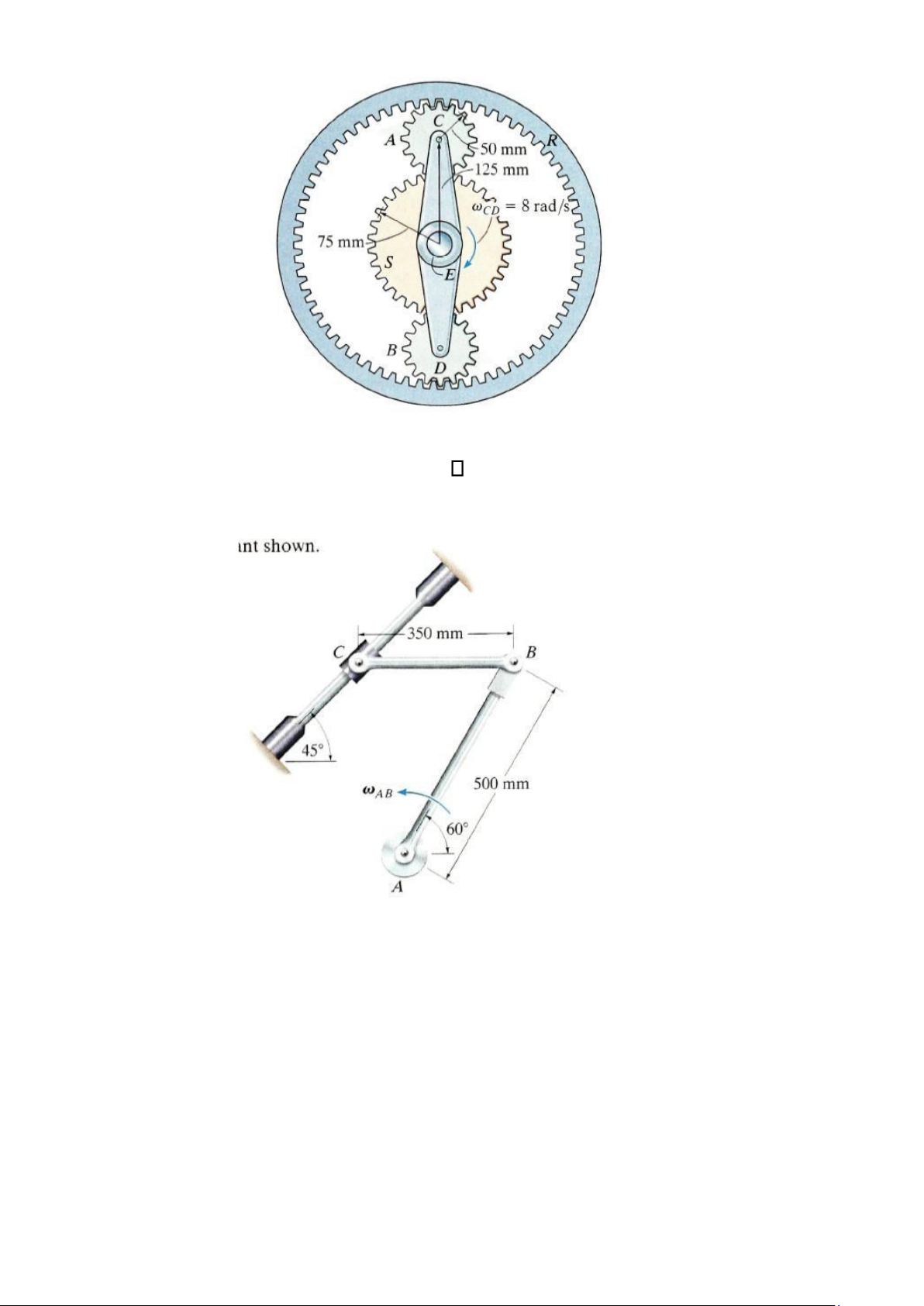
16-93. Trong một cơ cấu truyền động tự động,
các bánh răng hành tinh A và B quay trên các trục
Bài tập 16 - 92
được đỡ bởi giá đỡ CD. Như trong hình 16-93, CD
được gắn với trục tại E - đồng trục với tâm của bánh răng trung tâm cố định S. Trục này không
gắn chặt với bánh răng trung tâm. Nếu CD quay với vận tốc góc CD = 8 rad/s, xác định vận
tốc góc của vành răng R. lOMoAR cPSD| 58933639
Bài tập 16-93
16-94. Cho biết vận tốc góc của thanh AB là AB = 4 rad/s, hãy xác định vận tốc của vòng
đệm tại C và vận tốc góc của thanh CB tại thời điểm như hình vẽ. Biết thanh CB nằm ngang ở thời điểm này.
Hình 16 - 3
Bài tập 16-94/95
16-95. Nếu vòng đệm C chuyển động xuống dưới, sang trái với vận tốc vC = 8 m/s, hãy xác
định vận tốc góc của thanh AB tại thời điểm như hình vẽ.
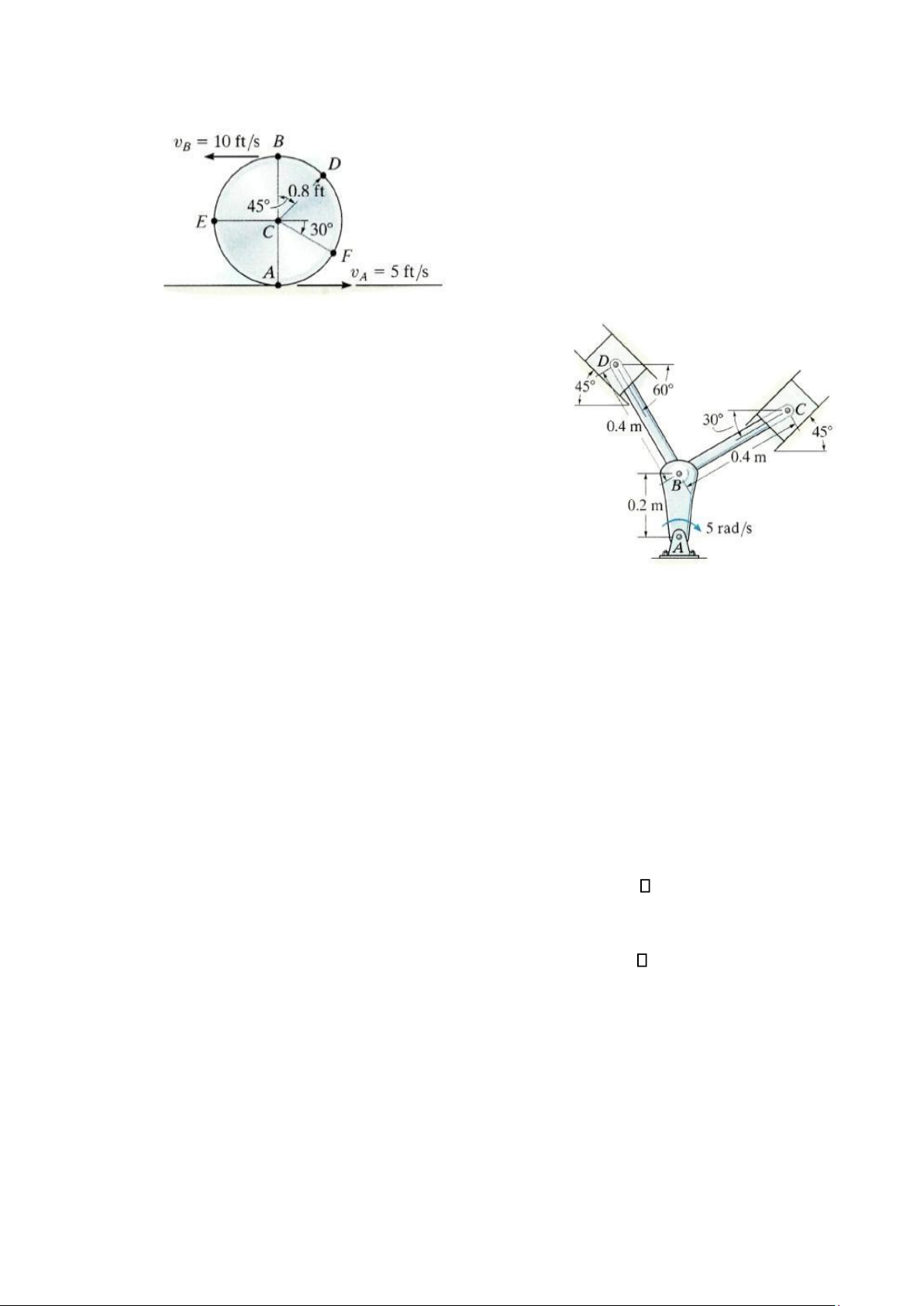
*16-96. Do xảy ra hiện tượng trượt nên các điểm A và B trên vành đĩa có vận tốc như trên
hình 16-96/97. Hãy xác định vận tốc của tâm C và điểm D tại thời điểm này. lOMoAR cPSD| 58933639 Bài tập 16-96/97 Bài tập 16-98/99
16-97. Do xảy ra hiện tượng trượt nên các điểm A và B trên vành đĩa có vận tốc như trên
hình 16-96/97. Hãy xác định vận tốc của tâm C và điểm E tại thời điểm này.
16-98. Cơ cấu được sử dụng trong động cơ của tàu biển bao gồm tay quay AB và hai thanh
nối BC và BD. Hãy xác định vận tốc của piston tại C khi tay quay ở vị trí như trong hình 16-
98/99 và có vận tốc góc là 5 rad/s.
16-99. Cơ cấu được sử dụng trong động cơ của tàu biển bao gồm tay quay AB và hai thanh
nối BC và BD. Hãy xác định vận tốc của piston tại D khi tay quay ở vị trí như trong hình 16-
98/99 và có vận tốc góc là 5 rad/s.
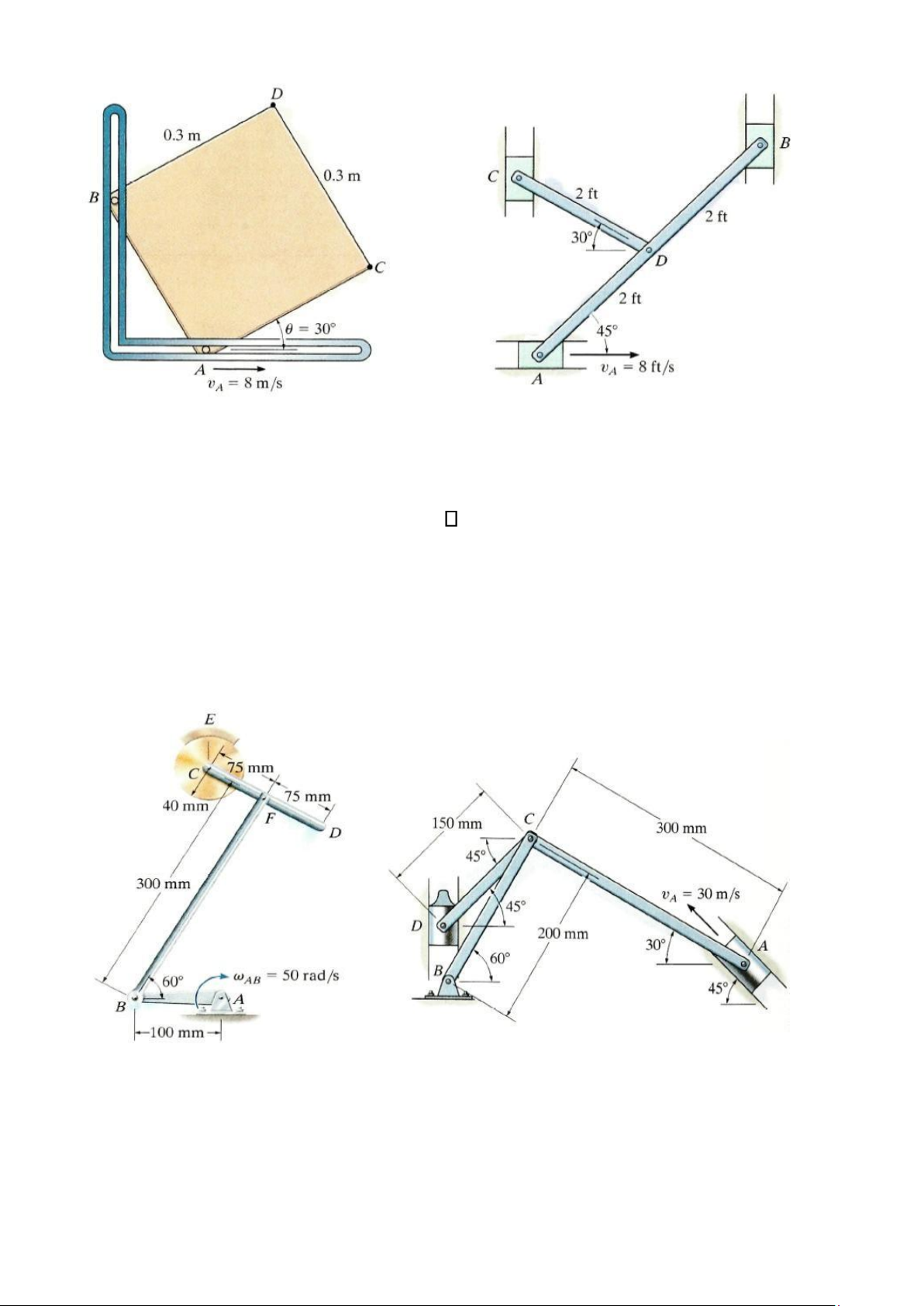
*16-100. Một tấm vuông được giữ trong các rãnh tại A và B. Khi = 300, điểm A di chuyển
với vận tốc vA = 8 m/s. Hãy xác định vận tốc của điểm C tại vị trí này.
16-101. Một tấm vuông được giữ trong các rãnh tại A và B. Khi = 300, điểm A di chuyển
với vận tốc vA = 8 m/s. Hãy xác định vận tốc của điểm D tại vị trí này. lOMoAR cPSD| 58933639 Bài tập 16-100/101 Bài tập 16-102
16-102. Nếu con trượt A chuyển động sang phải với vận tốc vA = 8 ft/s, hãy xác định vận
tốc của con trượt B và C tại vị trí như trong hình 16-102.
16-103. Tay quay AB quay với vận tốc góc AB = 50 rad/s quanh một trục cố định đi qua
điểm A, đĩa C được giữ cố định trên trục đỡ tại E. Hãy xác định vận tốc góc của thanh CD tại vị trí như hình 16-103.
*16-104. Cơ cấu trong hình 16-104 được sử dụng trong máy tán đinh. Nó bao gồm piston
truyền động A, ba thanh và một máy tán đinh gắn với con trượt D. Hãy xác định vận tốc của D
tại vị trí như trong hình vẽ, khi piston tại A có vận tốc vA = 30 m/s. Bài tập 16-103 Bài tập 16-104 lOMoAR cPSD| 58933639
16.7. Phân tích mối liên hệ chuyển động: Gia tốc
Phương trình quan hệ giữa gia tốc của hai
điểm trên một vật rắn chịu ràng buộc chuyển
động phẳng tổng quát có thể được xác định
bằng cách lấy vi phân của phương trình vận tốc v B
v vA B A/ theo thời gian. Từ đó, ta có
dvB dvA
dvB/ A dt dt dt
Các số hạng dvB/dt = aB và dvA/dt = aA
được tính từ hệ trục x và y cố định và biểu diễn
các gia tốc tuyệt đối của điểm B và A, số hạng
cuối cùng biểu diễn gia tốc của điểm B so với
điểm A xác định được khi người quan sát ở
trạng thái đứng yên so với các trục tịnh tiến x’
và y’, có điểm gốc trùng với điểm cơ sở A.
Trong phần 16.5, ta đã chứng minh rằng điểm
B coi như chuyển động trên một cung tròn có
bán kính cong là rB/A. Hệ quả là, aB/A có thể
được phân tích thành các thành phần pháp
tuyến và tiếp tuyến của chuyển động; tức là
aB/A = (aB/A)t +(aB/A)n, trong đó, (aB/A)t = rB/A
và (aB/A)n = 2 rB/A. Do đó, phương trình liên
hệ gia tốc có thể được viết như sau: a (16-
B = aA + (aB/A)t + (aB/A)n 17)
Trong đó, aB = gia tốc của điểm B aA = gia tốc của điểm A
(aB/A)t = thành phần gia tốc tiếp tuyến
tương đối của “B so với A”. Độ lớn của nó là
(aB/A)t = rB/A, và hướng của nó vuông góc với rB/A.
(aB/A)n = thành phần gia tốc pháp tuyến
tương đối của “B so với A”. Độ lớn của nó là
(aB/A)t = 2 rB/A, và nó có hướng từ B đến A. Hình 16-23
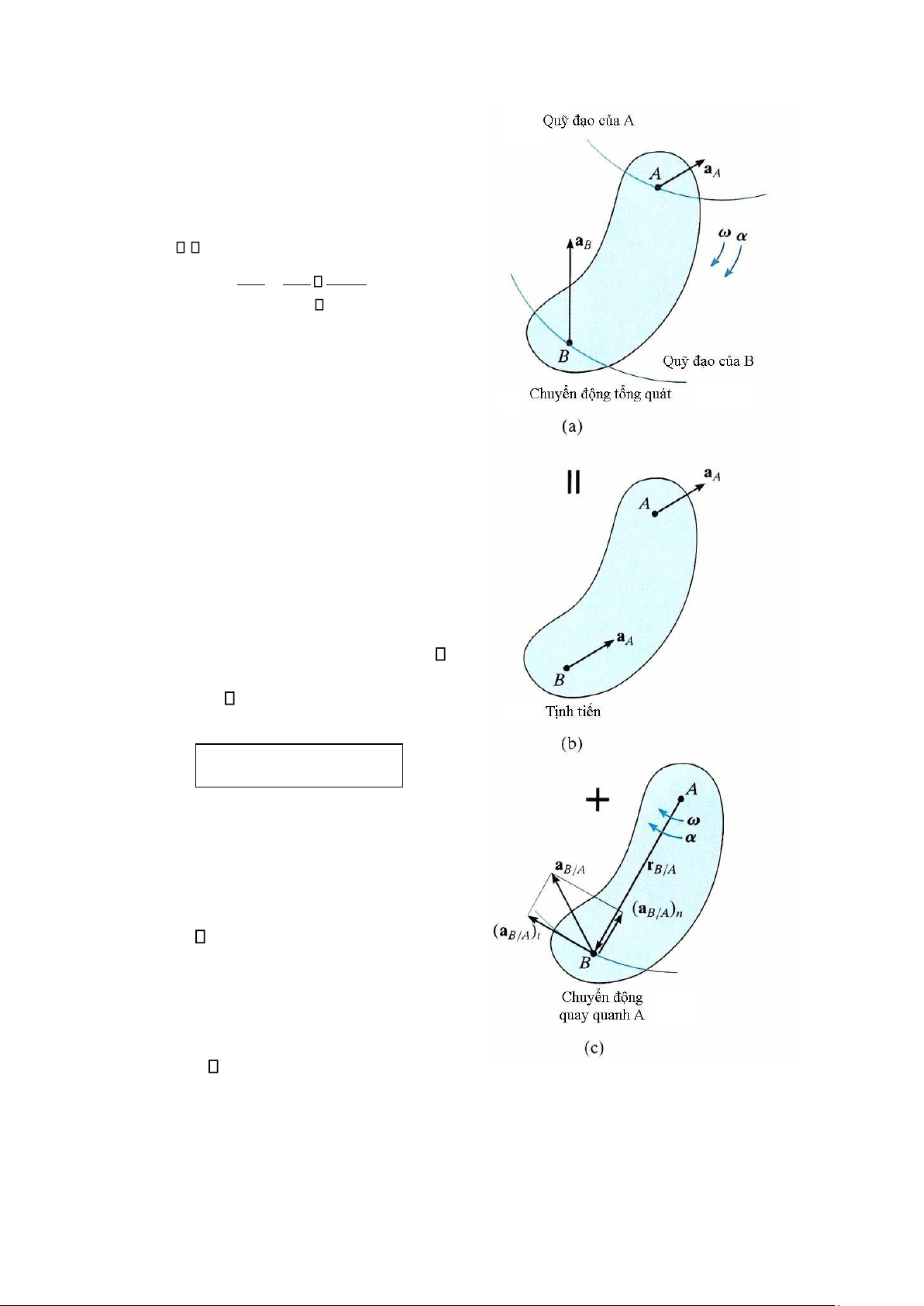
Mỗi số hạng trong phương trình 16-17 đều được biểu diễn trên sơ đồ động học trong hình
16-23. Ở đây, cho thấy gia tốc tức thời của B, hình 16-23a, được xác định bằng cách quan sát
vật chuyển động tịnh tiến với gia tốc aA, hình 16-23b, và đồng thời quay quanh điểm cơ sở A
với vận tốc góc tức thời ω và gia tốc góc α, hình lOMoAR cPSD| 58933639
16-23c. Sử dụng phép cộng véctơ và được áp dụng cho
điểm B, ta thu được aB, như trên hình 16-23d. Ta có thể
nhận thấy từ hình 16-23a, do các điểm A và B chuyển
động dọc theo các quỹ đạo cong nên gia tốc của các
điểm này đều có thể phân tích thành các thành phần
pháp tuyến và tiếp tuyến với quỹ đạo. (Nhớ lại Hình 16-23 d
rằng gia tốc của một điểm tiếp xúc với quỹ đạo chỉ khi
quỹ đạo của nó là thẳng hoặc khi nó là một điểm uốn trên đường cong). Quỹ đạo của B Hình 16-24
Do các thành phần gia tốc tương đối biểu diễn ảnh hưởng của chuyển động tròn được quan
sát từ các trục tịnh tiến có gốc ở điểm cơ sở A. Những thành phần này có thể được biểu diễn
bằng các phương trình (aB/A)t = α rB/A và (aB/A)n =
2 rB/A, phương trình 16-14. Do đó,
phương trình 16-17 trở thành
aB = a A + α rB/A 2 (16-18) trong
đó, aB = gia tốc của rB/A
điểm B aA = gia tốc của điểm cơ sở A α = gia tốc góc của vật
ω = vận tốc góc của vật
rB/A = vectơ vị trí tương đối được vẽ từ A tới B Nếu phương
trình 16-17 hoặc 16-18 được áp dụng vào thực tế để khảo sát
chuyển động không đều của một vật rắn được nối chốt với hai
vật khác, ta thấy rằng các điểm cùng nằm trên chốt chuyển động
với cùng một gia tốc do quỹ đạo chuyển động của chúng giống
nhau. Ví dụ như điểm B nằm trên thanh AB và điểm B nằm trên
thanh BC của cơ cấu tay quay trong hình 16-24a có cùng
gia tốc do các thanh này bị chốt lại với nhau tại B. Ở đây, B
chuyển động theo một quỹ đạo tròn nên aB có thể phân tích thành
các thành phần pháp và tiếp tuyến với quỹ
đạo. Tại đầu kia của thanh BC, điểm C chuyển Hình 16-25
động theo quỹ đạo thẳng tịnh tiến, được xác định bằng chuyển
động của piston. Do đó, aC nằm ngang, hình 16-24b. lOMoAR cPSD| 58933639
Nếu hai vật tiếp xúc với nhau mà không xảy ra hiện tượng trượt thì các điểm tại vị trí
tiếp xúc chuyển động theo các quỹ đạo khác nhau, khi đó các thành phần gia tốc tiếp tuyến
của các điểm này bằng nhau nhưng thành phần gia tốc pháp tuyến của chúng không bằng
nhau. Ví dụ, xét hai bánh răng ăn khớp với nhau trong hình 16-25a. Điểm A nằm trên bánh
răng B và điểm ăn khớp A’ nằm trên bánh răng C. Do chuyển động quay của hai bánh răng,
ta có (aA)t =
(aA’)t ; tuy nhiên, do hai điểm chuyển động theo các quỹ đạo khác nhau nên (aA)n (aA’)n và
do đó aA aA’ (Hình 16-25b).
Trình tự phân tích.
Phương trình liên hệ gia tốc có thể áp dụng cho hai điểm A và B trên một vật bằng
cách hoặc sử dụng phép phân tích vectơ Đề các, hoặc bằng cách viết trực tiếp phương trình
các thành phần vô hướng x và y.
Phân tích vận tốc
• Xác định vận tốc góc của vật bằng cách sử dụng phương pháp phân tích vectơ như
đã thảo luận trong phần 16.5 hoặc 16.6. Đồng thời xác định vận tốc vA và vB của các
điểm A và B nếu các điểm này chuyển động trên các quỹ đạo cong. Phân tích vectơ Sơ đồ động học
• Thiết lập hướng cho các toạ độ x, y cố định và vẽ sơ đồ động học của vật. Biểu diễn
các thành phần aA, aB, , , và rB/A.
• Nếu các điểm A và B chuyển động theo các quỹ đạo tròn thì gia tốc của chúng có thể
được phân tích thành hai thành phần pháp tuyến và tiếp tuyến, tức là, aA = (aA)t + (aA)n
và aB = (ab)t + (ab)n. Phương trình gia tốc
• Áp dụng phương trình aB = aA + α rB/A
2 rB/A để biểu diễn các vectơ dưới dạng
vectơ Đề các và thay chúng vào phương trình. Tính tích hữu hướng và cân bằng(đồng
nhất) các thành phần i và j để thu được hai phương trình vô hướng.
• Nếu bài toán cho ta kết quả âm đối với một biến chưa biết nào đó thì ta phải đổi hướng
của vectơ trong sơ đồ động học.
Phân tích vô hướng Sơ đồ động học
• Nếu muốn áp dụng phương trình aB = aA + (aB/A )t + (aB/A)n thì cần phải thiết lập độ
lớn và hướng của các thành phần gia tốc tương đối (aB/A )t và (aB/A)n. Để làm được
điều này, ta phải vẽ sơ đồ động học như trong hình 16-23c. Do vật được coi là bị chốt lOMoAR cPSD| 58933639
tức thời tại điểm cơ sở A, nên độ lớn của các thành phần gia tốc là (aB/A)t = rB/A và
(aB/A)n = 2 rB/A Hướng của chúng được thiết lập từ sơ đồ động học đó là, (aB/A )t có
phương vuông góc với rB/A, tuân theo chuyển động quay α của vật, và (aB/A)n có hướng từ B đến A.* Phương trình gia tốc
• Biểu diễn các vectơ trong phương trình aB = aA + (aB/A )t + (aB/A)n dưới dạng đồ thị
bằng cách biểu diễn hướng và độ lớn của chúng dưới mỗi số hạng. Các phương trình
vô hướng được xác định từ các thành phần x và y của các vectơ này.
Cơ cấu đóng, mở cửa sổ được minh hoạ như hình trên. Trong đó, CA quay quanh một trục cố định đi qua C và AB
có chuyển động phẳng tổng quát. Do điểm A chuyển động theo một quỹ đạo cong nên gia tốc của nó có thể phân
tích được thành hai thành phần trong khi điểm B chuyển động trên một đường thẳng và hướng gia tốc của nó là không đổi. lOMoAR cPSD| 58933639
* Việc kí hiệu aB = aA + (aB/A (chốt) )t + (aB/A (chốt))n giúp nhớ lại rằng A được giả sử là chốt quay. Ví dụ 16.13
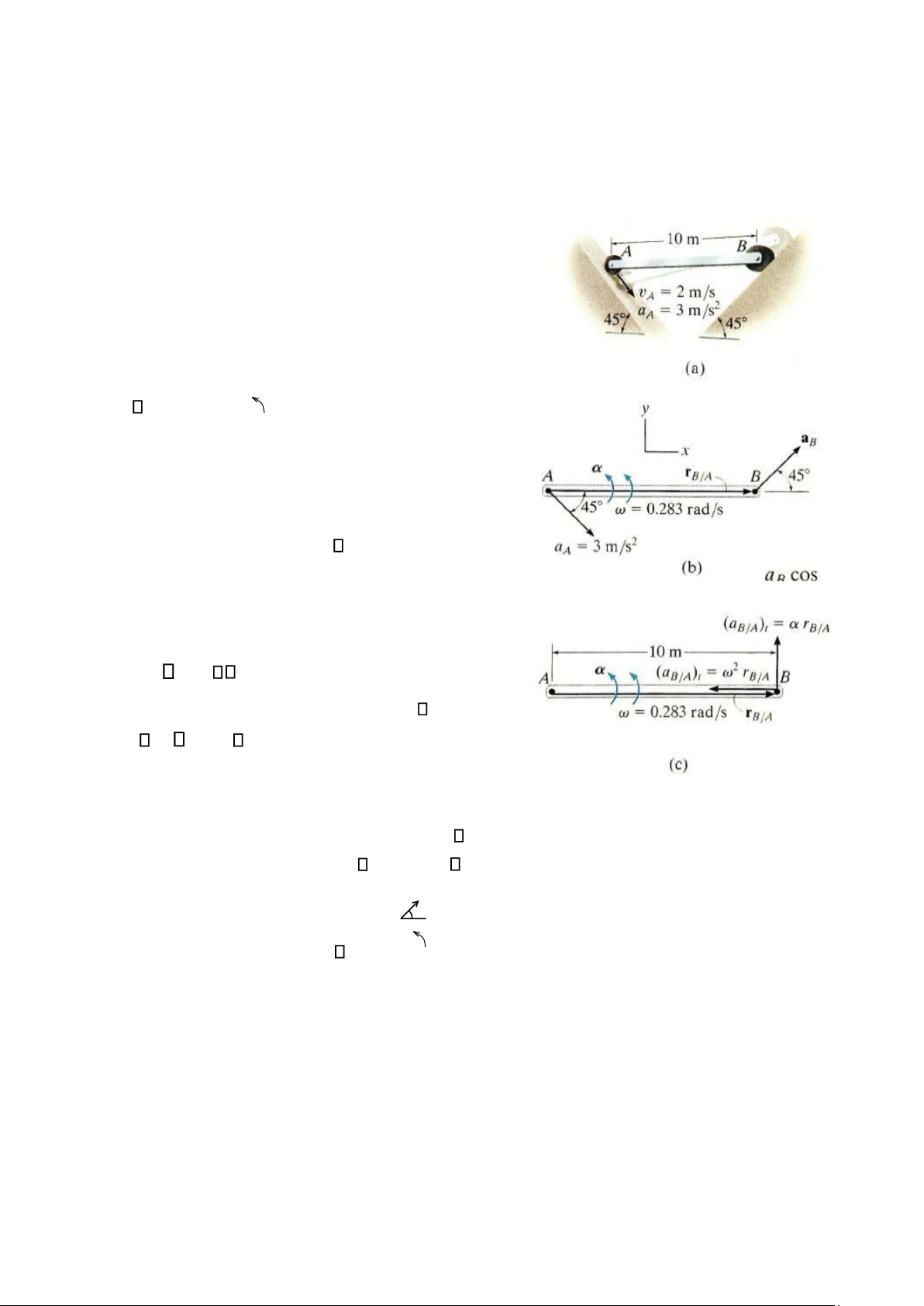
Thanh AB trong hình 16-26a chuyển động dọc theo mặt phẳng nghiêng tại A và B. Nếu
điểm A có gia tốc 3 m/s2 và vận tốc 2 m/s và cả hai có chiều hướng xuống mặt phẳng nghiêng
tại thời điểm thanh nằm ngang, hãy xác định gia tốc
góc của thanh tại vị trí này. Bài giải I (Phân tích véc tơ)
Ta sẽ áp dụng phương trình gia tốc cho các điểm
A và B trên thanh. Để làm được điều này, đầu tiên ta
phải xác định vận tốc góc của thanh. Chứng tỏ rằng
= 0.283 rad/s bằng cách sử dụng phương trình
vận tốc hoặc phương pháp tâm quay tức thời.
Sơ đồ động học. Do điểm A và B cùng chuyển
động trên một quỹ đạo thẳng, nên chúng không có
thành phần gia tốc pháp với quỹ đạo. Có hai ẩn số
trong hình 16-26b là aB và .
Phương trình gia tốc. Áp dụng phương trình
Hình 16 - 3
16-18 cho các điểm A và B trên thanh và biểu diễn
các vectơ dưới dạng các vectơ Đề các, ta có aB = aA
+ α rB/A 2 rB/A
aB cos 450i + aBsin 450j = 3 cos 450 i 3sin 450 j +
( k) (10i) (0.283)2(10i)
Thực hiện tính tích hữu hướng và cân bằng các
thành phần theo i, j, ta thu được Hình 16-26
aB cos 450 = 3 cos 450 (0.283)2 (10) (1) aB sin 450 = 3sin 450 + (10) (2)
Giải các phương trình trên, ta có aB = 1.87 m/s2 45 0 = 0.344 rad/s2
Bài giải II (Phân tích vô hướng)
Như một phương pháp loại trừ, ta có thể tính trực tiếp ra các phương trình của các thành
phần vô hướng 1 và 2. Từ sơ đồ động học, xét các thành phần của gia tốc tương đối (aB/A )t và
(aB/A)n, ta có:
aB = aA + (aB/A )t + (aB/A)n lOMoAR cPSD| 58933639 a45 2 B 0 3m s/ 0 (10 ) m
0.283rad s / 2 10m 45
Tính các thành phần x và y, ta thu được các phương trình 1 và 2 và có được kết quả như trên. Ví dụ 16.14
Tại vị trí cho trước, một khối trụ có bán kính r,
hình 16-27a, có vận tốc góc ω và gia tốc góc α. Hãy
xác định vận tốc và gia tốc tâm G của nó
nếu nó lăn không trượt. Bài giải (Phân tích véc tơ)
Khi khối trụ lăn, điểm G chuyển động theo một
quỹ đạo thẳng, và điểm A nằm trên vành của khối
trụ chuyển động trên một quỹ đạo cong - gọi là
cycloid, hình 16-27b. Ta sẽ áp dụng phương trình
vận tốc và gia tốc cho các điểm này. Quỹ đạo của A
Phân tích vận tốc. Do không xảy ra hiện tượng
trượt nên tại thời điểm khảo sát A tiếp xúc với đất
thì vA = 0. Do đó, từ biểu sơ động học trong hình Quỹ đạo của G
16-27c, ta có vG = vA + ω rG/A
vG i = 0 + ( k) (rj) vG = r (1)
Sơ đồ động học. Gia tốc của điểm G có phưong
ngang vì nó di chuyển theo quỹ đạo thẳng. Ngay
trước khi điểm A chạm đất thì vận tốc của nó hướng
xuống dưới dọc theo trục y, hình 16-27b, và ngay
sau khi chạm đất, vận tốc của nó có hướng lên trên.
Vì nguyên nhân này nên điểm A bắt đầu tăng tốc
lên trên khi nó rời mặt đất tại A, hình 16-27d. Độ
lớn của aA và aG chưa biết.
Phương trình gia tốc.
aG = aA + α rG/A
2 rG/A aG i = aA j + ( k) (rj) 2 (rj)
Thực hiện tích hữu hướng và cân bằng các Hình 16-27
thành phần theo i, j, ta thu được
aG = r (2) aA = 2 r (3) lOMoAR cPSD| 58933639
Chú ý: Các kết quả quan trọng vG = r và aG = r cũng đã thu được trong ví dụ 16-4.
Chúng đúng với bất cứ vật nào có hình tròn (như quả bóng, ròng rọc, đĩa, ...) lăn không trượt.
Ngoài ra, kết quả aA = 2 r cho thấy tâm quay tức thời có vận tốc bằng không, điểm A không
phải là điểm có gia tốc bằng không. Ví dụ 16.15
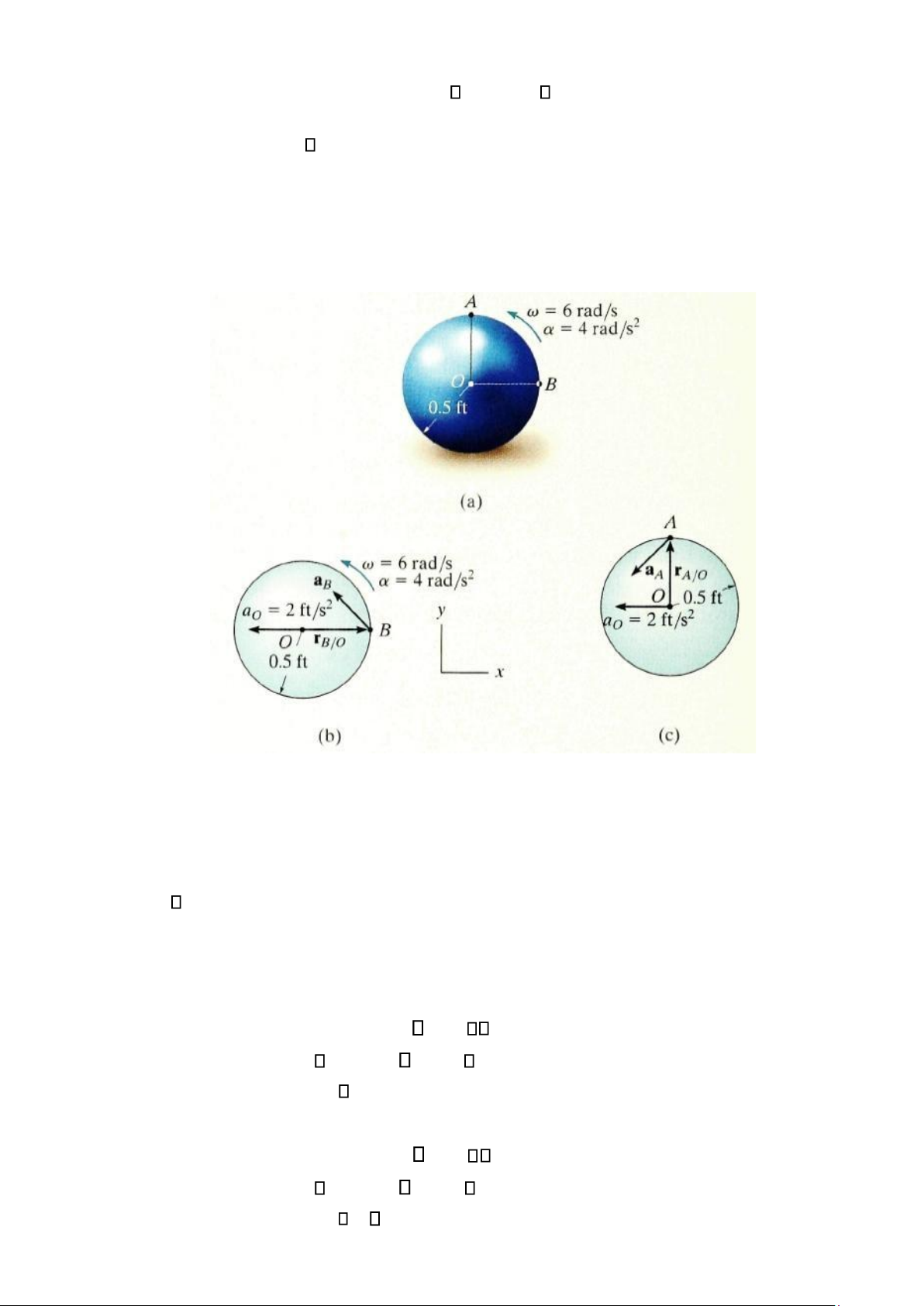
Quả bóng lăn không trượt có chuyển động góc như trong hình 16-28a. Hãy xác định gia
tốc của điểm A và B tại vị trí như trên hình vẽ. Hình 16-28
Bài giải (Phân tích véc tơ)
Sơ đồ động học. Sử dụng kết quả của ví dụ trước, ta có gia tốc của tâm quả bóng là
aO = r = (4 rad/s2) (0.5 ft) = 2 (ft/s2). Ta sẽ áp dụng phương trình gia tốc cho các điểm O
và điểm B, điểm O và điểm A.
Phương trình gia tốc. Áp
dụng cho điểm B (Hình 16-28b)
aB = aO + α rB/O
2 rB/O aB =
2i + (4k) (0.5i) (6)2 (0.5i) aB
= { 20i + 2j} ft/s2
Áp dụng cho điểm A (Hình 16-28c)
aA = aO + α rA/O
2 rA/O aA =
2i + (4k) (0.5j) (6)2 (0.5j) aB
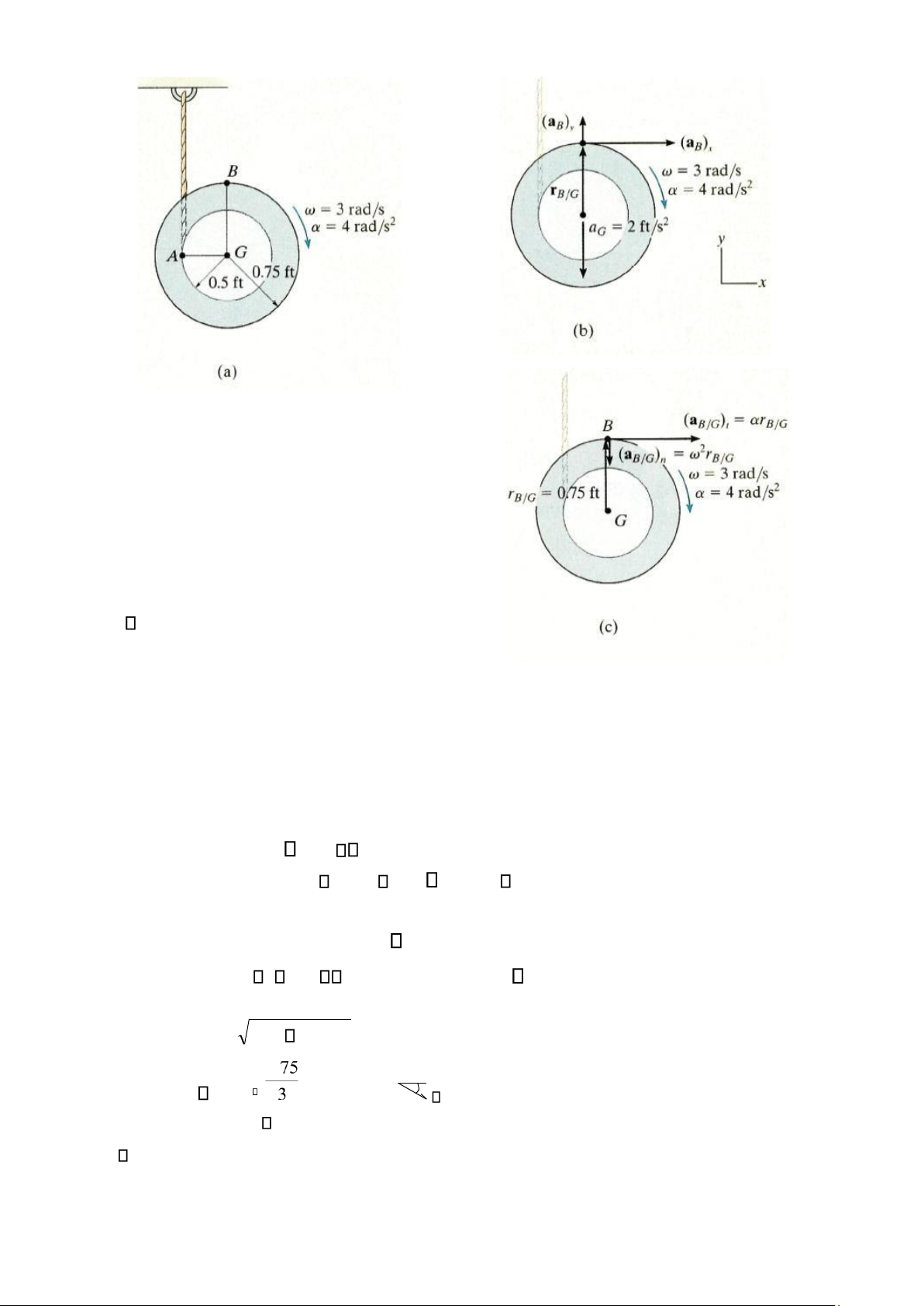
= { 4i 18j} ft/s2 lOMoAR cPSD| 58933639 Ví dụ 16.16 Ống cuộn (dây) biểu diễn trong hình 16-29a tời (tháo) ra từ sợi dây thừng.
Tại thời điểm khảo sát, nó có vận tốc góc là 3 rad/s và
gia tốc góc là 4 rad/s2. Hãy xác định gia tốc của điểm B.
Bài giải I (Phân tích véc tơ)
Ống cuộn có xu hướng lăn không trượt xuống
dưới tại điểm A. Do đó, ta có thể sử dụng kết quả của
ví dụ 16.14 để xác định gia tốc của điểm G, tức là
aG = r = 4 rad/s2 (0.5 ft) = 2 ft/s2
Ta sẽ áp dụng phương trình gia tốc cho điểm G và B.
Sơ đồ động học. Điểm B chuyển động dọc theo quỹ đạo cong với bán kính cong chưa xác
định. * Gia tốc của nó được biểu diễn bằng các thành phần x và y chưa biết như trên hình 16- 29b. Hình 16-29
Phương trình gia tốc.
aB = aG +α rB/G 2 rB/G
(aB)xi + (aB)yj = 2j + ( 4k) (0.75j) (3)2(0.75j)
Cân bằng các số hạng theo i và j, ta được các phương trình thành phần sau:
(aB)x = 4 (0.75) = 3 ft/s2 (1) (aB)y = 2 6.75 8.75 ft/s2 = 8.75 ft/s2 (2)
Do đó, độ lớn và hướng của aB là aB = (3)2 (8.75)2 = 9.25 ft/s2 8. = tan 1 = 71.10
* Nhận thấy bán kính cong không bằng bán kính của ống cuộn do ống cuộn không quay quanh điểm G. Hơn
nữa, không phải là khoảng cách từ A (IC) tới B do vị trí của điểm IC chỉ phụ thuộc vào vận tốc của một điểm
và không phụ thuộc vào hình dạng của quỹ đạo.