Bài giảng Chương 2: Hệ một bậc tự do môn Cơ học kết cấu | Trường Đại học Xây Dựng Hà Nội

Chương 2 Hệ một bậc tự do
Bộ môn Cơ học kết cấu Hà nội, 08 - 2024 Nội dung
2.1 Giới thiệu về hệ một bậc tự do
2.2 Phương trình động lực học 2.3 Dao động tự do
2.3.1 Dao động tự do không cản
2.3.2 Dao động tự do có cản Ví dụ áp dụng 2
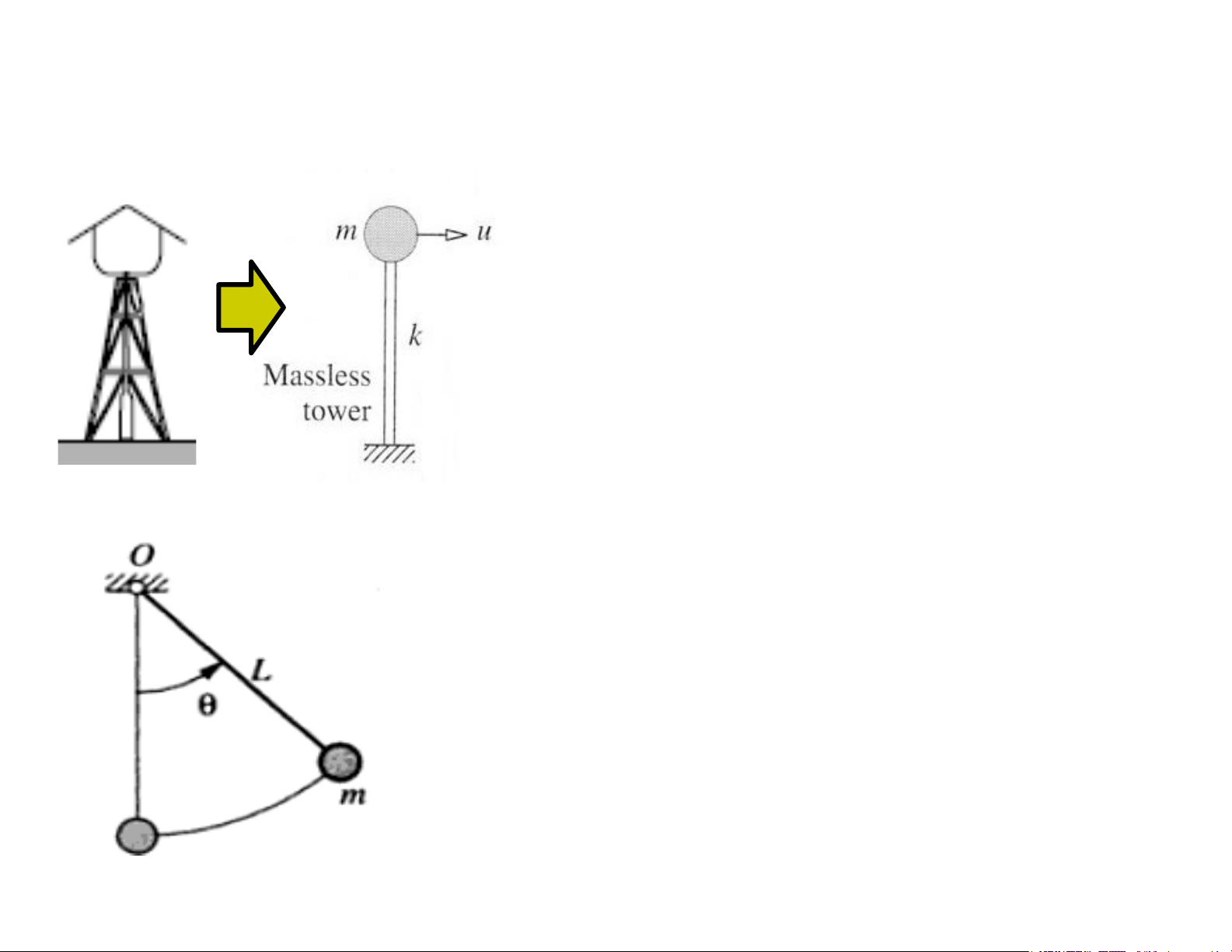
2.1 Giới thiệu về hệ một bậc tự do  Bể nước
 Khối lượng tập trung tại một điểm
 Kết cấu đỡ giả thiết không khối lượng
 Mô tả như là hệ một bậc tự do  Con lắc
 Thanh được giả thiết không khối lượng
 Chỉ xoay quanh bản lề
 Được mô phỏng là một bậc tự do 3
2.1 Giới thiệu về hệ một bậc tự do
Kết cấu công trình thực Sơ đồ lý tưởng 4
2.1 Giới thiệu về hệ một bậc tự do
Sơ đồ tính toán kết cấu (Idealized structure)?
Phương trình dao động (Equation of Motion)? 5
2.1 Giới thiệu về hệ một bậc tự do Sơ đồ tính toán
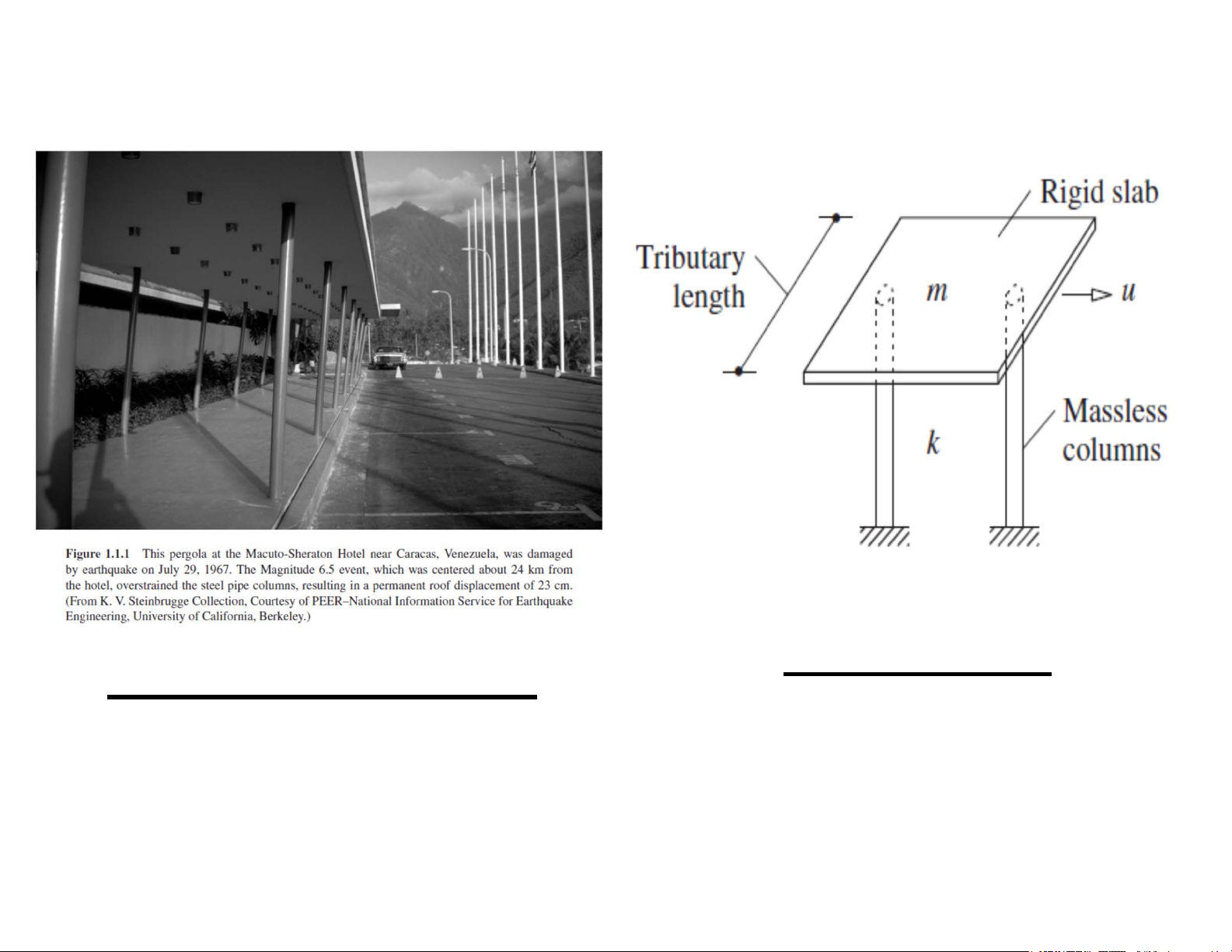
Kết cấu công trình thực:
k: Độ cứng kháng uốn của cột thép
Công trình 1 tầng có mái bê
m: khối lượng mái bê tông
tông cốt thép và hệ cột thép
u(t): Chuyển vị ngang của mái bê tông 6
2.1 Giới thiệu về hệ một bậc tự do
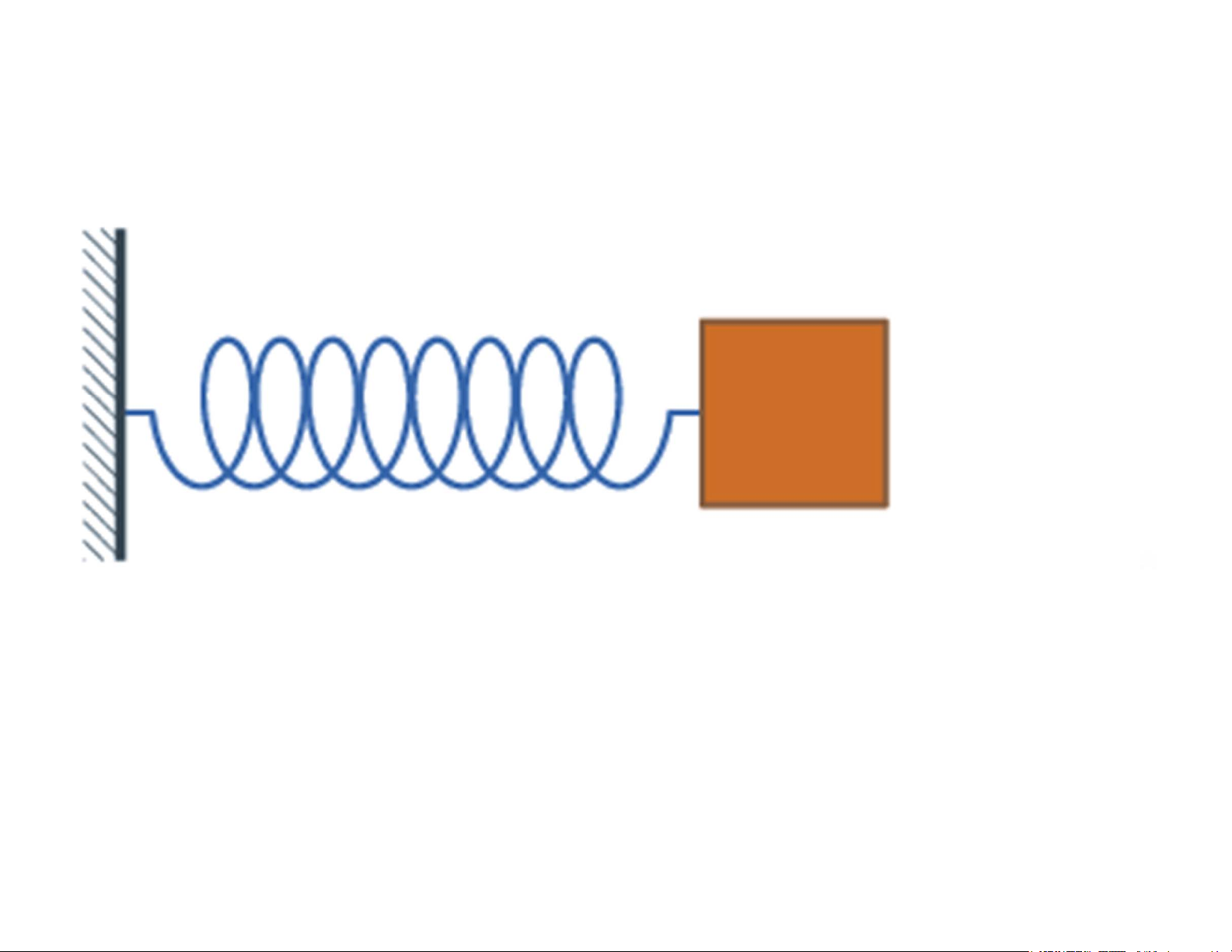
Hệ một bậc tự do có thể được đơn giản hóa bằng sơ đồ khối lượng
– lò xo (mass-spring system (Single-degree-of-freedom – SDOF) 7
2.2 Phương trình động lực học của hệ SDOF
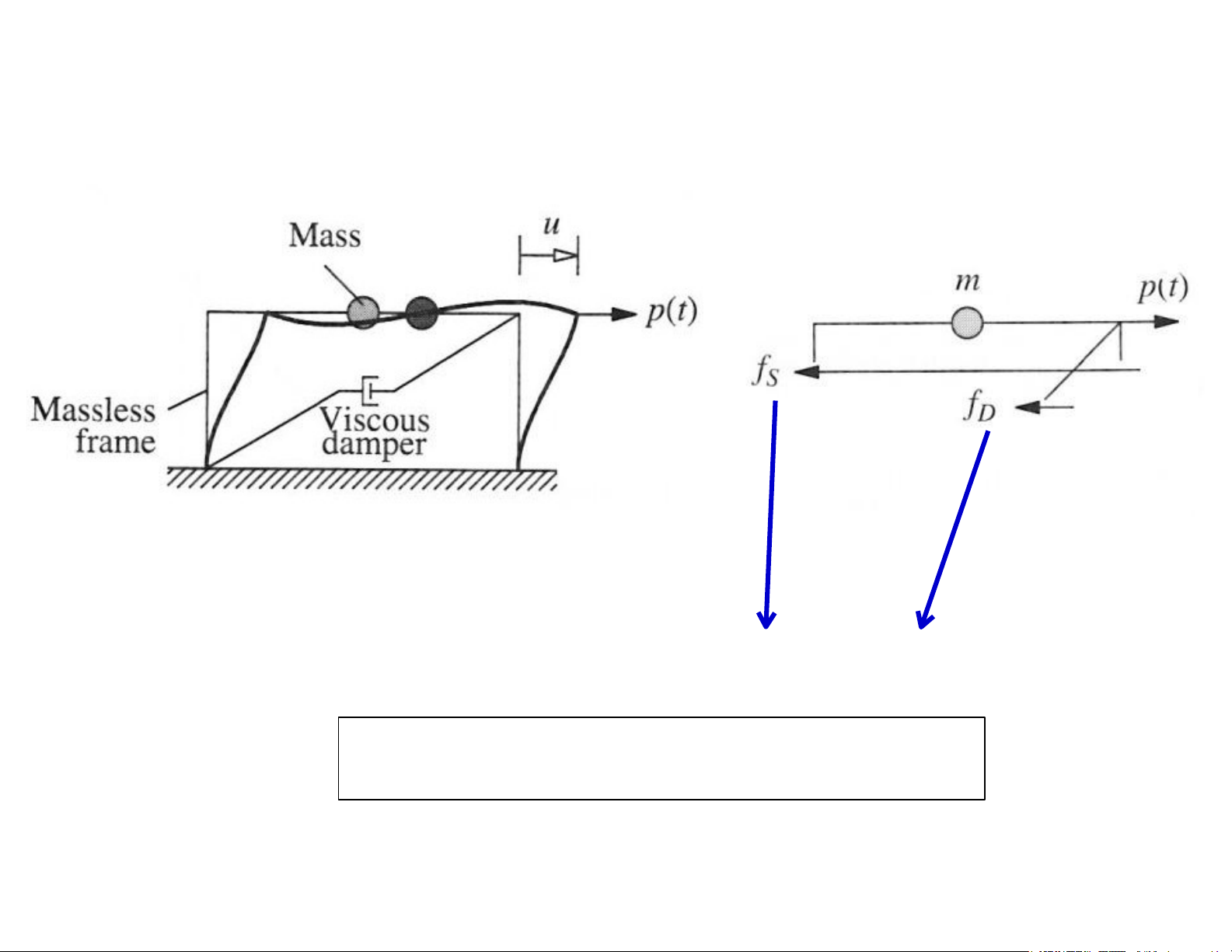
Hệ SDOF được thiết lập với 03 thông số động lực học:
- Khối lượng tham gia dao động m - Độ cứng k
- Hệ số cản nhớt c
- Ngoại lực p(t) 8
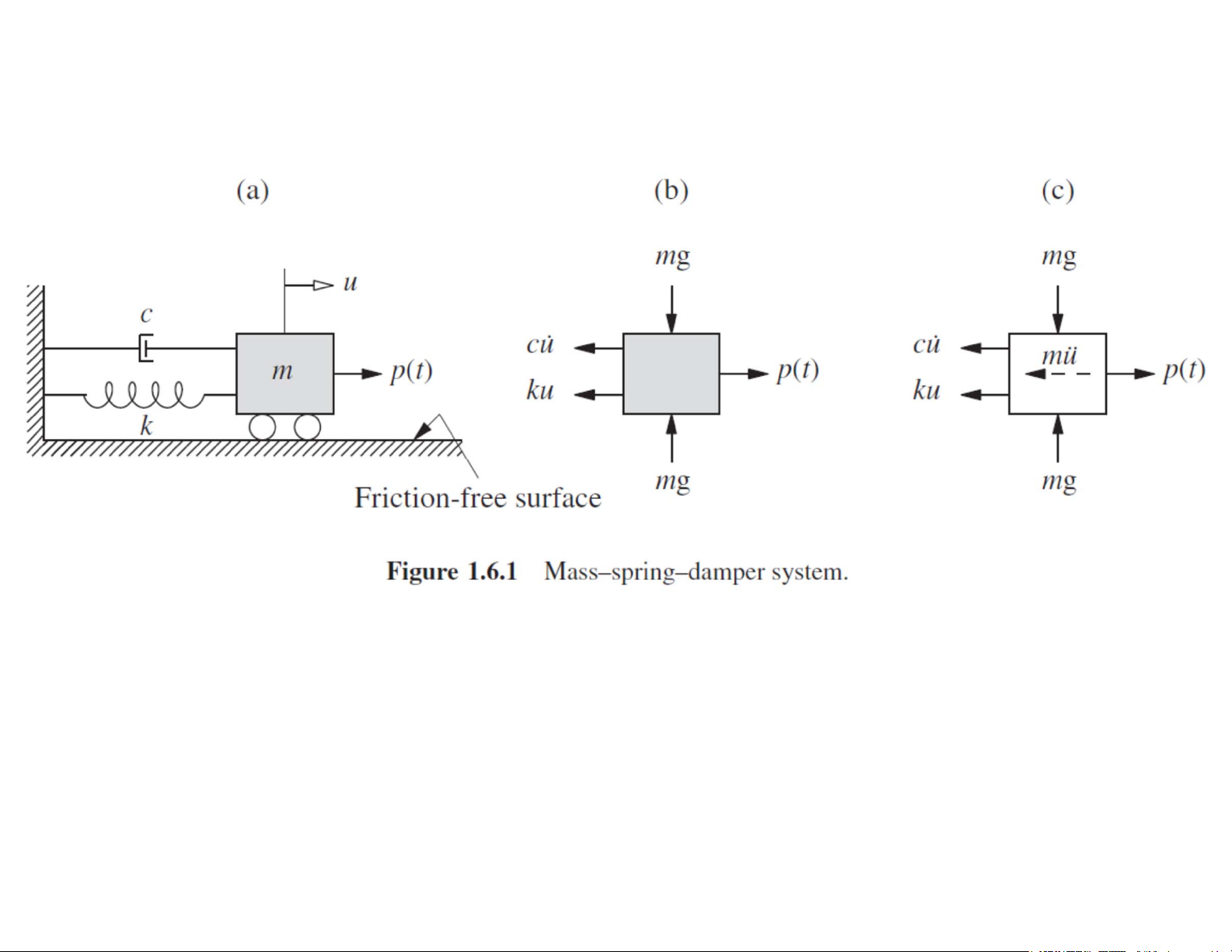
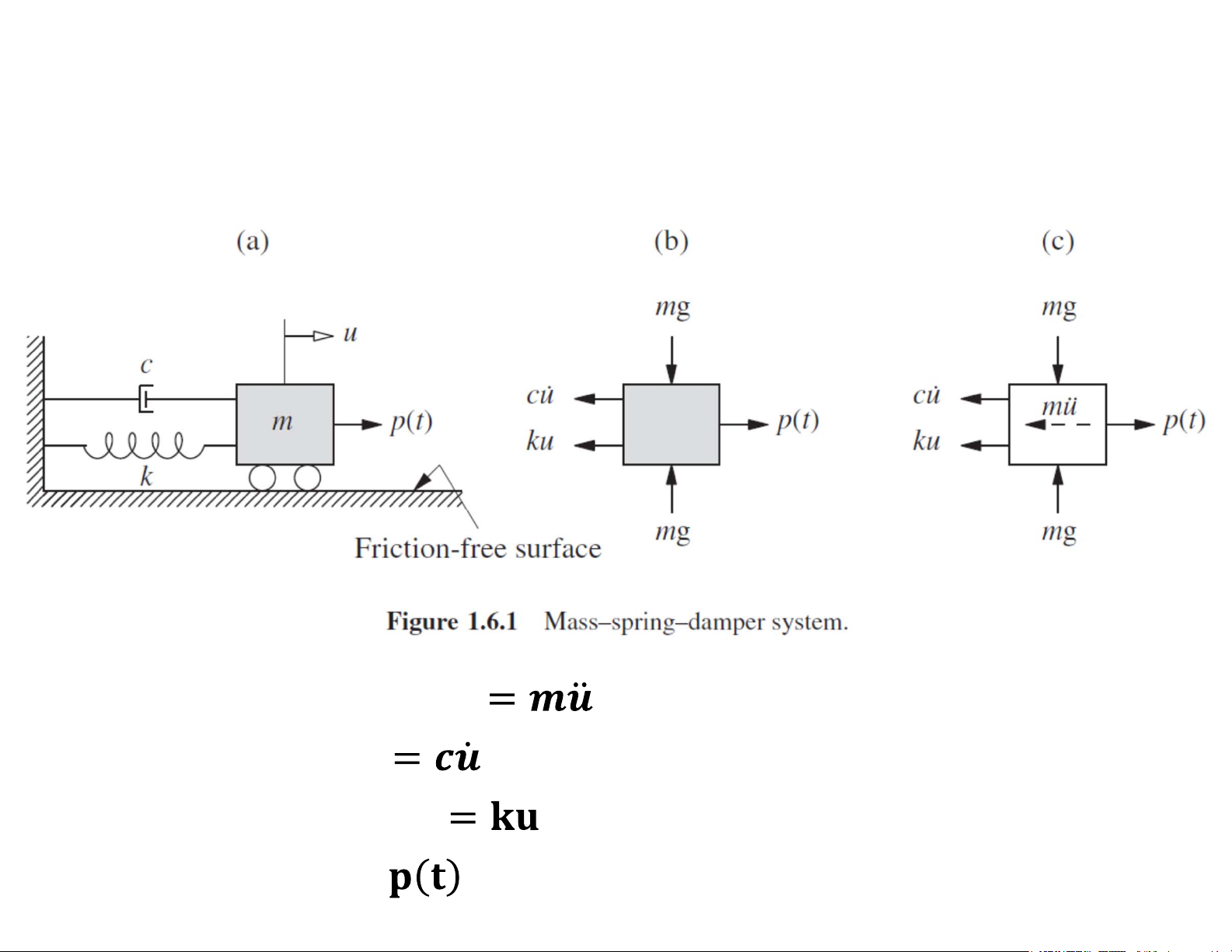
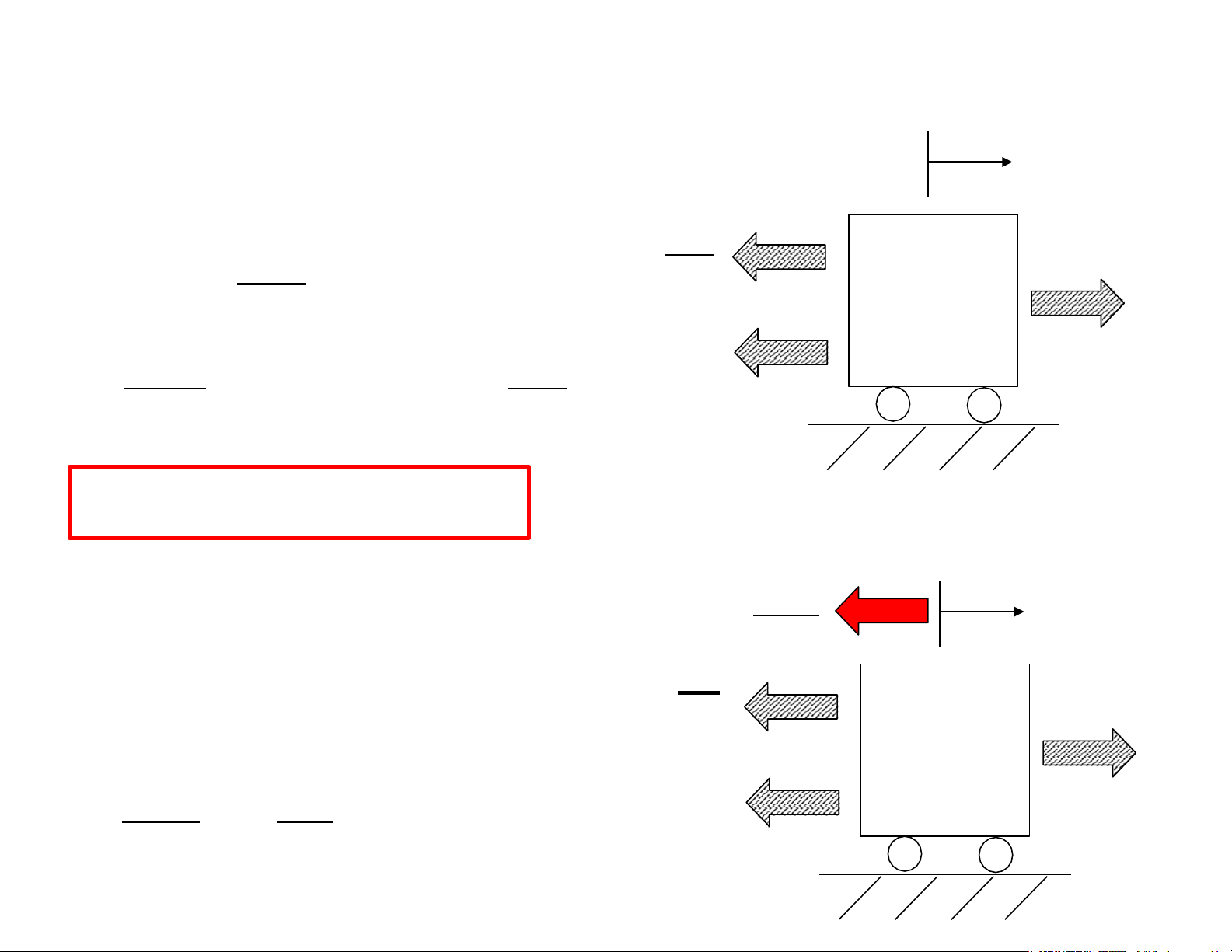
2.2 Phương trình động lực học của hệ SDOF Lực quán tính fi Lực cản fD
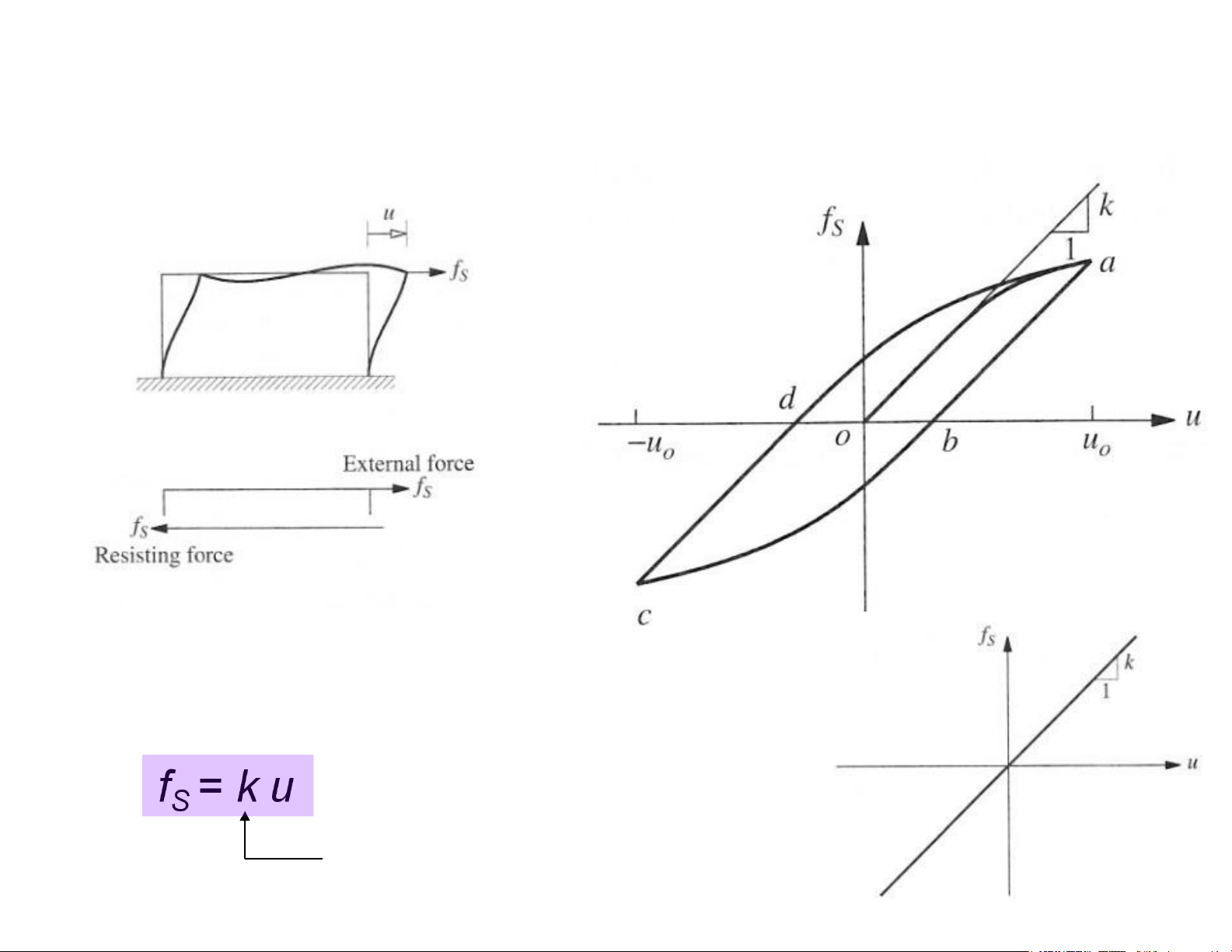
Lực đàn hồi fs Ngoại lực 9 Lực đàn hồi fs  Thực tế là phi tuyến 
Giả thiết tuyến tính cho biến dạng nhỏ f = S k u Độ cứng
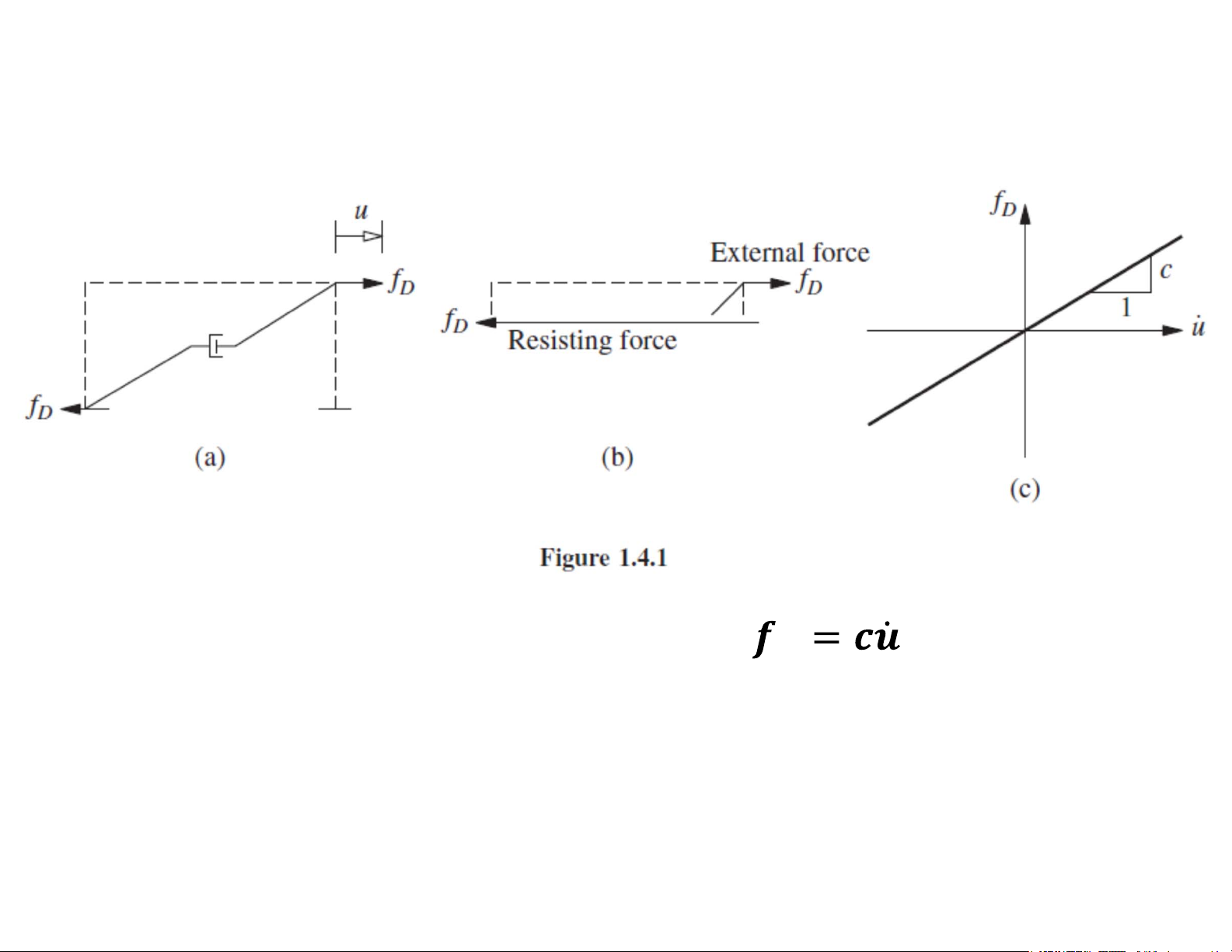
Lực cản nhớt fD (Damping force)
1. Tiêu tán năng lượng trong kết cấu
2. Xuất hiện trong kết cấu thực 3. Có rất nhiều nguồn Ma sát tại các mối nối Cản của vật liệu Cản nhớt (chất lỏng)
4. Có nhiều cách tính toán dựa trên các giả thiết cụ thể 11
Lực cản nhớt fD (Damping force)
Lực cản nhớt tỉ lệ thuận với vận tốc chuyển vị 𝑫
Hằng số c được gọi là hệ số cản nhớt (viscous damping coefficient)
c thường được xác định thông qua các nghiên cứu thực nghiệm 12
Lực cản nhớt fD (Damping force) du f  c D dt Vận tốc Units: m/s Lực cản Hệ số cản Units: N Units: Ns/m or kg/s Lưu ý:
 Hệ số cản c được xác định từ thực nghiệm
 Trong thực tế, hệ số cản trong kết cấu thường không phải là cản
nhớt. Tuy nhiên cho những giá trị cản nhỏ, lực cản được giả thiết
là tuyến tính nhằm đơn giản hóa. 33
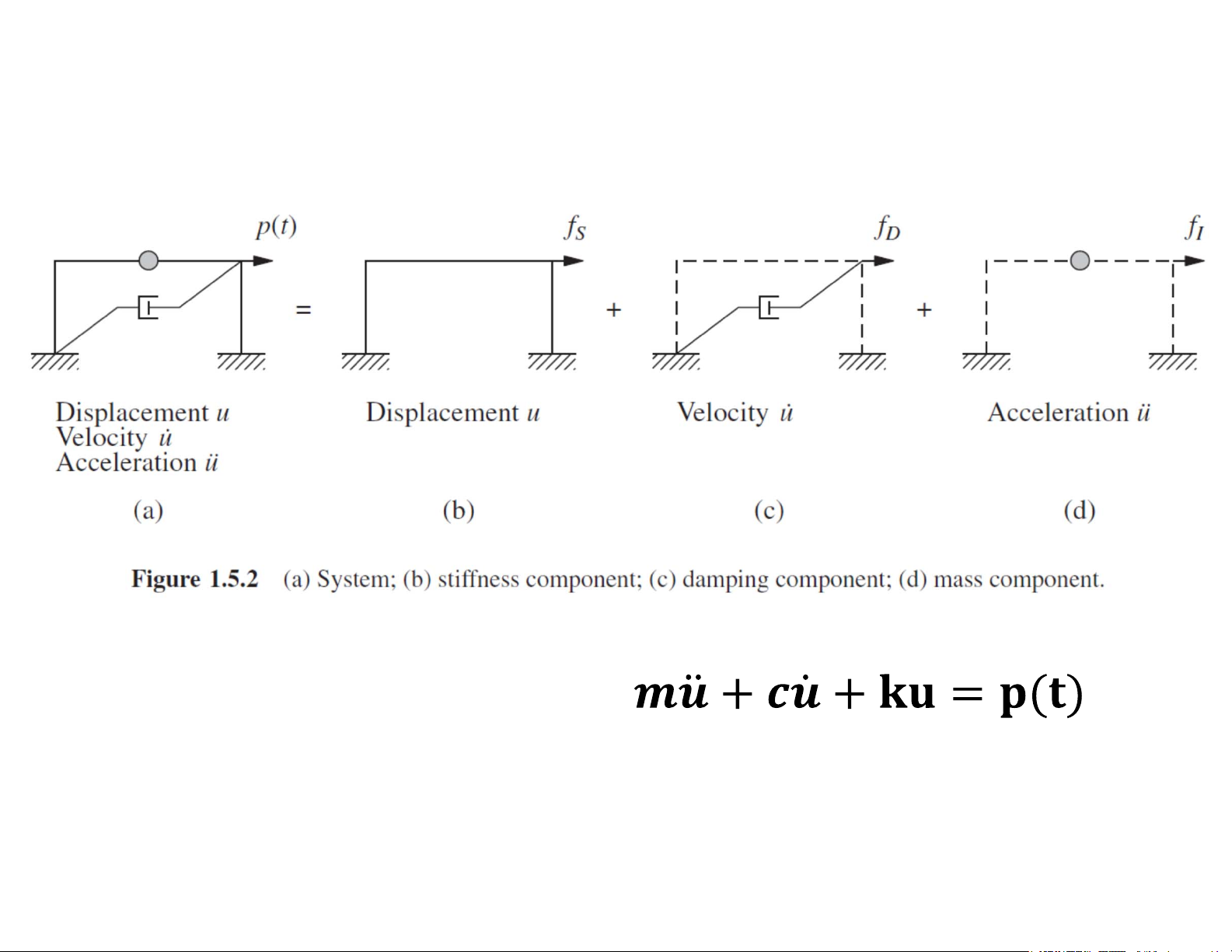
Phương trình chuyển động của hệ một bậc tự do u(t) Định luật 2 Newton du du2 c F  m d m t  2 dt (mass) p(t) du2 du ku m
 p(t)  ku  c dt2 dt
Mu’  cu’  ku  p(t ) du2 m u(t) Cân bằng động dt2 du c F  0 d m t (mass) p(t) du2 d  u m c
 ku  p(t) ku dt2 dt 14
Phương trình chuyển động của hệ một bậc tự do Định luật 2 Newton
F  ma  p(t)  ku(t)  cu’(t)  mu’’(t)
Mu’’(t)  cu’(t)  ku(t )  p(t) 15
Phương trình dao động do tác động ngoại lực Phương trình dao động: 16
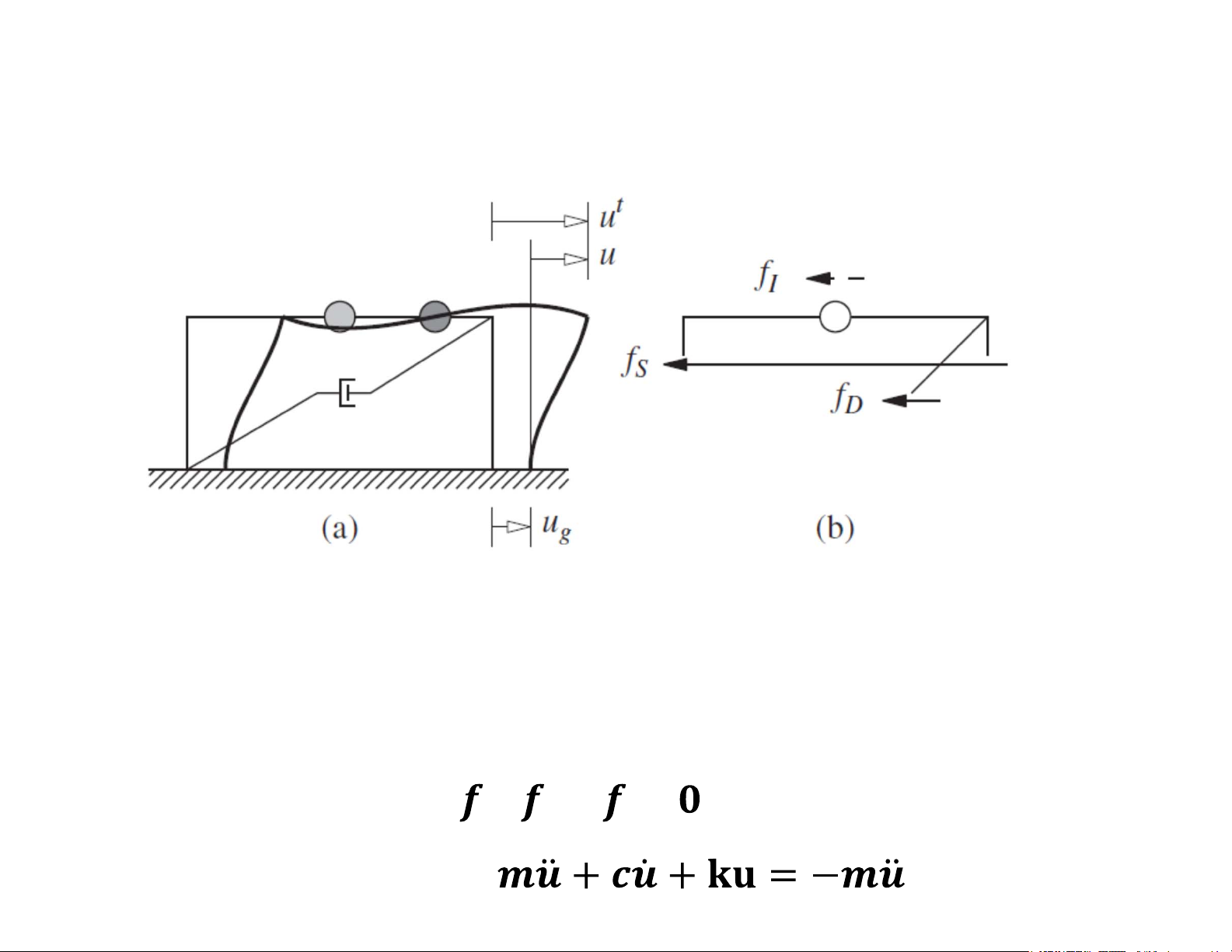
Phương trình dao động do động đất
ut(t)=u (t)+u(t) (1.7.1) g
Trong đó, ut(t) chuyển vị tuyệt đối (total displacement); ug(t): chuyển vị của
nền đất; u(t): chuyển vị tương đối giữa đất nền và khối lượng m
Phương trình cân bằng lực: 𝑰+ 𝑫+ 𝒔= (1.7.2)
Từ (1.7.1) và (1.7.2), ta có: (t) g 17
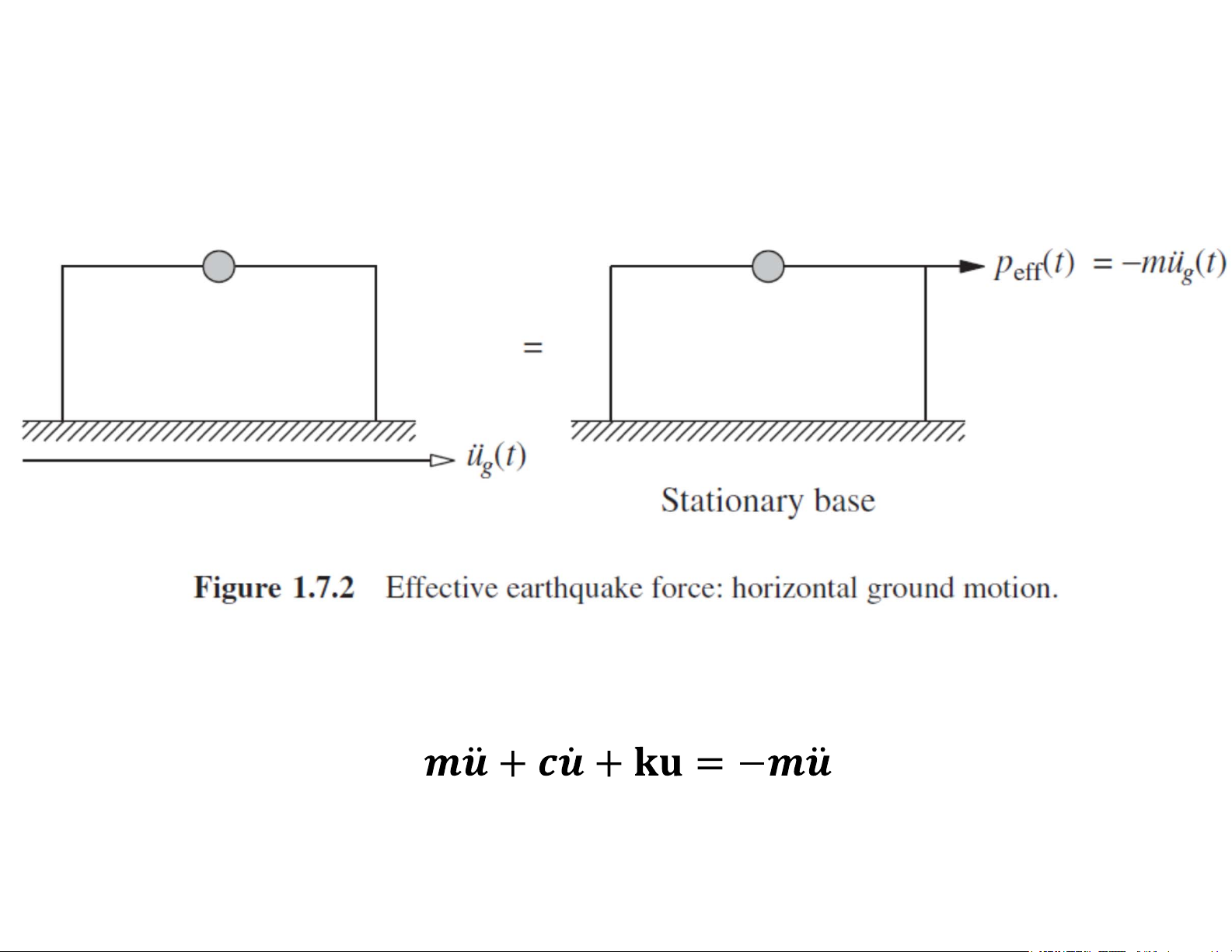
Phương trình dao động do động đất
ut(t)=ug(t)+u(t) (1.7.1) PTDĐ dạng tổng quát: (t) g 18
Các thông số cần tính toán trong phản ứng động PTDĐ do ngoại lực: PTDĐ do động đất: (t) g
a) Các thông số cần tính toán: Chuyển vị u(t); vận tốc (t); gia tốc (t)
b) Nội lực trong các cấu kiện kết cấu có thể được tính theo hai cách:
- Thông qua bảng tra hệ số độ cứng dựa trên chuyển vị tương đối u(t)
- Thông qua tĩnh lực tương đương (equivalent static force) fs=ku 19
Các phương pháp giải phương trình dao động PTDĐ do dạng tổng quát:
• Lời giải bằng tích phân từng phần cổ điển (classical solution)
• Tích phân Duhamel (Duhamel’s Integral)
• Tích phân theo miền tần số (Frequency-Domain Method)
• Phương pháp số (numerical methods) 20