Bài giảng Động lực học công trình môn Cơ học kết cấu | Trường Đại học Xây Dựng Hà Nội

ĐỘNG LỰC HỌC CÔNG TRÌNH (DYNAMICS OF STRUCTURES) BỘ B M ÔN N C Ơ C H ỌC C KẾ K T CẤ C U Ấ ĐẠ Đ I Ạ HỌ H C C XÂ X Y Â Y DỰNG N
3. SDOF – DAO ĐỘNG CƯỠNG BỨC GV G : V : NG N U G Y U ỄN N QU Q A U N A G N G HU H Y U hu h y u n y q n @h @ u h c u e c . e ed e u d . u vn v TẢI TRỌNG ĐIỀU HÒA 66
DYN – SDOF – DAO ĐỘNG CƯỠNG BỨC DO TẢI TRỌNG ĐIỀU HÒA K.Lượng F(t), u(t) Nội dung • Dao động điều hòa Cản Độ cứng
• Dao động tức thời & dao động bình ổn • Hệ số động Rd u
• Truyền / Cô lập dao động k m P(t) • Tải trọng tuần hoàn c 67
DYN – UNIT 3 – DAO ĐỘNG DO TẢI TRỌNG ĐIỀU HÒA
3.1. Dao động cưỡng bức
 Dao động cưỡng bức là dao động do tác dụng của tải trọng động p(t)
e.g. Dao động kết cấu (cầu, nhà cao tầng) do gió, động đất; dao động của đất nền do
các phương tiện giao thông, tàu cao tốc; dao động do các động cơ quay có khối lượng lệch tâm
𝑚𝑢̈ + 𝑐𝑢̇ + 𝑘𝑢 = 𝐹(𝑡)
 Phương trình dao động
𝑢̈ + 2𝜁𝜔 𝑢̇ + 𝜔 𝑢 = 𝐹(𝑡) / 𝑚
ĐK ban đầu: u│t=0 = u(0) , u̇│t=0 = u̇(0)
 Nghiệm tổng quát dạng: u(t) = uc(t) + up(t)
uc(t) ~ nghiệm tổng quát của PT thuần nhất (i.e. F(t) = 0 )
up(t) ~ nghiệm riêng của PTDĐ
 Phản ứng tức thời (transient response) & Phản ứng bình ổn (steady-state response) 68
DYN – UNIT 3 – DAO ĐỘNG DO TẢI TRỌNG ĐIỀU HÒA
3.2. Dao động cưỡng bức do tải trọng điều hòa Biên độ tải trọng, F0
 Tải trọng điều hòa F(t) = F0.sin(Ωt) / F(t) = F0.cos(Ωt)
F0 ~ biên độ tải trọng; Ω ~ tần số kích thích/tải trọng;
β = Ω/ωn ~ tỉ lệ tần số; δst = F0/k ~ chuyển vị tĩnh Chu kỳ của tải
 Nghiệm tổng quát dạng: u(t) = uc(t) + up(t) trọng, T=2π/Ω
uc(t) = A.sin(ωnt) + B.cos(ωnt)
A, B : hằng số được xác định từ đk ban đầu u(0) & u̇(0) up(t) = C.sin(Ωt)
C: hằng số được xác định từ tải trọng động p(t) 69
DYN – UNIT 3 – DAO ĐỘNG DO TẢI TRỌNG ĐIỀU HÒA
3.2.1 Dao động điều hòa không cản
 PTDĐ: mü + ku = Fo.sin(Ωt)
Xác định nghiệm riêng trước (C) sau  ĐK ban đầu: u│
đó dùng điều kiện ban đầu tìm A & B
t=0 = u(0) , u̇│t=0 = u̇(0)
 Nghiệm tổng quát dạng: u(t) = uc(t) + up(t)
uc(t) = A.cos(ωnt) + B.sin(ωnt)
A, B : hằng số được xác định từ đk ban đầu u(0) & u̇(0) up(t) = C.sin(Ωt)
C: hằng số được xác định từ tải trọng động p(t)  Nghiệm riêng 𝑢 (𝑡) = 𝐶 sin Ωt Đạo hàm hai lần:
𝑢̈ (𝑡) = −𝐶Ω sin 𝜔 𝑡 Thay vào PT F 1 F 1 ⇒ 𝐶 = hay 𝑢 (𝑡) = sin Ωt (𝜔 ≠ 𝜔 ) 𝑘 1 − (Ω/𝜔 ) 𝑘 1 − (Ω/𝜔 ) Nghiệm tổng quát F 1
𝑢(𝑡) = 𝐴 cos 𝜔 𝑡 + 𝐵 sin 𝜔 𝑡 + sin Ωt 𝑘 1 − (Ω/𝜔 ) 70
DYN – UNIT 3 – DAO ĐỘNG DO TẢI TRỌNG ĐIỀU HÒA
3.2.1 Dao động điều hòa không cản
 PTDĐ: mü + ku = po.sin(Ωt)
& ĐK ban đầu: u│t=0 = u(0) , u̇│t=0 = u̇(0)  Nghiệm tổng quát F 1
𝑢(𝑡) = 𝐴 cos 𝜔 𝑡 + 𝐵 sin 𝜔 𝑡 + sin Ωt 𝑘 1 − (Ω/𝜔 ) F Ω
⇒ 𝑢̇(𝑡) = −𝜔 𝐴 sin 𝜔 𝑡 + 𝜔 𝐵 cos 𝜔 𝑡 + cos Ωt 𝑘 1 − (Ω/𝜔 ) từ đk ban đầu 𝑢̇(0) F Ω/𝜔
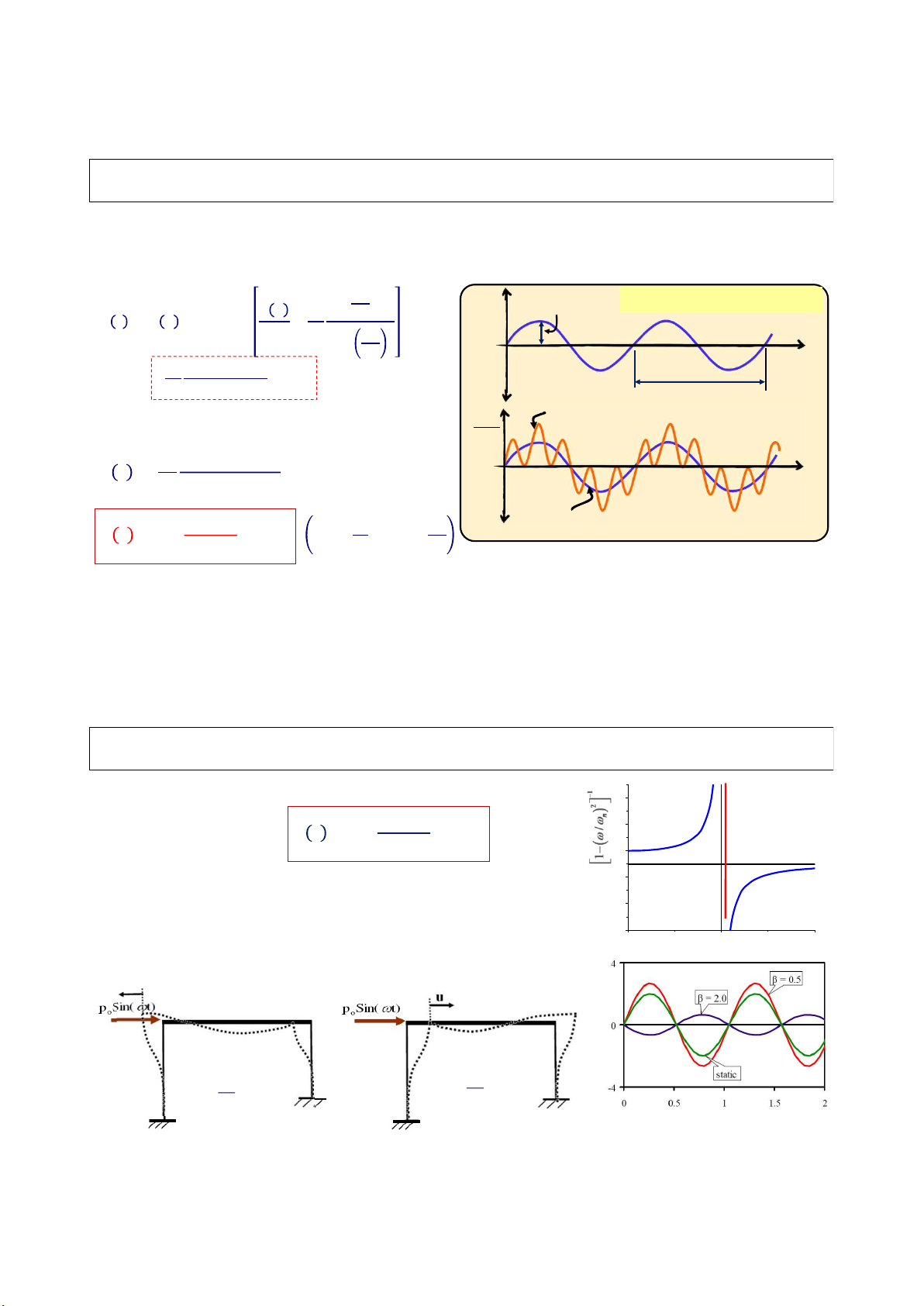
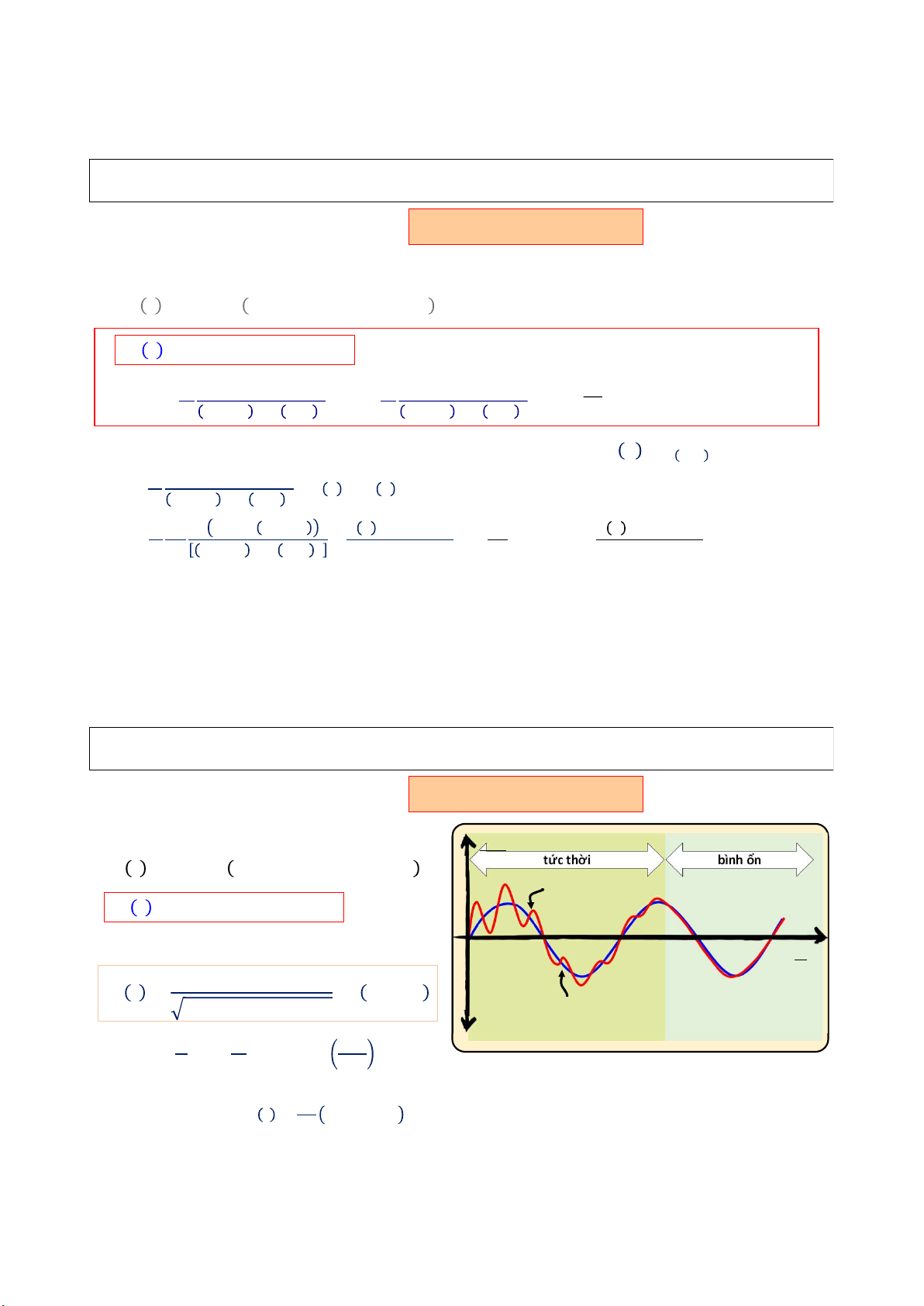
Dao động là tổ hợp của 2 sóng ⇒ 𝐴 = 𝑢(0); 𝐵 = − 𝜔 𝑘 1 − (Ω/𝜔 )
hàm ‘sin’; 1 sóng là dao động tự
nhiên của hệ & 1 sóng là dao
Dao động tức thời tồn tại khi đk ban đầu = 0
động theo kích thích bên ngoài. 𝑢̇(0) F Ω/𝜔 𝑝 1
𝑢(𝑡) = 𝑢(0) cos 𝜔 𝑡 + − sin 𝜔 𝑡 + sin Ωt 𝜔 𝑘 1 − (Ω/𝜔 ) 𝑘 1 − (Ω/𝜔 )
Dao động tức thời / dao động tự do
Dao động bình ổn / dao động cưỡng bức 71
DYN – UNIT 3 – DAO ĐỘNG DO TẢI TRỌNG ĐIỀU HÒA
3.2.1 Dao động điều hòa không cản
 PTDĐ: mü + ku = Fo.sin(Ωt)
& ĐK ban đầu: u│t=0 = u(0) , u̇│t=0 = u̇(0) Ω 𝑭(t)
Ω/𝜔 = 0.2; 𝑢(0) = 0; 𝑢̇(0) = 𝜔 F /𝑘 𝑢̇ 0 F 𝜔 Biên độ, F0
𝑢 𝑡 = 𝑢 0 cos 𝜔 𝑡 + − sin 𝜔 𝑡 𝜔 𝑘 Ω 1 − 𝜔 F 1 + sin Ω𝑡 𝑘 1 − (Ω/𝜔 ) Chu kỳ, 𝑇 = 2𝜋 𝜔 ⁄ Dao động tổng 𝑢(𝑡)
Thường chỉ xét dao động bình ổn (𝑢 ) F 1 𝑢 𝑡 = sin Ω𝑡 𝑘 1 − (Ω/𝜔 ) 1 F Ω Dao động bình ổn 𝑢 𝑡 = 𝛿 sin Ω𝑡 𝛿 = & 𝛽 = k 𝜔 1 − 𝛽 72
DYN – UNIT 3 – DAO ĐỘNG DO TẢI TRỌNG ĐIỀU HÒA
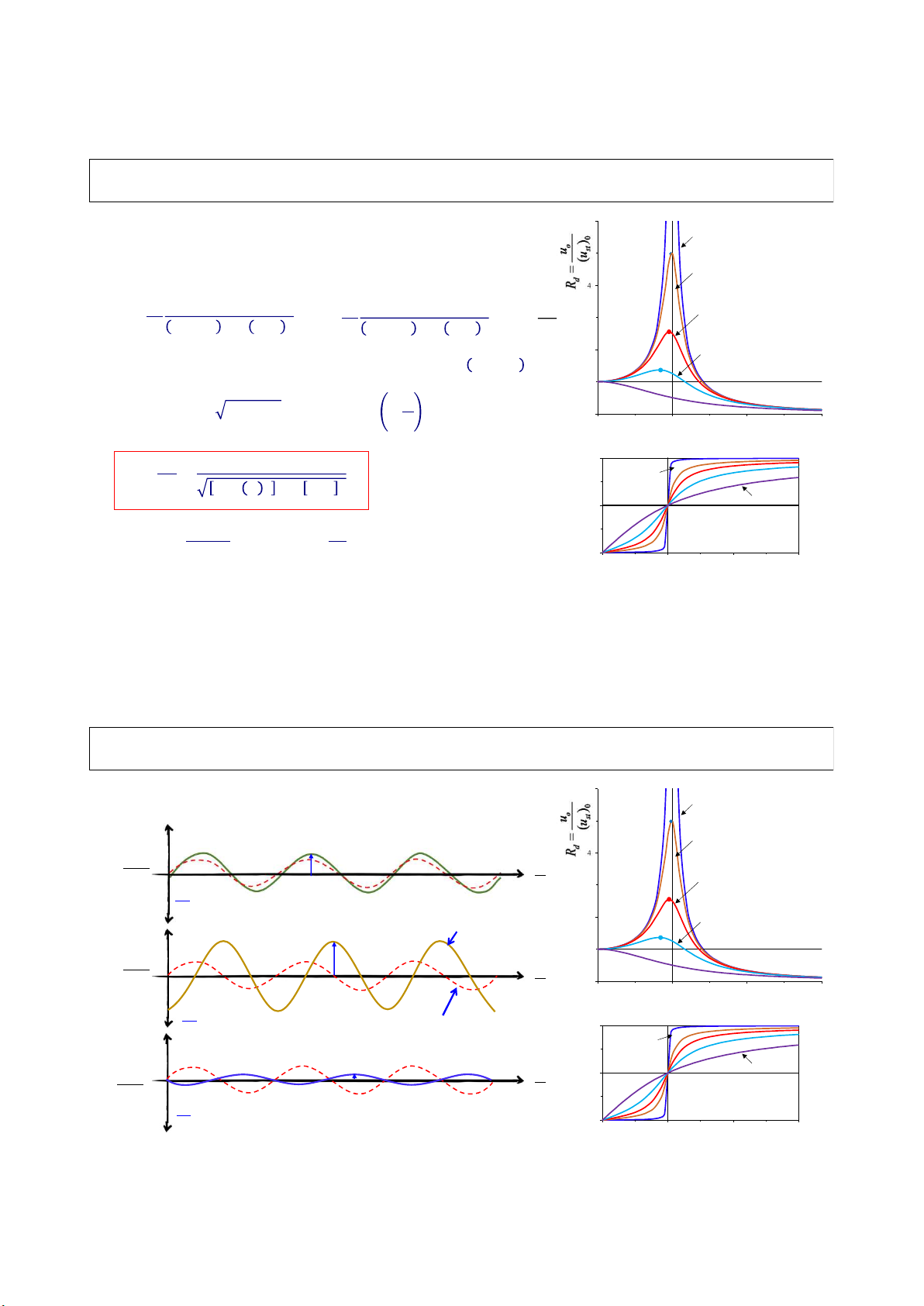
3.2.1 Dao động điều hòa không cản 5 1  Dao động bình ổn 𝑢 𝑡 = 𝛿 sin Ω𝑡 3 1 − 𝛽 1 -1
Biên độ dao động (bình ổn) phụ thuộc tỉ lệ tần số β -3  Ω < ω 𝜷 = 𝛀 𝝎
n (β < 1) → u(t) & p(t) cùng dấu; i.e cùng pha -5 0 1 2
 Ω > ωn (β >1) → u(t) & p(t) ngược dấu; i.e ngược pha 𝜔 𝜔 > 1 < 1 𝜔 𝜔 73
DYN – UNIT 3 – DAO ĐỘNG DO TẢI TRỌNG ĐIỀU HÒA
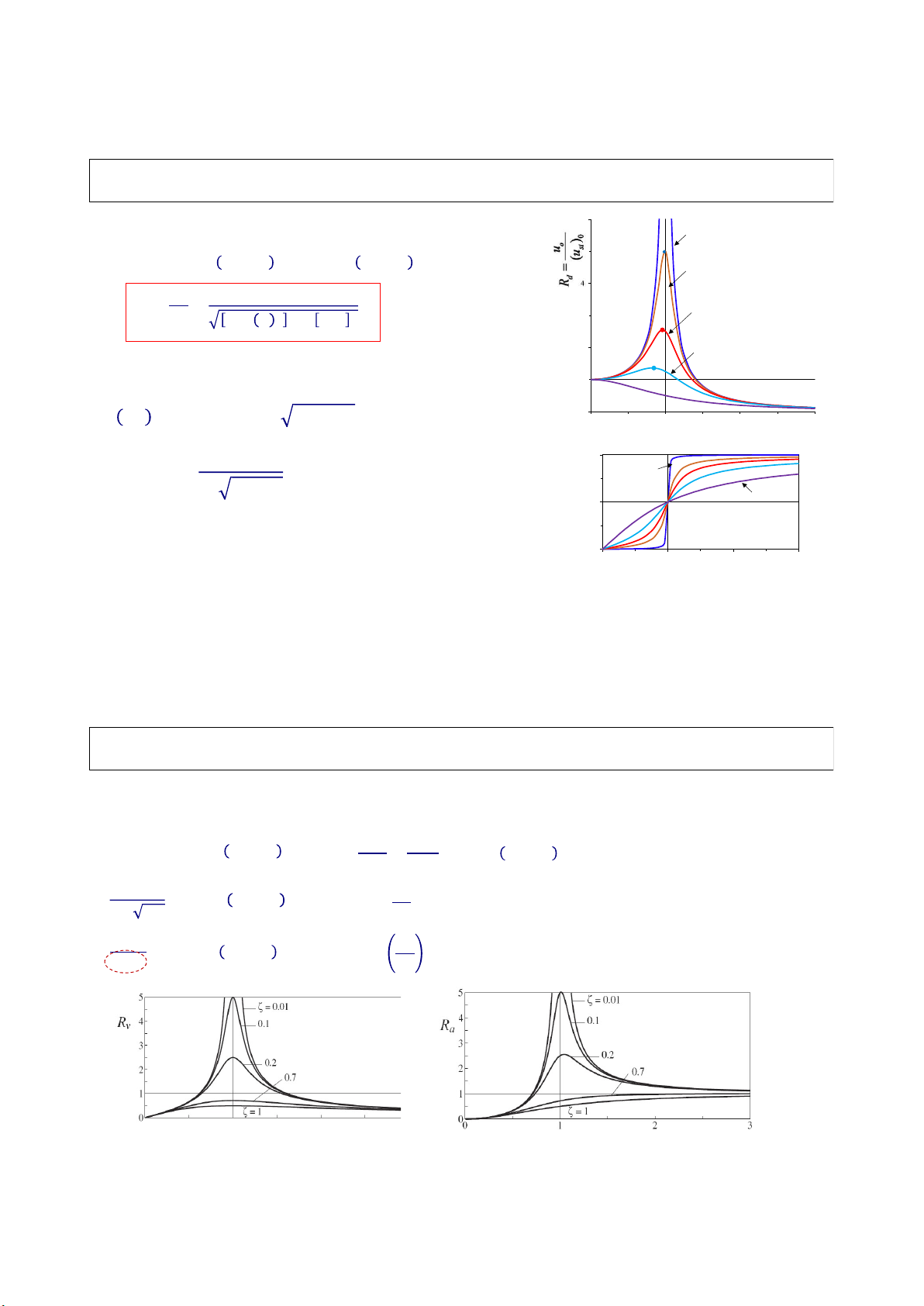
3.2.1 Dao động điều hòa không cản u u 1 6  Hệ số động R = = = Resonance 𝛿 𝛿 1 − 𝛽 4 𝐹 1 𝑢(𝑡) =
sin Ωt = 𝑢 sin( Ω𝑡 − 𝜙) = 𝛿 𝑅 sin( Ω𝑡 − 𝜙) 𝑘 1 − 𝛽 Slowly 2  R loaded
d ~ hệ số động (chuyển vị); u0 ~ biên độ dao động 1 Rapidly 0 Ω < 𝜔
→ u(t) thay đổi theo sin(Ωt) loaded  𝜙 = ϕ ~ pha dao động 180 Ω > 𝜔
→ u(t) thay đổi theo -sin(Ωt) 0 0 0.2 1 2 2 3 𝜷 = 𝛀 𝝎
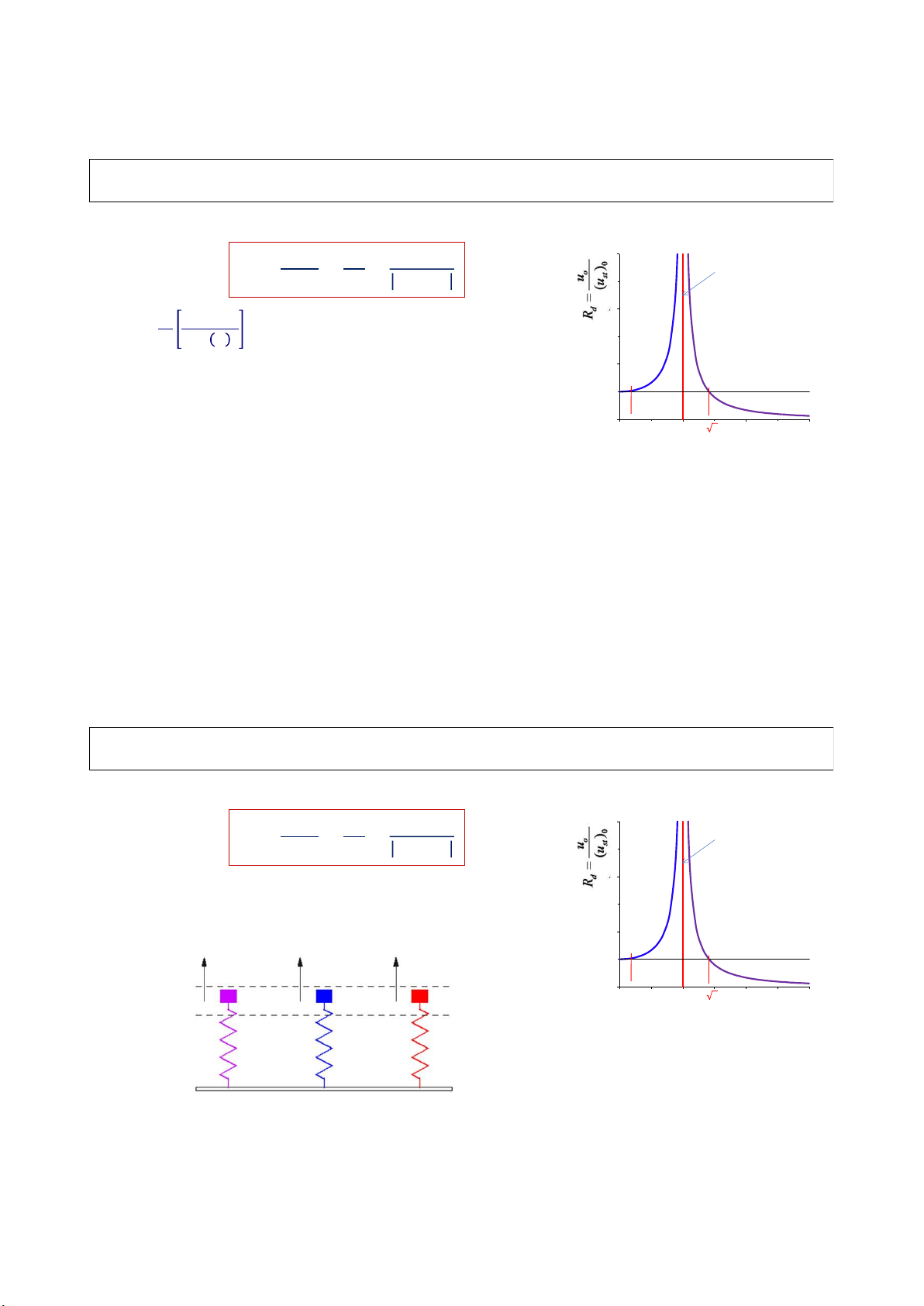
- (Ω/ωn) nhỏ, i.e. tải trọng tác dụng chậm ≈ tĩnh → Rd ~ 1
- (Ω/ωn) > √2 → Rd < 1, i.e. biên độ dao động nhỏ hơn chuyển vị tĩnh.
- (Ω/ωn) → ∞: Rd → 0, i.e. tải trọng tác dụng quá nhanh, kết cấu không kịp phản ứng
- (Ω/ωn) ≈ 1, Rd >>1, i.e. cộng hưởng 74
DYN – UNIT 3 – DAO ĐỘNG DO TẢI TRỌNG ĐIỀU HÒA
3.2.1 Dao động điều hòa không cản u u 1 6  Hệ số động R = = = Resonance 𝛿 𝛿 1 − 𝛽 4 Slowly 2 loaded 1 Rapidly loaded 0 0 0.2 1 2 2 3 𝜷 = 𝛀 𝝎
fΩ = 0.4 fn fD = 1.1 fn fD = 1.6 fn 75
DYN – UNIT 3 – DAO ĐỘNG DO TẢI TRỌNG ĐIỀU HÒA
3.2.1 Dao động điều hòa không cản 𝑢(𝑡) (𝑢 )
 Phản ứng khi cộng hưởng Ω = ω Đường 𝜋 n bao  Nghiệm riêng dạng
𝑢 (𝑡) = 𝐶𝑡 sin 𝜔 𝑡
Đạo hàm hai lần, thay vào PT được: F ⇒ 𝐶 = − 𝜔 𝑡 2𝑘 𝑇 F ⇒ 𝑢 (𝑡) = − 𝜔 𝑡 cos 𝜔 𝑡 (Ω = 𝜔 ) 2𝑘 ω=ωn; u(0)= v(0)=0 F
 Nghiệm 𝑢(𝑡) = 𝐴 cos 𝜔 𝑡 + 𝐵 sin 𝜔 𝑡 − 𝜔 𝑡 cos 𝜔 𝑡 2𝑘  chuyển vị tăng dần 𝑢̇(0) F
từ đk ban đầu ⇒ 𝐴 = 𝑢(0); 𝐵 = +  t = ∞ → u 𝜔 2𝑘 0 = ∞  ĐK ban đầu = 0 1 F 𝑢(𝑡) 1 2𝜋 2𝜋𝑡 2𝜋𝑡 𝑢(𝑡) = −
𝜔 𝑡 cos 𝜔 𝑡 − sin 𝜔 𝑡 ⇒ = − 𝑡 cos − sin 2 𝑘 (𝑢 ) 2 𝑇 𝑇 𝑇 76
DYN – UNIT 3 – DAO ĐỘNG DO TẢI TRỌNG ĐIỀU HÒA
3.2.1 Dao động điều hòa không cản
Ví dụ 1: sơ đồ kết cấu như hình vẽ. Quạt nặng 10kg; hoạt động ở tốc độ quay 15 rad/s; cánh
quạt coi như khối lượng 1.5kg lệch tâm 50 mm so với trục quay của cánh. Xác định biên độ dao
động bình ổn của hệ biết vị trí đặt quạt có chuyển vị 20 mm do trọng lượng của quạt. Ans: u0 = 6.35 mm 77
DYN – UNIT 3 – DAO ĐỘNG DO TẢI TRỌNG ĐIỀU HÒA
3.2.1 Dao động điều hòa không cản
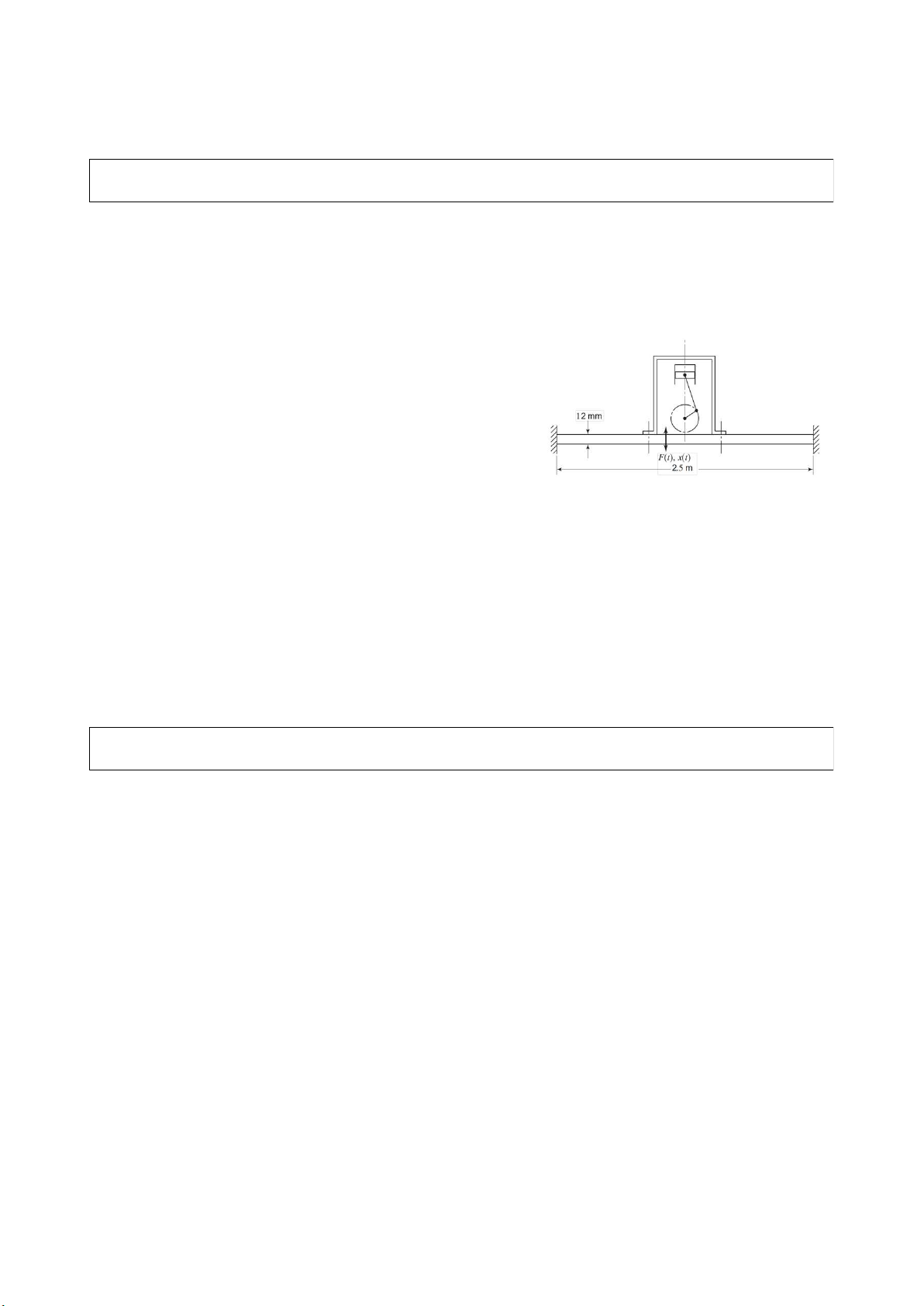
Ví dụ 2: Máy bơm ly tâm có trọng lượng 700 N được gắn vào giữa 1 tấm thép có chiều dày
12mm, chiều rộng 500mm, chiều dài (nhịp) 2.5m được ngàm chặt 2 đầu (hình vẽ). Khi hoạt
động, máy bơm tạo ra một lực điều hòa F(t) = 400cos(60t) (N). Xác định biên độ dao động bình ổn của tấm thép. Ans: u0 = 5 mm
Xem tấm thép như một dầm nhịp 2.5m; chiều rộng 500mm & chiều cao 12
mm; 2 đầu ngàm. Chuyển vị giữa dầm δst = (PL3)/(192EI) E = 200 GPa 78
DYN – UNIT 3 – DAO ĐỘNG DO TẢI TRỌNG ĐIỀU HÒA
3.2.1 Dao động điều hòa không cản
Ví dụ 3: Hệ SDOF có khối lượng 10 kg; tần số tự nhiên 80 rad/s; kích thích ban đầu = 0. Xác định biểu thức dao
động của hệ & vẽ đồ thị biểu diễn biểu thức đó khi hệ chịu tác dụng của: a) p(t) = 10sin(40t) N b) p(t) = 10 sin(80t) N Ans: 79
DYN – UNIT 3 – DAO ĐỘNG DO TẢI TRỌNG ĐIỀU HÒA
3.2.1 Dao động điều hòa không cản
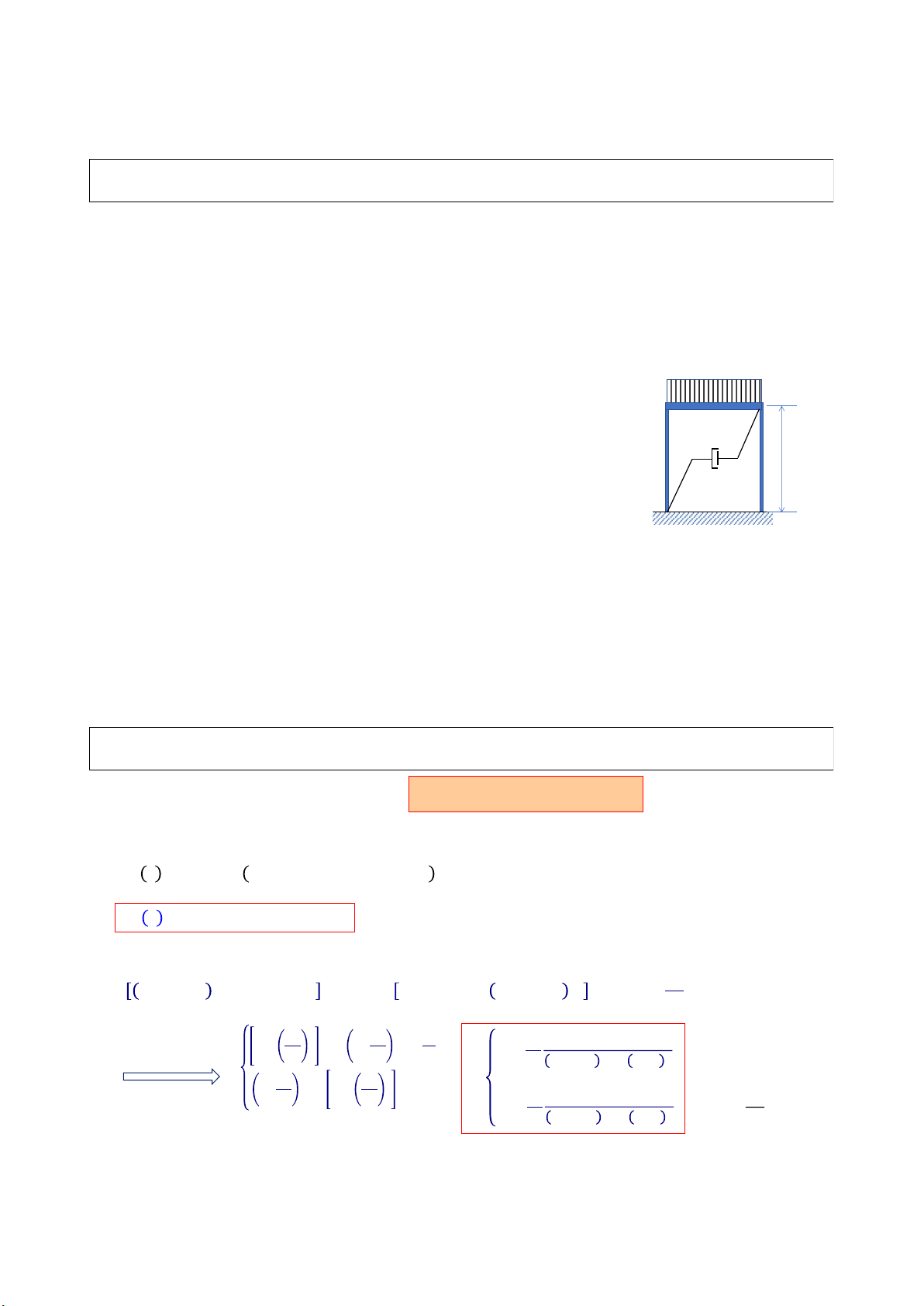
Bài tập 1: hệ kết cấu khung nhà 1 tầng như hình vẽ. Hệ có kích thích ban đầu u(0) = 3 cm & v(0)
= 20 cm/s; và chịu tác dụng của tải trọng điều hòa P(t) = 5000sin(Ωt) (kN). Vẽ đồ thị biểu diễn
dao động của hệ trong khoảng thời gian t = 0 – 0.25s; biết ζ = 0% và β = 0.1; 0.25; 0.6; 0.9; 1; 1.25 & 1.75 Ans: m = 25 tons EI ∞ 2 3 m 40x40 cm E= 23,500 MPa 80
DYN – UNIT 3 – DAO ĐỘNG DO TẢI TRỌNG ĐIỀU HÒA
3.2.2 Dao động điều hòa có cản
𝑚𝑢̈ + 𝑐𝑢̇ + 𝑘𝑢 = 𝐹 sin Ω𝑡
 Nghiệm tổng quát dạng: u(t) = uc(t) + up(t)
~ dao động tức thời, tắt nhanh do lực cản 𝑢 𝑡 = 𝑒
𝐴 cos 𝜔 𝑡 + 𝐵 sin 𝜔 𝑡
nên thường không cần xét đến/bỏ qua
𝑢 𝑡 = 𝐶 sin Ω 𝑡 + 𝐷 cos Ω 𝑡
~ dao động bình ổn theo tần số của tải trọng động F(t)
 lấy đạo hàm bậc 1 & 2 của uP(t), thay vào PTDĐ F
𝜔 − Ω 𝐶 − 2𝜁𝜔 Ω𝐷 sin Ωt + 2𝜁𝜔 Ω𝐶 + 𝜔 − Ω 𝐷 cos Ωt = sin Ωt k Ω Ω 𝑝 F 1 − 𝛽 1 − 𝐶 − 2𝜁 𝐷 = 𝜔 𝜔 𝑘 đúng tại 𝐶 = 𝑘 1 − 𝛽 + 2𝜁𝛽 Ω Ω ⇒ & 2𝜁 𝐶 + 1 − 𝐷 = 0 mọi t 𝜔 𝜔 F −2𝜁𝛽 Ω 𝐷 = 𝛽 = 𝑘 1 − 𝛽 + 2𝜁𝛽 𝜔 81
DYN – UNIT 3 – DAO ĐỘNG DO TẢI TRỌNG ĐIỀU HÒA
3.2.2 Dao động điều hòa có cản
𝑚𝑢̈ + 𝑐𝑢̇ + 𝑘𝑢 = 𝐹 sin Ω𝑡
 Nghiệm tổng quát dạng: u(t) = uc(t) + up(t) 𝑢 𝑡 = 𝑒
𝐴 cos 𝜔 𝑡 + 𝐵 sin 𝜔 𝑡
~ thường không cần xét đến/bỏ qua
𝑢 𝑡 = 𝐶 sin Ω 𝑡 + 𝐷 cos Ω 𝑡
~ dao động bình ổn theo tần số của tải trọng động F(t) F 1 − 𝛽 F −2𝜁𝛽 Ω với 𝐶 = & 𝐷 = 𝛽 = 𝑘 1 − 𝛽 + 2𝜁𝛽 𝑘 1 − 𝛽 + 2𝜁𝛽 𝜔
 Nếu cần thiết, A & B xác định từ các kích thích ban đầu u( ) = u 0 & u̇ = u̇(0) 𝐹 2𝜁𝛽 𝐴 = + 𝑢 0 = u 0 − D 𝑘 1 − 𝛽 + 2𝜁𝛽 𝐹 𝜔 𝛽 2𝜁 − 1 − 𝛽 𝑢̇ 0 + 𝑢(0)𝜔 𝜁 𝜔 𝑢̇ 0 + 𝑢(0)𝜔 𝜁 𝐵 = + = − (𝜁D + 𝛽C) + 𝑘 𝜔 1 − 𝛽 + 2𝜁𝛽 𝜔 𝜔 𝜔 82
DYN – UNIT 3 – DAO ĐỘNG DO TẢI TRỌNG ĐIỀU HÒA
3.2.2 Dao động điều hòa có cản
𝑚𝑢̈ + 𝑐𝑢̇ + 𝑘𝑢 = 𝐹 sin Ω𝑡
 Nghiệm tổng quát dạng: u(t) = uc(t) + up(t) 𝒖(𝒕) 𝜹𝒔𝒕 tức thời bình ổn 𝑢 𝑡 = 𝑒
𝐴 cos 𝜔 𝑡 + 𝐵 sin 𝜔 𝑡 Dao động tổng
𝑢 𝑡 = 𝐶 sin Ω 𝑡 + 𝐷 cos Ω 𝑡 hoặc dạng khác up(t) 𝑡 𝑇 𝛿 𝑢 𝑡 = sin Ω𝑡 − 𝜑 (1 − 𝛽 ) + 4𝜁 𝛽 Dao động bình ổn Ω/ωn=0.2, ζ = 0.05 u(0)=0; and v(0) =ωn F0/k với 𝛿 = ; 𝛽 = ; 𝜑 = tan 𝛿 Khi cộng hưởng: 𝑢 𝑡 = 𝑒
− 1 cos 𝜔 t với Ω = 𝜔 & 𝜔 ≈ 𝜔 2𝜁 83
DYN – UNIT 3 – DAO ĐỘNG DO TẢI TRỌNG ĐIỀU HÒA Resonance
3.2.2 Dao động điều hòa có cản: u 6 max & pha trễ 𝜙 ζ=0.01  Dao động bình ổn
𝑢(𝑡) = 𝐶 sin Ωt + 𝐷 cos Ωt ζ=0.1 4 F 1 − 𝛽 F −2𝜁𝛽 Ω 𝐶 = ; 𝐷 = ; 𝛽 = ζ=0.2 𝑘 1 − 𝛽 + 2𝜁𝛽 𝑘 1 − 𝛽 + 2𝜁𝛽 𝜔 2 ζ=0.4
 dạng khác: 𝑢(𝑡) = 𝑢 sin( Ω𝑡 − 𝜙) = 𝛿 𝑅 sin Ω𝑡 − 𝜙 Slowly loaded Rapidly ζ=1 loaded với: 𝐷 𝑢 = 𝐶 + 𝐷 ;
𝜙 = 𝑎𝑟𝑐𝑡𝑔 − 0 𝐶 0 1 2 3 𝜷 = 𝛀 𝝎
Phản ứng tần số / Frequency Response 𝑢 1 180 𝑅 = = ; 𝛿
→ hệ số động chuyển vị ζ=0.01 1 − 𝛽 + 2𝜁𝛽 (ngoài ra còn R ζ=1 v , Ra ) 90 ha trễ, ϕ 2𝜁𝛽 𝜙 P 𝜙 = tan
; 𝑡𝑖𝑚𝑒 𝑙𝑎𝑔 =
→ góc lệch pha (pha trễ) 𝜷 = 𝛀 𝝎 1 − 𝛽 2𝜋 0 0 1 2 3 84
DYN – UNIT 3 – DAO ĐỘNG DO TẢI TRỌNG ĐIỀU HÒA Resonance
3.2.2 Dao động điều hòa có cản: u 6 max & pha trễ 𝜙 ζ=0.01 ζ = 0.2 𝑅 = 1.29 Ω 𝜔 ⁄ = 0.5 ζ=0.1 4 𝑢(𝑡) 𝑡 (𝑢 ) 𝑇 ζ=0.2 𝜙 = 0.041 2𝜋 động u(t)/δ 2 ζ=0.4 Ω 𝜔 ⁄ = 1.0 𝑅 = 2.5 st Rapidly 𝑢(𝑡) ζ=1 𝑡 loaded (𝑢 ) 𝑇 0 0 1 2 3 𝜷 = 𝛀 𝝎 𝜙 = 0.25 2𝜋 tựa tĩnh F(t)/k 180 ζ=0.01 𝜔⁄𝜔 = 2 𝑅 = 0.32 ζ=1 𝑢(𝑡) 𝑡 90 ha trễ, ϕ (𝑢 ) 𝑇 P 𝜙 = 0.46 𝜷 = 𝛀 𝝎 2𝜋 0 0 1 2 3 85
DYN – UNIT 3 – DAO ĐỘNG DO TẢI TRỌNG ĐIỀU HÒA Resonance
3.2.2 Dao động điều hòa có cản: u 6 max & pha trễ 𝜙 ζ=0.01
 𝑢(𝑡) = 𝑢 sin Ω𝑡 − 𝜙 = 𝛿 𝑅 sin Ω𝑡 − 𝜙 ζ=0.1 4 𝑢 1 𝑅 = = ; 𝛿 ζ=0.2 1 − 𝛽 + 2𝜁𝛽 2 ζ=0.4
 0 < ζ < 1/√2 ~ Rd-max đạt được khi β < 1 Rapidly ζ=1 loaded 𝑅 = 0 ⟹ 𝛽 = 1 − 2𝜁 0 0 1 2 3 𝜷 = 𝛀 𝝎 1 180 R = ζ=0.01 2𝜁 1 − 𝜁 ζ=1 90 ha trễ, ϕ P 𝜷 = 𝛀 𝝎 0 0 1 2 3 86
DYN – UNIT 3 – DAO ĐỘNG DO TẢI TRỌNG ĐIỀU HÒA
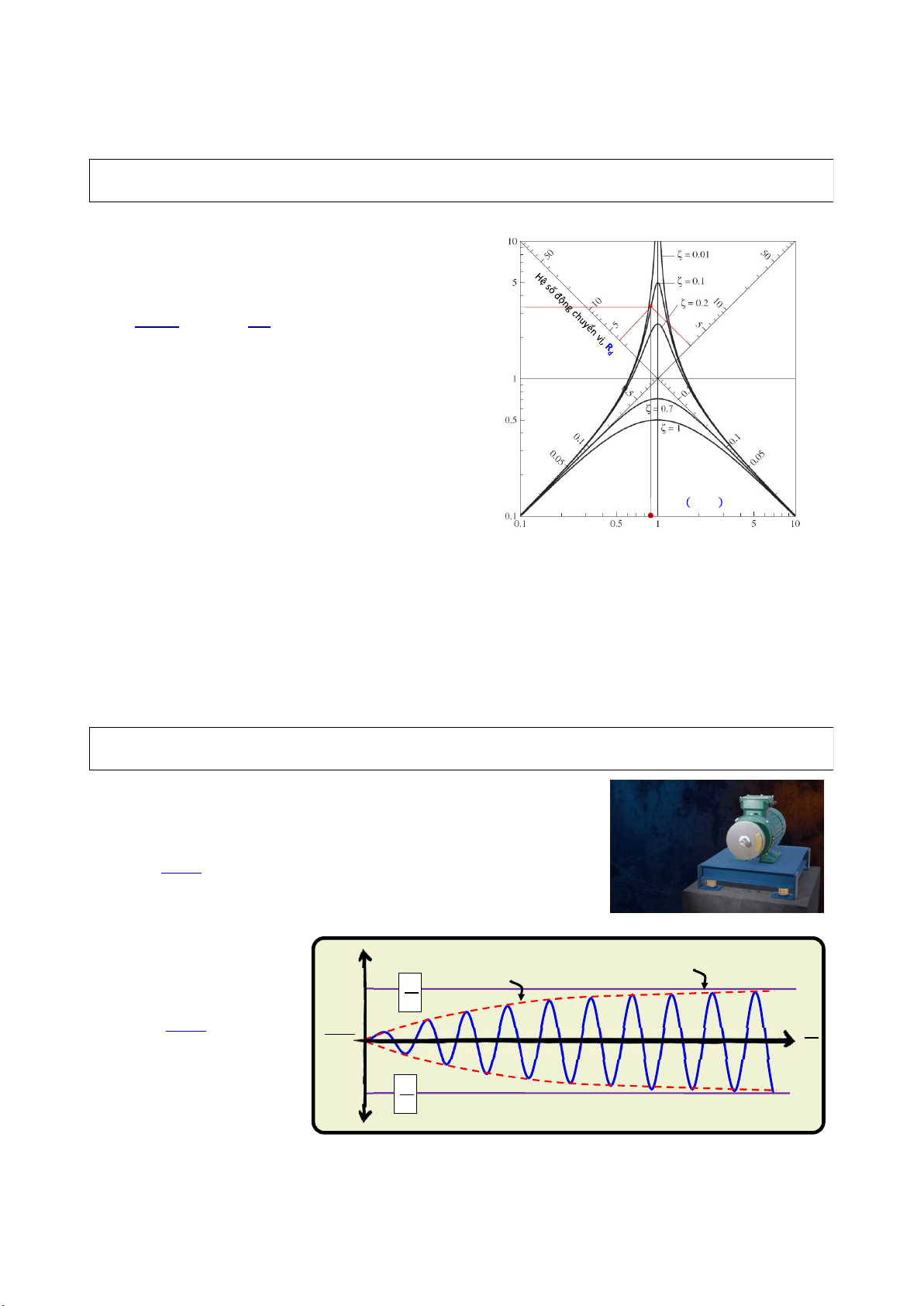
3.2.2 Dao động điều hòa có cản  Các hệ số động 𝑢(𝑡) 𝑢(𝑡)
𝑢(𝑡) = 𝛿 𝑅 sin Ω𝑡 − 𝜙 ℎ𝑎𝑦 = = 𝑅 sin Ω𝑡 − 𝜙 𝛿 𝐹 /𝑘 𝑢̇(𝑡) Ω = 𝑅 cos Ω𝑡 − 𝜙 với 𝑅 = 𝑅
→ hệ số động vận tốc F / 𝑘𝑚 𝜔 𝑢̈(𝑡) Ω = −𝑅 sin Ω𝑡 − 𝜙 với 𝑅 = 𝑅
→ hệ số động gia tốc F /𝑚 𝜔 = a 87
DYN – UNIT 3 – DAO ĐỘNG DO TẢI TRỌNG ĐIỀU HÒA
3.2.2 Dao động điều hòa có cản  Các hệ số động 𝑅 Ω = 𝑅 = 𝑅 Ω/𝜔 𝜔
ệ số động vận tốc, R v H
Hệ số động - Đồ thị logarit 4 Ω/𝜔
trục (four-way logarithmic plot) 88
DYN – UNIT 3 – DAO ĐỘNG DO TẢI TRỌNG ĐIỀU HÒA
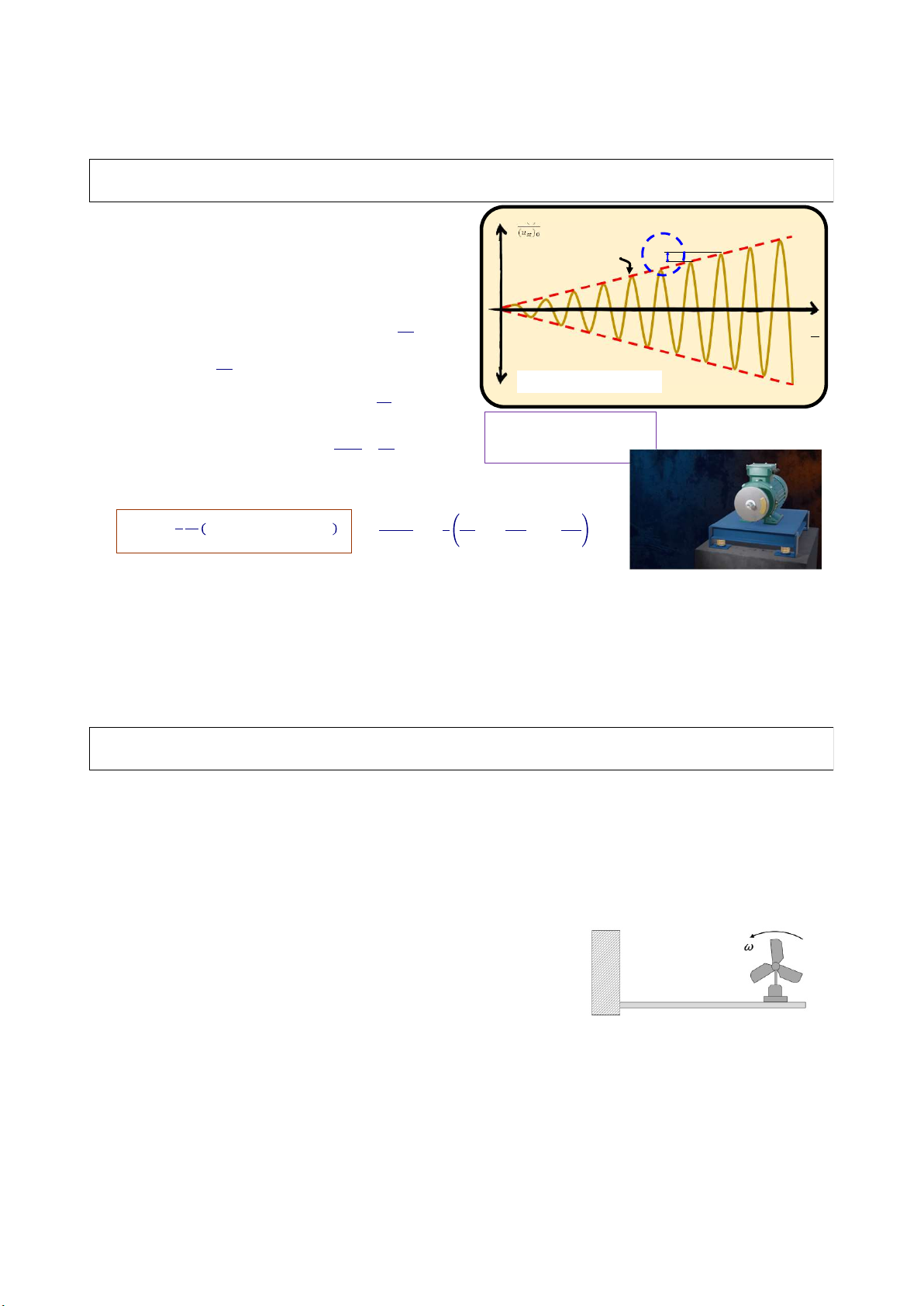
3.2.2 Dao động điều hòa có cản – cộng hưởng Ω = ωn  Biểu thức dao động (𝑢 ) 𝑢(𝑡) ≃ (𝑒 − 1) cos 𝜔 𝑡 2𝜁
i.e. dao động theo luật hàm cos; biên độ dao động tăng dần theo thời gian
- Giá trị tới hạn (1/2ζ) Biên độ bình ổn Đường bao - PT đường bao: 1 2𝜁 (𝑢 ) 𝑢(𝑡) = (𝑒 − 1) 𝑢(𝑡) 𝑡 2𝜁 (𝑢 ) 𝑇 1 2𝜁
ζ = 0.05 ;ω=ωn; u(0)= v(0)=0 89
DYN – UNIT 3 – DAO ĐỘNG DO TẢI TRỌNG ĐIỀU HÒA
3.2.2 Dao động điều hòa có cản – cộng hưởng Ω = ωn
 Tải trọng F(t) = F0cos(Ωt) Nghiệm riêng PTDĐ 𝑝 2𝜁𝛽 C = 𝑘 1 − 𝛽 + 2𝜁𝛽
𝑢 (𝑡) = 𝐶 sin 𝛺𝑡 + 𝐷 cos 𝛺𝑡 ⇒ & 𝑝 1 − 𝛽
D = 𝑘 1 − 𝛽 + 2𝜁𝛽 u 1 R = = 𝛿 1 − 𝛽 + 2𝜁𝛽
𝑢(𝑡) = 𝑢 cos 𝛺𝑡 − 𝜙 = 𝛿 𝑅 cos 𝛺𝑡 − 𝜙 2𝜁𝛽 𝜙 = tan 1 − 𝛽 90
DYN – UNIT 3 – DAO ĐỘNG DO TẢI TRỌNG ĐIỀU HÒA
3.2.2 Dao động điều hòa có cản
Ví dụ 4: khung thép như hình vẽ được dùng để đỡ một động cơ; khi hoạt động, động cơ gây ra
lực điều hòa F(t) = 1000sin(4t) (N) theo phương ngang tác dụng lên khung ở cao độ dầm đỡ. Giả
thiết, tỉ số cản 2% và dầm là tuyệt đối cứng; xác định:
a. Biên độ dao động bình ổn của khung
b. Ứng suất động lớn nhất trong cột m = 15 tons EI ∞ WF 250x125 4,5 m I = 4,050 cm4 E = 205,000 MPa 91
DYN – UNIT 3 – DAO ĐỘNG DO TẢI TRỌNG ĐIỀU HÒA
3.2.2 Dao động điều hòa có cản
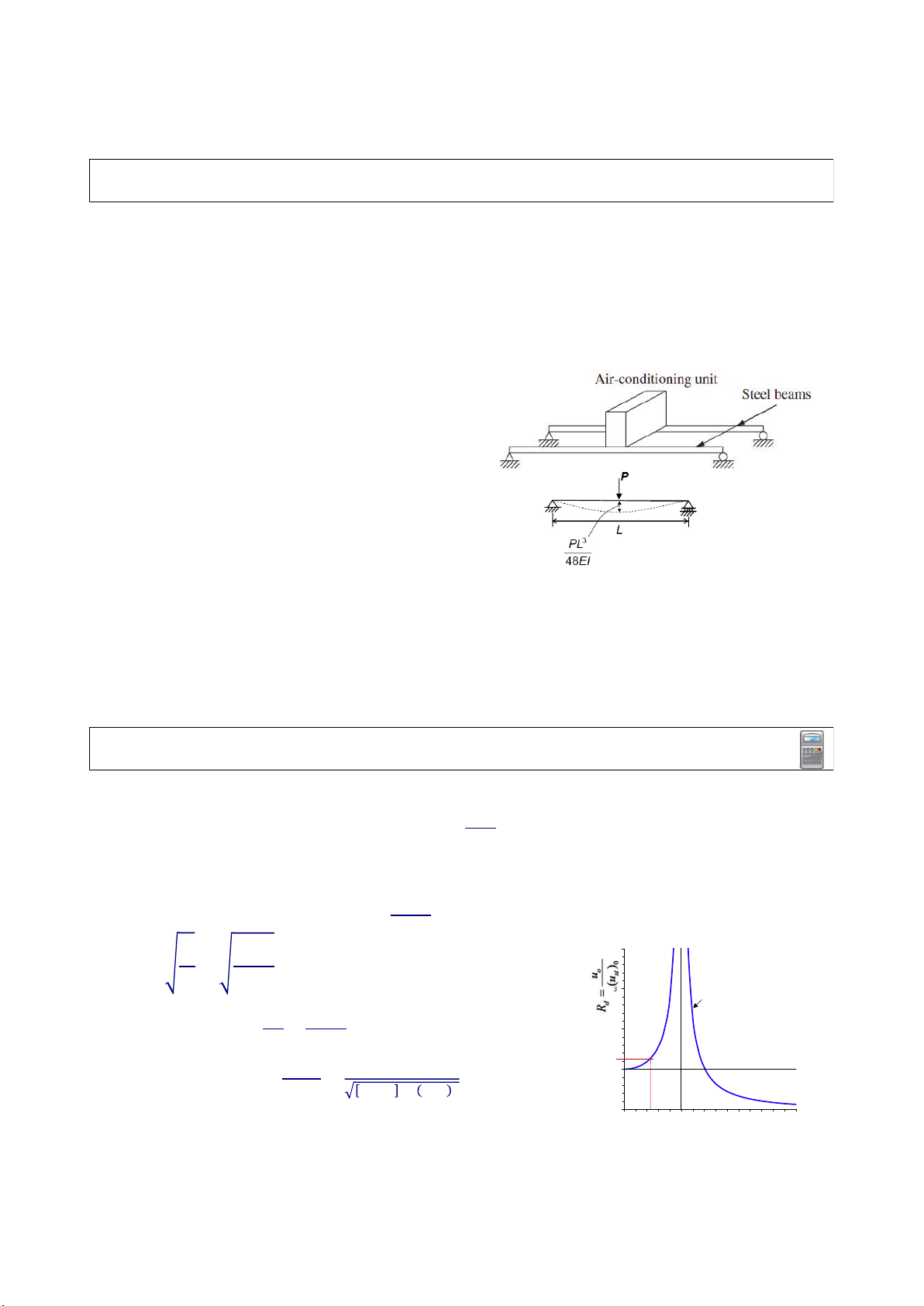
Ví dụ 5: Một chiếc điều hòa nặng 500 kg được lắp chặt vào 2 dầm đơn giản bằng thép (I = 1.0E-
6 m4 ; E = 200 GPa & L = 2 m). Mô tơ điều hòa hoạt động ở tốc độ 300 vòng/phút và tạo ra tải
trọng điều hòa có biên độ p0 = 300 N. Bỏ qua ảnh hưởng của khối lượng dầm. Xác định:
1. biên độ của chuyển vị và gia tốc tại điểm giữa dầm
2. mô men uốn lớn nhất trong dầm
 Độ cứng 𝑘 = 2400 kN/m
 Chuyển vị lớn nhất: 𝑢 = 1.6𝑥10 (𝑚)  gia tốc lớn nhất: 𝑢̈ = 1.56 (𝑚/𝑠 ) 92
DYN – UNIT 3 – DAO ĐỘNG DO TẢI TRỌNG ĐIỀU HÒA
3.2.2 Dao động điều hòa có cản 300
Ví dụ 5:  lực kích thích F = 300𝑁; Ω =
= 5 (vòng/s) = 5.2𝜋 = 10𝜋 (𝑟𝑎𝑑/ s) 60
𝑝(𝑡) = F sin( Ω𝑡) = 300 sin( 10𝜋𝑡)  tần số tự nhiên  48𝐸𝐼 n 𝑘 = 2𝑘 = 2
= 2400 𝑘𝑁/𝑚; 𝑚 = 0.5 𝑡𝑜𝑛 𝐿 𝑘 2400 4 𝜔 = = = 69.28 𝑟𝑎𝑑/𝑠 𝑚 0.5 3 ζ=0.01 𝜔 10𝜋  tỉ lệ tần số: 𝛽 = = = 0.453 2 𝜔 69.28 1.26  hệ số động: 1 𝑅 = = = 1.26 ( ) 0
(dầm thép, tỉ số cản  ≈ 1 %; R 0 0.45 1 2 3
d có thể tra trên biểu đồ phản ứng tần số) 𝜷 = 𝛀 𝝎 93
DYN – UNIT 3 – DAO ĐỘNG DO TẢI TRỌNG ĐIỀU HÒA
3.2.2 Dao động điều hòa có cản Fstatic Ví dụ 5: Fstatic  hệ số động: 𝑅 = = = 1.26 ( ) 0.095 kN.m 𝑝 0.3
 Chuyển vị lớn nhất: 𝑢 = 𝑅 . ≈ 1.26𝑥 = 1.6𝑥10 (𝑚) 𝑘 2400
 gia tốc lớn nhất: 𝑢̈ = Ω 𝑢 = 10𝜋 x 1 . 6 x 1 0 = 1.56 (𝑚/𝑠 ) 𝑢̈(𝑡) 𝑝 𝑝 𝜔
= −𝑅 sin( 𝜔𝑡 − 𝜙) ⇒ 𝑢̈ = 𝑅 = . . 𝑅 = 𝜔 𝑢 𝑝 /𝑚 𝑚 𝑚 𝜔 2400
 Lực tĩnh tương đương: Fstatic = u0.k/2 = 1.6 x 1 0 x = 0.19 (𝑘𝑁) 2
 Mô men uốn lớn nhất: 94
DYN – UNIT 3 – DAO ĐỘNG DO TẢI TRỌNG ĐIỀU HÒA
3.2.2 Dao động điều hòa có cản
Bài tập 2: hệ kết cấu khung nhà 1 tầng như hình vẽ. Hệ có kích thích ban đầu u(0) = 3 cm & v(0)
= 20 cm/s; và chịu tác dụng của tải trọng điều hòa P(t) = 5000sin(Ωt) (kN). Vẽ đồ thị biểu diễn
dao động của hệ trong khoảng thời gian t = 0 – 5s; biết ζ = 5% và β = 0.25; 0.6; 0.9; 1.25 & 1.75
(sử dụng công thức tại slide 82 hoặc 84) m = 25 tons EI ∞ 2 3 m 40x40 cm (b) E= 23,500 MPa 95
DYN – UNIT 3 – DAO ĐỘNG DO TẢI TRỌNG ĐIỀU HÒA
3.3 Truyền / Cô lập dao động
 Giảm thiểu (a) sự lan truyền dao động ra môi trường xung quanh & (b) ảnh hưởng do rung
động từ môi trường xung quanh lên kết cấu hoặc thiết bị nhạy cảm với dao động
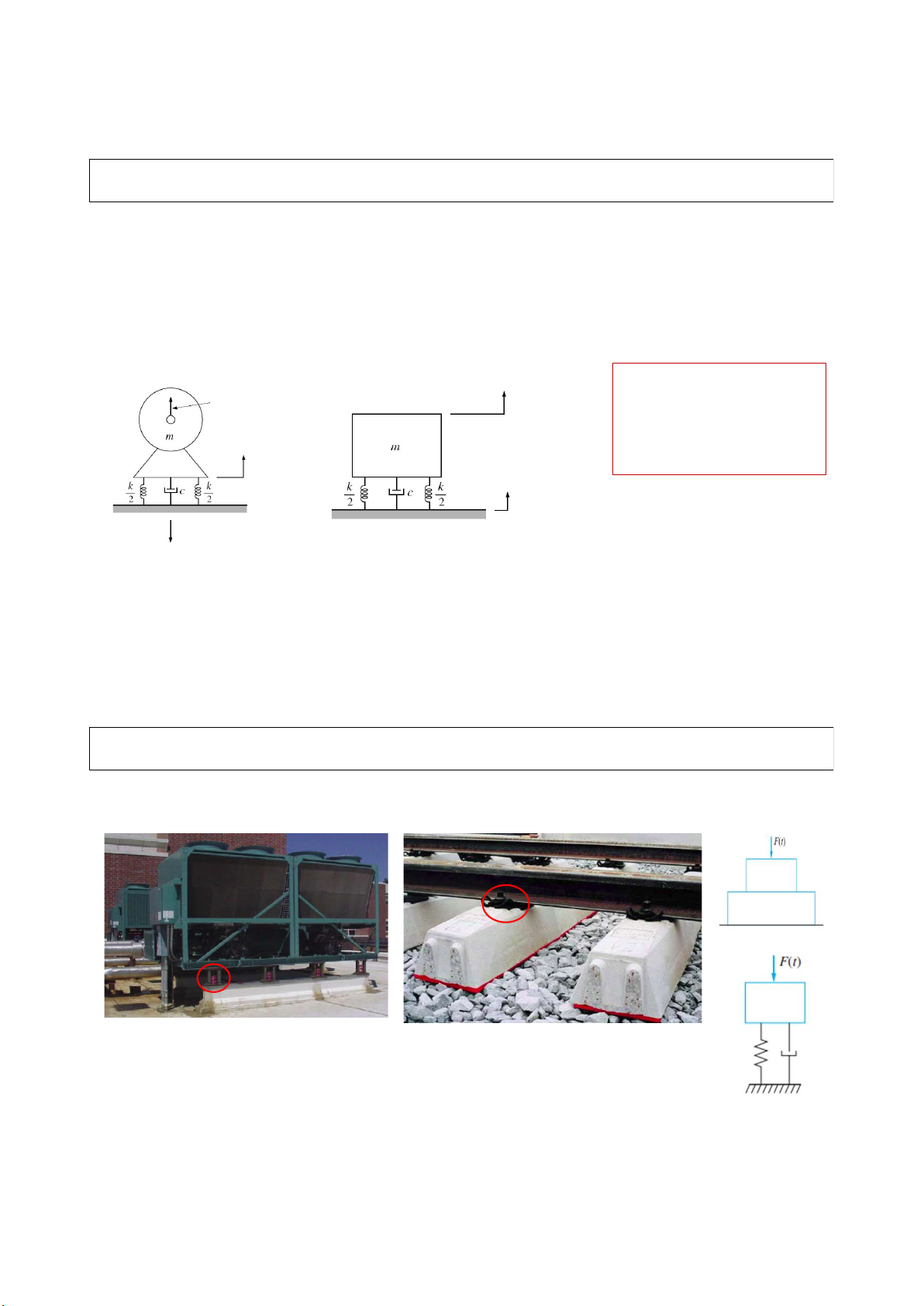
 Mô hình được xem là hệ SDOF; nối với môi trường xung quanh bằng lò xo k & bộ cản c (giá đỡ, bộ đệm...)
Với m, Ω cho trước, chọn 𝑢 (𝑡) F(𝑡) = F sin Ωt
k, c (ζ) để ảnh hưởng của
dao động là nhỏ nhất; i.e. 𝑢(𝑡)
𝑢 (𝑡) = 𝑢 (𝑡) + 𝑢(𝑡) (a) (b) lực truyền nhỏ nhất 𝑢 (𝑡) = 𝑢 sin Ωt 𝑓 = 𝑓 + 𝑓 96
DYN – UNIT 3 – DAO ĐỘNG DO TẢI TRỌNG ĐIỀU HÒA 3.3 Cô lập dao động 97
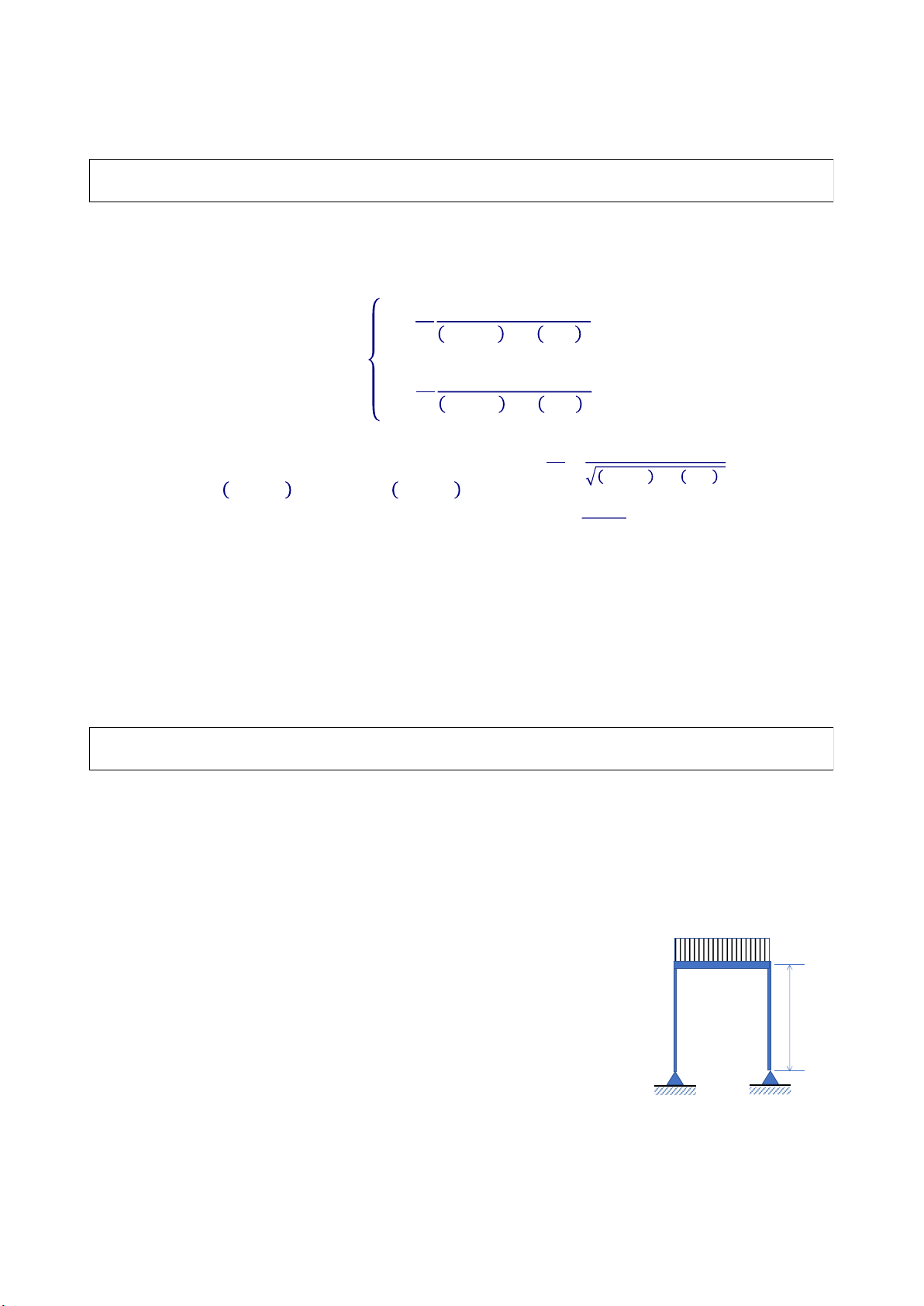
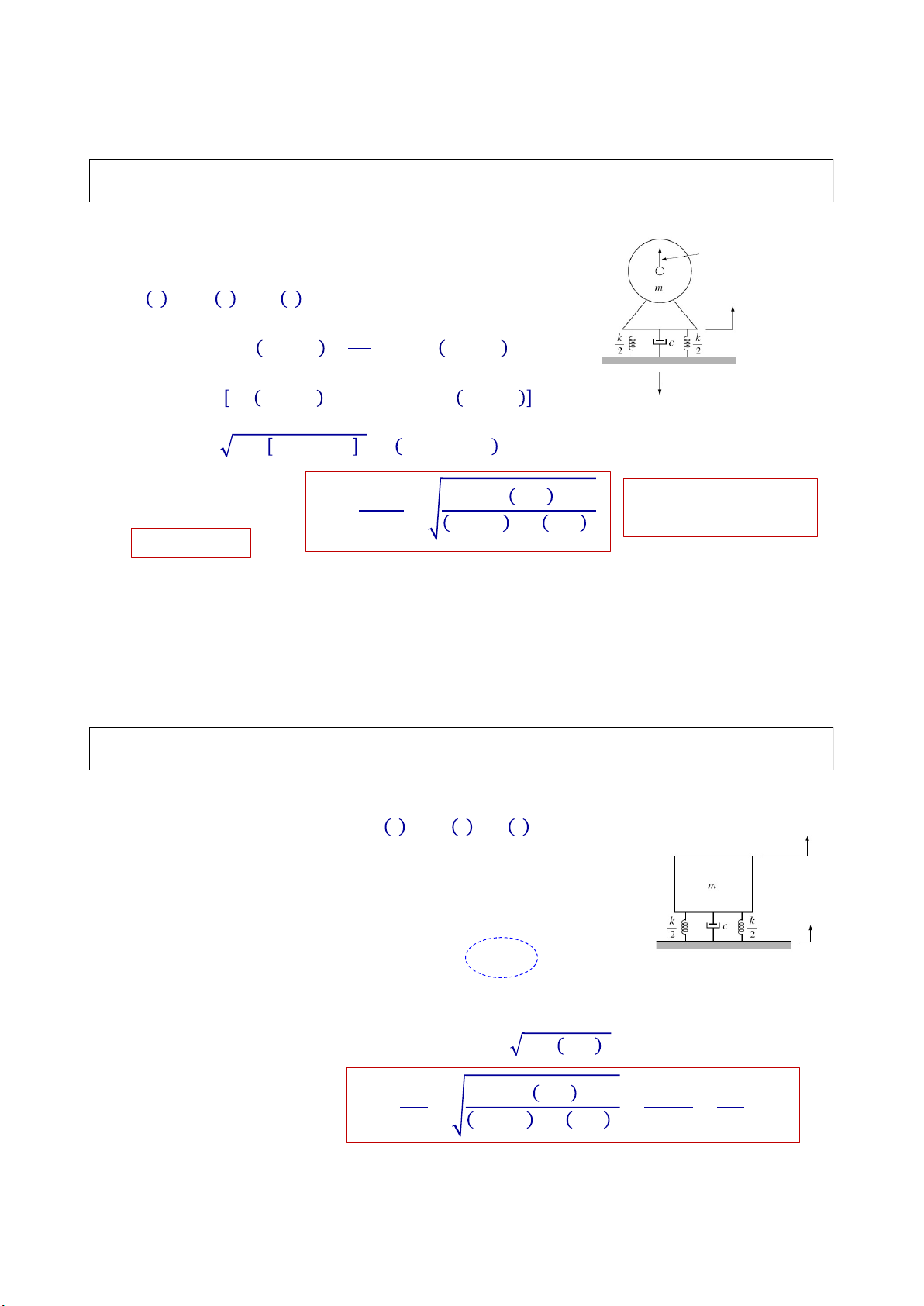
Máy điều hòa trung tâm (~ 10 tấn)
Rung động do xe lửa 25 – 50 Hz.
để trên mái nhà. Rung động trong
Dùng các tấm đệm đàn hồi để làm
các phòng ngay dưới vị trí để máy giảm rung động là 60 – 120 Hz 97
DYN – UNIT 3 – DAO ĐỘNG DO TẢI TRỌNG ĐIỀU HÒA 3.3 Cô lập dao động
 (a) Lực truyền xuống móng (dao động bình ổn) F(𝑡) = F sin Ω 𝑡
𝑓 𝑡 = 𝑘𝑢 𝑡 + 𝑐𝑢̇ 𝑡 𝑢(𝑡) (a)
= F 𝑅 sin Ω𝑡 − 𝜙 + 𝑅 Ω cos Ω𝑡 − 𝜙
= F 𝑅 sin Ω𝑡 − 𝜙 + 2𝜁(Ω/𝜔 ) cos Ω𝑡 − 𝜙 𝑓 = 𝑓 + 𝑓 = F 𝑅
1 + 2𝜁(Ω/𝜔 ) sin Ω𝑡 − 𝜙 + 𝛼
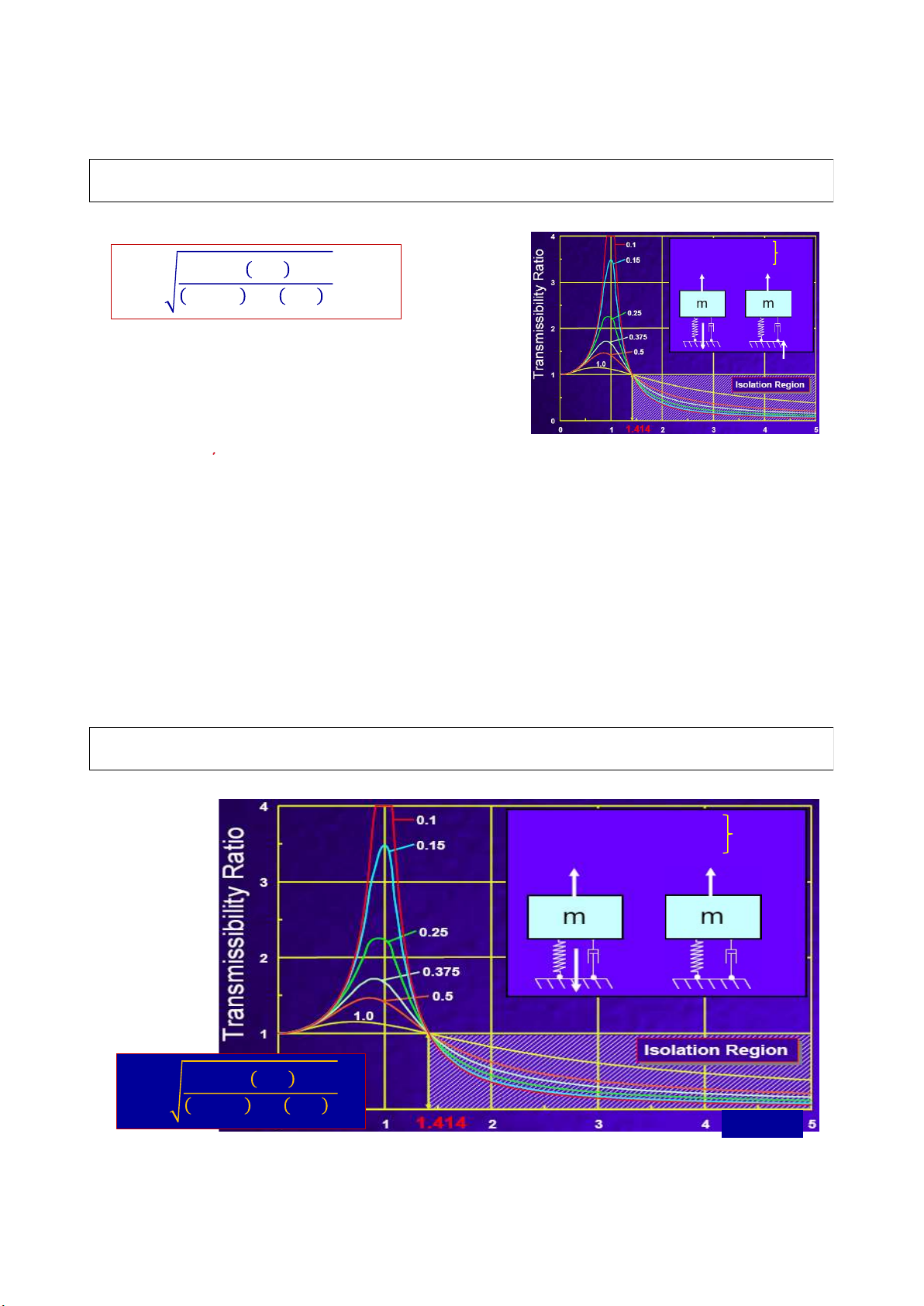
 Hệ số truyền dao động 𝑓 1 + 2𝜁𝛽
Chọn k, c (ζ) để TR nhỏ 𝑇𝑅 = = 𝐹 1 − 𝛽 + 2𝜁𝛽 nhất có thể. 𝑪𝑳 = 𝟏 − 𝑻𝑹 98
DYN – UNIT 3 – DAO ĐỘNG DO TẢI TRỌNG ĐIỀU HÒA 3.3 Cô lập dao động
(b) Do dao động từ móng/bệ đỡ 𝑢 𝑡 = 𝑢 𝑡 + 𝑢 𝑡 ; 𝑢 (𝑡) = 𝑢 𝑠𝑖𝑛 Ω𝑡 𝑢 (𝑡)
- ut(t): tổng dao động của khối lượng m
- ug(t): dao động của nền đất 𝑢 (𝑡)
- u(t): dao động tương đối của khối lượng m so với móng p0
 PTDĐ 𝑚𝑢̈(𝑡) + 𝑐𝑢̇(𝑡) + 𝑘𝑢(𝑡) = −𝑚𝑢̈ = 𝑚𝑢 Ω sin 𝜔 𝑡 = 𝑝 sin Ω 𝑡
 Dao động bình ổn 𝑢(𝑡) = 𝑢 (Ω/𝜔 ) 𝑅 sin( Ω𝑡 − 𝜙) ) = 𝑢̈ (1/𝜔 ) 𝑅 𝑠𝑖𝑛( 𝛺𝑡 − 𝜙)  Tổng dao động
𝑢 (𝑡) = 𝑢 (𝑡) + 𝑢(𝑡) = 𝑢 𝑅 1 + 2𝜁𝛽 sin( Ω𝑡 − 𝜙 + 𝛼) 𝑢 1 + 2𝜁𝛽 Ω 𝑢 𝑢̈
 Hệ số truyền dao động 𝑇𝑅 = = = = 𝑢 1 − 𝛽 + 2𝜁𝛽 Ω 𝑢 𝑢̈ 99
DYN – UNIT 3 – DAO ĐỘNG DO TẢI TRỌNG ĐIỀU HÒA
3.3 Cô lập dao động – hệ số truyền dao động TR m, P(t), ug(t) = const Tr k, c (z) ~ design min 1 + 2𝜁𝛽 P(t) ut(t) 𝑇𝑅 = 1 − 𝛽 + 2𝜁𝛽 k c k cug(t)
- Thành phần cản chỉ có tác dụng làm giảm sự truyền fT dao động khi β < √2
- Lực truyền lên bé hơn lực tác động khi β > √2 (i.e. k <
ω2.m/2); lúc này, lực cản lại làm tăng TR. Để có TR nhỏ, cần chọn ωn & ζ bé 𝜷 = 𝛀 𝝎 - Tuy nhiên, ω  k phải đủ cứng
n bé, i.e. k bé → (ust)0 quá lớn
- ζ quá bé, u0 có thể quá lớn khi tần số kích thích tăng lên và trùng tần số cộng hưởng.
- Cao su tự nhiên là vật liệu tốt để cô lập dao động (f = 25 – 50 Hz). 100
DYN – UNIT 3 – DAO ĐỘNG DO TẢI TRỌNG ĐIỀU HÒA
3.3 Cô lập dao động – hệ số truyền dao động TR m, P(t), ug(t) = const Trmin k, c (z) ~ design P(t) ut(t) k c k c ug(t) 1 + 2𝜁𝛽 𝑇𝑅 = 1 − 𝛽 + 2𝜁𝛽 𝜷 = 𝛀 𝝎 101
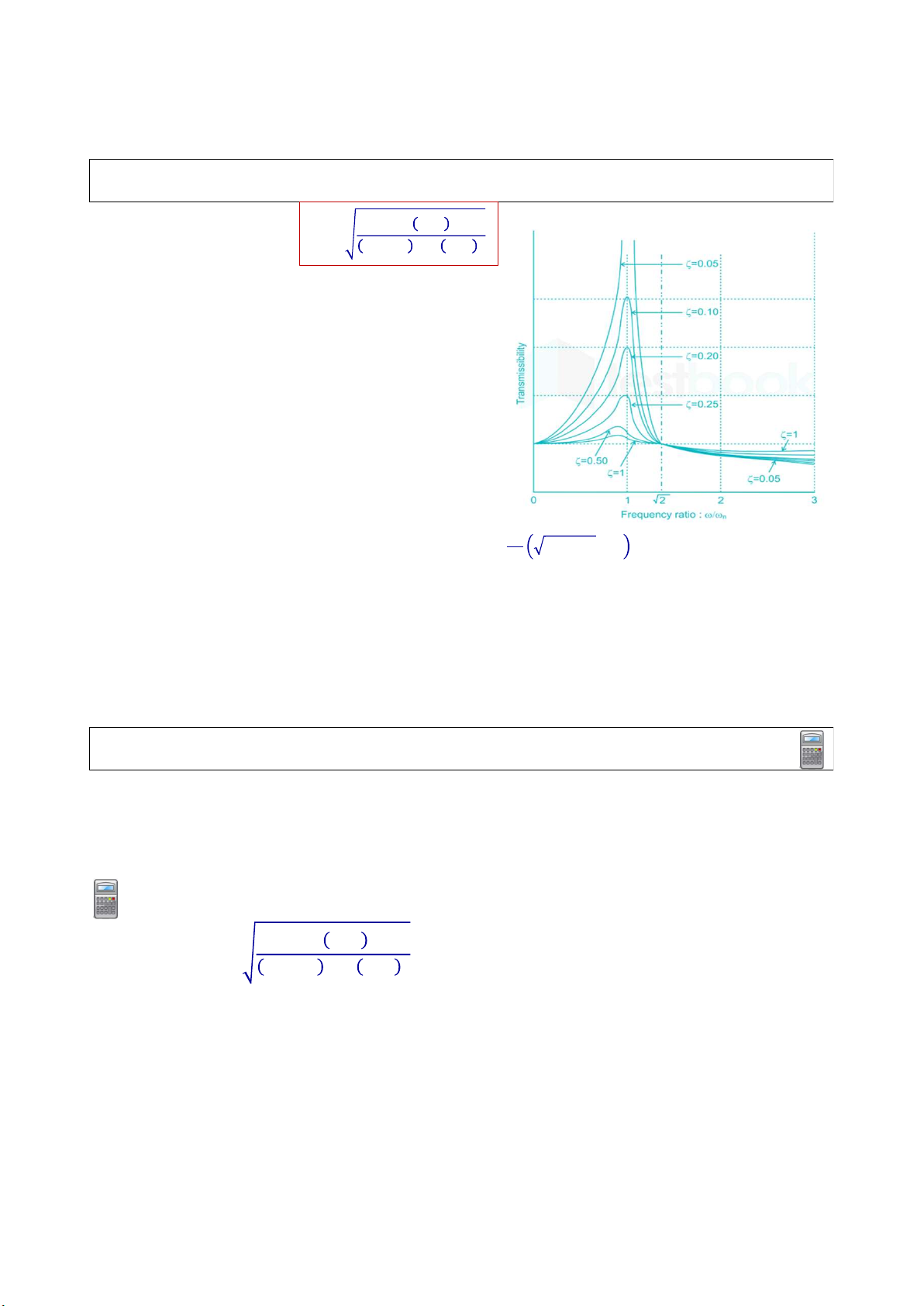
DYN – UNIT 3 – DAO ĐỘNG DO TẢI TRỌNG ĐIỀU HÒA 3.3 Cô lập dao động 1 + 2𝜁𝛽 𝑇𝑅 = 1 − 𝛽 + 2𝜁𝛽
• TR = 1 khi β = 0 & TR ≈ 1 khi β bé (với mọi giá trị của ζ; i.e. không phụ thuộc cản
• Hệ không cản (ζ = 0), TR →∞ khi cộng hưởng (β = 1)
• TR < 1 khi β > √2 (với mọi giá trị của ζ); i.e. lực truyền bé hơn
lực tác động (mục tiêu ~ vùng cô lập)
• TR = 1 khi β = √2 (với mọi giá trị của ζ)
• β < √2, nếu cản bé sẽ dẫn đến hệ số truyền lớn (i.e. lực truyền
lớn hơn lực tác động nhiều lần). Ngược lại, khi β > √2, cản bé
giúp làm giảm giá trị của TR 1
• TR đạt giá trị lớn nhất tại tỉ lệ tần số β 1 + 8𝜁 − 1 m (xét 0 < ζ < 1) 𝛽 = 2𝜁 102
DYN – UNIT 3 – DAO ĐỘNG DO TẢI TRỌNG ĐIỀU HÒA
Ví dụ 6: máy điều hòa không khí có trọng lượng 1 kN và động cơ hoạt động ở tốc độ 500 rpm.
Giá đỡ cần có chuyển vị tĩnh là bao nhiêu để đạt được độ cô lập dao động là 80% nếu giá đỡ có (a) ζ = 0 & (b) ζ = 10%
 Độ cô lập đạt 80% ~ lực truyền bằng (a) ζ = 0 1 + 2𝜁𝛽 𝑇𝑅 = 1 − 𝛽 + 2𝜁𝛽 103
DYN – UNIT 3 – DAO ĐỘNG DO TẢI TRỌNG ĐIỀU HÒA
Ví dụ 6: máy điều hòa không khí có trọng lượng 1 kN và động cơ hoạt động ở tốc độ 500 rpm.
Giá đỡ cần có chuyển vị tĩnh là bao nhiêu để đạt được độ cô lập dao động là 80% nếu giá đỡ có (a) ζ = 0 & (b) ζ = 10%
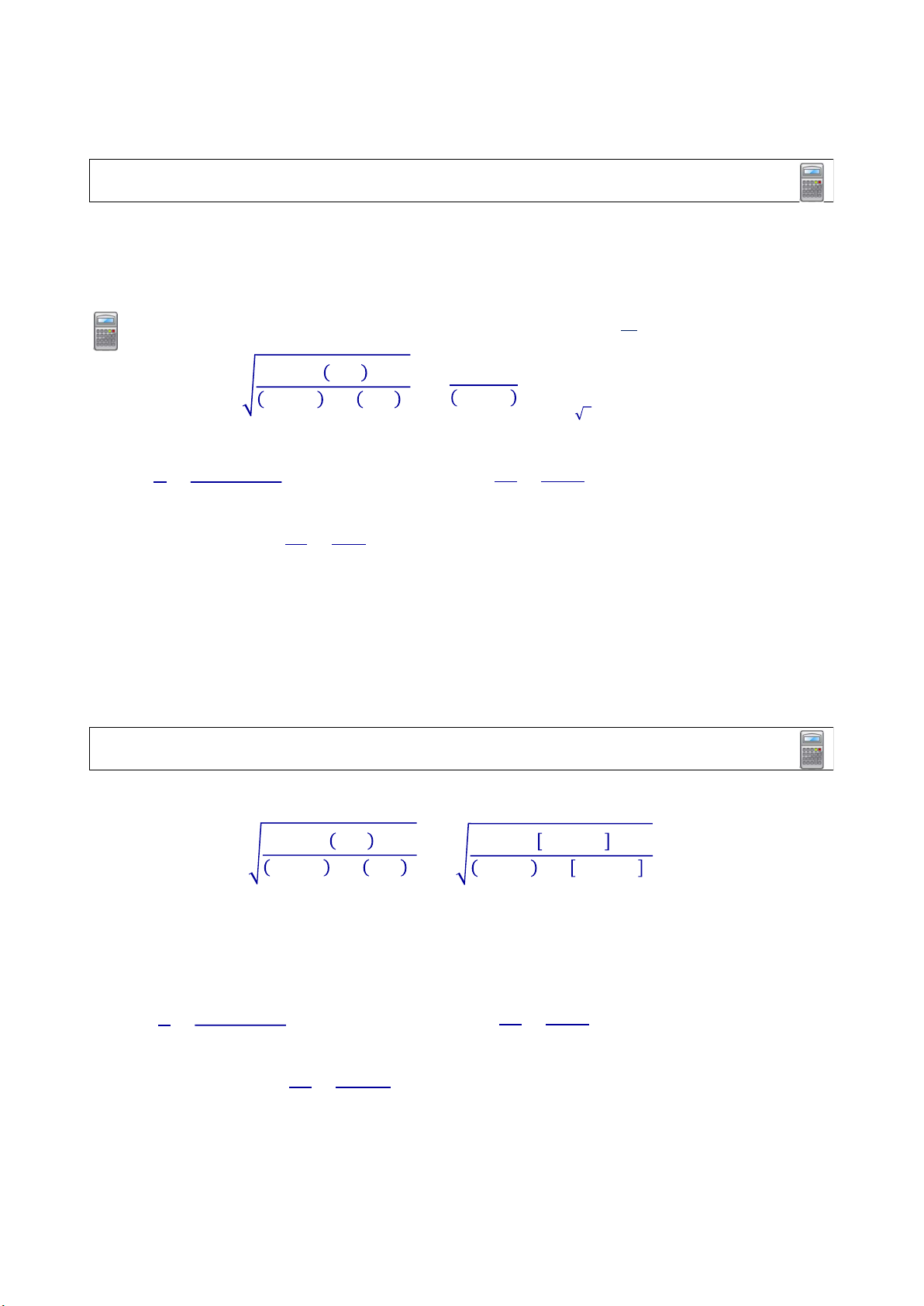
 Độ cô lập đạt 80% ~ lực truyền bằng 20% lực tác dụng 𝑇𝑅 = = 0.2 1 (a) ζ = 0 1 + 2𝜁𝛽 𝑇𝑅 = = = 0.2 → 𝛽 = 2.45 1 − 𝛽 + 2𝜁𝛽 𝛽 − 1
(𝛽 > 2 Để đạt được sự cô lập)
 Tần số tự nhiên lớn nhất của hệ để đạt được độ cách ly 80% Ω 500x2𝜋/60 g 9.81 𝜔 = = = 21.4 rad/s ⟹ 𝛿 = = = 0.02 m 𝛽 2.45 𝜔 21.4 W 1  Độ cứng ⟹ k = = = 50 kN/m 𝛿 0.02 104
DYN – UNIT 3 – DAO ĐỘNG DO TẢI TRỌNG ĐIỀU HÒA Ví dụ 6: (a) ζ = 0.1 1 + 2𝜁𝛽 1 + 2(0.1)𝛽 𝑇𝑅 = = = 0.2 1 − 𝛽 + 2𝜁𝛽 1 − 𝛽 + 2(0.1)𝛽
⟹ 𝛽 −2.9𝛽 − 24 = 0 ⟹ 𝛽 = 6.60 ⟹ 𝛽 = 2.57 (Note: lớn hơn giá trị khi ζ = 0)
 Tần số tự nhiên lớn nhất của hệ để đạt được độ cách ly 80% Ω 500x2𝜋/60 g 9.81 𝜔 = = = 20.4 rad/s ⟹ 𝛿 = = = 0.0236 m 𝛽 2.57 𝜔 20.4 W 1  Độ cứng ⟹ k = = = 42.4 kN/m 𝛿 0.0236 105