CHƯƠNG VI. MỘT SỐ YẾU TỐ THỐNG KÊ VÀ XÁC SUẤT
§1. THU THẬP VÀ PHÂN LOẠI DỮ LIỆU
Dạng 1. Thu thập dữ liệu
1. Các phương pháp thu thập dữ liệu trong mỗi trường hợp sau là trực tiếp hay gián tiếp?
a) Nam phỏng vấn các bạn trong lớp và ghi lại môn thể thao yêu thích của từng bạn.
b) Cách tra cứ và ghi lại số liệu vụ cháy trên địa bàn thành phố Hà Nội trên website của Cục Cảnh sát PCCC.
c) Nhân viên bán hoa quả đã thống kê và ghi lại số lượng từng loại hoa quả cửa hàng mình đã bán trong một ngày.
2. Để thu nhập dữ liệu sau, ta nên sử dụng phương pháp thu nhập dữ liệu nào? Đó là thu thập dữ liệu trực tiếp hay gián tiếp?
a) Dữ liệu về dân số của các tỉnh vùng núi và trung du phía Bắc.
b) Số liệu về lượng mưa trung bình trong sáu tháng đầu năm tại tỉnh Ninh Bình.
3. Nên sử dụng phương pháp thu thập dữ liệu nào để thu thập mỗi dữ liệu sau?
a) Tên các giống lúa được gieo trồng phổ biến tại Việt Nam.
b) Điểm kiểm tra học kì 1 môn Toán của các bạn trong lớp.
c) Thời gian đọc sách hằng ngày của các học sinh trong lớp.
4. Em hãy thu thập thông tim về vận động viên yêu thích của một số bạn trong lớp và cho biết phương
pháp thu thập thông tin mà em sử dụng là trực tiếp hay gián tiếp.
Dạng 2. Phân loại dữ liệu
5. Với mỗi câu hỏi sau, Thành đã hỏi năm bạn và ghi lại câu trả lời như sau. Mỗi dãy dữ liệu sau đó thuộc loại nào?
a) Số thành viên trong gia đình bạn? Kết quả 4;5;3;2;4.
b) Bạn thích chơi môn thể thao nào? Kết quả: 3 ; km 4, 2k ; m 6,8 ; km 7, 2k ; m 5km .
6. Dữ liệu thu được trong mỗi câu hỏi sau thuộc loại nào?
a) Lớp học của bạn có bao nhiêu học sinh cao trên 1,5 mét?
b) Nhiệt độ trung bình tại thành phố Đà Lạt trong năm 2022?
c) Các tháng có 31 ngày trong năm?
7. Để thu thập số liệu về thời gian chơi thể thao trong một ngày của một số bạn trong lớp, An đã phỏng vấn
5 bạn và ghi lại kết quả như sau: 2 giờ; 0,5 giờ; 1, 2 giờ; 30 giờ; 1,5 giờ. Dãy số liệu trên thuộc loại
nào? Trong dãy số liệu có giá trị nào không hợp lí không? Vì sao?
8. Trong các dãy số liệu sau, dãy số liệu nào là số liệu liên tục? Dãy số liệu nào là số liệu rời rạc?
a) Số tuổi của các thành viên trong gia đình bạn Trang: 54; 47; 25;24;14.
b) Quãng đường đi được của một xe ô tô trong ba tiếng liên tiếp: 50 ; km 93,5 ;134, km 9km. o
c) Nhiệt độ nóng chảy của một số kim loại (đơn vị C ): 1084,62 (đồng); 1538 (sắt); 1064,18 (vàng);
961,78 (bạc); 660,32 (nhôm).
9. Nối tên các loại dữ liệu và dãy dữ liệu phù hợp. A. Số liệu rời rạc
1. Đánh giá dịch vụ của khách hàng tại một quán ăn: Rất
tốt, Tốt, Bình thường, Kém. B. Số liệu liên tục
2. Thời gian chạy cự li 100 mét (đơn vị: giây) của năm
bạn học sinh 15, 4;16,32;14,9;17, 2;16.
C. Dữ liệu không là số, không thể sắp thứ tự 3. Sĩ số các lớp khối 8 tai một trường: 32;40;36;38;35
Dữ liệu không là số, có thể sắp thứ tự
4. Các loại hoa quả được gieo trồng tại Việt Nam: vải,
mít, thanh long, chối, dưa hấu,…
BÀI TẬP TỰ LUYỆN
1. Các phương pháp thu thập dữ liệu trong các trường hợp sau là trực tiếp hay gián tiếp?
a) An phát phiếu hỏi để thu thập thông tin về các hoạt động trong hè của các bạn học sinh trong trường.
b) An tra cứu thông tin trên internet về tên của các loài động vật quý hiếm được đưa vào danh sách đỏ.
2. Để nâng cao chất lượng phục vụ tại một khách sạn, nhân viên tiến hành khảo sát ý kiến đánh giá của các
khách hàng. Hãy đề xuất những phương pháp phù hợp để thu thập dữ liệu về ý kiến của khách hàng và
cho biết phương pháp đó là thu thập trực tiếp hay gián tiếp?
3. Hãy cho biết mỗi dữ liệu sau thuộc loại nào?
a) Tên các loài cây trong sân trường: Xà cừ, bàng, phượng, bằng lăng, hoa giấy, hoa hồng.
b) Số vật nuôi trong gia đình của các thành viên trong tổ 2;1;4;2;3;0;6.
c) Đánh giá xếp loại học lực của học sinh: Tốt, Khá, Đạt, Không đạt.
d) Chiều cao của một số bạn trong lớp 1,58 ;1 m ,63 ;1 m ,7 ;1 m ,55 ;1 m ,67 . m
4. Dữ liệu thu được trong mỗi câu hỏi sau thuộc loại nào?
a) Bạn có bao nhiêu anh, chị trong gia đình?
b) Vật nuôi bạn yêu thích nhất của bạn là gì?
c) Mỗi ngày bạn dành bao nhiêu thời gian để nghe nhạc?
5. Kết quả thu thập thông tin về các hộ gia đình trong một khu dân cư được trình bày trong bảng sau: Tên chủ hộ Năm sinh Nghề nghiệp Số con Nguyễn Văn Mạnh 1965 Bác sĩ 2 Trần Thanh Tùng 1971 Giáo viên 1 Nguyễn Anh Tuấn 1973 Kĩ sư 2 Phạm Thành Công 1969 Kế toán 3 Vũ Văn Thanh 1981 Nhà báo 1
6. Nam tra cứu và ghi lại tốc độ chạy của một số loài động vật vào bảng sau: Tên động vật Tốc độ (km/h) Báo 120 Dơi không đuôi 96,6 Linh dương 802 Thỏ nâu rừng 77 Ngựa 71
Dãy số liệu trên thuộc loại nào? Trong dãy số liệu có giá trị nào không hợp lí không? Vì sao?
§2. MÔ TẢ VÀ BIỂU DIỄN DỮ LIỆU TRÊN CÁC BẢNG, BIỂU ĐỒ
Dạng 1. Lựa chọn biểu đồ tranh hay biểu đồ cột
1. Biểu đồ sau biểu diễn số lượng học sinh lớp 8E yêu thích một số loài hoa.
Tên các loài hoa Số học sinh Hoa hồng 10 Hoa lan 8 Hoa cẩm tú cầu 16
a) Lập bảng thống kê số lượng học sinh lớp 8E yêu thích các loài hoa trên.
b) Vẽ biểu đồ cột biểu diễn số liệu đó.
2. Đầu năm học lớp 8A muốn may đồng phục lớp. Lớp trưởng thu thập cỡ áo của các bạn học sinh trong
lớp và tổng hợp thành báng sau: Cỡ áo S M L XL Số lượng 3 21 14 6
a) Vẽ biểu đồ cột biểu diễn số liệu trên.
b) Nếu muốn biểu diễn dữ liệu trên bảng bằng biểu đồ tranh, ta nên chọn mỗi biểu tượng biểu diễn cho bao nhiêu học sinh?
3. Trong chiến dịch trồng cây xanh do nhà trường tổ chức, số lượng cây trồng được của các khối được biểu diễn trong bảng sau: Khối 6 7 8 9 Số cây 145 178 205 193
Nếu muốn vẽ biểu đồ biểu diễn trên, ta nên dùng biểu đồ tranh hay biểu đồ cột? Vẽ biểu đồ đó.
Dạng 2. Lựa chọn biểu đồ cột hay biểu đồ đoạn thẳng
4. Bảng số liệu sau biểu diễn độ ẩm không khí trung bình tại một số trạm quan trắc năm 2021 Trạm quan  %  trắc
Độ ẩm không khí trung binh Lai Châu 82,8 Sơn La 77,9 Tuyên Quang 80,7 Hà Nội 75, 0 Nam Định 81,6
Chọn biểu đồ phù hợp để biểu diễn độ ẩm không khí trung bình tại một số trạm quan trắc năm 2021. Tại
sao em lại chọn biểu đồ đó?
5. Biểu đồ cột sau biểu diễn số trường đại học, học viện trên cả nước các nă, từ 2015 đến 2020.
a) Lập bảng thống kê cho dữ liệu trong biểu đồ trên.
b) Vẽ biểu đồ đoạn thẳng biểu diễn số liệu đó.
6. Bảng số liệu sau biểu diễn nhiệt độ không khí trung bình các tháng tại Hà Nội năm 2018. Tháng 1 2 3 4 5 6 7 8 9 10 11 12  oC  18,1 17,5 22,7 24, 4 29,5 30,6 30,1 29,1 29,0 26,1 24, 2 19,9 Nhiệt độ
a) Vẽ biểu đồ biểu diễn số liệu trên.
b) Để biểu diễn sự thay đổi của nhiệu độ không khí trung bình qua các tháng tại Hà Nội năm 2018 ta
nên sử dụng biểu đồ nào?
Dạng 3. Lựa chọn biểu đồ cột hay biểu đồ hình quạt tròn
7. Số học sinh được xếp loại học tập theo bốn mức trong HKI của mỗi lớp được thống kê ở bảng sau: Lớp Tốt Khá Đạt Chưa đạt 8A 10 15 5 1 8B 12 16 7 2
Vẽ biểu đồ để so sánh số học sinh được xếp loại theo từng mức của hai lớp.
8. Biểu đồ sau biểu diễn số huy chương Vàng, Bạc, Đồng của trường A và trường B khi tham gia hội thi
Thể dục thể thao cấp thành phố.
a) Lập bảng thống kê cho số liệu được biểu diễn ở biểu đồ trên.
b) Vẽ biểu đồ biểu diễn tỉ lệ số huy chương Vàng, Bạc, Đồng của trường A và trường B.
9. Biểu đồ sau biểu diễn tỉ lệ học sinh tham gia các câu lạc bộ của lớp 8A.
a) Lập bảng thống kê cho số liệu được biểu diễn ở biểu đồ trên.
b) Cho biết lớp 8A có 40 học sinh. Vẽ biểu đồ cột biểu diễn số lượng học sinh tham gia các câu lạc bộ của lớp 8A. BÀI TẬP RÈN LUYỆN
1. Bảng dữ liệu sua biểu diễn số lượng áo phông được bán trong một tuần của một cửa hàng quần áo. Ngày Thứ 2 Thứ 3
Thứ 4 Thứ 5 Thứ 6 Thứ 7 Chủ nhật Số lượng 100 131 83 91 152 205 224 (chiếc)
a) Vẽ biểu đồ cột để biểu diễn số liệu trong bảng thống kê trên.
b) Ta có nên sử dụng biểu đồ tranh để biểu diễn số liệu đó không? Vì sao?
2. Biểu đồ sau biểu diễn tỉ lệ hộ nghèo ở nước ta trong các năm từ 2015 đến 2020.
a) Lập bảng thống kê cho số liệu trong biểu đồ trên.
b) Vẽ biểu đồ đoạn thẳng biểu diễn tỉ lệ hộ nghèo ở nước ta qua các năm từ 2015 đến 2020.
3. Bảng số liệu sau biểu diễn kim ngạch xuất khẩu hạt tiêu tại Việt Nam các năm từ 2011 đến 2020. Năm 2011 2012 2013 2014 2015
Kim ngạch xuất khẩu hạt tiêu 793, 889, 1201, 1259, 732,5 (triệu đô la Mỹ) 7 8 9 9 Năm 2016 2017 2018 2019 2020
Kim ngạch xuất khẩu hạt tiêu 1429, (triệu đô la Mỹ) 1118 759 714,4 660,6 2
a) Để biểu diễn số liệu trong bảng trên ta có nên dùng biểu cột không? Vì sao?
b) Biểu đồ nào phù hợp để biểu diễn bảng số liệu trên?
4. Để quản lí chi tiêu, một người chia tổng thu nhập hàng tháng của mình thành sáu phần theo bảng sau: Tổng thu nhập 100% Chi tiêu cần thiết 55% Tiết kiệm dài hạn 10% Đầu tư sinh lời 10% Giáo dục 10% Hưởng thụ 5% Cho đi 10%
Ta nên sử dụng biểu đồ nào để biểu diễn tỉ lệ các danh mục chi tiêu so với tổng thu nhập hàng tháng? Vẽ biểu đồ đó.
5. Biểu đồ sau biểu diễn tình hình xuất khẩu gạo của Việt Nam và Thái Lan trong hai năm 2020 và 2022.
a) Lập bảng thống kê cho số liệu được biểu diễn trong biểu đồ trên.
b) Vẽ biểu đồ so sánh xuất khẩu gạo năm 2020 và 2022 của mỗi nước.
§3. PHÂN TÍCH VÀ XỬ LÍ DỮ LIỆU THU ĐƯỢC Ở DẠNG BẢNG, BIỂU ĐỒ 1. Cho hai biểu đồ sau:
a) Hai biểu đồ trên có biểu diễn cùng một tập dữ liệu không? Lập bảng thống kê cho dữ liệu đó.
b) Trong từng biểu đồ, so sánh tỉ lệ chiều cao của hai cột và tỉ lệ số liệu mà hai cột này biểu diễn. Tại sao có sự khác nhau đó? 2. Cho hai biểu đồ sau:
a) So sánh độ dốc của hai biểu đồ.
b) Tại sao biểu đồ b) dễ làm cho ta hiểu lầm rằng mật độ dân số tại thành phố Hà Nội năm 2020 tăng
đột biến so với trước?
c) Để thấy được xu thế của mật độ dân số tại thành phố Hà Nội, ta nên dùng biểu đồ nào? 3. Cho hai biểu đồ sau:
a) Nhận xét về xu thế thay đôi của hai biểu đồ?
b) Tỉ lệ trẻ em dưới 5 tuổi bị suy dinh dưỡng ở biểu đồ a) có giảm nhanh hơn tỉ lệ trẻ em dưới 5 tuổi bị
suy dinh dưỡng ở biểu đồ b) hay không?
c) Giải thích tại sao hai đường gấp khúc trên hai biểu đồ có độ dốc khác nhau? 4. Cho hai biểu đồ sau:
a) So sánh độ dốc của hai biểu đồ.
b) Tại sao biểu đồ b) dễ làm cho ta hiểu lầm rằng mật độ dân số tại thành phố Hà Nội năm 2020 tăng
đột biến so với trước?
c) Để thấy được xu thế của mật độ dân số tại thành phố Hà Nội, ta nên dùng biểu đồ nào?
Dạng 2. Phân tích số liệu từ biểu đồ
5. Cho biểu đồ sau biểu diễn lượng mưa các tháng trong năm 2021 tại Hà Nội và Nha Trang.
a) Lập bảng thống kê cho số liệu được biểu diễn trên biểu đồ.
b) Dựa vào biểu đồ, cho biết mùa mưa ở Hà Nội và Nha Trang rơi vào những tháng nào?
c) Những tháng nào lượng mưa ở hai nơi gần như nhau?
6. Biểu đồ sau biểu diễn cơ cấu sử dụng đất tại Việt Nam năm 2020.
a) Trong cơ cấu sử dụng đất tại Việt Nam năm 2020, loại đất nào chiếm diện tích lớn nhất?
b) Tính đến 12/2020, tổng diện tích đất tự nhiên của Việt Nam là 33 134,4 10 nghìn ha. Lập bảng thống
kê cho biết cơ cấu sử dụng đất tại Việt Nam
7. Biểu đồ sau biểu diễn số doanh nghiệp đăng kí thành lập mới tại Hà Nội và Thành phố Hồ Chí Minh từ năm 2016 đến 2021.
a) Nhận xét về xu thế của số doanh nghiệp đăng kí thành lập mới tại Hà Nội và Thành phố Hồ Chí
Minh các năm từ 2016 đến 2021.
b) Lập bảng thống kê số doanh nghiệp đăng kí thành lập mới tại Hà Nội và Thành phố Hồ Chí Minh trong giai đoạn này.
8. Hai biểu đồ sau biểu diễn cơ cấu lực lượng lao động từ 15 tuổi trở lên tại Việt Nam năm 2015 và năm 2020.
a) Lập bảng thống kê cho biết cơ cấu lực lượng lao động từ 15 tuổi (theo tỉ lệ %) năm 2020
b) Nhận xét về sự thay đổi cơ cấu lực lượng lao động từ 15 tuổi trở lên năm 2020 so với năm 2015. BÀI TẬP TỰ LUYỆN 1. Cho hai biểu đồ sau:
a) Hai biểu đồ trên có biểu diễn cùng một tập dữ liệu không? Lập bảng thống kê cho dữ liệu đó.
b) So sánh tỉ lệ chiều cao của cột học sinh nam và học sinh nữ ở mỗi biểu đồ. Giải thích tại sao có sự khác nhau đó.
2. Cho hai biểu đồ sau biểu diễn năng suất gieo trồng lúa tại các tỉnh Trung du và miền núi phía Bắc:
a) Nhận xét về năng suất gieo trồng lúa năm 2020 so với trước ở hai biểu đồ. Tại sao có sự khác biệt về xu thế đó?
b) Để thấy được xu thế của năng suất giao trồng lúa, ta nên dùng biểu đồ nào?
3. Biểu đồ sau biểu diễn tỉ lệ học sinh theo xếp loại học lực của lớp 8A.
a) Học sinh xếp loại nào chiếm đa số trong lớp 8A?
b) Biết lớp 8A có 15 học sinh đạt loại Tốt. Tính số học sinh lớp 8A.
c) Lập bảng thống kê số học sinh 4.
Biểu đồ sau biểu diễn số vụ tai nạn giao thông trên cả nước các năm từ 2015 đến 2020.
a) Nhận xét về xu thế của số vụ tai nạn giao thông trên cả nước từ năm 2015 đến 2020.
b) Số vụ tai nạn giao thông trên cả nước năm 2020 tăng hay giảm bao nhiêu phần trăm so với năm 2015? 5.
Biểu đồ sau biểu diễn số huy chương mà đoàn thể thao Việt Nam đạt được tại hai kì SEA Games 31 và SEA Games 32.
a) Lập bảng thống kê số huy chương các loại của đoàn thể thao Việt Nam tại hai kì SEA Games 31 và SEA Games 32.
b) So với SEA Games 31, tổng số huy chương của đoàn thể thao Việt Nam tại SEA Games 32 đã giảm bao nhiêu phần trăm?
§4. XÁC SUẤT CỦA BIẾN CỐ NGẪU NHIÊN
TRONG MỘT SỐ TRÒ CHƠI ĐƠN GIẢN
Dạng 1. Tính xác suất biến cố trong trò chơi tung đồng xu.
1. Tính xác suất thực nghiệm của biến cố “Mặt xuất hiện của đồng xu là mặt N trong mỗi trường hợp sau”:
a) Tung một đồng xu 20 lần liên tiếp, có 12 lần xuất hiện mặt N.
b) Tung một đồng xu 35 lần liên tiếp, có 7 lần xuất hiện mặt S.
2. Gieo hai đồng xu đồng chất và cân đối một lần. Tính xác suất sao cho hai đồng xu xuất hiện mặt giống nhau.
3. Gieo ba đông xu đồng chất và cân đối một lần. Tính xác suất sao cho ba đồng xu xuất hiện hai mặt giống nhau.
Dạng 2. Tính xác suất biến cố trong trò chơi vòng quay
4. Hình bên mô tả một đĩa tròn bằng bìa cứng được chia làm tám phần bằng nhau và ghi các số 1; 2; 3; 4;
5; 6; 7; 8. Chiếc kim được gắn cố định vào trục quay ở tâm của đĩa. Quay đĩa tròn một lần. Tính xác suất của các biến cố sau:
a) “Mũi tên chỉ vào hình quạt ghi số nhỏ hơn 4”.
b) “Mũi tên chỉ vào hình quạt ghi số là bội của 2”.
c) “Mũi tên chỉ vào hình quạt ghi số là ước của 6”.
d) “Mũi tên chỉ vào hình quạt ghi số lớn hơn 5 và nhỏ hơn hoặc bằng 7”
5. Một đĩa tròn bằng bìa cứng được chia làm hai mươi phần bằng nhau và ghi các số 1; 2; 3;...; 20. Chiếc
kim được gắn cố định vào trục quay ở tâm của đĩa. Quay đĩa tròn một lần. Tính xác suất của các biến cố sau:
a) “Mũi tên chỉ vào hình quạt ghi số chia hết cho 5 ”.
b) “Mũi tên chỉ vào hình quạt ghi số là bội của 9”.
c) “Mũi tên chỉ vào hình quạt ghi số có hai chữ số chia hết cho 6”.
Dạng 3. Tính xác suất biến cố trong trò chơi chọn ngẫu nhiên tượng từ một nhóm đối tượng
6. Câu lạc bộ nghệ thuật của trường gồm 3 nhóm: nhóm hát có 9 thành viên; nhóm nhảy có 15 thành viên;
nhóm múa có 10 thành viên. Thầy tổng phụ trách chọn ngẫu nhiên một bạn trong câu lạc bộ làm đội
trưởng. Tính xác suất của các biến cố sau:
a) A : “Bạn được chọn thuộc nhóm nhảy”;
b) B : “Bạn được chọn thuộc nhóm múa hoặc nhóm hát”.
7. Một túi đựng 15 quả bóng có kích thước giống nhau, được đánh số từ 1 đến 15. Lấy ngẫu nhiên một quả
bóng từ túi. Tính xác suất của các biến cố sau:
a) A : “Lấy được quả bóng ghi số chẵn”;
b) B : “Lấy được quả bóng ghi số nguyên tố.
c) C : “Lấy được quả bóng ghi số chia hết cho 5”.
8. An thực nghiệm gieo một con xúc xắc. Tính xác suất của các biến cố sau:
a) D : “Số chấm xuất hiện trên con xúc xắc là hợp số”;
b) E : “Số chấm xuất hiện trên con xúc xắc không lớn hơn 4.
9. Một hộp phấn màu có 10 viên phấn cùng kích thước, trong đó có 3 viên phấn màu vàng; 3 viên phấn
màu đỏ; 2 viên phấn màu xanh dương và 2 viên phấn màu xanh lá. Cô giáo lấy ngẫu nhiên một viên
phấn trong hộp để viết bảng. Tính xác suất của các biến cố :
a) Cô giáo lấy được viên phấn màu vàng
b) Cô giáo lấy được viên phấn màu đỏ hoặc màu xanh dương;
c) Cô giáo không lấy được viên phấn màu xanh lá.
10. Khuê mua vé xem một bộ phim yêu thích. Biết rạp chiếu phim có 8 hàng ghế ; A B;C; ; D E; F; ; G H mỗi
hàng có 10 ghế được đánh số từ 1 đến 10. Khuê chọn ngẫu nhiên một ghế trong rạp. Tính xác suất của các biến cố sau:
a) M : “Ghế được chọn thuộc hàng E ”;
b) N : “Ghế được chọn là ghế có số thứ tự 5”;
c) P : “Ghế được chọn thuộc hàng G và có số thứ tự là số chẵn”.
11. Một hộp kẹo cứng gồm có 24 viên kẹo cùng kích thước với hai vị dâu và cam, trong đó số viên kẹo vị
dâu gấp 2 lần số viên kẹo vị cam. Lấy ngẫu nhiên một viên kẹo từ trong hộp. Tính xác suất để lấy được viên kẹo vị cam.
12. Đội tuyển cầu lông của trường gồm 12 bạn tham dự giải cầu lông cấp quận. Thầy trưởng đoàn chọn
ngẫu nhiên một bạn lên bốc thăm thứ tự thi. Biết rằng xác suất để chọn được học sinh nam là Hỏi đội
tuyển có bao nhiêu thành viên nữ?
13. Một hộp gồm có 10 tấm thẻ giống nhau được đánh số từ 1 đến 10. Rút ngẫu nhiên hai tấm thẻ từ trong
hộp. Tính xác suất của các biến cố sau:
a) Số xuất hiện trên hai tấm thẻ là hai số tự nhiên liên tiếp;
b) Tổng hai số xuất hiện trên hai tấm thẻ bằng 10;
c) Hiệu hai số xuất hiện trên hai tấm lớn hơn 7.
14. Một hộp có 30 quả bóng được đánh số từ 1 đến 30, đồng thời các quả bóng từ 1 đến 10 được sơn màu
cam và các quả bóng còn lại được sơn màu xanh; các quả bóng có kích cỡ và khối lượng như nhau. Lấy
ngẫu nhiệm một quả bóng trong hộp. Tính xác suất của các biến cố sau:
a) “Quả bóng được lấy ra được sơn màu cam”;
b) “Quả bóng được lấy ra được sơn màu xanh”;
c) “Quả bóng được lấy ra ghi số tròn chục”;
d) “Quả bóng được lấy ra được sơn màu xanh và ghi số chia hết cho 3”.
15. Một hộp có 40 chiếc thể cùng loại, mỗi thẻ được ghi một trong các số 1; 2; 3; 4; ....; 39; 40; hai thẻ khác
nhau thì ghi hai số khác nhau. Rút ngẫu nhiên một thẻ trong hộp. Tính xác suất của mỗi biến cố sau:
a) “Số xuất hiện trên thẻ được rút ra là số chia hết cho cả 2 và 5”;
b) “Số xuất hiện trên thẻ được rút ra là số lẻ”
c) “Số xuất hiện trên thẻ được rút ra là số chẵn”
d) “Số xuất hiện trên thẻ được rút ra là lập phương của một số tự nhiên”. BÀI TẬP RÈN LUYỆN
1. Một bó hoa có 5 bông hoa hồng, 4 bông hoa cúc và 6 bông hoa ly. Lan chọn ngẫu nhiên một bông hoa
trong bó để tặng bạn. Tính xác suất của các biến cố sau:
a) Lan chọn được một bông hoa hồng
b) Lan chọn được một bông hoa cúc hoặc hoa ly.
2. Trong một chương trình bốc thăm trúng thưởng tại một cửa hàng phần thưởng là các phiếu quà tặng với
các mệnh giá 50 000 đồng, 100 000 đồng, 200 000 đồng, 300 000 đồng, 500 000 đồng và 1 000 000
đồng. Một khách hàng tham gia chương trình đã bốc thăm ngẫu nhiên được một trong các phiếu quà tặng trên biến cố sau:
a) Tỉnh xác suất để người đó bốc được thẻ quà tặng trị giá 200 000 đồng;
b) Tính xác suất để người đó bốc được thẻ quà tặng lớn hơn 300 000 đồng.
3. Một hộp đựng 100 tấm thẻ có kích thước giống nhau được đánh số từ 1 đến 100. Rút ngẫu nhiên một
tấm thẻ từ trong hộp. Tính xác suất của các
a) A : “Rút được tấm thẻ ghi số có hai chữ số”;
b) B : “Rút được tấm thẻ ghi số tròn chục”;
c) C : “Rút được tấm thẻ ghi số lớn hơn 50 và chia hết cho 5”.
4. Lớp 8A có 12 bạn học sinh nữ. Giáo viên chủ nhiệm chọn ngẫu nhiên một bạn học sinh trong lớp làm 5
lớp trưởng. Biết xác suất cô giáo chọn một bạn học sinh nam làm lớp trưởng là 9 . Hỏi lớp 8A có tất cả bao nhiêu học sinh?
5. Một bạn thực nghiệm gieo đồng thời hai con xúc xắc. Tính xác suất của các biến cố sau:
a) M : “Số chấm xuất hiện trên hai con xúc xắc là giống nhau”;
b) N : “Tổng số chấm xuất hiện trên hai con xúc xắc không bé hơn 10”.
6. Gieo ngẫu nhiên xúc xắc một lần.
a) Gọi A là tập hợp gồm các kết quả có thể xảy ra đối với mặt xuất hiện của xúc sắc. Tính số phần tử của tập hợp A .
b) Tính xác suất của mỗi biến cố sau:
- “Mặt xuất hiện của xúc xắc có số chấm là ước của 2”;
- “Mặt xuất hiện của xúc xắc có số chấm là số lớn hơn 6”;
- “Mặt xuất hiện của xúc xắc có số chấm là số không chia hết cho 3”.
§5. XÁC SUẤT THỰC NGHIỆM CỦA MỘT BIẾN CỐ
TRONG MỘT SỐ TRÒ CHƠI ĐƠN GIẢN
Dạng 1. Xác suất thực nghiệm của một biến cố
1. Tính xác suất thực nghiệm của biến cố “Mặt xuất hiện của đồng xu là mặt N” trong mỗi trường hợp sau :
a) Tung một đồng xu 20 lần liên tiếp, có 8 lần xuất hiện mặt N.
b) Tung một đồng xu 15 lần liên tiếp, có 9 lần xuất hiện mặt S .
2. a) Gieo một con xúc xắc 40 lần liên tiếp, có 18 lần xuất hiện của xúc xắc là mặt 6 chấm. Tính xác suất
thực nghiệm của biến cố “Mặt xuất hiện của xúc xắc là mặt 6 chấm”.
b) Gieo xúc xắc 20 lần liên tiếp, có 8 lần xuất hiện mặt 1 chấm. Tính xác suất thực nghiệm của biến cố
“Mặt xuất hiện của xúc xắc là mặt 1 chấm”.
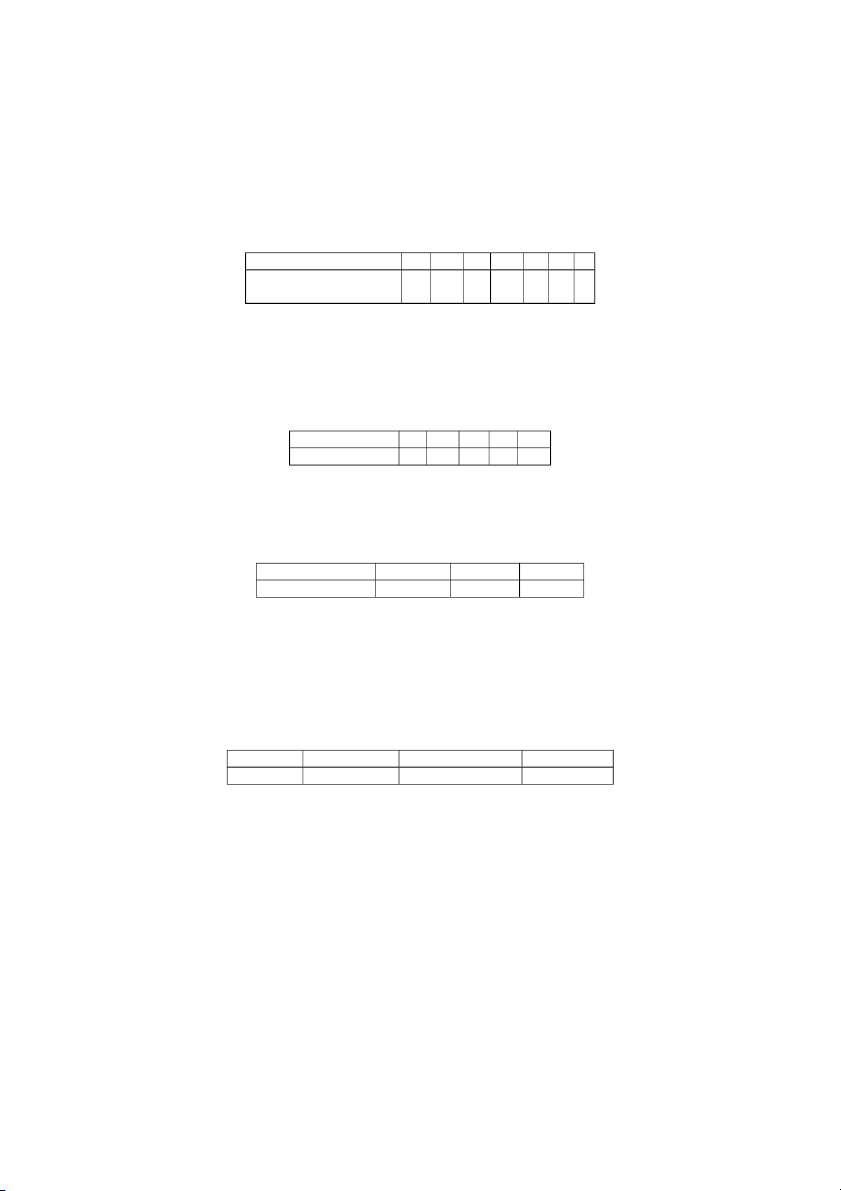
3. Đội cờ đỏ theo dõi và thống kê số học sinh đi học muộn mỗi ngày. Sau 2 tháng theo dõi, kết quả thu được như sau:
Số học sinh đi học muộn 0 1 2 3 4 5 6 Số ngày 4 15 1 11 8 7 3 2
a) Tính xác suất thực nghiệm của biến cố A : “Trong một ngày có 2 học sinh đi học muộn”
b) Tính xác suất thực nghiệm của biến cố B : “Trong một ngày có nhiều hơn 3 học sinh đi học muộn”
c) Tính xác suất thực nghiệm của biến cố C : “Trong một ngày nhất 2 học sinh đi học muộn”.
4. An làm thí nghiệm gieo 100 hạt đậu và theo dõi số hạt nảy mầm sau 1 ngày, 2 ngày, 3 ngày, 4 ngày và 5
ngày. Kết quả thu được Số ngày 1 2 3 4 5 Số hạt nảy mầm 15 29 32 13 11
a) Tính xác suất thực nghiệm của biến cố D : “Hạt đậu nảy mầm sau 1 ngày gieo hạt”
b) Tính xác suất thực nghiệm của biến cố E : “Hạt đậu nảy mầm sau ít nhất 4 ngày gieo hạt”
c) Tính xác suất thực nghiệm của biến cố F : “Hạt đậu nảy mầm trong vòng 3 ngày sau khi gieo hạt”
5. Một cửa hàng thời trang đã thống kê số lượng các loại áo bán được trong vòng một tháng vào bảng sau: Loại áo Áo phông Áo sơ mi Áo polo Số lượng (chiếc) 120 82 108
a) Tính xác suất thực nghiệm của biến cố M : “Áo sơ mi được bán trong Ta tháng đó tại cửa hàng”;
b) Tính xác suất thực nghiệm của biến cố N : “Áo sơ mi hoặc áo polo được bán trong tháng đó tại cửa hàng”.
6. Minh theo dõi và ghi lại thời gian đi từ nhà đến trường của chính mình trong 50 ngày. Kết quả thu được như sau: Thời gian Dưới 20 phút Từ 20 đến 30 phút Trên 30 phút Số ngày 15 32 3
a) Tính xác suất thực nghiệm của biến cố P : “Minh đi từ nhà đến trường mất không quá 20 phút”;
b) Tính xác suất thực nghiệm của biến cố Q : “Minh đi từ nhà đến trường mất ít nhất 20 phút”;
c) Biết Minh ra khỏi nhà lúc 7 giờ hằng ngày và trường Minh vào học lúc 8 giờ. Tính xác suất thực
nghiệm của biến cố “Minh bị muộn học”.
Dạng 2. Mối liên hệ giữa xác suất thực nghiệm với xác suất
7. Kiểm tra ngẫu nhiên 300 đơn hàng tại một công ty chuyển phát nhanh thì Suri sh có 5 đơn hàng bị ghi
nhầm địa chỉ giao hàng. Hãy ước lượng xác suất của biến cố E : “Một đơn hàng của công ty bị ghi nhầm địa chỉ”.
8. Theo một khảo sát, trong 1000 vụ cháy trên địa bàn thành phố Hà Nội có 798 vụ cháy có nguyên nhân
liên quan đến sự cố điện. Hãy ước lượng xác suất của biến cố E : “Vụ cháy có nguyên nhân liên quan đến sự cố điện”.
9. Khảo sát ngâu nhiên 500 học sinh tại trường A về thói quen đọc sách, có 172 học sinh đọc sách thường
xuyên; 112 học sinh không đọc sách và 216 học sinh thỉnh thoảng mới đọc sách. Hãy ước lượng xác suất của các biến cố sau:
a) E : “Học sinh đọc sách thường xuyên”,
b) F : “Học sinh có đọc sách”.
Dạng 3. Ứng dụng của xác suất thực nghiệm
10. Kiểm tra ngẫu nhiên 400 chiếc điện thoại được sản xuất tại một nhà máy thì thấy có 5 chiếc bị lỗi pin.
a) Tính xác suất thực nghiệm của biến cố E : “Một chiếc điện thoại được sản xuất tại nhà máy bị lỗi pin”;
b) Trong một lô hàng của nhà máy gồm 2000 chiếc điện thoại. Hãy dự đoán có bao nhiêu chiếc điện
thoại bị lỗi pin trong lô hàng đó.
11. An làm thí nghiệm gieo 100 hạt đậu và theo dõi số hạt nảy mầm sau 1 ngày, 2 ngày, 3 ngày, 4 ngày và 5
ngày. Kết quả thu được như sau: Số ngày 1 2 3 4 5 1 Số hạt nảy mầm 2 3 1 11 5 9 2 3
a) Có bao nhiêu hạt đậu đậu nảy mầm sau 1 ngày gieo hạt.
b) Có bao nhiêu hạt đậu đậu nảy mầm sau ít nhất 3 ngày gieo hạt.
c) Có bao nhiêu hạt đậu đậu nảy mầm trong vòng 4 ngày sau khi gieo hạt.
12. Một thử thách đường phố đã thu hút được 250 người qua đường tham gia. Trong đó có 45 người vượt
qua thử thách, 135 người hoàn thành 50% thử thách trở lên và 70 người chỉ hoàn thành được dưới 50% thử thách đó.
a) Tính xác suất thực nghiệm của biến cố E : “Người tham gia vượt qua thử thách” và biến cố F: “Người
tham gia hoàn thành ít nhất 50% thử thách”.
b) Giả sử có 600 người qua đường tham gia thử thách. Hãy dự đoán có bao nhiêu người vượt qua thử
thách và bao nhiêu người không vượt qua thử thách? BÀI TẬP RÈN LUYỆN
1. Tính xác suất thực nghiệm của biến cố “Mặt xuất hiện của đồng xu là mặt S " trong mỗi trường hợp sau:
a) Tung một đồng xu 18 lần liên tiếp, có 6 lần xuất hiện mặt S .
b) Tung một đồng xu 14 lần liên tiếp, có 7 lần xuất hiện mặt N .
c) Tung một đồng xu 28 lần liên tiếp, có 16 lần xuất hiện mặt S .
d) Tung một đồng xu 100 lần liên tiếp, có 45 lần xuất hiện mặt N .
2. a) Gieo một con xúc xắc 20 lần liên tiếp, có 10 lần xuất hiện mặt 2 chấm. Tính xác suất thực nghiệm của
biến cố “Mặt xuất hiện của xúc xắc là mặt 2 chấm”;