224 trang 3 lượt tải

Thực hành giải toán môn Toán 8 Kết Nối Tri Thức Với Cuộc Sống tập 2

5

Tài liệu gồm 224 trang, được biên soạn bởi tác giả Toán Họa, bao gồm tóm tắt lí thuyết và các dạng bài tập giúp học sinh lớp 8 thực hành giải toán môn Toán 8 bộ sách Kết Nối Tri Thức Với Cuộc Sống (KNTTVCS) tập 2, có đáp án và lời giải chi tiết.

Chủ đề: Tài liệu chung Toán 8 289 tài liệu

Môn: Toán 8 2.3 K tài liệu

Tác giả:

Profile

Linh Đan

2 tuần trước
Danh sách Quiz
/224
Bồi dưỡng năng lực học môn Toán 8
THỰC HÀNH GIẢI TOÁN LỚP 8
1
Bài 21: PHÂN THỨC ĐẠI SỐ
A. TÓM TẮT LÍ THUYẾT
Một phân thức đại số (hai nói gọn là phân thức) là biểu thức có dạng
A
B
,
trong đó
A
;
B
là hai đa thức và
B
khác đa thức
0
.
A được gọi là tử thức (hoặc tử) và
B
được gọi là mẫu thức (hoặc mẫu).
Nhận xét: Mỗi đa thức cũng được coi là một phân thức với mẫu bằng 1. Đặc
biệt, số 0 và số 1 cũng là những phân thức đại số.
Hai phân thức bằng nhau
Hai phân thức
A
B
và
gọi là bằng nhau nếu
.AD BC
AC
BD
nếu
.AD BC
Điều kiện xác định của phân thức
A
B
là điều kiện của biến để giá trị của mẫu
thức
B
khác
0
.
B. BÀI TẬP
Dạng 1: Chứng minh hai phân thức bằng nhau
1. Chứng minh hai phân thức bằng nhau.
a)
36
48
y xy
x
b)
2
2
3
3
9
xx y
xy
x
xx y
c)
2
2
24 2
2
2
xx x
x
x
d)
2
2
1 43
3
69
x xx
x
xx


e)
3
2
28
24
xx
x
xx x


f)
22
22
21 1
1
21
x y xy x y
xy
xy x



2. Vì sao các kết luận sau đúng?
a)
3 44
3
5
7
35
xy x y
xy
b)
2
2
2 ( 2)
2
4
xx
x
x

c)
2
2
( 3)
3
( 3)
xx x
x
xx
d)
22
87 67
11
xx xx
xx


Bồi dưỡng năng lực học môn Toán 8
THỰC HÀNH GIẢI TOÁN LỚP 8
2
3. Ba phân thức sau có bằng nhau không?
23
;
15
x
A
2
2 13 24
;
15 20
xx
B
x

2
10 11 6
75 30
xx
C
x

4. Chứng minh các đẳng thức sau:
a)
33
2
22
2x 4
xx
x
xx


0
x
b)
22
3x x
3x
y
xy
yx

xy
c)
2
2
3a
3a
9a
xy
xy
xy
0,a xy 
Dạng 2. Tìm điều kiện xác định của phân thức
5. Tìm điều kiện của
x
để các phân thức sau xác định
a)
2x
x
b)
1
3
x
x
c)
5
9 x
d)
3
2 10
x
x

e)
8
1
4
2
x
x
f)
1
4
5
3
6
2
x
x
6. Tìm điều kiện của
x
để các phân thức sau xác định
a)
4
13
x
xx

b)
2
9
1
x
c)
2
2
27xx
xx

d)
2
21
44
x
xx

e)
2
2
4
9 16
x
x
f)
2
2x 1
5x 6x

7. Tìm điều kiện của
x
để các phân thức sau xác định.
a)
2
54
2
x
xx
b)
2018
12xx x
c)
2
2
4
45
x
xx

d)
22
32
xy
xy

e)
2
54
6 10
xy
xx

f)
2
2018 2019
9 24 16
xy
xx

8. Chứng minh các phân thức sau luôn có nghĩa với mọi giá trị của
x
Bồi dưỡng năng lực học môn Toán 8
THỰC HÀNH GIẢI TOÁN LỚP 8
3
a)
2
7
5x
b)
2
6
14
x
x

c)
2
2
8
29
x
xx

d)
2
2 11
45
x
xx


e)
4 24
2
22
xy
x xy

e) e)
2
5
7
x
xx

Dạng 3. Tìm điều kiện của biến thoả mãn đẳng thức.
9. Tìm giá trị của
x
để giá trị của các phân thức sau bằng 0
a)
3
3
x
x
3x
b)
2
36
2
x
x
c)
2
2
5 125
1
x
x
d)
2
2
44
45
xx
xx


10. Tìm các giá trị nguyên của
x
để phân thức sau có giá trị nguyên
a)
3
21x
b)
2
5
1x
c)
2
7
1xx
Dạng 4: Toán thực tế
11. Ao Bà Om hay Ao Vuông, là một thắng cảnh độc đáo và nổi tiếng của tỉnh
Trà Vinh, Việt Nam. Mặt nước áo trong xanh và phẳng lặng được phủ bởi hoa
sen, hoa súng. Ao được bao bọc xung quanh bởi các gò cát mấp mô với các hàng
cây sao, cây dầu cổ thụ hàng trăm năm tuổi có rễ nổi lên khỏi mặt đất tạo nên
những hình thù kì lạ. Ao có hình chữ nhật có chiều rộng là
x
, chiều dài là
200x
mét, được đào ở trung tâm miếng đất hình vuông có cạnh là
400x
mét.
a) Tính diện tích của ao.
b) Tính diện tích phần đất còn lại sau khi đã đào ao.
12. Có một miếng đất hình vuông có cạnh là
()ab
mét. Người ta chừa ra phần
đất hình chữ nhật có chiều dài và chiều rộng lần lượt là
()ab
và
()ab
để lát
lối đi
0ab
. Viết biểu thức đại số tính diện tích phần đất còn lại để làm
vườn.
Bồi dưỡng năng lực học môn Toán 8
THỰC HÀNH GIẢI TOÁN LỚP 8
4
13. Một miếng bìa giấy hình vuông có cạnh bằng
20cm
. Người ta cắt bỏ bốn hình
vuông nhỏ ở bốn góc của miếng bìa có cạnh bằng
x
để khi gấp lại được một
hình hộp chữ nhật.
a) Viết biểu thức đại số tính độ dài cạnh của mặt đáy sau đó tính diện tích đáy
của hình hộp chữ nhật được gấp theo
x
.
b) Viết biểu thức đại số tính thể tích của hình hộp chữ nhật theo
x
.Biết công
thức tính thể tích của hình hộp chữ nhật
.V Sh
(
S
: diện tích đáy,
h
là chiều
cao).
c) Viết biểu thức đại số tính thể tích của hình hộp chữ nhật khi người ta cắt bỏ
4 hình vuông cá cạnh
x = 2cm
. Biết thể tích của hình hộp chữ nhật bằng tích 3
kích thước, hay bằng diện tích đáy
x
chiều cao.
14. Một miếng bìa hình chữ nhật có chiều dài hơn chiều rộng
30
cm
. Người ta
cắt 4 hình vuông nhỏ ở 4 góc của miếng bìa cùng có cạnh là 6cm. Sau khi gấp
lại được hình hộp chữ nhật có thể tích
3
3354 cm
. Biết thể tích của hình hộp chữ
nhật là
.V Sh
với
S
là diện tích đáy,
h
là chiều cao của hình hộp chữ nhật
a) Viết biểu thức đại số tính diện tích đáy của hình hộp chữ nhật sau khi gấp.
b) Tính các kích thước của miếng bìa lúc đầu.
15. Nhà trường tổ chức giải bóng đá mini mừng Xuân cho học sinh khối 8, mỗi
lớp cử một đội tham dự, mỗi đội lần lượt gặp đội của lớp bạn một lần.
Bồi dưỡng năng lực học môn Toán 8
THỰC HÀNH GIẢI TOÁN LỚP 8
5
a) Viết biểu thức đại số tính tổng số trận của khối lớp 8 nếu có
x
đội
*
x
tham dự.
b) Nếu số trận đấu là 10 thì khối 8 có bao nhiêu lớp tham dự?
Dạng 5: Tính giá trị biểu thức (dạng khó)
16. Tính giá trị của biểu thức
a)
2
2
23
,1
21
xx
Ax
xx
−−
= ≠
++
tại
3 10x −=
b)
2
2
, 2; 3
56
x
B xx
xx
−
= ≠≠
−+
tại
2
40x −=
17. Cho
1
3
x
x

. Tính giá trị của các biểu thức sau:
a)
2
2
1
Ax
x

b)
3
3
1
Bx
x

c)
4
4
1
Cx
x

d)
5
5
1
Dx
x

\
18. Cho ba số
,,abc
khác 0 và thỏa mãn:
0.abc
Tính
222 2 2 2 2 22
111
A
abc bca cab

 
Dạng 6: Tìm đa thức trong đẳng thức.
19. Tìm đa thức
A
thỏa mãn mỗi đẳng thức sau:
a)
2
2
4
Ax
x
x
b)
22
A xy
xy xy

c)
22
11xx x
xA

d)
32
11x xx
Ax

e)
22
22
2x xy y A
xy
xy

f)
22
22
2x xy y A
xy
xy

Bồi dưỡng năng lực học môn Toán 8
THỰC HÀNH GIẢI TOÁN LỚP 8
1
Bài 22: TÍNH CHẤT CƠ BẢN CỦA PHÂN THỨC ĐẠI SỐ
A. TÓM TẮT LÍ THUYẾT
Nếu nhân cả tử và mẫu của một phân thức với cùng một đa thức khác đa
thức
0
thì được một phân thức mới bằng phân thức đã cho.
.
.
A AM
B BM
(
M
là một đa thức khác đa thức
0
)
Nếu tử và mẫu của một phân thức có nhân tử chung thì khi chia cả từ và mẫu
cho nhân tử chung đó ta được một phân thức bằng phân thức đã cho.
:
:
A AN
B BN
(
N
là một nhân tử chung)
Muốn rút gọn một phân thức đại số ta làm như sau:
- Phân tích tử và mẫu thành nhân tử (nếu cần) để tìm nhân tử chung
- Chia cả tử và mẫu cho nhân tử chung đó.
Muốn quy đồng mẫu thức nhiều phân thức ta làm như sau:
- Phân tích các mẫu thức thành nhân tử rồi tìm mẫu thức chung;
- Tìm nhân tử phụ của mỗi mẫu thức bằng cách chia MTC cho mẫu thức đó;
- Nhân cả tử và mẫu của mỗi phân thức với nhân tử phụ tương ứng.
B. BÀI TẬP
Dạng 1: Tìm đa thức thoả mãn đẳng thức cho trước
1. Tìm đa thức
A
thỏa mãn mỗi đẳng thức sau:
a)
32
2
24
,
2
4
A xx
x
x
với
2;
x 
b)
22
5
55
,
3
xy
xy
A
với
xy
c)
23
8 2 16
,
21
x xx
xA

với
1
0,
2
xx
d)
,
2
yx xy
xA

với
2x
2. Tìm đa thức
A
thỏa mãn mỗi đẳng thức sau:
a)
2
2
693
49
bbb
A
b
với
3
;
2
b 
b)
2
nm mn
mA

với
2.m
Dạng 2: Biến đổi phân thức theo yêu cầu đề toán
3. a) Cho phân thức
2
43
5
x
x
. Biến đổi phân thức đã cho thành một phân thức
bằng nó và có tử thức là đa thức
2
12 9 .Axx
Bồi dưỡng năng lực học môn Toán 8
THỰC HÀNH GIẢI TOÁN LỚP 8
2
b) Biến đổi phân thức
2
8 82
4 2 15
xx
xx


thành một phân thức bằng nó và có tử
thức là
12Ax

4. a) Cho phân thức
2
12 12 3
2; 5
6 35
aa
aa
aa



. Biến đổi phân thức đã cho
thành một phân thức bằng nó và có tử thức là đa thức
12Aa
b) Biến đổi phân thức
2
73
;0
43 4
x
xx
x




thành một phân thức bằng nó và
có mẫu thức là
2
12 9B xx
5. Biến đổi mỗi phân thức sau thành một phân thức bằng nó và có tử thức là đa
thức
B
sau đây
a)
2
25
34
x
x
và
2
2 35
Bx x

b)
2
22
16
9 32
x xx
x xx


và
2
Bx

6. Tìm bộ ba đa thức
,,
ABC
thỏa mãn chuỗi đẳng thức sau:
23
3
4 3 27
AB C
x
xx x


với
1, 3 .xx
7. Tìm bộ ba đa thức
,,ABC
thỏa mãn chuỗi đẳng thức sau:
2 23
1
44 4 8
Ax
BC
xx x x


với
2
x 
8. Dùng tích chất cơ bản của phân thức để biến đổi mỗi cặp phân thức sau
thành một cặp phân thức bằng nó và có cùng tử thức:
a)
3
2x
và
1
5
x
x
b)
5
4
x
x
và
2
25
23
x
x
Dạng 3: Tính giá trị của phân thức
9. Tính giá trị của phân thức:
Bồi dưỡng năng lực học môn Toán 8
THỰC HÀNH GIẢI TOÁN LỚP 8
3
a)
2
22
21
x
xx

với
1x 
tại
1x
b)
2
2
33
1
xx
x
với
1x

tại
2x 
10. Tính giá trị của phân thức:
2
2
1
2 31
x
xx

với
1
1;
2
xx
tại
3 10x 
11. Tính giá trị của các biểu thức sau:
a)
23
32
ab
A
ab
với
12a
;
36b

b)
22
22
2
yx
B
x xy y

với
1
2
xy

c)
2
3
( 2)(2 2 )
( 1)(4 )
x xx
C
x xx


với
1
2
x
d)
2
32
3 31
x xy y y
D
yyy


với
31
;
42
xy

Dạng 4: Chứng minh cặp phân thức bằng nhau. Tìm giá trị của biến để phân
thức bằng nhau.
12. Cho cặp phân thức
2
96
3 3 22
x
x xx

và
2
3
3 33
1
xx
x

với
1x
và
2
.
3
x
Chứng tỏ cặp phân thức trên bằng nhau.
13. Cho hai phân thức
2
56
36
yy
y

và
2
2 53
63
yy
y

với
2y
và
1
.
2
y
Cặp
phân thức này có bằng nhau hay không?
14. Cho cặp phân thức
2
2
1
34
x
xx

và
2
2
23
1; 2; 4
2
xx
x xx
xx



a) Hai phân thức này có luôn bằng nhau không?
b) Tìm giá trị cụ thể của
x
để hai phân thức bằng nhau
Dạng 5: Rút gọn phân thức
15. Rút gọn các phân thức sau.
a)
532
24
14
21
xyz
xyz
b)
3
2
25 1
30 1
xy x
xy x
c)
3
35
12 5
xx
x
d)
3
2
60 3 2
45 2 3
xy x
xy x
Bồi dưỡng năng lực học môn Toán 8
THỰC HÀNH GIẢI TOÁN LỚP 8
4
16. Rút gọn phân thức
34
32
17
34
xy z
A
xyz
2
2
47
y xy
B
xy y
2
2
25
5
x
C
xx
2
2
x xz xy yz
D
x xz xy yz


2
45 3
15 3
xx
E
xx
22
3 2 23
33
yx
F
x x y xy y

17. Rút gọn phân thức
44
22
ax a x
A
a ax x

32
3
6
4
xx x
B
xx

2
22a ab
C
ac ad bc bd

2
2
22
4
96
xa x
D
a x ax


2
2
22
22
yx x y
E
xy y x


2
3
32
1
xx
F
x

18. Đơn giản các phân thức
a)
3
4
77
1
1
xx
x
x

b)
23
3
48 12 3
4
64
yyy
y
y


c)
22
22
12
12
x y xy
xy x


d)
2
2
x xz xy yz
x xz xy yz


e)
32
3
1
1
xxx
x

f)
42
3
21
32
xx
xx


Dạng 6: Tìm mẫu thức chung của các phân thức
19. Tìm mẫu thức chung của các phân thức sau:
a)
2
2
;
3
5
xy
xy
x
b)
2
35 3
;
7
2
x
xy
y

c)
2 32 3
21
;;
243
x xx
x y x y xy

d)
23 2
;
5
71
x
x

e)
37
;
13 3
x
xx

f)
2
15 7
;;
34 4
66
x
xx
xx
20. Tìm mẫu thức chung của các phân thức sau:
a)
2
3x
;
26
x
x
;
2
3
9x
b)
2
1
5xx
;
3
14
25xx
;
3 15
x
x
c)
3
3
1
x
x
;
2
1x
xx
;
2
5
1
x
xx

d)
2
1
32xx
;
1
1
x
;
1
24x
e)
2
222
72
;;
32 56 43
xx x
xx xx xx
 
Bồi dưỡng năng lực học môn Toán 8
THỰC HÀNH GIẢI TOÁN LỚP 8
5
Dạng 7: Quy đồng mẫu thức các phân thức
21. Quy đồng mẫu các phân thức sau:
a)
5
;
6
2
31
x
x
b)
2
;
55
x
2
33
x
x
c)
1
;
2x
5
;
10 10x
2
7
55
x
xx
22. Quy đồng mẫu các phân thức sau:
a)
1
24x
;
24
x
x
;
2
3
4 x
b)
2
1
2
xx
;
3
20
4xx
;
2
7
2xx
c)
3
1
x
x
;
2
1x
xx
;
2
2
1
x
xx

d)
2
1
32xx
;
2
1
1x
;
2
1
2
x
Dạng 8. Chứng minh đẳng thức. Chứng minh biểu thức không phụ thuộc vào
biến.
23. Chứng minh đẳng thức.
a)
2
32 2
21 1
33 3
bb b
bb b

b)
2
2
22
4
3
96
xa x
ax
ax
a x ax


c)
2
32
32 2
11
xx x
x xx


d)
2
xy x 2y 2 y 1
x2
4 4x x


e)
22
3 2 23
23 1
22
x xy y
xy
x x y xy y


24. Cho hai phân thức
223
32
44
48
xy x y x
P
x xy

và
2
2
22
44
xy x y x
Q
xx

với
0; 1; 2x x xy
. Chứng minh rằng
.PQ
25. Chứng minh biểu thức không phụ thuộc vào biến
x
.
22
xy
A
x y ay ax

;
2 22
2 22
(1 ) 1
(1 ) 1
x a a ax
B
x a a ax


Dạng 9. Chứng minh phân thức tối giản.
26. Chứng minh rằng các phân số sau tối giản với mọi số tự nhiên
n
:
a)
31
52
n
n
; b)
12 1
30 2
n
n
; c)
3
42
2
31
nn
nn

; d)
2
21
21
n
n
.
Bồi dưỡng năng lực học môn Toán 8
THỰC HÀNH GIẢI TOÁN LỚP 8
6
Dạng 10. Tìm x để phân thức có giá trị là số nguyên
27. Tìm số nguyên
x
để phân thức sau có giá trị là số nguyên:
a)
3
21x
; b)
2
5
1x
; c)
2
7
1xx
; d)
2
59
8
x
x
28. Tìm số hữu tỉ
x
để phân thức
2
10
1x
có giá trị là số nguyên.
Bồi dưỡng năng lực học môn Toán 8
THỰC HÀNH GIẢI TOÁN LỚP 8
1
Bài 23: PHÉP CỘNG VÀ PHÉP TRỪ PHÂN THỨC ĐẠI SỐ
A. TÓM TẮT LÍ THUYẾT
Quy tắc cộng hai phân thức cùng mẫu.
Muốn cộng hai phân thức có cùng mẫu thức, ta cộng các tử thức với nhau
và giữ nguyên mẫu thức
A B AB
MM M

Chú ý: Ta thường viết tổng dưới dạng rút gọn.
Quy tắc cộng hai phân thức không cùng mẫu.
Muốn cộng hai phân thức có mẫu thức khác nhau, ta quy đồng mẫu thức
rồi cộng các phân thức có cùng mẫu thức vừa tìm được.
Quy tắc trừ hai phân thức
Muốn trừ hai phân thức có cùng mẫu thức ta trừ các tử thức và giữ nguyên
mẫu thức.
A B AB
MM M

Muốn trừ hai phân thức có mẫu thức khác nhau, ta quy đồng mẫu thức rồi
trừ các phân thức có cùng mẫu thức vừa tìm được.
Rút gọn biểu thức có dấu ngoặc
Nếu trước dấu ngoặc có dấu
“”
thì bỏ dấu ngoặc và giữ nguyên các số hạng.
Nếu trước dấu ngoặc có dấu
““
thì bỏ dấu ngoặc và đổi dấu các số hạng
trong dấu ngoặc.
B. BÀI TẬP
Dạng 1: Cộng các phân thức đại số cùng mẫu
1. Thực hiện phép tính:
a)
4 10 8
14 14
xx 
b)
7 2 28
24 24
x xy
xy xy

c)
3 64
33
xy x y
xy xy


d)
3 4 7 12 4 3
25 25 25
xy x x
xy xy xy



2. Thực hiện phép tính.
Bồi dưỡng năng lực học môn Toán 8
THỰC HÀNH GIẢI TOÁN LỚP 8
2
a)
3 22
52 2 5
a
aa

b)
2 22
2 3 23x xy y xy y xy
xy yx xy



c)
22 2 2
632 2 6 3b bx ax a
ab ba


d)
2
3 2 23
22
22
xx
x xx xxx


3. Thực hiện phép tính:
a)
22
5 34 3
33
xy z x y z
xy xy

b)
22
2 2 75
3
33 3
a aa a
a
a aa



Dạng 2: Cộng các phân thức đại số khác mẫu.
4. Thực hiện phép tính:
a)
22 3
33
x ax x
a
b)
22 1abx
ab ax x b


c)
3 2 22
xy
xy x y

d)
2
2
3 23
1
1
x xy x
yx
xy


5. Thực hiện phép tính:
a)
2
5 72
2
4
x
x
x
b)
2
29 2
23
94
x
x
x
c)
22
4
22
xy
y xy x xy

d)
22
1 25
22
x
xx x

6. Thực hiện phép tính:
a)
2
32
23 1
1
1
11
x
Ax
x
x xx


b)
2
12 2 1
2 21
24
xx
B
xx
xx

c)
2
11 2
.
2 32 3
23
x
C
xx
xx



d)
22 2
11 1
.
2 2 ( 1) ( 3)
x
D
xx xx x x


7. Thực hiện phép tính.
a)
2 4 8 16
11 1 1 1 1
.
11
11 11
xx
xx xx



Bồi dưỡng năng lực học môn Toán 8
THỰC HÀNH GIẢI TOÁN LỚP 8
3
b)
433
yxzx yxyz yzxz

  
c)
22 2
12 3
3 2 12 35 7 10xx x x xx


8. Rút gọn rồi tính giá trị của phân thức thu gọn:
a)
2
23
1
11
2x
xxx

với
1x
tại
11x
b)
22
1
1 2
x
x
x
x
x
với
1, 0xx
tại
1
3
x
c)
2
2 212
42
14
1
42
xx
x
x
x
với
1
2
x 
tại
1
4
x
d)
5
233
52
xxy y
xy


với
5x
,
5
2
y
25yx
9. Rút gọn rồi tính giá trị của phân thức thu gọn:
a)
22
11
A
y xy x xy


, biết
1
xy 
b)
23
26
x xy
B
yx


, biết
36yx
c) Cho
,,xyz
là các số khác nhau và
2023xyz

.
Tính
333
( )( ) ( )( ) ( )( )
x yz
C
xyxz yzyx zxzy


10. Cho ba số
;b;ca
đôi một khác nhau. Chứng minh rằng biểu thức sau không
phụ thuộc vào
;;abc
:

bc ac ab
abac babc cacb

 
11. Với
,,abc
là 3 số khác nhau. Chứng minh tổng sau bằng 0.
111
.
( )(b ) (c )(a b) (b )(c a)ab c a c


Bồi dưỡng năng lực học môn Toán 8
THỰC HÀNH GIẢI TOÁN LỚP 8
4
Dạng 3: Tìm các hệ số thoả mãn điều kiện cho trước
12*. Hãy tìm giá trị của
,ab
để có các đẳng thức sau:
a)
5
.
( 2)( 3) 2 3
x ab
xx x x


b)
5 31
.
( 5)( 2) 5 2
x ab
xx x x


c)
22
35
.
1
( 1) ( 1)
x ab
x
xx


d)
22
81
.
3
( 3) ( 3)
x ab
x
xx


e)
1
.
( 1)( 2) ( 1) ( 1)( 2)
ab
xx x xx x x

 
13*. Xác định các số hữu tỷ
,,abc
sao cho:
a)
2
32
9 16 4
.
12
32
x x ab c
xx x
xxx




b)
2
22
21
.
12
( 1)( 2) ( 2)
xx a b c
xx
xx x




Dạng 4: Trừ các phân thức đại số cùng mẫu
14. Làm tính trừ các phân thức sau:
a)
22
2161
44
xx
xy xy

b)
3 2 25
2323
xx
xx


c)
17 11 1
32 2 3
xx
xx


d)
10 15 2 7
3 2 23
xx
xx


15. Làm tính trừ các phân thức sau:
a)
2
22
2 55 5
88
xy xy
xy xy

b)
2
75 45
3 ( 4)
3 12
xx
xx
xx

c)
2 18 2
666
x xx
xxx



. d)
2 22
333
5 4 2 38
888
x x x xx x
xxx



.
16. Làm tính trừ các phân thức sau:
Bồi dưỡng năng lực học môn Toán 8
THỰC HÀNH GIẢI TOÁN LỚP 8
5
a)
22
2 12
11 1
x xx x
x xx



. b)
51
11 1
y
y yy


.
c)
22
4 2 45
55 5
x xx x
x xx



. d)
2 92 1
6 66
xx
xx x



.
Dạng 5: Trừ các phân thức đại số khác mẫu.
17. Rút gọn các biểu thức:
a)
2
4 21
32
32
x
x
xx
b)
2
4
1
1
x
x
x

c)
32
12
1
1
x
x
xxx

d)
2
3 13 1 6
6 2 26
91
xx x
xx
x



18. Thực hiện các phép tính sau.
a)
21
22
a
a
. b)
37
12 2
x
xx

.
c)
7 7 31
5 5 15
x
x
. d)
44
22
22
2 xy
xy
xy

.
e)
2
31 1
1
1
x
x
x
. f)
2
29 1
23
94
x
x
x
.
19. Thực hiện các phép tính sau.
a)
22
11 2x
xy xy
xy


. b)
2
1 14
11
1
xx
xx
x



.
c)
2
13
22 22
1
x
xx
x


. d)
2
4
1
2
7 10
xx
x
xx


.
20. Thực hiện phép tính:
a)
2 32 2
12 1
32 4 4 56
x
x x x x xx x

 
b)
2
11 2
2 32 3
23
x
xx
xx



c)
22 2
11 1
2 2(1)(3)
x
xx xx x x


21. Thực hiện phép tính
Bồi dưỡng năng lực học môn Toán 8
THỰC HÀNH GIẢI TOÁN LỚP 8
6
a)
2 22
2 4 22 4
22
2
2
x xy y
A
x xy y
x yxy
xyxy




.
b)
2 4 8 16
1 1 2 4 8 16
11
111 1
B
xx
xxxx



.
22. Tính giá trị của biểu thức:
a)
2
2 1 12 2
4 24 2
14
xx
A
xx
x



với
1
4
x
b)
3 23
525
xy x y
B
xy



với
25yx
c)
2
22 4
22
4
ax ax a
Ca
xx
x



với
1
a
x
a
23. Chứng minh rằng:
11 1
1 ( 1)x x xx


. Vận dụng tính nhanh các phép tính
sau:
a)
11 1 1
( 1) ( 1)( 2) ( 2)(x 3) ( 3)( 4)xx x x x x x


b)
2222 2
11 1 1 11
5
32 56 712 920
x
xxxx xx xx xx

 
24. Chứng minh đẳng thức:
a)
2 2 2 22
2 22 2 2
4 ( 3) 9 (2 3)
1
9( 1) (2 3) 4 ( 3)
xx x x x
x x x xx



b)
222
( )( ) ( )( ) ( )( )
yz zx xy
xyxz yzyx zxzy xy yz zx



Dạng 6: Tìm phân thức thoả mãn yêu cầu
25. Tìm phân thức A biết
a)
2
23
4 224
1
11
xx
A
x
xx x


với
0, 1xx
b)
2
32 2
26 6 2
3
33 1
aa
A
a
a aa a


với
1, 3aa
Bồi dưỡng năng lực học môn Toán 8
THỰC HÀNH GIẢI TOÁN LỚP 8
7
c)
22 2
6 32 32
1 21 21
xx
A
x xx xx



với
1x 
Dạng 7: Rút gọn biểu thức có dấu ngoặc
26. Tính giá trị của biểu thức:
a)
2
321 3
11
1
x xx
xx
x





b)
11 11
xx y yx y xx y yy x







c)
33 2 2
13ab a b
ab
a b a ab b




d)

11 1
1
1 2 23
x
xx x x







27. Thực hiện phép tính (Tự luyện).
a)
3
2
2 32
2 15 1
33
21
4 4 1 8 12 6 1
xx x
xx
A
x
xx x xx









.
b)
22
2
2
2 22
22 2
4 3 23
25
35 4 9 25 415
x xx
x
B
x xxx x x









.
Bồi dưỡng năng lực học môn Toán 8
THỰC HÀNH GIẢI TOÁN LỚP 8
1
Bài 24: PHÉP NHÂN VÀ PHÉP CHIA PHÂN THỨC ĐẠI SỐ
A. TÓM TẮT LÍ THUYẾT
Quy tắc nhân hai phân thức.
Muốn nhân hai phân thức, ta nhân các tử thức với nhau, các mẫu thức với nhau
.
A C AC
B D BD
Chú ý: Ta thường viết tích dưới dạng rút gọn.
Các tính chất
Giao hoán:
AC C A
BD DB

Kết hợp:
A C E AC E
B DF BD F











Phân phối đối với phép cộng:
A C E AC E
B DF BD F











Quy tắc chia hai phân thức
Muốn chia phân thức
A
B
cho phân thức
C
D
khác 0, ta nhân
A
B
với phân thức
D
C
:
AC AD
B D BC

, với
0.
C
D
B. BÀI TẬP
Dạng 1: Nhân hai phân thức đại số
1. Thực hiện các phép tính sau
a)
3
22
14 2
5
xy
yx
b)
22
2
52
10
7
yx
y
y



c)
32
2
84
5 20
24
x xx
x
xx


d)
34
5
7
3.
9
z
xy
xy


2. Thực hiện các phép tính sau
a)
2
32
84
. 0; 0
15
xy
xy
yx

b)
22
3
99
. 3; 0
3
6
aa
aa
a
a

d)
22
4
47
. 0; 0
12
17
nm
mn
n
m



d)
32
3 6 2 18
. 2; 9
92
bb
bb
bb



Bồi dưỡng năng lực học môn Toán 8
THỰC HÀNH GIẢI TOÁN LỚP 8
2
3. Rút gọn biểu thức
a)
42 3
3 2 42
48 33
.. 1
2 2 12 1 4 8
tt t t
At
t t tt



b)
3
2
1
. 1 0; 1
21
yy
B yy y y
yy



c)
63 2
3 63
2 33 1
.. 1
1
1 23
x x xxx
Cx
x
x xx



d)
32
2 21 2 1
. 5; 2; 1
3 15 1 1 2
a aa
Da
a aa a





4. Tính hợp lí:
2 4 8 16
11 1 1 1 1
.....
11
1111
M
xx
xxxx


với
1x 
5. Thực hiện các phép tính sau
a)
3
2
11 1
24 1
1
mm
mm
mm





2; 1mm
b)
33
2001 2 16
..
2017 2 2017 2
u u uu
u uuu


2; 2017uu
c)
12 5 4 3 12 5 6 3
9 360 150 9 360 150
xx x x
xxxx



d)
34 2 3 3
33
xyxyxyxy
xyxy xyxy



6. Tính giá trị của các biểu thức sau.
a)
22
22
1.
2
x y xy
A
y
xy




Với
15x
,
15y 
b)
22
22
1
.
x y xy
B
y x xy
x xy y






Với
15x
,
5y
c)
222
2.
x yz
C x y z yz
xyz



Với
8, 6;x
2, 1, 4yz

Tài liệu khác của Toán 8

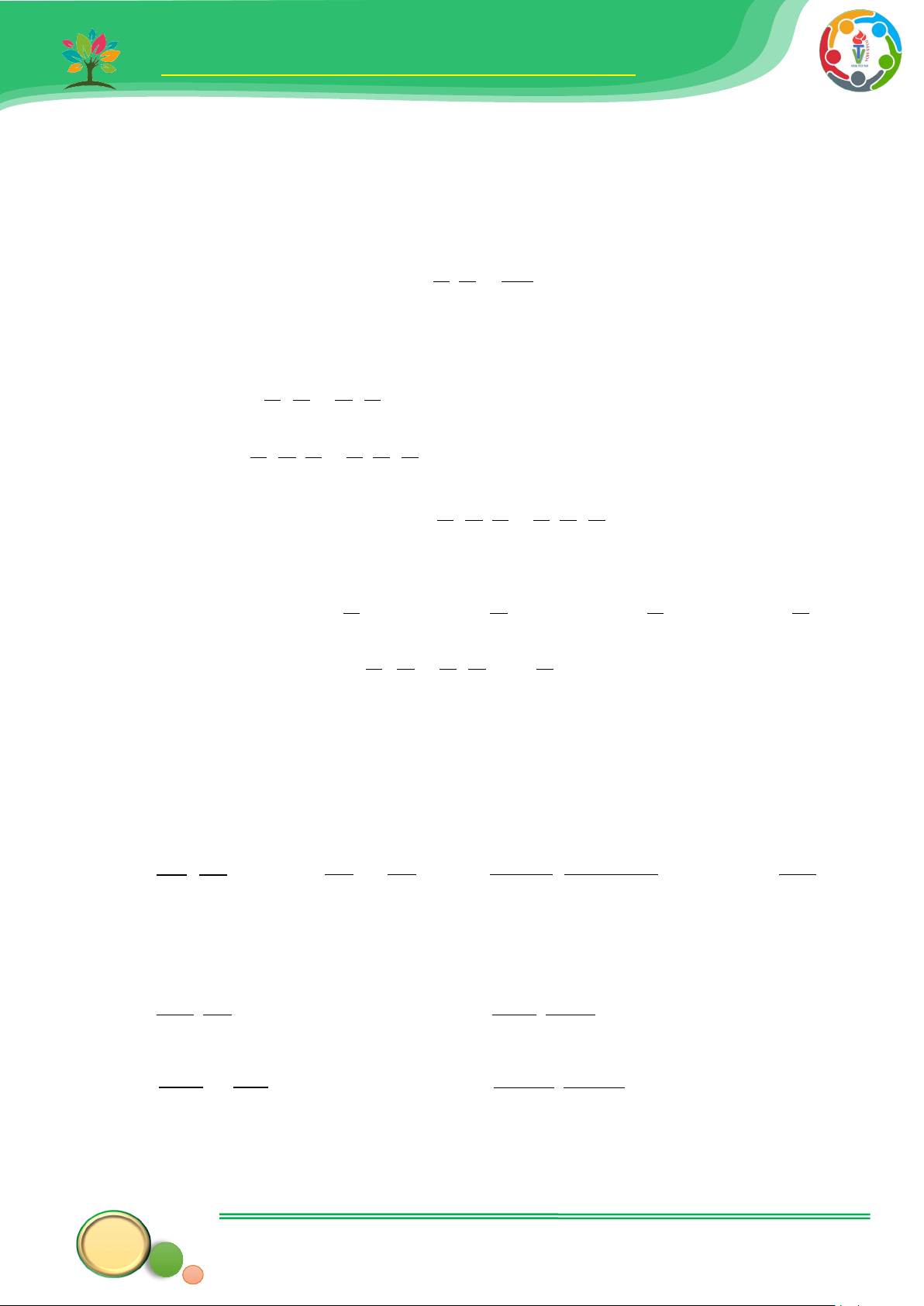
Preview text:

THỰC HÀNH GIẢI TOÁN LỚP 8
Bài 21: PHÂN THỨC ĐẠI SỐ
A. TÓM TẮT LÍ THUYẾT
Một phân thức đại số (hai nói gọn là phân thức) là biểu thức có dạng A , B
trong đó A ; B là hai đa thức và B khác đa thức 0 .
A được gọi là tử thức (hoặc tử) và B được gọi là mẫu thức (hoặc mẫu).
Nhận xét: Mỗi đa thức cũng được coi là một phân thức với mẫu bằng 1. Đặc
biệt, số 0 và số 1 cũng là những phân thức đại số.
Hai phân thức bằng nhau
Hai phân thức A và C gọi là bằng nhau nếu AD BC. B D A C
nếu AD BC. B D
Điều kiện xác định của phân thức A là điều kiện của biến để giá trị của mẫu B thức B khác 0 . B. BÀI TẬP
Dạng 1: Chứng minh hai phân thức bằng nhau
1. Chứng minh hai phân thức bằng nhau. 3x  x y x y 2 a) 3y 6xy  b)  4 8x 2 3x
9x x y 2 2 c) 2x  4x 2x x  1 x  4x  3  d)   2 x  2 x  2 2 x  3 x  6x  9 3 2 2 e) x  2 8  x       f) x y 2xy 1 x y 1  xx  2
x  2x  4 2 2
x y  2x  1 x y  1
2. Vì sao các kết luận sau đúng? 3 4 4 2 a) xy 5x y x  2 (x  2)  b)  3 7 35x y 2 x  2 x  4 2 2 2 c) x (x  3) x x  8x  7 x  6x  7  d)  2 x(x  3) x  3 x  1 x  1 1
Bồi dưỡng năng lực học môn Toán 8
THỰC HÀNH GIẢI TOÁN LỚP 8
3. Ba phân thức sau có bằng nhau không? 2x  3 2
2x  13x  24 2
10x  11x  6 A  ; B  ; C  15 15x  20 75x  30
4. Chứng minh các đẳng thức sau: 3 3 a) x  2 2  x   x  0 xx  2 x  2x  4 3xx 3x  y b)  x y   2 2 x y y x  3a x y x y 2 c) 
a  0,x y   2 3a 9a x y
Dạng 2. Tìm điều kiện xác định của phân thức
5. Tìm điều kiện của x để các phân thức sau xác định a) x  2 b) x  1 c) 5 x x  3 9  x 1 x  4 d) x  3 e) 8  x f) 5 2x  10 1 3 x  4 6  x 2 2
6. Tìm điều kiện của x để các phân thức sau xác định 2 a) x  4 9 x  2x  7  b) c) x   1 x  3 2 x  1 2 x x 2 d) 2x  1 e) x  4 f) 2x  1 2 x  4x  4 2 9x  16 2 x  5x  6
7. Tìm điều kiện của x để các phân thức sau xác định. 2 a) 5x  4 b) 2018 c) x  4 2 2x x x x   1 x  2 2 x   4x  5 d) x y e) 5x  4y
f) 2018x  2019y  2 2
x  2  y  2 3 2 x  6x  10
9x  24x  16
8. Chứng minh các phân thức sau luôn có nghĩa với mọi giá trị của x 2
Bồi dưỡng năng lực học môn Toán 8
THỰC HÀNH GIẢI TOÁN LỚP 8 2 a) 7 b) 6  x c) 8  x 2 x  5  2 x  2 1  4 x  2x  9 d) 2x 11 e) x  2y e) e) x  5 2 x   4x  5 4 2 4
x  2x y  2 2 x x  7
Dạng 3. Tìm điều kiện của biến thoả mãn đẳng thức.
9. Tìm giá trị của x để giá trị của các phân thức sau bằng 0 a) x  3  3x  6 x  3 b) x  3 2 x  2 2 2 c) 5x 125
d) x  4x  4 2 x  1 2 x  4x  5
10. Tìm các giá trị nguyên của x để phân thức sau có giá trị nguyên a) 3 b) 5 c) 7 2x  1 2 x  1 2 x x  1
Dạng 4: Toán thực tế
11. Ao Bà Om hay Ao Vuông, là một thắng cảnh độc đáo và nổi tiếng của tỉnh
Trà Vinh, Việt Nam. Mặt nước áo trong xanh và phẳng lặng được phủ bởi hoa
sen, hoa súng. Ao được bao bọc xung quanh bởi các gò cát mấp mô với các hàng
cây sao, cây dầu cổ thụ hàng trăm năm tuổi có rễ nổi lên khỏi mặt đất tạo nên
những hình thù kì lạ. Ao có hình chữ nhật có chiều rộng là x , chiều dài là
x  200mét, được đào ở trung tâm miếng đất hình vuông có cạnh làx  400 mét.
a) Tính diện tích của ao.
b) Tính diện tích phần đất còn lại sau khi đã đào ao.
12. Có một miếng đất hình vuông có cạnh là (a b)mét. Người ta chừa ra phần
đất hình chữ nhật có chiều dài và chiều rộng lần lượt là (a b) và (a b) để lát
lối đi a b  0. Viết biểu thức đại số tính diện tích phần đất còn lại để làm vườn. 3
Bồi dưỡng năng lực học môn Toán 8
THỰC HÀNH GIẢI TOÁN LỚP 8
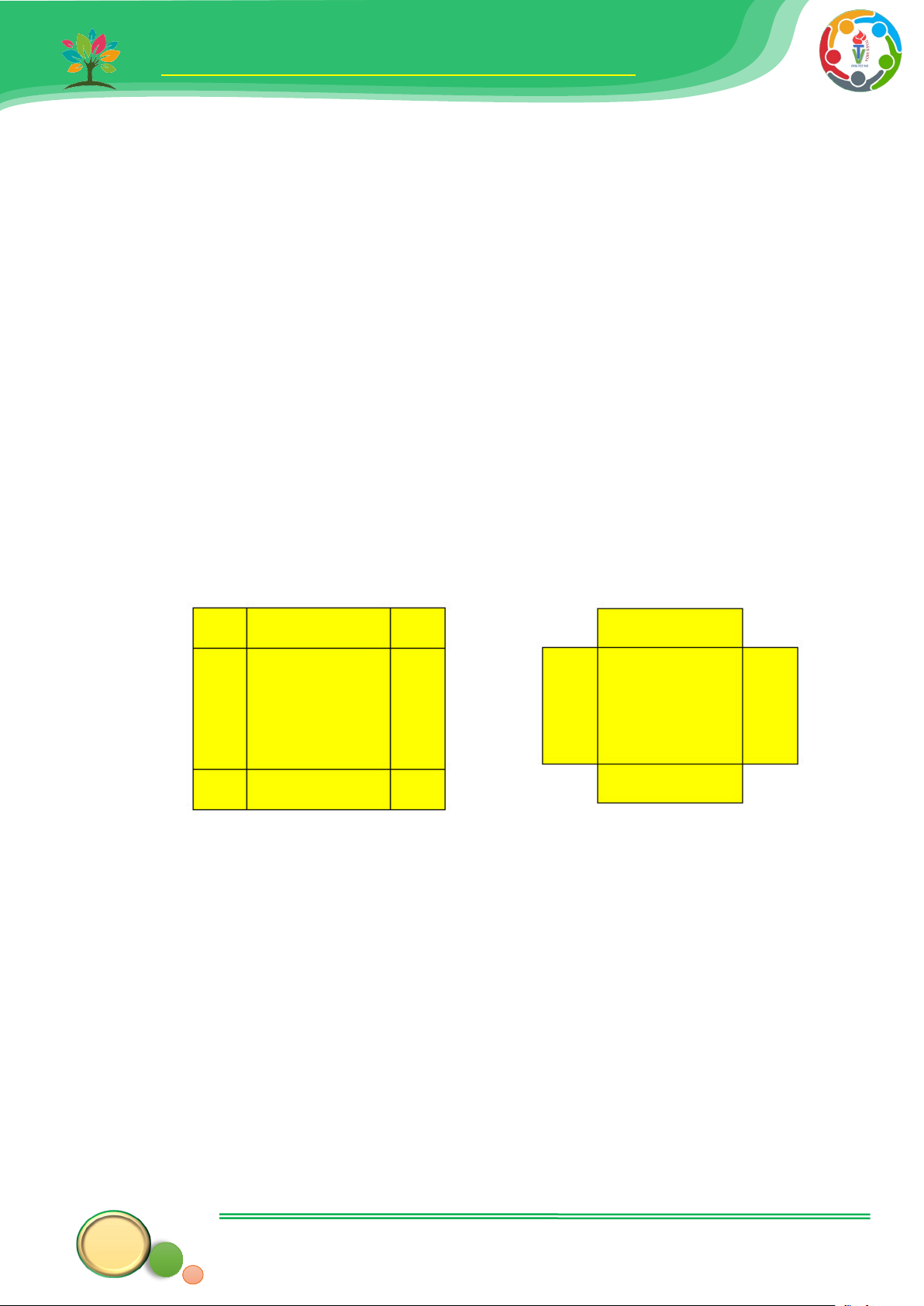
13. Một miếng bìa giấy hình vuông có cạnh bằng 20cm . Người ta cắt bỏ bốn hình
vuông nhỏ ở bốn góc của miếng bìa có cạnh bằng x để khi gấp lại được một hình hộp chữ nhật.
a) Viết biểu thức đại số tính độ dài cạnh của mặt đáy sau đó tính diện tích đáy
của hình hộp chữ nhật được gấp theo x .
b) Viết biểu thức đại số tính thể tích của hình hộp chữ nhật theo x .Biết công
thức tính thể tích của hình hộp chữ nhật V S.h (S : diện tích đáy, h là chiều cao).
c) Viết biểu thức đại số tính thể tích của hình hộp chữ nhật khi người ta cắt bỏ
4 hình vuông cá cạnh x = 2cm . Biết thể tích của hình hộp chữ nhật bằng tích 3
kích thước, hay bằng diện tích đáy x chiều cao.
14. Một miếng bìa hình chữ nhật có chiều dài hơn chiều rộng 30cm . Người ta
cắt 4 hình vuông nhỏ ở 4 góc của miếng bìa cùng có cạnh là 6cm. Sau khi gấp
lại được hình hộp chữ nhật có thể tích 3
3354 cm . Biết thể tích của hình hộp chữ
nhật là V S.h với S là diện tích đáy, h là chiều cao của hình hộp chữ nhật
a) Viết biểu thức đại số tính diện tích đáy của hình hộp chữ nhật sau khi gấp.
b) Tính các kích thước của miếng bìa lúc đầu.
15. Nhà trường tổ chức giải bóng đá mini mừng Xuân cho học sinh khối 8, mỗi
lớp cử một đội tham dự, mỗi đội lần lượt gặp đội của lớp bạn một lần. 4
Bồi dưỡng năng lực học môn Toán 8
THỰC HÀNH GIẢI TOÁN LỚP 8
a) Viết biểu thức đại số tính tổng số trận của khối lớp 8 nếu có x đội  * x    tham dự.
b) Nếu số trận đấu là 10 thì khối 8 có bao nhiêu lớp tham dự?
Dạng 5: Tính giá trị biểu thức (dạng khó)
16. Tính giá trị của biểu thức 2 a) x − 2x − 3 A =
, x ≠ 1 tại 3x −1 = 0 2 x + 2x +1 b) x − 2 B =
, x ≠ 2; x ≠ 3tại 2 x − 4 = 0 2 x − 5x + 6 17. Cho 1 x
 3 . Tính giá trị của các biểu thức sau: x a) 2 1 1 A x  b) 3 B x  2 x 3 x c) 4 1 1 C x  d) 5 D x  \ 4 x 5 x
18. Cho ba số a, ,bc khác 0 và thỏa mãn: a b c  0. Tính 1 1 1 A    2 2 2 2 2 2 2 2 2
a b c
b c a
c a b
Dạng 6: Tìm đa thức trong đẳng thức.
19. Tìm đa thức A thỏa mãn mỗi đẳng thức sau: 2 2 a) A x   b) A x y  2 x  4 x  2 x y x y 2 2 3 2
c) x x  1 1 x 1  x 1  x x  d)  x A A x 2 2 2 2
e) x  2xy y A
x  2xy y A  f)  2 2 x y x y 2 2 x y x y 5
Bồi dưỡng năng lực học môn Toán 8
THỰC HÀNH GIẢI TOÁN LỚP 8
Bài 22: TÍNH CHẤT CƠ BẢN CỦA PHÂN THỨC ĐẠI SỐ A. TÓM TẮT LÍ THUYẾT
Nếu nhân cả tử và mẫu của một phân thức với cùng một đa thức khác đa
thức 0 thì được một phân thức mới bằng phân thức đã cho. A . AM
(M là một đa thức khác đa thức 0 ) B B.M
Nếu tử và mẫu của một phân thức có nhân tử chung thì khi chia cả từ và mẫu
cho nhân tử chung đó ta được một phân thức bằng phân thức đã cho. A A : N
(N là một nhân tử chung) B B : N
Muốn rút gọn một phân thức đại số ta làm như sau:
- Phân tích tử và mẫu thành nhân tử (nếu cần) để tìm nhân tử chung
- Chia cả tử và mẫu cho nhân tử chung đó.
Muốn quy đồng mẫu thức nhiều phân thức ta làm như sau:
- Phân tích các mẫu thức thành nhân tử rồi tìm mẫu thức chung;
- Tìm nhân tử phụ của mỗi mẫu thức bằng cách chia MTC cho mẫu thức đó;
- Nhân cả tử và mẫu của mỗi phân thức với nhân tử phụ tương ứng. B. BÀI TẬP
Dạng 1: Tìm đa thức thoả mãn đẳng thức cho trước
1. Tìm đa thức A thỏa mãn mỗi đẳng thức sau: 3 2 x y 2 2 5 a) A 2x  4x   5x 5y , với x  2; b) 
, với x y 2 x  2 x  4 3 A 2 3 c) x  8 2x  16x y x x y  , với 1 x  0, x  d)  , với x  2 2x  1 A 2 2  x A
2. Tìm đa thức A thỏa mãn mỗi đẳng thức sau: 2 a) 6b  9b 3b n m m n  với 3 b   ; b)  với m  2. 2 4b  9 A 2 2  m A
Dạng 2: Biến đổi phân thức theo yêu cầu đề toán
3. a) Cho phân thức 4x  3 . Biến đổi phân thức đã cho thành một phân thức 2 x  5
bằng nó và có tử thức là đa thức 2
A  12x  9x. 1
Bồi dưỡng năng lực học môn Toán 8
THỰC HÀNH GIẢI TOÁN LỚP 8 2
b) Biến đổi phân thức 8x  8x  2 
thành một phân thức bằng nó và có tử
4x  215  x
thức là A  1 2x 2
4. a) Cho phân thức 12a 12a  3  a a
. Biến đổi phân thức đã cho
6a  35 a 2; 5
thành một phân thức bằng nó và có tử thức là đa thức A  1 2a 2  
b) Biến đổi phân thức x  7 3 x  
;x  0 thành một phân thức bằng nó và 4x  3  4  có mẫu thức là 2
B  12x  9x
5. Biến đổi mỗi phân thức sau thành một phân thức bằng nó và có tử thức là đa thức B sau đây a) 2x  5 và 2
B  2x  3x  5 2 3x  4
x  1 2x x  6 b) 
và B x  2 2 x   9  2 x  3x   2
6. Tìm bộ ba đa thức , A ,
B C thỏa mãn chuỗi đẳng thức sau: A B C  
với x  1,x  3. 2 3 x  3 x  4x  3 x  27
7. Tìm bộ ba đa thức , A ,
B C thỏa mãn chuỗi đẳng thức sau: Ax   1 B C  
với x  2 2 2 3 x  4x  4 x  4 x  8
8. Dùng tích chất cơ bản của phân thức để biến đổi mỗi cặp phân thức sau
thành một cặp phân thức bằng nó và có cùng tử thức: 2 a) 3 và x 1
b) x  5 và x  25 x  2 5x 4x 2x  3
Dạng 3: Tính giá trị của phân thức
9. Tính giá trị của phân thức: 2
Bồi dưỡng năng lực học môn Toán 8
THỰC HÀNH GIẢI TOÁN LỚP 8 2 a) 2x  2 với 3x  3x
x  1 tại x  1
với x  1 tại x  2 2 x  2x  1 b) 2 x  1 2
10. Tính giá trị của phân thức: x  1 với 1
x  1;x  tại 3x  1  0 2 2x  3x  1 2
11. Tính giá trị của các biểu thức sau: 2 3 a) a b A
với a  12 ; b  36 3 2 a b b) 2y  2xB  với 1 x y  2 2
x  2xy y 2 2 c)
(x  2)(2x  2x )  C  với 1 x  3
(x  1)(4x x ) 2 2 d)
x xy y yD  với 3 1 x  ;y  3 2
y  3y  3y  1 4 2
Dạng 4: Chứng minh cặp phân thức bằng nhau. Tìm giá trị của biến để phân thức bằng nhau. 2
12. Cho cặp phân thức 9x  6
và 3x  3x  3 với x  1 và 2 x  . 2
3x  3x  2x  2 3 x  1 3
Chứng tỏ cặp phân thức trên bằng nhau. 2 2
13. Cho hai phân thức y  5y  6 và 2y  5y  3 với y  2 và 1 y  . Cặp 3y  6 6y  3 2
phân thức này có bằng nhau hay không? 2 2
14. Cho cặp phân thức x 1 và x  2x  3 x  1;x  2;x  4 2   2 x  3x  4 x x  2
a) Hai phân thức này có luôn bằng nhau không?
b) Tìm giá trị cụ thể của x để hai phân thức bằng nhau
Dạng 5: Rút gọn phân thức
15. Rút gọn các phân thức sau. 5 3 2 3 3 a) 14x y z 2
25x y x   1
3x 5  x
60xy 3x  2 2 4 21x y z b) c) d)
30xy x   1 12x  53 2
45xy 2  3x 3
Bồi dưỡng năng lực học môn Toán 8
THỰC HÀNH GIẢI TOÁN LỚP 8
16. Rút gọn phân thức 3 4 17xy z 2 y xy 2 x  25 A B C  3 2 34x y z 2 4xy  7y 2 5x x 2
x xz xy yz 45x 3  x 2 2 y x D    F  2 E
x xz xy yz 3 2 2 3   
15x x  32 x 3x y 3xy y
17. Rút gọn phân thức 4 4 ax a x 3 2
x x  6x 2 2a  2ab A B C  2 2
a ax x 3 x  4x
ac ad bc bdx a2 2  4x y  2
2x x y  2 2 x  3x  2 D E F  3 2 2
a  9x  6ax x  2
2y y x  2 x  1
18. Đơn giản các phân thức 3 2 3 2 2 a) 7x  7x
48y  12y  3y
x y  1  2xy x  1 b) y  4 c) 3   4   x  1 y  64 2 2
x y  1  2x 2 3 2 4 2
d) x xz xy yz
e) x x x  1
f) x  2x  1 2
x xz xy yz 3 x  1 3 x  3x  2
Dạng 6: Tìm mẫu thức chung của các phân thức
19. Tìm mẫu thức chung của các phân thức sau: a) 2 x y 3 5  3x x  2 xx  1 ; b) ; c) ; ; 2 3xy 5x 2 7xy 2y 2 3 2 3 2x y 4x y 3xy d) 2 3x  2 3 7  x 1 5 x  7 ; e) ; f) ; ; 5 7x   1
x  1 3x  3 2
3x 4x  4 6x  6x
20. Tìm mẫu thức chung của các phân thức sau: a) 2 ; x ; 3 b) 1 ; 14 ; x x  3 2x  6 2 x  9 2 5x x 3
x  25x 3x  15
c) 3x ; x  1 ; x  5 d) 1 ; 1 ; 1 3 x  1 2 x x 2 x x  1 2
x  3x  2 x  1 2x  4 2 e) 7  x x 2x ; ; 2 2 2
x  3x  2 x  5x  6 x  4x  3 4
Bồi dưỡng năng lực học môn Toán 8
THỰC HÀNH GIẢI TOÁN LỚP 8
Dạng 7: Quy đồng mẫu thức các phân thức
21. Quy đồng mẫu các phân thức sau: a) 5 x  2 2 2  x 5 x  7 ; b) ; c) 1 ; ; 6 3x   1
5x  5 3x  3 2x 10x  10 2 5x  5x
22. Quy đồng mẫu các phân thức sau: a) 1 ; x ; 3 b) 1 ; 20 ; 7
2x  4 2x  4 2 4  x 2 x  2x 3 4x x 2 2x x
c) x ; x  1 ; x  2 d) 1 ; 1 ; 1 3 x  1 2 x x 2 x x  1 2
x  3x  2 x  2 1 x  22
Dạng 8. Chứng minh đẳng thức. Chứng minh biểu thức không phụ thuộc vào biến.
23. Chứng minh đẳng thức. 2 x a2 2  4x
a) b  2b  1 b  1 a x  b)  3 2 2 3b  3b 3b 2 2
a  9x  6ax a  3x 2
c) x  3x  2 x  2 xy  x  2y  2 y  1  d)  3 2 x  1 x x  1 2 4  4x  x x  2 2 2 e)
2x  3xy y 1  3 2 2 3
2x x y  2xy y x y 2 2 3 2
24. Cho hai phân thức
4xy  4x y x
2xy x  2y x P  và Q  với 3 2 4x  8x y 2 4x  4x
x  0;x  1;x  2y . Chứng minh rằng P Q.
25. Chứng minh biểu thức không phụ thuộc vào biếnx . 2 2 2 2 2 x y
x a(1a)a x 1 A   ; B
x yay ax  2x a 2 2
(1 a)  a x  1
Dạng 9. Chứng minh phân thức tối giản.
26. Chứng minh rằng các phân số sau tối giản với mọi số tự nhiên n : 3 a) 3n  1 ; b) 12n  1 ; c) n  2n ; d) 2n  1 . 5n  2 30n  2 4 2 n  3n  1 2 2n  1 5
Bồi dưỡng năng lực học môn Toán 8
THỰC HÀNH GIẢI TOÁN LỚP 8
Dạng 10. Tìm x để phân thức có giá trị là số nguyên
27. Tìm số nguyên x để phân thức sau có giá trị là số nguyên: 2 a) 3 ; b) 5 ; c) 7 ; d) x  59 2x  1 2 x  1 2 x x  1 x  8
28. Tìm số hữu tỉ 10 x để phân thức
có giá trị là số nguyên. 2 x  1 6
Bồi dưỡng năng lực học môn Toán 8
THỰC HÀNH GIẢI TOÁN LỚP 8
Bài 23: PHÉP CỘNG VÀ PHÉP TRỪ PHÂN THỨC ĐẠI SỐ A. TÓM TẮT LÍ THUYẾT
Quy tắc cộng hai phân thức cùng mẫu.
 Muốn cộng hai phân thức có cùng mẫu thức, ta cộng các tử thức với nhau
và giữ nguyên mẫu thức A B A B   M M M
Chú ý: Ta thường viết tổng dưới dạng rút gọn.
Quy tắc cộng hai phân thức không cùng mẫu.
 Muốn cộng hai phân thức có mẫu thức khác nhau, ta quy đồng mẫu thức
rồi cộng các phân thức có cùng mẫu thức vừa tìm được.
Quy tắc trừ hai phân thức
Muốn trừ hai phân thức có cùng mẫu thức ta trừ các tử thức và giữ nguyên mẫu thức. A B A B   M M M
Muốn trừ hai phân thức có mẫu thức khác nhau, ta quy đồng mẫu thức rồi
trừ các phân thức có cùng mẫu thức vừa tìm được.
Rút gọn biểu thức có dấu ngoặc
 Nếu trước dấu ngoặc có dấu “ ”
 thì bỏ dấu ngoặc và giữ nguyên các số hạng.
 Nếu trước dấu ngoặc có dấu “ “
 thì bỏ dấu ngoặc và đổi dấu các số hạng trong dấu ngoặc. B. BÀI TẬP
Dạng 1: Cộng các phân thức đại số cùng mẫu
1. Thực hiện phép tính:
a) x  4 10  8x
b) 7x  2 2  8xy  14 14 24xy 24xy c) 3x y 6x  4y xy   x x   d) 3 4 7 12 4 3   3x y 3x y 25xy 25xy 25xy
2. Thực hiện phép tính. 1
Bồi dưỡng năng lực học môn Toán 8
THỰC HÀNH GIẢI TOÁN LỚP 8 2 2 2 a) 3 2a  2     b) x 2xy 3y xy 2y 3xy   5  2a 2a  5 x y y x x y 2 c) 6b  3
2bx  2ax  6a  3 x  2 x  2  d)  2 2 2 2 a b b a 3 2 2 3
x  2x x
2x x x
3. Thực hiện phép tính: 2 2 2 2 a) 5xy  3z 4x y  3z 2 a a  2a 7  5a  b)   a  3 3xy 3xy a  3 3 a a  3
Dạng 2: Cộng các phân thức đại số khác mẫu.
4. Thực hiện phép tính: a) 2x 2ax  3x
a b x  b) 2 2 1  3 3a ab ax x b 2 c) 3x  2y 2 2       d) 3 2 3x xy x   xy x y 2 y  1 x x y   1
5. Thực hiện phép tính: a) 5 7  2x 2x  9 2  b)  2 x  2 x  4 2 9  4x 2x  3 c) x 4y   d) 1 2x 5  2 2 2y xy x  2xy 2 2 x x 2x  2
6. Thực hiện phép tính: 2 a) x  2 3 1 A    x  1 3 2   x  1 x x  1 1  x b) 1  2x 2x 1 B    2 2x 2x  1 2x  4x c) 1 1 x  2 C    . 2 2x  3 2x  3 2x x  3 d) 1 1 1  x D    . 2 2 2 x x  2 x x  2
(x  1)  (x  3)
7. Thực hiện phép tính. a) 1 1 1 1 1 1       . 2 4 8 16 1  x 1  x 1  x 1  x 1  x 1  x 2
Bồi dưỡng năng lực học môn Toán 8
THỰC HÀNH GIẢI TOÁN LỚP 8 b) 4 3 3   
y x z x y xy z y zx z c) 1 2 3   2 2 2 x  3x  2 x  12x  35 x  7x  10
8. Rút gọn rồi tính giá trị của phân thức thu gọn: 2 a) 1 x  2  với x  1 tại x  11 2 3 x x  1 x  1 b) x  1 x  2  
với x  1,x  0 tại 1 x  2 2 x x 1  x 3
c) 2x  1 1 2x 2   với 1 x   tại 1 x  2 4x  2 4x  2 1  4x 2 4
d) 3x y 2x  3y   với x  5 , 5 y y  2x  5 x  5 2y  5 2
9. Rút gọn rồi tính giá trị của phân thức thu gọn: a) 1 1 A   , biết xy  1 2 2 y xy x xy b) x 2x  3y B  
, biết 3y x  6 y  2 x  6 c) Cho x, ,
y z là các số khác nhau và x y z  2023 . 3 3 3 Tính x y z C   
(x y)(x z)
(y z)(y x)
(z x)(z y)
10. Cho ba số a;b;c đôi một khác nhau. Chứng minh rằng biểu thức sau không phụ thuộc vào a; ; b c : bc ac ab   
a ba c b ab c c ac b
11. Với a, ,bc là 3 số khác nhau. Chứng minh tổng sau bằng 0. 1 1 1   .
(a b)(bc) (ca)(a b) (bc)(c a) 3
Bồi dưỡng năng lực học môn Toán 8
THỰC HÀNH GIẢI TOÁN LỚP 8
Dạng 3: Tìm các hệ số thoả mãn điều kiện cho trước
12*. Hãy tìm giá trị của a,b để có các đẳng thức sau: a) 5x a b   .
(x  2)(x  3) x  2 x  3 b) 5x  31 a b   .
(x  5)(x  2) x  5 x  2 c) 3x  5 a b   . 2 2 (x  1) x  1 (x  1) d) 8x  1 a b   . 2 2 (x  3) x  3 (x  3) e) 1 a b   .
x(x  1)(x  2) x(x  1)
(x  1)(x  2)
13*. Xác định các số hữu tỷ a, ,bc sao cho: 2
a) 9x 16x  4 a b c    . 3 2
x  3x  2x x x  1 x  2 2
b) 2x x  1 a b c    . 2 2
(x  1)(x  2) x  1 x  2 (x  2)
Dạng 4: Trừ các phân thức đại số cùng mẫu
14. Làm tính trừ các phân thức sau:
a) 2x 1 6x 1 x   x  b) 3 2 2 5  2 2 4x y 4x y 2x  3 2x  3
c) x 17 11x  1 x x   d) 10 15 2 7  3  2x 2x  3 3x  2 2  3x
15. Làm tính trừ các phân thức sau: 2
a) 2xy  5 5xy  5    b) 7x 5 4x 5  2 2 8xy 8xy 2 3x(x  4) 3x  12x 2 2 2
c) x  2 18  x x  2   .
d) 5x x  4 x  2x x  3x  8   . x  6 x  6 x  6 3 3 3 x  8 x  8 x  8
16. Làm tính trừ các phân thức sau: 4
Bồi dưỡng năng lực học môn Toán 8
THỰC HÀNH GIẢI TOÁN LỚP 8 2 2 a) 2x x x  1 x  2 y   . b) 5 1   . x  1 1  x x  1 y  1 1  y y  1 2 2 c) 4  x 2x x 4x  5 x   x   . d) 2 9 2 1   . x  5 5  x x  5 x  6 x  6 6  x
Dạng 5: Trừ các phân thức đại số khác mẫu.
17. Rút gọn các biểu thức: 2 a) 4 2x  1 x   b) 4 x  1  2 3x  2 3x  2x x  1 c) 1 2x 3x  1 3x  1 6x  d)   3 2 x  1
x x x  1 2 6x  2 2  6x 9x  1
18. Thực hiện các phép tính sau. a) 2 a 1  x  . b) 3 7  . 2a 2 x  1 2x  2 2 4 4 x y 2 2  c) 7 7x  31  . d) x y  . 5 5x  15 2 2 x y e) 3x 1 1 2x  9 1  . f)  . 2 x  1 x  1 2 9  4x 2x  3
19. Thực hiện các phép tính sau. a) 1 1 2x x  1 x  1 4   . b)   . 2 2 x y x y x y 2 x  1 x  1 1  x c) x 1 3    . d) x 4 x   1 . 2 2x  2 x  1 2x  2 2 x  7x  10 2  x
20. Thực hiện phép tính: a) 1 2x 1   2 3 2 2 x  3x  2
x  4x  4x x  5x  6 b) 1 1 x  2   2 2x  3 2x  3 2x x  3 c) 1 1 1  x   2 2 2 x x  2 x x  2
(x  1)  (x  3)
21. Thực hiện phép tính 5
Bồi dưỡng năng lực học môn Toán 8
THỰC HÀNH GIẢI TOÁN LỚP 8 2 2 2 a) x 2xy y A    .
x y2 x y 4 2 2 4
x  2x y y  2 2
x y x y b) 1 1 2 4 8 16 B       . 2 4 8 16 x  1 x  1 x  1 x  1 x  1 x  1
22. Tính giá trị của biểu thức: a) 2x  1 1  2x 2 A    với 1 x  2 4x  2 4x  2 1  4x 4 b) 3x y 2x  3y B  
với y  2x  5 x  5 2y  5 c) 2a x 2a x 4a a C a    với x  2 2  x 2  x x  4 a  1
23. Chứng minh rằng: 1 1 1  
. Vận dụng tính nhanh các phép tính x x  1 x(x  1) sau: a) 1 1 1 1    x(x  1)
(x  1)(x  2) (x  2)(x 3)
(x  3)(x  4) b) 1 1 1 1 1 1      2 2 2 2 2 x x x  3x  2 x  5x  6 x  7x  12 x  9x  20 x  5
24. Chứng minh đẳng thức: 2 2 2 2 2
a) 4x (x  3) x  9 (2x  3)  x    1 2 2 2 2 2 9(x  1) (2x  3)  x 4x  (x  3) b) y z z x x y 2 2 2     
(x y)(x z)
(y z)(y x)
(z x)(z y) x y y z z x
Dạng 6: Tìm phân thức thoả mãn yêu cầu
25. Tìm phân thức A biết 2 a) 4 2 2x  4xA  
với x  0,x  1 2 3 x x  1 1  x x  1 2 b) 2a  6 6 2aA  
với a  1,a  3 3 2 2
a  3a a  3 a  3 1 a 6
Bồi dưỡng năng lực học môn Toán 8
THỰC HÀNH GIẢI TOÁN LỚP 8 c) 6 3x  2 3x  2 A    với x  1 2 2 2 x  1 x  2x  1 x  2x  1
Dạng 7: Rút gọn biểu thức có dấu ngoặc
26. Tính giá trị của biểu thức:   a) x  3 2x  1 x  3        2 x  1  x 1 x  1     b)  1 1   1 1        
x x yy x y x x yy y x       c) 1 3ab a b        3 3 2 2 a b a b
a ab b    d) 1  1 1      x  1
1  xx  2 x  2x  3  
27. Thực hiện phép tính (Tự luyện).  3 2    2  3 3
x x 1  5x x x 1 a) A       . 2 3 2 2x  1
4x  4x  1
8x  12x  6x  1     4x  32  x  2x  3 25 2 2 2  x b)  B      .
3x 52 4x 9x 2x 52 4x 152 2 2 2 x           7
Bồi dưỡng năng lực học môn Toán 8
THỰC HÀNH GIẢI TOÁN LỚP 8
Bài 24: PHÉP NHÂN VÀ PHÉP CHIA PHÂN THỨC ĐẠI SỐ A. TÓM TẮT LÍ THUYẾT
Quy tắc nhân hai phân thức.
Muốn nhân hai phân thức, ta nhân các tử thức với nhau, các mẫu thức với nhau A C AC .  B D BD
Chú ý: Ta thường viết tích dưới dạng rút gọn.
Các tính chất  Giao hoán: A C C A    B D D B      Kết hợp: A C   E A C E           
B D  F
B D F     
 Phân phối đối với phép cộng: A C   E A C E           
B D F
B D F 
Quy tắc chia hai phân thức
Muốn chia phân thức A cho phân thức C khác 0, ta nhân A với phân thức D B D B C A C A D C :   , với  0. B D B C D B. BÀI TẬP
Dạng 1: Nhân hai phân thức đại số
1. Thực hiện các phép tính sau 3 2 2   3 2   a) 14x 2y 5y  2x x  8 x  4x 7z  b)      c)  d) 3 4 3x y .     2 2   5y x 2 7y     10y  2
5x  20 x  2x  4 5  9xy 
2. Thực hiện các phép tính sau 2 2 2 a) 8x 4y 9a a  9 . x  0;y  0 b) .
a  3;a  0 3   3 2   15y x a  3 6a 2 2   d) 4n  7m
3b  6 2b  18 .   
m  0;n  0 d) .
b  2;b  9 3 2   4   
17m  12n 
b 9 b  2 1
Bồi dưỡng năng lực học môn Toán 8
THỰC HÀNH GIẢI TOÁN LỚP 8
3. Rút gọn biểu thức 4 2 3 a) t  4t  8 t 3t  3 A  . . t  1 3 2 4 2   2t  2
12t  1 t  4t  8 3   b) y  1  2 y B  . y   y  1    
y  0;y   1 2y  y  1 6 3 2 c) x  2x  3 3x x x  1 C  . . x  1 3 6 3   x  1
x  1 x  2x  3 3 2   d)
a  2a a  2 1 2 1 D  .      
a  5;2;  1 3a  15
a 1 a  1 a  2 4. Tính hợp lí: 1 1 1 1 1 1 M  . . . . .
với x  1 2 4 8 16
1  x 1  x 1  x 1  x 1  x 1  x
5. Thực hiện các phép tính sau 3   a) m 1 1 m  1      
m  2;m  1 2
2m  4 m  1 m m  1 3 3 b) u 2001  2u u u  16 .  .
u  2;u  2017 u  2017 u  2
u  2017 u  2 c) 12x  5 4x  3 12x  5 6  3x    x  9 360x  150 x  9 360x  150
d) x  3y 4x  2y x  3y x  3y    3x y x y
3x y x y
6. Tính giá trị của các biểu thức sau. 2 2   a) x yx y A    1. 
Với x  15, y  15 2 2  x y  2y 2 2     b) x y x y 1 B    .     
 Với x  15, y  5    2 2  y x
 x xy y
x y  c)     2 2 2 x y z C
x y z  2yz.
Với x  8,6; y  2,z  1,4
x y z 2
Bồi dưỡng năng lực học môn Toán 8

Tài liệu liên quan: